14-L.01 图的邻接矩阵、道路矩阵及Warshall算法
图的矩阵表示

4 4
2 6
6 51 215
1设G=<V,E>是简单图,令V={v1,v2,v3,…,vn}, G的
10 2 2 0 b)每行中1的个数为对应结点 1 vi与ej关联 12 0 0 2 从邻接矩阵看图的性质: 1 vi与vj邻接, 即(vi,vj)∈E 或 < vi,vj >∈E
010 01 0 0110
00010
01001
00010
01001
P=A∨A(2)∨A(3)∨A(4)∨A(5) A(5)=A(3)
11111 01011 P= 11111 01011 01011
G2 v1 v3
3*.用可达矩阵求强分图.
出有两个强分图:{v1,v3}和{v2,v4,v5} 下面看怎样用P求强分图.
例如,G2如图所示, 求它的 可达矩阵P.
G2
v1
v2
v3
v4
v5
00100
10010
01101
10010
00010
01011
01011
01011
A= 10010 A(2) = 01101 A(3) = 10010 A(4) = 01101 =A(2)
01001
00010
01000
00010
用的例v4求度如0传 数 ,0给递.0定0闭无1包0向的1图WGa1rs和ha有ll算向法1图0,G见012P如1116图610.所0示0:
21111
v1
1310
2
v2
v3
例 b这p)ij每如是= 行p,以T给中i结j定=1点1的A无与个向(结G 数图点为G1之)1对和间应有的结向邻点1图0接G1关12如系00图确00所定1示的1:矩阵.
基于gpu的所有点对的最短路径floyd-warshall算法

基于gpu的所有点对的最短路径
floyd-warshall算法
Floyd-Warshall 算法是一种用于计算图中所有点对之间的最短路径的算法。
该算法基于动态规划的思想,通过迭代更新节点之间的最短距离,最终得到所有点对之间的最短路径。
当使用 GPU 进行计算时,可以利用 GPU 的并行计算能力来加速 Floyd-Warshall 算法的执行。
以下是一个基于 GPU 的 Floyd-Warshall 算法的简要描述:
1. 数据准备:将图的邻接矩阵加载到 GPU 的内存中。
2. 外层循环:遍历图中的所有节点。
3. 内层循环:对于每个节点,遍历其与其他节点的连接。
4. 更新最短路径:根据当前节点和连接节点的距离,更新连接节点与其他节点的最短距离。
5. 重复步骤 2-4,直到所有节点都被遍历。
6. 获取结果:从 GPU 内存中读取更新后的最短距离矩阵。
通过将计算任务分配到多个 GPU 线程上并行执行,可以大大提高 Floyd-Warshall 算法的计算效率。
同时,需要注意 GPU 与主机之间的数据传输以及线程之间的同步问题。
这只是一个基于 GPU 的 Floyd-Warshall 算法的简单描述,实际实现可能会涉及到更多的细节和优化。
具体的实现方式会根据使用的 GPU 平台和编程语言而有所不同。
导航设备嵌入式软件的路线规划算法

导航设备嵌入式软件的路线规划算法导航设备已经成为了我们日常生活中不可或缺的一部分,无论是出行还是旅行,我们都需要依赖导航设备为我们提供准确的路线规划。
而导航设备的核心功能之一就是路线规划算法。
在导航设备嵌入式软件中,路线规划算法的作用是根据用户提供的起点和终点位置,计算出最优的路径,从而为用户提供可行和高效的导航路线。
路线规划算法的关键是在地图上寻找最短路径或最优路径的方法。
常见的路线规划算法主要有以下几种:1. Dijkstra算法Dijkstra算法是一种广泛应用的图搜索算法,用于从一个起点到其他所有点的最短路径问题。
在导航设备中,Dijkstra算法可以根据道路的权重(例如距离、交通状况等)计算出最短路径。
该算法通过不断更新起点到其他节点的距离,并选择距离最短的节点作为下一个起点,直到找到终点为止。
2. A*算法A*算法是一种启发式搜索算法,结合了Dijkstra算法的最短路径思想和迪克斯特拉算法的A算法,能够有效地解决路线规划问题。
A*算法通过引入启发函数,对距离和预估成本进行综合评估,以快速找到最短路径。
在导航设备中,A*算法可以根据预先设定的启发函数,计算出最优路径。
3. Floyd-Warshall算法Floyd-Warshall算法是一种动态规划算法,用于解决所有点对之间的最短路径问题。
在导航设备中,Floyd-Warshall算法通过构建图的邻接矩阵,利用动态规划的思想计算出每对节点之间的最短路径和距离。
该算法的优势在于可以同时计算多个起点和终点之间的最短路径。
4. 遗传算法遗传算法是一种模拟生物进化的搜索算法,通过模拟自然选择、交叉和变异等过程来搜索最优解。
在导航设备中,遗传算法可以用于求解复杂的路径规划问题,例如考虑多个因素(如距离、交通状况、道路类型等)的综合最优路径。
在实际应用中,以上算法往往会结合使用,以提高路线规划的准确性和效率。
例如,导航设备可以先利用A*算法进行粗略路径规划,然后再使用Dijkstra算法对具体道路进行细致的搜索。
图的邻接矩阵

1. 图的邻接矩阵(Adjacency Matrix)存储表示法设图 A = (V, E)是一个有n 个顶点的图, 图的邻接矩阵是一个二维数组 A.edge[n][n],用来存放顶点的信息和边或弧的信息。
定义为:(1)无向图的邻接矩阵是对称的;有向图的邻接矩阵可能是不对称的。
(2)在有向图中, 统计第i 行 1 的个数可得顶点i 的出度,统计第j 行 1 的个数可得顶点j 的入度。
在无向图中, 统计第i 行(列) 1 的个数可得顶点i的度。
图的邻接矩阵存储表示:#define INFINITY INT_MAX //最大值∞#define MAX_VERTEX_NUM 20 // 最大顶点个数typedef enum {DG, DN, AG, AN} GraphKind; //{有向图,有向网,无向图,无向网}typedef struct ArcCell {VRType adj; // VRType是顶点关系类型。
对无权图,用1或0表示相邻否;// 对带权图,则为权值类型。
InfoType *info; // 该弧相关信息的指针} ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef struct {VertexType vexs[MAX_VERTEX_NUM]; // 顶点向量AdjMatrix arcs; // 邻接矩阵int vexnum, arcnum; // 图的当前顶点数和弧(边)数GraphKind kind; // 图的种类标志} MGraph;构造一个具有n个顶点和e条边的无向网的时间复杂度为O(n2+e*n),其中O(n2)用于对邻接矩阵初始化。
2.图的邻接表(Adjacency List)存储表示法邻接表是图的一种链式存储结构,它对图中每个顶点建立一个单链表,第i个单链表中的结点表示依附于顶点vi的边(对有向图是以顶点vi为尾的弧),每个结点由三个域组成:邻接点域(adjvex)指示与顶点vi邻接的点在图中的位置,链域(nextarc)指示下一条边或弧的结点,数据域(info)存储和边或弧相关的信息(如权值)。
warshall算法

warshall算法传递关系闭包算法开始,先把关系集合转化为0,1矩阵,使得⽅便关系运算。
对于⼀般算法,通过矩阵点乘的来迭代的⽅式得到传递关系闭包的集合。
代码如下:typedef struct matrix{//定义关系矩阵int n;int a[10][10];}Matrix;Matrix getTranstiveClosure(Matrix matrixA,int matrix_n){for(int num=1;num<matrix_n;num++){//R^n,迭代n-1次按照C语⾔,0号位置为数组第⼀位for(int i=0;i<matrix_n;i++){//开始矩阵布尔积运算for(int j=0;j<matrix_n;j++){for(int k=0;k<matrix_n;k++){if(matrixA.a[i][j]==0)//优化或运算matrixA.a[i][j]=(matrixA.a[i][k]&matrixA.a[k][j]);}}}}return matrixA;}//M=getTranstiveClosure(matrixA);来得到传递闭包矩阵其中矩阵点乘的算法复杂度为O(n^3),迭代次数为n-1次(得到R^n为结果),算法复杂度为O(n^4)。
对于此类算法,特点为为了找到某⼀关系(a,b),要把其他的元素作为中间元素来判断是否存在传递关系。
例如:a,b,c,d,e属于A集合,R为A的关系集合,为了找到(a,b),需要把c,d,e作为中间元素,如假设(a,c)(c,b)∈R,(a,c)(c,b)->(a,b)∈R来得到传递关系。
简⾔之,针对所求的关系,去遍历中间元素的关系去判断。
下⾯我们来看看warshall算法。
代码如下:Matrix warshall(Matrix matrixB,int matrix_n){for(int k=0;k<matrix_n;k++){//K值选择中间量的元素来补全传递关系的路线for(int i=0;i<matrix_n;i++){//遍历新矩阵for(int j=0;j<matrix_n;j++){if(matrixB.a[i][j]==0){//优化或运算matrixB.a[i][j]=matrixB.a[i][k]&matrixB.a[k][j];}//如(a->b)&(b->c)-->(a->c)的关系}}}}warshall算法的算法复杂度为O(n^3),其巧妙之处就在于⽆需矩阵的迭代,通过固定中间元素来进⾏判断关系,并对中间元素逐次遍历,并对传递关系进⾏迭代,需要遍历的中间元素为n个,所求矩阵遍历操作为n^2,在n规模⾜够⼤的时候warshall算法能体现出优越性。
图论基础图的表示与常见算法

图论基础图的表示与常见算法图论是数学的一个分支,研究的是图这种数学结构。
图由节点(顶点)和边组成,是研究网络、关系、连接等问题的重要工具。
在图论中,图的表示和算法是非常重要的内容,本文将介绍图的表示方法以及一些常见的图算法。
一、图的表示1. 邻接矩阵表示法邻接矩阵是表示图的一种常见方法,适用于稠密图。
对于一个有n 个节点的图,邻接矩阵是一个n×n的矩阵,其中第i行第j列的元素表示节点i到节点j是否有边相连。
如果有边相连,则该元素的值为1或边的权重;如果没有边相连,则该元素的值为0或者无穷大。
邻接矩阵的优点是可以方便地进行边的查找和修改,但缺点是对于稀疏图来说,会浪费大量的空间。
2. 邻接表表示法邻接表是表示图的另一种常见方法,适用于稀疏图。
对于一个有n 个节点的图,邻接表是一个长度为n的数组,数组中的每个元素是一个链表,链表中存储了与该节点相连的其他节点。
邻接表的优点是节省空间,适用于稀疏图,但缺点是查找边的时间复杂度较高。
3. 关联矩阵表示法关联矩阵是表示图的另一种方法,适用于有向图。
对于一个有n个节点和m条边的图,关联矩阵是一个n×m的矩阵,其中第i行第j列的元素表示节点i和边j的关系。
如果节点i是边j的起点,则该元素的值为-1;如果节点i是边j的终点,则该元素的值为1;如果节点i与边j无关,则该元素的值为0。
关联矩阵适用于有向图,可以方便地表示节点和边之间的关系。
二、常见图算法1. 深度优先搜索(Depth First Search,DFS)深度优先搜索是一种用于遍历或搜索图的算法。
从起始节点开始,沿着一条路径一直向下搜索,直到到达叶子节点,然后回溯到上一个节点,继续搜索其他路径。
DFS可以用递归或栈来实现。
2. 广度优先搜索(Breadth First Search,BFS)广度优先搜索是另一种用于遍历或搜索图的算法。
从起始节点开始,先访问起始节点的所有邻居节点,然后再依次访问邻居节点的邻居节点,以此类推。
关系传递闭包Warshall算法之思想的图论解说

关系传递闭包Warshall算法之思想的一种解说摘要:Warshall算法是求二元关系传递闭包的一种高效的算法。
在左孝凌等编著的《离散数学》中提到了该算法,但并未对此算法作出解释,本文对该算法的思想作出一种比较通俗的解说。
关键词:Warshall算法;矩阵;Floyd算法1、引言Warshall在1962年提出了一个求关系的传递闭包的有效算法。
其具体过程如下,设在n个元素的有限集上关系R的关系矩阵为M:(1)置新矩阵A=M;(2)置k=1;(3)对所有i如果A[i,k]=1,则对j=1..n执行:A[i,j]←A[i,j]∨A[k,j];(4)k增1;(5)如果k≤n,则转到步骤(3),否则停止。
所得的矩阵A即为关系R的传递闭包t(R)的关系矩阵。
在左孝凌等编著的《离散数学》中提到了该算法,但并未对此算法作出解释。
下面本文将对该算法的思想作出一种比较通俗的解说。
2、对Warshall算法的解说设关系R的关系图为G,设图G的所有顶点为v1,v2,…,vn,则t(R)的关系图可用该方法得到:若G中任意两顶点vi和vj之间有一条路径且没有vi到vj的弧,则在图G中增加一条从vi到vj的弧,将这样改造后的图记为G’,则G’即为t(R)的关系图。
G’的邻接矩阵A 应满足:若图G中存在从vi到vj路径,即vi与vj连通,则A[i,j]=1,否则A[i,j]=0。
这样,求t(R)的问题就变为求图G中每一对顶点间是否连通的问题。
定义一个n阶方阵序列A(0),A(1),A(2),…,A(n),每个方阵中的元素值只能取0或1。
A(m)[i,j]=1表示存在从vi到vj且中间顶点序号不大于m的路径(m=1..n),A(m)[i,j]=0表示不存在这样的路径。
而A(0)[i,j]=1表示存在从vi到vj的弧,A(0)[i,j]=0表示不存在从vi到vj 的弧。
这样,A(n)[i,j]=1表示vi与vj连通,A(n)[i,j]=0表示vi与vj不连通。
warshall算法演示
பைடு நூலகம்
0101 0001 1111 1111
W3
1111 1111 1111 1111
W4
Second step:以2为过路顶点
1->2,2->4=>1->4; 3->2,2->4=>3->4
4->2,2->4=>4->4;
Third step:以3为过路点
4->3,3->1=>4->1
Fourth step:以4为过路点
可能有同学会问,为什么要有前面的C[i,j],因为后面括号里的值如果是0,不可能直接赋值 给C[i,j], 如果C[i,j]本来的值是1,直接赋值后就变为0,改变了原来的关系,所以一定要 有前面的C[i,j]并上后面括号。
0100 0001 1010 0110
第一行有1的位置划竖线 第一列有1的位置划横线 交叉点如果为1,则不改动
2->4,4->3=>2->3; 2->4,4->1=>2->1; 2->4,4->2=>2->2; 1-4->,4->1=>1->1; 1->4,4->3=>1->3
Warshall算法步骤
1.C=MR(先将R的关系矩阵赋值给一个新的变量C,目的是为了不影响原来的关系矩阵) 2.for k=1 to n (k相当于过路点)====for(k=1;k<=n;k++) 3.for i=1 to n 4.for j=1 to n 5.C[i,j]<-C[i,j]U(C[i,j]*C[ j,i]) (运用刚刚所讲的布尔积,可以得到C[i,j]的值)
warshall算法

——Warshall算法求二元关系的传递闭包t(R)设A={V1,V2,V3......Vn},t(R)=R1∪R2∪R3……Rn (n为集合A中元素的个数)——根据路径中所经过的节点数来推导递推公式,由递推公式计算Rn,即t(R)依次讨论Vi与Vj经过中间点(V1),(V1,V2),(V1,V2,V3),(V1,V2,V3…Vn)的情况且它们之间存在关系:后面讨论的情况总是包含前一项讨论的情况将A中的元素进行编号,例如:V1---1,V2---2,V3---3,Vn---n设Vi∈R Vj∈R定义R(k) 表示Vi 与Vj之间所经过节点的个数为k时的传递的集合R(0)=R 表示Vi 与Vj之间不经过节点的传递的集合R(1)表示Vi 与Vj之间经过第一个节点V1,若R(1)=1,说明Vi与Vj是连通的,若R(1)=0,说明Vi与Vj是不连通的有2条路径R(2)表示Vi与Vj之间经过第二个节点V2,且存在两个中间点V1,V2,有3条路径…………R(n)表示A中的所有元素都作为中间点,Vi与Vj之间有n条路径即Vi 不少于编号个数k的中间点的集合C Vj——递推关系(由R(k-1)推导R(k))设Vk ,表示Vi与Vj之间可能存在的节点k=1,2,3……n①Vk ∈C时此时Vi与Vj是否存在传递关系取决于Vi到Vk,Vk到Vj是否存在,若两者都存在,则Vi 中间点的集合C1 Vk 中间点的集合C2 VjRij(k)=Rik(k-1)∩Rkj(k-1)递推 2次②Vk ∈/C(不属于)时此时不在讨论的范围之内,Vi与Vj之间不存在新的连通关系,所以此时的Rij与上一次的相同,从而达到保留原来已算出的传递关系的目的Vi 不少于编号个数k的中间点的集合C VjRij(k)=Rij(k-1)综上所述,递推关系为:Rij(k)= Rij(k-1)∪{Rik(k-1)∩Rkj(k-1)}(为1)源代码#include<iostream.h>void main(){int i,j;int const n=4; //n为矩阵的阶数,可在此处改写int m[n][n];for(i=0;i<n;i++)for(j=0;j<n;j++)m[i][j]=0;int a,b,c; //输入关系矩阵Rcout<<"请输入矩阵"<<endl;c=1;while(c){cout<<"请分别输入矩阵中为1的行数和列数:"<<endl;cin>>a>>b;m[a-1][b-1]=1;cout<<"继续输入关系请按1,输入完成请按0"<<endl;cin>>c;}cout<<"输出关系矩阵R:"<<endl;for(i=0;i<n;i++){for(j=0;j<n;j++)cout<<m[i][j];cout<<endl;}int k; //warshall算法for(k=0;k<n;k++)for(i=0;i<n;i++)for(j=0;j<n;j++)if(m[i][j]==1||m[i][k]==1&&m[k][j]==1)m[i][j]=1;cout<<"R传递闭包是:"<<endl;for(i=0;i<n;i++){for(j=0;j<n;j++)cout<<m[i][j];cout<<endl;}}可执行文件。
邻接矩阵 检索-概述说明以及解释

邻接矩阵检索-概述说明以及解释1.引言1.1 概述:邻接矩阵是图论中一种常见的数据结构,用于描述图中各个顶点之间的连接关系。
在邻接矩阵中,图的顶点通常用矩阵的行和列来表示,矩阵的元素则表示顶点之间是否相连或具有何种关系。
邻接矩阵在图论中有着广泛的应用,可以用来表示网络结构、社交关系、路线规划等各种场景。
通过邻接矩阵,我们可以方便地进行图的遍历、查找、最短路径等操作,为解决各类实际问题提供了便利。
本文将重点介绍邻接矩阵的定义与概念,探讨邻接矩阵在图论中的应用,并详细介绍邻接矩阵检索算法,希望能够为读者提供对邻接矩阵及其应用的深入理解。
1.2文章结构1.2 文章结构本文主要分为三个部分,即引言、正文和结论。
在引言部分,将会对邻接矩阵进行概述,介绍文章的结构和目的。
其中,概述部分将对邻接矩阵的基本定义和概念进行简要介绍,为后续的正文部分做铺垫;文章结构部分将给出整篇文章的框架和布局,方便读者快速了解文章内容;而目的部分则会说明本文撰写的目的和意义。
在正文部分,将围绕着邻接矩阵展开讨论。
具体而言,将首先介绍邻接矩阵的定义与概念,让读者对其有一个清晰和全面的认识;接着将探讨邻接矩阵在图论中的应用,以便读者更深入地理解这一概念;最后将重点讨论邻接矩阵的检索算法,为读者提供一种快速高效地检索邻接矩阵信息的方法。
在结论部分,将对全文进行总结,回顾本文所涉及的内容和观点;同时也将展望邻接矩阵在未来的应用和发展方向,为读者呈现一幅邻接矩阵所展现出的无限可能;最后提出结论,总结本文的主要观点和贡献,为本文画上一个完整的句号。
1.3 目的邻接矩阵是图论中一种重要的数据结构,用于表示图中各个顶点之间的连通关系。
邻接矩阵检索算法则是基于邻接矩阵的数据结构,用于实现对图的快速检索和查询操作。
本文旨在探讨邻接矩阵检索算法的原理和实现方法,通过深入分析算法的逻辑结构和实用性,帮助读者更好地理解和应用邻接矩阵在图论中的作用。
通过本文的阐述,读者将能够了解邻接矩阵在图论中的重要性和应用价值,掌握邻接矩阵检索算法的具体实现方式,从而提升对图的处理和分析能力。
邻接矩阵计算

邻接矩阵:图的表示方法与计算方法
邻接矩阵是一种用于表示图(graph)的矩阵,其中每个元素表示两个节点之间的连接关系。
邻接矩阵是一个方阵,其行和列都对应图中的节点。
如果节点i和节点j之间存在一条边,则矩阵中的相应元素为1;否则为0。
在计算邻接矩阵时,首先需要确定图的顶点数和边数。
然后,根据这些信息可以创建一个空的矩阵,其行数和列数分别对应顶点的数量。
接下来,遍历图的每一条边,并标记邻接矩阵中相应位置的元素为1,以表示两个节点之间的连接关系。
如果图中存在自环边(即从节点到自身的边),则需要对邻接矩阵进行填充,使其对角线上的元素也为1。
最后,如果图是无向图,则需要对邻接矩阵进行补全,使得矩阵的上三角和下三角元素相等。
下面是一个简单的Python代码示例,用于计算邻接矩阵:
def compute_adjacency_matrix(vertices, edges):
adjacency_matrix = [[0] * vertices for _ in range(vertices)]
for edge in edges:
u, v = edge
adjacency_matrix[u-1][v-1] = 1
adjacency_matrix[v-1][u-1] = 1
return adjacency_matrix
在这个例子中,vertices参数表示顶点的数量,edges参数是一个包含边的列表,其中每个边都是一个包含两个顶点索引的元组。
该函数将创建一个大小为vertices x vertices的零矩阵,然后遍历边的列表,将邻接矩阵中相应位置的元素标记为1。
最后,该函数返回邻接矩阵。
图的矩阵表示

性,亦可用可达矩阵。
第9页/共29页
定义10.19 令 G=<V, E> 是一个简单有向图,V n ,
假定 G 的结点已编序,即 V={v1, v2, …, vn},定义
一个 n×n 矩阵P (pij ) 。其中
Pij
1,
从vi到v
至少存在一条路
j
0,
从vi到v
不存在路
j
称矩阵 P 是图 G 的可达性矩阵。
v3 0 1 1 1 0 0 0 V4,5 0 1 1 0 1 0 1
第21页/共29页
【例10.9】有向图(a)中合并结点 v2 和 v3。
解:合并时,删去自回路得图 (b)。其关联矩阵 M(G’) 是
由 M(G) 中将第 2 行加到第 3 行上面得到的。
v2
e1
v1
e7
e2
v4
e3 e8
e6
v3
第18页/共29页
设图 G 的结点 vi 与结点 vj 合并得到图 G′, 那么 M(G’) 是将 M(G) 中的第 i 行与第 j 行相加
而得到。因为若有关项中第 r 个对应分air量 ajr 1
有
,则说明 vi 与 vj 两者之中只有一
个结点是边 er 的端点,且将这两个结点合并后的结
点 vi,j 仍是 er 的端点。
有向图的完全关联矩阵也有类于无向图的一些性质。
定义10.22 对图 G 的完全关联矩阵中的两行相加如下:
若记 vi 对应的行为vi ,将第 i 行与第 j 行相加,规定
为:对有向图是指对应分量的加法运算,对无向图是指
对应分量的模 2 的加法运算,把这种运v算i 记v j vij
作
warshall算法原理

warshall算法原理
Warshall算法,又称为Floyd-Warshall算法,是解决“全源最
短路径”问题的一种动态规划算法。
在一个有向图中,每个点都有一个编号,假设有n个点,那么图
上所有的边可以用一个n×n的矩阵来表示,称为邻接矩阵。
邻接矩阵
中每个元素a[i][j]表示从i到j有一条边,a[i][j]=1。
如果没有边,则a[i][j]=0。
Warshall算法用动态规划的思想解决全源最短路径的问题。
定义
d[i][j]为从i到j的最短路径长度,k表示所有可能经过的中间点,
则状态转移方程为:d[i][j]=min(d[i][j], d[i][k]+d[k][j])。
其中i,j,k均为图中的点。
算法的步骤如下:
1. 将邻接矩阵复制给d数组。
2. 枚举所有节点k进行中间点的遍历,在此遍历中,如果通过
中间点k能够得到更短的路径,则更新对应的节点i到节点j的距离。
3. 遍历完所有中间节点后,d数组中保存的便是各个点到其他点的最短距离。
Warshall算法的时间复杂度为O(n^3),其中n为节点数。
虽然
算法复杂度较高,但是它适用于任意类型的有向图,包括存在负边权
的图,因此在实际使用中还是有一定的应用价值。
warshall算法
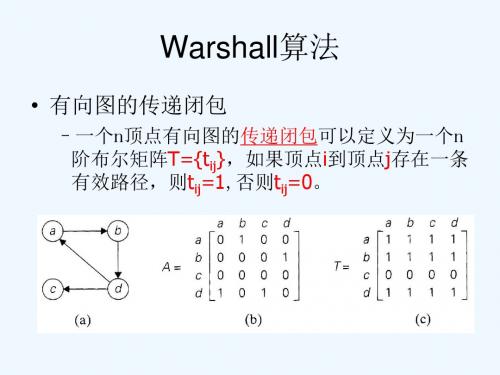
包含编号不大于3的中 间顶点a,b,c)的路径, 没有新路径
包含编号不大于2的中 间顶点(也就是a,b) 包含编号不大于4的中间顶 点(a,b,c,d)的路径.有五条新 路径
7
Warshald Mult_matrix( int c[][], int a[][], int b[][], int n) { // a、b 和 c 均为 n 阶方阵,且 c 是 a 和 b 的乘 积 for (i=1; i<=n; ++i) for (j=1; j<=n; ++j) { c[i,j] = 0; for (k=1; k<=n; ++k) c[i,j] += a[i,k]*b[k,j]; } }// Mult_matrix
Warshall算法思想
• 确定递推关系式
– 对于路径: vi,每个节点编号都不大于k的中间节点集C,vj – 情况1:Vk∈C,那么中间节点集合的节点编号定 不会大于k-1,因此有: rij(k)=rij(k-1) , Vk∈C – 情况2: Vk∈C ,则有路径:
vi,编号≤k-1的节点集,Vk,编号≤k-1的节点集, vj 此时节点i到节点j是否有路径,取决于两部分“编号≤k-1
R(0),…, R(k-1), R(k),…, R(n)
– 具体来说,当且仅当,从节点i到节点j存在一条 有向路径,且该路径上的每一个中间节点的编 号都不大于k时,矩阵R(k)的第i行第j列的元素 rij(k)=1。
vi,每个节点编号都不大于k的中间节点集,vj
• R(0)就只是有向图的邻接矩阵。 • R(1)包含可以用第一个顶点作为中间点的 路径信息。 • R(n)说明可以用所有的顶点作为中间点寻 找有向路径,所以R(n)就是我们要求的传 递闭包。 • 这个算法的中心是我们可以通过R(k-1)来 计算R(k)的所有元素。
邻接矩阵法

邻接矩阵法邻接矩阵法是图论中一种常用的表示图结构的方法。
它通过一个二维矩阵来表示图中各个顶点之间的连接关系。
在邻接矩阵中,矩阵的行和列分别代表图中的顶点,而矩阵中的元素则表示对应顶点之间是否存在边。
邻接矩阵的定义假设有一个无向图G=(V,E),其中V为顶点集合,E为边集合。
邻接矩阵A是一个n×n的方阵,其中n为图中顶点的个数。
邻接矩阵A满足以下条件:•如果顶点i和顶点j之间存在边,则A[i][j]=1;•如果顶点i和顶点j之间不存在边,则A[i][j]=0。
对于有向图来说,邻接矩阵也可以用来表示其连接关系,只是在有向图中,边具有方向性。
邻接矩阵的应用邻接矩阵作为一种常见的图表示方法,在许多算法和应用中都得到了广泛的应用。
下面介绍一些常见的应用场景:1. 图遍历通过邻接矩阵,我们可以方便地遍历图中的顶点和边。
对于一个顶点i,我们只需要遍历邻接矩阵的第i行(或第i列),就可以获取到与该顶点直接相连的所有顶点。
2. 最短路径算法邻接矩阵常被用于求解最短路径问题,例如Dijkstra算法和Floyd-Warshall算法。
在这些算法中,通过邻接矩阵来表示各个顶点之间的距离或权重,然后根据具体的算法逻辑来计算最短路径。
3. 最小生成树邻接矩阵也可以用于求解最小生成树问题,例如Prim算法和Kruskal算法。
在这些算法中,邻接矩阵用来表示图中各个顶点之间的连接关系,并根据具体的算法逻辑选择合适的边来构建最小生成树。
4. 图的连通性判断通过邻接矩阵,我们可以判断一个图是否是连通图。
如果一个无向图的邻接矩阵是对称且连通的,则说明该图是一个连通图。
如果一个有向图的邻接矩阵是强连通的,则说明该有向图是强连通图。
邻接矩阵的优缺点邻接矩阵作为一种图的表示方法,具有以下优点:•表示简单:邻接矩阵直观地表示了图中各个顶点之间的连接关系,易于理解和实现。
•查询高效:通过邻接矩阵,可以快速判断两个顶点之间是否存在边,时间复杂度为O(1)。
武汉大学2015–2016 学年第一学期期末考试《离散数学》试题

6 2 7
v2 11
1
1 v3
9
v1
3
8
v4 10
v6
4
5
v5
9. (9 分) 设 4 个城市 v1, v2, v3, v4 有航班如下图所示. 问从一个城市起飞, 可否达到其余 3 个城市? 试给出下图的邻接矩阵, 并用 Warshall 算法求可达性矩阵来证明你的答案.
v2
v3
v4
v1
四、数理逻辑 (本题满分 25 分)
3. (1) 这 100 个数分为 50 组互质的数: {1, 2}, {3, 4}, · · · , {99, 100}.
在选出的 51 个数中, 必有 2 个数属于同一组, 故它们是互质的. (2) 这 100 个数分为 50 组差为 50 的数:
{1, 51}, {2, 52}, · · · , {50, 100}. 在选出的 51 个数中, 必有 2 个数属于同一组, 故它们的差为 50.
1.
(9
分)
设
N
是自然数集,
定义
N
上的二元关系
R
=
{ ⟨x, y⟩
|
x, y
∈
N∧x+y
是偶数}.
(1) 证明 R 是一个等价关系;
(2) 求商集 N/R.
2. (10 分) 设 A = {a, b, c, d}, A 上的二元关系 R1 和 R2 定义如下:
{
}
R1 = ⟨a, b⟩, ⟨b, c⟩, ⟨c, d⟩, ⟨d, a⟩ ,
0 1
.
0011
自反性 反自反性 对称性 反对称性 传递性
R1
否
是
否
可达矩阵的Warshall算法实现

可达矩阵的Warshall算法实现叶红【摘要】A lot of important properties of graphs can be indicated by matrix through the graph , when adjacency matrix of the graph node set was regarded as the relationship matrix, the matrix could generate which could reflect the graph between the nodes if there were roads. Matrix could be obtained by Warshall algorithm. In this paper, the algorithm implemented VB.%通过图的矩阵表示可以得到图的很多重要性质,将邻接矩阵看作图的结点集的关系矩阵,由此可以产生可达矩阵,从而可以反映图中各结点间是否有路.可达矩阵可用Warshall算法求得,作者用VB实现了该算法.【期刊名称】《安徽大学学报(自然科学版)》【年(卷),期】2011(035)004【总页数】5页(P31-35)【关键词】图的矩阵;邻接矩阵;Warshall算法;VB;可达矩阵【作者】叶红【作者单位】安徽工业大学计算机学院,安徽马鞍山243000【正文语种】中文【中图分类】TP391图论[1-2]是近年来发展迅速且应用广泛的一门新兴学科,它最早起源于一些数学游戏的难题研究,如迷宫、匿门博奕、棋盘上马的路线、四色和哈密顿环球旅行等问题.图论中许多概论和定理的建立都与解决这些问题有关.随着实际的需要和科学技术的发展,在近半个世纪内,图论得到了迅猛的发展,受到工程界和数学界的特别重视,成为解决许多实际问题的基本工具之一.用矩阵表示图,便于用代数方法来研究图的性质及构造算法,也便于用计算机来处理图.图的矩阵表示的常用形式有:邻接矩阵、可达矩阵和关联矩阵.邻接矩阵和可达矩阵常用于研究图的各种道路问题.作者研究在用邻接矩阵表示图时,考虑如何将邻接矩阵看作图的结点集的关系矩阵R,这样可达矩阵即为R的传递闭包[3-4],实现可达矩阵也可以用Warshall算法计算得到.定义1 设G=(V,E)是一简单有向图,结点集为V= {v1,v2,…,vn }.构造矩阵A=(aij)n×n ,其中:图1所示为一有向图,则称矩阵A为有向图G的邻接矩阵.一般情况下,一个图的全体邻接矩阵都是置换等价的,只须选取G的任何一个邻接矩阵作为该图邻接矩阵的代表.给出了一个图的邻接矩阵,就等于给出了图的全部信息,可以从中直接判定图的某些性质.无向图的邻接矩阵是对称矩阵,其中反映的图的性质和有向图类似,在这里,只以有向图为例.定理1 设G=(V,E)是一个n阶的简单有向图,A是G的邻接矩阵.对k≥1,令则表示G中从vi到vj的、长度为k的有向道路数目.推论1 设A是n阶简单有向图G的邻接矩阵则对恒成立(i≠j),当且仅当从vi到vj 是不可达的.对于有向图中结点间的可达情况,可以用一个矩阵来描述[5].定义2 设G=(V,E)是一个n阶的有向简单图.定义矩阵P=(pij)n×n,其中:则称P是图G的可达性矩阵(或称道路矩阵).可达性矩阵表明了图中任何两个不同的结点之间是否存在至少一条道路,以及在任何结点处是否存在着回路.虽然它只记录了有关图的一部份信息,但是很有用处,如在很多实际问题中,常常要判断有向图的一个结点vi到另一个结点vj是否存在路的问题.如果利用邻接矩阵A,则可计算A,A2,…,An,…,当发现其中某个Al的aij(l)≥1,就表明两结点间是可达的.但这种计算比较繁琐,且Al不知计算到何时为止,但由定理1可知,如果有向图G有n个结点:V= {v1,v2,…,vn},vi到vj有一条路,则必有一条长度不超过n的路,因此只要考察aij(l)就可以了,且1≤L≤n.可以通过先构造A,A2,…,An、再构造Bn=A+A2+… +An来求可达性矩阵.又因为有:这样可以确定P的元素pij,从而构造出P.可见图1中任何两个结点之间都是相互可达的,是一个强连通图.显然,这种先求A,A2,A3,…,An,Bn再构造P的方法很费事.如果把邻接矩阵A当作关系矩阵,则求可达性矩阵就相当于求A的传递闭包,因此可以仿照集合论中求二元关系的传递闭包的办法,利用Warshall算法来求可达性矩阵P[6].Warshall算法描述如下:(1)置新矩阵A;(2)置i:=1;(3)对所有 j,如果 a(i,j)=1,则对 k=1,2,…,n,a(j,k):=a(j,k)+a(i,k);(4)i加1;(5)如果i≤n,则转到步骤(3),否则停止.因为在可达矩阵的运算过程中,考虑的只是图中两结点vi,vj间是否有路,表现在矩阵中即为aij是否为1.在具体的运算过程中,所有参加运算的矩阵都是布尔矩阵,即矩阵中所有的元素只有0,或者1.在 Warshall算法中,矩阵的加运算是逻辑加(∨),即0∨0=0,0∨1=1,1∨0=1,1∨1=1.步骤(3)中,如果 a(j,k),a(i,k)都为0,则a(j,k)=0,否则a(j,k)=1.因此,在代码实现中用If(a(i,j)and(a(i,k)or a(j,k)))then a(i,k)=1 来代替算法中的逻辑加的运算[7-8],这样效率更高,且用语言实现也更简单.图2~4是由图1在VB环境下利用Warshall算法生成可达矩阵的运行结果.图的矩阵运算是图中各结点之间连通性的判断的一个重要部分,大部分研究者侧重于数学方面的应用[9-12],作者则利用计算机语言来实现求解的过程.本来由邻接矩阵生成可达矩阵的过程很复杂,而作者利用Warshall算法,在VB环境下实现了该过程,使得该运算简单、迅速、有效,避免了对邻接矩阵的的多次求幂再相加的复杂运算,使得具体的运算更直观.【相关文献】[1]左孝凌.离散数学[M].上海:上海科学技术文献出版社,1982:123-124.[2]孙道德.离散数学[M].合肥:中国科学技术大学出版社,2010:228-253.[3]刘宏兵.二元关系传递闭包的Warshall算法及应用[J].信阳师范学院学报:自然科学版,2005,18(1):103-105.[4]吴鹏 .有限集上二元关系传递性的矩阵判别法[J].成都大学学报:自然科学版,2009,28(6):122-125[5]王欣欣.关于由邻接矩阵求可达矩阵的方法[J].吉林化工学院学报,2005,22(8):89-91. [6]孙凤芝.Warshall算法在判别传递性与求传递闭包中的应用[J].长春大学学报:自然科学版,2007,17(6):13-16.[7]潘煜.离散数学中R+算法的研究与实现[J].微计算机信息,2008,8(3):250-251.[8]张世龙.稀疏矩阵情况下Warshall算法的改进[J].计算机工程与应用,2008,44(28):60-61.[9]潘地林.Visual Basic程序设计[M].北京:高等教育出版社,2009.[10]潘地林.Visual Basic程序设计实训与考试指导[M].北京:高等教育出版社,2009:111-112.[11]郭志军.Warshall算法的C语言实现[J].长沙大学学报:自然科学版,2008,22(5):69-71. [12]刘任任.基于求传递闭包的Warshall算法的改进[J].计算机工程,2005(10):38-39.。
图的邻接矩阵表示法

图的邻接矩阵表⽰法 图常⽤的存储⽅法⼜邻接表表⽰法以及邻接矩阵表⽰法,邻接表适合稀疏矩阵的存储,但是缺点是稍微复杂⼀点,并且插⼊操作或者说更新图的操作实际上是⽐较复杂的,⽽邻接矩阵更加简单,再存储密集矩阵的时候更加合适,下⾯使⽤c++实现⼀个简单的邻接矩阵。
由于图⼀般简单的分为⼏种:1. ⽆向图 2.有向图 3.带权⽆向图 4.带权有向图下⾯可以构造的时候分别选择这⼏种⽅式来实现: 下⾯所提到的VType表⽰的是顶点的类型,⼀般设置成char或者string⽤于表⽰⽐较合适,ArcType表⽰的是弧的值类型,对于⽆权图⽤0,1分别表⽰⾮邻接以及邻接,⽽有全权图表⽰权重⼤⼩。
所有的private数据如下所⽰:1struct ArcCell{2 ArcType adj; //顶点对间关系类型,⽆权图为0或者1,表明相邻或者是不相邻,有权图代表的就是权值的⼤⼩3 };4 VType *vvec; //⽤于表⽰顶点的信息,例如char或者string等5 ArcCell ** arcs; //邻接矩阵6int vecNum; //顶点数⽬7int arcNum; //弧数⽬8 GraphKind kind; //图的种类,⾮别可以为带权有向图,⽆向图,不带权有向,⽆向图。
default constructor:1 Graph(int _vexNum = 0, GraphKind _kind = DG) :2 vecNum(_vexNum), arcNum(0), kind(_kind)3 {4 vvec = new VType[vecNum];5 arcs = new ArcCell *[vecNum];6for (int i = 0; i < vecNum; ++i){7 arcs[i] = new ArcCell[vecNum];8 }9 } destructor是non-trivial的,实际还是需要⾃⼰写⼀个的,代码如下:1 ~Graph()2 {3for (int i = 0; i < vecNum; ++i){4delete[] arcs[i];5 }6delete[] arcs;7delete[] vvec;8 } 下⾯是初始化所有的顶点信息:1void Init()2 {3 cout << "请输⼊每个顶点的关键字:" << endl;4 VType val;5for (int i = 0; i < vecNum; ++i){6 cin >> vvec[i];7 }8 ArcCell ac;9 ac.adj = 0;10for (int i = 0; i < vecNum; ++i){11for (int j = 0; j < vecNum; ++j){12 arcs[i][j] = ac;13 }14 }15 } 下⾯是根据不同类型来进⾏图的创建: 有向图:1void createDG()2 {3 Init();4int vhead, vtail;5 cout << " 请依次输⼊每条边的开始节点以及结束结点: " << endl;6while (cin >> vhead >> vtail){7 arcNum++;8 arcs[vhead][vtail].adj = 1;9 }10 } 带权有向图:1void createWDG()2 {3 Init();4int vhead, vtail;5 ArcType w;6 cout << " 请输⼊每条弧的开始顶点,结束顶点以及权值: " << endl;7while (cin >> vhead >> vtail >> w){8 arcNum++;9 arcs[vhead][vtail].adj = w;10 }11 } ⽆向图:1void createUDG()2 {3 Init();4int vhead, vtail;5 cout << "请输⼊每条弧的开始顶点,结束顶点: " << endl;6while (cin >> vhead >> vtail){7 arcNum+=2;8 arcs[vhead][vtail].adj = 1;9 arcs[vtail][vhead].adj = 1;10 }11 } 带权⽆向图:1void createWUDG()2 {3 Init();4int vhead, vtail;5 ArcType w;6 cout << "请输⼊每条弧的开始顶点,结束顶点以及弧的权重(总共的顶点数为: " << vecNum << ".)" << endl;7while (cin >> vhead >> vtail >> w){8 arcNum+=2;9 arcs[vhead][vtail].adj = w;10 arcs[vtail][vhead].adj = w;11 }12 } 图的显⽰部分:1void displayGraph()2 {3 cout << "顶点的总数为: " << vecNum << "个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学基础
•单元内容提示
−图的邻接矩阵
−有向图的道路矩阵
−求道路矩阵的 Warshall 算法
•定义. 无向图的邻接矩阵
−对无向图 G =(V,
E),n =|V|,构造矩阵 A=(a ij )n ×n ,其中称 A 是图 G 的邻接矩阵。
•定理1.
−设 A 1、
A 2 分别为图 G 1、G 2 的邻接矩阵,则 G 1≅G 2 当且仅当存在置换矩阵 P,使得 A 1=PA 2P T 。
•定理2.
−设 A n ×n 是有向图 G 的邻接矩阵,则连接 v i 与 v j (i ≠j ) 的长度为 l 的有向道路的条数等于 A l 的第 i 行第 j 列的元素的数值。
−这里的道路是有方向的,但不一定指初等道路。
−证明:
−设图 G=(V, A),V={v 1, v 2, …, v n }。
对 l 作数学归纳法。
−归纳基始:
»l =1 时,邻接矩阵 A 描述了 G 中任意两点 v i 与 v j 一步可达的的邻接关系。
−归纳假设:
»设 l =k 时,矩阵 A k 的元素 A k [i , j ] 的值是从 v i 到 v j (i ≠j ) 的长度为 k 的有向道路的条数。
−归纳过程:当 l =k +1 时, A k +1 = A k × A −此时:
2017-11-19
1
1[,][,][,]n
k k p A i j A i p A p j +==×∑ − 由归纳假设,A k
[i , p ] 是从 v i 到 v p 的长度为 k 的有向道路的条数。
当 A[p , j ]=1 时,可以将这些有向道路扩展为从 v i 到 v j 的经过 v p 的长度为 k +1 的有向道路。
取遍所有的可能性后,A k+1[i , j ] 的值就是从 v i 到 v j (i ≠j) 的长度为 k +1 的全部有向道路的条数。
• 定义. 有向图的道路矩阵
− 对有向图 G =(V, R),n =|V|,构造矩阵 P=(p ij )n ×n ,其中
称矩阵 P 是图 G 的道路矩阵或可达矩阵。
− 讨论:有向图 G =(V, R) 的道路矩阵 P 给出了关系 R 的传递闭包 t(R) 的关系矩阵。
• 算法. 求给定有向图 G 的道路矩阵 P
− 对有向图 G =(V, R),n =|V|∈Z +,设 A 为 G 的邻接矩阵,B = A+A 2+A 3+…+A n ‐1,则由[定理2],b ij 表示由 v i 至 v j 的长度为1,或2,或…,或 n ‐1 的路径数目,即为由 v i 至 v j 的全部路径总和。
令
即可求得 G 的道路矩阵 P 。
算法复杂度 O(n 4)。
• 定义. 二值元素的逻辑运算
− 0∨0 = 0,0∨1 = 1∨0 = 1,1∨1 = 1
− 0∧0 = 0,0∧1 = 1∧0 = 0,1∧1 = 1
• 定义. 二值矩阵的逻辑运算
− 设有 n ×n 阶矩阵 A = (a ij ),B = (b ij ),矩阵元素值域为 {0, 1},定义运算 A ∨B 和 A ⊗B :
1(),(),
()()ij ij ij ij ij ij n ij ik kj k A B a b A B a b A B a b =∨=∨∧=∧⊗=∨∧
• 定义.
− A (1) = A
− A (k ) = A (k −1) ⊗ A ( k ≥2 )
− 注意 A (k ) 与 A k 的区别。
• 定理3.
− 设 A n ×n 是有向图 G 的邻接矩阵,若从 v i 到 v j 存在长度为 l 的路,则 [A (l )]ij = 1,否则 [A (l )]ij = 0。
− 证明:对 l 作归纳;或直接引用[定理2]。
• 算法. 求给定有向图 G 的道路矩阵 P
− 对有向图 G =(V, R),n =|V|∈Z +,设 A 为 G 的邻接矩阵,则 G 的道路矩阵 P = A ∨A (2)∨A (3)∨ … ∨A (n ‐1),算法复杂度 O(n 4)。
• Warshall 算法. 设 A n ×n 是图 G 的邻接矩阵,求 G 的道路矩阵 P 。
(1) P ← A
(2) i ← 1
(3) j ← 1
(4) p jk ← p jk ∨ (p ji ∧ p ik ), k = 1 ... n
(5) j ← j +1, if j ≤n goto 4
(6) i ← i +1, if i ≤n goto 3
(7) Stop
• 定理4.
− Warshall 算法以计算复杂度 O(n 3) 在图 G 的道路矩阵 P 上结束。
− 证明:(略)
• 例:
− 有向图 G 的邻接矩阵 A 如下,使用 Warshall 算法求G 的道路矩阵 P 。
− 解:
P ← A ,i=1。
矩阵元素 p jk 处理次序:p 11, p 12, p 13, p 14, p 21, p 22, …, p 31,…, p 41,…, p 44。
− 按照 p jk ← p jk ∨ (p ji ∧ p ik ), j = 1 ... n , k = 1 ... n
p 11 = p 11∨(p 1i ∧p i1) = p 11∨(p 11∧p 11) = 0 ⎛⎞⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠01000011A = 11011000
p12 = p12∨(p2i∧p i2) = p12∨(p21∧p12) = 1
p13 = p13∨(p3i∧p i3) = p13∨(p31∧p13) = 0
…………
结果:
−考察第 i 次循环。
第 i 列的0元对应的第 j 行有 p ji=0,故
p jk=p jk∨(p ji∧p ik)=p jk∨(0∧p ik)=p jk;第 i 列的1元对应的第 j 行有 p ji=1,故
p jk=p jk∨(p ji∧p ik)= p jk∨p ik , 即将该行与第 i 行做“或”运算。
i =2 的迭代结果:
−(表上作业法) 第 i 次循环时,将第 i 行分别“叠加”到第 i 列的非0元对应的那些行,“叠加”运算是一对行向量各个对应元素的逻辑“或”运算。
如上例:
•例:
•进一步的讨论
−可见,{v1},{v3} 以及 {v2, v4, v5} 的导出子图分别构成强连通分量。
下一单元内容提示
−树的定义
−连通图的生成树
−有根树。
