插值算法与matlab代码
MATLAB实现:拉格朗日插值法示例代码及应用指南

下面是使用 MATLAB 编写的拉格朗日插值法的示例代码:参数:x 是已知点的 x 坐标数组,y 是已知点的 y 坐标数组,point 是要进行插值的点的 x 坐标。
该函数会返回在给定 x 坐标 point 处的插值结果。
算法的实现思路是根据拉格朗日插值公式计算插值多项式,然后将 point 带入多项式计算得到插值结果。
你可以按照以下步骤使用上述函数:定义已知点的 x 坐标数组 x 和对应的 y 坐标数组 y。
调用lagrange_interpolation函数,并将x、y 和要插值的point 作为参数传递进去。
函数将返回在 point 处的插值结果。
以下是一个使用示例:1.定义已知点的 x 和 y 坐标x = [0, 1, 2, 4];y = [1, 4, 3, 2];2.要进行插值的点的 x 坐标point = 3.5;3.调用 lagrange_interpolation 函数进行插值result = lagrange_interpolation(x, y, point);4.输出插值结果disp(['在x = ', num2str(point), ' 处的插值结果为:', num2str(result)]);在上述示例中,已知点的 x 坐标为 [0, 1, 2, 4],对应的 y 坐标为 [1, 4, 3, 2]。
我们要在point = 3.5 处进行插值,然后通过调用lagrange_interpolation 函数计算插值结果,并输出结果。
请注意,拉格朗日插值法适用于小样本量和较低次数的插值问题。
对于大样本量和更高次数的插值,可能需要考虑使用其他插值方法或数值计算库中提供的更高级的插值函数。
插值MATLAB实现(牛顿差商插值误差龙格现象切比雪夫插值)

插值MATLAB实现(牛顿差商插值误差龙格现象切比雪夫插值)插值是数值分析中的一种方法,通过已知数据点的函数值来估计函数在其他点的值。
MATLAB提供了多种方法来实现插值,包括牛顿差商插值、插值误差分析、龙格现象和切比雪夫插值。
下面将详细介绍这些方法的实现原理和MATLAB代码示例。
1.牛顿差商插值:牛顿差商插值是一种基于多项式插值的方法,其中差商是一个连续性的差分商。
该方法的优势在于可以快速计算多项式的系数。
以下是MATLAB代码示例:```matlabfunction [coeff] = newton_interpolation(x, y)n = length(x);F = zeros(n, n);F(:,1)=y';for j = 2:nfor i = j:nF(i,j)=(F(i,j-1)-F(i-1,j-1))/(x(i)-x(i-j+1));endendcoeff = F(n, :);end```该代码中,输入参数x和y分别表示已知数据点的x坐标和y坐标,返回值coeff表示插值多项式的系数。
2.插值误差分析:插值误差是指插值函数与原始函数之间的差异。
一般来说,通过增加插值节点的数量或使用更高次的插值多项式可以减小插值误差。
以下是MATLAB代码示例:```matlabfunction [error] = interpolation_error(x, y, x_eval)n = length(x);p = polyfit(x, y, n-1);y_eval = polyval(p, x_eval);f_eval = sin(pi*x_eval);error = abs(f_eval - y_eval);end```该代码中,输入参数x和y分别表示已知数据点的x坐标和y坐标,x_eval表示插值节点的x坐标,error表示插值误差。
3.龙格现象:龙格现象是插值多项式在等距插值节点上错误增长的现象。
用MATLAB作函数插值

1.先在三维坐标画出原始数据,画出粗糙的温度分布曲面图. 输入以下命令: x=1:5; y=1:3; temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86]; mesh(x,y,temps) 2.以平滑数据,在x、y方向上每隔0.2个单位的地方进行插值.
figure(5) subplot(1,3,1),contour(xi,yi,z1i,10,'r'); subplot(1,3,2),contour(xi,yi,z2i,10,'r'); subplot(1,3,3),contour(xi,yi,z3i,10,'r');
用MATLAB作散点数据的插值计算
例
已知飞机下轮廓线上数据如下,求x每改变0.1时的y值。
X Y
0 3 5 7 9 1 1 1 1 1 1 2 3 4 5 0 12 17 20 21 20 18 12 10 16 . . . . . . . . .
机翼下 轮廓线 y
x
x0=[0 3 5 7 9 11 12 13 14 15 ]; y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6 ]; x=0:0.1:15; y1=lagr1(x0,y0,x); y2=interp1(x0,y0,x); y3=interp1(x0,y0,x,'spline'); subplot(3,1,1) plot(x0,y0,'k+',x,y1,'r') grid title('lagrange') subplot(3,1,2) plot(x0,y0,'k+',x,y2,'r') grid title('piecewise linear') subplot(3,1,3) plot(x0,y0,'k+',x,y3,'r') grid title('spline')
用matlab编写拉格朗日插值算法的程序

用matlab编写拉格朗日插值算法的程序10[ 标签:matlab,插值算法,程序 ]用matlab编写拉格朗日插值算法的程序,并以下面给出的函数表为数据基础,在整个插值区间上采用拉格朗日插值法计算f(0.6),写出程序源代码,输出计算结果x -2.15 -1.00 0.01 1.02 2.03 3.25y 17.03 7.24 1.05 2.03 17.06 23.05匿名回答:1 人气:6 解决时间:2011-05-24 19:58满意答案好评率:83%做了一个测试,希望有所帮助。
代码:% 用matlab编写拉格朗日插值算法的程序,并以下面给出的函数表为数据基础,% 在整个插值区间上采用拉格朗日插值法计算f(0.6),写出程序源代码,输出计算结果% x -2.15 -1.00 0.01 1.02 2.03 3.25% y 17.03 7.24 1.05 2.03 17.06 23.05function main()clc;x = [-2.15 -1.00 0.01 1.02 2.03 3.25]; y = [17.03 7.24 1.05 2.03 17.06 23.05 ]; x0 = 0.6;f = Language(x,y,x0)function f = Language(x,y,x0)%求已知数据点的拉格朗日插值多项式%已知数据点的x坐标向量: x%已知数据点的y坐标向量: y%插值点的x坐标: x0%求得的拉格朗日插值多项式或在x0处的插值: f syms t l;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等!');return; %检错endh=sym(0);for (i=1:n)l=sym(y(i));for(j=1:i-1)l=l*(t-x(j))/(x(i)-x(j));end;for(j=i+1:n)l=l*(t-x(j))/(x(i)-x(j));end;h=h+l;endsimplify(h);if(nargin == 3)f = subs (h,'t',x0); %计算插值点的函数值elsef=collect(h);f = vpa(f,6); %将插值多项式的系数化成6位精度的小数end结果:f =0.0201>>如何用MATLAB编写的拉格朗日插值算法的程序、二阶龙格-库塔方法的程序和SOR迭代法的程序,要能运行的∮初夏戀雨¢回答:2 人气:29 解决时间:2009-12-08 19:04满意答案好评率:100%拉格朗日function y=lagrange(x0,y0,x)n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endSOR迭代法的Matlab程序function [x]=SOR_iterative(A,b)% 用SOR迭代求解线性方程组,矩阵A是方阵x0=zeros(1,length(b)); % 赋初值tol=10^(-2); % 给定误差界N=1000; % 给定最大迭代次数[n,n]=size(A); % 确定矩阵A的阶w=1; % 给定松弛因子k=1;% 迭代过程while k<=Nx(1)=(b(1)-A(1,2:n)*x0(2:n)')/A(1,1);for i=2:nx(i)=(1-w)*x0(i)+w*(b(i)-A(i,1:i-1)*x(1:i-1)'-A(i,i+1:n)*x0(i+1:n)')/A(i,i); endif max(abs(x-x0))<=tolfid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n'); fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'x的值\n\n');fprintf(fid, '%12.8f \n', x);break;endk=k+1;x0=x;endif k==N+1fid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n'); fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'超过最大迭代次数,求解失败!');fclose(fid);endMatlab中龙格-库塔(Runge-Kutta)方法原理及实现龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
matlab插值(详细 全面)

Matlab中插值函数汇总和使用说明MATLAB中的插值函数为interp1,其调用格式为: yi= interp1(x,y,xi,'method')其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量, 'method'表示采用的插值方法,MATLAB提供的插值方法有几种: 'method'是最邻近插值, 'linear'线性插值; 'spline'三次样条插值; 'cubic'立方插值.缺省时表示线性插值注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
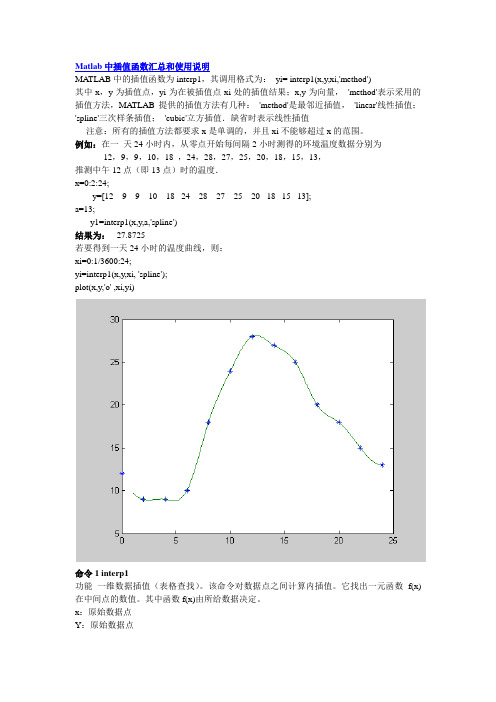
例如:在一天24小时内,从零点开始每间隔2小时测得的环境温度数据分别为12,9,9,10,18 ,24,28,27,25,20,18,15,13,推测中午12点(即13点)时的温度.x=0:2:24;y=[12 9 9 10 18 24 28 27 25 20 18 15 13];a=13;y1=interp1(x,y,a,'spline')结果为: 27.8725若要得到一天24小时的温度曲线,则:xi=0:1/3600:24;yi=interp1(x,y,xi, 'spline');plot(x,y,'o' ,xi,yi)命令1 interp1功能一维数据插值(表格查找)。
该命令对数据点之间计算内插值。
它找出一元函数f(x)在中间点的数值。
其中函数f(x)由所给数据决定。
x:原始数据点Y:原始数据点xi:插值点Yi:插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。
参量x 指定数据Y 的点。
若Y 为一矩阵,则按Y 的每列计算。
yi是阶数为length(xi)*size(Y,2)的输出矩阵。
matlab插值(详细 全面)范文

Matlab中插值函数汇总和使用说明MATLAB中的插值函数为interp1,其调用格式为:yi= interp1(x,y,xi,'method')其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量, 'method'表示采用的插值方法,MATLAB提供的插值方法有几种: 'method'是最邻近插值, 'linear'线性插值; 'spline'三次样条插值; 'cubic'立方插值.缺省时表示线性插值注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
例如:在一天24小时内,从零点开始每间隔2小时测得的环境温度数据分别为12,9,9,10,18 ,24,28,27,25,20,18,15,13,推测中午12点(即13点)时的温度.x=0:2:24;y=[12 9 9 10 18 24 28 27 25 20 18 15 13];a=13;y1=interp1(x,y,a,'spline')结果为: 27.8725若要得到一天24小时的温度曲线,则:xi=0:1/3600:24;yi=interp1(x,y,xi, 'spline');plot(x,y,'o' ,xi,yi)命令1 interp1功能一维数据插值(表格查找)。
该命令对数据点之间计算内插值。
它找出一元函数f(x)在中间点的数值。
其中函数f(x)由所给数据决定。
x:原始数据点Y:原始数据点xi:插值点Yi:插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。
参量x 指定数据Y 的点。
若Y 为一矩阵,则按Y 的每列计算。
yi 是阶数为length(xi)*size(Y,2)的输出矩阵。
Matlab求解插值问题

Matlab求解插值问题在应用领域中,由有限个已知数据点,构造一个解析表达式,由此计算数据点之间的函数值,称之为插值。
实例:海底探测问题某公司用声纳对海底进行测试,在5×5海里的坐标点上测得海底深度的值,希望通过这些有限的数据了解更多处的海底情况。
并绘出较细致的海底曲面图。
1、一元插值一元插值是对一元数据点(x i,y i)进行插值。
线性插值:由已知数据点连成一条折线,认为相临两个数据点之间的函数值就在这两点之间的连线上。
一般来说,数据点数越多,线性插值就越精确。
调用格式:yi=interp1(x,y,xi,’linear’) %线性插值zi=interp1(x,y,xi,’spline’) %三次样条插值wi=interp1(x,y,xi,’cubic’) %三次多项式插值说明:yi、zi、wi为对应xi的不同类型的插值。
x、y为已知数据点。
例:已知数据:求当x i=0.25时的y i的值。
程序:x=0:.1:1;y=[.3 .5 1 1.4 1.6 1 .6 .4 .8 1.5 2];yi0=interp1(x,y,0.025,'linear')xi=0:.02:1;yi=interp1(x,y,xi,'linear');zi=interp1(x,y,xi,'spline');wi=interp1(x,y,xi,'cubic');plot(x,y,'o',xi,yi,'r+',xi,zi,'g*',xi,wi,'k.-')legend('原始点','线性点','三次样条','三次多项式')结果:yi0 = 0.3500要得到给定的几个点的对应函数值,可用:xi =[ 0.2500 0.3500 0.4500]yi=interp1(x,y,xi,'spline')结果:yi =1.2088 1.5802 1.34542、二元插值二元插值与一元插值的基本思想一致,对原始数据点(x,y,z)构造见上面函数求出插值点数据(xi,yi,zi)。
(整理)matlab插值计算.

插值方法晚上做一个曲线拟合,结果才开始用最小二乘法拟合时,拟合出来的东西太难看了!于是尝试用其他方法。
经过一番按图索骥,终于发现做曲线拟合的话,采用插值法是比较理想的方法。
尤其是样条插值,插完后线条十分光滑。
方法付后,最关键的问题是求解时要积分,放这里想要的时候就可以直接过来拿,不用死去搜索啦。
呵呵插值方法的Matlab实现一维数据插值MATLAB中用函数interp1来拟合一维数据,语法是YI = INTERP1(X,Y,XI,方法)其中(X,Y)是已给的数据点,XI 是插值点,其中方法主要有'linear' -线性插值,默认'pchip' -逐段三次Hermite插值'spline' -逐段三次样条函数插值其中最后一种插值的曲线比较平滑例:x=0:.12:1; x1=0:.02:1;%(其中x=0:.12:1表示显示的插值点,x1=0:.02:1表示插值的步长)y=(x.^2-3*x+5).*exp(-5*x).*sin(x);plot(x,y,'o'); hold on;y1=interp1(x,y,x1,'spline');plot(x1,y1,':')如果要根据样本点求函数的定积分,而函数又是比较光滑的,则可以用样条函数进行插值后再积分,在MATLAB中可以编写如下程序:function y=quadspln(x0,y0,a,b)f=inline('interp1(x0,y0,x,''spline'')','x','x0','y0');y=quadl(f,a,b,1e-8,[],x0,y0);现求sin(x)在区间[0,pi]上的定积分,只取5点x0=[0,0.4,1,2,pi];y0=sin(x0);I=quadspln(x0,y0,0,pi)结果得到的值为2.01905,精确值为2求一段matlab插值程序悬赏分:20 - 解决时间:2009-12-26 19:57已知5个数据点:x=[0.25 0.5 0.75 1] y=[0 0.3104 0.6177 0.7886 1] ,求一段matlab插值程序,求过这5个数据点的插值多项式,并在x-y坐标中画出y=f(x)图形,并且求出f (x)与x轴围成图形的面积(积分),不胜感激!使用Lagrange 插值多项式的方法:首先把下面的代码复制到M文件中,保存成lagranfunction [C,L]=lagran(X,Y)% input - X is a vector that contains a list of abscissas% - Y is a vector that contains a list of ordinates% output - C is a matrix that contains the coefficients of the lagrange interpolatory polynomial%- L is a matrix that contains the lagrange coefficients polynomialw=length(X);n=w-1;L=zeros(w,w);for k=1:n+1V=1;for j=1:n+1if k~=jV=conv(V,poly(X(j)))/(X(k)-X(j));endendL(k,:)=V;endC=Y*L;然后在命令窗口中输入以下内容:x=[0 0.25 0.5 0.75 1];y=[0 0.3104 0.6177 0.7886 1];lagran(x,y)ans =3.3088 -6.3851 3.3164 0.7599 0得到的数据就是多项式各项的系数,注意最后一个是常数项,即x^0,所以表达式为:f=3.3088*x.^4-6.3851*x.^3+3.3164*x.^2 +0.7599*x求面积就是积分求解>> f=@(x)3.3088*x.^4-6.3851*x.^3+3.3164*x.^2 +0.7599*x;>> quad(f,0,1)ans =0.5509这些点肯定是通过这个多项式的!MATLAB插值与拟合§1曲线拟合实例:温度曲线问题气象部门观测到一天某些时刻的温度变化数据为:试描绘出温度变化曲线。
三种插值法原理及其代码

最临近插值法原理:这种算法就是根据原图像和目标图像的尺寸,计算缩放的比例,然后根据缩放比例计算目标像素所依据的原像素,过程中自然会产生小数,这时就采用四舍五入,取与这个点最相近的点。
图解如下:如果(i+u, j+v)落在A区,即u<0.5, v<0.5,则将左上角象素的灰度值赋给待求象素,同理,落在B区则赋予右上角的象素灰度值,落在C区则赋予左下角象素的灰度值,落在D区则赋予右下角象素的灰度值。
具体Matlab源代码实现:clear all;A=imread('12.png'); %读取图像信息imshow(A); %显示原图title('原图128*128');Row = size(A,1); Col = size(A,2); %图像行数和列数nn=8; %放大倍数m = round(nn*Row); %求出变换后的坐标的最大值n = round(nn*Col);B = zeros(m,n,3); %定义变换后的图像for i = 1 : mfor j = 1 : nx = round(i/nn); y = round(j/nn); %最小临近法对图像进行插值if x==0 x = 1; endif y==0 y = 1; endif x>Row x = Row; endif y>Col y = Col;endB(i,j,:) = A(x,y,:);endendB = uint8(B); %将矩阵转换成8位无符号整数figure;imshow(B); %显示输出图片title('最邻近插值法放大8倍1024*1024');运行程序后,原图如图1所示:图1用最邻近插值法放大8倍后的图如图2所示:图2双线性内插值法:计算过程简单了解,如图,已知Q12,Q22,Q11,Q21,但是要插值的点为P 点,这就要用双线性插值了,首先在x轴方向上,对R1和R2两个点进行插值,这个很简单,然后根据R1和R2对P点进行插值,这就是所谓的双线性插值。
双三次插值(bicubic interpolation)原理及MATLAB源码实现

%双三次插值具体实现clc,clear;fff=imread('E:\Documents\BUPT\DIP\图片\lena.bmp');ff = rgb2gray(fff);%转化为灰度图像[mm,nn]=size(ff); %将图像隔行隔列抽取元素,得到缩小的图像fm=mm/2;n=nn/2;f = zeros(m,n);for i=1:mfor j=1:nf(i,j)=ff(2*i,2*j);endendk=5; %设置放大倍数bijiao1 = imresize(f,k,'bilinear');%双线性插值结果比较bijiao = uint8(bijiao1);a=f(1,:);c=f(m,:); %将待插值图像矩阵前后各扩展两行两列,共扩展四行四列b=[f(1,1),f(1,1),f(:,1)',f(m,1),f(m,1)];d=[f(1,n),f(1,n),f(:,n)',f(m,n),f(m,n)];a1=[a;a;f;c;c];b1=[b;b;a1';d;d];ffff=b1';f1=double(ffff);g1 = zeros(k*m,k*n);for i=1:k*m %利用双三次插值公式对新图象所有像素赋值u=rem(i,k)/k; i1=floor(i/k)+2;A=[sw(1+u) sw(u) sw(1-u) sw(2-u)];for j=1:k*nv=rem(j,k)/k;j1=floor(j/k)+2;C=[sw(1+v);sw(v);sw(1-v);sw(2-v)];B=[f1(i1-1,j1-1) f1(i1-1,j1) f1(i1-1,j1+1) f1(i1-1,j1+2)f1(i1,j1-1) f1(i1,j1) f1(i1,j1+1) f1(i1,j1+2)f1(i1+1,j1-1) f1(i1+1,j1) f1(i1+1,j1+1) f1(i1+1,j1+2)f1(i1+2,j1-1) f1(i1+2,j1) f1(i1+2,j1+1) f1(i1+2,j1+2)];g1(i,j)=(A*B*C);endendg=uint8(g1);imshow(uint8(f)); title('缩小的图像'); %显示缩小的图像figure,imshow(ff);title('原图'); %显示原图像figure,imshow(g);title('双三次插值放大的图像'); %显示插值后的图像figure,imshow(bijiao);title('双线性插值放大结果'); %显示插值后的图像mse=0;ff=double(ff);g=double(g);ff2=fftshift(fft2(ff)); %计算原图像和插值图像的傅立叶幅度谱g2=fftshift(fft2(g));figure,subplot(1,2,1),imshow(log(abs(ff2)),[8,10]);title('原图像的傅立叶幅度谱'); subplot(1,2,2),imshow(log(abs(g2)),[8,10]);title('双三次插值图像的傅立叶幅度谱');基函数代码:function A=sw(w1)w=abs(w1);if w<1&&w>=0A=1-2*w^2+w^3;elseif w>=1&&w<2A=4-8*w+5*w^2-w^3;elseA=0;end算法原理双三次插值又称立方卷积插值。
插值算法与matlab代码
Matlab中插值函数汇总和使用说明MATLAB中的插值函数为interp1,其调用格式为: yi= interp1(x,y,xi,'method')其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量,'method'表示采用的插值方法,MA TLAB提供的插值方法有几种:'method'是最邻近插值,'linear'线性插值;'spline'三次样条插值;'cubic'立方插值.缺省时表示线性插值注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
例如:在一天24小时内,从零点开始每间隔2小时测得的环境温度数据分别为12,9,9,10,18 ,24,28,27,25,20,18,15,13,推测中午12点(即13点)时的温度.x=0:2:24;y=[12 9 9 10 18 24 28 27 25 20 18 15 13];a=13;y1=interp1(x,y,a,'spline')结果为:27.8725若要得到一天24小时的温度曲线,则:xi=0:1/3600:24;yi=interp1(x,y,xi, 'spline');plot(x,y,'o' ,xi,yi)命令1 interp1功能一维数据插值(表格查找)。
该命令对数据点之间计算内插值。
它找出一元函数f(x)在中间点的数值。
其中函数f(x)由所给数据决定。
x:原始数据点Y:原始数据点xi:插值点Yi:插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。
参量x 指定数据Y 的点。
若Y 为一矩阵,则按Y 的每列计算。
yi 是阶数为length(xi)*size(Y,2)的输出矩阵。
(2)yi = interp1(Y,xi)假定x=1:N,其中N 为向量Y 的长度,或者为矩阵Y 的行数。
Matlab插值算法程序集

Matlab插值算法程序集一、插值算法1.Atkenfunction f = Atken(x,y,x0)syms t;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等!');return;end %检错y1(1:n) = t; %符号函数数组要赋初值for(i=1:n-1)for(j=i+1:n)y1(j) = y(j)*(t-x(i))/(x(j)-x(i))+y(i)*(t-x(j))/(x(i)-x(j));endy = y1;simplify(y1);endif(nargin == 3)f = subs(y1(n),'t',x0); %计算插值点的函数值elsesimplify(y1(n)); %化简f = collect(y1(n)); %将插值多项式展开f = vpa(f,6); %将插值多项式的系数化成6位精度的小数end2.BSamplefunction f0 = BSample(a,b,n,y,y_1,y_N,x0)f0 = 0.0;h = (b-a)/n;c = zeros(n+3,1);b = zeros(n+1,1);for i=0:n-1if(a+i*h<=x0) && (a+i*h+h>=x0)index = i;break;endend %找到x0所在区间A = diag(4*ones(n+1,1));I = eye(n+1,n+1);AL = [I(2:n+1,:);zeros(1,n+1)];AU = [zeros(1,n+1);I(1:n,:)];A = A+AL+AU; %形成系数矩阵for i=2:nb(i,1) = 6*y(i);endb(1) = 6*y(1)+2*h*y_1;b(n+1) = 6*y(n+1)-2*h*y_N;d = followup(A,b); %用追赶法求出系数c(2:n+2) = d;c(1) = c(2) - 2*h*y_1; %c(-1)c(n+3) = c(3)+2*h*y_N; %c(n+1)x1 = (a+index*h-h-x0)/h;m1 = c(index+1)*(-((abs(x1))^3)/6+(x1)^2-2*abs(x1)+4/3); x2 = (a+index*h-x0)/h;m2 = c(index+2)*((abs(x2))^3/2-(x2)^2+2/3);x3 = (a+index*h+h-x0)/h;m3 = c(index+3)*((abs(x3))^3/2-(x3)^2+2/3);x4 = (a+index*h+2*h-x0)/h;m4 = c(index+4)*(-((abs(x4))^3)/6+(x4)^2-2*abs(x4)+4/3); f0 = m1+m2+m3+m4; %求出插值3.DCSfunction f = DCS(x,y,x0)syms t;if(length(x) == length(y))n = length(x);c(1:n) = 0.0;elsedisp('x和y的维数不相等!');return;endc(1) = y(1);for(i=1:n-1)for(j=i+1:n)y1(j) = (x(j)-x(i))/(y(j)-y(i));endc(i+1) = y1(i+1);y = y1;endf = c(n);for(i=1:n-1)f = c(n-i) + (t-x(n-i))/f;f = vpa(f,6);if(i==n-1)if(nargin == 3)f = subs(f,'t',x0);elsef = vpa(f,6);endendend;4.DHfunction fz = DH(x,y,x0,y0,zx,zy,zxy)n = length(x);m = length(y);for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index_x = i;break;endend %找到x0所在区间for i=1:mif(y(i)<=y0)&& (y(i+1)>=y0)index_y = i;break;endend %找到y0所在区间hx = x(index_x+1) - x(index_x);hy = y(index_y+1) - y(index_y);tx = (x0 - x(index_x))/hx; %插值坐标归一化ty = (y0 - y(index_y))/hy; %插值坐标归一化Hl = [(1-tx)^2*(1+2*tx) tx*tx*(3-2*tx) tx*(1-tx)^2 tx*tx*(tx-1)]; %左向量Hr = [(1-ty)^2*(1+2*ty); ty*ty*(3-2*ty); ty*(1-ty)^2 ; ty*ty*(ty-1)]; %右向量C = [Z(index_x, index_y) Z(index_x,index_y+1) zy(index_x, index_y) ...zy(index_x, index_y+1);Z(index_x+1, index_y) Z(index_x+1,index_y+1) zy(index_x+1, index_y) ...zy(index_x+1, index_y+1);zx(index_x, index_y) zy(index_x, index_y+1) zxy(index_x, index_y) ...zxy(index_x, index_y+1);zx(index_x+1, index_y) zy(index_x+1, index_y+1) zxy(index_x+1, index_y) ... zxy(index_x+1, index_y+1)]; %C矩阵fz = Hl*C*Hr;5.DLfunction fz = DL(x,y,Z,x0,y0,eps)n = length(x);m = length(y);for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index_x = i;break;endend %找到x0所在区间for i=1:mif(y(i)<=y0)&& (y(i+1)>=y0)index_y = i;break;endend %找到y0所在区间A = [1 x(index_x) y(index_y) x(index_x)* y(index_y);1 x(index_x+1) y(index_y+1) x(index_x+1)* y(index_y+1);1 x(index_x) y(index_y+1) x(index_x)* y(index_y+1);1 x(index_x+1) y(index_y) x(index_x+1)* y(index_y)];iA = inv(A);B = iA*[Z(index_x,index_y); Z(index_x+1,index_y+1); Z(index_x,index_y+1);Z(index_x+1,index_y)];fz = [1 x0 y0 x0*y0]*B;6.DTLfunction fz = DTL(x,y,Z,x0,y0)syms s t;f = 0.0;n = length(x);m = length(y);for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index_x = i;break;endend %找到x0所在区间for i=1:mif(y(i)<=y0)&& (y(i+1)>=y0)index_y = i;break;endend %找到y0所在区间if index_x == 1cx(1:3) = index_x:(index_x+2);elseif index_x == n-1cx(1:3) = (index_x-1):(index_x+1);elseif abs(x(index_x-1)-x0)>abs(x(index_x+2)-x0)cx(1:3) = (index_x):(index_x+2);elsecx(1:3) = (index_x-1):(index_x+1);endendend %找到离x0最近的三个x坐标if index_y == 1cy(1:3) = index_y:(index_y+2);elseif index_y == m-1cy(1:3) = (index_y-1):(index_y+1);elseif abs(y(index_y-1)-y0)>=abs(y(index_y+2)-y0)cy(1:3) = (index_y):(index_y+2);elsecy(1:3) = (index_y-1):(index_y+1);endendend %找到离y0最近的三个y坐标for i=1:3i1 = mod(i+1,3);if(i1 == 0)i1 = 3;endi2 = mod(i+2,3);if(i2 == 0)i2 = 3;endfor j=1:3j1 = mod(j+1,3);if(j1 == 0)j1 = 3;endj2 = mod(j+2,3);if(j2 == 0)j2 = 3;endf = f+Z(cx(i),cy(j))*((t-x(cx(i1)))*(t-x(cx(i2)))/(x(cx(i))-x(cx(i1)))/(x(cx(i))-x(cx(i2))))* ...(s-y(cy(j1)))*(s-y(cy(j2)))/(y(cy(j))-y(cy(j1)))/(y(cy(j))-y(cy(j2)));%插值多项式endendfz = subs(f,'[t s]',[x0 y0]);7.FCZfunction fz = DTL(x,y,Z,x0,y0)syms s t;f = 0.0;n = length(x);m = length(y);for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index_x = i;break;endend %找到x0所在区间for i=1:mif(y(i)<=y0)&& (y(i+1)>=y0)index_y = i;break;endend %找到y0所在区间if index_x == 1cx(1:3) = index_x:(index_x+2);elseif index_x == n-1cx(1:3) = (index_x-1):(index_x+1);elseif abs(x(index_x-1)-x0)>abs(x(index_x+2)-x0)cx(1:3) = (index_x):(index_x+2);elsecx(1:3) = (index_x-1):(index_x+1);endendend %找到离x0最近的三个x坐标if index_y == 1cy(1:3) = index_y:(index_y+2);elseif index_y == m-1cy(1:3) = (index_y-1):(index_y+1);elseif abs(y(index_y-1)-y0)>=abs(y(index_y+2)-y0)cy(1:3) = (index_y):(index_y+2);elsecy(1:3) = (index_y-1):(index_y+1);endendend %找到离y0最近的三个y坐标for i=1:3i1 = mod(i+1,3);if(i1 == 0)i1 = 3;endi2 = mod(i+2,3);if(i2 == 0)i2 = 3;endfor j=1:3j1 = mod(j+1,3);if(j1 == 0)j1 = 3;endj2 = mod(j+2,3);if(j2 == 0)j2 = 3;endf = f+Z(cx(i),cy(j))*((t-x(cx(i1)))*(t-x(cx(i2)))/(x(cx(i))-x(cx(i1)))/(x(cx(i))-x(cx(i2))))* ...(s-y(cy(j1)))*(s-y(cy(j2)))/(y(cy(j))-y(cy(j1)))/(y(cy(j))-y(cy(j2)));%插值多项式endendfz = subs(f,'[t s]',[x0 y0]);8.Gaussfunction f = Gauss(x,y,x0)if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等!');return;endxx =linspace(x(1),x(n),(x(2)-x(1)));if(xx ~= x)disp('节点之间不是等距的!');return;endif( mod(n,2) ==1)if(nargin == 2)f = GStirling(x,y,n);else if(nargin == 3)f = GStirling(x,y,n,x0);endendelseif(nargin == 2)f = GBessel(x,y,n);else if(nargin == 3)f = GBessel(x,y,n,x0);endendendfunction f = GStirling(x,y,n,x0)syms t;nn = (n+1)/2;f = y(nn);for(i=1:n-1)for(j=i+1:n)y1(j) = y(j)-y(j-1);endif(mod(i,2)==1)c(i) = (y1((i+n)/2)+y1((i+n+2)/2))/2;elsec(i) = y1((i+n+1)/2)/2;endif(mod(i,2)==1)l = t+(i-1)/2;for(k=1:i-1)l = l*(t+(i-1)/2-k);endelsel_1 = t+i/2-1;l_2 = t+i/2;for(k=1:i-1)l_1 = l_1*(t+i/2-1-k);l_2 = l_2*(t+i/2-k);endl = l_1 + l_2;endl = l/factorial(i);f = f + c(i)*l;simplify(f);f = vpa(f, 6);y = y1;if(i==n-1)if(nargin == 4)f = subs(f,'t',(x0-x(nn))/(x(2)-x(1)));endendendfunction f = GBessel(x,y,n,x0)syms t;nn = n/2;f = (y(nn)+y(nn+1))/2;for(i=1:n-1)for(j=i+1:n)y1(j) = y(j)-y(j-1);endif(mod(i,2)==1)c(i) = y1((i+n+1)/2)/2;elsec(i) = (y1((i+n)/2)+y1((i+n+2)/2))/2;endif(mod(i,2)==0)l = t+i/2-1;for(k=1:i-1)l = l*(t+i/2-1-k);endelsel_1 = t+(i-1)/2;l_2 = t+(i-1)/2-1;for(k=1:i-1)l_1 = l_1*(t+(i-1)/2-k);l_2 = l_2*(t+(i-1)/2-1-k);endl = l_1 + l_2;endl = l/factorial(i);f = f + c(i)*l;simplify(f);f = vpa(f, 6);y = y1;if(i==n-1)if(nargin == 4)f = subs(f,'t',(x0-x(nn))/(x(2)-x(1)));endendEnd9.Hermitefunction f = Hermite(x,y,y_1,x0)syms t;f = 0.0;if(length(x) == length(y))if(length(y) == length(y_1))n = length(x);elsedisp('y和y的导数的维数不相等!');return;endelsedisp('x和y的维数不相等!');return;endfor i=1:nh = 1.0;a = 0.0;for j=1:nif( j ~= i)h = h*(t-x(j))^2/((x(i)-x(j))^2);a = a + 1/(x(i)-x(j));endendf = f + h*((x(i)-t)*(2*a*y(i)-y_1(i))+y(i));if(i==n)if(nargin == 4)f = subs(f,'t',x0);elsef = vpa(f,6);endendEndnguagefunction f = Language(x,y,x0)syms t;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等!');return;end %检错f = 0.0;for(i = 1:n)l = y(i);for(j = 1:i-1)l = l*(t-x(j))/(x(i)-x(j));end;for(j = i+1:n)l = l*(t-x(j))/(x(i)-x(j)); %计算拉格朗日基函数end;f = f + l; %计算拉格朗日插值函数simplify(f); %化简if(i==n)if(nargin == 3)f = subs(f,'t',x0); %计算插值点的函数值elsef = collect(f); %将插值多项式展开f = vpa(f,6); %将插值多项式的系数化成6位精度的小数endendend11.Nevillefunction f = Neville(x,y,x0)syms t;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等!');return;endy1(1:n) = t;for(i=1:n-1)for(j=i+1:n)if(j==2)y1(j) = y(j)+(y(j)-y(j-1))/((t-x(j-i))/(t-x(j)))*(1-(y(j)-y(j-1))/y(j));elsey1(j) = y(j)+(y(j)-y(j-1))/((t-x(j-i))/(t-x(j)))*(1-(y(j)-y(j-1))/(y(j)-y(j-2)));endendy = y1;if(i==n-1)if(nargin == 3)f = subs(y(n-1),'t',x0);elsef = vpa(y(n-1),6);endendend12.Newtonfunction f = Newton(x,y,x0)syms t;if(length(x) == length(y))n = length(x);c(1:n) = 0.0;elsedisp('x和y的维数不相等!');return;endf = y(1);y1 = 0;l = 1;for(i=1:n-1)for(j=i+1:n)y1(j) = (y(j)-y(i))/(x(j)-x(i));endc(i) = y1(i+1);l = l*(t-x(i));f = f + c(i)*l;simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,'t',x0);elsef = collect(f); %将插值多项式展开f = vpa(f, 6);endendend13.Newtonbackfunction f = Newtonback(x,y,x0)syms t;if(length(x) == length(y))n = length(x);c(1:n) = 0.0;elsedisp('x和y的维数不相等!');return;endf = y(n);y1 = 0;xx =linspace(x(1),x(n),(x(2)-x(1)));if(xx ~= x)disp('节点之间不是等距的!');return;endfor(i=1:n-1)for(j=i+1:n)y1(j) = y(j)-y(j-1);endc(i) = y1(n);l = t;for(k=1:i-1)l = l*(t+k);end;f = f + c(i)*l/factorial(i);simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,'t',(x0-x(n))/(x(2)-x(1)));elsef = collect(f);f = vpa(f, 6);endend14.Newtonforwardfunction f = Newtonforward(x,y,x0)syms t;if(length(x) == length(y))n = length(x);c(1:n) = 0.0;elsedisp('x和y的维数不相等!');return;endf = y(1);y1 = 0;xx =linspace(x(1),x(n),(x(2)-x(1)));if(xx ~= x)disp('节点之间不是等距的!');return;endfor(i=1:n-1)for(j=1:n-i)y1(j) = y(j+1)-y(j);endc(i) = y1(1);l = t;for(k=1:i-1)l = l*(t-k);end;f = f + c(i)*l/factorial(i);simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,'t',(x0-x(1))/(x(2)-x(1)));elsef = collect(f);f = vpa(f, 6);endend15.SecSamplefunction [f,f0,fd0] = SecSample (x,y,y_1,x0)syms t;f = 0.0;f0 = 0.0;if(length(x) == length(y))if(length(y) == length(y_1))n = length(x);elsedisp('y和y的导数的维数不相等!');return;endelsedisp('x和y的维数不相等!');return;end %维数检查for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index = i;break;endend %找到x0所在区间d = y_1(1)*(x(2)-x(1))/2+y(1);for i=2:n-1d = d + y_1(i)*(x(i+1)-x(i-1))/2;endh = x(index+1) - x(index); %x0所在区间长度f = y_1(index+1)*(t-x(index))^2/2/h + ...y_1(index)*(t-x(index+1))^2/2/h + d; %x0所在区间的插值函数fd = (t-x(index))*y_1(index+1)/h + y_1(index)*(x(index+1)-t)/h;%x0所在区间的插值函数的导数f0 = subs(f,'t',x0); %x0处的插值fd0 = subs(fd,'t',x0); % x0处的导数插值16.SubHermitefunction [f,f0] = SubHermite(x,y,y_1,x0)syms t;f0 = 0.0;if(length(x) == length(y))if(length(y) == length(y_1))n = length(x);elsedisp('y和y的导数的维数不相等!');return;endelsedisp('x和y的维数不相等!');return;end %维数检查for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index = i;break;endend %找到x0所在区间h = x(index+1) - x(index); %x0所在区间长度fl = y(index)*(1+2*(t-x(index))/h)*(t-x(index+1))^2/h/h + ...y(index+1)*(1-2*(t-x(index+1))/h)*(t-x(index))^2/h/h; fr = y_1(index)*(t-x(index))*(t-x(index+1))^2/h/h + ...y_1(index+1)*(t-x(index+1))*(t-x(index))^2/h/h;f = fl + fr; %x0所在区间的插值函数f0 = subs(f,'t',x0); %x0处的插值17.ThrSample1function [f,f0] = ThrSample1 (x,y,y_1, y_N,x0)syms t;f = 0.0;f0 = 0.0;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等!');return;end %维数检查if(x(i)<=x0)&& (x(i+1)>=x0)index = i;break;endend %找到x0所在区间for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index = i;break;endend %找到x0所在区间A = diag(2*ones(1,n)); %求解m的系数矩阵u = zeros(n-2,1);lamda = zeros(n-1,1);c = zeros(n,1);for i=2:n-1u(i-1) = (x(i)-x(i-1))/(x(i+1)-x(i-1));lamda(i) = (x(i+1)-x(i))/(x(i+1)-x(i-1));c(i) = 3*lamda(i)*(y(i)-y(i-1))/(x(i)-x(i-1))+ ...3*u(i-1)*(y(i+1)-y(i))/(x(i+1)-x(i));A(i, i+1) = u(i-1);A(i, i-1) = lamda(i); %形成系数矩阵及向量cendc(1) = 2*y_1;c(n) = 2*y_N;m = followup(A,c); %用追赶法求解方程组h = x(index+1) - x(index); %x0所在区间长度f = y(index)*(2*(t-x(index))+h)*(t-x(index+1))^2/h/h/h + ...y(index+1)*(2*(x(index+1)-t)+h)*(t-x(index))^2/h/h/h + ...m(index)*(t-x(index))*(x(index+1)-t)^2/h/h - ...m(index+1)*(x(index+1)-t)*(t-x(index))^2/h/h;%x0所在区间的插值函数f0 = subs(f,'t',x0); %x0处的插值18. ThrSample2function [f,f0] = ThrSample2 (x,y,y2_1, y2_N,x0)syms t;f = 0.0;f0 = 0.0;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等!');return;end %维数检查for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index = i;break;endend %找到x0所在区间for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index = i;break;endend %找到x0所在区间A = diag(2*ones(1,n)); %求解m的系数矩阵A(1,2) = 1;A(n,n-1) = 1;u = zeros(n-2,1);lamda = zeros(n-1,1);c = zeros(n,1);for i=2:n-1u(i-1) = (x(i)-x(i-1))/(x(i+1)-x(i-1));lamda(i) = (x(i+1)-x(i))/(x(i+1)-x(i-1));c(i) = 3*lamda(i)*(y(i)-y(i-1))/(x(i)-x(i-1))+ ...3*u(i-1)*(y(i+1)-y(i))/(x(i+1)-x(i));A(i, i+1) = u(i-1);A(i, i-1) = lamda(i); %形成系数矩阵及向量cendc(1) = 3*(y(2)-y(1))/(x(2)-x(1))-(x(2)-x(1))*y2_1/2;c(n) = 3*(y(n)-y(n-1))/(x(n)-x(n-1))-(x(n)-x(n-1))*y2_N/2;m = followup(A,c); %用追赶法求解方程组h = x(index+1) - x(index); %x0所在区间长度f = y(index)*(2*(t-x(index))+h)*(t-x(index+1))^2/h/h/h + ...y(index+1)*(2*(x(index+1)-t)+h)*(t-x(index))^2/h/h/h + ...m(index)*(t-x(index))*(x(index+1)-t)^2/h/h - ...m(index+1)*(x(index+1)-t)*(t-x(index))^2/h/h;%x0所在区间的插值函数f0 = subs(f,'t',x0); %x0处的插值19.ThrSample3function [f,f0] = ThrSample3 (x,y,x0)syms t;f = 0.0;f0 = 0.0;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等!');return;end %维数检查for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index = i;break;endend %找到x0所在区间for i=1:nif(x(i)<=x0)&& (x(i+1)>=x0)index = i;break;endend %找到x0所在区间A = diag(2*ones(1,n-1)); %求解m的系数矩阵h0 = x(2)-x(1);h1 = x(3)–x(2);he = x(n)-x(n-1);A(1,2) = h0/(h0+h1);A(1,n-1) = 1 - A(1,2);A(n-1,1) = he/(h0+he);A(n-1,n-2) = 1 - A(n-1,1);c = zeros(n-1,1);c(1) = 3* A(1,n-1)*(y(2)-y(1))/h0 + 3* A(1,2)*(y(3)-y(2))/h1;for i=2:n-2u = (x(i)-x(i-1))/(x(i+1)-x(i-1));lamda = (x(i+1)-x(i))/(x(i+1)-x(i-1));c(i) = 3*lamda*(y(i)-y(i-1))/(x(i)-x(i-1))+ ...3*u*(y(i+1)-y(i))/(x(i+1)-x(i));A(i, i+1) = u;A(i, i-1) = lamda; %形成系数矩阵及向量cendc(n-1) = 3*( he*(y(2)-y(1))/h0+h0*( y(n)-y(n-1))/he)/(h0+he);m = zeros(n,1);[m(2:n),Q,R] = qrxq(A,c); %用qr分解法法求解方程组m(1) = m(n);h = x(index+1) - x(index); %x0所在区间长度f = y(index)*(2*(t-x(index))+h)*(t-x(index+1))^2/h/h/h + ...y(index+1)*(2*(x(index+1)-t)+h)*(t-x(index))^2/h/h/h + ... m(index)*(t-x(index))*(x(index+1)-t)^2/h/h - ...m(index+1)*(x(index+1)-t)*(t-x(index))^2/h/h;%x0所在区间的插值函数f0 = subs(f,'t',x0); %x0处的插值。
matlab牛顿插值法程序

matlab牛顿插值法程序牛顿插值法是一种数值分析方法,用于确定给定数据点之间的未知函数值。
该方法使用一个插值多项式,该多项式使得插值多项式通过给定的插值点,并且在插值点周围的函数值接近已知函数值。
该方法比其他插值方法更高,因为它使用被插值数据的微分。
下面是MATLAB中牛顿插值法的程序:function [f, c] = newton_interpolation(x, y)% x:插值节点不同的x值,必须有n个元素。
% y:相应在每个节点的y值,必须有n个元素。
% 返回:拟合的多项式和的权重向量c% 我们创建一个表格,其中包含x和y值的第一行n = length(x);delta=zeros(n,n);% 先把第一列设置为y值:delta(:,1)=y';%接下来,我们将使用牛顿插值法来填写余下的每个列for j=2:nfor i=j:ndelta(i,j) = ( delta(i,j-1) - delta(i-1,j-1) )/( x(i) - x(i-j+1));endend% 配置 c 数组% 从差分表中得出k次递归系数矩阵,目标是多项式系数c = zeros(1,n);c(1)=delta(1,1);% 获取插值多项式(通过牛顿插值法)syms t;L = c(1);for j=2:nprod = 1;for i=1:j-1prod = prod * ( t - x(i) );endL = L + c(j) * prod;end% 转换L成一个函数y=L(x)f = matlabFunction(L);end现在,当我们调用这个函数并输入我们想要插值的节点和相应的y值,我们会得到拟合的多项式和传递插值节点的权重向量。
lanczos插值 matlab代码

《深度探究:Lanczos插值在Matlab中的应用》在计算机图形学和数字图像处理领域,图像的放大和缩小是一项常见的任务。
而在这个过程中,插值算法则扮演着至关重要的角色。
本文将对Lanczos插值方法在Matlab中的应用进行深入探讨,旨在帮助读者更加深刻和全面地理解这一主题。
1. Lanczos插值简介Lanczos插值是一种用于信号处理和图像处理的插值算法。
它是由Cornelius Lanczos在20世纪初提出的,旨在解决插值过程中产生的模糊和失真问题。
Lanczos插值通过计算与窗函数相关的加权和来实现对目标像素的插值估计,能够有效地保持图像的边缘和细节信息,因此被广泛应用于数字图像处理中。
2. Lanczos插值算法原理在Matlab中,Lanczos插值算法可以通过内置函数实现。
其原理主要包括两个关键步骤:构建Lanczos核函数和应用核函数进行插值计算。
通过计算Lanczos核函数的系数和权重,可以得到一个离散的Lanczos核函数。
根据目标像素的位置和邻近像素的数值,将Lanczos核函数应用于图像,从而实现对目标像素的插值估计。
3. Lanczos插值在Matlab中的实现在Matlab中,可以使用内置的imresize函数来实现Lanczos插值。
通过设置插值方法参数为'lanczos3'或'lanczos8',可以选择使用3阶或8阶的Lanczos插值方法。
还可以根据具体需求调整滤波器的窗口大小和权重系数,以获得不同程度的插值效果。
4. 个人观点和理解作为一种高质量的插值算法,Lanczos插值在数字图像处理中具有广泛的应用前景。
在实际使用中,我们不仅可以根据图像的特点选择合适的Lanczos插值阶数和参数,还可以结合其他图像处理技术,如去噪和锐化,进一步提高图像的质量和清晰度。
我认为深入了解和掌握Lanczos插值算法在Matlab中的应用对于提升图像处理效果具有重要意义。
数值分析matlab方法插值法

其中,
n
【注】
x [a, b] w(x) (x x j ) j 0
(1)误差估计
Rn (x)
M n1 (n 1)!
w( x)
M n1
max
x( a ,b )
f
(n1) (x)
(2)余项与 x、M n1 节点的位置、个数 n 有关
(3)当 f (x)是 n 的多项式时Ln (x) f (x) n
M2 2!
(x
x0 )(x
x1 )
其中,
M2
max
x( x0 , x1 )
f
(x)
x
[
6
,
4
]
,所以
R1
(
5
24
)
sin
2!
4 (5
24
)( 5
6 24
)
4
0.0061
2)
抛物插值误差估计.因为
R2 (x)
M3 3!
(x
x0 )(x
x1)(x
x2 )
其中,
M3
max
x( x0 ,x2 )
f (x)
yiynewtonbackwardxyxicos035yi09394数值分析插值法55埃尔米特插值2n12n2数值分析插值法551埃尔米特插值多项式的存在唯一性2n1数值分析插值法数值分析插值法552埃尔米特插值余项553三次埃尔米特插值多项式maxsinxsin1数值分析插值法56561高次插值的病态性质0908原函数150706050405分段线性插值0302543214321055数值分析插值法562分段低次插值方法563分段低次插值余项090807060504030201090807060504030201543214321数值分析插值法57三次样条插值571三次样条插值572三弯矩法数值分析插值法573三次样条插值的误差估计与收敛性58插值运算的matlab函数581一维插值函数interp1yiinterp1xyximethod?linear?yiinterp1xyxilinear?1200135019
地震数据插值算法 matlab

地震数据插值算法是指在地震监测中,由于监测站点分布不均匀,导致某些区域的地震数据缺失或不完整,需要通过一定的算法来对这些缺失的数据进行估算和填补,以获得更加全面和准确的地震数据。
插值算法在地震监测中具有重要的作用,可以帮助地震学家更好地了解地震活动情况,为地震风险评估和地震预警提供重要依据。
在目前的地震监测中,常用的插值算法包括克里金插值、反距离加权插值、样条插值等。
而在实际的地震数据处理中,MATLAB编程语言可以为地震学家提供丰富的插值算法工具和强大的计算能力,能够有效地应用于地震数据的插值处理。
下面将介绍一些常用的地震数据插值算法及其在MATLAB中的实现。
一、克里金插值算法克里金插值是一种以地统计学原理为基础的插值算法,适用于地震数据的空间插值。
该算法假设地震数据之间的空间相关性受到某一半径范围内的数据影响,因此可以通过已知数据点的空间位置和数值来推断未知点的数值。
在MATLAB中,克里金插值算法可以利用Interp函数库来实现,用户只需提供已知数据点的空间位置和数值,即可利用克里金插值算法来对地震数据进行插值计算。
二、反距离加权插值算法反距离加权插值是一种基于距离权重的插值算法,适用于地震数据的点插值。
该算法假设地震数据点之间的距离越近,其数值之间的关联性越大,因此可以通过已知数据点的数值和距离来推断未知点的数值。
在MATLAB中,反距离加权插值算法可以利用Griddata函数库来实现,用户只需提供已知数据点的数值和距离,即可利用反距离加权插值算法来对地震数据进行插值计算。
三、样条插值算法样条插值是一种以局部插值为基础的插值算法,适用于地震数据的曲线插值。
该算法假设地震数据的变化过程是光滑的,因此可以通过已知数据点的数值和位置来推断未知点的数值。
在MATLAB中,样条插值算法可以利用Spline函数库来实现,用户只需提供已知数据点的数值和位置,即可利用样条插值算法来对地震数据进行插值计算。
MATLAB中的插值运算

MATLAB中的插值运算在数学中,有时需要查表,如对数表。
在具体查表时,需要的数据表中可能没有,这时一般可以先找出它相邻的数,再从表中查出其相应结果,然后按一定的关系把这些相邻的数以及它相应的结果加以修正,就可求出要查数的数据结果的近似值,这个修正关系就是一种插值。
在实践中,常常需要测量某些数据,但由于客观条件的限制,所测得的数据可能不够细密,满足不了实践的需要,这时便可以通过插值方法对数据进行加密处理。
此外,对于给定的离散数据对,如果要找一个函数来近似描述其对应关系,常常也需要插值。
与插值有关的MATLAB 函数(一) POLY2SYM 函数主要功能:把多项式的系数向量转换为符号多项式。
调用格式一:poly2sym (C)调用格式二:f1=poly2sym(C,'V') 或f2=poly2sym(C, sym ('V') ), (二) POLYVAL 函数主要功能:估计多项式的值。
调用格式:Y = polyval(P,X)(三) POLY 函数主要功能:把根转换为多项式的系数向量。
调用格式:Y = poly (V)(四) CONV 函数主要功能:计算卷积和多项式的和。
调用格式:C =conv (A, B)(五) DECONV 函数主要功能:计算逆卷积和多项式的除法、商和余式。
调用格式:[Q,R] =deconv (B,A)(六) roots(poly(1:n))命令调用格式:roots(poly(1:n))(七) det(a*eye(size (A)) - A)命令调用格式:b=det(a*eye(size (A)) - A)grange 插值方法介绍 对给定的n 个插值点12x ,,...n x x 及对应的函数值12,,...,n y y y ,利用n 次Lagrange 插值多项式,则对插值区间内任意x 的函数值y 可通过下式求的:11y()()n n j k k j k j j k x x x y x x ==≠-=-∑∏MATLAB 中没有直接实现拉格朗日算法的函数所以需建立M 文件:function y=lagrange (a,b,x)y=0;for i=1:length(a)l=1;for j=1:length(b)if j==il=l;elsel=l.*(x-a(j))/(a(i)-a(j));endendy=y+l*b(i);end算例:给出f(x)=ln(x)的数值表,用Lagrange计算ln(0.54)的近似值。
拉格朗日插值法matlab程序代码

拉格朗日插值法matlab程序代码拉格朗日插值法是一种常用的数值计算方法,用于在已知数据点的情况下,求解函数在其他点上的近似值。
它的基本思想是利用已知数据点构造一个多项式函数,使得该函数在这些点上与原函数完全相同。
在Matlab中实现拉格朗日插值法的代码如下:function [y] = LagrangeInterpolation(x, y, x0)% x为已知数据点的横坐标% y为已知数据点的纵坐标% x0为需要求解近似值的横坐标n = length(x); % 数据点个数L = ones(n, 1); % 初始化L矩阵for i = 1:nfor j = 1:nif i ~= jL(i) = L(i) * (x0 - x(j)) / (x(i) - x(j)); % 计算L(i)endendendy = sum(y .* L); % 计算插值结果end以上代码实现了拉格朗日插值法的核心部分。
首先定义了一个L矩阵,用于存储每个数据点对应的L(i)系数。
接着使用两层循环计算每个L(i)系数,并将它们乘起来得到多项式中第i项对应的系数。
最后将所有项相加即可得到插值结果。
需要注意的是,该代码只适用于已知数据点的横坐标互不相同的情况。
如果存在相同的横坐标,则需要对代码进行一定的修改。
在使用该代码时,可以先将已知数据点的横纵坐标存储在两个数组中,然后调用函数计算需要求解近似值的横坐标对应的插值结果即可。
例如:x = [1, 2, 3, 4];y = [1, 4, 9, 16];x0 = 2.5;y0 = LagrangeInterpolation(x, y, x0);以上代码将计算出在x=2.5处对应的近似值y0=6.25。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab中插值函数汇总和使用说明MATLAB中的插值函数为interp1,其调用格式为: yi= interp1(x,y,xi,'method')其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量,'method'表示采用的插值方法,MA TLAB提供的插值方法有几种:'method'是最邻近插值,'linear'线性插值;'spline'三次样条插值;'cubic'立方插值.缺省时表示线性插值注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
例如:在一天24小时内,从零点开始每间隔2小时测得的环境温度数据分别为12,9,9,10,18 ,24,28,27,25,20,18,15,13,推测中午12点(即13点)时的温度.x=0:2:24;y=[12 9 9 10 18 24 28 27 25 20 18 15 13];a=13;y1=interp1(x,y,a,'spline')结果为:27.8725若要得到一天24小时的温度曲线,则:xi=0:1/3600:24;yi=interp1(x,y,xi, 'spline');plot(x,y,'o' ,xi,yi)命令1 interp1功能一维数据插值(表格查找)。
该命令对数据点之间计算内插值。
它找出一元函数f(x)在中间点的数值。
其中函数f(x)由所给数据决定。
x:原始数据点Y:原始数据点xi:插值点Yi:插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。
参量x 指定数据Y 的点。
若Y 为一矩阵,则按Y 的每列计算。
yi 是阶数为length(xi)*size(Y,2)的输出矩阵。
(2)yi = interp1(Y,xi)假定x=1:N,其中N 为向量Y 的长度,或者为矩阵Y 的行数。
(3)yi = interp1(x,Y,xi,method)用指定的算法计算插值:’nearest’:最近邻点插值,直接完成计算;’linear’:线性插值(缺省方式),直接完成计算;’spline’:三次样条函数插值。
对于该方法,命令interp1 调用函数spline、ppval、mkpp、umkpp。
这些命令生成一系列用于分段多项式操作的函数。
命令spline 用它们执行三次样条函数插值;’pchip’:分段三次Hermite 插值。
对于该方法,命令interp1 调用函数pchip,用于对向量x 与y 执行分段三次内插值。
该方法保留单调性与数据的外形;’cubic’:与’pchip’操作相同;’v5cubic’:在MATLAB 5.0 中的三次插值。
对于超出x 范围的xi 的分量,使用方法’nearest’、’linear’、’v5cubic’的插值算法,相应地将返回NaN。
对其他的方法,interp1 将对超出的分量执行外插值算法。
(4)yi = interp1(x,Y,xi,method,'extrap')对于超出x 范围的xi 中的分量将执行特殊的外插值法extrap。
(5)yi = interp1(x,Y,xi,method,extrapval)确定超出x 范围的xi 中的分量的外插值extrapval,其值通常取NaN 或0。
例11.2.>>x = 0:10; y = x.*sin(x);3.>>xx = 0:.25:10; yy = interp1(x,y,xx);4.>>plot(x,y,'kd',xx,yy)复制代码例21.2.>> year = 1900:10:2010;3.>> product = [75.995 91.972 105.711 123.203 131.669 150.697 179.323 203.212 226.5054.249.633 256.344 267.893 ];5.>>p1995 = interp1(year,product,1995)6.>>x = 1900:1:2010;7.>>y = interp1(year,product,x,'pchip');8.>>plot(year,product,'o',x,y)复制代码插值结果为:1.2.p1995 =3.252.9885复制代码命令2 interp2功能二维数据内插值(表格查找)格式(1)ZI = interp2(X,Y,Z,XI,YI)返回矩阵ZI,其元素包含对应于参量XI 与YI(可以是向量、或同型矩阵)的元素,即Zi(i,j) ←[Xi(i,j),yi(i,j)]。
用户可以输入行向量和列向量Xi 与Yi,此时,输出向量Zi 与矩阵meshgrid(xi,yi)是同型的。
同时取决于由输入矩阵X、Y 与Z 确定的二维函数Z=f(X,Y)。
参量X 与Y 必须是单调的,且相同的划分格式,就像由命令meshgrid 生成的一样。
若Xi 与Yi 中有在X 与Y范围之外的点,则相应地返回nan(Not a Number)。
(2)ZI = interp2(Z,XI,YI)缺省地,X=1:n、Y=1:m,其中[m,n]=size(Z)。
再按第一种情形进行计算。
(3)ZI = interp2(Z,n)作n 次递归计算,在Z 的每两个元素之间插入它们的二维插值,这样,Z 的阶数将不断增加。
interp2(Z)等价于interp2(z,1)。
(4)ZI = interp2(X,Y,Z,XI,YI,method)用指定的算法method 计算二维插值:’linear’:双线性插值算法(缺省算法);’nearest’:最临近插值;’spline’:三次样条插值;’cubic’:双三次插值。
例3:1.2.>>[X,Y] = meshgrid(-3:.25:3);3.>>Z = peaks(X,Y);4.>>[XI,YI] = meshgrid(-3:.125:3);5.>>ZZ = interp2(X,Y,Z,XI,YI);6.>>surfl(X,Y,Z);hold on;7.>>surfl(XI,YI,ZZ+15)8.>>axis([-3 3 -3 3 -5 20]);shading flat9.>>hold off复制代码例4:1.2.>>years = 1950:10:1990;3.>>service = 10:10:30;4.>>wage = [150.697 199.592 187.6255.179.323 195.072 250.2876.203.212 179.092 322.7677.226.505 153.706 426.7308.249.633 120.281 598.243];9.>>w = interp2(service,years,wage,15,1975)复制代码插值结果为:1.2.w =3.190.6288复制代码命令3 interp3功能三维数据插值(查表)格式(1)VI = interp3(X,Y,Z,V,XI,YI,ZI)找出由参量X,Y,Z决定的三元函数V=V(X,Y,Z)在点(XI,YI,ZI)的值。
参量XI,YI,ZI 是同型阵列或向量。
若向量参量XI,YI,ZI 是不同长度,不同方向(行或列)的向量,这时输出参量VI 与Y1,Y2,Y3 为同型矩阵。
其中Y1,Y2,Y3 为用命令meshgrid(XI,YI,ZI)生成的同型阵列。
若插值点(XI,YI,ZI)中有位于点(X,Y,Z)之外的点,则相应地返回特殊变量值NaN。
(2)VI = interp3(V,XI,YI,ZI)缺省地,X=1:N ,Y=1:M,Z=1:P ,其中,[M,N,P]=size(V),再按上面的情形计算。
(3)VI = interp3(V,n)作n 次递归计算,在V 的每两个元素之间插入它们的三维插值。
这样,V 的阶数将不断增加。
interp3(V)等价于interp3(V,1)。
(4)VI = interp3(......,method) %用指定的算法method 作插值计算:‘linear’:线性插值(缺省算法);‘cubic’:三次插值;‘spline’:三次样条插值;‘nearest’:最邻近插值。
说明在所有的算法中,都要求X,Y,Z 是单调且有相同的格点形式。
当X,Y,Z 是等距且单调时,用算法’*linear’,’*cubic’,’*nearest’,可得到快速插值。
例51.2.>>[x,y,z,v] = flow(20);3.>>[xx,yy,zz] = meshgrid(.1:.25:10, -3:.25:3, -3:.25:3);4.>>vv = interp3(x,y,z,v,xx,yy,zz);5.>>slice(xx,yy,zz,vv,[6 9.5],[1 2],[-2 .2]); shading interp;colormap cool复制代码命令4 interpft功能用快速Fourier 算法作一维插值格式(1)y = interpft(x,n)返回包含周期函数x 在重采样的n 个等距的点的插值y。
若length(x)=m,且x 有采样间隔dx,则新的y 的采样间隔dy=dx*m/n。
注意的是必须n≥m。
若x 为一矩阵,则按x 的列进行计算。
返回的矩阵y 有与x 相同的列数,但有n 行。
(2)y = interpft(x,n,dim)沿着指定的方向dim 进行计算命令5 griddata功能数据格点格式(1)ZI = griddata(x,y,z,XI,YI)用二元函数z=f(x,y)的曲面拟合有不规则的数据向量x,y,z。
griddata 将返回曲面z 在点(XI,YI)处的插值。
曲面总是经过这些数据点(x,y,z)的。
输入参量(XI,YI)通常是规则的格点(像用命令meshgrid 生成的一样)。
XI 可以是一行向量,这时XI 指定一有常数列向量的矩阵。
类似地,YI 可以是一列向量,它指定一有常数行向量的矩阵。
(2)[XI,YI,ZI] = griddata(x,y,z,xi,yi)返回的矩阵ZI 含义同上,同时,返回的矩阵XI,YI 是由行向量xi 与列向量yi 用命令meshgrid 生成的。
