主动土压力 被动土压力 计算 excel
主动土压力 被动土压力 计算 excel

标题:深度探讨主动土压力和被动土压力的计算方法在土木工程和建筑领域,土压力是一个重要且复杂的问题。
主动土压力和被动土压力作为其中的重要概念,对土壤力学和结构设计有着重要的影响。
本文将深入探讨主动土压力和被动土压力的计算方法,并结合实际案例和Excel计算进行详细的分析和阐述。
一、主动土压力的计算1. 主动土压力的定义主动土压力是指土壤对于支撑结构施加的压力,通常是指土壤对于墙体的侧向压力。
在土木工程中,主动土压力是结构设计中必须考虑的重要参数之一。
2. 主动土压力的计算公式根据土力学的理论,主动土压力可以通过柯尔蒂斯公式来计算,公式如下:KaγH^2/2其中,Ka是土压力系数,γ是土的单位重,H是土壤高度。
通过这一公式,我们可以简单快速地计算出主动土压力的大小。
3. 实际案例分析举例来说,我们可以考虑一个简单的挡土墙结构,墙高5米,土的单位重为18kN/m³,土压力系数为0.35。
通过柯尔蒂斯公式的计算,我们可以得出挡土墙所受的主动土压力大小为315kN。
这个例子展示了主动土压力的计算方法以及其在实际工程中的应用。
二、被动土压力的计算1. 被动土压力的定义被动土压力是指支撑结构对土壤施加的反向压力,通常是指土壤对于桩基或承台的侧向压力。
在基础工程中,被动土压力是一个关键的设计参数。
2. 被动土压力的计算公式根据土力学的理论,被动土压力可以通过阿基米德原理来计算,公式如下:KpγH^2/2同样,其中Kp是土压力系数,γ是土的单位重,H是土壤高度。
通过这一公式,我们可以准确地计算出被动土压力的大小。
3. 实际案例分析假设我们有一个桩基基础工程,桩的长度为15米,土的单位重为20kN/m³,土压力系数为0.4。
通过阿基米德原理的计算,我们可以得出桩基所受的被动土压力大小为900kN。
这个例子展示了被动土压力的计算方法以及其在实际工程中的应用。
三、个人观点和总结回顾通过本文的深入探讨,我们了解了主动土压力和被动土压力的计算方法,并且结合实际案例进行了详细的分析。
(整理)土主动、被动土压力概念及计算公式

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin )1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直; (2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式σ1=σ3tg 2(45°+2ϕ)+2c ·tg(45°+2ϕ) σ3=σ1tg 2(45°-ϕ)-2c ·tg(45°-ϕ)当z=H 时p a =γHK a -2cK a在图中,压力为零的深度z 0,可由p a =0的条件代入式(6-3)求得a0K c 2z γ=(6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。
土体主动被动土压力概念及计算公式

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin )1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直;(2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算当z=H 时p a =γHK a -2cK a在图中,压力为零的深度z 0,可由p a =0的条件代入式(6-3)求得a 0K c2z γ= (6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。
墙背所受总主动土压力为P a ,其值为土压力分布图中的阴影部分面积,即γ+-γ=--γ=22c 2K cH 2K H 21)z H )(K c 2HK (21P a a 0a a a (6-5) 2)填土为无粘性土(砂土)时根据极限平衡条件关系方程式,主动土压力为a a zK )245(ztg p 2γ=ϕ-︒γ= (6-6) 上式说明主动土压力P a 沿墙高呈直线分布,即土压力为三角形分布,如图6-6所示。
土主动、被动土压力概念及计算公式

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin )1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直; (2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,ζz 仍保持不变,但ζx 将不断增大并超过ζz 值,当土墙挤压土体使ζx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,ζz 变为小主应力,ζx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式ζ1=ζ3tg 2(45°+2ϕ)+2c ·tg(45°+2ϕ) ζ3=ζ1tg 2(45°-ϕ)-2c ·tg(45°-ϕ)当z=H 时p a =γHK a -2cK a在图中,压力为零的深度z 0,可由p a =0的条件代入式(6-3)求得a0K c 2z γ=(6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。
土主动被动土压力概念及计算公式

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin )1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直; (2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式σ1=σ3tg 2(45°+2ϕ)+2c ·tg(45°+2ϕ) σ3=σ1tg 2(45°-ϕ)-2c ·tg(45°-ϕ)a0K c 2z γ=(6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。
墙背所受总主动土压力为P a ,其值为土压力分布图中的阴影部分面积,即γ+-γ=--γ=22c 2K cH 2K H 21)z H )(K c 2HK (21P a a 0a a a (6-5)2)填土为无粘性土(砂土)时根据极限平衡条件关系方程式,主动土压力为a a zK )245(ztg p 2γ=ϕ-︒γ= (6-6)上式说明主动土压力P a 沿墙高呈直线分布,即土压力为三角形分布,如图6-6所示。
土体主动被动土压力概念及计算公式

土体主动被动土压力概念及计算公式土体主动、被动土压力是土力学中常用的概念。
土体主动土压力指土体对支撑结构施加的压力,而被动土压力指支撑结构对土体施加的压力。
在土木工程设计和施工过程中,准确计算土体主动、被动土压力是保证结构安全和经济的关键。
首先,我们来讨论土体主动土压力。
土体主动土压力是土体对支撑结构施加的水平压力,通常被描述为土体在一定深度下的水平压力或水平力矩。
主动土压力的大小取决于土体的性质、土体参数以及土体与支撑结构之间的摩擦力。
常用的主动土压力计算公式有以下几种:1.集中力法集中力法是最常用的计算土体主动土压力的方法之一、该方法假设土体的压力是一个合力作用在支撑结构上,在计算时通常使用Coulomb公式:F=Ka*γ*H^2/2其中,F是土体对支撑结构施加的水平力,Ka是活动土压力系数,γ是土体的重度,H是土体的深度。
Ka的数值通常根据土体的稳定性和内摩擦角确定,可以通过试验和经验公式得到。
2.力均衡法力均衡法是另一种常用的计算土体主动土压力的方法。
该方法利用支撑结构处的力均衡条件,将土体的压力视为一个三角形分布,计算土体压力的大小以及作用点的位置。
土体主动土压力的计算公式可以根据具体情况进行修正和优化,例如考虑土体的非饱和状态、土壤侧向变形等因素。
接下来,我们来讨论土体被动土压力。
土体被动土压力是支撑结构对土体施加的水平压力,主要由支撑结构的刚度和应变引起。
当土体受到施加压力时,土体会发生侧向变形,从而形成被动土压力。
被动土压力的大小取决于支撑结构的刚度和土体的性质。
常用的被动土压力计算公式有以下几种:1. Rankine公式Rankine公式是最常用的计算土体被动土压力的方法之一、该方法假设土体的压力是一个合力作用在土体底部,在计算时通常使用以下公式:F=KP*γ*H其中,F是支撑结构对土体施加的水平力,KP是被动土压力系数,γ是土体的重度,H是土体的深度。
KP的数值通常根据土体的稳定性和内摩擦角确定,可以通过试验和经验公式得到。
土主动、被动土压力概念及计算公式.

基本原理
库伦于1776年根据研究挡土墙墙后滑动土楔体的静力平衡条件,提出了计算土压力的理论。他假定挡土墙是刚性的,墙后填土是无粘性土。当墙背移离或移向填土,墙后土体达到极限平衡状态时,填后填土是以一个三角形滑动土楔体的形式,沿墙背和填土土体中某一滑裂平面通过墙踵同时向下发生滑动。根据三角形土楔的力系平衡条件,求出挡土墙对滑动土楔的支承反力,从而解出挡土墙墙背所受的总土压力。
墙背所受总主动土压力为P a ,其值为土压力分布图中的阴影部分面积,即
γ+-γ=--γ=
22c 2K cH 2K H 21z H (K c 2HK (2
1
P a a 0a a a (6-5
2填土为无粘性土(砂土时
根据极限平衡条件关系方程式,主动土压力为
a a zK 2
45(ztg p 2γ=ϕ
-︒γ= (6-6
p p p K c zK tg c ztg p 22
45(2245(2+=+︒⋅++︒=γϕ
ϕγ (6-8
填土为无粘性土时
p p zK ztg p γϕ
γ=+
︒=2
45(2 (6-9
式中: P p ——沿墙高分布的土压力强度,kPa ;
K p ——被动土压力系数,2
45(2
ϕ
+
=tg Kp ;
其余符号同前。
取土楔ABC为脱离体,作用于滑动土楔体上的力有:①是墙对土楔的反力P ,其作用方向与墙背面的法线成δ角(δ角为墙与土之间的外摩擦角,称墙摩擦角;②是滑动面PC上的反力R ,其方向与BC面的法线φ角(φ为土的内摩擦角;③是土楔ABC的重力W。根据静力平衡条件W、P、R三力可构成力的平衡三角形。利用正弦定理,得:
土主动、被动土压力概念及计算公式

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin )1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直; (2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式σ1=σ3tg 2(45°+2ϕ)+2c ·tg(45°+2ϕ) σ3=σ1tg 2(45°-ϕ)-2c ·tg(45°-ϕ)当z=H 时p a =γHK a -2cK a在图中,压力为零的深度z 0,可由p a =0的条件代入式(6-3)求得a0K c 2z γ=(6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。
excel计算大全-房建-主动土压力计算(库仑、朗肯理论)
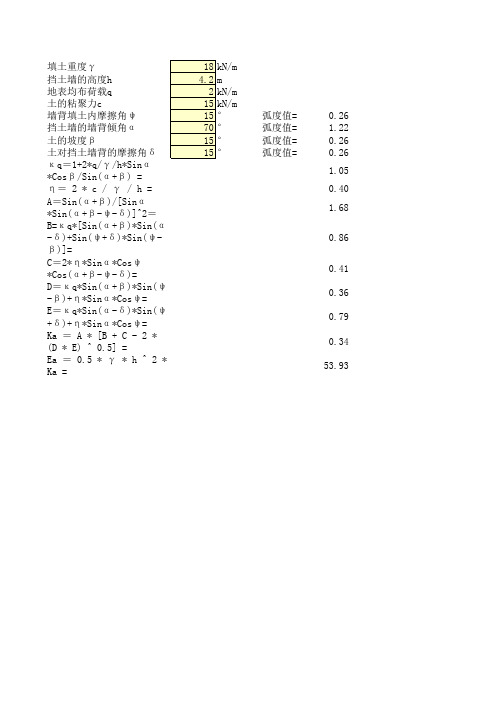
填土重度γ 18 kN/m 挡土墙的高度h 4.2 m 地表均布荷载q 2 kN/m 土的粘聚力c 15 kN/m 墙背填土内摩擦角ψ 15 ° 弧度值= 挡土墙的墙背倾角α 70 ° 弧度值= 土的坡度β 15 ° 弧度值= 土对挡土墙背的摩擦角δ 15 ° 弧度值= κq=1+2*q/γ/h*Sinα*Cosβ/Sin(α+β) = η= 2 * c / γ / h = A=Sin(α+β)/[Sinα*Sin(α+β-ψ-δ)]^2= B=κq*[Sin(α+β)*Sin(α-δ)+Sin(ψ+δ)*Sin(ψ-β)]= C=2*η*Sinα*Cosψ*Cos(α+β-ψ-δ)= D=κq*Sin(α+β)*Sin(ψ-β)+η*Sinα*Cosψ= E=κq*Sin(α-δ)*Sin(ψ+δ)+η*Sinα*Cosψ= Ka = A * [B + C - 2 * (D * E) ^ 0.5] = Ea = 0.5 * γ * h ^ 2 * Ka =
2017年整理】土体主动、被动土压力概念及计算公式

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体到达主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体到达被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比拟,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯根本理论朗肯土压力理论是英国学者朗肯〔Rankin 〕1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下根本假定。
(1)挡土墙是刚性的墙背垂直;(2)挡土墙的墙后填土外表水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体到达被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式当z=H 时p a =γHK a -2cK a在图中,压力为零的深度z 0,可由p a =0的条件代入式(6-3)求得a 0K c2z γ= (6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。
墙背所受总主动土压力为P a ,其值为土压力分布图中的阴影局部面积,即γ+-γ=--γ=22c 2K cH 2K H 21)z H )(K c 2HK (21P a a 0a a a (6-5) 2)填土为无粘性土(砂土)时根据极限平衡条件关系方程式,主动土压力为a a zK )245(ztg p 2γ=ϕ-︒γ= (6-6) 上式说明主动土压力P a 沿墙高呈直线分布,即土压力为三角形分布,如图6-6所示。
基坑支护excel计算明细

土压力计算 表格6.3.1-6.3.2

m kN/m3
弧度值
/ / / / / / 1.05 / 0.47 / /
参数输入 36644.89
1.15 1.00 31865.12 72952.65 162.22 60.00 90.00 27.00 2752.93 26.50
方案二 名称
修正后的主动岩石压力 增大系数 主动岩石压力修正系数 主动岩石压力合力标准值 四边形滑裂体自重 滑动面长度 缓倾的外倾软弱结构面的倾角
方案一
名称
修正后的主动岩石压力
增大系数
主动岩石压力修正系数
主动岩石压力合力标准值
四边形滑裂体自重
滑动面长度
缓倾的外倾软弱结构面的倾角
外倾软弱结构面的黏聚力
外倾软弱结构面内摩擦角
计算模型面积
平均重度
代号
Eak
/ β
Ea
G L θ cs φs源自A γ单位kN/m 1 1
kN/m kN/m
m ° kPa °
外倾软弱结构面的黏聚力
外倾软弱结构面内摩擦角
计算模型面积 平均重度
代号
Eak
/ β
Ea
G L θ cs
φs A γ
单位
kN/m 1 1
kN/m kN/m
m °
kPa
°
2
m kN/m3
弧度值
/ / / / / / 0.70 /
0.66
/ /
参数输入 -3201.97
1.15 1.35 -2062.46 8417.31 42.69 40.00
70.00
38.00
321.27 26.20
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主动土压力被动土压力计算 excel
【实用版】
目录
1.主动土压力和被动土压力的定义及区别
2.计算主动土压力和被动土压力的方法
3.使用 Excel 进行土压力计算的实践
正文
1.主动土压力和被动土压力的定义及区别
土压力是指土壤对挡土墙或地下室墙等建筑物的压力。
根据挡土墙的位移情况,土压力可分为静止、主动和被动三种。
静止土压力是指挡土墙不发生任何方向的位移,墙后填土施于墙背上的土压力。
主动土压力是指挡土墙在墙后填土作用下向前发生移动,致使墙后填土的应力达到极限平衡状态时,填土施于墙背上的土压力。
被动土压力是指挡土墙在某种外力作用下向后发生移动而推挤填土,致使墙后土体的应力达到极限平衡状态时,填土施于墙背上的土压力。
通俗一点说,主动土压力是土壤主动压向挡土墙,被动土压力则是挡土墙压向土壤。
主动土压力和被动土压力的量值关系为:Pa < P0 < Pp,其中 Pa 是主动极限平衡状态的最大值,Pp 是被动极限平衡状态的最小值。
2.计算主动土压力和被动土压力的方法
计算主动土压力和被动土压力通常采用库仑土压力理论。
库仑土压力理论是基于半空间理论的一种土压力计算方法,其基本假设是:土体与挡土墙之间存在一个滑动面,土体沿该滑动面发生滑动。
库仑土压力理论的计算公式为:
主动土压力:Pa = 0.5γz * (b - 3a)
被动土压力:Pp = 0.5γz * (3a - b)
其中,γz 为土壤的重度,a 为挡土墙的深度,b 为土壤的影响宽度。
3.使用 Excel 进行土压力计算的实践
要使用 Excel 计算主动土压力和被动土压力,需要按照以下步骤操作:
(1)在 Excel 中输入土壤的重度γz、挡土墙的深度 a 和土壤的影响宽度 b。
(2)使用 Excel 的 IF 函数判断挡土墙的位移情况,以确定应计算主动土压力还是被动土压力。
例如,如果挡土墙向前移动,则计算主动土压力;如果挡土墙向后移动,则计算被动土压力。
(3)使用 Excel 的 INDEX 和 MATCH 函数计算主动土压力或被动土压力。
以计算主动土压力为例,公式如下:
`=INDEX(IF({Array1>=Array2}, Array1, Array2), MATCH(1, (Array1>=Array2), 0))`
其中,Array1 为土壤的重度γz,Array2 为挡土墙的深度 a。
(4)根据计算结果,填写相应的单元格,即可完成土压力计算。
综上所述,通过使用 Excel,可以方便地计算主动土压力和被动土压力。
