习题课2

合集下载

高等数学习题课1-2 极限与连续

n
xn 1 x
n
( x 0)的连续性。
解当x [0,1)时, f ( x ) 0;
0, 0 x 1 1 1 即 f ( x) , x 1 当x 1时, f ( x ) ; 2 2 1, x 1 1 当x 1时, f ( x ) lim 1 n 1 n ( ) 1 x
x )
lim
x 0
e x sin 2 x e
2 x
x
2
1
例6 问x 1时, f ( x ) 3 x 2 x 1 ln x
2
是x 1的几阶无穷小 ?
解 f ( x ) 3 x 1 x 1 ln[1 ( x 1)]
lim
x 1
2
n
(2)设x0 1, xn 1
1 xn 1
(n 1, 2,), 试证{ xn }收敛 ,
并求 lim xn。
n
5.求极限
(1) lim
x 0
x 1 cos x
(2) lim
x a
tan x tan a xa xe
(a k

2
)
(3) lim
其中 x=0为跳跃间断点,
例 10 证明: 方程 tanx = x 有无穷多个实根。
分析从图形看 y=tanx与 y = x 有无穷多个交点。证设 f(x) = tan x- x (要在无穷个闭区间上用零点定理)
k Z ,
(1) k
lim
x ( k

2
f ( x ) ， lim
8. 设f ( x )在[0,1]上非负连续, 且f (0) f (1) 0, 则对任意实

工程热力学习题课(2)

三、小结
1.热力循环方向性的判断： Q
克劳修斯积分式
T
0
r
孤立系统熵增原理（既适应循环也适应过程方向的判断）
dSiso 0
卡诺定理
t c
2.对于求极值问题一般考虑可逆情况
3.应用孤立系统熵增原理计算每一对象的熵
变时，要以该对象为主题来确定其熵变的正负
谢谢大家！
Q1 W 264 .34kJ
气体定温过程熵变为：
T p p c p ln 2 R g ln 2 mR g ln 2 S m T1 p1 p1 10 6 1 287 ln 5 660 .8 J / K 10
热源熵变为：
1由热效率计算式可得热机e输出循环净功所以wnet40kj由热泵供暖系数计算公式可得供热量qnetnet1000290revnet7171290360360netrev3647114但这并不违反热力学第二定律以1为例包括温度为tnet100kj40kj60kjnet140kj40kj100kj就是说虽然经过每一循吸入热量60kj放出热量100kj净传出热量40kj给温度为t放出了100kj的热量所以40kj热量自低温传给高温热源是花了代价的这个代价就是100kj热量自高温传给了低温热源所以不违反热力学第二定律
因为为可逆过程，所以△Siso=0,即：
S iso S A S B dS 0
mc p ln
Tf T1
mc p ln
Tf T2
0
ln
T f2 T1T2
0
T f T1T2
可逆过程循环净功最大，为：
Wmax Q1 Q2 mc p T1 T f mc p T f T2 mc p T1 T2 2T f

习题课2(4~5章)

第四章习题讲解4.6 实训实训1【实训内容】简单if语句。

【实训目的】掌握简单if语句的使用。

【实训题目】分析下面两个程序，写出程序的功能并上机验证。

【程序1】#include <stdio.h>main(){float x,y,z;printf("Please enter x,y,z:");scanf("%f,%f,%f",&x,&y,&z);if(x<y) x=y;if(x<z) x=z;printf("%5.2f\n",x);}【程序2】#include <stdio.h>main(){float x,y,z,max;printf("Please enter x,y,z:");scanf("%f,%f,%f",&x,&y,&z);max=x;if(max<y) max=y;if(max<z) max=z;printf("%5.2f\n",max);}实训2【实训内容】if-else语句。

【实训目的】掌握if-else语句的使用。

【实训题目】简单加法练习程序。

阅读程序并上机调试，改正其中的错误，使之能正常运行。

#include <stdio.h>#include <stdlib.h>#include <time.h>main(){int num1,num2,answer;srand(time(NULL));num1=rand()%100;num2=rand()%100;printf("%d+%d=",num1,num2);scanf("%d",&answer);if(answer==num1+num2)printf("回答正确.\n");elseprintf("回答错误.\n");}实训3【实训内容】if嵌套【实训】编写程序，根据输入的某年某月，输出该月的天数。

09 11.2 习题课(2)

三角形全等证明思路
已知两边
找夹角（SAS））找直角（HL））找另一边（找另一边（SSS））边为角的对边找任一角（AAS）找任一角（）
找夹角的另一边（SAS）找夹角的另一边（）
已知一边一角
边为角的邻边找夹边的另一角（ASA）找夹边的另一角（）
找任一角（AAS））
A D C B M N
（D） AM∥CN
如图， AB上 AC上 B=∠C， 2、如图，D在AB上，E在AC上，且∠B=∠C，那么补充下列一个条件后，么补充下列一个条件后，仍无法判断 ABE≌△ACD的是的是（ △ABE≌△ACD的是（）（A） AD=AE B （B） ∠AEB=∠ADC D （C） BE=CD （D） AB=AC A E C
D E F A B C
5、已知，如图，AB、CD相交于点O，已知，如图，AB、CD相交于点O 相交于点 ACO≌△BDO，CE∥DF。求证：CE=DF。 △ACO≌△BDO，CE∥DF。求证：CE=DF。
C F E O D
A
B
6、已知，如图，AB⊥AC，AB＝AC，已知，如图，AB⊥AC，AB＝AC， AD⊥AE，AD＝AE。求证：BE＝CD。 AD⊥AE，AD＝AE。求证：BE＝CD。
找夹边
已知两角
（ASA））
找任一边（找任一边（AAS））
练习
如图，已知MB=ND MB=ND， MBA=∠NDC， 1、如图，已知MB=ND，∠MBA=∠NDC，下列条件不能判定△ABM≌△CDN的是（件不能判定△ABM≌△CDN的是（）的是（A） ∠M=∠N （ B）（ C） AB=CD AM=CN
15、已知，如图， ABC中 AB=AC， 15、已知，如图，△ABC中，AB=AC，∠BAC=900， AC的中点 AF⊥BD于的中点， BC于连结DF DF。 D是AC的中点，AF⊥BD于E，交BC于F，连结DF。求证： ADB=∠CDF。求证：∠ADB=∠CDF。 A 1 B 3 2 D E M N F C B 3 F M C A 2 1 D E

双曲线习题课(2)

2
5 5 2 或 k 即 28k 55k 25 0 解得 k 7 4 5 但 2 k 1 ∴ k 2 5 故直线AB的方程为 x y 1 0 2
2
设 C xc , yc ，则由已知 OA OB mOC
∵ A、B 在双曲线上，
y ①
2
x2 y 1 ∴ 4 2 (2 x )2 (2 y )2 1 4 2
由 ① - ② 得： x 2 y 1 0 .
2
②
M
2
o
. .N
2
x
2
即为所求直线的方程. AB
(2) 假设过N 的直线交双曲线于 ( x1 ， 1 ) ， ( x2 ， 2 ) ，则 C y D y
2
2

解： (1)设直线AB：y 1 k ( x 1) ，则
y kx 1 k 2 y2 x 1 4 2
2 2
2

2
M
2
o
. .N
2
x
(1 2k ) x 4k(1 k ) x 2(1 k ) 4 0 x1 x2 2k (1 k ) k1. 由 1 1 得 2 2 2 1 2k
得 x1, y1 x2 , y2 mxc , myc
x1 x2 y1 y2 ∴ xc , yc , m m
m 0
2k 2 4 5 ，y y (kx 1x (kx 1) k ( x1 ) 2 ) 22 又 x1 x 2 2 1 2 1 k 1 2k 2 2 2 8 即 y1 y 2 k 2 1 k 2 1
∴△ABC的面积 S 1 6 3 1

通信原理习题课(2)

解： AMI码：+1 0 -1 +1 0 0 0 0 0 0 0 0 0 -1 0 +1 AMI码如图6-18所示。 HDB3码：+1 0 -1 +1 0 0 0 +V –B 0 0 –V 0 +1 0 -1 HDB 3 码如图6-19所示
+E
0
-E 图6-18
+E
0
-E 图6-19
6-8 已知信息代码为101100101，试确定相应的双相码和 CIM码，并分别画出它们的波形图。
fsP(1 P)
G1( f
)G2(
2 f)
m
fs PG1(mfs)(1P)G2(mfs)
2 (f
mfs)
计算整理得：
Ps ()
fs
G( f
)2
1T6s 1 cos
fTs 2
0
f 1 Ts
其他
功率谱密度如下图所示。
Ps(ω)
Ts/4
Ts/16
-1/Ts
-1/2Ts
0 1/2Ts
ω 1/Ts
(2)不可以直接提取频率 fs 1/ Ts的位定时分量。
k(与t无关) 且
0 k 1 ，则脉冲序列将无
g2 (t)
离散谱。
解答：基带信号的功率谱分为稳态波功率谱和交变波功率谱两部分。其中只有稳态波功率谱有离散谱分量。由稳态波功率谱密度公式：
P ()
v
m
fs PG1(mfs)(1P)G2(mfs) 2g ( f
mf ) s
其中：
G1(mf s )
g(t)
A
t
-Ts/2
0
Ts/2
图P6-3

《数字电路与逻辑设计》习题课 (2)

10/10
状态定义： S0:初始状态。 S1:收到五角硬币。 S2:收到一元硬币。 S3:收到一元五角硬币。并入S0状态。
00/00 AB/YZ
S0
01/10 10/11
01/00 10/00
S2
S1 00/00 01/00
00/00 例1原始状态转移图
例2、分析图所示计数器电路，说明是模长为多少的计数器，并列出状态转移表。
6
C
&
1 1
A & ?
Z
X
&
N
A X
&
1 & J
1
C
R 1 & K
解：1）分析电路结构：该电路是由七个与非门及一个JKFF组成，且CP下降沿触发，属于米勒电路，输入信号X1，X2，输出信号Z。
2）求触发器激励函数：J=X1X2，K=X1X2 触发器次态方程：
Qn+1=X1X2Qn+X1X2Qn=X1X2Qn+(X1+X2)Q
第六章复习
计数器的分析
❖ 同步、异步分析步骤：由电路触发器激励函数(公式和图解）状态转移表分析模长和自启动性。用图解法，注意高低位顺序，一般数码越高位权越高：Q3Q0
❖ 移存型计数器属于同步计数器，只要求出第一级触发器的次态方程和初始状态，就可以写出状态转移表。
计数器的设计
❖ 同步计数器的设计：状态转移表激励函数和输出函数(自启动性检查)电路图。
❖ 7490只能异步级联，M=100。
❖ 74194级联可实现8位双向移存器
MSI实现任意进制计数器(M<N)
❖ 反馈法：异步清0法和同步置数法。注意：用LD端置全1（置最大数法）时，反馈状态对应编码中出现0的端口需通过非门送入反馈门。

习题课1、2、IP地址习题

习题课1（星期一）选择题Internet技术主要由一系列的组件和技术构成，Internet的网络协议核心是（C ）A. ISP/SPX B. PPPC. TCP/IPD. SLIP( A ) 是电话拨号上网的必备设备A. MODEMB. 网卡C. HUBD. 路由器INTRANET 是（C）A. 局域网B. 广域网C. 企业内部网D. INTERNET的一部分文件传输使用（D）协议。

A. SMTPB. TELNETC. ARPD. FTP新闻组是（A ）A. NEWSB. MOSAICC. FTPD. DNS中国教育科技网的英文缩写是（A）A. CERNETB. CSTNETC. CHINANETD. CHINAGBNINTERNET对每一台计算机的命名方案称为（C ）A. SMTPB. SNMPC. DNSD. FTP中国的Internet在B年开通A、1993B、1994C、1995D、1996TCP协议主要应用于（B）A、应用层B、传输层C、网络层D、数据层计算机网络的目的是实现（ D ）A、数据处理B、信息传输与数据处理C、文献查询D、资源共享与信息传输HTTP是（B ）A、超文本标记语言B、超文本传输协议C、搜索引擎D、文件传输协议我国的最高域名是（A ）A、cnB、twC、usD、ru与Web站点和Web页面密切相关的一个概念称为“URL”，它的中文意思是（ D ）A、用户申请语言B、超文本标识语言C、超级资源连接D、统一资源定位器用户要上网浏览WWW信息，须安装并运行以下（C ）软件A、sinaB、YahooC、浏览器D、万维网用户的电子邮箱是（ C ）A 通过邮局申请的个人信箱B、邮件服务器内存中的一块区域C、邮件服务器硬盘上的一块区域D、用户计算机硬盘上的一块区域用E-Mail发送信件时须知道对方的地址，下列表示中（ B ）是合法完整的E-Mail地址A、@user B、user@C、D、User$Outlook Express发送电子邮件时，其附件（ D ）A、只能是文本文件B、只能是二进制文件C、只能是ASCII文件D、可以是各种类型的文件电子邮件地址是yzj123@，则发送邮件服务器是（B ）A、yzj123B、C、yzj123@D、@判断题DNS是一个遍布在互联网上的分布式主机信息数据库系统采用客户机/服务器的工作模式。

多元函数微分学习题课 (2)

a
D，使
f
(最值定理)
(a) ;
(介值定理)
机动目录上页下页返回结束
思考与练习
1. 讨论二重极限 lim
xy
时, 下列算法是否正确?
(x,y)(0,0) x y
解法1
原式
lim
x0
y0
1 y
1
1 x
0
解法2 令 y kx,
解法3 令 x r cos , y r sin ,
f3
机动目录上页下页返回结束
例. 设 u f (x,t) , 而 t 是由 Fx, y, z 0确定，
其中f、F具有一阶连续偏导，
证明：
du dx
f F f F x t t x
f F F
t y t
三、多元函数微分法的应用
1. 极值与最值问题 • 极值的必要条件与充分条件 • 求条件极值的方法 (消元法, 拉格朗日乘数法)
f2 (x1, x2 , x3, y1, y2 ) y2 cos y1 6 y1 2x1 x3
x求0 由 (3,f2(,7x),Ty,)y0
0
(0,1)T
确定的隐函数
y
g(
x)在x0处的导数
机动目录上页下页返回结束
多元函数微分法
显式结构 1. 分析复合结构隐式结构
自变量个数 = 变量总个数 – 方程总个数自变量与因变量由所求对象判定 2. 正确使用求导法则注意正确使用求导符号 3. 利用一阶微分形式不变性
x y ( x, y)(0,0) 2
2
而其中 lim (x2 y2 ) ln( x2 y2 ) 0 ( x, y)(0,0)
lim

习题课2

Im o
Re
o -2 o
2j X 0 2
2j o Re 0 2
-2 o
-2j X (3)
-2j o (4)
Solution to 9.23
• Sol :
Property 1 in Sec.9.2.
e{ } 3 is in the ROC.
If x(t )e 3t is absolutely integrable, from the Dirichlet conditions of convergence of Fourier transform, the Fourier transform of x (t )e 3t exists. Thus, the Laplace of x(t ) exists at 3, or that X ( s ) converges at 3.
• Pole-zero Plot of Laplace Transform
– For a rational X(s), the roots of the numerator are referred to as zeros of the Laplace transform, whereas those of the denominator poles.
X
5j
o
X -5 -4
Im
55 / 2
Re
-7.5
o
X -5j
55 / 2
(b)
ROC is e{s} 4.
Solution to 9.21
• (i) x(t ) (t ) u(t );
1 s 1 Sol : X ( s ) 1 , s s ROC is e{s} 0.

习题课2

e−5 ⋅ 5k ≈∑ ≈ 0.986305. k! k=0
点评: 点评保险业是概率论的生长点和重要应用领域之一. 本例为简化起见, 不计利息与管理费. 域之一本例为简化起见不计利息与管理费
13
设随机变量X 在区间[2，上服从均匀例7 设随机变量在区间，5]上服从均匀分布，现对X 次独立观测，分布，现对进行 3 次独立观测，试求至少有两次观测值大于3的概率的概率。两次观测值大于的概率。设随机变量Y 解设随机变量是3次独立观测中观测值大次独立观测中观测值大的次数, 于3的次数则 Y ~ B(3, p),其中p是X大于3的概率. 的次数由题意知 X 的概率密度为
P( Ak ) = P( X = k) =
1 k 对k ≥ 1, P(B Ak ) = ( ) , 2 λk −λ 1 k P( Ak B) = P( Ak )P(B Ak ) = e ⋅ ( ) , k! 2
10
k!
e , k = 0,1,2,⋯
∴P(B) = P ∑Ak B = ∑P( Ak B) k=1 k=1
X − 200 P( A ) = P{X ≤ 200} = P ≤ −0.8 1 25 =φ−0.8) = 0.212; ( φ P( A2 ) = P{200 ≤ X ≤ 240}= 2 (0.8) − 1 = 0.576;
15
P( A3 ) = 1 − P( A ) − P( A2 ) = 0.212. 1
1
一般要学会做三类习题：一般要学会做三类习题： ①利用某些已知条件求出随机变量的分布律或密度函数；密度函数；利用分布律或分布函数，求出某些事件的概率； ②利用分布律或分布函数，求出某些事件的概率；利用分布律或密度函数，求出分布函数。 ③利用分布律或密度函数，求出分布函数。 4. 二维随机变量及其联合分布函数；二维随机变量及其联合分布函数；二维离散型随机变量及其联合分布律；二维离散型随机变量及其联合分布律；二维连续型随机变量及其联合概率密度。二维连续型随机变量及其联合概率密度。 5. 二维随机变量的边缘分布和条件分布。二维随机变量的边缘分布和条件分布。 6. 随机变量的相互独立性。随机变量的相互独立性。 7. 随机变量函数的分布。随机变量函数的分布。

有机单元习题课二

CH3 CH3
H COOC2H5 COOC2H5 H
CH3 CH3
H COOC2H5 COOC2H5 H
丁烯中少量的1 丁炔。四、用化学方法除去2 –丁烯中少量的 –丁炔。用化学方法除去丁烯中少量的丁炔
溶液洗涤，用Ag(NH3)2OH溶液洗涤，即可除去端炔。溶液洗涤即可除去端炔。
五、以乙炔、丙烯为原料（无机试剂任选）合成正戊醛。以乙炔、丙烯为原料（无机试剂任选）合成正戊醛。
7. CH2=CHCH2C CH
C2H5OH KOH ,
C2H5Br NaNH2 液 NH3
CH2=CHCH2C=CH2 OC2H5
A
Na 液 NH3
=
O
B:
CH3CCH3
8. CH3C
CH
B
Cl2
C 透视式
D 锯架式
E Newman式
F Fischer
CH3
H C=C C2H5
C:
Br C H3 C H C
一、写出下列化合物的最稳定构象：写出下列化合物的最稳定构象：
1. FCH2CH2OH
F H H H H O H
， 2. 顺 - 1，3- 环己二醇
O H H O H H
CH3 3. C2H5
H H C2H5 CH3 CH(CH3)2 H
(CH3)2CH H
CH(CH3)2
H 4. (CH3)2CH
分析：分析：
CH3CH2CH2CH2CHO 目标分子 CH3CH2CH2Br + NaC CH CH3CH2CH2 C CH
合成：合成：CH3CH=CH2
CH CH
NaNH2 液 NH3
HBr ROOR

广州大学线性代数习题课(2)

首页上页返回下页结束铃
一,内容提要
向量组的线性表示若向量组 B 中的任一向量都可由向量组 A 中的向量线性表示, 线性表示. 量线性表示就称向量组 B 可由向量组 A 线性表示矩阵方程 AX = B 有解的充分必要条件是矩阵 B 的有解的充分必要条件是: 任一列向量都可由矩阵 A 的列向量组线性表示. 的列向量组线性表示
首页上页返回下页结束铃
一,内容提要
向量在基下的坐标维向量空间, 设 V 为一个 r 维向量空间则 V 中任意 r 个线性无的一个基, 关向量 a1,…, ar 为 V 的一个基且有 …
V = L(a1 , , ar )
V 中任一向量 a 可唯一地表示为 a = k1a1 + + kr ar 下的坐标. 称 (k1,…, kr ) 为 a 在基 a1,…, ar 下的坐标 … …
线性相关性如果存在一组不全为设有向量组 a1 , , am , 如果存在一组不全为 0 的数
k1 , , km , 使
k1a1 + + km am = 0
那么, 称 a1 , , am 线性相关否则称 a1 , , am 线性无关线性相关. 否则, 线性无关. 那么基本性质 (1) 若向量 b 可由向量组 a1,…, am 线性表示则向量组线性表示, … 线性相关. b, a1,…, am 线性相关 … 当 a1,…, am 线性相关时表示式不唯一线性相关时, 表示式不唯一; … 当 a1,…, am 线性无关时表示式唯一线性无关时, 表示式唯一. …
首页上页返回下页结束铃
一,内容提要
定理向量组 b1,…, bl 与向量组 a1,…, am 等价的充分必 … … 要条件是

无穷级数习题课(2)

第七章无穷级数习题课 (一)
常数项级数
1
一、定义及性质
1．常数项级数 2．敛散性定义
an
n1
n
设Sn
k 1
an，如果
lim
n
Sn
s
存在，
3．性质
则级数收敛，否则级数发散。
必要性:
级数
an 收敛
n1
lim
n
an
0.
线性运算性质: 设级数 un s, vn , , 为常数
n1
n1
n1
No
Yes
| an 收| 敛
n1
lim an1 a n
n
lim
n
n
an
No
1
No
找正项收敛
级数 bn n1
找正项发散
级数 cn n1
an (1)n un No
Yes
an为交错级数
n1
用其它方法证明
1
Yes 1
an发散
n1
an收敛
n1
an bn
an收敛
n1
an cn
解：
由于
an
2n 1 3n
3n 3n
n1 3n
n 3n1
n1 3n
，由定义
Sn
(1
2) 3
(2 3
3 32
)
3 ( 32
4 33
)
(
n 3n1
n1 3n )
1
n1 3n
S
lim
n
Sn
lim(1
n
n1 3n )
1
所以原级数收敛，且和为1。
6
【例2】判别级数

《机械能守恒定律》习题课二

o A 《机械能守恒定律》习题课（二）系统机械能守恒刘彩丽2013 5.10 教学目标：1、复习巩固判断单个物体的机械能是否守恒的方法以及解决守恒问题2、学会运用机械能守恒定律解决两个物体组成的系统机械能守恒问题教学重点：1、2 课时：2节课一、复习巩固：1、机械能守恒的判断下面列举的各个实例中，那些情况下机械能是守恒的？（）①一小球在粘滞性较大的液体中匀速下落；②用细线拴着一个小球在竖直平面内做圆周运动；③用细线拴着一个小球在光滑水平面内做匀速圆周运动；④拉着一个物体沿光滑的斜面匀速上升；⑤一物体沿光滑的固定斜面向下加速运动A ．②③⑤B ．①②④C ．①③④D ．②③④2、单个物体的机械能守恒的应用质量为m 的小球，以初速度v 0由地面竖直上抛，空气阻力可忽略不计，小球到达最高点的高度为h ，当小球又落回到出发点时，小球具有的机械能为(以地面为重力势能的零点) mgh +mgh mv mgh mv 2D 21C B 21A 2020．．．．3.系统机械能是否守恒判断自主学习：1.系统机械能是否守恒的判断方法（1）系统以外的力是否对系统对做功，系统以外的力对系统做正功，系统的机械能就增加，做负功，系统的机械能就减少。

不做功，系统的机械能就不变。

（2）系统间的相互作用力做功，不能使其它形式的能参与和机械能的转换。

系统内物体的重力所做的功不会改变系统的机械能自我检测：一个轻弹簧固定于O 点，另一端系一重物，将重物从与悬点O 在同一水平面肯弹簧保持原长的A 点无初速度释放，让它自由下摆，不计空气阻力，在重物由A 摆到最低点的过程中，A 、重物的重力势能减少。

B 、重物的重力势能增加。

C 、系统的机械能不变。

D 、重物的机械能减少。

二．系统机械能守恒定律的应用自主学习：2.系统间的相互作用力分为三类：1）刚体产生的弹力：比如轻绳的弹力，斜面的弹力，轻杆产生的弹力等2）弹簧产生的弹力：系统中包括有弹簧，弹簧的弹力在整个过程中做功，弹性势能参与机械能的转换。

Java习题课(2)

P136 第8题
测试类： public class Test { public static void main(String[] args) { Shape square = new Square(2.0); //向上转型 Shape triangle = new Triangle(1.5,2.0); System.out.println(square.getArea()); System.out.println(triangle.getArea()); } }
多态性：方法覆盖和方法重载
方法的覆盖和重载是Java多态性的不同表现。覆盖是父类与子类之间多态性的一种表现，重载是一个类中多态性的一种表现。如果在子类中定义某方法与其父类有相同的名称和参数，我们说该方法被覆盖。子类的对象使用这个方法时，将调用子类中的定义，对它而言，父类中的定义如同被“屏蔽”了。如果在一个类中定义了多个同名的方法，它们或有不同的参数个数或有不同的参数类型，则称为方法的重载。方法覆盖必须满足下列条件 (1) 子类的方法的名称必须和所覆盖的方法相同 (2) 子类的方法的参数必须和所覆盖的方法相同 (3) 子类的方法返回类型必须和所覆盖的方法相同 (4) 子类方法不能缩小所覆盖方法的访问权限 (5) 子类方法不能抛出比所覆盖方法更多的异常重载方法必须满足下列条件 (1) 方法名必须相同 (2)方法的参数类型，个数顺序至少有一项不同 (3) 方法的返回类型和方法的修饰符可以不相同
P136 第8题
父类Shape： public abstract class Shape { public abstract double getArea(); } 正方形类Square： public class Square extends Shape{ private double length; public Square(double length) { this.length = length; } public double getArea() { System.out.println("square's area = length*length"); return length*length; } }

高数第二章习题课二

f ( x) f ( x0 ) f ( )( x x0 ) f ( x0 ) f ( ) x x0 f ( x0 ) M (b a) K
(定数)
10
可见对任意 x (a , b) , f ( x) K , 即得所证 .
例6
(a , b) 可导，且a 0, 设 f ( x) 在 [a , b] 连续，
代入上式
1 原式＝－ 6
12
四、导数应用
1. 研究函数的性态: 增减 , 极值 , 凹凸 , 拐点 , 渐近线 , 曲率
2. 解决最值问题
• 目标函数的建立与简化 • 最值的判别问题 3. 其他应用 : 求不定式极限 ; 几何应用 ;
证明不等式 ; 研究方程实根等.
13
1、利用函数的单调性证明不等式例1. 证明
有时也可考虑对导数用中值定理 .
(5) 若结论为不等式 , 要注意适当放大或缩小的技巧.
5
2x 2 arctan x , 例1：证明 arcsin 2 1 x 2x 证：令 f x arcsin 2 arctan x 2 1 x , f x 0 f x c
0
e
1 e

在 [ 1 , ) 只有唯一的极大点 x e , 因此在
处
又因中的最大项 .
也取最大值 .
22
例9 求曲线 x y 2 上点 A(1,1) 处的曲率半径。解方程两边对 x 求导
4
4
4 x 4 y y 0
方程两边再对 x 求导
3
3
x y y 0
5、利用泰勒公式证明不等式例7. 设函数 f ( x) 在 [0 ,1] 上具有三阶连续导数 ,

习题课-第二、三、四章

4
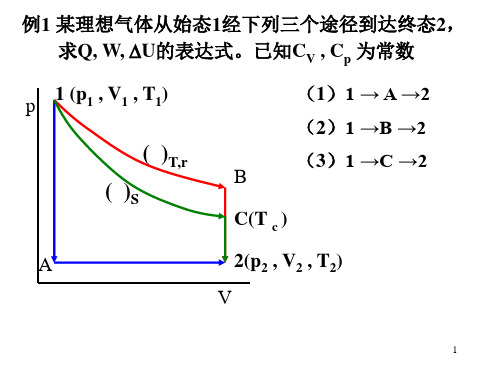
理想气体从300K，Pθ下等压加热到例3 2mol理想气体从理想气体从，下等压加热到800K，，求此过程的Δ 求此过程的ΔU、ΔH、ΔS、 ∆ A、ΔG。已知此理想气体的S 气体的Sθm (300K) =150.0J·K-1·mol-1， =30.0J·K-1·mol-1 Cp,m=30.0 解： ∆U=nCv,m(T2-T1)=-------=21.69kJ ∆H=nCp,m(T2-T1)=-------=30.00kJ ∆S =nCp,mln(T2/T1)=-------=58.85J·K-1 ∆S=n[ S m θ (800K)－Sθm (300K]，－， Sθm (800K)=----=179.4 J·K-1 ∆A＝ ∆U-∆(TS)＝ ∆U-(T2S2-T1S1)＝---=-76.83kJ ＝＝＝ ∆G =∆H-∆(TS)＝ ∆H- (T2S2－T1S1)＝---=-68.52kJ ＝＝ 5
3
是系统状态函数的改变量， ∆H、∆U是系统状态函数的改变量，只与始、终、是系统状态函数的改变量只与始、态有关，而与变化途径无关。即与做什么功，态有关，而与变化途径无关。即与做什么功，过程是否可逆无关。程是否可逆无关。 ∆H=285.6kJ 则是指反应 H2O(l) = H2(g) + 1/2O2(g) 的反应焓。的反应焓。即：∆rHmθ = 285.6 kJ⋅mol-1 = ΣνB∆fHm,Bθ ⋅ = - ∆fHmθ (H2O,l) 所以∆ 所以∆fHm,θ (H2O,l)= - 285.6kJ ⋅mol-1
7
8
例6. 将400K和101325Pa的一摩尔某液态物质向真空容器中蒸发成400K，101325Pa的气态物质(可视为理想气体)，已知此条件下该物质的标准摩尔气化热为16.74kJ·mol−1。 (a) (b) 计算该过程的∆vapS总，∆vapA，∆vapG； ∆ ∆ A ∆ G ∆vapS总，∆vapA，∆vapG是否均可用来判别这

习题课2

高等数学 习题课1-2 极限与连续

工程热力学习题课(2)

习题课2(4~5章)

09 11.2 习题课(2)

双曲线习题课(2)

通信原理习题课(2)

《数字电路与逻辑设计》习题课 (2)

习题课1、2、IP地址习题

多元函数微分学习题课 (2)

习题课2

习题课2

有机单元习题课二

广州大学 线性代数 习题课(2)

无穷级数习题课(2)

《机械能守恒定律》习题课二

Java习题课(2)

高数 第二章 习题课二

习题课-第二、三、四章

高等数学习题课1-2 极限与连续

广州大学线性代数习题课(2)

高数第二章习题课二