(完整版)六年级数学行程问题稍复杂题
(完整)六年级行程问题专题

六年级行程问题复习题【例题7】上午8点零8分,小明骑自行车从家里出发,8分钟后,爸爸骑摩托车去追他,在离家4千米的地方追上了他,然后爸爸立即回家,到家后又立即回头去追小明,再追上小明的时候,离家恰好是8千米。
问这时是几时几分?解法(一).从爸爸第一次追上小明到第二次追上这一段时间内,小明走的路程是8-4=4(千米),而爸爸行了4+8=12(千米),因此,摩托车与自行车的速度比是12∶4=3∶1.小明全程骑车行8千米,爸爸来回总共行4+12=16(千米),还因晚出发而少用8分钟,从上面算出的速度比得知,小明骑车行8千米,爸爸如同时出发应该骑24千米.现在少用8分钟,少骑24-16=8(千米),因此推算出摩托车的速度是每分钟1千米.爸爸总共骑了16千米追上小明,需16分钟,此时小明走了8+16=24(分钟),所以此时是8点32分.解法(二) 这从爸爸第一次追上小明到第二追上小明,小明走了4千米,爸爸走了三个4千米,所以小明的速度是时是爸爸速度的倍。
爸爸从家到第一次追上小明,比小明多走了4×(1-)=千米,共用了8分钟,所以小明的速度是÷8=米,从爸爸从家出发到第二次追上小明,小明共走了8千米,所用时间为8÷=24 分所以现在是8点32分解法(三)同上,先得出小明的速度是时是爸爸速度的倍. 爸爸从家到第一次追上小明,小明走了4千米,若爸爸与小明同时出发,则爸爸应走出12千米,但是由于爸爸晚出发8分钟,所以只走了4千米,所以爸爸8分钟应走8千米. 由于爸爸从出发到第二次追上小明共走了16千米, 所以爸爸用了16分钟,此时离小明出发共用了8+16=24分钟, 所以爸爸第二次追上小明时是8点32分题型二、航船问题航船问题中顺水时:速度=船速+水速逆水时:速度=船速-水速【例题1】甲、乙两港相距360千米,一艘轮船从甲港到乙港,顺水航行15小时到达,从乙港返回甲港,逆水航行20小时到达。
(word完整版)六年级奥数--行程问题

六年级奥数——行程问题(一)一、知识要点行程问题的三个基本量是距离、速度和时间。
其互逆关系可用乘、除法计算,方法简单,但应注意行驶方向的变化,按所行方向的不同可分为三种:(1)相遇问题;(2)相离问题;(3)追及问题。
行程问题的主要数量关系是:距离=速度×时间。
它大致分为以下三种情况:(1)相向而行:相遇时间=距离÷速度和(2)相背而行:相背距离=速度和×时间。
(3)同向而行:速度慢的在前,快的在后。
追及时间=追及距离÷速度差在环形跑道上,速度快的在前,慢的在后。
追及距离=速度差×时间。
解决行程问题时,要注意充分利用图示把题中的情节形象地表示出来,有助于分析数量关系,有助于迅速地找到解题思路。
二、精讲精练【例题1】两辆汽车同时从某地出发,运送一批货物到距离165千米的工地。
甲车比乙车早到8分钟,当甲车到达时,乙车还距工地24千米。
甲车行完全程用了多少小时?解答本题的关键是正确理解“已知甲车比乙车早刀8分钟,当甲车到达时,乙车还距工地24千米”。
这句话的实质就是:“乙48分钟行了24千米”。
可以先求乙的速度,然后根据路程求时间。
也可以先求出全程165千米是24千米的多少倍,再求甲行完全程要用多少小时。
解法一:乙车速度:24÷48×60=30(千米/小时)甲行完全程的时间:165÷30—4860=4.7(小时)解法二:48×(165÷24)—48=282(分钟)=4.7(小时)答:甲车行完全程用了4.7小时。
练习1:1、甲、乙两地之间的距离是420千米。
两辆汽车同时从甲地开往乙地。
第一辆每小时行42千米,第二辆汽车每小时行28千米。
第一辆汽车到乙地立即返回。
两辆汽车从开出到相遇共用多少小时?2、A、B两地相距900千米,甲车由A地到B地需15小时,乙车由B地到A地需10小时。
两车同时从两地开出,相遇时甲车距B地还有多少千米?3、甲、乙两辆汽车早上8点钟分别从A、B两城同时相向而行。
六年级第六讲较复杂的行程问题

求两个码头之间的距离,已知从A到B每天航行500千米, 从B到A每天航行400千米,只要求出从A到B的时间或从 B到A的时间就可以求出距离。
往返航行1次用 18÷5=3.6(天)
分析与思考
2
1
顺流与逆流的速度比为 500:400=5:4
A、B之间距离为 500×1.6=800(千米)
回顾运动过程
甲船从A到B需要4小时,每小时行全程的
乙船从B到A需要6小时,每小时行全程的
完全解题: 1÷( + )=2.4(小时)
小结
流水行船中的相遇问题,要结合工程问题的思想,将速度表示为每小时走全程的几分之几,再利用相遇问题的数量关系解决。
两船从两地同时出发,相向而行。 转化为相遇问题解决
顺流行60千米 + 逆流行120千米 用16小时
用时相等
顺流少行60千米
逆流多行40千米
顺流行60千米与逆流行40千米用时相等 即相同时间内,顺流与逆流航行的路程比为60:40=3:2
顺流行120千米 + 逆流行80千米 用16小时
1
顺流行 80÷2×3=120(千米)
全程: (千米)
船速: (千米/小时)
答:船在静水中的速度是17.5千米/小时。
分析与思考
例3、一艘轮船顺流航行120千米,逆流航行80千米共用16小时,顺流航行60千米,逆流航行120千米共用16小时。求水流速度。
顺流行120千米 + 逆流行80千米 用16小时
例2、一艘轮船在河流的两个码头之间航行,顺流需要6小时,逆流需要8小时,水流速度为2.5千米/时。求轮船在静水中的速度。
回顾例1的解题方法,用分率表示速度
小学六年级数学奥数行程问题20道详解(含答案)全国通用

行程问题50道详解一1、甲、乙二人以均匀的速度分别从A、B两地同时出发,相向而行,他们第一次相遇地点离A地4千米,相遇后二人继续前进,走到对方出发点后立即返回,在距B地3千米处第二次相遇,求两次相遇地点之间的距离.解:第二次相遇两人总共走了3个全程,所以甲一个全程里走了4千米,三个全程里应该走4*3=12千米,通过画图,我们发现甲走了一个全程多了回来那一段,就是距B地的3千米,所以全程是12-3=9千米,所以两次相遇点相距9-(3+4)=2千米。
2、甲、乙、丙三人行路,甲每分钟走60米,乙每分钟走67.5米,丙每分钟走75米,甲乙从东镇去西镇,丙从西镇去东镇,三人同时出发,丙与乙相遇后,又经过2分钟与甲相遇,求东西两镇间的路程有多少米?解:那2分钟是甲和丙相遇,所以距离是(60+75)×2=270米,这距离是乙丙相遇时间里甲乙的路程差所以乙丙相遇时间=270÷(67.5-60)=36分钟,所以路程=36×(60+75)=4860米。
3、A,B两地相距540千米。
甲、乙两车往返行驶于A,B两地之间,都是到达一地之后立即返回,乙车较甲车快。
设两辆车同时从A地出发后第一次和第二次相遇都在途中P地。
那么两车第三次相遇为止,乙车共走了多少千米?解:根据总结:第一次相遇,甲乙总共走了2个全程,第二次相遇,甲乙总共走了4个全程,乙比甲快,相遇又在P点,所以可以根据总结和画图推出:从第一次相遇到第二次相遇,乙从第一个P点到第二个P点,路程正好是第一次的路程。
所以假设一个全程为3份,第一次相遇甲走了2份乙走了4份。
第二次相遇,乙正好走了1份到B地,又返回走了1份。
这样根据总结:2个全程里乙走了(540÷3)×4=180×4=720千米,乙总共走了720×3=2160千米。
4、小明每天早晨6:50从家出发,7:20到校,老师要求他明天提早6分钟到校。
六年级数学 用比例解稍复杂行程问题_完整版题型训练 带详细答案

用比例解稍复杂行程问题【例题1】上午8点8分,小明骑自行车从家里出发,8分钟后,爸爸骑摩托车去追他,在离家4千米的地方追上了他.然后爸爸立即回家,到家后又立刻回头去追小明,再追上小明的时候,离家恰好是8千米,这时是几点几分?【练习1】欢欢和贝贝是同班同学,并且住在同一栋楼里.早晨7 : 40 ,欢欢从家出发骑车去学校,7 : 46 追上了一直匀速步行的贝贝;看到身穿校服的贝贝才想起学校的通知,欢欢立即调头,并将速度提高到原来的2倍,回家换好校服,再赶往学校;欢欢8 : 00赶到学校时,贝贝也恰好到学校.如果欢欢在家换校服用去6分钟且调头时间不计,那么贝贝从家里出发时是几点几分.【例题2】甲、乙两车分别同时从A、B两地相对开出,第一次在离A地95千米处相遇.相遇后继续前进到达目的地后又立刻返回,第二次在离B地25千米处相遇.求A、B两地间的距离?【练习2】(1)地铁有A,B 两站,甲、乙二人都要在两站间往返行走.两人分别从A,B 两站同时出发,他们第一次相遇时距A 站800 米,第二次相遇时距B 站500 米.问:两站相距多远?【例题3】(2)如右图,A,B 是圆的直径的两端,甲在 A 点,乙在B 点同时出发反向而行,两人在C 点第一次相遇,在D 点第二次相遇.已知 C 离 A 有80 米,D 离 B 有60 米,求这个圆的周长.【练习3】甲、乙两车同时从A地出发,不停地往返行驶于A、B 两地之间.已知甲车的速度比乙车快,并且两车出发后第一次和第二次相遇都在途中C 地.甲车的速度是乙车速度的多少倍?【例题4】每天早晨,小刚定时离家步行上学,张大爷也定时出家门散步,他们相向而行,并且准时在途中相遇.有一天,小刚提早出门,因此比平时早7 分钟与张大爷相遇.已知小刚步行速度是每分钟70 米,张大爷步行速度是每分钟40 米,那么这一天小刚比平时早出门多少分钟?【例题5】A、B 两地相距7200 米,甲、乙分别从A, B 两地同时出发,结果在距 B 地2400 米处相遇.如果乙的速度提高到原来的3倍,那么两人可提前10分钟相遇,则甲的速度是每分钟行多少米?【例题6】甲、乙二人分别从A、B 两地同时出发,相向而行,甲、乙的速度之比是 4 : 3,二人相遇后继续行进,甲到达B 地和乙到达A地后都立即沿原路返回,已知二人第二次相遇的地点距第一次相遇的地点30千米,则A、 B 两地相距多少千米?【练习6】甲、乙两车分别从A、B 两地出发,在A、B 之间不断往返行驶,已知甲车的速度是乙车的速度的3/7,并且甲、乙两车第2007 次相遇(这里特指面对面的相遇)的地点与第2008 次相遇的地点恰好相距120 千米,那么,A、B 两地之间的距离等于多少千米?【例题7】B地在A,C两地之间.甲从B地到A地去送信,甲出发10分后,乙从B地出发到C地去送另一封信,乙出发后10分,丙发现甲、乙刚好把两封信拿颠倒了,于是他从B地出发骑车去追赶甲和乙,以便把信调过来.已知甲、乙的速度相等,丙的速度是甲、乙速度的3倍,丙从出发到把信调过来后返回B地至少要用多少时间。
小学六年级奥数复杂行程问题例题10题详解

小学六年级奥数复杂行程问题1、甲、乙、丙三人沿着湖边散步,同时从湖边一固定点出发。
甲按顺序针方向行走,乙与丙按逆时针方向行走。
甲第一次遇到乙后411分遇到丙,再过433分钟第二次遇到乙。
已知乙的速度是甲的32,湖的周长为600米,求丙的速度。
武汉童老师分析:环形跑道的问题,相遇:合走1圈,相遇1次,合走几圈,相遇几次;反过来,相遇1次,合走1圈,相遇几次,合走几圈。
特别的地方:甲第一次遇到乙,之后又遇到了乙,这个很特别。
第一次遇到乙的时候,这个时候说明甲乙在同一个地方,之后他们两合走1圈就会第二次相遇,所以甲乙用:411+433=5分钟,所以得到,甲乙合走1圈用5分钟,所以甲乙5分钟合走600米,V 甲+V 乙=600÷5=120米/分又因为V 乙:V 甲=2:3,所以V 乙=48米/分钟,V 甲=72米/分钟。
甲乙同时出发,5分钟后甲乙第一次相遇,之后再过5/4分钟,甲丙相遇,即:甲和丙相遇1圈的时间为:5+5/4=25/4分钟所以,V 甲+V 丙=600÷25/4=96米/分钟因为V 甲=72米/分钟,所以V 丙=96-72=24米/分钟。
题目不是很难,但是关系要理清楚。
一个是甲乙第一次相遇,过5分钟甲乙第二次相遇,还有甲和丙是25/4分钟第一次相遇。
2、绕湖的一周是24千米,小张和小王在湖边某一地点同时出发反向而行。
小王以每小时4千米速度走1小时后休息5分钟,小张以每小时6千米速度每走50分钟后休息10分钟。
两人出发多少时间第一次相遇?武汉童老师分析:方法1:假设两个人都不休息,那么需要多少时间相遇?24÷(4+6)=2.4小时,再加上休息的时间,那么时间肯定大于2.4小时,所以两个人相遇时间一定需要行走2.4小时之后再继续走一段时间才可能相遇。
所以我们把2.4小时看成第一个阶段,先计算一下走2.4小时两个人还相距多少路程?(这里为实际时间2.4小时必须把休息时间计算在内。
六年级数学行程问题

六年级数学行程问题一、行程问题题目1. 甲、乙两地相距450千米,快车和慢车分别从甲、乙两地同时出发相向而行,快车每小时行60千米,慢车每小时行30千米。
问几小时后两车相遇?解析:两车相向而行,它们的相对速度就是两车速度之和,即公式千米/小时。
根据时间 = 路程÷速度,总路程是450千米,所以相遇时间为公式小时。
2. 一辆汽车从甲地开往乙地,速度是85千米/小时,用了6小时,返回时只用了5小时,返回时的速度是多少?解析:根据路程 = 速度×时间,从甲地到乙地的路程为公式千米。
返回时路程不变,时间为5小时,所以返回速度为公式千米/小时。
3. 小明和小红在周长为400米的环形跑道上跑步,小明的速度是6米/秒,小红的速度是4米/秒。
如果他们同时同地同向起跑,多少秒后小明第一次追上小红?解析:同向起跑时,小明第一次追上小红时,小明比小红多跑了一圈,即400米。
小明每秒比小红多跑公式米,所以追及时间为公式秒。
4. 两列火车同时从相距720千米的两地相对开出,一列火车每小时行50千米,另一列火车每小时行70千米。
经过几小时两车相遇?解析:两车相对开出,相对速度为公式千米/小时。
根据时间 = 路程÷速度,路程为720千米,所以相遇时间为公式小时。
5. 一辆客车和一辆货车分别从A、B两地同时出发,相向而行,客车的速度是每小时75千米,货车的速度是每小时65千米,经过3小时两车相遇。
A、B两地相距多少千米?解析:两车相向而行,它们的速度和为公式千米/小时,经过3小时相遇。
根据路程 = 速度×时间,所以A、B两地相距公式千米。
6. 甲、乙两人分别从相距24千米的两地同时出发相向而行,甲每小时走4千米,乙每小时走2千米,几小时后两人相遇?解析:两人相向而行,速度和为公式千米/小时。
根据路程÷速度= 时间,总路程24千米,所以相遇时间为公式小时。
7. 一辆汽车以每小时60千米的速度从甲地开往乙地,3小时后到达乙地,然后又以每小时45千米的速度返回甲地,求汽车往返的平均速度。
小学六年级奥数专项 行程问题

模块一发车问题【例1】某停车场有10辆出租汽车,第一辆出租汽车出发后,每隔4分钟,有一辆出租汽车开出.在第一辆出租汽车开出2分钟后,有一辆出租汽车进场.以后每隔6分钟有一辆出租汽车回场.回场的出租汽车,在原有的10辆出租汽车之后又依次每隔4分钟开出一辆,问:从第一辆出租汽车开出后,经过多少时间,停车场就没有出租汽车了?【例2】某人沿着电车道旁的便道以每小时4.5千米的速度步行,每7.2分钟有一辆电车迎面开过,每12分钟有一辆电车从后面追过,如果电车按相等的时间间隔以同一速度不停地往返运行.问:电车的速度是多少?电车之间的时间间隔是多少?【巩固】某人以匀速行走在一条公路上,公路的前后两端每隔相同的时间发一辆公共汽车.他发现每隔15分钟有一辆公共汽车追上他;每隔10分钟有一辆公共汽车迎面驶来擦身而过.问公共汽车每隔多少分钟发车一辆?【巩固】某人沿电车线路行走,每12分钟有一辆电车从后面追上,每4分钟有一辆电车迎面开来.假设两个起点站的发车间隔是相同的,求这个发车间隔.【例3】一条公路上,有一个骑车人和一个步行人,骑车人速度是步行人速度的3倍,每隔6分钟有一辆公共汽车超过步行人,每隔10分钟有一辆公共汽车超过骑车人,如果公共汽车始发站发车的时间间隔保持不变,那么间隔几分钟发一辆公共汽车?【巩固】从电车总站每隔一定时间开出一辆电车。
甲与乙两人在一条街上沿着同一方向步行。
甲每分钟步行82米,每隔10分钟遇上一辆迎面开来的电车;乙每分钟步行60米,每隔10分15秒遇上迎面开来的一辆电车。
那么电车总站每隔多少分钟开出一辆电车?【例4】甲城的车站总是以20分钟的时间间隔向乙城发车,甲乙两城之间既有平路又有上坡和下坡,车辆(包括自行车)上坡和下坡的速度分别是平路上的80%和120%,有一名学生从乙城骑车去甲城,已知该学生平路上的骑车速度是汽车在平路上速度的四分之一,那么这位学生骑车的学生在平路、上坡、下坡时每隔多少分钟遇到一辆汽车?【例5】甲、乙两地是电车始发站,每隔一定时间两地同时各发出一辆电车,小张和小王分别骑车从甲、乙两地出发,相向而行.每辆电车都隔4分钟遇到迎面开来的一辆电车;小张每隔5分钟遇到迎面开来的一辆电车;小王每隔6分钟遇到迎面开来的一辆电车.已知电车行驶全程是56分钟,那么小张与小王在途中相遇时他们已行走了分钟.【例6】小峰骑自行车去小宝家聚会,一路上小峰注意到,每隔9分钟就有一辆公交车从后方超越小峰,小峰骑车到半路,车坏了,小峰只好打的去小宝家,这时小峰又发现出租车也是每隔9分钟超越一辆公交车,已知出租车的速度是小峰骑车速度的5倍,那么如果公交车的发车时间间隔和行驶速度固定的话,公交车的发车时间间隔为多少分钟?【例7】某人乘坐观光游船沿顺流方向从A港到B港。
(完整)六年级行程问题综合

六年级行程问题综合(一)1. A、B两地相距720千米,大、小两辆汽车相向而行。
如果大车先行1.5小时, 小车再出发,两车就在中点相遇;若两车同时相向而行,5小时后,两车还相距180 千米。
大、小两辆汽车每小时各行()多少千米。
2. 两辆汽车从A 地同时出发开往B 地,快车比慢车每小时多行 6 千米。
快车比慢车早30 分钟通过中途的 C 地,当慢车到达C 地时,快车已经又行了30 千米并刚好到达B 地。
A、C 两地的距离是()。
3. 甲、乙两车同时从A、B 两地相向而行,两车第一次在距A 地32千米处相遇,相遇后两车继续行驶各自到达B、A 两地后,立即沿原路返回,第二次在距A 地64 千米处相遇。
则A、B 两地间的距离是()千米。
4. 有一项工程,甲队单独做20 天可以完成,乙队单独做30 天可以完成。
现在由甲乙两队合作来做完成这项工程,合作中甲队休息了 4 天,乙队休息了若干天,前后共15天完工。
则乙队休息了()天。
5 •甲、乙两车都是从A地出发经过B地驶往C地,A、B两地的距离等于B、C 两地的距离,乙车的速度是甲车速度的80%。
已知乙车比甲车早出发11 分钟,但在B地停留了7分钟,甲车则不停地驶往C地,最后乙车比甲车晚4分钟到达C地。
那么,乙车出发()分钟时,甲车就超过了乙车。
6. 某晚突然停电,房间里同时点燃了两支粗、细不同,但长短相同的蜡烛。
当来电时,同时吹灭两支蜡烛,发现其中较粗的那支蜡烛的剩余的长度是较细的蜡烛剩余长度的3 倍。
已知较粗的蜡烛从点燃到燃尽可维持5小时,较细的那支可维持3 小时。
这次停电持续了()小时。
7. 喜羊羊、美羊羊、懒羊羊它们分别从甲地驾船顺水航行地到乙地,喜羊羊用了6小时,喜羊羊、美羊羊、懒羊羊在顺水中划行的速度之比是5:4:3,那么懒羊羊从甲到乙顺水划行用了多少小时?8. 有一长方形跑道ABCD甲从顶点A出发,乙从C点出发,两人都按顺时针方向奔跑。
甲每秒跑5米,乙每秒跑4.5米,当甲第一次追上乙时,甲跑了()圈。
小升初重点专题练习:较复杂的行程问题(讲义)六年级下册数学北师大版

小升初重点专题练习----较复杂的行程问题一、行程问题三要素:路程、速度、时间路程=速度×时间速度=路程÷时间时间=路程÷速度二、相遇问题甲从A地到B地,乙从B地到A地,然后两人在途中相遇,实质上是甲和乙一起走了A,B之间这段路程,如果两人同时出发,那么:相遇路程=甲走的路程+乙走的路程=甲的速度×相遇时间+乙的速度×相遇时间=(甲的速度+乙的速度)×相遇时间=速度和×相遇时间相遇问题:路程和=速度和×相遇时间速度和=路程和÷相遇时间相遇时间=路程和÷速度和三、追及问题有两个人同时行走,一个走得快,一个走得慢,当走得慢的在前,走得快的过了一些时间就能追上慢者,这就是“追及问题”。
要算走得快的人在某一段时间内,比走得慢的人多走的路程,也就是要计算两人走的路程之差(追及路程)。
在相同的时间(追及时间)内(设甲走得快,乙走得慢):追及路程=甲走的路程-乙走的路程=甲的速度×追及时间-乙的速度×追及时间=(甲的速度-乙的速度)×追及时间=速度差×追及时间.追及问题:追及时间=路程差÷速度差路程差=速度差×追及时间速度差=路程差÷追及时间四、火车过桥问题(一)火车完全通过大桥火车完全过桥问题,首先要弄清列车通过一座桥是指从车头上桥到车尾离桥,列车过桥的总路程是桥长加车长。
基本数量关系:过桥的路程 = 桥长 + 车长完全通过桥的时间 =(桥长 + 车长)÷车速(二)火车完全在大桥上运行火车完全在大桥上运行,前提条件是桥长大于火车长,首先要弄清列车完全在大桥上运行是指从车尾上桥到车头离桥,总路程是桥长减车长。
基本数量关系:过桥的路程 = 桥长 - 车长完全在桥上的时间 =(桥长 -车长)÷车速典例精析:例1:(单人行程问题)淘气是一个自行车爱好者,正常骑自行车每小时行15千米。
(完整word版)六年级行程问题习题及答案
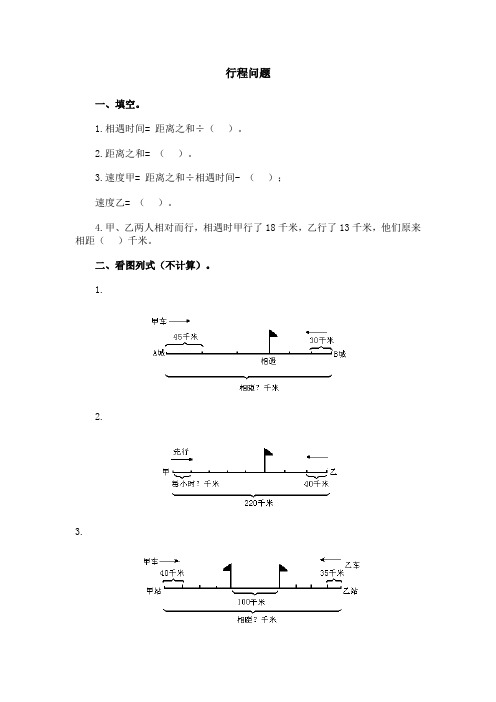
行程问题一、填空。
1.相遇时间= 距离之和÷()。
2.距离之和= ()。
3.速度甲= 距离之和÷相遇时间- ();速度乙= ()。
4.甲、乙两人相对而行,相遇时甲行了18千米,乙行了13千米,他们原来相距()千米。
二、看图列式(不计算)。
1.2.3.三、解应用题。
1.一列客车和一列货车同时从两个车站相对开出,货车每小时行35千米,客车每小时行45千米,2.5小时相遇,两车站相距多少千米?2.两个县城相距52.5千米,甲、乙二人分别从两城同时相对而行,甲每小时行5千米,乙每小时比甲快0.5千米,几小时后相遇?3.甲、乙二人分别从相距110千米的两地相对而行。
5小时后相遇,甲每小时行12千米,问乙每小时行多少千米?4.甲、乙两站相距486千米,两列火车同时从两站相对开出,5小时相遇。
第一列火车比第二列火车每小时快1.7千米,两列火车每小时的速度各是多少?5.两列火车同时从相距650千米的两地相向而行,甲列火车每小时行50千米,乙列火车每小时行52千米,4小时后还差多少千米才能相遇?6.大陈庄和小王庄相距90千米。
小刚和小牛分别由两庄同时反向出发。
2小时24分后两人相距46.6千米,如果小刚每小时行9.9千米,小牛每小时行多少千米?7.学校距活动站670米,小明从学校前往活动站每分钟行80米,2分钟后,小丽从活动站往学校走,每分钟行90米,小明出发多少分钟后和小丽相遇?相遇时二人各行了多少米?8.甲、乙两队合挖一条水渠,甲队从东往西挖,每天挖65米,乙队从西往东挖,每天比甲多挖2.5米。
两队合挖8天后还差52米,这条水渠全长多少米?9.张、李两位叔叔计划共同生产一种零件300个,二人一起生产了5小时后还差40个没完成。
已知张叔叔每小时生产24个,李叔叔每小时生产多少个?10.甲、乙两队合修一条长2400米的路,甲队每小时修126米,乙队每小时比甲队多修48米,求完工时两队各修路多少米?11.东西两村相距64千米。
小学六年级数学行程问题完整版

小学六年级数学行程问题HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】行程问题例1 甲乙两辆汽车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米。
辆车在距中点32千米处相遇。
东西两地相距多少千米?例2 快车和慢车同时从甲乙两地相向开出,快车每小时行40千米,经过3小时,快车已驶过中点25千米,这时快车与慢车还相距7千米。
慢车每小时行多少千米?例3 快车从甲站到达乙站需要8小时,慢车从乙站到达甲站需要12小时,如果快、慢两车同时从甲、乙两站相对开出,相遇是快车比慢车多行180千米,甲、乙两站相遇多少千米?例4 甲、乙两列火车同时从A、B两城相对开出,行了小时后,两列还相距全程的5/8, 两车还需要几小时才能相遇?例5 客车从甲地,货车从乙地同时相对开出。
一段时间后,客车行了全程的7/8,货车行的超过中点54千米,已知客车比货车多行了90千米,甲、乙两地相距多少千米?例6 甲、乙两车分别从A、B两地同时出发,当甲车行到全程的7/11时与乙车相遇,乙车继续以每小时40千米的速度前进,又行驶了154千米到达A地。
甲车出发到相遇用了多少小时?例7 客车从甲地到乙地要10小时,货车从乙地到甲地要15小时,两车同时从两地相对开出,相遇时客车比货车多行了90千米,甲、乙两地之间的距离是多少千米?相遇时客车和货车各行了多少千米?例8 客车和货车同时从甲、乙两地相向而行,在距离中点6千米处相遇,已知货车速度是客车速度的4/5,甲、乙两地相遇多少千米?例9 甲、乙两车同时从A、B两地相对开出,经过8小时相遇,相遇后两车继续前进,甲车又用了6小时到达B 地,乙车要用多少小时才能从B地到达A地。
例10 一辆汽车以每小时100千米的速度从甲地开往乙地,又以每小时60千米的速度从乙地开到甲地,这辆汽车的平均速度N 是多少千米?例11 小明上山每分钟行50米,16分钟到达山顶,再按每分钟80米的速度按原路下山,那么,上、下山每分钟平均行多少米?例12 甲、乙二人上午8时同时从东村骑车到西村去,甲每小时比乙快6千米。
复杂的奥数行程问题

比较复杂的行程问题多人行程例题多人行程这类问题主要涉及的人数为3人,主要考察的问题就是求前两个人相遇或追及的时刻,第三个人的位置,解题的思路就是把三人问题转化为寻找两两人之间的关系。
例1.甲乙丙三人同时从东村去西村,甲骑自行车每小时比乙快12公里,比丙快15公里,甲行3.5小时到达西村后立刻返回。
在距西村30公里处和乙相聚,问:丙行了多长时间和甲相遇?例2.甲、乙、丙三辆车同时从A地出发到B地去,甲、乙两车的速度分别为60千米/时和48千米/时。
有一辆迎面开来的卡车分别在他们出发后6时、7时、8时先后与甲、乙、丙三辆车相遇。
求丙车的速度。
例3、李华步行以每小时4千米的速度从学校出发到20.4千米外的冬令营报到。
0.5小时后,营地老师闻讯前来迎接,每小时比李华多走L2千米,又经过了1.5小时,张明从学校骑车去营地报到。
结果3人同时在途中某地相遇。
问:张明每小时行驶多少千米?例4:有甲、乙、丙三人同时同地出发,绕一个花圃行走,乙、丙二人同方向行走,甲与乙、丙相背而行。
甲每分钟走40米,乙每分钟走38米,丙每分钟走36米。
在途中,甲和乙相遇后3分钟和丙相遇。
问:这个花画的周长是多少米?4例5、AB两地相距30千米,甲乙丙三人同时从A到B,而且要求同时到达。
现在有两辆自行车,但不许带人,但可以将自行车放在中途某处,后来的人可以接着骑。
已知骑自行车的平均速度为每小时20千米,甲步行的速度是每小时5千米,乙和丙每小时4千米,那么三人需要多少小时可以同时到达?例6、有甲、乙、丙三人同时同地出发,绕一个花圃行走,乙、丙二人同方向行走,甲与乙、丙相背而行。
甲每分钟走40米,乙每分钟走38米,丙每分钟走36米。
在途中,甲和乙相遇后3分钟和丙相遇。
问:这个花圃的周长是多少米?二次相遇行程问题答题思路点拨:甲从A地出发,乙从B地出发相向而行,两人在C地相遇,相遇后甲继续走到B地后返回,乙继续走到A地后返回,第二次在D地相遇。
稍复杂的行程问题

稍复杂的行程问题例1:上午9:00小华骑自行车到市区去,8分钟后,爸爸骑摩托车去追小华,在离家8千米处追上小华,交待一句话后马上回家,回家后又当即骑摩托车去追,追上小华把钱交给他后,觉察现在离家已经有24千米,那么现在是何时?练习、上午8点8分,小明骑自行车从家里动身,8分钟后,爸爸骑摩托车去追他,在离家4千米的地址追上了他,然后爸爸当即回家,抵家后又立刻转头去追小明,再追上他的时候,离家恰好是8千米,这时是()点()分。
例2:一路电车的起点站和终点站别离是甲站和乙站,每隔5分钟有一辆电车从甲站发出开往乙站,全程要走15分钟。
有一个人从乙站动身沿电车线路骑车前去甲站,他动身的时候,恰好有一辆电车抵达乙站,在路上他又碰到了10辆迎面开来的电车,才抵达甲站。
这时,恰好又有一辆电车从甲站开出。
他从乙站到甲站用了多少分钟?练习、甲、乙两站从上午6时开始每隔8分钟同时相向发出一辆公共汽车,汽车单程运行需45分钟。
有一名乘客乘坐6点16分从甲站开出的汽车,途中他能碰到()辆从乙站开往甲站的公共汽车。
例3:甲、乙、丙三人中,甲每分钟走50米,乙每分钟走60米,丙每分钟走70米。
甲乙两人从东镇,丙一人从西镇同时动身,相向而行,丙碰到乙后2分钟再碰到甲,那么两镇的距离是多少米?练习、甲、乙、丙三人中,甲每分钟走50米,乙每分钟走60米,比丙每分钟少走10米。
甲乙两人从东镇,丙一人从西镇同时动身相向而行,丙碰到乙后3分钟再碰到甲,那么两镇的距离是()米。
例4:某考古队要越过一座山,他们上午8:00上山,每小时行3千米,抵达山顶休息1小时,下山比上山每小时多行2千米,下午2时抵达山底,全程共行了19千米。
那个考古队上山行了多少千米?下山行了多少千米?练习、王佳的奶奶住在山脚,每次王佳去奶奶家时都须越过一座山。
有一个双休日早上7:00,王佳以每小时4千米速度上山,抵达山顶休息半小时后马上下山,下山速度比上山快2千米,结果中午11:00恰好赶到奶奶家吃午饭,已知王佳全程共行17千米,那么她上山走了()千米,下山走了()千米。
(完整版)小学六年级奥数行程问题

行程问题(一)【知识点讲解】基本概念:行程问题是研究物体运动的,它研究的是物体速度、时间、路程三者之间的关系.基本公式:路程=速度X时间;路程士时间云度;路程士速度=时间关键:确定运动过程中的位置和方向。
相遇问题:速度和X相遇时间=相遇路程(请写出其他公式)追及问题:追及时间=路程差士速度差(写出其他公式)主要方法:画线段图法基本题型:已知路程(相遇路程、追及路程)、时间(相遇时间、追及时间)、速度(速度和、速度差)中任意两个量,求第三个量。
相遇问题:例1、甲乙两车同时从AB两地相对开出,第一次相遇后两车继续行驶,各自到达对方出发点后立即返回,第二次相遇时离B地的距离是AB全程的】。
已知甲5车在第一次相遇时行了120千米。
AB两地相距多少千米?例2、甲、乙两车分别从A、B两城同时相对开出,经过4小时,甲车行了全程的80%乙车超过中点35千米,已知甲车比乙车每小时多行10千米。
问A B 两城相距多少千米?例3、甲、乙和丙同时由东、西两城出发,甲、乙两人由东城到西城,甲步行每小时走5千米,乙骑自行车每小时行15千米,丙也骑自行车每小时20千米,已知丙在途中遇到乙后,乂经过1小时才遇到甲,求东、西城相距多少千米?例4、甲乙两站相距470千米,一列火车于中午1时从甲站出发,每小时行52 千米,另一歹0火车下午2时30分从乙站开出,下午6时两车相遇,求乙站开出的那辆火车的速度是多少?例5、小李从A城到B城,速度是50千米/小时,小兰从B城到A城,速度是40 千米/小时。
两人同时出发,结果在距A、B两城中点10千米处相遇。
求A、B 两城间的距离。
例6、绕湖的一周是24千米,小张和小王从湖边某一地点同时出发反向而行.小王以每小时4千米的速度每走1小时休息5分钟,小张以每小时6千米的速度每走5分休息10分钟.两人出发后多长时间第一次相遇?1、一列客车和一列货车同时从两地相向开出,经过18小时两车在某处相遇,已知两地相距1488千米,货车每小时比客车少行8千米,货车每行驶3小时要停驶1小时,客车每小时行多少千米?2、一个600米长的环形跑道上,兄弟两人如果同时从同一起点按顺时针反方向跑步,每隔12分钟相遇一次;如果两人同从同一起点反方向跑步,每隔4分中相遇一次。
六年级行程问题经典例题40题

六年级行程问题经典例题40题一、相遇问题1. 甲、乙两人分别从A、B两地同时出发,相向而行。
甲的速度是每小时5千米,乙的速度是每小时4千米,经过3小时后两人相遇。
求A、B两地的距离。
解析:根据相遇问题的公式,路程 = 速度和×相遇时间。
甲、乙的速度和为5 + 4 = 9(千米/小时),相遇时间是3小时,所以A、B两地的距离为9×3 = 27(千米)。
2. 两地相距600千米,上午8时,客车以每小时60千米的速度从甲地开往乙地,货车以每小时50千米的速度从乙地开往甲地。
要使两车在中点相遇,货车必须在上午几时出发?解析:两地中点距离为600÷2 = 300千米。
客车到达中点需要的时间为300÷60 = 5小时,货车到达中点需要的时间为300÷50 = 6小时。
客车上午8时出发,5小时后即13时到达中点,货车要6小时到达中点,所以货车必须提前1小时出发,也就是上午7时出发。
3. 甲、乙两车分别从A、B两地同时出发,相向而行,甲车每小时行70千米,乙车每小时行80千米,3小时后两车还相距50千米。
A、B两地相距多远?解析:甲、乙两车3小时行驶的路程之和为(70 + 80)×3=450千米,此时还相距50千米,所以A、B两地相距450+ 50 = 500千米。
二、追及问题4. 甲、乙两人在相距12千米的A、B两地同时出发,同向而行。
甲步行每小时行4千米,乙骑车在后面,每小时速度是甲的3倍。
几小时后乙能追上甲?解析:乙的速度是4×3 = 12千米/小时,乙与甲的速度差是12 4 = 8千米/小时。
追及路程是12千米,根据追及时间 = 追及路程÷速度差,可得追及时间为12÷8 = 1.5小时。
5. 一辆汽车从甲地开往乙地,每小时行40千米,开出5小时后,一列火车以每小时90千米的速度也从甲地开往乙地。
在甲乙两地的中点处火车追上汽车,甲乙两地相距多少千米?解析:汽车先开出5小时行驶的路程为40×5 = 200千米。
六年级复杂行程问题奥数例题

六年级复杂行程问题奥数例题六年级复杂行程问题奥数例题 1例题:王欣和陆亮两人同时从相距2000米的两地相向而行,王欣每分钟行110米,陆亮每分钟行90米。
如果一只狗与王欣同时同向而行,每分钟行500米,遇到陆亮后,立即回头向王欣跑去;遇到王欣后再回头向陆亮跑去。
这样不断来回,直到王欣和陆亮相遇为止,狗共行了多少米?分析与解答:要求狗共行了多少米,一般要知道狗的速度和狗所行的时间。
根据题意可知,狗的速度是每分钟行500米,关键是要求出狗所行的时间,根据题意可知:狗与主人是同时行走的,狗不断来回所行的时间就是王欣和陆亮同时出发到两人相遇的时间,即2000÷(110+90)=10分钟。
所以狗共行了500×10=5000米。
练习题:1、甲乙两队学生从相隔18千米的两地同时出发相向而行。
一个同学骑自行车以每小时15千米的速度在两队之间不停地往返联络。
甲队每小时行5千米,乙队每小时行4千米。
两队相遇时,骑自行车的同学共行多少千米?2、A、B两地相距400千米,甲、乙两车同时从两地相对开出,甲车每小时行38千米,乙车每小时行42千米。
一只燕子以每小时50千米的速度和甲车同时出发向乙车飞去,遇到乙车又折回向甲车飞去。
这样一直飞下去,燕子飞了多少千米,两车才能相遇?3、甲、乙两个车队同时从相隔330千米的两地相向而行,甲队每小时行60千米,乙队每小时行50千米。
一个人骑摩托车以每小时行80千米的速度在两车队中间往返联络,问两车队相遇时,摩托车行驶了多少千米?六年级复杂行程问题奥数例题 2例题:甲乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,乙每小时走4千米。
两人几小时后相遇?分析与解答:这是一道相遇问题。
所谓相遇问题就是指两个运动物体以不同的地点作为出发地作相向运动的问题。
根据题意,出发时甲乙两人相距20千米,以后两人的距离每小时缩短6+4=10千米,这也是两人的速度和。
所以,求两人几小时相遇,就是求20千米里面有几个10千米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解决问题(三)
1、邮递员去送信,已知回来时沿原路返回,但速度提高了25%。
并且来、回的
时间差是11
4小时。
求往返一次用多少小时?
2、甲、乙两车同时从A地去B地。
甲行全程的一半时,乙离B地还有54km。
当甲到达B地时,乙已经行了全程的80%。
求A、B两地的路程是多少km?
3、甲、乙两人分别从A、B两地同时出发,相向而行。
出发时他们的速度比是
3:2,他们第一次相遇后,甲的速度提高了20%,乙的速度提高了30%。
这样,当甲到达B地时,乙离A地还有280km。
那么A、B两地的路程是多少km?
4、水产商店计划以6元/kg的价格出售180kg的鲢鱼。
因购买鱼头的顾客较多,
所以商店决定把鱼按5:4的重量比分为鱼头和鱼尾。
已知鱼头和鱼尾的单价比为8:5,要使总收入不变,问鱼头和鱼尾的单价分别是多少?
5、一个圆锥的底面半径增加20%,要使体积不变,高应减少约百分之几。
6、甲、乙两人都骑车从A去B。
甲出发3小时后,乙才出发,结果乙比甲早一
小时到达B。
已知A、B两地相距120km,甲的速度是乙的2
3。
求甲、乙的
速度。
7、甲、乙两辆汽车同时从A去B,出发后,甲、乙两车的速度的比是5:4.当
甲车行至中点时,乙离中点还差60千米。
当乙车到达中点后,速度提高50%。
当甲到达B地时,乙离B地还有多少千米?
8、一杯牛奶,喝去20%。
加满水搅匀,再喝去60%后,杯中的纯牛奶只占原牛
奶的百分之几。
9、从装满100g浓度为80%的盐水杯中倒出40g盐水后,再用清水加满。
搅拌后
再倒出40g盐水,然后再用清水加满。
此时杯中盐水的浓度是百分之几。
10、某商品按20%的利润定价,如果打八折出售,每件就要亏损50元,这种
商品每件的成本是多少元?
11、一种商品,按进价的33%加价定价。
现在这种商品的进价降低了5%。
若仍按原定价出售,则这种商品现在的利润率是百分之几。
12、某商品销售一种皮衣,若按九折出售,可以赢利215元;如果按八折出
售,则亏损125元。
这件皮衣的进价是多少元?
13、甲、乙两个同样的被子,甲杯只有半杯清水,乙杯盛满了含盐30%的盐
水。
先将乙杯盐水的一半倒入甲杯,摇匀后,再将甲杯盐水的一半倒入乙杯。
这时甲杯的浓度是百分之几,乙杯的浓度是百分之几。
14、市场里卖一批白菜,上午以1.2元/kg的价钱卖出20kg,下午以1.1元/kg
的价钱卖出30kg,并且上午比下午少获利3元。
问白菜的进价是每千克多少元?
15、一件衣服如果打八折,可以优惠顾客60元,此时商家可获利润20%。
这
件衣服的成本是多少元?
16、原来3支笔的价钱相当于5个本的价钱。
现在由于本的价钱上涨,2支
笔的价钱相当于3个本的价钱。
求每个本上涨了百分之几?
17、甲、乙、丙三个队共同运完一批货。
乙队运了全部货物的40%,甲队运
货量与丙队的比是1:3。
已知乙队和丙队一共运了68吨。
求甲队比乙队少运多少吨?
18、一辆汽车从甲地到乙地用了6小时,返回时速度提高了25%,这样就少
用了几小时?
19、一件商品,原来按进价的20%赚取利润来定价出售。
现在由于进价上涨
了5%,而售价还保持不变,那么现在的利润减少了百分之几?
20、有一批零件,分给甲、乙各一半去加工。
当甲加工了他自己定额的2
3时,
乙还剩35个没有加工;当乙完成自己定额的一半时,甲还剩下他自己定额的20%没有加工。
求这批零件原有多少个?
21、某商品按定价的八折出售,仍可获利16%。
若按定价的六折出售,商家
是赚还是赔?赚或赔百分之几?
22、若干台机器同时加工一批零件,如果增加2台机器,完成任务用的时间
是原来的8
9;如果减少2台机器,完成任务就要多用
3
4时,如果用一台机器
加工全部零件要多少个小时?。
