理科实验班试题

合集下载

理科实验班招生考试物理试卷(一)

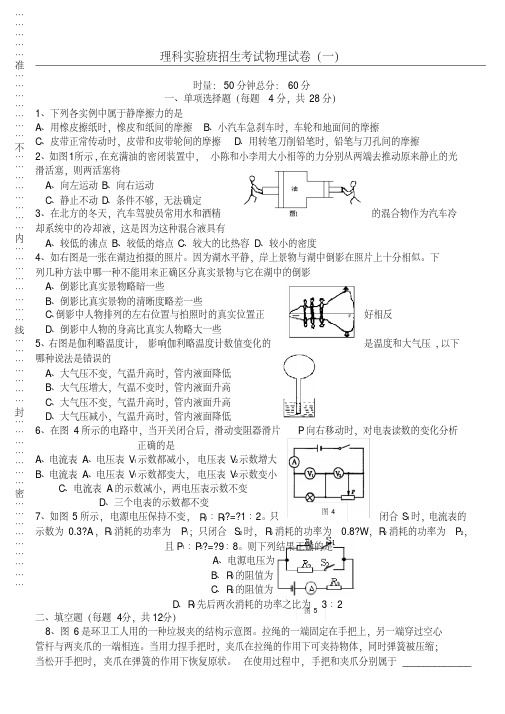
图4 理科实验班招生考试物理试卷（一）时量：50分钟总分：60分一、单项选择题（每题4分，共28分）1、下列各实例中属于静摩擦力的是A 、用橡皮擦纸时，橡皮和纸间的摩擦B 、小汽车急刹车时，车轮和地面间的摩擦C 、皮带正常传动时，皮带和皮带轮间的摩擦D 、用转笔刀削铅笔时，铅笔与刀孔间的摩擦2、如图1所示,在充满油的密闭装置中，小陈和小李用大小相等的力分别从两端去推动原来静止的光滑活塞，则两活塞将A 、向左运动B 、向右运动C 、静止不动D 、条件不够，无法确定3、在北方的冬天，汽车驾驶员常用水和酒精的混合物作为汽车冷却系统中的冷却液，这是因为这种混合液具有A 、较低的沸点B 、较低的熔点C 、较大的比热容D 、较小的密度4、如右图是一张在湖边拍摄的照片。

因为湖水平静，岸上景物与湖中倒影在照片上十分相似。

下列几种方法中哪一种不能用来正确区分真实景物与它在湖中的倒影A 、倒影比真实景物略暗一些B 、倒影比真实景物的清晰度略差一些C 、倒影中人物排列的左右位置与拍照时的真实位置正好相反D 、倒影中人物的身高比真实人物略大一些5、右图是伽利略温度计，影响伽利略温度计数值变化的是温度和大气压,以下哪种说法是错误的A 、大气压不变，气温升高时，管内液面降低B 、大气压增大，气温不变时，管内液面升高C 、大气压不变，气温升高时，管内液面升高D 、大气压减小，气温升高时，管内液面降低6、在图4所示的电路中，当开关闭合后，滑动变阻器滑片P 向右移动时，对电表读数的变化分析正确的是A 、电流表A 、电压表V 1示数都减小，电压表V 2示数增大B 、电流表A 、电压表V 1示数都变大，电压表V 2示数变小C 、电流表A 的示数减小，两电压表示数不变D 、三个电表的示数都不变7、如图5所示，电源电压保持不变，R 1∶R 2?=?1∶2。

只闭合S 1时，电流表的示数为0.3?A ，R 1消耗的功率为P 1；只闭合S 2时，R 0消耗的功率为0.8?W ，R 2消耗的功率为P 2，且P 1∶P 2?=?9∶8。

湖南师大附中理科实验班招生考试物理试题

师大附中理科实验班招生考试物理试题(物理）一．单项选择题（共7小题，每小题4分）1. 如图所示，s 为点光源，MN 为距s 水平距离为2m 的竖直墙壁，现有一小球在过s 的水平线上距离s 为1m 的位置开始由静止释放，设小球下落的距离d(米)与下落的时间t （秒）满足关系式d=5t 2，则有关小球在竖直墙上的影的速度的说法正确的是（）A ．影做匀速直线运动，且速度大小为5m/sB ．影做匀速直线运动，且速度大小为10 m/sC ．影的速度大小在增大。

D ．影的速度大小在减少。

2、如图所示，长方形水槽中漂浮一个木球，水槽底部中央有一个三棱柱支持着，恰好处于平衡状态，则下列判断正确的是（）A 、无论木球在何处，水槽仍可处于平衡状态B 、木球偏向左侧时，水槽向右侧倾斜C 、木球偏向左侧时，水槽向左侧倾斜D 、若用实心铁球代替木球，铁球无论在何处，水槽仍可处于平衡状态3、某校新建一个喷水池，在池底的中央安装了一只射灯。

池内无水时，射灯发出一束光照在池壁上，在S 点形成一个亮斑，如图所示。

现往池内注水，水面升至于a 位置时，站在池旁的人看到亮斑的位置在P 点；如果水面上升至b 位置时，人看到亮斑的位置在Q 点，则（）A 、P 点在S 点的上方，Q 点在S 点的上方B 、P 点在S 点的上方，Q 点在S 点的下方C 、P 点在S 点的下方，Q 点在S 点的下方D 、P 点在S 点的下方，Q 点在S 点的上方4、小明晚上做功课，把台灯插头插在书桌边的插座上，闭合台灯开关，发现台灯不亮．为了找出故障原因，小明把台灯插头插入其他插座，发现台灯能正常发光，用测电笔插入书桌边的插座孔进行检查，发现其中一个孔能使测电笔的氖管发光．故障原因可能是（）A 、进户线火线上的熔丝烧断B 、进户线零线断了C 、书桌边的插座与零线断开D 、书桌边的插座与火线断开5、有n 个完全相同的灯泡，并联后与R 1串联接入电路中，如图（1）所示，串联后再与R 2串联接入电路，如图（2）所示，若电路两端的电压均为U ，分别调节R 1 和R 2使所有灯都能正常发光，那么电路（1）（包括R 1）和电路（2）（包括R 2）所消耗的总功率之比（）A 、n 2∶1B 、n ∶1C 、1∶1D 、n 1/2∶16、某同学在一个较大的锥形瓶内注入水，然后将它放在水平桌面上，如图所示，此时水对锥形瓶底的压力为F 1，锥形瓶对桌面的压力为F 2。

普通高中理科实验班招生考试数学卷

普通高中理科实验班招生考试数学卷数学试题（满分150分，答题时间120分）一、选择题（本题共5小题，每小题10分，满分50．每小题均给出了代号为A 、B 、C 、D 的四个结论，其中只有一个是正确的，请将正确答案的代号填在题后的括号内）1．若mx 11-=是方程022=+-m mx 的根，则m x -的值为 ………【】 A ．0 B ．1 C ．－1 D ．22．内角的度数为整数的正n 边形的个数是 ………………………………【】 A ．24 B ．22 C ．20 D ．183．某商场五一期间举行优惠销售活动，采取“满一百元送二十元，并且连环赠送”的酬宾方式，即顾客每消费满100元（100元可以是现金，也可以是购物券，或二者合计）就送20元购物券，满200元就送40元购物券，依次类推，现有一位顾客第一次就用了16000元购物，并用所得购物券继续购物，那么他购回的商品大约相当于它们原价的 ………………………………………………………………【】 A ．90% B ．85% C ．80% D ．75%4．设x 为正整数，若1+x 是完全平方数，则它前面的一个完全平方数是【】 A ．x B ．12+-x x C ．112++-x x D ．212++-xx 5．横坐标、纵坐标都是整数的点叫做整点，函数1236-+=x x y 的图象上整点的个数是 ……………………………………………………………………………【】A ．3个B ．4个C ．6个D ．8个二、填空题（本题共5小题，每小题8分，共40分）6．计算：1＋2－3＋4＋5－6＋7＋8－9＋…＋97＋98－99＋100＝．7．已知实数x 满足012)(4)(222=----x x x x ，则代数式12+-x x 的值为．8．若方程组⎩⎨⎧+=--=+433235k y x k y x 的解为⎩⎨⎧==,,b y a x 且||k ＜3，则b a -的取值范围是．9．已知函数22)2(2a x a x y +++=的图象与x 轴有两个交点，且都在x 轴的负半轴上，则a 的取值范围是．10．如图，等腰梯形ABCD 中，AB ∥DC ，∠A ＝60°，AD ＝DC ＝10，点E ，F 分别在AD ，BC 上，且AE ＝4，BF ＝x ，设四边形DEFC 的面积为y ，则y 关于x 的函数关系式是（不必写自变量的取值范围）．三、（本题共4小题，满分60分）11．（本题满分15分）我们知道相交的两直线的交点个数是1，记两平行直线的交点个数是0；这样平面内的D CBAFE三条平行线它们的交点个数就是0，经过同一点的三直线它们的交点个数就是1；依次类推……（1）请你画图说明同一平面内的五条直线最多有几个交点？（2）平面内的五条直线可以有4个交点吗？如果有，请你画出符合条件的所有图形；如果没有，请说明理由．（3）在平面内画出10条直线，使交点数恰好是31．12．（本题满分15分）甲、乙两个粮库原来各存有整袋的粮食，如果从甲库调90袋到乙库，则乙库存粮是甲库的2倍；如果从乙库调若干袋到甲库，则甲库存粮是乙库的6倍．问甲库原来最少存粮多少袋？13．（本题满分15分）⊙O 1与⊙O 2相交于点A 、B ，动点P 在⊙O 2上，且在⊙O 1外，直线PA 、PB 分别交⊙O 1于点C 、D ．问：⊙O 1的弦CD 的长是否随点P 的运动而发生变化？如果发生变化，请你确定CD 最长或最短时点P 的位置；如果不发生变化，请给出你的证明．CB A··PDO O 2114．（本题满分15分）如图，函数221+-=x y 的图象交y轴于M ，交x 轴于N ，点P 是直线MN 上任意一点，PQ⊥x 轴，Q 是垂足，设点Q 的坐标为（t ，0），△POQ 的面积为S （当点P 与M 、N 重合时，其面积记为0）．（1）试求S 与t 之间的函数关系式；（2）在如图所示的直角坐标系内画出这个函数的图象，并利用图象求使得S ＝a （a ＞0）的点P 的个数．普通高中理科实验班招生考试数学试题参考答案及评分标准一、选择题（每小题10分，共50分）1．C 2．B 3．C 4．D 5．B 二、填空题（每小题8分，共40分）6．1684 7．7 8．－1＜b a -＜5 9．a ＞－1且a ≠010．35534+-=x y三、解答题（每小题15分，共60分）11．（本题满分15分）解（1）如图1，最多有10个交点； ……………………（4分）图1 图2（2）可以有4个交点，有3种不同的情形，如图2． ……（10分）⌒ ⌒ （3）如图3所示． …………………（15分）图312．（本题满分15分）解：设甲库原来存粮a 袋，乙库原来存粮b 袋，依题意可得 90)90(2+=-b a ．（1）再设乙库调c 袋到甲库，则甲库存粮是乙库的6倍，即)(6c b c a -=+．（2） ………………（5分）由（1）式得2702-=a b ．（3）将（3）代入（2），并整理得1620711=-c a ． ………………（10分）由于7)1(42327162011++-=-=a a a c ．又a 、c 是正整数，从而有7162011-a ≥1，即a ≥148；并且7整除)1(4+a ，又因为4与7互质，所以7整除1+a ．经检验，可知a 的最小值为152．答：甲库原来最少存粮153袋． …………………（15分） 13．当点P 运动时，CD 的长保持不变． …………………（4分）证法一：A 、B 是⊙O 1与⊙O 2的交点，弦AB 与点P 的位置无关．……（6分）连结AD ，∠ADP 在⊙O 1中所对的弦为AB ，所以∠ADP 为定值． ……………（10分） ∠P 在⊙O 2中所对的弦为AB ，所以∠P 为定值． ……………（12分）因为∠CAD ＝∠ADP ＋∠P ，所以∠CAD 为定值．在⊙O 1中∠CAD 所对弦是CD ，∴CD 的长与点P 的位置无关．………（15分）证法二：在⊙O 2上任取一点Q ，使点Q 在⊙O 1外，设直线QA 、QB 分别交⊙O 1 于C ＇、D ＇，连结C ＇D ＇．∵ ∠1＝∠3，∠2＝∠3，∠1＝∠2，∴ ∠3＝∠4． …………………（10分）∴ CC ＇＝DD ＇ ∴C ＇mD ＇＝CmD∴ CD ＝CD ． …………………（15分）14．（本题满分15分）解法1（1）① 当t ＜0时，OQ ＝t -，PQ ＝221+-t ． ∴ S ＝t t t t -=+--⋅241)221)((21； ② 当0＜t ＜4时，OQ ＝t ，PQ ＝221+-t ．∴ S ＝t t t t +-=+-⋅241)221(21；③ 当t ＞4时，OQ ＝t ，PQ ＝221)221(-=+--t t ．∴ S ＝t t t t -=-⋅241)221(21．④ 当t ＝0或4时，S ＝0．于是，⎪⎪⎩⎪⎪⎨⎧≤≤+-><-=)40(41)40(,4122t t t k t t t S 或 …………………………………………6分（2）⎪⎪⎩⎪⎪⎨⎧≤≤+--=+-><--=-=)40(1)2(4141)40(,1)2(41412222t t t t k t t t t S 或下图中的实线部分就是所画的函数图象． ……………………………………12分CBA··PDO O 21′′C D Q1234maS =观察图象可知：当0＜a ＜1时，符合条件的点P 有四个；当a ＝1时，符合条件的点P 有三个；当a ＞1时，符合条件的点P 只有两个． ………………………………………15分解法2：（1）∵ OQ ＝||t ，PQ ＝|221||221|-=+-t t ， ∴ S ＝|4|41|221|||212t t t t -=-⋅． ……………………………………4分（2）⎪⎪⎩⎪⎪⎨⎧≤≤+-><-=-=)40(41)40(,41|4|41222t t t k t t t t x S 或 ………………………6分以下同解法1．。

理科实验班招生考试物理试卷(一)

图4理科实验班招生考试物理试卷（一）时量：50分钟总分：60分一、单项选择题（每题4分，共28分）1、下列各实例中属于静摩擦力的是A 、用橡皮擦纸时，橡皮和纸间的摩擦B 、小汽车急刹车时，车轮和地面间的摩擦C 、皮带正常传动时，皮带和皮带轮间的摩擦D 、用转笔刀削铅笔时，铅笔与刀孔间的摩擦2、如图1所示,在充满油的密闭装置中，小陈和小李用大小相等的力分别从两端去推动原来静止的光滑活塞，则两活塞将A 、向左运动B 、向右运动C 、静止不动D 、条件不够，无法确定 3、在北方的冬天，汽车驾驶员常用水和酒精的混合物作为汽车冷却系统中的冷却液，这是因为这种混合液具有A 、较低的沸点B 、较低的熔点C 、较大的比热容D 、较小的密度4、如右图是一张在湖边拍摄的照片。

因为湖水平静，岸上景物与湖中倒影在照片上十分相似。

下列几种方法中哪一种不能用来正确区分真实景物与它在湖中的倒影 A 、倒影比真实景物略暗一些B 、倒影比真实景物的清晰度略差一些C 、倒影中人物排列的左右位置与拍照时的真实位置正好相反D 、倒影中人物的身高比真实人物略大一些 5、右图是伽利略温度计，影响伽利略温度计数值变化的是温度和大气压,以下哪种说法是错误的A 、大气压不变，气温升高时，管内液面降低B 、大气压增大，气温不变时，管内液面升高C 、大气压不变，气温升高时，管内液面升高D 、大气压减小，气温升高时，管内液面降低6、在图4所示的电路中，当开关闭合后，滑动变阻器滑片P 向右移动时，对电表读数的变化分析正确的是A 、电流表A 、电压表V 1示数都减小，电压表V 2示数增大B 、电流表A 、电压表V 1示数都变大，电压表V 2示数变小C 、电流表A 的示数减小，两电压表示数不变D 、三个电表的示数都不变7、如图5所示，电源电压保持不变，R 1∶R 2?=?1∶2。

只闭合S 1时，电流表的示数为0.3?A ，R 1消耗的功率为P 1；只闭合S 2时，R 0消耗的功率为0.8?W ，R 2消耗的功率为P 2，且P 1∶P 2?=?9∶8。

理科实验班招生考试物理试题

物理5一、选择题（每小题只有一个答案正确，每小题4分，共40分，答案填在后面的答题卡中） 1．如图所示，是我市金赛路两旁安装的隔音墙，其目的是减小车辆行驶时产生的噪声对公路两旁居民的危害。

这种减小噪声危害的方法主要是在下列哪个途径中实现的A ．噪声的产生B ．噪声的传播C ．噪声的接收D ．以上三种均是 2．在下列各种摩擦中，有害的摩擦是A ．小明上学时脚与地面间的摩擦B ．电动机运转时各转动部分间的摩擦C ．在家乐福人随电梯上行是人与电梯间的摩擦D ．小红骑自行车时后轮与地面间的摩擦3．为研究影响保温瓶保温效果的因素，某同学在保温瓶中灌入热水，先测量初始水温，经过一段时间下列研究方案中符合控制变量方法的是A ．若研究瓶内水量与保温效果的关系，可用序号2、4、6的数据。

B ．若研究初始水温与保温效果的关系，可用序号1、2、3的数据。

C ．若研究保温时间与保温效果的关系，可用序号4、5、6的数据。

D ．若研究瓶内水量与保温效果的关系，可用序号1、3、5的数据。

4．如图所示，A 、B 为完全相同的两条形磁铁，先将A 置于台秤的托盘上，忽略台秤与磁铁间的磁力作用，当平衡时台秤的示数为F 1，再将B 置于A 上，当平衡时台秤的示数为F 2，则F 1和F 2的大小关系是A ．F 2＝2F 1B ．F 2<2F 1C ．F 2>2F 1D ．F 2＝4F 15．家住山区的小明星期天上午8︰00出发，骑车去亲戚家，途经3个不同的路段：先是上坡路，然后是平直的路，最后是下坡路，于9︰30到达。

若三路段的长度相同，且他在3个路段的平均行驶速度之比为2︰3︰4，则9︰00时他行进在哪一路段A ．上坡路段B ．平直路段C ，下坡路段D ．刚好走完上坡路 6．小明在广场上游玩时，将一充有氢气的气球系于一辆玩具小汽车上，并将玩具小汽车放置在光滑的水平地面上，无风时细绳处于竖直方向，当一阵风沿水平方向吹向气球时，则下列说法中正确的是 A.小汽车可能被拉离地面 B.氢气球仍处于静止状态C.小汽车一定沿地面滑动D.小汽车仍处于静止状态7.在如右图所示的电路中，电源电压保持不变当闭合电键S 后，将滑动变阻器的滑片向左滑动时 A. 灯L 1、L 2变亮，灯L 3变暗 B. 灯L 2、L 3 变亮，灯L 1变暗 C. 灯L 1、L 3 变亮，灯 L 2变暗 D. 灯L 1、L 2 、L 3 都变亮8. 如图所示，甲、乙两个正方体物块放置在水平地面上，甲的边长小于乙的边长。

理科实验班模拟试题(四)

等腰直角 BCD ， E 是 CD 的中点，求证： AE EB .
21、(10 分) 绵阳中学为了进一步改善办学条件，决定计划拆除一部分旧校舍，建造新校舍。
拆除旧校舍每平方米需 80 元，建造新校舍每平方米需要 800 元，计划在年内拆除旧校舍
与建造新校舍共 9000 平方米，在实施中为扩大绿化面积，新建校舍只完成了计划的
A. －２
B.1
1 x2
1 x
x
4 ，则 4
C.－１或 2
1 的值是【
】
x
D.－２或 1
4、若直线 y 2x 1 与反比例函数 y k 的图像交于点 P(2, a) ， x
则反比例函数 y k 的图像还必过点【
】
x
A. ( －1,6)
B.(1, －6)
C.( －2, －3)
D.(2,12)
5、现规定一种新的运算： “* ”： m * n
P 点到达 D 点，即 M 与 D 重合
vQ 2.5cm / s SQ vQ t 2.5 12 30cm
N 点在 AB 之中点，即 AN BN
（2） vp 2m / s t 3s
Sp 6cm
AMN 为直角三角形
E 为 BD 的中点，又 BEF 与 AMN 相似
BEF 为直角三角形
① Q 到达 F1 处： vQ ＝ 3 ＝１cm/ s 3
16、下图是用火柴棍摆放的 1 个、２个、３个……六边形，那么
摆 100 个六边形，需要火柴棍 ______根。
17、在平面直角坐标系中，平行四边形四个顶点中，有三个顶点坐标分别是（－ 2，5），（－
3 ，－ 1 ），（ 1 ，－ 1 ），若另外一个顶点在第二象限，则另外一个顶点的坐标是

湖南长沙长郡中学理科实验班招生试题

湖南长沙长郡中学理科实验班招生试题长郡入学考试试题（1）一、选择题（每小题4分，共32分）1、如图，梯子跟地面的夹角为∠A ，关于∠A 的三角函数值与梯子的倾斜程度之间，叙述正确的是（）A sinA 的值越小，梯子越陡B ：cosA 的值越小，梯子越陡C ：tanA 的值越小，梯子越陡D ：陡缓程度与∠A 的函数值无关2、直线l :(3)2y m x n =-+-(m ,n 为常数)的图像如图，化简3m - ） A ： 3-m -n B ：5 C ：-1 D ：m +n -53、在一个凸n 边形的纸板上切下一个三角形后，剩下的是一个内角和为21600的多边形，则n 的值（）A ：只能为12 B ：只能为13 C ：只能为14 D ：以上都不对4、对于任意一个自然数n,m 能整除19999991n n --，则m 的最大值为（）A ：9B ：27C ：37D ：9995、半径为1的圆的外切直角三角的面积的最小值为（）A ：3-B ：3+C ：6-D ：6+6、某学生解一道没有实数解的二次方程20ax bx c ++=时，因看错了某一项的符号，得到的两根为，则b c a +的值为（）A ：1998 B ：1999 C ：1998或1999 D ：1999或2000 7、有两边高分别为4和12的三角形的内切圆半径r 的取值范围是（）A ：1223r <<B ：32r >C ：122r <<D ：322r <<8、点P 的正方形ABCD 在同一平面，且222PA PB PC +=。

则PD 的最大值为（）A ：4B ：2+C ：6D ：2+ 二、填空题（每小题4分，共32分）9、不等式组20260x x -<??-+11、将长为143cm 的铁丝截成n （3n ≥）小段，每小段不小于1cm ，若其中任意三小段都不能拼成三角形。

n 的最大值为。

12、三边都是整数的直角三角形叫做勾股三角形。

理科实验班招生考试化学试题

普通高中理科实验班招生考试（四）化学试题注意事项：1、本试卷共6页，包括三大题，25小题。

考试时间为90分，全卷满分100分。

2、答题前请先将密封线内的项目填写清楚。

相对原子质量：H 1 F 9 B 11 C 12 N 14 O 16 Na 23一、本大题包括15小题，每小题3分，共45分。

每小题有1个或2个选项符合题意。

如果该小题只有1个选项符合题意。

多选则不得分；如果该小题有2个选项符合题意，选对1个得1分，选对2个得3分，多选或错选均不得分。

1、通常人们所说的“酸雨”的主要成份是………………………………………………[ ]A.硫酸和盐酸B.盐酸和硝酸C.硫酸和硝酸D.硫酸、硝酸和盐酸2、在①石灰石②钟乳石③水垢④贝壳⑤蛋壳这5种物质上分别滴加稀盐酸时，会产生相同气体的……………………………………………………………………………………………………………[ ]A.只有①②B.只有④⑤C.只有①②④⑤D.是①②③④⑤3、目前，长寿卫星上需要的电能主要来自………………………………………………[ ]A.太阳能电池B.一次性化学电池C.核电池D.可充电电池4、绿色化学是人们逐渐熟悉的社会概念。

绿色食品的基本标准应该是下列各项中的①香甜可口②无污染③表面呈绿色④无化学添加剂⑤有营养价值……………………………………[ ]A.①②④⑤B.①③④⑤C.②④⑤D.①②③④⑤5、如果你晚上回到家中，开门后发现空气中由于液化气泄漏而充满了异臭味，这时你应该采取的第一个行动是…………………………………………………………………………………[ ]A.立即开灯，并闭液化气阀门，检查漏气原因B.立即开启排气风扇或排油烟机，尽快排出所泄漏的气体C.立即用家中电话报警，寻求110帮助D.立即关闭液化气阀门，打开门窗，让空气流通6、下列说法正确的是………………………………………………………………………[ ]A.物质一定都有固、液、气三态B.酸一定会使石蕊试液变红，碱一定会使石蕊试液变蓝C.在点燃可燃性气体前一定要检验其纯度D.酸式盐和碱反应一定生成正盐和水7、制备某种荧光粉所用的高纯氯化钙中含有镁离子，除去的方法是把氯化钙水溶液加热到90℃~95℃，在不断搅拌下加入适当的沉淀剂，使镁离子生成沉淀后，过滤除去。

理科实验班模拟试题(三)

7. 50°. 过 N 作 NG⊥PM于 G，可证 NG这 MP的中垂线
8. 4．提示：原式＝
2
7 3 10 2 21 10 2 21 10 2 21
2
2
( 7) ( 3)
4. 4
9. 1 2, 3 6 . 提示：作 AE ⊥ O于B E， CF ⊥ B于D F ，易求 OE＝ EB ＝ 1 ，B设F ＝ m，
理科实验班模拟试题（三）
一、选择题（每小题 6 分，共 30 分）
1. 若 0 a 1， 2 b
1，则 a 1
b2
ab
的值是【
a1 b2 ab
A．０
B．－１
C．－３
】 D．－４
2. 若
4x3m来自n2y2009 是关于 x, y 的二元一次方程，且
mn 0 ， 0 m n ≤ 3 ，则
m n 的值是【
的面积最小值是【
】
A．34
B．64
C．69
D．无法求出
5. 有铅笔、练习本、圆珠笔三种学习用品，若购铅笔
3 支、练习本 7 本、圆珠笔 1 支共需
6.3 元；若购铅笔 4 支、练习本 10 本、圆珠笔 1 支共需 8.4 元. 现购铅笔、圆珠笔各 1 支、
练习本 1 本，共需【
】元．
A．2.4
B．2.1
13. 如图，在⊙Ｏ中，弦 CD垂直于直径 AB，Ｍ是 OC的中点， AM的延长线交⊙Ｏ于点 E，DE 与 BC交于点 N.求证： BN＝CN.
14. 如图，在直角梯形 OABC中， OA∥BC，A、Ｂ两点的坐标分别为 A（13，0），B（11，12），动点 P、Ｑ从 O、Ｂ两点出发，点 P 以每秒 2 个单位的速度沿 OA向终点 A 运动，点 Q以每秒 1 个单位的速度沿 BC向 C 运动，当点 P 停止运动时，点 Q出同时停止运动 . 线段 OB、PQ

理科实验班分班考试(第二套)

理科实验班分班化学试题注童事项：1.本试卷共4页，分第I 卷选择题、第II 卷非选择题两部分，共21题。

2.满分60分，考试时间60分钟，请用钢笔或圆珠笔直接答在试卷上。

3.可能用到的相对原子质量 H-1 C-12 O-16 Cl-35.5 S-32第I 卷选择题（10分）注意：每小题只有一个选项符合题意。

1.下列变化中，只发生物理变化的是（） A.木柴燃烧 B. 消化食物 C.钢铁生锈 D.烧碱潮解2.下列物质中属于纯净物的是（） A. 生铁 B. 澄清石灰水 C. 石墨 D. 洁净空气3. 下列关于维生素C(化学式为C 6H 8O 6)的说法正确的是（） A ．该物质属于氧化物 B ．该物质中碳、氢、氧的质量比为3:4:3 C ．该物质的相对分子质量为l76 D ．其分子由碳原子、氢分子和氧分子构成4. ，下列有关认识中正确的是（） A.该反应中镁发生了还原反应 B.该反应属于置换反应 C.镁着火时可以用二氧化碳扑灭D.燃烧一定要有氧气助燃5.用100克9.8%的硫酸溶液恰好中和一定量的氢氧化钠溶液，如果改用等质量、等质量分数的稀盐酸，再滴入紫色石蕊试液，溶液显 ( )A 、紫色B 、蓝色C 、红色D 、无色 6. 下列装置或操作能达到实验目的的是（）7. 下列说法正确的是：（）A ．两份等质量的碳酸钙，一份与稀HCl 完全反应，一份高温煅烧产生的CO 2的质量相等B ．二氧化碳气体通人石蕊试液后，溶液变红，再经过加热，最后溶液的颜色为无色 C．向某种溶液中加入氯化钡溶液，产生白色沉淀，证明该溶液一定是SO 42-D ．C 、CO 、H 2都能还原氧化铜，使黑色粉末逐渐变成红色，同时发生置换反应8. 下列有关物质的性质和变化的归纳中，正确的是（） A .H 2、CO 、CH 4都能在空气里燃烧B. H 2、C 、CO 都能和CuO 发生置换反应C.浓硫酸、氢氧化钠固体、熟石灰都具有吸水性D. Fe 、Al 、Ag 都能从CuSO 4溶液中置换出Cu9.推理是化学学习中常用的思维方法，以下推理正确的是（） A ．有机物中含有碳元素，所以金刚石属于有机物B ．氢氧化钠溶液和氢氧化钙溶液能使酚酞变红，所以碱均能使酚酞变红C ．化学变化中分子种类发生改变，所有分子种类发生改变的变化一定是化学变化D ．置换反应生成单质和化合物，所以有单质和化合物生成的反应一定是置换反应 10.下列实验方案合理的是（） A 、除去CO 2中少量的CO ：通入空气后点燃B 、鉴别氢气、空气、二氧化碳、氧气：分别将燃着的木条伸入集气瓶中，观察现象C 、验证氢氧化钠溶液部分变质：取少量溶液，滴加适量稀盐酸D 、验证质量守恒定律：选用NH 4Cl 溶液和NaOH 溶液，比较反应前后烧杯内溶液的总质量第II 卷非选择题（共50分，11-15每空1分，16-19题每空2分）11. 铝元素的粒子结构和在元素周期表中的信息如图所示： ⑴铝元素的相对原子质量为；⑵若原子核外的电子层数与元素所在周期表中的周期数相同，则铝元素排在元素周期表的第周期； ⑶Al 3+可通过电子变成了Al （选填“得到”或“失去”）。

山东省重点高中2024年自主招生(理科实验班)提前预录考试化学模拟试题05(含解析)

2024年自主招生（理科实验班）提前预录考试化学模拟试题 05卷班级___________姓名___________学号____________分数____________（考试时间：70分钟试卷满分：70分）注意事项：1．答卷前，考生务必将自己的班级、姓名、学号填写在试卷上。

2．答卷时，将答案直接写在试卷上。

3．本卷可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 S-32 Cl-35.5 Zn-65 Ca-40 Fe-56 Cu-64 Ag-108 K-39 Ba-137一、选择题（本题共15小题，每小题只有一个选项符合题意。

每小题2分，共30分）1．化学与生活、技术密不可分。

下列说法中正确的是（）A. 用活性炭为焦糖脱色和用臭氧漂白纸浆原理相似B. 炒菜时加碘盐要在菜准备出锅时添加，是因为食盐中的碘受热易升华C. 汽油中添加含铅化合物Pb（C2H5）4，可提高汽油的抗爆震性能，有利于改善大气环境D. “熬胆矾铁釜，久之亦化为铜”，该过程发生了氧化还原反应2．以下装置（部分夹持仪器略）错误或达不到实验目的的是（）A. 图①由含有HCl的CO2获取纯净干燥的CO2B. 图②由海水获得淡水C. 图③过滤除去蔗糖水中的泥沙D. 图④蒸发结晶由NaCl溶液获取NaCl晶体3．有两瓶完全相同的氢氧化钠固体，其中一瓶是新开封的，将其用7.3%盐酸恰好中和消耗盐酸质量为a；另一瓶露置在空气中一段时间了，将其用7.3%的盐酸恰好完全反应，消耗盐酸质量为b，则a和b的关系为（）A. a=bB. a<bC. a>bD. 无法确定4．原子种类多种多样，组成了丰富多彩的世界万物。

已知，同种元素组成的结构不同的单质之间互称同素异形体。

符号H、D、T可以表示三种不同的氢原子。

以下说法错误的是（）A. 科学家近期发现的N5、N3与氮气互为同素异形体B. 中科院研发的“东方超环”（人造太阳）用到的H、D、T属于同一种元素C. 石墨、金刚石、富勒烯（如C60）结构不同，物理性质不同，化学性质相似D. 中科院大连物化所的科学家在H+HD→H2+D转化中，观测到化学反应中的量子干涉现象，HD与H2互为同素异形体5．下列说法正确的是（）A. 除去CO2中的HCl气体、水蒸气杂质，可通过饱和的Na2CO3溶液，再通过浓H2SO4B. 硝酸铵、苛性钠、氯化钠、碳酸钙四种白色固体用水不可以鉴别出来C. 用Zn、ZnO、Zn（OH）2、ZnCO3、CuCl2和盐酸6种物质制备ZnCl2的方法共有5种D. 检验氢氧化钠溶液是否部分变质，可取样加入适量的氯化钡溶液观察现象即可完成检验6．甲乙丁X的转化关系如图所示(反应条件和部分产物已略去，“→”表示一步转化)。

高中理科实验班招生考试理科综合试卷

高中理科实验班招生考试理科综合试卷（物理70分，化学50分，生物30分合计：150分考试时间：150分钟）物理部分（70分）一、单项选择题（每小题3分，共24分）1．在我国的许多地方，过春节人们喜爱放鞭炮（如图 1所示），下面是四位同学关于这件事的观点，你觉得谁的观点最正确（）A ．小芮：放鞭炮能增加节日的喜庆气氛，鞭炮声不能算作噪声B ．小嘉：放鞭炮虽然可以烘托节日气氛，但它会产生噪声、空气污染问题C ．小阳：放鞭炮没有任何好处D ．小曦：只要用收录机播放鞭炮的录音，就不存在噪声污染问题了 2．如图2所示，一平面镜放在圆筒的中心处，平面镜正对筒壁上一点光源S ，点光源发出一细光束垂直射向平面镜。

平面镜从图示位置开始绕圆筒中心轴O 匀速转动，在转动25°角时，点光源在镜中所成的像转过的角度为θ1，照射到筒壁上的反射光斑转过的角度为θ2，则（） A ．θ1 = 25°，θ2 = 25° B ．θ1 = 25°， θ2 = 50° C ．θ1 = 50°，θ2 = 25° D ．θ1 = 50°， θ2 = 50°3．重为G 的气象探测气球，在空中匀速下落过程中，不慎掉出一个重为G 0的小物体，之后气球又匀速上升，假若气球在上升或下降过程中，所受浮力大小均为F ，空气阻力大小均为f ，那么（）A ．F =GB ．F-f=G 0C ．G 0=2fD ．F=2G 0 4．如图4是我国新建成的“瓦良格”号航母，一架歼15正从航母跑道上起飞，由于受到条件的限制，舰船上的飞机跑道不能修得很长。

该战机在起飞时，要让飞机逆风起飞好？还是顺风起飞好？下列说法正确的是（） A ．应该让飞机顺风起飞好 B.应该让飞机逆风起飞好C ．飞机顺风、逆风没影响D.无法确定5．电工师傅常用一只标有“220V 400W ”的灯泡L 0（检验灯泡）取代保险丝图1图2图4来检查新安装的照明电路中每个支路的情况，如图5所示。

理科实验班招生考试模拟试题

物理训练题一、选择题（1*3=36）1、晴朗无风的早晨，当飞机从空中飞过，在蔚蓝的天空中会留下一条长长的“尾巴”，这种现象俗称为“飞机拉烟”。

产生这一现象的原因之一是飞机在飞行过程中排出的暖湿气体遇冷所致。

在这一过程中，暖湿气体发生的物态变化是（）A ．熔化B ．液化C ．蒸发D ．升华2、炎热无风的夏天，小宇走在被晒得发烫的柏油路上，看见前面的路面已被一辆洒水车洒水淋湿了。

他认为走在淋湿了的路面上一定比走在干燥的路面上感到凉爽，于是赶快走过去，结果在洒过水的路面上，他却感到更加闷热了。

你认为产生这种感觉的主要原因是（）A ．洒水车中的水经过曝晒后，内能增大，温度很高B ．地面上的水使被反射的阳光增多，身体获得更多热量C ．洒水后使附近的空气湿度增加，身上的汗液蒸发变慢D ．地面上的水蒸发时把热量带到了人的身上3、如图2平面镜放在圆筒的中心处，平面镜正对筒壁上一点光源S ，点光源发出一细光束垂直射向平面镜。

平面镜从图示位置开始绕圆筒中心轴O 匀速转动，在转动30角时，点光源在镜中所成的像转过的角度1θ，照射到筒壁上的反射光斑转过的角度2θ，则（）A ． 301=θ，302=θB ． 301=θ，602=θ C ． 601=θ， 302=θD ． 601=θ， 602=θ4、体离凸透镜22cm 时，能在光屏上得到一个清晰的倒立、缩小的像，则下列判断中正确的是 A ．如果物距小于11cm 时，一定不能成实像 B ．如果物距等于11cm 时，一定成放大的实像C ．如果物距稍大于11cm 时，一定成放大的实像D ．改变物距，当像距为22cm 时，在光屏上得到的是放大的像5、如图3置中，均匀木棒AB 的A 端固定在铰链上，悬线一端绕过一固定定滑轮，另一端用线套套在木棒上使棒保持水平。

现使线套逐渐向右移动，但始终使木棒保持水平，则悬线上的拉力T （棒和悬线足够长）（） A ．逐渐变小 B ．逐渐变大C ．先逐渐变大，后又逐渐变小D ．先逐渐变小，后又逐渐变大6、杂技节目表演中，一位杂技小丑穿着很长的大皮鞋，站在水平舞台上向观众鞠躬致意，双脚不动上身没有躬下，而是整个身子笔直缓慢向前倾斜却不倒下。

长郡中学理科实验班招生考试数学试卷

长郡中学理科实验班招生考试数学试卷满分：100 时量：70min一、选择题（本题有8小题，每小题4分，共32分） 1．函数y ＝1x -图象的大致形状是（）A B C D2．小明随机地在如图所示的正三角形及其内部区域投针，则针扎到其内切圆(阴影)区域的概率为（）A 、21B 、π63C 、π93D 、π33 3．满足不等式3002005<n的最大整数n 等于（）（A ）8 （B ）9 （C ）10 （D ）11 4．甲、乙两车分别从A ，B 两车站同时开出相向而行，相遇后甲驶1小时到达B 站，乙再驶4小时到达A 站. 那么，甲车速是乙车速的（A ）4倍（B ）3倍（C ）2倍（D ）1.5倍 5．图中的矩形被分成四部分，其中三部分面积分别为2，3，4，那么，阴影三角形的面积为（）（A ）5 （B ）6 （C ）7 （D ）86．如图，AB ，CD 分别是⊙O 的直径和弦，AD ，BC 相交于点E ，∠AEC=α，则△CDE 与△ABE 的面积比为（）（A ）cos α （B ）sin α （C ）cos 2α （D ）sin 2α7．两杯等量的液体，一杯是咖啡，一杯是奶油. 舀一勺奶油到咖啡杯里，搅匀后舀一勺混合液注入到奶油杯里. 这时，设咖啡杯里的奶油量为a ，奶油杯里的咖啡量为b ，那么a 和 b 的大小为（）（A ）b a > （B ）b a < （C ）b a = （D ）与勺子大小有关8．设A ，B ，C 是三角形的三个内角，满足B C B A 23,53<>，这个三角形是（）（A ）锐角三角形（B ）钝角三角形（C ）直角三角形（D ）都有可能二、填空题（本题有6小题，每小题5分，共30分）9．用数字1，2，3，4，5，6，7，8不重复地填写在下面连等式的方框中，使这个连等式成立：1＋□＋□=9＋□＋□=8＋□＋□=6＋□＋□10．如图，正三角形与正六边形的边长分别为2和1，正六边形的顶点O 是正三角形的中心，则四边形OABC 的面积等于 ______ . 11．计算：622633++++= ________ .yxOy xOy xOyxO……………..………….密………………..…………….封……………………………..线…………………….12．五支篮球队举行单循坏赛（就是每两队必须比赛1场，并且只比赛一场），当赛程进行到某天时，A 队已赛了4场，B 队已赛了3场，C 队已赛了2场，D 队已赛了1场，那么到这天为止一共已经赛了 __ 场，E 队比赛了 ___ 场.13．已知∠AOB=30°,C 是射线OB 上的一点，且OC=4，若以C 为圆心，半径为r 的圆与射线OA 有两个不同的交点，则r 的取值范围是_____________ 14．如图，△ABC 为等腰直角三角形，若AD=31AC ，CE=31BC ，则∠1 __ ∠2 （填“>”、“<”或“=”）三．解答题（共38分） 15. （１２分）今年长沙市筹备60周年国庆，园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A B ，两种园艺造型共50个摆放在五一大道两侧，已知搭配一个A 种造型需甲种花卉80盆，乙种花卉40盆，搭配一个B 种造型需甲种花卉50盆，乙种花卉90盆．（1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来．（2）若搭配一个A 种造型的成本是800元，搭配一个B 种造型的成本是960元，试说明（1）中哪种方案成本最低？最低成本是多少元？１６．（１２分）如图，ABC △是O 的内接三角形，AC BC =，D 为O 中AB 上一点，延长DA 至点E ，使CE CD =．（1）求证：AE BD =；（2）若AC BC ⊥，求证：2AD BD CD +=．（第14题）ＥＡＯＢ１７．（１４分）如图，在等腰梯形ABCD中，AD∥BC，AB=DC=50，AD=75，BC=135．点P从点B出发沿折线段BA-AD-DC以每秒5个单位长的速度向点C匀速运动；点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动，过点Q向上作射线QK⊥BC，交折线段CD-DA-AB于点E．点P、Q同时开始运动，当点P与点C重合时停止运动，点Q也随之停止．设点P、Q运动的时间是t秒（t＞0）．（1）当点P到达终点C时，求t的值，并指出此时BQ的长；（2）当点P运动到AD上时，t为何值能使PQ∥DC ？（3）设射线QK扫过梯形ABCD的面积为S，分别求出点E运动到CD、DA上时，S与t的函数关系式；（不必写出t的取值范围）（4）△PQE能否成为直角三角形？若能，写出t的取值范围；若不能，请说明理由．参考答案选择题 D C D C C C C B 9． 110．33 11． 26 12． 6场，2场 13．2r <≤ 14．＝1５．（１）解：设搭配A 种造型x 个，则B 种造型为(50)x -个，依题意，得：8050(50)34904090(50)2950x x x x +-⎧⎨+-⎩≤≤ ，解这个不等式组，得：3331x x ⎧⎨⎩≤≥，3133x ∴≤≤ x 是整数，x ∴可取313233，，，∴可设计三种搭配方案： ①A 种园艺造型31个 B 种园艺造型19个 ②A 种园艺造型32个 B 种园艺造型18个 ③A 种园艺造型33个 B 种园艺造型17个．（2）应选择方案③，成本最低，最低成本为42720元１６．证明：（1）在ABC △中，CAB CBA ∠=∠．在ECD △中，CAB CBA ∠=∠．CBA CDE ∠=∠，（同弧上的圆周角相等），ACB ECD ∴∠=∠． ACB ACD ECD ADE ∴∠-∠=∠-∠．ACE BCD∴∠=∠．在ACE △和BCD △中，ACE BCD CE CD AC BC ∠=∠==；； ACE BCD ∴△≌△．AE BD ∴=．（2）若AC BC ACB ECD ∠=∠⊥，．9045ECD CED CDE ∴∠=∴∠=∠=，． DE ∴=，又AD BD AD EA ED +=+=AD BD ∴+=１７．解：（1）t =（50＋75＋50）÷5=35（秒）时，点P 到达终点C ．此时，QC=35×3=105，∴BQ 的长为135－105=30．（2）如图8，若PQ ∥DC ，又AD∥BC ，则四边形PQCD 为平行四边形，从而PD=QC ，由QC=3t ，BA+AP=5t 得50＋75－5t=3t，解得t=1258．经检验，当t=1258时，有PQ ∥DC ．（3）①当点E 在CD 上运动时，如图9．分别过点A 、D 作AF ⊥BC 于点F ，DH ⊥BC 于点H ，则四边形 ADHF 为矩形，且△ABF ≌△DCH ，从而FH= AD=75，于是BF=CH=30．∴DH=AF=40．Q CDH=4t．又QC=3t，从而QE=QC·tanC=3t·CH（注：用相似三角形求解亦可）QE·QC=6t2；∴S=S⊿QCE =12②当点E在DA上运动时，如图8．过点D作DH⊥BC于点H，由①知DH=40，CH=30，又QC=3t，从而ED=QH=QC－CH=3t－30．(ED＋QC)DH =120 t－600．∴S= S梯形QCDE =12（4）△PQE能成为直角三角形．。

理科实验班考试模拟试题(答案)

理科实验班考试模拟试题一、选择题（本大题共有10小题，每小题4分，共40分） 1.下列运算正确的是【】A.22532b a ab ab =+ B.632a aa =⋅C.)0( 122≠=-a aaD.y x y x +=+ 2.如图，点A 在数轴上表示的实数为a ，则2-a 等于【】A.2-aB.2+aC.2--aD.2+-a 3.甲、乙两名运动员在10次的百米跑练习中，平均成绩分别为x甲7.10＝秒，x 乙7.10＝秒，方差分别为S 2甲054.0=，S 2乙103.0=，那么在这次百米跑练习中，甲、乙两名运动员成绩较为稳定的是【】A.甲运动员B.乙运动员C.甲、乙两人一样稳定D.无法确定4.如图，A 、B 、C 、D 是直线l 上顺次四点，M 、N 分别是AB 、CD 的中点，且6=MN cm ，1=BC cm ，则AD 的长等于【】A.10cmB.11cmC.12cmD.13cm5.已知等腰三角形的一个外角等于︒140，则这个三角形的三个内角的度数分别是【】A.︒20、︒20、︒140 B.︒40、︒40、︒100 C.︒70、︒70、︒40 D. ︒40、︒40、︒100或︒70、︒70、︒40 6.如图，点A 在函数=y x6-)0(<x 的图象上，过点A 作AE 垂直x 轴，垂足为E ，过点A 作AF 垂直y 轴，垂足为F ，则矩形AEOF 的面积是【】A.2B.3C.6D.不能确定7.用大小和形状完全相同的小正方体木块搭成一个几何体，使得它的正视图和俯视图如图所示，则搭成这样的一个几何体至少需要小正方体木块的个数为【】 A.22个 B.19个 C.16个 D.13个8.用半径为cm 6、圆心角为︒120的扇形做成一个圆锥的侧面, 则这个圆锥的底面半径是【】A.2cmB.3cmC.4cmD.6cm 9.若n 为整数，则能使11-+n n 也为整数的n 的个数有【】 A.1个 B.2个 C.3个 D.4个 10.已知a 为实数，则代数式221227a a +-的最小值为【】 A.0 B.3 C.33 D.9 二、填空题（本大题共有6小题，每小题4分，共24分） 11.函数12-+=x x y 的自变量x 的取值范围是． 12.分解因式：=+-xy y x 2733．13.把2007个边长为1的正方形排成如右图所示的图形，则这个图形的周长是．14.如图，正方形ABCD 的边长为4cm ，正方形AEFG 的边长为1cm ．如果正方形AEFG 绕点A 旋转，那么C 、F 两点之间的最小距离为 cm ．15.若规定：①{} m 表示大于m 的最小整数，例如：{}4 3 =，{}2 4.2-=-；②[] m 表示不大于m 的最大整数，例如：[]5 5 =，[]4 6.3-=-.则使等式{}[]4 2=-x x 成立的整数．．=x ．16.如图，E 、F 分别是□ABCD 的边AB 、CD 上的点，AF 与DE 相交于点P ，BF 与CE 相交于点Q ，若S△APD15=2cm ，S△BQC25=2cm ，则阴影部分的面积为______________2cm ．三、解答题（本大题共有7小题，共86分．其中第17题8分，第18、19题各10分，第20题12分，第21题14分，第22、23题各16分．请将解答过程写在答题卷的相应位置上）17.计算：2330tan 3)2(0----.18.先化简，再求值：⎪⎭⎫ ⎝⎛--+2122x x ÷24--x x，其中42-=x .19.将背面相同，正面分别标有数字1、2、3、4的四张卡片洗匀后，背面朝上放在桌面上.（1）从中随机抽取一张卡片，求该卡片正面上的数字是偶数的概率；（2）先从中随机抽取一张卡片（不放回．．．），将该卡片正面上的数字作为十位上的数字；再随机抽取一张，将该卡片正面上的数字作为个位上的数字，则组成的两位数恰好是4的倍数的概率是多少？请用树状图或列表法加以说明.20.为配合我市“创卫”工作，某中学选派部分学生到若干处公共场所参加义务劳动．若每处安排10人，则还剩15人；若每处安排14人，则有一处的人数不足14人，但不少于10人．求这所学校选派学生的人数和学生所参加义务劳动的公共场所个数.21.如图，四边形ABCD 是正方形，点N 是CD 的中点，M 是AD 边上不同于点A 、D 的点，若1010sin =∠ABM ，求证:MBC NMB ∠=∠.22.如图，抛物线的顶点坐标是⎪⎭⎫ ⎝⎛8925，－，且经过点) 14 , 8 (A . (1)求该抛物线的解析式；(2)设该抛物线与y 轴相交于点B ，与x 轴相交于C 、D 两点（点C 在点D 的左边），试求点B 、C 、D 的坐标；(3)设点P 是x 轴上的任意一点，分别连结AC 、BC ．试判断：PB PA +与BC AC +的大小关系，并说明理由.23.如图，AB 是⊙O 的直径，过点B 作⊙O 的切线BM ，点P 在右半圆上移动（点P 与点A 、B 不重合），过点P 作PC ⊥AB ，垂足为C ；点Q 在射线BM 上移动（点M 在点B 的右边），且在移动过程中保持OQ ∥AP .(1)若PC 、QO 的延长线相交于点E ，判断是否存在点P ，使得点E 恰好在⊙O 上？若存在，求出APC ∠的大小；若不存在，请说明理由； (2)连结AQ 交PC 于点F ，设PCPFk =，试问：k 的值是否随点P 的移动而变化？证明你的结论．理科实验班考试模拟试题参考答案及评分意见一、选择题（本大题共有10小题，每小题4分，共40分）题号 1 2 3 4 5 6 7 8 9 10 答案CAABDCDADB二、填空题（本大题共有6小题，每小题4分，共24分）11. 2-≥x 且1≠x 12. xy 3-)3(+x )3(-x （或)3)(3(3x x xy -+） 13. 4016 14．23 15．2 16．40 三、解答题（本大题共有7小题，共86分） 17．（8分）原式233331-+⨯-= …………………………………………6分 1-=………………………………………………………………8分 18．（10分）原式xx x x x --⋅---+=42212)2)(2( ………………………………2分 x x --=4162)4()4)(4(---+=x x x 4--=x ………………………7分∴当42-=x 时，原式=4)42(---2-= ……………………10分19．（10分）（1）（4分）42=偶数p 21= ………………………………………4分（2）①（4分）树状图为：或列表法为：13 24 2 3 1234（12）（13）（14）（21）（23）（24）（31）（32）（34）（41）（42）（ 43）（画出树状图或列出表格得4分） ……………………………………………4分 ②（2分）所以411234==的倍数p …………………………………………2分 20．（12分）解法一：设参加x 处公共场所的义务劳动，则学校派出)1510(+x 名学生^…………………………………………………………………………………2分依题意得：⎩⎨⎧≥--+<--+)2(10)1(14)1510()1(14)1(14)1510( x x x x ………………………6分由（1）得：433>x ，由（2）得：434≤x ∴434433≤<x ………………………………………………………………8分又x 为整数，∴4=x ……………………………………………………10分 ∴当4=x 时，551510=+x ………………………………………………11分答：这所学校派出55名学生，参加4处公共场所的义务劳动 …………12分解法二：设这所学校派出x 名学生，参加y 处公共场所的义务劳动……1分依题意得：⎩⎨⎧<--≤=+)2(14)1(1410)1(1510 y x x y ……………………………6分解得：434433≤<y …………………………………………………………8分 y 为整数，∴4=y ………………………………………………………10分 ∴当4=y 时，5515410=+⨯=x ………………………………………11分答：这所学校派出55名学生，参加4处公共场所的义务劳动 …………12分 21．（14分）证法一：如图，分别延长BC 、MN 相交于点E ………………1分设1=AM，∵1010sin=∠ABM，∴1010=BMAM，得10=BM………3分∴322=-=AMBMAB…………4分∵是正方形四边形ABCD，∴2=-=AMADDM，且2321===DCCNDN，在DMNRt∆中，2522=+=DNMDMN………………………………6分又∵∠=∠=∠RtECNMDN、ENCMND∠=∠，∴)(ASAECNMDN∆≅∆……………………………………………………9分∴2==MDCE、25==MNNE，………………………………………11分∴5=+=NEMNME、5=+=CEBCBE，∴BEME=…………13分∴MBCNMB∠=∠…………………………………………………………14分证法二：设1=AM，同证法一2522=+=DNMDMN………………6分如图，将ABM∆绕点A顺时针旋转︒90得到BCE∆，连结ME，∵∠=∠=∠RtBCDBCE，∴NCE∠是平角，即点ECN、、三点共线，………………………………………………………………………………… 7分∴BECBMA∠=∠……………………………8分1==AMCE、BMBE=…………………9分∴BEMBME∠=∠…………………………10分∵MNCECNNE==+=+=25123……11分∴NEMNME∠=∠…………………………12分∴NEMBEMNMEBME∠+∠=∠+∠∴AMBBECBMN∠=∠=∠………………13分又∵MBCAMB∠=∠BCN∴MBC BMN ∠=∠…………………………14分 22．（16分）（1）（4分）设抛物线的解析式为89252-⎪⎭⎫ ⎝⎛-=x a y ………………………1分∵抛物线经过)14,8(A ，∴89258142-⎪⎭⎫ ⎝⎛-a ＝，解得：21=a …………3分∴8925212-⎪⎭⎫ ⎝⎛-=x y （或225212+-=x x y ） …………………………4分（2）（4分）令0=x 得2=y ，∴)2,0(B ……………………………………1分令0=y 得0225212=+-x x ，解得11=x 、42=x ………………………3分 ∴)0 , 1(C 、) 0, 4(D …………………………………………………………4分（3）（8分）结论：BC AC PB PA +≥+ …………………………………1分理由是：①当点C P 与点重合时，有BC AC PB PA +=+ ………………………………2分②当时异于点点C P ，∵直线AC 经过点)14,8(A 、)0,1(C ，∴直线AC 的解析式为22-=x y ………3分设直线AC 与y 轴相交于点E ，令0=x ，得2-=y ， ∴)2,0(-E ，则)2,0()2,0(B E 与点-关于x 轴对称………………4分 ∴EC BC =，连结PE ，则PB PE =，∴AE EC AC BC AC =+=+， …………………5分∵在APE ∆中，有AE PE PA >+ …………………………………………6分 ∴BC AC AE PE PA PB PA +=>+=+…………………………………7分综上所得BC AC BP AP +≥+………………………………………………8分23．（16分）（1）（6分）解法一：当点E 在⊙O 上时，设OQ 与⊙O 交于点D ，∵PC AB ⊥，∴AP AE = ………………………1分 ∵AP ∥OQ ，∴PEQ APE ∠=∠ ………………2分⌒ ⌒⌒⌒∴PD AP =…………………………………………3分又BOD AOE ∠=∠，BD AE = …………………4分 APB AE 31=即………………………………………5分 ∴︒︒=⨯⨯=∠⨯=∠3018031213121AOB APE …6分解法二：设点E 在⊙O 上时，由已知有CP EC =， ……………………1分 ∴△≅EOC △PAC ，……………………………………………2分 ∴CA OC =，AP OE = …………………………………………3分在Rt △APC 中，212sin ====∠AC AC OA AC AP AC APC ……5分 ∴︒=∠30APC ……………………………………………………6分（2）（10分）k 值不随点P 的移动而变化.理由是:∵P 是⊙O 右半圆上的任意一点，且AP ∥OQ ，∴QOB PAC ∠=∠ ……………………………1分 ∵BM 是⊙O 的切线，∴∠=∠Rt ABQ ，又∵AB PC ⊥，∴∠=∠Rt ACP ， ∴ABQ ACP ∠=∠ ……………………………2分 ∴ACP ∆∽OBQ ∆ ……………………………3分 ∴QBPC OB AC =……………………………………4分又∵BAQ CAF ∠=∠、∠=∠=∠Rt ABQ ACF ，∴ACF ∆∽ABQ ∆……………………………………………………………6分⌒ ⌒⌒ ⌒ Q AB CEF P M O ．∴BQCF AB AC = …………………………………………………………………7分又∵OB AB 2=，∴BQ CF OB AC =2即BQ CF OB AC 2= …………………………8分 ∴CF PC 2= 即CF PF ＝ …………………………………………………9分 ∴==PC PF k 21，即k 值不随点P 的移动而变化. ………………………10分。

理科实验班模拟试题(7)

理科实验班模拟试题（7）一、选择题1．设532x ，则代数式(1)(2)(3)x x x x 的值为【】（A ）０（B ）１（C ）－１（D ）２2．已知x y z ，，为实数，且满足253xy z ，25x y z ，则222x y z 的最小值为【】（A ）111（B ）０（C ）５（D ）54113．点D E ，分别在△ABC 的边AB AC ，上，BE CD ，相交于点F ，设1234BDF BCF CEF EADFS S S S S S S S 四边形，，，，则13S S 与24S S 的大小关系为【】（A ）1324S S S S （B ）1324S S S S （C ）1324S S S S （D ）不能确定4．如图，菱形ABCD 中，点O 是对角线AC 上一点，OA ＝AD ，且OB ＝OC ＝OD ＝1，则该菱形的边长为【】A ．251B ．251C ．１D ．２5．如果x 和y 是非零实数，使得∣x ∣＋y ＝３和∣x ∣y ＋ｘ3＝0，那么x ＋ｙ等于【】A 、3;B 、13;C 、2131;D 、4－13二、填空题6．两条直角边长分别是整数a b ，（其中2011b ），斜边长是1b 的直角三角形的个数为.7．若112y xx 的最大值为a ，最小值为b ，则22a b 的值为8．如图，双曲线x y 2（x ＞0）与矩形OABC 的边CB ，BA 分别交于点E ，F ，且AF=BF ，连接EF ，则△OEF 的面积为.9．如图9，将长为4cm 宽为2cm 的矩形纸片ABCD 折叠，使点B 落在CD 边上的中点E 处，压平后得到折痕MN ，则线段AM 的长度为__________．10．已知二次函数的图象经过原点及点1124，，且图象与x 轴的另一交点到原点的距离为1，则该二次函数的解析式为．三、解答题11．如图，点H 为△ABC 的垂心，以AB 为直径的⊙1O 和△BCH 的外接圆⊙2O 相交于点D ，延长AD 交CH 于点P ，求证：点P 为CH 的中点．12．如图1，正方形ABCD 的边长为1，对角线AC 与BD 相交于点O ，点P 是AB 边上的一个动点（点P 不与点A 、Ｂ重合），CP 与BD 相交于点Q ．（1）若CP 平分∠ACB ，求证：AP ＝2QO ．（2）先按下列要求画出相应图形，然后求解问题．①把线段PC 绕点P 旋转90°，使点C 落在点E 处，并连接AE ．设线段BP 的长度为x ，△APE 的面积为S.试求S 与x 的函数关系式；②求出S 的最大值，判断此时点P 所在的位置．13．设a为整数,使得关于x的方程a2x－(a＋5)x＋a＋7＝０至少有一个有理根，试求方程所有可能的有理根．14．设k为正整数，证明：k也是两个连续正整数的乘积；1、如果k是两个连续正整数的乘积，那么256k是两个连续正整数的乘积，那么k也是两个连续正整数的乘积．2、如果256。