arima模型sas代码
用python做时间序列预测九:ARIMA模型简介

⽤python做时间序列预测九:ARIMA模型简介本篇介绍时间序列预测常⽤的ARIMA模型,通过了解本篇内容,将可以使⽤ARIMA预测⼀个时间序列。
什么是ARIMA?ARIMA是'Auto Regressive Integrated Moving Average'的简称。
ARIMA是⼀种基于时间序列历史值和历史值上的预测误差来对当前做预测的模型。
ARIMA整合了⾃回归项AR和滑动平均项MA。
ARIMA可以建模任何存在⼀定规律的⾮季节性时间序列。
如果时间序列具有季节性,则需要使⽤SARIMA(Seasonal ARIMA)建模,后续会介绍。
ARIMA模型参数ARIMA模型有三个超参数:p,d,qpAR(⾃回归)项的阶数。
需要事先设定好,表⽰y的当前值和前p个历史值有关。
d使序列平稳的最⼩差分阶数,⼀般是1阶。
⾮平稳序列可以通过差分来得到平稳序列,但是过度的差分,会导致时间序列失去⾃相关性,从⽽失去使⽤AR项的条件。
qMA(滑动平均)项的阶数。
需要事先设定好,表⽰y的当前值和前q个历史值AR预测误差有关。
实际是⽤历史值上的AR项预测误差来建⽴⼀个类似归回的模型。
ARIMA模型表⽰AR项表⽰⼀个p阶的⾃回归模型可以表⽰如下:c是常数项,εt是随机误差项。
对于⼀个AR(1)模型⽽⾔:当ϕ1=0 时,yt 相当于⽩噪声;当ϕ1=1 并且 c=0 时,yt 相当于随机游⾛模型;当ϕ1=1 并且 c≠0 时,yt 相当于带漂移的随机游⾛模型;当ϕ1<0 时,yt 倾向于在正负值之间上下浮动。
MA项表⽰⼀个q阶的预测误差回归模型可以表⽰如下:c是常数项,εt是随机误差项。
yt 可以看成是历史预测误差的加权移动平均值,q指定了历史预测误差的期数。
完整表⽰即: 被预测变量Yt = 常数+Y的p阶滞后的线性组合 + 预测误差的q阶滞后的线性组合ARIMA模型定阶看图定阶差分阶数d如果时间序列本⾝就是平稳的,就不需要差分,所以此时d=0。
ARIMA模型原理以及代码实现案例

ARIMA模型原理以及代码实现案例⼀、时间序列分析北京每年每个⽉旅客的⼈数,上海飞往北京每年的游客⼈数等类似这种顾客数、访问量、股价等都是时间序列数据。
这些数据会随着时间变化⽽变化。
时间序列数据的特点是数据会随时间的变化⽽变化。
随机过程的特征值有均值、⽅差、协⽅差等。
如果随机过程的特征随时间变化⽽变化,那么数据是⾮平稳的,相反,如果随机过程的特征随时间变化⽽不变化,则此过程是平稳的。
如图所⽰:⾮平稳时间序列分析时,若导致⾮平稳的原因是确定的,可以⽤的⽅法主要有趋势拟合模型、季节调整模型、移动平均、指数平滑等。
若导致⾮平稳的原因是随机的,⽅法主要有ARIMA,以及⾃回归条件异⽅差模型等。
⼆、ARIMA1、简介ARIMA通常⽤于需求预测和规划中。
可以⽤来对付随机过程的特征随着时间变化⽽⾮固定。
并且导致时间序列⾮平稳的原因是随机⽽⾮确定的。
不过,如果从⼀个⾮平稳的时间序列开始,⾸先需要做差分,直到得到⼀个平稳的序列。
模型的思想就是从历史的数据中学习到随时间变化的模式,学到了就⽤这个规律去预测未来。
ARIMA(p,d,q)d是差分的步长(差分的阶数指的是进⾏多少次差分。
⽐如步长为n的⼀阶差分diff(x) = f(x) - f(x - n),⽽⼆阶步长为n的差分: diff(x) = f(x) - f(x-n), diff(x-n) = f(x-n) - f(x - n - n), diff⼆阶差分(x - n) = diff(x) - diff(x-n)),⽤来得到平稳序列p为相应的⾃回归项q是移动平均项数2、⾃回归模型AR⾃回归模型描述当前值与历史值之间的关系,⽤变量⾃⾝的历史时间数据对⾃⾝进⾏预测。
⾃回归模型必须满⾜平稳性。
⾃回归模型需要先确定⼀个阶数p,表⽰⽤⼏期的历史值来预测当前值。
p阶⾃回归模型可以表⽰为:y t是当前值,u是常数项,p是阶数,r是⾃相关系数,e是误差AR的限制:⾃回归模型是⾃⾝的数据进⾏预测必须具有平稳性必须具有相关性如果⾃相关系数⼩⾬0.5,则不宜采⽤⾃回归只适⽤于预测与⾃⾝前期相关的现象3、移动平均模型MA移动平均模型关注的⾃回归模型中的误差项的累加,q阶⾃回归过程的公式定义如下:移动平均模型能有效地消除预测中的随机波动4、⾃回归移动平均模型ARMA⾃回归模型AR和移动平均模型MA模型相结合,我们就得到了⾃回归移动平均模型ARMA(p,q),计算公式如下:5、p、q的确定 (1) (2)结合最终的预测误差来确定p、q的阶数,在相同的预测误差情况下,根据奥斯卡姆剃⼑准则,模型越⼩越好。
ARIMA模型在汽车销量预测中的应用及SAS实现

J AN1 1
J AN1 2
图 1 汽 车 销 量 时 间 序 列 曲 线 图
二 、 处 理 预
A I A 建 模 方 法 是 以序 列 的 平 稳 性 为 前 提 的 .因此 首 RM 先 要 把 非 平 稳 序 列 转 换 为平 稳序 列 针 对 原 始 时 间 序 列具 有 季 节 性 变 化 同 时 有 增 大 的趋 势 . 用 对 数 变 换 消 除增 幅越 来 先
6 34 04 8 59 02 1 .3 l .8 1 .7 .0l
1 1 .11 .6 8 59 0 1 8 5 - 2 73 00 7 1 .2 .01 731
< .o 1 00 O
经 过 拟 合 后 比 较 发 现 , R(, )MA(,2 通 过 了 检 A 11 , 2 1 ) 1
JN6 A 0
d t ae
J 0 AN 7
JN8 A 0
JN9 A 0
J N1 A 0
J Nl A 1
J 1 AN 2
圈圃 囡 2  ̄ 0 1 0 4 1 1 2
管 理 荟
一
l l
萃
詈
( ) KI 二 A MA( ,,) (, Q) pdq x pD, z
由于 存 在 季 节 性 . 短 期 相 关 性 和季 节性 之 间 具有 乘 积 且 效 应 , 试 使 用 乘 积 模 型 来 拟合 序列 的发 展 。 尝
差 范 围 . 明差 分 中仍 蕴 含 着 非 常 显 著 的 季 节 效 应 。延 迟 1 说 步 的 自相 关 系 数 也 大 于 2倍 标 准 差 . 说 明 差分 后 序 列 还 具 这 有 短 期 相 关 性
( ) KI 一 A MA(,, pdq )
ARIMA模型在房屋销售价格指数预测中的应用及SAS实现

收稿日期: 2010-04-27 作者简介:孙淑珍 (1960-), 女 , 教授 , 研究方向为概率论与数理统计 .
2
湖 南 文 理 学 院 学 报(自 然 科 学 版)
2010 年
ARIMA(p, d, q)模型[3]:
⎧Φ ( B )∇d xt = Θ ( B ) εt , ⎪ 2 ⎨ E ( εt ) = 0, Var ( εt ) = σ t , E ( εs εt ) = 0, s ≠ t , ⎪ Ex ε = 0, ∀s < t. ⎩ s t
ˆa2 会下降,当达到 纵坐标画出残差方差图. 开始时 σ ˆa2 停止下降转为平缓甚 阶数的真值后会逐渐平稳. σ
或者:
ˆa2 ] + r ln( N ) / N . BIC( p, q) = ln[σ
选取不同的 p, q 及模型参数, 对 {εt } 进行拟合, 并计算该模型的 AIC 和 BIC 值, 然后改变模型阶数 和参数, 使 AIC 和 BIC 达到极小值的模型为最佳模 型. 1.2.3 模型参数估计 a. AR(p)模型的最小二乘估计. 这里假设 d1 , d 2 , , d p 为自回归系数 φ1 , φ2 , , φp 的估计,则有残差 ε j 的估计为:
运用统计分析软件(SAS)对房屋销售价格指数历史 数据的内部挖掘和分析,得出了精确的预测模型 . 同时预测了 2009 年 1 季度到 4 季度的房屋销售价格 指数.
ARIMA预测原理以及SAS实现代码
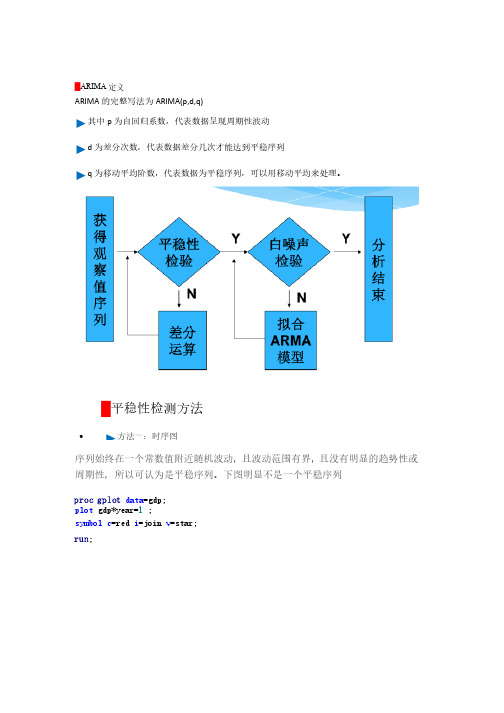
█ARIMA定义ARIMA的完整写法为ARIMA(p,d,q) ►其中p为自回归系数,代表数据呈现周期性波动►d为差分次数,代表数据差分几次才能达到平稳序列►q为移动平均阶数,代表数据为平稳序列,可以用移动平均来处理。
█平稳性检测方法·►方法一:时序图序列始终在一个常数值附近随机波动,且波动范围有界,且没有明显的趋势性或周期性,所以可认为是平稳序列。
下图明显不是一个平稳序列proc gplot data=gdp;plot gdp*year=1 ;=join v v=star;=red i i=joinsymbol c=redrun;·►方法二:自相关图自相关系数会很快衰减向0,所以可认为是平稳序列。
proc arima data= gdp;identify var=gdp=gdp stationaritystationarity =(adf=3)) nlagnlag=12; run;·►ADF单位根检验(精确判断)三个检验中只要有一个Pr<Rho小于0.05即可认定为平稳序列,主要是stationarity =(adf=3) 起作用起作用proc arima data= gdp;) nlagnlag=12;=gdp stationaritystationarity =(adf=3)identify var=gdprun;█白噪声检验白噪声检验Pr>卡方<0.05即可认定为通过白噪声检验。
proc arima data= gdp;) nlagnlag=12;stationarity =(adf=3)identify var=gdp=gdp stationarityrun;█非平稳序列转换为平稳序列方法一:将数据取对数。
方法一:将数据取对数。
函数 方法二:对数据取差分dif函数data gdp_log;set gdp;loggdp=log(gdp);cfloggdp=dif(loggdp);run;/**对数数据散点图**/proc gplot;plot loggdp*year=1 ;symbol c=black=join v v=star;=black i i=joinrun;/* 一阶差分对数数据散点图*/ proc gplot;plot cfloggdp*year=1;=dot i i=join; symbol c=green=green v v=dotrun;从上图中可以看出,一阶差分后序列已经变成平稳的了,因此,数列需要做一阶差分█转换完毕后再验证下面代码中的(1)就代表1阶差分,adf=3则代表平稳性检验0-3,/* 一阶差分对数数据的自相关图、偏自相关图、纯随机性检验、单位根检验 */ proc arima data=gdp_log;identify var=loggdp(1) ) stationaritynlag=12;stationarity =(adf=3) ) nlagrun;用Q LB 统计量作的c 2检验结果表明:对数差分后的GDP 序列的Q LB 统计量的P 值为0.0045(<0.05),故序列为非白噪声序列。
人大版应用时间序列分析(第5版)习题答案
第一章习题答案略第二章习题答案2.1答案:(1)不平稳,有典型线性趋势(2)1-6阶自相关系数如下(3)典型的具有单调趋势的时间序列样本自相关图2.2答案:(1)不平稳(2)延迟1-24阶自相关系数(3)自相关图呈现典型的长期趋势与周期并存的特征2.3答案:(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列2.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列(2)差分后序列为平稳非白噪声序列2.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
(2)单位根检验显示带漂移项0阶延迟的P值小于0.05,所以基于adf检验可以认为该序列平稳(3)如果使用adf检验结果,认为该序列平稳,则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳,那么一阶差分后序列为平稳非白噪声序列2.8答案(1)时序图和自相关图都显示典型的趋势序列特征(2)单位根检验显示该序列可以认为是平稳序列(带漂移项一阶滞后P值小于0.05)(3)一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--() 221112() 1.96110.7t Var x φ===--() 22213=0.70.49ρφ==()12122221110.490.7=0110.71ρρρφρρ-==-(4) 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有:,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=()1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=() 1112223340.70.15=0φρφφφ====-()3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩() ()模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩() 3.5证明:该序列的特征方程为:320c c λλλ--+=,解该特征方程得三个特征根:11λ=,2λ=3λ=无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
商 情 预 测 ARIMA (含SAS程序实例)

商情预测[ARIMA] 2012.11.16 廖崇廷整理以过去的观察值及干扰项(WHITE NOISE)来预测未来数值之方法一.ARIMA(p,d,q) = 连续性ARIMA= ARMA + 一般转移函数(或干预转移函数)EX:今年12月需考虑今年11月二.开列变数/回归式1. 决定符号±股价=F(货币供给,利率,汇率,开征证所税)+etY = F ( X, X, X,…. X) + e t反应变量自变量2. CHECK变量不重复(无共线性) 变量间相关系数矩阵之角对角在线下之值均< 0.8三.将序列数据绘图四.设定BOX-COX转换(直线/指数)1. 直线关系式: Y=f(X) 设定BOX-COX转换(直线/指数)因μ→1 直线型式可不必宣告λ→1 直线型式2. Log 关系式 :Log(Y)=Log(X)(1) 设定μ→0 指数型式μ= 0.01Xμ -1X0.01 -1X 作BOX-COX (即Log)转换X(μ)=-------- = ------------ = ㏒(X)μ0.01(2) 设定λ→0 指数型式λ= 0.01Yλ -1Y0.01 -1 Y 作BOX-COX (即Log)转换Y(λ)=-------- = ------------ = ㏒(Y)Λ 0.013. 进入ARIMA PROC*FILE 'C:\SAS\ARIMAT\STK;LIBNAME SAVE 'C:\SAS\ARIMAT\SASDATA';OPTION NONOTES NODATA LS=76 PS=60;%LET U=0.01;%LET L=0.01;%LET X=MS;%LET Y=SP;DATA D1;SET SAVE.STOCK;KEEP WEEK &X1 &X2 &X3 &Y;DATA D2;SET D1;&X=(&X**&U-1)/&U;&Y=(&Y**&L-1)/&L;PROC ARIMA;五.设定差分阶数及滤出AR/MA特质[找出序列之白噪音过程]IDENTIFY VAR=&Y(1) CROSSCORR=(&X(1)) NLAG=10;SAS程序撰写例:CHECK 残差项:自我相关P值> 0.05 表模式已消除虚假相关为平稳之白噪音序列可作ARIMA交互自我相关P值> 0.05六.设定结构转移函数Transfer Function (X,Y 关系式)1.一般转移函数型式( 略去下式中form4 , num4 )2.干预转移函数型式七.用Y[ARMA特质]+[一般转移函数(或干预转移函数)]──>预测八.预测期数Log(Y) 作反BOX-COX 转换(直线式则可不必做此转换)FORECAST LEAD=5 OUT=FORECAST NOPRINT;DATA FORECAST;MERGE D1 FORECAST;FORECAST=(&L*FORECAST+1)**(1/&L);STD=SQRT((FORECAST**(&L-1)**(-1)*(STD*2)));RESIDUAL=Y-FORECAST;L95=FORECAST-1.96*STD;U95=FORECAST+1.96*STD;PROC CORR NOSIMLE NOPROB;VAR &Y FORECAST;九.模式提报及检定1.2.SAS 报表提报ARIMA(p,d,q)模式: 设NUM1=X1 NUM2=X2NUM3=DUMMY十.解释模式(NUM1 - NUM1,1 B - NUM1,2 B2 - …)X1 λ(1)X1对Y之弹性系数=[X1 1%--> Y ?%]= -------------------------------------------------------- --------( 1 - DEN1,1 B - DEN1,2 B2 - …)Y(2)X2对Y之弹性系数=....(3)X3对Y之弹性系数=....( NUM3 - NUM1,1 B - NUM1,1 B2 - …)X1 1-λ(4)冲击乘数=干预函数对Y当期之影响= ------------------------------------------------------- ------( 1 - DEN1,1 B - DEN1,2 B2 - …)Y( NUM3 - NUM1,1 B - NUM1,1 B2 - …)X1 1-λ(5)长期乘数=干预函数对Y长期之影响= -------------------------------------------------------- ----( 1 - DEN1,1 B - DEN1,2 B2 - …)Y十一.摘要(SUMMRY)SAS程序范例解说Log(Y)=Log(X) %LET U=0.01%LET L=0.01BOX-COX转换&X1=(&X1**&U-1)/&U&X2=(&X2**&U-1)/&U&Y=(&Y**&L-1)/&LX1 差分阶数d=1 IDENTIFY VAR=&X1(1)滤出AR特质ESTIMATE P=(1,2)X2 差分阶数d=1 IDENTIFY VAR=&X2(1)滤出AR特质ESTIMATE P=(4)X3 差分阶数d=1 IDENTIFY VAR=&X3(1)滤出AR特质ESTIMATE P=(4,8)Y 差分阶数d=1 IDENTIFY VAR=&Y(1)CROSSCOR=(&X1(1) &X2(1) &X3(1))一般转移函数ESTIMATEINPUT=(4$(2)/&X1 &X2 1$(1)/&X3)设定AR1,1+MA1,1特质ESTIMATE P=(1) Q=(1) INPUT=(&X1 &X2 &X3)预测8期FORECAST LEAD=8[例一] 应用实务(DECODE 步骤):参考周文贤老师着[市场调查与营销策略研拟] 一书之例5.模式解释(1)弹性系数(2)成长率(3)生命周期(4)干预乘数:冲击/期间/长期[例二] 消费财产品预测3.预测流程:(5) POP=f(POP) POP--->ARIMA(p,1,q) --->POP Fcst(6) BBC Fcst = BBCP Fcst * POP Fcst(7) MOBIL Fcst = WLC Fcst - BBC Fcst(8) 产品预测= MOBIL Fcst * 市场占有率[例三]工业财产品预测1.变量说明: YEAR 年份GDP 每千家生产毛额EPP 静电式绘图机BUS 厂商数(千家)EPPP 每千家静电式绘图机2.关系式:EPPP=EPP/BUS3.预测流程:(2) BUS=f(BUS) BUS ---> ARIMA(p,1,q) --> BUS Fcst(3) EPP Fcst = EPPP Fcst * BUS Fcst[例四]民生财(所得弹性=0)产品预测。
Arima模型在SPSS中的操作

Arima模型在SPSS中的操作ARIMA是自动回归积分滑动平均模型,它主要使用与有长期趋势与季节性波动的时间序列的分析预测中。
ARIMA有6个参数,ARIMA (p,d,q)(sp,sd,sq),后三个是主要用来描述季节性的变化,前三个针对去除了季节性变化后序列。
为了避免过度训练拟合,这些参数的取值都很小。
p与sp的含义是一个数与前面几个数线性相关,这两参数大多数情况下都取0, 取1的情况很少,大于1的就几乎绝种了。
d与sd是差分,difference,d是描述长期趋势,sd是季节性变化,这两个参数的取值几乎也都是0,1,2,要做几次差分就取几作值。
q与sq是平滑计算次数,如果序列变化特别剧烈,就要进行平滑计算,计算几次就取几做值,这两个值大多数情况下总有一个为0,也很少超过2的。
ARIMA的思路很简单,首先用差分去掉季节性波动,然后去掉长期趋势,然后平滑序列,然后用一个线性函数+白噪声的形式来拟合序列,就是不断的用前p个值来计算下一个值。
用SPSS来做ARIMA大概有这些步骤:1定义日期,确定季节性的周期,菜单为Data-Define dates 2画序列图来观察数值变化,菜单为Graph-sequence /Time Series - autoregressive3若存在季节性波动,则做季节性差分,Graph- Time Series - autoregressive,先做一次,返回2观察,如果数列还存在季节性波动,就再做一次,需要做几次,sd就取几4若观察到差分后的数列中有某些值远远大于平均值,则需要做平滑,做几次sq就取几5然后看是否需要做去除长期趋势的差分,确定p与sp6然后在ARIMA模型中测试是否存在其他属性影响预测属性,如果Approx sig接近0,则说明该属性可以加入模型,作为独立变量,值得注意的是,如果存在突变,可以根据情况自定义变量,这个在判断突变的原因比重时特别有用。
SAS学习系列39.时间序列分析Ⅲ—ARIMA模型

39. 时间序列分析Ⅱ—-ARIMA 模型随着对时间序列分析方法的深入研究,人们发现非平稳序列的确定性因素分解方法(如季节模型、趋势模型、移动平均、指数平滑等)只能提取显著的确定性信息,对随机性信息浪费严重,同时也无法对确定性因素之间的关系进行分析。
而非平稳序列随机分析的发展就是为了弥补确定性因素分解方法的不足。
时间序列数据分析的第一步都是要通过有效手段提取序列中所蕴藏的确定性信息。
Box 和Jenkins 使用大量的案例分析证明差分方法是一种非常简便有效的确定性信息的提取方法。
而Gramer 分解定理则在理论上保证了适当阶数的差分一定可以充分提取确定性信息。
(一)ARMA 模型即自回归移动平均移动模型,是最常用的拟合平稳时间序列的模型,分为三类:AR 模型、MA 模型和ARMA 模型。
一、AR(p )模型——p 阶自回归模型 1。
模型:011t t p t p t x x x φφφε--=+++其中,0p φ≠,随机干扰序列εt 为0均值、2εσ方差的白噪声序列(()0t s E εε=, t ≠s ),且当期的干扰与过去的序列值无关,即E (x t εt )=0.由于是平稳序列,可推得均值011pφμφφ=---. 若00φ=,称为中心化的AR (p )模型,对于非中心化的平稳时间序列,可以令01(1)p φμφφ=---,*t t x x μ=-转化为中心化。
记B 为延迟算子,1()p p p B I B B φφΦ=---称为p 阶自回归多项式,则AR (p )模型可表示为:()p t t B x εΦ=.2. 格林函数用来描述系统记忆扰动程度的函数,反映了影响效应衰减的快慢程度(回到平衡位置的速度),G j 表示扰动εt —j 对系统现在行为影响的权数。
例如,AR(1)模型(一阶非齐次差分方程),1, 0,1,2,j j G j φ==模型解为0t j t j j x G ε∞-==∑.3。
ARIMA模型-[SPSSPython]
![ARIMA模型-[SPSSPython]](https://img.taocdn.com/s3/m/b8f63a846429647d27284b73f242336c1fb9305d.png)
ARIMA模型-[SPSSPython] 简介: ARIMA模型:(英语:Autoregressive Integrated Moving Average model),差分整合移动平均⾃回归模型,⼜称整合移动平均⾃回归模型(移动也可称作滑动),是时间序列预测分析⽅法之⼀。
AR是“⾃回归”,p为⾃回归项数;MA为“滑动平均”,q为滑动平均项数,d为使之成为平稳序列所做的差分次数(阶数)。
由于毕业论⽂要涉及到时间序列的数据(商品的销量)进⾏建模与分析,主要是对时间序列的数据进⾏预测,在对数据进⾏简单的散点图观察时,发现数据具有季节性,也就是说:数据波动呈现着周期性,并且前⾯的数据会对后⾯的数据产⽣影响,这也符合商品的销量随时间波动的影响。
于是选择了ARIMA模型,那为什么不选择AR模型、MA模型、ARMA模型 于是,通过这篇博客,你将学到: (1)通过SPSS操作ARIMA模型 (2)运⽤python进⾏⽩噪声数据判断 (3)为什么差分,怎么定阶 PS:在博客结尾,会附录上Python进⾏ARIMA模型求解的代码。
为什么会使⽤SPSS? 由于真⾹定理,在SPSS⾥有ARIMA、AR、MA模型的各种操作;还包括异常值处理,差分,⽩噪声数据判断,以及定阶。
⼀种很⽅便⼜不⽤编程还可以避免改代码是不是很爽… ARIMA模型的步骤 好啦,使⽤ARIMA模型的原因: 在过去的数据对今天的数据具有⼀定的影响,如果过去的数据没有对如今的数据有影响时,不适合运⽤ARIMA模型进⾏时间序列的预测。
使⽤ARIMA进⾏建模的步骤: 简单来说,运⽤ARIMA模型进⾏建模时,主要的步骤可以分成以下三步: (1)获取原始数据,进⾏数据预处理。
(缺失值填补、异常值替换) (2)对预处理后的数据进⾏平稳性判断。
如果不是平稳的数据,则要对数据进⾏差分运算。
(3)将平稳的数据进⾏⽩噪声检验;如果不是⽩噪声数据,则说明数据之间仍然有关联,需要进⾏ARIMA(p,d,q)重新定阶:p、q。
sas经济时间序列分各种模型分析

目录实验一分析太阳黑子数序列 (3)实验二模拟AR模型 (4)实验三模拟MA模型和ARMA模型 (6)实验四分析化工生产量数据 (8)实验五模拟ARIMA模型和季节ARIMA模型 (10)实验六分析美国国民生产总值的季度数据 (13)实验七分析国际航线月度旅客总数数据 (16)实验八干预模型的建模 (19)实验九传递函数模型的建模 (22)实验十回归与时序相结合的建模 (25)太阳黑子年度数据 (28)美国国民收入数据 (29)化工生产过程的产量数据 (30)国际航线月度旅客数据 (30)洛杉矶臭氧每小时读数的月平均值数据 (31)煤气炉数据 (35)芝加哥某食品公司大众食品周销售数据 (37)牙膏市场占有率周数据 (39)某公司汽车生产数据 (44)加拿大山猫数据 (44)实验一分析太阳黑子数序列一、实验目的:了解时间序列分析的基本步骤,熟悉SAS/ETS软件使用方法。
二、实验内容:分析太阳黑子数序列。
三、实验要求:了解时间序列分析的基本步骤,注意各种语句的输出结果。
四、实验时间:2小时。
五、实验软件:SAS系统。
六、实验步骤1、开机进入SAS系统。
2、创建名为exp1的SAS数据集,即在窗中输入下列语句:3、保存此步骤中的程序,供以后分析使用(只需按工具条上的保存按钮然后填写完提问后就可以把这段程序保存下来即可)。
4、绘数据与时间的关系图,初步识别序列,输入下列程序:ods html;ods listing close;5、run;提交程序,在graph窗口中观察序列,可以看出此序列是均值平稳序列。
6、识别模型,输入如下程序。
7、提交程序,观察输出结果。
初步识别序列为AR(2)模型。
8、估计和诊断。
输入如下程序:9、提交程序,观察输出结果。
假设通过了白噪声检验,且模型合理,则进行预测。
10、进行预测,输入如下程序:11、提交程序,观察输出结果。
12、退出SAS系统,关闭计算机。
总程序:data exp1;infile "D:\exp1.txt";input a1 @@;year=intnx('year','1jan1742'd,_n_-1);format year year4.;;proc print;run;ods html;ods listing close;proc gplot data=exp1 ;symbol i=spline v=dot h=1 cv=red ci=green w=1;plot a1*year/autovref lvref=2 cframe=yellow cvref=black ;title "太阳黑子数序列";run;proc arima data=exp1; identify var=a1 nlag=24 minic p=(0:5) q=(0:5); estimate p=3; forecast lead=6 interval=year id=year out=out; run; proc print data=out; run;选取拟合模型的规则:1.模型显著有效(残差检验为白噪声)2.模型参数尽可能少3.结合自相关图和偏自相关图以及minic 条件(BIC 信息量最小原则),选取显著有效的参数实验二 模拟AR 模型一、 实验目的:熟悉各种AR 模型的样本自相关系数和偏相关系数的特点,为理 论学习提供直观的印象。
R语言季节性arima模型案例附代码数据

R语言季节性arima模型案例代码数据文件sales.csv提供公司季度销售数据。
为这些数据构建时间序列图。
描述数据。
data=read.csv("sales.csv")head(data)## sales## 1 105715## 2 120136## 3 181669## 4 239813## 5 159980## 6 164760plot(as.numeric(data[,1]),type="l")# 分解为趋势和季节成分# 从数据来看,有明显得波动趋势,因此可能存在季节性趋势,需要进行季节性差分。
# 计算趋势(使用适当的移动平均线)和季节性成分。
将时间趋势,季节性因素和剩余序列与时间对应,并对您的地块进行评论。
kingstimeseries <-ts(as.numeric(data[,1]),frequency =12)kingstimeseries## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec## 1 3 8 19 25 14 15 24 29 21 23 28 33## 2 26 27 31 37 30 32 36 41 34 35 39 44## 3 38 40 47 50 42 43 51 55 45 46 54 4## 4 48 49 56 9 52 53 7 13 5 6 12 16## 5 10 11 18 22 17 20 2 1kingstimeseriescomponents <-decompose(kingstimeseries)kingstimeseriescomponents$seasonal # get the estimated values of the s easonal component## Jan Feb Mar Apr May Jun ## 1 -1.1649306 0.6059028 7.7934028 -4.4149306 5.3767361 7.1684028 ## 2 -1.1649306 0.6059028 7.7934028 -4.4149306 5.3767361 7.1684028 ## 3 -1.1649306 0.6059028 7.7934028 -4.4149306 5.3767361 7.1684028 ## 4 -1.1649306 0.6059028 7.7934028 -4.4149306 5.3767361 7.1684028 ## 5 -1.1649306 0.6059028 7.7934028 -4.4149306 5.3767361 7.1684028 ## Jul Aug Sep Oct Nov Dec ## 1 -2.1753472 2.7204861 -5.5503472 -4.2586806 1.4913194 -7.5920139 ## 2 -2.1753472 2.7204861 -5.5503472 -4.2586806 1.4913194 -7.5920139 ## 3 -2.1753472 2.7204861 -5.5503472 -4.2586806 1.4913194 -7.5920139 ## 4 -2.1753472 2.7204861 -5.5503472 -4.2586806 1.4913194 -7.5920139 ## 5 -2.1753472 2.7204861plot(kingstimeseriescomponents)# 从差分图来看,数据有明显得季节趋势,需要进行季节性差分。
ARIMA代码

ToEstMd = arima('ARLags',1:i,'Constant',0); %指定模型的结构
else
ToEstMd = a('ARLags',1:i,'MALags',1:j,'Constant',0); %指定模型的结构
m1=length(x); %原始数据的个数
%以天为周期进行差分,消除周期性
for i = s+1:m1
y(i-s) =x(i)-x(i-s);
end
%一阶差分消除趋势性
w = diff(y);
m2=length(w); %计算差分处理后的数据个数
k=0; %初始化试探模型的个数
%贝叶斯信息准则,BIC= Bayesian Information Criterions
n = 7*96; %预测数据的个数(更改此处)
r=input('输入阶数R=');m=input('输入阶数M=');
ToEstMd = arima('ARLags',1:r,'MALags',1:m,'Constant',0); %指定模型的结构
%compute Akaike and Bayesian Information Criteria
[aic(k),bic(k)] = aicbic(logL,numParams,m2);
end
end
fprintf('R,M,AIC,BIC的对应值如下\n %f'); %显示计算结果
area1data = area12014(:,2:size(area12014,2)); %(更改此处原始数据)
实验3-SAS模拟MA模型和ARMA模型

实验三模拟MA模型和ARMA模型一、实验目的:熟悉各种MA模型和ARMA模型的样本自相关系数和偏相关系数的特点,为理论学习提供直观的印象。
二、实验内容:随机模拟各种MA模型和ARMA模型。
三、实验要求:记录各MA模型和ARMA模型的样本自相关系数和偏相关系数,观察各序列的异同,总结MA模型和ARMA模型的样本自相关系数和偏相关系数的特点四、实验时间:2小时。
五、实验软件:SAS系统。
六、实验步骤1、开机进入SAS系统。
2、模拟情况,模拟过程。
3在edit窗中输入如下程序:data a;,a1=0;a2=0;do n=-50 to 250;a=rannor(32565);x=a+*a1+*a2;a2=a1;a1=a;if n>0 then output;end;run;4、观察输出的数据序列,输入如下程序,并提交程序。
)proc gplot data=a;symbol i=spline;plot x*n;run;5、观察样本自相关系数和偏相关系数,输入输入如下程序,并提交程序。
proc arima data=a;identify var=x nlag=10 outcov=exp1;run;proc gplot data=exp1;symbol1 i=needle c=red;plot corr*lag=1;·run;proc gplot data=exp1;symbol2 i=needle c=green;plot partcorr*lag=2;run;6、作为作业把样本自相关系数和偏相关系数记录下来。
7、估计模型参数,并与实际模型的系数进行对比,即输入如下程序,并提交。
proc arima data=a;identify var=x nlag=10 ;run;estimate q=2;`run;8、模拟情况,模拟过程。
重复步骤3-7即可(但部分程序需要修改,请读者自己完成)。
9、模拟情况,模拟过程。
SAS学习系列39 时间序列分析Ⅲ—ARIMA模型

39. 时间序列分析Ⅱ——ARIMA 模型随着对时间序列分析方法的深入研究,人们发现非平稳序列的确定性因素分解方法(如季节模型、趋势模型、移动平均、指数平滑等)只能提取显著的确定性信息,对随机性信息浪费严重,同时也无法对确定性因素之间的关系进行分析。
而非平稳序列随机分析的发展就是为了弥补确定性因素分解方法的不足。
时间序列数据分析的第一步都是要通过有效手段提取序列中所蕴藏的确定性信息。
Box 和Jenkins 使用大量的案例分析证明差分方法是一种非常简便有效的确定性信息的提取方法。
而Gramer 分解定理则在理论上保证了适当阶数的差分一定可以充分提取确定性信息。
(一)ARMA 模型即自回归移动平均移动模型,是最常用的拟合平稳时间序列的模型,分为三类:AR 模型、MA 模型和ARMA 模型。
一、AR(p )模型——p 阶自回归模型 1. 模型:011t t p t p t x x x φφφε--=+++其中,0p φ≠,随机干扰序列εt 为0均值、2εσ方差的白噪声序列(()0t s E εε=, t ≠s ),且当期的干扰与过去的序列值无关,即E(x t εt )=0.由于是平稳序列,可推得均值011pφμφφ=---. 若00φ=,称为中心化的AR (p )模型,对于非中心化的平稳时间序列,可以令01(1)p φμφφ=---,*t t x x μ=-转化为中心化。
记B 为延迟算子,1()p p p B I B B φφΦ=---称为p 阶自回归多项式,则AR (p )模型可表示为:()p t t B x εΦ=.2. 格林函数用来描述系统记忆扰动程度的函数,反映了影响效应衰减的快慢程度(回到平衡位置的速度),G j 表示扰动εt -j 对系统现在行为影响的权数。
例如,AR(1)模型(一阶非齐次差分方程),1, 0,1,2,j j G j φ==模型解为0t j t j j x G ε∞-==∑.3. 模型的方差对于AR(1)模型,2221()()1t jt j j Var x G Var εσεφ∞-===-∑. 4. 模型的自协方差对中心化的平稳模型,可推得自协方差函数的递推公式:用格林函数显示表示:200()()i j t j t k j j kj i j j k G G E GG γεεσ∞∞∞---+=====∑∑∑对于AR(1)模型,21121()(0)1k k k εσγφγφφ==- 5. 模型的自相关函数 递推公式:对于AR(1)模型,11()(0)k k k ρφρφ==.平稳AR(p )模型的自相关函数有两个显著的性质: (1)拖尾性指自相关函数ρ(k)始终有非零取值,不会在k 大于某个常数之后就恒等于零;(2)负指数衰减随着时间的推移,自相关函数ρ(k)会迅速衰减,且以负指数k iλ(其中i λ为自相关函数差分方程的特征根)的速度在减小。
ARIMA代码

%季节型模型用AIC准则寻求最优模型clc;clear;load water.txt; %把原始数据按照表中格式放在纯文本文件water.txt water=water';x=water(:)';s=12; %周期s=12n=12; %预报数据的个数m1=length(x); %原始数据的个数for i=s+1:m1y(i-s)=x(i)-x(i-s);endm2=length(y);%周期差分后数据的个数w=diff(y); %消除趋势性的差分运算m3=length(w); %计算最终差分后的数据的个数for i=0:3for j=0:s+1spec=garchset('R',i,'M',j,'Display','off');%指定模型结构[coeffX,errorsX,LLFX]=garchfit(spec,w); %拟合参数num=garchcount(coeffX); %计算拟合参数的个数%computer Akaike and Bayesian Information Criteria[aic,bic]=aicbic(LLFX,num,m3);fprintf('R=%d,M=%d,AIC=%f,BIC=%f\n',i,j,aic,bic); %显示计算结果endend%根据已有的季节型模型进行预测r=input('输入阶数R=');m=input('输入阶数M=');spec2=garchset('R',r,'M',m,'Display','off');%指定模型结构[coeffX,errorsX,LLFX]=garchfit(spec2,w);%拟合参数[sigmaForecast,w_Forecast]=garchpred(coeffX,w,n) %求w的预报值yhat=y(m2)+cumsum(w_Forecast) %求y的预报值for j=1:nx(m1+j)=yhat(j)+x(m1+j-s);endx_hat=x(m1+1:end) %复原到原始数据的预报值dbstop if errorclc,cleara=textread('6-9rain.txt'); %把原始数据按照原来的排列格式存放在纯文本文件rain.txt a=nonzeros(a')'; %按照原来数据的顺序去掉零元素r11=autocorr(a) %计算自相关系数r12=parcorr(a) %计算偏相关系数da=diff(a); %计算一阶差分r21=autocorr(da) %计算自相关系数r22=parcorr(da) %计算偏相关系数n=length(da); %计算差分后的数据个数for i=0:3for j=0:3spec=garchset('R',i,'M',j,'display','off'); %指定模型结构[coeffX,errorsX,LLFX]=garchfit(spec,da); %拟合参数num=garchcount(coeffX);%computer Akaike and Bayesian Information Criteria[aic,bic]=aicbic(LLFX,num,n);fprintf('R=%d,M=%d,aic=%f,bic=%f\n',i,j,aic,bic); %显示计算结果endendr=input('输入阶数R=');m=input('输入阶数M=');spec2=garchset('R',r,'M',m,'display','off');%指定模型结构[coeffX,errorsX,LLFX]=garchfit(spec2,da) %拟合参数[sigmaforecast,w_forecast]=garchpred(coeffX,da,5) %计算5步预测值x_pred=a(end)+cumsum(w_forecast) %计算原始数据的5步预测值dbstop if error由定义知,平稳性意味着:所有的tx都具有相同的分布;在整个时期内,任何两个相邻项的相关程度都相同。
