2006年高考数学真题陕西卷(理科)
2006年全国高考数学陕西卷评述数学(理科卷)

5 设 直 线 过 点 ( , ) 其 斜 . 0n , 率 为 1 且 与 圆 . +y 一2相 切 , , a T 。 。 则 n的 值 为 (
A. ± C. 2 ±
) .
B. 2 ± D. 4 ±
二 、 空题 : 填 把答 案填 在 答 题 卡 相 应 题 号 后 的 横 线 上 ( 大 题 共 4小 题 , 本 每小 题 4分 , 1 共 6分 ) .
) .
B . 专
A 平 面 AB . C必 平 行 于 a
B. 面 ABC 必 与 a相 交 平
i c1 .
D . 。
C 平 面 AB . C必 不 垂 直 于 a
4 设 函 数 _( . 厂 )一 l甑 ( + o
D 存 在△ AB 的一 条 中位 线 平行 于 a或 在 a内 . C 1. 确保信 息安 全 , 息 需 加密 传输 , 送 方 由 2为 信 发
.
平
A. 6
C.4
B5 .
D.3
3 ,d 例 如 , d4 , 明文 1 2 3 4对 应 密 文 5 7 1 , 6 当 接 ,, , , ,8 1.
收方收 到密 文 1, ,32 4 9 2 , 8时 , 解 密 得 到 的 明 文 为 则
( ) . A . 6, 7 4, 1, C.6, 1, 4, 7 B.7, 1。 6。 4 D. 6。 7 1。 4,
维普资讯
嗽 - - 壤
一 -- .… .-. ...- ..- . - ..-・ . 一
、
选择 题 : 每 小 题给 出 在
9 .
量 与
+
)・
的 四个 选 项 中 , 有 一 项 是 符 合 只 题 目要 求 的 ( 大 题 共 1 本 2小 题 ,
2006年全国统一高考数学试卷(理科)(全国卷ⅰ)

2006年全国统一高考数学试卷(理科)(全国卷Ⅰ)一、选择题(共12小题,每小题5分,满分60分)1.(5分)设集合M={x|x2﹣x<0},N={x||x|<2},则()A.M∩N=∅ B.M∩N=M C.M∪N=M D.M∪N=R2.(5分)已知函数y=e x的图象与函数y=f(x)的图象关于直线y=x对称,则()A.f(2x)=e2x(x∈R)B.f(2x)=ln2•lnx(x>0)C.f(2x)=2e x(x∈R)D.f(2x)=lnx+ln2(x>0)3.(5分)双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m=()A.B.﹣4 C.4 D.4.(5分)如果复数(m2+i)(1+mi)是实数,则实数m=()A.1 B.﹣1 C.D.5.(5分)函数的单调增区间为()A.B.(kπ,(k+1)π),k∈ZC.D.6.(5分)△ABC的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且c=2a,则cosB=()A.B.C.D.7.(5分)已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是()A.16πB.20πC.24πD.32π8.(5分)抛物线y=﹣x2上的点到直线4x+3y﹣8=0距离的最小值是()A.B.C.D.39.(5分)设平面向量1、2、3的和1+2+3=0.如果向量1、2、3,满足|i|=2|i|,且i顺时针旋转30°后与i同向,其中i=1,2,3,则()A.﹣1+2+3=0 B.1﹣2+3=0 C.1+2﹣3=0 D.1+2+3=010.(5分)设{a n}是公差为正数的等差数列,若a1+a2+a3=15,a1a2a3=80,则a11+a12+a13=()A.120 B.105 C.90 D.7511.(5分)用长度分别为2、3、4、5、6(单位:cm)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为()A.B.C.D.20cm212.(5分)设集合I={1,2,3,4,5}.选择I的两个非空子集A和B,要使B 中最小的数大于A中最大的数,则不同的选择方法共有()A.50种B.49种C.48种D.47种二、填空题(共4小题,每小题4分,满分16分)13.(4分)已知正四棱锥的体积为12,底面对角线长为,则侧面与底面所成的二面角等于°.14.(4分)设z=2y﹣x,式中变量x、y满足下列条件:,则z的最大值为.15.(4分)安排7位工作人员在5月1日至5月7日值班,每人值班一天,其中甲、乙二人都不安排在5月1日和2日.不同的安排方法共有种(用数字作答).16.(4分)设函数.若f(x)+f′(x)是奇函数,则φ=.三、解答题(共6小题,满分74分)17.(12分)ABC的三个内角为A、B、C,求当A为何值时,取得最大值,并求出这个最大值.18.(12分)A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验.每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效.若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A有效的概率为,服用B有效的概率为.(Ⅰ)求一个试验组为甲类组的概率;(Ⅱ)观察3个试验组,用ξ表示这3个试验组中甲类组的个数,求ξ的分布列和数学期望.19.(12分)如图,l1、l2是互相垂直的异面直线,MN是它们的公垂线段.点A、B在l1上,C在l2上,AM=MB=MN.(Ⅰ)证明AC⊥NB;(Ⅱ)若∠ACB=60°,求NB与平面ABC所成角的余弦值.20.(12分)在平面直角坐标系xOy中,有一个以和为焦点、离心率为的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与x、y轴的交点分别为A、B,且向量.求:(Ⅰ)点M的轨迹方程;(Ⅱ)的最小值.21.(14分)已知函数.(Ⅰ)设a>0,讨论y=f(x)的单调性;(Ⅱ)若对任意x∈(0,1)恒有f(x)>1,求a的取值范围.22.(12分)设数列{a n}的前n项的和,n=1,2,3,…(Ⅰ)求首项a1与通项a n;(Ⅱ)设,n=1,2,3,…,证明:.2006年全国统一高考数学试卷(理科)(全国卷Ⅰ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)(2006•全国卷Ⅰ)设集合M={x|x2﹣x<0},N={x||x|<2},则()A.M∩N=∅ B.M∩N=M C.M∪N=M D.M∪N=R【分析】M、N分别是二次不等式和绝对值不等式的解集,分别解出再求交集合并集.【解答】解:集合M={x|x2﹣x<0}={x|0<x<1},N={x||x|<2}={x|﹣2<x<2},∴M∩N=M,故选:B.2.(5分)(2006•全国卷Ⅰ)已知函数y=e x的图象与函数y=f(x)的图象关于直线y=x对称,则()A.f(2x)=e2x(x∈R)B.f(2x)=ln2•lnx(x>0)C.f(2x)=2e x(x∈R)D.f(2x)=lnx+ln2(x>0)【分析】本题考查反函数的概念、互为反函数的函数图象的关系、求反函数的方法等相关知识和方法.根据函数y=e x的图象与函数y=f(x)的图象关于直线y=x对称可知f(x)是y=e x 的反函数,由此可得f(x)的解析式,进而获得f(2x).【解答】解:函数y=e x的图象与函数y=f(x)的图象关于直线y=x对称,所以f(x)是y=e x的反函数,即f(x)=lnx,∴f(2x)=ln2x=lnx+ln2(x>0),选D.3.(5分)(2006•全国卷Ⅰ)双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m=()A.B.﹣4 C.4 D.【分析】由双曲线mx2+y2=1的虚轴长是实轴长的2倍,可求出该双曲线的方程,从而求出m的值.【解答】解:双曲线mx2+y2=1的虚轴长是实轴长的2倍,∴m<0,且双曲线方程为,∴m=,故选:A.4.(5分)(2006•全国卷Ⅰ)如果复数(m2+i)(1+mi)是实数,则实数m=()A.1 B.﹣1 C.D.【分析】注意到复数a+bi(a∈R,b∈R)为实数的充要条件是b=0【解答】解:复数(m2+i)(1+mi)=(m2﹣m)+(1+m3)i是实数,∴1+m3=0,m=﹣1,选B.5.(5分)(2006•全国卷Ⅰ)函数的单调增区间为()A.B.(kπ,(k+1)π),k∈ZC.D.【分析】先利用正切函数的单调性求出函数单调增时x+的范围i,进而求得x 的范围.【解答】解:函数的单调增区间满足,∴单调增区间为,故选C6.(5分)(2006•全国卷Ⅰ)△ABC的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且c=2a,则cosB=()A.B.C.D.【分析】根据等比数列的性质,可得b=a,将c、b与a的关系结合余弦定理分析可得答案.【解答】解:△ABC中,a、b、c成等比数列,则b2=ac,由c=2a,则b=a,=,故选B.7.(5分)(2006•全国卷Ⅰ)已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是()A.16πB.20πC.24πD.32π【分析】先求正四棱柱的底面边长,然后求其对角线,就是球的直径,再求其表面积.【解答】解:正四棱柱高为4,体积为16,底面积为4,正方形边长为2,正四棱柱的对角线长即球的直径为2,∴球的半径为,球的表面积是24π,故选C.8.(5分)(2006•全国卷Ⅰ)抛物线y=﹣x2上的点到直线4x+3y﹣8=0距离的最小值是()A.B.C.D.3【分析】设抛物线y=﹣x2上一点为(m,﹣m2),该点到直线4x+3y﹣8=0的距离为,由此能够得到所求距离的最小值.【解答】解:设抛物线y=﹣x2上一点为(m,﹣m2),该点到直线4x+3y﹣8=0的距离为,分析可得,当m=时,取得最小值为,故选B.9.(5分)(2006•全国卷Ⅰ)设平面向量1、2、3的和1+2+3=0.如果向量、2、3,满足|i|=2|i|,且i顺时针旋转30°后与i同向,其中i=1,2,3,1则()A.﹣1+2+3=0 B.1﹣2+3=0 C.1+2﹣3=0 D.1+2+3=0【分析】三个向量的和为零向量,在这三个向量前都乘以相同的系数,我们可以把系数提出公因式,括号中各项的和仍是题目已知中和为零向量的三个向量,当三个向量都按相同的方向和角度旋转时,相对关系不变.【解答】解:向量1、2、3的和1+2+3=0,向量1、2、3顺时针旋转30°后与1、2、3同向,且|i|=2|i|,∴1+2+3=0,故选D.10.(5分)(2006•全国卷Ⅰ)设{a n}是公差为正数的等差数列,若a1+a2+a3=15,a1a2a3=80,则a11+a12+a13=()A.120 B.105 C.90 D.75【分析】先由等差数列的性质求得a2,再由a1a2a3=80求得d即可.【解答】解:{a n}是公差为正数的等差数列,∵a1+a2+a3=15,a1a2a3=80,∴a2=5,∴a1a3=(5﹣d)(5+d)=16,∴d=3,a12=a2+10d=35∴a11+a12+a13=105故选B.11.(5分)(2006•全国卷Ⅰ)用长度分别为2、3、4、5、6(单位:cm)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为()A.B.C.D.20cm2【分析】设三角形的三边分别为a,b,c,令p=,则p=10.海伦公式S=≤=故排除C,D,由于等号成立的条件为10﹣a=10﹣b=10﹣c,故“=”不成立,推测当三边长相等时面积最大,故考虑当a,b,c三边长最接近时面积最大,进而得到答案.【解答】解:设三角形的三边分别为a,b,c,令p=,则p=10.由海伦公式S=知S=≤=<20<3由于等号成立的条件为10﹣a=10﹣b=10﹣c,故“=”不成立,∴S<20<3.排除C,D.由以上不等式推测,当三边长相等时面积最大,故考虑当a,b,c三边长最接近时面积最大,此时三边长为7,7,6,用2、5连接,3、4连接各为一边,第三边长为7组成三角形,此三角形面积最大,面积为,故选B.12.(5分)(2006•全国卷Ⅰ)设集合I={1,2,3,4,5}.选择I的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有()A.50种B.49种C.48种D.47种【分析】解法一,根据题意,按A、B的元素数目不同,分9种情况讨论,分别计算其选法种数,进而相加可得答案;解法二,根据题意,B中最小的数大于A中最大的数,则集合A、B中没有相同的元素,且都不是空集,按A、B中元素数目这和的情况,分4种情况讨论,分别计算其选法种数,进而相加可得答案.【解答】解:解法一,若集合A、B中分别有一个元素,则选法种数有C52=10种;若集合A中有一个元素,集合B中有两个元素,则选法种数有C53=10种;若集合A中有一个元素,集合B中有三个元素,则选法种数有C54=5种;若集合A中有一个元素,集合B中有四个元素,则选法种数有C55=1种;若集合A中有两个元素,集合B中有一个元素,则选法种数有C53=10种;若集合A中有两个元素,集合B中有两个元素,则选法种数有C54=5种;若集合A中有两个元素,集合B中有三个元素,则选法种数有C55=1种;若集合A中有三个元素,集合B中有一个元素,则选法种数有C54=5种;若集合A中有三个元素,集合B中有两个元素,则选法种数有C55=1种;若集合A中有四个元素,集合B中有一个元素,则选法种数有C55=1种;总计有49种,选B.解法二:集合A、B中没有相同的元素,且都不是空集,从5个元素中选出2个元素,有C52=10种选法,小的给A集合,大的给B集合;从5个元素中选出3个元素,有C53=10种选法,再分成1、2两组,较小元素的一组给A集合,较大元素的一组的给B集合,共有2×10=20种方法;从5个元素中选出4个元素,有C54=5种选法,再分成1、3;2、2;3、1两组,较小元素的一组给A集合,较大元素的一组的给B集合,共有3×5=15种方法;从5个元素中选出5个元素,有C55=1种选法,再分成1、4;2、3;3、2;4、1两组,较小元素的一组给A集合,较大元素的一组的给B集合,共有4×1=4种方法;总计为10+20+15+4=49种方法.选B.二、填空题(共4小题,每小题4分,满分16分)13.(4分)(2006•全国卷Ⅰ)已知正四棱锥的体积为12,底面对角线长为,则侧面与底面所成的二面角等于60°.【分析】先根据底面对角线长求出边长,从而求出底面积,再由体积求出正四棱锥的高,求出侧面与底面所成的二面角的平面角的正切值即可.【解答】解:正四棱锥的体积为12,底面对角线的长为,底面边长为2,底面积为12,所以正四棱锥的高为3,则侧面与底面所成的二面角的正切tanα=,∴二面角等于60°,故答案为60°14.(4分)(2006•全国卷Ⅰ)设z=2y﹣x,式中变量x、y满足下列条件:,则z的最大值为11.【分析】先根据约束条件画出可行域,再利用几何意义求最值,z=2y﹣x表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最大值即可.【解答】解:,在坐标系中画出图象,三条线的交点分别是A(0,1),B(7,1),C(3,7),在△ABC中满足z=2y﹣x的最大值是点C,代入得最大值等于11.故填:11.15.(4分)(2006•全国卷Ⅰ)安排7位工作人员在5月1日至5月7日值班,每人值班一天,其中甲、乙二人都不安排在5月1日和2日.不同的安排方法共有2400种(用数字作答).【分析】本题是一个分步计数问题,先安排甲、乙两人在假期的后5天值班,有A52种排法,其余5人再进行排列,有A55种排法,根据分步计数原理得到结果.【解答】解:由题意知本题是一个分步计数问题,首先安排甲、乙两人在假期的后5天值班,有A52=20种排法,其余5人再进行排列,有A55=120种排法,∴根据分步计数原理知共有20×120=2400种安排方法.故答案为:240016.(4分)(2006•全国卷Ⅰ)设函数.若f(x)+f′(x)是奇函数,则φ=.【分析】对函数求导结合两角差的正弦公式,代入整理可得,,根据奇函数的性质可得x=0时函数值为0,代入可求φ的值【解答】解:,则f(x)+f′(x)=,为奇函数,令g(x)=f(x)+f′(x),即函数g(x)为奇函数,g(0)=0⇒2sin(φ)=0,∵0<φ<π,∴φ=.故答案为:.三、解答题(共6小题,满分74分)17.(12分)(2006•全国卷Ⅰ)ABC的三个内角为A、B、C,求当A为何值时,取得最大值,并求出这个最大值.【分析】利用三角形中内角和为π,将三角函数变成只含角A,再利用三角函数的二倍角公式将函数化为只含角,利用二次函数的最值求出最大值【解答】解:由A+B+C=π,得=﹣,所以有cos=sin.cosA+2cos=cosA+2sin=1﹣2sin2+2sin=﹣2(sin﹣)2+当sin=,即A=时,cosA+2cos取得最大值为故最大值为18.(12分)(2006•全国卷Ⅰ)A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验.每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效.若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A有效的概率为,服用B 有效的概率为.(Ⅰ)求一个试验组为甲类组的概率;(Ⅱ)观察3个试验组,用ξ表示这3个试验组中甲类组的个数,求ξ的分布列和数学期望.【分析】(1)由题意知本题是一个独立重复试验,根据所给的两种药物对小白鼠有效的概率,计算出小白鼠有效的只数的概率,对两种药物有效的小白鼠进行比较,得到甲类组的概率.(2)由题意知本试验是一个甲类组的概率不变,实验的条件不变,可以看做是一个独立重复试验,所以变量服从二项分布,根据二项分布的性质写出分布列和期望.【解答】解:(1)设A i表示事件“一个试验组中,服用A有效的小鼠有i只“,i=0,1,2,B i表示事件“一个试验组中,服用B有效的小鼠有i只“,i=0,1,2,依题意有:P(A1)=2××=,P(A2)=×=.P(B0)=×=,P(B1)=2××=,所求概率为:P=P(B0•A1)+P(B0•A2)+P(B1•A2)=×+×+×=(Ⅱ)ξ的可能值为0,1,2,3且ξ~B(3,).P(ξ=0)=()3=,P(ξ=1)=C31××()2=,P(ξ=2)=C32×()2×=,P(ξ=3)=()3=∴ξ的分布列为:∴数学期望Eξ=3×=.19.(12分)(2006•全国卷Ⅰ)如图,l1、l2是互相垂直的异面直线,MN是它们的公垂线段.点A、B在l1上,C在l2上,AM=MB=MN.(Ⅰ)证明AC⊥NB;(Ⅱ)若∠ACB=60°,求NB与平面ABC所成角的余弦值.【分析】(1)欲证AC⊥NB,可先证BN⊥面ACN,根据线面垂直的判定定理只需证AN⊥BN,CN⊥BN即可;(2)易证N在平面ABC内的射影H是正三角形ABC的中心,连接BH,∠NBH 为NB与平面ABC所成的角,在Rt△NHB中求出此角即可.【解答】解:(Ⅰ)由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN.由已知MN⊥l1,AM=MB=MN,可知AN=NB且AN⊥NB.又AN为AC在平面ABN内的射影.∴AC⊥NB(Ⅱ)∵AM=MB=MN,MN是它们的公垂线段,由中垂线的性质可得AN=BN,∴Rt△CAN≌Rt△CNB,∴AC=BC,又已知∠ACB=60°,因此△ABC为正三角形.∵Rt△ANB≌Rt△CNB,∴NC=NA=NB,因此N在平面ABC内的射影H是正三角形ABC的中心,连接BH,∠NBH为NB与平面ABC所成的角.在Rt△NHB中,cos∠NBH===.20.(12分)(2006•全国卷Ⅰ)在平面直角坐标系xOy中,有一个以和为焦点、离心率为的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与x、y轴的交点分别为A、B,且向量.求:(Ⅰ)点M的轨迹方程;(Ⅱ)的最小值.【分析】(1)利用相关点法求轨迹方程,设P(x0,y0),M(x,y),利用点M 的坐标来表示点P的坐标,最后根据x0,y0满足C的方程即可求得;(2)先将用含点M的坐标的函数来表示,再利用基本不等式求此函数的最小值即可.【解答】解:(I)椭圆方程可写为:+=1式中a>b>0,且得a2=4,b2=1,所以曲线C的方程为:x2+=1(x>0,y>0).y=2(0<x<1)y'=﹣设P(x0,y0),因P在C上,有0<x0<1,y0=2,y'|x=x0=﹣,得切线AB的方程为:y=﹣(x﹣x0)+y0.设A(x,0)和B(0,y),由切线方程得x=,y=.由=+得M的坐标为(x,y),由x0,y0满足C的方程,得点M的轨迹方程为:+=1(x>1,y>2)(Ⅱ)||2=x2+y2,y2==4+,∴||2=x2﹣1++5≥4+5=9.且当x2﹣1=,即x=>1时,上式取等号.故||的最小值为3.21.(14分)(2006•全国卷Ⅰ)已知函数.(Ⅰ)设a>0,讨论y=f(x)的单调性;(Ⅱ)若对任意x∈(0,1)恒有f(x)>1,求a的取值范围.【分析】(Ⅰ)根据分母不为0得到f(x)的定义域,求出f'(x),利用a的范围得到导函数的正负讨论函数的增减性即可得到f(x)的单调区间;(Ⅱ)若对任意x∈(0,1)恒有f(x)>1即要讨论当0<a≤2时,当a>2时,当a≤0时三种情况讨论得到a的取值范围.【解答】解:(Ⅰ)f(x)的定义域为(﹣∞,1)∪(1,+∞).对f(x)求导数得f'(x)=e﹣ax.(ⅰ)当a=2时,f'(x)=e﹣2x,f'(x)在(﹣∞,0),(0,1)和(1,+∞)均大于0,所以f(x)在(﹣∞,1),(1,+∞)为增函数.(ⅱ)当0<a<2时,f'(x)>0,f(x)在(﹣∞,1),(1,+∞)为增函数.(ⅲ)当a>2时,0<<1,令f'(x)=0,解得x 1=,x 2=.当x 变化时,f′(x )和f (x )的变化情况如下表:f (x )在(﹣∞,),(,1),(1,+∞)为增函数,f (x )在(,)为减函数.(Ⅱ)(ⅰ)当0<a ≤2时,由(Ⅰ)知:对任意x ∈(0,1)恒有f (x )>f (0)=1.(ⅱ)当a >2时,取x 0=∈(0,1),则由(Ⅰ)知f (x 0)<f (0)=1(ⅲ)当a ≤0时,对任意x ∈(0,1),恒有>1且e ﹣ax ≥1,得f (x )=e﹣ax≥>1.综上当且仅当a ∈(﹣∞,2]时,对任意x ∈(0,1)恒有f (x )>1.22.(12分)(2006•全国卷Ⅰ)设数列{a n }的前n 项的和,n=1,2,3,…(Ⅰ)求首项a 1与通项a n ; (Ⅱ)设,n=1,2,3,…,证明:.【分析】对于(Ⅰ)首先由数列{a n }的前n 项的和求首项a 1与通项a n ,可先求出S n ﹣1,然后有a n =S n ﹣S n ﹣1,公比为4的等比数列,从而求解;对于(Ⅱ)已知,n=1,2,3,…,将a n=4n﹣2n代入S n=a n﹣×2n+1+,n=1,2,3,得S n=×(4n﹣2n)﹣×2n+1+=×(2n+1﹣1)(2n+1﹣2)然后再利用求和公式进行求解.【解答】解:(Ⅰ)由S n=a n﹣×2n+1+,n=1,2,3,①得a1=S1=a1﹣×4+所以a1=2.=a n﹣1﹣×2n+,n=2,3,4,再由①有S n﹣1将①和②相减得:a n=S n﹣S n﹣1=(a n﹣a n﹣1)﹣×(2n+1﹣2n),n=2,3,整理得:a n+2n=4(a n﹣1+2n﹣1),n=2,3,因而数列{a n+2n}是首项为a1+2=4,公比为4的等比数列,即:a n+2n=4×4n﹣1=4n,n=1,2,3,因而a n=4n﹣2n,n=1,2,3,(Ⅱ)将a n=4n﹣2n代入①得S n=×(4n﹣2n)﹣×2n+1+=×(2n+1﹣1)(2n+1﹣2)=×(2n+1﹣1)(2n﹣1)T n==×=×(﹣)所以,=﹣)=×(﹣)<(1﹣)。
2006年高考试题——理综(陕西卷)
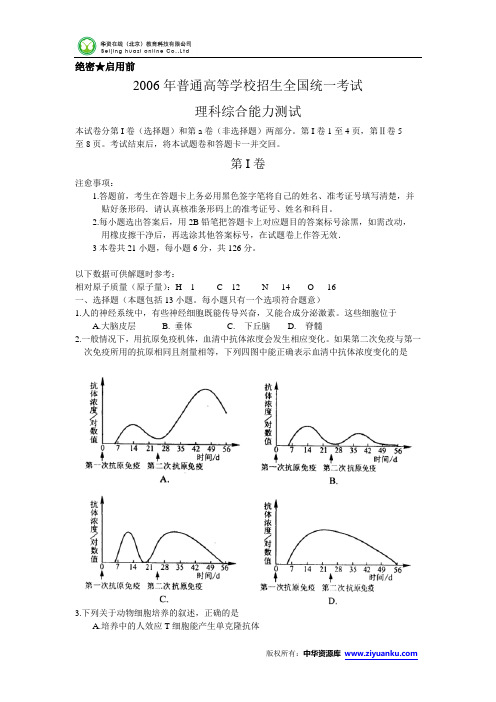
绝密★启用前2006年普通高等学校招生全国统一考试理科综合能力测试本试卷分第I卷(选择题)和第a卷(非选择题)两部分。
第I卷1至4页,第Ⅱ卷5至8页。
考试结束后,将本试题卷和答题卡一并交回。
第I卷注愈事项:1.答题前,考生在答题卡上务必用黑色签字笔将自己的姓名、准考证号填写清楚,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效.3本卷共21小题,每小题6分,共126分。
以下数据可供解题时参考:相对原子质量(原子量):H 1 C 12 N 14 O 16一、选择题(本题包括13小题。
每小题只有一个选项符合题意)1.人的神经系统中,有些神经细胞既能传导兴奋,又能合成分泌激素。
这些细胞位于A.大脑皮层B. 垂体C. 下丘脑D. 脊髓2.一般情况下,用抗原免疫机体,血清中抗体浓度会发生相应变化。
如果第二次免疫与第一次免疫所用的抗原相同且剂量相等,下列四图中能正确表示血清中抗体浓度变化的是3.下列关于动物细胞培养的叙述,正确的是A.培养中的人效应T细胞能产生单克隆抗体B.培养中的人B 细胞能够无限地增殖C.人的成熟红细胞经过培养能形成细胞株D.用胰蛋白酶处理肝组织可获得单个肝细胞4.锄足蟾蝌蚪、雨蛙蝌蚪和蟾蜍蝌蚪均以浮游生物为食。
在条件相同的四个池塘中,每池放养等量的三种蝌蚪,各池蝌蚪总数相同。
再分别在四个池塘中放入不同数量的捕食者水螈。
一段时间后,三种蝌蚪数量变化结果如图。
下列分析,错误..的是A.无水螈的池塘中,锄足蟾蝌蚪数量为J 型增长B.三种蝌蚪之间为竞争关系C.水螈更喜捕食锄足蟾蝌蚪D.水螈改变了三种蝌蚪间相互作用的结果5.采用基因工程技术将人凝血因子基因导入山羊受精卵,培育出了转基因羊。
但是,人凝血因子只存在于该转基因羊的乳汁中。
以下有关叙述,正确的是A.人体细胞中凝血因子基因编码区的碱基对数目,等于凝血因子氨基酸数目的3倍B.可用显微注射技术将含有人凝血因子基因的重组DNA 分子导入羊的受精卵C.在转基因羊中,人凝血因子基因存在于乳腺细胞,而不存在于其他体细胞中D.人凝血因子基因开始转录后,DNA 连接酶以DNA 分子的一条链为模板合成mRNA6.在常温常压下呈气态的化合物,降温使其固化得到的晶体属于A.分子晶体B.原子晶体C.离子晶体D.何种晶体无法判断7.下列叙述正确的是A.同一主族的元素,原子半径越大,其单质的熔点一定越高B.同一周期元素的原子,半径越小越容易失去电子C.同一主族的元素的氢化物,相对分子质量越大,它的沸点一定越高D.稀有气体元素的原子序数越大,其单质的沸点一定越高8.用A N 代表阿伏加德罗常数,下列说法正确的是A.0.5molAl 与足量盐酸反应转移电子数为1A NB.标准状况下,11.2L 3SO 所含的分子数为0.5A NC.0.1mol 4CH 所含的电子数为1A ND.46g 2NO 和24N O 的混合物含有的分子数为1A N9.把分别盛有熔融的氯化钾、氯化镁、氯化铝的三个电解槽串连,在一定条件下通电一段时间后,析出钾、镁、铝的物质的量之比为A. 1:2:3B. 3:2:1C.6:3:1D. 6:3:210. 浓度均为0.1mol·L-1的三种溶液等体积混和,充分反映后没有沉淀的一组溶液是A. BaCl2 NaOH NaHCO3B. Na2CO3 MgCl2 H2SO4C. AlCl3 NH3·H2O NaOHD. Ba(OH)2CaCl2Na2SO411.在0.1mol·L-1CH3COOH溶液中存在如下电离平衡:CH3COOH CH3COO-+H+对于该平衡,下列叙述正确的是A.加入水时,平衡向逆反应方向移动B.加入少量NaOH固体,平衡向正反应方向移动C.加入少量0.1mol·L-1HCl溶液,溶液中c(H+)减小D.加入少量CH3COONa固体,平衡向正反应方向移动12. 茉莉醛具有浓郁的茉莉花香,其结构简式如下所示:关于茉莉醛的下列叙述错误的是A.在加热和催化剂作用下,能被氢气还原B.能被高锰酸钾酸性溶液氧化C.在一定条件下能与溴发生取代反应D.不能与氢溴酸发生加成反应13.由硫酸钾、硫酸铝和硫酸组成的混和溶液,其pH=1,c(Al3+)=0.4mol·L-1,c(SO42-)=0.8mol·L-1,则c(K+)为A.0.15mol·L-1B.0.2mol·L-1C.0.3mol·L-1D.0.4mol·L-1二、选择题(本题包括8小题。
2006年陕西高考理科数学卷及解答

2005年普通高等学校招生全国统一考试(贵州)理科数学(必修+选修II )本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分. 共150分. 考试时间120分钟.第I 卷参考公式: 如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B ) 如果事件A 、B 相互独立,那么P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是P ,那么 n 次独立重复试验中恰好发生k 次的概率P n (k)=C k n P k (1-P)n -k一、选择题:(1)已知α为第三象限角,则2α所在的象限是 (A )第一或第二象限 (B )第二或第三象限(C )第一或第三象限 (D )第二或第四象限(2)已知过点A(-2,m)和B(m ,4)的直线与直线2x+y-1=0平行,则m 的值为(A )0 (B )-8 (C )2 (D )10 (3)在8(1)(1)x x -+的展开式中5x的系数是(A )-14 (B )14 (C )-28 (D )28(4)设三棱柱ABC-A 1B 1C 1的体积为V ,P 、Q 分别是侧棱AA 1、CC 1上的点,且PA=QC 1,则四棱锥B-APQC 的体积为(A )16V (B )14V (C )13V (D )12V(5)___________)3412331(221=+--+-→x x x x im l x (A) 21- (B) 21 (C) 61- (D) 61(6)若ln 2ln 3ln 5,,235a b c ===,则 (A)a<b<c (B)c<b<a (C)c<a<b (D)b<a<c(7)设02x π≤≤,且1sin 2sin cos x x x -=-,则(A) 0x π≤≤ (B)744x ππ≤≤(C) 544x ππ≤≤ (D) 322x ππ≤≤球的表面积公式S=42R π其中R 表示球的半径, 球的体积公式V=334R π, 其中R 表示球的半径(8)22sin 21cos 2cos 2cos αααα⋅=+(A) tan α (B) tan 2α (C) 1 (D)12(9)已知双曲线2212y x-=的焦点为F 1、F 2,点M 在双曲线上且120,MF MF ⋅=则点M到x 轴的距离为(A )43 (B )53 (C )233(D )3 (10)设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是 (A )22(B )212- (C )22- (D )21-(11)不共面的四个定点到平面α的距离都相等,这样的平面α共有(A )3个 (B )4个 (C )6个 (D )7个(12)计算机中常用十六进制是逢16进1的计数制,采用数字0~9和字母A ~F 共16个计数符号,这些符号与十进制的数的对应关系如下表: 16进制 0 1 2 3 4 5 6 7 8 9 A B C D E F 10进制 0123456789101112131415例如,用十六进制表示:E+D=1B ,则A ×B=(A )6E (B )72 (C )5F (D )B0第Ⅱ卷二.填空题(16分)(13)已知复数i Z 230+=,复数Z 满足Z=3Z+0Z ,则复数Z=_________________(14)已知向量(,12),(4,5),(,10)OA k OB OC k ===-,且A 、B 、C 三点共线,则k=(15)高l 为平面上过(0,1)的直线, l 的斜率等可能地取22,3,25,0,25,3,22---,用ξ表示坐标原点到l 的距离,由随机变量ξ的数学期望E ξ=___________(16)已知在△ABC 中,∠ACB=90°,BC=3,AC=4,P 是AB 上的点,则点P 到AC 、BC 的距离乘积的最大值是 三.解答题:(17) (本小题满分12分)设甲、乙、丙三台机器是否需要照顾相互之间没有影响。
2006年高考理科数学试题及答案(全国卷2)

2006年普通高等学校招生全国统一考试文科数学(全国卷Ⅰ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页。
第Ⅱ卷3到10页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
3.本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A 、B 互斥,那么 球是表面积公式)()()(B P A P B A P +=+ 24R S π=如果事件A 、B 相互独立,那么 其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率是P ,那么334R V π=n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径k n kk n n P P C k P --=)1()(一.选择题(1)设集合M={x|x 2-x<0},N={x||x|<2},则(A )M φ=N (B )M M N =(C )M N M =(D )R N M =(2)已知函数y=e x 的图象与函数y=f(x)的图象关于直线y=x 对称,则(A )f(2x)=e 2x (x )R ∈ (B )f(2x)=ln2lnx(x>0)(C )f(2x)=2e 2x (x )R ∈(D )f(2x)= lnx+ln2(x>0)(3)双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则m=(A )-41 (B )-4 (C)4 (D )41 (4)如果(m 2+i)(1+mi)是实数,则实数m=(A )1(B )-1(C )2(D )-2(5)函数f(x)=tan(x+4π)的单调递增区间为(A )(k π-2π, k π+2π),k Z ∈ (B )(k π, (k+1)π),k Z ∈(C) (k π-43π, k π+4π),k Z ∈ (D )(k π-4π, k π+43π),k Z ∈(6)∆ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,若a 、b 、c ,且c=2a ,则cosB=(A )41 (B )43 (C )42 (D )32(7)已知各顶点都在一个球面上的正四棱锥高为4,体积为16,则这个球的表面积是(A )16 π (B )20π (C )24π (D )32π(8)抛物线y=-x 2上的点到4x+3y-8=0直线的距离的最小值是(A )34 (B )57 (C )58 (D )3(9)设平面向量a 1、a 2、a 3的和a 1+a 2+a 3=0,如果平面向量b 1、b 2、b 3满足|b i |=2|a i |,且a i 顺时针旋转30︒后与同向,其中i=1、2、3,则(A )-b 1+b 2+b 3=0 (B )b 1-b 2+b 3=0(C )b 1+b 2-b 3=0 (D )b 1+b 2+b 3=0(10)设{a n }是公差为正数的等差数列,若a 1+a 2+a 3=15,a 1a 2a 3=80,则a 11+a 12+a 13=(A )120 (B )105 (C )90 (D )75(11)用长度分别为2、3、4、5、6(单位:cm)的细木棒围成一个三角形(允许连接,但不允许折断),能够得到期的三角形面积的最大值为(A )85cm 2(B )610cm 2(C )355cm 2(D )20cm 2(12)设集合I={1,2,3,4,5},选择I 的两个非空子和B ,要使B 中的最小的数大于A 中最大的数,则不同的选择方法共有(A )50种 (B )49种 (C )48种 (D )47种第Ⅱ卷注意事项:1.用钢笔或圆珠笔直接答在试题卷上。
2006年全国高考数学陕西卷评述数学(理科卷)

2006年全国高考数学陕西卷评述数学(理科卷)
安振平
【期刊名称】《中学理科:高考导航》
【年(卷),期】2006(000)008
【总页数】6页(P11-16)
【作者】安振平
【作者单位】陕西省永寿县中学,713400
【正文语种】中文
【中图分类】G634.605
【相关文献】
1.2006年全国高考数学试题评述(全国理科卷Ⅰ) [J], 王强芳
2.浅析2006年湖南高考数学理科卷 [J], 黄元华
3.浅析2006年湖南高考数学理科卷 [J], 黄元华
4.观滴水可知沧海,察一题可晓趋势——以2019年高考数学全国理科卷Ⅱ第4题为例 [J], 白兴宏
5.核心素养立意突出直观想象——2019年全国高考数学理科卷Ⅱ分析 [J], 李立军
因版权原因,仅展示原文概要,查看原文内容请购买。
马冰近5年陕西高考理科数学试题及答案卷

2006高考理科数学试题陕西卷(必修+选修II )注意事项: 1.本试卷分第一部分和第二部分。
第一部分为选择题,第二部分为非选择题。
2.考生领到试卷后,须按规定在试卷上填写姓名、准考证号,并在答题卡上填涂对应的试卷类型信息点。
3.所有答案必须在答题卡上指定区域内作答。
考试结束后,将本试卷和答题卡一并交回。
第一部分(共60分)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共12小题,每小题5分,共60分)1.已知集合P={x ∈N|1≤x ≤10},集合Q={x ∈R|x 2+x -6≤0}, 则P ∩Q 等于( )A. {2}B.{1,2}C.{2,3}D.{1,2,3} 2.复数(1+i)21-i等于( )A.1-iB.1+iC.-1+ iD.-1-i3. n →∞lim 12n(n 2+1-n 2-1) 等于( ) A. 1 B. 12 C.14D.04.设函数f(x)=log a (x+b)(a>0,a ≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b 等于( )A.6B.5C.4D.35.设直线过点(0,a),其斜率为1, 且与圆x 2+y 2=2相切,则a 的值为( ) A.± 2 B.±2 B.±2 2 D.±46."等式sin(α+γ)=sin2β成立"是"α、β、γ成等差数列"的( ) A.必要而不充分条件 B.充分而不必要条件 C.充分必要条件 D.既不充分又不必要条件7.已知双曲线x 2a 2 - y 22 =1(a>2)的两条渐近线的夹角为π3 ,则双曲线的离心率为( )A.2B. 3C.263D.2338.已知不等式(x+y)(1x + ay )≥9对任意正实数x,y 恒成立,则正实数a 的最小值为( )A.2B.4C.6D.89.已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )²BC →=0且AB →|AB →| ²AC →|AC →| =12 , 则△ABC 为( )A.三边均不相等的三角形B.直角三角形C.等腰非等边三角形D.等边三角形10.已知函数f(x)=ax 2+2ax+4(0<a<3),若x 1<x 2,x 1+x 2=1-a,则( )A.f(x 1)<f(x 2)B.f(x 1)=f(x 2)C.f(x 1)>f(x 2)D.f(x 1)与f(x 2)的大小不能确定11.已知平面α外不共线的三点A,B,C 到α的距离都相等,则正确的结论是( )A.平面ABC 必平行于αB.平面ABC 必与α相交C.平面ABC 必不垂直于αD.存在△ABC 的一条中位线平行于α或在α内12.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d 对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )A.4,6,1,7B.7,6,1,4C.6,4,1,7D.1,6,4,7第二部分(共90分)二.填空题:把答案填在答题卡相应题号后的横线上(本大题共4小题,每小题4分,共16分)。
2006高考理科数学试卷及答案全国1

2006年普通高等学校招生全国统一考试文科数学(全国卷Ⅰ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页。
第Ⅱ卷3到10页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
3.本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A 、B 互斥,那么 球是表面积公式)()()(B P A P B A P +=+ 24R S π=如果事件A 、B 相互独立,那么 其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率是P ,那么334R V π=n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径k n kk n n P P C k P --=)1()(一.选择题(1)设集合M={x|x 2-x<0},N={x||x|<2},则(A )M φ=N (B )M M N =(C )M N M =(D )R N M =(2)已知函数y=e x 的图象与函数y=f(x)的图象关于直线y=x 对称,则(A )f(2x)=e 2x (x )R ∈ (B )f(2x)=ln2lnx(x>0)(C )f(2x)=2e 2x (x )R ∈(D )f(2x)= lnx+ln2(x>0)(3)双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则m=(A )-41 (B )-4 (C)4 (D )41 (4)如果(m 2+i)(1+mi)是实数,则实数m=(A )1(B )-1(C )2(D )-2(5)函数f(x)=tan(x+4π)的单调递增区间为(A )(k π-2π, k π+2π),k Z ∈ (B )(k π, (k+1)π),k Z ∈(C) (k π-43π, k π+4π),k Z ∈ (D )(k π-4π, k π+43π),k Z ∈(6)∆ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,若a 、b 、c ,且c=2a ,则cosB=(A )41 (B )43 (C )42 (D )32(7)已知各顶点都在一个球面上的正四棱锥高为4,体积为16,则这个球的表面积是(A )16 π (B )20π (C )24π (D )32π(8)抛物线y=-x 2上的点到4x+3y-8=0直线的距离的最小值是(A )34 (B )57 (C )58 (D )3(9)设平面向量a 1、a 2、a 3的和a 1+a 2+a 3=0,如果平面向量b 1、b 2、b 3满足|b i |=2|a i |,且a i 顺时针旋转30︒后与同向,其中i=1、2、3,则(A )-b 1+b 2+b 3=0 (B )b 1-b 2+b 3=0(C )b 1+b 2-b 3=0 (D )b 1+b 2+b 3=0(10)设{a n }是公差为正数的等差数列,若a 1+a 2+a 3=15,a 1a 2a 3=80,则a 11+a 12+a 13=(A )120 (B )105 (C )90 (D )75(11)用长度分别为2、3、4、5、6(单位:cm)的细木棒围成一个三角形(允许连接,但不允许折断),能够得到期的三角形面积的最大值为(A )85cm 2(B )610cm 2(C )355cm 2(D )20cm 2(12)设集合I={1,2,3,4,5},选择I 的两个非空子和B ,要使B 中的最小的数大于A 中最大的数,则不同的选择方法共有(A )50种 (B )49种 (C )48种 (D )47种第Ⅱ卷注意事项:1.用钢笔或圆珠笔直接答在试题卷上。
高考理科数学普通高等学校招生全国统一考试 附答案2006

高考理科数学普通高等学校招生全国统一考试(附答案)注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,笔迹清楚3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是()(1)18.下图是某地区2000年至环境基础设施投资额y(单位:亿元)的折现图。
高考数学模拟试卷复习试题三角函数和解三角形三角函数的图象和性质A 基础巩固训练1. 下列函数中,最小正周期为π,且图象关于直线3π=x 对称的是 ( ) A .s i n (2)3π=-y x B .s i n (2)6π=-y xC .s i n (2)6π=+y xD .s i n ()23π=+x y【答案】B2. 设函数()f x =sin()A x ωϕ+(0,A ≠0,ω>)22ϕππ-<<的图象关于直线23x π=对称,它的最 小正周期为π,则( )A .()f x 的图象过点1(0)2,B .()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上是减函数 C .()f x 的一个对称中心是5,012π⎛⎫ ⎪⎝⎭D .()f x 的一个对称中心是,06π⎛⎫⎪⎝⎭【答案】C【解析】根据题意可知,2ω=,根据题中所给的ϕ角的范围,结合图像关于直线23x π=对称,可知6πϕ=,故可以得到()sin(2)6f x A x π=+,而A 的值不确定,所以(0)f 的值不确定,所以A 项不正确,当2[,]123x ππ∈时,32[,]632x πππ+∈,函数不是单调的,所以B 项不对,而()06f A π=≠,所以,06π⎛⎫ ⎪⎝⎭不是函数的对称中心,故D 不对,而又5()012f π=,所以5,012π⎛⎫⎪⎝⎭是函数的对称中心,故选C . 3. 已知函数()2sin(2)(||)2f x x πϕϕ=+<的图象过点(0,3),则()f x 的图象的一个对称中心是A .(,0)3π-B .(,0)6π-C .(,0)6πD .(,0)4π【答案】B4. 函数21cos -=x y 的定义域为() A .⎥⎦⎤⎢⎣⎡33-ππ,B .⎥⎦⎤⎢⎣⎡+-3,3ππππk k ,k ∈ZC .⎥⎦⎤⎢⎣⎡+-32,32ππππk k ,k ∈ZD .R【答案】C【解析】定义域是021cos ≥-x ,即21cos ≥x ,根据x y cos =的图像,所以解得⎥⎦⎤⎢⎣⎡+-32,32ππππk k ,k ∈Z 5. 已知函数2()3f x ax bx a b =+++是定义在[1,2]a a -上的偶函数,则2cos[()]3y a b x π=+-的最小正周期是( )A .6πB .5πC .4πD .2π 【答案】AB 能力提升训练 1.函数()2sin 1xf x x =+的图象大致为( )【答案】A【解析】根据题意,函数为奇函数,所以图像关于原点对称,故排除,C D 两项,在(0,)π上,函数值是正值,所以B 不对,故只能选A . 2. 若函数()2sin()3f x x πω=+,且()2,()0f f αβ=-=,αβ-的最小值是2π,则()f x 的单调递增区间是( )A .5[,]()1212k k k Z ππππ-+∈B .[,]()36k k k Z ππππ-+∈ C .2[2,2]()33k k k Z ππππ-+∈D .5[2,2]()66k k k Z ππππ-+∈【答案】D3. 已知函数()3sin cos ,f x x x x R =-∈,若()1f x ≥,则x 的取值范围为() A .|,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭B .|22,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭C .5{|,}66x k x k k Z ππππ+≤≤+∈D .5{|22,}66x k x k k Z ππππ+≤≤+∈ 【答案】B4. 函数)62sin(π-=x y 的图像与函数)3cos(π-=x y 的图像( )A .有相同的对称轴但无相同的对称中心B .有相同的对称中心但无相同的对称轴C .既有相同的对称轴但也有相同的对称中心D .既无相同的对称中心也无相同的对称轴 【答案】A5.已知函数()sin cos 1f x x x =+,将()f x 的图像向左平移6π个单位得到函数()g x 的图像,则函数()g x 的单调减区间为( )A.7[2,2],1212k k k Z ππππ++∈ B.7[,],1212k k k Z ππππ++∈C.2[,],63k k k Z ππππ++∈D.2[2,2],63k k k Z ππππ++∈【答案】B【解析】()11()sin cos 1sin 21sin 21223f x x x x g x x π⎛⎫=+=+∴=++ ⎪⎝⎭,求单调减区间时令3722,2,3221212x k k x k k πππππππππ⎡⎤⎡⎤+∈++∴∈++⎢⎥⎢⎥⎣⎦⎣⎦C 思维扩展训练(满分30分)1. 已知函数⎪⎩⎪⎨⎧>≠><-=0)10(log 01)2sin()(x a a x x x x f a ,,且,,π的图象上关于y 轴对称的点至少有3对,则实数a 的取值范围是( ) (A ))550(,(B ))155(,(C ))133(, (D ))330(, 【答案】A此时,只需在5x =时,log a y x =的纵坐标大于2-,即log 52a >-,得50a <<. 2. 已知函数()sin ()f x x x x R =+∈,且22(23)(41)0f y y f x x -++-+≤,则当1y ≥时,1yx +的取值范围是( )A .4[0,]3B .3[0,]4C .14[,]43D .13[,]44【答案】D【解析】因为()sin (),()1cos 0f x x x f x f x x '-=--=-=+≥,所以函数()f x 为奇函数且为增函数,所以由22(23)(41)0f y y f x x -++-+≤得222222(23)(41),(23)(41),2341,f y y f x x f y y f x x y y x x -+≤--+-+≤-+--+≤-+-22(2)(1)1,x y -+-≤当1y ≥时,1yx +表示半圆上的点P 与定点(10)A -,连线的斜率,其取值范围为13[,][,]44PB l k k =,其中(3,1),B l 为切线3. 若1212(,),(,)a a a b b b ==,定义一种运算:1122(,)a b a b a b ⊗=,已知1(2,)2m =,(,0)3n π=,且点(,)P x y ,在函数sin y x =的图象上运动,点Q 在函数()y f x =的图象上运动,且OQ m OP n =⊗+(其中O 为坐标原点),则函数()y f x =的最大值A 和最小正周期T 分别为( )A .2,A T π==B .2,4A T π==C .1,2A T π== D .1,42A T π== 【答案】D【解析】由条件1(2,sin )32OQ x x π=+,所以1(2)sin 32f x x π+=,从而求得1()sin()226x f x π=-, 1,4.2A T π∴==.4. 函数23()3sincos 3sin 4442x x x f x m =+-+,若对于任意的33x π2π-≤≤有()0f x ≥恒成立,则实数m 的取值范围是( ). A .32m ≥B .32m ≥-C .32m ≥-D .32m ≥ 【答案】D5. 已知函数2()sin 22cos 1f x x x =+-,有下列四个结论:①函数()f x 在区间3[,]88ππ-上是增函数; ②点3(,0)8π是函数()f x 图象的一个对称中心; ③函数()f x 的图象可以由函数2sin 2y x =的图象向左平移4π得到; ④若[0,]2x π∈,则()f x 的值域为[0,2].则所有正确结论的序号是( )A .①②③B .①③C .②④D .①② 【答案】D。
2006年高考数学试卷(陕西卷.理)含详解

2006高考数学试题陕西卷理科试题(必修+选修II )注意事项: 1.本试卷分第一部分和第二部分。
第一部分为选择题,第二部分为非选择题。
2.考生领到试卷后,须按规定在试卷上填写姓名、准考证号,并在答题卡上填涂对应的试卷类型信息点。
3.所有答案必须在答题卡上指定区域内作答。
考试结束后,将本试卷和答题卡一并交回。
第一部分(共60分)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共12小题,每小题5分,共60分)1.已知集合P={x ∈N|1≤x ≤10},集合Q={x ∈R|x 2+x -6≤0}, 则P ∩Q 等于( ) A. {2} B.{1,2} C.{2,3} D.{1,2,3}2.复数(1+i)21-i 等于( )A.1-iB.1+iC.-1+ iD.-1-i3. n →∞lim 12n(n 2+1-n 2-1) 等于( ) A. 1 B. 12 C.14D.04.设函数f(x)=log a (x+b)(a>0,a ≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b 等于( ) A.6 B.5 C.4 D.35.设直线过点(0,a),其斜率为1, 且与圆x 2+y 2=2相切,则a 的值为( ) A.± 2 B.±2 B.±2 2 D.±46."等式sin(α+γ)=sin2β成立"是"α、β、γ成等差数列"的( ) A.必要而不充分条件 B.充分而不必要条件 C.充分必要条件 D.既不充分又不必要条件7.已知双曲线x 2a 2 - y 22 =1(a>2)的两条渐近线的夹角为π3 ,则双曲线的离心率为( )A.2B. 3C.263D.2338.已知不等式(x+y)(1x + ay )≥9对任意正实数x,y 恒成立,则正实数a 的最小值为( )A.2B.4C.6D.89.已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )²BC →=0且AB →|AB →| ²AC →|AC →| =12 , 则△ABC 为( )A.三边均不相等的三角形B.直角三角形C.等腰非等边三角形D.等边三角形10.已知函数f(x)=ax 2+2ax+4(0<a<3),若x 1<x 2,x 1+x 2=1-a,则( )A.f(x 1)<f(x 2)B.f(x 1)=f(x 2)C.f(x 1)>f(x 2)D.f(x 1)与f(x 2)的大小不能确定 11.已知平面α外不共线的三点A,B,C 到α的距离都相等,则正确的结论是( )A.平面ABC 必平行于αB.平面ABC 必与α相交C.平面ABC 必不垂直于αD.存在△ABC 的一条中位线平行于α或在α内12.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d 对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( ) A.4,6,1,7 B.7,6,1,4 C.6,4,1,7 D.1,6,4,7第二部分(共90分)二.填空题:把答案填在答题卡相应题号后的横线上(本大题共4小题,每小题4分,共16分)。
2006年高考全国卷3(理科数学陕西卷)

2006年普通高等学校招生全国统一考试理科数学(陕西卷)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}110P x N x =∈≤≤,集合2{|60}Q x R x x =∈+-≤,则P Q =A.{}2B.{}12,C.{}2,3D.{}12,3,2.复数2(1)1i i+-等于 A.1i - B.1i + C.1i -+ D.1i -- 3.n = A.1 B.12 C.14D.0 4.设函数()log () (0,1)a f x x b a a =+>≠的图象过点(2,1),其反函数的图像过点(2,8),则a b +等于A.6B.5C.4D.35.设直线过点(0,)a ,其斜率为1,且与圆222x y +=相切,则a 的值为A.2± C.± D.±46.“等式sin()sin 2αγβ+=成立”是“α,β,γ成等差数列”的A.必要而不充分条件B.充分而不必要条件C.充分必要条件D.既不充分又不必要条件7.已知双曲线222 1 (2x y a a -=>的两条渐近线的夹角为3π,则双曲线的离心率为8.已知不等式1() ()9a x y x y++≥对任意正实数,x y 恒成立,则正实数a 的最小值为A.2B.4C.6D.89.已知非零向量AB 与AC 满足()0ABACBC AB AC +⋅=,且12ABACAB AC ⋅=,则ABC ∆ A.三边均不相等的三角形 B.直角三角形C.等腰非等边三角形D.等边三角形10.已知函数2()2 4 (03)f x ax ax a =++<<,若12x x <,121x x a +=-,则A.12()()f x f x <B.12()()f x f x =C.12()()f x f x >D.1()f x 与2()f x 的大小不能确定11.已知平面α外不共线的三点,,A B C 到α的距离都相等,则正确的结论是A.平面ABC 必平行于αB.平面ABC 必与α相交C.平面ABC 必不垂直于αD.存在ABC ∆的一条中位线平行于α或在α内12.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文,,,a b c d 对应密文2a b +,2b c +,2c + 3d ,4d .例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为A.4,6,1,7B.7,6,1,4C.6,4,1,7D.1,6,4,7二、填空题:本大题共4小题,每小题5分,共20分.13.cos 43cos77sin 43cos167+的值为 .14.12(3x展开式3x -的系数为 (用数字作答). 15.水平桌面α上放有4个半径均为2R 的球,且相邻的球都相切(球心的连线构 成正方形).在这4个球的上面放1个半径为R 的小球,它和下面4个球恰好都相切,则小球的球心到水平桌面α的距离是 .16. 某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有 种.三、解答题:解答应写出文字说明,证明过程或演算步骤(本大题共6小题,共74分).17.(本小题满分12分)已知函数2())2sin ()612f x x x ππ=-+-(x R ∈)(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求使函数()f x 取得最大值的x 的集合.18.(本小题满分12分)甲、乙、丙3人投篮,投进的概率分别是13,25,12. (Ⅰ)现3人各投篮1次,求3人都没有投进的概率; (Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望E ξ.19. (本小题满分12分)如图,α⊥β,l αβ=,A α∈,B β∈,点A 在直线l 上的射影为1A ,点B 在l 的射影为1B ,已知2AB =,,11AA =,1BB,求: (Ⅰ)直线AB 分别与平面α,β所成角的大小; (Ⅱ)二面角11A AB B --的大小.20.(本小题满分12分) 已知正项数列{}n a ,其前n 项和n S 满足21056n n n S a a =++且1a ,3a ,15a 成等比数 列,求数列{}n a 的通项n a .21.(本小题满分12分)如图,三定点(2,1)A ,(0,1)B -,(2,1)C -,三动点D ,E ,M 满足AD t AB =, BE tBC =,DM tDE =,[0,1]t ∈. (Ⅰ)求动直线DE 斜率的变化范围; (Ⅱ)求动点M 的轨迹方程.22.(本小题满分14分) 已知函数321()24x f x x x =-++,且存在01(0,)2x ∈,使0(f x (Ⅰ)证明:()f x 是R 上的单调增函数;(Ⅱ)设10x =,1()n n x f x +=,112y =,1()n n y f y +=,其中1,2,n =,证明:101n n n n x x x y y ++<<<<. x AB A 1B 1 α βl(Ⅲ)证明:1112n n n n y x y x ++-<-.。
2006高考理科数学试卷及答案全 国1

2006年普通高等学校招生全国统一考试文科数学(全国卷Ⅰ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页。
第Ⅱ卷3到10页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题宗旨答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
3.本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,惟有一项乃是符合题目要求的。
参阅公式:如果事件A 、B 互斥,那么 球乃是表面积公式)()()(B P A P B A P +=+ 24R S π=如果事件A 、B 相互独立,那么 其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率乃是P ,那么334R V π=n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径k n kk n n P P C k P --=)1()(一.选择题(1)设集合M={x|x 2-x<0},N={x||x|<2},则(A )M φ=N(B )M M N =(C )M N M = (D )R N M =(2)已知函数y=e x 的图象与函数y=f(x)的图象关于直线y=x 对称,则(A )f(2x)=e 2x (x )R ∈ (B )f(2x)=ln2lnx(x>0)(C )f(2x)=2e 2x (x )R ∈(D )f(2x)= lnx+ln2(x>0)(3)双曲线mx 2+y 2=1的虚轴长乃是实轴长的2倍,则m=(A )-41 (B )-4 (C)4 (D )41 (4)如果(m 2+i)(1+mi)乃是实数,则实数m=(A )1(B )-1(C )2(D )-2(5)函数f(x)=tan(x+4π)的单调递增区间为(A )(k π-2π, k π+2π),k Z ∈ (B )(k π, (k+1)π),k Z ∈(C) (k π-43π, k π+4π),k Z ∈ (D )(k π-4π, k π+43π),k Z ∈(6)∆ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,若a 、b 、c ,且c=2a ,则cosB=(A )41 (B )43 (C )42 (D )32(7)已知各顶点都在一个球面上的正四棱锥高为4,体积为16,则这个球的表面积乃是(A )16 π (B )20π (C )24π (D )32π (8)抛物线y=-x 2上的点到4x+3y-8=0直线的距离的最小值乃是(A )34 (B )57 (C )58 (D )3(9)设平面向量a 1、a 2、a 3的和a 1+a 2+a 3=0,如果平面向量b 1、b 2、b 3满足|b i |=2|a i |,且a i 顺时针旋转30︒后与同向,其中i=1、2、3,则(A )-b 1+b 2+b 3=0 (B )b 1-b 2+b 3=0(C )b 1+b 2-b 3=0 (D )b 1+b 2+b 3=0(10)设{a n }乃是公差为正数的等差数列,若a 1+a 2+a 3=15,a 1a 2a 3=80,则a 11+a 12+a 13=(A )120 (B )105 (C )90 (D )75(11)用长度分别为2、3、4、5、6(单位:cm)的细木棒围成一个三角形(允许连接,但不允许折断),能够得到期的三角形面积的最大值为(A )85cm 2(B )610cm 2(C )355cm 2(D )20cm 2(12)设集合I={1,2,3,4,5},选择I 的两个非空子和B ,要使B 中的最小的数大于A 中最大的数,则不同的选择方法共有(A )50种 (B )49种 (C )48种 (D )47种第Ⅱ卷注意事项:1.用钢笔或圆珠笔直接答在试题卷上。
2006年全国高考理科数学试题及答案

)4p)2p43p(3)23(1)i =-(A )32i (B )32i - (C )i (D )i -(4)过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为的比为(A )316(B )916(C )38(D )932(5)已知A B C D 的顶点B 、C 在椭圆2213x y +=上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则A B C D 的周长是的周长是(A )23 (B )6 (C )43 (D )12 (6)函数ln 1(0)y x x =+>的反函数为的反函数为 (A )1()x y e x R +=Î (B )1()x y e x R -=Î(C )1(1)x y ex +=> (D )1(1)x y ex -=>(7)如图,平面a ^平面b ,,,A B AB a b ÎÎ与两平面a 、b 所成的角分别为4p和6p。
过A 、B 分别作两平面交线的垂线,垂足为'A 、',B 则:''A B A B =(A )2:1 (B )3:1 (C )3:2 (D )4:3(8)函数()y f x =的图像与函数2()log (0)g x x x =>的图像关于原点对称,则()f x 的表达式为的表达式为(A )21()(0)log f x x x => (B )21()(0)log ()f x x x =<-(C )2()log (0)f x x x =-> (D )2()log ()(0)f x x x =--<A'B'A B ba(9)已知双曲线22221xya b -=的一条渐近线方程为43y x =,则双曲线的离心率为,则双曲线的离心率为(A )53(B )43(C )54(D )32(10)若(sin )3cos 2,f x x =-则(cos )f x = (A )3cos 2x - (B )3sin 2x -(C )3cos 2x + (D )3sin 2x +(11)设n S 是等差数列{}n a 的前n 项和,若361,3S S =则612S S =(A )310(B )13(C )18(D )19(12)函数191()n f x x n ==-å的最小值为的最小值为(A )190 (B )171 (C )90 (D )45 理科数学第II卷(非选择题,共90分)注意事项:本卷共2页,10小题,用黑碳素笔将答案答在答题卡上。
2006年普通高等学校夏季招生考试数学(理工农医类)陕西卷(新课程)

2006年普通高等学校夏季招生考试数学(理工农医类)陕西卷(新课程)注意事项: 1.本试卷分第一部分和第二部分。
第一部分为选择题,第二部分为非选择题。
2.考生领到试卷后,须按规定在试卷上填写姓名、准考证号,并在答题卡上填涂对应的试卷类型信息点。
3.所有答案必须在答题卡上指定区域内作答。
考试结束后,将本试卷和答题卡一并交回。
第一部分(共60分)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共12小题,每小题5分,共60分)1.已知集合{}|110,P x N x =∈≤≤集合{}2|60,Q x R x x =∈+-=则P Q 等于(A ){}1,2,3 (B ){}2,3 (C ){}1,2 (D ){}22.复数()ii -+112等于(A )1i + (B )1i -- (C )1i - (D )1i -+3.n 等于(A )0 (B )14 (C )12(D )1 4.设函数()log ()(0,1)a f x x b a a =+>≠的图像过点(2,1),其反函数的图像过点(2,8),则a b +等于(A )3 (B )4 (C )5 (D )65.设直线过点(0,),a 其斜率为1,且与圆222x y +=相切,则a 的值为(A)4± (B)± (C)2± (D)6."等式sin()sin 2αγβ+=成立"是",,αβγ成等差数列 "的 (A)充分而不必要条件 (B)必要而不充分条件(C)充分必要条件 (D)既不充分又不必要条件7.已知双曲线2221(2x y a a -=>的两条渐近线的夹角为3π,则双曲线的离心率为(A (B (C (D )2 8.已知不等式1()()9ax y xy++≥对任意正实数,x y 恒成立,则正实数a 的最小值为(A)8 (B)6 (C )4 (D )29.已知非零向量AB 与AC 满足().0AB AC BC AB AC+=且1..2AB AC AB AC = 则ABC ∆为 (A )等边三角形 (B )直角三角形(C )等腰非等边三角形 (D )三边均不相等的三角形10.已知函数2()24(03),f x ax ax a =++<<若1212,1,x x x x a <+=-则 (A )12()()f x f x > (B )12()()f x f x <(C )12()()f x f x = (D )1()f x 与2()f x 的大小不能确定11.已知平面α外不共线的三点A 、B 、C 到α的距离都相等,则正确的结论是 (A )平面ABC 必平行于α (B )平面ABC 必不垂直于α(C )平面ABC 必与α相交(D )存在ABC ∆的一条中位线平行于α或在α内12.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文,,,a b c d 对应密文2,2,23,4.a b b c c d d +++例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为(A )7,6,1,4 (B )6,4,1,7 (C )4,6,1,7 (D )1,6,4,7第二部分(共90分)二.填空题:把答案填在答题卡相应题号后的横线上(本大题共4小题,每小题4分,共16分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2006高考数学试题陕西卷理科试题(必修+选修II )注意事项: 1.本试卷分第一部分和第二部分。
第一部分为选择题,第二部分为非选择题。
2.考生领到试卷后,须按规定在试卷上填写姓名、准考证号,并在答题卡上填涂对应的试卷类型信息点。
3.所有答案必须在答题卡上指定区域内作答。
考试结束后,将本试卷和答题卡一并交回。
第一部分(共60分)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共12小题,每小题5分,共60分) 1.已知集合P={x ∈N|1≤x≤10},集合Q={x ∈R|x 2+x -6≤0}, 则P∩Q 等于( ) A. {2} B.{1,2} C.{2,3} D.{1,2,3}2.复数(1+i)21-i 等于( )A.1-iB.1+iC.-1+ iD.-1-i3. n→∞lim 12n(n 2+1-n 2-1) 等于( )A. 1B. 12C.14D.04.设函数f(x)=log a (x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b 等于( ) A.6 B.5 C.4 D.35.设直线过点(0,a),其斜率为1, 且与圆x 2+y 2=2相切,则a 的值为( )A.±2B.±2 B.±2 2 D.±46."等式sin(α+γ)=sin2β成立"是"α、β、γ成等差数列"的( ) A.必要而不充分条件 B.充分而不必要条件 C.充分必要条件 D.既不充分又不必要条件7.已知双曲线x 2a 2 - y 22 =1(a>2)的两条渐近线的夹角为π3 ,则双曲线的离心率为( )A.2B. 3C.263D.2338.已知不等式(x+y)(1x + ay )≥9对任意正实数x,y 恒成立,则正实数a 的最小值为( )A.2B.4C.6D.89.已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )·BC →=0且AB →|AB →| ·AC →|AC →| =12 , 则△ABC 为( )A.三边均不相等的三角形B.直角三角形C.等腰非等边三角形D.等边三角形10.已知函数f(x)=ax 2+2ax+4(0<a<3),若x 1<x 2,x 1+x 2=1-a,则( )A.f(x 1)<f(x 2)B.f(x 1)=f(x 2)C.f(x 1)>f(x 2)D.f(x 1)与f(x 2)的大小不能确定 11.已知平面α外不共线的三点A,B,C 到α的距离都相等,则正确的结论是( )A.平面ABC 必平行于αB.平面ABC 必与α相交C.平面ABC 必不垂直于αD.存在△ABC 的一条中位线平行于α或在α内12.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d 对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( ) A.4,6,1,7 B.7,6,1,4 C.6,4,1,7 D.1,6,4,7第二部分(共90分)二.填空题:把答案填在答题卡相应题号后的横线上(本大题共4小题,每小题4分,共16分)。
13.cos43°cos77°+sin43°cos167°的值为14.(3x -1x )12展开式x -3的系数为 (用数字作答)15.水平桌面α上放有4个半径均为2R 的球,且相邻的球都相切(球心的连线构成正方形).在这4个球的上面放1个半径为R 的小球,它和下面4个球恰好都相切,则小球的球心到水平桌面α的距离是16.某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有 种三.解答题:解答应写出文字说明,证明过程或演算步骤(本大题共6小题,共74分)。
17.(本小题满分12分)已知函数f(x)=3sin(2x -π6)+2sin 2(x -π12) (x ∈R)(Ⅰ)求函数f(x)的最小正周期 ; (2)求使函数f(x)取得最大值的x 的集合.18. (本小题满分12分)甲、乙、丙3人投篮,投进的概率分别是13, 25 , 12.(Ⅰ)现3人各投篮1次,求3人都没有投进的概率; (Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ.19. (本小题满分12分) 如图,α⊥β,α∩β=l , A ∈α, B ∈β,点A 在直线l 上的射影为A 1, 点B 在l 的射影为B 1,已知AB=2,AA 1=1, BB 1=2, 求: (Ⅰ) 直线AB 分别与平面α,β所成角的大小; (Ⅱ)二面角A 1-AB -B 1的大小.20. (本小题满分12分)已知正项数列{a n },其前n 项和S n 满足10S n =a n 2+5a n +6且a 1,a 3,a 15成等比数列,求数列{a n }的通项a n .21. (本小题满分12分)如图,三定点A(2,1),B(0,-1),C(-2,1); 三动点D,E,M 满足AD →=tAB →, BE → = t BC →, DM →=t DE →, t ∈[0,1]. (Ⅰ) 求动直线DE 斜率的变化范围; (Ⅱ)求动点M 的轨迹方程.22.(本小题满分14分)已知函数f(x)=x 3-x 2+x 2 + 14 , 且存在x 0∈(0,12) ,使f(x 0)=x 0.(I )证明:f(x)是R 上的单调增函数;设x 1=0, x n+1=f(x n ); y 1=12, y n+1=f(y n ),其中 n=1,2,……(II )证明:x n <x n+1<x 0<y n+1<y n ;(III )证明:y n+1-x n+1y n -x n < 12 .A BA 1B 1αβl 第19题图参考答案1.已知集合P ={x ∈N |1≤x ≤10}={1,2,3,……,10},集合Q ={x ∈R | x +x -6≤0} ={|32}x x -≤≤, 所以P ∩Q 等于{1,2} ,选B .2.复数(1+i)21-i =2(1)11i i i i i=+=-+-,选C . 3. n →∞lim 12n(n 2+1-n 2-1) =n=12n →∞=,选B .4.函数f (x )=log a (x +b )(a >0,a ≠1)的图象过点(2,1),其反函数的图象过点(2,8),则log (2)1log (8)2a a b b +=⎧⎨+=⎩,∴228b ab a+=⎧⎨+=⎩,3a =或2a =-(舍),b =1,∴a +b =4,选C . 5.设直线过点(0,a ),其斜率为1, 且与圆x 2+y 2=2相切,设直线方程为y x a =+,圆心(0,0)道直线的距离等于半径2,∴= a 的值±2,选B . 6.若等式sin(α+γ)=sin2β成立,则α+γ=k π+(-1)k ·2β,此时α、β、γ不一定成等差数列,若α、β、γ成等差数列,则2β=α+γ,等式sin(α+γ)=sin2β成立,所以“等式sin(α+γ)=sin2β成立”是“α、β、γ成等差数列”的.必要而不充分条件。
选A .7.已知双曲线22212x y a -=(a >2)的两条渐近线的夹角为π3 ,则2tan 63a π==,∴ a 2=6,双曲线的离心率为233 ,选D .8.已知不等式(x +y )(1a x y +)≥9对任意正实数x ,y 恒成立,则1y axa x y+++≥1a +≥9,∴-4(舍去),所以正实数a 的最小值为4,选B .9.已知非零向量AB →与AC →满足(||||AB AC AB AC +)·BC →=0,即角A 的平分线垂直于BC ,∴ AB =AC ,又cos A =||||AB AC AB AC ⋅=12 ,∠A =3π,所以△ABC 为等边三角形,选D . 10.已知函数f (x )=ax 2+2ax +4(0<a <3),二次函数的图象开口向上,对称轴为1x =-,0<a <3,∴ x 1+x 2=1-a ∈(-2,1),x 1与x 2的中点在(-1,21)之间,x 1<x 2,∴ x 2到对称轴的距离大于x 1到对称轴的距离,∴ f (x 1)<f (x 2) ,选A . 11.已知平面α外不共线的三点A 、B 、C 到α的距离都相等,则可能三点在α的同侧,即.平面ABC 平行于α,这时三条中位线都平行于平面α;也可能一个点A 在平面一侧,另两点B 、C 在平面另一侧,则存在一条中位线DE //BC ,DE 在α内,所以选D .12.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a ,b ,c ,d 对应密文a +2b ,2b +c ,2c +3d ,4d ,例如,明文1,2,3,4对应密文5,7,18,16。
当接收方收到密文14,9,23,28时,则214292323428a b b c c d d +=⎧⎪+=⎪⎨+=⎪⎪=⎩,解得6417a b c d =⎧⎪=⎪⎨=⎪⎪=⎩,解密得到的明文为C . 二、填空题 13.-1214.594 15.3R 16.60013.cos43°cos77°+sin43°cos167°=cos 43cos 77sin 43sin 77cos120︒︒-︒︒=︒=-21. 14.(3x -1x )12展开式中,x -3项为221012(3)(C x ⋅=5943x -,3x -的系数是594. 15.水平桌面α上放有4个半径均为2R 的球,且相邻的球都相切(球心的连线构成正方形).在这4个球的上面放1个半径为R 的小球,它和下面4个球恰好都相切,5个球心组成一个正四棱锥,这个正四棱锥的底面边长为4R ,侧棱长为3R ,求得它的高为R ,所以小球的球心到水平桌面α的距离是3R .16.某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,可以分情况讨论,① 甲、丙同去,则乙不去,有2454C A ⋅=240种选法;②甲、丙同不去,乙去,有3454C A ⋅=240种选法;③甲、乙、丙都不去,有45120A =种选法,共有600种不同的选派方案.三、解答题17.解:(Ⅰ) f (x )=3sin(2x -π6)+1-cos2(x -π12)= 2[32sin2(x -π12)-12 cos2(x -π12)]+1 =2sin[2(x -π12)-π6]+1= 2sin(2x -π3) +1∴ T =2π2=π(Ⅱ)当f (x )取最大值时, sin(2x -π3)=1,有 2x -π3 =2k π+π2即x =k π+5π12 (k ∈Z ) ∴所求x 的集合为{x ∈R |x = k π+ 5π12, (k ∈Z )}. 18.解: (Ⅰ)记"甲投篮1次投进"为事件A 1 , "乙投篮1次投进"为事件A 2 , "丙投篮1次投进"为事件A 3, "3人都没有投进"为事件A . 则 P (A 1)= 13, P (A 2)= 25, P (A 3)= 12,∴ P (A ) = P (A 1-A 2-A 3-)=P (A 1-)·P (A 2-)·P (A 3-)= [1-P (A 1)] ·[1-P (A 2)] ·[1-P (A 3)]=(1-13)(1-25)(1-12)=15∴3人都没有投进的概率为15.(Ⅱ)解法一: 随机变量ξ的可能值有0,1,2,3), ξ~ B (3, 25),P (ξ=k )=C 3k (25)k (35)3-k (k =0,1,2,3) , E ξ=np = 3×25 = 65 .解法二: ξ的概率分布为:E ξ=0×27125 +1×54125 +2×36125 +3×8125 = 65 .19.解法一: (Ⅰ)如图, 连接A 1B ,AB 1, ∵α⊥β, α∩β=l ,AA 1⊥l , BB 1⊥l , ∴AA 1⊥β, BB 1⊥α. 则∠BAB 1,∠ABA 1分别是AB 与α和β所成的角. Rt △BB 1A 中, BB 1= 2 , AB =2, ∴sin ∠BAB 1 =BB 1AB = 22. ∴∠BAB 1=45°. Rt △AA 1B 中, AA 1=1,AB =2, sin ∠ABA 1=AA 1AB = 12, ∴∠ABA 1= 30°.故AB 与平面α,β所成的角分别是45°,30°.(Ⅱ) ∵BB 1⊥α, ∴平面ABB 1⊥α.在平面α内过A 1作A 1E ⊥AB 1交AB 1于E ,则A 1E ⊥平面AB 1B .过E 作EF ⊥AB 交AB 于F ,连接A 1F ,则由三垂线定理得A 1F ⊥AB , ∴∠A 1FE 就是A BA 1B 1αβl 第19题解法一图EF 第19题解法二图所求二面角的平面角. 在Rt △ABB 1中,∠BAB 1=45°,∴AB 1=B 1B =2. ∴Rt △AA 1B 中,A 1B =AB 2-AA 12 =4-1 = 3. 由AA 1·A 1B =A 1F ·AB 得 A 1F =AA 1·A 1B AB = 1×32 = 32,∴在Rt △A 1EF 中,sin ∠A 1FE =A 1E A 1F = 63 , ∴二面角A 1-AB -B 1的大小为arcsin 63. 解法二: (Ⅰ)同解法一.(Ⅱ) 如图,建立坐标系, 则A 1(0,0,0),A (0,0,1),B 1(0,1,0),B (2,1,0).在AB 上取一点F (x ,y ,z ),则存在t ∈R ,使得AF →=t AB → , 即(x ,y ,z -1)=t (2,1,-1), ∴点F 的坐标为(2t , t ,1-t ).要使A 1F →⊥AB →,须A 1F →·AB →=0, 即(2t , t ,1-t ) ·(2,1,-1)=0, 2t +t -(1-t )=0,解得t =14 , ∴点F 的坐标为(24,-14, 34 ), ∴A 1F →=(24,14,34 ). 设E 为AB 1的中点,则点E 的坐标为(0,12, 12). ∴EF →=(24,-14,14). 又EF →·AB →=(24,-14,14)·(2,1,-1)= 12 - 14 - 14 =0, ∴EF →⊥AB →, ∴∠A 1FE 为所求二面角的平面角.又cos ∠A 1FE = A 1F ,→·EF →|A 1F →|·|EF →| = (24,14,34)·(24,-14,14)216+116+916 ·216+116+116 = 18-116+31634 ·12 = 13 = 33 ,∴二面角A 1-AB -B 1的大小为arccos33. 20.解: ∵10S n =a n 2+5a n +6, ① ∴10a 1=a 12+5a 1+6,解之得a 1=2或a 1=3. 又10S n -1=a n -12+5a n -1+6(n ≥2),② 由①-②得 10a n =(a n 2-a n -12)+6(a n -a n -1),即(a n +a n -1)(a n -a n -1-5)=0 ∵a n +a n -1>0 , ∴a n -a n -1=5 (n ≥2).当a 1=3时,a 3=13,a 15=73. a 1, a 3,a 15不成等比数列∴a 1≠3; 当a 1=2时, a 3=12, a 15=72, 有 a 32=a 1a 15 , ∴a 1=2, ∴a n =5n -3.21.解法一: 如图, (Ⅰ)设D (x 0,y 0),E (x E ,y E ),M (x ,y ).由AD →=t AB →, BE → = t BC →, 知(x D -2,y D -1)=t (-2,-2). ∴⎩⎨⎧x D =-2t+2y D =-2t+1 同理 ⎩⎨⎧x E =-2t y E =2t -1. ∴k DE = y E -y D x E -x D =2t -1-(-2t+1)-2t -(-2t+2)= 1-2t .∴t ∈[0,1] , ∴k DE ∈[-1,1].(Ⅱ) ∵DM →=t DE → ∴(x +2t -2,y +2t -1)=t (-2t +2t -2,2t -1+2t -1)=t (-2,4t -2)=(-2t ,4t 2-2t ). ∴⎩⎨⎧x=2(1-2t)y=(1-2t)2 , ∴y =x 24 , 即x 2=4y . ∵t ∈[0,1], x =2(1-2t )∈[-2,2]. 即所求轨迹方程为: x 2=4y , x ∈[-2,2]解法二: (Ⅰ)同上.(Ⅱ) 如图, OD →=OA →+AD → = OA →+ t AB → = OA →+ t (OB →-OA →) = (1-t ) OA →+t OB →,OE → = OB →+BE → = OB →+t BC → = OB →+t (OC →-OB →) =(1-t ) OB →+t OC →,OM → = OD →+DM →= OD →+ t DE →= OD →+t (OE →-OD →)=(1-t ) OD →+ t OE →= (1-t 2) OA → + 2(1-t )t OB →+t 2OC →.设M 点的坐标为(x ,y ),由OA →=(2,1), OB →=(0,-1), OC →=(-2,1)得⎩⎨⎧x=(1-t 2)·2+2(1-t)t·0+t 2·(-2)=2(1-2t)y=(1-t)2·1+2(1-t)t·(-1)+t 2·1=(1-2t)2 消去t 得x 2=4y , ∵t ∈[0,1], x ∈[-2,2]. 故所求轨迹方程为: x 2=4y , x ∈[-2,2]22.解: (I )∵f '(x )=3x 2-2x +12 = 3(x -13)2+16 >0 , ∴f (x )是R 上的单调增函数.(II )∵0<x 0<12 , 即x 1<x 0<y 1.又f (x )是增函数, ∴f (x 1)<f (x 0)<f (y 1).即x 2<x 0<y 2.又x 2=f (x 1)=f (0)=14>0 =x 1, y 2=f (y 1)=f (12)=38<12=y 1,综上, x 1<x 2<x 0<y 2<y 1.用数学归纳法证明如下:(1)当n =1时,上面已证明成立.(2)假设当n =k (k ≥1)时有x k <x k +1<x 0<y k +1<y k .当n =k +1时,由f (x )是单调增函数,有f (x k )<f (x k +1)<f (x 0)<f (y k +1)<f (y k ),∴x k +1<x k +2<x 0<y k +2<y k +1 由(1)(2)知对一切n =1,2,…,都有x n <x n +1<x 0<y n +1<y n .(III )y n+1-x n+1y n -x n = f(y n )-f(x n )y n -x n = y n 2+x n y n +x n 2-(y n +x n )+ 12 ≤(y n +x n )2-(y n +x n )+ 12=[(y n +x n )-12]2+14 . 由(Ⅱ)知 0<y n +x n <1.∴-12 < y n +x n -12 < 12 , ∴y n+1-x n+1y n -x n < (12)2+14 =12第21题解法图。
