高等电路分析动态非线性与混沌74页PPT

非线性电路分析解析ppt课件

则称函数关系f所描述的系统为线性系统。
5
非线性电路中至少包含
一个非线性元件，它的输出输入关系用非线性函数方程 v + 或非线性微分方程表示，右 –
图所示是一个线性电阻与二
极管组成的非线性电路。
Di
i
ZL
0
V0 v
二极管电路及其伏安特性
二极管是非线性器件，ZL为负载，V是所加信号源，幅度不大。设非线性元件的函数关系为i = f
所表征的电流。如果根据叠加原理，电流i应该是v1和 v2分别单独作用时所产生的电流之和，即
i
kv
2 1
kv
2 2
kV12m
sin2 1t
kV22m
sin2 2t
（6）
i kV12m sin2 1t kV22m sin2 2t 2kV1mV2m sin1t sin2t
（4）
18
i
kv
2 1
kv
28
(4) m次谐波(直流成分可视作零次、基波可视作一次)以及系数之和等于m的各组合频率成分，其振幅只与幂级数中等于及高于 m次的各项系数有关。例：直流成分与b0 、 b2都有关，而二次谐波及组合频率为1 + 2与1 - 2的各成分其振幅只与b2有关，而与b0无关。
29
(5) 因为幂级数展开式中含有两个信号的相乘项，起到乘法器的作用，因此，所有组合频率分量都是成对出现的，如有1 + 2就一定有1 – 2，有21 – 2，就一定有21 + 2，等等。
31
信号较大时，所有实际的非
线性元件，几乎都会进入饱和
ic
如右图所示半导体二 i
i
极管的伏安特性曲线。当 (a)
某一频率的正弦电压作

非线性电路理论与混沌现象

确定的系统与不确定的未来 ——非线性系统初始值的细微变化造成结果的巨大差差异
混沌现象的出
三体问题：一颗质量很小的卫星（灰尘）在两颗大质量的行星作用下运动。假定行星（灰尘）在它们之间的万有引力作用下绕其联线中心作圆周运动，而卫星（灰尘）质量很小，对行星运动的影响可以忽略。同时假定三个天体在同一平面内运动。现在要问：卫星在两颗行星作用下的运动情况如何呢？
使用了几个世纪的牛顿引力定律是广义相对论的弱场近似。只有当GmM/R << mc^2时牛顿引力定律才是正确的。
拉普拉斯曾写道：“我们应当把宇宙目前的状态视为其过去状态的结果和未来状态的原因。” ——拉普拉斯的世界不但是确定的，而且是可预测的。这就是牛顿世界中的决定论。
20世纪初，庞加莱首先意识到在确定论系统中有混沌现象的存在，对牛顿严格的决定论提出置疑，拉开了非线性研究的序幕。 20世纪50年代，由杨振宁和米尔斯建立的杨—米尔斯规范场论是非线性的，并且随后建立起来的弱电统一理论、量子色动力学也都是非线性的。而这些理论与实验符合得很好。物理学家断言：最后的大统一场论肯定也是非线性的。 ——整个世界，从宇观、宏观到微观本质上都是非线性的。
2. Intermittency Route to Chaos（或称为准周期道路）
使用和上面的实验相同的参数，当R进一步减小到系统产生3个极限环时，系统会形成另一种混沌现象：系统产生的信号几乎是周期性的，只是信号中存在一些没有规则的现象。也就是说信号中同时存在周期性的行为与没有规则的行为。产生这种混沌现象的方式为：在前一个实验中当系统产生三个稳定的极限环时，适当增加R的大小。
混沌基本特征
1、敏感性。表现在对系统结构参数敏感性和对初始条件敏感性。前者是指系统运动状态依赖于结构参数的变化，后者指初始条件的微小变化将导致系统运动行为的巨大差异。该特点违背了微分方程解对初始条件的连续依赖性，该特点形象的称为“蝴蝶效应” 。

高等电力系统分析--ppt课件

重写规范形式如下：
Y11V1 Y12V2 Y13V3 Y14V4 Y15V5 I1
Y21V1 Y22V2 Y23V3 Y24V4 Y25V5 I2
Y31V1
Y32V2
Y33V3
Y34V4
Y35V5
I3
Y41V1
Y42V2
Y43V3
Y44V4
Y45V5
I4
边界条件
I Sn AYU S AI S
节点电压方程简化为
YU I
nn
Sn
矩阵A反映了网络的拓扑约束， Y反映了网络的支路特性约束，
所以节点导纳矩阵集中了网络两种约束的全部信息。
2024/7/16
高等电力网络分析
19
若网络参数用阻抗形式表示，则节点网络方程有如下形式：
Z I U
n sn
n
Zn
.
I 1 Y11V1 Y12V2
.
I 2 Y21V1 Y22V2
.
I i Yi1V1 Yi2V2
.
I n Yn1V1 Yn2V2
Y1iVi
Y1nVn
Y2iVi Y2nVn
YiiVi
YinVn
YniVi YnnVn
节点自导纳Yii ＝节点i加单位电压，其它节点接地时，节点i向电网注入的电流。
V4
y1
y3
2
3
4
i1
i3
用节点电压方程描述电力网络的一个例子
y4
y5
i4
i5
1 V1
i6
y6
y2
V5
i2
5
V4
4
以基尔霍夫电流定律列出节点方程：

第七章非线性动力学与混沌讲义

二. 决定性系统与不可预测性
1. 力学决定论及其伟大成就
x m F (x, x, t ) x x 0 , x x 0

t t0

x(t ), x(t )
存在且唯一，可预测性
1757年，哈雷慧星（Hally comet）按预测回归。 1846年，海王星在预言的位置被发现。今天，日月蚀的准确预测，宇宙探测器的成功发射与回收。
ij (
f i )0 x j
11 12 0 21 22
T 11 22 系数矩阵的迹 11 22 12 21 系数行列式的值
A1 B 1 A2 B2
T 0
2
特征根
1, 2
T T 2 4 2
xi f i ( x1 , x2 ,, xn )
i 1,2,, n
优点：

四. 相空间（相图）的概念
相空间，也就是状态空间，是由广义坐标和广义动量（速度）张成的空间，也称相宇。相空间中运动状态的变化轨迹称为相图。
弹簧振子通解
x 0 x
2 0
x A cos( 0t ) x1 x A0 sin(0t ) x2
设想一位智者在某一瞬间得知激励大自然所有力及组成它的物体的相互位置，如果这位智者又能对众多的数据进行分析，把宇宙间最庞大的物体和最轻微的原子的运动凝聚在一个公式中，没有什么事物是不确定的，将来就像过去一样清晰地展现在眼前。
——拉普拉斯（Laplace，法国数学家，1749-1827）
2. 力学决定论不断受到挑战
x1 x, x2 x
x3 cos t , x4 x3

《非线性电路》课件

负载线的作用
2
探讨负载线在非线性电路中的重要作用
和影响。
3
非线性分析方法
4
介绍非线性电路分析的其他方法，如相位平面分析和哈特利分析。
分布式电路的频域分析
使用频域方法分析非线性电路中的分布式参数。
直接分析法和等效电路法
比较直接分析法和等效电路法在非线性电路分析中的应用。
IV. 非线性元件的应用
1
简单非线性电路的设计
给出一个简单非线性电路的设计示例，包括元件选择和参数调整。
2
复杂电路的应用和优化
分析一个复杂非线性电路的实际应用和性能优化。
VIII. 总结
1 非线性电路的应用前景
展望非线性电路在未来的应用领域，如通信、自动化等。
2 总结课程内容
总结本课件中涉及的主要知识点和重要概念。
3 答疑和交流
提供问答环节，鼓励学生提问和交流相和三极管
详细介绍二极管和三极管的工作原理、特性和应用。
发光二极管和光敏二极管
探讨发光二极管和光敏二极管在电路中的应用和性能特点。
晶体管
讲解晶体管的基本原理，包括 NPN和PNP两种类型。
集成电路
介绍集成电路及其在非线性电路中的应用和发展。
III. 非线性电路的分析
1
《非线性电路》PPT课件
非线性电路是电子领域中一项关键的研究内容，本课件将介绍非线性电路的基本概念、常见元件及其应用，并探讨非线性电路的分析、设计和优化方法。
I. 简介
什么是非线性电路
解释非线性电路的概念以及其与线性电路的区别和特点。
常见的非线性电路
介绍一些常见的非线性电路，如放大电路、振荡电路等。
讲解如何选择合适的电路参数以满足设计要求。

12.非线性电路混沌

非线性电路混沌长期以来，人们在认识和描述运动时，大多只局限于线性动力学描述方法，即确定的运动有一个完美确定的解析解.但是自然界在相当多情况下，非线性现象却起着很大的作用。

1963年美国气象学家LORENZ 在分析天气预报模型时，首先发现空气动力学中的混沌现象，该现象只能用非线性动力学来解释。

1975年混沌作为一个新的科学名词首次出现在科学文献中。

此后，非线性动力学迅速发展，并成为有丰富内容的研究领域，该学科涉及非常广泛的科学从电子学到物理学，从气象学到生态学，从数学到经济学等。

混沌通常相应于不规则或非周期性，这是由非线性系统本质产生的。

本实验将引导学生自己建立一个非线性电路，该电路包括有源非线性负阻、LC 振荡器和RC 移相器三部分；采用物理实验方法形容LC 振荡器产生的正弦波与经过RC 移相器三部分；采用物理实验方法研究LC 振荡器产生的正弦波与经过RC 移相器移相的正弦波合成的相图(李萨如图)，观测振动周期发生的分岔及混沌现象；测量非线性单元电路的电流—电压特性，从而对非线性电路及混沌现象有一初步了解；学会自己制作和测量一个带铁磁材料介质的电感器以及测量非线性器件伏安特性的方法［实验原理］1.非线性电路与非线性动力学实验电路如图1所示，图1中只有一个非线性元件R ，它是一个有源非线性负阻器件。

电感器L 和电容C 2组成一个损耗可以忽略的谐振回路；可变电阻R V 和电容器C 1串联将振荡器产生的正弦信号移相输出。

本实验中所用的非线性元件R 是一个三段分段线性元件。

图2所示的是该电阻的伏安特性曲线，从特性曲线显示中加在此非线性元件上电压与通过它的电流极性是相反的。

由于加在此元件上的电压增加时，通过它的电流却减小，因而将此元件称为非线性负阻元件。

图1非线性电路原理图图2非线性元件伏安特性图1电路的非线性动力学方程为： 1121)(1C C C C U g U U G dtdU C ⋅--⋅= L C C C i U U G dt dU C +-⋅=)(21122 (1)2C L U dtdi L -= 式中，导纳V R G /1=，1C U 和2C U 分别为表示加在电容器C 1和C 2上的电压，L i 表示流过电感器L 的电流，G 表示非线性电阻的导纳。

非线性电阻电路-混沌电路

非线性电阻电路-混沌电路姓名：陈文河学号. 0858210103班级：08582101指导老师：孙建红非线性电阻电路•混沌电路摘要：混沌的研究是20世纪物理学的重人事件。

混沌的研究表明，即使是非常简单的确定系统，由于自身的非线性作用，同样具有内在的随机性。

本文首先简略地介绍了混沌的基本概念,及其相关定义，概述了混沌运动的基本特征和混沌运动的判别方法。

利用非线性电阻的特性来设计混沌电路，然后通il Multisim 10.0软件来进行仿真计算，观察混沌现象。

分析结果衣明所谓混沌是指确定的非线性动力学系统中出现的貌似无规的类随机现象，此时系统运动轨道的时间行为对初始条件具有敏感性形成敏感参数，从而其长期行为变得混乱而无法预测，而整个系统长期行为的全局特征又与初始条件无关这种局部局域的不稳定性和整体上的稳定性必使它具有许多奇特性质。

混沌运动产生了层次和结构，混沌并不是真正意义上的无序和混乱，它是一种非周期的有序运动。

关键词：混沌，敏感参数，非线性电阻lo引言混沌(chaos)的英文意思是混乱的，无序的。

自1963年洛伦兹(E.N.Lorenz) 从三维自洽动力学系统中发现混沌以来，混沌动力学已迅速成为内容极为丰富，应用非常广泛的研究领域，它的概念和和方法逐步应用到自然科学，工程技术和社会科学的许多领域，并对于开阔和深化人们对自然界的认识起着越来越重要的作用。

混沌学揭示：世界是确定的，必然的，有序的，但同时又是随机的，偶然的，无序的。

有序运动会产生无序，无序的运动又包含着更高层次的有序，现实世界就是确定性和随机性，必然性和偶然性，有序性和无序性的辩证统一。

2. 实验目的2.1) 了解混沌现象的一些基本概念:混沌的定义，特征等。

2.2) 对设计电路进行调试，在示波器上观察相图中的倍周期分岔及混沌，奇怪吸引子等。

2.3) 测量有源非线性电阻的伏安特性。

3. 实验原理3.1非线性电路与非线性动力学实验电路如图1所示。

高等电路理论与技术PPT课件02 非线性电阻电路分析方法

Us
Uc
1
j1
2
1
2 3 1 j
6
3
j Us
1.3.3 分段线性化法
分段线性法(piecewise-linear technique)的基础是用若干直线段近似地表示非线性电阻元件的 ui 特性。
隧道二极管i u特性的分段线性近似
1.分段线性化方法
非线性元件的特性曲线可划分为许多区域，并且在每个区域中都可以用一段直线段来表示。每个区域中，用线性电路的分析方法来加以求解。
u(t) = U0 + u(t) i(t) = I0 + i(t)
代入KVL 方程 U sus(t)R siu
得 US+ uS(t )= RS [I0 + i(t) ]+ U0 + u(t)
直流工作状态： US= RSI0 + U0
小信号部分：
us(t)R s i(t) u(t)
要寻找△i(t)和△ u(t)的关系：
R1
US
R2
i3
R3
+ u_3
R
i3
U0
R3
+ u_3
其中
U0= US R2 /(R1+R2) , R=R1R2 /(R1+R2)
由此得
U0 =R i3 +20 i31/3 i3 曲线 u3
线性电路一般有唯一解。
非线性电阻电路可以有多个解或没有解。
i
iR + U-S
US +R -ud
A B
i = f ( ud ) C
(b)
is
1uu20 R3
10 3uu20
u* = 2 V

混沌电路的详解(课堂PPT)

蔡氏电路v1与v2信号输出波形
25
各种演变的相图如下图所示：
蔡氏电路相图中看到的混沌演变(v1-v2相图) 26
Chen氏混沌电路
Chen氏混沌系统是 Chen 等提出的一种新的吸引子。近年来 ,关于 Chen 氏系统本身特性的研究以及控制与同步的研究越来越多。目前，关于该系统的电路实现和同步控制的电路实现的研究报道不多。
20
蔡氏电路元件参数对运动形态的影响
蔡氏电路的运动形态因元件参数值的不同而有不同的拓扑性质。以电路元件参数值作为控制参数可以使蔡氏电路工作在不同的拓扑结构状态。
下面以下图电路为例，讨论R在1.298 kΩ～1.92 kΩ这一范围内变化时电路的状态。
iL
L
17mH
R
1.5k
C2
100nF
C1
10nF
12
(4) 洛伦兹(Lorenz)方程
x (y x)
y
x
y
xz
z
xy
z
(5) 蔡氏电路(Chua’s Cuicut，蔡少棠)方程
x α(y x G(x))
y
x
y
z
z
y
G (x)G bx1 2(G aG b)(x1x1)
(6) 洛斯勒(Rosslor)方程
x (y z)
y
(a) 稳定焦点，v1波形 (b)周期1，v1波形 (c)周期3，v1波形
(b)
(d)单涡旋，v1波形 (e)双涡旋，v1波形
蔡氏电路v1与v2信号输出波形
22
R为1.918 kΩ～1.820kΩ，周期2；R为1.819 kΩ～ 1.818kΩ，周期4；R+1.787kΩ，周期8；R=1.786kΩ，周期16；R继续减少至1.750kΩ为单涡旋图形，这是电路第一次进入单涡旋混沌，为洛斯勒形混沌吸引子。如图(d)所示。

非线性电路研究混沌现象

一、实验目的1．了解混沌的一些基本概念；2．测量有源非线性电阻的伏安特性；3．通过研究一个简单的非线性电路，了解混沌现象和产生混沌的原因。

二、实验原理实验所用电路原理图如图3.7-1所示。

电路中电感L 和电容C 1、C 2并联构成一个振荡电路。

R 是一有源非线性负阻元件，电感L 和电容器C 2组成一损耗可以忽略的谐振回路；可变电阻R 和电容器C 1串联将振荡器产生的正弦信号移相输出。

电路的非线性动力学方程如式（3.7-1）所示2121212d d )(d d )(d d 112C L C C C C L C C C U ti L gU U U G tU C i U U G tU C -=--=+-= （3.7－1）RL图3.7-1 电路原理图图3.7-2 非线性元件R 的U - I 特性这里，U C1、U C2是电容C 1、C 2上的电压，i L 是电感L 上的电流，G = 1/R 0是电导，g 为R 的伏安特性函数。

如果R 是线性的，g 是常数，电路就是一般的振荡电路，得到的解是正弦函数。

电阻R 0的作用是调节C 1 和C 2的位相差，把C 1 和C 2两端的电压分别输入到示波器的x ，y 轴，则显示的图形是椭圆。

如果R 是非线性的，它的伏安特性如图3.7-2所示，由于加在此元件上的电压增加时，通过它的电流却减小，因而此元件称为非线性负阻元件。

本实验所用的非线性元件R 是一个三段分段线性元件。

若用计算机编程进行数值计算，当取适当电路参数时，可在显示屏上观察到模拟实验的混沌现象。

除了计算机数学模拟方法之外，更直接的方法是用示波器来观察混沌现象，实验电路如图3.7-3所示。

图中，非线性电阻是电路的关键，它是通过一个双运算放大器和六个电阻组合来实现的。

电路中，LC 并联构成振荡电路，R 0的作用是分相，使A ，B 两处输入示波器的信号产生位相差，可得到x ，y 两个信号的合成图形。

双运放TL082的前级和后级正、负反馈同时存在，正反馈的强弱与比值R 3 /R 0，R 6/R 0有关，负反馈的强弱与比值R 2/R 1，R 5 /R 4有关．当正反馈大于负反馈时，振荡电路才能维持振荡。

电力系统稳态分析(ppt 74页)

i
i max
电压相角约束条件
线路的热极限约束、联络线潮流约束等
3.4电力网节点分类
电网中的节点因给定变量不同而分为三类： PQ节点
已知P、Q，待求U、δ；通常为给定PQ的电源节点和负荷节点。大多数节点为PQ节点。
PV节点
已知P、U，待求Q 、δ；通常为系统调压节点。数量少，可没有。
平衡节点
已知U、δ ，待求P、Q ；
承担电压参考和功率平衡的任务，又名松弛节点，比如系统调频节点或最
大电源节点，通常只设一个平衡节点。
3.4 实际的直角坐标潮流方程
n-1 个
m个 n-m-1 个
注：节点个数为n个，其中PQ节点个数为m个。
3.4 实际的直角坐标潮流方程
P1
x
e1
en1
2.1电力线路电压降落和损耗的分析
空载时，线路末端电压比始端高。
无功功率在电力线路中传输也产生有功功率损耗，同等大小的无功功率和有功功率在电力线路中传输产生的有功功率损耗相同。
由电压损耗纵分量可知降低电压损耗的方法有：提高电压等级；增大导线截面积；减小线路中流过的无功功率。
2.1变压器中的功率损耗
3.4直角坐标功率方程
e1
P1
x
en
f1
f
(
x
)
Pn
Q1
0
fn
Qn
未知数＝方程数
3.4 功率方程（极坐标系）
n
Pi jQi Uie ji ( Gij jBij )U je j j j 1
3.4极坐标功率方程
3.4 极坐标功率方程
1
P1
阻抗支路中损耗的功率为
导纳支路中的功率为

非线性电路混沌实验ppt课件

例如：
当=
31 3
时，0.7是周期一点。现用0.669去
迭代，就会出现周期二。迭代情况如下：
0.669---0.738---0.644---0.764---0.601---03 .799---
0.545---0.829---0.472---0.830---0.469---0.830---
0.470---0.830---0.470……
19
实验仪器介绍
LC组成的振荡电路
有源非线性电阻
20
实验内容
1. 连接电路，并将示波器打到合成档。 2. 通过调节电位器W1（粗调）和W2（细调），
在示波器上观察一倍周期李萨茹图、并记录之，
并分别观看1,2通道波形图并记录之。
3.
逐步减小
1 G
，李萨茹图开始出现分叉，即由1倍
周期变为2倍周期，记录之，并分别记录1,2通道
波形图。
4.逐步减小
1 G
，出现四倍周期，8倍周期，期与阵发混沌相
应图形。
21
实验内容
5.
再减小
1 G
，出现三倍周期，图像十分清楚稳定，
并记录相应图形。根据Yorke的著名论断“周期3意
味着混沌”，这说明电路即将出现混沌。
6.
继续减小
1 G
，则出现单个吸引子，并记录相应图
通信在我们的生活中的作用越来越重要,尤其是电子商务的兴起，对保密通信提出了更高的要求。利用混沌进行保密通信是现在十分热门的研究课题。混沌信号最本质的特征是对初始条件极为敏感，并导致了混沌信号的类随机特性。用它作为载波调制出来的信号当然也具有类随机特性。因而，调制混沌信号即使被敌方截获，也很难被破译，这就为混沌应用于保密通信提供了有利条件。因此利用混沌进行保密通信是目前十分热门的研究课题。混沌信号最本质的特征是对初始条件极为敏感，并由此信号又具有整体稳定性,当我们用同一个混沌信号去驱动两个相同的系统时，两个系统的某些部分将产生同步化的行为，这就为混沌应用于保密通信提供了可行性。

动态电路分析PPT课件

例、图示电路中，电源电动势为ε ，内阻不计，滑动变阻器最大阻值为R，负载电阻R0的阻值也为R ① 当开关K断开，滑动触头P滑动时R0两端的电压 U0变化的范围是多大？ ② 当K闭合，P滑动时，U0的变化范围是多大?
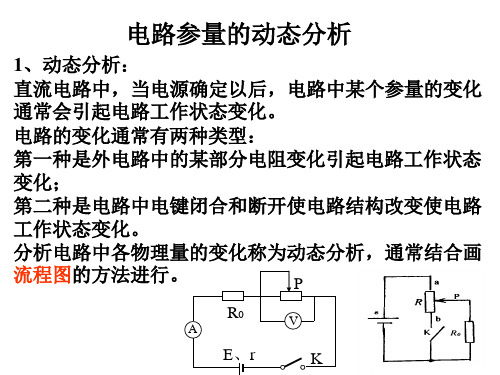
分析指导：电路变化由开关K的通断及滑动触头P的移动决定。 R被P分割为RaP和RPb两部分，P的变化引起两部分阻值变化，但它们的和恒等于R。
① K断开时：R0与RaP串联 P在b端时，由于R0=R，根据分压规律， R0上电压U0有最小值为ε /2P在a端时， RaP=0，R0上的电压是最大值为ε U0的变化范围是ε/2≤U0≤ε
② K闭合时：R0与Rpb并联，再与RaP串联 P在b端：
RPb=0，R0上电压U0有最小值为零。 P在a端：
电路参量的动态分析
1、动态分析：
直流电路中，当电源确定以后，电路中某个参量的变化
通常会引起电路工作状态变化。
电路的变化通常有两种类型：
第一种是外电路中的某部分电阻变化引起电路工作状态
变化；
第二种是电路中电键闭合和断开使电路结构改变使电路
工作状态变化。
分析电路中各物理量的变化称为动态分析，通常结合画
流程图的方法进行。
解题注意：当发现某一个物理量的变化难以确定时，应转向分析旁边支路，最后确定它的变化.
知识补充：
1）某部分电路电阻增大，总电阻增大；该部分电路两端电压增大
2）并联电路支路增加，总电阻减小
3）并联电路电阻代数和一定，当各支路电阻相等时总电阻最大
例1、（串联电路——分压作用）如图电路，当滑动变阻器滑片左移时，判断电流、电压表示数的变化？
器的滑动头向左移动时，下列判断正确的是（ AD ）
A．L1变暗 C．L2变暗

非线性振动与混沌简介PPT课件

d 2x dx x f cost
dt2 dt
三种情况： a. f= = = 0；b. f = =0；c. =0，相
应得出简谐振动、阻尼和受迫振动方程。
★简谐振动的相轨线：闭合圈---周期环---。
★阻尼振动的相轨线：从外向内收缩的螺旋线，最终停止于中点---不动点吸引子--- 。
★受迫振动：经过暂态之后趋于一稳定的闭合圈---周期吸引子或极限环。
单摆方程
ml
d2x dt 2
l
dx dt
mg
sin
x
F
cos t
按泰勒级数 sin x x 1 x3 6
取前两项近似，
适当代换，得到非线性振动方程（杜芬方程）
d 2x dx x x3 f cost
dt2 dt
讨论运动的演变
1. 线性近似下的单摆运动
21
第21页/共40页
1. 线性近似下的单摆运动令 =0，退化为线性方程
§3.2 混沌
一、混沌现象
混沌 ➢ 湍流
现象
雷诺实验
木星大红斑
障碍物后的流体
1
第1页/共40页
湍流
2
第2页/共40页
喷气混机沌尾现流
燃烧的蜡烛
象
➢洛仑兹水轮
3
第3页/共40页
➢滴水龙头
混沌现象
➢计算机迭代
x
x2 1的迭代
0.5
5
10 15 20 25 30
o
0.5
对周期点之间的距离之比，以及第相邻两次周期分
岔中的各对周期点之间的距离之比又趋于另一个常
数，称为标度因子或普适常数:
= 2.5029078750958928