哈工大数字信号处理实验报告
数字信号处理实验一 实验报告
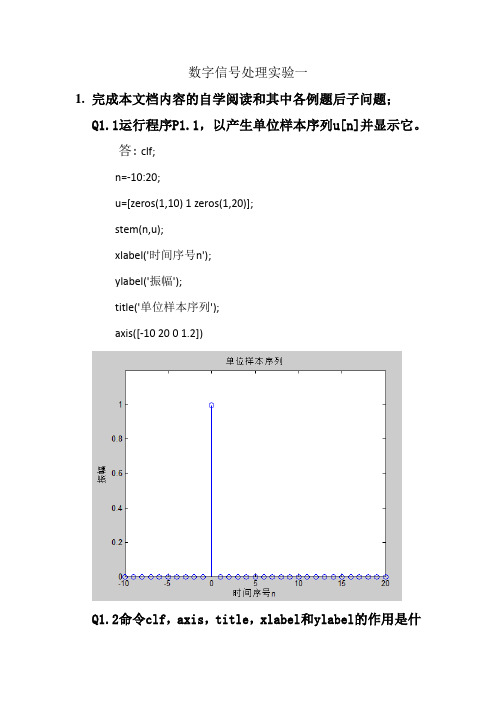
数字信号处理实验一1.完成本文档内容的自学阅读和其中各例题后子问题;Q1.1运行程序P1.1,以产生单位样本序列u[n]并显示它。
答: clf;n=-10:20;u=[zeros(1,10) 1 zeros(1,20)];stem(n,u);xlabel('时间序号n');ylabel('振幅');title('单位样本序列');axis([-10 20 0 1.2])Q1.2命令clf,axis,title,xlabel和ylabel的作用是什么?答:clf清除图对象,axis 控制轴刻度和风格的高层指令,title 设置图名,xlabel和ylabel设置横纵坐标轴名称。
Q1.3修改程序P1.1以产生带有延时11个单位样本的延迟单位样本序列ud[n]。
运行修改的程序并显示产生的序列。
答:clf;n=0:30;ud=[zeros(1,11) 1 zeros(1,19)];stem(n,ud);xlabel('时间序号n');ylabel('振幅');title('单位样本序列');axis([0 30 0 1.2])Q1.4修改程序P1.1以产生单位步长序列s[n].运行修改后程序并显示产生的序列。
答:clf;n = 0:30;u = [1.*n];stem(n,u);title('Unit Sample Sequence');axis([0 30 0 30])Q1.5修改程序P1.1,以产生带有超前7个样本的延时单位阶跃序列sd[n]。
运行修改后的程序并显示产生的序列。
答:clf;n = -15:30;s=[zeros(1,8) ones(1,38)];stem(n,s);xlabel('Time index n');ylabel('Amplitude'); title('Unit Sample Sequence');axis([-15 30 0 1.2]);Q1.6 运行程序P1.2,以产生复数值的指数序列。
哈尔滨工程大学数字信号处理实验四

t/T x (n )k X (k)t/T x (n)k X (k )一、 实验原理DFT 的快速算法FFT 利用了WN^(nk)的三个固有特性:(1)对称性,(WN^(nk))*=WN^(-nk),(2)周期性,WN^(nk)=WN^(n+N)k=WN^n(k+K),(3)可约性WN^(nk)=WmN^(nmk)和WN(nk)=WN/m^(nk/m)。
FFT 算法基本上可以分为两大类,即按时间抽选法和按频率抽选法。
MATLAB 中提供了进行快速傅里叶变换的fft 函数,X=fft(x),基2时间抽取FFT 算法,x 是表示离散信号的向量;X 是系数向量; X=fft(x ,N),补零或截断的N 点DFT ,当x 的长度小于N 时,对x 补零使其长度为N ,当x 的长度大于N 时,对x 截断使其长度为N 。
Ifft 函数计算IDFT ,其调用格式与fft 函数相同,参考help 文件。
例3.1程序及图形文件 >> k=8;>> n1=[0:19];>> xa1=sin(2*pi*n1/k); >> subplot(221) >> stem(n1,xa1)>> xlabel('t/T');ylabel('x(n)'); >> xk1=fft(xa1);>> xk1=abs(xk1);>> subplot(222)>> stem(n1,xk1)>> xlabel('k');ylabel('X(k)'); >> n2=[0:1:15]; >> xa2=sin(2*pi*n2/k); >> subplot(223) >> stem(n2,xa2)>> xlabel('t/T');ylabel('x(n)');>> xk2=fft(xa2);>> xk2=abs(xk2);>> subplot(224)>> stem(n2,xk2)>> xlabel('k');ylabel('X(k)');上两个图为N=20是的截取信号和DFT 结果,由于截取了两个半周期,频谱出现泄漏;下面的两个图为N=16时的截取信号和DFT 结果,由于截取了两个整周期,得到单一谱线的频谱。
哈工大数字信号处理实验2011

实验一 离散傅里叶变换的性质一、 实验目的1、 掌握离散傅里叶变换的性质,包括线性特性、时移特性、频移特性、对称性和循环卷积等性质;2、 通过编程验证傅里叶变换的性质,加强对傅里叶变换性质的认识。
二、 实验原理和方法 1. 线性特性1212DFT[()()]()()ax n bx n aX k bX k +=+2. 时移特性DFT[()]()DFT[()]()km kmx n m W X k x n m W X k -+=-=3. 频移特性()()nl N IDFT X k l IDFT X k W +=⎡⎤⎡⎤⎣⎦⎣⎦4. 对称性设由x(n) 延拓成的周期序列为 ()x n 则()()()e o xn x n x n =+ 共轭对称序列()()()*12e xn x n x N n ⎡⎤=+-⎣⎦ 共轭反对称序列()()()*12o x n x n x N n ⎡⎤=--⎣⎦ 将()e xn 和()o x n 截取主周期,分别得 ()()()ep e N x n x n R n = ()()()o p o N x n x n R n= 则()()()()()N ep op x n xn R n x n x n ==+ x(n)序列的实部和虚部的离散立叶变换(){}()Re ep DFT x n X k =⎡⎤⎣⎦ (){}()Im op DFT j x n X k =⎡⎤⎣⎦当x(n)为实数序列[][]()(())()()(())()()()(())()(())()()(())()(())()()()arg ()arg ()N N N N R R N N R N N I I N N I N N X k X k R k X k X N k R k X N k X k X k R k X N k R k X k X k R k X N k R k X k X N k X k X k *=-≅-=-≅-=-=-=--=--=-=--5. 循环卷积()312312()()()()()x n x n x n X k X k X k =⊗⇒=有限长序列线性卷积与循环卷积的关系 x1(n)和x2(n)的线性卷积:111212()()()()()N l m m x n x m x n m x m x n m -∞=-∞==-=-∑∑1120()()N m x m x n m -==-∑将x1(n)和x2(n)延拓成以N 为周期的周期序列11()()r xn x n rN ∞=-∞=+∑ 22()()q xn x n qN ∞=-∞=+∑ 则它们的周期卷积为14120()()()N p m x n xm x n m -==-∑ 1120()()N m x m xn m -==-∑ 1120()()N m q x m x n m qN -∞==-∞=-+∑∑1120()()N q m x m x n qN m ∞-=-∞=⎡⎤=+-⎢⎥⎣⎦∑∑ ()lq x n qN ∞=-∞=+∑x1(n)和x2(n)周期延拓后的周期卷积等于他们的线性卷积的的周期延拓。
数字信号处理实验报告_五个实验

实验一 信号、系统及系统响应一、 实验目的1、熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定理的理解;2、熟悉时域离散系统的时域特性;3、利用卷积方法观察分析系统的时域特性;4、掌握序列傅立叶变换的计算机实现方法,利用序列的傅立叶变换对连续信号、离散信号及系统响应进行频域分析。
二、 实验原理及方法采样是连续信号数字处理的第一个关键环节。
对采样过程的研究不仅可以了解采样前后信号时域和频域特性发生变化以及信号信息不丢失的条件,而且可以加深对傅立叶变换、Z 变换和序列傅立叶变换之间关系式的理解。
对一个连续信号)(t x a 进行理想采样的过程可用下式表示:)()()(^t p t t xx aa=其中)(^t x a 为)(t x a 的理想采样,p(t)为周期脉冲,即∑∞-∞=-=m nT t t p )()(δ)(^t x a的傅立叶变换为)]([1)(^s m a m j X T j a XΩ-Ω=Ω∑∞-∞=上式表明^)(Ωj Xa为)(Ωj Xa的周期延拓。
其延拓周期为采样角频率(T /2π=Ω)。
只有满足采样定理时,才不会发生频率混叠失真。
在实验时可以用序列的傅立叶变换来计算^)(Ωj X a 。
公式如下:Tw jw ae X j X Ω==Ω|)()(^离散信号和系统在时域均可用序列来表示。
为了在实验中观察分析各种序列的频域特性,通常对)(jw e X 在[0,2π]上进行M 点采样来观察分析。
对长度为N 的有限长序列x(n),有:n jw N n jw k ke m x eX--=∑=)()(1其中,k Mk πω2=,k=0,1,……M-1 时域离散线性非移变系统的输入/输出关系为 ∑∞-∞=-==m m n h m x n h n x n y )()()(*)()(上述卷积运算也可在频域实现)()()(ωωωj j j e H e X eY =三、 实验程序s=yesinput(Please Select The Step Of Experiment:\n 一.(1时域采样序列分析 s=str2num(s); close all;Xb=impseq(0,0,1); Ha=stepseq(1,1,10);Hb=impseq(0,0,3)+2.5*impseq(1,0,3)+2.2*impseq(2,0,3)+impseq(3,0,3); i=0;while(s);%时域采样序列分析 if(s==1) l=1; k=0;while(1)if(k==0)A=yesinput('please input the Amplitude:\n',...444.128,[100,1000]); a=yesinput('please input the Attenuation Coefficient:\n',...222.144,[100,600]); w=yesinput('please input the Angle Frequence(rad/s):\n',...222.144,[100,600]); end k=k+1;fs=yesinput('please input the sample frequence:\n',...1000,[100,1200]); Xa=FF(A,a,w,fs); i=i+1;string+['fs=',num2str(fs)]; figure(i)DFT(Xa,50,string); 1=yesinput 1=str2num(1); end%系统和响应分析else if(s==2)kk=str2num(kk);while(kk)if(kk==1)m=conv(Xb,Hb);N=5;i=i+1;figure(i)string=('hb(n)');Hs=DFT(Hb,4,string);i=i+1;figure(i)string('xb(n)');DFT(Xb,2,string);string=('y(n)=xb(n)*hb(n)');else if (kk==2)m=conv(Ha,Ha);N=19;string=('y(n)=ha(n)*(ha(n)');else if (kk==3)Xc=stepseq(1,1,5);m=conv(Xc,Ha);N=14;string=('y(n)=xc(n)*ha(n)');endendendi=i+1;figure(i)DFT(m,N,string);kk=yesinputkk=str2num(kk);end卷积定理的验证else if(s==3)A=1;a=0.5;w=2,0734;fs=1;Xal=FF(A,a,w,fs);i=i+1;figure(i)string=('The xal(n)(A=1,a=0.4,T=1)'); [Xa,w]DFT(Xal,50,string);i=i+1;figure(i)string =('hb(n)');Hs=DFT(Hb,4,string);Ys=Xs.*Hs;y=conv(Xal,Hb);N=53;i=i+1;figure(i)string=('y(n)=xa(n)*hb(n)');[yy,w]=DFT(y,N,string);i=i+1;figure(i)subplot(2,2,1)plot(w/pi,abs(yy));axis([-2 2 0 2]);xlabel('w/pi');ylabel('|Ys(jw)|');title(FT[x(n)*h(n)]');subplot(2,2,3)plot(w/pi,abs(Ys));axis([-2 2 0 2]);xlabel('w/pi');ylabel('|Ys(jw)|');title('FT[xs(n)].FT[h(n)]');endendend子函数:离散傅立叶变换及X(n),FT[x(n)]的绘图函数function[c,l]=DFT(x,N,str)n=0:N-1;k=-200:200;w=(pi/100)*k;l=w;c=x*Xc=stepseq(1,1,5);子函数:产生信号function c=FF(A,a,w,fs)n=o:50-1;c=A*exp((-a)*n/fs).*sin(w*n/fs).*stepseq(0,0,49); 子函数:产生脉冲信号function [x,n]=impseq(n0,n1,n2)n=[n1:n2];x=[(n-n0)==0];子函数:产生矩形框信号function [x,n]=stepseq(n0,n1,n2) n=[n1:n2];x=[(n-n0>=0)];四、 实验内容及步骤1、认真复习采样理论,离散信号与系统,线性卷积,序列的傅立叶变换及性质等有关内容,阅读本实验原理与方法。
哈尔滨工业大学威海校区_《数字信号处理》实验一

哈尔滨⼯业⼤学威海校区_《数字信号处理》实验⼀数字信号处理实验报告实验名称:实验⼀离散傅⾥叶变换的性质实验⽇期:2011.11.16姓名:尤伟学号:090240328哈尔滨⼯业⼤学(威海)实验⼀离散傅⾥叶变换的性质⼀、实验⽬的1、掌握离散傅⾥叶变换的性质,包括线性特性、时移特性、频移特性、对称性和循环卷积等性质;2、通过编程验证傅⾥叶变换的性质,加强对傅⾥叶变换性质的认识。
⼆、实验原理和⽅法1.线性特性1212D FT [()()]()()ax n bx n aX k bX k +=+ 2.时移特性DFT[()]()DFT[()]()km kmx n m W X k x n m WX k -+=-=3.频移特性()()nlN IDFT X k l IDFT X k W +=4. 对称性设由x(n)开拓成的周期序列为 ()p x n 则()()()p pe po x n x n x n =+ 偶序列()()()*12pe p p x n x n x N n ??=+-?奇序列()()()*12pop p x n x n x N n ??=--?? 将()pe x n 和()po x n 截取主周期,分别得()()()pet pe N x n x n R n = ()()()p o tp oN x n x n R n =则()()()()()p N pet pot x n x n R n x n x n ==+ x(n)序列的实部和虚部的离散⽴叶变换(){}()R e petD FT x n X k = (){}()Im potj x n Xk =[][]()()()()()()()()()()()arg ()arg ()R R R I I I X k X k X N k X k X k X N k X k X k X N k X k X N k X k X k * =-=-=-=-=--=--=-=-- 5.循环卷积()3123121()()()()()x n x n x n X k X k X k N=?=有限长序列线性卷积与循环卷积的关系 X1(n)和x2(n)的线性卷积:11312120()()()()()N m m x n x m x n m x m x n m -∞=-∞==-=-∑∑112()()N m x m xn m -==-∑将X1(n)和x2(n)开拓成以N 为周期的周期序列11()()p r x n x n rN ∞=-∞=+∑22()()p q x n x n qN ∞=-∞=+∑则它们的周期卷积为14120()()()N p p p m x n xm x n m -==-∑12()()N p m x m xn m -==-∑1120()()N m q x m x n m qN -∞==-∞=-+∑∑1120()()N q m x m x n qN m ∞-=-∞=??=+-∑∑ 3()q x n qN ∞=-∞=+∑X1(n)和x2(n)周期开拓后的周期卷积等于他们的线性卷积的的周期开拓。
哈尔滨工程大学数字信号处理实验八

一、实验原理1、频率(周期)检测对周期信号来说,可以用时域波形分析来确定信号的周期,也就是计算相邻的两个信号波峰的时间差或过零点的时间差。
这里采用过零点(ti)的时间差T(周期)。
频率即为f=1/T,由于能够求得多个T的值(ti有多个),故采用它们的平均值作为周期的估计值。
2、幅值检测在一个周期内,求出信号最大值ymax与最小值ymin的差的一半,即A=(ymax-ymin)/2,同样,也会求出多个A值,但第一个A值对应的ymax和ymin不是在一个周期内搜索得到的,故以除以第一个以外的A值的平均作为幅值的估计值。
3、相位检测采用过零法,即通过判断与同频零相位信号过零点时刻,计算其时间差,然后换成相应的相位差。
φ=2п(1-ti/T),同样,以φ的平均值作为相位的估计值。
频率、幅值和相位估计的流程图见实验讲义64页图3.13。
4、数字信号统计量估计(1)峰值p的估计在样本数据x中找出最大值与最小值,其差值为双峰值,双峰值的一半即为峰值。
(2)均值估计(3)均方值估计(4) 差估估计5、频谱分析原理时域分析只能反映信号的幅值随时间的变化情况,除单频谱分量的简单波形外,很难明确提示信号的频率组成的各频率分量的大小,而频域分析能很好的解决此问题。
(1)DFT与FFT对于给定的时域信号y,可以通过Fourier变换得到频域信息Y。
采样信号是一个不连续的频谱,不能算出所有点的值,所以采用离散Fourier变换DFT,但其计算效率较低,故实际中常用快速傅立叶变换。
(2)频率、周期的估计对于Y(k△f),如果当k△f=f~时,Y(k△f)取最大值,则f为频率的估计值,由于采样间隔的误差,f~也存在误差,其误差最大为△f/2。
周期T=1/f,从原理上可以看出,如果在标准信号中混有噪声,用上述方法仍能够精确地估计出原标准信号的频率和周期。
(3)频谱图为了直观地表示信号的频率特性,常常将傅立叶变换的结果用图形的方式表示,及频谱图。
数字信号处理实验报告

数字信号处理实验报告一、实验目的本次数字信号处理实验的主要目的是通过实际操作和观察,深入理解数字信号处理的基本概念和方法,掌握数字信号的采集、处理和分析技术,并能够运用所学知识解决实际问题。
二、实验设备与环境1、计算机一台,安装有 MATLAB 软件。
2、数据采集卡。
三、实验原理1、数字信号的表示与采样数字信号是在时间和幅度上都离散的信号,可以用数字序列来表示。
在采样过程中,根据奈奎斯特采样定理,为了能够准确地恢复原始信号,采样频率必须大于信号最高频率的两倍。
2、离散傅里叶变换(DFT)DFT 是将时域离散信号变换到频域的一种方法。
通过 DFT,可以得到信号的频谱特性,从而分析信号的频率成分。
3、数字滤波器数字滤波器是对数字信号进行滤波处理的系统,分为有限冲激响应(FIR)滤波器和无限冲激响应(IIR)滤波器。
FIR 滤波器具有线性相位特性,而 IIR 滤波器则在性能和实现复杂度上有一定的优势。
四、实验内容与步骤1、信号的采集与生成使用数据采集卡采集一段音频信号,或者在 MATLAB 中生成一个模拟信号,如正弦波、方波等。
2、信号的采样与重构对采集或生成的信号进行采样,然后通过插值算法重构原始信号,观察采样频率对重构信号质量的影响。
3、离散傅里叶变换对采样后的信号进行DFT 变换,得到其频谱,并分析频谱的特点。
4、数字滤波器的设计与实现(1)设计一个低通 FIR 滤波器,截止频率为给定值,观察滤波前后信号的频谱变化。
(2)设计一个高通 IIR 滤波器,截止频率为给定值,比较滤波前后信号的时域和频域特性。
五、实验结果与分析1、信号的采集与生成成功采集到一段音频信号,并在MATLAB 中生成了各种模拟信号,如正弦波、方波等。
通过观察这些信号的时域波形,对不同类型信号的特点有了直观的认识。
2、信号的采样与重构当采样频率足够高时,重构的信号能够较好地恢复原始信号的形状;当采样频率低于奈奎斯特频率时,重构信号出现了失真和混叠现象。
哈工程信号处理实验三

信号处理实验三实验要求:研究抽样过程,分析产生混叠效应的原因,实现不同的重建方案。
3.3.1>> n=0:80;>> f0=300;fs=8000;>> x=sin(2*pi*f0/fs*n+pi/3);>>stem(n,x)>>gtext('f0=300,fs=8k')>>plot(n,x)>>gtext('f0=300,fs=8k')>>gtext('Continue')b.>> n=0:80;>>fs=8000;>>subplot(221)>> x=sin(2*pi*100/fs*n+pi/3); >>stem(n,x);grid;gtext('f0=100') >>subplot(222)>> x=sin(2*pi*225/fs*n+pi/3); >>stem(n,x);grid;gtext('f0=225') >>subplot(223)>>stem(n,x);grid;gtext('f0=350') >>subplot(224)>> x=sin(2*pi*225/fs*n+pi/3); >>stem(n,x);grid;gtext('f0=475')d>> n=0:80;>>fs=8000;>>subplot(221)>> x=sin(2*pi*7525/fs*n+pi/3); >>stem(n,x);grid;gtext('f0=7525') >>subplot(222)>> x=sin(2*pi*7650/fs*n+pi/3); >>stem(n,x);grid;gtext('f0=7650') >>>>subplot(223)>> x=sin(2*pi*7775/fs*n+pi/3);>>stem(n,x);grid;gtext('f0=7675') >>subplot(224)>> x=sin(2*pi*7900/fs*n+pi/3); >>stem(n,x);grid;gtext('f0=7900')e>> n=0:80;fs=8000;>>subplot(221)x=sin(2*pi*32100/fs*n+pi/3); stem(n,x);grid;gtext('f0=32100') subplot(222)x=sin(2*pi*32225/fs*n+pi/3); stem(n,x);grid;gtext('f0=32225') subplot(223)x=sin(2*pi*32350/fs*n+pi/3); stem(n,x);grid;gtext('f0=32350') subplot(224)x=sin(2*pi*32475/fs*n+pi/3); stem(n,x);grid;gtext('f0=32475') >> t=0:1/80000:1000/80000; >> x=cos(2*pi*300*t+pi/6); >>stem(t,x)>> t=0:1/8000:1000/80000;>> x=cos(2*pi*300*t+pi/6);>>stem(t,x)>>fmagplot(x,1/80000)可以看到,当频率变化时,正弦信号并不是严格按信号频率变化的,而是呈周期的,有时变密有时变疏3.3.3>> t=0:1/80000:1000/80000;>> x=cos(2*pi*300*t+pi/6);>>stem(t,x)>> t=0:1/8000:1000/80000;>> x=cos(2*pi*300*t+pi/6);>>stem(t,x)>>fmagplot(x,1/80000)3.3.4>> n=0:100;>> t=n./80000;>> x=cos(2*pi*t*300+pi/6); >>stem(t./10,x)>> [X,W]=dtft(x,900);>>plot(W*10/pi,abs(X))3.3.5fs=8000;fsim=80000;fcut=2*(fs/2)/fsim;>> [b,a]=cheby2(9,60,fcut); %调用雪比滤波器>> [c,d]=freqz(b,a,1000,'whole');%1000点的频率响应>> d(501:1000)=d(501:1000)-2*pi; %d的位置全部左移2pi>> plot(d/2/pi/1000*fsim,abs(c));3.3.6fs=8000;fsim=80000;>> n=0:1000;>> l=length(n);>> x=cos(2*pi*300*n/fsim+pi/6);>> y=x(1:80000/8000:l);>> L=length(y); %取长度避免后面的维度不相等>> y2=zeros(1,length(x)); %置零序列>>for i=0:100;y2(i*10+1)=y(i+1); %取10倍数中的数,相当于抽样置零end>> t=0:0.001:1;>>plot(t,y2)>>fmagplot(y2,0.0000125)3.3.7fs=8000;fsim=80000;k=fsim/fs;n=0:1000;l=length(n);x=cos(2*pi*2000*n/fsim+pi/6);y=x(1:k:l);L=length(y);y2=zeros(1,length(x));for i=0:100;y2(i*10+1)=y(i+1);endt=0:0.001:1;y3=filter(b,a,y2); subplot(211);fmagplot(y3,0.0000125) subplot(212);plot(t,y3)gtext('2k')fs=8000;fsim=80000;k=fsim/fs;n=0:1000;l=length(n);x=cos(2*pi*6000*n/fsim+pi/6);y=x(1:k:l);L=length(y);y2=zeros(1,length(x));for i=0:100;y2(i*10+1)=y(i+1);endt=0:0.001:1;y3=filter(b,a,y2); subplot(211);fmagplot(y3,0.0000125) subplot(212);plot(t,y3)>>gtext('6k')x=cos(2*pi*7000*n/fsim+pi/6);y=x(1:k:l);L=length(y);y2=zeros(1,length(x));for i=0:100;y2(i*10+1)=y(i+1);endt=0:0.001:1;y3=filter(b,a,y2); subplot(211);fmagplot(y3,0.0000125) subplot(212);plot(t,y3)gtext('7k')x=cos(2*pi*9000*n/fsim+pi/6);y=x(1:k:l);L=length(y);y2=zeros(1,length(x));for i=0:100;y2(i*10+1)=y(i+1);endt=0:0.001:1;y3=filter(b,a,y2); subplot(211);fmagplot(y3,0.0000125) subplot(212);plot(t,y3)gtext('9k')x=cos(2*pi*10000*n/fsim+pi/6);y=x(1:k:l);L=length(y);y2=zeros(1,length(x));for i=0:100;y2(i*10+1)=y(i+1);endt=0:0.001:1;y3=filter(b,a,y2); subplot(211);fmagplot(y3,0.0000125) subplot(212);plot(t,y3)gtext('10k')x=cos(2*pi*15000*n/fsim+pi/6);y=x(1:k:l);L=length(y);y2=zeros(1,length(x));for i=0:100;y2(i*10+1)=y(i+1);endt=0:0.001:1;y3=filter(b,a,y2); subplot(211);fmagplot(y3,0.0000125) subplot(212);plot(t,y3)gtext('15k')x=cos(2*pi*17000*n/fsim+pi/6);y=x(1:k:l);L=length(y);y2=zeros(1,length(x));for i=0:100;y2(i*10+1)=y(i+1);endt=0:0.001:1;y3=filter(b,a,y2); subplot(211);fmagplot(y3,0.0000125) subplot(212);plot(t,y3)gtext('17k')x=cos(2*pi*18000*n/fsim+pi/6);y=x(1:k:l);L=length(y);y2=zeros(1,length(x));for i=0:100;y2(i*10+1)=y(i+1);endt=0:0.001:1;y3=filter(b,a,y2); subplot(211);fmagplot(y3,0.0000125) subplot(212);plot(t,y3)gtext('18k')x=cos(2*pi*19000*n/fsim+pi/6);y=x(1:k:l);L=length(y);y2=zeros(1,length(x));for i=0:100;y2(i*10+1)=y(i+1);endt=0:0.001:1;y3=filter(b,a,y2); subplot(211);fmagplot(y3,0.0000125) subplot(212);plot(t,y3)gtext('19k')x=cos(2*pi*20000*n/fsim+pi/6);y=x(1:k:l);L=length(y);y2=zeros(1,length(x));for i=0:100;y2(i*10+1)=y(i+1);endt=0:0.001:1;y3=filter(b,a,y2); subplot(211);fmagplot(y3,0.0000125) subplot(212);plot(t,y3)gtext('20k')从20k开始出现了混叠。
数字信号处理实验五 谱分析 哈工程

实验五谱分析一,试验目的:1 研究不同类型的窗函数,研究一些不同的方法来测试窗的性能;2 专注于有关窄带信号的几个不同的情形。
二,实验原理信号是无限长的,而在进行信号处理时只能采用有限长信号,所以需要将窄带信号“截断”。
在信号处理中,“截断”被看成是用一个有限长的“窗口”看无限长的信倍号,或者从分析的角度是无限长的信号x(t)乘以有限长的窗函数w(t),由傅立叶变换性质可知:x(t)w(t)==1/2πX(jw)W(jw)如果x(t)是频带有限信号,而w(t)是频带无限函数,截断后的信号也必是频带无限信号,从而产生所谓的频谱泄露。
频谱泄露是不可避免的,但是尽量减小,因此设计了不同的窗函数满足不同的要求。
从能量的角度,频谱泄露也是能量泄露,因为加窗后,是原来的信号集中在宅频带内的能量分散到无限的频带范围。
三,实验内容1.用MATLAB编程绘制各种窗函数的形状(1)矩形窗程序N=20;w=boxcar(N);nn=0:N-1;plot(nn,w)(2)汉宁窗程序N=20;w=hanning(N);nn=0:N-1;plot(nn,w)(3)汉明窗程序N=20;w=hamming(N);nn=0:N-1;plot(nn,w)(4)巴特利特窗程序N=20;w=bartlett(N);nn=0:N-1;plot(nn,w)(5)布莱克曼窗程序N=20;w=blackman(N);nn=0:N-1;plot(nn,w)(6)Triang窗程序N=20;w=triang(N); nn=0:N-1;plot(nn,w)(7)Kaiser窗程序N=20;w=kaiser(N,10); nn=0:N-1;plot(nn,w)(8)切比雪夫窗程序N=20;w=chebwin(N,30);nn=0:N-1;plot(nn,w)2,用MATLAB编程绘制各种窗函数的形状及其幅度响应。
(1)矩形窗N=20;w=boxcar(N);[H,W]=dtft(w,512);subplot(111),plot(W/2/pi,20*log(abs(H)));grid,title('MAGNITUDE RESPONSE')xlabel('NORMALIZED FREQUENCY'),ylabel('|H(w)|/dB')(2)汉宁窗N=20;w=hanning(N);[H,W]=dtft(w,512);subplot(111),plot(W/2/pi,20*log(abs(H)));grid,title('MAGNITUDE RESPONSE')xlabel('NORMALIZED FREQUENCY'),ylabel('|H(w)|/dB')(3)汉明窗N=20;w=hamming(N);[H,W]=dtft(w,512);subplot(111),plot(W/2/pi,20*log(abs(H)));grid,title('MAGNITUDE RESPONSE')xlabel('NORMALIZED FREQUENCY'),ylabel('|H(w)|/dB')(4)巴特利特窗N=20;w=bartlett(N);[H,W]=dtft(w,512);subplot(111),plot(W/2/pi,20*log(abs(H)));grid,title('MAGNITUDE RESPONSE')xlabel('NORMALIZED FREQUENCY'),ylabel('|H(w)|/dB')(5)布莱克曼窗N=20;w=blackman(N);[H,W]=dtft(w,512);subplot(111),plot(W/2/pi,20*log(abs(H)));grid,title('MAGNITUDE RESPONSE')xlabel('NORMALIZED FREQUENCY'),ylabel('|H(w)|/dB')(6)Triang窗N=20;w=triang(N);[H,W]=dtft(w,512);subplot(111),plot(W/2/pi,20*log(abs(H)));grid,title('MAGNITUDE RESPONSE')xlabel('NORMALIZED FREQUENCY'),ylabel('|H(w)|/dB')(7)Kaiser窗N=20;w=kaiser(N,10);[H,W]=dtft(w,512);subplot(111),plot(W/2/pi,20*log(abs(H)));grid,title('MAGNITUDE RESPONSE')xlabel('NORMALIZED FREQUENCY'),ylabel('|H(w)|/dB')(8)切比雪夫窗N=20;w=chebwin(N,30);[H,W]=dtft(w,512);subplot(111),plot(W/2/pi,20*log(abs(H)));grid,title('MAGNITUDE RESPONSE')xlabel('NORMALIZED FREQUENCY'),ylabel('|H(w)|/dB')3,绘制矩形窗的幅频响应,窗长度分别为:N=10,N=20,N=50,N=100。
数字信号处理实验报告11-12-10

《数字信号处理》实验报告专业学号姓名实验一 利用FFT 实现快速卷积一、实验目的1.加深理解FFT 在实现数字滤波(或快速卷积)中的重要作用,更好的利用FFT 进行数字信号处理。
2.掌握循环卷积和线性卷积两者之间的关系。
二、实验原理用FFT 来快速计算有限长度序列的线性卷积。
这种方法就是先将输入信号x(n)通过FFT 变换为它的频谱采样值()x k ,然后再和FIR 滤波器的频响采样值H(k)相乘,H(k)可事先存放在存储器中,最后再将乘积H(k)X(k)通过快速傅里叶变换(简称IFFT )还原为时域序列,即得到输出y(n)。
现以FFT 求有限长序列的卷积及求有限长度序列与较长序列间的卷积为例来讨论FFT 的快速卷积方法。
序列x(n)和h(n)的长差不多。
设x(n)的长为N 1,h(n)的长为N 2,要求∑-=-=⊗=1)()()()()(N m m n x m h n y n x n y用FFT 完成这一卷积的具体步骤如下:①为使两有限长序列的线性卷积可用其循环卷积代替而不发生混叠,必须选择循环卷积长度121-+≥N N N ,若采用基2-FFT 完成卷积运算,要求m N 2=(m 为整数)。
②用补零方法使x(n)和h(n)变成列长为N 的序列。
1122()01()01()01()01x n n N x n N n N h n n N h n N n N ≤≤-⎧=⎨≤≤-⎩≤≤-⎧=⎨≤≤-⎩③用FFT 计算x(n)和h(n)的N 点离散傅里叶变换。
④完成X(k)和H(k)乘积,)()()(k H k x k Y = ⑤用FFT 计算 ()Y k 的离散傅里叶反变换得*10*10)(1)(1)(⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=∑∑-=--=N k nk N nk N N k W k Y N W k Y N n y三、主要实验仪器及材料微型计算机、Matlab6.5教学版。
四、实验内容1.数字滤波器的脉冲响应为()22()1/2(),8nN h n R n N ==。
哈尔滨工业大学威海校区_《数字信号处理》实验三

数字信号处理实验报告实验名称:实验三FIR滤波器设计实验日期:2011.11.20姓名:尤伟学号:090240328哈尔滨工业大学(威海)实验三FIR滤波器设计一、实验目的1、熟悉FIR 滤波器设计的基本方法;2、掌握窗函数法设计FIR 滤波器的原理和方法;3、熟悉线性相位FIR 滤波器的幅频特性和相位特性;4、了解不同窗函数对滤波器性能的响应。
二、实验原理1、窗函数法设计FIR 滤波器原理采用理想滤波器的截断单位脉冲响应序列实现实际滤波器。
对理想低通滤波器的单位脉冲响应h(n)进行长度为N 的截取,得到长度为N 的序列h(n),截取时保证因果性和对滤波(d) 器线性相位的要求。
为减少吉布斯效应,对h(n)进行加窗,选择合适的窗函数以保证阻带衰减和过渡带要求。
注意窗函数的副瓣影响滤波器的阻带衰减,主瓣宽度影响滤波器的过渡带宽。
理想低通频率响应理想低通单位取样响应关于α偶对称,实序列全通系统的单位取样响应2、窗函数法设计FIR 低通过程1) 取理想低通单位取样响应的N 点,N 奇数(N-1 阶滤波器)2) 根据阻带衰减和过渡带要求选取窗函数—在保证阻带衰减满足要求的情况下,尽量选择主瓣窄的函数w(n)3) 得到加窗后的序列h(n)=hd(n)w(n) 。
w(n) 时关于(N-1)/2 偶对称,所以h(n)对称性取决于hd(n)4) 验证h(n)的频率响应是否满足设计要求。
若满足,则终止;否则重复2、3、4 步骤。
3、窗函数法设计高通高通= 全通—低通.与低通设计的不同只在第1)步骤,选取理想高通的单位取样响应序列N 点4、设计带通带通= 低通1 —低通2 带通截止频率为ωc1 >ωc2,选择低通1 截止频率ωc1,低通1 截止频率ωc2 5、设计带阻带阻= 低通+ 高通6、频率采样法设计FIR 滤波器原理若要求设计的滤波器Hd(ejw)公式复杂或者根本不能用封闭公式给出,对Hd(ejw)进行频率域取样,得到N 点离散取样值H(k), 用N 点频率取样值得到滤波器。
哈工程数字信号处理实验报告1

数字信号处理实验实验一:基本信号班级:姓名:学号:指导教师:2012年10月实验一:基本信号一:实验原理:本节专注于用MATLAB产生一些基本离散信号的问题。
主要是有那个MATLAB内部向量程序来产生信号。
用MATLAB的stem指令会出离散时间信号。
依据MATLAB的编址约定,标号n=0必须对应nn(1);必须给指定向量的第一个参数以得到正确的n轴。
二:实验内容:1.冲击信号产生并绘出下面的序列。
在每种情况下,水平n轴应该只在指定的区间上展开并应该相应标注。
使用stem指令使每个序列显示成离散时间信号。
x[n]=0.9δ[n-5] 1<=n<=20x[n]=0.8δ[n] -15<=n<=15x[n]=1.5δ[n-333] 300<=n<=350x[n]=4.5δ[n+7] -10<=n<=0L=20;nn=1:(L);imp=zeros(L,1);imp(5)=0.9;stem(nn,imp))L=31;nn=-15:(L-16);imp=zeros(L,1);imp(16)=0.8;stem(nn,imp))L=51;nn=300:350;imp=[zeros(L,1)]'; imp(34)=1.5 stem(nn,imp)L=11;nn=-10:(L-11);imp=zeros(L,1);imp(4)=4.5;stem(nn,imp)实验分析:所得4个图形均符合题目要求3、指数信号衰减的指数信号是数字信号是数字信号处理的基本信号。
因为它是线性常系数差分方程的解。
A.使用函数在区间n=0,1,2,。
,20上绘出信号x[n]=(0.9)ⁿ。
B.在许多推导中,指数信号序列aⁿu[n]须在有限区间上求和。
使用(a)中的函数产生一个指数信号然后对其求和并比较结果。
C.指数序列在信号处理中常常出现的一个原因是,时移并不改变其信号特征。
证明一有限长指数信号满足移位关系:y[n]=ay[n-1], 1<=n<=L-1比较向量y(2:L)和a*y(1:L-1)。
哈工大 数字信号处理实验报告

实验一: 用FFT 作谱分析实验目的:(1) 进一步加深DFT 算法原理和基本性质的理解(因为FFT 只是DFT 的一种快速算法, 所以FFT 的运算结果必然满足DFT 的基本性质)。
(2) 熟悉FFT 算法原理和FFT 子程序的应用。
(3) 学习用FFT 对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT 。
实验原理: DFT 的运算量:一次完整的DFT 运算总共需要2N 次复数乘法和(1)N N -复数加法运算,因而直接计算DFT 时,乘法次数和加法次数都和2N 成正比,当N 很大时,运算量很客观的。
例如,当N=8时,DFT 运算需64位复数乘法,当N=1024时,DFT 运算需1048576次复数乘法。
而N 的取值可能会很大,因而寻找运算量的途径是很必要的。
FFT 算法原理:大多数减少离散傅里叶变换运算次数的方法都是基于nk N W 的对称性和周期性。
(1)对称性()*()k N n kn knNN NW W W --==(2)周期性kn Nkn n N kn k NNN NNW W W W ++===由此可得()()/2(/2)1n N k N n k nk N N N N N k N k N N W W W W W W ---+⎧==⎪=-⎨⎪=-⎩这样:1.利用第三个方程的这些特性,DFT 运算中有些项可以合并;2.利用nk N W 的对称性和周期性,可以将长序列的DFT 分解为短序列的DFT 。
前面已经说过,DFT 的运算量是与2N 成正比的,所以N 越小对计算越有利,因而小点数序列的DFT 比大点数序列的DFT 运算量要小。
快速傅里叶变换算法正是基于这样的基本思路而发展起来的,她的算法基本上可分成两大类,即按时间抽取法和按频率抽取法。
我们最常用的是2M N =的情况,该情况下的变换成为基2快速傅里叶变换。
完成一次完整的FFT 计算总共需要2log 2N N次复数乘法运算和2log N N 次复数加法运算。
数字信号处理实验报告_完整版

实验1 利用DFT 分析信号频谱一、实验目的1.加深对DFT 原理的理解。
2.应用DFT 分析信号的频谱。
3.深刻理解利用DFT 分析信号频谱的原理,分析实现过程中出现的现象及解决方法。
二、实验设备与环境 计算机、MATLAB 软件环境 三、实验基础理论1.DFT 与DTFT 的关系有限长序列 的离散时间傅里叶变换 在频率区间 的N 个等间隔分布的点 上的N 个取样值可以由下式表示:212/0()|()()01N jkn j Nk N k X e x n eX k k N πωωπ--====≤≤-∑由上式可知,序列 的N 点DFT ,实际上就是 序列的DTFT 在N 个等间隔频率点 上样本 。
2.利用DFT 求DTFT方法1:由恢复出的方法如下:由图2.1所示流程可知:101()()()N j j nkn j nN n n k X e x n eX k W e N ωωω∞∞----=-∞=-∞=⎡⎤==⎢⎥⎣⎦∑∑∑ 由上式可以得到:IDFTDTFT( )12()()()Nj k kX e X k Nωπφω==-∑ 其中为内插函数12sin(/2)()sin(/2)N j N x eN ωωφω--= 方法2:实际在MATLAB 计算中,上述插值运算不见得是最好的办法。
由于DFT 是DTFT 的取样值,其相邻两个频率样本点的间距为2π/N ,所以如果我们增加数据的长度N ,使得到的DFT 谱线就更加精细,其包络就越接近DTFT 的结果,这样就可以利用DFT 计算DTFT 。
如果没有更多的数据,可以通过补零来增加数据长度。
3.利用DFT 分析连续信号的频谱采用计算机分析连续时间信号的频谱,第一步就是把连续信号离散化,这里需要进行两个操作:一是采样,二是截断。
对于连续时间非周期信号,按采样间隔T 进行采样,阶段长度M ,那么:1()()()M j tj nT a a a n X j x t edt T x nT e ∞--Ω-Ω=-∞Ω==∑⎰对进行N 点频域采样,得到2120()|()()M jkn Na a M kn NTX j T x nT eTX k ππ--Ω==Ω==∑因此,可以将利用DFT 分析连续非周期信号频谱的步骤归纳如下: (1)确定时域采样间隔T ,得到离散序列(2)确定截取长度M ,得到M 点离散序列,这里为窗函数。
数字信号处理实验报告s实验一和实验二

实验一离散时间信号的产生一、实验目的数字信号处理系统中的信号都是以离散时间形态存在的,所以对离散时间信号的研究是数字信号的基本所在。
而要研究离散时间信号,首先需要产生出各种离散时间信号。
使用MATLAB软件可以很方便地产生各种常见的离散时间信号,而且它还具有强大绘图功能,便于用户直观地处理输出结果。
通过本实验,学生将学习如何用MATLAB产生一些常见的离散时间信号,实现信号的卷积运算,并通过MATLAB中的绘图工具对产生的信号进行观察,加深对常用离散信号和信号卷积和运算的理解。
二、实验原理离散时间信号是指在离散时刻才有定义的信号,简称离散信号,或者序列。
离散序列通常用x(n)来表示,自变量必须是整数。
常见的离散信号如下:(1)单位冲激序列δ(n)如果δ(n)在时间轴上延迟了k个单位,得到δ(n-k),即长度为N的单位冲激序列δ(n)可以通过下面的MATLAB命令获得。
n=-(N-1):N-1x=[zeros(1,N-1) 1 zeros(1,N-1)];stem(n,x)延迟K个采样点的长度为N的单位冲激序列δ(n-k)(k<N)可以用下面命令获得:n=0:N-1y=[zeros(1,M) 1 zeros(1,N-M-1)];stem(n,y)(2)单位阶跃序列u(n)如果u(n)在时间轴上延迟了k个单位,得到u(n-k),即长度为N的单位阶跃序列u(n)可以通过下面的MATLAB命令获得。
n=-(N-1):N-1x=[zeros(1,N-1) ones(1,N)];stem(n,x)延迟的单位阶跃序列可以使用类似于单位冲激序列的方法获得。
(3)矩形序列矩形序列有一个重要的参数,就是序列的宽度N。
矩形序列与u(n)之间的关系为矩形序列等= u(n)— u(n-N)。
因此,用MATLAB表示矩形序列可利用上面的单位阶跃序列组合而成。
(4)正弦序列x(n)这里,正弦序列的参数都是实数。
与连续的正弦信号不同,正弦序列的自变量n 必须为整数。
哈尔滨工程大学数字信号处理实验六

哈尔滨工程大学数字信号处理实验六实验原理IIR数字滤波器一、脉冲响应不变法变换原理将模拟滤波器的s平面变换成数字滤波器的平面,而将模拟滤波器映射成数字滤波器。
MATLAB 信号处理工具箱中提供了IIR数字滤波器设计的函数,常用的函数:IIR滤波器的阶数选择Buttord----巴特沃斯滤波器阶数选择cheb1ord-----切比雪夫I型滤波器阶数选择cheb2ord ----切比雪夫Ⅱ型滤波器阶数选择IIR滤波器的设计Buttrer-----巴特沃斯滤波器设计cheby1-----切比雪夫I型滤波器设计cheby2 ----切比雪夫Ⅱ型滤波器设计maxflat----通用的巴特沃斯低通滤波器设计二、巴特沃斯滤波器设计巴特沃斯滤波器是通带,阻带都单调衰减的滤波器。
(1)调用buttord函数确定巴特沃斯滤波器的阶数,格式[N,Wc]=buttord(Wp,Ws,Ap,As)(2)调用butter函数设计巴特沃斯滤波器,格式[b,a]=butter(N,Wc,options)利用以上两个函数可以设计出模拟滤波器,格式为[N,Wc]=buttord(Wp,Ws,Ap,As,’s’)[b,a]=butter(N,Wc,options.’s’)三、切比雪夫I型滤波器的设计切比雪夫I型滤波器为通带波纹控制器;在通带呈现波纹特性,阻带单调衰减。
[N,Wc]= cheb1ord (Wp,Ws,Ap,As)[b,a]= cheby1 (N,Ap,Wc,options)四、切比雪夫Ⅱ型滤波器的设计切比雪夫Ⅱ型滤波器为阻带波纹控制器;在阻带呈现波纹特性,通带单调衰减。
[N,Wc]= cheb2ord (Wp,Ws,Ap,As)[b,a]= cheby2 (N,As,Wc,options)已知模拟滤波器。
可以利用脉冲响应不变法转换函数impinvar将其变为数字滤波器,调用格式为[bz,az]=impinvar(b,a,Fs).五、双线性变换原理采用非线性频率压缩方法,克服了脉冲响应不变法产生频率响应的混叠失真,使是s平面与z平面建立了一一对应的单值关系,消除多值变换性,频谱混叠现象。
哈工程 数字信号处理实验 实验一

实验一 基本信号一:实验原理使用MATLAB 内部向量程序来产生信号。
用MATLAB 的stem 指令绘出离散时间信号.用MATLAB 的stem 指令会出离散时间信号。
依据MATLAB 的编址约定,标号n=0必须对应nn (1);必须给指定向量的第一个参数以得到正确的n 轴。
二:实验内容2.正弦信号X 【n 】=Acos (ωn+ρ)使用MATLAB 的向量功能求解此问题,将向量赋予余弦或正弦函数,再利用一个函数调用。
在每种指定区间上展开并标注水平轴n 轴。
使用stem 指令显示每个序列。
A .X ₁【n 】=sin (πn /17) 0≤n ≤25 B .X ₂【n 】=sin (πn /17) -15≤n ≤25 C .X ₃【n 】=sin (3πn ﹢π/2) -10≤n ≤10 D . X ₄【n 】=sin (πn /√23) 0≤n ≤503.指数信号衰减的指数信号是数字信号处理中的基本信号,因为它是线性常系数方程的解。
A.利用functions 研究下面的MATLAB 函数,看他如何产生离线指数信号。
然后是用函数在区间n=0,1,2,3,. . . ,20上绘出指数信号x 【n 】=(0.9)ⁿ。
B.指数信号序列a ⁿu 【n 】须在有限区间上求和。
这个和以下面闭合时表示: a a a L nL n --=∑-=1110C.指数序列在信号处理中常常出现的一个原因是,时移并不改变其信号特征。
Y【n】=ay【n-1】,1≤n≤L-1D.产生指数信号另外的方法是使用查分方程给出的递归表示式。
当输入x【n】是一个冲击信号的时候,信号y【n】=aⁿu【n】是下面查分方程的解:y【n】-a【n-1】=x【n】,初始条件y【-1】=0三.实验程序2.正弦函数A.n=0:0.01:25y=sin(pi*n/17)plot(n,y)ylabel(‘y= sin(pi*n/17)’)gridgtext(‘n’)B.n=-15:0.01:25y=sin(pi*n/17)plot(n,y)ylabel(‘y= sin(pi*n/17)’)gridgtext(‘n’)C. n=-10:0.01:10y=sin(3*pi*n+pi/2)ylabel(‘y= sin(3*pi*n+pi/2)’)gridgtext(‘n’)D. n=0:0.01:50y=cos(pi*n/(23^0.5))plot(n,y)ylabel(‘cos(pi*n/(23^0.5)’)gridgtext(‘n’)3.指数信号A function y = genexp( b, n0, L)%GENEXP generate an exponential signal:b^n% usage:Y = genexp(B,N0,L)% B input scalar giving ratio between terns% N0 starting index (integer)% L length of geberated signal% Y output signal Y(1:L)if( L <= 0 )error('GENEXP:length not positive')endnn = n0 + [1 : L]'-1; %---vector of indices y =b .^ nn;endn=0:9;x1=genexp(0.9,0,20)stem(n,x1,'b')B. function y=signal(a,n0,L)if(L<=0)error('SIGNAL:length not positive') endnn=n0+[1:L]'-1y=(1-a.^nn)/(1-a)endu1=genexp(0.9,0,21)ss(1)=0;for i=1:19ss(i+1)=u1(i)+ss(i);endss(19)nn=[1:21]'-1;a=0.9y=(1-a.^nn)/(1-a)C. format compact, subplot(111)n=0:20;m=1:21;x1=genexp(0.9,0,21)subplot(211)stem(n,x1,'b')sum(x1(:))grid,title('Test1_3_3_1')x2=0.9*genexp(0.9,0,21)subplot(212)stem(m,x2,'b')grid,title('Test1_3_3_2')四.结果分析1.正弦函数A.BCD3.A.B.x1 =1.00000.90000.81000.72900.65610.59050.53140.47830.43050.38740.34870.31380.28240.25420.22880.20590.18530.16680.15010.13510.1216ans =8.9058用题目所给公式所求结果为8.9058,结果一致。
数字信号处理实验报告(全)
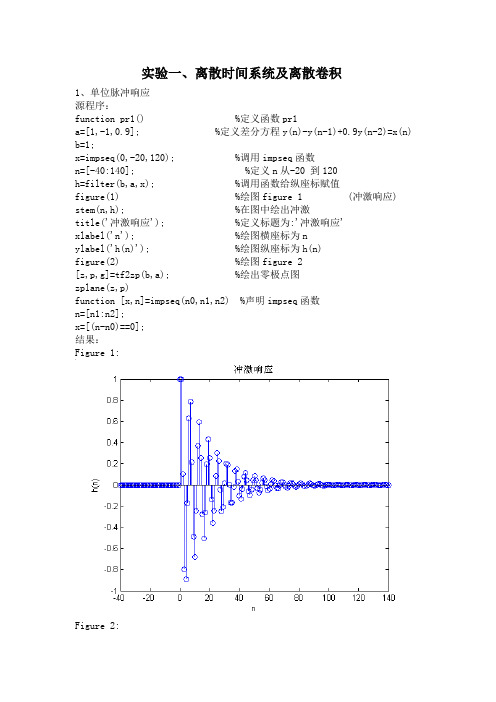
实验一、离散时间系统及离散卷积1、单位脉冲响应源程序:function pr1() %定义函数pr1a=[1,-1,0.9]; %定义差分方程y(n)-y(n-1)+0.9y(n-2)=x(n) b=1;x=impseq(0,-20,120); %调用impseq函数n=[-40:140]; %定义n从-20 到120h=filter(b,a,x); %调用函数给纵座标赋值figure(1) %绘图figure 1 (冲激响应) stem(n,h); %在图中绘出冲激title('冲激响应'); %定义标题为:'冲激响应'xlabel('n'); %绘图横座标为nylabel('h(n)'); %绘图纵座标为h(n)figure(2) %绘图figure 2[z,p,g]=tf2zp(b,a); %绘出零极点图zplane(z,p)function [x,n]=impseq(n0,n1,n2) %声明impseq函数n=[n1:n2];x=[(n-n0)==0];结果:Figure 1:Figure 2:2、离散系统的幅频、相频的分析源程序:function pr2()b=[0.0181,0.0543,0.0543,0.0181];a=[1.000,-1.76,1.1829,-0.2781];m=0:length(b)-1; %m从0 到3l=0:length(a)-1; %l从0 到3K=5000;k=1:K;w=pi*k/K; %角频率wH=(b*exp(-j*m'*w))./(a*exp(-j*l'*w));%对系统函数的定义magH=abs(H); %magH为幅度angH=angle(H); %angH为相位figure(1)subplot(2,1,1); %在同一窗口的上半部分绘图plot(w/pi,magH); %绘制w(pi)-magH的图形grid;axis([0,1,0,1]); %限制横纵座标从0到1xlabel('w(pi)'); %x座标为 w(pi)ylabel('|H|'); %y座标为 angle(H)title('幅度,相位响应'); %图的标题为:'幅度,相位响应' subplot(2,1,2); %在同一窗口的下半部分绘图plot(w/pi,angH); %绘制w(pi)-angH的图形grid; %为座标添加名称xlabel('w(pi)'); %x座标为 w(pi)ylabel('angle(H)'); %y座标为 angle(H)结果:3、卷积计算源程序:function pr3()n=-5:50; %声明n从-5到50u1=stepseq(0,-5,50); %调用stepseq函数声用明u1=u(n)u2=stepseq(10,-5,50); %调用stepseq函数声用明u2=u(n-10) %输入x(n)和冲激响应h(n)x=u1-u2; %x(n)=u(n)-u(n-10)h=((0.9).^n).*u1; %h(n)=0.9^n*u(n)figure(1)subplot(3,1,1); %绘制第一个子图stem(n,x); %绘制图中的冲激axis([-5,50,0,2]); %限定横纵座标的范围title('输入序列'); %规定标题为:'输入序列'xlabel('n'); %横轴为nylabel('x(n)'); %纵轴为x(n)subplot(3,1,2); %绘制第二个子图stem(n,h); %绘制图中的冲激axis([-5,50,0,2]); %限定横纵座标的范围title('冲激响应序列'); %规定标题为:'冲激响应序列'xlabel('n'); %横轴为nylabel('h(n)'); %纵轴为h(n)%输出响应[y,ny]=conv_m(x,n,h,n); %调用conv_m函数subplot(3,1,3); %绘制第三个子图stem(ny,y);axis([-5,50,0,8]);title('输出响应'); %规定标题为:'输出响应'xlabel('n');ylabel('y(n)'); %纵轴为y(n)%stepseq.m子程序%实现当n>=n0时x(n)的值为1function [x,n]=stepseq(n0,n1,n2)n=n1:n2;x=[(n-n0)>=0];%con_m的子程序%实现卷积的计算function [y,ny]=conv_m(x,nx,h,nh)nyb=nx(1)+nh(1);nye=nx(length(x))+nh(length(h));ny=[nyb:nye];y=conv(x,h);结果:实验二、离散傅立叶变换与快速傅立叶变换1、离散傅立叶变换(DFT)源程序:function pr4()F=50;N=64;T=0.000625;n=1:N;x=cos(2*pi*F*n*T); %x(n)=cos(pi*n/16)subplot(2,1,1); %绘制第一个子图x(n)stem(n,x); %绘制冲激title('x(n)'); %标题为x(n)xlabel('n'); %横座标为nX=dft(x,N); %调用dft函数计算x(n)的傅里叶变换magX=abs(X); %取变换的幅值subplot(2,1,2); %绘制第二个子图DFT|X|stem(n,X);title('DFT|X|');xlabel('f(pi)'); %横座标为f(pi)%dft的子程序%实现离散傅里叶变换function [Xk]=dft(xn,N)n=0:N-1;k=0:N-1;WN=exp(-j*2*pi/N);nk=n'*k;WNnk=WN.^nk;Xk=xn*WNnk;结果:F=50,N=64,T=0.000625时的波形F=50,N=32,T=0.000625时的波形:2、快速傅立叶变换(FFT)源程序:%function pr5()F=50;N=64;T=0.000625;n=1:N;x=cos(2*pi*F*n*T); %x(n)=cos(pi*n/16) subplot(2,1,1);plot(n,x);title('x(n)');xlabel('n'); %在第一个子窗中绘图x(n)X=fft(x);magX=abs(X);subplot(2,1,2);plot(n,X);title('DTFT|X|');xlabel('f(pi)'); %在第二个子图中绘图x(n)的快速傅%里叶变换结果:3、卷积的快速算法源程序:function pr6()n=0:14;x=1.^n;h=(4/5).^n;x(15:32)=0;h(15:32)=0;%到此 x(n)=1, n=0~14; x(n)=0,n=15~32% h(n)=(4/5)^n, n=0~14; h(n)=0,n=15~32subplot(3,1,1);stem(x);title('x(n)');axis([1,32,0,1.5]); %在第一个子窗绘图x(n)横轴从1到32,纵轴从0到1.5 subplot(3,1,2);stem(h);title('h(n)');axis([1,32,0,1.5]); %在第二个子窗绘图h(n)横轴从1到32,纵轴从0到1.5 X=fft(x); %X(n)为x(n)的快速傅里叶变换H=fft(h); %H(n)为h(n)的快速傅里叶变换Y=X.*H; %Y(n)=X(n)*H(n)%Y=conv(x,h);y=ifft(Y); %y(n)为Y(n)的傅里叶反变换subplot(3,1,3) %在第三个子窗绘图y(n)横轴从1到32,纵轴从0到6 stem(abs(y));title('y(n=x(n)*h(n))');axis([1,32,0,6]);结果:实验三、IIR数字滤波器设计源程序:function pr7()wp=0.2*pi;ws=0.3*pi;Rp=1;As=25;T=1;Fs=1/T;OmegaP=(2/T)*tan(wp/2); %OmegaP(w)=2*tan(0.1*pi) OmegaS=(2/T)*tan(ws/2); %OmegaS(w)=2*tan(0.15*pi)ep=sqrt(10^(Rp/10)-1);Ripple=sqrt(1/(1+ep.^2));Attn=1/10^(As/20);N=ceil((log10((10^(Rp/10)-1)/(10^(As/10)-1)))/(2*log10(OmegaP/OmegaS) ));OmegaC=OmegaP/((10.^(Rp/10)-1).^(1/(2*N)));[cs,ds]=u_buttap(N,OmegaC);[b,a]=bilinear(cs,ds,Fs);[mag,db,pha,w]=freqz_m(b,a);subplot(3,1,1); %在第一个子窗绘制幅度响应的图形plot(w/pi,mag);title('幅度响应');xlabel('w(pi)');ylabel('H');axis([0,1,0,1.1]);set(gca,'XTickmode','manual','XTick',[0,0.2,0.35,1.1]);set(gca,'YTickmode','manual','YTick',[0,Attn,Ripple,1]);grid;subplot(3,1,2); %在第二个子窗以分贝为单位绘制幅度响应的图形plot(w/pi,db);title('幅度响应(dB)');xlabel('w(pi)');ylabel('H');axis([0,1,-40,5]);set(gca,'XTickmode','manual','XTick',[0,0.2,0.35,1.1]);set(gca,'YTickmode','manual','YTick',[-50,-15,-1,0]);grid;subplot(3,1,3); %在第三个子窗绘制相位响应的图形plot(w/pi,pha);title('相位响应');xlabel('w(pi)');ylabel('pi unit');%axis([0,1,0,1.1]);set(gca,'XTickmode','manual','XTick',[0,0.2,0.35,1.1]);set(gca,'YTickmode','manual','YTick',[-1,0,1]);grid;function [b,a]=u_buttap(N,OmegaC)[z,p,k]=buttap(N);p=p*OmegaC;k=k*OmegaC.^N;B=real(poly(z));b0=k;b=k*B;a=real(poly(p));function [mag,db,pha,w]=freqz_m(b,a)[H,w]=freqz(b,a,1000,'whole');H=(H(1:501))';w=(w(1:501))';mag=abs(H);db=20*log10((mag+eps)/max(mag));pha=angle(H);结果:实验四、FIR数字滤波器的设计源程序:function pr8()wp=0.2*pi;ws=0.35*pi;tr_width=ws-wp;M=ceil(6.6*pi/tr_width)+1;n=0:M-1;wc=(ws+wp)/2;alpha=(M-1)/2;m=n-alpha+eps;hd=sin(wc*m)./(pi*m);w_ham=(hamming(M))';h=hd.*w_ham;[mag,db,pha,w]=freqz_m(h,[1]);delta_w=2*pi/1000;Rp=-(min(db(1:wp/delta_w+1)));As=-round(max(db(ws/delta_w+1:501)));subplot(2,2,1);stem(n,hd);title('理想冲激响应');axis([0,M-1,-0.1,0.3]);ylabel('hd(n)');subplot(2,2,2);stem(n,h);title('实际冲激响应');axis([0,M-1,-0.1,0.3]);ylabel('h(n)');subplot(2,2,3);plot(w/pi,pha);title('滤波器相位响应');axis([0,1,-pi,pi]);ylabel('pha');set(gca,'XTickmode','manual','XTick',[0,0.2,0.3,1.1]); set(gca,'YTickmode','manual','YTick',[-pi,0,pi]); grid;subplot(2,2,4);plot(w/pi,db);title('滤波器幅度响应');axis([0,1,-100,10]);ylabel('H(db)');set(gca,'XTickmode','manual','XTick',[0,0.2,0.3,1.1]); set(gca,'YTickmode','manual','YTick',[-50,-15,0]);function [mag,db,pha,w]=freqz_m(b,a)[H,w]=freqz(b,a,1000,'whole');H=(H(1:501))';w=(w(1:501))';mag=abs(H);db=20*log10((mag+eps)/max(mag));pha=angle(H);结果:。
哈工大数字信号处理大作业 (2)(word文档良心出品)

数字信号处理上机实验报告学号:姓名:实验题目一1. 实验要求:序列卷积计算(1)编写序列基本运算函数,序列相加、相乘、翻转、求和;(2)使用自定义函数计算序列线性卷积,并与直接计算结果相比较。
两个序列分别为:() 1,05 0,others n nx n≤≤⎧=⎨⎩,()2,030,othersn nx n≤≤⎧=⎨⎩2. 实验过程和步骤:包含题目分析,实验程序和流程图(程序要有必要的注释)3. 实验结果和分析:包含程序运行结果图,结果分析和讨论(一)基本运算函数1.原序列2.序列相加序列相加程序function [y,n]=sigadd(x1,n1,x2,n2)%implements y(n)=x1(n)+x2(n)%---------------------------------------------% [y,n] = sigadd(x1,n1,x2,n2)% y = sum sequence over n, which includes n1 and n2% x1 = first sequence over n1% x2 = second sequence over n2 (n2 can be different from n1)%n=min(min(n1),min(n2)):max(max(n1),max(n2)); %duration of y(n) y1=zeros(1,length(n));y2=y1;y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; %x1 with duration of y y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; %x2 with duration of y y=y1+y2; %sequence addition3.序列相乘序列相乘程序function [y,n]=sigmult(x1,n1,x2,n2)%implements y(n)=x1(n)*x2(n)%---------------------------------------------% [y,n] = sigmult(x1,n1,x2,n2)% y = product sequence over n, which includes n1 and n2% x1 = first sequence over n1% x2 = second sequence over n2 (n2 can be different from n1)%n=min(min(n1),min(n2)):m(min(n1),min(n2)) %duration of y(n)y1=zeros(1,length(n));y2=y1;y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; %x1 with duration of y y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; %x2 with duration of y y=y1.*y2; %sequence multiplication4.序列翻转序列翻转程序function [y,n]=sigfold(x, n)%implements y(n)=x(-n)%--------------------------------------------- % [y,n] = sigfold(x,n)%y=fliplr(x);n=-fliplr(n);5.序列移位序列移位程序function [y,n]=sigshift(x,m,n0)%implements y(n)=x(n-n0)%--------------------------------------------- % [y,n] = sigshift(x,m,n0)%n=m+n0;y=x;主程序x1=[0:5];x2=[0,1,2,3];n1=0:5;n2=0:3;%N=n1+n2-1;figure(1)subplot(211)stem(x1)xlabel('x1')subplot(212)stem(x2)xlabel('x2')title('原序列')x= sigadd(x1,n1,x2,n2);figure(2)stem(x)xlabel('x1+x2')title('序列相加')figure(3)[x,n] = sigfold(x1,n1);stem(n,x)xlabel('x1(-n)')title('序列翻转')[x,n] = sigshift(x,n,2);figure(4)stem(n,x)xlabel('x1(-n+2)')title('序列移位')x= sigmult(x1,n1,x2,n2);figure(5)stem(x)title('序列相乘')xlabel('x1*x2')(二)自定义函数计算线性卷积1.题目分析使用上一题中的序列相乘、翻转和求和子函数计算线性卷积,并与这直接用conv 函数计算的线性卷积结果相比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一: 用FFT 作谱分析实验目的:(1) 进一步加深DFT 算法原理和基本性质的理解(因为FFT 只是DFT 的一种快速算法, 所以FFT 的运算结果必然满足DFT 的基本性质)。
(2) 熟悉FFT 算法原理和FFT 子程序的应用。
(3) 学习用FFT 对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT 。
实验原理:DFT 的运算量:一次完整的DFT 运算总共需要2N 次复数乘法和(1)N N -复数加法运算,因而直接计算DFT 时,乘法次数和加法次数都和2N 成正比,当N 很大时,运算量很客观的。
例如,当N=8时,DFT 运算需64位复数乘法,当N=1024时,DFT 运算需1048576次复数乘法。
而N 的取值可能会很大,因而寻找运算量的途径是很必要的。
FFT 算法原理:大多数减少离散傅里叶变换运算次数的方法都是基于nk N W 的对称性和周期性。
(1)对称性()*()k N n kn kn N N N W W W --==(2)周期性()(mod`)()()kn N kn n N k n k N N N N N W W W W ++===由此可得()()/2(/2)1n N k N n k nk N N N N N k N k N N W W W W W W ---+⎧==⎪=-⎨⎪=-⎩这样:1.利用第三个方程的这些特性,DFT 运算中有些项可以合并;2.利用nk N W 的对称性和周期性,可以将长序列的DFT 分解为短序列的DFT 。
前面已经说过,DFT 的运算量是与2N 成正比的,所以N 越小对计算越有利,因而小点数序列的DFT 比大点数序列的DFT 运算量要小。
快速傅里叶变换算法正是基于这样的基本思路而发展起来的,她的算法基本上可分成两大类,即按时间抽取法和按频率抽取法。
我们最常用的是2M N =的情况,该情况下的变换成为基2快速傅里叶变换。
完成一次完整的FFT 计算总共需要2log 2N N 次复数乘法运算和2log N N 次复数加法运算。
很明显,N 越大,FFT 的优点就越突出。
实验步骤(1) 复习DFT 的定义、 性质和用DFT 作谱分析的有关内容。
(2) 复习FFT 算法原理与编程思想, 并对照DIT-FFT 运算流图和程序框图, 读懂本实验提供的FFT 子程序。
(3) 编制信号产生子程序, 产生以下典型信号供谱分析用:1423()()1,03()8470403()347x n R n n n x n n n n n x n n n =⎧+≤≤⎪=-≤≤⎨⎪⎩-≤≤⎧⎪=-≤≤⎨⎪⎩456()cos4()sin 8()cos8cos16cos 20x n n x n n x t t t t πππππ===++(4) 编写主程序。
(5) 按实验内容要求, 上机实验, 并写出实验报告。
实验程序与结果:(1)对x 1(n)进行FFT 变换(N=8和N=16)clear all;N=4;%读入长度x=[1,1,1,1];%调用信号产生子程序产生实验信号n=0:N-1;subplot(3,1,1);stem(n,abs(x));%调用绘图子程序(函数)绘制时间序列波形图title('原时间序列');N=8;%读入长度y1=fft(x,N);%调用FFT 子程序(函数)计算信号的DFTn=0:N-1;subplot(3,1,2);stem(n,fftshift(abs(y1)));holdon;plot(n,fftshift(abs(y1)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=8');N=16;%读入长度y2=fft(x,N);%调用FFT 子程序(函数)计算信号的DFTn=0:N-1;subplot(3,1,3);stem(n,fftshift(abs(y2)));holdon;plot(n,fftshift(abs(y2)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=16');结果图形实验误差分析:理论FFT频谱为一个抽样信号,由图形看出,随着采样率的提高,得到的FFT 频谱分辨率就越高,当N趋于无限时频谱包络接近理论的抽样函数。
(2)对x2(n)进行FFT变换(N=8和N=16)clear all;x=[1,2,3,4,4,3,2,1];%调用信号产生子程序产生实验信号N=8;%读入长度n=0:N-1;subplot(3,1,1);stem(n,abs(x));%调用绘图子程序(函数)绘制时间序列波形图title('原时间序列');N=8;%读入长度y1=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(3,1,2);stem(n,fftshift(abs(y1)));holdon;plot(n,fftshift(abs(y1)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=8');N=16;%读入长度y2=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(3,1,3);stem(n,fftshift(abs(y2)));holdon;plot(n,fftshift(abs(y2)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=16');结果图形实验误差分析:理论FFT频谱为一个抽样函数平方的信号,由图形看出,随着采样率的提高,得到的FFT频谱分辨率就越高,当N趋于无限时频谱包络接近理论的抽样函数。
(3)对x3(n)进行FFT变换(N=8和N=16)clear all;x=[4,3,2,1,1,2,3,4];%调用信号产生子程序产生实验信号N=8;%读入长度n=0:N-1;subplot(3,1,1);stem(n,abs(x));%调用绘图子程序(函数)绘制时间序列波形图title('原时间序列');N=8;%读入长度y1=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(3,1,2);stem(n,fftshift(abs(y1)));holdon;plot(n,fftshift(abs(y1)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=8');N=16;%读入长度y2=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(3,1,3);stem(n,fftshift(abs(y2)));holdon;plot(n,fftshift(abs(y2)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=16');结果图形实验误差分析:由图形看出,随着采样率的提高,得到的FFT频谱分辨率就越高,但对于这个函数来说,N仍然过小,因此幅频特性曲线与理论结果有较大差距。
(4)对x4(n)进行FFT变换(N=8和N=16)clear all;n=0:15;%读入长度x=cos(pi/4*n);%调用信号产生子程序产生实验信号subplot(3,1,1);stem(n,abs(x));%调用绘图子程序(函数)绘制时间序列波形图title('cos(pi/4*n)');N=8;%读入长度y1=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(3,1,2);stem(n,fftshift(abs(y1)));holdon;plot(n,fftshift(abs(y1)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=8');N=16;%读入长度y2=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(3,1,3);stem(n,fftshift(abs(y2)));holdon;plot(n,fftshift(abs(y2)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=16');结果图形:实验误差分析:这个函数的理论FFT抽样频谱为单位冲激函数,因此只要满足抽样定理,FFT 都可以与理论图形一样的曲线。
当N=8,16时,满足抽样定理。
(5)对x5(n)进行FFT变换(N=8和N=16)clear all;n=0:15;%读入长度x=sin(pi/8*n);%调用信号产生子程序产生实验信号subplot(3,1,1);stem(n,abs(x));%调用绘图子程序(函数)绘制时间序列波形图title('sin(pi/8*n)');N=8;%读入长度y1=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(3,1,2);stem(n,fftshift(abs(y1)));holdon;plot(n,fftshift(abs(y1)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=8');N=16;%读入长度y2=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(3,1,3);stem(n,fftshift(abs(y2)));holdon;plot(n,fftshift(abs(y2)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=16');结果图形:实验误差分析:这个函数的理论FFT抽样频谱为单位冲激函数,因此只要满足抽样定理,FFT 都可以与理论图形一样的曲线。
当N=8时,不满足抽样定理,因此产生了混叠失真,当N=8时,满足抽样定理,因此可得到与理论曲线一致的图形。
(6)对x6(n)进行FFT变换(N=16、N=32和N=64)clear all;n=0:64;%读入长度x=cos(pi/8*n)+cos(pi/4*n)+cos(pi/16*5*n);%调用信号产生子程序产生实验信号subplot(4,1,1);stem(n,abs(x));hold on;plot(n,abs(x),'r--');%调用绘图子程序(函数)绘制时间序列波形图title('cos(pi/8*n)+cos(pi/4*n)+cos(pi/16*5*n)');N=16;%读入长度y1=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(4,1,2);stem(n,fftshift(abs(y1)));holdon;plot(n,fftshift(abs(y1)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=16');N=32;%读入长度y2=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(4,1,3);stem(n,fftshift(abs(y2)));holdon;plot(n,fftshift(abs(y2)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=32');N=64;%读入长度y3=fft(x,N);%调用FFT子程序(函数)计算信号的DFTn=0:N-1;subplot(4,1,4);stem(n,fftshift(abs(y3)));holdon;plot(n,fftshift(abs(y3)),'r--');%调用绘图子程序(函数)绘制|X(k)|曲线title('N=64');结果图形:实验误差分析:这个函数的理论FFT抽样频谱为有三个不同频率分量的单位冲激函数,因此只要满足抽样定理,FFT都可以与理论图形一样的曲线。
