结构力学期末考试题型自己整理的
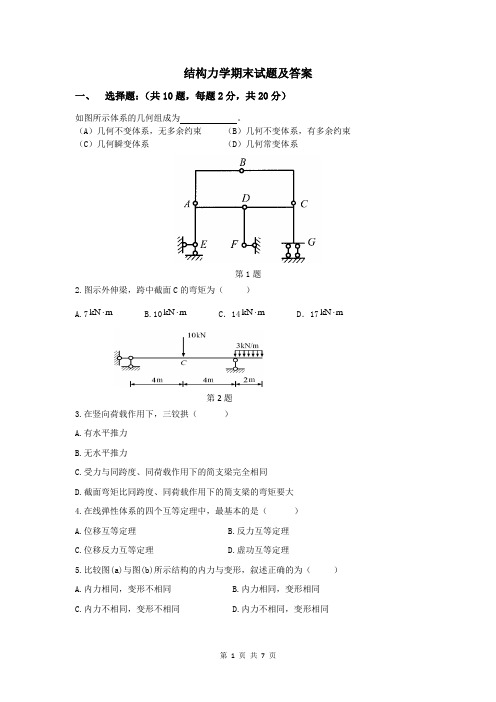
(完整版)结构力学期末考试及答案

铰A,C处M=Q
DE段无剪力,M不变。
BD段无外力,M为一直线,由已知 的D点和C点将直线延到B点。
AB段无外力,M为一直线,由已知 的B点和A点作直线。
由于W=0所以本体系为无多余约束的几何不变体系。
由C点弯矩为零可以判断支座F的 水平反力必须向右,得DF段M图。
由右部无垂直支承知梁BC要承担 剪力F。得BC段M图。BD段内无外力作 用,其M图必为一直线,得CD段M图。
F处的水平力只能由A点向左的水 平力平衡,所以得DA段M图。
BD段没有竖向剪力,M值不变。
6分)图示结构是多余约束的几何来自变体系(简述分析过程)
解:先计算体系的计算自由度W
如果以结点为观察对象:W=2j-b= 2X6-16=0
以刚片为对象:W=3m-2j-b= 3X12-2X16-4 =0
以三角形组成的不变体系I和II加大地为III组成三刚片 体系。刚片1和2以二平行的连杆组成平行于地面的无穷 远处虚铰,实铰(1,3)和(2,3)与此无穷远虚铰不成 一线,因而体系为几何不变。
结构力学期末试题及答案
1.图乘法的应用条件是什么?求变截面梁和拱的位移时可否用图乘法?
答.图乘法的应用条件:1)杆轴线为直线,2)杆端的EI为常数3)MP和M图中至少有一个为直线图形。否。(7分)
2.超静定结构的内力只与各杆件的刚度相对值有关,而与它们的刚度绝对值无关,对吗?为什么?
A.DE、AB段B.CD、DE段C.AB、BC段D.BC、CD段
二、填空题:(共10题,每题2分,共20分)
1.两刚片用一个铰和_________________相联,组成无多余约束的几何不变体系。
2.所示三铰拱的水平推力FH等于_______________。
3.图示结构,当支座A发生转角 时,引起C点的竖向位移为_____________。
4.用位移法计算图示结构,并绘其弯矩图,EI为常数。
5.用力矩分配法计算图示结构,并绘其弯矩图,EI为常数。
答案
一、选择题:(共10题,每小题2分,共20分)
1.A 2.D 3. A 4.D 5.A 6.C 7.D 8.B 9.C 10.C
二、填空题(共10空,每空2分,共20分)
1.不通过此铰的链杆 2. FP/2(→) 3.lθ(↓) 4. 刚体体系虚功原理 5.不变6.-1/2 7.6 8.(c) 9.反对称 10.无侧移的超静定结构
答:不对。仅受荷载作用的超静定结构,其内力分布与该结构中的各杆刚度相对值有关;而受非荷载因素作用的超静定结构,其内力则与各杆刚度的绝对值有关。(7分)
四、计算题. (1、2题8分,3题10分,4、5题12分,4题共计50分)
1.图示桁架,求1、2杆的轴力。
解:FN1=75KN,FN2= KN
2.图示刚架,求支座反力,并绘弯矩图。
结构力学考试题及答案

结构力学考试题及答案【篇一:《结构力学》期末考试试卷(a、b卷-含答案)】>一、填空题(20分)(每题2分)1.一个刚片在其平面内具有3 一个点在及平面内具有自由度;平面内一根链杆自由运动时具有 3 个自由度。
2.静定结构的内力分析的基本方法,隔离体上建立的基本方程是程。
3.杆系结构在荷载,温度变化,支座位移等因素作用下会产生和4.超静定结构的几何构造特征是5.对称结构在对称荷载作用下,若取对称基本结构和对称及反对称未知力,则其中反对称未知力等于零。
6.力矩分配法适用于。
7.绘制影响线的基本方法有8.单元刚度矩阵的性质有9.结构的动力特性包括;; 10. 在自由振动方程y(t)?2??y(t)??2y(t)?0式中,?称为体系的率,?称为阻尼比。
...二、试分析图示体系的几何组成(10分)(1)(2)答案:(1)答:该体系是几何不变体系且无余联系。
(2)答:该体系是几何不变体系且无多余联系。
三、试绘制图示梁的弯矩图(10分)(1)(2)答案:(1)(2)m图四、简答题(20分)1. 如何求单元等效结点荷载?等效荷载的含义是什么?答案:2.求影响线的系数方程与求内力方程有何区别?答案:3.动力计算与静力计算的主要区别是什么?答案:4.自由振动的振幅与那些量有关?答案五、计算题(40分)1、用图乘法计算如图所示简支梁a截面的转角?a。
已知ei=常量。
(10分)答案:解:作单位力状态,如图所示。
分别作出mp和m图后,由图乘法得:2.试作图示伸臂量的fby mk的影响线。
答案:fby的影响线mk的影响线3.试用力法计算单跨静定梁。
并作m图。
(10分)解:选取基本结构,并作出单位弯局矩图和荷载弯矩图如图所示4.试用位移法求作图示连续梁的内力图。
(10分)(型常数、载常数见附表)解:(c)m 解:(1)只有一个未知量,基本体系如图所示(d)mp (2)建立位移法典型方程k11z1?r1p?0(3)作m,mp如图所示(a)(b)11k11?7i;r1p?pl?ql2881(pl?ql2)(4)代入方程解得:z1??56i(5)叠加法绘制弯矩图(e)附表:型常数、载常数表(e)【篇二:结构力学试题及答案汇总(完整版)】. 图示体系的几何组成为:( a) a. 几何不变,无多余联系; b. 几何不变,有多余联系; c. 瞬变; d. 常变。
结构力学1期末考试及参考答案A

EI)
F P l
l
l
8. 根据图示结构特点,用位移法建立最简基本方程并求 MAE 和 MDF(不计各杆轴
向变形,各杆弯曲q 刚度皆为 EI)
E
D
F
l
A
B
C
l
l
l
9. 用力矩分配法绘制图示连续梁的弯矩图(保留到整数位)
12kN/m
A
EI
B EI
C EI
D
8m
8m
6m
10. 绘制图示静定结构的影响线(ILMB ,ILRD,ILFQB 右,ILRB),并确定给定移动荷
结构力学(I)试 题
题号 一 二 三 四 分数
作业
学号 姓名
其它
总分
1、 简述下列问题(每题 3 分,共 30 分)
1. 计算简图的简化原则是什么?
2. 描述刚结点的受力特征和几何特征。
3. 常用的杆件结构有哪几类?
4. 什么叫几何不变体系?分为哪两类结构?
5. 静定结构计算方法和超静定结构计算方法有何不同
8. x = (3 - 2 2)l ᄏ 0.172l
9.只需两个柱子的线刚度相等就能满足剪力相等的要求。
10.
2 y= a
3
2,3 荷载是临界荷载,当把荷载 2 放在尖点时是最不利荷载位置,对应的弯矩值是 10FPa/3Leabharlann 第 2 页 (共 2 页)
载对 RB 的最不利荷载位置和最不利反力值(其中 FP1=P,FP2=2P,d=l/3)。
F
F
P1
P2
A
d
B
C
D
l
l
l
第 3 页 (共 3 页)
结构力学(I) 答案
结构力学期末复习题及答案

结构力学期末复习题及答案结构力学是土木工程中非常重要的一门学科,它涉及到各种结构的力学性能和行为。
在期末复习中,学生们常常面临大量的习题和问题。
本文将为大家提供一些常见的结构力学复习题及其答案,希望能够帮助大家更好地复习和理解这门学科。
一、静力学题目1. 一个悬臂梁的长度为L,截面形状为矩形,宽度为b,高度为h。
如果梁的弯矩为M(x),则在梁的中点处的弯矩为多少?答案:对于悬臂梁,中点处的弯矩为M(L/2) = (3/8) * Mmax,其中Mmax为梁的最大弯矩。
2. 一根梁在两个支座之间均匀受到集中力P,支座之间的距离为L。
如果梁的弯矩为M(x),则在支座处的弯矩为多少?答案:在支座处,弯矩为M(0) = P * L / 4。
二、梁的挠度计算题目1. 一个悬臂梁的长度为L,截面形状为矩形,宽度为b,高度为h。
如果梁的弯矩为M(x),则梁的挠度为多少?答案:对于悬臂梁,挠度为δ(x) = (Mmax * x^2) / (2 * E * I),其中Mmax为梁的最大弯矩,E为材料的弹性模量,I为梁的截面惯性矩。
2. 一根梁在两个支座之间均匀受到集中力P,支座之间的距离为L。
如果梁的弯矩为M(x),则梁的挠度为多少?答案:在支座处,挠度为δ(0) = (P * L^3) / (48 * E * I)。
三、杆件的应力计算题目1. 一根杆件受到集中力P,杆件的截面形状为圆形,直径为d。
如果杆件的应力为σ,材料的弹性模量为E,则应力与应变之间的关系为什么?答案:应力与应变之间的关系为σ = E * ε,其中ε为应变。
2. 一根杆件受到集中力P,杆件的截面形状为矩形,宽度为b,高度为h。
如果杆件的应力为σ,材料的弹性模量为E,则应力与应变之间的关系为什么?答案:应力与应变之间的关系为σ = E * ε,其中ε为应变。
四、梁的破坏计算题目1. 一根梁的长度为L,截面形状为矩形,宽度为b,高度为h。
如果梁的弯矩为M(x),材料的抗弯强度为fy,则梁的破坏位置在哪里?答案:梁的破坏位置在弯矩达到抗弯强度的位置,即M(x) = fy * S,其中S为梁的截面面积。
结构力学期末考试复习题及参考答案-专升本
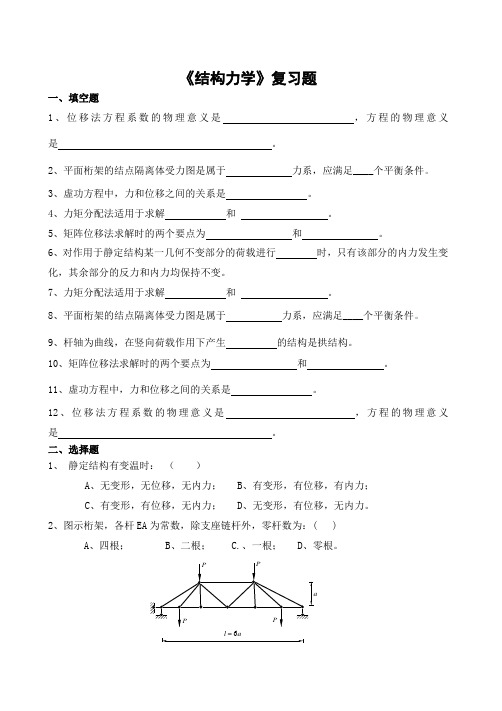
《结构力学》复习题一、填空题1、位移法方程系数的物理意义是,方程的物理意义是。
2、平面桁架的结点隔离体受力图是属于力系,应满足____个平衡条件。
3、虚功方程中,力和位移之间的关系是。
4、力矩分配法适用于求解和。
5、矩阵位移法求解时的两个要点为和。
6、对作用于静定结构某一几何不变部分的荷载进行时,只有该部分的内力发生变化,其余部分的反力和内力均保持不变。
7、力矩分配法适用于求解和。
8、平面桁架的结点隔离体受力图是属于力系,应满足____个平衡条件。
9、杆轴为曲线,在竖向荷载作用下产生的结构是拱结构。
10、矩阵位移法求解时的两个要点为和。
11、虚功方程中,力和位移之间的关系是。
12、位移法方程系数的物理意义是,方程的物理意义是。
二、选择题1、静定结构有变温时:()A、无变形,无位移,无内力;B、有变形,有位移,有内力;C、有变形,有位移,无内力;D、无变形,有位移,无内力。
2、图示桁架,各杆EA为常数,除支座链杆外,零杆数为:( )A、四根;B、二根; C.、一根; D、零根。
l= a63、绘制任一量值的影响线时,假定荷载是()A、一个方向不变的单位移动荷载B、一组移动荷载C、动力荷载D、单个移动荷载4、机动法作简支梁内力影响线所依据的原理是( )A、刚体系虚位移原理B、刚体系虚力原理C、变形体虚位移原理D、变形体虚力原理5、下列说法,哪一句是错的:()A.超静定结构具有多余约束;B.对于超静定结构支座位移、温度改变产生反力和内力;C.在荷载作用下超静定结构内力与各杆刚度的绝对值大小有关;D.在荷载作用下超静定结构内力与各杆刚度的相对比值有关;6、图示体系的几何组成为 ( )A.几何不变,无多余联系;B.几何不变,有多余联系;C. 瞬变;D.常变。
7、机动法作简支梁内力影响线所依据的原理是( )A.刚体系虚位移原理B.刚体系虚力原理C.变形体虚位移原理D.变形体虚力原理8、下列说法,哪一句是错的:()A.超静定结构具有多余约束;B.对于超静定结构支座位移、温度改变产生反力和内力;C.在荷载作用下超静定结构内力与各杆刚度的绝对值大小有关;D.在荷载作用下超静定结构内力与各杆刚度的相对比值有关;9、力法典型方程中δij的物理意义为:()A.在i处作用的单位力引起的j处的位移大小;B.在j处作用的单位力引起的i处的位移大小;C.在j处作用的单位位移引起的i处的力大小;D.在i处作用的单位位移引起的j处的力大小;10、静定结构的内力计算与()A、EI无关;B、 EI 相对值有关;C、EI绝对值有关;D、 E无关,I 有关。
结构力学期末复习题及答案全解

一、填空题。
1、在梁、刚架、拱、桁架四种常见结构中,主要受弯的是 梁 和 钢架 ,主要承受轴力的是拱 和 桁架 。
2、选取结构计算简图时,一般要进行杆件简化、支座 简化、 结点 简化和 荷载 简化。
3、分析平面杆件体系的几何组成常用的规律是两刚片法则、 三钢片 和二元体法则。
4、建筑物中用以支承荷载的骨架部分称为 结构 ,分为 板件 、 杆壳 和实体 三大类。
5、一个简单铰相当于 两个 个约束。
6、静定多跨梁包括 基础 部分和 附属 部分,内力计算从 附属 部分开始。
7、刚结点的特点是,各杆件在连接处既无相对 移动 也无相对 转动 ,可以传递 力 和 力矩 。
8、平面内一根链杆自由运动时的自由度等于三 。
二、判断改错题。
1、三刚片用三个铰两两相联不一定成为几何不变体系。
( )2、对静定结构,支座移动或温度改变不会产生内力。
( )3、力法的基本体系不一定是静定的。
( )4、任何三铰拱的合理拱轴不一定是二次抛物线。
( )5、图乘法不可以用来计算曲杆。
( ) 三、选择题。
1、图示结构中当改变B 点链杆方向(不能通过A 铰)时,对该梁的影响是( )A 、全部内力没有变化B 、弯矩有变化C 、剪力有变化D 、轴力有变化2、右图所示刚架中A 支座的反力A H 为( )A 、PB 、2P -C 、P -D 、2P3、右图所示桁架中的零杆为( )A 、CH BI DG ,,B 、BI AB BG DC DG DE ,,,,,C 、AJ BI BG ,,D 、BI BG CF ,,4、静定结构因支座移动,( ) A 、会产生内力,但无位移 B 、会产生位移,但无内力 C 、内力和位移均不会产生 D 、内力和位移均会产生5A 、θδ=+a cX B 、θδ=-a cXC 、θδ-=+a cXD 、θδ-=-acX四、对下图所示平面杆件体系作几何组成分析。
五、1‘用力法计算下图所示超静定组合结构,并画出梁式杆的M 图。
结构力学期末复习题及答案全解

一、填空题。
1在梁、刚架、拱、桁架四种常见结构中,主要受弯的是 _和 钢架,主要承受轴力的是拱 ____ 和桁架 。
2、 选取结构计算简图时, 一般要进行杆件简化、 支座 简化、结点 简化和 荷载 简化。
3、 分析平面杆件体系的几何组成常用的规律是两刚片法则、 三钢片 __________ 和二元体法则。
4、 建筑物中用以支承荷载的骨架部分称为 结构 ,分为________ 、 杆壳和实体 __________ 三大类。
5、 一个简单铰相当于 两个 个约束。
6、 静定多跨梁包括 基础 部分和 附属 部分,内力计算从 附属 部分开始。
7、 刚结点的特点是,各杆件在连接处既无相对 移动也无相对 转动,可以传递 力_和力矩 。
8、 平面内一根链杆自由运动时的自由度等于三。
、判断改错题。
1三刚片用三个铰两两相联不一定成为几何不变体系。
( ) 2、 对静定结构,支座移动或温度改变不会产生内力。
()3、 力法的基本体系不一定是静定的。
( )4、 任何三铰拱的合理拱轴不一定是二次抛物线。
()5、图乘法不可以用来计算曲杆。
( )三、选择题。
A 、全部内力没有变化B 弯矩有变化C 剪力有变化D 轴力有变化2、右图所示刚架中 A 支座的反力H A 为()P——C 2EIEI B1图示结构中当改变 B 点链杆方向(不能通过A 铰)时,对该梁的影响是(EI A3、右图所示桁架中的零杆为( )A DG,BI,CHB 、DE,DG, DC,BG, AB, BlC BG, Bl , AJD 、CF , BG,BI4、 静定结构因支座移动,() A 、会产生内力,但无位移 B 会产生位移,但无内力 C 内力和位移均不会产生 D 内力和位移均会产生5、 对右图所示的单跨超静定梁,支座A 产生逆时针转角 二,支座B 产生竖直沉降C ,若取简支梁为其基本结构,则力法方程为( )AX c» a ~c 八AB X— —□El 1 az1X Ca聿我績f $y C=-Q 1aABDX -C =-QX 『F 、—r 1—.ElIa四、对下图所示平面杆件体系作几何组成分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
W 2jb 269 3
例3 求图示体系的计算自由度W。
解: 结点数: j 6 链杆数: b 9
计算自由度:
W 2jb 269 3
例4 求图示体系的W。
解:
刚片数:m= 8 ( 曲杆ACDEB和FG、CG、GH、DH、HI、EI、IJ )
刚结数:g= 0 单铰数:h= 9 (C、D、E为单铰,G、H、I为复铰,每个复
M
L G
12kN 1m
16kN m
10kN m
6kN m
M
R G
12kN 1m 16kN m
4kN m
M
L B
16kN m
MH
ME
MF 2
ql 2 8
32kN m
MH
ME
MF 2
ql 2 8
32kN m
最大弯矩Mmax应在剪力为0的K截面。
2. 有若干个基本部分, 这些基本部分之间用附属部分相连。
3. 上述两种类型的组合。
多跨静定梁的受力特点 1.当力作用于基本部分或基本梁与附属梁的联结铰上时, 附属 部分不受力, 只有基本部分受力。 2.当力作用于附属部分时, 基本梁和附属梁均受力。
3. 在竖向荷载作用下:多跨静定梁中无轴力,附属梁向基本梁 只传递竖向分力。
2
平行。体系为几何不变,且
1
无多余约束。
例7 对图示体系作几何组成分析。
例7 对图示体系作几何组成分析。
Ⅰ
OⅡ, Ⅲ (在无穷远处)
Ⅲ
OⅠ, Ⅲ
OⅠ, Ⅱ
Ⅱ
⑴撤去支座,只分析上部体系; ⑵选择刚片及相应的联系; ⑶结论:三铰不共线,是无多余约束的几何不变体系。
例8 对图示体系作几何组成分析。
解: ⑴选择刚片及相应的联系;
3、试分析图示体系的几何构造。 4、试分析图示体系的几何构造。
5、试分析图示体系的几何构造。 6、试分析图示体系的几何构造。
7、试分析图示体系的几何构造。 8、试分析图示体系的几何构造。
9、试分析图示体系的几何构造。 10、试分析图示体系的几何构造。
11、试分析图示体系的几何构造。 12、试分析图示体系的几何构造。
1、试求图示梁的支座反力,并作其内力图(弯矩、剪 力)。
2、试求图示梁的支座反力,并作其内力图(弯矩、剪 力)。
3、不求支座反力,试作图所示多跨静定梁的内力图。 4、试求图示梁的弯矩图、剪力图和轴力图。
5、试求图示梁的支座反力,并作其内力图(弯矩、剪 力)。
附加例题
多跨静定梁常见组成方式: 1. 只有一个基本部分,在此基本部分上依次叠加附属部分。
铰均相当于2个单铰)
支杆数:b= 9
计算自由度:
W 3m 3g 2h b 38 30 29 9
3
例5 试分析图示体系的几何构造。
图b
图c
解:若按图b或图c所示的刚片划分,则刚片Ⅱ与基础刚片Ⅲ之
间均只有一根支座链杆直接联系,另一个为间接联系,不能直
接套用三刚片规则。
刚片Ⅰ、Ⅱ之间通过链杆ED和CF 相联,其延长后形成虚铰(Ⅰ,Ⅱ) ; 刚片Ⅰ、Ⅲ之间通过AD杆和支座 链杆相联,形成虚铰(Ⅰ, Ⅲ); 刚片 Ⅱ、Ⅲ之间通过AE杆和C支座链杆 相联,形成虚铰(Ⅱ, Ⅲ)。
g——单刚结个数;
h——单铰结个数; b——单链杆根数。
(2)链杆体系
W=2j-b
其中:j——结点数;
b——单链杆数。
等
注意:
效
平面体系计算自由度的公式
(1)刚片体系
W=3m-(3g+2h+b)
其中:m——刚片数;
g——单刚结个数;
h——单铰结个数; b——单链杆根数。
(2)链杆体系
W=2j-b
其中:j——结点数;
用截面法计算 控制截面弯矩。
M C 0 M A 20kN 1m 20kN m
M D 20kN 2m 58kN 1m 18kN m
M E 20kN 3m 58kN 2m 30kN 1m 26kN m
M F 12kN 2m 16kN m 10kN m 18kN m
Part 1 Part 2 Part 3 Part 4 Part 5 Part 6 Part 7
结构几何构造分析 静定梁的内力分析 静定刚架的内力分析 静定平面桁架的内力分析 结构位移计算 力法 位移法
CONTENTS
目
录
PART 结构的几何 01 构造分析
1、试分析图示体系的几何构造。 2、试分析图示体系的几何构造。
b——单链杆数。
等
注意:
效
例1 求图示体系的计算自由度W。
C
F
G
A
B
D
E
解: 以刚片的自由度为对象
刚片数:m=7;
单铰数:h =9; (D、E为复铰)
刚结数:g =0;
支杆数: b=3。
W 3m 3g 2h b 3 7 3 0 2 9 3 0
例2 求图示体系的计算自由度W。
解: 结点数: j 6 链杆数: b 9
13、试分析图示体系的几何构造。 14、试分析图示体系的几何构造。
15、试分析图示体系的几何构造。
图1
图2
图3
16、试分析图示体系的几何构造。
图1
图2
图3
17、计算下列各体系的自由度W。
(1)
(2)
(3)
(4)
附加例题
平面体系计算自由度的公式
(1)刚片体系
W=3m-(3g+2h+b)
其中:m——刚片数;
体系为几何不变,并且无多余约束。
例6 对图示体系作几何组成分析。
解: ⑴撤去支座链杆,分析上部体系;
⑵撤去二元体(DE,DI ) 和(AF,AJ ) ;
⑶寻找刚片和相应的联系:
刚片Ⅰ:CEGF 刚片Ⅱ:BJHI
链杆:FJ、GH、EI
⑷结论:刚片Ⅰ与刚片Ⅱ之间的联结
3
符合规律4。即:三根链杆
既不相交于一点,也不相互
⑵OⅡ, Ⅲ与OⅠ, Ⅲ 的连线与组成 无穷远铰OⅠ, Ⅱ 的两条平行线 平行。
⑶结论:虚铰OⅡ, Ⅲ与OⅠ, Ⅲ的连线 与形成虚铰OⅠ, Ⅱ 的两根 链杆平行,三铰共线, 为瞬变体系。
O Ⅰ, Ⅱ
(在无穷远处)
OⅠ, Ⅲ
E 刚片Ⅱ
D
C
O F Ⅱ, Ⅲ
刚片 Ⅲ
力分析
例1 试作图示梁的剪力图和弯矩图。
解:计算支反力。
由∑MB=0,得FA=58kN(↑) 由∑Fy=0,得FB=12kN(↑)
用截面法计算 控制截面剪力。
FSRC 20kN FSRA 20kN 58kN 38kN FSRD 20kN 58kN - 30kN 8kN FSRE FSRD 8kN FSRF 12kN FSRB 0
