MATLAB蛛网模型

合集下载

matlab patternnet算法原理

matlab patternnet算法原理patternnet算法是一种用于模式识别和分类问题的神经网络算法，在MATLAB中以函数patternnet实现。

该算法基于多层感知机（MLP）神经网络模型。

patternnet算法的原理如下：1. 数据准备：将输入数据和对应的目标输出数据进行预处理，确保输入数据和目标输出数据具有相同的维度和范围，并进行合适的数据归一化处理。

2. 网络结构：确定神经网络的结构，包括输入层、隐藏层和输出层的节点数以及它们之间的连接关系。

隐藏层的节点数和层数的选择需要根据具体问题进行调整。

3. 权重和偏差初始化：为网络中的权重和偏差赋予初始值。

通常使用随机数生成方法来初始化这些参数，以增加网络的灵活性。

4. 前向传播：通过将输入数据从输入层传递到隐藏层再传递到输出层，计算网络的输出值。

每个节点都会根据输入和相应的权重计算出一个加权和，并通过激活函数进行非线性映射得到节点的输出值。

5. 计算误差：根据网络的输出值和目标输出值之间的差异，计算网络的误差。

常用的误差函数包括均方误差（MSE）和交叉熵误差（cross-entropy error）。

6. 反向传播：根据误差，从输出层开始逐层地计算每个节点对误差的贡献，并根据链式法则，将误差反向传播到网络的每一层。

通过调整权重和偏差，使得网络的输出值逼近目标输出值。

7. 权重更新：根据反向传播算法计算得到的梯度信息，使用优化算法（如梯度下降法）来更新网络中的权重和偏差。

更新过程中可以设置学习率和动量等参数，以控制权重的调整速度和稳定性。

8. 重复迭代：重复执行步骤4至步骤7，直到网络的收敛或达到预定的迭代次数。

收敛表示网络的输出已经达到一个满意的精度，不再发生显著变化。

9. 模型评估：使用独立的测试数据集对训练好的模型进行评估，计算模型在新数据上的准确性、精度等指标，判断模型的性能和泛化能力。

以上就是patternnet算法的基本原理。

如何使用MATLAB进行网络分析与建模

如何使用MATLAB进行网络分析与建模网络分析与建模是数据科学领域中的重要研究方法之一，它涉及到了计算机科学、数学、统计学等多个学科领域。

而在现代信息爆炸的时代，网络数据的规模和复杂性不断增加，对于分析和建模工具的要求也越来越高。

MATLAB作为一个强大的数学计算软件，提供了丰富的功能和工具，可以帮助我们进行网络分析与建模。

本文将介绍如何使用MATLAB进行网络分析与建模。

第一部分：网络分析基础网络分析是研究网络结构、功能和演化规律的一种方法。

在网络分析中，我们通常需要描述网络的拓扑结构、节点与边的关系、节点的属性等信息。

而MATLAB提供了一些常用的工具和函数，可以方便地进行网络分析。

首先，我们需要将网络数据导入到MATLAB中。

MATLAB支持导入各种格式的网络数据，如邻接矩阵、边列表、节点属性等。

使用MATLAB的数据导入和读取函数，我们可以将网络数据转换成MATLAB中的矩阵或表格，方便后续的分析和建模。

其次，我们可以使用MATLAB提供的函数和工具来计算网络的基本属性，如网络的度分布、聚类系数、平均路径长度等。

这些属性可以帮助我们了解网络的结构和功能，并进行比较和分类。

MATLAB还提供了可视化工具，可以直观地展示网络的拓扑结构和属性分布。

第二部分：网络建模与预测网络建模是研究网络演化和行为规律的关键内容。

借助MATLAB的数学建模和机器学习工具，我们可以构建各种网络模型，并使用这些模型来预测网络的演化和行为。

常用的网络建模方法包括随机网络模型、小世界网络模型、无标度网络模型等。

我们可以使用MATLAB的随机数生成函数和图论工具，生成各种类型的网络模型，并进行参数调节和性能评估。

此外，MATLAB还提供了机器学习和深度学习工具箱，可以用于网络模型的训练和预测。

网络预测是网络分析与建模的重要应用之一。

通过分析网络的演化规律和行为模式，我们可以预测网络的未来走向和趋势。

MATLAB提供了一些预测模型和函数，如时间序列分析、回归分析、神经网络等。

关于房价的数学建模

一、问题重述房价问题事关国计民生，对国家经济发展和社会稳定有重大影响，一直是各国政府大力关注的问题。

我国自从取消福利分房制度以来，随着房价的不断飙升，房价问题已经成为全民关注的焦点议题之一，从国家领导人、地方政府官员，到开发商、专家学者、普通百姓通过各种媒体表达各种观点，但对于房价是否合理、未来房价的走势等关键问题，至今尚未形成统一的认识。

请根据中国国情，收集建筑成本、居民收入等与房价密切相关的数据，选取我国具有代表性的几类城市，解决以下几个方面的问题：问题一：房价的合理性，并进行定量分析；问题二：房价的未来走势，并进行定量分析；问题三：进一步探讨使得房价合理的具体措施；问题四：进一步探讨对经济发展产生的影响，并进行定量分析。

二、问题分析问题一分析：本问需要我们通过分析所选城市的房价以及其影响因素，找出影响房价的主要原因，然后依此建立数学模型。

同时，根据得出的结论分析判断房价相对于当今社会经济是否合理。

第一，目前房地产业蓬勃发展的关键是社会的各项指标，各项因素综合决定的，社会经济指标的发展是地产业持续发展的推动力。

由此，我们分析相关数据的目的是要得出几条对房地产影响较大的社会经济指标，从而为继续研究做好基础。

但是，要去逐一分析每一种经济因素是不可能办到的，只能抓住主要因素去着重分析，所以我们经过查询“中国统计年鉴网”中部分代表城市的房价数据和有关书籍中的资料，大致得出以下几条对房价影响缠身主导作用的因素：建安成本，市场供求变化，土地成本、各种税费以及当地居民人均收入等。

然而，针对本问，虽然我们从相关资料中获取了大量数据，但从实际出发来看这些数据只能作为理论支撑的基础，模型并不是针对某一个城市，而是具有普遍用途，这样才能完美的达到本题的目的所在。

通过以上准备发现，该问题适合用随机模型和蛛网模型来解决。

通过随机模型模拟出影响价格的因素，再根据得出的因素作出假设，运用蛛网模型分析房价的合理性。

其中，随机模型是一种非确定性模型，变量之间的关系是以统计制的形式给出的，如果模型中任意变量不确定，并且随着具体条件的改变而改变，则该模型就是随机模型。

人工神经网络建模matlab

• （5）神经网络可以用大规模集成电路来实现．如美国用 256个神经元组成的神经网络组成硬件用于识别手写体的邮政编码．
四、反向传播算法（B-P算法）
• Back propagation algorithm
• 算法的目的：根据实际的输入与输出数据，计算模型的参数（权系数）
• 1．简单网络的B-P算法
u (i) • (2) 设 k
表示第k层第i神经元所接收的信息
wk(i,j) 表示从第k-1层第j个元到第k层第i个元的权重，
ak (i) 表第k层第i个元的输出
• （3）设层与层间的神经元都有信息交换（否则，可设它们之间的权重为零）；但同一层的神经元之间无信息传输．
• (4) 设信息传输的方向是从输入层到输出层方向；因此称为前向网络．没有反向传播信息．
• 分类结果：(1.24，1.80)，(1.28，1.84)属于Af类；(1.40，2.04）属于 Apf类．
图2 分类直线图
• •缺陷：根据什么原则确定分类直线？
• 若取A=(1.46,2.10), B=(1.1,1.6)不变，则分类直线变为 y=1.39x+0.071
分类结果变为： (1.24,1.80)， (1.40,2.04) 属于Apf类； (1.28,1.84)属于Af类
• 问：如果抓到三只新的蚊子，它们的触角长和翼长分别为(l.24,1.80); (l.28，1.84)；（1.40，2.04）．问它们应分别属于哪一个种类？
• 解法一：
• 把翼长作纵坐标，触角长作横坐标；那么每个蚊子的翼长和触角决定了坐标平面的一个点.其中 6个蚊子属于 APf类；用黑点“·”表示； 9个蚊子属 Af类；用小圆圈“。”表示．

MATLAB中的神经网络模型构建与训练

MATLAB中的神经网络模型构建与训练神经网络模型是一种模拟人脑神经元活动的数学模型，其可以用于进行各种复杂的数据分析和问题求解。

在MATLAB中，我们可以利用其强大的工具和函数来构建和训练神经网络模型。

本文将介绍MATLAB中神经网络模型的构建过程及其相关训练方法。

一、神经网络模型简介神经网络模型是由一系列相互连接的神经元组成的网络结构。

每个神经元都有多个输入和一个输出，输入通过权重被加权后，经过激活函数激活输出。

神经网络可以分为三层：输入层、隐藏层和输出层。

输入层接收原始数据，隐藏层进行信息处理和特征提取，而输出层给出最终结果。

二、神经网络构建在MATLAB中，可以通过Neural Network Toolbox来构建神经网络。

首先，我们需要确定网络结构，包括输入层神经元数、隐藏层神经元数和输出层神经元数。

接下来，我们调用network函数来创建一个空的神经网络对象。

```matlabnet = network;```然后，我们可以通过net的属性来设置神经网络的各个参数，如输入层的大小、隐藏层的大小、激活函数等。

```matlabnet.numInputs = 1; % 设置输入层神经元数net.numLayers = 2; % 设置网络层数net.biasConnect = [1; 1]; % 设置偏置net.inputConnect = [1; 0]; % 设置输入连接yerConnect = [0 0; 1 0]; % 设置层连接net.outputConnect = [0 1]; % 设置输出连接yers{1}.size = 10; % 设置隐藏层神经元数yers{1}.transferFcn = 'tansig'; % 设置激活函数yers{2}.transferFcn = 'purelin'; % 设置激活函数```上述代码中，我们设置了一个具有10个隐藏层神经元的神经网络，其输入和输出分别为1个。

数学模型第四版(姜启源)作业对于6.4节蛛网模型讨论下列问题：【范本模板】

对于6。

4节蛛网模型讨论下列问题：（1）因为一个时段上市的商品不能立即售完，其数量也会影响到下一时段的价格，所以第k+1时段的价格1+k y 由第k+1和第k 时段的数量1+k x 和k x 决定。

如果设1+k x 仍只取决于k y ，给出稳定平衡的条件，并与6.4的结果进行比较。

（2）若除了1+k y 由1+k x 和k x 决定之外，1+k x 也由前两个时段的价格k y 和1-k y 决定，试分析稳定平衡的条件是否还会放宽。

解:（1)设1+k y 由1+k x 和k x 的平均值决定，即价格函数表示为：)2(11k k k x x f y +=++ 则 0),2(0101>-+-=-++ααx x x y y k k k 0),(001>-=-+ββy y x x k k消去y, 得到 012)1(22x x x x k k k +=++++αβαβαβ ,k=1，2，….该方程的特征方程为022=++αβαβλλ与6.4节中 )2(11-++=k k k y y g x 时的特征方程一样，所以0〈αβ〈2, 即为0p 点的稳定条件。

（2）设 )2(11k k k x x f y +=++ )2(11-++=k k k y y g x ，则有 0),2(0101>-+-=-++ααx x x y y k k k 0),2(0101>-+=--+ββy y y x x k k k 消去y ，得到0123)1(424x x x x x k k k k +=++++++αβαβαβαβ 该方程的特征方程为02423=+++αβαβλαβλλ令λ=x ,αβ=a ，即求解三次方程0a 2ax ax 4x 23=+++ 的根在matlab 中输入以下代码求解方程的根x ：syms x asolve(4*x^3+a*x^2+2＊a*x+a==0,x)解得 1x = （36＊a^2 — 216＊a — a^3 + 24＊3^（1/2）＊（-a^2＊（a — 27））^（1/2)）^（1/3）/12 — a/12 + (a*(a — 24))/（12＊（36*a^2 — 216＊a — a^3 + 24*3^（1/2)＊(-a^2＊（a — 27）)^（1/2))^(1/3）)；2x = -（2＊a*(36*a^2 - 216＊a — a^3 + 24＊3^（1/2）＊（—a^2＊(a - 27））^（1/2）)^（1/3） — 3^（1/2)*a*24＊i — 3^（1/2）*（36＊a^2 — 216＊a — a^3 + 24＊3^(1/2）＊(—a^2*(a — 27））^(1/2))^(2/3）*i - 24＊a + 3^(1/2)＊a^2*i+ (36*a^2 - 216＊a - a^3 + 24＊3^（1/2）*(-a^2＊（a — 27）)^（1/2）)^（2/3) + a^2)/（24*(36*a^2 — 216*a - a^3 + 24＊3^(1/2)＊（-a^2*（a — 27））^（1/2）)^（1/3））；3x =—（2＊a*（36*a^2 - 216*a — a^3 + 24＊3^（1/2)*(-a^2*（a - 27))^（1/2))^(1/3) + 3^(1/2)＊a ＊24*i + 3^（1/2）*(36＊a^2 - 216＊a — a^3 + 24*3^(1/2）＊(-a^2*(a - 27））^（1/2))^(2/3)*i — 24＊a - 3^（1/2)＊a^2＊i + (36＊a^2 - 216＊a - a^3 + 24*3^(1/2）*(-a^2＊（a - 27))^(1/2))^（2/3) + a^2）/（24＊（36＊a^2 — 216＊a — a^3 + 24*3^（1/2）*（—a^2*(a -27）)^(1/2）)^(1/3））；其中1x 为实根，2x 与3x 为一对共轭虚根。

MATLAB中常见的神经网络模型介绍

MATLAB中常见的神经网络模型介绍神经网络是一种模拟生物神经网络工作机制的数学模型。

它由许多人工神经元组成，这些神经元之间存在着连接，通过学习和优化，神经网络能够模拟和处理各种复杂的输入输出关系。

在MATLAB中，有许多常见的神经网络模型可供使用，下面将介绍其中几个。

一、前馈神经网络（Feedforward Neural Network）前馈神经网络是最常见和基本的神经网络模型之一。

它的结构由多层神经元组成，每一层的神经元与下一层的神经元完全连接，信号只能从输入层传输到输出层，不会反向传播。

前馈神经网络适用于分类、回归等问题。

在MATLAB中，创建一个前馈神经网络可以使用“feedforwardnet”函数。

可以设置隐藏层的大小、传递函数类型、训练算法等参数。

通过训练数据，可以使用MATLAB提供的各种优化算法进行网络模型的训练和预测。

二、循环神经网络（Recurrent Neural Network）循环神经网络是一种具有回路结构的神经网络模型。

它的每一个神经元都接受来自上一时刻输出的信号，并将当前的输入和上一时刻的输出作为输入，进行计算。

循环神经网络能够处理具有时序关系的数据，例如序列预测、语言模型等。

在MATLAB中，创建一个循环神经网络可以使用“layrecnet”函数。

可以设置回路层的大小、传递函数类型、训练算法等参数。

通过训练数据，同样可以使用MATLAB提供的优化算法进行网络模型的训练和预测。

三、自组织映射网络（Self-Organizing Map）自组织映射网络是一种无监督学习的神经网络模型。

它通过将输入数据投影到一个低维的节点空间中，并学习节点之间的拓扑结构。

自组织映射网络在数据聚类、特征提取等领域有广泛的应用。

在MATLAB中，创建一个自组织映射网络可以使用“selforgmap”函数。

可以设置节点空间的维度、拓扑结构、距离度量等参数。

通过输入数据，可以使用MATLAB提供的训练算法进行网络模型的训练和预测。

使用Matlab进行神经网络优化问题求解的方法

使用Matlab进行神经网络优化问题求解的方法一、引言在当今信息时代，神经网络已经成为解决复杂问题的重要工具。

随着计算能力的提升，神经网络优化问题的求解变得越来越重要。

而Matlab作为一种强大的科学计算软件，能够提供丰富的工具和函数来解决神经网络优化问题。

本文将介绍如何使用Matlab来解决神经网络优化问题。

二、神经网络优化问题的建模在使用Matlab解决神经网络优化问题之前，首先需要对问题进行建模。

通常来说，神经网络优化问题可以分为两类：单目标优化问题和多目标优化问题。

单目标优化问题是指希望优化网络的某个特定输出，常见的问题有回归问题和分类问题。

而多目标优化问题则是希望在多个指标上获得最优解，常见的问题有多目标分类和多目标回归问题。

在建模过程中，需要确定网络的结构和参数。

神经网络的结构通常由输入层、隐藏层和输出层组成。

输入层接受原始数据，隐藏层进行特征提取，输出层给出最终的结果。

而参数则包括权重和偏置，这些参数需要进行调整以达到最优解。

三、使用Matlab解决单目标优化问题1. 数据准备在解决单目标优化问题之前，首先需要准备好数据集。

数据集应该包含输入值和对应的目标值。

2. 网络训练使用Matlab的神经网络工具箱，可以方便地进行网络训练。

首先，需要创建一个神经网络对象，并设置好网络的结构和参数。

然后，使用训练函数对网络进行训练，常见的训练函数有Levenberg-Marquardt算法和梯度下降算法。

通过训练函数，可以不断调整网络的权重和偏置，直到达到最优解。

3. 网络评估训练完网络后，需要对网络进行评估。

可以使用测试数据集来评估网络的性能，通常采用预测误差、准确率等指标来评估网络的表现。

四、使用Matlab解决多目标优化问题解决多目标优化问题与解决单目标优化问题的方法类似，只是目标变成了多个。

可以使用多种方法来解决多目标优化问题，如加权法、约束法和分级法等。

1. 加权法加权法是一种常用的解决多目标优化问题的方法。

Matlab技术神经网络模型

Matlab技术神经网络模型一、引言在当今快速发展的信息化时代，神经网络模型被广泛应用于各个领域，如图像识别、语音处理、数据挖掘等。

Matlab作为一种功能强大的科学计算软件，提供了丰富的工具和函数，能够帮助研究人员和工程师设计、实现和优化神经网络模型。

本文将介绍Matlab技术在神经网络模型中的应用，探讨其优势和局限性。

二、Matlab与神经网络模型1. Matlab的优势Matlab作为一种高级编程语言，具有简洁、易读的语法，使得编写和调试神经网络模型变得更加简单。

同时，Matlab提供了丰富的函数库，包括多种神经网络工具箱，如神经网络工具箱(Neural Network Toolbox)、深度学习工具箱(Deep Learning Toolbox)等。

这些工具箱内置了大量的函数和算法，方便用户快速搭建并训练神经网络模型。

2. Matlab在神经网络模型中的应用Matlab提供了多种神经网络模型的实现方法，包括前馈神经网络(Feedforward Neural Network)、循环神经网络(Recurrent Neural Network)和深度神经网络(Deep Neural Network)等。

用户可以根据自己的需求选择合适的网络结构，并使用Matlab 提供的函数进行定义和训练。

在前馈神经网络模型中，Matlab提供的函数可以帮助用户构建网络的拓扑结构，并设置激活函数、损失函数和优化算法等参数。

用户可以通过调整这些参数来优化模型的性能。

此外，Matlab还提供了可视化工具，可帮助用户直观地理解神经网络的结构和训练过程。

在循环神经网络模型中，Matlab提供了LSTM(Long Short-Term Memory)、GRU(Gated Recurrent Unit)等常用的循环单元，以及Seq2Seq(Sequence to Sequence)结构等。

这些函数与演算法相结合，可以有效解决时间序列数据的处理问题，如语音识别、机器翻译等。

房地产市场非线性蛛网模型的构建

房地产市场非线性蛛网模型的构建立足于蛛网模型，建立房地产市场的非线性二次供给和需求函数，然后确定价格的调整机制，验证了在相关参数的调整下，价格会出现倍周期分岔和混沌。

通过数值模拟，计算价格机制的Lyapunov指数，证实了房地产价格混沌状态的出现，进而以天津市为例，探究和分析其价格系统的运行状态。

最后提出价格混沌的控制方法以及对房地产调控的现实启示。

标签：房地产；蛛网模型；倍周期分岔；混沌1 引言自2010年4月史上最严厉的房地产调控政策国十条出台以来，控房价、挤泡沫、保民生切实成为房市调控的主基调，后政策层面又陆续跟进国八条、新国五条，内容涵盖房源供应、土地政策、税制改革、金融监管各个层面，可见国家对于房地产调控的信心和决心。

在多方利益的博弈下，房地产走势不再是一个单纯的经济现象，它已经和很多社会、民生、安全问题联系起来了。

房地产业是周期性比较长的产业，具有供给滞后的特点，其外在表现为以成交量和成交均价等技术指标为主的房地产供求关系的周期波动。

从现实反映来看，其周期呈现突变性、非线性和非对称性的特点，因此，如何更好的利用模型契合其周期的变化趋势，使宏观调控政策有据可依，是值得研究的问题。

蛛网理论是由美国经济学家H. Schultz、意大利经济学家U.Ricel和荷兰经济学家J. Tinbergen提出，1934年由英国经济学家N.Kaldor命名的。

高鸿业在微观经济学第三版中，对蛛网模型是这样描述的，“引进时间变化的因素，通过对属于不同时期的需求量、供给量和价格之间相互作用的考察，用动态分析的方法论述诸如农产品、畜牧产品这类生产周期较长的商品的产量和价格在偏离均衡状态以后的实际波动过程及其结果”。

因此，可以利用蛛网理论来研究房地产的周期波动和价格变化等问题。

2 文献综述在国内来讲，具有代表性的是，王利根据北京市房地产市场的发展情况，在详列影响供给和需求的因素的基础上，建立了线性方程并进行回归，得出蛛网呈现发散的结论，需要国家的宏观调控。

MATLAB综合性实验报告8

一、实验目的：1.学会运用Matlab解决实际问题2.进一步掌握Matlab的一些基本操作3.通过范例体会Matlab的初步建模过程4学会用做动画二．实验仪器、设备或软件：电脑、MATLAB软件三．实验内容：1.已知前两年的猪肉的产量和猪肉的价格分别为：39吨，28吨，12元/公斤，17元/公斤，根据前一年的猪肉价格影响后一年猪肉产量当年猪肉产量影响当年猪肉价格的线性关系，编写程序，利用动画原理画出前十年猪肉的产量——价格的动态图形。

（参数设置为，c1=39,c2=28,c3=36,r1=12,r2=17,k=16)。

2．在地面上建有一座圆柱形水塔,水塔内部的直径为d,并且在地面处开了一个高为H的小门.现在要对水塔内部进行维修施工,施工方案要求把一根长为l(l>d)的水管运到水塔内部.请问水塔的门高H多高时,才有可能成功地把水管搬进水塔内。

四．实验记录：1．蛛网模型：实验代码：clear%c1为产量1, c2为产量2, c3为产量3, r1为%肉价1, r2为肉价2, k为K年后产量与肉价%是否稳定c1=39;c2=28;c3=36;hold offr1=12;r2=17;k=16;a1=[c1 1;c2 1];%系数矩阵b1=[r1,r2]';%列向量a2=[r1 1;r2 1];b2=[c2,c3]';a=a1\b1;b=a2\b2;%x0(1)=c1;for n=1:30y0(n)=a(1)*x0(n)+a(2); %a(1)a(2)为矩阵元素的引用，下行类似x0(n+1)=b(1)*y0(n)+b(2);x(n)=x0(n);y(n)=x0(n+1);endplot(x,y0,'-g',y,y0,'-b')hold onm=moviein(100);for n=1:kfor j=1:30t1=x0(n)+(j-1)*(x0(n+1)-x0(n))/30;t2=x0(n)+j*(x0(n+1)-x0(n))/30;if t2<t1t=t1;t1=t2;t2=t;%这样做方便画图elseendt=t1:0.01:t2;plot(t,y0(n),'.r')%划横线t1=y0(n)+(j-1)*(y0(n+1)-y0(n))/30;t2=y0(n)+j*(y0(n+1)-y0(n))/30;if t2<t1t=t1;t1=t2;t2=t;elseendt=t1:0.01:t2;plot(x(n+1),t,'.r')%划竖线endm(:,n)=getframe;endmovie(m,20)实验结果：ans =Columns 1 through 639.0000 28.0000 36.0000 30.1818 34.4132 31.3358 Columns 7 through 1233.5739 31.9462 33.1300 32.2691 32.8952 32.4398 Columns 13 through 1832.7710 32.5302 32.7053 32.5779 32.6706 32.6032 Columns 19 through 2432.6522 32.6166 32.6425 32.6236 32.6374 32.6274 Columns 25 through 3032.6346 32.6294 32.6332 32.6304 32.6324 32.6310 Column 3132.6320实验图像：2．水塔模型：实验代码：Clearfunction x=lt523(l,d,h) k1=0;a=0l=7;d=3ymax=0;k2=0;b=pi/2;h=3;while (b-a)>10^(-2)k2=k2+1;m=0;a=0;if k1==0n=ceil(b/h)-1 elsen=ceil(b/h);endfor i=1:n+1;x(i)=a+(i-1)*(b-a)/n;y(i)=l*sin(x(i))-d*tan(x(i));endfor i=1:nif y(i)>ymaxymax=y(i);a=x(i-1);else y(i)<ymaxb=x(i);endendm=m+1;k1=k1+1;h=(b-a)/5;endabx=(a+b)/2t=0:0.01:1.35y1=l*sin(t)-d*tan(t);plot(t,y1,'-b')方法：2syms h xh=8*sin(x)-2*tan(x);d1=0;d2=pi/2;d0=(d1+d2)/2;d=0.03;a=subs(h,x,d1);b=subs(h,x,d2);c=subs(h,x,d0);for n=d1:d:d2if (((c-a)/(d0-d1))*((b-c)/(d2-d0)))<0 d1=d1+d; d2=d2-d; d0=(d1+d2)/2;a=subs(h,x,d1);b=subs(h,x,d2);c=subs(h,x,d0);endendd0hold onaxis([0,pi/2,-5,5])x=0:0.05:pi/2;plot(x,8*sin(x)-2*tan(x),'-b')实验运行结果：五、实验总结：通过做此实验，让我对MATLAB有更进一步的了解，学会怎样才能正确运用MATLAB求解实际问题，了解如何利用数学模型去解释和分析社会经济问题，特别是这个典型经济问题的求解。

如何使用MATLAB进行神经网络建模

如何使用MATLAB进行神经网络建模使用MATLAB进行神经网络建模神经网络是一种模拟人脑神经系统运作的数学模型，它能够模拟人类的感知、学习和决策过程。

在现代科学和工程领域，神经网络被广泛应用于诸如模式识别、图像处理、时间序列预测等问题的解决中。

而MATLAB作为科学计算和数据分析的常用工具，也提供了一系列强大的神经网络建模工具。

接下来，我们将介绍如何使用MATLAB进行神经网络建模。

一、准备工作在使用MATLAB进行神经网络建模之前，我们需要准备一些必要的工作。

首先，需要安装MATLAB软件，并确保安装的是最新版本。

其次，需要了解MATLAB中神经网络建模的基本原理和概念。

二、数据准备与预处理在进行神经网络建模之前，我们首先需要准备好用于训练和测试的数据集。

通常情况下，我们需要将数据集分为训练集和测试集两部分。

训练集用于神经网络的训练，而测试集则用于评估神经网络的性能。

在准备好数据集后，我们还需要对数据进行一些预处理操作，例如数据归一化、数据标准化等。

这些操作有助于提高神经网络的性能和收敛速度。

三、神经网络建模使用MATLAB进行神经网络建模的核心步骤包括网络设计、网络训练和网络评估。

首先，我们需要确定神经网络的结构，包括输入层、隐藏层和输出层的神经元数量。

这需要根据具体问题的需求和特点进行调整。

然后，我们可以使用MATLAB提供的神经网络工具箱来建立神经网络模型。

根据问题的不同，有多种神经网络模型可供选择，例如前馈神经网络、递归神经网络、自适应神经网络等。

在建立好神经网络模型后，我们还需要选择合适的训练算法对网络进行训练。

常用的训练算法包括误差逆传播算法（Backpropagation）、Levenberg-Marquardt算法等。

最后，我们使用测试集对训练好的神经网络进行评估，得到模型的性能指标，如准确率、误差等。

四、模型调优与改进神经网络建模是一个不断调优与改进的过程。

在建立好初始模型后，我们可以通过修改网络结构、调整训练参数等方式来改进模型的性能。

蛛网模型的应用

科技天地55INTELLIGENCE························蛛网模型的应用湖南长沙中南大学土木建筑学院万毅曾华摘要：利用蛛网模型对市场猪肉的价格上涨现象做了初步的分析，主要通过一个简单的范例展现求解实际问题的初步建模过程，用MATLAB 做图并求解问题。

关键词：建模 matlab 蛛网模型蛛网模型是用需求曲线和供给曲线来分析市场变化的图示方法。

可以用来描述某商品市场变化的图形。

1.范例内容已知前两年的猪肉的产量和猪肉的价格分别为：25吨，28吨，12元/公斤，13元/公斤，根据前一年的猪肉价格影响后一年猪肉产量当年猪肉产量影响当年猪肉价格的线性关系，编写程序，利用动画原理画出前十年猪肉的产量——价格的动态图形。

（参数设置为，c1=25,c2=28,c3=26,r1=12，r2=13,k=15)2.详细设计在matlab 中输入如下程序：function [x0,y0]=zhuwangmoxing(c1,r1,c2,r2,c3,k)%c1为产量1, c2为产量2, c3为产量3, r1为%肉价1, r2为肉价2, k 为K 年后产量与肉价%是否稳定a1=[c1 1;c2 1];b1=[r1,r2]';a2=[r1 1;r2 1];b2=[c2,c3]';a=a1\b1;b=a2\b2;x0(1)=39;for n=1:30y0(n)=a(1)*x0(n)+a(2); x0(n+1)=b(1)*y0(n)+b(2); x(n)=x0(n); y(n)=x0(n+1);endplot(x,y0,'-g',y,y0,'-b')hold onfor n=1:k for j=1:30t1=x0(n)+(j-1)*(x0(n+1)-x0(n))/30; t2=x0(n)+j*(x0(n+1)-x0(n))/30; if t2<t1 t=t1; t1=t2; t2=t; else endt=t1:0.01:t2;plot(t,y0(n),'.r')t1=y0(n)+(j-1)*(y0(n+1)-y0(n))/30; t2=y0(n)+j*(y0(n+1)-y0(n))/30; if t2<t1 t=t1; t1=t2;t2=t; else endt=t1:0.01:t2;plot(x(n+1),t,'.r')end end3、实验结果>> zhuwangmoxing(25,12,28,13,26,15)ans =Columns 1 through 1239.0000 18.6667 32.2222 23.1852 29.2099 25.1934 27.8711 26.0860 27.2760 26.4827 27.0116 26.6590Columns 13 through 2426.8940 26.7373 26.8418 26.7721 26.8186 26.7876 26.8083 26.7945 26.8037 26.7976 26.8016 26.7989Columns 25 through 3126.8007 26.7995 26.8003 26.7998 26.8001 26.7999 26.80014、实验图像5、实验总结根据以上简单的范例，在影响消费者需求量大小的众多因素中商品的自身价格对需求量的影响是最重要的，由结果图像，知在其他因素不变的情况下，商品的需求量与其价格呈反比，这即是需求规律。

蛛网模型

目前，基于蛛网模型建模扩展主要是从以上三个方面，模型的思想主要从经济进程的动态性和状态变量的变化的随机性，使该种模型在经济计量方面越来越复杂，经济预测方面的精度越来越好。
二、蛛网模型的数学综述
（一）蛛网模型收敛性的充要条件
在数学模型中，供求函数都是设定为严格单调连续的可微函数，必要时还要假设供求函数为凸函数，在进行系统的分析中，通常对供求函数有如下关系， = (S( ))=G( ),该式可看作价格变化演进过程的表达，G为价格演化的一种映射，对于一阶差分方程 =G( )，其中G平滑可微，若为 =G( )的一个不动点，即
假设价格序列{ }收敛于，则序列{ }为递减序列，即| |<| |< <| |,( )( )<0,
则| |=|( - )-( - )|,| |=|( )-（ - ）|,
进一步可得
|( )-（ - ）|>|( - )-( - )|
对于D（P）,S(P),G(P)是严格单调连续可微函数，则价格序列收敛的充要条件是：
=G（）， = ，
| | <1,或者| |<1,又显然为单调递减函数 <0,所以0> ,又有对于任意的 , ,存在
|f( )-f( )| r| - |,
即 ,
可得，需求函数 =D（）和供给函数 =S( )，连续可微，= (S（P）)=G(P)单调递减连续可微，对于价格序列{ }收敛于的充要条件为
[2]高鸿业.西方经济学(第二版) [M].北京:中国人民出版社,2001年8月,58 -62 .
[3]王树和.微分方程模型与混沌[M].合肥：中国科技大学出版社，1998.
[4]龚德恩，雷勇.非均衡蛛网模型价格调节的稳定性分析[J].数学的实践与认识，2010,40（17）

如何利用Matlab进行网络分析与优化

如何利用Matlab进行网络分析与优化引言：在当今信息时代，网络技术的发展已经成为人们生活和工作的重要组成部分。

因此，网络的分析与优化，尤其是对于大规模网络的分析与优化，成为了重要的研究领域。

Matlab作为一种强大的科学计算软件，在网络分析与优化中扮演着重要的角色。

本文将围绕如何利用Matlab进行网络分析与优化展开探讨。

一、网络分析在网络分析中，我们可以利用Matlab进行网络的建模与分析。

首先，我们需要将网络表示为一个图，其中节点表示网络中的实体，边表示节点间的连接关系。

利用Matlab的图论工具包，我们可以方便地进行网络的可视化、统计特性的计算以及网络模型的构建。

1.1 网络可视化Matlab的图论工具包提供了各种绘制网络图的函数和工具，让我们能够直观地展示网络的拓扑结构。

通过对网络进行可视化，我们可以更好地理解网络的结构和特性，并有助于后续的分析与优化工作。

1.2 统计特性计算网络的统计特性是了解网络行为和性质的重要指标。

在Matlab中，我们可以利用图论工具包计算网络的度分布、聚类系数、路径长度等统计特性。

这些特性可以帮助我们深入了解网络的性质，为后续的优化工作提供基础。

1.3 网络模型构建为了更好地理解和分析网络，我们可以利用Matlab构建各种经典的网络模型，如随机网络、小世界网络和无标度网络等。

通过这些模型，我们可以模拟真实网络中的一些特性，从而更深入地研究网络的结构和行为。

二、网络优化网络优化旨在改善网络的性能和效率，使得网络能够更好地满足用户和应用的需求。

在网络优化中，我们可以利用Matlab进行网络流量优化、资源分配优化以及拓扑结构优化等方面的工作。

2.1 网络流量优化网络流量优化是指通过合理的路由和调度策略，使得网络中的数据能够以最优的方式传输，从而提高网络的传输效率和吞吐量。

在Matlab中，我们可以利用线性规划、整数规划和最优化算法等进行网络流量的优化设计，从而改善网络的性能和效果。

MATLAB在经济类线性代数中的应用

MATLAB在经济类线性代数中的应用摘要：文章针对经济类线性代数教学中出现的计算冗繁、与现代经济学科发展脱节的问题，提出将matlab引入教学，提高学生解决实际问题的能力，并举例说明matlab在计算与经济模型上的应用。

abstract: focusing on the problem of intricate calculation and abstract concept in the linear algebra, the matlab tools is introduced into the teaching of economics in this paper. the aim is to promote the combining theory with practice, and examples are given to illuminate the function of modeling and intuition.关键词：线性代数；matlab；应用key words: linear algebra；matlab；application0 引言现代的经济理论一般借助于数学推理导出经济行为的本质规律，以满足定性到定量思维分析的要求，这使得数学作为经济学科的专业基础课受到广泛的关注和重视。

而目前传统教学内容与经济学科的发展脱节，虽然学生学习了线性代数的数学理论,但由于经济数据的繁杂使得运算困难,在专业课的实际问题中仍难以得出结果，这就产生了将计算软件引人到计算中来的需要。

matlab具有丰富的经济计算函数，能轻松解决利用线性代数知识解决的许多实际经济问题，适合引入课程教学。

目前matlab在教学中的应用讨论主要集中在高等数学的微积分求解问题，在仿真绘图上的优势体现较少，经济类学生重点掌握的应用实例涉及更少，本文针对以上两种问题举例说明matlab的应用，以期表明软件教学可提高经济学科学生的应用能力，从而提高教学质量。

使用matlab工具箱创建神经网络模型

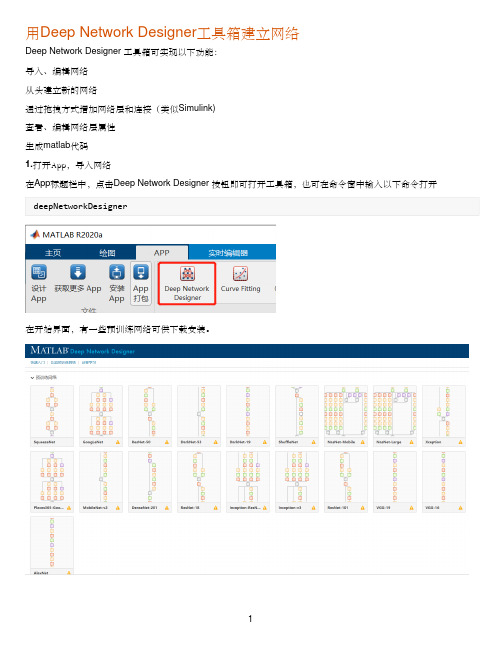
用Deep Network Designer工具箱建立网络Deep Network Designer 工具箱可实现以下功能：导入、编辑网络从头建立新的网络通过拖拽方式增加网络层和连接（类似Simulink)查看、编辑网络层属性生成matlab代码1.打开App，导入网络在App标题栏中，点击Deep Network Designer 按钮即可打开工具箱，也可在命令窗中输入以下命令打开在开始界面，有一些预训练网络可供下载安装。

一般通过新建或从工作区导入的方式创建网络2.增加/编辑网络层App提供了常用的网络层模块，可通过拖拽的方式添加，软件自带的层模块有：输入层（图片/序列输入）、卷积和全连接层（二维/三维卷积）、池化层、序列层（lstm、gru、NLP处理）、激活函数（relu、elu、tanh等）、归一化等工具（BN、dropout）、目标检测、输出层。

另外，可以通过命令行自己建立新的层，并添加到网络中。

在工作区中点击每个层，可以查看修改层属性参数，也可选中各层进行复制、剪切、删除等操作。

3.分析网络点击Analyze按钮可以检查分析网络，检查网络结构是否有问题，分析各层的可学习参数数量，errors为0时，网络可用于训练。

4.使用Deep Network Designer进行训练首先在Data 栏中，点击Import Data 按钮导入训练集，然后在Training栏中，进行网络训练。

App中可对训练集进行数据增强，可设置训练参数。

5.网络导出也可将建好的网络导出到matlab工作区，通过 trainNetwork 命令进行训练。

也可先在App中训练完毕，将训练好的网络导出到工作区，这样导出的网络包含已学习的权重参数。

MATLAB神经网络之各函数介绍

MATLAB神经网络之各函数介绍MATLAB是一种功能强大的计算机软件，用于数值计算、数据可视化以及机器学习等领域。

在神经网络的建模与训练过程中，MATLAB提供了一系列方便易用的函数，用来处理神经网络的构建、优化、训练和预测等任务。

本文将介绍一些MATLAB中常用的神经网络相关函数。

1. neuralnet：该函数用于构建和训练多层感知器（MLP）模型。

它可以指定模型的层数、每层的神经元个数和激活函数等参数，并通过反向传播算法来优化模型的权重和偏差。

该函数还提供了额外的选项，用于指定训练过程的终止条件和优化器等。

2. train：这个函数是神经网络训练的关键。

它采用输入和目标输出数据，以及神经网络模型作为输入参数，通过反向传播算法来更新神经网络的权重和偏差。

在训练过程中，该函数可用于指定训练次数、学习速率和正则化等参数，并返回训练后的神经网络模型。

3. sim：该函数用于根据给定的输入数据预测神经网络的输出结果。

它采用已经训练好的神经网络模型和输入数据作为输入参数，并返回神经网络的预测结果。

该函数还可以根据需要指定使用的输入和输出层，以及是否进行归一化等处理。

4. patternnet：与neuralnet函数类似，patternnet函数也用于构建和训练多层感知器模型。

不同的是，patternnet函数使用了一种特殊的网络结构，能够更好地适应分类问题。

该函数还提供了一些额外的选项，如正则化参数和错误权重等，用于调整模型的性能。

5. feedforwardnet：该函数用于构建和训练前馈神经网络模型。

前馈神经网络是最简单的神经网络形式，只包含输入层、隐藏层和输出层。

feedforwardnet函数通过指定隐藏层的神经元个数和激活函数等参数，来创建前馈神经网络模型。

该函数还可以通过设置训练函数和正则化参数等选项，来优化模型的性能。

6. perceptron：这个函数用于构建和训练感知器模型。

感知器是一种简单的神经网络结构，由一个输入层和一个输出层组成。