初中数学三角形专题
初中数学专题复习等腰三角形与直角三角形

初中数学专题复习等腰三角形与直角三角形在初中数学的学习中,等腰三角形和直角三角形是两个非常重要的几何图形。
它们具有独特的性质和定理,在解决数学问题时经常会用到。
下面我们就来对这两个图形进行一次系统的复习。
一、等腰三角形1、定义有两边相等的三角形叫做等腰三角形。
相等的两条边称为腰,另一边称为底边。
两腰所夹的角叫做顶角,底边与腰的夹角叫做底角。
2、性质(1)等腰三角形的两个底角相等(简写成“等边对等角”)。
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)。
3、判定(1)如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)。
(2)有两条边相等的三角形是等腰三角形。
4、等腰三角形中的常见计算(1)已知等腰三角形的顶角,求底角:底角=(180°顶角)÷ 2 。
(2)已知等腰三角形的底角,求顶角:顶角= 180° 2×底角。
5、等腰三角形的周长和面积(1)周长:等腰三角形的周长=腰长× 2 +底边。
(2)面积:通常可以通过作底边的高,将等腰三角形分成两个直角三角形,然后利用三角形面积公式 S = 1/2×底×高来计算。
二、直角三角形1、定义有一个角为 90°的三角形叫做直角三角形。
2、性质(1)直角三角形的两个锐角互余。
(2)直角三角形斜边上的中线等于斜边的一半。
(3)在直角三角形中,如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半。
(4)勾股定理:直角三角形两直角边的平方和等于斜边的平方。
3、判定(1)如果三角形的三边长 a、b、c 满足 a²+ b²= c²,那么这个三角形是直角三角形。
(2)如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形。
4、直角三角形中的常见计算(1)已知直角三角形的两条直角边 a、b,求斜边 c:c =√(a²+b²) 。
初中数学三角形专题训练50题含答案

初中数学三角形专题训练50题含答案(单选、填空、解答题)一、单选题1.如图,已知AO=OB ,OC=OD ,AD 和BC 相交于点E ,则图中全等三角形有( )对.A .1对B .2对C .3对D .4对 2.两个同心圆的半径分别是 5 和 4,则长为 6 的大圆的弦一定和小圆( ) A .相交 B .相切 C .相离 D .无法确定 3.在△ABC 中,AB =8,BC =15,AC =17,则下列结论正确的是( ) A .△ABC 是直角三角形,且△A =900B .△ABC 是直角三角形,且△B =900 C .△ABC 是直角三角形,且△C =900D .△ABC 不是直角三角形 4.若菱形ABCD 的对角线8AC =,60ABC ∠=,则菱形ABCD 的面积为( ) A .16 B .C .D .5.用10根等长的火柴棒拼成一个三角形(火柴棒不允许剩余,重叠和折断),这个三角形一定是( )A .等边三角形B .等腰三角形C .直角三角形D .不等边三角形 6.下列命题:△任何实数的0次幂都等于1;△有两个角相等的等腰三角形是等边三角形;△三角形三条边垂直平分线的交点到三角形三条边的距离相等;△若三角形一个外角的平分线平行于三角形的一边,则这个三角形是等腰三角形.正确的个数有( )A .0个B .1个C .2个D .3个 7.菱形的两条对角线分别是12和16,则该菱形的边长是( )A .10B .8C .6D .5 8.如图,下列条件中,不能证明△ABC △△DCB 的是( )A .AB =DC ,AC =DBB .AB =DC ,△ABC =△DCB C .△ACB =△DBC ,△A =△D D .AB =DC ,△DBC =△ACB 9.如图,把ABC 纸片沿EG 折叠,当点A 落在ABC 外部的点F 处,此时测得2104∠=︒,30A ∠=︒,则1∠的度数为( )A .40︒B .44︒C .46︒D .48︒ 10.如图,在边长为4的正方形ABCD 中,点E 、F 分别是BC 、CD 的中点,DE 、AF 交于点G ,AF 的中点为H ,连接BG 、DH .给出下列结论:△AF DE ⊥;△85DG =;△HD BG ∥;△ABG 与DFH 相似.其中正确的结论有( )个.A .1B .2C .3D .411.下列条件中,能判定△ABC△△DEF 的是( )A .AB=DE ,BC=EF ,△A=△EB .△A=△E ,AB=EF ,△B=△DC .△A=△D ,△B=△E ,△C=△F D .△A=△D ,△B=△E ,AC=DF 12.在Rt ABC △中,90A ∠=︒,6AB =,8AC =,点P 是ABC 所在平面内一点,则222PA PB PC ++取得最小值时,下列结论正确的是( )A .点P 是ABC 三边垂直平分线的交点B .点P 是ABC 三条内角平分线的交点 C .点P 是ABC 三条高的交点D .点P 是ABC 三条中线的交点13.下列命题中,真命题是( ) A .有两边和一角对应相等的两个三角形全等B .有两边和第三边上的高对应相等的两个三角形全等C .有两边和其中一边上的高对应相等的两个三角形全等D .有两边和第三边上的中线对应相等的两个三角形全等14.已知直角三角形两边的长分别为6和8,则此三角形的周长为( )A .24B .14C .14+24D .14+15.如图,点A 的坐标为(﹣3,2),△A 的半径为1,P 为坐标轴上一动点,PQ 切△A 于点Q ,在所有P 点中,使得PQ 长最小时,点P 的坐标为( )A .(0,2)B .(0,3)C .(﹣2,0)D .(﹣3,0) 16.如图1,已知AB AC =,D 为BAC ∠的角平分线上面一点,连接BD ,CD ;如图2,已知AB AC =,D 、E 为BAC ∠的角平分线上面两点,连接BD ,CD ,BE ,CE ;如图3,已知AB AC =,D 、E 、F 为BAC ∠的角平分线上面三点,连接BD ,CD ,BE ,CE ,BF ,CF ;…,依次规律,第n 个图形中有全等三角形的对数是( ).A .nB .21n -C .(1)2n n +D .3(1)n + 17.如图,若 AC 、BD 、EF 两两互相平分于点O ,那么图中的全等三角形共有( )A .3对B .4对C .5对D .6对 18.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm ,则正方形A ,B ,C ,D 的面积之和为( )A .27cmB .228cmC .242cmD .249 cm 19.如图,在□ABCD 中,AD =2AB ,F 是AD 的中点,作CE △AB ,垂足E 在线段AB上,连接EF 、CF ,则下列结论中:△△DCF =12△BCD ;△EF =CF ;△S △BEC <2S △CEF ;△△DFE =4△AEF .一定成立的有( )个.A .1B .2C .3D .420.如图,等边ABC 内部有一点D ,3DB =,4DC =,150BDC =∠︒,在AB 、AC 上分别有一动点E 、F ,且AE AF =,则DE DF +的最小值是( )A .5B .C .D .7二、填空题21.等腰三角形的两边长为2和3,则等腰三角形的周长为________.22.若3,m ,5=______. 23.如图,点P 是正方形ABCD 对角线BD 上的一点,且BP =BC ,则△DPC =______°.24.如图,在ABC 中,90C ∠=︒,70B ∠=︒,D ,E 分别是边AB 、AC 上的点,将A ∠沿DE 折叠,使点F 落在AB 的下方,当FDE 的边EF 与BC 平行时,ADE ∠的度数是_________.25.《九章算术)是我国古代数学名著,书中有下列问题:“今有户高多于广六尺,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺,门对角线距离恰好为1丈,问门高、宽各是多少?(1丈=10尺)如图,设门高AB 为x 尺,根据题意,可列方程为___________(将方程化简并写成一般形式).26.如图,ABC ∆和ABE 关于直线AB 对称,ABC ∆和ADC ∆关于直线AC 对称,CD 与AE 交于点F ,若32ABC ∠=︒,18ACB ∠=︒,则CFE ∠的度数为______.27.如图,有6个条形方格图,在由实线围成的图形中,全等图形有:(1)与__;(2)与__.28.如图,在△ABC 中,AB =AC ,△A =40°,CD ∥AB ,则△BCD 的度数是______.29.如图△ABC 中,△A =96°,延长BC 到D ,△ABC 的平分线与△ACD 的平分线交于点A 1,△A 1BC 的平分线与△A 1CD 的平分线交于点A 2,以此类推,△A 4BC 的平分线与△A 4CD 的平分线交于点A 5,则△A 5的大小是___30.ABC 中,AB 15=,BC 12=,AC 9=,圆O 是ABC 的内切圆,则图中阴影部分的面积为________.(结果不取近似值)31.如图所示,一水库迎水坡AB 的坡度1:2i =,则求坡角α的正弦值sin α______.32.一根旗杆在离地面4.5 m 的地方折断,旗杆顶端落在离旗杆底部6 m 外,则旗杆折断前的高度是________.33.如图,O 的弦AB 长为2,CD 是O 的直径,30,15ADB ADC ∠=︒∠=︒.△O 的半径长为_________.△P 是CD 上的动点,则PA PB +的最小值是_________.34.直角三角形斜边长是5,一直角边的长是3,则此直角三角形的面积为___________.35.如图,国旗上的五角星的五个角的度数是相同的,每一个角的度数都是____.36.在等边ABC 中,点D 在BC 边上,若4AB =,AD =BD 的长为______.37.如图,已知△MON =30°,点A 1,A 2,A 3,…在射线ON 上,点B 1,B 2,B 3,…在射线OM 上,△A 1B 1A 2,△A 2B 2A 3,△A 3B 3A 4,…均为等边三角形,若OA 1=2,则△A 5B 5A 6的边长为________.38.已知点G是面积为227cm的ABC的重心,那么AGC的面积等于____39.图示是一种“羊头”形图案,其作法是,从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,和2′,…,依次类推,若正方形7的边长为1cm,则正方形1的边长为__________cm.40.如图,平行四边形ABCD中,点P为边AD上一个动点,连接BP,将线段PB绕点B逆时针旋转60°得到BQ,连接AQ,若△ABC=60°,AB=2,BC=6,则线段AQ 的取值范围是______.三、解答题41.如图,已知ACB DBC AC BD,,求证:A D∠=∠=∠=∠.∠交AC于点D,E为AB中点,过点A作42.已知:如图ABC中,BD平分ABCAF BD,交DE延长线于点F.∥(1)求证:AF BD=(2)当ABC满足什么条件时,四边形AFBD是矩形?请证明你的结论.43.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,△B=90°,连接AC.(1)△ACD是直角三角形吗?为什么?(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?44.尺规作图=.(保留作图痕迹,不如图,ABC中,2B C∠=∠,在AC边上找一点P,使PB PC写作法)45.如图,在直角△ABC中,△ACB=90°,CD是高,△1=35°,求△2、△B与△A的度数.46.如图,在平行四边形ABCD中,E、F分别是AB、CD的中点.(1)求证:△AED△△CFB;(2)试判断四边形EBFD 的形状,并说明理由.47.如图,在△ABC 中,△ABC =△ACB ,E 为BC 边上一点,以E 为顶点作△AEF ,△AEF 的一边交AC 于点F ,使△AEF =△B .(1)如果△ABC =40°,则△BAC = ;(2)判断△BAE 与△CEF 的大小关系,并说明理由;(3)当△AEF 为直角三角形时,求△AEF 与△BAE 的数量关系.48.如图,在平面直角坐标系内有一正方形OABC ,点C 坐标为(0,4),点D 为AB 的中点,直线142y x =-+经过点C ,D 并交x 轴于点E ,BCD △沿着CD 折叠,顶点B 恰好落在OA 边上方F 处,连接BE ,点P 为直线CD 上的一动点,点Q 是线段BE 的中点.连接BP ,PQ .(1)求点F 的坐标;(2)求出点P 运动过程中,PO PA +的最小值;(3)是否存在点P ,使其在运动过程中满足EQP EBC △∽△,若存在,求出点P 坐标;若不存在,请说明理由.49.在Rt ACB △中,90ACB ∠=︒,AC BC =,D 为AB 上一点,连结CD ,将CD 绕C 点逆时针旋转90°至CE ,连结DE ,过C 作CF DE ⊥交AB 于F ,连结BE .(1)求证:AD BE=.(2)试探索线段AD,BF,DF之间满足的等量关系,并证明你的结论.(3)若15CD=,求BF.ACD=︒∠,1(注:在直角三角形中,30°所对的直角边等于斜边的一半)50.如图1,在ABC中,△A=90°,AB=AC+1,点D,E分别在边AB,AC 上,且AD=AE=1,连接DE.现将ADE绕点A顺时针方向旋转,旋转角为α(0°<α<180°),如图2,连接CE,BD,CD.(1)当0°<α<90°时,求证:CE=BD;(2)如图3,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;(3)在旋转过程中,求BCD的面积的最大值,并写出此时旋转角α的度数.参考答案:1.D【分析】由条件可证△AOD △△BOC ,可得△A =△B ,则可证明△ACE △△BDE ,可得AE =BE ,则可证明△AOE △△BOE ,可得△COE =△DOE ,可证△COE △△DOE ,可求得答案.【详解】解:在△AOD 和△BOC 中OA OBAOD BOC OD OC=⎧⎪∠=∠⎨⎪=⎩ △△AOD △△BOC (SAS ),△△A =△B ,△OC =OD ,OA =OB ,△AC =BD ,在△ACE 和△BDE 中A BAEC BEDAC BD∠=∠⎧⎪∠=∠⎨⎪=⎩△△ACE △△BDE (AAS ),△AE =BE ,在△AOE 和△BOE 中OA OBA BAE BE=⎧⎪∠=∠⎨⎪=⎩△△AOE △△BOE (SAS ),△△COE =△DOE ,在△COE 和△DOE 中OE OECOE DOEOD OC=⎧⎪∠=∠⎨⎪=⎩△△COE △△DOE (SAS ),故全等的三角形有4对,故选:D .【点睛】本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.2.B【分析】连接OB,作OC AB⊥,根据垂径定理求出132BC AB==,根据勾股定理求出OC,即可得到判断.【详解】解:连接OB,作OC AB⊥,△6AB=,△132BC AB==,在Rt OBC中,4OC=,△点C在小圆上,△OC AB⊥,△长为6的大圆的弦和小圆相切,故选:B.【点睛】此题考查了垂径定理,勾股定理,直线与圆的位置关系,正确理解垂径定理是解题的关键.3.B【详解】22281517+=, △△ABC是直角三角形,△AC是斜边,△△B=900,故B正确;故选B.4.C【分析】过A作AE△BC于E,由菱形性质和△ABC=60°,可得△ABC是等边三角形,解Rt△ABE求得AE即可解答;【详解】解:由题意作图如下,过A作AE△BC于E,由菱形的性质可得:AB=BC,△△ABC=60°,△△ABC是等边三角形,△AB=BC=AC=8,Rt△ABE中,AE=AB sin△B=△菱形ABCD面积=BC•AE=故选:C.【点睛】本题考查了菱形的性质,等边三角形的判定和性质,三角函数等知识;掌握菱形的性质是解题关键.5.B【分析】根据题意可知三角形的周长为10,再根据三角形的三边关系找到符合条件的三边,看符合哪类三角形即可.【详解】根据题意可知三角形的周长为10,又因为三角形任意两边之和大于第三边,△最大边要小于5,△三角形的三边可以为4,2,4或4,3,3.△这个三角形一定是等腰三角形.故选B.【点睛】此题考查了三角形的三边关系及等腰三角形的判定.三角形的三边关系:三角形任意两边之和大于第三边;任意两边之差小于第三边.6.B【分析】根据0指数幂的定义,等腰三角形三线合一,等边三角形的判定,线段垂直平分线性质逐个进行判断即可.【详解】解:△0的0次幂不存在,△△错误;△有一个角等于60°的等腰三角形是等边三角形,故△错误;△三角形三条边垂直平分线的交点到三角形三个顶点的距离相等,故△错误;△若三角形一个外角的平分线平行于三角形的一边,则这个三角形是等腰三角形,故△正确△正确的个数为:1个.故选:B .【点睛】本题考查了线段垂直平分线性质,0指数幂的定义,等腰三角形性质,等边三角形的判定的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等,任何不等于0的0次幂等于1,能理解性质和法则是解此题的关键.7.A【分析】首先根据题意画出图形,然后由菱形的两条对角线的长分别为12和16,求得OA 与OB ,再由勾股定理即可求得菱形的边长.【详解】如图,△菱形ABCD 中,A C=12,BD =16,△OA =12AC =6,OB =12BD =8,AC △BD ,△AB .即菱形的边长是10.故选:A.【点睛】此题考查了菱形的性质以及勾股定理.掌握菱形的对角线互相平分且垂直是解题的关键.8.D【详解】解:根据题意知,BC =BC .A 、由“SSS”可以判定△ABC △△DCB ,故本选项不符合题意;B 、由“SAS”可以判定△ABC △△DCB ,故本选项不符合题意;C 、由“AAS”可以判定△ABC △△DCB ,故本选项不符合题意;D 、由“SSA”不能判定△ABC △△DCB ,故本选项符合题意.故选:D .9.B【分析】设EF 与AB 交于D ,由折叠可得30F A ∠=∠=︒,根据三角形的外角性质得到21043074ADE A ∠=∠-∠=︒-︒=︒,1ADE F ∠=∠-∠,则由1ADE F ∠=∠-∠,即可求解.【详解】解:设EF 与AB 交于D ,如图,△21043074ADE A ∠=∠-∠=︒-︒=︒,又1ADE F ∠=∠-∠,1743044ADE F ∠=∠-∠=︒-︒=︒∴,故选:B .【点睛】本题考查三角形外角的性质,折叠的性质,熟练掌握三角形外角的性质与折叠的性质是解题的关键.10.B【分析】利用正方形的性质和线段中点性质,证明()SAS ADF DCE ≌,得到DAF CDE ∠=∠,即可判断△;利用勾股定理求AF =DG 的长,即可判断△;利用直角三角形的斜边中线等于斜边一半,得到DH HF =,进而得到HDF HFD ∠=∠,然后根据平行线的性质,得到HDF HFD BAG ==∠∠∠,由勾股定理求出AG =△;根据ABG DFH ∽,得到ABG DHF =∠∠,又因为AB AG ≠,得到ABG AGB ∠≠∠,进而得到AGB DHF ≠∠∠,即可判断△. 【详解】解:四边形ABCD 为正方形,90ADC BCD ,AD CD BC ==, E 、F 分别是BC 、CD 的中点,11222DF CD BC EC ∴====, 在ADF △和DCE 中,AD CD ADC BCD DF EC =⎧⎪∠=∠⎨⎪=⎩,()SAS ADF DCE ∴≌,DAF CDE ∴∠=∠,90ADG CDE ADC ∠+∠=∠=︒,90ADG DAF ∴∠+∠=︒,90AGD ∴∠=︒,AF DE ∴⊥,△结论正确;4AD =,122DF CD ==,AF ∴=,1122ADF S AD DF AG DG =⋅=⋅,AD DF DG AF ⋅∴==△结论错误; H 为AF 的中点,90ADC ∠=︒,12DH HF AF ∴=== HDF HFD ∴∠=∠,AB CD ∥,HFD BAG ∠=∠∴,HDF HFD BAG ∠=∠=∠∴,AG AD ==4AB =,52AG DF ∴==AB AB DH HF ==, AB AG DH DF∴=, ABG DFH ∴∽,△结论正确;ABG DHF ∴∠=∠,4AB =,AG = AB AG ∴≠,ABG AGB ∠≠∠∴,AGB DHF ∴∠≠∠,HD ∴与BG 不平行,△结论错误,综上可知,正确的结论为:△△,故选B .【点睛】本题考查了三角形全等的证明与判定,相似三角形的性质与判定,勾股定理,直角三角形的斜边中线等知识,熟练掌握全等三角形的判定和性质,相似三角形的判定和性质是解题关键.11.D【详解】解:A .AB=DE ,BC=EF ,△A=△E ,SSA 不能确定全等;B .△A=△E ,AB=EF ,△B=△D ,AB 和EF 不是对应边,不能确定全等;C .△A=△D ,△B=△E ,△C=△F ,AAA 不能确定全等;D .△A=△D ,△B=△E ,AC=DF ,根据AAS ,能判断△ABC△△DEF .故选D .12.D【分析】以点A 为坐标原点,AB 所在直线为x 轴,建立直角坐标系,则222PA PB PC ++=()22820032333x y ⎛⎫-+-+ ⎪⎝⎭,可得P (2,83)时,222PA PB PC ++最小,进而即可得到答案.【详解】以点A 为坐标原点,AB 所在直线为x 轴,建立直角坐标系,如图,则A (0,0),B (6,0),C (0,8),设P (x ,y ),则222PA PB PC ++=()()22222268x y x y x y ++-+++-=22331216100x y x y +--+=()22820032333x y ⎛⎫-+-+ ⎪⎝⎭, △当x =2,y =83时,即:P (2,83)时,222PA PB PC ++最小, △由待定系数法可知:AB 边上中线所在直线表达式为:883y x =-+, AC 边上中线所在直线表达式为:243y x =-+, 又△P (2,83)满足AB 边上中线所在直线表达式和AC 边上中线所在直线表达式,△点P是ABC三条中线的交点,故选D.【点睛】本题主要考查三角形中线的交点,两点间的距离公式,建立合适的坐标系,把几何问题化为代数问题,是解题的关键.13.D【分析】根据三角形全等的判定方法对A、D进行判断;利用三角形高的位置不同可对B、C进行判断.【详解】A、有两边和它们的夹角对应相等的两个三角形全等,所以A选项错误;B、有两边和第三边上的高对应相等的两个锐角三角形全等,所以B选项错误;C、有两边和其中一边上的高对应相等的两个锐角三角形全等,所以C选错误;D、有两边和第三边上的中线对应相等的两个三角形全等,所以D选项正确;故选:D.【点睛】本题考查了判断命题真假,以及全等三角形的判定,熟练掌握全等三角形的判定,仔细分类讨论是解题关键.14.C【分析】先设Rt△ABC的第三边长为x,由于8是直角边还是斜边不能确定,故应分8是斜边或x为斜边两种情况讨论.【详解】解:设Rt△ABC的第三边长为x,△当8为直角三角形的直角边时,x为斜边,由勾股定理得,10x=,此时这个三角形的周长=6+8+10=24;△当8为直角三角形的斜边时,x为直角边,由勾股定理得,22x8627,此时这个三角形的周长=△此三角形的周长为:24.故选:C.【点睛】本题考查的是勾股定理,二次根式的化简,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.15.D【分析】连接AQ、P A,如图,利用切线的性质得到△AQP=90°,再根据勾股定理得到PQ=AP△x轴时,AP的长度最小,利用垂线段最短可确定P点坐标.【详解】解:连接AQ、P A,如图,△PQ切△A于点Q,△AQ△PQ,△△AQP=90°,△PQ当AP的长度最小时,PQ的长度最小,△AP△x轴时,AP的长度最小,△AP△x轴时,PQ的长度最小,△A(﹣3,2),△此时P点坐标为(﹣3,0).故选:D.【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理,垂线段最短.16.C【分析】根据条件可得图1中△ABD△△ACD有1对三角形全等;图2中可证出△ABD△△ACD,△BDE△△CDE,△ABE△△ACE有3对三角形全等;图3中有6对三角形全等,根据数据可分析出第n个图形中全等三角形的对数.【详解】解:△AD是△BAC的平分线,△△BAD=△CAD.在△ABD与△ACD中,AB=AC,△BAD=△CAD,AD=AD,△△ABD△△ACD.△图1中有1对三角形全等;同理图2中,△ABE△△ACE,△BE=EC,△△ABD△△ACD.△BD=CD,又DE=DE,△△BDE△△CDE,△图2中有3对三角形全等;同理:图3中有6对三角形全等;由此发现:第n个图形中全等三角形的对数是()12n n+.故选:C.【点睛】此题主要考查了三角形全等的判定以及规律的归纳,解题的关键是根据条件证出图形中有几对三角形全等,然后寻找规律.17.D【分析】根据AC、BD、EF两两互相平分于点O,则有OE=OF,OA=OC,OB=OD;图中的对顶角有△AOB与△DOC,△AOE与△COF,△BOF与△DOE,△AOD与△BOC;根据两边和它们的夹角对应相等的两三角形全等(SAS)可得△AOB△△DOC;△AOE△△COF;再利用前面所证全等三角形,易证四边形ABCD是平行四边形,故△BOF△△DOE;△AOD△△BOC.【详解】解:△AC、BD、EF两两互相平分于点O△OE=OF,OA=OC,OB=OD;△△AOB=△DOC,△AOE=△COF,△BOF=△DOE,△AOD=△BOC;△△AOB△△DOC(SAS)△AOE△△COF(SAS)△OA=OC,OB=OD;△四边形ABCD是平行四边形,△ AD△BC,AD=BC△△EDO=△FBO,△AOD△△BOC△△BOF△△DOE故图中所有的全等三角形有6对,分别是△AOB△△DOC;△AOE△△COF;△BOF△△DOE;△AOD△△BOC;△ABD△△CDB;△ABC△△CDA.故选:D【点睛】本题考查了全等三角形的判定;找寻全等三角形时要从最明显的开始,由易到难,不重不漏.18.D【分析】根据正方形的面积公式,连续运用勾股定理,发现:四个小正方形的面积和等于最大正方形的面积,从而可解决问题.【详解】解:△所有的三角形都是直角三角形,所有的四边形都是正方形,△正方形A的面积=a2,正方形B的面积=b2,正方形C的面积=c2,正方形D的面积=d2,又△a2+b2=x2,c2+d2=y2,△正方形A、B、C、D的面积和=(a2+b2)+(c2+d2)=x2+y2=72=49(cm2).故选:D.【点睛】本题考查了勾股定理,注意掌握直角三角形中,两直角边的平方和等于斜边的平方.19.C【分析】△先证出AF =FD =CD ,得到△DFC =△DCF ,再根据平行线性质得到△DFC =△FCB ,即可得到△DCF =△BCF ,可得△DCF =12 △BCD ,故△正确;△做辅助线延长EF ,交CD 延长线于M ,先证△AEF △△DMF (ASA ),得到FE =MF 即12FE EM =,再通过在Rt ECM 中斜边上的中线等于斜边的一半得到12FC EM =,即可得到CF =EF ,故△正确;△根据EF =FM ,可得EFC CFM S S =,那么2ECM CFE S S =△△,再通过MC >BE ,得到BEC ECM S S △△<,即2BEC CEF S S △△<,故△的正确;△先证FC =FE ,设△FCE =x ,那么90DCF x ∠=︒-,再通过证△DCF =△DFC ,那么90DCF DFC x ∠=∠=︒-,则1802EFC x ∠=︒-,进一步证得9018022703EFD x x x ∠=︒-+︒-=︒-,即可证得3DFE AEF ∠=∠,故△错误.【详解】解:△△F 是AD 的中点,△AF =FD ,△在ABCD 中,AD =2AB ,△AF =FD =CD ,△△DFC =△DCF ,△//AD BC ,△△DFC =△FCB ,△△DCF =△BCF ,△△DCF =12△BCD ,故△正确;△延长EF ,交CD 延长线于M ,△四边形ABCD 是平行四边形,△//AB CD ,△△A =△MDF ,△F 为AD 中点,△AF =FD ,在△AEF 和△DFM 中,A FDM AF DFAFE DFM ∠∠⎧⎪⎨⎪∠∠⎩=== , △△AEF △△DMF (ASA ),△FE =MF ,即12FE EM =,△AEF =△M , △CE △AB ,△△AEC=90°,△△AEC =△ECD =90°, △12FC EM =△12FE EM =, △CF =EF ,故△正确;△△EF =FM ,△EFC CFM S S =,△2ECM CFE S S =△△,△MC >BE ,△BEC ECM S S △△<△2BEC CEF S S △△<故△正确;△设△FEC =x ,△CE △AB ,//AB CD ,△90ECD BEC ∠=∠=︒,△F 是EM 的中点,△FC =FE ,△△FCE =x ,△90DCF x ∠=︒-,△//AD BC△△FCB =△DFC△△DCF =△FCB ;△△DCF =△DFC△90DCF DFC x ∠=∠=︒-△1802EFC x ∠=︒-,△9018022703EFD x x x ∠=︒-+︒-=︒-,△90AEF x ∠=︒-,△△DFE =3△AEF ,故△错误.综上所述正确的是:△△△.故选:C .【点睛】此题主要考查了平行四边形的性质、全等三角形的判定与性质、直角三角形性质等知识,能准确找到边与边之间、角与角之间的关系是解答此题的关键.20.A【分析】过C 作HC CD ⊥于C ,使CH BD =,连接DH ,FH ,根据SAS 证明BED CFH ≅△△,得出FH DE =,则DE DF FH DF +=+,当FH DF +的最小时,DE DF +最小,当D 、F 、H 在同一条直线时,FH DF +最小,根据勾股定理算出结果即可.【详解】解:如图,过C 作HC CD ⊥于C ,使CH BD =,连接DH ,FH ,90HCA ACD ∴∠+∠=︒,150BDC ∠=︒,18015030DBC DCB ∴∠+∠=︒-︒=︒,()ABD ACD ABC ACB DBC DCB ∴∠+∠=∠+∠-∠+∠,△ABC 为等边三角形,60ABC ACB ∴∠=∠=︒,AB AC =,1203090ABD ACD ∴∠+∠=︒-︒=︒,HCA ABD ∴∠=∠, =AE AF ,BE CF ∴=,△在BED 和FCH 中BE CF HCA ABD CH BD =⎧⎪∠=∠⎨⎪=⎩,()SAS BED CFH ∴≅△△,FH DE ∴=,DE DF FH DF ∴+=+,∴当FH DF +的最小时,DE DF +最小,∴当D 、F 、H 在同一条直线时,FH DF +最小,在Rt DCH △中,3CH =,4DC =,5DH ∴,△DE DF +的最小值是5,故A 正确.故选:A .【点睛】本题主要考查了等边三角形的性质,全等三角形的判定和性质,勾股定理,余角的性质,解题的关键是作出辅助线,证明BED CFH ≅△△.21.7或8【分析】根据等腰三角形的性质,分两种情况:△当腰长为2时,△当腰长为3时,解答出即可.【详解】解:根据题意,△当腰长为2时,周长=2+2+3=7;△当腰长为3时,周长=3+3+2=8,故答案为:7或8.【点睛】本题主要考查了等腰三角形的性质,注意本题要分两种情况解答.22.3m ﹣18.【分析】先根据三角形三边关系确定m 的取值范围,然后利用二次根式的性质化简即可.【详解】△三角形的三边长分别为3、m 、5,△2<m <8,=|2﹣m |﹣2|m ﹣8|=m ﹣2﹣2(8﹣m )=3m ﹣18.故答案为:3m ﹣18.【点睛】本题主要考查三角形三边关系和二次根式的性质,掌握三角形三边关系和二次根式的性质是解题的关键.23.112.5【分析】根据正方形的性质,可以得到△PBC 的度数,再根据等腰三角形的性质和三角形内角和,求得△BPC 的度数,即可求得△DPC 的度数.【详解】解:△点P 是正方形ABCD 的对角线BD 上一点,△△PBC =45°,△BP =BC ,△△BPC =△BCP =180452︒-︒=67.5°, △△DPC =180°-△BPC =112.5°,故答案为:112.5.【点睛】本题考查正方形的性质、等腰三角形的性质,利用数形结合的思想解答是解答本题的关键.24.25︒或25度【分析】根据三角形内角和,得A ∠的角度,根据折叠得,A F ∠=∠,ADE EDF ∠=∠;又根据EF BC ∥,得90FEC C ∠=∠=︒,再根据三角形内角和,求出EGF ∠,最后根据三角形的外角和,即可求出ADE ∠.【详解】△ABC 中,90C ∠=︒,70B ∠=︒△18020A C B ∠=︒-∠-∠=︒△DEF 是DEA △折叠得到的△20A F ∠=∠=︒,ADE EDF ∠=∠△EF BC ∥△90FEC C ∠=∠=︒△18070EGF FEC F ∠=︒-∠-∠=︒△70EGF DGC ∠=∠=︒△70A ADG ∠+∠=︒△270A ADE ∠+∠=︒△25ADE ∠=︒.故答案为:25︒或25度.【点睛】本题考查三角形的知识,解题的关键是掌握三角形内角和、外角和定理. 25.26320x x --=【分析】先表示出BC 的长,再利用勾股定理建立方程即可.【详解】解:由题可知 1丈=10尺,门的对角线距离恰好为1丈,∴门的对角线距离恰好为10尺,△高比宽多6尺,设门高 AB 为x 尺,△()6BC x =-尺,△可列方程为:()222610x x +-=,整理得:26320x x --=故答案为:26320x x --=.【点睛】本题属于数学文化题,考查了勾股定理及其应用,解决本题的关键是读懂题意,能将文字语言转化为几何语言,能用含同一个未知数的式子表示出直角三角形的两条直角边,再利用勾股定理建立方程即可.26.118【分析】根据轴对称的性质得出角的度数,进而利用三角形外角的性质解答即可.【详解】解:∵△ABC和△ABE关于直线AB对称,△ABC和△ADC关于直线AC对称,∴∠DCA=∠ACB=18°,∠BAC=∠BAE,∵∠ABC=32°,∴∠BAC=180°-18°-32°=130°=∠BAE,∴∠EAC=360°﹣∠BAC﹣∠BAE=360°﹣130°﹣130°=100°,∴∠CFE=∠ACD+∠EAC=18°+100°=118°,故答案为:118°.【点睛】此题考查轴对称的性质,关键是根据轴对称的性质求出相关角的度数.27.(6)(3)(5)【分析】利用全等图形的概念可得答案.【详解】解:(1)与(6)是全等图形,(2)与(3)(5)是全等图形,故答案为:(6),(3)(5).【点睛】本题主要考查了全等图形,关键是掌握能够完全重合的两个图形叫做全等形.28.110°##110度【分析】根据等腰三角形性质,可得△B=△ACB=70°,再根据平行线的性质,即可求出△BCD的度数.【详解】解:△AB=AC,△A=40°,△△B=△ACB=12(180°-40°)=70°,△CD AB∥,△△B+△BCD=180°,△△BCD=110°.故答案为:110°【点睛】此题主要考查了等腰三角形的性质和平行线的性质,解题关键是熟练运用已知条件,进行正确的推理计算.29.3°##3度【分析】先利用外角等于不相邻的两个内角之和,以及角平分线的性质求△A1=12△A,再依此类推得,△A 2=212△A ;…△A 5=512 △A ;找出规律,从而求△A 5的值. 【详解】△BA 1C +△A 1BC =△A 1CD ,2△A 1CD =△ACD =△BAC +△ABC ,△2(△BA 1C +△A 1BC )=△BAC +△ABC ,2△BA 1C +2△A 1BC =△BAC +△ABC ,而2△A 1BC =△ABC ,△2△BA 1C =△BAC ,同理,可得2△BA 2C =△BA 1C ,2△BA 3C =△BA 2C ,2△BA 4C =△BA 3C ,2△BA 5C =△BA 4 C ,△△BA 5C =12 △BA 4C =14△BA 3C =18 △BA 2C =116 △BA 1C =132 △BAC =96°÷32=3°, 故△A 5=3°.故答案为:3°.【点睛】此题考查三角形的外角性质,解题关键在于找到规律30.549π-【分析】由15AB =,12BC =,9AC =,得到222AB BC AC =+,根据勾股定理的逆定理得到ABC 为直角三角形,于是得到ABC 的内切圆半径1291532+-==,图中阴影部分的面积等于直角三角形的面积减去圆的面积,分别利用它们的计算公式即可得到图中阴影部分的面积【详解】△ 15AB =,12BC =,9AC =,△ 222AB BC AC =+,△ ABC 为直角三角形,△ ABC 的内切圆半径1291532+-==, △ 图中阴影部分的面积2112935492ππ=⨯⨯-⋅=-. 故答案为549π-【点睛】本题考查了三角形的内切圆与内心、勾股定理的逆定理,对于不规则图形的面积要灵活转化为规则图形的求法是解题的关键31 【分析】过点A 作AC BC ⊥于C ,根据坡度与坡角的概念得1tan 2AC BC α==,设AC x =,2BC x =,根据勾股定理求出AB 的长,再根据锐角三角函数的概念即可求出答案.【详解】过点A 作AC BC ⊥于C ,△AB 的坡度1:2i =, △1tan 2AC BC α==, 设AC x =,2BC x =,△AC BC ⊥,△AB ,△sinAC AB α==【点睛】本题考查了坡度坡角的知识与解直角三角形的知识,熟练掌握坡度坡角的概念与勾股定理的应用是解本题的关键.32.12米【详解】解:如图所示,AC=6米,BC=4.5米,由勾股定理得,AB= =7.5(米). 故旗杆折断前高为:4.5+7.5=12(米).故答案为:12米.33. 2 【分析】△连接,OA OB ,易证AOB 是等边三角形,弦AB 长为2,2OA OB ==,即可得到答案;△先证90BOC AOB AOC ∠=∠+∠=︒,延长BO 交O 于点E ,连接AE 交CD 于点P ,连接BP ,则此时PA PB PA PE AE +=+=,即PA PB +的最小值是AE 的长,再用勾股定理求出AE 即可.【详解】解:△连接,OA OB ,△30,ADB ∠=︒△60AOB ∠=︒,△OA OB =,△AOB 是等边三角形,△弦AB 长为2,△2OA OB ==,即O 的半径长为2,故答案为:2△△15ADC ∠=︒,△230AOC ADC ︒∠=∠=,△90BOC AOB AOC ∠=∠+∠=︒,延长BO 交O 于点E ,连接AE 交CD 于点P ,连接BP ,则此时PA PB PA PE AE +=+=,即PA PB +的最小值是AE 的长,△60BAO ∠=︒,△2OA OE ==,△30OAE AEB ︒∠=∠=,△90BAE BAO OAE ∠=∠+∠=︒,△AE ==即PA PB+的最小值是故答案为:【点睛】此题考查了圆周角定理、勾股定理、等边三角形的判定和性质、轴对称最短路径等知识,熟练掌握相关定理并灵活应用是解题的关键.34.6【分析】利用勾股定理求解出另一条直角边,即可求解.【详解】解:△直角三角形斜边长是5,一直角边的长是3,△.×3×4=6.该直角三角形的面积S=12故答案为6.【点睛】本题考查了了勾股定理,解题的关键是掌握利用勾股定理求直角边.35.36°【分析】如图所示,△ABF中,根据内角和外角的关系,△2=△A+△B;△EDG中,△1=△D+△E;根据三角形内角和等于180°,得到△1+△2+△C=180度.于是△A+△B+△C+△D+△E=180°,由于五个角的度数是相同,即可求得每一个角的度数.【详解】△△2=△A+△B;△1=△D+△E,△1+△2+△C=180°,△△A+△B+△C+△D+△E=180°,△五个角的度数是相同,则每一个角的度数都是180°÷5=36°,故答案为36°【点睛】本题考查三角形的外角性质及三角形内角和定理,结合三角形内角和外角的关系,将所有角转化到一个三角形内,体现了数形结合思想和转化思想在解决数学问题时的魅力.36.1或3。
初中数学三角形专题练习

初中数学三角形专题练习三角形中的边角关系一、单选题1.(3分)下列长度的三条线段能组成三角形的是()A.4、5、6B.1、2、3C.3、3、6D.10、4、4 2.(3分)在△ABC中,∠C=100°,∠B=40°,则∠A的度数为()A.30°B.40°C.50°D.60°3.(3分)若一条长为31cm细线能围成一边长等于7cm的等腰三角形,该等腰三角形的腰长为()A.7cm B.9cm C.12cm D.7cm或12cm 4.(3分)如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=34°,则∠ACB的度数是()A.28°B.30°C.31°D.32°5.(3分)等腰三角形的一边长等于3,一边长等于7,则它的周长是()A.13B.17C.13或17D.126.(3分)如图,△ABC中,AB=AC,腰AB的垂直平分线DE交AB于点E,交AC 于点D,且∠DBC=15°,则∠A的度数是()A.50°B.36°C.40°D.45°7.(3分)如图,△ABC的三边的中线AD,BE,CF的公共点为G,且AG:GD=2:1,若S△ABC=12,则图中阴影部分的面积是()A .3B .4C .5D .68.(3分)如图,在△ABC 中,点D 是线段AB 的中点,DC ⊥BC ,作∠EAB =∠B ,DE ∥BC ,连接CE .若25BC AE =,设△BCD 的面积为S ,则用S 表示△ACE 的面积正确的是( )A .52SB .3SC .4SD .92S 9.(3分)如下图,已知∠AOB=α,在射线OA 、OB 上分别取点OA 1=OB 1,连结A 1B 1,在B 1A 1、B 1B 上分别取点A 2、B 2,使B 1B 2= B 1A 2,连结A 2 B 2按此规律下去,记∠A 2B 1 B 2=θ1,∠A 3B 2B 3=θ2,,∠A n+1B n B n+1=θn ,则θ2016-θ2015的值为( )A .20161802α+B .20161802α-C .20151802α+D .20151802α- 10.(3分)设△ABC 的面积为1,如图①将边BC 、AC 分别2等分,BE 1、AD 1相交于点O ,△AOB 的面积记为S 1;如图②将边BC 、AC 分别3等份,BE 1、AD 1相交于点O ,△AOB 的面积记为S 2;……, 依此类推,则S 5的值为( )A .18B .19C .110D .111二、填空题11.(3分)一个三角形三个内角的度数之比为2:3:7,这个三角形一定是______. 12.(3分)等腰三角形的周长为16cm ,底边长为xcm ,腰长为ycm ,则x 与y 之间的关系式为 ____________13.(3分)将一张等边三角形纸片沿着一边上的高剪开,可以拼成不同形状的四边形.试写出其中一种四边形的名称____________.14.(3分)如图,在Rt ABC △中,90C ∠=︒,边AB 的垂直平分线DE 交BC 于点D ,AD 平分BAC ∠,则B ∠=_______︒.15.(3分)如图,在Rt ABC 中,90ACB ∠=︒,BD 是ABC ∠的平分线,DE AB ⊥于E ,若3cm CD =,10cm AB =,则ABD △的面积为________.16.(3分)如图,D ,E 分别为ABC 两边AB ,AC 的中点,将ABC 沿线段DE 折叠,使点A 落在BC 上点F 处,若55B ∠=︒,则BDF ∠=________.17.(3分)如图,ABC 是钢架的一部分,为使钢架更加坚固,在其内部添加了一些钢管DE ,EF ,FG ,…,添加的这些钢管的长度与BD 的长度相等,如果10B ∠=︒,那么添加的这样钢管的根数最多是______.18.(3分)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.如:三个内角分别为120︒,40︒,20︒的三角形是“灵动三角形”.如图,60MON ∠=︒,在射线OM 上找一点A ,过点A 作AB OM ⊥交ON 于点B ,以A 为端点作射线AD ,交线段OB 于点C (规定090OAC ︒<∠<︒)当OAC ∠=________时,ABC 为“灵动三角形”.19.(3分)我们定义三边长均为整数的三角形叫做整三角形.已知△ABC 是整三角形,其周长为偶数,若AC - BC = 3.则边长AB 的最小值是__________20.(3分)在□ABCD 中AC =6cm ,BD =8cm ,则AB 的取值范围是__________.21.(3分)如图,在∠ABC 中,∠A=m°,∠ABC 和∠ACD 的平分线交于点A 1,得∠A 1;∠A 1BC 和∠A 1CD 的平分线交于点A 2,得∠A 2;…∠A 2012BC 和∠A 2012CD 的平分线交于点A 2013,则∠A 2013=____度.22.(3分)在等腰△ABC 中,AB=AC ,AC 腰上的中线BD 将三角形周长分为15和21两部分,则这个三角形的底边长为______.23.(3分)如图,在Rt ABC △中,90︒∠=C ,2BC =,30A ︒∠=,点D 是AB 的中点,P 是AC 边上一动点,连接DP ,将DPA 沿着DP 折叠,A 点落到F 处,DF 与AC 交于点E ,当DPF 的一边与BC 平行时,线段DE 的长为_____.24.(3分)如图,在正方形ABCD 中,E 是对角线BD 上一点,且满足BE =BC .连接CE 并延长交AD 于点F ,连接AE ,过B 点作BG ⊥AE 于点G ,延长BG 交AD 于点H .在下列结论中:∠AH =DF ; ∠∠AEF =45°; ∠AH =DE ;∠S 四边形EFHG =S △DEF +S △AGH ,其中正确的结论有_____.(填正确的序号)25.(3分)如图,在ABC ∆中,AB AC =,点D 在线段AC 上,现将ABC ∆沿着BD 翻折后得到A BD '∆,A B '交AC 于点E ,//A D BC '且A D BC '=,若BD =ABC ∆的面积为__________.三、解答题26.(4分)如图,在77⨯的网格中,A 、B 均在格点上,请只用无刻度的直尺作图.(保留作图痕迹,不写做法)(1)在图1中画格点C .使得ABC 为等腰三角形(请画出两个不同的C 点); (2)在图2中作出BAD ∠的角平分线.27.(5分)在ABC 中,,20A B C A B ∠+∠=∠∠-∠=︒,(1)求A ∠,B ,C ∠的度数;(2)ABC 按角分类,属于什么三角形ABC 按边分类,属于什么三角形?28.(4分)如图,在△ABC 中,∠B∠40°∠△ABC 的外角∠DAC 和∠ACF 的平分线交于点E ,求∠AEC 的度数.29.(6分)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题:∠1∠已知,如图1∠△ABC 中,P 点是∠ABC 和∠ACB 的角平分线的交点,求证:∠P=12∠A+90°∠ ∠2∠如图2,若P 点是∠ABC 和∠ACB 外角的角平分线的交点,∠A=80°,那么∠P=____°∠∠3∠如图3∠△ABC 中,若P 点是∠ABC 外角和∠ACB 外角的角平分线的交点,∠A=α,那么∠P=________(请用含α的代数式表示)30.(6分)如图,ABC ∆中,90BAC ︒∠=,40B ︒∠=,点D 在BC 边上,E 在BC 的延长上,且AB BD =,AC CE =.求DAE ∠的度数.参考答案1.A【分析】直接利用三角形的三边关系逐项判断即可.【详解】解:根据三角形任意两边的和大于第三边,得A 、4+5>6,能组成三角形;B 、1+2=3,不能组成三角形;C 、3+3=6,不能组成三角形;D 、4+4=8<10,不能组成三角形.故选:A .【点睛】本题主要考查了组成三角形三边的条件,掌握两较短边长的和大于最长边的长就能够组成三角形是解答本题的关键.2.B【分析】直接根据三角形内角和定理解答即可.【详解】解:ABC ∆中,40B ∠=︒,100C ,1801804010040A B C .故选:B .【点睛】本题考查的是三角形内角和定理,熟知三角形的内角和等于180︒是解答此题的关键. 3.C【分析】根据题意可分当腰长为7cm 时和当底边长为7cm 时,然后利用三角形三边关系进行判断求解即可.【详解】解:由题意易得:①当腰长为7cm 时,则底边为17cm ,17>7+7,根据三角形三边关系可知不符合题意;②当底边长为7cm时,则腰长为:317122cm-=,由三角形三边关系可知符合题意;∴该等腰三角形的腰长为12cm;故选C.【点睛】本题主要考查等腰三角形的性质及三角形的三边关系,熟练掌握等腰三角形的性质及三角形的三边关系是解题的关键.4.A【分析】连接OB,根据切线的性质,得∠OBA=90°,又∠A=34°,所以∠AOB=56°,再用三角形的外角性质可以求出∠ACB的度数.【详解】解:如图:连接OB,∵AB切⊙O于点B,∴∠OBA=90°,∵∠A=34°,∴∠AOB=90°﹣34°=56°,∵OB=OC,∴∠C=∠OBC,∵∠AOB=∠C+∠OBC=2∠C,∴∠C=28°.故选:A.【点睛】本题考查的是切线的性质和三角形的外角和定理,能够连接OB是解题的关键.5.B【分析】本题已知了等腰三角形的两边的长,但没有明确这两边哪边是腰,哪边是底,因此要分类讨论.【详解】解:当三边是3,3,7时,3+3=6<7,不符合三角形的三边关系;当三边是7,7,3时,符合三角形的三边关系,此时周长是7+7+3=17.因此等腰三角形的周长为17.故选:B.【点睛】此题主要考查等腰三角形的性质及三角形三边关系的运用;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.6.A【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,再根据等边对等角可得∠A=∠ABD,∠ABC=∠C,然后根据三角形的内角和等于180°方程求解即可.【详解】解:∵AB的垂直平分线DE交AC于D,∴AD=BD,∴∠A=∠ABD,∵AB=AC,∴∠ABC=∠C,∵∠DBC=15°,∴∠ABC=∠C=∠A+15°,在△ABC中,∠A+∠ABC+∠C=180°,∴∠A+∠A+15°+∠A+15°=180°,解得∠A=50°.故选:A.【点睛】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等边对等角的性质,三角形的内角和定理,熟记性质与定理并列出方程是解题的关键.7.B【分析】根据三角形的中线把三角形的面积分成相等的两部分,知△ABC的面积即为阴影部分的面积的3倍.【详解】∵△ABC的三条中线AD、BE,CF交于点G,∴S△CGE=S△AGE=13S△ACF,S△BGF=S△BGD=13S△BCF,∵S△ACF=S△BCF=12S△ABC=12×12=6,∴S△CGE=13S△ACF=13×6=2,S△BGF=13S△BCF=13×6=2,∴S阴影=S△CGE+S△BGF=4.故选:B.【点睛】此题主要考查根据三角形中线性质求解面积,熟练掌握,即可解题.8.C【分析】延长AE,BC交于点F,易得AE=DE,由DE∥BC,D为AB的中点,可知DE为中位线,所以BF=2DE,设BC=2x,AE=DE=5x,则BF=10x,CF=BF-BC=8x,在△ABF和△ACF中,分别利用同高的两个三角形面积之比等于底边之比,可推出面积关系.【详解】如图所示,延长AE,BC交于点F∵DE ∠BC ,∴∠ADE=∠B ,又∵∠EAB =∠B ,∴∠ADE=∠EAB ,∴AE=DE∵D 为AB 的中点,DE ∥BF ,∴DE 为△ABF 的中位线, ∴BF=2DE ,设BC=2x ,AE=DE=5x ,则BF=10x ,CF=BF -BC=8x , 在△ABC 中,∵D 是AB 的中点,∴S △ACD =S △BCD =S ∴S △ABC =2S , 在∠ABF 中,2184===ACFABC BC x CF x S S∠=8ACFSS在∠ACF 中,E 为AF 的中点, ∴1=42==ACECEFACFSSS S故选C. 【点睛】本题考查三角形的面积关系,根据同高的三角形面积比等于底边比,推出面积关系是关键. 9.B 【解析】∵OA 1=OB 1,∠AOB=α,∴∠A 1B 1O=12 (180°-α), ∴12(180°-α)+θ1=180, 整理得,θ1=1802α︒+ , ∵B 1B 2=B 1A 2,∠A 2B 1B 2=θ1,∴∠A 2B 2B 1=12(180°-θ1), ∴12(180°-θ1)+θ2=180°, 整理得,θ2=11802θ︒+=31804α⨯︒+, ∴θ2-θ1=31804α⨯︒+-1802α︒+=21802α︒-,同理可求θ3=21802θ︒+=71808α⨯︒+, ∴θ3-θ2=71808α⨯︒+-31804α⨯︒+=31802α︒-, …,依此类推,θ2016-θ2015 =20161802α︒-; 故选B . 10.D 【解析】如图1,连接OC,由1BE 、1AD 分别将边BC 、AC2等份,111122AD C BCE ABC S S S ∆∆∆===,所以111111AD C BCE CE OD CE OD S S S S ∆∆-=-四边形四边形,即11AOE BOD S S ∆∆=,根据等底同高的两个三角形的面积相等可得1111,,AOE COE BOD COD S S S S ∆∆∆∆== 所以11111122AOE COE COD AD C ABC S S S S S ∆∆∆∆∆++===,即可求得11116AOE COE COD S S S ∆∆∆===,所以111111114=63211ABC AOE COE COD BOD S S S S S S ∆∆∆∆∆=----=-⨯=⨯+;如图2,连接OC,OD 1,OE 2,由图(1)的方法可得 11222211215BOD D OD COD COE E OE AOE S S S S S S ∆∆∆∆∆∆======, 所以11222211221116=155221ABC BOD D OD COD COE E OE AOE S S S S S S S S ∆∆∆∆∆∆∆=------=-⨯=⨯+, 同样的方法可求得311=7231S =⨯+,以此类推可得511=25111S =⨯+.故选D.点睛:本题是规律探究题,主要考查等底同高的两个三角形的面积相等;能从图中观察,并能适当添加辅助线是解题的关键.. 11.钝角三角形 【分析】由一个三角形三个内角的度数之比为2:3:7,利用三角形的内角和定理,可求得这个三角形的最大角的度数,继而求得答案.【详解】解:∠一个三角形三个内角的度数之比为2:3:7,∠这个三角形的最大角为:180°×7237++=105°,∠这个三角形一定是钝角三角形.故答案为:钝角三角形.【点睛】此题考查了三角形的内角和定理.此题比较简单,注意求得三角形的最大角是关键.12.y=8-12x (0<x<8)【分析】根据等腰三角形周长公式可写出y与x的关系式.【详解】∵等腰三角形的周长为16cm,底边长为xcm,一腰长为ycm,∴x+2y=16,∴y=8-12 x,∵y-y<x<2y,x+2y=16,∴0<x<8,则y=8-12x (0<x<8).【点睛】此题主要考查等腰三角形的性质及三角形三边关系的综合运用.13.平行四边形(或矩形或筝形)【解析】解:将一张等边三角形纸片沿着一边上的高剪开,按位置摆放的不同,可以拼成平行四边形、矩形.故答案为平行四边形或矩形.14.30【分析】根据垂直平分线的性质和角平分线的定义得出EAD B CAD∠=∠=∠,然后利用直角三角形两锐角互余即可求出答案. 【详解】DE 垂直平分AB ,∴AD BD = ,EAD B ∴∠=∠.∵AD 平分BAC ∠,EAD CAD ∴∠=∠,EAD B CAD ∴∠=∠=∠.90C ∠=︒,90BAC B ∴∠+∠=︒, 390B ∴∠=︒ ,30B ∴∠=︒.故答案为:30. 【点睛】本题主要考查垂直平分线的性质,角平分线的定义和直角三角形两锐角互余,掌握垂直平分线的性质和角平分线的定义是解题的关键. 15.215cm 【分析】先根据角平分线的性质求得3DE cm =,再利用三角形面积公式即可求得答案. 【详解】解:∵BD 是ABC ∠的平分线,90ACB ∠=︒,DE AB ⊥ ∴3DE DC cm == ∵10AB cm = ∴21031522ABDAB DE Scm ⋅⨯===. 故答案是:215cm 【点睛】本题考查了角平分线的性质、三角形的面积公式,难度不大,能根据角平分线的性质求得3DE cm =是解决问题的关键. 16.70°利用折叠的性质求解. 【详解】解:由折叠的性质知,AD =DF , ∵点D 是AB 的中点,∴AD =BD ,由折叠可知AD =DF , ∴BD =DF ,∴∠DFB =∠B =55°,∠BDF =180°-2∠B =70°. 故答案为:70°. 【点睛】本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②中点的性质,等边对等角,三角形内角和定理求解. 17.8 【分析】根据已知利用等腰三角形的性质、三角形外角的性质找到图中存在的规律,根据规律和三角形内角和定理不难求解. 【详解】解:∵添加的钢管的长度与BD 的长度相等,10B ∠=︒ ∴10DEB B ∠=∠=︒ ∴20EDF DEB B ∠=∠+∠=︒ ∵ED EF =∴20EFD EDF ∠=∠=︒ ∴30FEG EFD B ∠=∠+∠=︒ ⋯⋯∴由此思路可知:第一个等腰三角形的底角是10︒,第二个底角是20︒,第三个底角是30,第四个底角是40︒,第五个底角是50︒,第六个底角是60︒,第七个底角是70︒,第八个底角是80︒,第九个底角是90︒(这时与三角形内角和是180︒产生矛盾)就不存在了 ∴加的这样钢管的根数最多是8个. 故答案是:8本题考查了等腰三角形的性质、三角形内角和定理、三角形外角的性质等,发现并运用规律是正确的解答本题的关键.18.80°或52.5°或30°【分析】分点C在线段OB和线段OB的延长线上两种情况,根据“灵动三角形”的定义计算.【详解】解:设∠OAC=x则∠BAC=90°-x,∠ACB=60°+x,∠ABC=30°∵△ABC为“灵动三角形”,当∠ABC=3∠BAC时,∴30°=3(90°-x),∴x=80°;当∠ABC=3∠ACB时,∴30°=3(60°+x)∴x=-50°(舍去)∴此种情况不存在;当∠BCA=3∠BAC时,∴60°+x=3(90°-x),∴x=52.5°,当∠BCA=3∠ABC时,∴60°+x=90°,∴x=30°;当∠BAC=3∠ABC时,∴90°-x=90°,∴x=0°(舍去);当∠BAC=3∠ACB时,∴90°-x=3(60°+x),∴x=-22.5°(舍去),∴此种情况不存在,∴综上所述:∠OAC=80°或52.5°或30°.故答案为:80°或52.5°或30°.本题考查的是三角形内角和定理、“灵动三角形”的概念,用分类讨论的思想解决问题是解本题的关键. 19.5 【分析】根据AC - BC = 3可得AC=BC+3,故三角形的周长为2BC+AB+3,其为偶数,故AB 为奇数,又因为AB >3,故AB 的最小值为5. 【详解】 ∵AC - BC = 3 ∴AC=BC+3∴三角形的周长=2BC+AB+3 ∵其周长为偶数,三边长均为整数 ∴AB 为奇数又∵AB >AC - BC 即AB >3 ∴AB 的最小值为5. 故答案为:5 【点睛】本题考查的是三角形的三边关系,掌握“两边之和大于第三边,两边之差小于第三边”是关键. 20.17AB <<; 【解析】如图,∵在平行四边形ABCD 中,AC=6cm∠BD=8cm∠∴OA=12AC=3cm,OB=12BD=4cm∠∴在△AOB 中,OB −OA<AB<OA+OB ,即1cm<AB<7cm. 故答案是:1cm<AB<7cm. 21.2013m 2 【解析】试题分析:∠A 1B 、A 1C 分别平分∠ABC 和∠ACD ,∠∠ACD=2∠A 1CD ,∠ABC=2∠A 1BC , 又∠∠A 1CD=∠A 1+∠A 1BC ,∠ACD=∠ABC+∠A ,∠∠A=2∠A 1,∠∠A 1=m2度.同理可得∠A 1=2∠A 2,即∠A=22∠A 2,∠∠A 2=2m2度. …… ∠∠A 2013=2013m2度. 22.16或8 【分析】本题由题意可知有两种情况,AB+AD=15或AB+AD=21.从而根据等腰三角形的性质及三角形三边关系可求出底边为8或16. 【详解】解:∵BD 是等腰△ABC 的中线,可设AD=CD=x ,则AB=AC=2x , 又知BD 将三角形周长分为15和21两部分, ∴可知分为两种情况①AB+AD=15,即3x=15,解得x=5,此时BC=21﹣x=21﹣5=16;②AB+AD=21,即3x=21,解得x=7;此时等腰△ABC 的三边分别为14,14,8. 经验证,这两种情况都是成立的. ∴这个三角形的底边长为8或16. 故答案为:16或8.【点睛】本题主要考查来了等边三角形的性质以及三角形的三边关系(两边之和大于第三边,两边只差小于第三边),注意求出的结果燕验证三角形的三边关系,掌握分类讨论思想是解题的关键.23.1或2【解析】 【分析】当DPF 的一边与BC 平行时,会有三种情况,需分别讨论,①://DF BC ,②//DP BC ,③://PF BC ,分别计算出每种情况时线段DE 的长即可. 【详解】当DPF 的一边与BC 平行时,有三种情况,分别讨论: ①://DF BC 如下图所示,当//DF BC 时,90AED C ︒∠=∠=,则在Rt AED △中,30A ︒∠=,2AD =,则12ADDE ==; ②: 如下图所示,当//DP BC 时,点A 的对应点F 与点C 、E 重合,由折叠的性质可知2AD DE ==;③: 当//PF BC 时,如下图所示,90CPF APF C ︒∠=∠=∠=,因为折叠,30A F ︒∠=∠=,过点D 作AC 边上的垂线,垂足为H ,则60DEH ︒∠=,根据中位线定理可知12BC DH ==,继而可DE = 【点睛】本题考查折叠的性质,中位线定理,熟知折叠的性质和中位线定理的应用是解题关键,本题属于三角形综合题 . 24.∠∠∠. 【分析】先判断出∠DAE =∠ABH ,再判断△ADE ≌△CDE 得出∠DAE =∠DCE =22.5︒,∠ABH =∠DCF ,再判断出Rt △ABH ≌Rt △DCF 从而得到①正确;根据三角形的外角求出∠AEF =45︒,得出②正确;结合①②可得DF =DE ,根据AH =DF 即可得③正确;连接HE ,判断出S △EFH ≠S △EFD 得出④错误. 【详解】∵BD 是正方形ABCD 的对角线,∴∠ABE =∠ADE =∠CDE =45︒,AB =BC , ∵BE =BC , ∴AB =BE , ∵BG ⊥AE ,∴BH 是线段AE 的垂直平分线,∠ABH =∠DBH =22.5︒, 在Rt △ABH 中,9067.5AHB ABH ∠=︒-∠=︒, ∵∠AGH =90︒,∴∠DAE =∠ABH =22.5︒, 在△ADE 和△CDE 中,45DE DE ADE CDE AD CD =⎧⎪∠=∠=︒⎨⎪=⎩, ∴△ADE ≌△CDE (SAS ), ∴∠DAE =∠DCE =22.5︒, ∴∠ABH =∠DCF , 在Rt △ABH 和Rt △DCF 中,BAH CDF AB CD ABH DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴Rt △ABH ≌Rt △DCF (ASA ),∴AH=DF,∠CFD=∠AHB=67.5︒,∵∠CFD=∠EAF+∠AEF,∴67.5︒=22.5︒+∠AEF,∴∠AEF=45︒,故∠∠正确;︒+︒=67.5︒,∵∠FDE=45︒,∠DFE=∠F AE+∠AEF=22.545︒-︒-︒=︒,∴∠DEF=1804567.567.5∴DF=DE,∵AH=DF,∴AH=DE,故∠正确;如图,连接HE,∵BH是AE垂直平分线,∴AG=EG,∴S△AGH=S△HEG,∵AH=HE,∴∠AHG=∠EHG=67.5︒,∴∠DHE=45︒,∵∠ADE=45︒,∴∠DEH=90︒,∠DHE=∠HDE=90︒,∴EH=ED,∴△DEH是等腰直角三角形,∵EF不垂直DH,∴FH≠FD,∴S△EFH≠S△EFD,∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故∠错误,∴正确的是∠∠∠,故答案为:∠∠∠.【点睛】本题考查正方形的性质,全等三角形的判定和性质以及三角形的内角和与外角和的应用,推断△ADE ≌△CDE 和作出辅助线是本题的关键,综合性较强.25.【分析】根据翻折的性质得到==ABD A BD A ED EBD S S S S ''+,由//A D BC '且A D BC '=,依据平行线的性质及ASA ,可得A DE '≌BCE ,通过等量代换得到BCD ABD S S =,从而得到CD AD =设为4a ,依据等量代换得到=4=CD a BC ,依据三角形外角的性质、翻折的性质、三角形内角和定理得到=4BE BC a =,连接B 与EC 的中点F ,依据三线合一求出两个有公共直角边的直角三角形,依据勾股定理列出关于a 的方程,解出可求得ABC 的底和高,再运用三角形面积公式即可.【详解】解:设=4AD a ,∵AB AC =,∴=C ABC ∠∠,∵将ABC 沿着BD 翻折后得到A BD ',∴==ABD A BD A ED EBD S S S S ''+,=4A D AD a '=,DBE DBA ∠=∠,∵//A D BC ',∴'=A DE C ∠∠,'=A CBE ∠∠,又∵=4A D BC a '=,∴A DE '≌BCE (ASA ), ∴12DE EC DC ==,A DE BCE S S '=, 又∵BCD BCE EBD SS S =+,=ABD A ED EBD S S S '+ ∴BCD ABD S S =,∴=4CD AD a =, ∴122DE EC DC a ===, ∵=4=CD a BC ,∴CBD CDB ∠=∠,又∵+CBD CBE DBE ∠=∠∠,+CDB A DBA ∠=∠∠,DBE DBA ∠=∠,∴=CBE A ∠∠,又∵=180BEC C EBC ∠︒-∠-∠,=180ABC C A ∠︒-∠-∠,=C ABC ∠∠∴=BEC ABC C ∠∠=∠,∴=4BE BC a =,如下图,连接B 与EC 的中点F ,则12FC FE EC a ===,3DF DE FE a =+=,∴BF AC ⊥,∴22222BD DF BF BC FC -==-,即22222(3)(4)a BF a a -==-(0a >),解得1a =,∴BF =88AC AD DC a +==,∴2ABC AC BF S ⋅==故答案为:【点睛】本题考查了翻折的性质、等腰三角形的等边对等角的性质、三线合一的性质、三角形等角对等边的性质、全等三角形的判定和性质、三角形的内角和定理和外角性质、勾股定理,解题的关键是发现D 是AC 的中点,三角形BCD 、三角形BCE 是等腰三角形,依据勾股定理列出关于a 的方程.26.(1)见解析;(2)见解析【分析】(1)根据等腰三角形的性质,构造边长为5的线段即可找出点C ;(2)利用等腰三角形的三线合一的思想解决问题即可.【详解】解:(1)如图,点C 即为所作;(2)如图,AE 即为所作.【点睛】本题考查作图-应用与设计,等腰三角形的性质,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.27.(1)∠A=55°,∠B=35°,∠C=90°;(2)ABC 按角分类属于直角三角形,按边分类属于不等边三角形【分析】(1)根据三角形内角和定理根据方程组即可解决问题.(2)根据三角形的分类解决问题即可.【详解】(1)由题意得:20180A B C A B A B C ∠+∠=∠⎧⎪∠-∠=︒⎨⎪∠+∠+∠=︒⎩,解得:553590A B C ∠=︒⎧⎪∠=︒⎨⎪∠=︒⎩,∴∠A=55°,∠B=35°,∠C=90°;(2)∵∠C=90°,∠A=55°,∠B=35°,∴按角分类,属于直角三角形,按边分类,属于不等边三角形.【点睛】本题考查了三角形内角和定理,三角形的分类等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.28.70°【详解】试题分析:先根据三角形内角和定理计算出∠BAC+∠BCA=180°-∠B=140°∠则利邻补角定义计算出∠DAC+∠FCA=180°-∠BAC+180°-∠BCA=220°,再根据角平分线定义得到∠EAC=12∠DAC∠∠ECA=12∠FCA ,所以∠EAC+∠ECA=12∠∠DAC+∠FCA∠=110°,然后再利用三角形内角和计算∠AEC 的度数.试题解析:在△ABC 中,∵∠B∠40°∠∴∠BAC∠∠BCA∠180°∠40°∠140°∠∵∠DAC∠∠BAC∠180°∠∠ACF∠∠ACB∠180°∠∴∠DAC∠∠ACF∠360°∠140°∠220°∠∵AE 平分∠DAC∠CE 平分∠ACF∠∴∠EAC∠∠ECA∠12(∠DAC∠∠ACF)∠110°∠∴∠AEC∠180°∠110°∠70°.29.(1)见解析(2)40°(3)90°-12α 【分析】根据角平分线的定义和三角形的外角等于不相邻的两个内角之和,推理出两角的关系.【详解】(1)证明∠由三角形内角和定理得, A ABC ACB 180∠∠∠++=︒∠P PBC PCB 180∠∠∠++=︒∠点P 是ABC ∠和ACB ∠的角平分线的交点 ∠11PBC ABC PCB ACB 22∠∠∠∠==, ∠11P ABC ACB 18022∠∠∠++=︒ 又∠A ABC ACB 180∠∠∠++=︒∴ABC ACB 180A ∠∠∠+=︒- ∠()1P 180A 1802∠∠+︒-=︒ ∠1P A 902∠∠=+︒ (2)由三角形的外角性质得ACD A ABC ∠∠∠=+∵点P 是ABC ∠和ACB ∠外角的角平分线的交点∴ABC 2PBC ∠∠= ACD 2PCD ∠∠=∴2PCD A 2PBC 802PBC ∠∠∠∠=+=︒+∴PCD 40PBC ∠∠=︒+∵PCD ∠是ABC 的外角∴PCD P PBC ∠∠∠=+∠40PBC P PBC ∠∠∠︒+=+∠P 40∠=︒(3)由三角形内角和定理得ABC ACB 180A ∠∠∠+=︒-∠点P 是ABC ∠外角和ACB ∠外角的角平分线的交点∴DBC 2PBC ∠∠= ECB 2PCB ∠∠=∴DBC ECB A ABC A ACB ∠∠∠∠∠∠+=+++=180A ∠︒+∠2PBC 2PCB 180A ∠∠∠+=︒+1PBC PCB 90A 2∠∠∠+=︒+∵PBC PCB 180P ∠∠∠+=︒- ∴1180P 90A 2∠∠︒-=︒+ 1P 90A 2∠∠=︒-∠A ∠α=∠1P 902∠∠α=︒- 【点睛】本题是一道探究问题∠考查的知识点是三角形的外角的性质以及角平分线的定义.认真阅读材料中提供的方法,是解决此类问题的关键.30.45DAE ︒∠=【分析】在ABD ∆中,根据等边对等角以及三角形内角和定理求出1(180)702BDA BAD B ∠=∠=︒-∠=︒,在ABC ∆中利用三角形内角和定理求出50∠=°ACB ,根据等边对等角以及三角形外角的性质得出1252CAE E ACB ∠=∠=∠=︒,根据三角形内角和,即可求出DAE ∠的度数.【详解】解:40B ︒∠=,AB BD =1(180)702BDA BAD B ∴∠=∠=︒-∠=︒ ,90,40ABC BAC B ∆∠=︒∠=︒中50ACB ∴∠=︒AC CE =1252CAE E ACB ︒∴∠=∠=∠= 180B BAD DAE E ∠+∠+∠+∠=︒180********DAE ∴∠=︒-︒-︒-︒=︒【点睛】本题考点涉及等腰三角形性质、直角三角形、三角形内角和定理以及三角形外角定理等知识点,属综合题,熟练掌握相关性质定理是解题关键.。
(专题精选)初中数学三角形难题汇编及答案解析

∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,∠AEB=60°,
∵AB= BC,
∴AE=BE= BC,
∴AE=CE,故①正确;
∴∠EAC=∠ACE=30°
∴∠BAC=90°,
∴S△ABC= AB•AC,故②错误;
∵BE=EC,
∴E为BC中点,O为AC中点,
(专题精选)初中数学三角形难题汇编及答案解析
一、选择题
1.如图,已知 ,若 , , ,下列结论:① ;② ;③ ;④ 与 互补;⑤ ,其中正确的有()
A.2个B.3个C.4个D.5个
【答案】C
【解析】
【分析】
根据平行线的判定得出AC∥DE,根据垂直定义得出∠ACB=∠CDB=∠CDA=90°,再根据三角形内角和定理求出即可.
∴S△ABE=S△ACE=2S△AOE,故③正确;
∵四边形ABCD是平行四边形,
∴AC=CO,
∵AE=CE,
∴EO⊥AC,
∵∠ACE=30°,
∴EO= EC,
∵EC= AB,
∴OE= BC,故④正确;
故正确的个数为3个,
故选:C.
【点睛】
此题考查平行四边形的性质,等边三角形的判定与性质.注意证得△ABE是等边三角形是解题关键.
15.如图,四边形 和 都是正方形,点 在 边上,点 在对角线 上,若 ,则 的面积是()
A.6B.8C.9D.12【答Βιβλιοθήκη 】B【解析】【分析】
根据正方形的性质得到∠DAC=∠ACD=45°,由四边形EFGH是正方形,推出△AEF与△DFH是等腰直角三角形,于是得到DE= EH= EF,EF= AE,即可得到结论.
全等三角形的六种模型全梳理(学生版)--初中数学专题训练

全等三角形的六种模型全梳理几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明三角形各种模型,或证明线段数量关系等,接来下我们针对其做出详细分析与梳理。
类型一、倍长中线模型目的:①构造出一组全等三角形;②构造出一组平行线。
将分散的条件集中到一个三角形中。
1【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:如图2,延长AD到点E,使DE=AD,连接BE.请根据小明的方法思考:(1)如图2,由已知和作图能得到△ADC≌△EDB的理由是.A.SSSB.SASC.AASD.ASA(2)如图2,AD长的取值范围是.A.6<AD<8B.6≤AD≤8C.1<AD<7D.1≤AD≤7【感悟】解题时,条件中若出现“中点”、“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论转化到同一个三角形中.【问题解决】(3)如图3,AD是△ABC的中线,BE交AC于点E,交AD于F,且AE=EF.求证:AC=BF.2(培优)已知△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AD,BE,点F为BE中点.AD;(1)如图1,求证:BF=12(2)将△DCE绕C点旋转到如图2所示的位置,连接AE,BD,过C点作CM⊥AD于M点.①探究AE和BD的关系,并说明理由;②连接FC,求证:F,C,M三点共线.1.如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AB=2AE.2.(1)如图1,已知△ABC中,AD是中线,求证:AB+AC>2AD;(2)如图2,在△ABC中,D,E是BC的三等分点,求证:AB+AC>AD+AE;(3)如图3,在△ABC中,D,E在边BC上,且BD=CE.求证:AB+AC>AD+AE.3.(1)阅读理解:如图①,在△ABC中,若AB=8,AC=5,求BC边上的中线AD的取值范围.可以用如下方法:将△ACD绕着点D逆时针旋转180°得到△EBD,在△ABE中,利用三角形三边的关系即可判断中线AD的取值范围是;(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=100°,以C为顶点作一个50°的角,角的两边分别交AB、AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并说明理由.类型二、截长补短模型截长补短法使用范围:线段和差的证明(往往需证2次全等)3如图,在五边形ABCDE中,AB=AE,CA平分∠BCD,∠CAD=12∠BAE.(1)求证:CD=BC+DE;(2)若∠B=75°,求∠E的度数.4(培优)在△ABC中,BE,CD为△ABC的角平分线,BE,CD交于点F.(1)求证:∠BFC=90°+12∠A;(2)已知∠A=60°.①如图1,若BD=4,BC=6.5,求CE的长;②如图2,若BF=AC,求∠AEB的大小.1.如图,△ABC为等边三角形,若∠DBC=∠DAC=α0°<α<60°,则∠BCD=(用含α的式子表示).2.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在直线BC、CD上,且∠BAD.∠EAF=12(1)当点E、F分别在边BC、CD上时(如图1),请说明EF=BE+FD的理由.(2)当点E、F分别在边BC、CD延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF、BE、FD之间的数量关系,并说明理由.3.阅读下面材料:【原题呈现】如图1,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6,求BC的长.【思考引导】因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图2).【问题解答】(1)参考提示的方法,解答原题呈现中的问题;(2)拓展提升:如图3,已知△ABC中,AB=AC,∠A=20°,BD平分∠ABC,BD=2.3,BC=2.求AD 的长.类型三、一线三等角模型应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解。
初中数学《三角形中的经典模型》九大题型含解析
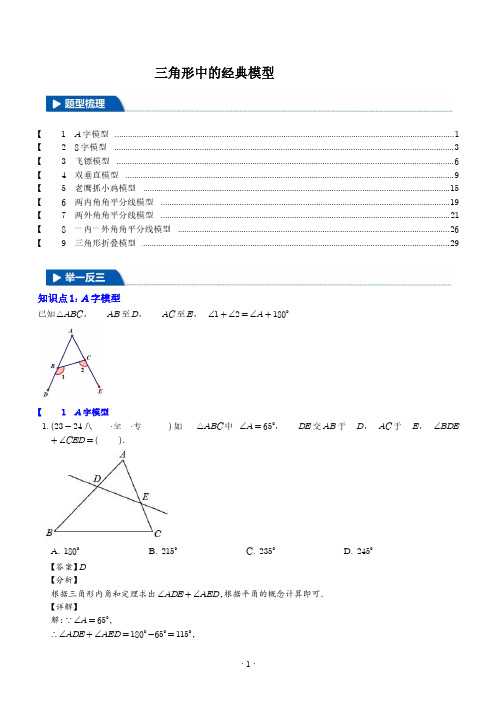
三角形中的经典模型【1A字模型 1【28字模型 3【3飞镖模型 6【4双垂直模型 9【5老鹰抓小鸡模型 15【6两内角角平分线模型 19【7两外角角平分线模型 21【8一内一外角角平分线模型 26【9三角形折叠模型 29知识点1:A字模型已知△ABC,AB至D,AC至E,∠1+∠2=∠A+180°【1A字模型1.(23-24八·全·专)如△ABC中∠A=65°,DE交AB于D,AC于E,∠BDE+∠CED=( ).A.180°B.215°C.235°D.245°【答案】D【分析】根据三角形内角和定理求出∠ADE+∠AED,根据平角的概念计算即可.【详解】解:∵∠A=65°,∴∠ADE+∠AED=180°-65°=115°,∴∠BDE+∠CED=360°-115°=245°,故选:D.【点睛】本题考查的是三角形内角和定理的应用,掌握三角形内角和等于180°是解题的关键.2.(23-24八年级·全国·专题练习)如图是某建筑工地上的人字架,若∠1=120°,那么∠3-∠2的度数为.【答案】60°【分析】根据平角的定义求出∠4,再利用三角形的外角的性质即可解决问题.【详解】解:如图∵∠1+∠4=180°,∠1=120°,∴∠4=60°,∵∠3=∠2+∠4,∴∠3-∠2=∠4=60°,故答案为:60°.【点睛】本题考查三角形外角的性质、平角的性质等知识,解题的关键是熟练掌握基本知识,属于中考基础题.3.(23-24八年级·河北沧州·期中)琪琪在操作课上将三角形剪掉一个角后得到四边形ABCD,则下列判断错误的是()A.变成四边形后对角线增加了两条B.变成四边形后内角和增加了360°C.外角和没有发生变化D.若剪掉的角的度数是60°,则∠1+∠2=240°【答案】B【分析】本题考查了多边形的对角线,内角和与外角和,三角形内角和定理,解题的关键是【详解】解:A、三角形没有对角线,变成四边形后对角线为两条,即增加了两条,故正确,不合题意;B、三角形内角和为180°,变成四边形后内角和为360°,增加了180°,故错误,不合题意;C、任意多边形的外角和是360°,故正确,不合题意;D、若剪掉的角的度数是60°,则∠A+∠B=120°,则∠1+∠2=360°-120°=240°,故正确,不合题意;故选:B.4.(23-24·浙江杭州·二模)将一把直尺与一块三角板在同一平面内按如图所示的方式放置,若∠1=130°,则∠2的度数为.【答案】40°/40度【分析】本题考查了平行线的性质,三角形的外角的性质,熟练掌握平行线的性质是解题的关键,根据平行线的性质可得∠FGH=∠1=130°,然后利用三角形外角的性质进行计算即可解答.【详解】解:如图:由题意得:AD∥BC,∴∠FGH=∠1=130°,∵∠FGH是△EFG的一个外角,∴∠FGH=∠2+∠E,∵∠E=90°,∴∠2=130°-90°=40°,故答案为:40°.知识点2:8字模型①已知AD,BC相交于O,则∠A+∠B=∠C+∠D②已知线段AP平分∠BAD,线段CP平分∠BCD,则∠P=12(∠B+∠D)【题型28字模型】5.(23-24八年级·浙江金华·期末)如图,BP平分∠ABC,交CD于点F,DP平分∠ADC交AB于点E,AB与CD相交于点G,∠A=42°.(1)若∠ADC=60°,求∠AEP的度数;(2)若∠C=38°,求∠P的度数.【答案】(1)72°;(2)40°.【分析】(1)根据角平分线的定义可得∠ADP=12∠ADC,然后利用三角形外角的性质即可得解;(2)根据角平分线的定义可得∠ADP=∠PDF,∠CBP=∠PBA,再根据三角形的内角和定理可得∠A+∠ADP=∠P+∠ABP,∠C+∠CBP=∠P+∠PDF,所以∠A+∠C=2∠P,即可得解.【详解】解:(1)∵DP平分∠ADC,∴∠ADP=∠PDF=12∠ADC,∵∠ADC=60°,∴∠ADP=30°,∴∠AEP=∠ADP+∠A=30°+42°=72°;(2)∵BP平分∠ABC,DP平分∠ADC,∴∠ADP=∠PDF,∠CBP=∠PBA,∵∠A+∠ADP=∠P+∠ABP,∠C+∠CBP=∠P+∠PDF,∴∠A+∠C=2∠P,∵∠A=42°,∠C=38°,∴∠P=12(38°+42°)=40°.【点睛】本题考查了三角形的内角和定理及三角形外角的性质,角平分线的定义,熟记定理并理解“8字形”的等式是解题的关键.6.(23-24八年级·河南漯河·期末)如图,AB和CD相交于点O,∠A=∠C,则下列结论中不能完全确定正确的是()A.∠B=∠DB.∠1=∠A+∠DC.∠2>∠DD.∠C=∠D【答案】D【分析】利用三角形的外角性质,对顶角相等逐一判断即可.【详解】∵∠A+∠AOD+∠D=180°,∠C+∠COB+∠B=180°,∠A=∠C,∠AOD=∠BOC,∴∠B=∠D,∵∠1=∠2=∠A+∠D,∴∠2>∠D,故选项A,B,C正确,故选D.【点睛】本题考查了对顶角的性质,三角形外角的性质,熟练掌握并运用两条性质是解题的关键.7.(23-24八年级·北京怀柔·期末)如图,在由线段AB,CD,DF,BF,CA组成的平面图形中,∠D=28°,则∠A+∠B+∠C+∠F的度数为( ).A.262°B.152°C.208°D.236°【答案】C【分析】如图标记∠1,∠2,∠3,然后利用三角形的外角性质得∠1=∠B+∠F=∠D+∠3,∠2=∠A+∠C,再利用∠2,∠3互为邻补角,即可得答案.【详解】解:如下图标记∠1,∠2,∠3,∵∠1=∠B+∠F=∠D+∠3,∵∠D=28°,∴∠3=∠B+∠F-28°,又∵∠2=∠A+∠C,∴∠2+∠3=∠A+∠C+∠B+∠F-28°,∵∠2+∠3=180°∴180°=∠A+∠C+∠B+∠F-28°,∴∠A+∠C+∠B+∠F=180°+28°=208°,故选C.【点睛】此题考查了三角形的外角性质与邻补角的意义,熟练掌握并灵活运用三角形的外角性质与邻补角的意义是解答此题的关键.8.(23-24八年级·全国·专题练习)如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H六个角的和.【答案】360°【分析】根据三角形内角和外角的性质可得:∠G+∠D=∠3,∠F+∠C=∠4,∠E+∠H=∠2,再根据三角形内角和定理可得答案.【详解】解:∵∠G+∠D=∠3,∠F+∠C=∠4,∠E+∠H=∠2,∴∠G+∠D+∠F+∠C+∠E+∠H=∠3+∠4+∠2,∵∠B+∠2+∠1=180°,∠3+∠5+∠A=180°,∴∠A+∠B+∠2+∠4+∠3=360°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°.【点睛】此题主要考查了三角形内角与外角的性质,关键是掌握三角形的一个外角等于和它不相邻的两个内角的和.知识点3:飞镖模型①已知四边形ABCD,则∠C=∠A+∠B+∠D②已知四边形ABCD,线段BO平分∠ABC,线段OD平分∠ADC,则∠O=12(∠A+∠C)【题型3飞镖模型】9.(23-24·河北秦皇岛·一模)如图,用铁丝折成一个四边形ABCD(点C在直线BD的上方),且∠A=70°,∠BCD=120°,若使∠ABC、∠ADC平分线的夹角∠E的度数为100°,可保持∠A不变,将∠BCD(填“增大”或“减小”)°.【答案】增大10【分析】利用三角形的外角性质先求得∠ABE+∠ADE=30°,根据角平分线的定义得到∠ABC+∠ADC= 60°,再利用三角形的外角性质求解即可.【详解】解:如图,连接AE并延长,连接AC并延长,∠BED=∠BEF+∠DEF=∠ABE+∠BAD+∠ADE=100°,∵∠BAD=70°,∴∠ABE+∠ADE=30°,∵BE,DE分别是∠ABC、∠ADC平分线,∴∠ABC+∠ADC=2(∠ABE+∠ADE)=60°,同上可得,∠BCD=∠BAD+∠ABC+∠ADC=130°,130°-120°=10°,∴∠BCD增大了10°.故答案为:增大,10.【点睛】本题考查了三角形的外角性质,三角形的内角和定理,角平分线的定义等知识,熟练运用题目中所给的结论是解题的关键.10.(23-24八年级·江苏苏州·阶段练习)在社会实践手工课上,小茗同学设计了如上图这样一个零件,如果∠A=52°,∠B=25°,∠C=30°,∠D=35°,∠E=72°,那么∠F=°.【答案】70【分析】延长BE、CF,交于点G,连接AG,根据三角形内角和定理和四边形的内角和为360°即可求解.【详解】解:延长BE、CF,交于点G,连接AG,如图,∴∠AGB=180°-∠B-∠BAG,∠AGC=180°-∠C-∠CAG,∴∠AGB+∠AGC=180°-∠B-∠BAG+180°-∠C-∠CAG=360°-∠B-∠C-∠BAC=253°,∴∠CGB=360°-∠AGB+∠AGC=107°.∵∠BED=72°,∴∠GED=108°,∴∠GFD=360°-∠GED-∠D-∠CGB=110°,∴∠CFD=70°.故答案为:70.【点睛】本题主要考查三角形内角和定理.正确的作出辅助线是解题关键.11.(23-24八年级·全国·专题练习)如图,若∠EOC=115°,则∠A+∠B+∠C+∠D+∠E+∠F=.【答案】230°【分析】根据三角形外角的性质,得到∠EOC=∠E+∠2=115°,∠2=∠D+∠C,∠EOC=∠1+∠F=115°,∠1=∠A+∠B,即可得到结论.【详解】解:如图∵∠EOC=∠E+∠2=115°,∠2=∠D+∠C,∴∠E+∠D+∠C=115°,∵∠EOC=∠1+∠F=115°,∠1=∠A+∠B,∴∠A+∠B+∠F=115°,∴∠A+∠B+∠C+∠D+∠E+∠F=230°,故答案为:230°.【点睛】本题主要考查三角形内角和定理和三角形外角的性质,解决本题的关键是要熟练掌握三角形外角性质.12.(23-24·河北邯郸·一模)嘉嘉在作业本上画了一个四边形,并标出部分数据(如图),淇淇说,这四个数据中有一个是标错的;嘉嘉经过认真思考后,进行如下修改:若∠A,∠B,∠BCD保持不变,则将图中∠D(填“增大”或“减小”)度,淇淇说,“改得不错”.【答案】增大5【分析】连接BD,利用三角形的内角和计算即可.【详解】解:连接BD,∵∠CDB+∠CBD=180°-∠A-∠ABC-∠ADC∠CDB +∠CBD =180°-∠BCD∴∠A +∠ABC +∠ADC =∠BCD∵∠A =90°,∠ABC =25°,∠BCD =145°∴∠ADC =145°-25°-90°=30°∴30°-25°=5°故答案为:增大,5【点睛】本题主要考查三角形的内角和,添加辅助线利用三角形内角和计算是解决本题的关键.知识点4:双垂直模型已知∠B =∠D =∠ACE =90°.则∠BAC =∠DCE ,∠ACB =∠CED .【证明】∵∠B =∠D =∠ACE =90°;∴∠BAC +∠ACB =90°;又∠ECD +∠ACB =90°;∴∠BAC =∠DCE 同理,∠ACB +∠DCE =90°,且∠CED +∠DCE =90°;∴∠ACB =∠CED ,得证.【题型4双垂直模型】13.(23-24八年级·广东珠海·期末)如图1,AB ⊥BC 于点B ,CD ⊥BC 于点C ,点E 在线段BC 上,且AE ⊥DE .(1)求证:∠EAB =∠CED ;(2)如图2,AF 、DF 分别平分∠BAE 和∠CDE ,则∠F 的度数是(直接写出答案即可);(3)如图3,EH 平分∠CED ,EH 的反向延长线交∠BAE 的平分线AF 于点G .求证:EG ⊥AF .(提示:三角形内角和等于180°)【答案】(1)见解析;(2)45°;(3)见解析【分析】(1)利用同角的余角相等即可证明;(2)过点F 作FM ∥AB ,利用∠DFA =∠DFM +∠AFM =12∠CDE +12∠EAB =12(∠CDE +∠EAB )即可解决问题;(3)想办法证明∠EAG +∠AEG =90°即可解决问题.【详解】解:(1)∵AB ⊥BC ,CD ⊥BC ,∴∠B =∠C =90°,∴∠BAE +∠AEB =90°,∵AE ⊥DE ,∴∠AED =90°,∴∠AEB +∠CED =90°,∴∠BAE =∠CED .(2)解:答案为45°;过点F 作FM ∥AB ,如图,∵AB ⊥BC ,CD ⊥BC ,∴∠B =∠C =90°,∴AB ∥CD ,∵∠C =90°,∴∠CED +∠CDE =90°,∵∠BAE =∠CED ,∴∠BAE +∠CDE =90°,∵AF 、DF 分别平分∠BAE 和∠CDE ,∴∠CDF =12∠CDE ,∠BAF =12∠BAE ,∴∠CDF +∠BAF =12(∠BAE +∠CDE )=45°,∵FM ∥AB ∥CD ,∴∠CDF =∠DFM ,∠BAF =∠AFM ,∴∠AFD =∠CDF +∠BAF =45°.(3)∵EH 平分∠CED ,∴∠CEH =12∠CED ,∴∠BEG =12∠CED ,∵AF 平分∠BAE ,∴∠BAG =12∠BAE ,∵∠BAE =∠CED ,∴∠BAG =∠BEG ,∵∠BAE +∠BEA =90°,∴∠BAG +∠GAE +∠AEB =90°,即∠GAE +∠AEB +∠BEG =90°,∴∠AGE =90°,∴EG ⊥AF .【点睛】本题考查三角形内角和定理、平行线的性质、角平分线的定义等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.14.(23-24八年级·陕西西安·期末)如图,在等腰Rt △ABC 中,∠ACB =90°,D 为BC 的中点,DE ⊥AB ,垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF .(1)求证:AD⊥CF.(2)连接AF,试判断△ACF的形状,并说明理由.【答案】(1)见解析(2)△ACF为等腰直角三角形;理由见解析【分析】本题考查了全等三角形的判定和性质及等腰三角形性质和判定.(1)欲求证AD⊥CF,先证明∠CAG+∠ACG=90°,需证明∠CAG=∠BCF,利用三角形全等,易证.(2)要判断△ACF的形状,看其边有无关系.根据(1)的推导,易证CF=AF,从而判断其形状.【详解】(1)证明:在等腰直角△ABC中,∵∠ACB=90°,∴∠CBA=∠CAB=45°,∵DE⊥AB,∴∠DEB=90°,∴∠BDE=45°,∵BF∥AC,∴∠CBF=180°-∠ACB=90°,∴∠BFD=45°=∠BDE,∴BF=DB,又∵D为BC的中点,∴CD=DB,即BF=CD,在△CBF和△ACD中,BF=CD∠CBF=∠ACD=90°CB=AC,∴△CBF≌△ACD(SAS).∴∠BCF=∠CAD.∵∠BCF+∠GCA=90°,∴∠CAD+∠GCA=90°,即AD⊥CF.(2)解:△ACF是等腰三角形,理由为:连接AF,如图所示,由(1)知:△CBF≌△ACD,∴CF=AD,∵△DBF是等腰直角三角形,且BE是∠DBF的平分线,∴BE垂直平分DF,∴AF=AD,∵CF=AD,∴CF=AF,∴△ACF是等腰三角形.15.(23-24八年级·山西晋中·期中)请把下面的证明过程补充完整如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F,求证:CF=CE.证明:∵AE平分∠CAB(已知),∴∠CAE=∠FAB(①),∵∠ACE=90°(已知),∴∠CAE+∠CEF=90°(②),∵CD是△ABC的高(已知),∴∠CDA=90°(三角形高的定义),∴(③),(直角三角形的两个锐角互余),∴∠CEF=∠AFD(④),∵∠CFE=∠AFD(⑤),∴∠CFE=∠CEF(⑥),∴CF=CE(⑦).【答案】①角平分线的定义;②直角三角形的两锐角互余;③∠FAD+∠AFD=90°;④等角的余角相等;⑤对顶角相等;⑥等量代换;⑦等角对等边【分析】本题考查的是直角三角形的性质、角平分线的定义,等腰三角形的判定,掌握直角三角形的两锐角互余是解题的关键.根据角平分线的定义、直角三角形的性质、对顶角相等、等角对等边解答即可.【详解】证明:∵AE平分∠CAB(已知),∴∠CAE=∠FAB(角平分线的定义),∵∠ACE=90°(已知),∴∠CAE+∠CEF=90°(直角三角形的两锐角互余),∵CD是△ABC的高(已知),∴∠CDA=90°(三角形高的定义),∴∠FAD+∠AFD=90°(直角三角形的两锐角互余),∴∠CEF=∠AFD(等角的余角相等),∵∠CFE=∠AFD(对顶角相等),∴∠CFE=∠CEF(等量代换),∴CF=CE(等角对等边).故答案为:角平分线的定义;直角三角形的两锐角互余;∠FAD+∠AFD=90°;等角的余角相等;对顶角相等;等量代换;等角对等边.16.(23-24八年级·江苏扬州·阶段练习)在Rt △ABC 中,∠CAB =90°,AB =AC ,点O 是BC 的中点,点P 是射线CB 上的一个动点(点P 不与点C 、O 、B 重合),过点C 作CE ⊥AP 于点E ,过点B 作BF ⊥AP 于点F ,连接EO ,OF.(问题探究)如图1,当P 点在线段CO 上运动时,延长EO 交BF 于点G .(1)求证:△AEC ≌△BFA ;(2)BG 与AF 的数量关系为:(直接写结论,不需说明理由);(拓展延伸)(3)①如图2,当P 点在线段OB 上运动,EO 的延长线与BF 的延长线交于点G ,∠OFE 的大小是否变化?若不变,求出∠OFE 的度数;若变化,请说明理由;②当P 点在射线OB 上运动时,若AE =2,CE =6,直接写出△OEF 的面积,不需证明.【答案】(1)见解析;(2)BG =AF ;(3)①∠OFE 的大小不变,∠OFE =45°;②满足条件的△OEF 的面积为8或16【分析】(1)根据等角的余角相等得出∠CAE =∠ABF ,证明△AEC ≌△BFA AAS ;(2)证明△COE ≌△BOG AAS 得出CE =BG ,则CE =AF ,等量代换可得AF =BG ;(3)①证明△AEC ≌△BFA AAS ,进而证明∠CEO =∠BGO 证明△COE ≌△BOG AAS 得出∠EFO =12∠EFG =45°;②根据题意画出图形,分类讨论,根据三角形的面积公式,即可求解.【详解】(1)证明:如图1中,∵CE ⊥AE ,BF ⊥AE ,∴∠AEC =∠BFA =∠CAB =90°,∴∠CAE +∠BAF =90°,∠BAF +∠ABF =90°,∴∠CAE =∠ABF ,在△AEC 和△BFA 中,∠AEC =∠BFA∠CAE =∠ABF AC =BA,∴△AEC ≌△BFA AAS ;(2)解:结论:BG =AF .理由:∵CE ⊥AE ,BF ⊥AE ,∴CE ∥BG ,∴∠CEO =∠BGO ,∵O 是BC 的中点,∴OC =OB ,在△COE 和△BOG 中,∠CEO =∠BGO∠AOE =∠BOG OC =OB,∴△COE ≌△BOG AAS ,∴CE =BG ,∵△AEC ≌△BFA ,∴CE =AF ,∴AF =BG .故答案为:BG =AF .(3)解:①如图2中,结论:∠OFE 的大小不变,∠OFE =45°.理由:∵CE ⊥AE ,BF ⊥AE ,∴∠AEC =∠BFA =∠CAB =90°,∴∠CAE +∠BAF =90°,∠BAF +∠ABF =90°,∴∠CAE =∠ABF ,在△AEC 和△BFA 中,∠AEC =∠BFA∠CAE =∠ABF AC =BA,∴△AEC ≌△BFA AAS ;∴CE =AF ,AE =BF ,∵CE ⊥AE ,BF ⊥AE ,∴CE ∥BG ,∴∠CEO =∠BGO ,∵O 是BC 的中点,∴OC =OB ,在△COE 和△BOG 中,∠CEO =∠BGO∠AOE =∠BOG OC =OB,∴△COE ≌△BOG AAS ,∴CE =BG ,OE =OG ,∴AF =BG ,∴EF =FG ,根据△EFO ≌△GFO SSS 可得:∠EFO =∠GFO∴∠EFO =12∠EFG =45°;②如图2中,当AE =2,CE=6时,EF =FG =6-2=4,∴S △EOF =12S △EFC =12×12×4×4=4如图3中,当AE =2,CE =6时,EF =FG =6+2=8,∴S △EOF =12S △EFG =12×12×8×8=16综上所述,满足条件的△OEF 的面积为8或16.【点睛】本题考查了全等三角形的证明与性质,等腰三角形的判定和性质,三角形的动点问题以及三角形求面积的问题,正确掌握知识点是解题的关键.知识点5:老鹰抓小鸡模型如图,∠A+∠O=∠1+∠2;口诀:腋下两角之和等于上下两角之和【题型5老鹰抓小鸡模型】17.(23-24八年级·江苏扬州·阶段练习)如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=95°,则∠2的度数为()A.24°B.35°C.30°D.25°【答案】D【分析】根据三角形内角和定理可得∠AEF+∠AFE=120°,再根据邻补角的性质可得∠FEB+∠EFC= 360°-120°=240°,再根据由折叠可得:∠B′EF+∠EFC′=∠FEB+∠EFC=240°,然后计算出∠1+∠2的度数,即可求得∠2的度数.【详解】∵∠A=60°,∴∠AEF+∠AFE=180°-60°=120°,∴∠FEB+∠EFC=360°-120°=240°,∵由折叠可得:∠B′EF+∠EFC′=∠FEB+∠EFC=240°,∴∠1+∠2=240°-120°=120°,∵∠1=95°,∴∠2=120°-95°=25°,故选D.【点睛】本题考查了三角形的内角和定理,翻折变换的性质,熟记定理及性质并准确识图是解题的关键.18.(23-24八年级·重庆渝北·阶段练习)如图,将△ABC沿着DE翻折,使B点与B 点重合,若∠1+∠2=80°,则∠B的度数为.【答案】40°/40度【分析】由翻折的性质可知,∠B=∠B ,∠BED=∠B ED,∠BDE=∠B DE,由∠BED+∠B ED+∠1= 180°,∠BDE+∠B DE+∠2=180°,∠1+∠2=80°,可得∠BED+∠BDE=140°,根据∠B=180°-∠BED+∠BDE,计算求解即可.【详解】解:由翻折的性质可知,∠B=∠B ,∠BED=∠B ED,∠BDE=∠B DE,∵∠BED+∠B ED+∠1=180°,∠BDE+∠B DE+∠2=180°,∠1+∠2=80°,∴∠BED+∠BDE=140°,∴∠B=180°-∠BED+∠BDE=40°,故答案为:40°.【点睛】本题考查了翻折的性质,三角形内角和定理.解题的关键在于对知识的熟练掌握与灵活运用.19.(23-24八年级·安徽铜陵·期中)如图,将△ABC纸片沿DE折叠,使点A落在点A′处,且A′B平分∠ABC,A′C平分∠ACB,若∠1+∠2=120°,则∠BA′C的度数为()A.120°B.110°C.100°D.90°【答案】A【详解】由∠BDE、∠CED是△ADE的两个外角知∠BDE=∠A+∠AED、∠CED=∠A+∠ADE,据此得∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,推出∠1+∠2=2∠A得到∠A=60°,根据BA'平分∠ABC,CA'平分∠ACB知∠A'BC+∠A'CB=12(∠ABC+∠ACB)=90°-12∠A.利用∠BA'C=180°-(∠A'BC+∠A'CB)可得答案.解:∵∠BDE、∠CED是△ADE的两个外角,∴∠BDE=∠A+∠AED,∠CED=∠A+∠ADE,∴∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,∴∠1+∠ADE+∠2+∠AED=2∠A+∠AED+∠ADE,即∠1+∠2=2∠A,∵∠1+∠2=120°,∴∠A=60°,∵BA'平分∠ABC,CA'平分∠ACB,∴∠A'BC+∠A'CB=12(∠ABC+∠ACB)=12(180°-∠A )=90°-12∠A .∴∠BA 'C =180°-(∠A 'BC +∠A 'CB ),=180°-90°-12∠A =90°+12∠A =90°+12×60°=120°.故选:A .【点睛】本题考查三角形的内角和定理、角平分线的定义、三角形的外角的性质等知识,解题的关键是灵活运用所学知识,属于中考常考题型.20.(23-24八年级·山东烟台·期中)折纸是我国一项古老的传统民间艺术,这项具有中国特色的传统文化在几何中可以得到新的解读.已知在△ABC 中,请根据题意,探索不同情境中∠1+∠2(或∠1-∠2)与∠A 的数量关系.(1)如图①,若∠A =80°,沿图中虚线DE 截去∠A ,则∠1+∠2=.(2)如图②,若∠A =80°,沿图中虚线DE 将∠A 翻折,使点A 落在BC 上的点A '处,则∠1+∠2=.(3)如图③,翻折后,点A 落在点A '处,若∠1+∠2=80°,求∠B +∠C 的度数(4)如图④,△ABC 纸片沿DE 折叠,使点A 落在点A '处,若∠1=80°,∠2=24°,求∠A 的度数.【答案】(1)260°(2)160°(3)∠B +∠C =140°(4)∠A =28°【分析】(1)根据三角形内角和定理得出∠B +∠C =180°-80°=100°,再由平角进行求解即可;(2)利用翻折的性质得出∠EDA '=∠ADE ,∠AED =∠DEA ',根据三角形内角和定理得出∠ADE +∠AED =100°,结合图形,由平角及各角之间的关系进行计算即可‘(3)连接AA .根据三角形外角的性质得出∠1=∠DAA '+∠DA 'A ,∠2=∠EAA '+∠EA 'A ,然后利用各角之间的数量关系得出∠EAD =40°,再由三角形内角和定理即可求解;(4)设AB 与DA 交于点F ,根据三角形外角得出∠1=∠DFA +∠A ,∠DFA =∠A +∠2,再由折叠的性质得出∠A =∠A ,结合图形及各角之间的数量关系进行求解即可【详解】(1)解:∵∠A=80°,∴∠ADE+∠AED=180°-80°=100°,∴∠1+∠2=360°-∠ADE-∠AED=260°,故答案为:260°;(2)∵∠A=80°,∴∠ADE+∠AED=180°-80°=100°,∵翻折,∴∠EDA'=∠ADE,∠AED=∠DEA',∴∠ADA'+∠AEA'=2(∠ADE+∠AED)=200°,∴∠1+∠2=360°-(∠ADA'+∠AEA')=160°,故答案为:160°;(3)解:连接AA .如图所示:∵∠1=∠DAA'+∠DA'A,∠2=∠EAA'+∠EA'A,∴∠1+∠2=∠DAA'+∠DA'A+∠EAA'+∠EA'A=∠EAD+∠EA'D,∵∠EAD=∠EA D,∴∠1+∠2=2∠EAD=80°,∴∠EAD=40°,∴∠B+∠C=180°-40°=140°.(4)解:如图,设AB与DA 交于点F,∵∠1=∠DFA+∠A,∠DFA=∠A +∠2,由折叠可得,∠A=∠A ,∴∠1=∠A+∠A +∠2=2∠A+∠2,又∵∠1=80°,∠2=24°,∴80°=2∠A+24°,∴∠A=28°.【点睛】题目主要考查三角形内角和定理及三角形外角的性质,平角的定义等,理解题意,作出相应辅助线求解是解题关键.知识点6:两内角角平分线模型在△ABC 中,BI 、CI 分别是∠ABC 和∠ACB 的角平分线,且相交于点I .则∠I =90°+12∠A【题型6两内角角平分线模型】21.(23-24八年级·河南信阳·开学考试)如图,AD ,CE 都是△ABC 的角平分线,且交于点O ,∠DAC =30°,∠ECA =35°,则∠ABO 的度数为.【答案】25°/25度【分析】本题考查了三角形内角和定理、角平分线,利用角平分线的定义结合三角形内角和定理找出∠ABO 的度数是解题的关键.根据角平分线的定义可得出∠BAC =60°、∠ACB =70°,结合三角形内角和可得出∠ABC =50°,由三角形的三条角平分线交于一点,可得出BO 平分∠ABC ,进而可得出∠ABO 的度数,此题得解.【详解】解:∵AD 平分∠BAC ,CE 平分∠ACB ,∠DAC =30°,∠ECA =35°,∴∠BAC =2∠DAC =60°,∠ACB =2∠ECA =70°,∴∠ABC =180°-∠BAC -∠ACB =50°.∵△ABC 的三条角平分线交于一点,∴BO 平分∠ABC ,∴∠ABO =12∠ABC =25°.故答案为:25°.22.(23-24八年级·全国·课后作业)如图,在△ABC 中,∠ABC 和∠ACB 的平分线BE ,CF 相交于点G ,若∠A =66°,则∠BGC 的度数为.【答案】123°/123度【分析】本题考查角平分线和三角形内角和定理,熟练利用角平分线的性质和三角形内角和定理找出题目中角的等量关系是解答本题的关键.由角平分线的性质可知∠GBC =12∠ABC ,∠GCB =12∠ACB ,再由三角形内角和定理可知∠BGC =180°-∠GBC +∠GCB ,即可求解.【详解】∵∠A =66°,∴∠ABC +∠ACB =180°-∠A =114°,∵BE 和CF 分别是∠ABC 和∠ACB 的平分线,∴∠GBC =12∠ABC ,∠GCB =12∠ACB ,∴∠BGC =180°-∠GBC +∠GCB =180°-12∠ABC +∠ACB =123°,故答案为:123°.23.(23-24八年级·河南信阳·开学考试)如图,在△ABC 中,AD 是BC 边上的高,AE ,BF 分别是∠BAC 和∠ABC 的角平分线,它们相交于点O ,∠AOB =125°.求∠CAD 的度数.【答案】∠CAD =20°.【分析】本题考查了角平分线的性质,三角形的内角和定理,以及余角的性质,解题的关键是熟练掌握所学的知识,正确求出∠C =70°,从而求出答案.根据角平分线的性质,由∠AOB =125°,得到∠CAB +∠CBA =110°,然后得到∠C ,由余角的性质,即可求出答案.【详解】解:∵AE ,BF 分别是∠BAC 和∠ABC 的角平分线,∴∠OAB =12∠BAC ,∠OBA =12∠ABC .∴∠CAB +∠CBA =2(∠OAB +∠OBA )=2180°-∠AOB∵∠AOB =125°,∴∠CAB +∠CBA =110°,∴∠C =70°.∵AD 是BC 边上的高∴∠ADC =90°,∴∠CAD =20°.24.(23-24八年级·山东烟台·期末)如图,在△ABC 中,∠A =90°,BE ,CD 分别平分∠ABC 和∠ACB ,且相交于F ,EG ∥BC ,CG ⊥EG 于点G ,则下列结论:①∠CEG =2∠DCA ;②∠DFE =130°;③∠EFC =12∠G :④∠ADC =∠GCD ;⑤△EGC 是等腰直角三角形,其中正确的结论是()A.①③④⑤B.①②③④C.①②③D.①③④【答案】D 【分析】本题主要考查了平行线的性质,角平分线的定义,三角形内角和定理,熟知平行线的性质,角平分线的定义是解题的关键.根据平行线的性质与角平分线的定义即可判断①;只需要证明∠ADC +∠ACD =90°,∠GCD +∠BCD =90°,即可判断④;根据角平分线的定义和三角形内角和定理先推出∠BFC=135°,即可判断②③;根据现有条件无法推出⑤.【详解】解:∵CD平分∠ACB,∴∠ACB=2∠DCA,∠ACD=∠BCD∵EG∥BC,∴∠CEG=∠ACB=2∠DCA,故①正确;∵∠A=90°,CG⊥EG,EG∥BC,∴∠ADC+∠ACD=90°,CG⊥BC,即∠BCG=90°,∴∠GCD+∠BCD=90°,又∵∠BCD=∠ACD,∴∠ADC=∠GDC,故④正确;∵∠A=90°,∴∠ABC+∠ACB=90°,∵BE,CD分别平分∠ABC,∠ACB,∴∠FBC=12∠ABC,∠FCB=12∠ACB,∴∠BFC=180°-∠FBC-∠FCB=180°-12(∠ACB+∠ABC)=135°,∴∠EFC=180°-∠BFC=45°,∵CG⊥EG∴∠G=90°,∴∠EFC=12∠G,故③正确;∵∠BFC=135°,∴∠DFE=∠BFC=135°,故②错误;∵∠G=90°∴△EGC是直角三角形,根据现有条件,无法推出CG=CE,即无法得到△EGC是等腰直角三角形,故⑤错误;∴正确的有①③④,故选:D.知识点7:两外角角平分线模型在△ABC中,BI、CI分别是△ABC的外角的角平分线,且相交于点O.则∠O=90°-12∠A.【证明】∵BO是∠EBC平分线,∴∠2=12∠EBC,∵CO是∠FCB平分线,∴∠5=12∠FCB由△BCO中内角和定理可知:∠O=180°-∠2-∠5=180°-12∠EBC-12∠FCB=180°-12(180°-∠ABC)-12(180°-∠ACB)=12(∠ABC+∠ACB)=12(180°-∠A)=∠O=90°-12∠A【题型7两外角角平分线模型】25.(23-24八年级·全国·专题练习)如图,在△ABC中,∠B=58°,三角形两外角的角平分线交于点E,则∠AEC=.【答案】61°【分析】先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF的度数,再根据角平分线的定义求得∠EAC+∠ECA的度数,即可解答.【详解】解:∵∠B+∠BAC+∠BCA=180°,∠B=58°,∴∠BAC+∠BCA=180°-∠B=180°-58°=122°,∵∠BAC+∠DAC=180°,∠BCA+∠ACF=180°,∴∠DAC+∠ACF=360°-(∠BAC+∠BCA)=360°-122°=238°,∵AE平分∠DAC,CE平分∠ACF,∴∠EAC=12∠DAC,∠ECA=12∠ACF,∴∠EAC+∠ECA=12(∠DAC+∠ACF)=119°,∵∠EAC+∠ECA+∠AEC=180°,∴∠AEC=180°-(∠EAC+∠ECA)=180°-119°=61°,故答案为:61°.【点睛】本题考查三角形的内角和定理、角平分线的定义、平角定义,熟练掌握三角形的内角和定理和角平分线的定义是解答的关键.26.(23-24八年级·河南郑州·阶段练习)如图,G是ΔAFE两外角平分线的交点,P是ΔABC的两外角平分线的交点,F,C在AN上,又B,E在AM上;如果∠FGE=66°,那么∠P=度.【答案】66【分析】利用角平分线的定义和三角形、四边形的内角和可求得:∠G=180°-12×[360°-(180°-∠A)]=90°-1 2∠A,∠P=180°-12×[360°-(180°-∠A)]=90°-12∠A,所以∠P=∠FGE=66°.【详解】解:因为G是△AFE两外角平分线的交点,∴∠FGE=180°-12×[360°-(180°-∠A)]=90°-12∠A,∵P是△ABC两外角平分线的交点,∴∠P=180°-12×[360°-(180°-∠A)]=90°-12∠A,∴∠P=∠FGE=66°.故答案为:66.【点睛】本题考查了三角形内角和定理、角平分线的性质和三角形外角的性质,结合图形熟练运用定理和性质进行求解是解题的关键.27.(23-24八年级·山东聊城·期末)如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACF与∠ABC平分线的交点,E是△ABC的两外角平分线的交点,若∠BOC=130°,则∠D的度数为()A.25°B.30°C.40°D.50°【答案】C【分析】根据角平分线的定义和平角定义可得∠OCD=∠ACO+∠ACD=90°,根据外角的性质可得∠BOC =∠OCD+∠D,继而即可求解.【详解】解:∵CO平分∠ACB,CD平分∠ABC的外角,∴∠ACO=12∠ACB,∠ACD=12∠ACF,∵∠ACB+∠ACF=180°,∴∠OCD=∠ACO+∠ACD=12∠ACB+∠ACF=90°,∴∠BOC=∠OCD+∠D,∴∠D=∠BOC-∠OCD=130°-90°=40°,故选择C.【点睛】本题考查角平分线的定义,平角定义,三角形的外角性质,解题的关键是根据角平分线定义和平角定义可得∠OCD=90°,根据外角的性质求得∠BOC=∠OCD+∠D.28.(23-24八年级·全国·课后作业)(分类讨论思想)△ABC的两外角平分线交于点F.(1)如图1,若∠A=30°,则∠BFC的度数为.(2)如图2,过点F作直线MN∥BC,分别交射线AB,AC于点M,N,若设∠MFB=α,∠NFC=β,则∠A与α+β的数量关系是.(3)在(2)的条件下,将直线MN绕点F转动.①如图3,当直线MN与线段BC没有交点时,试探索∠A与α,β之间的数量关系,并说明理由.②当直线MN 与线段BC 有交点时,试问①中∠A 与α,β之间的数量关系是否仍然成立?若成立,请说明理由;若不成立,请给出三者之间的数量关系.【答案】(1)75°(2)α+β-12∠A =90°(3)①α+β-12∠A =90°,见解析;②不成立,β-α-12∠A =90°或α-β-12∠A =90°【分析】(1)由三角形内角和定理可得∠ACB +∠ABC =180°-∠A ,从而可得∠CBD +∠BCE =180°+∠A ,再由角平分线的定义可得∠CBF +∠BCF =90°+12∠A ,最后由三角形内角和定理可得∠BFC =90°-12∠A ,进行计算即可;(2)由(1)可得由(1)可得∠BFC =90°-12∠A ,再由α+∠BFC +β=180°代入进行计算即可;(3)①根据(1)中的结论∠BFC =90°-12∠A ,以及平角的定义,即可得到答案;②分两种情况进行讨论:根据(1)中的结论∠BFC =90°-12∠A ,以及平角的定义,即可得到答案.【详解】(1)解:∵∠A +∠ACB +∠ABC =180°,∴∠ACB +∠ABC =180°-∠A ,∵∠ACB +∠BCE =180°,∠ABC +∠CBD =180°,∴∠CBD +∠BCE=180°-∠ABC +180-∠ACB=360°-∠ABC +∠ACB=360°-180°-∠A=180°+∠A ,∵BF 和CF 分别是∠DBC 和∠BCE 的平分线,∴∠CBF =12∠CBD ,∠BCF =12∠BCE ,∴∠CBF +∠BCF ,=12∠CBD +12∠BCE =12∠CBD +∠BCE =12×180°+∠A =90°+12∠A ,∵∠BFC +∠CBF +∠BCF =180°,∴∠BFC =180°-∠CBF +∠BCF =180°-90°+12∠A =90°-12∠A =75°,故答案为:75°;(2)解:α+β-12∠A =90°,由(1)可得∠BFC =90°-12∠A ,∵α+∠BFC +β=180°,∴α+β+90°-12∠A =180°,即α+β-12∠A =90°.(3)解:①当直线MN 与线段BC 没有交点时,α+β-12∠A =90°,理由如下:∵∠BFC =90°-12∠A ,∠MFB +∠NFC +∠BFC =180°,∴α+β+90°-12∠A =180°,即α+β-12∠A =90°;②当直线MN 与线段BC 有交点时,①中∠A 与α,β之间的数量关系不成立,需分两种情况讨论:a .如图1,当M 在线段AB 上,N 在射线AC 上时,β-α-12∠A =90°,,∵∠BFC =90°-12∠A ,∠BFC -∠MFB +∠NFC =180°,∴90°-12∠A -α+β=180°,即β-α-12∠A =90°,b .如图2,当M 在射线AB 上,N 在线段AC 上时,α-β-12∠A =90°,,∵∠BFC =90°-12∠A ,∠BFC -∠NFC +∠MFB =180°,∴90°-12∠A -β+α=180°,即α-β-12∠A =90°.【点睛】本题考查了三角形内角和定理、角平分线的定义、平角的定义等知识,熟练掌握以上知识点,采用分类讨论的思想解题,是解此题的关键.知识点8:一内一外角角平分线模型已知△ABC 中,BP 、CP 分别是△ABC 的内角和外角的角平分线,且相交于点P .则∠P =12∠A【证明】∵BP 是∠ABC 平分线,∴∠3=12∠ABC ∵CP 是∠ACE 平分线,∴∠1=12∠ACE 由△ABC 外角定理可知:∠ACE =∠ABC +∠A 即:2∠1=2∠3+∠A ⋯⋯①对①式两边同时除以2,得:∠1=∠3+12∠A⋯⋯②又在△BPC中由外角定理可知:∠1=∠3+∠P⋯⋯③比较②③式子可知:∠P=12∠A.【题型8一内一外角角平分线模型】29.(23-24八年级·江苏泰州·期末)如图,点B、C分别在AM、AN上运动(不与A重合),CD是∠BCN的平分线,CD的反向延长线交∠ABC的平分线于点P.知道下列哪个条件①∠ABC+∠ACB;②∠A;③∠NCD -∠ABP;④∠ABC的值,不能求∠P大小的是()A.①B.②C.③D.④【答案】D【分析】本题考查三角形外角的性质与内角和定理,根据三角形外角的性质及角平分线的定义可得∠P=∠NCD-∠ABP,可判断③,再利用三角形外角的性质得到∠A=∠NCB-∠ABC,等量代换可判断②,根据三角形内角和定理及等量代换可判断①和④,即可求解.【详解】解:∵CD是∠BCN的平分线,CD的反向延长线交∠ABC的平分线于点P,∴∠NCD=∠BCD,∠ABP=∠CBP,∵∠P=∠DCB-∠CBP,∴∠P=∠NCD-∠ABP,∴③能求出∠P的大小;∵∠A=∠NCB-∠ABC=2∠NCD-∠ABP,∠P=∠NCD-∠ABP∴∠P=12∠A,∴②能求出∠P的大小;∵∠ABC+∠ACB=180°-∠A,∴∠A=180°-∠ABC+∠ACB∵∠P=12∠A,∴∠P=12180°-∠ABC+∠ACB=90°-12∠ABC+∠ACB,∴①能求出∠P的大小,④不能求出∠P的大小;故选:D.30.(23-24八年级·四川遂宁·开学考试)如图,点D为△ABC边BC的延长线上一点,若∠A:∠ABC=3:4,∠ACD=140°,∠ABC的角平分线与∠ACD的角平分线交于点M,则∠M=度.【答案】30【分析】本题考查了三角形的外角定理,与角平分线有关的计算.解题的关键是掌握三角形的一个外角等于与它不相邻的两个内角之和,以及角平分线的定义.先根据∠A:∠ABC=3:4,∠ACD=140°,求出∠ABC=80°,进而得出∠CBM=12∠ABC=40°,∠CDM=12∠ACD=70°,最后根据三角形的外角定理即可解答.【详解】解:∵∠ACD=140°,∴∠A+∠ABC=140°∵∠A:∠ABC=3:4,∴∠ABC=140°×43+4=80°,∵BM平分∠ABC,CM平分∠ACD,∴∠CBM=12∠ABC=40°,∠CDM=12∠ACD=70°,∴∠M=∠DCM-∠CBM=30°,故答案为:30.31.(23-24八年级·四川眉山·开学考试)如图,∠ABC=∠ACB,AD、BD、CD分别平分∠EAC、∠ABC和∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③DB平分∠ADC;④∠ADC=90°-∠ABD.其中正确的结论有.(填序号)【答案】①②④【分析】证明∠EAD=∠DAC,由三角形外角得∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,得出∠EAD =∠ABC,再由平行线的判定即可判断出①是否正确;由AD∥BC,得出∠ADB=∠DBC,再由BD平分∠ABC,所以∠ABD=∠DBC,∠ABC=2∠ADB,进而可判断出②是否正确;假设DB平分∠ADC,推出与题干不符的结论,进而可判断出③是否正确,由∠ADC+∠CAD+∠ACD=180°,利用角的关系得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,进而可判断出④是否正确;【详解】解:①∵AD平分△ABC的外角∠EAC,∴∠EAD=∠DAC,∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,∴∠EAD=∠ABC,∴AD∥BC,故①正确;②由(1)可知AD∥BC,∴∠ADB=∠DBC,∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ABC=2∠ADB,∵∠ABC=∠ACB,∴∠ACB=2∠ADB,故②正确;③若DB 平分∠ADC ,∴∠ADB =∠CDB ,∵∠ADB =∠DBC =∠ABD ,∴∠ADB =∠DBC =∠ABD =∠CDB ,∴∠ABC =∠ADC ,与题干条件矛盾.故③错误.④在△ADC 中,∠ADC +∠CAD +∠ACD =180°,∵CD 平分△ABC 的外角∠ACF ,∴∠ACD =∠DCF ,∵AD ∥BC ,∴∠ADC =∠DCF ,∠ADB =∠DBC ,∠CAD =∠ACB ,∴∠ACD =∠ADC ,∠CAD =∠ACB =∠ABC =2∠ABD ,∴∠ADC +∠CAD +∠ACD =∠ADC +2∠ABD +∠ADC =2∠ADC +2∠ABD =180°,∴∠ADC +∠ABD =90°,∴∠ADC =90°-∠ABD ,故④正确;故答案为:①②④【点睛】此题考查三角形的外角性质,平行线的判定与性质,三角形的内角和定理的应用,解题关键在于掌握外角性质.32.(23-24八年级·河南开封·期末)如图,在△ABC 中,∠A =48°,△ABC 的内角∠ABC 与外角∠ACD 的平分线相交于点A 1,得到∠A 1;∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得到∠A 2;⋯⋯按此规律继续下去,∠A n -1BC 与∠A n -1CD 的平分线相交于点A n ,要使∠A n 的度数为整数,则n 的最大值为()A.3B.4C.5D.6【答案】B 【分析】本题主要考查了三角形的内角和,三角形的外角定理,角平分线的定义,熟练掌握三角形内角和是解题的关键.先根据外角和定理得出∠ACD =∠ABC +∠A ,再根据题意总结出规律,∠A n =12n ∠A 即可得到答案.【详解】解:∵∠ACD 是△ABC 的一个外角,∴∠ACD =∠ABC +∠A ,∵△ABC 的内角∠ABC 与外角∠ACD 的平分线相交于点A 1,得到∠A 1;∠A 1BC 与∠A 1CD 的平分线相交于点A 2,∴∠A 1BC =12∠ABC ,∠A 1CA =12∠ACD ,∴∠A 1=180°-∠A 1BC -∠A 1CB=180°-12∠ABC -(∠ACB +∠A 1CA )=180°-12∠ABC -∠ACB -12∠ACD =180°-12∠ABC -∠ACB -12(∠ABC +∠A )。
(专题精选)初中数学三角形难题汇编含答案

(专题精选)初中数学三角形难题汇编含答案一、选择题1.如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数()A.28°B.22°C.32°D.38°【答案】B【解析】【分析】延长AB交CF于E,求出∠ABC,根据三角形外角性质求出∠AEC,根据平行线性质得出∠2=∠AEC,代入求出即可.【详解】解:如图,延长AB交CF于E,∵∠ACB=90°,∠A=30°,∠ABC=60°,∵∠1=38°,∴∠AEC=∠ABC-∠1=22°,∵GH∥EF,∴∠2=∠AEC=22°,故选B.【点睛】本题考查了三角形的内角和定理,三角形外角性质,平行线性质的应用,主要考查学生的推理能力.2.如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A .8cmB .10cmC .12cmD .14cm【答案】B【解析】【分析】 根据“AAS”证明 ΔABD ≌ΔEBD .得到AD =DE ,AB =BE ,根据等腰直角三角形的边的关系,求其周长.【详解】∵ BD 是∠ABC 的平分线,∴ ∠ABD =∠EBD .又∵ ∠A =∠DEB =90°,BD 是公共边,∴ △ABD ≌△EBD (AAS),∴ AD =ED ,AB =BE ,∴ △DEC 的周长是DE +EC +DC=AD +DC +EC=AC +EC =AB +EC=BE +EC =BC=10 cm.故选B.【点睛】本题考查了等腰直角三角形的性质,角平分线的定义,全等三角形的判定与性质. 掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS 和HL )和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.3.如图,ABCD 的对角线AC 与BD 相交于点O ,AD BD ⊥,30ABD ∠=︒,若23AD =.则OC 的长为( )A .3B .3C 21D .6【答案】C【解析】【分析】 先根据勾股定理解Rt ABD △求得6BD =,再根据平行四边形的性质求得3OD =,然后根据勾股定理解Rt AOD △、平行四边形的性质即可求得OC OA ==【详解】解:∵AD BD ⊥∴90ADB ∠=︒∵在Rt ABD △中,30ABD ∠=︒,AD =∴2AB AD ==∴6BD ==∵四边形ABCD 是平行四边形 ∴132OB OD BD ===,12OA OC AC ==∴在Rt AOD △中,AD =3OD =∴OA =∴OC OA ==故选:C【点睛】本题考查了含30角的直角三角形的性质、勾股定理、平行四边形的性质等知识点,熟练掌握相关知识点是解决问题的关键.4.下列长度的三条线段能组成三角形的是( )A .2, 2,5B .C .3,4,8D .4,5,6【答案】D【解析】【分析】三角形的任何一边大于其他两边之差,小于两边之和,满足此关系的可组成三角形,其实只要最小两边的和大于最大边就可判断前面的三边关系成立.【详解】根据三角形三边关系可知,三角形两边之和大于第三边.A 、2+2=4<5,此选项错误;B 、<3,此选项错误;C 、3+4<8,此选项错误;D 、4+5=9>6,能组成三角形,此选项正确.故选:D .【点睛】此题考查三角形三边关系,解题关键在于掌握三角形两边之和大于第三边.即:两条较短的边的和小于最长的边,只要满足这一条就是满足三边关系.5.如图,已知AB ∥CD ,直线AB ,CD 被BC 所截,E 点在BC 上,若∠1=45°,∠2=35°,则∠3=( )A .65°B .70°C .75°D .80°【答案】D【解析】【分析】 由平行线的性质可求得∠C ,在△CDE 中利用三角形外的性质可求得∠3.【详解】解:∵AB ∥CD ,∴∠C =∠1=45°,∵∠3是△CDE 的一个外角,∴∠3=∠C+∠2=45°+35°=80°,故选:D .【点睛】本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a ∥b ,b ∥c ⇒a ∥c .6.将一个边长为4的正方形ABCD 分割成如图所示的9部分,其中ABE △,BCF ,CDG ,DAH 全等,AEH △,BEF ,CFG △,DGH 也全等,中间小正方形EFGH 的面积与ABE △面积相等,且ABE △是以AB 为底的等腰三角形,则AEH △的面积为( )A .2B .169C .32D 2【答案】C【解析】【分析】【详解】 解:如图,连结EG 并向两端延长分别交AB 、CD 于点M 、N ,连结HF ,∵四边形EFGH 为正方形,∴EG FH =,∵ABE △是以AB 为底的等腰三角形,∴AE BE =,则点E 在AB 的垂直平分线上,∵ABE △≌CDG ,∴CDG 为等腰三角形,∴CG DG =,则点G 在CD 的垂直平分线上,∵四边形ABCD 为正方形,∴AB 的垂直平分线与CD 的垂直平分线重合,∴MN 即为AB 或CD 的垂直平分线,则,EM AB GN CD ,EM GN ,∵正方形ABCD 的边长为4,即4AB CDAD BC , ∴4MN =, 设EM GN x ,则42EG FH x , ∵正方形EFGH 的面积与ABE △面积相等, 即2114(42)22x x ,解得:121,4x x ==,∵4x =不符合题意,故舍去,∴1x =,则S 正方形EFGH 14122==⨯⨯=ABE S , ∵ABE △,BCF ,CDG ,DAH 全等, ∴2====ABE BCF CDG DAHS S S S , ∵正方形ABCD 的面积4416=⨯=,AEH △,BEF ,CFG △,DGH 也全等, ∴1(4=AEH S S 正方形ABCD − S 正方形EFGH 134)(16242)42-=⨯--⨯=ABE S , 故选:C .【点睛】本题考查了正方形的性质、全等三角形的性质和等腰三角形的性质,解题的关键是求得ABE △的面积.7.图中的三角形被木板遮住了一部分,这个三角形是( )A .锐角三角形B .直角三角形C .钝角三角形D .以上都有可能【答案】D【解析】 从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角,故选D .8.如图,直线a b ∥,点A 、B 分别在直线a 、b 上,145∠︒=,若点C 在直线b 上,105BAC ∠︒=,且直线a 和b 的距离为3,则线段AC 的长度为( )A .32B .33C .3D .6【答案】D【解析】【分析】 过C 作CD ⊥直线a ,根据30°角所对直角边等于斜边的一半即可得到结论.【详解】过C 作CD ⊥直线a ,∴∠ADC =90°.∵∠1=45°,∠BAC =105°,∴∠DAC =30°.∵CD =3,∴AC =2CD =6.故选D .【点睛】本题考查了平行线间的距离,含30°角的直角三角形的性质,正确的理解题意是解题的关键.9.如图,在菱形ABCD 中,对角线AC =8,BD =6,点E ,F 分别是边AB ,BC 的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是()A.3 B.4 C.5 D.6【答案】C【解析】【分析】先根据菱形的性质求出其边长,再作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF 的最小值,再根据菱形的性质求出E′F的长度即可.【详解】解:如图∵四边形ABCD是菱形,对角线AC=6,BD=8,∴22,34作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF的最小值,∵AC是∠DAB的平分线,E是AB的中点,∴E′在AD上,且E′是AD的中点,∵AD=AB,∴AE=AE′,∵F是BC的中点,∴E′F=AB=5.故选C.10.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=12∠CGE.其中正确的结论是( )A.②③B.①②④C.①③④D.①②③④【答案】B【解析】【分析】根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案.【详解】①∵EG∥BC,∴∠CEG=∠ACB,又∵CD是△ABC的角平分线,∴∠CEG=∠ACB=2∠DCB,故正确;②∵∠A=90°,∴∠ADC+∠ACD=90°,∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠ADC+∠BCD=90°.∵EG∥BC,且CG⊥EG,∴∠GCB=90°,即∠GCD+∠BCD=90°,∴∠ADC=∠GCD,故正确;③条件不足,无法证明CA平分∠BCG,故错误;④∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,∴∠AEB+∠ADC=90°+12(∠ABC+∠ACB)=135°,∴∠DFE=360°-135°-90°=135°,∴∠DFB=45°=12∠CGE,,正确.故选B.【点睛】本题主要考查了角平分线的定义,平行线的性质,三角形内角和定理及多边形内角和,三角形外角的性质,熟知直角三角形的两锐角互余是解答此题的关键.11.如图,△ABC ≌△A E D ,∠C =40°,∠E AC =30°,∠B =30°,则∠E AD =( );A .30°B .70°C .40°D .110°【答案】D【解析】【分析】【详解】∵△ABC ≌△AED , ∴∠D=∠C=40°,∠C=∠B=30°,∴∠E AD=180°-∠D -∠E =110°,故选D.12.如图,在菱形ABCD 中,60BCD ∠=︒,BC 的垂直平分线交对角线AC 于点F ,垂足为E ,连接BF 、DF ,则DFC ∠的度数是( )A .130︒B .120︒C .110︒D .100︒【答案】A【解析】【分析】 首先求出∠CFB=130°,再根据对称性可知∠CFD=∠CFB 即可解决问题;【详解】∵四边形ABCD 是菱形,∴∠ACD =∠ACB =12∠BCD=25°, ∵EF 垂直平分线段BC ,∴FB=FC ,∴∠FBC=∠FCB=25°,∴∠CFB=180°-25°-25°=130°,根据对称性可知:∠CFD=∠CFB=130°,故选:A .【点睛】此题考查菱形的性质、线段的垂直平分线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.13.如图,在平面直角坐标系中,已知点A (﹣2,0),B (0,3),以点A 为圆心,AB 长为半径画弧,交x 轴的正半轴于点C ,则点C 的横坐标介于( )A .0和1之间B .1和2之间C .2和3之间D .3和4之间【答案】B【解析】【分析】 先根据点A ,B 的坐标求出OA ,OB 的长度,再根据勾股定理求出AB 的长,即可得出OC 的长,再比较无理数的大小确定点C 的横坐标介于哪个区间.【详解】∵点A ,B 的坐标分别为(﹣2,0),(0,3),∴OA =2,OB =3,在Rt △AOB 中,由勾股定理得:AB 222+313=∴AC =AB 13,∴OC 132,∴点C 132,0), ∵3134<< , ∴11322<< ,即点C 的横坐标介于1和2之间,故选:B .【点睛】本题考查了弧与x 轴的交点问题,掌握勾股定理、无理数大小比较的方法是解题的关键.14.满足下列条件的是直角三角形的是( )A .4BC =,5AC =,6AB =B .13BC =,14AC =,15AB = C .::3:4:5BC AC AB =D .::3:4:5A B C ∠∠∠= 【答案】C【解析】【分析】要判断一个角是不是直角,先要知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.【详解】A.若BC=4,AC=5,AB=6,则BC2+AC2≠AB2,故△ABC不是直角三角形;B.若13BC=,14AC=,15AB=,则AC2+AB2≠CB2,故△ABC不是直角三角形;C.若BC:AC:AB=3:4:5,则BC2+AC2=AB2,故△ABC是直角三角形;D.若∠A:∠B:∠C=3:4:5,则∠C<90°,故△ABC不是直角三角形;故答案为:C.【点睛】本题主要考查了勾股定理的逆定理,如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.15.等腰三角形的一个角比另一个角的2倍少20度,则等腰三角形顶角的度数是()A.140B.20或80C.44或80D.140或44或80【答案】D【解析】【分析】设另一个角是x,表示出一个角是2x-20°,然后分①x是顶角,2x-20°是底角,②x是底角,2x-20°是顶角,③x与2x-20°都是底角根据三角形的内角和等于180°与等腰三角形两底角相等列出方程求解即可.【详解】设另一个角是x,表示出一个角是2x-20°,①x是顶角,2x-20°是底角时,x+2(2x-20°)=180°,解得x=44°,∴顶角是44°;②x是底角,2x-20°是顶角时,2x+(2x-20°)=180°,解得x=50°,∴顶角是2×50°-20°=80°;③x与2x-20°都是底角时,x=2x-20°,解得x=20°,∴顶角是180°-20°×2=140°;综上所述,这个等腰三角形的顶角度数是44°或80°或140°.故答案为:D.【点睛】本题考查了等腰三角形两底角相等的性质,三角形的内角和定理,难点在于分情况讨论,特别是这两个角都是底角的情况容易漏掉而导致出错.16.如图,90ACB ∠=︒,AC CD =,过D 作AB 的垂线,交AB 的延长线于E ,若2AB DE =,则BAC ∠的度数为( )A .45°B .30°C .22.5°D .15°【答案】C【解析】【分析】 连接AD ,延长AC 、DE 交于M ,求出∠CAB=∠CDM ,根据全等三角形的判定得出△ACB ≌△DCM ,求出AB=DM ,求出AD=AM ,根据等腰三角形的性质得出即可.【详解】解:连接AD ,延长AC 、DE 交于M ,∵∠ACB=90°,AC=CD ,∴∠DAC=∠ADC=45°,∵∠ACB=90°,DE ⊥AB ,∴∠DEB=90°=∠ACB=∠DCM ,∵∠ABC=∠DBE ,∴∠CAB=∠CDM ,在△ACB 和△DCM 中CAB CDM AC CDACB DCM ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ACB ≌△DCM (ASA ),∴AB=DM ,∵AB=2DE ,∴DM=2DE ,∴DE=EM ,∵DE ⊥AB ,∴AD=AM ,114522.522BAC DAE DAC ︒︒∴∠=∠=∠=⨯= 故选:C .【点睛】 本题考查了全等三角形的性质和判定,等腰直角三角形,等腰三角形的性质和判定等知识点,能根据全等求出AB=DM 是解此题的关键.17.如图为一个66⨯的网格,在ABC ∆,A B C '''∆和A B C ''''''∆中,直角三角形有( )个A .0B .1C .2D .3【答案】C【解析】【分析】 根据题中的网格,先运用勾股定理计算出各个三角形的边长,再根据勾股定理的逆定理判断是否为直角三角形即可.【详解】设网格的小正方形的边长是1,由勾股定理(两直角边的平方等于斜边的平方)可知,ABC ∆的三边分别是:10,5,5; 由于2225510+=, 根据勾股定理的逆定理得:ABC ∆是直角三角形; '''A B C ∆的三边分别是:''A B 10, ''B C 5 ,''AC 13 由于22210513,根据勾股定理的逆定理得:'''A B C ∆不是直角三角形;A B C ''''''∆的三边分别是:A B ''''18B C ''''8 ,A C ''''26;由于22218826, 根据勾股定理的逆定理得:A B C ''''''∆是直角三角形;因此有两个直角等三角形;故选C .【点睛】本题主要考查了勾股定理和勾股定理的逆定理,能灵活运用所学知识是解题的关键.18.如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,3),点C的坐标为(12,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )A.132B.312C.3+192D.2 7【答案】B【解析】如图,作点A关于OB的对称点点D,连接CD交OB于点P,此时PA+PC最小,作DN⊥x 轴交于点N,∵B(33OA=3,AB3OB3BOA=30°,∵在Rt△AMO中,∠MOA=30°,AO=3,∴AM=1.5,∠OAM=60°,∴∠ADN=30°,∵在Rt△AND中,∠ADN=30°,AD=2AM=3,∴AN=1.5,DN 33 2∴CN=3-12-1.5=1,∴CD2=CN2+DN2=12+3322=314,∴CD=312.故选B.点睛:本题关键在于先借助轴对称的性质确定出P点的位置,然后结合特殊角30°以及勾股定理计算.19.如图,Rt△ABC中,∠C =90°,∠ABC的平分线BD交AC于D,若AD =5cm,CD=3cm,则点D到AB的距离DE是()A .5cmB .4cmC .3cmD .2cm【答案】C【解析】 ∵点D 到AB 的距离是DE ,∴DE ⊥AB ,∵BD 平分∠ABC ,∠C =90°,∴把Rt △BDC 沿BD 翻折后,点C 在线段AB 上的点E 处,∴DE=CD ,∵CD =3cm ,∴DE=3cm.故选:C.20.如图,在ABC 中,90C ∠=︒,60CAB ∠=︒,按以下步骤作图:①分别以A ,B 为圆心,以大于12AB 的长为半径画弧,两弧分别相交于点P 和Q . ②作直线PQ 交AB 于点D ,交BC 于点E ,连接AE .若4CE =,则AE 的值为( ) A .6B .2C .43D .8 【答案】D【解析】【分析】根据垂直平分线的作法得出PQ 是AB 的垂直平分线,进而得出∠EAB =∠CAE =30°,即可得出AE 的长.【详解】由题意可得出:PQ 是AB 的垂直平分线,∴AE =BE ,∵在△ABC中,∠C=90°,∠CAB=60°,∴∠CBA=30°,∴∠EAB=∠CAE=30°,∴CE=12AE=4,∴AE=8.故选D.【点睛】此题主要考查了垂直平分线的性质以及直角三角形中,30°所对直角边等于斜边的一半,根据已知得出∠EAB=∠CAE=30°是解题关键.。
初中数学八年级三角形及三角形全等专题练习题(附含答案)

初中数学八年级三角形及三角形全等专题练习题一、选择题1.如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE 的度数为何?()A.115B.120C.125D.1302.如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则下列结论,其中正确的是()①∠AFB∠∠AEC;②BF=CE;③∠BFC=∠EAF;④AB=BC.A.①②③B.①②④C.①②D.①②③④3.如图,平分,于,于,与的交点为,则图中全等三角形共有()A.2对B.3对C.4对D.5对4.如图,,且.、是上两点,,.若,,,则的长为()A.B.C.D.5.用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的识别方法是()A.SASB.ASAC.AASD.SSS6.下列判断正确的是()A.有两边和其中一边的对角对应相等的两个三角形全等B.有两边对应相等且有一角为30°的两个等腰三角形全等(8)C.有一角和一边相等的两个直角三角形全等D.有两角和一边对应相等的两个三角形全等7.如图所示,AB∠EF∠CD,∠ABC=90°,AB=DC,那么图中的全等三角形有()A.4对B.3对C.2对D.1对8.如图,在Rt∠ABC中,∠C=90°,AD是∠BAC的平分线,DE∠AB,垂足为E.若AB =10 cm,AC=6 cm,则BE的长度为()A.10 cm B.6 cm C.4 cm D.2 cm9.已知点A(a,1)与点B(5,b)关于y轴对称,则实数a,b的值分别是()A.5,1B.﹣5,1C.5,﹣1D.﹣5,﹣1 10.在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则()A.m=3,n=2B.m=﹣3,n=2C.m=2,n=3D.m=﹣2,n=﹣311.如图,等边的边长为3,点在边上,,线段在边上运动,,有下列结论:①与可能相等;②与可能相似;③四边形面积的最大值为;④四边形周长的最小值为.其中,正确结论的序号为()A.①④B.②④C.①③D.②③12.如图,已知等边三角形ABC边长为2,两顶点A、B分别在平面直角坐标系的x轴负半轴、轴的正半轴上滑动,点C在第四象限,连接OC,则线段OC长的最小值是()A.1B.3C.3D.13.已知实数x,y满足|x﹣4|+(y﹣8)2=0,则以x,y的值为两边长的等腰三角形的周长是()A.20或16B.20C.16D.以上答案均不对14.一个正方形周长与一个等腰角形的周长相等,若等腰三形的两边长为和,则这个正方形的对角线长为()A.B.C.D.15.如图所示,∠ABC中AC边上的高线是()A.线段DA B.线段BA C.线段BD D.线段BC二、综合题)16.(1)如图1,∠ABC中,作∠ABC、∠ACB的平分线相交于点O,过点O作EF∠BC 分别交AB、AC于E、F.① 求证:OE=BE;② 若∠ABC的周长是25,BC=9,试求出∠AEF的周长;(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,试探求∠BAC与∠PAC的数量关系式.17如图-1,的边在直线上,,且;的边也在直线上,边与边重合,且.(1)在图-1中,请你通过观察、测量,猜想并写出与关系;(2)将沿直线向左平移到图-2的位置时,交于点,连结,.猜想并写出与的关系,请证明你的猜想;(3)将沿直线向左平移到图-3的位置时,的延长线交的延长线于点,连结,.你认为(2)中所猜想的与的关系还成立吗?若成立,给出证明;若不成立,请说明理由.18、如图1,在∠ABC中,AB=AC,∠BAC=30°,点D是∠ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.(1)求∠ADE的度数;(2)求证:DE=AD+DC;参考答案一、选择题1、【答案】C∵三角形ACD为正三角形,∴AC=AD,∠ACD=∠ADC=∠CAD=60°,∵AB=DE,BC=AE,∴△ABC≌△DEA,∴∠B=∠E=115°,∠ACB=∠EAD,∠BAC=∠ADE,∴∠ACB+∠BAC=∠BAC+∠DAE=180°﹣115°=65°,∴∠BAE=∠BAC+∠DAE+∠CAD=65°+60°=125°,故选C.2、【答案】A∵∠EAF=∠BAC,∴∠BAF=∠CAE;在△AFB与△AEC中,,∴△AFB≌△AEC(SAS),∴BF=CE;∠ABF=∠ACE,∴A、F、B、C四点共圆,∴∠BFC=∠BAC=∠EAF;故①、②、③正确,④错误.故选A..3、【答案】C∵平分∴∠BOC=∠AOC又∵,∴∠AEO=∠BDO=90°又∵OC=OC∴∴OD=OE,CD=CE又∵∠BOD=∠AOE∴∴OA=OB,∠A=∠B∴又∵∠ACD=∠BCE∴故答案为C.4、【答案】D∵AB⊥CD,CE⊥AD,∴∠1=∠2,又∵∠3=∠4,∴180°-∠1-∠4=180°-∠2-∠3,即∠A=∠C.∵BF⊥AD,∴∠CED=∠BFD=90°,∵AB=CD,∴△ABF≌△CDE,∴AF=CE=a,ED=BF=b,又∵EF=c,∴AD=a+b-c.故选:D.5、【答案】D;6、【答案】D;7、【答案】B解:∵AB∥EF∥CD,∠ABC=90°,∴∠DCB=∠EFB=∠ABC=90°;在△ABC与△DCB中,,∴△ABC≌△DCB(SAS),∴∠ECB=∠EBC,∴EB=EC,BF=CF;同理可证△EFB≌EFC、△ABE≌△DCE;∴图中的全等三角形有3对,故选B.8、【答案】C9、【答案】B∵点A(a,1)与点A′(5,b)关于y轴对称,∴a=-5,b=1,故选B.10、【答案】B解:∵点A(m,2)与点B(3,n)关于y轴对称,∴m=-3,n=2.故选:B.11、【答案】D解:①∵线段在边上运动,,∴,∴与不可能相等,则①错误;②设,∵,,∴,即,假设与相似,∵∠A=∠B=60°,∴,即,从而得到,解得或(经检验是原方程的根),又,∴解得的或符合题意,即与可能相似,则②正确;③如图,过P作PE⊥BC于E,过D作DF⊥AB于F,设,由,,得,即,∴,∵∠B=60°,∴,∵,∠A =60°,∴,则,,∴四边形面积为:,又∵,∴当时,四边形面积最大,最大值为:,即四边形面积最大值为,则③正确;④如图,作点D关于直线的对称点D1,作D1D2∥PQ,连接CD2交AB于点P′,在射线P′A上取P′Q′=PQ,此时四边形P′CDQ′的周长为:,其值最小,∴D1Q′=DQ′=D2P′,,且∠AD1D2=180∠D1AB=180∠DAB =120°,∴∠D1AD2=∠D2AD1==30°,∠D2AC=90°,在△D1AD2中,∠D1AD2=30°,,∴,在Rt△AD2C中,由勾股定理可得,,∴四边形P′CDQ′的周长为:,则④错误,所以可得②③正确,故选:D.12、【答案】B解:如图所示:过点C作CE⊥AB于点E,连接OE,∵△ABC是等边三角形,∴CE=AC×sin60°=,AE=BE,∵∠AOB=90°,∴EO AB,∴EC-OE≥OC,∴当点C,O,E在一条直线上,此时OC最短,故OC的最小值为:OC=CE﹣EO=3故选B.13、【答案】B解:根据题意得,x﹣4=0,y﹣8=0,解得x=4,y=8,①4是腰长时,三角形的三边分别为4、4、8,∵4+4=8,∴不能组成三角形;②4是底边时,三角形的三边分别为4、8、8,能组成三角形,周长=4+8+8=20.所以,三角形的周长为20.故选:B.14、【答案】A解:①是腰,是底边时,两边的和小于第三边,不能构成三角形,舍去;②是底边和是腰时,等腰三角形的周长是,因而可得正方形的边长是,故这个正方形的对角线长是;故选:A.15、【答案】C由图可知,中AC边上的高线是BD.故选:C.二、综合题16、(1)∠BO平分∠ABC,∠∠EBO=∠OBC,∠EF∠BC,∠∠EDB=∠OBC,∠∠EOB=∠EBO,∠OE=BE (2)∠AEF的周长=AE+AF+EF=AE+AF+EB+FC=AB+AC=25-9=16(3)延长BA,证明P点在∠BAC外角的角平分线上,从而得到2∠PAC+∠BAC=180°17、解:(1)AB=AP;AB∠AP;(2)BQ=AP;BQ∠AP.证明:①由已知,得EF=FP,EF∠FP,∠∠EPF=45°.又∠AC∠BC,∠∠CQP=∠CPQ=45°.∠CQ=CP.在Rt∠BCQ和Rt∠ACP中,BC=AC,∠BCQ=∠ACP=90°,CQ=CP,∠Rt∠BCQ∠Rt∠ACP,∠BQ=AP.②如图,延长BQ交AP于点M.∠Rt∠BCQ∠Rt∠ACP,∠∠1=∠2.在Rt∠BCQ中,∠1+∠3=90°,又∠3=∠4,∠∠2+∠4=∠1+∠3=90°.∠∠QMA=90°.∠BQ∠AP;(3)成立.证明:①如图,∠∠EPF=45°,∠∠CPQ=45°.又∠AC∠BC,∠∠CQP=∠CPQ=45°.∠CQ=CP.在Rt∠BCQ和Rt∠ACP中,BC=AC,∠BCQ=∠ACP=90°,CQ=CP,∠Rt∠BCQ∠Rt∠ACP.∠BQ=AP.②如图,延长QB交AP于点N,则∠PBN=∠CBQ.∠Rt∠BCQ∠Rt∠ACP,∠∠BQC=∠APC.在Rt∠BCQ中,∠BQC+∠CBQ=90°,∠∠APC+∠PBN=90°.∠∠PNB=90°.∠QB∠AP.18、【答案】解:(1)∵△ABC中,AB=AC,∠BAC=30°,∴∠ABC=∠ACB==75°,∵DB=DC,∠DCB=30°,∴∠DBC=∠DCB=30°,∴∠ABD=∠ABC﹣∠DBC=45°,∵AB=AC,DB=DC,∴AD所在直线垂直平分BC,∴AD平分∠BAC,∴∠BAD=∠BAC=15°,∴∠ADE=∠ABD+∠BAD=60°;(2)如图1,在线段DE上截取DM=AD,连接AM,∵∠ADE=60°,DM=AD,∴△ADM是等边三角形,∴∠ADB=∠AME=120°∵AE=AB,∴∠ABD=∠E,在△ABD和△AEM中,,∴△ABD≌△AEM(AAS),∴BD=ME,∵BD=CD,∴CD=ME,∵DE=DM+ME,∴DE=AD+CD;-。
经典__初中数学三角形专题训练及例题解析

经典《三角形》专题训练知识点梳理考点一、三角形1、三角形的定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2、三角形的分类.⎪⎩⎪⎨⎧钝角三角形直角三角形锐角三角形⎪⎪⎩⎪⎪⎨⎧)(等边三角形等腰三角形不等边三角形 3、三角形的三边关系:三角形任意两边之和大于第三边,任意两边之差小于第三边. 4、三角形的重要线段①三角形的中线:顶点与对边中点的连线,三条中线交点叫重心②三角形的角平分线:内角平分线与对边相交,顶点和交点间的线段,三个角的角平分线的交点叫内心③三角形的高:顶点向对边作垂线,顶点和垂足间的线段.三条高的交点叫垂心(分锐角三角形,钝角三角形和直角三角形的交点的位置不同)5、三角形具有稳定性6、三角形的内角和定理及性质 定理:三角形的内角和等于180°. 推论1:直角三角形的两个锐角互补。
推论2:三角形的一个外角等于不相邻的两个内角的和。
推论3:三角形的一个外角大于与它不相邻的任何一个内角。
7、多边形的外角和恒为360° 8、多边形及多边形的对角线①正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.②凸凹多边形:画出多边形的任何一条边所在的直线,若整个图形都在这条直线的同一侧,这样的多边形称为凸多边形;,若整个多边形不都在这条直线的同一侧,称这样的多边形为凹多边形。
③多边形的对角线的条数:A.从n 边形的一个顶点可以引(n-3)条对角线,将多边形分成(n-2)个三角形。
B.n 边形共有2)3(-n n 条对角线。
9、边形的内角和公式及外角和①多边形的内角和等于(n-2)×180°(n ≥3)。
②多边形的外角和等于360°。
三角形 (按角分)三角形 (按边分)10、平面镶嵌及平面镶嵌的条件。
①平面镶嵌:用形状相同或不同的图形封闭平面,把平面的一部分既无缝隙,又不重叠地全部覆盖。
②平面镶嵌的条件:有公共顶点、公共边;在一个顶点处各多边形的内角和为360°。
人教版初中数学全等三角形考点专题训练

人教版初中数学全等三角形考点专题训练单选题1、如图,Rt △ACB 中,∠ACB =90°,△ABC 的角平分线AD 、BE 相交于点P ,过P 作PF ⊥AD 交BC 的延长线于点F ,交AC 于点H ,则下列结论:①∠APB =135°;②BF =BA ;③PH =PD ;④连接CP ,CP 平分∠ACB ,其中正确的是( )A .①②③B .①②④C .①③④D .①②③④答案:D解析:根据三角形内角和定理以及角平分线定义判断①;根据全等三角形的判定和性质判断②③;根据角平分线的判定与性质判断④.解:在△ABC 中,∵∠ACB=90°,∴∠BAC+∠ABC=90°,又∵AD 、BE 分别平分∠BAC 、∠ABC ,∴∠BAD+∠ABE=12(∠BAC+∠ABC)=12(180°-∠ACB)=12(180°-90°)=45°,∴∠APB=135°,故①正确.∴∠BPD=45°,又∵PF ⊥AD ,∴∠FPB=90°+45°=135°,∴∠APB=∠FPB ,又∵∠ABP=∠FBP ,BP=BP ,∴△ABP≌△FBP(ASA),∴∠BAP=∠BFP,AB=FB,PA=PF,故②正确.在△APH和△FPD中,∵∠APH=∠FPD=90°,∠PAH=∠BAP=∠BFP,PA=PF,∴△APH≌△FPD(ASA),∴PH=PD,故③正确.连接CP,如下图所示:∵△ABC的角平分线AD、BE相交于点P,∴点P到AB、AC的距离相等,点P到AB、BC的距离相等,∴点P到BC、AC的距离相等,∴点P在∠ACB的平分线上,∴CP平分∠ACB,故④正确,综上所述,①②③④均正确,故选:D.小提示:本题考查了角平分线的判定与性质,三角形全等的判定方法,三角形内角和定理.掌握相关性质是解题的关键.2、如图,已知∠ABC=∠DCB.添加一个条件后,可得△ABC≌△DCB,则在下列条件中,不能添加的是()A.AC=DB B.AB=DC C.∠A=∠D D.∠ABD=∠DCA答案:A解析:先要确定现有已知在图形上的位置,结合全等三角形的判定方法对选项逐一验证,排除错误的选项.解:∵∠ABC=∠DCB,∵BC=BC,A、添加AC=DB,不能得△ABC≌△DCB,符合题意;B、添加AB=DC,利用SAS可得△ABC≌△DCB,不符合题意;C、添加∠A=∠D,利用AAS可得△ABC≌△DCB,不符合题意;D、添加∠ABD=∠DCA,∴∠ACB=∠DBC,利用ASA可得△ABC≌△DCB,不符合题意;故选:A.小提示:本题主要考查三角形全等的判定,熟练掌握判定方法是解题的关键.3、工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA、OB上分别在取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.这里构造全等三角形的依据是()A.SAS B.ASA C.AAS D.SSS答案:D解析:根据全等三角形的判定条件判断即可.解:由题意可知OC=OD,MC=MD在△OCM和△ODM中{OC=OD OM=OM MC=MD∴△OCM≅△ODM(SSS)∴∠COM=∠DOM∴OM就是∠AOB的平分线故选:D小提示:本题考查全等三角形的判定及性质、角平分线的判定、熟练掌握全等三角形的判定是关键.4、如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD 的长为()A.a+c B.b+c C.a−b+c D.a+b−c 答案:D解析:分析:详解:如图,∵AB⊥CD,CE⊥AD,∴∠1=∠2,又∵∠3=∠4,∴180°-∠1-∠4=180°-∠2-∠3,即∠A=∠C.∵BF⊥AD,∴∠CED=∠BFD=90°,∵AB=CD,∴△ABF≌△CDE,∴AF=CE=a,ED=BF=b,∴AD=a+b-c.故选:D.点睛:本题主要考查全等三角形的判定与性质,证明△ABF≌△CDE是关键.5、如图,AC=BD,AO=BO,CO=DO,∠D=30°,∠A=95°,则∠AOB等于( )A.120°B.125°C.130°D.135°答案:B解析:在△AOC和△BOD中{AC=BD AO=BO CO=DO,∴△AOC≌△BOD(SSS),∴∠C=∠D,又∵∠D=30°,∴∠C=30°,又∵在△AOC中,∠A=95°,∴∠AOC=(180-95-30) °=55°,又∵∠AOC+∠AOB=180°(邻补角互补),∴∠AOB=(180-55)°=125 °.6、如图,△ABC和△EDF中,∠B=∠D=90°,∠A=∠E,点B,F,C,D在同一条直线上,再增加一个条件,不能判定△ABC≌△EDF的是( )A.AB=EDB.AC=EFC.AC∥EFD.BF=DC答案:C解析:根据全等三角形的判定方法即可判断.A. AB=ED,可用ASA判定△ABC≌△EDF;B. AC=EF,可用AAS判定△ABC≌△EDF;C. AC∥EF,不能用AAA判定△ABC≌△EDF,故错误;D. BF=DC,可用AAS判定△ABC≌△EDF;故选C.小提示:此题主要考查全等三角形的判定,解题的关键是熟知全等三角形的判定方法.7、如图,AB//DC,AB=DC,要使∠A=∠C,直接利用三角形全等的判定方法是()A.AASB.SASC.ASAD.SSS答案:B解析:根据平行线性质得出∠ABD=∠CDB,再加上AB=DC,BD=DB,根据全等三角形的判定定理SAS即可推出△ABD≌△CDB,从而推出∠A=∠C,即可得出答案.∵AB//DC,∴∠ABD=∠CDB,在△ABD和△CDB中,{AB=CD∠ABD=∠CDBBD=BD,∴△ABD≌△CDB(SAS),∴∠A=∠C,故选B.小提示:本题考查了平行线性质、全等三角形的判定与性质的应用,熟练掌握全等三角形的判定与性质定理是解题的关键.8、下列说法:①若AC=BC,则C为AB的中点②若∠AOC=12∠AOB,则OC是∠AOB的平分线③a>b,则a2>b2④若a=b,则|a|=|b|,其中正确的有()A.1个B.2个C.3个D.4个答案:A解析:根据直线中点、角平分线、有理数大小比较以及绝对值的性质,逐一判定即可.当三点不在同一直线上的时候,点C不是AB的中点,故错误;当OC位于∠AOB的内部时候,此结论成立,故错误;当a、b为负数时,a2<b2,故错误;若a=b,则|a|=|b|,故正确;故选:A.小提示:此题主要考查直线中点、角平分线、有理数大小比较以及绝对值的性质,熟练掌握,即可解题.填空题9、如图,MN∥PQ,AB⊥PQ,点A,D,B,C分别在直线MN和PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=_____.答案:7解析:由MN∥PQ,AB⊥PQ,可知∠DAE=∠EBC=90°,可判定△ADE≌△BCE,从而得出AE=BC,则AB=AE+BE=AD+BC=7.所以答案是:7.点睛:本题考查了直角三角形全等的判定和性质以及平行线的性质,是基础知识,比较简单.10、如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),点D在第二象限,且△ABD与△ABC全等,点D的坐标是__________.答案:(﹣4,3)或(﹣4,2)解析:分△ABD≌△ABC,△ABD≌△BAC两种情况,根据全等三角形对应边相等即可解答.解:当△ABD≌△ABC时,△ABD和△ABC关于y轴对称,如下图所示:∴点D的坐标是(-4,3),当△ABD’≌△BAC时,过D’作D’G⊥AB,过C点作CH⊥AB,如上图所示:△ABD’边AB上的高D’G与△BAC的边AB上高CH相等,∴D’G=CH=4,AG=BH=1,∴OG=2,∴点D’的坐标是(-4,2),所以答案是:(-4,3)或(-4,2).小提示:本题考查的是全等三角形的性质,坐标与图形的性质,掌握全等三角形的对应边相等是解题的关键.11、工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC.由此做法得△MOC≌△NOC的依据是____.答案:SSS##边边边解析:由作图过程可得MO=NO,NC=MC,再加上公共边CO=CO可利用SSS定理判定△MOC≌△NOC.解:∵在△ONC和△OMC中{ON=OM CO=CO NC=MC,∴△MOC≌△NOC(SSS),∴∠BOC=∠AOC,所以答案是:SSS.小提示:本题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.12、如图,已知AF=BE,∠A=∠B,AC=BD,经分析__________≌__________,依据是__________.答案:△ADF△BCE SAS解析:利用SAS 得出全等三角形.证明:∵AC =BD ,∴AD =BC ,在△ADF 和△BCE 中∵{AD =BC ∠A =∠B AF =BE,∴△ADF ≌△BCE (SAS ).所以答案是:①△ADF ,②△BCE ,③SAS .小提示:此题主要考查了全等三角形的判定,熟练掌握判定方法是解题的关键13、如图,已知AD =AE ,请你添加一个条件,使得△ADC ≌△AEB ,你添加的条件是_____.(不添加任何字母和辅助线)答案:AB =AC 或∠ADC =∠AEB 或∠ABE =∠ACD .解析:根据图形可知证明△ADC ≌△AEB 已经具备了一个公共角和一对相等边,因此可以利用ASA 、SAS 、AAS 证明两三角形全等.∵∠A =∠A ,AD =AE ,∴可以添加AB =AC ,此时满足SAS ;添加条件∠ADC=∠AEB,此时满足ASA;添加条件∠ABE=∠ACD,此时满足AAS,故答案为AB=AC或∠ADC=∠AEB或∠ABE=∠ACD;小提示:本题考查了全等三角形的判定,是一道开放题,解题的关键是牢记全等三角形的判定方法.解答题14、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,猜想DE、AD、BE之间的关系,并请给出证明.答案:(1)①见解析;②见解析;(2)AD−BE=DE,证明见解析.解析:(1)①利用“AAS”证明△ADC≌△CEB全等即可;②根据△ADC≌△CEB即可得到AD=CE,BE=CD,即可得到AD+BE=CE+CD=DE;(2)同(1)证明△ADC≌△CEB得到AD=CE,BE=CD,即可推出AD−BE=CE−CD=DE.证明(1)①∵AD⊥MN,BE⊥MN,∠ACB=90∘∴∠ADC=∠CEB=90°,∴∠DAC+∠DCA=∠DCA+∠BCE=90°,∴∠DAC=∠ECB,在△ADC和△CEB中,{∠ADC=∠CEB ∠DAC=∠ECBAC=CB,∴△ADC≌△CEB(AAS);②∵△ADC≌△CEB,∴AD=CE,BE=CD,∴AD+BE=CE+CD=DE;(2)关系:AD−BE=DE;证明:∵AD⊥MN,∠ACB=90∘,BE⊥MN,∴∠ADC=∠CEB=90°,∴∠DAC+∠ACD=90∘,∠ECB+∠ACD=90∘,∴∠DAC=∠ECB,在△ADC和△CEB中,{∠ADC=∠CEB ∠DAC=∠ECBAC=CB,∴△ADC≌△CEB(AAS),∴AD=CE,BE=CD,∴AD−BE=CE−CD=DE.小提示:本题主要考查了全等三角形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.15、如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点,连接DE并延长,交BC于点M,∠DAC的平分线交DM于点F.求证:AF=CM.答案:证明见解析.解析:先根据等腰三角形的性质可得∠B=∠C,再根据三角形的外角性质可得∠DAC=∠B+∠C=2∠C,然后根据角∠DAC=∠C,最后根据三角形全等的判定定理与性质即可得证.平分线的定义得∠EAF=12∵AB=AC,∴∠B=∠C,∴∠DAC=∠B+∠C=2∠C,∵AF是∠DAC的平分线,∴∠EAF=1∠DAC=∠C,2∵E是AC的中点,∴AE=CE,在△AEF和△CEM中,{∠EAF=∠CAE=CE∠AEF=∠CEM,∴△AEF≅△CEM(ASA),∴AF=CM.小提示:本题考查了等腰三角形的性质、角平分线的定义、三角形全等的判定定理与性质等知识点,熟练掌握三角形全等的判定方法是解题关键.。
初中数学三角形专题训练50题(含答案)

初中数学三角形专题训练50题含答案(单选、填空、解答题)一、单选题1.如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,AC的度数为100°,BC=2BD,动点P在线段AB上,则PC+PD的最小值为()C D RA.R B2.如图,在⊙ABCD中,连接AC,⊙ABC=⊙CAD=45°,AB=2,则BC的长是()AB.2C.D.43.如图点P是⊙BAC内一点,PE⊙AB于点E,PF⊙AC于点F,PE=PF,则直接得到⊙PEA⊙⊙PFA的理由是()A.HL B.ASA C.AAS D.SAS【答案】A【详解】解:⊙PE⊙AB于点E,PF⊙AC于点F,⊙⊙PEA=⊙PFA=90°,⊙PE=PF,AP=AP,⊙⊙PEA⊙⊙PFA(HL);4.如图,在平面直角坐标系中,菱形ABCD 的顶点A 在y 轴上,已知B(﹣3,0)、C(2,0),则点D 的坐标为( )A .(4,5)B .(5,4)C .(5,3)D .(4,3)5.适合下列条件的ABC ∆中,是直角三角形的共有( )⊙6a =,45A ∠=︒;⊙32A ∠=,58B ∠=︒;⊙2a =,2b =,4c =;⊙7a =,24b =,25c =.A .1个B .2个C .3个D .4个【答案】B 【分析】根据构成直角三角形三边关系的条件:三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形,最长边所对的角为直角,判定即可.【详解】⊙6a =,45A ∠=︒,不能判定ABC ∆中是直角三角形;⊙3258A B ︒︒==∠,∠,A B ∠∠=︒+90,是直角三角形;⊙2222222a b c +=+≠,不能判定ABC ∆中是直角三角形;⊙()()22222272425a b c +=+==,是直角三角形;【点睛】此题主要考查构成直角三角形条件的判定,熟练掌握,即可解题.=,点N在CD上,且6.如图,已知四边形ABCD是矩形,点M在BC上,BM CD=与BN交于点P,则:DN CM DM,DM BN=()A2B.C D.27.如图,已知正方形的面积为25,且AB比AC大1,BC的长为()A.3B.4C.5D.6【答案】A8.如图,在Rt ABC △中,90ACB ∠=︒,30ABC ∠=︒,若ABC A B C ''△≌△,且点A '恰好落在AB 上,则ACA ∠'的度数为( )A .30°B .45°C .50°D .60° 【答案】D 【分析】根据全等三角形的性质可得A C AC '=,从而得到60AA CA ,即可求解.【详解】解:⊙90ACB ∠=︒,30ABC ∠=︒,⊙⊙A =60°,⊙ABC A B C ''△≌△,⊙A C AC '=,⊙60AA C A ,⊙60ACA '∠=︒.故选:D【点睛】本题主要考查了全等三角形的性质,等腰三角形的性质,熟练掌握全等三角形的性质,等腰三角形的性质是解题的关键.9.如图,将三角板的直角顶点放在直尺的一边上,1=30∠︒,2=50∠︒,3=∠( )度A .10B .20C .30D .50 【答案】B 【分析】根据两直线平行,同位角相等求出⊙2的同位角,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解.【详解】解:如图:⊙⊙2=50°,直尺的两边互相平行,⊙⊙4=⊙2=50°,⊙⊙1=30°,⊙⊙3=⊙4-⊙1=50°-30°=20°.故选:B .【点睛】本题考查了两直线平行,同位角相等的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.10.在ABC 中,若90A C ∠+∠=︒,则( ).A .BC AB AC =+B .222AC AB BC =+ C .222AB AC BC =+D .222BC AB AC =+【答案】B【分析】由⊙A +⊙C =90°可得⊙B =90°,于是可确定AC 是Rt⊙ABC 的斜边,再根据勾股定理即得答案.【详解】解:⊙⊙A +⊙C =90°,⊙⊙B =90°,⊙AC 是Rt⊙ABC 的斜边,222【点睛】本题考查了勾股定理和三角形的内角和定理,由题意确定AC 是Rt ⊙ABC 的斜边是解题的关键.11.如图,直线AB CD ∥,AE CE ⊥于点E ,若140EAB ∠=︒,则ECD ∠的度数是( )A .120°B .130°C .150°D .160° 【答案】B 【分析】延长AE ,与DC 的延长线交于点F ,根据平行线的性质,求出⊙AFC 的度数,再利用外角的性质求出⊙ECF ,从而求出⊙EC D .【详解】解:延长AE ,与DC 的延长线交于点F ,⊙AB ⊙CD ,⊙⊙A +⊙AFC =180°,⊙⊙EAB =140°,⊙⊙AFC =40°,⊙AE ⊙CE ,⊙⊙AEC =90°,而⊙AEC =⊙AFC +⊙ECF ,⊙⊙ECF =⊙AEC -⊙F =50°,⊙⊙ECD =180°-50°=130°,故选:B .【点睛】本题考查平行线的性质和外角的性质,正确作出辅助线和正确利用平行线的性质是解题的关键.12.如图,在ABC 中,AB AC =,AD 是BAC ∠的平分线,DE AB ⊥,DF AC ⊥,垂足分别是E 、F ,下面给出的四个结论,其中正确的有( ).距离相等的点到DE 、DF 的距离也相等.A .1个B .2个C .3个D .4个 【答案】D 【分析】由等腰三角形“三线合一”可知AD⊙BC ,BD=DC ,得到AD 上的点到B 、C 两点的距离相等,根据角平分线性质定理可知DE=DF ,根据HL 证直角三角形全等,得到AE=AF ,从而得到AD 平分EDF ∠,即可得出答案.【详解】解:⊙AB AC =,AD 是BAC ∠的平分线,⊙AD⊙BC ,BD=DC ,⊙AD 上的点到B 、C 两点的距离相等,⊙⊙正确;⊙AD 是BAC ∠的平分线,DE AB ⊥,DF AC ⊥,⊙DE=DF ,⊙EDA=⊙FDA ,⊙AD 平分⊙EDF ,⊙⊙正确;在直角△AED 和直角△AFD 中,AD AD DE DF=⎧⎨=⎩ ⊙⊙AED⊙⊙AFD ,⊙AE=AF ,⊙AD 平分⊙BAC ,又⊙AD 是BAC ∠的平分线,⊙到AE 、AF 距离相等的点到DE 、DF 的距离也相等,⊙⊙、⊙正确,故选D .【点睛】本题考查了全等三角形的证明和性质,角平分线性质,等腰三角形的性质的应用,对条件的合理利用是解题的关键.13.如图,BO 、CO 分别平分⊙ABC 、⊙ACB ,OD ⊙BC 于点D ,OD =2,⊙ABC 的周长为28,则⊙ABC 的面积为( )A .28B .14C .21D .7在BOD 和△OEB OBE BO ∠=∠∠==BOD △≌△OE =OD =21122AB OE BC OD AC OF ++ )AB BC AC OD ++ 282⨯故选:A.【点睛】本题考查了角平分线的性质定理,求三角形的面积等知识,关键是根据条件构造适合角平分线性质定理条件的辅助线.14.如图,菱形ABCD的对角线AC与BD相交于点O,AE垂直平分CD,垂足为点E,则BAD∠=()A.100°B.120°C.135°D.150°【答案】B【分析】直接利用线段垂直平分线的性质得出AC=AD,再利用菱形的性质以及等边三角形的判定与性质得出答案.【详解】解:⊙AE垂直且平分边CD,⊙AC=AD,⊙四边形ABCD是菱形,⊙AD=DC,⊙ACB=⊙ACD,⊙⊙ACD是等边三角形,⊙⊙ACD=60︒,⊙⊙BCD=120︒.⊙⊙BAD=⊙BCD=120︒,故选:B.【点睛】此题主要考查了菱形的性质以及等边三角形的判定与性质,得出⊙ACD是等边三角形是解题关键.15.如图中字母A所代表的正方形的面积为()【详解】试题分析:根据勾股定理的几何意义解答.解:根据勾股定理以及正方形的面积公式知:以直角三角形的两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,所以A=289﹣225=64.故选D.16.三角形的三边长为a,b,c,且满足22-=-,则这个三角形是()()2a b c abA.等边三角形B.钝角三角形C.直角三角形D.锐角三角形【答案】C【分析】先利用完全平方公式化简已知等式,再根据勾股定理的逆定理即可得.【详解】由22a b c ab-=-得:222()2-+=-,a ab bc ab22即222a b c,+=,,a b c为三角形的三边长,∴这个三角形是直角三角形,故选:C.【点睛】本题考查了完全平方公式、勾股定理的逆定理,熟练掌握勾股定理的逆定理是解题关键.17.如图,⊙ABC的两边AB和AC的垂直平分线分别交BC于D,E,若⊙BAC+⊙DAE=150°,则⊙BAC的度数是()A.105B.110C.115D.120【答案】B【分析】根据垂直平分线性质,⊙B=⊙DAB,⊙C=⊙EAC.则有⊙B+⊙C+2⊙DAE=150°,即180°-⊙BAC+2⊙DAE=150°,再与⊙BAC+⊙DAE=150°联立解方程组即可.【详解】⊙⊙ABC的两边AB,AC的垂直平分线分别交BC于D,E,⊙DA=DB,EA=EC,⊙⊙B=⊙DAB,⊙C=⊙EAC.⊙⊙BAC+⊙DAE=150°,⊙⊙⊙B+⊙C+2⊙DAE=150°.⊙⊙B+⊙C+⊙BAC=180°,⊙180°-⊙BAC+2⊙DAE=150°,即⊙BAC-2⊙DAE=30°.⊙由⊙⊙组成的方程组150230BAC DAEBAC DAE∠+∠=︒⎧⎨∠-∠=︒⎩,解得⊙BAC=110°.故选B.【点睛】此题考查了线段的垂直平分线、等腰三角形的性质、三角形内角和定理等知识点,解题的关键是得到⊙BAC和⊙DAE的数量关系.18.如图,在平面直角坐标系中,已知A(﹣2,4)、P(﹣1,0),B为y轴上的动点,以AB为边构造⊙ABC,使点C在x轴上,⊙BAC=90°,M为BC的中点,则PM 的最小值为()A B C D【答案】C【分析】作AH⊙y轴,CE⊙AH,证明⊙AHB⊙⊙CEA,根据相似三角形的性质得到AE =2BH,求出点M的坐标,根据两点间的距离公式用x表示出PM,根据二次函数的性质解答即可.【详解】解:如图,过点A作AH⊙y轴于H,过点C作CE⊙AH于E,则四边形CEHO是矩形,⊙OH=CE=4,⊙⊙BAC=⊙AHB=⊙AEC=90°,19.如图,在ABC 和ADE 中,36CAB DAE ∠=∠=︒,AB AC =,AD AE =.连接CD ,连接BE 并延长交AC ,AD 于点F ,G .若BE 恰好平分ABC ∠,则下列结论错误的是( )A .ADC AEB ∠=∠B .//CD ABC .DE GE=D .2BF CF AC =⋅ 【答案】C 【分析】根据SAS 即可证明DAC EAB △≌△,再利用全等三角形的性质以及等腰三角形的性质,结合相似三角形的判定和性质,即可一一判断【详解】,,36AB AC AD AE CAB DAE ==∠=∠=︒DAC EAB ∴∠=∠AB AC=∴∠=ABCBE平分∴∠=ABEDAC△≌△∴∠ACD∴∠=ACDAD AE=∴∠=ADE∠=DGE∠即ADE∴≠DE GE∠=ABCCFB∴∠=∴=BC BF∴△∽△ABCBF CF∴=AB BC=AB ACBF CF∴=AC BF2=BF CF故答案选:【点睛】本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,相似三角20.如图,在Rt△ABC中,⊙ACB=90°,点D是AB边的中点,过D作DE⊙BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ 与PQ之间的数量关系是()A.AQ=52PQ B.AQ=3PQ C.AQ=83PQ D.AQ=4PQ⊙MN =PE ,ND =PC ,在△DNQ 和△CPQ 中,NDQ QCP NQD PQC DN PC ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊙⊙DNQ ⊙⊙CPQ ,⊙NQ =PQ ,⊙AN =NP ,⊙AQ =3PQ故选:B .【点睛】本题考查轴对称最短问题、全等三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是利用对称找到点P 位置,熟练掌握平行线的性质,属于中考常考题型.解两条线段之和最小(短)类问题,一般是运用轴对称变换将处于直线同侧的点转化为直线异侧的点,从而把两条线段的位置关系转换,再根据两点之间线段最短来确定方案,使两条线段之和转化为一条线段.二、填空题21.在Rt⊙ABC 中,⊙C =90°,若a =6,b =8,则c =________.【答案】10【详解】根据勾股定理2223664100c a b =+=+=c 为三角形边长,故c=10.22.在半径为5的圆中,弧所对的圆心角为90°,则弧所对的弦长是________.【点睛】本题考查利用半径和圆心角求弦长,难度不大,掌握勾股定理是解题的关键.23.在ABC 中,AB AC =,CD 是AB 边上的高,40ACD ∠=︒,则B ∠的度数为______.【答案】65︒或25︒【分析】分两种情况:当D 在线段AB 上时,根据题意,得出90ADC ∠=︒,再根据三角形的内角和定理,得出50A ∠=︒,再根据等边对等角,得出B ACB ∠=∠,再根据三角形的内角和定理,计算即可得出B ∠的度数;当D 在线段AB 的延长线上时,根据题意,得出90ADC ∠=︒,再根据三角形的内角和定理,得出50A ∠=︒,再根据等边对等角,得出B ACB ∠=∠,再根据三角形的外角的性质,计算即可得出B ∠的度数,综合即可得出答案.【详解】解:如图,当D 在线段AB 上时,⊙CD 是AB 边上的高,⊙90ADC ∠=︒,又⊙40ACD ∠=︒,⊙180904050A ∠=︒-︒-︒=︒,⊙AB AC =,⊙B ACB ∠=∠,⊙218018050130B A ∠=︒-∠=︒-︒=︒,⊙65B ∠=︒;如图,当D 在线段BA 的延长线上时,⊙CD 是AB 边上的高,⊙90ADC ∠=︒,又⊙40ACD ∠=︒,⊙180904050DAC ∠=︒-︒-︒=︒,⊙AB AC =,⊙B ACB ∠=∠,又⊙2DAC B ACB B ∠=∠+∠=∠,⊙250B ∠=︒,⊙25B ∠=︒,综上所述,B ∠的度数为65︒或25︒.故答案为:65︒或25︒.【点睛】本题考查了三角形的内角和定理、等边对等角、三角形的外角的性质,解本题的关键在熟练掌握相关的性质定理,分类讨论.24.如图,分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为4,则勒洛三角形的周长为:_________.25.边长为2的等边三角形的高与它的边长的比值为___________.【详解】解:等边三角形的边长是26.在Rt⊙ABC中,⊙C=90°,⊙A=30°,BC=2,则AC=_______ .27.如图,在四边形ABCD中,90∠=︒,2A==,BC=CD=AD AB∠的度数为________.ABC28.如图,在O 中,弦2BC =,点A 是圆上一点,且30BAC ∠=︒,则O 的半径是________.【答案】2【分析】连接OB ,OC ,先由圆周角定理求出BOC ∠的度数,再由OB OC =判断出BOC 是等边三角形,故可得出结论.【详解】解:连接OB ,OC ,⊙30BAC ∠=︒,⊙260BOC BAC ∠=∠=︒,⊙OB OC =,⊙BOC 是等边三角形,⊙2OB BC ==.故答案为:2【点睛】本题考查了圆周角定理,根据题意作出辅助线,构造出圆心角是解答此题的关键.29.如果等腰三角形的两边长分别为5cm 和10cm ,那么它的周长等于___________cm .【答案】25【分析】分5cm为腰和10cm为腰,两种情况求解.【详解】解:因为等腰三角形的两边长分别为5cm和10cm,当腰长为5cm时,三边长分别为5cm,5cm,10cm,+,因为55=10所以三角形不存在;当腰长为10cm时,三边长分别为5cm,10cm,10cm,+>,因为51010所以三角形存在;++=,所以三角形的周长为5101025(cm)故答案为:25.【点睛】本题考查了等腰三角形周长的分类计算,正确进行分类和判定三角形的存在性是解题的关键.30.等腰三角形的一边长为3,周长为15,则该三角形的腰长是______.31.如图,⊙O的半径为5cm,△ABC内接于⊙O,BC=5cm,则⊙A的度数为_____°.【答案】3032.如图,AD 、AE 分别是⊙ABC 的角平分线和高,⊙B =60°,⊙C =70°,则⊙EAD =______.【答案】5︒【分析】根据角平分线的性质及三角形内角和定理进行求解.【详解】解:由题意可知,⊙B =60°,⊙C =70°,所以18013050A ∠=-=°,所以25BAD ∠=°,在三角形BAE 中,906030BAE ∠=-=°,所以⊙EAD=5°故答案为:5°.【点睛】本题属于对角平分线和角度基本知识,解题的关键是进行变换求解.33.如图,正方形ABCD的对角线AC、BD相交于点O,点E、F分别在边AB、BC 上,且⊙EOF=90°,则S四边形OEBF⊙S正方形ABCD=___.34.图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD (点A与点B重合),点O是夹子转轴位置,O E⊙AC于点E,OF⊙BD于点F,OE=OF=1cm,AC=BD=6cm,CE=DF,CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动.(1)当E,F两点的距离最大值时,以点A,B,C,D为顶点的四边形的周长是_____cm.(2)当夹子的开口最大(点C与点D重合)时,A,B两点的距离为_____cm.35.如图,直线L 1、L 2、L 3分别过正方形ABCD 的三个顶点A 、D 、C ,且相互平行,若L 1、L 2的距离为1,L 2、L 3的距离为2,则正方形的边长为__________.AED DFC ≌,从而可得度.【详解】如图,过D ⊙123////L L L⊙13,EF L EF L ⊥⊥⊙AED DFC ≌1,DE CF AE DF ===22AD AE ED =+=故答案为:5.【点睛】本题考查了正方形与平行线的问题,掌握平行线的性质、全等三角形的性质以及判定定理、勾股定理是解题的关键.36.正方形ABCD 中.E 是AD 边中点.连接CE .作⊙BCE 的平分线交AB 于点F .则以下结论:⊙⊙ECD =30°.⊙⊙BCF 的外接圆经过点E ;⊙四边形AFCD 的面积是⊙BCF⊙BF AB =.其中正确的结论有 _____.(请填写所有正确结论的序号),易证BCF GCF ≅37.菱形ABCD中,AD=4,⊙DAB=60°,E、F、G、H分别是AD、AB、BC、CD上的点,且DH=FB,DE=BG,当四边形EFGH为正方形时,DH=____.38.已知菱形ABCD中,AC=6cm,BD=4cm.若以BD为边作正方形BDEF,则AF=__cm.⊙如图1,正方形BDEF在点A一侧时,延长CA交EF于点M.39.如图,正方形ABCD中,2AB=,AC,BD交于点O.若E,F分别是边AB,BC上的动点,且OE OF∆周长的最小值是__________.⊥,则OEF40.如图,在平行四边形ABCD 中,AC =3cm ,BD ,AC ⊙CD ,⊙O 是△ABD 的外接圆,则AB 的弦心距等于_____cm .【答案】116##516【分析】设AC、BD的交点为G,作圆的直径AN,连接BN,过点O作OF⊙AB于点三、解答题41.如图,AD⊙BC,⊙BAC=70°,DE⊙AC于点E,⊙D=20°.(1)求⊙B的度数,并判断⊙ABC的形状;(2)若延长线段DE恰好过点B,试说明DB是⊙ABC的平分线.【答案】(1)⊙ABC是等腰三角形,⊙B=40°;(2)见解析.【详解】分析:(1)、根据Rt⊙ADE的内角和得出⊙DAC=70°,根据平行线的性质得出⊙C=70°,从而根据有两个角相等的三角形是等腰三角形得出答案;(2)、根据等腰三角形底边上的三线合一定理得出DB为顶角的角平分线.详解:解:(1)⊙DE⊙AC于点E,⊙D=20°,⊙⊙CAD=70°,⊙AD⊙BC,⊙⊙C=⊙CAD=70°,又⊙⊙BAC=70°,⊙⊙BAC=⊙C,⊙AB=BC,⊙⊙ABC是等腰三角形,⊙⊙B=180°-⊙BAC-⊙C=180°-70°-70°=40°.(2)⊙延长线段DE恰好过点B,DE⊙AC,⊙BD⊙AC,⊙⊙ABC是等腰三角形,⊙DB是⊙ABC的平分线.点睛:本题主要考查的是等腰三角形的判定及性质,属于基础题型.明确等腰三角形底边上的三线合一定理是解决这个问题的关键.42.如图,小雪坐着轮船由点A出发沿正东方向AN航行,在点A处望湖中小岛M,测得小岛M在点A的北偏东60°,航行100米到达点B时,此时测得小岛M在点B的北偏东30°,求小岛M到航线AN的距离.Rt BDM 中,12BD MB ==2MD MB =答:小岛M 到航线【点睛】本题考查了方向角问题,勾股定理,等腰三角形的判定,含43.如图,BD 是⊙ABC 的高,AE 是⊙ABC 的角平分线,BD 交AE 于F ,若⊙BAC =44°,⊙C =80°,求⊙BEF 和⊙AFD 的度数.【答案】⊙BEF=102°;⊙AFD=68°【分析】根据BD是⊙ABC的高,AE是⊙ABC的角平分线,求得⊙ADB=90°,⊙BAE=⊙EAD=22°,根据三角形内角和定理即可求得⊙BEF和⊙AFD的度数.【详解】解:⊙BD是⊙ABC的高,AE是⊙ABC的角平分线,⊙BAC=44°,⊙C=80°,⊙⊙ADB=90°,⊙BAE=⊙EAD=22°,⊙⊙CBA=180°﹣44°﹣80°=56°,⊙⊙BEF=180°﹣22°﹣56°=102°,⊙AFD=180°﹣90°﹣22°=68°.【点睛】本题考查了三角形的高,角平分线,三角形内角和定理的应用,掌握三角形的高,角平分线的意义是解题的关键.44.(1)如图,90∠=∠=︒,O是AC的中点,求证:OB ODABC ADC=.(2)解方程:2430-+=.x x⊙()()130x x --=,即10,30x x -=-=,解得:121,3x x ==.【点睛】本题主要考查了直角三角形的性质,解一元二次方程,熟练掌握直角三角形斜边中线等于斜边的一半,一元二次方程的解法是解题的关键.45.如图,点E 在边长为10的正方形ABCD 内,6AE =,8BE =,请求出阴影部分的面积,AEB S =四边形ABCD =10ABCD ⨯AEB S =【点睛】本题主要考查了勾股定理的逆定理,熟知勾股定理的逆定理是解题的关键.46.图(a )、图(b )是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a )、图(b )中,分别画出符合要求的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.具体要求如下:(1)画一个底边长为4,面积为8的等腰三角形;(2)画一个面积为16的等腰直角三角形.47.如图,点A,B,C,D在同一条直线上,AB=DC,在四个论断“EA=ED,EF⊙AD,AB=DC,FB=FC”中选择二个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.已知、如图,点A,B,C,D在同一条直线上,.求证、.证明、.【答案】见解析【分析】已知:EA=ED ,EF⊙AD ,AB=DC ,求证FB=FC .想办法证明EF 是线段BC 的垂直平分线即可.(答案不唯一)【详解】已知:如图,EA=ED ,EF⊙AD ,AB=DC ,求证FB=FC .理由:延长EF 交BC 于H .⊙EA=ED ,EF⊙AD ,⊙AH=HD ,⊙AB=DC ,⊙BH=CH ,⊙FH⊙BC ,⊙FB=FC .故答案为EA=ED ,EF⊙AD ,AB=DC ;FB=FC ;延长EF 交BC 于H .⊙EA=ED ,EF⊙AD ,⊙AH=HD ,⊙AB=DC ,⊙BH=CH ,⊙FH⊙BC ,⊙FB=FC .【点睛】此题考查等腰三角形的判定和性质,线段的垂直平分线的性质,解题的关键是理解题意,灵活运用所学知识解决问题,属于开放性题目.48.如图,已知60AOB ∠︒=,OC 平分AOB ∠,CD ⊥OA 于点D .(1)实践与操作:作OC的垂直平分线分别交OA于点E;(要求:尺规作图,保留作图痕迹,不写作法)(2)连接CE,若DE的长为1,求OC的长.(1)解:如图所示,49.正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,A(-2,3),B(-3,1),C(-1,2),现将△ABC平移先向右平移3个单位长度,再向下平移2单位长度.(1)请画出平移后的A B C '''(点B C ''、分别是B 、C 的对应点);(2)写出点A B C '''、、三点的坐标;(3)求A B C '''的面积. 【答案】(1)画图见解析 (2)A '(1,1),B '(0,-1),C '(2,0)(3)1.5【分析】(1)根据所给的平移方式作图即可;(2)根据平移方式即可求出A 、B 、C 对应点A B C '''、、三点的坐标;(3)用A B C '''所在的正方形面积减去周围三个小三角形面积即可得到答案. (1)解:如图所示,A B C '''即为所求;(2)解:⊙A B C '''是△ABC 向右平移3个单位长度,向下平移2个单位长度得到的,A (-2,3),B (-3,1),C (-1,2),⊙A '(1,1),B '(0,-1),C '(2,0);(3)50.如图1,Rt⊙ABC中,⊙ABC=90°,P是斜边AC上一个动点,以BP为直径作⊙O交BC于点D,与AC的另一个交点为E(点E在点P右侧),连结DE、BE,已知AB=3,BC=6.(1)求线段BE的长;(2)如图2,若BP平分⊙ABC,求⊙BDE的正切值;(3)是否存在点P,使得⊙BDE是等腰三角形,若存在,求出所有符合条件的CP的长;若不存在,请说明理由.。
初中数学三角形专题训练50题含参考答案

初中数学三角形专题训练50题含答案(单选、填空、解答题)一、单选题1.如图,已知△ABC的六个元素,则图中甲、乙、丙三个三角形中和△ABC全等的图形个数是A.1B.2C.3D.02.如图,以点P为圆心,以x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为()A.B.(4,2)C.(4,4)D.(2,3.如图,等腰△ABC,BA=BC,点P是腰AB上一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似,满足这样条件的直线最多有()A.1个B.2个C .3个D .4个4.在学习“三角形的内角和外角”时,老师在学案上设计了以下内容:下列选项正确的是( )A .①处填ECD ∠B .①处填ECD ∠C .①处填A ∠D .①处填B ∠ 5.如图,在一块长方形草地上修速两条互相垂直且宽度相同的平行四边形通道,其中60KHB ∠=︒,已知20AB =米,30BC =米,四块草地总图积为2503m ,设GH 为x 米,则可列方程为( )A .2030503⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭B .(20)(30)503x x --=C .2203097x x x +-=D .232030974x x x +-= 6.下列四个命题中,是假命题的是( )A .过直线外一点,有且只有一条直线与已知直线平行B .两条直线被第三条直线所截,同位角相等C .三角形任意两边之和大于第三边D .如果a b =,a c =,那么b c =7.如图,BD 是①O 的直径,点A 、C 在圆上,且CD =OB ,则①BAC =( )A.120°B.90°C.60°D.30°8.已知:在平行四边形ABCD中,点M是BC的中点,MAD MDA∠=∠,则B∠=()A.60°B.90°C.100°D.120°9.两个直角三角形中:①有两条边相等;①一锐角和斜边对应相等;①斜边和一直角边对应相等;①两个锐角对应相等.能使这两个直角三角形全等的是()A.①①①B.①①C.①①D.①①①①10.如图,已知点O是正六边形ABCDEF的中心,扇形AOE的面积是12π,则正六边形的边长为()A.6B.C.D.1211.如图,△ABC和△DCE都是等边三角形,点B、C、E在同一条直线上,BC=1,CE=2,连接BD,则BD的长为()A.3B.C.D12.如图,在△ABC中,①ACB=90°,①B=40°,分别以点A和点B为圆心,以相同的长(大于12AB )为半径作弧,两弧相交于点M 和点N ,作直线MN 交AB 于点D ,交BC 于点E ,连接CD ,则①CDE 等于( )A .8°B .10°C .15°D .20° 13.已知菱形ABCD ,E 、F 是动点,边长为5,BE AF =,120BAD ∠=︒,则下列命题中正确的是( )①BEC AFC ≌;①ECF △为等边三角形;①ECF △的边长最小值为①若2AF =,则23FGC EGC S S =△△.A .①①B .①①C .①①①D .①①① 14.如图,在直角①O 的内部有一滑动杆AB ,当端点A 沿直线AO 向下滑动时,端点B 会随之自动地沿直线OB 向左滑动,如果滑动杆从图中AB 处滑动到A ′B ′处,那么滑动杆的中点C 所经过的路径是( )A .直线的一部分B .圆的一部分C .双曲线的一部分D .抛物线的一部分15.如图,平面内三点A 、B 、C ,AB =,AC =BC 为对角线作正方形BDCE ,连接AD ,则AD 的最大值是()A.5B.C.7D.16.在ABCD中,O是对角线AC,BD的交点.若AOB的面积是8,则ABCD□的面积是()A.16B.24C.32D.4017.如图,已知半圆O的直径8AB=,C是半圆上一点,沿AC折叠半圆得到弧ADC,交直径AB于点D,若DA、DB的长均不小于2,则AC的长可能是()A.7B.6C.5D.418.梯形的对角线互相垂直,其中一条对角线长为5,梯形的高为4,则梯形的面积为()A.5B.10C.503D.25319.如图,抛物线y=x2+bx+c与x轴的交点为A(x1,0)和B(x2,0),与y轴负半轴交点为C,点D为线段OC上一点.且满足c=x1+b,①ACO=①DBO,则下列说法:①b-c=1;①①AOC①①DOB;①若①DBC=30°,则抛物线的对称轴为直线x①当点B绕点D顺时针旋转90°后得到的点B'也在抛物线上,则抛物线的解析式为y=x2-2x-3.正确的是()A .①①①B .①①①C .①①①D .①①①①二、填空题20.如图,P 是MON ∠的平分线上一点,PA ON ⊥于点A ,Q 是射线OM 上一个动点,若8PA =,则PQ 的最小值为______.21.△ABC 中,①A=40o ,①B=60o ,则与①C 相邻外角的度数是______.22.在ABC 中,15,13AB AC ==,高12AD =,则ABC 的周长是 _____. 23.如图,已知ABC BAD ≌,A 和B ,C 和D 分别是对应顶点,且60C ∠=︒,35ABD ∠=︒,则BAD ∠ 的度数是_______24.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在AOB ∠的两边OA 、OB 上分别在取OC OD =,移动角尺,使角尺两边相同的刻度分别与点C 、D 重合,这时过角尺顶点M 的射线OM 就是AOB ∠的平分线.利用所学知识可知他构造全等三角形的依据是________.25.等腰三角形的周长18cm ,其中一边长为8cm ,则底边长为 ___________cm . 26.如图,在①ABC 中,AD 、AE 分别是BC 边上的中线和高,AE =6,S △ABD =15,则CD =_____.27.如图,为了防止门板变形,小明在门板上钉了一根加固木条,从数学的角度看,这样做的理由是利用了三角形的________.28.如图,在Rt △ABC 中,AB =BC ,①B =90°,AC =BDEF 是△ABC 的内接正方形(点D ,E ,F 在三角形的边上),则此正方形的面积是_______.29.如图, 正方形ABCD 和等边AEF △都内接于O EF ⊙,与BC CD ,分别相交于点G , H . 若6AE =, 则EG 的长为________.30.如图,在等边①ABC 中,BC =9,点O 是AC 上的一点,点D 是BC 上的一点,若①APO ①①COD ,AO =2.7,则BP =__________.31.平行四边形ABCD 中,E 为BA 延长线上的一点,CE 交AD 于F 点,若:1:3AE AB =,则:CDF ABCF S S =四边形________.32.如图,在Rt ①ABC 中,①ACB =90°,点D 是边AB 的中点,连接CD ,将①BCD 沿直线CD 翻折得到①ECD ,连接AE .若AC =6,BC =8,则①ADE 的面积为____.33.已知:如图,以Rt ABC 的三边为斜边分别向外作等腰直角三角形,若斜边AB=5,则图中阴影部分的面积为__.34.如图,在菱形ABCD 中,点E 是BC 上的点,AE ①BC ,若sin B =35,EC =3,P 是AB 边上的一个动点,则线段PE 最小时,BP 长为_____.35.如图,AB 为①O 的直径,弦CD①AB 于E ,已知CD =12,BE =2,则①O 半径为________.36.如图,在Rt①ABC 中,①ACB =90°,①B =35°,CD 是斜边AB 上的中线,如果将①BCD 沿CD 所在直线翻折,点B 落在点E 处,联结AE ,那么①CAE 的度数是_____度.37.如图,在菱形ABCD 中,=60B ∠︒,E 在CD 上,将ADE ∆沿AE 翻折至AD E '∆,且AD '刚好过BC 的中点P ,则D EC '∠=_________.38.如图,直线AM 的解析式为1y x =+与x 轴交于点M ,与y 轴交于点A ,以OA 为边作正方形ABCO ,点B 坐标为()1,1.过点B 作1EO MA ⊥交MA 于点E ,交x 轴于点1O ,过点1O 作x 轴的垂线交MA 于点1A 以11O A 为边作正方形1111O A B C ,点1B 的坐标为()5,3.过点1B 作12E O MA ⊥交MA 于1E ,交x 轴于点2O ,过点2O 作x 轴的垂线交MA 于点2A ,以22O A 为边作正方形2222O A B C ,,则点2020B 的坐标______.三、解答题39.如图,在ABC 中,44ABC ∠=︒,BD 平分ABC ∠,60C ∠=︒,22BDE ∠=︒.(1)求证:DE//AB;∠的度数.(2)求ADB40.如图,菱形ABCD对角线AC,BD相交于点O,点E是AD的中点,过点A作对角线AC的垂线,与OE的延长线交于点F,连接FD.(1)求证:四边形AODF是矩形;(2)若AD=10,①ABC=60°,求OF和OA的长.=,D是BC边上的中点,连结AD,BE平分①ABC交41.如图,在①ABC中,AB ACAC于点E,过点E作EF//BC交AB于点F.(1)若36∠=︒,求①BAD的度数;C(2)求证:点F在BE的垂直平分线上.42.如图,已知EF①BC,AD①BC,①1=①2,①判断DM与AB的位置关系,并说明理由;①若①BAC=70°,DM平分①ADC,求①ACB的度数.43.如图1,线段AD,BC相交于点O,32B︒∠=,38∠=.D︒(1)若60A ︒∠=,求AOB ∠和C ∠的度数;(2)在(1)的条件下,如图2,若BAO ∠、DCO ∠的平分线AM ,CM 相交于点M ,求M ∠度数;(3)若改变条件,设B α∠=,D β∠=,试用含αβ,的代数式表示M ∠的大小. 44.已知抛物线y =x 2+(12m ﹣2)x ﹣3,抛物线与坐标轴交于点A (3,0)、B 两点.(1)求抛物线解析式;(2)当点P (2,a )在抛物线上时.①如图1,过点P 不与坐标轴平行的直线l 1与抛物线有且只有一个交点,求直线l 1的方程;①如图2,若直线l 2:y =2x +b 交抛物线于M ,点M 在点P 的右侧,过点P (2,a )作PQ ①y 轴交直线l 2于点Q ,延长MQ 到点N 使得MQ =NQ ,试判断点N 是否在抛物线上?请说明理由.45.已知:如图,已知点B 、E 、F 、C 在同一直线上,AB =CD ,AE ⊥BC ,DF ⊥BC ,E ,F 是垂足,CE =BF ,求证:AB //CD .46.已知:如图所示,在Rt ABC ∆中,90ACB ∠=︒,AC BC =,点D 是BC 的中点,CE AD⊥,垂足为点E,BF AC交CE的延长线于点F,求证:AB垂直平分DF.47.求证:顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半.(1)根据题意补全下图,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.=,______;已知:在锐角ABC中,AB AC求证:______.(2)证明:48.如图,已知①ABC中,AB=AC,①A=108°,BD平分①ABC.求证:BC=AB+CD.参考答案:1.B【分析】根据全等三角形判定方法进行判断即可【详解】解:由已知,甲全等条件不具备,乙和△ABC满足两角夹边,故全等,丙和△ABC满足两角和其中一角的对边,故全等,因此,有两个三角形可以判定三角形全等. 2.C【分析】作PC①AB于C,如图,由点A和点B坐标得到AB=4,再根据垂径定理得到AC=BC=2,然后根据勾股定理计算出PC=4,于是可确定P点坐标.【详解】解:作PC①AB于C,如图,①点A的坐标为(2,0),点B的坐标为(6,0),①OA=2,OB=6,①AB=OB-OA=4,①PC①AB,①AC=BC=2,在Rt△P AC中,①P A AC=2,①PC,①OC=OA+AC=4,①P点坐标为(4,4).故选:C.【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理、坐标与图形性质.3.C【分析】根据相似三角形的判定,过点P分别BC,AC的平行线即可得到与原三角形相似的三角形,过点P作以点P为顶点的角与①A相等的角也可以得到原三角形相似的三角形.【详解】解:①BA=BC,①①A=①C,①作PE①BC,可得①APE①①ABC.①作PF①AC,可得①BPF①①BAC.①作①APG=①A,可得①AGP①①ABC,故选:C.【点睛】本题考查相似三角形的判定质,等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题.4.B【分析】延长BC到点D,过点C作CE①AB.依据平行线的性质以及平角的定义,即可得到①A+①B+①ACB=180°.【详解】延长BC到点D,过点C作CE①AB,①CE①AB.①①A=①ACE(两直线平行,内错角相等).①B=①ECD(两直线平行,同位角相等).①①ACB+①ACE+①ECD=180°(平角定义).①①A+①B+①ACB=180°(等量代换).故选:B.【点睛】本题主要考查了平行线的性质以及三角形内角和定理,解题时注意:两直线平行,内错角相等;两直线平行,同位角相等.5.D【分析】设GH为x米,根据矩形和平行四边形的面积公式,即可得出关于x的一元二次方程,此题得解.【详解】解:过H 作HM ①LG 于M ,①①KHB =60°,//LG KH ,①①HGM =①KHB =60°,①①HMG =90°,①HM , ①长方形的面积=20×30=600(cm )2,①四块草地总面积为503m 2,①通道的面积为:20x +30x -34x 2=97, 故选:D .【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.6.B【分析】根据平行公理,平行线的性质及三角形三边关系等逐项判断.【详解】A.过直线外一点,有且只有一条直线与已知直线平行,故A 不符合题意;B.两条平行线被第三条直线所截,同位角相等,故B 符合题意;C.三角形任意两边之和大于第三边,故C 不符合题意;D.如果a =b ,a =c ,那么b =c ,故D 不符合题意.故选:B .【点睛】本题考查命题与定理,解题的关键是掌握平行公理,平行线的性质及三角形三边关系等教材上的相关结论.7.C【分析】根据题意得OCD ∆为等边三角形,则60COD ∠=︒,根据圆周角定理得出BAC ∠的度数.【详解】解:连接OC ,CD OB =,OCD ∴∆为等边三角形,60COD ∴∠=︒,180120BOC COD ∴∠=︒-∠=︒,111206022BAC BOC ∴∠=∠=⨯︒=︒, 故选:C .【点睛】本题考查了圆周角定理、等边三角形的判定,解题的关键是掌握圆周角定理的内容.8.B【分析】由MAD MDA ∠=∠,得AM =DM ,再由平行四边形的性质得AB =CD ,AB ∥CD ,则①B +①C =180°,然后证△ABM ①△DCM (SSS ),得①B =①C ,即可求得①B 度数.【详解】解:如图,过点M 作MN ①AD 于N ,①MAD MDA ∠=∠,①AM =DM ,①平行四边形ABCD ,①AB =CD ,AB ∥CD ,①①B +①C =180°,①点M 是BC 的中点,在△ABM 与△DCM 中,AB DC BM CM AM DM =⎧⎪=⎨⎪=⎩,①△ABM ①△DCM (SSS ),①①B =①C ,①2①B =180°,①①B =90°,故选:B .【点睛】本题考查平行四边形的性质,等腰三角形的判定,全等三角形的判定与性质,熟练掌握相关性质与判定是解题的关键.9.B【分析】根据直角三角形全等的判定条件逐一分析即可得到答案.【详解】解:①两个直角三角形中有两条边相等,不能证明两个直角三角形全等,如一条直角边相等,另一个直角边与斜边相等;①两个直角三角形中一锐角和斜边对应相等,可用AAS 证明两个直角三角形全等; ①两个直角三角形中斜边和一直角边对应相等,可用HL 证明两个直角三角形全等; ①两个直角三角形中两个锐角对应相等,不能证明两个直角三角形全等;故选B .【点睛】本题主要考查了直角三角形全等的判定定理,熟知直角三角形的判定定理有AAS SAS ASA SSS HL ,,,,是解题的关键.10.A【分析】先求出中心角120AOE ∠︒=,证得OAF △是等边三角形,得到AF R =,根据扇形的面积求出圆的半径,即可得到正六边形的边长.【详解】解:连接OF ,设①O 的半径为R ,①O 是正六边形ABCDEF 的中心, ①360606AOF EOF ︒∠=∠==︒, ①120AOE ∠︒=,①OAF △是等边三角形,①AF OA R ==,①扇形AOE 的面积是12π, ①212012360R ππ=, ①236R = ,①6AF R ==,①正六边形的边长是6,故选:A .【点睛】本题考查了正多边形与圆,扇形的面积计算,解题的关键是求出正多边形的边长等于圆的半径.11.D【分析】作DF①CE 于F ,构建两个直角三角形,运用勾股定理逐一解答即可.【详解】过D 作DF①CE 于F ,根据等腰三角形的三线合一,得:CF=1,在直角三角形CDF 中,根据勾股定理,得:DF 2=CD 2-CF 2=22-12=3,在直角三角形BDF 中,BF=BC+CF=1+1=2,根据勾股定理得:故选D.【点睛】本题考查了等边三角形的性质,勾股定理等,正确添加辅助线、熟练应用相关的性质与定理是解题的关键.12.B【分析】由题意得MN 垂直平分AB ,得到AD =BD ,①ADE =90°,证得CD =AD =BD ,求出①ADC =2①B =80°,即可得到①CDE 的度数.【详解】解:由题意得MN 垂直平分AB ,①AD =BD ,①ADE =90°,①①ACB =90°,①CD =AD =BD ,①①BCD =①B =40°,①①ADC =2①B =80°,①①CDE =①ADE -①ADC =10°,故选:B .【点睛】此题考查了线段垂直平分线的作图方法,直角三角形斜边中线等于斜边一半的性质、等腰三角形的性质、三角形的外角性质,正确理解线段垂直平分线的作图是解题的关键.13.C【分析】根据菱形的性质可得AB =BC ,AD ①BC ,①BAC =①DAC =12①BAD =60°,从而可得①B =60°,进而证明△ABC 是等边三角形,然后得出BC =AC ,即可判断①;利用①的结论可得CE =CF ,①BCE =①ACF ,从而可得①BCA =①ECF =60°,即可判断①;当CE ①AB 时,ECF △的边长取最小值,根据含30度角的直角三角形的性质求出BE ,再利用勾股定理求出CE 即可判断①;过点E 作EM ①BC ,交AC 于点M ,求出EM =3,然后利用平行线分线段成比例求出23FG AF EG EM ==即可判断①. 【详解】解:①四边形ABCD 是菱形,120BAD ∠=︒,①AB =BC ,AD ①BC ,①BAC =①DAC =12①BAD =60°,①①B =180°−①BAD =60°,①①ABC 是等边三角形,①BC =AC ,①ACB =60°,在△BEC 和△AFC 中,BE AF B FAC BC AC =⎧⎪∠=∠⎨⎪=⎩,①①BEC ①①AFC (SAS ),①正确; ①CE =CF ,①BCE =①ACF ,①①BCE +①ACE =①ACF +①ACE , ①①BCA =①ECF =60°,①①ECF 是等边三角形,①正确; ①△ABC 是等边三角形,AB =BC =5, ①当CE ①AB 时,ECF △的边长取最小值, ①①B =60°,①此时①BCE =30°,①BE =1522BC =, ①CE①ECF △,①错误; 过点E 作EM ①BC ,交AC 于点M ,①①BEC ①①AFC ,①AF =BE =2,①AB =5,①AE =AB −BE =5−2=3,①EM ①BC ,①①AEM =①B =60°,①AME =①ACB =60°, ①①AEM 是等边三角形,①AE =EM =3,①AD①BC,①AF①EM①23 FG AFEG EM==,①23FGC EGCS S=△△,①正确;故选:C.【点睛】本题考查了菱形的性质,等边三角形的判定与性质,全等三角形的判定与性质,含30度角的直角三角形的性质,勾股定理以及平行线分线段成比例,灵活运用各性质进行推理是解题的关键.14.B【详解】连接OC、OC′,如图,①①AOB=90°,C为AB中点,①OC=12AB=12A′B′=OC′,①当端点A沿直线AO向下滑动时,AB的中点C到O的距离始终为定长,①滑动杆的中点C所经过的路径是一段圆弧.故选B.【点睛】考点:①圆的定义与性质;①直角三角形的性质.15.C【分析】如图,将①BDA绕点D顺时针旋转90°得到①CDM,由旋转的性质可得①ADM是等腰直角三角形,根据勾股定理推出AD,可知当AM的值最大时,AD的值最大,利用三角形的三边关系求出AM的最大值,即可解决问题.【详解】解:如图,将BDA△绕点D顺时针旋转90°得到CDM由旋转的性质可知:4AB CM ==,DA DM =,90ADM ∠=︒①ADM △是等腰直角三角形,①根据勾股定理222AD MD AM +=,①AD AM =, ①当AM 的值最大时,AD 的值最大,①AM AC CM ≤+,AC CM AB ===①AM ≤①AM 的最大值为①AD 的最大值为7,故选C .【点睛】本题考查了正方形的性质,旋转的性质,等腰直角三角形的判定和性质,勾股定理以及两点之间线段最短.解题的关键在于根据旋转的性质构造等腰直角三角形. 16.C【分析】根据平行四边形的性质可得BO =DO ,AO =CO ,由此可得8AOB AOD BOC COD S S S S ∆∆∆∆====,从而可得结论.【详解】解:①四边形ABCD 是平行四边形,①BO =DO ,AO =CO ,①8AOB AOD BOC COD S S S S ∆∆∆∆====,①平行四边形ABCD 的面积=4×8=32,故选:C【点睛】本题考查了平行四边形的性质和三角形中线的性质,解决本题的关键是理解平行四边形的对角线互相平分.17.A【分析】分如解图①,当点D 在圆心O 的左侧且2AD =时,如解图①,当点D 在圆心O 的右侧且2BD =时,两种情况求出AC 的长,从而确定AC 的取值范围即可得到答案.【详解】如解图①,当点D 在圆心O 的左侧且2AD =时,过C 作CE AB ⊥,垂足为E ,连接CD 、CO 、CB ,①AC ADC =,①CDB CBD ∠=∠,①CD CB =,①3DE BE ==,①2DO =,①1OE =,①5AE =,22215CE CO OE =-=,①AC =如解图①,当点D 在圆心O 的右侧且2BD =时,过C 作CE AB ⊥,垂足为E ,连接CD 、CO 、CB ,①AC ADC =,①CDB CBD ∠=∠,①CD CB =,①1DE BE ==,①3OE =,①7AE =,2227CE CO OE =-=,①AC =①若DA 、DB 的长均不小于2AC ≤①AC 的长可能是7,故选A .【点睛】本题主要考查了圆周角定理,等腰三角形的性质与判定,勾股定理,无理数的估算等等,利用分类讨论的思想求解是解题的关键.18.C【分析】过B 作BE AC ∥交DC 延长线于E ,过B 作BF DC ⊥于F ,如图所示,根据题意,分两种情况讨论:①当5BD =时;①当5AC =时,根据双垂直模型得到BDF EBF ∽△△,利用相似比得到未知线段,然后根据BDE ABCD S S =△梯形代值求解即可得到答案.【详解】解:过B 作BE AC ∥交DC 延长线于E ,过B 作BF DC ⊥于F ,如图所示:4BF ∴=,①当5BD =时,对角线相互垂直,即AC BD ⊥,BE BD ∴⊥,90DBF EBF ∴∠+∠=︒,BF DC ⊥,在Rt BDF △中,90,5,4DFB BD BF ∠=︒==,则3DF =, 90DBF BDF ∴∠+∠=︒,BDF EBF ∴∠=∠,90BFD BFE ∠=∠=︒,∴BDF EBF ∽△△,BD DF BE BF ∴=,即534BE =,203BE ∴=, ,AB CE AC BE ∥∥,∴四边形ABEF 是平行四边形,AB CE ∴=, ∴()()11111205052222233BDE ABCD S AB DC BF CE DC BF DE BF S BD BE =+⋅=+⋅=⋅==⋅=⨯⨯=△梯形;①当5AC =时,对角线相互垂直,即AC BD ⊥,BE BD ∴⊥,90DBF EBF ∴∠+∠=︒,BF DC ⊥,在Rt BEF △中,90,5,4EFB BE BF ∠=︒==,则3EF =, 90DBF BDF ∴∠+∠=︒,BDF EBF ∴∠=∠,90BFD BFE ∠=∠=︒,∴BDF EBF ∽△△,BD BF BE EF∴=,即453BD =, 203BD ∴=, ,AB CE AC BE ∥∥,∴四边形ABEF 是平行四边形,AB CE ∴=, ∴()()11111205052222233BDE ABCD S AB DC BF CE DC BF DE BF S BD BE =+⋅=+⋅=⋅==⋅=⨯⨯=△梯形;综上所述,梯形的对角线互相垂直,其中一条对角线长为5,梯形的高为4,则梯形的面积为503,【点睛】本题属于几何综合问题,考查梯形性质、梯形面积公式、勾股定理、两个三角形相似的判定与性质、平行四边形的判定与性质、三角形面积及双垂直模型等知识,熟练掌握相关几何图形的性质是解决问题的关键.19.B【分析】利用已知条件分别求得点A,B,C的坐标,表示出线段OA,OB,OC的长度,利用二次函数的性质,待定系数法与全等三角形的判定定理对每个结论进行逐一判断即可得出结论.【详解】解:将A(x1,0)代入物线y=x2+bx+c得:x12+bx1+c=0.①c=x1+b,①x12+bx1+x1+b=0,①x1(x1+1)+b(x1+1)=0,①(x1+b)(x1+1)=0,①c=x1+b≠0,①x1+1=0,①x1=-1,①A(-1,0),①OA=1,①c=-1+b,①b-c=1.①①的结论正确;①c=-1+b,①y=x2+bx+b-1,令y=0,则x2+bx+b-1=0,解得:x=-1或x=1-b,①B(1-b,0),①抛物线的对称轴在y轴的右侧,①b<0,①OB=1-b,①C(0,b-1),①OB =OC ,在△AOC 和△DOB 中,90ACO DBO OC OB AOC DOB ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ①①AOC ①①DOB (ASA ).①①的结论正确;若①DBC =30°,过点D 作DH ①BC 于点H ,如图,①①AOC ①①DOB ,①OA =OD =1,AC =BD ,①CD =OC -OD =-b ,①OB =OC ,①①OCB =①OBC =45°,①DH ①BC ,①DH, ①DH ①BC ,①DBC =30°,①BD =2DH,①ACb ,①OA 2+OC 2=AC 2,①12+(1−b ) 2=b ) 2.解得:b①b①抛物线的对称轴为直线x== ①①的结论不正确;当点B 绕点D 顺时针旋转90°后得到的点B '也在抛物线上时,过点B ′作B ′M ①y 轴于点M ,如图,由题意:DB =DB ′,①BDB ′=90°,①①MDB ′+①ODB =90°,①①ODB +①OBD =90°,①①MDB ′=①OBD ,在△MDB ′和△OBD 中,90DMB BOD MDB OBD DB BD ''∠=∠=︒⎧⎪∠=∠⎨⎪=⎩',①①MDB ′①①OBD (AAS ),①MD =OB =1-b ,MB ′=OD =1,①OM =OD +DM =2-b ,①B ′(1,b -2),①1+b +b -1=b -2,解得:b =-2,①c =b -1=-3,①此时抛物线的解析式为y=x2-2x-3,①①的结论正确;综上,正确的结论是:①①①.故选:B.【点睛】本题主要考查了待定系数法,数形结合法,二次函数的性质,抛物线与x轴的交点,抛物线上点的坐标的特征,图形的旋转的性质,全等三角形的判定与性质,勾股定理,含30°角的直角三角形的性质,熟练掌握二次函数的性质是解题的关键.20.8【分析】根据角平分线的性质定理解答.【详解】解:当PQ①OM时,PQ最小,①P是①MON角平分线上的一点,PA①ON,PQ①OM,①PQ=PA=8,故答案为:8.【点睛】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.21.100°##100度【分析】先根据三角形的内角和求出①C的度数,即可求出与①C相邻外角的度数【详解】①C=180°-①A-①B=80°,①①C相邻外角的度数为180°-80°=100°.故答案为:100°【点睛】此题主要考查邻补角的求解,解题的关键是熟知三角形的内角和为180°. 22.42或32##32或42【分析】分两种情况讨论:当高AD在ABC的内部时,当高AD在ABC的外部时,结合勾股定理,即可求解.【详解】解:当高AD在ABC的内部时,如图,在Rt ABD中,9BD,在Rt ACD中,5CD==,①14BC BD CD =+=,此时ABC 的周长是15141342AB BC AC ++=++=;当高AD 在ABC 的外部时,如图,在Rt ABD中,9BD ,在Rt ACD中,5CD ==,①4BC BD CD =-=,此时ABC 的周长是1541332AB BC AC ++=++=;综上所述,ABC 的周长是42或32.故答案为:42或32【点睛】此题考查了勾股定理的知识,在解本题时应分两种情况进行讨论,易错点在于漏解,同学们思考问题一定要全面,有一定难度.23.85︒【分析】根据全等三角形的性质和三角形内角和定理计算即可;【详解】①ABC BAD ≌,60C ∠=︒,35ABD ∠=︒,①60C D ∠=∠=︒,35DBA CAB ∠=∠=︒,①180180603585DAB D DBA ∠=︒-∠-∠=︒-︒-︒=︒.故答案是:85︒.【点睛】本题主要考查了全等三角形的性质和三角形内角和定理,准确分析计算是解题的关键.24.SSS【分析】根据全等三角形的判定定理SSS 推出①COM ①①DOM ,根据全等三角形的性质得出①COM =①DOM ,根据角平分线的定义得出答案即可.【详解】解:在①COM 和①DOM 中,,OC OD OM OM MC MD =⎧⎪=⎨⎪=⎩. ①①COM ①①DOM (SSS ),①①COM=①DOM,即OM是①AOB的平分线,故答案为:SSS.【点睛】本题考查了全等三角形的判定定理和性质定理,能熟记全等三角形的判定定理是解此题的关键.25.2或8.【详解】试题分析:由题意知,应分两种情况:当腰长为8cm时,则另一腰也为8cm,底边为18-2×8=2cm,①0<2<8+8,①边长分别为8cm,8cm,2cm,能构成三角形;当底边长为8cm时,腰的长=(18-8)÷2=5cm,①0<8<5+5=13,①边长为5cm,5cm,8cm,能构成三角形.故答案为2或8.考点:等腰三角形的性质.26.5【分析】由利用三角形的面积公式可求得BD的长,再由中线的定义可得CD=BD,从而得解.【详解】解:①S△ABD=15,AE是BC边上的高,BD•AE=15,①12×6BD=15,则12解得:BD=5,①AD是BC边上的中线,①CD=BD=5.故答案为:5.【点睛】本题主要考查三角形的中线,三角形的高,解答的关键是由三角形的面积公式求得BD的长.27.稳定性【分析】根据三角形的三边一旦确定,则形状大小完全确定,即三角形的稳定性.【详解】解:这样做的原因是:利用三角形的稳定性使门板不变形.故答案为:三角形具有稳定性.【点睛】本题主要考查三角形的稳定性在实际生活中的应用.28.36【分析】由△ABC 是等腰直角三角形,可得①A =①C =45°,从而证明△AEF 也是等腰直角三角形,设AF =x ,则BF =12﹣x ,列出方程并求出x 的值,再根据正方形的面积公式即可求得.【详解】解:①①ABC 是等腰直角三角形,①①A =①C =45°,①四边形BDEF 是△ABC 的内接正方形,①EF ①BC ,①①AEF =①C =45°,①①AEF 也是等腰直角三角形,①AF =EF ,设AF =x ,则BF =12﹣x ,①12﹣x =x ,①x =6,①此正方形的面积为6×6=36.故答案为:36.【点睛】本题考查了正方形的性质、等腰三角形的性质及判定.解题的关键是熟练掌握正方形的性质.29.3【分析】连接AC ,CE ,CF ,正方形ABCD 和等边AEF △都内接于O ,得证AC 是O 的直径,45ACG ∠=,60AEF AFE ∠=∠=,AE AF =,从而得证90AEC AFC ∠=∠=,30CEF CFE ∠=∠=,得到CE CF =,直线AC 是线段EF 的垂直平分线,从而得到90GMC ∠=,45CGM ∠=,得证CM GM =,30EAM ∠=,从而得证132EM AE ==,AM =2AC EC =,结合222AC EC AE =+,确定AC =CM GM AC AM ==-==,根据EG EM GM =-计算即可.【详解】如图,连接AC ,CE ,CF ,因为正方形ABCD 和等边AEF △都内接于O , 所以AC 是O 的直径,45ACG ∠=,60AEF AFE ∠=∠=,AE AF =,所以90AEC AFC ∠=∠=,30CEF CFE ∠=∠=,所以CE CF =,所以直线AC 是线段EF 的垂直平分线,所以90GMC ∠=,45CGM ∠=,所以CM GM =,30EAM ∠=,所以132EM AE ==,AM ==2AC EC =, 因为222AC EC AE =+, 所以2221()62AC AC =+,解得AC =所以CM GM AC AM ==-=所以EG EM GM =-=3故答案为:3【点睛】本题考查了正方形的性质,等边三角形的性质,线段垂直平分线的判定和性质,圆的基本性质,直角三角形的性质,勾股定理,等腰直角三角形的判定和性质,熟练掌握正方形的性质,圆的性质,等边三角形的性质,勾股定理是解题的关键.30.2.7【分析】根据全等可得OC =AP ,再根据等边三角形的性质可得AC =AB ,从而可得AO =BP ,即可得出结论【详解】解:①①ABC 为等边三角形,①AC =AB =BC =9,①①APO ①①COD ,AO =2.7,①AP =OC ,①BP =AO =2.7.故答案为:2.7.【点睛】本题考查全等三角形的性质,等边三角形的性质.正确理解性质得出线段之间的关系是解题关键.31.5:3.【分析】过C 做CG ①AD 交AD 延长线于G ,根据四边形ABCD 为平行四边形,可得CD∥AB 且CD =AB ,AD =BC ,利用平行线性质可得①CDF =①EAF ,①DCF =①E ,可证△DCF ①①AEF ,根据相似三角形性质可得31DF DC AF AE ==,设AF =m ,DF =3m ,则BC =AD = 4m ,求三角形与四边形面积S △CDF =1322DF CG mCG ⋅=,S 四边形ABCF =()()1154222AF BC CG m m CG mCG +⋅=+⋅=,再求两面积比即可. 【详解】解:过C 做CG ①AD 交AD 延长线于G ,①四边形ABCD 为平行四边形,①CD∥AB 且CD =AB ,AD =BC ,①①CDF =①EAF ,①DCF =①E ,①△DCF ①①AEF , ①31DF DC AF AE ==, 设AF =m ,DF =3m ,则BC =AD =AF +DF =4m ,①S △CDF =1322DF CG mCG ⋅=, S 四边形ABCF =()()1154222AF BC CG m m CG mCG +⋅=+⋅=, ①53::5:322CDF ABCF S S mCG mCG ==四边形. 故答案为5:3.【点睛】本题考查平行四边形的性质,三角形相似判定与性质,三角形面积与四边形面积,掌握平行四边形的性质,三角形相似判定与性质,三角形面积与四边形面积是解题关键.32.6.72【分析】连接BE,延长CD交BE与点H,作CF①AB,垂足为F.首先证明DC垂直平分线段BE,△ABE是直角三角形,利用三角形的面积求出EH,得到BE的长,在Rt△ABE 中,利用勾股定理即可解决问题.【详解】解:如图,连接BE,延长CD交BE与点H,作CF①AB,垂足为F.①①ACB=90°,AC=6,BC=8.①AB,①D是AB的中点,①AD=BD=CD=5,①S△ABC=12AC•BC=12AB•CF,①12×6×8=12×10×CF,解得CF=4.8.①将△BCD沿直线CD翻折得到△ECD,①BC=CE,BD=DE,①CH①BE,BH=HE.①AD=DB=DE,①①ABE为直角三角形,①AEB=90°,①S△ECD=S△ACD,①12DC•HE=12AD•CF,①DC=AD,①HE=CF=4.8.①BE=2EH=9.6.①①AEB=90°,①AE.①S△ADE=12EH•AE=12×2.8×4.8=6.72.故答案为:6.72.【点睛】本题考查了翻折变换(折叠问题),直角三角形斜边上的中线的性质,勾股定理,三角形的面积等知识,解题的关键是学会利用面积法求高,属于中考常考题型.33.【详解】试题分析:根据勾股定理和等腰直角三角形的面积公式,可以证明:以直角三角形的两条直角边为斜边的等腰直角三角形的面积和等于以斜边为斜边的等腰直角三角形的面积.则阴影部分的面积即为以斜边为斜边的等腰直角三角形的面积的2倍.解:在Rt①ABC中,AB2=AC2+BC2,AB=5,S阴影=S△AHC+S△BFC+S△AEB=×+×+×,=(AC2+BC2+AB2),=AB2,=×52=.故答案为.点评:本题考查了勾股定理的知识,要求能够运用勾股定理证明三个等腰直角三角形的面积之间的关系.34.48 5【分析】根据垂线段最短可知当EP①AB时,线段EP最短.根据12•AB•PE=12×BE×AE,只要求出AB、AE、BE、PE,即可解决问题.【详解】解:根据垂线段最短可知当PE①AB时,线段PE最短.①AE①BC于E,sinB=35=AEAB,设AE=3k,AB=BC=5k,则BE=4k,EC=k,①EC=3,①k=3,①BE=12,AB=15,AE=9,当PE①AB时,12•AB•PE=12×BE×AE,①PE=AE BEAB⨯=365,①线段PE的最小值为365,①BP 485.故答案为:485.【点睛】本题考查菱形的性质、解直角三角形、垂线段最短、锐角三角函数等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.35.10.【分析】连结OC,设①O半径为r,则OC=r,OE=r-2,根据垂径定理得到CE=DE=1 2CD=6,在Rt△OCE中,利用勾股定理列出关于r的等式,然后解方程求出r即可.【详解】解:连结OC,设①O半径为r,则OC=r,OE=r-BE=r-2,①CD①AB,CD=12①CE=DE=12CD=6,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级下册 第二十八章 锐角三角三角函数
三角函数 30° 45° 60°
sin a
1 2
2 2 2 2
1
3 2
1 2
cosa
tan a
3 2 3 3
求 边
3
求 角
正 弦
余 弦
正 切
计算 解直角三角形
俯仰 角角
方 位 角
坡 度
特殊值的运算
应用
定义 锐角三角函数
第28章锐角三角三角函数
九 年 级 下 册
三角形之间 的关系 三角形与其它 图形的关系
三角形
知识内容 三 角 形 专 题
五、立体整合
三角形知识内容之间的关系 等边三角形
相似三角形
拓展 和 延伸 相似比 为 1时
解直角三角形
等腰三角形
锐角三角函数 勾股定理
全等三角形
特殊三角形
三角形
领域间的
函数 联系和综合
三 角 形 专 题
八上 第11章全等三角形 第12章轴对称 等腰三角形
等 边 对 等 角
三 线 合 一
定 义
等 角 对 等 边
每 一 个 角 都 等
三 线 合 一
的三 三个 角角 形相 等
有 的一 三个 角角 形是
600
600
性质
判定
性质 等边三角形
第12章等腰三角形
判定
相关概念
等腰三角形
八 年 级 上 册
八年级下册 第十八章勾股定理
已知两边 求第三边
赵爽弦图 毕答哥拉斯 茄菲尔德
互逆命题
内容 内容
全等
证明
证明
知三边 定形状 应用
应用
勾股定理
勾股定理的逆定理
第18章勾股定理
八 年 级 下 册
九年级下册 第二十七章 相似
对应角相等 对应边成比例
对应中线的比=对应高的 比=对应角平分线的比= 相似比 周长的比=相似比 面积的比=相似比的平方
A字型 X字型
平行
两角对 应相等
相似三角形 的性质 相似三角形
A B C′ B′ C B C B′
C
F
2、让学生经历数学知识的形成过程 E △BCF≌△DAE或△ABF≌△CDE
全等证明不容易,三组元素要齐备. A′ A 要证明 BF=DE A′ 要想证明变简单,尽量找出相等边. 如等腰三角形“等边对等角”、“三线合一 A′ A A A′ 还差条件不用急,利用等角来补齐. B C ”性质的得出,可以先让学生剪出等腰三角 C′ B′ 公共边角对顶角,直接应用不用说. 3、注重分析思路,让学生学会思考问题 C 形,并进一步利用轴对称的性质思考相等的 B B B′ B ′ C A ′ 两边一角要正确,须是两边和夹角. 线段和相等的角,发现等腰三角形的性质。 利用边角证全等,反之全等证边角. 由操作过程得到启发:通过做出等腰三角形 的对称轴得到两个全等三角形,从而利用全 等证明等腰三角形的性质。 4、善于总结技术口决和基本图形
八下第18章勾股定理
论证几何开始 实验为主 出现推理
七下 第7章三角形
论证几何向 计算几何过渡 淡化证明 回归自然
九下第27章相似 第28章锐角三角函数
各年级的 侧重点不同 三 角 形 专 题
七年级下册 第七章三角形
定义
两边之和大 于第三边
中线 高
与三角形有关的角
多边形及 其内角和 镶嵌
三角形的 主要线段 角平分线
数学学习过程
评价建议
三 角 形
定性定量结合 在呈现评价结果时, 应重视定性评价的 作用,采用定性与 定量相结合的方法。
对学生数学学习过程的评价 包括参与数学活动的程度、 自信心、合作交流的意识, 以及独立思考的习惯、数学 思考的发展水平等方面。
八、课程资源开发 利用
生活材料 自身情况
学生资源
生活事件
知识与技能 课标要求
经历探索三角形基本性质的 过程;掌握三角形的基本性 质;掌握基本的识图、作图 等技能;体会证明的必要性, 能证明三角形的基本性质; 掌握基本的推理技能。
情感与态度 三 角 形
认识通过观察、实验、 归纳、类比、推断可以 获得数学猜想;体验数 学活动充满着探索性和 创造性;感受证明过程 的严谨性以及结论的确 定性。
圆
垂径定理的计算转 化为解直角三角形 问题 利用圆周角定理、切 线长定理可得到等腰 三角形和直角三角形
图三 形角 的形 关与 系其 他
六、教学建议
丰富多彩的图形世界给三角形的 以画思路图的方式说明证明题的思考方法(如: 学习提供了大量真实的素材,教 顺推、逆推、两头凑)启发学生自己说思路。 例题:已知:如图, AB=CD 学时要注意联系实际,从实际出 BC=DA E 、 F 是 AC A 发引入概念,并将所学知识应用 A′ 上两点,且 求证:A BF=DE . AE=CF A′ 1、注重联系实际 到实际生活中。如,用全等和相 分析:由已知可用SSS证△ABC≌△ CDA B 似的知识解决测量问题。 B′ C C′ B C B′ D ∠DAC=∠BCA 或 ∠DCA=∠BAC
三角形专题
一、课标要求
二、编写意图
三、体例安排
三角形
四、内容结构 五、立体整合 六、教学建议
七、评价建议
八、资源整合
一、课标要求
在探索图形的性 质中,初步建立 空间观念,发展 几何直觉。
数学思考
解决问题
尝试从不同角度 寻求解决问题的 方法并能有效地 解决问题;体会 在解决问题的过 程中与他人合作 的重要性。
老教材偏重于逻辑推 理,纯理论题占大多数; 新教材对于推理能力的 培养,按照“说点儿 理”“说理”“简单推 理”“符号表示推理” 等不同层次分阶段地安 排,逐步达到《课标》 要求。在七年级主要采 取渗透说理的方式,从 八年级上学期的“全等 三角形”开始正式出现 “证明”。
三、体例安排
体例安排
四、内容结构
与三角形有 关的线段 三角形的 稳定性
第7章三角形
七 年 级 下 册
八年级上册 第十一章全等三角形
对应边相等
对应角相等
三角形全等的条件
HL
全等三角形的性质
全等三角形
第11章全等三角形
全等三角形的概念
角平分线的性质
八 年 级 上 册
性质
判定
八年级上册 第十二章第三节等腰三角形
顶 角 和 底 角
腰 和 底 边
相似三角形 的判定
三边对应 成比例 两边成比例 且夹角相等
图形的相似
第27章相似
位似 画法、性质 用坐标表示 位似变换
位似中心是原点 对应点的坐标比 为k或-k
相似形
相似多边形
对应角相等, 对应边成比例, 周长的比=相似比 面积的比=相似比的平方
九 年 级 下 册
两图形位似 对应顶点的连线 交于一点 对应边平行
教材
教材资源
隐含材料 置换生疏
最大限度地利 用课内资源 课 程 资 源 开 发 合理开发 课外资源
信息资源
课堂表现
请各位专家多批评指正!
C′
A
B5、关注学生的学习兴趣和参程度七、评价建议应遵循《标准》的基本 自我评价、学生互评 理念,以本学段的知识 教师评价、家长评价 与技能目标为基准,考察 社会有关人员评价结合 发现解决问题 学生对基础知识和基本 技能的理解和掌握程序。 基础知识技能 主体方法多样化
从不同角度分析和解决 问题,与他人合作, 能用文字、字母、符号 表达解题过程。
多边形
正多边形的计算转 化为解直角三角形 问题
应用三角形全等知识 证明特殊四边形性质
应用三角形内角和 求多边形的内角和 三角形的外接圆 三角形的内切圆
四边形
三角形
由平行四边形的性质证 明了三角形的中位线定 理。由三角形中位线定 理又能得到梯形中位线 定理。 由矩形的性质得到” 直角三角形斜边上的 中线等于斜边的一半 ”
二、编写意图
教材设置了思考、探究、 讨论等栏目引导学生自主 探索,激发学生进行思考, 促进合作交流。
通过让学生观察 实际生活中的图 形,加强对图形 的直观认识和感 受,从中“发现” 几何图形,归纳 出几何图形的基 本特征,从而更 好地“把握图 形”。
加 大 了 探 索 交 流 的 空 间
编写意图
