中考真题专题汇编-综合计算题
中考计算真题专项练习100题

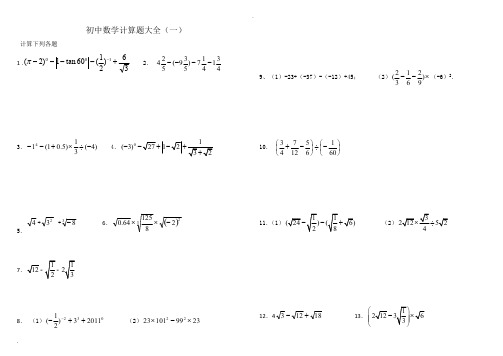
第 1 页中考计算真题专项练习100题12.6-6) 34.解下列方程:(1(256(用配方法解) 78.(本题4分)计算910.(1(2)已知:tan60°·sinα.11.计算(1).(2).-36) 12-313.解方程 (1)532436x x-=-; (2)431.60.20.5x x +--=- 14.计算:0323||()tan 60823ππ+-++︒+--.15.解不等式组,并把它们的解集在数轴上表示出来.(1)33213(1)8x x x x -⎧+≥⎪⎨⎪--<-⎩ (2)⎪⎩⎪⎨⎧<+>-3)4(2112x x 16.()()241940-+---17.(-5)×(-8)-(-28)÷4 18.12)1276521(⨯-+ 19.-22-(-2)2-23×(-1)2011 20.4932÷-+|-4|×0.52+292×(-121)2 21.(10分)计算:121()24234-+-⨯-.22.先化简,再求值:(21+a 1)212+-a a ,其中a =13+.23.先化简,再求值xx x x x x 41)111(22+÷-+++其x足方程0122=--x x .24.计算:0011124sin 60(3()3--+---π)25.计算:()0432--+-.26.21233(2)(2)x y x y ---÷第 3 页27.11122-+--+a aa a a 28.计算:2sin30°+4cos30°·tan60°-cos 245°29.先化简,再求值:)211(342--⋅--a a a ,其中3-=a . 30.(1−16 +34)×(−48)31.计算: |-4|2÷-(2-3)0+2)21(-- 32.计算221()a ba b a b b a-÷-+-33.计算 1a a-÷1a a a 22---1a 1- 34.解方程=--3x x 21-x31-35.先化简后求值。
中考化学真题分类汇编 计算题(含解析)-人教版初中九年级全册化学试题

综合计算题(一)1.(18某某)尿素[CO(NH2)2]是一种常见的氮肥,工业上制备反应如下:CO2+2NH3CO(NH2)2+H2O,请计算:(1)尿素中氮元素的质量分数。
(2)生产6t尿酸理论上需要氨气的质量是多少?化学试题参考答案及评分标准【答案】(1)46.7%t。
【解析】(1)尿素中氮元素的质量分数为:×100%=46.7%(2)设理论上需要氮气的质量为x。
CO2+2NH3CO(NH2)2+H2O3460x6tx tt。
2.(18某某)一种新型“人造树叶”可吸收二氧化碳并转化为乙醇(C2H5OH)燃料,化学方程式为2CO2+3H2O C2H5OH+3O2。
研究显示,一升“人造树叶”每天可从空气中吸收968gCO2。
(1)一升“人造树叶”工作一天可得到乙醇的质量是________?(2)若每天一棵树平均可吸收2,则一升“人造树叶”吸收的CO2相当于_______棵树吸收的CO2。
【答案】(1).506g(2).20【解析】根据反应的化学方程式计算解答。
(1)设一升“人造树叶”工作一天可得到乙醇的质量为x。
2CO2+3H2O C2H5OH +3O28846968gxx=506g(2)968g÷48.4g=20答:(1)一升“人造树叶”工作一天可得到乙醇的质量是506g;(2)若每天一棵树平均可吸收2,则一升“人造树叶”吸收的CO2相当于20棵树吸收的CO2。
3.(18某某)用溶质质量分数为5%的NaOH溶液中和73g的稀盐酸,反应过程中溶液的酸碱度变化如下图所示。
请计算:(1)用质量分数为10%的氢氧化钠溶液配制5%的氢氧化钠溶液100g,需要水__________克.(2)当a为80g时,所得溶液中溶质的质量分数是___________(结果精确到0.1%)?【答案】(1)50(2)3.8%【解析】(1)设需要水的质量为x,根据溶质在稀释前后质量不变。
100g×5%=(100g-x)×10%x=50g;(2)根据图像可知,当a为80g时,盐酸与氢氧化钠恰好完全反应。
中考数学真题《计算综合》专项测试卷(附答案)

中考数学真题《计算综合》专项测试卷(附答案)学校:___________班级:___________姓名:___________考号:___________1.(2024·北京海淀·二模)计算:020242sin 45|3|8-︒+-【答案】42【分析】本题主要考查实数的混合运算 掌握零次幂 特殊角的三角函数值的计算 二次根式的性质化简 绝对值的性质化简等知识是解题的关键.【详解】解:020242sin 4538-︒+-21232=-++42=2.(2024·北京海淀·二模)解不等式组:532342(1)x x x x +⎧<⎪⎨⎪->+⎩【答案】6x >【分析】本题考查了解一元一次不等式组 熟练掌握不等式组的解法是解题关键. 先分别求出两个不等式的解集 再找出它们的公共部分 即为不等式组的解集. 【详解】解:由532x x +< 解不等式可得1x > 由342(1)x x ->+解不等式可得6x >综上可得 不等式组的解集为6x >.3.(2024·北京海淀·二模)已知2230m n --= 求代数式2()2()m n n m n +-+的值.【答案】3【分析】本题主要考查了已知式子的值求代数式的值 根据2230m n --=可得出223m n -= 代数式2()2()m n n m n +-+提因式得到()()2m n m n n ++- 再用平方差公式即可得出22m n - 即可得到答案.【详解】解:2230m n --= 即223m n -= 2()2()m n n m n +-+()()2m n m n n =++- ()()m n m n =+-22m n =-3=4.(2024·北京东城·()13112tan6022-⎛⎫+--- ⎪⎭︒⎝.36【分析】本题考查了实数的混合运算 利用二次根式的性质 特殊角的三角函数值 负整数指数幂 乘方的意义进行化简 再计算加减即可 掌握运算法则是解此题的关键.()13112tan6022-⎛⎫+--- ⎪⎭︒⎝()()23328=---36=.5.(2024·北京东城·二模)解不等式组:()2154,611.3x x x x ⎧+<-⎪⎨+≥-⎪⎩【答案】2x >【分析】本题主要考查解一元一次不等式组 根据不等式的性质求出不等式的解集 根据找不等式组解集的规律找出不等式组的解集即可.【详解】解:()21546113x x x x ⎧+<-⎪⎨+≥-⎪⎩①② 解不等式① 得 2x > 解不等式① 得 43x ≥-所以 不等式组的解集为:2x >6.(2024·北京朝阳·二模)计算:113tan3027233-⎛⎫︒+- ⎪⎝⎭【答案】3【分析】本题考查特殊角的三角函数值 负整数指数幂 二次根式化简以及去绝对值 正确计算是解答本题的关键.先计算特殊角的三角函数值 负整数指数幂 化简二次根式以及去绝对值 再计算加减即可.【详解】解:113tan3027233-⎛⎫︒+- ⎪⎝⎭333333=+-333323=-3=.7.(2024·北京朝阳·二模)解不等式345(2)x x +<+ 并写出它的所有负整数解.【答案】不等式的解集是3x >- 其中所有负整数解为2- 1-【分析】此题考查一元一次不等式的整数解 解题关键在于掌握运算法则. 先解出不等式的解集 再求其负整数解. 【详解】解:34510x x +<+. 移项得 35104x x -<-. 合并同类项得 26x -<. 系数化为1得 3x >-.所以原不等式的所有负整数解为2- 1-.8.(2024·北京门头沟·()213220212sin 602π-⎛⎫-+++ ⎪⎝⎭°.【答案】5【分析】本题考查了含特殊角的三角函数值的实数的混合运算 根据相应的运算法则计算即可.()213220212sin 602π-⎛⎫-++︒+ ⎪⎝⎭23134=5=.9.(2024·北京门头沟·二模)解分式方程26111x x x -=+-【答案】5x =-【分析】本题考查了解分式方程 正确掌握解分式方程的法则及步骤是解题的关键.将分式方程去分母化为整式方程 解整式方程求出解并检验即可. 【详解】解:26111x x x -=+- 方程两边乘以(1)(1)x x +-得:(1)6(1)(1)--=+-x x x x 去括号:2261x x x --=- 移项:2216x x x --=-+ 合并同类项:5x -= 系数化1:5x =-.经检验:5x =-是原方程的解. ∴原方程的解是5x =-.10.(2024·北京门头沟·二模)已知:0x y -= 求()2222x yx y x xy y -⋅+++的值.【答案】2x y x y -+ 12- 【分析】本题考查分式化简求值问题 先通分 计算括号里的 再除法转化成乘法 计算括号外的 最后把x y =的值代入计算即可.【详解】解:()2222x yx y x xy y -⋅+++()()22x yx y x y -=⋅++2x yx y-=+ ①0x y -= ①x y = ①原式212x x x x -==-+. 11.(2024·北京昌平·1182sin 45122-⎛⎫-︒+ ⎪⎝⎭.【答案】2+1【分析】本题考查了二次根式 绝对值 负指数幂 特殊角的三角函数值的运算 熟悉运算法则是解题的关键.根据二次根式 绝对值 负指数幂 特殊角的三角函数值的运算 化简计算即可.【详解】解:原式222221=- 222221=221=.12.(2024·北京昌平·二模)解不等式组:38312x x x x -≥⎧⎪⎨->⎪⎩①②.【答案】4x ≥【分析】本题考查解一元一次不等式组.先解出每个不等式的解集 即可得到不等式组的解集.【详解】解:38312x x x x -≥⎧⎪⎨->⎪⎩①②.解不等式①得 4x ≥ 解不等式①得 1x >所以这个不等式的解集为4x ≥.13.(2024·北京昌平·二模)已知220x x +-= 求代数式212111x x ⎛⎫+÷ ⎪--⎝⎭的值.【答案】1【分析】本题考查的是分数的混合运算.将212111x x ⎛⎫+÷ ⎪--⎝⎭化简为22x x+ 再整体代入 求值. 【详解】解:原式211211x x x +-=÷--(1)(1)12x x x x +-=⋅-22x x += 220x x +-= 22x x ∴+=∴原式1=.14.(2024·北京顺义·二模)计算:13tan 302|1|12.︒--+-【答案】132【分析】本题考查实数的运算 熟练掌握特殊角的三角函数值 负整指数幂的运算法则是解题的关键.先把特殊角的三角函数值代入 并运用负整指数幂的运算法则计算和求绝对值 化简二次根式 再计算乘法 最后计算加减即可.【详解】解:13tan302112--+-3131232=+-13231232=+-132=15.(2024·北京顺义·二模)解不等式:2123x x -≥ 并求它的正整数解.【答案】2x ≤ 正整数解是2 1.【分析】此题考查了一元一次不等式的整数解 正确解不等式 求出解集是解答本题的关键 解不等式的基本步骤:去分母 去括号 移项 合并同类项 系数化为1 解不等式应根据不等式的基本性质.首先解不等式 然后确定不等式的解集中的正整数值即可. 【详解】解:342x x ≥-2x -≥-2x ≤正整数解是2 1.16.(2024·北京房山·二模)计算:()0π34sin60212--+-︒【答案】3【分析】本题主要考查了特殊角三角函数值和实数的混合运算 熟练掌握运算法则和特殊角三角函数值是解答本题的关键.先求出特殊角的三角函数值 幂的运算并对绝对值 二次根式化简 再进行计算即可.【详解】()0π34sin60212--+-︒31423=-++3=.17.(2024·北京房山·二模)解不等式组:12822x x x x +⎧<⎪⎨⎪->+⎩.【答案】1x <【分析】本题考查了解一元一次不等式组 熟练掌握知识点是解题的关键. 先解每一个一元一次不等式 再取解集的公共部分即可.【详解】解:原不等式组为12822x x x x +⎧<⎪⎨⎪->+⎩①② 解不等式① 得1x < 解不等式① 得2x < ∴原不等式组的解集为1x <.18.(2024·北京房山·二模)已知2210x x +-= 求代数式()()223x x x ++-的值.【答案】5【分析】本题考查了代数式求值 完全平方公式 整式的乘法 解决本题的关键是利用整体的思想求解.先将代数式展开得到224x x ++ 再将2210x x +-=化简为221x x += 整体代入求值即可. 【详解】解:()()223x x x ++- 22443x x x x =+++-224x x =++.2210x x +-= 221x x ∴+=∴原式2245x x =++=.19.(2024·北京·二模)计算:0(π2024)4sin 60512-+︒+-【答案】6【分析】本题考查实数的运算 熟练掌握相关运算法则是解题的关键.利用特殊锐角三角函数值 二次根式的性质 零整数指数幂 绝对值的性质计算即可 【详解】解:0(π2024)4sin 60512-+︒+-314523=+-6=.20.(2024·北京·二模)解不等式组:2123x x x x -≤⎧⎪⎨+>⎪⎩【答案】31-<≤x【分析】本题考查的是解一元一次不等式组 熟知“同大取大 同小取小 大小小大中间找 大大小小找不到”的原则是解答此题的关键.分别求出每一个不等式的解集 根据口诀:同大取大 同小取小 大小小大中间找 大大小小无解了确定不等式组的解集.【详解】解:原不等式组为2123x x x x -≤⎧⎪⎨+>⎪⎩①②解不等式① 得1x ≤ 解不等式① 得3x >-①原不等式组的解集为31-<≤x .21.(2024·北京·二模)已知340m n +-= 求代数式2226+69m nm mn n ++的值.【答案】12【分析】本题考查了分式的化简求值 熟练掌握因式分解是解题的关键.先算对分子分母进行因式分解 再约分 然后根据340m n +-=可以得到34m n +=然后代入化简后的式子即可. 【详解】解:2226+69m nm mn n ++22(3)(3)m n m n +=+23m n=+. ①340m n +-= ①34m n +=①原式21 42==.22.(2024·北京大兴·311232sin602-⎛⎫+--︒⎪⎝⎭.35【分析】本题考查了实数的运算分别根据二次根式化简负整数指数幂的运算法则化简绝对值特殊角的三角函数值计算出各数再进行合并计算即可熟知二次根式化简负整数指数幂的运算法则化简绝对值特殊角的三角函数值是解题的关键.【详解】解:原式3 3832=+-353 =35=.23.(2024·北京大兴·二模)解不等式组:()213 412x xxx⎧-<+⎪⎨+>⎪⎩【答案】152x -<<【分析】本题考查解一元一次不等式组 分别解出每个不等式的解集 然后确定不等式组的解集 熟练掌握不等式组的解法是解题的关键. 【详解】解:()213412x x x x ⎧-<+⎪⎨+>⎪⎩①② 解不等式① 得5x < 解不等式① 得12x >-①原不等式组的解集为:152x -<<.24.(2024·北京大兴·二模)已知50x y --= 求代数式2222x y x yy x x ⎛⎫+--÷ ⎪⎝⎭的值.【答案】10【分析】本题考查分式的化简求值 熟练掌握分式的混合运算法则是解题关键.先根据分式减法法则计算括号内的式子 再根据分式除法法则化简得出最简结果 把50x y --=变形后整体代入即可得答案.【详解】解:2222x y x yy x x ⎛⎫+--÷ ⎪⎝⎭ 2222x y xy xx x x y ⎛⎫+=-⋅⎪-⎝⎭ 2222x y xy x x x y⎛⎫+-=⋅⎪-⎝⎭()22x y xxx y-=⋅- ()2x y =-.①50x y --= ①5x y -=①原式()2=10x y =-.25.(2024·北京石景山·()0276tan3012024︒--+.3【分析】本题主要考查了实数的运算 求特殊角三角函数值 27=33 3tan 30︒=11-= 02024=1 再计算即可.【详解】解:原式333611=+ 333=326.(2024·北京石景山·二模)解不等式组:3452924x x xx -<+⎧⎪⎨-<⎪⎩【答案】31x -<<【分析】本题考查的是解一元一次不等式组 分别求出各不等式的解集 再求出其公共解集即可.熟知“同大取大 同小取小 大小小大中间找 大大小小找不到”的原则是解答此题的关键.【详解】解:原不等式组为3452924x x xx -<+⎧⎪⎨-<⎪⎩①② 解不等式① 得3x >-. 解不等式① 得1x <.∴原不等式组的解集为31x -<<.27.(2024·北京丰台·. 【答案】解:原式=22+3-2-2×22=22+3-2-2=2+1. 28.(2024·北京丰台·二模)解不等式组:【答案】解:解不等式① 得2<x解不等式① 得21->x∴不等式组的解集为221<<-x .29.(2024·北京丰台·二模)已知22360a a --= 求代数式(12)(12)3(12)a a a a +---的值. 【答案】解:原式=221436a a a --+=2123a a +-.①22360a a --= ①2236a a -=.①原式=16+=7.30.(2024·北京西城·二模)计算:4cos45°−√18+|−√2|−(π+3)0.118|3|2sin 452()°-+---22345,.x x x x +⎧<⎪⎨⎪-<+⎩【答案】31.(2024·北京西城·二模)解不等式组{3x−2<x+4x≥2x−35并写出它的所有整数解.【答案】32.(2024·北京西城·二模)已知x2+x﹣3=0 求代数式(1+3x−1)⋅3x2+4x+4的值.【答案】33.(2024•顺义区二模)如果1m n+=那么代数式22(1)m m nm n n--⋅-的值为()A.1-B.1C.2-D.2【答案】A【考点】分式的化简求值【分析】将所求式子化简然后将m n+的值代入计算即可.【解答】解:1m n +=∴22(1)m m n m n n--⋅- ()()m n m m n m n m n n--+-=⋅-()()n m n m n m n n-+-=⋅- ()m n =-+1=-故选:A .34.(2024•朝阳区二模)已知2220x x +-=,则代数式22(1)(1)(1)2x x x x +++-+的值为( ) A .4B .2C .1D .0【答案】A【考点】整式的混合运算—化简求值【分析】先根据完全平方公式和平方差公式进行计算 再合并同类项 求出222x x += 最后代入求出答案即可.【解答】解:22(1)(1)(1)2x x x x +++-+ 2222112x x x x =+++-+ 242x x =+ 2220x x +-= 222x x ∴+=∴原式22(2)224x x =+=⨯=.故选:A .35.(2024•东城区二模)在下列各式中 从左到右计算结果正确的是( ) A 862B .22(1)1x x -=- C 2(2)2--D .12111x x x -+=++ 【答案】D【考点】二次根式的加减法 完全平方公式 二次根式的性质与化简 分式的加减法【分析】直接利用二次根式的加减运算法则 完全平方公式 二次根式的性质 分式的加减运算法则分别化简 进而得出答案.【解答】解:A 86 故此选项不合题意B .22(1)21x x x -=-+ 故此选项不合题意C 2(2)2- 故此选项不合题意D .12111x x x -+=++ 故此选项符合题意. 故选:D .36.(2024•石景山区二模)若2310x x -+=,则代数式(2)(2)(6)x x x x +-+-的值为 .【答案】6-.【考点】整式的混合运算—化简求值【分析】先根据平方差公式和单项式乘多项式法则进行计算 再合并同类项 求出231x x -=- 最后代入求出答案即可.【解答】解:(2)(2)(6)x x x x +-+- 2246x x x =-+- 2264x x =-- 2310x x -+= 231x x ∴-=-∴原式22(3)42(1)4246x x =--=⨯--=--=-.故答案为:6-.37.(2024•东城区二模)若250m m +-=,则代数式22111()10m m m m--÷的值为 .【答案】2.【考点】分式的化简求值【分析】先利用异分母分式加减法法则计算括号里 再算括号外 然后把25m m +=代入化简后的式子进行计算即可解答.【解答】解:22111()10m m m m--÷第 21 页 共 21 页 2110(1)(1)m m m m m -=⋅+- 10(1)m m =+ 210m m=+ 250m m +-= 25m m ∴+= ∴当25m m +=时 原式1025== 故答案为:2.。
(完整版)初中数学中考计算题复习含答案
1 .23621601214314175395243 40431511454233862328125647--8123220113212399101232210601651274311121241318123214 1531246612131321620212529363181712312712661833218243352741581920112|4120131124212223231|1|3333325=14-9=5387431511441312318118741-44011536414233832527------813229200121012-992(101-99)21220091-3;210121-23+-37--12+45410-30=-45-606512743606560127604335+50=-3011121212121312131431323157.21113262969276161212233633231212122312231712233411851451424334155275424335274155424335274158019-2.+2-=-2.1. 2.201212352122232------------------------------------------------------------------63253--------71 220130 3|1|012013567 8 10 111213+|3|+1 151612120130+||222+412 17112013|7|+0121819122012302452211|3|+162320130222122312+124122512+12612272829201322012420113011一.解答题(共3011211+12121211101220130+1+13|1|01201312+1111212451141144362744421811139210+31111111212原式第一项利用立方根的定义化简,第二项利用负数的绝对值等于它的相反数计算法则计算,第四项利用负指数幂法则计算,第五项利用1181311321132132214 3.140+|3|+120131415221612120130+||222+412121122424242+4 17112013|7|+01211211115218原式第一项利用立方根的定义化简,第二项利用二次根式的化简公式化简,第三项利用零指数幂法则计算,1451912121114+1+|12|142121112012302452121222311416314211|3|+16232013021)原式第一项利用负数的绝对值等于它的相反数计算,第二项先计算乘方运算,再计算除法运算,第2131234622212121121313122312+11)原式第一项利用负数的绝对值等于它的相反数计算,第二项利用特殊角的三212172+1+324121)原式第一项利用绝对值的代数意义化简,第二项利用零指数幂法则计算,第三项利用负指数幂法则21+13+3213212512+112112+126121)原式第一项利用特殊角的三角函数值化简,第二项利用零指数幂法则计算,212211118272282129201322012420112011201122420112242011+522420110301819126-6 3020151351251513 223113415322 2215113656 709422023432852213222330 920121451012456011 ---3622337956347181213343144201232221113.解方程(本小题共61 2532436431.60.20.5140||6015 233218342101216241940 17582818 192221121276521223201120+|4|×0.5+21 21 49322922121212423424 25 0116033230148 31|4|201634232212117538131383171. 2. 3. 4. 5.62-36:-363-17.=-1+1-9-8=-174172312x-2=3x+5 2x-3x=2+5x=-7262(2x+1)-(5x-1)=6x=-354113【解析】先把第二个方程去分母得3x-4y=-2,4113622114211222212221117363236322182323931410123211212111-192-111=-9÷9-18=-1-18=-192753796418=-28+30-27+14=-111221311326313 1532436112171217129128122121543326452431.60.20.529362762732661361263616220561235414试题分析:原式第一项利用零指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用特殊角的三角函数值计算,最后一项利用立方根定义化简计算即可得到2. 3.153222123x-3+6≥2x332181-3x+3-8+x 0-23223421012122221161747 189190 2021-40--19-24=-40+19-24=-45 2-5-8--28 3-1256712=6+10-74-22--22-23-12011=-4-4+85-32+|-4|×0.52+2-12942912=-4+1+521 312124234 712166 102244124322421 1212423412166224001160341313200116034131322425 =2-1+230-76=-48+8-36=-76316412 95。
中考化学计算题综合题汇编含详细答案

一、中考初中化学计算题1.实验室有一瓶未知浓度的BaCl2溶液,某同学取出150g该溶液于烧杯中,向其中逐滴加入溶质质量分数为26.5%的Na2CO3溶液。
反应过程中生成沉淀的质量与所用Na2CO3溶液质量的关系如图所示。
已知:BaCl2+Na2CO3=BaCO3↓+2NaCl。
请计算:(1)配制26.5%的Na2CO3溶液80g,需要Na2CO3固体___g。
(2)BaCl2溶液的溶质质量分数是____?(写出计算过程,结果保留到0.1%)【答案】(1) 21.2g;(2)13.9%【解析】试题分析:(1)根据溶质质量分数计算的表达式:配制26.5%的Na2CO3溶液80g,需要Na2CO3固体质量=80g×26.5%=21.2g(2)从图甲中获知,当BaCl2完全转化为沉淀时消耗Na2CO3溶液的质量为40g,再根据化学反应方程式:BaCl2+Na2CO3=BaCO3↓+2NaCl中Na2CO3与BaCl2的质量关系,可求出BaCl2的质量,进而可求解BaCl2溶液的溶质质量分数解:设BaCl2的质量为xBaCl2+Na2CO3=BaCO3↓+2NaCl208106x40g×26.5%208∶106=X∶(40g×26.5%)x=208×40g×26.5%/106=20.8g该BaCl2溶液的溶质质量分数=(20.8g/150g)×100%=13.9%答:该BaCl2溶液的溶质质量分数为13.9%考点:溶质质量分数计算,根据化学方程式计算2.某中学化学课外活动小组对某工厂排放的含少量硫酸的废水进行抽样检测.取一定量的废水,用质量分数为1%的氢氧化钡溶液中和(其它物质不与氢氧化钡反应),当恰好中和时,消耗氢氧化钡溶液的质量为171g,过滤后,测得滤液的质量为268.67g.(不考虑过滤时滤液质量损失)(计算结果保留二位小数)求:①反应中生成沉淀的质量为多少?②该工厂排放的废水中所含硫酸的质量分数为多少?【答案】①2.33g ②0.98%【解析】解:①设生成沉淀的质量为x,废水样品中所含硫酸质量为y;H2SO4+Ba(OH)2═BaSO4↓+2H2O98 171 233 y 171g×1% x1711711%=233g x ⨯,x=2.33g ; 98=1711711%y g ⨯,y=0.98g ; ②根据质量守恒定律知:所取废水样品质量=(268.67+2.33)g-171g=100g ,该工厂排放的废水中硫酸的质量分数=0.98100gg×100%=0.98%; 答:①反应中生成沉淀的质量为2.33g ;②该工厂排放的废水中所含硫酸的质量分数为0.98%。
汇总)初中数学中考计算题(最全)-含答案

汇总)初中数学中考计算题(最全)-含答案.doc1.解答题(共30小题)1.1 计算题:① 2+3=5;②解方程:x+5=10,解得x=5.1.2 计算:π+(π﹣2013)=2π-2013.1.3 计算:|1﹣|﹣2cos30°+(﹣)×(﹣1)2013|=|1-|-2cos30°+(-1)×(-1)2013||=|1-|-2×√3/2+1||=|1-√3+1|=|2-√3|。
1.4 计算:﹣(-2)+(-3)=1.1.5 计算:√(5+2√6)+√(5-2√6)=√2+√3.1.6 计算:(2+√3)(2-√3)=1.1.7 计算:(1+√2)²=3+2√2.1.8 计算:(1-√3)²=4-2√3.1.9 计算:(√2+1)²=3+2√2.1.10 计算:(√2-1)²=3-2√2.1.11 计算:(3+√5)(3-√5)=4.1.12 计算:(√3+1)(√3-1)=2.1.13 计算:(√2+√3)²=5+2√6.1.14 计算:﹣(π﹣3.14)+|﹣3|+(﹣1)2013+tan45°=0.1.15 计算:√3+√2-√6=√3-√2+√6.1.16 计算或化简:1)计算2﹣1﹣tan60°+(π﹣2013)+|﹣|=-tan60°-2011;2)(a﹣2)²+4(a﹣1)﹣(a+2)(a﹣2)=-3a²+10a-6.1.17 计算:1)(﹣1)2013﹣|﹣7|+(√2)﹣1=-√2-8;2)(2+√3)÷(√3-1)=1+√3.1.18 计算:(1+√2)(1-√2)=﹣1.1.19 解方程:x²+2x+1=0,解得x=-1.1.20 计算:1)tan45°+sin230°﹣cos30°•tan60°+cos245°=√2-1;2)(√2+1)²-(√2-1)²=4√2.1.211)|﹣3|+16÷(﹣2)³+(2013﹣)﹣tan60°=2010;2)解方程:(1-2x)²=3,解得x=√2﹣1.1.222)求不等式组:{x²-2x0},解得0<x<1.1.232)先化简,再求值:(√3+1)÷(√3-1)=2.1.241)计算:tan30°=√3/3;2)解方程:x²-2x+1=0,解得x=1.1.25 计算:1)√2-√3+√6=(√2-1)(√3-1);2)先化简,再求值:(√2+1)²+(√2-1)²=8.1.261)计算:(1-√2)÷(1+√2)=-1+√2;2)解方程:x²-2x+2=0,解得x=1-√3.1.27 计算:1)(√2+√3)²-(√2-√3)²=4√6;2)先化简,再求值:(x²+2x+1)÷(x²-1)=1+x。
专题05解答基础题:计算综合(原卷版+解析)

专题05 计算综合题一、解答题(28题)专题05 计算综合题一、解答题(28题)1.(2023·重庆·统考中考真题)计算:(1)()()()211a a a a -++-; (2)22.211x x x x x x ⎛⎫÷- ⎪+++⎝⎭【答案】(1)21a - (2)11x + 【分析】(1)先计算单项式乘多项式,平方差公式,再合并同类项即可;(2)先通分计算括号内,再利用分式的除法法则进行计算.【详解】(1)解:原式2221a a a =-+-21a =-;(2)原式()222.11x x x x x x ⎛⎫+-=÷ ⎪++⎝⎭ ()22211x x x x =÷++ ()22211x x x x +=⋅+ 11x =+. 【点睛】本题考查整式的混合运算,分式的混合运算.熟练掌握相关运算法则,正确的计算,是解题的关键.2.(2023·重庆·统考中考真题)计算:(1)()()263x x x ++-; (2)2293n m n m m -⎛⎫+÷ ⎪⎝⎭. 【答案】(1)229x + (2)13m n- 【分析】(1)先根据单项式乘以多项式的法则、完全平方公式计算,再合并同类项; (2)根据分式混合运算的法则解答即可.【详解】(1)解:()()263x x x ++-22669x x x x =++-+229x =+; (2)解:2293n m n m m -⎛⎫+÷ ⎪⎝⎭ ()()333m n m m m n m n +=⋅+-13m n=-. 【点睛】本题考查了整式和分式的运算,属于基本计算题型,熟练掌握整式和分式混合运算的法则是解题的关键.3.(2022·重庆·统考中考真题)计算:(1)()()(2)x y x y y y +-+-; (2)2244124m m m m m -+⎛⎫-÷ ⎪⎝⎭-+. 【答案】(1)22x y - (2)22m - 【分析】(1)根据平方差公式和单项式乘多项式法则进行计算,再合并同类项即可;(2)先将括号里通分计算,所得的结果再和括号外的分式进行通分计算即可.【详解】(1)解:()()(2)x y x y y y +-+-=2222x y y y -+-=22x y -(2)解: 2244124m m m m m -+⎛⎫-÷ ⎪⎝⎭-+ =()()()222222m m m m m m -+-÷++- =()()()222222m m m m +-⨯+- =22m - 【点睛】本题考查了平方差公式、单项式乘多项式、合并同类项、分式的混合运算等知识点,熟练掌握运算法则是解答本题的关键.4.(2022·重庆·统考中考真题)计算:(1)()()224x x x ++-; (2)2212a a b b b -⎛⎫-÷ ⎪⎝⎭. 【答案】(1)224x + (2)2a b+ 【分析】(1)先计算乘法,再合并,即可求解;(2)先计算括号内的,再计算除法,即可求解.【详解】(1)解:原式22444x x x x =+++-224x =+(2)解:原式2()()a b b b a b a b -=⨯+- 2a b =+ 【点睛】本题主要考查了整式的混合运算,分式的混合运算,熟练掌握相关运算法则是解题的关键. 5.(2021·重庆·统考中考真题)计算(1)()()22x y x x y -++;(2)2241244a a a a a -⎛⎫-÷ ⎪+++⎝⎭. 【答案】(1)222x y +;(2)22a - 【分析】(1)利用完全平方公式和整式的乘法运算法则计算即可;(2)根据分式混合运算的运算法则计算即可.【详解】解:(1)()()22x y x x y -++=x 2﹣2xy +y 2+x 2+2xy=2x 2+y 2;(2)2241244a a a a a -⎛⎫-÷ ⎪+++⎝⎭ =22(2)(2))22(2)a a a a a a a ++--÷+++( =22(2)2(2)(2)a a a a +⨯++- =22a -. 【点睛】本题考查整式的混合运算、分式的混合运算、平方差公式、完全平方公式,熟练掌握运算法则是解答的关键.6.(2021·重庆·统考中考真题)计算:(1)2(23)()a a b a b ++-;(2)22293211x x x x x x ⎛⎫--÷+ ⎪+++⎝⎭. 【答案】(1)223++a ab b ;(2)-31x x + 【分析】(1)根据单项式乘以多项式以及完全平方公式计算即可;(2)利用分式的混合运算法则进行计算即可.【详解】解:(1)2(23)()a a b a b ++-2222+3+2+=a ab a ab b -22=3++a ab b(2)22293211x x x x x x ⎛⎫--÷+ ⎪+++⎝⎭()()()222+3-3+3=11+x x x x x x x ⎛⎫-÷ ⎪++⎝⎭()()()2+3-31=31x x x x x +++ -3=1x x + 【点睛】本题考查了整式的混合运算和分式的混合运算,熟练掌握运算法则是解题的关键.7.(2023·重庆沙坪坝·重庆八中校考一模)计算(1)()()()2223x y y x x y +-+-(2)2121211x x x x +⎛⎫÷+ ⎪-+-⎝⎭ 【答案】(1)22562x xy y -+(2)11x - 【分析】(1)根据平方差公式与完全平方公式将原式展开,再合并同类项即可;(2)现将分式中的多项式因式分解,以及通分括号里的式子,再根据分式的除法法则求解即可.【详解】(1)解:原式()()()2223y x y x x y =+-+-()()22222323y x x x y y =-+-⨯⋅+2222496y x x xy y =-+-+ ()()2222496x x xy y y =-+-++22562x xy y =-+.(2)解:原式()2112111x x x x x +-⎛⎫=÷+ ⎪--⎝⎭- ()21111x x x x ++⎛⎫=÷ ⎪-⎝⎭- ()21111x x x x +-=⋅+- 11x =-. 【点睛】本题考查了整式与分式的化简,需要熟练掌握平方差公式与完全平方公式,以及分式的混合运算,熟练掌握运算法则是解答本题的关键.8.(2023·重庆沙坪坝·重庆一中校考一模)计算:(1)()()2225x y x x y --- (2)221651m n n m n m n -⎛⎫÷- ⎪++⎝⎭ 【答案】(1)22xy y +(2)4m n +【分析】(1)根据完全平方公式,单项式乘以多项式进行计算即可求解;(2)根据分式的混合运算进行化简即可求解.【详解】(1)解:()()2225x y x x y ---()2222225x xy y x xy =-+-+ 22224225x xy y x xy =-+-+22xy y =+;(2)解:221651m n n m n m n -⎛⎫÷- ⎪++⎝⎭()()445m n m n m n n m n m n+-+-=÷++ ()()444m n m n m n m n m n+-+=⨯+- 4m n =+.【点睛】本题考查了整式的乘法以及分式的混合运算,熟练掌握整式的乘法运算以及分式的运算法则是解题的关键.9.(2023·重庆九龙坡·重庆市育才中学校考一模)计算:(1)()()22x y x y x +--; (2)224221121a a a a a a -⎛⎫-+÷ ⎪--+⎝⎭. 【答案】(1)222x y + (2)12a + 【分析】(1)根据完全平方公式,单项式乘以多项式进行计算即可求解;(2)根据分式的加减进行计算,同时将除法转化为乘法,根据分式的混合运算进行化简即可求解.【详解】(1)解:()()22x y x y x +--22222x xy y xy x =++-+ 222x y =+;(2)解:224221121a a a a a a -⎛⎫-+÷ ⎪--+⎝⎭()()()222141121a a a a a -+-=⨯-- ()()()()22+111211a a a a a -=⨯--+ 12a +=. 【点睛】本题考查了整式的化简,分式的混合运算,熟练掌握整式的运算法则以及分式的运算法则是解题的关键.10.(2023·重庆九龙坡·重庆实验外国语学校校考一模)计算:(1)(2)(2)(4)a b a b b a b +---; (2)222623969x x x x x ⎛⎫+÷ ⎪---+⎝⎭.【答案】(1)2a ab - (2)33x x --+ 【分析】(1)根据平方差公式与单项式乘以多项式进行计算即可求解;(2)根据分式的混合运算进行计算即可求解.【详解】(1)(2)(2)(4)a b a b b a b +---22244a b ab b =--+2a ab =-;(2)222623969x x x x x ⎛⎫+÷ ⎪---+⎝⎭ ()()()()26233332x x x x x -+-=⨯+- ()()()232332x x x x x--=⨯+- 33x x -=-+. 【点睛】本题考查了整式的乘法运算,分式的混合运算,熟练掌握以上运算法则是解题的关键. 11.(2023·重庆南岸·统考一模)计算:(1)()()212x x x ++-; (2)293()a a a a --÷ 【答案】(1)221x +(2)2a 3a +【分析】(1)根据完全平方公式、单项式乘以多项式法则计算解答即可;(2)根据分式乘除法则进行计算即可.【详解】(1)解:()()212x x x ++-=22212x x x x +++-=221x +.(2)解:293()a a a a --÷ =2(3)(3)3a a a a a +-⨯-【点睛】此题考查整式、分式的混合计算,关键是根据整式、分工的混合计算顺序和完全平方公式进行解答.12.(2023·重庆沙坪坝·统考一模)计算:(1)()()221x x x -++; (2)24122m m m -⎛⎫+÷ ⎪⎝⎭. 【答案】(1)41x + (2)2m m - 【分析】(1)先根据单项式乘以多项式,完全平方公式去括号,然后合并同类项即可;(2)根据分式的混合计算法则求解即可.【详解】(1)解:原式22221x x x x =-+++41x =+.(2)解:原式()()22222m m m m +-+=÷ ()()22222m m m m +=⋅+- 2m m =-. 【点睛】本题主要考查了分式的混合计算,知识的混合计算,熟知相关计算法则是解题的关键. 13.(2023·重庆开州·校联考一模)计算:(1)()()224--+x y x x y ; (2)2214411a a a a a -+⎛⎫-÷ ⎪--⎝⎭. 【答案】(1)284-+xy y (2)2a a - 【分析】(1)先根据完全平方公式,单项式乘多项式进行计算,再合并同类项即可;(2)先根据分式的减法法则进行计算,再根据分式的除法法则把除法变成乘法,最后根据分式的乘法法则进行计算即可.【详解】(1)解:()()224--+x y x x y=222444-+--x xy y x xy(2)解:2214411a a a a a -+⎛⎫-÷ ⎪--⎝⎭=()()211112-----a a a a a =()()21212----a a a a a =2a a - 【点睛】本题考查整式的混合运算和分式的混合运算,能正确根据整式的运算法则和分式的运算法则进行化简是解此题的关键,注意运算顺序.14.(2023·重庆合川·校考一模)计算:(1)(2)()(3)x y x y x x y ++-+;(2)2344(1)11x x x x x -+--÷++. 【答案】(1)22y(2)22x x +- 【分析】(1)先去括号再合并同类项即可;(2)先计算括号内的再乘以后面的式子的倒数即可.【详解】(1)解:原式222223x xy xy y x xy =+++--22y =.(2)解:原式2(1)(1)3111(2)x x x x x x -++⎡⎤=-⋅⎢⎥++-⎣⎦ 2(2)(2)11(2)x x x x x +-+=⋅+- x 2x 2+=-. 【点睛】本题考查了多项式乘以多项式,单项式乘以多项式,分式的混合运算,正确的计算是解题的关键. 15.(2023·重庆九龙坡·统考一模)化简:(1)()()()x y x y x x y -+--(2)22221211a a a a a a a ⎛⎫-÷-- ⎪-+-⎝⎭【答案】(1)2y xy -+ (2)1a a - 【分析】(1)先根据平方差公式和单项式乘多项式法则计算,再合并同类项即可;(2)根据分式的混合运算法则计算即可.【详解】(1)解:()()()x y x y x x y -+--222x y x xy =--+2y xy =-+;(2)解:22221211a a a a a a a ⎛⎫-÷-- ⎪-+-⎝⎭ 222(12)21(1)11a a a a a a a a ⎛⎫--+=÷- ⎪---⎝⎭ 2(12)12(1)1a a a a a --=÷-- 2(12)1(1)12a a a a a--=⨯-- 1a a =-. 【点睛】本题考查整式的混合运算,分式的混合运算.掌握各运算法则是解题关键.16.(2023·重庆九龙坡·重庆市育才中学校联考三模)化简(1)()()23x y x x y -++ (2)222111a a a a a a --⎛⎫+-÷ ⎪++⎝⎭ 【答案】(1)222x xy y ++ (2)1a a- 【分析】(1)根据完全平方公式及单项式乘以多项式的运算法则即可解答;(2)根据分式的混合运算法则即可解答.【详解】(1)解;()()23x y x x y -++()22223x xy y x xy =-+++22223x xy y x xy =-+++ 222x xy y =++;(2)解:222111a a a a a a --⎛⎫+-÷ ⎪++⎝⎭ ()()21122+111a a a a a a a a +-⎛⎫--=÷ ⎪+++⎝⎭ 2222111a a a a a a -+--=÷++ ()()21111a a a a a -=-÷++ ()()21111a a a a a -=+⨯+- 1a a-=; 【点睛】本题考查了完全平方差公式,单项式乘以多项式运算法则,分式的混合运算法则,掌握对应法则是解题的关键.17.(2023·重庆渝中·重庆巴蜀中学校考一模)计算:(1)()()232x x y x y -+- (2)22411369a a a a -⎛⎫-÷ ⎪+++⎝⎭ 【答案】(1)2275y xy x +- (2)31a a +-+ 【分析】()1原式利用单项式乘多项式法则,以及完全平方公式化简,去括号合并即可得到结果; ()2原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.【详解】(1)原式222344x xy x xy y =-+-+2257x xy y =-+(2)原式()()()21143333a a a a a a +-+⎛⎫=-÷ ⎪++⎝⎭+ ()()()2343311a a a a a +--=⋅++- ()()()231311a a a a a +-=-⋅++- 3.1a a +=-+【点睛】此题考查了分式的混合运算,单项式乘多项式,以及完全平方公式,熟练掌握运算法则及公式是解本题的关键.18.(2023·重庆沙坪坝·重庆南开中学校考二模)计算:(1)()223()31b ab a b b a ⋅+--+; (2)2222132193a a a a a a a ⎛⎫++++÷+- ⎪-+⎝⎭. 【答案】(1)22a ab - (2)13a a+- 【分析】(1)先根据单项式乘法法则、完全平方公式、单项式乘多项式法则进行展开,然后再合并同类项即可;(2)根据分式的基本性质和去括号法则进行分析判断,然后化简即可.【详解】(1)()223()31b ab a b b a ⋅+--+22222323ab a ab b ab b =+-+--22a ab =-(2)2222132193a a a a a a a ⎛⎫++++÷+- ⎪-+⎝⎭ ()()()()()2121÷1333a a a a a a a ⎡⎤+++=+-⎢⎥+-+⎣⎦ ()()()()()()()211321÷3333a a a a a a a a a ⎡⎤+++++=-⎢⎥+-++⎣⎦()()()()()()()211321333÷a a a a a a a a +++-++=+-+ ()()()()()()()213·331321a a a a a a a a ++=+-++-++ ()()()()()()213·33132a a a a a a a ++=+-⎡⎤++-+⎣⎦ ()211·31a a a +=-+ 13a a+=-.【点睛】本题主要考查分式的混合运算,掌握相关知识,及运算法则是解题的关键.19.(2023·重庆九龙坡·重庆市育才中学校联考二模)计算:(1)()()224a b a a b +-+; (2)22221121m m m m +⎛⎫+÷ ⎪--+⎝⎭. 【答案】(1)24b ; (2)12m - 【分析】(1)利用完全平方公式和单项式乘多项式的运算法则计算乘方和乘法,然后合并同类项进行化简; (2)先将小括号内的式子进行通分计算,然后再算括号外面的除法.【详解】(1)解:原式222444a ab b a ab =++--24b =;(2)解:原式()()22121111m m m m m +-⎛⎫=+÷ ⎪--⎝⎭- ()()211121m m m m -+=-+ 12m -= 【点睛】本题考查整式的混合运算,分式的混合运算,掌握完全平方公式、分式混合运算的运算顺序(先算乘方,然后算乘除,最后算加减,有小括号先算小括号里面的)和计算法则是解题关键.20.(2023·重庆渝中·重庆巴蜀中学校考二模)计算:(1)()()()()32242422a b a b b a b a b a b -++-÷-(2)222623969x x x x x ⎛⎫+÷ ⎪+--+⎝⎭. 【答案】(1)2a ab +(2)33x x -+ 【分析】(1)根据整式的混合运算法则计算即可;(2)根据分式的运算法则计算即可.【详解】(1)解:原式222244ab ab b a b =-++-2a ab =+(2)解:原式22(3)6(3)(3)(3)(3)(3)2x x x x x x x ⎡⎤--=+⋅⎢⎥+-+-⎣⎦ 22(3)(3)(3)2x x x x x-=⋅+- 33x x -=+ 【点睛】本题考查了整式混合运算和分式混合运算,熟练掌握整式除法、完全平方公式、平方差公式以及整式的运算法则,分式的运算法则是解题的关键.21.(2023·重庆·重庆实验外国语学校校考二模)化简:(1)()()()21214x x x x -+-+ (2)2192122x x x x --⎛⎫-÷ ⎪++⎝⎭ 【答案】(1)2341x x -- (2)23x -- 【分析】(1)先计算平方差、单项式乘多项式,再合并同类项;(2)先将括号内式子通分,再将分式除法变形为乘法,最后约分化简.【详解】(1)解:()()()21214x x x x -+-+()22=414x x x --+22=414x x x ---2=341x x --(2)解:2192122x x x x --⎛⎫-÷ ⎪++⎝⎭ ()()()33122121x x x x x x +----=÷++ ()()()()321133x x x x x -++=⋅++-23x =-- 【点睛】本题考查整式的混合运算,平方差公式的应用,分式的混合运算,掌握运算法则和运算顺序是解题的关键.22.(2023·重庆九龙坡·统考二模)化简:(1)()()()x y x y x x y -+-- (2)22221211a a a a a a a ⎛⎫-÷-- ⎪-+-⎝⎭【答案】(1)2y xy -+ (2)1a a - 【分析】(1)先计算平方差公式、单项式乘以多项式,再计算整式的加减法即可得;(2)先计算括号内的分式减法,再计算分式的除法即可得.【详解】(1)解:原式222x y x xy =--+2y xy =-+.(2)解:原式()()()222121111a a a a a a a --=÷--⎡⎤⎢⎥⎢-⎣⎦-⎥ ()()2221221111a a a a a a a a -⎛⎫-+=÷- ⎪---⎝⎭ ()()2121211a a a a a --=÷-- ()()2121121a a a a a --=⋅-- 1a a =-. 【点睛】本题考查了整式的混合运算、分式的减法与除法运算,熟练掌握整式和分式的运算法则是解题关键.23.(2023·重庆大渡口·统考二模)计算:(1)()()222x y y x y x -+-+; (2)22241244a a a a -⎛⎫+÷ ⎪--+⎝⎭. 【答案】(1)22x (2)2a a + 【分析】(1)根据完全平方公式和整式加减的运算法则计算即可;(2)根据分式的加减运算法则及乘除法运算法则计算即可.【详解】(1)()()222x y y x y x -+-+222222x xy y xy y x =-++-+ 22x x =+22x =;(2)22241244a a a a -⎛⎫+÷ ⎪--+⎝⎭ 222(2)2(2)(2)a a a a a -+-=⋅-+- 2a a =+. 【点睛】本题主要考查了整式及分式的混合运算,解题的关键是熟练运用整式与分式的混合运算法则,属于基础题.24.(2023·重庆江津·重庆市江津中学校校考二模)计算:(1)2(2)()()x y x y x y ---+; (2)2211211x x x x x -⎛⎫÷+ ⎪-+-⎝⎭. 【答案】(1)254y xy -(2)1【分析】(1)根据完全平方公式以及平方差公式即可求出答案;(2)先对前半部分分子分母进行因式分解,括号里的部分进行通分,再将分式除法转化为乘法,进行约分化简即可.【详解】(1)觧:2(2)()()x y x y x y ---+,222244x xy y x y =-+-+,254y xy =-;(2)2211211x x x x x -⎛⎫÷+ ⎪-+-⎝⎭, 2(1)11(1)11x x x x x x --⎛⎫=÷+ ⎪---⎝⎭, 2(1)(1)1x x x x x -=÷--, 2(1)1(1)x x x x x--=⋅-, 1=.【点睛】本题考查了整式的混合运算,分式的混合运算,解题的关键是熟练运用完全平方公式、平方差公式、分式运算法则是解答本题的关键.25.(2023·重庆渝中·统考二模)计算:(1)()()()233x x x x +--+;(2)(a b +﹣2b a b+)22241a b a ab -÷+. 【答案】(1)29x + (2)22a a b- 【分析】(1)先计算单项式乘多项式,再利用平方差公式计算,然后合并即可;(2)先把括号内通分和除法运算化为乘法运算,再把分子分母因式分解,然后约分即可.【详解】(1)()()()233x x x x +--+()2229x x x =+--2229x x x =+-+ 29x =+;(2)22224()b a b a b a b a ab-+-÷++ 22()()(2)(2)a b b a a b a b a b a b +-+=⋅++- ()()()222222a a b a ab b b a b a b a b +++-=⋅++- ()2a a b a b +=+()()()22a a b a b a b +⋅+- =22a a b-. 【点睛】本题考查了分式的混合运算:先乘方,再乘除,然后加减,有括号的先算括号里面的.也考查了完全平方公式.26.(2023·重庆九龙坡·重庆实验外国语学校校考三模)计算:(1)()()2a b a a b +-+ (2)283111m m m m m -⎛⎫+-÷ ⎪--⎝⎭ 【答案】(1)2ab b +(2)3m m+ 【分析】(1)根据完全平方公式和单项式乘以多项式进行运算,再合并同类项即可.(2)括号内的式子通分,根据分式的混合运算顺序进行运算即可.【详解】(1)解:原式2222a ab b a ab =++--2ab b =+;(2)解:原式()2318111m m m m m m -⎛⎫-=-÷ ⎪---⎝⎭ ()29113m m m m m --=⋅-- ()()()33113m m m m m m +--=⋅-- 3m m+=. 【点睛】本题考查了整式的混合运算以及分式的混合运算,熟练掌握运算法则及运算顺序是解题的关键. 27.(2023·重庆沙坪坝·重庆一中校考三模)计算:(1)()()222a b b b a a a ---+⋅ (2)2221214421x x x x x x x x x --++⎛⎫÷-⋅ ⎪++⎝⎭ 【答案】(1)23a a + (2)21x x +- 【分析】(1)根据完全平方公式,单项式乘以单项式,同底数幂的乘法进行计算即可求解;(2)根据分式的加减计算括号内的,同时将除法转化为乘法,再根据分式的性质化简【详解】(1)解:原式222322a ab b b ab a =-+-++23a a =+;(2)解:原式()()()()221122121x x x x x x x x x +-+-+=÷⋅++()()()()()22112211x x x x x x x x +-+=⨯++-21x x +=-. 【点睛】本题考查了整式的乘法与分式的混合运算,熟练掌握乘法公式以及分式的运算法则是解题的关键. 28.(2023·重庆渝中·重庆巴蜀中学校考三模)计算(1)()()()32242a a b a b a b ÷-++- (2)22311x x x x x -⎛⎫÷-+ ⎪++⎝⎭【答案】(1)224a ab - (2)212x x-+ 【分析】(1)先计算幂的乘方、单项式乘多项式、完全平方公式,再计算同底数幂的除法,然后计算加减法即可得;(2)先计算括号内的分式加法,再计算分式的除法即可得.【详解】(1)解:原式6422222a a ab b a ab b =÷--+-+224a a ab =+-224a ab =-.(2)解:原式()()()1112311x x x x x x x ⎡⎤-+-=÷+⎢⎥++⎣⎦+ ()2213111x x x x x x ⎛⎫--=÷+ ⎪++⎝⎭+ ()22411x x x x x --=÷++ ()()()12122x x x x x x -+=⋅+-+ ()12x x =-+ 212x x =-+. 【点睛】本题考查了幂的乘方、单项式乘多项式、完全平方公式、同底数幂的除法、分式的混合运算,熟练掌握各运算法则是解题关键.。
2024全国各地区数学中考真题汇编《第一期》

数学几何图形的相关计算1.(2024达州10题4分)如图,△ABC是等腰直角三角形,∠ABC=90°,AB=4,点D,CE,则下列E分别在AC,BC边上运动,连接AE,BD交于点F,且始终满足AD=√=√2;②∠DFE=135°;③△ABF面积的最大值是4√2-4;④CF的最小值是结论:①2√10-2√2.其中正确的是( )A.①③B.①②④C.②③④D.①②③④第1题图【推荐地区:安徽】解图①解图②第1题解图解直角三角形及其应用2.(2024遂宁19题8分)小明的书桌上有一个L型台灯,灯柱AB高40cm,他发现当灯带BC与水平线BM夹角为9°时(图①),灯带的直射宽DE(BD⊥BC,CE⊥BC)为35cm,但此时灯的直射宽度不够,当他把灯带调整到与水平线夹角为30°时(图②),直射宽度刚好合适,求此时台灯最高点C到桌面的距离.(结果保留1位小数)(sin9°≈0.16,cos9°≈0.99,tan9°≈0.16)图①图②第2题图【推荐地区:安徽、山西、浙江】【参考答案】2.解:如题图,∵BD⊥BC,CE⊥BC,∴BD∥CE.∵BM∥DE,∴四边形BDEM为平行四边形,∴BM=DE=35cm,∴BC=BM·cos9°≈34.65cm,如解图,过点C作D’E’的垂线分别交BM与点F,交D’E’于点G.在Rt△BCF中,CF=BC·sin30°≈17.3cm,∴CH=sin30°×cos9°×BM=×0.99×35=17.3(m),∴此时台灯最高处到左面的距离CG=CF+AB=17.3+40=57.3(cm).第2题解图一次函数与反比例函数的综合应用3.(2024自贡24题10分)如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数myx=的图象交于A(-6,1),B(1,n)两点.第3题图(1)求反比例函数和一次函数的解析式;(2)P是直线x=-2上的一个动点,△PAB的面积为21,求点P坐标;(3)点Q在反比例函数myx=位于第四象限的图象上,△QAB的面积为21,请直接写出Q点坐标.【推荐地区:安徽、江西、浙江】第3题解图,统计与概率4.(2024重庆B卷20题10分)数学文化有利于激发学生数学兴趣.某校为了解学生数学文化知识掌握的情况,从该校七、八年级学生中各随机抽取10名学生参加了数学文化知识竞赛,并对数据(百分制)进行整理、描述和分析(成绩均不低于70分,用x表示,共分三组:A.90≤x≤100,B.80≤x<90,C.70≤x<80),下面给出了部分信息:七年级10名学生的竞赛成绩是:76,78,80,82,87,87,87,93,93,97.八年级10名学生的竞赛成绩在B组中的数据是:80,83,88,88.八年级抽取的学生竞赛成绩扇形统计图七、八年级抽取的学生竞赛成绩统计表第4题图根据以上信息,解答下列问题:(1)填空:a=________,b=________,m=________;(2)根据以上数据,你认为该校七、八年级中哪个年级学生数学文化知识较好?请说明理由(写出一条理由即可);(3)该校七年级学生有500人,八年级学生有400人.估计该校七、八年级学生中数学文化知识为“优秀”(x≥90)的总共有多少人?【推荐地区:安徽、江西、浙江、湖南】【参考答案】4.(1)88,87,40;【解法提示】∵八年级10名学生的竞赛成绩在C组的有10×20%=2名,∴将八年级10名学生的竞赛成绩按照从小到大的顺序进行排列,在中间的两个数分别是88,88,∴=88;∵七年级10名学生的竞赛成绩中87出现的次数最多,∴b=87;∵八年级a=10名学生的竞赛成绩在B组的有4名,∴在A组的有10-2-4=4名,∴A组所占百分比为40%,即m=40.(2)八年级的数学文化知识较好,理由:七、八年级10名学生的竞赛成绩平均数相同,八年级的中位数和众数均大于七年级;(3)500×+400×40%=310(人).∴估计该校七、八年级学生中数学文化知识为“优秀”(x≥90)的总共有310人.。
中招考试综合计算专练

综合计算专练一 力学综合应用题(以力为主)(一)纯力学1.如图所示,某工人重,站在水平面上,用的拉力向下匀速拉动绳子,提起一浸没在 600 N 100 N 水中体积为,重的物体。
(物体始终浸没在水中,且忽略水对物体的阻力,1.2×10‒2 m 3 360 N ,)求:ρ水=1×103 kg/m 3 g =10N/kg (1)已知工人双脚与地面的总接触面积是,工人没有拉动绳子时对地面的压强;3×10‒2 m 2 (2)物体浸没在水中时受到的浮力;(3)提起物体时滑轮组的机械效率。
2.2014年5月17日,国外媒体报道了我国最先进的“翼龙”无人机出口沙特的消息,引起了人们对中国无人机的关注.翼龙无人机机身质量1.1吨,翼展14米,机长9米,最大升空高度5300米(16400英尺),其他参数如表格所示。
(1)翼龙无人机头部设计成流线型,且表面复合材料极其光滑,目的是 。
(2)翼龙无人机满载燃油,并以最大载荷量停在水平跑道上蓄势待发,此时无人机轮胎与地面接触的总面积为。
无人机对水平跑道的压强是多大?0.04 m 2(3)翼龙无人机若以正常巡航速度从某机场飞往相距2000千米的目的地执行任务,需飞行多少小时?最大飞行速度280千米/时正常巡航速度160千米/时最大续航时间20小时最大续航航程4000千米最大载荷量200千克最大载燃油量300千克3.“蛟龙号”创造了“中国深度”——下潜。
今年“蛟龙号”将远赴印度洋探索深 7062 m 2700 m 处活火山的奥秘。
已知:海水密度,声音在海水中的传播速度是ρ=1.03×103 kg/m 3 ,取。
问:1500 m /s g =10N/kg (1)“蛟龙号”下潜到深度时受到的海水压强是多少?2700 m (2)电磁波传播速度大,但是在海水中的传输距离很短,母船与“蛟龙号”的信息传递要借助于声呐。
在深处的“蛟龙号”收到正上方母船的指令需要多长时间?2700 m (3)“蛟龙号”到达海底扔掉部分配重后,排开水的重力是,它受到的浮力是多少?5×105 N (4)你认为“蛟龙号”面临的主要技术难题是什么(答出一条即可)?(二)力热综合4.“郑州宇通”是我省龙头企业之一,如图所示是宇通公司出产的专用校车车型。
中考数学真题分类汇编——几何综合题(含答案)

中考数学真题分类汇编——几何综合题(含答案)类型1 类比探究的几何综合题类型2 与图形变换有关的几何综合题类型3 与动点有关的几何综合题类型4 与实际操作有关的几何综合题类型5 其他类型的几何综合题类型1 类比探究的几何综合题(2018苏州)(2018烟台)(2018东营)(1)某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=33,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).请回答:∠ADB= °,AB= .(2)请参考以上解决思路,解决问题:如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=33,∠ABC=∠ACB=75°, BO:OD=1:3,求DC的长.(2018长春)(第24题图1) (第24题图2) (第24题图3)(2018陕西)(2018齐齐哈尔)(2018河南)(2018仙桃)问题:如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A 逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为;探索:如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;应用:如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.(2018襄阳)如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明与推断:①求证:四边形CEGF是正方形;的值为;②推断:AGBE(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE 之间的数量关系,并说明理由;(3)拓展与运用正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=22,则BC= .(2018淮安)(2018咸宁)(2018黄石)在△ABC 中,E 、F 分别为线段AB 、AC 上的点(不与A 、B 、C 重合). (1)如图1,若EF ∥BC ,求证:AEF ABC S AE AFS AB AC∆∆= (2)如图2,若EF 不与BC 平行,(1)中的结论是否仍然成立?请说明理由;(3)如图3,若EF 上一点G 恰为△ABC 的重心,34AE AB =,求AEFABC S S ∆∆的值.BBB(2018山西)(2018盐城)【发现】如图①,已知等边ABC ,将直角三角形的60角顶点D 任意放在BC 边上(点D 不与点B 、C 重合),使两边分别交线段AB 、AC 于点E 、F .(1)若6AB=,4AE=,2BD=,则CF=_______;(2)求证:EBD DCF∆∆.【思考】若将图①中的三角板的顶点D在BC边上移动,保持三角板与AB、AC的两个交点E、F都存在,连接EF,如图②所示.问点D是否存在某一位置,使ED平分BEF∠且FD平分CFE∠?若存在,求出BDBC的值;若不存在,请说明理由.【探索】如图③,在等腰ABC∆中,AB AC=,点O为BC边的中点,将三角形透明纸板的一个顶点放在点O处(其中MON B∠=∠),使两条边分别交边AB、AC于点E、F(点E、F均不与ABC∆的顶点重合),连接EF.设Bα∠=,则AEF∆与ABC∆的周长之比为________(用含α的表达式表示).(2018绍兴)(2018达州)(2018菏泽)(2018扬州)问题呈现如图1,在边长为1的正方形网格中,连接格点D、N和E、C,DN与EC相交于点P,求tan CPN∠的值.方法归纳求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中CPN∠不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点M、N,可得∠就变换到中Rt DMN∆.∠=∠,连接DM,那么CPNMN EC,则DNM CPN//问题解决(1)直接写出图1中tan CPN ∠的值为_________;(2)如图2,在边长为1的正方形网格中,AN 与CM 相交于点P ,求cos CPN ∠的值; 思维拓展(3)如图3,AB BC ⊥,4AB BC =,点M 在AB 上,且AM BC =,延长CB 到N ,使2BN BC =,连接AN 交CM 的延长线于点P ,用上述方法构造网格求CPN ∠的度数.(2018常德)已知正方形ABCD 中AC 与BD 交于O 点,点M 在线段BD 上,作直线AM 交直线DC 于E ,过D 作DH AE ⊥于H ,设直线DH 交AC 于N .(1)如图14,当M 在线段BO 上时,求证:MO NO =;(2)如图15,当M 在线段OD 上,连接NE ,当//EN BD 时,求证:BM AB =; (3)在图16,当M 在线段OD 上,连接NE ,当NE EC ⊥时,求证:2AN NC AC =⋅.(2018滨州)(2018湖州)(2018自贡)如图,已知AOB 60∠=,在AOB ∠的平分线OM 上有一点C ,将一个120°角的顶点与点C 重合,它的两条边分别与直线OA OB 、相交于点D E 、 .⑴当DCE ∠绕点C 旋转到CD 与OA 垂直时(如图1),请猜想OE OD +与OC 的数量关系,并说明理由;⑵当DCE ∠绕点C 旋转到CD 与OA 不垂直时,到达图2的位置,⑴中的结论是否成立?并说明理由; ⑶当DCE ∠绕点C 旋转到CD 与OA 的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给于证明;若不成立,线段OD OE 、与OC 之间又有怎样的数量关系?请写出你的猜想,不需证明.(2018嘉兴、舟山)O BOO B图3.(2018淄博)(1)操作发现:如图①,小明画了一个等腰三角形ABC ,其中AB AC =,在ABC ∆的外侧分别以,AB AC 为腰作了两个等腰直角三角形ABD ACE ,,分别取,BD CE ,BC 的中点,,M N G ,连接,GM GN .小明发现了:线段GM 与GN 的数量关系是 ;位置关系是 . (2)类比思考:如图②,小明在此基础上进行了深入思考.把等腰三角形ABC 换为一般的锐角三角形,其中AB AC >,其它条件不变,小明发现的上述结论还成立吗?请说明理由. (3)深入研究:如图③,小明在(2)的基础上,又作了进一步的探究.向ABC ∆的内侧分别作等腰直角三角形,ABD ACE ,其它条件不变,试判断GMN ∆的形状,并给与证明.类型2 与图形变换有关的几何综合题(2018宜昌)在矩形ABCD 中,12AB =,P 是边AB 上一点,把PBC 沿直线PC 折叠,顶点B 的对应点是点G ,过点B 作BE CG ⊥,垂足为E 且在AD 上,BE 交PC 于点F . (1)如图1,若点E 是AD 的中点,求证:AEB DEC ∆∆≌; (2) 如图2,①求证: BP BF =;②当AD 25=,且AE DE <时,求cos PCB ∠的值; ③当BP 9=时,求BE EF 的值.图1 图2 图2备用图 23.(1)证明:在矩形ABCD 中,90,A D AB DC ∠=∠==, 如图1,又AE DE =,图1∆≅∆,ABE DCE(2)如图2,图2①在矩形ABCD中,90∠=,ABC∆沿PC折叠得到GPC∆BPC∠=∠∴∠=∠=,BPC GPC PGC PBC90⊥BE CG∴,BE PG//∴∠=∠GPF PFBBPF BFP∴∠=∠∴=BP BFAD=时,②当25∠=BEC90∴∠+∠=,90AEB CED90AEB ABE ∠+∠=,CED ABE ∴∠=∠ 又90A D ∠=∠=,ABE DEC ∴∆∆∽AB DEAE CD∴=∴设AE x =,则25DE x =-,122512xx -∴=, 解得19x =,216x =AE DE <9,16AE DE ∴==, 20,15CE BE ∴==,由折叠得BP PG =,BP BF PG ∴==,//BE PG , ECF GCP ∴∆∆∽EF CEPG CG∴=设BP BF PG y ===,152025y y -∴=253y ∴=则253BP = 在Rt PBC ∆中,PC =,cos 10BC PCB PC ∠=== ③若9BP =,解法一:连接GF ,(如图3)90GEF BAE ∠=∠=, //,BF PG BF PG =∴四边形BPGF 是平行四边形BP BF =,∴平行四边形BPGF 是菱形//BP GF ∴, GFE ABE ∴∠=∠, GEF EAB ∴∆∆∽EF ABGF BE∴=129108BE EF AB GF ∴==⨯= 解法二:如图2,90FEC PBC ∠=∠=,EFC PFB BPF ∠=∠=∠, EFC BPC ∴∆∆∽EF CEBP CB∴=又90BEC A ∠=∠=, 由//AD BC 得AEB EBC ∠=∠,AEB EBC ∴∆∆∽AB CEBE CB∴=AE EFBE BP∴=129108BE EF AE BP ∴==⨯=解法三:(如图4)过点F 作FH BC ⊥,垂足为HBPF PFEGS BF BFS EF PG BE∆==+四边形图41212BFC BEC S BF EF BC EFBE S BC ∆∆⋅===⨯ 912EFBE ∴=129108BE EF ∴=⨯=(2018邵阳)(2018永州)(2018无锡)(2018包头)(2018赤峰)(2018昆明)(2018岳阳)(2018宿迁)(2018绵阳)(2018南充)(2018徐州)类型3 与动点有关的几何综合题(2018吉林)(2018黑龙江龙东)(2018黑龙江龙东)(2018广东)已知Rt△OAB,∠OAB=90o,∠ABO=30o,斜边OB=4,将Rt△OAB绕点O顺时针旋转60o,如图25-1图,连接BC.(1)填空:∠OBC=_______o;(2)如图25-1图,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)如图25-2图,点M、N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止.已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒.设运动时间为x秒,△OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?(结果可保留根号)(2018衡阳)(2018黔东南)如图1,已知矩形AOCB,6cm s的AB cm=,动点P从点A出发,以3/=,16BC cm速度向点O运动,直到点O为止;动点Q同时从点C出发,以2/cm s的速度向点B运动,与点P同时结束运动.(1)点P 到达终点O 的运动时间是________s ,此时点Q 的运动距离是________cm ; (2)当运动时间为2s 时,P 、Q 两点的距离为________cm ; (3)请你计算出发多久时,点P 和点Q 之间的距离是10cm ;(4)如图2,以点O 为坐标原点,OC 所在直线为x 轴,OA 所在直线为y 轴,1cm 长为单位长度建立平面直角坐标系,连结AC ,与PQ 相交于点D ,若双曲线ky x=过点D ,问k 的值是否会变化?若会变化,说明理由;若不会变化,请求出k 的值.(2018青岛)已知:如图,四边形ABCD ,//,AB DC CB AB ⊥,16,6,8AB cm BC cm CD cm ===,动点P 从点D 开始沿DA 边匀速运动,动点Q 从点A 开始沿AB 边匀速运动,它们的运动速度均为2/cm s .点P 和点Q 同时出发,以QA QP 、为边作平行四边形AQPE ,设运动的时间为()t s ,05t <<.根据题意解答下列问题: (1)用含t 的代数式表示AP ;(2)设四边形CPQB 的面积为()2S cm ,求S 与t 的函数关系式; (3)当QP BD ⊥时,求t 的值;(4)在运动过程中,是否存在某一时刻t ,使点E 在ABD ∠的平分线上?若存在,求出t 的值;若不存在,请说明理由.(2018广州)如图12,在四边形ABCD 中,∠B=60°,∠D=30°,AB=BC. (1)求∠A+∠C 的度数(2)连接BD,探究AD,BD,CD 三者之间的数量关系,并说明理由。
中考物理真题分类汇编专题22电热综合计算含解析

专题22电热综合计算1.(2005天津,31)质量为2kg ,温度为15℃的水,当吸收了1.68×105J 的热量后,温度升高到多少摄氏度[c 水=4.2×103J/(kg·℃)]?【答案】35℃【解析】由t cm Q ∆=,知℃℃202102.4J 1068.135=⨯⨯⨯==∆cm Q t ,即温度升高了20℃; 温度升高到℃℃℃3520150=+=∆+=t t t2.(2006天津,31)质量为500 g 的铁锅中放有3 kg 的水,把它们从15℃加热到85℃,吸收了多少热量?[c 铁=0.46×103J /(kg·℃),c 水=4.2×103J /(kg·℃)]【答案】8.981×105J【解析】Q=c 铁m 铁(t 2-t 1)+c 水m 水(t 2-t 1)=0.46×103J /(kg·℃)×0.5 kg×70 ℃+4.2×103J /(kg·℃)×3 kg×70 ℃ =8.981×105J3.(2007天津,31)把质量为2kg ,温度为30℃的铝块加热到100℃,铝块吸收的热量是多少焦耳?[铝的比热容为0.88×103J /(kg·℃)]【答案】1.232×105J【解析】Q=c 铝m 铝(t-t 0)=0.88×103J /(kg·℃)×2kg×(100℃-30℃)=1.232×105J4.(2008天津,24)已知铝的比热容是0.88×103J/(kg·℃).它表示质量是l kg 的铝块温度升高1℃时吸收吸收的热量为.依据上述比热容的物理意义.请计算:把质量为5 kg 、温度为20℃的铝块加热剑100℃.铝块吸收的热量是多少?【答案】0.88×103J ;3.52×105J【解析】比热容的物理意义为单位质量的某物体温度升高1℃时所吸收的热量; Q=c 铝m 铝(t-t 0)=0.88×103J /(kg·℃)×5kg×(100℃-20℃)=3.52×105J 。
中考复习专题——计算题50道专练(含答案)精编版

1.计算:(﹣1)2015+﹣()﹣2+sin45°.【答案】-7.【解析】试题分析:本题涉及零指数幂、乘方、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:原式=-1+2-9+1=-7.考点:实数的混合运算.2.计算:0114cos 452(5)()84π-︒--+-+-.【答案】3【解析】 试题分析:根据实数的运算性质计算,要注意2cos 452?,22-=,0(5)1π-=,11()44-=,822=.试题解析:解:原式=22412224-++-⨯=3.考点:实数混合运算 3.(本题6分)9+(21)-1-2sin45°+|-2013|【答案】2017【解析】试题分析:原式=3+2-1+2013 =2017考点: 实数的运算4.计算:()101122tan60201413-⎛⎫-︒+-- ⎪⎝⎭. 【答案】2-.【解析】试题分析:针对二次根式化简,特殊角的三角函数值,零指数幂,负整数指数幂4个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:解:原式=2323132-+-=-.考点:1.实数的运算;2.二次根式化简;3.特殊角的三角函数值;4.零指数幂;5.负整数指数幂.5.计算:020116sin30223275-⎛⎫⎛⎫--++- ⎪ ⎪-⎝⎭⎝⎭【答案】3.【解析】试题分析:针对负整数指数幂,特殊角的三角函数值,零指数幂,绝对值4个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:解:原式=146123243123232-⨯-++-=--++-=.考点:1.实数的运算;2.负整数指数幂;3.特殊角的三角函数值;4.零指数幂;5.绝对值.6.计算:()20012014sin 60323π-⎛⎫+-++- ⎪⎝⎭. 【答案】3122-.【解析】试题分析:针对负整数指数幂,零指数幂,特殊角的三角函数值,绝对值4个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:解:原式=3391231222+++-=-.考点:1.实数的运算;2.负整数指数幂;3.零指数幂;4.特殊角的三角函数值;5.绝对值.7.计算:100120142sin 3082-⎛⎫--+ ⎪⎝⎭. 【答案】22.【解析】试题分析:针对负整数指数幂,零指数幂,特殊角的三角函数值,二次根式化简4个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:解:原式=12122221122222--⨯+=--+=. 考点:1.实数的运算;2.负整数指数幂;3.零指数幂;4.特殊角的三角函数值;5.二次根式化简.8.计算:()()020141321sin452-+-+-︒; 【答案】2.【解析】试题分析:针对零指数幂,有理数的乘方,二次根式化简,特殊角的三角函数值4个考点分别进行计算,然后根据实数的运算法则求得计算结果. 试题解析:解:原式=2211222++-=. 考点:1.实数的运算;2.零指数幂;3.有理数的乘方;4.二次根式化简;5.特殊角的三角函数值. 9.计算:()20142sin45421--+︒+-【答案】3.【解析】试题分析:针对二次根式化简,有理数的乘方,特殊角的三角函数值,绝对值4个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:解:原式=22122212232+-⨯+=+-+=. 考点:1.实数的运算;2.二次根式化简;3.有理数的乘方;4.特殊角的三角函数值;5.绝对值. 10.计算:12-2sin60°+(-2014)0-(13)-1. 【答案】3-2.【解析】试题分析:根据零指数幂、负指数幂、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:原式=23-2×32+1-3 =23-3+1-3 =3-2.考点:1.实数的运算;2.零指数幂;3.负整数指数幂;4.特殊角的三角函数值.11.计算:4 cos45°-8+(π-3) +(-1)3; 【答案】0【解析】解:原式=4×22-22+1-1=012.计算:﹣25+(12)﹣1﹣|16﹣8|+2cos60°. 【答案】﹣33.【解析】试题分析:第一项利用乘方的意义化简,第二项利用负指数幂法则计算,第三项利用绝对值的代数意义化简,最后一项利用特殊角的三角函数值计算即可 .试题解析:原式=﹣32+2﹣4+1=﹣33.考点:1.实数的运算2.负整数指数幂3.特殊角的三角函数值.13.计算:(π﹣3.14)0+(﹣1)2015+|1﹣|﹣3tan30°.【答案】-1【解析】试题分析:按顺序依次利用零指数幂法则、乘方的意义、绝对值的代数意义、特殊角的三角函数值计算即可得到结果试题解析:原式=1﹣1+3﹣1﹣3×33=1﹣1+3﹣1﹣3=﹣1. 考点:1、实数的运算;2、零指数幂;3、绝对值;4、特殊角的三角函数值..14.计算:()10011820082cos 454π-⎛⎫---+ ⎪⎝⎭ 【答案】223+.°【解析】试题分析:原式第一项利用二次根式的化简公式计算,第二项利用零指数幂法则计算,第三项利用特殊角的三角函数计算,最后一项利用负指数幂法则,计算即可得到结果.试题解析:原式=232124=2232--⨯++. 考点:1.二次根式的化简2.零指数幂法则3.特殊角的三角函数4.负指数幂法则.15.计算:011(32)4cos30123||--++--()° 【答案】4.【解析】试题分析:分别用零指数次幂,负指数幂法则,特殊角的三角函数,绝对值的意义,进行化简,最后用实数的运算法则计算即可. 试题解析:原式3134122=++-⨯ 42323=+-4= . 考点:1.零指数次幂2.负指数幂法则3.特殊角的三角函数4.绝对值的意义. 16.计算: ()()202012312sin 302813π-︒⎛⎫---+--+- ⎪⎝⎭【答案】10-.【解析】试题分析:分别求出特殊角的三角函数,负指数次幂,零指数次幂,立方根,负数的偶次幂,再依据实数的运算法则计算即可.试题解析:原式=12912119121102-⨯-+-+=--+-+=-. 考点:1.特殊角的三角函数2.负指数次幂3.零指数次幂4.立方根.17.计算:|345tan |32)31()21(10-︒+⨯+-- 【答案】33.【解析】试题分析:原式第一项利用零指数幂法则计算,第二项利用负整数指数幂法则计算,第三项化为最简二次根式,最后一项利用绝对值的代数意义化简,计算即可得到结果.试题解析:原式=1+3×233+|1-3| =1+23+31- =33考点:1.实数的混合运算;2.零指数幂;3.负整数指数幂;4.特殊角的三角函数值.18.计算:|1﹣2|+(π﹣2014)0﹣2sin45°+(12)﹣2. 【答案】4.【解析】试题分析:先求出绝对值、零指数幂、负整指数幂、特殊角的三角函数值,然后根据实数的运算法则求得计算结果.试题解析:原式=2﹣1+1﹣2+4=4.考点:1.绝对值2.零指数幂3.负整指数幂4.特殊角的三角函数.19.计算:()21-︒-45sin 4+3-+8【答案】4【解析】试题分析:按照运算顺序计算,先算平方、特殊角的三角函数值、绝对值、二次根式的化简,然后按从左到右的顺序依次计算就可以试题解析:原式=1-4×22+3+22= 4 考点:1、平方;2、绝对值;3、实数的混合运算20.计算:. 【答案】3-7【解析】试题分析:先进行二次根式的化简、特殊角的三角函数值、零指数幂、负整数指数幂等运算,然后按照运算顺序进行计算即可.试题解析:原式=23﹣2×23+1﹣8=3-7 考点:1、二次根式的化简;2、零指数幂;3、负整数指数幂;4、特殊角的三角函数值.21.计算:20113015(1)()(cos68)338sin 602π---+++-. 【答案】-8+3【解析】原式31813382=--++-⨯ 83=-+22.计算:【答案】4.【解析】试题分析:根据特殊角的三角函数值进行计算.试题解析:考点:(1)二次根式的运算;(2)特殊角的三角函数.23.计算:01201314cos 452(5)()8(1)4π-︒--+-+---【答案】4.【解析】试题分析:先计算特殊角三角函数值、绝对值、零次幂、负整数指数幂、二次根式、有理数的乘方,再进行加减运算.试题解析:原式=242142212⨯-++-+ 224224=+-=考点:实数的混合运算.24.计算:0(3π)-++︒60tan 211()273--. 【答案】43-.【解析】试题分析:针对零指数幂,特殊角的三角函数值,负整数指数幂,二次根式化简4个考点分别进行计算,然后根据实数的运算法则求得计算结果. 试题解析:原式12333343=++-=-.考点:1.零指数幂;2.特殊角的三角函数值;3.负整数指数幂;4.二次根式化简. 25.计算:10012014122sin 605-⎛⎫-+- ⎪⎝⎭. 【答案】43+.【解析】试题分析:针对负整数指数幂,零指数幂,二次根式化简,特殊角的三角函数值 4个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:原式=351232432-+-⋅=+. 考点:1. 负整数指数幂;2.零指数幂;3.二次根式化简;4.特殊角的三角函数值.26.计算:1021182sin 45(32)32-⎛⎫-︒+- ⎪⎝⎭. 【答案】21-.【解析】试题分析:针对二次根式化简,特殊角的三角函数值,幂零指数幂,负整数指数4个考点分别进行计算,然后根据实数的运算法则求得计算结果. 试题解析:原式223221222212132=⨯-⨯+-=--=-. 考点:1. 二次根式化简;2.特殊角的三角函数值;3. 零指数幂.;4. 负整数指数幂27.计算:()101129tan 3042π-⎛⎫-︒+-- ⎪⎝⎭. 【答案】31--.【解析】试题分析:针对二次根式化简,特殊角的三角函数值,零指数幂,负整数指数幂4个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:原式=323912313=-⨯+-=--. 考点:1.二次根式化简;2.特殊角的三角函数值;3.零指数幂;4.负整数指数幂.28.计算: 10184sin 4520142-⎛⎫-︒-+ ⎪⎝⎭. 【答案】1-.【解析】试题分析:针对二次根式化简,特殊角的三角函数值,负整数指数幂,零指数幂4个考点分别进行计算,然后根据实数的运算法则求得计算结果试题解析:原式=22242+112-⨯-=-. 考点:1.二次根式化简;2.特殊角的三角函数值;3.负整数指数幂;4.零指数幂.29.计算:()1020140113tan 452-⎛⎫-+-π-+ ⎪⎝⎭ 【答案】-1【解析】原式= -1+1-2+1=-130.201(3)323tan 30π-+++-+︒【答案】2【解析】试题分析:先算乘方和去掉绝对值及三角函数的运算,再进行有理数的加减运算.试题解析:原式=-1+1+2-3+3×33=2-3+3=2 考点:有理数的混合运算.31.计算:101()3(3)3tan304-+--π-+︒ 【答案】323+.【解析】试题分析:针对负整数指数幂,绝对值,零指数幂,特殊角的三角函数值4个考点分别进行计算,然后根据实数的运算法则求得计算结果. 试题解析:101()3(3)3tan 343304133233-++--+⨯=-+︒=+-π.考点:1.负整数指数幂;2.绝对值;3.零指数幂;4.特殊角的三角函数值.32.计算:103130tan 3)23()12014(-⎪⎭⎫ ⎝⎛++--- 【答案】6【解析】试题分析:先进行零指数幂;负整数指数幂、三角函数值的运算和去括号,再进行加减运算. 试题解析:原式=103130tan 3)23()12014(-⎪⎭⎫ ⎝⎛++--- =1-32++333⨯ +113=1-32++3+3=6考点:1、零指数幂;2、负整数指数幂、3、三角函数值.33.计算:011|3|π12cos302---+--()() 【答案】1.【解析】试题分析:针对绝对值,零指数幂,负整数指数幂,特殊角的三角函数值4个考点分别进行计算,然后根据实数的运算法则求得计算结果. 试题解析:0113|3|π12cos303122=122---++-=-+-⨯()(). 考点:1.绝对值;2.零指数幂;3.负整数指数幂;4.特殊角的三角函数值.34.计算:︒+--+-⨯-+--60tan )31(64)2()1(42302013π 【答案】23-+.【解析】试题分析:根据绝对值、有理数的乘方、立方根、特殊角三角函数值的意义分别进行计算即可求出答案. 原式41493=-+-+ 23=-+.考点:实数的混合运算.35.计算:tan 245°-2sin 30°+(2﹣1)0 -21()2-= 【答案】-3.【解析】试题分析:根据零指数幂、负整指数幂、特殊角的三角函数值,可化简式子,根据实数的运算法则求得计算结果.原式=1-2×12+1−211()2=1-1+1-4=-3.考点:1.实数的运算;2.零指数幂;3.负整数指数幂;4.特殊角的三角函数值.36.计算:432328230232364cos -⨯+︒+-+-()() . 【答案】-6【解析】试题分析:先计算乘方和开方运算,再根据特殊角的三角函数值和平方差公式得到原式=1888316 2(23)(23)(23)42⨯⨯⨯+⨯+-+-- ,然后进行乘除运算后合并即可. 原式=1888316 2(23)(23)(23)42⨯⨯⨯+⨯+-+-- 834323=-++--()()8323=-++-=-6.考点:二次根式的混合运算;特殊角的三角函数值.37.3--(-4)-1+032π⎛⎫ ⎪-⎝⎭-2cos30° 【答案】54. 【解析】试题分析:先计算绝对值、负整数指数幂、零次幂、特殊角的三角函数值,再进行加减运算即可. 原式=1531344++-=. 考点:1.绝对值;2.零次幂;3.负整数指数幂;4.特殊角的三角函数值. 38.计算:︒+--+-⨯-+--60tan )31(64)2()1(42302013π 【答案】23-+.【解析】试题分析:根据绝对值、有理数的乘方、立方根、特殊角三角函数值的意义分别进行计算即可求出答案. 原式41493=-+-+23=-+.考点:实数的混合运算.39.计算:()02822sin 45π+-+--︒ 【答案】122+.【解析】试题分析:针对零指数幂,二次根式化简,绝对值,特殊角的三角函数值4个考点分别进行计算,然后根据实数的运算法则求得计算结果 ()02822sin 4512222122π+-+--︒=++-=+.考点:1.零指数幂;2.二次根式化简;3.绝对值;4.特殊角的三角函数值.40.计算:()10013tan 30132π-⎛⎫--+-+- ⎪⎝⎭ 【答案】1-.【解析】试题分析:针对负整数指数幂,特殊角的三角函数值,零指数幂,绝对值4个考点分别进行计算,然后根据实数的运算法则求得计算结果.原式=3231313--⨯++=-. 考点:1.负整数指数幂;2.特殊角的三角函数值;3.零指数幂;4.绝对值.41.计算: 10182cos 45()(2014)2--︒+-. 【答案】21+.【解析】试题分析:针对二次根式化简,特殊角的三角函数值,负整数指数幂,零指数幂4个考点分别进行计算,然后根据实数的运算法则求得计算结果.原式=222221212-⨯+-=+. 考点:1.二次根式化简;2.特殊角的三角函数值;3.负整数指数幂;1.零指数幂. 42.计算:-12003+()-2-|3-|+3tan60°。
2024年全国各省市数学中考真题汇编 专题5分式及其运算(37题)含详解

专题05分式及其运算(37题)一、单选题1.(2024·甘肃·中考真题)计算:4222a ba b a b-=--()A .2B .2a b-C .22a b-D .2a b a b--2.(2024·黑龙江绥化·中考真题)下列计算中,结果正确的是()A .()2139--=B .()222a b a b +=+C 93=±D .()3263x y x y -=3.(2024·黑龙江牡丹江·中考真题)下列计算正确的是()A .32622a a a ⋅=B .331(2)8a b a b-÷⨯=-C .()322a a a a a a++÷=+D .2233aa -=4.(2024·山东威海·中考真题)下列运算正确的是()A .5510x x x +=B .21m m n n n÷⋅=C .624a a a ÷=D .()325a a -=-5.(2024·广东广州·中考真题)若0a ≠,则下列运算正确的是()A .235a a a+=B .325a a a ⋅=C .235a a a⋅=D .321a a ÷=6.(2024·天津·中考真题)计算3311x x x ---的结果等于()A .3B .xC .1x x -D .231x -7.(2024·河北·中考真题)已知A 为整式,若计算22A y xy y x xy-++的结果为x yxy -,则A =()A .xB .yC .x y +D .x y-二、填空题8.(2024·四川南充·中考真题)计算---a ba b a b的结果为.9.(2024·湖北·中考真题)计算:111m m m +=++.10.(2024·广东·中考真题)计算:333a a a -=--.11.(2024·吉林·中考真题)当分式11x +的值为正数时,写出一个满足条件的x 的值为.12.(2024·山东威海·中考真题)计算:2422x x x+=--.13.(2024·四川内江·中考真题)在函数1y x=中,自变量x 的取值范围是;14.(2024·四川眉山·中考真题)已知11a x =+(0x ≠且1x ≠-),23121111,,,111-==⋯=---n n a a a a a a ,则2024a 的值为.三、解答题15.(2024·广东·中考真题)计算:011233-⨯-+.16.(2024·江苏盐城·中考真题)先化简,再求值:22391a a a a a ---÷+,其中4a =.17.(2024·四川泸州·中考真题)化简:2222y x y x y x x ⎛⎫-+-÷ ⎪⎝⎭.18.(2024·四川广安·中考真题)先化简2344111a a a a a ++⎛⎫+-÷⎪--⎝⎭,再从2-,0,1,2中选取一个适合的数代入求值.19.(2024·山东·中考真题)(11122-⎛⎫+-- ⎪⎝⎭;(2)先化简,再求值:212139a a a +⎛⎫-÷ ⎪+-⎝⎭,其中1a =.20.(2024·上海·中考真题)计算:102|124(1++-.21.(2024·江苏连云港·中考真题)计算0|2|(π1)-+-22.(2024·江苏连云港·中考真题)下面是某同学计算21211m m ---的解题过程:解:2121211(1)(1)(1)(1)m m m m m m m +-=---+-+-①(1)2m =+-②1m =-③上述解题过程从第几步开始出现错误?请写出完整的正确解题过程.23.(2024·江西·中考真题)(1)计算:0π5+-;(2)化简:888x x x ---.24.(2024·江苏苏州·中考真题)计算:()042-+-.25.(2024·福建·中考真题)计算:0(1)5-+-26.(2024·陕西·()()0723-+-⨯.27.(2024·湖南·中考真题)先化简,再求值:22432x x x x x-⋅++,其中3x =.28.(2024·北京·中考真题)已知10a b --=,求代数式()223232a b ba ab b -+-+的值.29.(2024·甘肃临夏·中考真题)计算:10120253-⎛⎫+ ⎪⎝⎭.30.(2024·甘肃临夏·中考真题)化简:21111a a a a a +⎛⎫++÷⎪--⎝⎭.31.(2024·浙江·中考真题)计算:1154-⎛⎫-- ⎪⎝⎭32.(2024·四川广元·中考真题)先化简,再求值:22222a a b a ba b a ab b a b--÷---++,其中a ,b 满足20b a -=.33.(2024·黑龙江牡丹江·中考真题)先化简,再求值:2669x x x x x --⎛⎫÷- ⎪⎝⎭,并从1-,0,1,2,3中选一个合适的数代入求值.34.(2024·山东烟台·中考真题)利用课本上的计算器进行计算,按键顺序如下:,若m 是其显示结果的平方根,先化简:27442393mm m m m m --⎛⎫+÷ ⎪--+⎝⎭,再求值.35.(2024·江苏苏州·中考真题)先化简,再求值:2212124x x xx x +-⎛⎫+÷ ⎪--⎝⎭.其中3x =-.36.(2024·贵州·中考真题)(1)在①22,②2-,③()01-,④122⨯中任选3个代数式求和;(2)先化简,再求值:()21122x x -⋅+,其中3x =.37.(2024·四川乐山·中考真题)先化简,再求值:22142x x x ---,其中3x =.小乐同学的计算过程如下:解:()()2212142222x x x x x x x -=---+--…①()()()()222222x x x x x x +=-+-+-…②()()2222x x x x -+=+-…③()()222x x x +=+-…④12x =-…⑤当3x =时,原式1=.(1)小乐同学的解答过程中,第______步开始出现了错误;(2)请帮助小乐同学写出正确的解答过程.专题05分式及其运算(37题)一、单选题1.(2024·甘肃·中考真题)计算:4222a ba b a b-=--()A .2B .2a b -C .22a b-D .2a b a b-【答案】A【分析】本题主要考查了同分母分式减法计算,熟知相关计算法则是解题的关键.【详解】解:()42422222222a b a b a b a b a a b a bb --===-----,故选:A .2.(2024·黑龙江绥化·中考真题)下列计算中,结果正确的是()A .()2139--=B .()222a b a b +=+C 93=±D .()3263x y x y -=【答案】A【分析】本题考查了负整数指数幂,完全平方公式,算术平方根,积的乘方,据此逐项分析计算,即可求解.【详解】解:A.()2139--=,故该选项正确,符合题意;B.()2222a b a ab b +=++,故该选项不正确,不符合题意;C.93=,故该选项不正确,不符合题意;D.()3263x y x y -=-,故该选项不正确,不符合题意;故选:A .3.(2024·黑龙江牡丹江·中考真题)下列计算正确的是()A .32622a a a ⋅=B .331(2)8a b a b-÷⨯=-C .()322a a a a a a++÷=+D .2233aa -=【答案】D【分析】本题考查了单项式的乘除法,多项式除以单项式,负整数指数幂,根据运算法则进行逐项计算,即可作答.【详解】解:A 、32522a a a ⋅=,故该选项是错误的;B 、33218(2)a a b b b-÷⨯=-,故该选项是错误的;C 、()3221a a a a a a ++÷=++,故该选项是错误的;4.(2024·山东威海·中考真题)下列运算正确的是()A .5510x x x +=B .21m m n n n÷⋅=C .624a a a ÷=D .()325a a -=-5.(2024·广东广州·中考真题)若0a ≠,则下列运算正确的是()A .235a a a +=B .325a a a ⋅=C .235a a a⋅=D .321a a ÷=6.(2024·天津·中考真题)计算11x x x ---的结果等于()A .3B .xC .1x x -D .231x -【答案】A【分析】本题考查分式加减运算,熟练运用分式加减法则是解题的关键;运用同分母的分式加减法则进行计算,对7.(2024·河北·中考真题)已知A 为整式,若计算22A y xy y x xy-++的结果为xy -,则A =()A .xB .yC .x y+D .x y-二、填空题8.(2024·四川南充·中考真题)计算-a b a b a b的结果为.9.(2024·湖北·中考真题)计算:111m m m +=.10.(2024·广东·中考真题)计算:333a a a -=--.【答案】1【分析】本题主要考查了同分母分式减法计算,根据同分母分式减法计算法则求解即可.11.(2024·吉林·中考真题)当分式11x +的值为正数时,写出一个满足条件的x 的值为.12.(2024·山东威海·中考真题)计算:22x x+=.13.(2024·四川内江·中考真题)在函数1y x=中,自变量x 的取值范围是;【答案】0x ≠【分析】本题考查函数的概念,根据分式成立的条件求解即可.熟练掌握分式的分母不等于零是解题的关键.【详解】解:由题意可得,0x ≠,故答案为:0x ≠.14.(2024·四川眉山·中考真题)已知11a x =+(0x ≠且1x ≠-),23121111,,,111-==⋯=---n n a a a a a a ,则2024a 的值为.三、解答题16.(2024·江苏盐城·中考真题)先化简,再求值:2391a a a a a---÷,其中4a =.17.(2024·四川泸州·中考真题)化简:2222y x y x y x x ⎛⎫-+-÷ ⎪⎝⎭.18.(2024·四川广安·中考真题)先化简111a a a ++⎛⎫+-÷⎪--⎝⎭,再从2-,0,1,2中选取一个适合的数代入求值.∴当0a =时,原式1=-;当2a =时,原式0=.19.(2024·山东·中考真题)(11122-⎛⎫+-- ⎪⎝⎭;(2)先化简,再求值:212139a a a +⎛⎫-÷ ⎪,其中1a =.21.(2024·江苏连云港·中考真题)计算0|2|(π1)-+-【答案】1-【分析】本题考查实数的混合运算,零指数幂,先进行去绝对值,零指数幂和开方运算,再进行加减运算即可.【详解】解:原式2141=+-=-22.(2024·江苏连云港·中考真题)下面是某同学计算21211m m ---的解题过程:解:2121211(1)(1)(1)(1)m m m m m m m +-=---+-+-①(1)2m =+-②1m =-③上述解题过程从第几步开始出现错误?请写出完整的正确解题过程.23.(2024·江西·中考真题)(1)计算:0π5+-;(2)化简:888x x x ---.24.(2024·江苏苏州·中考真题)计算:()042-+-.【答案】2【分析】本题考查了实数的运算,利用绝对值的意义,零指数幂的意义,算术平方根的定义化简计算即可.【详解】解:原式413=+-2=.25.(2024·福建·中考真题)计算:0(1)5-+-【答案】4【分析】本题考查零指数幂、绝对值、算术平方根等基础知识,熟练掌握运算法则是解题的关键.根据零指数幂、绝对值、算术平方根分别计算即可;【详解】解:原式152=+-4=.26.(2024·陕西·()()0723-+-⨯.27.(2024·湖南·中考真题)先化简,再求值:22x x x-⋅+,其中3x =.28.(2024·北京·中考真题)已知10a b --=,求代数式222a ab b -+的值.29.(2024·甘肃临夏·中考真题)计算:10120253-⎛⎫+ ⎪⎝⎭.【答案】0【分析】本题考查实数的混合运算,先进行开方,去绝对值,零指数幂和负整数指数幂的运算,再进行加减运算即可.【详解】解:原式2310=-+=.30.(2024·甘肃临夏·中考真题)化简:21111a a a a a +⎛⎫++÷ ⎪.31.(2024·浙江·中考真题)计算:1154-⎛⎫-- ⎪⎝⎭32.(2024·四川广元·中考真题)先化简,再求值:222a b a ab b a b--÷-,其中a ,b 满足20b a -=.33.(2024·黑龙江牡丹江·中考真题)先化简,再求值:x x x --⎛⎫÷- ⎪⎝⎭,并从1-,0,1,2,3中选一个合适的数代入求值.34.(2024·山东烟台·中考真题)利用课本上的计算器进行计算,按键顺序如下:,若m 是其显示结果的平方根,先化简:27442393m m m m m m --⎛⎫+÷ ⎪--+⎝⎭,再求值.35.(2024·江苏苏州·中考真题)先化简,再求值:2124x x +-⎛⎫+÷ ⎪--.其中3x =-.36.(2024·贵州·中考真题)(1)在①22,②2-,③()01-,④22⨯中任选3个代数式求和;(2)先化简,再求值:()21122x x -⋅,其中3x =.37.(2024·四川乐山·中考真题)先化简,再求值:242x x ---,其中3x =.小乐同学的计算过程如下:解:()()2212142222x x x x x x x -=---+--…①()()()()222222x x x x x x +=-+-+-…②()()2222x x x x -+=+-…③()()222x x x +=+-…④12x =-…⑤当3x =时,原式1=.(1)小乐同学的解答过程中,第______步开始出现了错误;(2)请帮助小乐同学写出正确的解答过程.。
中考数学计算题练习100道(2024年中考真题)

中考数学计算题练习100道(2024年中考真题)一、计算(1) (24年北京中考) 计算:()052sin 30π-+︒+(2) (24年福建中考)计算:0(1)5-+-(3) (24年深圳中考)计算:()112cos 45 3.1414π-⎛⎫-⋅︒+-++ ⎪⎝⎭.(4) (24年广东中考)计算:011233-⨯-+-. (5) (24年广西中考)计算:()()2342-⨯+-(6) (24年贵州中考)在①22,①2-,①()01-,①122⨯中任选3个代数式求和.(7) (24年河南中考)计算(01(8) (24年湖北中考)计算:()201322024-⨯-(9) (24年湖南中考)计算:|3|cos602-+-+︒ ⎪⎝⎭(10) (24年苏州中考)计算:()042-+-(11) (24年扬州中考)计算:0|3|2sin 302)π-+︒-(12) (24年青海中考)计算0tan 45π︒+-.(13) (24年枣庄中考)计算1122-⎛⎫-- ⎪⎝⎭(14) (24年上海中考)计算:102|124(1++.(15) (24年云南中考)计算:12117sin3062-⎛⎫++--- ⎪⎝⎭(16) (24()02sin 602024 2.π︒--(17) (24年山西中考)计算:2(6)()[(3)(1)]32--⨯-+-+-(18) (24年陕西中考)计算0(7)(2)3-+-⨯.(19) (24年重庆中考)计算:011(3)()2π--+=_____.(20) (24年新疆中考)计算:201(3)1)-+-.(21) (24年呼伦贝尔中考)计算:301tan602(π2024)2-⎛⎫--+︒+- ⎪⎝⎭. (22) (24年泰安中考)212tan60()2-︒+-(23) (24年赤峰中考)计算()0π12sin 602++︒+(24) (24年滨州中考)计算:()11222-⎫⎛+-⨯- ⎪⎝⎭(25) (24年乐山中考)计算:()03π2024-+-.(26) (24年武威中考)计算(27) (24年盐城中考)计算:()0214sin30π--++︒(28) (24年广安中考)计算:01π132sin 60|2|22-⎛⎫⎛⎫-+︒+- ⎪ ⎪⎝⎭⎝⎭(29) (24年泸州中考)计算:()11π20242sin 602-⎛⎫+--︒+ ⎪⎝⎭.(30) (24年德阳中考)计算212cos602-⎛⎫-︒ ⎪⎝⎭(31) (24年宜宾中考)计算:()022sin302︒-+--(32) (24年通辽中考)计算022sin60(π)+︒--.(33) (24年达州中考)计算:()2012sin 60π20242-⎛⎫-︒-- ⎪⎝⎭(34) (24年遂宁中考)计算:11sin4512021-⎛⎫︒+ ⎪⎝⎭.(35) (24年泰安中考)计算:212tan 602-⎛⎫︒+-+⎪⎝⎭(36) (24年连云港中考)02(1)π-+-二、化简求值(37) (24年北京中考)已知10a b --=,求代数式()223232a b ba ab b-+-+的值.(38) (24年深圳中考)先化简,再求值: 2221111a a a a -+⎛⎫-÷⎪++⎝⎭,其中 1a = (39) (24年广东中考)计算:333a a a -=--_______. (40) (24年贵州中考)先化简,再求值:()21122x x -⋅+,其中3x =.(41) (24年河南中考)化简:231124a a a +⎛⎫+÷ ⎪--⎝⎭. (42) (24年黑龙江龙东地区中考)先化简,再求值:22222111m m m m m m ⎛⎫-+÷- ⎪-+⎝⎭,其中cos60m =︒.(43) (24年湖北中考)计算:111m m m +=++______. (44) (24年湖南中考)先化简,再求值:22432x x x x x-⋅++,其中3x =.(45) (24年吉林中考)先化简,再求值:()()2111a a a +-++,其中a =(46) (24年苏州中考)先化简,再求值:2212124x x xx x +-⎛⎫+÷ ⎪--⎝⎭.其中3x =-. (47) (24年扬州中考)化简:2(2)1x x x -÷-+. (48) (24年江西中考)化简:888x x x ---.(49) (24年包头中考)先化简,再求值:()()2121x x +-+,其中x =(50) (24年青海中考)先化简,再求值:11xy y x y x ⎛⎫⎛⎫-÷-⎪ ⎪⎝⎭⎝⎭,其中2x y =-. (51) (24年枣庄中考)先化简,再求值:212139a a a +⎛⎫-÷ ⎪+-⎝⎭,其中1a =. (52) (24年天津中考)计算3311x x x --- (53) (24年山西中考)化简:2112(111x x x x ++÷-+-). (54) (24年陕西中考)先化简,再求值:2()(2),x y x x y ++-其中1,2x y ==-(55) (24年重庆中考)计算:()()22x x y x y -++;(56) (24年重庆中考)计算:22111a a a a -⎛⎫+÷ ⎪+⎝⎭.(57) (24年新疆中考)22222a b a ba ab b a b--÷+++ (58) (24年长春中考)先化简,再求值:32222x x x x ---,其中x . (59) (24年呼伦贝尔中考)先化简,再求值:22422324x xx x x -⎛⎫+-÷+ ⎪+-⎝⎭,其中72x =-.(60) (24年泰安中考)化简:2211()x x x x x---÷. (61) (24年赤峰中考)已知230a a --=,求代数式2(2)(1)(3)a a a -+-+的值.(62) (24年武威中考)先化简,再求值:()()()22222a b a b a b b ⎡⎤+-+-÷⎣⎦,其中2a =,1b .(63) (24年盐城中考)先化简,再求值:22391a a a a a---÷+,其中4a =.(64) (24年广安中考)先化简2344111a a a a a ++⎛⎫+-÷⎪--⎝⎭,再从2-,0,1,2中选取一个适合的数代入求值.(65) (24年南充中考)先化简,再求值:()23(2)3x x x x +-+÷,其中2 x =-.(66) (24年泸州中考)化简:2222y x y x y x x ⎛⎫-+-÷ ⎪⎝⎭.(67) (24年宜宾中考)计算:2211111a a a ⎫⎛÷- ⎪--+⎝⎭(68) (24年通辽中考)先化简,再求值:()()()()224+--+-a b a b a b a b ,其中2==a b .(69) (24年达州中考)先化简:22224x x x x x x x +⎛⎫-÷ ⎪-+-⎝⎭,再从2-,1-,0,1,2之中选择一个合适的数作为x 的值代入求值.(70) (24年遂宁中考)先化简:2121121x x x x -⎛⎫-÷ ⎪--+⎝⎭,再从1,2,3中选择一个合适的数作为x 的值代入求值.(71) (24年泰安中考)化简:2211x x x x x --⎛⎫+÷⎪⎝⎭(72) (24年连云港中考)21211m m --- 三、分式方程(73) (24年福建中考)解方程:3122x x x +=+-. (74) (24年广州中考)解方程:1325x x=-. (75) (24年武汉中考)分式方程131x x x x +=--的解是______. (76) (24年包头中考)解方程:2244x xx x --=--. (77) (24年成都中考)132x x=- (78) (24年陕西中考)解方程:22111xx x +=--四、方程(组)(79) (24年广西中考)解方程组:2321x y x y +=⎧⎨-=⎩(80) (24年苏州中考)解方程组:27233x y x y +=⎧⎨-=⎩. (81) (24年上海中考)解方程组:2234026x xy y x y ⎧--=⎨+=⎩①②. (82) (24年乐山中考)解方程组:425x y x y +=⎧⎨-=⎩ (83) (24年新疆中考)解方程:2(1)3x x --=.(84) (24年滨州中考)解方程:21132x x -+= (85) (24年广州中考)关于x 的方程2240x x m -+-=有两个不等的实数根.(1)求m 的取值范围;(2)化简:2113|3|21m m m m m ---÷⋅-+.(86) (24年滨州中考)解方程:240x x -=.五、不等式(组)(87) (24年黑龙江龙东地区中考)关于x 的不等式组420102x x a -≥⎧⎪⎨->⎪⎩恰有3个整数解,则a 的取值范围是________.(88) (24年武汉中考)求不等式组3121x x x +>⎧⎨-≤⎩①②的整数解. (89) (24年扬州中考)解不等式组260412x x x -≤⎧⎪⎨-<⎪⎩,并求出它的所有整数解的和. (90) (24年天津中考)解不等式组213317x x x +≤⎧⎨-≥-⎩①② (91) (24年成都中考)解不等式组231,11.23x x x +≥-⎧⎪-⎨-<⎪⎩ (92) (24年重庆中考)若关于x 的不等式组()411321x x x x a -⎧<+⎪⎨⎪+≥-+⎩至少有2个整数解,且关于y的分式方程13211ay y-=---的解为非负整数,则所有满足条件的整数a的值之和为______.(93)(24年武威中考)解不等式组:()223122x xxx⎧-<+⎪⎨+<⎪⎩(94)(24年德阳中考)解不等式组:2351124xx x-+≤-⎧⎪⎨-<+⎪⎩①②(95)(24年达州中考)解不等式组32 312 2xxx--<-⎧⎪⎨-≤+⎪⎩(96)(24年北京中考)解不等式组:() 3142,92.5x xxx⎧-<+⎪⎨-<⎪⎩(97)(24年广西中考)不等式7551x x+<+的解集为______.(98)(24年安徽中考)解不等式53.3xx++<并把它的解集在数轴上表示出来.(99)(24年盐城中考)求不等式113xx+≥-的正整数解.(100)(24年连云港中考)解不等式11 2xx-<+中考数学计算题练习100道答案(1)【答案】(2)【答案】4(3)【答案】4(4)【答案】2(5)【答案】8-(6)【答案】选择①,①,①和为7;选择①,①,①和为7;选择①,①,①和为6;选择①,①,①和为4(7)【答案】9(8)【答案】3(9)【答案】5 2(10)【答案】2(11)【答案】3π-(12)【答案】(13)【答案】3(14)【答案】(15)【答案】2(16)【答案】5(17)【答案】10-(18)【答案】2-(19) 【答案】3(20) 【答案】7(21) 【答案】11(22) 【答案】7(23) 【答案】6(24) 【答案】0(25) 【答案】1(26) 【答案】0(27) 【答案】3(28) 【答案】1(29) 【答案】3(30) 【答案】1(31)(32) 【答案】1(33) 【答案】3-(34) 【答案】2024(35) 【答案】7(36) 【答案】1-.(37) 【答案】3(38) 【答案】11a -,2(39) 【答案】1(40) 【答案】12x -,1 (41) 【答案】2a + (42) 【答案】1m -+,12 (43) 【答案】1(44) 【答案】1x x +,43(45) 【答案】22a ,6(46) 【答案】2x x +,13(47) 【答案】11x + (48) 【答案】1(49) 【答案】21x -,7(50) 【答案】1x y +,12(51) 【答案】3a -,2-(52) 【答案】3(53) 【答案】22x x + (54) 【答案】222,6x y +(55) 【答案】222x y +(56) 【答案】11a a +-. (57) 【答案】1(58) 【答案】2x ,2(59) 【答案】3x +,12- (60) 【答案】11x x -+ (61) 【答案】7(62) 【答案】2a b +,3(63) 【答案】23a +;27 (64) 【答案】22a a -+,0a =时,原式1=-,2a =时,原式0=. (65) 【答案】41x +,7-(66) 【答案】x y x y-+(67) 【答案】1(68) 【答案】3ab -,(69) 【答案】41x +,当1x =时,原式2=. (70) 【答案】1x -;2(71) 【答案】11x x -+. (72) 【答案】11m +. (73) 【答案】10x =.(74) 【答案】3x =(75) 【答案】3x =-(76) 【答案】3x =(77) 【答案】3x =(78) 【答案】3x =-是原分式方程的解.(79) 【答案】212x y =⎧⎪⎨=⎪⎩(80) 【答案】31x y =⎧⎨=⎩(81) 【答案】4x =,1y =或者6x =-,6y =.(82) 【答案】31x y =⎧⎨=⎩ (83) 【答案】5x =(84) 【答案】5x =(85) 【答案】(1)3m > (2)2-(86) 【答案】10x =,24x =.(87) 【答案】102a -≤< (88) 【答案】整数解为:1,0,1-(89) 【答案】132x <≤,整数和为6 (90) 【答案】31x -≤≤(91) 【答案】29.x -≤<(92) 【答案】16(93) 【答案】173x << (94) 【答案】46x ≤<(95) 【答案】15x -<≤(96) 【答案】17x -<<(97) 【答案】<2x -(98) 【答案】 2.x <-(99) 【答案】1,2. (100) 【答案】3x >-.。
2024年中考物理复习压轴真题专项汇编—计算题(功与简单机械综合23题)

2024年中考物理复习压轴真题专项汇编—计算题(功与简单机械综合23题)【题型1杠杆的平衡条件】1.(2023•呼和浩特)人类在漫长的历史长河中,创造了各种各样的工具,以无穷的智慧弥补了人类有限的力量,使工作更省力、更便捷,这些工具统称为机械。
杠杆便是其中最简单的机械之一。
如图所示,AB是一根长为1.6m的不计质量的杠杆,可以绕O点转动,在距O点0.4m的B端悬挂一质量为90kg,边长为30cm的匀质正方体合金块M,杠杆恰好在水平位置平衡。
求:(1)合金块M的密度为多少kg/m3;(2)A端施加的竖直向下拉力F A的大小。
【答案】(1)合金块M的密度为3.3×103kg/m3。
(2)A端施加的竖直向下拉力F A的大小为300N。
【解答】解:(1)边长为30cm的匀质正方体合金块M的体积为:V=l3=(30cm)3=2.7×104cm3=0.027m3;合金块M的密度为:。
(2)根据杠杆的平衡条件可知:F A×OA=G M×OB;所以:=。
答:(1)合金块M的密度为3.3×103kg/m3。
(2)A端施加的竖直向下拉力F A的大小为300N。
2.(2023•深圳)如图1是古时劳动人民用工具撬起木料的情景,如图二中已知其中BO:OC=1:5,木料的体积为4m3,木块的密度为0.5×103kg/m3。
(1)求木材所受重力?(2)如图2,在B端有一木材对绳子的力F1为1×104N,当F2为多大时,木料刚好被抬起?(3)随着时代发展,亮亮同学发现吊车能更方便地提起重物。
如图3用一吊车匀速向上提起木材,已知提升的功率为P=10kW,那这个吊车在10s内可以将该木料提升的高度为多高?【答案】(1)木材所受重力为2×104N;(2)当F2为2×103N时,木料刚好被抬起;(3)这个吊车在10s内可以将该木料提升的高度为5m。
2023年中考数学真题汇编几何综合压轴问题专项练习(共40题)(解析版)

几何综合压轴问题专项练习答案(40题)(1)将CDE 绕顶点C 旋转一周,请直接写出点M ,N 距离的最大值和最小值;(2)将CDE 绕顶点C 逆时针旋转120︒(如图2),求MN 【答案】(1)最大值为3,最小值为1(2)7【分析】(1)根据直角三角形斜边上的中线,得出,CM CN 解;(2)过点N 作NP MC ⊥,交MC 的延长线于点P ,根据旋转的性质求得进而可得1CP =,勾股定理解Rt ,Rt NCP MCP ,即可求解.【详解】(1)解:依题意,112CM DE ==,12CN AB =当M 在NC 的延长线上时,,M N 的距离最大,最大值为(2)解:如图所示,过点N 作NP MC ⊥,交MC 的延长线于点∵CDE 绕顶点C 逆时针旋转∴120BCE ∠=︒,∵45BCN ECM ∠=∠=︒,∴MCN BCM ECM ∠=∠-∠=∴60NCP ∠=︒,∴30CNP ∠=︒,∴112CP CN ==,在Rt CNP 中,2NP NC =-在Rt MNP △中,MP MC CP =+∴2234MN NP MP =+=+【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半,勾股定理,旋转的性质,含(1)如图1,求证:DE BF =;(2)如图2,若2AD BF =,的延长线恰好经过DE 的中点【答案】(1)见解析(2)22BE =+△∵点G 是DE 的中点,∴GH 是FCD 的中位线,∴11122GH CD AD ===,设BE a =,则CH EH ==(1)如图1,求AB边上的高CH的长.''.(2)P是边AB上的一动点,点,C D同时绕点P按逆时针方向旋转90︒得点,C D①如图2,当点C'落在射线CA上时,求BP的长.△是直角三角形时,求BP的长.②当AC D''∴90C PQ PC Q '∠+∠='︒∵90C PQ CPH ∠+∠='︒∴PC Q CPH ∠=∠'.由旋转知PC PC '=,设C D ''与射线BA 的交点为作CH AB ⊥于点H .∵PC PC ⊥',∴90CPH TPC ∠'+∠=︒,∵C D AT ''⊥,∴90PC T TPC ∠'+∠='︒,【答案】(1)①见解析;②AD DF BD =+,理由见解析;【分析】(1)①证明:ABE CBD ∠=∠,再证明ABE ≅△可得DF DC =.证明AE DF =,从而可得结论;(2)如图,过点B 作BE AD ⊥于点E ,得90BED ∠=︒,证明2DE BD =,证明2AB BC =,ABE CBD ∠=∠,可得②AD DF BD=+.理由如下:∵DF和DC关于AD对称,=.∴DF DC=,∵AE CD∴AE DF=.∴AD AE DE DF BD=+=+∵DF 和DC 关于AD 对称,∴DF DC =,ADF ADC ∠=∠.∵CD BD ⊥,∴45ADF ADC ∠=∠=︒,∴45EBD ∠=︒.∴2DE BD =.∵AB AC AF ==,∴()11222HF BF BD DF ==-=,222262210BC BD CD =+=+=∴2221022AF AC BC ===⨯=25HF (2)知识应用:如图2Y是菱形;①求证:ABCD②延长BC至点E,连接OE交【答案】(1)见解析5∴1BG BO GC OD==,∴115222CG BC AD ===,∴552OF GC .处从由60PC P C PCP ''=∠=︒,,可知PCP '△为①三角形,故PP PC '=,又P A PA ''=,故PA PB PC PA PB PP A B '''++=++≥,由②可知,当B ,P ,P ',A 在同一条直线上时,PA PB PC ++取最小值,如图2,最小值为(3)如图5,设村庄A ,B ,C 的连线构成一个三角形,且已知4km 23km AC BC ==,,建一中转站P 沿直线向A ,B ,C 三个村庄铺设电缆,已知由中转站P 到村庄A ,B ,C 元/km ,a 元/km ,2a 元/km ,选取合适的P 的位置,可以使总的铺设成本最低为___________用含的式子表示)∵ACP A CP ''∠=∠,∴ACP BCP A CP BCP ∠+∠=∠+∠''又∵60PCP '∠=︒过点A '作A H BC '⊥,垂足为H ,∵60ACB ∠=︒,90ACA '∠=︒,∴30A CH '∠=︒,1猜想证明:(1)如图2,试判断四边形AEDG的形状,并说明理由.问题解决;(2)如图3,将图2中左侧折叠的三角形展开后,重新沿MN折叠,使得顶点B与点∵1122 CHGS CH HG=⋅=∴154302CG HE⋅=⨯=,①求证:PD PB =;②将线段DP 绕点P 逆时针旋转,化时,DPQ ∠的大小是否发生变化?请说明理由;③探究AQ 与OP 的数量关系,并说明理由.【答案】(1)①见解析;②不变化,(2)AQ CP =,理由见解析【分析】(1)①根据正方形的性质证明②作,PM AB PN AD ⊥⊥,垂足分别为点∵四边形ABCD 是正方形,∴45DAC BAC ∠=∠=︒,∴四边形AMPN 是矩形,∴90MPN ∠=︒,∵四边形ABCD 是正方形,∴45BAC ∠=︒,90AOB ∠=∴45AEP ∠=︒,四边形OPEF=作PM AB⊥于点M,则QM MB=,∴QA BE=.∴AQ CP(1)求BCF ∠的度数;(2)求CD 的长.深入探究:(3)若90BAC ∠<︒,将BMN 绕点B 顺时针旋转α,得到BEF △,连接AE ,CF 满足0360α︒<<︒,点,,C E F 在同一直线上时,利用所提供的备用图探究BAE ∠与ABF ∠的数量关系,并说明理由.【答案】初步尝试:(1)1MN AC =;MN AC ∥;(2)特例研讨:(1)30BCF ∠=︒;(2)CD∵MN 是BAC 的中位线,∴MN AC ∥,∴90BMN BAC ∠=∠=︒∵将BMN 绕点B 顺时针旋转α∴,BE BM BF BN ==;BEF ∠=∵点,,A E F 在同一直线上时,2∵,ADN BDE ANB BED ∠=∠∠=∠∴ADN BDE ∽,∴2222DN AN DE BE ===,设DE x =,则2DN x =,在Rt ABE △中,2,2BE AE ==在Rt ADN △中,22AD DN AN =+∵AB AC =,∴A ABC CB =∠∠,设ABC ACB θ∠=∠=,则1802BAC θ∠=︒-,∵MN 是ABC 的中位线,∴MN AC∥∴MNB MBN θ∠=∠=,∵将BMN 绕点B 顺时针旋转α,得到BEF △,∴EBF MBN ≌,MBE NBF α∠=∠=,∴EBF EFB θ∠=∠=∴1802BEF θ∠=︒-,∵点,,C E F 在同一直线上,∴2BEC θ∠=∴180BEC BAC ∠+∠=︒,∴,,,A B E C 在同一个圆上,∴EAC EBC αθ∠=∠=-∴()()1802BAE BAC EAC θαθ∠=∠-∠=︒---180αθ=︒--∵ABF αθ∠=+,∴180BAE ABF ∠∠=+︒;如图所示,当F 在EC 上时,∵,BEF BAC BC BC∠=∠=∴,,,A B E C 在同一个圆上,设ABC ACB θ∠=∠=,则1802BAC BEF θ∠=∠=︒-,将BMN 绕点B 顺时针旋转α,得到BEF △,设NBF β∠=,则EBM β∠=,则360αβ+=︒,∴ABF θβ∠=-,∵BFE EBF θ∠=∠=,EFB FBC FCB∠=∠+∠∴ECB FCB EFB FBC θβ∠=∠=∠-∠=-,∵ EBEB =∴EAB ECB θβ∠=∠=-∴BAE ∠ABF=∠综上所述,BAE ABF ∠=∠或180BAE ABF ∠∠=+︒【点睛】本题考查了圆周角定理,圆内接四边形对角互补,相似三角形的性质与判定,旋转的性质,中位线的性质与判定,等腰三角形的性质与判定,三角形内角和定理,三角形外角的性质,勾股定理,熟练掌握以上知识是解题的关键.10.(2023·湖北黄冈·统考中考真题)【问题呈现】CAB △和CDE 都是直角三角形,90,,ACB DCE CB mCA CE mCD ∠=∠=︒==,连接AD ,BE ,探究AD ,BE 的位置关系.(1)如图1,当1m =时,直接写出AD ,BE 的位置关系:____________;(2)如图2,当1m ≠时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.【拓展应用】(3)当3,47,4m AB DE ===时,将CDE 绕点C 旋转,使,,A D E 三点恰好在同一直线上,求(2)解:成立;理由如下:∵90DCE ACB ∠=∠=︒,∴DCA ACE ACE ∠+∠=∠+(3)解:当点E 在线段AD设AD y =,则AE AD DE =+根据解析(2)可知,DCA △∴3BE BC m AD AC===,勾股定理,解题的关键是熟练掌握三角形相似的判定方法,画出相应的图形,注意分类讨论.(1)若点P 在AB 上,求证:A P AP '=;(2)如图2.连接BD .①求CBD ∠的度数,并直接写出当180n =时,x 的值;②若点P 到BD 的距离为2,求tan A MP '∠的值;∵PM 平分A MA '∠∴90PMA ∠=︒∴PM AB∥∴DNM DBA V V ∽∴DN DM MN DB DA BA ==∵8,6,90AB DA A ==∠=︒,∴2226BD AB AD =+=+∴2103sin 3BQ BP DBA ===∠,∵90PQB CBD DAB ∠=∠=∠=︒,∴90QPB PBQ DBA ∠=︒-∠=∠,∵A MP AMP ' ≌,∴90PA M A '∠=∠=︒,(2)如图②,在矩形ABCD 的BC 边上取一点E ,将四边形ABED 沿DE 翻折,使点B '处,若24,6BC CE AB ⋅==,求BE 的值;(3)如图③,在ABC 中,45,BAC AD BC ∠=︒⊥,垂足为点,10,D AD AE ==于点F ,连接DF ,且满足2DFE DAC ∠=∠,直接写出53BD EF +的值.∵EF BC ∥,∴2CDF DFE ∠=∠=∴CDH FDH ∠=∠,又∵DH DH =,CHD ∠∴(ASA CHD FHD ≌【点睛】本题考查矩形的性质、翻折性质、勾股定理、相似三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、锐角三角函数等知识,综合性强,较难,属于中考压轴题,熟练掌握相关知识的联系与运用,添加辅助线求解是解答的关键.13.(2023·湖南郴州·=,连接点E,使CE AD(1)如图1,当点D在线段AB上时,猜测线段CF与BD的数量关系并说明理由;(2)如图2,当点D在线段AB的延长线上时,①线段CF与BD的数量关系是否仍然成立?请说明理由;②如图3,连接AE.设4AB=,若AEB DEB∠=∠,求四边形BDFC的面积.【答案】(1)1CF BD=,理由见解析∴60,ADG ABC AGD ∠=∠=︒∠=∠∴ADG △为等边三角形,∴AD AG DG ==,∵AD CE =,AD AB AG AC -=-∴DG CE =,BD CG =,于点由①知:ADG △为等边三角形,∵ABC 为等边三角形,∴4,AB AC BC BH CH =====∴2223AH AB BH =-=,(1)若正方形ABCD 的边长为2,E 是AD 的中点.①如图1,当90FEC ∠=︒时,求证:AEF DCE ∽△△;②如图2,当2tan 3FCE ∠=时,求AF 的长;(2)如图3,延长CF ,DA 交于点G ,当1,sin 3GE DE FCE =∠=时,求证:,可得结论;正方形ABCD 中,①ADC BAD ∠=∠ ∴AEF CED ∠+∠=AEF ECD ∴∠=∠,延长DA ,CF 交于点G ,作GH CE ⊥,垂足为H ,90EDC EHG ∠=∠=︒ 且∠问题探究:(1)先将问题特殊化,如图(2),当90α=︒时,直接写出GCF ∠的大小;(2)再探究一般情形,如图(1),求GCF ∠与α的数量关系.问题拓展:(3)将图(1)特殊化,如图(3),当120α=︒时,若12DG CG =,求BE CE 的值.故答案为:45︒.(2)解:在AB上截取ANABC BAE AEB∠+∠+∠=∠=∠,ABC AEF22⎝⎭(3)解:过点A作CD的垂线交CD的延长线于点【点睛】此题考查菱形性质、三角形全等、三角形相似,解题的关键是熟悉菱形性质、三角形全等、三角形相似.16.(2023·山西·统考中考真题)问题情境:“综合与实践沿对角线剪开,得到两个全等的三角形纸片,表示为∠=∠=︒∠=∠.将ABCACB DEF A D90,和DFE△(1)数学思考:谈你解答老师提出的问题;(2)深入探究:老师将图2中的DBE绕点B逆时针方向旋转,使点问题.∠①“善思小组”提出问题:如图3,当ABE②“智慧小组”提出问题:如图AH的长.请你思考此问题,直接写出结果.【答案】(1)正方形,见解析(2)①AM BE=,见解析;【分析】(1)先证明四边形形;∠(2)①由已知ABE【点睛】本题考查了旋转的性质、全等三角形的判定与性质、正方形的判定与性质、相似三角形的判定与性质、三角函数、勾股定理等知识点,适当添加的辅助线、构造相似三角形是解题的关键.17.(2023·湖北十堰·统考中考真题)过正方形E ,连接AE ,直线AE 交直线(1)如图1,若25CDP ∠=︒,则DAF ∠=___________(2)如图1,请探究线段CD ,EF ,AF 之间的数量关系,并证明你的结论;(3)在DP 绕点D 转动的过程中,设AF a =,EF 【答案】(1)20︒。
全国各地中考化学真题分类汇编综合计算题含答案

全国各地中考化学真题分类汇编综合计算题含答案Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#2017中考真题专题汇编——综合计算题1.(2017甘肃)某化学兴趣小组同学为回收一块质量为40 g 的铜锌合金中的铜,将该合金放人烧杯中,逐渐加入稀硫酸至不再产生气泡时,恰好用去稀硫酸100 g ,烧杯内剩余固体27 g 。
请完成下列计算:(1)40 g 铜锌合金中锌的质量是________g 。
(2)计算所用稀硫酸中溶质的质量分数。
【答案】(1)40 g 铜锌合金中锌的质量为40 g-27 g=13 g (2)解:设所用稀硫酸中溶质的质量为x 。
Zn+H 2SO 4═ZnSO 4+H 2↑ 65 98 13 g xx98g 1365= x = g所用稀硫酸中溶质的质量分数:%6.19%100g100g19.6=⨯。
答:所用稀硫酸中溶质的质量分数是%。
2.(2017安顺)某锥形瓶盛有盐酸和氯化铜的混合溶液100g,向其中逐滴加入溶质质量分数为10%的氢氧化钠溶液,锥形瓶内溶液质量与滴入的氢氧化钠溶液的质量的变化关系如图所示。
请计算:(l)反应至A点时加入氢氧化钠溶液的质量为__________;(2)计算反应至B点时锥形瓶内所得溶液的溶质质量分数为多少(计算结果保留至%)【答案】(1)40g(1分);(2)%3.(2017河南)将30.9 g 氯酸钾(KClO3)和二氧化锰的固体混合物装入试管中,加热制取氧气,同时生成氯化钾。
待反应完全后,将试管冷却,称量,可以得到21.3 g 固体物质。
请计算原固体混合物中氯酸钾的质量。
【答案】生成氧气的质量为30.9g-21.3g=9.6g,设原混合物中氯酸钾的质量为x2KClO3 2KCl+3O2↑245 96x 9.6g96245=gx 6.9 解得x = 24.5g 4.(2017黄石)向克稀盐酸中加入锌粉(仅含不溶于酸的杂质),所加锌粉的质量与产生气体的质量的关系如下图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018中考真题专题汇编——综合计算题1.(2018甘肃)某化学兴趣小组同学为回收一块质量为40 g 的铜锌合金中的铜,将该合金放人烧杯中,逐渐加入稀硫酸至不再产生气泡时,恰好用去稀硫酸100 g ,烧杯内剩余固体27 g 。
请完成下列计算: (1)40 g 铜锌合金中锌的质量是________g 。
(2)计算所用稀硫酸中溶质的质量分数。
【答案】(1)40 g 铜锌合金中锌的质量为40 g-27 g=13 g (2)解:设所用稀硫酸中溶质的质量为x 。
Zn+H 2SO 4═ZnSO 4+H 2↑ 65 98 13 g xx98g 1365= x=19.6 g所用稀硫酸中溶质的质量分数:%6.19%100g100g19.6=⨯。
答:所用稀硫酸中溶质的质量分数是19.6%。
2.(2018安顺)某锥形瓶盛有盐酸和氯化铜的混合溶液100g ,向其中逐滴加入溶质质量分数为10%的氢氧化钠溶液,锥形瓶内溶液质量与滴入的氢氧化钠溶液的质量的变化关系如图所示。
请计算:(l )反应至A 点时加入氢氧化钠溶液的质量为__________;(2)计算反应至B 点时锥形瓶内所得溶液的溶质质量分数为多少?(计算结果保留至0.1%) 【答案】(1)40g (1分);(2)10.4%3.(2018河南)将30.9 g 氯酸钾(KClO 3)和二氧化锰的固体混合物装入试管中,加热制取氧气,同时生成氯化钾。
待反应完全后,将试管冷却,称量,可以得到21.3 g 固体物质。
请计算原固体混合物中氯酸钾的质量。
【答案】生成氧气的质量为30.9g -21.3g=9.6g ,设原混合物中氯酸钾的质量为x2KClO 32KCl+3O 2↑245 96x 9.6g96245=gx 6.9 解得x= 24.5g 4.(2018黄石)向l33.4克稀盐酸中加入锌粉(仅含不溶于酸的杂质),所加锌粉的质量与产生气体的质量的关系如下图所示。
求:(1)此过程产生气体的最大质量是______________; (2)原稀盐酸中溶质的质量分数为多少?(诗写出计算过程) 【答案】(1)0.4 (2)10.9%5.(2018武汉)钢是铁的合金。
为测定某钢样中铁的质量分数,取11.4g 钢样,向其中加入稀硫酸,产生氢气的质量与加入稀硫酸的质量关系如图所示(不考虑钢样中其它成分与稀硫酸的反应)。
(1)钢_____(填“是”或“不是”)金属材料。
(2)计算此钢样中铁的质量分数。
【答案】(1)是(2)98%6.(2018襄阳)把干燥、纯净的氯酸钾和二氧化锰的混合物31.5g装入大试管中,加热制取氧气。
待完全反应后,将试管冷却、称量,得到21.9g固体物质。
计算制得氧气多少克?21.9g固体物质中含有哪些物质?各多少克?【答案】9.6g;氯化钾14.9g、二氧化锰7g。
7.(2018孝感)某工厂排放的废水中含有亚硫酸钠(Na2SO3)未经处理,会造成污染。
化学兴趣小组的同学对废水处理设计了如图所示的实验方案:试计算:(l)反应完后生成亚硫酸钙沉淀的质量为_______g。
(2)废水中亚硫酸钠的质量分数(请写出计算过程)。
(温馨提示:Na2SO3+CaC12=CaSO3↓+2NaCl;氯化钙不与废水中的其它杂质反应)【答案】(1)6g;(2)12.6%。
8.(2107邵阳)某同学在实验室用氯酸钾和二氧化锰的混合物制取氧气,并对反应后固体剩余物进行回收、利用,实验操作流程及数据记录如下:请回答下列问题:(1)滤液可作化肥使用,你认为它属于_______肥。
(2)该同学制得氧气的质量_______g。
(3)计算滤液中溶质质量分数。
【答案】(1)钾或 K(1分)(2)4.8(1分)(3)14.9%9.(2018长沙)将适量二氧化碳通入100g氢氧化钠溶液中,恰好完全反应后,得到108.8g碘酸钠溶液。
请计算:(1)参加反应的二氧化碳的质量为_______g;(2)氢氧化钠溶液的溶质质量分数_________.【答案】(1) 8.8;(2)16%10.(2018宿迁)牙膏中的摩擦剂可以增强牙膏对牙齿的摩擦作用和去污效果。
己知某品牌牙膏中的摩擦剂是CaCO3和SiO2(SiO2不溶于水也不与稀盐酸反应)。
为了测定摩擦剂中CaCO3的质量分数,通过实验测得如图数据:(1)生成CO2质量为______g;(2)求摩擦剂中CaCO3的质量分数。
【答案】(1)2.2;(2)50%11.(2018江西)学习小组测定某工业废水(含有H2SO4、HNO3,不含固体杂质)中H2SO4的含量。
取100g废水于烧杯中,加入100gBaCl2溶液,恰好完全反应,经过滤得到176.7g溶液。
(可溶性杂质不参加反应,过滤后滤液的损失忽略不计)(1)充分反应后生成沉淀的质量为_______g;(2)该工业度水中硫酸的质量分数为多少?(写出计算过程)[来源:学科网](3)为避免工业废水污染环境,排放前应对废水进行中和处理,需加入的物质是________。
【答案】(1)100g+100g-176.7g=23.3g解:设100 g工业废水中硫酸的质量x(2)H2SO4+BaCl2=BaSO4↓+2HCl98 233x 23.3g98/233 = x/23.3gx = 9.8g9.8g/100g×100% = 9.8%答:该工业废水中硫酸的质量分数为9.8%。
(3)氢氧化钙等12.(2018呼和浩特)铁的氧化物有三种,分别是FeO、Fe2O3和Fe3O4。
某固体粉未可能含有一种或两种铁的氧化物。
取23.2克固体粉未,向其中通入足量一氧化碳并加热(假设固体完全反应),将反应生成的气体通入足量的澄清石灰水中。
生成40.0克沉淀。
试计算:(l)反应生成二氧化碳的质量为多少克?(要求写出计算过程)(2)固体粉末中含有的铁的氧化物可能为______或_______。
【答案】(1)17.6g;(2)Fe3O4;或FeO和Fe2O3。
13.(2018枣庄)一化工厂产生的废液中含有硫酸亚铁和硫酸铜(不考虑其它物质),为回收铜和硫酸亚铁,研究人员设计出“用铁处理”的发案,取100g上述废液,向其中加入2.8g铁粉,恰好完全反应,测得反应后溶液中溶质的质量分数为15%,求:(1)回收得到铜的质量为 g(2)回收得到硫酸亚铁的质量是多少?(写出计算过程)【答案】解:设2.8g铁完全反应生成的铜的质量为xFe+CuSO4=FeSO4+Cu56 642.8g x=x=3.2g硫酸亚铁质量为×15%=14.94g答:(1)回收得到铜的质量为 3.2gg(2)回收得到硫酸亚铁的质量是14.94g.14.(2018达州)NaCl和Na2CO3的固体混合物与一定质量的稀盐酸恰好完全反应,得到4.4gCO2和100g21.1%的NaCl溶液,求:⑴稀盐酸中溶质的质量为 g。
⑵原混合物中NaCl的质量分数(写出计算过程)。
【答案】⑴7.3g ⑵47%解:设碳酸钠的质量为x,反应生成的氯化钠质量为y,参加反应的盐酸中溶质质量为z。
Na2CO3+2HCl=2NaCl+H2O+CO2↑106 73 117 44x z y 4.4g106 x =73z=117y=444.4gx=10.6g y=11.7g z=7.3g原混合物中氯化钠的质量为:100g×21.1%-11.7g =9.4g原混合物中NaCl的质量分数=9.4g9.4g+10.6g×100%=47%15.(2018南充)某化学兴趣小组欲测定一瓶过氧化氢溶液中溶质的质量分数,实验操作及相关数据如图所示:(1)生成氧气的质量 g;(2)这瓶过氧化氢溶液中溶质的质量分数是多少?(写出计算过程). 解:(1)根据质量守恒定律,反应生成氧气的质量=68g+2g-68.4g=1.6g;故填:1.6(2)设68g过氧化氢溶液中含有过氧化氢的质量为x.2H2O22H2O + O2↑68 32x 1.6g解得,x=3.4g过氧化氢溶液的溶质的质量分数为16.(2018雅安) 化学兴趣小组用一瓶久置的过氧化氢溶液制取氧气并测量过氧化氢质量分数。
称量 68g 过氧化氢溶液和 0. 1g 二氧化锰进行实验, 反应前后质量随时间变化关系如图。
计算:( 1) 制得氧气的质量是 g。
( 2) 过氧化氢质量分数是多少?【答案】(1)0.8克(2分)(2)设参加反应的过氧化氢质量为x。
2H2O2 MnO2△2H2O + O2↑68 32x 0.8g68∶32=x∶0.8gx=1.7g过氧化氢质量分数:1.7g/68g *100%=2.5%答:过氧化氢质量分数是2.5%。
17.(2018湖州)军事上常用氢化锂( LiH)来制取氢气,反应的化学方程式为:LiH+H2O=LiOH+ H2↑现将12克氢化锂与991克水反应,反应后所得溶液中无LiOH析出。
求:(1)生成氢气的质量.(2)所得溶液的溶质质量分数。
【答案】(1)3g;(2)3.6%18.(2018温州)实验室有一变质的氢氧化钠样品(样品中只含碳酸钠杂质,且成分均匀),为测量样品中Na2CO3的质量分数,小明进行了如下实验。
①取质量、大小相同的3个烧杯,分别加入一定质量分数的稀盐酸100克,②向上述3个烧杯中分别加入3 份质量不同的样品;③充分反应后,再用电子天平称量烧杯及烧杯内物质的总质量(假设产生的气体完全逸出)。
实验数据记录如下:实验一实验二实验三反应前稀盐酸+烧杯质量(克)150 150 150反应前固体样品质量(克) 4 8 12反应后烧杯内物质+烧杯质量(克)m 155.8 158.7已知实验中发生的化学反应:NaOH+HCl=NaCl+H2ONa2CO3+ 2HCl=2NaCl+H2O+ CO2↑(1)分析表中教据,写出判断实验二中的样品已完全反应的理由__________。
(2)表中的m 值为________。
(3)根据实验二的数据计算样品中Na2CO3的质量分数。
【答案】(1)因为实验三产生的气体质量为150+12-158.7=3.3(克),实验三产生的气体质量为150+8-155.8=2.2(克),实验三产生的气体质量大于实验二,所以实验二中稀盐酸有剩余,8克样品已完全反应。
(2)152.9 (3)66.25%19.(2018重庆A)合成氨工业中,常用碳酸钾溶液吸收产生的二氧化碳得到碳酸氢钾,反应的化学方程式为:K2CO3+CO2+H2O=2KHCO3.现向碳酸钾溶液中通入二氧化碳,恰好完全反应,得到溶质的质量分数为10%的溶液50g,试计算:(1)碳酸钾中钾元素、碳元素、氧元素的质量比为_____________。
(2)若把该50g溶液,稀释为质量分数为4%的溶液,需要加入水的质量。
