激光原理、技术与应用课件:3_3 高斯光束的传播特性
合集下载
《高斯光束》PPT课件

W02
3.光斑半径:
Lin W(o) z0
W01W z0221/2W0
即:光斑半径等于束腰半径
4.横截面光强分布: 在束腰处(即z=0)基尔霍夫公式变为:
E (x ,y ,0 ) W A 0 0e x W r 0 2 2 p ex i( k p 0 0 ) i0 W A 0 0e x W r 0 2 2 p
W 0 2 2(R l2) 1 /4
( 2 6 )
即,已知激光器腔参数R、l可求得膜参数W0
例,设λ=0.6328×10-3mm,R=500 mm,l=250 mm,
则 W 0 (0 .63 21 2 3 0 )8 2(50 205 202 5 ) 1 /0 40 .2m 24m
* 基模发散角(远场发散角)——半角
( 28)
当ρ(通光孔径)=W(z),1.5W(z),2W(z),2.5W
(z),3W(z),∝时,N(ρ)值如下表:
ρ W ( z )1 .5 W ( z ) 2 W ( z ) 2 .5 W ( z ) ∝ ρ N ( )0 .8 6 4 0 .9 8 8 0 .9 9 7 0 .9 9 9 9 9 1
p()k A0 2
W 2(z)
oexW p2 2(rz2)2r.dr
图-2-5 在 r = ∝时,高斯光束的全部光强P(∝)
P( )kW A 20 (2z)o exW p2 2(rz2)2r.dr
设
p
k
N(P)P() o
P( ) k
o
e ex xW W p p2 2 2 2((rrzz2 2))2 2 rr..d d rr1expW 22 (2 z)
即,当限制孔径为计算出的高斯光斑半径2.5倍时其通过的能
3.3 高斯光束的振幅和强度分布 激光原理及应用 电子课件

2z0
x2 y2 12Lz0
2
z z 0 x 2 2 R 0 y 2 R 01 x 2 R 0 2 y 2 R 0R 0 2 x 2 y 2 R 0
R 0 2 x 2 y 2 z z 0 R 0 2
上一页 回首页 下一页 回末页 回目录
3.3.4 高斯光束的高亮度
第 三 章
激 光 器 的 输 出 特 性
3
3 高 斯 光 束 传 面在其法线方向上单位立体角范围内输出去的辐射功率。 B I SΩ
Ω(R)2 R22
2.一般的激光器是向着数量级约为10-6 sr的立体角范围内输出激光光束的。而普 通光源发光(如电灯光)是朝向空间各个可能的方向的,它的发光立体角为4πsr。 相比之下,普通光源的发光立体角是激光的约百万倍。
三 章
激 光 器
2(z)lz im 021z(z)(z02)222
2 2 L 0
的
输 2.由波动光学知道,在单色平行光照明下,一个半径为 r 的圆孔夫琅和费衍射角
出 (主极大至第一极小值之间的夹角) 0.61r 。与上式相比较可知.高斯光束
特 性
半角远场发散角在数值上等于以腰斑 0 为半径的光束的衍射角,即它已达到了衍 射极限。
§.
3 3.共焦腔基模光束的理论发散角具有毫弧度的数量缀,它的方向性相当好。
3 高 斯
4.由于高阶模的发散角是随着模的阶次的增大而增大,所以多模振荡时,光束的 方向性要比单基模振荡差。
光
束
传
播
特
性
上一页 回首页 下一页 回末页 回目录
共焦腔反射镜面是共焦场中曲率最大的等相位面
§.
3 4.共焦场中等相位面的分布如图(3-9)所示。
激光原理 高斯光束

| R(z) | 逐渐增加,曲率中心在 (− πω02 , πω02 ) λλ
Z=± ∞
|R(z)|≈|z|→ ∞ (无限远处等相面为平面)
光波面
ω(z)
F
ω0
z
−ω0
F
高斯光束 强度:
共焦腔心处:高斯分布平面波 其他:高斯分布球面波
非均匀球面波 变曲率中心球面波
2014/5/7
高斯光束的基本性质
NJUPT
高斯光束的基本性质
振幅分布及光斑半径
A(r)
A0
A0 e
0 r =ω(z) r
ω(z) =ω0
1+
z f
2
=ω0
λz 2
1
+
πω02
P67
=f π= ω02 1 L 共焦腔反射镜的焦距 λ2
NJUPT
高斯光束的基本性质
振幅分布及光斑半径
ω(z)
F
ω0
y, z)
=
A0 exp[−
ω(z)
(x2 + y2)
ω2(z) ]×
exp−
ik[
x2 + y2 2R(z)
+
z] +
iϕ ( z )
振幅因子
相位因子
NJUPT
高斯光束的基本性质
ω0 ——基模高斯光束的腰斑半径(束腰)
ω(z) ——高斯光束在z处的光斑半径 R(z) ——高斯光束在z处的波面曲率半径
1 =
q 2
C+ D q
=1 A+ B
q 1
(C + D ) − iλ D
高斯光束的传播特性ppt课件

复习:共焦腔内或腔外的一点的行波场的解析式:
umn x, y, z CmnHm
2 1
2
2 ws
x Hn
2 1
2
2 ws
y
exp
1
2
2
x2 y2 ws2
exp ix,
y, z
1. Hm
2 1
2
2 ws
x Hn
2 1 2
2 ws
y
exp
2 1
2
x2 y2 ws2
行波场横向振幅分布因子
束腰半径
0
1 2
s
L 2
f
等相面曲率半径 R(z) z [1 ( L )2 ] z [1 ( f )2 ] z [1 (02 )2 ]
2z
z
z
任意位置光斑 半径
(z) 0
1
(
z 02
)2
高斯光束的束腰半 径的大小和位置确
镜面光斑半径 远场发散角
s
20
L
2 2 0
定,就可以确定整
2、光斑尺寸
当场振幅为轴上( x2 y2 0 )的值的e-1倍,即强度为轴上的值的e-2倍时,
所对应的横向距离 z 即z 处截面内基模的光斑半径为
(z)
x2 y2 s
2
1 2 s
2
4z2 1 L2
§3.3.1 高斯光束的振幅和强度分布
(z) s 1 2 s
2
2
ωs xs2 ys2 L
k
L 2
1
2z L
1
2z L 2z
2
x2
L
y
2
2
z
k
umn x, y, z CmnHm
2 1
2
2 ws
x Hn
2 1
2
2 ws
y
exp
1
2
2
x2 y2 ws2
exp ix,
y, z
1. Hm
2 1
2
2 ws
x Hn
2 1 2
2 ws
y
exp
2 1
2
x2 y2 ws2
行波场横向振幅分布因子
束腰半径
0
1 2
s
L 2
f
等相面曲率半径 R(z) z [1 ( L )2 ] z [1 ( f )2 ] z [1 (02 )2 ]
2z
z
z
任意位置光斑 半径
(z) 0
1
(
z 02
)2
高斯光束的束腰半 径的大小和位置确
镜面光斑半径 远场发散角
s
20
L
2 2 0
定,就可以确定整
2、光斑尺寸
当场振幅为轴上( x2 y2 0 )的值的e-1倍,即强度为轴上的值的e-2倍时,
所对应的横向距离 z 即z 处截面内基模的光斑半径为
(z)
x2 y2 s
2
1 2 s
2
4z2 1 L2
§3.3.1 高斯光束的振幅和强度分布
(z) s 1 2 s
2
2
ωs xs2 ys2 L
k
L 2
1
2z L
1
2z L 2z
2
x2
L
y
2
2
z
k
激光原理与应用讲-第三章

§.
1
光 学
(3)
谐
振
腔
的
kL
2 2q
k 2 ν c
衍 射 理
νmn q 2 q Lc 2cL m n2 q Lc
论
图(3-4) 腔中允许的纵模数
上一页 回首页 下一页 回末页 回目录
第 三 章
激 光 器 的 输 出 特 性3
1
光 学 谐 振 腔 的 衍 射 理 论
§.
3.1.3 光学谐振腔谐振频率和激光纵模
光 器
u m C m n F m ( X n ) F n ( Y ) I m u m 2 n F m 2 n ( X ) F n 2 ( Y )
的
图(3-5)画出了m = 0,1,2和n = 0,1的 F m (X ) X 及 F n(Y ) Y 的变化曲线,同
输
时还画出了相应的光振动的镜面光强分布:
上一页 回首页 下一页 回末页 回目录
第 三 章
激
光 3.1.1 菲涅尔-基尔霍夫衍射公式
器
的
1.惠更斯-菲涅耳原理
输
出 特 性3
1
§.
为描述波的传播过程惠更斯提出了关于子波 的概念,认为波面上每一点可看作次球面子波的 波源,下一时刻新的波前形状由次级子波的包络
光 面所决定。
图3-1 惠更斯-菲涅耳原理
u m C n m H m n ( X ) H n ( Y ) e X 2 2 Y 2 ;其 X x 中 2 L ,Y y2 L
出
特 性3
i[k L(mn1)]
本征值近似解: mne
2
§.
2
对 称
Hm(X)和Hn(Y)均为厄密多项式,其表示式为:
高斯光束的传播特性

在近轴情况下,等相位面是顶点位于z 旋转抛物面,抛物面的焦距为 在近轴情况下,等相位面是顶点位于z0的旋转抛物面,抛物面的焦距为:
z0 f2 f '= + 2 2 z0
可以证明,在近轴情况下,共焦场的在z0处的等相位面近 可以证明,在近轴情况下,共焦场的在z 似为球面,其曲率半径为: 似为球面,其曲率半径为:
2
位相因子, exp (− iφ ( x, y , z )):位相因子,决定了共焦腔的位相分布
2 2 u mn ( x, y , z ) = C mn H m ⋅ 1+ ζ 2 w s
2 2 x H n ⋅ 1+ ζ 2 w s
2 x2 + y2 y ⋅ exp − 1 + ζ 2 ⋅ w 2 exp(− iφ ( x, y , z )) s
λz 2 1+ ( 2 ) πω 0
⇒ 2θ = 2
2λ 2λ = πL πω0
高阶模的发散角随阶次的增大而增大,方向性变差! 高阶模的发散角随阶次的增大而增大,方向性变差!
2λ 2λ 2θ = 2 = πL πω0
不同的腰半径的激光光束的远场发散角对比图
例:某共焦腔氦氖激光器,L=30cm, λ = 0.638µm 某共焦腔氦氖激光器,
一、等相位面的分布
1、等相位面——行波场中相位相同的点连成的曲面 、等相位面 行波场中相位相同的点连成的曲面 2、与腔轴线相交于z0的等相位面的方程 、与腔轴线相交于
φ (x, y, z ) = φ (0,0, z0 )
L 2z 2z L x2 + y2 π φ ( x, y, z ) = k[ (1 + ) + ] − (m + n + 1)( − ϕ ) = φ (0,0, z0 ) 2 L 1 + ( 2 z L) 2 L 2
高斯光束的传播特性课件

加精准,能够实现更高的光束质量和更稳定的传输。
动态调控
02
通过实时监测和反馈系统,实现对高斯光束的动态调控,以满
足不同应用场景的需求。
多光束控制
03
未来将实现多光束的独立控制和协同操作,提高光束的灵活性
和应用范围。
高斯光束在量子通信中的应用
1 2 3
安全性增强 高斯光束在量子通信中能够提供更强的安全性保 障,通过量子纠缠和量子密钥分发等技术,实现 更加安全的通信传输。
传输距离提升 随着量子通信技术的发展,高斯光束的应用将有 助于提高量子通信的传输距离和稳定性。
网络架构优化 高斯光束在量子通信网络架构中能够提供更灵活 和高效的光路设计,优化网络性能和扩展性。
高斯光束在其他领域的应用
生物医学成像
高斯光束在生物医学领域可用于光学显微镜、光谱仪等设备的成像 技术,提高成像质量和分辨率。
在生物医学成像中的应用
光学成像
高斯光束作为照明光源,能够提高光学成像的分辨率和对比度。
荧光成像
利用高斯光束激发荧光标记物,实现生物组织的荧光成像。
光声成像
结合高斯光束与光声效应,实现生物组织的高分辨率、高对比度 的光声成像。
05
高斯光束的未来展
高斯光束控制技术的发展
高精度控制
01
随着光学技术和计算机技术的发展,未来高斯光束的控制将更
高斯光束的强度分布和相位分 布都可以用高斯函数描述,这 使得高斯光束在许多领域都有 广泛的应用。
02
高斯光束的播特性
传播过程中的光强分布变化
01 02
光强分布变化规律
高斯光束在传播过程中,光强分布呈现中间高、两侧低的形态,类似于 钟形曲线。随着传播距离的增加,光强分布逐渐展宽,但中心峰值保持 不变。
《高斯光束》课件

02
高斯光束的数学模型
高斯光束的电场分布
描述高斯光束的电场分布通常使用高 斯函数,其形式为$E(r,z)=E_{0} frac{omega_{0}}{w(z)} exp(frac{r^{2}}{w(z)^{2}}) exp(ifrac{kr^{2}}{2R(z)}+ivarphi(z))$, 其中$E_{0}$是光束中心电场强度, $omega_{0}$是束腰半径,$w(z)$ 是光束半径,$R(z)$是光束的波前曲 率半径,$varphi(z)$是相位。
VS
高斯光束的电场分布具有中心强度高 、向外逐渐减小的特点,这种分布有 利于在一定范围内实现较高的能量集 中度。
高斯光束的能量分布
高斯光束的能量分布与电场分布类似,也呈现出中心强 度高、向外逐渐减小的特点。
在实际应用中,高斯光束的能量分布可以通过控制激光 器的参数和光束传输过程中的光学元件进行调整,以满 足不同应用需求。
高斯光束的特性
总结词
高斯光束具有许多独特的性质,包括光束宽度随传播距离增加、中心光强为零、能量集中于光束的腰斑等。
详细描述
高斯光束的一个重要特性是它的光束宽度随着传播距离的增加而增加,这是由于光束在传播过程中不断发生衍射 。此外,高斯光束的中心光强为零,即光束的最小值点位于中心。高斯光束的能量主要集中在腰斑处,即光束宽 度最小的地方,这使得高斯光束在远场具有很好的汇聚性能。
总结词
高斯光束在光学无损检测中能够穿透物质并检测其内部 结构和缺陷。
详细描述
高斯光束具有较好的穿透性和方向性,能够深入物质内 部并检测其结构和缺陷。在无损检测中,高斯光束被用 来检测材料内部的裂纹、气孔、夹杂物等缺陷,为产品 质量控制和安全性评估提供可靠的依据。这种检测方法 具有非破坏性和高灵敏度等优点,广泛应用于航空航天 、核工业等领域的安全监测和质量控制。
《激光原理》3.3高斯光束的传播特性(新)

共焦腔的反射镜面是两个等 相位面,与场的两个等相位 面重合,且曲率半径达到最小 值。
z = f, 即镜面处R最小,且等于镜面本身曲率半径
证 R(z) z f 2
z
dR
f2
dz 1 z2 0
zf
R( f ) ( f f 2 ) 2 f R f
z
-f 0
f
R02 x2 y2 z z0 R0 2
1.当 z0 0 时,R(z0 ) 2.当 z0 时,R(z0 ) 3.当 z0 f 时,R(z0 ) z0 4.当 z0 f 时,R(z0 ) L 2 f
束腰处的等相位面为平面, 曲 率中心在无穷远处
无穷远处等相位面为平 面,曲率中心在z=0处
光束可近似为一个 由z=0点发出的半径 为z的球面波。
由 0s 20 可知,镜面上的光斑尺寸,基模体积和远
V000
L
2 0
发散角等高斯光束的参数都可以通过
2 2 基模腰斑半径(“腰粗”)ω0来表征,故 0 “腰粗”是高斯光束的一个特征参数.
计算表明: 2 内含86.5%的光束总功率
Area
立体角的单位为sr,称为球面度。1sr是这样的 立体角:其顶点位于球心,它在球面上所截取 的面积等于以球半径为边长的正方形面积。
f ' z0 f 2 2 2z0
可以证明,在近轴情况下,共焦场的在z0处的等相位面近 似为球面,其曲率半径为:
R0
2
f
'
z0 [1
(
f z0
)2 ]
z0 [1
(L 2z0
)2 ]
(3 38)
则有:
z
z0
x2 y2 2R0
R0
x2 y2 1 R02 R0
z = f, 即镜面处R最小,且等于镜面本身曲率半径
证 R(z) z f 2
z
dR
f2
dz 1 z2 0
zf
R( f ) ( f f 2 ) 2 f R f
z
-f 0
f
R02 x2 y2 z z0 R0 2
1.当 z0 0 时,R(z0 ) 2.当 z0 时,R(z0 ) 3.当 z0 f 时,R(z0 ) z0 4.当 z0 f 时,R(z0 ) L 2 f
束腰处的等相位面为平面, 曲 率中心在无穷远处
无穷远处等相位面为平 面,曲率中心在z=0处
光束可近似为一个 由z=0点发出的半径 为z的球面波。
由 0s 20 可知,镜面上的光斑尺寸,基模体积和远
V000
L
2 0
发散角等高斯光束的参数都可以通过
2 2 基模腰斑半径(“腰粗”)ω0来表征,故 0 “腰粗”是高斯光束的一个特征参数.
计算表明: 2 内含86.5%的光束总功率
Area
立体角的单位为sr,称为球面度。1sr是这样的 立体角:其顶点位于球心,它在球面上所截取 的面积等于以球半径为边长的正方形面积。
f ' z0 f 2 2 2z0
可以证明,在近轴情况下,共焦场的在z0处的等相位面近 似为球面,其曲率半径为:
R0
2
f
'
z0 [1
(
f z0
)2 ]
z0 [1
(L 2z0
)2 ]
(3 38)
则有:
z
z0
x2 y2 2R0
R0
x2 y2 1 R02 R0
3-3激光器的输出特性-高斯光束传播特性
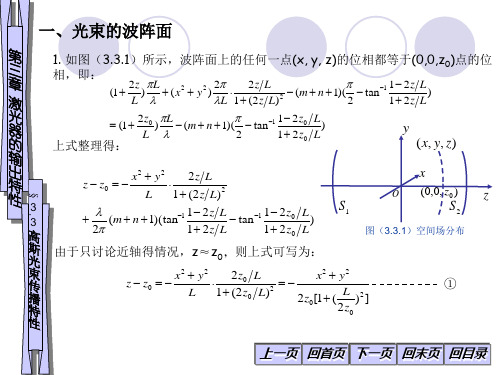
§ .
图(3.3.1)空间场分布
由于只讨论近轴得情况,z≈z0,则上式可写为:
2 z0 L x2 y2 x2 y2 z z0 L 2 L 1 ( 2 z0 L) 2 2 z0 [1 ( ) ] 2 z0
①
上一页 回首页 下一页 回末页 回目录
第 三 章 激 光 器 的 输 出 特 性
由于激光的发散角比普通光源的发散角小得多,因此激光的亮度要大得多。
5. 对高阶横模来说,光束的发散角比基横模大。 6. 高斯光束与球面波的区别:
2 0 L R0 z0 [1 ( )] z 0 1 ( z02 ) 2 7. 总结: 0 2 z0 0 1 2 20 2 2 0
x2 y2 2z L z z0 L 1 ( 2 z L) 2 1 2 z0 L 1 2z L (m n 1)(tan1 tan1 ) 2 1 2z L 1束 传 播 特 性
3 3
S1
(0,0, z0 )
S2
z
3 3
L 2 L2 R0 z0 z0 ( ) 2 z0 4 z0 R0 z0 越小。 看出,z0 越大,
高 斯 光 束 传 播 特 性
§ .
即波阵面离中心越远,其曲率中 心离腔中心越近,如图(3.3.5)所 示。
上一页 回首页 下一页 回末页 回目录
第 三 章 激 光 器 的 输 出 特 性
0
§ .
对近轴的波面有z≈z0,则上式可写为:
U 0 ( x, y, z ) U 0 ( x, y, z0 )
令
z
L [1 (2 z0 L) 2 ] 2
上一页 回首页 下一页 回末页 回目录
激光原理与技术-山西大学课件 第三章

数 q2 的高斯光束,于是有:
1 qi
1 Ri
i
i i2
X
iY
i 1, 2
(3.4.1)
n1
q1,1 RP1
RP2 q2 ,2
n2
a b
c
d
z
s1
s2
图3.4.1 高斯光束通过复杂光学系统的变换
由 q1 至 q2 的变换遵从ABCD定律:
1 C D / q1 q2 A B / q1
(3.4.2)
§3.1 高斯光束的基本性质
一、高斯光束是亥姆霍兹方程在 缓变振幅近似下的一个特解
二、高斯光束的基本性质
一、高斯光束是亥姆霍兹方程在缓变振幅近似下的一个特解
电磁场运动的普遍规律可用Maxwell方程组描写。稳态传输的光频 电磁场,只研究电矢量的波动方程,电矢量在光现象中起主要作用。在 标量近似下,波动方程可写为亥姆霍兹方程。高斯光束是亥姆霍兹方程 在缓变近似下的一个特解。
4.瑞利长度
瑞利长度的物理意义为:当 z z0 时,(z0 ) 20 。在实用中
常取 z z0 范围为高斯光束的准直范围,在这段长度内,高斯光束可以
近似认为是平行的。所以,瑞利长度越长,就意味着高斯光束的准直范围 越大,反之亦然。
5.远场发散角
lim 高斯光束的远场发散角可用下式定义:0
x
(3.3.8) (3.3.9)
将式(3.3.9)代入(3.3.8),利用方程式对任意r 成立条件,得到
s(z) 和q(z) 的微分方程组:
dq dz
1 2q2
1 ds 1
s dz q
(3.3.10) (3.3.11)
若传输常数 与z 无关,在边界条件 q(z) z0 s(z) z0 q1下,求得式
高斯光束的传播特性课件

高斯光束的未来发展趋势
01 发展现状分析
前景广阔
02 未来趋势探讨
挑战与机遇并存
03 科学研究发展
跨学科交叉
高斯光束在工业应用中的创新
制造工艺
高效精准 节约成本
设备应用
智能控制 自动化生产
材料加工
高质量 快速加工
能源利用
节能环保 绿色生产
● 07
第7章 高斯光束的传播特性 课件
高斯光束的重要性
折射率与热效应
热效应
高斯光束在介质中 传播时会产生热效
应。
折射率变化
热效应会导致折射率 发生变化,影响高斯 光束的传播和聚焦效
果。
总结
高斯光束的传播特性受到折射率、衍射效应、非线性光学和热 效应等因素的影响。理解这些因素对于光学应用和光束传输具 有重要意义。
● 03
第3章 高斯光束的光学系统
高斯光束的聚焦系统
● 04
第四章 高斯光束的传播实验
高斯光束的干涉实验
迈克尔逊干涉仪观测
利用迈克尔逊干涉 仪观测高斯光束的
干涉条纹
分析干涉条纹
分析干涉条纹的形状 和对比度,验证高斯
光束的传播特性
高斯光束的衍射实验
在衍射光栅实验中,观测高斯光束的衍射效 应是探究光栅对高斯光束的光斑形状和光强 分布的影响。通过实验,可以进一步了解光 的衍射现象,验证高斯光束在衍射过程中的 特性。
衍射效应
光束传播中的衍射 现象
散射效应
光束在物质中传播时 的散射现象
折射效应
光束在介质中传播时 的折射规律
高斯光束的调制特性
高斯光束可以通过调制改变其传播特性,例 如调制频率、相位等参数可以实现对光束的 精准控制。调制技术在光通信和激光加工中 有着重要的应用价值。
激光原理、技术与应用课件:3_3 高斯光束的传播特性

②饱和吸收染料选模。因TEM00模的功率密度高,在染料 中很容易饱和而使染料变得透明。但高阶横模其功率密度低, 不易“漂白”染料,两者的损耗具有较大的差异,从而达到选 基模的目的。
③调节腔镜选模。光学谐振腔的反射镜主光轴与激活介质的 轴线重合时,不同横模的衍射损耗都较小,当镜轴与腔轴偏离 时,则不同横模的衍射损耗都会相应增加。因高阶横模损耗大, 受到影响较大。而基横模损耗小,受到影响小,容易获得基模 输出,但输出功率会因此而下降。
R(z0) 0
zz 0 0
6.当 z0 0 时,
R(z0) 0 z z 0 0
——共焦腔的等相面是凹面向着腔的中心的球面
结论:在z < 0 处,光束是沿着z的方向传播的会聚球面波;
在z = 0处变成一个平面波;
在 z>0处又变成发散球面波。
三.共焦场的等相位面的分布图
共焦场等相面的分布 可以证明: 如果在场的任意一个等相位面处放上一块具有相应曲率的反 射镜片,则入射在该镜片上的场将准确地沿着原入射方向返 回,这样共焦场分布将不会受到扰动.这是非常重要的性质.
此法虽扩大了基模体积,但由于使用了二个透镜,增加了腔 内损耗,而且调整困难。腔内存在聚焦光束,使光阑处的光功率 密度过高,易使光阑烧坏,因此光阑材料须选用高熔点金属或蓝 宝石一类特殊材料。故不适用大功率、大能量激光器件。
补
补 ③“猫眼”谐振腔。将聚焦光阑装置再作改进,即将平面镜移到焦点处 贴近光阑,在透镜处放置另一个较大的光阑,此称为“猫眼”腔。它具 有高选模性、模体积大、腔长短、结构紧凑等优点。但腔镜处于焦点位 置,要求镜面能耐受强光照射。
介质能量的提取就大,对模 式振荡作贡献的粒子数越多, 就有可能获得大的输出功率。
图(3-8) 基模光斑半径随z按双曲线规律的变化
③调节腔镜选模。光学谐振腔的反射镜主光轴与激活介质的 轴线重合时,不同横模的衍射损耗都较小,当镜轴与腔轴偏离 时,则不同横模的衍射损耗都会相应增加。因高阶横模损耗大, 受到影响较大。而基横模损耗小,受到影响小,容易获得基模 输出,但输出功率会因此而下降。
R(z0) 0
zz 0 0
6.当 z0 0 时,
R(z0) 0 z z 0 0
——共焦腔的等相面是凹面向着腔的中心的球面
结论:在z < 0 处,光束是沿着z的方向传播的会聚球面波;
在z = 0处变成一个平面波;
在 z>0处又变成发散球面波。
三.共焦场的等相位面的分布图
共焦场等相面的分布 可以证明: 如果在场的任意一个等相位面处放上一块具有相应曲率的反 射镜片,则入射在该镜片上的场将准确地沿着原入射方向返 回,这样共焦场分布将不会受到扰动.这是非常重要的性质.
此法虽扩大了基模体积,但由于使用了二个透镜,增加了腔 内损耗,而且调整困难。腔内存在聚焦光束,使光阑处的光功率 密度过高,易使光阑烧坏,因此光阑材料须选用高熔点金属或蓝 宝石一类特殊材料。故不适用大功率、大能量激光器件。
补
补 ③“猫眼”谐振腔。将聚焦光阑装置再作改进,即将平面镜移到焦点处 贴近光阑,在透镜处放置另一个较大的光阑,此称为“猫眼”腔。它具 有高选模性、模体积大、腔长短、结构紧凑等优点。但腔镜处于焦点位 置,要求镜面能耐受强光照射。
介质能量的提取就大,对模 式振荡作贡献的粒子数越多, 就有可能获得大的输出功率。
图(3-8) 基模光斑半径随z按双曲线规律的变化
周炳坤激光原理与技术课件 第三章 高斯光束

结论:具有固定曲率中心的普通傍轴球面波可以由其曲率半径R来描述,它的 传
§ 3.2.2高斯光束q参数的变换规律———ABCD公式
一、高斯光束q参数在自由空间中的传播规律 根据式(2.9.9)表示的q参数的定义
λ 1 1 = −i q(z) R(z) πw 2 ( z )
(2.10.7)
(2.9.6)
1、用束腰半径 w0(或f)及束腰位置表征高斯光束 由式(2.9.1)与式(2.9.2)及ψ(z)式可知:一旦腰斑 w0及其位置确 定了,高斯光束的结构也就确定了。由f与 w0 的关系也可用f与束腰位置来表征 高斯光束。
2、用w(z)和R(z)表征高斯光束 由(2.9.4)和(2.9.6)式得到: πw 2 ( z ) 2 − 12 w 0 = w ( z )[1 + ( ) ] λR(z)
λ w(z) = w0
(2.9.2)
π w0 2 f = , w0 = λ
λf π
f 称为高斯光束的共焦参数或瑞利长度; R(z)为与传播轴线相交与z点的高斯光束等相位面的曲率半径。 当z等于f时, (z) 2w0 w = 对于一般稳定球面腔(R 、 2、 )所产生的高斯光束w 及f与 R 、 2、 的关系为 0 1R L 1R L
§ 3.2
高斯光束q参数的变换规律
§ 3.2.1普通球面波的传播规律
一、普通球面波的传播规律
图(2.10.1)普通球面波在自由空间的传播 如图普通球面波,曲率中心为0,曲率半径R(z)的传播规律为
R1 = R ( z1 ) = z1
R2 = R ( z 2 ) = z 2 R 2 = R1 + ( z 2 − z1 ) = R 1 + L
= q0 + l = qB + lC
高斯光束的传播特性新.ppt

x2
y2 L
2z0
x2 y2
1
L 2z0
2
R0
z 0 [1
(L 2z0
)2 ]
当 z0 0 时, R(z0 ) 当 z0 时, R(z0 )
当 z0 f
时,R(z ) L 0
腔中点或距腔中点无限 远处,等相面为平面
20为基模光束的发散角
由于高阶模的发散角是随着模的 阶次的增大而增大,所以多模振 荡时,光束的方向性要比单基模 振荡差。
由 0s 20 可知,镜面上的光斑尺寸,基模体积和远
V000
L
2 0
发散角等高斯光束的参数都可以通过
2 2 0
基模腰斑半径(“腰粗”)ω0来表征,故 “腰粗”是高斯光束的一个特征参数.
图3-7 计算腔内外光场分布的示意图
umnx, y, z CmnHm
2
1
2
2 ws
x Hn
2
1
2
2 ws
y
exp
2
1
2
x2 y2 ws2
exp
i x,
y,
z
( x,
y, z)
k
L 2
(1
)
1
2
x2
L
y
2
(m
n
1)(
2
)
arctg 1 arctg L 2z
1
L 2z
激光原理3.3高斯光束的传播特性(2014)_图文(精)

激光原理
高福斌
2013116
2013.11.6
/25 1
3.3 高斯光束的传播特性
回顾——求解对称开腔中的自再现模积分方程, 了解输出激光的具体场的分布——
前瞻研究高斯光束的传播特性
/22 2
一、等相位面的分布
等相位面 1、等相位面——行波场中相位相同的点连成的曲面(
, , x y z ϕx
z
z 0
(
00,0, z ϕ共焦场等相面的分布
/25
9
三 . 共焦场的等相位面的分布图
共焦场等相面的分布
可以证明:
如果在场的任意一个等相位面处放上一块具有相应曲率的反射镜片,则入射在该镜片上的场将准确地沿着原入射方向返 /25
16回,这样共焦场分布将不会受到扰动.这是非常重要的性质.
z 小结:高斯光束的基本性质
1. 高斯光束在其轴线附近可看作是一种非均匀高斯
球面波,
22. 在其传播过程中曲率中心不断改变
3. 其振幅在横截面内为一高斯光束
4. 强度集中在轴线及其附近
5. 等相位面保持球面/25 17
数值例 :
器件辐射能量脉冲时间 P
普通红宝石激光器 1J 10-4s 104W 1J 10910
调 Q 红宝石激光器 1J 10-9s 109W 调 Q 及锁模红宝石激光器 1J 10-12~10-13s 1012~1013W *输出能量一定时 , 激光器由于脉冲时间缩短可使△ I 很大 ; ,
而且因θ(或Ω 很小 , 故亮度 B 很大。
/25 23。
高斯光束的基本性质及特征参数课件

变换方法
通过使用各种光学元件,如反射镜、 棱镜等,可以对高斯光束进行各种形 式的变换,如旋转、平移、缩放等。
高斯光束的操控与调制
操控技术
利用光学元件对高斯光束进行操控,如改变光束方向、实现光束分裂等。
调制方法
通过在光束中加入外部信号,可以对高斯光束进行调制,实现信息传输和信号 处理等功能。
05
CHAPTER
高斯光束的聚焦
通过透镜可以将高斯光束聚焦到一点 ,聚焦点处的光强最大过程中,其传播方向呈发散状。
光强分布
高斯光束的光强呈高斯型分布,中心光强最大,向外逐渐减小。
衍射极限
高斯光束的衍射极限由波长和束腰宽度决定,短波长、小束腰宽度 的高斯光束具有更好的聚焦性能。
高斯光束的模拟与仿真
高斯光束的数值模拟方法
有限差分法
通过离散化高斯光束的波动方程,使用差分公式 求解离散点上的场值。
有限元法
将高斯光束的波动方程转化为变分问题,利用分 片多项式逼近解。
谱方法
将高斯光束的波动方程转化为频域或谱域的方程 ,通过傅里叶变换求解。
高斯光束的物理仿真实验
光学实验平台
搭建光学实验装置,通过实际的光路系统模拟高斯光束的传播。
光学成像
1 2 3
高分辨率成像
高斯光束在光学成像领域可用于实现高分辨率、 高清晰度的成像,从而提高图像的细节表现力和 清晰度。
荧光显微镜
高斯光束作为激发光,能够均匀地激发样品中的 荧光物质,提高荧光显微镜的成像质量和稳定性 。
光学共聚焦显微镜
利用高斯光束的聚焦和扫描特性,可以实现光学 共聚焦显微镜的高精度、高灵敏度成像。
激光加工
高效加工
01
高斯光束具有较高的亮度和能量集中度,能够实现高效、高精
通过使用各种光学元件,如反射镜、 棱镜等,可以对高斯光束进行各种形 式的变换,如旋转、平移、缩放等。
高斯光束的操控与调制
操控技术
利用光学元件对高斯光束进行操控,如改变光束方向、实现光束分裂等。
调制方法
通过在光束中加入外部信号,可以对高斯光束进行调制,实现信息传输和信号 处理等功能。
05
CHAPTER
高斯光束的聚焦
通过透镜可以将高斯光束聚焦到一点 ,聚焦点处的光强最大过程中,其传播方向呈发散状。
光强分布
高斯光束的光强呈高斯型分布,中心光强最大,向外逐渐减小。
衍射极限
高斯光束的衍射极限由波长和束腰宽度决定,短波长、小束腰宽度 的高斯光束具有更好的聚焦性能。
高斯光束的模拟与仿真
高斯光束的数值模拟方法
有限差分法
通过离散化高斯光束的波动方程,使用差分公式 求解离散点上的场值。
有限元法
将高斯光束的波动方程转化为变分问题,利用分 片多项式逼近解。
谱方法
将高斯光束的波动方程转化为频域或谱域的方程 ,通过傅里叶变换求解。
高斯光束的物理仿真实验
光学实验平台
搭建光学实验装置,通过实际的光路系统模拟高斯光束的传播。
光学成像
1 2 3
高分辨率成像
高斯光束在光学成像领域可用于实现高分辨率、 高清晰度的成像,从而提高图像的细节表现力和 清晰度。
荧光显微镜
高斯光束作为激发光,能够均匀地激发样品中的 荧光物质,提高荧光显微镜的成像质量和稳定性 。
光学共聚焦显微镜
利用高斯光束的聚焦和扫描特性,可以实现光学 共聚焦显微镜的高精度、高灵敏度成像。
激光加工
高效加工
01
高斯光束具有较高的亮度和能量集中度,能够实现高效、高精
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
exp ix,
y, z
二、基模振幅分布和光斑尺寸
1、振幅分布
对基横模TEM00
U 00
Cmn
exp
1
2
2
x2 y2
s2
基横模TEM00的光强
I 00
U
2 00
Cm2 n
exp
1
4
2
x2 y2
s2
——基模截面是高斯函数
2、光斑尺寸振幅下降为最大值1/e时的光斑半径
2z L
(z) s
2
1 2 s
在横截面内的场振幅分布按高斯函数所描述的规律从 中心(即传输轴线)向外平滑地降落。
花样:沿x方向有m条节线,沿y方向有n条节线。
2 exp ix, y, z :位相因子,决定了共焦腔的位相分布
umn x, y, z CmnHm
2 1
2
2 ws
x Hn
2 1
2
2 ws
yexp12 2x2 y2 ws2
由于透射、散射和吸收等因素而产生的损耗;δd为激光在谐振腔中因衍射
而产生的损耗。
因此,选横模的实质是使需要的横模(一般为基模TEM00)满足阈值条 件产生振荡,而使不需要的横模(一般为高阶模)不满足阈值条件而被抑 制,从而达到滤去高阶模的目的。由于G、δi、δm对不同横模来说是相 同的,因而满足振荡阈值条件主要由衍射损耗δd来决定。为了达到上述目 的,应当尽量减小δi和δm,或相对增长δd,使得腔的总损耗a中衍射损 耗δd能起决定作用,因而有利于选模。
L
镜面有效截面半径
3、 (z在) 纵截面上的表达式
( 0
z)
1 2
L [1 2 s
(
1 2
2z )2] L
L
(
z
)
0
1
(
z
2 0
)2
2 02
z2
(
2 0
)2
1
2 02
(
z
2 0
2
)
2
1
——光斑半径随z按照双曲线规律变化。
三、 模体积
1、定义:描述某一腔模在腔 内扩展的空间体积。
2、意义:模体积大。对激活
补
②聚焦光阑法。 小孔光阑法具有结构简单、调整方便等优点。但由于光阑较
小,使基模体积变小,使输出功率下降较大。所以此法仅适用于 增益较低的气体激光器。为了扩大基模体积,通常在谐振腔中安 置透镜进行选模。其原理是使腔内平行光束聚焦,再在焦点处插 入一个小孔光阑,使得只有沿轴向行进的平行光束才能通过小孔 往返振荡,而其它方向上的光速被小孔光阑所阻截。这种选模方 法,扩大了激活介质的基模体积,从而提高了激活晶体的利用率, 增大了激光输出功率(或能量)。
2
1
4z2 L2
(z) s 1 2 s
2
2
ωs xs2 ys2 L
1
4z2 L2
(z)
L [1 ( 2z )2 ] 2 L
①当 z=0 时,z 达到最小值
0
1 2
s
1 2
L
——高斯光束的基模腰斑半径(光腰或束腰)
②当 z f L 时,即在镜面上时,有: 2
z
20
介质能量的提取就大,对模 式振荡作贡献的粒子数越多, 就有可能获得大的输出功率。
图(3-8) 基模光斑半径随z按双曲线规律的变化
此外,还决定一个模式能 否振荡,与其它模式的竞 争情况等。
3、计算:对称共焦腔基模
的模体积:看成底半径为 ω0,高为L的圆柱体。
V000
L02
1 2
Ls2
L2
2
s
20
L
常遵循的原则是:
①必须尽量增大高阶横模与基模的衍射损耗比(差异),即尽量增大比值 δ10/δ00。使高阶横模相对基模而言更易于抑制而难于起振; ②必须尽量减小内部损耗δi及镜面上的损耗δm,而相对增大衍射损耗δd 在总损耗a中的比例。
补 2.横模选择的方法
横模选择是单频激光器所要求的必要条件。只有在单横模的基础上 选出单纵模才能获得激光的单频振荡。
高阶模:
Vm0n
1 2
L ms ns
(2 m
1)( 2n
1)L2
2
(2m 1)( 2n 1)V000
问题:模式竞争中,基模还是高阶 模更容易获得优势。
4 模体积的意义
模体积的概念在激光振荡及腔体设计中都具有重要意 义。定性地说,某一模式的模体积描述该模式在腔内所扩 展的空间范围。模体积大,对该模式的振荡有贡献的激发 态粒子数就多,因而,也就可能获得大的输出功率;模体 积小,则对振荡有贡献的激发态粒子数就少,输出功率就 小。(激光器件设计中的一个主要问题是,如何获得尽可能大的模体
积。)
一种模式能否振荡?能获得多大的输出功率?它与其 他模式的竞争能如何?所有这些不仅取决于该模式损耗的 高低,也与模体积的大小有密切的关系。
补
激光器横模选择技术
1.横模选择的原则。
(1)谐振腔的衍射损耗。
激光振荡的阈值条件为: G>a
a为总损耗系数,它可表示为:a=δi+δm+δd
其中δi为激光束通过增益介质产生的损耗;δm为激光束在谐振腔镜面上
此法虽扩大了基模体积,但由于使用了二个透镜,增加了腔 内损耗,而且调整困难。腔内存在聚焦光束,使光阑处的光功率 密度过高,易使光阑烧坏,因此光阑材料须选用高熔点金属或蓝 宝石一类特殊材料。故不适用大功率、大能量激光器件。
(1)光阑法选模。目前采用光阑法选模最为普遍,也十分简单,只需在 谐振腔中插入一个适当大小的小孔光阑,便可抑制高阶横模而获得基模 输出。此法具有以下几种不同形式: ①小孔光阑选模。由于基模具有最小的光斑尺寸,而其它高阶模的光斑 尺寸则依次变大。所以对气体激光器,可采用选择放电管的毛细管直径 的大小,来限制激活介质的横截面积,达到选模的目的。但对大多数固 体激光器而言,激活介质的直径不可能做得太细。故欲抑制高阶横模, 可在谐振腔中放置一个适当大小的小孔光阑,其孔径大小恰好阻止其余 高阶横模而让TEM00模顺利通过。
一、共焦腔内或腔外的一点的行波场的解析式:
umn x, y, z CmnHm
2 1
2
2 ws
x Hn
2 1
2
2 ws
y
exp
1
2
2
x2 y2 ws2
exp ix,
y, z
1
Hm
2 1
2
2 ws
x Hn
2 1
2
2 ws
y
exp
2 1
2
x2 y2 ws2
行波场横向振幅分布因子
—厄米—高斯函数
3.3 高斯光束的传播特性
回顾 ——求解对称开腔中的自再现模积分方程,了解输 出激光的具体场的分布
高阶模结线所致光斑强度分布的不均匀,限制了它的应用,基 模相对均匀,是高斯分布光束,高斯光束有和平面光束和球面 光束完全不同的传输特性。
前瞻 —— 研究高斯光束的传播特性
3.3.1 高斯光束的振幅和强度分布
