离散数学图论作业5-哈密顿图
应用离散数学图论欧拉图与哈密尔顿图题库试卷习题及答案
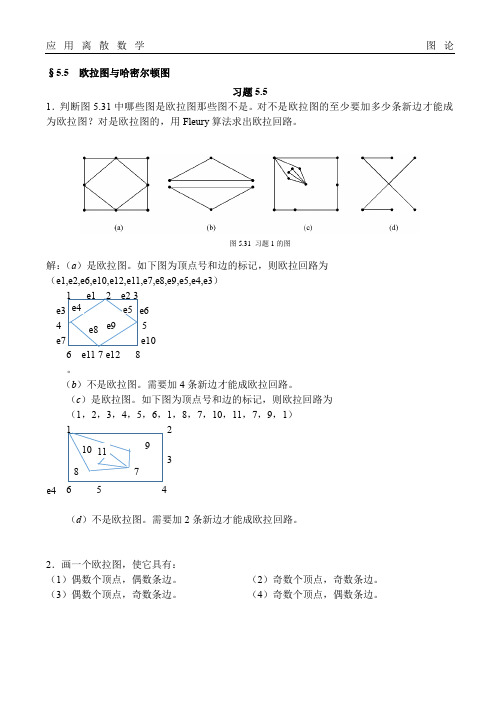
§5.5 欧拉图与哈密尔顿图习题5.51.判断图5.31中哪些图是欧拉图那些图不是。
对不是欧拉图的至少要加多少条新边才能成为欧拉图?对是欧拉图的,用Fleury算法求出欧拉回路。
图5.31 习题1的图解:(a)是欧拉图。
如下图为顶点号和边的标记,则欧拉回路为(e1,e2,e6,e10,e12,e11,e7,e8,e9,e5,e4,e3)e645e106 e117 e12 8。
(b)不是欧拉图。
需要加4条新边才能成欧拉回路。
(c)是欧拉图。
如下图为顶点号和边的标记,则欧拉回路为(1,2,3,4,5,6,1,8,7,10,11,7,9,1)236 5 4(d)不是欧拉图。
需要加2条新边才能成欧拉回路。
2.画一个欧拉图,使它具有:(1)偶数个顶点,偶数条边。
(2)奇数个顶点,奇数条边。
(3)偶数个顶点,奇数条边。
(4)奇数个顶点,偶数条边。
解 四个图按顺序分别如下:3.在k (k ≥2)个长度大于或等于3的无公共点的环型图之间至少加多少条边才能使它们组成一个简单欧拉图。
解:环形图中每个点的度是2,要形成欧拉回路,就要使新图是一个连通图,并且每个点的度仍保度偶数,因此,要让新图是欧拉图,则至少要加k 条边。
4.证明:可以从连通图中任意一点出发,经过这个图中每条边恰好两次,回到出发点。
解 将每条边都增加一条平行边,则得到一个多重图,此多重图的每个顶点的度数都是偶数,所以存在欧拉闭迹。
在欧拉闭迹中,将经过平行边改成第二次经过原来的边,定理即得证。
5.完全图p K 是欧拉图吗?是哈密尔顿图吗?完全二部图n m K ,是欧拉图吗?是哈密尔顿图吗?解 (1)K p ⎩⎨⎧不是欧拉图是欧拉图 为偶数时当为奇数时当p p K p (p ≥3)为哈密尔顿图((v 1,v 2,v 3,……,v p )即是一个哈密尔顿回路)。
(2)因为K m,n 中顶点的度数要么为m ,要么为n ,所以K m,n ⎩⎨⎧不是欧拉图是欧拉图 为奇数时或当为偶数时和当n m n m因为K m,n 的顶点数为m+n ,而任意两点的度数之和为2m 或2n 或m+n 。
哈密顿图论

哈密顿图十二面体中的哈密顿路径哈密顿图(英语:Hamiltonian path,或Traceable path)是一个无向图,由天文学家哈密顿提出,由指定的起点前往指定的终点,途中经过所有其他节点且只经过一次。
在图论中是指含有哈密顿回路的图,闭合的哈密顿路径称作哈密顿回路(Hamiltonian cycle),含有图中所有顶的路径称作哈密顿路径。
美国图论数学家奥勒在1960年给出了一个图是哈密尔顿图的充分条件:对于顶点个数大于2的图,如果图中任意两点度的和大于或等于顶点总数,那这个图一定是哈密尔顿图。
哈密尔顿回路问题与欧拉回路类似。
它是1859年哈密尔顿首先提出的一个关于12面体的数学游戏:能否在图10.4.9中找到一个回路,使它含有图中所有结点一次且仅一次?若把每个结点看成一座城市,连接两个结点的边看成是交通线,那么这个问题就变成能否找到一条旅行路线,使得沿着该旅行路线经过每座城市恰好一次,再回到原来的出发地呢?为此,这个问题也被称作周游世界问题(10.4.9)对图10.4.9 ,图中粗线给出了这样的回路。
定义10.4.3 给定图G,若有一条路通过G中每个结点恰好一次,则这样的路称为哈密尔顿路;若有一个圈,通过G个每个结点恰好一次,这样的圈称为哈密尔顿回路(或哈密尔顿圈)。
具有哈密尔顿回路的图称为哈密尔顿图。
尽管哈密尔顿回路与欧拉回路问题在形式上极为相似,但是到目前为止还不知道一个图为哈密尔顿图的充要条件,寻找该充要条件仍是图论中尚未解决的主要问题之一。
下面先给出一个简单而有用的必要条件。
定理10.4.4 设图G=〈V ,E〉是哈密尔顿图,则对于V的每个非空子集S,均有W(G-S)≤|S| 成立,其中W(G-S)是图G-S的连通分支数。
证明: 设α是G的哈密尔顿回路,S是V的任一非空子集。
在G-S中,α最多被分为|S|段,所以W(G-S)≤|S|利用本定理可判别某些图不为哈密尔顿图。
如在图10.4.10中,若取S={v1,v4},则G-S有3 个连通分支,故该图不是哈密尔顿图。
图论-哈密尔顿图-课内专题报告

{n-3,n-1},{n-1,1}组成。这条哈密顿圈与第一条圈没有公共边。当n ≥7时,按照这种
k 2 方法把图?中的圈旋转角度 n 1 ,其中2 ≤k ≤(n-3)/2,就得到总数为(n-1)/2条哈密顿
圈,它们满足任意两个圈没有公共边。所以这17名学生在此科学营地中一直可以共进 (17-1)/2=8天午餐,直到某些同学不得再次坐在其它人旁边。 5 5 7 n-2 3 3 2 4 1 n 2 1 n n-1 (b)
2014-4-14 图论之哈密尔顿图 16
Xi’an Jiaotong University
定理 3 设G =(V,E)是一个无环图并且|V| 2。如果对于所有的x,y V并且x y 都有deg(x)+deg(y) n-1,则G中有哈密顿路径。 使得x是C1中的一个顶点,y是C2中的一个顶点。设Ci具有n i 个顶点,其中i=1,2。 则deg(x) n1 1, deg( y ) n2 1, 从而有 deg( x) deg( y) ( n1 n2 ) 2, 这就与定理中 给出的条件矛盾。因此,G是连通的。 现在构造G中的一条哈密顿路径。对于m 2,pm是长度为m 1的路径
2
Xi’an Jiaotong University
哈密尔顿周游世界问题
1857年,著名的爱尔兰数学家Sir William Hamilton设计了一个游 戏:它是由一个木制的正十二面体构成,在它的每个棱角处标有当 时很有名的城市。游戏目的是“环球旅行”。为了容易记住被旅游 过的城市 ,在每个棱角上放上一个钉子,再用一根线绕在那些旅游 过的城市上(钉子),由此可以获得旅程的直观表示。给定世界上20个 城市,用一个代表地球的十二面体的20个顶点分别代表这20个城市。 从某一个顶点出发,沿着十二面体的棱,经过每个顶点恰好一次, 最后回到出发点。
离散数学中的图的哈密顿路径问题

离散数学中的图的哈密顿路径问题图论是离散数学中的一个重要研究方向,研究的是图的性质和图之间的关系。
图是由点和边组成的,哈密顿路径问题是图论中比较有名的问题之一,它的研究已经有了一定的发展。
什么是哈密顿路径哈密顿路径是一种在图中遍历每个顶点一次并恰好一次的路径。
换句话说,如果给定的路径经过了所有节点,则称该路径为哈密顿路径。
哈密顿路径问题哈密顿路径问题是指在给定的图中寻找哈密顿路径的问题。
哈密顿路径问题最早由爱尔兰数学家哈密顿提出,他曾经在利用拓扑方法解决多面体问题时,遇到了这个问题。
哈密顿路径问题的正确性还未得到证明,因此在应用中使用时需要适当的限制条件和剪枝技巧。
哈密顿路径的存在性对于一个无向图,若从一个结点开始,遍历每个节点一次,然后回到原来的结点,此时称这样的路径为哈密顿路径。
对于一个有向图,若从一个结点开始,经过每个结点恰好一次,最后回到开始的结点,则称这条路径为哈密顿回路。
哈密顿路径存在性问题是图论中的一个经典问题,它试图回答一个非常基本的问题:“对于任何一个图,该图是否存在哈密顿路径或哈密顿回路?”哈密顿回路的判断对于哈密顿回路的判断,通常使用的方法是基于邻接矩阵和搜索算法。
在搜索算法中,广度优先搜索和深度优先搜索分别应用于无向和有向图。
广度优先搜索:对于一个无向图G和其中的一个顶点v,如果存在一个哈密顿回路,则在G中从v出发的BFS树至少应该包含所有的顶点。
深度优先搜索:对于一个有向图G和其中的一个顶点v,如果存在一个哈密顿回路,则在G中从v出发的DFS树至少应该包含所有的顶点。
如果该树可以拓扑排序,则该图包含哈密顿回路。
哈密顿回路的求解在实际问题中,哈密顿路径/回路问题是非常重要的,其应用很广泛。
哈密顿回路的求解通常使用回溯法,可以按顺序搜索每个顶点,每次选择一个顶点进行搜索时,对于该点已经访问过的顶点进行标记,从未被访问过的顶点中选择一个进行搜索,如果可以找到一个哈密顿回路,则更新答案。
离散数学-图论-哈密顿图及其应用

离散数学-图论-哈密顿图及其应⽤哈密顿图⼀、定义概念1.哈密顿通路设G=<V,E>为⼀图(⽆向图或有向图).G中经过每个顶点⼀次且仅⼀次的通路称作哈密顿通路2.哈密顿回路G中经过每个顶点⼀次且仅⼀次的回路(通路基础上+回到起始点)称作哈密顿回路3.哈密顿图若G中存在哈密顿回路,则称它是哈密顿图4.定义详解:(1)存在哈密顿通路(回路)的图⼀定是连通图;(2)哈密顿通路是初级通路,哈密顿回路是初级回路;(3)若G中存在哈密顿回路,则它⼀定存在哈密顿通路,反之不真(看课本的话,是必要条件,⽽不是充分条件,故不可反推!)(4)只有哈密顿通路,⽆哈密顿回路的图不叫哈密顿图;即,哈密顿图是回路⼆、判定定理注意:⽬前还没有找到哈密顿图的简单的充要条件(1)设⽆向图G=<V,E>为哈密顿图,V1是V的任意真⼦集,则(注:n阶xx图指的是n个顶点,不要迷!)p(G-V1)<=|V1|其中,p(G-V1)为G中删除V1后的所得图的连通分⽀数⽬,|V1|为V1集合中包含的顶点个数。
【哈密顿图存在的必要条件】推论:有割点的图⼀定不是哈密顿图设v是图中的割点,则p(G-v)>=2,由上述定理知G不是哈密顿图(2)设G是n(n>=3)阶⽆向简单图,若对于G中的每⼀对不相邻的顶点u,v,均有d(u)+d(v)>=n-1则G中存在哈密顿通路。
⼜若d(u)+d(v)>=n则G中存在哈密顿回路,即G为哈密顿图。
【哈密顿图存在的充分条件,不是必要条件】其中d(u),d(v)分别代表顶点u,v的度数。
推论:设G是n(n>=3)阶⽆向简单图,若G的最⼩度>=n/2,则G是哈密顿图。
由推论知,对于完全图Kn,当n>=3时,是哈密顿图,完全⼆部图Kr,s当r==s>=2时是哈密顿图。
(3)在n(n>=2)阶有向图D=<V,E>中,如果略去所有有向边的⽅向,所得⽆向图中含⽣成⼦图Kn,则D中存在哈密顿通路。
图论05-哈密尔顿图

A F
B
A
C
F
B C
E
D
E
D
竞赛图
底图为K4的竞赛图: A
B
C
以上每个图可以看作4个选手参加的循环赛的一种结果
竞赛图与有向哈密尔顿通路
底图是完全图的有向图称为竞赛图。 利用归纳法可以证明竞赛图含有向哈密尔顿通路。
循环赛该如何排名次
A F
E
B
按照在一条有向Hamilton通路 (一定存在)上的顺序排名:
Ore定理的证明
Ore定理(1960) 设G是无向简单图,|G|=n3,若
对G中任意不相邻的顶点u和v, d(u)+d(v)n (*)
则G有哈密尔顿回图。
证明.反证法, 若存在满足(*)的图G,但是G没有Hamilton回 路. 不妨假设G是边极大的非Hamilton图,且满足(*)。若G不是 边极大的非Hamilton图,则可以不断地向G增加若干条边,把G 变成边极大的非Hamilton图G’,G’依然满足(*),因为对 vV(G), dG(v)dG’(v)。
设G是无向简单图, |G|=n2, 若G中任意不相邻的顶点对
u,v均满足:d(u)+d(v)n-1,则G是连通图。
假设G不连通,则至少含2个连通分支,设为G1, G2。取xVG1, yVG2, 则:d(x)+d(y)(n1-1)+(n2-1)n-2 (其中ni是Gi的顶பைடு நூலகம்个数), 矛盾。
有限图G是Hamilton图充分必要其闭合图C(G)是 Hamilton图.
闭合图(举例)
a
b
f
c e
d
判定定理的盲区
从“常识”出发个案处理
离散数学课件15欧拉图与哈密顿图

04
欧拉图与哈密顿图的应用 场景
欧拉图的应用场景
路径规划
欧拉图可以用于表示从一 个点到另一个点的路径, 常用于物流、交通和旅行 等领域。
网络流问题
欧拉图可以用于解决最大 流和最小割等问题,在网 络优化、资源分配和计划 制定等方面有广泛应用。
组合优化
欧拉图可以用于表示组合 优化问题,如旅行商问题、 排班问题等,是求解这些 问题的常用工具。
一个图存在哈密顿回路当且仅当其所有顶点的度都大于等于2 。
哈密顿图的性质
哈密顿图中的所有顶点的度都 大于等于2。
一个图存在哈密顿回路当且仅 当其所有顶点的度都大于等于2。回 路。
哈密顿图的构造方法
添加边法
在所有顶点的度都大于等于2的图 中,不断添加边,直到所有顶点的 度都大于等于2,最后得到的图就 是哈密顿图。
哈密顿图的应用场景
社交网络分析
哈密顿图可以用于表示社交网络 中的路径,分析人际关系和信息
传播路径。
生物信息学
哈密顿图可以用于表示基因组、蛋 白质组等生物信息数据,进行基因 序列比对、蛋白质相互作用分析等。
推荐系统
哈密顿图可以用于表示用户和物品 之间的关系,进行个性化推荐和智 能推荐。
欧拉图与哈密顿图在计算机科学中的应用
欧拉图的构造方法
欧拉图的构造方法1
总结词
通过添加一条边将所有顶点连接起来, 从而形成一个欧拉图。
详细描述了两种构造欧拉图的方法, 为实际应用中构造欧拉图提供了思路。
欧拉图的构造方法2
通过将两个欧拉图合并,并连接它们 的所有顶点,从而形成一个新的欧拉 图。
02
哈密顿图
哈密顿图的定义
哈密顿图(Hamiltonian Graph)是指一个图存在一个遍历其 所有边且每条边只遍历一次的路径,这个路径称为哈密顿路径, 如果该路径的起点和终点是同一点,则称这个路径为哈密顿回 路。
哈密顿图

定义4.3.1 经过图G 的每个顶点恰一次的路称为G 的Hamilton 路,简称为H 路。
经过图G 的每个顶点恰一次的圈称为G 的Hamilton 圈,简称为H 圈。
具有Hamilton 圈的图称为Hamilton 图,简称为H 图。
Hamilton 图的研究起源于一种十二面体上的游戏。
1857 年,爱尔兰著名数学家William Rowan Hamilton 爵士(他也是第一个给出复数的代数描述的人)制作了一种玩具,它是一个木制的正十二面体,在正十二面体的每个顶点上有一个木栓,并标有世界著名城市的名字。
游戏者用一条细线从一个顶点出发,设法沿着十二面体的棱找出一条路,通过每个城市恰好一次,最后回到出发点。
这个游戏当时称为Icosian 游戏,也称为周游世界游戏。
将正十二面体从一个面剖开并铺展到平面上得到的图形如下图所示,称为十二面体图。
周游世界游戏用图论术语来说就是判断十二面体图是否Hamilton 图,并设法找出其Hamilton 圈。
其中一条Hamilton 圈如图中粗边所示。
十二面体图是H 图判断一个图是否Hamilton 图与判断一个图是否Euler 图似乎很相似,然而二者却有本质的不同。
目前为止尚没有找到判别一个图是否是Hamilton 图的有效充要条件。
这是图论和计算机科学中未解决的重要难题之一。
本节给出一些经典的充分条件和必要条件。
一、必要条件定理4.3.1 设G 是二部图,若G 是H 图,则G 必有偶数个顶点。
证明:设G = (X, Y ) ,由于G 的边全在X 和Y 之间,因此如果G 有Hamilton 圈C,则G的所有顶点全在C 上,且必定是X 的点和Y 的点交替在C 上出现,因此G 必有偶数个顶点。
证毕。
这个定理给出了一个二部图不是Hamilton 图的简单判断条件:如果一个二部图有奇数个顶点,则它必定不是Hamilton 图。
例如,下列Herschel 图是二部图,但有奇数个顶点,故不是H 图。
离散-Hamilton图

定理4.4.2
➢若G=(P, L)是有限图, 3, /2,
则G是Hamilton图。其中,表示图G
中点数,即 =|P(G)|,表示G中点的
最小度。
= 5;
= 32
10
证明:
➢ 反证法,若G不是Hamilton图,则在G中一 定能找到其度</2的顶点。显然,G不是完 全图 。
若G不是极大非Hamilton图,则可以不断地 向G增加若干条边,把G变成极大非 Hamilton图G0,若G是极大非Hamilton图, 则 令 G0=G, 显 然 , 对 任 意 点 vP(G), dG(v)dG0(v),那么,如果在G0中能找到度 </2的点,在G中也一定能找到。
30
例:补图
G
H
31
➢ 用Km表示由m个点组成的完全图。将如 下三个图:
Kmc
Km
Kn-2m
1 m n/2
➢从左到右顺序连接起来构成的连接图记 为Cm,n。
32
例:
K2c
K2
K3
下图给出的是 C2,7的具体图
K2c
K2
K3
33
引理3
➢若1 m n/2 ,则图Cm,n 是非 Hamilton图。
6
例:
➢将图中点A,B,
C的集合记为S,
于是,删去S,
剩下的图的分支
数是4,而|S|=3。
由定理4.4.1知, 该图不是
A
Hamilton图。
C B
7
例:
8
§4.4.2 Hamilton图的充分条件
➢定义 设图G是非Hamilton图,若在G 中增加任意一条边uv,G∪{uv}就变成 Hamilton图,则G称为极大非 Hamilton图。
图论课件-哈密尔顿图

哈密尔顿图被用于解决DNA测序中的
排序问题,以确定基因排序的最密尔顿回路,将某个形状切割 成相等面积的小块,被应用于制造领 域。
总结
哈密尔顿图的实际应用
通过解决问题和优化路线,哈密尔顿图在各个领 域带来实际效益和成功案例。
哈密尔顿图的研究价值
了解和探索哈密尔顿图的特性,可以推动图论领 域的研究和未来的学术发展。
判断图中是否存在包含 所有顶点的哈密尔顿回 路。
2 哈密尔顿路径问题
判断图中是否存在包含 所有顶点的哈密尔顿路 径。
3 哈密尔顿图存在性
问题
判定一个图是否为哈密 尔顿图。
应用领域
1
网络拓扑布局
哈密尔顿图可以用于设计网络的拓扑
遗传学领域的DNA测序问题
2
结构,确保每个节点都可以直接连接 到其他节点。
哈密尔顿图的性质
哈密尔顿图一定是强连通的,每个顶点有且只有一条入边和一条出边。
判定哈密尔顿图的方法
线性时间的方法
使用策略或算法,如基于图的剖分和动态规划, 以线性时间判定图是否为哈密尔顿图。
构造性方法
应用数学原理和图的性质,通过构造合适的路 径或回路来判断图是否为哈密尔顿图。
相关问题
1 哈密尔顿回路问题
图论课件-哈密尔顿图
欢迎来到图论课件-哈密尔顿图!探索什么是哈密尔顿图,判定方法和相关问 题,以及其在网络布局、遗传学和切割问题中的应用。
什么是哈密尔顿图
哈密尔顿图的定义
具有一条包含所有顶点的哈密尔顿路径的图。
哈密尔顿回路与哈密尔顿路径
回路是一条从某个顶点出发并最终回到该顶点的路径。路径只需要包含所有顶点即可。
图论课件超哈密尔顿图问题共30页

(1) 假设是由a进入Ⅰ,要能够走 完P,必须遍历Ⅰ∪Ⅱ 的所有顶点后 由b进入Ⅲ,但这与断言2矛盾!
(2) 假设是由a进入Ⅳ,要能够走 完P,必须遍历Ⅲ∪Ⅳ 的所有顶点后 由b进入Ⅱ,但这也与断言2矛盾!
所以,情形1不能成立!
f
c
Ⅱ
Ⅰ
e
d
b
a
Ⅲ
Ⅳ
Thomassen图
12
1
f
c
Ⅱ
Ⅰ
e
d
b
a
Ⅲ
Ⅳ
Thomassen图 9
1
0.5 n 0
0.5
1 2 1.5 t1 0.5 00
1 0.8
0.6 0.4 x 0.2
定理证明分为两部分: (1) 证明G中不存在H路;(2) 证
明对G中任意点v,有G-v存在H路。
f
c
(1) 证明G中不存在H路。
Ⅱ
Ⅰ
如图所示,将G用虚线分成对称
e
2
4
3
G
4
3
G2
值得一提的是:在H问题研究中,H图中H圈的计数问题 也是一个研究方向。
21
1
0.5 n 0
0.5
1 2 1.5 t1 0.5 00
1 0.8
0.6 0.4 x 0.2
定理:每个3正则H图至少有3个生成圈。
我院张先迪、李正良教授曾经也研究过H图中H圈的计 数问题。90年在《系统科学与数学》学报上发表文章: “有限循环群上Cayley有向图的H回路”,得到了该类图 的H圈的计数公式。
0810604020xt0051152?1?050051n1本次课主要内容二e图和h图的关系超哈密尔顿图问题一超h图与超h迹0810604020xt0051152?1?050051n2定义1若图g是非h图但对于g中任意点v都有gv是是h图则称g是超h图
离散数学中的欧拉图与哈密顿图

欧拉图和哈密顿图是离散数学中的两个重要的图论概念。
它们分别研究了图中的路径问题,对于解决一些实际问题具有很大的应用价值。
欧拉图是指一个无向图中存在一条路径,经过图中的每条边一次且仅一次,这条路径称为欧拉路径。
如果这个路径的起点和终点重合,则称为欧拉回路。
而对于有向图,存在一条路径,使得经过每一个有向边恰好一次,称为欧拉有向路径,如果该路径起点和终点相同,则称为欧拉有向回路。
1722年,瑞士数学家欧拉首次提出了这个概念,并证明了一系列欧拉图的性质。
欧拉图的性质是其路径的存在性。
既然有了这个概念,那如何判断一个图是不是欧拉图就是一个非常重要的问题。
根据欧拉图的定义,我们可以发现,图中的每个节点的度数都应该是偶数,否则该节点无法成为路径中的中间节点。
因此,一个图是欧拉图的充分必要条件是该图中每个节点的度数都是偶数。
哈密顿图是指一个图中存在一条路径,经过图中的每个顶点一次且仅一次,这条路径称为哈密顿路径。
如果这个路径的起点和终点重合,则称为哈密顿回路。
哈密顿图的概念由19世纪初英国数学家哈密顿引入,其研究对象是关于骑士巡游问题。
与欧拉图不同的是,哈密顿路径并没有一个十分明显的判定条件。
唯一已知的是某些图是哈密顿图,比如完全图和圈图。
至于一般的图是否存在哈密顿路径,目前尚无通用的判定方法。
这也是全世界许多数学家所面临的一个著名且具有挑战性的开放问题,被命名为“哈密顿路径问题”。
欧拉图和哈密顿图在实际问题中具有广泛的应用。
欧拉图的应用包括电子电路和网络的设计,路线规划等。
而哈密顿图的应用更多地涉及路径的优化问题,比如旅行商问题。
在实际应用中,我们常常需要通过对欧拉图和哈密顿图的研究,来寻找最优解或者设计最佳路径。
总的来说,离散数学中的欧拉图和哈密顿图是两个重要的图论概念,它们研究的是图中的路径问题。
欧拉图的判定条件相对明确,而哈密顿图的判定则是一个尚未完全解答的开放问题。
这两个概念在实际中具有广泛的应用,对于解决一些路径优化问题具有重要的参考价值。
哈密顿图

13.2 哈密顿图13.2.1哈密顿图的定义与欧拉回路类似的是哈密顿回路问题。
它是1859年哈密顿首先提出的一个关于12面体的数学游戏:能否在下图中找到一个回路,使它含有图中所有结点一次且仅一次?若把每个结点看成一座城市,连接两个结点的边看成交通线,那么这个问题就变成能否找到一条旅行路线,使得沿着该旅行路线经过每座城市恰好一次,再回到原来的出发地呢?为此,这个问题也被称为周游世界问题。
定义13.3给定图G,若存在一条路经过图中的每一个结点恰好一次,这条路称作哈密顿(Hamilton)路。
若存在一条回路,经过图中的每一个结点恰好一次,这个回路称作哈密顿回路。
具有哈密顿回路的图称为哈密顿图。
具有哈密顿路但不具有哈密顿回路的图称为半哈密顿图。
(a)(b)(c)(a)中存在哈密顿路,不存在哈密顿回路,所以(a)是半哈密顿图,(b)中存在哈密顿回路,(b)是哈密顿图,(c)不是哈密顿图。
13.2.2哈密顿图的判定定理13.3(哈密顿回路的必要条件)若图G=<V, E>具有哈密顿回路,则对于结点集V的每一个非空子集S均有W(G−S)≤|S|成立。
其中W(G−S)是G−S中连通分支数。
定理13.4(奥尔定理,哈密顿路的充分条件)设G是具有n个结点的简单无向图,如果G中每一对不相邻顶点的度数之和大于等于n−1,则在G中存在一条哈密顿路。
例13.2某地有5个风景点。
若每个景点均有两条道路与其他景点相通,问是否可经过每个景点恰好一次而游完这5处?解将景点作为结点,道路作为边,则得到一个有5个结点的无向图。
由题意,对每个结点vi,有。
则对任意两点均有可知此图一定有一条哈密顿路,本题有解。
小结(1)深刻理解哈密顿图及半哈密顿图的定义;(2)分清哈密顿图的必要条件和充分条件,会用哈密顿图的必要条件证明某些图不是哈密顿图。
关于哈密顿图的思维形式注记图如图所示。
哈密顿图.doc

定义4.3.1 经过图G 的每个顶点恰一次的路称为G 的Hamilton 路,简称为H 路。
经过图G 的每个顶点恰一次的圈称为G 的Hamilton 圈,简称为H 圈。
具有Hamilton 圈的图称为Hamilton 图,简称为H 图。
Hamilton 图的研究起源于一种十二面体上的游戏。
1857 年,爱尔兰著名数学家William Rowan Hamilton 爵士(他也是第一个给出复数的代数描述的人)制作了一种玩具,它是一个木制的正十二面体,在正十二面体的每个顶点上有一个木栓,并标有世界著名城市的名字。
游戏者用一条细线从一个顶点出发,设法沿着十二面体的棱找出一条路,通过每个城市恰好一次,最后回到出发点。
这个游戏当时称为Icosian 游戏,也称为周游世界游戏。
将正十二面体从一个面剖开并铺展到平面上得到的图形如下图所示,称为十二面体图。
周游世界游戏用图论术语来说就是判断十二面体图是否Hamilton 图,并设法找出其Hamilton 圈。
其中一条Hamilton 圈如图中粗边所示。
十二面体图是H 图判断一个图是否Hamilton 图与判断一个图是否Euler 图似乎很相似,然而二者却有本质的不同。
目前为止尚没有找到判别一个图是否是Hamilton 图的有效充要条件。
这是图论和计算机科学中未解决的重要难题之一。
本节给出一些经典的充分条件和必要条件。
一、必要条件定理 4.3.1 设G 是二部图,若G 是H 图,则G 必有偶数个顶点。
证明:设G = (X, Y ) ,由于G 的边全在X 和Y 之间,因此如果G 有Hamilton 圈C,则G的所有顶点全在C 上,且必定是X 的点和Y 的点交替在C 上出现,因此G 必有偶数个顶点。
证毕。
这个定理给出了一个二部图不是Hamilton 图的简单判断条件:如果一个二部图有奇数个顶点,则它必定不是Hamilton 图。
例如,下列Herschel 图是二部图,但有奇数个顶点,故不是H 图。
哈密顿图

•= 13.2.1哈密顿图的定义
与欧拉回路类似的是哈密顿回路问题。它是1859年哈密顿首先提出的一 个 关于12面体的数学游戏:能否在下图中找到一个回路,使它含有图中所有
结点一次且仅一次?若把每个结点看成一座城市,连接两个结点的边看成交 通线,那么这个问题就变成能否找到一条旅行路线,使得沿着该旅行路线经 过每座城市恰好一次,再回到原来的出发地呢?为此,这个问题也被称为周
-小结
(1) 深刻理解哈密顿图及半哈密顿图的定义; (2) 分清哈密顿图的必要条件和充分条件,会用哈密顿图的 必
要条件证明某些图不是哈密顿图。关于哈密顿图的(半哈密顿图) f必要条件:W (G-S)<=|S|三〉判定籍不是哈密觥 [充 判定: 分条件:每一对结点度数之和大于等于n-1
虹例13.2 /
某地有5个风景点。若每个景点均有两条道路与其他景点 相通,问是否可经过每个景点恰好一次而游完这5处?
将景点作为结点,道路作为边,则得到一个有5个结点的 无向图。由题意,对每个结点vi,有de外)=¥丘况)则对任意两 点】.仲.」w ¥. }均有deg(】、,)+ deg(】、j ) = 2+2 = 4 = 5-1 可知此图一定有 —条哈密顿路,本题有解。
定义13.3
给定图G,若存在一条路经过图中的每一个结点恰好一次,这条路称作哈密
顿(Hamilton)路。若存在一条回路,经过图中的每一个结点恰好一次,这个 回路称作哈密顿回路。具有哈密顿回路的图称为哈密顿图。具有哈密顿路但不 具有哈密顿回路的图称为半哈密顿图。
(a) 中存在哈密顿路,不存在哈密顿回路,所以(a)是半哈密顿图, (b) 中存在哈密顿回路,(b)是哈密顿图,(c)不是哈密顿图。
•= 13.2.2哈密顿图的判定
离散数学图论作业5-哈密顿图

离散数学图论作业5-哈密顿图
Problem1
下方所示各图是否拥有哈密顿通路?若有哈密顿通路,则求出这样一条通路。
若没有哈密顿通路,则论证为什么这样的通路不存在。
(1)(2)(3)
Problem2
对哪些m和n值来说,完全二部图K m,n具有哈密顿回路?
Problem3
证明:每当n是正整数时,就存在n阶格雷码,或者等价地证明:n>1的n维立方体(n-cube)Q,总是具有哈密顿回路。
[提示:用数学归纳法,证明如何从n−1阶格雷码产生n阶格雷码。
]
证明:下图所示的彼得森图没有哈密顿回路,但删除任意顶点v和所有与v关联的边,所获得的子图都有哈密顿回路。
Problem5
若简单图G满足V(G)≥3且δ(G)≥V(G)−1
,证明或反驳:
2
a)G一定存在哈密顿回路。
b)G一定存在哈密顿通路。
Problem6
底图是完全图的有向图称为竞赛图,试证明:
a)竞赛图一定含有哈密顿通路。
b)竞赛图含有哈密顿回路的充分必要条件是强连通。
Problem7
考虑在15天安排15门课程的考试(每天考1门课),使得同一位老师所任的任意两门课程考试不排在接连的两天中,试证明如果没有老师担任多于8门课程,则符合上述要求的考试安排总是可能的。
考虑M×N的网格,以其中的方格作为点集,任意两个点之间有边当且仅当对应的两个方格相邻,构成图G。
a)当N是偶数且M>1时,给出一种哈密顿回路的构造方法。
b)当N和M都是大于1的奇数时,证明此时G没有哈密顿回路。
哈密顿图

procedure dfs(i:integer); Begin var j,k:integer; init; begin fillchar(visited,sizeof(visited),0); if (n=m)and(a[b[1],b[m]]=1) then print; found:=0; for j:=1 to n do m:=1; if (a[i,j]=1) and (visited[j]=0) then b[1]:=1; begin visited[1]:=1; visited[j]:=1; dfs(1); m:=m+1; if found=0 then writeln('no road'); b[m]:=j; end. dfs(j); visited[j]:=0; m:=m-1; end; end;
2 、安排座位
个客人围着一个桌子吃饭,每一个人都至少认识其他的2个客人。 n 个客人围着一个桌子吃饭 , 每一个人都至少认识其他的 2 个客人 。 请设计程 序求得n个人的一种坐法,使得每个人都认识他左右的客人。 序求得n个人的一种坐法,使得每个人都认识他左右的客人。 输入: 输入: 第一行:n(吃饭人的个数)。 第一行:n(吃饭人的个数)。 :n 以下n 以下n行:第i行的第一个数k表示第i个人认识的人数,后面k个数依次为i认识的 行的第一个数k表示第i个人认识的人数,后面k个数依次为i 人的编号。 人的编号。 输出:所有座法,要求第一个人为1号作为起点,按顺时针输出其它人的编号。 输出:所有座法,要求第一个人为1号作为起点,按顺时针输出其它人的编号。
Begin init; found:=0; for i:= 1 to n do begin fillchar(visited,sizeof(visited),0); m:=1; b[1]:=i; visited[i]:=1; dfs(i); end; if found=0 then writeln('no road'); end.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学图论作业5-哈密顿图
Problem1
下方所示各图是否拥有哈密顿通路?若有哈密顿通路,则求出这样一条通路。
若没有哈密顿通路,则论证为什么这样的通路不存在。
(1)(2)(3)
Problem2
对哪些m和n值来说,完全二部图K m,n具有哈密顿回路?
Problem3
证明:每当n是正整数时,就存在n阶格雷码,或者等价地证明:n>1的n维立方体(n-cube)Q,总是具有哈密顿回路。
[提示:用数学归纳法,证明如何从n−1阶格雷码产生n阶格雷码。
]
证明:下图所示的彼得森图没有哈密顿回路,但删除任意顶点v和所有与v关联的边,所获得的子图都有哈密顿回路。
Problem5
若简单图G满足V(G)≥3且δ(G)≥V(G)−1
,证明或反驳:
2
a)G一定存在哈密顿回路。
b)G一定存在哈密顿通路。
Problem6
底图是完全图的有向图称为竞赛图,试证明:
a)竞赛图一定含有哈密顿通路。
b)竞赛图含有哈密顿回路的充分必要条件是强连通。
Problem7
考虑在15天安排15门课程的考试(每天考1门课),使得同一位老师所任的任意两门课程考试不排在接连的两天中,试证明如果没有老师担任多于8门课程,则符合上述要求的考试安排总是可能的。
考虑M×N的网格,以其中的方格作为点集,任意两个点之间有边当且仅当对应的两个方格相邻,构成图G。
a)当N是偶数且M>1时,给出一种哈密顿回路的构造方法。
b)当N和M都是大于1的奇数时,证明此时G没有哈密顿回路。
