基于MATLAB的语音信号特技处理-延时与混响
如何在MATLAB中进行语音信号处理

如何在MATLAB中进行语音信号处理一、引言语音信号处理是一门充满挑战的学科,它涉及到声音的产生、捕捉、转换和处理等一系列过程。
在现代科技的支持下,MATLAB作为一种强大的工具,被广泛应用于语音信号处理领域。
本文将介绍如何使用MATLAB进行语音信号处理,包括信号预处理、语音分析和语音合成等方面。
二、信号预处理在进行语音信号处理之前,我们通常需要对信号进行预处理。
信号预处理的目标是将原始信号进行降噪、滤波和归一化等处理,以便后续的分析和处理。
在MATLAB中,我们可以使用一系列函数来实现信号预处理的过程。
首先,我们可以使用MATLAB提供的降噪算法对信号进行降噪处理。
常用的降噪算法有加性白噪声降噪算法、小波降噪算法等。
通过对原始信号进行降噪处理,可以有效提取出语音信号的有效信息。
其次,我们可以使用滤波技术对信号进行滤波处理。
滤波的目的是去除信号中的不必要成分,保留感兴趣的频率成分。
在MATLAB中,我们可以使用卷积和滤波函数来实现滤波过程。
最后,我们还可以对信号进行归一化处理。
归一化可以使信号的幅值范围在一个确定的范围内,方便后续的处理和比较。
在MATLAB中,我们可以使用归一化函数对信号进行归一化处理。
三、语音分析语音信号的分析是语音信号处理的关键步骤,它可以帮助我们了解信号的基本特征和结构。
在MATLAB中,我们可以使用一系列函数来实现语音信号的分析。
首先,我们可以使用MATLAB提供的时域分析函数对语音信号进行时域分析。
时域分析可以帮助我们了解信号的振幅、频率和相位等特征。
通过时域分析,我们可以得到语音信号的波形图、能谱图和自相关函数等。
其次,我们还可以使用频域分析函数对语音信号进行频域分析。
频域分析可以帮助我们了解信号的频率成分和频率分布等特征。
通过频域分析,我们可以得到语音信号的频谱图、功率谱密度图和谱线图等。
最后,我们还可以使用梅尔频率倒谱系数( MFCC)来提取语音信号的特征。
MFCC是一种广泛应用于语音识别领域的特征提取方法。
基于MATLAB的声音的延迟与混响

课程设计任务书学生:哲专业班级:通信gj1001指导教师:付琴工作单位:信息工程学院题目:基于MATLAB的声音延迟与混响初始条件:①MATLAB软件②数字信号处理与声音处理基础知识要求完成的主要任务:①较全面了解常用的数据分析与处理原理及方法;②能够运用相关软件进行模拟分析;③掌握基本的文献检索和文献阅读的方法;④提高正确地撰写论文的基本能力。
参考书目:1.泉,数字信号处理原理与实现(第二版),电子工业,2009;2.雄伟,DSP集成开发与应用实例,第1版,电子工业,2002;3. 洪涛等,数字信号处理,第一版,华中科技大学,20074. 启琮等,DSP技术的发展与应用,第二版,高等教育,20075. 述斌等,数字信号处理实践教程,第一版,华中科技大学,2007时间安排17周仿真设计18周鉴主15楼答辩指导教师签名:__________________年月日系主任(或责任教师)签名:____________年月日目录摘要 (4)1 绪论 (6)1.1设计任务 (7)1.2 设计要求 (7)2 设计的总体方案与原理 (8)2.1 设计的总体方案图 (8)2.2 程序流程图 (9)2.3 设计的详细原理 (10)2.3.1 信号采样 (10)2.3.2 混响与延时 (10)2.3.3 离散傅立叶变换 (12)2.3.4 滤波器设计 (13)3 程序设计的步骤和过程 (14)3.1 原始语音信号时域波形和频谱 (14)3.2 采样后语音信号的时域波形和频谱 (15)3.3 对采样后的信号延时 (15)3.4 对采样后的信号混响 (16)3.5 单回声滤波器程序设计 (17)3.6 多重回声滤波器程序设计 (18)3.7 无限个回声滤波器程序设计 (19)3.8 全通结构滤波器程序设计 (20)4 结果分析与体会 (21)5 设计心得体会 (29)6 主要参考文献 (31)附录:仿真总程序 (31)摘要数字信号处理技术自诞生以来,有了快速的发展,主要是研究用数字或符号序列表示和处理信号,被广泛应用于各个领域。
基于MATLAB的有噪声的语音信号处理的课程设计要点

基于MATLAB的有噪声的语音信号处理的课程设计要点一、设计背景随着科技的不断发展,语音信号处理愈发成为热门话题。
在语音数据中,常常会被噪声干扰,从而使得信号质量下降,影响了数据分析和处理的效果。
本课程设计旨在通过MATLAB来设计一套有噪声的语音信号处理方法,以提高对语音信号信噪比的分析和处理能力,为后续的语音处理研究奠定基础。
二、课程设计要点1. 语音信号的获取和预处理在本课程中,需要使用MATLAB语音处理工具箱中的audioread()函数获取.wav格式的语音信号,然后进行预处理操作,包括:•极化和采样:将语音信号从时间域转换到频域,并进行重采样处理,以适应后续处理操作的需求。
•去噪:根据信噪比的情况,选择合适的去噪算法对语音信号进行滤波,以减低信号的噪声干扰。
2. 基本的信号处理方法•频谱分析和频率域滤波:可以通过MATLAB处理语音信号的频域,进行谱分析、谱修复以及滤波的操作。
•时域滤波:应用IIR和FIR滤波器来消除噪声,提高信号质量。
•自适应滤波:通过模型建立和自适应滤波器设计,从语音信号中分离出噪声信号。
3. 压缩和解压缩•信号压缩:对语音信号进行压缩处理,以实现数据的高效管理和传输。
•信号解压缩:对压缩后的语音信号进行解压缩处理,还原原始的语音信号,以进行后续处理。
4. 语音识别•特征提取:通过分段处理,并进行特征提取,将信号的语音特征转换为相应的数字特征向量,为后续的语音识别做准备。
•语音识别:基于数字特征向量,采用各种识别算法,进行语音识别。
三、设计思路1.读入语音信号和噪声,可以通过audioread()函数和一些MATLAB工具箱实现。
同时,对输出语音信号进行噪声除去处理。
2.对语音信号进行频谱分析,并基于不同的SNR条件下,应用FIR和IIR滤波器对语音信号进行滤波处理。
进而利用多种去噪算法对含噪语音信号进行去噪处理。
3.对经过滤波处理的语音信号进行特征提取,并采用隐马尔可夫模型(HMM)对数字特征向量进行处理,进行不同说话人的识别。
基于MATLAB的语音信号的分析与处理

基于MATLAB的语音信号分析与处理[摘要]语音信号的处理是一门非常重要的学科,如今普遍应用在电话通信、助听器等方面。
本次设计主要是为了在MATLAB软件的帮助下处理一段加噪的声音信号,该过程会涉及到采样定理,傅立叶变换等理论和算法在设计过程中的实际应用。
在本次设计中,我们关注的是在驱除噪声污染是所需要的滤波器的选择,充分比较各种优缺点后,再利用滤波器来驱除杂音。
通过滤波前后的声音的频谱图的比较,来了解滤波器的特性和作用,并得到本次设计的结果。
[关键词]:语音信号;MATLAB;傅立叶变换;滤波器目录摘要 (Ⅰ)1 绪论 (1)1.1 课题的研究背景及意义 (1)1.1 设计任务 (1)2 语音信号处理的基本理论知识 (1)2.1 采样频率和采样位数 (1)2.2 采样定理 (1)2.3 IIR数字滤波器 (2)2.4 FIR数字滤波器 (2)2.5 IIR数字滤波器和FIR数字滤波器的比较 (3)2.6 倒谱 (3)3 语音信号处理和理论方案 (3)3.1 语音信号的采集 (3)3.2 语音信号的处理 (4)3.3 系统框图 (4)4 语音信号处理的实例分析. (5)4.1语音文件在MATLAB平台上的录入与打开 (5)4.2原始语音信号频谱分析及仿真 (5)4.3加噪语音信号频谱分析及仿真 (8)4.4去噪及仿真 (13)4.5 语音信号的回放 (18)4.6结合去噪后的频谱图对比两种方式滤波的优缺点 (18)5 总结. (19)6 致谢. (19)参考文献 (20)1绪论1.1课题的研究背景及意义语言是我们人类所特有的功能,它是传承和记载人类几千年文明史,没有语言就没有我们今天人类的文明。
语音是语言最基本的表现形式,是相互传递信息最重要的手段,是人类最重要、最有效、最常用和最方便的交换信息的形式。
语音信号处理属于信息科学的一个重要分支,大规模集成技术的高度发展和计算机技术的飞速前进,推动了这一技术的发展;它是研究用数字信号处理技术对语音信号进行处理的一门新兴学科,同时又是综合性的多学科领域和涉及面很广的交叉学科,因此我们进行语言信号处理具有时代的意义。
如何使用Matlab进行语音信号处理

如何使用Matlab进行语音信号处理引言:语音信号处理是一个重要的领域,在各种应用中都有广泛的应用,如语音识别、语音合成、音频编码等。
而Matlab是一个功能强大的工具,提供了许多用于语音信号处理的函数和工具箱,使得处理语音信号变得更加简单和高效。
本文将介绍如何使用Matlab进行语音信号处理的基本流程和一些常用的处理方法。
一、语音信号处理基础知识1.1 语音信号的特点语音信号是一种时变信号,具有时间和频率的特性。
它由一系列的声音波形组成,通过声音传感器(如麦克风)捕获并转换为电信号。
语音信号具有频谱的特征,包括基频、共振峰等。
了解语音信号的基本特点是进行语音信号处理的前提。
1.2 语音信号处理的基本流程语音信号处理的基本流程包括预处理、特征提取、模型建立、参数估计和应用等步骤。
预处理包括去噪、降采样等操作,特征提取包括MFCC(Mel频率倒谱系数)等方法,模型建立包括隐藏马尔可夫模型(HMM)等,参数估计通过最大似然估计等方法进行参数估计,应用包括语音识别、语音合成等。
二、使用Matlab进行语音信号处理的基本方法2.1 读取和保存语音文件Matlab提供了许多函数用于读取和保存语音文件。
可使用"audioread"函数读取.wav格式的语音文件,并得到语音信号的时域波形,可以使用"audiowrite"函数保存处理后的语音文件。
2.2 语音信号的时域和频域分析Matlab提供了许多函数用于对语音信号进行时域和频域分析。
可以使用"waveform"函数绘制语音信号的波形,使用"spectrogram"函数绘制语音信号的频谱图。
2.3 语音信号的预处理在语音信号处理之前,通常需要对语音信号进行预处理,如去除噪声、降低采样率等。
Matlab提供了丰富的函数和工具箱用于语音信号的预处理,如"noisegate"函数用于去除噪声,"resample"函数用于降低采样率。
基于某matlab的语音信号的合成(加入延迟混响)

中北大学课程设计说明书学生姓名:学号:学生姓名:学号:学生姓名:学号:学院:信息与通信工程学院专业:电子信息工程题目:信息处理实践:语言信号的合成指导教师:杨娜职称: 副教授2016 年 1月 3 日中北大学课程设计任务书15/16 学年第一学期学院:信息与通信工程学院专业:电子信息工程学生姓名:学号:学生姓名:学号:学生姓名:学号:课程设计题目:信息处理实践:语言信号的合成起迄日期:2016年1 月4日~2016年1月22 日课程设计地点:201,503,1号楼教室指导教师:杨娜系主任:王浩全下达任务书日期: 2016 年1月 3 日课程设计任务书课程设计任务书目录摘要 (1)1.MATLAB简介 (1)2.GUI简介 (1)一.设计方案........................................................................................................... 二.设计步骤及结果1.语音信号的采集..............................................2.语音信号的截取.................3.语音信号的合成.................4.合成语音的验证.........5.GUI界面设计及实现.........三.设计评述参考文献..............附录..............摘要语音信号处理是一门比较实用的电子工程专业课程,语音是人类获取信息的的重要来源和利用信息的重要手段。
通过语言相互传递信息是人类最重要的基本功能之一。
语音信号是一种非平稳的时变信号,它携带着各种信息。
在语音编码、语音合成、语音识别和语音增强等语音处理中无一例外需要提取语音中包含的各种信息。
Matlab是一个数据分析和处理功能十分强大的工程实用软件。
本文介绍了利用matlab软件及其中的图形用户界面(GUI)实现驱动声卡采集语音信号和语音信号采集后的文档处理方法,并通过实例利用matlab分析了语音信号处理的过程。
利用Matlab进行声音信号处理的技术方法

利用Matlab进行声音信号处理的技术方法引言:在现代科技飞速发展的时代,声音信号处理成为一个热门的技术领域。
利用Matlab这一功能强大的软件工具,可以进行各种声音信号处理的研究和应用。
本文将介绍利用Matlab进行声音信号处理的技术方法,包括声音信号采集、预处理、频域分析、音频特征提取、降噪以及语音识别等方面的内容。
一、声音信号采集声音信号采集是声音信号处理的第一步,它的质量直接影响后续处理的效果。
在Matlab中,我们可以利用声音输入和录音功能来实现声音信号的采集。
声音输入函数可以从外部声卡、麦克风等设备录取音频数据,而录音函数则可以通过计算机内部的声卡进行录音。
要进行声音信号采集,首先要设置好采样率和采样位数。
采样率表示每秒采样的次数,常用的采样率有8kHz、16kHz和44.1kHz等。
采样位数表示每个采样值的位数,一般为8位或16位。
在Matlab中,可以使用audiorecorder函数设置采样率和采样位数。
二、声音信号的预处理声音信号预处理是为了去除噪声和提高信号质量,以便后续处理。
常用的声音信号预处理方法包括去噪、滤波、归一化等。
去噪是声音信号预处理的重要步骤。
常见的去噪方法有时域滤波和频域滤波。
时域滤波是通过卷积运算对声音信号进行滤波,可以去除特定频率范围内的噪声。
频域滤波则是将声音信号从时域转换到频域,利用频域上的滤波器对噪声进行滤波。
滤波是声音信号预处理的另一种常用方法,它可以去除声音信号中的杂音和干扰信号。
低通滤波器可以去除高频噪声,而高通滤波器则可以去除低频噪声。
在Matlab中,可以使用fir1函数设计滤波器,然后使用filter函数进行滤波。
归一化是将声音信号的振幅范围缩放到合适的范围内,以便后续处理。
通过归一化,可以消除不同音频文件之间的振幅差异。
三、频域分析频域分析是声音信号处理中常用的方法之一。
在Matlab中,可以通过使用快速傅里叶变换(FFT)函数对声音信号进行频谱分析。
基于matlab语音信号合成与处理课程设计

摘要语音信号处理是研究用数字信号处理技术和语音学知识对语音信号进行处理的新兴学科,是目前发展最为迅速的学科之一,通过语音传递信息是人类最重要,最有效,最常用和最方便的交换信息的手段,所以对其研究就显得尤为重要。
Matlab语言是一种数据分析和处理功能十分强大的计算机应用软件,它可以讲声音文件变成离散的数据文件,然后用其强大的矩阵运算能力处理数据。
这为本次课程设计提供了强大并良好的环境。
本设计要求自己通过手机清唱一段歌曲,并用windows自带的录音机录制下来,保存格式为.wav格式,而且要求对所录的语音进行频率均衡和加入混响效果。
从网上下载相应的歌曲伴奏,经过截取、加噪、消噪后,与混响后的清唱语音进行合成,制作成一首歌曲。
采用语音合成可帮助学生加强理解,MATLAB里面有很多应用示波器滤波,利用这些滤波器可以很容易地实现语音信号的消噪过程,利用MATLAB的声音处理函数设计一组语音合成实验,配合Windows操作系统支持的语音媒体播放器可以很方便地将经过数字处理后的语音效果直观地体现出来,对于学生深刻理解数字信号处理中抽象数学运算的现实物理意义很有帮助。
关键字:信号处理语音合成加噪混响一、设计目的与任务录制各自的一段清唱歌曲语音信号,并对其进行频谱分析;然后在时域用数字信号处理的方法将信号加入延时与混响。
然后从网上下载一段该歌曲的伴奏,对伴奏进行截取、格式转换、加噪和去噪后,与伴唱歌曲进行合成,制作成一首歌曲,在分析其频谱,并与原始伴唱语音信号频谱进行比较。
通过数字信号处理的课程设计,巩固和运用数字信号处理课程中的理论知识和实践技能,掌握最基本的运用Matlab软件处理信号的理论和方法,培养发现问题,分析问题和解决问题的能力。
二、设计的基本要求1.录制的语音清晰,分析语音信号的特点;2.探讨语音分析、加噪、去噪、混响以及合成的基本方法;3.写出各个步骤的Matlab的程序代码;4.分析录制的语音信号的时域波形与频谱;分析加噪、去噪与合成前后的语音信号波形与频谱;5.熟悉加强滤波器的设计原理和滤波的过程;三、设计思路图-1语音合成的方案设计方框图整体设计思路:将录制的语音信号进行频谱分析,并进行频率均衡和加入混响效果。
基于MATLAB的语音信号的特技处理——时延和混响

设计任务书摘要(中文)数字信号处理(Digital Signal Processing)技术,从20世纪60年代以来,随着计算机科学和信息科学发展,数字处理技术应运而生并得以快速发展。
语言是人们进行信息沟通的主要方式之一,它具有直接、自然、方便等优点。
语音则是语言的物理层表达方式。
语音处理主要是对语音进行机器处理,以达到传输、自动识别、机器理解等目的。
进行了语音处理过程的滤波、采样、傅立叶变换和谱包络提取的算法实现研究,讨论了在算法的DSP实现方法,Matlab 语言是一种广泛应用于工程计算及数值分析领域的新型高级语言, Matlab 功能强大、简单易学、编程效率高。
特别是Matlab 还具有信号分析工具箱, 不需具备很强的编程能力, 就可以很方便地进行信号分析、处理和设计关键词语音信号处理 MATLAB语言滤波器频谱分析图形用户界面摘要(英文)Digital Signal Processing (Digital Signal Processing) technology from the1960s,along with the development of computer science and information science, digital processing techniques have emerged and to rapid development. Language is the communication of people to one of the main, it has a direct, natural, and easy. Voice is the language of the physical layer of expression. Voice processing machines mainly for voice processing, in order to achieve transmission, automatic recognition, machine understanding of other purposes. For voice processing filtering, sampling, Fourier transform and spectral envelope extraction algorithm research, discusses the implementation of DSP algorithms,Matlab language is a widely used engineering calculation and numerical analysis of the field of new high-level language, Matlab powerful, easy to learn, programming and high efficiency. Matlab also has a particular signal analysis toolbox, need not have strong programming skills, you can easily carry out signal analysis, processing and designKeywords Speech signal processing Spectral analysis of MATLAB Filter Spectrum analysis Graphical User Interface1 引言数字信号处理主要是研究用数字或符号序列表示和处理信号。
matlab报告基于matlab有噪声语音信号处理

Matlab课程设计报告题目:基于MATLAB有噪声语音信号处理系(院):计算机与信息工程学院专业:通信工程班级:10623102指导教师:学年学期:2011 ~ 2012 学年第2 学期简介:我们通信工程专业在实践中经常碰到需要对已接收信号进行处理的情况,而滤波器设计在数字信号处理中占有极其重要的地位。
本课题基于MATLAB有噪音语音信号处理的设计与实现,综合运用数字信号处理的理论知识对加噪语音信号进行时域、频域分析和滤波。
通过理论推导得出相应结论,再利用MATLAB作为编程工具进行计算机实现。
在设计实现的过程中,我们使用双线性变换法设计IIR数字滤波器,对模拟加噪语音信号进行低通滤波、高通滤波及带通滤波,并利用MATLAB作为辅助工具完成设计中的计算与图形的绘制。
1 绪论:数字信号处理是利用计算机或专用处理设备,以数值计算的方法对信号进行采集、抽样、变换、综合、估值与识别等加工处理,借以达到提取信息和便于应用的目的。
数字滤波器, 是数字信号处理中及其重要的一部分。
本课题采用IIR 滤波器对加噪声音信号进行处理。
IIR滤波器采用递归型结构,即结构上带有反馈环路。
IIR滤波器运算结构通常由延时、乘以系数和相加等基本运算组成,可以组合成直接型、正准型、级联型、并联型四种结构形式,都具有反馈回路。
同时,IIR数字滤波器在设计上可以借助成熟的模拟滤波器的成果,如巴特沃斯、契比雪夫和椭圆滤波器等,有现成的设计数据或图表可查,在设计一个IIR数字滤波器时,我们根据指标先写出模拟滤波器的公式,然后通过一定的变换,将模拟滤波器的公式转换成数字滤波器的公式。
2.原始语音信号采集与处理2.1语音信号的采集由于MATLAB只识别格式为.wav的声音文件,我们利用PC机上的声卡和WINDOWS操作系统进行数字信号的采集。
启动录音机进行录音,以文件名“Orisound”保存入原程序所属的文件夹中。
可以看到,文件存储器的后缀默认为.wav ,这是WINDOWS操作系统规定的声音文件存的标准。
如何使用MATLAB进行声音信号处理

如何使用MATLAB进行声音信号处理声音信号处理在现代通信、音频处理、语音识别等领域起着非常重要的作用。
MATLAB作为一款功能强大的科学计算软件,在声音信号处理方面具有广泛的应用。
本文将介绍如何使用MATLAB进行声音信号处理。
一、声音信号的基本概念和特征声音信号是一种通过空气、水等介质传播的机械波,具有振幅、频率和相位等特征。
在声音信号处理中,我们常用到的一些概念和特征包括频谱、语谱图、信噪比等。
频谱是声音信号在频域上的表现形式,可以通过傅里叶变换将时域信号转换为频域信号。
MATLAB提供了fft函数可以方便地进行傅里叶变换。
语谱图是声音信号在时间和频率上的三维表示,可以通过短时傅里叶变换(STFT)得到。
MATLAB的spectrogram函数可以实现语谱图的计算和绘制。
信噪比是衡量声音信号中有用信息和噪声之间比例的常用指标,可以通过计算信号的能量和噪声的能量比值得到。
MATLAB提供了snr函数可以计算信噪比。
二、声音信号的读取和保存在使用MATLAB进行声音信号处理之前,我们首先需要将声音信号读取到MATLAB中进行处理。
MATLAB的audioread函数可以实现读取常见音频格式的声音文件,例如.wav、.mp3等。
读取得到的声音信号可以保存在一个向量中,每个采样点的数值表示声音的振幅。
保存处理后的声音信号可以使用MATLAB的audiowrite函数。
我们可以指定保存的音频格式和保存的文件名。
三、声音信号的滤波处理滤波是声音信号处理中常用的技术,可以用来去除信号中的噪声或者增强信号中的某些频率成分。
MATLAB提供了fir1和butter函数可以用于设计和实现各种类型的滤波器。
fir1函数用于设计FIR滤波器,可以通过指定滤波器的阶数和截止频率来设计低通、高通、带通或带阻滤波器。
butter函数用于设计IIR滤波器,可以通过指定滤波器的阶数和截止频率来设计低通、高通、带通或带阻滤波器。
基于MATLAB语音信号处理(语音信号处理的综合仿真)

---------------------------------------------------------------范文最新推荐------------------------------------------------------ 基于MATLAB语音信号处理(语音信号处理的综合仿真)摘要:针对目前在嘈杂的环境中手机接听电话时人声不清楚的缺点,本文介绍了一个基于MATLAB的算法来对语音信号进行处理。
该算法通过计算机录音系统来实现对语音信号的采集,并且利用MATLAB的计算和信号处理能力进行频谱分析和设计滤波器,最终通过仿真得到滤波前后的波形,从而达到保留语音信号中的大部分人声并且滤除掉嘈杂噪声的目的。
仿真实验表明,采用低通滤波器保留人声的效果显著,失真较少。
本算法具有操作简单,运行速度快等优点。
关键词:语音信号;MATLAB;滤波;低通;噪声Speech Signal Processing Based on MATLAB1 / 17Abstract: At present, in view of the shortcomings of that the voice is not clear when people answering the phone in a noisy environment, this paper introduces a algorithm for speech signal processing based on MATLAB. The algorithm realizes the acquisition of the speech signal through a computer recording system. And the software can realize the capabilities of frequency spectrum analysis and filter design by the use of calculation and signal processing capabilities of MATLAB. Finally it can get the waveform before and after filtering through the simulation. So that we can retain most of the voices in the speech signal and at the same time remove noisy noise through filter. Simulation results show that the low pass filter has a remarkable effect of keeping voices and the distortion is little. This algorithm has the advantages of simple to operate and fast.Key Words: Speech signal; MATLAB; Filtering; Low pass; Noise目录---------------------------------------------------------------范文最新推荐------------------------------------------------------ 摘要1引言11.研究意义及研究现状21.1研究意义21.2研究现状22. 语音信号处理的总体方案2.1 研究的主要内容本课题主要介绍的是的语音信号的简单处理,目的就是为以后在手机上的移植打下理论基础。
基于MATLAB的语音处理
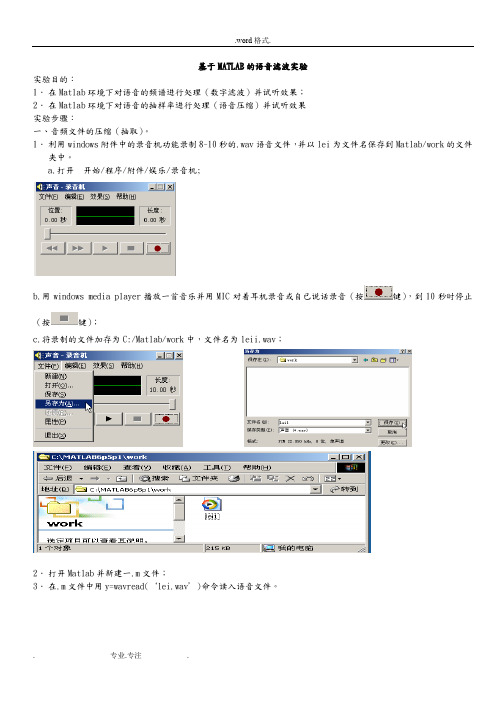
基于MATLAB的语音滤波实验实验目的:1.在Matlab环境下对语音的频谱进行处理(数字滤波)并试听效果;2.在Matlab环境下对语音的抽样率进行处理(语音压缩)并试听效果实验步骤:一、音频文件的压缩(抽取)。
1.利用windows附件中的录音机功能录制8~10秒的.wav语音文件,并以lei为文件名保存到Matlab/work的文件夹中。
a.打开开始/程序/附件/娱乐/录音机;b.用windows media player播放一首音乐并用MIC对着耳机录音或自已说话录音(按键),到10秒时停止(按键);c.将录制的文件加存为C:/Matlab/work中,文件名为leii.wav;2.打开Matlab并新建一.m文件;3.在.m文件中用y=wavread(‘lei.wav’)命令读入语音文件。
4.语音压缩:在m命令窗中输入如下命令:5.运行sample2.m之后会在work文件夹中生成一个名为lei2的.wav文件,如下图:6.双击lei2音频文件,用耳机试听效果,并跟lei1的效果比较。
7.在sample2.m文件中改变抽取倍率s (必须为正整数),重复4、5、6步,观察在不同抽取倍率s下的音频质量,(注意:在运行sample2.m之前必须将work中名为lei2的.wav音频文件删除,或在.m文件中wavwrite()中的保存文件名改为其它的名字。
)二、音频信号的时域滤波(音频数据的时域卷积)。
(一)、低通滤波1.打开Matlab并新建一.m文件,在.m文件中用y=wavread(‘lei.wav’)命令读入语音文件。
2.在m命令窗中输入如下命令,并加存为sample3.m,运行该m文件。
3.双击lei3音频文件,用耳机试听效果,并跟lei1的效果比较。
4.再加一级h(n)的低通滤波,重复2、3步,如下图:(注意:在运行lei2.m之前必须将work中名为lei3的.wav音频文件删除,或在.m文件中wavwrite()中的保存文件名改为其它的名字。
基于MATLAB的语音信号分析和处理

摘要本文主要描述的是基于MATLAB的一般声音信号的频谱分析过程包括:用电脑声卡录音、从WAV文件输入、从标准信号发生器输入;信号波形分析,包括幅值、频率、周期、相位的估计,以及统计量峰值、均值、均方值和方差的计算;信号频谱分析,频率、周期的估计,图形显示幅值谱、相位谱、实频谱、虚频谱和功率谱的曲线。
关键词:MATLAB,频谱分析,误差目录前言 (1)一、设计原理 (2)1.1系统整体设计原理 (2)1.2频谱分析原理 (3)1.3 频谱图 (4)1.4 模块划分 (4)二、详细设计步骤 (5)2.1语音信号的采集 (5)2.2采样分帧 (6)2.3 短时能量和短时平均幅度 (6)2.4短时过零率 (8)2.5短时自相关函数 (9)2.6语音信号的滤波 (11)三、设计结果及分析 (12)3.1语音信号的录入与打开 (12)3.2时域信号的FFT分析与加噪后的波形比较 (12)3.3滤波并比较滤波前后语音信号的波形 (14)3.4频率响应分析 (15)总结 (17)参考文献 (18)致谢 (19)附录 (20)前言随着软硬件技术的发展,仪器的智能化与虚拟化已成为未来实验室及研究机构的发展方向。
虚拟仪器技术的优势在于可由用户定义自己的专用仪器系统,且功能灵活,很容易构建,所以应用面极为广泛。
基于计算机软硬件平台的虚拟仪器可代替传统的测量仪器,如示波器、逻辑分析仪、信号发生器、频谱分析等。
从发展史看,电子测量仪器经历了由模拟仪器、智能仪器到虚拟仪器,由于计算机性能的飞速发展,已把传统仪器远远抛到后面,并给虚拟仪器生产厂家不断带来连锅端的技术更新速率。
目前已经有许多较成熟的频谱分析软件,如SpectraLAB、RSA Vu、dBFA等。
MATLAB是一个数据分析和处理功能十分强大的工程实用软件,他的数据采集工具箱为实现数据的输入和输出提供了十分方便的函数和命令。
本文将给出基于声卡与MATLAB的声音信号频谱分析的设计原理与实现方法。
基于MATLAB的语音信号特技处理-延时与混响

DSP应用课程设计(学年论文)说明书课题名称:DSP应用课程设计学生学号:专业班级:学生姓名:学生成绩:指导教师:课题工作时间:至武汉工程大学教务处制填写说明:1. 一、二、三项由指导教师在课程设计(学年论文)开始前填写并交由学生保管;2. 四、五两项由学生在完成课程设计后填写,并将此表与课程设计一同装订成册交给指导教师;3. 成绩评定由指导教师按评定标准评分。
4. 此表格填写好后与正文一同装订成册。
课程设计评审标准(指导教师用)(报告正文)一、课程设计目的综合运用数字信号处理的理论知识惊醒频谱分析和滤波器设计,通过理论推导得出相应结论,再利用MATLAB作为编程工具进行计算机实现,从而加深对所学知识的理解,建立概念。
二、课程设计要求1.熟悉离散信号和系统的时域特性。
2.熟悉语音信号的特点。
3.掌握数字信号处理的基本概念,基本理论和基本方法。
4.掌握序列快速傅里叶变换的基本方法。
5.学会MATLAB的使用,掌握MATLAB的程序设计方法。
6.掌握MATLAB设计各种数字滤波器的方法核对信号进行滤波的方法。
三、详细设计过程1.基本原理1.1信号采样(1)采样频率采样频率是指计算机每秒钟采集多少个声音样本,采样频率越高,即采样的间隔时间越短,则在单位时间内计算机得到的声音样本数据就越多,对声音波形的表示也越精确。
只有采样频率高于声音信号最高频率的两倍时,才能把数字信号表示的声音还原成为原来的声音。
(2)采样位数即采样值或取样值,用来衡量声音波动变化的参数,是指声卡在采集和播放声音文件时所使用数字声音信号的二进制位数。
声卡的位客观地反映了数字声音信号对输入声音信号描述的准确程度。
声卡的主要的作用之一是对声音信息进行录制与回放,在这个过程中采样的位数和采样的频率决定了声音采集的质量。
1.2混响与延时(1)混响效果主要是用于增加音源的融合感。
自然音源的延时声阵列非常密集、复杂,所以模拟混响效果的程序也复杂多变。
基于matlab的语音信号的合成(加入延迟混响)课案

中北大学课程设计说明书学生姓名:学号:学生姓名:学号:学生姓名:学号:学院:信息与通信工程学院专业:电子信息工程题目:信息处理实践:语言信号的合成指导教师:杨娜职称: 副教授2016 年 1月 3 日中北大学课程设计任务书15/16 学年第一学期学院:信息与通信工程学院专业:电子信息工程学生姓名:学号:学生姓名:学号:学生姓名:学号:课程设计题目:信息处理实践:语言信号的合成起迄日期:2016年1 月4日~2016年1月22 日课程设计地点:201,503,1号楼教室指导教师:杨娜系主任:王浩全下达任务书日期: 2016 年1月 3 日课程设计任务书课程设计任务书目录摘要 (1)1.MATLAB简介 (1)2.GUI简介 (1)一.设计方案........................................................................................................... 二.设计步骤及结果1.语音信号的采集..............................................2.语音信号的截取.................3.语音信号的合成.................4.合成语音的验证.........5.GUI界面设计及实现.........三.设计评述参考文献..............附录..............摘要语音信号处理是一门比较实用的电子工程专业课程,语音是人类获取信息的的重要来源和利用信息的重要手段。
通过语言相互传递信息是人类最重要的基本功能之一。
语音信号是一种非平稳的时变信号,它携带着各种信息。
在语音编码、语音合成、语音识别和语音增强等语音处理中无一例外需要提取语音中包含的各种信息。
Matlab是一个数据分析和处理功能十分强大的工程实用软件。
本文介绍了利用matlab软件及其中的图形用户界面(GUI)实现驱动声卡采集语音信号和语音信号采集后的文档处理方法,并通过实例利用matlab分析了语音信号处理的过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DSP应用课程设计(学年论文)说明书课题名称:DSP应用课程设计学生学号:专业班级:学生姓名:学生成绩:指导教师:课题工作时间:至武汉工程大学教务处制填写说明:1. 一、二、三项由指导教师在课程设计(学年论文)开始前填写并交由学生保管;2. 四、五两项由学生在完成课程设计后填写,并将此表与课程设计一同装订成册交给指导教师;3. 成绩评定由指导教师按评定标准评分。
4. 此表格填写好后与正文一同装订成册。
课程设计评审标准(指导教师用)(报告正文)一、课程设计目的综合运用数字信号处理的理论知识惊醒频谱分析和滤波器设计,通过理论推导得出相应结论,再利用MATLAB作为编程工具进行计算机实现,从而加深对所学知识的理解,建立概念。
二、课程设计要求1.熟悉离散信号和系统的时域特性。
2.熟悉语音信号的特点。
3.掌握数字信号处理的基本概念,基本理论和基本方法。
4.掌握序列快速傅里叶变换的基本方法。
5.学会MATLAB的使用,掌握MATLAB的程序设计方法。
6.掌握MATLAB设计各种数字滤波器的方法核对信号进行滤波的方法。
三、详细设计过程1.基本原理1.1信号采样(1)采样频率采样频率是指计算机每秒钟采集多少个声音样本,采样频率越高,即采样的间隔时间越短,则在单位时间内计算机得到的声音样本数据就越多,对声音波形的表示也越精确。
只有采样频率高于声音信号最高频率的两倍时,才能把数字信号表示的声音还原成为原来的声音。
(2)采样位数即采样值或取样值,用来衡量声音波动变化的参数,是指声卡在采集和播放声音文件时所使用数字声音信号的二进制位数。
声卡的位客观地反映了数字声音信号对输入声音信号描述的准确程度。
声卡的主要的作用之一是对声音信息进行录制与回放,在这个过程中采样的位数和采样的频率决定了声音采集的质量。
1.2混响与延时(1)混响效果主要是用于增加音源的融合感。
自然音源的延时声阵列非常密集、复杂,所以模拟混响效果的程序也复杂多变。
常见参数有以下几种:混响时间:能逼真的模拟自然混响的数码混响器上都有一套复杂的程序,其上虽然有很多技术参数可调,然而对这些技术参数的调整都不会比原有的效果更为自然,尤其是混响时间。
高频滚降:此项参数用于模拟自然混响当中,空气对高频的吸收效应,以产生较为自然的混响效果。
一般高频混降的可调范围为0.1~1.0。
此值较高时,混响效果也较接近自然混响;此值较低时,混响效果则较清澈。
扩散度:此项参数可调整混响声阵密度的增长速度,其可调范围为0~10,其值较高时,混响效果比较丰厚、温暖;其值较低时,混响效果则较空旷、冷僻。
预延时:自然混响声阵的建立都会延迟一段时间,预延时即为模拟次效应而设置。
声阵密度:此项参数可调整声阵的密度,其值较高时,混响效果较为温暖,但有明显的声染色;其值较低时,混响效果较深邃,切声染色也较弱。
频率调制:这是一项技术性的参数,因为电子混响的声阵密度比自然混响稀疏,为了使混响的声音比较平滑、连贯,需要对混响声阵列的延时时间进行调制。
此项技术可以有效的消除延时声阵列的段裂声,可以增加混响声的柔和感。
调治深度:指上述调频电路的调治深度。
(2)延时就是将音源延迟一段时间后,再欲播放的效果处理。
依其延迟时间的不同,可分别产生合唱、镶边、回音等效果。
当延迟时间在3~35ms之间时人耳感觉不到滞后音的存在,并且他与原音源叠加后,会因其相位干涉而产生"梳状滤波"效应,这就是镶边效果。
如果延迟时间在50ms以上时,其延迟音就清晰可辨,此时的处理效果才是回音。
回音处理一般都是用于产生简单的混响效果。
延时、合唱、镶边、回音等效果的可调参数都差不多,具体有以下几项:*延时时间(Dly),即主延时电路的延时时间调整。
*反馈增益(FB Gain),即延时反馈的增益控制。
*反馈高频比(Hi Ratio),即反馈回路上的高频衰减控制。
*调制频率(Freq),指主延时的调频周期。
*调制深度(Depth),指上述调频电路的调制深度。
*高频增益(HF),指高频均衡控制。
*预延时(Ini Dly),指主延时电路预延时时间调整。
*均衡频率(EQ F),这里的频率均衡用于音色调整,此为均衡的中点频率选择。
由于延时产生的效果都比较复杂多变,如果不是效果处理专家,建议使用设备提供的预置参数,因为这些预置参数给出的处理效果一般都比较好。
1.3离散傅立叶变换在MATLAB的信号处理工具箱中函数FFT和IFFT用于快速傅立叶变换和逆变换。
下面介绍这些函数。
函数FFT用于序列快速傅立叶变换。
函数的一种调用格式为y=fft(x)其中,x是序列,y是序列的FFT,x可以为一向量或矩阵,若x为一向量,y是x的FFT。
且和x相同长度。
若x为一矩阵,则y是对矩阵的每一列向量进行FFT。
如果x长度是2的幂次方,函数fft执行高速基-2FFT算法;否则fft执行一种混合基的离散傅立叶变换算法,计算速度较慢。
函数FFT的另一种调用格式为y=fft(x,N)式中,x,y意义同前,N为正整数。
函数执行N点的FFT。
若x为向量且长度小于N,则函数将x补零至长度N。
若向量x 的长度大于N,则函数截短x使之长度为N。
若x 为矩阵,按相同方法对x进行处理。
经函数fft求得的序列y一般是复序列,通常要求其幅值和相位。
MATLAB提供求复数的幅值和相位函数:abs,angle,这些函数一般和FFT同时使用。
函数abs(x)用于计算复向量x的幅值,函数angle(x)用于计算复向量的相角,介于和之间,以弧度表示。
函数unwrap(p)用于展开弧度相位角p ,当相位角绝对变化超过时,函数把它扩展至。
用MATLAB工具箱函数fft进行频谱分析时需注意:(1)函数fft返回值y的数据结构对称性。
(2) 频率计算。
(3) 作FFT 分析时,幅值大小与FFT 选择点数有关,但不影响分析结果。
1.4滤波器设计单回声滤波器的系统函数:R az z H -+=1)( , a <1 (3-1)无限个回声滤波器的系统函数:RRaz z z H ---=1)( , a <1 (3-2) 全通结构的混响器的系统函数:R Razz a z H --++=1)( , a <1 (3-3) 本次设计用IIR 滤波器对信号进行滤波,函数名为filter函数filter 的调用格式为 y=filter(b,a,x)该格式采用数字滤波器对数据进行滤波,既可以用于IIR 滤波器,也可以用于FIR 滤波器。
其中向量b 和a 分别表示系统函数的分子、分母多项式的系数,若a =1,此时表示FIR 滤波器,否则就是IIR 滤波器。
该函数是利用给出的向量b 和a ,对x 中的数据进行滤波,结果放入向量y 。
1.5 图形用户界面设计图形用户界面GUI (Graphics User Interface) 是由各种图形对象,如图形窗口、图轴、菜单、按钮、文本框等构建的用户界面,是人机交流信息的工具和方法。
GUI 设计即可以基本的MATLAB 程序设计为主,也可以鼠标为主利用GUIDE 工具进行设计。
GUIDE ( Graphics User Interface Design Environ2ment) 是一个专用于GUI 程序设计的快速开发环境,使用者通过鼠标就能迅速地产生各种GUI 控件,并随心所欲地改变它们的外形、大小及颜色等,从而帮助用户方便地设计出各种符合要求的图形用户界面。
调用GUIDE 的方法有2 种,在MATLAB 命令窗口中输入guide 命令,或在MATLAB 主菜单中点击File →New →GUI 即可打开一个可编辑的新窗口。
在GUIDE 设计环境中,需要用到的工具有属性编辑器、控件布置编辑器、菜单编辑器、对象浏览器、网格标尺设置编辑器以及GUI 应用属性设置编辑器等。
GUI 设计面板是GUI 设计工具应用的平台,面板上部提供了菜单和常用工具按钮,左边提供了多种GUI 控件,如按钮、单选按钮、复选框、文本框等。
进行GUI 设计时,首先单击GUI 面板左边所需的控件,然后在右边的图形界面编辑区中再次单击某一恰当的位置,这时将在该位置上为图形界面添加一相应的控件,接下来,通过属性编辑器和对齐编辑器对各控件设置相关属性和进行界面布置,以完善界面功能。
2.方案选择及设计(1)利用Windows 下的录音机或其他软件,录制一段自己的语音信号,时间控制在1s左右,并对录制的信号进行采样。
(2)语音信号的频谱分析,画出采样后语音信号的时域波形和频谱图。
(3)将信号加入延时和混响,再分析其频谱,并与原始信号频谱进行比较。
(4)设计几种特殊类型的滤波器:单回声滤波器,多重回声滤波器,无限个回声滤波器,全通结构的混响器,并画出滤波器的频域响应。
(5)用自己设计的滤波器对采集的语音信号进行滤波。
(6)分析得到信号的频谱,画出滤波后信号的时域波形和频谱,并对滤波前后的信号进行对比,分析信号的变化。
(7)回放语音信号。
3.程序设计流程四、调试分析1.软件中设置问题,通过edit—figure-copy-figure时发现粘贴到word里面的图形有问题通过设置图片属性可以解决此问题,通过这个问题的解决加深了对软件的了解,更加熟悉软件的运行。
2.GUI界面问题在界面运行时发现按钮覆盖住了图形,通过改变subplot函数的后面的参数,进行修改,改为subplot(2,15 ,[2 13])和subplot(2,15,[17,28])是按钮和图形分开。
3.程序中的细节问题a对信号进行采样时,采样区间为[20000 26000],做DFT变换点数应该为6001,刚开始做的时候就直接写为6000.b语音信号的音道问题,采取的语音信号为双声道,只需要取其中的一个声道进行分析,函数为y=y(:,1);五、结果分析与体会GUI设计界面运行结果:对信号采样后,信号时域波形出现了离散化的分布,不像原始图像那样密集分布,频谱图也是同样的变换,幅度和频率都是根据采样区间变化的从时域图出延时是让原来的波形向右移动300,频域的幅度发生了变化。
混响:在时域图看前面几乎没变化,后面的幅度有一定变化。
在频谱图幅度变化很大,中间的上下相互抵消,两边的跳动很大。
时域上形状大致相同,幅度有微小变化。
频谱上也是滤波前后两边跳动变换较大,幅度变化较大。
时域上波形变得稀疏了,幅度相对变化较大。
频谱上变化两边上下跳的动变化,中间变化抵消全通结构时域大致一样,滤波前比滤波后幅度有变化6000以后上下跳动抵消频域上变化的不为明显,幅度发生了变化。
设计心得体会此次课程设计综合了数字信号处理的理论知识和实践经验,经过两周的时间在查阅相关资料结合以前学过的数字信号处理和数字信号处理实验,如期完成了设计任务要求,并加深了对知识的理解,提高了自己的实践动手能力。
