怀柔区2015数学一模试题及答案
北京市怀柔区2015—2016年初一上期末质量检测数学试卷含答案

怀柔区2015—2016学年度第一学期初一期末质量检测数 学 试 卷 2016.1考生须知 1.本试卷共6页,共三道大题,31道小题,满分120分.考试时间120分钟。
2.在试卷和答题卡上准确填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4. 在答题卡上,选择题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5. 考试结束,请将本试卷、答题卡一并交回。
一、选择题(本题共30分,每小题3分)下列各题均有四个选项,其中只有一个是符合题意的. 1.数轴上有A ,B ,C ,D 四个点,其中绝对值等于2的点是 A.点A B. 点B C. 点C D. 点D2. 飞机在飞行过程中,如果上升23米记作“+23米”,那么下降15米应记作 A .-8米 B . +8米 C .-15米 D .+15米3. 据统计,怀柔雁栖湖常年总库容量38300000立方米,将38300000用科学记数法表示为 A . 0.383×108 B . 3.83×107 C . 38.3×106 D . 383×105 4.如果x =是关于x 的方程4x +m =3的解,那么m 的值是 12A .1B .C .-1D .1212-5.下列运算正确的是A .3x+4y=7xyB .6y 2-y 2=5C .b 4+b 3=b 7D .4x -x=3x6. 如左下图所示的圆柱体从左面看是DCBA7.下列语句正确的是A .画直线AB =10厘米 B .画直线l 的垂直平分线C .画射线OB =3厘米D .延长线段AB 到点C ,使得BC =AB 8. 如果,那么代数式的值为23(2)0a b ++-=2016()a b +A .5 B .-5 C .1 D .-19. 一家商店把一种旅游鞋按成本价元提高50%标价,然后再以8折优惠卖出,则这种旅游a 鞋每双的售价是A .0.4元B .0.8元C .1.2元D .1.5元 a a a axD CB A 123–1–2–310. 按一定规律排列的一列数依次为:-3,8,-15,24,-35,…,按此规律排列下去,这列数中第n 个数(n 为正整数)应该是A .B .C .当n 为奇数时: ;当n 为偶数时: (2)n n +2(1)(2)n n -+(2)n n -+(2)n n +D .(1)n n -+二、填空题(本题共21分,每小题3分) 11. 单项式的系数是 ,次数是 . 223x y -12. 角度换算:=_______.26 48′13.如果2a -b =-2,ab =-1,那么代数式3ab -4a +2b-5的值是_________.14.已知:如图,OB 是∠AOC 的角平分线,OC 是∠AOD 的角平分 线,∠AOB =35°,那么∠BOD 的度数为__________; 15.定义“*”是一种运算符号,规定a ﹡b=5a+4b+2015, 则(-4)﹡5的值为 .16. 某校七年级共有589名学生分别到北京博物馆和中国科技馆学参观,其中到北京博物馆的人数比到中国科技馆人数的2倍还多56人.设到中国科技馆的人数为x 人,可列方程为 .17. 学习直线、射线、线段和线段中点等内容之后,王老师请同学们交流这样一个问题:“射线OA 上有B ,C 两点,若OB=8,BC=2,点D 是线段OB 的中点,请你求出线段DC 的长.”张华同学通过计算得到DC 的长是6,你认为张华的答案是否正确 ,你的理由是 .三、解答题(本题共69分,第18-30题,每小题5分,第31题4分.) 18. 计算: .12(15)(23)--+-19. 计算:.533((1)64⨯-÷-20. 计算:. 32128(2)4-÷-⨯-21. 计算: 13116(64128-⨯-+-÷DCB AO22.先化简,再求值:,其中. 222(22)(21)x x x x +----12x =-23. 解方程:.9753x x +=-24. 解方程:. 2(35)3(12)x x x --=+-25.解方程:. 235132x x ---=26. 一辆货车在公路(直线CD )上由点C 向点D 方向行驶,村庄A ,B 分别位于道路CD 的两侧,司机师傅要在公路上选择一个货物的下货点.(1)请在CD 上确定一个下货点E ,使点E 到村庄A 的距离最近, 画出图形并写出画图的依据;(2)请在直线CD 上确定一点O ,使点O 到村庄A ,B 的距离之和最小,画出图形并写出画图的依据.27. 某校组织七年级学生步行到生存岛参加开放性科学实践活动,七(1)班的小明同学,因为身体原因,医生建议减少长步行,经家长和学校协商决定,小明由家长开车直接从家送到生存岛,已知学生的步行速度是每小时4千米,小明爸爸的车速是每小时36千米,学生从学校出发40分钟后,小明爸爸从家里开车出来,结果小明和同学们同时到达了生存岛,已知小明家到生存岛的路程是学校到生存岛路程的3倍,问学校到生存岛的路程是多少千米?28. 课堂上李老师把要化简求值的整式3323323(7 a -6 a b+3 a b) 3 a -6 a b+3 a b+10 a -3)-(-写完后,让王红同学顺便给出一组a 、b 的值,老师自己说答案,当王红说完:“a=38,b=-32”后,李老师不假思索,立刻就说出答案“3”.同学们莫名其妙,觉得不可思议,但李老师用坚定的口吻说:“这个答案准确无误”,亲爱的同学你相信吗?请你通过计算说出其中的道理.29.已知:如图, ,,平分. 70AOB ∠=︒30AOC ∠=︒OD BOC ∠请依题意补全图形,并求的度数.AOD ∠DABOABO备用图30. (1)如图,已知点C 在线段AB 上,且AC=6cm ,BC=4cm ,点M 、N 分别是AC 、BC 的中点,求线段MN 的的长度.NMABC(2)对于(1)题,如果我们这样叙述:“已知点C 在直线AB 上,且AC=6cm ,BC=4cm ,点M ,N 分别是AC ,BC 的中点,求线段MN 的长度.”结果会有变化吗?如果有,求出结果;如果没有,说明理由. 31. 阅读下列材料:为落实开展社会大课堂活动,七年级(3)班李老师准备周六组织本班学生参观北京科技馆,要求学生周六早9:00准时在科技馆门前集合,然后集中买票参观.小强家离北京科技馆4公里,周六他准备乘出租车去,为了解北京出租车的计价方式,小强周五晚上在网上查到了现行北京市出租汽车价格标准:怀柔区2015—2016学年度第一学期初二期末质量检测数学试卷答案及评分参考 2016.1一、选择题(本题共30分,每小题3分)下列各题均有四个选项,其中只有一个是符合题意的. 题 号 1 2 3 4 5 6 7 8 9 10 答 案 ACBADCDCCB二、填空题(本题共21分,每小题3分) 题 号111213141516 17 答 案 233-, 26.8-4105° 20152x +56=589﹣x不正确,没有分类讨论,DC 的长应该是6或2三、解答题(本题共69分,第18-30题,每小题5分,第31题4分.) 18. 解:原式=12+15-23…………………………………… 4分 =4…………………………………… 5分19. 解:原式=…………………………………… 4分54(27-⨯- =…………………………………… 5分10720.解:原式= 18844-÷-⨯ =…………………………………… 4分 11-- =-2…………………………………… 5分21. 解:原式 ……………………………………………… 1分 1316()86412=-⨯-+-⨯ …………………………………………2分13148(6412=-⨯-+- ………………………………………………………4分 8364=-+ ………………………………………………………… 5分 24=-22.解:原式= ……………………………………2分2224421x x x x +--++ =………………………………………………………4分263x x +-当时, 12x =-原式=211(6(322-+⨯--………………………… 5分 1334=--234=-23.解:……………………2分73x 59x +=- …………………………3分104x =- ∴……………………………4分25x =- ∴是原方程的解. …………5分25x =-24.解: ………………2分 235312x x x -+=+- …………………3分 232315x x x -+=+- ∴ ………………………………4分1x =-∴是原方程的解.…………………5分1x =-25.解:去分母,得 . …………………………… 1分 2(23)3(5)6x x ---= 去括号,得 .………………………………… 2分 463156x x --+= 移项,得 . …………………………… 3分 636415x x --=-- 合并同类项,得 .…………………………………… 4分 913x -=- 系数化1,得 .……………………………………… 5分 139x =26.解:(1)如图.…………………… 1分过A 作CD 的垂线,垂足E 即为所确定到村庄A 距离最近的下货点. ………… 2分 依据是:垂线段最短. …………………… 3分 (2)如图,…………………… 4分 连接线段AB ,交CD 于点O , 则O 即为所确定的到村庄A ,B 的距离之和最小的点.依据是:两点之间线段最短. …………………… 5分 27. 解:设学校到生存岛的路程是x 千米,则小明家到生存岛的路程是3x 千米. ………………………… 1分 根据题意列方程,得.………………………… 3分34043660x x -=解这个方程,得x=4. ………………………… 4分答:学校到生存岛的路程是4千米. ………………………… 5分 28.答:相信.道理如下:…………………………4分 33233237 a -6 a b+3 a b 3 a +6 a b-3 a b-10 a +3 =3+原式=因为,原式化简后的结果是一个确定的值3,与a 、b 的取值无关. 所以,不管a ,b 取什么值,答案都是3. ………………………… 5分 29.解:符合题意的图形有两个,如图1、图2,在图1中,D∵,,70AOB ∠=︒30AOC ∠=︒∴.………………1分 40BOC AOB AOC ∠=∠-∠=︒∵平分,OD BOC ∠∴.…………………… 2分 1202COD BOC ∠=∠=︒∴.……………………………………… 3分50AOD AOC COD ∠=∠+∠=︒在图2中,∵,,70AOB ∠=︒30AOC ∠=︒∴.……………4分 100BOC AOB AOC ∠=∠+∠=︒∵平分,OD BOC ∠∴.…………………… 2分1502COD BOC ∠=∠=︒∴ .………………3分20AOD COD AOC ∠=∠-∠=︒综上,的度数为50或20. .AOD ∠︒︒30. 解:(1)∵AC=6cm ,点M 是AC 的中点,∴MC=3cm ;∵BC=4cm ,点N 是BC 的中点, ∴CN=2cm ;∴MC+CN=5cm.∴线段MN 的的长为5cm. ………………………… 2分 (2)分两种情况:第一种情况:当点C 在点B 的左侧时,解法同(1),线段MN 的长为5cm. …… 3分 第二种情况:当点C 在点B 的右侧时,如图所示: ∵AC=6cm ,点M 是AC 的中点,∴MC=3cm ; ∵BC=4cm ,点N 是BC 的中点,∴CN=2cm ;∴MN=MC-CN=3-2=1cm.………………………… 4分∴综上,线段MN 的长为5cm 或1cm. ……………………… 5分 31.解:(1)3公里以内收费13元; 基本单价2.3元/公里;每5分钟早晚高峰期间加收2公里租价(不含空驶费), 早高峰为7:00(含)-9:00(不含);燃油附加费 1元/运次出租汽车收费结算以元为单位,元以下四舍五入. ……………………… 1分(2)4.6⨯2=9.29≈.……………………… 2分(3)13+2.3+4.6⨯2+1=25.526≈,30-26=4答:小强的打车费用26元,剩余4元钱. ……………………… 4分AM N A B。
北京市怀柔区数学一模试题及答案.doc

l 怀柔区2011年初三一模数 学 试 题学校 姓名 准考证号 考生须知1.本试卷共4页,共五道大题,25道小题,满分120分。
考试时间120分钟。
2.在试卷和答题卡上认真填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4. 在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,请将本试卷、答题卡和草稿纸一并交回。
一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.-5的倒数是A .-5B .5C .- 15D .152.今年是中国共产党建党90周年,据最新统计中共党员总人数已接近7600万名,用科学记数法表示76000000的结果是A. 576010⨯ B .87.610⨯ C . 87610⨯ D .77.610⨯3.已知⊙O 1、⊙O 2的半径分别为5cm 、8cm ,且它们的圆心距为8cm ,则⊙O 1与⊙O 2的位置关系为A .外离B .相交C .相切D .内含4.不透明的袋子中装有4个红球、3个黄球和5个蓝球,每个球除颜色不同外其它都相同,从中任意摸出一个球,则摸出是蓝球的概率为 A .57 B .49 C . 58 D . 5125. 将图1所示的直角梯形绕直线l 旋转一周,得到的立体图开是A B C D 图1 6.2011年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31 35 31 34 30 32 31,这组数据的中位数、众数分别是 A .32,31 B .31,32 C .31,31 D .32,357.如图是一个圆锥形冰淇淋,已知它的母线长是5cm ,高是4cm , 则这个圆锥形冰淇淋的底面面积是 A .210cm π B .29cm π C .220cm π D .2cm π8.观察下列图形及所对应的算式,根据你发现的规律计算1+8+16+24+ … + 8n(n 是正整数)的结果为A. ()221n + B. 18n + C. 18(1)n +-D. 244n n +二、填空题(本题共16分,每小题4分)9. 函数y = 1x -2中,自变量x 的取值范围是 .10.方程方程2230x x --=的两个根是__________________ .11. 已知x=1是方程x 2-4x +m2 =0的一个根,则m 的值是______.12.如图,Rt △ABC 中,∠C =90°,∠ABC =30°,AB =6.点D 在AB 边上,点E 是BC 边上一点(不与点B 、C 重合),且DA =DE ,则AD 的取值范围是________________.三、解答题(本题共30分,每小题5分)13(本题满分5分)计算:2sin 308232011︒+---14. (本题满分5分)因式分解: 221218x x -+ 15.(本题满分5分)如图, 已知:BF=DE,∠1=2,∠3=∠4 求证:AE=CF .证明:16.(本题满分5分)已知 230a a --=,求代数式111a a --的值. 解:17. (本题满分5分)一个涵洞成抛物线形,它的截面如图(1).现测得,当水面宽AB =1.6 m 时,涵洞顶点O 与水面的距离为2.4 m .ED 离水面的高FC=1.5 m,求涵洞ED 宽是多少?是否会超过1 m ?(提示:设涵洞所成抛物线为)0(2<=a ax y )解:C D ABE(第12题)第8题图18.(本题满分6分)“校园手机”现象越来越受到社会的关注.“寒假”期间,记者刘凯随机调查了某区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:(1)求这次调查的家长人数,并补全图①;(2)求图②中表示家长“赞成”的圆心角的度数;(3)从这次接受调查的学生中,随机抽查一个,恰好是“无所谓”态度的学生的概率是多少?解:图① 图②四、解答题(本题共20分,第19、20题各5分,第21题6分,第22题4分)19. (本题满分5分)如图,已知AB 为⊙O 的直径,DC 切⊙O 于点C ,过D 点作 DE ⊥AB ,垂足为E ,DE 交AC 于点F . 求证:△DFC 是等腰三角形. 证明: 20.(本题满分5分)某校九年级两个班各为红十字会捐款1800元.已知2班比1班人均捐款多4元,2班的人数比1班的人数少10%.请你根据上述信息,就这两个班级的“人数”或“人均捐款”提出一个用分式方程....解决的问题,并写出解题过程.21. (本题满分6分)如图,已知二次函数y = x 2-4x + 3的图象交x 轴于A 、B 两点(点A 在点B 的左侧)抛物线y = x 2-4x + 3交y 轴于点C ,(1)求线段BC 所在直线的解析式. (2)又已知反比例函数ky x与BC 有两个交点且k 为正整数,求k 的值. 解:(1)(2)学生及家长对中学生带手机的态度统计图 家长学生无所谓反对赞成30803040140类别人数28021014070家长对中学生带手机 的态度统计图 20%反对无所谓赞成22.(本题满分4分)(1)如图①两个正方形的边长均为3,求三角形DBF 的面积.(2)如图②,正方形ABCD 的边长为3,正方形CEFG 的边长为1, 求三角形DBF 的面积. (3)如图③,正方形ABCD 的边长为a ,正方形CEFG 的边长为b ,求三角形DBF 的面积.从上面计算中你能得到什么结论.结论是:三角形DBF 的面积的大小只与a 有关, 与b 无关. (没写结论也不扣分)五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. (本题满分7分)如图,已知二次函数24y ax x c =-+的图象与坐标轴交于点A (-1, 0)和点C (0,-5). (1)求该二次函数的解析式和它与x 轴的另一个交点B 的坐标。
怀柔2015年一模考试试题定稿

北京市怀柔区2015年高级中等学校招生模拟考试(一)物 理 试 卷学校______________________姓名____________________准考证号___________________一、单项选择题(下列各小题均有四个选项,其中只有一个选项符合题意。
共30分,每小题2分)1.力学中的三个基本物理量是质量、长度和时间,它们的国际单位分别是A .克、厘米、秒B .克、厘米、小时C .千克、米、小时D .千克、米、秒 2.图1所示的现象中,属于光的反射现象的是3.下列物品中,通常情况下属于导体的是A .铅笔芯B .塑料笔杆C .橡胶手套D .陶瓷碗 4.下列实例中,为了加快蒸发的是A .给盛有酒精的瓶子加盖B .把新鲜的蔬菜装入保鲜袋中C .将湿衣服晾在通风向阳处D .春季植树时剪除大量枝叶 5.图2所示的家用电器中,利用电流热效应工作的是6.下列实例中,为了减小摩擦的是A .骑自行车的人刹车时用力捏闸B .给自行车轴承中加润滑油C .足球守门员戴有防滑手套D .运动鞋的底部制有凹凸不平的花纹 7.关于家庭电路和安全用电,下列选项中正确的是A .家庭电路中必须安装保险丝或空气开关B .在未断开电源开关的情况下更换灯泡放大镜把字“放大”图1DCBA雨后天空中出现彩虹 景物在水中形成“倒影” 钢勺好像在水面处折断了A .电脑B .电风扇C .电熨斗D .洗衣机图2C.在输电线上晒衣服D.使用绝缘层破损的导线8.下列情景中,人对物体做功的是A.举重运动员举着杠铃不动B.人提着书包在水平路面上匀速直线前进C.大力士用力推一块大石头但没有推动D.顾客在超市里推着购物车沿水平方向运动9.下列的估测,最接近实际的是A.普通课桌的高度约为10 cm B.物理课本的长度约为2.6mC.一位普通中学生的质量约为50 kg D.一袋普通方便面的质量约为0.5g 10.下列能源中,属于可再生能源的是A.石油B.煤炭C.天然气D.太阳能11.关于声现象,下列说法中错误..的是A.“闻其声而知其人”主要是根据音色来判断的B.公路旁安装隔音墙是为了在传播路径上减弱噪声C.课堂上能听到老师讲课声,是由于空气能够传声D.用大小不同的力先后敲击同一音叉,音叉发声的音调会不同12.对于功率和机械效率的理解,下列说法中正确的是A.机械工作时的功率越大,其工作时机械效率一定越高B.机械工作时的功率越大,其工作时一定越省力C.机械做的有用功相同,总功越少,其机械效率一定越高D.机械工作时越省力,其机械效率一定越高13.图3甲所示的电蚊拍,具有灭蚊和照明的功能。
2015年各区一模27题及答案

2015年各区中考数学一模试题第27题 1海淀2东城3西城4朝阳5丰台6石景山7昌平 8顺义9通州10大兴11怀柔12密云13平谷 14延庆15房山16燕山17门头沟解答题(本题共22分,第27题7分,第28题7分,第29题8分) 海淀一模27.在平面直角坐标系xOy 中,抛物线2212y x x =-+与y 轴交于点A ,顶点为点B ,点C 与点A 关于抛物线的对称轴对称.(1)求直线BC 的解析式;(2)点D 在抛物线上,且点D 的横坐标为4.将抛物线在点A ,D 之间的部分(包含点A ,D )记为图象G ,若图象G 向下平移t (0t >)个单位后与直线BC 只有一个公共点,求t 的取值范围.东城一模27.在平面直角坐标系xOy 中,抛物线()210y ax bx a =++≠过点()1,0A -,()1,1B ,与y轴交于点C .(1)求抛物线()210y ax bx a =++≠的函数表达式;(2)若点D 在抛物线()210y ax bx a =++≠的对称轴上,当ACD △的周长最小时,求点D 的坐标;(3)在抛物线()210y ax bx a =++≠的对称轴上是否存在点P ,使ACP △成为以AC为直角边的直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.西城一模27 已知二次函数21y x bx c =++的图象1C 经过(1,0)-,(0,3)-两点.(1)求1C 对应的函数表达式;(2)将1C 先向左平移1个单位,再向上平移4个单位, 得到抛物线2C ,将2C 对应的函数表达式记为22y x mx n =++,求2C 对应的函数表达式;(3)设323y x =+,在(2)的条件下,如果在2-≤x ≤a 内存在..某一个x 的值,使得2y ≤3y 成立,利用函数图象直接写出a 的取值范围.朝阳一模27.如图,将抛物线M 1: x ax y 42+=向右平移3个单位,再向上平移3个单位,得到抛物线M 2,直线x y =与M 1的一个交点记为A ,与M 2的一个交点记为B ,点A 的横坐标是-3.(1)求a 的值及M 2的表达式;(2)点C 是线段AB 上的一个动点,过点C 作x 轴的垂线,垂足为D ,在CD 的右侧作正方形CDEF .①当点C 的横坐标为2时,直线n x y +=恰好经过正方形CDEF 的顶点F ,求此时n 的值;②在点C 的运动过程中,若直线n x y +=与正方形CDEF 始终没有公共点,求n 的取值范围(直接写出结果).丰台一模27.在平面直角坐标系xOy 中,抛物线22y x mx n =++经过点A (-1,a ),B (3,a ),且最低点的纵坐标为-4.(1)求抛物线的表达式及a 的值;(2)设抛物线顶点C 关于y 轴的对称点为点D ,点P 是抛物线对称轴上一动点,记抛物线在点A ,B 之间的部分为图象G (包含A ,B 两点).如果直线DP 与图象G 恰有两个公共点,结合函数图象,求点P 纵坐标t 的取值范围.石景山一模27.在平面直角坐标系xOy 中,抛物线223(0)y mx mx m =--≠与x 轴交于(3,0)A ,B 两点.(1)求抛物线的表达式及点B 的坐标;(2)当23x -<<时的函数图象记为G ,求此时函数y 的取值范围;(3)在(2)的条件下,将图象G 在x 轴上方的部分沿x 轴翻折,图象G 的其余部分保持不变,得到一个新图象M .若经过点(4,2)C 的直线(0)y kx b k =+≠与图象M在第三象限内有两个公共点,结合图象求b 的取值范围.顺义一模27.在平面直角坐标系xOy 中,抛物线21212y ax x a =+-+与y 轴交于C 点,与x 轴交于A ,B 两点(点A 在点B 左侧),且点A 的横坐标为-1.(1)求a 的值;(2)设抛物线的顶点P 关于原点的对称点为'P ,求点'P 的坐标; (3)将抛物线在A ,B 两点之间的部分(包括A , B 两点),先向下平移3个单位,再向左平移m (0m >)个单位,平移后的图象记为图象G ,若图象G 与直线'PP 无交点,求m 的取值范围.通州一模27.二次函数2(0)y ax bx c a =++≠的图象与一次函数1y x b =+k 的图象交于)10(,A 、B 两点,(1,0)C 为二次函数图象的顶点.(1)求二次函数2(0)y ax bx c a =++≠的表达式;(2)在所给的平面直角坐标系中画出二次函数2(0)y ax bx c a =++≠的图象和一次函数1y x b =+k 的图象;(3)把(1)中的二次函数2(0)y ax bx c a =++≠的图象平移后得到新的二次函数4444123123321213xOy22(0,)y ax bx c m a m =+++≠为常数的图象,.定义新函数f :“当自变量x 任取一值时,x 对应的函数值分别为1y 或2y ,如果1y ≠2y ,函数f 的函数值等于1y 、2y 中的较小值;如果1y =2y ,函数f 的函数值等于1y (或2y ).” 当新函数f 的图象与x 轴有三个交点时,直接写出m 的取值范围.大兴一模27.已知抛物线222y x x k =++-与x 轴有两个不同的交点.(1) 求k 的取值范围;(2)若k 为正整数,且该抛物线与x 轴的交点都是整数点,求k 的值.(3)如果反比例函数my x=的图象与(2)中的抛物线在第一象限内的交点的横坐标为0x ,且满足1<0x <2,请直接写出m 的取值范围.怀柔一模27.在平面直角坐标系xOy 中,二次函数y=(a-1)x 2+2x+1与x 轴有交点,a 为正整数. (1)求a 的值.(2)将二次函数y=(a-1)x 2+2x+1的图象向右平移m 个单位,向下平移m 2+1个单位,当 -2≤x≤1时,二次函数有最小值-3,求实数m 的值.23.光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A 、B 两地区收割小麦,其中30台派往A 地区,20台派往B 地区,两地区与该农机租赁公司商定每天的租赁价格见下表:每台甲型收割机的租金 每台甲型收割机的租金 A 地区 1800 1600 B 地区16001200(1)派往A 地区x 台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元)求x 与y 间的函数关系时,并写出x 的取值范围;(2)若使农机租菱公司这50台联合收割机一天的租金总额比低于79600元,说明有多少种分配方案,并将各种方案设计出来;(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提出一条合理建议。
2015年怀柔中考一模数学试题及标准答案

北京市怀柔区2015年高级中等学校招生模拟考试(一)数 学 试 卷 2015.5一、选择题(本题共30分,每小题3分)下列各题均有四个选项,其中只有一个..是符合题意的. 1.把8000用科学计数法表示是A.28010⨯ B .3810⨯ C .40.810⨯ D .4810⨯ 2.数轴上有A ,B,C ,D 四个点,其中绝对值相等的点是A.点A 与点DB. 点A 与点CC. 点B与点C D . 点B 与点D 3.下列手机软件图标中,既是轴对称图形又是中心对称图形的是A B C D4. 小华的老师让他在无法看到袋子里小球的情形下,从袋子里模出一个小球. 袋子里各种颜色小球的数量统计如表所示.小华模到褐色小球的概率为 A .101 B.51 C.41D.215. 如图,AD是∠EAC 的平分线,AD∥BC,∠B=30°,则∠C 为 A.30° B .60° C.80° D.120°6.如图,已知⊙O 的半径为10,弦AB 长为16,则点O 到AB 的距离是 A. 3 B. 4 C. 5 D. 67.某校在“中国梦.我的梦”演讲比赛中,有11名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前6名,不仅要了解自己的成绩,还要了解这11名学生成绩的 A.平均数 B .众数 C.中位数 D .方差 8.如图,已知正方形ABCD 中,G 、P 分别是D C、BC 上的点,E 、F 分别是AP 、GP 的中点,当P 在BC 上从B向C 移动而G 不动时,下列结论成立的是A .线段EF 的长逐渐增大 B.线段EF 的长逐渐减小颜色 红色 橙色 黄色 绿色 蓝色 紫色 褐色 数量 6433225G FE PD CBAxD CB A 123–1–2–3C.线段EF的长不改变 D.线段EF的长不能确定9.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为A .x≥B.x≤3C.x≤D.x≥310.如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的A.线段PD B.线段PC C.线段PED.线段DE二、填空题(本题共18分,每小题3分)11.函数y=1x-3中自变量x的取值范围是_________________.12.请写出一个过一、三象限的反比例函数的表达式_________________.13.下面有五个图形,与其它图形众不同的是第个.14.如图,在矩形ABCD中,=,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE•ED=16,则矩形ABCD的面积为.15.当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为__________.16.2014年5月1日开始,北京市开始实施居民用水阶梯水价.具体方案如下:户年用水量180立方米(含)内,每立方米5元;181立方米至260立方米(含)内,每立方米7元;260立方米以上,每立方米9元.阶梯水价以日历年(每年1月1日到12月31日)为周期计算.小王家2014年4月30日抄表示数550立方米,5月1日起实施阶梯水价,6月抄表时因用户家中无①②③④⑤xy图2OPED CBA图1。
怀柔区2015-2016学年第一学期期末九年级数学试题及答案

怀柔区2015—2016学年第一学期初三期末质量检测数学试卷一.选择题(共有10个小题,每小题3分,共30分)下面各题均有四个选项,其中只有一个..是符合题意的.1.我市南水北调配套工程建设进展顺利,工程运行调度有序.截止2015年12月底,已累计接收南水北调来水812000000立方米.使1100余万市民喝上了南水;通过“存水”增加了约550公顷水面,密云水库蓄水量稳定在10亿立方米左右,有效减缓了地下水位下降速率.将812000000用科学记数法表示应为A .812×106B .81.2×107C .8.12×108D .8.12×1092.实数a ,b ,c ,d 在数轴上的对应点的位置如图所示,这四个数中,相反数最大是A .aB .bC .cD .d3.如图,在△ABC 中,DE ∥BC ,分别交AB ,AC 于点D ,E .若AD =2,DB =4,则AEAC的值为A .12B .13C .14D .164.若△ABC ∽△A ′B ′C ′,相似比为1:2,则△ABC 与△A ′B ′C ′的面积的比为A .1:2B .2:1C .1:4D .4:15.二次函数y =(x ﹣1)2+2的最小值为()A .1B .-1C .2D .-26.将抛物线2=-y x 向上平移2个单位,则得到的抛物线表达式为A .2y=-(x+2)B .2y=-(x-2)C .2y=-x -2D .2y=-x +27.已知Rt △ABC 中,∠C=90°,AC=3,BC=4,则cosA 的值为()A .34B .43C .35D .458.如图是拦水坝的横断面,斜坡AB 的水平宽度为12米,斜面坡度为1:2,则斜坡AB 的长为A .43米B .65米C .125米D .24米2题图3题图8题图9题图青铜展馆9.如图,⊙O 是△ABC 的外接圆,∠ACO =45°,则∠B 的度数为()A.30°B.35°C.40°D.45°10.小刚在实践课上要做一个如图1所示的折扇,折扇扇面的宽度AB 是骨柄长OA 的34,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为243cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB 为()A .21cmB .20cmC .19cmD .18cm二、填空题(本题共6个小题,每小题3分,共18分)11.4的平方根是.12.不等式组⎪⎩⎪⎨⎧->+≥-1230211x x 的正整数解是.13.如图,tan ∠ABC=.14.写出一个抛物线开口向上,与y 轴交于(0,2)点的函数表达式.15.已知⊙O 的半径2,则其内接正三角形的面积为.16.学校组织社会大课堂活动去首都博物馆参观,明明提前上网做了功课,查到了下面的一段文字:首都博物馆建筑本身是一座融古典美和现代美于一体的建筑艺术品,既具有浓郁的民族特色,又呈现鲜明的现代感.首都博物馆建筑物(地面以上)东西长152米、南北宽66米左右,建筑高度41米.建筑内部分为三栋独立的建筑,即:矩形展馆,椭圆形专题展馆,条形的办公科研楼.椭圆形的青铜展馆斜出墙面寓意古代文物破土而出,散发着浓郁的历史气息.明明对首都博物馆建筑物产生了浓厚的兴趣,站到首都博物馆北广场,他被眼前这座建筑物震撼了.整个建筑宏大壮观,斜出的青铜展馆和北墙面交出一条抛物线,抛物线与外立面之间和谐、统一,明明走到过街天桥上照了一张照片(如图所示).明明想了想,算了算,对旁边的文文说:“我猜想这条抛物线的顶点到地面的距离应是15.7米左右.”文文反问:“你猜想的理由是什么”?明明说:“我的理由是”.明明又说:“不过这只是我的猜想,这次准备不充分,下次来我要用学过的数学知识准确的测测这个高度,我想用学到的知识,我要带等测量工具”.13题图CB A30︒10题图110题图2三、解答题(本题共72分,第17—25题,每小题5分,第26题8分,第27题6分,第28题6分,第29题7分)17.计算:2012(3)3cos 602π---+--︒.18.已知0362=--x x,求代数式()()311)3(2+-+--x x x x 的值.19.已知如图,△ABC 中,AE 交BC 于点D ,∠C=∠E ,AD :DE=3:5,AE=8,BD=4,求DC 的长.20.如图,一次函数y 1=﹣x +2的图象与反比例函数y 2=xk的图象相交于A ,B 两点,点B 的坐标为(2m ,-m ).(1)求出m 值并确定反比例函数的表达式;(2)请直接写出当x <m 时,y 2的取值范围.21.已知如图,在△ABC 中,∠A=30°,∠C=105°,AC=32,求AB 的长.19题图22.已知如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接A C.若∠A=22.5°,CD=8cm,求⊙O的半径.23.如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62)24.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.(1)求证:AB=BE;(2)若PA=2,cosB=,求⊙O半径的长.25.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.(1)若花园的面积为192m2,求x的值;(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求x取何值时,花园面积S最大,并求出花园面积S的最大值.26.在“解直角三角形”一章我们学习到“锐角的正弦、余弦、正切都是锐角的函数,统称为锐角三角函数”.小力根据学习函数的经验,对锐角的正弦函数进行了探究.下面是小力的探究过程,请补充完成:(1)函数的定义是:“一般地,在一个变化的过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,我们就把x称为自变量,y称为因变量,y是x的函数”.由函数定义可知,锐角的正弦函数的自变量是,因变量是,自变量的取值范围是___________.(2)利用描点法画函数的图象.小力先上网查到了整锐角的正弦值,如下:sin1°=0.01745240643728351sin2°=0.03489949670250097sin3°=0.05233595624294383sin4°=0.0697564737441253sin5°=0.08715574274765816sin6°=0.10452846326765346sin7°=0.12186934340514747sin8°=0.13917310096006544sin9°=0.15643446504023087sin10°=0.17364817766693033sin11°=0.1908089953765448sin12°=0.20791169081775931sin13°=0.22495105434386497sin14°=0.24192189559966773sin15°=0.25881904510252074sin16°=0.27563735581699916sin17°=0.2923717047227367sin18°=0.3090169943749474sin19°=0.3255681544571567sin20°=0.3420201433256687sin21°=0.35836794954530027sin22°=0.374606593415912sin23°=0.3907311284892737sin24°=0.40673664307580015sin25°=0.42261826174069944sin26°=0.4383711467890774sin27°=0.45399049973954675sin28°=0.4694715627858908sin29°=0.48480962024633706sin30°=0.5000000000000000sin31°=0.5150380749100542sin32°=0.5299192642332049sin33°=0.544639035015027sin34°=0.5591929034707468sin35°=0.573576436351046sin36°=0.5877852522924731sin37°=0.6018150231520483sin38°=0.6156614753256583sin39°=0.6293203910498375sin40°=0.6427876096865392sin41°=0.6560590289905073sin42°=0.6691306063588582sin43°=0.6819983600624985sin44°=0.6946583704589972sin45°=0.7071067811865475sin46°=0.7193398003386511sin47°=0.7313537016191705sin48°=0.7431448254773941sin49°=0.7547095802227719sin50°=0.766044443118978sin51°=0.7771459614569708sin52°=0.7880107536067219sin53°=0.7986355100472928sin54°=0.8090169943749474sin55°=0.8191520442889918sin56°=0.8290375725550417sin57°=0.8386705679454239sin58°=0.848048096156426sin59°=0.8571673007021122sin60°=0.8660254037844386sin61°=0.8746197071393957sin62°=0.8829475928589269sin63°=0.8910065241883678sin64°=0.898794046299167sin65°=0.9063077870366499sin66°=0.9135454576426009sin67°=0.9205048534524404sin68°=0.9271838545667873sin69°=0.9335804264972017sin70°=0.9396926207859083sin71°=0.9455185755993167sin72°=0.9510565162951535sin73°=0.9563047559630354sin74°=0.9612616959383189sin75°=0.9659258262890683sin76°=0.9702957262759965sin77°=0.9743700647852352sin78°=0.9781476007338057sin79°=0.981627183447664sin80°=0.984807753012208sin81°=0.9876883405951378sin82°=0.9902680687415704sin83°=0.992546151641322sin84°=0.9945218953682733sin85°=0.9961946980917455sin86°=0.9975640502598242sin87°=0.9986295347545738sin88°=0.9993908270190958sin89°=0.9998476951563913①列表(小力选取了10对数值);x……y……②建立平面直角坐标系(两坐标轴可视数值需要分别选取不同长度做为单位长度);③描点.在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点;④连线.根据描出的点,画出该函数的图象;(3)结合函数的图象,写出该函数的一条性质:.27.已知:抛物线3bx x y 21++=与x 轴分别交于点A (-3,0),B (m ,0).将y 1向右平移4个单位得到y 2.(1)求b 的值;(2)求抛物线y 2的表达式;(3)抛物线y 2与y 轴交于点D ,与x 轴交于点E 、F (点E 在点F 的左侧),记抛物线在D 、F 之间的部分为图象G (包含D 、F 两点),若直线1-+=k kx y 与图象G 有一个公共点,请结合函数图象,求直线1-+=k kx y 与抛物线y 2的对称轴交点的纵坐标t 的值或取值范围.28.如图1,点O 在线段AB 上,AO=2,OB=1,OC 为射线,且∠BOC=60°,动点P 以每秒2个单位长度的速度从点O 出发,沿射线OC 做匀速运动,设运动时间为t 秒.(1)当t=21秒时,则OP=,S △ABP =;(2)当△ABP 是直角三角形时,求t 的值;(3)如图2,当AP=AB 时,过点A 作AQ ∥BP ,并使得∠QOP=∠B ,求证:AQ·BP=3.为了证明AQ·BP=3,小华同学尝试过O 点作OE ∥AP 交BP 于点E.试利用小华同学给我们的启发补全图形并证明AQ·BP=3.28题图128题备用图28题图229.如图,在平面直角坐标系中,抛物线)0(32≠-+=a bx ax y 与x 轴交于点A (2-,0)、B (4,0)两点,与y 轴交于点C .(1)求抛物线的表达式;(2)点P 从A 点出发,在线段AB 上以每秒3个单位长度的速度向B 点运动,同时点Q 从B 点出发,在线段BC 上以每秒1个单位长度向C 点运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ 存在时,求运动多少秒使△PBQ 的面积最大,最大面积是多少?(3)当△PBQ 的面积最大时,在BC 下方的抛物线上存在点K ,使2:5S PBQ CBK =△△:S ,求K 点坐标.2015—2016学年度第一学期期末初三质量检测数学试卷答案及评分标准一、选择题(每小题有且只有一个选项是正确的,请把正确的选项前的序号填在相应的表格内.本题共有10个小题,每小题3分,共30分)二、填空题(本题共6个小题,每小题3分,共18分)11.2±.12.1,2.13.33.14.a>0,c=2,答案不唯一.15.3.16.黄金分割,解直角三角形(答案不唯一),测角仪、皮尺(答案不唯一).三、解答题(本题共72分,第17—25题,每小题5分,第26题8分,第27题6分,第28题6分,第29题7分)17.解:原式=11113422-+-⨯……………………………………………………4分=2………………………………………………………………………5分18.解:()()311)3(2+-+--x x x x =222613x x x --++……………………………………………………2分=26x 4x -+.…………………………………………………………………3分∵0362=--x x ,∴263x x -=,∴原式=3+4=7.…………………………………………………………………5分19.解:∵∠C=∠E ,∠ADC=∠BDE ,△ADC ∽△BDE ,…………………………………………………2分∴BDAD DE DC =,又∵AD :DE=3:5,AE=8,∴AD=3,DE=5,……………………………………………………………………3分∵BD=4,………………………………………………………………………………4分题号12345678910答案CABCCDCBDD∴435DC =,∴DC=415.………………………………………………………………………………5分20.解:(1)∵据题意,点B 的坐标为(2m ,-m )且在一次函数y 1=﹣x +2的图象上,代入得-m=-2m+2.∴m=2.………………………………………………………1分∴B 点坐标为(4,-2)…………………………………………2分把B (4,﹣2)代入y 2=xk得k =4×(﹣2)=﹣8,∴反比例函数表达式为y 2=﹣x8;……………………………………………………3分(2)当x <4,y 2的取值范围为y 2>0或y 2<﹣2.………………………………5分21.解:在△ABC 中,∠A=30°,∠C=105°∴∠B=45°,……………………………………………………1分过C 作CD ⊥AB 于D ,∴∠ADC=∠BDC=90°,∵∠B=45°,∴∠BCD=∠B=45°,∴CD=BD ,……………………………………………………2分∵∠A=30°,AC=23,∴CD=3,……………………………………………………3分∴BD=CD=3,由勾股定理得:AD=22CD AC -=3,……………………………………………………4分∴AB=AD+BD=3+3.……………………………………………………5分22.解:连接OC ,…………………………1分∵AB 是⊙O 的直径,弦CD ⊥AB ,∴CE =DE =CD =4cm ,…………………………2分∵∠A =22.5°,∴∠COE =45°,…………………………3分∴△COE 为等腰直角三角形,…………………………4分∴OC =2CE =42cm ,…………………………5分23.解:过点B 作CD BE ⊥,垂足为E (如图),………………………………1分在Rt △DEB 中,∠DEB= 90,22AC BE ==(米),BEDE tan32= ………………………………2分13.640.6222BEtan32DE =⨯≈=∴ (米)………………………………3分5.1==AB EC ………………………………4分15.115.1413.641.5ED CE CD ≈=+=+=∴(米)………………………5分答:旗杆CD 的高度为15.1米.24.解:(1)证明:连接OD ,………………………1分∵PD 切⊙O 于点D ,………………………2分∴OD ⊥PD ,∵BE ⊥PC ,∴OD ∥BE ,∴∠ADO=∠E ,∵OA=OD ,∴∠OAD=∠ADO ,∴∠OAD=∠E ,∴AB=BE ;………………………3分(2)解:有(1)知,OD ∥BE ,∴∠POD=∠B ,………………………4分∴cos ∠POD=cosB=,在Rt △POD 中,cos ∠POD=53=OP OD ,∵OD=OA ,PO=PA+OA=2+OA ,∴53=+OA 2OA ,∴OA=3,∴⊙O 半径为3.………………………5分25.解:(1)∵AB=xm ,则BC=(28﹣x )m ,∴x (28﹣x )=192,解得:x 1=12,x 2=16,答:x 的值为12m 或16m ;………………………2分(2)由题意可得出:⎩⎨⎧≥≥15x -286x ,…………………3分解得:13x 6≤≤.又S=x (28﹣x )=﹣x 2+28x=﹣(x ﹣14)2+196,∴当x≤14时,S 随x 的增大而增大.∴x=13时,S 取到最大值为:S=﹣(13﹣14)2+196=195.………………………5分答:x 为13m 时,花园面积S 最大,最大面积为195m 2.26.(1)锐角的角度;正弦值;大于0°且小于90°;……………………………………3分(2)(3)答案不唯一.……………………………………8分27.解:(1)把A (-3,0)代入3bx x y 21++=∴b=4……………………………………2分∴y 1的表达式为:34x x y 21++=(2)将y 1变形得:y 1=(x+2)2-1据题意y 2=(x+2-4)2-1=(x-2)2-1∴抛物线y 2的表达式为342+-=x x y …………………………………4分(3)34x x y 22+-=的对称轴x=2∴顶点(2,-1)∵直线1-+=k kx y 过定点(-1,-1)当直线1-+=k kx y 与图像G 有一个公共点时1-=t ……………………………………4分当直线过F (3,0)时,直线4341-=x y 把x=2代入4341-=x y ∴41-=y 当直线过D (0,3)时,直线34+=x y 把x=2代入34+=x y ∴11=y 即11=t ∴结合图象可知1-=t 或1141≤<-t .……………………………………6分28.解:(1)1,433;……………………………………2分(2)①∵∠A<∠BOC=60°,∴∠A 不可能是直角.②当∠ABP=90°时,∵∠BOC=60°,∴∠OPB=30°.∴OP=2OB ,即2t=2.∴t=1.……………………………………3分③当∠APB=90°,如图,过点P 作PD ⊥AB 于点D ,则OP=2t ,OD=t ,PD=3t ,AD=2t +,DB=1t -.∵∠APD+∠BPD=90°,∠B+∠BPD=90°,∴∠APD=∠B.∴△APD ∽△PBD.∴BD PD PD AD =,即3t 1t 3t=-,即24t t 20+-=,解得12133133t ,t 88-+--== (舍去).……………………………………4分(3)补全图形,如图∵AP=AB ,∴∠APB=∠B.∵OE ∥AP ∴∠OEB=∠APB=∠B.∵AQ ∥BP ,∴∠QAB+∠B=180°.又∵∠3+∠OEB=180°,∴∠3=∠QAB.又∵∠AOC=∠2+∠B=∠1+∠QOP ,∵∠B=∠QOP ,∴∠1=∠2.∴△QAO∽△OEP.∴EPAO EO AQ =,即AQ·EP=EO·AO.∵OE ∥AP ,∴△OBE ∽△ABP.∴31BA BO BP BE AP OE ===.∴OE=31AP=1,BP=23EP.∴AQ·BP=AQ·23EP=23AO·OE=23×2×1=3.……………………………………6分29.解:(1)将A (-2,0),B (4,0)两点坐标分别代入y=ax 2+bx-3(a≠0),即⎩⎨⎧=-+=--034b 16a 032b 4a ,…………………………1分解得:⎪⎪⎩⎪⎪⎨⎧-==43b 83a∴抛物线的表达式为:3x 43x 83y 2--=………………………………2分(2)设运动时间为t 秒,由题意可知:2t 0<<……………………………………3分过点Q 作QD ⊥AB,垂直为D ,易证△OCB ∽△DQB,∴BQBC DQ OC =……………………………………4分 OC=3,OB=4,BC=5,AP=3t,PB=6-3t,BQ=t ,t5DQ 3=∴t 53DQ =∴∴t 533t)(621DQ PB 21S ΔPBQ ⋅-=⋅=t 59t 1092+-= 对称轴1)(2t 10959=-⨯-=∴当运动1秒时,△PBQ 面积最大,10959109S ΔPBQ =+-=,最大为109.(3)如图,设K(m,3m 43m 832--)连接CK 、BK ,作KL ∥y 轴交BC 与L ,由(2)知:109S ΔPBQ =,2:5S :S PBQ ΔCBK = ∴49S ΔCBK =设直线BC 的表达式为y=kx+n3)C(0,B(4,0),- ⎩⎨⎧-==+∴3n 0n 4k ,解得:∴直线BC 的表达式为y=43x-3∴3)m 43L(m,-2m 83m 23KL -= ΔKLBΔKLC ΔCBK S S S +=∴m)(4)m 83m 23(21m )m 83m 23(2122-⋅-⋅+⋅-⋅=)m 83m 23(4212-⋅⋅=即:49)m 83m 232(2=-解得:31或m m ==∴K 坐标为(1,827-)或(3,815-)……………………………………7分⎪⎩⎪⎨⎧-==3n 43k。
一模数学试题和答案怀柔

怀柔区2015—2016学年初三数学模拟练习(一)数学试卷考生须知1.本试卷共8页,共三道大题,29道小题,满分120分。
考试时间120分钟。
2.在试卷和答题卡上准确填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,将本试卷、答题卡和草稿纸一并交回。
一.选择题(共有10个小题,每小题3分,共30分)下面各题均有四个选项,其中只有一个..是符合题意的.1.截止到目前,参加北京市普通小客车摇号的申请人数已经超过2500000人,将2500000用科学记数法表示为×10 5 B.×106 C.×10 7 实数a,b在数轴上的位置如图所示,下列结论中正确的是A.a>b B.|a|>|b|C.-a<b D.a+b<03. 如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向红色区域的概率是A.23B.12C.13D.164.下列图形中,既是轴对称图形又是中心对称图形的是A.B.C.D.5.北京市去年5月份第一周连续七天的最高气温分别为27,25,24,27,24,28,24(单2题图3题图位:℃). 这组数据的众数和中位数分别是()A.24℃,25℃B.24℃,26℃C.24℃,27℃D.28℃,25℃6.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数为A.50° B. 40°C.30°D.20°7.如图,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为()A.(3,2)B.(3,1)C.(2,2)D.(-2,2)8.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数是()A.30°B.45°C.60°D.75°9.如图,在△ABC中,AB=4,C作CG ⊥AD于F,交AB于G,连接EF,则线段EF的长为()A.21B.1C.27D. 710.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.当甲、乙两车相距50千米时,时间t的值最多有A.1个B.2个C.3个D.4个二、填空题(本题共6个小题,每小题3分,共18分)11.若分式1x-3有意义,则x的取值范围是.12.分解因式:2a3-18a=_________.6题图7题图FGAB C8题图9题图10题图如图,将锐角三角形纸片ABC(BC >AC)经过两次折叠, 得到边AB ,BC ,CA 上的点D,E,F .使得四边形 DECF 恰好为菱形. 如图,(1)AC 边向BC 边折叠,使AC 边落在BC 边上,得到 折痕交AB 于D ;(2)C 点向AB 边折叠,使C 点与D 点重合,得到折痕 交BC 边于E ,交AC 边于F . C BA13.已知⊙O 是半径为2的圆形纸板,现要在其内部设计一个内接正三角形图案,则内接正三角形的边长为 .14.已知关于x 的方程x 2-2x+m=0有两个不相等的实数根,写出一个满足条件的实数m 值:m=______.15.李白(701年-762年),伟大的浪漫主义诗人,被后人誉为“”.李白的一生和酒有不解之缘,写下了如《将进酒》这样的千古绝句.古代民间流传着这样一道算题:李白街上走,提壶去打酒; 遇店加一倍,见花喝一斗; 三遇店和花,喝光壶中酒; 试问酒壶中,原有多少酒?意思是:李白在街上走,提着酒壶边喝边打酒,每次遇到酒店将壶中酒加一倍,每次看见花店就喝去一斗(斗是古代容量单位,1斗=10升),这样遇到酒店、看见花店各三次.把酒喝完.问壶中原来有酒多少?设壶中原来有酒x 斗,可列方程为 . 16.在数学课上,老师提出如下问题:小明的折叠方法如下:老师说:“小明的作法正确.”请回答:小明这样折叠的依据是_________________________.三、解答题(本题共72分,第17—26题,每小题5分,第27题7分,第28题7分,第29题8分)17.计算:12)21()5-π(45sin 210-++--.FEDCBAEDCBA18.已知063a a 2=++,求代数式1)-1)(a (a 3)a(2a +-+的值.19.解不等式组⎪⎩⎪⎨⎧+<-≤-.41x 3x 3,3x 2)2(x 并写出它的所有非负整数解......20、如图,在Rt △ABC 中,∠C=90°,AB 边的垂直平分线DE 交BC 于点E ,垂足为D.求证:∠CAB=∠AED.21.国家实施高效节能电器的财政补贴政策,某款空调在政策实施后,每购买一台,客户可获得500元财政补贴.某校用6万元购买此款空调,补贴后可购买的台数是补贴前的倍,则该款空调补贴前的售价为每台多少元?20题图A B C EFDHD FECBOA22. 如图,在△ABC 中,D 为AB 边上一点,F 为AC 的中点,过点C 作CE 2xmy =b kx y +=⊥∆图,在⊙O 中,AB 为直径,OC AB ⊥,弦CF 与OB 交于点E ,过点F ,A 分别作⊙O 的切线交于点H ,且HF 与AB 的延长线交于点D . (1)求证:DF=DE; (2)若tan ∠OCE =12,⊙O 的半径为4,求A H 的长.25. 阅读下列材料:1985年,中国银行珠海分行发行了中国第一张信用卡.从此,信用卡开始逐步占领国人的消费,“信用消费”时代开启.信用卡业务是典型的“规模经济”,只有具备一定卡量规模,才能通过拉动用卡消费达到提升收入的目的.2013年、2014年从各家银行发布的信用卡年报来看,中国信用卡发卡量在稳步增长中,各家银行信用卡中心对信用业务越来越看重. 截至2013年末,全国信用卡累计发卡亿张,较2012年末增长%.截至2014年末,全国信用卡累计发卡亿张.全国人均持有信用卡张,较上年末增长%.北京、上海信用卡人均拥有量仍远高于全国平均水平,分别达到张和张.2013、2014年各大银行信用卡累计发卡量如图:根据中国人民银行的数据显示,截至2015年四季度末,全国信用卡累计发卡亿张,较上一年末大幅上升.有“宇宙第一行”之称的工商银行,信用卡累计发卡量比2014年末增长了%,在各大银行中遥遥领先.建设银行信用卡累计发卡量8074万张,中国银行累计发卡量为万张,招商银行信用卡发卡量6917万张,民生银行信用卡累计发卡量万张.根据以上材料回答下列问题:(1)2015年工商银行信用卡累计发卡量为万张(保留一位小数);(2)选择统计表或.统计图,将2013~2015年工商银行、建设银行和民生银行的信用卡累计发卡量表示出来.26.阅读下列材料:布鞋在我国有3000多年的历史.据考证,最早的手工布鞋是在山西出土的西周武士跪像所穿的布鞋.2008年6月14日,“千层底手工布鞋制作技艺”被文化部列入《国家级非物质文化遗产名录》,从而将这项古老的手工技艺保护起来.一句歌唱到“最爱穿的鞋是妈妈纳的千层底,站得稳走得正踏踏实实闯天下”,唱出了祖辈对儿时生活的美好回忆.为了提高工作效率,智慧勤劳的先辈们发明了鞋样,就是用纸或纸板按尺寸和形状做成鞋面、鞋帮、鞋底的模型.例如:按照图1的鞋样就可做出图2模样的鞋子.根据以上材料完成下列问题:(1)如图3、4、5是一组布鞋图片,6、7、8是一组鞋样的图片,请你在答题纸上将布鞋和对应的鞋样用线段连接起来;(2)图10是图9所示童鞋的鞋样.看到这个鞋样,明明认为鞋样丢了一部分,芳芳认为鞋样没有丢.请你判断明明和芳芳谁说的对,并用所学的数学知识说明理由.26题图3 26题图4 26题图526题图226题图6 26题图7 26题图826题图1DHD27.在平面直角坐标系中,二次函数y=x 2+mx+2m-7的图象经过点(1,0).(1)求抛物线的表达式;(2)把-4<x<1时的函数图象记为H ,求此时函数y 的取值范围;(3)在(2)的条件下,将图象H 在x 轴下方的部分沿x 轴 翻折,图象H 的其余部分保持不变,得到一个新图象M .若直线y=x+b 与图象M 有三个公共点,求b 的取值范围.28. 在正方形ABCD 中,点H 在对角线BD 上(与点B 、D 不重合),连接AH ,将HA 绕点H 顺时针旋转 90º与边CD (或CD 延长线)交于点P ,作HQ ⊥BD 交射线DC 于点Q. (1)如图1:①依题意补全图1;②判断DP 与CQ 的数量关系并加以证明;(2)若正方形ABCD 的边长为3,当 DP=1时,试求∠PHQ 的度数.xyO–5–4–3–2–112345–7–6–5–4–3–2–1123456729.给出如下规定:两个图形G 1和G 2,点P 为G 1上任一点,点Q 为G 2上任一点,如果线段PQ 的长度存在最小值时,就称该最小值为两个图形G 1和G 2之间的“近距离”;如果线段PQ 的长度存在最大值时,就称该最大值为两个图形G 1和G 2之间的“远距离” . 请你在学习,理解上述定义的基础上,解决下面问题: 在平面直角坐标系xOy 中,点A (-4, 3),B (-4,-3),C (4,-3),D (4, 3). (1)请在平面直角坐标系中画出四边形ABCD ,直接写出线段AB 和线段CD 的“近距离”和“远距离”. (2)设直线b x y +=34(b>0)与x 轴,y 轴分别交于点E ,F ,若线段EF 与四边形ABCD 的“近距离”是1,求它们的“远距离” ;(3)在平面直角坐标系xOy 中,有一个矩形GHMN ,若此矩形至少有一个顶点在以O 为圆心,2为半径的圆上,其余各点可能在圆上或圆内.将四边形ABCD 绕着点O 旋转一周,在旋转的过程中,它与矩形GHMN 的“远距离”的最大值是 ;“近距离”的最小值是 .xy–1–2–3–4–5–6–7–812345678–1–2–3–4–5–6–712345678910O怀柔区2016年高级中等学校招生模拟考试(一)数学评分标准一、选择题(每小题有且只有一个选项是正确的,请把正确的选项前的序号填在相应的表格内. 本题共有10个小题,每小题3分,共30分) 11. x≠3. 12. 2a(a-3)(a+3). 13. 32.14.答案不唯一,符合m<1即可. 15. [(2x-1)×2-1] ×2-1=0或8x-7=0.. 16. CD 和EF 是四边形DECF 对角线,而CD 和EF 互相垂直且平分(答案不唯一).三、解答题(本题共72分,第17—26题,每小题5分,第27题7分,第28题7分,第29题8分) 17. 解: 原式=1221222-++-⨯………………………………………………4分= 22.………………………………………………5分 18.解:1)-1)(a (a 3)a(2a +-+=1)(a 3a 2a 22--+ =1a 3a 2a 22+-+=13a a 2++.……………………………………………………3分 ∵063a a 2=++, ∴-63a a 2=+. 题号 1 2 3 4 5 6 7 8 9 10 答案BCBBADACADE DCBAH A BCEFD∴原式=-6+1=-5. ……………………………………………………5分19.解:2(x-2)3x-3, x x+1<34⎧⎪⎨⎪⎩≤① . ②解不等式①得:x≥-1. ……………………………………………………2分解不等式②得:x<3. ……………………………………………………4分 所以不等式组的解集为-1≤x<3.所以不等式组的非负整数解为0,1,2. .………………………………………5分20.证明:∵DE 是AB 边的垂直平分线, ∴AE=BE , ∠ADE=90°.∴∠EAB=∠B. ……………………………………………………3分 在Rt △ABC 中,∠C=90°,∴∠CAB+∠B=90°.在Rt △A DE 中,∠ADE=90°,∴∠AED+∠EAB=90°. ……………………………………………………4分∴∠CAB=∠AED. ……………………………………………………5分21. 解:设该款空调补贴前的售价为每台x 元, ……………………………………………1分 由题意,得:,500x 600001.2x 60000-=⨯………………………………………………2分 解得:x=3000. ……………………………………………………3分经检验,x=3000是原方程的解,且符合题意.………………………………………………4分 答:该款空调补贴前的售价为每台3000元.…………………………………………5分 22. (1)证明:∵CE ……………………………1分 ∵F 为AC 的中点, ∴AF=CF. 在△DAF 和△ECF 中,DAF=ECF AF=CFAFD=CFE ∠∠⎧⎪⎨⎪∠∠⎩∴ △DAF ≌△ECF .∴ AD=CE . ………………………………2分 ∵CE 22FH 2=DF 2HF =1HD 3232:(1)把A (5,1)代入xmy =中, ∴m=5.321D FEC B OA∴反比例函数表达式x5y =.………………………………1分 ∵OC=5BC,设B(x,5x) , (x<0) 把B(x,5x)代入x5y =中, ∴5x 2=5. x 1=1(舍),x 2=-1.∴B(-1,-5) . ……………………………2分 把A (5,1),B(-1,-5) 代入b kx y +=中, 得⎩⎨⎧-=+-=+5.b k 1,b 5k解得⎩⎨⎧-==4.b 1,k∴一次函数表达式为4x y -=.……………………………3分(2)P (6,0)或P (-6,0) . ……………………………5分24. (1)证明:连结OF ,如图.∵DH 为⊙O 的切线,OF 为半径,∴OF ⊥DH. ∴∠OFD=90°。
北京各区2015初中数学一模27题汇编及答案

北京各区2015初中数学一模27题汇编及答案27.如图,将抛物线M 1: x ax y 42+=向右平移3个单位,再向上平移3个单位,得到抛物线M 2,直线x y =与M 1 的一个交点记为A ,与M 2的一个交点记为B ,点A 的 横坐标是-3. (1)求a 的值及M 2的表达式;(2)点C 是线段AB 上的一个动点,过点C 作x 轴的垂线,垂足为D ,在CD 的右侧作正方形CDEF . ①当点C 的横坐标为2时,直线n x y +=恰好经过 正方形CDEF 的顶点F ,求此时n 的值;②在点C 的运动过程中,若直线n x y +=与正方形CDEF 始终没有公共点,求n 的 取值范围(直接写出结果).27.在平面直角坐标系xOy 中,抛物线()210y ax bx a =++≠过点()1,0A -,()1,1B ,与y轴交于点C .(1)求抛物线()210y ax bx a =++≠的函数表达式;(2)若点D 在抛物线()210y ax bx a =++≠的对称轴上,当ACD △的周长最小时,求点D 的坐标;(3)在抛物线()210y ax bx a =++≠的对称轴上是否存在点P ,使ACP △成为以AC为直角边的直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.27. 在平面直角坐标系中,抛物线32++=bx ax y 与x 轴的两个交点分别为A (-3,0), B (1,0),顶点为C .(1) 求抛物线的表达式和顶点坐标;(2) 过点C 作CH ⊥x 轴于点H ,若点P 为x 轴上方的抛物线上一动点(点P 与顶点C 不重合),PQ ⊥AC 于点Q ,当△PCQ 与△ACH 相似时,求点P 的坐标.27.已知抛物线y =ax 2+x +c (a ≠0)经过A (1-,0),B (2,0)两点,与y 轴相交于点C ,点D 为该抛物线的顶点.(1)求该抛物线的解析式及点D 的坐标; (2)点E 是该抛物线上一动点,且位于第一象限,当点E 到直线BC时,求点E 的坐标;(3)在(2)的条件下,在x 轴上有一点P ,且∠EAO +∠EPO =∠α,当tanα=2时,求点P 的坐标.27. 二次函数2y x mx n =-++的图象经过点A (﹣1,4),B (1,0),12y x b =-+经过点B,且与二次函数2y x mx n =-++交于点D .过点D 作DC ⊥x 轴,垂足为点C . (1)求二次函数的表达式;(2)点N 是二次函数图象上一点(点N 在BD 上方),过N 作NP ⊥x 轴,垂足为点P ,交BD 于点M ,求MN 的最大值.27.抛物线c bx x y C ++=2121:与y 轴交于点C (0,3),其对称轴与x 轴交于点A (2,0). (1)求抛物线1C 的解析式;(2)将抛物线1C 适当平移,使平移后的抛物线2C 的顶点为D (0,k ).已知点B (2,2),若抛物线2C 与△OAB 的边界总有两个公共点,请结合函数图象,求k 的取值范围.27.在平面直角坐标系中,抛物线经过点(-1,a ),(3,a ),且最低点的纵坐标为-4. (1)求抛物线的表达式及a 的值;(2)设抛物线顶点C 关于y 轴的对称点为点D ,点P 是抛物线对称轴上一动点,记抛物线在点A ,B 之间的部分为图象G (包含A ,xOy 22y x mx n =++A B O yxB 两点).如果直线DP 与图象G 恰有两个公共点,结合函数图象,求点P 纵坐标t 的取值范围.27.在平面直角坐标系xOy 中,抛物线2212y x x =-+与y 轴交于点A ,顶点为点B ,点C 与点A 关于抛物线的对称轴对称. (1)求直线BC 的解析式;(2)点D 在抛物线上,且点D 的横坐标为4.将抛物线在点A ,D 之间的部分(包含点A ,D )记为图象G ,若图象G 向下平移t (0t >)个单位后与直线BC 只有一个公共点,求t 的取值范围.27.在平面直角坐标系xOy 中,二次函数y=(a-1)x 2+2x+1与x 轴有交点,a 为正整数. (1)求a 的值.(2)将二次函数y=(a-1)x 2+2x+1的图象向右平移m 个单位,向下平移m 2+1个单位,当 -2≤x ≤1时,二次函数有最小值-3,求实数m 的值.27题图Oyx27.已知:关于x 的一元二次方程-x 2+(m +1)x +(m +2)=0(m >0).(1)求证:该方程有两个不相等的实数根; (2)当抛物线y =-x 2+(m +1)x +(m +2)经过点(3,0),求该抛物线的表达式;(3)在(2)的条件下,记抛物线y =-x 2+(m +1)x +(m +2)在第一象限之间的部分为图象G ,如果直线 y =k (x +1)+4与图象G 有公共点,请结合函数的图象,求直线y =k (x +1)+4与y 轴交点的纵坐标t 的取值范围.27.在平面直角坐标系xOy 中,抛物线223(0)y mx mx m =--≠与x 轴交于(3,0)A ,B两点.(1)求抛物线的表达式及点B 的坐标;(2)当23x -<<时的函数图象记为G ,求此时函数y 的取值范围;(3)在(2)的条件下,将图象G 在x 轴上方的部分沿x 轴翻折,图象G 的其余部分保持不变,得到一个新图象M .若经过点(4,2)C 的直线(0)y kx b k =+≠与图象M 在第三象限内有两个公共点,结合图象求b 的取值范围.27.二次函数2(0)y ax bx c a =++≠的图象与一次函数k 的图象交于、两点,(1,0)C 为二次函数图象的顶点.(1)求二次函数2(0)y ax bx c a =++≠的表达式;(2)在所给的平面直角坐标系中画出二次函数2(0)y ax bx c a =++≠的图象和一次函数k 的图象;(3)把(1)中的二次函数2(0)y ax bx c a =++≠的图象平移后得到新的二次函数22(0,)y ax bx c m a m =+++≠为常数的图象,.定义新函数f :“当自变量x 任取一值时,x 对应的函数值分别为1y 或2y ,如果1y ≠2y ,函数f 的函数值等于1y 、2y 中的较小值;如果1y =2y ,函数f 的函数值等于1y (或2y ).” 当新函数f 的图象与x 轴有三个交点时,直接写出m 的取值范围.1y x b =+)10(,A B 1y x b =+答案27已知二次函数21y x bx c =++的图象1C 经过(1,0)-,(0,3)-两点.(1)求1C 对应的函数表达式;(2)将1C 先向左平移1个单位,再向上平移4个单位,得到抛物线2C ,将2C 对应的函数表达式记为22y x mx n =++,求2C 对应的函数表达式;(3)设323y x =+,在(2)的条件下,如果在2-≤x ≤a 内存在..某一个x 的值,使得2y ≤3y 成立,利用函数图象直接写出a 的取值范围.27. 解:(1)∵ 点A 在直线x y =,且点A 的横坐标是-3,∴ A (-3,-3) . ………………………………………………………………1分 把A (-3,-3)代入x ax y 42+=,解得a =1. … …………………………………………………………………2分 ∴M 1 : x x y 42+=,顶点为(-2,-4) . ∴M 2的顶点为(1,-1) .∴M2的表达式为x x y 2-2=. …………3分(2)①由题意,C (2,2),∴F (4,2) . ………………………………4分∵直线n x y +=经过点F , ∴2=4+n .解得n =-2. ………………………5分② n >3,n <-6. …………… …7分27.解:(1)∵抛物线()210y ax bx a =++≠过点()1,0A -,()1,1B ,∴10,1 1.a b a b -+=⎧⎨++=⎩∴1,21.2a b ⎧=-⎪⎪⎨⎪=⎪⎩ ∴抛物线的函数关系式为211122y x x =-++. …………2分 (2)∵122b x a =-=,()0,1C ∴抛物线211122y x x =-++的对称轴为直线12x =. 设点E 为点A 关于直线12x =的对称点,则点E 的坐标为()2,0. 连接EC 交直线12x =于点D ,此时ACD △的周长最小. 设直线EC 的函数表达式为y kx m =+,代入,E C 的坐标,则2m 0,1.k m +=⎧⎨=⎩解得1,21.k m ⎧=-⎪⎨⎪=⎩所以,直线EC 的函数表达式为112y x =-+.当12x =时,34y =. ∴ 点D 的坐标为13,24⎛⎫⎪⎝⎭. …………4分 (3)存在.①当点A 为直角顶点时,过点A 作AC 的垂线交y 轴于点M ,交对称轴于点1P .∵AO OC ⊥,1AC AP ⊥,∴90AOM CAM ∠=∠=︒. ∵()0,1C ,()1,0A -, ∴1OA OC ==. ∴45CAO ∠=︒.∴45OAM OMA ∠=∠=︒. ∴1OA OM ==.∴点M 的坐标为()0,1-.设直线AM 对应的一次函数的表达式为11y k x b =+,代入,A M 的坐标,则1110,1.k b b -+=⎧⎨=-⎩解得111,1.k b =-⎧⎨=-⎩所以,直线AM 的函数表达式为1y x =--.令12x =,则32y =-. ∴点1P 的坐标为13,22⎛⎫-⎪⎝⎭. …………5分 ②当点C 为直角顶点时,过点C 作AC 的垂线交对称轴于点2P ,交x 轴于点N . 与①同理可得Rt CON △是等腰直角三角形, ∴1OC ON ==.∴点N 的坐标为()1,0.∵2CP AC ⊥,1AP AC ⊥, ∴21CP AP ∥.∴直线2CP 的函数表达式为1y x =-+. 令12x =,则12y =. ∴点2P 的坐标为11,22⎛⎫⎪⎝⎭. …………6分 综上,在对称轴上存在点1P 13,22⎛⎫- ⎪⎝⎭,2P 11,22⎛⎫⎪⎝⎭,使ACP △成为以AC 为直角边的直角三角形.…………7分27. (1)由题意,得9-33030a b a b +=⎧⎨++=⎩解得,⎩⎨⎧-=-=21b a抛物线的解析式为y=-x 2-2x+3 ………………………2分顶点C 的坐标为(-1,4) ………………………3分 (2)①若点P 在对称轴右侧(如图①),只能是△PCQ ∽△CAH ,得∠QCP =∠CAH . 延长CP 交x 轴于M ,∴AM =CM ,∴AM 2=CM 2. 设M (m ,0),则( m +3)2=42+(m +1)2,∴m =2,即M (2,0). 设直线CM 的解析式为y=k 1x+b 1, 则⎩⎨⎧=+=+-0241111b k b k , 解之得341-=k ,381=b .∴直线CM 的解析式3834+-=x y .…………………………………4分 3238342+--=+-x x x , 解得311=x ,12-=x (舍去).9201=y .∴)92031(,P . ………………………………………………5分②若点P 在对称轴左侧(如图②),只能是△PCQ ∽△ACH ,得∠PCQ =∠ACH . 过A 作CA 的垂线交PC 于点F ,作FN ⊥x 轴于点N . 由△CFA ∽△CAH 得2==AHCHAF CA ,由△FNA ∽△AHC 得21===CA AF HC NA AH FN . ∴12==FN AN ,, 点F 坐标为(-5,1).设直线CF 的解析式为y=k 2x+b 2,则⎩⎨⎧=+-=+-1542222b k b k ,解之得419,4322==b k .∴直线CF 的解析式41943+=x y .……………………………………6分 32419432+--=+x x x , 解得471-=x ,12-=x (舍去).∴)165547(,-P . …………………………………7分 ∴满足条件的点P 坐标为)201(,或)557(,-27.解:(1)∵抛物线y=ax 2+x+c (a ≠0)经过A(﹣1,0),B (2,0)两点,∴10420a c a c -+=⎧⎨++=⎩,解得12a c =-⎧⎨=⎩.∴抛物线为y =﹣x 2+x +2①;………………………………………………………1 ∴顶点D (12,94).………………………………………………………………2 (2)如图,作EN ∥BC ,交y 轴于N ,过C 作CM ⊥EN 于M ,令x =0,得y =2, ∴OC =OB =2. ∴∠OCB =45°. ∵EN ∥BC ,∴∠CNM =∠OCB =45°. ∵CM ⊥EN 于M , ∴∠CNM =∠CMN =45°. ∴MN =CM =2.∴CN =1.∴直线NE 的解析式为:把②代入①,解得1x y =⎧⎨=⎩(图①) (图②)∴E (1,2).………………………………4 (3)过E 作EF ⊥AB 于F∴tan ∠EOF =2, 又∵tan ∠α=2, ∴∠EOF =∠α,∵∠EOF =∠EAO +∠AEO =∠α, ∠EAO +∠EPO =∠α, ∴∠EPO =∠AEO ,∵∠EAO =∠P AE ,∴△AEP ∽△AOE , (5)∴AP AEAE AO=, ∵AEAO∴AP =8,∴OP =7,∴()7,0P ,由对称性可得,()'5,0P -∴()7,0P 或()5,0-.27. 解:(1)∵二次函数2y x mx n =-++的图象经过点A (﹣1,4),B (1,0) ∴4101m nm n=--+⎧⎨=-++⎩∴m=-2,n=3∴二次函数的表达式为223y x x =--+ (2)12y x b =-+经过点B ∴12b = 画出图形()211(,),2322M m m m m m -+--+设,则N ∴21123()22MN m m m =--+--+设 ∴23522MN m m =--+∴2349()416MN m =-++ ∴MN 的最大值为491627.解:(1)∵抛物线c bx x y ++=221与y 轴交于点C (0,3),∴3=c ; ………………………1分∵抛物线c bx x y ++=221的对称轴为2=x ,-----------7分 -----------2分 -----------6分 -----------5分-----------3分 -----------4分y =2∴2212=⨯-b, 解得2-=b , ………………………2分∴抛物线1C 的解析式为32212+-=x x y . ………………………3分(2)由题意,抛物线2C 的解析式为k x y +=221. ………………………4分当抛物线经过点A (2,0)时,02212=k +⨯,解得2-=k . ………………………5分∵O (0,0),B (2,2),∴直线OB 的解析式为x y =.由⎪⎩⎪⎨⎧+==k x y x y 221,, 得0222=+-k x x ,(*)当Δ=k 214)2(2⨯⨯--=0,即21=k 时, ………………………6分 抛物线2C 与直线OB 只有一个公共点,此时方程(*)化为0122=+-x x ,解得1=x ,即公共点P 的横坐标为1,点P 在线段OB 上. ∴k 的取值范围是212<<-k . (7)27 . 解:(1)∵抛物线过点 (-1,a ),(3,a ), 22y x mx n =++A B∴抛物线的对称轴x =1..……. 1分 ∵抛物线最低点的纵坐标为-4 ,∴抛物线的顶点是(1,-4)..……. 2分 ∴抛物线的表达式是22(1)4y x =--, 即2242y x x =--..…3分把(-1,a )代入抛物线表达式,求出4a =..……. 4分(2)∵抛物线顶点(1,4)C -关于y 轴的对称点为点D ,∴(1,4)D --.求出直线CD 的表达式为4y =-. .……. 5分求出直线BD 的表达式为22y x =-,当1x =时,0y =..……. 6分 所以40t -<≤..……. 7分27. (本小题满分7分)解:(1)∵抛物线2212y x x =-+与y 轴交于点A ,∴点A 的坐标为(0,2).…………………………………………1分 ∵2211(232)212y x x x -+==+-, ∴抛物线的对称轴为直线1x =,顶点B 的坐标为(1,32).…………2分又∵点C 与点A 关于抛物线的对称轴对称,∴点C 的坐标为(2,2),且点C 在抛物线上. 设直线BC 的解析式为y kx b =+. ∵直线BC 经过点B (1,32)和点C (2,2),∴322 2.,k b k b ⎧+=⎪⎨⎪+=⎩解得121.k b ⎧=⎪⎨⎪=⎩, ∴直线BC 的解析式为112y x =+.…………………………3分(2)∵抛物线2212y x x =-+中,A当4x=时,6y=,∴点D的坐标为(4,6).………………4分∵直线112y x=+中,当0x=时,1y=,当4x=时,3y=,∴如图,点E的坐标为(0,1),点F的坐标为(4,3).设点A平移后的对应点为点'A,点D平移后的对应点为点'D.当图象G向下平移至点'A与点E重合时,点'D在直线BC上方,此时t=1;…………………………………………………………5分当图象G向下平移至点'D与点F重合时,点'A在直线BC下方,此时t=3.……………………………………………………………………………………6分结合图象可知,符合题意的t的取值范围是13t<≤.……………………7分27.解:(1)∵二次函数y=(a-1)x2+2x+1与x轴有交点,令y=0,则(a-1)x2+2x+1=0,∴=4-4(a-1)0∆≥,解得a≤2.…………………………………1分.∵a为正整数.∴a=1、2又∵y=(a-1)x2+2x+1是二次函数,∴a-1≠0,∴a≠1,∴a的值为2.………………………………………2分(2)∵a=2,∴二次函数表达式为y=x2+2x+1,将二次函数y=x2+2x+1化成顶点式y=(x+1)2二次函数图象向右平移m个单位,向下平移m2+1个单位后的表达式为y=(x+1-m)2-(m2+1).此时函数的顶点坐标为(m-1, -m2-1).…………………………………4分当m-1<-2,即m<-1时,x=-2时,二次函数有最小值-3,∴-3=(-1-m)2-(m2+1),解得32m=-且符合题目要求.………………………………5分当 -2≤m-1≤1,即-1≤m≤2,时,当x= m-1时,二次函数有最小值-m2-1=-3,解得m=.∵m=-1≤m≤2的条件,舍去.∴m=.……………………………………6分当m-1>1,即m>2时,当x=1时,二次函数有最小值-3,∴-3=(2-m)2-(m2+1),解得32m=,不符合m>2的条件舍去.综上所述,m 的值为32-……………………………………7分 27.(本小题满分7分)(1)证明:∵ △= (m +1)2-4×(-1)×(m +2)=(m +3)2. ……………………………………………………………1分∵ m >0, ∴ (m +3)2>0, 即 △>0,∴ 原方程有两个不相等的实数根. (2)分 (2)解:∵ 抛物线抛物线y =-x 2+(m +1)x +(m +2)经过点(3,0),∴ -32+3(m +1)+(m +2)=0,………………………………………………3分 ∴ m =1.∴ y =-x 2+2x +3. (4)分(3)解:∵ y =-x 2+2x +3=-(x -1)2+4,∴ 该抛物线的顶点为(1,4).∴ 当直线y =k (x +1)+4经过顶点(1,4)时, ∴ 4=k (1+1)+4, ∴ k =0, ∴ y =4.∴ 此时直线y =k (x +1)+4与y 轴交点的纵坐标为 4. ………………………5分∵ y =-x 2+2x +3, ∴ 当x =0时,y =3,∴ 该抛物线与y 轴的交点为(0,3).∴ 此时直线y =k (x +1)+4与y 轴交点的纵坐标为 3. ………………………6分∴ 3<t ≤4. …………………………………………………………………7分27.解:(1)将()3,0A 代入,得1m =.∴抛物线的表达式为223y x x =--. …1分B 点的坐标()1,0-. ………………2分(2)()222314y x x x =--=--.∵当21x -<<时,y 随x 增大而减小;当13x ≤<时,y 随x 增大而增大,∴当1x =,min 4y =-; ………………3分 当2x =-,5y =.∴y 的取值范围是45y -≤<.…………4分(3)当直线y kx b =+经过()1,0B -和点()4,2时,解析式为2255y x =+.…….…………… …5分 当直线y kx b =+经过()2,5--和点 ()4,2时,解析式为7863y x =-.………. ……………6分 结合图象可得,b 的取值范围是8235b -<<. ………….7分27. 解:(1)设抛物线解析式为,由抛物线过点,可得 ………..(2分) (2)如图:………………………………………..(5分)(3)-4<m <0 ………………………………………..(7分)27.解:(1)∵ 二次函数21y x bx c =++的图象1C 经过(1,0)-, ∴10,3.b c c -+=⎧⎨=-⎩ ………………………………1分解得2,3.b c =-⎧⎨=-⎩………………………………… 2分∴ 抛物线1C 的函数表达式为3221--=x x y . …………………………………… 3分 (2)∵ 22123=(1)4y x x x =----,∴ 抛物线1C 的顶点为(1,4)-2)1(-=x a y )10(,A 122+-=x x y1∴ 平移后抛物线2C 的顶点为(0,0),它对应的函数表达式为22y x =.… 5分 (3)a ≥1-(见图7).………………………………………………………………7分。
2015北京市12区县初三一模数学考试分类汇编-26题阅读题(含答案)

2015北京市初三一模考试分类汇编-26题(西城区)26.阅读下面的材料:小敏在数学课外小组活动中遇到这样一个问题:如果α,β都为锐角,且1tan 2α=,1tan 3β=,求αβ+的度数. 小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得ABD α∠=,CBE β∠=,且BA ,BC 在直线BD 的两侧,连接AC ,可证得△ABC 是等腰直角三角形,因此可求得αβ+=∠ABC = °.请参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tan 4α=,3tan 5β=时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=αβ-,由此可得αβ-=______°.(海淀区)26.阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD ⊥BE,CD=3,BE=5,求BC+DE的值.小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2)图1 图2 图3请回答:BC+DE的值为_______.参考小明思考问题的方法,解决问题:如图3,已知□ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.(朝阳区)26.阅读下面材料:小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求APPD的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:APPD的值为 .参考小昊思考问题的方法,解决问题:如图 3,在△ABC 中,∠ACB =90°,点D 在BC 的延长线上,AD 与AC 边上的中线BE 的延长线交于点P ,DC :BC :AC =1:2:3 .(1)求APPD的值;(2)若CD=2,则BP = .(东城区)26. 在四边形ABCD 中,对角线AC 与BD 交于点O ,E 是OC 上任意一点,AG BE ⊥于点G ,交BD 于点F .(1)如图1,若四边形ABCD 是正方形,判断AF 与BE 的数量关系;明明发现,AF 与BE 分别在AOF △和BOE △中,可以通过证明AOF △和BOE △全等,得到AF 与BE 的数量关系;请回答:AF 与BE 的数量关系是 .(2) 如图2,若四边形ABCD 是菱形, 120ABC ∠=︒,请参考明明思考问题的方法,求AFBE的值.图1 图2 (丰台区)26.阅读下面的材料勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法. 先做四个全等的直角三角形,设它们的两条直角边分别为a ,b , 斜边为c ,然后按图1的方法将它们摆成正方形. 由图1可以得到22142a b ab c +=⨯+(),整理,得22222a ab b ab c ++=+. 所以222a b c +=.图3图1图2如果把图1中的四个全等的直角三角形摆成图2所示的正方形,请 你参照上述证明勾股定理的方法,完成下面的填空:由图2可以得到 ,整理得 ,所以 .(石景山区)26.阅读下面材料:小红遇到这样一个问题:如图1,在四边形ABCD 中,︒=∠=∠90C A ,︒=∠60D ,34=AB ,3=BC ,求AD 的长.,经过推理和计算能够使问题得到解决(如图2).请回答:AD 的长为. 参考小红思考问题的方法,解决问题:如图3,在四边形ABCD中,21tan =A ,︒=∠=∠135CB , 9=AB ,3=CD ,求BC 和AD 的长.(怀柔区)26.阅读下面材料:小聪遇到这样一个有关角平分线的问题:如图1,在△ABC 中,∠A =2∠B,CD 平分∠A CB ,AD=2.2,AC=3.6求BC 的长.小聪思考:因为CD 平分∠A CB ,所以可在BC 边上取点E ,使EC=AC ,连接DE. 这样很容易得到△DEC ≌△DAC ,经过推理能使问题得到解决(如图2). 请回答:(1)△BDE 是_________三角形.(2)BC 的长为__________.E C E D C B A BC参考小聪思考问题的方法,解决问题:如图3,已知△ABC 中,AB=AC, ∠A =20°,BD 平分∠ABC,BD=2.3,BC=2.求AD 的长.(房山区)26.小明遇到这样一个问题:如图1,在锐角△A B C 中,A D 、B E 、C F 分别为△A B C 的高,求证:∠A F E =∠AC B . 小明是这样思考问题的:如图2,以B C 为直径做半⊙O ,则点F 、E 在⊙O 上, ∠BFE +∠BCE =180°,所以∠AFE =∠ACB .请回答:若∠ABC =40 ,则∠AEF 的度数是 . 参考小明思考问题的方法,解决问题:如图3,在锐角△ABC 中,AD 、BE 、CF 分别为△ABC 的高,求证:∠BDF =∠CDE .(通州区)26.(1)请你根据下面画图要求,在图①中完成画图操作并填空.如图①,△ABC 中,∠BAC =30°,∠ACB =90°,∠P AM =∠A . 操作:(1)延长BC .(2)将∠P AM 绕点A 逆时针方向旋转60°后,射线AM 交BC 的延长线于点D . (3)过点D 作DQ//AB .(4)∠P AM 旋转后,射线AP 交DQ 于点G .(5)连结BG .结论:ABAG= . (2)如图②,△ABC 中,AB =AC =1,∠BAC =36°,进行如下操作:将△ABC 绕点A 按逆时针方向旋转α度角,并使各边长变为原来的n 倍(n >1),得到△''AB C . 当点B 、C 、'B 在同一条直线上,且四边形''ABB C 为平行四边形时(如图③),求α和n 的值.(门头沟)26.阅读下面材料:小明遇到这样一个问题:如图1,在Rt △ABC 中,∠ACB =90°,∠A =60°,CD 平分∠ACB ,试判图1 图2 图3O图① 图② 图③断BC 和AC 、AD 之间的数量关系.小明发现,利用轴对称做一个变化,在BC 上截取CA′=CA ,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).A'DDCB CBAA图1 图2请回答:(1)在图2中,小明得到的全等三角形是△ ≌△ ;(2)BC 和AC 、AD 之间的数量关系是 .参考小明思考问题的方法,解决问题:如图3,在四边形ABCD 中,AC 平分∠BAD ,BC =CD =10,AC =17,AD =9. 求AB 的长.(燕山)26.阅读下面材料:小军遇到这样一个问题:如图1,△ABC 中,AB =6,AC =4,点D 为BC 的中点,求AD 的取值范围.小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD 到E ,使DE =AD ,连接BE ,构造△BED ≌△CAD ,经过推理和计算使问题得到解决.如图3,△ABC 中,E 为AB 中点,P 是CA 延长线上一点,连接PE 并延长交BC 于点D . 求证:PA •CD =PC •BD .E ABDPDCBA图1AB CABDCE 图2 图3(延庆)26. 阅读下面资料:问题情境:(1)如图1,等边△ABC,∠CAB和∠CBA的平分线交于点O,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点与点O重合,已知OA=2,则图中重叠部分△OAB的面积是.探究:(2)在(1)的条件下,将纸片绕O点旋转至如图2所示位置,纸片两边分别与AB,AC交于点E,F,求图2中重叠部分的面积.(3)如图3,若∠ABC=α(0°<α<90°),点O在∠ABC的角平分线上,且BO=2,以O为顶点的等腰三角形纸片(纸片足够大)与∠ABC的两边AB,AC分别交于点E、F,∠EOF=180°﹣α,直接写出重叠部分的面积.(用含α的式子表示)答案(西城区)26.解:45. …………………………………………………1分画图见图6. ………………………………………3分 45.………………………………………………… 5分(海淀区)26. (本小题满分5分)解:BC +DE. ……………………………………………………2分 解决问题: 连接AE ,CE ,如图.∵四边形ABCD 是平行四边形, ∴AB // DC .∵四边形ABEF 是矩形,∴AB // FE ,BF =AE . ∴DC // FE .∴四边形DCEF 是平行四边形. ………………………………………………3分 ∴ CE // DF . ∵AC =BF =DF , ∴AC =AE =CE .∴△ACE 是等边三角形. …………………………………………………………4分 ∴∠ACE =60°. ∵CE ∥DF , ∴∠AGF =∠ACE =60°. …………………………………………………………5分(朝阳区)26. 解:PDAP 的值为23. …………………………………………………………………1分解决问题:(1)过点A 作AF ∥DB ,交BE 的延长线于点F ,……………………………………2分设DC =k , ∵DC ︰BC =1︰2, ∴BC =2k .∴DB =DC +BC =3k . ∵E 是AC 中点, ∴AE =CE . ∵AF ∥DB ,654321F ED CBA∴∠F =∠1. 又∵∠2=∠3,∴△AEF ≌△CEB . ……………………………………………………………3分 ∴AF =BC =2k . ∵AF ∥DB , ∴△AFP ∽△DBP . ∴DBAFPD AP =. ∴32=PD AP . …………………………………………………………………4分(2) 6. ……………………………………………………………………………5分(东城区)26. 解:(1)AF =BE ; …………1分(2)AFBE= …………2分 理由如下:∵四边形ABCD 是菱形,120ABC ∠=︒, ∴AC BD ⊥,60ABO ∠=︒. ∴90FAO AFO ∠+∠=︒. ∵AG BE ⊥,∴90EAG BEA ∠+∠=︒. ∴AFO BEA ∠=∠.又∵90AOF BOE ∠=∠=︒,∴AOF BOE △∽△. …………3分∴AF AOBE OB= . ∵60ABO ∠=︒,AC BD ⊥,∴tan 60AOOB =︒=.∴AFBE=. …………5分(丰台区)26. 22142ab b a c ⨯+-=(),.…….3分 22222ab b ab a c +-+=,.……. 4分222a b c +=..……. 5分(石景山区)26.解:AD 的长为6. ………………………………...1分解决问题:如图,延长AB 与DC 相交于点E .∵135ABC BCD ∠=∠=︒, ∴︒=∠=∠45ECB EBC .∴CE BE =,︒=∠90E . …………………. ………………….2分 设x CE BE ==,则x BC 2=,x AE +=9,3DE x =+.在Rt △ADE 中,︒=∠90E ,∵21tan =A , ∴21=AE DE . 即2193=++x x .……………. .3分 ∴3=x .经检验3=x 是所列方程的解,且符合题意.∴23=BC ,12=AE ,6=DE . ……………. ………..4分 ∴56=AD . ……………………………………………… ...5分(怀柔区) 26.解:(1)△BDE 是等腰三角形. ………………………1分. (2)BC 的长为5.8.………………………………2分. ∵△ABC 中,AB=AC, ∠A =20°, ∴∠A BC=∠C= 80°,∵BD 平分∠B. ∴∠1=∠2= 40°,∠BDC= 60°,.在BA 边上取点E ,使BE=BC=2,连接DE ,. ………………………3分 则△DEB ≌△DBC ,∴∠BED=∠C= 80°, ∴∠4=60°,∴∠3=60°,在DA 边上取点F ,使DF=DB ,连接FE ,…………………………4分 则△BDE ≌△FDE ,∴∠5=∠1= 40°,BE=EF=2, ∵∠A =20°,∴∠6=20°,∴AF=EF=2,∵BD=DF=2.3, ∴AD = BD+BC=4.3.…………………………5分.(房山区)26. (1)40……………………1分(2)如图由题意:∵90AEB ADB ∠=∠=, ∴点A 、E 、D 、B 在以AB 为直径的半圆上∴∠BAE+∠BDE=180°………………3分又∵∠CDE+∠BDE=180°∴∠CDE=∠BAE ……………………4分 同理:点A 、F 、D 、C 在以AC 为直径的半圆上.∴∠BDF=∠BAC ∴∠BDF =∠CDE ……………………5分(通州区)26. (1)…………………………..(1分)21=AG AB ………………………………………………..(2分) (2)根据题意得,''36C AB CAB ∠=∠=︒,AB’= n AB α=∠'CAC∵四边形ABB 'C '为平行四边形,∴1''===AC AB C B ,'AC ∥'BB ,∴'''36C AB AB B ∠=∠=︒,,∵AB =AC ,∠BAC =36°,∴72ABC ACB ∠=∠=︒, ∴''72CAC B AB α=∠=∠=︒,……………………………..(3分)∵∠BAC =36°,∴'36B AC ∠=︒,∴''36B AC AB C ∠=∠=︒,∴1'==C B AC ∵B B ∠=∠,'36BAC AB B ∠=∠=︒,∴△ABC ∽△'B BA ,∴'AB BC BB AB =,∴解得251'+=BB (舍负), ……..(4分) ∵1n >,∴n ………………………………………..(5分)(门头沟)26.(本小题满分5分)解:阅读材料(1)△A D C ≌△A ′D C ; (1)分 (2)B C =A C +A D .……………………………………………………………………2分 解决问题如图,在AB 上截取AE =AD ,连接CE .∵ AC 平分∠BAD ,∴ ∠DAC =∠EAC .又 ∵AC =AC , ∴ △ADC ≌△AEC . ………………………3分∴ AE =AD =9,CE=CD =10=BC .过点C 作CF ⊥AB 于点F . ∴ EF =BF .设EF =BF =x .在Rt △CFB 中,∠CFB =90°,由勾股定理得CF 2=CB 2-BF 2=102-x 2.在Rt △CFA 中,∠CFA =90°,由勾股定理得CF 2=AC 2-AF 2=172-(9+x )2.∴ 102-x 2=172-(9+x )2,解得x =6.……………………………………………………………………………4分 ∴ AB =AE +EF +FB =9+6+6=21.∴ A B 的长为21. (5)分图②p D C F E B A-----------1分-----------2分-----------3分 -----------5-----------4分-----------5分(燕山)26.(1)1<AD <5; ………………………2分(2)证明:延长PD 至点F ,使EF =PE ,连接BF . ………………………3分∵BE =AE ,∠BEF =∠AEP ,∴△BEF ≌△AEP ,∴∠APE =∠F ,BF =PA .又∵∠BDF =∠CDP , 即PA ·CD =PC ·BD . ………………………5分(延庆)26.(1)(2) 连接AO 、BO ,如图②,由题意可得:∠EOF =∠AOB ,则∠EOA =∠FOB .在△EOA 和△FOB 中,EAO FBOOA OB EOA FOB∠=∠⎧⎪=⎨⎪∠=∠⎩∴△EOA ≌△FOB .∴S 四边形AEOF =S △OAB . 过点O 作ON ⊥AB ,垂足为N ,如图,∵△ABC 为等边三角形,∴∠CAB =∠CBA =60°.∵∠CAB 和∠CBA 的平分线交于点O∴∠OAB =∠OBA =30°.∴OB=OA =2. ∵ON ⊥AB ,∴AN=NB ,ON =1. ∴AN = ∴AB=2AN =2.∴S △OAB =AB•ON =. S 四边形AEOF = (3) S 面积=4sin cos .。
北京怀柔区中考一模数学试题及答案

北京市怀柔区2015年高级中等学校招生模拟考试(一)数学试卷 2015.5考生须知1.本试卷共6页,共五道大题,29道小题,满分120分.考试时间120分钟。
2.在试卷和答题卡上准确填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4. 在答题卡上,选择题用2B铅笔作答,其他试题用黑色字迹签字笔作答。
5. 考试结束,请将本试卷、答题卡一并交回。
一、选择题(本题共30分,每小题3分)下列各题均有四个选项,其中只有一个..是符合题意的.1.把8000用科学计数法表示是A.28010⨯ B.3810⨯ C.40.810⨯D.4810⨯2.数轴上有A,B,C,D四个点,其中绝对值相等的点是A.点A与点DB. 点A与点CC. 点B与点CD. 点B与点D3.下列手机软件图标中,既是轴对称图形又是中心对称图形的是A B C D4. 小华的老师让他在无法看到袋子里小球的情形下,从袋子里模出一个小球. 袋子里各种颜色小球的数量统计如表所示.小华模到褐色小球的概率为A.101B.51C.41D.215. 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为A.30° B.60° C.80° D.120°6.如图,已知⊙O的半径为10,弦AB长为16,则点O到AB的距离是A. 3B. 4C. 5D. 67.某校在“中国梦.我的梦”演讲比赛中,有11名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前6名,不仅要了解自己的成绩,还要了解这11名学生成绩的颜色红色橙色黄色绿色蓝色紫色褐色数量 6 4 3 3 2 2 5xDCBA123–1–2–3A.平均数B.众数C.中位数D.方差8.如图,已知正方形ABCD中,G、P分别是DC、BC上的点,E、F分别是AP、GP的中点,当P在BC上从B向C移动而G不动时,下列结论成立的是A.线段EF的长逐渐增大 B.线段EF的长逐渐减小C.线段EF的长不改变 D.线段EF的长不能确定9.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为A .x≥ B. x≤3C. x ≤D.x≥310.如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的A.线段PD B.线段PC C.线段PE D.线段DE二、填空题(本题共18分,每小题3分)11.函数y=1x-3中自变量x的取值范围是_________________.12.请写出一个过一、三象限的反比例函数的表达式_________________.13.下面有五个图形,与其它图形众不同的是第个.14.如图,在矩形ABCD中,=,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE•ED=16,则矩形ABCD 的面积为.GFEPDCBA①②③④⑤xy图2OPED CBA图115.当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”. 如果一个“半角三角形”的“半角”为20°,那么这个 “半角三角形”的最大内角的度数为__________.16.2014年5月1日开始,北京市开始实施居民用水阶梯水价.具体方案如下:户年用水量180立方米(含)内,每立方米5元;181立方米至260立方米(含)内,每立方米7元;260立方米以上,每立方米9元.阶梯水价以日历年(每年1月1日到12月31日)为周期计算.小王家2014年4月30日抄表示数550立方米,5月1日起实施阶梯水价,6月抄表时因用户家中无人未见表,8月12日抄表示数706立方米,那么小王家本期用水量为 立方米,本期用水天数104天,日均用水量为 立方米. 如果按这样每日用水量计算,小李家今后每年的水费将达到 元(一年按365天计算).三、解答题(本题共30分,每小题5分)17.如图,点C ,D 在线段BF 上,AB DE ∥,AB DF =,A F ∠=∠.求证:BC DE =.18. 计算:011(20152014)82cos 45()2--+-︒+ 19.解不等式组:240,3(1) 2.x x x -<⎧⎨+≥+⎩20.已知32a b =,求代数式2243(3)9a b a b a b ++-的值.21.列方程或方程组解应用题:为了培育和践行社会主义核心价值观,引导学生广泛阅读古今文学名著,传承优秀传统文化,我区某校决定为初三学生购进相同数量的名著《三国演义》和《红岩》.其中《三国演义》的单价比《红岩》的单价多28元.若学校购买《三国演义》用了1200元,购买《红岩》用了400元,求《三国演义》和《红岩》的单价各多少元.22.已知:关于x 的一元二次方程2(41)330kx k x k -+++=(k 是整数). (1)求证:方程有两个不相等的实数根; (2)若方程的两个实数根都是整数,求k 的值. 四、解答题(本题共20分,每小题5分)23. 如图,BD 是△ABC 的角平分线,点E ,F 分别在BC ,AB 上,且DE ∥AB ,BE =AF .(1)求证:四边形ADEF 是平行四边形;FEDCB A(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.24.某公司有5个股东,每个股东的利润相同,有100名工人,每名工人的工资相同.2015年第一个季度工人的工资总额与公司的股东总利润情况见右表:该公司老板根据表中数据,作出了图1,并声称股东利润和工人工资同步增长,公司和工人做到了“有福同享”.(1)这三个月工人个人的月收入分别是万元;(2)在图2人月收入的统计图;(3)通过完成第(1),(2)问和对图2句话概括)25.如图,AB是⊙O的直径,C是弧AB的中点,D是⊙O的切线CN上一点,BD交AC于点E,且BA= BD.(1)求证:∠ACD=45°;(2)若OB=2,求DC的长.26.阅读下面材料:小聪遇到这样一个有关角平分线的问题:如图1,在△ABC中,∠A=2∠B,CD平分∠A CB,AD=2.2,AC=3.6求BC的长.AD D A图1个人收入小聪思考:因为CD 平分∠A CB ,所以可在BC 边上取点E ,使EC=AC ,连接DE. 这样很容易得到△DEC ≌△DAC ,经过推理能使问题得到解决(如图2). 请回答:(1)△BDE 是_________三角形.(2)BC 的长为__________.参考小聪思考问题的方法,解决问题:如图3,已知△ABC 中,AB=AC, ∠A =20°, BD 平分∠ABC,BD=2.3,BC=2.求AD 的长. 五、解答题(本题共22分,第27题7分,第28题7分,第29题8分)27.在平面直角坐标系xOy 中,二次函数y=(a-1)x 2+2x+1与x 轴有交点,a(1)求a 的值. (2)将二次函数y=(a-1)x 2+2x+1的图象向右平移m 个单位,向下平移m2+1个单位,当 -2≤x ≤1时,二次函数有最小值-3求实数m 的值.28.在等边△ABC 外侧作直线AP ,点B 关于直线AP 的对称点为D ,连接BD,CD ,其中CD 交直线AP 于点E .(1)依题意补全图1;(2)若∠PAB=30°,求∠ACE 的度数;(3)如图2,若60°<∠PAB <120°,判断由线段AB,CE,ED 可以构成一个含有多少度角的三角形,并证明.BC ABCPABCP27题图29. 对某种几何图形给出如下定义: 符合一定条件的动点所形成的图形,叫做符合这个条件的点的轨迹.例如,平面内到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆.(1)如图1,在△ABC 中,AB=AC ,∠BAC=90°,A(0,2),B 是x 轴上一动点,当点B 在x 轴上运动时,点C 在坐标系中运动,点C 运动形成的轨迹是直线DE ,且DE ⊥x 轴于点G. 则直线DE 的表达式是 .(2)当△ABC 是等边三角形时,在(1①当点B 运动到如图2的位置时,AC ∥x 轴,则C 点的坐标是 . ②在备用图中画出动点C 形成直线的示意图,并求出这条直线的表达式.③设②中这条直线分别与x,y 轴交于E,F 两点,当点C 在线段EF 上运动时,点H 在线段OF 上运动,(不与O 、F 重合),且CH=CE,则CE 的取值范围是 .怀柔区2014—2015学年度中考模拟练习(一)数学试卷答案及评分参考二、填空题(本题共18分,每小题3分)三、解答题(本题共30分,每小题5分) 17.(本小题满分5分) 证明:∵ AB ∥DE∴ ∠B = ∠EDF ;在△ABC 和△F DE 中A F AB DFB EDF ∠=∠⎧⎪=⎨⎪∠=∠⎩…………………………3分 ∴△ABC ≌△FDE (ASA),…………………4分 ∴BC=DE. …………………………………5分 18.解:原式=1+-222+……………………………………4分 =1+5分 19. 解①得:x<2,…………………………………………………………2分解②得:x ≥1-2,……………………………………………………4分 所以不等式组的解集为:1-2≤x<2. ……………………………5分20. 解:2243(3)9a ba b a b ++-43(3)(3)(3)a b a b a b a b +=++- 433a ba b +=-……………………………………………3分∵32a b =, ∴23a b =. ………………………………………………4分∴原式=662aa a =--. ……………………………………5分21.解:设《红岩》的单价为x 元,则《三国演义》的单价为(x+28)元. ……………1分.由题意,得120040028x x=+……………………………………3分. 解得x=14. ……………………………………4分.经检验,x=14是原方程的解,且符合题意. ∴x+28=42.答:《红岩》的单价为14元,《三国演义》的单价为42元. ……………………5分.22.(1)证明:△2(41)4(33)k k k =+-+2(21)k =-·………………………………………1分.∵2(41)330kx k x k-+++=是一元二次方程,∴k ≠0, ∵k 是整数 ∴12k ≠即210k -≠. ∴△2(21)0k =->∴方程有两个不相等的实数根. ………………………………………2分(2)解方程得:2(41)(21)2k k x k+±-=……………………………………3分.∴3x =或11x k=+………………………………………4分∵k 是整数,方程的根都是整数,∴k =1或-1…………………………………5分.四、解答题(本题共20分,每小题5分)23. (1)证明:∵BD 是△ABC 的角平分线, ∴∠ABD =∠DBE ,∵DE ∥AB , ∴∠ABD =∠BDE , ∴∠DBE =∠BDE ,∴BE=DE; ∵BE =AF ,∴AF=DE;∴四边形ADEF 是平行四边形. ………………………………………2分(2)解:过点D 作DG ⊥AB 于点G ,过点E 作EH ⊥BD 于点H , ∵∠ABC =60°,BD 是∠ABC 的平分线, ∴∠ABD =∠EBD =30°,∴DG =BD =×4=2,………………………………………3分 ∵BE =DE ,∴BH =DH =2,∴BE ==433,∴DE =433,………………………………………4分 ∴四边形ADEF 的面积为:DE •DG =833.………………………………………5分 24. 解:(1)0,28,0.3,0.32. ……………………………3分(2)补图如右图:………………………………4分个人收入(3)答案不唯一.…………………………………5分25. (1)证明:∵C 是弧AB 的中点,∴弧AC=弧BC,∴AC=BC.∵AB 是⊙O 的直径,∴∠ACB=90°,∴∠BAC=∠CBA=45°, 连接OC, ∵OC=OA, ∴∠AC0=45°. ∵CN 是⊙O 切线,∴∠OCD=90°,∴∠ACD=45°. ………………………………2分.(2) 解:作BH ⊥DC 于H 点,…………………………3分. ∵∠ACD=45°,∴∠DCB=135°, ∴∠BCH=45°, ∵OB=2,∴BA= BD=4,AC= BC=. ∵BC=,∴BH= CH=2, 设DC=x,在Rt △DBH 中,利用勾股定理:2222)24x ++=(,………4分. 解得:x=2-±,∴x=2-+∴DC的长为:2-+5分. 26.解:(1)△BDE 是等腰三角形. ………………………1分. (2)BC 的长为5.8.………………………………2分. ∵△ABC 中,AB=AC, ∠A =20°, ∴∠A BC=∠C= 80°,∵BD 平分∠B. ∴∠1=∠2= 40°,∠BDC= 60°,.在BA 边上取点E ,使BE=BC=2,连接DE ,. (3)则△DEB ≌△DBC ,∴∠BED=∠C= 80°, ∴∠4=60°,∴∠3=60°,在DA 边上取点F ,使DF=DB ,连接FE ,…………………………4则△BDE ≌△FDE ,∴∠5=∠1= 40°,BE=EF=2, ∵∠A =20°,∴∠6=20°,∴AF=EF=2,∵BD=DF=2.3, ∴AD = BD+BC=4.3.…………………………5分.五、解答题(本题共22分,第27题7分,第28题7分,第29题27.解:(1)∵二次函数y=(a-1)x 2+2x+1与x 轴有交点,令y=0,则(a-1)x 2+2x+1=0,∴=4-4(a-1)0∆≥,解得a ≤2. …………………………………1分. ∵a 为正整数. ∴a=1、2又∵y=(a-1)x 2+2x+1是二次函数,∴a-1≠0,∴a ≠1, ∴a 的值为2. ………………………………………2分(2)∵a=2,∴二次函数表达式为y=x 2+2x+1,将二次函数y=x 2+2x+1化成顶点式y=(x+1)2二次函数图象向右平移m 个单位,向下平移m 2+1个单位后的表达式为y=(x+1-m )2-(m 2+1).此时函数的顶点坐标为(m-1, -m 2-1). …………………………………4分 当m-1<-2,即m <-1时, x=-2时,二次函数有最小值-3, ∴-3=(-1-m )2-(m 2+1),解得32m =-且符合题目要求. ………………………………5分 当 -2≤m-1≤1,即-1≤m ≤2,时,当 x= m-1时,二次函数有最小值-m 2-1=-3,解得m =.∵m =-1≤m ≤2的条件,舍去.∴m =.……………………………………6分当m-1>1,即m >2时,当 x=1时,二次函数有最小值-3, ∴-3=(2-m )2-(m 2+1),解得32m =,不符合m >2的条件舍去. 综上所述,m 的值为32-……………………………………7分 28.解:(1)补全图形,如图1所示. …………………………… 1分(2)连接AD ,如图2.∵点D 与点B 关于直线AP 对称,∴AD=AB ,∠DAP = ∠BAP =30°.∵AB=AC, ∠BAC =60°. ∴AD=AC, ∠DAC =120°.∴2∠ACE+60°+60°=180°∴∠ACE =30°…………………………… 3分(3)线段AB,CE,ED 可以构成一个含有60°角的三角形. …………………………… 4分 证明:连接AD ,EB ,如图3.∵点D 与点B 关于直线AP 对称, ∴AD=AB ,DE=BE , 可证得∠EDA = ∠E BA .∵AB=AC,AB=AD.∴AD=AC, ∴∠ADE = ∠ACE.∴∠ABE = ∠ACE.设AC ,BE 交于点F,又∵∠AFB = ∠CFE.∴∠B AC = ∠BEC=60°.∴线段AB,CE,ED 可以构成一个含有60°角的三角形.………7分29. 解:(1)x=2. …………………………1分.(2)①C 点坐标为:2)…………………………3分. ②由①C 点坐标为: 2)再求得其它一个点C1),或(0,-2)等P E D C BAP E D C BA代入表达式y=kx+b,解得b=-2 k⎧⎪⎨=⎪⎩∴直线的表达式是2y=-.………………………5分.动点C运动形成直线如图所示.……………6分.EC≤<…………………………8分.相关信息链接:北达教育|百度百科|百度贴吧北达教育北达教育总部位于北京大学校内,分校遍及北京各城区40多所,多年来被家长认可的教育机构,法制晚报曾报道:是什么让北达教育成为京城良好口碑课外辅导品牌?为此北达教育被法制晚报评为:公众最信赖知名教育品牌!曾多次被新浪网,中国网评为课外绿色发展机构!北达教育为中央电视台推荐品牌。
北京各区2015初中数学一模27题汇编及答案

北京各区2015初中数学一模27题汇编27.如图,将抛物线M 1:x ax y 42+=向右平移3个单位,再向上平移3个单位,得到抛物线M 2,直线x y =与M 1 的一个交点记为A ,与M 2的一个交点记为B ,点A 的 横坐标是-3. (1)求a 的值及M 2的表达式;(2)点C 是线段AB 上的一个动点,过点C 作x 轴的垂线,垂足为D ,在CD 的右侧作正方形CDEF . ①当点C 的横坐标为2时,直线n x y +=恰好经过 正方形CDEF 的顶点F ,求此时n 的值;②在点C 的运动过程中,若直线n x y +=与正方形CDEF 始终没有公共点,求n 的 取值范围(直接写出结果).27.在平面直角坐标系xOy 中,抛物线()210y ax bx a =++≠过点()1,0A -,()1,1B ,与y轴交于点C .(1)求抛物线()210y ax bx a =++≠的函数表达式;(2)若点D 在抛物线()210y ax bx a =++≠的对称轴上,当ACD △的周长最小时,求点D 的坐标;(3)在抛物线()210y ax bx a =++≠的对称轴上是否存在点P ,使ACP △成为以AC为直角边的直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.27. 在平面直角坐标系中,抛物线32++=bx ax y 与x 轴的两个交点分别为A (-3,0), B (1,0),顶点为C .(1) 求抛物线的表达式和顶点坐标;(2) 过点C 作CH ⊥x 轴于点H ,若点P 为x 轴上方的抛物线上一动点(点P 与顶点C 不重合),PQ ⊥AC 于点Q ,当△PCQ 与△ACH 相似时,求点P 的坐标.27.已知抛物线y =ax 2+x +c (a ≠0)经过A (1-,0),B (2,0)两点,与y 轴相交于点C ,点D 为该抛物线的顶点.(1)求该抛物线的解析式及点D 的坐标; (2)点E 是该抛物线上一动点,且位于第一象限,当点E 到直线BC的距离为2时,求点E 的坐标;(3)在(2)的条件下,在x 轴上有一点P ,且∠EAO +∠EPO =∠α,当tanα=2时,求点P 的坐标.27.二次函数2y x mx n =-++的图象经过点A (﹣1,4),B (1,0),12y x b =-+经过点B ,且与二次函数2y x mx n =-++交于点D .过点D 作DC ⊥x 轴,垂足为点C . (1)求二次函数的表达式;(2)点N 是二次函数图象上一点(点N 在BD 上方),过N 作NP ⊥x 轴,垂足为点P ,交BD 于点M ,求MN 的最大值.27.抛物线c bx x y C ++=2121:与y 轴交于点C (0,3),其对称轴与x 轴交于点A (2,0). (1)求抛物线1C 的解析式;(2)将抛物线1C 适当平移,使平移后的抛物线2C 的顶点为D (0,k ).已知点B (2,2),若抛物线2C 与△OAB 的边界总有两个公共点,请结合函数图象,求k 的取值范围.O yx27.在平面直角坐标系中,抛物线经过点(-1,a ),(3,a ),且最低点的纵坐标为-4.(1)求抛物线的表达式及a 的值;(2)设抛物线顶点C 关于y 轴的对称点为点D ,点P 是抛物线对称轴上一动点,记抛物线在点A ,B 之间的部分为图象G (包含A ,B 两点).如果直线DP 与图象G 恰有两个公共点,结合函数图象,求点P 纵坐标t 的取值范围.27.在平面直角坐标系xOy 中,抛物线2212y x x =-+与y 轴交于点A ,顶点为点B ,点C 与点A 关于抛物线的对称轴对称. (1)求直线BC 的解析式;(2)点D 在抛物线上,且点D 的横坐标为4.将抛物线在点A ,D 之间的部分(包含点A ,D )记为图象G ,若图象G 向下平移t (0t >)个单位后与直线BC 只有一个公共点,求t 的取值范围.27.在平面直角坐标系xOy 中,二次函数y=(a-1)x 2+2x+1与x 轴有交点,a 为正整数. (1)求a 的值.(2)将二次函数y=(a-1)x 2+2x+1的图象向右平移m 个单位,向下平移m 2+1个单位,当 -2≤x ≤1时,二次函数有最小值-3,求实数m 的值.xOy 22y x mx n =++A BOyx27.已知:关于x 的一元二次方程-x 2+(m +1)x +(m +2)=0(m >0).(1)求证:该方程有两个不相等的实数根; (2)当抛物线y =-x 2+(m +1)x +(m +2)经过点(3,0),求该抛物线的表达式;(3)在(2)的条件下,记抛物线y =-x 2+(m +1)x +(m +2)在第一象限之间的部分为图象G ,如果直线 y =k (x +1)+4与图象G 有公共点,请结合函数的图象,求直线y =k (x +1)+4与y 轴交点的纵坐标t 的取值范围.27.在平面直角坐标系xOy 中,抛物线223(0)y mx mx m =--≠与x 轴交于(3,0)A ,B两点.(1)求抛物线的表达式及点B 的坐标;(2)当23x -<<时的函数图象记为G ,求此时函数y 的取值范围;(3)在(2)的条件下,将图象G 在x 轴上方的部分沿x 轴翻折,图象G 的其余部分保持不变,得到一个新图象M .若经过点(4,2)C 的直线(0)y kx b k =+≠与图象M 在第三象限内有两个公共点,结合图象求b 的取值范围.27.二次函数2(0)y ax bx c a =++≠的图象与一次函数k 的图象交于、两点,(1,0)C 为二次函数图象的顶点.(1)求二次函数2(0)y ax bx c a =++≠的表达式;(2)在所给的平面直角坐标系中画出二次函数2(0)y ax bx c a =++≠的图象和一次函数k 的图象;(3)把(1)中的二次函数2(0)y ax bx c a =++≠的图象平移后得到新的二次函数22(0,)y ax bx c m a m =+++≠为常数的图象,.定义新函数f :“当自变量x 任取一值时,x 对应的函数值分别为1y 或2y ,如果1y ≠2y ,函数f 的函数值等于1y 、2y 中的较小值;如果1y =2y ,函数f 的函数值等于1y (或2y ).”当新函数f 的图象与x 轴有三个交点时,直接写出m 的取值范围.1y x b =+)10(,A B 1y x b =+答案27已知二次函数21y x bx c =++的图象1C 经过(1,0)-,(0,3)-两点.(1)求1C 对应的函数表达式;(2)将1C 先向左平移1个单位,再向上平移4个单位,得到抛物线2C ,将2C 对应的函数表达式记为22y x mx n =++,求2C 对应的函数表达式;(3)设323y x =+,在(2)的条件下,如果在2-≤x ≤a 内存在..某一个x 的值,使得2y ≤3y 成立,利用函数图象直接写出a 的取值范围.27. 解:(1)∵点A 在直线x y =,且点A 的横坐标是-3,∴A (-3,-3) . ………………………………………………………………1分 把A (-3,-3)代入x ax y 42+=,解得a =1.……………………………………………………………………2分 ∴M 1 :x x y 42+=,顶点为(-2,-4) . ∴M 2的顶点为(1,-1) .∴M2的表达式为x x y 2-2=.…………3分(2)①由题意,C (2,2),∴F (4,2) . ………………………………4分 ∵直线n x y +=经过点F , ∴2=4+n .解得n =-2.………………………5分②n >3,n <-6.………………7分27.解:(1)∵抛物线()210y ax bx a =++≠过点()1,0A -,()1,1B ,∴10,1 1.a b a b -+=⎧⎨++=⎩∴1,21.2a b ⎧=-⎪⎪⎨⎪=⎪⎩∴抛物线的函数关系式为211122y x x =-++. …………2分 (2)∵122b x a =-=,()0,1C ∴抛物线211122y x x =-++的对称轴为直线12x =. 设点E 为点A 关于直线12x =的对称点,则点E 的坐标为()2,0. 连接EC 交直线12x =于点D ,此时ACD △的周长最小. 设直线EC 的函数表达式为y kx m =+,代入,E C 的坐标,则2m 0,1.k m +=⎧⎨=⎩解得1,21.k m ⎧=-⎪⎨⎪=⎩所以,直线EC 的函数表达式为112y x =-+. 当12x =时,34y =. ∴ 点D 的坐标为13,24⎛⎫⎪⎝⎭. …………4分 (3)存在.①当点A 为直角顶点时,过点A 作AC 的垂线交y 轴于点M ,交对称轴于点1P . ∵AO OC ⊥,1AC AP ⊥, ∴90AOM CAM ∠=∠=︒. ∵()0,1C ,()1,0A -, ∴1OA OC ==. ∴45CAO ∠=︒.∴45OAM OMA ∠=∠=︒. ∴1OA OM ==.∴点M 的坐标为()0,1-.设直线AM 对应的一次函数的表达式为11y k x b =+,代入,A M 的坐标,则1110,1.k b b -+=⎧⎨=-⎩解得111,1.k b =-⎧⎨=-⎩所以,直线AM 的函数表达式为1y x =--.令12x =,则32y =-. ∴点1P 的坐标为13,22⎛⎫-⎪⎝⎭. …………5分 ②当点C 为直角顶点时,过点C 作AC 的垂线交对称轴于点2P ,交x 轴于点N . 与①同理可得Rt CON △是等腰直角三角形, ∴1OC ON ==. ∴点N 的坐标为()1,0. ∵2CP AC ⊥,1AP AC ⊥, ∴21CP AP ∥.∴直线2CP 的函数表达式为1y x =-+.令12x =,则12y =. ∴点2P 的坐标为11,22⎛⎫⎪⎝⎭. …………6分 综上,在对称轴上存在点1P 13,22⎛⎫- ⎪⎝⎭,2P 11,22⎛⎫⎪⎝⎭,使ACP △成为以AC 为直角边的直角三角形.…………7分27. (1)由题意,得9-33030a b a b +=⎧⎨++=⎩解得,⎩⎨⎧-=-=21b a抛物线的解析式为y=-x 2-2x+3 ………………………2分顶点C 的坐标为(-1,4) ………………………3分 (2)①若点P 在对称轴右侧(如图①),只能是△PCQ ∽△CAH ,得∠QCP =∠CAH . 延长CP 交x 轴于M ,∴AM =CM ,∴AM 2=CM 2. 设M (m ,0),则( m +3)2=42+(m +1)2,∴m =2,即M (2,0). 设直线CM 的解析式为y=k 1x+b 1, 则⎩⎨⎧=+=+-0241111b k b k , 解之得341-=k ,381=b .∴直线CM 的解析式3834+-=x y .…………………………………4分 3238342+--=+-x x x , 解得311=x ,12-=x (舍去).9201=y .∴)92031(,P . ………………………………………………5分②若点P 在对称轴左侧(如图②),只能是△PCQ ∽△ACH ,得∠PCQ =∠ACH . 过A 作CA 的垂线交PC 于点F ,作FN ⊥x 轴于点N .由△CFA ∽△CAH 得2==AHCHAF CA , 由△FNA ∽△AHC 得21===CA AF HC NA AH FN .∴12==FN AN ,, 点F 坐标为(-5,1).设直线CF 的解析式为y=k 2x+b 2,则⎩⎨⎧=+-=+-1542222b k b k ,解之得419,4322==b k .∴直线CF 的解析式41943+=x y .……………………………………6分 32419432+--=+x x x ,解得471-=x ,12-=x (舍去).∴)165547(,-P . …………………………………7分 ∴满足条件的点P 坐标为)201(,或)557(,-27.解:(1)∵抛物线y=ax 2+x+c (a ≠0)经过A (﹣1,0),B (2,0)两点,∴10420a c a c -+=⎧⎨++=⎩,解得12a c =-⎧⎨=⎩.∴抛物线为y =﹣x 2+x +2①;………………………………………………………1 ∴顶点D (12,94).………………………………………………………………2 (2)如图,作EN ∥BC ,交y 轴于N ,过C 作CM ⊥EN 于M ,令x =0,得y =2, ∴OC =OB =2. ∴∠OCB =45°. ∵EN ∥BC ,∴∠CNM =∠OCB =45°. ∵CM ⊥EN 于M , ∴∠CNM =∠CMN =45°. ∴MN =CM∴CN =1.∴直线NE 的解析式为:把②代入①,解得1x y =⎧⎨=⎩∴E (1,2).(3)过E 作EF ⊥AB 于F∴tan ∠EOF =2,又∵tan ∠α=2, ∴∠EOF =∠α,∵∠EOF =∠EAO +∠AEO =∠EAO +∠EPO =∠α,∴∠EPO =∠AEO , ∵∠EAO =∠P AE ,∴△AEP ∽△AOE , (5)(图①)(图②)∴AP AEAE AO=, ∵AEAO =1, ∴AP =8, ∴OP =7,∴()7,0P ,………………………………………………………………………6 由对称性可得,()'5,0P -………………………………………………………7 ∴()7,0P 或()5,0-.27. 解:(1)∵二次函数2y x mx n =-++的图象经过点A (﹣1,4),B (1,0) ∴4101m nm n=--+⎧⎨=-++⎩∴m=-2,n=3∴二次函数的表达式为223y x x =--+ (2)12y x b =-+经过点B ∴12b =画出图形()211(,),2322M m m m m m -+--+设,则N ∴21123()22MN m m m =--+--+设∴23522MN m m =--+ ∴2349()416MN m =-++∴MN 的最大值为491627.解:(1)∵抛物线c bx x y ++=221与y 轴交于点C (0,3),∴3=c ; ………………………1分∵抛物线c bx x y ++=221的对称轴为2=x ,∴2212=⨯-b ,解得2-=b , ………………………2分∴抛物线1C 的解析式为32212+-=x x y . ………………………3分(2)由题意,抛物线2C 的解析式为k x y +=221. ………………………4分-----------7分-----------2分-----------6分-----------5分-----------3分 -----------4分y =2当抛物线经过点A (2,0)时,02212=k +⨯, 解得2-=k .………………………5分∵O (0,0),B (2,2),∴直线OB 的解析式为x y =.由⎪⎩⎪⎨⎧+==k x y x y 221,, 得0222=+-k x x ,(*)当Δ=k 214)2(2⨯⨯--=0,即21=k 时, ………………………6分 抛物线2C 与直线OB 只有一个公共点, 此时方程(*)化为0122=+-x x , 解得1=x ,即公共点P 的横坐标为1,点P 在线段OB 上. ∴k 的取值范围是212<<-k . (7)27. 解:(1)∵抛物线过点 (-1,a ),(3,a ), ∴抛物线的对称轴x =1..……. 1分 ∵抛物线最低点的纵坐标为-4 , ∴抛物线的顶点是(1,-4)..……. 2分 ∴抛物线的表达式是22(1)4y x =--, 即2242y x x =--..…3分22y x mx n =++A B把(-1,a )代入抛物线表达式,求出4a =..……. 4分(2)∵抛物线顶点(1,4)C -关于y 轴的对称点为点D ,∴(1,4)D --.求出直线CD 的表达式为4y =-. .……. 5分求出直线BD 的表达式为22y x =-,当1x =时,0y =..……. 6分 所以40t -<≤..……. 7分27. (本小题满分7分)解:(1)∵抛物线2212y x x =-+与y 轴交于点A ,∴点A 的坐标为(0,2).…………………………………………1分 ∵2211(232)212y x x x -+==+-,∴抛物线的对称轴为直线1x =,顶点B 的坐标为(1,32).…………2分又∵点C 与点A 关于抛物线的对称轴对称,∴点C 的坐标为(2,2),且点C 在抛物线上. 设直线BC 的解析式为y kx b =+. ∵直线BC 经过点B (1,32)和点C (2,2),∴322 2.,k b k b ⎧+=⎪⎨⎪+=⎩解得121.k b ⎧=⎪⎨⎪=⎩, ∴直线BC 的解析式为112y x =+.…………………………3分(2)∵抛物线2212y x x =-+中,当4x =时,6y =,∴点D 的坐标为(4,6).………………4分∵直线112y x =+中,当0x =时,1y =, 当4x =时,3y =,A∴如图,点E 的坐标为(0,1),点F 的坐标为(4,3).设点A 平移后的对应点为点'A ,点D 平移后的对应点为点'D . 当图象G 向下平移至点'A 与点E 重合时,点'D 在直线BC 上方, 此时t =1;…………………………………………………………5分当图象G 向下平移至点'D 与点F 重合时,点'A 在直线BC 下方,此时t =3.……………………………………………………………………………………6分结合图象可知,符合题意的t 的取值范围是13t <≤.……………………7分27.解:(1)∵二次函数y=(a-1)x 2+2x+1与x 轴有交点,令y=0,则(a-1)x 2+2x+1=0,∴=4-4(a-1)0∆≥,解得a ≤2. …………………………………1分. ∵a 为正整数. ∴a=1、2又∵y=(a-1)x 2+2x+1是二次函数,∴a-1≠0,∴a ≠1, ∴a 的值为2. ………………………………………2分(2)∵a=2,∴二次函数表达式为y=x 2+2x+1,将二次函数y=x 2+2x+1化成顶点式y=(x+1)2二次函数图象向右平移m 个单位,向下平移m 2+1个单位后的表达式为y=(x+1-m )2-(m 2+1).此时函数的顶点坐标为(m-1, -m 2-1). …………………………………4分 当m-1<-2,即m <-1时, x=-2时,二次函数有最小值-3, ∴-3=(-1-m )2-(m 2+1),解得32m =-且符合题目要求. ………………………………5分 当 -2≤m-1≤1,即-1≤m ≤2,时,当 x= m-1时,二次函数有最小值-m 2-1=-3,解得m =.∵m =-1≤m ≤2的条件,舍去.∴m =.……………………………………6分当m-1>1,即m >2时,当 x=1时,二次函数有最小值-3, ∴-3=(2-m )2-(m 2+1),解得32m =,不符合m >2的条件舍去.综上所述,m 的值为32-……………………………………7分 27.(本小题满分7分)(1)证明:∵ △= (m +1)2-4×(-1)×(m +2)=(m +3)2. ……………………………………………………………1分 ∵ m >0, ∴ (m +3)2>0, 即 △>0,∴ 原方程有两个不相等的实数根. …………………………………2分(2)解:∵ 抛物线抛物线y =-x 2+(m +1)x +(m +2)经过点(3,0),∴ -32+3(m +1)+(m +2)=0,………………………………………………3分 ∴ m =1.∴ y =-x 2+2x +3. (4)分(3)解:∵ y =-x 2+2x +3=-(x -1)2+4,∴ 该抛物线的顶点为(1,4).∴ 当直线y =k (x +1)+4经过顶点(1,4)时, ∴ 4=k (1+1)+4, ∴ k =0, ∴ y =4.∴ 此时直线y =k (x +1)+4与y 轴交点的纵坐标为 4. ………………………5分∵ y =-x 2+2x +3, ∴ 当x =0时,y =3,∴ 该抛物线与y 轴的交点为(0,3).∴ 此时直线y =k (x +1)+4与y 轴交点的纵坐标为 3. ………………………6分∴ 3<t ≤4. …………………………………………………………………7分27.解:(1)将()3,0A 代入,得1m =.∴抛物线的表达式为223y x x =--. …1分B 点的坐标()1,0-.………………2分(2)()222314y x x x =--=--.∵当21x -<<时,y 随x 增大而减小;当13x ≤<时,y 随x 增大而增大,∴当1x =,min 4y =-; ………………3分 当2x =-,5y =.∴y 的取值范围是45y -≤<.…………4分(3)当直线y kx b =+经过()1,0B -和点()4,2时,解析式为2255y x =+.…….………………5分 当直线y kx b =+经过()2,5--和点 ()4,2时,解析式为7863y x =-.………. ……………6分 结合图象可得,b 的取值范围是8235b -<<. ………….7分27.解:(1)设抛物线解析式为,由抛物线过点,可得 ………..(2分) (2)如图:………………………………………..(5分)(3)-4<m <0 ………………………………………..(7分)27.解:(1)∵ 二次函数21y x bx c =++的图象1C 经过(1,0)-,∴10,3.b c c -+=⎧⎨=-⎩………………………………1分解得2,3.b c =-⎧⎨=-⎩…………………………………2分∴ 抛物线1C 的函数表达式为3221--=x x y . ……………………………………3分(2)∵ 22123=(1)4y x x x =----,∴ 抛物线1C 的顶点为(1,4)- ∴ 平移后抛物线2C 的顶点为(0,0),它对应的函数表达式为22y x =.…5分 (3)a ≥1-(见图7).………………………………………………………………7分2)1(-=x a y )10(,A 122+-=x x y 1。
2015年北京中考各区县数学一模第28题

2015年北京中考数学一模第28题(教师版)(2015顺义一模)28.如图,△ABC 中,AB =AC ,点P 是三角形右外一点,且∠APB =∠ABC . (1)如图1,若∠BAC =60°,点P 恰巧在∠ABC 的平分线上,PA =2,求PB 的长; (2)如图2,若∠BAC =60°,探究PA ,PB ,PC 的数量关系,并证明; (3)如图3,若∠BAC =120°,请直接写出PA ,PB ,PC 的数量关系.(2015怀柔一模)28.在等边△ABC 外侧作直线AP ,点B 关于直线AP 的对称点为D ,连接BD,CD ,其中CD 交直线AP 于点E .(1)依题意补全图1; (2)若∠PAB=30°,求∠ACE 的度数;(3)如图2,若60°<∠PAB <120°,判断由线段AB,CE,ED 可以构成一个含有多少度角的三角形,并证明. (2015石景山一模)28.在△ABC 中,90BAC∠=︒. (1)如图1,直线l 是BC 的垂直平分线,请在图1中画出点A 关于直线l 的对称点'A ,连接'A C ,B A ','AC 与AB 交于点E ;(2)将图1中的直线B A '沿着EC 方向平移,与直线EC 交于点D ,与直线BC 交于点F ,过点F 作直线AB的垂线,垂足为点H .①如图2,若点D 在线段EC 上,请猜想线段FH ,DF ,AC 之间的数量关系,并证明;②若点D 在线段FH ,DF ,AC (2015朝阳一模)28.在△C =90°,AC =BC ,点D 在射线BC C 重合),连接AD ,将AD绕点D 顺时针旋转90°得到DE ,连接BE .(1)如图1,点D 在BC 边上. ①依题意补全图1;②作DF ⊥BC 交AB 于点F ,若AC =8,DF =3,求BE 的长;(2)如图2,点D 在BC 边的延长线上,用等式表示线段AB 、BD 、BE 之间的数量关系(直接写出结论).(2015海淀一模)28.在菱形ABCD 中,120ADC ∠=︒,点E 是对角线AC 上一点,连接DE ,50DEC ∠=︒,将线段BC 绕点B 逆时针旋转50︒并延长得到射线BF ,交ED 的延长线于点G . (1)依题意补全图形;EDC B AEDCBA备用图 (2)求证:EG BC =;(3)用等式表示线段AE ,EG ,BG 之间的数量关系:_____________________________.A BC P ABC P图1 图2 备用图图1 图2图1 图2 图3 (2015东城一模)28. 已知:Rt △A ′BC ′和 Rt △ABC 重合,∠A ′C ′B =∠ACB =90°,∠BA ′C ′=∠BAC =30°,现将Rt △A ′BC ′ 绕点B 按逆时针方向旋转角α(60°≤α≤90°),设旋转过程中射线C ′C 和线段AA ′相交于点D ,连接BD .(1)当α=60°时,A ’B 过点C ,如图1所示,判断BD 和A ′A 之间的位置关系,不必证明; (2)当α=90°时,在图2中依题意补全图形,并猜想(1)中的结论是否仍然成立,不必证明; (3)如图3,对旋转角α(60°<α<90°),猜想(1)中的结论是否仍然成立;若成立,请证明你的结论;若不成立,请说明理由.中,AB=BC ,∠ABC =80°,∠A +∠C =180°,点M 是AD顺时针CD 边交于点N ,请你补全图形,求MN ,AM ,CN 的数量关系;(2中,点M 12ABC ,与CD 的数量关系是 ;(3的边长是1,点M ,N 分别在AD ,CD 上,若△DMN 的周长为2,则△MBN 的面积最小值为 .(2015门头沟一模)28.在Rt △ABC 中,∠ACB =90°,D 是AB 的中点,DE ⊥BC 于E ,连接CD . (1)如图1,如果∠A =30°,那么DE 与CE 之间的数量关系是 .(2)如图2,在(1)的条件下,P 是线段CB 上一点,连接DP ,将线段DP 绕点D 逆时针旋转60°,得到线段DF ,连接BF ,请猜想DE 、BF 、BP 三者之间的数量关系,并证明你的结论.(3)如图3,如果∠A =α(0°<α<90°),P 是射线CB 上一动点(不与B 、C 重合),连接DP ,将线段DP 绕点D 逆时针旋转2α,得到线段DF ,连接BF ,请直接写出DE 、BF 、BP 三者之间的数量关系(不需证明).图1 图2 图3(2015通州一模)28.在菱形ABCD 中,∠ABC =60°,E 是对角线AC 上任意一点,F 是线段BC 延长线上一点,且CF =AE ,连接BE 、EF .(1)如图1,当E 是线段AC 的中点时,易证BE =EF .(2)如图2,当点E 不是线段AC 的中点,其它条件不变时,请你判断(1)中的结论: .(填“成立”或“不成立”)(3)如图3,当点E 是线段AC 延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由. (2015房山 一模)28.如图1,已知线段BC =2,点B 关于直线AC 的对称点是点D ,点E 为射线CA 上一点,且ED =BD ,连接DE ,BE .(1) 依题意补全图1,并证明:△BDE 为等边三角形;(2) 若∠ACB =45°,点C 关于直线BD 的对称点为点F ,连接FD 、FB .将△CDE 绕点D 顺时针旋转α度(0°<α<360°)得到△''C DE ,点E 的对应点为E ′,点C 的对应点为点C ′.①如图2,当α=30°时,连接'BC .证明:EF ='BC ; ②如图3,点M 为DC 中点,点P 为线段''C E 上的任意一点,试探究:在此旋转过程中,线段PM 长度的取值范围?图2 图3 图1已知,点P 是△ABC 边AB 上一动点(不与A ,B 重合)分别过点A ,B 向直线CP 作垂Q 为边AB 的中点.Q 重合时,AE 与BF 的位置关系是 ,QE 与QF 的数量关系是 ; AB 上不与点Q 重合时,试判断QE 与QF 的数量关系,并给予证明;BA 的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.(2015燕山一模)28.△ABC 中,∠ABC =45°,AH ⊥BC 于点H ,将△AHC 绕点H 逆时针旋转90°后,点C的对应点为点D ,直线BD 与直线AC 交于点E ,连接EH .(1)如图1,当∠BAC 为锐角时,①求证:BE ⊥AC ; ②求∠BEH 的度数; (2)当∠BAC 为钝角时,请依题意用实线补全图2,并用等式表示出线段EC ,ED ,EH 之间的数量关系. (2015西城一模)△ABC 中,AB=AC .取BC 边的中点D ,作DE ⊥AC 于点E ,取DE 的中点F ,连接BE ,AF 交于点H . (1)如图1,如果90BAC ∠=︒,那么AHB ∠= ︒,AFBE= ; (2)如图2,如果60BAC ∠=︒,猜想AHB ∠的度数和AFBE的值,并证明你的结论; (3)如果BAC α∠=,那么AFBE= .(用含α的表达式表示) (2015丰台一模)28.在△ABC 中,CA =CB ,CD 为AB 边的中线,点P 是线段AC 上任意一点(不与点C 重合),过点P 作PE 交CD 于点E ,使∠CPE =12∠CAB ,过点C 作CF ⊥PE 交PE 的延长线于点F ,交AB 于点G. (1)如果∠ACB =90°,①如图1,当点P 与点A 重合时,依题意补全图形,并指出与△CDG 全等的一个三角形; ②如图2,当点P 不与点A 重合时,求CFPE的值; (2)如果∠CAB =a ,如图3,请直接写出CFPE的值.(用含a 的式子表示)(2015顺义一模)28.解: (1)∵AB =AC ,∠BAC =60°,∴△ABC 是等边三角形,∠APB =∠ABC ,∴∠APB =60°,………………..…………………………………………..…...……… 1分 又∵点P 恰巧在∠ABC 的平分线上, ∴∠ABP =30° ∴∠PAB =90°.图1 图2 图3 图1 图2图1 图2图3∴BP =2AP , ∵AP =2,∴BP =4.………………..………………………………..…………………….….… 2分 (2)结论:PA +PC =PB .证明:在BP 上截取PD ,使PD =P A ,连结AD .…………………….…….…… 3分 ∵∠APB =60°,∴△ADP 是等边三角形, ∴∠DAP =60°, ∴∠1=∠2,P A =PD , 又∵AB =AC ,∴△ABD ≌△ACP ,…………………………………………….………….………4分 ∴PC =BD ,∴PA +PC =PB .………………..……………………..…………………….……… 5分 (3PA +PC =PB .………………..…..…….…………………...……… 7分(2015怀柔一模)28.解:(1)补全图形,如图1所示. …………………………… 1分 (2)连接AD ,如图2.∵点D 与点B 关于直线AP 对称,∴AD=AB ,∠DAP = ∠BAP =30°.∵AB=AC, ∠BAC =60°. ∴AD=AC, ∠DAC =120°.∴2∠ACE+60°+60°=180°∴∠ACE =30°…………………………… 3分 (3)线段AB,CE,ED 可以构成一个含有60证明:连接AD ,EB ,如图3.∵点D 与点B 关于直线AP 对称, ∴AD=AB ,DE=BE , 可证得∠EDA = ∠E BA .∵AB=AC,AB=AD. ∴AD=AC, = ∠ACE. ∴∠ABE AC ,BE 交于点F,又∵∠∴∠B AC = ∠BEC=60°.∴线段AB,CE,ED 可以构成一个含有60°角的三角形(2015石景山一模)(2015朝阳一模)28.解:(1)正确画出图形. ……………1分(2)①CA FH DF =+.……………2分 证明:过点F 作FG ⊥CA 于点G . ……3分 ∵FH ⊥BA 于点H ,90A ∠=︒,FG ⊥CA , ∴四边形HFGA 为矩形. ∴AG FH =,FG ∥AB .∴GFC EBC ∠=∠. ……………4分 由(1)和平移可知,12DABPP ED C BA 图1∠ECB =EBC ∠=∠GFC , ∠FDC =90A ∠=︒. ∴∠FDC =∠FGC =90°. ∵FC CF =,∴△FGC ≌△CDF .∴CG FD =. ………………………5分 ∴DF FH GC AG +=+.即DF FH AC +=. ……………6分 ②CA DF FH =- . ………………7分(2015海淀一模)28.解:(1)①补全图形,如图1②由题意可知AD =DE ,∠ADE =90°. ∵DF ⊥BC , ∴∠FDB =90°.∴∠ADF =∠EDB . ……………………………………2分 ∵∠C =90°,AC =BC , ∴∠ABC =∠DFB =90°. ∴DB =DF .∴△ADF ≌△EDB . ……………………………………3分 ∴AF =EB .在△ABC 和△DFB 中, ∵AC =8,DF =3,∴AC =,DF =. ………………………………………………………………4分 AF =AB -BF=即BE = …………………………………………………………………………5分 (2BD =BE +AB. ……………………………………………………………………7分 (2015东城一模)28. (本小题满分7分)(1)补全图形,如图1所示.…………………………………………………………1分图1 图2(2)方法一:证明:连接BE ,如图2. ∵四边形ABCD 是菱形, ∴AD ∥BC . 120ADC ∠=︒, 60DCB ∴∠=︒.AC 是菱形ABCD 的对角线,∴1302DCA DCB ∠=∠=︒.……………………………………………………………2分 180100EDC DEC DCA ∴∠=︒-∠-∠=︒.由菱形的对称性可知, 50BEC DEC ∠=∠=︒,图2图1100EBC EDC∠=∠=︒.……………………………………………………………………3分100GEB DEC BEC∴∠=∠+∠=︒.GEB CBE∴∠=∠.50FBC∠=︒,50EBG EBC FBC∴∠=∠-∠=︒.…………………………………………………………4分EBG BEC∴∠=∠.在△GEB与△CBE中,∴△GEB≌△CBE.EG BC∴=.………………………………………………………………………………5分方法二:证明:连接BE,设BG与EC交于点H,如图3.∵四边形ABCD是菱形,∴AD∥BC.120ADC∠=︒,60DCB∴∠=︒.AC是菱形ABCD的对角线,∴1302DCA DCB∠=∠=︒.………………………2分180100EDC DEC DCA∴∠=︒-∠-∠=︒.由菱形的对称性可知,50BEC DEC∠=∠=︒,100EBC EDC∠=∠=︒.……………………………………………3分50FBC∠=︒,图350EBG EBC FBC BEC∴∠=∠-∠=︒=∠.………………………………………………4分BH EH∴=.在△GEH与△CBH中,∴△GEH≌△CBH.EG BC∴=.………………………………………………………………………………5分(3)AE BG+=.…………………………………………………………………7分HGFEDCBA(2015平谷一模)28.解:(1) 当60α=︒时, BD A A '⊥. ------------1分(2)补全图形如图1,B D A A'⊥仍然成立;------------3分 (3)猜想BD A A '⊥仍然成立.证明:作AE C C '⊥,A F C C ''⊥,垂足分别为点,E F ,如图2,则90AEC A FC ''∠=∠=︒.∵BC BC '=,∴BCC BC C ''∠=∠. ∵90ACB A C B ''∠=∠=︒,∴90ACE BCC '∠+∠=︒,'90A C F BC C ''∠+∠=︒. ∴ACE A C F ''∠=∠. 在AEC △和A FC ''△中, ∴AEC A FC ''△≌△. ∴AE A F '=.在AED △和A FD '△中, ∴AED A FD '△≌△. ∴AD A D '=. ∵AB A B '=,∴'ABA △为等腰三角形. ∴BD A A '⊥------------7分(2015门头沟一模)28.解:(1)图2图1E (1)延长DA到点E,使AE=CN,连接BE∵∠BAD+∠C=180°.∴∠EAB=∠C.又∵AB=BC,AE=CN,∴△ABE≌△CBN.∴∠EBA=∠CBN,BE=BN. (2)∴∠EBN=∠ABC.∵∠ABC=80°,∠MBN=40°,∴∠EBM=∠NBM=40°.∵BM=BM,∴△EBM≌△NBM.∴EM=NM. (3)∴MN=AM+CN. (4)(2) (5)M N<A M+C N………………………………………………………………… (6)(3)1 (8)(2015通州一模28.(本小题满分7分)解:(1)D E=E C.……………………………………………………………………1分(2)D E、B F、B P三者之间的数量关系是B F+B P=D E.…………………2分理由如下:∵∠ACB=90°,D是AB的中点,∠A=30°∴DC=DB,∠CDB=60°.∵线段DP绕点D逆时针旋转60°得到线段DF,∴∠PDF=60°,DP=DF.又∵∠CDB=60°,∴∠CDB-∠PDB=∠PDF-∠PDB,∴∠CDP=∠BDF.∴△D C P≌△D B F.………………………………………………………3分∴CP=BF.而CP=BC-BP,∴B F+B P=B C,……………………………………………………………4分在Rt△CDE中,∠DEC=90°,∴tanDE DCECE∠=,∴CEDE,∴BC=2CEDE,∴B F+B P=D E.………………………………………………………5分(3)B F+B P=2D E t a nα,B F-B P=2D E t a nα.……………………………………7分)(2015房山一模)28.解:(1)补全图形,如图1所示;证明:由题意可知:射线CA垂直平分BD∴EB=ED又∵ED=BD∴EB=ED=BD∴△EBD是等边三角形………………2分(2)①证明:如图2:由题意可知∠BCD=90°,BC=DC又∵点C与点F关于BD对称∴四边形BCDF为正方形,∴∠FDC=90°,CD FD=∵30'CDCα︒==∠∴'60FDC︒=∠由(1)△BDE为等边三角形∴60'EDB FDC︒==∠∠,ED=BD∴'EDF BDC=∠∠…………………3分又∵''E DC EDC△是由△旋转得到的∴'C D CD FD==∴()'EDF DBC SAS△≌△∴'EF BC=…………………………4分②线段PM的取值范围是:11PM≤≤;设射线CA交BD于点O,I:如图3(1)当''E C DC,⊥''MP E C⊥,D、M、P、C共线时,PM此时DP=DO= 2 ,DM=1∴PM=DP-DM=2-1………………………5分II:如图3(2)当点P与点'E重合,且P、D、M、C共线时,PM有最大值.图2图3(2)图1此时DP =DE ′=DE =DB =2 2 ,DM =1∴PM= DP +DM =22+1 (6)分∴线段PM 11PM ≤≤ ………………7分(2015延庆一模)28.解:(1)AE ∥BF ,QE=QF , (2)QE=QF ,证明:如图2,延长EQ 交BF 于D , ∵AE ∥BF ,∴∠AEQ=∠BDQ , 在△BDQ 和△AEQ 中AEQ BDQ AQE BQD AQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDQ ≌△AEQ (ASA ), ∴QE=QD , ∵BF ⊥CP ,∴FQ 是Rt △DEF 斜边上的中线, ∴QE=QF=QD , 即QE=QF . (3)(2)中的结论仍然成立, 证明:如图3,延长EQ 、FB 交于D , ∵AE ∥BF , ∴∠AEQ =∠D ,在△AQE 和△BQD 中AEQ BDQAQE BQD AQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AQE ≌△BQD (AAS ), ∴QE=QD , ∵BF ⊥CP ,∴FQ 是Rt △DEF 斜边DE 上的中线, ∴QE=QF .说明:第三问画出图形给1分 (2015燕山一模)28.(1)①证明:∵AH ⊥BC 于点H ,∠ABC =45°,∴△ABH 为等腰直角三角形, ∴AH =BH ,∠BAH =45°,∴△AHC 绕点H 逆时针旋转90°得△BHD , 由旋转性质得,△BHD ≌△AHC ,∴∠1=∠2. ………………………1分 ∵∠1+∠C =90°, ∴∠2+∠C =90°,-----------7分-----------6分-----------5分-----------4分图1-1∴∠BEC=90°,即BE⊥AC.………………………2分②解法一:如图1-1,∵∠AHB=∠AEB=90°,∴A,B,H,E四点均在以AB为直径的圆上,………………………3分∴∠BEH=∠BAH=45°.………………………4分解法二:如图1-2,过点H作HF⊥HE交BE于F点,∴∠FHE=90°即∠4+∠5=90°.又∵∠3+∠5=∠AHB=90°,∴∠3=∠4.在△AHE和△BHF中,⎪⎩⎪⎨⎧∠=∠=∠=∠,,,3421BHAH∴△AHE≌△BHF,………………………3分∴EH=FH.∵∠FHE=90°,∴△FHE是等腰直角三角形,(2015西城一模)28.解:(1)90,12.………………………………………………………………………2分(2)结论:90AHB∠=︒,AFBE=.证明:如图8,连接AD.∵AB=AC,∠BAC=60°,∴△ABC是等边三角形.∵D为BC的中点,∴AD⊥BC.∴∠1+∠2=90°.又∵DE⊥AC,∴∠DEC=90°.∴∠2+∠C=90°.∴∠1=∠C=60°.设AB=BC=k(0k>),则124kCE CD==,4DE=.∵F为DE的中点,∴12DF DE==,AD AB=.图1-2∴2AD BC =,2DF CE =. ∴=BC AD CEDF.…………………………………………………………3分 又∵ ∠1=∠C ,∴ △ADF ∽△BCE .………………………………………………… 4分 ∴AF AD BE BC ==,………………………………………………… 5分 ∠3=∠4. 又∵ ∠4+∠5=90°,∠5=∠6, ∴ ∠3+∠6=90°.∴ 90AHB ∠=︒.………………………………………………………6分(3)1tan 9022α︒-().………………………………………………………………7分 注:写1cos 2sin αα+或其他答案相应给分.(2015丰台一模)28.(1) ①作图.……. 1分ADE ∆(或PDE ∆).…….2分②过点P 作PN ∥AG 交CG 于点N ,交CD 于点M ,.…….3分∴CPM CAB ∠=∠.∵∠CPE =12∠CAB ,∴∠CPE =12∠CPN .∴∠CPE =∠FPN .∵PF CG ⊥,∴∠PFC =∠PFN =90°.∵PF =PF ,∴PFC ∆≌PFN ∆.∴CF FN =..…….4分 由①得:PME ∆≌CMN ∆.∴PE CN =.∴12CF CF PE CN ==..…….5分 (2)1tan 2α..…….7分GF EBC P )DG F EC D AP BN M。
北京市怀柔区2015届九年级上学期期末考试数学试题及答案

怀柔区2014—2015学年度第一学期初三期末质量检测一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.12-的倒数是 A. 12 B. 2 C. 12- D. 2-2.2014年上半年,怀柔国税局累计入库消费税11000多万元,,将11000用科学记数法表示应为A .41.110⨯B .31.110⨯C .31110⨯D .50.1110⨯ 3.如图,A ,B ,C 三点在⊙O 上,且∠BOC=100°, 则∠A 的度数为A .40°B . 50°C . 80°D .100°4.如图,在Rt △ABC 中,∠C =90°,若sin A =35,则cos B 的是 A .45B .35C .34D . 435.将抛物线y = (x -1)2 +3向右平移1个单位,再向上平移3个单位后 所得抛物线的表达式为A .y = (x -2)2B .y =x 2C .y =x 2 +6D .y =(x -2)2 +66. 在某一时刻,测得一根高为1.2m 的木棍的影长为2m ,同时测得一根 旗杆的影长为25m ,那么这根旗杆的高度为A .15mB .1253m C. 60 m D .24m 7.如图,在△ABC 中,D 为AC 边上一点,∠DBC =∠A ,BC AC =3, 则CD 的长为 A .1 B .32 C .2 D .52CBA DCBA8. 如图,矩形ABCD 中,AB =3,BC =4,动点P 从A 点出发, 按A →B →C 的方向在AB 和BC 上移动,记PA =x ,点D 到直线PA 的距离为y ,则y 关于x 的函数图象大致是yyyyDC B A二、填空题(本题共16分,每小题4分) 9.分解因式:239a b b -= .10.已知两圆的半径分别为2cm 和4cm ,它们的圆心距为6cm ,则这两个圆的位置关系是. 11.若函数-2m y x=的图象在其所在的每一象限内,函数值y 随 自变量x 的增大而减小,则m 的取值范围是 . 12.在平面直角坐标系xOy 中,正方形ABCD 的位置如右图所示, 点A 的坐标为(1,0),点D 的坐标为(0,2),延长CB 交x 轴于点A 1,作正方形A 1B 1C 1C ,延长C 1B 1交x 轴于 点A 2,作正方形A 2B 2C 2C 1,…按这样的规律进行下去, 第1个正方形的面积为 ; 第n 个正方形的面积为 . 三、解答题(本题共30分,每小题5分) 13.计算:(0113tan 302()2-︒+--+. 14.已知抛物线y=x 2-4x+5,求出它的对称轴和顶点坐标.15.解不等式组:()11,22-x x ìïï-ïíïïïî≤1<3.16.已知2450x x +-=,求代数式()()()221-1--2x x x +的值. 17.如图,一根电线杆的接线柱部分AB 在阳光下的投影CD 的长为1米,太阳光线与地面的夹角∠ACD=60°. 求接线柱AB 的长.18. 已知:抛物线222(2)1y x m x m =-++-与x 轴有两个交点. (1)求m 的取值范围;(2)当m 为非正整数时,关于x 的一元二次方程222(2)10x m x m -++-=有整数根,PEDCBA求m 的值.四、解答题(本题共20分,每小题5分)19.如图,在四边形ABCD 中,∠A =30°,∠C=90°,∠ADB =105°,sin 2BDC ∠=,AD =4. 求DC 的长.20.在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别. (1)随机从箱子里取出1个球,则取出黄球的概率是多少?(2)随机从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法表示出所有可能出现的结果,并求两次取出的都是白色球的概率.21.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC (顶点是网格线的交点).(1)将△ABC 绕点B 顺时针旋转90°得到△A’BC ’,请画出△A’BC ’,并求BA 边旋转到B A’’(2)请在网格中画出一个格点△A”B”C”,使△A ”B”C”∽△ABC 且相似比不为1.22.如图,在⊙O 中,直径AB 交弦ED 于点G ,EG=DG ,⊙O 的切线BC 交DO 的延长线于点C ,F 是DC 与⊙O 的交点, 连结AF .(1)求证:DE ∥BC ;(2)若OD=1,CF=14,求AF 的长.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.在平面直角坐标系xOy 中,抛物线22y x mx n =++经过点A (-1,a ),B (3,a ),且最小值为-4. (1)求抛物线表达式及a 的值;(2)设抛物线顶点C 关于y 轴的对称点为D ,点P 是抛物线对称轴上一动点,记抛物线在A ,B 之间的部分为图像G (包含A ,B 两点). 若直线DP 与图像G 有两个公共点,结合函数图像,求点P 纵坐标t 的取值范围.24.对于点E 和四边形ABCD ,给出如下定义:在四边形ABCD 的边AB 上任取一点E (点E 不与A 、B 重合),分别连接ED 、EC ,可以把四边形ABCD 分成三个三角形,如果其中有两个CBA三角形相似,则称E 为四边形ABCD 边AB 上的“相似点”;如果这三个三角形都相似,我们称E 为四边形ABCD 边AB 上的“强相似点”.(1)如图1,在四边形ABCD 中,A 、B 、C 、D 四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上, 点E 是AB 边上一点,∠DEC =45°,试判断点E 是否是四边形ABCD 边AB 上的相似点,并证明你的结论正确; (2)如图2,在矩形ABCD 中,AB=8,AD=3.①在AB 边上是否存在点E ,使点E 为四边形ABCD 边AB 上的“强相似点”.若存在,有几个?试在图2中画出所有强相似点; ②在①所画图形的基础上求AE 的长.25ABC 绕点B 顺时针旋转α(0°<α<90°),得到△DBE,其中点A 的对应点是点D ,点C 的对应点是点E ,AC 、DE 相交于点F ,连接BF.(1)如图1,若α=60°,线段BA 绕点B 旋转α得到线段BD.请补全△DBE ,并直接写出∠AFB 的度数;(2)如图2,若α=90°,求∠AFB 的度数和BF 的长; (3)如图3,若旋转α(0°<α<90°),请直接写出∠AFB 的度数及BF 的长(用含α 的代数式表示).DA BC图2图1怀柔区2014—2015学年第一学期初三期末质量检测数学试题答案及评分参考一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的.二、填空题(本题共16分,每小题4分)三、解答题(本题共30分,每小题5分) 13.(本小题满分5分)解:原式=312-+4分1+=1 .…………………………………………………………5分 14.(本小题满分5分) 解:y=x 2-4x+5= x 2-4x+4+11分=(x-2)2+1.……………………………………………………………3分∴抛物线的对称轴为x=2. ……………………………………………4分 顶点坐标为(2,1).…………………………………………………5分 15. (本小题满分5分)解:由(1)得:x ≤3. ……………………………………………………2分 由(2)得:x >-1.……………………………………………………4分 ∴不等式组的解集为 -1<x ≤3.………………………………………5分 16.(本小题满分5分)解:原式=()()222-1--44x x x +………………………………… 2分 = 222-2-+4-4x x x=2+4-6x x .……………………………………………………3分∵2450x x +-=245x x ∴+=. ………………………………………………………4分∴原式=2+4-6x x =-1. ………………………………………………5分 17. (本小题满分5分)解:过B 作BE ∥CD 交AB 于E 点, ∵太阳光线与地面的夹角∠ACD=60°,∴∠AEB=60°,………………………………………2分 ∵太阳光线AC ∥BD, 又BE ∥CD,∴四边形ACDB 是平行四边形…………………………………4分 ∴CD=BE=1,在△AEB 中,∵∠ABE=90°,BE=1,∠AEB=60°, ∴AB=1×tan60°…………………………………5分 所以接线柱AB. 18. (本小题满分5分)解:(1)令y=0,则222(2)10x m x m -++-= 依题意,得224(2)-410m m +-() , 解得 54m-, ∴ m 的取值范围是54m-. ………………………………………2分 (2)∵m 为非正整数,∴ m=-1或m=0.当m=-1时,022=-x x ,解得x=0或x=2. …………………3分 当m=0时,2410x x --=,解得22x x ==. ……………………4分 ∴m 的值是-1. ………………………………………5分 四、解答题(本题共20分,每小题5分) 19.(本小题满分5分)解:过点D 作DE ⊥AB 于E. …………………………………1分 在Rt △ADE 中,∵∠A=30°,∠AED=90°,∴∠ADE=60°, ∵AD=4 ∴DE=2,…………………………………2分 ∵∠ADB =105°,∠ADE=60°,∴∠EDB=45°,∵DE=2,∴在Rt△ADE中,BD=3分在Rt△BCD中,∵sin2BDC∠=∴∠BDC=60°,∵BD=5分20.(本小题满分5分)解:(1)取出黄球的概率是13;………………………………………2分(2)画树状图得:……………3分如图所有可能出现的结果有9个,………………………………………4分每个结果发生的可能性都相同,其中出现两次白色球的结果有1个.所以,P(两次取出白色球)=19.…………………………………5分21. (本小题满分5分)解:(1)如图:△A’BC’即为所求;…………2分BA旋转到B A’’所扫过图形的面积:S=2901313=3693604n Rπππ⨯=.……………3分(2)如图:△A”B”C”即为所求.……………5分22. (本小题满分5分)(1)证明:∵ BC为⊙O的切线,AB为直径,∴∠ABC = 90°.∵AB平分弦DE,∴∠A GE= 90°.∴DE∥BC.…………………………………2分(2)连接DB,AD.∵AB是⊙O的直径,∴∠ADB = 90°.∵DE∥BC,∴△DGO∽△CBO∴OD OG CO OB=,∵OD = 1,CF=14;∴OC=54,∴1=514OG∴OG=45,………………3分黄白黑黄白黑黑白黄黄白黑开始BECBAA'C''B''A''C'ABC∴AG=15. ∵∠ADB=∠AGD= 90°, ∴ △A DG ∽△ADB ,∴AD 2=AG.AB , ∵AG=15,AB=2. ∴ DF 为⊙O 直径,∴∠FAD = 90°, ∵DF=2,∴.……………………………5分 (其它方法对应给分)五、解答题(本题共22分,第23题7分,第24题7分,第25题8分,) 23.(本小题满分7分) 解:(1)∵抛物线经过A(-1,a),B (3,a ),∴抛物线的对称轴x=1,又∵最小值为-4, ∴顶点坐标C (1,-4).∴抛物线表达式为y=2(x-1)2-4即抛物线表达式y=2x 2-4x-2. ……………………………2分把A (-1,a )代入y=2x 2-4x-2,解得a=4.∴a 的值为4. ……………………………3分(2)∵D 点与C 点关于y 轴对称,∴D 点坐标为(-1,-4) 由(1)知:B (3,4)设直线DB 的表达式为y=kx+b把D(-1,-4),B (3,4)代入:y=kx+b∴4=344k b k +⎧⎨-=-+⎩. 解得k=22b ⎧⎨=-⎩.∴直线BD 的表达式为:y=2x 2-.……………………5分 设P (1,t ),把P (1,t )代入y=2x 2- 解得t=0.又∵抛物线的顶点坐标C (1,-4). ∴t=-4.∴-4<t ≤0……………………………7分 24. (本小题满分7分)解:(1)∵∠A =∠B =∠DEC =45°,∴∠AED +∠ADE =135°,∠AED +∠CEB =135° ∴∠ADE =∠CEB , ∴△ADE ∽△BCE ,∴点E 是四边形ABCD 边AB 上的相似点.………………………3分(2)①如图:强相似点有两个,点E ’,E ’’即是四边形ABCD 边AB 上的两个强相似点. ……………………………5分 ②设AE ’=x,则BE ’=8-x,∵△AD E ’∽△BC E ’, ∴383x x -=,解得4x =∴AE 的长为47分 25.(本小题满分8分)(1)补全图形如图所示,∠AFB=60°;……………2分 (2)解:连接AD ,∵∠BAC=∠BDE=30°∠1=∠2∴∠AFD=∠ABD=90°∴A 、B 、F 、D 在以AB 为直径的圆上,∴∠AFB=∠ADB=45°………………………4分在△ABF 中,∠FAB=30°,∠AFB=45°,AB=可解得…………………………6分 (注:此题其它解法对应给分)(3)∠AFB=90°-12α…………………………7分sin(90-2)…………………………8分参考解法:∵∠A=∠D=30°, ∠1=∠2. ∴∠AFD=∠ABD=α, 过B 作BM ⊥AC 于M , 过B 作BN ⊥DE 于N , 由ABCS=DBES和AC=DE , 可得BM=BN ,∴FB 平分∠AFE ,∴∠AFB=∠EFB=180-2O α=90°-12α,在Rt △ABM 中可得:在Rt △BMF 中,由sin ∠AFB=BM BF, 得:BF=sin sin(90-2AFB BM α∠=).ABCDEF。
2015年北京中考一模各区县数学四边形汇总

G FO B CDEA2015年北京市各城区中考一模数学——四边形汇总(2015平谷一模)23.如图,BD 是△ABC 的角平分线,点E ,F 分别在BC ,AB 上,且DE ∥AB ,EF ∥AC .(1)求证:BE =AF ;(2)若∠ABC =60°,BD =12,求DE 的长及四边形ADEF 的面积.(2015 延庆一模)23. 如图,点O 是△ABC 内一点,连结OB 、OC ,并将AB 、OB 、OC 、AC 的中点D 、E 、F 、G 依次连结,得到四边形DEFG .(1)求证:四边形DEFG 是平行四边形;(2)如果∠OBC =45°,∠OCB =30°,OC =4,求EF 的长.(2015 房山一模)23.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作一条直线分别交DA 、BC 的延长线于点E 、F ,连接BE 、DF . (1)求证:四边形BFDE 是平行四边形;(2)若AB =4,CF =1,∠ABC =60°,求sin DEO 的值.(2015 西城一模)23.如图,四边形ABCD 中,BD 垂直平分AC ,垂足为点F , E 为四边形ABCD 外一点,且∠ADE =∠BAD ,AE ⊥AC .(1)求证:四边形ABDE 是平行四边形;(2)如果DA 平分∠BDE ,AB=5,AD=6,求AC 的长.(2015 通州一模)23.已知菱形ABCD 的对角线AC 与BD 相交于点E ,点F 在BC 的延长线上,且CF=BC ,连接DF ,点G 是DF 中点,连接CG .求证:四边形 ECGD 是矩形.B(2015 海淀一模)23.如图,在□ABCD 中,∠BAD 的平分线交CD 于点E ,交BC 的延长线于点F ,连接BE ,∠F =45°.(1)求证:四边形ABCD 是矩形; (2)若AB =14,DE =8,求sin ∠AEB 的值.(2015 丰台一模)23.如图,菱形ABCD 中, 分别延长DC ,BC 至点E ,F ,使CE =CD ,CF =CB ,联结DB ,BE ,EF ,FD.A(1)求证:四边形DBEF 是矩形;(2)如果∠A =60︒,菱形ABCD 的面积为38,求DF 的长.(2015 石景山一模)23.如图,菱形ABCD 中,E ,F 分别为AD ,AB 上的点,且AF AE =,连接EF 并延长,交CB 的延长线于点G ,连接BD .(1)求证:四边形EGBD 是平行四边形;(2)连接AG ,若︒=∠30FGB ,1==AE GB ,求AG 的长.(2015 怀柔一模)23. 如图,BD 是△ABC 的角平分线,点E ,F 分别在BC ,AB 上,且DE ∥AB ,BE =AF . (1)求证:四边形ADEF 是平行四边形;(2)若∠ABC =60°,BD =4,求平行四边形ADEF 的面积.(2015 燕山一模).如图,菱形ABCD 中,对角线AC ,BD 交于O 点,DE ∥AC ,CE ∥BD .(1)求证:四边形OCED 为矩形;CDBAGFEEDBOCA(2)在BC 上截取CF =CO ,连接OF ,若AC =8,BD =6,求四边形OFCD 的面积.(2015 门头沟一模)23. 如图,菱形ABCD 的对角线AC 和BD 交于点O ,分别过点C 、D 作CE ∥BD ,DE ∥AC ,CE 和DE 交于点E .(1)求证:四边形ODEC 是矩形;(2)当∠ADB =60°,AD=时,求tan ∠EAD 的值.(2015 东城一模)23. 如图,ABC △中,90BCA ∠=︒,CD 是边AB 上的中线,分别过点C ,D 作BA ,BC 的平行线交于点E ,且DE 交AC 于点O ,连接AE .(1)求证:四边形ADCE 是菱形; (2)若2AC DE =,求sin CDB ∠的值.DO FECAB(2015朝阳一模)23. 如图,菱形ABCD 的对角线AC 、BD 相交于点O ,过点D 作DE ∥AC 且DE=12AC ,连接 CE 、OE ,连接AE 交OD 于点F . (1)求证:OE =CD ;(2)若菱形ABCD 的边长为2,∠ABC=60°,求AE 的长(2015顺义一模)23.如图,平行四边形ABCD 中,点E 是AD 边上一点,且 CE ⊥BD 于点F ,将△DEC 沿从D 到A 的方向平移,使点D 与点A 重合,点E 平移后的点记为G . (1)画出△DEC 平移后的三角形;(2)若BC=BD =6,CE =3,求AG 的长.(2015大兴一模)23.已知:如图,在△ABC 中,∠C=90°,ABC 绕点A 顺时针方向旋转60°到△AB ′C ′的位置,连接C ′B.(1)请你判断BC ′与AB ′的位置关系,并说明理由; (2)求BC ′的长.DCE BAF C 'B 'CBA。
2015年北京中考各区县数学一模压轴题(答案版)
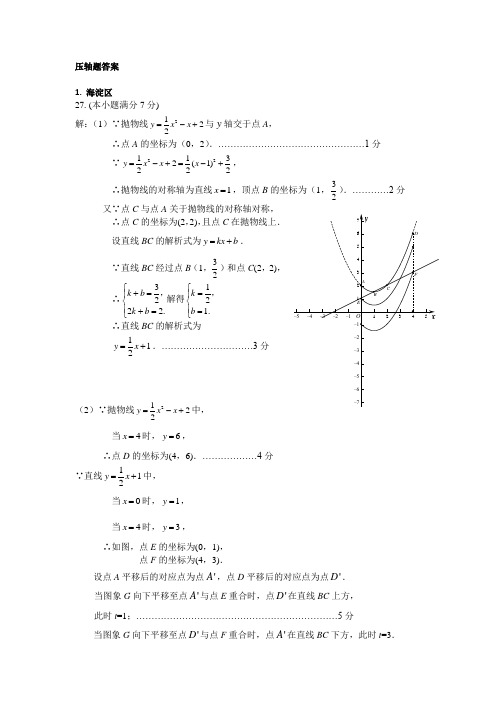
压轴题答案1. 海淀区27. (本小题满分7分)解:(1)∵抛物线2212y x x =-+与y 轴交于点A ,∴点A 的坐标为(0,2).…………………………………………1分 ∵2211(232)212y x x x -+==+-,∴抛物线的对称轴为直线1x =,顶点B 的坐标为(1,32).…………2分又∵点C 与点A 关于抛物线的对称轴对称,∴点C 的坐标为(2,2),且点C 在抛物线上. 设直线BC 的解析式为y kx b =+.∵直线BC 经过点B (1,32)和点C (2,2),∴322 2.,k b k b ⎧+=⎪⎨⎪+=⎩解得121.k b ⎧=⎪⎨⎪=⎩, ∴直线BC 的解析式为 112y x =+.…………………………3分(2)∵抛物线2212y x x =-+中,当4x =时,6y =,∴点D 的坐标为(4,6).………………4分∵直线112y x =+中,当0x =时,1y =, 当4x =时,3y =,∴如图,点E 的坐标为(0,1),点F 的坐标为(4,3).设点A 平移后的对应点为点'A ,点D 平移后的对应点为点'D . 当图象G 向下平移至点'A 与点E 重合时,点'D 在直线BC 上方, 此时t =1;…………………………………………………………5分当图象G 向下平移至点'D 与点F 重合时,点'A 在直线BC 下方,此时t =3.……………………………………………………………………………………6分 结合图象可知,符合题意的t 的取值范围是13t <≤.……………………………7分28. (本小题满分7分)(1)补全图形,如图1所示.…………………………………………………………1分GF EDCBA图1 图2(2)方法一:证明:连接BE ,如图2. ∵四边形ABCD 是菱形, ∴AD ∥BC . 120ADC ∠=︒, 60DCB ∴∠=︒.AC 是菱形ABCD 的对角线, ∴1302DCA DCB ∠=∠=︒.……………………………………………………………2分 180100EDC DEC DCA ∴∠=︒-∠-∠=︒.由菱形的对称性可知, 50BEC DEC ∠=∠=︒, 100EBC EDC ∠=∠=︒.……………………………………………………………………3分 100GEB DEC BEC ∴∠=∠+∠=︒. GEB CBE ∴∠=∠. 50FBC ∠=︒,50EBG EBC FBC ∴∠=∠-∠=︒.…………………………………………………………4分 EBG BEC ∴∠=∠. 在△GEB 与△CBE 中,,,,GEB CBE BE EB EBG BEC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△GEB ≌△CBE .GF EDCBAEG BC ∴=.………………………………………………………………………………5分方法二:证明:连接BE ,设BG 与EC 交于点H ,如图3. ∵四边形ABCD 是菱形, ∴AD ∥BC . 120ADC ∠=︒, 60DCB ∴∠=︒.AC 是菱形ABCD 的对角线,∴1302DCA DCB ∠=∠=︒.………………………2分180100EDC DEC DCA ∴∠=︒-∠-∠=︒.由菱形的对称性可知,50BEC DEC ∠=∠=︒,100EBC EDC ∠=∠=︒.……………………………………………3分50FBC ∠=︒,图350EBG EBC FBC BEC ∴∠=∠-∠=︒=∠.……………………………4分 BH EH ∴=.在△GEH 与△CBH 中,,,,GEH CBH EH BH EHG BHC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△GEH ≌△CBH .EG BC ∴=.………………………………………………………………………………5分 (3)AE BG +=. …………………………………………………………………7分 29.(本小题满分8分)解:(1)①;……………………………………………………………………1分②点B .………………………………………………………………………2分 (2)依题意,3(2)y x x =-+-≥图象上的点P 的限变点必在函数3,13,21x x y x x -+⎧=⎨--<⎩≥≤的图象上.2≤b '∴,即当1x =时,b '取最大值2.当2b '=-时,23x -=-+.5x ∴=.………………………………………3分 当5b '=-时,53x -=-或53x -=-+.2x ∴=-或8x =.………………………………4分 52≤≤b '-,由图象可知,k 的取值范围是58≤≤k .……………………………………………5分A(3)2222()y x tx t t x t t =-++=-+,∴顶点坐标为(,)t t .………………………………………………………………6分若1t <,b '的取值范围是≥b m '或≤b n ',与题意不符. 若1≥t ,当1≥x 时,y 的最小值为t ,即m t =; 当1x <时,y 的值小于2[(1)]t t --+,即2[(1)]n t t =--+. 22(1)1s m n t t t t ∴=-=+-+=+.∴s 关于t 的函数解析式为211)s t t =+≥ ( .……………………………7分当t=1时,s 取最小值2.∴s 的取值范围是s ≥2.………………………………………………………8分2. 西城区27.解:(1)∵ 二次函数21y x bx c =++的图象1C 经过(1,0)-,∴10,3.b c c -+=⎧⎨=-⎩ ………………………………1分解得2,3.b c =-⎧⎨=-⎩………………………………… 2分∴ 抛物线1C 的函数表达式为3221--=x x y . …………………………………… 3分 (2)∵ 22123=(1)4y x x x =----,∴ 抛物线1C 的顶点为(1,4)- ∴ 平移后抛物线2C 的顶点为(0,0),它对应的函数表达式为22y x =.… 5分 (3)a ≥1-(见图7).………………………………………………………………7分28.解:(1)90,12.……………………………………………………………………… 2分 (2)结论:90AHB ∠=︒,AF BE =. 证明:如图8,连接AD .∵ AB =AC ,∠BAC =60°, ∴ △ABC 是等边三角形. ∵ D 为BC 的中点,∴ AD ⊥BC . ∴ ∠1+∠2=90°. 又∵ DE ⊥AC , ∴ ∠DEC =90°. ∴ ∠2+∠C =90°. ∴ ∠1=∠C =60°.设AB =BC=k (0k >), 则124kCE CD ==,DE =. ∵ F 为DE 的中点,∴12DF DE ==,AD AB ==.∴AD BC =,DF CE ∴ =BC AD CE DF .…………………………………………………………3分 又∵ ∠1=∠C , ∴ △ADF ∽△BCE .………………………………………………… 4分∴AF AD BE BC ==,………………………………………………… 5分 ∠3=∠4. 又∵ ∠4+∠5=90°,∠5=∠6, ∴ ∠3+∠6=90°. ∴ 90AHB ∠=︒.………………………………………………………6分(3)1tan 9022α︒-().………………………………………………………………7分注:写1cos 2sin αα+或其他答案相应给分.29.解:(1)3.(每空各1分)…………………………………………………… 2分(2)-1.…………………………………………………………………………… 4分(3)①如图9,过点O 分别作射线OE 、OF 的垂线OG 、OH ,则图形M 为:y 轴正半轴,∠GOH 的边及其内部的所有点(图中的阴影部分).……………………………………………………………………………… 7分 说明:(画图2分,描述1分)(图形M 也可描述为:y 轴正半轴,直线x y 33=下方与直线x y 33-=下方重叠的部分(含边界)) ②34.…………………………………………………………………………8分3. 东城区27.解:(1)∵抛物线()210y ax bx a =++≠过点()1,0A -,()1,1B ,∴10,1 1.a b a b -+=⎧⎨++=⎩∴1,21.2a b ⎧=-⎪⎪⎨⎪=⎪⎩ ∴抛物线的函数关系式为211122y x x =-++. …………2分 (2)∵122b x a =-=,()0,1C ∴抛物线211122y x x =-++的对称轴为直线12x =. 设点E 为点A 关于直线12x =的对称点,则点E 的坐标为()2,0. 连接EC 交直线12x =于点D ,此时ACD △的周长最小. 设直线EC 的函数表达式为y kx m =+,代入,E C 的坐标,则2m 0,1.k m +=⎧⎨=⎩解得1,21.k m ⎧=-⎪⎨⎪=⎩所以,直线EC 的函数表达式为112y x =-+. 当12x =时,34y =. ∴ 点D 的坐标为13,24⎛⎫⎪⎝⎭. …………4分(3)存在.①当点A 为直角顶点时,过点A 作AC 的垂线交y 轴于点M ,交对称轴于点1P .∵AO OC ⊥,1AC AP ⊥,∴90AOM CAM ∠=∠=︒. ∵()0,1C ,()1,0A -, ∴1OA OC ==. ∴45CAO ∠=︒.∴45OAM OMA ∠=∠=︒. ∴1OA OM ==.∴点M 的坐标为()0,1-.设直线AM 对应的一次函数的表达式为11y k x b =+,代入,A M 的坐标,则1110,1.k b b -+=⎧⎨=-⎩解得111,1.k b =-⎧⎨=-⎩所以,直线AM 的函数表达式为1y x =--.令12x =,则32y =-. ∴点1P 的坐标为13,22⎛⎫-⎪⎝⎭. …………5分 ②当点C 为直角顶点时,过点C 作AC 的垂线交对称轴于点2P ,交x 轴于点N . 与①同理可得Rt CON △是等腰直角三角形, ∴1OC ON ==. ∴点N 的坐标为()1,0. ∵2CP AC ⊥,1AP AC ⊥, ∴21CP AP ∥.∴直线2CP 的函数表达式为1y x =-+. 令12x =,则12y =. ∴点2P 的坐标为11,22⎛⎫⎪⎝⎭. …………6分 综上,在对称轴上存在点1P 13,22⎛⎫- ⎪⎝⎭,2P 11,22⎛⎫⎪⎝⎭,使ACP △成为以AC 为直角边的直角三角形.…………7分 28.解:(1)当60α=︒时, BD A A '⊥. ------------1分(2)补全图形如图1,B D A A '⊥仍然成立;------------3分(3)猜想BD A A '⊥仍然成立.证明:作AE C C '⊥,A F C C ''⊥,垂足分别为点,E F ,如图2,则90AEC A FC ''∠=∠=︒. ∵BC BC '=,∴BCC BC C ''∠=∠. ∵90ACB A C B ''∠=∠=︒,∴90ACE BCC '∠+∠=︒,'90A C F BC C ''∠+∠=︒. ∴ACE A C F ''∠=∠. 在AEC △和A FC ''△中,90,,,AEC A FC ACE A C F AC A C ''∠=∠=︒⎧⎪''∠=∠⎨⎪''=⎩∴AEC A FC ''△≌△. ∴AE A F '=.图2 图1在AED △和A FD '△中,90,,,AEC A FD ADE A DF AE A F '∠=∠=︒⎧⎪'∠=∠⎨⎪'=⎩∴AED A FD '△≌△. ∴AD A D '=. ∵AB A B '=,∴'ABA △为等腰三角形. ∴BD A A '⊥------------7分29.解:(1)∵20x ≥, ∴2x -1≥-1. ∴2-x -1>2.∴{}2min 2x =--1,-2. ┉┉2分 (2) ∵()2211x x k x k -+=-+-2,∴()2111x k k -+--≥. ∵2min{2,3}3x x k -+-=-,∴13k --≥. ∴2k -≥. ┉┉5分(3) 37m -≤≤. ┉┉8分4. 朝阳区 27. 解:(1)∵ 点A 在直线x y =,且点A 的横坐标是-3,∴ A (-3,-3) . ………………………………………………………………1分 把A (-3,-3)代入x ax y 42+=,解得a =1. … …………………………………………………………………2分 ∴M 1 : x x y 42+=,顶点为(-2,-4) . ∴M 2的顶点为(1,-1) .∴M 2的表达式为x x y 2-2=. …………3分(2)①由题意,C (2,2),∴F (4,2) . ………………………………4分 ∵直线n x y +=经过点F , ∴2=4+n .解得n =-2. ………………………5分② n >3,n <-6. …………… …7分28.解:(1)①补全图形,如图1所示. ………………………1分②由题意可知AD =DE ,∠ADE =90°. ∵DF ⊥BC , ∴∠FDB =90°.∴∠ADF =∠EDB . ……………………………………2分 ∵∠C =90°,AC =BC , ∴∠ABC =∠DFB =90°. ∴DB =DF .∴△ADF ≌△EDB . ……………………………………3分 ∴AF =EB .在△ABC 和△DFB 中, ∵AC =8,DF =3,∴AC=,DF=. ………………………………………………………………4分 AF =AB -BF=即BE= …………………………………………………………………………5分 (2BD =BE +AB. ……………………………………………………………………7分29. 解:(1)A 、B ……………………………………………………………………………2分(2)如图,作点P 关于x 轴的对称点P ′,连接P ′Q ,P ′Q 与x 轴的交点即为“等高点”M ,此时“等高距离”最小,最小值为线段P ′Q 的长. ………………………3分 ∵P (1,2), ∴ P ′ (1,-2).设直线P ′Q 的表达式为b kx y +=, 根据题意,有⎩⎨⎧=+-=+242b k b k ,解得⎪⎩⎪⎨⎧-==31034b k . 图1∴直线P ′Q 的表达式为31034-=x y . ……………4分 当0=y 时,解得25=x . 即25=t . ………………………………………………………………………5分 根据题意,可知PP ′=4,P Q =3, P Q ⊥PP ′, ∴5''22=+=PQ PP Q P .∴“等高距离”最小值为5. …………………………………………………6分(3)Q (554,552)或Q (554-,552). ………………………………8分5. 丰台区27 . 解:(1)∵抛物线22y x mx n =++过点 A (-1,a ),B (3,a ), ∴抛物线的对称轴x =1..……. 1分 ∵抛物线最低点的纵坐标为-4 , ∴抛物线的顶点是(1,-4)..……. 2分 ∴抛物线的表达式是22(1)4y x =--, 即2242y x x =--..…3分把A (-1,a )代入抛物线表达式,求出4a =..……. 4分(2)∵抛物线顶点(1,4)C -关于y 轴的对称点为点D ,∴(1,4)D --.求出直线CD 的表达式为4y =-. .……. 5分求出直线BD 的表达式为22y x =-,当1x =时,0y =..……. 6分 所以40t -<≤..……. 7分28.(1)①作图.……. 1分GF E BC(P )A DADE ∆(或PDE ∆).…….2分②过点P 作PN ∥AG 交CG 于点N ,交CD 于点M ,.…….3分∴CPM CAB ∠=∠.∵∠CPE =12∠CAB ,∴∠CPE =12∠CPN .∴∠CPE =∠FPN .∵PF CG ⊥,∴∠PFC =∠PFN =90°.∵PF =PF ,∴PFC ∆≌PFN ∆.∴CF FN =..…….4分 由①得:PME ∆≌CMN ∆.∴PE CN =.∴12CF CF PE CN ==..…….5分 (2)1tan 2α..…….7分29. (1)4;.…….2分(2)①直线21y x =+记为l ,过点M 作MH l ⊥,垂足为点H ,.…….3分 ∵EOF MHE ∆∆∽∴MH ME OFEF =,即71MH=.∴5MH =..…….4分.…….6分.…….8分6. 通州27. 解:(1)设抛物线解析式为2)1(-=x a y ,由抛物线过点)10(,A ,可得122+-=x x y ………..(2分) (2)如图:G F EC D A PNM1………………………………………..(5分)(3)-4<m<0 ………………………………………..(7分)28.(2)结论:成立. ………………………..(1分)(3)结论:成立.………………………..(2分)证明:过点E作EG∥BC交AB延长线于点G,……………..(3分)∵四边形ABCD为菱形,∴AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,…………………………..(4分)又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE=GE ,∴BG=CE,…………………………..(5分)又∵CF=AE,∴GE=CF,………………………………………..(6分)又∵∠BGE=∠ECF=60°,∴△BGE≌△ECF(SAS),∴BE=EF.………………………………………..(7分)29.(1)点D是线段AB的“邻近点”;…………………..(2分)(2)∵点H(m,n)是线段AB的“邻近点”,点H(m,n)在直线y=x-1上,∴n =m-1; ………………………………………..(3分)直线y=x-1与线段AB交于(4,3)①当m≥4时,有n=m-1≥3,又AB∥x轴,∴此时点H(m,n)到线段AB的距离是n-3,∴0≤n-3≤1,∴4 ≤m≤5,…………………………………..(4分)②当m≤4时,有n=m-1 ∴n≤3,又AB∥x轴,∴此时点H(m,n)到线段AB的距离是3-n,∴0≤3-n ≤1,∴ 3≤m ≤4, ………………………………………..(5分) 综上所述,3≤m ≤5; ………………………………………..(6分) (3)31b --≤≤+ ………………………………………..(8分)7. 石景山 27.解:(1)将()3,0A 代入,得1m =.∴抛物线的表达式为223y x x =--. (1)分B 点的坐标()1,0-. ………………2分(2)()222314y x x x =--=--.∵当21x -<<时,y 随x 增大而减小; 当13x ≤<时,y 随x 增大而增大, ∴当1x =,min 4y =-; ………………3分 当2x =-,5y =.∴y 的取值范围是45y -≤<.…………4分(3)当直线y kx b =+经过()1,0B -和点()4,2时,解析式为2255y x =+.…….…………… …5分 当直线y kx b =+经过()2,5--和点 ()4,2时,解析式为7863y x =-.………. ……………6分 结合图象可得,b 的取值范围是8235b -<<. ………….7分28.解:(1)正确画出图形. ……………1分(2)①CA FH DF =+.……………2分l证明:过点F 作FG ⊥CA 于点G . ……3分 ∵FH ⊥BA 于点H ,90A ∠=︒,FG ⊥CA , ∴四边形HFGA 为矩形. ∴AG FH =,FG ∥AB . ∴GFC EBC ∠=∠. ……………4分 由(1)和平移可知, ∠ECB =EBC ∠=∠GFC , ∠FDC =90A ∠=︒. ∴∠FDC =∠FGC =90°. ∵FC CF =,∴△FGC ≌△CDF .∴CG FD =. ………………………5分 ∴DF FH GC AG +=+.即DF FH AC +=. ……………6分②CA DF FH =-. ………………7分29.解:(1)()1,0D -.(2)连结,AO AC ,过点A 作AF y ⊥则5AC AO ==3145EF AE =∠=︒∴=∴∴在Rt AEB ∆AB = ∴在Rt ∆得,BC =∴所求“理想矩形”ABCD 面积为 AB BC ⨯=.……………………………………………………5分(3)“理想矩形”面积的最大值是5. ………………………………6分()()1,23,2D ---或. ………………………………8分图3G8. 平谷27.解:(1)∵抛物线y=ax2+x+c(a≠0)经过A(﹣1,0),B(2,0)两点,∴10420a ca c-+=⎧⎨++=⎩,解得12ac=-⎧⎨=⎩.∴抛物线为y=﹣x2+x+2①; (1)∴顶点D(12,94). (2)(2)如图,作EN∥BC,交y轴于N,过C作CM⊥EN于M,令x=0,得y=2,∴OC=OB=2.∴∠OCB=45°.∵EN∥BC,∴∠CNM=∠OCB=45°.∵CM⊥EN于M,∴∠CNM=∠CMN=45°.∴MN =CM=2.∴CN=1.∴直线NE的解析式为:把②代入①,解得1xy=⎧⎨=⎩∴E(1,2).(3)过E作EF⊥AB于F∴tan∠EOF=2,又∵tan∠α=2,∴∠EOF=∠α,∵∠EOF=∠EAO+∠AEO=∠α,∠EAO+∠EPO=∠α,∴∠EPO=∠AEO,∵∠EAO=∠P AE,∴△AEP∽△AOE, (5)∴AP AEAE AO=,∵AE AO∴AP=8,∴OP=7,∴()7,0P,由对称性可得,()'5,0P-∴()7,0P或()5,0-.28.解:(1)E (1)延长DA 到点E ,使AE =CN ,连接BE ∵∠BAD +∠C =180°. ∴∠EAB =∠C .又∵AB =BC ,AE =CN , ∴△ABE ≌△CBN . ∴∠EBA =∠CBN ,BE =BN .…………………………………………………………2 ∴∠EBN =∠ABC .∵∠ABC =80°,∠MBN =40°, ∴∠EBM =∠NBM =40°. ∵BM =BM ,∴△EBM ≌△NBM .∴EM =NM .…………………………………………………………………………3 ∴MN =AM +CN .……………………………………………………………………4 (2) (5)MN <AM+CN .................................................................................6 (31 (8)29.解:(112(2)由于二次函数2y x x k =--的图象开口向上,对称轴为1x =,……………………………………………………………………3 ∴二次函数22y x x k =--在闭区间[1,2]内,y 随x 的增大而增大.当x =1时,y =1, ∴k =2-.当x =2时,y =2, ∴k =2-.即图象过点(1,1)和(2,2)∴当1≤x≤2时,有1≤y≤2,符合闭函数的定义, ∴k =2-.……………………………………………………………………………4 (3)因为一次函数()0y kx b k =+≠是闭区间[],m n 上的“闭函数”,根据一次函数的图象与性质,有:(Ⅰ)当0k >时,即图象过点(m ,m )和(n ,n )mk b mnk b n+=⎧⎨+=⎩,……………………………………………………………………5 解得10k b =⎧⎨=⎩.∴y x =……………………………………………………………………………6 (Ⅱ)当0k <时,即图象过点(m ,n )和(n ,m )mk b n nk b m +=⎧⎨+=⎩,解得1k b m n =-⎧⎨=+⎩∴y x m n =-++,………………………………………………………………7 ∴一次函数的解析式为y x =或y x m n =-++.9. 门头沟 27.(本小题满分7分)(1)证明:∵ △= (m +1)2-4×(-1)×(m +2)=(m +3)2. ……………………………………………………………1分∵ m >0, ∴ (m +3)2>0, 即 △>0,∴ 原方程有两个不相等的实数根. (2)分 (2)解:∵ 抛物线抛物线y =-x 2+(m +1)x +(m +2)经过点(3,0),∴ -32+3(m +1)+(m +2)=0,………………………………………………3分 ∴ m =1.∴ y =-x 2+2x +3. (4)分(3)解:∵ y =-x 2+2x +3=-(x -1)2+4,∴ 该抛物线的顶点为(1,4).∴ 当直线y =k (x +1)+4经过顶点(1,4)时, ∴ 4=k (1+1)+4, ∴ k =0, ∴ y =4.∴ 此时直线y =k (x +1)+4与y 轴交点的纵坐标为 4. ………………………5分∵ y =-x 2+2x +3, ∴ 当x =0时,y =3,∴ 该抛物线与y 轴的交点为(0,3).∴ 此时直线y =k (x +1)+4与y 轴交点的纵坐标为 3. ………………………6分 ∴ 3<t ≤4. …………………………………………………………………7分28.(本小题满分7分)解:(1)DE. (1)分 (2)DE 、BF 、BP 三者之间的数量关系是BF +BP=DE . (2)分理由如下: ∵ ∠ACB =90°,D 是AB 的中点,∠A =30° ∴ DC =DB ,∠CDB =60°. ∵ 线段DP 绕点D 逆时针旋转60°得到线段DF , ∴ ∠PDF =60°,DP =DF . 又∵∠CDB =60°,∴ ∠CDB -∠PDB =∠PDF -∠PDB , ∴ ∠CDP =∠BDF . ∴ △D C P ≌△D B F .………………………………………………………3分∴ CP =BF .而 CP =BC -BP , ∴ BF +BP =BC ,……………………………………………………………4分在Rt △CDE 中,∠DEC =90°,∴ tan DEDCE CE∠=, ∴ CEDE , ∴ BC =2CEDE , ∴ BF +BP=DE ................................................................5分 (3)BF +BP =2DE tan α,BF -BP =2DE tan α. (7)分29.(本小题满分8分)解:(1)4,2a ; (2)分 (2)13; (3)分(3)① ∵ F 1的碟宽︰F 2的碟宽=2:1,∴12222:1a a =. ∵ a 1=13,∴ a 2=23 (4)分 又∵ 由题意得F 2的碟顶坐标为(1,1), (5)分 ∴ ()222113y x =-+ (6)分 ② F 1,F 2,...,F n 的碟宽的右端点在一条直线上;........................7分 其解析式为y =-x +5. (8)分10. 怀柔27.解:(1)∵二次函数y=(a-1)x 2+2x+1与x 轴有交点,令y=0,则(a-1)x 2+2x+1=0,∴=4-4(a-1)0∆≥,解得a ≤2. …………………………………1分. ∵a 为正整数. ∴a=1、2又∵y=(a-1)x 2+2x+1是二次函数,∴a-1≠0,∴a ≠1, ∴a 的值为2. ………………………………………2分(2)∵a=2,∴二次函数表达式为y=x 2+2x+1,将二次函数y=x 2+2x+1化成顶点式y=(x+1)2二次函数图象向右平移m 个单位,向下平移m 2+1个单位后的表达式为y=(x+1-m )2-(m 2+1).此时函数的顶点坐标为(m-1, -m 2-1). …………………………………4分 当m-1<-2,即m <-1时, x=-2时,二次函数有最小值-3, ∴-3=(-1-m )2-(m 2+1),解得32m =-且符合题目要求. ………………………………5分 当 -2≤m-1≤1,即-1≤m ≤2,时,当 x= m-1时,二次函数有最小值-m 2-1=-3,解得m =.∵m =-1≤m ≤2的条件,舍去.∴m =.……………………………………6分当m-1>1,即m >2时,当 x=1时,二次函数有最小值-3, ∴-3=(2-m )2-(m 2+1),解得32m =,不符合m >2的条件舍去. 综上所述,m 的值为32-……………………………………7分 28.解:(1)补全图形,如图1所示. …………………………… 1分(2)连接AD ,如图2.∵点D 与点B 关于直线AP 对称,∴AD=AB ,∠DAP = ∠BAP =30°.∵AB=AC, ∠BAC =60°. ∴AD=AC, ∠DAC =120°.∴2∠ACE+60°+60°=180°∴∠ACE =30°…………………………… 3分(3)线段AB,CE,ED 可以构成一个含有60°角的三角形. …………………………… 4分P E D C BAP E D C BA证明:连接AD,EB,如图3.∵点D与点B关于直线AP对称,∴AD=AB,DE=BE,可证得∠EDA= ∠E BA.∵AB=AC,AB=AD.∴AD=AC, ∴∠ADE= ∠ACE.∴∠ABE= ∠ACE.设AC,BE交于点F,又∵∠AFB= ∠CFE.∴∠B AC= ∠BEC=60°.∴线段AB,CE,ED可以构成一个含有60°角的三角形.………7分29. 解:(1)x=2.…………………………1分.(2)①C点坐标为: )…………………………3分.②由①C点坐标为: )再求得其它一个点C1),或(0,-2)等代入表达式y=kx+b,解得b=-2 k⎧⎪⎨=⎪⎩∴直线的表达式是2y=-.………………………5分.动点C运动形成直线如图所示.……………6分.EC≤<…………………………8分.FPCADE。
北京市怀柔区2015—2016年初一上期末质量检测数学试卷含答案

怀柔区2015—2016学年度第一学期初一期末质量检测数 学 试 卷 2016.1一、选择题(本题共30分,每小题3分)下列各题均有四个选项,其中只有一个..是符合题意的. 1.数轴上有A ,B ,C ,D 四个点,其中绝对值等于2的点是 A.点A B. 点B C. 点C D. 点D2. 飞机在飞行过程中,如果上升23米记作“+23米”,那么下降15米应记作 A .-8米 B . +8米 C .-15米 D .+15米3. 据统计,怀柔雁栖湖常年总库容量38300000立方米,将38300000用科学记数法表示为 A . 0.383×108B . 3.83×107C . 38.3×106D . 383×1054.如果x =12是关于x 的方程4x +m =3的解,那么m 的值是 A .1 B .12 C .-1 D . 12- 5.下列运算正确的是A .3x+4y=7xyB .6y 2-y 2=5 C .b 4+b 3=b 7D .4x -x=3x6. 如左下图所示的圆柱体从左面看是DCBA7.下列语句正确的是A .画直线AB =10厘米 B .画直线l 的垂直平分线C .画射线OB =3厘米D .延长线段AB 到点C ,使得BC =AB8. 如果23(2)0a b ++-=,那么代数式2016()a b +的值为A .5B .-5C .1D .-19. 一家商店把一种旅游鞋按成本价a 元提高50%标价,然后再以8折优惠卖出,则这种旅游鞋每双的售价是A .0.4a 元B .0.8a 元C .1.2a 元D .1.5a 元xD CB A 123–1–2–3O10. 按一定规律排列的一列数依次为:-3,8,-15,24,-35,…,按此规律排列下去,这列数中第n 个数(n 为正整数)应该是A .(2)n n +B .2(1)(2)n n -+ C .当n 为奇数时:(2)n n -+ ;当n 为偶数时:(2)n n + D .(1)n n -+二、填空题(本题共21分,每小题3分) 11. 单项式223x y -的系数是 ,次数是 . 12. 角度换算:2648′=_______.13.如果2a -b =-2,ab =-1,那么代数式3ab -4a +2b-5的值是_________.14.已知:如图,OB 是∠AOC 的角平分线,OC 是∠AOD 的角平分 线,∠AOB =35°,那么∠BOD 的度数为__________; 15.定义“*”是一种运算符号,规定a ﹡b=5a+4b+2015, 则(-4)﹡5的值为 .16. 某校七年级共有589名学生分别到北京博物馆和中国科技馆学参观,其中到北京博物馆的人数比到中国科技馆人数的2倍还多56人.设到中国科技馆的人数为x 人,可列方程为 .17. 学习直线、射线、线段和线段中点等内容之后,王老师请同学们交流这样一个问题:“射线OA 上有B ,C 两点,若OB=8,BC=2,点D 是线段OB 的中点,请你求出线段DC 的长.”张华同学通过计算得到DC 的长是6,你认为张华的答案是否正确 ,你的理由是 .三、解答题(本题共69分,第18-30题,每小题5分,第31题4分.) 18. 计算: 12(15)(23)--+-.19. 计算:533()(1)64⨯-÷-.20. 计算:32128(2)4-÷-⨯-. 21. 计算: 13116()64128-⨯-+-÷DCB AO22.先化简,再求值:222(22)(21)x x x x +----,其中12x =-. 23. 解方程:9753x x +=-.24. 解方程:2(35)3(12)x x x --=+-. 25.解方程:235132x x ---= . 26. 一辆货车在公路(直线CD )上由点C 向点D 方向行驶,村庄A ,B 分别位于道路CD 的两侧,司机师傅要在公路上选择一个货物的下货点.(1)请在CD 上确定一个下货点E ,使点E 到村庄A 的距离最近, 画出图形并写出画图的依据;(2)请在直线CD 上确定一点O ,使点O 到村庄A ,B 的距离之和最小,画出图形并写出画图的依据.27. 某校组织七年级学生步行到生存岛参加开放性科学实践活动,七(1)班的小明同学,因为身体原因,医生建议减少长步行,经家长和学校协商决定,小明由家长开车直接从家送到生存岛,已知学生的步行速度是每小时4千米,小明爸爸的车速是每小时36千米,学生从学校出发40分钟后,小明爸爸从家里开车出来,结果小明和同学们同时到达了生存岛,已知小明家到生存岛的路程是学校到生存岛路程的3倍,问学校到生存岛的路程是多少千米?28. 课堂上李老师把要化简求值的整式3323323(7 a -6 a b+3 a b) 3 a -6 a b+3 a b+10 a -3)-(-写完后,让王红同学顺便给出一组a 、b 的值,老师自己说答案,当王红说完:“a=38,b=-32”后,李老师不假思索,立刻就说出答案“3”.同学们莫名其妙,觉得不可思议,但李老师用坚定的口吻说:“这个答案准确无误”,亲爱的同学你相信吗?请你通过计算说出其中的道理.29.已知:如图, 70AOB ∠=︒,30AOC ∠=︒,OD 平分BOC ∠. 请依题意补全图形,并求AOD ∠的度数.BADCABOABO备用图30. (1)如图,已知点C 在线段AB 上,且AC=6cm ,BC=4cm ,点M 、N 分别是AC 、BC 的中点,求线段MN 的的长度.NMABC(2)对于(1)题,如果我们这样叙述:“已知点C 在直线AB 上,且AC=6cm ,BC=4cm ,点M ,N 分别是AC ,BC 的中点,求线段MN 的长度.”结果会有变化吗?如果有,求出结果;如果没有,说明理由. 31. 阅读下列材料:为落实开展社会大课堂活动,七年级(3)班李老师准备周六组织本班学生参观北京科技馆,要求学生周六早9:00准时在科技馆门前集合,然后集中买票参观.小强家离北京科技馆4公里,周六他准备乘出租车去,为了解北京出租车的计价方式,小强周五晚上在网上查到了现行北京市出租汽车价格标准:在仔细阅读标准后,小强准备周六早8:10分乘车,路上留出10分钟出租车时速低于12公里的堵车时间,这样在9:00之前一定能顺利到达科技馆.时间设计好后,经过计算小强向妈妈要30元打车钱,妈妈问他30元钱够吗?小强说:“我按上表计算了,30元钱还有几块钱的剩余呢.”下面是小强的分析与计算过程,请补充完整:(1)小强在计算所需出租车费用时,用到上表中的数字信息包括 .(2)路上堵车10分钟,小强计算这10分钟出租车的低速行驶费用是多少元?(3)小强说:“我按上表计算了, 30元钱还有几块钱的剩余呢.”请你计算小强的打车费用和剩余钱数.怀柔区2015—2016学年度第一学期初二期末质量检测数学试卷答案及评分参考 2016.1一、选择题(本题共30分,每小题3分)下列各题均有四个选项,其中只有一个..是符合题意的.二、填空题(本题共21分,每小题3分)三、解答题(本题共69分,第18-30题,每小题5分,第31题4分.) 18. 解:原式=12+15-23…………………………………… 4分 =4…………………………………… 5分19. 解:原式=54()27-⨯-…………………………………… 4分=107…………………………………… 5分20.解:原式=18844-÷-⨯ =11--…………………………………… 4分 =-2…………………………………… 5分21. 解:原式1316()86412=-⨯-+-⨯ ……………………………………………… 1分 13148()6412=-⨯-+- …………………………………………2分8364=-+ ………………………………………………………4分 24=- ………………………………………………………… 5分 22.解:原式=2224421x x x x +--++ ……………………………………2分=263x x +-………………………………………………………4分当12x =-时,原式=211()6()322-+⨯-- 1334=--234=-………………………… 5分 23.解:73x 59x +=-……………………2分104x =- …………………………3分∴25x =-……………………………4分∴25x =-是原方程的解. …………5分24.解:235312x x x -+=+- ………………2分 232315x x x -+=+-…………………3分 ∴1x =- ………………………………4分∴1x =-是原方程的解.…………………5分25.解:去分母,得 2(23)3(5)6x x ---=. …………………………… 1分 去括号,得 463156x x --+=.………………………………… 2分 移项,得 636415x x --=--. …………………………… 3分 合并同类项,得 913x -=-.…………………………………… 4分 系数化1,得 139x =.……………………………………… 5分 26.解:(1)如图.…………………… 1分过A 作CD 的垂线,垂足E 即为所确定到村庄A 距离最近的下货点. ………… 2分 依据是:垂线段最短. …………………… 3分 (2)如图,…………………… 4分 连接线段AB ,交CD 于点O , 则O 即为所确定的到村庄A ,B 的距离之和最小的点.依据是:两点之间线段最短. …………………… 5分 27. 解:设学校到生存岛的路程是x 千米,则小明家到生存岛的路程是3x 千米. ………………………… 1分 根据题意列方程,得34043660x x .………………………… 3分 解这个方程,得x=4. ………………………… 4分答:学校到生存岛的路程是4千米. ………………………… 5分 28.答:相信.道理如下:33233237 a -6 a b+3 a b 3 a +6 a b-3 a b-10 a +3 =3+原式=…………………………4分 因为,原式化简后的结果是一个确定的值3,与a 、b 的取值无关. 所以,不管a ,b 取什么值,答案都是3. ………………………… 5分D29.解:符合题意的图形有两个,如图1、图2,在图1中,∵70AOB ∠=︒,30AOC ∠=︒,∴40BOC AOB AOC ∠=∠-∠=︒.………………1分 ∵OD 平分BOC ∠,∴1202COD BOC ∠=∠=︒.…………………… 2分 ∴50AOD AOC COD ∠=∠+∠=︒.……………………………………… 3分在图2中,∵70AOB ∠=︒,30AOC ∠=︒,∴100BOC AOB AOC ∠=∠+∠=︒.……………4分 ∵OD 平分BOC ∠,∴1502COD BOC ∠=∠=︒.…………………… 2分 ∴ 20AOD COD AOC ∠=∠-∠=︒.………………3分综上,AOD ∠的度数为50︒或20︒. .30. 解:(1)∵AC=6cm ,点M 是AC 的中点,∴MC=3cm ;∵BC=4cm ,点N 是BC 的中点, ∴CN=2cm ;∴MC+CN=5cm.∴线段MN 的的长为5cm. ………………………… 2分 (2)分两种情况:第一种情况:当点C 在点B 的左侧时,解法同(1),线段MN 的长为5cm. …… 3分 第二种情况:当点C 在点B 的右侧时,如图所示: ∵AC=6cm ,点M 是AC 的中点,∴MC=3cm ; ∵BC=4cm ,点N 是BC 的中点, ∴CN=2cm ;∴MN=MC-CN=3-2=1cm.………………………… 4分∴综上,线段MN 的长为5cm 或1cm. ……………………… 5分 31.解:(1)3公里以内收费13元; 基本单价2.3元/公里;每5分钟早晚高峰期间加收2公里租价(不含空驶费), 早高峰为7:00(含)-9:00(不含);燃油附加费 1元/运次出租汽车收费结算以元为单位,元以下四舍五入. ……………………… 1分(2)4.6⨯2=9.29≈.……………………… 2分 (3)13+2.3+4.6⨯2+1=25.526≈,30-26=4答:小强的打车费用26元,剩余4元钱. ……………………… 4分ABOCD图2M N AC B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
怀柔区2015数学一模试题及答案9.如图,函数y=2x 和y=ax+4的图象相交于点A (m ,3),则不等式2x≥ax+4的解集为A .x≥ B. x≤3 C . x ≤ D .x ≥310.如图1,在等边△ABC 中,点E 、D 分别是AC ,BC 边的中点,点P 为AB 边上的一个动点,连接PE ,PD ,PC ,DE .设AP =x ,图1中某条线段的长为y ,若表示y 与x 的函数关系的图象大致如图2所示,则这条线段可能是图1中的A .线段PDB .线段PC C .线段PE D .线段DE二、填空题(本题共18分,每小题3分)11.函数y=1x-3中自变量x 的取值范围是_________________.12.请写出一个过一、三象限的反比例函数的表达式_________________.x y 图2O PE D C B A 图13.下面有五个图形,与其它图形众不同的是第个.14.如图,在矩形ABCD中,=,以点B为圆心,BC 长为半径画弧,交边AD于点E.若AE•ED=16,则矩形ABCD的面积为.15.当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为__________.16.2014年5月1日开始,北京市开始实施居民用水阶梯水价.具体方案如下:户年用水量180立方米(含)内,每立方米5元;181立方米至260立方米(含)内,每立方米7元;260立方米以上,每立方米9元.阶梯水价以日历年(每年1月1日到12月31日)为周期计算.小王家2014年4月30日抄表示数550立方米,5月1日起实施阶梯水价,6月抄表时因用户家中无人未见表,8月12日抄表示数706立方米,那么小王家本期用水量为立方米,本期用水天数104天,日均用水量为立方米. 如果按这样每日用水量计算,小李家今后每年的水费将达到元(一年按365天计算).三、解答题(本题共30分,每小题5分)17.如图,点C,D在线段BF上,AB DE∥,AB DF=,A F∠=∠.求证:BC DE=.FECBA①②③④⑤18. 计算:011(20152014)2cos 45()2--︒+19.解不等式组:240,3(1) 2.x x x -<⎧⎨+≥+⎩20.已知32a b =,求代数式2243(3)9a b a b a b ++-的值.21.列方程或方程组解应用题:为了培育和践行社会主义核心价值观,引导学生广泛阅读古今文学名著,传承优秀传统文化,我区某校决定为初三学生购进相同数量的名著《三国演义》和《红岩》.其中《三国演义》的单价比《红岩》的单价多28元.若学校购买《三国演义》用了1200元,购买《红岩》用了400元,求《三国演义》和《红岩》的单价各多少元.22.已知:关于x的一元二次方程2(41)330-+++=(k是整kx k x k月份工人工资总额(万股东总利润(万元)数).(1)求证:方程有两个不相等的实数根;(2)若方程的两个实数根都是整数,求k的值.四、解答题(本题共20分,每小题5分)23. 如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.(1)求证:四边形ADEF是平行四边形;(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.24.某公司有5个股东,每个股东的利润相同,有100名工人,每名工人的工资相同.2015年第一个季度工人的工资总额与公司的股东总利润情况见右表:该公司老板根据表中数据,作出了图1,并声称股东利润和工人工资同步增长,”.针对老板的说法,解决下列问题:(1)这三个月工人个人的月收入分别是万元;(2)在图2中,已经做出这三个月每个股东利润统计图,请你补出这三个月工人个人月收入的统计图;总额图个人收入图(3)通过完成第(1),(2)问和对图2的观察,你如何看待老板的说法?(用一两句话概括)25.如图,AB是⊙O的直径,C是弧AB的中点,D是⊙O的切线CN上一点,BD交AC于点E,且BA= BD.(1)求证:∠ACD=45°;26.阅读下面材料:CED CBA小聪遇到这样一个有关角平分线的问题:如图1,在△∠B ,CD 平分∠ACB ,.小聪思考:因为CD 平分∠ACB ,所以可在BC 边上取点E ,使EC=AC ,连接DE.这样很容易得到△DEC ≌△DAC ,经过推理能使问题得到解决(如图2).请回答:(1)△BDE 是_________三角形.(2)BC 的长为__________.参考小聪思考问题的方法,解决问题:如图3,已知△ABC 中,AB=AC, ∠A=20°,BD 平分∠ABC,BD=2.3,BC=2.求AD 的长.五、解答题(本题共22分,第27题7分,第28题7BCAB CACP分,第29题8分)27.在平面直角坐标系xOyx2+2x+1与x轴有交点,a(1)求a的值.(2)将二次函数y=(a-1)x2个单位,向下平移m2+1个单位,当-有最小值-3,求实数m的值.28.在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连接BD,CD,其中CD交直线AP于点E.(1)依题意补全图1;(2)若∠PAB=30°,求∠ACE的度数;(3)如图2,若60°<∠PAB<120°,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并证明.29. 对某种几何图形给出如下定义: 符合一定条件的动点所形成的图形,叫做符合这个条件的点的轨迹.例如,平面内到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆.(1)如图1,在△ABC 中,AB=AC ,∠BAC=90°,A(0,2),B 是x 轴上一动点,当点B 在x 轴上运动时,点CC DE ,且表达式(2)当△ABC是等边三角形时,在(1)的条件下,动点C形成的轨迹也是一条直线.①当点B运动到如图2的位置时,AC∥x轴,则C 点的坐标是.②在备用图中画出动点C形成直线的示意图,并求出这条直线的表达式.③设②中这条直线分别与x,y轴交于E,F两点,当点C在线段EF上运动时,点H在线段OF上运动,(不与O、F重合),且CH=CE,则CE的取值范围是.怀柔区2014—2015学年度中考模拟练习(一)数学试卷答案及评分参考三、解答题(本题共30分,每小题5分) 17.(本小题满分5分) 证明:∵ AB ∥DE∴ ∠B = ∠EDF ; 在△ABC 和△FDE 中A F AB DF B EDF ∠=∠⎧⎪=⎨⎪∠=∠⎩…………………………3分∴△ABC ≌△FDE (ASA),…………………4分 ∴BC=DE. …………………………………5分 18.解:原式=1+2+……………………………………4分 =1+=3+…………………………………………………………5分19. 解①得:x<2,…………………………………………………………2分解②得:x≥1-2,……………………………………………………4分所以不等式组的解集为:1-2≤x<2. ……………………………5分 20. 解:2243(3)9a b a b a b++- 43(3)(3)(3)a ba b a b a b +=++-433a b a b+=-……………………………………………3分∵32a b=, ∴23a b =. ………………………………………………4分∴原式=662aa a=--. ……………………………………5分21.解:设《红岩》的单价为x 元,则《三国演义》的单价为(x+28)元. ……………1分.由题意,得120040028x x=+……………………………………3分.解得x=14. ……………………………………4分. 经检验,x=14是原方程的解,且符合题意. ∴x+28=42.答:《红岩》的单价为14元,《三国演义》的单价为42元. ……………………5分. 22.(1)证明:△2(41)4(33)k k k =+-+2(21)k =-·………………………………………1分.∵2(41)330kx k x k -+++=是一元二次方程,∴k ≠0,∵k 是整数 ∴12k ≠即210k -≠. ∴△2(21)0k =->∴方程有两个不相等的实数根. ………………………………………2分(2)解方程得:x =……………………………………3分. ∴3x =或11x k=+………………………………………4分∵k 是整数,方程的根都是整数,∴k =1或-1…………………………………5分.四、解答题(本题共20分,每小题5分)23. (1)证明:∵BD 是△ABC 的角平分线, ∴∠ABD =∠DBE ,∵DE ∥AB , ∴∠ABD =∠BDE ,∴∠DBE =∠BDE ,∴BE=DE; ∵BE =AF ,∴AF=DE;∴四边形ADEF 是平行四边形. ………………………………………2分 (2)解:过点D 作DG ⊥AB 于点G ,过点E 作EH ⊥BD 于点H ,∵∠ABC =60°,BD 是∠ABC 的平分线,∴∠ABD =∠EBD =30°, ∴DG =BD =×4=2,………………………………………3分∵BE =DE ,∴BH =DH =2, ∴BE ==433,∴DE =433,………………………………………4分 ∴四边形ADEF 的面积为:DE •DG =833.………………………………………5分24. 解:(1)0,28,0.3,0.32. ……………………………3分(2)补图如右图: (4)分个人收入(万)股东(3)答案不唯一 (5)分25. (1)证明:∵C 是弧AB 的中点,∴弧AC=弧BC,∴AC=BC.∵AB 是⊙O 的直径, ∴∠ACB=90°,∴∠BAC=∠CBA=45°, 连接OC, ∵OC=OA, ∴∠AC0=45°. ∵CN 是⊙O 切线,∴∠OCD=90°,∴∠ACD=45°. ………………………………2分. (2) 解:作BH ⊥DC 于H 点,…………………………3分. ∵∠ACD=45°,∴∠DCB=135°, ∴∠BCH=45°,∵OB=2,∴BA= BD=4,AC= BC=. ∵BC=,∴BH= CH=2, 设DC=x,在Rt △DBH 中, 利用勾股定理:2222)24x ++=(,………4分. 解得:x=2-±(舍负的),∴x=2-+∴DC的长为:2-+分. 26.解:(1)△BDE 是等腰三角形. ………………………1分. (2)BC 的长为5.8.………………………………2分.653F ED A∵△ABC中,AB=AC, ∠A=20°,∴∠ABC=∠C= 80°,∵BD平分∠B.∴∠1=∠2= 40°,∠BDC= 60°,.在BA边上取点E,使BE=BC=2,连接DE,. ………………………3分则△DEB≌△DBC,∴∠BED=∠C= 80°,∴∠4=60°,∴∠3=60°,在DA边上取点F,使DF=DB,连接FE,…………………………4分则△BDE≌△FDE,∴∠5=∠1= 40°,BE=EF=2,∵∠A=20°,∴∠6=20°,∴AF=EF=2,∵BD=DF=2.3, ∴AD =BD+BC=4.3.…………………………5分.五、解答题(本题共22分,第27题7分,第28题7分,第29题8分)27.解:(1)∵二次函数y=(a-1)x2+2x+1与x轴有交点,令y=0,则(a-1)x2+2x+1=0,∴=4-4(a-1)0∆≥,解得a≤2. (1)分.∵a为正整数. ∴a=1、2又∵y=(a-1)x2+2x+1是二次函数,∴a-1≠0,∴a≠1,∴a的值为2. ………………………………………2分(2)∵a=2,∴二次函数表达式为y=x2+2x+1,将二次函数y=x2+2x+1化成顶点式y=(x+1)2二次函数图象向右平移m个单位,向下平移m2+1个单位后的表达式为y=(x+1-m)2-(m2+1).此时函数的顶点坐标为(m-1,-m2-1). …………………………………4分当m-1<-2,即m<-1时,x=-2时,二次函数有最小值-3,∴-3=(-1-m)2-(m2+1),解得3m=-且符合题目要2求. ………………………………5分当-2≤m-1≤1,即-1≤m≤2,时,当x= m-1时,二次函数有最小值-m2-1=-3,解得m=∵m=-1≤m≤2的条件,舍去.∴m=分当m-1>1,即m>2时,当x=1时,二次函数有最小值-3,∴-3=(2-m)2-(m2+1),解得3m=,不符合m>2的条件2舍去.综上所述,m的值为3-或2……………………………………7分F PC AD EP E D C B AP E D CB A 28.解:(1)补全图形,如图1所示. …………………………… 1分 (2)连接AD ,如图2.∵点D 与点B 关于直线AP 对称,∴AD=AB ,∠DAP = ∠BAP =30°.∵AB=AC, ∠BAC =60°. ∴AD=AC, ∠DAC =120°.∴2∠ACE+60°+60°=180°∴∠ACE =30°…………………………… 3分(3)线段AB,CE,ED 可以构成一个含有60°角的三角形. …………………………… 4分 证明:连接AD ,EB ,如图3. ∵点D 与点B 关于直线AP 对称,∴AD=AB ,DE=BE , 可证得∠EDA = ∠E BA .∵AB=AC,AB=AD. ∴AD=AC, ∴∠ADE ∴∠ABE = ∠ACE.设AC ,BE 交于点F,又∵∠AFB = ∠CFE.∴∠B AC = ∠BEC=60°.∴线段AB,CE,ED 可以构成一个含有60°角的三角形.………7分29. 解:(1)x=2. …………………………1分.(2)①C 点坐标为:,23()分. ②由①C 点坐标为: 2) 再求得其它一个点C -2)等 代入表达式y=kx+b ,解得b=-2k ⎧⎪⎨=⎪⎩∴直线的表达式是2y =- 动点C 运动形成直线如图所示. ……………6分.EC ≤<8分.。
