数值传热_数值传热学大作业3gg
数值传热课后学习题及答案(权威版)

习题 4-14
充分发展区的温度控制方程如下:
c
p
u
T x
1 r
r
(r
T r
)
对于三种无量纲定义 T Tw 、 T T 、 T Tw 进行分析如下
Tb Tw
Tw T
T Tw
1)由 T Tw 得: Tb Tw
T (Tb Tw ) Tw
由 T 可得:
T [(Tb Tw ) Tw ] Tb (1 ) Tw
x
x
x
x
T r
[(Tb
Tw ) Tw ] r
(Tb
Tw
)
r
(1 ) Tw r
由 Tb 与 r
无关、
与 x 无关以及
T x
、
T r
的表达式可知,除了 Tw 均匀的情况外,该无量
纲温度定义在一般情况下是不能用分离变量法的;
2)由 T T 得: Tw T
T (Tw T ) T
由 T 可得:
节点 3:
T2 4T3 75
求解结果:
T2 85 , T3 40
对整个控制容积作能量平衡,有:
qB Sx h f (T f T3 ) Sx 15 (20 40) 150 2 0
即:计算区域总体守恒要求满足
习题 4-5
在 4-2 习题中,如果 h 10 (T3 T f )0.25 ,则各节点离散方程如下:
coematrix(n,n)=A(1,n); if n>=2
coematrix(n,n-1)=-1*B(1,n); end if n<mdim
coematrix(n,n+1)=-1*C(1,n); end end %计算 D 矢量 D=(coematrix*T')'; %由已知的 A、B、C、D 用 TDMA 方法求解 T %消元 P(1,1)=C(1,1)/A(1,1); Q(1,1)=D(1,1)/A(1,1); for n=2:mdim P(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1)); Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end %回迭 Tcal(1,mdim)=Q(1,mdim); for n=(mdim-1):-1:1 Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n);
数值传热大作业

放置竖直孤立平板的二维围场内的空气流动与换热的数值分析(西安交通大学能源与动力工程学院,710049,西安)摘要:针对内部放置孤立平板的二维围场内的空气流动与换热问题,在稳态、常物性和壁面温度以及孤立平板温度恒定的条件下,采用SIMPLER算法,对围场内部的空气进行了流动与换热的数值模拟计算。
在瑞利数Ra=10000时,计算得到了二维围场内的流线、等温线以及热线。
关键词:SIMPLER算法、孤立平板、流线、等温线、热线Abstract:Inorder to investigate the fluxion and heat transfer of air in a 2D square enclosure with an isolated plate. SIMPLER algorithm was adopted based on the Reylonds conservation equations of the steady-state constant property laminar flow and a constant temperature of the isolated plate and the inner walls of the enclosure condition. Slove fluid velocity and temperature fields inthe enclosure for Ra=10000,and draw the diagrams of stream lines ,isotherms and heat lines.Key words:SIMPLER algorithm; isolated plate; stream lines; isotherms; heat lines主要符号表R瑞利数aP普朗特数rν空气运动粘度m2/sg重力加速度kg.m/s2 k空气导热系数W/(m℃) β空气体膨胀系数1/℃c空气比热容J/kg.℃pρ空气密度kg/(m3s)T金属板温度℃hT围场壁面温度℃c∆温差℃T一、引言封闭空腔内孤立物体自然对流换热是一个重要的研究课题,从某种角度讲,大空间自然对流是封闭腔内孤立物体自然对流的一个特例。
传热与流体数值计算大作业

大作业一、假设0,1x y≤≤的方腔内充满不可压缩流体,左、右、下壁面固定,上壁面以()22161u x x=--运动。
试求腔内的定常解。
(流体的物性取20℃的水。
同时,可以使用20℃的甘油作为对比)二、求解二维圆柱坐标中的Poisson-Nernst-Plack(PNP)方程,PNP方程来描述纳米孔内带电离子在浓度梯度及电场作用下的迁移行为和离子浓度分布。
具体方程如下所示:其中i=+/-,分别代表阴阳离子。
以及连续性方程:其中Φ是局域的电动势,c i表示i种离子的浓度,左侧边界上c+=10,c-=10,右侧边界上c+=1,c-=1。
j i表示离子流,D i为离子的扩散系数2×10-9,z i为离子的带电量,z i=1,T为溶液的温度,T=300。
e是电子电量1.602×10-19,ε0×εr=80,k B为波尔兹曼常数,k B=1.38×10-23。
边界上的电势Φ由高斯定律决定:对于带电的纳米孔壁(图中红色实线所示),有σs=σ(σ为纳米孔的表面电荷密度,数值为0.05);对于其余区域有σs=0。
离子流j i在边界上的法向分量为零,即,求解φ、浓度c i以及ij的场。
(备注:求解区域为一圆柱形区域,长度为1200,直径为d=10。
建议步骤:可首先猜想浓度场c+和c-,并求解电动势场φ,通过连续性方程修正离子流场ij)大作业要求:1-3人为一组,完成以上任选一题目。
最终截止时间为12月26日。
在最终截止时间之前可以提交1次,若不满意得分可以继续修改。
大作业以报告形式提交,内容至少包括计算域的网格划分、方程的离散化、边界条件的处理、计算收敛的判据、计算的结果、结果的图形化显式、结果分析等。
源代码作为附录附在报告的最后。
数值传热_数值传热学大作业3gg

数值传热学 2009-2010 学年第一学期大作业 3
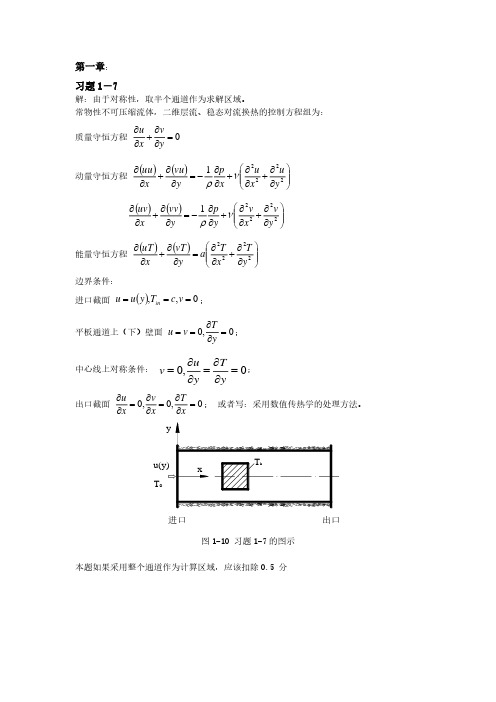
阶 梯 形 标 量 场 ( 长 宽 均 为 1 ) 的 纯 对 流 传 递 ( θ = 340 ), 控 制 方 程 为 u ∂φ + v ∂φ = 0 ,上游的边界条件都是第一类的,即给定了φ 的分布,下游按开
∂x ∂y 口边界的方式处理。
图 1 示意图
(2)从图中可以得知:数值计算在剧烈变化区域(y=0.5 处),采用 CD、 SUD、QUICK 格式时,产生越界现象。
(3)计算过程中采用 STOIC 格式,计算效果最好。 (4)采用不同的格式时,其表达式在 CBC 线内,则会出现稳定解,否则会 出现解得越界现象,越界现象与对流稳定性不同。 (5)编程过程中,采用 SOR 低松弛迭代方法,所得结果比较理想,计算速 度远远 Gauss—Seidel 方法。在本次作业中,松弛系数取为 0.8。 (6)编程过程中,要将边值点带入循环进行计算,否则会导致计算结果出 错。进而也证明了,对流现象是具有方向性,其扰动只能沿下游传播。
要求:
1、分别利用 FUD,CD,SUD,QUICK,CLAM,EULER,MINMOD,MUSCL,OSHER,SMART, STOIC 来离散对流项,观察它们的计算结果有何不同。 2、用延迟修正进行求解。 3、写出详细的离散过程和求解方法。 4、用 TECPLOT 软件画出整个流场中φ 的分布,并画出 y = 0.5 时,φ 随 x 的 分布。 5、编程采用 C/C++或 FORTRAN 语言。 6、将源程序附于作业之后,程序中要有详细的注释,以反映出思路。 7、源程序电子版和打印版上交时间:截止 2009 年 12 月 28 日。 8、每组交一份作业,给出每位同学的贡献度。(总和为 100%)
数值传热学--作业

数值传热学大作业—淬火过程的瞬态热分析专业:材料工程班级:研1303班学号:S2*******指导教师:孙斌煜姓名:李康一、问题描述某零件材料为45钢,按照国标GB/T6912-1999规定的45钢推荐热处理制度为840C 。
淬火.600C 。
回火,淬火介质为水,试计算零件温度随时间的我变化曲线和最后时刻的温度场云图 (1)45钢弹性模量:200GPa 泊松比:0.3质量密度:78503/m kg膨胀系数:15.5e-6m/C 。
比热:448C J kg / 导热系数:70()C m W .*/ (2)水 密度:9963/m kg 比热:4185C J kg / 导热系数:2()C m W .*/水沸腾对流换热系数:1200()C m W .*2/初始45钢温度840,水的初始温度为20C 。
,水槽宽1m,中间位零件最大截面60mm ,下图为淬火过程的零件截面。
图-1二、创建模型1.建立分析项目(1)在Windows系统下执行“开始”—“所有程序”—“ANSYS14.0”—“Mechanical APDL(ANSYS)14.0”命令,启动Mechanical APDL(ANSYS)14.0,进入主界面。
(2)选择热分析过滤菜单GUI:选择菜单Main Menu —Preprocessor,弹出分析项目对话框,选择Thermal 热分析,如图2 所示,完成后单击OK按钮结束。
2.更改分析名称和标题(1)改变工作项目标题GUI:File→Change Title,弹出对话框,输入“Thermal01”如下图,单击OK结束。
(2)更改项目名称GUI:File→Change Title,弹出对话框,输入“Thermal01”下方的复选框,如下图所示,完成单击OK完成。
3.创建材料模型要点:创建模型顺序依次为工件,水(1)添加导热系数GUI:Main Menu →Preprocessor→Material Prop→Material Models→Thermal→Conductivity→Isotropic,弹出对话框,输入导热系数70,如下图完成后单击OK 结束输入(2)添加比热容GUI:Main Menu →Preprocessor→Material Prop→Material Models→Thermal→Specific Heat.弹出比热容输入对话框,在文本框中输入工件比热容448,如下图,成后单击OK结束输入(3)添加密度GUI:Main Menu →Preprocessor→Material Prop→Material Models→Thermal→Density,弹出密度输入对话框,在文本框中输入工件比热容7785,如下图,成后单击OK结束输入(4)创建材料2依照上述步骤添加水的比热容4185,密度996,导热系数25.选择单元GUI:Main Menu →Preprocessor→Element type→add/Edit/Delete→add,弹出下图所示单元对话框,选择Thermal Solide的Quad 8node77单元,按OK键结束设置单元选项GUI:Main Menu →Preprocessor→Element type→add/Edit/Delete→add,弹出Element type对话框,单击对话框中的Option,弹出设置单元对话框,在单元形状K3文本框选择Plane Thickness,如下图,单击OK结束关闭对话框。
传热大作业-数值解法-清华-传热学

一维非稳态导热的数值解法一、导热问题数值解法的认识(一)背景所谓求解导热问题,就是对导热微分方程在规定的定解条件下的积分求解。
这样获得的解称为分析解。
近100年来,对大量几何形状及边界条件比较简单的问题获得了分析解。
但是,对于工程技术中遇到的许多几何形状或边界条件复杂的导热问题,由于数学上的困难目前还无法得出其分析解。
另一方面,在近几十年中,随着计算机技术的迅速发展,对物理问题进行离散求解的数值方法发展十分迅速,并得到日益广泛的应用。
这些数值方法包括有限差分法、有限元法及边界元法等。
其中,有限差分法物理概念明确,实施方法简便,本次大作业即采用有限差分法。
(二)基本思想把原来在时间、空间坐标系中连续的物理量的场,如导热物体的温度场,用有限个离散点上的值的集合来代替,将连续物理量场的求解问题转化为各离散点物理量的求解问题,将微分方程的求解问题转化为离散点被求物理量的代数方程的求解问题。
(三)基本步骤(1)建立控制方程及定解条件。
根据具体的物理模型,建立符合条件的导热微分方程和边界条件。
(2)区域离散化。
用一系列与坐标轴平行的网格线把求解区域划分成许多子区域,以网格线的交点作为需要确定温度值的空间位置,称为节点。
每一个节点都可以看成是以它为中心的一个小区域的代表,将小区域称之为元体。
(3)建立节点物理量的代数方程。
建立方法主要包括泰勒级数展开法和热平衡法。
(4)设立迭代初场。
(5)求解代数方程组。
(6)解的分析。
对于数值计算所获得的温度场及所需的一些其他物理量应作仔细分析,以获得定性或定量上的一些结论。
对于不符合实际情况的应作修正。
二、问题及求解(一)题目一厚度为0.1m 的无限大平壁,两侧均为对流换热边界条件,初始时两侧流体温度与壁内温度一致,1205f f t t t ===℃;已知两侧对流换热系数分别为h 1=11 W/m 2K 、h 2=23W/m 2K ,壁的导热系数λ=0.43W/mK ,导温系数a=0.3437×10-6 m 2/s 。
数值传热学 习题答案

数值传热学习题答案数值传热学习题答案数值传热学是热力学的一个重要分支,主要研究热量在物质中传递的机理和规律。
在实际工程中,我们经常会遇到各种与传热有关的问题,通过数值计算可以得到准确的答案。
下面我将为大家提供一些数值传热学习题的答案,希望能够帮助大家更好地理解和应用这门学科。
1. 一个铝制热交换器的表面积为10平方米,其表面温度为100摄氏度,环境温度为20摄氏度。
已知铝的导热系数为200 W/(m·K),求热交换器的传热速率。
答:根据传热定律,传热速率与传热面积、传热系数和温度差之间成正比。
传热速率 = 传热系数× 传热面积× 温度差。
将已知数据代入公式中,可得传热速率= 200 × 10 × (100 - 20) = 160,000 W。
2. 一个房间的尺寸为5米× 5米× 3米,墙壁和天花板的厚度为0.2米,墙壁和天花板的导热系数为0.5 W/(m·K),室内温度为25摄氏度,室外温度为10摄氏度。
求房间的传热损失。
答:房间的传热损失可以通过计算墙壁和天花板的传热速率来得到。
墙壁和天花板的传热速率 = 传热系数× 传热面积× 温度差。
墙壁和天花板的传热面积 = 2 × (5 × 5) + 2 × (5 × 3) = 70平方米。
将已知数据代入公式中,可得墙壁和天花板的传热速率= 0.5 × 70 × (25 - 10) = 525 W。
因此,房间的传热损失为525瓦特。
3. 一个水箱的体积为1立方米,初始温度为20摄氏度,水的密度为1000千克/立方米,比热容为4186 J/(千克·摄氏度),水箱的表面积为2平方米,表面温度为100摄氏度。
已知水的传热系数为0.6 W/(m^2·K),求水箱内水的温度随时间的变化。
数值传热学作业-第四章

4-1解:采用区域离散方法A 时;内点采用中心差分123278.87769.9T T T ===22d T T=0dx - 有 i+1i 122+T 0i i T T T x---=∆ 将2点,3点带入 321222+T 0T T T x --=∆ 即321209T T -+= 432322+T 0T T T x --=∆4321322+T 0T T T x --=∆ 即4321209T T T -+-= 边界点4(1)一阶截差 由x=1 1dT dx =,得 4313T T -=(2)二阶截差 11B M M q x x xT T S δδλλ-=++V所以 434111. 1.36311T T T =++即 43122293T T -=采用区域离散方法B22d TT=0dx - 由控制容积法 0w edT dT T x dT dT ⎛⎫⎛⎫--∆= ⎪ ⎪⎝⎭⎝⎭ 所以代入2点4点有322121011336T T T T T ----= 即 239028T T -=544431011363T T T T T ----= 即3459902828T T T -+= 对3点采用中心差分有432322+T 013T T T --=⎛⎫⎪⎝⎭即2349901919T T T -+= 对于点5 由x=11dT dx =,得 5416T T -= (1)精确解求左端点的热流密度由 ()21x x eT e e e -=-+所以有 ()2220.64806911x xx x dT e e q e e dxe e λ-====-+=-=++ (2)由A 的一阶截差公式210.247730.743113x T T dT q dxλ=-=-==⨯= (3)由B 的一阶截差公式0.216400.649213x dTq dxλ=-=-== (4)由区域离散方法B 中的一阶截差公式:210.108460.6504()B BT T dT dx x δ-⎛⎫==⨯= ⎪⎝⎭ 通过对上述计算结果进行比较可得:区域离散B 有控制容积平衡法建立的离散方程与区域离散方程A 中具有二阶精度的格式精确度相当!4-3解: 对平板最如下处理:1 2 3 4由左向右点分别表述为1、2、3、4点,x 的正方向为由左向右; 控制方程为λd 2tdx +S =0 (1)边界条件为X=0,T=75℃;X=0.1,λdTdx +ℎ(T −T f )=0;则2、3点采用二阶截差格式,有 则有以下两式:λT3−2T2+T1∆x+S=0(2)λT4−2T3+T2∆x2+S=0(3)一阶截差公式可由λdTdx+ℎ(T−T f)=0变形得到λ(T4−T3∆x)=h(T4−T f)再变形得到T4=[T3+h×∆xλT f]/(1+h×∆xλ)(4)二阶截差公式可以联立λT5−2T4+T3∆x2+S=0和λ(T5−T32∆x)=h(T4−T f),可得以下公式T4=[T3+∆x2S2λ+h×∆xλ]/(1+h×∆xλ)(5)分别联立2、3、4式与2、3、5式,把S=50×103W/m3,λ=10W/m∙℃,h=50 W/m∙℃,T f=25℃,T1=75℃,∆x= 1/30带入到式子中,则有联立2、3、4式的解为:T2=78.58℃,T3=76.59℃,T4=69.03℃联立3、4、5式的解为:T2=80.42℃,T3=80.28℃,T4=74.58℃对控制方程进行积分,并将边界条件带入,则有关于T的方程T=−2500x2+250x+75(6)把x2=130,x3=230,x3=0.1代入上述6式则有:T2=80.56℃,T3=80.56℃,T4=75.1℃相比之下,对右端点采用二阶截差的离散更接近真实值4-4解:对平板作如下分析:1 2 3 4 5 由左向右分别对点编号为1、2、3、4、5 控制方程与4-3相同,为λd 2tdx +S =0 (1)边界条件为X=0,T=75℃;X=0.1,λdTdx +ℎ(T −T f )=0;设1点和2点的距离为∆x ,另1点对2点进行泰勒展开,有d 2t dx =(T 1−T 2+dT dx ∆x )2∆x其中dT dx=T 3−T 22∆x,则有λ2T 1−3T 2+T 3∆x 2+S =0 (2)对3点进行离散有λT 4−2T 3+T 2∆x 2+S =0 (3)对右端点有: [a p +A 1ℎ+(δx )5λ]T 4=a w T 3+[S/∆x +AT f 1ℎ+(δx )5λ]代入数据有T 3−3T 2+155.56=0 T 4−2T 3+T 2=−5.56342.85T4-300T3=1681解得:T2=78.1℃,T3=78.7℃,T4=73.8℃由导热定律有T4−T3∆x =2T5−T4∆x则有T5=71.35℃4—12编写程序:M=rand(10,3)A=M(:,1);B=M(:,2);C=M(:,3);B(10)=0;C(1)=0;T=12:21;D(1)=A(1)*T(1)-B(1)*T(2)for i=2:9;D(i)= A(i)*T(i)-B(i)*T(i+1)-C(i)*T(i-1)endD(10)= A(10)*T(10)-C(10)*T(9);P(1)=B(1)/A(1);Q(1)= D(1)/A(1);for i=2:10;P(i)=B(i)/(A(i)-C(i)*P(i-1));Q(i)=(D(i)+C(i)*Q(i-1))/(A(i)-C(i)*P(i-1)); endfor i=10:-1:2;t(10)=Q(10);t(i-1)=P(i-1)*t(i)+Q(i-1);enddisp(D(1:10))disp(T(1:10))disp(t(1:10))运行结果:由运行结果可知:无论系数怎样变化,T与t都是一致的。
西安交通大学数值传热学大作业

5
数值传热学论文
能量方程: u 边界条件:
T T 2T 2T v ( 2 2 ) x y x y
T ( x, Tp ) T ( x,0)
(4)
(5) (6) (7) (8) (9) (10)
u( x, Tp ) u( x,0)
v( x, T v( x, 0 ) p )
图 2 网格划分
百叶窗翅片通道内周期性充分发展流动与换热的控制方程如下: 连续性方程: 动量方程: u
u v 0 x y
(1) (2) (3)
u u 1 p 2 u 2u v v( 2 2 ) x y x x y u v v 1 p 2v 2v v v( 2 2 ) x y y x y
2
数值传热学论文
主要符号表
f
Nu m
摩擦因数 平均 Nusselt 数 Prandtl(普朗特)数 雷诺数 竖直平板和封闭方腔壁面间的距离,热扩散系数(定义 u r ) 表面换热系数 导热系数 温度 平均温度 内部翅片的温度 W/(m2℃) W/(m℃) ℃ ℃ ℃ m/s m m m Pa W/m2
数值传热学论文
数值传热学大作业
1
数值传热学论文
百叶窗翅片流动换热的数值模拟
(西安交通大学能源与动力工程学院,710049,西安) 摘要: 针对具有一定倾斜角度的流动和换热已经进入周期性充分发展的百叶窗换 热问题,在稳态、层流、常物性和翅片温度恒定的条件下,采用 SIMPLER 算法, 对百叶窗的一个翅片单元进行了数值模拟计算。在翅片倾角θ =25°,雷诺数 Re 在 10 到 500 范围内变化时,得到了平均 Nusselt 数与阻力系数 f 的计算结果。计 算结果表明:随着 Re 的增大,平均 Nusselt 数逐渐增大,f 却随之逐渐减少。 关键词:百叶窗;周期性发展;数值模拟;SIMPLER 算法
数值传热学习题答案(汇总版)
2-4-9
= rP rS
式(2-4-9)也可以写成 a PTP = a E TE + aW TW + b 的形式。而且两种结果是一致的。
2—6:
n n TE −TW dT P , n = 解:将 , dx 2x n n TE −2TPn + TW d 2T P , n = , dx2 x 2
dk = f (x ) 代入原方程,得: dx
令
2-4-4
rk rk a E = , aW = , a P = a E + aW , b x w x e
= SrP r ,
式(2-4-4)可以写成 a PTP = a E TE + aW TW + b 的形式。 2. 再用 Taylor 展开法导出 k
2 2 uE + uP u = , 2 2 e
2 2 uW + uP u = 2 2 w
t u ut N − uP y = (y ) , n n
t
t ut u p − uS y = (y ) 。 s s
t
(y ) n = (y ) s = y
n n n n TE −TW TE −2TPn + TW k + f (x ) +S=0 整理得: 2x x 2
4kT P= 2k + xf ( x)T E+2k − xf ( x)T W +2x 2 S
− 2k 时, a E 会成为负值, x 2k 当 f(x)> 时, aW 会成为负值。 x
rk dr = rk r r dr dr dr
w
e
1 d
数值传热学

数值传热学数值传热又称计算传热,是传热学与数值方法相结合的一门交叉学科,它采用数值方法描述流动和传热问题的控制方程,并用计算机求解。
数值换热,其基本思想是将原始坐标在空间和时间上连续的物理量场(如速度场、温度场和浓度场等),用一系列有限个离散点上的数值来代替,通过一定的原理建立离散点变量值之间的关系代数方程(称为离散方程)。
通过求解所建立的代数方程组,得到求解变量的近似值。
1简介数值传热学(numerical heat transfer)数值传热学,又称计算传热学,是指对描写流动与传热问题的控制方程采用数值方法,通过计算机求解的一门传热学与数值方法相结合的交叉学科。
数值传热学的基本思想是把原来在空间与时间坐标中连续的物理量的场(如速度场,温度场,浓度场等),用一系列有限个离散点上的值的集合来代替,通过一定的原则建立起这些离散点变量值之间关系的代数方程(称为离散方程)。
求解所建立起来的代数方程已获得求解变量的近似值。
2发展简史数值传热学,主要由20世纪中叶,S.V. Patankar和D.B.Spalding 等人在总结前人的研究基础上所提出。
E.M.Sparrow对数值传热学的发展也起到了一定的促进作用。
国内比较知名的学者是陶文铨教授。
陶文铨3研究方法数值传热学常用的数值方法1.有限差分法历史上最早采用的数值方法,对简单几何形状中的流动与换热问题最容易实施的数值方法。
其基本点是:将求解区域中用于坐标轴平行的一系列网格的交点所组成的点的集合来代替,在每个节点上,将控制方程中每一个导数用相应的差分表达式来代替,从而在每个节点上,形成一个代数方程,每个方程中包括了本节点及其附近一些节点上的未知值,求解这些代数方程就获得了所需的数值解。
2.有限容积法将所计算的区域划分成一系列控制容积划分为一系列控制容积,每个控制容积都有一个节点做代表。
通过将守恒型的控制方程对控制容积坐积分导出离散方程。
在导出过程中,需要对界面上的被求函数本身及其一阶导数的构成做出假定,是目前流动与换热问题的数值计算中应用最广的一种方法。
数值传热学

平壁导热问题的有限差分解法摘要:在求解平壁导热问题时,应用分析解法,包括直接积分法和分离变量法,计算量都是相当巨大的,对于复杂的几何形状的物体和非线性边界条件下的导热问题,应用分析解法几乎是不可能。
在这种情况下,建立在有限差分法、有限元法和边界元法基础上的数值计算法是求解导热问题的十分有效的方法。
本文通过对一维非稳态平壁导热过程的微分方程进行离散,并采用有限差分法对其进行求解。
关键词:平壁导热 离散方程 有限差分一、 离散方程的建立方法建立离散方程基本上有两种方法,一种是泰勒级数展开法,另一种是热平衡法。
1、 泰勒级数展开法应用泰勒级数展开式,把导热微分方程中的各阶导数用相应的差分表达式来替代。
例如,用节点),(j i 的温度参数来表示节点),1(j i +的温度j i t ,1+时,根据泰勒级数展开式...!3)(!2)()(3,332,22,,,1+∆∂∂+∆∂∂+∆∂∂+=+x xt x x t x x t t t j i j i j i j i ji (1)归并上式中右边第三项以及以后的各个尾项,移项整理,可以得到节点),(j i 的温度对x 的一阶导数)(0)(,,1,x xt t x tj i j i j i ∆+∆-=∂∂+ (2)式中,)(0x ∆代表了二阶导数和更高阶导数项之和,称为截断误差。
它表示随着x ∆的趋近于零,用xt t ji j i ∆-+,,1来代替j i xt,)(∂∂时,截断误差小于或等于||x c ∆,此处,c 是与x 无关的正实数。
式(2)称为一阶截差公式。
类似地,可以用节点),(j i 的温度参数来表示节点),1(j i -的温度,它的泰勒级数展开式是 ...!3)(!2)()(3,332,22,,,1+∆∂∂-∆∂∂+∆∂∂-=-x x t x x t x x t t t j i j i j i ji j i (3) 同样的,只取式(3)右边前两项,归并右边第三项以及以后的各个尾项,移项整理可得)(0)(,1,,x xt t x tj i j i j i ∆+∆-=∂∂- (4)式(4)是节点),(j i 一阶导数的向后差分表达式,而式(2)节点),(j i 一阶导数的向前差分表达式,两者都是一阶截差公式。
数值传热学

数值传热学数值传热学是一门研究如何采用计算机技术模拟传热过程的学科。
它的出现,使得传热学在进行理论分析和数值计算方面更加具有实际意义。
以前要进行传热问题的求解,需要有丰富经验的工程师去积累相应的数据,而且也只能做到相对比较好的效果,这对于我们来说也并非难事,但是就目前情况来看,人工建立一个数值模型对于复杂的传热过程进行求解将会变得更加困难。
而且传统的工业过程模拟中大多都是依靠经验,但是这种经验往往又是片面的、偶然的。
因此,建立一个完整的数值传热学体系就成了当务之急。
然而数值传热学作为一门年轻的学科,它的许多思想都源于传热学的实际应用。
因此,对于传热学基础理论知识的掌握以及综合应用能力的培养对于该课程学习至关重要。
在教学过程中,除了注重学生自身素质的培养外,还应该结合教学内容,创新教学方法,在充分调动学生主观能动性的基础上,发挥他们的创造性思维,让学生参与其中。
另外,还可以借助多媒体教学等现代化教学手段,提高课堂效率,增强教学效果。
从而促进学生对于课程的理解,提升教学质量。
传统的传热学模型很难完全适用于现代化传热分析与设计。
针对于传热模型方面,首先,需要增加数值传热学模型,在原有的基础上引入新的概念和规则;其次,模型的编制需要精确考虑每一个单元模块之间的关联,在保证各个模块都能够单独准确地计算出结果的同时,还必须将他们联系起来。
例如,对于燃烧室内传热问题,由于温度的分布情况是非常复杂的,因此我们需要构造适当的网格进行相应的计算,将所有网格划分成细小的区域,再逐步地建立起燃烧室内温度场的整体结构,进而达到一个有效的、清晰的计算结果。
除此之外,计算结果的收敛速度和计算的精确度也是影响分析效率的两个主要因素。
但是随着对于这些相关领域研究人员的不断增多,一些技术已经可以得到大幅度的改善,甚至部分可以直接用于商业用途。
而计算流体力学( CFD)就是在计算机运算能力不断增强的基础上逐渐形成的一门新兴学科,它可以通过在计算机上建立一些专门的数学模型,利用计算机仿真软件进行求解,最终获取相应的物理图像或者曲线,帮助工程师快速地找到解决方案。
数值传热学第二章作业

数值传热学第二章作业2—1:POWER=input('POWER=?');L1=input('L1=?');M1=input('M1=?');XL=input('XL=?');YL=input('YL=?');for i=2:L1XF(i)=XL*((i-2)/(L1-2))^POWER;endfor j=2:M1YF(j)=YL*((j-2)/(M1-2))^POWER;endX(1)=0;for i=2:L1-1X(i)=(XF(i)+XF(i+1))/2;endX(L1)=XF(L1);Y(1)=0;for j=2:M1-1Y(j)=(YF(j)+YF(j+1))/2;endY(M1)=YF(M1);for j=2:M1-1plot(X(1),Y(j),'b.');plot(X(1),Y(2), 'b.');plot(X(L1),Y(j),'b.');hold onendfor i=2:L1-1for j=1:M1plot(X(i),Y(j),'b.');hold onendendfor i=2:L1m=[XF(i),XF(i)];n=[0,M1];plot(m,n,'b-.');hold onendfor j=2:M1m=[YF(j),YF(j)];n=[0,L1];plot(n,m,'b-.');hold onendxlabel('x');ylabel('y');title('POWER= ') 运行结果如下:2—3: 解:由2221()u2u u u xxyη∂∂∂===∂∂∂得:原方程的守恒形式为:222()2u u xyη∂∂=∂∂对方程两端在t ∆时间间隔内对其控制容积积分,把可积的部分积出后得:22()t tsne wtu u dtdy +∆-⎰⎰= 2t t e wtn s u u dtdx y y η+∆⎡⎤⎛⎫⎛⎫∂∂-⎢⎥ ⎪ ⎪∂∂⎝⎭⎝⎭⎣⎦⎰⎰选定2u 随y 而变化的型线,这里取为阶梯式,即在控制容积内沿y 方向不变,则2222()=y ()t tt ts ne we w ttu u dtdy u u dt +∆+∆-∆-⎰⎰⎰选定2u 随t 而变化的规律,这里采用阶梯式显式,则22()t te w ty u u dt +∆∆-⎰= ()()22t te w u u t y ⎡⎤-∆∆⎢⎥⎣⎦选定u y∂∂随x 而变化的型线,这里取为阶梯式,即在控制容积内沿x方向不变,则22t t t t ewtt n s n s u u u u dtdx x dt y y y y ηη+∆+∆⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂∂-=∆-⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎰⎰⎰选定u y∂∂随t 而变化的规律,这里采用阶梯显式,则2t t tn s u u x dt y y η+∆⎡⎤⎛⎫⎛⎫∂∂∆-⎢⎥ ⎪ ⎪∂∂⎝⎭⎝⎭⎣⎦⎰= 2t t n s u u t xy y η⎡⎤⎛⎫⎛⎫∂∂-∆∆⎢⎥ ⎪ ⎪∂∂⎢⎥⎝⎭⎝⎭⎣⎦进一步选取u 随x,y 分段线性变化,则2222E Pe u u u +=, 222w 2W Pu u u +=()nt Pt N ty u u y u δ-=⎪⎪⎭⎫ ⎝⎛∂∂n , ()stS t p ts y u u yu δ-=⎪⎪⎭⎫ ⎝⎛∂∂。
数值传热大作业报告

目录一、物理问题的描述及分析 (2)二、离散过程及算法分析 (2)2.1 离散过程………………………………………………………………………………...错误!未定义书签。
2.2 算法分析……………………………………………………………………...................错误!未定义书签。
装三、结果演示 (2)四、结论 (11)五、心得体会 (11)六、附件 (12)订线一、物理问题的描述及分析对如图所示的二维方腔顶盖驱动流问题,顶盖拖动速度为u top ,方腔的长度和高度均为H ,流体密度为ρ、动力粘度为μ。
流动与传热的控制方程如下:0u v x y∂∂+=∂∂ 22221u u u p u u u v t x y x x y μρρ⎛∂∂∂∂∂∂++=-++ ∂∂∂∂∂∂⎝其中,u 、v 分别为x 、y 方向速度分量,p 为压力。
用高度H 、流体密度ρ和拖动速度u top 作为无量纲标尺,将控制方程无量纲化,流场初始状态为静止,Re =1000 (top u HRe ρμ=),求流动达到稳定状态时,x 方向中垂线(/2x H =)上的无量纲速度U x ,y 方向中垂线(/2y H =)上的无量纲速度V ,绘制出速度分布曲线 ;绘出压力场、速度场。
二、离散过程及算法分析2.1 离散过程无量纲化后的控制方程:0U VX Y∂∂+=∂∂ (1) 22221Re U U U P U U U V X Y X X Y τ⎛⎫∂∂∂∂∂∂++=-++ ⎪∂∂∂∂∂∂⎝⎭ (2) 22221Re V V V P V V U V X Y Y X Y τ⎛⎫∂∂∂∂∂∂++=-++ ⎪∂∂∂∂∂∂⎝⎭(3) 利用有限差分,同位网格方法对其进行离散,空间项采用中心差分,速度用显式,压力用隐式:u22221v v v p v v u v t x y y x y μρρ⎛∂∂∂∂∂∂++=-++ ∂∂∂∂∂∂⎝1,,n ni j i jU U U ττ+-∂=∂∆ (4a ) 1,1,,2n n i j i j n i j U U U U U X X +--∂=∂∆;,1,1,2n ni j i j n i j U U U V V Y Y+--∂=∂∆ (4b ) 111,,n n i j i jP P P X X+++-∂-=-∂∆ (4c ) 21,,1,222n n n i j i j i j U U U U X X +--+∂=∂∆;2,1,,1222n n ni j i j i j U U U U Y Y +--+∂=∂∆ (4d ) 以下对边界邻点进行特殊处理:U 的左边界邻点:()1,,1,2,343i j i j i ji jU U U UO X X X+-+-∂=+∆∂∆ ()21,,1,2,2281243i j i j i ji jU U U U O X X X -+-+∂=+∆∂∆U 的右边界邻点:()1,,1,2,433i j i j i ji jU U U U O X X X+---∂=+∆∂∆ ()21,,1,2,221283i j i j i ji jU U U U O X X X-+-+∂=+∆∂∆U 的下边界邻点:(),1,,12,343i j i j i j i jU U U U O Y Y Y+-+-∂=+∆∂∆ ()2,1,,12,2281243i j i j i j i jU U U U O Y Y Y -+-+∂=+∆∂∆U 的上边界邻点:(),1,,12,433i j i j i j i jU U U U O Y Y Y+---∂=+∆∂∆ ()2,1,,12,221283i j i j i j i jU U U U O Y Y Y-+-+∂=+∆∂∆同理,可以写出V 的边界邻点的表达式,这里不再赘述。
数值传热学大作业

数值传热学大作业燃烧室出口换热与流动的数值模拟学院专业班级学号姓名燃烧室出口换热与流动的数值模拟摘要:本文针对稳态、层流、常物性的燃烧室出口的换热与流动问题,采用商业软件FLUENT 进行了数值模拟。
通过数值模拟,本文得到了温度分布和速度分布,计算得到三种流体各自的换热量以及漏斗状壁面两侧烟气和空气的局部的表面对流换热系数。
1物理问题描述某圆柱形燃烧室出口截面结构如图1-1所示,燃烧产生的高温烟气从燃烧室流出后在图1标号为①的位置进入图中漏斗结构,最终从②流出。
冷却水从标号为⑤的位置进入“水套”结构,由⑥流出;常温空气从标号为③的位置流入空气流道,分别与高温烟气和冷却水发生热交换,最终从④流出。
图1-1 燃烧室出口结构:①烟气入口;②烟气出口;③空气流道入口;④空气流道出口⑤冷却水入口;⑥冷却水出口表1给出了该结构的几何参数,漏斗状的结构(图1中标号为A的结构)、水套(图1中标号为B的结构)的壁厚均为5mm,材料为钢,过程是稳态。
给定工况和给定的流体参数如表2所示:表2 工质工矿与流体参数为了方便计算,在数值模拟中,本文做了一些假设:(1)流体的物性都是固定的;(2)流体中的粘性耗散度忽略不计;(3)流动及换热处于稳态、层流、充分发展状态;(4)假设流体流动过程中不存在热辐射的情况。
2控制方程及求解方法考虑几何对称性,将问题简化为一个2D模型,则该问题中的控制方程如下。
连续性方程:动量方程:能量方程:本文采用了SIMPLE算法进行求解。
SIMPLE算法自1972年问世以来在世界各国计算流体力学及计算传热学界得到了广泛的应用,这种算法提出不久很快就成为计算不可压流场的主要方法,随后这一算法以及其后的各种改进方案成功的推广到可压缩流场计算中,已成为一种可以计算任何流速的流动的数值方法。
SIMPLE 算法的基本假设:速度场的假定与压力场的假定各自独立进行,二者无任何联系。
对假定压力场的修正通过已求解的速度场的质量守恒条件得到。
西安交通大学西安交通大学《《《《数值传热学数值传热学

西安交通大学西安交通大学《《《《数值传热学数值传热学西安交通大学西安交通大学《《数值传热学数值传热学》》课程大作业20140114一. 题目(1)百叶窗翅片的二维模型如图1 所示。
在流动与换热已经进入周期性充分发展的阶段,可以取出一个翅片单元进行传热与流动阻力的分析计算。
在稳态,层流,常物性,翅片温度恒定的条件下,对于表1给定的几何尺寸,进行Re =10-500 范围内的数值模拟,揭示每个计算单元的平均Nu 数与阻力系数f 与Re 的关系;Nu ,f 以及Re 定为:112()Re ;;0.5pm m m dp dx L u L h L f Nu u νρλ==?=其中m u 为来流平均速度;m h 为每块条片的平均换热系数。
表1 几何参数L1/mmTp/mm Lp/mm Delta/mm /θ 30 18.6 30 1.5 25图1 百叶窗翅片二维模型图2 阶梯型逼近二. 建议建议与要求与要求1. 为便于处理流固耦合问题,计算可对图1中打阴影线的区域进行;2. 可采用图2 所示的阶梯型网格处理倾斜的翅片;3. 按照《西安交通大学学报》的论文格式撰写本报告;4. 2014年4月30号前交课程论文到东三楼204房间。
三. 参考文献[1] 陶文铨编著,数值传热学(第二版),2001,西安交通大学出版社,节11.2[2] Wang L B, Tao, W Q. Numerical analysis on heat transfer and fluid flow for arrays of non-uniform plate length aligned at angles to the flow direction. Int J Numerical Methods for Heat and Fluid Flow , 1997, 7(5,6):496[3] Gong L. Li Z Y, He Y L, Tao W Q. Discussion on numerical treatment of periodic boundary condition for temperature. Numerical Heat Transfer, Part B , 2007, 52(5):429-448。
数值传热学习题答案权威版

数值传热学习题答案权威版习题4-2⼀维稳态导热问题的控制⽅程:022=+??S xTλ依据本题给定条件,对节点2节点3采⽤第三类边界条件具有⼆阶精度的差分格式,最后得到各节点的离散⽅程:节点1: 1001=T 节点2: 1505105321-=+-T T T 节点3:75432=+-T T 求解结果:852=T ,403=T对整个控制容积作能量平衡,有:02150)4020(15)(3=?+-?=?+-=?+x S T T h x S q f f B即:计算区域总体守恒要求满⾜习题4-5在4-2习题中,如果25.03)(10f T T h -?=,则各节点离散⽅程如下:节点1: 1001=T节点2: 1505105321-=+-T T T节点3:25.03325.032)20(4015])20(21[-?+=-?++-T T T T对于节点3中的相关项作局部线性化处理,然后迭代计算;求解结果:818.822=T ,635.353=T (迭代精度为10-4)迭代计算的Matlab 程序如下: x=30; x1=20;while abs(x1-x)>0.0001a=[1 0 0;5 -10 5;0 -1 1+2*(x-20)^(0.25)]; b=[100;-150; 15+40*(x-20)^(0.25)]; t=a^(-1)*b; x1=x; x=t(3,1); endtcal=t习题4-12的Matlab程序%代数⽅程形式A i T i=C i T i+1+B i T i-1+D imdim=10;%计算的节点数A=cos(x);%TDMA的主对⾓元素B=sin(x);%TDMA的下对⾓线元素C=cos(x)+exp(x); %TDMA的上对⾓线元素T=exp(x).*cos(x); %温度数据%由A、B、C构成TDMAcoematrix=eye(mdim,mdim);for n=1:mdimcoematrix(n,n)=A(1,n);if n>=2coematrix(n,n-1)=-1*B(1,n);endif ncoematrix(n,n+1)=-1*C(1,n);endend%计算D⽮量D=(coematrix*T')';%由已知的A、B、C、D⽤TDMA⽅法求解T%消元P(1,1)=C(1,1)/A(1,1);Q(1,1)=D(1,1)/A(1,1);for n=2:mdimP(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1));Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end%回迭Tcal(1,mdim)=Q(1,mdim);for n=(mdim-1):-1:1Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n);endTcom=[T;Tcal];%绘图⽐较给定T值和计算T值plot(Tcal,'r*')hold on结果⽐较如下,由⽐较可知两者值⾮常切合(在⼩数点后8位之后才有区别):习题4-14充分发展区的温度控制⽅程如下:)(1rTr r r x T uc p =??λρ对于三种⽆量纲定义w b w T T T T --=Θ、∞∞--=ΘT T T T w 、ww T T T T --=Θ∞进⾏分析如下1)由wb wT T T T --=Θ得:w w b T T T T +Θ-=)(由T 可得:x T x T x T T T x T w b w w b ??Θ-+??Θ=?+Θ-?=??)1(])[(rT r T T r T T T r T w w b w w b ??Θ-+?Θ?-=?+Θ-?=??)1()(])[( 由b T 与r ⽆关、Θ与x ⽆关以及x T ??、rT的表达式可知,除了w T 均匀的情况外,该⽆量纲温度定义在⼀般情况下是不能⽤分离变量法的; 2)由∞∞--=ΘT T T T w 得: ∞∞+Θ-=T T T T w )(由T 可得:xT x T T T x T w w ??Θ=?+Θ-?=??∞∞])[(rx T ??、rT的表达式可知,在常见的四种边界条件中除了轴向及周向均匀热流const q w =的情况外,有0=??rT w,则该⽆量纲温度定义是可以⽤分离变量法的; 3)由wwT T T T --=Θ∞得: w w T T T T +Θ-=∞)(由T 可得:xT x T T T x T w w w ??Θ-=?+Θ-?=??∞)1(])[(rT r T T r T T T r T w w w w ??Θ-+?Θ-=+Θ-?=??∞∞)1()(])[( 同2)分析可知,除了轴向及周向均匀热流const q w =温度定义是可以⽤分离变量法的;习题4-181)采⽤柱坐标分析,写出统⼀的稳态柱坐标形式动量⽅程:S r r r r r r x x w r v r r r u x +++=??+??+??)(1)(1)()(1)(1)(θφλθφλφλφρθφρφρ x 、r 和θ分别是圆柱坐标的3个坐标轴,u 、v 和w 分别是其对应的速度分量,其中x 是管内的流动⽅向;对于管内的层流充分发展有:0=v 、0=w ,0=??xu;并且x ⽅向的源项:x pS ??-=r ⽅向的源项:r pS ??-=r S 1由以上分析可得到圆柱坐标下的动量⽅程: x ⽅向:0)(1)(1=??-+x pu r r r u r r r θλθλ r ⽅向:0=??r pθ⽅向:0=??θp边界条件: R r =,0=u0=r ,0=??r u ;对称线上,0=??θu不考虑液体的轴向导热,并简化分析可以得到充分发展的能量⽅程为:)(1)(1θλθλρ+=??Tr r r T r r r x T uc p 边界条件: R r =,w q r T =??λ;0=r ,0=??rTπθ/0=,0=??-θλT2)定义⽆量纲流速:dxdp R uU 2-=λ并定义⽆量纲半径:R r /=η;将⽆量纲流速和⽆量纲半径代⼊x ⽅向的动量⽅程得:0))1((1))1((122=??-?-+?-xp U dx dp R R R R U dx dp R RR R θληλθηηλληηη上式化简得:ηθηηηηηU U 边界条件:1=η,0=U0=η,0=??ηU;对称线上,0=??θU 定义⽆量纲温度:λ/0R q T T b -=Θ其中,0q 是折算到管壁表⾯上的平均热流密度,即:Rq q wπ=0;由⽆量纲温度定义可得:b T Rq T +Θ=λ将T 表达式和⽆量纲半径η代⼊能量⽅程得:)(1)(100θληλθηηλληηηρ?Θ+?Θ=??R q R R R R q R R R x T uc b p 化简得:)1(1)(10θηθηηηηηρ?Θ+?Θ=??x T u c q R b p (1)由热平衡条件关系可以得:mm m b m p b p p RU U q R u u R q A u u dx dT A u c x T u c x T u c 020221221)(===??=??ππρρρ将上式代⼊式(1)可得:)1(1)(12θηθηηηηη?Θ+?Θ=m U U 边界条件:0=η,0=?Θ?η;1=η,R q q w πη10==?Θ?0=?Θ?θ;πθ=,0=?Θθ单值条件:由定义可知:0/0=-=ΘλR q T T b b b 且: ??Θ=ΘAAb U d AU d A 即得单值性条件:0=Θ??AA UdAUdA3)由阻⼒系数f 及Re 定义有:228)(2/Re ??? ??=-=D D U D u u dx dp D f e m e m me νρ且:m W b m W b m W R q T T D T T q Nu ,0,,0~2)/(2Θ=-=-=λλ5-21.⼀维稳态⽆源项的对流-扩散⽅程如下所⽰:xx u 22??Γ=??φφρ(取常物性)边界条件如下:L L x x φφφφ====,;,00上述⽅程的精确解如下:11)/(00--=--?PeL x Pe L e e φφφφΓ=/uL Pe ρ 2.将L 分成20等份,所以有:=P Pe 201 2 3 4 5 6 ………… …………… 17 18 19 20 21 对于中⼼差分、⼀阶迎风、混合格式和QUICK 格式分别分析如下: 1)中⼼)5.01()5.01(11-?+?++-=i i i P P φφφ 20,2 =i2)⼀阶迎风中间节点: ?-?++++=P P i i i 2)1(11φφφ 20,2 =i3)混合格式当1=?P 时,中间节点:2)5.01()5.01(11-?+?++-=i i i P P φφφ20,2 =i当10,5=?P 时,中间节点: 1-=i i φφ 20,2 =i 4) QUICK 格式*12111)35(8122121---++++++=+--??-??+?i i i i i i i P P P P P φφφφφφφ 2≠i *1111)336(8122121--++++++=+-?-??+?i i i i i i P P P P P φφφφφφ 2=i数值计算结果与精确解的计算程序如下:%except for HS, any other scheme doesnt take Pe<0 into consideration %expression of exact solution y=dsolve('a*b*Dy=c*D2y','y(0)=y0,y(L)=yL','x')y=subs(y,'L*a*b/c','t')y=simple(subs(y,'a*b/c*x','t*X'));ysim=simple(sym(strcat('(',char(y),'-y0)','/(yL-y0)')))y=sym(strcat('(',char(ysim),')*(yL-y0)','+y0'))% in the case of Pe=0y1=dsolve('D2y=0','y(0)=y0,y(L)=yL','x')%grid Pe numbertt=[1 5 10];%dimensionless lengthm=20;%mdim is the number of inner nodemdim=m-1;X=linspace(0,1,m+1);%initial value of variable during calculationy0=1;yL=2;%cal exact solutionfor n=1:size(tt,2)t=m*tt(1,n);if t==0yval1(n,:)=eval(y1);elseyval1(n,:)=eval(y);endend%extra treatment because max number in MATLAB is 10^308 if max(isnan(yval1(:)))yval1=yval1';yval1=yval1(:);indexf=find(isnan(yval1));for n=1:size(indexf,1)if rem(indexf(n,1),size(X,2))==0yval1(indexf(n),1)=yL;elseyval1(indexf(n),1)=y0;endendyval1=reshape(yval1,size(X,2),size(yval1,1)/size(X,2));yval1=yval1';endd=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*tt(1,n))*y0;d(n,mdim)=0.5*(1-0.5*tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval2=TDMA(a,b,c,d,mdim);yval2=[repmat([1],size(tt,2),1),yval2,repmat([2],size(tt,2),1)]; Fig(1,X,yval1,yval2,tt); title('CD Vs. Exact Solution')% FUS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval3=TDMA(a,b,c,d,mdim);yval3=[repmat([1],size(tt,2),1),yval3,repmat([2],size(tt,2),1)]; Fig(2,X,yval1,yval3,tt); title('FUS Vs. Exact Solution')% HS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);t=tt(1,n);if t>2b(n,:)=repmat([0],1,mdim);c(n,:)=repmat([1],1,mdim);d(n,1)=y0;elseif t<-2b(n,:)=repmat([1],1,mdim);c(n,:)=repmat([0],1,mdim);d(n,mdim)=yL;elseb(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*t)*y0;d(n,mdim)=0.5*(1-0.5*t)*yL;endendc(:,1)=0;b(:,mdim)=0;% numerical cal by using TDMA subfuctionyval4=TDMA(a,b,c,d,mdim);yval4=[repmat([1],size(tt,2),1),yval4,repmat([2],size(tt,2),1)]; Fig(3,X,yval1,yval4,tt); title('HS Vs. Exact Solution')%QUICK Solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval5=zeros(size(tt,2),mdim);yval5com=yval5+1;counter=1;%iterativewhile max(max(abs(yval5-yval5com)))>10^-10if counter==1yval5com=TDMA(a,b,c,d,mdim);endfor nn=1:size(tt,2)for nnn=1:mdimif nnn==1d(nn,nnn)=((6*yval5com(nn,nnn)-3*y0-3*yval5com(nn,nnn+1))*tt(1,nn))/(8*(2+tt(1, nn)))+((1+tt(1,nn))/(2+tt(1,nn))*y0);elseif nnn==2d(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-y0)*tt (1,nn))/(8*(2+tt(1,nn)));elseif nnn==mdimd(nn,nnn)=((5*yval5com(nn,nnn)-3*yL-yval5com(nn,nnn-1)-yval5com(nn,nnn-2))*tt (1,nn))/(8*(2+tt(1,nn)))+(1/(2+tt(1,nn))*yL); elsed(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-yval5 com(nn,nnn-2))*tt(1,nn))/(8*(2+tt(1,nn))); endendendyval5=TDMA(a,b,c,d,mdim);temp=yval5;yval5=yval5com;yval5com=temp;counter=counter+1;endyval5=yval5com;yval5=[repmat([1],size(tt,2),1),yval5,repmat([2],size(tt,2),1)];Fig(4,X,yval1,yval5,tt);title('QUICK Vs. Exact Solution')%-------------TDMA SubFunction------------------function y=TDMA(a,b,c,d,mdim)%form a b c d resolve yval2 by using TDMA%eliminationp(:,1)=b(:,1)./a(:,1);q(:,1)=d(:,1)./a(:,1);for n=2:mdimp(:,n)=b(:,n)./(a(:,n)-c(:,n).*p(:,n-1));q(:,n)=(d(:,n)+c(:,n).*q(:,n-1))./(a(:,n)-c(:,n).*p(:,n-1));end%iterativey(:,mdim)=q(:,mdim);for n=(mdim-1):-1:1y(:,n)=p(:,n).*y(:,n+1)+q(:,n);end%-------------ResultCom SubFunction------------------ function y=ResultCom (a,b,c)for n=1:max(size(c,2))y(2*n-1,:)=a(n,:);y(2*n,:)=b(n,:);end%-------------Fig SubFunction------------------ function y=Fig(n,a,b,c,d)figure(n);plot(a,b);hold onplot(a,c,'*');str='''legend(';for n=1:size(d,2)if n==size(d,2)str=strcat(str,'''''Pe=',num2str(d(1,n)),''''')''');elsestr=strcat(str,'''''Pe=',num2str(d(1,n)),''''',');endendeval(eval(str));精确解与数值解的对⽐图,其中边界条件给定10=φ,2=L φ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
=
1 2)
(1 +
) φC
)
= φC
0
≤
) φC
≤
1 2
1 2
≤
) φC
≤1
其它范围
)) φf = 2φC
MUSCL:
=
1 4
+
) φC
=1 )
= φC
0
≤
) φC
≤
1 4
1 4
≤
) φC
≤
3 4
3 4
≤
) φC
≤
1
其它范围
) φf
=
3 2
) φC
OSHER: = 1 )
= φC
0
≤
) φC
≤
2 3
五、心得体会
通过此次大作业,我们认识到大家合作的重要性,同时也锻炼了我们共同处
理问题的能力。此次作业中遇到了很困惑的一个问题,就是一开始采用规正变量 后得不到收敛解,原因是计算规正变量时分母会出现为 0 的情况,一开始的做法 是当分母为 0 时在分母上加上一个很小的数,这样做的话或导致分数值很大,导 致最终不收敛。最后我们的做法是,当分母为 0 时,所计算的边界值采用一阶迎 风形式。从这次亲身体会,我们认识到在得到离散的格式之后,不要盲目的去算, 而是应该判断其特点,然后再进行程序的编写,并且,在编程过程中要熟知语句 的用法,这样不仅会节省很多时间,而且容易发现错误。同时,我们学会了解决 问题的一些基本思想,并可以应用这些基本思想解决其它学科中所遇到的问题。
+ w
− φW
)
− ue (
f
+ e
− φP ))∆y
+
(vs (
f
+ s
− φS
)
− vn (
f
+ n
− φP ))∆x
设沿斜线的对流速度为 f,则可知:
ue = uw = f cosθ , vn = vs = f sinθ
其中对
f
+ w
,
f
+ e
,
f
+ n
,
f
+ s
引入规正变量,进行延迟修正处理,且对于不同的格
b
=
(uw (
f
+ w
− φW
)
− ue (
f
+ e
− φP ))∆y
/2+
(vs (
f
+ s
− φS
)−
vn (
f
+ n
− φP ))∆x
特殊处理:
在计算边界处的
f
+ w
,
f
+ s
时按一阶迎风格式近似处理来求解其值。
具体编程处理: 取网格数为 100×100,所以 x、y 方向空间步长分别为 0.01,进行编程计算。
,0
](
f
+ s
−φS
)
−[
−
(v)s
,0
](
f
− s
−φP
))∆x
若对流方向沿斜线向上,则 u 的方向为从左向右,v 的方向为从下向上。可
将以上各式进行化简,如下所示: aE = 0, aN = 0, aW = uw∆y, aS = vs ∆x,a P = ue∆y + vn∆x
b
=
(uw (
f
一.采用有限容积法对方程进行进行离散
原方程: u ∂φ + v ∂φ = 0
(1)
∂x ∂y
开始离散处理:视 u、v 为常数,对(1)式进行积分:
∫ ∫n
s
e w
u
∂φ dxdy ∂x
=
[(uφ ) e
−
(uφ) w
]∆y
(2)
N● n
W● w P● e E● s S●
∫ ∫e w
n s
v
∂φ ∂y
引入规正变量,采用延迟修正方法,采用 SOR 进行迭代(w=0.8),当累积误差 err<10-5 时,迭代终止,输出各网格点数据并绘制图形。
二、程序
见附页。
三、y=0.5 时的图形
见附页
四、计算结果分析
(1)计算过程中引入规正变量,采用延迟修正处理,保证编程过程中方程 对角占优,从而易于求得稳定解。
∂x ∂y 口边界的方式处理。
图 1 示意图
要求:
1、分别利用 FUD,CD,SUD,QUICK,CLAM,EULER,MINMOD,MUSCL,OSHER,SMART, STOIC 来离散对流项,观察它们的计算结果有何不同。 2、用延迟修正进行求解。 3、写出详细的离散过程和求解方法。 4、用 TECPLOT 软件画出整个流场中φ 的分布,并画出 y = 0.5 时,φ 随 x 的 分布。 5、编程采用 C/C++或 FORTRAN 语言。 6、将源程序附于作业之后,程序中要有详细的注释,以反映出思路。 7、源程序电子版和打印版上交时间:截止 2009 年 12 月 28 日。 8、每组交一份作业,给出每位同学的贡献度。(总和为 100%)
+
(
f
− w
− φP )]
(5)
(vφ ) n
= [ (v)n ,0 ][φP
+
(
f
+ n
− φP )] − [ − (v)n ,0 ][φN
+
(
f
− n
− φN )]
(6)
(vφ ) s
= [ (v)s ,0 ][φS
+
(
f
+ s
− φS )] − [ − (v)s ,0 ][φP
+
(
f
− s
− φP )]
六、每个小组成员承担工作
工作 姓名
禹国军
编程 王晏林
王岩
绘图 韩立涛
报告、ppt 刘文婷
附页
(FUD)
(SUD)
(CD) (CLAM)
(QUICK) (EULER)
(MINMOD)
(MUSCL)
(OSHER)
(SMART)
(STOIC)
− φC )
= φC
) φ=
φ −φU
φD − φU
0 ≤ ϕ)C ≤ 1 其它范围
f
●
●
●
UC D
) φf = EULER: = 3
4) = φC
)) ) φ(C 1− φC))3 − φC2
1− 2φC
) 0 ≤ φC ≤ 1 ) φC = 0.5 其它范围
) φf
=
3 2
) φC
MINMOD:
≤
1 5
1 5
≤
) φC
≤
1 2
1 2
≤
) φC
≤
5 6
5 6
≤
) φC
≤1
其它范围
由于 ∂φ = 0, ∂φ = 0 ,因此,将上边界与右边界做绝热处理,认为边界处值 ∂y ∂x
等于内点值;在左上边界处φ = 1 ,因此,将边界值可赋值为 1,紧邻边界点的内 点计算时按划分网格的一半计算系数参数来近似处理。 aE = 0, aN = 0, aW = uw∆y, aS = vs ∆x / 2,a P = ue ∆y + vn∆x / 2
将式(4)、(5)、(6)、(7)分别代入式(2)、(3),整理可得:
(([ (u)e ,0 ] + [ − (u)w ,0 ])∆y + ([ (v)n ,0 ] + [ − (v)s ,0 ])∆x)φP
= [ (u)w ,0 ]∆yφW + [ − (u)e ,0 ]∆yφE + [ − (v)n ,0 ]∆xφN + [ (v)s ,0 ]∆xφS
aS = [ (v)s ,0 ]∆x
b
=
([
−
(u)e ,0 ](
f
− e
−φE
)
−[
(u)e ,0
](
f
+ e
−φP
)
+[
(u)w ,0
](
f
+ w
− φW
)
−[
−
(u)w ,0
](
f
− w
− φP
))∆y
+
([
−
(v)n
,0
](
f
+ n
−φP)+ [
−
(v)n
,0 ](
f
− n
−φN
)
+[
(v)n
dxdy
=
[(vφ
)n
− (vφ)s ]∆x
已知:
(3)
图 1 局部网格
(uφ ) e
=
[ (u)e ,0 ][φP
+
(
f
+ e
− φP )] − [ − (u)e ,0 ][φE
+
(
f
− e
− φE )]
(4)
(uφ) w
= [ (u)w ,0 ][φW
+
(
f
+ w
− φW
)] − [ − (u)w ,0 ][φP
,0
](
f
− s
−
φP
))∆x
因此可知:
aP = ([ (u)e ,0 ] + [ − (u)w ,0 ])∆y + ([ (v)n ,0 ] + [ − (v) s ,0 ])∆x
