流体力学_06气体射流
合集下载
流体力学第6章讲解

2、射孔的形状,圆孔口和方孔显然其扩张的情况不会相同。不同的射口形状有 不
同的实验值。用φ表示这个影响因素, 对圆断面射流 φ=3.4,长条缝射孔 φ=2.44。
圆孔综口合射这流两:个t影g响因素K:x k=Kφα 3.4a
x
R 1 3.4 as 3.4( as 0.294)
r0
vm
vm r0 1
1
v0 R
2
1
[(11.5 )2 ]2d
0
9
第二节圆断面射流的运动分析
1
n
1
n
[(1 1.5 )2 ] d Bn; [(1 1.5 )2 ] d Cn
0
0
n
1
1.5
2
2.5
3
Bn
0.0985
0.064
0.0464
0.0359
0.0286
第一节无限空间淹没紊流射流特性
二、紊流系数a及几何特征
其斜率即:tga=常数=k。 对于不同的条件,k值是不同的常数,也叫实验常数。 通过实验发现,k值的影响因素有两个主要的因素:
1、射孔出口截面上气流的紊流强度。 紊流强度的大小用紊流系数a(A)来表示:a大紊流的强度就大,因此,紊
流 系数的大小可以反映出射流的扩张能力,所以,a也叫表征射流流动结构的 特征系数。另一方面,由于a反映的是射流混合能力的大小,因此,a还可以反 映孔口出口截面上的速度均匀程度。a越小,则混合能力越差,说明流速越均匀 。
二、断面流量Q
R
微环面的流量表达式 Q 2vydy Q0 r02v0
0
主体段:
R
Q
v r 0
y
y
2 ( )( )d( )
《流体力学》第六章气体射流ppt课件

1
6.8
as r0
11.56
as r0 as r0
2
1 0 .4 3 a s
v1 v0
1
b0 2 .4 4 a s
b0
段
质量平均 v 2
流速
v2 v0
10.76as r0
1
2
1.32
as r0
v2 v0
1
1 0.43 as
b0
ppt精选版
27
段名 参数名称 符号 圆断面射流
ppt精选版
14
Bn和Cn值
n
1
1.5
2
2.5
3
Bn 0.0985 0.064 0.0464 0.0359 0.0286
Cn 0.3845 0.3065 0.2585 0.2256 0.2015
Bn
1
(
v
)nd
0 vm
Cn
1
(
v
)n d
0 vm
rR02vvm 0 22B220.0464
v 3.28 r m
ppt精选版
17
射流参数的计算
段 名
参数名称
符号
圆断面射流
平面射流
主 扩散角 α tg3.4a tg2.44a
体
段 射流直径 或半高度
D b
D d0
6.8
as d0
0.147
b b0
2.44
as b0
0.41
ppt精选版
18
段名 参数名称 轴心速度
主
流量
体 断面平均 流速
段 质量平均 流速
符号
vm
Q
圆断面射流
(完整版)第六章气体射流

6.4 温差或浓差射流
温差(浓差)射流—本身温度(浓度)与周围有差异的射流 射流内边界层 温度内边界层
温度外边界层 射流外边界层
为简化,忽略温度(浓度)与射流速度边界的差
对于温差射流
出口截面与外界温差 轴心与外界温差
T0 T0 Te
Tm Tm Te
截面上某点与外界温差 T T Te
对于浓差射流
Q0v0 r02v02
任意截面动量
R
v2 ydyv
R 2v2 ydy
0
0
动量守恒
r02v02
R 2v2 ydy
0
6.2 圆断面射流的运动分析
根据紊流射流的特征来研究圆断面射流的速度、流量沿 射程的变化规律。
□ 6.2.1 轴心速度vm
方程两端同除 R2vm2 :
r02v02
喷嘴种类
带有收缩口的喷嘴 圆柱形管 带有导板的轴流式风机 带有导板的直角弯管 带有金属网的轴流式风机 收缩极好的平面喷口 平面壁上锐缘狭缝
具有导叶磨圆边口的风道纵向缝
a 0.066 0.08 0.12 0.20 0.24 0.108 0.118
0.155
2α 25o20' 29o00' 44o30' 68o30' 78o40' 29o30' 32o10'
41o20'
喷嘴上装置不同型式的风板栅栏,则出口截面上气流的扰动紊乱程度不同, 因而紊流系数 a 不同。扰动大的紊流系数 a 值增大,扩散角 α 也增大。
◇ 圆断面射流半径沿射程的变化规律
射流半径的沿程变化规律
R r0
3.4
as r0
0.294
流体力学第六章 气体射流

6.1 无限空间淹没紊流射流的特征
2.运动特征:速度分布具有相似性。 特留彼尔在轴对称射流主体段的实验结果,以及阿勃拉莫 维奇在起始段内的测定结果,见图6-2(a)及图6-3(a)。
6.1 无限空间淹没紊流射流的特征
6.1 无限空间淹没紊流射流的特征
3.动力特征 射流中的压强与周围流体中的压强相等。 可得各横截面上轴向动量相等——动量守恒,动量守 恒方程式为:
6.4 温差或浓度差射流
6.4 温差或浓度差射流
三.射流弯曲 温差射流或浓差射流由于密度与周围密度不同, 所受的重力与浮力不相平衡,使整个射流将发生向下或向上弯 曲。通过推导可得出无因次轨迹方程为
6.4 温差或浓度差射流
[例6-3]工作地点质量平均风速要求3m/s,工作面直径D=2.5m 送风温度为15℃,车间空气温度30 ℃,要求工作地点的质量 平均温度降到25 ℃ ,采用带导叶的轴流风机,紊流系数 = 0.12。求(1)风口的直径及速度;(2)风口到工作面的距离。 [解]温差 =15-30=-15 ℃
6 气体射流
6.1 无限空间淹没紊流射流的特征
一.射流结构 出流到无限大空间中,流动不受固体边壁的限制,为无限 空间射流,又称自由射流。射流的流动特性及结构图:
6.1 无限空间淹没紊流射流的特征
二.射流的特性 1. 几何特性: 外边界线为一直线。tan a 紊流系数 a 是表征射流流动结构的特征系数。它与出口断 面上紊流强度有关,紊流强度越大。各种不同形状喷嘴的紊 流系数和扩散角的实测值列于表6-1。
一.特点:1.温度边界层与速度边界层不重合。 2.射流发生弯曲。
6.4 温差或浓度差射流
二.特性: 1.温差特性: 试验得出,截面上温差(浓度差分布)分布具有相 似性。 与速度分布关系如下:
流体力学第六章 气体射流

的过程中,是否受到某固体边界的约束,可分为自由
射流、半限制射流和限制射流。
4.按射流流体在扩散流动过程中是否旋转,可分 为旋转射流和非旋转射流。 5.按射流管嘴出口截面形状不同,可分为圆形射 流(又称轴对称射流)、矩形射流、条缝射流(可按平 面射流处理)、环状射流和同心射流等。 对于矩形射流,当长宽比小于3时,可按轴对称
=>
2
习 题 解 析
例6-3 工作带质量平均流速要求为3m/s,工作面直径 为2.5m,送风温度为15℃,车间温度为30℃,要求工作带的
温差或浓差射流分析,主要 是研究温差或浓差场的分布规律, 同时讨论由温差或浓差引起的射 流弯曲的轴心轨迹。
(一) 温差射流的特征 1. 几何特征 除常规射流的动量、质量交换,温差射流还存在 热量交换。由于热扩散略快于动量扩散,因此温度 边界层比速度边界层发展要快些厚些。但在处理实 际问题时,为简化起见,认为二者相同。 2. 温差(或浓差)分布的相似性.
说明工作区在射流主体段内。 (2) 由表9-1中主体段质量平均流速计算式,得喷口流速为
( u0 as R0 0 . 455 0 . 294 ) u ( 0 . 08 3 . 86 0 . 15 0 . 455 0 . 294 ) 3 15 . 5 m/s
喷口流量为
Q0 1 4
R 3 .4 R 0 ( as R0 0 . 294 ) 3 . 4 a s R 0
所以,喷口至工作区的距离为
s R R0 3 .4 a 1 . 2 0 . 15 3 . 4 0 . 08 3 . 86 m
射流起始段长度为
习 题 解 析
s n 0 . 672 R0 a 0 . 672 0 . 15 0 . 08 1 间存在着 温度差或浓度差,则这样的射流就称为温差射 流或浓差射流。 举例:
射流、半限制射流和限制射流。
4.按射流流体在扩散流动过程中是否旋转,可分 为旋转射流和非旋转射流。 5.按射流管嘴出口截面形状不同,可分为圆形射 流(又称轴对称射流)、矩形射流、条缝射流(可按平 面射流处理)、环状射流和同心射流等。 对于矩形射流,当长宽比小于3时,可按轴对称
=>
2
习 题 解 析
例6-3 工作带质量平均流速要求为3m/s,工作面直径 为2.5m,送风温度为15℃,车间温度为30℃,要求工作带的
温差或浓差射流分析,主要 是研究温差或浓差场的分布规律, 同时讨论由温差或浓差引起的射 流弯曲的轴心轨迹。
(一) 温差射流的特征 1. 几何特征 除常规射流的动量、质量交换,温差射流还存在 热量交换。由于热扩散略快于动量扩散,因此温度 边界层比速度边界层发展要快些厚些。但在处理实 际问题时,为简化起见,认为二者相同。 2. 温差(或浓差)分布的相似性.
说明工作区在射流主体段内。 (2) 由表9-1中主体段质量平均流速计算式,得喷口流速为
( u0 as R0 0 . 455 0 . 294 ) u ( 0 . 08 3 . 86 0 . 15 0 . 455 0 . 294 ) 3 15 . 5 m/s
喷口流量为
Q0 1 4
R 3 .4 R 0 ( as R0 0 . 294 ) 3 . 4 a s R 0
所以,喷口至工作区的距离为
s R R0 3 .4 a 1 . 2 0 . 15 3 . 4 0 . 08 3 . 86 m
射流起始段长度为
习 题 解 析
s n 0 . 672 R0 a 0 . 672 0 . 15 0 . 08 1 间存在着 温度差或浓度差,则这样的射流就称为温差射 流或浓差射流。 举例:
流体力学课件6气体射流

状态方程
总结词
描述气体在不同状态下的物理属性。
详细描述
状态方程是描述气体在不同压力、温度和密 度下的物理属性的关系式。在气体射流中, 状态方程可以用于计算气体的密度、压力和 温度等物理量,进而用于求解其他方程。
04
气体射流的数值模拟方法
有限差分法
有限差分法是一种基于离散化的数值方法,通过将连续的 物理量离散化为有限个离散点上的数值,并建立差分方程 来求解物理量的变化规律。
特性
气体射流具有方向性、扩散性和扰动 性等特性,这些特性决定了气体射流 的运动规律和作用效果。
分类与形式
分类
根据不同的分类标准,气体射流可以分为多种类型,如按流 动形态可分为自由射流、受限射流和冲击射流等;按气体性 质可分为可压缩气体射流和不可压缩气体射流等。
形式
气体射流的形式多样,常见的有喷嘴射流、燃烧室射流、透 平射流等,这些形式的应用范围和作用效果各不相同。
随着气体射流远离喷口,压力逐渐减小,这是由于气体流动过程中能量损失导致 的。
温度分布与变化
温度分布
气体射流中的温度分布与压力分布类 似,中心区域温度较高,边缘区域温 度较低。
温度变化
射流过程中,由于气体与周围介质之 间的热量交换,温度会发生变化。通 常情况下,射流会逐渐冷却。
密度分布与变化
密度分布
射流的基本方程
01
02
03
连续性方程
描述了气体射流中质量守 恒的规律,即流入和流出 射流区域的质量流量相等 。
动量方程
描述了气体射流中动量守 恒的规律,即流入和流出 射流区域的动量流量相等 。
能量方程
描述了气体射流中能量守 恒的规律,即流入和流出 射流区域的能量流量相等 。
流体力学第六章

r0 d0
(3)起始段质量平均温差∆T2 将起始段的 qv 0 / qv代入T2 / T0 qv 0 / qv ,即得起始段 质量平均温差计算式为
T2 qv 0 T0 qv
1 as as 1 0 .76 1 .32 r0 r 0
2
二、射流弯曲
质量平均流速为轴心流速的 47%。因此用v2 代表使用区 v2 :不仅在数值上 v1 、 的流速要比 v1 更合适些。但必须注意, 不同,更重要的是在定义上根本不同,不可混淆。
五、起始段核心长度 Sn 及核心收缩角
r0 s n 0.672 a
r0 tg 1.49a sn
§6-4 平面射流
一、有限空间射流结构
C :漩涡中心
Ⅰ-Ⅰ断面也称第一临界断面, Ⅱ-Ⅱ断面也称第二临界断面 ,
橄榄形流场由三部分组成: 射流出口至断面Ⅰ-Ⅰ为自由扩张段
Ⅰ-Ⅰ断面至Ⅱ-Ⅱ断面为有限扩张段
Ⅱ-Ⅱ断面至Ⅳ-Ⅳ为收缩区段
二、有限空间射流动力特征与半经验公式
有限空间射流研究起来较自由射流困难得多。 有限空间射流不同于自由射流的重要特征是橄榄形边界 外部与固体边壁形成与射流方向相反的回流区。而空调工程 中,工作区通常就设在回流区内,因此对其风速需要限制。 计算回流区速度v 的半经验公式:
三、射流的动力特征
射流过流断面间的动量变化规律为射流的动力特征。
实验表明,射流中任意一点上的压强均等于周围气体的 压强。根据动量方程可以导出,射流各断面上的动量相等。 这就是射流的动力特征。
三、射流的动力特征
以圆断面射流为例,它的任意断面上的动量可表示为
Q0 v0 r v 2 u 2 y dy
得: 令
(3)起始段质量平均温差∆T2 将起始段的 qv 0 / qv代入T2 / T0 qv 0 / qv ,即得起始段 质量平均温差计算式为
T2 qv 0 T0 qv
1 as as 1 0 .76 1 .32 r0 r 0
2
二、射流弯曲
质量平均流速为轴心流速的 47%。因此用v2 代表使用区 v2 :不仅在数值上 v1 、 的流速要比 v1 更合适些。但必须注意, 不同,更重要的是在定义上根本不同,不可混淆。
五、起始段核心长度 Sn 及核心收缩角
r0 s n 0.672 a
r0 tg 1.49a sn
§6-4 平面射流
一、有限空间射流结构
C :漩涡中心
Ⅰ-Ⅰ断面也称第一临界断面, Ⅱ-Ⅱ断面也称第二临界断面 ,
橄榄形流场由三部分组成: 射流出口至断面Ⅰ-Ⅰ为自由扩张段
Ⅰ-Ⅰ断面至Ⅱ-Ⅱ断面为有限扩张段
Ⅱ-Ⅱ断面至Ⅳ-Ⅳ为收缩区段
二、有限空间射流动力特征与半经验公式
有限空间射流研究起来较自由射流困难得多。 有限空间射流不同于自由射流的重要特征是橄榄形边界 外部与固体边壁形成与射流方向相反的回流区。而空调工程 中,工作区通常就设在回流区内,因此对其风速需要限制。 计算回流区速度v 的半经验公式:
三、射流的动力特征
射流过流断面间的动量变化规律为射流的动力特征。
实验表明,射流中任意一点上的压强均等于周围气体的 压强。根据动量方程可以导出,射流各断面上的动量相等。 这就是射流的动力特征。
三、射流的动力特征
以圆断面射流为例,它的任意断面上的动量可表示为
Q0 v0 r v 2 u 2 y dy
得: 令
6气体射流
• 射流边界基本是直线。并且有:
tan 3.4 a
• 射流各断面处的速度分布具有相似特征,可表示 1.5 2 为: u y
1 um R
• 射流各断面上的动量守恒,即任一断面处的动量 等于出口处的动量
2 2 u dA u A0 0 0 A
• 自由淹没射流可分为两个部分。 保持射流出口流速U0不变的部分,称为射流核心。 因卷吸与掺混作用流速小于U0的部分,即射流核心与静止液体之间的部 分,称为射流边界层。 沿射流方向从出口断面至射流核心开始消失的所谓转折截面,称为射流 初始段;转折截面以后的部分,称为射流主体段。
射流有以下基本特征:
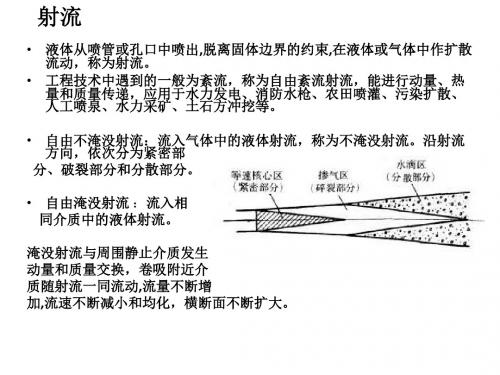
射流
• 液体从喷管或孔口中喷出,脱离固体边界的约束,在液体或气体中作扩散 流动,称为射流。 • 工程技术中遇到的一般为紊流,称为自由紊流射流,能进行动量、热 量和质量传递,应用于水力发电、消防水枪、农田喷灌、污染扩散、 人工喷泉、水力采矿、土石方冲挖等。 • 自由不淹没射流:流入气体中的液体射流,称为不淹没射流。沿射流 方向,依次分为紧密部 分、破裂部分和分散部分。 • 自由淹没射流 :流入相 同介质中的液体射流。 淹没射流与周围静止介质发生 动量和质量交换,卷吸附近介 质随射流一同流动,流量不断增 加,流速不断减小
tan 3.4 a
• 射流各断面处的速度分布具有相似特征,可表示 1.5 2 为: u y
1 um R
• 射流各断面上的动量守恒,即任一断面处的动量 等于出口处的动量
2 2 u dA u A0 0 0 A
• 自由淹没射流可分为两个部分。 保持射流出口流速U0不变的部分,称为射流核心。 因卷吸与掺混作用流速小于U0的部分,即射流核心与静止液体之间的部 分,称为射流边界层。 沿射流方向从出口断面至射流核心开始消失的所谓转折截面,称为射流 初始段;转折截面以后的部分,称为射流主体段。
射流有以下基本特征:
射流
• 液体从喷管或孔口中喷出,脱离固体边界的约束,在液体或气体中作扩散 流动,称为射流。 • 工程技术中遇到的一般为紊流,称为自由紊流射流,能进行动量、热 量和质量传递,应用于水力发电、消防水枪、农田喷灌、污染扩散、 人工喷泉、水力采矿、土石方冲挖等。 • 自由不淹没射流:流入气体中的液体射流,称为不淹没射流。沿射流 方向,依次分为紧密部 分、破裂部分和分散部分。 • 自由淹没射流 :流入相 同介质中的液体射流。 淹没射流与周围静止介质发生 动量和质量交换,卷吸附近介 质随射流一同流动,流量不断增 加,流速不断减小
流体力学气体射流PPT课件

条边界线ABC与DEF延长交于喷口内M点,该点称为射流的极点。两边界线夹角的一半称为射流的极角或 扩散角,以符号α表示。 • 从喷口轴心延长的x轴方向为圆断面射流的对称轴,射流任一断面的轴心到边界线的距离为该截面的半径R (对平面射流称为半高度b)。射流的任一断面的半径(或半高度)与该断面到极点的距离成正比。
• 当扩散角确定后,射流边界相应也被确定,因此射流只能以这样的扩散角作扩散运动。即射流各断面的半 径(对平面射流为半高度)是成比例的,这就是射流的几何特征。
• 根据这一特征,就可以计算圆断面射流各断面半径沿射程的变化规律,对照图6.1有
• 以直径表示
R x0 s 1 s 1 3.4a s 3.4( as 0.294 )
9
第9页/共29页
6.1 无限空间淹没紊流射流
• 就整个射流而言,沿射程各断面上的流速沿程不断衰减,但卷吸进来的流体与射流气体之间的动量交换强 度是从外向内逐渐减弱,因此各断面轴心处的流速为最大,从轴心向外,流速由最大值逐渐减小到零。因 此各断面流速分布虽然不同,但对大量实验所得数据的无因次化整理,找出了射流主体段各断面的无因次 速度与无因次距离之间具有同一性。在这里无因次速度,是指射流横断面上任意一点流速u与同一断面上轴 心流速um的比值,即
6.1 无限空间淹没紊流射流
• 按照喷口形状,又可分为圆射流、矩形射流和条缝射流。圆形射流是轴对称射流。如矩形喷口的长短边之 比(a:b)不超过3:1时,矩形射流能够迅速发展为圆形射流,只需要根据当量直径,就可采用圆形射流 公式进行计算。当矩形喷口长短边之比超过10:1时,就属于条缝射流,条缝射流又称为平面射流。
• 从上式可以看出,射流极角的大小取决于紊流系数,紊流强度越大,射流卷吸能力越强,被带入射流的周 围气体数量越多,扩散角也相应增大。
• 当扩散角确定后,射流边界相应也被确定,因此射流只能以这样的扩散角作扩散运动。即射流各断面的半 径(对平面射流为半高度)是成比例的,这就是射流的几何特征。
• 根据这一特征,就可以计算圆断面射流各断面半径沿射程的变化规律,对照图6.1有
• 以直径表示
R x0 s 1 s 1 3.4a s 3.4( as 0.294 )
9
第9页/共29页
6.1 无限空间淹没紊流射流
• 就整个射流而言,沿射程各断面上的流速沿程不断衰减,但卷吸进来的流体与射流气体之间的动量交换强 度是从外向内逐渐减弱,因此各断面轴心处的流速为最大,从轴心向外,流速由最大值逐渐减小到零。因 此各断面流速分布虽然不同,但对大量实验所得数据的无因次化整理,找出了射流主体段各断面的无因次 速度与无因次距离之间具有同一性。在这里无因次速度,是指射流横断面上任意一点流速u与同一断面上轴 心流速um的比值,即
6.1 无限空间淹没紊流射流
• 按照喷口形状,又可分为圆射流、矩形射流和条缝射流。圆形射流是轴对称射流。如矩形喷口的长短边之 比(a:b)不超过3:1时,矩形射流能够迅速发展为圆形射流,只需要根据当量直径,就可采用圆形射流 公式进行计算。当矩形喷口长短边之比超过10:1时,就属于条缝射流,条缝射流又称为平面射流。
• 从上式可以看出,射流极角的大小取决于紊流系数,紊流强度越大,射流卷吸能力越强,被带入射流的周 围气体数量越多,扩散角也相应增大。
流体力学泵与风机第6章

sn
0.671r0 a
0.671 0.3 0.12
1.68
m 10
m
所计算断面 在主体段内
vm 0.965
0.965
0.225
v0 as 0.294 0.1210 0.294
r0
0.3
vm 0.225v0 2.25 m/s
Q
4.4(
as d0
0.147)Q0
4.4( 0.1210 0.147) 3.14 0.32 10 26.7 m3/s 0.6
v0 A Q0 Q0 R
3.4ax ax
v1 0.2vm
四、主体段质量平均流速v2 定义v2 :用v2乘以质量即得真实动量
Q0v0 Qv2
v2 Q0 1 0.4545 v0 Q 2.2ax ax
v2 0.47vm
五、起始段核心长度sn及核心收缩角θ
过渡断面vm=v0 ,s=sn,代入
vm v0
r0
r0
r0
1 6.8 as 11.56( as)2
r0
r0
八、起始段质量平均流速v2
v2 Q0
1
v0 Q 1 0.76 as 1.32( as)2
r0
r0
[例6-1] 用轴流风机水平送风,风机直径d0=600mm。出口风速 v0= 10m/s,求距出口10m处的轴心速度和风量。
解: 由表6-1查得紊流系数a=0.12。先求起始段核心长度sn
3.86 m
r0 3.4a 0.15
3.4 0.08
(2)先求起始段核心长度sn
sn
0.671r0 a
0.671 0.15 1.26 0.08
m 3.86
m
工程流体力学课件第六章 气体射流

旋风除尘器
几何特征: tg Kx K 3.4a x
K—试验系数,对圆断面射流K=3.4 a,平面射流K=2.44 a; a—紊流系数,由实验决定,是表示射流流动结构的特征系数。
紊流系数a确定,射流边界层的外边界线确定了,射流即按一定的扩散角 向前
作扩散运动,形成圆锥形流场,这就是圆形喷嘴紊流射流的几何特征。
动力特征
(1) 射流内部的压强是变化的,随射程的增大而增大,直至端头 末尾压强最大,达到稳定后数值比周围环境大气压强稍高一点。
(2) 射流中各横截面上的动量不再守恒,沿程逐渐减小,在第二 临界断面后,动量很快减小以至消失。
旋转射流
气体本身一面旋转,一面向周围介质中扩散前进, 其特征与自由射流和有限空间射流大不相同。
本章简要介绍无限空间射流和有限空间射流
一、自由湍流射流
右图为射流结构示意图
自由湍流射流特征
起始段和主体段
射流边界层从出口沿射程不断向外扩散,带动周围介质进入边界层,同时边界层也向 射流中心扩展,至出口如图的BOE面处,边界层扩展到射流轴心线,核心区域消失。
起始段:出口断面至过渡断面之间的部分称为射流起始段 主体段:过渡断面以后称为射流主体段
(2) 轴心流速 vm :
vm
0.965 as 0.294 v0
as
0.48 v0
0.147
r0
d0
(3) 断面平均流速v1 :
v1
Q A
as
0.19 0.294
v0
0.095 as 0.147
v0
r0
d0
(4) 质量平均流速 v2 :
Q 0.4545
0.23
v2
A
as
v0 0.294
几何特征: tg Kx K 3.4a x
K—试验系数,对圆断面射流K=3.4 a,平面射流K=2.44 a; a—紊流系数,由实验决定,是表示射流流动结构的特征系数。
紊流系数a确定,射流边界层的外边界线确定了,射流即按一定的扩散角 向前
作扩散运动,形成圆锥形流场,这就是圆形喷嘴紊流射流的几何特征。
动力特征
(1) 射流内部的压强是变化的,随射程的增大而增大,直至端头 末尾压强最大,达到稳定后数值比周围环境大气压强稍高一点。
(2) 射流中各横截面上的动量不再守恒,沿程逐渐减小,在第二 临界断面后,动量很快减小以至消失。
旋转射流
气体本身一面旋转,一面向周围介质中扩散前进, 其特征与自由射流和有限空间射流大不相同。
本章简要介绍无限空间射流和有限空间射流
一、自由湍流射流
右图为射流结构示意图
自由湍流射流特征
起始段和主体段
射流边界层从出口沿射程不断向外扩散,带动周围介质进入边界层,同时边界层也向 射流中心扩展,至出口如图的BOE面处,边界层扩展到射流轴心线,核心区域消失。
起始段:出口断面至过渡断面之间的部分称为射流起始段 主体段:过渡断面以后称为射流主体段
(2) 轴心流速 vm :
vm
0.965 as 0.294 v0
as
0.48 v0
0.147
r0
d0
(3) 断面平均流速v1 :
v1
Q A
as
0.19 0.294
v0
0.095 as 0.147
v0
r0
d0
(4) 质量平均流速 v2 :
Q 0.4545
0.23
v2
A
as
v0 0.294
流体力学第六章 气体射流

✓出口断面上紊流强度 ✓出口断面上速度分布的均匀性 ✓喷嘴结构
射流半径沿程的线形增长性。
R = 3.4a( x0 + s)
R
as
=ቤተ መጻሕፍቲ ባይዱ3.4( + 0.294)
r0
r0
2、运动特征
轴心速度 最大,从轴心 向边界层边缘, 速度逐渐减小 至零。
距喷嘴距 离越远边界层 厚度越大,而 轴心速度则越 小,也就是速 度分布曲线不 断地扁平化了。
在定义上根本不同,不可混淆。
矩形喷嘴运动参数
以上分析出圆断面射流主 体段内运动参数变化规律,这 些规律亦适用于矩形喷嘴。但 要将矩形换算成为流速当量直 径代人进行计算。换算公式按 第四章所述。
五、起始段核心长度 sn及核心 收缩角 θ
【例题6.3】圆射流以Q0=0.55m3/s,从d0=0.3m管嘴
BO 为圆断面射流截面的半径 R, R称为 ⑨ 射流半径。
三、紊流射流的特征
1、几何特征
射流半径和从极点起算的距离成正比, 即 BO =Kx。
扩散角α为一定值,其正切值
式中 K ― 试验系数,对圆断面射流 K = 3.4a 。
a ― 紊流系数,由实验决定,是表 示射流流动结构的特征系数。
紊流系数的影响因素
研究内容
浓度扩散与温度相似。在实 际应用中,为了简化起见,可以 认为,温度、浓度内外的边界与 速度内外的边界相同。于是参数 R 、 Q 、 vm 、 v1、 v2等可 使用前两节所述公式,仅对轴心 温差 △ Tm ,平均温差等沿射程 的变化规律进行讨论。
定义参数:以足标e表示周围气体的符号
截面上温差分布,浓差分布
第二节 圆断面射流的运动分析
一、轴心速度 vm
射流半径沿程的线形增长性。
R = 3.4a( x0 + s)
R
as
=ቤተ መጻሕፍቲ ባይዱ3.4( + 0.294)
r0
r0
2、运动特征
轴心速度 最大,从轴心 向边界层边缘, 速度逐渐减小 至零。
距喷嘴距 离越远边界层 厚度越大,而 轴心速度则越 小,也就是速 度分布曲线不 断地扁平化了。
在定义上根本不同,不可混淆。
矩形喷嘴运动参数
以上分析出圆断面射流主 体段内运动参数变化规律,这 些规律亦适用于矩形喷嘴。但 要将矩形换算成为流速当量直 径代人进行计算。换算公式按 第四章所述。
五、起始段核心长度 sn及核心 收缩角 θ
【例题6.3】圆射流以Q0=0.55m3/s,从d0=0.3m管嘴
BO 为圆断面射流截面的半径 R, R称为 ⑨ 射流半径。
三、紊流射流的特征
1、几何特征
射流半径和从极点起算的距离成正比, 即 BO =Kx。
扩散角α为一定值,其正切值
式中 K ― 试验系数,对圆断面射流 K = 3.4a 。
a ― 紊流系数,由实验决定,是表 示射流流动结构的特征系数。
紊流系数的影响因素
研究内容
浓度扩散与温度相似。在实 际应用中,为了简化起见,可以 认为,温度、浓度内外的边界与 速度内外的边界相同。于是参数 R 、 Q 、 vm 、 v1、 v2等可 使用前两节所述公式,仅对轴心 温差 △ Tm ,平均温差等沿射程 的变化规律进行讨论。
定义参数:以足标e表示周围气体的符号
截面上温差分布,浓差分布
第二节 圆断面射流的运动分析
一、轴心速度 vm
流体力学课件6气体射流

u 任意一断面上任意 一点的流速 um 同一断面上轴心流速
11
6.1 无限空间淹没紊流射流
而无因次距离,是指上述射流横断面上任意一点到轴 心的距离y与同一断面上射流半径R的比值,即
y 横断面上流速为u的点到轴心的距离 R 同一断面上的射流半径
射流主体段任一断面的无因次速度和无因次距离之间 具有这样的相似性 u y 1.5 2
17
6.1 无限空间淹没紊流射流
从圆形喷口或矩形喷口喷出的射流,是以喷口轴心延长线为 对称轴的圆截面轴对称射流。但当矩形喷口长短边之比超过 10:1时,从喷口喷出的射流只能在垂直长度的平面上作扩 散运动。如果条缝相当长,这种流动可视为平面运动,故称 为平面射流。 平面射流的喷口高度以2b0 (b0为喷口半高度)表示,紊流系 数a值见表6.1或查阅通风空调设计手册相关内容。条缝形喷 口的形状系数φ=2.44。 在平面射流的计算公式中b0是条缝喷口的半高度,其余各参 数的意义都与圆截面射流相同。
3
6.1 无限空间淹没紊流射流
图6.1 射流的结构
4
6.1 无限空间淹没紊流射流
射流的动量交换和卷吸作用是从外向内逐渐发展的, 在距喷口断面距离较短的范围内,射流中心的气体还 没来得及与周围气体相互作用,仍保持原喷口流速的 区域,称为射流核心,如图6.1所示的AOD部分。而 射流核心以外的区域流速小于v0,称为边界层。由于 卷吸的不断加强,参与动量交换的气体数量不断增加。 射流边界层的范围从喷口沿射流方向不断扩大,射流 核心区沿程不断减小,如图所示到达距喷口sn处,也 就是断面BOE处,边界层扩展到射流轴心,射流核心 消失,这个断面称为过渡断面或临界断面。 以过渡断面为界,从喷口到过渡断面称为射流的起始 段。过渡断面以后的射流称为射流主体段。起始段射 流轴心的速度都为v0,而主体段轴心速度沿x方向不断 下降。
11
6.1 无限空间淹没紊流射流
而无因次距离,是指上述射流横断面上任意一点到轴 心的距离y与同一断面上射流半径R的比值,即
y 横断面上流速为u的点到轴心的距离 R 同一断面上的射流半径
射流主体段任一断面的无因次速度和无因次距离之间 具有这样的相似性 u y 1.5 2
17
6.1 无限空间淹没紊流射流
从圆形喷口或矩形喷口喷出的射流,是以喷口轴心延长线为 对称轴的圆截面轴对称射流。但当矩形喷口长短边之比超过 10:1时,从喷口喷出的射流只能在垂直长度的平面上作扩 散运动。如果条缝相当长,这种流动可视为平面运动,故称 为平面射流。 平面射流的喷口高度以2b0 (b0为喷口半高度)表示,紊流系 数a值见表6.1或查阅通风空调设计手册相关内容。条缝形喷 口的形状系数φ=2.44。 在平面射流的计算公式中b0是条缝喷口的半高度,其余各参 数的意义都与圆截面射流相同。
3
6.1 无限空间淹没紊流射流
图6.1 射流的结构
4
6.1 无限空间淹没紊流射流
射流的动量交换和卷吸作用是从外向内逐渐发展的, 在距喷口断面距离较短的范围内,射流中心的气体还 没来得及与周围气体相互作用,仍保持原喷口流速的 区域,称为射流核心,如图6.1所示的AOD部分。而 射流核心以外的区域流速小于v0,称为边界层。由于 卷吸的不断加强,参与动量交换的气体数量不断增加。 射流边界层的范围从喷口沿射流方向不断扩大,射流 核心区沿程不断减小,如图所示到达距喷口sn处,也 就是断面BOE处,边界层扩展到射流轴心,射流核心 消失,这个断面称为过渡断面或临界断面。 以过渡断面为界,从喷口到过渡断面称为射流的起始 段。过渡断面以后的射流称为射流主体段。起始段射 流轴心的速度都为v0,而主体段轴心速度沿x方向不断 下降。
流体力学泵与风机-第6章-气体射流ppt课件

射流讨论的是出流后的流速场、温度场和浓度场。
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
§6.1
无限空间淹没紊流射流的特征
一、过渡断面(转折断面)、起始段、主体段
射流核心:u=u0 边界层: u<u0
主体段: 轴心u<u0 , u沿程下降 射流特征:几何?速度等?
出口截面动量流量
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
§6.2
圆断面射流的运动分析
一、主体段轴心速度vm
R
2v2ydyr02v02 0
两端同除以R2vm2 ,在一个断面上vm可视为常数进行计算
(r0)2(v 0)2 2R (v)2ydy () 21 (1 1 .5)4d 0 .09 Rv m 0 v m RR 0
r 0 3 .4 a 0 .15 3 .4 0 .08
(2)先求起始段核心长度sn
sn 0 .6r 7 a 0 1 0 .6 7 0 0 ..0 1 1 8 5 1 .2m 6 3 .8m 6所在求主断体面段内
v2 0.4545 0.4545 0.193
v0 as0.2940.0 83.860.294
三、运动特征
主 y--体-断速段面度:上分任布意: 点至vvm 轴心距[1离(R y问)1.题5]2:[1v m如1.5何]2确定?
R---该断面射流半径 v---y点的速度 vm---轴心速度
起始段:
y---断面上任意点 至核心边界的距离
R---同断面的边界层厚度 v---y点的速度 vm---核心速度v0
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
§6.1
无限空间淹没紊流射流的特征
一、过渡断面(转折断面)、起始段、主体段
射流核心:u=u0 边界层: u<u0
主体段: 轴心u<u0 , u沿程下降 射流特征:几何?速度等?
出口截面动量流量
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
§6.2
圆断面射流的运动分析
一、主体段轴心速度vm
R
2v2ydyr02v02 0
两端同除以R2vm2 ,在一个断面上vm可视为常数进行计算
(r0)2(v 0)2 2R (v)2ydy () 21 (1 1 .5)4d 0 .09 Rv m 0 v m RR 0
r 0 3 .4 a 0 .15 3 .4 0 .08
(2)先求起始段核心长度sn
sn 0 .6r 7 a 0 1 0 .6 7 0 0 ..0 1 1 8 5 1 .2m 6 3 .8m 6所在求主断体面段内
v2 0.4545 0.4545 0.193
v0 as0.2940.0 83.860.294
三、运动特征
主 y--体-断速段面度:上分任布意: 点至vvm 轴心距[1离(R y问)1.题5]2:[1v m如1.5何]2确定?
R---该断面射流半径 v---y点的速度 vm---轴心速度
起始段:
y---断面上任意点 至核心边界的距离
R---同断面的边界层厚度 v---y点的速度 vm---核心速度v0
第6章气体射流正式

同绘在一个无因次坐标 无因次温差分布线, 上,无因次温差分布线, 在无因次速度分布线的 外部
51
6·4 温差或浓差射流 4 一、概述
5、计算温差、浓差射流假定条件 计算温差、 1、几何特征 2、运动特征
比热单位, 比热单位, KJ/Kg·℃ KJ/Kg ℃
3、等温射流的动力特征变为热力特征:在等压的情
19
送、回风的形式与特点(一)上送
20
送、回风的形式与特点(一)上送
21
送、回风的形式与特点(一)上送
22
送、回风的形式与特点(一)上送
23
送、回风的形式与特点(一)上送
24
送、回风的形式与特点(一)上送
25
送、回风的形式与特点(二)中送
26
风口
(二)类型
27
风口
(二)类型
百叶风口
用0·35替代0·11更与 实验吻合
61
6·4 温差或浓差射流 4
2、射流的轨迹方程
(4)积分
y = y’+ xtgα x s= cos α
Ar阿基米德准数, Ar阿基米德准数,它是决定射流弯曲程度的主要 阿基米德准数 因素。Ar大 随射程x变化的y值变化也大, 因素。Ar大,随射程x变化的y值变化也大,射流 弯曲大。 Ar绝对值小于 001 绝对值小于0 001时 弯曲大。当Ar绝对值小于0·001时,可忽略射流 的弯曲而按等温射流计算。Ar愈小 愈小, 的弯曲而按等温射流计算。Ar愈小,贴附长度愈 长。
47
6·4 温差或浓差射流 4 一、概述
2、温差、浓差射流的特点: 温差、浓差射流的特点: 射流中横向动量交换、旋涡的出现。质量交换, (1)射流中横向动量交换、旋涡的出现。质量交换,热量交 浓度发生交换的射流形成过程中, 换,浓度发生交换的射流形成过程中,射流轴线的轨迹发生 弯曲。 弯曲。 在温差射流中,由于热量扩散比动量扩散要快些, (2)在温差射流中,由于热量扩散比动量扩散要快些,所以 温度边界层比速度边界层发展要快些。 温度边界层比速度边界层发展要快些。浓度扩散温度扩散也 类似。在工程实际中,为了简化,可以忽略边界层的差别。 类似。在工程实际中,为了简化,可以忽略边界层的差别。 所以, vm、v1、v2可用前面的公式 所以,R、Q、vm、v1、v2可用前面的公式
流体力学第六章

r0 0.15 s n = 0.672 = 0.672 × = 1.26m a 0.08
s n < s = 2.1m
所求截面在主体段内 。
⎛ as ⎞ ⎛ 0.08×2.1 ⎞ ⎟ R = 3.4⎜ +0.294r0 = 3.4×⎜ +0.294 ×0.15= 0.721 m ⎟ ⎜r ⎟ ⎝ 0.15 ⎠ ⎝0 ⎠
(三)、射流轴线的弯曲
温差射流或浓差射流的密度与周围流体介质的密度不同, 致使作用于射流质点上的重力与浮力不平衡,造成整个射流 向上或向下弯曲,如图9-6所示。但这时整个射流仍可看作是 对称于轴线的,因此,只要了解射流轴线的弯曲情况,便可知 道整个射流的弯曲情况。一般热射流和含轻密度物质的射流 向上弯曲;而冷射流和含重密度物质的射流向下弯曲。 温差射流或浓差射流的密度不仅沿程有变化,而且在同一 射流截面上的不同点也是不同的,要精确计算射流轴线的弯曲 轨迹比较复杂,我们采用近似的计算方法。
gΔT0 ⎛ a 3 2⎞ s + 0.115 ⎟ y′ = 2 ⎜ 0.51 ⎜ ⎟ υ0 Te ⎝ 2r0 ⎠
由实验修正, 将0.115改为0.355。
=>
gΔT0 ⎛ a 3 2⎞ y′ = 2 ⎜ 0.51 s + 0.335 ⎟ ⎟ 2r0 υ0 Te ⎜ ⎠ ⎝
习 题 解 析
例6-3 工作带质量平均流速要求为3m/s,工作面直径 为2.5m,送风温度为15℃,车间温度为30℃,要求工作带的 质量平均温度降到25℃,采用风机送风,取β0=1, =3.5。 x 求:(1)风口直径和风口至工作面的距离;(2)风口的风速和风 量;(3)工作面中心点温度;(4)射流在工作带下降的距离。 已知:u ′ =3.0m/s,R=1.25m,β0=1, =3.5。 x T0=288K, Ta=303K,T′=298K, ΔT0=T0-Ta=288-303=-15K, ΔT′=T′-Ta=298-303=-5K 解:(1) 由式(9-6)得
s n < s = 2.1m
所求截面在主体段内 。
⎛ as ⎞ ⎛ 0.08×2.1 ⎞ ⎟ R = 3.4⎜ +0.294r0 = 3.4×⎜ +0.294 ×0.15= 0.721 m ⎟ ⎜r ⎟ ⎝ 0.15 ⎠ ⎝0 ⎠
(三)、射流轴线的弯曲
温差射流或浓差射流的密度与周围流体介质的密度不同, 致使作用于射流质点上的重力与浮力不平衡,造成整个射流 向上或向下弯曲,如图9-6所示。但这时整个射流仍可看作是 对称于轴线的,因此,只要了解射流轴线的弯曲情况,便可知 道整个射流的弯曲情况。一般热射流和含轻密度物质的射流 向上弯曲;而冷射流和含重密度物质的射流向下弯曲。 温差射流或浓差射流的密度不仅沿程有变化,而且在同一 射流截面上的不同点也是不同的,要精确计算射流轴线的弯曲 轨迹比较复杂,我们采用近似的计算方法。
gΔT0 ⎛ a 3 2⎞ s + 0.115 ⎟ y′ = 2 ⎜ 0.51 ⎜ ⎟ υ0 Te ⎝ 2r0 ⎠
由实验修正, 将0.115改为0.355。
=>
gΔT0 ⎛ a 3 2⎞ y′ = 2 ⎜ 0.51 s + 0.335 ⎟ ⎟ 2r0 υ0 Te ⎜ ⎠ ⎝
习 题 解 析
例6-3 工作带质量平均流速要求为3m/s,工作面直径 为2.5m,送风温度为15℃,车间温度为30℃,要求工作带的 质量平均温度降到25℃,采用风机送风,取β0=1, =3.5。 x 求:(1)风口直径和风口至工作面的距离;(2)风口的风速和风 量;(3)工作面中心点温度;(4)射流在工作带下降的距离。 已知:u ′ =3.0m/s,R=1.25m,β0=1, =3.5。 x T0=288K, Ta=303K,T′=298K, ΔT0=T0-Ta=288-303=-15K, ΔT′=T′-Ta=298-303=-5K 解:(1) 由式(9-6)得
《流体力学第六章》

.
一、射流的几何特征
对于圆断面射流, tan 3.4a由几何关有 :
R r0
3.4ar0s
0.294
或
D d0
6.8das0
0.147
上式是用数学关系表示的射流几何特征。
.
二、射流的运动特征
轴心速度最大,从轴心向边界层边缘,速度逐渐减小 至零。
距喷嘴距离越远边界层厚度越大,而轴心速度则越小, 也就是速度分布曲线不断地扁平化了。
.
三、射流的动力特征
以圆断面射流为例,它的任意断面上的动量可表示为
Q 0v 0 r 0 2v 0 20 R 2 u 2y dy
式中: —射流气体密度,kg m3
Q 0 —射流出口断面上的体积流量,m3 s 其它同前。
.
§6-3 圆断面射流的运动分析
一、轴心速度um
轴心速度沿射程的变化规律可根据射流动力特征,即各 断面动量守恒的原理导出。
.
2、射流的结构
(6)实验结果及半经验理论都得出射流外边界是一条直 线,如图上的 AB 及 DE 线。
(7)AB、DE 反向延长至喷嘴内交于 M 点,此点称为极 点,∠AMD的一半称为极角(α),又称扩散角。
(8)BO为圆断面射流截面的半径(R),R称为射流半径。
.
§6-2 无限空间淹没紊流射流的特征
一、射流的几何特征
射流外边界扩散的变化规律称为射流的几何特征。
射流扩散半径 R与射程 S 之间的关系:
1 AMD
2 射流扩散角 的大小与紊流强度和喷口断面的形状有关, 可按下式计算:
tana
a为紊流系数,大小取决于喷口结构形式和气流经过喷口 时受扰动的程度,a值越大表示紊流强度越大.
为射流喷口的形状系数。
一、射流的几何特征
对于圆断面射流, tan 3.4a由几何关有 :
R r0
3.4ar0s
0.294
或
D d0
6.8das0
0.147
上式是用数学关系表示的射流几何特征。
.
二、射流的运动特征
轴心速度最大,从轴心向边界层边缘,速度逐渐减小 至零。
距喷嘴距离越远边界层厚度越大,而轴心速度则越小, 也就是速度分布曲线不断地扁平化了。
.
三、射流的动力特征
以圆断面射流为例,它的任意断面上的动量可表示为
Q 0v 0 r 0 2v 0 20 R 2 u 2y dy
式中: —射流气体密度,kg m3
Q 0 —射流出口断面上的体积流量,m3 s 其它同前。
.
§6-3 圆断面射流的运动分析
一、轴心速度um
轴心速度沿射程的变化规律可根据射流动力特征,即各 断面动量守恒的原理导出。
.
2、射流的结构
(6)实验结果及半经验理论都得出射流外边界是一条直 线,如图上的 AB 及 DE 线。
(7)AB、DE 反向延长至喷嘴内交于 M 点,此点称为极 点,∠AMD的一半称为极角(α),又称扩散角。
(8)BO为圆断面射流截面的半径(R),R称为射流半径。
.
§6-2 无限空间淹没紊流射流的特征
一、射流的几何特征
射流外边界扩散的变化规律称为射流的几何特征。
射流扩散半径 R与射程 S 之间的关系:
1 AMD
2 射流扩散角 的大小与紊流强度和喷口断面的形状有关, 可按下式计算:
tana
a为紊流系数,大小取决于喷口结构形式和气流经过喷口 时受扰动的程度,a值越大表示紊流强度越大.
为射流喷口的形状系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
查表6-2 ,B1=0.0985 ; 再将(6-1-2),(6-2-1)式代入
Q as as 2.2( 0.294) 4.4( 0.147) Q0 r0 d0
2016/1/17
(6 2 2)
22
四、主体段断面平均流速 1
无因次断面平均流速为:
1 QA0 Q r0 2 ( ) 0 Q0 A Q0 R
2016/1/17 24
例6—1 用轴流风机水平送风,风机直径 d0=600 mm 。出口风 速 10 m/s ,求距出口 10 m 处的轴心速度和风量。 解 由表6—1查得 a=0.12。用(6—2—1)式
m 0.48 0.48 0.225 0 as 0.147 0.1210 0.147
y
y
x
1 2
x0
y
s x
图 6-5 射流计算式的推证
2016/1/17
17
§6-2 圆断面射流的运动分析
现在根据紊流射流特征来研究圆断面射流的速度 ,流 量Q 沿射程 s (或 x )的变化规律。 一、主体段轴心速度m 应用式6-4
r 22 ydy
2 2 0 0 0
R
第六章
气体射流
§6–1 无限空间淹没紊流射流的特征
§6–2 圆断面射流的运动分析
§6–3 平面射流
§6–4 温差或浓差射流
§6–6 有限空间射流
2016/1/17
1
第六章
气体射流
气体自孔口、状态,叫做紊流射 流。工程上所应用的射流,多为气体紊流射流。
用半经验公式表示射流各横截面上的无因次速度分布如下:
令
y 1.5 2 [1 ( ) ] m R y R [1 1.5 ]2 m
(6 — 3)
(6 — 3a)
由此得出 y/R 从轴心或核心边界到射流外边界的变化范围为 / m 从轴心或核心边界到射流边界的变化范围为1 0。 0 1。
由于射流为紊流型,紊流的横向脉动造成射流与周围介 质之间不断发生质量、动量交换,带动周围介质流动,使射 流的质量流量、射流的横断面积沿 x 方向不断增加,形成了 向周围扩散的锥体状流动场,如图6—1所示的锥体CAMDF。
2016/1/17
3
紊流射流的结构及特性。
C
起始段
B
A
主体段
M
D
核心
边
o
E
界
1
n Cn ( ) d 0 m
2016/1/17
19
r0 2 0 2 于是( )( ) 2 B2 2 0.0464 R m
m r 3.28 0 0 R
再将射流半径R沿程变化规律(6—2)式代入,得
m 0.965 0.48 0 as 0.294 as 0.147
d0 0.6
m 0.225 0 0.22510 2.25 m/s
Q as 4.4( 0.147) 4.4 2.147 9.45 Q0 d0 Q 9.45Q0 9.45
4
d 02 0 9.45
4
(0.6) 2 10 26.7 m 3 /s
三、主体段断面流量 Q
取无因次流量,
R Q 2 0 ydy y y rs 2 ( )( ) d ( ) 2 0 Q0 r0 0 0 r0 r0 R
m y y R 再用 = ; 代换 0 m 0 r0 R r0
m R 2 1 y Q y 2 ( ) ( )( ) d ( ) Q0 0 r0 0 m R R
2016/1/17 15
四、动力特征 实验证明,射流中任意点上的静压强均等于周围气体的 压强。现取6-5中1-1、2-2所截的一段射流脱离体,分析其上 受力情况。因各面上所受静压强均相等,则 x 轴外力之和为 零。据动量方程可知,各横截面上动量相等—动量守恒,这 就是射流的动力学特征。 以圆断面射流为例应用动量守恒原理
1
18
按前述
y 及 的变化范围,B2 的数值列于表6—2。 R m
Bn和Cn
n
Bn Cn
1
值
2
表 6—2
2 .5 0.0359 0.2256 3 0.0286 0.2015
1 .5 0.064 0.3065
0.0985 0.3845
0.0464 0.2585
1
n Bn ( ) d 0 m
在上式中,0.5vm点表示速度为轴心速度的一半之处的点。
阿勃拉莫维奇整理起始段时,所用无因次量为
2016/1/17
14
经过这样整理使得出书中图6—3b。可以看到原来各截面不 同的速度分布曲线,经过这样变换均成为同一条无因次分布线。 这种同一性说明.射流各截面上速度分布的相似性。这就是射 流的运动特征。
2 Q0 0.4545 0.23 0.4545 0 Q as 0.294 as 0.147 ax
r0 d0 (6 — 2 — 4)
2 0.47m 。因此用2 比较(6—2—1)与(6—2—4)式, 2 不仅在 代表使用区的流速要比 1 更合适。但必须注意, 1 、 数值上不同,更重要的是在定义上根本不同,不可混淆。
290 00
44030 68030
0.24 收缩极好的平面喷口 0.108 平面壁上锐缘狭缝 0.118 具有导叶且加工磨圆边口 0.155 的风道上纵向缝
2016/1/17
7
由(6—1)式可知, a 值确定,射流边界层的外边界线 也就被确定,射流即按一定的扩散角 a 向前作扩散运动,这 就是它的几何特征。应用这一特征,对圆断面射流可求出射 流半径沿射程的变化规律。
2
2
九、起始段质量平均流速
Q0 v2 v0 Q Q 1 as as 1 0.76 1.32 r0 r0
2
2016/1/17
28
§6-3 平面射流
气体从狭长缝隙中外射运动时,射流只能在垂直条缝长度 的平面上扩散运动。如果条缝相当长,这种流动可视为平面运 动,故称为平面射流。 平面射流喷口高度以2b0(b0半高度)表示,a值见表6-1 后三项;j值为2.44,于是tan a=2.44a。而几何、运动、动力 特征则完全与圆断面射流相似。所以各运动参数规律的推导 基本与圆断面类似,这里不再推导,列公式于表6-3中。
2 以R2m 除两端,得: 1 r0 2 0 2 y 2 y ( )( ) 2 ( ) d( ) 0 R m m R R y 应用式( 6 1 3) =[1 ( )1.5 ]2 代入,则 m R
2016/1/17
1.5 2 2 [(1 ) ] d B2 0
层
F
x0
s0
s
x
图 6—1
2016/1/17
射流结构
4
一、过流断面(又称转折断面)起始段及主体段 刚喷出的射流速度仍然是均匀的。沿 x 方向流动,射流 不断代入周围介质,不仅使边界扩张,而且使射流主体的速 度逐渐降低,速度为 u0 的部分(如图其6—1 AoD 锥体)称为 射流核心,其余部分速度小于 u0 称为边界层。射流边界层从 出口开始沿射程不断地向外扩散,带动周围介质进入边界层, 同时向射流中心扩展,至某一距离处,边界层扩展到射流轴 心线,核心区域消失,只有轴心上速度为 u0 。射流这一断面 为图6—1上的 BoE ,称为过渡断面或转折断面。以过渡断面分 界,出口断面至过渡断面称为射流起始段。过渡断面以后称 为射流主体段。
2016/1/17 5
二、紊流系数 a 及几何特征 射流外边界层是一条直线,如图6—1上的 AB及 DE 线。 AB 、 DE 延至喷嘴内交于 M 点,此点称为极点, AMD 的 一半称为极角 ,又称扩散角 。 Bo为圆断面射流截面的半径 R(或平面射流边界层的 半宽度 yb )。它和从极点起点算的距离成正比,即 Bo = Kx 。 oM 是从极点起算的 x 距离。由图看出,Bo/oM =tan a , 故 Kx tan K a =3.4a (6-1) x 式中 K—试验常数;
0.0 6 6 0.0 7 1
喷 嘴 种 类 带有收缩口的喷嘴 圆柱形管 带有导风板的轴流式通风 机带导流板的直角弯管
喷 嘴 种 类
表6—1 2
780 40 290 30 32010 410 20
250 20 27 10
0
带金属网格的轴流风机
0.0 7 6 0.0 8 0 .1 2 0 .2 0
r0 d0 (6 5)
2016/1/17
20
二、起始段核心长度 s n 及核心收缩角
起始段核心长度 sn 由式(6-2-1),将 vm=v0 ,s=sn ,代入
r0 sn 0.671 , a
核心收缩角
sn 0.671 sn r0 a
r0 tg 1.49a sn
2016/1/17 21
经计算化简得整个截面上流量为:
as Q Q Q as 1 0.76 1.32 Q0 Q0 r0 r0
2
2016/1/17
27
八、起始段断面平均流速
v1 v0 as as 1 0.76 1.32 r0 r0 as as 1 6.8 11.56 r0 r0
R x0 s s s as 1 1 3.4 3.4( 0.294) r0 x0. r0 / tan r0 r0
R r0 3.4as
(6—2)
x0 s R x0 / r0 s / r0 3.4 ( x0 s) 3.4ax r0 x0. / r0 1/ tan
D as 6.8( 0.147) d0 d0
Q as as 2.2( 0.294) 4.4( 0.147) Q0 r0 d0
2016/1/17
(6 2 2)
22
四、主体段断面平均流速 1
无因次断面平均流速为:
1 QA0 Q r0 2 ( ) 0 Q0 A Q0 R
2016/1/17 24
例6—1 用轴流风机水平送风,风机直径 d0=600 mm 。出口风 速 10 m/s ,求距出口 10 m 处的轴心速度和风量。 解 由表6—1查得 a=0.12。用(6—2—1)式
m 0.48 0.48 0.225 0 as 0.147 0.1210 0.147
y
y
x
1 2
x0
y
s x
图 6-5 射流计算式的推证
2016/1/17
17
§6-2 圆断面射流的运动分析
现在根据紊流射流特征来研究圆断面射流的速度 ,流 量Q 沿射程 s (或 x )的变化规律。 一、主体段轴心速度m 应用式6-4
r 22 ydy
2 2 0 0 0
R
第六章
气体射流
§6–1 无限空间淹没紊流射流的特征
§6–2 圆断面射流的运动分析
§6–3 平面射流
§6–4 温差或浓差射流
§6–6 有限空间射流
2016/1/17
1
第六章
气体射流
气体自孔口、状态,叫做紊流射 流。工程上所应用的射流,多为气体紊流射流。
用半经验公式表示射流各横截面上的无因次速度分布如下:
令
y 1.5 2 [1 ( ) ] m R y R [1 1.5 ]2 m
(6 — 3)
(6 — 3a)
由此得出 y/R 从轴心或核心边界到射流外边界的变化范围为 / m 从轴心或核心边界到射流边界的变化范围为1 0。 0 1。
由于射流为紊流型,紊流的横向脉动造成射流与周围介 质之间不断发生质量、动量交换,带动周围介质流动,使射 流的质量流量、射流的横断面积沿 x 方向不断增加,形成了 向周围扩散的锥体状流动场,如图6—1所示的锥体CAMDF。
2016/1/17
3
紊流射流的结构及特性。
C
起始段
B
A
主体段
M
D
核心
边
o
E
界
1
n Cn ( ) d 0 m
2016/1/17
19
r0 2 0 2 于是( )( ) 2 B2 2 0.0464 R m
m r 3.28 0 0 R
再将射流半径R沿程变化规律(6—2)式代入,得
m 0.965 0.48 0 as 0.294 as 0.147
d0 0.6
m 0.225 0 0.22510 2.25 m/s
Q as 4.4( 0.147) 4.4 2.147 9.45 Q0 d0 Q 9.45Q0 9.45
4
d 02 0 9.45
4
(0.6) 2 10 26.7 m 3 /s
三、主体段断面流量 Q
取无因次流量,
R Q 2 0 ydy y y rs 2 ( )( ) d ( ) 2 0 Q0 r0 0 0 r0 r0 R
m y y R 再用 = ; 代换 0 m 0 r0 R r0
m R 2 1 y Q y 2 ( ) ( )( ) d ( ) Q0 0 r0 0 m R R
2016/1/17 15
四、动力特征 实验证明,射流中任意点上的静压强均等于周围气体的 压强。现取6-5中1-1、2-2所截的一段射流脱离体,分析其上 受力情况。因各面上所受静压强均相等,则 x 轴外力之和为 零。据动量方程可知,各横截面上动量相等—动量守恒,这 就是射流的动力学特征。 以圆断面射流为例应用动量守恒原理
1
18
按前述
y 及 的变化范围,B2 的数值列于表6—2。 R m
Bn和Cn
n
Bn Cn
1
值
2
表 6—2
2 .5 0.0359 0.2256 3 0.0286 0.2015
1 .5 0.064 0.3065
0.0985 0.3845
0.0464 0.2585
1
n Bn ( ) d 0 m
在上式中,0.5vm点表示速度为轴心速度的一半之处的点。
阿勃拉莫维奇整理起始段时,所用无因次量为
2016/1/17
14
经过这样整理使得出书中图6—3b。可以看到原来各截面不 同的速度分布曲线,经过这样变换均成为同一条无因次分布线。 这种同一性说明.射流各截面上速度分布的相似性。这就是射 流的运动特征。
2 Q0 0.4545 0.23 0.4545 0 Q as 0.294 as 0.147 ax
r0 d0 (6 — 2 — 4)
2 0.47m 。因此用2 比较(6—2—1)与(6—2—4)式, 2 不仅在 代表使用区的流速要比 1 更合适。但必须注意, 1 、 数值上不同,更重要的是在定义上根本不同,不可混淆。
290 00
44030 68030
0.24 收缩极好的平面喷口 0.108 平面壁上锐缘狭缝 0.118 具有导叶且加工磨圆边口 0.155 的风道上纵向缝
2016/1/17
7
由(6—1)式可知, a 值确定,射流边界层的外边界线 也就被确定,射流即按一定的扩散角 a 向前作扩散运动,这 就是它的几何特征。应用这一特征,对圆断面射流可求出射 流半径沿射程的变化规律。
2
2
九、起始段质量平均流速
Q0 v2 v0 Q Q 1 as as 1 0.76 1.32 r0 r0
2
2016/1/17
28
§6-3 平面射流
气体从狭长缝隙中外射运动时,射流只能在垂直条缝长度 的平面上扩散运动。如果条缝相当长,这种流动可视为平面运 动,故称为平面射流。 平面射流喷口高度以2b0(b0半高度)表示,a值见表6-1 后三项;j值为2.44,于是tan a=2.44a。而几何、运动、动力 特征则完全与圆断面射流相似。所以各运动参数规律的推导 基本与圆断面类似,这里不再推导,列公式于表6-3中。
2 以R2m 除两端,得: 1 r0 2 0 2 y 2 y ( )( ) 2 ( ) d( ) 0 R m m R R y 应用式( 6 1 3) =[1 ( )1.5 ]2 代入,则 m R
2016/1/17
1.5 2 2 [(1 ) ] d B2 0
层
F
x0
s0
s
x
图 6—1
2016/1/17
射流结构
4
一、过流断面(又称转折断面)起始段及主体段 刚喷出的射流速度仍然是均匀的。沿 x 方向流动,射流 不断代入周围介质,不仅使边界扩张,而且使射流主体的速 度逐渐降低,速度为 u0 的部分(如图其6—1 AoD 锥体)称为 射流核心,其余部分速度小于 u0 称为边界层。射流边界层从 出口开始沿射程不断地向外扩散,带动周围介质进入边界层, 同时向射流中心扩展,至某一距离处,边界层扩展到射流轴 心线,核心区域消失,只有轴心上速度为 u0 。射流这一断面 为图6—1上的 BoE ,称为过渡断面或转折断面。以过渡断面分 界,出口断面至过渡断面称为射流起始段。过渡断面以后称 为射流主体段。
2016/1/17 5
二、紊流系数 a 及几何特征 射流外边界层是一条直线,如图6—1上的 AB及 DE 线。 AB 、 DE 延至喷嘴内交于 M 点,此点称为极点, AMD 的 一半称为极角 ,又称扩散角 。 Bo为圆断面射流截面的半径 R(或平面射流边界层的 半宽度 yb )。它和从极点起点算的距离成正比,即 Bo = Kx 。 oM 是从极点起算的 x 距离。由图看出,Bo/oM =tan a , 故 Kx tan K a =3.4a (6-1) x 式中 K—试验常数;
0.0 6 6 0.0 7 1
喷 嘴 种 类 带有收缩口的喷嘴 圆柱形管 带有导风板的轴流式通风 机带导流板的直角弯管
喷 嘴 种 类
表6—1 2
780 40 290 30 32010 410 20
250 20 27 10
0
带金属网格的轴流风机
0.0 7 6 0.0 8 0 .1 2 0 .2 0
r0 d0 (6 5)
2016/1/17
20
二、起始段核心长度 s n 及核心收缩角
起始段核心长度 sn 由式(6-2-1),将 vm=v0 ,s=sn ,代入
r0 sn 0.671 , a
核心收缩角
sn 0.671 sn r0 a
r0 tg 1.49a sn
2016/1/17 21
经计算化简得整个截面上流量为:
as Q Q Q as 1 0.76 1.32 Q0 Q0 r0 r0
2
2016/1/17
27
八、起始段断面平均流速
v1 v0 as as 1 0.76 1.32 r0 r0 as as 1 6.8 11.56 r0 r0
R x0 s s s as 1 1 3.4 3.4( 0.294) r0 x0. r0 / tan r0 r0
R r0 3.4as
(6—2)
x0 s R x0 / r0 s / r0 3.4 ( x0 s) 3.4ax r0 x0. / r0 1/ tan
D as 6.8( 0.147) d0 d0
