高中电路化简(1)
高三物理电路化简复习

二、例题选解
1.如图,画等效电路。
A R2 B R3 A、D接电源时
R1 A R2 R3 D R4 A R2
R1
R4
C
D A、B接电源时
R1 R4 R3 B
• 如图,画等效电路。
R1 R2 R3 R4
A
1
R5
B
2 A
5 4
3 B
2.画下图的等效电路。
R2 A R1
R3
B
R1 R2 A R3 B
B
6
8 B
A
9
7.画下图的等效电路。 R4 R3 R1 R2 R7 A R5 R6 B A R1
R3
R6
R4
R5
R2
R7
B
R3R6R4 R1R2R5断开时:
A
R7
1
B 3 6
2
7
5
4
R3
R6
R4 R1 R2
R5
闭合时:
A
R7
1 A 2
B 4
3
5 7
6 B
求:φ A, φ B的大小关系。
R 2R 结论:相等
A B
2R 4R
若在间连一根导线呢? 或接一个电阻呢? 结论:无电流
.画下图的等效电路。
; 恒耀娱乐 恒耀娱乐公司 ; 2019.1 ;
突围." 李小克给他点上烟,两人坐在一起吐着烟圈. "耶夫洛夫,还是想想现在吧.我们歼灭了一小股党卫军,位置已经暴露,敌人必然很快就要向我们进攻.我们的总兵力有三千,那是很大的数目.德国人到底有多少我不知道,但是他们一定部署在森林外,其目的就是堵截我军大部队的突围." "所 以我们现在反而非常危险?"耶夫洛夫问道. &#
专题:电路的简化

A.电流表读数变大,电压表读数变小
B.灯泡L1变亮
C.电容器C上电荷量减小
D.电源的输出功率可能变大
例5.如图所示的电路中,开关S闭合后,由于电阻发 生短路或者断路故障,电压表和电流表的读数都增大 ,则肯定出现了下列哪种故障( A )
A.R1短路
C.R3短路
A
B.R2短路
D.R1断路
R1 R2 E r V R3 s
例3.四个电阻R1、R2 、R3、R4如图所示连接,若 R1=R2=R3=R4=2Ω,且R1两端的电压为4V,求:
(1)电路的总电阻.
(2)电阻R2两端的电压
a R2
R1
b R3 c R4 d
R总=1.2Ω U2=6V
a R2 R3 R1 c R4 b d
例4.如图所示的电路中,闭合开关S,灯泡L1和L2均正 常发光,由于某种原因,L2灯丝突然烧断,其余用电器均 不会损坏,则下列结论正确的是 ( D )
高中物理选修3-1
第二章
恒定电流
专题:电路的简化
电路的等效化简
高中物理恒定电流知识学习中,化简电路是应当掌握 的基本技能之一,现在介绍两种常见的电路化简方法。
1、化简原则
(1).理想导线可任意长短。
(2).无电流支路可去掉。
(3).等电势点可合并。
(4).理想电压表可看成断路,理想电流表可看成短路,
例6.将规格为“6 V,6 W”和“6 V,4 W”的A灯和B 灯接入电压为 12 V 的电路中,既要使两灯都能正常发 光,又要使整个电路消耗的电功率最小,如图所示的 四种接法最合理的是( D )
例2、三个电阻R1、R2 、R3 如图所示连接,若 R1=R2=R3=2Ω,求:电路的总 电阻.
高中电路化简(1)

电路化简2.4.1、 等效电源定理实际的直流电源可以看作电动势为ε,内阻为零的恒压源与内阻r 的串联,如图2-4-1所示,这部分电路被称为电压源。
不论外电阻R 如何,总是提供不变电流的理想电源为恒流源。
实际电源ε、r 对外电阻R 提供电流I 为r R rr r R I +⋅=+=εε其中r /ε为电源短路电流0I ,因而实际电源可看作是一定的内阻与恒流并联的电流源,如图2-4-2所示。
实际的电源既可看作电压源,又可看作电流源,电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。
利用电压源与电流源的等效性可使某些电路的计算简化。
等效电压源定理又叫戴维宁定理,内容是:两端有源网络可等效于一个电压源,其电动势等于网络的开路电压,内阻等于从网络两端看除电源以外网络的电阻。
如图2-4-3所示为两端有源网络A 与电阻R 的串联,网络A可视为一电压源,图2-4-1图2-4-2图2-4-3图2-4-4等效电源电动势0ε等于a 、b 两点开路时端电压,等效内阻0r 等于网络中除去电动势的内阻,如图2-4-4所示。
等效电流源定理 又叫诺尔顿定理,内容是:两端有源网络可等效于一个电流源,电流源的0I 等于网络两端短路时流经两端点的电流,内阻等于从网络两端看除电源外网络的电阻。
例4、如图2-4-5所示的电路中,Ω=Ω=Ω=Ω=Ω===0.194,5.43,0.101,0.12,5.01,0.12,0.31R R R R r r V V εε (1)试用等效电压源定理计算从电源()22r 、ε正极流出的电流2I ;(2)试用等效电流源定理计算从结点B 流向节点A 的电流1I 。
分析: 根据题意,在求通过2ε电源的电流时,可将ABCDE 部分电路等效为一个电压源,求解通过1R 的电流时,可将上下两个有源支路等效为一个电流源。
解: (1)设ABCDE 等效电压源电动势0ε,内阻0r ,如图2-4-6所示,由等效电压源定理,应有VR R R r R 5.1132111=+++=εε()Ω=+++++=5321132110R R R r R R r R r电源00r 、ε与电源22r 、ε串联,故Ar R r I 02.0240022-=+++=εε2图2-4-5图2-4-62I <0,表明电流从2ε负极流出。
人教版高中物理全套教案和导学案2.4.电路化简

§2. 4、电路化简2.4.1、 等效电源定理实际的直流电源可以看作电动势为ε,内阻为零的恒压源与内阻r 的串联,如图2-4-1所示,这部分电路被称为电压源。
不论外电阻R 如何,总是提供不变电流的理想电源为恒流源。
实际电源ε、r 对外电阻R 提供电流I 为r R rr r R I +⋅=+=εε其中r /ε为电源短路电流0I ,因而实际电源可看作是一定的内阻与恒流并联的电流源,如图2-4-2所示。
实际的电源既可看作电压源,又可看作电流源,电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。
利用电压源与电流源的等效性可使某些电路的计算简化。
等效电压源定理又叫戴维宁定理,内容是:两端有源络可等效于一个电压源,其电动势等于络的开路电压,内阻等于从络两端看除电源以外络的电阻。
如图2-4-3所示为两端有源络A 与电阻R 的串联,络A 可视为一电压源,等图2-4-1图2-4-2图2-4-3图2-4-4效电源电动势0ε等于a 、b 两点开路时端电压,等效内阻0r 等于络中除去电动势的内阻,如图2-4-4所示。
等效电流源定理 又叫诺尔顿定理,内容是:两端有源络可等效于一个电流源,电流源的0I 等于络两端短路时流经两端点的电流,内阻等于从络两端看除电源外络的电阻。
例4、如图2-4-5所示的电路中,Ω=Ω=Ω=Ω=Ω===0.194,5.43,0.101,0.12,5.01,0.12,0.31R R R R r r V V εε (1)试用等效电压源定理计算从电源()22r 、ε正极流出的电流2I ;(2)试用等效电流源定理计算从结点B 流向节点A 的电流1I 。
分析: 根据题意,在求通过2ε电源的电流时,可将ABCDE 部分电路等效为一个电压源,求解通过1R 的电流时,可将上下两个有源支路等效为一个电流源。
解: (1)设ABCDE 等效电压源电动势0ε,内阻0r ,如图2-4-6所示,由等效电压源定理,应有VR R R r R 5.1132111=+++=εε()Ω=+++++=5321132110R R R r R R r R r电源00r 、ε与电源22r 、ε串联,故Ar R r I 02.0240022-=+++=εε2图2-4-5图2-4-62I <0,表明电流从2ε负极流出。
高考物理 二轮专题复习 专题:电路化简新人教版

UCB= UCD+ UDB= I3R3+ IR2= 18(V)
(2)如果在ab间接入一只理想电流表,如图2所示,电流表的读数为流过R3、R4的电流之和.此时电路的总电阻为3Ω,则电路的总电流为
I = U/R = 24/3 = 8(A);
流过R1的电流I1= 2A;
流过R3的电流I3= 2/3A;
流过R4的电流I4= 6A;
故电流表的读数为:IA= I3+ I4= 6.67A.
(2)问中关键是弄清两只电流表测量的是哪些支路上的电流.最后由学生计算.
二、等势点化简电路法(步骤)
1、将电路中的所有理想安培表视为短路,所有理想电压表视为开路;
2、寻找电路中的所有等势点:凡是用无阻导线相连点,都是电势相等的点。
3、将电路中电势不等的点用不同的字母标示出来;
4、按电流的流向将电势不同的点按电势降低顺次序从左向右排列出来;
【教学难点】通过电路的计算培养学生应用数学工具解决物理问题的能力.
主备教案
自备教案
一、以例题为引入:
[例1]下图电路中,R1=R2=R3=R4=3欧,则:
(1)A、B间的总电阻多少?(2)若在导线CE上接电流表A1、DF上接电流表A2,且UAB=4V,则A1、A2的读数分别为多大?
引导:(1)确定等势点,利用节器按对号入座的原则放到相应的等势点中去;
6、再按原电路图,将电流表和电压表放到相应位置上去;
物理电路化简节点法与万能法则十条 经典化简例题
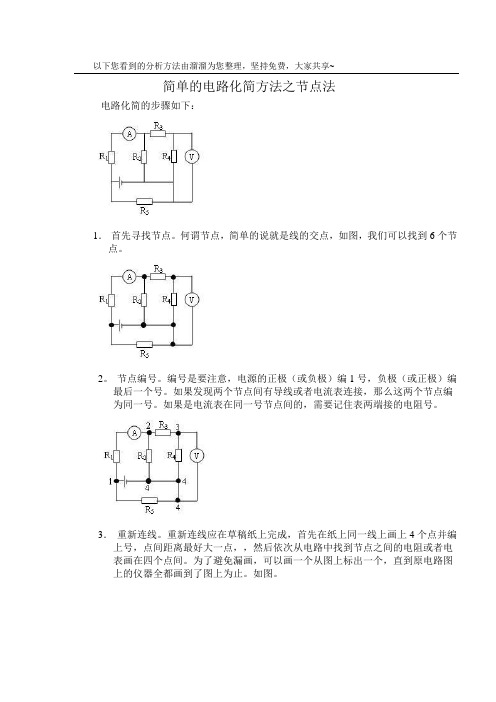
以下您看到的分析方法由溜溜为您整理,坚持免费,大家共享~简单的电路化简方法之节点法电路化简的步骤如下:1.首先寻找节点。
何谓节点,简单的说就是线的交点,如图,我们可以找到6个节点。
2。
节点编号。
编号是要注意,电源的正极(或负极)编1号,负极(或正极)编最后一个号。
如果发现两个节点间有导线或者电流表连接,那么这两个节点编为同一号。
如果是电流表在同一号节点间的,需要记住表两端接的电阻号。
3.重新连线。
重新连线应在草稿纸上完成,首先在纸上同一线上画上4个点并编上号,点间距离最好大一点,,然后依次从电路中找到节点之间的电阻或者电表画在四个点间。
为了避免漏画,可以画一个从图上标出一个,直到原电路图上的仪器全都画到了图上为止。
如图。
4.转化为规范化电路图。
相信做完上一步后,您已经可以看出电路的组成了,如果发现点与点之间有断开的情况,只要将点适当的移位就可。
关于这道题的规范化电路图,在此就省略吧。
在使用过程中觉得此方法非常的简单,而且解题过程非常机械。
当然有时因为节点编号的问题出现画完以后还是看不出来的问题,不过只要将点进行简单的移位,便可以一目了然。
下面是化简的万能十条法则。
电路的等效变化高中生在处理较复杂的混联电路问题时,常常因不会画等效电路图,难以求出等效电阻而直接影响解题。
为此,向同学们介绍一种画等效电路图的方法《快速三步法》。
快速三步法画等效电路图的步骤为:⑴标出等势点。
依次找出各个等势点,并从高电势点到低电势点顺次标清各等势点字母。
⑵捏合等势点画草图。
即把几个电势相同的等势点拉到一起,合为一点,然后假想提起该点“抖动”一下,以理顺从该点向下一个节点电流方向相同的电阻,这样逐点依次画出草图。
画图时要注意标出在每个等势点处电流“兵分几路”及与下一个节点的联接关系。
⑶整理电路图。
要注意等势点、电阻序号与原图一一对应,整理后的等效电路图力求规范,以便计算。
例1、图1所示电路中,R1=R2=R3=3Ω, R4=R5=R6=6Ω,求M、N两点间的电阻。
7电路的化简方法

*选学内容:电路的化简方法★知识要点1. 稍复杂的混联电路的等效化简方法: (1) 电路化简时的原则:① 无电流的支路化简时可去除,为什么? ② 等电势的点化简时可合并,为什么? ③ 理想..导线可任意长短; ④ 理想..电流表可认为短路,理想..电压表可认为断路; ⑤ 电压稳定..的电容器可认为断路. (2) 常用等效化简方法: ① 电流分支法:a. 先将各结点用字母标上;b. 判定各支路元件的电流方向(若电路原无电压电流,可假设在总电路两端加上电压后判定);c. 按电流流向,自左到右将各元件、结点、分支逐一画出;d. 将画出的等效电路图加工整理. ② 等势点排列法:a. 将各结点用字母标上;b. 判定各结点电势的高低(若原电路未加电压,可先假设加上电压);c. 将各结点按电势高低自左到右排列,再将各结点间的支路画出;d. 将画出的等效电路图加工整理.注意:若能将以上两种方法结合使用,效果更好. 2. 含有电容器的直流电路的分析方法: (1) 电路稳定时,电容器是断路的,其两端电压等于所并联的电路两端的电压. (2) 电路的电流、电压变化时,将会引起电容器的充(放)电. 如果电容器两端电压升高,电容器将充电;如果电压降低,电容器将通过与并联的电路放电.★应用演练【例1】如右图所示,R 1=R 2=R 3= R 4=R ,求:电键S 闭合和开启时,A 、B 两端电阻之比. 解析:化简时可假设电键S 开启,而无电流的支路化简时可去除,等化简结束后再补上.方法(一):用电流分支法化简电路.设A 点电势高于B 点电势,判断各支路上的电流情况:甲乙电流由A 经R 1到B 为第一支路;电流由A 经R 2到C ,再到B 为第二支路;电流由A 经R 3到D ,再经R 4到B 为第三支路. 沿电流方向画出电路图,然后在C 、D 间补上电键S (如图乙).S 闭合:R 4短路,相当于R 1、R 2、R 3并联,故R AB =R/3.S 开启:相当于R 3、R 4串联后再和R 1、R 2并联,故12341111AB R R R R R =++'+,R AB ′=2R/5.∴R AB :R AB ′=5:6. 方法(二):用等电势排列法化简电路. 设A 点电势高于B 点电势,判断电路上各点的电势情况:φA >φD >φC =φB .在A 、B 之间有三条支路并联:第一条为R 1;第二条为R 2;第三条为R 3和R 4的串联电路.由等电势的点化简时可合并可得:S 与R 4并联. 答案:5:6〖点评〗对于复杂的电路化简时应交替使用分支法和等势法 【例2】如右图所示,R 1=R 2=R 3=R 4=R ,则:A 、B 两端总电阻是多大?解析:方法(一):用电流分支法化简电路.设A 点电势高于B 点电势,判断各支路上的电流情况(如A 图所示). 沿电流方向画出电路图(如B 图所示),经整理得到C 图.故R AB =R 1+R 并=R +R/3=4R/3.方法(二):用等电势排列法化简电路. 设A 点电势高于B 点电势,判断电路上各点的电势情况(电势相同的点标相同的字母):φA >φC >φB . 在A 、C 之间有R 1;在C 、B 之间有R 2、R 3、R 4三个电阻并联.★同步练习1. 如右图所示,AB 之间的总电阻为:甲图R AB = Ω;乙图R AB = Ω;丙图S 断开时R AB = Ω,S 闭合时R AB ′= Ω;丁图S 断开时R AB = Ω,S 闭合时R AB ′= Ω. 0、12/13、4、2、3、D 图乙甲丙丁A 图B 图C 图2. 用三个完全相同的金属环,将其相互垂直放置,并把相交点焊接起来成为如右图所示的球形骨架,如每个圆环的周长导线电阻阻值为4Ω,则A 、C 间的总电阻阻值R AC = Ω. 0.5 解析:设A 点接高电势,B 点接低电势. 由题目的对称性可推断出B 、D 、E 、F 各点的电势相等,因此B 、D 、E 、F 各点可合并为一点. 电路可简化为右图所示电路. 则A 、C 间的总电阻阻值R AC =(R/4)/4×2=R/8=0.5Ω.3. 如下图所示的电路,R 1=R 2=4Ω,R 3=R 4=2Ω,U AB =6V ,求:A. 安培表A 1和A 2的示数(不计安培表的内阻); I A1=1.5A ;I A2=1.0AB. R 1与R 4两端电压之比. U 1:U 4=1:2解析:⑴ R 1、R 2与R 3相并联,再跟R 4相串联,其等效电路如右图所示. 根据并联电路的性质,可知R 1、R 2、R 3三个电阻并联的总电阻R 并,即:1231111R R R R =++并. ∴R 并=1Ω.根据欧姆定律,干路中电流为4ABU I R R =+并=2A.并联部分的电压为:U 并=I·R 并=2V . 则通过R 1、R 2、R 3的电流分别为:1U I R =并1=0.5A ,22U I R =并=0.5A ,33U I R =并=1.0A.由图可知,安培表A 1的示数是通过R 2与R 3的电流之和,则有:I A1=I 2+I 3=1.5A. 安培表A 2的示数是通过R 1与R 2的电流之和,则有:I A2=I 1+I 2=1.0A. ⑵ 根据串联电路电压分配关系可知:1444R U 1U U U R ==并并=2.-A2。
高中物理电路简化教案

高中物理电路简化教案
教学目标:
1. 了解电路中的基本元件和符号。
2. 理解串联和并联电路的特点。
3. 能够简化复杂电路并计算电流和电压。
教学内容:
1. 电路中的基本元件:电池、电阻、电流表、电压表。
2. 串联电路和并联电路的特点及应用。
3. 电路简化的方法和计算电流、电压的公式。
教学步骤:
一、引入:
通过引入一个简单的电路图,让学生猜测每个元件的作用,并介绍电路中的基本元件和符号。
二、讲解:
1. 介绍串联电路和并联电路的定义和特点,通过示意图和实例进行讲解。
2. 分别介绍串联电路和并联电路的公式,讲解计算电流和电压的方法。
三、示范:
展示一个复杂电路图,让学生分别简化为串联和并联电路,并计算电流和电压。
四、练习:
让学生进行简化电路图和计算电流、电压的练习,并进行互相核对和订正。
五、总结:
总结串联和并联电路的特点,强调简化电路的重要性和计算方法。
六、作业:
布置作业,要求学生简化一个复杂的电路图并计算电流、电压。
教学反思:
本节课重点介绍了串联和并联电路的特点和计算方法,通过实例的讲解和练习,帮助学生加深理解。
在布置作业时应注意难易度的把握,避免出现太过复杂的题目,确保学生能够独立完成。
高考物理中复杂电路的简化方法——百度文库

R1 b R2
R3 d R4
R5 b R6
R7 d
第 2 步——梳理节点。将 A、a、b、c、d、B 节点依次标在一条直线上,如图所示。
A
a
b
c
d
B
第 3 步——嵌入元件。分别将 R1~R7 共 7 个元件嵌入第 1 步标示的 2 个节点之间。
A
a
R1
b
R2
c
R3
d
B
R5
R6
R7
R4
第 4 步——整理计算。把电阻和导线整理成直角拆线样式,根据串并联关系计算。
A1
R2
R3
R1 A2
S
解析:第 1 步——标节点序号。原电路中的节点如图所示,A、B 为电路中电源外电路 的两个端口。
A1
b1 R2
R3 b2
a1 R1
a2
A2
S
AB
第 2 步——梳理节点。将 A、a1、a2、b1、b2、B 节点依次标在一条直线上,如图所示。
A
a1
a2
b1 b2
B
第 3 步——嵌入元件。分别将 R1~R3、A1 表、A2 表共 5 个元件嵌入第 1 步标示的 2 个 节点之间。
并联关系,利用电阻的串并联公式计算电阻。
【实例 1】(电路简化——节点法)如图所示,电路中的各个电阻值均为 10Ω,则两个
端口 A、B 间的电阻 RAB=________。
A
B
R1
R2
R3
R4
R5
R6
R7
解析:第 1 步——标节点序号。原电路中的节点如图所示,A、B 为电路的两个端口。
Aa
c
a
c
高中物理电路的简化已用
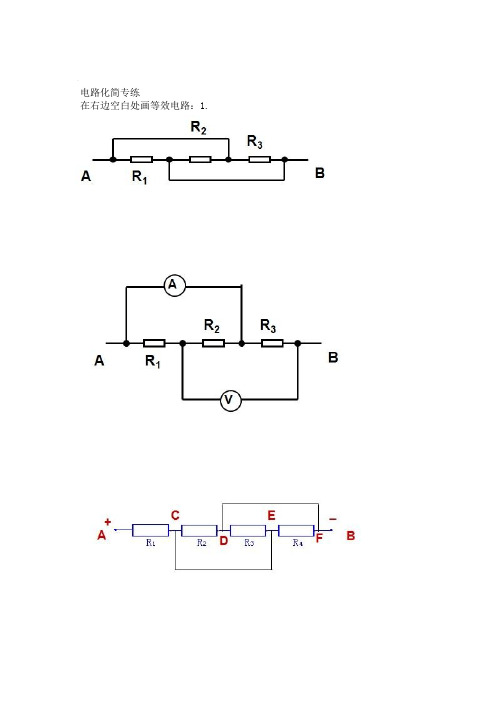
电路化简专练在右边空白处画等效电路:1.、R电阻都是精选资料,欢迎下载。
接电源时的等效电路图:分别画出AD接电源和AB2.3..画出电键断开和闭合时的等效电路图:4.含电容器、电流表、电压表的复杂电路KSU闭A、B两点间的电压。
当=1.如图所示,当电键断开时,AB U A、B两点间的电压。
=合时,AB SSSS是极板水平放置的平行板电均闭合、在如图电路中,电键2..C、、4123PP会向下运动容器,板间悬浮着一油滴,断开哪一个电键后SSSS.A.B.DC.4123R与平行板电容器组如图是一个由电池、电阻3(多选). 成的串联电路,在增大电容器两极板间距离的过程中R B.电容器的电容变小A.电阻中没有电流bRa中有从的电流流向C.电阻abR的电流流向D.电阻中有从C极板是水平放置的,它和一平行板电容器,).4(多选m的带电油滴悬浮在.今有一质量为三个可变电阻及电源联接成如图所示的电路 .要使油滴上升,可采用的办法是两极板之间静止不动RR A.增大增大B.21RR D.减小增大C.23CRRE)闭=6 Ω,=4 Ω,1F,电池内阻可忽略。
求(15.如图所示,10 V=,=21RKKR的总2的电流;()然后将开关断开,求这以后通过合开关,求稳定后通过11.电量RRBA、内电阻可忽略的直流电源,,电阻、如图所示,6.在、两点间接一电压为U21R C,电流表的内阻不计,求:(1)电流表的读数.,电容器的电容为的阻值为R3R (2)电容器所带的电荷量.的电荷量(3)断开电源后,通过2答案精选资料,欢迎下载。
0 2.C 3.BC 4.CD 5.(1)1A (2)6C (3)1C 6.(1)U/R (2)CU(3)CU/2 1.U、5.含电容器、电流表、电压表的复杂电路:画等效电路时,可以注意以下原则:与电容器、电容器、电压表视为断路(若考虑内阻,则将其视为一个大电阻),①电流表视为导线,电压表串联的用电器视为短路即可。
高中物理电路的简化的方法

高中物理电路的简化的方法?[标签:高中物理,电路]解决时间:2009-09-26 00:33满意答案好评率:66%1、节点法就是标出所有的连接点(电路元件左右两端),用导线直接连在一起的算一个连接点,用同一个字符来标示,然后画出串、并联关系非常明确的等效电路图,再进行简化。
2、局部化简法从局部入手,找出其中的串联、并联部分。
例,某段电路有R1、R2两个电阻串联,又与R3并联。
则把R1、R2这两个电阻去掉,换成一个电阻,记为R12,连入原图中。
然后把R12和R3都去掉,换成一个电阻,记为R(12)/3连入原图中。
你会发现这样下去,电路图越来越简单,并且看你自己标记的电阻符号,你就知道其关系了。
如果1、2两电阻串联,3、4两电阻串联,然后再并上。
记为R(12)/(34)如2、3并联,前串1、后串4,记为R1(2/3)4求高中物理电路图简化方法2009-1-23 13:52浏览次数:1426次2009-1-23 13:55最佳答案:1、元件的等效处理,理想电压表--开路、理想电流表--短路;2、电流流向分析法:从电源一极出法,依次画出电流的分合情况。
注意:○1有分的情况,要画完一路再开始第二路,不要遗漏。
○2一般先画干路,再画支路。
3、等势点分析法:先分析电路中各点电势的高低关系,再依各点电势高低关系依次排列,等电势的点画在一起,再将各元件依次接入相应各点,就能看出电路结构了。
4、弄清结构后,再分析各电表测量的是什么元件的电流或电压。
说明:2、3两点往往是结合起来用的。
这是我复制来的,多做些题目仔细体会一下高中物理串联、并联电路的简化来源:4221学习网整理| 作者:未知| 本文已影响683 人在我们平常所遇到的串联、并联电路问题中,最头痛的莫过于碰到一个复杂的电路而不知如何下手。
其实,对于物理中的复杂电路计算,可采取简化电路的方法,化为几个简单的问题进行解决。
简化电路的原则是根据题目提出的要求,取消被短路与开路的器件,保留通路的器件,从而简化出其等效电路。
电路化简

电路化简2.4.1、 等效电源定理实际的直流电源可以看作电动势为ε,内阻为零的恒压源与内阻r 的串联,如图2-4-1所示,这部分电路被称为电压源。
不论外电阻R 如何,总是提供不变电流的理想电源为恒流源。
实际电源ε、r 对外电阻R 提供电流I 为r R rr r R I +⋅=+=εε其中r /ε为电源短路电流0I ,因而实际电源可看作是一定的内阻与恒流并联的电流源,如图2-4-2所示。
实际的电源既可看作电压源,又可看作电流源,电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。
利用电压源与电流源的等效性可使某些电路的计算简化。
等效电压源定理又叫戴维宁定理,内容是:两端有源网络可等效于一个电压源,其电动势等于网络的开路电压,内阻等于从网络两端看除电源以外网络的电阻。
如图2-4-3所示为两端有源网络A 与电阻R 的串联,网络A 可视为一电压源,等效电源电动势0ε等于a 、b 两点开路时端电压,等效内阻0r 等于网络中除去电动势的内阻,如图2-4-4所示。
等效电流源定理又叫诺尔顿定理,内容是:两端有源网络可等效于一个电流源,电流图2-4-1图2-4-2图2-4-3图2-4-4源的0I 等于网络两端短路时流经两端点的电流,内阻等于从网络两端看除电源外网络的电阻。
例4、如图2-4-5所示的电路中,Ω=Ω=Ω=Ω=Ω=Ω===0.194,5.43,0.52,0.101,0.12,5.01,0.12,0.31R R R R r r V V εε(1)试用等效电压源定理计算从电源()22r 、ε正极流出的电流2I ;(2)试用等效电流源定理计算从结点B 流向节点A 的电流1I 。
分析: 根据题意,在求通过2ε电源的电流时,可将ABCDE 部分电路等效为一个电压源,求解通过1R 的电流时,可将上下两个有源支路等效为一个电流源。
解: (1)设ABCDE 等效电压源电动势0ε,内阻0r ,如图2-4-6所示,由等效电压源定理,应有VR R R r R 5.11321110=+++=εε()Ω=+++++=5321132110R R R r R R r R r电源00r 、ε与电源22r 、ε串联,故Ar R r I 02.0240022-=+++=εε2I <0,表明电流从2ε负极流出。
逻辑电路化简公式

逻辑电路化简公式
逻辑电路的化简是电子数字电路设计中的重要环节。
它通过对逻辑电路的布尔函数进行简化,实现对电路的优化,从而减少电路中的元器件数量,降低电路的功耗和成本,提高电路的可靠性和性能。
化简逻辑电路的核心是化简其布尔函数,而化简布尔函数又有以下几种方法。
1.代数化简法
代数化简法是一种基本的布尔函数化简方法,其基本思想是通过代数运算,把布尔表达式转化为简化的形式。
常用的代数化简方法有吸收律、分配律、德摩根定理等。
例如,在化简布尔表达式AB+AC时,可以使用吸收律将其简化为
A(B+C)。
2.卡诺图法
卡诺图法是一种重要的逻辑电路化简方法,它通过绘制卡诺图,把同样的几个布尔函数合并在一起,以达到化简的目的。
例如,在化简布尔表达式A’C’+A’BC+AB’C时,可以使用卡诺图法得到如下的化简结果:
3.奎因-麦克拉斯基方法
奎因-麦克拉斯基方法是一种基于二进制数的逻辑电路化简方法,它通过求取二进制数的最小项和最大项,以及使用二进制加法和减法等运算,实现对布尔表达式的化简。
例如,在化简布尔表达式A’B’C+ABC’+ABC时,可以使用奎因-麦克拉斯基方法得到如下的化简结果:
4.逻辑代数法
逻辑代数法是一种类比于传统代数的逻辑演算方法,它在布尔代数理论的基础上,将逻辑运算符与代数运算符联系起来,以期达到逻辑电路的简单化,化简的方法是精品。
以上四种化简方法可以互相结合使用,以达到更好的效果。
在实际的电路设计中,根据不同的应用场景和要求,选择合适的化简方法,可以大幅提高电路的性能和可靠性。
电路化简之节点法

节点法
1.寻找节点
何谓节点,电路中三条或三条以上导线的汇交点,称为
节点。借助节点排列的规范化来作出等效电路的方法,称为
节点法。
如图,我们可以找到6个节点。
2.节点编号
编号是要注意,电源的正极(或负极)编1号,负极(或 正极)编最后一个号。如果发现两个节点间只有导线(电流表、 闭合的开关)连接,那么这两个节点编为同一号。如果是电流 表在同一号节点间的,需要记住表两端接的用电器号。
4.当S1、S2 均闭合且滑片P 滑到a 端时; 当S1、S2 均断开且滑片P 在a 端时
3.重新连线
重新连线应在草稿纸上完成,首先在纸上同一线上画上4 个点并编上号,点间距离最好大一点,然后依次从电路中找到 节点之间的电阻或者电表画在四个点间。为了避免漏画,可以 画一个从图上标出一个,直到原电路图上的元件全都画到了图 上为止。过程如下:
重新画线第一步:画出所有的节点
1
2
3
4
3.重新连线
重新画线第二步:按顺序依次画出所有电路步:转化为规范化电路图。第二步中规范绘制
也就是规范电路图。
V
A
1
R1
2
R3
3
R4
4
R2 R5
4 . 节 点 法 化 简 电 路 练习化简电路图
练习化简电路图
(1)当闭合开关S0、S1,断 开开关S2时; (2)当闭合开关S2,断开开 关S0、S1时;
高中物理高二简化电路(共10张PPT)

(1)a 图S1,S2都闭合时;(2)a 图
S1,S2都断开时;(3)S1闭合,S2 例5、如图8,R1=R2=20Ω,V1表的示数U1=6V,V2表的示数U2=9V,问:(1)R1、R2、R3的连接形式是
一个或哪两个电阻两端的电压?则R3.
;(2)V1、V2分别测哪
其原则是:将电流表视为短路;
断开时;(4)s1断开,s2闭合时。 (3)电阻不计的导线可以伸长、缩短或者弯曲,电路中同一条导线的两端可以看成是一点。
(2)V1、V2分别测哪一个或哪两个电阻
两端的电压?则R3.= ,电源电压U=
V
器为并联;
简化电路方法:
节点法:在识别电路时,不论导线有多
长,只要其间没有电源、用电器,导线
两端均可看成同一点(看成是等势点)。按照 电流的流向将电路中的各节点依次标上A、 B、C、D等,然后将各用元件连在相对应 的节点位置即可。
简化电路应注意以下几点:
(1)开关闭合时将其连成一条线,开关 断开时可去掉。
(1)开关闭合时将其连成一条线,开关断开时可去掉。 1)电流法:让电流从电源正极流经各用电器回到电源的负极,途中电流只有一条通路,这些用电器为串联;
例4、画出下图电路的等效电路图:
丁图开关S1和S2均闭合时 与 是
(1)a 图S1,S2都闭合时;(2)a 图S1,S2都断开时;(3)S1闭合,S2断开时;(4)s1断开,s2闭合时。
(3)电阻不计的导线可以伸长、缩短或者弯曲,电路中同一条导线的两端可以看成是一点。
例1:根据下图甲、乙、丙、丁四个电路图识别小灯泡是怎样连接的?
例2、在图3所示电路中,开关都闭合灯连接方式如何?
简化电路先判断串联或是并联:
按照电流的流向将电路中的各节点依次标上A、B、C、D等,然后将各用元件连在相对应的节点位置即可。
电路化简(14张PPT)剖析讲解

如何理解电流经过电阻后降压 U=IR
R1
R2R3AB源自U1=IR1 U2=IR2
U3=IR3
一、化简方法
1.电流分支法 2.等电势法
二、化简原则
1.理想导线可任意长短 2.无电流支路可去掉 3.等电势点可合并 4.摘表:理想电压表可看成断路,理想电流表可看成短 路,电流稳定后,电容器可看成断开。 5判断电阻串、并联关系,两个电阻并联后可看成一个 整体。 6两法并用:假想高低电势点,电流从高电势点流入, 从低电势点流出,看经过哪些支路。
A1
R2
结点电流原理:流 入某个结点的电流 强度等于流出该点 电流大小。 R3
A
R1
B
A2
A1电流表示数为I2+I3 A2电流表示数为I1+I2
4.若已知UAB=U,R=R1=R2=R3,求
电流表读数:U/R 电压表读数:U
A
R2
R3
A
R1
B
V
A
R2
R3
A
R1
B
V
5.画右图的等
R5
效电路。 R3
二、例题选解
1.如图,画等效电路。
A
R1
C
B A、D接电源时
R2 R3
R4 D
A、B接电源时
R1 R4
R1 R4
R3
A
DA
R2 R3
R2
B
• 如图,画等效电路。
R1
R3
R2
A
R4
B
R5
R1 R2
R3 R4
A
R5
B
2.画下图的等效电路。
R1
A
R2
B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电路化简2.4.1、 等效电源定理实际的直流电源可以看作电动势为ε,内阻为零的恒压源与内阻r 的串联,如图2-4-1所示,这部分电路被称为电压源。
不论外电阻R 如何,总是提供不变电流的理想电源为恒流源。
实际电源ε、r 对外电阻R 提供电流I 为其中r /ε为电源短路电流0I ,因而实际电源可看作是一定的内阻与恒流并联的电流源,如图2-4-2所示。
实际的电源既可看作电压源,又可看作电流源,电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。
利用电压源与电流源的等效性可使某些电路的计算简化。
等效电压源定理又叫戴维宁定理,内容是:两端有源网络可等效于一个电压源,其电动势等于网络的开路电压,内阻等于从网络两端看除电源以外网络的电阻。
如图2-4-3所示为两端有源网络A 与电阻R 的串联,网络A 可视为一电压源,等效电源电动势0ε等于a 、b 两点开路时端电压,等效内阻0r 等于网络中除去电动势的内阻,如图2-4-4所示。
图2-4-1图2-4-2图2-4-3图2-4-4等效电流源定理 又叫诺尔顿定理,内容是:两端有源网络可等效于一个电流源,电流源的0I 等于网络两端短路时流经两端点的电流,内阻等于从网络两端看除电源外网络的电阻。
例4、如图2-4-5所示的电路中,Ω=Ω=Ω=Ω=Ω===0.194,5.43,0.101,0.12,5.01,0.12,0.31R R R R r r V V εε (1)试用等效电压源定理计算从电源()22r 、ε正极流出的电流2I ;(2)试用等效电流源定理计算从结点B 流向节点A 的电流1I 。
分析: 根据题意,在求通过2ε电源的电流时,可将ABCDE 部分电路等效为一个电压源,求解通过1R 的电流时,可将上下两个有源支路等效为一个电流源。
解: (1)设ABCDE 等效电压源电动势0ε,内阻0r ,如图2-4-6所示,由等效电压源定理,应有VR R R r R 5.1132111=+++=εε电源00r 、ε与电源22r 、ε串联,故2I <0,表明电流从2ε负极流出。
(2)将A 、B 两个节点短接,构成等效电流源(00r I 、)如图2-4-7所示,由等效电流源定理,0I 为原电路流经A 、B 短接后的支路电流。
因为有21εε、两电源,必须用线性叠加原理,所谓叠加原理与力学中“力的独立作用原理”极为相似,其内容为:若电路中有多个电源,则通过任一支路的电流等于各个电动势单独存在时该支路产生的电流之和。
2图2-4-5图2-4-6由叠加原理 由0r '和1R 的分流关系2.4.2、 Y —△变换在某些复杂的电路中往往会遇到电阻的Y 型或△,如图2-4-8所示,有时把Y 型联接代换成等效的△型联接,或把△型联接代换成等效的Y 型联接,可使电路变为串、并联,从而简化计算,等效代换要求Y 型联接三个端纽的电压312312U U U 、、及流过的电流321I I I 、、与△型联接的三个端纽相同。
在Y 型电路中有 可解得 在△型电路中 等效即满足:即 313322112R R R R R R R R ++=①213322131R R R R R R R R ++=②类似方法可得 113322123R R R R R R R R ++= ③①、②、③式是将Y 型网络变换到△型电路中的一组变换。
同样将△型电路变换到Y 型电路,变换式可由①、②、③式求得:④、⑤、⑥31231231121R R R R R R ++=④1图2-4-7图2-4-831231223122R R R R R R ++=⑤ 31231223313R R R R R R ++=⑥例5、试求如图2-4-9所示电路中的电流。
分析: 这是包含一个Y 型电路和一个△型电路的网络,解决问题的方向可将左边Y 型网络元变换成△型网络元,或将右侧△型网络元变换成Y 型网络元。
解: 将左侧Y型网络换成△型,如图2-4-10Ω===1321R R R所示已知 则有Ω=++=3213322131R R R R R R R R由图2-4-10,可进一步电路整理为图2-4-11所示。
Ω=34总R将右侧△型网络元换成Y 型网络元同样可求得Ω=34总R ,这里不再叙述。
2.4.3、 对称性原理①等势节点的断接法在一个复杂电路中,如果能找到一些完全对称的点,(以两端连线为对称轴),那么可以将接在等电势节点'图2-4-9'图2-4-10V4图2-4-11AC间的导线或电阻或不含电源的支路断开(即去掉),也可以用导线或电阻或不含电源的支路将等电势节点连接起来,且不影响电路的等效性。
例6、用导线连接成如图2-4-12所示的框架,ABCD 和ABCE 是正四面体,每段导线的电阻都是1Ω。
求AB 间的总电阻。
解: 设想A 、B 两点上存在电势差B AU U -,由于电路的对称性可以知道D 、C 、两点的电势都应该介乎A U 与B U 的中间,即2/)(B A U U U-=,所以两点应是等电势的。
这样,去掉CD 段导线,对A 、B 间的总电阻不会有影响。
当去掉CD 段导线后,就成为三路并联,即A —D —B ,A —C —B ,和AB 。
于是:②电流分布法设有电流I 从A 点流入、B 点流出,应用电流分流的思想和网络中两点间不同路径等电压的思想,(即基耳霍夫定理),建立以网络中各支路的电流为未知量的方程组,解出各支路电流与总电流I 的关系,然后经任一路径计算A 、B 两点间的电压AB U ,再由I U R ABAB =即可求出等效电阻。
例7、10根电阻均为r 的电阻丝接成如图2-4-13所示的网络,试求出A 、B 两点之间的等效电阻AB R 。
由结构对称性,要求电流I 从A 点流入后在A 点的电流分布应与电流I 从B 点流出前的电流分布相同,中间四方形必具有上、下电流分布对称和左、右电流分布对称,因此网络内电流分布应如图2-4-14所示。
对图中C 点和D 点,有电流关联解得II I 2121=+ ①图2-4-13由A 、E 两点间不同路线等电压的要求,得 即 I I I =-123②解①、②两式得 选择线路AEDB ,可得 因此,A 、B 间等效电阻便为2.4.4、无穷网络等效变换法若,⋯++++=a a a a x(a >0)在求x 值时,x 注意到是由无限多个a 组成,所以去掉左边第一个+a 对x 值毫无影响,即剩余部分仍为x ,这样,就可以将原式等效变换为x a x +=,即02=--a x x。
所以这就是物理学中解决无限网络问题的基本思路。
例8、如图2-4-15所示,框架是用同种金属丝制成的,单位长度的电阻为ρ,一连串内接等边三角形的数目可认为趋向无穷,取AB 边长为a ,以下每个三角形的边长依次减小一半,则框架上A 、B 两点间的电阻为多大?从对称性考虑原电路可以用如图2-4-16所示的等效电路来代替,同时我们用电阻为2/AB R 的电阻器来代替由无数层“格子”所构成的“内”三角,并且电阻是AB R 这样的,x AB R R =,ρa R =因此解此方程得到2.4.5、 电流叠加法AB图2-4-15B2/图2-4-16解题步骤是:先考虑一支流入或流出系统的电流,把它看作在给系统充电或放电,利用对称性求出系统中的电荷分布和电流场分布,求出每一支电流造成的分布后进行叠加,使得电荷分布全部抵消,而电流场叠加作为所求的电流场。
例9、有一个无限平面导体网络,它由大小相同的正六边形网眼组成,如图2-4-17所示。
所有六边形每边的电阻为0R ,求:(1)结点a 、b 间的电阻。
(2)如果有电流I 由a 点流入网络,由g 点流出网络,那么流过de 段电阻的电流 I de 为多大。
解: (1)设有电流I 自a 点流入,流到四面八方无穷远处,那么必有3/I 电流由a 流向c ,有6/I 电流由c 流向b 。
再假设有电流I 由四面八方汇集b 点流出,那么必有6/I电流由a 流向c ,有3/I 电流由c 流向b 。
将以上两种情况综合,即有电流I 由a 点流入,自b 点流出,由电流叠加原理可知263I I I I ac =+=(由a 流向c ) 263I I I I cb =+=(由c 流向b )因此,a 、b 两点间等效电阻(2)假如有电流I 从a 点流进网络,流向四面八方,根据对称性,可以设 应该有I I I A =+B 63因为b 、d 两点关于a 点对称,所以同理,假如有电流I 从四面八方汇集到g 点流出,应该有图2-4-17最后,根据电流的叠加原理可知以上几种方法可实现电路的化简。
其中,电流分布法特别适合于纯电阻电路及求复杂导体和等效电阻,当为纯电容电路时,可先将电容换成电阻为解等效阻值,最后只需将R 换成C 1即可。
例10、十个电容为C 的电容器按图2-4-17个方式连接,求AB 间等效电容AB C 。
解: 将电容全部换成阻值为r 的电阻,由“电容分布法”中的例题可知用C 1代替R ,则图2-4-17。
