2016年四川省特岗数学真题
四川省特岗教师招聘考试真题2016年

四川省特岗教师招聘考试真题2016年(总分:100.00,做题时间:90分钟)一、单项选择题(总题数:30,分数:30.00)1.教育学史上第一个正式提出的有关教育起源的学说是______(分数:1.00)A.神话起源论B.生物起源论√C.心理起源论D.劳动起源论解析:[解析] 生物起源说是第一个正式提出的有关教育起源的学说。
2.在世界教育学史上被认为是“现代教育学之父”的教育学家是______(分数:1.00)A.夸美纽斯B.杜威C.康德D.赫尔巴特√解析:[解析] 赫尔巴特在世界教育史上被认为是“现代教育学之父”或“科学教育学的奠基人”。
3.教师仅凭考试成绩来评价学生,从而导致学生产生“书呆子型”成就中心的偏向。
这是考试的______ (分数:1.00)A.显性正向功能B.显性负向功能C.隐性正向功能D.隐性负向功能√解析:[解析] 负向教育功能是指阻碍社会进步和个体发展的消极影响和作用,隐性教育功能是指伴随显性功能而出现的非预期的功能。
题干中的“书呆子型”即体现了伴随着考试的评价功能而出现的阻碍个体发展的隐性功能。
4.下列选项中,不属于教育目的的功能的是______(分数:1.00)A.对教育活动的定向功能B.对教育活动的调控功能C.对教育活动的监督功能√D.对教育活动的评价功能解析:[解析] 教育目的的功能包括:(1)对教育活动的定向功能;(2)对教育活动的调控功能;(3)对教育活动的评价功能。
5.“家有一斗粮,不当孩子王。
”这种说法反映了中国传统社会中教师普遍较低的______(分数:1.00)A.政治地位B.经济地位√C.法律地位D.专业地位解析:[解析] 教师职业的经济地位指将教师职业与其他职业相比较,其劳动报酬的差异状况及其经济生活状态。
它是教师社会地位的最直接体现。
自古以来,除少数大师鸿儒外,普通教师的经济地位一直比较低下,“家有一斗粮,不当孩子王”“两袖清风”等正是这种情况的真实写照。
【真题】2018年四川省特岗教师初中数学学科专业知识试卷全解析版
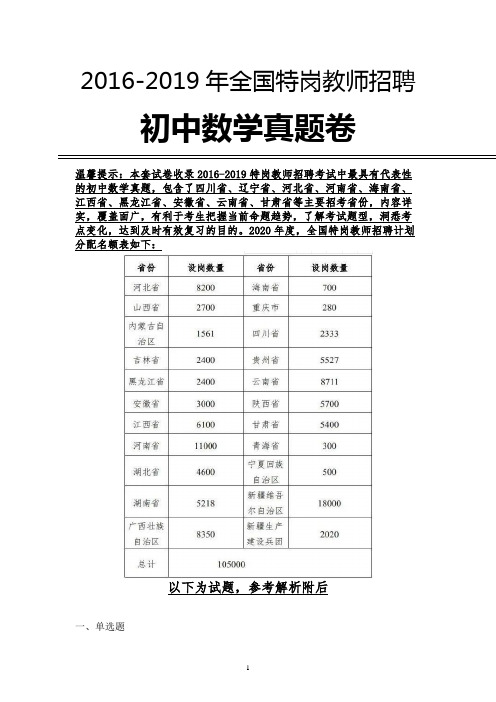
2016-2019年全国特岗教师招聘初中数学真题卷温馨提示:本套试卷收录2016-2019特岗教师招聘考试中最具有代表性的初中数学真题,包含了四川省、辽宁省、河北省、河南省、海南省、江西省、黑龙江省、安徽省、云南省、甘肃省等主要招考省份,内容详实,覆盖面广,有利于考生把握当前命题趋势,了解考试题型,洞悉考点变化,达到及时有效复习的目的。
2020年度,全国特岗教师招聘计划分配名额表如下:以下为试题,参考解析附后一、单选题1.5的相反数是()A.﹣5 B.5 C.D.【答案】A【解析】试题分析:5的相反数是﹣5,故选A.考点:相反数.2.估计6+1的值在()A.2到3之间B.3到4之间C.4到5之间D.5到6之间3.如图,数轴上的点A,B,O,C,D分别表示数-2,-1,0,1,2,则表示数25的点P应落在()A.线段AB上B.线段BO上C.线段OC上D.线段CD上4.数轴上有A,B,C,D四个点,其中绝对值大于2的点是()A.点A B.点B C.点C D.点D5.按照如图所示的操作步骤,若输入的值为3,则输出的值为()A.54 B.55 C.60 D.616.下列四边形中,是中心对称而不是轴对称图形的是()A.平行四边形B.矩形C.菱形D.正方形7.已知数据:2,1,4,6,9,8,6,1.则这组数据的中位数是()A.4 B.5 C.6 D.4和68.如图所示,将长方形ABCD的一角沿AE折叠,若∠BAD′=40°,那么∠EAD′的度数为()A.20 B.25°C.40°D.50°9.如图,把一张长方形的纸片ABCD沿EF折叠,若∠AED′=40°,则∠DEF 的度数为()A.40°B.50°C.60°D.70°10.94的值等于()A.32B.32-C.32±D.811611.△ABC中,AB=7,BC=24,AC=25.在△ABC内有一点P到各边的距离相等,则这个距离为()A.1 B.2 C.3 D.412.如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=12BC=1,则下列结论:①∠CAD=30°②BD=7③S平行四边形ABCD =AB•AC④OE=14AD⑤S△APO=312,正确的个数是()A.2 B.3 C.4 D.5 13.下图中是中心对称图形而不是轴对称图形的共有()。
【必备】2019年四川省特岗教师初中数学学科专业知识试卷全解析版
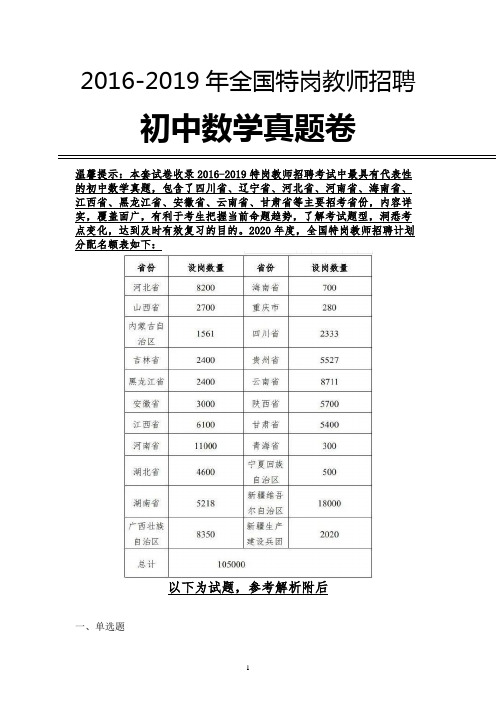
2016-2019年全国特岗教师招聘初中数学真题卷温馨提示:本套试卷收录2016-2019特岗教师招聘考试中最具有代表性的初中数学真题,包含了四川省、辽宁省、河北省、河南省、海南省、江西省、黑龙江省、安徽省、云南省、甘肃省等主要招考省份,内容详实,覆盖面广,有利于考生把握当前命题趋势,了解考试题型,洞悉考点变化,达到及时有效复习的目的。
2020年度,全国特岗教师招聘计划分配名额表如下:以下为试题,参考解析附后一、单选题1.下列图案属于轴对称图形的是()A.B.C.D.2.如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放.若∠EMB=75°,则∠PNM度数是()A.45°B.25°C.30°D.20°3.如图所示是由5个相同的小正方体组成的立体图形,这个立体图形的俯视图是()A.B.C.D.4.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E 处,若∠AGE=32°,则∠GHC等于()A .112°B .110°C .108°D .106°5.如图,AD 是ABC ∆的角平分线,DE AB ⊥,垂足为E ,若7ABC S ∆=,2DE =,4AB =,则AC 的长为( )A .6B .5C .4D .36.下列运算正确的是( )A .a 2 + a 3 = a 5B .(- b 2)3 =— b 6C .2x ∙ 2x 2 = 2x 3D .(m —n )2 = m 2 — n 2 7.在同一直角坐标系中,函数y mx m =+和函数222y mx x =-++(m 是常数,且0m ≠)的图象可能是( )A .B .C .D .8.如图,一次函数y 1=ax+b 图象和反比例函数y 2=k x图象交于A(1,2),B(﹣2,﹣1)两点,若y 1<y 2,则x 的取值范围是( )。
2016年特岗教师招聘中学数学专业知识试题及答案

2010年特岗教师招聘中学数学专业知识试题及答案特岗教师招聘考试中学数学试卷中学数学试卷(满分为100分)一、单项选择题(在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的代号填入题后括号内。
本大题共12小题,每小题3分,共36分。
)1.若不等式x2-x≤0的解集为M,函数f(x)=ln(1-|x|)的定义域为N,则M∩N为()。
A. [0,1)B. (0,1)C. [0,1]D. (-1,0]2.将函数y=2x+1的图像按向量a平移得到函数y=2x+1的图像,则a等于()。
A. (-1,-1)B.(1,-1)C.(1,1)D.(-1,1)3.已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,则AB1与底面ABC所成角的正弦值等于()。
A. 13B. 23C. 33D. 234.若不等式组x≥0, x+3y≥4, 3x+y≤4,所表示的平面区域被直线y=kx+43分为面积相等的两部分,则k的值是()。
A. 73B. 37C. 43D. 345.一个等差数列首项为32,该数列从第15项开始小于1,则此数列的公差d的取值范围是()。
A. -3113≤d<-3114B. -3113<d<-3114C. d<3114D. d≥-31136.∫π2-π2(1+cosx)dx等于()。
A. πB. 2C. π-2D. π+27.在相距4k米的A、B两地,听到炮弹爆炸声的时间相差2秒,若声速每秒k米,则爆炸地点P 必在()。
A. 以A、B为焦点,短轴长为3k米的椭圆上B. 以AB为直径的圆上C. 以A、B为焦点, 实轴长为2k米的双曲线上D. 以A、B为顶点, 虚轴长为3k米的双曲线上8.通过摆事实、讲道理,使学生提高认识、形成正确观点的德育方法是()。
A. 榜样法B. 锻炼法C. 说服法D. 陶冶法9.一次绝对值不等式|x|>a(a>0)的解集为x>a或x<a,|x|<a(a>0)的解集为-a<x <a。
2015年四川省特岗数学真题

2015年四川特岗教师招聘考试《小学数学》真题及解析一、选择题(本大题共15小题,每小题3分,共45分)1已知集合A={-1,0,1},集合B={x∣x2+x=0},则集合A∪B=( )。
A、{-1,0,1}B、{-1,0}C、{0,1}D、{-1,1}2函数f(x)=x2的图像关于( ).A、y轴对称B、直线y=x对称C、坐标原点对称D、直线y=-x对称3若向量a=(2,6),向量b=(3,x),且a∥b,则x=( )。
A、-1B、1C、4D、94若角α的终边在第二象限,则点P(sinα,cosα)在( )·A、第一象限B、第二象限C、第三象限D、第四象限5函数f(x)=2的x次方+3x的零点所在的一个区间是( )·A、(-2,-1)B、(-1,0)C、(0,1)D、(1,2)6下列函数中,在区间(0,+∞)上为减函数的是( ).A、y=2xB、y=lnxC、D、7设i为虚数单位,则复数A、-1-iB、-2+iC、2-i8有两张卡片,一张的正反面分别写着数字1与2,另一张的正反面分别写着3与4,将两张卡片排在一起组成一个两位数,则所组成的两位数为奇数的概率是( ).9已知三棱锥的底面是边长为1的正三角形,其正视图如图所示,则此三棱锥的体积为( ).10双曲线的离心率是( ).11为了得到函数的图像,只需把函数y=sinx的图像上所有的点( ).12圆(x-1)2+y2=1的圆心到直线x+y-2=0的距离是( ).13若正实数x和y满足x+2y=1,则xy的最大值是( ).14抛物线y2=4x上一点P到点F(1,0)的距离是3,则点P到y轴的距离为( ).A、1C、3D、415若α、β为两个不同的平面,m为平面α上一条直线,则“α⊥β”是“m⊥β”的( ).A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件二、填空题(本大题共5小题,每小题3分.共15分)16lg2+lg5= .17一支田径队有男运动员28人,女运动员21人,现按性别用分层抽样的方法,从中抽取14位运动员进行健康检查,则男运动员应抽取人.18执行如图所示的程序框图,输出的S的值是 .19已知,则sin2α= .20设变量x,y满足约束条件,则目标函数z=4x+y的最大值为 .三、解答题(本大题共5小题,每小题8分,共40分.解答应写出文字说明,证明过程或演算步骤)21已知△ABC的内角A、B、C所对的边分别为a、b、C,(Ⅰ)求cosC的值;(Ⅱ)求△ABC的面积.22已知公差不为0的等差数列{an}的首项为2,且a1、a2、a4成等比数列.(Ⅰ)求数列{an}的通项公式;(Ⅱ)设数列{an}的前n项和为Sn,求数列的前n项和.在正方体ABCD-A1B1C1D1中,点M、N分别是棱AB、C1D1的中点. (Ⅰ)证明:直线MN⊥直线B1C;(Ⅱ)证明:直线CM∥平面AA1N。
四川特岗教师考试试题(中学数学)

)
。
A. 简单随机抽样
B. 按性别分层抽样
C. 按学段分层抽样
D. 系统抽样
5. 已知在正项等比数列 {an} 中,a7·a1=256,则 a4 =(
A. 8
B. 16
C. 32
D. 256
6. 若一个几何体的三视图都是三角形,则该几何体是(
A. 圆锥
B. 圆台
C. 三棱锥
15. 程序如图所示,S=_________。
44
特岗教师 数学・题本-修改版本.indd 44
2020/7/14 19:58:11
2018年四川特岗教师考试试题(中学数学)
16.
sin cos
3 ,则 tan 2θ=_________。
sin cos
三、解答题(本大题共 5 小题,17~20 小题每小题 7 分,21 小题 8 分,共 36 分)
10
8. 若直线 x+y—2=0 与圆 x 2 ( y a ) 2 2 相交,则实数 a 的取值范围是(
A. [0,4]
B.(0,4)
C.(—∞,4)
D.(—∞,4)∪(4,+ ∞)
9. 函数 f(x)=sin 2x(cos2x—sin2x)是(
)
。
π
A. 最小正周期为 的奇函数
2
π
B. 最小正周期为 的偶函数
2. 下列函数为奇函数的是(
)
。
A. y=cosx
2
B. y = x
C. y=lnx+x
1
D. y =
x
3. 设 i 为虚数单位,则复数
)
【数学】2019年四川省特岗教师初中数学学科专业知识试卷全解析版

初中数学真题卷Leabharlann 温馨提示:本套试卷收录 2016-2019 特岗教师招聘考试中最具有代表性 的初中数学真题,包含了四川省、辽宁省、河北省、河南省、海南省、 江西省、黑龙江省、安徽省、云南省、甘肃省等主要招考省份,内容详 实,覆盖面广,有利于考生把握当前命题趋势,了解考试题型,洞悉考 点变化,达到及时有效复习的目的。2020 年度,全国特岗教师招聘计划 分配名额表如下:
()
3
A.abc<0
B.b2﹣4ac<0 C.a﹣b+c<0
D.2a+b=0
12.下列运算正确的是( )
A.a2+a2=a4 C.2x•2x2=2x3
B.(﹣b2)3=﹣b6 D.(m﹣n)2=m2﹣n2
13.在一个口袋中有 4 个完全相同的小球,把它们分别标号为 1,2,3,4,随
机地摸出一个小球然后放回,再随机地摸出一个小球.则两次摸出的小球的标
A.调查某班学生的身高情况,适采用抽样训查
B.对端午节期间市场上粽子质量情况的调查适合采用全面调查
C.小南抛掷两次硬币都是正面向上,说明抛掷硬币正面向上的率是 1
D.“若 m, n 互为相反数,则 m n 0 ”,这一事件是必然事件
8.四个实数﹣ 2 ,1,0,﹣2.5 中,最小的实数是( ) 3
A.﹣ 2 3
B.1
9.下列运算正确的是( )
C.0
D.﹣2.5
A.a2•a3=a6
B.(a2)3=a6
C.a6÷a2=a3
D.2﹣3=﹣6
10.在△ABC 中,AB=10,AC=2 10 ,BC 边上的高 AD=6,则另一边 BC 等于
()
2016年四川省特岗教师招聘(初中数学)真题试卷(精选)(题后含答

2016年四川省特岗教师招聘(初中数学)真题试卷(精选)(题后含答案及解析)题型有:1. 单项选择题 3. 简答题 5. 填空题单项选择题1.已知集合P={x|x2-x-2≤0},Q={x|log2(x-1)≤1),则等于( ).A.(-∞,-1]U[3,+∞)B.[2,3]C.(∞,-1]U(3,+∞)D.(2,3]正确答案:D解析:对于集合P:z。
x2-x-2≤0,整理得(x-2)(x+1)≤0,解得-1≤x≤2,所以P={x|-1≤x≤2},={x|x<-1或x>2};对于集合Q:log2(x-1)≤1=log22,得到0<x-1≤2,解得1<x≤3,即Q={x|1<x≤3}.所以,()∩Q={x|2<x≤3}.答案选择D项.2.反比例函数f(x)=k/x(k为常数)的图像如右图所示,下列说法正确的是( ).A.常数k<-1B.函数f(x)在定义域范围内,y随x的增大而减小C.若点a(-1,m)和点b(2,n)在函数f(x)的图像上,则m<nD.函数f(x)图像的对称轴的直线方程是y=x正确答案:C解析:由图像可知,k>0,故A项错误;因为反比例函数的定义域为x≠0,故不能说在定义域内,y随x的增大而减小,只能说函数分别在(-∞,0)和(0,+∞)内,y随x的增大而减小,故B项错误;当x=-1时,,当x=2时,n=k/2,又因为k>0,因此-k<k/2,即m<n,故C项正确;因为k>0,故函数f(x)图像的对称轴的直线方程是y=-x,故D项错误.因此本题选C3.计算=( ).A.2B.-2C.2iD.-2i正确答案:A解析:.4.若sinθcosθ>0,则θ在( ).A.第一、二象限B.第一、三象限C.第一、四象限D.第二、四象限正确答案:B解析:由正弦、余弦函数的性质可知:又因为sinθcosθ>0,即故θ应在第一、三象限.5.在△ABC中,三边a,b,c成等差数列,也成等差数列,则△ABC是( ).A.正三角形B.等腰三角形C.直角三角形D.钝角三角形正确答案:A解析:故△ABC是正三角形.6.设不等式表示的平面区域为D,在区域D内随机抽取一个点,则此点到坐标原点的距离大于2的概率是( ).A.B.C.D.正确答案:D解析:如图阴影部分表示到坐标原点的距离大于2的点,则概率为P=7.在平面直角坐标系中,设A(-2,3),B(3,-2)沿x轴把直角坐标系折成120°二面角后,则AB的长度是( ).A.B.C.D.正确答案:C解析:题目化为求右图所示四棱锥中AB的长度,已知AD⊥DE,四边形BCDE为矩形,AD=3,DE=5,BE=2,∠ADC=120°.根据余弦定理,,所以AC=,所以AB=8.将直线x+y=1先绕点(1,0)顺时针旋转90°,再向上平移1个单位后,与圆x2+(y-1)2=r2相切,则半径r的值是( ).A.B.C.D.正确答案:A解析:经过一系列变化之后的直线为x-y=0,此直线到圆心(0,1)的距离即为r,9.双曲线的右准线与两渐近线交于A、B两点,右焦点为F,且,则双曲线的离心率为( )A.B.C.D.正确答案:C解析:双曲线准线方程为x=a2/c,渐近线方程为,则·F(c,0),又因为,得10.展开式中,x4的系数为( ).A.-10B.10C.40D.45正确答案:D解析:x4的系数为11.若a+1=b(a和b是不为0的自然数),那a和b的最小公倍数是( ).A.aB.bC.abD.(a+1)b正确答案:C解析:a与a+1互素,故a、b互素,所以两者的最小公倍数为ab.12.在平面直角坐标系中,点P(-4,5)关于原点对称的点的坐标为( ).A.(4,5)B.(4,-5)C.(-4,-5)D.(5,-4)正确答案:B13.下列性质中,等腰三角形具有而直角三角形不一定具有的是( ).A.两边之和大于第三边B.有一个角的平分线垂直于这个角的对边C.有两个锐角的和等于90°D.内角和等于180°正确答案:B解析:等腰三角形中顶角的平分线垂直于对边,但直角三角形不一定具有该性质,两边之和大于第三边、内角和等于180°是所有三角形都具有的性质,两个锐角的和等于90°是直角三角形具有的性质,但等腰三角形不一定具有.故本题选B14.一个无盖的正方体盒子的平面展开图可以是图中的( ).A.①B.①②C.②③D.①③正确答案:D15.若命题甲是命题乙的充分不必要条件,命题丙是命题乙的必要不充分条件,命题丁是命题丙的充要条件,则命题丁是命题甲的( ).A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件正确答案:B解析:由题意,命题甲可以推出命题乙,命题乙推出命题丙,命题丙推出命题丁,即命题甲推出命题丁,但反之则不行,所以命题丁是命题甲的必要不充分条件.简答题在△ABC中,角A,B,C所对的边分别是a,b,c且满足csinA=acosC,16.求角C的大小;正确答案:由正弦定理a/sinA=c/sinC,得asinC=csinA,又因为csinA=acosC,所以sinC=cosC,又因为cosC≠0,所以tanC=1,则C=π/4.17.求的最大值,并求取得最大值时角A、B的大小.正确答案:由上题结果C=π/4可知A+B=3π/4,所以题中原式可变为:.当时,该式有最大值2.此时.如图,在正方体ABCD-A1B1C1D]1中,棱长AA1=2,E为CC1的中点.18.求证:B1D1⊥AE;正确答案:以D为原点,DA为x轴正向、DC为y轴正向,DD1为z轴正向建立空间直角坐标系,则A(2,0,0),B(2,2,0),C(0,2,0),D(0,0,0),A1(2,0,2),B1(2,2,2),C1(0,2,2),D1(0,0,2),E(0,2,1).证明:因为,所以=-2×(-2)+(-2)×2+0×1=0.所以B1D1⊥AE.19.求二面角C-AE-B的平面角的正切值;正确答案:由题意可知,平面CAE的法向量m=(1,1,0),平面BAE的法向量n=(1,0,2),设平面角所求平面角为a,则,求得tanα=3.20.求点D1到平面EAB的距离.正确答案:平面EAB的方程为x+2z-2=0,点D1到平面EAB的距离为等差数列{an}的公差不为零,a4=7,a1,a2,a5成等比数列.21.求{an}的通项公式;正确答案:设等差数列{an}的通项公式为an=a1+(n-1)d(d≠0),则由已知可得解得即an=1+2(n-1)=2n-122.若数列{Tn}满足Tn=a2+a4+a8+…+a2n,求Tn正确答案:如图所示,一次函数y=kx+b的图像与反比例函数y=m/x的图像交于A(1,2),B(-m,-1)两点.23.求反比例函数和一次函数的解析式;正确答案:将两点代入得所以所求直线为y=x+1,反比例函数为y=2/x.24.根据图像直接写出使一次函数的值大于反比例函数的值的x的取值范围.正确答案:由题意可知,当取同-x值时,一次函数的点位于反比例函数的点上方,说明一次函数的值大于反比例函数的值.故观察图像得x∈(-2,0)∪(1,+∞).25.义务教育数学课程标准在各个学段都安排了数与代数的学习内容,小学生在第二学段将进一步学习整数、分数、小数和百分数及有关运算,进一步发展数感,假如你是小学第二学段的数学教师,你在教学中将会从哪些方面去培养学生的数感?(至少写出三个方面的观点)正确答案:(1)体会感知、萌芽数感只有当学生把所学知识与生活经验联系起来,才能更好地掌握知识,内化知识.数学是人们对客观世界定性把握和定量刻画的科学,它源自于生活,并优化于生活.数学教学要紧密联系学生的生活实际,只有当学生在生动、丰富的现实情境中,才能真正激起学生主动学习的欲望,才会有由具体理解上升到抽象与概括的层次提升.数感不是通过传授而得以培养的,而是让学生自己去感知、去发现,主动地去探索与体会,让学生在学习中感受到数学其实就在自己身边,让学生意识到运用所学到的数学知识可以解释生活中的数学现象,解决现实世界中的一些数学问题,感受到学习数学的作用.(2)思考方法,建立数感数学姓“数”,要进行数学式地学习,要让学生学会数学式地思考问题,会用数学的方法理解、解释并解决实际现象和问题,能从生活情境中看出数学的本质问题,这就是学生数感建立的过程.教师在教学中,可以通过自己的教学,有目的、有步骤逐步渗透、探索与实践,注重学生数学感悟素养的培养.(3)应用反思,巩固数感让学生了解数在现实中的应用,有助于使他们体会到数的意义,从而巩固数感.学生通常对于某个数的读与写、和与分等掌握得非常到位,但对于这个数的意义的理解,特别是这个数在现实生活中的应用还不甚了解.此时如果教师能在教学中将数与现实生活的应用相结合,将会让学生在现实情境中更好地把握数的意义,有助于数感的巩固与提高.填空题26.已知直线l过点A(0,2),且倾斜角的正切值为1,则直线l的方程为________________.正确答案:y=x+2解析:设直线l的方程为y=kx+b,根据题意,k=1,b=2,则直线方程为y=x+2.27.已知正方体的棱长为1,则这个正方体的外接球的直径为_______________.正确答案:解析:正方体的棱长为1,其体对角线为,则这个正方体的外接球的直径为.28.在等差数列{an}中,若a3=3,a5=7,则a7=_________________.正确答案:11解析:由题意可知,a5=a3+2d,得2d=4,则a7=a5+2d=7+4=11.29.一个锐角的补角比这个角的余角大____________度.正确答案:90解析:设这个锐角为A,它的补角为180°-A,余角为90-A,则(180°-A)-(90°-A)=90°.30.已知函数,则f(x)的最小值为_______________.正确答案:12解析:因为x>0,所以12/x>0,3x>0,则有,当且仅当12/x=3x,即x=2时,“=”成立,故f(x)min=12。
[四川卷]2016年四川卷理科数学(全解析)
![[四川卷]2016年四川卷理科数学(全解析)](https://img.taocdn.com/s3/m/9af55fd8050876323112125d.png)
结束输出v i =i 1 v =vx +ii ≥ 0?i =n 1v = 1 开始 输入n, x 否 是2016年四川卷理科数学试题逐题详解考试时间:2016年 6月 7日(星期二)15:00~17:00本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分 150分.考试时间 120分钟.第Ⅰ卷(选择题 共 50分)一、 选择题:本大题共 10小题,每小题 5分,共 50 分.在每小题给出的四个选项中,只有一项是 符合题目要求的.1. 设集合 { }22 A x x =-££ ,Z 为整数集,则集合A Z I 中元素的个数是( )A .3B .4C .5D .6【解析】C ;由题可知, { } 2,1,0,1,2 A =-- Z I ,则 A Z I 中元素的个数为5. 2. 设i 为虚数单位,则( ) 6i x + 的展开式中含 4x 的项为( )A . 4 15x -B . 415x C . 4 20i x - D . 420i x【解析】A ;由题可知,含 4x 的项为 24246 C i 15 x x =- .3. 为了得到函数 π sin 2 3 y x æö =- ç÷ èø的图象,只需把函数 sin 2 y x = 的图象上所有的点( )A .向左平行移动 π 3 个单位长度B .向右平行移动 π 3 个单位长度C .向左平行移动 π6个单位长度D .向右平行移动 π6个单位长度【解析】D ;因为 ππ sin 2sin 2 36 y x x éù æöæö =-=- ç÷ç÷ êú èøèø ëû ,所以只需把 sin 2 y x = 的图象向右平移 6 p个单位. 4. 用数字1,2,3,4,5构成没有重复数字的五位数,其中奇数的个数为( )A .24B .48C .60D .72【解析】D ;由题可知,五位数要为奇数,则个位数只能是1,3,5;分为两步:先从1,3,5三个数中选一个作为个位数有 13 C ,再将剩下的4个数字排列得到 44 A ,则满足条件的五位数有 1434 C A 72 ×= .5. 某公司为激励创新,计划逐年加大研发资金投入,若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12% ,则该公司全年投入的研发资金开始超过200万元的年 份是( )(参考数据:lg1.120.05 » ,lg1.30.11 » ,lg 20.30 = ) A .2018年B .2019年C .2020年D .2021年【解析】B ;设x 年后该公司全年投入的研发资金为200万元,由题可知,( )130112%200 x+= ,解得 1.12200lg 2lg1.3 log 3.80 130lg1.12x - ==» ,因资金需 超过200万,则x 取4,即2019年.6. 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示 的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n ,x 的值 分别为3,2.则输出v 的值为( ) A .9B .18C .20D .35【解析】B ;初始值 3,2 n x == ,程序运行过程: 2 i = , 1224 v =´+= ; 1 i = ,详解提供: 南海中学 钱耀周(1,1) C (2,1) B (1,0)A (0,1)Oy xy =1y = x+1y =x 1P MFxO y4219 v =´+= ; 0 i = , 92018 v =´+= ; 1 i =- ,跳出循环,输出 18 v = .7. 设 p :实数 , x y 满足( ) ( ) 22 112 x y -+-£ ,q :实数 , x y 满足 11 1 y x y x y ³- ì ï³- í ï £ î,则 p 是q 的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件【解析】A ;如图,( ) ( ) 22112 x y -+-£ ①表示圆心为( ) 1,1 ,半径为 2 的圆内区域所有点(包括边界); 11 1 y x y x y ³- ì ï³- í ï £ î② 表示 ABC D 内部区域所有点(包括边界).实数 , x y 满足②则必然满足①,反之不成立,则 p 是q 的必要不充分条件.8. 设O 为坐标原点,P 是以F 为焦点的抛物线 22 y px = ( 0 p > )上任意一点,M 是线段PF 上的点,且2 PM MF = ,则直线OM 斜率的最大值为( )A .3 3B .2 3C .2 2D .1【解析】C ;如图,由题可知 ,0 2 p F æö ç÷ èø ,设P 点坐标为 2 00 , 2 y y p æö ç÷ èø,显然,当 0 0y < 时, 0 OM k < ; 0 0 y > 时, 0 OM k > ,要求 OM k 最大值,不妨设 0 0 y > ,则OM OF FM =+= uuuu r uuu r uuuu r OF +uuu r( )200 1112 , 3333633 y y p FP OF OP OF OP OF p æö=+-=+=+ ç÷ èø uuu r uuu r uuu r uuu r uuu r uuu r , 020 0 02 32 63 OM y k y p y p p y p == + +2 22 £ 2 2 = ,当且仅当 220 2 y p = 等号成立.[或]设 ( ) 2 2,2 P pt pt , ( ) , M x y ,则 2 2,2 2 p FP pt pt æö =- ç÷ èø uuu r , 又 1 3 FM FP = uuuu r uuu r ,所以 2 2 236 p p p x t -=- 且 2 3 pt y = ,即 2 2 33 p p x t =+ 且 2 3 pt y = ,所以 OM k =2 2112 1 212 12 2 2t t t t =£= + + ,所以( ) max2 2 OM k = . 9. 设直线 1 l , 2 l 分别是函数 ( ) ln ,01 ln ,1 x x f x x x -<< ì= í > î 图象上点 1 P , 2 P 处的切线, 1 l 与 2 l 垂直相交于点P ,且1 l ,2 l 分别与 y 轴相交于点 , A B ,则 PAB D的面积的取值范围是( ) A .( )0,1 B .( )0,2 C .( )0,+¥ D .( )1,+¥ 【解析】A ;由题设知,不妨设 12 , P P 点的坐标分别为 ( ) ( ) 111222 ,,, P x y P x y ,其中 12 01 x x <<< ,则由于 12, l l 分别是点 12 , P P 处的切线,由导数几何意义可知 1 l 的斜率 1 k 为 1 1 x - , 2 l 的斜率 2 k 为 21x ;又 1 l 与 2 l 垂直, 且 12 0 x x << ,可得: 1112 1211 11 k k x x x x ×=-×=-Þ×= ,且 1 l 的方程为: ( ) 11 1 1ln y x x x x =--- ①, 2 l2D P C (3, 3)C (3, 3) x A y PAMCBxDy的方程分别为 ( ) 22 2 1ln y x x x x=-+ ②,此时点 A 的坐标为( ) 1 0,1ln x - , B 的坐标为( ) 2 0,1ln x -+ ,由此可得: ( ) 1212 2ln ln 2ln 2 AB x x x x =--=-×= ,①、②两式联立可解得交点P 的横坐标为x =121212 2ln 2 x x x x x x - = ++ , PAB D 的面积为 12 1 1 1122 21 1 22 PAB xS AB P x x x x D =×=´´=£ + + ,当且仅当 1 1 1x x=即 1 1 x = 时等号成立,而 1 01 x << ,所以 1 PAB S D < . 10.在平面内,定点 ,,, A B C D 满足 == DA DB DC uuu r uuu r uuu r , 2 DA DB DB DC DC DA ×=×=×=- uuu r uuu r uuu r uuu r uuu r uuu r,动点P ,M满足 =1 AP uuu r ,PM MC = uuuu r uuu u r ,则 2BM uuuu r 的最大值是( )A .434B .494 C . 3763 4 + D .37233 4+ 【解析】B ;由题意, DA DB DC == uuu r uuu r uuu r,所以 D 到 ,, A B C 三点的距离相等, D 是 ABC D 的外心;2 DA DB DB DC DC DA ×=×=×=- uuu r uuu r uuu r uuu r uuu r uuu r ( )0 DA DB DB DC DB DA DC DB CA Þ×-×=×-=×= uuu r uuu r uuu r uuu r uuu r uuu r uuu r uuu r uuu r ,所以DB AC ^ ,同理可得, , DA BC DC AB ^^ ,从而D 是 ABC D 的垂心; 所以 ABC D 的外心与垂心重合,因此 ABC D 是正三角形,且D 是 ABC D 的中心, cos DA DB DA DB ADB DA DB ×=Ð= uuu r uuu r uuu r uuu r uuu r uuu r 1 2 2 æö´-=-ç÷ èø所以 2 DA = uuu r,所以正三角形 ABC D 的边长为23,以 A 为原点建立直角坐标系, ,, B C D 三点坐标分别为 ( ) ( )3,3,3,3 B C - , ( ) 2,0 D ,由 1 AP = uuu r,设 ( ) cos ,sin P q q ,其中 [ ) 0,2π q Î ,而PM MC = uuuu r uuu u r,即M 是PC 的中点,可以写出M 的坐标为 3cos 3sin , 22 M q q æö++ ç÷ ç÷ èø,则 22 cos3 2 BM q - æö =+ ç÷ èø uuuu r 23712sin 33sin 371249 6 2444 p q q æö +- ç÷ æö ++ èø =£= ç÷ ç÷ èø,当 2 3 q p = 时, 2 BM uuuu r 取得最大值 49 4 . [或]甴已知易得 120 ADC ADB BDC Ð=Ð=Ð=°, 2 DA DB DC === uuu r uuu r uuu r,以D 为原点,直线DA 为x 轴建立平面直角坐标系,则 ( ) 2,0 A , ( )1,3 B -- , ( )1,3 C - ,设 ( ) , P x y ,由已知 1 AP = uuu r ,得( ) 2 2 21 x y -+= ,又PM MC = uuuu r uuu u r ,所以 13 , 22 x y M æö -+ ç÷ ç÷ èø ,所以 133 , 22 x y BM æö ++ =ç÷ ç÷ èøuuuu r ,所以 ( ) ( )222 133 4x y BM -++ = uuuu r ,它表示圆( ) 2 221 x y -+= 上点( ) . x y 与点 ( )1,33 -- 距离平方的 1 4 ,所以 ( )( )22 2 2max 149 3331 44 BM æö =+-+= ç÷ èøuuuu r .13 3CBAP1133第Ⅱ卷(非选择题 共 100 分)二、填空题:本大题共 5 小题,每小题 5 分,满分 25 分.11. 22 ππ cos sin = 88- __________.【解析】2 2 ; 22 πππ2 cos sin cos 8842-== (直接考查二倍角公式). 12.同时抛掷两枚质地均匀的硬币,当至少有一枚硬币正面向上时,就说这次试验成功,则在2次试验中成功次数X 的均值是__________.【解析】 3 2 ; 由题可知,在一次试验中,试验成功(即至少有一枚硬币正面向上)的概率为 113 1 224P =-´= , 因为 2次独立试验成功次数X 满足二项分布 3 ~2, 4 X B æö ç÷ èø,则 ( ) 33 2 42E X =´= 13.已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是_________.【解析】 33;由题可知,因为三棱锥每个面都是腰为2的等腰三角形,由正视图可得几何体P ABC - ,且三棱锥高为 1 h = ,则体积 13V Sh ==113 2311 323 æö´´´´= ç÷ èø. 14.已知函数 ( ) f x 是定义在R 上的周期为2的奇函数,当01 x << 时, ( ) 4 xf x = ,则 5 2 f æö-+ ç÷ èø ( ) 1 f = __________.【解析】 2 - ;由周期性知 ( ) ( ) 11 f f =- ,由奇函数知 ( ) ( ) 11 f f =-- ,即 ( ) 10 f = ,又 5 2 f æö -= ç÷ èø11 22 f f æöæö-=- ç÷ç÷ èøèø12 42 =-=- ,所以 ( ) 5 12 2 f f æö-+=- ç÷ èø. 15.在平面直角坐标系中,当 ( ) , P x y 不是原点时,定义P 的“伴随点”为 2222 , y x Px y x y æö- ¢ ç÷++ èø;当P 是 原点时,定义P 的“伴随点”为它自身,平面曲线C 上所有点的“伴随点”所构成的曲线C ¢定义为曲线C 的“伴随曲线”,现有下列命题:① 若点A 的“伴随点”是点A ¢,则点A ¢的“伴随点”是点A ;② 单位圆的“伴随曲线”是它自身;③ 若曲线C 关于x 轴对称,则其“伴随曲线” ' C 关于 y 轴对称; ④ 一条直线的“伴随曲线”是一条直线.其中的真命题是__________(写出所有真命题的序号).【解析】②③;①设 ( ) , A x y ,伴随点 2222 , y x Ax y x y æö- ¢ ç÷++ èø , A ¢的伴随点横坐标为 2222 2222x x yy x x y x y - + æöæö - + ç÷ç÷ ++ èøèøx =- ,同理可得纵坐标为 y - ,故 ( ) , A x y ¢¢ -- ,错误;② 设单位圆上的点P 的坐标为( ) cos ,sin q q ,则 P 的伴随点的坐标为 ( ) sin ,cos P q q ¢ -= ππ cos ,sin 22 q q æö æöæö -- ç÷ç÷ ç÷ èøèø èø ,所以P ¢也在单位圆上,即P ¢点是P 点延顺时针方向旋转 π2 .正确;③设曲线C 上点 A 的坐标( ) , x y ,其关于x 轴对称的点 ( )1 , A x y - 也在曲线C 上,所以点 A 的伴随点 2222 , y x Ax y x y æö - ¢ ç÷ ++ èø ,点 1 A 的伴随点 1 2222 , y x A x y x y æö -- ¢ ç÷ ++ èø, A ¢与 1 A ¢ 关于 y 轴对称.正确;④反例:例如 1y = 这条直线,则 ( ) 0,1 A , ( ) 1,1 B , ( ) 2,1 C ,而这三个点的伴 随点分别是 ( ) 1112 1,0,,,, 2255 A B C æöæö¢¢¢ -- ç÷ç÷ èøèø,而这三个点不在同一直线上.下面给出严格证明:设点 ( ) , P x y 在直线 :0 l Ax By C ++= ,P 点的伴随点为 ( ) 00, P x y ¢ ,则 0 22 0 22 y x x yx y x y ì = ï + ï í - ï = ï + î ,解得 022 000 2200y x x y x y x y - ì = ï + ï í ï = ï + î , 代入直线方程可知 00222200000 y x AB C x y x y - ++= ++ ,化简得 ( ) 22 0000 0 Ay Bx C x y -+++= ,当 0 C = 时, ()2200 C x y + 是一个常数, ' P 的轨迹是一条直线;当 0 C ¹ 时, ()2200 C x y + 不是一个常数,P ¢的轨迹不是一条直线.所以,直线“伴随曲线”不一定是一条直线. 错误.三、解答题:本大题共 6 小题,共 75 分,解答须写出必要的文字说明、证明过程或演算步骤.16.(本小题满分 12分)我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟 确定一个合理的月用水量标准x (吨),一位居民的月用水量不超过x 的部分按平价收费,超出x 的部分按议 价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按 照[ ) 0,0.5 ,[ ) 0.5,1 ,…,[ ] 4,4.5 分成9组,制成了如图所示的频率分布直方图. (Ⅰ) 求直方图中a 的值;(Ⅱ) 设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由; (Ⅲ) 若该市政府希望使85%的居民每月均用水量不超过标准x (吨),估计x 的值,并说明理由.a 0.52 0.40 0.160.12 0.08 0.044.5 43.532.521.510.5月均用水量(吨)组距频率 【解析】(Ⅰ)由直方图得 ( ) 0.50.080.160.40.520.120.080.0421 a ´+++++++= ,解得 0.3 a = .(Ⅱ)由图,不低于3吨人数所占百分比为 ( ) 0.50.120.080.04=12% ´++ , 所以全市月均用水量不低于3吨的人数为:3012%=3.6 ´ (万) (Ⅲ)由图可知,月均用水量小于2.5吨的居民人数所占百分比为:EPDCBAG M FAB CDPE( ) 0.50.080.160.30.40.520.73 ´++++= ,即73%的居民月均用水量小于2.5吨,同理,88%的居民月均用水量小于3吨,故2.53 x << , 假设月均用水量平均分布,则 ( ) 85%73%0.5 2.50.5 2.9 0.3x -¸ =+´= (吨).所以,估计用水量为2.9吨时,85%的居民每月均用水量不超过标准. 17.(本小题满分 12分)在 ABC D 中,角 ,, A B C 所对的边分别是 ,, a b c ,且cos cos sin A B Ca b c+= . (Ⅰ) 证明:sin sin sin A B C = ; (Ⅱ) 若 2226 5b c a bc +-= ,求tan B .【解析】(Ⅰ)依题意,结合正弦定理得 cos cos sin 1 sin sin sin A B CA B C+== ,两边同时乘以sin sin A B ,可得sin cos sin cos sin sin B A A B A B += ,又sin cos sin cos B A A B += ( ) ( ) sin sin sin A B C C p +=-= ,从而sin sin sin A B C = .(Ⅱ)由题 22265 b c a bc +-= ,根据余弦定理可知, 2223 cos 25b c a A bc +- == ,又 ( ) 0, A p Î ,sin 0 A > ,则 234sin 1 55A æö =-= ç÷ èø ,即 cos 3 sin 4 A A = ,由(Ⅰ)可知 cos cos sin 1 sin sin sin ABC A B C +== ,所以 cos 11 sin tan 4 B B B ==所以tan 4 B = .18.(本小题满分 12分)如图,在四棱锥P ABCD - 中, // AD BC , 90 ADC PAB Ð=Ð=°, 12BC CD AD == ,E 为棱 AD 的中点,异面直线PA 与CD 所成的角为90°.(Ⅰ) 在平面PAB 内找一点M ,使得直线 // CM 平面PBE ,并说明理由;(Ⅱ) 若二面角P CD A -- 的大小为45°,求直线PA 与平面PCE 所成角的正弦值.【解析】(Ⅰ)延长AB ,交直线CD 于点M ,因为E 为 AD 中点,所以 1 = 2AE ED AD = ,因为 1 = 2BC CD AD = ,所以ED BC = ,因为 // AD BC 即 // ED BC ,所以四边形BCDE 为平行四边形, // BE CD ,即 // CM BE ,又BE Ì 面PBE ,CM Ë 面PBE ,所以 // CM 面PBE .此时M 在DC 延长线上,且DC CM = . (事实上:延长AP 至N 使AP PN = ,则所找的点可以是MN 上任意一点!)(Ⅱ)过A 作 AF EC ^ 交EC 于点F ,连结PF ,过A 作 AG PF ^ 交PF 于点G , 因为 90 PAB =° ∠ ,PA 与CD 所成角为90°,所以PA AB ^ ,PA CD ^ ,又 = AB CD M I , 所以PA ^平面 ABCD ,又EC Ì面ABCD ,所以PA EC ^ ,因为EC AF ^ 且 AF AP A = I ,z E PD C BAx M y 所以CE ^面PAF ,又 AG Ì面PAF ,所以AG CE ^ ,因为 AG PF ^ 且 AG AF A = I , 所以AG ^面PFC ,所以 APF ∠ 为所求PA 与面PCE 所成的角,因为PA ^面 ABCD , 90 ADC =° ∠ 即 AD DC ^ .所以 PDA ∠ 为二面角P CD A -- 所成的平面角, 由题意可得 45 PDA =° ∠ ,而 90 PAD =° ∠ ,所以PA AD = ,因为BC CD = ,四边形BCDE 是平行四边形, 90 ADM =° ∠ ,所以四边形BCDE 是正方形, 所以 45 BEC =° ∠ ,所以=45 AEF BEC = o∠∠ ,因为 90 AFE = o∠ ,所以 2= 2AF AE , 所以 22 4 tan == 4 AD AF APF AP AP = ∠ ,所以 1sin = 3APF ∠ , 所以直线PA 与平面PCE 所成角的正弦值为 13.向量法:由已知CD PA ^ ,CD AD ^ ,PA AD A = I ,所以CD ^平面PAD ,于是CD PD ^ ,故 PDA Ð 为二面角P CD A -- 的平面角,所以 45 PDA =° ∠ ,由PA AB ^ ,PA CD ^ ,又 = AB CD M I ,所以PA ^平面ABCD ,不妨设 1 BC = , 则在Rt PAD D 中, 2 PA AD == ,以 A 为原点,建立空间直角坐标系 A xyz - 如图所示,则( ) 0,0,0 A , ( ) 0,0,2 P , ( ) 2,1,0 C , ( ) 1,0,0 E , () 1,0,2 PE =- uuu r , ( ) 1,1,0 EC = uuu r , ( ) 0,0,2 AP = uuu r, 设平面PCE 的法向量为 ( ) ,, x y z = n ,则 0 0 PE EC ì ×= ïí ×= ï îuuu r uuu r n n ,得 20 0 x z x y -= ì í += î ,解得 2 2 x z y z = ì í=- î , 令 1 z = ,得 ( ) 2,2,1 =- n ,设直线PA 与平面PCE 所成角为q ,则 21sin 233AP AP q × === ´ uuu ruuu r n n , 所以直线PA 与平面PCE 所成角的正弦值为 13. 19.(本小题满分 12分)已知数列{ } n a 的首项为1, n S 为数列{ } n a 的前n 项和, 1 1 n n S qS + =+,其中 0 q > , *n ÎN . (Ⅰ) 若 232 2,,2 a a a + 成等差数列,求{ }n a 的通项公式; (Ⅱ) 设双曲线 2 22 1 ny x a -= 的离心率为 n e ,且 253 e = ,证明: 12 1 43 3 n nn n e e e - - ++×××+> . 【解析】(Ⅰ)当 1 n = 时, 21 1 S qS =+ ,即 121 1 a a qa +=+ ,又 1 1 a = ,所以 2 a q = .当 2 n ³ 时, 1 1 n n S qS + =+ , 1 1 n n S qS - =+ ,相减得 1 n n a qa + = ,又 21 a qa q == , 所以{ }n a 是首项为1,公比为q 的等比数列. 又 232 2,,2 a a a + 成等差数列,所以 3222 22232 a a a a =++=+ ,即 22320 q q --= , 解得 2 q = 或 12q =- (舍去),所以 1* 2, n n a n - =ÎN .(Ⅱ) 2221 =1 1n n n a e a + =+ ,由(Ⅰ)可得,{ } n a 为首项为1,公比为q 的等比数列,故 22225 11 3 e a q =+=+= ,即 4 3 q = ,所以 14 3 n n a - æö= ç÷ èø,所以 22221444 1 333 n n n n e --- æöæöæö =+>= ç÷ç÷ç÷ èøèøèø所以 21 123 1 4 1 44443 3 ...1... 4 3333 1 3nn n nn n e e e e - - æö- ç÷ - æöæö èø ++++>++++== ç÷ç÷ èøèø - ,不等式得证.20.(本小题满分 13分)已知椭圆E : 2222 1 x y a b+= ( 0 a b >> )的两个焦点与短轴的一个端点是直角三角形的3个顶点,直线l : 3 y x =-+ 与椭圆E 有且只有一个公共点T .(Ⅰ) 求椭圆E 的方程及点T 的坐标;(Ⅱ) 设O 是坐标原点,直线l ¢平行于OT ,与椭圆E 交于不同的两点A 、B ,且与直线l 交于点P .证明: 存在常数l ,使得 2PTPA PB l =× ,并求l 的值.【解析】(Ⅰ)设短轴一端点为 ( ) 0, C b ,左,右焦点分别为 ( ) 1 ,0 F c - , ( ) 2 ,0 F c ( 0 c > ),则 222c b a += .由题意, 12 F F C D 为直角三角形,所以 2221212 F F FC F C =+ ,解得 22b c a == , 所以E : 22 22 1 2 x y b b += ,代入 3 y x =-+ 消去 y 整理得 223121820 x x b -+-= (*),由 ( ) 2212121820 b D =--= ,解得 2=3 b ,所以椭圆E 的方程为 221 63x y += .此时(*)为 2440 x x -+= ,解得 2 x = ,则 31 y x =-+= ,所以T 的坐标为( ) 21 , .(Ⅱ)设l ¢: 1 2 y x m =+ ( 0 m ¹ ),联立直线l 的方程可解得 22 2,1 33 m m P æö -+ ç÷ èø,故 2 2 8 9 PT m = ,设 ( ) ( ) 1122 ,,, A x y B x y ,联立直线l ¢与椭圆E 的方程消去 y 整理得22344120 x mx m ++-= , 由 ( ) 2216124120 m m D =--> ,解得 3232 22 m -<< ,且 12 4 3 mx x +=- , 212 412 3m x x - = , 所以 22111 2252 212 3323 m m m PA x y x æöæö=--++-=-- ç÷ç÷ èøèø,同理 2 52 2 23 m PB x =-- ,所以 12 522 22 433 m m PB PB x x æöæö ×=---- ç÷ç÷ èøèø ( ) 21212 522 22 433 m m x x x x æöæö =---++ ç÷ç÷ èøèø2 2 5224412 (2)(2)() 43333m m m m - =----+210 9 m = , 故存在常数 45l = ,使得 2PTPA PB l =× .[参数方程法]设 ( ) 00 ,3 P x x - 在l 上,由 12 OT k = ,l ¢平行OT ,得l ¢的参数方程为 0 02 3 x x t y x t =+ ì í =-+ î ,代入椭圆E 整理可得 2200 24440 t t x x ++-+= ,设两根为 A t , B t ,则有 ( ) 20 2 2A B x t t - =,而 ( ) ( )()( ) 22222000 23122 PTx x x =-+--=- , 5 A PA t = , 5 B PB t = ,故有 ( ) 2 0 5 552 2A B PA PB t t x ×=×=- ,由题意 2PT PA PB l =× , 所以 2220 2(2) 4 5 5 (2) 2PT x PA PB x l - === × - ,故存在常数 4 5 l = ,使得 2 PT PA PB l =× ,21.(本小题满分 14分)设函数 ( ) 2ln f x ax a x =-- ,其中a ÎR .(Ⅰ) 讨论 ( ) f x 的单调性;(Ⅱ) 确定a 的所有可能取值,使得 ( ) 1 1 e xf x x- >- 在区间( ) 1,+¥ 内恒成立(其中e 2.718 = …为自然 对数的底数).【解析】(Ⅰ)由题意, ( ) 2121'2 ax f x ax x x- =-= ( 0 x > ),① 当 0 a £ 时, 2210 ax -£ , ( ) 0 f x ¢ £ , ( ) f x 在( ) 0,+¥ 上单调递减.② 当 0 a > 时,当 1 0, 2 x a æöÎç÷ ç÷ èø 时, ( ) 0 f x ¢ < ;当 1 , 2 x a æö Î+¥ ç÷ ç÷ èø时, ( ) 0 f x ¢ > . 故 ( ) f x 在 1 0, 2a æöç÷ ç÷ èø 上单调递减,在 1 , 2a æö +¥ ç÷ ç÷ èø上单调递增. (Ⅱ)原不等式等价于 ( ) 1 1 e 0 xf x x - -+> 在 ( ) 1, x Î+¥ 上恒成立.一方面:令 ( ) ( ) 121 11 e ln e x xg x f x ax x a x x-- =-+=--+- ,只需 ( ) g x 在( ) 1,+¥ 上恒大于0即可,又 ( ) 10 g = ,故 ( ) g x ¢ 在 1 x = 处必大于等于0,令 ( ) ( ) 1 2 112e x F x g x ax x x- ¢ ==-+- , ( ) 10 g ¢ ³ ,可得 12 a ³ .另一方面:当 1 2 a ³ 时, ( ) 3 111 2323312122 2e 1e e x xx x x F x a x x x x x--- +- ¢ =+-+³+-+=+ , 因为 ( ) 1, x Î+¥ ,故 3 20 x x +-> ,又 1 e 0 x - > ,故 ( ) F x ¢ 在 12a ³ 时恒大于0.所以当 12a ³ 时, ( ) F x 在 ( ) 1, x Î+¥ 单调递增.所以 ( ) ( ) 1210 F x F a >=-³ ,故 ( ) g x 也在 ( ) 1, x Î+¥ 单调递增.所以 ( ) ( ) 10 g x g >= ,即 ( ) g x 在 ( ) 1, x Î+¥ 上恒大于0. 综上,a 的所有可能取值为 12a ³ .[法二]令 ( ) 1 11ex g x x - =- , ( ) 1 e x s x x - =- ,则 ( ) 1 e 1 x s x - ¢ =- ,当 1 x > 时, ( ) 0 s x ¢ > ,故 ( ) s x 递增, 又由 ( ) 10 s = ,有 ( ) 0 s x > ,从而当 1 x > 时, ( ) 0 f x > ,当 0 a £ , 1 x > 时, ( ) ( )2 1ln 0 f x a x x =--< , 故当 ( ) ( ) f x g x > 在区间( ) 1,+¥ 内恒成立时,必有 0 a > . 当 10 2a << 时,1 1 2a > ,由(Ⅰ)由 ( ) 1 102 f f a æö <= ç÷ èø ,从而 1 0 2g a æö > ç÷ èø , 所以此时 ( ) ( ) f x g x > 在区间( ) 1,+¥ 内不恒成立. 当 12a ³ 时,令 ( ) ( ) ( ) h x f x g x =- ( 1 x ³ ),当 1 x > 时, ( ) 32 1 2222111112121 2e 0 xx x x x h x ax x x x x x x x x - -+-+ ¢ =-+->-+-=>> ,因此, ( ) h x 在( ) 1,+¥ 上递增,又 ( ) 10 h = ,所以当 1 x > 时, ( ) 0 h x > ,即 ( ) ( ) f x g x > 恒成立, 综上,a 的所有可能取值为 12a ³ .。
四川省特岗教师教育公共基础知识真题精选文档

四川省特岗教师教育公共基础知识真题精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-2016年四川省特岗教师招聘考试教育公共基础笔试试题?(考试时间:120分钟满分:100分)一、单项选择题(本大题共30小题,每小题1分,共30分。
在每小题列出的四个备选项中只有一个是符合题目要求的。
请将答题卡的相应位置涂黑,错涂、多涂或未涂均无分)?1.教育学史上第一个正式提出有关教育起源的学说是( )。
?A.神话起源说? B.生物起源说? C.心理起源说? D.劳动起源说?2.在世界教育学史上被认为是“现代教育学之父”的教育学家是( )。
?A.夸美纽斯? B.杜威? C.康德? D.赫尔巴特? 3.教师仅凭考试成绩来评价学生,从而导致学生产生“书呆子”型成就中心的偏向,这是考试的( )。
?A.显性正向功能? B.显性负向功能?C.隐性正向功能? D.隐性负向功能?4.下列选项中。
不属于教育目的的功能是( )。
?A.对教育活动的定向功能? B.对教育活动的调控功能?C.对教育活动的监督功能? D.对教育活动的评价功能? 5.“家有三斗粮。
不当孩子王”,这种说法反映中国传统社会中教师普遍较低的( )。
?A.政治地位? B.经济地位? C.法律地位? D.专业地位? 6.坚持知识统一性观点.而且可以发挥学习者的迁移能力的课程类型是( )。
?A.学科课程? B.活动课程? C.综合课程? D.核心课程? 7.世界上最早系统地论述教育教学思想的专着是( )。
?A.《学记》? B.《论演说家的教育》? C.《大教学论》D.《普通教育学》?8.对班级教学的实施产生重要推动作用的是( )。
?A.“道尔顿制”? B.“巴达维亚法”? C.“圣路易编制法”? D.“导生制”?9.班级组织的设计者和指导者是( )。
?A.班主任? B.班委会? C.任课教师? D.班长?10.贯穿于校本课程各个阶段或整个过程的评价是( )。
四川省特岗教师招聘考试真题2016年

四川省特岗教师招聘考试真题2016年一、单项选择题(总题数:30,分数:30.00)1.教育学史上第一个正式提出的有关教育起源的学说是______A.神话起源论B.生物起源论√C.心理起源论D.劳动起源论解析:生物起源说是第一个正式提出的有关教育起源的学说。
2.在世界教育学史上被认为是“现代教育学之父”的教育学家是______A.夸美纽斯B.杜威C.康德D.赫尔巴特√解析:赫尔巴特在世界教育史上被认为是“现代教育学之父”或“科学教育学的奠基人”。
3.教师仅凭考试成绩来评价学生,从而导致学生产生“书呆子型”成就中心的偏向。
这是考试的______A.显性正向功能B.显性负向功能C.隐性正向功能D.隐性负向功能√解析:负向教育功能是指阻碍社会进步和个体发展的消极影响和作用,隐性教育功能是指伴随显性功能而出现的非预期的功能。
题干中的“书呆子型”即体现了伴随着考试的评价功能而出现的阻碍个体发展的隐性功能。
4.下列选项中,不属于教育目的的功能的是______A.对教育活动的定向功能B.对教育活动的调控功能C.对教育活动的监督功能√D.对教育活动的评价功能解析:教育目的的功能包括:(1)对教育活动的定向功能;(2)对教育活动的调控功能;(3)对教育活动的评价功能。
5.“家有一斗粮,不当孩子王。
”这种说法反映了中国传统社会中教师普遍较低的______A.政治地位B.经济地位√C.法律地位D.专业地位解析:教师职业的经济地位指将教师职业与其他职业相比较,其劳动报酬的差异状况及其经济生活状态。
它是教师社会地位的最直接体现。
自古以来,除少数大师鸿儒外,普通教师的经济地位一直比较低下,“家有一斗粮,不当孩子王”“两袖清风”等正是这种情况的真实写照。
6.坚持知识统一性观点,而且可以发挥学习者的迁移能力的课程类型是______A.学科课程B.活动课程C.综合课程√D.核心课程解析:综合课程坚持知识统一性的观点,把所有的知识视为一个整体,采用综合课程的形式教授。
【必备】2018年四川省特岗教师初中数学学科专业知识试卷全解析版
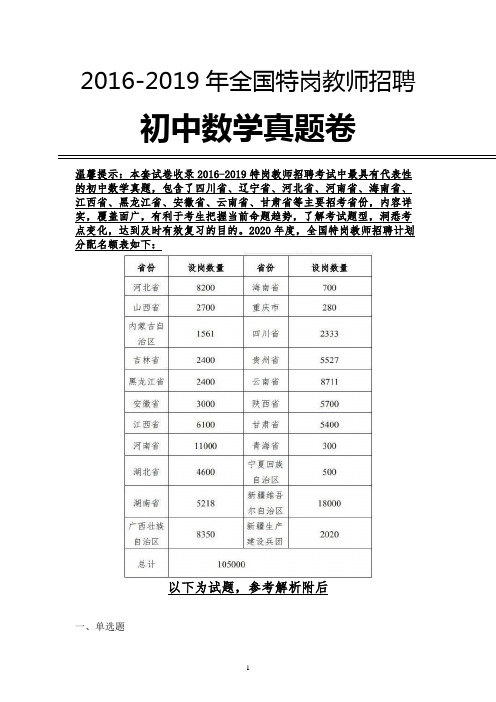
2016-2019年全国特岗教师招聘初中数学真题卷温馨提示:本套试卷收录2016-2019特岗教师招聘考试中最具有代表性的初中数学真题,包含了四川省、辽宁省、河北省、河南省、海南省、江西省、黑龙江省、安徽省、云南省、甘肃省等主要招考省份,内容详实,覆盖面广,有利于考生把握当前命题趋势,了解考试题型,洞悉考点变化,达到及时有效复习的目的。
2020年度,全国特岗教师招聘计划分配名额表如下:以下为试题,参考解析附后一、单选题1.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为()。
A.60 °B.75°C.85°D.90°2.如图,一座石拱桥是圆弧形其跨度AB=24米,半径为13米,则拱高CD为()A.35米B.5米C.7米D.8米3.已知二次函数y=x2 + bx +c 的图象与x轴相交于A、B两点,其顶点为P,若S△APB=1,则b与c满足的关系是()A.b2 -4c +1=0 B.b2 -4c -1=0 C.b2 -4c +4 =0 D.b2 -4c -4=0 4.如图,在⊙O中,OC⊥AB,∠ADC=35°,则∠OBA的度数是()A.35 B.30°C.25°D.20°5.-2019的相反数是()A.2019 B.-2019 C.12019D.120196.某班进行中招体育项目模拟考试:抽查15名女生的一分钟跳绳成绩如下表跳绳(个/分)165 172 173 174 175 171 跳绳人数 1 3 2 3 5 1这些女生跳绳成绩的中位数和众数分别是()A.174,175 B.175,174 C.175,175 D.3,57.如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中正确的个数是()A.1 B.2 C.3 D.48.实数a在数轴上的位置如图所示,则22(4)(11)a a---化简后为()A.7 B.﹣7 C.2a﹣15 D.无法确定9.如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B 等于()A.30°B.35°C.40°D.50°10.计算sin45︒的结果等于()A.12B.22C.32D.111.如图所示,菱形ABCD中,直线l⊥边AB,并从点A出发向右平移,设直线。
【特岗真题】2019年四川省特岗教师初中数学学科专业知识试卷全解析版
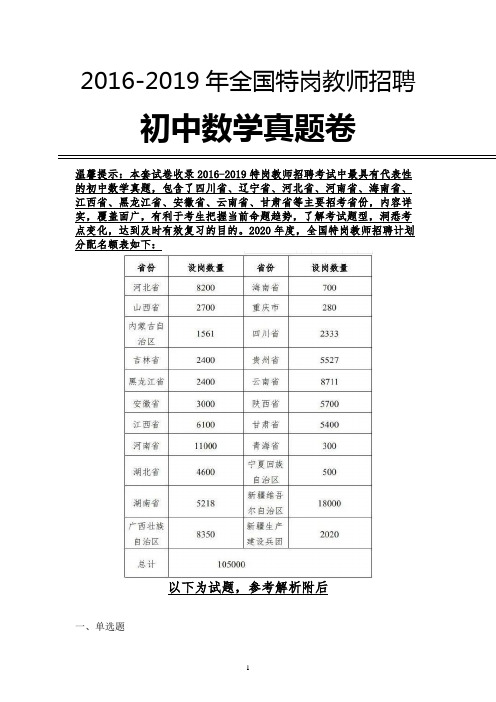
2016-2019年全国特岗教师招聘初中数学真题卷温馨提示:本套试卷收录2016-2019特岗教师招聘考试中最具有代表性的初中数学真题,包含了四川省、辽宁省、河北省、河南省、海南省、江西省、黑龙江省、安徽省、云南省、甘肃省等主要招考省份,内容详实,覆盖面广,有利于考生把握当前命题趋势,了解考试题型,洞悉考点变化,达到及时有效复习的目的。
2020年度,全国特岗教师招聘计划分配名额表如下:以下为试题,参考解析附后一、单选题1.如图,四边形ABHK 是边长为6的正方形,点C 、D 在边AB 上,且AC=DB=1,点P 是线段CD 上的动点,分别以AP 、PB 为边在线段AB 的同侧作正方形AMNP 和正方形BRQP ,E 、F 分别为MN 、QR 的中点,连接EF ,设EF 的中点为G ,则当点P 从点C 运动到点D 时,点G 移动的路径长为( )A .1B .2C .3D .62.计算6m 3÷(-3m 2)的结果是( )A .-3mB .-2mC .2mD .3m3.一组数据是4,x ,5,10,11共五个数,其平均数为7,则这组数据的众数是( )A .4B .5C .10D .114.已知一组数3、﹣2、1、﹣4、0,那么这组数的极差是( )A .3B .4C .6D .75.如图,抛物线21(2)3y a x =+-与221(3)12y x =-+交于点(1,3)A ,过点A 作x 轴的平行线,分别交两条抛物线于点,B C ,则以下结论:①无论x 取何值,2y 的值总是正数;②1a =;③23AB AC =其中正确结论是( )A .①②B .①③C .②③D .都正确6.计算sin45︒的结果等于( )A .12B .22C .32D .17.如图,四边形ABCD 中,AC 平∠DAB ,∠ADC =∠ACB =90°,E 为AB 的中点,若AD =4,AB =6,则AC AF 的值为( )A .2B .74C .32D .628.如图,在平行四边形ABCD 中,按以下步骤作图:①以A 为圆心,AB 长为半径画弧,交边AD 于点;②再分别以B ,F 为圆心画弧,两弧交于平行四边形ABCD 内部的点G 处;③连接AG 并延长交BC 于点E ,连接BF ,若BF =3,AB =2.5,则AE 的长为( )A .2B .4C .8D .5 9.若方程323x x k =++的根为正数,则k 的取值范围是 ( ) A .k<2B .-3<k<2C .k ≠-3D .k<2且k ≠-310.下列方程,是一元二次方程的是( )①3x 2+x=20,②2x 2-3xy+4=0,③x 2-1x =4,④x 2=0,⑤x 2-3x +3=0 A .①② B .①④⑤ C .①③④ D .①②④⑤11.如图,山上有一座高塔,山脚下有一圆柱形建筑物平台,高塔及山的剖面与圆柱形建筑物平台的剖面ABCD 在同一平面上,在点A 处测得塔顶H 的仰角为35°,在点D 处测得塔顶H 的仰角为45°,又测得圆柱形建筑物的上底面直径AD 为6m ,高CD 为2.8m ,则塔顶端H 到地面的高度HG 为( )(参考数据:sin350.57︒≈,cos350.82︒≈,tan350.70︒≈2 1.41≈)。
【真题】2017年四川省特岗教师初中数学学科专业知识试卷全解析版

2016-2019年全国特岗教师招聘初中数学真题卷温馨提示:本套试卷收录2016-2019特岗教师招聘考试中最具有代表性的初中数学真题,包含了四川省、辽宁省、河北省、河南省、海南省、江西省、黑龙江省、安徽省、云南省、甘肃省等主要招考省份,内容详实,覆盖面广,有利于考生把握当前命题趋势,了解考试题型,洞悉考点变化,达到及时有效复习的目的。
2020年度,全国特岗教师招聘计划分配名额表如下:以下为试题,参考解析附后一、单选题1.如图,正方形ABCD 内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为( )A .14B .12C .8π D .4π 2.在﹣1、0、1、2这四个数中,最小的数是( ) A .﹣1 B .0 C .1 D .13.我校举行了“建设宜居中山,关注环境保护”的知识竞赛,某班学生的成绩统计如下: 成绩(分) 60 70 80 90 100 人数 4812115则该班学生成绩的众数和中位数分别是( ) A .70分,80分B .80分,80分C .90分,80分D .80分,90分4.根据某网站公布的实时数据,截至2016年11月11日24时,某网购商城“双11全球狂欢节”总交易额约1207亿元,把这个数据用科学记数法表示为( ). A .8120710⨯元B .1012.0710⨯元C .81.20710⨯元D .111.20710⨯元5.下列运算正确的是( )A .5a 2+3a 2=8a 4B .a 3·a 4=a 12C .a +2b =2abD .a 5÷a 2=a 3 6.如图//AB CD ,点E 是CD 上一点,EF 平分AED ∠交AB 于点F ,若42AEC ∠=,则AFE ∠的度数为( )A .42B .65C .69D .717.9的平方根是()A.3 B.±3C.3D.±38.在“朗读者”节目的影响下,某中学开展了“好书伴我成长”读书活动.为了解5月份八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:册数0 1 2 3 4人数 4 12 16 17 1关于这组数据,下列说法正确的是()A.中位数是2 B.众数是17 C.平均数是2 D.方差是29.如图,一个空间几何体的主视图和左视图都是正三角形,俯视图是一个圆,那么这个几何体是()A.三角形B.三棱柱C.三棱锥D.圆锥10.如图是由棱长为1的正方体搭成的某几何体三视图,则图中棱长为1的正方体的个数是()A.9 B.8 C.7 D.611.2018的相反数是( )A.8102 B.﹣2018 C.12018D.201812.下表是摄氏温度和华氏温度之间的对应表,则字母a的值是( ) 华氏°F 23 32 41 a 59。
2016四川省特岗教师《教育公共基础知识》真题

2016四川省特岗教师《教育公共基础知识》真题2016年四川省特岗教师招聘考试教育公共基础笔试试题(考试时间:120分钟满分:100分)一、单项选择题(本大题共30小题,每小题1分,共30分。
在每小题列出的四个备选项中只有一个是符合题目要求的。
请将答题卡的相应位置涂黑,错涂、多涂或未涂均无分)1.教育学史上第一个正式提出有关教育起源的学说是( )。
A.神话起源说B.生物起源说C.心理起源说D.劳动起源说2.在世界教育学史上被认为是“现代教育学之父”的教育学家是( )。
A.夸美纽斯B.杜威C.康德D.赫尔巴特3.教师仅凭考试成绩来评价学生,从而导致学生产生“书呆子”型成就中心的偏向,这是考试的( )。
A.显性正向功能B.显性负向功能C.隐性正向功能D.隐性负向功能4.下列选项中。
不属于教育目的的功能是( )。
A.对教育活动的定向功能B.对教育活动的调控功能C.对教育活动的监督功能D.对教育活动的评价功能5.“家有三斗粮。
不当孩子王”,这种说法反映中国传统社会中教师普遍较低的( )。
A.政治地位B.经济地位C.法律地位D.专业地位6.坚持知识统一性观点.而且可以发挥学习者的迁移能力的课程类型是( )。
A.学科课程B.活动课程C.综合课程D.核心课程7.世界上最早系统地论述教育教学思想的专著是( )。
A.《学记》B.《论演说家的教育》C.《大教学论》D.《普通教育学》8.对班级教学的实施产生重要推动作用的是( )。
A.“道尔顿制”B.“巴达维亚法”C.“圣路易编制法”D.“导生制”9.班级组织的设计者和指导者是( )。
A.班主任B.班委会C.任课教师D.班长10.贯穿于校本课程各个阶段或整个过程的评价是( )。
A.诊断性评价B.发展性评价C.形成性评价D.终结性评价11.某班级中出现了一些基于需求、兴趣、游戏倾向等类似因素结合起来的小团体,由此可判断该班级组织处于( )。
A.个人属性之间的矛盾阶段B.团体要求与个人属性之间的矛盾阶段C.团体要求架构内的矛盾阶段D.团体要求与团体文化之间的矛盾阶段12.在个体心理发展中起主导作用的是( )。
2017年四川特岗教师招聘考试-数学真题及解析

2017年四川特岗教师-小学数学试题一、单向选择题(本题共12题,每题4分,共48分)1、已知集合A={-2,-1,0,1,2},集合B={x|-1<x<2},则集合A ∩B=( )。
A.∅B.{-1,0,1,2}C.{0,1}D.{-2,-1,0,1,2}答案:C2、函数1ln -=x x y 的定义域是( )。
A.(0,+ ∞)B.(1,+∞)C.(-∞,1)U(1,+∞)D.(0,1)U(1,+∞)答案:D3、设i 为虚数单位,则复数i(2+i)=( )。
A.-1+2iB.1+2iC.-1-2iD.1-2i答案:A4、已知{an}为等差数列,若a3+a7=8,则a5=( )。
A.3B.4C.5D.8答案:B解析:{an}为等差数列,则a3+a7=2a5=8,故a5=45、函数f(x)=sinxcosx 是()。
A.最小正周期为π的奇函数B.最小正周期是π的偶函数C.最小正周期为2π的奇函数D.最小正周期为2π的偶函数答案:A解析:f (x )=sinxcosx=21sin2x 为奇函数,最小正周期为ππ==22T 6 、经过圆x2+y2-4y=0的圆心,且与直线x+y=0垂直的直线方程是( )。
A.x-y-2=0B.x-y+2=0C.x+y-2=0D.x+y+2=0答案:B解析:圆x2+y2-4y=0化为标准方程x2+(y-2)=4,圆心坐标为(0.2);直线与x+y=0垂直,即斜率为1,又过点(0,2),则直线的方程为x-y+2=07、掷两颗均匀的骰子,点数和为7的概率为( )。
A.181 B.121 C.61 D.51 答案:C解析:事件是抛掷两颗骰子,共有6X6=36种结果,满足点数和为7的事件可列举为(1,6)(2,5)(3,4)(4,3)(5,2)(6,1),共有6种结果 ,所以出现点数和为7的概率为61366 8、已知变量x 与y 正相关,变量y,z 满足z=-0.3y+2,则( )。
四川省特岗教师教育公共基础考试真题2016年

四川省特岗教师教育公共基础考试真题2016年一、单项选择题(本大题共30小题,每小题1分,共30分。
在每小题列出的四个备选项中只有一个是符合题目要求的。
请将答题卡的相应位置涂黑,错涂、多涂或未涂均无分)(总题数:30,分数:30.00)1.教育学史上第一个正式提出有关教育起源的学说是( )。
A.神话起源说B.生物起源说√C.心理起源说D.劳动起源说解析:神话起源学说是人类关于教育起源的最古老的观点,生物起源说是第一个正式提出的有关教育起源的学说。
2.在世界教育学史上被认为是“现代教育学之父”的教育学家是( )。
A.夸美纽斯B.杜威C.康德D.赫尔巴特√解析:赫尔巴特是近代德国著名的心理学家和教育学家,在世界教育史上被认为是“现代教育学之父”或“科学教育学的奠基人”。
3.教师仅凭考试成绩来评价学生,从而导致学生产生“书呆子”型成就中心的偏向,这是考试的( )。
A.显性正向功能B.显性负向功能C.隐性正向功能D.隐性负向功能√解析:教育的正向功能指教育有助于社会进步和个体发展的积极影响和作用。
负向功能指阻碍社会进步和个体发展的消极影响和作用。
显性功能指教育活动依照教育目的,在实际运行中所出现的与之相吻合的结果。
隐性功能指伴随显性教育功能所出现的非预期性的功能。
根据题干描述,学生的表现没有达到预期效果.并产生了消极影响,体现出考试的隐性负向功能。
4.下列选项中。
不属于教育目的的功能是( )。
A.对教育活动的定向功能B.对教育活动的调控功能C.对教育活动的监督功能√D.对教育活动的评价功能解析:教育目的是教育活动的出发点和归宿,其层次的多样性,使其具有多方面的功能:①对教育活动的定向功能。
任何社会的教育活动,都是通过教育目的才得以定向的。
②对教育活动的调控功能。
一是通过价值的方式进行调控;二是通过标准的方式进行调控;三是通过目标的方式进行调控。
③对教育活动的评价功能。
教育目的是衡量和评价教育实施效果的根本依据和标准。
教师招聘_2015四川特岗教师招聘考试小学数学真题

2021 四川特岗教师招聘考试小学数学真题本试卷分为第一卷(选择题)和第二卷(非选择题),总分值100分。
考试时间120分钟.第一卷(选择题共45分)一、选择题(本大题共l5小题,每题3分,共45分)1.集合A={-1,0,1},集合B={x∣x2+x=0},那么集合A∪B=( )。
A.{-1,0,1}B.{-1,0}C.{0,1}D.{-1,1}2.函数f(x)=x2的图像关于( ).A.y轴对称B.直线y=x对称C.坐标原点对称D.直线y=-x对称3. 假设向量a=(2,6),向量b=(3,x),且a∥b,那么x=( )。
A.-1C.4α的终边在第二象限,那么点P(sinα,cosα)在( )·A.象限B.第二象限C.第三象限D.第四象限5.函数f(x)=2x+3x的零点所在的一个区间是( )·A.(-2,-1)B.(-1,0)C.(0,1)D.(1,2)6.以下函数中,在区间(0,+∞)上为减函数的是( ).A.y=2xB.y=lnxD.y=1/x7.设i为虚数单位,那么复数A.-l-iB.-2+iC.-2-iD.2+i8.有两张卡片,一张的正反面分别写着数字1与2,另一张的正反面分别写着3与4,将两张卡片排在一起组成一个两位数,那么所组成的两位数为奇数的概率是( ).9.三棱锥的底面是边长为1的正三角形,其正视图如下图,那么此三棱锥的体积为( ).14.抛物线y2=4x上一点P到点F(1,o)的距离是3,那么点P到y轴的距离为( ).A.1C.3α、β为两个不同的平面,m为平面α上一条直线,那么“α⊥β〞是“m⊥β〞的( ).A.充分不必要条件B.必要不充分条件C.充要条件第二卷(非选择题共55分)二、填空题(本大题共5小题,每题3分.共15分)16.lg2+lg5= .17.一支田径队有男运发动28人,女运发动21人,现按性别用分层抽样的方法,从中抽取14位运发动进展安康检查,那么男运发动应抽取人.18.执行如下图的程序框图,输出的S的值是______.三、解答题(本大题共5小题,每题8分,共40分.解容许写出文字说明,证明过程或演算步骤)△ABC的内角A、B、C所对的边分别为a、b、C,(Ⅰ)求cosC的值;(Ⅱ)求△ABC的面积.22.公差不为0的等差数列{an}的首项为2,且a1、a2、a4成等比数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设数列{a n}的前n项和为S n,求数列的前n项和.23.在正方体ABCD-A1B1C1D1中,点M、N分别是棱AB、C1D1的中点.(Ⅰ)证明:直线MN⊥直线B1C;(Ⅱ)证明:直线CM∥平面AA1N。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年四川特岗教师招聘考试《小学数学》真题及
解析
一、选择题(本大题共15小题,每小题3分,共45分)
1
已知集合P={x∣x2-x-2≤0),Q={x∣log2(x-1)≤1),
A、(-∞,-1]∪[3,+∞)
B、[2,3]
C、(-∞,-1]∪(3,+∞)
D、(2,3]
2
反比例函数f(x)=(k为常数)的图像如右图所示,下列说法正确的是( ).
A、常数k<-1
B、函数f(x)在定义域范围内,y随x的增大而减小
C、若点a(-1,m)和点b(2,n)在函数f(x)的图像上,则m<n
D、函数f(x)图像的对称轴的直线方程是y=x
3
A、2
B、-2
C、2i
D、-2i
4
若sinθcosθ>0,则θ在( ).
A、第一、二象限
B、第一、三象限
C、第一、四象限
D、第二、四象限
5
在△ABC中,三边a,b,c成等差数列,也成等差数列,则△ABC是( ).
A、正三角形
B、等腰三角形
C、直角三角形
D、钝角三角形
6
设不等式表示的平面区域为D,在区域D内随机抽取一个点,则此点到坐标原点的距离大于2的概率是( ).
7
在平面直角坐标系中,设A(-2,3),B(3,-2,)沿x轴把直角坐标系折成120°二面角后,则AB的长度是( ).
8
将直线x+y=1先绕点(1,0)顺时针旋转90°,再向上平移1个单位后,与圆x2+(y-1)2=r2相切,则半径r的值是( ).
9
双曲线的右准线与两渐近线交于A、B两点,右焦点为F,
双曲线的离心率为( ).
10
展开式中,x4的系数为( ).
A、-10
B、10
C、40
D、45
11
若a+1=b(a和b是不为0的自然数),那a和b的最小公倍数是( )
A、a
B、b
C、ab
D、(a+1)b
12
在平面直角坐标系中,点P(-4,5)关于原点对称的点的坐标为( ).
A、(4,5)
B、(4,-5)
C、(-4,-5)
D、(5,-4)
13
下列性质中,等腰三角形具有而直角三角形不一定具有的是( ).
A、两边之和大于第三边
B、有一个角的平分线垂直于这个角的对边
C、有两个锐角的和等于90°
D、内角和等于180°
14
一个无盖的正方体盒子的平面展开图可以是图中的( ).
A、①
B、①②
C、②③
D、①③
15
若命题甲是命题乙的充分不必要条件,命题丙是命题乙的必要不充分条件,命题丁是命题丙的充要条件,则命题丁是命题甲的( ).
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
二、填空题(本大题共5小题,每小题3分,共15分)
16
已知直线l过点A(0,2),且倾斜角的正切值为1,则直线l的方程为.
17
已知正方体的棱长为1,则这个正方体的外接球的直径为.
18
在等差数列{an}中,若a3=3,a5=7,则a7= .
19
一个锐角的补角比这个角的余角大度.
20
已知函数则f(x)的最小值为.
三、简答题(本大题共5小题.每小题8分.共40分.解答应写出文字说明.证明过程或演算步骤)
21
在△ABC中,角A,B,C所对的边分别是a,b,C且满足csinA=acosC.
(1)求角C的大小;
(2)求的最大值,并求取得最大值时角A、B的大小.
22
如图,在正方体ABCD-A1B1C1D1中,棱长AA1=2,E为CC1的中点。
(1) 求证:B1D1 ⊥AE;
(2) 求二面角C-AE-B的平面角的正切值;
(3) 求点D1到平面EAB的距离.
23
等差数列{an}的公差不为零,a4=7,以a1,a2,a5成等比数列。
(1)求{an}的通项公式;
(2)若数列{Tn}满足Tn=a2+a4+a8+ …+a2n,求Tn。
24
如图所示,一次函数y=kx+b的图像与反比例函数的图像交于A(1,2),B(-m,-1)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图像直接写出使一次函数的值大于反比例函数的值的x的取值范围.
25
义务教育数学课程标准在各个学段都安排了数与代数的学习内容。
小学生在第二学段将进一步学习整数、分数、小数和百分数及有关运算,进一步发展数感,假如你是小学第二学段的数学教师,你在教学中将会从哪些方面去培养学生的数感?(至少写出三个方面的观点)。
