【精编】资料分析满分必备计算公式
资料分析计算公式整理
(2) 公式可变换为：
X%
增长量=现期量汉——甘出
1+x%， 其中
X%为增函数，所以现期量大，增长率
1+x%
大的情况下，增长量一定大。
增长率计算
（13）已知基期量与增长量
丄出【/皆增长量
增长率_ ”里 基期量
（1） 截位直除法
（2） 插值法
（14）已知现期量与基期量
增长率 现期量-基期量
基期量
现期量=基期量+基期量xM
=基期量x(1+M)
估算法
(7)已知基期量，增长量N
现期量=基期量+N
尾数法，估算法
4■苗上昌H苗
(8)已知基期量与现期量
增长量=现期量-基期量
尾数法
(9)已知基期量与增长率x%
增长量=基期量汉X%
特殊分数法
(10)已知现期量与增长率X%
增长量=现期量沢X%
1+x%
1
(1)特殊分数法，当X%可以被视为-时，n
1+x%
（1）截位直除法（2）如果现期量差距较 大，增长率相差不大，可直接比较现期量。
（3）化同法
分数大小比较：
（1） 直除法（首位判断或差量比较）
（2） 化冋法，差分法或其它
现期量计算
（5）已知基期量，增长率X%
现期量=基期量+基期量汉X%
=基期量（nx%）
特殊分数法，估算法I
(6)已知基期量，相对基期量增加M倍
截位直除法
（15）如果基期量为A，经N期变为B,平均 增长率为X%
x% =N_-1
\A
代入法或公式法
（16）两期混合增长率：如果第二期与第二期
资料分析公式汇总
资料分析公式汇总在进行资料分析时，掌握一些关键的公式可以帮助我们更高效、准确地处理和解读数据。
以下是为大家汇总的一些常用公式：一、增长相关公式1、增长量＝现期量基期量增长量用于衡量数据在一定时期内的绝对增长幅度。
2、增长率＝增长量÷基期量×100%这个公式反映了数据增长的相对速度。
3、基期量＝现期量÷（1 ＋增长率）当我们已知现期量和增长率，要求出之前某个时期的量时，就会用到这个公式。
4、现期量＝基期量×（1 ＋增长率）通过基期量和增长率来计算当前时期的量。
二、比重相关公式1、比重＝部分÷整体×100%比重表示部分在整体中所占的比例。
2、整体＝部分÷比重已知部分和其占整体的比重，可求出整体的量。
3、部分＝整体×比重根据整体的量和部分所占的比重，能计算出部分的量。
三、平均数相关公式1、平均数＝总数÷个数这是计算平均数最基本的公式。
2、总数＝平均数×个数当已知平均数和个数时，可求出总数。
四、倍数相关公式1、 A 是 B 的几倍：A÷B直接用 A 的数值除以 B 的数值，得到 A 是 B 的倍数。
2、 A 比 B 多几倍：（A B）÷B先计算 A 与 B 的差值，再除以 B 的数值。
五、隔年增长相关公式1、隔年增长率＝现期增长率＋间期增长率＋现期增长率×间期增长率例如，今年的增长率为 r1，去年的增长率为 r2，那么隔年增长率就是 r1 ＋ r2 ＋ r1×r2 。
2、隔年基期量＝现期量÷（1 ＋隔年增长率）六、年均增长相关公式1、年均增长量＝（末期量初期量）÷年份差用于计算在一定年份内平均每年的增长量。
2、年均增长率＝（末期量÷初期量）＾（1÷年份差) 1七、混合增长率相关公式整体增长率介于部分增长率之间，且偏向于基期量大的部分增长率。
(完整版)资料分析计算公式
资料分析计算公式
基本概念：
基期：统计中计算指数或变化情况等动态指标时，作为参照标准的时期。
（参照物）现期：相对基期而言，是与基期相比较的后一时期。
同比增长：与上一年同一时期相比的增长情况。
环比增长：与之紧紧相邻的上一个统计周期相比较的增长情况。
贸易顺差与贸易逆差
贸易顺差：进口额< 出口额
贸易顺差= 出口额—进口额
贸易逆差：进口额> 出口额
贸易逆差= 进口额—出口额
年均增长率、年均增长量：
现期量= 基期量()N
⨯，其中n为相差年数；
+
1年均增长率
年均增长量= ()n÷
现期量，其中n为相差年数；
-基期量。
行测资料分析必背公式
行测资料分析必背公式在行测中，公式是解题的重要工具之一、熟练掌握行测中常用的公式，能够提高解题速度和准确度。
下面是行测中常见的几类公式及其应用。
一、百分数公式1.百分数与小数、分数的相互转换关系：小数=百分数÷100，分数=百分数÷100。
例如：80%=0.80，20%=1/52.若一个变量y与它的百分数x成正比，则有以下关系：y = kx ÷ 100，其中k为比例系数。
如果变量y与x成反比，则有：y = k ÷ x。
3.百分数的连乘与连除：若A=B×C×D，其中B、C、D均为百分数，则A也为百分数；若A=B÷C÷D，其中B、C、D均为百分数，则A也为百分数。
例如：75%×50%=(75×50)÷100=37.5%；80%÷20%=(80÷20)×100=400%。
二、利息计算公式1.简单利息的计算公式：利息=本金×利率×时间，其中本金为P，利率为r，时间为t。
例如：笔本金为5000元，年利率为5%，存款期限为2年，则利息计算为：利息=5000×0.05×2=500元。
2.复利的计算公式：复利=本利和-本金，其中本利和为P(1+r/100)^t，本金为P，利率为r，时间为t。
例如：笔本金为5000元，年利率为5%，存款期限为2年，则复利计算为：复利=5000×(1+0.05)^2-5000=525元。
三、速度、距离、时间的关系1.速度、距离、时间的关系：距离=速度×时间，速度=距离÷时间，时间=距离÷速度。
例如：如果小明骑自行车以20km/h的速度骑了2小时，则他所走的距离为：距离= 20 × 2 = 40km。
四、比例相关问题中的公式1.比例的计算：若两个变量之间的比例为a:b，则有a/b=c/d；若已知a/b=c/d，且已知其中一个变量的值为x，则可以根据比例计算其他变量的值：a=x×c/d，b=x×d/c。
资料分析常用公式
资料分析常用公式1. 平均数公式平均数（Mean）是表示一组数据集中趋势的量数，计算公式为：$$\text{平均数} = \frac{\sum_{i=1}^{n} x_i}{n}$$其中，$ x_i $ 表示第 $ i $ 个数据，$ n $ 表示数据总数。
平均数适用于描述一组数据的总体水平，常用于市场调研、人口统计等领域。
2. 中位数公式中位数（Median）是将一组数据按大小顺序排列后位于中间位置的数，计算公式为：$$\text{中位数} =\begin{cases}\frac{x_{\frac{n+1}{2}} + x_{\frac{n}{2}}}{2} & \text{当 } n \text{ 为偶数时} \\x_{\frac{n+1}{2}} & \text{当 } n \text{ 为奇数时}\end{cases}$$其中，$ x_i $ 表示第 $ i $ 个数据，$ n $ 表示数据总数。
中位数适用于描述一组数据的中间水平，常用于描述收入、房价等分布不均的数据。
3. 标准差公式标准差（Standard Deviation）是衡量一组数据离散程度的量数，计算公式为：$$\sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i \mu)^2}{n}}$$其中，$ x_i $ 表示第 $ i $ 个数据，$ \mu $ 表示平均数，$ n $ 表示数据总数。
标准差适用于描述一组数据的波动程度，常用于质量控制、风险评估等领域。
4. 相关系数公式相关系数（Correlation Coefficient）用于衡量两个变量之间的线性关系程度，计算公式为：$$r = \frac{\sum_{i=1}^{n} (x_i \bar{x})(y_i\bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i \bar{x})^2}\sqrt{\sum_{i=1}^{n} (y_i \bar{y})^2}}$$其中，$ x_i $ 和 $ y_i $ 分别表示两个变量中的第 $ i $ 个数据，$ \bar{x} $ 和 $ \bar{y} $ 分别表示两个变量的平均数，$ n $ 表示数据总数。
资料分析相关公式汇总
增长量相关1. 基期量已知现期量、增长率，基本公式：基期量=现期量/(1+增长率)。
已知现期量、增长量，基本公式：基期量=现期量-增长量。
2. 增长率已知基期量、增长量。
基本公式：增长率=增长量/基期量。
已知现期量、基期量。
基本公式: 增长率=(现期量-基期量)/基期量。
已知现期量、增长量。
基本公式：增长率=增长量/(现期量-基期量)。
3. 隔年增长率已知现期与间期的增长率，那么现期相对于基期的增长率为：隔年增长率=现期增长率+间期增长率+现期增长率*间期增长率。
比重相关1. 现期比重已知部分值、整体值，求比重。
基本公式：比重=部分值/整体值已知整体值、比重，求部分值。
基本公式：部分值=整体值*比重已知部分值、比重，求整体值。
基本公式：整体值=部分值/比重2. 基期比重部分值的现期量A，部分值的现期增长率q A，整体值的现期量B，整体值的现期增长率q B，则基期比重为：3. 比重变化分子部分所对应的增长速度>分母部分所对应的增长速度，则现期比重>基期比重，即比重值上升。
反之，平均数与倍数1. 平均数已知总体值、份数，求平均数。
基本公式：平均数=总数/份数2. 年均增长量已知末期值、初期値与年份差，求年均增长量。
基本公式：年均增长量=(末期量-初期量)/年份差3. 年均增长率已知末期值、初期值与年份差，求年均增长率。
基本公式：末期值=初期值×（1+年均增长率）N资料分析公式非常多，往往求解一个量就会有三四个公式，这时候就要求考生先看材料给了哪些数据，根据所给出的数据来决定用哪个公式，比如求解增长率的时候，给出增长量、基期值所用的公式和给出增长量、现期值所用的公式是不一样的，求解基期比重的时候，给出现期值、增长量和给出现期值、增长率所用的公式也是不一样的。
这里就要求各位考生熟悉掌握每一个公式和提前阅读材料。
大家如果记住了上面的公式，加上一些思维技巧，速度会很快提上来，就会做到事半功倍。
资料分析满分必备计算公式
增长率 现期量 - 基期量 基期量
增长率计算
（ 15）如果基期量为 A ，经 N 期变为 B ，平均 增长率为 x%
（ 16）两期混合增长率：如果第二期与第三期
B x% N 1
A
增长率分别为 r1与r2 ，那么第三期相对第一期增 长率 r3
r3 r1 r2 r1r2
增长率比较
（ 17）合成增长率：整体分为 A 、B 两个部分， 分别增长 a%与 b%，整体增长率 r% （ 18）混合增长率：整体为 A，增长率为 rA， 分为两个部分 B 和 C，增长率为 rB 和 rC
；
1n
（ 2）估算法 （倍数估算） 或分数的近似计 算（看大则大，看小则小）
直除法
（ 1）特殊分数法， 当 x%可以被视为 1 时， n
公式可被化简为： 增长量
现期量 1n
（2）公 式可变换 为：
x% 增长量 现期量
1 x% ， 其 中
（ 13）已知基期量与增长量
增长率 增长量 基期量
（ 14）已知现期量与基期量
拉动增长 比重计算
（ 22）如果 B 是 A 的一部分， B 拉动 A 增长 x% x% B的增长量 A的基期量
（ 1）截位直除法 （ 2）插值法
（ 23）某部分现期量为 A ，整体现期量为 B
现期比重
（ 24）某部分基期量为 A ，增长率 a%，整体基 期量为 B，增长率 b%
现期比重
A B
A (1 a%) B (1 b%)
（ 25）某部分现期量为 A 增长率 a%，整体现期 量 B，增长率 b%
基期比重
A 1 b% B 1 a%
两期比重差值计算：
（ 1）截位直除法
（ 2）插值法
资料分析满分速算技巧
资料分析满分速算技巧补充技巧1：两年混合增长率公式：1、如果第二期与第三期增长率分别为r1与r2，那么第三期相对于第一期的增长率为：r1＋r2＋r1× r22、如果第二期的值为A，增长率为r，则第一期的值A′：A′＝A/1＋r≈A×（1-r）（实际上左式略大于右式，r越小，则误差越小，误差量级为r2）3、平均增长率近似公式：如果N年间的增长率分别为r1、r2、r3……rn，则平均增长率：r≈r1＋r2＋r3＋……rn/n（实际上左式略小于右式，增长率越接近，误差越小）4、“分子分母同时扩大/缩小型分数”变化趋势判定：①A/B中若A与B同时扩大，则①若A增长率大，则A/B扩大②若B增长率大，则A/B缩小；A/B中若A与B同时缩小，则①若A减少得快，则A/B缩小②若B减少得快，则A/B扩大。
②A/A＋B中若A与B同时扩大，则①若A增长率大，则A/A＋B扩大②若B增长率大，则A/A＋B缩小；A/A＋B中若A与B同时缩小，则①若A减少得快，则A/A＋B 缩小②若B减少得快，则A/A＋B扩大。
5、多部分平均增长率：如果量A与量B构成总量“A＋B”，量A增长率为a，量B增长率为b，量“A＋B”的增长率为r，则A/B=r-b/a-r，一般用“十字交叉法”来简单计算：注意几点问题：1.r一定是介于a、b之间的，“十字交叉”相减的时候，一个r在前，另一个r在后；2.算出来的A/B=r-b/a-r是未增长之前的比例，如果要计算增长之后的比例，应该在这个比例上再乘以各自的增长率，即A′/B′=（r-b）×（1＋a）/（a-r）×（1＋b）。
6、等速率增长结论：如果某一个量按照一个固定的速率增长，那么其增长量将越来越大，并且这个量的数值成“等比数列”，中间一项的平方等于两边两项的乘积。
【例1】2005年某市房价上涨16.8%，2006年房价上涨了6.2%，则2006年的房价比2004年上涨了（）。
公务员考试资料分析重要公式
单一数据相关计算公式：
现期值相关计算公式：
增长量增长率增长量增长率）（基期值增长量基期值现期值+=+⨯=+=1
现期值题目问法：时间与材料一致，问具体数值为多少。
基期值相关计算公式：
增长率增长量增长率现期值增长量现期值基期值=+==1-
基期值题目问法：时间比材料靠前，问具体数值为多少。
增长量相关计算公式：
增长量=现期值-基期值=基期值×增长率=增长率
现期值+1×增长率 增长量题目问法：有增长含义+带单位的表述。
增长率相关计算公式：
增长量现期值增长量基期值增长量基期值基期值现期值增长率--===
增长率相关问法：有增长含义+不带单位的表述。
两数之比相关计算公式： 现期：B
A （倍数、比重、平均数） 基期：A
B q q ++⨯11B A （倍数、比重、平均数） 增长量：A
B A q q q +-⨯1B A （比重、平均数） 增长率：
B B A q q q +-1（平均数） 两数之比的问法都会涉及到自身概念，比如问倍数就会出现倍数的相关字眼，比重平均数也
是一样，再者问的是哪一个内容就和前面的单一数据一样，例如问增长量就会出现增长的含义+带单位的具体数值，只是在主体中会有两数之比的表述。
2024国考考前必背资料分析常用公式大盘点
2024国考考前必背资料分析常用公式大盘点在资料分析中，熟悉并掌握常用的公式是非常重要的，可以帮助我们更加高效地进行数据分析和决策。
下面就是一些在资料分析过程中常用的公式的大盘点：1. 平均数（Mean）：用于计算一组数据的平均值。
公式为：平均数= 总和 / 数据个数。
2. 中位数（Median）：用于确定一组数据的中间值。
当数据量为奇数时，中位数为排序后的中间值，当数据量为偶数时，中位数为排序后的两个中间值的平均值。
3. 众数（Mode）：用于确定一组数据中出现次数最多的数值。
4. 方差（Variance）：用于衡量一组数据的离散程度。
公式为：方差= (∑(数据 - 平均数)^2) / 数据个数。
5. 标准差（Standard Deviation）：用于衡量一组数据的离散程度，是方差的平方根。
6. 相关系数（Correlation Coefficient）：用于衡量两个变量之间的线性关系强度和方向。
相关系数的取值范围在-1到1之间，值越接近1表示正相关关系，值越接近-1表示负相关关系。
7. 百分位数（Percentile）：表示一组数据中特定百分比的数据所对应的值。
例如，第75百分位数表示75%的数据小于或等于该值。
8. 累计百分比（Cumulative Percentage）：表示一组数据中小于等于一些值的数据所占的百分比。
9. 折算率（Discount Rate）：用于计算资金的现值或未来值。
折算率反映了资金的时间价值。
折算率越高，未来的价值就越低。
10. 利息（Interest）：代表投资或贷款所产生的收益或成本。
利息的计算公式为：利息 = （本金× 利率× 时间）/ 36512. 弹性系数（Elasticity）：用于衡量需求或供应对价格变动的敏感度。
公式为：弹性系数 = （% 变动的需求量 / % 变动的价格）。
14. 现值（Present Value）：将未来的现金流折算到现在的价值。
公考资料分析公式最全集合
资料分析公式集合●基期现期
基期=现期-增长量= 现期
1+r
=现期-现期×r
现期=基期+增长量=基期×（1+r）
●增长率
增长率=A
B −1=现期−基期
基期
倍数=增长率+1
给百分比的增长率时，高减低加
●增长率的比较
当现期和基期相差大，用现期
基期
比较大小
当现期和基期相差小，用现期−基期
基期
比较大小●增长量
给增长率r，|r|=1
N ，增长量=现期
N+1
，减少量=现期
N−1
●增长量的比较
同增同减时，现期量大，增长幅度大，增长量也大（大大则大）一大一小时，可以先相乘，相差较小的话，必须百分比
●年均增长量
现期−基期
年份差
（例外：十三五规划，五年规划的年份差都是五）
●番数
番N倍=原来的2N倍。
资料分析公式汇总
资料分析公式汇总速算技巧一、估算法精度要求不高的情况下，进行粗略估值的速算方式。
选项相差较大，或者在被比较的数字相差必须比较大，差距的大小将直接决定对“估算”时对精度的要求。
二、直除法在比较或者计算较复杂的分数时，通过“直接相除”的方式得到商的首位（首一位、首两位、首三位），从而得出正确答案的速算方式。
常用形式： 1.比较型：比较分数大小时，若其量级相当，首位最大∕小数为最大∕小数2.计算型：计算分数大小时，选项首位不同，通过计算首位便可得出答案。
难易梯度：1.基础直除法：①可通过直接观察判断首位的情形；②需要通过手动计算判断首位的情形。
2.多位直除法：通过计算分数的“首两位”或“首三位”判断答案情形。
三、插值法1.“比较型”插值法如果A与B的比较，若可以找到一个数C，使得A﹥C，而B﹤C，既可以判定A﹥B；若可以找到一个数C，使得A﹤C，而B﹥C，既可以判定A﹤B；2.“计算型”插值法若A﹤C﹤B，则如果f﹥C，则可以得到f=B;如果f﹤C，则可以得到f=A；若A﹥C﹥B，则如果f﹥C，则可以得到f=A;如果f﹤C，则可以得到f=B。
四、放缩法当计算精度要求不高时，可以将中间结果进行大胆的“放”（扩大）或者“缩”（缩小），从而迅速得到精度足够的结果。
常用形式：1. A﹥B,C﹥D,则有A+C﹥B+D；A-D﹥B-C；2. A﹥B﹥0，C﹥D﹥0，则有A×C﹥B×D；A÷D﹥B÷C五、割补法在计算一组数据的平均值或总和值时，首先选取一个中间值，根据中间值将这组数据“割”（减去）或“补”（追上），进而求取平均值或总和值。
常用形式:1.根据该组数据，粗略估算一个中间值；2.将该组值分别减去中间值得到一组数值；3.将得到的新数值相加得到和值，用和值除以该组数值的项数得到商值，将商值加上中间值，即为该组数值的精确平均值；4.用中间值乘以数据项数再加上最后的和值即为总和值。
资料分析公式总结
资料分析公式总结1 现期值=基期值*（1+增长率）基期值=现期值/1+增长率2 增长量：✧增长量=现期值-基期值=（现期值/1+增长率）x增长率✧考点识别：增长（增加）+具体数值？（多少）+单位（元、吨…）✧常用方法：特殊分数化简法1/2=50% 1/3=33.3% 1/4=25% 1/5=20% 1/6=16.7% 1/7=14.3%1/8=12.5% 1/9=11.1% 1/10=10% 1/11=9.1% 1/12=8.3% 1/13=7.7%1/14=7.1% 1/15=6.7% 2/7=28.6% 3/8=37.5% 2/9=22.2% 2/11=18.2% ✧增长量=现期值/1+增长率x增长率=(现期值/1+1/n)x1/n=现期值/n+1（注意：增长率为正数时，n取正数，增长率为负数时，n取负数）✧特殊题型：增长量比大小口诀：大大则大，一大一小看倍数1)大大则大：现期值大，增长率达，则增长量一定大；2)一大一小看倍数（乘积），分别计算两者现期值之间的倍数关系与增长率之间的倍数关系，锁定倍数关系明显大的那一组（如现期值是5倍关系，增长率是3倍关系，就看现期值），其中数值大的（在刚才那个例子中就是现期值）增长量大。
（注意：口诀适用于增长率小于50%的题目）3 增长率=现期值/基期值-14 年均增长量=现期值-基期值/增长次数（年份差）5 年均增长率=现期值/基期值开根号下年份差次方 -1 （年均增长率约等于 (a/b-1）/n)6 隔年增长量=现期值-基期值7 隔年增长率=现期增长率+基期增长率+现期增长率x基期增长率比重：A（部分）占B（整体）的比重比重=部分/整体x100%基期比重=现期比重x（1+整体增长率/1+部分增长率）比重变化=现期比重x（部分增长率-整体增长率）/部分增长率判断：部分增长率>整体增长率比重上升部分增长率=整体增长率比重不变部分增长率<整体增长率比重下降平均数✧平均数=总量/份数✧考点识别：平均、均、每、单位（单位面积产量）✧列示形式：后/前✧常考题型：1)平均数计算2)平均数大小比较3)两期平均数（现期基期平均数大小比较，通过a%、b%的大小关系判断）平均数增长率=总量增长率-份数增长率/1+份数增长率判断：总量增长率>份数增长率平均数增加总量增长率<份数增长率平均数减少4）连续求两次平均数5）特殊题型：N个较为接近的数值求平均数例如：35.2 33.4 36.8 38.4 39.7 求平均数以35为基准，第一个多0.2、第二个少1.6…以此类推，最后可把多余部分相加除以5，再加上35。
资料分析计算公式整理
资料分析计算公式整理在进行资料分析时，掌握一些常用的计算公式能够帮助我们更高效、准确地处理数据和得出结论。
以下是对一些重要的资料分析计算公式的整理。
一、增长类计算公式1、增长量＝现期量基期量例如，2022 年某公司的销售额为 100 万元，2021 年为 80 万元，那么增长量就是 100 80 ＝ 20 万元。
2、增长率＝增长量 ÷基期量 × 100%用上例的数据，增长率为（20 ÷ 80）× 100% ＝ 25% 。
3、基期量＝现期量 ÷（1 ＋增长率）假设 2023 年某产品的销量为 120 万件，同比增长 20%，则 2022 年的销量（基期量）为 120 ÷（1 ＋ 20%）＝ 100 万件。
4、现期量＝基期量 ×（1 ＋增长率）如果已知 2021 年某地区的人口为 50 万人，预计每年以 5%的速度增长，那么 2025 年的人口（现期量）为 50 ×（1 ＋ 5%）＾4 万人。
二、比重类计算公式1、比重＝部分量 ÷整体量 × 100%比如，某班级男生有 20 人，全班共有 50 人，那么男生所占比重为（20 ÷ 50）× 100% ＝ 40% 。
2、部分量＝整体量 ×比重若已知某公司总利润为 1000 万元，其中 A 产品的利润占比为 30%，则 A 产品的利润为 1000 × 30% ＝ 300 万元。
3、整体量＝部分量 ÷比重比如某企业中研发部门的人数为 50 人，占总人数的 20%，则该企业总人数为 50 ÷ 20% ＝ 250 人。
三、平均数类计算公式1、平均数＝总数 ÷个数例如，某班级5 名学生的数学成绩分别为80、90、85、95、75 分，那么平均成绩为（80 ＋ 90 ＋ 85 ＋ 95 ＋ 75）÷ 5 ＝ 85 分。
资料分析计算公式整理之欧阳术创编
相当于分数大小比较，同上述做法
发展速度
（20）已知现期量与基期量
（1）截位直除法
（2）插值法
增长贡献率
（21）已知部分增长量与整体增长量
（1）截位直除法
（2）插值法
拉动增长
（22）如果B是A的一部分，B拉动A增长x%
（1）截位直除法
（2）插值法
比重计算
（23）某部分现期量为A，整体现期量为B
（3）截位直除法
（4）插值法
（24）某部分基期量为A，增长率a%，整体基期量为B，增长率b%
一般先计算 ，然后根据a和b的大小判断大小
（25）某部分现期量为A增长率a%，整体现期量B，增长率b%
一般先计算 ，然后根据a和b的大小判断大小
（26）基期比重－现期比重：某部分现期量为A增长率a%，整体现期量B，增长率b%
两期比重差值计算：
（1）先根据a与b的大小判断差值计算结果是正数还是负数；
（2）答案小于丨a－b丨
（3）估算法（近似取整估算）
比重比较
（27）某部分现期量为A，整体现期量为B
相当于分数大小比较，同上述做法
（28）基期比重与现期比重比较：某部分现期量为A，增长率a%，整体现期量为B，增长率b%
当部分增长率大于整体增长率，则现期比重大于基期比重。（方法为“看”增长率）
（3）化同法
分数大小比较：
（1）直除法（首位判断或差量比较）
（2）化同法，差分法或其它
现期量计算
（5）已知基期量，增长率x%
特殊分数法，估算法
（6）已知基期量，相对基期量增加M倍
估算法
（7）已知基期量，增长量N
尾数法，估算法
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
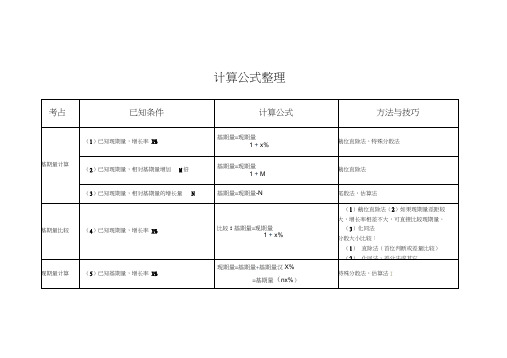
计算公式整理
考点
已知条件
计算公式
方法与技巧
基期量计算
（1）已知现期量，增长率
x%
x%1现期量基期量
截位直除法，特殊分数法
（2）已知现期量，相对基期量增加M 倍
M 1现期量基期量
截位直除法
（3）已知现期量，相对基期量的增长量N
N
-现期量基期量
尾数法，估算法
基期量比较（4）已知现期量，增长率x%
比较:x%
1现期量基期量
（1）截位直除法（2）如果现期量差距较大，增长率相差不大，可直接比较现期量。
（3）化同法分数大小比较：
（1）直除法（首位判断或差量比较）（2）化同法，差分法或其它
现期量计算（5）已知基期量，增长率x%
）
（基期量基期量
基期量现期量x%1x%
特殊分数法，估算法
（6）已知基期量，相对基期量增加M 倍
）
（基期量基期量
基期量现期量M M
1估算法
（7）已知基期量，增长量N N
基期量
现期量尾数法，估算法增长量计算
（8）已知基期量与现期量
基期量现期量增长量
-尾数法
（9）已知基期量与增长率x%
x%
基期量
增长量
特殊分数法
（10）已知现期量与增长率
x%
x%
x%
1现期量增长量
（1）特殊分数法，当x%可以被视为
n
1时，
公式可被化简为：
n
1现期量增长量
；
（2）估算法（倍数估算）或分数的近似计算（看大则大，看小则小）
（11）如果基期量为A ，经N 期变为B ，平均
增长量为x
N
A
B x
直除法
增长量比较（12）已知现期量与增长率x%
x%
x%
1现期量增长量
（1）特殊分数法，当x%可以被视为
n
1时，
公式可被化简为：n
1现期量增长量
（
2
）
公
式
可
变
换为：%
1%x x 现期量
增长量，
其
中
%
1%x x 为增函数，所以现期量大，增长率
大的情况下，增长量一定大。
增长率计算
（13）已知基期量与增长量
基期量
增长量增长率
（1）截位直除法（2）插值法
（14）已知现期量与基期量
基期量
基期量
现期量增长率
-截位直除法
（15）如果基期量为A ，经N 期变为B ，平均
增长率为x%
1
%
N
A
B x 代入法或公式法
（16）两期混合增长率：如果第二期与第三期增长率分别为21r r 与，
那么第三期相对第一期增长率3
r 2
1213r r r r r 简单记忆口诀：连续增长，最终增长大于
增长率之和；连续下降，最终下降小于增长率之和
（17）合成增长率：整体分为A 、B 两个部分，分别增长a%与b%，整体增长率
r%
B
A b
B a A r %%
%
B
A
a b B a r %)%
(%
%（18）混合增长率：整体为A ，增长率为
r A ，
分为两个部分
B 和
C ，增长率为r B 和r C
则r A 介于r B 和r C 之间
混合增长率大小居中
增长率比较（19）已知现期量与增长量
比较基期量
现期量增长率代替增长率进行
大小比较
相当于分数大小比较，同上述做法
发展速度（20）已知现期量与基期量
增长率
基期量
现期量发展速度
1（1）截位直除法（2）插值法增长贡献率（21）已知部分增长量与整体增长量
整体增长量
部分增长量增长贡献率
（1）截位直除法（2）插值法拉动增长（22）如果B 是A 的一部分，B 拉动A 增长x% 的基期量
的增长量
A B x%
（1）截位直除法（2）插值法比重计算
（23）某部分现期量为A ，整体现期量为 B
B
A 现期比重（1）截位直除法（2）插值法（24）某部分基期量为A ，增长率a%，整体基
期量为B ，增长率b% )b%1()a%1(B A 现期比重
一般先计算B
A ，然后根据a 和b 的大小判断大小（25）某部分现期量为A 增长率a%，整体现期
量B ，增长率b%
a%
1b%1B A 基期比重
一般先计算B
A ，然后根据a 和b 的大小判断大小
（26）基期比重－现期比重：某部分现期量为
A
增长率a%，整体现期量
B ，增长率b%
两期比重差值计算：
%
1b%-a%)%1%11(a%1b%1a B
A a b
B A B A B A －－
现期比重－基期比重
（1）先根据a 与b 的大小判断差值计算结果是正数还是负数；（2）答案小于丨
a －
b 丨
（3）估算法（近似取整估算）
比重比较（27）某部分现期量为A，整体现期量为 B
B
A
现期比重相当于分数大小比较，同上述做法
（28）基期比重与现期比重比较：某部分现期
量为A，增长率a%，整体现期量为B，增长率
b%
)
a%
1(
)
b%
1(
B
A
基期比重当部分增长率大于整体增长率，则现期比
重大于基期比重。
（方法为“看”增长率）
平均数计算（29）已知N个量的值，求平均数
N n
n
n N
2
1
平均数凑整法直接读数类
（30）方法：读题做标记，辅助工具（直尺）
综合分析题（31）四项基本原则：题干短原则，不计算原
则（时间与材料时间一致），信息易得原则，简单计算原则。