椭圆曲线算法循环群生成器
椭圆曲线算法循环群生成器

椭圆曲线算法循环群生成器椭圆曲线算法(Elliptic Curve Cryptography,ECC)是一种在密码学中广泛应用的公钥加密算法。
它借助于椭圆曲线上的离散对数难题,实现了在相对较短的密钥长度下提供与传统RSA算法相当的安全性。
其中,循环群生成器是椭圆曲线算法中非常重要的一部分,它用于生成椭圆曲线上的循环群,为加密和签名提供了基础。
循环群是群中的一个子集,它包含了群中所有元素的某个整数倍。
在椭圆曲线上,循环群的生成器是一个基点(Base Point),我们通常用G来表示。
循环群生成器的选择对椭圆曲线算法的安全性和性能都具有重要影响。
生成循环群的具体过程如下:1. 选择一个椭圆曲线方程椭圆曲线方程通常采用Weierstrass方程形式,如y^2 = x^3 + ax + b。
其中,a和b是曲线参数。
这里的选择需要满足方程判别式不为0,且曲线上的点满足一些特定的性质,这样才能保证椭圆曲线的安全性和性能。
2. 选择一个基点G基点G是椭圆曲线上的一个点,用来生成循环群。
通常基点G的选择应具有随机性,并且不易预测和计算其离散对数。
基点G必须属于椭圆曲线上,并且不是无穷远点。
椭圆曲线上的每个点都可以通过基点重复相加来生成循环群中的其他点。
3. 创建循环群利用基点G,我们可以通过重复相加运算来生成循环群中的其他点。
具体来说,设两点A和B,若A与B在椭圆曲线上相交,则它们的交点C也在椭圆曲线上。
椭圆曲线上的两个点相加运算可以定义为:C = A + B。
重复相加运算即可生成循环群。
4. 验证循环群性质生成循环群后,我们需要验证其具有循环群的性质,即存在一个整数n,使得nG = O(其中O为无穷远点)。
这个整数n称为基点的阶(Order),nG表示将基点G与自身相加n次后得到的结果。
循环群生成器在椭圆曲线算法中发挥着至关重要的作用。
它不仅为加密和签名提供了基础,还保证了算法的安全性和性能。
通过选择合适的曲线方程和基点,我们可以生成强大且具有循环群性质的椭圆曲线,从而实现安全高效的密码学应用。
椭圆曲线密码(ECC)加解密算法的实现

毕业论文论文题目椭圆曲线密码(ECC)加解密算法的实现学生姓名学号院别数学与信息科学学院专业信息与计算科学班级指导教师完成时间 2011 年 04 月椭圆曲线密码(ECC)加解密算法的实现摘要本文首先介绍椭圆曲线密码体制(ECC);并简明地给出了椭圆曲线的定义;接着以ElGamal公钥体制的ECC加解密的实现为例具体说明了其实现流程;最后分析了实现结果,安全性能和概述了ECC的发展现状,并对其未来的发展作了展望.关键词椭圆曲线密码;公钥密码,数字签名1引言随着政府部门和行业对网络环境和网络资源依赖程度的增强,涉及国家安全和社会公共安全的所有重大问题都在网络上表现出来. 为了确保信息的保密性,完整性,可用性,可控性,避免国家或个人的信息受到非法获取,破坏,篡改等形式的威胁,人们便提出了用密码技术来保障以电子形式保存或传送的数据. 1985年,N. Koblitz和V. Miller分别独立提出了椭圆曲线密码体制 (ECC),这是一种高安全性,高效率的公钥密码体系,它在密钥强度,加解密的处理速度和存储开销上都有着明显的优势. 采用椭圆曲线密码技术使密钥协商协议可充分利用椭圆曲线密码的优势,在更小密钥量下提供了更大的安全性,所需带宽明显减少,而且还大大降低了用户端的计算负担和存储要求.2椭圆曲线密码体制2.1密码体制的含义密码体制分为对称密码体制和非对称密码体制.非对称密码体制是指在加密过程中,密钥被分为一对.这对密钥中的任何一个密钥都可以作为公开密钥通过非保密方式向他人公开, 而另一把作为私有密钥加以保存. 这对密钥具有这样一个特点: 当知道密钥对中的一个密钥时, 要检测出另一个密钥, 在计算上是不可能的. 公开密钥用来对信息进行加密, 则私有密钥用来对信息进行解密, 反之亦然. 在这个系统中, 每个通信实体都有一个加密密钥和一个紧密相关的解密密钥.通信的双方只要知道对方的公钥,就可以进行安全的通信.2.2 椭圆曲线密码体制椭圆曲线密码体制,即基于椭圆曲线离散对数问题的各种公钥密码体制. 最早由Miller和Koblitz [1] 于1985年分别独立地提出. 它是利用有限域上椭圆曲线的有限点群代替基于离散对数问题密码体制中的有限循环群所得到的一类密码体制. 对于椭圆曲线密码系统(ECC)的安全性,其数学基础是计算椭圆曲线离散对数问题(ECDLP)的难解性[2] . 一般来说,ECC没有亚指数攻击,所以它的密钥长度大大地减少,256bit的ECC密码体制成为目前已知公钥密码体制中每位提供加密强度最高的一种体制.3.椭圆曲线的定义所谓椭圆曲线指的是由韦尔斯特拉斯 (Weierstrass)方程:所确定的平面曲线[1].若F是一个域,满足方程的数偶称为域F上的椭圆曲线 E的点. F域可以是有理数域, 也可以是复数域, 还可以是有限域. 椭圆曲线通常用 E 表示.4.ECC算法的设计思想设, 称为Weierstrass多项式. 当在任意点P成立, 则椭圆曲线称为光滑的或非奇异的. 若E是定义在有限域Fq上的椭圆曲线且其(p为素数), 这样的p称为有限域Fq的特征值. E中恰好有一个Z坐标为0的点(0, 1, 0), 我们称它为椭圆曲线的无穷远点, 用O表示. 椭圆曲线上有理点的个数称为该椭圆曲线的阶, 若亦表示椭圆曲线的阶, 则由(其中), 即Hasse定理. 如果椭圆曲线E定义在域Fq上, 其特征值不等于2和3, 则E 的Weierstrass等式可以简化, 做变换, 进而Weierstrass等式变换为, 其中, 判别式, 此式为椭圆曲线的一般形式. 若令, 则等式变为.根据椭圆曲线进行加密通信的过程:1) 用户A选定一条椭圆曲线,并取椭圆曲线上一点, 作为基点G.2) 用户A选择一个私有密钥k, 并生成公开密钥.3) 用户A将和点K, G传给用户B.4) 用户B接到信息后, 将待传输的明文编码到上一点M(编码方法很多,这里不作讨论),并产生一个随机整数r ( r < n ).5) 用户B计算点.6) 用户B将C1、C2传给用户A.7) 用户A接到信息后,计算, 结果就是点M, 即明文.因为再对点M进行解码就可以得到明文. 密码学中,描述一条上的椭圆曲线,常用到六个参量:,其中p、a、b 用来确定一条椭圆曲线,G为基点,n为点G的阶,h 是椭圆曲线上所有点的个数m与n相除的整数部分[3].5. 椭圆曲线参数的选取和基点的确定5.1 选取参数和确定基点的理论分析在基于椭圆曲线的加解密和数字签名的实现方案中,首先要给出椭圆曲线域的参数来确定一条椭圆曲线. 但并不是所有的椭圆曲线都适合加密,是一类可以用来加密的椭圆曲线,也是最为简单的一类. 下面我们就选用作为我们的加密曲线. 这条曲线定义在Fq上: 两个满足下列条件的小于p (p为素数) 的非负整数a、b:则满足下列方程的所有点,再加上无穷远点∞,构成一条椭圆曲线.其中 x, y属于0到p - 1间的整数,并将这条椭圆曲线记为.参数p的选取:p当然越大越安全,但越大,计算速度会变慢,200位左右可以满足一般安全要求,我们将p取为200比特位的素数.参数a、b的选取: 先随机产生小于p - 1的正整数作为参数a, 然后依据条件,判断随机产生的小于p - 1的正整数是否适合作为参数b.基点的确定:随着参数a, b, p确定,这条曲线就定下来了. 先随机产生0到p - 1间的整数作为基点x坐标,计算的结果再开方就得出基点y坐标.5.2 选取参数和确定基点的具体程序实现具体程序实现如下:……{//GetPrime(b,40); //先随机产生一个参数Bmp_expt_d(a, 3, &temp1);mp_sqr(b, &temp2);mp_mul_d(&temp1, 4, &temp3);mp_mul_d(&temp2, 27, &temp4);mp_add(&temp3, &temp4, &temp5);mp_mod(&temp5,p,&temp);if(mp_cmp(&temp, &compare)!=0 ){break; //满足条件跳出循环}}//, 随机产生X坐标,根据X坐标计算Y坐标GetPrime(x1,30); // 随机产生30比特长的X坐标mp_expt_d(x1, 3, &temp6);mp_mul(a, x1, &temp7);mp_add(&temp6, &temp7, &temp8);mp_add(&temp8, b, &tempx);mp_sqrt(&tempx, y1); // 得到Y坐标……私钥的确定:随机选取1到P - 1之间的素数作为私钥d.公钥的确定:由d 乘我们所确定的基点得到公钥K,即.6. 椭圆曲线密码的算法6.1 椭圆曲线密码算法的特点6.1.1 离散性密码算法需要的是离散值的定点运算,而不是连续值的浮点运算,在密码算法中不允许舍入.6.1.2 大数运算密码算法往往是大数运算,椭圆曲线密码体制要求160位的大数运算,但现有微机的CPU最多只支持64位的运算.1) 要求大容量的数据存储.密码运算通常都要利用大容量的数据表,即用空间来换取时间上的加速. 这就要求运算部件具有大容量的存储.2) 包含大量的并行性.6.2 椭圆曲线密码体制中的有关计算6.2.1 椭圆曲线密码体制中的运算类型作为公开密钥算法的一种,椭圆曲线密码体制要用到点乘、点加、模乘、模加、模逆、模幂这些基本运算,它们的执行速度直接决定着椭圆曲线的加密速度. 为了提高它们的速度,可从以下两方面考虑:(1) 采用高速的算法.(2) 实现算法的并行性(以便在硬件设计中利用多处理器进行并行运算):1) 大数乘、大数取模属于整数域上的运算;2) 模加、模乘、模逆、模幂属于有限域上的运算;3) 点加和点乘属于椭圆曲线的点加群上的运算.6.2.2 简述椭圆曲线的点加和纯量乘法由于本人能力有限,短时间内很难做出一些深层次的研究和探讨,因此只能在这里做一点表面文章. 所以本文在这一部分就结合前面对有关大数计算算法进行的阐述,做一些力所能及的事情. 对于一般的椭圆曲线方程,设点,和的坐标.的计算公式如下:,,其中.当P ≠ Q时,.当P = Q时, 对于椭圆曲线方程, 上述的公式变为:,,其中当P ≠ Q时,.当P=Q时, 由上述运算公式, 可以得出点积mP的运算, 即mP = P + P + … + P, 共m个P相加, 这里m∈N.6.3椭圆曲线的点积的具体程序算法设m的二进制表示为,其中, Q = P, 从左到右依次计算:for( i = n - 2 to 0){ Q = 2Q;if(==1) Q=Q+P;}则Q=mP.Return;函数原形为:bool Ecc_points_mul(mp_int*qx, mp_int*qy, mp_int*px, mp_int*py, mp_int*d, mp_int *a,mp_int *p)成功返回true.int Two_points_add(mp_int*x1, mp_int*y1, mp_int*x2, mp_int*y2, mp_int*x3, mp_int *y3, mp_int *a, bool zero, mp_int*p)成功返回1.7.加密文件的读入与输出7.1椭圆曲线的加密体制在Diffe-Hellman公钥系统体制中,具体的椭圆曲线、曲线上点P及P的周期大素数N都是公开信息.A和B要进行通讯,首先得到椭圆曲线E、点P及素数N. 然后用户A将[1, N-1]中随机选取的整数a作为私钥, A将作为自己的公钥传送给用户B, 与此同时B将 [1, N-1]中随机选取的整数b作为私钥, 并将作为自己的公钥传送给A. A、B各自将自己的私钥点乘于对方传过来的公钥得到, 这样就完成了密钥的交换过程.当用户A需要将待传数据m传送给用户B时, A 利用m和生成, 当用户B得到后, 利用密钥交换过程自己生成的和从用户A处得到的加密数据生成数据m.见下图[5]:7.2加密文件的读入与输出的具体程序实现mp_digit只用28比特,因此一个单元最多可存放三个半字节. 为充分利用存取空间,采用一个单元放三个半字节.7.2.1函数putin()的实现函数putin()的实现的作用: 将明文的二进制比特串赋给mp_int数a. 主要循环部分及说明如下:// chlong为要存入的字符数组长for(j=0; j<<="(mp_digit)CHAR_BIT;" *temp 存入字符 255); 左移8位存入高8位并向左移8位,以便放入下一个字符 temp跳过前一个单元,先存入后一单元 *++temp 每次跳七个字符 i + ="7"; 的两个单元中以7个字符为单元循环,把七个字符放入的mp_int 7; j++){(>> 4); //存放被切分的字符的高四位,temp跳回前一个单元//存入第一单元*temp |= (mp_digit) (ch[i-4] & yy); //存放被切分的字符的低四位yy=(mp_digit)15;*temp <<= (mp_digit)CHAR_BIT; //向左移8位,以便放入下一个字符*temp |= (mp_digit)(ch[i-5] & 255); //存入字符*temp <<= (mp_digit)CHAR_BIT; //左移8位*temp |= (mp_digit)(ch[i-6] & 255); //存入字符*temp <<= (mp_digit)CHAR_BIT; //左移8位*temp++ |= (mp_digit)(ch[i-7] & 255);//存放被切分的字符的低四位,temp跳到后一个单元temp++; //再向后跳一单元,这样和下次的++temp实现每次循环跳两个单元}函数原型为:int putin(mp_int*a, char*ch, int chlong)成功返回0.7.2.2函数chdraw( )的实现函数chdraw()实现将mp_int数a中的比特串还原为字符串并赋给字符串ch: chdraw和putin是相反过程,将putin存入字符的过程反过来取出字符.函数原型为:int chdraw(mp_int* a, char*ch)成功返回0.8.密文的存取和读入此过程难点是如何保证存入文件后,再从文件中读取密文并存入mp_int型数后,和原存放密文的mp_int型数不能有一个比特位的改变.存取时先存 *mp->dp的最高8位,再依次往下存后面3个8位. 依据 *mp->dp的特点,最高8位为0000xxxx,因此,可将255作为一个密文段的结束标志,把前一密文段和后一密文段区分开. 这样在密文文件中,密文的存取结构为:0000xxxx|xxxxxxxx|xxxxxxxx|xxxxxxxx|0000xxxx|……|11111111|0000xxxx|xxxxxxxx|…..0字节 1字节 2字节 3字节 4字节 4x字节下一加密段 x为1或0利用fgetc每次读取一个字符,并赋值给一个字符数组. 当a[i]=255,且i%4=0时截止.读出之后赋值就简单了.存密文:int chmistore(mp_int*a, FILE*fp) 成功返回0把密文赋给mp_int型数a: int miwendraw(mp_int*a, char*ch, int chlong) 成功返回0.9. ECC加密的实现9.1 ECC加密实现的理论依据加密时因P长度取值为200比特,所以所取明文长度应在0到199比特之间,另外需要一个附加的标志字节char(255),所以一次取明文最大长为191比特. 在本程序中一次取20字节. 和RSA不同,ECC运算是基于点的运算. 一个点有两个参数,一个X坐标,一个Y坐标. 所以取明文时需一次取两段,前一段做X坐标,后一段做Y坐标. 因此,一次加密明文为40字节. 由于每次加密要取两段,引发了另外一个问题:当加密文件末尾所剩明文长度小于20字节时的处理. 在本程序中,我们的解决是将剩余明文取作X,而将Y取作0,且不加标志字节char(255),这样解密时,程序在Y中找不到标志字节char(255),就不会往解密文中存任何东西.取得明文后,产生一个随机整数r, 计算点;. 将点、坐标,,,依次存入密文文件[6].9.2 ECC加密的具体程序实现for(i=0; i 0) // Residue为剩余字符数{if (Residue <= enlongtemp ){fread(miwenx,1, Residue, fp); //读入字符串miwenx[Residue]=char(255);putin(&mx, miwenx,Residue+1); //文件存入mp_zero(&my);}else{fread(miwenx,1,enlongtemp,fp); //读入字符串miwenx[enlongtemp]=char(255);fread(miweny,1,Residue-enlongtemp,fp); //读入字符串miweny[Residue-enlongtemp]=char(255);putin(&mx, miwenx,enlongtemp+1); //文件存入putin(&my, miweny,Residue-enlongtemp+1); //文件存入}//加密Ecc_points_mul(&c2x,&c2y,px,py,&r,a,p); //C2=rGEcc_points_mul(&tempx,&tempy,qx,qy,&r,a,p); // rKTwo_points_add(&mx,&my,&tempx,&tempy,&c1x,&c1y,a,zero,p); // C1=M+rK//保存密文chmistore(&c1x,fq);chmistore(&c1y,fq);chmistore(&c2x,fq);chmistore(&c2y,fq);}函数原型为:void Ecc_encipher(mp_int*qx, mp_int*qy, mp_int*px,mp_int*py, mp_int*a, mp_int*p);10.ECC解密的实现10.1ECC解密实现的理论依据解密时,依据存密文时放入的结束标志255,读入密文. 依次取4段, 调用miwendraw将密文存入mp_int型数中,还原为加密时存入的点C1和C2坐标c1x, c1y, c2x, c2y. 依据. 计算(d为私钥),得到明文点坐标,. 其中两点减的计算可如下:;计算完毕后调用chdraw取出mp_int中的明文比特串,依次存入解密文件中,完成解密[6].10.2 ECC解密的具体程序实现while(!feof(fp)){//取C1点X坐标i=0;while(1){stemp[i]=fgetc(fp);if(i%4==0){if(int(stemp[i]&0xFF) == 255 ) goto L1;}i++;}L1: miwendraw(&, stemp, i); //取其他坐标Ecc_points_mul(&tempx, &tempy, &, &, k, a, p); // 计算mp_neg(&tempy, &temp); // -Q=(X,-Y)Two_points_add(&,&, &tempx, &temp, &, &, a, zero, p);int chtem;chtem=chdraw(&,stemp); //从ming中取出字符串//保存解密结果for(int kk=0;kk < chtem;kk++){fprintf(fq,"%c",stemp[kk]);}chtem=chdraw(&,stemp); //从ming中取出字符串//保存解密结果for(kk=0; kk < chtem; kk++){fprintf(fq, "%c", stemp[kk]);}}函数原型为:void Ecc_decipher(mp_int*k, mp_int*a, mp_int*p);11. 测试结果及分析为验证系统的加密解密功能,对系统进行了如下测试:测试环境Intel p4; CPU 1.5G; 256M RAM; Windows XP DEV - C++测试结果利用系统对文本文件、BMP、WORD、EXCEL、EXE等文件进行加密,然后解密. 验证结果表明,给定的明文经系统加密后再解密的结果完全一致, 没有一个比特的偏差,较好的实现了ECC的功能.12.结束语目前,国际上公认的比较安全实用的公钥密码体制是 1985年 Koblitz和Miller分别独立提出的建立在椭圆曲线上的离散对数难题基础上的椭圆曲线密码体制(ECC). 经过长期的理论研究和科学实践,ECC得到了迅猛的发展. 现在椭圆曲线密码体制不仅是一个重要的理论研究领域,而且已经从理论研究转化为实际可用的密码算法,促使民用安全技术走向产业化. 当前,国内外很多生产密码产品的公司都在致力于ECC产品的开发. 椭圆曲线加密算法ECC的安全性,是基于计算有限域上椭圆曲线点集所构成的可交换群上定义的离散对数的困难性. 该算法具有安全性能高,计算量小,处理速度快,存储空间占用小和带宽要求低等特点,已在强调速度的领域如PDA,手机,智能卡等方面得到应用.参考文献:[1] 杨超, 高海燕. 椭圆曲线密码体制理论与其安全性研究[J]电脑知识与技术, 2006,(17).[2] 孙跃刚. 椭圆曲线密码体制中若干问题的研究[D]. 吉林大学 2009. [3] 于彬. 椭圆曲线密码算法的研究与实现[D]. 沈阳工业大学.[4] 王庆先. 有限域运算和椭圆曲线数乘运算研究[D]. 电子科技大学2006.[5] 李学俊. 基于椭圆曲线离散对数问题的公钥密码及其算法研究[D].[6] 杨君辉, 戴宗铎, 杨栋毅, 刘宏伟. 关于椭圆曲线密码的实现[J]通信技术,2001(06).On the Realization of the Elliptic Curve Encryption Algorit hmYan MeitingAbstract: In this paper, we first introduce the elliptic curve encryption algorithm, then give the definition of the elliptic curve briefly. The ElGamal public encryption system is based on the elliptic curve theory, and we analyze the process and the security of this encryption system. At last we realize it in c++ and offer the source code.Keywords: elliptic curve encryption algorithm; public-key password, digital signatures。
电子护照PACE协议映射机制原理解析与芯片实现

电子护照PACE协议映射机制原理解析与芯片实现郭小波【摘要】2012年5月我国正式启动了电子护照,ICAO对电子机读旅行证件的相关规范做了多次升级修订,2013年出版的新版规范中增加了SAC协议,其中包括PACE、CA以及TA协议.PACE协议中最重要的流程是建立映射机制,映射主要分为三种通用映射、综合映射和芯片认证映射.主要解析符合PACE协议的映射机制和原理,并通过确定的安全域参数进行协议的算法实现,可从根本上理解协议.同时,在解析符合PACE协议的映射机制和原理的基础上,简要描述确定安全域参数的PACE协议算法,并在现有芯片平台上进行编码实现,可提高我国电子护照的安全应用技术水平,推动相关芯片产品的成果应用与推广.【期刊名称】《警察技术》【年(卷),期】2016(000)005【总页数】4页(P67-70)【关键词】电子护照;PACE协议;补充访问控制;基本访问控制【作者】郭小波【作者单位】公安部第一研究所【正文语种】中文2004年,国际民航组织(ICAO)发布了电子机读旅行证件基本访问控制(Basic Access Control,简称BAC)协议和扩展访问控制(Extended Access Control,简称EAC)协议,通过协议的实现保证了电子护照应用的安全和互通性;2013年,ICAO发布了访问控制的增补协议---补充访问控制(Supp lemental Access Control,简称SAC)协议,可进一步提高访问控制的安全性。
ICAO最新增补协议包括三个部分:基于口令认证连接建立(Password Authenticated Connection Establishment,简称PACE)协议、芯片认证(Chip Authentication,简称CA)协议和以及终端认证(Term inal Authentication,简称TA)协议。
PACE协议是在BAC和EAC访问控制协议的基础上提出的更高安全性的访问控制协议,可替代BAC和EAC协议。
信息安全技术SM2椭圆曲线公钥密码算法

信息安全技术SM2椭圆曲线公钥密码算法1 范围GB/T XXXXX 的本部分规定了SM2椭圆曲线公钥密码算法涉及的必要数学基础知识与相关密码技术,以帮助实现其它各部分所规定的密码机制。
本部分适用于基域为素域和二元扩域的椭圆曲线公钥密码算法的设计、开发、使用。
2 符号和缩略语B MOV 阈。
正数B ,使得求取B q F 上的离散对数至少与求取q F 上的椭圆曲线离散对数一样困难。
deg ( f ) 多项式f (x )的次数。
E 有限域上由a 和b 定义的一条椭圆曲线。
E (F q ) q F 上椭圆曲线E 的所有有理点(包括无穷远点O )组成的集合。
ECDLP 椭圆曲线离散对数问题。
F p 包含p 个元素的素域。
F q 包含q 个元素的有限域。
F q * 由F q 中所有非零元构成的乘法群。
m 2F 包含m 2个元素的二元扩域。
G 椭圆曲线的一个基点,其阶为素数。
gcd(x , y ) x 和y 的最大公因子。
h 余因子,h=#E (F q )/n ,其中n 是基点G 的阶。
LeftRotate ( ) 循环左移运算。
l max 余因子h 的最大素因子的上界。
m 二元扩域F 2m 关于F 2的扩张次数。
mod f (x ) 模多项式f (x )的运算。
若f (x )是二元域上的多项式,则所有系数执行模2运算。
mod n 模n 运算。
例如,23 mod 7=2。
n 基点G 的阶(n 是#E (F q )的素因子)。
O 椭圆曲线上的一个特殊点,称为无穷远点或零点,是椭圆曲线加法群的单位元。
P P = (x P , y P ) 是椭圆曲线上除O 之外的一个点,其坐标x P ,y P 满足椭圆曲线方程。
P 1+P 2 椭圆曲线E 上两个点P 1与P 2的和。
p 大于3的素数。
q 有限域F q 中元素的数目。
a, b q F 中的元素,它们定义q F 上的一条椭圆曲线E 。
r min 基点G 的阶n 的下界。
椭圆曲线算法循环群生成器

椭圆曲线算法循环群生成器
椭圆曲线算法是一种流行的加密算法,它建立在数论基础上,它的安全性广受认可。
这个算法的核心是使用椭圆曲线上的点来生成一个循环群,我们可以利用这个循环群来进行加密和解密操作。
首先,让我们了解一下什么是椭圆曲线。
椭圆曲线是一个特殊的曲线,它可以表示成一个方程式y²=x³+ax+b,其中a、b是常数。
这个曲线在平面上呈现出来就是一个类似于椭圆的形状,但是它们具有很强的数学性质,被广泛应用于密码学领域。
接下来,我们来看一下如何利用椭圆曲线上的点来生成一个循环群。
首先,选择一个大素数p作为我们的模数,并且选取一条椭圆曲线。
这个椭圆曲线需要满足一些条件,例如它的点数要很大。
然后,我们选取一个点G作为曲线上的基点,这个基点G也需要满足一些条件,例如它不能是曲线上的奇点,同时它的阶(order)要很大。
接下来,我们用G来生成一个循环群。
我们可以定义这个循环群为集合{G,G+G,G+G+G,…},其中加号是椭圆曲线上的加法运算。
由于G的阶可以很大,因此我们可以生成非常多的点,这个循环群也会非常大。
最后,我们需要选择一个私有密钥d来加密我们的消息。
我们可以将这个私钥d作为一个整数,然后使用椭圆曲线上的点G来生成一
个公钥Q=dG。
这个公钥我们可以与别人分享,他们可以使用这个公钥来加密消息,我们可以使用私钥d来解密。
总的来说,椭圆曲线算法循环群生成器是一个非常强大的密码学工具,它可以帮助我们实现加密和解密操作。
在使用时要注意算法的使用条件和密钥的生成,以确保我们的数据安全。
一种基于ECC算法的安全认证方法
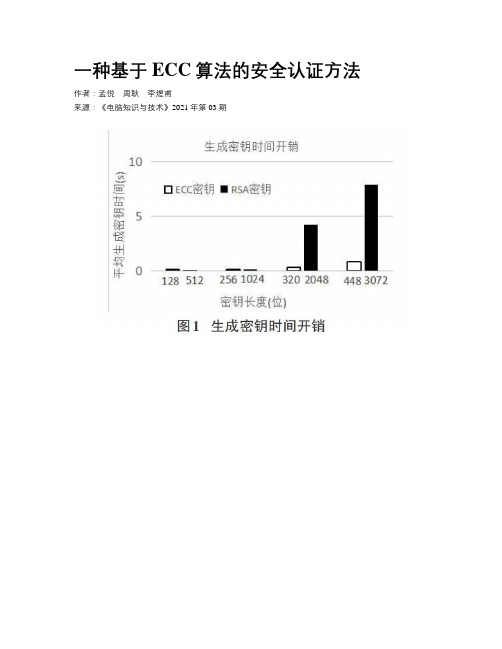
一种基于ECC算法的安全认证方法作者:孟悦周耿李煜甫来源:《电脑知识与技术》2021年第03期摘要:为了解决传统基于RSA算法的身份认证方法不能满足无人机网络轻量级认证需求的问题,该文设计并实现了基于椭圆曲线ECC(Elliptic Curve Cryptography)算法的身份认证方法。
使用ECC数字证书作为合法节点的身份证明,基于椭圆曲线的ECDSA(Elliptic Curve Digital Signature Algorithm)签名算法对节点身份进行签名验证,同时使用ECDH密钥交换算法生成通信所需要的会话密钥,实现以较短长度密钥和较小运算量完成节点间身份认证。
关键词:无人机网络;身份认证;椭圆曲线中图分类号:TP393 文献标识码:A文章编号:1009-3044(2021)03-0075-02Abstract: In order to solve the problem that the traditional authentication method based on RSA algorithm cannot meet the lightweight authentication requirements of the UAV network. This paper designed and implemented an identity authentication scheme based on Elliptic Curve Cryptography algorithm. The ECC digital certificate is used as the identity proof of the legal node, the ECDSA (Elliptic Curve Digital Signature Algorithm) signature algorithm based on the elliptic curve is used to verify the identity of the node, and the ECDH key exchange algorithm is used to generate the session key required for communication, so as to realize the end-to-end authentication between nodes with short length key and small amount of computation.Key words: UAV network;identity authentication;elliptic curve嵌入式系統具有有限的系统资源,如无人机网络中设备物理资源和计算能力[1-3]非常有限,针对传统身份认证方案中资源开销大的问题,基于椭圆曲线ECC算法实现了轻量级身份认证方案。
secp256k1椭圆曲线算法

secp256k1椭圆曲线算法【1】椭圆曲线算法简介椭圆曲线算法(Elliptic Curve Cryptography,简称ECC)是一种公钥加密算法,基于椭圆曲线上的数学问题。
这种算法在1985年由W.Duever和V.Shamir提出。
与RSA、DSA等公钥加密算法相比,椭圆曲线算法具有相同的安全级别,但所需的密钥长度较短,因此在实际应用中具有更高的效率。
【2】SECP256k1椭圆曲线参数SECP256k1(Secure Curve 256-bit Key Length 1)是一种常见的椭圆曲线算法,其参数如下:- 曲线方程:y^2 = x^3 + ax + b- 生成元:G = (x, y)- 椭圆曲线阶:n = 2^256 - 1- 素数p:p = 2^256 - 1- 系数a、b:a = 0,b = 7【3】SECP256k1算法应用SECP256k1算法广泛应用于加密货币、网络通信等领域。
以下是SECP256k1算法在比特币(Bitcoin)中的应用示例:1.密钥生成:用户生成一个私钥,对其进行椭圆曲线运算,得到一个对应的公钥。
2.数字签名:用户用自己的私钥对交易信息进行签名,生成数字签名。
3.验证签名:交易接收方使用发送方的公钥验证数字签名,确保交易的真实性和完整性。
【4】安全性与性能分析SECP256k1算法的安全性依赖于椭圆曲线上的数学难题,目前尚未找到高效的破解方法。
然而,随着计算能力的提升,未来可能会出现针对SECP256k1的攻击手段。
因此,研究人员正在寻求更高安全性的椭圆曲线算法,如SECG 曲线。
在性能方面,SECP256k1算法相较于其他公钥加密算法具有较高的运算速度。
但这仍取决于具体的实现和硬件条件。
在实际应用中,可以采用优化算法和硬件加速手段进一步提高性能。
【5】总结SECP256k1椭圆曲线算法作为一种高效、安全的公钥加密算法,在现代密码学和加密货币领域具有重要地位。
椭圆曲线运算的verilog实现

椭圆曲线运算的Verilog实现近年来,随着网络安全领域的快速发展,椭圆曲线密码学作为一种重要的加密算法逐渐受到广泛关注。
椭圆曲线密码学以其优越的安全性和高效性成为各种信息安全领域的重要工具,而椭圆曲线运算作为其核心内容之一,受到了越来越多的关注和研究。
本文将针对椭圆曲线运算的Verilog实现展开深入探讨,帮助读者对这一重要的主题有更加全面和深入的了解。
1. 椭圆曲线密码学简介椭圆曲线密码学是建立在椭圆曲线运算基础之上的一种密码学方法。
在椭圆曲线密码学中,椭圆曲线的离散对数问题被用来构建公钥密码系统,并被广泛应用于数字签名、密钥交换、身份验证等领域。
因其所需的密钥长度相对较短,安全性高,运算速度快等优点,椭圆曲线密码学逐渐成为了信息安全领域的热门研究方向。
2. 椭圆曲线运算的基本原理椭圆曲线运算主要包括点的加法、点的乘法、点的倍乘等运算。
在椭圆曲线密码学中,点的加法和点的乘法是常用的运算方式,而点的倍乘则是用于生成公钥和私钥的关键操作。
3. Verilog实现椭圆曲线运算的挑战在实际应用中,椭圆曲线密码学需要在各种硬件评台上进行实现和部署,以满足不同场景下的安全需求。
然而,由于椭圆曲线运算涉及大量的高精度浮点运算和模运算等复杂操作,因此在硬件评台上实现椭圆曲线运算是一项具有挑战性的任务。
Verilog作为一种硬件描述语言,可以用来描述和实现具体的硬件电路,因此在Verilog上实现椭圆曲线运算成为了一种可行的选择。
4. Verilog实现椭圆曲线运算的关键技术要在Verilog上实现椭圆曲线运算,首先需要深入理解椭圆曲线运算的基本原理,并转化为硬件电路。
重点包括点的加法、点的乘法、点的倍乘等运算的转化方法,以及如何利用Verilog语言描述这些操作。
还需要考虑如何优化硬件电路结构,以提高运算速度和减小硬件资源占用。
5. Verilog实现椭圆曲线运算的未来发展随着硬件技术的不断进步,椭圆曲线运算的Verilog实现将会得到更加广泛的应用。
椭圆曲线加密算法(ECC)原理和C++实现源码(摘录)

椭圆曲线加密算法(ECC)原理和C++实现源码(摘录)/* 1、⽤户A选定⼀条适合加密的椭圆曲线Ep(a,b)(如:y2=x3+ax+b),并取椭圆曲线上⼀点,作为基点G。
2、⽤户A选择⼀个私有密钥k,并⽣成公开密钥K=kG。
3、⽤户A将Ep(a,b)和点K,G传给⽤户B。
4、⽤户B接到信息后,将待传输的明⽂编码到Ep(a,b)上⼀点M,并产⽣⼀个随机整数r(r<n)。
5、⽤户B计算点C1=M+rK;C2=rG。
6、⽤户B将C1、C2传给⽤户A。
7、⽤户A接到信息后,计算C1-kC2,结果就是点M。
因为C1-kC2=M+rK-k(rG)=M+rK-r(kG)=M 再对点M进⾏解码就可以得到明⽂。
密码学中,描述⼀条Fp上的椭圆曲线,常⽤到六个参量:T=(p,a,b,G,n,h)。
(p 、a 、b ⽤来确定⼀条椭圆曲线,G为基点,n为点G的阶,h 是椭圆曲线上所有点的个数m与n相除的整数部分) 这⼏个参量取值的选择,直接影响了加密的安全性。
参量值⼀般要求满⾜以下⼏个条件: 1、p 当然越⼤越安全,但越⼤,计算速度会变慢,200位左右可以满⾜⼀般安全要求; 2、p≠n×h; 3、pt≠1 (mod n),1≤t<20; 4、4a3+27b2≠0 (mod p); 5、n 为素数; 6、h≤4。
*/#include <stdio.h>#include <string.h>#include <stdlib.h>#include <iostream.h>#include "tommath.h"#include <time.h>#define BIT_LEN 800#define KEY_LONG 128 //私钥⽐特长#define P_LONG 200 //有限域P⽐特长#define EN_LONG 40 //⼀次取明⽂字节数(x,20)(y,20)//得到lon⽐特长素数int GetPrime(mp_int *m,int lon);//得到B和G点X坐标G点Y坐标void Get_B_X_Y(mp_int *x1,mp_int *y1,mp_int *b, mp_int *a, mp_int *p);//点乘bool Ecc_points_mul(mp_int *qx,mp_int *qy, mp_int *px, mp_int *py,mp_int *d,mp_int *a,mp_int *p);//点加int Two_points_add(mp_int *x1,mp_int *y1,mp_int *x2,mp_int *y2,mp_int *x3,mp_int *y3,mp_int *a,bool zero,mp_int *p);//⼆进制存储密⽂int chmistore(mp_int *a,FILE *fp);//把读取的字符存⼊mp_int型数int putin(mp_int *a,char *ch,int chlong);//ECC加密void Ecc_encipher(mp_int *qx,mp_int *qy, mp_int *px, mp_int *py,mp_int *a,mp_int *p);//ECC解密void Ecc_decipher(mp_int *k, mp_int *a,mp_int *p);//实现将mp_int数a中的⽐特串还原为字符串并赋给字符串ch:int chdraw(mp_int *a,char *ch);//取密⽂int miwendraw(mp_int *a,char *ch,int chlong);int myrng(unsigned char *dst, int len, void *dat){int x;for (x = 0; x < len; x++) dst[x] = rand() & 0xFF;return len;}void main(){cout<<"\n 本程序实现椭圆曲线的加密解密"<<endl;cout<<"\n------------------------------------------------------------------------\n"<<endl;mp_int GX;mp_int GY;mp_int K;//私有密钥mp_int A;mp_int QX;mp_int QY;mp_int P;//Fp中的p(有限域P)mp_init(&GX);mp_init(&GY);mp_init(&K);mp_init(&A);mp_init(&B);mp_init(&QX);mp_init(&QY);mp_init(&P);time_t t;srand( (unsigned) time( &t ) );printf("椭圆曲线的参数如下(以⼗进制显⽰):\n");GetPrime(&P,P_LONG);printf("有限域 P 是:\n");char temp[800]={0};mp_toradix(&P,temp,10);printf("%s\n",temp);GetPrime(&A,30);char tempA[800]={0};printf("曲线参数 A 是:\n");mp_toradix(&A,tempA,10);printf("%s\n",tempA);Get_B_X_Y(&GX,&GY,&B,&A,&P);char tempB[800]={0};printf("曲线参数 B 是:\n");mp_toradix(&B,tempB,10);printf("%s\n",tempB);char tempGX[800]={0};printf("曲线G点X坐标是:\n");mp_toradix(&GX,tempGX,10);printf("%s\n",tempGX);char tempGY[800]={0};printf("曲线G点Y坐标是:\n");mp_toradix(&GY,tempGY,10);printf("%s\n",tempGY);//------------------------------------------------------------------GetPrime(&K,KEY_LONG);char tempK[800]={0};printf("私钥 K 是:\n");mp_toradix(&K,tempK,10);printf("%s\n",tempK);Ecc_points_mul(&QX,&QY,&GX,&GY,&K,&A,&P);char tempQX[800]={0};printf("公钥X坐标是:\n");mp_toradix(&QX,tempQX,10);printf("%s\n",tempQX);char tempQY[800]={0};printf("公钥Y坐标是:\n");mp_toradix(&QY,tempQY,10);printf("%s\n",tempQY);printf("\n------------------------------------------------------------------------\n"); Ecc_encipher(&QX,&QY,&GX,&GY,&A,&P);//加密printf("\n------------------------------------------------------------------------\n"); Ecc_decipher(&K,&A,&P);//解密printf("\n------------------------------------------------------------------------\n"); char cc;cout<<"\n\n请击⼀键退出!\n";mp_clear(&GX);mp_clear(&GY);mp_clear(&K);//私有密钥mp_clear(&A);mp_clear(&B);mp_clear(&QX);mp_clear(&QY);mp_clear(&P);//Fp中的p(有限域P)}int GetPrime(mp_int *m,int lon){mp_prime_random_ex(m, 10, lon,(rand()&1)?LTM_PRIME_2MSB_OFF:LTM_PRIME_2MSB_ON, myrng, NULL); return MP_OKAY;}void Get_B_X_Y(mp_int *x1,mp_int *y1,mp_int *b, mp_int *a, mp_int *p){mp_int tempx,tempy;mp_int temp;mp_int compare;mp_int temp1;mp_int temp2;mp_int temp3;mp_int temp4;mp_int temp5;mp_int temp6;mp_int temp7;mp_int temp8;mp_init_set_int (&compare, 0);mp_init(&tempx);mp_init(&tempy);mp_init(&temp);mp_init(&temp1);mp_init(&temp2);mp_init(&temp3);mp_init(&temp4);mp_init(&temp5);mp_init(&temp6);mp_init(&temp7);mp_init(&temp8);while(1){//4a3+27b2≠0 (mod p)GetPrime(b,40);mp_expt_d(a, 3, &temp1);mp_sqr(b, &temp2);mp_mul_d(&temp1, 4, &temp3);mp_mul_d(&temp2, 27, &temp4);mp_add(&temp3, &temp4, &temp5);mp_mod(&temp5,p,&temp);if(mp_cmp(&temp, &compare)!=0 ){break;}}//y2=x3+ax+b,随机产⽣X坐标,根据X坐标计算Y坐标GetPrime(x1,30);mp_expt_d(x1, 3, &temp6);mp_mul(a, x1, &temp7);mp_add(&temp6, &temp7, &temp8);mp_add(&temp8, b, &tempx);mp_sqrt(&tempx, y1);mp_clear(&tempx);mp_clear(&tempy);mp_clear(&temp);mp_clear(&temp1);mp_clear(&temp2);mp_clear(&temp3);mp_clear(&temp4);mp_clear(&temp5);mp_clear(&temp8);}bool Ecc_points_mul(mp_int *qx,mp_int *qy, mp_int *px, mp_int *py,mp_int *d,mp_int *a,mp_int *p){mp_int X1, Y1;mp_int X2, Y2;mp_int X3, Y3;mp_int XX1, YY1;mp_int A,P;int i;bool zero=false;char Bt_array[800]={0};char cm='1';mp_toradix(d,Bt_array,2);mp_init_set_int(&X3, 0);mp_init_set_int(&Y3, 0);mp_init_copy(&X1, px);mp_init_copy(&X2, px);mp_init_copy(&XX1, px);mp_init_copy(&Y1, py);mp_init_copy(&Y2, py);mp_init_copy(&YY1, py);mp_init_copy(&A, a);mp_init_copy(&P, p);for(i=1;i<=KEY_LONG-1;i++){mp_copy(&X2, &X1);mp_copy(&Y2, &Y1);Two_points_add(&X1,&Y1,&X2,&Y2,&X3,&Y3,&A,zero,&P);mp_copy(&X3, &X2);mp_copy(&Y3, &Y2);if(Bt_array[i]==cm){mp_copy(&XX1, &X1);mp_copy(&YY1, &Y1);Two_points_add(&X1,&Y1,&X2,&Y2,&X3,&Y3,&A,zero,&P);mp_copy(&X3, &X2);mp_copy(&Y3, &Y2);}}if(zero){cout<<"It is Zero_Unit!";return false;//如果Q为零从新产⽣D}mp_copy(&X3, qx);mp_copy(&Y3, qy);mp_clear(&X1);mp_clear(&Y1);mp_clear(&X2);mp_clear(&Y2);mp_clear(&X3);mp_clear(&Y3);mp_clear(&XX1);mp_clear(&YY1);mp_clear(&A);mp_clear(&P);return true;}//两点加int Two_points_add(mp_int *x1,mp_int *y1,mp_int *x2,mp_int *y2,mp_int *x3,mp_int *y3,mp_int *a,bool zero,mp_int *p) {mp_int x2x1;mp_int y2y1;mp_int tempk;mp_int tempy;mp_int temp1;mp_int temp2;mp_int temp3;mp_int temp4;mp_int temp5;mp_int temp6;mp_int temp7;mp_int temp8;mp_int temp9;mp_int temp10;mp_init(&x2x1);mp_init(&y2y1);mp_init(&tempk);mp_init(&tempy);mp_init(&tempzero);mp_init(&k);mp_init(&temp1);mp_init(&temp2);mp_init_set(&temp3,2);mp_init(&temp4);mp_init(&temp5);mp_init(&temp6);mp_init(&temp7);mp_init(&temp8);mp_init(&temp9);mp_init(&temp10);if(zero){mp_copy(x1, x3);mp_copy(y1, y3);zero=false;goto L;}mp_zero(&tempzero);mp_sub(x2, x1, &x2x1);if(mp_cmp(&x2x1,&tempzero)==-1){mp_add(&x2x1, p, &temp1);mp_zero(&x2x1);mp_copy(&temp1, &x2x1);}mp_sub(y2, y1, &y2y1);if(mp_cmp(&y2y1,&tempzero)==-1){mp_add(&y2y1, p, &temp2);mp_zero(&y2y1);mp_copy(&temp2, &y2y1);}if(mp_cmp(&x2x1, &tempzero)!=0){mp_invmod(&x2x1,p,&tempk);mp_mulmod(&y2y1, &tempk, p, &k);}else{if(mp_cmp(&y2y1, &tempzero)==0){mp_mulmod(&temp3,y1,p,&tempy); mp_invmod(&tempy,p,&tempk);mp_sqr(x1, &temp4);mp_mul_d(&temp4, 3, &temp5);mp_add(&temp5, a, &temp6);mp_mulmod(&temp6, &tempk, p, &k); }else{zero=true;goto L;}}mp_sqr(&k, &temp7);mp_sub(x1, x3, &temp9);mp_mul(&temp9, &k, &temp10);mp_submod(&temp10, y1, p, y3);L:mp_clear(&x2x1);mp_clear(&y2y1);mp_clear(&tempk);mp_clear(&tempy);mp_clear(&tempzero);mp_clear(&k);mp_clear(&temp1);mp_clear(&temp2);mp_clear(&temp3);mp_clear(&temp4);mp_clear(&temp5);mp_clear(&temp6);mp_clear(&temp7);mp_clear(&temp8);mp_clear(&temp9);mp_clear(&temp10);return1;}//⼆进制存储密⽂int chmistore(mp_int *a,FILE *fp){int i,j;char ch;char chtem[4];mp_digit yy=(mp_digit)255;for (i=0; i <= a->used - 1; i++) {chtem[3]=(char)(a->dp[i] & yy);chtem[2]=(char)((a->dp[i] >> (mp_digit)8) & yy); chtem[1]=(char)((a->dp[i] >> (mp_digit)16) & yy); chtem[0]=(char)((a->dp[i] >> (mp_digit)24) & yy);for(j=0;j<4;j++){fprintf(fp,"%c",chtem[j]);}}ch=char(255);fprintf(fp, "%c", ch);return MP_OKAY;}//把读取的字符存⼊mp_int型数int putin(mp_int *a,char *ch,int chlong){mp_digit *temp,yy;int i,j,res;if(a->alloc<chlong*2/7+2){if((res=mp_grow(a,chlong*2/7+2))!=MP_OKAY)return res;}a->sign=0;mp_zero(a);temp=a->dp;i=0;yy=(mp_digit)15;if(chlong<4){for(j=chlong-1;j>=0;j--){*temp |= (mp_digit)(ch[j] & 255);*temp <<= (mp_digit)CHAR_BIT;}return MP_OKAY;}if(chlong<7){i+=4;*++temp |= (mp_digit)(ch[i-1] & yy);*temp <<= (mp_digit)CHAR_BIT;*temp |= (mp_digit)(ch[i-2] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp |= (mp_digit)(ch[i-3] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp-- |= (mp_digit)(ch[i-4] & 255); //存放被切分的字符的低四位for(j=chlong-1;j>=i;j--){*temp |= (mp_digit)(ch[j] & 255);*temp <<= (mp_digit)CHAR_BIT;}*temp >>= (mp_digit)4;*temp |= (mp_digit)((ch[i-1] & 255) >> 4); //存放被切分的字符的⾼四位 a->used=2;return MP_OKAY;}//以7个字符为单元循环,把七个字符放⼊的mp_int 的两个单元中for(j=0;j<chlong/7;j++){i+=7;*++temp |= (mp_digit)(ch[i-1] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp |= (mp_digit)(ch[i-2] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp |= (mp_digit)(ch[i-3] & 255);*temp <<= (mp_digit)4;*temp-- |= (mp_digit)((ch[i-4] & 255) >> 4); //存放被切分的字符的⾼四位 *temp |= (mp_digit)(ch[i-4] & yy); //存放被切分的字符的低四位*temp <<= (mp_digit)CHAR_BIT;*temp |= (mp_digit)(ch[i-5] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp |= (mp_digit)(ch[i-6] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp++ |= (mp_digit)(ch[i-7] & 255);temp++;}if((chlong>=7)&&(chlong%7!=0)) //剩余字符的存放{if(chlong%7 < 4) //剩余字符少余4个时,只需⼀个mp_digit单元存放 {for(j=chlong-1;j>=i;j--){*temp |= (mp_digit)(ch[j] & 255);*temp <<= (mp_digit)CHAR_BIT;}*temp >>= (mp_digit)8;a->used=chlong*2/7+1;}else{ //剩余字符不⼩于4个时,需两个mp_digit单元存放i+=4;*temp |= (mp_digit)(ch[i-1] & yy);*temp <<= (mp_digit)CHAR_BIT;*temp |= (mp_digit)(ch[i-2] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp |= (mp_digit)(ch[i-3] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp++ |= (mp_digit)(ch[i-4] & 255); //存放被切分的字符的低四位for(j=chlong-1;j>=i;j--){*temp |= (mp_digit)(ch[j] & 255);*temp <<= (mp_digit)CHAR_BIT;}*temp >>= (mp_digit)4;*temp |= (mp_digit)((ch[i-1] & 255) >> 4); //存放被切分的字符的⾼四位}}else{a->used=chlong*2/7;}return MP_OKAY;}void Ecc_encipher(mp_int *qx,mp_int *qy, mp_int *px, mp_int *py,mp_int *a,mp_int *p){ //公钥X、Y坐标,曲线G点X、Y坐标,曲线参数A,有限域P mp_int mx, my;mp_int c1x, c1y;mp_int c2x, c2y;mp_int r;mp_int tempx, tempy;bool zero=false;FILE *fp,*fq;int i;char miwenx[280]={0};char miweny[280]={0};char stemp[650]={0};mp_init(&mx);mp_init(&my);mp_init(&c1x);mp_init(&c1y);mp_init(&c2x);mp_init(&c2y);mp_init(&r);mp_init(&tempx);mp_init(&tempy);GetPrime(&r, 100);char filehead[60],filefoot[20],filename[85]={0};cout<<"请输⼊您要加密⽂件的存放路径和⽂件名(如: c:\\000\\⼤整数运算 ):"<<endl;cin>>filehead;cout<<"请输⼊您要加密⽂件的扩展名(如: .doc ):"<<endl;cin>>filefoot;strcpy(filename,filehead);strcat(filename,filefoot);//打开要加密⽂件if((fp=fopen(filename,"rb"))==NULL){printf("can not open the file!");exit(1);}unsigned int FileLong=0;//⽂件字符长度char ChTem;//临时字符变int Frequency=0;int Residue=0;while( !feof(fp) )//找⽂件字符长度{ChTem = fgetc( fp );FileLong++;}--FileLong;Frequency = FileLong/EN_LONG;Residue = FileLong%EN_LONG;int enlongtemp=EN_LONG/2;//printf("%d\n",Frequency);//printf("%d\n",Residue);char filemi[85];strcpy(filemi,filehead);strcat(filemi,"密⽂");strcat(filemi,filefoot);//打开保存密⽂⽂件if((fq=fopen(filemi,"wb"))==NULL)exit(1);}printf("\n开始加密...\n");rewind(fp);for(i=0; i<Frequency; i++){fread(miwenx,1,enlongtemp,fp);//读⼊字符串miwenx[enlongtemp]=char(255);fread(miweny,1,enlongtemp,fp);//读⼊字符串miweny[enlongtemp]=char(255);putin(&mx, miwenx,enlongtemp+1);//⽂件存⼊putin(&my, miweny,enlongtemp+1);//⽂件存⼊Ecc_points_mul(&c2x,&c2y,px,py,&r,a,p);//加密Ecc_points_mul(&tempx,&tempy,qx,qy,&r,a,p);Two_points_add(&mx,&my,&tempx,&tempy,&c1x,&c1y,a,zero,p);//保存密⽂chmistore(&c1x,fq);chmistore(&c1y,fq);chmistore(&c2x,fq);chmistore(&c2y,fq);}//剩余字符处理if ( Residue > 0){if (Residue <= enlongtemp ){fread(miwenx,1,Residue,fp);//读⼊字符串miwenx[Residue]=char(255);putin(&mx, miwenx,Residue+1);//⽂件存⼊mp_zero(&my);}else{fread(miwenx,1,enlongtemp,fp);//读⼊字符串miwenx[enlongtemp]=char(255);fread(miweny,1,Residue-enlongtemp,fp);//读⼊字符串miweny[Residue-enlongtemp]=char(255);putin(&mx, miwenx,enlongtemp+1);//⽂件存⼊putin(&my, miweny,Residue-enlongtemp+1);//⽂件存⼊}Ecc_points_mul(&c2x,&c2y,px,py,&r,a,p);//加密Ecc_points_mul(&tempx,&tempy,qx,qy,&r,a,p);Two_points_add(&mx,&my,&tempx,&tempy,&c1x,&c1y,a,zero,p);//保存密⽂chmistore(&c1x,fq);chmistore(&c1y,fq);chmistore(&c2x,fq);chmistore(&c2y,fq);}cout<<"\nok!加密完毕!"<<endl;cout<<"密⽂以⼆进制保存"<<endl;cout<<"密⽂存放路径为 "<<filemi<<endl ;mp_clear(&mx);mp_clear(&my);mp_clear(&c1x);mp_clear(&c1y);mp_clear(&c2x);mp_clear(&c2y);mp_clear(&r);mp_clear(&tempx);mp_clear(&tempy);}//取密⽂int miwendraw(mp_int *a,char *ch,int chlong){mp_digit *temp;int i,j,res;if(a->alloc<chlong/4){if((res=mp_grow(a,chlong/4))!=MP_OKAY)return res;}a->alloc=chlong/4;a->sign=0;mp_zero(a);temp=a->dp;i=0;for(j=0;j<chlong/4;j++){i+=4;*temp |= (mp_digit)(ch[i-4] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp |= (mp_digit)(ch[i-3] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp |= (mp_digit)(ch[i-2] & 255);*temp <<= (mp_digit)CHAR_BIT;*temp++ |= (mp_digit)(ch[i-1] & 255);}a->used=chlong/4;return MP_OKAY;}//实现将mp_int数a中的⽐特串还原为字符串并赋给字符串ch:int chdraw(mp_int *a,char *ch){int i,j;mp_digit *temp,xx,yy;temp=a->dp;i=0;yy=(mp_digit)255; //⽤于位与运算,取⼋位⽐特串xx=(mp_digit)15; //⽤于位与运算,取四位⽐特串for(j=0;j<a->used/2;j++) //以两个单元为循环,把两个单元的⽐特串赋给7个字符 {i+=7;ch[i-4]=(char)(*++temp & xx);ch[i-3]=(char)((*temp >> (mp_digit)4) & yy);ch[i-2]=(char)((*temp >> (mp_digit)12) & yy);ch[i-1]=(char)((*temp-- >> (mp_digit)20) & yy);ch[i-7]=(char)(*temp & yy);ch[i-6]=(char)((*temp >> (mp_digit)8) & yy);ch[i-5]=(char)((*temp >> (mp_digit)16) & yy);ch[i-4] <<= 4;ch[i-4]+=(char)((*temp++ >> (mp_digit)24) & xx);temp++;}if(a->used%2!=0) //剩于⼀个单元的处理{ch[i++] = (char)(*temp & yy);ch[i++] = (char)((*temp >> (mp_digit)8) & yy);ch[i++] = (char)((*temp >> (mp_digit)16) & yy);}--i;while(int(ch[i]&0xFF) != 255 && i>0) i--;return i;void Ecc_decipher(mp_int *k, mp_int *a,mp_int *p){mp_int c1x, c1y;mp_int c2x, c2y;mp_int tempx, tempy;mp_int mx, my;mp_int temp;mp_init(&temp);mp_init(&c1x);mp_init(&c1y);mp_init(&c2x);mp_init(&c2y);mp_init(&tempx);mp_init(&tempy);mp_init(&mx);mp_init(&my);mp_int tempzero;mp_init(&tempzero);int i;char stemp[700]={0};FILE *fp,*fq;bool zero=false;char filehead[60],filefoot[20],filename[85]={0};cout<<"请输⼊您要解密的⽂件的存放路径和⽂件名(如: c:\\000\\⼤整数运算 ):"<<endl; cin>>filehead;cout<<"请输⼊您要解密的⽂件的扩展名(如: .doc ):"<<endl;cin>>filefoot;strcpy(filename,filehead);strcat(filename,filefoot);printf("\n开始解密\n");if((fp=fopen(filename,"rb"))==NULL){printf("can not open the file!");exit(1);}//打开保存解密结果⽂件char filemi[80];strcpy(filemi, filehead);strcat(filemi, "解密");strcat(filemi, filefoot);if((fq=fopen(filemi,"wb"))==NULL){printf("can not open the file!");exit(1);}rewind(fp);while(!feof(fp)){i=0;while(1){stemp[i]=fgetc(fp);if(i%4==0){if(int(stemp[i]&0xFF) == 255 ) goto L1;}i++;}L1: miwendraw(&c1x, stemp, i);i=0;while(1){stemp[i]=fgetc(fp);if(i%4==0){if(int(stemp[i]&0xFF) == 255 ) goto L2;}i++;}L2: miwendraw(&c1y, stemp, i);i=0;while(1){stemp[i]=fgetc(fp);if(i%4==0){if(int(stemp[i]&0xFF) == 255 ) goto L3;}i++;}L3: miwendraw(&c2x, stemp, i);i=0;while(1){stemp[i]=fgetc(fp);if(i%4==0){if(int(stemp[i]&0xFF) == 255 ) goto L4;}i++;}L4: miwendraw(&c2y, stemp, i);mp_zero(&tempzero);if(mp_cmp(&c1x, &tempzero)==0) break;Ecc_points_mul(&tempx, &tempy, &c2x, &c2y, k, a, p);mp_neg(&tempy, &temp);Two_points_add(&c1x,&c1y,&tempx,&temp,&mx,&my,a,zero,p);int chtem;chtem=chdraw(&mx,stemp);//从ming中取出字符串//保存解密结果for(int kk=0;kk<chtem;kk++){fprintf(fq,"%c",stemp[kk]);}chtem=chdraw(&my,stemp);//从ming中取出字符串//保存解密结果for(kk=0;kk<chtem;kk++){fprintf(fq,"%c",stemp[kk]);}}cout<<"\nok!解密完毕!"<<endl;cout<<"解密后的⽂字存放路径为 "<<filemi<<endl;fclose(fq);fclose(fp);mp_clear(&c1x);mp_clear(&c1y);mp_clear(&c2x);mp_clear(&c2y);mp_clear(&tempx);mp_clear(&tempy);mp_clear(&mx);mp_clear(&my);mp_clear(&temp);}。
椭圆曲线技术工作原理解析

椭圆曲线技术工作原理解析
大多数加密资产使用与比特币完全相同的椭圆曲线,称为secp256k1 。
这使得重新使用比特币的许多椭圆曲线库和工具成为可能。
椭圆曲线密码学(英语:Elliptic Curve Cryptography,缩写为ECC)是一种基于椭圆曲线数学的公开密钥加密算法。
下图示例大多数加密资产使用与比特币完全相同的椭圆曲线,称为secp256k1 。
这使得重新使用比特币的许多椭圆曲线库和工具成为可能。
椭圆曲线技术用于创建由私钥派生出来的公钥。
椭圆曲线技术工作原理
以一个随机生成的数字_k_的私钥开始,我们通过将它乘以称为_generator point_ G_的曲线上的预定点,在曲线上的其他位置产生另一个点,这是相应的公钥_K。
生成点被指定为+secp256k1+标准的一部分,对于+secp256k1+的所有实现始终相同,并且从该曲线派生的所有密钥都使用相同的点_G_:
K = k * G
k 是私钥
G 是预定点
K 是生成的公钥,曲线上的某一点
由于所有比特币用户曲线上的预定点总是相同的,私钥k乘以G将得到的公钥K始终相同.k和K之间的关系是固定的,但这种情况只存在于单向运算,即只能从k到K。
这就是比特币地址(从K派生)可以与任何人共享并且不会泄露用户的私钥(k)的原因。
为了将一个点与整数相乘可视化,我们将使用比实数更简单的椭圆曲线来描述,旨在找到曲线上的预定点G的多个kG。
这个运算逻辑与将G自身连续相加k次相同。
在椭圆曲线中,向自身添加一个点相当于在点上绘制切线并再次找到它与曲线相交的位置,然后在x轴上反映该点。
椭圆曲线

例如,若E是 F7上椭圆曲线 y2 = x3 + 2x + 4 则 E7 (a,b) 上的点是 E7 (2,4) = {O,(0,2),(0,5),(1,0),(2,3),(2,4),(3,3),(3,4),
(6,1), (6, 6)}
(1) ElGamal密码体制的原理 密钥产生过程: 首先选择一素数p以及两个小
这里 ∞ 为无穷远点.
一条椭圆曲线E指的是由韦尔斯特拉斯(Weierstrass)方程: y2 + axy + by = x3 + cx2 + dx + e
所确定的平面曲线,它是由方程的全体解(x, y)再加上 一个无穷远点∞ 构成的集合。其中系数a,b,c,d, e 是满足一些简单条件的实数。亦即:椭圆曲线
• A的私钥取为nA=121,公钥为 PA=121(2,2)=(115,48)。 • B的秘密钥取为nB=203,公开钥 PB=203(2,2)=(130,203)。 • 由此得到的共享密钥为
121(130,203)=203(115,48)=(161,169)
如果选整数作为共享密钥,则可简单地取其中的一 个,如取 x 坐标,或取 x 坐标的某一简单函数。
在椭圆曲线构成的Abel群Ep(a,b)上考虑方程 Q=kP,其中P,Q∈ Ep(a,b) ,k<p,则由k和P易求 Q,但由P、Q求k则是困难的,这就是椭圆曲线上 的离散对数问题,可应用于公钥密码体制。DiffieHellman密钥交换和ElGamal密码体制是基于有限 域上离散对数问题的公钥体制,下面考虑如何用椭 圆曲线来实现这两种密码体制。
9P = (4, 7) 10P = (22, 5) 11P = (10, 5) 12P = (17, 9)
椭圆曲线数字签名算法

椭圆曲线数字签名算法(ECDSA)原文The Elliptic Curve Digital Signature Algorithm (ECDSA)CERTICOM公司李鹤帅译(部分内容有删节)摘要椭圆曲线数字签名算法(ECDSA)是使用椭圆曲线对数字签名算法(DSA)的模拟。
ECDSA 于1999年成为ANSI标准,并于2000年成为IEEE和NIST标准。
它在1998年既已为ISO所接受,并且包含它的其他一些标准亦在ISO的考虑之中。
与普通的离散对数问题(discrete logarithm problem DLP)和大数分解问题(integer factorization problem IFP)不同,椭圆曲线离散对数问题(elliptic curve discrete logarithm problem ECDLP)没有亚指数时间的解决方法。
因此椭圆曲线密码的单位比特强度要高于其他公钥体制。
本文将详细论述ANSI X9.62标准及其协议和实现方面的问题。
1、介绍数字签名算法(DSA)在联邦信息处理标准FIPS中有详细论述。
它的安全性基于素域上的离散对数问题。
椭圆曲线密码(ECC)由Neal Koblitz和Victor Miller于1985年发明。
它可以看作是椭圆曲线对先前基于离散对数问题(DLP)的密码系统的模拟,只是群元素由素域中的数换为有限域上的椭圆曲线上的点。
椭圆曲线密码体制的安全性基于椭圆曲线离散对数问题(ECDLP)的难解性。
椭圆曲线离散对数问题远难于离散对数问题,椭圆曲线密码系统的单位比特强度要远高于传统的离散对数系统。
因此在使用较短的密钥的情况下,ECC可以达到于DL系统相同的安全性。
这带来的好处就是计算参数更小,密钥更短,运算速度更快,签名也更加短小。
因此椭圆曲线密码尤其适用于处理器速度、带宽及功耗受限的场合。
ECDSA是椭圆曲线对DSA的模拟。
ECDSA首先由Scott Vanstone在1992年为了响应NIST 对数字签名标准(DSS)的要求而提出。
基于STM32的硬件狗设计与实现

基于STM32的硬件狗设计与实现滕广超;郎建军;杜奇才;林嘉宇【摘要】信息技术的快速发展,对党政军机要部门的信息安全保密提出了新的要求.为了满足各系统的需要,被保护的软件不被非授权访问或使用,提出一种基于USB接口的硬件狗对保密软件系统进行保护的方法.首先介绍硬件狗的基本原理,然后详细说明其算法实现,最后阐述其在STM32硬件平台上的具体设计与实现.【期刊名称】《微处理机》【年(卷),期】2013(034)006【总页数】3页(P70-72)【关键词】保密软件;算法;STM32;硬件狗;保护【作者】滕广超;郎建军;杜奇才;林嘉宇【作者单位】国防科学技术大学电子科学与工程学院,长沙 410073;武警黄金一总队通信科,哈尔滨 150086;武警黄金一总队通信科,哈尔滨 150086;特种作战学院侦查系,广州 510500;国防科学技术大学电子科学与工程学院,长沙 410073【正文语种】中文【中图分类】TP368.11 引言随着人们对软件的依赖性越来越高,党、政、军的各机要部门借助软件管理信息、调度、自动化、仿真等应用也越来越广泛。
同时,软件系统的安全操作等方面存在着巨大隐患。
为了防止失泄密事故的发生,保证需要被保护的软件操作和访问的合法性,要在技术防范方面提高水平,加强拒绝非法访问的手段和防范措施,以技术为手段的保护成为保护软件的最重要方法[1]。
对软件的常用保护技术通常有软保护和硬保护两种。
软保护是通过在程序中使用一些独特手段来实现加密变换,验证使用者的合法性,重点在如何反拷贝、防静态分析、防动态跟踪等方面[2]。
硬保护是一种需要外插额外硬件的加密手段,软件必须通过访问指定的硬件,并与其进行数据交换才能执行。
由于硬保护依赖硬件,相比于软保护来说具有不易复制性,所以硬保护更加可靠。
现有最常见的硬保护设备主要是硬件狗(加密锁),它可以有效地保护软件不被非法复制和非授权访问或使用,从而达到保护软件的目的。
一种椭圆曲线快速生成算法

一种椭圆曲线参数生成的快速算法谷勇浩 刘勇(北京邮电大学通信网络综合技术研究所)摘要:椭圆曲线密码体制是公钥密码中的研究热点。
该文介绍了椭圆曲线密码体制的基本概念及相关知识,讨论了目前基于离散对数问题的椭圆曲线密码的研究动态。
本文的创新点是针对目前椭圆曲线研究重点之一——椭圆曲线参数生成算法,给出了一种生成参数a 、b 的快速算法。
这种算法利用了Jacobi 符号和二次剩余的理论,并且用matlab 计算出利用这种算法生成一个椭圆曲线的平均时间,最后我们分析了今后椭圆曲线密码系统的研究方向和重点。
关键词:椭圆曲线;离散对数问题;Jacobi 符号;二次剩余;阶1976年Diffie 和Hellman 提出公钥密码思想以来,国际上提出了许多种公钥密码体制的实现方案。
一些已经被攻破,一些被证明是不可行的。
目前,只有3类公钥密码体制被认为是安全有效的,按照其所依据的数学难题划分为:基于大整数分解问题(IFP ),如RSA 体制和Rabin 体制;基于有限域离散对数问题(DLP ),如Diffie-Hellman 体制和ElGamal 体制;基于椭圆曲线离散对数问题(ECDLP ),如椭圆密码体制。
椭圆曲线应用到密码学上最早是由Neal Koblitz 和Victor Miller 在1985年分别独立提出的。
它是目前已知的公钥体制中,对每一比特所提供加密强度最高的一种体制。
它具有安全性高、密钥量小、灵活性好的特点,受到了国际上的广泛关注。
而SET(Secure Electronic Transaction)协议的制定者已把它作为下一代SET 协议中缺省的公钥密码算法。
深入研究基于椭圆曲线离散对数问题的公钥密码具有很大的现实意义。
1建立椭圆曲线公钥密码体制1.1椭圆曲线域的参数在基于椭圆曲线的加解密和数字签名的实现方案中,首先要给出椭圆曲线域的参数来确定一条椭圆曲线。
在 IEEE P1363标准中,定义其参数为一个七元组:T=(q,FR,a,b,G,n,h),其中q 代表有限域GF(q),q 为素数或2m;FR 为域表示法,如f(x)为2mF 域元素的不可约多项式的表示法;曲线的方程,当q 为素数时,方程为23ax b yx =++,当q 为2m时,方程为232xy a b yx x +=++,a,b 是方程中的系数;G 为基点;n 为大素数并且等于点G的阶,h 是小整数称为余因子且#()/qh E n F=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
椭圆曲线算法循环群生成器
椭圆曲线算法(ECDSA)是一种非对称加密算法,是现代加密系统中广泛应用的一种算法。
它通过利用椭圆曲线上的点来实现加密和签名的功能,具有高度的安全性和可靠性。
椭圆曲线算法可以使用循环群生成器来生成相关的密钥对和签名。
循环群是一种数学对象,它包含一个有限的集合和一种二元运算,其满足三个公理:封闭性、结合律和单位元素。
在密码学中,循环群生成器是一种算法,它能够生成一个循环群,并在其中选择一个随机数作为密钥。
循环群生成器是非常重要的密码学工具,它可以用来生成加密密钥、数字签名和身份验证证书等。
椭圆曲线算法循环群生成器可以通过以下步骤生成相关的密钥对和签名:
1. 选择一个椭圆曲线E,并确定一个有限域Fp上的质数p和曲线上的一点G作为群的生成元。
曲线E可以用以下公式表示:
y^2 = x^3 + ax + b(mod p)
其中,a和b是有限域Fp上的常数,p是一个大质数,x和y 是有限域Fp上的元素。
2. 选择一个任意的私钥k,并计算公钥P。
私钥k通常是一个大素数,并且需要保密。
公钥P是曲线E上的一点,其值为
k*G,即P=kG。
3. 使用私钥k和一个哈希函数H生成一个签名r和s。
具体的签名算法可以用以下公式表示:
r = x1(mod n)
s = ((H(m) + xr)/k)mod n
其中,m是待签名的消息,x1和y1是曲线E上的一点,n是一个大素数。
4. 验证签名。
验证签名可以用以下公式表示:
u1 = H(m)/s(mod n)
u2 = r/s(mod n)
X = u1G + u2P
如果X的x坐标等于r,则验证成功。
椭圆曲线算法循环群生成器的安全性是基于离散对数问题的,即在有限域Fp上,给定一个群的生成元G和一个点P,找出一个整数k,使得kG=P。
离散对数问题是一个困难的问题,因此椭圆曲线算法具有高度的安全性。
总的来说,椭圆曲线算法循环群生成器是一种非常重要的密码学工具,它可以用来生成加密密钥、数字签名和身份验证证书
等。
在实际应用中,我们需要选择安全的椭圆曲线和合适的参数来保证算法的安全性。
除此之外,我们还需要对密钥和签名进行正确的管理和使用,以保护系统的安全性。
