露顶式平面钢闸门设计答案
闸门重力计算
闸门行走支承系数Kz 材料系数Kc 孔口高度系数Kg闸门行走支承系数Kz材料系数Kc 孔口高度H(m)闸门工作性质系数K 1孔口高宽比修正系数K 2水头修正系数K 3闸门工作性质系数K 1孔口高宽比修正系数K 2水头修正系数K 3④露顶式弧形钢闸门Kg---孔口高度系数,当H<5m时,Kg=0.156;5m≤H≤8m时,Kg=0.13;③潜孔式平面滑动闸门G=0.022×K 1×K 2×K 3×A 1.34×Hs 0.63K 1---闸门工作性质系数,工作闸门,K 1=1.0;检修门与导流门,K 1=0.9;K 2---孔口高度比修正系数,当H/B≥2时,K 2=0.93;H/B<1时,K 2=1.1;其他情况,K 2=1.0;K 3---水头修正系数,当H S ≥60m时,K 3=(H S /A)0.25;H S <60m时,K 3=1.0;②潜孔式平面滚轮闸门G=0.073×K 1×K 2×K 3×A 0.93×H s 0.79Kc---材料系数,闸门材料为普通碳素结构钢时,Kc=1.0;为普通低合金结构钢时,Kc=0.8;Kz---闸门行走支承系数,对于滑动式支承,Kz=0.81;对于滚轮式支承,Kz=1.0;对于台车式支承1)钢闸门 ①露顶式平面钢闸门 ⅰ,5m≤H≤8m G=0.012×K z ×K c ×H 1.43×B 0.88ⅱ,H>8m G=0.012×K z ×K c ×H 1.65×B 1.85K 1---闸门工作性质系数,工作闸门,K 1=1.1;检修门与导流门,K 1=1.0;K 2---孔口高度比修正系数,当H/B≥2时,K 2=0.93;H/B<1时,K 2=1.1;其他情况,K 2=1.0;K 3---水头修正系数,当H S ≥70m时,K 3=(H S /A)0.25;H S <70m时,K 3=1.0;输入数据输入数据数据输入输入数据浙江水利水电专科学校水利工程系孔口高度H(m)孔口宽度B(m) 闸门重力G(10kN)孔口宽度B(m) 闸门重力G(10kN)式支承,Kz=1.3;;孔口面积A(m3)设计水头H s(m)闸门重力G(10kN)=1.0;孔口面积A(m3)设计水头H s(m)闸门重力G(10kN)=1.0;K c=0.8; 20m时,K b=1.0;。
露顶式平面钢闸门设计答案

露顶式平面钢闸门设计说明书一、设计资料⑴闸门型式:露顶式平面钢闸门 ⑵孔口净宽:8.0 m ⑶设计水头:7.0m⑷结构材料:Q235F A -⑸焊条:焊条采用E 43型手工焊⑻止水橡皮:侧止水用P 型橡皮,底止水用条形橡皮;行走支承:采用胶木滑道,压合胶木为2-MCS⑼混泥土强度等级:C20⑾规范:《水利水电工程钢闸门设计规范》 (SL 74-1995)二、闸门结构的型式及布置 1. 闸门尺寸的确定:⑴ 闸门高度:考虑风浪所产生的水位超高为0.2 m ,故闸门高度5.2+0.2=5.4 m ⑵ 闸门的荷载跨度为两侧止水间的间距L D =8.0 m ⑶ 闸门计算跨度L=L 0+2d=8+2×0.3=8.6 m2. 主梁的型式主梁的型式应根据水头和跨度大小而定,本闸门属于中等跨度(L=5~10),为了便于制造和维护,采用实腹式组合梁,焊接组合截面。
3. 主梁的布置根据闸门的高垮比L H =8.65.2 =1.65>1.55,决定采用双主梁,为使两根主梁在设计水位时所受水压力相等,两根主梁的位置应对称于水压力合力的作用线y=H 3 =53 =1.67 m ,并要求下悬臂a ≥0.12H 和a ≥0.4 m ,上悬臂c ≤0.45H 和c <3.6 m 。
且使底主梁到底止水的距离尽量符合底缘布置要求(即α>30°),先取a=0.12H=0.6 m ,则主梁间距:2b=2(y-a)=2×(1.67-0.6)=2.14 m 4. 梁格的布置和形式格采用复式布置和高等连接,三根水平次梁穿过横隔板上的预留孔并被横隔板所支承。
水平次梁为连续梁,其间距上疏下密,面板各区格所需要的厚度大致相等。
梁格的布置及具体尺寸如下图所示: 5. 联结系的布置和形式(1)横向联结系:根据主梁的跨度,采用布置3道横隔板,横隔板兼作竖直次梁,其横向联结间距为L=8.64=2.15 m(2)纵向联结系:采用斜杆式桁架,布置在两根主梁下翼缘的竖平面内,并设有4根等肢角钢的斜杆。
露顶式平面钢闸门设计答案

组合截面形心到槽钢中心线的距离: 516×8×74
e= 5978 =51 mm
mm2
跨中组合截面的惯性矩及截面模量为: Ι次中=5637000+1851×512+516×8×
可编辑
精品
计算列表如下 :
梁号 1(顶梁) 2
梁轴线水 梁间距
压强度 p (KN/m
(m) 1.50
a上 a下 q=p
2
a上 a下
(m)
2
(mm)
2.7(m6 )
2) 14.70
0.96
1.230 18.08
备注:
顶梁荷载按下图下式计算
1.30 14.7 1.30
R1=
2
3
1.50
=2.76KN/m2
6
=77625 mm3
考虑利用面板作为次梁截面的一部分,初选 槽钢 14a 由附表查得:A=1851 mm2 ;
可编辑
精品
WX =80500 mm2 ; I X =5637000 mm4 ; b1 =58 mm; d=6 mm
面板参加次梁翼缘工作的有效宽度按下式计算,然后取最小值。
B≤ b1 +60t=58+60×8=538 mm
2. 主梁的型式 主梁的型式应根据水头和跨度大小而定,本闸门属于中等跨度(L=5~10),为了便于制造和 维护,采用实腹式组合梁,焊接组合截面。
3. 主梁的布置 L 8.6
根据闸门的高垮比H =5.2 =1.65>1.55,决定采用双主梁,为使两根主梁在设计水位时所
可编辑
精品
H5 受水压力相等,两根主梁的位置应对称于水压力合力的作用线 y=3 =3 =1.67 m,并要求 下悬臂 a≥0.12H 和 a≥0.4 m,上悬臂 c≤0.45H 和 c<3.6 m。且使底主梁到底止水的距离 尽量符合底缘布置要求(即α>30°),先取 a=0.12H=0.6 m,则主梁间距:2b=2(y-a)=2 ×(1.67-0.6)=2.14 m
露顶式平面钢闸门课程设计-《钢结构》 (1)

露顶式平面钢闸门课程设计-《钢结构》 (1)一、课题背景及意义随着建筑都市化的深入发展,涉及到门类型的多样化,钢闸门也在这一过程中有了很大的发展。
配套安装了顶式平面钢闸门,可以清楚地观察到它的优点,从而更好地满足建筑和工程工程的要求,在维护人们的安全作用以及节约能源的作用上起到了重要的作用,而顶式平面钢闸门是坚固耐用的一类门。
因此,本课题将深入分析顶式平面钢闸门的结构特点,为专业人员和未来相关领域进行开展学习、研究和应用打下基础,将为安全提供更好的性能及更高的使用效率而努力。
二、目的和任务1.熟悉钢结构的知识,并详细了解钢结构及其技术特征。
2.了解顶式平面钢闸门,掌握其设计、制作材料、结构及施工要求;3.分析顶式平面钢闸门的优点和特点,提出相应的设计方案;4.优化顶式平面钢闸门的结构设计,考虑其使用效果和安全性。
三、基础理论及资料准备1.本课题需准备《钢结构》、《钢结构及铝合金结构》、《钢结构设计手册》以及相关的标准规范。
2.从专业角度准备涉及的基础理论及制作要求,对顶式平面钢闸门进行实际应用。
3.参考相关文档,进行原理理论分析,结合现实情况,找出可行的设计方案。
四、技术应用1.根据所采用的钢结构规范分析这种类型钢闸门的结构设计,并参考结构规范中关于钢结构设计的基本要求,对顶式平面钢闸门的制作采用合理的合金规范。
2.结合材料的性能,考虑现有的情况,分析门的框架结构,以满足材料、结构和维护性能的要求;4.在安装完成后,测试闸门的控制功能,检查设计的是否符合标准,以及闸门开闭是否正常,一定要严格把握,及时处理出现的问题。
五、总结通过本课程的学习,系统学习和了解了钢结构的基本知识及其特性,以及顶式平面钢闸门的设计、制作材料、结构及施工要求。
在掌握知识基础上,并结合实际,本课题利用一系列技术工具,通过分析顶式平面钢闸门的特点和优点,制定有效的实施方案,形成了运用钢结构实现顶式平面钢闸门设计和制作的思路。
露顶钢闸门课程设计

一、设计资料:①闸门型式:露顶式平面钢闸门②孔口尺寸(宽⨯高): 14 m ⨯ 12 m③上游水位: m④下游水位: m⑤闸底高程: 0 m⑥启闭方式:⑦材料钢结构:Q235-A.F;焊条:E43型;行走支承:滚轮支承或胶木滑道止水橡皮:侧止水用P型橡皮,底止水用条形橡皮⑧制造条件金属结构制造厂制造,手工电弧焊,满足Ⅲ级焊缝质量检验标准规范:《水利水电工程钢闸门设计规范SL 1974-2005》二、闸门结构的形式及布置1.闸门尺寸的确定闸门高度:考虑风浪所产生的水位超高0.2m,故闸门高度=12+0.2=12.2(m);闸门的荷载跨度为两侧止水的间距:L1=14m;闸门计算跨度:L=L0+2d=14+2*0.2=14.40(m)整个闸门的荷载为作于和闸门距离闸底H/3的P=706.32 KN/m的均布荷载2.主梁的形式主梁的形式根据水头和跨度大小而定,本闸门属偏大跨度,为了方便制造和维护,决定采用实腹式组合梁。
3.主梁的布置①根据闸门的高跨比:当L小于等于H时采用多主梁形式,当L大于等于1.5H 时候采用双主梁形式,根据设计资料为14*12孔口尺寸,本设计采用3根主梁②主梁位置的确定:主梁位置的设计原则是根据每个主梁承受相等水压力的原则确定。
对于露顶式闸门:假定水面至门底的距离为H,主梁的个数为n,第K根主梁至水面的距离为Yk,则Yk=2H/3√n[K1.5 -(K-1)1.5 ]根据公式:Y1=2*12/3√3[11.5 -(1-1)1.5 ]=4.6(m)Y2=2*12/3√3[21.5 -(2-1)1.5 ]=8.5 (m)Y3=2*12/3√3[31.5 -(3-1)1.5 ]=10.9(m)考虑到后面梁格的布置和面板的选取将第三根主梁的位置下调0.5m所以Y3=11.4(m)。
4.梁格的布置和形式对于露顶式大跨度闸门采用复式布置和等高连接,水平次梁穿过横隔板上的预留孔并被横隔板所支撑,水平次梁为连续梁,其间距应上疏下密,使面板各区格需要的厚度大致相等,梁格布置的尺寸详见下图5.连接系的布置和形式①横向连接系,根据主梁的跨度,决定布置7道横隔板,其间距为1.75m,横隔板兼做竖直次梁,②纵向连接系,设在两两主梁下翼缘的竖平面内,采用斜杆式桁架。
水利水电工程钢结构课程设计Y--某小型钢闸门设计及小型拦污栅的设计

课程设计说明书课程名称 :水利水电工程钢结构课程设计课程代码 :8203281题目 :某小型钢闸门设计及小型拦污栅的设计学生姓名 :学号 :年级/专业/班:学院(直属系):能源与环境学院指导教师 :徐良芳实验总成绩:水利水电钢闸门设计一、 设计资料:1、 露顶式平面钢闸门设计:①闸门形式:露顶式平面钢闸门 ②孔口尺寸(宽×高):7.5m ×8.0m ③上游水位:7.8m ④下游水位:0.1m ⑤闸底高程:0m⑥启闭方式:电动固定式启闭机 ⑦材料 钢结构:Q235-A.F ; 焊条:E43型;行走支承:滚轮支承或胶木滑道止水橡皮:侧止水用P 型橡皮,底止水用条形橡皮⑧制造条件 金属结构制造厂制造,手工电弧焊,满足Ⅲ级焊缝强度质量检验标准⑨规范:《水利水电工程钢结构闸门设计规范 SL 1974-2005》 2、拦污栅设计: ①拦污栅型式:固定式平面拦污栅②尺寸(宽×高):7.5m ×8.0m ③水头:4m二、 闸门结构的型式及布置1.闸门尺寸的确定:上游水面高度7.8,考虑风浪因素闸门应高出0.2m ,故闸门高度H=7.8+0.2=8m 闸门净高:8.0m 闸门高度:8.0m闸门的荷载跨度为两侧止水之间的间距:L=7.5m闸门的计算跨度:L= L 0+2d = 7.5+2×0.2 = 7.9m 2.主梁的形式:本闸门属于小跨度中水头闸门,所以主梁采用实腹式组合梁。
3.主梁的布置因为闸门跨度L 小于闸门高度H ,所以采用主梁式。
根据闸门的高跨比,决定采用3主梁。
水面至门底的距离为H ,主梁个数为3,设第K 根主梁至水面的距离为Y k 则根据以下公式求得:露顶式闸门:()[]5.15.1132--=K K nH y k计算结果及分布如下图所示:1.连接系的布置和形式(1)横线连接系,根据主梁的跨度,决定布置3道横隔板,其间距为中央三隔板间距2m,隔板与边梁间距1.95m,横隔板兼做竖直次梁。
露顶式平面钢闸门设计答案

露顶式平面钢闸门设计说明书、设计资料⑴闸门型式:露顶式平面钢闸门⑵孔口净宽:8.0 m⑶设计水头:7.0m⑷结构材料:Q235A F⑸焊条:焊条采用E43型手工焊⑻止水橡皮:侧止水用P型橡皮,底止水用条形橡皮;行走支承:采用胶木滑道,压合胶木为MCS 2⑼混泥土强度等级:C20(11)规范:《水利水电工程钢闸门设计规范》(SL 74-1995)图8-1 ¥価钢阿门门叶结构立体示意图、闸门结构的型式及布置1. 闸门尺寸的确定:⑴闸门高度:考虑风浪所产生的水位超高为0.2 m,故闸门高度5.2+0.2=5.4 m⑵ 闸门的荷载跨度为两侧止水间的间距L D=8.0 m⑶ 闸门计算跨度L=L 0+2d=8+2 X 0.3=8.6 m2. 主梁的型式主梁的型式应根据水头和跨度大小而定, 本闸门属于中等跨度(L=5~10),为了便于制造和维护,采用实腹式组合梁,焊接组合截面。
3. 主梁的布置L 8.6根据闸门的高垮比 ==1.65>1.55,决定采用双主梁,为使两根主梁在设计水位时所受H 5.2水压力相等,两根主梁的位置应对称于水压力合力的作用线 臂a >0.12H 和a > 0.4 m ,上悬臂c < 0.45H 和c v 3.6 m 。
且使底主梁到底止水的距离尽量符合底缘布置要求(即 a >30 °),先取 a=0.12H=0.6 m ,则主梁间距:2b=2(y-a)=2 X (1.67-0.6)=2.14m4. 梁格的布置和形式格采用复式布置和高等连接,三根水平次梁穿过横隔板上的预留孔并被横隔板所支承。
水联结系:根据主梁的跨度,采用布置3道横隔板,横隔板兼作竖直次梁,其横向联8.6结间距为L 盲吃15 mH 5y=- =3 =1.67 m ,并要求下悬3 3 平次梁为连 续梁,其间距上疏下 密,面板各 区格所需要 的厚度大致 相等。
梁格 的布置及具 体尺寸如下 图所示: 5.联结系 的布置和形 式 (1)横向I \、、顶梁"n主梁\/X / / ,“ \ /主孤ZVI导-1215021500I&UO丄;3Ln-(2) 纵向联结系:采用斜杆式桁架,布置在两根主梁下翼缘的竖平面内,并设有 肢角钢的斜杆。
闸门设计

一.设计资料闸门形式:引水道露顶式平面钢闸门;孔口净宽:10.00m;设计水头:7.00m;结构材料:平炉热轧碳素钢A3;焊条:E43;止水橡皮:侧止水用P型橡皮,底止水用条形橡皮;行走支承:采用胶木滑道,压合胶木为MCS -- 2;混凝土标号:采用C25号混凝土;二.闸门详细设计过程主要包括:荷载计算、门叶结构设计、梁的连接设计、闸门的外部结构设计。
Ⅰ:荷载计算主要包括:静水压力、闸门自重、地震动水压力、计算荷载的确定。
1.静水压力:对于闸门高度,考虑风浪所引起的波动,门顶超高0.2 m,H=7+0.2=7.2 m ;下图(1)是静水压力计算图,由公式q=12γ H S 2Bg其中,H s-----水高,B-----孔口净宽,γ---水的容重,淡水取γ =1.0 g/cm3。
∴q=12γ H S 2Bg=12×1×72×10×9.8=2401 KN ; p=240.1 kN/m ;合力作用线至顶部的距离H C=23×H S=4.7 m图(1)静水压力计算图图(2)闸门主要尺寸图2.估算闸门自重根据经验公式:对于5m≤H≤8m时,G=K z×K C×K g×H1.43×B0.88其中,G-----闸门自重(kN)H------闸门高度(m)B------孔口宽度(m)K z----闸门行走支承系数,对于滚动支承,K z=1.0K c ----材料系数,普通碳素结构钢,K c =1.0 K g ----闸门高度系数,5m ≤H ≤8m ,K g =0.13 将以上数据带入得:G=K z ×K C ×K g ×H 1.43×B 0.88 =1.0×1.0×0.13×7.21.43×100.88=162.61 kN 即闸门的自重为162.61 kN. 3.地震动水压力水深为y 处的地震动水压力P 0̅=K h ×C Z ×f y ×γ0×H 0 设计地震烈度为7级,查表知:K h =0.2, 综合影响系数 C z =0.25 将数据带入公式得:P 0̅=K h ×C Z ×f y ×γ0×H 0=0.65×0.1×0.25×1×72×9.8=15.6 kN/m整个闸门所承受的地震动水压力为 P ̅=P 0̅×B =15.6×10=156 kN其作用点距离水面的距离为0.54H 0=0.54×7.0=3.78 m,其作用线到门底的距离为h z ,则h z =7-3.78=3.22 m.4.计算荷载的确定根据设计规范对于设计荷载的规定,对作用在闸门上的荷载作如下组合: 设计荷载: 静水压力+闸门自重校核荷载: 静水压力+闸门自重+地震动水压力钢闸门在做结构设计时不计自重,则设计荷载为:2401 kN ,其作用线到门底的距离为 h 设计=2.33 m 。
水工钢结构课程设计平面刚闸门

水工刚结构露顶式焊接平面钢闸门设计计算书 一、 设计资料闸门形式:溢洪道露顶式平面钢闸门; 孔口净宽:9.00m ; 设计水头:5.50m ; 结构材料:Q235钢; 焊条:E43;止水橡皮:侧止水用P 型橡皮;行走支承:采用胶木滑道,压和胶木为MCS-2; 混凝土强度等级:C20;二、 闸门结构的形式及布置(1)闸门尺寸的确定(图1) 1)闸门高度:考虑风浪所产生的水位超高为0.2m ,故闸门高度=5.5+0.2=5.7(m); 2)闸门的荷载跨度为两侧止水的间距:19L m =;图1图23)闸门计算跨度:1L L 2d 920.29.40=+=+⨯= (m)。
(2)主梁的形式。
主梁的形式应根据水头和跨度大小而定,本闸门属于中等跨度,为了方便制造和维护,决定采用实腹式组合梁。
(3)主梁的布置。
根据闸门的高跨比,决定采用双主梁。
为使两个主梁设计水位时所受的水压力相等,两个主梁的位置应对称于水压合力的作用线y=H/3=1.8m 。
(图2)并要求下悬臂a ≥0.12H 和a ≥0.4m 、上悬臂0.45c H ≤,今取 a=0.7≈0.12H=0.66(m)主梁间距 2b=2(Y —a)×(1.83—0.66)≈2.4(m) 则 c=H-2b-a=5.5-2.2-0.7=2.4(m)≈0.45H(满足要求) (4)梁格的布置和形式。
梁格采用复式布置和高等连接,水平次梁穿过横隔板上的预留孔并被横隔板所支承。
水平次梁为连续梁,其间距应上疏下密,使面板各区格所需要的厚度大致相等,梁格的布置具体尺寸见图3。
图3(5)连接系的布置和形式。
1)横向连接系,根据主梁的跨度,决定布置3道横隔板,其间距为2.35m ,横隔板兼做竖直次梁。
2)纵向连接系,设在两个主梁下翼缘的竖平面内,采用斜杆式桁架。
(6)边梁与行走支承。
边梁采用单复试,行走支承采用胶木滑道。
三、 面板设计根据《钢闸门设计规范》(SL74-95)及2006修订送审稿,关于面板的设计,先估算面板厚度,在主梁截面选择之后再验算面板的局部弯曲与主梁整体弯曲的折算应力。
水工钢结构露顶式平面钢闸门设计计算书-水利水电工程钢结构课程设计

目录一、设计资料 (2)二、闸门结构的形式及布置 (2)三、面板设计 (4)四、水平次梁、顶梁和底梁的设计 (5)五、主梁设计 (10)六、横隔板设计 (16)七、纵向连接系设计 (17)八、边梁设计 (18)九、行走支承设计 (20)十、滚轮轨道设计 (21)十一、闸门启闭力和吊耳计算 (22)十二、液压式启闭机 (23)水工刚结构露顶式焊接平面钢闸门设计计算书一、设计资料1、闸门形式:露顶式平面钢闸门;2、孔口尺寸(宽*高):18m*15m;3、上游水位:14.8m;4、下游水位:0.2m;5、闸底高程:0m;6、启闭方式:液压式启闭机;7、材料:钢结构:Q235-A.F;焊条:E43型;行走支承:滚轮支承;止水橡皮:侧止水用p型橡皮,底止水用条形橡皮;8、制造条件:金属结构制造厂制造,手工电弧焊,满足III级焊缝质量检验标准9、规范:《水利水电工程闸门设计规范SL 1947-2005》二、闸门结构的形式及布置1、闸门尺寸的确定(如下图)闸门高度:考虑风浪所产生的水位超高为0.2m,故闸门高度=14.8+0.2=15m;闸门的荷载跨度为两侧止水的间距:L1=15m;闸门的计算跨度:L=L0+2×0.2=18+0.4=18.4m。
2、主梁的形式主梁的形式根据水头合跨度大小而定,本闸门属中等跨度为了便于制造和维护,决定采用实腹式组合梁。
3.主梁的布置因为L=18.00<1.5H=1.5X15=22.5所以是选取7跟主梁。
根据公式计算每一根主梁距水面的距离,K及第K跟主梁,得:y1=3.78m; y2=6.91m; y3=8.95; y4=10.60m; y5=12.02m; y6=13.29m;y7=14.45m 具体布置见下图:4梁格的布置和形式梁格采用复式布置和等高连接,水平次梁穿过横隔板上的预留孔并被横隔板所支承。
水平次梁为连续梁,其间距应上疏下密,使面板各区格所需要的厚度大致相等,梁格的布置具体尺寸见下页图。
水利水电工程钢结构课程设计-水工刚结构露顶式焊接平面钢闸门设计计算书.

水工刚结构露顶式焊接平面钢闸门设计计算书一、设计资料闸门形式:炉鼎是平面钢闸门;空口尺寸(宽×高): 26m×12m上游水位:11.8m下游水位:0.1m闸底高程:0m启闭方式:电动固定式启闭机材料:钢结构Q235-A.F;焊条:E43型;行走支承:滚轮支承;止水橡皮:侧止水用P型橡皮,底止水用条形橡皮。
制造条件:金属结构制造厂制造,手工电弧焊,满足Ⅲ级焊缝质量检验标准规范:水利水电工程钢闸门设计规范SL 1974-2005二、闸门结构的形式及布置1.闸门尺寸的确定闸门高度:考虑风浪所产生的水位超高为0.2m,故闸门高度H=11.8+0.2=12m;闸门的荷载跨度为两侧止水的间距:L1=26m;闸门计算跨度:L=L0+2d=22+2×0.2=26.40m。
2.主梁的形式主梁的形式应根据水头和跨度大小而定,本闸门应用实腹式组合梁。
3.主梁的布置因为L=26.40>1.5H=1.5×12=18所以采取双主梁。
为使两根主梁在设计水位时所受的水压力相等,两根主梁的位置应对称与水压力合力的作用线y=H/3=4.0m,并要求下旋臂a≧0.12H和a≧0.4m、上悬臂c≦0.45H,现取a=1.5m ≈0.12H=1.44(m)主梁间距: 2b=2(y﹣a)=2×2.5=5(m)则 c=H-2b-a=12-5-1.5=5.5(m)=0.458H (满足要求)(单位:m)4梁格的布置和形式梁格采用复式布置和等高连接,水平次梁穿过横隔板上的预留孔并被横隔板所支承。
水平次梁为连续梁,其间距应上疏下密,使面板各区格所需要的厚度大致相等,梁格的布置具体尺寸见下页图。
5.连接系的布置和形式(1)横向连接系,根据主梁的跨度决定布置16道横隔板,其间距为1.65m ,横隔板兼做竖直次梁。
(2)纵向连接系,设在两个主梁下翼缘的竖平面内,采用斜杆式桁架。
6.边梁与行走支承。
边梁采用单复试,行走支承采用胶木滑道。
露顶式平面钢闸门设计(附答案)

B=ξ1b( 对跨间正弯矩段); B=ξ2b(对支座负弯矩段); 按 5 号梁进行计算,设该梁平均间距 b=(b12+b2) =6602+630 =645 mm,对于第一跨中正弯矩
段,零点之间的距离: l0 0.8l 0.8 2150 1720mm,对于支座负弯矩段取: l0 0.4l 0.4 2150 860mm,根据 L0/b 查表 2—1; 由 l0 1720 2.667 得ξ1=0.80,则 B=ξ1b=0.80×645=516 mm
(2) 主梁荷载:P= 1 H2= 1 ×9.8×5.02=122.5 KN/m, q = p =61.25 KN/m
22
2
(3) 横隔板间隔:2.15m。
(4)
主梁容许绕度:
w L
=
1 600
。
(二)主梁设计 1. 截面选择
(1)主梁内力分析如图: 主梁简支于边梁上,最大弯矩在跨中, 最大剪力在支承处
245×8×74 组合截面形心到槽钢中心线的距离:e= 3811 =38 mm
支座处截面的惯性矩及截面模量为:Ι次 B=5637000+1851×382+245×8×362=10850004 mm4
10850004 Wmin= 108
=100463
mm2
2. 水平次梁的强度验算
支座 B 处弯矩最大,截面模量也较大,跨中弯矩小,故两处截面的抗弯强度都需要验算。
⑾规范:《水利水电工程钢闸门设计规范》 (SL 74-1995)
二、闸门结构的型式及布置 1. 闸门尺寸的确定: ⑴ 闸门高度:考虑风浪所产生的水位超高为 0.2 m,故闸门高度 5.2+0.2=5.4 m ⑵ 闸门的荷载跨度为两侧止水间的间距 LD=8.0 m ⑶ 闸门计算跨度 L=L0+2d=8+2×0.3=8.6 m
溢洪道露顶式平面钢闸门设计模板

溢洪道露顶式平面钢闸门设计一:基本资料及设计计算说明书的内容1、基本资料如下①闸门形式:溢洪道露顶式平面钢闸门。
②孔口净宽:8.00m;③设计水头:5.00m;④结构材料:平炉热轧碳素钢Q235A-F;⑤焊条:E43;⑥止水橡皮:侧止水用P型橡皮,底止水用条形橡皮。
⑦行走支承:采用胶木滑道,压合木为MCS-2.⑧混凝土强度等级:C30.2、设计计算说明书的内容包括:①闸门结构的形式及其布置(包括闸门尺寸确定、主梁的形式、数目及位置、梁格的布置和形式、联接系的布置和形式面板设计);②水平次梁、顶梁和底梁设计;③主梁设计;④横隔板设计;⑤纵向联接系设计;⑥边梁设计;⑦行走支承设计;⑧闸门启闭力和吊座计算;二:闸门结构的形式及其布置1.闸门尺寸的确定。
闸门高度:考虑风浪所产生的水位超高为0.2m,故闸门高度H闸= H设+H超=5+0.2=5.2(m);闸门的荷载跨度为两侧止水的间距:L1=8m;闸门的计算跨度:L=L0+2d=8+2×0.2=8.40(m);2.主梁的形式主梁的形式根据水头合跨度大小而定,本闸门属中等跨度为了便于制造和维护,决定采用实腹式组合梁。
3.主梁(数目与位置)布置根据闸门的高跨比,决定采用双主梁。
为使两个主梁在设计水位时所承受的水压力相等,两个主梁的位置应对称于水压力合力的作用线y=H设/3=1.67m,如图一所示。
并要求下悬臂a≥0.12H和a≥0.4m,上悬臂c≤0.45 H设,今取,a=0.57m≈0.12 H设=0.6m主梁间距:2b=2(y-a)=2*(1.67-0.57)=2.2m.则c= H设-2b-a=5-2.2-0.57=2.23m<0.45 H设(满足要求)。
4.梁格的布置和形式梁格采用复式布置和等高连接,水平次梁穿过横隔板上的预留孔并被横隔板所支承。
水平次梁为连续梁,其间应上疏下密,使面板各区格所需要的厚度大致相等,梁布置的具体尺寸如图二。
钢闸门课程设计--露顶式平面钢闸门

\课程设计说明书课程名称:水利水电工程钢结构课程设计课程代码:题目:露顶式平面钢闸门学院(直属系) :能源与环境学院年级/专业/班:2009级/水利水电工程学生姓名:学号:指导教师:开题时间:2011年12 月日完成时间:2011年12月日目录1.设计资料………………………………………………………………………………………2.闸门结构的型式及布置………………………………………………………………………3.面板设计………………………………………………………………………………………4.水平次梁、顶梁和底梁的设计………………………………………………………………5.主梁设计………………………………………………………………………………………6.面板参加主(次)梁工作的折算应力验算…………………………………………………7.横隔板设计……………………………………………………………………………………8.纵向连接系设计………………………………………………………………………………9.边梁设计………………………………………………………………………………………10.行走支承设计…………………………………………………………………………………11.轨道设计………………………………………………………………………………………12.闸门启闭力和吊耳计算………………………………………………………………………工程概况:闸门是用来关闭、开启或者局部开启水工建筑物中过水孔口的活动结构。
其主要作用是控制水位、调节流量。
闸门是水工建筑物的重要组成部分,它的安全与适用,在很大程度影响着整个水工建筑物的原行效果。
水工刚结构露顶式焊接平面钢闸门设计计算书一、设计资料及有关规定:闸门形式:楼顶式平面钢闸门孔口尺寸(宽⨯高):10m⨯11m上游水位:10.8m下游水位:0.1m闸底高程:0.0m启闭方式:电动固定式启闭机材料钢结构:Q235-A.F;焊条:E43型;行走支承:滚轮支承;止水橡皮:侧止水用P型橡皮,底止水用条形橡皮制造条件金属结构制造厂制造,手工电弧焊,满足Ⅲ级焊缝质量检验标准规范:《水利水电工程钢闸门设计规范SL 1974-2005》二、闸门结构的形式及布置1. 闸门尺寸的确定闸门高度:考虑风浪所产生的水位超高0.2m,故闸门高度=10.8+0.2=11m;闸门的荷载跨度为两侧止水的间距:L=10m1L+d2=10+2⨯0.2=10.4m闸门计算跨度:L=图12.主梁的形式主梁的形式应根据水头和跨度大小而定,本闸门属中等跨度,为了制造和维护,决定采用实腹式组合梁。
钢闸门重量计算
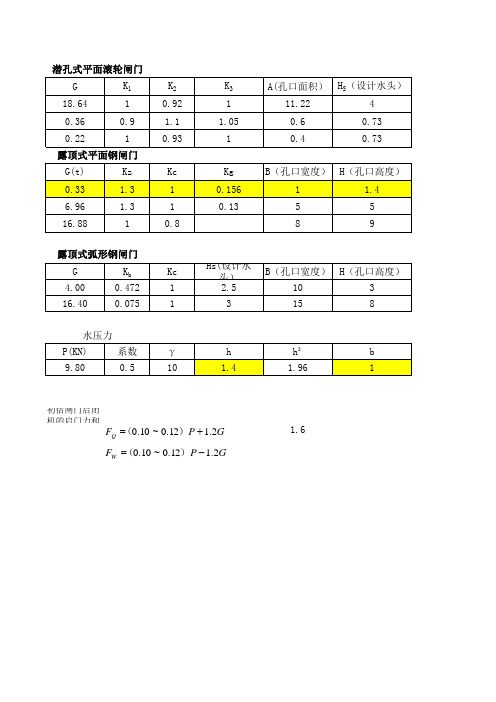
1.6
FW (0.10 ~ 0.12)P 1.2G
K1 工作门、事故门 检修门、导流门
K2 H/B≥2 H/B<1 其他情况
K3 Hs<60m Hs≥60m
备注 H<5m 5m<H<8m H>8m
KZ--闸门行走支承系数;滑动支承取0.81,滚轮支承取1.0,台车式支承取 Kc--材料系数;闸门用普通碳素钢取1.0,用低合金钢取0.8。
B(孔口宽度) H(孔口高度)
1
1.4
5
5
8
9
露顶式弧形钢闸门
G 4.00
Kb
Kc
0.472
1
Hs(设计水 头)
B(孔口宽度) H(孔口高度)
2.5
10
3
16.40
0.075
1
3
15
8
水压力
P(KN)
系数
γ
h
h²
b
9.80
0.5
10
1.4
1.96
1
初估闸门启闭
机的启门力和
FQ (0.10 ~ 0.12)P 1.2G
Kg--孔口高度系数;当H<5m时,取0.156;当5m<H<8m时,取0.13。H>8m时 计算G=0.012KzKcH1.65B1.85
备注 B≤10m B>10m
Kb--孔口宽度系数;当B≤5m时,Kb=0.29,5m<B≤10m时,Kb=0.472,10m<B< Kb=0.075,B>20m时,Kb=0.105。
潜孔式平面滚轮闸门
G
K1
18.64
1
0.36
0.9
第六章平面钢闸门. 文档

第六章平面钢闸门一、单项选择题1、设置在开敞式泄水孔口的闸门,需设置三面止水的闸门称为:【】3 (分数:1分)A. 检修闸门B. 施工导流闸门C. 露顶式闸门D. 潜孔式闸门正确答案:C2、钢闸门结构采用【】法进行结构强度验算(分数:1分)A. 极限应力法B. 极限应变法C. 经验推算法D. 容许应力法正确答案:D3、用来封闭和开启孔口的活动挡水结构是:【】(分数:1分)A. 承重结构B. 行走支承C. 门叶结构D. 主梁正确答案:C4、用来挡水,直接承受水压的是【】(分数:1分)A. 梁格B. 面板C. 垂直支承D. 系杆正确答案:B5、在大跨度的露顶式闸门中常采用的主梁数目是【】(分数:1分)A. 单主梁式B. 双主梁式C. 多主梁式D. 无具体要求正确答案:B 6、对于实腹式主梁的工作闸门,一般使底主梁的下翼缘到底止水边缘连线的倾角不应小于【】(分数:1分)A. 30度B. 45度C. 60度D. 90度正确答案:A 7、水平次梁和竖直次梁直接与面板相连,主梁放在竖直次梁后面的梁格连接形式称为【】(分数:1分)A. 齐平连接B. 降低连接C. 层叠连接D. 竖直连接正确答案:C8、下列关于单腹式边梁叙述正确的是【】(分数:1分)A. 抗扭刚度强B. 广泛用于定轮闸门中C. 便于设置滚轮和吊轴D. 主要用于滑道式支承的闸门正确答案:D9、对于大跨度的闸门,宜采用【】(分数:1分)A. 型钢梁B. 桁架式主梁C. 实腹式组合梁D. 变高度的主梁正确答案:B二、多项选择题10、平面钢闸门的承重结构由下列哪几项构成:【】(分数:2分)A. 面板B. 梁格C. 节点板D. 纵向联结系E. 横向联结系正确答案:ABDE11、闸门的行走支承包括:【】(分数:2分)A. 止水B. 滑道支承C. 吊耳D. 启闭力E. 滚轮支承正确答案:BE12、按照闸门的设置部位,闸门可以分为下列哪几类【】(分数:2分)A. 露顶式闸门B. 潜孔式闸门C. 工作闸门D. 事故闸门E. 检修闸门正确答案:AB13、结构布置图包括:【】(分数:2分)A. 立体图B. 平面图C. 节点图D. 侧面图E. 剖面图正确答案:BDE。
露顶式钢闸门课程设计计算书6.5×3.5

挡洪闸工作闸门计算书(6.5m×3.5m)2016.7.10一.设计资料(1)闸门型式:提升式平面钢闸门(露顶式) (2)孔口尺寸(宽×高):6.50×3.50m 2 (3)上游水位:▽35.81m (4)下游水位:无(5)闸底高程:▽32.5m (6)启闭设备:QPQ2x10 (7)闸门所用材料:门叶承重钢结构:Q235.B 钢焊 条:E43型行走支承:采用滚轮,材料为铸钢ZG45止水橡皮:侧止水——P 形橡皮;底止水——条形橡皮(9)制造条件:金属结构制造厂制造,手工电焊,满足Ⅲ级焊缝质量检验标准。
(10) 采用的规范:《水利水电工程钢闸门设计规范SL74—95》 二.闸门结构的型式及布置 (1)闸门尺寸的确定 闸门总宽:bL d L B a +++=20L 0 ——孔口宽度d ——行走支承到闸墙边缘的距离(0.135m) L a ——边梁两腹板中到孔中距离(0.16m) b ——边梁下翼缘宽度(0.19m))(12.716.019.0135.025.6m B =++⨯+=闸门高度:H=校核洪水位+超高△H))(5.319.05.3281.35m H =+-=闸门的荷载跨度为两侧止水的间距:)(58.604.025.604.020m L L q =⨯+=⨯+=闸门的计算跨度:)(77.6135.025.620m d L L =⨯+=+=(2)主梁的数目型式及位置。
2.186.15.3/5.6/0>==H L主梁数目:采用双主梁主梁形式:单轴对称工字形截面焊接组合梁主梁位置:根据等荷载原则,两根主梁的位置应对称于水压力合力的作用线,且应满足:Ha 12.0≥且m 4.0≥且m mm D 66.060=+≥H c 45.0≤且m 6.3≤(式中H 取闸门止水压力作用高度,取孔口高度+100mm )数解法。
露顶闸门第K 根主梁到水面的距离ky 按下式确定:()[]5.15.11n32--=K K H y k()[]()[]m02.3122235.32m65.1111235.325.15.125.15.11=--⨯==--⨯=y y式中:n 为主梁根数;K 为由门顶算起的主梁根数;H 为水面至门底的距离。
露顶钢闸门课程设计

露顶钢闸门课程设计水利水电工程钢结构课程设计 ----露顶式平面闸门一、设计资料:①闸门型式:露顶式平面钢闸门②孔口尺寸: 14 m 12 m ③上游水位:m ④下游水位:m ⑤闸底高程: 0 m ⑥启闭方式:⑦材料钢结构:;焊条:E43型;行走支承:滚轮支承或胶木滑道止水橡皮:侧止水用P型橡皮,底止水用条形橡皮⑧制造条件金属结构制造厂制造,手工电弧焊,满足Ⅲ级焊缝质量检验标准规范:《水利水电工程钢闸门设计规范SL 1974-20XX》二、闸门结构的形式及布置 1.闸门尺寸的确定闸门高度:考虑风浪所产生的水位超高,故闸门高度=12+=;闸门的荷载跨度为两侧止水的间距:L1=14m;闸门计算跨度:L=L0+2d=14+2*=整个闸门的荷载为作于和闸门距离闸底H/3的P= KN/m 的均布荷载2.主梁的形式主梁的形式根据水头和跨度大小而定,本闸门属偏大跨度,为了方便制造和维护,决定采用实腹式组合梁。
3.主梁的布置①根据闸门的高跨比:当L小于等于H时采用多主梁形式,当L大于等于时候采用双主梁形式,根据设计资料为14*12孔口尺寸,本设计采用3根主梁②主梁位置的确定:主梁位置的设计原则是根据每个主梁承受相等水压力的原则确定。
对于露顶式闸门:假定水面至门底的距离为H,主梁的个数为n,第K根主梁至水面的距离为Yk,则Yk=2H/3√n[ - ] 根据公式:Y1=2*12/3√3[ - ]=5水利水电工程钢结构课程设计 ----露顶式平面闸门Y2=2*12/3√3[2 - ]= Y3=2*12/3√3[ - ]=考虑到后面梁格的布置和面板的选取将第三根主梁的位置下调所以Y3=。
4.梁格的布置和形式对于露顶式大跨度闸门采用复式布置和等高连接,水平次梁穿过横隔板上的预留孔并被横隔板所支撑,水平次梁为连续梁,其间距应上疏下密,使面板各区格需要的厚度大致相等,梁格布置的尺寸详见下图 5.连接系的布置和形式①横向连接系,根据主梁的跨度,决定布置7道横隔板,其间距为,横隔板兼做竖直次梁。
溢洪道露顶式平面钢闸门

溢洪道露顶式平面钢闸门1基本资料闸门形式:溢洪道露顶式平面钢闸门; 孔口净宽:9.00m ; 设计水头:5.50m ; 结构材料:Q235钢; 焊条:E43;止水橡皮:侧止水用p 形橡皮;行走支承:采用胶木滑道,压合胶木为MCS-2; 混凝土强度等级:C20。
2闸门结构的形式及布置 (1)闸门尺寸的确定(图1)。
1)闸门高度:考虑风浪所产生的水位超高为m,故闸门高度m 7.52.05.5=+=2)闸门的荷载跨度为两侧止水的间距:m L 91=; 3)闸门计算跨度:m d L L 40.92.02920=⨯+=+=(2)主梁的形式。
主梁的形式应根据水头的大小和跨度的大小而定,本闸门属于中等跨度,为了方便制造和维护,决定采用实复式组合梁。
(3)主梁的布置。
根据闸门的高跨比,决定采用双主梁。
为使两个主梁设计水位时所受的水压力相等,两个主梁的位置应对称于水压力合理的作用线m H y 8.13/==(图1)并要求下悬臂a H 12.0≥和m a 4.0≥,上悬臂H c 45.0≤,今取m H a 66.012.06.0=≈=主梁间距m2=⨯=(2=-a)b4.2y2.12则H--=2==(满足要求)5.5--=c45b4.2mHa6.05.2.0图1 闸门主要尺寸图(4)梁格的布置和形式。
梁格采用复式布置和等高连接,水平次Array梁穿过横隔板上的预留孔并被横隔板所支撑。
水平次梁为连续梁,其间距应上疏下密,使面板各区格需要的厚度大致相等,梁格布置具体尺寸如图2所示。
图2 梁格布置尺寸图(5)连接系的布置和形式。
1)横向连接系,根据主梁的跨度,决定布置3道横隔板,其间距为2.6m,横隔板兼作竖直次梁。
2)纵向连接系,设在两个主梁下翼缘的竖平面内,采用斜杆式桁架。
(6)边梁与行走支撑。
边梁采用单复式,行走支撑采用胶木滑道。
3面板设计根据《钢闸门设计规范》(SL74-95)及2006修订送审稿,关于面板的计算,先估算面板厚度,在主梁截面选择之后在验算面板的局部弯曲与主梁整体弯曲的折算应力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
露顶式平面钢闸门设计说明书一、设计资料⑴闸门型式:露顶式平面钢闸门 ⑵孔口净宽:8.0 m ⑶设计水头:7.0m⑷结构材料:Q235F A -⑸焊条:焊条采用E 43型手工焊⑻止水橡皮:侧止水用P 型橡皮,底止水用条形橡皮;行走支承:采用胶木滑道,压合胶木为2-MCS⑼混泥土强度等级:C20⑾规范:《水利水电工程钢闸门设计规范》 (SL 74-1995)二、闸门结构的型式及布置 1. 闸门尺寸的确定:⑴ 闸门高度:考虑风浪所产生的水位超高为0.2 m ,故闸门高度5.2+0.2=5.4 m ⑵ 闸门的荷载跨度为两侧止水间的间距L D =8.0 m ⑶ 闸门计算跨度L=L 0+2d=8+2×0.3=8.6 m2. 主梁的型式主梁的型式应根据水头和跨度大小而定,本闸门属于中等跨度(L=5~10),为了便于制造和维护,采用实腹式组合梁,焊接组合截面。
3. 主梁的布置根据闸门的高垮比L H =8.65.2 =1.65>1.55,决定采用双主梁,为使两根主梁在设计水位时所受水压力相等,两根主梁的位置应对称于水压力合力的作用线y=H 3 =53 =1.67 m ,并要求下悬臂a ≥0.12H 和a ≥0.4 m ,上悬臂c ≤0.45H 和c <3.6 m 。
且使底主梁到底止水的距离尽量符合底缘布置要求(即α>30°),先取a=0.12H=0.6 m ,则主梁间距:2b=2(y-a)=2×(1.67-0.6)=2.14 m 4. 梁格的布置和形式格采用复式布置和高等连接,三根水平次梁穿过横隔板上的预留孔并被横隔板所支承。
水平次梁为连续梁,其间距上疏下密,面板各区格所需要的厚度大致相等。
梁格的布置及具体尺寸如下图所示: 5. 联结系的布置和形式(1)横向联结系:根据主梁的跨度,采用布置3道横隔板,横隔板兼作竖直次梁,其横向联结间距为L=8.64=2.15 m(2)纵向联结系:采用斜杆式桁架,布置在两根主梁下翼缘的竖平面内,并设有4根等肢角钢的斜杆。
6. 边梁与行走支承采用单腹式边梁,行走支承采用双股式滚动行走支承。
三、面板设计1. 估算面板厚度假定梁格布置如图所示,面板厚度由公式t=[]σ92.0kpa,且t max -t min ≤2 mm当b /a ≤3时,α=1.5,则t==⨯⨯1605.19.0kpa0.068a kp当b/a >3时,α=1.4,则t==⨯⨯1604.19.0kpa 0.07a kp现列表计算如下:根据计算结果,选用面板厚度t=8 mm 四、水平次梁、顶梁和底梁的设计 1. 荷载与内力计算水平次梁和顶、底梁都是支承横隔板的连续梁,作用在上面的水压力按q=p 2下上a a +计算 计算列表如下 :据表中结果,水平次梁计算荷载取最大值25.10KN/m ,水平次梁为四跨连续梁,跨度为2.15m 。
水平次梁计算结构简图及弯矩图如下:水平次梁边跨中的正弯矩为:M 次中=0.077qL=0.077×25.10×2.152=8.93 KN/m支座B 处的负弯矩为:M 次B =0.107ql=0.107×25.10×2.152=12.42 KN/m2、截面选择 []σ M =1601042.126⨯=776253mm考虑利用面板作为次梁截面的一部分,初选槽钢14a 由附表查得:A=1851 2mm ;X W =80500 2mm ;X I =5637000 4mm ;1b =58 mm; d=6 mm面板参加次梁翼缘工作的有效宽度按下式计算,然后取最小值。
B ≤1b +60t=58+60×8=538 mm B=ξ1b( 对跨间正弯矩段);B=ξ2b(对支座负弯矩段);按5号梁进行计算,设该梁平均间距b=(b1+b2)2 =660+6302 =645 mm ,对于第一跨中正弯矩段,零点之间的距离:mm l l 172021508.08.00=⨯==,对于支座负弯矩段取:mm l l 86021504.04.00=⨯==,根据L 0/b 查表2—1;由667.264517200==b l 得ξ1=0.80,则B=ξ1b=0.80×645=516 mm 由333.16458600==b l 得ξ2=0.380,则B=ξ2b=0.380×645=245 mm 对于第一跨中,选用B=516 mm ,则水平次梁的组合截面积:A=1851+516×8=5978mm2组合截面形心到槽钢中心线的距离:e=516×8×745978=51 mm跨中组合截面的惯性矩及截面模量为:Ι次中=5637000+1851×512+516×8×232=12635136mm 4,W min =12635136121=104423 mm2组合截面形心到槽钢中心线的距离: e=516×8×745978=51 mm对于支座段,选用B=245 mm ,则水平次梁的组合截面积:A=1851+245×8=3811 mm 2组合截面形心到槽钢中心线的距离:e=245×8×743811=38 mm支座处截面的惯性矩及截面模量为:Ι次B =5637000+1851×382+245×8×362=10850004 mm4W min =10850004108=100463 mm 22. 水平次梁的强度验算支座B 处弯矩最大,截面模量也较大,跨中弯矩小,故两处截面的抗弯强度都需要验算。
次中σ=min W M 次中=1044231093.86⨯=85.52 N/ mm 2 <[]σ=160 N/mm2B 次σ=min BW M 次=100463108.7116⨯=123.63 N/ mm 2 <[]σ=160 N/mm 2综上可知水平次梁选用[14a 满足弯应力强度要求。
3. 水平次梁的扰度验算水平次梁为受均布荷载的四跨连续梁,其最大扰度发生在边跨,已求得M 次B =12.42 KN/m ,Ι次B =10850004 mm 4, 四跨连续梁0063.0''=k ,⎥⎦⎤⎢⎣⎡L w =2501=0.004 L w =B 30''次I E ql k =0.0063×004.10851006.21015.210.25553⨯⨯⨯⨯=0.0007<⎥⎦⎤⎢⎣⎡L w =0.004,满足挠度要求。
4. 顶梁和底梁底梁计算简图和弯矩图支座M =0.107q 2l =0.107×15.29×2.152 =7.56 KN ·m需W =[]σ支座M =33625.4747250160106.57cm mm ==⨯ 选用[12σW =62.1373cm >需W =325.47cm 底梁弯应力强度验算:σ=23/67.121137.621056.7M mm N W y=⨯=支座<[]σ=160 N/2cm ,满足弯应力要求。
底梁刚度验算:L w =B 3''次I E ql k =0.0063×466.3911006.21015.229.15553⨯⨯⨯⨯=0.00119<⎥⎦⎤⎢⎣⎡L w =0.004满足刚度要求。
顶梁采用和底梁相同的槽钢即[12σ,顶梁弯应力强度验算:支座M =0.107q 2l =0.107×2.76×2.152=1.37 KN ·m σ=23/05.22137.621037.1M mm N W y=⨯=支座<[]σ=160 N/2cm 满足应力强度要求。
顶梁的刚度验算:L w =B 3''次I E ql k =0.0063×466.3911006.21015.276.2553⨯⨯⨯⨯=0.00021<⎥⎦⎤⎢⎣⎡L w =0.004满足刚度要求。
五、主梁设计 (一)已知条件(1) 主梁跨度:净跨度1l =8.0m ,计算跨度L=8.6m ,荷载跨度l =8.0m (2) 主梁荷载:P=21γH 2=21×9.8×5.02=122.5 KN/m ,q =2p=61.25 KN/m (3) 横隔板间隔:2.15m 。
(4) 主梁容许绕度:⎥⎦⎤⎢⎣⎡L w =6001。
(二)主梁设计1. 截面选择(1)主梁内力分析如图:主梁简支于边梁上,最大弯矩在跨中,最大剪力在支承处max M =)2(4l L ql-=5.563)286.8(64825.61=-⨯⨯ KN ·m max V =245825.612121=⨯⨯=ql KN(2)需要的截面抵抗矩(考虑闸门自重引起的附加应力的影响)W =[]33max 382816092.0105.56392.0cm M =⨯⨯=σ (3)腹板高度h 0选择(刚度条件求得最小梁高h min )min h =0.96×0.208×[][]L W E L /σ0.96×0.208×()cm 62.73600/11006.292.0106.816052=⨯⨯⨯⨯⨯ec h =3.15/2W=3.1×cm 05.8438285/2=经济梁高选取的梁高h 一般应大于min h 但比ec h 稍小,故应选取h=80 cm 。
(4)腹板厚度选择:腹板厚度w t =11h =81.01180=,选w t =1.0cm (5)翼缘截面选择: 每个翼缘所需截面为:A 1=6800.1803828600⨯-=-h t h W w =34.522cm 下翼缘选用cm t A b cm t 26.17252.34,0.21111====,因此需要选用cm b 251=。
(在cm hh 163255.2-=-之间),上翼缘的部分截面面积可利用面板,故只需设置较小的上翼缘板同面板相连,选用cm b cm t 14,0.211==。
面板兼做主梁上翼缘的有效宽度B=1b +5t=14+50×0.8=54cm 上翼缘截面面积212.718.0540.214cm A =⨯+⨯= (6)弯应力强度验算:主梁跨中截面的几何特性如下表; 部位 截面尺寸 cm 2 截面面积 cm 2各形心离面板表面距离y ' 'Ay各形心离中心轴距离y=y '-y2Ay面板部分 54×0.8 43.2 0.4 17.28 -37.78 61660.59 上翼缘板 14×2.0 28.0 1.8 50.4 -36.38 37058.12 腹板 80×1.0 80 42.8 3424 4.62 1707.55 下翼缘板 25×2.0 50 83.8419045.62104059.22 合计201.27681.68204485.48主梁跨中截面形心距面板表面的距离y 1=∑∑A Ay '=cm 18.382.20158.7681=截面惯性矩为:4323024715248.20448512800.112cm Ay h t I w =+⨯=+=∑截面抵抗矩为:上翼缘顶边21max 647318.38247152cm y I W ===下翼缘底边22min 591082.41247152cm y I W ===弯应力2min max /53.959101005.563cm KN M M =⨯==σ<0.92×23=21.16 KN/2cm ,安全 (7)主梁支承端剪应力强度验算()3134.17894.082.418.054cm S =-⨯⨯=,()56.11208.182.412142=-⨯⨯=S 3219.290956.112034.1789cm S S S =+=+=2433max /85.280.110247152109.290910245mm N It S V w =⨯⨯⨯⨯⨯==τ<[]2/95mm N =τ (8)整体稳定与刚度验算。
