第10讲 控制系统工具箱中的GUI工具
GUI控制系统典型环节的演示
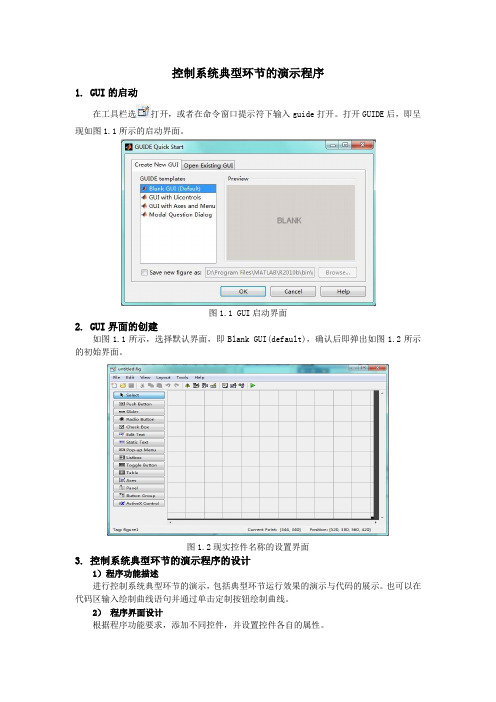
控制系统典型环节的演示程序1. GUI的启动在工具栏选打开,或者在命令窗口提示符下输入guide打开。
打开GUIDE后,即呈现如图1.1所示的启动界面。
图1.1 GUI启动界面2. GUI界面的创建如图1.1所示,选择默认界面,即Blank GUI(default),确认后即弹出如图1.2所示的初始界面。
图1.2现实控件名称的设置界面3. 控制系统典型环节的演示程序的设计1)程序功能描述进行控制系统典型环节的演示,包括典型环节运行效果的演示与代码的展示。
也可以在代码区输入绘制曲线语句并通过单击定制按钮绘制曲线。
2)程序界面设计根据程序功能要求,添加不同控件,并设置控件各自的属性。
1)添加Axes控件,用来显示演示图形,双击调出属性编辑器进行各种属性设置,Tag 属性设为“myAxes”。
如图1.3所示。
图1.3Axes控件属性设置2)添加Panel控件用来盛放其他控件,如图1.4所示。
这里我们盛放Edit Text控件。
Tag属性设为“uipanel”,Title属性设为空。
图1.4 添加Panel控件3)添加Edit Text控件盛放于Panel控件中,此处作为代码区,如图1.5所示。
Tag 属性设为“strCode”,String属性设为空,可以看到该控件中心“Edit Text”字样消失,及背静颜色等的设置。
图1.5 Edit Text控件的添加4)添加Static Button控件作为标识。
Tag属性设为“textDemo”,String属性设为“典型环节演示”。
5)添加ListBox控件来从中选择4个不同的典型环节选项。
Tag属性设为“lstBox”,String属性设为:6)添加两个Push Button控件。
一个用于定制曲线的绘制,用户在代码区输入绘制曲线语句后,单击此按钮进行曲线的绘制。
Tag的属性设为“btnDraw”,String属性设为“定制曲线”,TooltipString属性设为“在代码区中输入曲线参数,绘制任意曲线”。
控制系统工具箱简介

SISO设计工具
在命令空间中输入sisotool既可进入SISO补 偿设计窗口,也可直接指定设计对象,调用形式 为sisotool(sys)。
该工具允许使用 根轨迹、波特图、尼 科尔斯图等手段进行 系统补偿设计。同时 可对系统进行阶跃响 应等各种LTI分析。
SISO设计工具的使用
导入系统数据:包括系统结构及相应模型
二、控制系统工具箱使用
控制系统工具箱用于完成一般控制系统工程设计是, 主要内容包括以下三个方面:
模型建立:描述如何建立线性模型、模型连接, 确定模型特征,离散时间模型和连续时间模型之间的转 换,模型的降阶处理。
模型分析:图形化用户界面(GUI)的设计工 具—LTI Viewer,使得观察系统响应变得非常简单。
通过 ltidemo 分别 执行模型建立、离散时 间模型、访问模型数据、 模型连接、模型类型转 换、连续/离散转换等 演示。熟悉工具箱中函 数用法。
图形化的模型分析工具LTI Viewer
LTI Viewer 可以对系统进行阶跃响应、脉冲响应、 波特图、奈奎斯特图等的分析,同时还可以直接从 SIMULINK环境下的结构图中指定输入输出点所产生 的系统进行分析。
一、MATLAB工具箱的简介
功能型工具箱:主要用来扩充MATLAB的符号计 算功能、图形建模仿真功能、文字处理功能以及与硬件 实时交互功能,可用于多种学科中;
领域型工具箱:是专业性很强的工具箱,如控制 系统工具箱、信号处理工具箱、神经网络工具箱等。
注意:在每个工具箱中有一个Contents文件,在文 件中将该工具箱里的所有函数其作用功能一一列出,可 以在使用前先看此文件,找到要用的函数后,在命令空 间里键入help 文件名,即可查到相应函数的调用格式。
PYTHONGUI开发工具介绍

PYTHONGUI开发工具介绍Python是一种功能强大、易于学习和使用的编程语言,广泛用于各种科学计算、数据分析和web开发等领域。
开发Python GUI(图形用户界面)应用程序可以使用户更加直观地与程序进行交互,提升用户体验。
在Python中,有许多GUI开发工具可供选择,包括以下几种常用的:1. Tkinter:Tkinter是Python标准库中的一个GUI工具包,它提供了开发简单且强大的GUI应用程序的功能。
Tkinter基于Tcl/Tk库,并且与Python语言紧密集成,因此使用起来非常方便。
Tkinter的优点包括易于学习、跨平台性强、丰富的小部件库等。
然而,Tkinter的外观较为简单,并且在处理复杂界面和高级功能时可能会受限。
2. PyQt:PyQt是基于Qt库的一个Python绑定库,它是一个强大而灵活的GUI开发工具。
PyQt提供了丰富的小部件库和高级功能,可以轻松创建复杂的GUI应用程序。
PyQt还支持与Qt Designer(可视化的GUI设计器)的集成,使得开发过程更加快捷。
PyQt的缺点是学习曲线较陡峭,并且根据其许可协议的不同,可能需要付费使用。
3. wxPython:wxPython是基于wxWidgets库的Python绑定库,它提供了一个跨平台的GUI开发工具。
wxPython的优点包括可扩展性强、外观美观、丰富的小部件库和良好的文档支持。
wxPython的不足之处在于相对于其他GUI工具,它的学习曲线稍陡,并且可能在安装和设置上稍有复杂。
4. PyGTK:PyGTK是Python绑定库,用于开发基于GTK+(GIMP Toolkit)的GUI应用程序。
GTK+是一个用于创建图形用户界面的开源工具集,可用于多种操作系统,如Linux、Windows和Mac OS。
PyGTK的优点包括易于学习、跨平台性强、功能丰富、外观美观等。
然而,由于GTK+在Windows上的支持相对较弱,所以在Windows平台上使用PyGTK可能会遇到一些问题。
Matlab控制系统工具箱的高级应用教程

Matlab控制系统工具箱的高级应用教程Matlab是一种强大的数学软件,广泛应用于科学研究和工程领域。
控制系统工具箱(Control System Toolbox)是Matlab中一个重要的工具包,提供了许多用于设计、分析和模拟控制系统的函数和工具。
在这篇文章中,我将介绍一些Matlab控制系统工具箱的高级应用,以帮助读者更好地利用这个工具包。
首先,让我们从控制系统的建模开始。
控制系统的建模是设计和分析控制系统的第一步。
在Matlab中,你可以使用Transfer Function模型(传递函数模型)或State Space模型(状态空间模型)来描述控制系统。
对于简单的系统,你可以使用Transfer Function模型,它是用输入和输出之间的传递函数来表示系统的模型。
对于更复杂的系统,你可以使用State Space模型,它是用系统的状态变量和它们之间的关系来表示系统的模型。
使用这两种模型,你可以方便地进行控制系统的分析和设计。
一旦你得到了控制系统的模型,你可以使用Matlab控制系统工具箱中提供的函数来进行控制系统的分析。
例如,你可以使用"step"函数来绘制控制系统的阶跃响应,从而判断系统的稳定性和性能。
你也可以使用"bode"函数来绘制系统的频率响应曲线,从而分析系统的幅频特性和相频特性。
此外,你还可以使用"Sensitivity"函数来分析系统对参数的敏感性,以评估系统的鲁棒性。
除了控制系统的分析,Matlab控制系统工具箱还提供了许多函数和工具来进行控制系统的设计。
例如,你可以使用"LQG"函数来设计线性二次高斯(LQG)控制器,它是一种常用的最优控制器设计方法。
你也可以使用"H∞"函数来设计H∞控制器,它是一种用于鲁棒控制的设计方法。
此外,你还可以使用"PID Tuner"工具箱来进行PID控制器的调参,以满足控制系统的性能要求。
GUI教程——精选推荐

GUI教程第⼗章图形⽤户界⾯GUI 制作⽤户界⾯(或接⼝)是指:⼈与机器(或程序)之间交互作⽤的⼯具和⽅法。
如键盘、⿏标、跟踪球、话筒都可成为与计算机交换信息的接⼝。
图形⽤户界⾯(Graphical User Interfaces ,GUI )则是由窗⼝、光标、按键、菜单、⽂字说明等对象(Objects )构成的⼀个⽤户界⾯。
⽤户通过⼀定的⽅法(如⿏标或键盘)选择、激活这些图形对象,使计算机产⽣某种动作或变化,⽐如实现计算、绘图等。
假如读者所从事的数据分析、解⽅程、计算结果可视⼯作⽐较单⼀,那么⼀般不会考虑GUI 的制作。
但是如果读者想向别⼈提供应⽤程序,想进⾏某种技术、⽅法的演⽰,想制作⼀个供反复使⽤且操作简单的专⽤⼯具,那么图形⽤户界⾯也许是最好的选择之⼀。
MATLAB 为表现其基本功能⽽设计的演⽰程序demo 是使⽤图形界⾯的最好范例。
MATLAB 的⽤户,在指令窗中运⾏demo 打开那图形界⾯后,只要⽤⿏标进⾏选择和点击,就可浏览那丰富多彩的内容。
即便⽐较熟悉MATLAB 的读者,在他初次编写GUI 程序时,也会感到棘⼿。
为使读者获得制作⾃⼰GUI 的体验,本章“⼊门”节提供了⼀个简单的⽰例。
读者只要输⼊所提供的程序,就可引出相应的界⾯。
本章第2节叙述图形⽤户界⾯的设计原则和⼀般制作步骤。
第3、4节分别介绍⽤户菜单、⽤户控件的制作。
出于“由浅⼊深”的考虑,前4节制作GUI 是通过M 脚本⽂件实现的。
利⽤M 函数⽂件制作GUI ,需要解决数据传递问题,为此专设第5节给予阐述和⽰例。
这前5节内容对读者理解交互图形界⾯的⼯作原理很有帮助。
本章第6节专述MATLAB6.5提供的界⾯设计⼯作台的使⽤。
值得指出:该设计⼯作台与MATLAB5.3版的设计⼯具有很⼤不同。
新的设计⼯作台显得更成熟、⽅便。
在此提醒读者,假如要⽐较准确的理解本章程序和掌握本章内容,请先阅读第9章关于图柄的内容。
10.1 ⼊门【例10.1-1】对于传递函数为1212++=s s G ζ的归⼀化⼆阶系统,制作⼀个能绘制该系统单位阶跃响应的图形⽤户界⾯。
gui教程

gui教程图形用户界面(Graphical User Interface,简称GUI)是一种用户界面,通过图形化的方式给用户展示信息和实现交互操作。
相对于传统的命令行界面,GUI更加直观和易于操作,广泛应用于各种软件和系统中。
本文将介绍GUI的基本原理和用法,希望对初学者有所帮助。
首先,GUI的基本原理是通过图形化的界面元素,如按钮、文本框、菜单等,来展示和接收用户的操作。
用户可以通过鼠标点击、键盘输入等方式与界面进行交互。
GUI的主要优点是直观和可视化,使用户更容易理解和掌握软件的功能和操作方式。
在GUI的设计中,需要考虑到界面的布局、颜色、字体等各个方面。
一个好的GUI设计应该具备简洁、美观、易用的特点,同时要符合用户的习惯和预期。
一般来说,GUI的设计需要结合软件的功能和用户的需求进行综合考虑。
在实际应用中,GUI的开发可以采用各种编程语言和开发工具。
常见的GUI开发工具有Visual Studio、Eclipse、Qt等。
这些工具提供了丰富的库和组件,可以方便地创建各种界面元素,并进行布局和交互设置。
在GUI的开发中,需要掌握一些基本的概念和技巧。
比如,掌握界面元素的创建和设置方法,了解布局管理器的使用,熟悉事件处理和消息传递机制。
此外,还需要学习一些UI设计的原则和技巧,如色彩搭配、字体选择、图标设计等。
总结一下,GUI是一种直观和易用的用户界面,广泛应用于各种软件和系统中。
GUI的开发需要掌握一些基本的概念和技巧,如界面元素的创建和设置、布局管理器的使用、事件处理和消息传递机制等。
希望本文能够对初学者了解GUI有所帮助。
gui基础知识点总结

gui基础知识点总结一、什么是GUI?GUI通常被翻译成“图形用户界面”,它是指在计算机程序中提供给用户的图形化界面。
与传统的命令行界面相比,GUI更加直观、易用,并且更容易被普通用户所接受。
用户通过在屏幕上的图形界面上进行点击、拖拽和输入来与计算机程序进行交互。
二、GUI的发展历程1. 文字界面时代:早期的计算机系统使用文字界面进行交互,用户需要通过输入命令来操作计算机程序,这种方式需要用户具备一定的计算机知识,操作起来相对繁琐。
2. 图形界面时代:20世纪80年代,苹果公司和微软公司推出了第一代图形用户界面操作系统,分别是苹果的Macintosh系统和微软的Windows系统。
这些系统首次将图形化界面带入了个人计算机领域,取代了传统的命令行界面,大大提升了用户的操作体验。
3. 现代GUI:随着技术的不断发展,GUI的设计越来越美观、交互方式也越来越多样化,包括触摸屏、手势操作等。
现代GUI不仅仅是单纯的界面展示,还承担了很多其他功能,如数据可视化、用户行为分析等。
三、GUI的基本元素1. 窗口(Window):窗口是GUI界面的基本单元,它是一个独立的用户界面组件,用户可以通过拖拽和放大来调整窗口的大小和位置。
2. 控件(Widget):控件是指GUI界面上的各种可交互的元素,比如按钮、文本框、下拉框、复选框等。
控件用来与用户进行交互,用户可以通过它们来输入数据、选择选项、执行命令等。
3. 布局(Layout):布局是指控件在窗口中的排列方式,常见的布局包括流式布局、网格布局、绝对布局等。
良好的布局可以使界面看起来更加美观、整洁,并且提高用户的使用体验。
4. 事件处理(Event Handling):GUI程序通常会响应用户的各种操作,比如点击按钮、拖拽元素、键盘输入等。
这些操作会触发相应的事件,程序需要能够捕获并处理这些事件,从而做出相应的响应。
5. 图形渲染(Graphics Rendering):GUI界面中可能会包含一些图形元素,比如图片、图标、图表等。
gui介绍

Matlab/GUI 设计介绍日期:2006-8-22 来源:ChinaUI|图形用户界面(GUI)是用户与计算机程序之间的交互方式,是用户与计算机进行信息交流的方式。
计算机在屏幕显示图形和文本,若有扬声器还可产生声音。
用户通过输入设备,如:键盘、鼠标、跟踪球、绘制板或麦克风,与计算机通讯。
用户界面设定了如何观看和如何感知计算机、操作系统或应用程序。
通常,多是根据悦目的结构和用户界面功能的有效性来选择计算机或程序。
图形用户界面或GUI是包含图形对象,如:窗口、图标、菜单和文本的用户界面。
以某种方式选择或激活这些对象,通常引起动作或发生变化。
最常见的激活方法是用鼠标或其它点击设备去控制屏幕上的鼠标指针的运动。
按下鼠标按钮,标志着对象的选择或其它动作。
MATLAB在demo命令中包含了GUI功能的极好例子。
>> demo研究该命令,以了解uimenu和uicontrol如何给MATLAB函数提供交互输入。
在运行了demo 例子后,很可能会问“为什么要在MATLAB 中建立一个GUI?”这是一个很好的问题,简单的回答是可能并不需要.使用MATLAB来分析数据,求解问题,绘制结果的绝大多数的人,并不会发现GUI 工具很有用。
但另一方面,GUI可以在MATLAB中生成非常有效的工具和应用程序,或是建立演示工作的交互式界面。
对“句柄图形”的理解是设计和实现GUI的先决条件。
由图形命令生成的每一事物是一个图形对象。
图形对象不仅包括uimenu和uicontrol对象,而且还包括图形、坐标轴和他们的子对象。
让我们从另一个角度来看这一层次结构。
计算机的屏幕本身是根结点,图形是根对象的子对象,坐标轴,uimenu ,uicontrol是图形的子对象。
根可以包括多个图形,每个图形含有一组或多组坐标轴以及其子对象,每个图形也可以有一个或多个与坐标轴无关的uimenu和uicontrol。
虽然uicontrol对象无子对象结点,但他们确实具有多种类型。
MATLAB GUI设计入门与实战PPT课件:第10章 GUI经典案例分析与应用

第十章
YCrCb彩色模型是一种彩色传输模型,主要用于彩色电视信号传输标准方面,被广泛的 应用在电视的色彩显示等领域中。这是由于YCrCb彩色空间模型具有如下的优点:
(1)YCrCb色彩格式具有与人类视觉感知过程相类似的构成原理。 (2)YCrCb色彩格式被广泛地应用在电视显示等领域中,也是许多视频压缩编码,如 MPEG和JPEG等标准中普遍采用的颜色表示格式。 (3)YCrCb色彩格式具有与HSV等其他一些色彩格式相类似的将色彩中的亮度分量分 离出来的优点。 (4)相比HSV等其他一些色彩格式,YCrCb色彩格式的计算过程和空间坐标表示形式 比较简单。 (5)实验结果表明在YCrCb色彩空间中的肤色聚类特性比较好。
第十章
第10章 GUI经典案例分析与应用
第十章
本章主要围绕GUI案例设计应用展开,具体包括数据概率密度函数统计软件设计、 曲线线型及颜色更改软件设计、数据拟合GUI设计、倒立摆系统GUI设计、图像颜色空 间转换GUI设计、图像灰度处理GUI设计、图像滤波去噪GUI设计、图像边缘检测GUI设 计、彩色图像分割GUI设计、医学图像分割GUI设计、粒子群算法模型求解设计、遗传 算法模型求解GUI设计、蚁群算法TSP动态GUI设计、Pareto多目标求解GUI设计等。
RGB彩色空间是一个立方体状彩色空间,如图10-77所示。 由于彩色图像是多光谱图像的一种特殊情况,对应于人类视觉的三基色即红、绿、 蓝三个波段,是对人眼的光谱量化性质的近似,因此利用R、G、B三基色这三个分量来 表征颜色是很自然的一种格式,而且多数的图像采集设备都是以CCD技术为核心,直接 感知色彩的R、G、B三个分量,这也使得三基色模型成为图像成像、显示、打印等设备 的基础,具有十分重要的作用。RGB颜色模型主要应用于CRT监视器和图形刷新设备中 。
GUI的基础知识总结

图形用户界面GUI(Graphical User Interfaces)就是一种用户与计算机进行信息交流得工具与方法,由各种图形对象组成,在这种用户界面下,用户得命令与对程序得控制就是通过鼠标等输入设备“选择”各种图形对象来实现得。
软件开发者只需在由软件开发工具自动生成得程序代码中添加自己得运算或控制代码,就可以完成应用程序得设计。
目前90%以上得应用程序与软件都就是在GUI下运行得。
ﻫTLAB提供得图形用户界面开发环境GUIDE中得图形用户界面开发工具得GUI创建方式制作.这里主要介绍基于GUIDE得创建方式。
在GUI得设计中应注意在面板上进行按钮得静态布置时一定要事先预算好按钮得个数.更重要得一点就是如果您放置了一个按钮并且对此按钮得属性进行了某种操作,那么该按钮得痕迹将永远保存在您所建得面板上,您将该按钮删除,然后重新建一个按钮,并将其属性值设置与上一个按钮一模一样,那并不能保证您将上一按钮覆盖,在程序进行运行得过程中它只会识别上一按钮(已经删除得按钮),而您将上一按钮得删除则造成程序运行中得错误或就是得不到您预想得界面效果,为了避免这种情况,在进行设计得时候对任一按钮属性得设置不要与已经删除按钮得属性相同.Matlab为GUI设计一共准备了4种模板,分别就是:ﻫBlank GUI(Default)(空白模板,默认);ﻫGUI with Uicontrols (带控件对象得GUI模板); ﻫGUI with Axes and Menu(带坐标轴与菜单得GUI模板);ﻫModal Question Dialog (带模式问题对话框得GUI模板)。
ﻫ当用户选择不同得模板时,在GUI设计模板界面得右边就会显示出与该模板对应得GUI 图形。
在GUI设计模板中选中一个模板,然后单击OK按钮,就会显示GUI设计窗口。
选择不同得GUI设计模式时,在GUI设计窗口中显示得结果就是不一样得。
图形用户界面GUI设计窗口由菜单栏、工具栏、控件工具栏以及图形对象设计区等4个功能区组成。
控制系统工具箱

八.控制系统工具箱系统常用的数学模型有:传递函数模型,状态方程模型,零极点增益模型,部分分式模型;(1) 传递函数描述系统在MATLAB 中可以方便地由分子和分母系数构成的两个向量唯一地确定出来,这两个向量分别用num 和den 表示。
num=[b1,b2,…,bm,bm+1]den=[a1,a2,…,an,an+1]调用格式:G=tf(num,den)注意:它们都是按s 的降幂进行排列的。
num=[12,24,0,20];den=[2 4 6 2 2];G=tf(num,den)num=4*conv([1,2],conv([1,6,6],[1,6,6]));den=conv([1,0],conv([1,1],conv([1,1],conv([1,1],[1,3,2,5]))));G=tf(num,den)(1)G.variable='p'Transfer function:4 p^5 + 56 p^4 + 288 p^3 + 672 p^2 + 720 p + 288-----------------------------------------------------p^7 + 6 p^6 + 14 p^5 + 21 p^4 + 24 p^3 + 17 p^2 + 5 pG.td=0.5Transfer function:4 p^5 + 56 p^4 + 288 p^3 + 672 p^2 + 720 p + 288exp(-0.5*p) * -----------------------------------------------------p^7 + 6 p^6 + 14 p^5 + 21 p^4 + 24 p^3 + 17 p^2 + 5 p(2)G=tf(num,den,'inputdelay',0.5)Transfer function:4 s^5 + 56 s^4 + 288 s^3 + 672 s^2 + 720 s + 288exp(-0.5*s) * -----------------------------------------------------s^7 + 6 s^6 + 14 s^5 + 21 s^4 + 24 s^3 + 17 s^2 + 5 s(3)set(G,'variable','s','Td',0.7)get(G)num: {[0 0 4 56 288 672 720 288]}den: {[1 6 14 21 24 17 5 0]}ioDelay: 0Variable: 's'Ts: 0InputDelay: 0.7OutputDelay: 0InputName: {''}22642202412)(23423++++++=s s s s s s s G )523()1()66)(2(4)(23322+++++++=s s s s s s s s s GOutputName: {''}InputGroup: [1x1 struct]OutputGroup: [1x1 struct]Name: ''Notes: {}UserData: [](2)零极点增益模型调用格式 G=zpk(z,p,k);结果是零极点形式的;函数tf2zp()可以用来求传递函数的零极点和增益:[z,p,k] = tf2zp(num,den)例 求零极点增益模型num=[1 11 30];den=[1 9 45 87 50];[z, p,k]=tf2zp(num,den);G=zpk(z,p,k)(3)部分分式展开 实际就是对residue 的应用 例 将tf 转化为部分分式的形式num=[2 0 9 1];den=[1 1 4 4 ];[r p k]=residue(num,den);[num den]=residue(r,p,k)num =2.0000 -0.0000 9.0000 1.0000den =1.0000 1.0000 4.0000 4.0000(4)状态空间描述B 的列数为输入的个数,C 的行数为输出的个数;D 的维数为C 的行*B 的列数 G=ss (A,B,C,D ); 例 可以看出: >> A=[1 6 9 10;3 12 6 8;4 7 9 11;5 12 13 14]; >> B=[4 6; 2 4; 2 2;1 0];>> C=[0 0 2 1;8 0 2 2]; >> D=zeros(2); >> G=ss(A,B,C,D)a =x1 x2 x3 x4x1 1 6 9 10x2 3 12 6 8x3 4 7 9 11x4 5 12 13 1450874593011)(23423++++++=s s s s s s s s G 44192)(233+++++=s s s s s s G DuCx y Bu Ax x+=+= x y u x x ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=22081200012242641413125119748612310961b =u1 u2x1 4 6x2 2 4x3 2 2x4 1 0c =x1 x2 x3 x4y1 0 0 2 1y2 8 0 2 2d =u1 u2y1 0 0y2 0 0Continuous-time model.>> G=tf(G) 得到四个传递函数;分别为11;12;21;21(5)模型之间的相互转换模型转换的函数包括:residue :传递函数模型与部分分式模型互换ss2tf : 状态空间模型转换为传递函数模型ss2zp : 状态空间模型转换为零极点增益模型tf2ss : 传递函数模型转换为状态空间模型tf2zp : 传递函数模型转换为零极点增益模型zp2ss : 零极点增益模型转换为状态空间模型zp2tf : 零极点增益模型转换为传递函数模型也就是tf ss zpk 之间可以相互转化;举例说明:1. 状态空间模型:(单输入,单输出) A=[0 1;1 -2];B=[0;1];C=[1 3];D=1; G=ss(A,B,C ,D); [num,den]=ss2tf(A,B,C,D,[1])[Z P K]=ss2zp(A,B,C,D,[1]);2. 单入三出的模型的传递函数如下:(这里的分子和分母是矩阵)61162)(61165)(61162)()()(23231232123111++++=+++--=+++-==s s s ss s G s s s s s G s s s s u s y s Gnum=[0 0 -2;0 -1 -5 ;1 2 0];den=[ 1 6 11 6];[A B C D]=tf2ss(num,den);[]u x y u x x +=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=31102110>> g=tf(num,den)??? Error using ==> tf.tf at 239The values of the "num" and "den" properties must be rowvectors or cell arrays of row vectors, where each vectoris nonempty and containing numeric data. Type "ltipropstf" for more information.也就是tf 只能对行向量进行转化;可以直接G=ss(A,B,C,D);G=tf(G)生成多个传递函数3. 系统的零极点增益模型 )5)(2)(1()3(6)(++++=s s s s s G z=[-3];p=[-1 -2 -5];k=[6];g=zpk(z,p,k);[num,den]=zp2tf(z,p,k);[a,b,c,d]=zp2ss(z,p,k)4.模型的结构A 串联 G=G1*G2;B.并联G=G1+G1C.反馈G=feedback(G1,G2,SIGN);5.控制系统工具箱(控制系统的分析稳定性分析,时域分析,频域分析,根轨迹分析) LTI 对象有如下三种:ss 对象;tf 对象;zpk 对象;(1) 稳定性判据;判稳及找出是否为最小相角系统 例 a=[1 2 -1 2;2 6 3 0;4 7 -8 -5;7 2 1 6]; b=[-1;0 ;0;1]; c=[-2 5 6 1]; d=[7]; [z p k]=ss2zp(a,b,c,d); Ii=find(real(p)>0) %找出右半平面的极点下标,以列向量给出pzmap(p,z); %汇出系统的零极点图2.num=[3 16 41 28 ]; den=[1 14 110 528 1494 2117 112]; [z p k]=tf2zp(num,den);pzmap(p,z)(2) 时域分析求取系统单位阶跃响应:step()求取系统的脉冲响应:impulse() 本身就可以处理多输入,多输出的问题 求系统的稳态值 :dcgain(sys)Pole(G) zero(G) 以列向量形式返回极点和零点例101113220)(234++++=s s s s s G o 系统的开环传递函数,求单位反馈下的阶跃响应曲线。
Control_System_Toolbox(控制系统工具箱)

Control System Toolbox设计和分析控制系统产品概览1:56Control System Toolbox™为系统地分析、设计和调节线性控制系统提供行业标准算法和工具。
您可以将您的系统指定为传递函数、状态空间、零极点增益或频率响应模型。
通过交互式工具和命令行函数(如阶跃响应图和波特图),您可以实现时域和频域中系统行为的可视化效果。
可以使用自动PID 控制器调节、波特回路整形、根轨迹方法、LQR/LQG 设计及其他交互式和自动化方法来调节补偿器参数。
您可以通过校验上升时间、超调量、稳定时间、增益和相位裕度及其他要求来验证您的设计。
Control System ToolboxDesign and analyze control systemsProduct Overview1:56Control System Toolbox™ provides industry-standard algorithms and tools for systematically analyzing, designing, and tuning linear control systems. You can specify your system as a transfer function, state-space, pole-zero-gain, or frequency-response model. Interactive tools and command-line functions, such as step response plot and Bode plot, let you visualize system behavior in time domain and frequency domain. You can tune compensator parameters using automatic PID controller tuning, Bode loop shaping, root locus method, LQR/LQG design, and other interactive and automated techniques. You can validate your design by verifying rise time, overshoot, settling time, gain and phase margins, and other requirements.简介Control System Toolbox™为系统地分析、设计和调节线性控制系统提供行业标准算法和工具。
ch10-GUI-GUI基本知识-01

事件处理模型介绍
Java GUI设计中,通过注册监听器的方式对所关注的事件 源进行监控。 注册监听器时应该指明该监听器监控(感兴趣)的事件种
类。
当事件源发生了某种类型的事件时,只触发事先已就该种 事件类型注册过的监听器。
事件源:能够产生事件的GUI组件对象,如按钮、文本框。 事件监听器:调用事件处理方法的对象 事件处理方法:能够接受、解析和处理事件类对象,实现与用户交 互功能的方法。
单击 是事件对象中的一种 触发事件 按钮是事件源 响应事件 显示开始菜单
必须由事件监听器 调用相关方法
组件基本定位
Java组件在容器中的定位有布局管理器来决定。 如果要人工控制组件在容器中的定位,可取消布局管理器 ,然后使用Component类的下述成员方法:
setLocation()
setSize() setBounds() GUI坐标系:
容器
容器(Container)实际上是Component的子类,因此容 器类对象本身也是一个组件,具有组件的所有性质,另 外还具有容纳其他组件和容器的功能。 容器的特点:
容器类对象可使用方法add()添加组件
两种主要的容器类型:
• Java.awt.Window:常用他的子类Frame,可以自由的停泊在顶级
说明
标签类 包含内容可变的条目的列表框组件 菜单条组件 菜单组件 菜单项组件 基本容器类,不能单独停泊 弹出式菜单组件 滚动条组件 带水平及垂直滚动条的容器组件
常见组件和容器
组件类型
Python GUI工具包

Python GUI工具包一、Python GUI工具包简介Python是一种高级编程语言,具有简单易学、可读性强、代码规范等特点。
Python的GUI工具包可以让开发者快速构建跨平台的图形用户界面,提高开发效率和用户体验。
二、常见的Python GUI工具包1. TkinterTkinter是Python自带的GUI工具包,也是最常用的GUI工具包之一。
它提供了丰富的控件和布局管理器,可以创建各种类型的窗口和对话框。
Tkinter支持多国语言,可以在Windows、Mac OS X和Linux等平台上运行。
2. PyQtPyQt是一套基于Qt库的Python GUI工具包,提供了丰富的控件和布局管理器,可以创建复杂的GUI应用程序。
PyQt支持多国语言,可以在Windows、Mac OS X和Linux 等平台上运行。
3. KivyKivy是一个开源的Python GUI工具包,支持多点触控和多线程。
Kivy提供了丰富的控件和布局管理器,可以创建各种类型的窗口和对话框。
Kivy支持多国语言,可以在Windows、Mac OS X和Linux等平台上运行。
4. PyGTKPyGTK是一套基于GTK库的Python GUI工具包,提供了丰富的控件和布局管理器,可以创建复杂的GUI应用程序。
PyGTK支持多国语言,可以在Windows、Mac OS X 和Linux等平台上运行。
三、选择适合自己的GUI工具包在选择Python GUI工具包时,需要考虑以下几个方面:1. 功能需求不同的GUI工具包提供的功能不同,需要根据自己的需求选择合适的工具包。
例如,如果需要创建复杂的窗口和对话框,可以选择PyQt或Kivy;如果只需要创建简单的窗口和对话框,可以选择Tkinter。
2. 平台支持不同的GUI工具包支持的平台不同,需要根据自己的开发环境和目标平台选择合适的工具包。
例如,如果需要在Windows上开发GUI应用程序,可以选择Tkinter或PyQt;如果需要在Mac OS X上开发GUI应用程序,可以选择PyQt 或Kivy。
自动控制原理实验的GUI设计

自动控制原理实验的GUI设计作者:孙凤玲来源:《中国新通信》 2018年第7期一、GUI 的组成在GUI 设计中需要利用的软件有MATLAB,这是目前在编程中一种比较新的编程语言,是一种可视化的工具,较之之前的编程工具具有明显的优势特点。
其中比较明显的优势就是其强大的显示图形和处理数据的功能。
针对GUI 的主要组成部分,包含按键、菜单、说明、文字、光标、窗口等几个方面的内容,用户在使用的过程中需要将这些对象的图标进行激活处理,这需要依靠合适的方法进行激活,在实际的操作过程中主要进行GUI 设计的主要元素有以下几个方面:1、组件。
组件是整个GUI 设计中最基本的部分,在其中每一个设计的项目都属于一个图形化的组件,一般来讲组件主要分为三种类型,分别是静态的元素、图形化的控件以及菜单和坐标系三种类型,在其中窗口就属于静态的元素,编辑框、列表等就属于图形化的控件,并且不同的组件由不同的函数来进行创建。
2、图形窗口。
图形窗口主要的功能是用来进行GUI 中每个组件的安排工作,在进行数据图像的设计工作中,图像窗口会进行自动创建,如果出现没有自动创建的情况,可以借助函数figure 来进行创建图形窗口。
3、回应。
回应主要是指在进行信息的录入或者是单击时,要保障程序有相应的动作来进行回应,在进行工作的过程中,如果利用MATLAB 程序进行函数的运行,相关的MATLAB 函数就能够得到及时的回应。
二、实验界面和平台的设计工作进行试验界面和平台的设计工作中,首先应该进行界面和平台草图的绘制,在进行实验界面和平台的设计工作中,经常利用的工具有数学模型的建立,波特图的绘制以及性能的分析等,在进行设计的过程中,进行波特图的绘制工作要用到两个坐标轴,进行草图构建都需要按照相应的标准进行设计,具体的步骤大致为以下几步。
1、控件的绘制。
首先应该将MATLAB 程序打开,根据界面的标识将GUI 界面进行打开处理,然后根据之前设计好的草图,将各个控件的位置进行准确摆放。
《控制系统工具箱》课件

案例一:温度控制系统
总结词
通过PID控制器实现温度稳定
详细描述
介绍如何使用控制系统工具箱中的PID控制器,对加热炉或空调系统等温度控制 系统进行建模、分析和优化,实现温度的快速稳定和精确控制。
案例二:液位控制系统
总结词
利用串级控制提高液位控制精度
详细描述
阐述如何利用控制系统工具箱构建串级液位控制系统,通过两个控制回路的协同工作,提高液位控制的稳定性和 精度,降低因扰动或参数变化对系统的影响。
未来展望
强化实时性能
随着工业自动化和实时控制要求的提高, 控制系统工具箱将进一步强化实时性能,
提高系统响应速度和稳定性。
强化人机交互
为了更好地服务于用户,控制系统工具箱 将进一步优化人机安全威胁的增加,控制系统工具 箱将更加注重安全性设计,加强数据保护 和系统防御。
解决方案
检查网络连接是否正常、账号密码是否正确、服务 器是否正常运行。
解决方案
检查安装包是否完整、操作系统版本是否兼容 、安装目录权限是否正确。
问题2
无法登录控制系统工具箱。
问题3
工具箱界面显示异常。
解决方案
尝试重启工具箱或更换浏览器/操作系统版本,检查浏 览器插件是否冲突。
04
CATALOGUE
它可以帮助工程师和科研人员更好地理解和优化控制系统,提高系统的性能和稳 定性。
03
CATALOGUE
控制系统工具箱的使用方法
控制系统工具箱的安装与配置
下载与安装
从官方网站下载控制系统工具箱的安装包,按照 提示进行安装。
配置环境
根据操作系统和软件要求,配置合适的环境变量 和运行权限。
GUI优化工具箱的使用.ppt

图5-5 无约束优化实例
无约束优化(fminsearch求解器)
启动优化工具:
然后在Solver下拉选框中选择 fminsearch;
目标函数栏输入@(x)abs(x^23*x+2);
初始点输入-7,其余参数默认;
单击Start按钮运行。
运行就可得到极小值和对应的 值
图5-7 用fminsearch求解非光滑优化问题
优化工具箱中的智能优化算法包括 遗传算法(ga)和模拟退火算法 (simulannealbnd),MATLAB中的 ga求解器功能非常强大,既能求解 无约束优化问题,也能求解约束优 化问题,而且约束条件可以是非线 性的,但是simulannealbnd求解器只 能求解无约束优化问题。
在Solver下拉选框中选择ga; 在适应函数栏输入@(x)x^4-
5.3.2 GUI优化工具的界面
GUI优化工具的界面 主要分为三大块:
左边为优化问题的描 述及计算结果显示 (Problem Setup and Results);
中间为优化选项的设 置(Options);
右边为帮助(Quick Reference)。
为了界面的简洁,可 以单击右上角的“<<” 按钮将帮助隐藏起来。
(1)在命令行上 输入optimtool;
(2)在MATLAB 主界面单击左下角 的“Start”按钮, 然后依次选择 “Toolboxes→Opti
mization→Optimiza tion tool(optimtool)。
图5-2 优化工具图形界面的菜单启动方式 图5-3 优化工具图形界面
3*x^3+x^2-2; 变量个数输入1,其余参数默认; 单击Start按钮运行。
gui-命令

MATLAB中的图形用户界面(GUI)工具功能类别命令函数说明GUI函数dragrect 用鼠标拖动“异或”矩形selectmoveresize 交互地选择,移动,改变大小或者拷贝对象uicontrol 创建用户界面控件uimenu 创建用户界面菜单uirestore 恢复图形的交互状态uiresume 继续执行先前停止执行的程序uistack 控制对象的堆栈顺序uisuspend 挂起图形的交互状态uiwait 停止执行程序并等待恢复waitforbuttonpress 在图形中等待按键/按钮waitfor 停止执行程序并等待事件GUI设计工具align 排列UI控件和轴guide 设计GUI inspect 检查对象的属性propedit 编辑属性对话框axlimdlg 轴范围对话框dialog 创建对话框errordlg 出错对话框helpdlg 帮助对话框imageview 利用缩放图形显示图像inputdlg 输入对话框listdlg 列表选择对话框menu 为用户输入产生选择菜单movieview 利用重放按钮显示动画图形msgbox 消息对话框pagedlg 页面位置对话框pagesetupdlg 页面设置对话框printdlg 打印对话框printpreview 预览待打印的图形questdlg 提问对话框soundview 以图形和播放的形式显示声音uigetfile 标准的打开文件对话框uigetpref 支持优先级的提问对话框uiimport 为输入数据(Import Wizard)而启动GUI uiload显示打开文件对话框并在结果中调用“1oad”uiopen显示打开文件对话框并在结果中调用“open”uiputfile 标准的保存文件对话框uisave显示打开文件对话框并在结果中调用“save”uisetcolor 颜色选择对话框uisetfont 字体选择对话框waitbar 显示等待条warndlg 警告对话框菜单函数makemenu 创建菜单结构menubar 对MenuBar属性而言计算机所依赖的默认设置umtoggle 切换uimenu对象的“checked”状态winmenu 给“窗口”菜单项目创建子菜单工具栏按钮组件函数btndown 在工具栏按钮组件中压下按钮btnresize 改变按钮组件的大小btngroup 创建工具栏按钮组件btnpress 工具栏按钮组件的按钮管理btnstate 提问工具栏按钮组件的状态btnup 在工具栏按钮组件中弹起按钮优先权addpref 添加优先权getpref 获取优先权.ispref 测验优先权的存在情况rmpref 去除优先权setpref 设置优先权其他函数allchild 获取所有对象的子类clipboard 输给系统剪贴板以及来自系统剪贴板的拷贝和粘贴字符串edtext 轴文本对象的交互编辑findall 搜索所有的对象findfigs 搜索图形超出屏幕的部分getptr 获取图形指针getstatus 获取图形中文本字符串的状态guidata 储存或恢复应用数据guihandles 返回句柄的一个结构hidegui 隐藏/显示GUIlistfonts 从单元数组中获取可用的系统字体列表movegui 将GUI移到屏幕的指定部分overobj 获取指针结束时的对象句柄popupstr 获取上拉式菜单的选项字符串remapfig 变换图形对象的位置setptr 设置图形指针setstatus 设置图形中文本字符串的状态uiclearmode 清除当前激活的交互模式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
07:57
6/9
系统仿真
格式2:增加补偿器C作系统分析。 格式3:给定系统的各环节G、C、H、F,作系统分 析。其中 G:系统对象模型 C:补偿器对象模型 H;反馈对象模型 F:前置滤波器模型 格式4:指定view的作图类型,view可以为 rlocus,根轨迹图; bode,博德图; nichols,尼柯尔斯图线; filter,前置滤波器的博德图。
07:57 2/9
系统仿真
格式 2:sysl,…为系统对象。 plottype:为分析方法作图,选项如下所述。 step:阶跃响应分析。 impulse:脉冲响应分析。 bode:博德图。 bodemag:博德图稳定裕度分析。 nyquist:奈奎斯特图。 nichols:尼柯尔斯图线。 sigma:奇异值绘图。 pzmap:零点极点绘图。 格式3:任意输入响应分析。 u:输人信号向量。 t:时间向量。 x0: 初值向量。
07:57
4/9
系统仿真
例 2、系统传递函数为
4 G s 2 s s4
使用 LTI Viewer 工具,并作系统时域性能分析。 num=[4]; den=[1 1 4]; sys=tf(num,den); ltiview(sys)
07:57
5/9
系统仿真
二、sisotool
sisotool为单输入单输出系统的GUI设计工具。格式 如下: sisotool(G) sisotool(G,C) sisotool(G,C,H,F) sisotool(view,G,…) 格式1:给定线性系统的开环对象模型G可以是tf, zpk,ss对象任意一种。作系统 分析。
07:57 7/9
系统仿真
例3、 系统开环传递函数为
4 G s 2 s s
使用 sisotool 工具,并作系统分析。 num=[4]; den=[1 1 0]; sys=tf(num,den); sisotool(sys) sisotool({bode,nichols},sys)
07:57
07:57 3/9
系统仿真
下面两个例题,一为命令行方式使用ltiview,一为命 令行与ltiview交互方式使用。
例 1、系统传递函数为
4 G s 2 s s4
使用 ltiview 工具,并作系统时域性能分析。 num=[4]; den=[1 1 4]; sys=tf(num,den); ltiview({'step';'bode'},sys)
8/9
系统仿真
谢谢大家!
07:57
9/9
系统仿真
Байду номын сангаас
第十讲 控制系统工具箱中的 GUI工具
07:57
1/9
系统仿真
一、ltiview
ltiview命令打开一个系统分析窗口界面,用于 线性系统的时域分析或者频域分析。应用 格式为: ltiview(sys1,…) ltiview(plottype,sysl,…) ltiview(‘lsim’,sysl,sys2,u,t,xO) 格式1:做系统对象sysl,sys2,…的阶跃响 应曲线(默认)。
