流体机械04讲-流体机械速度三角形分析与欧拉方程_486101757
《流体力学与流体机械》最全知识点

Dρ ,而将气体视为可压缩流体。 = 0 ,∇⋅u = 0 ) Dt
4、粘性是流体反抗发生剪切变形的特性,粘性只有在流体质点之间具有相对运动时才表 现出来( τ = 0 ,能否说明是理想流体? )。牛顿流体作一维层流流动时,其粘性内摩擦切应力 符合牛顿内摩擦定律(牛顿剪切公式) : τ = µ du dy 。 µ 是表征流体动力特性的粘度,称为动 力粘度。ν 是表征流体运动特性的粘度( ν = µ ρ ) ,称为运动粘度。 当温度升高时,液体的 粘性降低,而气体的粘性增大。 应用牛顿内摩擦定律做相关计算:平行和旋转缝隙内的剪切流动
等压面的两个重要特性: (1)在平衡的流体中,通过任意一点的等压面,必与该点所受的质量力互相垂直; (2)当两种互不相混的液体处于平衡时,它们的分界面必为等压面。 5、流体静力学基本方程式: z +
p = c 或 p = p0 + ρ gh γ
适用条件:(1)质量力只有重力;(2)不可压缩流体。 6、液体的相对平衡 (1) 等加速直线运动容器中液体的相对平衡(与坐标系选取有关)
u = u ( x, y , z , t ) , p = p ( x, y, z, t )
在同一时刻,上述欧拉表达式就描绘出流动参数在流场中的分布情况。 2、欧拉法中速度的质点导数: a = Du ∂u ∂u ∂u ∂u ∂u = + u ⋅∇u = + ux + uy + uz Dt ∂t ∂t ∂x ∂y ∂z
《流体力学与流体机械》复习
《流体力学》部分 第一章 流体及其物理性质
1、流体是一种很容易发生剪切变形的物质,流动性是其主要特征。连续介质假定是为以 及流体的宏观机械运动而提出的一种流体模型。质点是构成宏观流体的最小单元,质点本身 的物理量可以进行观测。 2、单位体积流体所包含的质量称为密度 ρ ;重度 γ 是单位体积流体具有的重量, γ = ρ g 。 3、流体受压体积减小的性质称为压缩性;流体受热体积增大的性质称为膨胀性。液体的 可压缩性和膨胀性都比较小,气体的可压缩性和膨胀性都比较大,所以 ,通常可将其视为不 可压缩流体(
流体机械原理完整精选ppt

No Image
第四章 固定元件 ▪ 第一节 吸气室 ▪ 第二节 无叶扩压器 ★ ▪ 第三节 叶片扩压器 ★ ▪ 第四节 叶轮主要参数对级性能的影响 ★ ▪ 第五节 半开式、混流式叶轮
第五章 相似原理在离心压缩机中的应用 ★ ▪ 第一节 相似原瑗的基础知识 ▪ 第二节 离心压缩机的相似条件 ▪ 第三节 相似原理的应用 ▪ 第四节 相似模化设计 ▪ 第五节 性能换算
.2010年 B72班
No Image
流体机械
▪ 流体机械的定义 流体机械是以流体(液体或气体)为工作介质与能 量载体的机械设备
▪ 流体机械的分类 流体机械分为原动机与工作机 原动机:将流体的能量转换为机械能的机械设备。
水轮机、汽轮机、燃气轮机、风力机、气动工具等
工作机:将机械能转换为流体的能量。
No Image
.2010年 B72班
No Image
.2010年 B72班
No Image
.2010年 B72班
No Image
螺杆压缩机
.2010年 B72班
No Image
螺杆压缩机的运行
.2010年 B72班
No Image
螺杆式制冷压缩机结构和工作原理
.2010年 B72班
No Image
.2010年 B72班
No Image
第八章 实际气体 ▪ 第一节 实际气体的压缩性系数 ▪ 第二节 实际混合气体 ▪ 第三节 实际气体的热力学性质 ▪ 第四节 实际气体的压缩过程
第九章 离心式压缩机热力设计 ▪ 第一节 中间冷却与分段 ▪ 第二节 热力设计概述 ▪ 第三节 压缩机中各段各级主要参数的选择 ▪ 第四节 级通流部分基本尺寸的确定 ▪ 第五节 计算例题
流体力学--第四章流体动力学基础

∂uy ∂uy ∂uy 1 ∂p 1 2 Ydy− dy = uy ( dx + dy + dz) = d(uy ) ⑤ ρ ∂y ∂x ∂y ∂z 2 ∂uz ∂uz ∂uz 1 ∂p 1 2 Zdz− dz = uz ( dx + dy + dz) = d(uz ) ⑥ ρ ∂z ∂x ∂y ∂z 2
(2)动能积分
u2 α v2 dQ = ρg∫ ρ gQ Q 2g 2g
式中α 称为动能修正系数,即实际动能与平均动能之比值 。
α=
流速分布较均匀 流速分布不均匀
u3dA ∫ v3 A
α = 1.05 ~ 1.10
流体机械原理
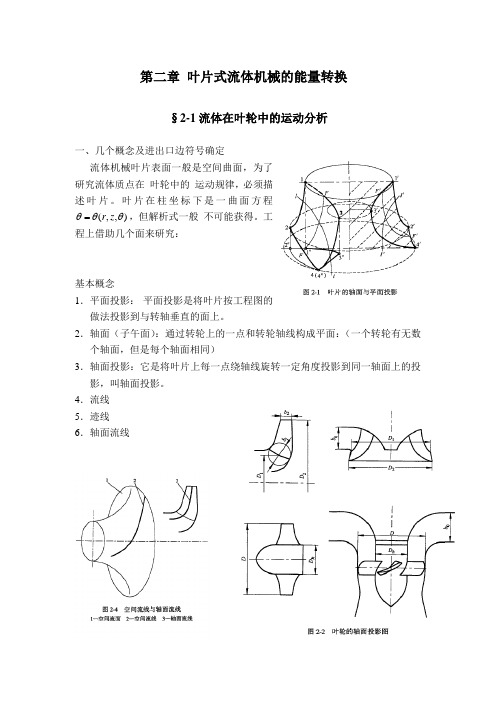
第二章 叶片式流体机械的能量转换§2-1流体在叶轮中的运动分析一、几个概念及进出口边符号确定流体机械叶片表面一般是空间曲面,为了研究流体质点在 叶轮中的 运动规律,必须描述叶片。
叶片在柱坐标下是一曲面方程),,(θθθz r =,但解析式一般 不可能获得。
工程上借助几个面来研究: 基本概念1.平面投影: 平面投影是将叶片按工程图的做法投影到与转轴垂直的面上。
2.轴面(子午面):通过转轮上的一点和转轮轴线构成平面:(一个转轮有无数个轴面,但是每个轴面相同)3.轴面投影:它是将叶片上每一点绕轴线旋转一定角度投影到同一轴面上的投影,叫轴面投影。
4.流线5.迹线 6.轴面流线进出边符号确定:(本书规定) P 代表高压边 P 对风机,泵,压缩机,一般S 代表低压边 出口边对水轮机进口边S 对风机,泵,压缩机,一般是进口边,对水轮机是出口边二、叶轮中的介质运动 1.速度的合成与分解:流体机械的叶片表面是空间曲面,而转轮又是绕定轴旋转的,故通常用圆柱坐标系来描述叶片形式及流体介质在转轮中的运动。
在柱坐标中,空间速度矢量式可分解为圆周,径向,轴向三个分量。
u z r C C C C++= 将C z ,C r 合成得C m , z r m C C C+= C m 位于轴面内(和圆周方向垂直的面),故又叫轴面速度。
2.绝对运动和相对运动:在流体机械的叶轮中,叶片旋转,而流体质点又有相对转轮的运动,这样根据理论力学知识质:叶轮的旋转是牵连运动。
流体质点相对于叶轮的运动叫相对运动,其速度叫相对速度,这样,流体质点的绝对速度为 这两速度的合成,即 u w C += 其中 u是叶轮内所研究的流体质点的牵连速度在流体机械的静止部件内,没有牵连速度,相对运动的轨迹和绝对运动重合。
用速度三角形,表示上述关系,即得:依速度合成分解,将C 分解为沿圆周方向的分量C u 及轴面上的分量C m ,从速度三角形知:C m =W m u u W C u +=或u u W C u-=叶轮内,每一点都可作出上述速度三角形。
第04章理想流体动力学

y
2 t
(4-3)
(U p v2 ) 0
z
2 t
括弧内函数不随空间坐标(x,y,z)变化,
只可能是时间的函数。
所以
p v2
U F (t)
2 t
(4 - 4)
若流体的质量力只有重力,取z轴铅直向上,
有U=-gz,故
gUz
p
v2 2
t
F (t)
(4
- 4')
7
t
为书写简单,引入 F (t)dt 0
分常数C 只在同一条流线上不变,不同流线取 l
值不同,称为流线常数或者说拉氏积分在整个空 间成立,而伯氏积分只在同一条流线上成立。
18
为了工程上的应用,现将伯氏方程推广到 有限大的流束。
渐变流动:流线近似平行,而且流线的曲率很小 的流动,否则称为急变流动。
渐变流动特点:(z p) 项在整个过水(过流) 断面上为常数。
z p 称为静压
v2 称为动压
2
28
伯努利方程的应用
实例一:小孔口出流(如水桶壁上破一洞) 图示容器装有液体,在重力作 用下从小孔流出。求流量。
设小孔面积比容器中液面 面积小很多,液面高度h近似 认为不变(近似为定常流),
不计流体粘性,此时流体的质量力只有重 力。满足伯氏方程来求解的前提。
29
取小孔轴线为基准,整个容器看成一个大流管 取容器液面为截面
将Φ对x,y,z求偏导数,仍为速度的投影
x
x
Vx
y
y
Vy
z
z
Vz
引入Φ后,式(4-4)可改写成:
U p V 2
2
t
(4-5)
8
若流体的质量力只有重力,式(4 - 4')可写成:
流体力学课件第四章 流体动力学基础 共131页

教学的目的和要求
了解从动量守恒原理导出的纳维—斯托克斯 方程及其各项的物理意义。
了解理想流体运动的欧拉方程及欧拉方程的 边界条件。
了解定常流动的欧拉方程积分──伯努利定理 的物理意义;掌握伯努利定理的应用实例;了解 不定常流动的欧拉方程积分──拉格朗日—柯西积 分。
uy z
pzz
p2uz
z
zxxzuxz
ux z
(3) 粘性流体运动微分方程
推导方法类似无粘性流体远动微分方程的推导。
§4.1 流体的运动微分方程
第四章 流体动力学基础
2、粘性流体运动微分方程: (2). 应力与变形速度(应变率)的关系
本构方 程
Bemoulli,D. (1700~1782)根据能
量原理给出了类似的 公式,为纪念他。
§4.2 元流的伯努利方程
第四章 流体动力学基础
2 v1g2 gp1 z1v22g2gp2 z2
物理意义和几何意义:
v12
b 总水头
2g c
p1
1
z1
a
v
2 2
b'
2g
c'
p2
H
2
z2
a'
单位重量流体的动能+压力势能+高度势能-----总机械能守恒 速度水头 压强水头 位置水头----------总水头沿流线相等。
x方向:
p p dx x 2
z y
O
x
dz p(x,y)
a
c
dy dx
p p dx x 2
水力学 第3章 流体力学基本方程PPT课件

积分得:
p u2 gzppρt精选版 2 cons. t
19
例1:已知:u = x+t,v = -y+t, w = 0。
求t=0时,经过点A(-1,-1)的流线方程。
解:t=0时,u=x, v=-y, w=0;代入流线微分方程, 有:
dx dy x y
ln xln yC 1
xyc
流线过点(-1,-1) ∴ C =1
流线方p程 pt精选为 版 x: y 1
这里:
Vuivjwk
aaxiay jazk
2.欧拉法:
以流场作为研究对象,研究各流场空间点上流体质 点的各运动要素随时间与空间的变化的分布规律。
流场:运动流体所占据的空间。
在欧拉法中,是以速度场来描述流体运动的,流体质点的运
动速度(即速度函数)是定义ppt在精选空版 间点上的,它们是空间点坐
标(x, y, z)的函数:
因为: V // ds
因此,两矢量的分量对应成比例:
ppt精选版
dx dy dz
u vw 15
四.流管、流束、元流、总流:
1.流管:
在流场中任意绘一条非流线的封 闭曲线,在该曲线上的每一点作流 线,这些流线所围成的管状面称为 流管。
由于流管的“管壁”是由流线构成的,因而流体质点的 速度总是与“管壁”相切,不会有流体质点穿过“管壁”流 入或者流出流管。流管内的流体就像是在一个真实的管子里 流动一样:从一端流入,从另一端流出。
二.恒定流与非恒定流:
1.恒定流(定常流动):
流场中各点处的所有流动参数均不随时间而变化的流动。
特征 u : v w 0 , p0 等。
t t t
t
2.非恒定流(非定常流动):
流体力学与流体机械Ⅰ主要公式及方程

《流体力学与流体机械》(上)主要公式及方程式1.流体的体积压缩系数计算式:pp V V d d 1d d 1p ρρβ=-= 流体的体积弹性系数计算式:ρρd d d d pV p VE =-= 流体的体积膨胀系数计算式:TT V V d d 1d d 1T ρρβ-==2.等压条件下气体密度与温度的关系式:tβρρ+=10t , 其中2731=β。
3.牛顿内摩擦定律公式:yuAT d d μ±= 或 y u A T d d μτ±==恩氏粘度与运动粘度的转换式:410)0631.00731.0(-⨯-=EE ν 4.欧拉平衡微分方程式: ⎪⎪⎪⎭⎪⎪⎪⎬⎫=∂∂-=∂∂-=∂∂-010101z p f y p f x pf z y x ρρρ 和 ⎪⎪⎪⎭⎪⎪⎪⎬⎫=∂∂-=∂∂-=∂∂-010101z pf r p f r p f z r ρθρρθ欧拉平衡微分方程的全微分式: )d d d (d z f y f x f p z y x ++=ρ )d d d (d z f r f r f p z r ++=θρθ 5.等压面微分方程式: 0d d d =++z f y f x f z y x0d d d =++z f r f r f z r θθ 6.流体静力学基本方程式:C z p=+γ或2211z p z p +=+γγ或 2211z g p z g p ρρ+=+相对于大气时: C z g p a m =-+)(ρρ 或 2211)()(z g p z g p a m a m ρρρρ-+=-+ 7.水静力学基本方程式:h p p γ+=0,其中0p 为自由液面上的压力。
8.水平等加速运动液体静压力分布式:)(0gz ax p p +-=ρ;等压面方程式:C z g ax =+;自由液面方程式:0=+z g ax 。
注意:p 0为自由液面上的压力。
9.等角速度旋转液体静压力分布式:)2(220z gr p p -+=ωγ;等压面方程式:C z g r =-222ω;自由液面方程式:0222=-z g r ω。
过程流体机械的重点总结讲解

过程流体机械整体概念:过程是指事物状态变化在时间上的持续和空间上的延伸,它描述的是事物发生状态变化的经历、生产过程是人们利用生产工具改变劳动对象以适应人们需要的过程。
流体机械是以流体或流体与固体的混合体为对象进行能量转换、处理、也包括提高其压力进行输送的机械,它是过程装备的重要组成部分。
流体机械的分类:(能量:原动机、工作机)(介质:压缩机、泵、分离机)(结构:往复式结构的流体机械、旋转式结构的流体机械)第一篇活塞式压缩机1.循环功:什么是理论循环功?什么是实际循环功?循环:被压缩气体进入工作腔内完成一次气体压缩称为一级,每个级由进气、压缩、排气等过程组成,完成一次该过程称为一个循环。
理论循环:1.汽缸没有余隙容积,被压缩气体能全部排出汽缸。
2.进排气过程无压力损失,压力波动、热交换、吸排气压力为定值。
3.压缩过程和排气过程无气泄漏。
4.所压缩的气体为理想气体,其过程指数为定值。
5.压缩过程为等温或绝热过程。
1.往复压缩机的理论循环与实际环的差异是什么?1.汽缸有余隙容积2.进、排气通道及气阀有阻力3.气体与汽缸各接触壁面间存在温差4气缸容积不可能绝对密封 5.阀室容积不是无限大6.实际气体性质不同于理想气体7.在特殊的条件下使用压缩机容积系数λv=1-α(ε^1/m-1)=1-V0/Vs[(pd/ps)^1/n-1]α:相对余隙容积,α=V0(余隙容积)/Vs(行程容积);α=0.07~0.12低压,0.09~0.14中压,0.11~0.16高压,>0.2超高压。
ε:名义压力比(进排气管口可测点参数),ε=pd/ps=p2/p1,一般单级ε=3~4;n:膨胀过程指数,一般n<=m压缩过程指数。
2.什么是设计循环示功图?什么是实际循环示功图?3.说明容积系数,压力系数,温度系数以及漏泄系数的意义.容积系数:λv=1-α(ε^1/m-1)=1-V0/Vs[(pd/ps)^1/n-1]α:相对余隙容积,α=V0(余隙容积)/Vs(行程容积);α=0.07~0.12低压,0.09~0.14中压,0.11~0.16高压,>0.2超高压。
流体运动的基本方程

同理,
u u u u u v w t x y z v v v v ay u v w t x y z w w w w az u v w t x y z ax
加速度矢量
DV V a (V ) V Dt t
一、拉格朗日法: 描述每一个流体质点在不同时刻的运动。怎样区分每一 个流体质点?
r (a, b, c, t )
x x(a, b, c, t ) y y(a, b, c, t ) z z (a, b, c, t )
(a, b, c)
初始时刻流体质点的标示参数 (a, b, c) 对于任意物理量 B : B F (a, b, c, t )
V V V V x y z t dV x y z t a lim t 0 dt t V V V V Vx Vy Vz t x y z
t
x 方向加速度:
du u u dx u dy u dz ax dt t x dt y dt z dt u u u u ax u v w t x y z
第3章流体运动的基本方程
3.1 流体运动的描述方法 3.2 随体导数 3.3 流动分类 3.4 流体微团的运动分析 3.5 作用在流体上的力 3.6 流体运动的基本方程 3.7 流体运动基本方程的运用
3.2 流体质点加速度 (Euler法)
时:V ( M 0 ) V ( x, y, z , t ) t t 时:V (M 1 ) V ( x x, y y, z z, t t )
第3章流体运动的基本方程
3.1 流体运动的描述方法 3.2 随体导数 3.3 流动分类 3.4 流体微团的运动分析 3.5 作用在流体上的力 3.6 流体运动的基本方程 3.7 流体运动基本方程的运用
第四讲 流体运动描述方法及速度场_9670922

第四讲:流体流动描述方法及速度场流体流动描述方法及速度场一、流场及其描述方法二、流体流动的速度场三、迹线与流线流体运动学:用几何的观点研究流体流动现象及其规律;不涉及引起运动变化的原因,即力的作用。
描述流体运动的困难拉格朗日坐标•以一组数(a,b,c)作为标记,如质点初始时刻t=t0的位置坐标(a,b,c),来识别运动流体的一个质点,这组数称为拉格朗日坐标或随体坐标。
•流体不管什么时候,运动到哪,其拉格朗日坐标不变1-1 拉格朗日法●着眼于流体的质点,流体质点表示为拉格朗日坐标和时间的函数。
●流体质点运动轨迹:k z j y i x r t c b a z z t c b a y y t c b a x x ++=⇒⎪⎩⎪⎨⎧===迹线方程),,,(),,,(),,,(),,,(t c b a r=1-2 欧拉法✓欧拉坐标●以固定于空间的坐标系中的一组坐标,来表示流体质点在不同时刻运动到空间的一个位置,称为欧拉坐标。
●由连续性假设,流体质点与空间点,从而与欧拉坐标是一一对应的。
✓欧拉法(空间描述法)●着眼于空间点,将流体的运动和物理参数直接表示为空间坐标和时间的函数,而不是沿运动轨迹去追踪质点。
●任意空间点(x,y,z)处流体速度:●同理●流动问题有关任意物理量(矢量或标量)(,,,),(,,,)x y z t p p x y z t ρρ==(,,,)x y z t ϕϕ=ϕ(,,,)V V x y z t = k t z y x w j t z y x v i t z y x u ),,,(),,,(),,,(++=欧拉法把流场的运动要素和物理量都用场的形式表达,为在分析流体力学问题时直接运用场论的数学知识创造了便利条件。
•欧拉法是描述流体运动常用的一种方法。
●关注沙尘暴(风暴)的走向,拉格朗日法描述。
●关注某一地区的天气情况,欧拉法描述拉格朗日描述与欧拉描述流场:流体由无穷多个质点构成,流体质点存在相对运动和相互作用。
第四章 流体动力学微分形式的基本方程

第四章流体动力学微分形式的基本方程§4-1运动流体中的应力张量流体中的应力一、运动流体中的应力张量作微元四面体,如图()cos ,x n nA A n x A Δ=Δ=Δx n ()cos ,y n nA A n y A Δ=Δ=Δy n ()cos ,z n nA A n z A Δ=Δ=Δz n00当()00,0,0dv dx dy dz →→→→n x y zA A A A Δ=Δ+Δ+Δn x y z p p p p n x n y n z nA n A n A n A Δ=Δ+Δ+Δn x y z p p p pn n n =++x y zxx xy xzp p p =++n x y z x p p p p p i j k yx yy yzzx zy zzp p p p p p =++=++y z p i j k p i j k y 分量公式:nx ny nzp p p =++n p i j k nx x xx y yx z zxp n p n p n p =++ny x xy y yy z zynz x xz y yz z zz p n p n p n p p n p n p n p =++=++⎛xx xy xz p p p ⎞⎜⎟=为对称张量yxyyyz zxzy zz P p p p p p p ⎜⎟⎜⎟⎝⎠ 为对称张量P =++x y z ip jp kp x y z n n n P=++=i 依赖于通过某点的面元方位P是的函数n x y z p p p p n (),t 依赖于通过某点的面元方位,P是的函数.n p r二、理想流体中的应力00p αβαβ≠⎧=⎨1111222233330= nn nn nn p n n p p n n p p n n p βαβ≠⎩===112233nn p p p p ∴===理想流体任一方向应力分量都相等p P p δ=−=−n p n+∇i V =0()t ρ∂t∂:适用惯性坐标系,非惯性坐标系,理想流体和非理想流体.⎛()()200v e ,t ,A A t 2φφφττ⎞==×=+==⎜⎟⎝⎠V, r V ,d d 00D D Dt Dt ττρτρτ=∫∫∫∫∫∫V VD ∫∫∫∫∫∫∫∫ A Dt ττD ⎛⎞V ∴0d Dt τρρτ−−∇=⎜⎟⎝⎠∫∫∫f P i1yz xz zz z P P w w w w P u v w f t x y z x y z ρ∂⎛⎞∂∂∂∂∂∂+++++⎜⎟∂∂∂∂∂∂∂⎝⎠=+各项物理意义y x dx dy ∂⎛⎞∂⎛⎞⎟⎟P P z dxdydz+dydz+dxdz x y D +dz dxdy dxdydz ρρ⎜⎜∂∂⎝⎠⎝⎠∂⎛⎞ =f P V (牛顿第二定律)z Dt ⎜⎟∂⎝⎠2Dt ⎝⎠()()()221122R V V e e +q T t λρρ⎛⎞⎛⎞∂++∇+=∇+∇∇⎜⎟⎜⎟∂i i i i i V f V +P V 或⎝⎠⎝⎠§4-5 方程组的封闭性三大方程连续方程动量方程(个)能量方程:连续方程、动量方程(3个)、能量方程。
4流体动力学详解

工程流体力学
4.流体动力学
§4.1 理想流体的运动微分方程
在流动的理想流体中,取出一个微元平行六面体的微 团,它的各边长度分别为dx、dy和dz,如图4-1所示。由 于是理想流体,没有黏性,运动时不产生内摩擦力,所以 作用在流体微团上的外力只有质量力和压强。该压强与静 压强一样,垂直向内,作用在流体微团的表面上。假设六 面体形心的坐标为x、y、z,压强为p。 先分析x方向的运动,在垂直于x轴的左右两个平面中 p dx 心点上的压强各等于 p dx p p x 2 x 2 由于是微元面积,所以这些压强可以作为各表面上的
(4-3)
假如流体微团沿流线的微小位移ds在三个坐标轴上的投影为 dx、dy和dz。现用dx、dy和dz分别乘以式的第一式、第 二式和第三式,则可得到
8
工程流体力学
4.流体动力学
1 p u u u Xdx dx u dx v dx w dx x x y z 1 p v v v Ydy dy u dy v dy w dy y x y z 1 p w w w Zdz dz u dz v dz w dz z x y z
23
工程流体力学
4.流体动力学
特点: • 有效断面面积减小 基本原理: • 当管路中的流体流经节流装置时,在收缩断 面处流速增加,压力降低,使节流装置前后 产生压差,可通过测量压差来计量流量。 流量计公式: • 公式推导根据能量方程和连续性方程。
24
工程流体力学
4.流体动力学
节流式流量计工作原理
1 p p p ( Xdx Ydy Zdz ) dx dy dz x y z udu vdv wdw
(4-40)
流体机械的基本方程流体机械的基本方程75页PPT

流体机械的基本方程流体机械的基本 方程
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
ቤተ መጻሕፍቲ ባይዱ
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
混流式(HL) Mixed-flow Type
贯流式(GL) Tubular Flow Type
斜流式(XL) Diagonal-flow Type
冲击式(CJ)-平面投影图
Impulse Type Plan Projection Drawing
王正伟 13601363209
4
2
2008-11-8
K K K K K K 径向分量(radial component) 轴向分量(axial component) 圆周分量(circumferential component)
vr , wr
vz , wz
vu , wu
在旋转的流体机械中,只有径向分量和轴向分量对通过叶轮的流量有贡献
In rotary fluid machinery, only radial component and axial component make contribution to flow rate through impeller
在旋转的流体机械中,将这径向分量和轴向分量合成
K K In rotary fluid machinery, compose radial component and axial component together
引入wK轴m 面=速wK度r :+
vKm wz
,
wmK vm
=
K vr
+
K vz
Wu
由a-点的轴面投影 Axial Region Projection Of Point
b-轴面流线
Axial Region Streamline
c-导叶
Guide Vane
d-相对运动迹线 Relative Velocity Trace Line
e-转轮叶片
Impeller Wheel Blade
f-绝对运动迹线 Absolute Velocity Trace Line
如何表示空间叶片的形状?
How to represent the shape of space blade?
两个二维平面 Two Two-dimension Plan
平面投影图 Plan Projection Drawing
轴面投影图 Pinacoidal Projection Drawing
(r,θ)坐标 (r,θ) Coordinate
2008-11-8
混流式水轮机中的绝对与相对运动 Absolute Velocity And Relative Velocity
Inside Mixed-Flow Turbine
0-导叶出口
Guide Vane Outlet
1-转轮进口
Impeller Inlet
2-转轮出口
Impeller Outlet
2008-11-8
王正伟 13601363209
3
几种典型水轮机的轴面投影
Axial Region Projections of Several Typical Turbines
辐流式(FL) Radial Flow Type
轴流式(ZL) Axial Flow Type
叶片形状及图示方法
Blade Shape and Graphic Method
Pascal
2
4
6
Pascal
8
10
12
14
16
18
Time / s
7000
6000
5000
4000
3000
展开流面 Developed Stream Surface
轴面流线 Axial Region Streamline
旋转流面 Revolved Stream Surface
流面展开 Stream Surface Development
1.流线 2.轴面流线 3.旋转流面 4.两类流面 5.过流断面
Streamline Axial Region Streamline Revolved Stream Surface Two Kinds Of Stream Surfaces Cross Section
2008-11-8
王正伟 13601363209
1
流体机械的能量转化过程
Energy Transformation Process of Fluid Machinery
流体能
Fluid Energy
水轮机Turbine
机械能
Mechanical Energy
来流 Incoming Flow
来流 Incoming Flow Vu=0
2008-11-8
王正伟 13601363209
5
过流断面 Flow Stream Cross Surface
·在轴面上作若干轴面流线
·Make several axial region streamlines on an axial region ·再作一曲线与所有轴面流线正交
·And then make a curve orthogonal to all streamlines ·该曲线绕轴旋转一周形成的回转面称为过流断面
2008-11-8
4.1 流体机械的能量转化过程 Energy transformation process of fluid machinery 4.2 叶片形状及图示方法 Blade shape and graphic method 4.3 几种典型水轮机的轴面投影 Pinacoidal projections of several typical turbines 4.4 展开流面 Developed stream surface 4.5 过流流面 Cross‐section 4.6 速度三角形的定义 Definition of velocity triangle 4.7 叶片式流体机械欧拉方程 Euler equation of vane type fluid machinery 4.8 叶片式流体机械的反击度 Reactiondegree of vanetypefluid machinery 4.9 不同工作条件下的速度三角形-自学分析 Self study and analyze: velocity triangle under different operating conditions
Vu=0 出流 Efferent Flow
2008-11-8
Vu=0 出流 Efferent Flow
机械能
Mechanical Energy
水泵Pump
王正伟 13601363209
流体能
Fluid Energy
2
1
2008-11-8
叶片形状及图示方法
Blade Shape and Graphic Method
Vu=0
叶片 Blade:M=0→M≠0
导叶 Guide Vane:
部分压能→动能 Partial Pressure Energy→Kinetic Energy
Vu≠0
Vu≠0
导叶 Guide Vane:
部分动能→压能 Partial Kinetic Energy→Pressure Energy
叶片 Blade: 动量矩M≠0→M=0
王正伟 13601363209
8
4
2008-11-8
速度三角形的定义 Definition Of Velocity Triangle
在旋转机械中,往往将各速度在柱坐标系下分解成 In rotary, velocity is usually resoluted in column coordinate
2008-11-8
王正伟 13601363209
6
3
2008-11-8
速度三角形的定义 Definition Of Velocity Triangle
·在流体机械旋转叶轮内的流动区域中任取一点,考察该点流体的运动速度 Take any point in flowing area of fluid machinery rotating impeller; observe kinematic velocity of fluid on this point. ·观察者站在相对于地球静止的固定坐标系下观察到的为绝对速度 Absolute velocity is observed when observer stands on stable fixed coordinate relative to the earth. ·观察者站在与叶轮一起旋转的相对坐标系下观察到的是相对速度 Relative velocity is observed when observer stands on relative coordinate rotating with impellers. ·观察者可以非常清楚地观察流体在转轮内的运动状态 Observer can observe fluid motion state inside impeller wheel clearly. ·绝对速度和相对速度间存在如下关系:
vK = uK + wK Absolute velocity and relative velocity have relation represented as below:
2008-11-8
王正伟 13601363209
7
速度三角形的定义 Definition Of Velocity Triangle
Velocity of following runs along circumferential direction,
Therefore velocity components have relation as belowing
