股票定价的奥尔森模型成立条件
剩余收益法在建筑企业价值评估中的应用

B +∑
式中, 为基期的企业股权价值; B 为账面净资产 ; r 为股东权益资金
成本 ; ( )表示企业在 t 时刻的剩余收益 的期望值。该公示反映企业的价 值应为公司所有者权益价值和未来预期的剩余收益现值之和 J 。
( 四 ) 剩余 收 益 法的 评 价
剩余收益模 型的提 出引起了人们的广泛关注 ,它不仅可 以对 企业的 价值进行评估 ,还可以用于行业水平的分析、商誉价值的测算。在国内,已 有学者运用剩余收益法对银行商誉进行测算、上市公司企业价值评估应用等 等。已 有的研究表明,在应用剩余收益 法对企业价值评估 的解释远远优于 自 由现金流模型和股权折现模型,并且对于各国的证券市场都适用。 剩余收益模型的优点在于 目标企业的价值不受会计选择 的影响,实际 的操作中适用性很强 ] 。R I M与 E V A显示计算资本成本时相同,同时考虑 了负债 和权 益 的资本成 本 ,并且 只有 收益大 于成本 时企 业 才有 价值 。R IM 吸 收会计稳健性的优点又将投资者在证券市场上对公司未来预计收益预测结 合在一起 ,是企业 内在价值定义更加 明确 ,评估结果更合理。 二 . 建筑 企 业价 值 评 估 ( 一 ) 建筑 企 业 价 值 评 估 现 状 我国的资产评估工作开展较晚 ,有关企业价值评估的理论研 究和实 践积累都相对落后 ,与发达 国家相 比还有一定的差距 。无论 实业界 ,还 是理论界对建筑企业究竟从哪些方面评估 ,采用什么方法进行评 估还处 于研究之 中,还没有形 成一套科学的评估体 系。 目前我国建筑企业进行企业价值评估时以成本法 为主 ,市场 比较法 和收益法为辅 。在 2 0 0 7 年之前上 市的建筑企业 大多只使 用成本法 一种 评估方法 ,2 0 0 7年之后上市 的建筑企业一般选用成本法作为主要评估方 法,用 收益法进行验证 。这种现状的成 因主要有三个方面 : ( 1 )经济政策的原 因。国家 国有资产管 理局制 定的 《 资产 评估操 作规范意见》 ( 国资办发 1 9 9 6 1 2 3号),第 1 1 5条 明确指 出 “ 近期内,对
简述merton模型的基本思路与求解思路

简述merton模型的基本思路与求解思路一、引言Merton模型是金融领域中的经典模型之一,它是基于随机过程理论和期权定价理论构建而成的。
该模型能够帮助企业或个人评估其违约风险,并根据这种风险来确定其债券和股票的定价。
本文将对Merton模型的基本思路和求解思路进行详细阐述。
二、Merton模型的基本思路Merton模型是由美国经济学家罗伯特·C·默顿于1974年提出的。
该模型主要用于评估企业或个人违约风险,进而确定其债券和股票的定价。
该模型假设企业或个人的资产遵循几何布朗运动,即资产价格随时间呈连续性变化,并且变化幅度服从正态分布。
在Merton模型中,企业或个人的资产可以分为两部分:有价值资产和无价值资产。
有价值资产是指能够为持有者带来收益的资产,如股票、债券等;无价值资产则是指不能为持有者带来收益的资产,如现金、短期债务等。
当企业或个人违约时,其有价值资产将被用来偿还债务。
因此,违约风险的大小取决于有价值资产与债务的比例。
当有价值资产低于债务时,企业或个人就会违约。
三、Merton模型的求解思路Merton模型可以通过期权定价理论来求解。
期权定价理论是指根据某个金融资产的价格,预测该资产在未来某个时间点的价格,并根据这种预测来确定期权的价格。
在Merton模型中,假设企业或个人发行了一种零息债券,到期日为T,面值为V。
如果企业或个人在到期日T前违约,则债券持有者将无法收回本金。
因此,在该模型中,债券持有者所面临的风险就是违约风险。
为了确定该零息债券的价格,需要先估计企业或个人违约的概率。
Merton模型假设企业或个人资产遵循几何布朗运动,并且有价值资产与无价值资产之间存在一定的关系。
因此,在该模型中,可以通过计算有价值资产与债务之间的比例来估计违约概率。
具体地说,假设企业或个人的有价值资产为A,无价值资产为B,债务为D,则有:A +B = S其中,S表示企业或个人的总资产。
《货币金融学》米什金 第07专题 股票市场、理性预期和有效市场假说(E

4. 预期的预测误差平均为0,且事先不可知。
六为金融的挑战,提高有效性的措施? ★★
(一)假设(有效市场假说建立在三个依次减弱的前提假定上) ①理性 ②独立的理性偏差 ③套利 判断1:若市场有效,则定价有效,那么所有的风险都会有回报。(错) 风险是指系统性风险β,所以需要基金行业来分散非系统性风险。 判断2:有效市场假说提倡消极投资策略,比如指数基金。(对) 判断3:即使是有效市场,也需要有基金经理。(对) 有效市场要求有完善的套利机制,基金行业保证了套利机制完善。
四,如何购买国外股票?如何国外购买我国股票? 购买外国股票,优点是投资组合分散化,缺点是购买不方便。 方法有ADRs(美国存托凭证),由一家银行购买美国股票,并打包成资产池发售给国内 投资者,实现了国内投资者投资美国股票的目的。类似的,我国的CDR是可以实现外国 购买中国股票的金融工具,也有利于我国金融市场的国际化。
#第07专题 股票市场、理性预期和有效市场假说(EMH)★
一,股票的权利? (一)投票权 (二)剩余价值索取权
二,股票如何定价?★
(一)市场法——指通过一些公司指标,如市盈率、市净率等指标,与类似的公司股价比 较,确定本公司股价。
(二)收益法
1. 自由现金流模型(FTE、WACC)
2. 股利贴现模型(单期股利贴现模型推广到多期股利贴现模型,最后简化到戈登 公式)
(二)内涵 市场价格反映所有可得信息,市场不存在任何套利机会
(三)类型 ①弱式有效市场:市场价格包括一切历史信息,此时技术分析无效。 ②半强式有效市场:市场价格包括一切公开信息,此时基本面分析无效 ③强式有效市场:市场价格包括一切信息,此时内幕交易无效
(四)如何检验这三级有效市场? 1,检验弱有效市场——序列相关性,在弱势有效市场上,序列自相关系数为0,股票 后一期收益与前一期收益无关。 2,检验半强有效市场——事件研究/共同基金记录(基金经理业绩) 3,检验强有效市场——公司内部人员交易的超额利润
grinold-kroner模型推导原理

grinold-kroner模型推导原理
Grinold-Kroner模型是一种用于预测股票市场收益的模型,它基于基本面分析和市场估值两个方面的因素来解释股票市场的预期收益。
该模型可以通过以下步骤推导:
1. 首先,根据基本面分析,模型考虑了股票市场的预期收益由股利收入、盈利增长和股息率决定。
具体来说,模型将股票市场的预期收益(E(Ri))表示为三个因素的加权和:
E(Ri) = D/P + g + ∆PE
其中,D/P表示股利收入占股票价格的比例,g表示盈利增长率,∆PE表示市盈率的变化。
2. 然后,模型考虑了市场估值对股票市场收益的影响。
它使用市盈率的变化(∆PE)来衡量市场估值的变动,并假设股票市场收益与市盈率变化呈正相关关系。
∆PE = (PE_t - PE_t-1) / PE_t-1
其中,PE_t表示当前时期的市盈率,PE_t-1表示前一时期的市盈率。
3. 最后,模型进一步将市盈率的变化分解为两个因素:市场估值的改善(PE_t > PE_t-1)和回归到均值(PE_t < PE_t-1)。
这些因素可以用来解释市盈率变化对股票市场收益的影响。
根据Grinold-Kroner模型的推导原理,考虑基本面和市场估值
因素可以帮助预测股票市场的预期收益。
基于这些因素的分析,投资者可以在股票市场中做出更明智的投资决策。
然而,需要注意的是,该模型的预测能力可能受到多种因素的影响,包括市场情绪、宏观经济环境等。
因此,在使用该模型进行预测时,需要综合考虑其他因素并进行合理的风险管理。
浅议剩余收益估价模型和动态金融资产计价模型

他率先将 股利折现模 型用剩余收益 表达 并对之 进行 系统论
述 ,最 终确立 了具 有经典 意义的剩 余收益 估价模 型 ( s u1 Red a i Ic meV lao dl剩余收益定价模型 ) 也称奥尔森模型 no a t nMo e, ui ,
( -o d1。剩 余 收 益 的 含义 是 本 期 综 合收 益 减 去 资 本 的 Obsn Mo e) l
成 为 迫 切 需 解 决 的 问题 。本 文 通 过 简要 介 绍 西 方 经 济 学 中的 剩 余 收 益 估 价 模 型 和 动 态金 融 资 产计 价模 型 , 为我 国 资 本 市 场 的 发展 和 经济 理 论 的 完善 提 供 借 鉴 。
第一 , 企业价值 ( 股票价格 ) 等于企业未来期 间的预期股利
美国投资公 司也利用基 于剩 余收益 估价模型 的指令 系统进行 有效 的投资决策。
基础 , 以它没有被 当时的会计界所 普遍接受 。 所
奥 尔森 ( l n 19 Ohs )95年在 《 o 当代 会 计研 究》 上发 表文 章 { a i s o k Va e,ad D v ed n E ut Va ao ) E r n ,B o l s n ii n si q i l t n , n g u d y ui )
的现值 , 即股利贴现模 型 :
V =
T l \ … ,
其中 , 【 v 为企业 t 期的股票 价值 ,t t d为 期支付 的股利 ,为 r
经过风险调整 的回报率 ( 资本成 本率 )它 是一种机 会成本 , , 并
假定 不变 。
第二 , 业 的 会 计 处 理 满 足 净 盈 余 会 计 关 系 ( l n S rls 企 Ce upu a
BLACK-SCHOLES期权定价模型

BLACK-SCHOLES期权定价模型Black-Scholes期权定价模型(Black-Scholes Option Pricing Model),1997年10月10日,第二十九届诺贝尔经济学奖授予了两位美国学者,哈佛商学院教授罗伯特·默顿(RoBert Merton)和斯坦福大学教授迈伦·斯克尔斯(MyronScholes)。
他们创立和发展的布莱克-斯克尔斯期权定价模型(Black Scholes Option Pricing Model)为包括股票、债券、货币、商品在内的新兴衍生金融市场的各种以市价价格变动定价的衍生金融工具的合理定价奠定了基础,特别是为评估组合保险成本、可转换债券定价及认股权证估值等提供了依据。
BLACK-SCHOLES期权定价模型- 简介斯克尔斯与他的同事、已故数学家费雪·布莱克(Fischer Black)在70年代初合作研究出了一个期权定价的复杂公式(看涨和看跌)。
与此同时,默顿也发现了同样的公式及许多其它有关期权的有用结论。
结果,两篇论文几乎同时在不同刊物上发表。
所以,布莱克—斯克尔斯定价模型亦可称为布莱克—斯克尔斯—默顿定价模型(含红利的)。
默顿扩展了原模型的内涵,使之同样运用于许多其它形式的金融交易。
瑞士皇家科学协会(The Royal Swedish Academyof Sciencese)赞誉他们在期权定价方面的研究成果是今后25年经济科学中的最杰出贡献。
BLACK-SCHOLES期权定价模型- 其假设条件(一)B-S模型有5个重要的假设1、金融资产收益率服从对数正态分布;(股票价格走势遵循几何布朗运动)2、在期权有效期内,无风险利率和金融资产收益变量是恒定的;3、市场无摩擦,即不存在税收和交易成本;4、该期权是欧式期权,即在期权到期前不可实施;5、金融资产在期权有效期内无红利及其它所得(该假设后被放弃);6、不存在无风险套利机会;7、证券交易是持续的;8、投资者能够以无风险利率借贷。
剩余收益价值估值模型的思想渊源

剩余收益价值估值模型的思想渊源崔侠2013170629 剩余收益模型是充分利用现有的会计信息,以公司权益的账面价值和预期剩余收益的现值来表示股票内在价值的数理模型。
相比传统的现金流量折现模型,剩余收益模型具备很大的优点,因此成了美国财务学界近十年来非常流行的研究主题,并在实践中取得了良好的应用效果。
本文对该模型进行了较详细的阐述,并以国内上市公司的实例进行了说明。
企业契约理论认为企业可以视为许多契约的集合。
这些契约中的一个主要条款即是所有者对企业资产和现金的剩余索取权。
而股票就是股东对企业剩余收益的所有权。
近年来,剩余收益(Residual Income)理论受到了理论界的重视。
一、剩余收益估价模型概述剩余收益模型(RIM)又被称为EBO模型,最早是由爱德华兹(Edwards)和贝尔(Bell)于1961年提出的,但并没有引起财务理论界多大的重视,沉寂了很长一段时间。
1995年美国学者奥尔森(Olson)在其文章《权益估价中的收益、账面价值和股利》中,对这一模型公司权益价值与会计变量之间的关系,再次进行了系统的阐述,使该模型重新得到理论界的重视,并成为近十年来美国财务学界最热门的研究主题之一。
所谓剩余收益是指公司的净利润与股东所要求获得的报酬之差。
企业只有赚取了超过股东要求的报酬的净利润,才算是获得了正的剩余收益;如果只能获得相当于股东要求的报酬的利润,仅仅是实现了正常收益。
即剩余收益t t t rBV NI RI -=++11,其中,1+t RI 代表t+1期的剩余收益,1+t NI 代表t+1期的企业净收益,t BV 是t 期企业权益的账面价值,r 是投资者要求的必要报酬率。
剩余收益需要进行资本成本的调整,从而反映会计上未加确认但事实上存在的权益资本的机会成本。
剩余收益模型是使用公司权益的账面价值和预期剩余收益的现值,来表示股票的内在价值。
在考虑货币时间价值以及投资者所要求的风险报酬的情况下,将企业折价,主要取决其初始评估价值的评估方法。
论ohlson模型的成立条件

论股票定价奥尔森模型的成立条件内容摘要:根据奥尔森(Ohlson)1995年给出的RIV模型,公司股票市值等于帐面净值加上未来预期超常收益的贴现值,因此对公司股票的估值只需预测其未来的盈利而不用考虑现金流和股息政策。
我们发现该模型的成立是有条件的,通过研究不同的股息分配政策,利用会计理论模型,推导出了该模型的成立条件。
我们的研究表明该模型在许多正常的经营情况下并不成立,因此股票定价模型并不能够回避掉未来现金流和股息的影响。
关键词:股票定价,奥尔森模型,股息政策中图分类号:F272.5 文献标识码:GAbstract:According to the RIV model given by Ohlson in 1995, the market value of a firm equals to the present value of expected abnormal earnings (or residual income value RIV) of the firm, so to estimate the value of the firm, it is no longer necessary to forecast cash flow and dividends. We find that there exists a theoretical fault in the Ohlson model RIV. We have studied different dividend policies, find that the RIV model works only under some specific conditions, and in ordinary business operation the RIV doesn’t work. So to estimate the market value of a firm, we still have to take into account the influence of cash flow and dividends.Key words: market value, Ohlson model, dividends一、引言奥尔森1995年发表了著名的《股价估值中的盈利、帐面价值和股息》(Ohlson,1995)一文。
07Milgrom-Roberts垄断限价模型

入者L 进入, x D1L ,一般有 x D1L ,故必有 M1L 他所以选 p1L
x M 1L
D1L 。
而不是短L 期L垄断价,L 必然L是有 L
(7.44)
或
M 1 ( p1 ) M 1 M 1 D1
M 1L M 1L ( p1L ) (M 1L D1L )
(7.45)
条件(7.42)和(7.43)的含义 p1L 尽管可阻是止低进成入本,在却位在者总的利这润样上一比种不价模格仿,直它接低暴得露使自高己成本高模成仿本无身意份义(,从因而模引仿致
M
L 1
(
p1
)
0
或
M 1H ( p1 ) M 1L
p1
( p1 )
当(SM)条件成立时,可证明存在区间
p~~,p~p1
,使任何
pL 1
~p, ~p 都满足条
件(7.42)和(7.44),即构成一个分离均衡价格。另可证条件(7.46)意味着
~p
p
L m
,故为了得到分离均衡,低成本在位者需要选一个足够低的价格(低于
M1
D1H M 1H ( p1 ) M 1H
(7.42)
或
H
L
M 1H M 1H ( p1L ) (M 1H D1H )
(7.43)
低 成 本 在 位 者 选 p1L 并 能 阻 止 进 入 ( 分 离 均 衡 中 ), 其 总 利 润 为
M1 ( p1L ) M1L ,若他选短期垄断价,其总利润为 M1L x ,在最坏情况下,进
Milgrom–Roberts 垄断限价模型
Milgrom 和 Roberts (1982)的垄断限制性定价模型(limit pricing model)是
费尔森-奥尔森估价模型实证检验

pt=bt+α1Xta+α2vt
(7)
公式(7)中,α1=ω/(1+γ-ω) α2=(1+r)/[(1+γ-ω)(1+r-γ)]
这 一 估 值 函 数 ,即 不 需 要 预 测 未 来 股 利 ,也 不 需 要
关于终值的假设,而是通 过 以 上 修 正 回 归 模 型 来 估 计
执业会员,硕士研究生。
36
徐 红 军 :费 尔 森 - 奥 尔 森 估 价 模 型 的 实 证 检 验
Pt=n∑∞=1Et[bt+n-(11++xrt)+nn-bt+n]
(3)
经代数计算可将(3)式写成:
pt=bt+n∑∞=1Et[xt+(1n-+rrb)tn+n-1]-E(1t[+btr+)∞∞]
应计制会计在估值方面 优 于 现 金 制 会 计,则 费 尔 森 -
奥尔森模型的有用性应更多建立在会计数据的特性上。尔 森 - 奥 尔 森 模 型
的实证意义依赖于其第 三 假 设,即 剩 余 收 益 的 信 息 动
态性。这一假设赋予了费尔森-奥尔森模型严格的约
型 的 一 种 重 新 表 述 ,由 以 上 推 演 过 程 可 以 清 楚 地 看 到 ,
它并不依赖于会计数据 的 特 性,而 是 依 赖 于 净 剩 余 会
计 关 系 。Frankel、Lee(1998)证 明 尽 管 股 利 折 现 模 型 的
剩余收益表达形式表面上具有依赖于会计数据的特
点 ,但 从 实 证 角 度 却 没 有 任 何 意 义 。 因 为 ,如 果 要 说 明
一模型 提 出 了 相 对 于 其 他 模 型 更 加 全 面 的 估 值 方 法 。[5-6]但 这 些 实 证 研 究 忽 视 了 剩 余 收 益 的 信 息 动 态 性 特征,将该模型变成了用 剩 余 收 益 代 替 的 股 利 折 现 模 型的衍生模型,导致这一模型失去了其内核。 笔者认为,剩余收益 模 型 所 依 赖 的 理 论 基 础 仍 然
black-scholes几种推导方法

第3章 期权定价理论3.1 期权定价理论的发展3.1.1 早期模型早在公元前1200年的古希腊和古尼基国的贸易中就已经出现了期权交易的雏形,只不过当时条件下不可能对其有深刻认识。
法国学者路易斯·巴舍利耶(Louis Bachelier)是迄今为止所知最早的用理论模型研究期权定价问题的提出者。
1900年,他在博士论文《投机理论》中,假设股票价格按无漂移和每单位时间具有2σ的绝对布朗运动变化,得到不分红股票的欧式买入期权的定价公式为:(,)c S T SN KNσ=-+ 其中:S 为股票价格,K 为执行价格,T 为期权到期的时间,(),c S T 为欧式买入期权价格,σ收益的瞬时标准差,()N 为标准正态分布的分布函数,()n 为标准状态分布的概率密度函数。
该公式允许有负的证券价格和期权价格,而且没有考虑资金的时间价值[50]。
巴舍利耶的研究成果为后人指引了方向。
但是他在建模时有3个缺陷:(1)假设股票价格服从正态分布,使得股价出现负值的概率大于0;(2)认为买权价值在离到期日足够远的时候价值可能大于标的股票的价值;(3)假设股票的期望收益为零。
这都是与实际情况不符合的。
在巴舍利耶以后,期权定价理论的进展主要是在应用计量经济模型方面。
其中经典的成果是卡苏夫(Kassouf)的工作,他利用下面式子估计看涨期权价格:()111S C X X γγ⎧⎫⎪⎪⎡⎤=+-⎨⎬⎢⎥⎣⎦⎪⎪⎩⎭,1γ≤<∞其中,S X 分别为期权执行价格和股票价格。
这一公式限定了看涨期权的最高价格是股票价格,最低价格至实值()max 0,S X -。
卡苏夫通过到期时间,股票收益和其他变量估计参数γ,从而确定期权定价模型。
卡苏夫计量模型的不足是缺乏微观基础。
20世纪60年代,期权定价理论取得新的进展。
1961年斯普林克尔(Sprenkle)假设股票价格的动态过程满足对数正态分布,而且股票价格具有固定平均值和方差,进一步通过在随机游走过程中引入正向漂移,这样就直接排除了证券是非正价的可能性。
股权激励第一类 black-scholes 模型

股权激励第一类black-scholes 模型股权激励第一类Blackscholes模型是一种用于估值股权激励计划的数学模型。
该模型在金融学中被广泛应用,特别是在股票期权定价方面。
本文将一步一步回答关于这一模型的问题,并提供详细的解释。
第一步:介绍股权激励和Blackscholes模型为了理解股权激励第一类Blackscholes模型,首先需要了解股权激励计划和Blackscholes模型的基本概念。
股权激励计划是一种用于激励员工的管理工具,它通常包括股票期权和股票奖励等形式。
股票期权可以理解为员工以特定价格购买公司股票的权利,而股票奖励则是公司直接向员工授予一定数量的公司股票。
Blackscholes模型是股票期权定价的经典模型之一,该模型由费舍尔·布莱克和默顿·斯科尔斯共同提出。
该模型基于随机几何布朗运动,假设股票价格的变动服从对数正态分布,根据股票价格、行权价格、无风险利率、期权到期时间和波动率等因素来计算期权的价格。
第二步:模型的基本假设Blackscholes模型建立在一些基本假设的基础上,这些假设对于计算期权的价格至关重要。
以下是Blackscholes模型的基本假设:1. 股票价格服从几何布朗运动。
2. 股票价格变动的波动率是常数。
3. 没有红利支付。
4. 期权到期前无法行权。
5. 市场没有摩擦,例如无交易费用和无税收。
这些假设对于Blackscholes模型的有效性至关重要,如果假设不成立,模型将无法准确估计期权的价格。
第三步:模型的计算公式基于上述假设,可以推导出Blackscholes模型的计算公式。
根据股票价格、行权价格、无风险利率、期权到期时间和波动率等因素,Blackscholes 模型的计算公式如下:C = S * N(d1) - X * e^(-r * T) * N(d2)其中,C表示期权的价格,S表示股票价格,N(d)表示标准正态分布,d1和d2的计算公式如下:d1 = (ln(S / X) + (r + 0.5 * σ^2) * T) / (σ* sqrt(T))d2 = d1 - σ* sqrt(T)在这些公式中,X表示行权价格,r表示无风险利率,T表示期权到期时间,σ表示股票价格的波动率。
大智慧L2 欧奈尔相对强弱指标解决方案
大智慧L2 欧奈尔相对强弱指标解决方案(申请加精)利用长假,重新阅读经典书籍,回顾检讨近期操作,欧奈尔主要的一个指标就是相对强弱(RPS),在网上搜索了一下,竟然没有找到能够完全体现欧奈尔思路的,书中说明的是年相对强弱:股票当前价格与一年前价格相比的涨跌幅度为个股相对强弱,与市场中所有股票排序相比,取值0-99,为个股在市场中其他股票相比的年度相对强弱。
大于80以上才可能是龙头目标。
因此,RPS指标的目的是发现市场中相对强势的股票。
网络上普遍存在的公式是用个股涨跌幅与大盘相比,实际上个股与市场平均涨跌幅的相对强弱,一定程度上能够反映强弱,但与RPS原意还存在差距。
经过一段时间的思考,终于找到合适的解决方案,共享给大家。
第一步:编写个股相对强弱公式,源码如下:INPUT:N(250,1,1000);StockRPS:((C-REF(C,N))/REF(C,N))*100;取名为“RPS引用”。
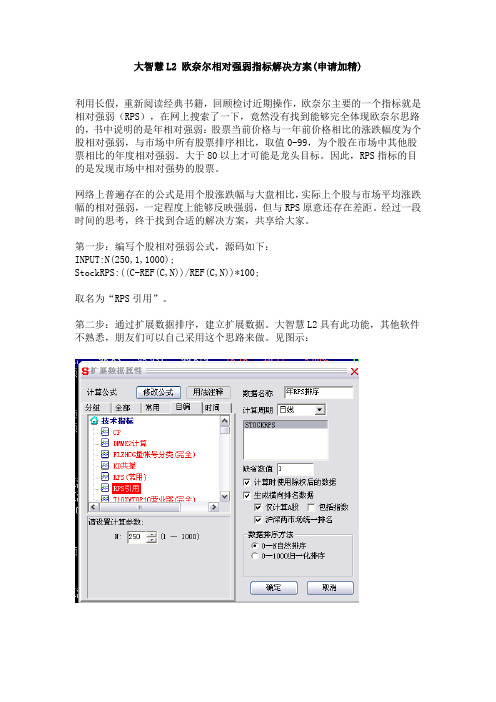
第二步:通过扩展数据排序,建立扩展数据。
大智慧L2具有此功能,其他软件不熟悉,朋友们可以自己采用这个思路来做。
见图示:上图是扩展数据建立的设置,下图是需要建立的几个排序周期,分别是年、周、月、季度,通过上面的设置参数来实现,周是5日、月是20日,季度是60日。
希望动态更新的可以选中上面的“同步更新动态数据”。
每日收盘时会自动更新这些数据。
好了,这样我们就对所有股票进行了强弱排序,这还不够,此种排序是1-1575,因为两市加起来是1575只股票。
是个股涨跌幅排序,不是相对强弱排序。
第三步:编写指标,调用扩展数据,进行相对强弱排序,源码如下:INPUT:N(1575,1,5000);BETA系数:BETA(10),COLORYELLOW,LINETHICK0;周RPS:(1-EXTDATA(2)/N)*100,COLORCYAN,PRECIS2;月RPS:(1-EXTDATA(3)/N)*100,COLORYELLOW,LINETHICK2,PRECIS2; PARTLINE(月RPS,月RPS>=90,RGB(255,0,0)),LINETHICK2,PRECIS2;季RPS:(1-EXTDATA(4)/N)*100,COLORMAGENTA,PRECIS2;年RPS:(1-EXTDATA(1)/N)*100,COLORGREEN,PRECIS2,LINETHICK2;BETA系数与相对强弱无关,反应了风险收益,作为参考。
股票投资价值灰色系统模型及应用

股票投资价值灰色系统模型及应用股票投资价值灰色系统模型及应用发布时间:20XX-3-2 作者:聂祖荣李波内容提要格雷厄姆和多德在《证券分析》一书中对股票价格波动的本质进行了分析,说明了“股票内在价值”对于投资的重要性,随后,这个领域的研究引起了众多经济金融学家的兴趣,经过几十年的探索,得到了大量的重要研究成果,而且不乏广泛应用的方法,但是,对于新兴市场和普通投资者却难以采用。
这里,我们希望借用20世纪80年代兴起的灰色系统理论,探索一套简便易用的股票投资价值预测方法。
本文探讨了灰色预测方法及其在股票价格预测中应用的理论基础和方法,以期能为投资者的决策行为提供一定的指导作用。
1. 问题的提出我们知道,股票市场的价格走势是极为复杂且难以预测的。
股票价格对市场信息如何进行反应,即使最高明最富经验的分析师也难以稳操胜券,这是因为,我们缺乏信息对市场影响的传导系统的结构和系统传导模型,不能准确把握金融政策、利率政策、公司状况、国际市场及投资者心理承受能力等因素的变化及其对市场的影响方式和作用,只能似是而非地对价格走势进行把握,其结果可想而知。
于是,如何判断或预测股票市场价格走势引起了众多经济金融学家和市场分析人员的极大兴趣,在许多经济学家的共同努力下,股票定价方法向着量化方向发展,建立了大量令人振奋的定价方法。
格雷厄姆和多德在1934年《证券分析》一书对1929年美国股票市场价格暴跌的深刻反思,认为股票价格的波动是建立在股票“内在价值”基础上的,股票价格会由于各种非理性原因偏离“内在价值”,但随着时间的推移这种偏离会得到纠正而回到“内在价值”,因此,股票价格的未来表现可通过与“内在价值”的比较而加以判断。
但“内在价值”取决于公司未来盈利能力,因此,对公司未来盈利能力及其现金流的准确把握将是非常关键的。
此后,戈登在对“内在价值”进行深入的量化分析的基础上,提出了著名的股票定价的现金流量模型即“戈登模型”,然而,公司未来现金流是不确定的,为该模型的广泛应用带来麻烦,为此,关于股票定价的早期研究就集中在确定公司未来现金流。
O-F模型与合理市盈率研究——中国股市泡沫的实证分析

益的定价模型 )导出衡量股市泡沫的合理市盈率计算公式, 以此考察 了中国的股市泡沫。通过 分析发现 市盈 率的合理 , 并
值是一个动态值 , 主要 由企业各期的净 资产 、 收益 、 净资产收益率、 持续盈利能力 等内生变量决定 , 不存 在一 个固定的合 理
市盈率来 测量股市的泡沫程度。 计算表明中国的股市泡沫 白 19 年 以来呈明显下降趋势 , 2 0 逐步形成 以来 , 93 且 01 我国股
我 国股 市 的 泡 沫 问题 。
一
、
股 票 内在 投 资 价 值 与 O F模欧文 ・ 费雪 (r h i e 在 13 年开创性地提出在确定条件下的 Lv gF hr 90 i s ) 价值评估理论——投资项 目的价值就是未来各期现金流量按照一定利率折现后的现值 。在他这一思想 的指导下 , 派生 出一 些经 典 的企业价 值评 估模 型 , wii 如 la lms的股利贴 现模 型 、 o i aiM珊e 的 MM M d in— r
就 世界 范 围而 言 ,市 盈 率 是被 广 泛 用 来衡 量 股票 投 资 价值 和测 量 股 市 泡沫 风 险 的 一 个 重 要 指
标 。股票市盈率高则说 明股票投资价值低 , 或者说股市 泡沫风 险高 ; 之 , 反 股票市盈率低则说 明股 票 投 资价 值 高 , 者 说 股 市 泡沫 风 险 低 。认 定 股 票 市盈 率 的 高低 , 须 有 一 个参 照 系一 一 合 理 市盈 或 必
理论 以及 自由现金流模 型 。然 而 , 模型 , 以上 存在 以下 缺陷 :1使 用 的财 务数 据较少 ;2 忽略 了企业 现 () ()
期净资产对企业价值的影响 ; ) ( 这些模型的基本思路是把股东财富归于价值分配, 3 批评者认为应从企
有效市场假说概述

有效市场假说概述有效市场假说(Efficient Markets Hypothesis,简称EMH)是由尤金·法玛(Eugene Fama)于1970年深化并提出的。
“有效市场假说”起源于20世纪初,这个假说的奠基人是一位名叫路易斯·巴舍利耶的法国数学家,他把统计分析的方法应用于股票收益率的分析,发现其波动的数学期望值总是为零。
1964年奥斯本提出了“随机漫步理论”,他认为股票价格的变化类似于化学中的分子“布朗运动”(悬浮在液体或气体中的微粒所做的永不休止的、无秩序的运动),具有“随机漫步”的特点,也就是说,它变动的路径是不可预期的。
1970年法玛也认为,股票价格收益率序列在统计上不具有"记忆性",所以投资者无法根据历史的价格来预测其未来的走势。
这个结论不免使许多在做股价分析的人有点沮丧,他们全力研究各家公司的会计报表与未来前景以决定其价值,并试图在此基础上做出正确的金融决策。
难道股价真的是如此随机,金融市场就没有经济学的规律可循吗?萨缪尔森的看法是,金融市场并非不按经济规律运作,恰恰相反,这正是符合经济规律的作用而形成的一个有效率的市场。
“有效市场假说”包含以下几个要点:第一,在市场上的每个人都是理性的经济人,金融市场上每只股票所代表的各家公司都处于这些理性人的严格监视之下,他们每天都在进行基本分析,以公司未来的获利性来评价公司的股票价格,把未来价值折算成今天的现值,并谨慎地在风险与收益之间进行权衡取舍。
第二,股票的价格反映了这些理性人的供求的平衡,想买的人正好等于想卖的人,即,认为股价被高估的人与认为股价被低估的人正好相等,假如有人发现这两者不等,即存在套利的可能性的话,他们立即会用买进或卖出股票的办法使股价迅速变动到能够使二者相等为止。
第三,股票的价格也能充分反映该资产的所有可获得的信息,即"信息有效",当信息变动时,股票的价格就一定会随之变动。
股票定价的奥尔森模型成立条件

∑R
-τ f
Et ( x
a τ t+
) 是未来超常收益的贴现值 。 因此 , 一个
公司的市值等于其账面净值加上其预期的未来超常收 益 (剩余收入 ) 的贴现值 , 而与现金流和股息无关 。 另 外 , 根据第三个假设 , 奥尔森 ( O h lson, 1995 ) 还导出了 一个线性自回归信息动态模型 L I M: a a x t+1 = ωx t + V t +ε 1 t+1 V t+1 = γ V t +ε 2 t +1
τ= 1 ∞
∑R ∑R
-τ f
E1 ( x1 + τ) ( r′ - r) E1 ( y ) 呈正相关 ;
( 3 ) 市场对剩余收益的定价乘
很明显 , P1 = 0即 PV ED 是对的 ,按 R I V 给出的定 价 P′ 1 是错误的 。 由此可见 , 由于不考虑股息和现金流 , 奥尔森
Cond ition s of Establishm en t of R IV M odel of Stock Pr ic i ng WANG W en - hui, ZHANG W ei
( S chool of M anagem en t, T ian jin U n iversity, T ian jin 300072, Ch ina )
0 ( Π t = 1, 2, ……) , 又假定该公司是每年按年初报表
( r′> r ) 制造报 上的账面净值的固定 (一定 ) 比例 r′
①
将 ( 4 ) 代入 ( 1 ) , 整理后可得 :
∞
P t = yt +
τ= 1
∑R
拓展RIV模型的推导

b t bt 1 NI t d t (2)
其中 b t ,b t -1 分别表示 t 和 t-1 时刻公司权益的账面价,NI t 表示从时刻 t-1 到时刻 t 的期间内的会计收益, d t 为 t 时刻的股利。 将(2)带入(1)得到:
xt1 xt vt 1,t 1 (9)
vt 1 vt 2,t 1 ( 10)
其中 vt 表示未来剩余收益, xt 为 t 期剩余收益,r 为折现率, 为期望值为 0 的干扰项, 和 为 0 到 1 之间常数。 将上面两式带入 6 式得到:
因为资本扩张率
bt 1 b bt 1 ,所以 bt 1 t 1 NI t ,所以 NI t ROEt * bt b1
净资产收益率 ROEt
所以我们有
Pt bt * [1 a1 ( ROEt
r )] a 2 vt ( 13) 1 r a 2 vt ( 14) 1
Pt bt a1bt * ROEt a1 * bt *
Pt bt (1 a1
r ) a1et a2 vt ( 15) 1
由于 vt 的存在,我们不能用上述方程直接进行回归,但是我们可以根据上述 方程得出一些有价值的推论,并根据推论建立回归方程。 推论 1:企业每股收益与股价正相关,因为 a2 大于 0. 推论 2:公司的成长能力与股价正相关,因为企业较高的资本扩张率彰显着 企业良好的成长性。当 越大的时候 P 越大。 推论 3:公司盈利能力与股价正相关,因为 vt 是企业的未来剩余收益,跟企 业的盈利能力密切相关,企业盈利能力越强,剩余收益越高。企业现在或者未来 的盈利决定着股价的高低。 推论 4:公司股价与公司偿债能力正相关,因 为公司偿债能力 r 1 a1 0 越强,资本成本越低。公式也显示 r 越小 P 越 大。 1 推论 5:股价与每股净资产正相关,因为 基于以上推论,我们可以建立如下回归模型:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
出模型中所用的各个变量的定义 , 如无特别说明 , 以
下变量均是对每股取值 。
Pt =t时刻公司股票的市场价格 。 dt =t时刻发放的净股息 r=无风险利率
Rf =无风险利率加 1 Et[· ] =根据 t时刻的信息对随机变量取期望值 xt =时间区间 (t-1, t)内产生的盈利 yt =t时刻的净账面价值 xa t =时间区间 (t-1, t)内产生的超常收益或剩 余收入 (abnormalearningAE或 residualincomeRI),
余收益 )呈正相关 ; (3)市场对剩余收益的 定价乘 数低于对收益的定价乘数 。
虽然很多对 Ohlson模 型的实证检 验都声称支 持
该模型 , 但这种支持仅仅是因为它的实证解释能力较
以前使用的股利贴现模型和现金流贴现模型高 。 对于
解释能力的提高 , 有人发现这些研究在进行横截面回
归分析时 , 没有 对公司 的规模 和必要 贴现 率进行 调
整 , 因而受规模效应的影响 , 其结果是有偏的 , 并非
奥尔森模型所显示的股价与现金流和股利无关 。
二 、 奥尔森模型 RIV存在的问题 :一个示例
按照传统的财务理论 , 一个公司股票的内在价值
是其未来提供给股东的现金流 , 即股息的贴现值 , 而
股票的 市场价 格是 其内 在价 值的 无偏 估计 , 即
∞
∑ PVED:Pt = R-fτEt[ dt+τ] 。 τ=1
股息的发放直接取决于公司的盈利情况 公司的
现金流状况 、 公司的股利政策 。 会计报表可以直接提
供当期的第一项内容 , 间接计算第二项内容 , 但无法
主观设定第三项 。 面对 “股息谜局 ”, 研究人员的对
策是利用有效市场假设加以回避 , 从一开始就排除了
为小于 1的固定正常数 。模型 (7)RIV、(8)LIM构成了
完整的奥尔森 (Ohlson, 1995)模型体系 OM。在后续研 究中 , 由于 Vt很难把握 , 绝大部分相 关文献都是 基于 RIV模型的研究 , 理论界对奥尔森 (Ohlson, 1995)模型
的赞誉也主要是针对 RIV模型的 。
奥尔森模型发表之后 , 研究人员进行了大 量的基
于这一模型的实证研究 。研究显示相比较最早 的现金
流贴现模型 , 奥尔森 模型对于股价的解释能力 有明显
的提高 。研究发现 : (1)收益 、 净资产 、 剩余收益 、
流通股比例和规模都具有价值相 关性 。 (2 )与 Ohl-
son的模型预测一致 , 股票价格与收益 (净资 产和剩
(6)
于是 , (5)变成 :
∞
∑ Pt =yt + Rf-τEt(xat+τ) τ=1
(7)
这就是著名的奥尔森模型中的超常收入模型或剩
余收入模型 RIV。该模型中 , yt是 t时刻的净账面价值 ,
∞
∑ Rf-τEt(xat+τ)是未来超常收益的贴现值 。因此 , 一个
τ=1
公司的市值等于其账面净值加上其预期的未来超常收
一 、 奥尔森模型回顾 奥尔森 1995 年发表了著名论 文 《股价估 值中的 盈利 、 账面价值和股息 》, 利用干净盈余关系 (clean surplusrelation, CSR)研究了股票估值与盈利 、 账面 价值和股息之间的关系 , 建立了奥尔森模型体系 。 奥 尔森模型体系基于三个 基本假设 :假 设 1.股 票价格 等于其未来期望股息的 贴现值 。 假设 2.会计 数据和 股息满足干净盈余关系 , 即导致权益变化的净利润等 于利润表中的净利润 。 假设 3.作为随机变量 的超常 收益 , 其时间序列运动满足线性自回归关系 。 根据以上假设 , 奥尔森 (Ohlson, 1995)按照如 下步骤推导出了一个关于股价估值的模型体系 。 先给
通过研究发现市场的偏差或者是市场尚未反应的信息
的可能性 。 然而当 市场有效 性不 足的证 据越 来越多
股票定价的奥尔森模型成立条件
摘要 :根据奥尔森 (Ohlson)1995 年提出的 RIV模型 , 对公司 股票的估值只需预测其未 来的盈利而 不用考虑现金流和股息政策 。 通过研究不同的股息分配政策 , 利用会计理论模型 , 推导出该模型的成 立条件 。 研究表明该模型在许多正常的经营情况下并不成立 , 股票定价模型不能回避未来现金流和股 息的影响 。 关键词 :股票定价 ;奥尔森模型 ;股息政策
(1) (2) (3)
由 (2)(3)可得 : dt =xat -yt +Rfyt-1 将 (4)代入 (1), 整理后可得 :
(4)
∑ Pt
∞
=yt + τ=1
Rf-τEt(xat+τ)-τl→im ∞ (Et 1(+yt+rτ))τ
(5)
奥尔森给定 :
τl→im∞ (Et1(+yt+rτ))τ =0
奥尔森 (Ohlson) 1995 年发表 了著 名的 《股 价 估值中的盈 利 、 账 面价值 和股息 》 一 文 。 根据他 的 RIV模型 , 公司股票的市值等于其账面净值加上未来 预期超常收益的贴现值 , 对公司股票的估值只需预测 其未来的盈利 、 不用考虑未来现金流和股息政策 。 奥 尔森模型提出之后 , 不仅在西方会计 、 金融界 , 而且 在东方学术界也引起很大反响 。 但是 , 该模型的成立 需要很强的条件 , 而一般条件下该模型是不成立的 。
即该时间区间内产生的盈利减去当期开始时的净账面
价值所要求的无风险收益 。 [ ·~ ] =某一变量对应的随机变量表示 。
根据上面的定义和三个假设 , 奥尔森建立如下等
式:
∞
∑ Pt = Rf-τEt[ dt+τ] PVED τ=1
yt -yt-1 =xt -dt(CSR) xa t =xt -(Rf -1)yt-1 =xt -ryt-1
益 (剩余收入 )的贴现值 , 而与现金流和股息无关 。另
外 , 根据第三个假设 , 奥尔森 (Ohlson, 1995)还导出了
一个线性自回பைடு நூலகம்信息动态模型 LIM:
xa t+1
=ωxat +Vt +ε1t+1
Vt+1 =γVt +ε2t+1
(8)
此模型假设的是超常收益 的时间序列行为 , Vt为
与公司价值有关但未包含在 xa t中的 “其他信息 ” , ω、γ
