推理技术习题以及答案

合集下载

直言推理练习题及答案

一直言推理1.三年级已发现有同学考试作弊。

如果上述断定是真的，那么在下述三个断定中不能确定真假的是：I.三年级没有同学不作弊。

II.三年级有的同学没作弊。

III.三年级所有的同学都未作弊。

A．只有I和II。

B．只有I。

C．只有I和III。

D．只有II。

E．I、II和III。

答案：A2.所有的三星级饭店都搜查过了，没有发现犯罪嫌疑人的踪迹。

如果上述断定为真，则在下面四个断定中：Ⅰ.没有三星级饭店被搜查过。

Ⅱ.有的三星级饭店被搜查过。

Ⅲ.有的三星级饭店没有被搜查过。

Ⅳ.犯罪嫌疑人躲藏的三星级饭店已被搜查过。

可确定为假的是：A.仅Ⅰ和Ⅱ。

B.仅Ⅰ和Ⅲ。

C.仅Ⅱ和Ⅲ。

D.仅Ⅰ、Ⅲ和Ⅳ。

E.Ⅰ、Ⅱ、Ⅲ和Ⅳ。

答案：B3.设“并非无商不奸”为真，则以下哪项一定为真：A.所有的商人都是奸商。

B.所有商人都不是奸商。

C.并非有的商人不是奸商。

D.并非有的商人是奸商。

E.有的商人不是奸商。

答案：E4.并非不参加辅导班的同学都是不努力的。

下列哪项与上述命题含义相同?A.所有不参加辅导班的同学都不是不努力的。

B.不参加辅导班的同学中有不努力的。

C.有的不参加辅导班的同学是努力的。

D.没有一个不参加辅导班的同学不是不努力的。

E.有的参加辅导班的同学是不努力的。

答案：C5.有球迷喜欢所有参赛球队。

如果上述断定为真，则以下哪项不可能为真？A.所有参赛球队都有球迷喜欢。

B.有球迷不喜欢所有参赛球队。

C.所有球迷都不喜欢某个参赛球队。

D.有球迷不喜欢某个参赛球队。

E.每个参赛球队都有球迷不喜欢。

答案：C6.在一次歌唱竞赛中，每一名参赛选手都有评委投了优秀票。

如果上述断定为真，则以下哪项不可能为真？I.有的评委投了所有参赛选手优秀票。

II.有的评委没有给任何参赛选手投优秀票。

III.有的参赛选手没有得到一张优秀票。

A.只有IB.只有IIC.只有IIID.只有I和IIE.只有I和III答案：C7. 学院路街道发现有保姆未办暂住证。

如果上述断定为真，则以下哪项不能确定真假? Ⅰ.学院路街道所有保姆都未办暂住证。

小学数学推理题及答案练习题及答案

小学数学推理题及答案练习题及答案一、选择题1. 12的因数有（）个。

A. 4B. 5C. 6D. 7答案：C2. 一个数如果能被2整除，那么它一定是（）数。

A. 整数B. 正数C. 0D. 负数答案：A3. 已知三角形ABC中，∠ABC=60°，则∠ACB等于（）。

A. 90°B. 60°C. 80°D. 120°答案：A4. 小明去书店买了一本书，花了25元，剩下的钱是40元。

小明原来有多少钱？A. 25元B. 40元C. 50元D. 65元答案：D5. 一个矩形的长是它宽的两倍，如果宽是5cm，那么长是（）cm。

A. 5B. 10C. 15D. 20答案：B二、填空题1. 请写出下列数字的英文名：① 13： thirteen② 20： twenty③ 52： fifty-two④ 100： one hundred2. 请判断下列各题的计算结果是正数、负数还是零。

① (+3) × (+5) = 正数② (-6) × (+8) = 负数③ (-4) × (-2) = 正数④ (-7) × 0 = 零3. 请用适当的符号（>, <, =）填空。

① 8 + 6 ______ 14： <② 7 × 2 ______ 13： <③ 35 ÷ 7 ______ 6： >4. 请写出下列数的阿拉伯数字：①三十五： 35②九十八： 98③一百二十一：121④五百： 500三、计算题1. A、B两家饭店合作举办美食节，A家每天卖出50份套餐，B家每天卖出40份套餐。

已知美食节举办7天，两家饭店一共卖出多少份套餐？答案：(50 + 40) × 7 = 630份2. 小明买了一本书，花了32元，还剩下12元。

小明原来有多少钱？答案：32 + 12 = 44元3. 计算 75 ÷ 3 × 5 + 10 = ？答案：(75 ÷ 3) × 5 + 10 = 125四、解答题1. Alice、Bob和Cindy是小学三年级的同学，他们参加了一个游戏。

逻辑推理习题及答案

逻辑推理习题及答案逻辑推理习题及答案⼀、填空题1. 甲、⼄、丙三⼈进⾏跑步⽐赛.A、B、C三⼈对⽐赛结果进⾏预测.A说:“甲肯定是第⼀名.”B说:“甲不是最后⼀名.”C说:“甲肯定不是第⼀名.”其中只有⼀⼈对⽐赛结果的预测是对的.预测对的是 .2. A、B、C、D、E和F六⼈⼀圆桌坐下.B是坐在A右边的第⼆⼈.C是坐在F右边的第⼆⼈.D坐在E的正对⾯,还有F和E不相邻.那么,坐在A和B之间的是 .3. 甲、⼄、丙、丁与⼩明五位同学进⼊象棋决赛.每两⼈都要⽐赛⼀盘,每胜⼀盘得2分,和⼀盘得1分,输⼀盘得0分.到现在为⽌,甲赛了4盘,共得了2分；⼄赛了3盘,得了4分；丙赛了2盘，得了1分；丁赛了1盘，得了2分.那么⼩明现在已赛了盘，得了分.4. 曹、钱、刘、洪四个⼈出差，住在同⼀个招待所.⼀天下午,他们分别要找⼀个单位去办事.甲单位星期⼀不接待,⼄单位星期⼆不接待,丙单位星期四不接待,丁单位只在星期⼀、三、五接待，星期⽇四个单位都不接待.曹:“两天前,我去误了⼀次,今天再去⼀次,还可以与⽼洪同⾛⼀条路.”钱:“今天我⼀定得去,要不明天⼈家就不接待了.”刘:“这星期的前⼏天和今天我去都能办事.”洪:“我今天和明天去,对⽅都接待.”那么,这⼀天是星期 ,刘要去单位,钱要去单位,曹要去单位,洪要去单位.5. 四位外国朋友住在⼗⼋层⾼的饭店⾥,他们分别来⾃埃及、法国、朝鲜和墨西哥.(1)A住的层数⽐C住的层数⾼,但⽐D住的层数低；(2)B住的层数⽐朝鲜⼈住的层数低；(3)D住的层数恰好是法国⼈住的层数的5倍；(4)如果埃及⼈住的层数增加2层,他与朝鲜⼈相隔的层数,恰好和他与墨西哥⼈相隔的层数⼀样；(5)埃及⼈住的层数是法国⼈和朝鲜⼈住的层数的和.根据上述情况,请你确定A是⼈,住在层；B是⼈,住在层；C是⼈,住在层；D是⼈,住在层.6. ⼩赵的电话号码是⼀个五位数,它由五个不同的数字组成.⼩张说：“它是84261.”⼩王说：“它是26048.”⼩李说：“它是49280.”⼩赵说：“谁说的某⼀位上的数字与我的电话号码上的同⼀位数字相同，就算谁猜对了这个数字.现在你们每⼈都猜对了位置不相邻的两个数字.”这个电话号码是 .7. ⼩赵的电话号码是⼀个五位数,它由五个不同的数字组成.⼩王说：“它是93715.”⼩张说：“它是79538.”⼩李说：“它是15239.”⼩赵说：“谁说的某⼀位上的数字与我的电话号码上的同⼀位数字相同，就算谁猜对了这个数字.现在你们三⼈猜对的数字个数都⼀样,并且电话号码上的每⼀个数字都有⼈猜对.⽽每个⼈猜对的数字的数位都不相邻”.这个电话号码是 .8. A、B、C、D四⼈定期去图书馆，四⼈中A、B⼆⼈每隔8天(中间空7天,下同)、C每隔6天、D每隔4天各去⼀次，在2⽉份的最后⼀天，四⼈刚好都去了图书馆，那么从3⽉1⽇到12⽉31⽇只有⼀个⼈来图书馆的⽇⼦有____ 天.9. 六年级六个班组织乒乓球单打⽐赛,每班派甲、⼄两⼈参赛，根据规则每两⼈之间⾄多赛⼀场，且同班的两⼈之间不进⾏⽐赛.⽐赛若⼲场后发现,除⼀班队员甲以外,其他每⼈已⽐赛过的场数各不相同,那么⼀班队员⼄已赛过____场.10. ⼈的⾎型通常为A型,B型,O型,AB型.⼦⼥的⾎型与其⽗母⾎型间的关系如下表所⽰:⽗母的⾎型⼦⼥可能的⾎型O,O OO,A A,OO,B B,OO,AB A,BA,A A,OA,B A,B,AB,OA,AB A,B,ABB,B B,OB,AB A,B,ABAB,AB A,B,AB现有三个分别⾝穿红,黄,蓝上⾐的孩⼦,他们的⾎型依次为O,A,B.每个孩⼦的⽗母都戴着同颜⾊的帽⼦,颜⾊也分红,黄,蓝三种,依次表⽰所具有的⾎型为AB,A,O.那么穿红、黄、蓝上⾐的孩⼦的⽗母戴帽⼦的颜⾊是、、 .⼆、解答题11. 刘毅、马宏明、张健三个男孩都有⼀个妹妹,六⼈在⼀起打乒乓球,进⾏男⼥混合双打,事先规定:兄妹不搭档.第⼀盘:刘毅和⼩萍对张健和⼩英；第⼆盘:张健和⼩红对刘毅和马宏明的妹妹.⼩萍、⼩红和⼩英各是谁的妹妹？12. 四位运动员分别来⾃北京、上海、浙江和吉林,在游泳、⽥径、乒乓球和⾜球四项运动中,每⼈只参加了⼀项,且四⼈的运动项⽬各个不相同,除此以外,只知道⼀些零碎情况：(1)张明是球类运动员,不是南⽅⼈；(2)胡⽼纯是南⽅⼈,不是球类运动员；(3)李勇和北京运动员、乒乓球运动员三⼈同住⼀个房间；(4)郑永禄不是北京运动员,年龄⽐吉林运动员和游泳运动员两⼈的年龄⼩；(5)浙江运动员没有参加游泳⽐赛.根据这些条件,请你分析⼀下:这四名运动员各来⾃什么地⽅?各参加什么运动?13. ⽼吴、⽼周、⽼杨分别是⼯程师、会计师和农艺师，还分别是业余作家、画家和⾳乐家,但不知道每⼈的职业及业余爱好,只知道：(1)业余⾳乐家、作家常和⽼吴⼀起看电影； (2)画家常请会计师讲经济学的道理； (3)⽼周⼀点也不爱好⽂学；(4)⼯程师埋怨⾃⼰对绘画、⾳乐⼀窍不通. 请你指出每个⼈的职业和爱好.14. 四个⼈聚会,每⼈各带了2件礼品,分赠给其余三个⼈中的⼆⼈,试证明:⾄少有两对⼈,每对⼈是互赠过礼品的.———————————————答案——————————————————————1. CA 、C 的预测截然相反,必⼀对⼀错.因为只有⼀⼈对,不论A 、C 谁对,B 必错,所以甲是最后⼀名,C 对. 2. E如右图,E 坐在A 、B 之间.3. 2,3.由题意可画出⽐赛图,已赛过的两⼈之间⽤线段引连(见右图).由图看出⼩明赛了2盘.因为⼀共赛了六盘,共得12分,所以⼩明得了12-(2+4+1+2)=3(分).4. 三,丙,丁,甲,⼄.由刘的讲话,知这⼀天是星期三,刘要去丙单位.钱要去丁单位,曹去的是甲单位,洪去的是⼄单位.5. 埃及,8；法国，3；朝鲜，5；墨西哥，15.容易知道,墨西哥⼈住得最⾼,埃及⼈次之,朝鲜⼈⼜次之,法国⼈最低,各层次分别15,8,5和3.由(2)知B 是法国⼈,由(3)和D 是墨西哥⼈,由(1)知A 是埃及⼈,⽽C 是朝鲜⼈.6. 86240.因为每⼈猜对两个数字,三⼈共猜对张:842 1 2 3=6(个)数字,⽽电话号码只有5位, 王:26048 所以必有⼀位数字被两⼈同对猜对.如右李:49?80图所⽰,猜对的是左起第三位数字2.因为每⼈猜对的两个数字不相邻,所以张、李猜对的另⼀个数字分别在两端,推知王猜对的数字是6和4,进⼀步推知张猜对8,李猜对0.电话号码是86240.甲丁⼩明7. 19735.因为每个数字都有⼈猜对,所以每⼈⾄少猜对两个数字.下页右上图中,同⼀位数中只有⽅框中的两个数相同,如果每⼈猜对的数字多于两位,相同的数字⾄少有3?3-5=4(组),所以每⼈恰好猜对两个数字. 王: 9 3 7 1 5三⼈共猜对2?3=6(个)数字,因为电话号码只有张: 7 9 5 3 85位,所以相同的⼀组是正确的,即左起第四位是李: 1 5 2 3 93.因为每⼈猜对的数字不相邻,所以张、李猜对的另⼀个数字都在前两位,王猜对的两个数字是7和5,进⽽推知张猜对9,李猜对1.电话号码是19735.8. 51天.):天, 306÷24=12…18，所以所求天数为4?12+3=51(天).9. 5根据题意,有11名队员⽐赛场数各不相同,并且每⼈最多⽐赛10场,所以除甲外的11名队员⽐赛的场数分别为0~10.已赛10场的队员与除已赛0场外的所有队员都赛过,所以已赛10场的队员与已赛0场的队员同班；已赛9场的队员与除已赛0、1场外的所有队员都赛过,所以已赛9场的队员与已赛1场的队员同班；同理,已赛8、7、6场的队员分别与已赛2、3、4场的队员同班；所以甲与已赛5场的队员同班,即⼄赛过5场.注本题可以求出甲也赛了5场,分别与已赛10、9、8、7、6场的队员各赛1场.10. 蓝、黄、红.解法⼀题中表明,每个孩⼦的⽗母是同⾎型的.具有B型⾎的孩⼦,其⽗母同⾎型时,由表中可见,只能是B型或AB型,但题中没有同具B型⾎的⽗母,所以戴红帽⼦的⽗母的孩⼦穿蓝上⾐.具有A型⾎的孩⼦的同⾎型的⽗母,只可能同为A型⾎或同为AB型⾎.今已知有⼀对⽗母为AB型⾎者,所以穿黄上⾐的孩⼦的⽗母戴黄帽⼦.由表中可见,其孩⼦为O型⾎时,⽗母⾎型只能同为A型或B型或O型.今已知不具有同为B型⾎的⽗母,⽽同为A型⾎的⽗母的孩⼦已知具有A型⾎.把代表孩⼦的点与他的可能双亲的代表点之间连⼀直线段,便可得下⾯的图；由于孩⼦与其⽗母之间是唯⼀搭配的,所以,保存下来的只有连着红、蓝；黄，黄及蓝，红的三条边.所以,穿红上⾐(O型⾎)孩⼦的⽗母戴蓝帽⼦.孩⼦⾐服颜⾊⽗母帽⼦颜⾊(O型⾎)(AB型⾎)(A型⾎)黄黄(A型⾎)(B型⾎)蓝蓝(O型⾎)所以,穿红上⾐的孩⼦的⽗母戴蓝帽⼦；穿黄上⾐的孩⼦的⽗母戴黄帽⼦；穿蓝上⾐的孩⼦的⽗母戴红帽⼦. ,张健和⼩萍分别是兄妹.12.13.表解如下:由(3)北京运动员是乒乓球运动员, 故张是⾜球运动员郑是乒乓球运动员由(4)吉林运动员不是游泳运动员,故李是⽥径运动员,⽽胡是游泳运动员由(5)知胡是上海运动员⽽郑是浙江运动员.张明是北京选⼿李勇是吉林选⼿14. 设此四⼈为甲、⼄、丙、丁并⽤画在平⾯上的四个点分别表⽰他们，称为它们的代表点,当某⼈(例如甲)赠了1件礼品给另⼀个(例如⼄)时,就由甲向⼄的代表点画⼀条有指向的线,⽆⾮有以下两个可能:(1)甲、⼄、丙、丁每⼈各收到了2件礼品.(2)上⾯的情形不发⽣.这时只有以下⼀个可能,即有⼀个⼈接受了3件礼品 (即多于2件礼品；因为⼀⼈之外总共还有三个⼈，所以⾄多收到3件礼品).(或许会有⼈说,还有两个可能:有⼈只收到1件礼品及有⼈什么礼品也没收到.其实,这都可归以“有⼀⼈接受了3件礼品”这个情形.因为,当有⼀⼈(例如甲)只接受了1件礼品的情形发⽣时,四⼈共带来的8件礼品中还剩下7件在甲以外的三个⼈中分配,如果他们每⼈⾄多只收到2件礼品,则收受礼品数将不超过6件,这不可能,所以⾄少有⼀⼈收到2件以上(即3件)礼品,同样,当甲未收到礼品时,8件礼品分给⼄、丙、丁三⼈，也必定有⼈收到3件礼品).当(1)发⽣时,例如甲收到⼄、丙的礼品,由于甲发出的礼品中⾄少有1件给了⼄或丙,为确切计,设⼄收到了甲的礼品,于是我们先有了⼀对⼈:(甲、⼄),他们互赠了礼品，如果丙也收到甲的礼品,那么⼜有了第⼆对互赠了礼品的⼈(甲、丙)；如果收到甲礼品的另⼀⼈是丁(如右图)丁的2件礼品必定分赠了⼄及丙(甲已收⾜了本情形中限定的2件礼品)丙或⼄的另⼀件礼品给了丁,则问题也解决(这时另⼀对互赠了礼品的⼈便是(⼄、丁)或(丙、丁)但丙的另⼀件礼品只能给丁,因为这时⼄已收⾜了2件礼品,所以，当本情形发⽣时,⾄少能找到两对互赠过1件礼品的⼈.当(2)发⽣时,不失⼀般性,设甲收到了来⾃⼄、丙、丁的各1件礼品，但甲⼜应向他们之中的某两⼈(例如⼄、丙)各赠送1件礼品,于是(甲、⼄),(甲、丙)便是要找的两对⼈.总上可知,证明完毕.⽼吴是业余画家,⽼周是业余⾳乐家,⽼杨是业余作家.⼯程师是⽼杨,会计师是⽼周农艺师是⽼吴.。

数字推理专项习题50道(附答案)

Ａ．186 Ｂ．208 Ｃ．158 Ｄ．132 2． 1， 5， 19， 81， 411，（）Ａ．2473 Ｂ．2485 Ｃ．1685 Ｄ．1857 3． 3， 3， 12， 21， 165，（）Ａ．649 Ｂ．606 Ｃ．289 Ｄ．343 4． 0，，，，，（）Ａ．Ｂ．Ｃ．Ｄ．5． 7， 11， 16， 25， 54，（）Ａ．98 Ｂ．127 Ｃ．172 Ｄ．203 6． 3， 7， 16， 41， 90，（）Ａ．121 Ｂ．211 Ｃ．181 Ｄ．256 7． 3， 12， 30， 63， 117，（）Ａ．187 Ｂ．198 Ｃ．193 Ｄ．196 8． 3， 8， 22， 62， 178，（）Ａ．518 Ｂ．516 Ｃ．548 Ｄ．546 9． 3， 2，，，，（）Ａ．Ｂ．Ｃ．Ｄ．10． 1， 3， 8， 33， 164，（）Ａ．999 Ｂ．985 Ｃ．1024 Ｄ．1048A.12B.16C.20D.2412. 4， -6， 6， -8， 7.5，（）A．-7.5 B.-8 C.-8.5 D.-9.613. 16， 8， 12， 30， 105，（）A.215B.365.5C.425D.472.514. -3， 5， 7， 4， 14， 18，（）A.29B.23C.21D.1715. 1234， 1360， 1396， 2422， 2458，（）A.2632B.2584C.2864D.297616. -2， 2， 6， 10， 46，（）A.78B.86C.124D.14617. 4， 12， 40， 112， 352，（）A.625B.784C.832D.99618. -32， 36， -30， 38， -29，（）A.39B.45C.51D.6319. 1， 5， 11， 20， 34， 56，（）A.68B.71C.82D.9120. ， 3， 2， 10， 9， 31， 37，（）A.94B.72C.56D.4821. 13610， 25714， 26816， 35715， 43714，（）A.48524B.48718C.46212D.4681322. 1， 2， 3， 7， 7， 17，（）， 37A.21B.23C.25D.1523. 1， 4， 11， 27， 61， 133，（）A.324B.279C.221D.18624. 4， 3， 5， 14， 55，（）A.98B.146C.252D.27425． 1， 2， 6， 9， 15，（）A．20 B．24 C．25 D．3026． 2， 3， 8， 27， 112，（）A．452 B．562 C．565 D．73027． 2， 7， 15， 32， 85，（）A．312 B．314 C．318 D．32228．，，，，，（）A． B． C． D．29． 6， 10， -18， 22，（）Ａ．0 Ｂ． 20 Ｃ． -24 Ｄ．-2030． 0， 3， 3， 15， 63，（）Ａ．1023 Ｂ．511 Ｃ．127 Ｄ．731． 1， 3， 8， 29， 237，（）A．6878 B．6890 C．6989 D．701232． 69， 84， 96， 111， 114，（）A．116 B．120 C．124 D．12833． 5， 16， 60， 236， 940，（）A．3752 B．3756 C．3760 D．376434． 2， 4， 8， 24， 88，（）A．176 B．342 C．568 D．66435． 101， 84， 73， 76， 117，（）A．109 B．171 C．212 D．26836． 18， 48， 125， 252， 539，（）A．729 B．832 C．922 D．101437． 256， 144， 217， 107， 182，（）A．96 B．85 C．74 D．11738． 112， 134， 186， 294，（）A．322 B．410 C．458 D．51239． -3， 3， 25， 127， 341，（）A．627 B．717 C．731 D．102240． 8， 16， 43， 107， 232，（）A．448 B．472 C．511 D．56641． -3，4，， 1，，（）A．1 B．0 C． D．42． 17， 49， 193， 961，（）A．2083 B．3007 C．5761 D．778543． 7， 9， 32， 123， 620，（）A．3720 B．3715 C．3705 D．368044． 64， 100， 121， 178， 256，（）A．289 B．350 C．361 D．39145． 12， 15， 15， 24， 6，（）A．8 B．27 C．44 D．6946． 51， 84， 126， 176， 236，（）A．276 B．302 C．315 D．32847．，， 1，，，（）A． B． C． D．48． 1， 3， 4， 13， 53，（）A．267 B．531 C．690 D．89149．， 0， 6， 15， 28，（）A．15 B．31 C．32 D．2650. 5， 8， 12， 24， 72，（）A．108 B．144 C．324 D．6481．【答案】Ｃ。

逻辑推理专项习题100道(附答案)

1．某市口腔医院的一项统计结果显示，65岁至74岁老年人中，10人中就有一个全口无牙，调查结果表明，受教育程度越高的老人，全口无牙的比例越低，这说明这些老人对口腔保健比较重视，而大部分人受旧观念的影响认为人老了就应该掉牙，因此忽视了中老年人的口腔保健，使简单易治、痛苦小、治疗费用较低的龋齿、牙龈炎发展成治疗复杂、令人痛苦、治疗费用较高的牙髓病和牙周炎。

如果这段文字所表述的内容是真实的，则以下哪一项也一定是真实的？A．某些观念、卫生习惯的改变，会影响一个人年老后患牙齿疾病的风险B．如果一个人受教育的程度比较低，年老后患牙齿疾病的风险就比较大C．定期检查，发现疾病及时治疗是老年人的预防口腔疾病有效方法D．80岁的老人至少应有20颗功能牙，也就是20颗能够正常咀嚼食物、不松动的牙齿2．联合国粮农组织拉丁美洲地区代表日前表示，全球投资基金和美元疲软在很大程度上应该对世界食品价格高涨负责。

近来从面包到牛奶在内的各种食品都出现了全球性涨价，并在一些国家推动了通胀，他说：“这场危机是由投机造成的，并将持续下去，对美元的信心不足已经使得投资基金转向商品寻求更高回报，首先是金属，然后是食品。

”由此可以推出：A．投资基金投机行为造成全球食品上涨B．投资基金原来的投资对象是美元C．加拿大食品价格上涨与美元疲软有关D．投机行为也导致全球金属价格提高3.有以下几个条件成立：（1）如果小王是工人，那么小张不是医生；（2）或者小李是工人，或者小王是工人；（3）如果小张不是医生，那么小赵不是学生；（4）或者小赵是学生，或者小周不是经理。

以下哪项如果为真，可得出“小李是工人”的结论？A.小周不是经理B.小王是工人C.小赵不是学生D.小周是经理4.乒乓球单打决赛在甲、乙、丙、丁四位选手中进行，赛前，有些人预测比赛的结果，A说：甲第4。

B说：乙不是第2，也不是第4。

C说：丙的名次在乙的前面。

D说：丁将得第1。

比赛结果表明，四个人中只有一个人预测错了。

图形推理练习题答案

<一>1.【答案】C。

中公解析：第一、三个图都由直线组成;第二、四个图都由一条曲线和一条直线组成。

2.【答案】C。

中公解析：①③⑤都是水平对称图形，②④⑥都是竖直对称图形。

3.【答案】C。

中公解析：第一组图形的直线数分别为8、16、32，成等比数列，第二组图形的直线数应为1、2、(4)，应选择C。

4.【答案】D。

中公解析：每个图形都有5个交点，只有D符合。

5.【答案】A。

中公解析：每行来看，第一个图形的第一行星星依次减少一个得到第二、三个图形。

6.【答案】D。

中公解析：1个菱形换算为2个三角形，则每个图形都相当于有12个三角形。

7.【答案】C。

中公解析：每一行图形中，前两个图形去除与黑点相连接的线，然后叠加得到第三个图形。

由此选择C。

8.【答案】A。

中公解析：每行三个图形封闭区域数之和均为8，问号处图形应只有1个封闭区域，选择A。

9.【答案】D。

中公解析：前两个图形中心重合相叠加并去掉外框得到第三个图形，因此选择D。

10.【答案】A。

中公解析：观察题干中的6组图形，可发现这6组图形都含有两个小黑点。

仔细观察小黑点的位置关系，可发现在①③⑥中，黑点是不相通的;在②④⑤中，黑点是相通的。

<二>1.【答案】Ｃ。

中公解析：第二、三、四个图形中的斜线都可以在第一个图形中找到。

选项中只有Ｃ项满足这一规律。

2.【答案】Ｄ。

中公解析：1个菱形换算为2个三角形，则每个图形都相当于有12个三角形。

【考点点拨】对于这种存在两种小图形的题目，首先考查两种图形各自的数量变化，发现没有明显规律，再考查这两个图形整体的数量变化，依然没有发现规律，此时应该考虑图形间的数量等价转换。

3.【答案】Ｂ。

中公解析：“时针”和“分针”的夹角依次为30°、60°、90°、120°、（150°）。

4.【答案】Ｄ。

中公解析：各图形的交点个数依次为8、7、6、5、（4）。

小学生逻辑思维推理题训练题及答案

小学生逻辑思维推理题训练题及答案1、有两个桶，一个三斤，一个五斤，水无限，如何得出精确的四斤水。

2、夜晚过一桥，甲过需要一分钟，乙两分钟，丙五分钟，丁十分钟。

桥一次最多只能承受两人，过桥必须使用手电筒，现在只有一只手电筒。

请问4人如何在17分钟内全部过桥。

3、小赵的店里来了一位顾客，挑了20元的货，顾客拿出50元，小赵没零钱找不开，就到隔壁小韩的店里把这50元换成零钱，回来给顾客找了30元零钱。

过一会，小韩来找小赵，说刚才的是假钱，小赵马上给小李换了张真钱。

问：在这一过程中小赵赔了多少钱4、鸡妈妈领着自己的孩子出去觅食，为了防止小鸡丢失，她总是数着，从后向前数到自己是8，从前向后数，数到她是9。

鸡妈妈最后数出来她有17个孩子，可是鸡妈妈明明知道自己没有这么多孩子。

那么这只糊涂的鸡妈妈到底有几个孩子呢鸡妈妈为什么会数错5、用水果刀平整地去切一个大西瓜，一共切10刀，最多能将西瓜切成多少块最少能切多少块6、小李有40元钱，他想用他们买饮料，老板告诉他，2元钱可以买一瓶饮料，4个饮料瓶可以换一瓶饮料。

那么，小李可以买到多少瓶饮料7、有一口深4米的井，井壁非常光滑。

井底有只青蛙总是往井外跳，但是，这只青蛙每次最多能跳3米，你觉得这只青蛙几次能跳到井外去吗为什么8、小红和小丽一块到新华书店去买书，两个人都想买《综合习题》这本书，但钱都不够，小红缺少4.9元，小丽缺少0.1元，用两个人合起来的钱买一本，但是钱仍然不够，那么，这本书的价格是多少呢9、明明牵着一只狗和两只小羊回家，路上遇到一条河，没有桥，只有一条小船，并且船很小，他每次只能带狗或一只小羊过河。

你能帮他想想办法，把狗和羊都带过河去，又不让狗咬到小羊。

10、如果有9个乒乓球，要分别装在4个袋里，保证每个袋里有乒乓球，并且每个袋里的乒乓球个数是单数，你能想出办法吗11、盗贼从窗户潜入三楼一卧室内盗走了梳妆台上的一枚钻石戒指。

经实地调查，此盗贼未携带任何作安案具，看来其身体敏捷，功夫也不一般，但却在梳妆台上留下了明显的指纹。

奥数四年级简单推理习题+答案

奥数四年级简单推理习题+答案一、知识要点解答推理问题，要从许多条件中找出关键条件作为推理的突破口。

推理要有条理地进行，要充分利用已经得出的结论，作为进一步推理的依据。

二、精讲精练【例题1】一包巧克力的重量等于两袋饼干的重量，4袋牛肉干的重等于一包巧克力的重量，一袋饼干等于几袋牛肉干的重量？练习1：（1）一只菠萝的重量等于4根香蕉的重量，两只梨子的重量等于一只菠萝的重量，一只梨子的重量等于几根香蕉的重量？（2）3包巧克力的重量等于两袋糖的的重量，12袋牛肉干的重量等于3包巧克力的重量，一袋糖的重量等于几袋牛肉干的重量？（3）一只小猪的重量等于6只鸡的重量，3只鸡的重量等于4只鸭的重量。

一只小猪的重量等于几只鸭的重量？【例题2】一头象的重量等于4头牛的重量，一头牛的重量等于3匹小马的重量，一匹小马的重量等于3头小猪的重量。

一头象的重量等于几头小猪的重量？练习2：（1）一只西瓜的重量等于两个菠萝的重量，1个菠萝的重量等于4个苹果的重量，1个苹果的重量等于两个橘子的重量。

1只西瓜的重量等于几个橘子的重量？（2）一头牛一天吃草的重量和一只兔子9天吃草的重量相等，也和6只羊一天吃草的重量相等。

已知一头牛每天吃青草18千克，一只兔子和一只羊一天共吃青草多少千克？（3）一只小猪的重量等于6只鸡的重量，3只鸡的重量等于4只鸭的重量，两只鸭的重量等于6条鱼的重量。

问：两只小猪的重量等于几条鱼的重量？【例题3】根据下面两个算式，求○与□各代表多少？○＋○＋○=18 ○＋□=10练习3：（1）根据下面两个算式，求□与△各代表多少？□＋□＋□＋□=32 △ －□=20（2）根据下面两个算式，求○与□各代表多少？○＋○＋○=15 ○＋○＋□＋□＋□=40（3）根据下面两个算式，求○与△各代表多少？○－△=8 △＋△＋△=○【例题4】根据下面两个算式，求○与△各代表多少？△－○=2 ○＋○＋△＋△＋△=56练习4：（1）根据下面两个算式求□与○各代表多少？□－○=8 □＋□＋○＋○=20（2）根据下面两个算式，求△与○各代表多少？△＋△＋△＋○＋○=78 △＋△＋○＋○＋○=72（3）根据下面两个算式，求△与□各代表多少？△＋△＋△－□－□=12 □＋□＋□－△－△=2【例题5】甲、乙、丙三人分别是一小、二小和三小的学生，在区运动会上他们分别获得跳高、跳远和垒球冠军。

逻辑推理习题及答案(3)

【例题1】所有的亲戚我都问过了，谁也不知道明明的下落。

上述断定为假，以下判定可以确定为真的是:A.有的亲戚不知道明明的下落B.有的亲戚知道明明的下落C.没有亲戚知道明明的下落D.知道明明下落的亲戚没有问到【例题2】有些不是鱼的动物外表像鱼。

与以上判断等值的是:A.有些外表像鱼的动物不是鱼B.有些外表像鱼的动物是鱼C.有些不是鱼的动物外表不像鱼D.有些鱼外表不像鱼【例题3】如果“我们班有的同学不会使用计算机”是一个真判断，下面不能确定其真假的是:A.我们班至少有一个同学不会使用计算机B.我们班所有的同学都会使用计算机C.我们班有的同学会使用计算机D.不会使用计算机的有些是我们班的同学【例题4】某人说:“不可能所有的人都会投他的赞成票。

”与以上判断的意思最相近的是:A.可能所有的人都会投他的赞成票B.可能所有的人都不会投他的赞成票C.必然所有的人都会投他的赞成票D.必然有的人不会投他的赞成票【例题5】调查人员发现，被害人曾两次向朋友提到了被威胁的事，一次是1996年5月，她向男朋友周某提出分手，周某威胁要毁她的容。

另一次没有说时间，只说她在6年里经常受到周某的威胁。

以上事实最好地支持了下面哪项?A.被害人1996年5月开始受到周某的威胁B.周某威胁了被害人6年C.被害人是被周某杀害的D.被害人因要和周某分手而经常受到威胁【例题6】所有的聪明人都是近视眼,我近视得很厉害,所以我很聪明。

以下哪项与上述推理的逻辑结构一致?()A.我是个笨人,因为所有的聪明人都是近视眼,而我的视力那么好B.所有的猪都有四条腿,但这种动物有八条腿,所以它不是猪C.小陈十分高兴,所以小陈一定长得很胖;因为高兴的人都能长胖D.所有的鸡都是尖嘴,这种总在树上呆着的鸟是尖嘴,所以它是鸡【例题7】母亲要求儿子从小就努力学外语。

儿子说:“我长大了又不想当翻译,何必学外语。

”以下哪项是儿子的回答中包含的前提?()A.要当翻译,需要学外语B.只有当翻译,才需要学外语C.学习外语也不得见得能当翻译D.学了外语才能当翻译【例题8】已知:第一,《神鞭》的首次翻译出版用的或者是英语或者是日语,二者必居其一。

图形推理专项习题100道(附答案)

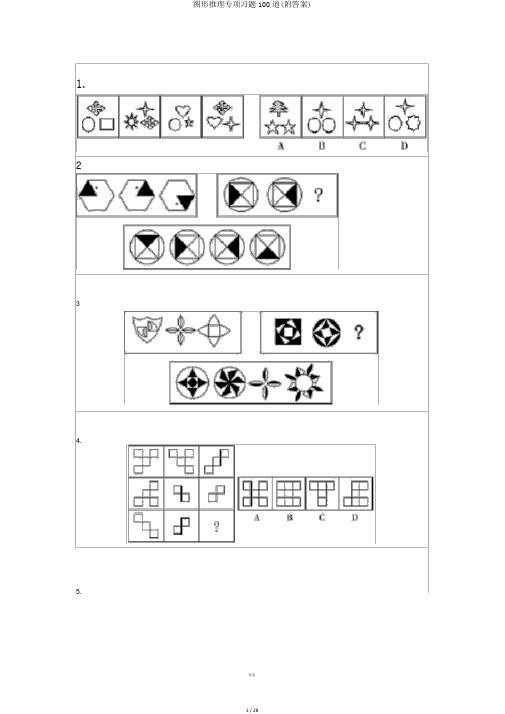
1. 2 34.5.6.7.8.9.10.11.12.13.14.15.16. 将下边左图进行折叠后，获得的图形是（）17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：51.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：52.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：53.左边给定的是纸盒的表面面，下边哪一项能由它折叠而成？54.左边给定的是纸盒的表面面，下边哪一项能由它折叠而成？55.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：56.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：57.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：58.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：59.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：60.左边给定的是纸盒的表面面，下边哪一项能由它折叠而成？61.左边给定的是纸盒的表面面，下边哪一项能由它折叠而成？62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.80.81.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：82.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：83.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：84.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：85.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：86.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：87.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：88.从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：89.左边给定的是纸盒的表面面，下边哪一项能由它折叠而成？90.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：91.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：92.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：93.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：94.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：95.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性96.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：97.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：98.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：99.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：100.请从所给的四个选项中，选择最适合的一个填入问号处，使之体现必定的规律性：1．【答案】Ｄ。

小学数学推理练习题答案

小学数学推理练习题答案1. 推理题答案：1) 答案：C。

解析：根据题干中的条件，小明今天买了苹果和香蕉，且香蕉的数量是苹果的两倍。

假设小明买了苹果a个，香蕉2a个。

又知道总共花费了12元，每个苹果1元，每个香蕉2元。

所以可以列出方程：a + 2a = 12，解得a = 4。

因此，小明买了4个苹果。

2) 答案：A。

解析：根据题干中的条件，Jeffrey比小明多看了6页书，而小明读了书中的前1/5。

设书共有x页。

小明读了前1/5，即x/5页；Jeffrey比小明多看了6页，即x/5 + 6页。

根据题意，他们两人一共看了1/2的书，即(x/5) + (x/5 + 6) = x/2。

解得x = 60。

所以，书共有60页。

2. 推理题答案：1) 答案：C。

解析：根据题干中的条件，每班有40名同学，3个班级一共有120名同学。

而每名同学捐献1元，所以筹集的善款为120元。

2) 答案：B。

解析：根据题干中的条件，每天总共骑行150米，10天总共骑行的距离为150 × 10 = 1500米。

由于1千米等于1000米，所以1500米等于1.5千米。

因此，小明总共骑行了1.5千米。

3. 推理题答案：1) 答案：B。

解析：根据题干中的条件，小王每天比小李多骑行3公里，而小李每天骑行15公里。

设小王每天骑行的公里数为x，则小王每天骑行15 + x公里。

根据题意，小王和小李一共骑行了6天，所以总公里数为(15 + x) × 6公里。

又知道总骑行距离为102公里，所以(15 + x) × 6 = 102。

解得x = 3。

因此，小王每天骑行15 + 3 = 18公里。

2) 答案：A。

解析：根据题干中的条件，小明每天至少骑行5公里，而小王每天至少骑行4公里。

设小明每天骑行的公里数为x，小王每天骑行的公里数为y。

可得不等式组：x + y ≤ 24，x ≥ 5，y ≥ 4。

求解该不等式组得出x的最大值为x = 19。

小学数学《逻辑推理》练习题(含答案)

小学数学《逻辑推理》练习题（含答案）（一）条件分析【例1】小东、小南和小北是好朋友，他们中一位是教师，一位是医生，一位是司机，现在只知道，小北比司机年纪大，小东和医生不同岁，医生比小南年龄小，请问：谁是教师，谁是医生，谁是司机？分析：我们可以通过列表法解答这道题：根据“小北比司机年纪大”判断出小北不是司机；根据“小东和医生不同岁”判断出小东不是医生；根据“医生比小南年龄小”判断出小南不是医生，所以小北是医生；根据年龄大小来判断：小北比小南年龄小，小北比司机年纪大，所以小南也比司机年龄大，所以小南是教师，小东是司机.[巩固]小王、小张和小李一位是工人，一位是农民，一位是教师，现在只知道：小李比教师年龄大；小王与农民不同岁；农民比小张年龄小．问：谁是工人？谁是农民？谁是教师？分析：由题目条件可以知道：小李不是教师，小王不是农民，小张不是农民．由此得到左下表．表格中打“√”表示肯定，打“×”表示否定．因为左上表中，任一行、任一列只能有一个“√”，其余是“×”，所以小李是农民，于是得到右上表．因为农民小李比小张年龄小，又小李比教师年龄大，所以小张比教师年龄大，即小张不是教师．因此得到左下表，从而得到右下表，即小张是工人，小李是农民，小王是教师．采用列表法，使得各种关系更明确．为了讲解清楚，例题中画了几个表，实际解题时，不用画这么多表，只在一个表中先后画出各种关系即可．需要注意的是：①第一步应将题目条件给出的关系画在表上，然后再依次将分析推理出的关系画在表上；②每行每列只能有一个“√”，如果出现了一个“√”，它所在的行和列的其余格中都应画“×”．【例2】森林里举行动物运动会，小猴、小兔、小马、小羊和小鹿参加赛跑．小马在小羊和小猴之前跑到终点，小猴没有小羊跑得快，小兔紧跟着小马之后跑到终点，有两只小动物在小鹿和小羊之间跑到终点，这五只小动物的名次分别是多少呢？分析：可以用画图的方法进行分析．因为“小马在小猴和小羊之前跑到终点，小猴没有小羊跑得快“，所以小马比小猴和小羊都跑得快，用下图表示：又因为“小兔紧跟着小马之后跑到终点，有两只小动物在小鹿和小羊之间跑到终点”，可以判断小兔在小马后面，小鹿应该是第一名，如图所示：【例3】中关村一小举办歌咏比赛，六个年级排名次，比赛的最后结果得分情况如下：（1）四年级的得分比一年级高；（2）五年级的得分比二年级高，但比一年级低；（3）三年级的得分比四年级低，但比一年级高．请你判断哪个年级在这次歌咏比赛中得了第1名？分析：建议教师在本题的讲解中强调“数轴定位”的数学方法.我们先将题目中所列举的条件翻译一下：由（1）知，四年级的得分＞一年级的得分，在数轴上表示为：一年级四年级由（2）知，一年级的得分＞五年级的得分＞二年级的得分，在数轴上表示为：二年级五年级一年级四年级由（3）知，四年级的得分＞三年级的得分＞一年级的得分，在数轴上表示为：三年级二年级五年级一年级四年级于是我们可以知道四年级的得分是本次歌咏比赛的五个年级中最高的，所以四年级得了第一名．【例4】编号分别为1，2，3，4的四位同学参加了学校的110米栏比赛，获得了全校的前四名，1号同学说：“3号比我先到达终点.”得第三名的同学说：“1号不是第四名.”而另一位同学说：“我们的号码与我们所得的名次都不相同.”聪明的同学们，你们能说出这四位同学各自所得到的名次吗？分析：从得第三名同学的话中可以推知：1号不是第三名，也不是第四名；而1号同学又说“3号比我先到终点”，这说明1号同学不是第一名，这样我们可以得知1号同学是第二名，于是3号同学是第一名，而另一位同学说：“我们的号码与我们所得的名次都不相同.”，这样4号不是第四名，只能是第三名，所以获得第四名的同学是2号.[拓展]小刚在纸条上写了一个四位数，让小明猜．小明问：“是603l 吗?”小刚说：“猜对了1个数字，且位置正确．”小明问：“是5672吗?”小刚说：“猜对了2个数字，但位置都不正确．”小明问：“是4796吗?”小刚说：“猜对了4个数字，但位置都不正确．”根据以上信息，可以推断出小刚所写的四位数多少？分析：由两人的第3次问答可知小刚所写的四位数是由数字4，7，9，6组成的．因为数字6在603l 中出现，所以据小刚的第1次回答知四位数的千位数字就是6．又数字7在5672和4796中均出现过，且小刚说其位置均不正确，所以7应该出现在个位．数字9在4796中出现，但它的位置也不正确，所以9只能在百位，进而4是十位数字．综上所述，所求的四位数是6947．（一般电子辞典等学习工具中会有类似这种题目的小游戏，可以锻炼学生的逻辑思维）【例5】一个粉笔盒的六个面分别涂上了红、黄、绿、蓝、黑、白六种颜色．从三个不同角度看到粉笔盒如下视图，请你判断每种颜色的对面是什么颜色?⑶⑵⑴黑黄黑蓝绿白红绿白分析：本题的要点在于“相邻的面不同色”，所以本题可以采用排除法解决.由第一个图，红色与白色、与绿色相邻，所以红色的对面不可能是白色与绿色，同理，白色对面不是红、绿色，绿色对面不是红、白色，如图（1）（建议老师用红笔连线表示不对面，绿色表示对面）：黑黄蓝绿白红黑黄蓝绿白红黑黄蓝绿白红（1）（2）（3）由第二个图，白色对面不可能是蓝色与黑色，蓝色对面不可能是黑、白色，黑色对面不可能是蓝、白色如图（2）；由第三个图，绿色对面不可能是黄色与黑色，黑色对面不是黄、绿色，黄色对面不是黑、绿色，如图（3）.现在看图（3），绿色的对面只能是蓝色；白色对面只能是黄色；黑色对面只能是红色.【例6】宝宝、贝贝、聪聪每人有两个外号，人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们，此外：（1）数学博士夸跳高冠军跳的高（2）跳高冠军和大作家常与宝宝一起看电影（3）短跑健将请小画家画贺年卡（4）数学博士和小画家关系很好（5）贝贝向大作家借过书（6）聪聪下象棋常赢贝贝和小画家问：宝宝、贝贝、聪聪各有哪两个外号吗？分析：由（2）知，宝宝不是跳高冠军和大作家；由（5）知，贝贝不是大作家；由（6）知，贝贝、聪聪都不是小画家，可以得到下表：因为宝宝是小画家，所以由（3）（4）知宝宝不是短跑健将和数学博士，推知宝宝是歌唱家，因为聪聪是大作家，所以由（2）知聪聪不是跳高冠军，推知贝贝是跳高冠军，因为贝贝是跳高冠军，所以由（1）所以，宝宝是小画家和歌唱家，贝贝是短跑健将和跳高冠军，聪聪是数学博士和大作家.[开心数学]有个学生请教爱因斯坦学习逻辑推理有什么用，爱因斯坦问他：“两个人从烟囱里爬出去，一个满脸烟灰，一个干干净净，你认为哪一个该去洗澡？”“当然是脏的那个．”学生说，爱因斯坦回答：“不对．脏的那个看见对方干干净净，以为自己也不会脏，哪里会去洗澡？”（二）真假判断【例7】四个小朋友宝宝、星星、强强和乐乐在院子里踢足球，一阵响声，惊动了正在读书的王老师，王老师跑出来查看，发现一块窗户玻璃被打破了．王老师问：“是谁打破了玻璃？”宝宝说：“是星星无意打破的．”星星说：“是乐乐打破的．”乐乐说：“星星说谎．”强强说：“反正不是我打破的．”如果只有一个孩子说了实话，那么这个孩子是谁？是谁打破了玻璃？分析：因为星星和乐乐说的正好相反，所以必是一对一错，可以逐一假设检验假设星星说得对，即玻璃窗是乐乐打破的，那么强强也说对了，这与“只有一个孩子说了实话”矛盾，所以星星说错了．假设乐乐说对了，按题意其他孩子就都说错了．由强强说错了，推知玻璃是强强打破的．宝宝、星星确实都说错了．符合题意．所以是强强打破了玻璃．［拓展］动物王国发生了一起盗窃案，由狮子法官审理，它对涉及到的四名嫌疑犯狐狸、松鼠、老虎、黄鼠狼进行了审问．四人分别供述如下：狐狸说：“罪犯在松鼠、老虎、黄鼠狼三人之中．”松鼠说：“我没有做案，是老虎偷的．”老虎说：“在狐狸和黄鼠狼中间有一人是罪犯．”黄鼠狼说：“松鼠说的是事实．”经过充分的调查，证实这四人中有两人说了真话，另外两人说的是假话．同学们，你能确认谁是罪犯吗？分析：松鼠和黄鼠狼是盗窃犯．如果狐狸说的是假话，那么剩下三人中有一人说的也是假话，另外两人说的是真话．可是松鼠和黄鼠狼两人的观点一致，所以在剩下的三人中只能是老虎说了假话，松鼠和黄鼠狼说的都是真话．即“老虎是盗窃犯”．这样一来，狐狸说的也是对的，不是假话．这样，前后就产生了矛盾．所以狐狸说的不可能是假话，只能是真话．同理，剩下的三人中只能是老虎说真话．松鼠和黄鼠狼说的是假话，即老虎不是罪犯，松鼠是罪犯．又由狐狸所述为真话，即狐狸不是罪犯．再由老虎所述为真话，即黄鼠狼是罪犯．注意：用假设法解决逻辑问题，就是根据题目的几种可能情况，逐一假设，如果推出矛盾，那么假设不成立；如果推不出矛盾，那么符合题意，假设成立.【例8】小猫、小狗、小兔子和小松鼠在比较它们的身高，小猫说：“我最高”．小狗说：“我不最矮”小兔子说：“我没有小猫高，但是还有人比我矮”小松鼠说：“我最矮”．经过测量，有一只小动物说错了，请将它们按身高次序从高到矮排列出来．分析：小松鼠不可能说错，否则就没有最矮的了，由此推出小狗也没有说错，假设小猫也没有说错，那么小兔子说的也就是对的了，所以，说错话的是小猫，可以推出它们的高矮顺序是：小狗、小猫、小兔子、小松鼠.【例9】小白兔、小黑兔、小花兔和小灰兔进行赛跑，比赛结束后，小白兔、小黑兔、小花兔说了以下几句话，小灰兔没有说话．小白兔：小花兔第一名，我第三名小黑兔：我第一名，小灰兔第四名小花兔：小灰兔第二名，我第三名比赛成绩公布后，发现它们都只说对了一半，你能说出它们的名次是如何排列的吗？分析：因为每只小兔子说的两句话中，有一半是对的，即一句对一句错，我们可以先假设某一句话是对的来进行推理，如果出现矛盾，就说明这句话是错的．假设小白兔说的前半句是对的，即小花兔是第一名，那么它说的第二句话“我第三名”就是错的；因为小花兔是第一名，那么小黑兔说的第一句就是错的，它说的小灰兔第四名就是对的；因为小灰兔是第四名，那么小花兔说的小灰兔第二名就是错的，它说的“我第三名”是对的，即小花兔是第三名，这样，小花兔既是第一名又是第三名，发生矛盾，所以假设是错误的，即小白兔说的前半句话不可能是对的．由上面的假设，小白兔说的后半句话一定是对的，即小白兔第三名，那么小花兔说的“我第三名”就是错的，它说的“小灰兔第二名”是对的，推出小黑兔说的“小灰兔第四名”是错的，从而小黑兔是第一名，所以小花兔是第四名．名次排列为：小黑兔、小灰兔、小白兔、小花兔.［拓展］三年级一班新转来三名学生，班主任问他们三人的年龄．刘强说：“我12岁，比陈红小2岁，比李丽大1岁．”陈红说：“我不是年龄最小的，李丽和我差3岁，李丽是15岁．”李丽说：“我比刘强年岁小，刘强13岁，陈红比刘强大3岁．”这三位学生在他们每人说的三句话中，都有一句是错的．请你帮助班主任分析出他们三人各是多少岁？分析：经过审题，仔细分析这九句话，不难发现有两句话是相互矛盾的．一句话是刘强说的第一句话：“我12岁”，另一句话是李丽说的第二句话：“刘强13岁”．这两句话不能都真，必有一句是假的．为了确定这两句话的真假性．可以先假设某一句为真，如果推不出矛盾，本题就获得了解决；如果推出矛盾，就说明这句话是假的，从而也就找到了突破口．先假设刘强说的第一句话“我12岁”为真，那么李丽说的第二句话“刘强13岁”就为假，因此李丽的另外两句话就应该是真话，从“陈红比刘强大3岁”就推出陈红是15岁；又从“我比刘强年岁小”推出李丽小于12岁．可是这样一来，陈红说的三句话中，“李丽和我差3岁”和“李丽15岁”这两句话都不能成立，这与本题中的要求（“每人说的三句话中，都有一句是错的”，即三句话中有两句话是真的）相矛盾．因此，刘强说的“我12岁”这句话是假的．由于刘强说的第一句话是假的，所以后两句话就是真的．因此，李丽说的第三句话“陈红比刘强大3岁”就是假的，所以，李丽说的第二句话“刘强13岁”就是真的．于是就可以推出：李丽12岁，陈红15岁，刘强13岁．【例10】在神话王国内，居民不是骑士就是骗子，骑士不说谎，骗子永远说谎，有一天国王遇到该国的居民小白、小黑、小蓝，小白说：“小蓝是骑士，小黑是骗子．”，小蓝说：“小白和我不同，一个是骑士，一个是骗子．”国王很快判断出谁是骑士，谁是骗子．你能判断出吗？分析：假设小白是骑士（说实话），则小蓝是骑士，小黑是骗子；又因为小蓝是骑士，那么小白、小蓝不同，一个是骑士，一个是骗子，与小白、小蓝均为骑士矛盾．假设小白是骗子（说假话），那么小蓝是骗子，小黑是骑士，又因为小蓝是骗子，所以小白、小蓝不同是假话．因此，小白、小蓝是骗子，小黑是骑士.[拓展]甲、乙、丙三人，一个总说谎，一个从不说谎，一个有时说谎．有一次谈到他们的职业．甲说：“我是油漆匠，乙是钢琴师，丙是建筑师．”乙说：“我是医生，丙是警察，你如果问甲，甲会说他是油漆匠．”丙说：“乙是钢琴师，甲是建筑师，我是警察．”你知道谁总说谎吗？分析：甲．如果甲从不说谎，那么乙的最后一句、丙的第一句都对，没有总说谎的人，矛盾；同理，如果丙从不说谎，也将推出矛盾．【例11】数学竞赛后，小明、小华和小强各获得一枚奖牌，其中一人得金牌，一人得银牌，一人得铜牌．老师猜测：“小明得金牌，小华不得金牌，小强不得铜牌．”结果老师只猜对了一个，那么谁得金牌，谁得银牌，谁得铜牌？分析：小华得金牌，小强得银牌，小明得铜牌．（1）若小明得金牌，小华一定“不得金牌”，这与“老师只猜对了一个”相矛盾，不合题意．（2）若小华得金牌，那么“小明得金牌”与“小华不得金牌”这两句都是错的，那么“小强不得铜牌”应是正确的，那么小强得银牌，小明得铜牌．（三）分析计算【例12】三年级举行乒乓球单循环比赛，王同、李涛、韩伟、张洪、付文五人参加．胜者得2分，负者不得分，已知比赛结果如下：（1）王同与付文并列第一名；（2）李涛是第三名；（3）韩伟与张洪并列第四名．求李涛的得分．分析：共五名选手比赛，每人都要赛4场，每名选手得分均为偶数，且最少0分，最多8分，又有两个并列第一和两个并列第四，所以，没有四场全胜，也没有4场全败的.五人参加比赛：4×5÷2=10（场），十场球总得分：2×10=20（分），由于有两个并列第一，两个并列第四，所以没有全胜的，也没有全败的，即没有得8分的，也没有得0分的，因此，并列第一只能得6分，6×2=12（分）；并列第四得2分，2×2=4（分），所以，第三名得20-12-4=4（分），即李涛得4分.［拓展］某次考试，A，B，C，D，E五人的得分是互不相同的整数．A说：“我得了94分．”B说：“我在五人中得分最高．”C说：“我的得分是A和D的平均分．”D说：“我的得分恰好是五人的平均分．”E说：“我比C多得2分，在我们五人中是第二名．”问：这五个人各得多少分？（总分100分）分析：B，E，D，C，A依次得98，97，96，95，94分．由B，E所说，推知B第一、E第二；由C，D所说，推知C，D都不是最低，所以A最低；由A最低及C 所说，推知C在A，D之间，即D第三、C第四．五个人得分从高到底的顺序是B，E，D，C，A．因为C是A，D的平均分，A是94分，所以D的得分必是偶数，只能是96或98．如果D是98分，则C是（98＋94）÷2＝96（分）， E是96＋2＝98（分），与D得分相同，与题意不符．因此D是96分，C得95分，E得97分， B得96×5－（94＋95＋96＋97）＝98（分）．B，E，D，C，A依次得98，97，96，95，94分．[韵律小诗]逻辑推理有规律，基本方法有两个；已知条件必相关，活用“假设”与“排除”．严密分析做假设，排除一切不可能；逐步归纳与总结，正确答案轻松找；运用“假设”与“画图”，还有列表等方法；此类问题常见到，生活处处有学问；冷静仔细逐一对，条理清楚不慌张；掌握逻辑善推理，聪明过人办法多；不仅益于学数学，其它学科亦有助.[小规律]逻辑推理必须遵守四条基本规律：（1）同一律．在同一推理过程中，每个概念的含义，每个判断都应从始至终保持一致，不能改变．（2）矛盾律．在同一推理过程中，对同一对象的两个互相矛盾的判断，至少有一个是错误的．例如，“这个数大于8”和“这个数小于5”是两个互相矛盾的判断，其中至少有一个是错的，甚至两个都是错的．（3）排中律．在同一推理过程中，对同一对象的两个恰好相反的判断必有一个是对的，它们不能同时都错．例如“这个数大于8”和“这个数不大于8”是两个恰好相反的判断，其中必有一个是对的，一个是错的．（4）理由充足律．在一个推理过程中，要确认某一判断是对的或不对的，必须有充足的理由．1.（例1）甲、乙、丙分别是来自中国、日本和英国的小朋友．甲不会英文，乙不懂日语却与英国小朋友热烈交谈．问：甲、乙、丙分别是哪国的小朋友？分析：乙不懂日语却与英国小朋友热烈交谈说明乙不是日本人和英国人，所以乙是中国人，甲不懂英文，说明甲是日本人，丙是英国人．2.（例5）有一个正方体，每个面上分别写有1、2、3、4、5、6.有三个学生从不同的角度观察，结果如图4-5-2．问这个正方体每个数字的对面各是什么数字?分析：1的对面是5，2的对面是4，3的对面是63.（例6）徐、王、陈、赵四位师傅分别是工厂的木工、车工、电工和钳工，他们都是象棋迷．（1）车工只和电工下棋；（2）王、陈两位师傅经常与木工下棋；（3）徐师傅与电工下棋互有胜负；（4）陈师傅比钳工下得好．问：徐、王、陈、赵四位师傅各从事什么工种？分析：由（2）（3）（1）可画出右表：徐是车工，王是钳工，陈是电工，赵是木工．4.（例9）学校新来了一位老师，五个学生分别听到如下的情况：（1）是一位姓王的中年女老师，教语文课；（2）是一位姓丁的中年男老师，教数学课；（3）是一位姓刘的青年男老师，教外语课；（4）是一位姓李的青年男老师，教数学课；（5）是一位姓王的老年男老师，教外语课．他们听到的情况各有一项正确，请问：真实情况如何？分析：姓刘的老年女老师，教数学．假设是男老师，由（2）（3）（5）知，他既不是青年、中年，也不是老年，矛盾，所以是女老师．再由（1）知，她不教语文，不是中年人．假设她教外语，由（3）（5）知她必是中年人，矛盾，所以她教数学．由（2）（4）知她是老年人，由（3）知她姓刘．5.（例12）有1克、2克、4克和8克的砝码各一个，其中丢了一个砝码，所以在砝码放在一端，只能称一次的情况下，无法称出12克和7克的重量，问丢的那个砝码是几克重的？分析：注意题目中的重要条件：在砝码放在一端，只能称一次的情况下，无法称出12克和7克的重量，要称12克的重量必有8克砝码，要称7克重量必有4克砝码，以此为突破口进行推理．因为8+4=12，所以称12克的重量必有8克和4克的砝码，又因为1+2+4=7，所以称7克的重量必有1克、2克、4克的砝码，综上所述，因为称12克与7克的重量都要用4克的砝码，所以丢失的砝码是4克重的.。

小学数学《逻辑推理》练习题(含答案)

小学数学《逻辑推理》练习题（含答案）例题分析【例1】（☆☆）有一天，李强、王雷、丁红、孙丽四名运动员围坐在桌旁聊天。

已知： ⑴ 丁红的对面是足球运动员；⑵ 李强的左边是篮球运动员；⑶ 孙丽的对面是王雷；⑷ 篮球运动员与乒乓球运动员不相邻；⑸ 排球运动员的右边是孙丽。

根据上面的情况判断，王雷是什么球类运动员？分析：由⑶、⑸可知图一，由⑴可进一步知道图二，再由⑴可补充画出图三，最后由⑵可得图四：所以王雷是乒乓球运动员。

【例2】（☆☆）在一列国际列车上，有A ，B ，C ，D 四位不同国籍的旅客，他们分别穿蓝、黑、灰、褐色的大衣，面对面每边两人地坐在同一张桌子上。

已知：⑴ 英国旅客坐在B 先生左侧；⑵ A 先生穿褐色大衣；⑶ 穿黑色大衣的坐在德国旅客右侧；⑷ D 先生的对面坐着美国旅客；⑸ 俄国旅客穿着灰色大衣。

问：A ，B ，C ，D 分别是哪国人？分别穿着什么颜色的大衣？分析：由⑶、⑸可知德国旅客穿的大衣不可能是黑色和灰色，由⑴、⑶可知德国旅客和英国旅客斜对面，即德国旅客与B 先生面对面，与C 先生相邻，因此四位旅客的国籍与大衣颜色如上右表：【例3】（☆☆）有八个球编号是①至⑧，其中有六个球一样重，另外两个球都轻1克，为了找出这两个轻球，用天平称了三次，结果如下：第一次①+②比③+④重，第二次⑤+⑥比⑦+⑧轻，第三次①+③+⑤与②+④+⑧一样重。

那么两个轻球的编号是？分析：从第一次称重和第二次称重的情况来看，③号球和④号球中必有一个轻球，⑤号球和⑥号球中必有一个轻球，其它球都是标准球。

我们再来看第三次称重的情况，②号和⑧号都是标准球，如果④号也是标准球，从“一样重”可推出③号、⑤号也都是标准球，这就与“③号、④号球中必有一轻球”不符合，可见④号球是轻球。

④号球是轻球，可知③号球是标准球，再由第三次的“一样重”，得到⑤号球是轻球。

所以两个轻球的编号是④号和⑤号。

【例4】（☆☆☆）小赵的电话号码是一个五位数，它由五个不同的数字组成。

推理技术习题以及答案

习题三求下列谓词公式的子句集。

(1)∃x∃y(P(x,y) ∧Q(x,y))解：去掉存在量词变为：P(a,b)∧Q(a,b)变成子句集{ P(a,b),Q(a,b)}(2)∀x ∀y(P(x,y) →Q(x,y))解：去掉蕴涵符号变为：∀x ∀y(¬ P(x,y) ∨ Q(x,y))去掉全称量词变为：¬ P(x,y) ∨ Q(x,y)变成子句集{ ¬ P(x,y) ∨ Q(x,y)}(3)∀x∃y((P(x,y) ∨Q(x,y)) →R(x,y))解：去掉蕴涵符号变为：∀x ∃y(¬ (P(x,y) ∨ Q(x,y)) ∨ R(x,y)) 否定符号作用于单个谓词变为：∀x ∃y((¬ P(x,y) ∧¬ Q(x,y)) ∨ R(x,y)) 去掉存在量词变为：∀x ((¬ P(x,f(x)) ∧¬ Q(x,f(x))) ∨ R(x,f(x))) 去掉全称量词变为：(¬ P(x,f(x)) ∧¬ Q(x,f(x))) ∨ R(x,f(x)化合取范式为：(¬ P(x,f(x)) ∨ R(x,f(x))∧(¬ Q(x,f(x)) ∨ R(x,f(x))变元：(¬ P(x,f(x)) ∨ R(x,f(x)))∧(¬ Q(y,f(y)) ∨ R(y,f(y)))变成子句集{ ¬ P(x,f(x)) ∨ R(x,f(x)), ¬ Q(y,f(y)) ∨ R(y,f(y))} (4)∀x (P(x) →∃y (P(y) ∧R(x,y)))解：去掉蕴涵符号变为：∀x (¬ (P(x) ∨∃y (P(y) ∧R(x,y))) 去掉存在量词变为：∀x (¬ (P(x) ∨ (P(f(x)) ∧R(x,f(x)))去掉全称量词变为：(¬ (P(x) ∨ (P(f(x)) ∧R(x,f(x)))化合取范式为：(¬ (P(x) ∨ P(f(x))) ∧(¬ (P(x) ∨R(x,f(x)))变元：(¬ (P(x) ∨ P(f(x))) ∧(¬ (P(y) ∨R(y,f(y)))变为子句集：{¬ (P(x) ∨ P(f(x)),¬ (P(y) ∨R(y,f(y))}(5)∃x(P(x) ∧∀x(P(y) →R(x,y)))解：去掉蕴涵符号变为：∃x(P(x) ∧∀x(¬P(y) ∨R(x,y)))去掉存在量词变为：P(a) ∧∀x(¬P(y) ∨R(a,y))去掉全称量词变为：P(a) ∧ (¬P(y) ∨R(a,y))变成子句集：{ P(a) ，¬P(y) ∨R(a,y) }(6)∃x∃y∀z ∃u∀v ∃w(p(x,y,z,u,v,w) ∧(Q(x,y,z,u,v,w) ∨¬R(x,z,w))) 解：去掉存在量词变为：∀z ∀v (p(a,b,z,f(z),v,g(z,v)) ∧(Q(a,b,z,f(z),v, g(z,v) ∨¬R(a,z, g(z,v))) 去掉全称量词变为：p(a,b,z,f(z),v,g(z,v)) ∧(Q(a,b,z,f(z),v, g(z,v) ∨¬R(a,z, g(z,v))变元：p(a,b,x,f(x),y,g(x,y)) ∧(Q(a,b,z,f(z),v, g(z,v) ∨¬R(a,z, g(z,v))化成子句集：{p(a,b,x,f(x),y,g(x,y)) , Q(a,b,z,f(z),v, g(z,v) ∨¬R(a,z, g(z,v)) } 3. 试判断下列子句集中哪些是不可满足的。

小学数学《简单的逻辑推理》练习题（含答案）

⼩学数学《简单的逻辑推理》练习题（含答案）⼩学数学《简单的逻辑推理》练习题（含答案）列表分析法【例1】⼩王、⼩张和⼩李⼀位是⼯⼈，⼀位是农民，⼀位是教师，现在只知道：⼩李⽐教师年龄⼤；⼩王与农民不同岁；农民⽐⼩张年龄⼩. 问：谁是⼯⼈？谁是农民？谁是教师？分析：这道题⽬并不难，聪明的⼩朋友思考⼀下就能得到答案，但是今天我们通过这道题⽬⼀起来学习⼀个⼗分有⽤的⽅法：列表分析法. 由题⽬条件可以知道：⼩李不是教师，⼩王不是农民，⼩张不是农民.由此得到左下表。

表格中打“√”表⽰肯定，打“×”表⽰否定.因为左上表中，任⼀⾏、任⼀列只能有⼀个“√”，其余是“×”，所以⼩李是农民，于是得到右上表.因为农民⼩李⽐⼩张年龄⼩，⼜⼩李⽐教师年龄⼤，所以⼩张⽐教师年龄⼤，即⼩张不是教师。

因此得到左下表，从⽽得到右下表，即⼩张是⼯⼈，⼩李是农民，⼩王是教师.例题中采⽤列表法，使得各种关系更明确. 为了讲解清楚，例题中画了⼏个表，实际解题时，不⽤画这么多表，只在⼀个表中先后画出各种关系即可.需要注意的是：①第⼀步应将题⽬条件给出的关系画在表上，然后再依次将分析推理出的关系画在表上；②每⾏每列只能有⼀个“√”，如果出现了⼀个“√”，它所在的⾏和列的其余格中都应画“×”.【巩固】⼩王、⼩张和⼩李原来是邻居，后来当了医⽣、教师和战⼠。

只知道：⼩李⽐战⼠年纪⼤，⼩王和教师不同岁，教师⽐⼩张年龄⼩。

请同学们想⼀想：谁是医⽣，谁是教师，谁是战⼠？分析：⼩李是教师，⼩王是战⼠，⼩张是医⽣。

【例2】甲、⼄、丙每⼈有两个外号，⼈们有时以“数学博⼠”、“短跑健将”、“跳⾼冠军”、“⼩画家”、“⼤作家”和“歌唱家”称呼他们。

此外：（1）数学博⼠夸跳⾼冠军跳得⾼；（2）跳⾼冠军和⼤作家常与甲⼀起去看电影；（3）短跑健将请⼩画家画贺年卡；（4）数学博⼠和⼩画家很要好；（5）⼄向⼤作家借过书；（6）丙下象棋常赢⼄和⼩画家。

推理测试题和答案

推理测试题和答案1. 以下是一则推理测试题，包含情节描述和问题。

请仔细阅读并思考每个问题的答案。

情节描述：昨天晚上，一名年轻女子在她的公寓楼中被发现惨遭杀害。

调查员对现场进行勘查，发现以下证据：- 公寓的前门锁着，没有任何迹象表明有人非法进入。

- 除了被害者的指纹外，没有找到其他任何可疑的指纹。

- 在被害者手中，有一缕细长的黑发。

问题：1) 谁是最有可能是凶手？为什么？2) 凶手是如何进入公寓的？3) 指纹是否可以用来找到凶手？答案：1) 最有可能是凶手的是被害者的室友。

因为公寓的前门是锁着的，没有迹象表明有人非法进入，这意味着凶手很有可能是公寓内的人员。

而作为室友，她有机会接近被害者并犯罪。

2) 凶手是可能利用钥匙进入公寓的。

作为室友，她极有可能掌握了公寓的钥匙，因此轻易进入了公寓而不引起任何怀疑。

3) 指纹可以作为潜在的证据，但并不一定能准确找到凶手。

由于公寓是被害者和室友共同居住的地方，室友的指纹在场景中是正常的。

因此，只有确认指纹与凶手有关才能确切证明其罪行。

2. 继续阅读下一个推理测试题，请按照合适的格式进行回答。

情节描述：昨天下午五点，警察接到一通报案电话，称一家珠宝店发生了抢劫。

警方立即赶往现场，进行了勘查和询问。

根据调查人员提供的情报，以下是案发现场的情况：- 珠宝店入口的玻璃被粗暴破坏，外面有残留的玻璃碎片。

- 看起来店内的保险箱被人打开，里面的珠宝和贵重物品全部被盗走。

- 视频监控显示，案发时间是下午三点左右，但是没有录像显示任何可疑人员进出店内。

问题：1) 誰是最有可能是犯罪嫌疑人？为什么？2) 入室的方式是什么？3) 为什么没有录像显示可疑人员进出店内？答案：1) 最有可能是犯罪嫌疑人的是一名店员。

作为内部工作人员，他对店内的保险措施比其他人更加了解。

此外，他是唯一一个有机会接触保险箱并熟悉内部布局的人。

2) 犯罪嫌疑人很有可能使用了一种高超的技巧来打开保险箱。

由于保险箱的锁并未受到破坏或剧烈撞击的痕迹，可以推断其可能具备开锁技能。

一年级推理练习题带答案

一年级推理练习题带答案小明和小红是一年级的学生，他们喜欢玩推理游戏。

今天，老师给他们出了一些推理练习题，让我们一起来帮助他们解答吧！题目一：小明有5个苹果，他给了小红2个苹果。

请问小明现在有几个苹果？答案：小明原来有5个苹果，给了小红2个，所以现在有 5 - 2 = 3个苹果。

题目二：小红有3个橘子，她又从家里拿了2个橘子。

现在小红一共有多少个橘子？答案：小红原来有3个橘子，又拿了2个，所以现在有 3 + 2 = 5个橘子。

题目三：小明和小红一共有10个苹果，如果小明有6个苹果，小红有多少个苹果？答案：小明和小红一共有10个苹果，小明有6个，所以小红有 10 - 6 = 4个苹果。

题目四：如果小明有5个苹果，小红比小明多2个苹果，那么小红有多少个苹果？答案：小明有5个苹果，小红比小明多2个，所以小红有 5 + 2 = 7个苹果。

题目五：小明有5个苹果，小红有3个苹果，他们决定平均分苹果。

请问他们每人会得到多少个苹果？答案：小明和小红一共有 5 + 3 = 8个苹果。

如果他们平均分，每人会得到8 ÷ 2 = 4个苹果。

题目六：小明有3个苹果，小红有4个苹果。

如果他们交换1个苹果，小明和小红各有几个苹果？答案：小明给小红1个苹果，小明剩下 3 - 1 = 2个苹果；小红收到1个苹果，小红有 4 + 1 = 5个苹果。

题目七：小明有4个苹果，小红有2个苹果。

如果小明给小红2个苹果，他们每人会有几个苹果？答案：小明给小红2个苹果，小明剩下 4 - 2 = 2个苹果；小红收到2个苹果，小红有 2 + 2 = 4个苹果。

题目八：小明有7个苹果，小红有5个苹果。

如果他们各自吃掉1个苹果，他们还剩下多少个苹果？答案：小明吃掉1个苹果，剩下 7 - 1 = 6个苹果；小红吃掉1个苹果，剩下 5 - 1 = 4个苹果。

题目九：小明有3个苹果，小红有2个苹果。

如果他们各自吃掉1个苹果，然后交换剩下的苹果，他们各自会有几个苹果？答案：小明吃掉1个苹果，剩下 3 - 1 = 2个苹果；小红吃掉1个苹果，剩下 2 - 1 = 1个苹果。

小学数学逻辑推理练习题及答案

小学数学逻辑推理练习题及答案以下是一份关于小学数学逻辑推理的练习题和答案：一、选择题1. 在一个学校的150名学生中，有80名学生是女生，剩下的学生是男生。

那么男生人数是：A. 50B. 70C. 100D. 120答案：B. 702. 小华拥有10支铅笔，小明有他的3倍铅笔数，小红有他们两个人的总和铅笔数。

小红最少有几支铅笔？A. 20B. 30C. 40D. 50答案：C. 403. 一辆公交车上有30名乘客，其中有5名是老人，8名是学生。

那么剩下的乘客是成年人的人数是多少？A. 9B. 12C. 15D. 18答案：B. 124. 三个数字a、b、c构成一个三位数abc，其中a > b > c。

如果abc = 589，那么a、b、c的值分别是多少？A. a = 9, b = 8, c = 5B. a = 8, b = 9, c = 5C. a = 5, b = 8, c = 9D. a = 9, b = 5, c = 8答案：D. a = 9, b = 5, c = 8二、填空题1. 用阿拉伯数字表示："六百四十五万零三十二"。

答案：645,0322. 请将下列数字从小到大排列：20, 10, 50, 5。

答案：5, 10, 20, 503. 请写出一个比65大且能被8整除的最小正整数。

答案：724. 一个正方形的边长是8个单位，请计算它的周长。

答案：32个单位三、解答题1. 一共有6个苹果和3个橘子，小明拿走了2个苹果和1个橘子。

请问还剩下几个水果？答案：4个水果（4个苹果和2个橘子）2. 小华在一家商店里买了一条裤子，裤子原价120元，商店正在举行打折活动，打8折。

请问小华需要支付多少钱？答案：96元3. 如果一个矩形的长是8个单位，宽是2个单位，那么它的面积是多少？周长是多少？答案：面积为16个单位，周长为20个单位。

以上是关于小学数学逻辑推理的练习题和答案。