扩散系数
扩散系数和有效扩散系数的关系

扩散系数和有效扩散系数的关系扩散系数和有效扩散系数是在物理学和化学领域中常用的两个概念,它们用于描述物质在介质中的扩散行为。
扩散是指分子或离子从浓度高的区域向浓度低的区域移动的过程。
在此文章中,我们将分步回答关于扩散系数和有效扩散系数之间的关系的问题。
第一步:定义扩散系数和有效扩散系数在物理学和化学中,扩散系数是一种描述物质扩散速度的物理量。
它定义为单位时间内通过单位面积的物质流量与浓度梯度之间的比值。
扩散系数通常由D来表示,其单位为平方厘米每秒(cm²/s)。
有效扩散系数是一种考虑了介质非均匀性的扩散系数。
介质的非均匀性可以由于介质中存在微观不均匀的缺陷或异质性而引起。
有效扩散系数定义为介质中实际扩散通量与理想均匀介质中的扩散通量之比。
有效扩散系数通常由D*来表示,其单位也是平方厘米每秒(cm²/s)。
第二步:扩散系数和有效扩散系数的关系扩散系数和有效扩散系数之间存在着一定的关系。
有效扩散系数可以看作是扩散系数在非均匀介质中的修正。
如果介质是均匀的,即没有任何非均匀性或缺陷,那么扩散系数和有效扩散系数将相等。
然而,当介质存在非均匀性时,有效扩散系数将小于扩散系数。
这是因为非均匀性会导致扩散过程中出现额外的阻力,使得物质的扩散速度减慢。
有效扩散系数考虑了这种额外阻力,因此会小于扩散系数。
具体来说,有效扩散系数可以通过下述公式计算:D* = D / f其中,D*是有效扩散系数,D是扩散系数,f是修正因子。
修正因子f通常小于1,它反映了介质中非均匀性对物质扩散的影响程度。
修正因子的具体值取决于介质的性质和非均匀性的程度。
第三步:确定修正因子修正因子的确定是一个复杂的过程,需要考虑介质的具体情况以及实验或模拟的数据。
一些常用的方法用于确定修正因子,包括统计方法、数值模拟和实验测量。
统计方法可以通过对介质的非均匀性进行统计分析,并根据统计结果估计修正因子。
数值模拟可以使用计算流体力学等方法对介质中的扩散过程进行模拟,并根据模拟结果计算修正因子。
扩散系数计算

扩散系数计算WTD standardization office【WTD 5AB- WTDK 08- WTD 2C】扩散系数费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、 气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5210/m s -。
通常对于二元气体A、B 的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即AB BA D D D ==。
表7-1给出了某些二元气体在常压下(51.01310Pa ⨯)的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:1/31/32[()()]A B D P v v =+∑∑ (7-19)式中,D -A、B 二元气体的扩散系数,2/m s ;P -气体的总压,Pa ;T -气体的温度,K;A M 、B M -组分A、B 的摩尔质量,/kg kmol ;Av∑、Bv∑-组分A、B 分子扩散体积,3/cm mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
51.01310Pa ⨯式7-19的相对误差一般小于10%。
二、 液体中的扩散系数由于液体中的分子要比气体中的分子密集得多,因此也体的扩散系数要比气体的小得多,其量级为9210/m s -。
表7-3给出了某些溶质在液体溶剂中的扩散系数。
式估算:150.6()7.410T B AB A M TD V -φ=⨯μ 2/m s (7-21)式中,AB D -溶质A在溶剂B中的扩散系数(也称无限稀释扩散系数),2/m s ;T -溶液的温度,K; μ-溶剂B的粘度,.Pa s ;B M -溶剂B的摩尔质量,/kg kmol ;φ-溶剂的缔合参数,具体值为:水;甲醇;乙醇;苯、乙醚等不缔合的溶剂为;A V -溶质A 在正常沸点下的分子体积,3/cm mol ,由正常沸点下的液体密度来计算。
扩散系数计算

7.2.2扩散系数费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、 气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5210/m s -。
通常对于二元气体A、B的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即AB BA D D D ==。
表7-1给出了某些二元气体在常压下(51.01310Pa ⨯)的扩散系数。
150.67.410B AB A D V -=⨯μ 2/m s (7-21)式中,AB D -溶质A在溶剂B中的扩散系数(也称无限稀释扩散系数),2/m s ;T -溶液的温度,K;μ-溶剂B的粘度,.Pa s ;B M -溶剂B的摩尔质量,/kg kmol ;φ-溶剂的缔合参数,具体值为:水2.6;甲醇1.9;乙醇1.5;苯、乙醚等不缔合的溶剂为1.0;A V -溶质A 在正常沸点下的分子体积,3/cm mol ,由正常沸点下的液体密度来计算。
若缺乏此密度数据,则可采用Tyn-Calus 方法估算: 1.0480.285c V V =,其中c V 为物质的临界体积(属于基本物性),单位为3/cm mol ,见表7-4。
从(7-21)可见,溶质A在溶剂B中的扩散系数AB D 与溶质B在溶质A中的扩散系数BAD 不相等,这一点与气体扩散系数的特性明显不同,需引起注意。
对给定的系统,可由温度1T 下的扩散系数1D 推算2T 下的2D (要求1T 和2T 相差不大),如下:21211()T D D T 2μ=μ (7-22)三、 生物物质的扩散系数表7-5给出了一些生物溶质在水溶液中的扩散系数。
表7—5 生物溶质在水溶液中的扩散系数PM其中,.atm)。
** P M的单位:m3溶质(标准状态)/(s?m2?atm/m)。
扩散系数计算

它表达某个组分在介质中扩 0.0101T 1.75(7—19)722扩散系数费克定律中的扩散系数D 代表单位浓度梯度下的扩散通量, 散的快慢,是物质的一种传递性质。
一、气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为10 m 2/s 。
通常对于二元气体A 、B 的相互扩散,A 在 B 中的扩散系数和 B 在A 中的扩散系数相等,因此可略去下标而用同一符号D 表示,即 D AB = D BA =D。
表7 — 1给出了某些二元气体在常压下(1.013 105Pa )的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:p[c V A )1/3 e V B )1/3]22式中,D —A 、B 二元气体的扩散系数,m /s ;P —气体的总压,Pa ;T —气体的温度,K ;MA 、MB —组分A 、B 的摩尔质量,kg/kmol ;7 V A 7 V B3、—组分A 、B 分子扩散体积,cm 3/mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
表7-1某些二元气体在常压下(5)的扩散系数系统温度/K 扩散系数/(10-5m 2/s)系统温度/K-5 2扩散系数/(10 m/s)H 2—空气 273 6.11 甲醇一空气 273 1.32 He —空气 317 7.56 乙醇一空气 273 1.0202—空气 273 1.78 正丁醇-空气 273 0.703 Cl 2 —空气 273 1.24 苯-空气 298 0.962 H 2O —空气273 2.20 甲醇一空气298 0.844 298 2.56 H 2— CO 273 6.513323.05 H 2— CO 2 273 5.50 NH 3 —空气 273 1.98H 2— N 2 273 6.89 CO 2 —空气273 1.38294 7.632981.64 H 2— NH 3 298 7.83 SO 2 —空气 2931.22He — Ar2987.297-2 原子扩散体积3v/(cm /mol) 分子扩散体积 3工 V /( cm /mol)原子扩散体积3v/(cm /mol)分子扩散体积3工 V /( cm /mol)C15.9 He 2.67 S22.9CO 18.0,其扩散系数常用 Wilke-Cha ng 公式估算:2 /m/S(7 — 21)AB= 7.4 10‘5(M B )T T 」V A 0.6式7 — 19的相对误差一般小于1 0%。
扩散系数的公式

扩散系数的公式扩散系数(Diffusion coefficient)是描述物质扩散能力的物理量。
一、菲克定律与扩散系数。
1. 菲克第一定律。
- 表达式为J = -D(dc)/(dx),这里J是扩散通量(单位时间内通过单位面积的物质的量),D就是扩散系数,(dc)/(dx)是浓度梯度(沿x方向的浓度变化率)。
- 由该定律可以推导出扩散系数D=(-J)/(frac{dc){dx}}(在已知扩散通量J和浓度梯度(dc)/(dx)的情况下)。
2. 菲克第二定律。
- 表达式为(∂ c)/(∂ t)=Dfrac{∂^2c}{∂ x^2}(在一维扩散情况下),其中c是浓度,t是时间,x是空间坐标。
- 在一些特定的初始条件和边界条件下,通过求解菲克第二定律的方程,可以得到扩散过程中浓度随时间和空间的分布,进而可以确定扩散系数D的值。
例如在简单的扩散问题中,假设扩散物质初始时局限于某一区域,随着时间的推移,根据浓度分布的变化情况来计算D。
- 如果已知浓度c随时间t和空间x的函数关系c(x,t),可以通过对(∂ c)/(∂ t)和frac{∂^2c}{∂ x^2}求导,然后根据菲克第二定律计算D=(frac{∂ c)/(∂ t)}{frac{∂^2c}{∂ x^2}}。
二、爱因斯坦 - 斯托克斯方程(适用于稀溶液中的球形粒子扩散)1. 公式为D = (kT)/(6πeta r),其中k是玻尔兹曼常量(k = 1.38×10^-23J/K),T 是绝对温度,eta是溶剂的粘度,r是球形粒子的半径。
2. 这个公式的推导基于分子运动论和流体力学原理。
它表明扩散系数与温度成正比,与溶剂粘度和粒子半径成反比。
例如,在研究胶体溶液中球形胶粒的扩散时,可以通过测量温度T、溶剂粘度eta以及已知胶粒半径r,利用该公式计算扩散系数D。
扩散系数方程

扩散系数方程摘要:一、扩散系数的定义与性质1.扩散系数的含义2.扩散系数的性质二、扩散系数的计算方法1.菲克定律2.莫根堡公式3.斯托克斯公式三、扩散系数在实际应用中的意义1.在生物学中的应用2.在物理学中的应用3.在化学中的应用四、扩散系数与相关概念的区分1.扩散系数与扩散速度2.扩散系数与扩散常数3.扩散系数与浓度梯度正文:扩散系数是一个描述物质在介质中扩散过程的物理量,它在不同学科中有广泛的应用。
本文将对扩散系数的定义、性质、计算方法以及在实际应用中的意义进行详细阐述。
一、扩散系数的定义与性质1.扩散系数的含义扩散系数是指单位时间内,物质通过扩散过程在单位面积上的物质的量。
扩散系数是一个无量纲的量,它反映了物质在介质中扩散的快慢程度。
2.扩散系数的性质扩散系数的值取决于物质的性质、温度、压力以及介质的几何形状等因素。
在不同的条件下,扩散系数的值会有所不同。
二、扩散系数的计算方法1.菲克定律菲克定律是一种常用的计算扩散系数的方法,它表示物质的扩散量与扩散系数成正比,与扩散面积成反比。
菲克定律的数学表达式为:J = D * (C)。
其中,J 是扩散量,D 是扩散系数,C 是浓度梯度。
2.莫根堡公式莫根堡公式是另一种计算扩散系数的方法,它主要用于计算在球对称条件下的扩散系数。
莫根堡公式的数学表达式为:D = k * (1 / r^2)。
其中,k 是扩散系数,r 是距离。
3.斯托克斯公式斯托克斯公式是计算扩散系数的一种更一般的方法,它可以用于计算任意形状的介质中的扩散系数。
斯托克斯公式的数学表达式为:D = (k * C) / (1 -(C)^2)。
其中,k 是扩散系数,C 是浓度梯度的二阶梯度算子。
三、扩散系数在实际应用中的意义1.在生物学中的应用在生物学中,扩散系数被用来研究生物分子在细胞内的扩散过程,这对于理解生命现象有着重要的意义。
2.在物理学中的应用在物理学中,扩散系数被用来研究气体和液体的扩散现象,这对于理解热传导和质量传输等过程有着重要的作用。
[整理版]扩散系数计算
![[整理版]扩散系数计算](https://img.taocdn.com/s3/m/fae65b1a77c66137ee06eff9aef8941ea76e4b7b.png)
7.2.2扩散系数费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5210/m s -。
通常对于二元气体A、B 的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即AB BA D D D ==。
表7-1给出了某些二元气体在常压下(51.01310Pa ⨯)的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:1/31/32[()()]A B D P v v =+∑∑ (7-19)式中,D -A、B 二元气体的扩散系数,2/m s ;-气体的总压,Pa ;-气体的温度,K;A M 、B M -组分A、B 的摩尔质量,/kg kmol ;Av∑、Bv∑-组分A、B 分子扩散体积,3/cm mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
表7-1 某些二元气体在常压下(51.01310Pa ⨯)的扩散系数式7-19的相对误差一般小于10%。
二、液体中的扩散系数由于液体中的分子要比气体中的分子密集得多,因此也体的扩散系数要比气体的小得多,其量级为9210/m s -。
表7-3给出了某些溶质在液体溶剂中的扩散系数。
表7-3 溶质在液体溶剂中的扩散系数(溶质浓度很低)对于很稀的非电解质溶液(溶质A+溶剂B),其扩散系数常用Wilke-Chang 公式估算: 150.6()7.410T B AB A M TD V -φ=⨯μ 2/m s (7-21)式中,AB D -溶质A在溶剂B中的扩散系数(也称无限稀释扩散系数),2/m s ;-溶液的温度,K;-溶剂B的粘度,.Pa s ;B M -溶剂B的摩尔质量,/kg kmol ;φ-溶剂的缔合参数,具体值为:水2.6;甲醇1.9;乙醇1.5;苯、乙醚等不缔合的溶剂为1.0;A V -溶质A 在正常沸点下的分子体积,3/cm mol ,由正常沸点下的液体密度来计算。
扩散系数计算

7.2.2扩散系数费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5210/m s -。
通常对于二元气体A、B 的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即AB BA D D D ==。
表7-1给出了某些二元气体在常压下(51.01310Pa ⨯)的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:1/31/32[()()]A B D P v v =+∑∑ (7-19)式中,D -A、B 二元气体的扩散系数,2/m s ;P -气体的总压,Pa ; T -气体的温度,K;A M 、B M -组分A、B 的摩尔质量,/kg kmol ;Av∑、Bv∑-组分A、B 分子扩散体积,3/cm mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
51.01310Pa ⨯式7-19的相对误差一般小于10%。
二、液体中的扩散系数由于液体中的分子要比气体中的分子密集得多,因此也体的扩散系数要比气体的小得多,其量级为9210/m s -。
表7-3给出了某些溶质在液体溶剂中的扩散系数。
表7-3 溶质在液体溶剂中的扩散系数(溶质浓度很低)对于很稀的非电解质溶液(溶质A+溶剂B),其扩散系数常用Wilke-Chang 公式估算:150.6()7.410T B AB A M TD V -φ=⨯μ 2/m s (7-21)式中,AB D -溶质A在溶剂B中的扩散系数(也称无限稀释扩散系数),2/m s ;T -溶液的温度,K; μ-溶剂B的粘度,.Pa s ;B M -溶剂B的摩尔质量,/kg kmol ;φ-溶剂的缔合参数,具体值为:水2.6;甲醇1.9;乙醇1.5;苯、乙醚等不缔合的溶剂为1.0;A V -溶质A 在正常沸点下的分子体积,3/cm mol ,由正常沸点下的液体密度来计算。
扩散系数d的计算公式

扩散系数d的计算公式扩散系数d的计算公式简介扩散系数是描述物质在介质中扩散能力的一个重要参数。
在科学研究和工程实践中,准确计算和预测物质扩散现象对于材料选择、工艺设计等方面具有重要意义。
本文将介绍几种常见的扩散系数计算公式,并通过具体例子进行解释说明。
离子扩散系数的计算公式斯托克斯-爱因斯坦方程(Stokes-Einstein equation)扩散系数与粘度(η)和温度(T)之间的关系可以通过斯托克斯-爱因斯坦方程来描述:equationequation其中,D表示扩散系数,k_B为玻尔兹曼常数,T为温度,η为粘度,r为扩散物质的半径。
丁尼斯方程(Daniels’ equation)对于一维扩散情况下的离子扩散系数计算,丁尼斯方程给出了如下关系式:[equation](其中,D表示扩散系数,X为晶格常数,z为离子价数,F为法拉第常数,r为离子半径。
分子扩散系数的计算公式弗里克方程(Fick’s law)弗里克方程描述了分子扩散的速率与浓度梯度之间的关系:[equation](其中,J表示扩散通量,D表示扩散系数,c表示浓度,x表示距离。
举例说明以计算离子在水中的扩散系数为例,假设温度为300K,粘度为mPa s,离子半径为1 Å。
根据斯托克斯-爱因斯坦方程可以计算得到扩散系数:[equation](计算结果为D≈×10^-10 m^2/s。
对于分子在空气中的扩散系数计算,假设扩散物质为氧气(O2),浓度梯度为 mol/L,扩散距离为1 mm。
根据弗里克方程可以计算得到扩散系数:[equation](计算结果为D≈1×10^-9 m^2/s。
通过以上两个例子可以看出,扩散系数的计算公式可以在不同情况下根据实际需求进行选择和应用,以准确描述物质的扩散现象。
以上就是关于扩散系数d的计算公式的介绍和举例说明。
希望对读者有所帮助!流体动力学方程(Navier-Stokes equation)对于流体中扩散现象的计算,可以采用流体动力学方程。
扩散第一定律 扩散系数

扩散第一定律扩散系数
扩散是物质分子之间的无序运动,它会使分子从浓度高的地方向浓度低的地方移动,直到浓度达到平衡。
扩散现象在自然界和工业生产中都有广泛的应用。
扩散系数是衡量物质在单位时间内扩散的距离的物理量,通常用 D 表示。
扩散系数的大小与分子的大小、形状、质量和温度等因素有关。
扩散系数越大,分子在单位时间内就能扩散更远的距离。
根据扩散的第一定律,扩散通量与扩散浓度梯度成正比,通量的比例系数就是扩散系数。
也就是说,如果将扩散物质放在一段长度为 L 的管道中,管道两端的浓度分别为 C1 和 C2,那么扩散通量 J 等于 D(C2-C1)/L。
扩散系数的值通常在实验室中通过测量扩散速率、扩散距离和浓度梯度等参数来确定。
在工程设计中,扩散系数也是一个重要的参数,因为它决定了物质在空气、水、土壤等介质中的分布和传输过程。
- 1 -。
扩散系数计算(仅限借鉴)
7.2.2扩散系数费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5210/m s -。
通常对于二元气体A、B 的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即AB BA D D D ==。
表7-1给出了某些二元气体在常压下(51.01310Pa ⨯)的扩散系数。
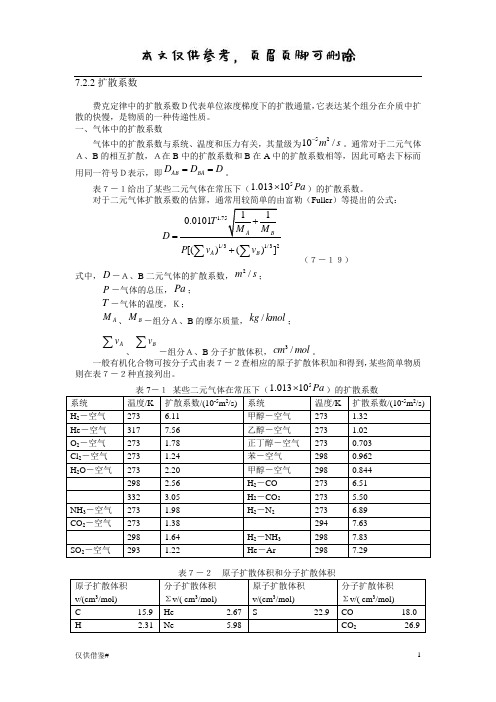
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:1.751/31/32110.0101[()()]A BA B T M M D P v v +=+∑∑ (7-19)式中,D -A、B 二元气体的扩散系数,2/m s ;P -气体的总压,Pa ; T -气体的温度,K;A M 、B M -组分A、B 的摩尔质量,/kg kmol ;Av∑、Bv∑-组分A、B 分子扩散体积,3/cm mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
51.01310Pa ⨯系统 温度/K 扩散系数/(10-5m 2/s) 系统 温度/K 扩散系数/(10-5m 2/s)H 2-空气 273 6.11 甲醇-空气 273 1.32 He -空气 317 7.56 乙醇-空气 273 1.02 O 2-空气 273 1.78 正丁醇-空气 273 0.703 Cl 2-空气 273 1.24 苯-空气 298 0.962 H 2O -空气 273 2.20 甲醇-空气 298 0.844 298 2.56 H 2-CO 273 6.51332 3.05 H 2-CO 2 273 5.50 NH 3-空气 273 1.98 H 2-N 2 273 6.89 CO 2-空气 273 1.38 294 7.63298 1.64 H 2-NH 3 298 7.83 SO 2-空气2931.22He -Ar2987.29原子扩散体积v/(cm 3/mol)分子扩散体积 Σv/( cm 3/mol) 原子扩散体积 v/(cm 3/mol) 分子扩散体积 Σv/( cm 3/mol)C 15.9 He 2.67 S 22.9 CO 18.0 H 2.31 Ne 5.98CO 2 26.9O 6.11 Ar 16.2 N 2O 35.9 N 4.54 Kr 24.5 NH 3 20.7 芳香族环 -18.3 Xe 32.7H 2O 13.1 杂环 -18.3 H 2 6.12 SF 6 71.3 F 14.7 D 2 6.84 Cl 2 38.4 CL 21.0 N 2 18.5Br 2 69.0 Br 21.9O 2 16.3SO 2 41.8I 29.8 空气 19.7式7-19的相对误差一般小于10%。
第七讲 扩散系数

2、论文要求
1、格式要求:(20分)
格式示例:
题目:润滑油基础油中硫、氮化合物的氧化性能研究
作者: 周亚松,林世雄
专业班级: (石油大学 重质油国家重点实验室,北京102200) 摘 要:用动态循环吸氧的方法研究了吲哚和喹啉对饱和烃 氧化特征的影 正文: 结论: 参考文献:
1、 [Maleville X, et al. Oxidation of mineral base oils of petroleum original: The relationship between chemical composition, thickening, and composition of degradation products [J]. Lubr Sci, 1996,9(1),3-59.
Brobaw式
2)经验关联型 Wilke—Lee
2、高压气体D计算
此研究很少,有一种简单的对比态法
Tr=T/Tc Tc=yATCA+yBTCB
Pr=P/Pc Pc=yAPCA+yBPCB
(DABP)* 为低压方法计算得的值 再由右图的Tr Pr查得后计算得 DABP
3、多组分气体系统D
Wilke根据Stefan—Maxwell方程提出:
3)Tyn—Calus 式
简化
4)Huyduk---Minhas 式 正构烷烃 含水溶液
适用:C5~C32正构烷烃为溶质 C5~C16正构烷烃为溶剂
4)Huyduk---Minhas 式 非水溶液(非电解质溶液)
推荐:(1)用Tyn—Calus, Huyduk—Minhas式 均需[P]或表面张力
4、液体(二元稀溶液,xi<5%)
新版扩散系数-新版.pdf

7.2.2扩散系数费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、一、气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5210/m s 。
通常对于二元气体A、B 的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即AB BAD D D 。
表7-1给出了某些二元气体在常压下(51.01310Pa )的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:1.751/31/32110.0101[()()]A B A B T M M DP v v (7-19)式中,D -A、B 二元气体的扩散系数,2/m s ;P -气体的总压,Pa ;T -气体的温度,K;A M 、B M -组分A、B 的摩尔质量,/kg kmol ;A v 、Bv -组分A、B 分子扩散体积,3/cm mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
表7-1某些二元气体在常压下(51.01310Pa )的扩散系数系统温度/K 扩散系数/(10-5m 2/s) 系统温度/K 扩散系数/(10-5m 2/s) H 2-空气273 6.11 甲醇-空气273 1.32 He -空气317 7.56 乙醇-空气273 1.02 O 2-空气273 1.78 正丁醇-空气273 0.703 Cl 2-空气273 1.24 苯-空气298 0.962 H 2O -空气273 2.20 甲醇-空气298 0.844 298 2.56 H 2-CO 273 6.51 3323.05 H 2-CO 2 273 5.50 NH 3-空气273 1.98 H 2-N 2 273 6.89 CO 2-空气273 1.38 294 7.63 298 1.64 H 2-NH 3 298 7.83 SO 2-空气2931.22He -Ar2987.29表7-2原子扩散体积和分子扩散体积原子扩散体积v/(cm 3/mol) 分子扩散体积Σv/( cm 3/mol) 原子扩散体积v/(cm 3/mol)分子扩散体积Σv/( cm 3/mol) C 15.9 He 2.67 S22.9CO 18.0 H 2.31Ne5.98 CO 226.9 O6.11 Ar16.2N 2O35.9N 4.54 Kr 24.5 NH320.7 芳香族环-18.3 Xe 32.7 H2O 13.1 杂环-18.3 H2 6.12 SF671.3 F 14.7 D2 6.84 Cl238.4 CL 21.0 N218.5 Br269.0 Br 21.9 O216.3 SO241.8 I 29.8 空气19.7注:已列出分子扩散体积的,以后者为准。
扩散系数计算
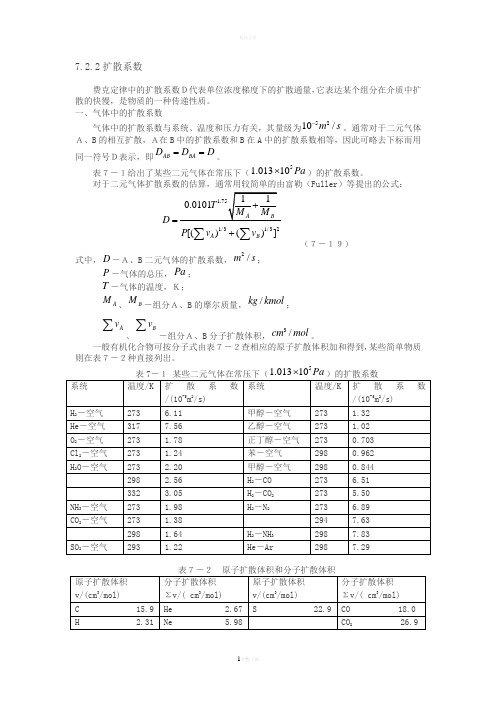
7.2.2扩散系数费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5210/m s -。
通常对于二元气体A、B 的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即AB BA D D D ==。
表7-1给出了某些二元气体在常压下(51.01310Pa ⨯)的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:1/31/32[()()]A B D P v v =+∑∑ (7-19)式中,D -A、B 二元气体的扩散系数,2/m s ;P -气体的总压,Pa ; T -气体的温度,K;A M 、B M -组分A、B 的摩尔质量,/kg kmol ;Av∑、Bv∑-组分A、B 分子扩散体积,3/cm mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
51.01310Pa ⨯式7-19的相对误差一般小于10%。
二、液体中的扩散系数由于液体中的分子要比气体中的分子密集得多,因此也体的扩散系数要比气体的小得多,其量级为9210/m s -。
表7-3给出了某些溶质在液体溶剂中的扩散系数。
对于很稀的非电解质溶液(溶质A+溶剂B),其扩散系数常用Wilke-Chang 公式估算:150.6()7.410T B AB A M TD V -φ=⨯μ 2/m s (7-21)式中,AB D -溶质A在溶剂B中的扩散系数(也称无限稀释扩散系数),2/m s ;T -溶液的温度,K;μ-溶剂B的粘度,.Pa s ;B M -溶剂B的摩尔质量,/kg kmol ;φ-溶剂的缔合参数,具体值为:水2.6;甲醇1.9;乙醇1.5;苯、乙醚等不缔合的溶剂为1.0;A V -溶质A 在正常沸点下的分子体积,3/cm mol ,由正常沸点下的液体密度来计算。
扩散系数计算

扩 散 系 数费克定律中的扩散系数D 代表单位浓度梯度下的扩散通量, 散的快慢,是物质的一种传递性质。
一、气体中的扩散系数A 、B 的相互扩散,A 在 B 中的扩散系数和 B 在A 中的扩散系数相等,因此可略去下标而 用同一符号D 表示,即 D AB D BA D 。
5表7 — 1给出了某些二元气体在常压下(1.013 10 Pa )的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:1/31/3 2P[( V A ) ( V B )](7—19)2 式中,D —A 、B 二元气体的扩散系数, m /s ;P —气体的总压,Pa ; T —气体的温度,K ; M A 、MB —组分A 、 B 的摩尔质量,kg/kmol ;V AV B3、—组分A 、B 分子扩散体积,cm /mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到, 某些简单物质则在表7-2种直接列出。
5表7-1某些二元气体在常压下(1.013 10 Pa )的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5 210 m /s 。
通常对于二元气体它表达某个组分在介质中扩式7 —19的相对误差一般小于1 0%。
、液体中的扩散系数由于液体中的分子要比气体中的分子密集得多,因此也体的扩散系数要比气体的小得9 2多,其量级为10 m /s。
表7 —3给出了某些溶质在液体溶剂中的扩散系数。
表7 — 3 溶质在液体溶剂中A E),其扩散系数常用Wilke-Cha ng公式估算:式中,D AB—溶质A在溶剂E中的扩散系数(也称无限稀释扩散系数),m2/s ;T —溶液的温度,K;-溶剂E的粘度,Pa.s ;M B—溶剂E的摩尔质量,kg/ kmol ;—溶剂的缔合参数,具体值为:水 2.6 ;甲醇1.9 ;乙醇1.5 ;苯、乙醚等不缔合的溶剂为1.0;VA—溶质A在正常沸点下的分子体积,cm3/mol,由正常沸点下的液体密度来计D AB 7.4 10 15(M B)TV A0.6 2 /m /S (7 — 21)算。
msd 扩散系数

msd 扩散系数
MSD(Mean Square Displacement)是指扩散分子在一定时间内移动的平均距离的平方。
扩散系数(Diffusion Coefficient)是描述扩散分子运动速度和距离的一个物理量。
扩散系数可通过MSD计算得到。
在离散的时间点上,扩散分子的位置可以表示为(x(i), y(i), z(i)),其中i为时间点。
扩散分子的MSD可以通过以下公式计算:MSD = <(x(i) - x(0))^2 + (y(i) - y(0))^2 + (z(i) - z(0))^2>其中<>表示对所有时间点求平均。
扩散系数D可以由Einstein关系得到:MSD = 6Dt其中t为时间。
因此,扩散系数可以通过MSD与时间的关系进行计算。
在实际实验或模拟中,可以通过观察分子在时间内的移动轨迹,计算出其MSD 并通过拟合得到扩散系数。
扩散系数

7.2.2扩散系数
费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、 一、气体中的扩散系数
气体中的扩散系数与系统、温度和压力有关,其量级为5
2
10/m s -。
通常对于二元气体A、B 的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即
AB BA D D D ==。
表7-1给出了某些二元气体在常压下(5
1.01310Pa ⨯)的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:
1/31/32
[()()]A B D P v v =
+∑∑ (7-19)
式中,D -A、B 二元气体的扩散系数,2
/m s ;
P -气体的总压,Pa ; T -气体的温度,K;
A M 、
B M -组分A、B 的摩尔质量,/kg kmol ;
A
v
∑、B
v
∑-组分A、B 分子扩散体积,3
/cm mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
5。
扩散系数计算

扩散系数费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5210/m s -。
通常对于二元气体A、B 的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即AB BA D D D ==。
表7-1给出了某些二元气体在常压下(51.01310Pa ⨯)的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:1/31/32[()()]A B D P v v =+∑∑ (7-19)式中,D -A、B 二元气体的扩散系数,2/m s ;P -气体的总压,Pa ; T -气体的温度,K;A M 、B M -组分A、B 的摩尔质量,/kg kmol ;Av∑、Bv∑-组分A、B 分子扩散体积,3/cm mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
表7-1 某些二元气体在常压下(51.01310Pa ⨯)的扩散系数表7-2 原子扩散体积和分子扩散体积式7-19的相对误差一般小于10%。
二、液体中的扩散系数由于液体中的分子要比气体中的分子密集得多,因此也体的扩散系数要比气体的小得多,其量级为9210/m s 。
表7-3给出了某些溶质在液体溶剂中的扩散系数。
表7-3 溶质在液体溶剂中的扩散系数(溶质浓度很低)对于很稀的非电解质溶液(溶质A+溶剂B),其扩散系数常用Wilke-Chang 公式估算:150.6()7.410T B AB A M TD V -φ=⨯μ 2/m s (7-21)式中,AB D -溶质A在溶剂B中的扩散系数(也称无限稀释扩散系数),2/m s ;T -溶液的温度,K; μ-溶剂B的粘度,.Pa s ;B M -溶剂B的摩尔质量,/kg kmol ;φ-溶剂的缔合参数,具体值为:水;甲醇;乙醇;苯、乙醚等不缔合的溶剂为;A V -溶质A 在正常沸点下的分子体积,3/cm mol ,由正常沸点下的液体密度来计算。
扩散系数

图9 微量CdCl2掺杂的NaCl单晶中Na+的自扩散系数与温度的关系
Patterson等人测定了NaCl单晶中Na+离子和C1-离子 的本征与非本征扩散系数以及由此实测值计算出的扩 散活化能。 NaCl单晶中自扩散活化能
活 本征扩散 Na C1
+
化
能
(KJ /ml) ΔHf 199 199
非本征扩散 (ΔHm) 74 161
这便是由于两种扩散的活化能差异所致, 这种弯曲或转折相当于从受杂质控制的非本 征扩散向本征扩散的变化。在高温区活化能 大的应为本征扩散,在低温区的活化能较小 的应为非本征扩散。
700
600
T(℃) 500 400
350
10-9
10-11
10-13
1.00
1.20 1.40 103/T(K-1)
1.60
1、空位扩散系数
空位扩散属于无序扩散,可用无序扩散系数来描述。在
空位扩散机理中,只有当邻近的结点上有空位时,质点才 能够跃迁。所以单位时间内空位的跃迁次数(n/t 或q)与
晶体内的空位浓度或缺陷浓度(Nν)、质点跃迁到邻近空位
的跃迁频率(γ)以及与可供空位跃迁的结点数(A)有关,即: n/t=A Nv γ
因此,在考虑沿特定方向原于的扩散时,上 述反向跃迁所造成的结果是:示踪原子自扩散 系数(D*)小于无序扩散系数(Dr),或者说示踪 原子的自扩散系数只相当于无序扩散系数的一 个分数。 D*=f Dr 式中的系数(f )叫相关系数或相关因数 (correlation factor),它是由晶体结构和扩散 机理所决定的小于1的常数,
第三节 扩散系数
通常,扩散系数可作为表征扩散的一个 参量。它不仅与扩散机构,也与扩散介质 和外部条件有关。因此可以认为扩散系数 是物质的一个物性指标。
扩散系数d的计算公式(一)

扩散系数d的计算公式(一)扩散系数d的计算公式简介在科学研究和工程设计中,扩散系数d是描述物质在空气或溶液中扩散能力的重要参数。
本文将介绍几种常用的扩散系数计算公式,并通过具体例子解释其用途和计算方法。
Fick定律Fick定律是描述物质扩散过程的基本规律,通过扩散流量和浓度梯度之间的关系来表达。
根据Fick定律,扩散系数d可计算如下:d = J / (A * ΔC / Δx)其中,d代表扩散系数,J代表扩散流量,A代表扩散面积,ΔC 代表浓度差,Δx代表扩散路径长度。
浓度梯度法浓度梯度法是通过测量物质浓度沿某一方向的变化来求解扩散系数的方法。
具体计算公式如下:d = (m / (A * t)) / (ΔC / Δx)其中,d代表扩散系数,m代表物质的质量,A代表扩散面积,t 代表扩散时间,ΔC代表浓度差,Δx代表扩散路径长度。
例如,某实验室内放置了一块导热板,板上有一定量的物质,通过测量物质在板上的浓度分布情况,可以计算扩散系数。
假设测得物质的质量为30克,测量时间为60秒,扩散宽度为10厘米,扩散长度为5厘米,浓度差为8克/立方厘米,那么扩散系数的计算如下:d = (30 / (10 * 60)) / (8 / 5) = cm²/s基于物质传输速率的方法基于物质传输速率的方法是通过测量物质在单位时间内通过某一面的质量来计算扩散系数的方法。
d = m / (A * t * ΔC / Δx)其中,d代表扩散系数,m代表物质的质量,A代表扩散面积,t 代表扩散时间,ΔC代表浓度差,Δx代表扩散路径长度。
例如,某实验中放置了一块薄膜,通过测量物质通过薄膜的质量变化来计算扩散系数。
假设测得物质的质量为20克,测量时间为30秒,扩散面积为100平方厘米,扩散长度为2厘米,浓度差为4克/立方厘米,那么扩散系数的计算如下:d = 20 / (100 * 30 * 4 / 2) = cm²/s结论本文介绍了扩散系数的计算公式,并通过具体例子解释了这些公式的用途和计算方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非稳态扩散d/dt0 扩散通量为J1的物质 经过体积元后的变化 浓度和距离的瞬时变化
通量和距离的瞬时关系 x
© meg/aol ‘02
在体积元(Adx)内 积存速率 = 流入速率 - 流出速率
- (JA) dx x
J1A
J2A=J1A+
( JA) x
dx
体积元内扩散物质质量的积存速率:
A dx = - J A dx
应用:测定碳在-Fe中的扩散系数
2r2
l>>r l
1000C [C]
2r1
平视方向
2r2
2r1
俯视方向
© meg/aol ‘02
稳态时: 单位时间内通过半径为r(r2<r<r1) 的圆柱管壁的碳量为常数: q/t
径向通量:J=
q
2rlt
=
d
-D dr
由菲克第一定律得: q
2rlt
=
-D
d
d ln r
t
x
= - J
t x
= (D )
t x x
菲克第二定律
© meg/aol ‘02
若D与浓度无关,则:
= D 2
t
x 2
对三维各向同性的情况:
2 2 2
= D( )
t
x2 y 2 z 2
© meg/aol ‘02
菲克定律描述了固体中存在浓度 梯度时发生的扩散,称为化学扩散
当扩散不依赖于浓度梯度,仅由 热振动而引起时,则称为自扩散
=常数
结论:
1. 当lnr与呈直线关系时,
D与碳浓度无关
2. 当lnr与为曲线关系时,
-lnr 实测的lnr与关系
D是碳浓度的函数
© meg/aol ‘02
4.1.2 菲克第二定律(Fick’s second law)
+
推
导
过A
程
:
菲
质 量
克浓
第
度
一
定
律
质
通 量
量
守
恒
x1
J1
x2
J2
dx
J1 J2
§ 4. 1 表象理论(Phenomenological laws)
扩散(diffusion): 在一个相内因分子或原子的热激活运动导 致成分混合或均匀化的分子合
时间
完全混合
© meg/aol ‘02
碳的扩散方向 Fe-C合金
高碳含量区域
低碳含量区域
© meg/aol ‘02
4.1.1 菲克第一定律(Fick’s first law)
稳态扩散 (d = 0)
dt
dx
1
2
(1>2)
J
=
d -D
dx
J
J: 扩散通量(mass flux), kg/(m2•s) D: 扩散系数(diffusivity), m2/s : 质量浓度,kg/m3
d
dx:
浓度梯度
© meg/aol ‘02
第四章 固体中原子及分子的运动
物质的传输方式
气体: 扩散+对流
金属
固体: 扩散
离 子 键
陶瓷
液体: 扩散+对流
高分子
扩散机制不同
© meg/aol ‘02
本章内容
• 扩散的表象理论 • 扩散的原子机制 • 影响扩散的因素 • 陶瓷材料中扩散的主要特征 • 高分子材料中分子运动的规律
© meg/aol ‘02
lim ( )- J
定义:自扩散系数 Ds= ρ 0
x
x
© meg/aol ‘02
