第4章 二维列联表
高中数学 第四章 典型统计案例 4.3 列联表独立性分析案例课件 湘教版选修1-2

解 将问题中的数据写成2×2列联表:
服用该药品 不服用该药品
合计
患A疾病 5 18 23
不患A疾病 100 400 500
合计 105 418 523
将上述数据代入公式χ2=
nad-bc2 a+bc+da+cb+d
中,计算
可得χ2≈0.041 4,因为0.0414<3.841,故没有充分理由认为 该保健药品对预防A疾病有效.
预习测评 1.若事件 A 与事件 B 相互独立,则下列各式不正确的是
( ). A.P( A B )=P( A )+P( B ) B.P( A B)=P( A )P(B) C.P(A B )=P(A)P( B ) D.P(AB)=P(A)P(B)
答案 A
2.在一个2×2列联表中,由其数据计算得χ2=13.097,则其
[正解] B
纠错心得 本题是利用χ2公式求出χ2的值,再利用与临界值 的大小关系来判断假设是否成立,解题时应注意准确代数与 计算,不可错用公式,要准确进行比较与判断.
4.3 列联表独立性分析案例
【课标要求】 1.通过典型案例的探究,了解独立性检验(只要求2×2列联
表)的基本思想、方法及其简单应用. 2.本节的重点和难点是独立性检验的思想、方法及其初步
应用.
自学导引
1.在 2×2 列联表中,χ2 统计量的计算公式为
nad-bc2
a+bc+da+cb+d
χ2=
,
n= a+b+c+d .
两个变量间有关系的可能性为
( ).
A.99%
B.95%
C.90%
D.无关系
解析 因为χ2=13.097,13.097>6.635,所以两个变量间有
关系的可能性为99%.
第4章二维列联表

一致性的检验
• 一般认为,计算的Kappa小于0时,属于偶然一致, 即期望一致率大于观测一致率; • 只有在Kappa大于0时,才进行一致性检验; • 在计算kappa系数的方差基础上,可以构造检验统 计量:
U D( ) ~ N (0,1)
• 经计算,例4.3的kappa=0.361,kappa的标准误 =0.0844,故U=4.277 • 很明显,原假设不成立,即不是偶然一致。
• 在保持边缘和不变的前提下,解出期望频数。 • 有的情况下期望频数的极大似然估计难以直接得 到,需要通过迭代算法求解。 • 迭代算法就是在保持边缘和不变时,寻找 i j 放 入不完备列联表的非空格中,也就是满足以上方 程组成立。
迭代估计法
p1 j p1 prj pr p1 j p1 prj pr p j
• 如果A与B独立,则对任意i都与j无关
pi1 p1 pic pi1 p c p1 pic pi p c
独立性与齐性
• 此时,称属性A与B有齐性关系。 • 齐性关系描述了Ai类中Bj的条件概率完全相 同,或在Bj 类中Ai的条件概率完全相同。 • 因此,对于二维列联表属性A与B相互独立, 等价于二者之间有齐性关系。 • 需要指出的是,在四格表中相互独立等价 于不相关,可以用相关系数描述二者的关 联程度。但在二维列联表中则不能使用。
• 当TA=TB=TAB时,说明每一行、每一列只有一个 非零值; • 当从左上角到右下角的对角线元素外的其余元素 都等于0时,为完全正相合; • 当从右上角到左下角的对角线元素外的其余元素 都等于0时,为完全负相合;
Gamma系数
• 除肯德尔的τ外,相合性度量还有伽马系数 Gamma: GH
第4章 二维列联表

相合性的度量与检验
τ相关系数基本思路:
认为二维列联表均可定义为有序表; 对有序变量的赋值可以确定由小到大的顺序关 系,但不影响相合关系的度量;最简单的赋值 方法就是令 x i, i 1,, r y j , j 1,, c 在二维表中,
x i 1 r 数据对 , 如数据对 有n11对, 有nrc 对 y j 1 c
该系数取值范围在[-1,1],常用于2×c或者r×2的 列联表,前者适用于列属性依赖于行属性的情况, 后者适用于行属性依赖于列属性的情况。 三个系数的比较:
B1 B2 B3 B4 B5 A1 * * * 0 0 A2 0 0 * * *
B1 B2 B3 B4 B5 A1 * * * 0 0 A2 0 0 0 * *
i j
i 1 i 1
ij
n(n 1) C G H TA TB TAB 2
2 n
相合性的度量与检验
从τ系数的计算公式可知,在属性A与B正相 合时,G 比较大而H 比较小;反之在A与B 负相合时, G 比较小而H 比较大。因此, (G-H)的方向决定了相合性的方向。 在存在同分对的情况下,需要对相合性的 度量进行修正。
其中(xi ,yi )、(x j ,y j )为数据对的等级或顺序
相合性的度量与检验
同分对可以有三种类型
因此有,
属性A方向的同分对,即行等级或顺序相同的 r 数据对,记为TA ;TA Cn2 i 1 属性B方向的同分对,即列等级或顺序相同的 c 数据对,记为TB ;TB Cn2 i 1 属性A与B的同分对,即行顺序与列顺序相等的 r c 数据对,记为TAB ;TAB Cn2
二维表

1.数据模型有三种:层次模型、网状模型、关系模型2.关系型数据库三种基本操作:选择操作、投影操作、联接操作3.结构化程序设计三种结构:顺序结构、选择结构(分支)、循环(重复)结构物理联接:1.定义:是对两个表按相同的公共字段进行联接,联接后生成一个新的表。
2.格式:JOIN WITH <非当前工作区别名>TO <新表>[范围][FOR<条件表达式>表1.公共字段=表2.公共字段][FIEL <字段名表>].. 3.功能:(1)两个表按相同的公共字段进行物理联接,联接后生成一个新的表。
(2)两个表进行联接时,必须有公共字段。
(3)联接的结果放入一个新表中。
要想看到联接的结果,必须打开联接后的新表。
(4)联接的方法是:首先把主表指针指向第一条记录,然后在子表的N条记录中进行查找,如果找到满足相同条件的记录,就把结果放入新表中,接着子表指针继续下移,按相同的条件继续查找,方法同上。
当把子表中的N条记录查找完后,主表指针下移到第二条记录,按照上述方法在子表的N条记录中重新查找。
方法同上。
这样当主表有M条记录,子表有N条记录,查找的过程将执行M*N次。
第二部分常用的命令一、格式:命令动词 [范围][字段名表][for<条件>] [其它…]二、几个重要的概念:1.指针:指向表中的某一条记录,通过记录号实现。
2.刚打开的表文件,指针指向表文件的第一记录。
3.绝对定位:(1)第N条记录:NGOTO NGO RECO NGO NDISP(2)顶部Go topGo top 与Go 1不是总一样,在索引文件中。
(3)底部Go bottGo bott 与go n(最后一条记录)不是总一样,在索引文件中不一样。
4.相对移动(1) SKIP向下移一条记录SKIP 1(2) SKIP +(-)N不包括当前记录,向下(上)移N条,而不是记录号向下(上)数N个。
5.几个常用的函数BOF()、文件首EOF()、文件尾RECC()、当前表中实际的记录个数RECN()当前的记录号必考的18个字:数据模型种类:层次、网状、关系关系型三种基本操作:选择、投影、联接结构化程序设计三种结构:顺序、选择、循环VF的工作方式有两种:交互方式(命令方式、菜单方式和向导方式)、程序方式1、s=1+2+3+..+100分别用5种不同的方法编写.2、从键盘任意输入10个不同的数,求这 10个不同数的和.3、S=1+(1+2)+(1+2+3)+(1+2+3+4)+...+(1+2+3+ (10)4、S=1!+2!+3!+ (10)5、S=2!+4!+6!+8!+10!6、S=1-2+3-4+5-6+7-87、打开成绩表,用循环的方法求出成绩表中总分的和。
二维表

性质
性质
关系模型采用二维表来表是有限的——元组个数有限性; (2)二维表中元组均不相同——元组的唯一性; (3)二维表中元组的次序可以任意交换——元组的次序无关性; (4)二维表中元组的分量是不可分割的基本数据项——元组分量的原子性; (5)二维表中属性名各不相同——属性名唯一性; (6)二维表中属性与次序无关,可任意交换——属性的次序无关性; (7)二维表属性的分量具有与该属性相同的值域——分量值域的统一性。
关键字
关键字
在一个关系中有这样一个或几个字段,它(们)的值可以唯一地标识一条记录,称之为关键字(Key)。例 如,在学生关系中,学号就是关键字。
关系模式对关系的描述称为关系模式,其格式为: 关系名(属性名1,属性名2,…,属性名n) 一个关系模式对应一个关系的结构,它是命名的属性集合。
生活中
生活中
二维表
数据结构
01 基本介绍
03 生活中
目录
02 关键字 04 性质
基本信息
二维表,数据结构,是一个关系名,意思是指关系模型中,数据结构的表示方法。
基本介绍
基本介绍
二维表名就是关系名。表中的第一行通常称为属性名,表中的每一个元组和属性都是不可再分的,且元组的 次序是无关紧要的。
常用的关系术语如下: 记录二维表中每一行称为一个记录,或称为一个元组。 字段二维表中每一列称为一个字段,或称为一个属性。 域一组具有相同数据类型的值。例如:自然数就是一个域
谢谢观看
二维表在生活中的应用广泛,例如成绩单、工资表、人员花名册、价格表、物料清单等
excel就是一个二维表,功能强大!!!
二维表就是由行列组成的,知道行号列号就可以确定一个表中的数据,这是二维表的特点。在关系数据库中, 存放在数据库中的数据的逻辑结构以二维表为主.
基本数学模型-列联表

M :被告是白人 M :被告是黑人
S :被告被判处死刑 S :被告未被判处死刑 P(S | M ) 19 0.119
160 P(S | M ) 17 0.102
166
独立性检验 2 0.22105
4
Simpson悖论
被告人 种族
被害人 种族
判决情况 死刑 非死刑
总计
V :被害人是白人 V :被害人是黑人
Kendall
Ammon
(1907-1983) (1842-1916)
Ammon, O. G., Zur Anthropologie der Badener
英国统计学家 德国人类学家
(On the anthropology of the people of Baden), 1899
Kendall, M. G., The Advanced Theory of Statistics, 1945
1
二维列联表
• 假设 n 个个体可根据两个属性进行分类,属性 A
有 r 类 A1, A2, , Ar,属性 B 有 c 类 B1, B2, , Bc。既属 于 Ai 类又属于B j类的个体有 nij 个。nij可显示在一张 二维列联表(contingency table)中
B1 A1 n11
Ar nr1
运筹与统计
列联表
头发与眼睛
• 头发颜色与眼睛颜色是否相关
头发 眼睛
浅色
棕
黑
红 总计
蓝 1768 807 189 47 2811
灰或绿 946 1387 746 53 3132
棕 115 438 288 16 857 Maurice George Otto Georg
王静龙定性数据分析第四章二维列联表答案
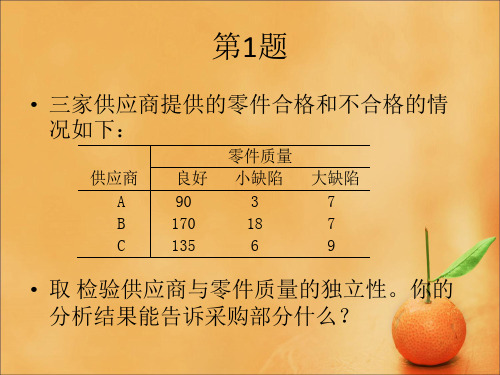
回答
非常满意 比较满意 比较不满意 不满意
提出的问题 你满意吗 你不满意吗 139 128 82 69 12 20 10 23
• 问:这两种提问方式对被调查者回答问题有没有影响?
第3题
• H0:这两种提问方式对被调查者回答问题无影响的 • H1:这两种提问方式对被调查者回答问题有影响
2
n n 1 / 2 TA n n 1 / 2 TB 正相合
(2)相合性的检验
GH
0.4245 0
H0:A(年龄)和B(冠状动脉硬化的程度)相互独立 H1:A和B正相合
第5题
2
n n n n ( z) 1942119
• 年龄越大的人,冠状动脉硬化的程度是否有越重的趋势? • (取水平 =0.05 )
第5题
• (1) 相合性的度量 G 15880 H 4324
4
TA
i 1
ni ni 1 2
10070
TB
j 1
4
n j n j 1 2
12442
= D(nij)
E ( )
2 i j
r
c
D(nij ) ni n j / n
( n r 1) c 1 n 1
• 9、假设二维
r r 概率方表为:
B1 … …
Br p1r
合计 p1+
A1
p11
Ar
合计
pr+ n
pr1 p+1
„ „
prr p+r
D(q1 ) 2 (1 q2 )
二维表_精品文档

二维表什么是二维表?二维表,又称为表格,是一种常见的数据结构,用于存储和组织数据。
二维表由行和列组成,其中每行代表一个记录,每列代表一个字段。
二维表可以看作是一张由行和列交叉形成的网格,每个交叉点处存储着特定的数据。
二维表的结构二维表通常由一行作为表头和多行作为数据组成。
表头包含了字段名称,用于描述每一列的数据类型或含义。
而数据行则包含了实际的数据。
一个简单的二维表示例如下所示:ID Name Age Gender1 Alice 25 Female2 Bob 30 Male3 Carol 35 Female在这个例子中,表头包含了四个字段:ID、Name、Age和Gender。
数据行则表示了三个人的信息,包括ID、用户名、年龄和性别。
二维表的特点二维表具有以下几个特点:1.行和列的关系:二维表可以看作是行和列的交叉点,每个交叉点处存储着具体的数据。
2.可扩展性:二维表可以随着需要增加行和列,以适应数据的变化。
3.数据的一致性:每个字段在表头中都有明确定义,确保了数据在同一列中具有一致的数据类型或含义。
4.查询和排序:通过对二维表进行查询和排序操作,可以方便地获取特定的数据。
5.关系和连接:多个二维表之间可以通过共同的字段进行关联和连接,以便于获取更加复杂的数据。
二维表的应用二维表广泛应用于各个领域,包括但不限于:•数据库管理系统:二维表是关系型数据库的基本概念之一,用于存储和管理大量的结构化数据。
•电子表格软件:电子表格软件使用二维表的形式来展示和计算数据,如Microsoft Excel、Google Sheets等。
•数据分析和报表:二维表可以用于存储数据,进行数据分析和生成报表,帮助用户更好地理解和利用数据。
•Web开发:二维表作为后端数据的存储形式,可以被 Web 开发中的数据库或其他数据存储工具所使用。
总结二维表是一种常见的数据结构,用于组织和存储数据。
它由行和列组成,表头包含了字段名称,数据行包含了具体的数据。
二维列联表 英文文章

二维列联表英文文章二维列联表在英文中通常被称为 "2D contingency table"。
以下是一篇关于二维列联表的英文文章:The 2D Contingency Table: A Powerful Tool for Data AnalysisThe 2D contingency table is a fundamental tool in the field of statistics, particularly in the analysis of categorical data. This table provides a structured way to organize and analyze data that has two categorical variables. By breaking down the data into various categories, the 2D contingency table allows for a more comprehensive understanding of the relationships between the variables.In its simplest form, a 2D contingency table consists of rows and columns. The rows represent one categorical variable, while the columns represent the other categorical variable. Each cell of the table contains the frequency or count of observations that fall into a specific category combination. For example, if we have twocategorical variables: species (cat, dog) and color (white, black), a 2D contingency table could look like this:Species Color FrequencyCat White 10Cat Black 5Dog White 8Dog Black 3The information in a 2D contingency table can be used to perform various statistical tests and calculations to assess the relationship between the variables. Commonly used measures include the chi-square test, odds ratio, and correlation coefficient. These measures help to determine if there is a significant association between the variables and to what extent they are related.The 2D contingency table is particularly useful when dealing with data that has two categorical variables with multiple levels. Itprovides a structured framework for organizing and visualizing the data, enabling researchers to easily identify patterns and trends within the data. By breaking down the data into smaller categories, researchers can gain a more nuanced understanding of the relationships between the variables, which can lead to valuable insights and conclusions.In conclusion, the 2D contingency table is a valuable tool for statisticians and researchers who work with categorical data. It allows for a comprehensive analysis of relationships between two categorical variables, providing insights that can inform further research and decision-making.。
列联表ppt课件

精选PPT课件
4
一维多项分类分析
将总体按照某种特性分为A1,A2,……Ak, 计k个类型,每一个体仅属于其中一个类型, 总体中属于k个类型的比例P1,P2,……Pk。 现从总体中随机抽查n个样本单位,其中属 于类Ai有ni个,i=1,2,…k。现作原假设: P1 = P2 =……= Pk 。
精选PPT课件
其中,p i.为属性A处于类型i的概率,p . j 为属性B处于
类型j的概率。
精选PPT课件
16
列联表
特征A
A1 A2 ‥ ‥ Aj ‥ ‥
B1 n11 n12 ‥ ‥
精选PPT课件
13
列联表原理
在利用列联表进行分析时,首先表示出列 联表,列联表实际上是一个交叉的频数表, 利用所给频数构造一个卡方统计量,根据 样本数据计算得来的卡方值与一定自由度 下卡方临界值进行对比,从而判断是否接 受原假设。
实质上是品质相关的问题
精选PPT课件
14
列联表分析在处理两个或几个定性变量间 是否有真正意义上的独立问题是独具魅力。 其原因有三:
每个试验的结果都落在k组中的某一组内
某个试验的结果落在某一特定组的概率在试验之间保持
不变。且有
k
pi 1
试验是独立的 i1
试验者关心的n1,n2,…nk,这里ni等于试验落在组i的数目。 注意,n1+n2+…+nk=n
精选PPT课件
8
例2.1
某信息咨询公司受委托调查了解顾客对甲、 乙、丙三种品牌矿泉水的喜好程度,随机 观察了150名购买者的购买情况,并作如 下统计。
处于类型j的个体数在表中记为nij 。并且,
a
b
n. j nij
《二至四维列联表》课件

三维列联表
定义和概念
三维列联表是一种在二维列联表 的基础上,增加了另一个变量进 行分析的工具。
制作方法
制作三维列联表需要收集涉及三 个变量的数据,并进行适当的整 理和计算。
应用场景
三维列联表广泛用于市场营销、 企业管理等领域,帮助决策者进 行更全面的数据分析。
四维列联表
1
定义和概念
四维列联表是在三维列联表的基础上,引入了第四个变量进行进一步的数据探索。
《二至四维列联表》PPT 课件
# 二至四维列联表 PPT课件 本次课程介绍二至四维列联表的基本知识和使用方法。
二维列联表
定义和概念
二维列联表是一种统计分析工具,用于研究两个变量之间的关系。
制作方法
制作二维列联表需要收集数据,并按照指定的格式进行整理和计算。
应用场景
二维列联表常用于市场调研、社会调查等领域,以了解不同变量之间的关联程度。
2
制作方法
制作四维列联表需要收集包含四个变量的数据,并进行逐步的整理、计算和分析。
3
应用场景
四维列联表常用于医学研究、市场பைடு நூலகம்测等领域,帮助发现多个变量之间的复杂关 系。
实战应用案例
基于列联表的数据分析案例分析
通过实际案例,展示如何运用列联表进行深入的数据分析,揭示隐藏在数据背后的规律。
基于列联表的决策分析案例分析
参考资料
• 参考书籍 • 网络资源 • 相关软件工具
以实际决策场景为例,演示列联表在辅助决策过程中的应用,帮助做出更明智的决策。
总结
制作列联表的注意事项
列联表制作过程中要注意数据收 集的准确性、格式的统一性和分 析的合理性。
列联表在数据分析和决策 中的重要性
第四章统计量的计算分解

根据Eviews给出的拒绝零假设犯第一类错误的概率可 以判断是否拒绝零假设,这个概率值是检验的相伴概 率,简称为P值。
P值指JB统计量取值大于样本计算的JB值的概率。以检 验水平5%为例,如果这个概率大于0.05,说明JB值落 在了原假设的接受域,应该接受原假设;如果这个概 率小于0.05,说明JB值落在了原假设的拒绝域,应该 拒绝原假设。
直方图反应序列值在各区间的分布频率,直方图右边的框里 列出了根据当前样本值测算得到描述统计量值。
一、序列窗口下的描述性统计量
以工作文件“余额宝二月收益”中序列对象“annreturn”为 例来进行说明:
“Mean”表示均值,即序列对象观测值的平均值; “Median”表示中位数,即从小到大排列的序列对象观测值的 中间值,是对序列分布中心的一个大致估计; “Maximum”表示最大值,是该序列观测值中的最大值 “Minimum”表示最小值,是该序列观测值中的最小值;
Series/Group for Classify:分类的序列或序列组,填入用 于分类的一个序列或一组序列,这些序列可以把指定序 列划分为不同的组或子序列。
操作练习
3. 做出序列“TRDVOL”的统计表将结果固化,命名为 “Table01”。
4. 按照中间值和偏度做出序列“CLPR”和“TRDVOL” 的描述性统计量,将结果固化,命名为“Table02”。
第三个选项是“Stats by Classification”(分类统计量), 把指定序列按不同的属性种类(以一个序列或一组序列表示) 划分为几个子序列,然后分别计算子序列的描述统计量。
分类统计量
Statistics:输出统计量的种类,包括均值(Mean)、求和 (Sum)、中位数(Median)、极大值(Maximum)、极小值 (Minimum)、标准差(Std. Dev.)、偏度(Skewness)、峰度 (Kurtosis)、无观测值个数(# of NAs)、观测值个数(Obs)。
二维列联表

因此有,
i =1 i =1
ij
2 Cn =
n(n 1) = G + H + TA + TB TAB 2
相合性的度量与检验
从τ系数的计算公式可知,在属性A与B正 相合时,G 比较大而H 比较小;反之在A与 B负相合时, G 比较小而H 比较大.因此, (G-H)的方向决定了相合性的方向. 在存在同分对的情况下,需要对相合性的 度量进行修正.
相合性的检验
从前面几个相关系数的计算公式可以看出, 对二维列联表的相关性的检验,主要是对 同序对与异序对的差进行检验,即检验G-H 是否等于0. 令 z = G H ,于是有:
z U= N (0,1) σ ( z)
z2 χ2 =U2 = 2 χ 2 (1) σ ( z)
由于其标准误计算较为复杂,通常使用统 计软件进行计算.
方表的一致性检验
二维表中当r=c时,形成方表. 方表有一致性检验问题. 【例4.3】两位检验员分别对72件产品进行检验的结 果见表:
问:他们的检验结果是否一致?
一致性的度量
在二维列联表的相合性度量中,当除从左上角到 右下角的对角线元素外其余都为0时,两种属性完 全正相合. 在方表中,一致性可以理解为:从左上角到右下 角的对角线元素表示结果一致,其值越大,表示 一致性越高.因此,q1 可以反映一致性的大小, 称为观测一致率:
GH τ= [n(n 1) / 2 TA ][n(n 1) / 2 TB ]
相合性的度量与检验
τ系数的取值范围为[-1,1]之间
–当H=0,且TA=TB=TAB时,完全正相合;
当r=c时,τ=1;
–当G=0,且TA=TB=TAB时,完全负相合;
《二维表的关联》教学案例.doc

《二维表的关联使用》教学案例一、教学目标:1、理解二维表关联的意义及建立关关联的条件,掌握建立关联的命令、方法及步骤。
2、能够利用二维表的关联,来引用多个二维表中的数据,灵活地操作多个工作表,实现VF中多个表Z间的数据杳询。
3、通过对多个表的关联操作,使学生理解各事物不是独立存在的,是普遍联系的,联系是有其内在规律的,学会用全局的观点看问题想事情。
二、教学方法:1、讲述和演示相结合,引导学生提出问题,发现新知。
2、任务驱动下的案例教学法。
三、教学重点:1、二维表关联的前提条件。
2、建立关联后,如何引用关联工作区上的数据。
四、教学难点:1、两个或两个以上的表同时关联到一个工作区。
2、父表和子表的选择及各工作区的切换。
五、课时安排:1课时六、课具准备:多媒体七、教学过程:1、回顾旧知,引入新知上堂课我们学习了多工作区的概念及多个表同时使用,请同学们回顾这两个问题:1、怎样选择多工作区?2、如何在当前工作区引用其它工作区上的数据。
同学们踊跃举手,冋答止确,接着设问:当我们操作当前表引用其它表中数据时, 同们发现有什么局限吗?是不是只能引用其它表的当而记录中的数据,也就是说当前表的记录指针随着二维表的操作在变化时,被引用表的记录指针不变化,当我们需要被引用表中的记录指针随当前表的操作发牛同步变化时,我们有什么办法吗?这就是我们今天耍学的关联。
2、创造情景,提出任务我们上堂课已接触了两个表,学生表(学号,姓名,性别,毕业学校,电话号码)和段考成绩表(学号,语文,数学,英语,计算机),这两个属性是来自于相同的实体,如下图所示我们可单独显示两个表。
段考成绩表:学牛表:现在有一个这样的任务,我们要把叨个表连到一起来查询,要得到姓名、语文、数学、计算机、总分等字段,耍达到这样的冃标,就必须把两个表按学号字段关联起來。
我们先來学习关联。
3、环环相扣,讲解新知(1)、概念:所谓表文件的关联是把当前工作区屮打开的表与另一个工作区屮打开的表进行逻辑连接,而不生成新的表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不完备列联表的检验
对拟独立的不完备列联表的ML估计后,需要进行 拟独立性检验;同时,考虑不完备子集的拟独立 性也是研究完备表的一种方法。
原假设应为:
H0 : 存在i (i 1, , r)和 j ( j 1, , c),使得mij i j
对独立性的期望频数定义公式可以通过取对数将 乘法转换为加法,即:
ln mij ln i ln j
这就是对数线性模型(第7章)。
不完备列联表
当某些nij=0时,称这些格为空格;有空格的列联 表称为不完备的列联表。
对于一般完备列联表讨论独立性,对不完备列联 表讨论拟独立性。
属性A方向的同分对,即行等级或顺序相同的 r
数据对,记为TA
;TA
C2 ni
属性B方向的同分对,即i1 列等级或顺序相同的 c
数据对,记为TB
; TB
C2 n j
属性A与B的同分对,即i行1 顺序与列顺序相等的
数据对,记为TAB ;TAB r
c
C2 nij
相合性的度量与检验
在四格表中,用来判断属性A与B关联情况 (相合性检验)的统计量U、χ2均包含一个 共同因子:
n11n22-n12n21>0时,四格表正相合; n11n22-n12n21<0时,四格表负相合;
有序属性数据相合关系的度量:
Pearson的矩相关系数 Spearman的等级相关系数 Kendall的τ相关系数——使用最多
对不完备列联表中元素的估计,可以在假定完全 随机泊松分布的基础上,得到似然方程组:
ii ni , i 1, , r j j n j , j 1, , c
在保持边缘和不变的前提下,解出期望频数。 有的情况下期望频数的极大似然估计难以直接得
到,需要通过迭代算法求解。 迭代算法就是在保持边缘和不变时,寻找 i j放入
检验统计量为:
2
(nij mˆ ij )2 ~ 2 ((r 1)(c 1) m)
(i, j )S
mˆ ij
G2
2
(i, j )S
nij
ln
mˆ ij nij
二维列联表的独立性检验
二维列联表独立性检验实质上是带参数的 分类数据的检验问题。
二维列联表的独立性检验
【例4.1】为了解男性和女性对三种啤酒的偏 好差异分别调查了1353个男性和636个女性, 结果见表:
问男性与女性对啤酒的偏好是否有显著差异。
二维列联表的独立性检验
通过计算检验统计量的值得到:
mˆ i(j2)
mˆ i(j1)
mˆ i(j1)
n j
{i:(i, j )S}
迭代估计法
4、将第二次迭代得到的值作为初始估计,重复前面的 步骤2和步骤3;
5、直至相邻两次迭代得到的估计仅有比较小的差别, 最后得到的迭代估计就是期望频数的极大似然估计。
以上步骤可以在表格上完成,每次估计所有非空 格的迭代值,直到精度符合要求即可。
因此有, i1 i1
Cn2
n(n 1) 2
G
H
TA
TB
TAB
相合性的度量与检验
从τ系数的计算公式可知,在属性A与B正相 合时,G 比较大而H 比较小;反之在A与B 负相合时, G 比较小而H 比较大。因此, (G-H)的方向决定了相合性的方向。
在存在同分对的情况下,需要对相合性的 度量进行修正。
其中,mij为期望频数(证明见P96)。 主要用来描述完全随机泊松分布变量的抽样方式
下,属性A与B的相互独立问题,即:
nij ~ P(mij ) P(i j )
完全随机泊松分布情况下,属性A与B独立性检验 与带参数的分类数据检验完全相同。
独立性的期望频数定义
公式 mij i 可j 以理解为: 在A和B相互独立时, i 和 j是与 mij 有关的两 个量。 由 nij ~ P(mij )可知,E(nij ) mij i j ,因此,可 以认为 i 和 j分别是属性A和B的效应。
当从左上角到右下角的对角线元素外的其余元素 都等于0时,为完全正相合;
当从右上角到左下角的对角线元素外的其余元素 都等于0时,为完全负相合;
Gamma系数
除肯德尔的τ外,相合性度量还有伽马系数 Gamma: G H
GH
伽马的取值在[-1,1]之间,越接近1说明越趋向正 相合,越接近-1说明为负相关。
很明显,原假设不成立,即不是偶然一致。
独立性的期望频数定义
对于二维表,独立性的定义除基本的联合概率等 于边缘概率乘积的方法外,还可以用期望频数。
若存在 i (i 1, , r)和 j ( j 1, ,, c)使任意的 i 和 j 都有:mij i j ,则称属性A和B相互独立。
独立性与齐性
如果对任意的i和j,都有:pi j pi p j,则称 属性A与B独立。
如果A与B独立,则对任意j都与i无关
p1 j p1
prj p1 j pr p1
prj pr
p j
如果A与B独立,则对任意i都与j无关
pi1 p1
pic pi1 pc p1
相合性的度量与检验
τ相关系数基本思路:
认为二维列联表均可定义为有序表; 对有序变量的赋值可以确定由小到大的顺序关
系,但不影响相合关系的度量;最简单的赋值 方法就是令 x i,i 1, , r
y j, j 1, , c
在二维表中,
数据对
x y
一致性的检验
一般认为,计算的Kappa小于0时,属于偶然一致, 即期望一致率大于观测一致率;
只有在Kappa大于0时,才进行一致性检验;
在计算kappa系数的方差基础上,可以构造检验统
计量:
U ~ N (0,1) D( )
经计算,例4.3的kappa=0.361,kappa的标准误 =0.0844,故U=4.277
相合性的度量与检验
相合性用来描述属性变量之间的相关情况,包括 关联的方向和强度。
二维列联表根据属性的类型分为三类:
双向无序列联表 一向无序、一向有序列联表 双向有序列联表
实际上即使无序也可以定义为有序,或假设有序。 这样,相合关系有两类:
正相合:属性A大的个体,属性B也往往较大; 负相合:属性A大的个体,属性B往往较小;
i j
,
如数据对11
有n11对, cr
有nrc
对
相合性的度量与检验
在不考虑同分对的情况下,τ系数以数据对中同 序对与异序对的差为分子,以样本容量n可能 形成的总数据对数为分母;即
ns nd Cn2
2 n(n 1) (ns
nd )
其中:在二维表的任意两个单元格之间,若:
2 90.685,p P( 2 (2) 90.685) 0 G2 90.065,p P( 2 (2) 90.065) 0
说明男性与女性对啤酒的偏好有显著差异 可见,独立性问题的讨论仅仅是说明属性A
与B有无关系,或是否相互独立,但不能给 出关系的方向与强弱。
果见表:
问:他们的检验结果是否一致?
一致性的度量
在二维列联表的相合性度量中,当除从左上角到 右下角的对角线元素外其余都为0时,两种属性完 全正相合。
在方表中,一致性可以理解为:从左上角到右下 角的对角线元素表示结果一致,其值越大,表示 一致性越高。因此,q1 可以反映一致性的大小, 称为观测一致率:
令 z G H,于是有:
U z N (0,1)
(z)
2
U2
z2 2 (z)
2 (1)
由于其标准误计算较为复杂,通常使用统
计软件进行计算。
方表的一致性检验
二维表中当r=c时,形成方表。 方表有一致性检验问题。 【例4.3】两位检验员分别对72件产品进行检验的结
GH
[n(n 1) / 2 TA][n(n 1) / 2 TB ]
相合性的度量与检验
τ系数的取值范围为[-1,1]之间
当H=0,且TA=TB=TAB时,完全正相合;
当r=c时,τ=1;
当G=0,且TA=TB=TAB时,完全负相合;
当r=c时, τ=-1;
当TA=TB=TAB时,说明每一行、每一列只有一个非 零值;
不完备列联表的非空格中,也就是满足以上方程 组成立。
迭代估计法
迭代算法的步骤:
1、令非空格上的期望频数估计的初始值为1,
mˆ i(j0) 1, (i, j) S
2、调整该估计值,令:
mˆ i(j1)
mˆ i(j0)
mˆ i(j0)
ni
{ j:(i, j )S}
3、继续调整以上估计值,令:
q1 (n11 n22 nrr ) / n
但这一度量值存在平均值为正的缺陷,由Cohen 于1960年提出了Kappa系数。
一致性度量
一致性的检验
Kappa 系数中的π0就是q1 , πe是π0的期望或均值,
称为期望一致率,即两次试验结果由于偶然机会所 造成的一致率; 当方表中左上到右下对角线以外元素均为0时, Kappa 系数达到最大值1,即完全一致;当完全不 一致时, Kappa 等于0; Kappa 系数的取值在[0,1]之间; Kappa <0.4时,认为一致性较差; Kappa >0.8时,认为一致性较好; 0.4>Kappa <0.8时,认为一致性一般。
