初中几何中线段和与差最值问题学习资料
中考复习线段和差的最大值与最小值(拔高)

中考二轮复习之线段和(差)的最值问题一、两条线段和的最小值。
填空题:1.如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是.2.如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则P A+PC的最小值是.3.如图,在锐角△ABC中,AB=42,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是.4.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________.5.已知A(-2,3),B(3,1),P点在x轴上,若P A+PB长度最小,则最小值为.若P A—PB长度最大,则最大值为.6.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为.7、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为8、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD 和AE上的动点,则DQ+PQ的最小值为.综合题:1.如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.第1题第2题第3题第4题2.如图,已知平面直角坐标系,A ,B 两点的坐标分别为A (2,-3),B (4,-1)设M ,N 分别为x 轴和y 轴上的动点,请问:是否存在这样的点M (m ,0),N (0,n ),使四边形ABMN 的周长最短?若存在,请求出m =______,n = ______(不必写解答过程);若不存在,请说明理由.中考赏析:1.著名的恩施大峡谷(A )和世界级自然保护区星斗山(B )位于笔直的沪渝高速公路X 同侧,AB =50km 、B 到直线X 的距离分别为10km 和40km ,要在沪渝高速公路旁修建一服务区P ,向A 、B 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(AP 与直线X 垂直,垂足为P ),P 到A 、B 的距离之和S 1=P A +PB ,图(2)是方案二的示意图(点A 关于直线X 的对称点是A',连接BA'交直线X 于点P ),P 到A 、B 的距离之和S 2=P A +PB . (1)求S 1、S 2,并比较它们的大小; (2)请你说明S 2=P A +PB 的值为最小;(3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B 到直线Y 的距离为30km ,请你在X 旁和Y 旁各修建一服务区P 、Q ,使P 、A 、B 、Q 组成的四边形的周长最小.并求出这个最小值.2.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.3、在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC 绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F.(1)求经过A、B、C三点的抛物线的解析式;(2)当BE经过(1)中抛物线的顶点时,求CF的长;(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ 的周长最小,求出P、Q两点的坐标.4.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.5、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题 (运用三角形两边之差小于第三边)1.直线2x-y-4=0上有一点P ,它与两定点A (4,-1)、B (3,4)的距离之差最大,则P 点的坐标是 .2.已知A 、B 两个村庄的坐标分别为(2,2),(7,4),一辆汽车(看成点P )在x 轴上行驶.试确定下列情况下汽车(点P )的位置:(1)求直线AB 的解析式,且确定汽车行驶到什么点时到A 、B 两村距离之差最大? (2)汽车行驶到什么点时,到A 、B 两村距离相等?3. 如图,抛物线y =-14x 2-x +2的顶点为A ,与y 轴交于点B .(1)求点A 、点B 的坐标;(2)若点P 是x 轴上任意一点,求证:P A -PB ≤AB ; (3)当P A -PB 最大时,求点P 的坐标.4. 如图,已知直线y =21x +1与y 轴交于点A ,与x 轴交于点D ,抛物线y =21x 2+bx +c 与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B (1)求该抛物线的解析式;(3)在抛物线的对称轴上找一点M ,使|AM -MC |大,求出点M 的坐标.5. 如图,直线y =-3x +2与x 轴交于点C ,与y 轴交于点B ,点A 为y 轴正半轴上的一点,⊙A 经过点B 和点O ,直线BC 交⊙A 于点D . (1)求点D 的坐标;(2)过O ,C ,D 三点作抛物线,在抛物线的对称轴上是否存在一点P ,使线段PO 与PD 之差的值最大?若存在,请求出这个最大值和点P 的坐标.若不存在,请说明理由.好题赏析:原型:已知:P 是边长为1的正方形ABCD 内的一点,求P A +PB +PC 的最小值.例题:如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM . (1)求证:△AMB ≌△ENB ;(2)①当M 点在何处时,AM +CM 的值最小;②当M 点在何处时,AM +BM +CM 的值最小,并说明理由; (3)当AM +BM +CM 的最小值为3+1时,求正方形的边长.变式:如图四边形ABCD 是菱形,且∠ABC =60,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM ,则下列五个结论中正确的是( )①若菱形ABCD 的边长为1,则AM +CM 的最小值1; ②△AMB ≌△ENB ;③S 四边形AMBE =S 四边形ADCM ;④连接AN ,则AN ⊥BE ;⑤当AM +BM +CM 的最小值为23时,菱形ABCD 的边长为2. A .①②③ B .②④⑤ C .①②⑤三、其它非基本图形类线段和差最值问题1、求线段的最大值与最小值需要将该条线段转化到一个三角形中,在该三角形中,其他两边是已知的,则所求线段的最大值为其他两线段之和,最小值为其他两线段之差。
初中几何中线段和差的最大值与最小值典型分析(最全)

初中几何中线段和差的最大值与最小值典型分析(最全)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:(对称轴为:动点所在的直线上)一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧: (3)两个点都在内侧:mm A Bm B mA Bmnmnnmn(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:n点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、点与圆在直线两侧:2、点与圆在直线同侧:m nmnmnmmm三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解)(1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
初中几何中线段和差的最大值与最小值典型分析(最全)

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:(对称轴为:动点所在的直线上)一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: (4)、台球两次碰壁模型变式一:已知点A 、B线m,n 的内侧,在直线n 、m 求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧,在直线m、n 别上求点P 、Q 点PA+PQ+QA 周长最短. 二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解)(1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧: 练习题?1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为?????????????.nn m m2、 如图1,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 分别是AD 和AB上的动点,则BM+MN 的最小值为?????????????.3、如图,在锐角三角形ABC 中,AB=∠BAC=45,BAC的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少?4、如图4所示,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为?????????.5、如图3,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时,PB 的长为__________.6、 如图4,等腰梯形ABCD 中,AB=AD=CD=1,∠ABC=60°,P 是上底,下底中点EF 直线上的一点,则PA+PB 的最小值为??????????????.7、如图5菱形ABCD 中,AB=2,∠BAD=60°,E 是AB 的中点,P 是对角线AC 上的一个动点,则PE+PB 的最小值为????????????.8、如图,菱形ABCD 的两条对角线分别长6和8,点P 是对角线AC 上的一个动点,点M 、N 分别是边AB 、BC 的中点,则PM+PN 的最小值是????????????9、如图,圆柱形玻璃杯,高为12cm ,底面周长为18cm ,在杯内离杯底3cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为________cm .10、如图,菱形ABCD 中,AB=2,∠A=120°,点P ,Q ,K 分别为线段BC ,CD ,BD 上的任意一点,则PK+QK 的最小值为?????????????11、如图,正方形ABCD 的边长为2,E 为AB 的中点,P 是AC 上一动点.则PB +PE 的最小值是12、 如图6所示,已知正方形ABCD 的边长为8,点M 在DC 上,且DM=2,N 是AC 上的一个动点,则DN+MN 的最小值为???????????. 13、如图,正方形ABCD 的边长是2,∠DAC 的平分线交DC 于点E ,若点P 、Q 分别是AD 和AE 上的动点,则DQ+PQ 的最小值15、如图,⊙O 的半径为2,点A 、B 、C 在⊙O 上,OA ⊥OB ,∠AOC =60°,P 是OB 上一动点,则PA +PC 的最小值是.16、如图8,MN 是半径为1的⊙O 的直径,点A 在⊙O 上,∠AMN =30°,B 为AN 弧的中点,P 是直径MN 上一动点,则PA +PB 的最小值为(???)(A)2???(B)?????(C)1???(D)2Q解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.?3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y=x2-x+3和y轴的交点为A,M为OA的中点,若有一动点P,自M点处出发,沿直线运动到x轴上的某点(设为点E),再沿直线运动到该抛物线对称轴上的某点(设为点F),最后又沿直线运动到点A,求使点P运动的总路程最短的点E,点F的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x 轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F.(1)求经过A、B、C三点的抛物线的解析式;(2)当BE经过(1)中抛物线的顶点时,求CF的长;(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ 的周长最小,求出P、Q两点的坐标.?6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题(运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,差小于第三边,P ’A —P ’B <AB ,而PA —时最大,因此点P 为所求的点。
初中几何中线段和差的最大值与最小值典型分析(最全)

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:(对称轴为:动点所在的直线上)一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:m m mmABmn m nnmn(3)两个点都在内侧:(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:nnm Bnn2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:mnmmmmm过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧: 练习题1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为 .2、 如图1,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为 . 3、如图,在锐角三角形ABC 中 ,AB=52,∠BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少mABB'EQ PmABQPQ4、如图4所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为.5、如图3,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB 上一个动点,当PC+PD的和最小时,PB的长为__________.6、如图4,等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF直线上的一点,则PA+PB的最小值为.7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2 (B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A 点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F . (1)求经过A 、B 、C 三点的抛物线的解析式; (2)当BE 经过(1)中抛物线的顶点时,求CF 的长;(3)在抛物线的对称轴上取两点P 、Q (点Q 在点P 的上方),且PQ =1,要使四边形BCPQ 的周长最小,求出P 、Q 两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x 轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.v1.0 可编辑可修改二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
初中数学线段和差最值问题(史上最全版)

初中数学线段和差最值问题(史上最全版)⼀、知识依据1.线段公理:两点之间,线段最短;2.对称的性质:①关于⼀条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三⾓形的三边关系:①三⾓形两边之和⼤于第三边;②三⾓形两边之差⼩于第三边。
4.垂直线段最短。
⼆、从“将军饮马”说起话说在古罗马时代,在亚历⼭⼤城有⼀位精通数学和物理的学者,名叫海伦。
⼀天,⼀位罗马将军专程去拜访他,向他请教⼀个百思不得其解的问题:将军每天从军营A出发,先到河边饮马,然后再去河岸同侧B地开会,应该怎样⾛才能使路程最近?从此,这个被称为“将军饮马”的问题⼴泛流传。
这个问题的解决并不难,据说海伦略作思考就解决了它。
为了解决“将军饮马”问题,我们先看下⾯的问题。
(⼀)点A、B在直线m的异侧,在直线m上,求⼀点P,使PA+PB最⼩由两点之间线段最短知,由A到B⾛直线距离最短,所以连接AB与直线m交于点P,此时PA+PB最⼩。
我们选取除P之外的任意⼀点P’,由三⾓形的三边关系可以证明。
综上,我们可知点A、B在直线m异侧时,连接AB与直线m交于点P,即为所求。
搞清楚上⾯这个问题后,我们再来研究“将军饮马”问题就简单了。
(⼆)点A、B在直线m的同侧,在直线m上,求⼀点P,使PA+PB最⼩作图步骤:①作点A关于直线m的对称点A,②连接BA,,与直线L相交于点P③此时PA+PB最⼩。
看到这个问题后,我们会怎么思考呢?结合上⾯的问题及解答思路,我们会想到将直线m同侧的两个点转化到直线m异侧,那么问题就迎刃⽽解了。
所以,我们作A关于直线m的对称点A’(做B的对称点也⼀样),则将同侧的两点A、B转化到了异侧两点A’、B。
此时,连接A’B与直线m交于点P,即为所求。
综上,我们可知“将军饮马”问题转化为对称点,则问题就轻松解决了。
三、“将军饮马”的拓展延伸总结“将军饮马”问题,我们发现是两个顶点及定直线上的⼀个动点问题,那么接下来我们将刚才的问题进⾏升级。
初中几何中线段和与差最值问题
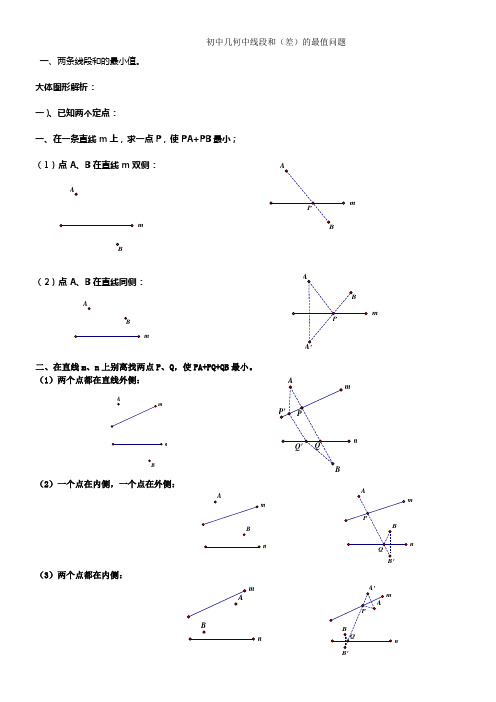
初中几何中线段和(差)的最值问题一、两条线段和的最小值。
大体图形解析: 一)、已知两个定点:一、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 双侧:(2)点A 、B 在直线同侧:二、在直线m 、n 上别离找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mmABmA Bmn mnnmnm(4)、台球两次碰鼻模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 别离上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 别离上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点:(一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 一、两点在直线双侧:二、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 一、点与圆在直线双侧:二、点与圆在m nmnm nmmm三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解)(1)点A 、B 在直线m 双侧:作法:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,现在P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:基础题1.如图1,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 别离是OA 、OB 上的动点,求△PQR 周长的最小值为 .二、如图2,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 别离是AD 和AB 上的动点,那么BM+MN 的最小值为 .3、如图3,在锐角三角形ABC 中 ,AB=52,∠BAC=45,BAC 的平分线交BC 于D ,M 、N 别离是AD 和AB 上的动点,那么BM+MN 的最小值是 。
初中几何中线段和与差最值问题

v1.0可编辑可修改初中几何中线段和(差)的最值问题、两条线段和的最小值。
基本图形解析:)、已知两个定点:1、在一条直线m上,求一点P,使PA+PB最小;(1 )点A B在直线m两侧:(2)点A B在直线同侧:*A'2、在直线m n上分别找两点P、Q,使PA+PQ+Q最小。
(1)两个点都在直线外侧:B(2)一个点在内侧,一个点在外侧:QB' (3)两个点都在内侧:m22(4 )、台球两次碰壁模型变式一:已知点 A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得变式二:已知点A 位于直线m,n 的内侧,在直线m二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线 m 上找一点P ,使PA+PB 最小(在图中画出点 P 和点B )1、两点在直线两侧:2、两点在直线同侧:围成的四边形ADEB 周长最短.n 分别上求点P 、Q 点PA+PQ+Q 周长最短.A"33(二)动点在圆上运动点B 在O O 上运动,在直线 m 上找一点P ,使PA+PB 最小(在图中画出点 P 和点B ) 1、点与圆在直线两侧:三)、已知A B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定 在直线m 上要求P 、Q 两点,使得PA+PQ+Q 的值最小。
(原理用平移知识解)(1 )点A 、B 在直线m 两侧:A■- m作法:过A 点作AC// m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为 P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:2、点与圆在直 m线同侧:基础题1.如图1, / AOB45。
,P是/ AOB^一点,PO1Q, Q R分别是OA 0B上的动点,求厶PQR周长的最小值为 _____________________________分别是AD和AB上的动点,贝U BM+M的最小值为___________________________3、如图3,在锐角三角形ABC中,AB=5j2,/ BAC=45 BAC的平分线交BC于D, M N分别是AD和AB上的动点,贝U BM+MN勺最小值是______________ 。
(完整版)初中几何中线段和差的最大值与最小值典型分析(最全)
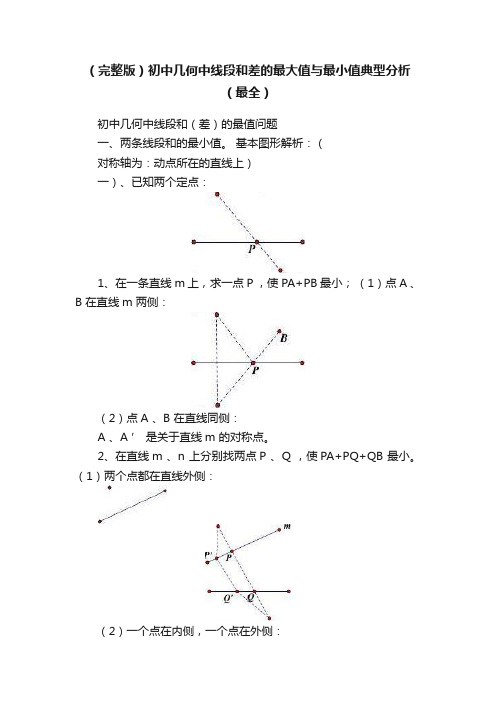
(完整版)初中几何中线段和差的最大值与最小值典型分析(最全)初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:(对称轴为:动点所在的直线上)一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小;(1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mm ABm B mA Bmn m nn m nnnm B(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点:(一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:m nmnmnm(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:mmmmQ Q练习题1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR周长的最小值为.2、如图1,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为. 3、如图,在锐角三角形ABC 中,AB=52,∠BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少?4、如图4所示,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为 .5、如图3,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时,PB 的长为__________.6、如图4,等腰梯形ABCD 中,AB=AD=CD=1,∠ABC=60°,P 是上底,下底中点EF 直线上的一点,则PA+PB 的最小值为.Q7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN 的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC 上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则P A+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2 (B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P 和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F .(1)求经过A 、B 、C 三点的抛物线的解析式;(2)当BE 经过(1)中抛物线的顶点时,求CF 的长;(3)在抛物线的对称轴上取两点P 、Q (点Q 在点P 的上方),且PQ =1,要使四边形BCPQ 的周长最小,求出P 、Q 两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x 轴、y轴的正半轴上,OA=3,OB=4,D为边OB 的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF 的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题(运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
中考数学专题复习求线段和差的最值问题(共26张PPT)

第一步 寻找、构造几何模型
要求四边形MNFE F/
F
的周长最小?
使线段PO与PD之差最大?若存在,请求出这个最大值和点P的坐标。
N
E
⑵练习①:当已M知点二在次何函处数时图,像AM的+顶C点M坐的标值为最C小(3;,-2),且在x轴上截得的线段AB的长为4,在y轴上有一点P,使△APC的周长最小,求P点
线段和差的最值问题解题策略 一、两条线段和的最小值
例4:在矩形ABCD中,F是BC的三等分点,E是AB的二等分点,在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如
y 果存在,求出周长的最小值;如果不存在,请说明理由.
点A为 y 轴正半轴上的一点,⊙A经过点B和点O,直线BC交⊙A与点D。
(1)点A、B在直线m两侧:
(2)点A、B在直线同侧:
A
A
m B
m P
A
B
A
B m
B m
P
A'
一、求两条线段之和的最小值
例1:在△ABC中,AC=BC=2,
∠ACB=90O,D是BC边的中点,E是AB
上的一动点,则EC+ED的最小值
为
。
A
p
E
C
D
.
B
2、抛物线在坐标系中的位置如图:对 在其称轴上找一点P,使得△PBC的周 长最小,请求出点P的坐标 .
举一反三
典例2 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F
在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿
直线EF翻折,点C落在点P处,则点P到边AB距离的最小
值是
.
1.2
中考专题复习
中考专题复习-----线段和差地最大值与最小值
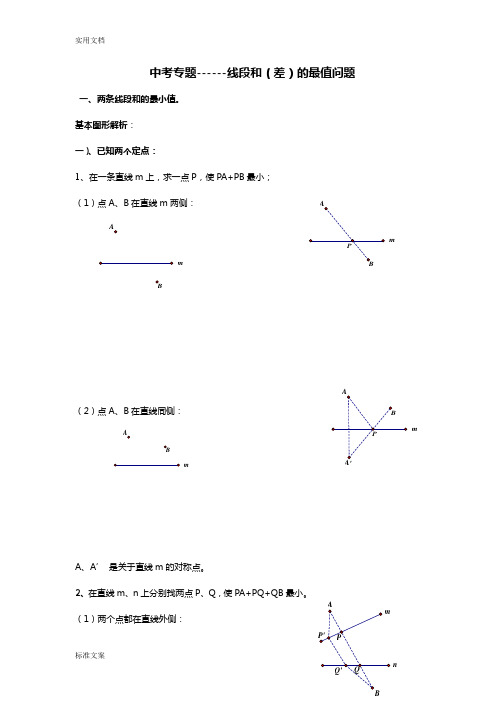
中考专题------线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:m m BmABm(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)、台球两次碰壁模型nmnmnnnm变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点:(一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动m nmnmnm点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:mmmm过A点作AC∥m,且AC长等于PQ长,连接BC,交直线m于Q,Q向左平移PQ长,即为P点,此时P、Q即为所求的点。
(2)点A、B在直线m同侧:练习题QQ1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR周长的最小值为 .2、 如图1,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为 .3、如图,在锐角三角形ABC 中 ,AB=52,∠BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少?4、如图4所示,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为 .Q5、如图3,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________.6、如图4,等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF 直线上的一点,则PA+PB的最小值为.7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N 分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC 上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC 上一动点,连接PB、PQ,则△PBQ周长的最小值为 cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2(B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC 绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F.(1)求经过A、B、C三点的抛物线的解析式;(2)当BE经过(1)中抛物线的顶点时,求CF的长;(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ 的周长最小,求出P、Q两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x 轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题(运用三角形两边之差小于第三边)基本图形解析:1、在一条直线m上,求一点P,使PA与PB的差最大;A(1)点A、B在直线m同侧:AB解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
“线段和差最值问题”专题学习 ppt

专题学习
1、如图,直线L外有点A与点B,点P是L 上一 动点,当PA+PB最小时,试确定点P的位置.
2、如图,射线AC外有一点B,点P是射线AC 上一动点,当PB + 1 PA最小时,试确定点 P
2 的位置.
◆如图,平面直角坐标系中,OA =2, 点P为 x 轴正半轴上一动点, ∠POA=30 °. 求:OP+2PA的最小值。分别是y轴与x轴上的动点, 当 MC+MN — 2 AN最小时,试确定动
2
点M、N 的位置,并求 MC+MN — 2 AN
2
的最小值。
◆如图,射线AC外有一点B,点P是射线AC 上一动点,
当PB — 1 PA 最小时,试确定点 P 的位置. 2
◆如图,点A在第一象限,点B在x轴正半轴上,点M、N分别是y轴与x轴上
的动点,当 MA+MN + 1 BN最小时,试在坐标系中确定动点M、N 的位置。 2
【思考】如图,抛物线 y x2 2x 3 与x轴交于A、B两点,抛物线的
初级中学几何中线段和差的最大值与最小值典型分析(完整)
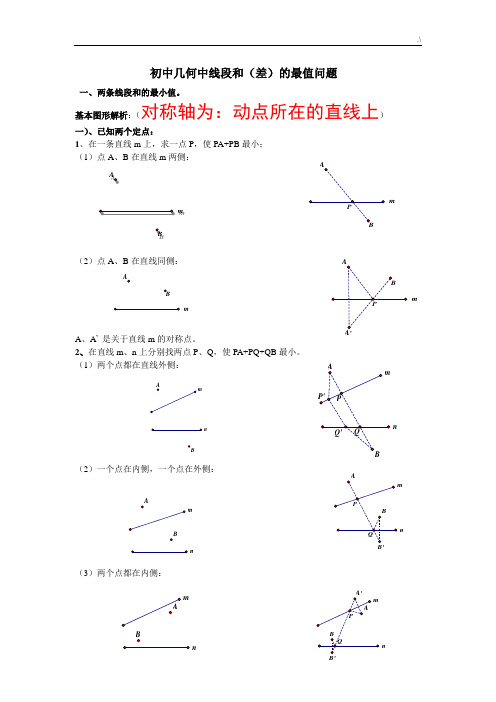
初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:(对称轴为:动点所在的直线上)一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mm ABm B mA Bmn m nn m nnnm B(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:m nmnmnm(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:mmmmQ Q练习题1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为 .2、 如图1,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为 . 3、如图,在锐角三角形ABC 中 ,AB=52,∠BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少?4、如图4所示,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为 .5、如图3,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时,PB 的长为__________.6、 如图4,等腰梯形ABCD 中,AB=AD=CD=1,∠ABC=60°,P 是上底,下底中点EF 直线上的一点,则PA+PB 的最小值为 .Q7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则P A+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2 (B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F . (1)求经过A 、B 、C 三点的抛物线的解析式;(2)当BE 经过(1)中抛物线的顶点时,求CF 的长; (3)在抛物线的对称轴上取两点P 、Q (点Q 在点P 的上方),且PQ =1,要使四边形BCPQ 的周长最小,求出P 、Q 两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x 轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
线段及差最值问题
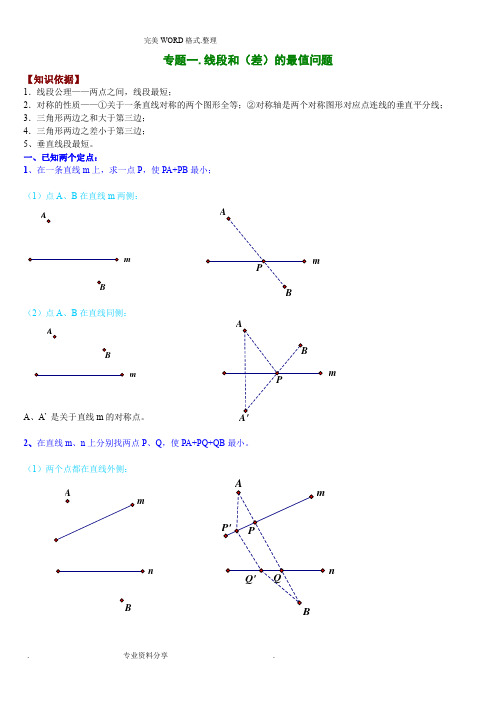
专题一.线段和(差)的最值问题【知识依据】1.线段公理——两点之间,线段最短;2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三角形两边之和大于第三边;4.三角形两边之差小于第三边;5、垂直线段最短。
一、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小;(1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:P m A B m A B m A BPm A B A'n m A B Q P n m A B P'Q'(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.n m A B QP n m A B B'Q P nm A B B'A' n m A B m n A B E D m n A B A'B'm n A P Q m n A A'二、一个动点,一个定点:(一)动点在直线上运动: 点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动:点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、点与圆在直线两侧:2、点与圆在直线同侧:m n A P m n A B m n A Pm n A A'B m O A P'P m O B A B' m O A P m O A B A'三、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
2020详解初中几何线段和(差)的最值问题

2020详解初中几何线段和(差)的最值问题2020详解初中几何线段和(差)的最值问题:
一、两条线段和的最小值问题
基本图形解析:(对称轴为:动点所在的直线上)
一)、已知两个定点:
二)、一个动点,一个定点:
三)、已知A、B是两个定点,P、Q是直线m上的两个动点,P
在Q的左侧,且PQ间长度恒定,在直线m上要求P、Q两点,使得PA+PQ+QB的值最小。
(原理用平移知识解)
一、在三角形背景下探求线段和的最小值
1.1 在锐角三角形中探求线段和的最小值
1.2在等边三角形中探求线段和的最小值
二、在四边形背景下探求线段和的最小值
2.1在直角梯形中探求线段和的最小值
2.2在等腰梯形中探求线段和的最小值
2.3在菱形中探求线段和的最小值
2.4在正方形中探求线段和的最小值
三、在圆背景下探求线段和的最小值
四、在反比例函数图象背景下探求线段和的最小值
五、在二次函数背景下探求线段和的最小值
六、在平面直角坐标系背景下探求线段和的最小值
二、求两线段差的最大值问题 (运用三角形两边之差小于第三边)
三、其它非基本图形类线段和差最值问题。
最新中考数学之_线段和(差)的最值问题

求线段和(差)的最值问题【知识依据】:1.线段公理——两点之间,线段最短;2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三角形两边之和大于第三边;4.三角形两边之差小于第三边。
5、垂直线段最短 一、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:mm ABm ABm n mn(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.nm Annnm二、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:m nm nm nmmmmm三、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左移动PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:四、求两线段差的最大值问题(运用三角形两边之差小于第三边) 1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:(2)点A 、B 在直线m 异侧:过B 作关于直线m 的对称点B ’,连接AB ’交点直线m 于P,此时PB=PB ’,PA-PB 最大值为AB ’BmmmmQ m Q一、在线段之和的最值问题中酝酿与构建,借用线段公理求解例1 (湖北荆门)如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN =30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )A 2BC 1D 2解析:PA+PB的线段之和最小值求法的依据是“平面几何中,两点之间线段最短”的数学模型与原理,故可作B关于MN的对称点是H,连接AH交MN于点P,AH的长就是PA+PB的线段之和的最小值,借助圆圆周角定理,可知根据∠AOH=90°,巧妙构造Rt△OAH,根据题意运用勾股定理可求出AH=,所以PA+PB的最小值为故选B。
初中几何中线段和差的最大值与最小值模型解析

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧: (4)台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.mnnm填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. 二)一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、点与圆在直线两侧:2、点与圆在直线同侧:(三)已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解)m(1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:二、求两线段差的最大值问题 (运用三角形两边之差小于第三边)基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mm B mA Bmn mnn mnnn m(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:m n mnm n mm2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:作法:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:基础题 1.如图1,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为 .2、如图2,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N分别是AD 和AB 上的动点,则BM+MN 的最小值为 .mmQ Q3、如图3,在锐角三角形ABC中,AB=BAC=45,BAC的平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是。
4、如图4所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为.5、如图5,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB 上一个动点,当PC+PD的和最小时,PB的长为__________.6、如图6,等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF直线上的一点,则PA+PB的最小值为.7、如图7菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图8,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是9、如图9,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图10所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为.11、如图11,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2 (B) (C)1 (D)2压轴题1、如图,正比例函数x y 21=的图象与反比例函数xky =(k ≠0)在第一象限的图象交于A 点,过A 点作x 轴的垂线,垂足为M ,已知三角形OAM 的面积为1.(1)求反比例函数的解析式;(2)如果B 为反比例函数在第一象限图象上的点(点B 与点A 不重合),且B 点的横坐标为1,在x 轴上求一点P ,使PA+PB 最小.2、如图,一元二次方程0322=-+x x 的二根1x ,2x (1x <2x )是抛物线c bx ax y ++=2与x 轴的两个交点B ,C 的横坐标,且此抛物线过点A (3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P ,对称轴与AC 相交于点Q ,求点P 和点Q 的坐标; (3)在x 轴上有一动点M ,当MQ+MA 取得最小值时,求M 点的坐标.3、如图,在平面直角坐标系中,点A 的坐标为(1,3) ,△AOB 的面积是3. (1)求点B 的坐标;(2)求过点A 、O 、B 的抛物线的解析式; (3)在(2)中抛物线的对称轴上是否存在点C ,使△AOC 的周长最小?若存在,求出点C 的 坐标;若不存在,请说明理由.4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F . (1)求经过A 、B 、C 三点的抛物线的解析式;(2)当BE 经过(1)中抛物线的顶点时,求CF 的长;(3)在抛物线的对称轴上取两点P 、Q (点Q 在点P 的上方),且PQ =1,要使四边形BCPQ 的周长最小,求出P 、Q 两点的坐标.6.如图,已知平面直角坐标系,A ,B 两点的坐标分别为A (2,-3),B (4,-1)若C (a ,0),D (a+3,0)是x 轴上的两个动点,则当a 为何值时,四边形ABDC 的周长最短.7、如图,在平面直角坐标系中,矩形的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA=3,OB=4,D 为边OB 的中点.(1)若E 为边OA 上的一个动点,当△CDE 的周长最小时,求点E 的坐标;(2)若E 、F 为边OA 上的两个动点,且EF=2,当四边形CDEF 的周长最小时,求点E 、F 的坐标.二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
B(2)点A 、B 在直线m 异侧:解析:过B 作关于直线m 的对称点B ’,连接AB ’交点直线m 于P,此时PB=PB ’,PA-PB 最大值为AB ’ 练习题1. 如图,抛物线y =-14x 2-x +2的顶点为A ,与y 轴交于点B .(1)求点A 、点B 的坐标;(2)若点P 是x 轴上任意一点,求证:PA -PB ≤AB ; (3)当PA -PB 最大时,求点P 的坐标.2. 如图,已知直线y =21x +1与y 轴交于点A ,与x 轴交于点D ,抛物线y =21x 2+bx +c 与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为(1,0). (1)求该抛物线的解析式;(2)在抛物线的对称轴上找一点M ,使|AM -MC |的值最大,求出点M 的坐标.3、在直角坐标系中,点A 、B 的坐标分别为(-4,-1)和(-2,-5);点P 是y 轴上的一个动点:⑴点P 在何处时,PA +PB 的和为最小?并求最小值. ⑵点P 在何处时,∣PA—PB∣最大?并求最大值.4. 如图,直线y =-3x +2与x 轴交于点C ,与y 轴交于点B ,点A 为y 轴正半轴上的一点,⊙A 经过点B 和点O ,直线BC 交⊙A 于点D . (1)求点D 的坐标;(2)过O ,C ,D 三点作抛物线,在抛物线的对称轴上是否存在一点P ,使线段PO 与PD 之差的值最大?若存在,请求出这个最大值和点P 的坐标.若不存在,请说明理由.5、抛物线的解析式为223y x x =-++,交x 轴与A 与B,交y 轴于C. ⑴在其对称轴上是否存在一点P ,使⊿APC 周长最小,若存在,求其坐标;⑵在其对称轴上是否存在一点Q ,使∣QB—QC∣的值最大,若存在求其坐标.6、已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.(1)试直接写出点D的坐标;(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连接OP.①若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标;②试问在抛物线的对称轴上是否存在一点T,使得|TO-TB|的值最大?7、如图,已知抛物线C1的解析式为y=-x2+2x+8,图象与y轴交于D点,并且顶点A在双曲线上.(1)求过顶点A的双曲线解析式;(2)若开口向上的抛物线C2与C1的形状、大小完全相同,并且C2的顶点P始终在C1上,证明:抛物线C2一定经过A点;(3)设(2)中的抛物线C2的对称轴PF与x轴交于F点,且与双曲线交于E点,当D、O、E、F四点组成的四边形的面积为16.5时,先求出P点坐标,并在直线y=x上求一点M,使|MD-MP|的值最大.8、如图,已知抛物线243y x bx c =++ 经过A(3,0),B(0,4) . (1)求此抛物线解析式;(2)若抛物线与x 轴的另一交点为C ,求点C 关于直线AB 的对称点C ’的坐标;(3) 若点D 是第二象限内点,以D 为圆心的圆分别与x 轴、y 轴、直线AB 相切于点E 、F 、H ,问在抛物线的对称轴上是否存在一点一点P ,使得|PH -PA |的值最大?若存在,求出该最大值;若不存在,请说明理由。
三、其它非基本图形类线段和差最值问题1、求线段的最大值与最小值需要将该条线段转化到一个三角形中,在该三角形中,其他两边是已知的,则所求线段的最大值为其他两线段之和,最小值为其他两线段之差。
