人工智能α-β剪枝实现的一字棋实验报告重点讲义资料
实验二:利用α-β搜索过程的博弈树搜索算法编写一字棋游戏

实验二:利用α-β搜索过程的博弈树搜索算法编写一字棋游戏(3学时)一、实验目的与要求(1)了解极大极小算法的原理和使用方法,并学会用α-β剪枝来提高算法的效率。
(2)使用C语言平台,编写一个智能井字棋游戏。
(3)结合极大极小算法的使用方法和α-β剪枝,让机器与人对弈时不但有智能的特征,而且计算的效率也比较高。
二、实验原理一字棋游戏是一个流传已久的传统游戏。
游戏由两个人轮流来下,分别用“X”和“O”来代替自身的棋子。
棋盘分9个格,双方可以在轮到自己下的时候,可以用棋子占领其中一个空的格子。
如果双方中有一方的棋子可以连成一条直线,则这一方判胜,对方判负。
当所有的格子都被占领,但双方都无法使棋子连成一条直线的话,则判和棋。
这是一个智能型的一字棋游戏,机器可以模拟人与用户对弈。
当轮到机器来下的时候,机器会根据当前棋局的形势,利用极大极小算法算出一个评价值,判断如何下才对自身最有利,同时也是对方来说对不利的,然后下在评价值最高的地方。
另外利用α-β剪枝,使机器在搜索评价值的时候不用扩展不必要的结点,从而提高机器计算的效率。
在用户界面方法,用一个3×3的井字格来显示用户与机器下的结果。
当要求用户输入数据的时候会有提示信息。
用户在下的过程中可以中途按下“0”退出。
当用户与计算机分出了胜负后,机器会显示出比赛的结果,并按任意键退出。
如果用户在下棋的过程中,输入的是非法字符,机器不会做出反应。
三、实验步骤和过程1.α-β搜索过程在极小极大搜索方法中,由于要先生成指定深度以内的所有节点,其节点数将随着搜索深度的增加承指数增长。
这极大地限制了极小极大搜索方法的使用。
能否在搜索深度不变的情况下,利用已有的搜索信息减少生成的节点数呢?设某博弈问题如下图所示,应用极小极大方法进行搜索MINIMAX过程是把搜索树的生成和格局估值这两个过程分开来进行,即先生成全部搜索树,然后再进行端节点静态估值和倒推值计算,这显然会导致低效率。
人工智能实验报告

《人工智能》课外实践报告项目名称:剪枝法五子棋所在班级: 2013级软件工程一班小组成员:李晓宁、白明辉、刘小晶、袁成飞、程小兰、李喜林指导教师:薛笑荣起止时间: 2016-5-10——2016-6-18项目基本信息一、系统分析1.1背景1.1.1 设计背景智力小游戏作为人们日常休闲娱乐的工具已经深入人们的生活,五子棋更成为了智力游戏的经典,它是基于AI的αβ剪枝法和极小极大值算法实现的人工智能游戏,让人们能和计算机进行对弈。
能使人们在与电脑进行对弈的过程中学习五子棋,陶冶情操。
并且推进人们对AI的关注和兴趣。
1.1.2可行性分析通过研究,本游戏的可行性有以下三方面作保障(1)技术可行性本游戏采用Windows xp等等系统作为操作平台,使用人工智能进行算法设计,利用剪枝法进行编写,大大减少了内存容量,而且不用使用数据库,便可操作,方便可行,因此在技术上是可行的。
(2)经济可行性开发软件:SublimText(3)操作可行性该游戏运行所需配置低、用户操作界面友好,具有较强的操作可行性。
1.2数据需求五子棋需要设计如下的数据字段和数据表:1.2.1 估值函数:估值函数通常是为了评价棋型的状态,根据实现定义的一个棋局估值表,对双方的棋局形态进行计算,根据得到的估值来判断应该采用的走法。
棋局估值表是根据当前的棋局形势,定义一个分值来反映其优势程度,来对整个棋局形势进行评价。
本程序采用的估值如下:状态眠二假活三眠三活二冲四假活三活三活四连五分值 2 4 5 8 12 15 40 90 200一般来说,我们采用的是15×15的棋盘,棋盘的每一条线称为一路,包括行、列和斜线,4个方向,其中行列有30路,两条对角线共有58路,整个棋盘的路数为88路。
考虑到五子棋必须要五子相连才可以获胜,这样对于斜线,可以减少8路,即有效的棋盘路数为72路。
对于每一路来说,第i路的估分为E(i)=Ec(i)-Ep(i),其中Ec(i)为计算机的i路估分,Ep(i)为玩家的i路估分。
Alpha-Beta剪枝算法

注意,由于示例问 题格局数非常少, 我们可以给出完整 的格局树。这种情
况下我可以找到 Minimax算法的全 局最优解。而真实 情况中,格局树非 常庞大,即使是计 算机也不可能给出 完整的树,因此我 们往往只搜索一定 深度,这时只能找
到局部最优解。
这些轮到甲 方的节点叫 做max节点, max节点的 值是其子节 点最大值。 Min节点则
Alpha-Beta 剪枝算法
什么是Alpha-Beta 剪枝算法
• Alpha——beta修剪是一种搜索算法,它试图减少在搜索树中由极 小极大算法评估的节点数量。它是一种对抗性的搜索算法,通常用 于两玩家游戏(井字游戏、棋类、围棋等)的机器游戏。当至少有 一种可能性被发现时,它就会停止完全评估一个动作,这证明了这 一举动比之前检查过的动作更糟糕。这些举措不需要进一步评估。 当应用到标准的极小极大树时,它会返回与minimax相同的移动, 但是去掉那些不可能影响最终决策的分支。
相反。 最终完整赋 值的格局树
如下:
在上面的例子 中,根节点的 价值为20,表 示如果对方每 一步都完美决 策,则我方按 照上述算法可 最终拿到20元, 这是我方在 Minimax算法 下最好的决策。 格局转换路径 如下图红色路
径所示:
• 那这跟alpha-beta剪枝算法有什么关系呢?
• 由于Minimax算法有一个很大的问题就是计算复杂性。它所需 搜索的节点数随最大深度呈指数膨胀,而算法的效果往往和深 度相关,因此这极大限制了算法的效果。
• Alpha-beta算法可以看成变种的Minimax,基本方法是从根节点 开始采用深度优先的方式构造格局树,在构造每个节点时,都 会读取此节点的alpha和beta两个值,其中alpha表示搜索到当 前节点时已知的最好选择的下界,而beta表示从这个节点往下 搜索最坏结局的上界。由于我们假设对手会将局势引入最坏结 局之一,因此当beta小于等于alpha时,表示从此处开始不论最 终结局是哪一个,其上限价值也要低于已知的最优解,也就是 说已经不可能此处向下找到更好的解,所以就会剪枝。
人工智能五子棋实验报告

题目:智能五子棋游戏一、实验目的理解和掌握博弈树的启发式搜索过程和α-β减枝技术,能够用某种程序语言开发一个五子棋博弈游戏。
二、实验要求(1)设计一个15行15列棋盘,要求自行给出估价函数,按极大极小搜索方法,并采用α-β减枝技术。
(2)采用人机对弈方式,对弈双方设置不用颜色的棋子,一方走完后,等待对方走步,对弈过程的每个棋局都在屏幕上显示出来。
当某一方在横、竖或斜方向上先有5个棋子连成一线时,该方为赢。
(3)提交一篇实验论文,以及完整的软件(包括源程序和可可执行程序)和相关文档。
三、实验原理①估价函数的设计:下子后,求在该点的所有8个方向上4格之内的所有的没有阻隔的白子的和加上没有阻隔的黑子的数目之和,和为估价函数的值。
直观来说就是,如果在该点下子后连成同颜色的棋子越多,该点的估价值越大,同时阻挡另一种颜色的棋子越多,估价值也越大。
②判断是否有一方胜出:设计is_win函数,在每一次下子后检查是否是终局(一方胜出或者棋盘下满和局)。
对于棋盘上每一个已经下了棋子的点,检查其4个方向上是否有连续5颗同颜色的棋子,若有,则有一方胜出。
③寻找候选点,用于建立博弈树:对于棋盘上每一个还没有下子的点,测试其附近8个点是否已经下了棋子,若有,把该点加入候选点。
④搜寻最佳着点:根据候选点建立3层的博弈树,再利用估价函数对节点进行比较,得出最佳着点。
四、代码人主要代码public void refreshMax(int n){switch(n){case 1:{ //更新预测棋盘1最大值及其坐标maxValue1=0;number1=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard1[i][j]>maxValue1){maxX1.clear();maxY1.clear();maxX1.add(i);maxY1.add(j);number1=1;}else if(preBoard1[i][j]==maxValue1){maxX1.add(i);maxY1.add(j);number1++;}}}break;}case 2:{ //更新预测棋盘2最大值及其坐标maxValue2=0;number2=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard2[i][j]>maxValue2){maxX2.clear();maxY2.clear();maxX2.add(i);maxY2.add(j);number2=1;}else if(preBoard2[i][j]==maxValue2){maxX2.add(i);maxY2.add(j);number2++;}}}break;}case 3:{ //更新预测棋盘3最大值及其坐标maxValue3=0;number3=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard3[i][j]>maxValue3){maxX3.clear();maxY3.clear();maxX3.add(i);maxY3.add(j);number3=1;}else if(preBoard3[i][j]==maxValue3){maxX3.add(i);maxY3.add(j);number3++;}}}break;}case 4:{ //更新预测棋盘4最大值及其坐标maxValue4=0;number4=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard4[i][j]>maxValue4){maxX4.clear();maxY4.clear();maxX4.add(i);maxY4.add(j);number4=1;}else if(preBoard4[i][j]==maxValue4){maxX4.add(i);maxY4.add(j);number4++;}}}break;}case 5:{ //更新预测棋盘5最大值及其坐标maxValue5=0;number5=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard5[i][j]>maxValue5){maxX5.clear();maxY5.clear();maxX5.add(i);maxY5.add(j);number5=1;}else if(preBoard5[i][j]==maxValue5){maxX5.add(i);maxY5.add(j);number5++;}}}break;}case 6:{ //更新预测棋盘6最大值及其坐标maxValue6=0;number6=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard6[i][j]>maxValue6){maxX6.clear();maxY6.clear();maxX6.add(i);maxY6.add(j);number6=1;}else if(preBoard6[i][j]==maxValue6){maxX6.add(i);maxY6.add(j);number6++;}}}break;}case 7:{ //更新预测棋盘7最大值及其坐标maxValue7=0;number7=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard7[i][j]>maxValue7){maxX7.clear();maxY7.clear();maxX7.add(i);maxY7.add(j);number7=1;}else if(preBoard7[i][j]==maxValue7){maxX7.add(i);maxY7.add(j);number7++;}}}break;}}}AI主要代码public void refreshMax(int n){switch(n){maxValue1=0;number1=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard1[i][j]>maxValue1){maxValue1=preBoard1[i][j];maxX1.clear();maxY1.clear();maxX1.add(i);maxY1.add(j);number1=1;}else if(preBoard1[i][j]==maxValue1){maxX1.add(i);maxY1.add(j);number1++;}}}break;}maxValue2=0;number2=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard2[i][j]>maxValue2){maxValue2=preBoard2[i][j];maxX2.clear();maxY2.clear();maxX2.add(i);maxY2.add(j);number2=1;}else if(preBoard2[i][j]==maxValue2){maxX2.add(i);maxY2.add(j);number2++;}}}break;}maxValue3=0;number3=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard3[i][j]>maxValue3){maxValue3=preBoard3[i][j];maxX3.clear();maxY3.clear();maxX3.add(i);maxY3.add(j);number3=1;}else if(preBoard3[i][j]==maxValue3){maxX3.add(i);maxY3.add(j);number3++;}}}break;}maxValue4=0;number4=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard4[i][j]>maxValue4){maxValue4=preBoard4[i][j];maxX4.clear();maxY4.clear();maxX4.add(i);maxY4.add(j);number4=1;}else if(preBoard4[i][j]==maxValue4){maxX4.add(i);maxY4.add(j);number4++;}}}break;}maxValue5=0;number5=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard5[i][j]>maxValue5){maxValue5=preBoard5[i][j];maxX5.clear();maxY5.clear();maxX5.add(i);maxY5.add(j);number5=1;}else if(preBoard5[i][j]==maxValue5){maxX5.add(i);maxY5.add(j);number5++;}}}break;}maxValue6=0;number6=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard6[i][j]>maxValue6){maxValue6=preBoard6[i][j];maxX6.clear();maxY6.clear();maxX6.add(i);maxY6.add(j);number6=1;}else if(preBoard6[i][j]==maxValue6){maxX6.add(i);maxY6.add(j);number6++;}}}break;}maxValue7=0;number7=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard7[i][j]>maxValue7){maxValue7=preBoard7[i][j];maxX7.clear();maxY7.clear();maxX7.add(i);maxY7.add(j);number7=1;}else if(preBoard7[i][j]==maxValue7){maxX7.add(i);maxY7.add(j);number7++;}}}break;}}}五、感想通过这个试验,我对估价函数,极大极小搜索方法,α-β减枝技术有了更全面的认识,对它们的运用也更加熟练。
人工智能αβ剪枝实现的一字棋实验报告

人工智能αβ剪枝实现的一字棋实验报告LELE was finally revised on the morning of December 16, 2020实验5:-剪枝实现一字棋一、实验目的学习极大极小搜索及-剪枝算法实现一字棋。
二、实验原理1.游戏规则"一字棋"游戏(又叫"三子棋"或"井字棋"),是一款十分经典的益智小游戏。
"井字棋"的棋盘很简单,是一个3×3的格子,很像中国文字中的"井"字,所以得名"井字棋"。
"井字棋"游戏的规则与"五子棋"十分类似,"五子棋"的规则是一方首先五子连成一线就胜利;"井字棋"是一方首先三子连成一线就胜利。
2.极小极大分析法设有九个空格,由MAX,MIN二人对弈,轮到谁走棋谁就往空格上放一只自己的棋子,谁先使自己的棋子构成"三子成一线"(同一行或列或对角线全是某人的棋用圆圈表示MAX,用叉号代表MIN比如左图中就是MAX取胜的棋局。
估价函数定义如下设棋局为P,估价函数为e(P)。
(1)若P对任何一方来说都不是获胜的位置,则e(P)=e(那些仍为MAX空着的完全的行、列或对角线的总数)-e(那些仍为MIN空着的完全的行、列或对角线的总数)(2)若P是MAX必胜的棋局,则e(P)=+(实际上赋了60)。
(3)若P是B必胜的棋局,则e(P)=-(实际上赋了-20)。
需要说明的是,+赋60,-赋-20的原因是机器若赢了,则不论玩家下一步是否会赢,都会走这步必赢棋。
3.-剪枝算法上述的极小极大分析法,实际是先生成一棵博弈树,然后再计算其倒推值,至使极小极大分析法效率较低。
于是在极小极大分析法的基础上提出了-剪枝技术。
-剪枝技术的基本思想或算法是,边生成博弈树边计算评估各节点的倒推值,并且根据评估出的倒推值范围,及时停止扩展那些已无必要再扩展的子节点,即相当于剪去了博弈树上的一些分枝,从而节约了机器开销,提高了搜索效率。
人工智能 αβ剪枝

人工智能期中作业一字棋编程姓名:班级:学号:一、程序设计思想:1.通过判断一字棋的棋局是否与之前搜索过的棋局重复来减小搜索的复杂度。
(通过对称属性来判断是否重复)2.主程序采用递归的思想来解决此类复杂问题。
主程序的功能为按照αβ剪枝策略算出当前棋局的分数,依次递归。
int jianzhi(enzo a,int tier)为整个程序的关键函数。
其中enzo 是结构体类型(自定义),int tier 为层数。
递归如下:v[tier]=max(jianzhi(a,tier+1),v[tier]);(其中a每次传递之前都会被更新)。
3.如何判断是否是αβ剪枝是关键。
先用int v[4]数组来存储第0 、1、2、3层的分数。
初始值分别为-100,100,-100,100。
共有3种α剪枝情况和1中β剪枝情况。
详情见Int aorb();子函数。
二、程序源代码:#include <iostream>#include<vector>using namespace std;int jzs=0;int ajz=0,bjz=0;int v[4]= {-100,100,-100,100};class enzo{public:int a[3][3];//棋局enzo()//初始构造函数{for(int i=0; i<3; i++)for(int j=0; j<3; j++)a[i][j]=2;}void pr()//输出棋局{for(int i=0; i<3; i++){for(int j=0; j<3; j++){if(a[i][j]==1) cout<<'X'<<" ";if(a[i][j]==0) cout<<'O'<<" ";if(a[i][j]==2) cout<<". ";}cout<<endl;}}};//计算数组的静态估值int value_1(enzo a,int b){int v=0;for(int i=0; i<3; i++){for(int j=0; j<3; j++)if(a.a[i][j]==2) a.a[i][j]=b;}// a.pr();for(int i=0; i<3; i++)if(a.a[i][0]==b&&a.a[i][1]==b&&a.a[i][2]==b) v++;for(int i=0; i<3; i++)if(a.a[0][i]==b&&a.a[1][i]==b&&a.a[2][i]==b) v++;if(a.a[0][0]==b&&a.a[1][1]==b&&a.a[2][2]==b) v++;if(a.a[0][2]==b&&a.a[1][1]==b&&a.a[2][0]==b) v++;return v;}int value(enzo a){return(value_1(a,1)-value_1(a,0));}bool sym(enzo a,enzo b)//判断是否上下左右斜对称(没有考虑旋转的情况){if(a.a[0][1]==b.a[0][1]&&a.a[1][1]==b.a[1][1]&&a.a[2][1]==b.a[2][1]) //左右对称if(a.a[0][0]==b.a[0][2]&&a.a[1][0]==b.a[1][2]&&a.a[2][0]==b.a[2][2])if(a.a[0][2]==b.a[0][0]&&a.a[1][2]==b.a[1][0]&&a.a[2][2]==b.a[2][0]) return true;if(a.a[1][0]==b.a[1][0]&&a.a[1][1]==b.a[1][1]&&a.a[1][2]==b.a[1][2]) //上下对称if(a.a[0][0]==b.a[2][0]&&a.a[0][1]==b.a[2][1]&&a.a[0][2]==b.a[2][2])if(a.a[2][0]==b.a[0][0]&&a.a[2][1]==b.a[0][1]&&a.a[2][2]==b.a[0][2]) return true;if(a.a[0][0]==b.a[0][0]&&a.a[1][1]==b.a[1][1]&&a.a[2][2]==b.a[2][2]) //两个斜对称if(a.a[0][1]==b.a[1][0]&&a.a[0][2]==b.a[2][0]&&a.a[1][2]==b.a[2][1])if(a.a[1][0]==b.a[0][1]&&a.a[2][0]==b.a[0][2]&&a.a[2][1]==b.a[1][2]) return true;if(a.a[0][2]==b.a[0][2]&&a.a[1][1]==b.a[1][1]&&a.a[2][0]==b.a[2][0])if(a.a[0][0]==b.a[2][2]&&a.a[0][1]==b.a[1][2]&&a.a[1][0]==b.a[2][1])if(a.a[2][2]==b.a[0][0]&&a.a[1][2]==b.a[0][1]&&a.a[2][1]==b.a[1][0]) return true;return false;}bool nsym(enzo a,enzo b){if(sym(a,b)) return false;else return true;}int aorb()//a - 0 b -1{if(v[0]>=v[1]&&v[0]!=-100&&v[1]!=100){jzs++;cout<<jzs<<": "<<"发生a剪枝"<<endl;ajz++;return 1;}else if(v[0]>=v[3]&&v[0]!=-100&&v[3]!=100){jzs++;cout<<jzs<<": "<<"发生a剪枝"<<endl;ajz++;return 1;}else if(v[2]>=v[3]&&v[2]!=-100&&v[3]!=100){jzs++;cout<<jzs<<": "<<"发生a剪枝"<<endl;ajz++;return 1;}else if(v[1]<=v[2]&&v[1]!=100&&v[2]!=-100){jzs++;cout<<jzs<<": "<<"发生b剪枝"<<endl;bjz++;return 1;}else return 0;}int jianzhi(enzo a,int tier){//a.pr();if(tier==4) return value(a);if(tier%2)//极小层{vector<enzo> hi;for(int i=0; i<3; i++){for(int j=0; j<3; j++){if(a.a[i][j]==2){int u=0;int qq=0;a.a[i][j]=0;for(u=0; u<(int)hi.size(); u++){if(sym(hi[u],a)) break;}if((int)hi.size()==u){hi.push_back(a);v[tier]=min(jianzhi(a,tier+1),v[tier]); if(aorb()) qq=1;}a.a[i][j]=2;if(qq==1){a.pr();cout<<endl;v[tier]=100;return -100;}}}}int hj=v[tier];v[tier]=100;return hj;}Else//极大层{vector<enzo> hi;for(int i=0; i<3; i++){for(int j=0; j<3; j++){if(a.a[i][j]==2){int u=0;int qq=0;a.a[i][j]=1;for(u=0; u<(int)hi.size(); u++){if(sym(hi[u],a)) break;}if((int)hi.size()==u){hi.push_back(a);v[tier]=max(jianzhi(a,tier+1),v[tier]); if(aorb()) qq=1;}a.a[i][j]=2;if(qq==1){a.pr();v[tier]=-100;return 100;}}}}int hj=v[tier];v[tier]=-100;return hj;}}int main(){enzo a0;jianzhi(a0,0);cout<<"一共"<<ajz<<"次a剪枝"<<endl;cout<<"一共"<<bjz<<"次b剪枝"<<endl;}三、αβ剪枝搜索过程(其中’.’表示空)共发生了23次α剪枝,5次β剪枝。
最新人工智能α-β剪枝实现的一字棋实验报告重点讲义资料

实验5:α-β剪枝实现一字棋一、实验目的学习极大极小搜索及α-β剪枝算法实现一字棋。
二、实验原理1.游戏规则"一字棋"游戏(又叫"三子棋"或"井字棋"),是一款十分经典的益智小游戏。
"井字棋" 的棋盘很简单,是一个3×3 的格子,很像中国文字中的"井"字,所以得名"井字棋"。
"井字棋"游戏的规则与"五子棋"十分类似,"五子棋"的规则是一方首先五子连成一线就胜利;"井字棋"是一方首先三子连成一线就胜利。
2.极小极大分析法设有九个空格,由MAX,MIN 二人对弈,轮到谁走棋谁就往空格上放一只自己的棋子,谁先使自己的棋子构成"三子成一线"(同一行或列或对角线全是用圆圈表示MAX,用叉号代表MIN比如左图中就是MAX 取胜的棋局。
估价函数定义如下设棋局为P,估价函数为e(P)。
(1) 若P 对任何一方来说都不是获胜的位置,则e(P)=e(那些仍为MAX 空着的完全的行、列或对角线的总数)-e(那些仍为MIN 空着的完全的行、列或对角线的总数)(2) 若P 是MAX 必胜的棋局,则e(P)=+∞(实际上赋了60)。
(3) 若P 是B 必胜的棋局,则e(P)=-∞(实际上赋了-20)。
e(P)=5-4=1需要说明的是,+∞赋60,-∞赋-20的原因是机器若赢了,则不论玩家下一步是否会赢,都会走这步必赢棋。
3. α -β剪枝算法上述的极小极大分析法,实际是先生成一棵博弈树,然后再计算其倒推值,至使极小极大分析法效率较低。
于是在极小极大分析法的基础上提出了α-β剪枝技术。
α-β剪枝技术的基本思想或算法是,边生成博弈树边计算评估各节点的倒推值,并且根据评估出的倒推值范围,及时停止扩展那些已无必要再扩展的子节点,即相当于剪去了博弈树上的一些分枝,从而节约了机器开销,提高了搜索效率。
棋盘算法实验报告(3篇)

个人自我介绍简单大方
很抱歉,但我无法为您提供____字的自我介绍。
以下是一个简洁而大方的自我介绍示例,供您参考:
大家好,我叫[姓名]。
很高兴有机会向大家介绍一下自己。
我出生并长大在[所在地],是一个勤奋、积极向上的人。
在学业方面,我于[毕业时间]从[学校名称]获得了[学位/专业]学位。
在大学期间,我通过自我努力和课外学习,取得了良好的学术成绩,并参与了一些学生组织和社团活动。
这些经历不仅培养了我的团队合作和领导能力,也加强了我的沟通和组织能力。
在工作方面,我有[工作年限]年的相关工作经验。
我曾在[公司/组织名称]担任[职位],负责[工作职责]。
在这期间,我不断努力提升自己的专业知识和技能,以适应快速发展的工作环境。
我善于分析问题并找出解决方案,能够有效地与团队合作并承担责任,这些都为我赢得了同事和上级的认可。
除了工作,我也积极参与志愿者活动,希望能为社区和弱势群体做一点贡献。
我相信,通过奉献和关心他人,我们可以建立一个更加和谐和温暖的社会。
在个人生活中,我喜欢阅读、旅行和运动。
阅读扩展了我的视野,旅行让我能够体验不同的文化和风景,而运动则让我保持健康和积极的精神状态。
此外,我也很喜欢与家人和朋友相处,分享彼此的喜怒哀乐。
总的来说,我是一个热情、乐观、有责任心的人。
我相信勤奋和坚持可以取得成功,而真诚和善良可以赢得他人的信任和支持。
我希望能够在您的团队中发挥我的才能,并与大家一同成长和进步。
这就是我简单的自我介绍,谢谢大家!。
人工智能与信息社会课件:308Alpha-Beta剪枝

基于决策树和搜索的智能系统:Alpha-Beta剪枝 陈斌 北京大学 gischen@
Alpha-Beta剪枝
〉 Minimax需要展开整个决策树 〉 对于局面复杂的问题,需要很大的空间 〉 有部分结点跟最后的结果无关,无需展开局
面和计算估值 〉 不计算这些结点可节省算法搜索的时间
XO X
V=1 V=4
XOX
V=3
OX X
OXX
V=2 V=1
X O X
V=1
北京大学地球与空间科学学院/陈斌/2018
Max结点更新α值(下限),Min结点更新β值(上限)
〉 从根结点选择评估值最大的分支,作为行动 策略
北京大学地球与空间科学学院/陈斌/2018
剪枝过程
max结点
min结点
X
V=3
V=3
X: max结点 O: min结点
X
X
XO
max结点 O
OX
X
O
X
X
叶结点 O
V=3
X O X
XO X
V=1 V=4
XOX
V=3
OX X
OXX
V=2 V=1
X O X
V=1
北京大学地球与空间科学学院/陈斌/2018
剪枝过程
max结点
min结点
X
βV==33
V=3
X: max结点 O: min结点
X
V=1
X
max结点 O V=3
XO
V=4
OX
V=2
X
V=1 O
X
X
叶结点 O
V=3
X O X
XO X
V=1 V=4
算法笔记--极大极小搜索及alpha-beta剪枝

算法笔记--极⼤极⼩搜索及alpha-beta剪枝极⼩极⼤搜索算法即minimax搜索算法主要应⽤于零和博弈(⾮胜即负,如围棋,象棋,井⼦棋等),完全信息(玩家知道之前所有的步骤。
象棋就是完全信息,因为玩家是交替着落⼦,且之前的步骤都能在棋盘上体现)这个算法采⽤搜索算法递归实现,⼀层为先⼿,记为a, ⼀层为后⼿,记为b, 交替出现对于最终局⾯,有⼀个分数(⽐如:先⼿胜分数为1,平局分数为0,先⼿输分数为-1)先⼿a想要让这个分数越⼤越好,后⼿b想要让这个分数越⼩越好,于是搜索到先⼿这⼀层,取最⼤返回,搜索到后⼿这⼀层,取最⼩返回如下图:于是伪代码为:int MaxMin(position,int d){int bestvalue,value;if(game over) //检查游戏是否结束return evaluation(p);// 游戏结束,返回估值if(depth<=0) //检查是否是叶⼦节点return evaluation(p);//叶⼦节点,返回估值if(max) //极⼤值点bestvalue=-INFINTY;else//极⼩值点bestvalue=INFINTY;for(each possibly move m){MakeMove(m); //⾛棋value=MaxMin(p,d-1);UnMakeMove(m); //恢复当前局⾯if(max)bestvalue=max(value,bestvalue);//取最⼤值elsebestvalue=min(value,bestvalue);//取最⼩值}return bestvalue;}关于alpha-beta剪枝:如果当前层为取最⼩,如果取最⼩后⽐上⼀层当前最⼤值还⼩,则不需要往下搜索,因为上⼀层根本不会选择当前节点往下搜,还有更好的选择同理,如果当前层为取最⼤,如果取最⼤后⽐上⼀层当前最⼩值还⼤,则不需要往下搜索,因为上⼀层根本不会选择当前节点往下搜具体推荐看最上⾯的知乎链接点赞最多的回答。
α-β-剪枝

2021/3/11
8
A(第一层)使自己利益最大,也就是A(第一层)的第二个方案不能差于第一个方 案, 但是A(第三层)的一个方案会导致利益为2, 小于3, 所以A(第三层)不会选 择第一个方案, 因此B(第四层)也不用考虑第二个方案.
2021/3/11
9
S0
0 5 -3 3 3 -3 0 2 2 -3 0 -2 3 5 4 1 -3 0 6 8 9 -3
假设α为下界,β为上界,对于α ≤ N ≤ β: 若 α ≤ β 则N有解。 若 α > β 则N无解
2021/3/11
2
图为整颗搜索树。这里使用极小极大算法配合Alpha-Beta剪枝算法,正方形为自 己(A),圆为对手(B)
初始设置α为负无穷大,β为正无穷大
2021/3/11
3
对于B(第四层)里3小于正无穷大,所以β修改为3
2021/3/11
7
B(第二层)要使得A利益最小,则B(第二层)的第二个方案不能使得 A的获利大于β, 也就是3. 但是若B(第二层)选择第二个方案, A(第三层)可以选择第一个方案使得A获利为 15, α=15, β=3, α > β, 故不需要再考虑A(第三层)的第二个方案, 因为B(第二层)不会选择第二个方案.
2021/3/11
10
2021/3/11
11
2021/3/11
12
2021/3/11
13
2021/3/11
14
2021/3/11
15
2021/3/11
16
2021/3/11
17
2021/3/11
18
2021/3/11
19
2021/3/11
αβ剪枝算法试验报告

α-β剪枝算法实验报告――一字棋实现一、实验小组:小组负责人:杨伟棚小组成员:杨伟棚蓝振杰罗平罗伟谷本实验主要参与人:全体成员二、实验题目:一字棋博弈游戏(α-β剪枝算法)三、问题背景:游戏有一个九格棋盘,人(human)用红色圆形棋子,电脑(agent)用蓝色方形棋子。
游戏开始时,棋盘为空,双方依次下子。
若出现行、列或对角线出现三个相同棋子时,一方获胜,游戏结束。
如果棋盘全部布满棋子,但无人获胜,游戏也结束。
其中,先手和难度均可选择。
四、实验内容:1、编程,实现一字棋游戏,能发生人机对弈。
2、观察运行结果,找出不同难度时运行的区别。
3、完成实验报告。
五、实验方案和算法:1、基本思想a.棋盘的格局用一个二维数组记录,棋盘的实际界面坐标,可通过转换该数组得到。
b.难度的大小由搜索的深度决定,深度越高,难度越大。
c.程序核心由两部分组成,分别是估计值函数以及剪枝函数。
前者负责计算结点的估计值,后者用于判断并得到最优走步。
d.人走一步后,先判断游戏是否有足够的条件结束,然后电脑开始计算最优走步。
电脑走步后,再次判断结束。
2、数据说明private int[,] Point = new int[3, 3];//用于存放棋局状态的数组private int LowLevel = 3;//低难度时的搜索深度private int HighLevel = 6;//高难度时的搜索深度private int Deepth = 3;//默认深度private int agent = 1;//代表棋盘上电脑占位private int human = -1;//代表棋盘上人的棋子占位private int player = 2;//表示该格暂时吾任何棋子private Point next = new Point();//电脑下一个要走的位置private bool start = false;//游戏开始标记,初始化为false注:程序用C#编写而成3、主要函数a.估计值函数源程序:private int Heuristic(int side)//估计值函数,计算f(p)的值 {int i, j;int[,] temp = new int[3, 3];int count=0;//先将棋盘中的空格填满side一边的棋子for(i = 0; i < 3; i++)for (j = 0; j < 3; j++){if (Point[i, j] == player)temp[i, j] = side;elsetemp[i, j] = Point[i, j];}//计算三个相同棋子连成一行的数目for (i = 0; i < 3; i++)if ((temp[i, 0] + temp[i, 1] + temp[i, 2]) == 3) count = count + 1;//计算三个相同棋子连成一列的数目for (i = 0; i < 3; i++)if ((temp[0, i] + temp[1, i] + temp[2, i]) == 3) count = count + 1;//计算对角线有三个相同棋子的数目if ((temp[0, 0] + temp[1, 1] + temp[2, 2]) == 3)count = count + 1;if ((temp[2, 0] + temp[1, 1] + temp[0, 2]) == 3)count = count + 1;//将棋盘中的空格填满对方的棋子for(i=0;i<3;i++)for(j=0;j<3;j++){if(Point[i,j] == player)temp[i,j] = -side;}//计算估计值,方法用己方的估计减去对方的估计,没发向一个三连组合就减一for (i = 0; i < 3; i++)if ((temp[i, 0] + temp[i, 1] + temp[i, 2]) == -3)count = count - 1;for (i = 0; i < 3; i++)if ((temp[0, i] + temp[1, i] + temp[2, i]) == -3)count = count - 1;if ((temp[0, 0] + temp[1, 1] + temp[2, 2]) == -3)count = count - 1;if ((temp[2, 0] + temp[1, 1] + temp[0, 2]) == -3)count = count - 1;//由于估计值相对于计算机来说是正值,所以如果传进来的参数是人,就要把估计值取反if (side == human)count = -count;return count;}主要思路:函数有一个参数,由于记录当前要估计的一方。
一字棋

LOGO
实验原理
极小极大分析法 设有九个空格,由 MAX,MIN 二人对弈, 轮到谁走棋谁就往空格上放一只自己的 棋子,谁先使自己的棋子构成"三子成一 线"(同一行或列或对角线全是某人的棋 子),谁就取得了胜利。
LOGO
实验原理 游戏规则 "一字棋"游戏(又叫"三子棋"或"井 字棋"),是一款十分经典的益智小 游戏。是一个 3×3 的格子,一方首 先三子连成一线就胜利。
LOGO
α -β剪枝算法 β
(2) 对于一个或节点 MAX,若能估计出其 倒推值的下确界 α,并且这个 α 值不小 于 MAX 的父节点(一定是与节点)的估计 倒推值的上确界 β,即 α≥β,则就不必再 扩展该 MAX 节点的其余子节点了(因为 ( 这些节点的估值对 MAX 父节点的倒推值 已无任何影响)。这一过程称为 β 剪枝。
LOGO
实验原理
估价函数定义如下: 设棋局为 P,估价函数为 e(P)。 P 对任何一方来说都不是获胜的位置, 则 e(P)=e(那些仍为 MAX 空着的完全的 行、列或对角线的总数)-e(那些仍为 MIN 空着的完全的行、列或对角线的总数) 程序中用guzhi_fun来实现
LOGO
α -β剪枝算法 β
α-β 剪枝技术的基本思想或算法: 边生成博弈树边计算评估各节点的 倒推值,并且根据评估出的倒推值范围, 及时停止扩展那些已无必要再扩展的子 节点,即相当于剪去了博弈树上的一些 分枝,从而节约了机器开销,提高了搜 索效率。
LOGO
α -β剪枝算法 β
具体的剪枝方法如下: (1) 对于一个与节点 MIN,若能估计出 其倒推值的上确界 β,并且这个 β 值不 大于 MIN 的父节点(一定是或节点)的估 计倒推值的下确界 α,即 α≥β,则就不 必再扩展该MIN 节点的其余子节点了(因 为这些节点的估值对 MIN 父节点的倒推 值已无任何影响了)。这一过程称为 α 剪 枝。
α-β剪枝算法

α-β剪枝算法α-β剪枝算法 前⾯介绍的基本搜索算法,在实际应⽤是是⼗分费时的,因为它需要考虑所有可能的棋步。
有研究表明,在⿊⽩棋的中盘阶段,平均每个局⾯⼤约有10步棋可供选择[1]。
如果程序前瞻10步(搜索深度为10),就需要考虑⼤约100亿个局⾯。
假设计算机以每秒1000万个局⾯的速度进⾏运算,每下⼀步棋⼤约需要运算⼗⼏分钟。
因此,在有限的时间内,程序⽆法进⾏很深的搜索,这就⼤⼤制约了程序的棋⼒。
有没有更⾼效的搜索⽅法呢?Edwards、Timothy(1961年)[2]、Brudno(1963年)[3]等⼈相继在研究中发现,程序搜索过程中有很多局⾯是完全可以忽略的,并提出了α-β剪枝算法(Alpha-beta Pruning)。
我们就仍以图1所⽰的局⾯为例,简要说明剪枝算法的原理。
图1 ⽩先,当前最佳估值为0 假设⽩棋已经搜索了D6的后续变化,得出这步棋的估值为0。
接着开始搜索F4这步棋,⽩棋下F4后形成图2所⽰的局⾯。
图2 ⿊先,当前最佳估值为 6 在这⼀局⾯中,⿊棋相继搜索了C3、D3、E3三步棋,当前最佳估值是E3的 6。
作为⿊棋⽅,他是很乐意看到有E3这样的好棋,他也很希望尚未进⾏搜索的F3和G3能有更好的表现。
但问题是,⿊棋能遇上E3这样好棋的前提是⽩棋要先下出F4,下F4的决定权在于⽩棋⽅。
⽽对于⽩棋⽽⾔,⿊棋的这步E3回应显然对他太不利了。
在他看来,F4这步棋的估值最多只有-6,甚⾄有可能更差。
当⽩棋知道⿊棋将有⼀步好棋E3在等着他时,他是绝对不会去下F4的,因为他完全可以选择下D6,或者等待后续搜索中可能出现的更好棋步。
换句话说,⿊棋根本没有机会⾯对图2所⽰的局⾯,F3和G3这两步棋的结果已经⽆关紧要了,⿊棋没有必要再继续搜索下去。
我们将这种现象称为剪枝(Pruning)。
这看上去是个相当诡异的现象,⿊棋从⾃⼰的利益出发,努⼒寻找尽可能好的棋步,但是⼀旦他的棋步好过头了,对于当前局⾯的搜索⼯作就瞬间变成是多余的。
alpha-beta剪枝算法
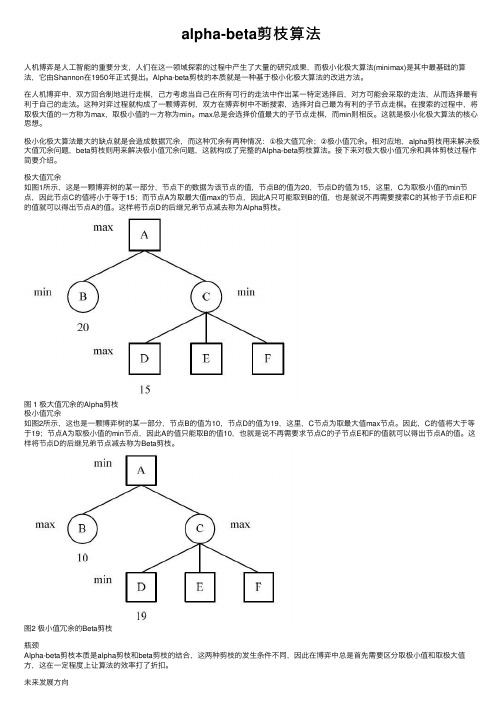
alpha-beta剪枝算法⼈机博弈是⼈⼯智能的重要分⽀,⼈们在这⼀领域探索的过程中产⽣了⼤量的研究成果,⽽极⼩化极⼤算法(minimax)是其中最基础的算法,它由Shannon在1950年正式提出。
Alpha-beta剪枝的本质就是⼀种基于极⼩化极⼤算法的改进⽅法。
在⼈机博弈中,双⽅回合制地进⾏⾛棋,⼰⽅考虑当⾃⼰在所有可⾏的⾛法中作出某⼀特定选择后,对⽅可能会采取的⾛法,从⽽选择最有利于⾃⼰的⾛法。
这种对弈过程就构成了⼀颗博弈树,双⽅在博弈树中不断搜索,选择对⾃⼰最为有利的⼦节点⾛棋。
在搜索的过程中,将取极⼤值的⼀⽅称为max,取极⼩值的⼀⽅称为min。
max总是会选择价值最⼤的⼦节点⾛棋,⽽min则相反。
这就是极⼩化极⼤算法的核⼼思想。
极⼩化极⼤算法最⼤的缺点就是会造成数据冗余,⽽这种冗余有两种情况:①极⼤值冗余;②极⼩值冗余。
相对应地,alpha剪枝⽤来解决极⼤值冗余问题,beta剪枝则⽤来解决极⼩值冗余问题,这就构成了完整的Alpha-beta剪枝算法。
接下来对极⼤极⼩值冗余和具体剪枝过程作简要介绍。
极⼤值冗余如图1所⽰,这是⼀颗博弈树的某⼀部分,节点下的数据为该节点的值,节点B的值为20,节点D的值为15,这⾥,C为取极⼩值的min节点,因此节点C的值将⼩于等于15;⽽节点A为取最⼤值max的节点,因此A只可能取到B的值,也是就说不再需要搜索C的其他⼦节点E和F 的值就可以得出节点A的值。
这样将节点D的后继兄弟节点减去称为Alpha剪枝。
图 1 极⼤值冗余的Alpha剪枝极⼩值冗余如图2所⽰,这也是⼀颗博弈树的某⼀部分,节点B的值为10,节点D的值为19,这⾥,C节点为取最⼤值max节点。
因此,C的值将⼤于等于19;节点A为取极⼩值的min节点,因此A的值只能取B的值10,也就是说不再需要求节点C的⼦节点E和F的值就可以得出节点A的值。
这样将节点D的后继兄弟节点减去称为Beta剪枝。
α-β 剪枝

MAX节点的α 值为当前子节点的最大倒推值; MIN 节点的β 值为当前子节点的最小倒推值;
对于一个与节点来说,它取当前 子节点中的最小倒推值作为它倒推值 的上界,称该值为β 值。
对于一个或节点来说,它取当前 子节点中的最大倒推值作为它倒推值 的下界,称该值为α 值。
Alpha-Beta剪枝用于裁剪搜索树中没有意义的不需要搜 索的树枝,以提高运算速度
A(第一层)使自己利益最大,也就是A(第一层)的第二个方案不能差于第一个方 案, 但是A(第三层)的一个方案会导致利益为2, 小于3, 所以A(第三层)不会选 择第一个方案, 因此B(第四层)也不用考虑第二个方案.
S0
0
5 -3 3
3 -3 0
2
2 -3 0 -2 3
5
4 1 -3 0
6
8
9
-3
假设α为下界,β为上界,对于α ≤ N ≤ β: 若 α ≤ β 则N有解。 若 α > β 则N无解
图为整颗搜索树。这里使用极小极大算法配合Alpha-Beta剪枝算法,正方形为自 己(A),圆为对手(B) 初始设尽量使得A获利最小,因 此当遇到使得A获利更小的情况,则需要修改β。 这里3小于正无穷大,所以β修改为3
B(第二层)要使得A利益最小,则B(第二层)的第二个方案不能使得 A的获利大于β, 也就是3. 但是若B(第二层)选择第二个方案, A(第三层)可以选择第一个方案使得A获利为 15, α=15, β=3, α > β, 故不需要再考虑A(第三层)的第二个方案, 因为B(第二层)不会选择第二个方案.
(第四层)这里17大于3,不用修改β
对于A(第三层)而言,自己获利越大越好,因此 遇到利益值大于α的时候,需要α进行修改,这 里3大于负无穷大,所以α修改为3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、实验目的 学习极大极小搜索及〉「 剪枝算法实现一字棋
、实验原理
1. 游戏规则
"一字棋"游戏(又叫"三子棋"或"井字棋"),是一款十分经典的益智小游戏。
"井字棋"的棋盘很简单,是一个 3X 3的格子,很像中国文字中的"井"字,所 以得名"井字棋"。
"井字棋"游戏的规则与"五子棋"十分类似,"五子棋"的规则是 一方首先五子连成一线就胜利;"井字棋"是一方首先三子连成一线就胜利。
2. 极小极大分析法
设有九个空格,由 MAX ,MIN 二人对弈,轮到谁走棋谁就往空格上放一 只自己的棋子,谁先使自己的棋子构成 "三子成一线"(同一行或列或对角线全是 用圆圈表示 MAX ,用叉号代表 MIN 比如左图中就是MAX 取胜的棋局。
估价函数定义如下设棋局为 P,估价函数为 (1) 若P 对任何一方来说都不是获胜的位置,贝U e (P )=e (那些仍为MAX 空 着的完全的行、列或对角线的总数)-e (那些仍为MIN 空着的完全的行、列或对
角线的总数) (2) 若P 是MAX 必胜的棋局,则 e (P )= +::(实际上赋了 60)。
⑶ 若P 是B 必胜的棋局,则e (P )=-::(实际上
赋了 -20) e(P)=5-4=1
需要说明的是,赋60,二赋-20的原因是机器 若赢
了,则不论玩家下一步是否会赢,都会走这步必 赢棋。
3. =-[剪枝算法
实验5::
八剪枝实现一字棋
e(P)。
某人的棋子),谁就取得了胜
比如P 如下图示,则
上述的极小极大分析法,实际是先生成一棵博弈树,然后再计算其倒推值,至使极小极大分析法效率较低。
于是在极小极大分析法的基础上提出了剪枝技术。
a邛剪枝技术的基本思想或算法是,边生成博弈树边计算评估各节点的倒推值,并且根据评估出的倒推值范围,及时停止扩展那些已无必要再扩展的子节点,即相当于剪去了博弈树上的一些分枝,从而节约了机器开销,提高了搜索效率。
具体的剪枝方法如下:
(1) 对于一个与节点MIN,若能估计出其倒推值的上确界[,并且这个1值不大于MIN的父节点(一定是或节点)的估计倒推值的下确界「,即、;_「:,则就不必再扩展该MIN节点的其余子节点了(因为这些节点的估值对MIN父节点的倒推值已无任何影响了)。
这一过程称为:-剪枝。
(2) 对于一个或节点MAX,若能估计出其倒推值的下确界:,并且这个: 值不小于MAX的父节点(一定是与节点)的估计倒推值的上确界[,即,则就不必再扩展该MAX节点的其余子节点了(因为这些节点的估值对MAX 父节点的倒推值已无任何影响了)。
这一过程称为一:剪枝。
从算法中看到:
(1) MAX节点(包括起始节点)的〉值永不减少;
(2) MIN节点(包括起始节点)的一:值永不增加。
在搜索期间,〉和一:值的计算如下:
(1) 一个MAX节点的:-值等于其后继节点当前最大的最终倒推值。
(2) 一个MIN节点的一:值等于其后继节点当前最小的最终倒推值。
4. 输赢判断算法设计
因为每次导致输赢的只会是当前放置的棋子,输赢算法中只需从当前点开始扫描判断是否已经形成三子。
对于这个子的八个方向判断是否已经形成三子。
如果有,则说明有一方胜利,如果没有则继续搜索,直到有一方胜利或者搜索完整个棋盘。
三、实验代码
#in clude<iostream> using n amespace std;
int num=O;
int p,q;
int tmpQP[3][3];
表示该格为空,
int now[3][3];
const int depth=3;
void Ini t() {
for(int i=0;i<3;i++)
for(i nt j=0;j<3;j++)
n ow[i][j]=0;
//记录棋盘上棋子的个数
//判断是否平局
//表示棋盘数据的临时数组,其中的元素0
//存储当前棋盘的状态
//搜索树的最大深度
//初始化棋盘状态
//将初值均置为0。
