计算机图形学代码_CS法直线段裁剪

计算机图形学Cohen-Sutherland直线裁剪算法源码c++

Cohen-Sutherland直线段裁减算法实验报告
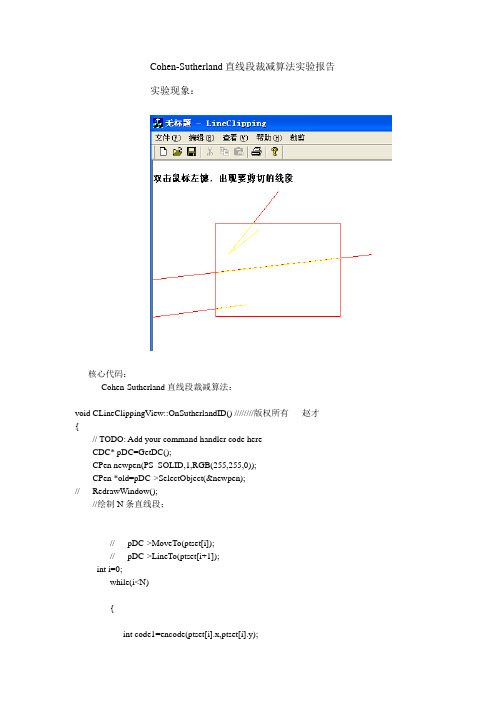
实验现象：
核心代码：
Cohen-Sutherland直线段裁减算法：
void CLineClippingView::OnSutherlandID() ////////版权所有赵才
{
// TODO: Add your command handler code here
pDC->LineTo(ptset[i+1]);
i+=2;
continue;
}
else
{
if((code1 & code2)!=0)//简弃
{
i+=2;
continue;
}
else
{
if(code1==0)
{
int tx,ty,ct;
ct=code1;
code1=code2;
code2=ct;
tx=ptset[i].x;
ptset[i].y=YT;
continue;
}
if(code1 & BOTTOM)
{
//
ptset[i].x=int(1.0/k*(YB-ptset[i].y)+ptset[i].x+0.5);
ptset[i].y=YB;
continue;
}
}
}
}
}
int encode(int x,int y) //确定端点编码
if(code1 & LEFT)
{
//
ptset[i].y=int(k*(XL-ptset[i].x)+ptset[i].y+0.5);
ptset[i].x=XL;

计算机图形学代码_CS法直线段裁剪

这段代码主要是用CS法对一个直线段进行裁剪。

运行在VC环境下。

typedef struct{float x,y;}Point;typedef struct{unsigned all;unsigned left,right,top,bottom;}OutCode;void CompOutCode(Point p,RECT* rect,OutCode *outCode){outCode->all=0;outCode->top=outCode->bottom=0;if(p.y>(float)rect->bottom){outCode->top=1;outCode->all+=1;}else if(p.y<(float)rect->top){outCode->bottom=1;outCode->all+=1;}outCode->left=outCode->right=0;if(p.x>(float)rect->right){outCode->right=1;outCode->all+=1;}else if(p.x<(float)rect->left){outCode->left=1;outCode->all+=1;}}void Cohen_SutherlandLineClip(Point p0,Point p1,RECT *rect,CDC* pDC) {bool accept=false,done=false;OutCode outCode0,outCode1;OutCode *outCodeOut;Point p;CompOutCode(p0,rect,&outCode0);CompOutCode(p1,rect,&outCode1);do{if(!outCode0.all&&!outCode1.all)accept=done=true;else if((outCode0.all&outCode1.all)!=0)done=true;else{if(outCode0.all)outCodeOut=&outCode0;elseoutCodeOut=&outCode1;if(outCodeOut->left){p.y=p0.y+(p1.y-p0.y)*(rect->left-p0.x)/(p1.x-p0.x);p.x=(float)rect->left;}else if(outCodeOut->top){p.x=p0.x+(p1.x-p0.x)*(rect->top-p0.y)/(p1.y-p0.y);p.y=(float)rect->top;}else if(outCodeOut->right){p.y=p0.y+(p1.y-p0.y)*(rect->right-p0.x)/(p1.x-p0.x);p.x=(float)rect->right;}else if(outCodeOut->bottom){p.x=p0.x+(p1.x-p0.x)*(rect->bottom-p0.y)/(p1.y-p0.y);p.y=(float)rect->bottom;}if(outCodeOut->all==outCode0.all){p0.x=p.x;p0.y=p.y;CompOutCode(p0,rect,&outCode0);}else{p1.x=p.x;p1.y=p.y;CompOutCode(p1,rect,&outCode1);}}}while(!done);if(accept){pDC->MoveTo((int)p0.x,(int)p0.y);pDC->LineTo((int)p1.x,(int)p1.y);}}void CCohen_SutherlandView::OnDraw(CDC* pDC) {CCohen_SutherlandDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);// TODO: add draw code for native data hereRECT rect={50,100,150,200};pDC->Rectangle(&rect);Point p0,p1;p0.x=40;p0.y=90;p1.x=140;p1.y=190;Cohen_SutherlandLineClip(p0,p1,&rect,pDC);}。

计算机图形学裁剪技术

求交测试顺序固定(左右下上）最坏情形，线段求交四次。
裁剪
直线段裁剪
Cohen-Sutherland算法中点分割算法参数化裁剪算法 Liang-Barskey算法
多边形裁剪
Sutlerland_Hodgman算法
Weiler-Athenton算法
字符裁剪
裁剪

裁剪：确定图形中哪些部分落在显示区之内，哪些落在显示区之外 , 以便只显示落在显示区内的那部分图形。这个选择过程称为裁剪。在进行裁剪时，画面中对应于屏幕显示的那部分区域称为窗口。
Cohen-Sutherland算法

将区域码的各位从右到左编号，则坐标区域与各位的关系为：
任何位赋值为1，代表端点落在相应的位置上，否则该位为0。若端点在剪取矩形内，区域码为0000。如果端点落在矩形的左下角，则区域码为0101。
直线段裁剪

裁剪线段与窗口的关系：(1)线段完全可见；(2) 显然不可见；(3)其它提高裁剪效率：快速判断情形(1)(2)，对于情形(3)，设法减少求交次数和每次求交时所需的计算量。
常用的线段裁剪方法三种：

Cohen-Sutherland算法中点分割算法参数化裁剪算法
Cohen-Sutherland裁剪

基本思想：
对于每条线段P1P2分为三种情况处理: （1）若P1P2完全在窗口内，则显示该线段P1P2。（2）若P1P2明显在窗口外，则丢弃该线段。
（3）若线段不满足（1）或（2）的条件，则在交点处把线段
分为两段。其中一段完全在窗口外，可弃之。然后对另一段重复上述处理。

如何实现上述的处理呢？
实现方法：采用下面的编码方法

[计算机图形学]复习Cohen-Sutherland直线段裁剪算法

[计算机图形学]复习Cohen-Sutherland直线段裁剪算法
关于Cohen-Sutherland 直线段裁剪算法思想概述
直线段裁剪是⼆维图形裁剪的基础，本质是判断直线段是否与窗⼝边界相交，如相交则进⼀步确定直线段上位于窗⼝内的部分。

算法思想：直线的端点赋予⼀组4位⼆进制码，称为RC（区域编码），裁剪窗⼝的四条边所在的直线可以把平⾯分为9个区域，对各个区域的编码也是四位，C3C2C1C0，分别代表上下右左四个窗⼝边界。

裁剪窗⼝所在的区域为0000，对于直线段上的端点进⾏编码，等于该端点所在的区域的编码。

编码后就容易判断两个端点的情况：
⽐如两个端点求与不等于0，即RC0&RC1≠0；说明该线段在裁剪窗⼝之外，应简弃；
两个端点RC编码按位或为0，即RC0|RC1=0。

说明直线段两个端点都在窗⼝内，应简取。

还有第三种情况：不满⾜前两种情况的，说明直线段与边界或其延长线有交点，要进⾏求交判断：
①此时直线段与边界相交，P0P1和两个边界相交，按左右下上的顺序计算交点，设交点为P，注意：总是要让直线段的⼀个顶点处于窗⼝之外，例如P0点。

这样P0点到交点P的直线段必然不可见，故可以将交点外的线段简弃。

②直线段与边界的延长线相交，直线段在窗⼝外，也不在窗⼝同⼀侧。

依旧按照左右下上顺序计算，将延长线与线段交点定为P，有PP0，位于窗⼝某侧，被简弃。

如果求裁剪后窗⼝内直线段的端点坐标，（那⼀般是求P1，以实际题⽬为准，看剪了哪部分），两点求直线⽅程，然后带⼊相交边界的x或y值可得。

实验一编程实现直线段的裁剪算法

实验一编程实现直线段的裁剪算法课程名称：图形学任课老师谢伙生老师年级03级班级计算机（6）班姓名沈睿汀学号S030300833一、实验要求1、裁剪算法选用Cohen-Sutherland算法；2、界面设计友好、直观。

二、实验环境说明(1)本系统基于JA V A编程环境，使用JBuilder X作为相关的开发工具，因此系统的运行与其它用VC++开发的系统略有不同。

(2)在WINDOWS-XP下运行本程序的时候,请先安装j2re-1_4_2_04-windows-i586-p.exe,然后,才能正常运行，windows环境下双击030300833Cutline.exe。

三、算法与数据结构（程序设计）核心算法Cohen-Sutherland的编写过程如下(在Sutherland.java文件中可以看到具体代码)：（1）新建一个类Sutherland，并在类在声明一个构造函数Sutherland(int wyt, int wyb, int wxl, int wxr) ，传递矩形的四个边界参数，并对类中的共有属性进行初始化。

（2）声明一个端点编码方法private void codingPoint(int x, int y, int[] p)，根据书上的编码规则对端点进行编码。

（3）声明一个方法public void setPoint(int x1, int y1, int x2, int y2)来设置直线段的两端点坐标。

（4）声明两个方法private int OR(int[] op1, int[] op2)和private int AND(int[] op1, int[] op2)来分别实现编码后的端点的相或和相与。

并编写一个方法isInWindow(int[] op)来判断点op是否在窗口中。

（5）编写两个方法private int caculateY(int x1, int y1, int x2, int y2, int x) 和private int caculateX(int x1, int y1, int x2, int y2, int y)来分别求出未知的端点坐标，接着利用这两个方法又编写一个方法private void caculateCrossPoint()来对直线段和相应的窗口边界进行求交处理。

直线段裁剪直接求交算法

直线段裁剪直接求交算法
直线段裁剪直接求交算法是一种用于判断直线段与矩形窗口相交的算法。

该算法通过比较直线段上的点与窗口的边界来确定直线段是否与窗口相交。

算法步骤如下：
1. 初始化变量：
`left`、`right`、`top`、`bottom` 分别表示窗口的左、右、上、下边界坐标。

`x1`、`y1`、`x2`、`y2` 分别表示直线段的起点和终点的x 和y 坐标。

`px`、`py` 表示直线段上的任意一点的坐标。

2. 如果直线段的起点或终点在窗口边界上，则认为直线段与窗口相交。

3. 如果直线段完全位于窗口内部，则认为直线段与窗口相交。

4. 如果直线段完全位于窗口外部，则认为直线段与窗口不相交。

5. 如果直线段与窗口的边界相交，则计算交点坐标，并判断交点是否位于直线段上。

如果交点位于直线段上，则认为直线段与窗口相交。

6. 返回结果：如果直线段与窗口相交，则返回 True；否则返回 False。

以下是该算法的 Python 代码实现：
例如，对于直线段 `(1, 1, 3, 3)` 和窗口 `(0, 0, 4, 4)`，该算法将返回 True，因为直线段与窗口相交。

对于直线段 `(2, 2, 1, 1)` 和窗口 `(0, 0, 4, 4)`，该算法将返回 False，因为直线段与窗口不相交。

计算机图形学实验三

太原工业学院实验报告GetClientRect(&rect);//获得客户区的大小pDC->SetMapMode(MM_ANISOTROPIC);//pDC自定义坐标系pDC->SetWindowExt(rect.Width(),rect.Height());//设置窗口范围pDC->SetViewportExt(rect.Width(),-rect.Height());//设置视区范围,x轴水平向右，y轴垂直向上pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);//客户区中心为原点CDC memDC;//内存DCCBitmap NewBitmap,*pOldBitmap;//内存中承载的临时位图memDC.CreateCompatibleDC(pDC);//创建一个与显示pDC兼容的内存memDCNewBitmap.CreateCompatibleBitmap(pDC,rect.Width(),rect.Height());//创建兼容位图pOldBitmap=memDC.SelectObject(&NewBitmap);//将兼容位图选入memDCmemDC.FillSolidRect(rect,pDC->GetBkColor());//按原来背景填充客户区，否则是黑色memDC.SetMapMode(MM_ANISOTROPIC);//memDC自定义坐标系memDC.SetWindowExt(rect.Width(),rect.Height());memDC.SetViewportExt(rect.Width(),-rect.Height());memDC.SetViewportOrg(rect.Width()/2,rect.Height()/2);rect.OffsetRect(-rect.Width()/2,-rect.Height()/2);DrawWindowRect(&memDC);//绘制窗口if(PtCount>=1){memDC.MoveTo(Round(P[0].x),Round(P[0].y));memDC.LineTo(Round(P[1].x),Round(P[1].y));}pDC->BitBlt(rect.left,rect.top,rect.Width(),rect.Height(),&memDC,-rect.Width()/2,-rect.Height()/2,SRCCOPY);//将内存memDC中的位图拷贝到显示pDC中memDC.SelectObject(pOldBitmap);//恢复位图NewBitmap.DeleteObject();//删除位图}（2）绘制裁剪窗口void CTestView::DrawWindowRect(CDC* pDC)//绘制裁剪窗口{// TODO: Add your message handler code here and/or call defaultpDC->SetTextColor(RGB(128,0,255));pDC->TextOut(-10,Wyt+20,CString("窗口"));CPen NewPen3,*pOldPen3;//定义3个像素宽度的画笔NewPen3.CreatePen(PS_SOLID,3,RGB(255,128,0));pOldPen3=pDC->SelectObject(&NewPen3);pDC->Rectangle(Wxl,Wyt,Wxr,Wyb);pDC->SelectObject(pOldPen3);NewPen3.DeleteObject();}（3）Cohen-Sutherland算法void CTestView::Cohen()//Cohen-Sutherland算法{CP2 p;//交点坐标EnCode(P[0]);//起点编码EnCode(P[1]);//终点编码while(P[0].rc!=0 || P[1].rc!=0)//处理至少一个顶点在窗口之外的情况{if((P[0].rc & P[1].rc)!=0)//简弃之{PtCount=0;return;}if(0==P[0].rc)//确保P[0]位于窗口之外{CP2 Temp;Temp=P[0];P[0]=P[1];P[1]=Temp;}UINT RC=P[0].rc;double k=(P[1].y-P[0].y)/(P[1].x-P[0].x);//直线段的斜率//窗口边界按左、右、下、上的顺序裁剪直线段if(RC & LEFT)//P[0]点位于窗口的左侧{p.x=Wxl;//计算交点y坐标p.y=k*(p.x-P[0].x)+P[0].y;}else if(RC & RIGHT)//P[0]点位于窗口的右侧{p.x=Wxr;//计算交点y坐标p.y=k*(p.x-P[0].x)+P[0].y;}else if(RC & BOTTOM)//P[0]点位于窗口的下侧{p.y=Wyb;//计算交点x坐标p.x=(p.y-P[0].y)/k+P[0].x;}else if(RC & TOP)//P[0]点位于窗口的上侧{p.y=Wyt;//计算交点x坐标p.x=(p.y-P[0].y)/k+P[0].x;}EnCode(p);P[0]=p;}}void CTestView::EnCode(CP2 &pt)//端点编码函数{pt.rc=0;if(pt.x<Wxl)pt.rc=pt.rc|LEFT;else if(pt.x>Wxr)pt.rc=pt.rc|RIGHT;if(pt.y<Wyb)pt.rc=pt.rc|BOTTOM;else if(pt.y>Wyt)pt.rc=pt.rc|TOP;}（4）人机交互void CTestView::OnDrawpic(){// TODO: Add your command handler code herePtCount=0;bDrawLine=TRUE;MessageBox(CString("鼠标画线，剪刀裁剪"),CString("提示"),MB_OKCANCEL);Invalidate(FALSE);}运行结果：实验拓展：在屏幕上显示一个直线构成的图案，使用鼠标选择两点绘制矩形代表窗口对图案矩形裁剪。

计算机图形学之裁剪算法

窗口特别小的场合。
2、中点裁剪法
中点分割裁剪法是将Cohen-Sutherland 算法中求线段与窗口边界的交点的过程用折半查找（即求中点）的方法来代替。仍然采用对线段端点进行编码的方式判断完全可见和显然完全不可见的线段，对于与窗口有交点的线段，该算法分别求离两个端点最近（或最远）的可见点。这两个可见点之间的线段即是原线段的可见部分。
计算P1P2的最近可见点Pma和 Pmb ：（一）直线段P1P2的一个端点可见， P1 另一个端点不可见。只需解算不可见端点的最近的可见点。 1）设P1不可见，计算P1P2的中点Pm1。
P1
pm
P2
P2
判断中点Pm1如果落在（接近）窗口边上，则确定该中点为最近可见点。裁剪结束。否则，
2）判断Pm1是否可见：如果Pm1可见，以Pm1取代P2 ，返回到 1）计算 P1Pm1的中点Pm2，判断Pm2 如果Pm1不可见，以Pm1取代P1 ，返回到 1）计算Pm1P2的中点Pm2，判断Pm2
关键：根据多边形的边表，逐次对每一段边与裁剪线 (窗口边直线)比较，判别输入顶点的个数和坐标，并联结成封闭多边形。
不可见侧
2
多边形边与裁剪线相对位置的四种
情况与处理方法： (1) 位于可见一侧：输出终点作为新多边形顶点 (2) 位于不可见一侧：不输出 (3) 由可见到不可见：输出与裁剪
P2
两种线段裁剪算法的比较
Cohen-Sutherland算法是最早的、使用最广泛的线
段裁剪算法之一。在裁剪窗口很大，大部分线段完全
可见，或裁剪窗口很小，大部分线段完全不可见的情况下，该算法特别有效；在一般情况下，该算法有时要做不必要的求交运算，因而效率不是太高.

计算机图形学实验报告三图形裁剪算法

图形裁剪算法1.实验目的：理解地区编码设计直线裁剪算法编程实现直线裁剪算法2.实验描绘：设置裁剪窗口坐标为：wxl=250;wxr=850;wyb=250;wyt=450;裁剪前以下列图所示：裁剪后结果为：3.算法设计：直线裁剪算法：假定裁剪窗口是标准矩形，由上（y=wyt ）、下（ y=wyb ）、左（ x=wxl ）、右（ x=wxr ）四条边构成，以下列图所示。

延伸窗口四条边形成9 个地区。

依据被裁剪直线的任一端点P(x， y)所处的窗口地区地点，能够给予一组 4 位二进制地区码C4C3C2C1 。

编码定义规则：第一位 C1：若端点位于窗口之左边，即第二位 C2：若端点位于窗口之右边，即第三位 C3：若端点位于窗口之下侧，即第四位 C4：若端点位于窗口之上侧，即X<WxlX>WxrY<WybY>Wyt，则，则，则，则C1=1 ，不然C2=1 ，不然C3=1 ，不然C4=1 ，不然C1=0。

C2=0。

C3=0 。

C4=0。

裁剪步骤：1.若直线的两个端点的地区编码都为0，即 RC1|RC2=0 （两者按位相或的结果为 0，即2.若直线的两个端点的地区编码都不为0，即 RC1&RC2 ≠ 0（两者按位相与的结果不为0，即 RC1≠0 且 RC2≠ 0，即直线位于窗外的同一侧，说明直线的两个端点都在窗口外，应“ 简弃”。

3.若直线既不知足“ 简取” 也不知足“ 简弃” 的条件，直线段必定与窗口订交，需要计算直线与窗口界限的交点。

交点将直线分为两段，此中一段完整位于窗口外，可“ 简弃”。

对另一段给予交点处的地区编码，再次测试，再次求交，直至确立完整位于窗口内的直线段为止。

4.实现时，一般按固定次序左（ x=wxl ）、右（ x=wxr ）、下（ y=wyb ）、上（ y=wyt ）求解窗口与直线的交点。

4.源程序：class CTestView : public CView{.protected:double Pointx[2],Pointy[2];//用户绘制的直线int wxl,wxr,wyb,wyt;//左上与右下CDC Picture;// 内存 (预存 )DC, 防备屏幕闪耀char m_i; // 第一个点仍是第二个点BOOL m_Attatch;BOOL m_Draw;unsigned int RC,RC0,RC1;..}CTestView::CTestView(){//窗口地点坐标wxl=250;wxr=850;wyb=250;wyt=450;m_Attatch=FALSE;m_i=0;m_Draw=FALSE;RC0=0;RC1=0;}void CTestView::OnDraw(CDC* pDC){CTestDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);//装载位图CRect Rect;GetClientRect(&Rect);// 获取客户区的大小CBitmap Bitmap,*pBitmap;Bitmap.LoadBitmap(IDB_BITMAP);CDC MemDC;MemDC.CreateCompatibleDC(GetDC());pBitmap=MemDC.SelectObject(&Bitmap);MemDC.BitBlt(0,0,Rect.Width(),Rect.Height(),&Picture,0,0,SRCCOPY);MemDC.TextOut((wxl+wxr)/2,wyb-20,"窗口");//窗口标题//绘制窗口和直线CPen Pen3,*pOldPen3;// 定义 3 个像素宽度的画笔Pen3.CreatePen(PS_SOLID,3,RGB(0,0,0));pOldPen3=MemDC.SelectObject(&Pen3);MemDC.MoveTo(wxl,wyt);MemDC.LineTo(wxr,wyt);MemDC.LineTo(wxr,wyb);MemDC.LineTo(wxl,wyb);MemDC.LineTo(wxl,wyt);MemDC.SelectObject(pOldPen3);Pen3.DeleteObject();CPen Pen1,*pOldPen1;// 定义 1 个像素宽度的画笔Pen1.CreatePen(PS_SOLID,1,RGB(0,0,255));pOldPen1=MemDC.SelectObject(&Pen1);if(m_i>=1){MemDC.MoveTo(ROUND(Pointx[0]),ROUND(Pointy[0]));MemDC.LineTo(ROUND(Pointx[1]),ROUND(Pointy[1]));}MemDC.SelectObject(pOldPen1);Pen1.DeleteObject();CDC *dc=GetDC();dc->BitBlt(0,0,Rect.Width(),Rect.Height(),&MemDC,0,0,SRCCOPY);MemDC.SelectObject(pBitmap);}void CTestView::OnMENUClip()//裁剪菜单函数{Cohen();Invalidate(FALSE);}unsigned int CTestView::EnCode(double LinePx,double LinePy)//端点编码函数{// 次序左右下上RC=0;if(LinePx<wxl){RC=RC | LEFT;}if(LinePx>wxr){RC=RC | RIGHT;}if(LinePy<wyb){RC=RC | BOTTOM;}if(LinePy>wyt){RC=RC | TOP;}return RC;}void CTestView::OnMENUDrawLine()//绘制直线菜单函数{//TODO: Add your command handler codehere if(FALSE==m_Attatch){Picture.CreateCompatibleDC(GetDC());CBitmap *Bitmap,*pBitmap;Bitmap=new CBitmap;Bitmap->LoadBitmap(IDB_BITMAP);pBitmap=Picture.SelectObject(Bitmap);m_Attatch=TRUE;}m_Draw=TRUE;m_i=0;Invalidate(FALSE);AfxGetMainWnd()->SetWindowText("事例10：Cohen-Sutherland直线裁剪算法");// 显示标题MessageBox(" 请使用鼠标在屏幕上绘制直线，而后点击裁剪按钮进行裁剪"," 提示",MB_OKCANCEL);}void CTestView::OnLButtonDown(UINT nFlags, CPoint point)//单击鼠标左键函数{//TODO: Add your message handler code here and/or call defaultif(TRUE==m_Draw){if(m_i<2){Pointx[m_i]=point.x;Pointy[m_i]=point.y;m_i++;}}CView::OnLButtonDown(nFlags, point);}void CTestView::OnMouseMove(UINT nFlags, CPoint point) //鼠标挪动函数{//TODO: Add your message handler code here and/or call defaultif(TRUE==m_Draw){if(m_i<2){Pointx[m_i]=point.x;Pointy[m_i]=point.y;Invalidate(FALSE);}}CView::OnMouseMove(nFlags, point);}void CTestView::Cohen()//Cohen － Sutherland 算法{BOOL Change;double x,y;RC0=EnCode(Pointx[0],Pointy[0]);RC1=EnCode(Pointx[1],Pointy[1]);while(TRUE){Change=FALSE;if(0 == (RC0|RC1)){// 简取之return;}else if(0!=(RC0 & RC1)){// 简弃之return;}else{if(0==RC0)// 假如P0 点在窗口内，互换P0 和P1,保证p0 点在窗口外{//互换点的坐标值double TPointx,TPointy;TPointx=Pointx[0];TPointy=Pointy[0];Pointx[0]=Pointx[1];Pointy[0]=Pointy[1];Pointx[1]=TPointx;Pointy[1]=TPointy;//互换点的编码值unsigned int TRC;TRC=RC0;RC0=RC1;RC1=TRC;}//按左、右、下、上的次序裁剪if(RC0 & LEFT )//P0点位于窗口的左边{x=wxl;// 求交点 yy=Pointy[0]+(Pointy[1]-Pointy[0])*(x-Pointx[0])/(Pointx[1]-Pointx[0]);Pointx[0]=x;Pointy[0]=y;Change=TRUE;RC0=EnCode(Pointx[0],Pointy[0]);RC1=EnCode(Pointx[1],Pointy[1]);}if(RC0 & RIGHT )//P0点位于窗口的右边{x=wxr;// 求交点 yy=Pointy[0]+(Pointy[1]-Pointy[0])*(x-Pointx[0])/(Pointx[1]-Pointx[0]);Pointx[0]=x;Pointy[0]=y;Change=TRUE;RC0=EnCode(Pointx[0],Pointy[0]);RC1=EnCode(Pointx[1],Pointy[1]);}if(RC0 & BOTTOM )//P0点位于窗口的下侧{y=wyb;// 求交点 xx=Pointx[0]+(Pointx[1]-Pointx[0])*(y-Pointy[0])/(Pointy[1]-Pointy[0]);Pointx[0]=x;Pointy[0]=y;Change=TRUE;RC0=EnCode(Pointx[0],Pointy[0]);RC1=EnCode(Pointx[1],Pointy[1]);}if(RC0 & TOP )//P0点位于窗口的上侧{y=wyt;// 求交点 xx=Pointx[0]+(Pointx[1]-Pointx[0])*(y-Pointy[0])/(Pointy[1]-Pointy[0]);Pointx[0]=x;Pointy[0]=y;Change=TRUE;RC0=EnCode(Pointx[0],Pointy[0]);RC1=EnCode(Pointx[1],Pointy[1]);}if(FALSE==Change){return;}}}}5.运转结果：。

在Opengl应用框架下实现C-S裁剪算法。

《计算机图形学》上机实验报告if(code1 != 0){code=code1;}else{code=code2;}if((code & LIFT) != 0){x=XL;float k=(float)(y2-y1)/(x2-x1);y=int(k*(XL-x1)+y1+0.5);}else if((code & RIGHT) != 0){x=XR;float k=(float)(y2-y1)/(x2-x1);y=int(k*(XR-x1)+y1+0.5);}else if((code & BOTTOM) != 0){y=YB;float k=(float)(x2-x1)/(y2-y1);x=int(k*(y-y1)+x1+0.5);}else if((code & TOP) != 0){y=YT;float k=(float)(x2-x1)/(y2-y1);x=int(k*(y-y1)+x1+0.5);}if(code==code1){x1=x;y1=y;code1=encode(x,y);}else if(code==code2){x2=x;y2=y;code2=encode(x,y);}}void init(void){glClearColor(1.0, 1.0, 1.0, 0.0); // 设置背景颜色glMatrixMode(GL_PROJECTION); // 设置投影参数gluOrtho2D(0.0, 600.0, 0.0, 400.0); // 设置场景的大小}void draw(void){glClear(GL_COLOR_BUFFER_BIT);glColor3f(1.0, 0.0, 0.0); // 设置画图颜色glBegin(GL_LINE_LOOP);glVertex2i(XL, YB); // 绘制几何图形glVertex2i(XR, YB);glVertex2i(XR, YT);glVertex2i(XL, YT);glEnd( );glBegin(GL_LINES);glVertex2i(x1, y1); // 绘制几何图形glVertex2i(x2, y2);glEnd( );CSLineClip(x1,y1,x2,y2,XL,XR,YB,YT);glColor3f(1.0, 0.0, 0.0);glLineWidth(3.0);glBegin(GL_LINES);glVertex2i(x1, y1); // 绘制几何图形glVertex2i(x2, y2);glEnd( );glFlush( ); // 处理绘图pipeLine}void main(int argc, char** argv){glutInit(&argc, argv); // 初始化GLUT环境glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); // GLUT显示模式：单缓冲区、RGB颜色模型glutInitWindowPosition(50, 100); // 窗口左上角的位置glutInitWindowSize(600, 450); // 显示窗口的大小glutCreateWindow("An Example of OpenGL"); // 创建显示窗口，加上标题注：表格高度可根据内容自己调整。

计算机图形学-实验五直线和多边形的裁剪

贵州大学实验报告学院：计算机科学与信息学院专业：软件工程班级： 102班姓名学号实验组实验时间指导教师成绩实验项目名称实验五直线和多边形的裁剪实验目的掌握直线段的裁剪算法以及多边形的裁剪算法实验要求熟练掌握直线段的裁剪算法以及多边形的裁剪算法的基本原理，并编写测试代码进行实验。

实验原理Cohen-Sutherland直线剪裁算法以区域编码为基础，将窗口及其周围的，8个方向以4 bit的二进制数进行编码。

右图所示的编码方法将窗口及其邻域分为5个区域：⑴内域：区域(0000)。

⑵上域：区域(1001, 1000, 1010)。

⑶下域：区域(0101, 0100, 0110)。

⑷左域：区域(1001, 0001, 0101)。

⑸右域：区域(1010, 0010, 0110)。

当线段的两个端点的编码的逻辑“与”非零时，线段为显然不可见的，对某线段的两个端点的区号进行位与运算，可知这两个端点是否同在视区的上、下、左、右；Cohen-Sutherland直线剪裁算法的算法思想是：对于每条线段P1P2分为三种情况处理。

（1）若P1P2完全在窗口内，则显示该线段实验内容一、直线段裁剪算法的核心代码为：计算（x,y）点的编码的方法：private int encode(double x, double y) { == edge[1].y) && (edge[0].x < edge[1].x)) {if >= edge[0].y) {return true;}}== edge[1].y) && (edge[0].x > edge[1].x)) {if <= edge[0].y) {return true;}}== edge[1].x) && (edge[0].y < edge[1].y)) {if <= edge[0].x) {return true;}}== edge[1].x) && (edge[0].y > edge[1].y)) {if >= edge[0].x) {return true;}}return false;}直线段与窗口边界求交：实验数据一、直线段裁剪算法的结果显示：（1）运行程序，点击“W”键，显示出裁剪窗口，用鼠标在画布上点击两点作为直线段的起点和终点，点击“A”键，进行直线段的裁剪，进行下一次的线段裁剪时，点击“R”键进行画布的清除，再重复上述过程进行实验：第一种情况：线段在裁剪窗口的外部，线段完全不可见。

计算机图形学裁剪核心代码

// 裁剪Dlg.cpp : implementation file//#include "stdafx.h"#include "裁剪.h"#include "裁剪Dlg.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif/////////////////////////////////////////////////////////////////////////////// CAboutDlg dialog used for App Aboutclass CAboutDlg : public CDialog{public: CAboutDlg();// Dialog Data//{{AFX_DATA(CAboutDlg)enum { IDD = IDD_ABOUTBOX };//}}AFX_DATA// ClassWizard generated virtual function overrides//{{AFX_VIRTUAL(CAboutDlg)protected:virtual void DoDataExchange(CDataExchange* pDX); // DDX/DDV support //}}AFX_VIRTUAL// Implementationprotected://{{AFX_MSG(CAboutDlg)virtual void OnOK();//}}AFX_MSGDECLARE_MESSAGE_MAP()};CAboutDlg::CAboutDlg() : CDialog(CAboutDlg::IDD){//{{AFX_DATA_INIT(CAboutDlg)//}}AFX_DATA_INIT}void CAboutDlg::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CAboutDlg)//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CAboutDlg, CDialog)//{{AFX_MSG_MAP(CAboutDlg)//}}AFX_MSG_MAPEND_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CMyDlg dialogCMyDlg::CMyDlg(CWnd* pParent /*=NULL*/): CDialog(CMyDlg::IDD, pParent){//{{AFX_DATA_INIT(CMyDlg)// NOTE: the ClassWizard will add member initialization here //}}AFX_DATA_INIT// Note that LoadIcon does not require a subsequent DestroyIcon in Win32 m_hIcon = AfxGetApp()->LoadIcon(IDR_MAINFRAME);ldb = FALSE;step = 0;top = 0,but = 0,lef = 0,rig = 0;lxb = 0,lyb = 0;lxe = 0,lye = 0;}void CMyDlg::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CMyDlg)// NOTE: the ClassWizard will add DDX and DDV calls here //}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CMyDlg, CDialog)//{{AFX_MSG_MAP(CMyDlg)ON_WM_SYSCOMMAND()ON_WM_PAINT()ON_WM_QUERYDRAGICON()ON_BN_CLICKED(IDC_BUTTON4, OnButton4)ON_BN_CLICKED(IDC_BUTTON1, OnButton1)ON_BN_CLICKED(IDC_BUTTON2, OnButton2)ON_WM_LBUTTONDOWN()ON_WM_LBUTTONUP()ON_WM_MOUSEMOVE()ON_BN_CLICKED(IDC_BUTTON3, OnButton3)//}}AFX_MSG_MAPEND_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CMyDlg message handlersBOOL CMyDlg::OnInitDialog(){CDialog::OnInitDialog();// Add "About..." menu item to system menu.// IDM_ABOUTBOX must be in the system command range.ASSERT((IDM_ABOUTBOX & 0xFFF0) == IDM_ABOUTBOX);ASSERT(IDM_ABOUTBOX < 0xF000);CMenu* pSysMenu = GetSystemMenu(FALSE);if (pSysMenu != NULL){CString strAboutMenu;strAboutMenu.LoadString(IDS_ABOUTBOX);if (!strAboutMenu.IsEmpty()){pSysMenu->AppendMenu(MF_SEPARATOR);pSysMenu->AppendMenu(MF_STRING, IDM_ABOUTBOX, strAboutMenu);}}// Set the icon for this dialog. The framework does this automatically// when the application's main window is not a dialogSetIcon(m_hIcon, TRUE); // Set big iconSetIcon(m_hIcon, FALSE); // Set small icon// TODO: Add extra initialization hereCPaintDC dc(this);pic.CreateCompatibleDC(&dc);CBitmap * bp1,*obp1;bp1 = new CBitmap;bp1->LoadBitmap(IDB_B);obp1 = pic.SelectObject(bp1);obp1->DeleteObject();return TRUE; // return TRUE unless you set the focus to a control}void CMyDlg::OnSysCommand(UINT nID, LPARAM lParam){if ((nID & 0xFFF0) == IDM_ABOUTBOX){CAboutDlg dlgAbout;dlgAbout.DoModal();}else{CDialog::OnSysCommand(nID, lParam);}}// If you add a minimize button to your dialog, you will need the code below// to draw the icon. For MFC applications using the document/view model, // this is automatically done for you by the framework.void CMyDlg::OnPaint(){CPaintDC dc(this); // device context for paintingif (IsIconic()){SendMessage(WM_ICONERASEBKGND, (WPARAM) dc.GetSafeHdc(), 0);// Center icon in client rectangleint cxIcon = GetSystemMetrics(SM_CXICON);int cyIcon = GetSystemMetrics(SM_CYICON);CRect rect;GetClientRect(&rect);int x = (rect.Width() - cxIcon + 1) / 2;int y = (rect.Height() - cyIcon + 1) / 2;// Draw the icondc.DrawIcon(x, y, m_hIcon);}else{CDialog::OnPaint();}CDC mdc;CBitmap bmp,*bp;bmp.LoadBitmap(IDB_B);mdc.CreateCompatibleDC(GetDC());bp = mdc.SelectObject(&bmp);pic.BitBlt(0,0,500,320,&mdc,0,0,SRCCOPY);mdc.SelectObject(bp);CDC * dc1;CWnd * wd1;wd1 = this->GetDlgItem(IDC_S);dc1 = wd1->GetDC();pic.MoveTo(lxb,lyb);pic.LineTo(lxe,lye);pic.MoveTo(lef,top);pic.LineTo(rig,top);pic.LineTo(rig,but);pic.LineTo(lef,but);pic.LineTo(lef,top);dc1->BitBlt(1,1,496,309,&pic,0,0,SRCCOPY);}// The system calls this to obtain the cursor to display while the user drags // the minimized window.HCURSOR CMyDlg::OnQueryDragIcon(){return (HCURSOR) m_hIcon;}void CMyDlg::OnButton4(){// TODO: Add your control notification handler code hereOnOK();}void CMyDlg::OnButton1(){// TODO: Add your control notification handler code herestep = 1;}void CMyDlg::OnButton2(){// TODO: Add your control notification handler code herestep = 2;}void CMyDlg::OnLButtonDown(UINT nFlags, CPoint point) //鼠标点下，线段始点{// TODO: Add your message handler code here and/or call defaultif(step){if(point.x>11&&point.x<508&&point.y>11&&point.y<321){ldb = TRUE;switch(step){case 1:top = point.y-12;lef = point.x-12;break;case 2:lxb = point.x-12;lyb = point.y-12;break;}}}CDialog::OnLButtonDown(nFlags, point);}void CMyDlg::OnLButtonUp(UINT nFlags, CPoint point) //鼠标抬起，线段另一点{// TODO: Add your message handler code here and/or call defaultif(ldb){ldb = FALSE;int ti;switch(step){case 1:but = point.y-12;rig = point.x-12;if(but<top){ti = but;but = top;top = ti;}if(lef>rig){ti = lef;lef = rig;rig = ti;}break;case 2:lxe = point.x-12;lye = point.y-12;break;}Invalidate(FALSE);}CDialog::OnLButtonUp(nFlags, point);}void CMyDlg::OnMouseMove(UINT nFlags, CPoint point) //鼠标移动{// TODO: Add your message handler code here and/or call defaultif(ldb){switch(step){case 1:but = point.y-12;rig = point.x-12;break;case 2:lxe = point.x-12;lye = point.y-12;break;}Invalidate(FALSE);}CDialog::OnMouseMove(nFlags, point);}#define LEFT 1#define RIGHT 2#define BOTTOM 4#define TOP 8int CMyDlg::code(int x,int y){ //编码函数int c = 0;if(x<lef)c = c|LEFT;else if(x>rig)c = c|RIGHT;if(y>but)c = c|BOTTOM;else if(y<top)c = c|TOP;return c;}void CMyDlg::OnButton3(){// TODO: Add your control notification handler code hereint code1,code2,tcode;code1 = code(lxb,lyb);code2 = code(lxe,lye);int x,y;while(code1!=0||code2!=0){if((code1&code2)!=0){lxb = 0,lyb = 0;lxe = 0,lye = 0;break;}tcode = code1;if(code1 == 0){tcode = code2;}if((tcode&LEFT)!=0){//交左边界x = lef;y = lyb + (int)(float(lye - lyb)*float(lef-lxb)/float(lxe - lxb));}else if((tcode&RIGHT)!=0){//右边界相交x = rig;y = lyb + int(float(lye - lyb)*float(rig - lxb)/float(lxe - lxb));}else if((tcode&BOTTOM) != 0){//与下边界相交y = but;x = lxb + int(float(lxe - lxb) * float(but - lyb)/float(lye - lyb));}else if((tcode&TOP)!=0){//与上边界相交y = top;x = lxb + int(float(lxe - lxb) * float(top - lyb)/float(lye - lyb));}if(tcode == code1){lxb = x;lyb = y;code1 = code(x,y);}else{lxe = x;lye = y;code2 = code(x,y);}}Invalidate(FALSE);}void CAboutDlg::OnOK(){// TODO: Add extra validation hereCDialog::OnOK();}。

计算机图形学实验四二维图形的裁剪

西北农林科技大学实习报告学院名称：理学院专业班级：姓名：学号：课程：计算机图形学实验报告日期：第十五周实验四二维图形的裁剪一、实验目的1）加深直线段的剪裁算法的理解。

2）熟练掌握一种裁剪算法的编程方法。

二、实验步骤1）分析直线段和矩形窗口的位置关系，选定比较合理算法流程。

2）画出程序流程图。

3）编写程序的源程序。

4）编辑源程序并进行调试。

5）进行特殊模式的运行测试，并结合情况进行调整。

三、实验内容1）在编码算法、中点分割算法、Liang-Barsky算法三种中任选一种作为编程模型。

2）编写直线段裁剪的源程序。

3）建议有能力的学生编写多边形裁剪程序。

4）在计算机上编辑编译运行，实现直线段的裁剪。

原理1．直线和窗口的关系：直线和窗口的关系可以分为如下3类：（1）整条直线在窗口内。

此时，不需剪裁，显示整条直线。

（2）整条直线在窗口外，此时，不需剪裁，不显示整条直线。

（3）部分直线在窗口内，部分直线在窗口外。

此时，需要求出直线与窗框的交点，并将窗口外的直线部分剪裁掉，显示窗口内的直线部分。

直线剪裁算法有两个主要步骤。

首先将不需剪裁的直线挑出，即删去在窗外的直线。

然后，对其余直线，逐条与窗框求交点，并将窗口外的部分删去。

2．Cohen-Sutherland直线剪裁算法：（1）输入直线段的两端点坐标p1(x1,y1)，p2(x2,y2)，以及窗口的4条边界坐标，y wt ,y wb,y wl,y wr.（2）对p1，p2进行编码，点p1的编码为code1，点p2的编码为code2.（3）若code1| code2=0，对直线p1p2“简取”之，转（6）；否则，若code1& code2≠0，对直线段“简弃”之，转（7）；当上述两条均不满足时，进行步骤（4）。

（4）确保p1在窗口外部。

若p1在窗口内，则交换p1和p2的坐标值和编码。

（5）根据p1编码从低位开始寻找值为1的地方，从而确定p1在窗口外的哪一侧，然后求出直线段与相应窗口边界的交点S，并用交点S的坐标值替换p1的坐标值，即在交点S处把线段一分为二，因此可以去掉p1S。

计算机图形学编码裁剪算法c语言程序

编码裁剪算法
一，
二，实验目的和意义：窗口内的图形显示，超出窗口边框的图形不予显示。这个过程就是裁剪过程,它在图形显示及窗视口变换中经常用到，对工程图形进行裁剪时，编码裁剪是一种有效的裁剪方法，通过该实验，了解和掌握编码裁剪的原理和方法。从而快速地处理显示区内的图形。
三，实验原理；将绘图所在平面分成九个区域，每个区域用一个四位的二进制数来表示，0000、0001、0010、1001、1000、1010、0101、0100、0110，如果线段两个端点的4位编码全为0，表示线段全部在窗口内，可直接接受并加以显示；如果对线段两个端点的4位编码进行逻辑与运算，结果为非0，则此线段全部在窗口外，可直接舍弃加以裁减；否则，计算直线和窗口边框线的交点，再计算交点的特征码；重复这一过程，直到全部线段均被裁减掉或接受为止。
{
x=x1;
y=y1+(long)(y2-y1)*(xl-x1)/(x2-x1);
}
else if((RIGHT&code)!=0)
/*线段与右边界相交*/
{
x=xr;
y=y1+(long)(y2-y1)*(xr-x1/x2-x1);
}
else if((BOTTOM&code)!=0)
/*线段与上边界相交*/
{
y=yb;
x=x1+(long)(x2-x1)*(yb-y1)/(y2-y1);
}
else if((TOP&code)!=0)
/*线段与下边界相交*/
{
y=yt;
x=x1+(long)(x2-x1)*(yt-y1)/(y2-y1);
}
if(code==code1)
{x1=x;

计算机图形学实验五直线段裁剪

计算机图形学实验报告黔南民族师范学院信息与计算科学撰写人姓名： __ 撰写时间：2010年5月5日审查人姓名：实验过程记录一、实验目的：1、通过实验，进一步理解和掌握直线段的裁剪算法；2、通直线段的裁剪。

二、实验内容：要求：•1 、进一步理解并掌握线段的裁剪算法，并可以实践至少一种线段的裁剪算法；•2、注意：本次作业要求学生不能直接使用系统提供的线段裁剪函数，但是可以调用相关的画点、画线函数。

三、实验设备及软件软件需求：windows98以上操作系统、Turbo C 2.0 、Turbo C＋＋3.0、Visual C＋＋软件、Microsoft Word 97或2000。

硬件需求：建议Pentium IV CPU处理器、64MB以上内存、1GB以上硬盘空间的计算机、激光打印机四、实验方法及步骤1 实验准备上该实验课前将针对解决实验内容问题的C语言程序编制好，在实验课上，对编制完的程序进行调试、修改和分析,熟悉TurboC2.0的菜单，以及编译，运行程序和调试程序的方法，并编写程序。

2. 调试程序；程序一：#define LEFT 1#define RIGHT 2#define BOTTOM 4#define TOP 8#define XL 150#define XR 350#define YB 150#define YT 300#include <math.h>#include"graphics.h"main(){ int gdriver=DETECT,gmode;initgraph(&gdriver,&gmode,"c:\\tc");setcolor(12);line(XL,YT,XR,YT);line(XL,YB,XR,YB);line(XL,YT,XL,YB);line(XR,YT,XR,YB);setcolor(9);draw_ett();getch();closegraph();}encode (x,y,code)int x,y;int *code;{ int c;c=0;if (x<XL) c=c|LEFT;else if (x>XR) c=c|RIGHT;if (y<YB) c=c|BOTTOM;else if (y>YT) c=c|TOP;*code=c;return;}draw_ett(){ int x1,x2,y1,y2,x,y;int code1,code2,code;/* printf("XL=150,XR=350,YB=150,YT=300\n");scanf("%d,%d,%d,%d",&x1,&y1,&x2,&y2);*/x1=50;y1=210;x2=300;y2=100;setcolor(2);line(x1,y1,x2,y2);encode(x1,y1,&code1);encode(x2,y2,&code2);while ((code1!=0)||(code2!=0)) {if ((code1&code2)!=0) return;code=code1;if (code1==0) code=code2;if ((LEFT&code)!=0){x=XL;y=y1+(y2-y1)*(XL-x1)/(x2-x1);}else if ((RIGHT&code)!=0){x=XR;y=y1+(y2-y1)*(XR-x1)/(x2-x1);}else if ((BOTTOM&code)!=0) {y=YB;x=x1+(x2-x1)*(YB-y1)/(y2-y1); }else if ((TOP&code)!=0){y=YT;x=x1+(x2-x1)*(YT-y1)/(y2-y1);}if (code==code1){ x1=x;y1=y;encode(x,y,&code1);}else{ x2=x;y2=y;encode(x,y,&code2);}}setcolor(14);line(x1,y1,x2,y2);return;}运行结果：程序二：请按书上P109的Cohen-Sutherland算法写出完整的程序，并运行出效果图，可参考以上程序一#define XL 150#define XR 350#define YB 150#define YT 300#define FALSE 0#define TRUE 1#include <math.h>#include"graphics.h"typedef struct{int xmin,xmax,ymin,ymax;}Rectangle;typedef int boolean;typedef struct{unsigned all;unsigned left,right,top,bottom;}OutCode;void CompOutCode(float x,float y,Rectangle *rect,OutCode *outCode){outCode->all=0;outCode->top=outCode->bottom=0;if(y>(float)rect->ymax){outCode->top=1;outCode->all+=1;}else if(y<(float)rect->ymin){outCode->bottom=1;outCode->all+=1;}outCode->right=outCode->left=0 ; if(x>(float)rect->xmax){outCode->right=1;outCode->all+=1;}else if(x<(float)rect->xmin){outCode->left=1;outCode->all+=1;}}void CSLineClip(float x0,float y0,float x1,float y1,Rectangle *rect){boolean accept,done;OutCode outCode0,outCode1;OutCode *outCodeOut;float x,y;accept=FALSE;done=FALSE;CompOutCode(x0,y0,rect,&outCode0);CompOutCode(x1,y1,rect,&outCode1);do{if(outCode0.all==0&&outCode1.all==0){accept=TRUE;done=TRUE;}else if(outCode0.all&outCode1.all!=0)done=TRUE;else{if(outCode0.all!=0)outCodeOut=&outCode0;elseoutCodeOut=&outCode1;if(outCodeOut->left){y=y0+(y1-y0)*(rect->xmin-x0)/(x1-x0);x=(float)rect->xmin;}else if(outCodeOut->top){x=x0+(x1-x0)*(rect->ymax-y0)/(y1-y0);y=(float)rect->ymax;}else if(outCodeOut->right){y=y0+(y1-y0)*(rect->xmax-x0)/(x1-x0);x=(float)rect->xmax;}else if(outCodeOut->bottom){x=x0+(x1-x0)*(rect->ymin-y0)/(y1-y0);y=(float)rect->ymin;}if(outCodeOut->all==outCode0.all){x0=x;y0=y;CompOutCode(x0,y0,rect,&outCode0);}else{x1=x;y1=y;CompOutCode(x1,y1,rect,&outCode1);}}}while(!done);if(accept){line((int)x0,(int)y0,(int)x1,(int)y1);}}main(){ int gdriver=DETECT,gmode;Rectangle rect;rect.xmin=XL;rect.xmax=XR;rect.ymin=YB;rect.ymax=YT;initgraph(&gdriver,&gmode,"c:\\tc"); setcolor(12);line(XL,YT,XR,YT);line(XL,YB,XR,YB);line(XL,YT,XL,YB);line(XR,YT,XR,YB);setcolor(2);line(100,100,300,400);setcolor(WHITE);CSLineClip(100,100,300,400,&rect);getch();closegraph();}成绩评定：指导教师：。

一编程实现直线段的裁剪算法

实验一编程实现直线段的裁剪算法课程名称：图形学任课老师谢伙生老师年级03级班级计算机（6）班姓名沈睿汀学号S030300833一、实验要求1、裁剪算法选用Cohen-Sutherland算法；2、界面设计友好、直观。

二、实验环境说明(1)本系统基于JA V A编程环境，使用JBuilder X作为相关的开发工具，因此系统的运行与其它用VC++开发的系统略有不同。

(2)在WINDOWS-XP下运行本程序的时候,请先安装j2re-1_4_2_04-windows-i586-p.exe,然后,才能正常运行，windows环境下双击030300833Cutline.exe。

三、算法与数据结构（程序设计）核心算法Cohen-Sutherland的编写过程如下(在Sutherland.java文件中可以看到具体代码)：（1）新建一个类Sutherland，并在类在声明一个构造函数Sutherland(int wyt, int wyb, int wxl, int wxr) ，传递矩形的四个边界参数，并对类中的共有属性进行初始化。

（2）声明一个端点编码方法private void codingPoint(int x, int y, int[] p)，根据书上的编码规则对端点进行编码。

（3）声明一个方法public void setPoint(int x1, int y1, int x2, int y2)来设置直线段的两端点坐标。

（4）声明两个方法private int OR(int[] op1, int[] op2)和private int AND(int[] op1, int[] op2)来分别实现编码后的端点的相或和相与。

并编写一个方法isInWindow(int[] op)来判断点op是否在窗口中。

（5）编写两个方法private int caculateY(int x1, int y1, int x2, int y2, int x) 和private int caculateX(int x1, int y1, int x2, int y2, int y)来分别求出未知的端点坐标，接着利用这两个方法又编写一个方法private void caculateCrossPoint()来对直线段和相应的窗口边界进行求交处理。

计算机图形学常用算法及代码大全

2.1.1 生成直线的DDA算法数值微分法即DDA法(Digital Differential Analyzer)，是一种基于直线的微分方程来生成直线的方法。

一、直线DDA算法描述：设(x1，y1)和(x2，y2)分别为所求直线的起点和终点坐标，由直线的微分方程得可通过计算由x方向的增量△x引起y的改变来生成直线：也可通过计算由y方向的增量△y引起x的改变来生成直线：式(2－2)至(2－5)是递推的。

二、直线DDA算法思想：选定x2－x1和y2－y1中较大者作为步进方向(假设x2－x1较大)，取该方向上的增量为一个象素单位(△x=1)，然后利用式(2－1)计算另一个方向的增量(△y=△x·m=m)。

通过递推公式(2－2)至(2－5)，把每次计算出的(x i+1，y i+1)经取整后送到显示器输出，则得到扫描转换后的直线。

之所以取x2－x1和y2－y1中较大者作为步进方向，是考虑沿着线段分布的象素应均匀，这在下图中可看出。

另外，算法实现中还应注意直线的生成方向，以决定Δx及Δy是取正值还是负值。

三、直线DDA算法实现：1、已知直线的两端点坐标：(x1，y1)，(x2，y2)2、已知画线的颜色：color3、计算两个方向的变化量：dx=x2－x1dy=y2－y14、求出两个方向最大变化量的绝对值：steps=max(|dx|，|dy|)5、计算两个方向的增量(考虑了生成方向)：xin=dx/stepsyin=dy/steps6、设置初始象素坐标：x=x1,y=y17、用循环实现直线的绘制：for(i=1；i<=steps；i++){ putpixel(x，y，color)；/*在(x，y)处，以color色画点*/x=x+xin；y=y+yin；}五、直线DDA算法特点：该算法简单，实现容易，但由于在循环中涉及实型数的运算，因此生成直线的速度较慢。

//@brief 浮点数转整数的宏实现代码#define FloatToInteger(fNum)((fNum>0)?static_cast<int>(fNum+0.5):static_cast<int>(fNum-0.5))/*!* @brief DDA画线函数** @param pDC [in]窗口DC* @param BeginPt [in]直线起点* @param EndPt [in]直线终点* @param LineCor [in]直线颜色* @return 无*/void CDrawMsg::DDA_DrawLine(CDC *pDC,CPoint &BeginPt,CPoint &EndPt,COLORREF LineCor){l ong YDis = (EndPt.y - BeginPt.y);l ong XDis = (EndPt.x-BeginPt.x);l ong MaxStep = max(abs(XDis),abs(YDis)); // 步进的步数f loat fXUnitLen = 1.0f; // X方向的单位步进f loat fYUnitLen = 1.0f; // Y方向的单位步进f YUnitLen = static_cast<float>(YDis)/static_cast<float>(MaxStep);f XUnitLen = static_cast<float>(XDis)/static_cast<float>(MaxStep);// 设置起点像素颜色p DC->SetPixel(BeginPt.x,BeginPt.y,LineCor);f loat x = static_cast<float>(BeginPt.x);f loat y = static_cast<float>(BeginPt.y);// 循环步进f or (long i = 1;i<=MaxStep;i++){x = x + fXUnitLen;y = y + fYUnitLen;pDC->SetPixel(FloatToInteger(x),FloatToInteger(y),LineCor);}}2.1.2 生成直线的B resenham算法从上面介绍的DDA算法可以看到，由于在循环中涉及实型数据的加减运算，因此直线的生成速度较慢。

计算机图形学裁剪算法详解

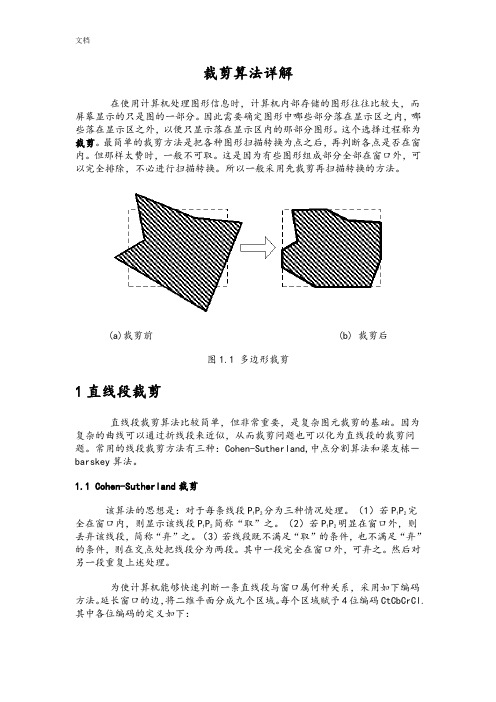
裁剪算法详解在使用计算机处理图形信息时，计算机内部存储的图形往往比较大，而屏幕显示的只是图的一部分。

因此需要确定图形中哪些部分落在显示区之内，哪些落在显示区之外，以便只显示落在显示区内的那部分图形。

这个选择过程称为裁剪。

最简单的裁剪方法是把各种图形扫描转换为点之后，再判断各点是否在窗内。

但那样太费时，一般不可取。

这是因为有些图形组成部分全部在窗口外，可以完全排除，不必进行扫描转换。

所以一般采用先裁剪再扫描转换的方法。

(a)裁剪前(b) 裁剪后图1.1 多边形裁剪1直线段裁剪直线段裁剪算法比较简单，但非常重要，是复杂图元裁剪的基础。

因为复杂的曲线可以通过折线段来近似，从而裁剪问题也可以化为直线段的裁剪问题。

常用的线段裁剪方法有三种：Cohen-Sutherland,中点分割算法和梁友栋－barskey算法。

1.1 Cohen-Sutherland裁剪该算法的思想是：对于每条线段P1P2分为三种情况处理。

（1）若P1P2完全在窗口内，则显示该线段P1P2简称“取”之。

（2）若P1P2明显在窗口外，则丢弃该线段，简称“弃”之。

（3）若线段既不满足“取”的条件，也不满足“弃”的条件，则在交点处把线段分为两段。

其中一段完全在窗口外，可弃之。

然后对另一段重复上述处理。

为使计算机能够快速判断一条直线段与窗口属何种关系，采用如下编码方法。

延长窗口的边，将二维平面分成九个区域。

每个区域赋予4位编码CtCbCrCl.其中各位编码的定义如下：图1.2 多边形裁剪区域编码图5.3线段裁剪裁剪一条线段时，先求出P1P2所在的区号code1,code2。

若code1=0,且code2=0，则线段P1P2在窗口内，应取之。

若按位与运算code1&code2≠0，则说明两个端点同在窗口的上方、下方、左方或右方。

可判断线段完全在窗口外，可弃之。

否则，按第三种情况处理。

求出线段与窗口某边的交点，在交点处把线段一分为二，其中必有一段在窗口外，可弃之。

计算机图形学直线裁剪代码

using System;using ;using ponentModel;using System.Data;using System.Drawing;using System.Text;using ;namespace LineCut_Cohen{public partial class Form1 : Form{public Form1(){InitializeComponent();}//定义钻石参数int x0 = 100;int y0 = 100;int n = 13;int r = 50;int[] x;int[] y;////计算钻石顶点 by tiantian//public void ZuanShi(){float t = (float)3.14159 * 2 / n;x = new int[n];y = new int[n];for (int i = 0; i < n; i++){x[i] = (int)(r * Math.Cos(i * t) + x0);y[i] = (int)(r * Math.Sin(i * t) + y0);}}////计算点(x,y)的编码//void CompOutCode(int x, int y, Rectangle rect, OutCode outCode){outCode.all = 0;outCode.top = outCode.bottom = 0;if (y < rect.Top) //rect类的top相当于我们惯常用的坐标系的bottomby:tiantian{outCode.bottom = 1;outCode.all += 1;}else if (y > rect.Bottom)//rect类的bottom相当于我们惯常用的坐标系的top by:tiantian{outCode.top = 1;outCode.all += 1;}outCode.right = outCode.left = 0;if (x > rect.Right){outCode.right = 1;outCode.all += 1;}else if (x < rect.Left){outCode.left = 1;outCode.all += 1;}}////线段裁剪，p0(x0,y0),p1(x1,y1)为待裁剪线断，rect为裁剪窗口//bool ChoenSutherlandLineClip(ref int x0, ref int y0, ref int x1, ref int y1, Rectangle rect) //这里必须是引用传递！by:tiantian{Boolean accept, done;OutCode outCode0 = new OutCode();OutCode outCode1 = new OutCode();OutCode outCodeOut = new OutCode();int x = 0;int y = 0;accept = false;done = false;CompOutCode(x0, y0, rect, outCode0);CompOutCode(x1, y1, rect, outCode1);do{int code0 = outCode0.Code();int code1 = outCode1.Code();if ((outCode0.all == 0) && (outCode1.all == 0)) //完全可见{accept = true;done = true;}else if ((code0 & code1) != 0) //显然不可见 by ttdone = true;else //进行求交测试{if (outCode0.all != 0) //判断哪一点位于窗口之外outCodeOut = outCode0;else outCodeOut = outCode1;if (outCodeOut.left == 1)//线段与窗口的左边相交{x = rect.Left;y = y0 + (y1 - y0) * (x - x0) / (x1 - x0);}else if (outCodeOut.right == 1)//线段与窗口的右边相交{x = rect.Right;y = y0 + (y1 - y0) * (x - x0) / (x1 - x0);}else if (outCodeOut.top == 1)//线段与窗口的上边相交{y = rect.Bottom;x = x0 + (x1 - x0) * (y - y0) / (y1 - y0);}else if (outCodeOut.bottom == 1)//线段与窗口的下边相交{y = rect.Top;x = x0 + (x1 - x0) * (y - y0) / (y1 - y0);}//以交点为界，将线段位于窗口边所在的直线的外侧的部分丢弃。

计算机图形学代码_CS法直线段裁剪

计算机图形学Cohen-Sutherland直线裁剪算法源码c++