南京清江花苑严老师数列综合题

合集下载

南京清江花苑严老师高中数学必修2+必修5测试题

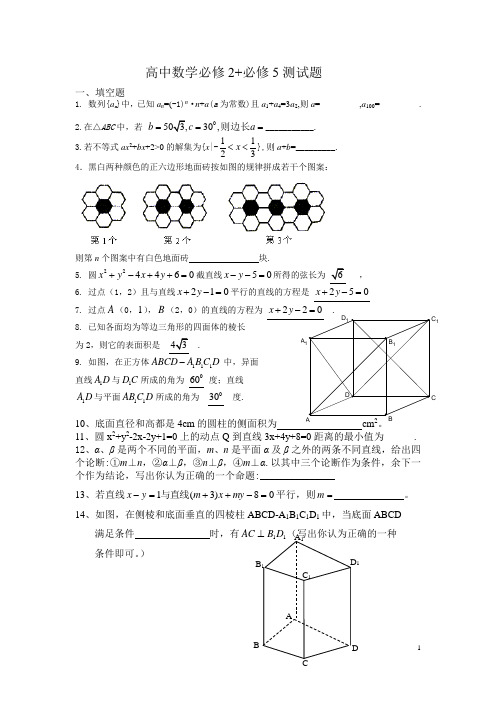
高中数学必修2+必修5测试题一、填空题1. 数列{a n }中，已知a n =(-1)n ·n +a (a 为常数)且a 1+a 4=3a 2,则a =_________,a 100=_________.2.在△ABC 中，若030,b c a ===则边长___________. 3.若不等式ax 2+bx +2>0的解集为{x |-3121<<x },则a +b =_________. 4．黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：则第n 个图案中有白色地面砖块.5. 圆224460x y x y +-++=截直线50x y --=所得的弦长为， 6. 过点（1，2）且与直线210x y +-=平行的直线的方程是 250x y +-= 7. 过点A （0，1），B （2，0）的直线的方程为 220x y +-= . 8. 已知各面均为等边三角形的四面体的棱长为2，则它的表面积是9. 如图，在正方体111ABCD A BC D -中，异面直线1A D 与1D C 所成的角为 060 度；直线1A D 与平面11AB C D 所成的角为 030 度.10、底面直径和高都是4cm 的圆柱的侧面积为 cm 2。

11、圆x 2+y 2-2x-2y+1=0上的动点Q 到直线3x+4y+8=0距离的最小值为______. 12、α、β是两个不同的平面，m 、n 是平面α及β之外的两条不同直线，给出四个论断:①m ⊥n ，②α⊥β，③n ⊥β，④m ⊥α.以其中三个论断作为条件，余下一个作为结论，写出你认为正确的一个命题:_______________13、若直线08)3(1=-++=-my x m y x 与直线平行，则=m 。

14、如图，在侧棱和底面垂直的四棱柱ABCD-A 1B 1C 1D 1中，当底面ABCD满足条件时，有11D B AC ⊥（写出你认为正确的一种条件即可。

南京清江花苑严老师八年级上学期数学期末复习试卷1401

八年级上学期数学期末复习试卷1401一、选择题（每空3 分，共30 分）1、下列说法正确的是（）A、有一个外角的平分线平行于一边的三角形不是等腰三角形。

B、等腰三角形的高、中线、角平分互相重合C、有两个内角分别为70°和40°的三角形是等腰三角形。

D、等腰三角形一边不可以是另一边的2倍2、下列数中，3.14159，，，，，,无理数的个数有 ( )A．1个 B．2个 C．3个 D．4个3、以下列数组中的三个数分别为三边长，能构成直角三角形的是 ( )4、A．1，1， B．，， C．2，3，5 D．，，4、若，，且，则的值为 ( )A．-1或11 B．-1或-11 C ． 1 D ．115、如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1，则其旋转中心可能是 ( )A．点D B．点C C．点B D．点A6、函数y＝的自变量x的取值范围是（）Ａ．x≥-2 Ｂ.x＞-2 Ｃ．x≤-2 Ｄ．x＜-2 7、.一根弹簧原长12cm，它所挂的重量不超过10kg，并且挂重1kg就伸长1.5cm，写出挂重后弹簧长度y（cm）与挂重x（kg）之间的函数关系式是（）Ａ．y＝1.5（x+12）(0≤x≤10) Ｂ．y＝1.5x+12 (0≤x≤10)Ｃ．y＝1.5x+10 (0≤x) Ｄ．y＝1.5(x－12) (0≤x≤10)8、无论m 为何实数，直线与的交点不可能在（）A.第一象限B.第二象限C.第三象限D.第四象限9、某兴趣小组做实验，将一个装满水的啤酒瓶倒置（如图），并设法使瓶里的水从瓶中匀速流出.那么该倒置啤酒瓶内水面高度随水流出的时间变化的图象大致是（）A B C D10、已知函数 , 当-1＜x≤1时，y的取值范围是（）A. B. C. D.二、填空题(每题3分，共30分）11、若x2－11＝0，则x的值等于______________.12、地球上七大洲的总面积约为149480000 km2，保留2个有效数字约为km²13、如图，将△AOB绕点O按逆时针方向旋转40°后得到△A＇OB＇，若∠AOB=15°，则∠AOB＇的度数是_______.14、如图,以直角三角形一边向外作正方形,其中两个正方形的面积为 100和64,则正方形A的面积为。

南京清江花苑严老师高三年级调研测试(含答案)

高三年级调研测试数学试题参考公式：锥体的体积公式为V ＝13Sh ，其中S 是锥体的底面积，h 是锥体的高．一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置．．．．．．．上．1．已知集合A ＝{2α，3}，B ＝{2，3}，若A ∪B ＝{1，2，3}，则实数a 的值是． 2．函数f (x )＝sin x cos x 的最小正周期是．3．若复数z ＝1－m i2＋i（i 是虚数单位）是纯虚数，则实数m 的值是．4．盒子中有大小相同的3只白球，2只黑球．若从中随机地摸出两只球，则两只球颜色相同的概率是．5．根据2012年初我国发布的《环境空气质量指数AQI 技术规定(试行)》，AQI 共分为六级：(0，50]为优，(50，100]为良，(100，150]为轻度污染，(150，200]为中度污染， (200，300]为重度污染，300以上为严重污染．2012年12月1日出版的《A 市早报》对A 市2012年11月份中30天的AQI 进行了统计，频率分布直方图如图所示．根据频率分布直方图，可以看出A 市该月环境空气质量优良的总天数为．6．运行如图所示的算法流程图，则输出的n 的值是．开始 S ←1 n ←0S ←S ＋3nn ←n ＋1结束输出n S ≥20 N Y (第6题)0.0010.002 0.004 0 50 100 150 200 300 AQI 频率组距0.006(第5题)7．已知圆锥的侧面展开图是一个半径为3cm ，圆心角为2π3的扇形，则此圆锥的高为 cm ．8．在平面直角坐标系xOy 中，设过原点的直线l 与圆C ：(x －3)2＋(y －1)2＝4 交于M ，N 两点．若MN ≥23，则直线l 的斜率k 的取值范围为．9．设数列{a n }是公差不为零的等差数列，S n 为其前n 项和，且满足a 21＋a 22＝a 23＋a 24，S 5＝5，则a 7的值是．10．若函数f (x )为定义在R 上的奇函数，当x ＞0时，32)(1-=-x x f ，则不等式f (x )＞1的解集为．11．在△ABC 中，已知AB ＝2，BC ＝3，∠ABC ＝60°，BD ⊥AC ，D 为垂足，则BD →·BC →的值为．12．若关于x 的不等式(2ax －1)ln x ≥0对任意x ∈(0，＋∞)恒成立，则实数a 的值为． 13．在平面直角坐标系xOy 中，双曲线C ：x 24－y 23＝1．设过点M (0，1)的直线l 与双曲线C 交于A ，B 两点，若AM →＝2MB →，则直线l 的斜率为．14．已知数列{a n }的通项为 a n ＝7n ＋2，数列{b n }的通项为b n ＝n 2，若将数列{a n }，{b n } 中相同的项按从小到大顺序排列后记作数列{c n }，则c 9的值是．二、解答题：本大题共6小题，共90分．请在答题卡指定区域内．．．．．．．．作答，解答时应写出文字说明、证明过程或演算步骤． 15．(本小题满分14分)在△ABC 中，已知角A ，B ，C 所对的边分别是a ，b ，c ，cos C cos B ＝2a －cb．（1）求B ；（2）若tan(A ＋π4)＝7，求cos C 的值．16．(本小题满分14分)如图，在四棱锥P －ABCD 中，底面ABCD 为直角梯形，AD ∥BC ，PB ⊥平面ABCD ，CD ⊥BD ，PB ＝AB ＝AD ＝1，点E 在线段PA 上，且满足PE ＝2EA ．（1）求三棱锥E －BAD 的体积；（2）求证：PC ∥平面BDE ．17．(本小题满分14分)如图，某广场中间有一块扇形状绿地OAB ，其中O 为扇形所在圆的圆心，∠AOB ＝60 ．广场管理部门欲在绿地上修建一条观光小路：在⌒AB 上选一点C ，过C 修建与OB 平行的小路CD ，修建与OA 平行的小路CE ．问C 应选在何处，才能使得修建的道路CD 与CE 的总长最大，并说明理由．18．(本小题满分16分)已知数列{a n }的各项都为正数，且对任意n ∈N *，a 2n ＋1＝a n a n ＋2＋k (k 为常数)．（1）若k ＝(a 2－a 1)2，求证：a 1，a 2，a 3成等差数列；（2）若k ＝0，且a 2，a 4，a 5成等差数列，求a 2a 1的值；（3）已知a 1＝a ，a 2＝b (a ，b 为常数)，是否存在常数λ，使得a n ＋a n ＋2＝λa n ＋1对任意n ∈N *都成立？若存在，求出λ；若不存在，说明理由．BOCDE A(第17题)P ABCD(第16题)E19．(本小题满分16分)在平面直角坐标系xOy 中，椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)过点A (a 2，a2)和点B (3，1)．（1）求椭圆C 的方程；（2）已知点P (x 0，y 0)在椭圆C 上，F 为椭圆的左焦点，直线l 的方程为x 0x ＋3y 0y －6＝0．①求证：直线l 与椭圆C 有唯一的公共点；②若点F 关于直线l 的对称点为Q ，求证：当点P 在椭圆C 上运动时，直线PQ 恒过定点，并求出此定点的坐标．20．(本小题满分16分)设函数f (x )＝x 2－(a －2)x －a ln x ．（1）求函数f (x )的单调区间；（2）若函数f (x )有两个零点，求满足条件的最小正整数a 的值；（3）若方程 f (x )＝c 有两个不相等的实数根x 1，x 2，求证：0)2(21>+'x x f .2012—2013学年度高三年级第三次调研测试数学附加题 2013．0321．【选做题】在A 、B 、C 、D 四小题中只能选做2题，每小题10分，共20分．请在答．卷卡指定区域内．．．．．．．作答．解答应写出文字说明、证明过程或演算步骤． A ．选修4—1：几何证明选讲如图，⊙O 是等腰三角形ABC 的外接圆，AB ＝AC ，延长BC 到点D ，使得CD ＝AC ，连结AD 交⊙O 于点E ，连结BE 与AC 交于点F ，证明：AE 2＝EF ·BE ． B ．选修4—2：矩阵与变换已知二阶矩阵A ＝⎣⎡⎦⎤3 50－2．（1）求矩阵A 的特征值和特征向量；（2）设向量β＝⎣⎢⎡⎦⎥⎤1－1，求A 5β．C ．选修4—4：坐标系与参数方程已知直线l ：⎩⎨⎧x ＝1－55t ，y ＝－1＋255t（t 为参数）和曲线C ：⎩⎨⎧x ＝1＋t ，y ＝1＋t 2（t 为参数）．若点P 是曲线C 上任意一点，求点P 到直线l 的距离的最小值及此时点P 的坐标．D ．选修4—5：不等式选讲若正数a ，b 满足a ＋b ＝1，求13a ＋2＋43b ＋2的最小值．AOECDBF(第21题A )【必做题】第22题、第23题，每题10分，共20分．请在答．题卡指定区域内．．．．．．．作答．解答应写出文字说明、证明过程或演算步骤． 22．(本小题满分10分)如图，在直三棱柱ABC －A 1B 1C 1中，CA ＝4，CB ＝4，CC 1＝22，∠ACB ＝90°，点M 在线段A 1B 1上．（1）若A 1M ＝3MB 1，求异面直线AM 与A 1C 所成角的余弦值；（2）若直线AM 与平面ABC 1所成角为30°，试确定点M 的位置．23．(本小题满分10分)设f (x )＝(1＋x ) (1＋2x )·…·(1＋nx )，(n ∈N*且n ≥2)，其展开后含rx 项的系数记作r a （r ＝0，1，2，…，n ）．（1）求a 1(用含n 的式子表示)；（2）求证：a 2＝3n ＋24C 3n ＋1．数学参考答案及评分标准一、填空题：本大题共l4小题．每小囊5分．共70分． 1.0 π.2 2.3 52.4 12.5 5.6 22.7 ]43,0.[8 9.9 10.),3()0,2(+∞- 727.11 21.12 .1321± 961.14二、解答题：本大题共6小题。

南京清江花苑严老师七年级数学9月月考试卷1602.doc

七年级数学9月月考试卷1602一、选择题：1・下列运算中，正确的是() 、O 0 O , 、 r a OA. (a+b) n+rB. ( - x - y) n~+2xy+y-C. (x+3) (x-2) =X 2-6D. ( -a-b) (a+b) =a 2 - b 23. a, b, c, d 四根竹签的长度分别为2cm, 3cm, 4cm, 6cm,若从中任意选取三根首尾依次相接围成不同的三角形，则围成的三角形共有（）A. 1个B. 2个C. 3个D. 4个4.在下列多项式的乘法中，可以川平方差公式计算的是（） (a+b 2) 5. 一个多边形的每个内角都是144°,这个多边形是（）A.八边形B.十边形C.十二边形D.十四边形 66 具备下列条件的AABC 中，不是直角三角形的是（）A. ZA+ZB=ZCB. ZA=^ZB=^ZCC. ZA ： ZB ： ZC=1： 2： 3D. ZA=2ZB=3ZC V Z4+ZD=180°, •••AD 〃BCD. T Z4+ZB=180°, .I AB //CDA. (x+3) (3+x)B.c. (-x+y) (x - y) D. (a 2-b) 如图，下列推理中正确的是2. B. C. VZ1 = Z3, AAD/7BC (a+~^b)A. AABC 中，AD 是边BC ±的高B. AABC 中，GC 是边BC ±的高C. AGBC 中，GC 是边BC ±的高D. AGBC 中，CF 是边BG 上的高8. 通过计算儿何图形的面积可表示一些代数恒等式，如图可表示的代数恒等式是（C. 2a (a+b) =2a 2+2abD. (a+b) (a-b) =a 2 - b 2二•填空题：9. _____________________________ 计算：3x 3* （ -2x ） 2= 10. _________________________________________________ 若x 2+kx+9是一个二项整式的平方，则k 的值是 _______________________________________II. 一个等腰三介形的两边长分别是3cm 和7cm,则它的周长是 _______________ cm.(a+b) 2=a 2+2ab+b 2B.ZC=50°,若沿图中虚线剪去ZC,则Zl+Z2=13.如图，AB〃CD, AD〃BC, ZB=110。

南京清江花苑严老师高三数学上学期期末复习

高三数学上学期期末复习0010一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应的位置上． 1．已知全集U =R ，集合{}10A x x =+>，则U A =ð ▲ ．2．已知复数z =32i i -(i 是虚数单位)，则复数z 所对应的点位于复平面的第 ▲ 象限．3．已知正四棱锥的底面边长是6，这个正四棱锥的侧面积是 ▲ ． 4．定义在R 上的函数()f x ，对任意x ∈R 都有(2)()f x f x +=，当(2,0)x ∈- 时，()4x f x =，则(2013)f = ▲ ．5．已知命题p ：“正数a 的平方不等于0”，命题q ：“若a 不是正数，则它的平方等于0”，则p 是q 的 ▲ ．（从“逆命题、否命题、逆否命题、否定”中选一个填空）6．已知双曲线22221y x a b-=的一个焦点与圆x 2+y 2－10x =0的圆心重合，，则该双曲线的标准方程为 ▲ ．7．若S n 为等差数列{a n }的前n 项和，S 9=－36，S 13=－104，则a 5与a 7的等比中项为 ▲ ．8．已知实数x ∈[1，9]，执行如右图所示的流程图，则输出的x 不小于55的概率为 ▲ ．9．在△ABC 中，若AB =1，AC||||AB AC BC +=u u u r u u u r u u u r ，则||BA BC BC ⋅u u u r u u u r u u u r = ▲．10．已知01a <<，若log (21)log (32)a a x y y x -+>-+，且x y <+λ，则λ的最大值为 ▲ ． 11．曲线2(1)1()e (0)e 2x f f x f x x '=-+在点(1，f (1))处的切线方程为 ▲ ． 12．如图，点O 为作简谐振动的物体的平衡位置，取向右方向为正方向，若振幅为3cm ，周期为3s ，且物体向右运动到距平衡位置最远处时开始计时．则该物体5s 时刻的位移为 ▲ cm ．13．已知直线y =ax +3与圆22280x y x ++-=相交于A ，B 两点，点00(,)P x y 在直线y =2x 上，且PA =PB ,则0x 的取值范围为 ▲ ．14．设P (x ，y )为函数21y x =-(x >图象上一动点，记353712x y x y m x y +-+-=+--，则当m 最小时，点 P 的坐标为 ▲ ．(第12题)二、解答题：本大题共6小题，共计90分．请把答案写在答题卡相应的位置上．解答时应写出文字说明，证明过程或演算步骤． 15．(本题满分14分)如图，在正三棱柱ABC －A 1B 1C 1中，E 是侧面AA 1B 1B 对角线的交点，F 是侧面AA 1C 1C 对角线的交点，D 是棱BC 的中点．求证：（1）//EF 平面ABC ；（2）平面AEF ⊥平面A 1AD ．16.（本题满分14分）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，sin sin tan cos cos A B C A B +=+．（1）求角C 的大小；（2）若△ABC 的外接圆直径为1，求22a b +的取值范围．17.（本题满分14分）ABCDEF A 1 B 1C 1(第15题)某公司为一家制冷设备厂设计生产一种长方形薄板，其周长为4米，这种薄板须沿其对角线折叠后使用．如图所示，()ABCD AB AD >为长方形薄板，沿AC 折叠后，AB '交DC 于点P ．当△ADP 的面积最大时最节能，凹多边形ACB PD '的面积最大时制冷效果最好．（1）设AB =x 米，用x 表示图中DP 的长度，并写出x 的取值范围；（2）若要求最节能，应怎样设计薄板的长和宽？（3）若要求制冷效果最好，应怎样设计薄板的长和宽？18.（本题满分16分）已知数列{a n }中，a 2=1，前n 项和为S n ，且1()2n n n a a S -=．（1）求a 1；（2）证明数列{a n }为等差数列，并写出其通项公式；（3）设1lg 3n n na b +=，试问是否存在正整数p ，q (其中1<p <q )，使b 1，b p ，b q 成等比数列？若存在，求出所有满足条件的数组(p ，q )；若不存在，说明理由．19.（本题满分16分）A BCD（第17题）B 'P已知左焦点为F (－1，0)的椭圆过点E (1．过点P (1，1)分别作斜率为k 1，k 2的椭圆的动弦AB ，CD ，设M ，N 分别为线段AB ，CD 的中点．（1）求椭圆的标准方程；（2）若P 为线段AB 的中点，求k 1；（3）若k 1+k 2=1，求证直线MN 恒过定点，并求出定点坐标．20.（本题满分16分）已知函数()(0ln x f x ax x x=->且x ≠1)．（1）若函数()f x 在(1,)+∞上为减函数，求实数a 的最小值；（2）若212,[e,e ]x x ∃∈，使f (x 1)≤2()f x a '+成立，求实数a 的取值范围．A B EFDCO(第21A 题)数学附加题21．【选做题】本题包括A ，B ，C ，D 共4小题，请从这4题中选做2小题，每小题10分，共20分．请在答题卡上准确填涂题目标记，解答时应写出文字说明、证明过程或演算步骤．A ．选修4－1：几何证明选讲如图，△ABC 是⊙O 的内接三角形，若AD 是△ABC 的高，AE 是⊙O 的直径，F 是»BC的中点．求证：（1）AB AC AE AD ⋅=⋅；（2）FAE FAD ∠=∠．B ．选修4－2：矩阵与变换已知曲线2:2C y x = ，在矩阵M 1002⎡⎤=⎢⎥⎣⎦对应的变换作用下得到曲线1C ，1C 在矩阵N 0110-⎡⎤=⎢⎥⎣⎦对应的变换作用下得到曲线2C ，求曲线2C 的方程．C ．选修4－4：坐标系与参数方程已知极坐标系的极点在直角坐标系的原点，极轴与x 轴的正半轴重合．曲线C 的极坐标方程为2222cos 3sin 3+=ρθρθ，直线l的参数方程为,1x y t⎧=⎪⎨=+⎪⎩(t 为参数，t ∈R)．试在曲线C 上求一点M ，使它到直线l 的距离最大．D ．选修4－5：不等式选讲已知0,0,a b >>且21a b +=，求224S a b =--的最大值．22．(本小题满分10分)．解答时应写出文字说明、证明过程或演算步骤．如图，已知定点R (0，－3)，动点P ，Q 分别在x 轴和y 轴上移动，延长PQ至点M ，使12PQ QM =u u u r u u u u r，且0PR PM ⋅=u u u r u u u u r ．（1）求动点M 的轨迹C 1；（2）圆C 2： 22(1)1x y +-=，过点(0，1)的直线l 依次交C 1于A ，D 两点（从左到右），交C 2于B ，C 两点（从左到右），求证：AB CD ⋅u u u r u u u r 为定值．23．(本小题满分10分)．解答时应写出文字说明、证明过程或演算步骤．已知数列{a n }满足：1*1122,1()n a n a a a a n -+=-=+∈N ．（1）若1a =-，求数列{a n }的通项公式；（2）若3a =，试证明：对*n ∀∈N ，a n 是4的倍数．（第22题）。

南京清江花苑严老师中考数学模拟试卷

中考数学精品模拟试卷1605一、选择题（本大题共8小题，每小题3分，共24分，在每小题给出的四个选项中国，只有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应的位置上）1．的值等于（）A．4 B．﹣4 C．±4 D．2．如图，数轴上有A，B，C，D四个点，其中到原点距离相等的两个点是（）A．点B与点D B．点A与点C C．点A与点D D．点B与点C3．如图，一个由5个大小相同、棱长为1的正方体搭成的几何体，下列关于这个几何体的说法正确的是（）A．主视图的面积为5 B．左视图的面积为3C．俯视图的面积为5 D．俯视图的面积为34．某中学为了解学生的视力情况，需要抽取部分学生进行调查，下列抽取方法中最合适的是（）A．随机抽取一部分男生B．随机抽取一个班级的学生C．随机抽取一个年级的学生D．在各个年级中，每班各随机抽取20名学生5．若a=b﹣3，则b﹣a的值是（）A．﹣3 B．3 C．0 D．66．小超同学在“百度”搜索引擎中输入“中国梦，我的梦”，能搜索到与之相关结果的条数是1650000，这个数用科学记数法表示为（）A．165×104B．1.65×105C．1.65×106D．0.165×1077．如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是（）A．同位角相等，两直线平行B．内错角相等，两直线平行C．两直线平行，同位角相等D．两直线平行，内错角相等8．如图，表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动．甲、乙两人前往目的地所行驶的路程S（千米）随时间t（分）变化的函数图象，则每分钟乙比甲多行驶的路程是（）A．0.5千米B．1千米C．1.5千米D．2千米二、填空题（本大题共10小题，每小题3分，共30分，不需写出解答过程，请把答案直接填写在答题卡相应位置上）9．使式子有意义的x的取值范围是．10．因式分解：x2y﹣9y=．11．若（m+2）2+=0，则m﹣n=．12．化简分式：=．13．如表记录了一名球员在罚球线上投篮的结果．那么，这名球员投篮一次，投中的概率约为（精确到0.1）．投篮次数（n）50 100 150 200 250 300 500投中次数（m）28 60 78 104 123 152 251投中频率（m/n）0.56 0.60 0.52 0.52 0.49 0.51 0.5014．如图，以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′，若OA=4，OA′=8，则四边形ABCD和四边形A′B′C′D′的周长的比为．15．一元二次方程x2+mx+2m=0的两个实根分别为x1，x2，若x1+x2=1，则x1x2=．16．如图，将三角板的直角顶点放在直尺的一边上，若∠1=55°，则∠2的度数为°．17．如图，D、E分别是AC和AB上的点，AD=DC=4，DE=3，DE∥BC，∠C=90°，将△ADE沿着AB边向右平移，当点D落在BC上时，平移的距离为．18．若x是不等于1的实数，我们把称为x的差倒数，如2的差倒数是=﹣1，﹣1的差倒数为=．现已知x1=﹣，x2是x1的差倒数，x3是x2的差倒数，x4是x3的差倒数，…，依此类推，则x2016的值为．三、解答题（本大题共10小题，共96分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）19．（1）计算：﹣|﹣2|﹣4cos60°．（2）解不等式2x﹣3＜，并把解集在数轴上表示出来．20．已知4x=3y，求代数式（x﹣2y）2﹣（x﹣y）（x+y）﹣2y2的值．21．甲、乙、丙三位歌手进入“我是歌手”的冠、亚、季军的决赛，他们通过抽签来决定演唱顺序．（1）求甲第一位出场的概率；（2）用树状图或列表格写出所有可能的出场顺序，并求出甲比乙先出场的概率．22．如图，在平面直角坐标系中，一次函数y=kx+b与反比例函数y=﹣的图象交于A（﹣1，m），B（n，﹣3）两点，一次函数y=kx+b的图象与y轴交于点C．（1）求一次函数的解析式；（2）点P是x轴上一点，且△BOP的面积是△BOC面积的2倍，求点P的坐标．23．如图，已知点E，F分别是▱ABCD的边BC，AD上的中点，且∠BAC=90°．（1）求证：四边形AECF是菱形；（2）若∠B=30°，BC=10，求菱形AECF面积．24．为了推动阳光体育运动的广泛开展，引导学生积极参加体育锻炼，某校九年级准备购买一批运动鞋供学生借用，现从九年级各班随机抽取了部分学生的鞋号，绘制了如下的统计图①和图②，请根据相关信息，解答下列问题：（1）接受随机抽样调查的学生人数为，图①中m的值为；（2）在本次调查中，学生鞋号的众数为号，中位数为号；（3）根据样本数据，若该年级计划购买100双运动鞋，建议购买35号运动鞋多少双？25．如图，某校一幢教学大楼的顶部竖有一块“传承文明，启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°，沿山坡向上走到B处测得宣传牌顶部C的仰角为45°．已知山坡AB的坡度i=1：，AB=10米，AE=15米，求这块宣传牌CD的高度．（测角器的高度忽略不计，结果精确到0.1米．参考数据：≈1.414，≈1.732）26．已知：如图，△ABC内接于⊙O，AB为直径，∠CBA的平分线交AC于点F，交⊙O于点D，DE⊥AB于点E，且交AC于点P，连结AD．（1）求证：∠DAC=∠DBA；（2）求证：P是线段AF的中点；（3）连接CD，若CD﹦3，BD﹦4，求⊙O的半径和DE的长．27．已知一次函数y=﹣x+1与抛物线y=x2+bx+c交于A（0，1），B两点，B点纵坐标为10，抛物线的顶点为C．（1）求b，c的值；（2）判断△ABC的形状并说明理由；（3）点D、E分别为线段AB、BC上任意一点，连接CD，取CD的中点F，连接AF，EF．当四边形ADEF为平行四边形时，求平行四边形ADEF的周长．28．【发现证明】（1）如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图1证明上述结论．【类比引申】（2）如图2，点E、F分别在正方形ABCD的边CB、CD的延长线上，∠EAF=45°，连接EF，请直接写出EF、BE、DF之间的数量关系，不需证明；【联想拓展】（3）如图3，如图，∠BAC=90°，AB=AC，点E、F在边BC上，且∠EAF=45°，若BE=1，CF=2，求EF的长．。

南京清江花苑严老师八年级10月月考数学试卷1602.doc

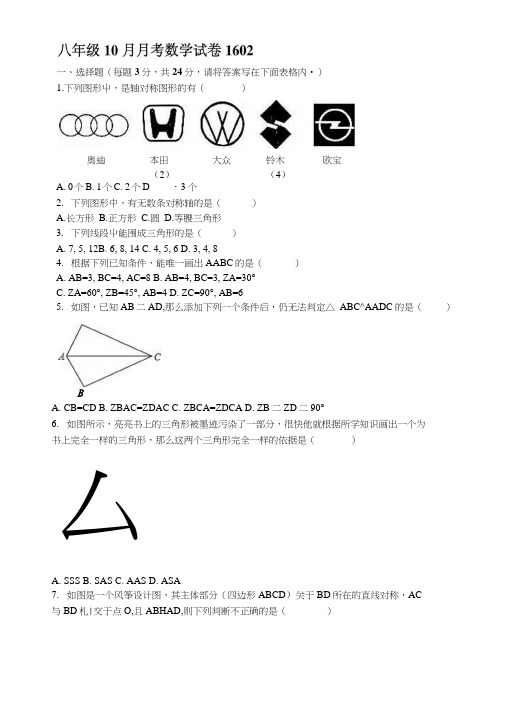
・3个A. 0个B. 1个C. 2个D 2. 下列图形中，有无数条对称轴的是（）A.长方形B.正方形C.圆D.等腰三角形3. 下列线段屮能围成三角形的是（）A. 7, 5, 12B. 6, 8, 14C. 4, 5, 6D. 3, 4, 84. 根据下列已知条件，能唯一画出AABC 的是（）A. AB=3, BC=4, AC=8B. AB=4, BC=3, ZA=30°C. ZA=60°, ZB=45°, AB=4D. ZC=90°, AB=65. 如图，已知AB 二AD,那么添加下列一个条件后，仍无法判定△ ABC^AADC 的是（） BA. CB=CDB. ZBAC=ZDACC. ZBCA=ZDCAD. ZB 二ZD 二90°6. 如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个为书上完全一样的三角形，那么这两个三角形完全一样的依据是（）厶A. SSSB. SASC. AASD. ASA7. 如图是一个风筝设计图，其主体部分（四边形ABCD ）关于BD 所在的直线对称，AC 与BD 札|交于点O,且ABHAD,则下列判断不正确的是（）一、选择题（每题3分，共24分，请将答案写在下面表格内•） 1.下列图形屮，是轴对称图形的有（）奥迪大众欧宝本田（2）铃木（4）A. AABD^ACBDB. AABC^AADCC. AAOB^ACOBD. AAOD^ACOD8.将一匸方形纸片按图中（1）、（2）的方式依次对折后，再沿（3）中的虚线裁剪，最后将（4）中的纸片打开铺平，所得图案应该是下面图案中的（）二、填空题（每题3分，共24分）ZB=100°, ZBAC=30°,那么ZAED=如图，Z1 = Z2,要使△ABE9ZXACE,还需添加一个条件是的一个条件即可）.12.如图，AABC屮，AD丄BC于D,要使△ABD/AACD,若根据“HL〃判定，还需加条件 .度.（填上你认为适当10.14.如图，AD=AE, BE=CD, Z1 = Z2=1OO°, ZBAE=60°,那么ZCAE= ____________15.女（1 图，ZA=ZE, AC±BE, AB=EF, BE二10, CF=4,贝lj AC= _______=60°, AABC与B' C1关于直线1对称，则ZB二三、解答题（共72分）17.如图所示，画出AABC关于直线MN的轴对称图形.18.如图，已知：点B、F、C、E 在一•条直线上，FB=CE, AC=DF. ZA=ZD=90°；求证:AB//DE.20. 如图，己矢U AC 丄AB, DB 丄AB, AC=BE, AE 二BD,试猜想线段CE 与DE 的大小与位迸关系，并证明你的结论.21. 如图，在厶ABC ^IIAABD 中，AC 与 BD 相交于点 E, AD 二BC, ZDAB=ZCBA,求 II ： AOBD.且 AC=DB, AB=DC ・求证：ZA=ZD.A22.如图，AC 和BD 相交于点O, OA=OC, OB=OD.求证：DC//AB.23.如图，已知点A、F、E、C 在同一直线上，AB〃CD, ZABE=ZCDF, AF=CE.（1）从图中任找两组全等三角形；（2）从（1）中任选一组进行证明.24.如图①A、E、F、C在一•条直线上，AE=CF,过E、F分别作DE丄AC, B F丄AC,若AB二CD.（1）图①中冇 ____ 对全等三角形，并把它们写出来______（2）求证：BD与EF互相平分于G；（3）若将AABF的边AF沿GA方向移动变为图②时，其余条件不变，第（2）题中的结论是否成立，如果成立，请予证明.图①。

2015南京清江花苑严老师等差与等比数列求和习题02

1南京清江花苑严老师等差与等比数列求和习题021.设{a n }是首项为1的正项数列，且()011221=+-+++n n n n a a na a n (n =1,2,3,…)，则n a =________. 2.数列{a n }中，a 1 =1，当n ≥2时，n 2= a 1 a 2 a n 恒成立，则=n a .3.数列{a n }中,a 1+2a 2+3a 3+…+na n =n (n +1)(n +2) ,则=n a .4.已知数列{a n }的前n 项和S n =1－5+9－13+…+(－1)n +1(4n －3)，则S 15+S 22－S 31= .5.已知数列{a n }中，11++=n n a n ，则S n= . 6.=++++++++)1(2113211211n .7.设函数f (x )满足2f (n +1)=2f (n )+n ，f (1)=2则f (20)= .8.已知等比数列的前n 项和为S n ，若S 3 :S 2=3:2，则公比q = .9.在等差数列{a n }中，若S 4=21,a n －3+a n －2+a n －1+a n =67, S n =286,则n = .10.已知数列{a n }，（1）若11=a ，)2(121≥-+=-n n a a n n ，则=n a ；（2）若11=a ，n n a n na 11+=+，则=n a ；（3）若11=a ，)2(121≥+=-n a a n n ，则=n a ；（4）若前n 项和S n =3n 2+n +1，则=n a ；（5）若211=a ，n n a n S 2=，则=n a ；11.设a 1=2,a 2=4，b n =a n +1－a n ，b n +1=2b n +2，（1）求证：数列{b n +2}是公比为2的等比数列；（2）求数列{a n }的通项公式.12．已知数列{a n }的前n 项为S n ，且满足21),2(0211=≥=⋅+-a n S S a n n n（1）求证⎭⎬⎫⎩⎨⎧n S 1是等差数列；（2）求n a .2南京清江花苑严老师 13.设数列{a n }满足211233333n n n a a a a -++++=…，a ∈*N ．（1）求数列{a n }的通项；（2）设a n b n =n ，求数列{b n }的前n 项和S n ．14.正数数列{a n }的前n 项和为n S ，且12+=n n a S ，求：（1）数列{a n }的通项公式；（2）设11+=n n na ab ，数列{b n }的前n 项的和为B n ，求证：2B n <115.数列{a n }中，a 1=8,a 4=2,，满足a n +2－2a n +1+a n =0,n=1,2, …（1）数列{a n }的通项公式；（2）设n n n n b b b S N n a n b ++=∈-=21*),()12(1，是否存在最大的整数m ，使得任意的n 均有32m S n >总成立，若存在求出m ，若不存在说明理由.。

2015南京清江花苑严老师高一数学期末复习1-1

1-1题目1．不等式01x x <-的解集为 ▲ . 2．直线l：30x +=的倾斜角为 ▲ .3．在相距2千米的,A B 两点处测量目标C ，若75CAB ∠=，60CBA ∠=，则,A C 两点之间的距离是 ▲ 千米（结果保留根号）.5．等比数列{}n a 的公比为正数，已知23954a a a ⋅=，22a =，则1a = ▲ .9．若数列{}n a 满足：112a =，112n n n a a n++=（*n N ∈），则{}n a 的通项公式为n a = ▲ . 11．已知函数()2x f x =，()()8f a f b ⋅=，若0a >且0b >，则14a b +的最小值为 ▲ . 12．等比数列{}n a 的公比12q =，前5项的和为3164．令12log n n b a =，数列11{}n n b b +的前n 项和为n T ，若n T c <对*n N ∈恒成立，则实数c 的最小值为 ▲ .13．ABC ∆中，角A ，B ，C 所对的边为,,a b c ．若2b ac =，则sin cos tan sin cos tan A A C B B C ++的取值范围是 ▲ .16．在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，且满足2cos cos cos b A c A a C =+．（1）求角A 的大小；（2）若b c +=，ABC ∆的面积S =，求a 的长．17．数列{}n a 的前n 项和为n S ，满足22n S n n =+．等比数列{}n b 满足：143,81b b ==．（1）求证：数列{}n a 为等差数列；（2）若312123n n na a a a Tb b b b =++++，求n T ． 18．如图，ABCD 是长方形海域，其中10AB =海里，AD =域失事，两艘海事搜救船在A 处同时出发，沿直线AP 、AQ 向前联合搜索，且4PAQ π∠=（其中P 、Q 分别在边BC 、CD 上），搜索区域为平面四边形APCQ 围成的海平面．设PAB θ∠=，搜索区域的面积为S ．（1）试建立S 与tan θ的关系式，并指出tan θ的取值范围；（2）求S 的最大值，并指出此时θ的值．20．（1）公差大于0的等差数列{}n a 的前n 项和为n S ，{}n a 的前三项分别加上1，1，3后顺次成为某个等比数列的连续三项，525S =．①求数列{}n a 的通项公式；②令(0)n Sn b t t =>，若对一切*n N ∈，都有2122n n n b b b ++>，求t 的取值范围；（2）是否存在各项都是正整数的无穷数列{}n c ，使2122n n n c c c ++>对一切*n N ∈都成立，若存在，请写出数列{}n c 的一个通项公式；若不存在，请说明理由．Q P D C BA。

2014-2015南京清江花苑严老师高三数学上学期期末复习1502

高三数学上学期期末复习1502第Ⅰ卷（必做题共160分）一、填空题（本题共14小题，每小题5分，共70分）1、复数(1)(2)i i ++的模等于 .2、已知集合U ＝{2,3,6,8}，A ＝{2,3}，B ＝{2,6,8}，则(∁U A )∩B ＝．3、命题“对∀R x ∈，都有02≥x ”的否定为4、如图所示的算法中，输出的结果是．5、在所有的两位数中，任取一个数，则这个数能被2或整除的概率是6、若双曲线22221x y a b -=（0,0a b >>）与直线y =无交点，则离心率e 的取值范围是________．7、设y kx z +=,其中实数y x ,满足⎪⎩⎪⎨⎧≤--≥+-≥-+04204202y x y x y x ,若z 的最大值为12,则实数=k ________.8、要使46sin 4m mαα-=-有意义，则实数m 的范围是________． 9、若正三棱锥的底面边长为2，侧棱长为1，则此三棱锥的体积为 .10、已知各项均为正数的等比数列{}n a 中，4a 与14a 的等比中项为，则7112a a +的最小值为 .11、在平面直角坐标中，设圆M 的半径为1，圆心在直线10x y --=上,若圆M 上存在点N ，使12NO NA =，其中(0,3)A ，则圆心M 横坐标的取值范围__ ____． 12、已知ABC ∆是边长为4的正三角形，D 、P 是ABC ∆内部两点，且满足11(),48AD AB AC AP AD BC =+=+uuu r uu u r uuu r uu u r uuu r uu u r，则APD ∆的面积为13、若R b a ∈,，且9422≤+≤b a ，则22b ab a +-的范围是____________.( 第4题 )14、设12,x x 是函数)0()(223>-+=a x a bx ax x f 的两个极值点，且22||||21=+x x 则b 的最大值为_________二、解答题（本题共6题，共90分，其中15、16、17每小题14分，18、19、20每小题16分）15、在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .已知cos A －2cos C cos B ＝2c －ab .(1)求sin Csin A 的值；(2)若cos B ＝14，△ABC 的周长为5，求b 的长．16、在三棱柱111ABC A B C -中，1A A B C⊥，160A AC ︒∠=，11AA AC BC ===，1A B =（1）求证：平面1A BC ⊥平面11ACC A ；（2）如果D 为AB 的中点，求证：BC ∥平面1ACD .（第16题图）17、某商场为促销要准备一些正三棱锥形状的装饰品，用半径为10cm 的圆形包装纸包装．要求如下：正三棱锥的底面中心与包装纸的圆心重合，包装纸不能裁剪，沿底边向上翻折，其边缘恰好达到三棱锥的顶点，如图所示．设正三棱锥的底面边长为xcm ，体积为3Vcm ．在所有能用这种包装纸包装的正三棱锥装饰品中，V 的最大值是多少？并求此时x 的值．18、已知椭圆的中点为坐标原点O ，椭圆短轴长为2，动点(2,)(0)M t t >在椭圆的准线上． (1)求椭圆的标准方程．(2)求以OM 为直径且被直线3450x y --=截得的弦长为2的圆的方程；(3)设点F 是椭圆的右焦点，过点F 作OM 的垂线FH ，且与以OM 为直径的圆交于点N ，求证：线段ON 的长为定值，并求出这个定值．19、设各项均为正数的数列{}n a 的前n 项和为ns，已知11a =，且11()(1)n n n n S a S a λ+++=+对一切*n ∈N 都成立．（1）若1λ=，求数列{}n a 的通项公式；（2）求λ的值，使数列{}n a 是等差数列．20、已知()2ln f x x x =，2()3g x x ax =-+-.(1)求函数 ()f x 的最小值；(2)若存在 (0,)x ∈+∞，使()()f x g x ≤成立，求实数a 的取值范围； (3)证明对一切(0,)x ∈+∞，都有2()2()x x f x e e>-成立．21． B ．（矩阵与变换选做题）设矩阵A a b c d ⎡⎤=⎢⎥⎣⎦，矩阵A 属于特征值11λ=-的一个特征向量为111 ⎡⎤=⎢⎥-⎣⎦α，属于特征值 24λ=的一个特征向量为232⎡⎤=⎢⎥⎣⎦α，求ad －bc 的值．C 极坐标与参数方程：已知点P是曲线2cos ,:(,x C y θθπθπθ=⎧⎪≤≤⎨=⎪⎩为参数，2)上一点，O 为原点．若直线OP 的倾斜角为3π，求点P 的直角坐标．22．（本小题满分10分）一批产品需要进行质量检验，质检部门规定的检验方案是：先从这批产品中任取3件作检验，若3件产品都是合格品，则通过检验；若有2件产品是合格品，则再从这批产品中任取1件作检验，这1件产品是合格品才能通过检验；若少于2件合格品，则不能通过检验，也不再抽检. 假设这批产品的合格率为80%，且各件产品是否为合格品相互独立.(1)求这批产品通过检验的概率；(2)已知每件产品检验费为125元，并且所抽取的产品都要检验，记这批产品的检验费为ζ元，求ζ的概率分布及数学期望.23．（本小题满分10分）如图，在直三棱柱111ABC A B C -中，已知1CA CB ==，12AA =，o 90BCA ∠=．（1）求异面直线1BA 与1CB 夹角的余弦值；（2）求二面角1B AB C --平面角的余弦值．（第23题图）ABC A 1B 1C 1。

南京清江花苑严老师中考数学精品模拟试卷1604.doc

中考数学精品模拟试卷1604一、选择题（共8小题，每小题3分，满分24分）1.4的算术平方根是（）A.±V2B. V2 c. ±2 D. 22.下列运算正确的（）A. a3 - a2=aB. a2*a3=a6C. （a3）2=a6D. （3a）3=9a33.下列说法疋确的是（）A.两名同学5次成绩的平均分相同，则方差较大的同学成绩更稳定B.某班选出两名同学参加校演讲比赛，结果一定是一名男生和一名女生C.学校气象小组预报明天下雨的概率为0.8,则明天下雨的可能性较人D.为了解我是学校“阳光体育〃活动开展情况，必须采用普查的方式4.与Jg最接近的整数是（）A. 4B. 3C. 2D. 15.如图，已知AB〃CD, AD和BC相交于点O, ZA=50°, ZAOB=105°,则ZC等于（）H ------- 知A. 20°B. 25°C. 35°D. 45°6.下列函数中，当x>0时，y随x增大而增大的是（）1 9A. y= - xB. y=— C・ y=3 - 2x D. y=x~x7.如图，AB是半圆的直径，点D是丘的屮点，ZABC=50°,贝IJZDAB等于（）A. 55°B. 60°C. 65°D. 70°8.如图，菱形OABC的顶点C的处标为（3, 4）•顶点A在x轴的正半轴上，反比例函数y」（x二、填空题（共10小题，每小题3分，满分30分）99. 反比例函数尸M 中自变量x 的取值范围 ____________ . x10. 分解因式：2x 2 - 2= ____________ .11・一纽•数据1, 3, 2, 5, 2, a 的众数是a,这组数据的屮位数是 __________________ .12. "五一〃期间，小明与小亮两家准备从古黄河入海口、马荡风景区、金沙沪旅游度假区中选择一景点游玩，小明与小亮通过抽签方式确定景点，则两家抽到同一景点的概率是 ______________ . 13. 己知圆心角为150。

2015南京清江花苑严老师高三数学午时30分钟训练29

高三数学午时30分钟训练29班级姓名1．设数列{}n a 的前n 项和为n S （N ∈n ）. 关于数列{}n a 有下列三个命题：（1）若{}n a 既是等差数列又是等比数列，则)(1N ∈=+n a a n n ；（2）若()R ∈+=b a n b n a S n 、2，则{}n a 是等差数列；（3）若()nn S 11--=，则{}n a 是等比数列. 这些命题中，真命题的序号是 .2．在数列{}n a 中，已知前n 项的和2100781,n S n n a =-+=则 .3．数列{}n a 是项数为偶数的等差数列，它的奇数项之和为24，偶数项之和为30，若它的末项比首项大10.5，则数列的项数是 .4．三数成等比数列，若将第三数减去32，则成等差数列；若将该等差数列中项减去4，又成等比数列，则原三数为 .5．设等差数列112{}0,9,n k k a d a d a a a =的公差不为若是与的等比中项，则k 等于．6．已知等差数列{}n a 的前n 项的和为n S ，若1200OB a OA a OC =+,且A ，B ，C 三点共线（该直线不过原点O ），则200S = .7．已知数列{}n a 、{}n b 都是公差为1的等差数列，其首项分别为11a b 、，且115a b +=，11,.()n n b a b N c a n N **∈=∈设,则数列{}n c 的前10项和等于 .8．等差数列{}n a 的首项为a ，公差为1，n n n a a b +=1，若对+∈∀N n 都有8b b n ≥成立，则实数a 的取值范围是9．已知无穷数列0121555510,10,10,10,,n -探究：（1）这个数列是等比数列吗？（2）这个数列的任意两项的积还在这个数列中吗？1. （1）、（2）、（3）①不妨设数列}{n a 的前三项为d a a d a +-,,，则其又成等比数列，故222d a a -=，∴0=d ，即1+=n n a a ；②由n S 的公式，可求出b a n a n +-=)12(，故}{n a 是等差数列；③由n S 可求由1)1(2--=n n a ，故数列}{n a 是等比数列. 故选D .【总结点评】本题主要考查等差、等比数列的概念，n S 与n a 的关系，思维的灵活性.2.；3.8；4.；226338,,999； 5.4；6.100；7.85；8.(8,7)--；9.（1）是，（2）在数列当中.。

南京清江花苑严老师高三上学期期初测试数学(理)试题

南京清江花苑严老师高三上学期期初测试数学(理)试题高三上学期期初测试数学（理）试题数学（理科）试题一、填空题（本大题共14小题，每小题5分，共70分，请将答案填写在答题卷相应位置）01，2}，则A B 1．已知集合A {__ 0}，B { 1，，2．命题：“ x R，3 0”的否定是．3．用反证法证明命题“a,b N，ab可被5整除，那么a,b中至少有一个能被5整除”时，应反设为4．“x4”是“tan 1”的（从“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中，选出适当的一种填空）n4 n25．用数学归纳法证明：1 2 3 n ，则当n k 1时，左端在n k时的左端加上了22．x2x 46．方程C11的解为C11．7．四位外宾参观某校，需配备两名安保人员．六人依次进入校门，为安全起见，首尾一定是两名安保人员，则六人的入门顺序共有▲ 种不同的安排方案（用数字作答）．8．已知复数z满足z 3 4i 2，则z的最大值为．9．设数列{an}满足a1 3，an 1 an2 2nan 2，n 1,2,3, ，通过计算a2，a3，a4，试归纳出这个数列的通项公式an ．10．从4红球和2名白球中任选3个球，设随机变量表示所选3个球中白球的个数，则“所选3个球中白球个数1”的概率为▲ ．11．从0，1，2，3，4，5这六个数字中任取两个奇数和两个偶数，组成没有重复数字的四位数的个数为（用数字作答）22212．命题p：x 2x 3 0，命题q：x ax 2a 0，若命题p是命题q的必要不充分条件，则实数a的取值范围为▲ ．13．给出下面类比推理命题（其中R为实数集，C为复数集）：①“若a,b R,则a b 0 a b”类比推出“若a,b C,则a b 0 a b”；②“若a,b R,则ab 0 a 0或b 0”类比推出“若a,b C,则ab 0 a 0或b 0”；③“若a,b R,则a b 0 a b” 类比推出“若a,b C,则a b 0 a b”；④“若a,b R,则a b 0”类比推出“若a,b C,则a b 0” 所有命题中类比结论正确的序号是▲ ．2222m14．从装有n 1个球（其中n个白球，1个黑球）的口袋中取出m个球0 m n,m,n N ,共有Cn 1种m0m取法，这Cn 1种取法可分成两类：一类是取出的m个球中，没有黑球，有C1 Cn种取法，另一类是取m1m 1m1m 1出的m个球中有一个是黑球，有C1种取法，由此可得等式：C10 Cn+C1=Cn Cn Cn 1．则根据上m1m 1m 2m k0述思想方法，当1 k m n,k,m,n N时，化简CkCn Ck Cn Ck2 Cn Ckk Cn．（用符号表示）二、解答题：15. （本小题满分14分）在极坐标系中，曲线C1：ρ2cos θ＋sin θ)＝1与曲线C2：ρ＝a(a0)的一个交点在极轴上，求a的值．11 12B 16. （本小题满分14分）已知矩阵A ，23 . 23（Ⅰ）求矩阵A的逆矩阵A-1；（Ⅱ）求直线x+y-1=0在矩阵A-1B对应的线性变换作用下所得曲线的方程.17. （本小题满分15分）已知复数z1 3 m i, z2 1 2 i, m R （1）若z1是纯虚数，求实数m的值；z2 i（2）若|z1 z2| |z1 z2|，求z1 z218. （本小题满分15分）设命题p：函数f(x) lg(x2 ax 1)的定义域为R；命题q：函数f(x) x2 2ax 1在( , 1]上单调递减．（1）若命题“p q”为真，“p q”为假，求实数a的取值范围；（2）若关于x的不等式(x m)(x m 5) 0(m R)的解集为M；命题p为真命题时，a的取值集合为N．当M N M时，求实数m的取值范围．19. （本小题满分16分）设(1 （1）求(1 （2）求(1 （3）求(11mx) a0 a1x a2x2 a3x3 .... amxm，若a0,a1,a2成等差数列．21mx)展开式的中间项；21mx)展开式中所有含x奇次幂的系数和；21m 6x)展开式中系数最大项. 220. （本小题满分16分）设数列{an}的前n项和为Sn，且方程x2－anx－an＝0有一根为Sn－1，n＝1,2,3，。

南京市鼓楼区清江花苑严老师高二12月月测数学试题1402

高二12月月测数学试题1402一．填空题1．在△ABC 中，a ＝3，b ＝7，c ＝2，那么B ＝_____2．已知数列{}n a 的前n 项和为kn n S n +=25，且182=a ，则k = ．3．关于x 的不等式x 2-ax +2a <0的解集为A ,若集合A 中恰有两个整数,则实数a 的取值范围是_________.4．边长为5,7,8的三角形的最大角与最小角的和是________ 5．椭圆22137x y +=的准线方程是． 6．数列1，211+，3211++，，n++++ 3211的前n 项和为______． 7．设等差数列}{n a 中，31-=a ，且从第5项开始是正数，则公差的范围是． 8．若直线mx ny +-=30与圆x y 223+=没有公共点，则以（m ，n ）为点P 的坐标，过点P 的一条直线与椭圆22173x y +=的公共点有_________个。

9．已知双曲线2221(0)x y a a-=>的一条准线与抛物线y 2=－6x 的准线重合，则该双曲线的离心率是．10. 已知P:|x-a|<4;q:(x-2)(3-x)>0,若⌝p 是⌝q 的充分不必要条件,则a 的取值范围为________________.【答案】16a -≤≤11.不等式组⎪⎪⎩⎪⎪⎨⎧≤+≤+≥≥62363200y x y x y x 的所有点中，使目标函数y x z -=取得最大值点的坐标为 . 12．已知n S 是数列{}n a 的前n 项和，且有21n S n =+，则数列{}n a 的通项n a = ．13. 已知抛物线)0(22>=p px y ，过定点（p,0）作两条互相垂直的直线121,,l l l 与抛物线交于P 、Q 两点，l 2与抛物线交于M 、N 两点，l 1斜率为k.某同学已正确求得弦PQ 的中点坐标为（k p p k p ,2+），请你写出弦MN 的中点坐标： .14.在平面直角坐标系xOy 中，抛物线y 2＝2x 的焦点为F . 设M 是抛物线上的动点，则MO MF 的最大值为 .二．解答题15．在△ABC 中，角A ，B ，C 所对的边分别为a,b,c,设S 为△ABC 的面积，满足222)4S a b c =+-。