实验2 分治法算法设计
二分搜索算法实验报告

二分搜索算法实验报告篇一:实验报告2--二分搜索技术注意:红色的部分需要用自己的代码或内容进行替换。
湖南涉外经济学院实验报告实验课程:算法设计与分析实验项目:二分搜索技术学院专业实验地点分组组号实验时间 XX年 3 月 10 日星期一第 12节指导老师【实验目的和要求】1. 理解分治法的原理和设计思想;2.要求实现二分搜索算法;3.要求交互输入一组关键字序列,输入需要查找的关键字;4. 要求显示结果。
【系统环境】操作系统:Windows XP 操作系统开发工具:VC++6.0英文企业版开发语言:C,C++【实验原理】1、问题描述给定已排好序的n个元素a[0…n-1],现要在这n个元素中找出一特定元素x。
2、实验原理二分搜索方法充分利用了元素间的次序关系(但也局限于此),采用分治策略,将n个元素分成个数大致相同的两半,取a[n/2]与x进行比较。
如果x=a[n/2],则找到x,算法终止。
如果xa[n/2],则只要在数组a的右半部继续搜索x。
【实验任务与步骤】1、实验步骤(可以根据自己的程序修改)(1) 实现顺序搜索。
(2) 实现二分搜索算法的递归算法。
(3) 实现二分搜索算法的非递归算法。
(4) 编写主函数,调用所写的三个算法进行测试,并进行输出。
2、源程序代码// 此处为解决问题的完整源程序,要求带注释,代码必须符合书写规范。
(1) 顺序搜索(2) 递归的二分搜索(3) 非递归的二分搜索(原文来自:小草范文网:二分搜索算法实验报告)……【实验结论(包括实验数据处理、问题与解决办法、心得体会、意见与建议等)】// 此处为程序运行的结果,要求有程序运行输入输出实例,要求至少有两组实验结果。
// 必须写心得体会、意见与建议等,或者遇到的问题、难题等。
……篇二:查找排序实验报告实验十:查找、排序计算机学院 12级2班 12110XX 李龙实验目的:1.掌握折半查找算法的思想。
2.实现折半查找的算法。
3.掌握常见的排序算法(插入排序、交换排序、选择排序等)的思想、特点及其适用条件。
分治算法的实验报告

一、实验背景分治算法是一种常用的算法设计方法,其基本思想是将一个复杂问题分解成若干个相互独立的小问题,然后将小问题递归求解,最终将子问题的解合并为原问题的解。
分治算法具有高效性、可扩展性和易于实现等优点,被广泛应用于各个领域。
本实验旨在通过实现分治算法解决实际问题,掌握分治算法的设计思想,并分析其时间复杂度。
二、实验目的1. 理解分治算法的基本思想;2. 掌握分治算法的递归实现方法;3. 分析分治算法的时间复杂度;4. 应用分治算法解决实际问题。
三、实验内容本实验选择两个分治算法:快速排序和合并排序。
1. 快速排序快速排序是一种高效的排序算法,其基本思想是将待排序序列分为两个子序列,其中一个子序列的所有元素均小于另一个子序列的所有元素,然后递归地对两个子序列进行快速排序。
(1)算法描述:① 选择一个基准值(pivot),通常取序列的第一个元素;② 将序列分为两个子序列,一个子序列包含所有小于基准值的元素,另一个子序列包含所有大于基准值的元素;③ 递归地对两个子序列进行快速排序。
(2)代码实现:```cvoid quickSort(int arr[], int left, int right) {if (left < right) {int pivot = arr[left];int i = left;int j = right;while (i < j) {while (i < j && arr[j] >= pivot) {j--;}arr[i] = arr[j];while (i < j && arr[i] <= pivot) {i++;}arr[j] = arr[i];}arr[i] = pivot;quickSort(arr, left, i - 1);quickSort(arr, i + 1, right);}}```2. 合并排序合并排序是一种稳定的排序算法,其基本思想是将待排序序列分为两个子序列,分别对两个子序列进行排序,然后将排序后的子序列合并为一个有序序列。
分治算法实验报告
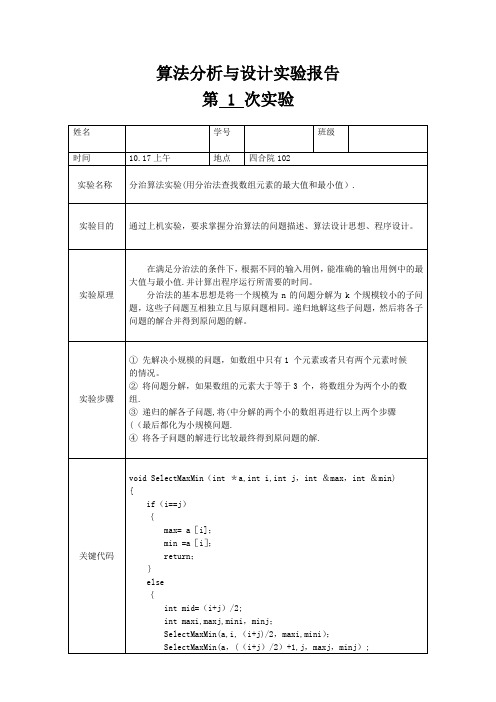
算法分析与设计实验报告第 1 次实验if(maxi>maxj)max=maxi;elsemax=maxj;if(mini<minj)min=mini;elsemin=minj;return;}}srand((unsigned int)time(NULL));cout <〈”随机产生的数据(0—100):”;for(int i=0; i〈m; i++)a[i] = rand()%100;测试结果附录:完整代码SelectMaxMin.cpp:#include <iostream>#include <ctime>#include 〈cstdio>#include <iomanip>#include 〈cstdlib〉using namespace std;void SelectMaxMin(int *a,int i,int j,int &max,int &min) {if(i==j){max= a[i];min =a[i];return;}else{int mid=(i+j)/2;int maxi,maxj,mini,minj;SelectMaxMin(a,i,(i+j)/2,maxi,mini);SelectMaxMin(a,((i+j)/2)+1,j,maxj,minj);if(maxi〉maxj)max=maxi;elsemax=maxj;if(mini<minj)min=mini;elsemin=minj;return;}}int main(){clock_t start,end,over;start=clock();end=clock();over=end—start;start=clock();//freopen("in。
txt",”r",stdin);//freopen(”out。
txt”,”w",stdout);int m;cout 〈<"Please input the number : ”;cin>〉 m;int a[m];srand((unsigned int)time(NULL));cout 〈〈 "随机产生的数据(0-100):";for(int i=0; i〈m; i++)a[i] = rand()%100;for(int i=0; i〈m; i++)cout <〈 a[i] 〈< " ";cout 〈< endl;int max,min;SelectMaxMin(a,0,m-1,max,min);cout 〈< "max = " 〈〈 max 〈〈 endl;cout <〈”min = " <〈 min 〈〈 endl;end=clock();printf(”The time is %6.3f”,(double)(end-start—over)/CLK_TCK); }。
《算法设计与分析》实验报告实验一...

《算法设计与分析》实验报告实验一递归与分治策略应用基础学号:**************姓名:*************班级:*************日期:2014-2015学年第1学期第九周一、实验目的1、理解递归的概念和分治法的基本思想2、了解适用递归与分治策略的问题类型,并能设计相应的分治策略算法3、掌握递归与分治算法时间空间复杂度分析,以及问题复杂性分析方法二、实验内容任务:以下题目要求应用递归与分治策略设计解决方案,本次实验成绩按百分制计,完成各小题的得分如下,每小题要求算法描述准确且程序运行正确。
1、求n个元素的全排。
(30分)2、解决一个2k*2k的特殊棋牌上的L型骨牌覆盖问题。
(30分)3、设有n=2k个运动员要进行网球循环赛。
设计一个满足要求的比赛日程表。
(40分)提交结果:算法设计分析思路、源代码及其分析说明和测试运行报告。
三、设计分析四、算法描述及程序五、测试与分析六、实验总结与体会#include "iostream"using namespace std;#define N 100void Perm(int* list, int k, int m){if (k == m){for (int i=0; i<m; i++)cout << list[i] << " ";cout << endl;return;}else{for (int i=m; i<k; i++){swap(list[m], list[i]);Perm(list, k, m+1);swap(list[m], list[i]);}}}void swap(int a,int b){int temp;temp=a;a=b;b=temp;}int main(){int i,n;int a[N];cout<<"请输入排列数据总个数:";cin>>n;cout<<"请输入数据:";for(i=0;i<n;i++){cin>>a[i];}cout<<"该数据的全排列:"<<endl;Perm(a,n,0);return 0;}《算法设计与分析》实验报告实验二递归与分治策略应用提高学号:**************姓名:*************班级:*************日期:2014-2015学年第1学期一、实验目的1、深入理解递归的概念和分治法的基本思想2、正确使用递归与分治策略设计相应的问题的算法3、掌握递归与分治算法时间空间复杂度分析,以及问题复杂性分析方法二、实验内容任务:从以下题目中任选一题完成,要求应用递归与分治策略设计解决方案。
分治算法设计(求第K个最小数)

福建工程学院计算机与信息科学系实验报告2010 – 2011 学年第一学期任课老师:实验题目1.设计程序利用分治策略求n个数的最大值和最小值。
2.利用分治策略,在n个不同元素中找出第k个最小元素。
实验时间实验开始日期:报告提交日期:实验目的、要求一、算法设计技术当我们求解某些问题时,由于这些问题要处理的数据相当多,或求解过程相当复杂,使得直接求解法在时间上相当长,或者根本无法直接求出。
对于这类问题,我们往往先把它分解成几个子问题,找到求出这几个子问题的解法后,再找到合适的方法,把它们组合成求整个问题的解法。
如果这些子问题还较大,难以解决,可以再把它们分成几个更小的子问题,以此类推,直至可以直接求出解为止。
这就是分治策略的基本思想。
下面通过实例加以说明。
【例】在n个元素中找出最大元素和最小元素。
我们可以把这n个元素放在一个数组中,用直接比较法求出。
算法如下:void maxmin1(int A[],int n,int *max,int *min){ int i;*min=*max=A[0];for(i=2;i < n;i++){ if(A[i] > *max) *max= A[i];if(A[i] < *min) *min= A[i];}}上面这个算法需比较2(n-1)次。
能否找到更好的算法呢?我们用分治策略来讨论。
把n个元素分成两组:A1={A[1],...,A[int(n/2)]}和A2={A[int(N/2)+1],...,A[N]}分别求这两组的最大值和最小值,然后分别将这两组的最大值和最小值相比较,求出全部元素的最大值和最小值。
如果A1和A2中的元素多于两个,则再用上述方法各分为两个子集。
直至子集中元素至多两个元素为止。
例如有下面一组元素:-13,13,9,-5,7,23,0,15。
用分治策略比较的过程如下:图中每个方框中,左边是最小值,右边是最大值。
从图中看出,用这种方法一共比较了10次,比直接比较法的14次减少4次,即约减少了1/3。
分治法实验心得

分治法实验心得分治法实验心得分治法是一种常见的算法设计策略,它将原问题划分成若干个规模较小但结构与原问题相似的子问题,然后递归地求解这些子问题,最终将子问题的解合并得到原问题的解。
在本次实验中,我们实现了两个基于分治法的算法:归并排序和快速排序,并对它们进行了性能测试和比较。
一、归并排序1. 原理归并排序是一种典型的分治算法。
它将待排序数组不断地二分为两个子数组,直到每个子数组只剩下一个元素。
然后将相邻的两个子数组合并成一个有序数组,再将相邻的两个有序数组合并成一个更大的有序数组,直到最终合并成整个待排序数组。
2. 实现我们采用了自顶向下的递归方式实现了归并排序。
具体来说,我们定义了一个merge函数用于合并两个有序子数组,并定义了一个sort 函数用于递归地对左右两个子数组进行排序和合并。
3. 性能测试与比较我们使用Python内置的time模块对不同规模(10^2 ~ 10^6)的随机整数列表进行了性能测试,并绘制出了运行时间随数组规模增大的变化曲线。
结果表明,归并排序的时间复杂度为O(nlogn),与理论分析相符。
二、快速排序1. 原理快速排序也是一种分治算法。
它选择一个基准元素,将数组中小于等于它的元素放在其左侧,大于它的元素放在其右侧。
然后递归地对左右两个子数组进行同样的操作,直到每个子数组只剩下一个元素。
2. 实现我们实现了两个版本的快速排序:递归版本和非递归版本。
其中,递归版本采用了经典的Lomuto分区方案,而非递归版本则采用了更高效的Hoare分区方案。
3. 性能测试与比较我们同样使用Python内置的time模块对不同规模(10^2 ~ 10^6)的随机整数列表进行了性能测试,并绘制出了运行时间随数组规模增大的变化曲线。
结果表明,快速排序具有很好的平均时间复杂度(O(nlogn)),但最坏情况下时间复杂度会退化到O(n^2)。
三、总结与思考通过本次实验,我们深入理解了分治算法设计策略,并学会了如何实现归并排序和快速排序。
算法设计与分析:递归与分治法-实验报告(总8页)

算法设计与分析:递归与分治法-实验报告(总8页)实验目的:掌握递归与分治法的基本思想和应用,学会设计和实现递归算法和分治算法,能够分析和评价算法的时间复杂度和空间复杂度。
实验内容:1.递归算法的设计与实现3.算法的时间复杂度和空间复杂度分析实验步骤:1)递归定义:一个函数或过程,在其定义或实现中,直接或间接地调用自身的方法,被成为递归。
递归算法是一种控制结构,它包含了解决问题的基础情境,也包含了递归处理的情境。
2)递归特点:递归算法具有以下特点:①依赖于递归问题的部分解被划分为若干较小的部分。
②问题的规模可以通过递推式递减,最终递归终止。
③当问题的规模足够小时,可以直接求解。
3)递归实现步骤:①确定函数的定义②确定递归终止条件③确定递归调用的过程4)经典实例:斐波那契数列递推式:f(n) = f(n-1) + f(n-2)int fib(int n) {if (n <= 0)return 0;else}5)优化递归算法:避免重复计算例如,上述斐波那契数列的递归算法会重复计算一些中间结果,影响效率。
可以使用动态规划技术,将算法改为非递归形式。
int f1 = 0, f2 = 1;for (int i = 2; i <= n; i++) {f1 = f2;使用循环避免递归,重复计算可以大大减少,提高效率。
1)分治算法的定义:将原问题分解成若干个规模较小且类似的子问题,递归求解子问题,然后合并各子问题得到原问题的解。
2)分治算法流程:②将问题分解成若干个规模较小的子问题。
③递归地解决各子问题。
④将各子问题的解合并成原问题的解。
3)分治算法实例:归并排序归并排序是一种基于分治思想的经典排序算法。
排序流程:②分别对各子数组递归进行归并排序。
③将已经排序好的各子数组合并成最终的排序结果。
实现源代码:void mergeSort(int* arr, int left, int right) {if (left >= right)while (i <= mid && j <= right)temp[k++] = arr[i] < arr[j] ? arr[i++] : arr[j++];temp[k++] = arr[i++];1) 时间复杂度的概念:指完成算法所需的计算次数或操作次数。
算法设计与分析实验报告

实验一找最大和最小元素与归并分类算法实现(用分治法)一、实验目的1.掌握能用分治法求解的问题应满足的条件;2.加深对分治法算法设计方法的理解与应用;3.锻炼学生对程序跟踪调试能力;4.通过本次实验的练习培养学生应用所学知识解决实际问题的能力。
二、实验内容1、找最大和最小元素输入n 个数,找出最大和最小数的问题。
2、归并分类将一个含有n个元素的集合,按非降的次序分类(排序)。
三、实验要求(1)用分治法求解问题(2)上机实现所设计的算法;四、实验过程设计(算法设计过程)1、找最大和最小元素采用分治法,将数组不断划分,进行递归。
递归结束的条件为划分到最后若为一个元素则max和min都是这个元素,若为两个取大值赋给max,小值给min。
否则就继续进行划分,找到两个子问题的最大和最小值后,比较这两个最大值和最小值找到解。
2、归并分类使用分治的策略来将一个待排序的数组分成两个子数组,然后递归地对子数组进行排序,最后将排序好的子数组合并成一个有序的数组。
在合并过程中,比较两个子数组的首个元素,将较小的元素放入辅助数组,并指针向后移动,直到将所有元素都合并到辅助数组中。
五、源代码1、找最大和最小元素#include<iostream>using namespace std;void MAXMIN(int num[], int left, int right, int& fmax, int& fmin); int main() {int n;int left=0, right;int fmax, fmin;int num[100];cout<<"请输入数字个数:";cin >> n;right = n-1;cout << "输入数字:";for (int i = 0; i < n; i++) {cin >> num[i];}MAXMIN(num, left, right, fmax, fmin);cout << "最大值为:";cout << fmax << endl;cout << "最小值为:";cout << fmin << endl;return 0;}void MAXMIN(int num[], int left, int right, int& fmax, int& fmin) { int mid;int lmax, lmin;int rmax, rmin;if (left == right) {fmax = num[left];fmin = num[left];}else if (right - left == 1) {if (num[right] > num[left]) {fmax = num[right];fmin = num[left];}else {fmax = num[left];fmin = num[right];}}else {mid = left + (right - left) / 2;MAXMIN(num, left, mid, lmax, lmin);MAXMIN(num, mid+1, right, rmax, rmin);fmax = max(lmax, rmax);fmin = min(lmin, rmin);}}2、归并分类#include<iostream>using namespace std;int num[100];int n;void merge(int left, int mid, int right) { int a[100];int i, j,k,m;i = left;j = mid+1;k = left;while (i <= mid && j <= right) {if (num[i] < num[j]) {a[k] = num[i++];}else {a[k] = num[j++];}k++;}if (i <= mid) {for (m = i; m <= mid; m++) {a[k++] = num[i++];}}else {for (m = j; m <= right; m++) {a[k++] = num[j++];}}for (i = left; i <= right; i++) { num[i] = a[i];}}void mergesort(int left, int right) { int mid;if (left < right) {mid = left + (right - left) / 2;mergesort(left, mid);mergesort(mid + 1, right);merge(left, mid, right);}}int main() {int left=0,right;int i;cout << "请输入数字个数:";cin >> n;right = n - 1;cout << "输入数字:";for (i = 0; i < n; i++) {cin >> num[i];}mergesort(left,right);for (i = 0; i < n; i++) {cout<< num[i];}return 0;}六、运行结果和算法复杂度分析1、找最大和最小元素图1-1 找最大和最小元素结果算法复杂度为O(logn)2、归并分类图1-2 归并分类结果算法复杂度为O(nlogn)实验二背包问题和最小生成树算法实现(用贪心法)一、实验目的1.掌握能用贪心法求解的问题应满足的条件;2.加深对贪心法算法设计方法的理解与应用;3.锻炼学生对程序跟踪调试能力;4.通过本次实验的练习培养学生应用所学知识解决实际问题的能力。
常见算法设计实验报告(3篇)

第1篇一、实验目的通过本次实验,掌握常见算法的设计原理、实现方法以及性能分析。
通过实际编程,加深对算法的理解,提高编程能力,并学会运用算法解决实际问题。
二、实验内容本次实验选择了以下常见算法进行设计和实现:1. 排序算法:冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序。
2. 查找算法:顺序查找、二分查找。
3. 图算法:深度优先搜索(DFS)、广度优先搜索(BFS)、最小生成树(Prim算法、Kruskal算法)。
4. 动态规划算法:0-1背包问题。
三、实验原理1. 排序算法:排序算法的主要目的是将一组数据按照一定的顺序排列。
常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序和堆排序等。
2. 查找算法:查找算法用于在数据集中查找特定的元素。
常见的查找算法包括顺序查找和二分查找。
3. 图算法:图算法用于处理图结构的数据。
常见的图算法包括深度优先搜索(DFS)、广度优先搜索(BFS)、最小生成树(Prim算法、Kruskal算法)等。
4. 动态规划算法:动态规划算法是一种将复杂问题分解为子问题,通过求解子问题来求解原问题的算法。
常见的动态规划算法包括0-1背包问题。
四、实验过程1. 排序算法(1)冒泡排序:通过比较相邻元素,如果顺序错误则交换,重复此过程,直到没有需要交换的元素。
(2)选择排序:每次从剩余元素中选取最小(或最大)的元素,放到已排序序列的末尾。
(3)插入排序:将未排序的数据插入到已排序序列中适当的位置。
(4)快速排序:选择一个枢纽元素,将序列分为两部分,使左侧不大于枢纽,右侧不小于枢纽,然后递归地对两部分进行快速排序。
(5)归并排序:将序列分为两半,分别对两半进行归并排序,然后将排序好的两半合并。
(6)堆排序:将序列构建成最大堆,然后重复取出堆顶元素,并调整剩余元素,使剩余元素仍满足最大堆的性质。
2. 查找算法(1)顺序查找:从序列的第一个元素开始,依次比较,直到找到目标元素或遍历完整个序列。
分治算法实验(用分治法查找数组元素的最大值和最小值)

算法分析与设计实验报告第一次实验附录:完整代码(分治法)#include<iostream>#include<time.h>#include<iomanip>using namespace std;//当数组中的元素个数小于3时,处理最大值int compmax(int A[],int start,int end){int max;if(start<end) //有两个元素{if(A[start]<=A[end])max=A[end];elsemax=A[start];}else//有一个元素max=A[start];return max;}//当数组中元素的个数小于2时,处理最小值int compmin(int A[],int start,int end){int min;if(start<end) //有两个元素{if(A[start]<=A[end])min=A[start];elsemin=A[end];}else//有一个元素min=A[start];return min;}//分治法处理整个数组,求最大值与最小值void merge(int a[],int left,int right,int &Max,int &Min) //Max,Min用来保存最大值与最小值//之所以使用&引用,是由于如果只是简单的使用变量,并不会改变Max与Min的值,使用指针也可以{int max1=0,min1=0,max2=0,min2=0;if(right-left>2) //当数组中元素个数大于等于3时,进行分治{int mid=(right+left)/2;merge(a,left,mid,max1,min1); //左半边递归调用自身,求出最大值最小值,分别保存在max1,min1中merge(a,mid+1,right,max2,min2); //右半边递归调用自身,求出最大值最小值,分别保存在max2,min2中if(max1>=max2) //子序列两两合并,求出最大值与最小值,保存在Max与Min中Max=max1;elseMax=max2;if(min1<=min2)Min=min1;elseMin=min2;}else//数组中元素个数小于3时的情况,直接赋值{Max=compmax(a,left,right);Min=compmin(a,left,right);}}void ran(int *input,int n) //随机生成数组元素函数{int i;srand(time(0));for(i=0;i<n;i++)input[i]=rand();input[i]='\0';}int a[1000000]; //定义全局变量用来存放要查找的数组int main(){int n;int i;int max;int min;cout<<"请输入要查找的序列个数:"<<endl;for(i=0;i<5;i++){cin>>n;ran(a,n);clock_t start,end,over; //计算程序运行时间的算法start=clock();end=clock();over=end-start;start=clock();merge(a,0,n-1,max,min); //调用分治法算法cout<<max<<" "<<min<<endl;end=clock();printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显示运行时间}system("pause"); //停止运行窗口return 0;}完整代码(非递归方法)#include<iostream>#include<time.h>#include<iomanip>using namespace std;void ran(int *input,int n) //随机生成数组元素函数{int i;srand(time(0));for(i=0;i<n;i++)input[i]=rand();input[i]='\0';}int a[1000000];int main(){int max=a[0],min=a[0];int i,j,n;cout<<"请输入数据规模:"<<endl;for(j=0;j<5;j++){cin>>n;ran(a,n);clock_t start,end,over; //计算程序运行时间的算法start=clock();end=clock();over=end-start;start=clock();for(i=1;i<n;i++){if(a[i]>max)max=a[i];if(a[i]<min)min=a[i];}cout<<max<<" "<<min<<endl;end=clock();printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显示运行时间}system("pause");return 0;}。
分治法实验报告

算法实验报告一分治法实验一、实验目的及要求利用分治方法设计大整数乘法的递归算法,掌握分治法的基本思想和算法设计的基本步骤。
要求:设计十进制的大整数乘法,必须利用分治的思想编写算法,利用c语言(或者c++语言)实现算法,给出程序的正确运行结果。
(必须完成)设计二进制的大整数乘法,要求利用分治的思想编写递归算法,并可以实现多位数的乘法(利用数组实现),给出程序的正确运行结果。
(任选)二、算法描述1、输入两个相同位数的大整数u,v 输出uv的值判断大整数的位数i;w=u/10^(i/2);y=v/10^(i/2);x=u-w*10^(i/2);z= v-y*10^(i/2);然后将w,x,y,z代入公式求得最后结果uv=wy10^i+((w+x)(y+z)-wy-xz)10^(i/2)+xz三、调试过程及运行结果在实验中我遇到的问题:原来以为这两个大整数的位数不同,结果题目要求是相同位数的大整数在写10的多少次方时,写的是10^(i/2),10^(i),结果不对,我就将它改成了for循环语句四、实验总结在本次实验中,我知道了分治算法,以及分治算法的基本思想。
我还掌握了编写大整数乘法的算法与步骤,以及如何修改在编写程序时遇到的问题。
五、附录(源程序代码清单)1、#include<iostream.h> int weishu(int x){int i;while(x!=0){ x=x/10;i++;}return i;}void main(){int u,v;cout<<输入两个位数相同的大整数:<<endl; cin>>u;cin>>v;int i,j,m,n;int p,x,y,z,w;int a=1;int b=1;i=weishu(u);for(int k=1;k<=i;k++){a=a*10;}for(int q=1;q<=i/2;q++) {b=b*10;}w=u/b;y=v/b;x=u-w*b;z=v-y*b;p=w*y*a+((w+x)*(y+z)-w*y-x*z)*b+x*z; cout<<u<<*<<v<<=<<p; }教师评语:成绩:√优良中及格不及格算法实验报告二动态规划法实验一、实验目的及要求利用动态规划方法设计背包问题算法,掌握动态规划法的基本思想和算法设计的基本步骤。
二分治专题座PPT课件

时间复杂度
令t(n)表示MaxMin需要的元素比较次数, 存在下列递推关系
0
n1
t(n)
1
n2
t(n/2)t(n/2)2 n2
当n是2的幂时, 即对于某个正整数k, n=2k, 有
t(n)=2t(n/2)+2 = 2(2t(n/4)+2)+2 = 4t(n/4)+4+2
=2k-1t(2)+
2i
=2k-1+2k-2 1ik 1
else b[k++]=a[h++]; } if(l>mid)
while (h<=high) b[k++]=a[h++]; /* 转储剩余部分 */ else
while(l<=mid) b[k++]=a[l++]; a[low : high]=b[low : high]; /* 将b数组转储到a */ }
已分类的部分
未分类的部分
a[1] … a[j-1] a[j] a[j+1] … a[n]
插入分类算法
InsertSort(int n) { for(j=1; j<n; j++)
{ for( unsorted=a[j], k=j-1; (k>=0)&&(unsorted <a[k]); k-- ) a[k+1]=a[k];
a[k+1]= unsorted; } }
时间复杂度
考虑内层for循环中元素比较的次数T(n)
最好情况: 最坏情况:
T(n)=O(n) T(n)==1+2+…n-1==O(n2)
分治法实验报告

分治法实验报告分治法实验报告一、引言分治法是一种重要的算法设计策略,它将一个大问题分解成若干个小问题,并通过递归的方式解决这些小问题,最终将它们的解合并起来得到原问题的解。
本实验旨在通过实际案例,探索分治法的应用和效果。
二、背景在计算机科学领域,分治法常常被用于解决一些复杂的问题,如排序、搜索、图算法等。
它的核心思想是将问题划分为更小的子问题,然后分别解决这些子问题,最后将它们的解合并起来得到原问题的解。
通过这种方式,我们可以降低问题的复杂度,提高算法的效率。
三、实验目的本实验旨在通过实际案例,验证分治法在问题解决中的有效性,并探索其在不同问题上的应用效果。
通过对比不同算法的运行时间和结果准确性,评估分治法在不同场景下的适用性。
四、实验过程本次实验选取了两个典型的问题,分别是最大子数组和快速排序。
首先,我们使用分治法来解决最大子数组问题。
该问题要求在一个给定的数组中,找到一个连续子数组,使得该子数组的和最大。
我们将数组分为两半,分别求解左半部分和右半部分的最大子数组,然后再考虑跨越中点的最大子数组。
通过递归的方式,最终得到整个数组的最大子数组。
接着,我们使用分治法来实现快速排序算法。
快速排序是一种高效的排序算法,它的核心思想是通过选择一个基准元素,将数组分为两个部分,使得左边的元素都小于等于基准元素,右边的元素都大于等于基准元素。
然后,对左右两个部分分别递归地进行快速排序,最终得到有序的数组。
五、实验结果通过对最大子数组和快速排序问题的实验,我们得到了以下结果。
首先,分治法在解决最大子数组问题上表现出色。
通过将问题划分为更小的子问题,我们可以在较短的时间内找到最大子数组,大大提高了算法的效率。
其次,在快速排序问题上,分治法同样展现了强大的能力。
通过不断地划分数组并进行排序,我们可以快速得到有序的结果。
六、实验分析分治法作为一种重要的算法设计策略,具有许多优点。
首先,它可以将复杂的问题分解为简单的子问题,降低了问题的复杂度,提高了算法的效率。
分治法实验(最小值问题)python

南阳理工学院算法设计与分析报告册开课学院:计算机与软件工程学院实验项目:分治算法实验实验时间:实验地点:指导教师:学生姓名:学生学号:专业班级:18大数据2019-2020学年第2学期一、实验目的1.了解分治策略算法思想及基本原理2.掌握使用分治法求解问题的一般特征3.掌握分解、治理的方法4.能够针对实际问题,能够正确的分解、治理,设计分治算法。
5.能够正确分析算法的时间复杂度和空间复杂度二、实验平台1.Windows操作系统或Linux操作系统2.Python3.x3.pyCharm或sublime或jupyter notebook三、实验内容最小值问题:求n个元素的最小值四、算法设计1.问题分析要用分治法求列表的最小值,就要将列表中的元素进行分组,分开求最小值,最后再求总的最小值。
2.问题建模采用先分后治的思想将元素分成两部分求解,最后再合起来求解。
3.算法描述先创建一个tlist列表用于存n个元素,然后定义一个函数getmin求最小值,getmin函数传入1个列表和两个整数作为参数,然后定义一个分治的中点,分别从中点的左侧和右侧调用递归的方式进行求最小值,最后再将两个解进行合并求总的最小值。
五、算法源码def getmin(l,low,high):min1=0 #左边最小值min2=0 #右边最小值if(low==high): #当问题的规模为1时return l[low]elif(low==high-1): #只剩两个值时if(l[low]<l[high]):return l[low]else:return l[high]else:mid=(low+high)//2 #选取分治的中点# 调用递归min1=getmin(l,low,mid) #求左边的最小值min2=getmin(l,mid,high) #求右边的最小值return min(min1,min2) #合并n=int(input("请输入数字个数:"))print("数字分别为:")tlist=[0]*nfor i in range(n):tlist[i]=int(input())min=getmin(tlist,0,len(tlist)-1)print("最小值为:%d" %min)六、测试数据请输入数字个数:512 19 3 45 100最小值为:3请输入数字个数:625 19 34 9 1 0最小值为:0七、程序运行结果(要求:截图说明算法运行的结果)八、算法分析(分析算法的时间复杂度和空间复杂度)因为需要对n个数字进行比较所以时间复杂度为:O(n)。
算法分析与设计第四章2分治法归并分类PPT课件

{
item=a[j];i=j-1;
while(i>=1&&item<a[i])
{
a[i+1]=a[i];i=i-1;
}
a[i+1]=item;
}
}
2008-09-01
i指示的是j之前的一位, 即当前已排序子表的 最末一个元素的下标
4
性能分析
输入数据按非增次序排列,每次内层while循 环执行j次(j=1,2,…, n-1)。
i 1 2 3 4 5 6 7 8 9 10 a[i] 6 7 8 9 2 3 4 5 0 1
i 1 2 3 4 5 6 7 8 9 10 a[i] 2 3 4 5 6 7 8 9 0 1
步骤4:length=8
i 1 2 3 4 5 6 7 8 9 10 a[i] 0 1 2 3 4 5 6 7 8 9
16
public static void MergeSort(int n,int DataLength) { //n为待合并数据个数
int i,t; //循环计数变量 i=1; //还有两段长度为DataLength的list可合并 while(i<=(n-2*DataLength+1)) {
Merge(i, i+DataLength-1, i+2*DataLength-1); i=i+2*DataLength; } if(i+DataLength<n) {//合并两段list,一段长度为DataLength,另一段长度不足DataLength Merge(i, i+DataLength-1, n); } else {//将剩下一段长度不足DataLength的list中的值不变 } }
算法分析与设计实验报告-最大子段和、0-1背包问题

实验报告课程计算机算法设计与分析实验名称最大子段和、0-1背包问题学号姓名实验日期:实验二最大子段和、0-1背包问题一.实验目的(1)学习最大子段和问题的简单算法,掌握原理,运用C++编程实现。
(2)学习0-1背包问题的简单算法,掌握原理,运用C++编程实现。
二.实验内容(1)设计最大子段和问题的算法,上机编程实现。
(2)设计0-1背包问题的算法,上机编程实现。
三.实验代码1 .分治法实现最大子段和程序如下:#include<iostream.h>int MaxSum(int a[],int left,int right){int sum=0;if (left==right){if (a[left]>0)sum=a[left];elsesum=0;}else{int center=(left+right)/2;int leftsum=MaxSum(a,left,center);int rightsum=MaxSum(a,center+1,right);int s1=0;int lefts=0;for(int i=center;i>=left;i--){lefts+=a[i];if(lefts>s1)s1=lefts;}int s2=0;int rights=0;for(int j=center+1;j<=right;j++){rights+=a[j];if(rights>s2)s2=rights;}sum=s1+s2;if(sum<leftsum)sum=leftsum;if(sum<rightsum)sum=rightsum;}return sum;}void main(){int n,a[100],m,maxsum;cout<<"分治法求解"<<endl;cout<<"请输入待求的元素数目"<<endl;cin>>n;cout<<"请输入各元素"<<endl;for(m=1;m<=n;m++)cin>>a[m];maxsum=MaxSum(a,1,n);cout<<"当前序列最大子段和为:"<<maxsum<<endl; }(2)0-1背包问题程序如下:#include<iostream>#include<cstdio>#include<conio.h>#include<iomanip>using namespace std;template<class ty>class Knap{ public:friend void Init();friend void Knapsack();friend void Backtrack(int i);friend float Bound(int i);bool operator<(Knap<ty> a)const{ if(fl<a.fl)return true;elsereturn false; }private:ty w; //重量ty v; //价值float fl; //单位重量的价值v/wint kk; //记录第几个物品int flag; //记录是否放入包中};template<class ty>void Sort(Knap<ty> *li,int n){ int i,j,k;Knap<ty> minl;for(i=1;i<n;i++){ minl=li[0];k=0;for(j=1;j<=n-i;j++){ if(minl<li[j]){ minl=li[j];swap(li[j],li[k]);k=j; } } } }namespace jie //命名空间{ int c=0,n=0;int *x=NULL;Knap<int> *bag=NULL;int cp=0,cw=0; int bestp=0; }using namespace jie;void Init(){ int i=0;cout<<endl;cout<<"请输入物品数量n = ";cin>>n;cout<<endl;cout<<"请输入背包容量C = ";cin>>c;cout<<endl;bag=new Knap<int> [n];x=new int[n];cout<<"请依次输入"<<n<<"个物品的重量W:"<<endl; for(i=0;i<n;i++)cin>>bag[i].w;cout<<endl;cout<<"请依次输入"<<n<<"个物品的价值P:"<<endl; for(i=0;i<n;i++)cin>>bag[i].v;for(i=0;i<n;i++){ bag[i].flag=0;bag[i].kk=i;bag[i].fl=1.0*bag[i].v/bag[i].w;}}void Backtrack(int i) { if(i>=n) //到达叶节点{ bestp=cp; //更新最优价值return; }if(cw+bag[i].w<=c) //进入左子树{ bag[i].flag=1;cw+=bag[i].w;cp+=bag[i].v;Backtrack(i+1);cw-=bag[i].w;cp-=bag[i].v; }if(Bound(i+1)>bestp)//进入右子树{ bag[i].flag=0;Backtrack(i+1); } } //计算当前节点处的上界float Bound(int i){ int cleft = c-cw; //剩余容量float b = cp;while (i<n&&bag[i].w<=cleft){ //以物品单位重量价值递减序装入cleft-=bag[i].w;b+=bag[i].v;i++; } //装满背包if (i<n) b+=1.0*bag[i].v/bag[i].w * cleft;return b; }void Knapsack() //计算最优解和变量值{ int L(0); //用L累计价值,初始价值设置为0for(int k=0;k<n;k++){ x[bag[k].kk]=bag[k].flag; //x=0表示未放入背包,x=1表示放入背包L+=bag[k].flag*bag[k].v; //价值累加}cout<<endl;cout<<"当前最优价值为:"<<L<<endl;cout<<"变量值x = ";for(int i=1;i<=n;i++){ cout<<x[i-1]; }delete []bag;bag=NULL;delete []x;x=NULL;cout<<endl;getch(); }int main(){ cout<<endl;cout<<"|**********回溯法解0-1背包问题**********|"<<endl;Init();Backtrack(0);Knapsack();return 0;}四.实验结果(1)分治法最大子段和问题运行结果如下:(2)0-1背包问题运行结果如下:五.总结与思考。
实验报告

合肥师范学院实验报告册2016/ 2017 学年第 1 学期系别计算机学院实验课程算法设计与分析专业软件工程班级一班姓名杨文皇学号1310421071指导教师程敏实验一:分治算法一、实验目的1、理解分治策略的基本思想;2、掌握用分治法解决问题的一般技巧。
二、实验内容利用分治算法在含有n个不同元素的数组a[n]中同时找出它的最大的两个元素和最小的两个元素,编写出完整的算法,并分析算法的时间复杂度。
三、实验源程序。
1、算法设计思想利用分治法思想,n个不同元素的数组不断进行划分,化为若干个个子问题,其与原问题形式相;解决子问题规模较小而容易解决则直接解决:即当n的规模为只有一个或两个,三个或四个;否则再继续直至更小的子问题:即当n的规模大于四时。
将已求得的各个子问题的解,逐步合并原问题的解:即将左右两边求得的子问题进行比较,在四个数据中的得到两个最大(最小)值。
为了简化空间,采用了对每一个小规模问题的排序,以及合并原问题时,对四个数据进行排序,获得当前或合并的最大(最小)值2、算法实现#include<iostream>using namespace std;int a[10]={4,5,6,2,3,9,8,13,1};int b[4];int sort(int i,int j){int temp,k;for(;i<j;i++){for(k=i;k<j;k++)if(a[k]>a[k+1]){temp=a[k];a[k]=a[k+1];a[k+1]=temp;}}return 0;}int sort1(int lmin1,int lmin2,int rmin1,int rmin2){int i,j,temp;b[0]=lmin1;b[1]=lmin2;b[2]=rmin1;b[3]=rmin2;for(i=0;i<=1;i++)for(j=i;j<=3;j++){if(b[i]>b[j]){temp=b[i];b[i]=b[j];b[j]=temp;}}return 0;}int maxmin(int i,int j,int &fmin1,int &fmin2,int &fmax1,int &fmax2) {int mid;int lmin1,lmin2,lmax1,lmax2;int rmin1,rmin2,rmax1,rmax2;if(i==j || i==j-1){sort(i,j);fmin1=a[i];fmin2=a[i];fmax1=a[j];fmax2=a[j];}elseif(i==j-2 || i==j-3){sort(i,j);fmin1=a[i];fmin2=a[i+1];fmax1=a[j-1];fmax2=a[j];}else{mid=(i+j)/2;maxmin(i,mid,lmin1,lmin2,lmax1,lmax2);maxmin(mid+1,j,rmin1,rmin2,rmax1,rmax2);sort1(lmin1,lmin2,rmin1,rmin2);fmin1=b[0];fmin2=b[1];sort1(lmax1,lmax2,rmax1,rmax2);fmax1=b[2];fmax2=b[3];}return 0;}int main(){int fmin1,fmin2,fmax1,fmax2;int i;maxmin(0,8,fmin1,fmin2,fmax1,fmax2);cout<<endl;cout<<"该组数据为:";for(i=0;i<=8;i++)cout<<a[i]<<" ";cout<<endl<<endl<<"最小值是:"<<fmin1<<",第二小值是:"<<fmin2<<endl;cout<<endl<<"第二大值是:"<<fmax1<<",最大值是:"<<fmax2<<endl<<endl;return 0;}3、程序结果4、算法分析用T(n)元素表示数,则导出的递推关系式是:在理想的情况下,即每一小规模的子问题中的数据都是递增序列,则:当n<=4时,T(n)=1; 当n>4时,T(n)= T(n/2)+ T(n/2)(均向下取整);在非理想情况下,即每一小规模的子问题中的数据都是递减序列,则:当n=1时,T(n)=1;当n=2时,T(n)=2;当n=3时,T(n)=3;当n=4时,T(n)=6;当n>4时,T(n)= T(n/2)+ T(n/2)(均向下取整)+12。
《算法设计与分析》实验二

14210501022017 3 281234121010 3201741112//枢轴元素t为数组最左侧的元素//i往右移动j往左移动当指向同一位置时扫描完成//如果右侧指针元素比轴测元素大,指针元素左移//确保i在j左边//当右侧指针元素比轴测元素小时,交换两指针指向数的位置//如果左侧指针元素比轴测元素小,指针元素右移//确保i在j左边//当左侧指针元素比轴测元素大时,交换两指针指向数的位置//对左边进行排序//对右边进行排序printf("\n");system("pause");getchar();}运行结果经验归纳结合以前学的数据结构及应用算法,较容易理解。
题目二:对用户输入的杂乱无序的数字序列按照由小到大的顺序排序:合并排序题目分析合并排序的基本思想是:将待排序的元素分成大小大相同的两个子集合,分别对两个子集合进行排序,最终将排序好的子集合合并成所要求的拍好序的集合。
算法构造核心代码来自书上:MergePass(Type x[],Type y[],int s,int n)//合并大小为s的相邻序列子数组Merge(Type c[],Type d[],int l,int m,int r) //合并c[l,m]和x[m+1,r]到y[l,r]算法实现//将a中的元素合并到数组b//将b中的元素合并到数组a//合并c[l,m]和x[m+1,r]到y[l,r]//合并大小为s的相邻序列子数组//合并大小为s的相邻2字段数组//合并x[i,i+s-1]和x[i+s,i+2*s-1]到y[i,i+2*s-1] //处理剩下的元素少于2sfor(int j=i;j<=n-1;j++)y[j]=x[j];}void main(){int a[100],i,n;printf("请输入要进行合并排序的数字的个数:\n");scanf_s("%d",&n);for( i=0;i<n;i++){printf("请输入要进行合并排序的第%d个数字:\n",i+1);scanf_s("%d",&a[i]);}MergeSort(a,n);printf("合并排序的结果:\n");for(i=0;i<n;i++)printf("%d,",a[i]);printf("\n");system("pause");}运行结果经验归纳结合以前学的数据结构及应用算法,用心理解还能明白。
《算法设计与分析》实验目的

《算法设计与分析》实验指导书曹严元计算机与信息科学学院2007年5月目录实验一递归算法与非递归算法 (2)实验二分治算法 ................................................... 错误!未定义书签。
实验三贪心算法 (3)实验四动态规划 (2)实验五回溯法 (3)实验六分枝—限界算法 (4)实验七课程设计 (4)实验一递归与分治算法实验目的1.了解并掌握递归的概念,掌握递归算法的基本思想;2.掌握分治法的基本思想方法;3.了解适用于用递归与分治求解的问题类型,并能设计相应递归与分治算法;4.掌握递归与分治算法复杂性分析方法,比较同一个问题的递归算法与循环迭代算法的效率。
实验二动态规划实验目的1.掌握动态规划的基本思想方法;2.了解适用于用动态规划方法求解的问题类型,并能设计相应动态规划算法;3.掌握动态规划算法复杂性分析方法。
实验三贪心算法实验目的1.掌握贪心法的基本思想方法;2.了解适用于用贪心法求解的问题类型,并能设计相应贪心法算法;3.掌握贪心算法复杂性分析方法分析问题复杂性。
实验五回溯法实验目的1.掌握回溯法的基本思想方法;2.了解适用于用回溯法求解的问题类型,并能设计相应回溯法算法;3.掌握回溯法算法复杂性分析方法,分析问题复杂性。
实验六 分枝—限界算法实验目的1. 掌握分枝—限界的基本思想方法;2. 了解适用于用分枝—限界方法求解的问题类型,并能设计相应动态规划算法;3. 掌握分枝—限界算法复杂性分析方法,分析问题复杂性。
实验七 课程设计实验目的1. 在已学的算法基本设计方法的基础上,理解算法设计的基本思想方法;2. 掌握对写出的算法的复杂性分析的方法,理解算法效率的重要性;3. 能运用所学的基本算法设计方法对问题设计相应算法,分析其效率,并建立对算法进行改进,提高效率的思想意识。
预习与实验要求1. 预习实验指导书及教材的有关内容,回顾所学过的算法的基本思想;2. 严格按照实验内容进行实验,培养良好的算法设计和编程的习惯;3. 认真听讲,服从安排,独立思考并完成实验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《算法分析与设计》实验报告实验2 分治法算法设计姓名XXX 学号XXX 班级XXXXXX时间:XXXX-XX-XX 地点:XXX同组人:无指导教师:XXX实验目的a)掌握分治法算法设计的一般思想和方法。
b)理解并掌握二分查找、归并分类、快速分类算法。
c)能熟练运用分治法求解问题。
d)实验中所准备的数据是有代表性的。
实验内容a)写一个顺序查找算法,将其与二分查找算法一起转换成程序,上机验证。
b)选择不同规模的数据集运行上二程序,统计它们的时间开销并比较。
c)归并分类、快速分类算法转换成程序并验证之。
d)选择不同规模的数据集运行上二程序,统计它们的时间开销并比较。
e)准备一定规模的数据集用于实验。
此数据集越大越有得于验证算法,可以考虑最终的数据个数超过10000个。
f)编写归并分类、快速分类程序,将上数据集中的数据分类。
可以使用较少的数据调试程序时。
g)用规模从小到大的数据集运行上述程序,统计它们的运行时间,并作对比分析。
h)编写顺序查找、二分查找程序。
i)将查找程序与分类程序结合起来,用不同规模的数据集运行,统计程序运行时间。
实验环境硬件: Intel(R) Pentium(R) CPU RAM:4G软件:Myeclipse2013实验前准备2、程序设计:见附1实验步骤a)准备一定规模的随机数据集用于实验,存于数组A中,A为全程数组,此数据集越大越有得于验证算法,可以考虑最终的数据个数超过10000个。
使用randomInt(int min, int max, int num)方法产生不小于min,小于max的num个随机数(其中A[0]和A[n]作为数组的上界和下界,供方便排序用,不参与实际排序),在分析程序效率时可修改num来达到产生不同数量的随机数:b)分别编写归并分类MergeSort、快速分类程序QuickSort(),将上数据集中的数据分类。
可以使用较少的数据调试程序时。
/*归并算法,主程序调用f.MergeSort(0,f.getSize());*/public void MergeSort(int low,int high){if(low < high){int mid =(low + high)/2;// 求两个集合的分割点this.MergeSort(low, mid);// 将一个子集合分类this.MergeSort(mid +1, high);// 将另一个子集合分类this.Merge(low, mid, high);// 归并两个已分类的子集合}}/* 使用辅助数组归并两个已分类的集合 */private void Merge(int low,int mid,int high){// arry[n]是一个全程数组int[] B =new int[high - low +1];int h = low;// 子序列第一个开始等待进入B数组中int i =0;// B数组接收两个子序列进队int j = mid +1;// 子序列从第一个开即行等等待进入B数组中while(h <= mid && j <= high){// 当两个集合都没取尽时if(A[h]<= A[j]){// 集合1的小时集合1的进队BB[i]= A[h];h++;}else{// 集合2的小时集合2的进队BB[i]= A[j];j++;}i++;}if(h > mid)// 处理剩余元素for(int k = j; k <= high; k++){B[i]= A[k];i++;}elsefor(int k = h; k <= mid; k++){B[i]= A[k];i++;}for(int k = low; k <= high; k++){// 将已归并的集合复制到AA[k]= B[k - low];}}// 改进后的归并排序private int Merge1(int q,int r){// TODO Auto-generated method stubint i = q;int j = r;int k =0;while(i !=0&& j !=0){if(A[i]<= A[j]){Link[k]= i;k = i;i = Link[i];}else{Link[k]= j;k = j;j = Link[j];}}if(i ==0)Link[k]= j;elseLink[k]= i;return Link[0];}public int MergeSort1(int low,int high){if(high - low +1<16){return this.insertionSort(low, high);}else{int mid =(low + high)/2;int q =this.MergeSort1(low, mid);int r =this.MergeSort1(mid +1, high);return this.Merge1(q, r);}}// 插入排序public int insertionSort(int low,int high){int item;Link[0]= low;for(int j = low +1; j <= high; j++){item = A[j];int p =0;int q = Link[p];while(q !=0&& item > A[q]){p = q;q = Link[p];}Link[p]= j;Link[j]= q;}return Link[0];}/* 快速排序,在主程序中的调用为f.QuickSort(0,f.getSize()); */ public void QuickSort(int low,int high){if(low < high){int mid = high +1;mid =this.partition(low, mid);// 进行一次划分,并返回划分点this.QuickSort(low, mid -1);// 对划分的前半部分进行快速排序this.QuickSort(mid +1, high);// 对划分的后半部分进行快速排序}}// 划分,并返回划分元素所在的下标private int partition(int low,int high){int temp = A[low];// A[m]是划分元素int i = low;while(true){do{low++;}while(A[low]< temp);do{high--;}while(A[high]> temp);if(low < high){int t = A[low];A[low]= A[high];A[high]= t;}elsebreak;}A[i]= A[high];// 划分元素在位置highA[high]= temp;return high;}c)用规模从小到大的数据集运行上述程序,统计它们的运行时间,并作对比分析,即改变n的值,使每次随机产生的数的个数不同,并将其复制三份,统计三种算法M(默认100)次的排序时间int M =100;int a=0,b=10000;int n=10000;for(int i =0; i < M; i++){FenZhi f =new FenZhi(a, b,n);//new一个对象,n决定每次排序的规模FenZhi f1 =(FenZhi) f.clone();//复制三份,以保证三次排序的条件相同FenZhi f2 =(FenZhi) f.clone();FenZhi f3 =(FenZhi) f.clone();t1 = System.currentTimeMillis();f1.MergeSort(1, f1.getSize()-1);//归并排序t2 = System.currentTimeMillis();f2.MergeSort1(1, f2.getSize());//改进后的归并排序t3 = System.currentTimeMillis();f3.QuickSort(1, f2.getSize()-1);//快速排序t4 = System.currentTimeMillis();T1 += t2 - t1;T2 += t3 - t2;T3 += t4 - t3;}System.out.println("归并排序执行所需要的时间为:"+(T1)+"毫秒\n改进后的归并排序执行所需要的时间为:"+(T2 )+"毫秒\n快速排序执行所需要的时间为:"+(T3 )+"毫秒");}d)可以明显看到快速排序最快,改进后的归并排序次之,最慢的是普通的归并排序:n(100次)10000 15000 20000 25000 30000 35000 40000 45000 50000 MergeSort 165 285 331 416 525 616 685 770 863 MergeSort1 139 164 233 281 337 407 463 527 600 QuickSort 100 135 181 244 296 327 370 426 467 d)编写顺序查找、二分查找程序。
// 顺序查找public int srch(int x){for(int i =0; i <this.size; i++){if(x == A[i]){return i;}}return-1;}// 二分查找;public int binSrch(int x){int low =0;int high =this.size;int mid;while(low <= high){mid =(low + high)/2;if(x < A[mid]){high = mid -1;}else if(x > A[mid]){low = mid +1;}elsereturn mid;}return-1;}e)将查找程序与分类程序结合起来,用不同规模的数据集运行,统计程序运行时间,因为查找所需要的时间极短,所以我们统计查找10000次的结果,放大时间效果,并且数据规模的起始值设为50000,每次增10000设有n个运动员要进行网球循环赛。
设计一个满足以下要求的比赛日程表。
①每个选手必须与其它n-1选手各赛一次;②每个选手一天只能赛一次。
