数字电路与数字电子技术-课后答案第七章
王海光数字电子技术基础 第7章 可编程逻辑器件

载了不同设计的同型号芯片,以及进行产品的质量跟踪等。
7.3 复杂可编程逻辑器件CPLD
随着数字电子系统功能日益复杂,规模迅速加大,GAL在集 成度和性能方面很快又难以满足要求,集成度高、功能更强大的 CPLD应运而生。为便于使用,如今的CPLD普遍集成了编程所需 的高压脉冲产生电路以及编程控制电路 ,成了在系统可编程 (ISP,In System Programmable)器件,编程时无须另外编 程器,也无须将器件从系统中拔出。
synac0ac1n工作模式电路结构组态简化电路图组合单向模式与用输入结构图716a与用输出结构图716b组合双向模式组合输入输出结构图716c寄存器模式时序电路中的组合io结构图716d寄存器输出结构图716e表721olmc的5种电路结构组态图724olmc的5种电路结构组态简化电路图中nc表示不连接722输出逡辑宏单元olmcsynac0ac1n工作模式电路结构组态简化电路图组合单向模式与用输入结构图716a与用输出结构图716b组合双向模式组合输入输出结构图716c寄存器模式时序电路中的组合io结构图716d寄存器输出结构图716e表721olmc的5种电路结构组态图724olmc的5种电路结构组态简化电路图中nc表示不连接722输出逡辑宏单元olmcsynac0ac1n工作模式电路结构组态简化电路图组合单向模式与用输入结构图716a与用输出结构图716b组合双向模式组合输入输出结构图716c寄存器模式时序电路中的组合io结构图716d寄存器输出结构图716e表721olmc的5种电路结构组态图724olmc的5种电路结构组态简化电路图中nc表示不连接722输出逡辑宏单元olmc需要说明的是结构控制字的内容无需设计人员逐位设定而是由eda设计开収工具软件根据用户的引脚安排以及要实现的电路功能自动生成于编程下载时自动写入芯片内部的
数字电子技术第七章数字电子技术第三章ch5

二、 连线的检查
调试前,还需认真检查电路的接线是否正确,以 避免接错线、少接线和多接线。多接线一般是因为接 线时看错引脚,或在改接线时忘记去掉原来的接线而 造成的。这种情况在实验中经常发生,而查线又很难 被发现,调试中则往往会给人造成错觉,以为问题是 元器件故障造成的。如把输出电平一高一低的 两个 TTL 门的输出端无意中连在一起而引起输出电平下降 时,则很容易错误地认为是元器件损坏了。
整机联调一般只观察结果,将测得的参数与设计指标 逐一对比,找出问题,然后进行电路参数的修改,直到完 全符合要求为止。
3.5.3 调试注意事项
一、 熟悉仪器的使用
调试前,先要熟悉仪器的使用方法,并仔细加以检查,以避 免由于仪器使来自不当或出现故障而作出错误判断。
二、 将仪器和被测电路的地线连在一起
分块调试的一般步骤如下:
1. 静态测试
不加输入信号,测试调整模拟电路的静态工作点。对 于数字电路,则加入固定电平,再根据器件的逻辑功能测 试电路各点电位,以判断电路的工作是否正常。这样,可 发现电路存在的问题和找出损坏的元器件。静态测量时, 应选用高内阻 ( 2×104Ω/V ) 万用表或数字万用表进行测量。 对于 A / D 转换器和运算放大器,则需要内阻更高的仪器 (如数字电压表)进行测量。
二、 分块调试
在数字电路中,逻辑值 0 和 1 不是一个固定不变的 值,而是一个数值范围。
数字集成电路的逻辑电平标准
电路类型 参数名称
电源电压 / V
UOH / V UOL / V UIH / V UIL / V
HTTL
5 ≥2.4 ≤0.4 ≥2 ≤0.8
STTL
5 ≥2.7 ≤0.5 ≥2 ≤0.8
三、 调试前的准备
《数字电子技术》黄瑞祥第六七章习题答案

《数字电⼦技术》黄瑞祥第六七章习题答案第六章6-1答:ROM 只能读不能写,⽽RAM 可随机读写。
6-2 输⼊B 3B 2B 1B 0为四位⼆进制,输出Y 7Y 6Y 5Y 4Y 3Y 2Y 1Y 0为B 3B 2B 1B 0的平⽅,逻辑图:存储内容(数据)B B B B 3210Y Y Y Y 7654Y Y Y Y数据0000010021110000115……000000011000000000D 7D 6D 5D 4D 3D 2D 1D 0地址6-3输⼊B 7B 6B 5B 4B 3B 2B 1B 0为⼋位⼆进制,输出Y 7Y 6Y 5Y 4Y 3Y 2Y 1Y 0为格雷码,逻辑图:存储内容(数据)3210Y Y Y Y 7654Y Y Y Y数据0000001121000000015……000000011000000000D 7D 6D 5D 4D 3D 2D 1D 0地址6-4 X=0为加法计数,X=1为减法法计数,逻辑图:存储内容(数据)32100011111000010001100111001100000000010~150100101000 (1000001001)00000100010000026~31(00010000010000100000)数据地址6-5 可编程器件有PROM 、PAL 、GAL 低密度PLD 和 CPLD 、FPGA ⾼密度PLD 。
它们共同特点可实现⾼速的数字逻辑。
6-6 相同点:结构上均采⽤“与-或”结构,不同点:GAL 和PAL 输出结构不同,PAL 采⽤固定输出结构,GAL 输出采⽤可编程的宏单元结构。
6-7 共享扩展项作⽤:实现复杂的⾼扇⼊函数,但会增加输出时延。
并联扩展项作⽤:实现快速复杂的⾼扇⼊函数。
6-8 MAX7000系列采⽤“与-或”结构实现逻辑函数,⽽FLEX10K 系列采⽤“查找表”结构实现逻辑函数。
6-9 利⽤级联链,FLEX10K 结构可以实现扇⼊很多的逻辑函数。
数字电子技术基础习题册答案
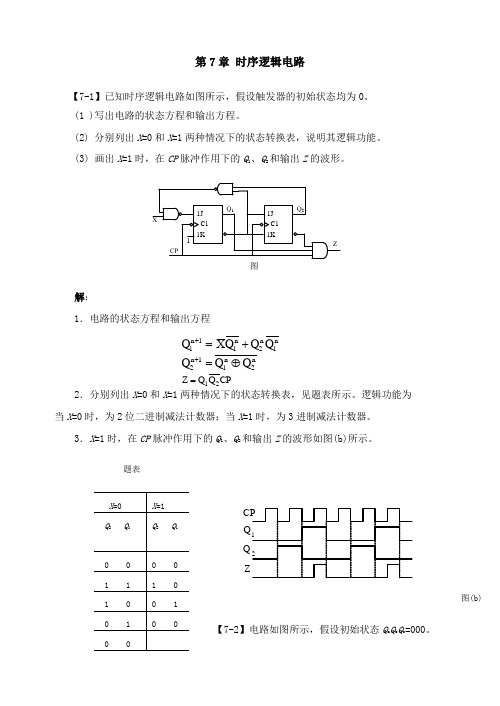
第7章 时序逻辑电路【7-1】已知时序逻辑电路如图所示,假设触发器的初始状态均为0。
(1 )写出电路的状态方程和输出方程。
(2) 分别列出X =0和X =1两种情况下的状态转换表,说明其逻辑功能。
(3) 画出X =1时,在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形。
1J 1KC11J 1KC1Q 1Q 2CPXZ1图解:1.电路的状态方程和输出方程n 1n2n 11n 1Q Q Q X Q +=+n 2n 11n 2Q Q Q ⊕=+ CP Q Q Z 21=2.分别列出X =0和X =1两种情况下的状态转换表,见题表所示。
逻辑功能为 当X =0时,为2位二进制减法计数器;当X =1时,为3进制减法计数器。
3.X =1时,在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形如图(b)所示。
题表Q Q Z图(b)【7-2】电路如图所示,假设初始状态Q a Q b Q c =000。
(1) 写出驱动方程、列出状态转换表、画出完整的状态转换图。
(2) 试分析该电路构成的是几进制的计数器。
Q c图解:1.写出驱动方程1a a ==K J ncn a b b Q Q K J ⋅== n b n a c Q Q J = n a c Q K = 2.写出状态方程n a 1n a Q Q =+ n a n a n a n a n c n a 1n b Q Q Q QQ Q Q +=+ nc n a n c n b n a 1n b Q Q Q Q Q Q +=+3.列出状态转换表见题表,状态转换图如图(b)所示。
图7.2(b)表7.2状态转换表CP na nbc Q Q Q 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 16 0 0 0n4.由FF a 、FF b 和FF c 构成的是六进制的计数器。
【7-3】在二进制异步计数器中,请将正确的进位端或借位端(Q 或Q )填入下表解:题表7-3下降沿触发 由 Q 端引出进位 由Q 端引出借位触发方式 加法计数器 减法计数器上升沿触发 由Q 端引出进位 由Q 端引出借位【7-4】电路如图(a)所示,假设初始状态Q 2Q 1Q 0=000。
《数字电子技术基础》课后习题及参考答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
数字电子技术习题答案

习题答案第一章数制和码制1.数字信号和模拟信号各有什么特点?答:模拟信号——量值的大小随时间变化是连续的。
数字信号——量值的大小随时间变化是离散的、突变的(存在一个最小数量单位△)。
2.在数字系统中为什么要采用二进制?它有何优点?答:简单、状态数少,可以用二极管、三极管的开关状态来对应二进制的两个数。
3.二进制:0、1;四进制:0、1、2、3;八进制:0、1、2、3、4、5、6、7;十六进制:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。
4.(30.25)10=( 11110.01)2=( 1E.4)16。
(3AB6)16=( 0011101010110110)2=(35266)8。
(136.27)10=( 10001000.0100)2=( 88.4)16。
5.B E6.ABCD7.(432.B7)16=( 010*********. 10110111)2=(2062. 556)8。
8.二进制数的1和0代表一个事物的两种不同逻辑状态。
9.在二进制数的前面增加一位符号位。
符号位为0表示正数;符号位为1表示负数。
这种表示法称为原码。
10.正数的反码与原码相同,负数的反码即为它的正数原码连同符号位按位取反。
11.正数的补码与原码相同,负数的补码即为它的反码在最低位加1形成。
12.在二进制数的前面增加一位符号位。
符号位为0表示正数;符号位为1表示负数。
正数的反码、补码与原码相同,负数的反码即为它的正数原码连同符号位按位取反。
负数的补码即为它的反码在最低位加1形成。
补码再补是原码。
13.A:(+1011)2的反码、补码与原码均相同:01011;B: (-1101)2的原码为11101,反码为10010,补码为10011.14.A: (111011)2 的符号位为1,该数为负数,反码为100100,补码为100101. B: (001010)2 的符号位为0,该数为正,故反码、补码与原码均相同:001010.15.两个用补码表示的二进制数相加时,和的符号位是将两个加数的符号位和来自最高有效数字位的进位相加,舍弃产生的进位得到的结果就是和的符号。
数字电子技术第7章习题答案

数字电子技术第7章习题答案
1. 什么是逻辑门?
答:逻辑门是数字电路中的基本组件,用于对输入进行逻辑运算并产生输出。
2. 列举几种常见的逻辑门。
答:与门、或门、非门、异或门、与非门、或非门等。
3. 什么是真值表?
答:真值表是一种用来展示逻辑函数输入与输出关系的表格,其中列出了所有可能的输入和对应的输出。
4. 什么是逻辑电路?
答:逻辑电路是指由逻辑门组成的电路,用于对输入进行逻辑运算并产生输出。
5. 什么是卡诺图?
答:卡诺图是一种用于最小化逻辑函数的图形化工具,通过将函数的真值表转化为图形,可快速找到最小化的逻辑表达式。
6. 什么是多路复用器?
答:多路复用器是一种数字电路,可以选择不同的输入并将其发送到一个输出线上。
7. 什么是解码器?
答:解码器是一种数字电路,用于将二进制数字输入转换为对应的输出,通常用于驱动其他数字电路中的寄存器、计数器等。
8. 什么是编码器?
答:编码器是一种数字电路,用于将多个输入端连接到一个二进制数字输出端,也可以实现将多个开关等输入转换为一个数字信号输出。
9. 什么是计数器?
答:计数器是一种数字电路,可用于记录电路所经过的时间或事件数量,通常用于计时器、频率计等应用。
10. 什么是触发器?
答:触发器是一种数字电路,可用于存储和控制数字信号,通常用于存储器、寄存器等应用。
《数字电子技术(第二版)》课后习题参考答案
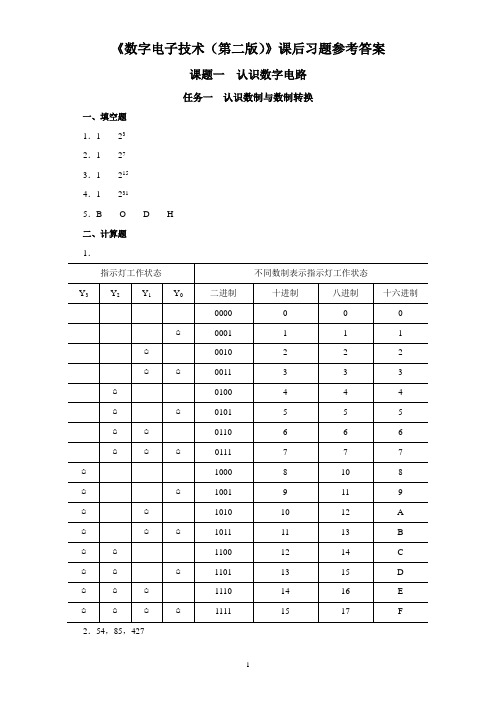
《数字电子技术(第二版)》课后习题参考答案课题一认识数字电路任务一认识数制与数制转换一、填空题1.1 232.1 273.1 2154.1 2315.B O D H二、计算题1.2.54,85,4273.0101,1100,1 1000,11 01114.17O,37O,66 O5.110B,010 111B,001 101 110B6.0FH,36H,0AE63H7.0001 0110B,0010 1010B,1111 1100 0000B任务二学习二进制数算术运算一、计算题(给出的二进制均是无符号数)1.(1)1 0000 (2)1 0000 10012.(1)10 1010 (2)1010 11113.(1)1 0100 (2)110 00004.(1)101 (2)11二、写出下列带符号位二进制数(原码)所表示的十进制数(1)+110 (2)-15 (3)-42 (4)+127 (5)+111(6)-63 (7)+0 (8)+32 767 (9)-32 768三、问答题1.(1)答:左移,移动3位,应作乘以8运算。
(2)答:左移,移动4位,应作乘以16运算。
(3)答:右移,移动7位,应作除以128运算。
(4)答:右移,移动3位,应作除以8运算。
2.答:4位二进制无符号数的最大值是15。
3.答:8位二进制无符号数、有符号数的最大值分别是255和+127。
4.答:16位二进制有符号数的最大值是+32 767。
任务三学习二进制代码一、填空题1.二进制数2.43.8,4,2,1二、判断题1.×2.× 3.√ 4.× 5.× 6.×三、计算题1.36,55,892.[0011 0010]8421,[0101 0010 0111]8421,[0001 0011 0110 1001]8421任务四认识基本逻辑关系并测试逻辑门一、填空题1.与或非2.13.04.1 05.Y=AB6.Y=A+B7.Y=A8.Y=AB9.Y=A+B10.Y=A B=AB+AB二、选择题1.D 2.A 3.B,C 4.A,D三、判断题1.× 2.× 3.× 4.√四、问答题1.答:Y1=ABCD2.答:Y2=A+B+C+D五绘图题1.2.3.4.任务五测试TTL集成门电路1.答:TTL集成门电路电源电压范围为4.75~5.25V之间,额定电压为5V。
数字电子技术课后习题及答案

第二章2.2 证明下列异或运算公式(1)A0A证明:左侧A0 A 0A得证(2)A1A证明:左侧 A 1 A 1A得证(3)A A0证明:左侧 A A A A得证(4)AA A证明:左侧 A A A AA得证(5)ABAB证明:右侧A B A BA B A BA B得证(6)(A B) C A (B C)证明:等式右侧 A (B C) A (BC BC)A(BC BC) A (BC BC)A(BC BC) A BC A BCA (B C)( B C)ABC A BCA (BB BC BC CC)ABC ABCABC ABC ABC ABC(A B AB)C (AB A B)C(A B)C (A B)C(将看成一个整体 (A B) ,用M来表示MC MCM C再替换 M ,则)(A B)C得证2.3 用逻辑代数法将下列逻辑函数式化简为最简与或表达式(1) L=AB(BC+A)解: L=AB(BC+A)=ABC+AB=AB(C+1)=AB(2)L=AB AB B解:L= AB AB B= AB (A1)B=AB B=AB B+A=A+B(3)L A ABC ABC BC BC解: L A ABC ABC BC BCA(1 BC ABC) C(B B)A C(4)L A B BD DCE AD解: L AB (A B)D DCEA B A BD DCEA B D DCEA B D (1CE)A B D(5)L( A B)AB A B AB解: L( A B)( A B)AB(A B)ABA B AB ABA B AB AB ABA (B B)B(A A )A B(6)L (A B C) (D E)(A B C DE )解: L(A B C) (D E)(A B C DE)(( A B C)(D E))(ABC DE )(A BC DE)(ABC DE )(0 DE( ABC ) ABCDE DE )DE2.4 已知函数L(A ,B,C)ABC ABC ABC 。
数字电子技术基础数电第六版阎石课后答案第七章

数字电子技术基础数电第六版阎石课后答案第七章第七章:逻辑门和逻辑代数1. 本章节内容概述本章介绍了逻辑门和逻辑代数的基础知识。
首先介绍了逻辑电平和逻辑门的概念,然后详细介绍了与门、或门、非门等基本逻辑门的原理、特性和应用。
接着介绍了与非门、或非门、异或门等组合逻辑门的原理和应用。
最后介绍了逻辑代数的基本概念和运算规则。
2. 逻辑门逻辑门是数字电子电路中使用的基本元件,用于进行逻辑运算。
逻辑门有多种类型,其中最基本的有与门(AND)、或门(OR)和非门(NOT)。
2.1 与门(AND)与门是一种逻辑门,其输出信号仅在所有输入信号都为高电平时才为高电平,否则为低电平。
与门的逻辑符号如下:AND gateAND gate2.2 或门(OR)或门是一种逻辑门,其输出信号在任何输入信号中有一个或多个为高电平时就为高电平,只有所有输入信号都为低电平时才为低电平。
或门的逻辑符号如下:OR gateOR gate2.3 非门(NOT)非门是一种逻辑门,其输出信号和输入信号相反。
当输入信号为低电平时,输出信号为高电平;当输入信号为高电平时,输出信号为低电平。
非门的逻辑符号如下:NOT gateNOT gate3. 组合逻辑门除了基本逻辑门之外,还有一些由基本逻辑门组合而成的组合逻辑门,例如与非门(NAND)、或非门(NOR)和异或门(XOR)等。
3.1 与非门(NAND)与非门是由与门和非门组成的组合逻辑门。
其输出信号在所有输入信号都为高电平时为低电平,否则为高电平。
与非门的逻辑符号如下:NAND gateNAND gate3.2 或非门(NOR)或非门是由或门和非门组成的组合逻辑门。
其输出信号在任何输入信号中有一个或多个为高电平时为低电平,只有所有输入信号都为低电平时才为高电平。
或非门的逻辑符号如下:NOR gateNOR gate3.3 异或门(XOR)异或门是一种比较特殊的组合逻辑门,其输出信号在输入信号中有奇数个高电平时为高电平,否则为低电平。
数字电子技术课后习题答案

ABACBC
BC
A
00 01 11 10
00
1
0
1
11
0
1
0
Y ABC
❖ 3.13某医院有一、二、三、四号病室4间,每室设有 呼叫按钮,同时在护士值班室内对应的装有一号、 二号、三号、四号4个指示灯。
❖ 现要求当一号病室的按钮按下时,无论其它病室的 按钮是否按下,只有一号灯亮。当一号病室的按钮 没有按下而二号病室的按钮按下时,无论三、四号 病室的按钮是否按下,只有二号灯亮。当一、二号 病室的按钮都未按下而三号病室的按钮按下时,无 论四号病室的按钮是否按下,只有三号灯亮。只有 在一、二、三号病室的按钮均未按下四号病室的按 钮时,四号灯才亮。试用优先编码器74148和门电路 设计满足上述控制要求的逻辑电路,给出控制四个 指示灯状态的高、低电平信号。
HP RI/BIN
I0
0/ Z1 0 10 ≥1
I1
1/ Z1 1 11
I2
2/ Z1 2 12 18
YS
I3
3/ Z1 3 13
I4
4/ Z1 4 14
YEX
I5
5/ Z1 5 15
I6
6/ Z1 6 16
I7
7/ Z1 7 17
Y0
V18
Y1
ST
E N
Y2
(b)
74148
(a)引脚图;(b)逻辑符号
A
00 01 11 10
00
0
0
1
11
1
0
1
Y AB BC AC
由于存在AC 项,不存在相切的圈,故无冒险。
❖ 4.1在用或非门组成的基本RS触发器中,已知 输入SD 、RD的波形图如下,试画出输出Q, Q
数字电子技术应用基础习题答案赵景波数字电子技术书后习题参考答案

第1章习题答案一、填空题 1、模拟、数字 2、高、低3、逻辑、逻辑、逻辑、与逻辑、或逻辑、非逻辑4、基数、位权、基、位权5、8421、2421、余3、格雷6、进位制、数、按位权展开求和7、除2取余、乘2取整8、二进、二进制、三位、四位 9、8、4、2、1、二进制、0~9 10、原码、反码、补码、补码11、分配、结合、交换、反演、非非 12、或项、与项13、最小项、相邻、最小项、一位变量 14、“1”、“0” 二、判断题1、错2、错3、错4、对5、错6、错7、对 三、选择题1、B2、C3、B4、A四、简答题1、答:数字信号是离散的,模拟信号是连续的,这是它们的最大区别。
它们之中,数字电路的抗干扰能力较强。
2、答:数制是指计数的进制,如二进制码、十进制码和十六进制码等等码制是指不同的编码方式,如各种BCD 码、循环码等。
在本书介绍的范围内,8421BCD 码和2421BCD 码属于有权码余3码和格雷码属于无权码。
3、答:用卡诺图化简时,合并的小方格应组成正方形或长方形,同时满足相邻原则。
利用卡诺图化简逻辑函数式的步骤如下:①根据变量的数目,画出相应方格数的卡诺图;②根据逻辑函数式,把所有为“1”的项画入卡诺图中;③用卡诺圈把相邻最小项进行合并,合并时就遵照卡诺圈最大化原则;④根据所圈的卡诺圈,消除圈内全部互非的变量,每一个圈作为一个“与”项,将各“与”项相或,即为化简后的最简与或表达式。
五、计算题1、(1)C B A + (2)B C A + (3)BC B A AB ++ (4)C B D C B A ++2、(1)(365)10=(101101101)2=(555)8=(16D )16 (2)(11101.1)2=(29.5)10=(35.4)8=(1D.8)16(3)(57.625)10=(71.5)8=(39.A )163、(1)D C AD Y += (2)AD B C B A Y ++=(3)C B BC B A Y ++= (4)D B A ACD BC A D C A Y +++=第2章习题答案一、填空题1、门电路、与门、或门2、异或、同或3、开关、双极、单极、双极、单极4、或非、有1出1,全0出0、与非5、图腾、高电平“1”、低电平“0”、“1”、“0”、高阻6、三态、OC7、TTL 、CMOS 、CMOS8、PMOS 、NMOS 、输入、输出、控制 9、并、并、并 10、“与”、悬空、“或”、低、高、低、悬空 二、判断题 1、对 2、错三、选择题1、B2、D3、B四、分析题1、F 1是与门电路,F 2是或门电路,波形如下图所示。
数字电子技术基础课后答案全解__主编_杨春玲_王淑娟

数字电子技术基础课后答案全解__主编_杨春玲_王淑娟(总43页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除第3章 逻辑代数及逻辑门【3-1】 填空1、与模拟信号相比,数字信号的特点是它的 离散 性。
一个数字信号只有两种取值分别表示为0 和1 。
2、布尔代数中有三种最基本运算: 与 、 或 和 非 ,在此基础上又派生出五种基本运算,分别为与非、或非、异或、同或和与或非。
3、与运算的法则可概述为:有“0”出 0 ,全“1”出 1;类似地或运算的法则为 有”1”出”1”,全”0”出”0” 。
4、摩根定理表示为:A B ⋅=A B + ;A B +=A B ⋅。
5、函数表达式Y=AB C D ++,则其对偶式为Y '=()A B C D +⋅。
6、根据反演规则,若Y=AB C D C +++,则Y =()AB C D C ++⋅ 。
7、指出下列各式中哪些是四变量A B C D 的最小项和最大项。
在最小项后的( )里填入m i ,在最大项后的( )里填入M i ,其它填×(i 为最小项或最大项的序号)。
(1) A +B +D (× ); (2) ABCD (m 7 ); (3) ABC ( × ) (4)AB (C +D ) (×); (5) A B C D +++ (M 9 ) ; (6) A+B+CD (× ); 8、函数式F=AB+BC+CD 写成最小项之和的形式结果应为m ∑(3,6,7,11,12,13,14,15),写成最大项之积的形式结果应为M (∏0,1,2,4,5,8,9,10 )9、对逻辑运算判断下述说法是否正确,正确者在其后( )内打对号,反之打×。
(1) 若X +Y =X +Z ,则Y=Z ;( × ) (2) 若XY=XZ ,则Y=Z ;( × ) (3) 若X ⊕Y=X ⊕Z ,则Y=Z ;(√ ) 【3-2】用代数法化简下列各式(1) F 1 =1ABC AB += (2) F 2 =ABCD ABD ACD AD ++=(3)3F AC ABC ACD CD A CD =+++=+ (4) 4()()F A B C A B C A B C A BC =++⋅++⋅++=+【3-3】 用卡诺图化简下列各式(1) 1F BC AB ABC AB C=++=+ (2) 2F AB BC BC A B=++=+(3) 3F AC AC BC BC AB AC BC=+++=++ (4) 4F ABC ABD ACD CD ABC ACD A D=+++++=+或AB AC BC ++(5) 5F ABC AC ABD AB AC BD=++=++ (6) 6F AB CD ABC AD ABC A BC CD=++++=++(7) 7F AC AB BCD BD ABD ABCD A BD BD=+++++=++ (8) 8 F AC AC BD BD ABCD ABCD ABCD ABCD=+++=+++(9) 9()F A C D BCD ACD ABCD CD CD =⊕+++=+(10)F 10=10F AC AB BCD BEC DEC AB AC BD EC =++++=+++【3-4】 用卡诺图化简下列各式(1) P 1(A ,B ,C )=(0,1,2,5,6,7)m AB AC BC =++∑(2) P 2(A ,B ,C ,D )=(0,1,2,3,4,6,7,8,9,10,11,14)m AC AD B CD =+++∑ (3)P 3(A ,B ,C ,D )=(0,1,,4,6,8,9,10,12,13,14,15)m AB BC AD BD =+++∑ (4) P 4 (A ,B ,C ,D )=17M M A BC BC D •=+++【3-5】用卡诺图化简下列带有约束条件的逻辑函数(1)()1,,,(3,6,8,9,11,12)(0,1,2,13,14,15)()d P A B C D m AC BD BCD ACD =+=++∑∑或 (2) P 2(A ,B ,C ,D )=(0,2,3,4,5,6,11,12)(8,9,10,13,14,15)d m BC BC D +=++∑∑ (3) P 3 =()A C D ABCD ABCD AD ACD BCD ABD ++++=++或 AB +AC =0 (4) P 4 =A B ABCD ABCD +=+(A B C D 为互相排斥的一组变量,即在任何情况下它们之中不可能两个同时为1)【3-6】 已知: Y 1 =AB AC BD ++ Y 2 =ABCD ACD BCD BC +++ 用卡诺图分别求出Y Y 12⋅, Y Y 12+, Y Y 12⊕。
《数字电子技术》课后习题答案

第1单元能力训练检测题(共100分,120分钟)一、填空题:(每空0.5分,共20分)1、由二值变量所构成的因果关系称为逻辑关系。
能够反映和处理逻辑关系的数学工具称为逻辑代数。
2、在正逻辑的约定下,“1”表示高电平,“0”表示低电平。
3、数字电路中,输入信号和输出信号之间的关系是逻辑关系,所以数字电路也称为逻辑电路。
在逻辑关系中,最基本的关系是与逻辑、或逻辑和非逻辑。
4、用来表示各种计数制数码个数的数称为基数,同一数码在不同数位所代表的权不同。
十进制计数各位的基数是10,位权是10的幂。
5、8421 BCD码和2421码是有权码;余3码和格雷码是无权码。
6、进位计数制是表示数值大小的各种方法的统称。
一般都是按照进位方式来实现计数的,简称为数制。
任意进制数转换为十进制数时,均采用按位权展开求和的方法。
7、十进制整数转换成二进制时采用除2取余法;十进制小数转换成二进制时采用乘2取整法。
8、十进制数转换为八进制和十六进制时,应先转换成二进制,然后再根据转换的二进数,按照三个数码一组转换成八进制;按四个数码一组转换成十六进制。
9、逻辑代数的基本定律有交换律、结合律、分配律、反演律和非非律。
10、最简与或表达式是指在表达式中与项中的变量最少,且或项也最少。
13、卡诺图是将代表最小项的小方格按相邻原则排列而构成的方块图。
卡诺图的画图规则:任意两个几何位置相邻的最小项之间,只允许一位变量的取值不同。
14、在化简的过程中,约束项可以根据需要看作1或0。
二、判断正误题(每小题1分,共10分)1、奇偶校验码是最基本的检错码,用来使用PCM方法传送讯号时避免出错。
(对)2、异或函数与同或函数在逻辑上互为反函数。
(对)3、8421BCD码、2421BCD码和余3码都属于有权码。
(错)4、二进制计数中各位的基是2,不同数位的权是2的幂。
(对)3、每个最小项都是各变量相“与”构成的,即n个变量的最小项含有n个因子。
(对)4、因为逻辑表达式A+B+AB=A+B成立,所以AB=0成立。
《数字电子技术基础》课后习题答案

《数字电子技术基础》课后习题答案《数字电路与逻辑设计》作业教材:《数字电子技术基础》(高等教育出版社,第2版,2012年第7次印刷)第一章:自测题:一、1、小规模集成电路,中规模集成电路,大规模集成电路,超大规模集成电路5、各位权系数之和,1799、01100101,01100101,01100110;11100101,10011010,10011011二、1、×8、√10、×三、1、A4、B练习题:1.3、解:(1) 十六进制转二进制: 4 5 C0100 0101 1100二进制转八进制:010 001 011 1002 13 4十六进制转十进制:(45C)16=4*162+5*161+12*160=(1116)10所以:(45C)16=(10001011100)2=(2134)8=(1116)10(2) 十六进制转二进制: 6 D E . C 80110 1101 1110 . 1100 1000二进制转八进制:011 011 011 110 . 110 010 0003 3 3 6 . 6 2十六进制转十进制:(6DE.C8)16=6*162+13*161+14*160+13*16-1+8*16-2=(1 758.78125)10所以:(6DE.C8)16=(011011011110. 11001000)2=(3336.62)8=(1758.78125)10(3) 十六进制转二进制:8 F E . F D1000 1111 1110. 1111 1101二进制转八进制:100 011 111 110 . 111111 0104 3 7 6 . 7 7 2十六进制转十进制:(8FE.FD)16=8*162+15*161+14*160+15*16-1+13*1 6-2=(2302.98828125)10所以:(8FE.FD)16=(100011111110.11111101)2=(4376.772)8=(2302.98828125)10(4) 十六进制转二进制:7 9 E . F D0111 1001 1110 . 1111 1101二进制转八进制:011 110 011 110 . 111 111 0103 6 3 6 . 7 7 2十六进制转十进制:(79E.FD)16=7*162+9*161+14*160+15*16-1+13*16 -2=(1950. 98828125)10所以:(8FE.FD)16=(011110011110.11111101)2=(3636.772)8=(1 950.98828125)101.5、解:(74)10 =(0111 0100)8421BCD=(1010 0111)余3BCD (45.36)10=(0100 0101.0011 0110)8421BCD=(0111 1000.0110 1001 )余3BCD(136.45)10=(0001 0011 0110.0100 0101)8421BCD=(0100 0110 1001.0111 1000 )余3BCD (374.51)10=(0011 0111 0100.0101 0001)8421BCD=(0110 1010 0111.1000 0100)余3BCD1.8、解(1)(+35)=(0 100011)原= (0 100011)补(2)(+56 )=(0 111000)原= (0 111000)补(3)(-26)=(1 11010)原= (1 11101)补(4)(-67)=(1 1000011)原= (1 1000110)补第二章:自测题:一、1、与运算、或运算、非运算3、代入规则、反演规则、对偶规则二、2、×4、×三、1、B3、D5、C练习题:2.2:(4)解:Y=AB̅+BD+DCE+A̅D=AB̅+BD+AD+A̅D+DCE=AB̅+BD+D+DCE=AB̅+D (B +1+CE ) =AB̅+D (8)解:Y =(A ̅+B ̅+C ̅)(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅(A ̅+B ̅+C ̅+DE ) =[(A ̅+B ̅+C ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅+(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅](A ̅+B ̅+C ̅+DE ) =(ABC +DE )(ABC ̅̅̅̅̅̅+DE ) =DE 2.3:(2)证明:左边=A +A ̅(B +C)̅̅̅̅̅̅̅̅̅̅̅̅ =A +A ̅+(B +C)̅̅̅̅̅̅̅̅̅̅=A +B̅C ̅ =右式所以等式成立(4)证明:左边= (A̅B +AB ̅)⨁C = (A̅B +AB ̅)C ̅+ (A ̅B +AB ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅C = (A ̅BC ̅+AB ̅C ̅)+A ̅B ̅̅̅̅⋅AB̅̅̅̅̅⋅C =A̅BC ̅+AB ̅C ̅+(A +B ̅)(A ̅+B )C =A̅BC ̅+AB ̅C ̅+(AB +A ̅B ̅)C =A̅BC ̅+AB ̅C ̅+ABC +A ̅B ̅C 右边= ABC +(A +B +C )AB ̅̅̅̅⋅BC ̅̅̅̅⋅CA̅̅̅̅ =ABC +(A +B +C )[(A̅+B ̅)(B ̅+C ̅)(C ̅+A ̅)] =ABC +(A +B +C )(A̅B ̅+A ̅C ̅+B ̅+B ̅C ̅)(C ̅+A ̅)=ABC +(A +B +C )(A̅B ̅C ̅+A ̅C ̅+B ̅C ̅+A ̅B ̅) =ABC +AB̅C ̅+A ̅BC ̅+A ̅B ̅C 左边=右边,所以等式成立 2.4(1)Y ′=(A +B ̅C ̅)(A ̅+BC) 2.5(3)Y ̅=A ̅B ̅(C ̅+D ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ C ̅D ̅(A ̅+B ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 2.6:(1)Y =AB +AC +BC=AB (C +C̅)+AC (B +B ̅)+BC (A +A ̅) =ABC +ABC ̅+AB ̅C +A ̅BC 2.7:(1)Y =A ̅B ̅+B ̅C ̅+AC +B ̅C 卡诺图如下: B C A 00 0111100 1 1 1111所以,Y=B̅+AC2.8:(2)画卡诺图如下:B C A 0001 11 100 1 1 0 11 1 1 1 1Y(A,B,C)=A+B̅+C̅2.9:(1)画Y(A,B,C,D)=∑m(0,1,2,3,4,6,8)+∑d(10,11,12,13,14)如下:CDAB00 01 11 1000 1 1 1 101 1 111 ×××10 1 ××Y (A,B,C,D )=A̅B ̅+D ̅ 2.10:(3)解:化简最小项式: Y =AB +(A̅B +C ̅)(A ̅B ̅+C ) =AB +(A̅B A ̅B ̅+A ̅BC +A ̅B ̅C ̅+C ̅C ) =AB (C +C̅)+A ̅BC +A ̅B ̅C ̅ =ABC +ABC ̅+A ̅BC +A ̅B ̅C ̅ =∑m (0,3,6,7)最大项式:Y =∏M(1,2,4,5) 2.13:(3)Y =AB̅+BC ̅+AB ̅C ̅+ABC ̅D ̅ =AB̅(1+C ̅)+BC ̅(1+AD ̅) =AB̅+BC ̅ =AB̅+BC ̅̿̿̿̿̿̿̿̿̿̿̿̿ = AB̅̅̅̅̅∙BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅技能题:2.16 解:设三种不同火灾探测器分别为A 、B 、C ,有信号时值为1,无信号时为0,根据题意,画卡诺图如下:B C A 00 01 11 10 0 0 0 1 0 1 0 1 1 1Y =AB +AC +BC=AB +AC +BC ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=AB ̅̅̅̅⋅AC ̅̅̅̅⋅BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=(A ̅+B ̅)(A ̅+C ̅)(B ̅+C ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅+B ̅̅̅̅̅̅̅̅̅+A ̅+C ̅̅̅̅̅̅̅̅̅+B ̅+C ̅̅̅̅̅̅̅̅̅第三章:自测题:一、1、饱和,截止7、接高电平,和有用输入端并接,悬空;二、1、√8、√;三、1、A4、D练习题:3.2、解:(a)因为接地电阻4.7k Ω,开门电阻3k Ω,R>R on ,相当于接入高电平1,所以Y =A ̅B ̅1̅̅̅̅̅̅=A +B +0=A +B(e) 因为接地电阻510Ω,关门电0.8k Ω,R<R off ,相当于接入高电平0,所以、Y =A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A̅⋅B ̅∙1̅̅̅̅̅̅̅̅̅̅=A +B +0=A +B3.4、解:(a) Y1=A+B+0̅̅̅̅̅̅̅̅̅̅̅̅̅=A+B̅̅̅̅̅̅̅̅(c) Y3=A+B+1̅̅̅̅̅̅̅̅̅̅̅̅̅=1̅=0(f) Y6=A⋅0+B⋅1̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅3.7、解:(a) Y1=A⨁B⋅C=(A̅B+AB̅)C=A̅BC+AB̅C3.8、解:输出高电平时,带负载的个数2020400===IHOHOH I I NG 可带20个同类反相器输出低电平时,带负载的个数78.1745.08===ILOLOL I I NG 反相器可带17个同类反相器3.12EN=1时,Y 1=A , Y 2=B ̅EN=0时,Y 1=A ̅, Y 2=B3.17根据题意,设A为具有否决权的股东,其余两位股东为B、C,画卡诺图如下,BCA00 01 11 100 0 0 0 01 0 1 1 1则表达结果Y的表达式为:Y=AB+AC=AB+AC̿̿̿̿̿̿̿̿̿̿̿̿=AB̅̅̅̅⋅AC̅̅̅̅̅̅̅̅̅̅̅̅̅̅逻辑电路如下:技能题:3.20:解:根据题意,A、B、C、D变量的卡诺图如下:CD AB00 01 11 1000 0 0 0 001 0 0 0 011 0 1 1 110 0 0 0 0Y =ABC +ABD =ABC +ABD ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=ABC ̅̅̅̅̅̅⋅ABD ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅电路图如下:第四章:自测题:一、2、输入信号,优先级别最高的输入信号7、用以比较两组二进制数的大小或相等的电路,A>B 二、3、√4、√三、5、A7、C练习题:4.1;解:(a) Y =A⨁B +B ̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅B +AB ̅+B ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅B +B ̅̅̅̅̅̅̅̅̅̅̅=A ̅+B̅̅̅̅̅̅̅̅̅=AB ,所以电路为与门。
阎石《数字电子技术基础》(第6版)章节题库-第7章 脉冲波形的产生和整形电路【圣才出品】

第7章脉冲波形的产生和整形电路一、选择题1.为了提高多谐振荡器频率的稳定性,最有效的方法是()。
A.提高电容、电阻的精度B.提高电源的稳定度C.采用石英晶体振荡器C.保持环境温度不变【答案】C【解析】石英晶体多谐振荡器的振荡频率取决于石英晶体的固有谐振频率,而与外接电阻、电容无关,具有极高的频率稳定性。
2.已知时钟脉冲频率为f cp,欲得到频率为0.2f cp的矩形波应采用()A.五进制计数器B.五位二进制计数器C.单稳态触发器C.多谐振荡器【答案】A【解析】频率变为原来的五分之一,是五分频,只需要每五次脉冲进一位即可实现。
3.在图7-1用555定时器组成的施密特触发电路中,它的回差电压等于()A.5VB.2VC.4VD.3V图7-1【答案】B【解析】555组成的施密特触发器中,当不接外接电压时,得到电路的回差电压为2V CC/3-V cc/3=V cc/3;5脚为外部参考电压输入V CO,如果参考电压由外接的电压V CO供给,这时V T+=V CO;V T-=V CO/2,回差电压为V CO/2=4V/2=2V,可以通过改变V CO值可以调节回差电压的大小。
4.电路如下图7-2(图中为上升沿JK触发器),触发器当前状态Q3Q2Q1为“100”,请问在时钟作用下,触发器下一状态(Q3Q2Q1)为()。
图7-2A.“101”B.“100”C.“011”D.“000”【答案】C【解析】JK触发器特征方程为Q n+1=JQ_n+K_Q n,由图7-2可得,三个触发器的驱动方程均为J=K=1,即特性方程均为Q n+1=Q_n,Q1的时钟是CP,Q2的时钟是Q1,Q3的时钟是Q2,当前Q3Q2Q1的状态是100,由于触发器在上升沿被触发,CP上升沿Q1状态被触发,变为1;同时触发了Q2,Q2变为1;同理Q3为0。
5.多谐振荡器可产生的波形是()A.正弦波B.矩形脉冲C.三角波D.锯齿波【答案】B【解析】“多谐”指矩形波中除了基波成分外,还含有丰富的高次谐波成分。
《数字电子技术基础》课后习题答案

《数字电路与逻辑设计》作业教材:《数字电子技术基础》(高等教育出版社,第2版,2012年第7次印刷)第一章:自测题:一、1、小规模集成电路,中规模集成电路,大规模集成电路,超大规模集成电路5、各位权系数之和,1799、01100101,01100101,01100110;11100101,10011010,10011011二、1、×8、√10、×三、1、A4、B练习题:1.3、解:(1)十六进制转二进制:45 C010*********二进制转八进制:010*********2134十六进制转十进制:(45C)16=4*162+5*161+12*160=(1116)10所以:(45C)16=(10001011100)2=(2134)8=(1116)10(2)十六进制转二进制:6D E.C8011011011110.11001000二进制转八进制:011011011110.1100100003336.62十六进制转十进制:(6DE.C8)16=6*162+13*161+14*160+13*16-1+8*16-2=(1758.78125)10所以:(6DE.C8)16=(011011011110. 11001000)2=(3336.62)8=(1758.78125)10(3)十六进制转二进制:8F E.F D100011111110.11111101二进制转八进制:100011111110.1111110104376.772十六进制转十进制:(8FE.FD)16=8*162+15*161+14*160+15*16-1+13*16-2=(2302.98828125)10所以:(8FE.FD)16=(100011111110.11111101)2=(437 6.772)8=(2302.98828125)10 (4)十六进制转二进制:79E.F D011110011110.11111101二进制转八进制:011110011110.1111110103636.772十六进制转十进制:(79E.FD)16=7*162+9*161+14*160+15*16-1+13*16-2=(1950. 98828125)10所以:(8FE.FD)16=(011110011110.11111101)2=(3636.772)8=(1950.98828125)101.5、解:(74)10 =(0111 0100)8421BCD=(1010 0111)余3BCD(45.36)10 =(0100 0101.0011 0110)8421BCD=(0111 1000.0110 1001 )余3BCD(136.45)10 =(0001 0011 0110.0100 0101)8421BCD=(0100 0110 1001.0111 1000 )余3BCD (374.51)10 =(0011 0111 0100.0101 0001)8421BCD=(0110 1010 0111.1000 0100)余3BCD1.8、解(1)(+35)=(0 100011)原= (0 100011)补(2)(+56 )=(0 111000)原= (0 111000)补(3)(-26)=(1 11010)原= (1 11101)补(4)(-67)=(1 1000011)原= (1 1000110)补第二章:自测题:一、1、与运算、或运算、非运算3、代入规则、反演规则、对偶规则 二、 2、×4、× 三、 1、B 3、D5、C练习题:2.2:(4)解:Y =AB̅+BD +DCE +A D =AB̅+BD +AD +A D +DCE =AB̅+BD +D +DCE =AB̅+D (B +1+CE ) =AB̅+D (8)解:Y =(A +B ̅+C )(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅(A +B ̅+C +DE ) =[(A +B ̅+C )̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅+(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅](A +B ̅+C +DE ) =(ABC +DE )(ABC ̅̅̅̅̅̅+DE ) =DE2.3:(2)证明:左边=A +A (B +C)̅̅̅̅̅̅̅̅̅̅̅̅ =A +A +(B +C)̅̅̅̅̅̅̅̅̅̅ =A +B̅C ̅ =右式所以等式成立(4)证明:左边= (A B +AB̅)⨁C = (A B +AB ̅)C + (A B +AB̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅C = (A BC +AB ̅C )+A B ̅̅̅̅⋅AB̅̅̅̅⋅C =A BC +AB̅C +(A +B ̅)(A +B )C =A BC +AB̅C +(AB +A B ̅)C =A BC +AB̅C +ABC +A B ̅C 右边= ABC +(A +B +C )AB̅̅̅̅⋅BC ̅̅̅̅⋅CA ̅̅̅̅ =ABC +(A +B +C )[(A +B̅)(B ̅+C )(C +A )]=ABC +(A +B +C )(A B̅+A C +B ̅+B ̅C )(C +A ) =ABC +(A +B +C )(A B̅C +A C +B ̅C +A B ̅) =ABC +AB̅C +A BC +A B ̅C 左边=右边,所以等式成立 2.4(1)Y ′=(A +B̅C )(A +BC) 2.5(3)Y ̅=A B ̅̅̅̅(C +D ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅ C D ̅̅̅̅̅(A +B ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 2.6:(1)Y =AB +AC +BC=AB (C +C̅)+AC (B +B ̅)+BC (A +A ̅) =ABC +ABC̅+AB ̅C +A ̅BC 2.7:(1)Y =A B̅+B ̅C +AC +B ̅C 卡诺图如下:所以,Y =B2.8:(2)画卡诺图如下:Y(A,B,C)=A +B̅+C2.9:(1)画Y (A,B,C,D )=∑m (0,1,2,3,4,6,8)+∑d(10,11,12,13,14)如下:Y (A,B,C,D )=A B̅+D ̅2.10:(3)解:化简最小项式:Y =AB +(A B +C )(A B̅+C ) =AB +(A B A B̅+A BC +A B ̅C +C C ) =AB (C +C )+A BC +A B̅C =ABC +ABC ̅+A BC +A B ̅C =∑m (0,3,6,7)最大项式:Y =∏M(1,2,4,5)2.13:(3)Y =AB̅+BC +AB ̅C +ABC D ̅ =AB̅(1+C )+BC (1+AD ̅) =AB ̅+BC =AB ̅+BC ̿̿̿̿̿̿̿̿̿̿̿̿ = AB ̅̅̅∙BC ̅̅̅̅̅̅̅̅̅̅̅技能题:2.16 解:设三种不同火灾探测器分别为A 、B 、C ,有信号时值为1,无信号时为0,根据题意,画卡诺图如下:Y =AB +AC +BC =AB +AC +BC ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿ =AB ̅̅̅̅⋅AC̅̅̅̅⋅BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ =(A +B ̅)(A +C )(B ̅+C )̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ =A +B ̅̅̅̅̅̅̅̅+A +C ̅̅̅̅̅̅̅̅+B ̅+C̅̅̅̅̅̅̅̅第三章:自测题:一、1、饱和,截止7、接高电平,和有用输入端并接,悬空; 二、 1、√ 8、√; 三、 1、A 4、D练习题:3.2、解:(a)因为接地电阻4.7k Ω,开门电阻3k Ω,R>R on ,相当于接入高电平1,所以Y =A B 1̅̅̅̅̅̅=A +B +0=A +B (e) 因为接地电阻510Ω,关门电0.8k Ω,R<R off ,相当于接入高电平0,所以、 Y =A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅⋅B ̅∙1̅̅̅̅̅̅̅̅̅̅=A +B +0=A +B3.4、解:(a) Y 1=A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A +B ̅̅̅̅̅̅̅(c) Y 3=A +B +1̅̅̅̅̅̅̅̅̅̅̅̅̅=1̅=0(f) Y 6=A ⋅0+B ⋅1̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅3.7、解:(a) Y 1=A⨁B ⋅C =(A B +AB̅)C =A B C +AB ̅C3.8、解:输出高电平时,带负载的个数2020400===IH OH OH I I N G 可带20个同类反相器输出低电平时,带负载的个数78.1745.08===IL OL OL I I N G 反相器可带17个同类反相器3.12EN=1时,Y 1=A , Y 2=B̅ EN=0时,Y 1=A̅, Y 2=B3.17根据题意,设A 为具有否决权的股东,其余两位股东为B 、C ,画卡诺图如下,则表达结果Y 的表达式为:Y =AB +AC =AB +AC ̿̿̿̿̿̿̿̿̿̿̿=AB ̅̅̅̅⋅AC̅̅̅̅̅̅̅̅̅逻辑电路如下:技能题:3.20:解:根据题意,A 、B 、C 、D 变量的卡诺图如下:Y =ABC +ABD =ABC +ABD ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=ABC̅̅̅̅̅̅⋅ABD ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅电路图如下:第四章:自测题:一、2、输入信号,优先级别最高的输入信号7、用以比较两组二进制数的大小或相等的电路,A>B 二、 3、√ 4、√ 三、 5、A 7、C练习题:4.1;解:(a) Y =A⨁B +B ̅̅̅̅̅̅̅̅̅̅̅̅̅=A B +AB ̅+B ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A B +B ̅̅̅̅̅̅̅̅̅̅̅=A +B ̅̅̅̅̅̅̅̅=AB ,所以电路为与门。
哈工大数字电子技术基础习题册-标准答案-章

哈工大数字电子技术基础习题册2010-答案6-7章————————————————————————————————作者:————————————————————————————————日期:2第6章 触发器【6-1】已知由与非门构成的基本RS 触发器的直接置“0”端和直接置“1”端的输入波形如图6.1所示,试画出触发器Q 端和Q 端的波形。
R d S d Q Q图 6.1解:基本RS 触发器Q 端和Q 端的波形可按真值表确定,要注意的是,当d R 和d S 同时为“0”时,Q 端和Q 端都等于“1”。
d R 和d S 同时撤消,即同时变为“1”时,Q 端和Q 端的状态不定。
见图6.1(b )所示,图中Q 端和Q 端的最右侧的虚线表示状态不定。
R d S d QQ不定状态图6.1(b ) 题6-1答案的波形图【6-2】触发器电路如图 6.2(a)所示,在图(b)中画出电路的输出端波形,设触发器初态为“0”。
QQR d S dd S d Q QR(a) (b)图6.2解:此题是由或非门构成的RS 触发器,工作原理与由与非门构成的基本RS 触发器一样,只不过此电路对输入触发信号是高电平有效。
参照题6-1的求解方法,即可画出输出端的波形,见图6.2(c)。
d S d Q QR 不定状态图6.2(c)【6-3】试画出图6.3所示的电路,在给定输入时钟作用下的输出波形,设触发器的初态为“0”。
C11J 1K R SQ“1”CPYZCP图 6.3解:见图6.3(b)所示,此电路可获得双相时钟。
CPQQYZ图6.3(b)【6-4】分析图6.4所示电路,列出真值表,写出特性方程,说明其逻辑功能。
Q QD CP图6.4解:1.真值表(CP=0时,保持;CP=1时,如下表)D n Q n Q n+10 0 00 1 01 0 11 1 12.特性方程Q n+1=D n3.该电路为锁存器(时钟型D触发器)。
CP=0时,不接收D的数据;CP=1时,把数据锁存,但该电路有空翻。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 时序逻辑电路1.电路如图P7.1所示,列出状态转换表,画出状态转换图和波形图,分析电路功能。
图P7.1 解:(1)写出各级的W.Z 。
D 1=21Q Q ,D 2=Q 1,Z=Q 2CP( 2 ) 列分析表( 3 ) 状态转换表(4图7.A1 本电路是同步模3计数器。
2. 已知电路状态转换表如表P7.1所示,输入信号波形如图P7.2所示。
若电路的初始状态为Q2Q1 = 00,试画出Q2Q1的波形图(设触发器的下降沿触发)。
Q 2 Q 1 D 2 D 1 Q 2n+1 Q 1n+1 Z 0 0 0 1 0 1 0 0 1 1 0 1 0 0 1 0 0 0 0 0 1 1 1 1 0 1 0 1Q 2 Q 1 Q 2n+1 Q 1n+1 Z 0 0 0 1 0 0 1 1 0 0 1 0 0 0 1 1 1 1 0 1 CP表P7.1 XQ 2 Q 1 0 1 00 01 10 11 01/1 10/0 10/0 01/1 11/1 10/0 11/0 00/1Q 2n+1 Q 1n+1/ZCP XQ 1 0 Q 2 0 Z 图P7.2 CPQ 1 0 Q 1 0 Z ( b ) Q 2 Q 1 /Z( a )01/0 11/1 10/1 00/0解:由状态转换表作出波形图3. 试分析图P7.3所示电路,作出状态转换表及状态转换图,并作出输入信号为0110111110相应的输出波形(设起始状态Q 2Q 1 = 00)。
( a )( b )解:(1)写W.Z 列分析表J 1 = XQ 2 J 2 = X Z =12Q Q X K 1 = X K 2 =1Q X( 2 ) 作出状态转换表及状态转换图XQ 2 Q 10 1 00 01 10 11 00/1 00/1 00/1 00/1 10/1 11/1 01/111/0 Q 2n+1 Q 1n+1/ZX Q 2 Q 1 J 2 K 2 J 1 K 1 Q 2n+1 Q 1n+1 Z 0 0 0 0 1 0 1 0 0 1 0 0 1 0 1 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 0 1 1 0 1 0 1 0 0 1 1 0 0 1 1 0 0 1 0 11 0 1 1 0 0 0 1 1 1 1 1 0 1 1 1 0 0 1 1 1 1 1 1 0 1 0 1 1 0 CP X图P7.3CP X Q 1 0 Q 1 0Z 图P7.A2 0 /10 /1 0 /1 1/1 1/1 0/1 1/0 1/1图P7.A3 ( a )01 11 1000(3)作出输出波形图:1 根据状态转换表,作出状态的响应序列,设y = Q 2Q 1 X : 0 1 1 0 1 1 1 1 1 0 y n : 0 02 1 0 2 13 3 3 y n+1: 0 2 1 0 2 1 3 3 3 0 Z : 1 1 1 1 1 1 1 0 0 12 根据状态响应序列画响应的输出波形。
4.X :Z :0 0 0 0 0 0 0 0 0 0 1 1 0 0 … 解:(1)建立原始的状态转换图和状态转换表 设:A --- 输入“0”以后的状态。
B --- 输入1个“1”以后的状态。
C --- 输入2个“1”以后的状态。
D --- 输入3个“1”以后的状态。
E --- 输入4个“1”以后的状态。
(2(3)状态分配:画出分配后的状态转换表和状态转换图设:A(4)画出动作卡诺图,触发器选型,确定电路激励输入,确定外输出Z。
图P7.A4(d )选用JK触发器,J是a必圈0必不圈,其余无关,K是β必圈1必不圈,其余无关。
J2 = XQ1J2 =2QX Z =12QQXK2 =X K1=X+Q2 =2QX(5)画出逻辑电路图图P7.A4(e )5. 已知某计数器电路中图P7.4所示,分析它是几进制计数器,并画出工作波形,设电路初始状态Q2Q1 = 00。
0 /00/0 1/01/1 0/0 0/01/0 1/0图P7.A4 ( c )01110010XQ2Q10 10001111000/000/000/000/001/011/010/010/1Q2n+1 Q1n+1/ZXQ2 Q1 0 100011110W20 00αβ 1β 1XQ2 Q1 0 100011110Z0 000000 1XQ2 Q1 0 100011110W10 αβ 1ββ0 0图P7.4解:列出分析表:D1=1Q,D2=21Q⊕Q设计数器为4进制计数器,画出工作波形图如下:6. 分析图P7.5所示计数器电路,画出状态转换图,说明是几进制计数器,有无自启功能。
图P7.5解:(1)写出激励函数,列分析表J1=32QQ J2=1Q J3=Q2Q1Q2 Q1D2 D1Q2n+1Q1n+10 0 0 1 0 10 1 1 0 1 01 0 1 1 1 11 1 0 0 0 0图P7.A5(a )00011110CPQ1 0Q1 0图P7.A5 ( b )K 1=1K2= 31Q Q =Q 1+Q 3 K 3=1设计数器是具有自启动能力的模4计数器。
路是否具有自启动能力。
图P7.6解:(1) 写出激励函数,列分析表J 1=1 J 2 = Q 13Q J 3 = Q 2Q 1K 1=1 K 2= Q 13Q K 3 = Q 1( 2 )画出状态转换图图P7.A6000 001 111 110 100 101 010 011 Q 3 Q 2 Q 1 J 3 K 3 J 2 K 2 J 1 K 1 Q 3n+1 Q 2n+1 Q 1n+1 0 0 0 0 1 0 0 1 1 0 0 1 0 0 1 0 1 1 1 0 1 0 1 0 0 1 0 0 1 0 0 0 1 0 1 1 0 1 1 1 1 1 1 0 1 1 0 0 1 0 0 0 1 0 1 1 1 0 0 1 1 0 1 0 1 1 1 1 1 0 1 0 1 1 0 0 1 0 1 0 1 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0(2)写出各级触发器特征方程,画出状态转换图。
Q 1 n+1 = [1Q ]CP ↓Q 2 n+1 = [Q13Q 2Q +231Q Q Q ]CP ↓ Q 3 n+1 = [Q 2Q 13Q +1Q Q 3] CP ↓设计数器是具有自启能力的模68. 用JK 触发器设计同步模9 加法计数器。
解:(1)列出状态转换表,画出动作卡诺图图P7.A8( a )(2) 由动作卡诺图写出各触发器的激励函数。
J 4 = Q 3Q 2Q 1 J 3 = Q 2Q 1 J 2 = Q 1 J 1 =4Q Z = Q 4 K 4 = 1 K 3 = Q 2Q 1 K 2 = Q 1 K 1 =1图P7.A8( b )(3)检查是否具有自启能力。
具有自启动能力 (4)画出逻辑电路图图P7.A8( d )9. 用D 触发器设计模7同步加法计数器。
Q 4 Q 3 Q 2 Q 1 J 4 K 4 J 3 K 3 J 2 K 2 J 1 K 1 Q 3n+1 Q 2n+1 Q 1n+1 Z 1 0 0 1 0 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 0 0 0 0 0 1 0 0 1 0 1 1 0 1 1 0 1 1 1 1 1 0 1 0 1 0 0 1 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 0 0 1 0 0 0 0 0 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 0 0 111 11 11 11 10 10 10 10 10 10 10 1011 11 11 11图P7.A8( c )0000 0110 0000 0010 0001 1101 11100101 1011 01001100 1000 0011 0000 0000 0111 Q 4 Q 3 Q 2 Q 1 00 01 11 10 00 01 11 10 Z 0 0 X 1 0 0 X X 0 0 X X0 0 X X解:(1) 画出状态转换卡诺图,求出激励函数。
由于D 触发器Q n+1 = D ,所以可以Q n+1直接求出D 。
D 3 = Q 321 2 12D 1 = 3Q 1Q +2Q 1Q Z = Q 3Q 2 (2)检查是否自启动具有自启动能力(3)画出逻辑电路图图P7.A9( c )10. 用JK 触发器设计模7同步减法计数器 解:(1)列出状态转换表,画出动作卡诺图图P7.A10( )(2)根据动作卡诺图求出激励函数 J 3=2Q J 2=2Q +3Q =31Q Q J 1=1 Z=23Q Q K 3=2Q 1Q K 2= 1Q K 1=Q 2+Q 3=32 (3)检查是否自启动Q 3 Q 2 Q 1 Q 3n+1 Q 2n+1 Q 1n+1 W 3 W 2 W 1 Z 1 1 1 1 1 0 1 1 β 0 1 1 0 1 0 1 1 β α 0 1 0 1 1 0 0 1 0 β 01 0 0 0 1 1 β α α 0 0 1 1 0 1 0 0 1 β 0 0 1 0 0 0 1 0 β α 0 0 0 1 1 1 1 α α 1 1Q 3 Q 2 Q 1 J 3 K 3 J 2 K 2 J 1 K 1 Q 3n+1 Q 2n+1 Q 1n+1 Z 0 0 0 1 1 1 1 0 1 1 1 1 Q3 Q2Q1 00 01 11 101 ZX 0 0 01 0 0 0Q3 Q2Q1 00 01 11 10 01W2X β βα α 1 1 0Q3 Q2 Q1 00 01 11 10 01W3X 0 1 β α 0 1 1Q3 Q2Q1 00 01 11 10 01 W1X α αα 1 β β β具有自启动能力 (4)画出逻辑电路图图P7.A10( c )11.用JK 触发器设计一个可控计数器,X=0为7进制同步加法计数,X=1为模5同步加法计数。
解:(1)画出状态转换卡诺图,从而画出动作卡诺图图P7.A11( a )图P7.A11( a )(2)根据动作卡诺图求出激励函数J 3 = Q 2Q 1 J 2 = Q 1 J 1 =3Q +X 2Q =23Q X •Q K 3 = X K 2 = Q 1+Q 3 =31Q Q K 1=1 (3) 检查是否自启动X Q 3 Q 2 Q 1 00 01 11 10 00 01 11 10 Q 3n+1 Q 2n+1 Q 1n+1 001 101 000 001 010 110 xxx 010 100 xxx xxx 100 011 000 xxx 011 X Q 3 Q 2 Q 1 00 01 11 10 00 01 11 10 W 20 0 0 0 α α X αβ X X β 1 β X 1 X Q 3 Q 2 Q 1 00 01 11 10 00 01 11 10 W 3 0 0 β 0 0 1 X 0α X X α 0 β X 0 X Q 3 Q 2 Q 1 00 01 11 10 00 01 11 10 W 1 αα0α β β X β β X X β α 0 X α有自启动能力(4) 画出逻辑电路图图P7.A11(c )图P7.A12 ( 1 )( a )2 从次态卡诺图求出激励函数D A =Q A C Q +Q A D Q +A Q Q C Q D D B =C Q Q D +Q B D Q D C = Q C D Q +Q B C Q Q D D D =D Q3 检查是否自启动图P7.A12 ( 1 )( c )(2) 画出状态转换卡诺图,从而得到动作卡诺图 图P7.A12 ( 2 )( a ) (3) 采用JK 触发器在动作卡诺图上求出各触发器激励函数.J A = Q B C Q D Q J B = Q C D Q J C =B Q Q D K A =00B Q K B = Q A K C = Q B Q D J D = Q B Q C + A Q B Q C Q = C B A C B Q Q Q •Q QK D = Q B C Q +B Q Q C = C B C B Q Q •Q Q(4)Q A Q BQ C Q D 00 01 11 10 00 01 11 10 Q 4n+1 Q 3n+1 Q 2n+1 Q 1n+1 0001 0101 1101 10010100 0110 1110 1100 xxxx 1000 0000 xxxx xxxx 0111 1111 xxxx Q A Q BQ C Q D 00 01 11 10 00 011110Q A n+10 0 1 10 0 1 1 X 1 0 X X 0 1 X Q A Q B Q C Q D 00 01 11 10 00 01 11 10 Q C n+1 0 0 0 0 0 1 1 0 X 0 0 X X 1 1 X Q A Q B Q C Q D 00 01 11 10 00 01 11 10 Q D n+1 1 1 1 1 0 0 0 0 X 0 0 X X 1 1 X Q A Q BQ C Q D 00 01 11 1000 01 11 10 Q B n+10 1 1 0 1 1 1 1 X 1 1 X X 1 1 XQ A Q B Q C Q D J A K A J B K B J C K C J D K D Q A n+1 Q B n+1 Q C n+1 Q D n+1 1 0 0 1 0 1 0 1 1 0 0 0 0 0 1 1 1 0 1 0 0 1 1 1 0 0 0 1 0 1 1 0 1 0 1 1 0 1 0 1 1 0 0 1 0 0 1 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 0 1 1 1 1 1 1 0 0 0 1 0 1 0 0 1 0 0 1图P7.A12 ( 2 )( b )电路具有自启动能力(5)图P7.A12 ( 2 )( c )13.分析图P7.7所示电路逻辑功能,画出状态转换图,说明电路是否具有自启动能力图P7.7解:本电路是异步时序电路,用特征方程法进行分析(1) 写出各触发器的激励函数及特征方程J1 = K1 = 1 J2 = Q3 J3 =1 J4 = K4 = 1CP1= CP↓K2 = 1 K3 = Q2CP4 = Q3↓CP2 = Q1↓CP3 = CP↓11011000 000010011100 0100 010100010111 0110 10100011 00101111 11101011Z =CP Q Q Q Q 4321 Q 1n+1 = [1Q ]CP ↓ Q 2n+1 = [Q 32Q ]Q 1↓Q 3n+1 = [3Q +2Q Q 3] CP ↓= [3Q +2Q ] CP ↓= [23Q Q ] CP ↓ Q 4n+1 = [4Q ] Q 3↓(2)根据特征方程列出状态转换表,画出转换图本电路是异步模8计数器,有自启动能力分析图P7.8所示电路,写出特征方程,画出状态转换图及在CP 作用下Q 1,Q 2,Q 3,Q 4和的工作波形.图P7.8解:(1) 写出各触发器的激励函数,列分析表J 1= K 1=1 J 2 =431Q Q •Q =1Q (Q 3+Q 4) J 3 = Q 41Q K 2 = 1Q K 3 =2Q 1QJ 4 =2Q 3QF=4Q 3Q 2Q 1QK 4 =1Q表P7.A13Q 4 Q 3 Q 2 Q 1 Q 4n+1 Q 3n+1 Q 2n+1 Q 1n+1 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 00 1 1 0 1 0 1 1 1 0 1 1 1 1 1 0 1 1 0 0 1 1 0 11 1 0 1 1 1 0 0 1 1 1 0 0 0 1 1 0 0 1 1 0 1 1 0 0 1 0 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 1 0 0 0 0 1 0 0 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 0 1 0 0图P7.A1300011010 0010 1000 0111 0000 1100 0101 0110 1111 1101 0100 0011 1110Q 1n+1 Q 2n+1 = [1Q (Q 3+Q 4) 2Q +Q 1Q 2] CP ↓ Q 3n+1 = [Q 41Q 3Q +12Q Q Q 3]↓Q 4n+1 = [2Q 3Q 4Q +Q 1Q 4] CP ↓15. 分析图P7.9所示电路,并画出在CP 作用下Q 2输出与CP 之间的关系图P7.9解:(1) 写出特征方程Q 1n+1 = [1Q][ Q2+CP]↑当Q3=1时, CP1 =CP↑,即CP1=CP↓Q2n+1 = [1Q] Q1↑当Q3 = 0时, CP1=CP↑Q3n+1 = [1Q] Q1↑根据特征方程画出工作波形图(1)画波形图CPQ10Q20Q30图P7.A15CP脉冲与Q2之间的关系是Q2的周期为3.5 T CP (T CP为CP的周期)16. 分析图P7.10所示电路,写出特征方程,并画出在CP作用下,输出a、b、c、d、e、f下的各点波形,说明该电路完成什么逻辑功能。
