数学建模logistic人口增长模型

合集下载

基于人口增长模型的数学建模(DOC)

数学建模论文题目：人口增长模型的确定专业、姓名：专业、姓名：专业、姓名：人口增长模型摘要随着人口的增加，人们越来越认识到资源的有限性，人口与资源之间的矛盾日渐突出，人口问题已成为世界上最被关注的问题之一。

问题给出了1790—1980年间美国的人口数据，通过分析近两百年的美国人口统计数据表，得知每10年的人口数的变化。

预测美国未来的人口。

对于问题我们选择建立Logistic模型(模型2)现实中，影响人口的因素很多，人口也不能无限的增长下去，Logistic 模型引进常数N 表示自然资源和环境所能承受的最大人口数，因而得到了一个贝努利方程的初值问题公式，从实际效果来看，这个公式较好的符合实际情况的发展，随着时间的递增，人口不是无限增长的，而是趋近于一个数，这个即为最大承受数。

我们还同时对数据作了深入的探讨，作数据分析预测，通过观测比较选择一个比较好的拟合模型（模型3）进行预测。

预测接下来的每隔十年五次人口数量，分别为251.4949， 273.5988 ， 293.4904 ， 310.9222 325.8466。

关键词：人口预测Logistic模型指数模型一、问题重述1790-1980年间美国每隔10年的人口记录如下表所示。

试用以上数据建立马尔萨斯(Malthus)人口指数增长模型，并对接下来的每隔十年预测五次人口数量，并查阅实际数据进行比对分析。

如果数据不相符，再对以上模型进行改进，寻找更为合适的模型进行预测。

二、问题分析人口预测是一个相当复杂的问题，影响人口增长除了人口数与可利用资源外，还与医药卫生条件的改善，人们生育观念的变化等因素有关…….可以采取几套不同的假设，做出不同的预测方案，进行比较。

人口预测可按预测期长短分为短期预测 (5年以下)、中期预测(5～20年)和长期预测(20～50年)。

在参数的确定和结果讨论方面，必须对中短期和长期预测这两种情况分开讨论。

中短期预测中所用的各项参数以实际调查所得数据为基础，根据以往变动趋势可较准确加以估计，推算结果容易接近实际，现实意义较大。

(完整版)数学建模logistic人口增长模型

Logistic 人口发展模型一、题目描述建立Logistic 人口阻滞增长模型，利用表1中的数据分别根据从1954年、1963年、1980年到2005年三组总人口数据建立模型，进行预测我国未来50年的人口情况.并把预测结果与《国家人口发展战略研究报告》中提供的预测值进行分析比较。

分析那个时间段数据预测的效果好?并结合中国实情分析原因。

表1 各年份全国总人口数（单位：千万）二、建立模型阻滞增长模型（Logistic 模型）阻滞增长模型的原理：阻滞增长模型是考虑到自然资源、环境条件等因素对人口增长的阻滞作用，对指数增长模型的基本假设进行修改后得到的。

阻滞作用体现在对人口增长率r 的影响上，使得r 随着人口数量x 的增加而下降。

若将r 表示为x 的函数)(x r 。

则它应是减函数。

于是有：0)0(,)(x x x x r dt dx== （1）对)(x r 的一个最简单的假定是，设)(x r 为x 的线性函数，即 )0,0()(>>-=s r sxr x r （2）设自然资源和环境条件所能容纳的最大人口数量mx ，当mx x =时人口不再增长，即增长率)(=m x r ，代入（2）式得m x rs =，于是（2）式为)1()(mx x r x r -= （3）将（3）代入方程（1）得：⎪⎩⎪⎨⎧=-=0)0()1(x x x x rx dtdxm （4）解得：rt mme x x x t x --+=)1(1)(0（5）三、模型求解用Matlab 求解，程序如下： t=1954:1:2005;x=[60.2,61.5,62.8,64.6,66,67.2,66.2,65.9,67.3,69.1,70.4,72.5,74.5,76.3,78.5,80.7,83,85.2,87.1,89.2,90.9,92.4,93.7,95,96.259,97.5,98.705,100.1,101.654,103.008,104.357,105.851,107.5,109.3,111.026,112.704,114.333,115.823,117.171,118.517,119.85,121.121,122.389,123.626,124.761,125.786,126.743,127.627,128.453,129.227,129.988,130.756];x1=[60.2,61.5,62.8,64.6,66,67.2,66.2,65.9,67.3,69.1,70.4,72.5,74.5,76.3,78.5,80.7,83,85.2,87.1,89.2,90.9,92.4,93.7,95,96.259,97.5,98.705,100.1,101.654,103.008,104.357,105.851,107.5,109.3,111.026,112.704,114.333,115.823,117.171,118.517,119.85,121.121,122.389,123.626,124.761,125.786,126.743,127.627,128.453,129.227,129.988];x2=[61.5,62.8,64.6,66,67.2,66.2,65.9,67.3,69.1,70.4,72.5,74.5,76.3,78.5,80.7,83,85.2,87.1,89.2,90.9,92.4,93.7,95,96.259,97.5,98.705,100.1,101.654,103.008,104.357,105.851,107.5,109.3,111.026,112.704,114.333,115.823,117.171,118.517,119.85,121.121,122.389,123.626,124.761,125.786,126.743,127.627,128.453,129.227,129.988,130.756];dx=(x2-x1)./x2; a=polyfit(x2,dx,1);r=a(2),xm=-r/a(1)%求出xm 和rx0=61.5;f=inline('xm./(1+(xm/x0-1)*exp(-r*(t-1954)))','t','xm','r','x0');%定义函数 plot(t,f(t,xm,r,x0),'-r',t,x,'+b');title('1954-2005年实际人口与理论值的比较') x2010=f(2010,xm,r,x0) x2020=f(2020,xm,r,x0) x2033=f(2033,xm,r,x0)解得：x(m)= 180.9516(千万)，r= 0.0327/(年),x(0)=61.5得到1954-2005实际人口与理论值的结果：根据《国家人口发展战略研究报告》我国人口在未来30年还将净增2亿人左右。

数学应用典型案例模型1马尔萨斯人口增长(指数增长)模型

xc e hx
C
其中 C 为任意常数，可由初始条件确定。
捕食----被捕食模型有着广泛的应用。当一个包含两个群体的系统中，只要
两个群体相互依存、相互制约，均可用捕食----被捕食模型来描述。例如，鲨鱼
与食用鱼、寄生虫与其宿主、害虫与其天敌、肿瘤细胞与正常细胞等都可用该模
型来描述。下图表明了狐狸----野兔（数量）随着时间 t 所发生的周而复始的变
化，正是这种变化维持着该系统的生态平衡。
在狐狸----野兔生态系统中，生态系统的平衡点就是使 dx 0, dy 0 的点。 dt dt
即
a byx 0 c hxy 0
(3-2)
只求非零解，可知平衡点为： x c , y a 。也就是说，当野兔数量保持在 c ，
设人类生存空间及可利用资源（食物、水、空气）等环境因素所能容纳的最大人口容量为 K（称为饱和系数）.人口数量 N（t）的增长速率不仅与现有人口数量成正比，而且还与人口尚未实现的部分（相对最大容量 K 而言）所占比例 K N 成比例，比例系数为固有增长率 r.于是，修改后的模型为
K
dN

hb
h
狐狸数量保持在 a 时，就能维持狐狸----野兔生态系统的平衡。 b
图 3-2
例狐狸----野兔模型为
dx dt

0.03x

0.001xy
dy dt

0.9 y 0.002xy
(3-3)
试问：狐狸、野兔的数目各为多少时，该系统才达到平衡？
解：由 dx 0 ，得 y狐狸 0.03 3（0 只）；
模型 3 捕食——被捕食模型所用知识：微分方程组内容介绍：

基于logistic模型对中国未来人口的预测分析

基于logistic模型对中国未来人口的预测分析中国人口是世界上最多的国家之一，人口数量的变化对中国社会经济的发展具有重大影响。

本文将基于logistic模型对中国未来人口的预测分析进行探讨。

我们需要了解logistic模型的基本原理。

logistic模型是一种常用的人口增长模型，它基于人口增长的两个关键因素：增长速率和容量。

增长速率表示人口每年的增长率，容量表示人口可以达到的最大数量。

logistic模型的基本形式如下：N(t) = K / [1 + (K/N0 - 1) * exp(-r * t)]N(t)表示时间t时刻的人口数量，K表示最大人口容量，N0表示初始人口数量，r表示人口增长速率。

在对中国未来人口进行预测分析时，我们需要确定模型的参数。

初始人口数量可以根据历史数据进行估计。

人口增长速率可以根据过去几十年的人口增长率进行计算。

最大人口容量需要根据中国国情和可持续发展的要求进行估算。

中国的人口增长速率在过去几十年一直处于较高水平，但随着经济社会发展和计划生育政策的实施，人口增长速率逐渐趋缓。

在未来，可以预计中国的人口增长速率将继续下降。

根据logistic模型对中国未来人口的预测分析，可以得出以下结论：随着时间的推移，中国人口数量将继续增长，但增长速率将逐渐减缓。

最终，人口数量将趋于一个稳定的最大容量，同时与资源和环境保持平衡。

需要注意的是，logistic模型是基于过去数据进行的预测分析，未来人口发展受到许多因素的影响，例如经济、政策、社会文化等，这些因素可能会引起人口变动的不确定性。

基于logistic模型的预测分析可以为中国未来人口发展提供一定的指导和参考，但在制定政策和决策时，还需要综合考虑多种因素，并及时更新模型参数，以保证预测结果的准确性和可靠性。

Logistic模型人口增长到一定数量后-Read

tr
N (t) rm p(s, t)ds 0
0
f (t)
t
生育率的分解
k(r, t) ~ (女性)性别比函数
b(r, t ) ~ (女性)生育数
[r1 , r2 ] ~ 育龄区间
f (t ) r2b(r, t )k(r, t ) p(r, t )dr r1
h(r,t) h(r)
1
,
s1 s2
12
,
,
s1
s2 sn1
n1 1

T
• 若L矩阵存在bi, bi+1>0, 则 k 1, k 2,3, , n
且
lim
k
x(k )
1k

cx*
,
c是由bi,
si,
x(0)决定的常数
解释
x(k) Lk x(0) L对角化 L P[diag(1 , n )]P 1
2、阻滞增长模型(Logistic模型)
此模型最初由19世纪比利时社会学家P.F.Verhulst提出的人口增长到一定数量后，增长率下降的原因：资源、环境等因素对人口增长的阻滞作用且阻滞作用随人口数量增加而变大
模型假设
1、地球上的资源有限,不妨设为1;
2、一个人的正常生存需要占用资源(这里事实上也内在的假定了地球的极限承载人口数有限);
~ 各年龄组种群数量不变
=1时 Lx* x* x* 1, s1, s1s2, s1s2 sn1 T
b1

s1

L

0
b2 0
s2

bn1 0
0
sn1

中国人口增长预测-数学建模

中国人口增长的预测和人口的结构分析摘要本文是在已知国家政策和人口数据的前提下对未来人口的发展进行预测和评估，选择了两种模型分别对人口发展的短期和长期进行预测。

模型一中我们在人口阻滞增长模型logistic模型的基础上进行改进，弥补了logistic原始模型仅仅能表示环境对人口发展趋势影响的缺陷，加入了社会因素的影响作为改进，保证了logistic改进模型的有效性和短期预测的正确性。

多次运用拟合的方法（非线性单元拟合，线性多元拟合）对数据进行整合，得到的改进模型对短期预测具有极高的准确性，证明了我们的修正方式与模型改进具有一定的正确性。

模型二中我们分别考虑了城、乡、镇人口的发展情况，利用不同年龄段存活率和死亡率的不同，采用迭代的方式也就是Leslie矩阵的方式对人口发展进行预测，迭代的方式不同于拟合，具有逐步递进的准确性，在参数正确的前提下，能够保证每一年得到的人口都有正确性，同时我们分男女两方面来考虑模型，不仅仅用静态的男女比例来估算人口总数，具有更高的准确性。

然而Leslie模型涉及的参数较多，如果采用动态模型的方式，计算量过大，我们首先用均值的方式对模型进行简化，同样得到迭代矩阵后的人口数值，发展趋势与预测相同，能够很好的预测中国人口的长期发展，同时，由于Leslie矩阵涉及多个参数，所以我们用最终的结果来表征老龄化程度，城乡比，抚养比等多个评价社会发展的参数，得到了较好的估计值，使模型在估算人口的基础上得到了推广和应用。

通过logistic改进模型和Leslie模型我们分别对中国人口发展进行短期和中长期预测，均能得到很好的效果，说明了我们的模型在适用范围内的准确性和实用性。

关键词：人口发展预测；logistic模型改进；参数拟合；Leslie迭代模型；一、问题重述中国是世界上人口最多的发展中国家, 人口问题始终是制约我国发展的关键因素之一，人口众多、资源相对不足、环境承载能力较弱是中国现阶段的基本国情,短时间内难以改变。

数学建模-人口增长模型

数学建模-人口增长模型人口增长模型是一种基于数理统计学方法的计算机模型，用于描绘全球各地的人口增长情况。

人口增长模型能够预测人口数量、年龄分布、死亡率、出生率、移民等方面的变化趋势，为社会规划带来指导性的建议，具有很高的实用价值。

本文将从多个方面来探究人口增长模型。

一、人口增长的三个阶段第一阶段：原始社会阶段，这个时期的人口增长缓慢。

由于食物水平低下和医疗条件落后，死亡率非常高，而出生率仍然很高。

第二阶段：传统社会阶段，人口增长迅速。

由于改进了农业技术、医疗技术以及水、电、煤等基础设施建设的改善，死亡率降低，但出生率仍然很高。

第三阶段：现代社会阶段，人口增长开始放缓。

由于生育规律的改变，人们生育晚、生育次数减少，导致出生率下降。

另一方面，医疗技术和生活水平的提高，使得人们的寿命增加，死亡率下降。

人口增长模型是一种以数学为基础、能够预测人口增长变化趋势的计算机模型。

它解决了传统的统计分析方法难以预测未来人口增长趋势的问题，方便了研究人口增长对于社会经济发展的影响。

目前，常用的人口模型有四种：1.经验模型：该模型主要是针对已有数据进行平衡分析，所以只能反映人口变动的历史趋势，难以预测未来人口变化。

2. 非参数回归模型：它又称为核回归模型，它是一种无参数模型，可以从数据本身中学习出应该如何比较好地去拟合数据，因此预测效果相较于经验模型提高了不少。

3. 参数回归模型：这种模型较为复杂，它基于特定的模型，通过拟合已有的数据，建立一个完整的模型，目的是预测新的数据变化趋势。

4. 知识驱动模型：该模型结合了经验模型和参数回归模型的基本特点，它将专家的知识与历史数据相结合，通过精细化的调整，建立能够反映人口增长趋势的模型。

该模型可广泛应用于国家人口预测、社会福利计划等领域。

人口增长有其基本的规律，这些规律可以帮助我们更好地了解和解决人口问题。

1.现代社会阶段的人口增长趋势是死亡率下降，而出生率下降，且死亡率的下降速度比出生率的下降速度快。

基于logistic模型对中国未来人口的预测分析

基于logistic模型对中国未来人口的预测分析中国是世界上人口最多的国家，人口问题一直是中国社会经济发展的重要因素之一。

通过对中国未来人口的预测分析，可以为政府制定相关政策提供依据，以应对可能出现的社会问题。

logistic模型是一种常用的人口预测模型，它基于数学和统计方法，能够通过对历史人口数据的分析，预测未来的人口趋势。

该模型假设人口增长具有一个饱和度，即人口增长速度随着人口数量的增加逐渐减缓，并最终趋于稳定。

要进行中国未来人口的预测分析，首先需要收集和整理大量的历史人口数据，包括人口数量和相关的社会经济指标。

然后，可以利用logistic模型对这些数据进行拟合，得出一个适合中国人口增长情况的数学模型。

logistic模型的数学表达式为：P(t) = K / (1 + A * e ^ (-B * t))P(t)表示时间t对应的人口数量，K表示人口达到饱和时的最大值，A和B是待定参数，e表示自然对数的底。

对于中国未来人口的预测分析，需要首先确定人口的饱和最大值K。

这可以通过对历史数据的分析，结合中国的社会经济发展情况，来估计中国的人口饱和状态。

考虑到资源的限制和生活质量的改善，人口不可能无限制地增长。

相关的政策和社会变化也需要考虑在内。

确定了人口饱和最大值后，可以使用历史数据拟合logistic模型，得到模型的参数A 和B。

然后，可以根据参数和已有的时间数据，预测未来的人口趋势。

logistic模型的预测结果需要进行验证和修正。

由于人口预测是一个复杂的问题，涉及到许多因素，如经济发展、社会政策、生育率和死亡率等，因此需要综合考虑其他相关的因素。

不同地区之间的差异也需要进行分析和预测。

在进行中国未来人口的预测分析时，还需要考虑到数据的可靠性和准确性。

历史数据的收集和整理需要尽可能的全面和准确，以提高模型的预测效果。

使用多种数据源并进行数据验证可以提高模型的准确性。

基于logistic模型进行中国未来人口的预测分析可以为政府决策提供参考依据，但需要注意模型的合理性和数据的可靠性，以及综合考虑其他相关因素。

【logistic人口阻滞增长模型】-与数共舞：数学建模与实验系列07

【logistic人口阻滞增长模型】-与数共舞：数学建模与实验系列07
我们将在下一篇的微文中继续探索 Logistic 人口模型的一种简化模型, 从而了解混沌以及特点.
上面就是利用 Mathematica (Wolfram语言) 创造出来动手中学习人口论模型的例子.
好了, 现在让我们在下一篇的数学实验与建模课堂再见. 这里感谢各位每一位看到这里的老师和
朋友!
Thanks! Happy Weekend!
相关文章:
【马尔萨斯人口模型】- 与数共舞: 06
【人口模型中的两种级数】- 与数共舞: 05
【线性规划】-与数共舞: 04
【神秘数字π的计算】-与数共舞: 03
【购房贷款的选择】-与数共舞: 02
【购房贷款的选择】-与数共舞: 01
【挥舞翅膀的函数】- 数学函数可视化之魅 I。

人口指数增长模型和Logistic模型学习资料

根据美国人口从1790年到1990年间的人口数据（如下表），确定人口指数增长模型和Logistic 模型中的待定参数，估计出美国2010年的人口，同时画出拟合效果的图形。

表1 美国人口统计数据1860 1870 1880 1890 1900 1910 指数增长模型：rt e x t x 0)(=Logistic 模型：()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭解：模型一:指数增长模型。

Malthus 模型的基本假设下，人口的增长率为常数，记为r ，记时刻t 的人口为 )(t x ，（即)(t x 为模型的状态变量）且初始时刻的人口为0x ，因为⎪⎩⎪⎨⎧==0)0(x x rxdt dx由假设可知0()rt x t x e = 经拟合得到：}2120010120()ln ()ln ,ln (),,ln rt a y a t a x t x e x t x rt r a x e y x t a r a x =+=⇒=+⇒=====程序：t=1790:10:1980;x(t)=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5123.2 131.7 150.7 179.3 204.0 226.5 ];y=log(x(t));a=polyfit(t,y,1) r=a(1),x0=exp(a(2)) x1=x0.*exp(r.*t); plot(t,x(t),'r',t,x1,'b') 结果：a = 0.0214 -36.6198r= 0.0214 x0= 1.2480e-016所以得到人口关于时间的函数为：0.02140()t x t x e =，其中x0 = 1.2480e-016，输入：t=2010;x0 = 1.2480e-016; x(t)=x0*exp(0.0214*t)得到x(t)= 598.3529。

数学建模预测中国人口增长

数学建模预测中国人口增长并就“全面二胎”政策对未来几年人口影响做出思考一、摘要日益增长的人口数量导致了资源短缺，环境恶化。

通过对1900年到2017年的全国人口数量的统计数据，结合所学知识，建立数学模型logistic模型。

模型通过假设条件，根据假设建立合理的模型，以及MATLAB对数据的处理，并且运用数据拟合求模型的解r，最后通过的的r预测中国未来几年内的人口变化规律，从而可以合理的有计划的利用资源，使环境和资源实现可持续发展。

另外，全面二胎政策2016年正式实施，对于人口结构有问题中国，全面二胎政策将可能对人口模式造成怎样的影响。

通过查阅大量文献资料，对二胎政策的影响做出思考。

关键词：人口模型中国人口数量全面二胎政策二、问题的提出人口问题是当今世界的三大问题之一，人口的剧烈增长导致资源日益短缺，环境日益恶化，认识和了解人口数量的变化规律，做出较准确的估测，从而有效地控制人口增长以及合理有效地开发能源和环境保护，通过1900年到2017年的人口数据变化的规律，对2018年到2023年全国人口数量做出合理的预测。

三、问题分析通过对数据的观察，运用MATLAB的画图功能，可以看出随着时间增长，人口数量也在急剧增长，而且图像与指数模型吻合，所以不妨假设人口模型符合指数模型，建立第一个数学模型。

但是通过对指数模型和实际数据的比对，发现指数模型在1978年到2003年间与实际较符合，但是2005到2018期间误差越来越大，通过对指数的性质可以了解到，当自变量无穷大时，函数趋于去穷大，这与事实相悖，因为现实资源是有限的，当人口到达某一数值后，由于各种资源、环x，境因素的限制，人口数量将达到某一稳定值，所以，不妨假设最大人口数为m当人口数达到最大的时候，增长率为0，建立logistic阻滞增长数学模型。

四、模型假设与简化1 假设：表中所给出的数据是中国人口的真实值。

2 假设：一些大型自然灾害不考虑在内，如战争，地震等。

Logistic模型的参数估计及人口预测

Logistic模型的参数估计及人口预测一、本文概述本文旨在探讨Logistic模型的参数估计及其在人口预测中的应用。

Logistic模型是一种广泛应用于生物学、生态学、社会科学等领域的统计模型，尤其在人口增长预测中发挥着重要作用。

本文将首先介绍Logistic模型的基本原理和参数估计方法，包括模型的构建、参数求解以及模型的检验与评估。

随后，本文将重点分析Logistic模型在人口预测中的应用。

通过收集相关人口数据，运用Logistic模型进行参数估计，并对未来人口增长趋势进行预测。

本文还将探讨不同参数设置对预测结果的影响，以提高预测的准确性和可靠性。

本文将对Logistic模型在人口预测中的优势和局限性进行分析，并提出相应的改进建议。

通过本文的研究，旨在为人口预测提供更为科学、有效的方法，为政府决策、人口规划和社会经济发展提供有力支持。

二、Logistic模型的基本原理Logistic模型，也称为逻辑增长模型，是一种广泛应用于生态学和人口学等领域的数学模型。

该模型基于生物种群增长规律，尤其是当种群增长受到环境资源限制时的情况。

Logistic模型的基本原理在于它假设种群的增长速度在开始时由于资源充足而迅速增加，但随着种群密度的增加，资源限制和种内竞争导致增长速度逐渐减慢，直到最终种群达到其最大可能规模，即环境容纳量。

\frac{dN}{dt} = rN\left(1 - \frac{N}{K}\right) ]其中，(N) 是种群数量，(t) 是时间，(r) 是种群的内禀增长率（即在没有环境限制时的最大增长率），而 (K) 是环境容纳量，即种群数量的最大可能值。

这个模型的核心在于其非线性项 (1 - \frac{N}{K})，它反映了种群增长速度随种群密度的变化。

当种群数量 (N) 远小于环境容纳量 (K) 时，(1 - \frac{N}{K}) 接近1，种群增长迅速。

随着 (N) 接近 (K)，这个项趋于0，种群增长速度减慢，最终停止增长。

人口增长logistic模型的拟合1

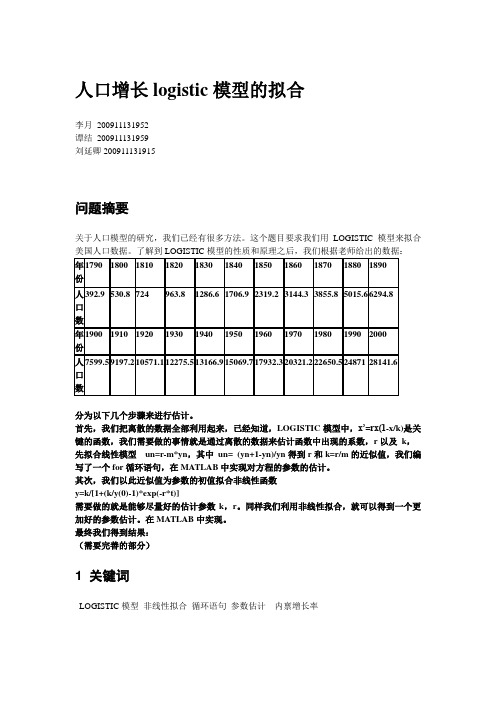
人口增长logistic模型的拟合李月200911131952谭结200911131959刘延卿200911131915问题摘要关于人口模型的研究，我们已经有很多方法。

这个题目要求我们用LOGISTIC模型来拟合美国人口数据。

了解到LOGISTIC模型的性质和原理之后，我们根据老师给出的数据：分为以下几个步骤来进行估计。

首先，我们把离散的数据全部利用起来，已经知道，LOGISTIC模型中，x’=rx(1-x/k)是关键的函数，我们需要做的事情就是通过离散的数据来估计函数中出现的系数，r以及k，先拟合线性模型un=r-m*yn，其中un= (yn+1-yn)/yn得到r和k=r/m的近似值，我们编写了一个for循环语句，在MATLAB中实现对方程的参数的估计。

其次，我们以此近似值为参数的初值拟合非线性函数y=k/[1+(k/y(0)-1)*exp(-r*t)]需要做的就是能够尽量好的估计参数k，r。

同样我们利用非线性拟合，就可以得到一个更加好的参数估计。

在MATLAB中实现。

最终我们得到结果：（需要完善的部分）1 关键词LOGISTIC模型非线性拟合循环语句参数估计内禀增长率2 问题的重述3 问题的分析问题的关键是要做一个LOGISTIC模型。

在模型的建立中，至关重要的是对参数的估计。

我们知道的LOGISTIC模型，x’=rx(1-x/k)是这个模型的基础，所以我们最重要的任务就是要合理估计参数。

分为以下几个步骤来进行估计。

1我们把离散的数据全部利用起来，已经知道，LOGISTIC模型中，x’=rx(1-x/k)是关键的函数，我们需要做的事情就是通过离散的数据来估计函数中出现的系数，r以及k，2先拟合线性模型un=r-m*yn，其中un= (yn+1-yn)/yn得到r和k=r/m的近似值，我们编写了一个for循环语句，在MATLAB中实现对方程的参数的估计。

3我们以此近似值为参数的初值拟合非线性函数y=k/[1+(k/y(0)-1)*exp(-r*t)]需要做的就是能够尽量好的估计参数k，r。

人口增长的Logistic模型分析及其应用资料讲解

人口增长的L o g i s t i c模型分析及其应用人口增长的Ｌｏｇｉｓｔｉｃ模型分析及其应用作者：熊波来源：《商业时代》2008年第27期◆中图分类号：C923 文献标识码：A内容摘要：本文运用迭代的方法计算出人口极限值xm和人口增长率r，用 Logistic模型预测了我国人口未来的发展趋势，并根据预测的结果提出了相应的对策与建议。

关键词：人口 Logistic模型迭代人口增长问题相关研究最早注意人口问题的是英国经济学家马尔萨斯，他在1798 年提出了人口指数增长模型。

这个模型的基本假设是：人口的增长率是一个常数。

记t时刻的人口总数为x(t)。

初始时刻t=0时的人口为x0。

人口增长率为r，r表示单位时间内x(t)的增量与x(t)的比例系数。

那么，时刻t到时刻t+Δt内人口的增量为x(t+Δt)-x(t)=rx(t)Δt。

于是x(t)满足下列微分方程的初值问题，他的解为x(t)=x0ert。

在r>0时，人口将按指数规律增长。

但是不管生物是按算术级数、几何级数还是按指数曲线变化，随着时间增长生物数量将趋于无穷大。

然而，实际情况却不然，实验指出在有限的空间内，一开始生物以较快速度增长，到一定时期生物增长量就会减缓，生物数量趋于稳定。

历史上的人口统计数据也表明，当一个国家的社会稳定时，一定时期内马尔萨斯模型是符合实际的，但是如果时间比较长或社会发生动荡时，马尔萨斯模型就不能令人满意了。

原因是随着人口的增加，自然资源、环境条件等因素对人口增长开始起阻滞作用，因而人口增长率不断下降。

基于以上考虑荷兰生物学家Verhaust对原人口发展模型进行了改造，于1838 年提出了以昆虫数量为基础的Logistic 人口增长模型。

这个模型假设增长率r是人口的函数，它随着x的增加而减少。

最简单的假定是r是x的线性函数，其中r称为固有增长率，表示x→0时的增长率。

由r（x）的表达式可知，x=xm时r=0。

xm表示自然资源条件能容纳的最大人口数。

数学建模与人口增长问题

跨学科合作：加强数学建模与其他学科的合作，如生物学、经济学等，共同研究人口增长问题，推动相关领域的发展。
数学建模在人口增长问题中的应用：通过建立数学模型，对人口增长进行预测和模拟，为政策制定提供科学依据。
未来发展方向：随着大数据和人工智能技术的不断发展，数学建模将更加精准地预测人口增长趋势，为可持续发展提供有力支持。
定义变量：人口数量、出生率、死亡率等
求解模型：通过数学方法求解模型，得到未来人口数量
添加标题
添加标题
添加标题
添加标题
建立模型：根据人口增长规律和影响因素，建立数学模型
应用模型：将模型应用于实际人口数据，预测未来人口趋势
模型假设：对人口增长进行合理假设，简化问题模型建立：根据假设建立数学模型，描述人口增长规律模型求解：采用适当的数学方法求解模型，得出人口增长预测结果模型验证：通过实际数据与预测结果进行对比，检验模型的准确性和可靠性
模型验证与评估：验证所建模型的准确性和可靠性，以及在实际应用中的效果和价值
预测未来人口趋势，为政策制定提供科学依据优化资源配置，提高人口管理和服务水平揭示人口发展规律，促进人口与经济社会协调发展创新人口研究方法，推动人口科学的发展
挑战：数据获取与处理
机遇：预测未来人口增长趋势
添加标题
和可靠性
拓展研究领域，探究人口增长与其他领域（如气候变化、资源利用等）之间的联
系和影响
汇报人：XX
通过数学建模，我们可以评估不同的人口政策对人口增长的影响，增长的规律和趋势，为经济和社会发展提供参考。
深入研究不同数学模型在人口增长问题中的应用和效果
探索人口增长与社会、经济、环境等多因素之间的相互作

数学应用典型案例模型1马尔萨斯人口增长(指数增长)模型

xt x0ert (1-4)
这个解表明人口将按指数规律增长，这就是世界著名的 Malthus 人口模型。 1.6 模型分析
上述数学模型是在所给出的模型假设条件下得到的。如果人口的发展确实是按照这个假设条件在发展，那么这个模型应该是对的。用 19 世纪以前欧洲一些地区人口统计数据检验这个模型，得到令人满意的结果。但是，人口的发展真的是按照这样的规律发展吗？在 Malthus 以前的 100 年里，人口发展基本上是按照这个规律发展的。那么，以后人口的发展是否还将按照这个规律发展？从这个模型本身用纯粹的数学方法就可分析出结论。
图 3-1
我们用 x（t）表示在时间 t 时野兔的数量，y（t）表示在时间 t 时狐狸的数量。
根据上述分析，野兔（被捕食）的增长速率 dx 一方面与自身数量 x 成正比； dt
另一方面，由于狐狸（捕食）的存在又制约了野兔的增长速率，故模型又假设野兔的增长速率是一个与狐狸数量成正比的量的减函数。因此，被捕食方程（野兔
模型 3 捕食——被捕食模型所用知识：微分方程组内容介绍：
设在一个海岛上考察狐狸----野兔生态系统。狐狸吃野兔，野兔吃草（假设草总是充足的）。野兔（被捕食）的数量取决于两个方面：自身数量与狐狸（捕食）的数量。狐狸的数量也取决于两个方面：自身数量与野兔的数量。每个群体的改变必然引起另一群体的改变。例如，野兔数量增加，狐狸容易捕食，狐狸的数量也随着增加；狐狸数量的增加，吃掉许多野兔，引起野兔的数量减少，狐狸进入饥饿状态，狐狸的数量又减少，但这又引起野兔的数量增加；从而出现反复循环。下图所画曲线表示狐狸----野兔生态系统岁时间而变化的情况。
天津工业大学数学建模教学团队编写
数学应用典型案例
模型 1 马尔萨斯人口增长（指数增长）模型所用知识：常微分方程内容介绍：

数学建模人口增长模型

人口增长预测模型摘要本文建立了我国人口增长的预测模型，对各年份全国人口总量增长的中短期和长期趋势作出了预测，并对人口老龄化、人口抚养比等一系列评价指标进行了预测。

最后提出了有关人口控制与管理的措施。

模型Ⅰ：建立了Logistic人口阻滞增长模型，利用附件2中数据，结合网上查找补充的数据，分别根据从1954年、1963年、1980年到2005年三组总人口数据建立模型，进行预测，把预测结果与附件1《国家人口发展战略研究报告》中提供的预测值进行分析比较。

得出运用1980年到2005年的总人口数建立模型预测效果好，拟合的曲线的可决系数为0.9987。

运用1980年到2005年总人口数据预测得到2010年、2020年、2033年我国的总人口数分别为13.55357亿、14.18440亿、14.70172亿。

模型Ⅱ：考虑到人口年龄结构对人口增长的影响，建立了按年龄分布的女性模型（Leslie模型）：以附件2中提供的2001年的有关数据，构造Leslie矩阵，建立相应Leslie模型；然后，根据中外专家给出的人口更替率1.8，构造Leslie矩阵，建立相应的 Leslie模型。

首先，分别预测2002年到2050年我国总人口数、劳动年龄人口数、老年人口数（见附录8），然后再用预测求得的数据分别对全国总人口数、劳动年龄人口数的发展情况进行分析，得出：我国总人口在2010年达到14.2609亿人，在2020年达到14.9513亿人，在2023年达到峰值14.985亿人；预测我国在短期内劳动力不缺，但须加强劳动力结构方面的调整。

其次，对人口老龄化问题、人口抚养比进行分析。

得到我国老龄化在加速，预计本世纪40年代中后期形成老龄人口高峰平台，60岁以上老年人口达4.45亿人，比重达33.277%；65岁以上老年人口达3.51亿人，比重达25.53%；人口抚养呈现增加的趋势。

再次，讨论我国人口的控制，预测出将来我国育龄妇女人数与生育旺盛期育龄妇女人数，得到育龄妇女人数在短期内将达到高峰，随后又下降的趋势的结论。

数学建模模版之人口增长问题

p1=1050, n1=10, p1/n1=105 p2=1000, n2=10, p2/n2=100 p1/n1– p2/n2=5 但后者对A的不公平程度已大大降低!
“公平”分配方法
若 p1/n1> p2/n2 ，定义
将绝对度量改为相对度量
p1 / n1 p2 / n2 rA (n1 , n2 ) ~ 对A的相对不公平度 p2 / n2
0
t
x(t)~S形曲线, x增加先快后慢
阻滞增长模型(Logistic模型)
参数估计用指数增长模型或阻滞增长模型作人口预报，必须先估计模型参数 r 或 r, xm
• 利用统计数据用最小二乘法作拟合例：美国人口数据（单位~百万）
1860 1870 1880 …… 1960 1970 1980 1990 31.4 38.6 50.2 …… 179.3 204.0 226.5 251.4
2
6
2
模型应用
回答提出的问题：由模型算得 n = 4450 时 t = 116.4分，剩下的录像带能录 184-116.4= 67.6分钟的节目。揭示了“t 与 n 之间呈二次函数关系”这一普遍规律，当录像带的状态改变时，只需重新估计 a,b 即可。
第三章
3.1
3.2 3.3
简单的优化模型
ni (ni 1)
, i 1,2， , m
该席给Q值最大的一方
Q 值方法
三系用Q值方法重新分配 21个席位
按人数比例的整数部分已将19席分配完毕
甲系：p1=103, n1=10 乙系：p2= 63, n2= 6 丙系：p3= 34, n3= 3
用Q值方法分配第20席和第21席

logistic人口模型代码

logistic人口模型代码Logistic人口模型是一种用于描述人口增长的数学模型。

它基于人口增长受到资源限制的假设，通过考虑出生率、死亡率和迁移率等因素，预测未来人口的变化趋势。

本文将介绍Logistic人口模型的原理、应用以及相关的计算代码。

Logistic人口模型的原理是基于人口增长的S型曲线。

在初始阶段，人口增长呈指数增长，但随着资源的有限性，人口增长逐渐趋于饱和，增长速度放缓。

模型的基本方程如下：dP/dt = r * P * (1 - P/K)其中，dP/dt表示单位时间内人口数量的变化率，r表示人口增长率，P表示当前时间的人口数量，K表示环境的承载能力，即最大人口数量。

Logistic人口模型的代码实现可以使用各种编程语言，例如Python。

下面是一个简单的Python代码示例：```pythonimport numpy as npimport matplotlib.pyplot as pltdef logistic_population_growth(r, K, P0, t):P = []P.append(P0)for i in range(1, len(t)):dP = r * P[i-1] * (1 - P[i-1]/K)P.append(P[i-1] + dP)return Pr = 0.02 # 人口增长率K = 1000 # 环境的承载能力P0 = 100 # 初始人口数量t = np.linspace(0, 100, 100) # 时间范围population = logistic_population_growth(r, K, P0, t)plt.plot(t, population)plt.xlabel('Time')plt.ylabel('Population')plt.title('Logistic Population Growth')plt.show()```上述代码使用了NumPy库来生成时间范围，matplotlib库用于绘制人口变化趋势图。

人口增长的Logistic模型分析及其应用

人口增长的Ｌｏｇｉｓｔｉｃ模型分析及其应用本文运用迭代的方法计算出人口极限值xm和人口增长率r，用Logistic模型预测了我国人口未来的发展趋势，并根据预测的结果提出了相应的对策与建议。

关键词：人口Logistic模型迭代人口增长问题相关研究最早注意人口问题的是英国经济学家马尔萨斯，他在1798 年提出了人口指数增长模型。