基于MATLAB的信道编码分析

合集下载

信道编码实验报告

信道编码实验报告引言：信道编码是一种常用的通信技术，用于增强数据传输的可靠性和效率。

通过在发送端对数据进行编码，并在接收端进行解码，可以有效地纠正或检测在信道传输过程中产生的错误。

本实验旨在研究不同的信道编码方法，并分析它们在不同信道条件下的性能。

一、实验目的：1.了解信道编码的概念和基本原理；2.掌握常用的信道编码方法和相关算法；3.通过实验验证不同信道编码方法的性能；4.分析信道编码在不同信道条件下的适用性。

二、实验原理：1.信道编码概述：信道编码主要分为前向纠错编码（Forward Error Correction, FEC）和自动重传请求（Automatic Repeat reQuest, ARQ）两类。

其中，FEC方法通过在数据流中引入冗余信息，使接收端能够检测和纠正一定数量的错误。

而ARQ方法则是通过接收端向发送端发送请求进行重传，从而实现数据的可靠传输。

2.常用的信道编码方法：在实验中，我们主要研究了以下几种常用的信道编码方法：（1）奇偶校验编码：奇偶校验编码是最简单的一种编码方式，它通过在数据末尾添加一个校验位来实现错误检测。

若校验位与数据位中的奇偶性不一致，则认为出现错误。

（2）海明码编码：海明码是一种通过添加冗余位来实现错误检测和纠正的编码方法。

通过在数据位中插入冗余位，接收端可以检测到并纠正一定数量的错误。

（3）卷积码编码：卷积码是一种递归线性均匀的编码方法，通过引入冗余信息来增强信号的可靠性。

它具有较好的纠错性能，广泛应用于无线通信领域。

三、实验过程：1.实验环境准备：在实验中，我们使用了Matlab软件进行信道编码的仿真实验。

通过编写相应的算法和程序，可以模拟不同的信道编码方法，并分析它们的性能。

2.编写奇偶校验编码程序：首先，我们编写了奇偶校验编码的程序，通过向数据流中添加校验位实现错误检测。

然后，对不同的信道条件进行仿真实验，并记录不同错误率下的传输性能。

3.编写海明码编码程序：接下来，我们编写了海明码编码的程序，通过插入冗余位实现错误检测和纠正。

基于matlab的信道编码仿真(可编辑)

基于matlab的信道编码仿真（可编辑）基于matlab的信道编码仿真海南大学毕业论文(设计)题目:基于matlab的信道编码仿真学号:姓名:年级:学院:信息科学技术学院系别:电子信息工程专业:电子信息工程指导教师: 完成日期:摘要通信技术的飞速发展,信道编码已经成功地应用于各种通信系统中。

以及各种传输方式对可靠性要求的不断提高,信道编码技术作为抗干扰技术的一种重要的手段,在数字通信技术领域和数字传输系统中显示出越来越重要的作用。

信道编码的目的是为了改善通信系统的传输质量。

由于实际信道存在噪声和干扰,使发送的码字与信道传输后所接收的码字之间存在差异,称这种差异为差错。

一般情况下,信道噪声、干扰越大,码字产生差错的概率也就越大。

本文利用matlab对二进制对称信道BSC,高斯白噪声信道AWGN两种信道的仿真,(7,4)Hamming码对信道的仿真,通过误码率的曲线图来了解信道的编码。

并利用matlab的simulink模块仿真,运用simulink里的卷积码viterbi译码器来对二进制对称信道和高斯白噪声信道的仿真,观察误码率的曲线图来了解2个信道的不同。

关键字:matlab,信道,编码,译码,Simulink。

AbstractWith the rapid development of communication technology, channelcoding has been successfully applied to various communications systems. And a variety of transmission of the continuous improvement ofreliability requirements, anti-jamming channel coding technology as an important means of technology in the field of digital communications technology and digital transmission systems in a more and more important role The purpose of channel coding is to improve the transmissionquality of communications systems. As the actual existence of thechannel noise and interference, the transmitted codewords and channel transmission received after the difference between code words, said this difference is wrong. Under normal circumstances, channel noise, the greater the interference, the code word generated the greater the probability of errorIn this paper, matlab binary symmetric channel BSC, Gaussian white noise channel AWGN two channel simulation, 7,4 Hamming code simulation of the channel, through the bit error rate curve to understand the channel coding. Using matlab to simulink block simulation, using simulink in the viterbi decoder to convolutional codes on the binary symmetric channel and Gaussian white noise channel simulation, observation error rategraphs to understand the two different channelsKeywords: matlab, channel, coding, decoding, Simulink.目录1引言 11.1选题的目的和意义 11.2本选题的理论依据、研究内容 12.信道编码以及其运行环境MATLAB的介绍 2 2.1 信道编码的概念及分类 22.2 信道编码定理及信道编码中所包含的各种码类的简介 22.2.1卷积码 22.2.2线性分组码 32.2.3循环码 32.3 MATLAB语言的简介 42.4 Simulink 53.信道 53.1二进制对称信道(BSC) 53.2二进制删除信道(BEC) 63.3高斯白噪声信道AWGN 64. Hamming码 74.1汉明码 74.2校验方法 74.3汉明码编码 94.3.1汉明码对高斯白噪声信道 94.3.2汉明码对二进制对称信道的仿真 115.卷积码 155.1卷积码定义与原理 155.2维特比译码原理 155.3卷积码译码器对高斯白噪声信道的设计与仿真 18 5.3.1卷积码译码器的设计与仿真 195.3.2简化维特比译码器的仿真 225.3.3卷积码译码器的误码率分析 245.4卷积编码器在二进制对称信道(BSC)中的性能 256.卷积码译码器对二进制对称信道和高斯白噪声信道仿真比较 307.总结 31致谢 32参考文献 33附录1: 34附录2: 37附录3: 40附录4: 411引言1.1选题的目的和意义数字信号在传输中往往由于各种原因,使得在传送的数据流中产生误码,从而使接收端产生图象跳跃、不连续、出现马赛克等现象。

基于MATLAB的信道编码教学实验软件设计与实现

第24卷第1期 2005年1月实验室研究与探索RESEARCH AND EXPLORATION IN LABORATORYVol.24No.1 Jan.2005基于MATLAB 的信道编码教学实验软件设计与实现张海涛, 王福昌(华中科技大学电工电子教学基地湖北武汉430074)摘要:介绍了基于MATLAB 的信道编码教学实验软件,主要包括实验操作界面制作以及循环码和卷积码编译码。

关键词: 矩阵实验室软件包;循环码;卷积码;编译码;界面中图分类号:TN911.22文献标识码:B文章编号:1006 7167(2005)01 0046 04Design and Realization of the Teaching ExperimentalSoftware on Channel Coding with MATLABZ HANG Hai tao , WANG Fu chang(Instruction Base of Electrotechnics&Electtronics,Huazhong Univ.of Science and Technology,W uhan 430074,China)Abstract :This paper introduceds a teaching experimentel software based on channel coding with MATLAB,including the design of experiment interface ,the encode decode process of cyclic code and convolutional code.Key words :MATLAB (Matrix Laboratory);cyclic code;convolutional code;encode decode;interface收稿日期:2004 04 09作者简介:张海涛(1978-),男,汉族,湖北红安人,硕士研究生三年级,主要从事通信与信号处理方面的科研。

基于matlab的调制解调与信道编译码仿真

基于MATLAB 的调制解调与信道编译码仿真摘要:随着信息时代的步伐，通信技术得到了全面的发展，信息技术已成为了21世纪最强大的国际化动力。

在通信技术中，信息的调制、解调和误码纠错都占有重要的地位。

MATLAB 作为一款功能强大的数学工具软件，在通信领域中得到了很广泛的应用。

本文基于MATLAB 对信号进行模拟仿真设计，实现对二进制相移键控、循环码的纠错仿真、BPSK 的调制解调等进行仿真设计。

关键字：MATLAB 、调制解调、2PSK 、BPSK 、重复码。

一、二进制和四进制相移键控调制仿真设计1.1 二进制相移键控（2PSK ）原理相移键控是利用载波的相位变化来传递数字信息的，而振幅和频率保持不变。

在2PSK 中常用0和π分别表示二进制“0”和“1”，2PSK 的信号时域表达式为:2t )e c pskn w t ϕ+（）=Acos( n ϕ表示为第n 个符号的绝对相位，因此上式可改写为:2Acosw t -Acosw t 1-P Pe {psk c c t （）=概为概率为率由于表示信号的两种码形完全相同，极性相反，故2PSK 信号一般表示一个双极性全占空矩形脉冲序列与一个正弦载波相乘。

2p ()sk e t =s(t)cosw c t其中：s(t)=∑n a g(t-nTs);这里，g(t)为脉宽Ts 的单个矩形脉冲；n a 的统计特征为 n a =概率为概率为即发送二进制“0”时（a 1n =+），2p ()sk t e 取0相位；发送二进制符号“1”时（a 1n =+），2p()sk t e 取π相位。

这种以载波的不同相位直接法去表示相应二进制数字信号的调制方式，称为二进制绝对相移方式。

2PSK信号时间波形2PSK信号的调制原理如下图所示，与2ASK的产生方法相比，只是对s(t)的要求不同，在2ASK中s(t)是单极性的，而在2PSK中s(t)是双极性的基带信号。

（a）模拟调制方法（b）键控法2PSK信号的解调通常采用相干解调法，解调原理如下原理框图所示，在相干解调中，如何得到与接受的2PSK信号同频同相的相干载是关键问题，后续进一步介绍。

基于MATLAB的通信系统信道编码的研究及其仿真

本科毕业设计论文题目：基于MATLAB的通信系统信道编码的研究及其仿真所在系：电气与信息工程系专业：电子信息工程班级：学号学生姓名：指导老师：摘要论文题目：基于MATLAB的通信系统信道编码的研究及仿真学科专业：电子信息工程姓名：班级：电信学号：指导教师：摘要现代社会发展要求通信系统功能越来越强，性能越来越高，构成越来越复杂:另一方面，要求通信系统技术研究和产品开发缩短周期，降低成本，提高水平。

这样尖锐对立的两个方面的要求，只有通过使用强大的计算机辅助分析设计技术和工具才能实现。

现代计算机科学技术快速发展，已经研发出了新一代的可视化的仿真软件。

这些功能强大的仿真软件，使得通信系统仿真的设计和分析过程变得相对直观和便捷，由此也使得通信系统仿真技术得到了更快的发展。

通信系统仿真贯穿着通信系统工程设计的全过程. 对通信系统的发展起着举足轻重的作用。

通信系统仿真具有广泛的适应性和极好的灵活性，有助于我们更好地研究通信系统性能。

本文首先介绍了通信系统仿真的墓本内容，包括通信系统仿真的一般步骤MATLAB中的一种可视化仿真工具Simulink 以及S-函数的相关概念。

从理论上对通信系统进行深入细致的研究是非常必要的。

本文对通信系统中的一些重要环节，包括信道、噪声、模拟信号的数字化传输、信道编码以及信号调制的原理、方法和过程进行了详细的阐述。

理论知识是用来指导具体实践的。

本文在深刻理解通信系统理论的基础上利用MATLAB强大的仿真功能，设计了许多具体的通信系统仿真模型。

在仿真模型设计过程中，本文对模型设计的目的、具体的结构组成、仿真流程以及仿真结果都给出了具体详实的分析和说明。

最后,本文对所做的研究工作进行了总结，并且提出了今后的工作和研究方向。

关键词：通信系统，仿真，MATLAB. S-函数，系统设计西安交通大城市学院本科生毕业设计（论文）ABSTRACTTitle: The communications system based on MATLAB simulation research and channel codingApplicant: Li JieSpeciality: Electronic information projectABSTRACTModern social development requirements will increasingly communication system, performance and high, more and more complex, on the other hand, the requirement communication system technology research and product development and shorten the cycle, reduce cost, improve level. So sharp opposition in two aspects, only through the use of powerful computer aided analysis and design techniques and tools to achieve. The modern computer science and technology development, have developed a new generation of visual simulation software. These powerful simulation software, communication system design and analysis of the simulation process relatively intuitive and convenient, which also makes communication system simulation technology faster development. Communication system simulation through the communication system design process of the development of communication system. Plays an important role. Communication system Simulation has extensive adaptability and good flexibility and help us to better research communications system performance. This paper introduces the system simulation of the content, including the communication system of general steps of MATLAB simulation of a visualization simulation tools and Simulink related concepts - function. From the theory of communication system intensive study is very necessary. This paper is an important link of some of the communication system, including channel simulation signal and noise, the digital transmission, channel coding modulation signal and the principle, method and process in detail. Knowledge is used to guide practice. Based on the profound understanding of the communication system based on the theory of MATLAB simulation, the design of the function of many specific communication system simulation model. In the design process simulation model, this model is designed, specific structure, simulation process and the simulation results are given detailed analysis and explanation. Finally, this paper studies are summarized, and working for the future work and puts forward research direction.KEY WORDS: communication system, simulation of MATLAB. S - function, systemdesign西安交通大城市学院本科生毕业设计（论文）目录目录摘要 (I)ABSTRACT (III)1 绪论 (1)1.1选题意义 (1)1.2 选题目的 (2)1.3 国内外研究现状 (2)1.4 主要研究内容及技术方法 (2)1.5研究课题的方案设计 (3)2 通信原理及通信系统仿真简介 (5)2.1 通信发展及趋势 (5)2.1.1 通信发展史简介 (5)2.2 通信的基本概念 (6)2.3 通信系统仿真及其重要作用 (7)2.3.1 通信系统仿真的概念 (7)2.3.2 通信系统仿真的重要作用 (8)3 通信系统仿真相关内容概述 (11)3.1 通信系统仿真的一般步骤 (11)3.1.1 仿真建模 (11)3.1.2 仿真实验 (11)3.1.3 仿真分析 (12)3.2 用于仿真的软件 (12)3.2.1 MATLAB (12)3.2.2 MATLAB的发展及特点 (13)3.2.3 MATLAB在通信仿真中的应用 (14)3.3 SIMULINK (15)3.3.1 Simulink概述 (15)3.3.2 Simulink仿真过程 (19)3.4 S-函数 (20)4 通信系统信道编码的研究及仿真 (23)4.1 信道编码概念 (23)4.1.1 信道编码概念及任务 (23)4.2 信道编码的分类 (23)4.2.1分组编码 (23)4.2.2循环冗余码 (24)西安交通大城市学院本科生毕业设计（论文）4.2.3卷积编码 (24)4.3仿真系统设计 (25)4.3.1 RS编码纠错性能分析 (25)4.3.2 CRC-16编码检错性能分析 (32)4.3.3卷积编码软判决译码和硬判决译码性能分析 (40)5.1 总结 (49)5.2展望 (49)致谢 (51)参考文献 (53)1 绪论1 绪论1.1选题意义随着现代通信系统的飞速发展,计算机仿真已成为今天分析和设计通信系统的主要工具,在通信系统的研发和教学中具有越来越重要的意义。

信道编码-MATLAB仿真实验中的应用

⚫ 输入参数2——trellis，卷积码编码器的网格结构；
⚫ 输入参数3——tblen，a positive integer scalar，用于规定回溯深度。If the code rate is 1/2, a typical value for tblen is about five times the constraint length of the code；
⚫ 输入参数1——msg，未编码的信息符号序列，二进制矢量形式； ⚫ 输入参数2——trellis，卷积码编码器的网格结构； ⚫ 输出参数——code，编码后的卷积码符号序列，二进制矢量形式。
⚫ 卷积码译码的MATLAB函数为：
⚫ vitdec
卷积码的维特比译码（二进制数据）
⚫ 最常用的函数格式为：
⚫ 输入参数5—— dectype，指示译码器的判决类型。其取值不同，对应的输入参数1——code的数据类型也不同。其取值如下表：
Values of Meaning dectype Input
'unquant' 软判决，code的数据类型为实数（未量化），其中1表示逻辑‘0’，-1表示逻辑‘1’ 。
decoded = vitdec(code,trellis,tblen,opmode,dectype)；
decoded = vitdec(code,trellis,tblen,opmode,'soft',nsdec)
⚫ 输入参数1——code，维特比译码器的输入符号序列，矢量形式。以前述2/3码率的编码器结构为例，每个符号代表编码器输出的3个bit；
一、信道编码概述四、卷积码译码
二、卷积码的结构描述
三、卷积码编码
⚫ 信道编码又称检纠错编码，通过增加一定的冗余度以提高数字通信系统的可靠性。

基于MATLAB的信道编码仿真毕设汇总

4 卷积码 .......................................................... 17 4.1 卷积码基本理论 .............................................. 17 4.1.1 卷积码的基本概念......................................... 17
In this paper, the linear block codes and convolutional codes are compiled and analyzed, and the simulation is carried out with MATLAB. Linear block code to (7,4) Hamming code as an example, using MATLAB to the over a binary symmetric channel (BSC), additive white Gaussian noise (AWGN) simulation, the bit error rate curve to analyze performance of Hamming code. The convolutional code is verified by MATLAB for simulation and error correction, and the error rate is analyzed under different SNR and different decision modes.Simulation results show that the Hamming code with increase of the signal to noise ratio, bit error rate is getting smaller and smaller, and for convolutional codes, signal-to-noise ratios were slightly higher will greatly reduce the bit error rate (BER) and using a soft decision decoding error rate is lower, a better effect. Keywords: channel coding MATLAB bit error rate

基于matlab的信道编码仿真(可编辑)

信道编码的目的是为了改善通信系统的传输质量。

由于实际信道存在噪声和干扰,使发送的码字与信道传输后所接收的码字之间存在差异,称这种差异为差错。

一般情况下,信道噪声、干扰越大,码字产生差错的概率也就越大。

本文利用matlab对二进制对称信道BSC,高斯白噪声信道AWGN两种信道的仿真,(7,4)Hamming码对信道的仿真,通过误码率的曲线图来了解信道的编码。

关键字:matlab,信道,编码,译码,Simulink。

基于matlab的信源编码实验系统的设计

标题：深度探讨基于matlab的信源编码实验系统的设计在信息科学与技术领域中，信源编码是指利用编码技术对信号源产生的信号进行编码，以便更有效地传输和存储。

基于matlab的信源编码实验系统的设计，是目前研究热点之一。

本文将从信源编码的基本概念出发，深入探讨基于matlab的信源编码实验系统的设计，让读者在阅读后对该主题有一个全面、深刻的理解。

一、信源编码的基本概念1.1 信源编码的定义和作用在通信领域，信源编码是指利用编码技术对信源产生的信号进行编码，以便更有效地传输和存储。

其作用在于减少数据传输或存储时所需要的比特数，提高传输效率和降低成本。

1.2 信源编码的分类信源编码主要分为无损编码和有损编码两种。

无损编码是指编码解码过程中不会有信息丢失，有损编码则是在编码解码过程中会有信息丢失。

其中，无损编码包括霍夫曼编码、算术编码等；有损编码包括JPEG、MP3等。

二、基于matlab的信源编码实验系统的设计2.1 实验系统的基本组成基于matlab的信源编码实验系统主要包括信源编码器、信道编码器、调制器、信道、调制解调器、信道解码器等组成。

其中，信源编码器用于对信号进行编码，信道编码器用于对数据进行处理以应对信道传输中的噪声，调制器用于将数据转换为模拟信号，信道用于传输信号，调制解调器用于将模拟信号转换为数字信号，信道解码器用于对数据进行解码。

2.2 实验系统的设计原理在实验系统的设计中，需要考虑不同编码方式的选择和实现，以及信道传输中可能出现的噪声和干扰。

还需要考虑编码器和解码器之间的匹配和信道编码器的选择等因素。

三、个人观点和理解在我看来，基于matlab的信源编码实验系统的设计是一个复杂且具有挑战性的任务。

在设计过程中，需要深入理解信源编码的基本原理和各种编码方式的特点，同时还需要考虑到实际应用中可能出现的各种问题和挑战。

只有全面了解和深入思考，才能设计出高效、稳定的实验系统。

总结与回顧本文首先介绍了信源编码的基本概念，包括其定义、作用和分类，然后深入探讨了基于matlab的信源编码实验系统的设计，包括实验系统的基本组成和设计原理。

基于某MATLAB地信道编码分析报告

实用文档题目：基于MATLAB的通信系统仿真———信道编码对通信系统性能的影响专业：通信工程：校通学号： 6日期: 2016.12.22目录一、引言 (2)二、信道编码理论 (2)2.1、信道编码的目的 (2)2.2、信道编码的实质 (3)2.3、信道编码公式 (3)三、线性分组码的编译码原理 (3)3.1、线性分组码的基本概念 (3)3.2、生成矩阵和校验矩阵 (4)四、MATLAB仿真 (5)4.1仿真 (5)4.1.1原理说明 (5)4.1.2各子函数说明 (5)4.2仿真源程序 (5)4.2.1信道编码 (5)4.2.2信道解码 (6)4.2.3交织 (6)4.2.4解交织 (7)4.2.5信道衰落 (7)六程序及仿真图 (8)1、 file1：信道编码对通信系统性能的影响，有无信道编码的影响 (8)2、file2：在周期性深衰落的信道条件下，交织对通信系统性能的影响. 103、 file3：在交织条件下，不同时长的周期性深衰落对系统性能影响的比较 (13)基于MATLAB的通信系统仿真———信道编码对通信系统性能的影响摘要：简述信道编码理论，详细说明分组码的编译原理、实现方法及检错纠错能力，用MATLAB仿真有无信道编码条件下对通信系统性能的影响及信道编码在不同信道下对通信系统性能的影响，如AWGN信道和深衰落信道。

关键词：信道编码、分组码、MATLAB仿真、性能一、引言提高信息传输的有效性和可靠性始终是通信技术所追求的目标，而信道编码能够显著的提升信息传输的可靠性。

1948年,信息论的奠基人C.E.Shannon在他的开创性论文“通信的数学理论”中,提出了著名的有噪信道编码定理.他指出：对任何信道,只要信息传输速率R不大于信道容量C, 就一定存在这样的编码方法：在采用最大似然译码时,其误码率可以任意小.该定理在理论上给出了对给定信道通过编码所能达到的编码增益的上限,并指出了为达到理论极限应采用的译码方法.在信道编码定理中,香农提出了实现最佳编码的三个基本条件：(1 )采用随机编译码方式 ; (2 )编码长度Ｌ→∞ , 即分组的码组长度无限 ; (3)译码采用最佳的最大似然译码算法。

基于matlab通信系统仿真——信源编解码课程设计报告

一、设计题目◆基于MATLAB通信系统仿真——信源编解码。

二、实验内容及要求◆内容：完成对一模拟信号的抽样、量化、编码，然后利用Huffman信源编码对其进行数据压缩，再利用（15，11）的线性分组码进行信道编码，然后采用DPSK调制方式调制，接着通过信道；在接收端进行其逆过程，即先解调（可采用相干解调或差分相干解调），再依次为信道译码，Huffman信源译码，PCM译码。

◆要求：利用相关知识，建立系统模型，完成各个模块的代码设计。

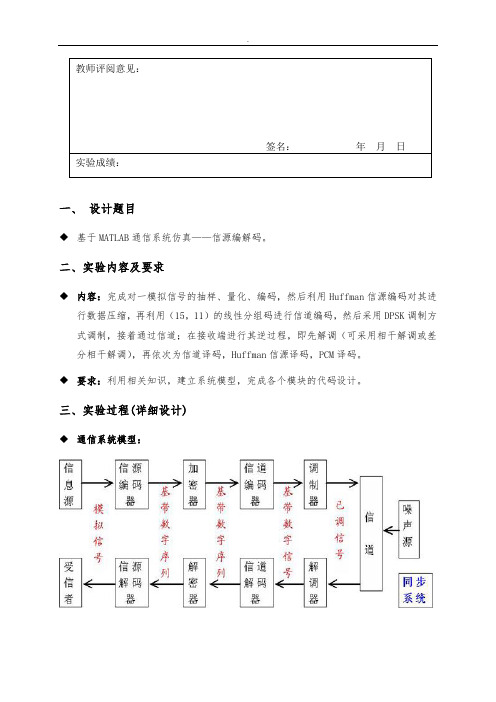
三、实验过程(详细设计)◆通信系统模型：◆ 本实验主函数框图：◆ 分步设计：抽样部分([sg1,sg2]=Sampling(fs))：函数功能：对原始信号进行抽样；函数参数：fs 抽样频率（须大于等于两倍的信号最高频率）；函数返回值：sg1表示原始信号，sg2表示抽样信号；实现：根据抽样频率fs 在一个周期里抽取fs 个值即可。

进制转换部分([h]=dextobin(n,n_no)):函数功能：将十进制数转换成二进制数；函数参数：n 表示待转换的十进制数，n_no 表示要将n 转换为二进制数的位数；函数返回值：h 表示n 的n_no 位二进制数；实现：首先判定n 是否为整数，如果不是则将其先进行四舍五入处理，然后将处理后的n ’转换成位数与n_no 相同的二进制数，前面多余的位用零表示。

PCM 编码部分（[pc]=PCM_code(sg2)）：函数功能：对抽样值sg2进行PCM 编码；函数参数：sg2表示通过抽样函数Sampling 抽样后的离散值；函数返回值：pc 表示sg2中的每一个值通过PCM 编码后的8位二进制码组的十进制数形式（说明：之所以转换成十进制数，是为了在Huffman 编码时的方便）。

实现：以一个实际的数为例，首先确定这个数拥有多少个量化单位（1/2048），然后编码，如果为负则第一位为0，否则为1；接着根据刚才计算得到的量化单位判断其段落，得到段落码；最后确定段内码，方法：先计算每一端的量化间隔22i i D -=（注意：此处的i D 是一量化单位为基础的，而不是最小量化间隔）i 为段落值，然后再利用计算式(2)((2)/)i i G fix x D +=-，得到段内段落数G ，再将G 转换成二进制数，完成编码。

OFDM信道估计MATLAB代码

echo off; % 关闭回显clear all; % 从内存中清除变量和函数close all; % 关闭所有图形fprintf( '\n OFDM仿真\n \n') ; % 设置显示格式% --------------------------------------------- %% 参数定义%% --------------------------------------------- %IFFT_bin_length = 1024; % 发送端的IFFT变换长度, 接收端的FFT变换长度，R代表接受，T代表发送carrier_count = 200; % 子载波数bits_per_symbol = 2; % 位数/符号symbols_per_carrier = 50; % 符号数/载波cp_length = input('cp length = '); % 输入循环前缀长度d4 = input('d4 = '); % 输入最大多径时延扩展a4 = input('a4 = '); % 输入最大多径时延扩展的系数SNR = input('SNR = '); % 输入信道信噪比(dB) % --------------------------------------------- %% 初始参数设置完毕%% --------------------------------------------- %baseband_out_length = carrier_count * symbols_per_carrier * bits_per_symbol; % 计算发送的二进制序列长度：基带传送长度=载波数×符号数/载波×位数/符号carriers = (1:carrier_count) + (floor(IFFT_bin_length/4) - floor(carrier_count/2)); % 载波（坐标）：(1:200) + 256 - 100 = 157:356conjugate_carriers = IFFT_bin_length - carriers + 2; % 载波变换（坐标）：1024 - (157:356) + 2 = 1026 - (157:356) = (869:670)%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% 构造共轭时间－载波矩阵，以便应用所谓的RCC，Reduced Computational Complexity算法，即ifft之后结果为实数% 也可以用flipdim函数构造对称共轭矩阵%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% --------------------------------------------- %% 发送信号%% --------------------------------------------- %%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% Generate a random binary output signal:% - a row of uniform random numbers (between 0 and 1), rounded to 0 or 1% - this will be the baseband signal which is to be transmitted.%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－baseband_out = round(rand(1,baseband_out_length));%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% round：朝最近的整数取整，rand:产生均匀分布的随机数矩阵（1×baseband_out_length 阶）% Convert to 'modulo N' integers where N = 2^bits_per_symbol% - this defines how many states each symbol can represent% - first, make a matrix with each column representing consecutive bits% from the input stream and the number of bits in a column equal to the% number of bits per symbol% - then, for each column, multiply each row value by the power of 2 that% it represents and add all the rows% - for example: input 0 1 1 0 0 0 1 1 1 0% bits_per_symbol = 2% convert_matrix = 0 1 0 1 1% 1 0 0 1 0% modulo_baseband = 1 2 0 3 2%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－convert_matrix = reshape(baseband_out,bits_per_symbol,length(baseband_out)/bits_per_symbol) ;%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% RESHAPE Change size. 把baseband_out变为M×N阶的矩阵% RESHAPE(X,M,N) returns the M-by-N matrix whose elements% are taken columnwise from X. An error results if X does% not have M*N elements.%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－for k = 1:(length(baseband_out)/bits_per_symbol)modulo_baseband(k) = 0 ;for i = 1:bits_per_symbolmodulo_baseband(k) = modulo_baseband(k) + convert_matrix(i,k)*2^(bits_per_symbol - i) ; endend%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% Serial to Parallel Conversion 串并转换% - convert the serial modulo N stream into a matrix where each column% represents a carrier and each row represents a symbol% - for example:% serial input stream = a b c d e f g h i j k l m n o p% parallel carrier distribution =% C1/s1=a C2/s1=b C3/s1=c C4/s1=d% C1/s2=e C2/s2=f C3/s2=g C4/s2=h% C1/s3=i C2/s3=j C3/s3=k C4/s3=l% . . . .% . . . .%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－carrier_matrix = reshape(modulo_baseband, carrier_count, symbols_per_carrier)'; %生成时间－载波矩阵（carrier_count×symbols_per_carrier）%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% Apply differential coding to each carrier string% - append an arbitrary start symbol (let it be 0, that works for all% values of bits_per_symbol) (note that this is done using a vertical% concatenation [x;y] of a row of zeros with the carrier matrix, sweet!)% - perform modulo N addition between symbol(n) and symbol(n-1) to get the% coded value of symbol(n)% - for example:% bits_per_symbol = 2 (modulo 4)% symbol stream = 3 2 1 0 2 3% start symbol = 0%% coded symbols = 0 + 3 = 3% 3 + 2 = 11 = 1% 1 + 1 = 2% 2 + 0 = 2% 2 + 2 = 10 = 0% 0 + 3 = 3%% coded stream = 0 3 1 2 2 0 3%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% --------------------------------------------- %% QDPSK调制%% --------------------------------------------- %carrier_matrix = [zeros(1,carrier_count);carrier_matrix]; % 添加一个差分调制的初始相位，为0for i = 2:(symbols_per_carrier + 1)carrier_matrix(i,:) = rem(carrier_matrix(i,:)+carrier_matrix(i-1,:),2^bits_per_symbol); % 差分调制（rem除后取余）end%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% Convert the differential coding into a phase% - each phase represents a different state of the symbol% - for example:% bits_per_symbol = 2 (modulo 4)% symbols = 0 3 2 1% phases =% 0 * 2pi/4 = 0 (0 degrees)% 3 * 2pi/4 = 3pi/2 (270 degrees)% 2 * 2pi/4 = pi (180 degrees)% 1 * 2pi/4 = pi/2 (90 degrees)%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－carrier_matrix = carrier_matrix * ((2*pi)/(2^bits_per_symbol)); % 产生差分相位%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% Convert the phase to a complex number% - each symbol is given a magnitude of 1 to go along with its phase% (via the ones(r,c) function)% - it is then converted from polar to cartesian (complex) form% - the result is 2 matrices, X with the real values and Y with the imaginary% - each X column has all the real values for a carrier, and each Y column% has the imaginary values for a carrier% - a single complex matrix is then generated taking X for real and% Y for imaginary%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－[X,Y] = pol2cart(carrier_matrix, ones(size(carrier_matrix,1),size(carrier_matrix,2))); % 由极坐标向复数坐标转化第一参数为相位第二参数为幅度%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% Carrier_matrix contains all the phase information and all the amplitudes are the same,‘1’% 函数说明：极或柱坐标变为直角坐标% POL2CART Transform polar to Cartesian coordinates.% [X,Y] = POL2CART(TH,R) transforms corresponding elements of data% stored in polar coordinates (angle TH, radius R) to Cartesian% coordinates X,Y. The arrays TH and R must the same size (or% either can be scalar). TH must be in radians.% [X,Y,Z] = POL2CART(TH,R,Z) transforms corresponding elements of% data stored in cylindrical coordinates (angle TH, radius R, height Z)% to Cartesian coordinates X,Y,Z. The arrays TH, R, and Z must be% the same size (or any of them can be scalar). TH must be in radians.%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－complex_carrier_matrix = complex(X,Y);%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% 函数说明：% COMPLEX Construct complex result from real and imaginary parts.% C = COMPLEX(A,B) returns the complex result A + Bi, where A and B are% identically sized real N-D arrays, matrices, or scalars of the same data type.%% Assign each carrier to its IFFT bin% - each row of complex_carrier_matrix represents one symbol period, with% a symbol for each carrier% - a matrix is generated to represent all IFFT bins (columns) and all% symbols (rows)% - the phase modulation for each carrier is then assigned to the% appropriate bin% - the conjugate of the phase modulation is then assigned to the% appropriate bin% - the phase modulation bins and their conjugates are symmetric about% the Nyquist frequency in the IFFT bins% - since the first bin is DC, the Nyquist Frequency is located% at (number of bins/2) + 1% - symmetric conjugates are generated so that when the signal is% transformed to the time domain, the time signal will be real-valued% - example% - 1024 IFFT bins% - bin 513 is the center (symmetry point)% - bin 1 is DC% - bin 514 is the complex conjugate of bin 512% - bin 515 is the complex conjugate of bin 511% - ....% - bin 1024 is the complex conjugate of bin 2 (if all bins% were used as carriers)% - So, bins 2-512 map to bins 1024-514%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% % 添加训练序列% %－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% training_symbols = [ 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 ...-j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 ...1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 ...-1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j ...-1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 1 j j 1 -1 -j -j -1 ];%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% 25 times "1 j j 1"% 25 times "-1 -j -j -1"% totally 200 symbols as a row%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－training_symbols = cat(1, training_symbols, training_symbols) ;training_symbols = cat(1, training_symbols, training_symbols) ;%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% Production of 4 rows of training_symbols% 函数说明：串接成高维数组% CAT Concatenate arrays.% CAT(DIM,A,B) concatenates the arrays A and B along the dimension DIM.% CAT(2,A,B) is the same as [A,B].% CAT(1,A,B) is the same as [A;B].% B = CAT(DIM,A1,A2,A3,A4,...) concatenates the input% arrays A1, A2, etc. along the dimension DIM.%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－complex_carrier_matrix = cat(1, training_symbols, complex_carrier_matrix);%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% 训练序列与数据合并，串接成高维数组% block-type pilot symbols%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－IFFT_modulation = zeros(4 + symbols_per_carrier + 1, IFFT_bin_length);%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% Here a row vector of zeros is between training symbols and data symbols% 4 training symbols and 1 zero symbol% every OFDM symbol takes a row of "IFFT_modulation"%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－IFFT_modulation(:,carriers) = complex_carrier_matrix;IFFT_modulation(:,conjugate_carriers) = conj(complex_carrier_matrix);%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% Find the indices of zeros% Description% ZC = conj(Z) returns the complex conjugate of the elements of Z.% AlgorithmIf Z is a complex array: conj(Z) = real(Z) - i*imag(Z)%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－time_wave_matrix = ifft(IFFT_modulation'); % 进行IFFT操作time_wave_matrix = time_wave_matrix'; % 进行矩阵转置cp_add = zeros(4 + symbols_per_carrier + 1,cp_length);for i = 1:4 + symbols_per_carrier + 1cp_add(i,:) = time_wave_matrix(i,(IFFT_bin_length - cp_length + 1) : IFFT_bin_length);endtime_wave_matrix_cp = [cp_add,time_wave_matrix];for i = 1: 4 + symbols_per_carrier + 1 % windowed_time_wave_matrix(i,:) = real(time_wave_matrix(i,:)) .* hamming(IFFT_bin_length)';windowed_time_wave_matrix_cp(i,:) = real(time_wave_matrix_cp(i,:));end%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% Serialize the modulating waveform% - sequentially take each row of windowed_time_wave_matrix and construct a row vector % - the row vector will be the modulating signal% - note that windowed_time_wave_matrix is transposed, this is to account for the way the % Matlab 'reshape' function works (reshape takes the columns of the target matrix and% appends them sequentially)% get the real part of the result of IFFT% 这一步可以省略，因为IFFT结果都是实数% 由此可以看出，只是取了IFFT之后载波上的点，并未进行CP的复制和添加end%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ofdm_modulation = reshape(windowed_time_wave_matrix_cp', 1, (IFFT_bin_length + cp_length)*(4 + symbols_per_carrier+1)); % P2S operation%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－Tx_data = ofdm_modulation;%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% 信道模拟%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－% The channel model is Gaussian (AWGN) only% - Rayleigh fading would be a useful addition%－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－d1 = 40; a1 = 0.2; d2 = 50; a2 = 0.3; d3 = 60; a3 = 0.4;%d4 = 160; a4 = 0.9;copy1 = zeros(size(Tx_data)) ;for i = 1 + d1: length(Tx_data)copy1(i) = a1*Tx_data( i - d1) ;endcopy2 = zeros(size(Tx_data) ) ;for i = 1 + d2: length( Tx_data)copy2(i) = a2*Tx_data( i - d2) ;endcopy3 = zeros(size(Tx_data) ) ;for i = 1 + d3: length(Tx_data)copy3(i) = a3*Tx_data ( i - d3) ;endcopy4 = zeros(size(Tx_data) ) ;for i = 1 + d4: length( Tx_data)copy4(i) = a4*Tx_data(i - d4) ;endTx_data = Tx_data + copy1 + copy2 + copy3 + copy4; % 4 multi-pathsTx_signal_power = var(Tx_data);%-------------------------------------------------------------------------% 函数说明：% VAR Variance.% For vectors, Y = VAR(X) returns the variance of the values in X. For% matrices, Y is a row vector containing the variance of each column of% X.%-------------------------------------------------------------------------linear_SNR = 10^(SNR/10);noise_sigma = Tx_signal_power/linear_SNR;noise_scale_factor = sqrt(noise_sigma);%noise = randn(1, length(Tx_data))*noise_scale_factor;Rx_Data = Tx_data + noise;%Rx_Data = Tx_data;%-------------------------------------------------------------------------% 函数说明：产生正态分布的随机函数% Y = randn(m,n) or Y = randn([m n]) returns an m-by-n matrix of random% entries.% The randn function generates arrays of random numbers whose elements are% normally distributed with mean 0 and variance 1.%-------------------------------------------------------------------------% --------------------------------------------- %% 信号接收%% --------------------------------------------- %%-------------------------------------------------------------------------Rx_Data_matrix_cp = reshape(Rx_Data, IFFT_bin_length + cp_length, 4 + symbols_per_carrier + 1);Rx_Data_matrix_cp = Rx_Data_matrix_cp';Rx_Data_matrix = zeros(4 + symbols_per_carrier + 1,IFFT_bin_length);for i = 1:4 + symbols_per_carrier + 1Rx_Data_matrix(i,:) = Rx_Data_matrix_cp(i,(cp_length + 1):(IFFT_bin_length + cp_length)); endRx_Data_matrix = Rx_Data_matrix';%-------------------------------------------------------------------------% Transform each symbol from time to frequency domain% - take the fft of each column%-------------------------------------------------------------------------Rx_spectrum = fft(Rx_Data_matrix);%-------------------------------------------------------------------------% Suppose precise synchronazition between Tx and RxRx_carriers = Rx_spectrum(carriers,:)';Rx_training_symbols = Rx_carriers( (1: 4) , : ) ;Rx_carriers = Rx_carriers((5: 55), : ) ;% --------------------------------------------- %% 信道估计%% --------------------------------------------- %Rx_training_symbols = Rx_training_symbols./ training_symbols;Rx_training_symbols_deno = Rx_training_symbols.^2;Rx_training_symbols_deno = Rx_training_symbols_deno(1,:)+Rx_training_symbols_deno(2,:)+Rx_training_symbols_deno(3,:)+ Rx_training_symbols_deno(4,:) ;Rx_training_symbols_nume = Rx_training_symbols(1, : ) +Rx_training_symbols(2, : ) + Rx_training_symbols(3, : ) +Rx_training_symbols(4, : ) ;Rx_training_symbols_nume = conj(Rx_training_symbols_nume) ;%-------------------------------------------------------------------------% 取4个向量的导频符号是为了进行平均优化% 都是针对“行向量”即单个的OFDM符号进行操作% 原理：寻求1/H，对FFT之后的数据进行频域补偿% 1/H = conj(H)/H^2 because H^2 = H * conj(H)%-------------------------------------------------------------------------Rx_training_symbols = Rx_training_symbols_nume./Rx_training_symbols_deno;Rx_training_symbols_2 = cat(1, Rx_training_symbols,Rx_training_symbols) ;Rx_training_symbols_4 = cat(1, Rx_training_symbols_2,Rx_training_symbols_2) ;Rx_training_symbols_8 = cat(1, Rx_training_symbols_4,Rx_training_symbols_4) ;Rx_training_symbols_16 = cat(1, Rx_training_symbols_8, Rx_training_symbols_8) ;Rx_training_symbols_32 = cat(1, Rx_training_symbols_16, Rx_training_symbols_16) ;Rx_training_symbols_48 = cat(1, Rx_training_symbols_32, Rx_training_symbols_16) ;Rx_training_symbols_50 = cat(1, Rx_training_symbols_48, Rx_training_symbols_2) ;Rx_training_symbols = cat(1, Rx_training_symbols_50,Rx_training_symbols) ;Rx_carriers = Rx_training_symbols.*Rx_carriers;%-------------------------------------------------------------------------% 进行频域单抽头均衡%-------------------------------------------------------------------------Rx_phase = angle(Rx_carriers)*(180/pi);phase_negative = find(Rx_phase < 0);%-------------------------------------------------------------------------% 函数说明：找出非零元素的索引号% FIND Find indices of nonzero elements.% I = FIND(X) returns the linear indices of the array X that are nonzero.% X may be a logical expression. Use IND2SUB(I,SIZE(X)) to calculate% multiple subscripts from the linear indices I.%---------------------------------------------------------------------------Rx_phase( phase_negative );Rx_phase(phase_negative) = rem(Rx_phase(phase_negative) + 360, 360) ;% 把负的相位转化为正的相位Rx_decoded_phase = diff(Rx_phase) ;% 这也是为什么要在前面加上初始相位的原因% “Here a row vector of zeros is between training symbols and data symbols”%-------------------------------------------------------------------------% 函数说明：% DIFF Difference and approximate derivative.% DIFF(X), for a vector X, is [X(2)-X(1) X(3)-X(2) ... X(n)-X(n-1)].% DIFF(X), for a matrix X, is the matrix of row differences,% [X(2:n,:) - X(1:n-1,:)].%------------------------Test Codes --------------------------------------% a = [1 2 3; 4 5 6; 7 8 9; 10 11 12];% b = a;% for i = 2:4% b(i,:) = b(i-1,:) + b(i,:);% end% c = diff(b);%-----------------------Test Result --------------------------------------% a = Modulating signal% 1 2 3% 4 5 6% 7 8 9% 10 11 12% b = Modulated signal% 1 2 3% 5 7 9% 12 15 18% 22 26 30% c = Recovered signal% 4 5 6% 7 8 9% 10 11 12% ----------------------------------------------------------------------------% Name Size Bytes Class% Rx_phase 51x200 81600 double array% Rx_decoded_phase 50x200 80000 double array% ----------------------------------------------------------------------------phase_negative = find(Rx_decoded_phase < 0) ;Rx_decoded_phase(phase_negative)= rem(Rx_decoded_phase(phase_negative) + 360, 360) ;% ----------------------------------------------------------------------------% Extract phase differences (from the differential encoding)% - the matlab diff( ) function is perfect for this operation% - again, normalize the result to be between 0 and 359 degrees% 再次把负的相位转化为正的相位% ----------------------------------------------------------------------------% --------------------------------------------- %% QDPSK解调%% --------------------------------------------- %base_phase = 360 /2^bits_per_symbol;delta_phase = base_phase /2;Rx_decoded_symbols = zeros(size(Rx_decoded_phase,1),size(Rx_decoded_phase,2)) ;%for i = 1: (2^bits_per_symbol - 1)center_phase = base_phase*i;plus_delta = center_phase + delta_phase; % Decision threshold 1minus_delta = center_phase - delta_phase; % Decision threshold 2decoded = find((Rx_decoded_phase <= plus_delta)&(Rx_decoded_phase > minus_delta)) ;Rx_decoded_symbols(decoded) = i;end% ----------------------------------------------------------------------------% 仅仅对三个区域进行判决% 剩下的区域就是零相位的空间了% 这个区域在定义解调矩阵时已经定义为零% ----------------------------------------------------------------------------Rx_serial_symbols = reshape(Rx_decoded_symbols',1,size(Rx_decoded_symbols, 1)*size(Rx_decoded_symbols,2)) ;for i = bits_per_symbol: -1: 1if i ~= 1Rx_binary_matrix(i, : ) = rem(Rx_serial_symbols, 2) ;Rx_serial_symbols = floor(Rx_serial_symbols/2) ;elseRx_binary_matrix( i, : ) = Rx_serial_symbols;endend % Integer to binarybaseband_in = reshape(Rx_binary_matrix, 1,size(Rx_binary_matrix, 1)*size(Rx_binary_matrix, 2) ) ; % --------------------------------------------- %% 误码率计算%% --------------------------------------------- %bit_errors = find(baseband_in ~= baseband_out) ; % find的结果其每个元素为满足逻辑条件的输入向量的标号，其向量长度也就是收发不一样的bit的个数bit_error_count = size(bit_errors, 2) ;total_bits = size( baseband_out, 2) ;bit_error_rate = bit_error_count/ total_bits;fprintf ( '%f \n',bit_error_rate) ;。

基于matlab的信源编码实验系统的设计

基于matlab的信源编码实验系统的设计基于Matlab的信源编码实验系统的设计1. 引言在数字通信领域，信源编码是一项核心技术，用于对信号进行压缩和重构，以便在传输过程中节省带宽和能量消耗。

在本文中，我们将探讨基于Matlab的信源编码实验系统的设计，旨在通过对信源编码的理论与实际结合，为读者提供对该领域的全面理解。

2. 信源编码原理介绍信源编码是一种将信号进行离散表示和编码的技术，其核心原理是通过对信号的统计特性进行分析，找到其中的冗余信息并进行压缩。

常见的信源编码原理包括霍夫曼编码、算术编码、熵编码等。

这些方法在不同场景下有各自的适用性，对于不同类型的信号也有不同的效果。

3. Matlab在信源编码中的应用Matlab作为一个强大的数学计算软件，提供了丰富的工具箱和函数，可以用于对信源编码原理进行建模、仿真和实验。

通过Matlab，可以方便地对信号进行采样、量化、编码和解码，以及对各种编码方法的效果进行比较和评估。

4. 信源编码实验系统的设计基于前述原理和Matlab的应用，我们设计了一套完整的信源编码实验系统。

该系统包括信号生成模块、编码器、解码器和性能评估模块。

在信号生成模块中，我们可以生成不同类型的信号，如语音信号、图像信号等，用于后续的编码实验。

编码器和解码器模块则实现了常见的信源编码方法，用户可以选择不同的编码算法进行实验。

性能评估模块可以对不同编码算法的效果进行定量分析，如压缩比、失真度等指标。

5. 实验结果与分析我们通过该实验系统对不同的信号和编码方法进行了实验，得到了丰富的数据和结果。

我们发现，对于不同类型的信号，不同的编码方法有着不同的效果。

在一些情况下，算术编码可能表现更好，而在另一些情况下，霍夫曼编码可能更适用。

我们也发现了一些编码方法的局限性，比如在某些高压缩比情况下，可能会出现严重的失真问题。

这些结果为我们提供了对信源编码方法的深入理解，并指导了我们在实际应用中的选择。

基于MATLAB的通信编码仿真数字通信课程设计

数字通信课程设计题目：MATLAB信道编码仿真院系：专业：学号：姓名：数字通信课程设计2：基于MATLAB的信道编码仿真数字信号在传输中往往由于各种原因，使得在传送的数据流中产生误码，从而使接收端产生图象跳跃、不连续、出现马赛克等现象。

所以通过信道编码这一环节，对数码流进行相应的处理，使系统具有一定的纠错能力和抗干扰能力，可极大地避免码流传送中误码的发生，提高信道可靠性。

误码的处理技术有纠错、交织、线性内插等。

本实验将以以线性分组码和交织编码为例，讨论信道编码对于误码率的影响，通过比较信道编码前后的信噪比和误码率曲线，总结出采用信道编码信道与不采用信道编码信道在误码率上的区别。

验证信道编码对于信道可靠性的提高，以及对信道性能的改善。

内容要求1：MATLAB仿真信道编码对信噪比和误码率的影响仿真条件：✓ 1 信道输入:s(t), s(t)可以取为MPSK 信号✓ 2 考虑常数AWGN信道✓ 3 噪声设为n(t)✓ 4 信道输出为y(t)=As(t)+n(t)仿真要求：✓ 1 利用线性分组码或者卷积码进行信道编码✓ 2 画出SER VS SNR的结果图，SNR取0－10dB✓SER：符号差错率✓SNR：信噪比本仿真实验对传统基带系统模型进行简化，假设基带系统模型的框图如图1，只考虑AWGN信道和噪声的干扰，其简化模型如图1：图1 基带传输系统简化模型在实际仿真实验中，采用了正交相移键控（QPSK），考虑常数AWGN信道，噪声为加性高斯白噪声。

利用（7，4）线性分组码进行信道编码。

输入信号为s(t)，每个码元s(t)可以表示两个比特，其QPSK星座图如图2：图2 QPSK调制星座图噪声n(t)采用均值为1，方差为0的标准正态分布，通过信号发送峰值电平A来控制信号的发送功率和信噪比SNR，信噪比SNR与峰值电平A 的关系为：SNR = A2 / 2σ2（1）由于噪声采用均值为0，方差为1的标准正态分布，即σ2=1，故公式（1）可简化为：SNR = A2 / 2（2）利用MA TLAB进行QPSK调制解调的仿真如图3：图3 QPSK调制时的信噪比误码率曲线通过对上图分析可知，对于发送QPSK信号，随着同样信噪比的提高，误码率逐渐减小，这满足AWGN信道中信噪比和误码率的一般关系。

基于matlab的信道编码分析

题目：基于MATLAB的通信系统仿真———信道编码对通信系统性能的影响专业：通信工程：崔校通学号：201300484316日期: 2016.12.22目录一、引言 (2)二、信道编码理论 (2)2.1、信道编码的目的 (2)2.2、信道编码的实质 (3)2.3、信道编码公式 (3)三、线性分组码的编译码原理 (3)3.1、线性分组码的基本概念 (3)3.2、生成矩阵和校验矩阵 (4)四、MATLAB仿真 (5)4.1仿真 (5)4.1.1原理说明 (5)4.1.2各子函数说明 (5)4.2仿真源程序 (5)4.2.1信道编码 (5)4.2.2信道解码 (6)4.2.3交织 (6)4.2.4解交织 (7)4.2.5信道衰落 (7)六程序及仿真图 (8)1、file1：信道编码对通信系统性能的影响，有无信道编码的影响 (8)2、file2：在周期性深衰落的信道条件下，交织对通信系统性能的影响 (10)3、file3：在交织条件下，不同时长的周期性深衰落对系统性能影响的比较 (13)基于MATLAB的通信系统仿真———信道编码对通信系统性能的影响摘要：简述信道编码理论，详细说明分组码的编译原理、实现方法及检错纠错能力，用MATLAB仿真有无信道编码条件下对通信系统性能的影响及信道编码在不同信道下对通信系统性能的影响，如AWGN信道和深衰落信道。

1948年,信息论的奠基人C.E.Shannon在他的开创性论文“通信的数学理论”中,提出了著名的有噪信道编码定理.他指出：对任何信道,只要信息传输速率R不大于信道容量C, 就一定存在这样的编码方法：在采用最大似然译码时,其误码率可以任意小.该定理在理论上给出了对给定信道通过编码所能达到的编码增益的上限,并指出了为达到理论极限应采用的译码方法.在信道编码定理中,香农提出了实现最佳编码的三个基本条件：(1 )采用随机编译码方式; (2 )编码长度Ｌ→∞ , 即分组的码组长度无限; (3)译码采用最佳的最大似然译码算法。

信道编码实验报告BCH码

信道编码实验报告
一、实验内容
利用matlab 设计一个长度为127，纠错能力为6的BCH 码，并用matlab 实现系统码的编码和彼得森译码，并验证正确。

二、实验目的
1. 利用matlab 设计一个长度为127，纠错能力为6的BCH 码；
2. 用matlab 实现系统码的编码和彼得森译码。

三、实验原理
1. BCH 码
2. 彼得森译码四、程序框图
（1）编码框图
（2）译码框图（彼得森）
五、实验分析
1. 先以n=15,进行仿真，输入数据如下：（1）输入g(x)的根（2）输入生成多项式次数（3）输入纠错能力（4）输入错误位个数
创新点：
（1）接收端的码多项式加入了信道干扰的影响；（2）生成的多项式也是随机的，具有普适性。

举例如下：
n=15，t=3，生成元为65432
,,,,,ααααα
α，m=4。

Matlab 结果如下：
2.再以n=127进行仿真
(1)e=3
由结果可视，原码元应为全0码
(2)e=5
如图可以看出，在第1,29,41,86,92位为1，其余位为0。

信道编码matlab

信道编码在通信系统中是为了提高通信系统的可靠性和性能而采用的一种技术。

常见的信道编码包括奇偶校验码、循环冗余校验码（CRC）、卷积码和纠错码等。

在 MATLAB 中，你可以使用内置的函数或者通信工具箱来实现信道编码。

以下是使用 MATLAB 进行一些常见信道编码的示例：
1. 奇偶校验码：
2. 卷积码：
3. 纠错码（Reed-Solomon 码）：
4. Turbo 码：
这只是一些常见信道编码的示例。

实际上，信道编码的选择取决于通信系统的要求和特定的应用场景。

你可以根据需要选择适当的编码方案，并使用 MATLAB 中相关的函数或工具箱进行实现。

基于MATLAB的信道编译码系统设计学士学位论文

学士学位论文基于MATLAB的信道编译码系统设计毕业设计（论文）原创性声明和使用授权说明原创性声明本人郑重承诺：所呈交的毕业设计（论文），是我个人在指导教师的指导下进行的研究工作及取得的成果。

尽我所知，除文中特别加以标注和致谢的地方外，不包含其他人或组织已经发表或公布过的研究成果，也不包含我为获得及其它教育机构的学位或学历而使用过的材料。

对本研究提供过帮助和做出过贡献的个人或集体，均已在文中作了明确的说明并表示了谢意。

作者签名：日期：指导教师签名：日期：使用授权说明本人完全了解大学关于收集、保存、使用毕业设计（论文）的规定，即：按照学校要求提交毕业设计（论文）的印刷本和电子版本；学校有权保存毕业设计（论文）的印刷本和电子版，并提供目录检索与阅览服务；学校可以采用影印、缩印、数字化或其它复制手段保存论文；在不以赢利为目的前提下，学校可以公布论文的部分或全部内容。

作者签名：日期：学位论文原创性声明本人郑重声明：所呈交的论文是本人在导师的指导下独立进行研究所取得的研究成果。

除了文中特别加以标注引用的内容外，本论文不包含任何其他个人或集体已经发表或撰写的成果作品。

对本文的研究做出重要贡献的个人和集体，均已在文中以明确方式标明。

本人完全意识到本声明的法律后果由本人承担。

作者签名：日期：年月日学位论文版权使用授权书本学位论文作者完全了解学校有关保留、使用学位论文的规定，同意学校保留并向国家有关部门或机构送交论文的复印件和电子版，允许论文被查阅和借阅。

本人授权大学可以将本学位论文的全部或部分内容编入有关数据库进行检索，可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。

涉密论文按学校规定处理。

作者签名：日期：年月日导师签名：日期：年月日注意事项1.设计（论文）的内容包括：1）封面（按教务处制定的标准封面格式制作）2）原创性声明3）中文摘要（300字左右）、关键词4）外文摘要、关键词5）目次页（附件不统一编入）6）论文主体部分：引言（或绪论）、正文、结论7）参考文献8）致谢9）附录（对论文支持必要时）2.论文字数要求：理工类设计（论文）正文字数不少于1万字（不包括图纸、程序清单等），文科类论文正文字数不少于1.2万字。

信道编码之线性编码译码matlab

clc;clear all;k=input('输入信息元\n');g=[1,0,0,1,0,0,1;0,1,0,1,1,1,0;0,0,1,0,1,1,1];[row,col]=size(g);rest=rem(length(k),row);if(rest==0) %输入的信元0补余，保证满足能和生成矩阵相乘的形式co=1;elseco=1;rest1=row-rest+length(k);k(length(k):rest1)=0;endfor n=1:row:length(k); %编码过程c(co,:)=k(n:n+row-1)*g;co=co+1;end[row,col]=size(c);for n=1:row %编码后的码字展开c1(col*n-col+1:col*n)=c(n,:);endy=c1;%过高斯信道% c=mod(c,2);h=[1,1,0,1,0,0,0;0,1,1,0,1,0,0;0,1,1,0,0,1,0;1,0,1,0,0,0,1]; gni=pinv(g); %生成矩阵的逆矩阵，译码用[row,col]=size(h);co=1;for n=1:col:length(y); %整合接收码字与校验矩阵相乘验证传输正确性cy(co,:)=y(n:n+col-1);co=co+1;endt=cy*h';t=mod(t,2);if(t==0)disp('接收码字正确');m=cy*gni; %译码[row,col]=size(m);for n=1:rowk1(col*n-col+1:col*n)=m(n,:);endk1=round(abs(k1))elsedisp('接收码字错误');End注意输入时候请按这样的格式输入信息元[1,0,1,0,0,1,0,1,0,1,0,1,0,1,0,0,1,0,1,0]输出结果为：接收码字正确k1 =Columns 1 through 171 0 1 0 0 1 0 1 0 1 0 1 0 1 0 0 1Columns 18 through 210 1 0 0>>。

基于MATLAB的信道编码分析

信道编码实验报告

基于matlab的信道编码仿真(可编辑)

基于MATLAB的信道编码教学实验软件设计与实现

基于matlab的调制解调与信道编译码仿真

基于MATLAB的通信系统信道编码的研究及其仿真

信道编码-MATLAB仿真实验中的应用

基于MATLAB的信道编码仿真 毕设汇总

基于matlab的信道编码仿真(可编辑)

基于matlab的信源编码实验系统的设计

基于某MATLAB地信道编码分析报告

基于matlab通信系统仿真——信源编解码课程设计报告

OFDM信道估计MATLAB代码

基于matlab的信源编码实验系统的设计

基于MATLAB的通信编码仿真 数字通信课程设计

基于matlab的信道编码分析

信道编码实验报告BCH码

信道编码matlab

基于MATLAB的信道编译码系统设计学士学位论文

信道编码之线性编码译码matlab

基于MATLAB的信道编码仿真毕设汇总

基于MATLAB的通信编码仿真数字通信课程设计