第五章 第一节
第五章第一节 热带植被类型

新几内亚岛南部接近的生物类型。位于澳洲北部地
区的卡卡杜国家公园是澳大利亚最大最重要的国家 公园,也是澳洲第一批被列为世界自然遗产的国家 公园。
5、季雨林类型及我国季雨林(自习)
热带季雨林可以分成几种不同的类型。
1)半常绿季雨林:在水热条件比较好的地方,热
带季雨林中只有最高大的第一层乔木有部分落叶的 现象,整个森林的外貌是终年常绿的,这种热带季 雨林被称作半常绿季雨林。半常绿季雨林中木质藤 本、绞杀植物、附生植物、老茎生花和板状根等各
第五章
第一节
世界植被地理
热带的植被类型
一、热带雨林(tropical rain forest)
(一)环境特征 1、气候条件_____赤道气候 终年高温多雨,雨量充沛均匀、大于1800毫米,有 些地方达3500毫米。温差小、白天温度一般在30摄 氏度左右,夜间约20摄氏度。无显著冬季和旱季。 这里无明显的季节变化。 2、土壤条件_____砖红壤,酸性、含营养盐类和腐 殖质很少,土壤营养物质显得贫乏,但与其它环境 因素配合,仍是植物种类最丰富地区。热带雨林中 土壤和岩石的风化作用强烈,其风化壳可达100米。 这类土壤虽富含铝、铁氧化物、氢氧化物和高岭石, 但其他一些矿物质却因淋溶和侵蚀作用而流失。另 外,在高温高湿条件下,有机物分解很快,能迅速 被饥饿的树根和真菌所吸收。所以,这里的土壤其 实并不肥沃。
悉尼皇家国家公园亚热带雨林中的附生植物
悉尼蓝山暖温带雨林中的桫椤和攀援植物
茎花现象
藤本植物
板状根
7、动物种类很多,但个体数量较少,特有种类较
多。生活于冠层的树叶之间的大多数草食性动物很
少降到地面,它们善于摆动、攀爬、滑行和跳跃,
猩猩、犀、象等在地面生活,犰狳、盲螈、等则穴
第五章 第一节 细菌和真菌在自然界中的作用

讨论:
有些细菌真菌寄生在动植物、人体内,使
他们生病;而有些细菌真菌却能够与动植物、 人体共生。那么,你怎么看待细菌真菌与动植 物和人类的关系呢?
有些细菌和真菌可以导致植物患病
玉米黑粉病
小麦叶锈病
三、与动植物共生
豆 科 植 物 的 根
根 瘤 根 瘤 菌
豆科植物与根瘤菌共生时,能摄取空中之游离氮素其中,真菌向藻类提供 水分和无机盐,藻类向真菌提供营养物质。
壳状地衣
针叶林下的枝状地衣
动物体
动、植物遗体
植物体
2.二氧化碳、 和_______
1.被
和
分解
二、引起动植物患病
肺炎双球菌
金黄葡萄球菌
各 种 各 样 的 癣
真 菌
梅毒皮 肤症状
控诉日本细菌战:他们究竟对我们做了什么?
细菌战亦称“生物战”。是利 用细菌或病毒作武器,以毒害
人、畜及农作物,造成人工瘟
疫的一种灭绝人性的罪行。
第五章 细菌和真菌在生物圈中的作用
如果没有植物,地球将失去绿色,动物和人都要饿死。 如果没有动物,生态平衡也难以维持。
如果没有细菌和真菌呢?
第一节 细菌和真菌 在自然界中的作用
第一节 细菌和真菌在自然界中的作用
如果没有细菌和真
菌的分解,
动植物的遗体就会 堆积如山。
地球将成为一个巨
大的坟场!
一、作为分解者 参与物质循环
其中的藻类通常为绿藻,真菌多 为子囊菌或担子菌
•藻类光合作用制造的有机 物,大部分被菌类所夺取、 藻类和外界环境隔绝,不能 从外界吸取水分、无机盐和 二氧化碳,只好依靠菌类供 给,它们是1种特殊的共生 关系 .
与动物共生
与动物共生
第五章第一节:宗教改革的背景(共17张PPT)

“物必先腐而后生虫,教会之所以 出现改革的诉求,皆因自身的腐败”
——摘自《西方宗教史》
结论
向近代过渡的西欧 --新旧文明的冲突,改革的必然
火刑柱 插图画 中世纪
思考:为什么西欧早期的反封建斗争采取了宗教“异
端”的形式?
1、宗教异端——早期欧洲的反封建斗争
事件:
失败
①12C,法国南部“异端”运动
主张:否定正统宗教仪式和教阶制度
失败
②14C-15C,英国人威克里夫的“异端”学说
主张:信徒与上帝之间不需要教会和教士
③捷克人胡司对教会的批判
切寄人托于是来神世的。附属,为信仰而生活。
组织“十字军东征”,垄断军事; 兜售赎罪券,掠夺财富; 导致封建王权衰落。
十字军东征
兜售赎罪卷
二、宗教改革前的西欧
①天主教的神权统治,人们的思想和行动受到严格控制 ②资本主义不发达,资产阶级力量较弱,不得不借助宗教 外衣。
异端裁判所的一次公开审判 托莱多 版画 罗马 1498年
而罗马帝国内忧外患——312年,君士坦丁受洗皈依,次年6月 发布《米兰敕令》(das Tolerantedikt von Mailand)成为基 督教发展史上的重要转折点,结束了对基督教的长期迫害,恢 复了信仰自由与和平。 ❖ 5.公元329年,狄奥多西一世诏令全国,正式承认基督教为罗马 帝国国教——基督教成为罗马帝国唯一合法宗教。
思想文化上:教会垄断学校教育,文学艺术 也蒙上浓厚的宗教愚色人彩船 布罗尼穆斯·博斯
油画 荷兰 1470年 这幅画描绘了在荒宴中
纵情声色的修女和修士们, 他们正试图咬下悬在空中的 糕点。中世纪教会中所谓圣 者的愚蠢与自负加上他们生 活中的堕落、益发使他们成 为了人们嘲弄的对象。
第五章 第一节流水地貌

坡面流水是雨水或冰雪融水在地表形成的薄
层片流或细流,随地表起伏而流动,没有固定 的流路,因而面状而均匀地冲刷地表松散物质。 如果植被稀疏、地表物质疏松、降水量多且强 度大、坡面形态有利于加快径流流速和增多流 水,那么坡面流水的侵蚀就强烈。坡面流水冲 刷下来的物质或汇入沟谷与河流,是江河泥沙 的主要来源;或在缓坡、坡麓和洼地堆积,成 为坡积物。 当坡面流水和细流增大到一定程度时,会自动 汇集为线状集流,再进一步汇集成沟谷水流。 沟谷流水比较集中,有较固定的流路,其侵蚀 能力比坡面流水显著增强,是形成沟谷地貌的 主要营力。 沟谷进一步发展,或得到地下水补给,就形 成有常流水的河谷,河谷中的常流水就是河流。
(一)、河谷地貌 河流是一种经常性的线状流水,它有固定的流路,较稳定的流量和流 速,作用力比较强大,由它所造成的槽形谷地,称为河谷。 河谷是由河流长期侵蚀而成的线状延伸的凹地,它的底部有着经常性 的水流,至于其他成因如构造运动所成的谷地如果没有河流出现,都 不能称为河谷。河谷的长短不一,大的河谷长达数千公里,如亚马逊 河为6516千米,尼罗河为6484千米,长江为6380千米。 1. 河谷的形态
(二)沟谷流水地貌 沟谷流水在不同的部 位其作用方式和强度都不 同,因而产生三种地貌: 即上游集水盆、中游沟谷 和下游扇形地。 (1)沟谷 它是沟谷 流水侵蚀所成的槽形洼地, 小的仅长10余米,大的可 达数十公里。按其发育程 度又可分为四种类型: 1)细沟:它是最初 发育的小沟,深、宽度不 及0.5m,沟的两坡没有明 显的沟缘(图6.18A), 纵剖面与坡面形态大致相 同。
2)切沟:由细沟发展而成,宽、 深度达到1~2m,长数十米以上, 横剖面是“V”形,沟缘明显, 纵剖面与坡面不一致,其下部 成为下凹形(图6.18B)。 3)冲沟:由切沟进一步侵 蚀而成,是沟谷发育的最盛期 的形态,下切作用强烈,深数 米至百米不等,长可达数公里 至数十公里,横剖面呈峡谷状, 纵剖面崎岖起伏,多陡坎和瓯 穴(图6.18C)。 4)坳沟:沟谷发育晚期的 形态,以侧蚀作用为主,谷坡 迅速扩宽,谷底堆积物增厚, 纵剖面比较平缓,横剖面呈宽 槽形。在我国南方的坳沟多开 辟成“坑田”(图6.18D)。
第五章 第一节 新中国的成立和巩固政权的斗争.

11.1952年底我国已基本完成了土地改革,至 此确立了 A.生产资料公有制 B.人民公社体制 C.农民阶级土地所有制 D.家庭联产承包责任制
12.据统计数字:1951年全国粮食产量比1949 年增加28%,1952年比1949年增加40%,超过 抗战前最高产量的9%,据此得出的结论错误是 A.土地改革提高了农民的生产积极性 B.土地改革使农业走上了社会主义的道路 C.土地改革加速国民经济的恢复 D.土地改革大大解放了农村生产力
1949年10月1日—1956年底:过渡时期 (新民主主义社会向社会主义社会过渡)
①1949.10—1952年底:巩固政权和恢复国民经济 ②1953—1956年底:社会主义制度建立 用3年时间巩固政权和恢复经济 用4年时间完成了三大改造,建立了社会主义制度
并通过1953~1957年一五计划建设发展了经济
新中国成立后,中共对农村生产关系的调整
农民土地所有制(土地改革) 农业合作社 (农业社会主义改造) 人民公社化 家庭联产承包责任制
三反、五反运动(1951年) (1)背景: 不法资本家非法攫取暴利,破坏经济秩序 五毒横行、干部中“糖衣炮弹” (2)三反: 范围:国家机关和企业 内容:
意义:纯洁干部队伍,抑制腐蚀
5.下列关于“三反”运动的表述,正确的是 A.主要在私营企业中进行 B.纯洁了干部队伍,抵制了资产阶级的腐蚀 C.杜绝了腐败和投机现象 D.在工商业领域进行了一次普遍的守法教育
6.1949年中华人民共和国成立标志着 A.社会主义制度的基本建立 B.美国遏制中国政策的失败 C.新民主主义革命的基本胜利 D.社会主义三大改造的开始
②建国第一年与苏联等17个国家正式建立外交 关系
③提出“和平共处五项原则” ④出席了日内瓦会议和亚非国际会议,在亚非 会议上提出了“求同存异”的方针
第五章第一节:启蒙主义文学概述

英国的资本主义经济最为发达, 英国的资本主义经济最为发达, 的资本主义经济最为发达 基本完成了资本主义原始积累; 基本完成了资本主义原始积累; 对英国资产阶级而言, 对英国资产阶级而言,主要任 务是“将革命进行到底” 务是“将革命进行到底”;
法国封建社会已腐朽不堪, 法国封建社会已腐朽不堪,尖 封建社会已腐朽不堪 锐的社会矛盾,导致1789年 锐的社会矛盾,导致 年 资产阶级革命, 资产阶级革命,是启蒙运动的 标本” 中心” “标本”和“中心”。
(一)、英国 )、英国
英国的启蒙运 动是在资产阶 级取得政权之 后发生的。 后发生的。
任务: 任务: 扫除封建主义因素是英国启 蒙运动的一大任务; 蒙运动的一大任务; 同时也批判资本主义制度下 的一些丑恶现象。 的一些丑恶现象。
主要成就: 主要成就: 现实主义小说 这是18世纪英国文学的主要 这是 世纪英国文学的主要 贡献。 贡献。
第一节 概 述 一、影响文学的诸因素 二、启蒙运动与文艺复兴运动 的比较 三、启蒙文学的基本特征 四、启蒙文学发展概况
一、影响文学的诸因素 18世纪仍然是欧洲社会、欧洲 世纪仍然是欧洲社会、 世纪仍然是欧洲社会 文化的理性调整时代。 理性调整时代 文化的理性调整时代。 18世纪是欧洲先进知识分子大 世纪是欧洲先进知识分子大 张旗鼓的进行思想启蒙和张扬 理性的时代。 理性的时代。
后者充满着个性解放的激情, 后者充满着个性解放的激情, 充满着个性解放的激情 前者则以冷静而又富有哲理的 前者则以冷静而又富有哲理的 眼光透视现实生活, 眼光透视现实生活,更能把握 其本质。 其本质。 启蒙现实主义更鲜明地表现出 启蒙现实主义更鲜明地表现出 客观性、社会性和理性的特征。 客观性、社会性和理性的特征。
发展经历: 发展经历: 1.17世纪末——18世纪30 世纪末——18世纪30年 1.17世纪末——18世纪30年 形成时期。 代,形成时期。 诗歌方面的代表:蒲柏, 诗歌方面的代表:蒲柏,英 国第一个启蒙文学作家。 国第一个启蒙文学作家。 现实主义小说的代表: 现实主义小说的代表:笛福 斯威夫特。 和斯威夫特。
第五章 第一节透镜

第一节 透镜
C
目录
ONTENT S 1 学习目标导航
2 3
4
课前自主预习
课堂合作探究 课后作业
2
学习目标导航
学习目标 1、认识凸透镜、凹透镜,了解主光轴、光心、焦 点、焦距等基本概念。 2、知道凸透镜和凹透镜对光的作用,会作出相关 的光路图。 学习重点 1.通过观察和实验,了解凸透镜对光线起会聚作用 和凹透镜对光线起发散作用。 2.凸透镜对光线起会聚作用和凹透镜对光线起发散 作用,会正确作出光路图。 知识链接:光的折射规律
课堂合作探究
(2)、平行于主光轴的光线,经凸透镜后经 过焦点 ;平行于主光轴的光线,经凹透镜后向外 发散,但其反向延长线(必须用虚线画出反向延 长线且不能带箭头)必过异侧的 焦点 ,完成下图:
课堂合作探究 (3)、过凸透镜焦点的光线,经凸透镜后平行 于主光轴;射向凹透镜异侧焦点的光线,经凹透镜 后平行于 主光轴,完成下图:
课后作业
19.(2014佛山)如图所示,S为蜡烛,S′为蜡烛通 过凸透镜所成的像,请根据凸透镜成像特点,画图 确定并标出凸透镜光心O点的位置及两侧焦点F的 位置.
课后作业 20.(2016莆田期末)在如图所示的方框中,填入 适当的透镜.
21.(2014•盐城)将凸透镜正对太阳光,其下方 的纸上呈现一个并非最小的光斑,这时光斑到凸透 镜的距离为l.若凸透镜远离纸的过程中光斑一直 变大,则该凸透镜的焦距( A )
课堂合作探究 5、讨论3:请在图16中画出合适的透镜。 点拨: (1)会聚和发散是折射光线相对于入射光线而言 的。若折射光线相对于入射光线变窄即会聚就是 凸透镜。若折射光线相对于入射光线变宽即发散 就是凹透镜。 (2)光线会聚不一定相交,光线发散不一定不相 交。
第五章第一节:植被 (17张PPT)

森林——常绿阔叶林
主要分布地区
亚热带季风气候和亚热带湿润区
气候特征
夏季炎热多雨,冬季温和且无明显干季
植被特征
森林常绿,乔木多革质叶片,大部分植物花期 集中在春末夏初。与热带雨林相比,垂直结构 较简单,少板根和茎花现象
森林——落叶阔叶林
分布:温带季风气候区或温带海洋气候区
气候特征:夏季炎热或温暖,冬季寒冷 特征:乔木叶片宽阔,春季发芽,秋冬落叶,
一、植被与环境
植被概念:
自然界成群生长的各种植物的整体称为植被。
植被分类
人工花卉
天然植被 人工植被
天然形成的植被 人工栽培和经营管理的植被
人工草场
经济林
更多的植物生长,直至形成稳定的植被
少数植被改造其生长的土壤、水分等环境条件
裸地
光照强度 强
气温越高、降水量越多的地方, 植被高度越大,植物种的数量 越多,垂直结构越丰富。
47. 不是境况造就人,而是人造就境况。48. 你想成为幸福的人吗?但愿你首先学会吃得起苦。——屠格涅夫49. 成功的时候,都说是朋友。但只有母亲——她是失败时的伴侣。——郑振峄 50.在我们的一生中,没有人会为你等待,没有机遇会 为你停留,成功也需要速度 51.不论做什么事,都要相信你自己,别让别人的一句话将你击倒。人生没有对错,只有选择后的坚持,不后悔,走下去,走着走着,花就开了。52.吃别人吃不了的苦,忍别人受不了的气,付出比别人更多的,才 会享受的比别人更多。53.我们每个人的人生之舟都需要自己掌舵,自己掌控。懂得,是跌倒了依然会选择站起,失败了依然会选择重来,受伤了依然会选择坚强;懂得,是在黑暗中依然不迷失方向,在生死关头依然不乱了方寸,在灾难包围 中依然会微笑前行。54.思路清晰远比卖力苦干重要,心态正确远比现实表现重要,选对方向远比努力做事重要,做对的事情远比把事情做对重要。成长的痛苦远比后悔的痛苦好,胜利的喜悦远比失败的安慰好。55.再大的事,到了明天就是 小事,再深的痛,过去了就把它忘记,就算全世界都抛弃了你,——你依然也要坚定前行,因为,你就是自己最大的底气。56.人生路上常有风雨,需要一个好的心态。再难的路,只要不放弃,一直走下去,总会走到终点;再重的担子,笑着 是挑,哭着也是挑,又何必让自己难堪;再不顺的生活,撑一撑,也就过去了,笑容,最终会出现在脸上。57.最精美的宝石,受匠人琢磨的时间最长。最贵重的雕刻,受凿的打击最多。58.只有对过去既往不咎,才能甩掉沉重的包袱;只有能 够看轻自己,才能做到轻装上阵。只要不放弃,就没有什么能让自己退缩;只要够坚强,就没有什么能把自己打垮。59.学会驾驭自己的生活,即使困难重重,也要满怀信心的向前。不自怜不自卑不哀怨,一日一日过,一步一步走,那份柳暗 花明的喜乐和必然的抵达,在于我们自己的修持。真正想做成一件事,不取决于你有多少热情,而是看你能多久坚持。60.永远不要沉溺在安逸里得过且过,能给你遮风挡雨的,同样能让你不见天日。只有让自己更加强大,才能真正的撑起一 片天。61.人生中谁都有梦想,但要立足现实,在拼搏中靠近,在忍耐中坚持,别把它挂在嘴边,常立志者无志。62.人这一辈子,其实做不了几件事,所以想做的事就赶紧去做,并且尽量把它做到最好,这样才不会留下太多的遗憾和悔恨。 淡看人生苦痛,淡薄名利,心态积极而平衡,有所求而有所不求,有所为而有所不为,不用刻意掩饰自己,不用势利逢迎他人,只是做一个简单真实的自己。63.你所做的事情,也许暂时看不到成果,但不要灰心或焦虑,你不是没有成长,而 是在扎 64.无论你从事什么行业,只要做好两件事就够了:一个是专业、一个是人品。专业决定了你的存在,人品决定了你的人脉;剩下的就是坚持。65.给自己的三句话:一、年轻,什么都还来得及;二、不要纠缠于小事;三、你现在遇到的 事都是小事。66.生活只有两种选择:重新出发,做自己生命的主角;抑或停留在原地,做别人的配角。67.决定你的人生高度的,不是你的才能,而是你的人生态度!限制你的,从来就不是什么年龄,而是你的心态!68.水再浑浊,只要长久 沉淀,依然会分外清澄;人再愚钝,只要足够努力,一样能改写命运!69.人最大的对手,就是自己的懒惰;做一件事并不难,难的在于坚持;坚持一下也不难,难的是坚持到底;你全力以赴了,才有资格说自己运气不好;感觉累,也许是因 为你正处于人生的上坡路;只有尽全力,才能迎来美好的明天!70.有理想,有目标,攒足力量向前冲;有勇气,有信心,艰苦奋斗不放松;有恒心,有毅力,百折不挠不认输;加把劲,提提神,前途光明见曙光。71.想要体面生活,又觉得打拼 辛苦;想要健康身体,又无法坚持运动。人最失败的,莫过于对自己不负责任,连答应自己的事都办不到,又何必抱怨这个世界都和你作对?72.人生从来没有固定的路线,决定你能够走多远的,并不是年龄,而是你的努力程度。无论到了什 么时候,只要你还有心情对着糟糕的生活挥拳宣战,都不算太晚。迟做,总比不做好!73.任何打击都不应该成为你堕落的借口,你改变不了这个世界,但你可以改变自己,选择一条正确的路,坚定的走下去。74.也许你一生中走错了不少路, 看错不少人 ,承受了许多的叛逆,落魄得狼狈不胜, 但都无所谓,只要还活着,就总有盼望,余生很长, 何必慌张 75.这世界上,没有能回去的感情。就算真的回去了,你也会发现,一切已经面目全非回去的,只是存于心底的记忆。是的, 回不去了,所以,我们只能一直往前。76.鸡汤再有理,终究是别人的总结。故事再励志,也只是别人的经历,只有你自己才能改变自己。77.理想艰险,遇到再大的困难,想着为自己的理想奋斗,也不会选择放弃。即使在阴霾的云沙下,也 会想到苍天苏醒的风和日丽。即使在封闭的角落中也会让心灵驰骋在广阔的草原上。78.只要勇于去博,英勇去闯,就可闯出一片属于自己天地,以实现人生出色。不管结局能否完美,至少你享受拼搏的过程,就是人生的成功,就是胜者。79. 一个人想要优秀,你必须接受挑战!一个人想要尽快优秀,就要寻找挑战!80.人最大的对手,就是自己的懒惰;做一件事并不难,难的在于坚持;坚持一下也不难,难的是坚持到底;你全力以赴了,才有资格说自己运气不好;感觉累,也许 是因为你正处于人生的上坡路;只有尽全力,才能迎来美好的明天!81.每个人都有一行热泪,苦也要面对,因为坚强;每个人都有无言的伤,痛也要承受,因为成长。82.每一份坚持都是成功的累积!只要相信自己,总会遇到惊喜;每一种 生活都有各自的轨迹!记得肯定自己,不要轻言放弃;每一个清晨都是希望的开始,记得鼓励自己!83.我没有靠山,自己就是山!我没有天下,自己打天下!我没有资本,自己赚资本!这世界从来没有什么救世主。我弱了,所有困难就强了。 我强了,所有阻碍就弱了!活着就该逢山开路,遇水架桥。生活,你给我压力,我还你奇迹!.你要记得,在这个世界上,你是独一无二的,没人像你,你也不需要去代替谁。在你的人生舞台上,你是自己的主角,不需要去做谁
《汉字通论》第五章第一节 第一节 衣食住行

—— 纨 纨,细致洁白的薄绸,“纨绔”是富贵人穿的胫衣,后来
绔
指代富贵人家不务正业的子弟。
衣食住行:衣
上古无棉花,制衣材料除皮毛之外只有丝和麻。富贵者穿丝织品,庶人穿 麻织品。丝织品统称为“帛”,因此跟衣服有关的汉字大都以“衣”、 “丝”、“帛”作为偏旁。
末,食用。有点类似于今天的肉松。
脍 一种烹饪法。将肉切成细丝,越细越好。
衣食住行:食
醢 肉酱。肉酱的制作过程很复杂:先把肉制成肉干,然后铡碎,在碎肉中加
入酒曲和盐搅拌,再用好酒浸渍,密封在瓶子里,经过一百天才可食用。 工序这样多,做工这样细,其美味可想而知。醢不是单独食用的食物,而 是放在其他肉食中一道食用,所以醢相当于一种调料。
第五章 汉字文化
第一节 衣食住行
衣食住行:衣
绅 古人上衣外面要系腰带,腰带打结后余下的部分延伸下垂,叫做“绅”。
—— 缙 本作“搢绅”,搢者,插也,谓插笏于带,这是古代官员
绅
的装束,因而也作为官员的代称。
常 现代汉语里,人们把衣服称为“衣裳”,但在古代“衣”和“裳”是分
开的,“衣”是上衣,“裳”是下裙。“裳”本作“常”。上衣可袒,
或者天生的秃头,或者头发脱落,就要戴假发来装饰(因为妇女不
戴冠,头发是裸露在外的)。
沐 因为头发很重要,也因为头发长,洗起来很麻烦,所以造了个词来专指
洗头发。
衣食住行:食
食
下边是器皿装满了食物,两个点表示食物满得要溢出了,上边三
角形是盖子;也有人认为,上边的三角形是人的口,两个点是人
对着食物流下的口水。总之“食”字与食物或吃的动作有关。作
上冠,戴上冠之后要用簪子横插过头发与冠,使其固定。
第五章 第一节 三种方法表示点的运动的比较
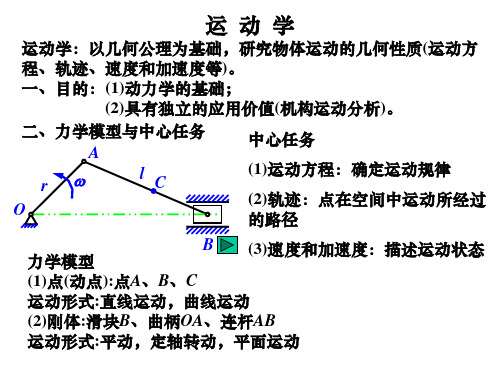
x
第一节 三种方法表示点的运动的比较
a r
O z a r O y M z x v y M v 直角坐标法 自然法 x=f1(t) 运 y=f2(t) 动 s = f(t) r = r(t) z=f3(t) 方 r=xi+yj+zk 程 g1(x,y)=0 轨 已知 矢端曲线 g2(x,z)=0 迹 vx = x vy= y 速 v=dr/dt r v =s vz = z = 度 沿轨迹切线 v = vt v= vxi+vy j+vzk a=at+an ax= v x 加 ay= v x =att+ann r 速 a= v = az= v z at= v an=v2/r 度 a=axi+ay j+azk an指向曲率中心 矢量法
第五章 点的运动学
本章将研究点的运动 包括点的运动方程、运动轨迹、速度、加速度等。 三种方法: (1)矢量法(主要用于理论分析) (2)直角坐标法(主要用于实际应用) (3) 自然法(主要用于实际应用) 还有柱坐标法和球坐标法(略)
第一节 三种方法表示点的运动的比较
a r
O z a r O y M z x v y M v 直角坐标法 x=f1(t) 运 y=f2(t) 动 z=f3(t) 方 r = r(t) r=xi+yj+zk 程 g1(x,y)=0 轨 矢端曲线 g2(x,z)=0 迹 vx = x vy= y 速 v=dr/dt r vz = z = 度 沿轨迹切线 v= vxi+vy j+vzk ax= v x 加 ay= v x r 速 a= v = az= v z 度 a=axi+ay j+azk 矢量法 自然法
第五章第一节质量守恒定律

点燃
磷 + 氧气 → 五氧化二磷
M1 =
M2
PO 2 点 燃 P 2O 5
铁钉与硫酸铜溶液反应前后质量 的测定
反应前
反应后
实验二:现象与结论
产生的现象:铁钉表面覆盖一层红色物质,
溶液由蓝色变成浅绿色,天平保持平衡
得出结论:化学反应前后物质的质量 和相等
第五章
第一节
质量守恒定律
对比思考:
反应前物质(或物体)
反应后物质(或物体)
锥形瓶 细砂 橡皮塞 气球 白磷
锥形瓶 细砂 橡皮塞 气球 五氧化二磷
氧气 氮气
(空气)
氮气
(剩余气体)
稀有气体等
稀有气体等
白磷质量+氧气质量=五氧化二磷质量
实验一:现象与结论
产生的现象为:产生大量白烟,放热,气
球先膨胀后收缩,天平保 持平衡
化学反应前后
物质பைடு நூலகம் 总质量 呢?
可能改变
宏观
微观
元素种类 六 原子种类 元素质量 不 原子数目 物质的总质量 变 原子质量
物质的种类 改变 分子的种类
可能改变
分子数目
理解质量守恒定律的定义时要注意:
1.质量守恒定律是关于化学反应的普遍 规律,其运用范围是化学变化。一切化学 反应都遵循质量守恒定律。
铁+硫酸铜→铜 +硫酸亚铁
F Me + 1C u S O = C u F e MS O 2
质量守恒定律:(所有的化学反应都遵循质
量守恒定律)
参加反应的 各物质的质
量总 和
生生成成的各物 质的质量
总和
参加化学反应的各物质的质量总和 等于反应后生成的各物质的质量总和。
_第五章_第一节校园礼仪

(二)爱幼
四、邻里团结
(一)相互了解
1、主动接近。 2、掌握情况。 3、严守口风。
(二)相互体谅
1、注意整洁。 2、保持安静。 3、管教孩子。 4、分清财物。
(三)相互关心
1、主动照顾。 2、热情相助。
第三节 公共场所礼仪
公共场所是为社会公众提供服务的地方。
一、交通礼仪
(一)行走礼仪
1、守法。 2、礼让。 3、问候。 4、卫生。 5、位置。 6、举止。 7、围观。
四、体育场礼仪
1、公平 2、守纪
五、景点游览礼仪
1、保护环境 2、不伤风化
营造文明、和谐的旅游环境,关系到每位游客的切身利益。做文明游 客是我们大家的义务,请遵守以下公约: 1、维护环境卫生。不随地吐痰和口香糖,不乱扔废弃物,不在禁烟场 所吸烟。 2、遵守公共秩序。不喧哗吵闹,排队遵守秩序,不并行挡道,不在公 众场所高声交谈。 3、保护生态环境。不踩踏绿地,不摘折花木和果实,不追捉、投打、 乱喂动物。 4、保护文物古迹。不在文物古迹上涂刻,不攀爬触摸文物,拍照摄像 遵守规定。 5、爱惜公共设施。不污损客房用品,不损坏公用设施,不贪占小便宜, 节约用水用电,用餐不浪费。 6、尊重别人权利。不强行和外宾合影,不对着别人打喷嚏,不长期占 用公共设施,尊重服务人员的劳动,尊重各民族宗教习俗。 7、讲究以礼待人。衣着整洁得体,不在公共场所袒胸赤膊;礼让老幼 病残,礼让女士;不讲粗话。 8、提倡健康娱乐。抵制封建迷信活动,拒绝黄、赌、毒。
1、课堂礼仪
(1)课间。
(2)课前两分钟。 (3)迟到。
坐姿端正
起立站直
(4)遵守课堂纪律。
遵守课堂纪律既是对教师辛勤劳动的尊重,也是学 生的一种基本的礼貌礼仪。 (5)注意着装。
第五章 第一节 生态工程的基本原理

)
『本节小结』
物质循环再生 原理:物质能在生态系统中循环往复, 1)_______________ 分层分级利用 _______________ 物种多样性 原理:物种繁多复杂的生态系统具有较 2)_______________ 高的_______________ 抵抗力稳定性 协调与平衡 原理:生态系统的生物数量不能超过 3)_______________ _______________ 环境承载力 (环境容纳量)的限度 4)_______________ 原理:生态系统建设要考虑自然、 整体性 _____________ 、____________ 经济 社会 的整体影响 功能 原理: 系统学和工程学 原理 系统的结构决定_________ 5)_______________ 要通过改善和优化系统结构改善功能 比例关系 ,使得 系统整体性原理:系统各组分间要有适当的_________ 能量、物质、信息等的转换和流通顺利完成,并实现总体功 之和 的效果,即“1+1>2” 能大于各部分______
没有物质循环的系 统,就会产生废弃物, 造成环境污染,并最终 影响么系统的稳定和发 展。
三、生态工程所遵循的基本原理
资料分析讨论
2、物种多样性原理
为什么樟子松林的松毛虫会肆虐,几十亿株杨树会毁于一旦? 而珊瑚礁区却能够在养分稀少的深海中,保持着很高的生物多样性? 纯樟子松林、杨树林的生物多样性低,食物链短而单调,缺少 松毛虫、天牛的天敌,而成片单一的林木又为其提供了丰富的食物 来源,因而会导致了树林的毁坏。 珊瑚礁区的生物多样性高,食物链复杂,不同的生物占据了不 同的时间位、空间位和资源位,因而充分利用了珊瑚礁生态系统的 环境。例如,氮、磷等养分就能够在该区生物体间充分地循环利用 而很少流出系统外。
第五章第一节基因突变和基因重组

6、若一对夫妇所生育子女中,性状差异甚多,这种变 异主要来自 A.基因突变 B.基因重组 C.环境影响 D.染色体变异
7、生物界是千姿百态,多种多样的,这都要建立在生 物丰富变异的基础上。生物丰富的变异主要来源于 A.基因重组 C.染色体变异 B.基因突变 D.环境变化
8、右图是人类镰刀型细胞贫血症病因图解,请据图回答:
A.减数第一次分裂 B.四分体时期 C.减数第一次分裂的间期 D.有丝分裂间期
跟踪训练
2、如果将一个镰刀型细胞贫血症的患者血液, 输给一个血型相同的正常人,将使正常人 A、 基因产生突变,使此人患病 B、无基因突变,性状不遗传给此人 C、基因重组,将病遗传给此人 D、无基因突变,此人无病,其后代患病
“一猪生九仔,连母十个样”——这种 个体的差异,产生的主要原因是什么?
基因重组
二、基因重组
1、概念:
在生物进行有性生殖过程中, 控制不同性状的基因的自由组合。
基因重组——自由组合
减数第一次分裂后期
b
B
Ab 和 aB
B b
AB 和 ab
基因重组——交叉互换
减数第一次分裂前期
AB 和 ab
b
B
b
表现型与基因型有什么样的关系
表现型 (改变)
= 基因型 + 环境条件
(改变) (改变)
将小麦种子种植在肥沃的土壤中, 给予充足的阳光和水分,结出的是粒多 饱满的种子;但是把这些种子种到贫瘠 的土壤中,结出的就是普通的种子。
不可遗传的变异
太空椒(经过太空辐射的青椒)和普 通青椒相比,太空具有明显的优势, 果实 肥大, 把其种下去后结出的仍是太空椒。
跟踪训练
4、一种植物在正常情况下只开红花,但偶然会出现一 朵白花,如果将白花种子种下去,它的后代全部开 白花,出现这种现象的原因是 A. 自然杂交 B. 自然选择 C. 基因突变 D. 基因重组 5、进行有性生殖的生物其亲子代之间总是存在着一定 的差异的主要原因是 A. 基因重组 B. 基因突变 C. 染色体变异 D. 生活条件改变
人教版物理八年级上册-第5章 第1节 透镜(共46张PPT)

知课 识时 管作 理业
1.透镜 分 类:(1)凸透镜是中间 厚 、边缘 薄 的透镜。 (2)凹透镜是中间 薄 、边缘 厚 的透镜。 概 念:(1)主光轴(主轴):通过两个球面球心的直线。
(2)光心(O):薄透镜的中心。 性质:通过光心的光传播方向不改变。 (3)焦点(F):凸透镜能使跟主光轴平行的光会聚在主光轴上的一点,这个点叫 焦点。 (4)焦距(f):焦点到凸透镜光心的距离。
6.(对应例 3)[2017·云南昆明模拟]如图所示,请在图中作出两条入射光线经凹 透镜折射后的折射光线。
【解析】 根据延长线过另一侧焦点的光线经凹透镜折射后将平行于主光轴; 平行于主光轴的光线经凹透镜折射后,其折射光线的反向延长线过焦点分别作出 对应的折射光线,如图所示:
7.(对应例 1)[2017·江西南昌期中](多选)关于透镜的焦点和焦距,下列说法正 确的是( AC )
7.(对应例 4)[2017·湖北老河口模拟]如图所示,请画出光线通过透镜后的光 路图。
【解析】 平行于主光轴的光线经凸透镜折射后将过焦点;过焦点的光线经 凸透镜折射后,平行于主光轴,如图所示:
分课 层时 作 业
1.(对应例 1)[2017·海南定安一模]如图所示,下列透镜属于凸透镜的是( A )
(2)光线经过凸透镜折射后不一定能会聚于一点,比如通过焦点的光线经凸透 镜折射后将平行于主光轴;
(3)通过凸透镜的光线可能是会聚的,也可能是发散的; (4)除了过光心的光线方向不变以外,凹透镜对光线有发散作用,通过凹透镜 的光线可能是发散的,也可能是平行的,还有可能是会聚的(相比原传播方向)。
类型之三 会根据三条特殊光线完成光路图 [2017·四川眉山]在图中完成光路图。
3.(对应例 1、例 2)[2017·湖南益阳自主招生]下列有关透镜对光线作用的说法 中正确的是( A )
第五章第一节染色体和染色质
• ③在细胞的寿命、衰老和死亡中起作用。
染色体端粒
端粒酶
特点:
1. 由RNA和蛋白质构成的复合物 2. 为特殊的逆转录酶,能以自身的RNA为 模板逆转录合成端粒DNA
• 功能:
合成端粒DNA,维持端粒的长度
端粒及端粒酶的意义:
• 在中期染色体上常位于染色体的着丝 粒区,端粒区、次缢痕等部位;
功能:
• 1、具有遗传惰性,不转录也不编 码蛋白质;
• 2、在复制行为上,较常染色质早 聚缩晚复制
• 2)兼性异染色性:
• 作用:
• 染色质的压缩折叠可能是关闭基因 活性的一种途径。
常、异染色质的区别
常染色质 异染色质
螺旋化程度 低
7、染色体的三个关键元素
• 染色体要确保在细胞世代中保持稳定,必须具有 自主复制、保证复制的完整性、遗传物质能够平 均分配到2个子细胞中的能力,与这些能力相关 的结构序列是:
• (1)自主复制DNA序列:
• (2)着丝粒DNA序列:
• (3) 端粒DNA序列:
• 为一段短的正向重复序列,在人类TTAGGG 的高度重复序列。
染色质的二级结构:
• 螺线管 螺线管是染色质的二级结构,6个 核小体缠绕一圈形成的中空性管. 外 30nm; 内10nm,组蛋白H1位于螺旋管内 侧。
内10nm
组蛋白H1
一、二级结构与四级结构模型一致:核小体 (10nm),螺线管(30nm)
30nm螺线管 形成袢环
袢环模型(loop model)
2)着丝粒:
• 着丝粒:由高度重复的异染色质组成,是中期 染色单体相互联系在一起的特殊位;在很多高 等真核生物中,着丝粒看起来像是在染色体一 个点上的浓缩区域,这个区域包含着丝点又称 主缢痕也就是在两个染色单体相连处,染色体 上出现向内凹陷的縊痕,被称为主縊痕。此是 细胞分裂时纺锤丝附着之处。在大部分真核生 物中每个纺锤丝附着在不同的着丝粒上。如啤 酒酵母)附着在每个着丝粒上仅一条纺锤丝。广 义上说着丝粒也常指着丝点﹐然而狭义上的着 丝点是将染色体和纺锤丝微管相结合的蛋白质 复合体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节数列的概念与简单表示法1.数列的有关概念n n 若数列{a n }的前n 项和为S n ,则a n =⎩⎪⎨⎪⎧S 1,n =1,S n -S n -1,n ≥2.5.数列的分类1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)根据数列的前几项归纳出数列的通项公式可能不止一个.( ) (2)1,1,1,1,…,不能构成一个数列.( )(3)任何一个数列不是递增数列,就是递减数列.( )(4)如果数列{a n }的前n 项和为S n ,则对∀n ∈N *,都有a n +1=S n +1-S n .( ) 答案:(1)√ (2)× (3)× (4)√2.已知数列{a n }的通项公式为a n =9+12n ,则在下列各数中,不是{a n }的项的是( ) A .21 B .33 C .152D .153解析:选C 由9+12n =152,得n =14312∉N *.3.在数列{a n }中,a 1=1,a n =1+1a n -1(n ≥2),则a 4=( ) A.32 B.53 C.74D.85解析:选B 由题意知,a 1=1,a 2=1+1a 1=2,a 3=1+1a 2=32,a 4=1+1a 3=53.4.已知数列{a n }满足a 1=1,a n =a n -1+2n (n ≥2),则a 7=( ) A .53 B .54 C .55D .109解析:选C 由题意知,a 2=a 1+2×2,a 3=a 2+2×3,……,a 7=a 6+2×7,各式相加得a 7=a 1+2(2+3+4+…+7)=55.5.数列1,23,35,47,59,…的一个通项公式a n =________.解析:由已知得,数列可写成11,23,35,…,故通项公式可以为a n =n 2n -1.答案:n2n -16.已知数列{a n }的前n 项和S n =2n -3,则数列{a n }的通项公式是________________. 解析:当n =1时,a 1=S 1=2-3=-1,当n ≥2时,a n =S n -S n -1=(2n -3)-(2n -1-3)=2n -2n -1=2n -1.又a 1=-1不适合上式,故a n =⎩⎪⎨⎪⎧-1,n =1,2n -1,n ≥2.答案:a n =⎩⎪⎨⎪⎧-1,n =1,2n -1,n ≥2考点一 由a n 与S n 的关系求通项a n (基础送分型考点——自主练透)[考什么·怎么考]n n 1.已知S n =3n +2n +1,则a n =____________. 解析:因为当n =1时,a 1=S 1=6; 当n ≥2时,a n =S n -S n -1=(3n +2n +1)-[3n -1+2(n -1)+1]=2·3n -1+2,由于a 1不适合此式,所以a n =⎩⎪⎨⎪⎧6,n =1,2·3n -1+2,n ≥2.答案:⎩⎪⎨⎪⎧6,n =1,2·3n -1+2,n ≥22.(2017·全国卷Ⅲ改编)设数列{a n }满足a 1+3a 2+…+(2n -1)a n =2n ,则a n =____________.解析:因为a 1+3a 2+…+(2n -1)a n =2n , 故当n ≥2时,a 1+3a 2+…+(2n -3)a n -1=2(n -1). 两式相减得(2n -1)a n =2, 所以a n =22n -1(n ≥2). 又由题设可得a 1=2,满足上式, 从而{a n }的通项公式为a n =22n -1(n ∈N *). 答案:22n -1(n ∈N *) [题型技法] 已知S n 求a n 的3步骤 (1)先利用a 1=S 1求出a 1;(2)用n -1替换S n 中的n 得到一个新的关系,利用a n =S n -S n -1(n ≥2)便可求出当n ≥2时a n 的表达式;(3)注意检验n =1时的表达式是否可以与n ≥2的表达式合并. 考法(二) 由S n 与a n 的关系,求a n ,S n3.设数列{a n }的前n 项和为S n ,且S n =2(a n -1)(n ∈N *),则a n =( ) A .2n B .2n -1 C .2nD .2n -1解析:选C 当n =1时,a 1=S 1=2(a 1-1),可得a 1=2,当n ≥2时,a n =S n -S n -1=2a n -2a n -1,∴a n =2a n -1,∴数列{a n }为首项为2,公比为2的等比数列,所以a n =2n .4.(2015·全国卷Ⅱ)设S n 是数列{a n }的前n 项和,且a 1=-1,a n +1=S n S n +1,则S n =________.解析:∵a n +1=S n +1-S n ,a n +1=S n S n +1, ∴S n +1-S n =S n S n +1.∵S n ≠0,∴1S n -1S n +1=1,即1S n +1-1S n=-1.又1S 1=-1,∴⎩⎨⎧⎭⎬⎫1S n 是首项为-1,公差为-1的等差数列. ∴1S n=-1+(n -1)×(-1)=-n ,∴S n =-1n .答案:-1n[题型技法] S n 与a n 关系问题的求解思路根据所求结果的不同要求,将问题向不同的两个方向转化. (1)利用a n =S n -S n -1(n ≥2)转化为只含S n ,S n -1的关系式,再求解. (2)利用S n -S n -1=a n (n ≥2)转化为只含a n ,a n -1的关系式,再求解.考点二 由递推关系式求数列的通项公式 (基础送分型考点——自主练透)[考什么·怎么考]1.在数列{a n }中,a 1=1,a n =n -1n a n -1(n ≥2),则数列{a n }的通项公式为__________. 解析:∵a n =n -1n a n -1(n ≥2),∴a n -1=n -2n -1a n -2,a n -2=n -3n -2a n -3,…,a 2=12a 1.以上(n -1)个式子相乘得 a n =a 1·12·23·…·n -1n =a 1n =1n .当n =1时,a 1=1,上式也成立.∴a n =1n (n ∈N *). 答案:a n =1n (n ∈N *)[方法点拨] 叠乘法求通项公式的4步骤方法(二)叠加法求通项公式2.设数列{a n}满足a1=1,且a n+1-a n=n+1(n∈N*),则数列{a n}的通项公式为________________.解析:由题意有a2-a1=2,a3-a2=3,…,a n-a n-1=n(n≥2).以上各式相加,得a n-a1=2+3+…+n=(n-1)(2+n)2=n2+n-22.又∵a1=1,∴a n=n2+n2(n≥2).∵当n=1时也满足上式,∴a n=n2+n2(n∈N*).答案:a n=n2+n2(n∈N*)[方法点拨]叠加法求通项公式的4步骤方法(三)构造法求通项公式3.已知数列{a n}满足a1=1,a n+1=3a n+2,则数列{a n}的通项公式为________________.解析:∵a n+1=3a n+2,∴a n+1+1=3(a n+1),∴a n+1+1a n+1=3,∴数列{a n+1}为等比数列,公比q=3,又a1+1=2,∴a n+1=2·3n-1,∴a n=2·3n-1-1(n∈N*).答案:a n=2·3n-1-1(n∈N*)[方法点拨] 构造法求通项公式的3步骤[怎样快解·准解]1.正确选用方法求数列的通项公式(1)对于递推关系式可转化为a n +1a n=f (n )的数列,并且容易求数列{f (n )}前n 项的积时,采用叠乘法求数列{a n }的通项公式.(2)对于递推关系式可转化为a n +1=a n +f (n )的数列,通常采用叠加法(逐差相加法)求其通项公式.(3)对于递推关系式形如a n +1=pa n +q (p ≠0,1,q ≠0)的数列,采用构造法求数列的通项. 2.避免2种失误(1)利用叠乘法,易出现两个方面的问题:一是在连乘的式子中只写到a 2a 1,漏掉a 1而导致错误;二是根据连乘求出a n 之后,不注意检验a 1是否成立.(2)利用构造法求解时应注意数列的首项的正确求解以及准确确定叠加、叠乘后最后一个式子的形式.考点三 数列的性质及应用 (重点保分型考点——师生共研)1.已知数列{a n }满足a n +1=11-a n,若a 1=12,则a 2 018=( )A .-1 B.12 C .1D .2解析:选D 由a 1=12,a n +1=11-a n ,得a 2=11-a 1=2,a 3=11-a 2=-1,a 4=11-a 3=12,a 5=11-a 4=2,…, 于是可知数列{a n }是以3为周期的周期数列,因此a 2 018=a 3×672+2=a 2=2. 2.已知数列{a n }满足a n =n +13n -16(n ∈N *),则数列{a n }的最小项是第________项.解析:因为a n =n +13n -16,所以数列{a n }的最小项必为a n <0,即n +13n -16<0,3n -16<0,从而n <163.又n ∈N *,所以当n =5时,a n 的值最小.答案:5[解题师说]1.解决数列周期性问题的方法先根据已知条件求出数列的前几项,确定数列的周期,再根据周期性求值. 2.判断数列单调性的2种方法(1)作差比较法:比较a n +1-a n 与0的大小.(2)作商比较法:比较a n +1a n 与1的大小,注意a n 的符号.3.求数列最大项或最小项的方法(1)利用不等式组⎩⎪⎨⎪⎧a n -1≤a n ,a n ≥a n +1(n ≥2)找到数列的最大项;(2)利用不等式组⎩⎪⎨⎪⎧a n -1≥a n ,a n ≤a n +1(n ≥2)找到数列的最小项.[冲关演练]1.已知数列{a n }满足a 1=1,a n +1=a 2n -2a n +1(n ∈N *),则a 2 018=( )A .1B .0C .2 018D .-2 018解析:选B ∵a 1=1,a n +1=a 2n -2a n +1=(a n -1)2,∴a 2=(a 1-1)2=0,a 3=(a 2-1)2=1,a 4=(a 3-1)2=0,…,可知数列{a n }是以2为周期的数列,∴a 2 018=a 2=0,选B.2.等差数列{a n }的公差d <0,且a 21=a 211,则数列{a n }的前n 项和S n 取得最大值时的项数n 的值为( )A .5B .6C .5或6D .6或7解析:选C 由a 21=a 211,可得(a 1+a 11)(a 1-a 11)=0,因为d <0,所以a 1-a 11≠0,所以a 1+a 11=0, 又2a 6=a 1+a 11,所以a 6=0. 因为d <0,所以{a n }是递减数列,所以a 1>a 2>…>a 5>a 6=0>a 7>a 8>…,显然前5项和或前6项和最大,故选C.(一)普通高中适用作业A 级——基础小题练熟练快1.已知数列1,2,7,10,13,…,则219在这个数列中的项数是( ) A .16 B .24 C .26D .28解析:选C 因为a 1=1=1,a 2=2=4,a 3=7,a 4=10,a 5=13,…,所以a n=3n -2.令a n =3n -2=219=76,解得n =26.2.数列{a n }的前n 项和S n =2n 2-3n (n ∈N *),若p -q =5,则a p -a q =( ) A .10 B .15 C .-5D .20解析:选D 当n ≥2时,a n =S n -S n -1=2n 2-3n -[2(n -1)2-3(n -1)]=4n -5,当n =1时,a 1=S 1=-1,符合上式,所以a n =4n -5,所以a p -a q =4(p -q )=20.3.(2017·河南许昌二模)已知数列{a n }满足a 1=1,a n +2-a n =6,则a 11的值为( ) A .31 B .32 C .61D .62解析:选A ∵数列{a n }满足a 1=1,a n +2-a n =6,∴a 3=6+1=7,a 5=6+7=13,a 7=6+13=19,a 9=6+19=25,a 11=6+25=31. 4.(2018·云南检测)设数列{a n }的通项公式为a n =n 2-bn ,若数列{a n }是单调递增数列,则实数b 的取值范围为( )A .(-∞,-1]B .(-∞,2]C .(-∞,3)D.⎝⎛⎦⎤-∞,92 解析:选C 因为数列{a n }是单调递增数列,所以a n +1-a n =2n +1-b >0(n ∈N *),所以b <2n +1(n ∈N *),所以b <(2n +1)min =3,即b <3.5.(2018·湖南湘潭一中、长沙一中等六校联考)已知数列{a n }满足:∀m ,n ∈N *,都有a n ·a m =a n +m ,且a 1=12,那么a 5=( )A.132B.116C.14D.12解析:选A ∵数列{a n }满足:∀m ,n ∈N *,都有a n ·a m =a n +m ,且a 1=12,∴a 2=a 1a 1=14,a 3=a 1·a 2=18,∴a 5=a 3·a 2=132. 6.数列{a n }满足a n +a n +1=12(n ∈N *),a 2=2,S n 是数列{a n }的前n 项和,则S 21为( )A .5B.72C.92D.132解析:选B ∵a n +a n +1=12,a 2=2,∴a n =⎩⎪⎨⎪⎧-32,n 为奇数,2, n 为偶数.∴S 21=11×⎝⎛⎭⎫-32+10×2=72. 7.已知数列{a n }的前n 项和S n =n 2+2n +1(n ∈N *),则a n =________. 解析:当n ≥2时,a n =S n -S n -1=2n +1, 当n =1时,a 1=S 1=4≠2×1+1,因此a n =⎩⎪⎨⎪⎧4,n =1,2n +1,n ≥2.答案:⎩⎪⎨⎪⎧4,n =1,2n +1,n ≥28.已知数列{a n }为12,14,-58,1316,-2932,6164,…,则数列{a n }的一个通项公式是________.解析:各项的分母分别为21,22,23,24,…,易看出从第2项起,每一项的分子都比分母少3,且第1项可变为-2-32,故原数列可变为-21-321,22-322,-23-323,24-324,…故其通项公式为a n =(-1)n·2n -32n ,n ∈N *.答案:a n =(-1)n·2n -32n ,n ∈N *9.数列{a n }的前n 项和为S n ,若S n +S n -1=2n -1(n ≥2,n ∈N *),且S 2=3,则a 1+a 3的值为________.解析:∵S n +S n -1=2n -1(n ≥2),令n =2, 得S 2+S 1=3,由S 2=3得a 1=S 1=0, 令n =3,得S 3+S 2=5,所以S 3=2,则a 3=S 3-S 2=-1,所以a 1+a 3=0+(-1)=-1. 答案:-110.在一个数列中,如果∀n ∈N *,都有a n a n +1a n +2=k (k 为常数),那么这个数列叫做等积数列,k 叫做这个数列的公积.已知数列{a n }是等积数列,且a 1=1,a 2=2,公积为8,则a 1+a 2+a 3+…+a 12=________.解析:依题意得数列{a n }是周期为3的数列,且a 1=1,a 2=2,a 3=4,因此a 1+a 2+a 3+…+a 12=4(a 1+a 2+a 3)=4×(1+2+4)=28.答案:28B 级——中档题目练通抓牢1.若a 1=12,a n =4a n -1+1(n ≥2),则a n >100时,n 的最小值为( )A .3B .4C .5D .6解析:选C 由a 1=12,a n =4a n -1+1(n ≥2)得,a 2=4a 1+1=4×12+1=3,a 3=4a 2+1=4×3+1=13,a 4=4a 3+1=4×13+1=53,a 5=4a 4+1=4×53+1=213>100.2.(2018·咸阳模拟)已知正项数列{a n }中,a 1+a 2+…+a n =n (n +1)2(n ∈N *),则数列{a n }的通项公式为( )A .a n =nB .a n =n 2C .a n =n2D .a n =n 22解析:选B ∵a 1+a 2+…+a n =n (n +1)2, ∴a 1+a 2+…+a n -1=n (n -1)2(n ≥2), 两式相减得a n =n (n +1)2-n (n -1)2=n (n ≥2), ∴a n =n 2(n ≥2).又当n =1时,a 1=1×22=1,a 1=1,适合上式,∴a n =n 2,n ∈N *.故选B.3.若数列{a n }满足:a 1=19,a n +1=a n -3(n ∈N *),则数列{a n }的前n 项和数值最大时,n 的值为( )A .6B .7C .8D .9解析:选B ∵a 1=19,a n +1-a n =-3,∴数列{a n }是以19为首项,-3为公差的等差数列, ∴a n =19+(n -1)×(-3)=22-3n . 设{a n }的前k 项和数值最大,则有⎩⎪⎨⎪⎧ a k ≥0,a k +1≤0k ∈N *,∴⎩⎪⎨⎪⎧22-3k ≥0,22-3(k +1)≤0,∴193≤k ≤223, ∵k ∈N *,∴k =7.∴满足条件的n 的值为7.4.在数列{a n }中,a n >0,且前n 项和S n 满足4S n =(a n +1)2(n ∈N *),则数列{a n }的通项公式为________.解析:当n =1时,4S 1=(a 1+1)2,解得a 1=1; 当n ≥2时,由4S n =(a n +1)2=a 2n +2a n +1, 得4S n -1=a 2n -1+2a n -1+1,两式相减得4S n -4S n -1=a 2n -a 2n -1+2a n -2a n -1=4a n ,整理得(a n +a n -1)(a n -a n -1-2)=0,因为a n >0,所以a n -a n -1-2=0,即a n -a n -1=2, 又a 1=1,故数列{a n }是首项为1,公差为2的等差数列, 所以a n =1+2(n -1)=2n -1. 答案:a n =2n -15.已知数列{a n }的通项公式为a n =(-1)n ·2n +1,该数列的项排成一个数阵(如图),则该数阵中的第10行第3个数为________.a 1 a 2 a 3 a 4 a 5 a 6 ……解析:由题意可得该数阵中的第10行第3个数为数列{a n }的第1+2+3+…+9+3=9×102+3=48项,而a 48=(-1)48×96+1=97,故该数阵中的第10行第3个数为97. 答案:976.已知数列{a n }的通项公式是a n =n 2+kn +4.(1)若k =-5,则数列中有多少项是负数?n 为何值时,a n 有最小值?并求出最小值; (2)对于n ∈N *,都有a n +1>a n ,求实数k 的取值范围. 解:(1)由n 2-5n +4<0,解得1<n <4. 因为n ∈N *,所以n =2,3,所以数列中有两项是负数,即为a 2,a 3. 因为a n =n 2-5n +4=⎝⎛⎭⎫n -522-94, 由二次函数性质,得当n =2或n =3时,a n 有最小值,其最小值为a 2=a 3=-2. (2)由a n +1>a n ,知该数列是一个递增数列,又因为通项公式a n =n 2+kn +4,可以看作是关于n 的二次函数,考虑到n ∈N *,所以-k 2<32,解得k >-3.所以实数k 的取值范围为(-3,+∞).7.已知二次函数f (x )=x 2-ax +a (a >0,x ∈R),有且只有一个零点,数列{a n }的前n 项和S n =f (n )(n ∈N *).(1)求数列{a n }的通项公式;(2)设c n =1-4a n(n ∈N *),定义所有满足c m ·c m +1<0的正整数m 的个数,称为这个数列{c n }的变号数,求数列{c n }的变号数.解:(1)依题意,Δ=a 2-4a =0, 所以a =0或a =4. 又由a >0得a =4, 所以f (x )=x 2-4x +4. 所以S n =n 2-4n +4.当n =1时,a 1=S 1=1-4+4=1; 当n ≥2时,a n =S n -S n -1=2n -5.所以a n =⎩⎪⎨⎪⎧1,n =1,2n -5,n ≥2.(2)由题意得c n =⎩⎪⎨⎪⎧-3,n =1,1-42n -5,n ≥2. 由c n =1-42n -5可知,当n ≥5时,恒有c n >0. 又c 1=-3,c 2=5,c 3=-3,c 4=-13,c 5=15,c 6=37,即c 1·c 2<0,c 2·c 3<0,c 4·c 5<0, 所以数列{c n }的变号数为3. C 级——重难题目自主选做1.已知数列{a n }的通项公式为a n =(n +2)⎝⎛⎭⎫910n (n ∈N *),则数列{a n }的最大项是( ) A .a 6或a 7 B .a 7或a 8 C .a 8或a 9D .a 7解析:选B 因为a n +1-a n =(n +3)⎝⎛⎭⎫910n +1-(n +2)⎝⎛⎭⎫910n =⎝⎛⎭⎫910n ·7-n 10,当n <7时,a n+1-a n >0,即a n +1>a n ;当n =7时,a n +1-a n =0,即a n +1=a n ;当n >7时,a n +1-a n <0,即a n +1<a n ,则a 1<a 2<…<a 7=a 8>a 9>a 10>…,所以此数列的最大项是第7项或第8项,即a 7或a 8.故选B.2.(2018·成都诊断)在数列{a n }中,a 1=1,a n =n 2n 2-1a n -1(n ≥2,n ∈N *),则a n =________.解析:由题意知a n a n -1=n 2n 2-1=n 2(n -1)(n +1),所以a n =a 1×a 2a 1×a 3a 2×…×a na n -1=1×2222-1×3232-1×…×n 2n 2-1=22×32×42×…×n 2(2-1)×(2+1)×(3-1)×(3+1)×(4-1)×(4+1)×…×(n -1)×(n +1) =22×32×42×…×n 21×3×2×4×3×5×…×(n -1)×(n +1)=2nn +1. 答案:2nn +1(二)重点高中适用作业A 级——保分题目巧做快做1.已知数列1,2,7,10,13,…,则219在这个数列中的项数是( ) A .16 B .24 C .26D .28解析:选C 因为a 1=1=1,a 2=2=4,a 3=7,a 4=10,a 5=13,…,所以a n=3n -2.令a n =3n -2=219=76,解得n =26.2.(2018·郑州模拟)已知数列{a n }满足a 1=1,a n +2-a n =6,则a 11的值为( ) A .31 B .32 C .61D .62解析:选A ∵数列{a n }满足a 1=1,a n +2-a n =6, ∴a 3=6+1=7,a 5=6+7=13,a 7=6+13=19, a 9=6+19=25,a 11=6+25=31.3.数列{a n }的前n 项和S n =2n 2-3n (n ∈N *),若p -q =5,则a p -a q =( ) A .10 B .15 C .-5D .20解析:选D 当n ≥2时,a n =S n -S n -1=2n 2-3n -[2(n -1)2-3(n -1)]=4n -5,当n =1时,a 1=S 1=-1,符合上式,所以a n =4n -5,所以a p -a q =4(p -q )=20.4.(2018·湖南湘潭一中、长沙一中等六校联考)已知数列{a n }满足:∀m ,n ∈N *,都有a n ·a m =a n +m ,且a 1=12,那么a 5=( )A.132B.116C.14D.12解析:选A ∵数列{a n }满足:∀m ,n ∈N *,都有a n ·a m =a n +m ,且a 1=12,∴a 2=a 1a 1=14,a 3=a 1·a 2=18,∴a 5=a 3·a 2=132. 5.若数列{a n }满足:a 1=19,a n +1=a n -3(n ∈N *),则数列{a n }的前n 项和最大时,n 的值为( )A .6B .7C .8D .9解析:选B ∵a 1=19,a n +1-a n =-3,∴数列{a n }是以19为首项,-3为公差的等差数列, ∴a n =19+(n -1)×(-3)=22-3n . 设{a n }的前k 项和最大,则有⎩⎪⎨⎪⎧ a k ≥0,a k +1≤0k ∈N *,∴⎩⎪⎨⎪⎧22-3k ≥0,22-3(k +1)≤0, ∴193≤k ≤223, ∵k ∈N *,∴k =7. ∴满足条件的n 的值为7.6.(2018·河北唐山一模)设数列{a n }的前n 项和为S n ,且S n =a 1(4n -1)3,若a 4=32,则a 1=________.解析:∵S n =a 1(4n -1)3,a 4=32,∴S 4-S 3=255a 13-63a 13=32,∴a 1=12. 答案:127.已知数列{a n }为12,14,-58,1316,-2932,6164,…,则数列{a n }的一个通项公式是________.解析:各项的分母分别为21,22,23,24,…,易看出从第2项起,每一项的分子都比分母少3,且第1项可变为-2-32,故原数列可变为-21-321,22-322,-23-323,24-324,…故其通项公式为a n =(-1)n·2n -32n ,n ∈N *.答案:a n =(-1)n·2n -32n ,n ∈N *8.在一个数列中,如果∀n ∈N *,都有a n a n +1a n +2=k (k 为常数),那么这个数列叫做等积数列,k 叫做这个数列的公积.已知数列{a n }是等积数列,且a 1=1,a 2=2,公积为8,则a 1+a 2+a 3+…+a 12=________.解析:依题意得数列{a n }是周期为3的数列,且a 1=1,a 2=2,a 3=4,因此a 1+a 2+a 3+…+a 12=4(a 1+a 2+a 3)=4×(1+2+4)=28.答案:289.已知数列{a n }的前n 项和S n =-12n 2+kn ,k ∈N *,且S n 的最大值为8.试确定常数k ,并求数列{a n }的通项公式.解:因为S n =-12n 2+kn =-12(n -k )2+12k 2,其中k 是常数,且k ∈N *,所以当n =k时,S n 取最大值12k 2,故12k 2=8,k 2=16,因此k =4,从而S n =-12n 2+4n .当n =1时,a 1=S 1=-12+4=72;当n ≥2时,a n =S n -S n -1=⎝⎛⎭⎫-12n 2+4n --12(n -1)2+4(n -1)=92-n . 当n =1时,92-1=72=a 1,所以a n =92-n .10.已知数列{a n }的通项公式是a n =n 2+kn +4.(1)若k =-5,则数列中有多少项是负数?n 为何值时,a n 有最小值?并求出最小值; (2)对于n ∈N *,都有a n +1>a n ,求实数k 的取值范围. 解:(1)由n 2-5n +4<0,解得1<n <4. 因为n ∈N *,所以n =2,3,所以数列中有两项是负数,即为a 2,a 3. 因为a n =n 2-5n +4=⎝⎛⎭⎫n -522-94, 由二次函数性质,得当n =2或n =3时,a n 有最小值,其最小值为a 2=a 3=-2. (2)由a n +1>a n ,知该数列是一个递增数列,又因为通项公式a n =n 2+kn +4,可以看作是关于n 的二次函数,考虑到n ∈N *,所以-k 2<32,解得k >-3.所以实数k 的取值范围为(-3,+∞). B 级——拔高题目稳做准做1.(2018·云南检测)设数列{a n }的通项公式为a n =n 2-bn ,若数列{a n }是单调递增数列,则实数b 的取值范围为( )A .(-∞,-1]B .(-∞,2]C .(-∞,3)D.⎝⎛⎦⎤-∞,92 解析:选C 因为数列{a n }是单调递增数列,所以a n +1-a n =2n +1-b >0(n ∈N *),所以b <2n +1(n ∈N *),所以b <(2n +1)min =3,即b <3.2.已知数列{a n }满足a n +1=a n +2n ,且a 1=33,则a nn 的最小值为( ) A .21 B .10 C.212D.172解析:选C 由已知条件可知,当n ≥2时, a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1) =33+2+4+…+2(n -1)=n 2-n +33,又n =1时,a 1=33满足此式. 所以a n n =n +33n -1.令f (n )=a n n =n +33n-1,则f (n )在[1,5]上为减函数,在[6,+∞)上为增函数. 又f (5)=535,f (6)=212,则f (5)>f (6), 故f (n )=a n n 的最小值为212.3.(2018·成都质检)在数列{a n }中,a 1=1,a n =n 2n 2-1a n -1(n ≥2,n ∈N *),则a n =________.解析:由题意知a n a n -1=n 2n 2-1=n 2(n -1)(n +1),所以a n =a 1×a 2a 1×a 3a 2×…×a na n -1=1×2222-1×3232-1×…×n 2n 2-1=22×32×42×…×n 2(2-1)×(2+1)×(3-1)×(3+1)×(4-1)×(4+1)×…×(n -1)×(n +1) =22×32×42×…×n 21×3×2×4×3×5×…×(n -1)×(n +1)=2nn +1. 答案:2nn +14.已知数列{a n }的通项公式为a n =(-1)n ·2n +1,该数列的项排成一个数阵(如图),则该数阵中的第10行第3个数为________.a 1 a 2 a 3 a 4 a 5 a 6 ……解析:由题意可得该数阵中的第10行第3个数为数列{a n }的第1+2+3+…+9+3=9×102+3=48项,而a 48=(-1)48×96+1=97,故该数阵中的第10行第3个数为97. 答案:975.已知二次函数f (x )=x 2-ax +a (a >0,x ∈R),有且只有一个零点,数列{a n }的前n 项和S n =f (n )(n ∈N *).(1)求数列{a n }的通项公式;(2)设c n =1-4a n(n ∈N *),定义所有满足c m ·c m +1<0的正整数m 的个数,称为这个数列{c n }的变号数,求数列{c n }的变号数.解:(1)依题意,Δ=a 2-4a =0,所以a =0或a =4. 又由a >0得a =4, 所以f (x )=x 2-4x +4. 所以S n =n 2-4n +4.当n =1时,a 1=S 1=1-4+4=1; 当n ≥2时,a n =S n -S n -1=2n -5.所以a n =⎩⎪⎨⎪⎧1,n =1,2n -5,n ≥2.(2)由题意得c n =⎩⎪⎨⎪⎧-3,n =1,1-42n -5,n ≥2. 由c n =1-42n -5可知,当n ≥5时,恒有c n >0. 又c 1=-3,c 2=5,c 3=-3,c 4=-13,c 5=15,c 6=37,即c 1·c 2<0,c 2·c 3<0,c 4·c 5<0, 所以数列{c n }的变号数为3.6.已知{a n }是公差为d 的等差数列,它的前n 项和为S n ,S 4=2S 2+4,在数列{b n }中,b n =1+a na n.(1)求公差d 的值;(2)若a 1=-52,求数列{b n }中的最大项和最小项的值;(3)若对任意的n ∈N *,都有b n ≤b 8成立,求a 1的取值范围. 解:(1)∵S 4=2S 2+4,∴4a 1+3×42d =2(2a 1+d )+4,解得d =1.(2)∵a 1=-52,∴数列{a n }的通项公式为a n =-52+(n -1)×1=n -72,∴b n =1+a n a n =1+1a n=1+1n -72.∵函数f (x )=1+1x -72在⎝⎛⎭⎫-∞,72和⎝⎛⎭⎫72,+∞上分别是单调减函数, ∴b 3<b 2<b 1<1,当n ≥4时,1<b n ≤b 4,∴数列{b n }中的最大项是b 4=3,最小项是b 3=-1. (3)由b n =1+1a n,得b n =1+1n +a 1-1.又函数f (x )=1+1x +a 1-1在(-∞,1-a 1)和(1-a 1,+∞)上分别是单调减函数,且x <1-a 1时,y <1;当x >1-a 1时,y >1.∵对任意的n ∈N *,都有b n ≤b 8, ∴7<1-a 1<8,∴-7<a 1<-6, ∴a 1的取值范围是(-7,-6).。
