用标准孔板流量计测量天然气流量计算实例
孔板流量计理论流量计算公式

二.煤气计算书(省略)
三.程序分析
1.瞬时量
温度量:必须转换成绝对摄氏温度;即+273.15
压力量:必须转换成绝对压力进行计算。即表压+大气压力
补偿计算根据计算公式,数据保存在PLC的寄存器内。同时在intouch画面上做监视。
2.累积量
采用2秒中一个扫描上升沿触发进行累积,即将补偿流量值(Nm3/h)比上1800单位转换成每2S的流量值,进行累积求和,画面带复位清零功能。
Q = 0.004714187 *d^2*ε*@sqr(ΔP/ρ) Nm3/h 0C101.325kPa
也即是画面要求显示的0度标准大气压下的体积流量。
在根据密度公式:
ρ= P*T50/(P50*T)* ρ50
其中:ρ、P、T表示任意温度、压力下的值
ρ50、P50、T50表示50度表压为0.04MPa下的工艺基准点
2009-05-10 17:11:29|分类:技术资料|标签:|字号大中小订阅
引用
蝈蝈的孔板流量理论流量计算公式
(1)差压式流量计
差压式流量计是以伯努利方程和流体连续性方程为依据,根据节流原理,当流体流经节流件时(如标准孔板、标准喷嘴、长径喷嘴、经典文丘利嘴、文丘利喷嘴等),在其前后产生压差,此差压值与该流量的平方成正比。在差压式流量计中,因标准孔板节流装置差压流量计结构简单、制造成本低、研究最充分、已标准化而得到最广泛的应用。孔板流量计理论流量计算公式为:
Q = 0.004714187 *d^2*ε*@sqr(ΔP/ρ)Nm3/h 0C101.325kPa
也即是画面要求显示的0度标准大气压下的体积流量。
在根据密度公式:
ρ= P*T50/(P50*T)* ρ50
化工实验-流量计-数据处理计算过程举例

数据处理计算过程举例以第四组为例1、孔板流量计性能测定(1)流体粘度μ=0.000001198+EXP(1972.53/(273.15+27.7))=0.695×10-3(Pa·s)(2)流体密度ρ=-0.003589285×27.72-0.0872501×27.7+1001.44 =996.1(kg·m3)(3)流体流量qv=6.0(m3÷h)÷3600(s)=1.67×10-3(m3÷s)(4)因流速u=qv÷A=qv÷(3.14×d²÷4)=1.67×10-3÷(3.14×(0.0262)÷4=3.14(m·s)(5)因qv =C×A×√(2ΔP÷ρ)则孔流系数C0=qv/((A×√(2ΔP/ρ))=1.67×10-3/[(3.14×0.0172÷4)×√(2×36.2×1000÷996.1)] =0.862(6)雷诺数Re=d×u×ρ÷μ=0.026×1.67×996.1÷(0.695×10-3)=1170882、文丘里流量计性能测定(1)流体粘度μ=0.000001198+EXP(1972.53/(273.15+29.8))=0.673×10-3(Pa·s)(2)流体密度ρ=-0.003589285×29.82-0.0872501×29.8+1001.44=995.7(kg·m3)(3)流体流量qv=6.9(m3·h)÷3600(s)=1.92×10-3(m3÷s)(4)因流速u=qv ÷A=qv÷(3.14×d²÷4)=1.92×10-3÷(3.14×(0.0262)÷4 =3.61(m·s)(5)因qv =Cv×A×√(2ΔP÷ρ)则孔流系数Cv =qv/((A×√(2ΔP/ρ))=1.92×10-3/[(3.14×0.0152÷4)×√(2×6.0÷995.7)]=0.998(7)雷诺数Re=d×u×ρ÷μ=0.026×1.67×996.1÷(0.695×10-3)=139023 3、转子流量计性能测定涡轮流体流量qv=2.3(m3·h)÷3600(s)=6.39×10-4(m3·s) 流体密度ρ=-0.003589285×25.82-0.0872501×25.8+1001.44=996.8(kg·m3)校正后转子流量:由公式qv ’/qv=√[ρ(ρf-ρ’)]÷√[ρ’(ρf-ρ)]=2.2×√[996.779(7900-996.8)]÷√[996.8(7900-996.779)]÷3600 =6.1×10-4 (m3·s)4、用最大误差法对节流式流量计的流量系数进行误差估算和分析。
孔板流量计理论流量计算公式

孔板流量计理论流量计算公式Modified by JACK on the afternoon of December 26, 2020如果你没有计算书,你只需要向制造厂提供下列数据:管道(法兰)尺寸,管道(法兰)材质,介质,流体的最大和常用流量,温度,压力和你现有的孔板外圆尺寸,生产厂会根据你的数据重新计算,然后你根据计算书重新调整你的差压变送器和流量积算仪引用孔板流量计理论流量计算公式2009-05-10 17:11:29|?分类: |?标签: |字号大中小订阅?引用的(1)差压式流量计差压式流量计是以伯努利方程和流体连续性方程为依据,根据节流原理,当流体流经节流件时(如标准孔板、标准喷嘴、长径喷嘴、经典文丘利嘴、文丘利喷嘴等),在其前后产生压差,此差压值与该流量的平方成正比。
在差压式流量计中,因标准孔板节流装置差压流量计结构简单、制造成本低、研究最充分、已标准化而得到最广泛的应用。
孔板流量计理论流量计算公式为:式中,qf为工况下的体积流量,m3/s;c为流出系数,无量钢;β=d/D,无量钢;d为工况下孔板内径,mm;D为工况下上游管道内径,mm;ε为可膨胀系数,无量钢;Δp为孔板前后的差压值,Pa;ρ1为工况下流体的密度,kg/m3。
对于天然气而言,在标准状态下天然气积流量的实用计算公式为:式中,qn为标准状态下天然气体积流量,m3/s;As为秒计量系数,视采用计量单位而定,此式As=×10-6;c为流出系数;E为渐近速度系数;d为工况下孔板内径,mm;FG为相对密度系数,ε为可膨胀系数;FZ为超压缩因子;FT为流动湿度系数;p1为孔板上游侧取压孔气流绝对静压,MPa;Δp为气流流经孔板时产生的差压,Pa。
差压式流量计一般由节流装置(节流件、测量管、直管段、流动调整器、取压管路)和差压计组成,对工况变化、准确度要求高的场合则需配置压力计(传感器或变送器)、温度计(传感器或变送器)流量计算机,组分不稳定时还需要配置在线密度计(或色谱仪)等。
用标准孔板流量计测量天然气流量

用标准孔板流量计测量天然气流量(SY/T6143—2004)1、适用范围本标准规定了标准孔板的结构形式、技术要求;节流装置的取压方式、使用方法、安装和操作条件、检验要求;天然气在标准参比条件下体积流量、质量流量以及测量不准确度的计算方法;同时还给出了计算流量及其有关不确定度等方面必需的资料。
本标准适用于取压方式为法兰取压和角接取压的节流装置,用标准孔板对气田或油田采出的以甲烷为主要成分的混合气体的流量测量。
本标准不适用于孔板开孔直径小于12.5mm,测量管内径小于50mm和大于1000mm,直径比小于0.1和大于0.75,管径诺雷数小于5000的场合。
对改建或新建的计量系统应满足本标准要求。
本标准不强调更新已建计量系统。
如果计量系统不满足本标准要求,由于流动条件和上游直管不相适应,就可能存在计量系统附加误差。
2、气流条件1)气流通过节流装置的流动应是保持亚音速的,稳定的或仅随时间缓慢变化的。
本标准不适用于脉动流的流量测量。
2)气流应是均匀单项的牛顿流体。
若气体含有质量成分不超过2%的固体或流体微粒,且呈均匀分散状态,也可以认为是均匀单项的牛顿流体。
3)气流流经孔板以前,其流束应与管道轴线平行,气流流动应为充分发展紊流且无漩涡,管道横截面所有点上的旋涡角小于2°,即认为无旋涡。
4)为进行流量测量,应保持孔板下游侧静压力与上游侧静压力之比等于或大于0.75。
5)可接受的速度剖面条件为:横截面上任一点局部留苏与最大流速的必至于很长直管段(超过100D)后管道横截面上流速比值在5%之内一致。
3、标准参比条件:本标准规定投入气体及流量计量的标准参比条件和发热量测量的燃烧标准参比条件均为绝对压力P n等于101.325kPa 和热力学温度Tn等于293.15K。
也可以采用合压力和合同温度作为参比条件。
4、安装要求1)节流装置应安装在两段具有等直径的圆形横截面的直管段之间,在此中间,除了取压孔、测温孔外,无本标准规定之外的障碍和连接支管。
(完整版)孔板流量计的流量计算公式

孔板流量计的流量计算公式简单来说差压值要开方输出才能对应流量实际应用中计算比较复杂一般很少自己计算的这个都是用软件来计算的下面给你一个实际的例子看看吧一.流量补偿概述差压式流量计的测量原理是基于流体的机械能相互转换的原理。
在水平管道中流动的流体,具有动压能和静压能(位能相等),在一定条件下,这两种形式的能量可以相互转换,但能量总和不变。
以体积流量公式为例:Q v = CεΑ/sqr(2ΔP/(1-β^4)/ρ1)其中:C 流出系数;ε 可膨胀系数Α 节流件开孔截面积,M^2ΔP 节流装置输出的差压,Pa;β 直径比ρ1 被测流体在I-I处的密度,kg/m3;Qv 体积流量,m3/h按照补偿要求,需要加入温度和压力的补偿,根据计算书,计算思路是以50度下的工艺参数为基准,计算出任意温度任意压力下的流量。
其实重要是密度的转换。
计算公式如下:Q = 0.004714187 *d^2*ε*@sqr(ΔP/ρ) Nm3/h 0C101.325kPa也即是画面要求显示的0度标准大气压下的体积流量。
在根据密度公式:ρ= P*T50/(P50*T)* ρ50其中:ρ、P、T表示任意温度、压力下的值ρ50、P50、T50表示50度表压为0.04MPa下的工艺基准点结合这两个公式即可在程序中完成编制。
二.煤气计算书(省略)三.程序分析1.瞬时量温度量:必须转换成绝对摄氏温度;即+273.15压力量:必须转换成绝对压力进行计算。
即表压+大气压力补偿计算根据计算公式,数据保存在PLC的寄存器内。
同时在intouch画面上做监视。
2.累积量采用2秒中一个扫描上升沿触发进行累积,即将补偿流量值(Nm3/h)比上1800单位转换成每2S的流量值,进行累积求和,画面带复位清零功能。
用标准孔板流量计测量天然气流量精品

用标准孔板流量计测量天然气流量(SY/T6143—2004)1、适用范围本标准规定了标准孔板的结构形式、技术要求;节流装置的取压方式、使用方法、安装和操作条件、检验要求;天然气在标准参比条件下体积流量、质量流量以及测量不准确度的计算方法;同时还给出了计算流量及其有关不确定度等方面必需的资料。
本标准适用于取压方式为法兰取压和角接取压的节流装置,用标准孔板对气田或油田采出的以甲烷为主要成分的混合气体的流量测量。
本标准不适用于孔板开孔直径小于12.5mm,测量管内径小于50mm和大于1000mm,直径比小于0.1和大于0.75,管径诺雷数小于5000的场合。
对改建或新建的计量系统应满足本标准要求。
本标准不强调更新已建计量系统。
如果计量系统不满足本标准要求,由于流动条件和上游直管不相适应,就可能存在计量系统附加误差。
2、气流条件1)气流通过节流装置的流动应是保持亚音速的,稳定的或仅随时间缓慢变化的。
本标准不适用于脉动流的流量测量。
2)气流应是均匀单项的牛顿流体。
若气体含有质量成分不超过2%的固体或流体微粒,且呈均匀分散状态,也可以认为是均匀单项的牛顿流体。
3)气流流经孔板以前,其流束应与管道轴线平行,气流流动应为充分发展紊流且无漩涡,管道横截面所有点上的旋涡角小于2°,即认为无旋涡。
4)为进行流量测量,应保持孔板下游侧静压力与上游侧静压力之比等于或大于0.75。
5)可接受的速度剖面条件为:横截面上任一点局部留苏与最大流速的必至于很长直管段(超过100D)后管道横截面上流速比值在5%之内一致。
3、标准参比条件:本标准规定投入气体及流量计量的标准参比条件和发热量测量的燃烧标准参比条件均为绝对压力P n等于101.325kPa和热力学温度Tn等于293.15K。
也可以采用合压力和合同温度作为参比条件。
4、安装要求1)节流装置应安装在两段具有等直径的圆形横截面的直管段之间,在此中间,除了取压孔、测温孔外,无本标准规定之外的障碍和连接支管。
天然气流量计算公式

和差压计组成,
对工况变化、
准确度要求高的场合则需配置压力计
(传感器
或变送器)、温度计(传感器或变送器)流量计算机,组分不稳定时还需要配置
在线密度计(或色谱仪)等。
(
2
)速度式流量计
速度式流量计是以直接测量封闭管道中满管流动速度为原理的一类流量计。
工业
应用中主要有:
①涡轮流量计:当流体流经涡轮流量传感器时,在流体推力作用下涡轮受力旋
贸易天然气)
,
则另配置在线色谱仪连续分析混合气体的组分或物性值计算压缩
因子、密度、发热量等。
(
3
)容积式流量计
在容积式流量计的内部,
有一构成固定的大空间和一组将该空间分割成若干个已
知容积的小空间的旋转体,如腰轮、皮膜、转筒、刮板、椭圆齿轮、活塞、螺杆
等。
旋转体在流体压差的作用下连续转动,
不断地将流体从已知容积的小空间中
沿顺流方向和沿逆流方向的传播速度则不同。在较宽的流量(雷诺数)范围内,
该时差与被测流体在管道中的体积流量
(平均流速)
成正比。
超声波流量计的流
量方程式为:
式中,
qf
为工况下的体积流量,
m3/s
;
V
为流体通过超声换能器皿
1
、
2
之间传
播途径上的声道长度,
m
;
L
为超声波在换能器
1
、
2
之间传播途径上的声道长度,
时,
无需补偿就能得到准确结果。
如果有一个或一个以上
?
不一致,
可用式
(
3.34
)
进行补偿。
qv=Aiqmax=
气体流量计算公式

气体流量计算公式 Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】(1)差压式流量计差压式流量计是以伯努利方程和流体连续性方程为依据,根据节流原理,当流体流经节流件时(如标准孔板、标准喷嘴、长径喷嘴、经典文丘利嘴、文丘利喷嘴等),在其前后产生压差,此差压值与该流量的平方成正比。
在差压式流量计中,因标准孔板节流装置差压流量计结构简单、制造成本低、研究最充分、已标准化而得到最广泛的应用。
孔板流量计理论流量计算公式为:式中,qf为工况下的体积流量,m3/s;c为流出系数,无量钢;β=d/D,无量钢;d为工况下孔板内径,mm;D为工况下上游管道内径,mm;ε为可膨胀系数,无量钢;Δp为孔板前后的差压值,Pa;ρ1为工况下流体的密度,kg/m3。
对于天然气而言,在标准状态下天然气积流量的实用计算公式为:式中,qn为标准状态下天然气体积流量,m3/s;As为秒计量系数,视采用计量单位而定,此式As=×10-6;c为流出系数;E为渐近速度系数;d为工况下孔板内径,mm;FG为相对密度系数,ε为可膨胀系数;FZ为超压缩因子;FT为流动湿度系数;p1为孔板上游侧取压孔气流绝对静压,MPa;Δp为气流流经孔板时产生的差压,Pa。
差压式流量计一般由节流装置(节流件、测量管、直管段、流动调整器、取压管路)和差压计组成,对工况变化、准确度要求高的场合则需配置压力计(传感器或变送器)、温度计(传感器或变送器)流量计算机,组分不稳定时还需要配置在线密度计(或色谱仪)等。
(2)速度式流量计速度式流量计是以直接测量封闭管道中满管流动速度为原理的一类流量计。
工业应用中主要有:① 涡轮流量计:当流体流经涡轮流量传感器时,在流体推力作用下涡轮受力旋转,其转速与管道平均流速成正比,涡轮转动周期地改变磁电转换器的磁阻值,检测线圈中的磁通随之发生周期性变化,产生周期性的电脉冲信号。
气体流量计算公式

(1)差压式流量计差压式流量计是以伯努利方程和流体连续性方程为依据,根据节流原理,当流体流经节流件时(如标准孔板、标准喷嘴、长径喷嘴、经典文丘利嘴、文丘利喷嘴等),在其前后产生压差,此差压值与该流量的平方成正比。
在差压式流量计中,因标准孔板节流装置差压流量计结构简单、制造成本低、研究最充分、已标准化而得到最广泛的应用。
孔板流量计理论流量计算公式为:式中,qf为工况下的体积流量,m3/s;c为流出系数,无量钢;β=d/D,无量钢;d为工况下孔板内径,mm;D为工况下上游管道内径,mm;ε为可膨胀系数,无量钢;Δp为孔板前后的差压值,Pa;ρ1为工况下流体的密度,kg/m3。
对于天然气而言,在标准状态下天然气积流量的实用计算公式为:式中,qn为标准状态下天然气体积流量,m3/s;As为秒计量系数,视采用计量单位而定,此式As=3.1794×10-6;c为流出系数;E为渐近速度系数;d为工况下孔板内径,mm;FG 为相对密度系数,ε为可膨胀系数;FZ为超压缩因子;FT为流动湿度系数;p1为孔板上游侧取压孔气流绝对静压,MPa;Δp为气流流经孔板时产生的差压,Pa。
差压式流量计一般由节流装置(节流件、测量管、直管段、流动调整器、取压管路)和差压计组成,对工况变化、准确度要求高的场合则需配置压力计(传感器或变送器)、温度计(传感器或变送器)流量计算机,组分不稳定时还需要配置在线密度计(或色谱仪)等。
(2)速度式流量计速度式流量计是以直接测量封闭管道中满管流动速度为原理的一类流量计。
工业应用中主要有:① 涡轮流量计:当流体流经涡轮流量传感器时,在流体推力作用下涡轮受力旋转,其转速与管道平均流速成正比,涡轮转动周期地改变磁电转换器的磁阻值,检测线圈中的磁通随之发生周期性变化,产生周期性的电脉冲信号。
在一定的流量(雷诺数)范围内,该电脉冲信号与流经涡轮流量传感器处流体的体积流量成正比。
涡轮流量计的理论流量方程为:式中n为涡轮转速;qv为体积流量;A为流体物性(密度、粘度等),涡轮结构参数(涡轮倾角、涡轮直径、流道截面积等)有关的参数;B为与涡轮顶隙、流体流速分布有关的系数;C为与摩擦力矩有关的系数。
孔板流量计(流量)计算表
2.8920
20.000 54
##
中间任意 孔径
6
0.##
中间任意 孔径
30
54
0.0000
54
####### 6(10%)
66.1068
150.000 6(10%)
最大孔径 ####### 30(50%) 147.5542
最大孔径 150.000 30(50%)
#######
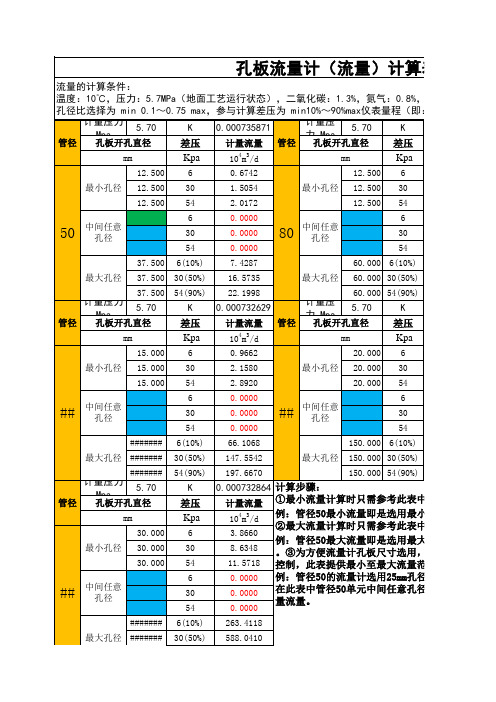
例:管径50的流量计选用25mm孔径时所对应的气量 在此表中管径50单元中间任意孔径绿色单元格处填 量流量。
####### 6(10%) 263.4118
最大孔径 ####### 30(50%) 588.0410
量流量。
最大孔径 ####### 54(90%)
787.7825
)计算表(自编)
气:0.8%,相对密度:0.6,大气压力:0.089MPa,等熵指数:1.3
孔板流量计(流量)计算表(自编)
流量的计算条件:
温度:10℃,压力:5.7MPa(地面工艺运行状态),二氧化碳:1.3%,氮气:0.8%,相对密度:0.6,
孔径比选择为 min 0.1~0.75 max,参与计算差压为 min10%~90%max仪表量程(即:6~54KPa)
计量压力 Mpa
5.70
50
中间任意 孔径
6
0.0000
6
30
0.0000
80
中间任意 孔径
30
54
0.0000
54
37.500 6(10%)
7.4287
60.000 6(10%)
最大孔径 37.500 30(50%) 16.5735
最大孔径 60.000 30(50%)
天然气流量计算公式

1)差压式流量计差压式流量计是以伯努利方程和流体连续性方程为依据,根据节流原理,当流体流经节流件时(如标准孔板、标准喷嘴、长径喷嘴、经典文丘利嘴、文丘利喷嘴等),在其前后产生压差,此差压值与该流量的平方成正比。
在差压式流量计中,因标准孔板节流装置差压流量计结构简单、制造成本低、研究最充分、已标准化而得到最广泛的应用。
孔板流量计理论流量计算公式为:式中, qf 为工况下的体积流量, m3/sc 为流出系数,无量钢;β=d/D,无量钢; d 为工况下孔板内径, mmD 为工况下上游管道内径, mmε为可膨胀系数,无量钢;Δ p 为孔板前后的差压值, Paρ1为工况下流体的密度,kg/m3。
对于天然气而言,在标准状态下天然气积流量的实用计算公式为:式中, qn 为标准状态下天然气体积流量, m3/sAs 为秒计量系数,视采用计量单位而定,此式As=3.1794×10-6c 为流出系数;E 为渐近速度系数; d为工况下孔板内径, mmFG 为相对密度系数,ε为可膨胀系数;FZ 为超压缩因子;FT 为流动湿度系数; p1 为孔板上游侧取压孔气流绝对静压, MPaΔ p 为气流流经孔板时产生的差压,Pa差压式流量计一般由节流装置(节流件、测量管、直管段、流动调整器、取压管路)和差压计组成,对工况变化、准确度要求高的场合则需配置压力计(传感器或变送器)、温度计(传感器或变送器)流量计算机,组分不稳定时还需要配置在线密度计(或色谱仪)等。
(2)速度式流量计速度式流量计是以直接测量封闭管道中满管流动速度为原理的一类流量计。
工业应用中主要有:①涡轮流量计:当流体流经涡轮流量传感器时,在流体推力作用下涡轮受力旋转,其转速与管道平均流速成正比,涡轮转动周期地改变磁电转换器的磁阻值,检测线圈中的磁通随之发生周期性变化,产生周期性的电脉冲信号。
在一定的流量(雷诺数)范围内,该电脉冲信号与流经涡轮流量传感器处流体的体积流量成正比。
sy-t_6143-1996天然气流量的标准孔板计量方法

sy-t_6143-1996天然气流量的标准孔板计量方法全文共四篇示例,供读者参考第一篇示例:SY/T 6143-1996《天然气流量的标准孔板计量方法》是中国石油天然气行业的一项标准,旨在规范使用孔板计量方法对天然气流量进行准确测量。
天然气是一种重要的清洁能源,在生产、储运和使用过程中需要进行流量计量,以确保生产运行的安全和生产数据的准确性。
而孔板计量方法是一种简单、经济、可靠的流量测量方法,被广泛应用于天然气计量领域。
孔板计量方法是基于伯努利方程和连续方程建立的一种流量计算方法,通过孔板上的压差测量来得出天然气的流量。
孔板计量方法适用于对干燥、无腐蚀性、无凝积性气体进行流量计量,具有结构简单、安装方便、维护成本低等优点。
SY/T 6143-1996标准详细规定了孔板计量方法的应用范围、计算公式、试验装置、试验步骤等内容,以确保孔板计量方法在实际应用中能够获得准确可靠的流量数据。
该标准要求在进行孔板计量之前,要对孔板进行严格的检查和校准,确保孔板的几何尺寸和表面光洁度符合标准要求。
在孔板计量过程中,应注意避免气体泄漏、管道振动等因素对测量结果的影响,同时要及时记录测量数据和环境条件,以备后续分析和核查。
第二篇示例:天然气是一种重要的能源资源,在很多领域都有着广泛的应用。
为了有效地监测和计量天然气的流量,我们需要使用一些特殊的设备和方法。
标准孔板计量方法是一种非常常用和有效的计量方法。
本文将详细介绍和解释sy-t_6143-1996天然气流量的标准孔板计量方法。
一、标准孔板的特点标准孔板是一种测量流体流量的装置,通常用于中小口径管道中的流量测量。
标准孔板具有以下特点:1. 结构简单:标准孔板由一块金属板上开有一个孔构成。
2. 安装方便:标准孔板安装在管道内部,与管道之间不存在密封接触,不会对管道内部的流体造成阻力。
3. 测量准确:标准孔板通过测量差压来计算流量,精度高,适用范围广。
二、标准孔板计量方法标准孔板计量方法是通过测量差压和温度来计算天然气的流量。
差压式流量测量技术问答_五_节流装置计算及温压补偿计算

②计算雷诺数ReD 正常流量雷诺数:
(4)结果
56
AUTOMATION PANORAMA 2011.05
34 内锥式流量计与标准节流装置相比在计算方法 上有什么不同?
根据工程的要求,标准节流装置的计算方法大致分为两大 类: 一类是根据已知的管内径、流量以及流体的物理性质等数 据,选择一个合理的差压,计算出节流装置的孔径。这类方法通 常称为设计计算,是主要的计算方法; 另一类是根据节流装置的孔径、差压、管内径以及流体的物 理性质等数据,核算流量的大小,这类方法通常称为校验计算。 内锥式流量计计算时,根据实际工程和机械加工技术的需要, 常常把内锥体的直径与管内径固定下来,用等效直径比βV表示:
Column
专栏
[专家Q&A]
差压式流量测量技术问答(五)
节流装置计算及温压补偿计算
天津石化炼油厂
汪玉忠
33 用实例说明采用行标(SY/T6143)是如何计 算天然气流量的孔板孔径?
(1)已知条件 ①天然气正常流量:qvcon=8.15m3/s,最大流量qvmax=11.25 m3/s, 最小流量qvmin=4.00 m3/s ②天然气操作温度t1=15℃ ③测量管内径:D20=259.38 mm ④正常差压:Δp=12500 Pa,(最大差压ΔP=2500 0Pa) ⑤管道静压:p1=1.48 MPa ⑥当地常用大气压:pa=0.0981 MPa ⑦介质真实相对密度:Gr=0.6640 ⑧介质等熵系数K=1.36,介质动力粘度μ=0.01096 ⑨管道材质热膨胀系数 ⑩孔板材质热膨胀系数 (2)辅助计算 ①操作条件下的管内径D /℃ /℃
最大流量雷诺数:
最小流量雷诺数:
(3)计算 ③求β′的近似值: 由本题数据求出(也可以查图SY/T6143—2004 88页) FG=1.2272 ε=0.9975 FZ=1.0216 FT=1.0086 设β0=0.6 E=1.0719 C=0.06043 则:
孔板流量计理论流量计算公式

孔板流量计,可广泛应用于石油、化工、天然气、冶金、电力、制药等行业中,各种液体、气体、天燃气以及蒸汽的体积流量或质量流量的连续测量。但是许多人不知道孔板流量计是怎么计算出来,今天我就和大家探讨一下孔板流量计的计算公式
Q v = CεΑ/sqr(2ΔP/(1-β^4)/ρ1)
其中:C流出系数;
ε可膨胀系数
Α节流件开孔截面积,M^2
ΔP节流装置输出的差压,Pa;
β直径比
ρ1被测流体在I-I处的密度,kg/m3;
Qv体积流量,m3/h
按照补偿要求,需要加入温度和压力的补偿,根据计算书,计算思路是以50度下的工艺参数为基准,计算出任意温度任意压力下的流量。其实重要是密度的转换。计算公式如下:
Q = 0.004714187 *d^2*ε*@sqr(ΔP/ρ)Nm3/h 0C101.325kPa
也即是画面要求显示的0度标准大气压下的体积流量。
在根据密度公式:
ρ= P*T50/(P50*T)* ρ50
其中:ρ、P、T表示任意温度、压力下的值
ρ50、P50、T50表示50度表压为0.04MPa下的工艺基准点
简单来说差压值要开方输出才能对应流量
实际应用中计算比较复杂一般很少自己计算的这个都是用软件来计算的下面给你一个实际的例子看看吧
一.流量补偿概述
差压式流量计的测量原理是基于流体的机械能相互转换的原理。在水平管道中流动的流体,具有动压能和静压能(位能相等),在一定条件下,这两种形式的能量可以相互转换,但能量总和不变。以体积流量公式为例:
孔板流量计流量计算方法

孔板流量计算方法本方法所需配置:适宜的孔板流量计,空盒气压计,压差计,温度计,瓦斯浓度测定仪。
孔板流量计由抽采瓦斯管路中加的一个中心开孔的节流板、孔板两侧的垂直管段和取压管等组成。
当气体流经管路内的孔板时,流束将形成局部收缩,在全压不变的条件下,收缩使流速增加、静压下降,在节流板前后便会产生静压差。
在同一管路截面条件下,气体的流量越大,产生的压差也越大,因而可以通过测量压差来确定气体流量。
混合气体流量由下式计算:Q=Kb△hδPδT(1)该公式系数计算如下:K=189.76a0mD2(2)b=(1/(1-0.00446x))(3)K—孔板流量计系数,由实验室确定;b—瓦斯浓度校正系数,由有关手册查取;△h—孔板两侧的静压差,mmH2O,由现场实际测定获取;δP—压力校正系数;δT—温度校正系数;x--混合气体中瓦斯浓度,%;t--同点温度,℃;a0--标准孔板流量系数;(在相关手册中查出)m--孔板截面与管道截面比;D--管道直径,米;PT--孔板上风端测得的绝对压力,毫米水银柱;抽采的纯瓦斯流量,采用下式计算:Qw=x·Q(6)式中x—抽采瓦斯管路中的实际瓦斯浓度,%。
孔板流量计在安装时要注意孔板与瓦斯管的同心度,不能装偏。
在钻场内安装流量计时,应保证孔板前后各1m段应平直,不要有阀门和变径管。
在抽采巷瓦斯管末端安装流量计应保证孔板前后各5m段应平直,不要有阀门和变径管。
煤矿抽放瓦斯使用孔板流量计计算抽放要领及参考系数孔板流量计由抽采瓦斯管路中扩展的一个焦点开孔的节流板、孔板两侧的垂直管段和取压管等组成,如下图。
煤矿。
当气体流经管路内的孔板时,流束将造成局限缩短,孔板流量计原理。
在全压不变的条件下,缩短使流速扩展、静抬高落,孔板流量计原理。
在节流板前后便会出现静压差。
学习孔板流量计计算公式。
在同一管路截面条件下,计算公式。
气体的流量越大,你知道流量计。
出现的压差也越大,是以能够经历丈量压差来肯定气体流量。
用标准孔板流量计测量天然气流量-5页word资料

用标准孔板流量计测量天然气流量(SY/T6143—2019)1、适用范围本标准规定了标准孔板的结构形式、技术要求;节流装置的取压方式、使用方法、安装和操作条件、检验要求;天然气在标准参比条件下体积流量、质量流量以及测量不准确度的计算方法;同时还给出了计算流量及其有关不确定度等方面必需的资料。
本标准适用于取压方式为法兰取压和角接取压的节流装置,用标准孔板对气田或油田采出的以甲烷为主要成分的混合气体的流量测量。
本标准不适用于孔板开孔直径小于12.5mm,测量管内径小于50mm和大于1000mm,直径比小于0.1和大于0.75,管径诺雷数小于5000的场合。
对改建或新建的计量系统应满足本标准要求。
本标准不强调更新已建计量系统。
如果计量系统不满足本标准要求,由于流动条件和上游直管不相适应,就可能存在计量系统附加误差。
2、气流条件1)气流通过节流装置的流动应是保持亚音速的,稳定的或仅随时间缓慢变化的。
本标准不适用于脉动流的流量测量。
2)气流应是均匀单项的牛顿流体。
若气体含有质量成分不超过2%的固体或流体微粒,且呈均匀分散状态,也可以认为是均匀单项的牛顿流体。
3)气流流经孔板以前,其流束应与管道轴线平行,气流流动应为充分发展紊流且无漩涡,管道横截面所有点上的旋涡角小于2°,即认为无旋涡。
4)为进行流量测量,应保持孔板下游侧静压力与上游侧静压力之比等于或大于0.75。
5)可接受的速度剖面条件为:横截面上任一点局部留苏与最大流速的必至于很长直管段(超过100D)后管道横截面上流速比值在5%之内一致。
3、标准参比条件:本标准规定投入气体及流量计量的标准参比条件和发热量测量的燃烧标准参比条件均为绝对压力P n等于101.325kPa和热力学温度Tn等于293.15K。
也可以采用合压力和合同温度作为参比条件。
4、安装要求1)节流装置应安装在两段具有等直径的圆形横截面的直管段之间,在此中间,除了取压孔、测温孔外,无本标准规定之外的障碍和连接支管。
天然气流量计算公式

1)差压式流量计差压式流量计是以伯努利方程和流体连续性方程为依据,根据节流原理,当流体流经节流件时(如标准孔板、标准喷嘴、长径喷嘴、经典文丘利嘴、文丘利喷嘴等),在其前后产生压差,此差压值与该流量的平方成正比。
在差压式流量计中,因标准孔板节流装置差压流量计结构简单、制造成本低、研究最充分、已标准化而得到最广泛的应用。
孔板流量计理论流量计算公式为:式中, qf 为工况下的体积流量, m3/sc 为流出系数,无量钢;β=d/D,无量钢; d 为工况下孔板内径, mmD 为工况下上游管道内径, mmε为可膨胀系数,无量钢;Δ p 为孔板前后的差压值, Paρ1为工况下流体的密度,kg/m3。
对于天然气而言,在标准状态下天然气积流量的实用计算公式为:式中, qn 为标准状态下天然气体积流量, m3/sAs 为秒计量系数,视采用计量单位而定,此式As=3.1794×10-6c 为流出系数;E 为渐近速度系数; d为工况下孔板内径, mmFG 为相对密度系数,ε为可膨胀系数;FZ 为超压缩因子;FT 为流动湿度系数; p1 为孔板上游侧取压孔气流绝对静压, MPaΔ p 为气流流经孔板时产生的差压,Pa差压式流量计一般由节流装置(节流件、测量管、直管段、流动调整器、取压管路)和差压计组成,对工况变化、准确度要求高的场合则需配置压力计(传感器或变送器)、温度计(传感器或变送器)流量计算机,组分不稳定时还需要配置在线密度计(或色谱仪)等。
(2)速度式流量计速度式流量计是以直接测量封闭管道中满管流动速度为原理的一类流量计。
工业应用中主要有:①涡轮流量计:当流体流经涡轮流量传感器时,在流体推力作用下涡轮受力旋转,其转速与管道平均流速成正比,涡轮转动周期地改变磁电转换器的磁阻值,检测线圈中的磁通随之发生周期性变化,产生周期性的电脉冲信号。
在一定的流量(雷诺数)范围内,该电脉冲信号与流经涡轮流量传感器处流体的体积流量成正比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所以: β= d / D =150.24/259.37=0.5792
B.1.2.2 求天然气的相对密度 Gr:按 A.1.2 规定:
压力降低,在孔板前后产生静压力差(差压) ,气体的流速越大,孔板前后的差
压也越大,从而可通过测量差压来衡量天然气流过节流装置的流量大小。这种测
量流量的方法是以能量守恒定律和流动连续性方程为基础的。
8.3.1.1 天然气质量流量计算基本公式为:
qm =
C ε π d2 1− β4 4
2∆pρ1
………………(14)
1
1
(2-1)
式中:
C—为了补偿任意两点的摩擦影响所引入的一个经验系数,称为流出系数,
它与节流件几何形状、取压位置及雷诺数等有关,通常由试验确定;
3
ν—平均比容,m /kg;
P—静压力,Pa;
1
U—流体质点的线速度,m/s;
∫ 2 ν dp —为从点 1 到点 2 所测量的压头变化; 1
∫ 2 UdU —为从点 1 到点 2 所测量的速头变化。 1
对式(2-1)积分后得:
C 2 (P2
− P1 )ν
=
−
(U
2 2
−
U
2 1
)
2
对上式整理后得:
U
2 2
−
U
2 1
=
2C 2 (P1
−
P2 )ν
(2-2)
又根据连续性方程,通过各截面的体积流量恒等:
A1U1=A2U2=qv
(2-3)
2
式中:A1、A2 分别为测量管横截面积和孔板开孔面积,m ;
U1、U2 分别为 A1、A2 处的流速,m/s;
7
FZ =
Zn Z1
称为超压缩因子;
联解公式(16)、(17) 和(18),整理后得到天然气在标准参比条件下的体积
流量计算实用公式(19)。
qvn = AvnCEd 2FGεFz FT P1∆p
………(19)
式中:
qvn—天然气在标准参比条件下的体积流量;
3
Avn—体积流量计量系数视采用计量单位而定。秒体积流量(m /s)计量系数
-6
3
3
Avns=3.1795×10 ;小时体积流量(m /h)计量系数 Avnh=0.011446;日体积流量(m /d)
计量系数 Avnd=0.27471;
C—流出系数,按 8.4.2.1 确定;
E—渐近速度系数,按 8.4.2.2 确定;
d—孔板开孔直径,mm,按 8.4.2.3 确定;
FG—相对密度系数,按 8.4.2.4 确定;
Gi 替代 Mg=GiMa)时,则有:
ρ1
=
G1M a P1 Z1 RT1
(2-22)
ρn
=
G1M a Pn Z n RTn
(2-23)
然后将式(2-22)和(2-23)中的 Gi 以式(2-21)中的真实相对密度 Gr 替
代后,则有:
ρ1
=
M a Z n G r P1 RZ a Z 1T 1
……………..(2-24)
Gr—天然气的真实相对密度。
ρn
=
M aGr Pn RZ aTn
……………(18)
令:
E=
1 1− β 4
称为渐近速度系数,将ρ1 和ρn 代入(16)式后,则有:
Qn
=
CE
π 4
ε 1d
2
2 ∆ p r Z N M a P1 RZ a Z 1T1
G r M a Pn
RZ aT n
将分母平方后进入根号,经整理并把部分常数项提到前面后,则有:
式中:
3
ρ1—天然气在操作条件下上游取压孔处的密度,可通过计算或实测得出,kg/ m 。
8.3.1.2 天然气在标准参比条件下的体积流量计算基本公式为:
qvn
=
qm ρn
qvn =
C ε π d2 1− β4 4
2∆pρ1 / ρn
…………………(16)
式中:
3
ρn—天然气在标准参比条件下的密度,可通过计算或实测得出,kg/ m 。
令:
β = d , 则 β 2 = ( d )2 = A2
D
D
A1
2
将β 代入式(2-4),则可求出孔板开孔面积 A2 处的流速:
U
2 2
=
C2 1− β
4
× 2(P1
−
P2 )ν
等式两边同时开平方并以平均密度ρ代替平均比容后得:
U2 =
C 1− β 4
2(P1 − P2 )ρ
(2-5)
2
根据连续性方程,质量流量有:
2 孔板流量计的流量基本方程推导
图 1 孔板节流原理示意图
在孔板前后取断面 1 和 3(如图 1 所示)。按理第一个断面应取流体未收缩
以前处,第二个断面应取孔板后收缩最小处(即断面 3 处,由于它的截面无法测
量,故一般取孔板开孔截面 2 处)。实际上由于流量大小不同时两个断面位置也
是不固定的,因此在制造节流装置时,有意识地把取压孔安排在孔板前后固定的
qm = qv1ρ1 = qv2 ρ2 = qv ρ
根据式(2-3)便有:
qm = U 2 A2 ρ
(2-6)
将式(2-5)代入式(2-6)并令 ∆P = P1 − P2 后得:
qm =
C 1− β 4
• A2
2∆Pρ
(2-7)
令:α = C / 1 − β 4 称为流量系数。
令: E = 1/ 1− β 4 称为渐近速度系数。故,流出系数 C 与流量系数α的关系为:
C=α/E
于是,方程(2-7)可改写为下面形式:
qm
=
CE π 4
d2
2∆Pρ
(2-8)
对气体而言,在流经孔板时,由于流速和压力的改变而伴随着密度的改变(气
体从 P1 降为 P2 因膨胀而使密度减小),为适应此种变化以修正因假设密度等于
常量而对流量引起的偏差,固此必须加入一个系数,这个系数被称为可膨胀性系
求出 d、D:
-6
查表 A.4 得:1Cr18Ni9Ti 的膨胀系数 16.60×10 ,
-6
20 号钢的新无缝钢管的膨胀系数 11.16×10 ,
-5
d=150.25×[1+1.660×10 ×(15-20)]=150.24mm
-5
D=259.38×[1+1.116×10 ×(15-20)]=259.37mm
Tn—标准状态下热力学温度(Tn=293.15K);
Zn—标准状态下,天然气的压缩因子。
其它符号解释同前。
同样,对空气亦可写成与式(2-15)相同的形式:
ρa
=
M a Pn Z a RTn
(2-16)
3
式中:ρa—标准状态下干空气密度,kg/m ;
Za—标准状态下,干空气的压缩因子(Za=0.99963);
8.3.2 天然气流量计算实用公式
按天然气在操作条件下和在标准参比条件下密度与其温度、压力的关系,并
引入与干空气的相对性推导流量计算实用公式。
8.3.2.1 天然气在标准参比条件下的体积流量计算实用公式
根据:
ρ1
=
M a Z n G r P1 RZ a Z T1 1
……………(17)
式中:
Ma—干空气的摩尔质量,其值为 28.9626,kg/kmol;
3
R—通用气体常数,其值为 0.00831451,MPa·m /kmol·K;
Za—干空气在标准参比条件下的压缩因子,其值为 0.99963;
Zn —天然气在标准参比条件下的压缩因子;
6
P1—天然气在操作条件下上游侧取压孔的绝对压力,MPa;
T1—天然气在操作条件下的气流热力学温度,K;
Z1—天然气在操作条件下的压缩因子;
烷
烷
化碳
摩尔 0.8682 0.0625 0.0238 0.0072 0.0064 0.0025 0.0034 0.0027 0.0004 0.0004 0.0068 0.0157 分数
B.1.2 辅助计算
B.1.2.1 求直径比β:
因为β=d/D,
按公式(25)d=d20[1+Λd(t1- t20)]和公式(A.4)D=D20[1+ΛD(t1- t20)]
Qn
=
CE ε 1
π 4
d2
RZ aTn M a Pn2
2 Tn Z n G rT1Z1
∆PP1
将常数 π R Za Tn Pa Ma 等代入后得:
Qn = 3.1794×10−6 CEε1d 2
1 Gr
Tn T1
Zn Z1
∆PP1
令:
FG =
1 Gr
称为相对密度系数;
FT =Tn T1Biblioteka 称为流动温度系数;ρn
=
M aGr Pn RZ aTn
…………….(2-25)
通过求解式(2-24)和(2-25)我们便可通过真实气体的相对密度 Gr 求出
流量方程中的气体真实密度ρ1 和ρn,进而求出天然气在标准状态下的体积流量。
5
8.3 天然气流量计算方法
8.3.1 天然气流量计算基本公式
天然气流经节流装置时,流束在孔板处形成局部收缩,从而使流速增加,静
位置上,其误差将通过水力试验校正之。由于取压孔位置的不同,因而才有了所
谓的不同取压方式,也就有了不同的校正系数(即不同的流量系数或流出系数)。
根据前面假设,在绝热稳定流动过程中,圆管内沿流线水平方向,断面 1
和断面 2 上的流体质点之间将遵守下面的能量方程式:
