《垂直平分线》练习题(含答案)
鲁教版七年级线段的垂直平分线练习50题及参考答案(难度系数0.6)

线段的垂直平分线(难度系数0.6)一、单选题(共20题;共40分)1.如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.下列说法正确的是()A. 甲、乙都正确B. 甲、乙都错误C. 甲正确,乙错误D. 甲错误,乙正确【答案】D【考点】线段垂直平分线的性质,线段垂直平分线的判定2.如图,在△ABC中,DE是边AB的垂直平分线,BC=8cm,AC=5cm,则△ADC的周长为()A. 14cmB. 13cmC. 11cmD. 9cm【答案】B【考点】线段垂直平分线的性质3.已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是70cm和48cm,则△ABC的腰和底边长分别为()A. 24cm和22cmB. 26cm和18cmC. 22cm和26cmD. 23cm和24cm【答案】C【考点】线段垂直平分线的性质4.如图,AC=AD,BC=BD,则有()A. AB与CD互相垂直平分B. CD垂直平分ABC. AB垂直平分CDD. CD平分∠ACB【答案】C【考点】线段垂直平分线的性质5.如图,△ABC中,AB的垂直平分线DE交AB于E,交BC于D,若AC=6,BC=10,则△ACD的周长为()A. 16B. 14C. 12D. 10【答案】A【考点】线段垂直平分线的性质6.如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE 的度数为()A. 70°B. 80°C. 40°D. 30°【答案】D【考点】线段垂直平分线的性质,等腰三角形的性质7.下列说法中正确的是()A. 轴对称图形只有一条对称轴B. 两个三角形关于某直线对称,不一定全等C. 两个全等三角形一定成轴对称D. 直线MN垂直平分线段AB,则直线MN是线段AB的对称轴【答案】D【考点】线段垂直平分线的性质,轴对称的性质8.下列说法中,正确的有()个.①两个全等的三角形一定关于某直线对称;②关于某条直线对称的两个图形,对称点所连线段被对称轴垂直平分;③等腰三角形的高、中线、角平分线互相重合;④等腰三角形一腰上的高与底边的夹角等于顶角的一半;⑤若三角形一个外角的平分线平行于三角形的一边,则这个三角形为等腰三角形.A. 1B. 2C. 3D. 4【答案】B【考点】平行线的性质,线段垂直平分线的性质,轴对称的性质9.如图,△ABC中,AB=AC,AD是∠BAC的平分线,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是()A. 2对B. 3对C. 4对D. 5对【答案】C【考点】三角形全等的判定,线段垂直平分线的性质,等腰三角形的性质10.如图所示,在Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中不一定相等的线段有()A. AC=AE=BEB. AD=BDC. AC=BDD. CD=DE【答案】C【考点】线段垂直平分线的性质11.如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为()A. 75°B. 65°C. 63°D. 61°【答案】B【考点】线段垂直平分线的性质12.如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为()A. 6B. 14C. 18D. 24【答案】B【考点】线段垂直平分线的性质13.如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD.若△ABC的周长是17cm,AE=2cm,则△ABD的周长是()A. 13cmB. 15cmC. 17cmD. 19cm【答案】A【考点】线段垂直平分线的性质14.如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,则∠EBC的度数是()A. 30°B. 40°C. 70°D. 80°【答案】A【考点】线段垂直平分线的性质15.如图,在△ABC中,∠ACB=90°,DE垂直平分AB,垂足为D,如果∠A=30°,AB=6√3cmcm,那么CE等于()A. 3cmB. 2cmC. 4cmD. √3cm【答案】A【考点】线段垂直平分线的性质16.如图,在已知的△ABC中,按以下步骤作图:BC的长为半径作弧,两弧相交于两点M,N;①分别以B,C为圆心,以大于12②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为()A. 90°B. 95°C. 100°D. 105°【答案】D【考点】全等三角形的性质,线段垂直平分线的性质17.如图,在△ABC中,已知AB=AC,DE垂直平分AC,且AC=8,BC=6,则△BDC的周长为()A. 20B. 22C. 10D. 14【答案】D【考点】线段垂直平分线的性质18.在Rt△ABC中,∠C=90°,∠A=15°,AB的垂直平分线和AC相交于点M,则CM:MA等于()A. 1:√3B. √3:1C. 2:√3D. √3:2【答案】 D【考点】线段垂直平分线的性质19.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,ED垂直平分AB于点D,若AB=6,则AE的值是()A. 3√3B. 2√3C. 3D. 2【答案】B【考点】线段垂直平分线的性质,含30度角的直角三角形二、填空题(共12题;共12分)20.如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC=________.【答案】30o【考点】线段垂直平分线的性质,等腰三角形的性质21.如图,△ABC中AB=AC,AB的垂直平分线MN交AC于点D.若AC+BC=10cm,则△DBC的周长为________.【答案】10cm【考点】线段垂直平分线的性质22.如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC 的度数是________.【答案】115°【考点】线段垂直平分线的性质23.如图,△ABC中,AB+AC=6cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为________cm.【答案】6【考点】线段垂直平分线的性质24.如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC=________°.【答案】30【考点】线段垂直平分线的性质,等腰三角形的性质25.如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD的周长为13cm,则△ABC的周长是________ cm.【答案】19【考点】线段垂直平分线的性质26.如图,△ABC中,边AB的中垂线分别交BC、AB于点D、E,AE=3cm,△ADC的周长为9cm,则△ABC 的周长是________cm.【答案】15【考点】线段垂直平分线的性质27.在△ABC中,AB=AC,AB的中垂线于AC所在的直线相交所得的锐角为40°,则底角∠B的大小为________【答案】65°或25°【考点】线段垂直平分线的性质28.如图,在△ABC中,AB=AC,点D、F分别在AB,AC上,DF垂直平分AB,E是BC的中点,若∠C=70°,则∠EDF=________【答案】50°【考点】线段垂直平分线的性质29.如图,在△ABC中,AB=10cm,AC=6cm,BC的垂直平分线交AB于点D,交BC于点E,则△ACD的周长为________cm.【答案】16【考点】线段垂直平分线的性质30.在Rt△ABC中,∠C=90°,CB=8cm,若斜边AB的垂直平分线交CB于点D,CD=2cm,则AD=________ cm.【答案】6【考点】线段垂直平分线的性质31.如图,在△ABC中,AB=6cm,AC=4cm,BC的垂直平分线分别角AB、BC于D、E,则△ACD的周长为________cm.【答案】10【考点】线段垂直平分线的性质三、解答题(共7题;共35分)32.如图,直线AB,CD相交于点O,OE平分∠BOC,OF⊥CD于点O,∠BOD:∠EOB= 2:3,请补全图形,并求出∠AOF的度数.【答案】解:①若OF在CD上方时,如图所示,∵∠BOD:∠EOB=2:3设∠BOD=2x,∠EOB=3x∵OE平分∠BOC∴∠BOC=2 ∠EOB=6x∵∠BOC+∠BOD=180°∴6x+2x=180°解得:x=22.5°∴∠AOC=∠BOD=2×22.5°=45°∵OF⊥CD∴∠COF=90°∴∠AOF=∠AOC+∠COF=135°②若OF在CD下方时,如图所示,∵∠BOD:∠EOB=2:3设∠BOD=2x,∠EOB=3x∵OE平分∠BOC∴∠BOC=2 ∠EOB=6x∵∠BOC+∠BOD=180°∴6x+2x=180°解得:x=22.5°∴∠AOC=∠BOD=2×22.5°=45°∵OF⊥CD∴∠COF=90°∴∠AOF=∠COF-∠AOC=45°综上所述:∠AOF=135°或45°.【考点】角平分线的性质,线段垂直平分线的性质,根据数量关系列出方程33.利用尺规作三角形的三条边的垂直平分线,观察这三条垂直平分线的位置关系,你发现了什么?再换一个三角形试一试。
线段的垂直平分线经典习题及答

线段的垂直平分线(含答案)一、选择题(共8小题)1、(2011•绍兴)如图,在△ABC中,分别以点A和点B为圆心,大于的AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为()A、7B、14C、17D、202、(2011•丹东)如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D.若AC=9,则AE的值是()A、6B、4C、6D、43、(2010•义乌市)如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为()A、6B、5C、4D、34、(2010•烟台)如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于()A、80°B、70°C、60°D、50°5、(2010•台湾)如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:(甲)作∠ACP、∠BCP之角平分线,分别交AB于D、E,则D、E即为所求;(乙)作AC、BC之中垂线,分别交AB于D、E,则D、E即为所求.对于甲、乙两人的作法,下列判断何者正确()A、两人都正确B、两人都错误C、甲正确,乙错误D、甲错误,乙正确6、(2010•三明)如图,在Rt△ABC中,∠C=90°,∠B=30°.AB的垂直平分线DE交AB于点D,交BC于点E,则下列结论不正确的是()A、AE=BEB、AC=BEC、CE=DED、∠CAE=∠B7、(2010•巴中)如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在()A、△ABC的三条中线的交点B、△ABC三边的中垂线的交点C、△ABC三条角平分线的交点D、△ABC三条高所在直线的交点8、(2009•钦州)如图,AC=AD,BC=BD,则有()C、AB与CD互相垂直平分D、CD平分∠ACB二、填空题(共12小题)9、(2011•长春)如图,在△ABC中,∠B=30°,ED垂直平分BC,ED=3.则CE长为_________.10、(2010•无锡)如图,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE=_________度.11、(2010•黄石)如图,等腰三角形ABC中,已知AB=AC,∠A=30°,AB的垂直平分线交AC于D,则∠CBD的度数为_________°.12、(2009•泉州)如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC 与四边形AEDC的周长之差为12,则线段DE的长为_________.13、(2009•临沂)如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB= _________度.14、(2008•孝感)如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠ADC=_________度._________度.16、(2004•陕西)如图,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有_________个不同的四边形.17、(2004•湖州)已知如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于_________.18、(2002•天津)如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形.请写出正确结论的序号_________(把你认为正确结论的序号都填上)19、(2002•广西)如图,△ABC的周长为19cm,AC的垂直平分线DE交BC于D,E为垂足,AE=3cm,则△ABD的周长为_________ cm.20、(2002•安徽)在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC的度数是_________°.三、解答题(共6小题)21、(2011•株洲)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.(1)求∠ECD的度数;(2)若CE=5,求BC长.22、(2011•乐山)如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.1、(2011•绍兴)如图,在△ABC中,分别以点A和点B为圆心,大于的AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为()A、7B、14C、17D、20考点:线段垂直平分线的性质。
北师大版数学八年级下线段的垂直平分线 同步练习含答案

线段的垂直平分线第1课时线段垂直平分线的性质定理及其逆定理1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=3 cm,则线段PB的长为()A.6 cm B.5 cmC.4 cm D.3 cm第1题图第2题图2.如图,AB是CD的垂直平分线.若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是()A.3.9 cm B.7.8 cmC.4 cm D.4.6 cm3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.若BC=6,AC =5,则△ACE的周长为()A.8 B.11C.16 D.17第3题图第4题图4.如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB.若∠A=50°,则∠B的度数为.5.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.6.如图,AC=AD,BC=BD,则有()A.AB垂直平分CDB.CD垂直平分ABC.AB与CD互相垂直平分D.CD平分∠ACB第6题图第7题图7.如图,已知△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是()A.P是AC的垂直平分线与AB的交点B.P是BC的垂直平分线与AB的交点C.P是∠ACB的平分线与AB的交点D.P是以点B为圆心,AC长为半径的弧与边AB的交点8.如图,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC交AC于点D.求证:点D在AB的垂直平分线上.9.在△ABC中,AB=AC,边AB的垂直平分线与边AC所在的直线相交所得的锐角为50°,则∠C的度数为.10.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB;②若PA=PB,EA=EB,则直线PE是线段AB的垂直平分线;③若EA=EB,则直线EP是线段AB的垂直平分线;④若PA=PB,则点P在线段AB的垂直平分线上.其中正确的有()A.1个B.2个C.3个D.4个11.如图,在△ABC中,DE是AC的垂直平分线,AC=6 cm,且△ABD的周长为13 cm,则△ABC的周长为()A.13 cm B.19 cmC.10 cm D.16 cm第11题图第12题图12.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=.13.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为.第13题图第14题图14.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=39°,则∠AOC=.15.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,DE交AC于点F.求证:点E在AF的垂直平分线上.16.如图1,在△ABC中,AB=AC,点D是△ABC外的一点(点D与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.(1)求证:AD垂直平分BC;(2)请从A,B两题中任选一题作答,我选择________题.A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.第2课时三角形三边的垂直平分线1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定()A.是边AB的中点B.在边AB的中线上C.在边AB的高上D.在边AB的垂直平分线上2.在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形()A.三条中线的交点B.三条角平分线的交点C.三条边的垂直平分线的交点D.三条高的交点3.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是()A.锐角三角形B.钝角三角形C.等边三角形D.直角三角形4.如图,已知直线MN为△ABC的边BC的垂直平分线.若AB,AC两边的垂直平分线相交于点O,当顶点A的位置移动时,点O始终在()A.直线MN上B.直线MN的左侧C.直线MN的右侧D.直线MN的左侧或右侧5.下列作图语句正确的是()A.过点P作线段AB的垂直平分线B.在线段AB的延长线上取一点C,使AB=ACC.过直线a和直线b外一点P作直线MN,使MN∥a∥bD .过点P 作直线AB 的垂线6.如图,点E ,F ,G ,Q ,H 在一条直线上,且EF =GH ,我们知道按如图所作的直线l 为线段FG 的垂直平分线.下列说法正确的是( )A .l 是线段EH 的垂直平分线B .l 是线段EQ 的垂直平分线C .l 是线段FH 的垂直平分线D .EH 是l 的垂直平分线第6题图 第7题图7.如图,在Rt △ABC 中,∠B =90°,分别以点A ,C 为圆心,大于12AC 的长为半径画弧,两弧相交于点M ,N ,连接MN ,分别与AC ,BC 交于点D ,E ,连接AE ,则:(1)∠ADE = ;(2)AE EC ;(填“=”“>”或“<”)(3)当AB =3,AC =5时,△ABE 的周长等于 .8.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P ,使P 到该镇A 村、B 村、C 村所属的村委会所在地的距离都相等(A ,B ,C 不在同一直线上,地理位置如图),请你用尺规作图的方法确定点P 的位置.要求:写出已知、求作,不写作法,保留作图痕迹.A 村 ·B 村 ·C 村·9.在平面内,到三点A,B,C距离相等的点()A.只有一个B.有两个C.有三个或三个以上D.有一个或没有10.如图,在△ABC中,∠BAC=90°,AB>AC.按下列步骤作图:①分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;②作直线MN,与边AB相交于点D,连接CD.下列说法不一定正确的是()A.∠BDN=∠CDN B.∠ADC=2∠BC.∠ACD=∠DCB D.2∠B+∠ACD=90°11.等腰三角形的底角为40°,两腰的垂直平分线交于点P,则()A.点P在三角形内B.点P在三角形外C.点P在三角形底边上D.点P的位置与三角形的边长有关12.如图,由于水资源缺乏,B,C两地不得不从黄河上的扬水站A引水,这就需要A,B,C之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,AD垂直BC于点D;在图③中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知△ABC恰好是一个边长为a的等边三角形,那么通过计算,你认为最好的铺设方案是方案.13.如图所示,已知线段a,b,求作等腰三角形,使高为a,腰长为b(a<b,尺规作图,保留作图痕迹).14.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.(1)若∠ACB=120°,求∠MCN的度数;(2)若△CMN的周长为15 cm,求AB的长;(3)若∠MFN=70°,求∠MCN的度数.【变式】如图,在△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.(1)求∠PAQ的度数;(2)若△APQ周长为12,BC长为8,求PQ的长.参考答案:第1课时线段垂直平分线的性质定理及其逆定理1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=3 cm,则线段PB的长为(D)A.6 cm B.5 cmC.4 cm D.3 cm第1题图第2题图2.如图,AB是CD的垂直平分线.若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是(B)A.3.9 cm B.7.8 cmC.4 cm D.4.6 cm3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.若BC=6,AC =5,则△ACE的周长为(B)A.8 B.11C.16 D.17第3题图第4题图4.如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB.若∠A=50°,则∠B的度数为30°.5.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.证明:∵DE是AB的垂直平分线,∴EA=EB.∴∠EAB=∠B.∵∠C=90°,∴∠CAB+∠B=90°.又∵∠AED+∠EAB=90°,∴∠CAB=∠AED.6.如图,AC=AD,BC=BD,则有(A)A.AB垂直平分CDB.CD垂直平分ABC.AB与CD互相垂直平分D.CD平分∠ACB第6题图第7题图7.如图,已知△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是(B)A.P是AC的垂直平分线与AB的交点B .P 是BC 的垂直平分线与AB 的交点 C .P 是∠ACB 的平分线与AB 的交点D .P 是以点B 为圆心,AC 长为半径的弧与边AB 的交点8.如图,在△ABC 中,∠C =90°,∠A =30°,BD 平分∠ABC 交AC 于点D.求证:点D 在AB 的垂直平分线上.证明:∵∠C =90°,∠A =30°, ∴∠ABC =90°-30°=60°. ∵BD 平分∠ABC , ∴∠ABD =12∠ABC =30°.∴∠A =∠ABD. ∴DA =DB.∴点D 在AB 的垂直平分线上.9.在△ABC 中,AB =AC ,边AB 的垂直平分线与边AC 所在的直线相交所得的锐角为50°,则∠C 的度数为20°或70°.10.下列说法:①若直线PE 是线段AB 的垂直平分线,则EA =EB ;②若PA =PB ,EA =EB ,则直线PE 是线段AB 的垂直平分线;③若EA =EB ,则直线EP 是线段AB 的垂直平分线;④若PA =PB ,则点P 在线段AB 的垂直平分线上.其中正确的有(C)A .1个B .2个C .3个D .4个11.如图,在△ABC 中,DE 是AC 的垂直平分线,AC =6 cm ,且△ABD 的周长为13 cm ,则△ABC 的周长为(B)A .13 cmB .19 cmC .10 cmD .16 cm第11题图 第12题图12.如图,在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于点D ,将AB 边沿AD 折叠,发现B 点的对应点E 正好在AC 的垂直平分线上,则∠C =30°.13.如图,在Rt △ABC 中,∠ACB =90°,BC =3,AC =4,AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为76.第13题图 第14题图14.(2020·南京)如图,线段AB ,BC 的垂直平分线l 1,l 2相交于点O.若∠1=39°,则∠AOC =78°.15.如图,在△ABC 中,∠ACB =90°,D 是BC 延长线上一点,E 是BD 的垂直平分线与AB 的交点,DE 交AC 于点F.求证:点E 在AF 的垂直平分线上.证明:∵E 是BD 的垂直平分线上的一点, ∴EB =ED. ∴∠B =∠D. ∵∠ACB =90°,∴∠A=90°-∠B,∠CFD=90°-∠D.∴∠CFD=∠A.又∵∠AFE=∠CFD,∴∠AFE=∠A.∴EF=EA.∴点E在AF的垂直平分线上.16.如图1,在△ABC中,AB=AC,点D是△ABC外的一点(点D与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.(1)求证:AD垂直平分BC;(2)请从A,B两题中任选一题作答,我选择________题.A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.解:(1)证明:∵AB=AC,∴点A在线段BC的垂直平分线上.∵DB=DC,∴点D在线段BC的垂直平分线上.∴AD垂直平分BC.(2)选择A,证明:由(1),得AD⊥BC,又∵AB=AC,∴∠BAF=∠CAF.∵DE∥AC,∴∠CAF=∠ADE.∴∠BAF=∠ADE.∴DE=AE.选择B,线段DE,AC,BE之间的等量关系为DE=BE+AC.证明:由(1),得AF⊥BC,又∵AB=AC,∴∠BAF=∠CAF.∵DE∥AC,∴∠EDA=∠CAF.∴∠BAF=∠EDA.∴AE=DE.∵AE=EB+AB,AB=AC,∴DE=BE+AC.第2课时三角形三边的垂直平分线1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定(D)A.是边AB的中点B.在边AB的中线上C.在边AB的高上D.在边AB的垂直平分线上2.在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形(C)A.三条中线的交点B.三条角平分线的交点C.三条边的垂直平分线的交点D.三条高的交点3.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是(D) A.锐角三角形B.钝角三角形C.等边三角形D.直角三角形4.如图,已知直线MN为△ABC的边BC的垂直平分线.若AB,AC两边的垂直平分线相交于点O,当顶点A的位置移动时,点O始终在(A)A.直线MN上B.直线MN的左侧C.直线MN的右侧D.直线MN的左侧或右侧5.下列作图语句正确的是(D)A.过点P作线段AB的垂直平分线B.在线段AB的延长线上取一点C,使AB=ACC.过直线a和直线b外一点P作直线MN,使MN∥a∥bD.过点P作直线AB的垂线6.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是(A)A.l是线段EH的垂直平分线B.l是线段EQ的垂直平分线C.l是线段FH的垂直平分线D.EH是l的垂直平分线第6题图 第7题图7.如图,在Rt △ABC 中,∠B =90°,分别以点A ,C 为圆心,大于12AC 的长为半径画弧,两弧相交于点M ,N ,连接MN ,分别与AC ,BC 交于点D ,E ,连接AE ,则:(1)∠ADE =90°;(2)AE =EC ;(填“=”“>”或“<”) (3)当AB =3,AC =5时,△ABE 的周长等于7.8.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P ,使P 到该镇A 村、B 村、C 村所属的村委会所在地的距离都相等(A ,B ,C 不在同一直线上,地理位置如图),请你用尺规作图的方法确定点P 的位置.要求:写出已知、求作,不写作法,保留作图痕迹.解:已知:A ,B ,C 三点不在同一直线上. 求作:作一点P ,使PA =PB =PC. 如图所示,点P 即为所求的点.9.在平面内,到三点A ,B ,C 距离相等的点(D) A .只有一个B .有两个C .有三个或三个以上D .有一个或没有10.如图,在△ABC 中,∠BAC =90°,AB >AC.按下列步骤作图:①分别以点B 和点C 为圆心,大于BC 一半的长为半径作圆弧,两弧相交于点M 和点N;②作直线MN,与边AB相交于点D,连接CD.下列说法不一定正确的是(C)A.∠BDN=∠CDN B.∠ADC=2∠BC.∠ACD=∠DCB D.2∠B+∠ACD=90°11.等腰三角形的底角为40°,两腰的垂直平分线交于点P,则(B)A.点P在三角形内B.点P在三角形外C.点P在三角形底边上D.点P的位置与三角形的边长有关12.如图,由于水资源缺乏,B,C两地不得不从黄河上的扬水站A引水,这就需要A,B,C之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,AD垂直BC于点D;在图③中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知△ABC恰好是一个边长为a的等边三角形,那么通过计算,你认为最好的铺设方案是方案③.13.如图所示,已知线段a,b,求作等腰三角形,使高为a,腰长为b(a<b,尺规作图,保留作图痕迹).解:作法:(1)作线段AD=a;(2)过点D作直线MN⊥AD于点D;(3)以点A为圆心,b为半径画弧,交MN于B,C两点,连接AB,AC,△ABC即为所求,如图所示.14.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.(1)若∠ACB=120°,求∠MCN的度数;(2)若△CMN的周长为15 cm,求AB的长;(3)若∠MFN=70°,求∠MCN的度数.解:(1)∵DM,EN分别垂直平分AC和BC,∴AM=CM,CN=BN.∴∠A=∠ACM,∠B=∠BCN.∴∠MCN=180°-(∠CMN+∠CNM)=180°-(2∠A+2∠B)=180°-2(180°-∠ACB)=60°.(2)∵AM=CM,BN=CN,∴△CMN的周长为CM+MN+CN=AM+MN+BN=AB.∵△CMN的周长为15 cm,∴AB=15 cm.(3)∵∠MFN=70°,∴∠MNF+∠NMF=180°-70°=110°.∵∠AMD=∠NMF,∠BNE=∠MNF,∴∠AMD+∠BNE=∠NMF+∠MNF=110°.∴∠A+∠B=90°-∠AMD+90°-∠BNE=70°.又∵∠A=∠ACM,∠B=∠BCN,∴∠MCN=180°-2(∠A+∠B)=40°.【变式】如图,在△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.(1)求∠PAQ的度数;(2)若△APQ周长为12,BC长为8,求PQ的长.解:(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,∵MP和NQ分别垂直平分AB和AC,∴AP=PB,AQ=CQ.∴∠B=∠BAP=x+z,∠C=∠CAQ=x+y.∵∠BAC=80°,∴∠B+∠C=100°,即x+y+z=80°,x+z+x+y=100°.∴x=20°.∴∠PAQ=20°.(2)∵△APQ周长为12,∴AQ+PQ+AP=12.∵AQ=CQ,AP=PB,∴CQ+PQ+PB=12,即BC+2PQ=12.∵BC=8,∴PQ=2.21。
鲁教版七年级垂直平分线练习50题及参考答案(难度系数0.7)

七年级垂直平分线(难度系数0.7)一、单选题(共21题;共42分)1.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是()A. 12B. 13C. 14D. 15【答案】B【考点】线段垂直平分线的性质2.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是()A. 8B. 10C. 12D. 14【答案】B【考点】线段垂直平分线的性质3.若一个三角形两边的垂直平分线的交点在第三边上,则这个三角形是()A. 锐角三角形B. 钝角三角形C. 直角三角形D. 不能确定【答案】C【考点】线段垂直平分线的性质4.如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC于E,则△ADE的周长等于()A. 8B. 4C. 12D. 16【答案】A【考点】线段垂直平分线的性质5.如图,已知AB=AC,AB=5,BC=3,以AB两点为圆心,大于1AB的长为半径画圆弧,两弧相交于点M、2N,连接MN与AC相交于点D,则△BDC的周长为()A. 8B. 10C. 11D. 13【答案】A【考点】线段垂直平分线的性质6.如图,直线DE是△ABC的边AB的垂直平分线,已知AC=5cm,△ADC的周长为17cm,则BC的长为()A. 7cmB. 10cmC. 12cmD. 22cm【答案】C【考点】线段垂直平分线的性质7.如图,在△ABE中,AE的垂直平分线MN交BE于点C,∠E=30°,且AB=CE,则∠BAE的度数是()A. 80°B. 85°C. 90°D. 105°【答案】C【考点】线段垂直平分线的性质8.如图,在△ABC中,DE是边AB的垂直平分线,BC=8cm,AC=5cm,则△ADC的周长为()A. 14cmB. 13cmC. 11cmD. 9cm【答案】B【考点】线段垂直平分线的性质9.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为()A. 8B. 11C. 16D. 17【答案】B【考点】线段垂直平分线的性质10.在联欢晚会上,有A,B,C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在△ABC的()A. 三边中线的交点 B. 三边垂直平分线的交点 C. 三边上高的交点 D. 三条角平分线的交点【答案】B【考点】线段垂直平分线的性质AB的长为半径画圆,两弧相交11.如图,已知AB=AC,AB=5,BC=3,以AB两点为圆心,大于12于点M,N,连接MN与AC相较于点D,则ΔBDC的周长为()A. 8B. 10C. 11D. 13【答案】A【考点】线段垂直平分线的性质12.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为()A. AB>AC=CEB. AB=AC>CEC. AB>AC>CED. AB=AC=CE【答案】D【考点】线段垂直平分线的性质13.如图,在△ABC中,边BC的垂直平分线l与AC相交于点D,垂足为E,如果△ABD的周长为10cm,BE=3cm,则△ABC的周长为()A. 9 cmB. 15 cmC. 16 cmD. 18 cm【答案】C【考点】线段垂直平分线的性质14.如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为13cm,则△ABC的周长为()cm.A. 19B. 13C. 10D. 16【答案】A【考点】线段垂直平分线的性质15.(2015•达州)如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为()A. 48°B. 36°C. 30°D. 24°【答案】A【考点】线段垂直平分线的性质16.如图,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长为().A. 16B. 18C. 26D. 28【答案】B【考点】线段垂直平分线的性质17.如图在△ABC中,BC=8,AB,AC的垂直平分线与BC分别交于E,F两点,则△AEF的周长为( )A. 2B. 4C. 8D. 不能确定【答案】C【考点】线段垂直平分线的性质18.如图,在△ABC中,分别以点A和点B为圆心,大于1AB长为半径画弧,两弧分别相交于点M,N,2作直线MN,交BC于点D,连结AD.若△ADC的周长为10,AB=7,则△ABC的周长为()A. 27B. 14C. 17D. 20【答案】C【考点】线段垂直平分线的性质19.如图,在ΔABC中,∠A=90°,CE平分∠ACB,ED垂直平分BC,CE=5,ED= 1,则AB的长为( )A. 5B. 6C. 10D. 12【答案】B【考点】线段垂直平分线的性质20.如图,在△ABC中,AC=10,BC=8,AB垂直平分线交AB于点M,交AC于点D,则△BDC的周长为()A. 14B. 16C. 18D. 20【答案】C【考点】线段垂直平分线的性质21.已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是70cm和48cm,则△ABC的腰和底边长分别为()A. 24cm和22cmB. 26cm和18cmC. 22cm和26cmD. 23cm和24cm【答案】C【考点】线段垂直平分线的性质二、填空题(共18题;共18分)22.如图,△ABC中,线段BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC=________ °.【答案】96【考点】线段垂直平分线的性质23.已知点O为△ABC三边垂直平分线的交点,点O到顶点A的距离为6cm,则OA+OB+OC=________. 【答案】18cm【考点】线段垂直平分线的性质24.如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为________.【答案】19【考点】线段垂直平分线的性质25.如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于________.【答案】6cm【考点】线段垂直平分线的性质26.如图,在△ABC中,AB=7cm,AC=4cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为________ cm.【答案】11【考点】线段垂直平分线的性质27.如图,△ABC的AC边的垂直平分线DE交BC于点E,若BC=4,AB=3,则△ABE的周长为________【答案】7【考点】线段垂直平分线的性质28.如图,DE是三角形ABC的边AB的垂直平分线,分别交AB、BC于D、E,AE平分∠BAC,若∠B=30度,则∠C=________ 度.【答案】90【考点】线段垂直平分线的性质29.如图,△ABC中,AC=6,BC=4,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.【答案】10【考点】线段垂直平分线的性质30.如图,在△ABC中,AC=10,BC=6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是________.【答案】16【考点】线段垂直平分线的性质31.如图,△ABC的周长为19cm,AC的垂直平分线DE交BC于D,E为垂足,AE=3cm,则△ABD的周长为________cm.【答案】13【考点】线段垂直平分线的性质32.如图,CD是线段AB的垂直平分线,若AC=2cm,BD=4cm,则四边形ACBD的周长是________cm.【答案】12【考点】线段垂直平分线的性质33.如图所示,在△ABC中,DM,EN分别垂直平分AB和AC,交BC于点D,E,若△ADE的周长为19 cm,则BC=________【答案】19【考点】线段垂直平分线的性质34.如图,在△ABC中,AB=8,BC=6,AC的垂直平分线MN交边AB、AC于点M、N.则△BCM的周长为________.【答案】14【考点】线段垂直平分线的性质35.如图,AB+AC=7,D是AB上一点,若点D在BC的垂直平分线上,则△ACD的周长为________.【答案】7【考点】线段垂直平分线的性质36.如图,在周长为10 cm的□ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为________.【答案】5cm【考点】线段垂直平分线的性质37.已知如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于________ .【答案】8【考点】线段垂直平分线的性质38.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC与点E,若三角形BCE的周长等于50,则BC的长为________.【答案】23【考点】线段垂直平分线的性质39.如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=________.【答案】32°【考点】线段垂直平分线的性质三、解答题(共9题;共45分)40.如图,在△ABC中,AB的垂直平分线ED交AC于D,如果AC=7,BC=5,求△BDC的周长.【答案】解:∵ED是AB的垂直平分线,∴AD=BD,∵△BDC的周长=DB+BC+CD,∴△BDC的周长=AD+BC+CD=AC+BC=7+5=12【考点】线段垂直平分线的性质41.如图,在△ABC中,AD是高,在线段DC上取一点E,使DE=BD,已知AB+BD=DC.求证:E点在线段AC的垂直平分线上.【答案】证明:∵AD是高,∴AD⊥BC,又∵BD=DE,∴AD所在的直线是线段BE的垂直平分线,∴AB=AE,∴AB+BD=AE+DE,又∵AB+BD=DC,∴DC=AE+DE,∴DE+EC=AE+DE∴EC=AE,∴点E在线段AC的垂直平分线上【考点】线段垂直平分线的性质42.△ABC中,DE是AC的垂直平分线,AE=5cm,△CBD的周长为24cm,求△ABC的周长。
垂直平分线的性质第1课时线段的垂直平分线的性质和判定练习新版新人教版含答案
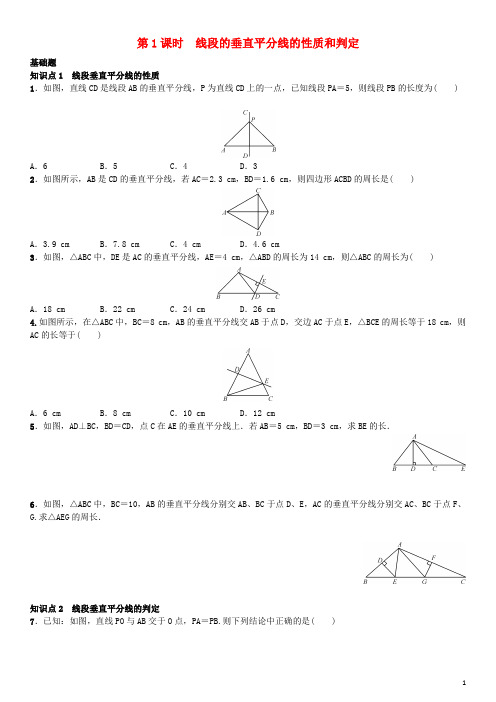
第1课时线段的垂直平分线的性质和判定基础题知识点1 线段垂直平分线的性质1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )A.6 B.5 C.4 D.32.如图所示,AB是CD的垂直平分线,若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是( )A.3.9 cm B.7.8 cm C.4 cm D.4.6 cm3.如图,△ABC中,DE是AC的垂直平分线,AE=4 cm,△ABD的周长为14 cm,则△ABC的周长为( )A.18 cm B.22 cm C.24 cm D.26 cm4.如图所示,在△ABC中,BC=8 cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18 cm,则AC的长等于( )A.6 cm B.8 cm C.10 cm D.12 cm5.如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上.若AB=5 cm,BD=3 cm,求BE的长.6.如图,△ABC中,BC=10,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.求△AEG的周长.知识点2 线段垂直平分线的判定7.已知:如图,直线PO与AB交于O点,PA=PB.则下列结论中正确的是( )A.AO=BOB.PO⊥ABC.PO是AB的垂直平分线D.P点在AB的垂直平分线上8.如图所示,AB=AC,DB=DC,E是AD延长线上的一点,BE是否与CE相等?试说明理由.知识点3 经过直线外一点作已知直线的垂线9.如图,已知钝角△ABC,其中∠A是钝角,求作AC边上的高BH.中档题10.(临沂中考)如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )A.AB=AD B.AC平分∠BCDC.AB=BD D.△BEC≌△DEC11.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB∶∠CAE=3∶1,则∠C等于( )A.28°B.25°C.22.5° D.20°12.已知:如图,AC是线段BD的垂直平分线,E是AC上的一点,则图中全等的三角形共有( )A.3对B.4对C.5对D.6对13.在锐角△ABC内一点P,满足PA=PB=PC,则点P是△ABC( )A.三条角平分线的交点B.三条中线的交点C.三条高的交点D.三边垂直平分线的交点14.如图,在△ABC中,AB=AC,AB的垂直平分线交AB,AC于点D,E,△BCE的周长是8,AB-BC=2,则△ABC 的周长是( )A.13 B.12 C.11 D.1015.如图所示,直线MN是线段AB的对称轴,点C在MN外,CA与MN相交于点D,如果CA+CB=8 cm,那么△BCD 的周长等于________cm.16.如图,△ABC中,边AB,BC的垂直平分线交于点P,且AP=5,那么PC=________.17.已知直线l与线段AB交于点O,点P在直线l上,且AP=PB,下列结论:①OA=OB;②PO⊥AB;③∠APO=∠BPO;④点P在线段AB的垂直平分线上,其中正确的有________.18.如图,四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A,连接AC,求证:点A在CD的垂直平分线上.综合题19.如图,已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC 交AC于点G.求证:(1)BF =CG ;(2)AF =12(AB +AC).参考答案1.B 2.B 3.B 4.C 5.∵AD⊥BC,BD =CD ,∴AB =AC.∵点C 在AE 的垂直平分线上,∴AC =CE.∵AB=5 cm ,BD =3 cm ,∴CE =5 cm ,CD =3 cm.∴BE =BD +DC +CE =11 cm. 6.∵DE 是AB 的垂直平分线,∴AE =BE.同理:AG =CG.∴△AEG 的周长为AE +AG +EG =BE +CG +EG =BC =10.7.D 8.相等.连接BC ,∵AB =AC ,∴点A 在线段BC 的垂直平分线上.同理:D 点也在线段BC 的垂直平分线上.∵两点确定一条直线,∴AD 是线段BC 的垂直平分线.∵E 是AD 延长线上的一点,∴BE =CE. 9.图略 10.C 11.A 12.D 13.D 14.A 15.816.5 17.④ 18.证明:∵MN 垂直平分BC ,∴AB =AC.∵AB=AD ,∴AC =AD.∴点A 在CD 的垂直平分线上. 19.证明:(1)连接BE 、CE.∵AE 平分∠BAC,EF ⊥AB ,EG ⊥AC ,∴EF =EG.∵DE 垂直平分BC ,∴EB =EC.在Rt △EFB 和Rt △EGC 中,⎩⎪⎨⎪⎧EF =EG ,EB =EC ,∴Rt △EFB ≌Rt △EGC(HL).∴BF=CG.(2)∵BF=CG ,∴AB +AC =AB +BF +AG =AF +AG.又易证Rt △AEF ≌Rt △AEG(HL),∴AF =AG.∴AF=12(AB +AC).。
专题 垂直平分线的性质(含答案)

专题垂直平分线的性质一.解答题(共12小题)1.如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,求∠DBC的度数.2.如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB、BC于D、E两点,连接AE,若AE平分∠BAC,求∠C的度数.3.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,求∠C的度数.4.如图所示,在△ABC中,MP和NQ分别垂直平分AB和AC,MP分别交AB、BC于M、P两点,NQ分别交AC、BC于N、Q两点,连接AP、AQ.(1)若△APQ的周长为18,求BC的长;(2)若∠BAC=110°,求∠P AQ的度数.5.如图,△ABC中,边AB、AC的垂直平分线ED、GF分别交AB、AC于点E、G,交BC于点D、F,连接AD,AF,若∠DAF=40°,求∠BAC的度数.6.如图,在△ABC中,∠C=90°,边AB的垂直平分线DE交AC于D.CA=16cm,BC=8cm,求DC的长度;7.如图,在△ABC中,BC边的垂直平分线交AC边于点D,连接BD.(1)如图CE=4,△BDC的周长为18,求BD的长.(2)求∠ADM=60°,∠ABD=20°,求∠A的度数.8.如图,在△ABC中,∠C=90°,DE为AB的垂直平分线,DE交AC于点D,连接BD.若∠ABD=2∠CBD,求∠A的度数.9.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.(1)若∠BAE=40°,求∠C的度数;(2)若△ABC周长13cm,AC=6cm,求DC长.10.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.(1)若BC=10,则△ADE周长是多少?为什么?(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?11.在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC、BC 于点M、N,连接AE,AN.(1)如图1,若∠BAC=100°,求∠EAN的度数;(2)如图2,若∠BAC=70°,求∠EAN的度数;专题垂直平分线的性质参考答案与试题解析一.解答题(共12小题)1.【解答】解:∵AB=AC,∴∠ABC=∠ACB ==70°,∵MN的垂直平分AB,∴DA=DB,∴∠A=∠ABD=40°,∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.故答案为:30°.2.【解答】解:∵DE是线段AB的垂直平分线,∠B=30°,∴∠BAE=∠B=30°,∵AE平分∠BAC,∴∠EAC=∠BAE=30°,即∠BAC=60°,∴∠C=180°﹣∠BAC﹣∠B=180°﹣60°﹣30°=90°.3.【解答】解:∵∠B=90°,∠BAE=10°,∴∠BEA=80°.∵ED是AC的垂直平分线,∴AE=EC,∴∠C=∠EAC.∵∠BEA=∠C+∠EAC,∴∠C=40°.4.(【解答】解:(1)∵MP和NQ分别垂直平分AB和AC,∴P A=PB,QA=QC,∵△APQ的周长为18,∴AP+PQ+AQ=BP+PQ+QC=18,∴BC=18;(2)∵∠BAC=110°,∴∠B+∠C=70°,∵P A=PB,QA=QC,∴∠P AB=∠B,∠QAC=∠C,∴∠P AB+∠QAC=∠B+∠C=70°,∴∠P AQ=40°.5.【解答】解:在△ADF中,∵∠DAF=40°,∴∠ADF+∠AFD=180°﹣40°=140°,∵边AB、AC的垂直平分线ED、GF分别交AB、AC于点E、G,∴AD=BD,AF=CF,∴∠BAD=∠B,∠CAF=∠C,∴∠ADF=∠BAD+∠B=2∠B,∠AFD=∠CAF+∠C=2∠C,∴2∠B+2∠C=∠ADF+∠AFD=140°,∴∠B+∠C=70°,∴∠BAC=180°﹣(∠B+∠C)=110°.6.【解答】解:(1)∵DE垂直平分线段AB,∴DA=DB,设CD=x,则AD=BD=(16﹣x)cm,在Rt△BDC中,∵BD2=CD2+BC2,∴(16﹣x)2=x2+82,∴x=6,∴CD=6cm.7.【解答】解:(1)∵MN垂直平分BC,∴DC=BD,CE=EB,又∵EC=4,∴BE=4,又∵△BDC的周长=18,∴BD+DC=10,∴BD=5;(2)∵∠ADM=60°,∴∠CDN=60°,又∵MN垂直平分BC,∴∠DNC=90°,∴∠C=30°,又∵∠C=∠DBC=30°,∠ABD=20°,∴∠ABC=50°,∴∠A=180°﹣∠C﹣∠ABC=100°.8.【解答】解:∵DE为AB的垂直平分线,∴∠A=∠ABD,又∵∠ABD=2∠CBD,∴∠A=∠ABD=2∠CBD,设∠A=α,则∠ABD=α,∠CBD =α,又∵∠C=90°,∴∠A+∠ABC=90°,即α+α+α=90°,解得α=36°,∴∠A=36°.9.【解答】解:(1)∵AD垂直平分BE,EF垂直平分AC,∴AB=AE=EC,∴∠C=∠CAE,∵∠BAE=40°,∴∠AED=70°,∴∠C =∠AED=35°;(2)∵△ABC周长13cm,AC=6cm,∴AB+BE+EC=7cm,即2DE+2EC=7cm,∴DE+EC=DC=3.5cm.10.【解答】解:(1)C△ADE=10.(1分)∵AB、AC的垂直平分线分别交BC于D、E,∴AD=BD,AE=CE.(3分)C△ADE=AD+DE+AE=BD+DE+CE=BC=10.(4分)(2)∠DAE=76°.(5分)∵AB、AC的垂直平分线分别交BC于D、E,∴AD=BD,AE=CE.∴∠B=∠BAD,∠C=∠CAE.∵∠BAC=128°,∴∠B+∠C=52°.(7分)∴∠DAE=∠BAC﹣(∠BAD+∠CAE)=∠BAC﹣(∠B+∠C)=76°.(8分)11.【解答】解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得:∠CAN=∠C,∴∠EAN=∠BAC﹣∠BAE﹣∠CAN,=∠BAC﹣(∠B+∠C),在△ABC中,∠B+∠C=180°﹣∠BAC=80°,∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=100°﹣80°=20°;(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得:∠CAN=∠C,∴∠EAN=∠BAE+∠CAN﹣∠BAC,=(∠B+∠C)﹣∠BAC,在△ABC中,∠B+∠C=180°﹣∠BAC=110°,∴∠EAN=∠BAE+∠CAN﹣∠BAC=110°﹣70°=40°;。
部编数学八年级上册专题08线段的垂直平分线性质问题(解析版)含答案

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!2023--2024学年度人教版数学八年级上册期末复习核心考点三种题型精炼专题08 线段的垂直平分线性质问题一、选择题1. (2023长春)如图,用直尺和圆规作MAN Ð的角平分线,根据作图痕迹,下列结论不一定正确的是( )A. AD AE= B. AD DF = C. DF EF = D. AF D E^【答案】B 【解析】根据作图可得,AD AE DF EF ==,进而逐项分析判断即可求解.根据作图可得,AD AE DF EF ==,故A ,C 正确;∴,A F 在DE 的垂直平分线上,∴AF D E ^,故D 选项正确,而DF EF =不一定成立,故B 选项错误,故选:B .【点睛】本题考查了作角平分线,垂直平分线的判定,熟练掌握基本作图是解题的关键.2.如图所示,底边BC 为2,顶角A 为120°的等腰△ABC 中,DE 垂直平分AB 于D ,则△ACE 的周长为( )A .2+2B .2+C .4D .3【答案】A 【解析】本题考查了线段垂直平分线性质,三角形的内角和定理,等腰三角形的性质,含30度角的直角三角形性质等知识点,主要考查运用性质进行推理的能力.过A作AF⊥BC于F,根据等腰三角形的性质得到∠B=∠C=30°,得到AB=AC=2,根据线段垂直平分线的性质得到BE=AE,即可得到结论.过A作AF⊥BC于F,∵AB=AC,∠A=120°,∴∠B=∠C=30°,∴AB=AC=2,∵DE垂直平分AB,∴BE=AE,∴AE+CE=BC=2,∴△ACE的周长=AC+AE+CE=AC+BC=2+23.如图,BD是△ABC 的角平分钱,AE⊥BD ,垂足为F. 若∠ABC=35°,∠C=50°,则∠CDE的度数为()A.35°B.40°C.45°D.50°【答案】C【解析】本题考查角平分线的性质,因为BD平分∠ABC,AE⊥BD,所以△ABF≌△EBF,所以BD是线段AE的垂直平分线,所以AD=ED,所以∠BAD=∠BED=180°-35°-50°=95°,所以∠CDE=180°-∠C=95°-50°=45°,故选C.1. (2023湖北荆州)如图,60AOB Ð=°,点C 在OB 上,OC =P 为AOB Ð内一点.根据图中尺规作图痕迹推断,点P 到OA 的距离为___________.【答案】1【解析】首先利用垂直平分线的性质得到12OQ OC ==,利用角平分线,求出BOP Ð,再在POQ △中用勾股定理求出1PQ =,最后利用角平分线的性质求解即可.【详解】如图所示,由尺规作图痕迹可得,PQ 是OC 的垂直平分线,∴12OQ OC ==,∴1302BOP BOA Ð=Ð=°,设PQ x =,则2PO x =,∵222PQ OQ OP +=,∴()2222x x +=,∴1x =,由尺规作图痕迹可得,PO 是AOB Ð的平分线,∴点P 到OA 的距离等于点P 到OB 的距离,即PQ 的长度,∴点P 到OA 的距离为1.故答案为:1 .【点睛】本题考查角平分线和垂直平分线的性质,勾股定理,数形结合思想是关键.2. (2023四川广元)如图,a b ∥,直线l 与直线a ,b 分别交于B ,A 两点,分别以点A ,B 为圆心,大于12AB 的长为半径画弧,两弧相交于点E ,F ,作直线EF ,分别交直线a ,b 于点C ,D ,连接AC ,若34CDA Ð=°,则CAB Ð的度数为 _____.【答案】56°##56度【解析】先判断EF 为线段AB 的垂直平分线,即可得CAB CBA Ð=Ð,ACD BCD Ð=Ð,再由a b ∥,可得34CDA BCD Ð=Ð=°,即有34ACD BCD Ð=Ð=°,利用三角形内角和定理可求CAB Ð的度数.【详解】由作图可知EF 为线段AB 的垂直平分线,∴AC BC =,∴CAB CBA Ð=Ð,ACD BCD Ð=Ð,∵a b ∥,∴34CDA BCD Ð=Ð=°,∴34ACD BCD Ð=Ð=°,∵180ACD BCD CAB CBA Ð+Ð+Ð+Ð=°,∴56CAB Ð=°,故答案为:56°.【点睛】本题考查了垂直平分线的作图、垂直平分线的性质、平行线的性质以及三角形内角和定理等知识,判断EF 为线段AB 的垂直平分线是解答本题的关键.3.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.(1)∠ECD的度数为 ;(2)若CE=5,求BC长为 .【答案】(1)∠ECD的度数是36°;(2)BC长是5.【解析】(1)∵DE垂直平分AC∴CE=AE,∴∠ECD=∠A=36°(2)∵AB=AC,∠A=36°,∴∠B=∠ACB=72°,∴∠BEC=∠A+∠ECD=72°,∴∠BEC=∠B,∴BC=EC=5.4.如图,在Rt V ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为________.【答案】40°【解析】根据直角三角形的性质求得∠AEB=80°;根据线段垂直平分线的性质得AE=CE,则∠C=∠EAC,再根据三角形的外角的性质即可求解.∵∠B=90°,∠BAE=10°,∴∠BEA=80°.∵ED是AC的垂直平分线,∴AE=EC,EB ∴∠C=∠EAC .∵∠BEA=∠C+∠EAC ,∴∠C=40°.故答案为:40°.【点睛】此题考查了线段垂直平分线性质,涉及到三角形的外角的性质以及等腰三角形的性质的知识,难度适中.三、解答题1.如图,在直角△ABC 中,∠C=90°,∠CAB 的平分线AD 交BC 于D ,若DE 垂直平分AB ,求∠B 的度数.【答案】30°.【解析】∵DE 垂直平分AB ,∴∠DAE=∠B ,∵在直角△ABC 中,∠C=90°,∠CAB 的平分线AD 交BC 于D ,∴∠DAE=(90°﹣∠B )/2=∠B ,∴3∠B=90°,∴∠B=30°.2.如图,在ABC D 中,CD 是AB 边上的高,BE 是AC 边上的中线,且BD CE =。
人教版数学八年级上册 第十三章 13.1.2 线段的垂直平分线的性质 同步练习 (含答案)

人教版数学八年级上册第十三章13.1.2 线段的垂直平分线的性质同步练习一、选择题1.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是()A.AB=AD B.AC平分∠BCDC.AB=BD D.△BEC≌△DEC2. 如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是()A.PB>PC B.PB=PCC.PB<PC D.PB=2PC3. 如图,在△ABC中,△ACB=90°,△B=22.5°,AB边的垂直平分线交BC于点D,则下列结论中错误的是()A.△ADC=45° B.△DAC=45°C.BD=AD D.BD=DC4. 在数学课上,老师提出如下问题:如图,已知△ABC中,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PB=BC.下面是四名同学的作法,其中正确的是()5. 如图,在△ABC 中,DE 是AC 的垂直平分线,且分别交BC ,AC 于点D 和E ,△B =60°,△C =25°,则△BAD 为( )A .50°B .70°C .75°D .80°6. 如图,在△ABC 中,DE 垂直平分AB ,交AB 于点E ,交BC 于点D ,若AD=4,BC=3DC ,则BC 等于 ( )A.4B.4.5C.5D.67. 如图,C ,E 是直线l 两侧的点,以点C 为圆心,CE 的长为半径画弧交直线l于A ,B 两点.又分别以点A ,B 为圆心,大于12AB 的长为半径画弧,两弧交于点D ,连接CA ,CB ,CD ,则下列结论不一定正确的是 ( )A .CD△直线lB .点A ,B 关于直线CD 对称C .点C ,D 关于直线l 对称D .CD 平分△ACB 8. 如图,在Rt ABC 中,90ACB ∠=︒,分别以点B 和点C 为圆心,大于12BC 的长为半径作弧,两弧相交于D E ,两点,作直线DE 交AB 于点F ,交BC 于点G ,连接CF .若3AC =,2CG =,则CF 的长为( )A .52 B .3 C .2 D .72 9. 如图,在△ABC 中,AB 的垂直平分线交AB 于点D ,交BC 于点E ,若BC=6,AC=5,则△ACE 的周长为( )A .8B .11C .16D .1710. 如图,在△ABC 中,直线MN 为BC 的垂直平分线,交BC 于点E ,点D 在直线MN 上,且在△ABC 的外面,连接BD ,CD ,若CA 平分△BCD ,△A=65°,△ABC=85°,则△BCD 是( )A.等边三角形B.等腰三角形C.直角三角形D.等腰直角三角形二、填空题11. 如下图,△ABC 中,AB=AC=14cm ,D 是AB 的中点,DE△AB 于D 交AC 于E ,△EBC 的周长是24cm ,则BC= .12. 如图,在Rt△ABC中,△C=90°,边AB的垂直平分线交BC点D,AD平分△BAC,则△B度数为.13. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.14. 如图,DE是△ABC的边AC的垂直平分线,若BC=9,AD=4,则BD=________.15. 如图,在△ABC中,△C=90°,DE是AB的垂直平分线,AD恰好平分△BAC.若DE=1,则BC的长是________.三、解答题16.现要在三角地带ABC内(如图)建一座中心医院,使医院到A,B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请你确定这座中心医院的位置.17. 如图,已知△ABC.(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.18. 如图,在△ABE中,AD△BE于点D,C是BE上一点,DC=BD,且点C在AE的垂直平分线上.若△ABC的周长为22 cm,求DE的长.19. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D 和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG 的周长为16,GE=3,求AC的长.20. 如图,点P是△AOB外的一点,点Q与P关于OA对称,点R与P关于OB 对称,直线QR分别交OA、OB于点M、N,若PM=PN=4,MN=5.(1)求线段QM、QN的长;(2)求线段QR的长.21. 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. (1)若∠B=70°,则∠MNA的度数是.(2)连接NB,若AB=8cm,△NBC的周长是14cm.①求BC的长;②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.22. 如图,△ABC中,△ABC=30°,△ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.(1)直接写出△BAC的度数;(2)求△DAF的度数,并注明推导依据;(3)若△DAF的周长为20,求BC的长.人教版数学八年级上册第十三章13.1.2 线段的垂直平分线的性质同步练习--参考答案一、选择题1.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是()A.AB=AD B.AC平分∠BCDC.AB=BD D.△BEC≌△DEC【答案】C2. 如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是()A.PB>PC B.PB=PCC.PB<PC D.PB=2PC【答案】B[解析] 如图,连接AP.△线段AB,AC的垂直平分线相交于点P,△AP=PB,AP=PC.△PB=PC.3. 如图,在△ABC中,△ACB=90°,△B=22.5°,AB边的垂直平分线交BC于点D,则下列结论中错误的是()A.△ADC=45° B.△DAC=45°C.BD=AD D.BD=DC【答案】D[解析] △AB的垂直平分线交BC于点D,△AD=BD,故C正确;△AD=BD,△△B=△BAD=22.5°.△△ADC=45°,故A正确;△DAC=90°-△ADC=90°-45°=45°,故B正确.故选D.4. 在数学课上,老师提出如下问题:如图,已知△ABC中,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PB=BC.下面是四名同学的作法,其中正确的是()【答案】C[解析] △PA+PB=BC,而PC+PB=BC,△PA=PC.△点P为线段AC的垂直平分线与BC的交点.显然只有选项C符合题意.5. 如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,△B=60°,△C=25°,则△BAD为()A.50°B.70°C.75°D.80°【答案】B6. 如图,在△ABC中,DE垂直平分AB,交AB于点E,交BC于点D,若AD=4,BC=3DC,则BC等于()A.4B.4.5C.5D.6【答案】D[解析] △DE垂直平分AB,AD=4,△BD=AD=4.△BC=3DC,△BD=2CD.△CD=2.△BC=BD+CD=6.故选D.7. 如图,C,E是直线l两侧的点,以点C为圆心,CE的长为半径画弧交直线l于A,B两点.又分别以点A,B为圆心,大于12AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,则下列结论不一定正确的是()A .CD△直线lB .点A ,B 关于直线CD 对称C .点C ,D 关于直线l 对称D .CD 平分△ACB 【答案】C [解析] 由作法可知CD 垂直平分AB ,故选项A ,B 正确; △CD 垂直平分AB ,△CA =CB.设CD 与AB 交于点G ,易证Rt△ACG△Rt△BCG ,△△ACG =△BCG , 即CD 平分△ACB ,故选项D 正确;△AB 不一定平分CD ,故选项C 错误.故选C.由线段垂直平分线的性质可得PA =PB ,但不能得到OP =OF.8. 如图,在Rt ABC 中,90ACB ∠=︒,分别以点B 和点C 为圆心,大于12BC 的长为半径作弧,两弧相交于D E ,两点,作直线DE 交AB 于点F ,交BC 于点G ,连接CF .若3AC =,2CG =,则CF 的长为( )A .52B .3C .2D .72【答案】A【解析】由作法得GF 垂直平分BC ,∴FB FC =,2CG BG ==,FG BC ⊥, ∵90ACB ∠=︒,∴FG AC ∥,∴BF CF =,∴CF 为斜边AB 上的中线,∵5AB ==,∴1522CF AB ==.故选A . 9. 如图,在△ABC 中,AB 的垂直平分线交AB 于点D ,交BC 于点E ,若BC=6,AC=5,则△ACE 的周长为( )A.8B.11C.16D.17【答案】答案为:B.10. 如图,在△ABC中,直线MN为BC的垂直平分线,交BC于点E,点D在直线MN上,且在△ABC的外面,连接BD,CD,若CA平分△BCD,△A=65°,△ABC=85°,则△BCD是()A.等边三角形B.等腰三角形C.直角三角形D.等腰直角三角形【答案】A二、填空题11. 如下图,△ABC中,AB=AC=14cm,D是AB的中点,DE△AB于D交AC 于E,△EBC的周长是24cm,则BC=.【答案】10cm12. 如图,在Rt△ABC中,△C=90°,边AB的垂直平分线交BC点D,AD平分△BAC,则△B度数为.【答案】答案为:30°13. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.【答案】13【解析】△DE垂直平分AB,△AE=BE,△AE+EC=8,△EC+BE=8,△△BCE的周长为BE+EC+BC=13.14. 如图,DE是△ABC的边AC的垂直平分线,若BC=9,AD=4,则BD=________.【答案】515. 如图,在△ABC中,△C=90°,DE是AB的垂直平分线,AD恰好平分△BAC.若DE=1,则BC的长是________.【答案】3[解析] △AD平分△BAC,且DE△AB,△C=90°,△CD=DE=1.△DE是AB的垂直平分线,△AD=BD.△△B=△DAB.△△DAB=△CAD,△△CAD=△DAB=△B.△△C=90°,△△CAD+△DAB+△B=90°.△△B=30°.△BD=2DE=2.△BC=BD+CD=2+1=3.三、解答题16.现要在三角地带ABC内(如图)建一座中心医院,使医院到A,B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请你确定这座中心医院的位置.【答案】解:作线段AB的垂直平分线EF,作△BAC的平分线AM,EF与AM相交于点P,则点P处即为这座中心医院的位置.17. 如图,已知△ABC.(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.【答案】解:(1)如图所示.(2)证明:如图,连接OA.△l1是AB的垂直平分线,△OA=OB.同理,OA=OC.△OB=OC.18. 如图,在△ABE中,AD△BE于点D,C是BE上一点,DC=BD,且点C在AE的垂直平分线上.若△ABC的周长为22 cm,求DE的长.【答案】解:△BD=DC,AD△BE,△AB=AC.△点C在AE的垂直平分线上,△AC=CE.△△ABC的周长是22 cm,△AC+AB+BD+CD=22 cm.△AC+CD=11 cm.△DE=CD+CE=CD+AC=11 cm.19. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D 和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG 的周长为16,GE=3,求AC的长.【答案】解:△DE垂直平分线段AB,GF垂直平分线段BC,△EB=EA,GB=GC.△△BEG的周长为16,△EB+GB+GE=16.△EA+GC+GE=16.△GA+GE+GE+GE+EC=16.△AC+2GE=16.△GE=3,△AC=10.20. 如图,点P是△AOB外的一点,点Q与P关于OA对称,点R与P关于OB对称,直线QR分别交OA、OB于点M、N,若PM=PN=4,MN=5.(1)求线段QM、QN的长;(2)求线段QR的长.【答案】【解答】解:(1)△P,Q关于OA对称,△OA垂直平分线段PQ,△MQ=MP=4,△MN=5,△QN=MN﹣MQ=5﹣4=1.(2)△P,R关于OB对称,△OB垂直平分线段PR,△NR=NP=4,△QR=QN+NR=1+4=5.21. 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. (1)若∠B=70°,则∠MNA的度数是.(2)连接NB,若AB=8cm,△NBC的周长是14cm.①求BC的长;②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.【答案】解:(1) 50(2) ①∵MN垂直平分AB.∴NB=NA,又∵△NBC的周长是14cm,∴AC+BC=14cm,∴BC=6cm.②当点P与点N重合时,由点P、B、C构成的△PBC的周长值最小,最小值是14cm.22. 如图,△ABC中,△ABC=30°,△ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.(1)直接写出△BAC的度数;(2)求△DAF的度数,并注明推导依据;(3)若△DAF的周长为20,求BC的长.【答案】【解答】解:(1)△△ABC+△ACB+△BAC=180°,△△BAC=180°﹣30°﹣50°=100°;(2)△DE是线段AB的垂直平分线,△DA=DB,△△DAB=△ABC=30°,同理可得,△FAC=△ACB=50°,△△DAF=△BAC﹣△DAB﹣△FAC=100°﹣30°﹣50°=20°;(3)△△DAF的周长为20,△DA+DF+FA=20,由(2)可知,DA=DB,FA=FC,△BC=DB+DF+FC=DA+DF+FA=20.。
初二线段垂直平分线练习题带答案

初二线段垂直平分线练习题带答案题目一:在平面直角坐标系中,已知线段AB的坐标分别为A(-2,1)和B(4,-3),求线段AB的垂直平分线方程。
解析:要求线段AB的垂直平分线方程,我们需要找到线段AB的中点以及线段AB的斜率。
线段AB的中点坐标为:x坐标:(x_A + x_B)/2 = (-2 + 4)/2 = 2/2 = 1y坐标:(y_A + y_B)/2 = (1 + (-3))/2 = -2/2 = -1所以线段AB的中点为M(1, -1)。
线段AB的斜率为:斜率 k = (y_B - y_A)/(x_B - x_A)= (-3 - 1)/(4 - (-2))= -4/6= -2/3由于垂直平分线与线段的斜率乘积为-1,所以垂直平分线的斜率为斜率 k 的相反数的倒数:k_2 = -1/(-2/3) = 3/2。
通过中点和斜率,我们可以得到垂直平分线的方程:y - y_M = k_2(x - x_M)y - (-1) = (3/2)(x - 1)y + 1 = (3/2)(x - 1)2(y + 1) = 3(x - 1)2y + 2 = 3x - 32y = 3x - 5所以线段AB的垂直平分线方程为2y = 3x - 5。
题目二:在平面直角坐标系中,直线L过点A(-3,3),且与直线x = -1垂直,求直线L的方程。
解析:首先,直线L与直线x = -1垂直,说明直线L的斜率为0。
由于直线L过点A(-3,3),我们可以确定直线L的y截距为3。
所以直线L的方程为y = 3。
题目三:在平面直角坐标系中,已知线段CD的两个端点分别为C(-4,2)和D(6,2),求线段CD的垂直平分线方程。
解析:要求线段CD的垂直平分线方程,我们需要找到线段CD的中点以及线段CD的斜率。
线段CD的中点坐标为:x坐标:(x_C + x_D)/2 = (-4 + 6)/2 = 2/2 = 1y坐标:(y_C + y_D)/2 = (2 + 2)/2 = 4/2 = 2所以线段CD的中点为N(1, 2)。
垂直平分线专项练习30题(有答案)ok

垂直平分线专项练习30题(有答案)1.如图,在△ABC中,∠BAC=2∠B,DE⊥AB于点D,交BC于点E,AC=AD=BD,请你猜想∠C的度数并证明.2.如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN⊥AB于N,PM⊥AC 于点M,求证:BN=CM.3.如图,在△ABC中,D是BC的垂直平分线DH上一点,DF⊥AB于F,DE⊥AC交AC的延长线于E,且BF=CE.(1)求证:AD平分∠BAC;(2)若∠BAC=80°,求∠DCB的度数.4.如图,在△ABC中,AB=AC,∠A=52°,AB的垂直平分线MN交AC于点D.求∠DBC的度数.5.如图,在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC 交AF的延长线于E.求证:BC垂直且平分DE.6.已知△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F.求证:∠BAF=∠ACF.7.如图,△ABC中,边AB、BC的垂直平分线交于点P.(1)求证:PA=PB=PC;(2)点P是否也在边AC的垂直平分线上?由此你还能得出什么结论?8.如图,在Rt△ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,求BD的长.9.如图,在△ABC中,AD平分∠BAC,AD的垂直平分线EF交BC的延长线于点F,连接AF,求证:∠CAF=∠B.10.如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB、BC延长线于F、E.求证:(1)∠EAD=∠EDA;(2)DF∥AC;(3)∠EAC=∠B.11.如图所示,AD是△ABC中∠BAC的平分线,AD的垂直平分线EF交BC的延长线于F,试说明∠BAF=∠ACF 的理由.12.如图所示,在△ABC中,AB=AC=16cm,D为AB的中点,DE⊥AB交AC于E,△BCE的周长为26cm,求BC的长.13.如图,在△ABC中,EN,DM分别是AB,AC边的垂直平分线,BC=8cm.求△AED的周长.14.如图,在△ABC中,0E,OF分别是AB,AC的中垂线,∠ABO=20°,∠ABC=45°,求∠BAC和∠ACB的度数.15.如图所示,△ABC中,∠BAC的平分线与BC的垂直平分线相交于点E,EF⊥AB,EG⊥AC,垂足分别为F、G,则BF=CG吗?说明理由.16.在△ABC中,BC边的垂直平分线DE交BC于D,交AB于E,BE=5,△BCE的周长为18 即BE+CE+BC=18,求BC的长?17.如图1,△ABC中,AB=AC,∠BAC=130°,边AB、AC的垂直平分线交BC于点P、Q.(1)求∠PAQ的度数;(2)如图2,△ABC中,AB>AC,且90°<∠BAC<180°,边AB、AC的垂直平分线交BC于点P、Q.①若∠BAC=130°,则∠PAQ=_________°,若∠BAC=α,则∠PAQ用含有α的代数式表示为_________;②当∠BAC=_________°时,能使得PA⊥AQ;③若BC=10cm,则△PAQ的周长为_________cm.18.如图,△ABC中,AB=AC=14cm,D是AB的中点,DE⊥AB于D交AC于E,△EBC的周长是24cm,求BC 的长度.19.已知:如图,在△ABC中,AB=AC=32,AB的垂直平分线DE分别交AB、AC于点E、D.(1)若△DBC的周长为56,求BC的长;(2)若BC=21,求△DBC的周长.20.在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE 的周长为6cm.(1)求BC的长;(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.21.如图,在△ABC中,E、F分别是AB、AC上的点,AD平分∠BAC,DE⊥AB,DF⊥AC,求证:AD垂直平分EF.22.如图,AD是△ABC的角平分线,AD的垂直平分线交BC的延长线于点F.求证:∠FAC=∠B.23.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于P、Q.(1)若BC=10,求△APQ周长是多少?(2)若∠BAC=110°,求∠PAQ的度数是多少?24.已知,如图,AD是BC的垂直平分线,DE⊥AB于点E,DF⊥AC于点F,求证:(1)∠ABD=∠ACD;(2)DE=DF.25.如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,连接EF.求证:AD垂直平分EF.26.如图,△ABC中,E是BC边上的中点,DE⊥BC于E,DM⊥AB于M,DN⊥AC于N,BM=CN 试证明:点D在∠BAC的平分线上.27.如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.求△AEG的周长.28.如图,在△ABC中,M为BC的中点,DM⊥BC,DM与∠BAC的角平分线交于点D,DE⊥AB,DF⊥AC,E、F为垂足,求证:BE=CF.29.已知,如图,DE为△ABC的边AB的垂直平分线,CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,求证:AN=BM.30.如图所示,在△ABC中,AB=8,AC=4,∠BAC的平分线与BC的垂直平分线交于点D,过点D作DE⊥AB 于点E,DF⊥AC(或AC的延长线)于点D.(1)求证:BE=CF;(2)求AE的长.参考答案:1.解:∠C=90°.证明:如图,连接AE,在Rt△AED和Rt△BED中,,∴△AED≌△BED(HL),∴∠DAE=∠B,又∵∠BAC=2∠B,∴∠DAE=∠CAE,在△AED和△BED中,,∴△ACE≌△ADE,∴∠C=∠ADE=90°.2.证明:连接PB,PC,∵AP是∠BAC的平分线,PN⊥AB,PM⊥AC,∴PM=PN,∠PMC=∠PNB=90°,∵P在BC的垂直平分线上,∴PC=PB,在Rt△PMC和Rt△PNB中,∴Rt△PMC≌Rt△PNB(HL),∴BN=CM.3.(1)证明:如图,连接BD,∵DH垂直平分BC,∴BD=CD,在Rt△BDF和Rt△CDE中,,∵DF⊥AB于F,DE⊥AC,∴AD平分∠BAC;(2)解:∵Rt△BDF≌Rt△CDE,∴∠CDE=∠BDF,∴∠BDC=∠EDF,∵∠BAC=80°,∴∠EDF=360°﹣90°×2﹣80°=100°,∴∠BDC=100°,∵BD=CD,∴∠DCB=(180°﹣100°)=50°4.解:∵AB=AC,∠A=52°,∴∠ABC=∠ACB==64°,∵AB的垂直平分线MN,∴AD=BD,∠A=∠ABD=52°,∴∠DBC=∠ABC﹣∠ABD=64°﹣52°=12°5.证明:在△ADC中,∠DAH+∠ADH=90°,∠ACH+∠ADH=90°,∴∠DAH=∠DCA,∵∠BAC=90°,BE∥AC,∴∠CAD=∠ABE=90°.又∵AB=CA,∴在△ABE与△CAD中,∴△ABE≌△CAD(ASA),∴AD=BE,又∵AD=BD,∴BD=BE,在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,故∠ABC=45°.∵BE∥AC,∴∠EBD=90°,∠EBF=90°﹣45°=45°,∴△DBP≌△EBP(SAS),∴DP=EP,即可得出BC垂直且平分DE6.证明:∵AD是∠BAC的平分线,∴∠1=∠2,∵FE是AD的垂直平分线,∴FA=FD(线段垂直平分线上的点到线段两端的距离相等),∴∠FAD=∠FDA(等边对等角),∵∠BAF=∠FAD+∠1,∠ACF=∠FDA+∠2,∴∠BAF=∠ACF7.证明:(1)∵边AB、BC的垂直平分线交于点P,∴PA=PB,PB=PC.∴PA=PB=PC.还可得出结论:①三角形三边的垂直平分线相交于一点.②这个点与三顶点距离相等8.解:因为CE垂直平分AD,所以AC=CD=5cm.所以∠ACE=∠ECD.因为CD平分∠ECB,所以∠ECD=∠DCB.因为∠ACB=90°,所以∠ACE=∠ECD=∠DCB=30°.所以∠A=90°﹣∠ACE=60°.所以∠B=90°﹣∠A=30°.所以∠DCB=∠B.所以BD=CD=5cm9.证明:∵EF垂直平分AD,∴AF=DF,∠ADF=∠DAF,∵∠ADF=∠B+∠BAD,∠DAF=∠CAF+∠CAD,又∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠CAF=∠B10.解:(1)∵EF是AD的垂直平分线,∴AE=DE,∴∠EAD=∠EDA;(2)∵EF是AD的垂直平分线,∴AF=DF,∴∠FAD=∠FDA,∵AD是∠BAC平分线,∴∠FAD=∠CAD,∴∠FDA=∠CAD,∴DF∥AC;(3)∵∠EAC=∠EAD﹣∠CAD,∠B=∠EDA﹣∠BAD,且∠BAD=∠CAD,∠EAD=∠EDA,∴∠EAC=∠B11.解:∵EF垂直平分AD,∴AF=DF,∴∠FAD=∠FDA.又∵AD平分∠BAC,∴∠BAD=∠CAD,∵∠BAF=∠BAD+∠FAD,∠ACF=∠DAC+∠FDA,∴∠BAF=∠ACF12.解:∵点D中AB的中点,DE⊥AB,∴DE是AB的中垂线,∴AE=BE,∴△BCE的周长=BE+EC+BC=AE+EC+BC=AC+BC=26,∴BC=26﹣AC=26﹣16=10cm13.解:∵EN,DM分别是AB,AC边的垂直平分线,∴BE=AE,CD=AD,14.解:连接AO并延长,交BC于点D,∵0E,OF分别是AB,AC的中垂线,∴OB=OA,OC=OA,∴OC=OB,∠ABO=∠BAO=20°,∠CBO=∠BCO,∠CAO=∠ACO,∵∠ABC=45°,∴∠CBO=∠BCO=25°,∴∠BOC=180°﹣∠CBO﹣∠BCO=130°,∵∠BOD=∠ABO+∠BAO,∴∠BOD=40°,∠COD=90°.∵∠COD=∠CAO+∠ACO,∴∠CAO=45°,∴∠BAC=∠BAO+∠CAO=65°,∠ACB=∠BCO+∠ACO=70°15.解:BF=CG;理由如下:因为点E在BC的垂直平分线上,所以BE=CE.因为点E在∠BAC的角平分线上,且EF⊥AB,EG⊥AC,所以EF=EG,在Rt△EFB和Rt△EGC中,因为BE=CE,EF=EG,所以Rt△EFB≌Rt△EGC(HL).所以BF=CG16.解:∵BC边的垂直平分线DE,∴BE=CE=5,∵BE+CE+BC=18,∴BC=18﹣5﹣5=8,答:BC的长是817.解:(1)∵边AB、AC的垂直平分线交BC于点P、Q,∴AP=BP,AQ=CQ,∴∠BAP=∠B,∠CAQ=∠C,∵∠BAC=130°,∴∠B+∠C=180°﹣∠BAC=50°,∴∠BAP+∠CAQ=50°,∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=130°﹣50°=80°;(2)①∵边AB、AC的垂直平分线交BC于点P、Q,∴AP=BP,AQ=CQ,∴∠BAP=∠B,∠CAQ=∠C,∵∠BAC=130°,∴∠B+∠C=180°﹣∠BAC=50°,∴∠BAP+∠CAQ=50°,∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=130°﹣50°=80°;∵边AB、AC的垂直平分线交BC于点P、Q,∴AP=BP,AQ=CQ,∴∠BAP=∠B,∠CAQ=∠C,∵∠BAC=α,∴∠B+∠C=180°﹣∠BAC=180°﹣α,∴∠BAP+∠CAQ=180°﹣α,∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=α﹣(180°﹣α)=2α﹣180°;②当∠PAQ=90°,即2α﹣180°=90°时,PA⊥AQ,解得:α=135°,∴当∠BAC=135°时,能使得PA⊥AQ;③∵边AB、AC的垂直平分线交BC于点P、Q,∴AP=BP,AQ=CQ,∵BC=10cm,即BP+PQ+CQ=AP+PQ+AQ=10cm,∴△PAQ的周长为10cm.故答案为:①80,2α﹣180°;②135;③1018.解:在△ABE中,∵D是AB的中点,DE⊥AB于D交AC于E,∴AE=BE;在△ABC中,∵AB=AC=14cm,AC=AE+EC,又∵CE+BE+BC=24cm,∴BC=10cm19.解:(1)∵DE是线段AB的垂直平分线,∴AD=BD,∴AD+CD=BD+CD=AC,∵△DBC的周长为56,AC=32,∴BC=56﹣32=24;(2)∵AD=BD,AC=32,∴AD+CD=BD+CD=AC=32,∵BC=21,∴△DBC的周长=BD+CD+BC=32+21=53.故答案为:24;5320.解:(1)∵DF、EG分别是线段AB、AC的垂直平分线,∴AD=BD,AE=CE,∴AD+DE+AE=BD+DE+CE=BC,∵△ADE的周长为6cm,即AD+DE+AE=6cm,∴BC=6cm;(2)∵AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,∴OA=OC=OB,∵△OBC的周长为16cm,即OC+OB+BC=16,∴OC+OB=16﹣6=10,∴OC=5,∴OA=OC=OB=5.21.证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,∠EAD=∠FAD,∠AED=∠AFD=90°,∴∠EDA=180°﹣∠AED﹣∠EAD,∠FDA=180°﹣∠AFD﹣∠FAD,∴∠EDA=∠FDA,∵DE=DF(已证),∴DG垂直平分EF(三线合一),即AD垂直平分EF.22.证明:∵EF是AD的垂直平分线,∴AF=DF,∴∠FAD=∠FDA,∵∠FAD=∠FAC+∠CAD,∠FDA=∠B+∠BAD,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠FAC=∠B23.解:(1)∵MP、NQ分别是AB、AC的垂直平分线,∴AP=BP,AQ=CQ,∴△APQ周长=AP+PQ+AQ=BP+PQ+QC=BC,∵BC=10,∴△APQ周长=10;(2)∵∠BAC=110°,∴∠B+∠C=180°﹣110°=70°,∵AP=BP,AQ=CQ(已证),∴∠BAP=∠B,∠CAQ=∠C,∴∠PAQ=∠BAC﹣∠BAP﹣∠CAQ=∠BAC﹣∠B﹣∠C=110°﹣70°=40°24.证明:(1)∵AD是BC的垂直平分线,∴AB=AC,BD=CD,∴∠ABC=∠ACB,∠DBC=∠DCB,∴∠ABD=∠ACD;(2)∵AB=AC,AD是BC的垂直平分线,∴∠BAD=∠CAD,∵DE⊥AB,DF⊥AC,∴DE=DF25.证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,在△ADE和△ADF中,,∴△ADE≌△ADF(HL),∴AE=AF,又∵AD平分∠BAC,∴AD垂直平分EF26.证明:如图,连接BD、CD,∵DE⊥BC,E是BC边上的中点,∴BD=CD,在△BDM和△CDN中,,∴△BDM≌△CDN(HL),∴DM=DN,又∵DM⊥AB,DN⊥AC,∴点D在∠BAC的平分线上.27.解:∵DE为AB的中垂线,∴AE=BE,∵FG是AC的中垂线,∴AG=GC,△AEG的周长等于AE+EG+GA,分别将AE和AG用BE和GC代替得:△AEG的周长等于BE+EG+GC=BC,所以△AEG的周长为BC的长度即7.故答案为:728.解:连接DB.∵点D在BC的垂直平分线上,∴DB=DC;∵D在∠BAC的平分线上,DE⊥AB,DF⊥AC,∴DE=DF;∵∠DFC=∠DEB=90°,在Rt△DCF和Rt△DBE中,,∴Rt△DCF≌Rt△DBE(HL),∴CF=BE(全等三角形的对应边相等).29.证明:∵DE为△ABC的边AB的垂直平分线,∴AD=BD,∵CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,∴DN=DM,在Rt△ADN和Rt△BDM中,,∴Rt△ADN≌Rt△BDM(HL),∴AN=BM.30.(1)证明:连结BD,CD.∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴∠AED=∠BED=∠AFD=90°,DE=DF.∵DE垂直平分BC,∴DB=DC.在Rt△DEB和Rt△DFC中,∴Rt△DEB≌Rt△DFC(HL),∴BE=CF;(2)解:在Rt△ADE和Rt△ADF中,,∴Rt△ADE≌Rt△ADF(HL).∴AE=AF.∵AB=AE+BE,∴AB=AF+EB,∴AB=AC+CF+EB.∵AB=8,AC=4,∴8=4+CF+EB,∴CF+EB=4,∴2EB=4,∴EB=2.∴AE=8﹣2=6.答:AE的长为6.。
《垂直平分线的性质》热点专题高分特训(含答案)

A.ED=CD
B.∠DAC=∠B
C.
D.∠B+∠ADE=90°
答案:D 解题思路:
试题难度:三颗星知识点:垂直平分线的性质 4.如图,四边形 ABCD 中,AC 垂直平分 BD,垂足为 E,下列结论不一定成立的是( )
A.AB=AD B.AC 平分∠BCD C.AB=BD D.△BEC≌△DEC 答案:C 解题思路:
试题难度:三颗星知识点:垂直平分线的性质 5.如图,在 Rt△ABC 中,∠C=90°,斜边 AB 的垂直平分线 DE 交 AB 于点 D,交 BC 于点 E, 且 AE 平分∠BAC,下列关系式不成立的是( )
垂直平分线的性质(人教版)
一、单选题(共 12 道,每道 8 分) 1.下列命题中正确的命题有( ) ①线段垂直平分线上任一点到线段两端距离相等;②线段上任一点到垂直平分线两端距 离相等;③经过线段中点的直线只有一条;④点 P 在线段 AB 外且 PA=PB,过 P 作直线 MN,则 MN 是线段 AB 的垂直平分线;⑤过线段上任一点可以作这条线段的中垂线. A.1 个 B.2 个 C.3 个 D.4 个 答案: Nhomakorabea 解题思路:
A.AC=2EC B.∠B=∠CAE C.∠DEA=2∠B D.BC=3EC 答案:A 解题思路:
试题难度:三颗星知识点:垂直平分线的性质 6.如图,有 A、B、C 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物 超市,使超市到三个小区的距离相等,则超市应建在( )
A.在 AC,BC 两边高线的交点处 B.在 AC,BC 两边中线的交点处
八年级数学上册《第二章 线段的垂直平分线》练习题-含答案(湘教版)

八年级数学上册《第二章线段的垂直平分线》练习题-含答案(湘教版)一、选择题1.下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,则对应选项中作法错误..的是( ) A.① B.② C.③ D.④2.如图,已知线段AB,分别以A,B为圆心,大于12AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为( )A.40°B.50°C.60°D.70°3.如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,适当长度(大于BC长的一半)为半径作圆弧,两弧相交于点M和N;②作直线MN交AB于点D,连接CD.若AB=9,AC=4,则△ACD的周长是( )A.12B.13C.17D.184.如图,已知AB=AC,AB=5,BC=3,以A,B两点为圆心,大于12AB的长为半径画圆弧,两弧相交于点M,N,连接MN与AC相交于点D,则△BDC的周长为( )A.8B.10C.11D.135.如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于12BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若AD=AC,∠A=80°则∠ACB的度数为( )A.65°B.70°C.75°D.80°6.如图,AB∥CD,BE垂直平分AD,DC=BC,若∠A=70°,则∠C=( )A.100°B.110°C.115°D.120°7.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则( )A.BC>PC+APB.BC<PC+APC.BC=PC+APD.BC≥PC+AP8.如图,已知在直角坐标系中,点A在y轴上,BC⊥x轴于点C,点A关于直线OB的对称点D 恰好在BC上,点E与点O关于直线BC对称,∠OBC=35°,则∠OED的度数为( )A.10°B.20°C.30°D.35°二、填空题9.如图,在△ABC中,AB=AC=8,BC=6,AB的垂直平分线交AC于点E,垂足为点D,连接BE,则△BEC的周长为 .10.如图,DE是△ABC边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为 .11.如图,若△ACD的周长为7cm,DE为AB边的垂直平分线,则AC+BC= cm.12.小军做了一个如图所示的风筝,其中EH=FH,ED=FD,小军说不用测量就知道DH是EF的垂直平分线.其中蕴含的道理是 .13.如图,在△ABC中,∠C=35°,AB=AD,DE是AC的垂直平分线,则∠BAD=度.14.如图所示,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2.连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为.三、作图题15.尺规作图(不写作法,保留作图痕迹):已知线段a和∠AOB,点M在OB上(如图所示).(1)在OA边上作点P,使OP=2a;(2)作∠AOB的平分线;(3)过点M作OB的垂线.四、解答题16.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于点D,垂足为E,且∠CAD∶∠CAB=1∶3,求∠B的度数.17.在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,交AC于点E. (1)若∠ABE=38°,求∠EBC的度数;(2)若△ABC的周长为36cm,一边为13cm,求△BCE的周长.18.如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.19.如图,AD平分∠BAC,EF垂直平分AD交BC的延长线于F,连接AF.求证:∠B=∠CAF.20.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.(1)若∠B=70°,则∠NMA的度数是________.(2)连接MB,若AB=8cm,△MBC的周长是14cm.①求BC的长;②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P 的位置并求△PBC的周长最小值;若不存在,说明理由.参考答案1.C.2.B.3.B.4.A.5.C.6.D.7.C8.B.9.答案为:14.10.答案为:28cm.11.答案为:7.12.答案为:与线段两个端点距离相等的点在这条线段的垂直平分线线上.13.答案为:40.14.答案为:6.15.解:(1)点P为所求作;(2)OC为所求作;(3)MD为所求作;16.解:设∠CAD=x°则∠CAB=3x°,∠BAD=2x°.∵DE是AB的垂直平分线∴DA=DB∴∠B=∠BAD=2x°.∵∠C=90°∴∠CAB+∠B=90°即3x+2x=90,解得x=18∴∠B=2×18°=36°.17.解:∵DE是AB的垂直平分线∴AE=BE∴∠A=∠ABE=38°∵AB=AC∴∠ABC=∠C=71°∴∠EBC=∠ABC-∠ABE=71°-38°=33°由△ABC的周长为36cmAB>BC,AB=AC可知AB=AC=13cm BC=10cm△BCE的周长=BE+CE+BC=AC+BC=13+10=23(cm) 18.解:∵AD平分∠BAC∴∠BAD=∠DAE∵∠BAD=29°∴∠DAE=29°∴∠BAC=58°∵DE垂直平分AC∴AD=DC∴∠DAE=∠DCA=29°∵∠BAC+∠DCA+∠B=180°∴∠B=93°.19.证明:∵EF垂直平分AD∴AF=DF,∠ADF=∠DAF∵∠ADF=∠B+∠BAD,∠DAF=∠CAF+∠CAD又∵AD平分∠BAC∴∠BAD=∠CAD∴∠B=∠CAF.20.解:(1)50°(2)猜想的结论为:∠NMA=2∠B﹣90°.理由:∵AB=AC∴∠B=∠C∴∠A=180°﹣2∠B又∵MN垂直平分AB∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)=2∠B﹣90°. 如图:①∵MN垂直平分AB.∴MB=MA又∵△MBC的周长是14cm∴AC+BC=14cm∴BC=6cm.②当点P与点M重合时,PB+CP的值最小,最小值是8cm.。
专题 垂直平分线的性质(含答案)

专题垂直平分线的性质一.解答题(共12小题)1.如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,求∠DBC的度数.2.如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB、BC于D、E两点,连接AE,若AE平分∠BAC,求∠C的度数.3.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,求∠C的度数.4.如图所示,在△ABC中,MP和NQ分别垂直平分AB和AC,MP分别交AB、BC于M、P两点,NQ分别交AC、BC于N、Q两点,连接AP、AQ.(1)若△APQ的周长为18,求BC的长;(2)若∠BAC=110°,求∠PAQ的度数.5.如图,△ABC中,边AB、AC的垂直平分线ED、GF分别交AB、AC于点E、G,交BC于点D、F,连接AD,AF,若∠DAF=40°,求∠BAC的度数.6.如图,在△ABC中,∠C=90°,边AB的垂直平分线DE交AC于D.CA=16cm,BC=8cm,求DC的长度;7.如图,在△ABC中,BC边的垂直平分线交AC边于点D,连接BD.(1)如图CE=4,△BDC的周长为18,求BD的长.(2)求∠ADM=60°,∠ABD=20°,求∠A的度数.8.如图,在△ABC中,∠C=90°,DE为AB的垂直平分线,DE交AC于点D,连接BD.若∠ABD=2∠CBD,求∠A的度数.9.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.(1)若∠BAE=40°,求∠C的度数;(2)若△ABC周长13cm,AC=6cm,求DC长.10.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.(1)若BC=10,则△ADE周长是多少?为什么?(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?11.在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC、BC于点M、N,连接AE,AN.(1)如图1,若∠BAC=100°,求∠EAN的度数;(2)如图2,若∠BAC=70°,求∠EAN的度数;专题垂直平分线的性质参考答案与试题解析一.解答题(共12小题)1.【解答】解:∵AB=AC,∴∠ABC=∠ACB ==70°,∵MN的垂直平分AB,∴DA=DB,∴∠A=∠ABD=40°,∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.故答案为:30°.2.【解答】解:∵DE是线段AB的垂直平分线,∠B=30°,∴∠BAE=∠B=30°,∵AE平分∠BAC,∴∠EAC=∠BAE=30°,即∠BAC=60°,∴∠C=180°﹣∠BAC﹣∠B=180°﹣60°﹣30°=90°.3.【解答】解:∵∠B=90°,∠BAE=10°,∴∠BEA=80°.∵ED是AC的垂直平分线,∴AE=EC,∴∠C=∠EAC.∵∠BEA=∠C+∠EAC,∴∠C=40°.4.(【解答】解:(1)∵MP和NQ分别垂直平分AB和AC,∴PA=PB,QA=QC,∵△APQ的周长为18,∴AP+PQ+AQ=BP+PQ+QC=18,∴BC=18;(2)∵∠BAC=110°,∴∠B+∠C=70°,∵PA=PB,QA=QC,∴∠PAB=∠B,∠QAC=∠C,∴∠PAB+∠QAC=∠B+∠C=70°,∴∠PAQ=40°.5.【解答】解:在△ADF中,∵∠DAF=40°,∴∠ADF+∠AFD=180°﹣40°=140°,∵边AB、AC的垂直平分线ED、GF分别交AB、AC于点E、G,∴AD=BD,AF=CF,∴∠BAD=∠B,∠CAF=∠C,∴∠ADF=∠BAD+∠B=2∠B,∠AFD=∠CAF+∠C=2∠C,∴2∠B+2∠C=∠ADF+∠AFD=140°,∴∠B+∠C=70°,∴∠BAC=180°﹣(∠B+∠C)=110°.6.【解答】解:(1)∵DE垂直平分线段AB,∴DA=DB,设CD=x,则AD=BD=(16﹣x)cm,在Rt△BDC中,∵BD2=CD2+BC2,∴(16﹣x)2=x2+82,∴x=6,∴CD=6cm.7.【解答】解:(1)∵MN垂直平分BC,∴DC=BD,CE=EB,又∵EC=4,∴BE=4,又∵△BDC的周长=18,∴BD+DC=10,∴BD=5;(2)∵∠ADM=60°,∴∠CDN=60°,又∵MN垂直平分BC,∴∠DNC=90°,∴∠C=30°,又∵∠C=∠DBC=30°,∠ABD=20°,∴∠ABC=50°,∴∠A=180°﹣∠C﹣∠ABC=100°.8.【解答】解:∵DE为AB的垂直平分线,∴∠A=∠ABD,又∵∠ABD=2∠CBD,∴∠A=∠ABD=2∠CBD,设∠A=α,则∠ABD=α,∠CBD =α,又∵∠C=90°,∴∠A+∠ABC=90°,即α+α+α=90°,解得α=36°,∴∠A=36°.9.【解答】解:(1)∵AD垂直平分BE,EF垂直平分AC,∴AB=AE=EC,∴∠C=∠CAE,∵∠BAE=40°,∴∠AED=70°,∴∠C =∠AED=35°;(2)∵△ABC周长13cm,AC=6cm,∴AB+BE+EC=7cm,即2DE+2EC=7cm,∴DE+EC=DC=3.5cm.10.【解答】解:(1)C△ADE=10.(1分)∵AB、AC的垂直平分线分别交BC于D、E,∴AD=BD,AE=CE.(3分)C△ADE=AD+DE+AE=BD+DE+CE=BC=10.(4分)(2)∠DAE=76°.(5分)∵AB、AC的垂直平分线分别交BC于D、E,∴AD=BD,AE=CE.∴∠B=∠BAD,∠C=∠CAE.∵∠BAC=128°,∴∠B+∠C=52°.(7分)∴∠DAE=∠BAC﹣(∠BAD+∠CAE)=∠BAC﹣(∠B+∠C)=76°.(8分)11.【解答】解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得:∠CAN=∠C,∴∠EAN=∠BAC﹣∠BAE﹣∠CAN,=∠BAC﹣(∠B+∠C),在△ABC中,∠B+∠C=180°﹣∠BAC=80°,∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=100°﹣80°=20°;(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得:∠CAN=∠C,∴∠EAN=∠BAE+∠CAN﹣∠BAC,=(∠B+∠C)﹣∠BAC,在△ABC中,∠B+∠C=180°﹣∠BAC=110°,∴∠EAN=∠BAE+∠CAN﹣∠BAC=110°﹣70°=40°;温馨提示:最好仔细阅读后才下载使用,万分感谢!。
人教版八年级数学上册13.1.2《线段的垂直平分线的性质》同步训练习题(含答案)

13.1.2 线段的垂直平分线的性质同步训练习题一、单选题1. 下列图案中不是轴对称图形的是()2. 到△ABC的三个顶点距离相等的点是( )A.三条中线的交点B.三条角平分线的交点C.三条高线的交点D.三条边的垂直平分线的交点3. 平面内与A、B、C(不在同一直线上)三点等距离的点()A、没有B、只有1个C、有2个D、有4个4. 如图△ABC中,AB=AC,AB的垂直平线交BC于D,M是BC的中点,若∠BAD=30°则图中等于30°的角还有()个.A.1个B.2个C.3个D.4个5. 已知,如图,AC=BC,AD=BD,下列结论不正确的是()A.CO=DO B.AO=BO C.AB⊥CD D.△ACO≌△BCO6. 如图,△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=4cm,则△ABD 的周长是()A.22cm B.20 cm C.18cm D.15cm7.如图,在中,,是的垂直平分线,交于点,交于点.已知,则的度数为()A .B.C .D .二、填空题8. 在△中,,点在上,垂直平分,垂足为点,且,则.9. 已知点P在线段AB的垂直平分线上,PA=6,则PB=10. 如图,∠A=30°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD 于点E,连接EC,则∠AEC的度数是____________11.如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=2,则AC=.12.如图:△ABC中,∠ACB=90°,DE是AB的垂直平分线,且∠BAD∶∠CAB=1∶3,则∠B等于_______度.三、解答题13. 某地有两座工厂和两条交叉的公路,图中点M、N表示工厂,OA、OB表示公路,现计划修建一座物资仓库,希望仓库到两工厂的距离相同,到两条公路的的距离相同,你能确定出仓库P应该建在什么位置吗?请在图中画出你的设计。
八年级数学线段的垂直平分线的性质和判定(人教版)(基础)(含答案)

线段的垂直平分线的性质和判定(人教版)(基础)一、单选题(共11道,每道9分)1.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的一条直线垂直平分线段AB.其中不正确的个数有( )A.1个B.2个C.3个D.4个答案:A解题思路:根据线段垂直平分线的性质定理和判定定理,①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB,符合性质定理,是正确的;②若PA=PB,EA=EB,则直线PE垂直平分线段AB,符合判定定理,是正确的;③若PA=PB,则点P必是线段AB的垂直平分线上的点,符合判定定理,是正确的;④若EA=EB,则点E在AB垂直平分线上,但是平面内过一点的直线有无数条,不能确定是垂直平分线,所以错误;综上④错误,故选A试题难度:三颗星知识点:略2.如图,AC=AD,BC=BD,则有( )A.CD垂直平分ABB.AB垂直平分CDC.AB与CD互相垂直平分D.CD平分∠ACB答案:B解题思路:AC=AD,根据到线段两个端点距离相等的点在这条线段的垂直平分线上,所以A在CD的垂直平分线上;BC=BD,所以B在CD的垂直平分线上.两点确定一条直线,则AB垂直平分CD.故选B.试题难度:三颗星知识点:略3.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D,下列结论不一定成立的是( )A.DE=CEB.OE平分∠DECC.OE垂直平分CDD.CD垂直平分OE答案:D解题思路:A:因为OE平分∠AOB,EC⊥OA,ED⊥OB,所以DE=CE成立;B:由题可知∠DOE=∠COE,∠ODE=∠OCE=90°,可证△DOE≌△COE(AAS)所以∠OED=∠OEC,故OE平分∠DEC成立;C:由选项A,B可知DE=CE,OD=OC,所以点E和点O分别在线段CD的垂直平分线上,所以OE垂直平分CD成立;D:点C和点D均不在线段OE的垂直平分线上,所以CD垂直平分OE不成立;故选D试题难度:三颗星知识点:略4.平面内,过直线外一点作已知直线的垂线最终都转化为下列哪一种基本作图( )A.作一个角等于已知角B.作一条线段等于已知线段C.作已知角的角平分线D.作已知线段的垂直平分线答案:D解题思路:过直线外一点作已知直线的垂线可以先在直线上作一条线段,使直线外的一点在这条线段的垂直平分线上,再作这条线段的垂直平分线.故选D.试题难度:三颗星知识点:略5.如图1,已知A为直线MN外一点,求作直线AB,使AB⊥MN.如图2用尺规作图作出直线AB,下列叙述:①任取一点P;②以点A为圆心,AP长为半径作弧,交MN于C,D两点;③分别以点C,点D为圆心,以大于长为半径作弧,两弧交MN下方于一点B;④作直线AB.直线AB即为所求.其中错误的是( )A.①B.②C.③D.④答案:A解题思路:过点A作直线AB,使AB⊥MN的作法为:①任取一点P,使点P和点A位于直线MN的异侧;②以点A为圆心,AP长为半径作弧,交MN于C,D两点;③分别以点C,点D为圆心,以大于长为半径作弧,两弧交MN下方于一点B;④作直线AB.直线AB即为所求.要保证以AP为半径的弧与直线MN有交点,点P与点A应位于直线MN异侧,①错误.故选A.试题难度:三颗星知识点:略6.如图1,已知线段MN,在MN上求作一点O,使OM=ON.如图2用尺规作图作出了点O,下列作图语言叙述正确的是( )A.分别以点M,点N为圆心,任意长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求.B.分别以点M,点N为圆心,以大于长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求.C.以点M为圆心,任意长为半径作弧,再以点N为圆心,大于长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求.D.分别以点M,点N为圆心,任意长为半径作弧,两弧相交于点A和点B;作直线AB,直线AB即为所求.答案:B解题思路:在MN上求作一点O,使OM=ON可以转化为作线段MN的垂直平分线,与MN的交点即为点O.正确作法为:分别以点M,点N为圆心,以大于长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求;要找到MN垂直平分线上的两点,需要保证以相同长为半径作弧,且两弧有交点,所以此半径应大于,故选项A,C,D错误.故选B.试题难度:三颗星知识点:略7.如图,以C为圆心,以大于点C到AB的距离为半径作弧交AB于点D,E,再以D,E为圆心,以大于DE为半径作弧,两弧交于点F,作射线CF,则( )A.CF平分∠ACBB.CF垂直平分DEC.CF平分ABD.CF垂直平分AB答案:B解题思路:由题意可知,点C到D,E两点的距离相等,点F到D,E两点的距离相等,所以点C和点F 均在线段DE的垂直平分线上,所以CF垂直平分DE;故选B试题难度:三颗星知识点:略8.如图,某地由于居民增多,要在公路边增加一个公共汽车站,A,B是路边两个新建小区,要使两个小区到车站的路程一样长,这个公共汽车站C应建在( )A.点A到l的垂线与l的交点处B.线段AB的垂直平分线上任意某点处C.线段AB的垂直平分线和l的交点处D.点B到l的垂线与l的交点处答案:C解题思路:由题意可得,点C到A,B两点的距离相等,所以C在AB的垂直平分线上,因为C在l上,所以这个公共汽车站C应建在线段AB的垂直平分线和l的交点处.故选C试题难度:三颗星知识点:略9.如图,某公园的三个出口A,B,C构成△ABC,想要在公园内修建一个公共厕所,要求到三个出口距离都相等,则公共厕所应该在( )A.三条边的垂直平分线的交点B.三个角的角平分线的交点C.三角形三条高的交点D.三角形三条中线的交点答案:A解题思路:∵公共厕所到出口A,B的距离相等∴公共厕所在线段AB的垂直平分线上,同理,公共厕所在线段BC的垂直平分线上所以,公共厕所应该在三条边的垂直平分线的交点故选A试题难度:三颗星知识点:略10.电信部门要在S区修建一座手机信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OC,OD的距离也必须相等,则发射塔应建在( )A.∠COD的平分线上任意某点处B.线段AB的垂直平分线上任意某点处C.∠COD的平分线和线段AB的交点处D.∠COD的平分线和线段AB垂直平分线的交点处答案:D解题思路:由题意可得,发射塔到两个城镇A,B的距离相等,所以发射塔要建在AB的垂直平分线上,又因为发射塔到两条高速公路OC,OD的距离也相等,所以发射塔要建在∠COD的平分线上,所以发射塔应建在线段AB垂直平分线和∠COD的平分线的交点处;故选D试题难度:三颗星知识点:略11.如图,△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB,下列描述正确的是( )A.P是AC的垂直平分线与AB的交点B.P是BC的垂直平分线与AB的交点C.P是∠ACB的平分线与AB的交点D.P是以点B为圆心,AC长为半径的弧与边AB的交点答案:B解题思路:因为PA+PB=AB,要使PA+PC=AB即PB=PC,即点P在BC的垂直平分线上所以点P为线段BC的垂直平分线与AB的交点故选B试题难度:三颗星知识点:略。
鲁教版七年级下册数学-线段的垂直平分线素养提升练习(含解析)

4 线段的垂直平分线基础过关全练知识点1 线段垂直平分线的性质定理1.如图所示,AC垂直平分BD,若AB=3 cm,CD=5 cm,则四边形ABCD的周长是( )A.11 cmB.13 cmC.16 cmD.18 cm2.如图,在△ABC中,AB=AC,∠A=42°,AB的垂直平分线MN交AC于D点,连接BD,则∠DBC的度数是( )A.22°B.27°C.32°D.40°3.(2021山东济南期末)如图,∠ABC=90°,∠C=15°,线段AC的垂直平分线DE交AC 于D,交BC于E,CE=10 cm,则AB=( )A.4 cmB.5 cmC.6 cmD.不能确定4.(2022内蒙古鄂尔多斯中考)如图,在△ABC中,边BC的垂直平分线DE交AB于点D,连接DC,若AB=3.7,AC=2.3,则△ADC的周长是 .5.如图,在Rt△ABC中,∠C=90°,直线DE是线段AB的垂直平分线,交AC于点E,连接BE.(1)若∠A=35°,求∠CBE的度数;(2)若∠A=30°,△BCE的周长为15+53,求△ABC的面积.知识点2 线段垂直平分线的判定定理6.已知:C、D是线段AB外不重合的两点,AC=BC,AD=BD,点P在直线CD上.若AP=5,则BP的长为( )A.2.5B.5C.10D.257.(2023陕西西安高陵期末)如图,已知∠ACB=∠BDA=90°,BC与AD交于点E,AC=BD.求证:点E在线段CD的垂直平分线上.8.【一题多解】如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,EH垂直平分BD,连接DE交AC于F,求证:点E在线段AF的垂直平分线上.知识点3 三角形三条边的垂直平分线的性质9.(2023河北石家庄赵县二模)A、B、C三地所在的位置如图所示,若想建立一个货物中转仓,使其到这三地的距离相等,则中转仓的位置应选在( )A.△ABC的三边垂直平分线的交点处B.△ABC的三边中线的交点处C.△ABC的三条角平分线的交点处D.△ABC的三边上的高所在直线的交点处能力提升全练10.(2023山东济南历下期末,10,★★☆)如图,在锐角三角形ABC中,直线l为边BC的垂直平分线,射线BP为∠ABC的平分线,且直线l与射线BP相交于点P.若∠A=64°,∠ACP=26°,则∠ABP的度数为( )A.30°B.32°C.34°D.36°11.(2023山东威海荣成十六校联盟期中,8,★★☆)如图,在△ABC中,∠BAC=80°,AB 边的垂直平分线交AB于点D,交BC于点E,AC边的垂直平分线交AC于点F,交BC 于点G,连接AE,AG,则∠EAG的度数为( )A.15°B.20°C.25°D.30°12.【新考法】(2022湖北宜昌中考,6,★★☆)如图,在△ABC中,分别以点B和点C为BC长为半径画弧,两弧相交于点M,N.作直线MN,交AC于点D,交BC于圆心,大于12点E,连接BD.若AB=7,AC=12,BC=6,则△ABD的周长为( )A.25B.22C.19D.1813.(2023浙江丽水中考,13,★★☆)如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是 .14.(2023山东淄博张店期中,12,★★☆)如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠AOC=68°,则∠ABC= .15.(2022山东青岛胶州期中,14,★★☆)如图,在△ABC中,AB=AC=10,BC=12,点D 是边BC的中点,直线MN是线段AB的垂直平分线,点E是MN上的一个动点,则△BDE周长的最小值是 .16.【方程思想】(2022山东济南章丘期末,23,★★☆)如图,在△ABC中,∠C=90°,点P 在AC上运动,点D在AB上运动,PD始终与PA相等,线段BD的垂直平分线交BC于点E,交BD于点F,连接DE.(1)判断DE与PD的位置关系,并说明理由;(2)若AC=3,BC=4,PA=1,求线段DE的长.素养探究全练17.【推理能力】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC.若△ADE的周长为12 cm,△OBC的周长为32 cm.(1)求线段BC的长;(2)连接OA,求线段OA的长;(3)若∠BAC=n°(n>90),求∠DAE的度数.(用含n的式子表示)答案全解全析基础过关全练1.C ∵AC 垂直平分BD,∴AD=AB=3 cm,BC=CD=5 cm,∴四边形ABCD 的周长=AD+AB+BC+CD=16 cm.故选C.2.B ∵AB=AC,∠A=42°,∴∠ABC=12(180°-∠A)=12(180°-42°)=69°,∵MN 垂直平分AB,∴AD=BD,∴∠ABD=∠A=42°,∴∠DBC=∠ABC-∠ABD=69°-42°=27°.故选B.3.B ∵DE 垂直平分AC,∴AE=CE=10 cm,∴∠EAC=∠C=15°,∴∠AEB=30°,∵∠ABC=90°,∴AB=12AE=5 cm,故选B.4.答案 6解析 ∵边BC 的垂直平分线DE 交AB 于点D,∴BD=CD,∵AB=3.7,AC=2.3,∴△ADC 的周长为AD+CD+AC=AB+AC=6,故答案为6.5.解析 (1)∵∠C=90°,∠A=35°,∴∠ABC=90°-35°=55°,∵直线DE 是线段AB 的垂直平分线,∴EA=EB,∴∠EBA=∠A=35°,∴∠CBE=55°-35°=20°.(2)∵∠C=90°,∠A=30°,∴∠ABC=60°,∵EB=EA,∴∠ABE=∠A=30°,∴∠CBE=30°,∴BE=2CE,设CE=x,则BE=2x,∴BC=BE 2−CE 2=3x,∴3x +3x =15+53,∴x =5,∴BC =53,EA=EB=10,∴AC=CE+EA=15,∴△ABC 的面积=12×CA ×BC =7532.6.B ∵C 、D 是线段AB 外不重合的两点,AC=BC,AD=BD,∴直线CD 是线段AB 的垂直平分线,∵点P 在直线CD 上,AP=5,∴BP=AP=5,故选B.7.证明 ∵∠ACB=∠BDA=90°,AC=BD,且AB=BA,∴Rt△ACB≌Rt△BDA(HL),∴AD=BC,∠ABC=∠BAD,∴AE=BE,∴EC=ED,∴点E在线段CD的垂直平分线上.8.证明 证法一:∵EH垂直平分BD,∴BE=DE,EH⊥BD,∴∠BEH=∠DEH,∵∠ACB=90°,∴AC⊥BD,∴EH∥AC,∴∠BEH=∠A,∠DEH=∠AFE,∴∠A=∠AFE,∴AE=EF,∴点E在线段AF的垂直平分线上.证法二:∵∠ACB=90°,∴∠A+∠B=90°,∠D+∠DFC=90°,∵EH垂直平分BD,∴EB=ED,∴∠B=∠D,∴∠A=∠DFC,∵∠DFC=∠AFE,∴∠A=∠AFE,∴EA=EF,∴点E在线段AF的垂直平分线上.9.A ∵中转仓到A、B、C三地的距离相等,∴中转仓的位置应选在△ABC的三边垂直平分线的交点处,故选A.能力提升全练10.A ∵直线l为边BC的垂直平分线,∴PB=PC,∴∠PBC=∠PCB,∵BP为∠ABC的平分线,∴∠ABP=∠CBP,∴∠PBC=∠PCB=∠ABP,∵∠ABC+∠ACB+∠A=180°,∴3∠ABP+∠A+∠ACP=180°,∵∠A=64°,∠ACP=26°,∴∠ABP=30°.故选A.11.B ∵AB边的垂直平分线交BC于点E,AC边的垂直平分线交BC于点G,∴AG=CG,AE=BE,∴∠C=∠CAG,∠B=∠BAE,∴∠BAE+∠CAG=∠B+∠C=180°-∠BAC=100°,∴∠EAG=∠BAE+∠CAG-∠BAC=100°-80°=20°,故选B.12.C 由题意可得,MN垂直平分BC,∴DB=DC,∴△ABD的周长=AB+BD+AD=AB+DC+AD=AB+AC,∵AB=7,AC=12,∴AB+AC=19,∴△ABD的周长是19,故选C.13.答案 4解析 ∵∠B=∠ADB,AB=4,∴AD=AB=4,∵直线DE是边AC的垂直平分线,∴DC=AD=4,故答案为4.14.答案 34°解析 连接OB,AC,如图所示,∵线段AB,BC的垂直平分线l1,l2相交于点O,∴OA=OB,OC=OB,∴∠OBA=∠OAB,∠OBC=∠OCB,∵∠AOC=68°,∴∠OAC+∠OCA=180°-68°=112°,∵∠OAC+∠OCA+∠OAB+∠OBA+∠OBC+∠OCB=180°,∴112°+2∠OBA+2∠OBC=180°,∴2(∠OBA+∠OBC)=68°,∴∠OBA+∠OBC=34°,即∠ABC=34°.15.答案 14解析 如图,连接AD,AE,∵直线MN是线段AB的垂直平分线,∴AE=BE,∵AB=AC,D是BC的中点,∴AD⊥BC,BD=CD=6,∴△BDE的周长=BD+DE+BE=BD+DE+AE≥BD+AD,∴当A、E、D 三点共线时,△BDE的周长最小,∵∠ADB=90°,AB=10,BD=6,∴AD=AB2−BD2=8,∴△BDE周长的最小值为6+8=14,故答案为14.16.解析 (1)DE⊥DP.理由:∵PD=PA,∴∠A=∠PDA,∵直线EF是线段BD的垂直平分线,∴EB=ED,∴∠B=∠EDB,∵∠C=90°,∴∠A+∠B=90°,∴∠PDA+∠EDB=90°,∴∠PDE=180°-90°=90°,∴DE⊥DP.(2)如图,连接PE,CP=AC-AP=2,PD=PA=1,设DE=x,则EB=ED=x,∴CE=4-x,∵∠C=∠PDE=90°,∴PC2+CE2=PE2=PD2+DE2,即22+(4-x)2=12+x 2,解得x=198,故DE=198.素养探究全练17.解析 (1)∵l 1是AB 边的垂直平分线,∴DA=DB,∵l 2是AC 边的垂直平分线,∴EA=EC,∵△ADE 的周长为12 cm,∴DA+DE+EA=12 cm,∴BC=BD+DE+EC=DA+DE+EA=12 cm.(2)如图,∵l 1是AB 边的垂直平分线,∴OA=OB,∵l 2是AC 边的垂直平分线,∴OA=OC,∵△OBC 的周长为32 cm,∴OB+OC+BC=32 cm,∴OA=OB=OC=32−122=10(cm).(3)∵∠BAC=n°,∴∠ABC+∠ACB=(180-n)°,∵DA=DB,EA=EC,∴∠BAD=∠ABC,∠EAC=∠ACB,∴∠DAE=∠BAC-∠BAD-∠EAC=n°-(180°-n°)=2n°-180°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1题A B E C 2题D A B C 3题D A
B E
C 4题A B C O 5题
D A B
E C 11题D A B E C O 12题D A B E C 13题D A B E C 14题D A B E C 15题D A B E C
6题
D A B
E C 8题D A B E C 7题D A B E C 10题
'9题《垂直平分线》练习题
1.如图,△ABC 的边AB 的垂直平分线交AC 于点E,若AE=23,则BE= 。
2.如图,△ABC 中,AB=AC ,AB 的垂直平分线交AC 于点D, △ABC 和△DBC 的周长分别为60㎝和38㎝,则△ABC 的腰长为 ,底边长为 。
3.如图,△ABC 中,∠ACB=90°,CB 的垂直平分线DE 交AB 于点D,垂足为E ,①若∠B=20°,则∠ADC 的度数为 ;②若△ADC 的周长为14,AC=4,则AB= ;③若AB=8㎝,则CD= 。
4.如图,△ABC 中,∠A=52°,AB 、AC 的垂直平分线交于点O ,则∠BOC 的度数为 。
5.如图,∠ABC=50°,AD 垂直平分线段BC ,交BC 于点D ,∠ABC 的角平分线BE 交AD 于点E ,连接EC ,则∠AEC 的度数为 。
6.如图,△ABC 中,AC 的垂直平分线交BC 于点D ,垂足为E ,△ABD 的周长为12㎝,AC=5㎝,则△ABC 的周长为 。
7.如图,△ABC 中,AB=AC ,AB 的垂直平分线交AC 于点E ,垂足为D, ∠EBC ∶∠EBA=1∶2,则∠A 的度数为 。
8.如图,平行四边形ABCD 中,AB=3,BC=5,AC 的垂直平分线交AD 与点E,则△CDE 的周长为 。
9.如图,某广告公司为一厂家设计的商标图案,AD 垂直平分线段BC ,E 、F 都在线段AD 上,若AB=5,BC=6,则图中阴影部分面积为 。
10.如图,△ABC 中,AB=BC=2,∠ABC=90°,D 为BC 的中点,且它关于AC 的对称点D ’,则 BD ’= 。
11.如图,平行四边形ABCD 中,AC 、BD 交于点O ,过O 作AC 的垂线交AB 于点E ,连接CE ,若平行四边形ABCD 的周长为20㎝,则△EBC 的周长为 。
12.如图,△ABC 中,AB=AC ,∠A=36°,AB 的中垂线DE 交AC 于点E ,,垂足为D ,则图中的等腰三角形有 。
13.如图,△ABC 中,∠C=90°,AB 的垂直平分线交BC 于点D,垂足为E ,∠CAD=2∠B,若BD=2,则AC= 。
14.如图,△ABC 中,∠C=90°,DE 垂直平分AB ,∠CAD ∶∠BAD=2∶3,则∠ADB= 。
15.如图,△ABC 中,∠B=45°, ∠C=30°,AB 、AC 的垂直平分线分别交BC 于点D 、E ,若CE=2,
则BC= ,AB= 。
16题D A B M 17题
18题D A B E C 19题D A B E C 20题A B C P M Q N 21题D A B E C
甲
26题A C a 16.如图,△ABC 中,AB=AC ,AB 的垂直平分线交BC 于点D,M 为BC 的中点,若∠BAD=30°,则图中等于30°的角还有 。
17.如图,分别作出点P 关于OA 、OB 的对称点P 1、P 2,连接P 1、P 2分别交OA 、OB 与点C 、D ,若△PCD 的周长为10㎝,则P 1P 2= 。
18.如图,△ABC 中,∠C=90°,DE 垂直平分AB ,AB =2AC,BC =18㎝, 则BE 的长度为 。
19.如图,△ABC 中,∠C=90°, ∠B=15°,AB 的垂直平分线交BC 于点D ,交AB 于点E ,BD=10㎝, 则AC= 。
20.如图,△ABC 中, MP 、NQ 分别垂直平分AB 、AC ,①若∠BAC=130°,则∠PAQ 的度数为 ;②若AB=AC ,∠BAC=120°,BC=15㎝,则PQ= ;③若BC=12㎝,则△PAQ 的周长为 。
21.如图,△ABC 中,∠C=90°, DE 垂直平分AB ,且AD 平分∠BAC ,则∠B 的度
数为 。
22.一个三角形两边的垂直平分线的交点在第三边上,则这个三角形的形状
为 。
23.到三角形的三个顶点的距离相等的点是 。
24.已知线段AB ,用尺规作AB 的垂直平分线CD ,垂足为E ,在CD 上取
一点F,使EF= 12 AB ,连接AF 、BF ,则∠AFB 的度数为 。
25.如图,甲乙两村要合资修建一所变电站,地点想选在两村旁边的一条公路附近,由于两村出资相同,所以变电站的位置要离两村距离相等,请
你帮助他们确定变电站的位置。
(保留痕迹,不写作法)
26.某企业集团,下设三个厂A,B,C ,如图,分别生产某机器的相关零件,试问该集团的总厂设在何处,可使总厂到各分厂的距离相等?
27.已知:线段a.求作:△ABC ,使AB=AC ,BC=a,且BC 边上的高=2a. (要求:尺规作图,保留痕迹,不写作法)
29题D A B C E P F Q 28题D A B
C 28.如图,△ABC 中,AB=BC ,∠B=120°,AB 的垂直平分线交AC 于点
D 。
求证:AD= 12 CD
29. 如图,△ABC 中,∠B=22.5°,AB 的垂直平分线交AB 于点Q ,交BC 于点P ,PE ⊥AC 于点E , AD ⊥BC 于点D ,AD 、PE 交于点F 。
求证:DF=DC 。
答案:
1.2 3
2.22㎝ 16㎝
3.40°10 4㎝
4.104°
5.115°
6.17㎝
7.45°
8.8 9.6 10. 5 11.10㎝ 12.△ABC、△AEB、△BEC 13. 2 14.112.5°15.3+ 3 6 16.∠B、∠C、∠DAB 17.10㎝ 18.12㎝ 19.5㎝
20. ①80°②5㎝③12㎝ 21.30° 22.直角三角形 23.三条垂直平分线的角点24.90° 25.略 26.略 27.略 28.略 29.略。
