初二数学 勾股定理常考压轴题专题练习汇总(含解析)
八年级勾股定理压轴题

八年级勾股定理压轴题八年级勾股定理选择压轴题一、单选题1.下列各组数中,是勾股数的是( )A. 12,15,18B. 12,35,36C. 2,3,4D. 5,12,13【答案】D2.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )A. 1-B. 1-C.D.【答案】D【解析】试题分析:设CD与B′C′相交于点O,连接OA.根据旋转的性质,得∠BAB′=30°,则∠DAB′=60°.3.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )A. 5B. 25C. 10 +5D. 35【答案】B【解析】试题解析:将长方体展开,连接A、B,根据两点之间线段最短,(1)如图,BD=10+5=15,AD=20,由勾股定理得:AB= .4.在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=( )A. 4B. 5C. 6D. 7【答案】A【解析】解:由勾股定理的几何意义可知:S1+S2=1,S2+S3=2,S3+S4=3,S1+S2+S3+S4=4,故选A.5.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为81,小正方形面积为16,若用x,y表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是( )A. x2+y2=81B. x+y=13C. 2xy+16=81D. x-y=4【答案】B6.如图,带阴影的长方形面积是( )A. 9 cm2B. 24 cm2C. 45 cm2D. 51 cm2【答案】C【解析】试题解析:由图可知,△ABC是直角三角形,∵AC=8cm,BC=12cm,∴AB= =15cm,∴S阴影=15×3=45cm2.故选C.7.“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是3和6,则大正方形与小正方形的面积差是( )A. 9B. 36C. 27D. 34【答案】B【解析】大正方形的面积为32+62=45,小正方形的面积为(6-3)2=9,则面积差为45-9=36.故选B.8.如图所示,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为( )A. B. C. 3 D. 2【答案】B故选B.9.如图,一棵大树在一次强台风中于离地面5m处折断倒下,倒下后树顶落在树根部大约12m处。
勾股定理中的常考问题(6种类型48道)—2024学年八年级数学上册(解析版)

勾股定理中的常考问题6种类型48道【类型一用勾股定理解决折叠问题】1.如图,将长方形ABCD沿着AE折叠,点D落在BC边上的点F处,已知AB=8,BC=10,则EC的长为()A.4B.3C.5D.2【答案】B【分析】长方形ABCD沿着AE折叠,得AD=AF=BC=10,EF=ED,根据勾股定理得BF=6,则CF=4,设EC=x,ED=8−x,根据勾股定理得EF2=EC2+CF2,即可解得EC的长.【详解】解:∵四边形ABCD是长方形,∴AD=BC=10,DC=AB=8,∵长方形ABCD沿着AE折叠,∴AD=AF=BC=10,EF=ED,∴BF=√AF2−AB2=√100−64=6,CF=BC−BF=4,设EC=x,ED=8−x,∴EF2=EC2+CF2,即(8−x)2=x2+42,解得x=3,所以EC=3,故选:B.【点睛】本题主要考查了图形折叠以及勾股定理等知识内容,掌握图形折叠的性质是解题的关键.2.如图,有一块直角三角形纸片,∠C=90°,AC=4,BC=3,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则BD的长为()【答案】C【分析】利用勾股定理求得AB=5,由折叠的性质可得AB=AE=5,DB=DE,求得CE=1,设DB=DE=x,则CD=3−x,根据勾股定理可得12+(3−x)2=x2,进而求解即可.【详解】解:∵∠C=90°,AC=4,BC=3,∴AB=√32+42=5,由折叠的性质得,AB=AE=5,DB=DE,∴CE=1,设DB=DE=x,则CD=3−x,在Rt△CED中,12+(3−x)2=x2,,解得x=53故选:C.【点睛】本题考查勾股定理、折叠的性质,熟练掌握勾股定理是解题的关键.【答案】B【分析】根据图形翻折变换的性质可知,AE=BE,设AE=x,则BE=x,CE=8−x,再Rt△BCE中利用勾股定理即可求出CE的长度.【详解】解:∵△ADE翻折后与△BDE完全重合,∴AE=BE,设AE=x,则BE=x,CE=8−x,∵在Rt△BCE中,CE2=BE2−BC2,即(8−x)2=x2−62,解得,x=7,4.∴CE=74故选:B【点睛】本题考查了图形的翻折变换,解题中应注意折叠是一种对称变换,属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.4.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,AD为∠BAC的平分线,将△DAC沿AD向上翻折得到△DAE,使点E在射线AB上,则DE的长为()【答案】B【分析】根据勾股定理求得BC,进而根据折叠的性质可得AE=AC,可得BE=2,设DE=x,表示出BD,DE,进而在Rt△BDE【详解】解:∵在Rt△ABC中,∠ABC=90°,AB=3,AC=5,∴BC=√AC2−AB2=√52−32=4,∵将△DAC沿AD向上翻折得到△DAE,使点E在射线AB上,∴AE=AC,设DE=x,则DC=DE=x,BD=BC−CD=4−x,BE=AE−AB=5−3=2,在Rt△BDE中,BD2+BE2=DE2,即(4−x)2+22=x2,解得:x=52,即DE的长为52故选:B.【点睛】本题考查了勾股定理与折叠问题,熟练掌握勾股定理是解题的关键.5.如图,矩形纸片ABCD的边AB长为4,将这张纸片沿EF折叠,使点C与点A重合,已知折痕EF长为2√5,则BC长为()A.4.8B.6.4C.8D.10【答案】C【分析】过点F作FG⊥BC于点G,则四边形ABGF是矩形,从而FG=AB=4,在Rt△EFG中,利用勾股定理求得EG=√EF2−FG2=√(2√5)2−42=2.设BE=x,则BG=BE+EG=x+2.由∠AFE=∠CEF=∠AEF 得到AE=AF=BG=x+2,从而在Rt△ABE中,有AB2+BE2=AE2,代入即可解得x的值,从而得到BE,CE的长,即可得到BC.【详解】过点F作FG⊥BC于点G∵在矩形ABCD中,∠DAB=∠B=90°∴四边形ABGF是矩形∴FG=AB=4∴在Rt△EFG中,EG=√EF2−FG2=√(2√5)2−42=2设BE=x,则BG=BE+EG=x+2∵在矩形ABCD中,BC∥AD∴∠AFE=∠CEF由折叠得∠CEF=∠AEF∴AE=AF∵在矩形ABGF中,AF=BG=x+2∴AE=AF=x+2∵在Rt△ABE中,AB2+BE2=AE2∴42+x2=(x+2)2解得x=3即BE=3,AE=5∴由折叠可得CE=AE=5∴BC=BE+EC=3+5=8故选:C【点睛】本题考查矩形的性质,勾股定理的应用,利用勾股定理构造方程是解决折叠问题的常用方法.A.7B.136【答案】B【分析】根据题意可得AD=AB=2,∠B=∠ADB,CE=DE,∠C=∠CDE,可得∠ADE=90°,继而设AE=x,则CE=DE=3−x,根据勾股定理即可求解.【详解】解:∵沿过点A的直线将纸片折叠,使点B落在边BC上的点D处,∴AD=AB=2,∠B=∠ADB,∵折叠纸片,使点C与点D重合,∴CE=DE,∠C=∠CDE,∵∠BAC=90°,∴∠B+∠C=90°,∴∠ADB+∠CDE=90°,∴AD2+DE2=AE2,设AE=x,则CE=DE=3−x,∴22+(3−x)2=x2,,解得x=136即AE=13,6故选:B【点睛】本题考查了折叠的性质,勾股定理,掌握折叠的性质以及勾股定理是解题的关键.7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边BC沿CE翻折,点B落在点F处,连接CF交AB于点D,则FD的最大值为()【答案】D【分析】根据将边BC沿CE翻折,点B落在点F处,可得FD=CF−CD=4−CD,即知当CD最小时,FD最大,此时CD⊥AB,用面积法求出CD,即可得到答案.【详解】解:如图:∵将边BC沿CE翻折,点B落在点F处,∴CF=BC=4,∴FD=CF−CD=4−CD,当CD最小时,FD最大,此时CD⊥AB,∵∠ACB=90°,AC=3,BC=4,∴AB=√AC2+BC2=√32+42=5,∵2S△ABC=AC⋅BC=AB⋅CD,∴CD=AC⋅BCAB =3×45=125,∴FD=CF−CD=4−125=85,故选:D.【点睛】本题考查直角三角形中的翻折问题,涉及勾股定理及应用,解题的关键是掌握翻折的性质.A.73B.154【答案】B【分析】先求出BD=2,由折叠的性质可得DN=CN,则BN=8−DN,利用勾股定理建立方程DN2= (8−DN)2+4,解方程即可得到答案.【详解】解:∵D是AB中点,AB=4,∴AD=BD=2,∵将Rt△ABC折叠,使点C与AB的中点D重合,∴DN=CN,∴BN=BC−CN=8−DN,在Rt△DBN中,由勾股定理得DN2=BN2+DB2,∴DN2=(8−DN)2+4,∴DN=17,4,∴BN=BC−CN=154故选:B.【点睛】本题主要考查了勾股定理与折叠问题,正确理解题意利用方程的思想求解是解题的关键.【类型二杯中吸管问题】9.如图,有一个透明的直圆柱状的玻璃杯,现测得内径为5cm,高为12cm,今有一支15cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度最少为()A.1cm B.2cm C.3cm D.不能确定【答案】B【分析】吸管露出杯口外的长度最少,即在杯内最长,可用勾股定理解答.【详解】解∶∵CD=5cm,AD=12cm,∴AC=√CD2+AD2=√52+122,露出杯口外的长度为=15−13=2(cm).故答案为:B.【点睛】本题考查勾股定理的应用,所述问题是一个生活中常见的问题,与勾股定理巧妙结合,可培养同学们解决实际问题的能力.10.如图,一支笔放到圆柱形笔筒中,笔筒内部底面直径是9cm,内壁高12cm.若这支笔长18cm,则这支笔在笔筒外面部分的长度是()A.6cm B.5cm C.3cm D.2cm【分析】根据勾股定理求得AC的长,进而即可求解.【详解】解:根据题意可得图形:AB=12cm,BC=9cm,在Rt△ABC中:AC=√AB2+BC2=√122+92=15(cm),所以18−15=3(cm).则这只铅笔在笔筒外面部分长度为3cm.故选:C.【点睛】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.11.如图,一支笔放到圆柱形笔筒中,笔筒内部底面直径是9cm,内壁高12cm.若这支笔长18cm,则这支笔在笔筒外面部分的长度是()A.6cm B.5cm C.4cm D.3cm【答案】D【分析】首先根据题意画出图形,利用勾股定理计算出AC的长度.然后求其差.【详解】解:根据题意可得:AB BC=9cm,在Rt△ABC中∶AC=√AB2+BC2=√122+92=15(cm),所以18−15=3(cm),则这只铅笔在笔筒外面部分长度为3cm.故选:D.【点睛】此题主要考查了勾股定理的应用,正确得出笔筒内铅笔的最短长度是解决问题的关键.12.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度ℎcm,则ℎ的取值范围是()A.ℎ≤17cm B.ℎ≥16cm C.5cm<ℎ≤16cm D.7cm<ℎ≤16cm【分析】根据勾股定理及直径为最大直角边时即可得到最小值,当筷子垂直于底面时即可得到最大值即可得到答案;【详解】解:由题意可得,当筷子垂直于底面时ℎ的值最大,ℎmax=24−8=16cm,当直径为直角边时ℎ的值最小,根据勾股定理可得,ℎmin=24−√82+152=7cm,∴7cm<ℎ≤16cm,故选D.【点睛】本题考查勾股定理的运用,解题的关键是找到最大与最小距离的情况.13.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度ℎcm,则ℎ的取值范围是()A.ℎ≤17cm B.ℎ≥16cm C.5cm<ℎ≤16cm D.7cm≤ℎ≤16cm【答案】D【分析】如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出的取值范围.【详解】解:如图1所示,当筷子的底端在D点时,筷子露在杯子外面的长度最长,=24−8=16cm,∴ℎ最大如图2所示,当筷子的底端在A点时,筷子露在杯子外面的长度最短,在Rt△ABD中,AD=15cm,BD=8cm,∴AB=√AD2+BD2=17cm,=24−17=7cm,∴此时ℎ最小∴的取值范围是7cm≤h≤16cm.故选:D.【点睛】本题主要考查了勾股定理的应用,明确题意,准确构造直角三角形是解题的关键.A.5B.7C.12D.13【答案】A【分析】根据勾股定理求出h的最短距离,进而可得出结论.【详解】解:如图,当吸管、底面直径、杯子的高恰好构成直角三角形时,h最短,此时AB=√92+122=15(cm),故ℎ=20−15=5(cm);最短故选:A.【点睛】本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.15.如图,某同学在做物理实验时,将一支细玻璃棒斜放入了一只盛满水的烧杯中,已知烧杯高8cm,玻璃棒被水淹没部分长10cm,这只烧杯的直径约是()A.9cm B.8cm C.7cm D.6cm【答案】D可.【详解】解:由题意,可得这只烧杯的直径是:√102−82=6(cm).故选:D.【点睛】本题考查了勾股定理的应用,能够将实际问题转化为数学问题是解题的关键.16.如图,一根长18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中,牙刷露在杯子外面的长度为h cm,则h的取值范围是()A.4<h<5B.5<h<6C.5≤h≤6D.4≤h≤5【答案】C【分析】根据题意,求出牙刷在杯子外面长度最小与最大情况即可得出取值范围.【详解】解:根据题意,当牙刷与杯底垂直时,ℎ最大,如图所示:故ℎ最大=18−12=6cm;∵当牙刷与杯底圆直径、杯高构成直角三角形时,ℎ最小,如图所示:在RtΔABC中,∠ACB=90°,AC=5cm,BC=12cm,则AB=√BC2+AC2=√52+122=13cm,∵牙刷长为18cm,即AD=18cm,∴ℎ最小=AD−AB=18−13=5cm,∴h的取值范围是5≤h≤6,故选:C.【点睛】本题考查勾股定理解实际应用题,读懂题意,根据牙刷的放置方式明确牙刷在杯子外面长度最小与最大情况是解决问题的关键.【类型三楼梯铺地毯问题】17.如图在一个高为3米,长为5米的楼梯表面铺地毯,则地毯至少需要().A.3米B.4米C.5米D.7米【答案】D【分析】当地毯铺满楼梯时的长度是楼梯的水平宽度与垂直高度的和,根据勾股定理求得水平宽度,即可求得地毯的长度.【详解】解:由勾股定理得:楼梯的水平宽度=√52−32=4(米),∵地毯铺满楼梯的长度应该是楼梯的水平宽度与垂直高度的和,∴地毯的长度至少是3+4=7(米).故选:D.【点睛】此题考查了生活中的平移现象以及勾股定理,属于基础题,利用勾股定理求出水平边的长度是解答本题的关键.18.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要()【分析】当地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,根据勾股定理求得水平宽度,然后求得地毯的长度即可.【详解】解:由勾股定理得:楼梯的水平宽度=√132−52=12m,∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,∴地毯的长度至少是12+5=17(m).故选B.【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解答本题的关键.19.如图是楼梯的示意图,楼梯的宽为5米,AC=5米,AB=13米,若在楼梯上铺设防滑材料,则所需防滑材料的面积至少为()A.65m2B.85m2C.90m2D.150m2【答案】B【分析】勾股定理求出BC,平移的性质推出防滑毯的长为AC+BC,利用面积公式进行求解即可.【详解】解:由图可知:∠C=90°,∵AC=5米,AB=13米,∴BC=√AB2−AC2=12米,由平移的性质可得:水平的防滑毯的长度=BC=12(米),铅直的防滑毯的长度=AC=5(米),∴至少需防滑毯的长为:AC+BC=17(米),∵防滑毯宽为5米∴至少需防滑毯的面积为:17×5=85(平方米).故选:B.【点睛】本题考查勾股定理.解题的关键是利用平移,将防滑毯的长转化为两条直角边的边长之和.A.13cm B.14cm C.15cm D.16cm【答案】A【分析】根据勾股定理即可得出结论.【详解】如图,由题意得AC=1×5=5(cm),BC=2×6=12(cm),故AB=√122+52=13(cm).故选:A.【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.21.如图所示:某商场有一段楼梯,高BC=6m,斜边AC是10米,如果在楼梯上铺上地毯,那么需要地毯的长度是()A.8m B.10m C.14m D.24m【答案】C【分析】先根据直角三角形的性质求出AB的长,再根据楼梯高为BC的高=6m,楼梯的宽的和即为AB的长,再把AB、BC的长相加即可.【详解】∵△ABC是直角三角形,BC=6m,AC=10m∴AB=√AC2−BC2=√102−62=8(m),∴如果在楼梯上铺地毯,那么至少需要地毯为AB+BC=8+6=14(米).故选C【点睛】本题考查的是勾股定理的应用,解答此题的关键是找出楼梯的高和宽与直角三角形两直角边的等量关系.22.某酒店打算在一段楼梯面上铺上宽为2米的地毯,台阶的侧面如图所示,如果这种地毯每平方米售价为80元,则购买这种地毯至少需要()A.2560元B.2620元C.2720元D.2840元【答案】C【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.【详解】利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为√132−52=12米、5米,∴地毯的长度为12+5=17米,地毯的面积为17×2=34平方米,∴购买这种地毯至少需要80×34=2720元.故选C.【点睛】本题考查的知识点是勾股定理的应用,生活中的平移现象,解题关键是要注意利用平移的知识,把要求的所有线段平移到一条直线上进行计算.23.如图所示:是一段楼梯,高BC是3m,斜边AC是5m,如果在楼梯上铺地毯,那么至少需要地毯()A.5m B.6m C.7m D.8m【答案】C【详解】楼梯竖面高度之和等于AB的长.由于AB=√AC2−BC2=√52−32=4,所以至少需要地毯长4+3=7(m).故选C24.如图,是一段楼梯,高BC是1.5m,斜边AC是2.5m,如果在楼梯上铺地毯,那么至少需要地毯()A.2.5m B.3m C.3.5m D.4m【答案】C【分析】当地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,根据勾股定理求得AB,然后求得地毯的长度即可.【详解】解:由勾股定理得:AB=√2.52−1.52=2因为地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和所以地毯的长度至少是1.5+2=3.5(m)故选C.【点睛】本题考查了图形平移性质和勾股定理,解决本题的关键是要熟练掌握勾股定理.【类型四最短路径问题】25.如图,透明圆柱的底面半径为6厘米,高为12厘米,蚂蚁在圆柱侧面爬行.从圆柱的内侧点A爬到圆柱的外侧点B处吃食物,那么它爬行最短路程是厘米.(π≈3)【答案】30【分析】把圆柱的侧面展开,根据勾股定理即可得到结论.【详解】解:∵透明圆柱的底面半径为6厘米,∴透明圆柱的底面周长为2×6π=厘米≈36厘米,作点A关于直线EF的对称点A′,连接A′B,则A′B的长度即为它爬行最短路程,×36=18厘米,∴A′A=2AE=24厘米,AB=12∴A′B=√AB2+A′A2=√182+242=30(cm),故答案为:30.【点睛】本题考查平面展开-最短路径问题,解题的关键是计算出圆柱展开后所得长方形的长和宽的值,然后用勾股定理进行计算.【答案】10【分析】将圆柱侧面展开,由图形可知蚂蚁在圆柱侧面爬行,从点A爬到点B的最短路程即为AB的长,再由勾股定理求出.【详解】解:根据圆柱侧面展开图,cm,高为8cm,∵圆柱的底面半径为6π∴底面圆的周长为2×6×π=12cm,π×12=6cm,∴BC=8cm,AC=12由图形可知蚂蚁在圆柱侧面爬行,从点A爬到点B的最短路程即为AB的长,AB=√AC2+BC2=10cm,故答案为:10.【点睛】本题考查了平面展开最短路线问题,勾股定理,将立体图形转化成平面图形求解是解题的关键.27.如图有一个棱长为9cm的正方体,一只蜜蜂要沿正方体的表面从顶点A爬到C点(C点在一条棱上,距离顶点B 3cm处),需爬行的最短路程是cm.【答案】15【分析】首先把正方体展开,然后连接AC,利用勾股定理计算求解即可.【详解】解:如图,连接AC,由勾股定理得,AC=√92+(9+3)2=15,故答案为:15.【点睛】本题考查了正方体的展开图、勾股定理的应用,解题的关键在于明确爬行的最短路线.28.如图,桌上有一个圆柱形玻璃杯(无盖),高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的内壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是厘米.【答案】10【分析】将杯子侧面展开,作A关于杯口的对称点A′,根据两点之间线段最短可知A′P的长度即为所求,再结合勾股定理求解即可.【详解】解:如图所示:将杯子侧面展开,作A关于杯口的对称点A′,连接PA′,最短距离为PA′的长度,)2+(6−1.5+1.5)2=10(厘米),PA′=√PE2+EA′2=√(162最短路程为PA ′=10厘米.故答案为:10.【点睛】本题考查了平面展开−最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.【答案】20【分析】先把圆柱的侧面展开,连接AS ,利用勾股定理即可求得AS 的长.【详解】解:如图,∵在圆柱的截面ABCD 中,AB =24π,BC =32,∴AB =12×24π×π=12,BS =12BC =16, ∴AS =√AB 2+BS 2=20,故答案为:20.【点睛】本题考查平面展开图−最短路径问题,根据题意画出圆柱的侧面展开图,利用勾股定理求解是解题的关键.30.如图,圆柱形玻璃杯的杯高为9cm ,底面周长为16cm ,在杯内壁离杯底4cm 的点A 处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿1cm ,且与蜂蜜相对的点B 处,则蚂蚁从外壁B 处到内壁A 处所走的最短路程为 cm .(杯壁厚度不计)【答案】10【分析】如图(见解析),将玻璃杯侧面展开,作B关于EF的对称点B′,根据两点之间线段最短可知AB′的长度即为所求,利用勾股定理求解即可得.【详解】解:如图,将玻璃杯侧面展开,作B关于EF的对称点B′,作B′D⊥AE,交AE延长线于点D,连接AB′,BB′=1cm,AE=9−4=5(cm),由题意得:DE=12∴AD=AE+DE=6cm,∵底面周长为16cm,×16=8(cm),∴B′D=12∴AB′=√AD2+B′D2=10cm,由两点之间线段最短可知,蚂蚁从外壁B处到内壁A处所走的最短路程为AB′=10cm,故答案为:10.【点睛】本题考查了平面展开——最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.31.如图所示,ABCD是长方形地面,长AB=20m,宽AD=10m.中间竖有一堵砖墙高MN=2m.一只蚂蚱从A点爬到C点,它必须翻过中间那堵墙,则它要走的路程s取值范围是.【答案】s≥26m【分析】连接AC,利用勾股定理求出AC的长,再把中间的墙平面展开,使原来的长方形长度增加而宽度不变,求出新长方形的对角线长即可得到范围.【详解】解:如图所示,将图展开,图形长度增加4m,原图长度增加4m,则AB=20+4=24m,连接AC,∵四边形ABCD是长方形,AB=24m,宽AD=10m,∴AC=√AB2+BC2=√242+102=26m,∴蚂蚱从A点爬到C点,它要走的路程s≥26m.故答案为:s≥26m.【点睛】本题考查的是平面展开最短路线问题及勾股定理,根据题意画出图形是解答此题的关键.【答案】5【分析】要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理.【详解】解:将圆柱表面切开展开呈长方形,则彩灯带长为2个长方形的对角线长,∵圆柱高3米,底面周长2米,∴AC2=22+1.52=6.25,∴AC=2.5,∴每根柱子所用彩灯带的最短长度为5m.故答案为5.【点睛】本题考查了平面展开−最短路线问题,勾股定理的应用.圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.【类型五旗杆高度问题】【答案】6m【分析】设AD=x,在△ABC中,利用勾股定理列出方程,解之即可.【详解】解:∵BF=2m,∴CE=2m,∵DE=1m,∴CD=CE−DE=1m,设AD=x,则AB=x,AC=AD−CD=x−1,由题意可得:BC⊥AE,在△ABC中,AC2+BC2=AB2,即(x−1)2+32=x2,解得:x=5,即AD=5,∴旗杆AE的高度为:AD+DE=5+1=6m.【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理的相关知识并在直角三角形中正确运用是解题的关键.34.荡秋千是深受人们喜爱的娱乐项目,如图,小丽发现,秋千静止时踏板离地面的垂直高度DE=0.5m,将它往前推送至点B,测得秋千的踏板离地面的垂直高度BF=1.1m,此时水平距离BC=EF=1.8m,秋千的绳索始终拉的很直,求绳索AD的长度.【答案】3m【分析】设绳索AD的长度为xm=(x−0.6)m,在Rt△ABC中,由勾股定理得出方程,解方程即可.【详解】解:设秋千的绳索AD长为xm,则AB为xm,∵四边形BCEF是矩形,∴BF=CE=1.1m,∵DE=0.5m,∴CD=0.6m则AC为(x−0.6)m在Rt△ABC中,由勾股定理得:AC2+BC2=AB2,即:(x−0.6)2+1.82=x2解得:x=3∴绳索AD的长度为3m.【点睛】本题考查了勾股定理的应用,由勾股定理得出方程是解题的关键.35.如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),聪明的小红发现:先测出垂到地面的绳子长,再将绳子拉直(如图2),测出绳子末端C到旗杆底部B的距离n,利用所学知识就能求出旗杆的长,若m=1米,n=5米,求旗杆AB的长.【答案】12米【分析】设旗杆的高为x米,在Rt△ABC中,推出x2+52=(x+1)2,可得x=12,由此解决问题.【详解】解:设AB=x米,因为∠ABC=90°,所以在Rt△ABC中,根据勾股定理,得:x2+52=(x+1)2,解之,得:x=12,所以,AB的长为12米,答:旗杆AB的长为12米.【点睛】本题考查直角三角形、勾股定理等知识,解题的关键是理解题意,学会构建方程.【答案】风筝的高度CE为61.68米.【分析】利用勾股定理求出CD的长,再加上DE的长度,即可求出CE的高度.【详解】解:在Rt△CDB中,由勾股定理,得CD=√CB2−BD2=√652−252=60(米).∴CE=CD+DE=60+1.68=61.68(米).答:风筝的高度CE为61.68米.【点睛】本题考查了勾股定理的应用,熟悉勾股定理,能从实际问题中抽象出勾股定理是解题的关键.37.看着冉冉升起的五星红旗,你们是否想过旗杆到底有多高呢?某数学兴趣小组为了测量旗杆高度,进行以下操作:如图1,先将升旗的绳子拉到旗杆底端,发现绳子末端刚好接触到地面;如图2,再将绳子末端拉到距离旗杆8m处,发现绳子末端距离地面2m.请根据以上测量情况,计算旗杆的高度.【答案】17米【分析】根据题意画出示意图,设旗杆高度为xm,可得AC=AD=x m,AB=(x−2)m,BC=8m,在Rt△ABC中利用勾股定理可求出x.【详解】解:如图所示设旗杆高度为x m,则AC=AD=x m,AB=(x−2)m,BC=8m,在Rt△ABC中,AB2+BC2=AC2(x−2)2+82=x2解得:x=17,答:旗杆的高度为17m.【点睛】本题考查了勾股定理的应用,解题的关键是构造直角三角形.38.同学们想利用升旗的绳子、卷尺,测算学校旗杆的高度.爱动脑的小华设计了这样一个方案:如图,将升旗的绳子拉直刚好触底,此时测得绳子末端C到旗杆AB的底端B的距离为1米,然后将绳子末端拉直到距离旗杆5米的点E处,此时测得绳子末端E距离地面的高度DE为1米.请你根据小华的测量方案和测量数据,求出学校旗杆的高度.【答案】12.5米【分析】过点E作EF⊥AB,垂足为F,在Rt△ABC和Rt△AEF中,根据勾股定理得出AC2=AB2+BC2,AE2= AF2+EF2,根据AC=AE,得出AB2+12=(AB−1)2+52,求出AB的长即可.【详解】解:过点E作EF⊥AB,垂足为F,如图所示:由题意可知:四边形BDEF是长方形,△ABC和△AEF是直角三角形,∴DE=BF=1,BD=EF=5,BC=1,在Rt△ABC和Rt△AEF中,根据勾股定理可得:AC2=AB2+BC2,AE2=AF2+EF2,即AC2=AB2+12,AE2=(AB−1)2+52,又∵AC=AE,∴AB2+12=(AB−1)2+52,解得:AB=12.5.答:学校旗杆的高度为12.5米.【点睛】本题主要考查了勾股定理的应用,解题的关键是根据勾股定理列出关于AB方程AB2+12= (AB−1)2+52.39.学过《勾股定理》后,某班兴趣小组来到操场上测量旗杆AB的高度,得到如下信息:①测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1米(如图1);②当将绳子拉直时,测得此时拉绳子的手到地面的距离CD为1米,到旗杆的距离CE为6米(如图2).根据以上信息,求旗杆AB的高度.【答案】9米【分析】设AB=x,则AC=x+1,AE=x−1,再根据勾股定理可列出关于x的等式,解出x即得出答案.【详解】解:设AB=x依题意可知:在Rt△ACE中,∠AEC=90°,AC=x+1,AE=x−1,CE=6,根据勾股定理得:AC2=AE2+CE2,即:(x+1)2=(x−1)2+62,解得:x=9答:旗杆AB的高度是9米.【点睛】本题考查勾股定理的实际应用.结合题意,利用勾股定理列出含未知数的等式是解题关键.40.如图,学校要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),同学们首先测量了多出的这段绳子长度为1米,再将绳子拉直(如图2),测出绳子末端C到旗杆底部B的距离为5米,求旗杆的高度.【答案】12米【分析】因为旗杆、绳子、地面正好构成直角三角形,设旗杆的高度为x米,则绳子的长度为(x+1)米,根据勾股定理即可求得旗杆的高度.【详解】解:设旗杆的高度AB为x米,则绳子AC的长度为(x+1)米,在Rt△ABC中,根据勾股定理可得:x2+52=(x+1)2,解得,x=12,答:旗杆的高度为12米.【点睛】本题考查了勾股定理的应用,熟知勾股定理是解题关键.【类型六航海问题】【答案】30海里/小时【分析】先根据题意结合方位角的描述求出∠ABC=90°以及AB、BC的长,再利用勾股定理求出AC的长即可得到答案.【详解】解:如图所示,由题意得,∠HAB=90°−60°=30°,∠MBC=90°−∠EBC=60°,∵AH∥BM,∴∠ABM=∠BAH=30°,∴∠ABC=∠ABM+∠MBC=90°,∵巡逻艇沿直线追赶,半小时后在点C处追上走私船,∴BC=18×0.5=9海里,在Rt△ABC中,∠ABC=90°,AB=12海里,BC=9海里,∴AC=√AB2+BC2=15海里,∴我军巡逻艇的航行速度是15=30海里/小时,0.5答:我军巡逻艇的航行速度是30海里/小时.【点睛】本题主要考查了勾股定理的实际应用,正确理解题意在Rt△ABC中利用勾股定理求出AC的长是解题的关键.(1)求点A与点B之间的距离;(2)若在点C处有一灯塔,灯塔的信号有效覆盖半径为处有一艘轮船准备沿直线向点多能收到多少次信号?(信号传播的时间忽略不计)【答案】(1)AB=1000海里(2)最多能收到14次信号【分析】(1)由题意易得∠ACB是直角,由勾股定理即可求得点A与点B之间的距离;(2)过点C作CH⊥AB交AB于点H,在AB上取点M,N,使得CN=CM=500海里,分别求得NH、MH的长,可求得此时轮船过MN时的时间,从而可求得最多能收到的信号次数;【详解】(1)由题意,得:∠NCA=54°,∠SCB=36°;。
初二下学期压轴题练习- 勾股定理的应用(含答案)

专题04勾股定理的应用一.选择题1.(2021秋•朝阳区期末)如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm.若这支铅笔长为18cm,则这只铅笔在笔筒外面部分长度不可能的是()A.3cm B.5cm C.6cm D.8cm2.(2020秋•碑林区校级期末)有长为5cm,13cm的两根木条,现想找一根木条和这两根木条首尾顺次相连组成直角三角形,则下列木条长度适合的是()A.10cm B.12cm C.18cm D.20cm3.(2021秋•兴平市期中)国庆假期间,妍妍与同学去玩寻宝游戏,按照藏宝图,她从门口A处出发先往东走9km,又往北走3km,遇到障碍后又往西走7km,再向北走2km,再往东走了4km,发现走错了之后又往北走1km,最后再往西走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.3km B.10km C.6km D.km4.(2021秋•赣榆区期中)在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈(10尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面()尺.A.4B.3.6C.4.5D.4.555.(2020秋•长沙期末)如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为()A.1米B.米C.2米D.4米6.(2021秋•高新区校级月考)如图,一棵大树在离地面6m,10m两处折成三段,中间一段AB恰好与地面平行,大树顶部落在离大树底部12m处,则大树折断前的高度是()A.14m B.16m C.18m D.20m7.(2021秋•高州市校级月考)国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.20km B.14km C.11km D.10km8.(2021春•爱辉区期末)如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要()A.4米B.5米C.6米D.7米9.(2020秋•新城区校级月考)如图,八年级一班的同学准备测量校园人工湖的深度,他们把一根竹竿AB 竖直插到水底,此时竹竿AB离岸边点C处的距离CD=0.8米.竹竿高出水面的部分AD长0.2米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则人工湖的深度BD为()A.1.5米B.1.7米C.1.8米D.0.6米二.填空题10.(2020春•鹿城区期中)图1是小红在“淘宝•双11”活动中所购买的一张多挡位可调节靠椅,挡位调节示意图如图2所示.已知两支脚AB=AC,O为AC上固定连接点,靠背OD=10分米.挡位为Ⅰ挡时,OD∥AB,挡位为Ⅱ挡时,OD′⊥AC,过点O作OG∥BC,则∠DOG+∠D′OG=°当靠椅由Ⅰ挡调节为Ⅱ挡时,靠背顶端D向后靠至D′,此时点D移动的水平距离是2分米,即ED′=2分米.DH⊥OG 于点H,则D到直线OG的距离为分米.11.(2020秋•仪征市期末)如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB、AC 长分别为13米、20米,主梁AD的高度为12米,则固定点B、C之间的距离为米.12.(2020秋•苏州期末)“东方之门”座落于美丽的金鸡湖畔,高度约为301.8米,是苏州的地标建筑,被评为“中国最高的空中苏式园林”.现以现代大道所在的直线为x轴,星海街所在的直线为y轴,建立如图所示的平面直角坐标系(1个单位长度表示的实际距离为100米),东方之门的坐标为A(6,﹣4),小明所在位置的坐标为B(﹣2,2),则小明与东方之门的实际距离为米.13.(2021春•越秀区校级期中)如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有学校,点A到公路MN的距离为80m.现有一卡车在公路MN上以5m/s的速度沿PN方向行驶,卡车行驶时周围100m以内都会受到噪音的影响,请你算出该学校受影响的时间为秒.14.(2014秋•招远市期中)小明家有一块如图所示的地,其中阴影部分是两个正方形,其他的是两个直角三角形和一个正方形,大直角三角形的斜边和一条直角边的长分别为34米,30米,小明家打算在阴影部分的土地上种花生,则种花生的面积为米2.15.(2021秋•茂名期中)如图所示,校园内有两棵树相距8m,一棵树高13m,另一棵树高7m,一只小鸟从一棵树顶端飞到另一棵树的顶端,小鸟至少要飞米.16.(2021•盂县一模)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是寸.17.(2020秋•石景山区期末)我国古代的数学名著《九章算术》中有这样一道题目“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵索沿地面退行,在离木柱根部8尺处时,绳索用尽.问绳索长是多少?”示意图如图所示,设绳索AC的长为x尺,木柱AB的长用含x的代数式表示为尺,根据题意,可列方程为.三.解答题18.(2021秋•紫金县期末)如图,一个直径为12cm(即BC=12cm)的圆柱形杯子,在杯子底面的正中间点E处竖直放一根筷子,筷子露出杯子外2cm(即FG=2cm),当筷子GE倒向杯壁时(筷子底端不动),筷子顶端正好触到杯D,求筷子GE的长度.19.(2021秋•济宁期末)一架云梯长25m,如图那样斜靠在一面墙上,云梯顶端离地面24m.(1)这架云梯的底端距墙角有多远?(2)如果云梯的顶端下滑了4m,那么它的底部在水平方向滑动了多少m?20.(2021秋•长春期末)如图,长方形ABCD为一个花园,其中AB=15米,BC=8米,在花园内修一条长13米的笔直小路EF,小路出口一端E选在AD边上距D点3米处,另一端出口F应选在AB边上距B点几米处?21.(2021秋•铁西区期中)甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6千米/小时的速度向正东行走.1小时后乙出发,他以5千米/小时的速度向正北行走.上午10:00,甲、乙二人相距多远?22.(2020秋•重庆期末)如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,在A处有一所中学,AP=120米,此时有一辆消防车在公路MN上沿PN方向以每秒5米的速度行驶,假设消防车行驶时周围100米以内有噪音影响.(1)学校是否会受到影响?请说明理由.(2)如果受到影响,则影响时间是多长?23.(2021秋•淮阴区期中)为整治城市街道的汽车超速现象,交警大队在某街道旁进行了流动测速.如图,一辆小汽车在某城市街道上直行,某一时刻刚好行驶到离车速检测仪A处60m的C处,过了4s后,小汽车到达离车速检测仪A处100m的B处.(1)求BC的长;(2)已知该段城市街道的限速为70km/h,这辆小汽车超速了吗?请通过计算说明.24.(2021春•饶平县校级期中)如图,某校科技创新兴趣小组用他们设计的机器人,在平坦的操场上进行走展示.输入指令后,机器人从出发点A先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米到达终止点B.求终止点B与原出发点A的距离AB.25.(2021春•吉林期末)如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16nmile,“海天”号每小时航行12nmile.它们离开港口一个半小时后分别位于点Q,R处,且相距30nmile.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?26.(2021秋•重庆期末)如图是俱乐部新打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26米,长方形ADCG和长方形DEFC均为木质平台的横截面,点G在AB上,点C在GF上,点D在AE上,经过现场测量得知:CD=1米,AD=15米.(1)小敏猜想立柱AB段的长为10米,请判断小敏的猜想是否正确?如果正确,请写出理由,如果错误,请求出立柱AB段的正确长度;(2)为加强游戏安全性,俱乐部打算再焊接一段钢索BF,经测量DE=3米,请你求出要焊接的钢索BF的长.(结果不必化简成最简二次根式)专题04勾股定理的应用一.选择题1.(2021秋•朝阳区期末)如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm.若这支铅笔长为18cm,则这只铅笔在笔筒外面部分长度不可能的是()A.3cm B.5cm C.6cm D.8cm【思路引导】首先根据题意画出图形,利用勾股定理计算出AC的长度.然后求其差.【完整解答】解:根据题意可得图形:AB=12cm,BC=9cm,在Rt△ABC中:AC===15(cm),所以18﹣15=3(cm),18﹣12=6(cm).则这只铅笔在笔筒外面部分长度在3cm~6cm之间.观察选项,只有选项D符合题意.故选:D.【考察注意点】此题主要考查了勾股定理的应用,正确得出笔筒内铅笔的最短长度是解决问题的关键.2.(2020秋•碑林区校级期末)有长为5cm,13cm的两根木条,现想找一根木条和这两根木条首尾顺次相连组成直角三角形,则下列木条长度适合的是()A.10cm B.12cm C.18cm D.20cm【思路引导】根据勾股定理即可得到结论.【完整解答】解:∵52+132=()2,132﹣52=122,∴木条长度适合的是12cm,故选:B.【考察注意点】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.3.(2021秋•兴平市期中)国庆假期间,妍妍与同学去玩寻宝游戏,按照藏宝图,她从门口A处出发先往东走9km,又往北走3km,遇到障碍后又往西走7km,再向北走2km,再往东走了4km,发现走错了之后又往北走1km,最后再往西走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.3km B.10km C.6km D.km【思路引导】根据题意先求A、B两地的水平距离和竖直距离,运用勾股定理求AB的长.【完整解答】解:过点B作BC⊥AC,垂足为C.观察图形可知AC=9﹣7+4﹣1=5(km),BC=3+2+1=6(km),在Rt△ACB中,AB=(km).答:门口A到藏宝点B的直线距离是km,故选:D.【考察注意点】本题考查了矩形的性质以及勾股定理的应用,解题的关键是结合图形,读懂题意,根据题意找到需要的数量关系,运用勾股定理求线段的长度.4.(2021秋•赣榆区期中)在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈(10尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面()尺.A.4B.3.6C.4.5D.4.55【思路引导】画出图形,设折断处离地面x尺,则AB=(10﹣x)尺,由勾股定理得出方程,解方程即可.【完整解答】解:如图,由题意得:∠ACB=90°,BC=3尺,AC+AB=10尺,设折断处离地面x尺,则AB=(10﹣x)尺,在Rt△ABC中,由勾股定理得:x2+32=(10﹣x)2,解得:x=4.55,即折断处离地面4.55尺.故选:D.【考察注意点】此题主要考查了勾股定理的应用,正确应用勾股定理得出方程是解题的关键.5.(2020秋•长沙期末)如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为()A.1米B.米C.2米D.4米【思路引导】作CF⊥AB,根据勾股定理求得AF的长,可得BF的长度.【完整解答】解:过点C作CF⊥AB于点F,根据题意得:AB=AC=5,CF=DE=3,由勾股定理可得AF2+CF2=AC2,∴AF=,∴BF=AB﹣AF=5﹣4=1,∴此时木马上升的高度为1米,故选:A.【考察注意点】本题主要考查勾股定理的应用,添加辅助线构建直角三角形是解题的关键.6.(2021秋•高新区校级月考)如图,一棵大树在离地面6m,10m两处折成三段,中间一段AB恰好与地面平行,大树顶部落在离大树底部12m处,则大树折断前的高度是()A.14m B.16m C.18m D.20m【思路引导】作BO⊥DC于点O,首先由题意得:AD=BO=6m,AB=OD=4m,然后根据DC=6米,得到OC=8米,最后利用勾股定理得BC的长度即可.【完整解答】解:如图,作BO⊥DC于点O,由题意得:AD=BO=6m,AB=OD=4m,∵DC=12m,∴OC=8m,∴由勾股定理得:BC=(m),∴大树的高度为10+10=20(m),故选:D.【考察注意点】本题考查了勾股定理的应用,正确的构造直角三角形是解答本题的关键.7.(2021秋•高州市校级月考)国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.20km B.14km C.11km D.10km【思路引导】根据题意先求A、B两地的水平距离和竖直距离,运用勾股定理求AB的长.【完整解答】解:过点B作BC⊥AC,垂足为C.观察图形可知AC=AF﹣MF+MC=8﹣3+1=6(km),BC=2+5=7(km),在Rt△ACB中,AB===10(km).答:登陆点到宝藏埋藏点的直线距离是10km,故选:D.【考察注意点】本题考查了矩形的性质以及勾股定理的应用,解题的关键是结合图形,读懂题意,根据题意找到需要的数量关系,运用勾股定理求线段的长度.8.(2021春•爱辉区期末)如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要()A.4米B.5米C.6米D.7米【思路引导】先求出AC的长,利用平移的知识可得出地毯的长度.【完整解答】解:在Rt△ABC中,AC==4米,故可得地毯长度=AC+BC=7米,故选:D.【考察注意点】此题考查了勾股定理的应用及平移的知识,属于基础题,利用勾股定理求出AC的长度是解答本题的关键.9.(2020秋•新城区校级月考)如图,八年级一班的同学准备测量校园人工湖的深度,他们把一根竹竿AB 竖直插到水底,此时竹竿AB离岸边点C处的距离CD=0.8米.竹竿高出水面的部分AD长0.2米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则人工湖的深度BD为()A.1.5米B.1.7米C.1.8米D.0.6米【思路引导】设BD的长度为xm,则AB=BC=(x+0.2)m,根据勾股定理构建方程即可解决问题.【完整解答】解:设BD的长度为xm,则AB=BC=(x+0.2)m,在Rt△CDB中,0.82+x2=(x+0.2)2,解得x=1.5.故选:A.【考察注意点】本题考查勾股定理的应用,解题的关键是理解题意,学会利用参数构建方程解决问题.二.填空题10.(2020春•鹿城区期中)图1是小红在“淘宝•双11”活动中所购买的一张多挡位可调节靠椅,挡位调节示意图如图2所示.已知两支脚AB=AC,O为AC上固定连接点,靠背OD=10分米.挡位为Ⅰ挡时,OD∥AB,挡位为Ⅱ挡时,OD′⊥AC,过点O作OG∥BC,则∠DOG+∠D′OG=°当靠椅由Ⅰ挡调节为Ⅱ挡时,靠背顶端D向后靠至D′,此时点D移动的水平距离是2分米,即ED′=2分米.DH⊥OG 于点H,则D到直线OG的距离为分米.【思路引导】先利用平行线的性质与等腰三角形的性质证明∠DOG=∠COG,再利用等量代换计算出∠DOG+∠D′OG=∠COD′=90°;先构造Rt△OMD′,再利用全等的性质以及勾股定理计算DH的长即可.【完整解答】解:设AB与OH交于点N,作D′M⊥OG于M,∵OD∥AB,OG∥BC,∴∠DOG=∠ANO,∠ANO=∠ABC,∠ACB=∠COG,∵AB=AC,∴∠ABC=∠ACB,∴∠DOG=∠ABC=∠ACB=∠COG,∵OD′⊥AC,∴∠COD′=90°,∴∠DOG+∠D′OG=∠COD′=∠COG+∠D′OG=∠COD′=90°;∵DH⊥OG,D′M⊥OG,∴∠OHD=∠OMD′=90°,在Rt△OHD中∠DOG+∠ODH=90°,又∠DOG+∠D′OG=90°,∴∠ODH=∠D′OG,∵当靠椅由Ⅰ挡调节为Ⅱ挡时,靠背顶端D向后靠至D′,即OD旋转到OD′,在△ODH和△D′OM中∴,∵△ODH≌△D′OM,∴DH=OM,又∵HM=ED′=2,∴DH=OM=OH+HM=OH+2,设OH=x,则DH=x+2,在Rt△OHD中,OD=10,由勾股定理得:OH2+DH2=OD2,即x2+(x+2)2=102,解得:x1=6,x2=﹣8(舍去),∴点D到直线OG的距离为DH=x+2=8.故答案为:90,8.【考察注意点】本题考查了全等三角形的性质和判定,勾股定理,等腰三角形的性质,解题的关键是构造全等三角形.11.(2020秋•仪征市期末)如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB、AC 长分别为13米、20米,主梁AD的高度为12米,则固定点B、C之间的距离为21米.【思路引导】根据勾股定理即可得到结论.【完整解答】解:∵AD⊥BC,∴∠ADB=∠ADC=90°,∵AB、AC长分别为13米、20米,AD的高度为12米,∴BD=(米),DC=(米)∴BC=BD+DC=5+16=21(米),故答案为:21.【考察注意点】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.12.(2020秋•苏州期末)“东方之门”座落于美丽的金鸡湖畔,高度约为301.8米,是苏州的地标建筑,被评为“中国最高的空中苏式园林”.现以现代大道所在的直线为x轴,星海街所在的直线为y轴,建立如图所示的平面直角坐标系(1个单位长度表示的实际距离为100米),东方之门的坐标为A(6,﹣4),小明所在位置的坐标为B(﹣2,2),则小明与东方之门的实际距离为1000米.【思路引导】根据两点之间的距离和勾股定理解答即可.【完整解答】解:小明与东方之门的实际距离=,10×100=1000(米),故答案为:1000.【考察注意点】此题考查勾股定理的应用,关键是根据两点之间的距离和勾股定理解答.13.(2021春•越秀区校级期中)如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有学校,点A到公路MN的距离为80m.现有一卡车在公路MN上以5m/s的速度沿PN方向行驶,卡车行驶时周围100m以内都会受到噪音的影响,请你算出该学校受影响的时间为24秒.【思路引导】设卡车开到C处刚好开始受到影响,行驶到D处时结束,在Rt△ACB中求出CB,继而得出CD,再由卡车的速度可得出所需时间.【完整解答】解:设卡车开到C处刚好开始受到影响,行驶到D处时结束了噪声的影响.则有CA=DA=100m,在Rt△ABC中,CB==60(m),∴CD=2CB=120(m),则该校受影响的时间为:120÷5=24(s).答:该学校受影响的时间为24秒,故答案为:24.【考察注意点】本题考查了勾股定理的应用,解答本题的关键是熟练掌握勾股定理的表达式,画出示意图,另外要求掌握时间=路程÷速度.14.(2014秋•招远市期中)小明家有一块如图所示的地,其中阴影部分是两个正方形,其他的是两个直角三角形和一个正方形,大直角三角形的斜边和一条直角边的长分别为34米,30米,小明家打算在阴影部分的土地上种花生,则种花生的面积为256米2.【思路引导】两个阴影正方形的面积和等于直角三角形另一未知边的平方.利用勾股定理即可求出.【完整解答】解:两个阴影正方形的面积和为342﹣302=256(米2).故种花生的面积为256米2.故答案为:256.【考察注意点】本题考查了直角三角形中勾股定理的运用,考查了正方形面积的计算,本题中根据勾股定理求阴影部分的边长是解题的关键.15.(2021秋•茂名期中)如图所示,校园内有两棵树相距8m,一棵树高13m,另一棵树高7m,一只小鸟从一棵树顶端飞到另一棵树的顶端,小鸟至少要飞10米.【思路引导】根据“两点之间线段最短”可知:小鸟沿着两棵树的顶端进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.【完整解答】解:两棵树高度相差为AE=13﹣7=6m,之间的距离为BD=CE=8m,即直角三角形的两直角边,故斜边长AC==10m,即小鸟至少要飞10m.故答案为:10.【考察注意点】本题考查勾股定理的应用,主要是将小鸟的飞行路线转化为求直角三角形的斜边,利用勾股定理解答即可.16.(2021•盂县一模)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是101寸.【思路引导】取AB的中点O,过D作DE⊥AB于E,根据勾股定理解答即可得到结论.【完整解答】解:取AB的中点O,过D作DE⊥AB于E,如图2所示:由题意得:OA=OB=AD=BC,设OA=OB=AD=BC=r寸,则AB=2r(寸),DE=10寸,OE=CD=1寸,∴AE=(r﹣1)寸,在Rt△ADE中,AE2+DE2=AD2,即(r﹣1)2+102=r2,解得:r=50.5,∴2r=101(寸),∴AB=101寸,故答案为:101.【考察注意点】本题考查了勾股定理的应用,弄懂题意,构建直角三角形是解题的关键.17.(2020秋•石景山区期末)我国古代的数学名著《九章算术》中有这样一道题目“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵索沿地面退行,在离木柱根部8尺处时,绳索用尽.问绳索长是多少?”示意图如图所示,设绳索AC的长为x尺,木柱AB的长用含x的代数式表示为x﹣3尺,根据题意,可列方程为x2﹣(x﹣3)2=82.【思路引导】设绳索长为x尺,根据勾股定理列出方程解答即可.【完整解答】解:设绳索长为x尺,根据题意得:x2﹣(x﹣3)2=82,故答案为:x﹣3;x2﹣(x﹣3)2=82.【考察注意点】本题考查了勾股定理的应用,找准等量关系,正确列出一元二次方程是解题的关键.三.解答题18.(2021秋•紫金县期末)如图,一个直径为12cm(即BC=12cm)的圆柱形杯子,在杯子底面的正中间点E处竖直放一根筷子,筷子露出杯子外2cm(即FG=2cm),当筷子GE倒向杯壁时(筷子底端不动),筷子顶端正好触到杯D,求筷子GE的长度.【思路引导】根据题意可得DE=GE,EF=GE﹣2,在Rt△DFE中,根据勾股定理列出方程,解方程即可求解.【完整解答】解:设筷子GE的长度是xcm,那么杯子的高度是(x﹣2)cm,∵杯子的直径为12cm,∴杯子半径为6cm,∴(x﹣2)2+62=x2,即x2﹣4x+4+36=x2,解得:x=10,答:筷子GE的长度是10cm.【考察注意点】本题考查勾股定理的应用,解题的关键是理解题意,学会利用参数构建方程解决问题.19.(2021秋•济宁期末)一架云梯长25m,如图那样斜靠在一面墙上,云梯顶端离地面24m.(1)这架云梯的底端距墙角有多远?(2)如果云梯的顶端下滑了4m,那么它的底部在水平方向滑动了多少m?【思路引导】(1)在RtADE中,利用勾股定理即可求出DE的长;(2)首先求出A′E的长,利用勾股定理可求出D′E的长,进而得到DD′=ED′﹣ED的值.【完整解答】解:(1)在Rt△ADE中,由勾股定理得AE2+DE2=AD2,即DE2+242=252,∴DE==7(m),答:这架云梯的底端距墙角有7m远;(2)∵云梯的顶端A下滑了4m至点A′,∴A′E=AE﹣AA′=24﹣4=20(m),在Rt△A′ED′中,由勾股定理得A′E2+D′E2=A′D′2,即202+D′E2=252,∴D′E==15(m),∴DD′=ED′﹣ED=15﹣7=8(m),答:梯子的底端在水平方向也滑动了8m.【考察注意点】本题考查了勾股定理在实际生活中的应用,本题中根据梯子长不会变的等量关系求解是解题的关键.20.(2021秋•长春期末)如图,长方形ABCD为一个花园,其中AB=15米,BC=8米,在花园内修一条长13米的笔直小路EF,小路出口一端E选在AD边上距D点3米处,另一端出口F应选在AB边上距B点几米处?【思路引导】根据勾股定理直接求出AF的长,即可得出FB即可得出答案.【完整解答】解:由题意知EF=13米,EA=5米.在Rt△EAF中,由勾股定理,得AF2=EF2﹣EA2,即AF2=132﹣52=144,则AF=12(取正值).所以FB=15﹣12=3(米),即另一端出口F应选在AB边上距B点3米处.【考察注意点】此题主要考查了勾股定理的应用,正确的记忆勾股定理确定好斜边与直角边是解决问题的关键.21.(2021秋•铁西区期中)甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6千米/小时的速度向正东行走.1小时后乙出发,他以5千米/小时的速度向正北行走.上午10:00,甲、乙二人相距多远?【思路引导】要求甲、乙两人的距离,就要确定甲、乙两人在平面的位置关系,由于甲往东、乙往北,所以甲所走的路线与乙所走的路线互相垂直,然后求出甲、乙走的路程,利用勾股定理,即可求得甲、乙两人的距离.【完整解答】解:如图,甲从上午8:00到上午10:00一共走了2小时,走了12千米,即OA=12.乙从上午9:00到上午10:00一共走了1小时,走了5千米,即OB=5.在Rt△OAB中,AB2=122十52=169,∴AB=13,因此,上午10:00时,甲、乙两人相距13千米.∵15>13,∴甲、乙两人还能保持联系.答:上午10:00甲、乙两人相距13千米,两人还能保持联系.【考察注意点】本题勾股定理的应用,方位角等知识,学会用转化的思想思考问题,属于中考常考题型.22.(2020秋•重庆期末)如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,在A处有一所中学,AP=120米,此时有一辆消防车在公路MN上沿PN方向以每秒5米的速度行驶,假设消防车行驶时周围100米以内有噪音影响.(1)学校是否会受到影响?请说明理由.(2)如果受到影响,则影响时间是多长?【思路引导】(1)作AB⊥MN于B,根据含30度的直角三角形三边的关系得到AB=PA=60m,由于这个距离小于100m,所以可判断拖拉机在公路MN上沿PN方向行驶时,学校受到噪音影响;(2)以点A为圆心,100m为半径作⊙A交MN于C、D,根据垂径定理得到BC=BD,再根据勾股定理计算出BC=80m,则CD=2BC=160m,根据速度公式计算出拖拉机在线段CD上行驶所需要的时间.【完整解答】解:(1)学校受到噪音影响.理由如下:作AB⊥MN于B,如图1,∵PA=120m,∠QPN=30°,∴AB=PA=60m,而60m<100m,∴消防车在公路MN上沿PN方向行驶时,学校受到噪音影响;(2)以点A为圆心,100m为半径作⊙A交MN于C、D,如图,∵AB⊥CD,∴CB=BD,在Rt△ABC中,AC=100m,AB=60m,CB==80m,∴CD=2BC=160m,∵消防车的速度5m/s,∴消防车在线段CD上行驶所需要的时间=160÷5=32(秒),∴学校受影响的时间为32秒.【考察注意点】本题考查了勾股定理的应用,直线与圆的位置关系:设⊙O的半径为r,圆心O到直线。
【勾股定理 期末压轴题训练】2022-2023学年八年级数学下册(人教版)含解析
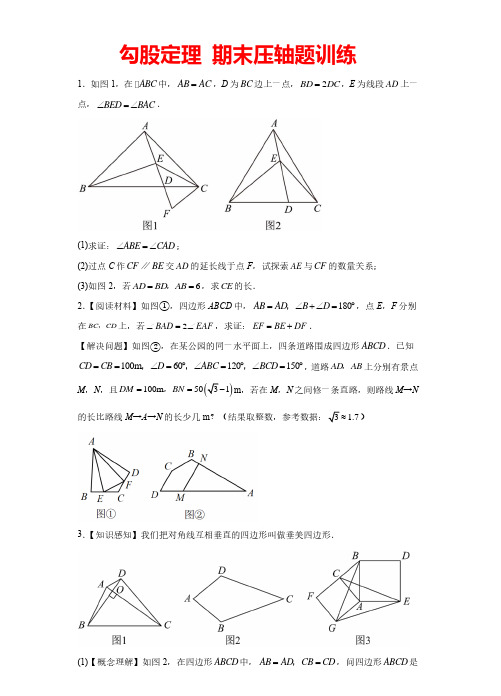
,在ABC 中,BAC ∠(1)求证:ABE CAD ∠=∠;(2)过点C 作CF BE ∥交AD 的延长线于点F ,试探索AE 与CF (3)如图2,若6AD BD AB ==,,求CE 的长.2.【阅读材料】如图①,四边形ABCD 中,AB AD B =∠+∠,3.【知识感知】我们把对角线互相垂直的四边形叫做垂美四边形.Rt ACB的直角边,,,BG GE,在ABC中,在整个运动过程中,当BCP是等腰三角形时,求,在平面直角坐标系中,点AQ CP交于点M,则在P、Q运动的过程中,(1)如图1,连接,(填“会”或“不会”);(2)如图1,当PBQ是直角三角形时,求点P的坐标;在ABC中,.在等腰直角ABC中,,延长BC∠=∠;(1)求证:MQB PAC(2)若22,,求DQ DH==(3)用等式表示线段MB与CP.在ABC中,(2)如图2,若点D在线段AB上,取.在ABC 中,(1)如图1,当ABC 为锐角三角形时,①依题意补全图形,猜想BAE ∠与BCD ∠之间的数量关系并证明;②用等式表示线段AE ,CE ,DE 的数量关系,并证明.(2)如图2,当ABC ∠为钝角时,直接写出线段问题解决:(1)先考虑特殊情况:①如果点E刚好和点A重合,或者点B刚好和点F重合时,AE “>”,“<”或“=”);形ABC和△⊥BC AD正方形的三个顶点,可得ABC ,则,在ABC 中,是BC .如图,ABC 是等腰直角三角形,上一点.时,求DEF 的面.和CDE 中,AC 上,连接(1)如图1,若30EDC ∠=︒,6EF =,求AEF △的面积;(2)如图2,若BD AE =,求AF 、AE 、BC 之间的数量关系;(3)如图3,移动点D ,使得点F 是线段AB 的中点时,3DB =,4AB =别是线段AC ,BC 上的动点,且AP CQ =,连接DP ,FQ ,求DP FQ +(1)如图1,若45CBD ∠=︒①求BCG ∠的度数;②求证:CE DG =;(2)如图2,若60CBD ∠=︒,当6AC DE −=时,求CE 的值(2)如图2,ABC ∆中,2B C ∠=∠,线段AC 的垂直平分线交AC 于点E ,交BC 于点D .求证:AD 是ABC ∆的一条双腰分割线;(3)如图3,已知ABC ∆中,AD 是三角形ABC 的双腰分割线,且AB AD =.①若64B ∠=︒,求C ∠的度数;②若3AB =,5AC =,求BC 的长.参考答案:1.(1)见解析(2)AE CF =【分析】(1)利用三角形外角的性质以及角的和差定义解决问题即可.(2)如图1中,在AF 上截取AJ ,使得AJ BE =.证明SAS ABE CAJ ≌(),推出AE CJ =,再证明CF CJ =即可解决问题.(3)如图2中,过点B 作BK AD ⊥于K ,作CF BE ∥交AD 的延长线于F ,过点C 作CQ DF⊥于Q .首先证明BE BD =, CD DF =,再证明EK DK =,DQ FQ =,2DK DQ =,2BK CQ =,AE DE CD CF ===,利用参数构建方程解决问题即可.【解析】(1)证明:∵BED ABE BAE BAC BAE CAD ∠=∠+∠∠=∠+∠,,又∵BED BAC ∠=∠,∴ABE BAE BAE CAD ∠+∠=∠+∠,∴ABE CAD ∠=∠.(2)解:结论:AE CF =.理由:如图1中,在AF 上截取AJ ,使得AJ BE =.∵BA AC ABE CAJ BE AJ =∠=∠=,,,∴SAS ABE CAJ ≌(),∴AE CJ AEB AJC =∠=∠,,∴BED CJF ∠=∠,∵BE CF ∥,∴BEJ F ∠=∠,∴CJF F ∠=∠,∴CJ CF =,∴AE CF =.(3)如图2中,过点B 作BK AD ⊥于K ,作CF BE ∥交AD 的延长线于F ,过点C 作CQ DF ⊥于Q .设ABE CAD x CBE y ∠=∠=∠=,,∵AB AC DB DA ==,,∴DBA DAB ACB x y ∠=∠=∠=+,∴22BED ABE DAB x y BDE ACB CAD x y ∠=∠+∠=+∠=∠+∠=+,,∴BED BDE ∠=∠,∴BE BD =,∵AB CA ABE CAD =∠=∠,,∴AAS ABE CAD ≌(),∴AE CD BE AD ==,,∵CF BE ∥,∴F BED ∠=∠,∴F CDF ∠=∠,∴CD CF =,∵BE BD BK DE CD CF CQ DF =⊥=⊥,,,,∴EK KD DQ QF ==,,∵CQ BK ∥,∴:::1:2DQ DK CD BD CQ BK ===,∴可以假设2DQ m DK m ==,,∵222BD BE AD CD CF AE =====,∴48AE DE m AD BD m ====,,∴BK ==,∴CQ =,在Rt ABK △中,∵222AB AK BK=+,∴()()22266m =+,∴m, ∴DQ =,CQ ,5EQ m ==,∵90CQE ∠=︒,∴CE =.【点评】本题属于三角形综合题,考查了等腰三角形的判定和性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.2.阅读材料:见解析;解决问题:少370m【分析】阅读材料:延长CB 到点M ,使BM DF =,连接AM ,如图,利用已知条件可得D ABM ∠=∠,进而可证明ABM ADF ≅,可得,AM AF MAB DAF =∠=∠,再证明AEM AEF ≅,可得=ME EF ,进而可得结论;解决问题:如图,作辅助线,构建阅读材料的图形,先根据四边形的内角和定理证明90G ∠=︒ ,分别计算,,,CG DG AD AG 的长,由线段的和与差可得,AM AN 的长,最后由阅读材料的结论可得MN 的长,计算AM AN MN +−可得答案.【解析】阅读材料:证明:延长CB 到点M ,使BM DF =,连接AM ,如图,∵180ABC D ∠+∠=︒,180ABC ABM ∠+∠=︒,∴D ABM ∠=∠,∵,,AB AD ABM D BM DF =∠=∠=,∴ABM ADF ≅,∴,AM AF MAB DAF =∠=∠,∵2BAD EAF ∠∠=,∴BAE DAF BAE BAM EAM EAF ∠+∠=∠+∠=∠=∠,又∵,AM AF AE AE ==,∴AEM AEF ≅,∴=ME EF ,∴EF MB BE BE DF =+=+;解决问题:解:如图,延长DC AB ,交于点G ,连接CN CM ,,∵60120150D ABC BCD ∠=︒∠=︒∠=︒,,,∴3606012015030A ∠=︒−︒−︒−︒=︒,∴90G ∠=︒,∴2AD DG =,在Rt CGB △中,18015030BCG ∠=︒−︒=︒,∴1502BG BC CG ===,∴100DG CD CG =+=+∴2200150AD DG AG ==+==+∵100DM =,∴200100100AM AD DM =−=+=+∵)50501BG BN ==,,∴)150********AN AG BG BN =−−=+−=+GN BG BN =+= ∵60CD DM D =∠=︒,,∴DCM △ 是等边三角形,∴60DCM ∠=︒,∵GC GN ==∴CGN 是等腰直角三角形,∴45GCN ∠=︒,∴453015BCN ∠=︒−︒=︒, ∴11506015752MCN BCD ∠=︒−︒−︒=︒=∠,由【阅读材料】的结论得:)10050150MN DM BN =+=+=+∵()10015050200370AM AN MN +−=++=+≈(m ). ∴路线M→N 的长比路线M→A→N 的长少370m .【点评】此题主要考查了含30︒的直角三角形的性质,勾股定理,等腰直角三角形的判定与性质、等边三角形的判定与性质、全等三角形的判定和性质,二次根式的混合运算等知识与方法,解题的关键是作出所需要的辅助线,构造含30︒的直角三角形,再利用线段的和与差进行计算.3.(1)是,见解析(2)2222AD BC AB CD ++=,见解析【分析】(1)根据垂直平分线的判定定理证明即可;(2)根据垂直的定义和勾股定理解答即可;(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算.【解析】(1)如图2,四边形ABCD 是垂美四边形.证明:连接AC BD 、交于点E ,∵AB AD =,∴点A 在线段BD 的垂直平分线上,∵CB CD =,∴点C 在线段BD 的垂直平分线上,∴直线AC 是线段BD 的垂直平分线,∴AC BD ⊥,即四边形ABCD 是垂美四边形;(2)猜想结论2222AD BC AB CD ++=.如图1,已知四边形ABCD 中,∵AC BD ⊥,∴90AOD AOB BOC COD ∠=∠=∠=∠=︒,由勾股定理得,222222AD BC AO DO BO CO +=+++,222222AB CD AO BO DO CO +=+++,∴2222AD BC AB CD ++=;(3)如图3,连接CG BE 、,∵90CAG BAE ∠=∠=︒,∴CAG BAC BAE BAC ∠+∠=∠+∠,即GAB CAE ∠∠=,在GA B 和CAE V 中,AG AC GAB CAEAB AE =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS GAB CAE V V ≌, ∴ABG AEC ∠=∠,又90AEC AME ∠+∠=︒,∴90ABG BMN ∠+∠=︒,∴90BNC ∠=︒,即CE BG ⊥,∴四边形CGEB 是垂美四边形,由(2)得,2222CG BE CB GE +=+,∵810AC AB ==,,∴6BC CG ==,BE =∴((22222226292GE CG BE CB =+−=+−=,∴GE ==【点评】本题考查的是正方形的性质、全等三角形的判定和性质、垂直的定义、勾股定理的应用,正确理解垂美四边形的定义、灵活运用勾股定理是解题的关键.4.(1)4,4t − (2)52t = (3)1或535或9.5或10【分析】(1)利用勾股定理求出AC ,利用CP AC AP =−,求出CP ;(2)过点P 作PD AB ⊥,交AB 于点D ,利用勾股定理列式求解即可;(3)分,,BC CP BP CP BC BP ===,三种情况进行讨论求解即可.【解析】(1)解:∵90,5,3ACB AB BC ∠=︒==,∴4AC =;∵点P 从点A 出发,以每秒1个单位长度的速度沿路线A C B A →→→运动,∴当点P 在AC 上时,AP t =,∴4CP AC AP t =−=−;故答案为:4,4t −;(2)解:点P 作PD AB ⊥,交AB 于点D ,则:90PDA PDB ∠=∠=︒,∵点P 在ABC ∠的角平分线上,90ACB ∠=︒,∴90ACB PDB ∠=∠=︒,PD PC =,又∵BP BP =,∴()HL PBD PBC ≌,∴3BD BC ==,∴2AD AB BD =−=,由(1)知,4AP t CP t ==−,∴4PD PC t ==−,在Rt ADP 中,222AP PD AD =+,即:()22242t t =−+, 解得:52t =; (3)解:P 点运动的总时间为:()543112++÷=秒,当BCP 是等腰三角形时: ①当BC CP =,点P 在AC 上时:如图,此时:43t −=,解得:1t =;当BC CP =,点P 在AB 上时:如图,过点C 作CE AB ⊥,交AB 于点E ,则:72BP t AC BC t BE =−−=−=, ∵1122ABC S AC BC AB CE =⋅=⋅,即:435CE ⨯=, ∴125CE =,∴95BE ==, ∴1875BP t =−=, ∴535t =; ②当BP CP =时,如图:由①可知:912,7,55BE BP t CE ==−=, ∴97,75PE t CP t =−−=−,在Rt PEC 中,222CP PE CE =+,即:()2224412755t t ⎛⎫⎛⎫−=−+ ⎪ ⎪⎝⎭⎝⎭, 解得:9.5t =;③当BC BP =时,如图:此时:73BP t =−=,解得10t =;综上:当BCP 是等腰三角形时,t 的值为:1或535或9.5或10.【点评】本题考查三角形上的动点问题.熟练掌握勾股定理,以及等腰三角形的定义是解题的关键.注意,分类讨论.5.(1)不会(2)当PBQ 是直角三角形时,点P的坐标为43⎛ ⎝⎭或23⎛ ⎝⎭(3)(1,P −,120CMQ ∠=︒【分析】(1)先利用SAS 证明ABQ CAP ≌,得BAQ ACP ∠=∠,利用外角的性质并进行等量代换可得60CMQ ACP CAM BAQ CAM BAC ∠=∠+∠=∠+∠=∠=︒(2)分90,90PQB BPQ ︒∠=︒∠=两种情况, 利用直角三角形中30度角所对直角边等于斜边的一半列式求解(3)作PM x ⊥轴,先根据30度角的性质和勾股定理求出1MB =cm和MP =cm ,进而求出(1,P −,再根据SAS 证明ACQ CBP ≌,最后根据外角的性质并进行等量代换作答即可【解析】(1)解:在等边三角形ABC 中,60AB AC CBA CAP ︒=∠=∠=且点A 、点Q 同时出发,且它们的速度都为1cm/s AP =BQ ∴(SAS)ABQ CAP ∴≌BAQ ACP ∴∠=∠60CMQ ACP CAM BAQ CAM BAC ∴∠=∠+∠=∠+∠=∠=︒故答案为:不会(2)解:设运动时间为t 秒,则,4AP BQ t PB t ===−①当90PQB ∠=︒时60ABC ∠=︒30BPQ ∠=︒∴12BQ PB ∴=,即1(4)2t t =− 解得43t = 即48433BP =−= 60ABC ∠=︒∴43P ⎛ ⎝⎭ ②当90BPQ ∠=︒时60ABC ∠=︒30PQB ∴∠=︒12PB BQ ∴=,即142t t −= 解得83t = 即84433BP =−=60ABC ∠=︒∴23P ⎛ ⎝⎭ ∴当PBQ 是直角三角形时,点P的坐标为43⎛ ⎝⎭或23⎛ ⎝⎭ (3)∵12BP BC =∴2BP =cm作PM x ⊥轴∵60ABC ∠=︒∴60PBM ∠=︒∴60PBM ∠=︒∴30MPB ∠=︒∴1MB =cm由勾股定理得MP =cm∴(1,P −在等边三角形ABC 中,60BC AC ABC ACB ︒=∠=∠=∵点A 、点Q 同时出发,且它们的速度都为1cm/sBP CQ ∴=,120PBC ACQ ∠=∠=︒(SAS)ACQ CBP ∴≌CMQ APM PAM APM PAC CAQ AQB PAC CAQ ∴∠=∠+∠=∠+∠+∠=∠+∠+∠180AQB PAC CAQ ABC ∠+∠+∠+∠=︒,60ABC ∠=︒18060120CMQ ∴∠=︒−︒=︒【点评】本题考查了全等三角形的判定和性质,外角的性质,直角三角形30度角的性质,勾股定理,熟练掌握各知识点是解题的关键.6.(1)见解析(2)(1)是,证明见解析;(2)存在,66013CP =.【分析】(1)根据阅读材料给出的定义结合已经学过的三角形的知识点,推到即可得出结论;(2)根据已知条件利用相似三角形即可得出①中的作法是符合条件的;第②小题根据已知条件画出图形,再根据图形得出结论.【解析】(1)解:①∵BD 为△ABC 的角平分线,∠ABC =2∠C∴∠=∠DBC C∴BD CD =∴图中相等的线段有BD CD =∵A A ∠=∠,2ADB ABC C ∠=∠=∠∴ADB ABC ∽∴图中相似的三角形有:ADB 和ABC②∵AC 的中垂线交边BC 于点E∴AE EC =∴AEC △是等腰三角形∵2AEB C ∠=∠,2ABC C ∠∠=∴AB AE =∴ABE 是等腰三角形(2)解:①符合要求,延长EF 交AD 于N ,则四边形ABEN 为矩形∴48AB EN ==,1662AN BE EC BC ====∵33EF =∴483315NF EN EF =−=−=∵PN BC ∥∴PFN CFE ∽ ∴PN NF PF EC EF FC == ∴153366PN = ∴1553311PF FC == ∴663036AP AN PN =−=−=∵90A ∠=︒∴60BP = ∴60513211BP FC == ∴BP PF BC FC = 作FK BP ⊥于K ∴BPF BCF SPF S FC =∴1212FK BP PF FCEF BC ⋅=⋅∴FK EF =∵FK BP ⊥,FE BC ⊥ ∴BF 平分PBC ∠∴1FBE PBC 2∠=∠∵F 在BC 的垂直平分线上∴FB FC =∴FBC FCB ∠=∠∴2PBC PCB ∠=∠∴符合要求②存在, 66013CP =.I.若P 在AD 上时,连接BD ,如图所示,∴PBC DBC ∠>∠,PCB DCB ∠<∠取BD 的中垂线交BC 与G ,作DH BC ⊥于H∴四边形ABHD 为矩形∴48HD AB ==,68BH AD ==,DG GB =,1326864CH BC BH =−=−=,∴80DC =,设GH x =,则68BG DG x ==−∵90DHG ∠=︒∴由勾股定理222GH DH DG +=∴()2226848x x −=+∴22136684811620x =−=⨯ ∴2906417x =<在CH 上取点M ,使29017HM GH ==,连接DM∴DMB DCB PCB ∠>∠>∠∵DG BG =∴DBC GDB ∠=∠∴22DGC GDB DBC DBC PBC ∠=∠+∠=∠<∠∴HM GH =,DH MG ⊥∴DG DM =∴DMB DGC ∠=∠∴2PBC PCB ∠>∠∴在AD 上所有点都满足2PBC PCB ∠>∠∴不存在;II. 若P 在AB 上时,如图所示,∵BP AB BC <<,∴45BCP ∠<︒,∴2PBC BCP ∠≠∠,∴在AB 上不存在其它满足要求的△BCP ;III. 若P 在AB 上时,如图所示,作BC 的垂直平分线交AD 于点L 、交BC 于点R ,作BCD ∠的平分线交RL 于点O ,连结BO 并延长交DC 于点P ,此时有22BCD BCO PBC ∠=∠=∠, ∴△BCP 是以BC 为底边的倍角三角形,作OU DC ⊥于点U ,连结OA 、OD ,∵CO 平分BCD ∠,OR BC ⊥,OU DC ⊥,∴OR OU =,设OR x =,则OU x =,48OL x =−,由AOB BOC COD AOD ABCD S S S S S =+++梯形得11111(68132)4848661328068(48)22222x x x ⨯+⨯=⨯⨯+⨯+⨯+⨯⨯−,解得:22x =在Rt BOR 中,OB =∴OC OB ==∵OCP OCB PBC ∠=∠=∠,2POC PBC OCB PBC PCB ∠=∠+∠=∠=∠,∴PBC PCO ~,∴CP BP BC OP CP OC ==∴OP =,BP =, 由BP OP OB −=得= 解得,66013CP =【点评】本题考查了角的倍数关系,角平分线的性质,相似三角形的判定等相关知识,明确题意根据已知条件画出图形是解题的关键.7.(1)45,=(2)(3)【分析】(1)根据等腰直角三角形的三线合一即可得到90,ADC AD CD BD ∠=︒==,由此推出,45BC BA AD D C ⊥∠=︒=∠,证明ADE CDF △△≌,得到,DE DF ADE CDF =∠=∠,求出DEF 是等腰直角三角形,勾股定理得到EF =DE ;(2)证明(SAS)ADE CDF ≌V V ,得到DE DF =,ADE CDF ∠=∠,推出DE DF ⊥,再由勾股定理得到答案;(3)分两种情况,①当H 在线段AC 上时,②当H 在线段AC 的延长线上时,连接MC ,过点M 作MF AC ⊥于F ,由等腰三角形的性质及等腰直角三角形的性质可得出答案.【解析】(1)解:在ABC 中,90BAC ∠=︒,AB AC =,45B BCA ∠=∠=︒,D 是BC 的中点,∴,45BC BA AD D C ⊥∠=︒=∠,∴90,ADC AD CD BD ∠=︒==,∵AE CF =,∴ADE CDF △△≌(SAS ),∴,DE DF ADE CDF =∠=∠,∵90CDF ADF ADC ∠+∠=∠=︒,∴90ADE ADF ∠+∠=︒,∴DEF 是等腰直角三角形,∴EF ==,故答案为:45,=(2)解:∵AB AC =,90BAC ∠=︒,∴45B ACD ∠=∠=︒,∵AB AC =,点D 是BC 的中点,∴AD BC ⊥,45BAD CAD ∠=∠=︒∴AD CD =,90ADC ∠=︒,∴BAD ACD ∠=∠,∴180180BAD ACD ︒−∠=︒−∠,即EAD FCD ∠=∠,∵45ACD CAD ∠=∠=︒,∴AD CD =,在ADE V 和CDF 中,AD CD EAD FCD AE CF =⎧⎪∠=∠⎨⎪=⎩,∴(SAS)ADE CDF ≌V V ,∴DE DF =,ADE CDF ∠=∠,∴90EDF CDF EDC ADE EDC ADC ∠=∠+∠=∠+∠=∠=︒,∴DE DF ⊥,在Rt EDF 中,DE DF =,4EF =,∴DE EF ==(3)解:①当H 在线段AC 上时,如图,连接MC ,过点M 作MF AC ⊥于F ,∵,AD BC BD CD ⊥=,∴AM 是线段BC 的中垂线,∴MB MC =,∴MBC MCB ∠=∠,∵AB AC =,∴A ABC CB =∠∠,∴ABM ACM ∠=∠,又∵90BAC BMH ∠=∠=︒,360BAH ABM BMH AHM ∠+∠+∠+∠=︒,∴180ABM AHM ∠+∠=︒,∵180AHM MHC ∠+∠=︒,∴ABM MHC ∠=∠,∴MCH MHC ∠=∠,∴MH MC =,∵2CH =, ∴112HF CF CH ===, ∵6AC =,∴615AF AC CF =−=−=,∵45DAC ∠=︒,∴5AF MF ==,∴AM =∵6AB AC ==,90BAC ∠=︒,D 是BC 的中点,∴12AD BC ==∴DM AM AD =−=②当H 在线段AC 的延长线上时,如图,连接MC ,过点M 作MF AC ⊥于F , 同理可得1CF HF ==,∴617AF AC CF =+=+=,∴AM =∴DM AM AD =−=综上,DM 的长为【点评】此题是三角形的综合题,主要考查了直角三角形的性质,等腰三角形的判定和性质,全等三角形的判定和性质及等腰直角三角形的判定和性质,根据已知得出ADE CDF V V ≌是解题的关键.8.(1)见解析(2)HM =(3)MB ,证明见解析【分析】(1)由直角三角形两个锐角互余即可得出90APC PAC ∠+∠=︒,90MQB APC ∠+∠=︒,从而得出MQB PAC ∠=∠;(2)连接AQ ,DP .由题意易得出AC 为线段QP 的垂直平分线,即得出2DP DQ ==,QAC PAC ∠=∠,AP AQ =,从而由勾股定理可求出PH DH .进而易证(AAS)DAH PQH ≌,得出2AH QH DQ DH ==+=,再根据勾股定理可求出2AQ ==.又易证QAM QMA ∠=∠,即得出2QM QA ==,从而由HM QM DH =−求解即可;(3)作ME QB ⊥于点E ,易证(AAS)APC QME ≌,即得出PC ME =.再根据MEB 是等腰直角三角形,即得出MB =,从而得出MB .【解析】(1)∵90ACB ∠=︒,QH AP ⊥,∴90APC PAC ∠+∠=︒,90MQB APC ∠+∠=︒,∴MQB PAC ∠=∠;(2)如图,连接AQ ,DP .∵CQ CP =,90ACB ∠=︒,∴AC 为线段QP 的垂直平分线,∴2DP DQ ==,QAC PAC ∠=∠,AP AQ =,∴PH DH =.又∵DAH PQH ∠=∠,90AHD QHP ∠=∠=︒,∴(AAS)DAH PQH ≌,∴2AH QH DQ DH ==+=∴2AQ ==.∵45QAM QAC CAB QAC ∠=∠+∠=∠+︒,45QMA MQB B BQM ∠=∠+∠=∠+︒, ∴QAM QMA ∠=∠,∴2QM QA ==,∴2(2HM QM DH =−=−=(3)MB .证明如下,如图,作ME QB ⊥于点E ,由(2)可知AP AQ QM ==,又∵90MQE PAC ACP QEM ∠=∠∠=∠=︒,,∴(AAS)APC QME ≌,∴PC ME =.∵MEB 是等腰直角三角形,∴BE ME =.∵222BE ME MB +=,∴MB ,∴MB =.【点评】本题考查等腰三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理.正确作出辅助线是解题的关键.9.(1)见解析(2)①见解析;②2AE CF =;证明见解析【分析】(1)根据“SAS ”证明≌ACD BCE V V ,得出AD BE =,DAC CBE ∠=∠,证明ABE为直角三角形,根据勾股定理得出222AB BE AE +=,即可得出答案;(2)①根据题意补全图形即可;②延长CF ,截取FG CF =,连接BG ,证明CFD GFB ≌,得出CD BG =,GBF CDF ∠=∠,证明()SAS ACE CBG ≌即可得出结论.【解析】(1)证明:∵90ACB ∠=︒,AC BC =,∴190452CAB CBA ∠=∠=⨯︒=︒,∵90DCE ∠=︒,∴90DCA ACE ACE ECB ∠+∠=∠+∠=︒,∴DCA ECB ∠=∠,∵AC BC =,CE CD =,∴()SAS ACD BCE △≌△,∴AD BE =,DAC CBE ∠=∠,∵180135DAC CAB ∠=︒−∠=︒,∴135CBE ∠=︒,∴90ABE CBE CBA ∠=∠−∠=︒,∴ABE 为直角三角形,∴222AB BE AE +=,∴222AB AD AE +=.(2)解:①依题意补全图2如图所示:②2AE CF =;理由如下:如图,延长CF ,截取FG CF =,连接BG ,∵F 为BD 的中点,∴BF DF =,∵CFD GFB ∠=∠,CF FG =,∴()SAS CFD GFB ≌,∴CD BG =,GBF CDF ∠=∠,∵CD CE =,∴BG CE =,∵45CDF DCA CAD DCA ∠=∠+∠=∠+︒,∴45GBF CDF DCA ∠=∠=∠+︒,∴454590CBG FBG CBA DCA DCA ∠=∠+∠=∠+︒+︒=∠+︒,∵90ACE DCA DCE DCA ∠=∠+∠=∠+︒,∴ACE CBG ∠=∠,∵AC BC =,CE BG =,∴()SAS ACE CBG ≌,∴2AE CG CF FG CF ==+=.【点评】本题主要考查了三角形全等的判定和性质,勾股定理,等腰三角形的性质,三角形外角的性质,余角的性质,解题的关键是作出辅助线,构造全等三角形.10.(1)见解析(2)见解析(3)22AD =,20AB =【分析】(1)由“SAS ”可证AOB ≌COD △,可得OB OD =;(2)由AOB ≌COD △得OAB OCD ∠=∠,AOB COD ∠=∠,从而得出AOC BOD ∠=∠,AOC APC ∠=∠,根据180APC APD ∠+∠=︒和1902APD COB ∠=︒+∠进一步得出结论;(3)作BF OD ⊥于F ,作CG OA ⊥于G ,设2BD OE a ==,根据1122BOD S OD BF BD OE =⋅=⋅,BF =,从而45BF OB ,设4BF k =,5OD OB k ==,则3OF k =,根据B F O C G O ,表示各边,并求出OG 和CG ,根据AB CD =列出方程,从而求得k ,进一步求得结果.【解析】(1)证明:在AOB 和COD △中,OA OC BAO DCOAB CD =⎧⎪∠=∠⎨⎪=⎩,∴AOB ≌COD △,∴OB OD =;(2)证明:由(1)知:AOB ≌COD △,∴OAB OCD ∠=∠,AOB COD ∠=∠,∴AOB BOC COD BOC ∠−∠=∠−∠,即:AOC BOD ∠=∠.∵180A P C O C D C E P ∠=︒−∠−∠,180A O C B A O A E O ∠=︒−∠−∠,∴AOC APC ∠=∠.∵180APC APD ∠+∠=︒,∴180A O C A P D ∠+∠=︒. ∵1902APD COB ∠=︒+∠, ∴1(90)1802AOC COB ∠+︒+∠=︒,∴2180A O C B O C ∠+∠=︒,∴180A O C B O D B O C ∠+∠+∠=︒,∴A ,O ,D 三点共线;(3)解:如图,作BF OD ⊥于F ,作CG OA ⊥于G ,设2BD OE a ==,∵OB OD =,∴BE DE a ==.∵90BEO ∠=︒,∴OD OB ===. ∵1122BOD S OD BF BD OE =⋅=⋅,22BF a a ⋅=⋅,∴BF =,∴45BF OB=, ∴设4BF k =,5OD OB k ==,则3OF k =,∵AOC BOD ∠=∠,90B F O C G O ∠=∠=︒,∴B F O C G O ,∴::::3:4:5O G C G O C O F B F O B ==,设3OG x =,4CG x =,5OC x =,∴57x =, 解得75x =, ∴2135OG x ==,2845CG x ==,在Rt CDG △和Rt AFB 中,由勾股定理得,222D C C G D G =+,222AB AF BF =+,且AB CD =, ∴22222821()(5)(37)(4)55k k k ++=++,解得3k =,∴412BF k ==,15OB OD ==,39OF k ==,33716A F =⨯+=,∴71522AD OA OD =+=+=.∵222221216400A B B F A F =+=+=,∴20AB =.【点评】本题主要考查了等腰三角形性质,勾股定理,全等三角形判定和性质等知识,解决问题的关键是作辅助线,根据面积法求得线段间关系.11.(1)①图形见解析;猜想:BAE BCD ∠=∠, 理由见解析;②见解析;(2)线段AE ,CE ,DE 的数量关系:CE AE =.【分析】(1)①依题意补全图形,由直角三角形的性质得出90BAE B ∠+∠=︒,90BCD B ∠+∠=︒,即可得出BAE BCD ∠=∠;②在AE 上截取AF CE =,可证出ACD 是等腰直角三角形,得出AD CD =,可证明()ADF CDE SAS ≌△△,得出DF DE =,ADF CDE ∠=∠,可推出90CDE FDC EDF ∠︒+∠=∠=,证出EDF 是等腰直角三角形,即可得出结论CE AE =;(2) 在CE 上截取CF AE =,连接DF ,由CD AD ⊥,AE BC ⊥,可得EAD DCF ∠=∠,由45BAC ∠=︒可得AD CD =,可证()ADE CDF SAS △≌△,可得ED DF =,ADE CDF ∠=∠,可推出90EDF ∠=︒,可得EDF 是等腰直角三角形故EF ,即可得线段AE ,CE ,DE 的数量关系.【解析】(1)解:①依题意,补全图形,如图1所示.猜想:BAE BCD ∠=∠,理由如下:∵CD AB ⊥,AE BC ⊥,∴90BAE B ∠+∠=︒,90BCD B ∠+∠=︒,∴BAE BCD ∠=∠,②证明:如图2,在AE 上截取AF CE =,连接DF∵45BAC ∠=︒,CD AB ⊥,∴ACD 是等腰直角三角形,∴AD CD =,在ADF △和CDE 中,DA CD BAE BCDAF CE =⎧⎪∠=∠⎨⎪=⎩∴()ADF CDE SAS ≌△△,∴DF DE =,ADF CDE ∠=∠,∵AB CD ⊥,∴90ADF FDC ∠+∠=︒,∴90CDE FDC EDF ∠︒+∠=∠=,∴EDF 是等腰直角三角形,∴EF =,∵AF EF AE +=,∴CE AE =.(2)解:依题意补全图形,如图3所示,在CE 上截取CF AE =,连接DF ,∵CD AD ⊥,AE BC ⊥,∴90ADC AEC ∠=∠=︒,∴90EAB ABE ∠+∠=︒,90DBC DCF ∠+∠=︒,ABE CBD ∠=∠,∴EAD DCF ∠=∠,∵45BAC ∠=︒,∴45DCA ∠=︒,∴AD CD =,在ADE V 和CDF 中,AD CD EAD DCFCF AE =⎧⎪∠=∠⎨⎪=⎩∴()ADE CDF SAS △≌△,∴ED DF =,ADE CDF ∠=∠,∵90CDF ADF ∠+∠=︒,∴90ADE ADF ∠+∠=︒,∴90EDF ∠=︒,∴EDF 是等腰直角三角形,∴EF =,∵CE CF EF =+,∴CE AE =,∴线段AE ,CE ,DE 的数量关系:CE AE =.【点评】本题考查了全等三角形的判定与性质等腰直角三角形的判定与性质、直角三角形的性质等知,证明三角形全等是解题的关键.12.(1)①=,②>(2)>(3)【分析】(1)①连接BD ,先证明CDB △是等边三角形,即60ACB CBD BDC ∠=︒=∠=∠,当F 点与B 点重合时,即0BF =,根据“三线合一”可得AE EF =,即有AE BF EF +=,同理:如果点E 刚好和点A 重合,同样有AE BF EF +=;问题得解;②先证明DEF 是等边三角形,根据等腰三角形的性质可得AE EF =,再结合含30︒角的直角三角形的性质可以求出BF AC =,即问题得解; (2)将DF 绕D 点逆时针旋转120°至DM ,连接AM ME ,,先证明DEM DEF ≌V V ,再证明ADM BDF ≌△△,问题即可得解;(3)将DF 绕D 点逆时针旋转120︒至DN ,连接AN NE ,,根据(2)中的方法,同理可证明:DEN DEF ≌V V ,ADN BDF ≌V V ,再证明ANE 是直角三角形,90ANE ∠=︒,结合含30︒角的直角三角形的性质即可求解.【解析】(1)①如图,连接BD ,根据题意有90ABC ∠=︒,60ACB ∠=︒,即30CAB ∠=︒,∵点D 为AC 中点, ∴12AD DC BD AC ===,∴CDB △是等边三角形,(此结论也适用于第(2)和(3)问)∴60ACB CBD BDC ∠=︒=∠=∠,∵30CAB ∠=︒,∴在Rt ABC △中,12BC AC =,∴AB AC ,当F 点与B 点重合时,如上图左图,即0BF =,∵60EDF DBC ∠=︒=∠,∴DE BC ∥,∴90AED ABC ∠=∠=︒,∴DE AF ⊥,∵AD BD =,∴AE EF =,∵0BF =,∴AE BF EF +=,同理:如果点E 刚好和点A 重合,同样有AE BF EF +=,故答案为:=;②当30ADE ∠=︒时,如图,∵30ADE ∠=︒,30DAE ∠=︒,∴60DEF ∠=︒,AE DE =,∵60EDF ∠=︒,∴DEF 是等边三角形,90ADF Ð=°,∴DE EF =,∴AE EF =,∵90ADF Ð=°,30DAE ∠=︒,∴在Rt ADF 中,12DF AF =,∴AF AB =,∴AF AC =,∴BF AB AF AC AC AC =−==,∵AE EF =,BF AC ,∴AE BF EF +>,故答案为:>;(2)AE BF EF +>,理由如下:将DF 绕D 点逆时针旋转120︒至DM ,连接AM ME ,,如图,根据旋转的性质有:120MDF ∠=︒,DF DM =,∵60FDE ∠=︒,∴60MDE ∠=︒,∵DE DE =,∴DEM DEF ≌V V ,∴EM EF =,∵60CDB ∠=︒,∴120ADB ∠=︒,即:ADB MDF ∠=∠,∵ADB ADF FDB ∠=∠+∠,MDF ADF ADM ∠=∠+∠,∴BDF ADM ∠=∠,∵AD BD =,MD DF =,∴ADM BDF ≌△△, ∴AM BF =,∴在AME △中,AM AE ME +>,∴BF AE EF +>,故答案为:>;(3)将DF 绕D 点逆时针旋转120︒至DN ,连接AN NE ,,如图,根据(2)中的方法,同理可证明:DEN DEF ≌V V ,ADN BDF ≌V V ,∴AN BF =,NE EF =,DBF DAN ∠=∠,∵222BF EF AE +=,∴222AN NE AE +=,∴ANE 是直角三角形,90ANE ∠=︒,∵在(1)中已证明60CBD ∠=︒,∴30DAN DBF ∠=∠=︒,∴60NAE DAN CAB ∠=∠+∠=︒,∴30AEN ∠=︒, ∴12AN AE =,∴NE AE ,∴EF NE AE AE=. 【点评】本题主要考查了全等三角形的判定与性质,含30︒角直角三角形的性质,等腰三角形的判定与性质,勾股定理及其逆定理等知识,合理构筑辅助线,证明三角形全等是解答本题的关键.13.(1)见解析(2) (3)94x =【分析】(1)表示出三个图形的面积进行加减计算可证222+=a b c ;(2)计算出ABC 的面积,再根据三角形的面积公式即可求得AB 边上的高;(3)运用勾股定理在Rt ABD 和Rt ADC 中求出2AD ,列出方程求解即可;【解析】(1)证明:∵2 12ABCD S c =四边形,() 12AEDC S b a b =+梯形,()12BED S a b a =−△, BED ABCD AEDC S S S =+△四边形梯形 ∴()()2111222c b a b a b a =++− ∴2221111122222c b ab a ab =++− ∴222+=a b c(2)111442424226222ABC S =⨯−⨯⨯−⨯⨯−⨯⨯=,AB =11622ABC S AB h =⨯=⨯=, 655h =即AB 边上的高是(3)解:在Rt △ABD 中,由勾股定理得222222416AD AB BD x x =-=-=-∵6BD CD BC +==,∴6CD BC BD x =−=−在Rt ACD △中,由勾股定理得()222222561112AD AC CD x x x =−=−−=−+−∴22161112x x x -=-+-, ∴94x =【点评】此题主要考查了梯形,证明勾股定理,勾股定理的应用,证明勾股定理常用的方法是利用面积证明,是解本题的关键.构造出直角三角形DEF 是解本题的难点.14.(1)见解析(2)(3)【分析】(1)证明ACE BCF △△≌,即可解决问题; (2)先由全等三角形的性质和三角形的外角性质,证出90ACD DFB ∠=∠=︒,再由勾股定理即可解决问题;(3)作FH BC ⊥于H .先证明BCF △是底角为30°的等腰三角形,再求出CF FB FH ,,的长,然后根据DEF ECD CDF ECF S S S S =+−计算即可.【解析】(1)证明:∵ABC ECF ,都是等腰直角三角形,∴90CA CB CE CF ACB ECF ==∠=∠=︒,,,∴ACE BCF ∠=∠,∴()SAS ACE BCF ≌,∴CAE CBF ∠=∠;(2)解:∵90AC BC ACB ==∠=︒,∴AB ==由(1)得:CAD DBF ∠=∠,∵ADB CAD ACD DBF DFB ∠=∠+∠=∠+∠,∴90DFB ACD ∠=∠=︒,∴AF == (3)解:过点F 作FH BC ⊥于H ,如图3所示:∵ABC 是等腰直角三角形,90ACB AC BC ∠=︒=,,∴45BAC ABC ∠=∠=︒,∵15BAD ∠=︒,∴451530CAE ∠=︒−︒=︒,∴30ACE CAE ∠=∠=︒,∴==AE CE CF ,同(1)得:()SAS ACE BCF ≌,∴30BF AE ACE BCF =∠=∠=︒,,∴CF BF =,∴30BCF CBF ∠=∠=︒,∵FC FB FH BC =⊥,,∴12CH BH BC ===,32FH ==,23CF BF FH ===,∵60903060CED CAE ACE ECD ∠=∠+∠=︒∠=︒−︒=︒,,∴ECD 是等边三角形,∴3EC CF CD ===,∴DEF ECD CDF ECF S S S S =+−21313333222=+⨯⨯−⨯⨯=.【点评】本题属于三角形综合题,考查了等腰直角三角形的性质,等边三角形的判定和性质,含30°角的直角三角形的性质,全等三角形的判定和性质,等腰三角形的性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.15.(1)AEFS =;AC BD =+,证明见解析;(3)DP FQ +【分析】(1)过点F 作FG AC ^于点G ,在Rt EFG △中利用勾股定理求得GF 的长,在等腰直角三角形AFG 中即可求得AG 的长,从而可得答案;(2)过点E 作EH AC ⊥交AB 于点H ,过点H 作HM BC ⊥于点M ,通过证明HEF DBF ≌,利用全等三角形的性质与等腰直角三角形的性质即可得出结论;(3)过点F 作FM AC ⊥于点M ,延长FM 至F '使F M FM '=,则F '与F 关于AC 对称,过点F '作F N BC '⊥,交BC 的延长线于点N ,证明APF CQF ≌,利用轴对称解决路径最短问题即可求得结论.【解析】(1)解:过点F 作FG AC ^于点G ,如图,∵90,ACB AC BC ∠=︒=,∴45A ABC ∠=∠=︒,∵90,30ECD EDC ∠=︒∠=︒,∴60DEG ∠=︒.∵,6FG AC EF ⊥=, ∴132EG EF ==,∴FG ==∵,45FG AC A ⊥∠=︒,∴AG FG ==∴3AE AG EG =−=.∴)11322AEF S AE FG ==⨯=. (2)解:过点E 作EH AC ⊥交AB 于点H ,过点H 作HM BC ⊥于点M ,如图,∵,45EH AC A ⊥∠=︒,∴,AE EH AH ==.∵BD AE =,∴EH BD =.∵,EH AC DC AC ⊥⊥,∴HE CD ∥,∴HEF D ∠=∠.在HEF 和DBF 中,HEF D HFE BFD EH DB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()AAS HEF DBF ≌. ∴12HF BF BH ==.∵90HEC ACB HMC ∠=∠=∠=︒,则90EHM ∠=︒,∴HM AC ∥,而HE CD ∥,∴由平行线间的距离处处相等可得:,CM HE HM CE ==,∵,45HM BC ABC ⊥∠=︒,∴EC HM ==,∴12AF AH HF BH =++. ∴2AE BH =,即:AE AE CE AE AC =++=+. ∴AC BD =+.(3)解:∵AB = F 是线段AB 的中点,90ACB ∠=︒,∴4,45,AF FB FC AC BC A ABC CF AB =====∠=∠=︒⊥.∴45FCQ A ∠=∠=︒.在APF 和CQF △中,AP CQ A FCQ AF FC =⎧⎪∠=∠⎨⎪=⎩,∴APF CQF ≌.∴PF FQ =. ∴DP FQ DP PF +=+.过点F 作FN AC ⊥于点M ,延长FM 至F '使F M FM '=,则F '与F 关于AC 对称, 连接DF '交AC 于点P ,如图,则此时DP FP DF '+=,取得最小值, 过点F '作F N BC '⊥,交BC 的延长线于点N ,∵90,,45AFC FM AC A ∠=︒⊥∠=︒, ∴112,222AM MC AC FM AC =====. ∴2F M FM '==.。
勾股定理(10个考点梳理+题型解读+提升训练)(原卷版)24-25学年八年级数学上学期期中考点

勾股定理(10个考点梳理+题型解读+提升训练)【清单01】勾股定理直角三角形两直角边的平方和等于斜边的平方如图:直角三角形ABC 的两直角边长分别为,斜边长为,那么.注意:(1)勾股定理揭示了一个直角三角形三边之间的数量关系.(2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.(3)理解勾股定理的一些变式:a b ,c 222a b c +=,, .运用:1.已知直角三角形的任意两条边长,求第三边;2.用于解决带有平方关系的证明问题;3.利用勾股定理,作出长为的线段【清单02】勾股定理的证明方法一:将四个全等的直角三角形拼成如图(1)所示的正方形. 图(1)中,所以. 方法二:将四个全等的直角三角形拼成如图(2)所示的正方形. 图(2)中,所以.方法三:如图(3)所示,将两个直角三角形拼成直角梯形.,所以.【清单03】勾股定理逆定理 222a c b =-222b c a =-()222c a b ab =+-1.定义:如果三角形的三条边长,满足,那么这个三角形是直角三角形.注意:(1)勾股定理的逆定理的作用是判定某一个三角形是否是直角三角形.(2)勾股定理的逆定理是把“数”转为“形”,是通过计算来判定一个三角形是否为直角三角形.2.如何判定一个三角形是否是直角三角形(1)首先确定最大边(如).(2)验证与是否具有相等关系.若,则△ABC 是∠C =90°的直角三角形;若,则△ABC 不是直角三角形.注意:当时,此三角形为钝角三角形;当时,此三角形为锐角三角形,其中为三角形的最大边.【清单04】勾股数像 15,8,17 这样,能够成为直角三角形三条边长的三个正整数,称为勾股数 。
勾股数满足两个条件:①满足勾股定理 ②三个正整数【清单05】勾股定理应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论. 本专题分类进行巩固解决以下生活实际问题【考点题型一】一直直角三角形的两边,求第三边长【典例1】已知一直角三角形两直角边的长分别为9,12,则它的斜边长为( )A .15B .16C .17D .25【变式1-1】如图,在△ABC 中,∠C =90°,AC =8,AB =10,则BC 的长为( )a b c ,,222a b c +=c 2c 22a b +222c a b =+222c a b ¹+222a b c +<222a b c +>cA.6B C.24D.2【变式1-2】如图,一个零件的形状如图所示,已知∠CAB=∠CBD=90°,AC=3cm,AB=4cm,BD=12cm,则CD长为()cm.D.15A.5B.13C.1445【变式1-3】如图,∠C=∠ABD=90∘,AC=4,BC=3,BD=12,则AD的长等于.【考点题型二】等面积法斜边上的高【典例2】如图,在Rt△ABC中,∠ACB=90°,若AC=6,CB=8.(1)求AB的长;(2)求AB边上的高CD是多少?【变式2-1】已知直角三角形的两直角边长分别为5和12,则此直角三角形斜边上的高长为()A.52B.6C.132D.6013【变式2-2】如图,在△ABC中,∠ACB=90°,CD是高,AB=4,AC=2,则CD的长为.【变式2-3】在△ABC中,∠ACB=90°,AC=12,BC=5,则高CD=.【考点题型三】作无理数的线段【典例3】如图,在数轴上点A表示的数为a,则a的值为()A B.―1C.―1+D.―1―【变式3-1】如图,点B,D在数轴上,OB=3,OD=BC=1,∠OBC=90°,DC长为半径作弧,与数轴正半轴交于点A,则点A表示的是()A B+1C1D【变式3-2】如图,OC=2,BC=1,BC⊥OC于点C,连接OB,以点O为圆心,OB长为半径画弧与数轴交于点A,若点A表示的数为x,则x的值为()A B.C―2D.2―【变式3-3】如图的数轴上,点A,C对应的实数分别为1,3,线段AB⊥AC于点A,且AB长为1个单位长度,若以点C为圆心,BC长为半径的弧交数轴于0和1之间的点P,则点P表示的实数为()A3B.3―C3D.3―【考点题型四】勾股定理的证明【典例4】用图1所示的四个全等的直角三角形可以拼成图2的大正方形.请根据信息解答下列问题:(1)请用含a,b,c的代数式表示大正方形的面积.方法1:______.方法2:______.(2)根据图2,求出a,b,c之间的数量关系.(3)如果大正方形的边长为10,且a+b=14,求小正方形的边长.【变式4-1】下面四幅图中,能证明勾股定理的有()A.一幅B.两幅C.三幅D.四幅【变式4-2】勾股定理在数学和许多其他领域中都有广泛的应用,勾股定理是一个非常重要的数学定理,它在几何学、三角学、物理学、工程学等多个领域都有重要的应用.关于勾股定理的证明方法到现在为止有500多种,勾股定理常见的一些证明方法是:几何证明、代数证明、向量证明、复数证明、面积证明等.当两个全等的直角三角形按图1或图2摆放时,都可以用“面积法”来证明,以下是利用图1证明勾股定理的完整过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2证明:连接BD ,过点D 作DF ⊥BC 交BC 延长线于点F ,则DF =EC =b ―a∵S 四边形ADCB =S △ACD +S △ABC =12b 2+12ab 又∵S 四边形ADCB =S △ADB +S △DCB =12c 2+12a (b ―a )∴∴12b 2+12ab =12c 2+12a (b ―a )∴a 2+b 2=c 2请参照上述证明方法,利用图2完成下面的证明.将两个全等的直角三角形按图2所示摆放,其中∠DAB =90°,求证:a 2+b 2=c 2.【变式4-3】我国是最早了解勾股定理的国家之一,汉代数学家赵爽为了证明勾股定理,创制了一幅如图1所示“赵爽弦图”(边长为c 的大正方形中放四个全等的直角三角形,两直角边长分别为a ,b ,斜边长为c ).(1)如图1,请用两种不同方法表示图中空白部分面积.方法1:S 阴影=______;方法2:S 阴影=______;根据以上信息,可以得到等式:______;(2)小亮将“弦图”中的4个三角形进行了运动变换,得到图2,请利用图2证明勾股定理;(3)如图3,将图2的2个三角形进行了运动变换,若a=6,b=3,求阴影部分的面积.【考点题型五】直角三角形的判定【典例5】下列长度的三条线段,能构成直角三角形的是()A.1,2,3B.2,3,4C.3,4,5D.8,12,13【变式5-1】以下列各组数据为三角形三边,能构成直角三角形的是()A.4,8,7B.5,12,14C.2,2,4D.7,24,25【变式5-2】下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是()A B.1,C.6,7,8D.2,3,4【变式5-3】下列几组数中,不能构成直角三角形的是()A.9,12,15B.15,36,39C.10,24,26D.12,35,36【考点题型六】勾股定理的逆定理的运用【典例6】如图,一块四边形的空地,∠B=90°,AB的长为9m,BC的长为12m,CD的长为8m,AD的长为17m.为了绿化环境,计划在此空地上铺植草坪,若每铺植1m2草坪需要花费50元,则此块空地全部铺植草坪共需花费多少元?【变式6-1】绿都农场有一块菜地如图所示,现测得AB=12m,BC=13m,CD=4m,AD=3m,∠D=90°,求这块菜地的面积.【变式6-2】定义:顶点都在网格点上的多边形叫格点多边形.如图,在正方形网格中,每个小正方形的边长为1,四边形ABCD的每一个顶点都在格点上,(1)求∠ABC的度数;(2)求格点四边形ABCD的面积.【变式6-3】如图,已知一块四边形的草地ABCD,其中∠B=90°,AB=20m,BC=15m,CD=7m,DA=24m,求这块草地的面积.【考点题型七】勾股数的应用【典例7】勾股数,又名毕氏三元数,则下列各组数构成勾股数的是( )A .13,14,512B .1.5,2,2.5C .5,15,20D .9,40,41【变式7-1】下列各组数中,是勾股数的是( )A .13,14,15B .3,4,7C .6,8,10D .12【变式7-2】下列数组是勾股数的是( )A .2,3,4B .0.3,0.4,0.5C .5,12,13D .8,12,15【变式7-3】下列各组数中是勾股数的是( )A .4,5, 6B .1.5,2, 2.5C .11,60, 61D .12【考点题型八】构造直角三角形解决实际问题【典例8-1】如图,一架2.5m 长的梯子斜靠在墙上,此时梯足B 距底端O 为0.7m .(1)求OA 的长度.(2)如果梯子下滑0.4m ,则梯子滑出的距离是否等于0.4m ?请通过计算来说明理由.【典例8-2】小强和小伟都喜欢放风筝.一天放学后他们互相配合又放起了风筝(如图所示),小伟想测量风筝的铅直高度CE ,于是他进行了如下测量:①测得小强牵线的手到风筝的水平距离BD 为15m ;②根据小强手中剩余线的长度计算出风筝线BC (假设BC 是直的线)的长为39m ;③小强牵线的手离地面的距离DE 为1.5m .(1)求此时风筝的铅直高度CE.(2)若小强想使风筝沿CD方向下降16m(不考虑其他因素),则他应该收线多少米?【典例8-3】台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.(1)求∠ACB的度数;(2)海港C受台风影响吗?为什么?(3)若台风中心的移动速度为25千米/时,则台风影响该海港持续的时间有多长?【变式8-1】一支铅笔斜放在圆柱体的笔筒中,如图所示,笔筒的内部底面直径是6cm,内壁高8cm.若这支铅笔在笔筒外面部分长度是5cm,则这支铅笔的长度是()cm.A.10B.15C.20D.25【变式8-2】如图是台阶的示意图,若每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB的长度是()A.185cm B.195cm C.205cm D.215cm【变式8-3】如图,庭院中有两棵树,小鸟要从一棵高10m的树顶飞到一棵高4m的树顶上,两棵树相距8m,则小鸟至少要飞米.【变式8-4】如图,大风把一棵树刮断,量得AC=4m,BC=3m,则树刮断前的高度为m.【变式8-5】我图古代数学著作《九章算术》中有这样一个问题:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深几何?(注:丈、尺是长度单位,1丈=10尺)意思为:如图,有一个边长为1丈的正方形水池,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的岸边,它的顶端恰好碰到池边的水面.则这根芦苇的长度是尺【变式8-6】如图,开州大道上A,B两点相距14km,C,D为两商场,DA⊥AB于A,CB⊥AB于B.已知DA=8km,CB=6km.现在要在公路AB上建一个土特产产品收购站E,使得C,D两商场到E站的距离相等,(1)求E站应建在离A点多少km处?(2)若某人从商场D以5km/h的速度匀速步行到收购站E,需要多少小时?【变式8-7】某市夏季经常受台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,当AC⊥BC时,A点到B,C两点的距离分别为500km和300km,以台风中心为圆心周围250km以内为受影响区域.(1)求BC;(2)海港C受台风影响吗?为什么?【典例9】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD 折叠,使点C落在边AB的C′点.(1)求DC′的长度;(2)求△ABD的面积.【变式9-1】如图,长方形ABCD中,AB=9,BC=6,将长方形折叠,使A点与BC的中点F重合,折痕为EH ,则线段BE 的长为( )A .53B .4C .52D .5【变式9-2】如图,折叠长方形的一边AD ,点D 落在BC 边的点F 处,已知AB =8cm ,BC =10cm ,则EC 的长为( )A .3cmB .4cmC .3.5cmD .5cm【变式9-3】如图,将长方形纸片ABCD 沿AE 折叠,使点D 恰好落在BC 边上点F 处,若AB =3,AD =5,求EC 的长.【考点题型十】面展开图-最短路径问题【典例10-1】如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 .【典例10-2】如图,圆柱形杯子容器高为18cm,底面周长为24cm,在杯子内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子外壁,离杯子上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为cm.【变式10-1】临汾是帝尧之都,有着尧都之称.尧都华表柱身祥云腾龙,顶蹲冲天吼,底座浮雕长城和黄河壶口瀑布,是中华民族历史悠久、文化灿烂的标志.如图,在底面周长约为6米且带有层层回环不断的云朵石柱上,有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到达柱顶正上方(从点A到点C,B为AC 的中点),每根华表刻有雕龙的部分的柱身高约16米,则雕刻在石柱上的巨龙至少为()A.20米B.25米C.30米D.15米【变式10-24cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是()A.9B.+6C.D.12【变式10-3】如图是放在地面上的一个长方体盒子,其中AB=9cm,BC=6cm,BF=5cm,点M在棱AB上,且AM=3cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为cm.【变式10-4】如图,圆柱的底面周长是10cm,圆柱高为12cm,一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B,那么它爬行的最短路程为.【变式10-5】如图,是一个三级台阶,它的每一级的长、宽,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,则蚂蚁沿着台阶面爬到B点的最短路程是.【变式10-6】如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,其实他们仅仅少走了m,却踩伤了花草.【变式10-7】如图,在一个边长为6cm的正方形纸片ABCD上,放着一根长方体木块,已知该木块的较长边与AD平行,横截面是边长为的正方形,一只蚂蚁从点A爬过木块到达蜂蜜C处需爬行的最短路程是cm.。
期末考试勾股定理与几何翻折压轴题专项训练—2023-2024学年八年级数学下学期(人教版)(解析版)

期末考试勾股定理与几何翻折压轴题专项训练【例题精讲】例1.(三角形翻折问题)如图,在Rt ABC △中,9086ABC AB BC ∠=︒==,,,分别在AB AC ,边上取点E F ,,将AEF △沿直线EF 翻折得到A EF '△,使得点A 的对应点A '恰好落在CB 延长线上,当60EA B '∠=︒时,AE 的长为 ,当A F AC '⊥时,AF 的长为 .【答案】 32− 407【分析】由折叠的性质可得AE A E '=,先求出30A EB '∠=︒,从而可得1122A B A E AE ''==,再由勾股定理可得BE AE =,最后由AE BE AB +=,进行计算即可;令A F '交AB 于G ,连接CG ,由折叠的性质可得:A EA F '∠=∠,AFE A FE '∠=∠,AEF A EF '∠=∠,AF A F '=,由A F AC '⊥得出90A FA A FC ''∠=∠=︒,45AFE A FE '∠=∠=︒,证明()ASA A FC AFG '≌得到CF FG =,设CF FG x ==,则10AF x =−,AG ,根据1122ACG S AC FG AG BC =⋅=⋅建立方程,解方程即可得出CF 的长,即可求解.【详解】解:由折叠的性质可得:AE A E '=,90ABC ∠=︒,18090A BE ABC '∴∠=︒−∠=︒,60EA B '∠=︒,9030A EB EA B ''∴∠=︒−∠=︒,1122A B A E AE ''∴==,BE AE∴==,AE BE AB+=,8AE AE∴=,32AE∴=−如图,令A F'交AB于G,连接CG,A F AC'⊥,90A FA A FC''∴∠=∠=︒,由折叠的性质可得:A EA F'∠=∠,AFE A FE'∠=∠,AEF A EF'∠=∠,AF A F'=,90AFE A FE'∠+∠=︒,45AFE A FE'∴∠=∠=︒,设A EA Fα'∠=∠=,则45FEB AFEα∠=∠=+︒,180135AEF FEB A EFα'∴∠=︒−∠=︒−=∠,()13545902A EB A EF BEFααα''∴∠=∠−∠=︒−−︒+=︒−,902EA B A EBα''∴∠=︒−∠=,FA C EA B EA F Aα'''∴∠=∠−∠==∠,在A FC'和AFG中,CA F AA F AFA FC AFG∠=∠⎧⎪=⎨⎪∠=∠''⎩',()ASAA FC AFG'∴≌,CF FG∴=,在Rt ABC△中,9086ABC AB BC∠=︒==,,,10AC∴,设CF FG x==,则10AF x=−,AG∴==1122ACGS AC FG AG BC=⋅=⋅,106x∴⋅=,整理得:271809000x x+−=,即29014400749x⎛⎫+=⎪⎝⎭,9012077x∴+=±,解得:307x=或30x=−(不符合题意,舍去),307CF∴=,30401077AF AC CF∴=−=−=,故答案为:32−407.【点睛】本题考查了折叠的性质、全等三角形的判定与性质、勾股定理、三角形的面积公式、等腰直角三角形的判定与性质、三角形外角的定义及性质、三角形内角和定理等知识,熟练掌握以上知识点,添加适当的辅助线是解此题的关键.例2.(坐标系中折叠问题)如图,在平面直角坐标系中,长方形ABCO的边OC OA、分别在x轴、y轴上,6AB=,点E在边BC上,将长方形ABCO沿AE折叠,若点B的对应点F 恰好是边OC的三等分点,则点E的坐标是.【答案】⎛−⎝⎭或(−【分析】本题主要考查了勾股定理与折叠问题,坐标与图形,由折叠的性质可得6AF AB==,BE EF=,90AFE B∠=∠=︒,再分当点F靠近点C时,24CF OF==,,当点F靠近点O 时,则42CF OF==,,两种情况利用勾股定理先求出OA的长,进而得到BC的长,设出CE 的长,进而得到EF的长,在Rt EFC△中,由勾股定理建立方程求解即可.【详解】解:在长方形ABCO 中,6CO AB ==,90BCO B AOC ∠=∠=∠=︒, 由折叠的性质可得6AF AB ==,BE EF =,90AFE B ∠=∠=︒,F 恰好是边OC 的三等分点,∴当点F 靠近点C 时,24CF OF ==,,在Rt AFO V中,OA =,∴BC OA ==设CE x =,则BE EF x ==,在Rt EFC △中,由勾股定理得到222EF CF CE =+,∴()2222xx =+,解得x =,∴点E的坐标是⎛− ⎝⎭; 当点F 靠近点O 时,则42CF OF ==,,在Rt AFO V中,OA ==∴BC OA ==设CE x =,则BE EF x ==,在Rt EFC △中,由勾股定理得到222CF CE =+,∴()2224x x =+,解得x =∴点E的坐标是(−;综上所述,点E的坐标是⎛− ⎝⎭或(−,故答案为:⎛− ⎝⎭或(−.例3.(四边形折叠问题)如图,已知矩形ABCD ,4AB =,5BC =,点P 是射线BC 上的动点,连接AP ,AQP △是由ABP 沿AP 翻折所得到的图形.(1)当点Q 落在边AD 上时,QC = ;(2)当直线PQ 经过点D 时,求BP 的长;(3)如图2,点M 是DC 的中点,连接MP 、MQ .①MQ 的最小值为 ;②当PMQ 是以PM 为腰的等腰三角形时,请直接写出BP 的长.【答案】(2)2BP =或8BP =(3) 2.9BP =或4BP =或10BP =【分析】(1)根据折叠的性质和勾股定理进行求解即可;(2)分点P 在线段BC 上,点P 在线段BC 的延长线上,两种情况,进行讨论求解;(3)①连接AM ,勾股定理求出AM 的长,折叠求出AQ 的长,根据MQ AM AQ ≥−,求出最小值即可;②分PM MQ =和PM PQ =两种情况,再分点P 在线段BC 上,点P 在线段BC 的延长线上,进行讨论求解即可.【详解】(1)解:当点Q 落在边AD 上时,如图所示,∵矩形ABCD ,4AB =,5BC =,∴4,5CD AB AD BC ====,90BAD B BCD ADC ∠=∠=∠=∠=︒,∵翻折,∴4,90AQ AB AQP B ==∠=∠=︒,∴1DQ AD AQ =−=,在Rt CDQ △中,CQ ==(2)当直线PQ 经过点D 时,分两种情况:当点P 在线段BC 上时,如图:∵翻折,∴4AQ AB ==,90AQP B ∠=∠=︒,BP PQ =,∴90AQD ∠=︒,∴3DQ ==,设BP PQ x ==,则:5PC BC BP x =−=−,3DP DQ PQ x =+=+,在Rt PCD △中,222DP CP CD=+,即:()()222345x x +=+−,∴2x =;∴2BP =;②当P 在线段BC 的延长线上时:∵翻折,∴4,90AQ AB Q B ==∠=∠=︒,BP PQ =,∴3DQ ==,设BP PQ x ==,则:5PC BP BC x =−=−,3DP PQ DQ x =−=−,在Rt PCD △中,222DP CP CD =+,即:()()222345x x −=+−,∴8x =;∴8BP =;综上:2BP =或8BP =;(3)①连接AM ,∵M 是CD 的中点, ∴122DM CM CD ===,∴AM =∵翻折,∴4AQ AB ==,∵MQ AM AQ ≥−,∴当,,A Q M 三点共线时,MQ 的值最小,即:4MQ AM AQ =−=4;②当PM PQ =时,如图:∵翻折,∴BP PQ PM ==,设BP x =,则:,5PM x CP BC BP x ==−=−,在Rt PCM 中,222PM CM PC =+,即:()22225x x =+−,解得: 2.9x =,即: 2.9BP =;当PM QM =,点P 在线段BC 上时,如图:∵,QM PM DM CM ==,90D C ∠=∠=︒,∴()HL MDQ MCP ≌,∴CP DQ =,点Q 在AD 上,由(1)知:1DQ =,∴1CP DQ ==,∴4BP BC CP =−=;当点P 在BC 的延长线上时:如图:此时点M 在AP 上,连接BM ,∵翻折,∴BM MQ PM ==,∵MC BP ⊥,∴210BP BC ==;综上: 2.9BP =或4BP =或10BP =.质,综合性强,难度大,属于压轴题.利用数形结合和分类讨论的思想进行求解,是解题的关键.【模拟训练】1.如图,在长方形ABCD 中,点E 是AD 的中点,将ABE 沿BE 翻折得到FBE ,EF 交BC 于点H ,延长BF DC 、相交于点G ,若8DG =,10BC =,则DC = .【答案】258【分析】本题考查了全等三角形的判定与性质,折叠的性质,勾股定理,连接EG ,根据点E 是AD 的中点得DE AE EF ==,根据四边形ABCD 是长方形得90D A ∠=∠=︒,根据将ABE 沿BE 翻折得到FBE 得90BFE D A ∠=∠=∠=︒,利用HL 证明Rt Rt EFG EDG △≌△,得8FG DG ==,设DC x =,则8CG DG DC x =−=−,8BG BF FG AB FG DC FG x =+=+=+=+,在Rt BCG V △中,根据勾股定理得,222CG BC BG +=,进行计算即可得.【详解】解:如图所示,连接EG ,∵点E 是AD 的中点,∴DE AE EF ==,∵四边形ABCD 是长方形,∴90D A ∠=∠=︒,∵将ABE 沿BE 翻折得到FBE ,∴90BFE D A ∠=∠=∠=︒在Rt EFG △和Rt EDG △中,EF ED EG EG =⎧⎨=⎩,∴()Rt Rt HL EFG EDG V V ≌,∴8FG DG ==,设DC x =,则8CG DG DC x =−=−,8BG BF FG AB FG DC FG x =+=+=+=+,在Rt BCG 中,根据勾股定理得,222CG BC BG +=,∴222(8)10(8)x x −+=+,解得258x =,故答案为:258.2.如图,在Rt ABC △中,90ACB ∠=︒,254AB =,154=AC ,点D 是AB 边上的一个动点,连接CD ,将BCD △沿CD 折叠,得到CDE ,当DE 与ABC 的直角边垂直时,AD 的长是 .【答案】154或54【分析】本题考查了勾股定理,平行四边形的判定和性质,折叠的性质,全等三角形的判定和性质,分DE BC ⊥和DE AB ⊥两种情况进行求解即可得到答案,根据题意,正确画出图形是解题的关键.【详解】解:如图,当DE BC ⊥时,延长ED 交BC 于点F ,CE 与AB 相交于点M ,∵EF BC ⊥,∴90EFC EFB ∠=∠=︒,∴90E ECF ∠+∠=︒,由折叠得,B E ∠=∠,CE CB =,MCD FCD ∠=∠,∴90B ECF ∠+∠=︒,∴90CMB ∠=︒,即C M A B ⊥,∵90ACB ∠=︒,254AB =,154=AC ,∴5BC ==, ∵1122ABC S AC BC AB CM ==△,∴11512552424CM ⨯⨯=⨯⨯,解得3CM =,∴4BM =,∵90CFD CMD FCD MCD CD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ∴()AAS CFD CMD ≌,∴3CF CM ==,DF DM =,∴532BF BC CF =−=−=,设DF DM x ==,则4BD x =−,在Rt BFD 中,222DF BF BD +=,∴()22224x x +=−, 解得32x =, ∴35422BD =−=, ∴25515424AD AB BD =−=−=;当DE AB ⊥时,如图,设DE 与AC 相交于点M ,由折叠可得,BCD ECD ∠=∠,DE DB =,ED BD =,5EC BC ==,∵DE AB ⊥,90ACB ∠=︒,∴DE BC ∥,∴EDC BCD ∠=∠,∴EDC ECD ∠=∠,∴5ED EC ==,∴5BD ED ==, ∴255544AD AB BD =−=−=;综上,AD 的长是154或54, 故答案为:154或54.3.如图,等边三角形ABC 中,16AB BD AC =⊥,于点D ,点E F 、分别是BC DC 、上的动点,沿EF 所在直线折叠CEF △,使点C 落在BD 上的点C '处,当BEC '△是直角三角形时,BE 的值为 .【答案】24−或323【分析】本题考查了翻折变换,等边三角形的性质,折叠的性质,熟练运用折叠的性质是本题的关键.由等边三角形的性质可得30DBC ∠=︒,分9090BEC BC E ''∠=︒∠=︒,两种情况讨论,由直角三角形的性质即可求解.【详解】解:ABC 是等边三角形,BD AC ⊥,30,DBC ∴∠=︒ 由折叠的性质可得:,CE C E '=若90,BEC ∠'=︒且30,C BE ∠'=︒,2,BE E B E C C ∴='''=16,BE CE BC +==16,CE +=8,E E C C ∴'==24BE ∴=−若90,30,E C B E C B ∠'=︒='∠︒2,,BE E B C E C ∴'''=16,BE CE BC +==16,3CE E C =='∴ 32.3BE ∴=故答案为∶ 24−323.4.如图,在ABC 中,120ACB ∠=︒,8AC =,4BC =,将边BC 沿CE 翻折,使点B 落在AB 上的点D 处,再将边AC 沿CF 翻折,使点A 落在CD 的延长线上的点A '处,两条折痕与斜边AB 分别交于点E 、F ,则线段FA '的长为 .【答案】【分析】本题考查了折叠的性质,勾股定理,直角三角形的性质,添加恰当辅助线构造直角三角形是本题的关键.过点A 作AH BC ⊥交BC 的延长线于H ,由直角三角形的性质可求142HC AC ==,AH =AB 的长,由面积法可求CE 的长,由折叠的性质可求90BEC DEC ∠=∠=︒,BCE DCE ∠=∠,ACF DCF ∠=∠,然后再求解即可.【详解】解:如图,过点A 作AH BC ⊥,交BC 的延长线于H ,120ACB ∠=︒,ACB H HAC ∠=∠+∠,30HAC ∴∠=︒,142HC AC ∴==,AH ==,448BH ∴=+=,AB ∴1122ACB S BC AH AB CE =⨯⨯=⨯⨯,4CE ∴=,CE ∴,将边BC 沿CE 翻折,使点B 落在AB 上的点D 处,再将边AC 沿CF 翻折,90BEC DEC ∴∠=∠=︒,BCE DCE ∠=∠,ACF DCF ∠=∠,1602ECF ACB ∴∠=∠=︒,30CFE ∴∠=︒,EF ∴,在Rt BCE中,BE ===,AF AB EF BE ∴=−−==FA AF '∴==故答案为:5.如图,点D 是ABC 的边AB 的中点,将BCD △沿直线CD 翻折能与ECD 重合,若4AB =,2CD =,1AE =,则点C 到直线AB 的距离为 .【答案】【分析】连接BE ,延长CD 交BE 于点G ,作CH AB ⊥于点H ,如图所示,由折叠的性质及中点性质可得AEB △为直角三角形,且G 为BE 中点,从而CG BE ⊥,由勾股定理可得BE的长,再根据2ABC BDC S S =△△,即11222AB CH CD BG ⋅=⨯⋅,从而可求得CH 的长.【详解】解:连接BE ,延长CD 交BE 于点G ,作CH AB ⊥于点H ,如图所示,由折叠的性质可得:BD ED =,CB CE =,∴CG 为BE 的中垂线, ∴12BG BE =,∵点D 是AB 的中点,4AB =,2CD =,1AE =, ∴122BD AD AB ===,CBD CAD S S =,AD DE =,∴DBE DEB ∠=∠,DEA DAE ∠=∠,∵180EDA DEA DAE ∠+∠+∠=︒,即22180DEB DEA ∠+∠=︒,∴90DEB DEA ∠+∠=︒,即90BEA ∠=︒,∴BE∴12BG BE ==, ∵2ABC BDCS S =△△, ∴11222AB CH CD BG ⋅=⨯⋅,∴422CH =⨯,∴CH ,∴点C 到直线AB 的距离为.故答案为:.【点睛】本题考查翻折变换,线段中垂线的判定,等腰三角形的性质,点到直线的距离,直角三角形的判定,勾股定理,利用面积相等求相应线段的长,解题的关键是得出CG 为BE 的中垂线,2ABC BDC S S =△△.6.如图,在ABC 中,90,A AB AC ∠=︒==D 为AC 边上一动点,将C ∠沿过点D 的直线折叠,使点C 的对应点C '落在射线CA 上,连接BC ',当Rt ABC '△的某一直角边等于斜边BC '长度的一半时,CD 的长度为 .【答案】 或 【分析】由翻折得,12CD CC '=,分三种情况:①当点C '在边AC 上,且12AC BC ''=(即2BC AC ''=)时;②当点C '在CA 的延长线上,且12AC BC ''=(即2BC AC ''=)时;③当点C '在CA 的延长线上,且12AB BC '=(即2BC AB '==时,分别根据勾股定理求出AC '的长,再求出CC '的长即可 【详解】解:由翻折得,12CD CC '=,分三种情况:①当点C '在边AC 上,且12AC BC ''=(即2BC AC ''=)时,90,A AB AC ∠=︒==∴由勾股定理得,222BC AC AB ''−=,即222(2)AC AC ''−=,AC '∴=CC '∴CD ∴;②当点C '在CA 的延长线上,且12AC BC ''=(即2BC AC ''=)时,同理得AC 'CC '∴CD ∴;③当点C '在CA 的延长线上,且12AB BC '=(即2BC AB '==由勾股定理得,222AC BC AB ''=−,即22218AC '=−=,AC '∴=CC '∴CD ∴=,0>,CD AB ∴>,此时点D 不在边AC 上,不符合题意,舍去,综上,当Rt ABC '△的某一直角边等于斜边BC '长度的一半时,CD 的长度为或.故答案为:或.【点睛】本题主要考查图形的翻折变换(折叠问题),勾股定理,等腰直角三角形的性质等知识,灵活运用折叠的性质及勾股定理是解答本题的关键,同时要注意分类思想的运用.7.如图,在ABC 中,90ACB ∠=︒,3AC =,4BC =,P 为斜边AB 上的一动点(不包含A ,B 两端点),以CP 为对称轴将ACP △翻折得到A CP ',连结BA '.当A P AB '⊥时,BA '的长为 .【答案】【分析】当A P AB '⊥时,过点C 作CD AB ⊥于D ,可知125CD =,95AD =,得出PDC △为等腰直角三角形,得到PD CD =,求出PA '和BP 的长,利用勾股定理即可求出BA '的长.【详解】过点C 作CD AB ⊥于D ,在Rt ADC 中,90ACB ∠=︒,3AC =,4BC =,∴5AB = ∵1122AC BC AB CD ⨯=⨯,125CD ∴=,在Rt ADC 中,3AC =∴95AD ==,当A P AB '⊥时,如图由折叠性质可知12∠=∠,PA PA '=,又1290A PA '∠=∠+∠=︒145∠=∠2=︒∴,又2390∠+∠=︒,345∴∠=︒,23∴∠=∠,125PD CD ∴==,又PA PD AD =+,12921555PA ∴=+=,又PA PA '=,215PA '∴=,又BP AB PA =−,214555BP ∴=−=,在Rt BPA '△中,90BPA ∠='︒,222BP PA BA ∴='+,2224214575525BA ⎛⎫⎛⎫'∴=+= ⎪ ⎪⎝⎭⎝⎭,BA '∴=,故答案为:.【点睛】本题考查了勾股定理的应用,折叠问题,熟练掌握勾股定理是解题的关键.8.如图,在ABC 中,90ACB ∠=︒,AC BC =,D 为AB 上一点,连接DC ,将BDC 沿DC 翻折,得到EDC △,连接AE ,若AE CE =,4BC =,则D 到CE 的距离是 .【答案】2【分析】本题考查等腰直角三角形中的折叠问题,涉及等边三角形判定与性质,勾股定理应用、面积法等知识.设BE 交CD 于G ,过E 作EF BC ⊥交BC 延长线于F ,根据将BDC 沿DC 翻折,得到EDC △,AC BC =,AE CE =,可得ACE △是等边三角形,即知60ACE ∠=︒,而90ACB ∠=︒,故150BCE ∠=︒,30ECF ∠=︒,可得75BCD ECD ∠=∠=︒,122EF CE ==,CF =BE =15CBE ∠=︒,可得90BGC ∠=︒,即CG BE ⊥,从而12BG BE GE ===,由勾股定理得CG ,在Rt BDG △中,DG ,即得CD DG CG =+,由面积法可得D 到CE 的距离是2. 【详解】解:设BE 交CD 于G ,过E 作EF BC ⊥交BC 延长线于F ,如图:将BDC 沿DC 翻折,得到EDC △,4BC CE ∴==,BCD ECD ∠=∠,AC BC =,AE CE =,AC BC CE AE ∴===,ACE ∴是等边三角形,60ACE ∴∠=︒,90ACB ∠=︒,150BCE ∴∠=︒,30ECF ∠=︒,75BCD ECD ∴∠=∠=︒,122EF CE ==,CF =在Rt BEF △中,BE ==BCE 中,BC CE =,150BCE ∠=︒,15CBE ∴∠=︒,18090BGC BGC BCD ∴∠=︒−∠−∠=︒,即CG BE ⊥,12BG BE GE ∴==,CG ∴===,45ABC ∠=︒,15CBE ∠=︒,30DBG ∴∠=︒,在Rt BDG△中,DG =,CD DG CG ∴=+=,设D 到CE 的距离是h ,2DCE S CE h DC GE ∆=⋅=⋅,324DC GE h CE ⋅∴===,故答案为:2.9.在生活中、折纸是一种大家喜欢的活动、在数学中,我们可以通过折纸进行探究,探寻数学奥秘.【纸片规格】三角形纸片ABC ,120ACB ∠=︒,CA CB =,点D是底边AB 上一点.【换作探究】(1)如图1,若6AC =,AD =CD ,求CD 的长度;(2)如图2,若6AC =,连接CD ,将ACD 沿CD 所在直线翻折得到ECD ,点A 的对应点为点.E 若DE 所在的直线与ABC 的一边垂直,求AD 的长;(3)如图3,将ACD 沿CD 所在直线翻折得到ECD ,边CE 与边AB 交于点F ,且DE BC ∥,再将DFE △沿DF 所在直线翻折得到DFG ,点E 的对应点为点G ,DG 与CE 、BC 分别交于H ,K ,若1KH =,请直接写出AC 边的长.【答案】(1)(2)3或(3)3【分析】(1)作CE AB ⊥于E ,求得30A B ==︒∠∠,从而得出132CE AC ==,AE AC =进而得出DE AE AD =−=(2)当DE AB ⊥时,连接AE ,作CG AB ⊥于G ,依次得出45DAE DEA ∠=∠=︒,304575CAE CAD DAE ∠=∠+∠=︒+︒=︒,75CEA CAE ∠=∠=︒,30ACE ∠=︒,15ACD DCE ∠=∠=︒,45CDG CAB DAC ∠=∠+∠=︒,从而DG CG =,进一步得出结果;当ED AC ⊥时,设ED 交AC 于点W CE ,交AB 于V ,可推出90AVC ∠=︒,60ACE ∠=︒,从而30ACD DCE ∠=∠=︒,进一步得出结果;当DE BC ⊥时,可推出180ACB BCE ∠+∠=︒,从而90ACD DCE ∠=∠=︒,进一步得出结果;(3)可推出CKH 和CDH △及CHK 是直角三角形,且30HCK ∠=︒,30HDF ∠=︒,45DCH ∠=︒,进一步得出结果.【详解】(1)解:如图1,作CE AB ⊥于E ,90AEC ∴∠=︒,CA CB =,120ACB ∠=︒,30A B ∴∠=∠=︒,132CE AC ∴==,AE =,DE AE AD ∴=−==CD ∴=;(2)解:如图2,当DE AB ⊥时,连接AE ,作CG AB ⊥于G ,由翻折得:AD DE =,CAD CED =∠∠,AC CE =,45DAE DEA ∠∠∴==︒,304575CAE CAD DAE ∴∠=∠+∠=︒+︒=︒,75CEA CAE ∴∠=∠=︒,30ACE ∴∠=︒,15ACD DCE ∴∠=∠=︒,45CDG CAB DAC ∴∠=∠+∠=︒,DG CG ∴=,由(1)知:3CG =,AG =3AD AG DG ∴=−=;如图3,当ED AC ⊥时,设ED 交AC 于点W CE ,交AB 于V ,90E ACE ∴∠+∠=︒,E A ∠=∠,90A ACE ∴∠+∠=︒,90AVC ∴∠=︒,60ACE∴∠=︒,30ACD DCE∴∠=∠=︒,ACD A∴∠=∠,AD CD∴=,3CV =,CD∴=,AD CD∴==如图4,当DE BC⊥时,30E A∠=∠=︒,60BCE∴∠=︒,180ACB BCE∴∠+∠=︒,90ACD DCE∴∠=∠=︒,AD∴=,综上所述:3AD=或(3)解:如图5,∵DE BC ∥,30B C ∠=∠=︒,30BCF E ∴∠=∠=︒,30EDF B ∠=∠=︒,120ACB ∠=︒,90ACE ∴∠=︒,1452ECD ACD ACE ∴∠=∠=∠=︒,将DFE △沿DF 所在直线翻折得到DFG ,30GDF EDF ∴∠=∠=︒,60EDG ∴∠=︒,90CHK EHD ∴∠=∠=︒,DH CH ∴=1FH ∴==,1CF CH FH ∴=+,3AC ∴==.【点睛】本题考查了等腰三角形的判定和性质,直角三角形的性质等知识,解决问题的关键是正确分类,画出图形.10.如图,在ABC 中,90BAC ∠=︒,AB AC =,点D 为线段BC 延长线上一点,以AD 为腰作等腰直角DAF △,使90DAF ∠=︒,连接CF .(1)请判断CF 与BC 的位置关系,并说明理由;(2)若8BC =,4CD BC =,求线段AD 的长;(3)如图2,在(2)的条件下,将DAF △沿线段DF 翻折,使点A 与点E 重合,连接CE ,求线段CE 的长.【答案】(1)CF BC ⊥,理由见解析(2)(3)【分析】(1)证明()SAS ABD ACF △≌△,则ADB AFC ∠=∠,如图1,记AD CF 、的交点为O ,根据180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠,AOF COD ∠=∠,可得90FAO DCO ∠=∠=︒,进而可得CF BC ⊥;(2)如图2,过A 作AH BC ⊥于H ,则142BH CH AH BC ====,6DH =,由勾股定理得,AD =(3)由翻折的性质可知,DE AD =,45EDF ADF ∠=∠=︒,90ADE ∠=︒,如图3,过A 作AM BC ⊥于M ,过E 作EN BC ⊥于N ,证明()AAS ADM DEN ≌,则46DN AM EN DM ====,,6CN =,由勾股定理得,CE =计算求解即可.【详解】(1)解:CF BC ⊥,理由如下:∵等腰直角DAF △,90DAF ∠=︒,∴AD AF =,又∵90BAC ∠=︒,∴BAC CAD DAF CAD ∠+∠=∠+∠,即BAD CAF ∠=∠,∵AB AC =,BAD CAF ∠=∠,AD AF =,∴()SAS ABD ACF △≌△,∴ADB AFC ∠=∠,如图1,记AD CF 、的交点为O ,∵180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠,AOF COD ∠=∠,∴90FAO DCO ∠=∠=︒,∴CF BC ⊥;(2)解:∵8BC =,4CD BC =,∴2CD =,如图2,过A 作AH BC ⊥于H ,∵ABC 是等腰直角三角形, ∴142BH CH AH BC ====,∴6DH =,由勾股定理得,AD =∴线段AD 的长为(3)解:由翻折的性质可知,DE AD =,45EDF ADF ∠=∠=︒,∴90ADE ∠=︒,如图3,过A 作AM BC ⊥于M ,过E 作EN BC ⊥于N ,∴90AMD DNE ∠=︒=∠,同理(2)可知,4AM =,6MD =,∵90ADM EDN EDN DEN ∠+∠=︒=∠+∠,∴ADM DEN ∠=∠,∵90AMD DNE ∠=︒=∠,ADM DEN ∠=∠,AD DE =,∴()AAS ADM DEN ≌,∴46DN AM EN DM ====,,∴6CN =,由勾股定理得,CE =,∴线段CE 的长为【点睛】本题考查了全等三角形的判定与性质,三角形内角和定理,勾股定理,折叠的性质,等腰三角形的性质.熟练掌握全等三角形的判定与性质,折叠的性质是解题的关键.11.如图1,在Rt ABC △中,90C ∠=︒,5AC =,12BC =,点D 为BC 边上一动点,将ACD 沿直线AD 折叠,得到AFD △,请解决下列问题.(1)AB =______;当点F 恰好落在斜边AB 上时,CD =______;(2)连接CF ,当CBF V 是以CF 为底边的等腰三角形时,请在图2中画出相应的图形,并求出此时点F 到直线AC 的距离;(3)如图3,E 为边BC 上一点,且4,连接EF ,当DEF 为直角三角形时,CD = .(请写出所有满足条件的CD 长)【答案】(1)13,103(2)画图见解析,600169(3)52或或5或10【分析】(1)根据勾股定理可得AB 的长,再利用等积法求出CD 即可;(2)过点F 作FG AC ^,交CA 的延长线于G ,首先由等积法求出CH 的长,再根据勾股定理求出AH 的长,再次利用等积法可得FG 的长;(3)分90DEF ∠=︒或90EDF ∠=︒或90EFD ∠=︒分别画出图形,从而解决问题.【详解】(1)解:在Rt ABC △中,由勾股定理得,13AB ,当点F 落在AB 上时,由折叠知,CD DF =, ∴111222AC CD AB DF AC BC ⋅+⋅=⋅,51360CD CD ∴+=,103CD ∴=,故答案为:13,103;(2)过点F 作FG AC ^,交CA 的延长线于G ,BC BF =,AC AF =,AB ∴垂直平分CF , 由等积法得6013AC BC CH AB ⋅==,在Rt ACH 中,由勾股定理得,2513AH ===, 1122ACF S AC FG CF AH =⋅=⋅△,6025260013135169CF AH FG AC ⨯⨯⋅∴===;(3)当90DEF ∠=︒时,当点D 在CE 上时,作FH AC ⊥于H ,则4HF CE ==,5AF AC ==,3AH ∴=,2CH EF AC AH ∴==−=,设CD x =,则4DE x =−,在Rt EDF 中,由勾股定理得,222(4)2x x =−+, 解得52x =,52CD ∴=, 当点D 在EB 上时,同理可得538CH AC AH =+=+=,设CD DF x ==,则4DE x =−,在Rt EDF 中,由勾股定理得,222(4)8x x −+=,解得10x =,10CD ∴=,当90DFE ∠=︒时,由勾股定理得AE设CD DF x ==,则520x +=,x ∴,CD ∴=;当90FDE ∠=︒时,则45ADC ADF ∠=∠=︒,5CD AC ∴==,综上:52CD =或或5或10,故答案为:52或或5或10.【点睛】本题是三角形综合题,主要考查了翻折的性质,直角三角形的性质,勾股定理,等腰直角三角形的判定与性质等知识,利用等积法求垂线段的长是解题的关键.。
部编数学八年级下册难点特训(一)和勾股定理有关的压轴大题(解析版)含答案

难点特训(一)和勾股定理有关的压轴大题1.正方形ABCD 中,E ,F 分别为CD ,AD 上一点,CE DF =,BE ,CF 交于点G ,O 为BD 的中点.(1)求证:BCE V ≌CDF V ;(2)求证:BE CF ^;(3)求证:BG CG -2.在平面直角坐标系xOy中,点B、C的坐标分别为(0,0)、(12,0),点A在第一象限,且△ABC 是等边三角形.点D的坐标为(4,0),E是边AB上一动点,连接DE,以DE为边在DE右侧作等边△DEF.(1)求出A点坐标;(2)当点F落在边AC上时,△CDF与△BED全等吗?若全等,请给予证明;若不全等,请说明理由;(3)连接CF,当△CDF是等腰三角形时,BE=______.∵C(6,0),∵FD=FC,FT⊥CD,3.在□ABCD 中,连接BD ,若BD CD ^,点E 为边AD 上一点,连接CE .(1)如图1,点G 在BD 上,连接CG ,过G 作GH CE ^于点H ,连接DH 并延长交AB 于点M .求证:HGD DCE Ð=Ð;(2)如图1,在(1)的前提下,若HG BM =,DG DC =.求证:BM DB +=;(3)如图2,120ABC Ð=°,AB =点N 在BC 边上,4BC CN =,若CE 是DCB Ð的角平分线,线段PQ (点P 在点Q 的左侧)在线段CE 上运动,PQ =,连接BP ,NQ ,求BP PQ QN ++的最小值.4.如图,在矩形ABCD中,AB=8,BC=16,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是每秒1个单位,连接PQ、AQ、CP,设点P、Q运动的时间为t秒.(1)当t= 时,四边形ABQP是矩形;(2)当t=6时,判断四边形AQCP的形状,并说明理由;(3)直接写出以PQ为对角线的正方形面积为96时t的值;(4)整个运动当中,线段PQ扫过的面积是 .【点睛】本题考查了正方形的判定与性质、矩形的判定与性质、菱形的判定、勾股定理、平行四边形的判定、三角形面积公式以及分类讨论等知识;熟练掌握正方形的判定与性质和勾股定理是解题关键.5.已知,如图,在△ABC中,AB=AC=20cm,BD⊥AC于D,且BD=16cm.点M从点A出发,沿AC方向匀速运动,速度为4c m/s;同时点P由B点出发,沿BA方向匀速运动,速度为lc m/s,过点P的动直线PQ∥AC,交BC于点Q,连结PM,设运动时间为t(s)(0<t<5),解答下列问题:(1)线段AD=___cm;(2)求证:PB=PQ;(3)当t为何值时,以P、Q、D、M为顶点的四边形为平行四边形.根据题意得:PQ=BP=t,AM=4t,AD∴MD=AD-AM=12-4t,∵PQ∥AC,∴PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,∴t=12-4t,根据题意得:PQ=BP=t,AM=4t,AD∴MD=AM-AD=4t-12,∵PQ∥AC,∴PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,∴t=4t-12,解得:t=4(s);6.平面直角坐标系中,矩形AOBC的顶点C的坐标为(m,n),m、n满足m﹣8=(1)m=______,n=_______;(2)如图1,连接AB、OC交于点D,过点D作DM⊥DB交x轴于点M,求点M的坐标;(3)如图2,E、F分别为OB、BC上的动点,以AE、EF为边作矩形AEFQ,连接EQ、CQ,当EQ=2CQ时,求点Q的纵坐标.∵m=8,n=4,∴C(8,4),∵四边形AOBC是矩形,∴AO=4,BO=8,AD=BD,∵DM⊥DB,∵四边形AEFQ是矩形,∴AF=EQ,PF=PA12AF=,PE=PQ∴PF12EQ =,7.如图,点P为正方形ABCD的对角转AC上一动点,过点P作PE⊥PB交射线DC于点E.(1)如图1,当点E在边CD上时,求证:PB=PE;(2)如图2,当点E在DC的延长线上时,探求线段PA、PC、CE的数量关系并加以证明;(3)如图3,在(1)的条件下,连接BE交AC于点F,若正方形ABCD的边长为4,当点E为CD的中点,则PF= (请直接写出结果).8.如图,我们把对角线互相垂直的四边形叫做“垂美四边形”.(1)性质探究:如图1.已知四边形ABCD 中,AC ⊥BD .垂足为O ,求证:AB 2+CD 2=AD 2+BC 2;(2)解决问题:已知AB =BC =△ABC 的边BC 和AB 向外作等腰Rt △BCE 和等腰Rt △ABD ;①如图2,当∠ACB =90°,连接DE ,求DE 的长;②如图3.当∠ACB≠90°,点G、H分别是AD、AC中点,连接GH.若GH=,则S△ABC = .②连DC、AE相交于点F【点睛】本题主要考查了四边形的综合问题,等腰直角三角形的性质,全等三角形的性质与判定,9.已知平行四边形ABCD中,AD=2AB.(1)作∠ABC的平分线BM交AD于M,连CM.①如图1,求∠BMC的度数;②如图2,若∠ADC=90°,点P是AD延长线上一点,BP交CM于N,CG⊥BP垂足为H,交AD于G,求证:BN=CG+GN;(2)如图3,若∠ADC=60°,AB=4,E是AB的中点,P是BC边上一动点,将EP逆时针旋转90°得到线段EQ,连DQ,直接写出DQ的最小值 .310.在正方形ABCD中,点E是边BC上一动点(不含端点B、C).(1)如图1,AE⊥EP,AE=EF,连接CF.①求∠ECF的大小;②如图2,N为CF的中点,连接DN、DE,求证:DE DN;BE+DE的最小值.(2)如图3.若AD=12则AH EC =,BHE D 为等腰直角三角形,45BHE HEBÐ=Ð=°,45BHE HAE AEH Ð=Ð+Ð=°Q ,180180459045AEH FEC AEF HEB Ð+Ð=°-Ð-Ð=°-°-°=°,HAE FEC \Ð=Ð,在HAE D 和CFE D 中,HAE FEC AH ECAE EF Ð=Ðìï=íï=î,()HAE CFE SAS \D @D ,180********ECF AHE BHE \Ð=Ð=°-Ð=°-°=°,ECF \Ð的大小为135°;②延长DN 到Q 时DN QN =,连接FQ 、EN ,设FQ 交BC 的延长线于点R ,在DNC D 和QNF D 中,DN QN DNC QNF CN FN =ìïÐ=Ðíï=î,()DNC QNF SAS \D @D ,CD FQ \=,CDQ FQD Ð=Ð,//CD FQ \,而CD BR ^,则FQ BR ^,90EFR FER \Ð+Ð=°,11.在平面直角坐标系中,O 为坐标原点,A ,D 两点坐标分别为A (0,a ),D (b ,b ),且a ﹣b =.(1)求A ,D 两点坐标;(2)点B ,C 是x 轴上两动点(B 在C 左侧),且使四边形ABCD 为平行四边形.①如图,当点B ,C 分别在原点两侧时,连接DO ,过点O 作OG ⊥DO 交AB 于点G ,连接DG ,取DG 中点H ,在DO 上截取DE ,使DE =GO ,求证:4AH 2+DE 2=2AE 2;②当点B 在原点左侧时,过点O 的直线MN ⊥AB ,分别交AB ,CD 于M ,N ,试探究OM ,BM ,CN 三条线段之间的数量关系.【答案】(1)A (0,5),D (5,5);(2)见解析;(3)OM =CN +BM 或OM =BM -CN .【分析】(1)根据算术平方根有意义的条件可得50b -³,3150b -³,由此可得5b =,进而可求得5a =,由此可得A ,D 两点的坐标;(2)①延长AH 交CD 于点F ,连接GF ,GE ,先证AOG ADE △≌△,可得AG =AE ,∠GAO =∠EAD ,进而可得GE ²=2AE ²,再证AGF EAO △≌△(SAS ),可得OE = 2AH ,最后再根据OE ²+OG ²=GE ²等量代换,即可得证;②分两种情况讨论:点C 在点O 的右侧时,点C 在点O 的左侧时,画出相应的图形,作出正确的辅助线,证明KCB MAO △≌△(AAS ),由此可得结论.【详解】解:∵50b -³,∴5b £,∵3150b -³,∴5b ³,又∵HG=HD,∴四边形AGFD为平行四边形,∴GF=AD=AO,AD//GF,∴∠AGF+∠GAD=180°,即∠AGF+∠GAO+∠OAD=180°,∴∠AGF+∠GAO=180°-∠OAD=90°,又∵∠OAE+∠EAD=90°,∠GAO=∠EAD,∴∠AGF=∠OAE,∴AGF EAO△≌△(SAS),∴OE=AF=2AH,∵∠GOD=90°,∴OE²+OG²=GE²,∴(2AH)²+DE²=2AE²,即:4AH2+DE2=2AE2;②如图,当点C在点O的右侧时,过点C作CK⊥AB于点K,∵四边形ABCD为平行四边形,∴AD=BC,又∵AO=AD,∴AO=BC,∵MN⊥AB,CK⊥AB,∴∠AMO=∠CKB=90°,MN//CK,∴∠KBC+∠KCB=90°,∵∠AOB=90°,∴∠ABO+∠BAO=90°,∴∠KCB=∠BAO,∴KCB MAO△≌△(AAS),∴OM=KB=KM+BM,∵AB//CD,MN//CK,∴四边形MNCK为平行四边形,∴KM=CN,∴OM=CN+BM,如图,当点C在点O的左侧时,过点C作CK⊥AB于点K,同理可得:KCB MAO△≌△(AAS),∴OM=KB=BM-KM,又∵KM=CN,∴OM=BM-CN,综上所述:OM,BM,CN三条线段之间的数量关系为OM=CN+BM或OM=BM-CN.【点睛】本题考查了算术平方根有意义的条件,平行四边形的判定与性质,全等三角形的判定与性质,勾股定理,熟练掌握平行四边形和全等三角形的判定与性质是解决本题的关键.12.如图,在平面直角坐标系中,A,B两点的坐标分别为A(0,a),点B(b,0),且a,b满足:b+4,点C与点B关于y轴对称,点P,点E分别是x轴,直线AB上的两个动点.(1)则点C的坐标为 ;(2)连接PA,PE.①如图1,当点P在线段BO(不包括B,0两个端点)上运动,若△APE为直角三角形,F为斜边PA的中点,连接EF,OF,试判断EF与OF的关系,并说明理由;②如图2,当点P在线段OC(不包括O,C两个端点)上运动,若△APE为等腰三角形,M为底边AE的中点,连接MO,试探索PA与OM的数量关系,并说明理由;(3)如图3,连PA,CE,设它们所在的直线交于点G,设CE交y轴于点F,连接BG,若OP=OF,则BG的最小值为 .∵C(4,0)A(0,4)∴OA=OC=4,又OP=OF ∠AOP=∠COF=90°∴△AOP≌△COF(SAS)13.如图,在平面直角坐标系中,O为坐标原点,A点的坐标为(18,0),B点的坐标为(0,24).(1)求AB的值;(2)点C在OA上,且BC平分∠OBA,求点C的坐标;(3)在(2)的条件下,点M在第三象限,点D为y轴上的一个点,连接DM交x轴于点H,连接CM,点F为BC的中点,点E为AD的中点,AD与BC交于点G,点H为DM的中点,当∠MCG-∠DGF=∠OAB,且AD=CM时,求线段EF的长.14.若△ABC和△ADE均为等腰三角形,且AB=AC=AD=AE,当∠ABC和∠ADE互余时,称△ABC 与△ADE互为“底余等腰三角形”,△ABC的边BC上的高AH叫做△ADE的“余高”.(1)如图1,△ABC与△ADE互为“底余等腰三角形”.①若连接BD,CE,判断△ABD与△ACE是否互为“底余等腰三角形”:_______ (填“是”或“否”);②当∠BAC=90°时,若△ADE的“余高”AH DE=_______;③当0°<∠BAC<180°时,判断DE与AH之间的数量关系,并证明;(2)如图2,在四边形ABCD中,∠ABC=60°,DA⊥BA,DC⊥BC,且DA=DC.①画出△OAB与△OCD,使它们互为“底余等腰三角形”;②若△OCD的“余高”长为a,则点A到BC的距离为_______(用含a的式子表示).①如图1,连接BD 、CE ,∵AB AC AD AE ===,∴A ABC CB =Ð∠,ADE AED Ð=Ð,ABD Ð∵90ABC ADE Ð+Ð=°,∴90ACB AED Ð+Ð=°,∵四边形BCDE 的内角和为360°,∴(3609090)290ABD AEC Ð+Ð=°-°-°¸=∴ABD △与ACE △互为“底余等腰三角形”,①如图2,连接BD ,取BD 中点为点∵DA BA ^,DC BC ^,∴BAD V ,BCD △都是直角三角形,∴OA OB OD OC ===,在Rt BAD V 与Rt BCD △中,AD CD BD BD =ìí=î,∴Rt BAD Rt BCD @△△,115.如图1,点,A 点B 的坐标分别为()(),0,0,a b ,且4,b =将线段BA 绕点B 逆时针旋转90o 得到线段BC .(1)直接写出=a __,b =__ _,点C 的坐标为 _;(2)如图2,作CD x ^轴于点,D 点M 是BD 的中点,点N 在OBD V 内部,,ON DN ^求证:.ON DN +=(3)如图3,点P 是第二象限内的一个动点,若90,OPB Ð=°求线段CP 的最大值.1a \=-,4b \=,\点()1,0A -,点()0,4B ,如图,过点C 作CE BO ^于E ,Q 将线段BA 绕点B 逆时针旋转90°得到线段BC .BA BC \=,90ABC Ð=°,90ABO CBE \Ð+Ð=°,且90ABO BAO Ð+Ð=°,BAO CBE \Ð=Ð,且AB BC =,90AOB CEB Ð=Ð=°,()ABO BCE AAS \D @D 1BE AO \==,4BO CE ==,3OE \=,\点()4,3C 故答案为:1-,4,()4,3(2)连接OM ,作MF MN ^交DN 于F ,CD x ^Q 轴,4OD BO \==,45MDO \Ð=°,Q 点M 是BD 的中点,OM MD \=,90OMD OND Ð=°=Ð,NOM MDN \Ð=Ð,。
新人教版八年级下数学第十七章勾股定理提高练习与常考难题和培优题压轴题(含解析)-

新人教版八年级下第十七章勾股定理提高练习与常考难题和培优题压轴题(含解析)一.选择题(共8小题)1.直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C.D.2.下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2D.在Rt△ABC中,∠B=90°,所以a2+b2=c23.如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm4.如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺5.如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C.﹣D.﹣1+6.一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米7.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.48.如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169二.填空题(共5小题)9.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是.10.如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为米.11.已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于.12.观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是(只填数,不填等式)13.观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b=,c=.三.解答题(共27小题)14.a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.15.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.16.如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.17.如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100km到达B点,然后再沿北偏西30°方向走了100km到达目的地C点,求出A、C两点之间的距离.18.如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?19.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC 边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t 秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.20.在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.(1)△ABC的面积为:.(2)若△DEF三边的长分别为、、,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为.(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是m2.21.(1)在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.请你将△ABC的面积直接填写在横线上.思维拓展:(2)已知△ABC三边的长分别为a(a>0),求这个三角形的面积.我们把上述求△ABC面积的方法叫做构图法.如图2,网格中每个小正方形的边长都是a,请在网格中画出相应的△ABC,并求出它的面积.类比创新:(3)若△ABC三边的长分别为(m>0,n >0,且m≠n),求出这个三角形的面积.如图3,网格中每个小长方形长、宽都是m,n,请在网格中画出相应的△ABC,用网格计算这个三角形的面积.22.有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?23.(拓展创新)在教材中,我们通过数格子的方法发现了直角三角形的三边关系,利用完全相同的四个直角三角形采用拼图的方式验证了勾股定理的正确性.问题1:以直角三角形的三边为边向形外作等边三角形,探究S′+S″与S的关系(如图1).问题2:以直角三角形的三边为斜边向形外作等腰直角三角形,探究S′+S″与S 的关系(如图2).问题3:以直角三角形的三边为直径向形外作半圆,探究S′+S″与S的关系(如图3).24.如图,在平面坐标系中,点A、点B分别在x轴、y轴的正半轴上,且OA=OB,另有两点C(a,b)和D(b,﹣a)(a、b均大于0);(1)连接OD、CD,求证:∠ODC=45°;(2)连接CO、CB、CA,若CB=1,C0=2,CA=3,求∠OCB的度数;(3)若a=b,在线段OA上有一点E,且AE=3,CE=5,AC=7,求△OCA的面积.25.11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题“小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻飞去抓鱼,并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树根有多远?26.(1)先化简,再求值:x(x﹣2)﹣(x+1)(x﹣1),其中x=10.(2)已知,求代数式(x+1)2﹣4(x+1)+4的值.(3)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图:①从点A出发在图中画一条线段AB,使得AB=;②画出一个以(1)中的AB为斜边的等腰直角三角形,使三角形的三个顶点都在格点上,并根据所画图形求出等腰直角三角形的腰长.27.[问题情境]勾股定理是一条古老的数学定理,它有很多种证明方法.我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数学关系”(勾股定理)带到其它星球,作为地球人与其他星球“人”进行第一次“谈话”的语言;[定理表述]请你根据图1中的直角三角形叙述勾股定理;[尝试证明]以图1中的直角三角形为基础,将两个直角边长为a,b,斜边长为c 的三角形按如图所示的方式放置,连接两个之间三角形的另外一对锐角的顶点(如图2),请你利用图2,验证勾股定理;[知识扩展]利用图2中的直角梯形,我们可以证明<,其证明步骤如下:∵BC=a+b,AD=又∵在直角梯形ABCD中,有BCAD(填大小关系),即∴.28.观察、思考与验证(1)如图1是一个重要公式的几何解释,请你写出这个公式;(2)如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°;(3)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的《新英格兰教育日志》上),请你写出验证过程.29.超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?(参考数据:=1.41,=1.73)30.中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C 处截住了渔船.(1)请用直尺和圆规作出C处的位置;(2)求我国海监船行驶的航程BC的长.31.在一次“构造勾股数”的探究性学习中,老师给出了下表:m 2 3 3 4…n1123…a22+1232+1232+2242+32…b4 6 1224 …c22﹣1232﹣1232﹣2242﹣32…其中m、n为正整数,且m>n.(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=,b=,c=.(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.32.如图1,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<8).(1)请在4×8的网格纸图2中画出t为6秒时的线段PQ.并求其长度;(2)当t为多少时.△PQB是以BP为底的等腰三角形.33.阅读下面的情景对话,然后解答问题:(1)理解:①根据“奇异三角形”的定义,请你判断:“等边三角形一定是奇异三角形”吗?(填是或不是)②若某三角形的三边长分别为1、、2,则该三角形(是或不是)奇异三角形.(2)探究:若Rt△ABC是奇异三角形,且其两边长分别为2、2,则第三边的长为,且这个直角三角形的三边之比为(从小到大排列,不得含有分母).(3)设问:请提出一个和奇异三角形有关的问题.(不用解答)34.观察下列各式,你有什么发现?32=4+5,52=12+13,72=24+25,92=40+41,…用你的发现解决下列问题:(1)填空:112=+ ;(2)请用含字母n(n为正整数)的关系式表示出你发现的规律:;(3)结合勾股定理有关知识,说明你的结论的正确性.35.小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?36.如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.37.如图,四边形ABCD的三边(AB、BC、CD)和BD的长度都为5厘米,动点P从A出发(A→B→D)到D,速度为2厘米/秒,动点Q从点D出发(D→C→B→A)到A,速度为2.8厘米/秒.5秒后P、Q相距3厘米,试确定5秒时△APQ的形状.38.一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B 处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由.39.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地°送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺),此时踏板升高离地五尺(BD=5尺),求秋千绳索(OA或OB)的长度.40.如图,∠AOB=90°,OA=45cm,OB=15cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?1.已知直角三角形两边的长为3和4,则此三角形的周长为()A.12 B.7+C.12或7+D.以上都不对2.图中字母所代表的正方形的面积为144的选项为()A.B.C.D.3.如图,数轴上的点A所表示的数为x,则x的值为()A.B.﹣C.2 D.﹣24.如图,带阴影的正方形面积是.5.如图,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=.6.正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,(1)在图①中,画一个面积为10的正方形;(2)在图②、图③中,分别画两个不全等的直角三角形,使它们的三边长都是无理数.初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)参考答案与试题解析一.选择题(共8小题)1.(2016秋•吴江区期中)直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C.D.【分析】首先根据勾股定理,得:斜边==13.再根据直角三角形的面积公式,求出斜边上的高.【解答】解:由题意得,斜边为=13.所以斜边上的高=12×5÷13=.故选D.【点评】运用了勾股定理.注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.2.(2016春•抚顺县期中)下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2D.在Rt△ABC中,∠B=90°,所以a2+b2=c2【分析】在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角,根据此就可以直接判断A、B、C、D选项.【解答】解:在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角.A、不确定c是斜边,故本命题错误,即A选项错误;B、不确定第三边是否是斜边,故本命题错误,即B选项错误;C、∠C=90°,所以其对边为斜边,故本命题正确,即C选项正确;D、∠B=90°,所以斜边为b,所以a2+c2=b2,故本命题错误,即D选项错误;故选C.【点评】本题考查了勾股定理的正确运用,只有斜边的平方才等于其他两边的平方和.3.(2016春•临沭县期中)如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm【分析】作出直角三角形后分别求得直角三角形的两直角边的长后即可利用勾股定理求得斜边AB的长.【解答】解:如图,由题意得:AC=15×5=75cm,BC=30×6=180cm,故AB===195cm.故选A.【点评】本题考查了勾股定理的应用,解题的关键是从实际问题中抽象出直角三角形,难度不大.4.(2015春•青山区期中)如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺【分析】找到题中的直角三角形,设水深为x尺,根据勾股定理解答.【解答】解:设水深为x尺,则芦苇长为(x+1)尺,根据勾股定理得:x2+()2=(x+1)2,解得:x=12,芦苇的长度=x+1=12+1=13(尺),故选D.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.5.(2016春•南陵县期中)如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C.﹣D.﹣1+【分析】点A在以O为圆心,OB长为半径的圆上,所以在直角△BOC中,根据勾股定理求得圆O的半径OA=OB=,然后由实数与数轴的关系可以求得a的值.【解答】解:如图,点A在以O为圆心,OB长为半径的圆上.∵在直角△BOC中,OC=2,BC=1,则根据勾股定理知OB===,∴OA=OB=,∴a=﹣1﹣.故选A.【点评】本题考查了勾股定理、实数与数轴.找出OA=OB是解题的关键.6.(2015春•蓟县期中)一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米【分析】先根据梯子的顶端下滑了0.4米求出A′C的长,再根据勾股定理求出B′C 的长,进而可得出结论.【解答】解:(1)∵在Rt△ABC中,AB=2.5m,BC=0.7m,∴AC===2.4(m).∵梯子的顶端下滑了0.4米,∴A′C=2m,∵在Rt△A′B′C中,A′B′=2.5m,A′C=2m,∴B′C==1.5m,∴BB′=B′C﹣BC=1.5﹣0.7=0.8m.故选C.【点评】此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.7.(2015春•罗田县期中)在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.4【分析】根据勾股定理求出AB的长即可解答.【解答】解:在Rt△ABC中,根据勾股定理,AB==13,又∵AC=12,BC=5,AM=AC,BN=BC,∴AM=12,BN=5,∴MN=AM+BN﹣AB=12+5﹣13=4.故选D.【点评】本题综合考查了勾股定理的应用,找到关系MN=AM+BN﹣AB是关键.8.(2016春•重庆校级期中)如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169【分析】根据勾股定理,知两条直角边的平方等于斜边的平方,此题中斜边的平方即为大正方形的面积13,2ab即四个直角三角形的面积和,从而不难求得(a+b)2的值.【解答】解:(a+b)2=a2+b2+2ab=大正方形的面积+四个直角三角形的面积和=13+(13﹣1)=25.故选C.【点评】考查了勾股定理的证明,注意完全平方公式的展开:(a+b)2=a2+b2+2ab,还要注意图形的面积和a,b之间的关系.二.填空题(共5小题)9.(2016春•固始县期中)将一根24cm的筷子,置于底面直径为15cm,高8cm 的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是7cm≤h≤16cm.【分析】如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出h的取值范围.【解答】解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,∴h=24﹣8=16cm;当筷子的底端在A点时,筷子露在杯子外面的长度最短,在Rt△ABD中,AD=15,BD=8,∴AB==17,∴此时h=24﹣17=7cm,所以h的取值范围是7cm≤h≤16cm.故答案为:7cm≤h≤16cm.【点评】本题考查了勾股定理的应用,求出h的值最大值与最小值是解题关键.10.(2015春•汕头校级期中)如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为(1+)米.【分析】根据题意利用勾股定理得出BC的长,进而得出答案.【解答】解:由题意得:在直角△ABC中,AC2+AB2=BC2,则12+22=BC2,∴BC=,∴则树高为:(1+)m.故答案为:(1+).【点评】此题主要考查了勾股定理的应用,熟练利用勾股定理得出BC的长是解题关键.11.(2016春•高安市期中)已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于24cm2.【分析】利用勾股定理列出关系式,再利用完全平方公式变形,将a+b与c的值代入求出ab的值,即可确定出直角三角形的面积.【解答】解:∵Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,∴由勾股定理得:a2+b2=c2,即(a+b)2﹣2ab=c2=100,∴196﹣2ab=100,即ab=48,则Rt△ABC的面积为ab=24(cm2).故答案为:24cm2.【点评】此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.12.(2016春•嘉祥县期中)观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是15,112,113(只填数,不填等式)【分析】通过观察,得出规律:这类勾股数分别为2n+1,2n(n+1),2n(n+1)+1,由此可写出第7组勾股数.【解答】解:∵第1组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,第2组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,第3组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,第4组:9=2×4+1,40=2×4×(4+1)41=2×4×(4+1)+1,∴第7组勾股数是2×7+1=15,2×7×(7+1)=112,2×7×(7+1)+1=113,即15,112,113.故答案为:15,112,113.【点评】此题考查的知识点是勾股数,属于规律性题目,关键是通过观察找出规律求解.13.(2009春•武昌区期中)观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b=84,c=85.【分析】认真观察三个数之间的关系:首先发现每一组的三个数为勾股数,第一个数为从3开始连续的奇数,第二、三个数为连续的自然数;进一步发现第一个数的平方是第二、三个数的和;最后得出第n组数为(2n+1),(),(),由此规律解决问题.【解答】解:在32=4+5中,4=,5=;在52=12+13中,12=,13=;…则在13、b、c中,b==84,c==85.【点评】认真观察各式的特点,总结规律是解题的关键.三.解答题(共27小题)14.(2016春•黄冈期中)a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.【分析】现对已知的式子变形,出现三个非负数的平方和等于0的形式,求出a、b、c,再验证两小边的平方和是否等于最长边的平方即可.【解答】解:由a2+b2+c2+338=10a+24b+26c,得:(a2﹣10a+25)+(b2﹣24b+144)+(c2﹣26c+169)=0,即:(a﹣5)2+(b﹣12)2+(c﹣13)2=0,由非负数的性质可得:,解得,∵52+122=169=132,即a2+b2=c2,∴∠C=90°,即三角形ABC为直角三角形.【点评】本题考查勾股定理的逆定理的应用、完全平方公式、非负数的性质.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.15.(2016秋•永登县期中)如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.【分析】连接AC,则在直角△ABC中,已知AB,BC可以求AC,根据AC,AD,CD的长可以判定△ACD为直角三角形,(1)根据∠BAD=∠CAD+∠BAC,可以求解;(2)根据四边形ABCD的面积为△ABC和△ACD的面积之和可以解题.【解答】解:(1)连接AC,∵AB⊥CB于B,∴∠B=90°,在△ABC中,∵∠B=90°,∴AB2+BC2=AC2,又∵AB=CB=,∴AC=2,∠BAC=∠BCA=45°,∵CD=,DA=1,∴CD2=5,DA2=1,AC2=4.∴AC2+DA2=CD2,由勾股定理的逆定理得:∠DAC=90°,∴∠BAD=∠BAC+∠DAC=45°+90°=135°;(2)∵∠DAC=90°,AB ⊥CB 于B ,∴S △ABC =,S △DAC =,∵AB=CB=,DA=1,AC=2, ∴S △ABC =1,S △DAC =1而S 四边形ABCD =S △ABC +S △DAC ,∴S 四边形ABCD =2.【点评】本题考查了勾股定理在直角三角形中的运用,考查了根据勾股定理逆定理判定直角三角形,考查了直角三角形面积的计算,本题中求证△ACD 是直角三角形是解题的关键.16.(2016春•邹城市校级期中)如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.【分析】直接利用网格结合勾股定理求出答案.【解答】解:如图所示:△ABC 即为所求.【点评】此题主要考查了勾股定理,正确借助网格求出是解题关键.17.(2015春•平南县期中)如图所示,在一次夏令营活动中,小明坐车从营地A 点出发,沿北偏东60°方向走了100km到达B点,然后再沿北偏西30°方向走了100km到达目的地C点,求出A、C两点之间的距离.【分析】根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.【解答】解:∵AD∥BE∴∠ABE=∠DAB=60°∵∠CBE=30°∴∠ABC=180°﹣∠ABE﹣∠CBE=180°﹣60°﹣30°=90°,在Rt△ABC中,∴==200,∴A、C两点之间的距离为200km.【点评】本题考查勾股定理的应用,先确定是直角三角形后,根据各边长,用勾股定理可求出AC的长,且求出∠DAC的度数,进而可求出点C在点A的什么方向上.18.(2015秋•新泰市期中)如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?【分析】(1)过A作AE⊥BD于E,线段AE的长即为台风中心与气象台A的最短距离,由含30°角的直角三角形的性质即可得出结果;(2)根据题意得出线段CD就是气象台A受到台风影响的路程,求出CD的长,即可得出结果.【解答】解:(1)过A作AE⊥BD于E,如图1所示:∵台风中心在BD上移动,∴AE的长即为气象台距离台风中心的最短距离,在Rt△ABE中,∠ABE=90°﹣60°=30°,∴AE=AB=160,即台风中心在移动过程中,与气象台A的最短距离是160km.(2)∵台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响,∴线段CD就是气象台A受到台风影响的路程,连接AC,如图2所示:在Rt△ACE中,AC=200km,AE=160km,∴CE==120km,∵AC=AD,AE⊥CD,∴CE=ED=120km,∴CD=240km.∴台风影响气象台的时间会持续240÷20=12(小时).【点评】本题考查了勾股定理在实际生活中的应用、垂径定理、含30°角的直角三角形的性质等知识;熟练掌握垂径定理和勾股定理,求出CD是解决问题(2)的关键.19.(2015春•阳东县期中)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.。
勾股定理的应用十种最常考类型(解析版) 八年级数学下册专题训练

专题05勾股定理的应用十种最常考类型(解析版)类型一大树折断问题【典例1】(2023春•德庆县期末)如图,一棵高为16m的大树被台风刮断,若树在离地面6m处折断,树顶端刚好落在地面上,此处离树底部8m处.【思路引领】首先设树顶端落在离树底部x米处,根据勾股定理可得62+x2=(16﹣6)2,再解即可.【解答】解:设树顶端落在离树底部x米处,由题意得:62+x2=(16﹣6)2,解得:x1=8,x2=﹣8(不合题意舍去).故答案为:8.【总结提升】此题主要考查了勾股定理的应用,关键是正确理解题意,掌握直角三角形中两直角边的平方和等于斜边的平方.【变式训练】1.(2023•南宁模拟)在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈(10尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面()尺.A.4B.3.6C.4.5D.4.55【思路引领】画出图形,设折断处离地面x尺,则AB=(10﹣x)尺,由勾股定理得出方程,解方程即可.【解答】解:如图,由题意得:∠ACB=90°,BC=3尺,AC+AB=10尺,设折断处离地面x尺,则AB=(10﹣x)尺,在Rt△ABC中,由勾股定理得:x2+32=(10﹣x)2,解得:x=4.55,即折断处离地面4.55尺.故选:D.【总结提升】此题主要考查了勾股定理的应用,正确应用勾股定理得出方程是解题的关键.类型二水杯中的筷子问题及类似问题【典例2】(2023春•陕州区期中)如图是一个饮料罐,下底面半径是5,上底面半径是8,高是12,上底面盖子的中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是()A.12≤a≤13B.12≤a≤15C.5≤a≤12D.5≤a≤13【思路引领】如图,过A作AB⊥BC于B,根据勾股定理即可得到结论.【解答】解:如图,过A作AB⊥BC于B,∵下底面半径是5,高是12,∴AB=12,BC=5,∴AC=B2+B2=122+52=13,∴a的长度的取值范围是12≤a≤13,故选A.【总结提升】本题考查正确运用勾股定理.善于观察题目的信息,正确理解题意是解题的关键.【变式训练】1.(2023春•盐山县期末)如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为()尺.A.10B.12C.13D.14【思路引领】找到题中的直角三角形,设水深为x尺,根据勾股定理解答.【解答】解:设水深为x尺,则芦苇长为(x+1)尺,根据勾股定理得:x2+(102)2=(x+1)2,解得:x=12,芦苇的长度=x+1=12+1=13(尺),答:芦苇长13尺.故选:C.【总结提升】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.2.(2022秋•安阳县期末)从前有一个人拿着竹竿进城,横拿竖拿都进不去,横着比城门宽43,竖着比城门高23,另一个人告诉他沿着城门的两对角斜着拿竿,这个人一试,不多不少刚好进去了,则竹竿的长度为103.【思路引领】设竹竿的长为x米,根据门框的边长的平方和等于竹竿的长的平方列方程,解一元二次方程即可.【解答】解:设竹竿的长为x米,由题意得:(−43)2+(−23)2=2,解得:1=103,2=23(舍去),故答案为:103.【总结提升】本题考查一元二次方程的应用;得到门框的边长和竹竿长的等量关系是解决本题的关键.类型三梯子滑动问题【典例3】(2020春•硚口区期中)如图,一个梯子AB斜靠在一竖直的墙AO上,测得AO=8米.若梯子的顶端沿墙面向下滑动2米,这时梯子的底端在水平的地面也恰好向外移动2米,则梯子AB的长度为()A.10米B.6米C.7米D.8米【思路引领】首先设BO=x米,则DO=(x+2)米,利用勾股定理可列出方程,再解可得BO长,然后再利用勾股定理计算出AB长.【解答】解:由题意得:AC=BD=2米,∵AO=8米,∴CO=6米,设BO=x米,则DO=(x+2)米,由题意得:62+(x+2)2=82+x2,解得:x=6,AB=82+62=10(米),故选:A.【总结提升】此题主要考查了勾股定理的应用,关键是掌握直角三角形两直角边的平方和等于斜边的平方.【变式训练】1.(2023秋•新泰市期中)如图,一架梯子若靠墙直立时比窗户的下沿高1m.若斜靠在墙上,当梯子的下端离墙5m时,梯子的上端恰好与窗户的下沿对齐.则梯子的长度为()A.13m B.12m C.15m D.172【思路引领】设梯子的长度为x m,根据勾股定理列方程即可得到结论.【解答】解:设梯子的长度为x m,根据勾股定理得,52+(x﹣1)2=x2,解得x=13,答:梯子的长度为13m,故选:A.【总结提升】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.2.(2023秋•北京期末)如图,小巷左右两侧是竖直的墙,已知小巷的宽度CE是2.2米.一架梯子AB斜靠在左墙时,梯子顶端A与地面点C距离是2.4米.如果保持梯子底端B位置不动,将梯子斜靠在右墙时,梯子顶端D与地面点E距离是2米.求此时梯子底端B到右墙角点E的距离是多少米.【思路引领】设此时梯子底端B到右墙角点E的距离是x米,则BC为(2.2﹣x)米,在Rt△ABC和Rt △DBE中,根据勾股定理列出方程,解方程即可.【解答】解:设此时梯子底端B到右墙角点E的距离是x米,则BC为(2.2﹣x)米,由题意可知,AC=2.4米,DE=2米,AB=DB,在Rt△ABC和Rt△DBE中,由勾股定理得:AB2=BC2+AC2,DB2=BE2+DE2,∴BC2+AC2=BE2+DE2,即(2.2﹣x)2+2.42=x2+4,解得:x=1.5,答:此时梯子底端B到右墙角点E的距离是1.5米.【总结提升】本题考查了勾股定理的应用,根据勾股定理列出方程是解题的关键.3.(2023秋•宝丰县期末)如图是盼盼家新装修的房子,其中三个房间甲、乙、丙,他将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作MA,如果梯子的底端P不动,顶端靠在对面墙上,此时梯子的顶端距离地面的垂直距离记作NB.(1)当盼盼在甲房间时,梯子靠在对面墙上,顶端刚好落在对面墙角B处,若MA=1.6米,AP=1.2米,则甲房间的宽度AB= 3.2米.(2)当他在乙房间时,测得MA=2.4米,MP=2.5米,且∠MPN=90°,求乙房间的宽AB;(3)当他在丙房间时,测得MA=2.8米,且∠MPA=75°,∠NPB=45°.①求∠MPN的度数;②求丙房间的宽AB.【思路引领】(1)根据勾股定理即可得到结论;(2)证明△AMP≌△BPN,从而得到MA=PB=2.4米,PA=NB=0.7米,即可求出AB=PA+PB;(3)①根据平角的定义即可求出∠MPN=60°;②根据PM=PN以及∠MPN的度数可得到△PMN为等边三角形.利用相应的三角函数表示出MN,MP的长,可得到房间宽AB和AM长相等.【解答】解:(1)在Rt△AMP中,∵∠A=90°,MA=1.6米,AP=1.2米,∴PM=B2+B2=1.62+1.22=2,∵PB=PM=2,∴甲房间的宽度AB=AP+PB=3.2米,故答案为:3.2;(2)∵∠MPN=90°,∴∠APM +∠BPN =90°,∵∠APM +∠AMP =90°,∴∠AMP =∠BPN .在△AMP 与△BPN 中,∠B =∠B ∠B =∠B =90°B =B,∴△AMP ≌△BPN ,∴MA =PB =2.4,∵PA =B2−B 2=0.7,∴AB =PA +PB =0.7+2.4=3.1;(3)①∠MPN =180°﹣∠APM ﹣∠BPN =60°;②过N 点作MA 垂线,垂足点D ,连接NM .设AB =x ,且AB =ND =x .∵梯子的倾斜角∠BPN 为45°,∴△BNP 为等腰直角三角形,△PNM 为等边三角形(180°﹣45°﹣75°=60°,梯子长度相同),∠MND =15°.∵∠APM =75°,∴∠AMP =15°.∴∠DNM =∠AMP ,∵△PNM 为等边三角形,∴NM =PM .∴△AMP ≌△DNM (AAS ),∴AM =DN ,∴AB =DN =AM =2.8米,即丙房间的宽AB 是2.8米.【总结提升】此题考查了勾股定理的应用,全等三角形的应用,解直角三角形的应用,根据PM=PN以及∠MPN的度数得到△PMN为等边三角形是解题的关键.类型四立体图形中的最短距离问题【典例4】(2021春•饶平县期末)如图,长方体的底面边长均为3cm,高为5cm,如果用一根细线从点A 开始经过4个侧面缠绕一圈达到点B,那么所用细线最短需要13cm.【思路引领】把立体图形转化为平面图形解决即可.【解答】解:将长方体展开,连接AB,根据两点之间线段最短,AB=52+122=13cm;故答案为:13【总结提升】本题考查了平面展开﹣最短路径问题,本题就是把长方体的侧面展开“化立体为平面”,用勾股定理解决.【变式训练】1.(2023秋•沙坪坝区期中)如图,圆柱形容器中,高为12cm,底面周长为32cm,在容器内壁离容器底部2cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿2cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为20cm.(容器厚度忽略不计)【思路引领】将容器侧面展开,建立A关于EC的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.【解答】解:如图,将容器侧面展开,作A关于EC的对称点A′,连接A′B交EC于F,则A′B即为最短距离.∵高为12cm,底面周长为32cm,在容器内壁离容器底部2cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿2cm与蚊子相对的点A处,∴A′D=16cm,BD=12cm,∴在直角△A′DB中,A′B=162+122=20(cm).故答案为:20.【总结提升】本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.2.(2022春•桦甸市期末)如图,是一块长,宽,高分别为6cm,4cm和3cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的外表面,到长方体的另一个顶点B处吃食物,则它需要爬行的最短路径长是85cm.【思路引领】把这个长方体中蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.【解答】解:第一种情况:把我们所看到的左面和上面组成一个平面,则这个长方形的长和宽分别是9和4,则所走的最短线段是AB=92+42=97(cm).第二种情况:把我们看到的前面与上面组成一个长方形,则这个长方形的长和宽分别是7和6,所以走的最短线段是AB=72+62=85(cm).第三种情况:把我们所看到的前面和右面组成一个长方形,则这个长方形的长和宽分别是10和3,所以走的最短线段是AB=102+32=109(cm).∴它需要爬行的最短路径是85cm.故答案为:85cm.【总结提升】本题主要考查的是平面展开﹣最短路径问题,解决此题的关键是明确线段最短这一知识点,然后把长方体的一些面展开到一个平面内,求出最短的线段.3.(荆州中考)如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为()A.42dm B.22dm C.25dm D.45dm【思路引领】要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.【解答】解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.∵圆柱底面的周长为4dm,圆柱高为2dm,∴AB=2dm,BC=BC′=2dm,∴AC2=22+22=4+4=8,∴AC=22dm,∴这圈金属丝的周长最小为2AC=42dm.故选:A.【总结提升】本题考查了平面展开﹣最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.类型五选址满足条件问题【典例5】(2023春•永善县期中)如图,河CD的同侧有A、B两个村,且AB=213km,A、B两村到河的距离分别为AC=2km,BD=6km.现要在河边CD上建一水厂分别向A、B两村输送自来水,铺设水管的工程费每千米需2000元.请你在河岸CD上选择水厂位置0,使铺设水管的费用最省,并求出铺设水管的总费用w(元).【思路引领】作A点关于CD的对称点为A',连接A'B交CD于点O,过点A作AF⊥BD于点F,过点A'作A'E⊥BD交BD的延长线于点E,分别利用勾股定理求出AF和A'B的长即可.【解答】解:如图所示,作A点关于CD的对称点为A',连接A'B交CD于点O,过点A作AF⊥BD于点F,过点A'作A'E⊥BD交BD的延长线于点E,此时AO+BO最小,∵AC=2km,BD=6km,∴BF=4km,DE=2km,∵AB=213km,∴AF=(213)2−42=6(km),在Rt△BA'E中,由勾股定理得:A'B=′2+B2=62+(6+2)2=10(km),∴AO+BO=10(km),∴铺设水管的总费用W=10×2000=20000(元).【总结提升】本题主要考查了勾股定理的应用,构造直角三角形运用勾股定理是解题的关键.【变式训练】1.(2023春•红塔区期中)如图,在笔直的铁路上A,B两点相距20km,C、D为两村庄,DA=8km,CB=14km,DA⊥AB于点A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等,求AE=13.3km.【思路引领】设AE=x km,即可得到EB=(20﹣x)km,结合DA⊥AB于点A,CB⊥AB于B根据勾股定理列式求解即可得到答案.【解答】解:设AE=x km,则EB=(20﹣x)km,∵DA⊥AB,CB⊥AB,DA=8km,CB=14km,∴DE2=x2+82=x2+64,DE2=(20﹣x)2+142=x2﹣40x+596,∵C、D两村到E站的距离相等,∴x2﹣40x+596=x2+64,解得:x=13.3,故答案为:13.3.【总结提升】本题考查勾股定理的应用,解题的关键是根据相等列等式求解.类型六航海问题【典例6】(2023春•黄陂区期中)如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一小时后分别位于点Q,R处,且相距20海里.如果知道“远航”号沿北偏东50°方向航行,你能判断“海天”号沿哪个方向航行吗?请说明理由.【思路引领】利用勾股定理逆定理以及方向角得出答案.【解答】解:由题意可得:RP=12海里,PQ=16海里,QR=20海里,∵162+122=202,∴△RPQ是直角三角形,∴∠RPQ=90°,∵“远航”号沿北偏东50°方向航行,∴∠RPN=40°,∴“海天”号沿北偏西40°方向航行.【总结提升】此题主要考查了勾股定理的逆定理以及解直角三角形的应用,正确得出各线段长是解题关键.【变式训练】1.(2023秋•泰山区期末)如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时30分,我国反走私A艇发现正东方有一走私艇C以8海里/时的速度偷偷向我领海驶来,便立即通知正在MN线上巡逻的我国反走私艇B密切注意.反走私艇A和走私艇C的距离是20海里,A、B两艇的距离是12海里;反走私艇B测得距离C艇16海里,若走私艇C的速度不变,最早会在什么时候进入我国领海?【思路引领】由勾股定理的逆定理得△ABC为直角三角形,且∠ABC=90°,再由三角形面积求出BE=485海里,然后由勾股定理得CE=645海里,即可解决问题.【解答】解:由题意可知,∠BEC=90°,∵AB2+BC2=122+162=202=AC2,∴△ABC为直角三角形,且∠ABC=90°,∵MN⊥AC,∴走私艇C进入我国领海的最短距离是CE,=12AB•BC=12AC•BE,∵S△ABC∴BE=B⋅B B=12×1620485(海里),∴CE=B2−B2==645(海里),∴645÷8=85(小时)=96分,∴9时30分+96分=11时6分.答:走私艇C最早在11时6分进入我国领海.【总结提升】本题考查了勾股定理的应用、勾股定理的逆定理以及三角形面积等知识,熟练掌握勾股定理和勾股定理的逆定理是解题的关键.类型七受台风或噪声影响问题【典例7】(2022秋•清水县月考)如图,A城气象台测得台风中心在A城的正西方300千米处,以每小时107千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.(1)问A城是否会受到这次台风的影响?为什么?(2)若A城受到这次台风的影响,那么A城遭受这次台风影响的时间有多长?【思路引领】(1)作AC⊥BF,则距点A最近的点即为C点,计算AC的长,若AC>200千米,则不受影响,反之,则受影响.(2)求出A城所受影响的距离DE,又有台风移动的速度,即可求解出其影响的时间.【解答】解:(1)A城市受影响.如图,过点A作AC⊥BF,则距离点C最近的距离为AC,∵AB=300,∠ABC=30°,∴AC=12AB=150<200,所以A城会受到这次台风的影响;(2)如图,∵距台风中心200千米的范围内是受这次台风影响的区域,则AD=AE=200,即DE为A城遭受这次台风的距离,CD=A2−B2=507,∴DE=1007,则t===10小时.故A城遭受这次台风影响的时间10小时.【总结提升】本题主要考查了方向角问题以及解直角三角形的简单运用,能够熟练掌握.【变式训练】1.(2022春•紫云县期末)如图,有两条公路OM,ON相交成30°,沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿道路ON的方向行驶时,以P为圆心,50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大,若重型运输卡车P沿道路ON方向行驶的速度为5米/秒.(1)求卡车P对学校A的噪声影响最大时,卡车P与学校A的距离;(2)求卡车P沿道路ON方向行驶一次,它给学校A带来噪声影响的总时间.【思路引领】(1)过点A作AH⊥ON于H,利用含30°角的直角三角形的性质可得答案;(2)当AC=AN=50米时,则卡车在CD段对学校A有影响,利用勾股定理求出CH的长,再根据等腰三角形的性质可得CD的长,从而求出时间.【解答】解:(1)过点A作AH⊥ON于H,∵∠O=30°,OA=80米,∴AH=12OA=40米,∴卡车P对学校A的噪声影响最大时,卡车P与学校A的距离为40米;(2)当AC=AN=50米时,则卡车在CD段对学校A有影响,由(1)知AH=40米,∴CH=B2−B2=502−402=30(米),∴CN=2CH=60(米),∴t=60÷5=12(秒),∴卡车P沿道路ON方向行驶一次,它给学校A带来噪声影响的总时间为12秒.【总结提升】本题主要考查了勾股定理的实际应用,含30°角的直角三角形的性质,等腰三角形的性质,垂线段最短等知识,根据题意,构造出直角三角形是解题的关键.类型八求旗杆(大树)高度问题【典例8】(2023秋•开封期末)如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为(滑轮上方的部分忽略不计)()A.14m B.15m C.16m D.17m【思路引领】根据题意画出示意图,设旗杆高度为x m,可得AC=AD=x m,AB=(x﹣2)m,BC=8m,在Rt△ABC中利用勾股定理可求出x.【解答】解:设旗杆高度为x m,过点C作CB⊥AD于B,则AC=AD=x m,AB=(x﹣2)m,BC=8m,在Rt△ABC中,AB2+BC2=AC2,即(x﹣2)2+82=x2,解得:x=17,即旗杆的高度为17米.故选:D.【总结提升】本题考查了勾股定理的应用,解答本题的关键是构造直角三角形,构造直角三角形的一般方法就是作垂线.【变式训练】1.(2023春•岳阳楼区期末)小华和小侨合作,用一块含30°的直角三角板,旗杆顶端垂到地面的绳子,测量长度的工具,测量学校旗杆的高度,如图,测得AD=0.5米,绳子部分长CD=6米,则学校旗杆AB的高度为()A.6.5米B.(63+0.5)米C.12.5米D.(65+0.5)米【思路引领】根据含30°角的直角三角形的性质得出2DC=BC,进而利用勾股定理解答即可.【解答】解:由题意知∠ABC=30°,CD⊥AB,∴BC=2CD=12米,A=63米,∵AD=0.5米,∴B=(63+0.5)米,故选:B.【总结提升】本题考查了含30度直角三角形的性质及勾股定理的应用,熟悉勾股定理,能从实际问题中抽象出勾股定理是解题的关键.2.(2023秋•岱岳区期中)学习完《勾股定理》后,张老师要求数学兴趣小组的同学测量学校旗杆的高度.同学们发现系在旗杆顶端的绳子垂到了地面并多出了一段,但这条绳子的长度未知.如图,经测量,绳子多出的部分长度为2米,将绳子拉直,且绳子底端与地面接触,此时绳子端点距离旗杆底端5米,则旗杆的高度为214米.【思路引领】在Rt△ABC中,由勾股定理得出关于AB的方程求解即可.【解答】解:如图,由题意可知,BD=2米,BC=5米,AC=AB+BD=(AB+2)米,在Rt△ABC中,由勾股定理得,AB2+BC2=AC2,即AB2+52=(AB+2)2,解得AB=214,∴旗杆的高度为214米.故答案为:214.【总结提升】本题考查了勾股定理的应用,熟记勾股定理是解题的关键.3.(2023秋•秦安县期末)如图,在一棵树的10米高B处,有两只猴子,一只猴子爬下树走到离树20米处的池塘A处,另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树的高度为15米.【思路引领】根据两只猴子所经过的距离相等,将两只猴子所走的路程表示出来,根据勾股定理列出方程求解.【解答】解:如图,设树的高度为x米,因两只猴子所经过的距离相等都为30米.由勾股定理得:x2+202=[30﹣(x﹣10)]2,解得x=15m.故这棵树高15m.【总结提升】把实际问题转化为数学模型,构造直角三角形,然后利用勾股定理解决.类型九小鸟飞行距离问题【典例9】(2022秋•嵩县期末)如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行()米.A.6B.8C.10D.12【思路引领】根据“两点之间线段最短”可知:小鸟沿着两棵树的树尖进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.【解答】解:两棵树的高度差为8﹣2=6m,间距为8m,根据勾股定理可得:小鸟至少飞行的距离=82+62=10m.故选:C.【总结提升】本题主要考查了勾股定理的应用,解题的关键是将现实问题建立数学模型,运用数学知识进行求解.【变式训练】1.(2023秋•青羊区期中)如图,一只小鸟旋停在空中A点,A点到地面的高度AB=20米,A点到地面C 点(B,C两点处于同一水平面)的距离AC=25米.(1)求出BC的长度;(2)若小鸟竖直下降到达D点(D点在线段AB上),此时小鸟到地面C点的距离与下降的距离相同,求小鸟下降的距离.【思路引领】(1)在直角三角形中运用勾股定理即可求解;(2)在Rt△BDC中,根据勾股定理即可求解.【解答】解:(1)由题意知∠B=90°,∵AB=20米,AC=25米.∴BC=252−202=15米,(2)设AD=x,则CD=x,BD=20﹣x,在Rt△BDC中,DC2=BD2+BC2,∴x2=(20﹣x)2+152,解得x=1258,∴小鸟下降的距离为1258米.【总结提升】本题考查勾股定理,熟练掌握勾股定理是解题关键.类型十利用勾股定理表示无理数【典例10】(2022春•武昌区期末)平面直角坐标系中,点P(﹣4,2)到坐标原点的距离是()A.2B.4C.23D.25【思路引领】利用勾股定理计算可得结论.【解答】解:由题意得,点P到坐标原点的距离为:42+22=20=25.故选:D.【总结提升】本题考查了勾股定理,掌握勾股定理的内容是解决本题的关键.【变式训练】1.(2023•大连)如图,在平面直角坐标系中,点A,B的坐标分别为(1,0)和(0,2),连接AB,以点A为圆心、AB的长为半径画弧,与x轴正半轴相交于点C,则点C的横坐标是+1.【思路引领】由勾股定理求出AB的长,进而得到AC的长,再求出OC的长,得出点C的坐标,即可解决问题.【解答】解:∵点A,B的坐标分别为(1,0)和(0,2),∴OA=1,OB=2,∵∠AOB=90°,∴AB=B2+B2=12+22=5,∵以点A为圆心,以AB长为半径画弧,∴AC=AB=5,∴OC=AC+OA=5+1,∵交x轴正半轴于点C,∴点C的坐标为(5+1,0).故答案为:5+1.【总结提升】本题考查了勾股定理以及坐标与图形性质等知识,熟练掌握勾股定理是解题的关键.2.(2022秋•芗城区月考)用尺规作图在数轴上作出表示实数=10的点P(保留作图痕迹,不写作法).【思路引领】过表示1的点A作数轴的垂线AB,在垂线上截取AB=3,连接OB,以O为圆心,OB为半径作弧交数轴于P,则P即为所求的点.【解答】解:如图:点P表示的数即为10.【总结提升】此题主要考查了勾股定理以及作图,关键是掌握10是两直角边长分别为1和3的直角三角形的斜边长.3.(2023•长阳县一模)如图,在3×3的正方形网格中,每个小正方形边长为1,点A,B,C,D均为格点,以A为圆心,AB长为半径作弧,交网格线CD于点E,则C,E两点间的距离为()A.3B.3−3C.3+12D.3−12【思路引领】如图:连接AE,则AE=2、AD=1,由勾股定理可求出DE,然后运用线段的和差即可解答.【解答】解:如图:连接AE,则AE=2,AD=1,∴DE=B2−A2=22−12=3,∴CE=CD﹣DE=3−3.故选B.【总结提升】本题主要考查了勾股定理的应用以及线段的和差,根据题意运用勾股定理求得DE是解答本题的关键.4.(2022秋•埇桥区期中)如图,网格中每个小正方形的边长均为1,点A、B,C都在格点上,以A为圆心,AB为半径画弧,交最上方的网格线于点D,则CD的长为()A.3−1B.3−5C.5D.22【思路引领】连接AD,则AD=AB=3,在Rt△AED中,利用勾股定理求出DE即可得出答案.【解答】解:连接AD,由题意知:AD=AB=3,在Rt△AED中,由勾股定理得:ED=A2−B2=32−22=5,∴CD=CE﹣DE=3−5,故选:B.【总结提升】本题主要考查了勾股定理,求出DE的长是解题的关键.。
初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析) 之欧阳史创编

初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)时间:2021.02.10 创作:欧阳史一.选择题(共8小题)1.直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C.D.2.下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2D.在Rt△ABC中,∠B=90°,所以a2+b2=c23.如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm4.如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺5.如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C.﹣ D.﹣1+6.一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米7.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.48.如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169二.填空题(共5小题)9.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是.10.如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为米.11.已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC 的面积等于.12.观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是(只填数,不填等式)13.观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b=,c=.三.解答题(共27小题)14.a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.15.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB 于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.16.如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.17.如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100km到达B点,然后再沿北偏西30°方向走了100km到达目的地C点,求出A、C两点之间的距离.18.如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD 方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?19.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.20.在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△AB C三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.(1)△ABC的面积为:.(2)若△DEF三边的长分别为、、,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为.(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是m2.21.(1)在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.请你将△ABC的面积直接填写在横线上.思维拓展:(2)已知△ABC三边的长分别为a(a>0),求这个三角形的面积.我们把上述求△ABC面积的方法叫做构图法.如图2,网格中每个小正方形的边长都是a,请在网格中画出相应的△ABC,并求出它的面积.类比创新:(3)若△ABC三边的长分别为(m >0,n>0,且m≠n),求出这个三角形的面积.如图3,网格中每个小长方形长、宽都是m,n,请在网格中画出相应的△ABC,用网格计算这个三角形的面积.22.有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?23.(拓展创新)在教材中,我们通过数格子的方法发现了直角三角形的三边关系,利用完全相同的四个直角三角形采用拼图的方式验证了勾股定理的正确性.问题1:以直角三角形的三边为边向形外作等边三角形,探究S′+S″与S的关系(如图1).问题2:以直角三角形的三边为斜边向形外作等腰直角三角形,探究S′+S″与S的关系(如图2).问题3:以直角三角形的三边为直径向形外作半圆,探究S′+S″与S的关系(如图3).24.如图,在平面坐标系中,点A、点B分别在x轴、y轴的正半轴上,且OA=OB,另有两点C(a,b)和D(b,﹣a)(a、b均大于0);(1)连接OD、CD,求证:∠ODC=45°;(2)连接CO、CB、CA,若CB=1,C0=2,CA=3,求∠OCB的度数;(3)若a=b,在线段OA上有一点E,且AE=3,CE=5,AC=7,求△OCA的面积.25.11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题“小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻飞去抓鱼,并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树根有多远?26.(1)先化简,再求值:x(x﹣2)﹣(x+1)(x﹣1),其中x=10.(2)已知,求代数式(x+1)2﹣4(x+1)+4的值.(3)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图:①从点A出发在图中画一条线段AB,使得AB=;②画出一个以(1)中的AB为斜边的等腰直角三角形,使三角形的三个顶点都在格点上,并根据所画图形求出等腰直角三角形的腰长.27.[问题情境]勾股定理是一条古老的数学定理,它有很多种证明方法.我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数学关系”(勾股定理)带到其它星球,作为地球人与其他星球“人”进行第一次“谈话”的语言;[定理表述]请你根据图1中的直角三角形叙述勾股定理;[尝试证明]以图1中的直角三角形为基础,将两个直角边长为a,b,斜边长为c的三角形按如图所示的方式放置,连接两个之间三角形的另外一对锐角的顶点(如图2),请你利用图2,验证勾股定理;[知识扩展]利用图2中的直角梯形,我们可以证明<,其证明步骤如下:∵BC=a+b,AD=又∵在直角梯形ABCD中,有BCAD(填大小关系),即∴.28.观察、思考与验证(1)如图1是一个重要公式的几何解释,请你写出这个公式;(2)如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°;(3)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的《新英格兰教育日志》上),请你写出验证过程.29.超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?(参考数据:=1.41,=1.73)30.中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.(1)请用直尺和圆规作出C处的位置;(2)求我国海监船行驶的航程BC的长.31.在一次“构造勾股数”的探究性学习中,老师给出了下表:m 2 3 3 4 …n 1 1 2 3 …a 22+12 32+12 32+22 42+32 …b 4 6 12 24 …c 22﹣12 32﹣12 32﹣22 42﹣32 …其中m、n为正整数,且m>n.(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=,b=,c=.(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.32.如图1,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t (0<t<8).(1)请在4×8的网格纸图2中画出t为6秒时的线段PQ.并求其长度;(2)当t为多少时.△PQB是以BP为底的等腰三角形.33.阅读下面的情景对话,然后解答问题:(1)理解:①根据“奇异三角形”的定义,请你判断:“等边三角形一定是奇异三角形”吗?(填是或不是)②若某三角形的三边长分别为1、、2,则该三角形(是或不是)奇异三角形.(2)探究:若Rt△ABC是奇异三角形,且其两边长分别为2、2,则第三边的长为,且这个直角三角形的三边之比为(从小到大排列,不得含有分母).(3)设问:请提出一个和奇异三角形有关的问题.(不用解答)34.观察下列各式,你有什么发现?32=4+5,52=12+13,72=24+25,92=40+41,…用你的发现解决下列问题:(1)填空:112=+;(2)请用含字母n(n为正整数)的关系式表示出你发现的规律:;(3)结合勾股定理有关知识,说明你的结论的正确性.35.小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?36.如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.37.如图,四边形ABCD的三边(AB、BC、CD)和BD的长度都为5厘米,动点P从A出发(A→B→D)到D,速度为2厘米/秒,动点Q从点D出发(D→C→B→A)到A,速度为2.8厘米/秒.5秒后P、Q相距3厘米,试确定5秒时△APQ的形状.38.一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B 处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由.39.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地°送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺),此时踏板升高离地五尺(BD=5尺),求秋千绳索(OA或OB)的长度.40.如图,∠AOB=90°,OA=45cm,OB=15cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?1.已知直角三角形两边的长为3和4,则此三角形的周长为()A.12 B.7+ C.12或7+D.以上都不对2.图中字母所代表的正方形的面积为144的选项为()A.B. C.D.3.如图,数轴上的点A所表示的数为x,则x的值为()A.B.﹣ C.2 D.﹣24.如图,带阴影的正方形面积是.5.如图,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=.6.正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,(1)在图①中,画一个面积为10的正方形;(2)在图②、图③中,分别画两个不全等的直角三角形,使它们的三边长都是无理数.初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)参考答案与试题解析一.选择题(共8小题)1.(2016秋•吴江区期中)直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C.D.【分析】首先根据勾股定理,得:斜边==13.再根据直角三角形的面积公式,求出斜边上的高.【解答】解:由题意得,斜边为=13.所以斜边上的高=12×5÷13=.故选D.【点评】运用了勾股定理.注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.2.(2016春•抚顺县期中)下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2D.在Rt△ABC中,∠B=90°,所以a2+b2=c2【分析】在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角,根据此就可以直接判断A、B、C、D选项.【解答】解:在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角.A、不确定c是斜边,故本命题错误,即A选项错误;B、不确定第三边是否是斜边,故本命题错误,即B选项错误;C、∠C=90°,所以其对边为斜边,故本命题正确,即C选项正确;D、∠B=90°,所以斜边为b,所以a2+c2=b2,故本命题错误,即D选项错误;故选 C.【点评】本题考查了勾股定理的正确运用,只有斜边的平方才等于其他两边的平方和.3.(2016春•临沭县期中)如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm【分析】作出直角三角形后分别求得直角三角形的两直角边的长后即可利用勾股定理求得斜边AB的长.【解答】解:如图,由题意得:AC=15×5=75cm,BC=30×6=180cm,故AB===195cm.故选A.【点评】本题考查了勾股定理的应用,解题的关键是从实际问题中抽象出直角三角形,难度不大.4.(2015春•青山区期中)如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺【分析】找到题中的直角三角形,设水深为x尺,根据勾股定理解答.【解答】解:设水深为x尺,则芦苇长为(x+1)尺,根据勾股定理得:x2+()2=(x+1)2,解得:x=12,芦苇的长度=x+1=12+1=13(尺),故选D.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.5.(2016春•南陵县期中)如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C.﹣ D.﹣1+【分析】点A在以O为圆心,OB长为半径的圆上,所以在直角△BOC中,根据勾股定理求得圆O的半径OA=OB=,然后由实数与数轴的关系可以求得a的值.【解答】解:如图,点A在以O为圆心,OB长为半径的圆上.∵在直角△BOC中,OC=2,BC=1,则根据勾股定理知OB===,∴OA=OB=,∴a=﹣1﹣.故选A.【点评】本题考查了勾股定理、实数与数轴.找出OA=OB是解题的关键.6.(2015春•蓟县期中)一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米【分析】先根据梯子的顶端下滑了0.4米求出A′C的长,再根据勾股定理求出B′C的长,进而可得出结论.【解答】解:(1)∵在Rt△ABC中,AB=2.5m,BC=0.7m,∴AC===2.4(m).∵梯子的顶端下滑了0.4米,∴A′C=2m,∵在Rt△A′B′C中,A′B′=2.5m,A′C=2m,∴B′C==1.5m,∴BB′=B′C﹣BC=1.5﹣0.7=0.8m.故选C.【点评】此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.7.(2015春•罗田县期中)在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.4【分析】根据勾股定理求出AB的长即可解答.【解答】解:在Rt△ABC中,根据勾股定理,AB==13,又∵AC=12,BC=5,AM=AC,BN=BC,∴AM=12,BN=5,∴MN=AM+BN﹣AB=12+5﹣13=4.故选D.【点评】本题综合考查了勾股定理的应用,找到关系MN=AM+BN﹣AB是关键.8.(2016春•重庆校级期中)如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169【分析】根据勾股定理,知两条直角边的平方等于斜边的平方,此题中斜边的平方即为大正方形的面积13,2ab即四个直角三角形的面积和,从而不难求得(a+b)2的值.【解答】解:(a+b)2=a2+b2+2ab=大正方形的面积+四个直角三角形的面积和=13+(13﹣1)=25.故选C.【点评】考查了勾股定理的证明,注意完全平方公式的展开:(a+b)2=a2+b2+2ab,还要注意图形的面积和a,b之间的关系.二.填空题(共5小题)9.(2016春•固始县期中)将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是7cm≤h≤16cm.【分析】如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出h 的取值范围.【解答】解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,∴h=24﹣8=16cm;当筷子的底端在A点时,筷子露在杯子外面的长度最短,在Rt△ABD中,AD=15,BD=8,∴AB==17,∴此时h=24﹣17=7cm,所以h的取值范围是7cm≤h≤16cm.故答案为:7cm≤h≤16cm.【点评】本题考查了勾股定理的应用,求出h的值最大值与最小值是解题关键.10.(2015春•汕头校级期中)如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为(1+)米.【分析】根据题意利用勾股定理得出BC的长,进而得出答案.【解答】解:由题意得:在直角△ABC中,AC2+AB2=BC2,则12+22=BC2,∴BC=,∴则树高为:(1+)m.故答案为:(1+).【点评】此题主要考查了勾股定理的应用,熟练利用勾股定理得出BC的长是解题关键.11.(2016春•高安市期中)已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于24cm2.【分析】利用勾股定理列出关系式,再利用完全平方公式变形,将a+b与c的值代入求出ab的值,即可确定出直角三角形的面积.【解答】解:∵Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,∴由勾股定理得:a2+b2=c2,即(a+b)2﹣2ab=c2=100,∴196﹣2ab=100,即ab=48,则Rt△ABC的面积为ab=24(cm2).故答案为:24cm2.【点评】此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.12.(2016春•嘉祥县期中)观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是15,112,113 (只填数,不填等式)【分析】通过观察,得出规律:这类勾股数分别为2n+1,2n (n+1),2n(n+1)+1,由此可写出第7组勾股数.【解答】解:∵第1组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,第2组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,第3组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,第4组:9=2×4+1,40=2×4×(4+1)41=2×4×(4+1)+1,∴第7组勾股数是2×7+1=15,2×7×(7+1)=112,2×7×(7+1)+1=113,即15,112,113.故答案为:15,112,113.【点评】此题考查的知识点是勾股数,属于规律性题目,关键是通过观察找出规律求解.13.(2009春•武昌区期中)观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b= 84 ,c= 85 .【分析】认真观察三个数之间的关系:首先发现每一组的三个数为勾股数,第一个数为从3开始连续的奇数,第二、三个数为连续的自然数;进一步发现第一个数的平方是第二、三个数的和;最后得出第n组数为(2n+1),(),(),由此规律解决问题.【解答】解:在32=4+5中,4=,5=;在52=12+13中,12=,13=;…则在13、b、c中,b==84,c==85.【点评】认真观察各式的特点,总结规律是解题的关键.三.解答题(共27小题)14.(2016春•黄冈期中)a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.【分析】现对已知的式子变形,出现三个非负数的平方和等于0的形式,求出a、b、c,再验证两小边的平方和是否等于最长边的平方即可.【解答】解:由a2+b2+c2+338=10a+24b+26c,得:(a2﹣10a+25)+(b2﹣24b+144)+(c2﹣26c+169)=0,即:(a﹣5)2+(b﹣12)2+(c﹣13)2=0,由非负数的性质可得:,解得,∵52+122=169=132,即a2+b2=c2,∴∠C=90°,即三角形ABC为直角三角形.【点评】本题考查勾股定理的逆定理的应用、完全平方公式、非负数的性质.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.15.(2016秋•永登县期中)如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.【分析】连接AC,则在直角△ABC中,已知AB,BC可以求AC,根据AC,AD,CD的长可以判定△ACD为直角三角形,(1)根据∠BAD=∠CAD+∠BAC,可以求解;(2)根据四边形ABCD的面积为△ABC和△ACD的面积之和可以解题.【解答】解:(1)连接AC,∵AB⊥CB于B,∴∠B=90°,在△ABC中,∵∠B=90°,∴AB2+BC2=AC2,又∵AB=CB=,∴AC=2,∠BAC=∠BCA=45°,∵CD=,DA=1,∴CD2=5,DA2=1,AC2=4.∴AC2+DA2=CD2,由勾股定理的逆定理得:∠DAC=90°,∴∠BAD=∠BAC+∠DAC=45°+90°=135°;(2)∵∠DAC=90°,AB⊥CB于B,∴S△ABC=,S△DAC=,∵AB=CB=,DA=1,AC=2,∴S△ABC=1,S△DAC=1而S四边形ABCD=S△ABC+S△DAC,∴S四边形ABCD=2.【点评】本题考查了勾股定理在直角三角形中的运用,考查了根据勾股定理逆定理判定直角三角形,考查了直角三角形面积的计算,本题中求证△ACD是直角三角形是解题的关键.16.(2016春•邹城市校级期中)如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.【分析】直接利用网格结合勾股定理求出答案.【解答】解:如图所示:△ABC即为所求.【点评】此题主要考查了勾股定理,正确借助网格求出是解题关键.17.(2015春•平南县期中)如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100km 到达B点,然后再沿北偏西30°方向走了100km到达目的地C点,求出A、C两点之间的距离.【分析】根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.【解答】解:∵AD∥BE∴∠ABE=∠DAB=60°∵∠CBE=30°∴∠ABC=180°﹣∠ABE﹣∠CBE=180°﹣60°﹣30°=90°,在Rt△ABC中,∴==200,∴A、C两点之间的距离为200km.【点评】本题考查勾股定理的应用,先确定是直角三角形后,根据各边长,用勾股定理可求出AC的长,且求出∠DAC的度数,进而可求出点C在点A的什么方向上.18.(2015秋•新泰市期中)如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?【分析】(1)过A作AE⊥BD于E,线段AE的长即为台风中心与气象台A的最短距离,由含30°角的直角三角形的性质即可得出结果;(2)根据题意得出线段CD就是气象台A受到台风影响的路程,求出CD的长,即可得出结果.【解答】解:(1)过A作AE⊥BD于E,如图1所示:∵台风中心在BD上移动,∴AE的长即为气象台距离台风中心的最短距离,在Rt△ABE中,∠ABE=90°﹣60°=30°,∴AE=AB=160,即台风中心在移动过程中,与气象台A的最短距离是160km.(2)∵台风中心以每小时20km的速度沿北偏东60°的BD 方向移动,在距离台风中心200km内的地方都要受到其影响,∴线段CD就是气象台A受到台风影响的路程,连接AC,如图2所示:在Rt△ACE中,AC=200km,AE=160km,∴CE==120km,∵AC=AD,AE⊥CD,∴CE=ED=120km,∴CD=240km.∴台风影响气象台的时间会持续240÷20=12(小时).【点评】本题考查了勾股定理在实际生活中的应用、垂径定理、含30°角的直角三角形的性质等知识;熟练掌握垂径定理和勾股定理,求出CD是解决问题(2)的关键.19.(2015春•阳东县期中)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B 开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理。
2023-2024学年八年级数学下册 专题04 勾股定理常考压轴题汇总(解析版)

专题04勾股定理常考压轴题汇总一.选择题(共23小题)1.我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成一个大正方形.如图,直角三角形的直角边长为a、b,斜边长为c.若b﹣a=2,c=10,则a+b的值为()A.12B.14C.16D.18【答案】B【解答】解:由图可得,a2+b2=c2,∴且a、b均大于0,解得,∴a+b=6+8=14,故选:B.2.如图,长方体的长为3,宽为2,高为4,一只蚂蚁从点A出发,沿长方体表面到点B处吃食物,那么它爬行最短路程是()A.B.C.D.【答案】B【解答】解:第一种情况:把我们所看到的前面和上面组成一个平面,则这个长方形的长和宽分别是6和3,则所走的最短线段是=3;第二种情况:把我们看到的左面与上面组成一个长方形,则这个长方形的长和宽分别是5和4,所以走的最短线段是=;第三种情况:把我们所看到的前面和右面组成一个长方形,则这个长方形的长和宽分别是7和2,所以走的最短线段是=;三种情况比较而言,第二种情况最短.所以它需要爬行的最短路线的长是,故选:B.3.如图,以Rt△ABC的三条边作三个正三角形,则S1、S2、S3、S4的关系为()A.S1+S2+S3=S4B.S1+S2=S3+S4C.S1+S3=S2+S4D.不能确定【答案】C【解答】解:如图,设Rt△ABC的三条边AB=c,AC=b,BC=a,∵△ACG,△BCH,△ABF是等边三角形,∴S1=S△ACG﹣S5=b2﹣S5,S3=S△BCH﹣S6=a2﹣S6,∴S1+S3=(a2+b2)﹣S5﹣S6,∵S2+S4=S△ABF﹣S5﹣S6=c2﹣S5﹣S6,∵c2=a2+b2,∴S1+S3=S2+S4,故选:C.4.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI 上,若AC+BC=6,空白部分面积为10.5,则AB的长为()A.3B.C.2D.【答案】B【解答】解:∵四边形ABGF是正方形,∴∠FAB=∠AFG=∠ACB=90°,∴∠FAC+∠BAC=∠FAC+∠ABC=90°,∴∠FAC=∠ABC,在△FAM与△ABN中,,∴△FAM≌△ABN(ASA),=S△ABN,∴S△F AM=S四边形FNCM,∴S△ABC∵在△ABC中,∠ACB=90°,∴AC2+BC2=AB2,∵AC+BC=6,∴(AC+BC)2=AC2+BC2+2AC•BC=36,∴AB2+2AC•BC=36,=10.5,∵AB2﹣2S△ABC∴AB2﹣AC•BC=10.5,∴3AB2=57,解得AB=或﹣(负值舍去).故选:B.5.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.3cm2B.4cm2C.6cm2D.12cm2【答案】C【解答】解:将此长方形折叠,使点B与点D重合,∴BE=ED.∵AD=9cm=AE+DE=AE+BE.∴BE=9﹣AE,根据勾股定理可知AB2+AE2=BE2.解得AE=4.∴△ABE的面积为3×4÷2=6.故选:C.6.如图,阴影部分表示以Rt△ABC的各边为直径向上作三个半圆所组成的两个新月形,面积分别记作S1和S2.若S1+S2=7,AC=3,则BC长是()A.3.5B.C.4D.5【答案】B【解答】解:以AC为直径的半圆的面积=×π×=π,同理:以BC为直径的半圆的面积=π,以AB为直径的半圆的面积=π,∴S1+S2=π+π+△ABC的面积﹣π,∵∠ACB=90°,∴AC2+BC2=AB2,∴S1+S2=△ABC的面积=AC•BC=7,∵AC=3,∴BC=.故选:B.7.如图,在长方体ABCD﹣EFGH盒子中,已知AB=4cm,BC=3cm,CG=5cm,长为10cm 的细直木棒IJ恰好从小孔G处插入,木棒的一端I与底面ABCD接触,当木棒的端点Ⅰ在长方形ABCD内及边界运动时,GJ长度的最小值为()A.(10﹣5)cm B.3cm C.(10﹣4)cm D.5cm【答案】A【解答】解:当GI最大时,GJ最小,当I运动到点A时,GI最大,此时GI=cm,而AC2=AB2+BC2=42+32=25,∴GI===5(cm),∴GJ长度的最小值为(10﹣5)cm.故选:A.8.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=6,BC=10,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为()A.420B.440C.430D.410【答案】B【解答】解:如图,延长AB交KL于P,延长AC交LM于Q,由题意得,∠BAC=∠BPF=∠FBC=90°,BC=BF,∴∠ABC+∠ACB=90°=∠PBF+∠ABC,∴∠ACB=∠PBF,∴△ABC≌△PFB(AAS),同理可证△ABC≌△QCG(AAS),∴PB=AC=8,CQ=AB=6,∵图2是由图1放入长方形内得到,∴IP=8+6+8=22,DQ=6+8+6=20,∴长方形KLMJ的面积=22×20=440.故选:B.9.国庆假期间,妍妍与同学去玩寻宝游戏,按照藏宝图,她从门口A处出发先往东走9km,又往北走3km,遇到障碍后又往西走7km,再向北走2km,再往东走了4km,发现走错了之后又往北走1km,最后再往西走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.3km B.10km C.6km D.km【答案】D【解答】解:过点B作BC⊥AC,垂足为C.观察图形可知AC=9﹣7+4﹣1=5(km),BC=3+2+1=6(km),在Rt△ACB中,AB=(km).答:门口A到藏宝点B的直线距离是km,故选:D.10.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AB=9,BC=6,则BD的长为()A.3B.4C.5D.6【答案】B【解答】解:∵∠ACB=90°,AB=9,BC=6,∴,∵,∴AC•BC=AB•CD,,,∵CD⊥AB,∴∠CDB=90°,∴,故选:B.11.如图,某小区有一块长方形花圃,为了方便居民不用再走拐角,打算用瓷砖铺上一条新路,居民走新路比走拐角近()A.2m B.3m C.3.5m D.4m【答案】D【解答】解:根据勾股定理求得,AB==10(m),∴AC+BC﹣AB=6+8﹣10=4(m),故选:D.12.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是()A.148B.100C.196D.144【答案】A【解答】解:设将CA延长到点D,连接BD,根据题意,得CD=12×2=24,BC=7,∵∠BCD=90°,∴BC2+CD2=BD2,即72+242=BD2,∴BD=25,∴AD+BD=12+25=37,∴这个风车的外围周长是37×4=148.故选:A.13.如图,四边形ABCD中,AD⊥CD于点D,BC=2,AD=8,CD=6,点E是AB的中点,连接DE,则DE的最大值是()A.5B.C.6D.【答案】C【解答】解:如图,连接AC,取AC的中点为M,连接DM、EM,∵AD⊥CD,∴∠ADC=90°,∵AD=8,CD=6,∴AC=,∵M是AC的中点,∴DM=AC=5,∵M是AC的中点,E是AB的中点,∴EM是△ABC的中位线,∵BC=2,∴EM=BC=1,∵DE≤DM+EM(当且仅当点M在线段DE上时,等号成立),∴DE≤6,∴DE的最大值为6.故选:C.14.如图,长为8cm的橡皮筋放置在数轴上,固定两端A和B,然后把中点C垂直向上拉升3cm到D点,则橡皮筋被拉长了()A.2cm B.3cm C.4cm D.1cm【答案】A【解答】解:∵点C为线段AB的中点,∴AC=AB=4cm,在Rt△ACD中,CD=3cm;根据勾股定理,得:AD==5(cm);∵CD⊥AB,∴∠DCA=∠DCB=90°,在△ADC和△BDC中,,∴△ADC≌△BDC(SAS),∴AD=BD=5cm,∴AD+BD﹣AB=2AD﹣AB=10﹣8=2(cm);∴橡皮筋被拉长了2cm.故选:A.15.如图的数轴上,点A,C对应的实数分别为1,3,线段AB⊥AC于点A,且AB长为1个单位长度,若以点C为圆心,BC长为半径的弧交数轴于0和1之间的点P,则点P表示的实数为()A.B.C.D.【答案】A【解答】解:由题意可得∠BAC=90°,AB=1,AC=3﹣1=2,则CB==,那么点P表示的实数为3﹣,故选:A.16.“四千年来,数学的道理还是相通的”.运用祖冲之的出入相补原理也可证明勾股定理.若图中空白部分的面积是11,整个图形(连同空白部分)的面积是25,则大正方形的边长是()A.B.C.D.【答案】D【解答】解:如下图,设图中直角三角形的两条直角边长分别为a、b,斜边为c,∵图中空白部分的面积是11,整个图形(连同空白部分)的面积是25,∴可有,解得c2=18,解得或(不合题意,舍去),∴大正方形的边长是.故选:D.17.如图所示的一段楼梯,高BC是3米,斜边AB长是5米,现打算在楼梯上铺地毯,至少需要地毯的长度为()A.5米B.6米C.7米D.8米【答案】C【解答】解:∵△ABC是直角三角形,BC=3m,AB=5m∴AC==4(m),∴如果在楼梯上铺地毯,那么至少需要地毯为AC+BC=7米,故选:C.18.勾股定理是人类早期发现并证明的重要数学定理之一,是数形结合的重要细带.数学家欧几里得利用如图验证了勾股定理.以直角三角形ABC的三条边为边长向外作正方形ACKJ,正方形ABFE,正方形BCIH,连接AH.CF,具中正方形BCIH面积为1,正方形ABFE面积为5,则以CF为边长的正方形面积为()A.4B.5C.6D.10【答案】D【解答】解:过点C作CM⊥EF于点M,交AB于点N,∵正方形ABFE面积为5,正方形BCIH面积为1,∴CN⊥AB,BC=1,AB=MN=,BN=FN,∵△ABC是直角三角形,∠ACB=90°,∴AC===2,∴,即=CN,∴CN=,∴BN=FM===,∴CM=CN+MN==,∴CF=10,∴以CF为边长的正方形面积为10.故选:D.19.如图,Rt△ABC中,∠C=90°.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN.四块阴影部分的面积如图所示分别记为S、S1、S2、S3,若S=10,则S1+S2+S3等于()A.10B.15C.20D.30【答案】C【解答】解:如图,过E作BC的垂线交ED于D,连接EM.在△ACB和△BDE中,∠ACB=∠BDE=90°,∠CAB=∠EBD,AB=BD,∴△ACB≌△BND(AAS),同理,Rt△GDE≌Rt△HCB,∴GE=HB,∠EGD=∠BHC,∴FG=EH,∴DE=BC=CM,∵DE∥CM,∴四边形DCME是平行四边形,∵∠DCM=90°,∴四边形DCME是矩形,∴∠EMC=90°,∴E、M、N三点共线,∵∠P=∠EMH=90°,∠PGF=∠DGE=∠BHC=∠EHM,∴△PGF≌△MHE(AAS),∵图中S1=S Rt△EMH,S△BHC=S△EGD,∴S1+S3=S Rt△ABC.S2=S△ABC,∴S1+S2+S3=Rt△ABC的面积×2=20.故选:C.20.如图,在Rt△ABC中,∠C=90°,分别以AB、AC、BC为直径向外作半圆,它们的面积分别记作S1、S2、S3,若S1=25,S3=16,则S2为()A.9B.11C.32D.41【答案】A【解答】解:在Rt△ABC中,∠C=90°,∴AB2=AC2+BC2.∵S1=(AB)2π=AB2=25,∴AB2=25×.同理BC2=16×.∴AC2=AB2﹣BC2=25×﹣16×=9×.∴S1=(AC)2π=AC2=×9×=9.故选:A.21.如图,在Rt△ABC中,∠ACB=90°,分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4.若已知S△ABC=S,则下列结论:①S4=S;②S2=S;③S1+S3=S2;④S1+S2+S3+S4=2.5S.其中正确的结论是()A.①②③B.①②④C.①③④D.②③④【答案】A【解答】解:由题意有Rt△EBD≌Rt△ABC,∴S4=S;故①正确;过F作AM的垂线交AM于N,由题意,得Rt△ANF≌Rt△ABC,Rt△NFK≌Rt△CAT,所以S2=S,故②正确;连接FP,FQ,由题意,可得△AQF≌△ACB,则F,P,Q三点共线,由Rt△NFK≌Rt△CAT可得Rt△FPT≌Rt△EMK,∴S3=S△FPT,可得Rt△AQF≌Rt△ACB,∴S1+S3=S Rt△AQF=S,故③正确;S1+S2+S3+S4=(S1+S3)+S2+S4+S Rt△ABC+S Rt△ABC=S Rt△ABC×3=S Rt△ABC=3S,故④不正确.故选:A.22.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为()尺.A.10B.12C.13D.14【答案】C【解答】解:设水深为x尺,则芦苇长为(x+1)尺,根据勾股定理得:x2+()2=(x+1)2,解得:x=12,芦苇的长度=x+1=12+1=13(尺),答:芦苇长13尺.故选:C.23.将四个全等的直角三角形作为叶片按图1摆放成一个风车形状,形成正方形ABCD和正方形EFGH.现将四个直角三角形的较长直角边分别向外延长,且A′E=ME.B′F =NF,C′G=PG,D′H=HQ,得到图2所示的“新型数学风车”的四个叶片,即△A′EF,△B′FG,△C′CH.△D′HE.若FM平分∠BFE,正方形ABCD和正方形EFGH 的边长比为1:5.若”新型数学风车”的四个叶片面积和是m,则正方形EFCH的面积是()A.B.C.3m D.【答案】B【解答】解:∵将四个全等的直角三角形作为叶片按图1摆放成一个风车形状,形成正方形ABCD和正方形EFCH.正方形ABCD和正方形EFGH的边长比为1:5.∴设正方形ABCD的边长为a,则正方形EFGH的边长为5a,设AE=BF=CG=DH=x,在△BEF中,BE2+BF2=EF2,即(x+a)2+x2=(5a)2,x2+ax﹣12a2=0,(x+4a)(x﹣3a)=0,x=﹣4a(舍去)或x=3a,∴BE=4a,BF=3a,EF=5a,∵FM平分∠BFE,∴△EMF边EF上的高为BM,+S△MBF=S△BEF,则S△BMF即,∴,∴BM=,∵A'E=ME=BE﹣BM=4a﹣a,若”新型数学风车”的四个叶片面积和是m,=S△EF A'=m,∴S△EMF∴,∴a m,∴a=∴EF=5a=,=EF=,∴S正方形EFCH故选:B.二.填空题(共14小题)24.如图①,四个全等的直角三角形与一个小正方形,恰好拼成一个大正方形,这个图形是由我国汉代数学家赵爽在为《周髀算经》作注时给出的,人们称它为“赵爽弦图”.如果图①中的直角三角形的长直角边为7cm,短直角边为3cm,连结图②中四条线段得到如图③的新图案,则图③中阴影部分的周长为32cm.【答案】32.【解答】解:由题意得:BD=7cm,AB=CD=3cm,∴BC=7﹣3=4(cm),由勾股定理得:AC==5(cm),∴阴影的周长=4(AB+AC)=4×(3+5)=32(cm).故答案为:32.25.如图,在△ABC中,已知:∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发,沿射线BC以1cm/s的速度运动,设运动的时间为t秒,连接PA,当△ABP为等腰三角形时,t的值为16或10或.【答案】16或10或.【解答】解:在△ABC中,∠ACB=90°,由勾股定理得:BC=cm,∵△ABP为等腰三角形,当AB=AP时,则BP=2BC=16cm,即t=16;当BA=BP=10cm时,则t=10;当PA=PB时,如图:设BP=PA=x cm,则PC=(8﹣x)cm,在Rt△ACP中,由勾股定理得:PC2+AC2=AP2,∴(8﹣x)2+62=x2,解得x=,∴t=.综上所述:t的值为16或10或.故答案为:16或10或.26.如图,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的“勾股分割点”.已知点M,N是线段AB的“勾股分割点”,若AM=4,MN=5,则斜边BN的长为.【答案】.【解答】解:当BN为最大线段时,∵点M,N是线段AB的勾股分割点,∴BN===,故答案为:.27.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示“垂美”四边形ABCD,对角线AC,BD交于点O,若AB=6,CD=10,则AD2+BC2=136.【答案】136.【解答】解:∵BD⊥AC,∴∠COB=∠AOB=∠AOD=∠COD=90°,∴BO2+CO2=CB2,OB2+OA2=AB2=36,OA2+OD2=AD2,OC2+OD2=CD2=100,∴BO2+CO2+OA2+OB2=36+100,∴AD2+CB2=BO2+CO2+OA2+OB2=136;故答案为:136.28.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(30,0)(0,12),点D是OA的中点,点P在BC上运动,当△ODP是腰长为15的等腰三角形时,点P 的坐标为(9,12)或(3,12)或(24,12).【答案】(9,12)或(6,12)或(24,12).【解答】解:由题意,当△ODP是腰长为15的等腰三角形时,有三种情况:(1)如答图①所示,PD=OD=15,点P在点D的左侧.过点P作PE⊥x轴于点E,则PE=12.在Rt△PDE中,由勾股定理得:DE===9,∴OE=OD﹣DE=15﹣9=6,∴此时点P坐标为(6,12);(2)如答图②所示,OP=OD=15.过点P作PE⊥x轴于点E,则PE=4.在Rt△POE中,由勾股定理得:OE===9,∴此时点P坐标为(9,12);(3)如答图③所示,PD=OD=5,点P在点D的右侧.过点P作PE⊥x轴于点E,则PE=4.在Rt△PDE中,由勾股定理得:DE===9,∴OE=OD+DE=15+9=24,∴此时点P坐标为(24,12).综上所述,点P的坐标为:(9,12)或(6,12)或(24,12);故答案为:(9,12)或(6,12)或(24,12).29.《勾股》中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合2寸,问门广几何?”意思是:如图推开两扇门(AD和BC),门边沿D,C两点到门槛AB的距离是1尺(1尺=10寸),两扇门的间隙CD为2寸,则门槛AB长为101寸.【答案】101.【解答】解:设OA=OB=AD=BC=r寸,如图,过D作DE⊥AB于点E,则DE=10寸,OE=CD=1(寸),AE=(r﹣1)寸,在Rt△ADE中,由勾股定理得:AE2+DE2=AD2,即(r﹣1)2+102=r2,解得:r=50.5,∴2r=101,即门槛AB长为101寸,故答案为:101.30.如图,在某次军事演习中,舰艇1号在指挥中心(O处)北偏西30°的A处,舰艇2号在指挥中心南偏东60°的B处,并且OA=OB.接到行动指令后,舰艇1号向正东方向以60海里/小时的速度前进,舰艇2号沿北偏东60°的方向以m海里/小时的速度前进.1.5小时后,指挥中心观测到两舰艇分别到达点E,F处,若∠EOF=75°,EF=210海里,则m的值为80.【答案】80.【解答】解:延长AE、BF相交于点C,∵∠AOB=30°+90°+30°=150°,∠EOF=75°,∴∠EOF=∠AOB,又∵OA=OB,∠OAC+∠OBC=(90°﹣30°)+(60°+60°)=180°,延长FB至D,使BD=AE,连接OD,∵∠OBD=∠OBC,∴.∠OBD=∠A,∴△OBD≌△OAE(SAS),∴OD=OE,∠BOD=∠AOE,∵∠EOF=∠AOB=∠EOD,∴.∠EOF=∠DOF,又∵OF=OF,∴△EOF≌△DOF(SAS),∴EF=AE+BF,即EF=1.5×(60+m)=210.解得m=80.故答案为:80.31.如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形EFGH组成,恰好拼成一个大正方形ABCD.连结EG并延长交BC于点M.若AB=5,EF=1,则GM的长为.【解答】解:由图可知∠AED=90°,AB=5,EF=1,∵大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成,故AE=BF=GC=DH,设DE=x,则在Rt△AED中,AD=AB=5,AE=1+x,根据勾股定理,得AD2=DE2+AE2,即52=x2+(1+x)2,解得:x1=3,x2=﹣4(舍去).过点M作MN⊥FB于点N,如图所示.∵四边形EFGH为正方形,EG为对角线,∴△EFG为等腰直角三角形,∴∠EGF=∠NGM=45°,故△GNM为等腰直角三角形.设GN=NM=a,则NB=GB﹣GN=3﹣a,∵MN∥AF,∴△BMN∽△BAF,∴=,将MN=a,AF=3,BN=3﹣a,BF=4代入,得=,解得a=,∴MN=GN=,在Rt△MGN中,由勾股定理,得GM===.32.如图,铁路上A、D两点相距25千米,B,C为两村庄,AB⊥AD于A,CD⊥AD于D,已知AB=15km,CD=10km,现在要在铁路AD上建一个土特产品收购站P,使得B、C 两村到P站的距离相等,则P站应建在距点A10千米.【答案】10.【解答】解:设AP=x千米,则DP=(25﹣x)千米,∵B、C两村到P站的距离相等,∴BP=PC.在Rt△APB中,由勾股定理得BP2=AB2+AP2,在Rt△DPC中,由勾股定理得PC2=CD2+PD2,∴AB2+AP2=CD2+PD2,又∵AB=15km,CD=10km,∴152+x2=102+(25﹣x)2,∴x=10.故答案为:10.33.如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为20cm(杯壁厚度不计).【答案】见试题解答内容【解答】解:如图:将杯子侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B===20(cm).故答案为20.34.如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD⊥BC.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是.【答案】.【解答】解:如图,连接BP,在△ABC中,AB=AC=10,BC=12,AD=8,∴BD=DC,∴BP=PC,∴PC+PQ=BP+PQ=BQ,∴当B,P,Q共线时,PC+PQ的值最小,∴当BQ⊥AC时,BQ的值最小,令AQ'=a,则CQ'=10﹣a,∵BQ'⊥AC,∴AB2﹣AQ'2=BC2﹣CQ'2,即102﹣a2=122﹣(10﹣a)2,解得a=,∴BQ'==,∴PC+PQ的最小值为,故答案为:.35.如图,在△ABC中,∠ABC=45°,AB=,AC=6,BC>4,点E,F分别在BC,AC边上,且AF=CE,则AE+BF的最小值为2.【答案】2.【解答】解:过A点作AG∥BC,截取AG=AC,连接FG,BG,过B作BR⊥AG,交AG的反向延长线于R,则∠RBC=∠BRA=90°,∴∠GAF=∠ACE,在△AFG和△CEA中,,∴△AFG≌△CEA(SAS),∴GF=AE,∴AE+BF的最小值,即为BG的长,∵∠ABC=45°,∴∠RAB=∠EBA=45°,∵AB=4,∴BR=AR=4,∵AC=6,∴AG=AC=6,∴RG=AR+AG=4+6=10,∴BG===2,即AE+BF的最小值为2.故答案为:2.36.如图,在△ABC中,AB=9cm,AC=12cm,BC=15cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是cm.【答案】.【解答】解:∵在△ABC中,AB=9cm,AC=12cm,BC=15cm,∴BC2=AB2+AC2,∴∠A=90°,∵MD⊥AB,ME⊥AC,∴∠A=∠ADM=∠AEM=90°,∴四边形ADME是矩形,∴DE=AM,当AM⊥BC时,AM的长最短,根据三角形的面积公式得:AB•AC=BC•AM,∴9×12=15AM,AM=,即DE的最小值是cm.故答案为:.37.如图,Rt△ABC中,.点P为△ABC内一点,PA2+PC2=AC2.当PB的长度最小时,△ACP的面积是.【答案】.【解答】解:如图所示,取AC中点O,连接PO,BO,∵PA2+PC2=AC2,∴∠APC=90°,∴,∵BP+OP≥OB,∴当B、P、O三点共线时BP+OP有最小值,即此时BP有最小值,∵∠ACB=90°,∴,∴BP=BO﹣OP=2,∴BP=PO,又∠ACB=90°,∴PC=BO=2,∴PC=PO=CO,∴△OPC是等边三角形,∴∠PCO=60°,∠PAC=30°∴AP==2,∴,故答案为:.三.解答题(共4小题)38.如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A 出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?【答案】见试题解答内容【解答】解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,∴BC=CA.设AC为x,则OC=9﹣x,由勾股定理得:OB2+OC2=BC2,又∵OA=9,OB=3,∴32+(9﹣x)2=x2,解方程得出x=5.∴机器人行走的路程BC是5cm.39.如图,在Rt△ABC中,∠ACB=90°,AB=10cm,AC=6cm,动点P从B出发沿射线BC以1cm/s的速度运动,设运动时间为t(s).(1)求BC边的长.(2)当△ABP为等腰三角形时,求t的值.【答案】或10或16.【解答】解:在Rt△ABC中,∠ACB=90°,AB=10cm,AC=6cm,∴BC=,当AP=BP时,如图1,则AP=t,PC=BC﹣BP=8﹣t,在Rt△ACP中,AC2+CP2=AP2,∴62+(8﹣t)2=t2,解得t=;当AB=BP时,如图2,则BP=t=10;当AB=AP时,如图3,则BP=2BC;∴t=2×8=16,综上,t的值为或10或16.40.今年第6号台风“烟花”登陆我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB =500km,经测量,距离台风中心260km及以内的地区会受到影响.(1)海港C受台风影响吗?为什么?(2)若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?【答案】(1)海港C受台风影响,理由见解答过程;(2)台风影响该海港持续的时间为小时.【解答】解:(1)海港C受台风影响,理由:∵AC=300km,BC=400km,AB=500km,∴AC2+BC2=AB2,∴△ABC是直角三角形,∠ACB=90°;过点C作CD⊥AB于D,∵△ABC是直角三角形,∴AC×BC=CD×AB,∴300×400=500×CD,∴CD=240(km),∵以台风中心为圆心周围260km以内为受影响区域,∴海港C受台风影响;(2)当EC=260km,FC=260km时,正好影响C港口,∵ED=(km),∴EF=2ED=200km,∵台风的速度为28千米/小时,∴200÷28=(小时).答:台风影响该海港持续的时间为小时.41.请阅读下列材料:已知:如图(1)在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D,使问题得到解决.请你参考小明的思路探究并解决下列问题:(1)猜想BD、DE、EC三条线段之间存在的数量关系式,直接写出你的猜想;(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;(3)已知:如图(3),等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.【答案】见试题解答内容【解答】解:(1)DE2=BD2+EC2;(2)关系式DE2=BD2+EC2仍然成立.证明:将△ADB沿直线AD对折,得△AFD,连FE∴△AFD≌△ABD,∴AF=AB,FD=DB,∠FAD=∠BAD,∠AFD=∠ABD,又∵AB=AC,∴AF=AC,∵∠FAE=∠FAD+∠DAE=∠FAD+45°,∠EAC=∠BAC﹣∠BAE=90°﹣(∠DAE﹣∠DAB)=45°+∠DAB,∴∠FAE=∠EAC,又∵AE=AE,∴△AFE≌△ACE,∴FE=EC,∠AFE=∠ACE=45°,∠AFD=∠ABD=180°﹣∠ABC=135°∴∠DFE=∠AFD﹣∠AFE=135°﹣45°=90°,∴在Rt△DFE中,DF2+FE2=DE2,即DE2=BD2+EC2;解法二:将△EAC绕点A顺时针旋转90°得到△TAB.连接DT.∴∠ABT=∠C=45°,AT=AE,∠TAE=90°,∵∠ABC=45°,∴∠TBC=∠TBD=90°,∵∠DAE=45°,∴∠DAT=∠DAE,∵AD=AD,∴△DAT≌△DAE(SAS),∴DT=DE,∵DT2=DB2+EC2,∴DE2=BD2+EC2;(3)当AD=BE时,线段DE、AD、EB能构成一个等腰三角形.如图,与(2)类似,以CE为一边,作∠ECF=∠ECB,在CF上截取CF=CB,可得△CFE≌△CBE,△DCF≌△DCA.∴AD=DF,EF=BE.∴∠DFE=∠1+∠2=∠A+∠B=120°.若使△DFE为等腰三角形,只需DF=EF,即AD=BE,∴当AD=BE时,线段DE、AD、EB能构成一个等腰三角形,且顶角∠DFE为120°.。
初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析) 之欧阳生创编

初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)时间:2021.02.08 创作人:欧阳生一.选择题(共8小题)1.直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C.D.2.下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2D.在Rt△ABC中,∠B=90°,所以a2+b2=c23.如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm4.如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺5.如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C.﹣ D.﹣1+6.一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米7.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.48.如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169二.填空题(共5小题)9.将一根24cm的筷子,置于底面直径为15cm,高8cm 的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是.10.如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为米.11.已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于.12.观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是(只填数,不填等式)13.观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b=,c=.三.解答题(共27小题)14.a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.15.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.16.如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.17.如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100km到达B点,然后再沿北偏西30°方向走了100km到达目的地C点,求出A、C 两点之间的距离.18.如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?19.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.20.在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△A BC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.(1)△ABC的面积为:.(2)若△DEF三边的长分别为、、,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为.(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是m2.21.(1)在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.请你将△ABC的面积直接填写在横线上.思维拓展:(2)已知△ABC三边的长分别为a(a>0),求这个三角形的面积.我们把上述求△ABC面积的方法叫做构图法.如图2,网格中每个小正方形的边长都是a,请在网格中画出相应的△ABC,并求出它的面积.类比创新:(3)若△ABC三边的长分别为(m>0,n>0,且m≠n),求出这个三角形的面积.如图3,网格中每个小长方形长、宽都是m,n,请在网格中画出相应的△ABC,用网格计算这个三角形的面积.22.有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?23.(拓展创新)在教材中,我们通过数格子的方法发现了直角三角形的三边关系,利用完全相同的四个直角三角形采用拼图的方式验证了勾股定理的正确性.问题1:以直角三角形的三边为边向形外作等边三角形,探究S′+S″与S的关系(如图1).问题2:以直角三角形的三边为斜边向形外作等腰直角三角形,探究S′+S″与S的关系(如图2).问题3:以直角三角形的三边为直径向形外作半圆,探究S′+S″与S的关系(如图3).24.如图,在平面坐标系中,点A、点B分别在x轴、y轴的正半轴上,且OA=OB,另有两点C(a,b)和D(b,﹣a)(a、b均大于0);(1)连接OD、CD,求证:∠ODC=45°;(2)连接CO、CB、CA,若CB=1,C0=2,CA=3,求∠OCB 的度数;(3)若a=b,在线段OA上有一点E,且AE=3,CE=5,AC=7,求△OCA的面积.25.11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题“小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻飞去抓鱼,并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树根有多远?26.(1)先化简,再求值:x(x﹣2)﹣(x+1)(x﹣1),其中x=10.(2)已知,求代数式(x+1)2﹣4(x+1)+4的值.(3)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图:①从点A出发在图中画一条线段AB,使得AB=;②画出一个以(1)中的AB为斜边的等腰直角三角形,使三角形的三个顶点都在格点上,并根据所画图形求出等腰直角三角形的腰长.27.[问题情境]勾股定理是一条古老的数学定理,它有很多种证明方法.我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数学关系”(勾股定理)带到其它星球,作为地球人与其他星球“人”进行第一次“谈话”的语言;[定理表述]请你根据图1中的直角三角形叙述勾股定理;[尝试证明]以图1中的直角三角形为基础,将两个直角边长为a,b,斜边长为c的三角形按如图所示的方式放置,连接两个之间三角形的另外一对锐角的顶点(如图2),请你利用图2,验证勾股定理;[知识扩展]利用图2中的直角梯形,我们可以证明<,其证明步骤如下:∵BC=a+b,AD=又∵在直角梯形ABCD中,有BCAD(填大小关系),即∴.28.观察、思考与验证(1)如图1是一个重要公式的几何解释,请你写出这个公式;(2)如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°;(3)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的《新英格兰教育日志》上),请你写出验证过程.29.超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?(参考数据:=1.41,=1.73)30.中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.(1)请用直尺和圆规作出C处的位置;(2)求我国海监船行驶的航程BC的长.31.在一次“构造勾股数”的探究性学习中,老师给出了下表:m 2 3 3 4 …n 1 1 2 3 …a 22+12 32+12 32+22 42+32 …b 4 6 12 24 …c 22﹣12 32﹣12 32﹣22 42﹣32 …其中m、n为正整数,且m>n.(1)观察表格,当m=2,n=1时,此时对应的a、b、c 的值能否为直角三角形三边的长?说明你的理由.(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=,b=,c=.(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.32.如图1,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<8).(1)请在4×8的网格纸图2中画出t为6秒时的线段PQ.并求其长度;(2)当t为多少时.△PQB是以BP为底的等腰三角形.33.阅读下面的情景对话,然后解答问题:(1)理解:①根据“奇异三角形”的定义,请你判断:“等边三角形一定是奇异三角形”吗?(填是或不是)②若某三角形的三边长分别为1、、2,则该三角形(是或不是)奇异三角形.(2)探究:若Rt△ABC是奇异三角形,且其两边长分别为2、2,则第三边的长为,且这个直角三角形的三边之比为(从小到大排列,不得含有分母).(3)设问:请提出一个和奇异三角形有关的问题.(不用解答)34.观察下列各式,你有什么发现?32=4+5,52=12+13,72=24+25,92=40+41,…用你的发现解决下列问题:(1)填空:112=+;(2)请用含字母n(n为正整数)的关系式表示出你发现的规律:;(3)结合勾股定理有关知识,说明你的结论的正确性.35.小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m (在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?36.如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.37.如图,四边形ABCD的三边(AB、BC、CD)和BD的长度都为5厘米,动点P从A出发(A→B→D)到D,速度为2厘米/秒,动点Q从点D出发(D→C→B→A)到A,速度为2.8厘米/秒.5秒后P、Q相距3厘米,试确定5秒时△APQ的形状.38.一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由.39.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地°送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺),此时踏板升高离地五尺(BD=5尺),求秋千绳索(OA或OB)的长度.40.如图,∠AOB=90°,OA=45cm,OB=15cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?1.已知直角三角形两边的长为3和4,则此三角形的周长为()A.12 B.7+C.12或7+D.以上都不对2.图中字母所代表的正方形的面积为144的选项为()A.B. C.D.3.如图,数轴上的点A所表示的数为x,则x的值为()A.B.﹣ C.2 D.﹣24.如图,带阴影的正方形面积是.5.如图,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=.6.正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,(1)在图①中,画一个面积为10的正方形;(2)在图②、图③中,分别画两个不全等的直角三角形,使它们的三边长都是无理数.初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)参考答案与试题解析一.选择题(共8小题)1.(2016秋•吴江区期中)直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C.D.【分析】首先根据勾股定理,得:斜边==13.再根据直角三角形的面积公式,求出斜边上的高.【解答】解:由题意得,斜边为=13.所以斜边上的高=12×5÷13=.故选D.【点评】运用了勾股定理.注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.2.(2016春•抚顺县期中)下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2D.在Rt△ABC中,∠B=90°,所以a2+b2=c2【分析】在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角,根据此就可以直接判断A、B、C、D选项.【解答】解:在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角.A、不确定c是斜边,故本命题错误,即A选项错误;B、不确定第三边是否是斜边,故本命题错误,即B选项错误;C、∠C=90°,所以其对边为斜边,故本命题正确,即C选项正确;D、∠B=90°,所以斜边为b,所以a2+c2=b2,故本命题错误,即D选项错误;故选C.【点评】本题考查了勾股定理的正确运用,只有斜边的平方才等于其他两边的平方和.3.(2016春•临沭县期中)如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm【分析】作出直角三角形后分别求得直角三角形的两直角边的长后即可利用勾股定理求得斜边AB的长.【解答】解:如图,由题意得:AC=15×5=75cm,BC=30×6=180cm,故AB===195cm.故选A.【点评】本题考查了勾股定理的应用,解题的关键是从实际问题中抽象出直角三角形,难度不大.4.(2015春•青山区期中)如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺【分析】找到题中的直角三角形,设水深为x尺,根据勾股定理解答.【解答】解:设水深为x尺,则芦苇长为(x+1)尺,根据勾股定理得:x2+()2=(x+1)2,解得:x=12,芦苇的长度=x+1=12+1=13(尺),故选D.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.5.(2016春•南陵县期中)如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C.﹣ D.﹣1+【分析】点A在以O为圆心,OB长为半径的圆上,所以在直角△BOC中,根据勾股定理求得圆O的半径OA=OB=,然后由实数与数轴的关系可以求得a的值.【解答】解:如图,点A在以O为圆心,OB长为半径的圆上.∵在直角△BOC中,OC=2,BC=1,则根据勾股定理知OB===,∴OA=OB=,∴a=﹣1﹣.故选A.【点评】本题考查了勾股定理、实数与数轴.找出OA=OB 是解题的关键.6.(2015春•蓟县期中)一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米【分析】先根据梯子的顶端下滑了0.4米求出A′C的长,再根据勾股定理求出B′C的长,进而可得出结论.【解答】解:(1)∵在Rt△ABC中,AB=2.5m,BC=0.7m,∴AC===2.4(m).∵梯子的顶端下滑了0.4米,∴A′C=2m,∵在Rt△A′B′C中,A′B′=2.5m,A′C=2m,∴B′C==1.5m,∴BB′=B′C﹣BC=1.5﹣0.7=0.8m.故选C.【点评】此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.7.(2015春•罗田县期中)在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.4【分析】根据勾股定理求出AB的长即可解答.【解答】解:在Rt△ABC中,根据勾股定理,AB==13,又∵AC=12,BC=5,AM=AC,BN=BC,∴AM=12,BN=5,∴MN=AM+BN﹣AB=12+5﹣13=4.故选D.【点评】本题综合考查了勾股定理的应用,找到关系MN=AM+BN﹣AB是关键.8.(2016春•重庆校级期中)如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169【分析】根据勾股定理,知两条直角边的平方等于斜边的平方,此题中斜边的平方即为大正方形的面积13,2ab即四个直角三角形的面积和,从而不难求得(a+b)2的值.【解答】解:(a+b)2=a2+b2+2ab=大正方形的面积+四个直角三角形的面积和=13+(13﹣1)=25.故选C.【点评】考查了勾股定理的证明,注意完全平方公式的展开:(a+b)2=a2+b2+2ab,还要注意图形的面积和a,b之间的关系.二.填空题(共5小题)9.(2016春•固始县期中)将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是7cm≤h≤16cm.【分析】如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出h 的取值范围.【解答】解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,∴h=24﹣8=16cm;当筷子的底端在A点时,筷子露在杯子外面的长度最短,在Rt△ABD中,AD=15,BD=8,∴AB==17,∴此时h=24﹣17=7cm,所以h的取值范围是7cm≤h≤16cm.故答案为:7cm≤h≤16cm.【点评】本题考查了勾股定理的应用,求出h的值最大值与最小值是解题关键.10.(2015春•汕头校级期中)如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为(1+)米.【分析】根据题意利用勾股定理得出BC的长,进而得出答案.【解答】解:由题意得:在直角△ABC中,AC2+AB2=BC2,则12+22=BC2,∴BC=,∴则树高为:(1+)m.故答案为:(1+).【点评】此题主要考查了勾股定理的应用,熟练利用勾股定理得出BC的长是解题关键.11.(2016春•高安市期中)已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于24cm2.【分析】利用勾股定理列出关系式,再利用完全平方公式变形,将a+b与c的值代入求出ab的值,即可确定出直角三角形的面积.【解答】解:∵Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,∴由勾股定理得:a2+b2=c2,即(a+b)2﹣2ab=c2=100,∴196﹣2ab=100,即ab=48,则Rt△ABC的面积为ab=24(cm2).故答案为:24cm2.【点评】此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.12.(2016春•嘉祥县期中)观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是15,112,113 (只填数,不填等式)【分析】通过观察,得出规律:这类勾股数分别为2n+1,2n(n+1),2n(n+1)+1,由此可写出第7组勾股数.【解答】解:∵第1组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,第2组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,第3组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,第4组:9=2×4+1,40=2×4×(4+1)41=2×4×(4+1)+1,∴第7组勾股数是2×7+1=15,2×7×(7+1)=112,2×7×(7+1)+1=113,即15,112,113.故答案为:15,112,113.【点评】此题考查的知识点是勾股数,属于规律性题目,关键是通过观察找出规律求解.13.(2009春•武昌区期中)观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b= 84 ,c= 85 .【分析】认真观察三个数之间的关系:首先发现每一组的三个数为勾股数,第一个数为从3开始连续的奇数,第二、三个数为连续的自然数;进一步发现第一个数的平方是第二、三个数的和;最后得出第n组数为(2n+1),(),(),由此规律解决问题.【解答】解:在32=4+5中,4=,5=;在52=12+13中,12=,13=;…则在13、b、c中,b==84,c==85.【点评】认真观察各式的特点,总结规律是解题的关键.三.解答题(共27小题)14.(2016春•黄冈期中)a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.【分析】现对已知的式子变形,出现三个非负数的平方和等于0的形式,求出a、b、c,再验证两小边的平方和是否等于最长边的平方即可.【解答】解:由a2+b2+c2+338=10a+24b+26c,得:(a2﹣10a+25)+(b2﹣24b+144)+(c2﹣26c+169)=0,即:(a﹣5)2+(b﹣12)2+(c﹣13)2=0,由非负数的性质可得:,解得,∵52+122=169=132,即a2+b2=c2,∴∠C=90°,即三角形ABC为直角三角形.【点评】本题考查勾股定理的逆定理的应用、完全平方公式、非负数的性质.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.15.(2016秋•永登县期中)如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.【分析】连接AC,则在直角△ABC中,已知AB,BC可以求AC,根据AC,AD,CD的长可以判定△ACD为直角三角形,(1)根据∠BAD=∠CAD+∠BAC,可以求解;(2)根据四边形ABCD的面积为△ABC和△ACD的面积之和可以解题.【解答】解:(1)连接AC,∵AB⊥CB于B,∴∠B=90°,在△ABC中,∵∠B=90°,∴AB2+BC2=AC2,又∵AB=CB=,∴AC=2,∠BAC=∠BCA=45°,∵CD=,DA=1,∴CD2=5,DA2=1,AC2=4.∴AC2+DA2=CD2,由勾股定理的逆定理得:∠DAC=90°,∴∠BAD=∠BAC+∠DAC=45°+90°=135°;(2)∵∠DAC=90°,AB⊥CB于B,∴S△ABC=,S△DAC=,∵AB=CB=,DA=1,AC=2,∴S△ABC=1,S△DAC=1而S四边形ABCD=S△ABC+S△DAC,∴S四边形ABCD=2.【点评】本题考查了勾股定理在直角三角形中的运用,考查了根据勾股定理逆定理判定直角三角形,考查了直角三角形面积的计算,本题中求证△ACD是直角三角形是解题的关键.16.(2016春•邹城市校级期中)如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.【分析】直接利用网格结合勾股定理求出答案.【解答】解:如图所示:△ABC即为所求.【点评】此题主要考查了勾股定理,正确借助网格求出是解题关键.17.(2015春•平南县期中)如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100km到达B点,然后再沿北偏西30°方向走了100km 到达目的地C点,求出A、C两点之间的距离.【分析】根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.【解答】解:∵AD∥BE∴∠ABE=∠DAB=60°∵∠CBE=30°∴∠ABC=180°﹣∠ABE﹣∠CBE=180°﹣60°﹣30°=90°,在Rt△ABC中,∴==200,∴A、C两点之间的距离为200km.【点评】本题考查勾股定理的应用,先确定是直角三角形后,根据各边长,用勾股定理可求出AC的长,且求出∠DAC的度数,进而可求出点C在点A的什么方向上.18.(2015秋•新泰市期中)如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km 的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?【分析】(1)过A作AE⊥BD于E,线段AE的长即为台风中心与气象台A的最短距离,由含30°角的直角三角形的性质即可得出结果;(2)根据题意得出线段CD就是气象台A受到台风影响的路程,求出CD的长,即可得出结果.【解答】解:(1)过A作AE⊥BD于E,如图1所示:∵台风中心在BD上移动,∴AE的长即为气象台距离台风中心的最短距离,在Rt△ABE中,∠ABE=90°﹣60°=30°,∴AE=AB=160,即台风中心在移动过程中,与气象台A的最短距离是160km.(2)∵台风中心以每小时20km的速度沿北偏东60°的BD 方向移动,在距离台风中心200km内的地方都要受到其影响,∴线段CD就是气象台A受到台风影响的路程,连接AC,如图2所示:在Rt△ACE中,AC=200km,AE=160km,∴CE==120km,∵AC=AD,AE⊥CD,∴CE=ED=120km,∴CD=240km.∴台风影响气象台的时间会持续240÷20=12(小时).【点评】本题考查了勾股定理在实际生活中的应用、垂径定理、含30°角的直角三角形的性质等知识;熟练掌握垂径定理和勾股定理,求出CD是解决问题(2)的关键.19.(2015春•阳东县期中)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.【分析】(1)我们求出BP、BQ的长,用勾股定理解决即可.(2)△PQB形成等腰三角形,即BP=BQ,我们可设时间为t,列出方程2t=8﹣1×t,解方程即得结果.(3)直线PQ把原三角形周长分成相等的两部分,根据勾股定理可知AC=10cm,即三角形的周长为24cm,则有BP+BQ=12,即2t+(8﹣1×t)=12,解方程即可.。
初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)-

初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)一.选择题(共8小题)1.直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C .D .2.下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2D.在Rt△ABC中,∠B=90°,所以a2+b2=c23.如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm4.如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺5.如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C .﹣D.﹣1+6.一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米7.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.48.如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169二.填空题(共5小题)9.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在第1页(共38页)杯子外面的长度为hcm,则h的取值范围是.10.如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为米.11.已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于.12.观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是(只填数,不填等式)13.观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b= ,c= .三.解答题(共27小题)14.a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.15.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.16.如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.17.如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100km 到达B点,然后再沿北偏西30°方向走了100km到达目的地C点,求出A、C两点之间的距离.18.如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?第2页(共38页)(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?19.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.20.在△ABC中,AB、BC、AC 三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.(1)△ABC的面积为:.(2)若△DEF 三边的长分别为、、,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为.(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ 之间的数量关系,并证明你的结论.(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是m2.21.(1)在△ABC中,AB、BC、AC 三边的长分别为、、,求这个三角形的面积.如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC 的高,而借用网格就能就算出它的面积.请你将△ABC的面积直接填写在横线上.思维拓展:(2)已知△ABC 三边的长分别为a(a>0),求这个三角形的面积.我们把上述求△ABC面积的方法叫做构图法.如图2,网格中每个小正方形的边长都是a,请在网格中画出相应的△ABC,并求出它的面积.第3页(共38页)类比创新:(3)若△ABC 三边的长分别为(m>0,n>0,且m≠n),求出这个三角形的面积.如图3,网格中每个小长方形长、宽都是m,n,请在网格中画出相应的△ABC,用网格计算这个三角形的面积.22.有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?23.(拓展创新)在教材中,我们通过数格子的方法发现了直角三角形的三边关系,利用完全相同的四个直角三角形采用拼图的方式验证了勾股定理的正确性.问题1:以直角三角形的三边为边向形外作等边三角形,探究S′+S″与S的关系(如图1).问题2:以直角三角形的三边为斜边向形外作等腰直角三角形,探究S′+S″与S的关系(如图2).问题3:以直角三角形的三边为直径向形外作半圆,探究S′+S″与S的关系(如图3).24.如图,在平面坐标系中,点A、点B分别在x轴、y轴的正半轴上,且OA=OB,另有两点C(a,b)和D(b,﹣a)(a、b均大于0);(1)连接OD、CD,求证:∠ODC=45°;(2)连接CO、CB、CA,若CB=1,C0=2,CA=3,求∠OCB的度数;(3)若a=b,在线段OA上有一点E,且AE=3,CE=5,AC=7,求△OCA的面积.25.11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题“小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻飞去抓鱼,并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树根有多远?26.(1)先化简,再求值:x(x﹣2)﹣(x+1)(x﹣1),其中x=10.(2)已知,求代数式(x+1)2﹣4(x+1)+4的值.(3)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图:①从点A出发在图中画一条线段AB,使得AB=;②画出一个以(1)中的AB为斜边的等腰直角三角形,使三角形的三个顶点都在格点上,并根据所第4页(共38页)画图形求出等腰直角三角形的腰长.27.[问题情境]勾股定理是一条古老的数学定理,它有很多种证明方法.我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数学关系”(勾股定理)带到其它星球,作为地球人与其他星球“人”进行第一次“谈话”的语言;[定理表述]请你根据图1中的直角三角形叙述勾股定理;[尝试证明]以图1中的直角三角形为基础,将两个直角边长为a,b,斜边长为c的三角形按如图所示的方式放置,连接两个之间三角形的另外一对锐角的顶点(如图2),请你利用图2,验证勾股定理;[知识扩展]利用图2中的直角梯形,我们可以证明<,其证明步骤如下:∵BC=a+b,AD=又∵在直角梯形ABCD中,有BCAD(填大小关系),即∴.28.观察、思考与验证(1)如图1是一个重要公式的几何解释,请你写出这个公式;(2)如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°;(3)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的《新英格兰教育日志》上),请你写出验证过程.29.超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?(参考数据:=1.41,=1.73)30.中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO 方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.(1)请用直尺和圆规作出C处的位置;(2)求我国海监船行驶的航程BC的长.第5页(共38页)31.在一次“构造勾股数”的探究性学习中,老师给出了下表:其中m、n为正整数,且m>n.(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a= ,b= ,c= .(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.32.如图1,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<8).(1)请在4×8的网格纸图2中画出t为6秒时的线段PQ.并求其长度;(2)当t为多少时.△PQB是以BP为底的等腰三角形.33.阅读下面的情景对话,然后解答问题:(1)理解:①根据“奇异三角形”的定义,请你判断:“等边三角形一定是奇异三角形”吗?(填是或不是)②若某三角形的三边长分别为1、、2,则该三角形(是或不是)奇异三角形.(2)探究:若Rt△ABC是奇异三角形,且其两边长分别为2、2,则第三边的长为,且这个直角三角形的三边之比为(从小到大排列,不得含有分母).(3)设问:请提出一个和奇异三角形有关的问题.(不用解答)34.观察下列各式,你有什么发现?32=4+5,52=12+13,72=24+25,92=40+41,…第6页(共38页)用你的发现解决下列问题:(1)填空:112= +;(2)请用含字母n(n为正整数)的关系式表示出你发现的规律:;(3)结合勾股定理有关知识,说明你的结论的正确性.35.小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?36.如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.37.如图,四边形ABCD的三边(AB、BC、CD)和BD的长度都为5厘米,动点P从A出发(A→B→D)到D,速度为2厘米/秒,动点Q从点D出发(D→C→B→A)到A,速度为2.8厘米/秒.5秒后P、Q相距3厘米,试确定5秒时△APQ的形状.38.一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由.39.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地°送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺),此时踏板升高离地五尺(BD=5尺),求秋千绳索(OA或OB)的长度.40.如图,∠AOB=90°,OA=45cm,OB=15cm,一机器人在点B处看见一个小球从点A出发沿着AO 方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?1.已知直角三角形两边的长为3和4,则此三角形的周长为()A.12 B.7+C.12或7+D.以上都不对2.图中字母所代表的正方形的面积为144的选项为()第7页(共38页)A. B .C .D .3.如图,数轴上的点A所表示的数为x,则x的值为()A.B .﹣C.2 D.﹣24.如图,带阴影的正方形面积是.5.如图,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD= .6.正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,(1)在图①中,画一个面积为10的正方形;(2)在图②、图③中,分别画两个不全等的直角三角形,使它们的三边长都是无理数.初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)参考答案与试题解析一.选择题(共8小题)1.(2016秋•吴江区期中)直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C .D .【分析】首先根据勾股定理,得:斜边==13.再根据直角三角形的面积公式,求出斜边上的高.【解答】解:由题意得,斜边为=13.所以斜边上的高=12×5÷13=.故选D.【点评】运用了勾股定理.注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.2.(2016春•抚顺县期中)下列说法中正确的是()第8页(共38页)A.已知a,b,c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2D.在Rt△ABC中,∠B=90°,所以a2+b2=c2【分析】在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角,根据此就可以直接判断A、B、C、D选项.【解答】解:在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角.A、不确定c是斜边,故本命题错误,即A选项错误;B、不确定第三边是否是斜边,故本命题错误,即B选项错误;C、∠C=90°,所以其对边为斜边,故本命题正确,即C选项正确;D、∠B=90°,所以斜边为b,所以a2+c2=b2,故本命题错误,即D选项错误;故选 C.【点评】本题考查了勾股定理的正确运用,只有斜边的平方才等于其他两边的平方和.3.(2016春•临沭县期中)如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm【分析】作出直角三角形后分别求得直角三角形的两直角边的长后即可利用勾股定理求得斜边AB 的长.【解答】解:如图,由题意得:AC=15×5=75cm,BC=30×6=180cm,故AB===195cm.故选A.【点评】本题考查了勾股定理的应用,解题的关键是从实际问题中抽象出直角三角形,难度不大.4.(2015春•青山区期中)如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺【分析】找到题中的直角三角形,设水深为x尺,根据勾股定理解答.【解答】解:设水深为x尺,则芦苇长为(x+1)尺,第9页(共38页)根据勾股定理得:x2+()2=(x+1)2,解得:x=12,芦苇的长度=x+1=12+1=13(尺),故选D.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.5.(2016春•南陵县期中)如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C .﹣D.﹣1+【分析】点A在以O为圆心,OB长为半径的圆上,所以在直角△BOC中,根据勾股定理求得圆O 的半径OA=OB=,然后由实数与数轴的关系可以求得a的值.【解答】解:如图,点A在以O为圆心,OB长为半径的圆上.∵在直角△BOC中,OC=2,BC=1,则根据勾股定理知OB===,∴OA=OB=,∴a=﹣1﹣.故选A.【点评】本题考查了勾股定理、实数与数轴.找出OA=OB是解题的关键.6.(2015春•蓟县期中)一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米【分析】先根据梯子的顶端下滑了0.4米求出A′C的长,再根据勾股定理求出B′C的长,进而可得出结论.【解答】解:(1)∵在Rt△ABC中,AB=2.5m,BC=0.7m,∴AC===2.4(m).∵梯子的顶端下滑了0.4米,∴A′C=2m,∵在Rt△A′B′C中,A′B′=2.5m,A′C=2m,∴B′C==1.5m,∴BB′=B′C﹣BC=1.5﹣0.7=0.8m.故选C.第10页(共38页)【点评】此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.7.(2015春•罗田县期中)在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.4【分析】根据勾股定理求出AB的长即可解答.【解答】解:在Rt△ABC中,根据勾股定理,AB==13,又∵AC=12,BC=5,AM=AC,BN=BC,∴AM=12,BN=5,∴MN=AM+BN﹣AB=12+5﹣13=4.故选D.【点评】本题综合考查了勾股定理的应用,找到关系MN=AM+BN﹣AB是关键.8.(2016春•重庆校级期中)如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169【分析】根据勾股定理,知两条直角边的平方等于斜边的平方,此题中斜边的平方即为大正方形的面积13,2ab即四个直角三角形的面积和,从而不难求得(a+b)2的值.【解答】解:(a+b)2=a2+b2+2ab=大正方形的面积+四个直角三角形的面积和=13+(13﹣1)=25.故选C.【点评】考查了勾股定理的证明,注意完全平方公式的展开:(a+b)2=a2+b2+2ab,还要注意图形的面积和a,b之间的关系.二.填空题(共5小题)9.(2016春•固始县期中)将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是7cm≤h≤16cm .第11页(共38页)【分析】如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出h的取值范围.【解答】解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,∴h=24﹣8=16cm;当筷子的底端在A点时,筷子露在杯子外面的长度最短,在Rt△ABD中,AD=15,BD=8,∴AB==17,∴此时h=24﹣17=7cm,所以h的取值范围是7cm≤h≤16cm.故答案为:7cm≤h≤16cm.【点评】本题考查了勾股定理的应用,求出h的值最大值与最小值是解题关键.10.(2015春•汕头校级期中)如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为(1+)米.【分析】根据题意利用勾股定理得出BC的长,进而得出答案.【解答】解:由题意得:在直角△ABC中,AC2+AB2=BC2,则12+22=BC 2,∴BC=,∴则树高为:(1+)m.故答案为:(1+).【点评】此题主要考查了勾股定理的应用,熟练利用勾股定理得出BC的长是解题关键.11.(2016春•高安市期中)已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于24cm2.【分析】利用勾股定理列出关系式,再利用完全平方公式变形,将a+b与c的值代入求出ab的值,即可确定出直角三角形的面积.【解答】解:∵Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,∴由勾股定理得:a2+b2=c2,即(a+b)2﹣2ab=c2=100,∴196﹣2ab=100,即ab=48,第12页(共38页)则Rt△ABC 的面积为ab=24(cm2).故答案为:24cm2.【点评】此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.12.(2016春•嘉祥县期中)观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是15,112,113 (只填数,不填等式)【分析】通过观察,得出规律:这类勾股数分别为2n+1,2n(n+1),2n(n+1)+1,由此可写出第7组勾股数.【解答】解:∵第1组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,第2组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,第3组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,第4组:9=2×4+1,40=2×4×(4+1)41=2×4×(4+1)+1,∴第7组勾股数是2×7+1=15,2×7×(7+1)=112,2×7×(7+1)+1=113,即15,112,113.故答案为:15,112,113.【点评】此题考查的知识点是勾股数,属于规律性题目,关键是通过观察找出规律求解.13.(2009春•武昌区期中)观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b= 84 ,c= 85 .【分析】认真观察三个数之间的关系:首先发现每一组的三个数为勾股数,第一个数为从3开始连续的奇数,第二、三个数为连续的自然数;进一步发现第一个数的平方是第二、三个数的和;最后得出第n组数为(2n+1),(),(),由此规律解决问题.第13页(共38页)【解答】解:在32=4+5中,4=,5=;在52=12+13中,12=,13=;…则在13、b、c中,b==84,c==85.【点评】认真观察各式的特点,总结规律是解题的关键.三.解答题(共27小题)14.(2016春•黄冈期中)a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.【分析】现对已知的式子变形,出现三个非负数的平方和等于0的形式,求出a、b、c,再验证两小边的平方和是否等于最长边的平方即可.【解答】解:由a2+b2+c2+338=10a+24b+26c,得:(a2﹣10a+25)+(b2﹣24b+144)+(c2﹣26c+169)=0,即:(a﹣5)2+(b﹣12)2+(c﹣13)2=0,由非负数的性质可得:,解得,∵52+122=169=132,即a2+b2=c2,∴∠C=90°,即三角形ABC为直角三角形.【点评】本题考查勾股定理的逆定理的应用、完全平方公式、非负数的性质.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.15.(2016秋•永登县期中)如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.【分析】连接AC,则在直角△ABC中,已知AB,BC可以求AC,根据AC,AD,CD的长可以判定△ACD为直角三角形,(1)根据∠BAD=∠CAD+∠BAC,可以求解;第14页(共38页)(2)根据四边形ABCD的面积为△ABC和△ACD的面积之和可以解题.【解答】解:(1)连接AC,∵AB⊥CB于B,∴∠B=90°,在△ABC中,∵∠B=90°,∴AB2+BC2=AC2,又∵AB=CB=,∴AC=2,∠BAC=∠BCA=45°,∵CD=,DA=1,∴CD2=5,DA2=1,AC2=4.∴AC2+DA2=CD2,由勾股定理的逆定理得:∠DAC=90°,∴∠BAD=∠BAC+∠DAC=45°+90°=135°;(2)∵∠DAC=90°,AB⊥CB于B,∴S△ABC =,S△DAC=,∵AB=CB=,DA=1,AC=2,∴S△ABC =1,S△DAC=1而S四边形ABCD =S△ABC+S△DAC,∴S四边形ABCD=2.【点评】本题考查了勾股定理在直角三角形中的运用,考查了根据勾股定理逆定理判定直角三角形,考查了直角三角形面积的计算,本题中求证△ACD是直角三角形是解题的关键.16.(2016春•邹城市校级期中)如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.【分析】直接利用网格结合勾股定理求出答案.【解答】解:如图所示:△ABC即为所求.【点评】此题主要考查了勾股定理,正确借助网格求出是解题关键.17.(2015春•平南县期中)如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100km到达B点,然后再沿北偏西30°方向走了100km到达目的地C点,求出A、C两点之间的距离.第15页(共38页)【分析】根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.【解答】解:∵AD∥BE∴∠ABE=∠DAB=60°∵∠CBE=30°∴∠ABC=180°﹣∠ABE﹣∠CBE=180°﹣60°﹣30°=90°,在Rt△ABC 中,∴==200,∴A、C两点之间的距离为200km.【点评】本题考查勾股定理的应用,先确定是直角三角形后,根据各边长,用勾股定理可求出AC 的长,且求出∠DAC的度数,进而可求出点C在点A的什么方向上.18.(2015秋•新泰市期中)如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?【分析】(1)过A作AE⊥BD于E,线段AE的长即为台风中心与气象台A的最短距离,由含30°角的直角三角形的性质即可得出结果;(2)根据题意得出线段CD就是气象台A受到台风影响的路程,求出CD的长,即可得出结果.【解答】解:(1)过A作AE⊥BD于E,如图1所示:∵台风中心在BD上移动,∴AE的长即为气象台距离台风中心的最短距离,在Rt△ABE中,∠ABE=90°﹣60°=30°,∴AE=AB=160,即台风中心在移动过程中,与气象台A的最短距离是160km.(2)∵台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响,∴线段CD就是气象台A受到台风影响的路程,连接AC,如图2所示:第16页(共38页)在Rt△ACE中,AC=200km,AE=160km,∴CE==120km,∵AC=AD,AE⊥CD,∴CE=ED=120km,∴CD=240km.∴台风影响气象台的时间会持续240÷20=12(小时).【点评】本题考查了勾股定理在实际生活中的应用、垂径定理、含30°角的直角三角形的性质等知识;熟练掌握垂径定理和勾股定理,求出CD是解决问题(2)的关键.19.(2015春•阳东县期中)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.【分析】(1)我们求出BP、BQ的长,用勾股定理解决即可.(2)△PQB形成等腰三角形,即BP=BQ,我们可设时间为t,列出方程2t=8﹣1×t,解方程即得结果.(3)直线PQ把原三角形周长分成相等的两部分,根据勾股定理可知AC=10cm,即三角形的周长为24cm,则有BP+BQ=12,即2t+(8﹣1×t)=12,解方程即可.【解答】解:(1)出发2秒后,AP=2,BQ=4,∴BP=8﹣2=6,PQ==2;(3分)(2)设时间为t,列方程得2t=8﹣1×t,解得t=;(6分)(3)假设直线PQ能把原三角形周长分成相等的两部分,由AB=8cm,BC=6cm,根据勾股定理可知AC=10cm,第17页(共38页)。
专题01 勾股定理与几何综合的三种考法(原卷版)-2024年常考压轴题攻略(8年级上册北师大版)

专题01勾股定理与几何综合的三种考法类型一、翻折问题【变式训练1】如图,在等腰两点,连接DE,将BDE△BB'交于点F,则折痕类型二、最值问题例1.(垂线段最值)将ABD △沿BD 折叠,【变式训练1】如图,C为线段AC,EC.已知AB=2,DE=(1)用含x的代数式表示AC+CE(2)探究:当点C满足什么条件时,(3)根据(2)中的结论,请构造图形求代数式A.21cm B.15类型三、解三角形问题A.13B.△Rt ABC【变式训练2】如图,在长方形△ABE 的轴对称图形△于点F ,已知AB =9【变式训练3】如图,ABC 26AD BC ==,:5:AB BC =A .32B .52课后训练1.如图,将矩形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上点F 处,已知3CE =,8AB =,则图中阴影部分的面积为()A .20B .24C .28D .303.如图所示,将一张矩形纸片沿着BF 折叠(其中点F 为:3:5BCF BGF S S =△△,且AB 5.如图,在Rt ABC △中,C ∠折后,点A 落在点E 处,如果7.如图,在矩形ABCD 称点分别是点M 、N .如果直线8.如图,在四边形ADC B DAE ∠=∠+∠9.如图,如果四边形ABCD 13DC =,9FC =,则10.如图,在矩形ABCD 中,已知为,MN 连接.CN CDN △的面积与11.如图的实线部分是由Rt ABC∆沿高CH折叠,使点B∆经过两次折叠得到的.首先将Rt ABC落在斜边上的点B'处,再沿CM折叠,使点A落在CB'的延长线上的点A'处.若图中BC=,20cm∠=︒,15cmAC=,则MB'的长为______.90ACB12.如图,矩形ABCD中,5V沿AE折叠,AD=,7AB=,点E为DC上一个动点,把ADE∠的角平分线上时,DE的长为______.当点D的对应点D¢落在ABC。
八年级数学勾股定理30道必做题(含答案和解析)

八年级数学勾股定理30道必做题(含答案和解析)1、如图,四边形ABCD ,EFGH ,NHMC 都是正方形,边长分别为a ,b ,c. A ,B ,N ,E ,F 五点在同一直线上,则c = .(用含有a ,b 的代数式表示).答案:√a 2+b 2.解析:由三个正方形如图的摆放.∵四边形ABCD ,EFGH ,NHMC 都是正方形. ∴∠CNB +∠ENH =90°.又∵∠CNB +∠NCB =90°,∠ENH +∠EHN =90°. ∴∠CNB =∠EHN ,∠NCB =∠ENH. 在△CBN 和△NEH 中:{∠BNC =∠EHNNC =HN ∠NCB =∠HNE .∴△CBN ≌△NEH (ASA ). ∴HE =BN.在Rt △CBN 中,BC 2+BN 2=CN 2.又已知三个正方形的边长分别为a ,b ,c. 则有a 2+b 2=c 2. ∴c =√a 2+b 2.考点:三角形——全等三角形——全等三角形的性质——全等三角形的判定.三角形——直角三角形——勾股定理. 四边形——正方形——正方形的性质.2、在Rt △ABC 中,斜边长BC =3,AB 2+AC 2+BC 2的值为( ). A.9 B.18 C.6 D. 无法计算答案:B.解析:在Rt△ABC中,斜边长BC=3.BC2=AB2+AC2=9.∴AB2+AC2+BC2=9+9=18.考点:三角形——直角三角形——勾股定理.3、三角形三边长分别为① 3,4,5;② 9,40,41;③ 5,12,13;④ 6,8,10;⑤ 7,24,25;⑥ 8,15,17.其中能构成直角三角形的有.答案:①②③④⑤⑥.解析:① 3,4,5;② 9,40,41;③ 5,12,13;④ 6,8,10;⑤ 7,24,25;⑥ 8,15,17.全都能构成直角三角形.考点:三角形——直角三角形——勾股数.4、已知点A(3,5),B(-1,1)那么线段AB的长度为().A.4B.3√2C.4√2D.5答案:C.解析:已知A(3,5)和B(-1,1),由两点间的距离公式可知AB=√(3+1)2+(5−1)2=4√2.考点:函数——平面直角坐标系——坐标与距离.5、等腰直角三角形的斜边为10,则腰长为,斜边上的高为.答案:1.5√2.2.5.解析:等腰三角形的三边关系为1∶1∶√2.因为等腰直角三角形的斜边为10,则腰长为5√2.斜边上的高,即为斜边的中线,为斜边的一半,长为5.考点:三角形——直角三角形——等腰直角三角形——勾股定理.6、若正方形的周长为40,则其对角线长为().A.100B.20√2C.10√2D.10答案:C.解析:正方形边长为10,根据勾股定理得对角线长为10√2.考点:三角形——直角三角形——勾股定理.四边形——正方形——正方形的性质.7、在Rt△ABC中,∠C=90°,∠A=30°,BC=1,则AC的长是().A.2B.√32C.√3D.√3+2答案:C.解析:略.考点:三角形——直角三角形——勾股定理.8、等边三角形的边长为4,则它的面积是.答案:4√3 .解析:等边三角形的面积=√34×42=4√3.考点:三角形——直角三角形——含30°角的直角三角形.9、已知一个直角三角形的两条直角边分别为3,4,则此三角形斜边是__________,斜边上的高为__________.A.5;125B.6;145C.6;125D.5;145答案:A.解析:略.考点:三角形——三角形基础——三角形面积及等积变换.直角三角形——勾股定理.10、直角三角形两直角边长分别为5和12,则它的斜边上的高为.答案:6013.解析:设斜边的长为c,斜边上的高为h.∵直角三角形的两直角边长分别为5和12.∴c=√52+122=13.∴5×12=13h,解得h=60.13考点:三角形——三角形基础——三角形面积及等积变换.三角形——直角三角形——勾股定理.11、如图所示,小明同学在距离某建筑物6米的点A处测得条幅两端点B,C点的仰角分别为60°和30°,则条幅的高度BC为米(结果可以保留根号).答案:4√3.=2√3,BC=BD−CD=4√3.解析:依题可知,BC=6√3,CD=√3考点:三角形——直角三角形——含30°角的直角三角形.三角形——锐角三角函数——解直角三角形.12、一张直角三角形的纸片,按图所示折叠,使两个锐角的顶点A,B重合,若∠B=30°,AC=√3,则DC的长为.答案:1.解析:由题知∠DAE=∠B=30°.∴∠DAC=90°-∠B-∠DAE=30°.AC=1.∴在Rt△ADC中,DC=√33考点:三角形——直角三角形——含30°角的直角三角形.13、已知:如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,D是AB延长线上一点且∠CDB=45°.求DB与DC的长.答案:证明见解析.解析:过C作CE⊥AB于E.在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4.∴BC=2,∠ABC=60°.∴∠BCE=30°.∴BE=1,CE=√3.在Rt△CDE中,∠CED=90°,∠CDB=45°.∴∠ECD=45°.∴DE=CE=√3.∴CD=√CE2+DE2=√6.∴BD=√3-1.考点:三角形——直角三角形——含30°角的直角三角形——等腰直角三角形——勾股定理.14、如图,数轴上有两个Rt△OAB,Rt△OCD,OA,OC是斜边,且OB=1,AB=1,CD=1,OD=2,分别以O为圆心,OA,OC为半径画弧交x轴于E,F,则E,F分别对应的数是.答案:−√2,√5.解析:在Rt△OAB中,OA=√OB2+AB2=√2.∴OE=√2.∴点E对应的数为−√2.在Rt△OCD中,OC=√OD2+CD2=√5.∴OF=√5.∴点F对应的数为√5.考点:数——有理数——数轴.三角形——直角三角形——勾股定理.15、在△ABC中,三条边的长分别为AB=√5,BC=√10,AC=√13,求这个三角形的面积.小宝同学在解答这道题时,先建立一个正方形网格,其中每个小正方形的边长为1,再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样就不需求△ABC的高,而借用网格就能计算出它的面积.(1)请你将△ABC的面积直接填写在横线上.(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为√2a,√13a,√17a(a>0).请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积填写在横线上.(3)若△ABC中有两边的长分别为√2a,√10a(a>0).且△ABC的面积为2a2,试运用构图法在图3的正方形网格(每个小正方形的边长为a)中画出所有符合题意的△ABC(全等的三角形视为同一种情况),并求出它的第三条边长填写在横线上..答案:(1)72a2.(2)52(3)4a或2√2a.解析:(1)△ABC的面积为72.(2)△ABC的面积为52a2.(3)图中三角形为符合题意的三角形.第三边的长度为4a或2√2a.考点:函数——平面直角坐标系——坐标与面积.三角形——三角形基础——三角形面积及等积变换.三角形——直角三角形——勾股定理.16、在Rt△ABC中,∠C=90°,若a+b=5,c=4,则S△ABC=.答案:94.解析:在Rt△ABC中,由勾股定理得,a2+b2=c2.又有(a+b)2=a2+b2+2ab,∴(a+b)2-c2=2ab.∴S△ABC=12ab=94.考点:三角形——直角三角形——勾股定理.17、已知Rt△ABC的周长为2+√6,其中斜边AB=2,则这个三角形的面积为.答案:12.解析:在Rt△ABC中,设BC=a,AC=b.由勾股定理得a2+b2=4.由题意得a +b +2=2+√6. ∴a +b =√6. ∴ab =(a+b)2−(a 2+b 2)2=6−42=1.∴s =12ab =12.考点:式——整式——完全平方公式.三角形——直角三角形——勾股定理.18、在直角三角形中,一条直角边为11cm ,另两边是两个连续自然数,则此直角三角形的周长为 . 答案:132cm. 解析:略.考点:三角形——直角三角形——勾股定理.19、如图所示,在平静的湖面上,有一支红莲,高出水面1m ,一阵风吹来,红莲吹到一边,花朵齐及水面,已知红莲移动的水平距离为2m ,求水深是多少?答案:水深为1.5米.解析:设水深AC 为x 米.则红莲的长是(x +1)米.在Rt △ABC 中,根据勾股定理得,AC 2+BC 2=AB 2. ∴(x +1)2=x 2+4. 解得x =1.5. 答:水深为1.5米.考点:三角形——直角三角形——勾股定理——勾股定理的应用.20、如图,点C 为线段AB 上一点,将线段CB 绕点C 旋转,得到线段CD ,若DA ⊥AB ,AD =1,BD =√17,则BC 的长为 ..答案:178解析:在Rt△ABD中,由勾股定理可知,AD=1,BD=√17,AB=4.设BC=BD=x,AC=4-x..由勾股定理可知12+(4-x)2=x2,解得x=178考点:三角形——直角三角形——勾股定理.21、如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于.答案:6.解析:∵AB=10,EF=2.∴大正方形的面积是100,小正方形的面积是4.∴四个直角三角形的面积和为100-4=96.ab=96.设AE=a,DE=b,即4×12∴2ab=96,a2+b2=100.∴a+b=14.∵a-b=2.解得a=8,b=6.∴AE=8,DE=6.∴AH=8-2=6.考点:方程与不等式——二元一次方程组——解二元一次方程组.三角形——直角三角形——勾股定理.四边形——正方形——正方形的性质.22、在Rt△ABC中,AC=5,BC=12,则AB边的长是.答案:13或√119.解析:若AC=5,BC=12都是直角边,则AB=13.若BC=12是斜边,则AB=√122−52=√119.考点:三角形——直角三角形——勾股定理.23、等腰三角形的一边长为12,另一边长是10,则其面积为.答案:48或5√119.解析:作出底边上的高AD.当AB=AC=12,BC=10时,BD=5.由勾股定理得:AD=√AB2−BD2=√119.∴S=12BC×AD=12×10×√119=5√119.当AB=AC=10,BC=12时,BD=6.由勾股定理得:AD=√AB2−BD2=√102−62=8.∴S=12BC×AD=48.考点:三角形——直角三角形——勾股定理.24、在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为cm2.答案:66或126.解析:如图所示,分如下两种情况:由勾股定理可得,B1H=B2H=5,CH=16.∴CB1=21,CB2=11.∴△ABC的面积为66或126cm2.考点:三角形——三角形基础——三角形面积及等积变换.三角形——直角三角形——勾股定理.25、下列各组数中,不能构成直角三角形的是().A.3,4,5B.1,1,√2C.5,12,13D.4,6,8答案:D.解析:∵32+42=52,∴选项A正确.∵12+12=(√2)2,∴选项B正确.∵52+122=132,∴选项C正确.∵42+62≠82,∴选项D错误.考点:三角形——直角三角形——勾股定理的逆定理.26、在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,如果三边长满足b2-a2=c2,那么△ABC中互余的一对角是.答案:∠A和∠C.解析:∵b2-a2=c2.∴b2=a2+c2.∴△ABC为直角三角形,且∠B=90°.∴∠A+∠C=90°.考点:几何初步——角——余角和补角.三角形——直角三角形——勾股定理的逆定理.27、如图所示,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=14CD.求证:△AEF 是直角三角形.答案:证明见解析.解析:如图所示,延长FE交AB的延长线于点G.∵∠C=∠GBE=90°,CE=BE,∠1=∠2.∴△CEF≌△BEG.∴EF=EG,CF=BG.设正方形ABCD的边长为a,则CF=14a,DF=34a.在Rt△ADF中,根据勾股定理,得AF2=AD2+DF2=a2+(34a)2=2516a2.∴AF=54a,BG=14a.∴AG=54a.∴AF=AG.∵EF=EG.∴AE⊥FG.∴∠AEF=90°.∴△AEF是直角三角形.考点:三角形——全等三角形——全等三角形的应用.三角形——等腰三角形——等腰三角形的性质.三角形——直角三角形——勾股定理——勾股定理的逆定理.28、如图,四边形ABCD中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,求四边形ABCD的面积.答案:四边形ABCD的面积为1+√5.解析:连接AC.∵∠ABC=90°,AB=1,BC=2.∴AC=√AB2+BC2=√5.在△ACD中,AC2+CD2=5+4=9=AD2.∴△ACD是直角三角形.∴S四边形ABCD=12AB×BC+12AC×CD=12×1×2+12×√5×2=1+√5.故四边形ABCD的面积为1+√5.考点:三角形——三角形基础——三角形面积及等积变换.三角形——直角三角形——勾股定理——勾股定理的逆定理.29、在△ABC中,点D为BC的中点,点M,N分别为AB,AC上的点,且MD⊥ND.(1)若∠A=90°,以线段BM,MN,CN为边能否构成一个三角形?若能,该三角形是锐角三角形,直角三角形或钝角三角形?(2)如果BM2+CN2=DM2+DN2,求证AD2=14(AB2+AC2).答案:(1)能,该三角形是直角三角形.(2)证明见解析.解析:(1)略.(2)延长ND至E,使DE=DN,连接EB,EM,MN.因为DE=DN,DB=DC,∠BDE=∠CDN,则△BDE≌△CDN.从而BE=CN,∠DBE=∠C.而DE=DN,∠MDN=90°,故ME=MN.因此DM2+DN2=MN2=ME2.即BM2+BE2=ME2,则∠MBE=90°.即∠MBD+∠DBE=90°.因为∠DBE=∠C,故∠MBD+∠C=90°.则∠BAC=90°.AD为Rt△ABC斜边BC上的中线.BC.故AD=12(AB2+AC2).由此可得AD2=14考点:三角形——全等三角形——全等三角形常用辅助线——倍长中线.三角形——全等三角形——全等三角形的性质——全等三角形的判定.三角形——直角三角形——勾股定理.30、阅读下面材料:小伟遇到这样一个问题:如图1,在正三角形ABC内有一点P,且PA=3,PB=4,PC=5,求∠APB的度数.小伟是这样思考的:如图2,利用旋转和全等的知识构造△AP’C,连接PP’,得到两个特殊的三角形,从而将问题解决.(1)图1中∠APB的度数等于.(2)如图3,在正方形ABCD内有一点P,且PA=2√2,PB=1,PD=√17,则∠APB的度数等于,正方形的边长为.(3)如图,在正六边形ABCDEF内有一点,且PA=2,PB=1,PF=√13,则∠APB的度数等于,正六边形的边长为(并写出解答过程).答案:(1)150°.(2)1.135°.2.√13.(3)1.120°.2.√7.解析:(1)∵△ABC为正三角形,PA=P’A.∴△AP P’为正三角形.∴∠A P’P=60°,P’P=AP=3.∵P’C=PB=4,PC2=P’P2+P’C2.∴∠PP’C=90°.∴∠APB=∠AP’C=150°.(2)1.135°;2.√13.(3)图4中∠APB的度数等于120°,正六边形的边长为√7.将△APB绕点A逆时针旋转120°得到△A P’F,连接P’P.过点A作AN⊥P’P,过点A作AH⊥FP’于点H.∵△APB绕点A逆时针旋转120°得到△A P’F.∴∠PAP’=120°,P’A=PA=2,P’F=PB=1.∴∠AP’P=30°.在Rt△ANP’中,P’A=2AN=2.∴P’N=√3.∴PP’=2√3.在△FPP’中,PF=√13,PP’=2√3,P’F=2.∴PF2=P’F2+P’P2.∴∠FP’P=90°.∴∠APB=∠FP’A=∠FP’P+∠AP’P=120°.∴∠HP’A=60°.在Rt△HP’A中,AP’=2, ∠P’AH=30°.∴HP’=1.在Rt△HFA中,FA2=FH2+HA2.∴FA=√FH2+HA2=√7.考点:三角形——直角三角形——勾股定理——勾股定理的逆定理.几何变换——图形的旋转——旋转全等.。
完整版八年级数学经典压轴题勾股定理综合

(完整版)八年级数学经典压轴题:勾股定理综合在八年级数学中,勾股定理是一个非常重要的定理。
它是数学中的经典定理之一,也是几何学中最基础的定理之一。
勾股定理的应用非常广泛,不仅在数学中有很多应用,而且在物理学、工程学等其他领域中也有很多应用。
今天,我们来看看一些关于勾股定理的综合题。
1. 已知直角三角形的直角边分别为3cm和4cm,求斜边的长度。
解:根据勾股定理,斜边的长度可以通过直角边的长度计算得出。
直角边分别为3cm和4cm,那么斜边的长度为:斜边的长度= √(3^2 + 4^2) = √(9+ 16) = √25 = 5cm所以,斜边的长度为5cm。
2. 已知直角三角形的斜边长度为10cm,其中一直角边的长度为6cm,求另一直角边的长度。
解:根据勾股定理,直角边的长度可以通过斜边的长度计算得出。
斜边的长度为10cm,其中一直角边的长度为6cm,那么另一直角边的长度为:另一直角边的长度= √(10^2 - 6^2) = √(100 - 36) = √64 = 8cm所以,另一直角边的长度为8cm。
3. 已知两条直角边的长度分别为5cm和12cm,求斜边的长度。
解:根据勾股定理,斜边的长度可以通过直角边的长度计算得出。
直角边的长度分别为5cm和12cm,那么斜边的长度为:斜边的长度= √(5^2 + 12^2) = √(25 + 144) = √169 = 13cm所以,斜边的长度为13cm。
4. 已知三角形的三边长分别为6cm、8cm和10cm,判断该三角形是否为直角三角形。
解:根据勾股定理,如果一个三角形的三边满足勾股定理的条件,那么这个三角形就是直角三角形。
三角形的三边长分别为6cm、8cm和10cm,将这三条边的长度按从小到大的顺序排列得到6cm、8cm和10cm。
根据勾股定理,如果一个三角形是直角三角形,那么它的最长边的平方等于其他两边的平方之和。
这个三角形的最长边为10cm,其他两边的平方之和为6^2 + 8^2 = 36 + 64 = 100,显然不等于10^2 = 100,所以这个三角形不是直角三角形。
勾股定理 期末压轴题训练(含答案) 2022—2023学年人教版数学八年级下册
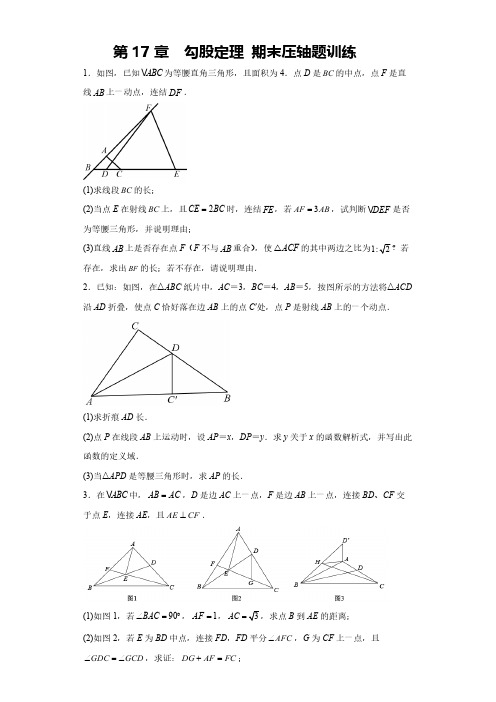
1.如图,已知 VABC 为等腰直角三角形,且面积为 4.点 D 是 BC 的中点,点 F 是直 线 AB 上一动点,连结 DF .
(1)求线段 BC 的长; (2)当点 E 在射线 BC 上,且 CE 2BC 时,连结 FE ,若 AF 3AB ,试判断 VDEF 是否 为等腰三角形,并说明理由; (3)直线 AB 上是否存在点 F(F 不与 AB 重合),使△ACF 的其中两边之比为1: 2 ?若 存在,求出 BF 的长;若不存在,请说明理由. 2.已知:如图,在△ABC 纸片中,AC=3,BC=4,AB=5,按图所示的方法将△ACD 沿 AD 折叠,使点 C 恰好落在边 AB 上的点 C′处,点 P 是射线 AB 上的一个动点.
(1)如图 1,若 BAC 90 , AF 1, AC 3 ,求点 B 到 AE 的距离; (2)如图 2,若 E 为 BD 中点,连接 FD,FD 平分 AFC ,G 为 CF 上一点,且 GDC GCD ,求证: DG AF FC ;
(3)如图 3,若 BAC 120 , BC 12 ,将△ABD 沿着 AB 翻折得△ABD ,点 H 为 BD 的中点,连接 HA、HC,当△HAC 周长最小时,请直接写出 AD 的值.
(1)如图 1,△ABC 与△ADE 互为“底余等腰三角形”. ①若连接 BD,CE,判断△ABD 与△ACE 是否互为“底余等腰三角形”:_______ (填 “是”或“否”) ;
②当∠BAC=90°时,若△ADE 的“余高”AH= 5 ,则 DE=_______;
③当 0°<∠BAC<180°时,判断 DE 与 AH 之间的数量关系,并证明; (2)如图 2,在四边形 ABCD 中,∠ABC=60°,DA⊥BA,DC⊥BC,且 DA=DC. ①画出△OAB 与△OCD,使它们互为“底余等腰三角形”; ②若△OCD 的“余高”长为 a,则点 A 到 BC 的距离为_______(用含 a 的式子表示). 7.已知:△ABC 是等腰直角三角形,动点 P 在斜边 AB 所在的直线上,以 PC 为直角 边作等腰直角三角形 PCQ,其中∠PCQ=90°,探究并解决以下问题: (1)如图 1,若点 P 在线段 AB 上,且 AC=4,PA= 2 ,则①线段 PB= ,PC= .② 猜想: PA2, PB2, PQ2 三者之间的数量关系为 .
第一章 勾股定理压轴题考点训练(解析版)-2024年常考压轴题攻略(8年级上册北师大版)

第一章勾股定理压轴题考点训练,,A.《周髀算经》【答案】D【分析】运用《九章算术注》相关知识即可直接解答.【详解】解:由于《九章算术注》是我国学者编撰的最早的一部测量数学著作,该书第一卷【分析】根据八个直角三角形全等,四边形ABCD ,EFGH ,MNKT 是正方形,得出CG NG =,CF DG NF ==,再根据三个正方形面积公式列式相加:12312S S S ++=,求出2GF 的值,从而可以计算结论即可.【详解】解: 八个直角三角形全等,四边形ABCD ,EFGH ,MNKT 是正方形,CG NG ∴=,CF DG NF ==,21()S CG DG ∴=+,222CG DG CG DG =++⋅,22GF CG DG =+⋅,22S GF =,2223()2S NG NF NG NF NG NF =-=+-⋅,2222212322312S S S GF CG DG GF NG NF NG NF GF ∴++=+⋅+++-⋅==,24GF ∴=,24S ∴=,12312S S S ++= ,138S S ∴+=,故选:D .【点睛】此题主要考查了勾股定理的应用,用到的知识点是勾股定理和正方形、全等三角形的性质,根据已知得出2312GF =是解决问题的关键.7.如图,四个全等的直角三角形围成一个正方形ABCD 和正方形EFGH ,即赵爽弦图,连接AC ,FN 交EF ,GH 分别于点M ,N 已知AH=3DH ,且S 正方形ABCD 21=,则图中阴影部分的面积之和为()A .3B .2【答案】C 【分析】过点K 作KM CF ⊥,与CF 的延长线交于点再求得22AK KF EF ==,2MK MF ==果.∵222AH DH ==,∴2DH GH ==,∵EFGH 是正方形,∴EF FG GH HE ===∴DH HE =,A.0.8米B.2米【答案】D【分析】先根据勾股定理求出梯子的长,进而根据勾股定理可得出小巷的宽度.【详解】解:如图,由题意可得:A.①②④B.①④【答案】A【分析】①根据正方形的性质和平角的定义可求得∠②根据正方形的性质求得OE2221(3∴=+=+CF FG CG【答案】3或6【分析】分两种情况分别求解,AED=∠AED′=45′,得DE=(2)当∠ED′A=90°时,如图得A、D′、C在同一直线上,根据勾股定理得∵∠CED′=90°,根据轴对称的性质得∠AED∵∠D=90°,∴△ADE是等腰直角三角形,∴DE=AD=6;根据轴对称的性质得∠AD′E 即∠CD′E=90°,∴∠AD′E+∠CD′E=180°,∴A、D′、C在同一直线上,=根据勾股定理得AC AD35【答案】5或4【分析】本题按照题意合理画图,尽可能想到各种情况,然后根据等腰直角三角形的性质以及以此构造全等三角形,结合正切函数的概念,即可求解.【详解】分两种情况:第一种情况:如图,延长DE 交CA 于A ',∵CDE 是等腰直角三角形,∴45CDE ∠=︒.又=90ACD ∠︒,∴45D C A ∠='︒.由已知45DAC ∠=︒,且点C 、点A 、点A '在同一条直线上,∴A 与A '是同一点(或重合).又∵tan 3QBP ∠=,且CBE △为直角三角形.∴3CE BE =,又由AE AB BE CE =+=得,103BE BE +=,解得:5BE =.第二种情况:如下图,分别自C 、D 作AE 的垂线,垂足为点O 、点F ,过D 作CO 延长线的垂线,与CO 的延长线交于点N .设CD 与AE 交于R .∵AC CD N DN ⊥⊥,C ,∴9090ACO OCR CDN OCR ∠=︒-∠∠=︒-∠,,∴ACO CDN ∠=∠.又∵90,AOC CND AC CD ∠=∠=︒=,∴ACO CDN =△△.①2ADC CAE ∠=∠;③若60BED ∠=︒,则4BE DE =【答案】①②③④【分析】根据直角三角形斜边中线的性质,∴∠DAE=∠DBM,∵∠ADE=∠BDM,AD=BD,∴△ADE≌△BDM(AAS),∴DE=DM,若∠BED=60°,则BE=2EM=4DE【答案】22【分析】通过等腰直角三角形构建一线三等角模型求解即可.【详解】解:如图所示,分别过A 、D 作AE BC ⊥于E ,DF ∴90AEP DFP ∠=∠=︒∴90APE PAE ∠+∠=︒,90DPF PDF ∠+∠=︒∵90APD ∠=︒【答案】2.6【分析】将木块展开,根据两点之间线段最短及勾股定理即可求出答案.【答案】3或18或22【分析】分当点P 在线段AB 上运动时,当点P 在线段BC 上运动且在点E 的左边时三种情况讨论,即可求出【详解】解:∵90C ∠=︒,BC ∴2221612AB AC BC =+=+当点P 在线段BC 上运动且在点同理可知12cm 2CP CE ==∴()1282118t =+-÷=秒;故答案为∶3或18或22.【点睛】本题考查了三角形的面积公式的运用,勾股定理,以及中线的性质,分类讨论的数学思想,解答时分类讨论是是关键.18.如图,一个长方体纸箱,长是点B ,它所走的最短路线的长是(1)如图1,由题意知AC=4,BC=6+4=10由勾股定理得:AB=(2)如图(2)即为所求,正方形的边长为【点睛】本题考查勾股定理的应用,熟练掌握勾股定理是解题关键面积公式求解即可.【详解】解:(1)证明:如图,过点G 作GH ∥AB ,因为AB ∥CD ,所以GH ∥CD ,所以∠AMG =∠MGH ,∠CFG =∠FGH ,∴∠MGF ═∠AMG +∠CFG∴∠AMG 、∠CFG 与∠M GF 之间的数量关系为∠G =∠AMG +∠CFG .(2)∵2180GME AMG ∠+∠=︒,而∠AMG+∠GME+∠EMB=180°,∴∠GME=∠EMG过点E 作EJ//AB ,如图,∴∠MEJ=∠EMB=∠GME∵60GME E ∠-∠=︒∴∠MEG-∠E=60°=∠GEJ∵EJ//AB ,AB//CD ,∴EJ//CD∴∠GFC=∠GEJ=60°而∠GFC=∠FGN+∠GNC∴∠FGN=∠GFC-∠GNC=60°-25°=35°∵NG 平分∠MGF∴∠MGH=∠FGN=35°∴∠MGE=∠MGN+∠FGN=35°+35°=70°(3)∵KNE KHF ∠=∠,24FEN FHE AMG∠=∠+∠又15,60AMG FNE ∠=︒∠=︒由(2)得,∴BCE ACD ∠=∠而BC kAC =∴BC EC k AC DC==,AB=,FG=,(+)2DF,﹣DF•BD∴△(∵在Rt △ABC 中,22BC=AC AB =33-∵CH 平分∠BCA ,∴∠HCB=在△HCB 和△HCG 中HGC=HBC HCB=HCG CH=CH ∠∠⎧⎪∠∠⎨⎪⎩∴△HCB ≌△HCG (AAS )∴BH=HG ,CG=BC③若AE=EC,如图所示,由PE=PC可知P点在CE的中垂线上,的交点即为P点,设AE=EC=x,则BE=BC EC=33x--在Rt△ABE中,由勾股定理得,()222-,解得x=2333x+3=x∴EC=23又∵PM垂直平分EC,∴MC=3。
初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析) 之欧阳德创编

初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)时间:2021.03.07 创作:欧阳德一.选择题(共8小题)1.直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C.D.2.下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2 B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2 D.在Rt△ABC中,∠B=90°,所以a2+b2=c2 3.如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB 等于()A.195cm B.200cm C.205cm D.210cm 4.如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺 C.12尺D.13尺5.如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣ B.1﹣C.﹣D.﹣1+6.一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米7.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.48.如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169二.填空题(共5小题)9.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是.10.如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为米.11.已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于.12.观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是(只填数,不填等式)13.观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b=,c=.三.解答题(共27小题)14.a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.15.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.16.如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.17.如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100km到达B点,然后再沿北偏西30°方向走了100km到达目的地C 点,求出A、C两点之间的距离.18.如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?19.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.20.在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△AB C三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC 的高,而借用网格就能计算出它的面积.这种方法叫做构图法.(1)△ABC的面积为:.(2)若△DEF三边的长分别为、、,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为.(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA 的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是m2.21.(1)在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.请你将△ABC的面积直接填写在横线上.思维拓展:(2)已知△ABC三边的长分别为a(a >0),求这个三角形的面积.我们把上述求△ABC面积的方法叫做构图法.如图2,网格中每个小正方形的边长都是a,请在网格中画出相应的△ABC,并求出它的面积.类比创新:(3)若△ABC三边的长分别为(m>0,n>0,且m≠n),求出这个三角形的面积.如图3,网格中每个小长方形长、宽都是m,n,请在网格中画出相应的△ABC,用网格计算这个三角形的面积.22.有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?23.(拓展创新)在教材中,我们通过数格子的方法发现了直角三角形的三边关系,利用完全相同的四个直角三角形采用拼图的方式验证了勾股定理的正确性.问题1:以直角三角形的三边为边向形外作等边三角形,探究S′+S″与S的关系(如图1).问题2:以直角三角形的三边为斜边向形外作等腰直角三角形,探究S′+S″与S的关系(如图2).问题3:以直角三角形的三边为直径向形外作半圆,探究S′+S″与S的关系(如图3).24.如图,在平面坐标系中,点A、点B分别在x轴、y轴的正半轴上,且OA=OB,另有两点C(a,b)和D(b,﹣a)(a、b均大于0);(1)连接OD、CD,求证:∠ODC=45°;(2)连接CO、CB、CA,若CB=1,C0=2,CA=3,求∠OCB的度数;(3)若a=b,在线段OA上有一点E,且AE=3,CE=5,AC=7,求△OCA的面积.25.11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题“小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻飞去抓鱼,并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树根有多远?26.(1)先化简,再求值:x(x﹣2)﹣(x+1)(x﹣1),其中x=10.(2)已知,求代数式(x+1)2﹣4(x+1)+4的值.(3)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图:①从点A出发在图中画一条线段AB,使得AB=;②画出一个以(1)中的AB为斜边的等腰直角三角形,使三角形的三个顶点都在格点上,并根据所画图形求出等腰直角三角形的腰长.27.[问题情境]勾股定理是一条古老的数学定理,它有很多种证明方法.我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数学关系”(勾股定理)带到其它星球,作为地球人与其他星球“人”进行第一次“谈话”的语言;[定理表述]请你根据图1中的直角三角形叙述勾股定理;[尝试证明]以图1中的直角三角形为基础,将两个直角边长为a,b,斜边长为c的三角形按如图所示的方式放置,连接两个之间三角形的另外一对锐角的顶点(如图2),请你利用图2,验证勾股定理;[知识扩展]利用图2中的直角梯形,我们可以证明<,其证明步骤如下:∵BC=a+b,AD=又∵在直角梯形ABCD中,有BCAD(填大小关系),即∴.28.观察、思考与验证(1)如图1是一个重要公式的几何解释,请你写出这个公式;(2)如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°;(3)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的《新英格兰教育日志》上),请你写出验证过程.29.超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?(参考数据:=1.41,=1.73)30.中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.(1)请用直尺和圆规作出C处的位置;(2)求我国海监船行驶的航程BC的长.31.在一次“构造勾股数”的探究性学习中,老师给出了下表:m 2 3 3 4 …n 1 1 2 3 …a 22+12 32+12 32+22 42+32 …b 4 6 12 24 …c 22﹣12 32﹣12 32﹣22 42﹣32 …其中m、n为正整数,且m>n.(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=,b=,c=.(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.32.如图1,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<8).(1)请在4×8的网格纸图2中画出t为6秒时的线段PQ.并求其长度;(2)当t为多少时.△PQB是以BP为底的等腰三角形.33.阅读下面的情景对话,然后解答问题:(1)理解:①根据“奇异三角形”的定义,请你判断:“等边三角形一定是奇异三角形”吗?(填是或不是)②若某三角形的三边长分别为1、、2,则该三角形(是或不是)奇异三角形.(2)探究:若Rt△ABC是奇异三角形,且其两边长分别为2、2,则第三边的长为,且这个直角三角形的三边之比为(从小到大排列,不得含有分母).(3)设问:请提出一个和奇异三角形有关的问题.(不用解答)34.观察下列各式,你有什么发现?32=4+5,52=12+13,72=24+25,92=40+41,…用你的发现解决下列问题:(1)填空:112=+;(2)请用含字母n(n为正整数)的关系式表示出你发现的规律:;(3)结合勾股定理有关知识,说明你的结论的正确性.35.小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l 与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?36.如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C 分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.37.如图,四边形ABCD的三边(AB、BC、CD)和BD的长度都为5厘米,动点P从A出发(A→B→D)到D,速度为2厘米/秒,动点Q从点D出发(D→C→B→A)到A,速度为2.8厘米/秒.5秒后P、Q相距3厘米,试确定5秒时△APQ的形状.38.一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由.39.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地°送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺),此时踏板升高离地五尺(BD=5尺),求秋千绳索(OA或OB)的长度.40.如图,∠AOB=90°,OA=45cm,OB=15cm,一机器人在点B处看见一个小球从点A出发沿着AO 方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?1.已知直角三角形两边的长为3和4,则此三角形的周长为()A.12 B.7+C.12或7+D.以上都不对2.图中字母所代表的正方形的面积为144的选项为()A.B.C.D.3.如图,数轴上的点A所表示的数为x,则x的值为()A.B.﹣C.2 D.﹣24.如图,带阴影的正方形面积是.5.如图,在Rt△ABC中,∠BCA=90°,点D是BC 上一点,AD=BD,若AB=8,BD=5,则CD=.6.正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,(1)在图①中,画一个面积为10的正方形;(2)在图②、图③中,分别画两个不全等的直角三角形,使它们的三边长都是无理数.初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)参考答案与试题解析一.选择题(共8小题)1.(2016秋•吴江区期中)直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C.D.【分析】首先根据勾股定理,得:斜边==13.再根据直角三角形的面积公式,求出斜边上的高.【解答】解:由题意得,斜边为=13.所以斜边上的高=12×5÷13=.故选D.【点评】运用了勾股定理.注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.2.(2016春•抚顺县期中)下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2 B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2 D.在Rt△ABC中,∠B=90°,所以a2+b2=c2【分析】在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角,根据此就可以直接判断A、B、C、D选项.【解答】解:在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角.A、不确定c是斜边,故本命题错误,即A选项错误;B、不确定第三边是否是斜边,故本命题错误,即B选项错误;C、∠C=90°,所以其对边为斜边,故本命题正确,即C选项正确;D、∠B=90°,所以斜边为b,所以a2+c2=b2,故本命题错误,即D选项错误;故选C.【点评】本题考查了勾股定理的正确运用,只有斜边的平方才等于其他两边的平方和.3.(2016春•临沭县期中)如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm 【分析】作出直角三角形后分别求得直角三角形的两直角边的长后即可利用勾股定理求得斜边AB的长.【解答】解:如图,由题意得:AC=15×5=75cm,BC=30×6=180cm,故AB===195cm.故选A.【点评】本题考查了勾股定理的应用,解题的关键是从实际问题中抽象出直角三角形,难度不大.4.(2015春•青山区期中)如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺 C.12尺D.13尺【分析】找到题中的直角三角形,设水深为x尺,根据勾股定理解答.【解答】解:设水深为x尺,则芦苇长为(x+1)尺,根据勾股定理得:x2+()2=(x+1)2,解得:x=12,芦苇的长度=x+1=12+1=13(尺),故选D.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.5.(2016春•南陵县期中)如图所示,在数轴上点A 所表示的数为a,则a的值为()A.﹣1﹣ B.1﹣C.﹣D.﹣1+【分析】点A在以O为圆心,OB长为半径的圆上,所以在直角△BOC中,根据勾股定理求得圆O的半径OA=OB=,然后由实数与数轴的关系可以求得a的值.【解答】解:如图,点A在以O为圆心,OB长为半径的圆上.∵在直角△BOC中,OC=2,BC=1,则根据勾股定理知OB===,∴OA=OB=,∴a=﹣1﹣.故选A.【点评】本题考查了勾股定理、实数与数轴.找出OA=OB是解题的关键.6.(2015春•蓟县期中)一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米【分析】先根据梯子的顶端下滑了0.4米求出A′C的长,再根据勾股定理求出B′C的长,进而可得出结论.【解答】解:(1)∵在Rt△ABC中,AB=2.5m,BC=0.7m,∴AC===2.4(m).∵梯子的顶端下滑了0.4米,∴A′C=2m,∵在Rt△A′B′C中,A′B′=2.5m,A′C=2m,∴B′C==1.5m,∴BB′=B′C﹣BC=1.5﹣0.7=0.8m.故选C.【点评】此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.7.(2015春•罗田县期中)在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.4【分析】根据勾股定理求出AB的长即可解答.【解答】解:在Rt△ABC中,根据勾股定理,AB==13,又∵AC=12,BC=5,AM=AC,BN=BC,∴AM=12,BN=5,∴MN=AM+BN﹣AB=12+5﹣13=4.故选D.【点评】本题综合考查了勾股定理的应用,找到关系MN=AM+BN﹣AB是关键.8.(2016春•重庆校级期中)如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169【分析】根据勾股定理,知两条直角边的平方等于斜边的平方,此题中斜边的平方即为大正方形的面积13,2ab即四个直角三角形的面积和,从而不难求得(a+b)2的值.【解答】解:(a+b)2=a2+b2+2ab=大正方形的面积+四个直角三角形的面积和=13+(13﹣1)=25.故选C.【点评】考查了勾股定理的证明,注意完全平方公式的展开:(a+b)2=a2+b2+2ab,还要注意图形的面积和a,b之间的关系.二.填空题(共5小题)9.(2016春•固始县期中)将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是7cm≤h≤16cm.【分析】如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出h的取值范围.【解答】解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,∴h=24﹣8=16cm;当筷子的底端在A点时,筷子露在杯子外面的长度最短,在Rt△ABD中,AD=15,BD=8,∴AB==17,∴此时h=24﹣17=7cm,所以h的取值范围是7cm≤h≤16cm.故答案为:7cm≤h≤16cm.【点评】本题考查了勾股定理的应用,求出h的值最大值与最小值是解题关键.10.(2015春•汕头校级期中)如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为(1+)米.【分析】根据题意利用勾股定理得出BC的长,进而得出答案.【解答】解:由题意得:在直角△ABC中,AC2+AB2=BC2,则12+22=BC2,∴BC=,∴则树高为:(1+)m.故答案为:(1+).【点评】此题主要考查了勾股定理的应用,熟练利用勾股定理得出BC的长是解题关键.11.(2016春•高安市期中)已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于24cm2.【分析】利用勾股定理列出关系式,再利用完全平方公式变形,将a+b与c的值代入求出ab的值,即可确定出直角三角形的面积.【解答】解:∵Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,∴由勾股定理得:a2+b2=c2,即(a+b)2﹣2ab=c2=100,∴196﹣2ab=100,即ab=48,则Rt△ABC的面积为ab=24(cm2).故答案为:24cm2.【点评】此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.12.(2016春•嘉祥县期中)观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是15,112,113 (只填数,不填等式)【分析】通过观察,得出规律:这类勾股数分别为2n+1,2n(n+1),2n(n+1)+1,由此可写出第7组勾股数.【解答】解:∵第1组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,第2组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,第3组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,第4组:9=2×4+1,40=2×4×(4+1)41=2×4×(4+1)+1,∴第7组勾股数是2×7+1=15,2×7×(7+1)=112,2×7×(7+1)+1=113,即15,112,113.故答案为:15,112,113.【点评】此题考查的知识点是勾股数,属于规律性题目,关键是通过观察找出规律求解.13.(2009春•武昌区期中)观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b= 84 ,c= 85 .【分析】认真观察三个数之间的关系:首先发现每一组的三个数为勾股数,第一个数为从3开始连续的奇数,第二、三个数为连续的自然数;进一步发现第一个数的平方是第二、三个数的和;最后得出第n组数为(2n+1),(),(),由此规律解决问题.【解答】解:在32=4+5中,4=,5=;在52=12+13中,12=,13=;…则在13、b、c中,b==84,c==85.【点评】认真观察各式的特点,总结规律是解题的关键.三.解答题(共27小题)14.(2016春•黄冈期中)a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.【分析】现对已知的式子变形,出现三个非负数的平方和等于0的形式,求出a、b、c,再验证两小边的平方和是否等于最长边的平方即可.【解答】解:由a2+b2+c2+338=10a+24b+26c,得:(a2﹣10a+25)+(b2﹣24b+144)+(c2﹣26c+169)=0,即:(a﹣5)2+(b﹣12)2+(c﹣13)2=0,由非负数的性质可得:,解得,∵52+122=169=132,即a2+b2=c2,∴∠C=90°,即三角形ABC为直角三角形.【点评】本题考查勾股定理的逆定理的应用、完全平方公式、非负数的性质.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.15.(2016秋•永登县期中)如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.【分析】连接AC,则在直角△ABC中,已知AB,BC 可以求AC,根据AC,AD,CD的长可以判定△ACD 为直角三角形,(1)根据∠BAD=∠CAD+∠BAC,可以求解;(2)根据四边形ABCD的面积为△ABC和△ACD的面积之和可以解题.【解答】解:(1)连接AC,∵AB⊥CB于B,∴∠B=90°,在△ABC中,∵∠B=90°,∴AB2+BC2=AC2,又∵AB=CB=,∴AC=2,∠BAC=∠BCA=45°,∵CD=,DA=1,∴CD2=5,DA2=1,AC2=4.∴AC2+DA2=CD2,由勾股定理的逆定理得:∠DAC=90°,∴∠BAD=∠BAC+∠DAC=45°+90°=135°;(2)∵∠DAC=90°,AB⊥CB于B,∴S△ABC=,S△DAC=,∵AB=CB=,DA=1,AC=2,∴S△ABC=1,S△DAC=1而S四边形ABCD=S△ABC+S△DAC,∴S四边形ABCD=2.【点评】本题考查了勾股定理在直角三角形中的运用,考查了根据勾股定理逆定理判定直角三角形,考查了直角三角形面积的计算,本题中求证△ACD是直角三角形是解题的关键.16.(2016春•邹城市校级期中)如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.【分析】直接利用网格结合勾股定理求出答案.【解答】解:如图所示:△ABC即为所求.【点评】此题主要考查了勾股定理,正确借助网格求出是解题关键.17.(2015春•平南县期中)如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100km到达B点,然后再沿北偏西30°方向走了100km到达目的地C点,求出A、C两点之间的距离.【分析】根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.【解答】解:∵AD∥BE∴∠ABE=∠DAB=60°∵∠CBE=30°∴∠ABC=180°﹣∠ABE﹣∠CBE=180°﹣60°﹣30°=90°,在Rt△ABC中,∴==200,∴A、C两点之间的距离为200km.【点评】本题考查勾股定理的应用,先确定是直角三角形后,根据各边长,用勾股定理可求出AC的长,且求出∠DAC的度数,进而可求出点C在点A的什么方向上.18.(2015秋•新泰市期中)如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?【分析】(1)过A作AE⊥BD于E,线段AE的长即为台风中心与气象台A的最短距离,由含30°角的直角三角形的性质即可得出结果;(2)根据题意得出线段CD就是气象台A受到台风影响的路程,求出CD的长,即可得出结果.【解答】解:(1)过A作AE⊥BD于E,如图1所示:∵台风中心在BD上移动,∴AE的长即为气象台距离台风中心的最短距离,在Rt△ABE中,∠ABE=90°﹣60°=30°,∴AE=AB=160,即台风中心在移动过程中,与气象台A的最短距离是160km.(2)∵台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响,∴线段CD就是气象台A受到台风影响的路程,连接AC,如图2所示:在Rt△ACE中,AC=200km,AE=160km,∴CE==120km,∵AC=AD,AE⊥CD,∴CE=ED=120km,∴CD=240km.∴台风影响气象台的时间会持续240÷20=12(小时).【点评】本题考查了勾股定理在实际生活中的应用、垂径定理、含30°角的直角三角形的性质等知识;熟练掌握垂径定理和勾股定理,求出CD是解决问题(2)的关键.19.(2015春•阳东县期中)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t 秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.【分析】(1)我们求出BP、BQ的长,用勾股定理解决。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
别这个三角形的形状. 15.如图:四边形 ABCD 中,AB=CB= ,CD= ,DA=1,且 AB⊥CB 于 B. 试求:(1)∠BAD 的度数; (2)四边形 ABCD 的面积.
16.如图,小华准备在边长为 1 的正方形网格中,作一个三边长分别为 4,5, 的三角形,请你帮助小华作出来.
17.如图所示,在一次夏令营活动中,小明坐车从营地 A 点出发,沿北偏东 60°方向走了 100 km 到达 B 点,然后再沿北偏西 30°方向走了 100km 到达目 的地 C 点,求出 A、C 两点之间的距离.
11.已知 Rt△ABC 中,∠C=90°,a+b=14cm,c=10cm,则 Rt△ABC 的面积等 于 . 12.观察下列勾股数 第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1 第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1 第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1 第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1 …观察以上各组勾股数组成特点,第 7 组勾股数是 (只填数,不填等式) 13.观察下列一组数: 列举:3、4、5,猜想:32=4+5; 列举:5、12、13,猜想:52=12+13; 列举:7、24、25,猜想:72=24+25; … 列举:13、b、c,猜想:132=b+c; 请你分析上述数据的规律,结合相关知识求得 b= ,c= . 三.解答题(共 27 小题) 14.a,b,c 为三角形 ABC 的三边,且满足 a2+b2+c2+338=10a+24b+26c,试判
9.将一根 24cm 的筷子,置于底面直径为 15cm,高 8cm 的圆柱形水杯中,如 图所示,设筷子露在杯子外面的长度为 hcm,则 h 的取值范围是 .
10.如图,一场暴雨过后,垂直于地面的一棵树在距地面 1 米的点 C 处折断, 树尖 B 恰好碰到地面,经测量 AB=2 米,则树高为 米.
19.如图,已知△ABC 中,∠B=90°,AB=8cm,BC=6cm,P、Q 分别为 AB、 BC 边上的动点,点 P 从点 A 开始沿 A⇒B 方向运动,且速度为每秒 1cm,点 Q 从点 B 开始 B→C 方向运动,且速度为每秒 2cm,它们同时出发;设出发的 时间为 t 秒. (1)出发 2 秒后,求 PQ 的长; (2)从出发几秒钟后,△PQB 能形成等腰三角形? (3)在运动过程中,直线 PQ 能否把原三角形周长分成相等的两部分?若能 够,请求出运动时间;若不能够,请说等腰 Rt△ABE 和等腰 Rt△ACF,过点 E、F 作射 线 GA 的垂线,垂足分别为 P、Q.试探究 EP 与 FQ 之间的数量关系,并证明 你的结论. (4)如图 4,一个六边形的花坛被分割成 7 个部分,其中正方形 PRBA, RQDC,QPFE 的面积分别为 13m2、25m2、36m2,则六边形花坛 ABCDEF 的面 积是 m2.
初二数学 勾股定理常考压轴题专题练习汇总(含解析)
一.选择题(共 8 小题) 1.直角三角形两直角边长度为 5,12,则斜边上的高( ) A.6 B.8 C. D. 2.下列说法中正确的是( ) A.已知 a,b,c 是三角形的三边,则 a2+b2=c2 B.在直角三角形中两边和的平方等于第三边的平方 C.在 Rt△ABC 中,∠C=90°,所以 a2+b2=c2 D.在 Rt△ABC 中,∠B=90°,所以 a2+b2=c2 3.如图,是台阶的示意图.已知每个台阶的宽度都是 30cm,每个台阶的高度 都是 15cm,连接 AB,则 AB 等于( )
18.如图,在气象站台 A 的正西方向 320km 的 B 处有一台风中心,该台风中 心以每小时 20km 的速度沿北偏东 60°的 BD 方向移动,在距离台风中心 200km 内的地方都要受到其影响. (1)台风中心在移动过程中,与气象台 A 的最短距离是多少?
(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时 间会持续多长?
A.195cm B.200cm C.205cm D.210cm 4.如图,在水池的正中央有一根芦苇,池底长 10 尺,它高出水而 1 尺,如果 把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是 ( )
A.10 尺 B.11 尺 C.12 尺 D.13 尺 5.如图所示,在数轴上点 A 所表示的数为 a,则 a 的值为( )
A.﹣1﹣ B.1﹣ C.﹣
D.﹣1+
6.一架 2.5 米长的梯子底部距离墙脚 0.7 米,若梯子的顶端下滑 0.4 米,那么
梯子的底部在水平方向滑动了( )
A.1.5 米 B.0.9 米 C.0.8 米 D.0.5 米 7.在△ABC 中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则 MN 的 长为( )
A.2 B.2.6 C.3 D.4 8.如图,是 2002 年北京第 24 届国际数学家大会会徽,由 4 个全等的直角三角 形拼合而成,如果大正方形的面积是 13,小正方形的面积是 1,直角三角形的 短直角边为 a,较长直角边为 b,那么(a+b)2 的值为( )
A.13 B.19 C.25 D.169 二.填空题(共 5 小题)
20.在△ABC 中,AB、BC、AC 三边的长分别为 、 、 ,求这个三角 形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的 边长为 1),再在网格中画出格点△ABC(即△ABC 三个顶点都在小正方形的顶 点处),如图 1 所示.这样不需求△ABC 的高,而借用网格就能计算出它的面 积.这种方法叫做构图法. (1)△ABC 的面积为: . (2)若△DEF 三边的长分别为 、 、 ,请在图 2 的正方形网格中画出 相应的△DEF,并利用构图法求出它的面积为 . (3)如图 3,△ABC 中,AG⊥BC 于点 G,以 A 为直角顶点,分别以 AB、
