冲击系数计算
喷嘴冲击力计算

喷嘴冲击力的计算需要考虑到喷嘴的设计、喷出物的速度、喷嘴与目标物体的距离、以及目标的材质等因素。
以下是一个基本的计算公式和说明:公式:F = 1/2 * CD * π* r2 * v2解释:* F:冲击力* CD:冲击系数,取决于喷出物的速度和喷嘴口径的相对大小,具体数值可以在相关文献或软件中查询。
* r:喷嘴到目标物体的距离(单位:米)* v:喷出物的速度(单位:米/秒)* π:圆周率通常来说,对于相同的设计和喷出物速度,喷嘴离目标越近,冲击力越大。
这是因为距离变小,喷嘴的射程也会相应变短,所以更多的能量会集中在较小的范围内,造成了更大的冲击力。
对于液体喷嘴,冲击力还可能受到目标物体材质的影响。
一般来说,硬度较高的物体可能会对喷嘴造成磨损。
这是因为液体在喷出时会携带一部分能量,这些能量在撞击到物体后会有一部分转化为对物体的冲击力。
所以,选择合适的喷嘴和目标物体是非常重要的。
另外,对于某些特定的应用场景,可能需要考虑其他因素,如喷出物的粘度、喷嘴的口径、形状、以及喷嘴与目标物体的角度等。
这些因素都会影响到喷嘴的冲击力和实际效果。
在实际应用中,可以根据上述公式和说明,结合具体情况进行计算和调整。
需要注意的是,这个公式只是一个基本的计算方法,实际应用中可能还需要考虑其他因素,如液体种类、环境温度、压力等因素的影响。
此外,不同的喷嘴和液体组合可能会有不同的效果,需要进行实验和测试来确定最佳的方案。
总的来说,喷嘴冲击力的计算是一个涉及到多个因素的过程,需要综合考虑设计、速度、距离、目标物体材质等因素的影响。
通过合理的选择和调整,可以获得最佳的效果和安全性。
冲击系数

冲击系数说明书、冲击系数原理1一般,桥梁动载实验中,动力荷载作用与桥梁结构上产生的动挠度或动应变较同样的静荷载所产生的相应的静挠度(静应变)要大。
以动挠度为例,动挠度。
由于挠度反映了桥梁结)与相应的静挠度的比值称为活荷载的冲击系数(1+μ因此活载冲击系数综合反映了动力是衡量结构刚度的主要指标,构的整体变形,车辆行驶速活载冲击系数与桥梁结构的结构形式、荷载对桥梁结构的动力作用。
应使车辆以不同为了测定桥梁结构的冲击系数,度、桥梁的平整度等因素有关。
的速度驶过桥梁,逐次记录跨中截面的挠度时程曲线,按照冲击系数的定义有:Y ???1max Y meanY----动载作用下该测点最大动挠度值;式中:axm Y----相应的静载荷作用下该测点最大挠度值,简称最大静挠度值,其值mean可由动挠度曲线求得:1)YY?Y?(minmaxmean2YY相应的最小挠度值。
如图1为与所示。
其中meaninm图1 移动荷载作用下桥梁动挠度曲线同理,在动载实验中测试动应变时,产生的冲击系数(1+μ)的计算公式如下:1 / 2S??1?max S mean式中:----动载作用下该测点最大动应变值;S axm----相应的静载荷作用下该测点最大应变值,其值可由动应变曲线求S mean得:1 )?SS?(S minmeanmax2 为与相应的最小应变值。
其中SS meanmin另外,在测试动应变时程曲线时,由于应变片的贴法的正负极性不同,用户实测的动应变曲线的主峰很可能往下(为负值),在这种情况下,冲击系数的计SS、都将有所改变,具体如下:、算公式不变,但是S meanaxmmin S----动载作用下该测点最大动应变的绝对值;axm S----相应的静载荷作用下该测点最大应变的绝对值;mean S相应的最小应变的绝对值。
与----S meanmin(范文素材和资料部分来自网络,供参考。
可复制、编制,期待你的好评与关注)2 / 2。
冲击系数

冲击系数说明书1、冲击系数原理桥梁动载实验中,动力荷载作用与桥梁结构上产生的动挠度或动应变,一般较同样的静荷载所产生的相应的静挠度(静应变)要大。
以动挠度为例,动挠度与相应的静挠度的比值称为活荷载的冲击系数(1+μ)。
由于挠度反映了桥梁结构的整体变形,是衡量结构刚度的主要指标,因此活载冲击系数综合反映了动力荷载对桥梁结构的动力作用。
活载冲击系数与桥梁结构的结构形式、车辆行驶速度、桥梁的平整度等因素有关。
为了测定桥梁结构的冲击系数,应使车辆以不同的速度驶过桥梁,逐次记录跨中截面的挠度时程曲线,按照冲击系数的定义有: mean Y Y max 1=+μ式中:m ax Y ----动载作用下该测点最大动挠度值;mean Y ----相应的静载荷作用下该测点最大挠度值,简称最大静挠度值,其值可由动挠度曲线求得:)(21min max Y Y Y mean += 其中m in Y 为与mean Y 相应的最小挠度值。
如图1所示。
图1 移动荷载作用下桥梁动挠度曲线同理,在动载实验中测试动应变时,产生的冲击系数(1+μ)的计算公式如下:mean S S max 1=+μ式中:m ax S ----动载作用下该测点最大动应变值;mean S ----相应的静载荷作用下该测点最大应变值,其值可由动应变曲线求得:)(21min max S S S mean +=其中min S 为与mean S 相应的最小应变值。
另外,在测试动应变时程曲线时,由于应变片的贴法的正负极性不同,用户实测的动应变曲线的主峰很可能往下(为负值),在这种情况下,冲击系数的计算公式不变,但是m ax S 、mean S 、min S 都将有所改变,具体如下:m ax S ----动载作用下该测点最大动应变的绝对值;mean S ----相应的静载荷作用下该测点最大应变的绝对值;min S ----与mean S 相应的最小应变的绝对值。
混凝土曲线箱梁桥面板局部冲击系数计算方法研究

精品文档供您编辑修改使用专业品质权威编制人:______________审核人:______________审批人:______________编制单位:____________编制时间:____________序言下载提示:该文档是本团队精心编制而成,希望大家下载或复制使用后,能够解决实际问题。
文档全文可编辑,以便您下载后可定制修改,请根据实际需要进行调整和使用,谢谢!同时,本团队为大家提供各种类型的经典资料,如办公资料、职场资料、生活资料、学习资料、课堂资料、阅读资料、知识资料、党建资料、教育资料、其他资料等等,想学习、参考、使用不同格式和写法的资料,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!And, this store provides various types of classic materials for everyone, such as office materials, workplace materials, lifestylematerials, learning materials, classroom materials, reading materials, knowledge materials, party building materials, educational materials, other materials, etc. If you want to learn about different data formats and writing methods, please pay attention!混凝土曲线箱梁桥面板局部冲击系数计算方法探究混凝土曲线箱梁桥是一种高速公路桥梁的主要类型,其桥面板在运营中会受到各种不同形式的荷载作用,其中一种重要的荷载类型是局部冲击荷载。
铁路桥涵挖孔桩计算

铁路桥涵顶进挖孔桩计算及施工安全的探讨工程概述随着交通运输的发展,框架桥顶进施工技术已经广泛应于铁路既有线改造、增建二线以及公路、铁路平改立交工程中。
挖孔桩在框架顶进过程中起着非常重要的作用;挖孔桩计算必须要严格把关,确保铁路运输安全正常。
采用人工挖孔桩架设D型施工便梁和工字钢对京广铁路上下行线路进行架空,主跨采用2套D16型施工便梁,副跨采用24片56#工字钢和112片32#工字钢组成(采用横抬法)。
一、荷载计算挖孔桩所受列车运营荷载如图(一)冲击系数不限速时:1+μ=1+28/(40+L P)限速时:1+vμ=1+ v28/(40+L P)V—冲击力系数的折减系数=V/(2V KP-V) V KP 一般取80,L P——计算跨度(m)。
列车慢行45km/h冲击系数=1+vμ=1+ v28/(40+L P)=1+ V/(2V KP-V) ×28/(40+L P)=1+45/(2×80-45) ×28/(40+16)=1.2(二)列车活载列车活载=5×220+92×(L-5×1.5)=5×220+92×(16.4-5×1.5)=1919KN L—计算跨度。
(三)线路静载D16便梁查说明可得重245.5KN线路自重= 7.31KN/m×16=108KN56#工字钢=12m×6片×123.9kg=7657kg=76.57KN32#工字钢=2股×(12/0.6)片×62.7=2496kg=25KN(四)线路中间单桩承载力计算检算时,取最不利线路中间主挖孔桩进行计算P=冲击系数×(列车荷载+线路静载)=1.2×[(1919+245.5+108)×2/4+76.57/2+25×2/2]=1440KN二、挖孔桩允许承载力计算挖孔桩开挖位置为人工填土路堤,硬塑黏土。
汽车荷载冲击系数计算(自编)
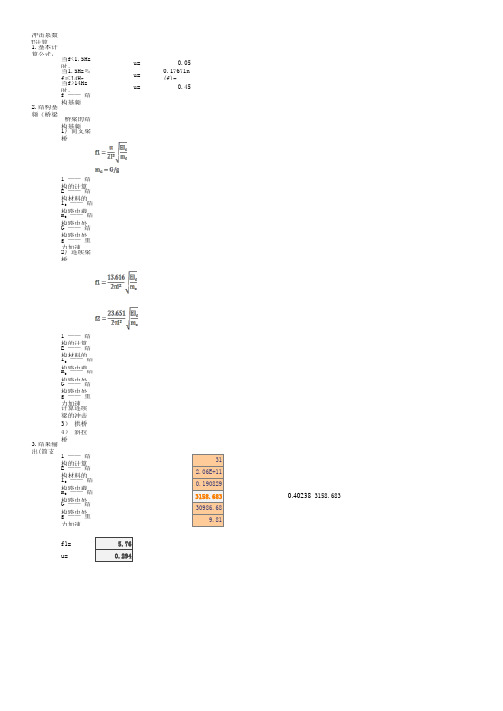
冲击系数U计算1.基本计算公式:当f<1.5Hz时,u=0.05当1.5Hz≤f≤14Hz时,u=0.1767ln(f)-0.0157当f>14Hz时,u=0.45f —— 结构基频(桥梁自振频率)2.结构基频(桥梁自振频率)计算公式:桥梁的结构基频(桥梁自振频率)宜采用有限元方法计算,对于常规结构,也可采用下列公式估算。
1) 简支梁桥l —— 结构的计算跨径(m)E —— 结构材料的弹性模量(N/m2)I c —— 结构跨中截面的截面惯性矩(m4)m c —— 结构跨中处的单位长度质量(kg/m)G —— 结构跨中处延米结构重力(N/m)g —— 重力加速度,g=9.81(m/s2)2) 连续梁桥l —— 结构的计算跨径(m)E —— 结构材料的弹性模量(N/m2)I c —— 结构跨中截面的截面惯性矩(m4)m c —— 结构跨中处的单位长度质量(kg/m)G —— 结构跨中处延米结构重力(N/m)g —— 重力加速度,g=9.81(m/s2)计算连续梁的冲击力引起的正弯矩效应和剪力效应时,采用f1;计算连续梁的冲击力引起的负弯矩效应时,采用f2。
3) 拱桥4) 斜拉桥3.结果输出(简支梁):l —— 结构的计算跨径(m)31E —— 结构材料的弹性模量(N/m2) 2.06E+11I c —— 结构跨中截面的截面惯性矩(m4)0.190829m c —— 结构跨中处的单位长度质量(kg/m)3158.6830.402383158.683G —— 结构跨中处延米结构重力(N/m)30986.68g —— 重力加速度,g=9.81(m/s2)9.81f1= 5.76u=0.294。
桥梁冲击系数计算

桥梁冲击系数计算
桥梁冲击系数是指桥梁在受到外力作用时所承受的冲击程度。
它是一个紧密关联桥梁结构安全的重要指标之一,其计算方法主要包含以下几个步骤:
1. 首先需要确定所受外力的种类,如车辆荷载、风荷载、地震荷载等。
2. 然后需要根据外力特性、桥墩类型及间跨距等因素来确定桥梁的动力特性,如自振周期、阻尼比等参数。
3. 根据特性值来计算桥梁的加速度响应谱,即动力特性下所受外力对桥梁的加速度响应值。
4. 最后根据加速度响应谱与外力谱之间的比值,即为桥梁冲击系数,通常用于计算桥梁的动态响应和疲劳破坏等安全问题。
需要注意的是,在计算桥梁冲击系数时,必须要考虑多种因素,如桥梁的几何形态、材料性质、荷载类型、工作状态等,以获取准确的计算结果。
三相短路实用计算中,冲击系数

三相短路实用计算中,冲击系数1. 前言在电力系统中,短路计算是非常重要的一项工作。
短路会造成电力设备的损坏,甚至引发火灾或事故。
正确地进行短路计算,对于保障电力系统的安全稳定运行至关重要。
而在三相短路实用计算中,冲击系数则是一个关键的参数。
2. 三相短路计算概述三相短路是指电力系统中的三相导线之间发生的短路故障。
在进行三相短路计算时,需要考虑诸如电阻、电抗、传输线路参数等多个因素。
而其中的一个重要参数就是冲击系数。
3. 冲击系数的定义冲击系数是指系统在短路状态下电流的最大值与额定电流之比。
冲击系数越大,代表电流峰值与额定电流的差距就越大。
在实际工程中,考虑到冲击系数可以更准确地评估短路时的过载程度。
4. 冲击系数的计算方法在三相短路实用计算中,冲击系数的计算可以通过如下公式得出:\[ K_{\text{冲击}} = \frac {I_{\text{短路峰值}}}{I_{\text{额定}}} \]式中,\( K_{\text{冲击}} \) 表示冲击系数,\( I_{\text{短路峰值}} \) 表示短路时电流的峰值,\( I_{\text{额定}} \) 表示额定电流。
5. 冲击系数的影响因素冲击系数是由多个因素共同影响而形成的,主要包括以下几点:- 电力系统的负载特性- 发电机及变电设备的参数- 电力系统的阻抗特性- 系统的短路电流限制等等。
6. 冲击系数和保护装置的关系冲击系数的大小直接影响到保护装置的选择和设置。
在短路状态下,电流的瞬时峰值可能远大于额定电流,如果保护装置的选择不当,可能会导致保护装置动作不准确,甚至失灵。
在进行保护装置的设置时,必须充分考虑冲击系数的影响。
7. 冲击系数的实际应用在电力系统设计和建设中,对冲击系数的准确计算和评估是非常重要的。
通过合理地评估冲击系数,可以确定合适的保护装置、设备参数,从而保证电力系统在短路状态下的安全可靠运行。
8. 结论在三相短路实用计算中,冲击系数是一个重要的评估参数。
