斯坦纳定理(My God)
斯氏定理(斯坦沃特定理)

斯氏定理、斯坦沃特定理,任意三角形ABC中,D是底边BC上一点,联结AD,则有:AB^2×CD+AC^2×BD-AD^2×BC=BD×DC×BC也可以有另一种表达形式:设BD=u,DC=v,则有:AD^2=(b^2×u+c^2×v)/a-uv2证明过点A作AE⊥BC于E, 设DE = x(假设底边四点从左到右顺序为B、D、E、C)则 AE^2 = b^2 - (v-x)^2 = c^2 - (u+x)^2 = AD^2 - x^2若E在BC的延长线上,则v-x换成x-v所以有 AD^2 = b^2 - v^2 + 2vxAD^2 = c^2 - u^2 - 2ux1*u式+2*v式得AD^2(u+v) = b^2u + c^2v - uv(u + v)故 AD^2 = (b^2u + c^2v)/a - uv1)当AD是△ABC中线时, u = v = 1/2a AD^2 = (b^2+c^2-(a^2)/2)/22)当AD是△ABC内角平分线时,由三角形内角平分线的性质,得u = ac/(b+c), v =ab/(b+c)设s = (a+b+c)/2得 AD^2 = 4/(b+c)^2 *(bcs(s-a))3)当AD是△ABC高时, AD^2 = b^2 - u^2 = c^2 - v^2再由 u+v = a得AD^2 = 1/4a^2(2a^2b^2 + 2b^2c^2 + 2c^2a^2 - a^4 - b^4 - c^4)证明方法2:不妨设角ADB=θ。
AD=t由余弦定理可得:c^2=t^2+u^2-2tu·cosθ ①b^2=t^2+v^2+2tv·cosθ ②①×v+②×u得:b^2u+c^2v=at^2+auv整理即可得:t^2=(b^2×u+c^2×v)/a-uv证毕3推广角平分线长定理已知AD为三角形ABC的角分线,则AD^2=AB·AC-DB·DC中线定理(pappus定理),又称阿波罗尼奥斯定理,是欧氏几何的定理,表述三角形三边和中线长度关系。
八年级数学上册 17.5 反证法 谈谈斯坦纳—雷姆斯定理素材 (新版)冀教版

谈谈斯坦纳——雷姆斯定理1840年,雷姆斯(C.L ehmus)向著名几何大师瑞士人斯坦纳(J.Steiner)提出了一个看起来十分简单的几何问题,要求给以证明。
问题是:命题三角形两个底角平分线相等便是等腰三角形。
斯氏答应研究它,但他直到1844年才发表定理的征明。
后来该命题就以斯坦纳—雷姆斯定理而闻名于世。
150多年来,经常有论述它的文章发表。
笔者见过斯—雷定理的证明30余种,比较而言,觉得还是以斯氏原证为佳。
问题在△ABC中,∠B、∠C的平分线分别为BD,CE,且BD=CE。
求证:AB=AC。
斯坦纳原证如图1,假设AB>AC。
则∠B<∠C,从而∠BEC>∠BDC(1)在△BCE与△CBD中,∵BD=CE,BC公共,∠BCE>∠CBD,∴BE>CD。
作平行四边形BDCF,连接EF。
∵BE>CD=BF。
∴∠1<∠2。
∵CE=BD=CF 。
∴∠3=∠4。
∴∠BEC<∠BFC=∠BDC (2)(1)与(2)矛盾。
∴AB≯AC。
同理AC≯AB。
故 AB=AC。
之所以说斯氏原证好,是因为它不仅简洁优美,而且另一些证明三角形等腰的问题也可仿照斯氏原证证明。
请同学们看以下三例。
例1 如图2,在△ABC中,AT⊥BC于T,垂足T在BC上,H为垂心,P为HT上任意一点,将BP交 AC于D,CP交AB于E,且BD=CE。
求证:AB=AC。
证明:假设AB>AC,则BT>CT,BP>CP,∠5>∠6。
在△BCE与△CBD中,又因CD=BD,BC公共,∴BE>CD。
设CH⊥AB于I,BH⊥AC于K。
在Rt△CIE与Rt△BKD中,∵CE=BD,由AB>AC,知CI<BK,∴∠8<∠7。
∴∠BEC>∠BDC (1)作平行四边形BDCF,连接EF,∵BE>CD=BF,∴∠1<∠2。
∵CE=BD=CF,∴∠3=∠4。
∴∠BEC<∠BFC=∠BDC(2)(1)与(2)矛盾。
∴AB≯AC。
同理AC≯AB。
故AB=AC。
例2 在△ABC中,点M,N分别在AB,AC上,AM=AN。
几何中的著名定理大全
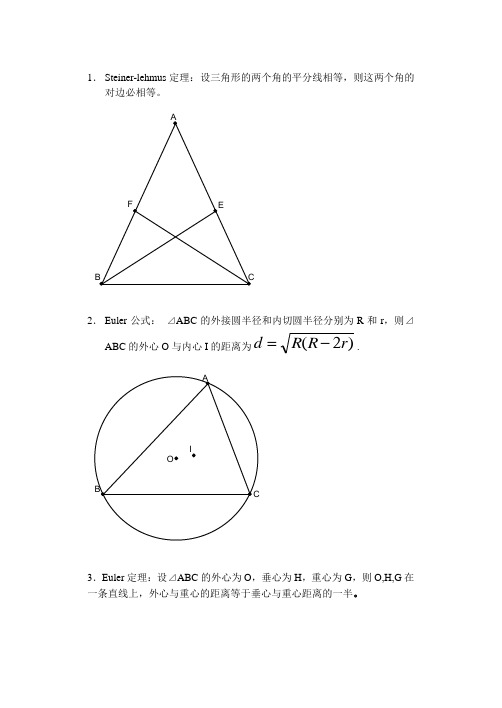
1.Steiner-lehmus定理:设三角形的两个角的平分线相等,则这两个角的对边必相等。
2.Euler公式:⊿ABC的外接圆半径和内切圆半径分别为R和r,则⊿ABC的外心O与内心I的距离为)2(rRRd-=.3.Euler定理:设⊿ABC的外心为O,垂心为H,重心为G,则O,H,G在一条直线上,外心与重心的距离等于垂心与重心距离的一半。
4.九点圆(Euler圆Feuerbach圆)定理:在⊿ABC中,三边的中点,从三顶点向三边做垂线所得垂足,三个顶点与垂心连线的中点,这九个点共圆。
4.已知非等腰锐角三角形ABC的外心、内心和垂心分别是O、I、H,∠A,若三角形ABC的三条高线分别是AD、BE、CF,则三角60=形OIH 的外接圆半径与三角形DEF 的外接圆半径之比为 .5. Euler 定理2:四边形ABCD 两对角线AC,BD 的中点分别是M,N,则22222224MN BD AC DA CD BC AB ++=+++6.Carnot 定理:设G 为⊿ABC 的重心,P 为⊿ABC 所在平面上任意一点,则)(313322222222222c b a PG PG GC GB GA PC PB PA +++=+++=++,其中后一等式为Leibnitz 公式。
6. 张角公式:已知⊿ABC 之BC 边上一点D ,设∠BAD=α,∠DAC=β,则.ABAC AD βαβαsin sin )sin(+=+7.Newton定理:设⊙O的外切四边形ABCD的对角线AC,BD的中点分别为E,F,则E,O,F共线。
8.Newton线定理:任意四边形的两条对角线的中点,两组对边延长线交点所构成的线段的中点,这三点在一条直线上。
BH10.Ptolemy 定理:圆内接四边形ABCD 的两组对边乘积的和等于他对角线的乘积。
BD AC BC AD CD AB⋅=⋅+⋅11.Morley 定理:⊿ABC 的各角的三等分线交点做成⊿DEF,则⊿DEF 是正三角形.AC12.Stewart 定理:⊿ABC 的边BC 上任取一点D,若BD=u,DC=v,AD=t,则uv av c u b t -+=222.D13.Ceva 定理:在⊿ABC 内任取一点P,直线AP,BP,CP 分别与边BC,CA,AB 相交于D,E,F,则1=⋅⋅FBAFEA CE DC BD ,其中点P 称为⊿ABC 的西瓦点. Ceva -1定理:在⊿ABC 的边BC,CA,AB 上分别取点D,E,F,如果1=⋅⋅FBAFEA CE DC BD ,那么直线AD,BE,CF 相交于一点.D14.Menelaus 定理:一直线与⊿ABC 的三边BC,CA,AB 或延长线分别交于X,Y ,Z,则1=⋅⋅YACYXC BX ZB AZ ,其中直线XYZ 称为⊿ABC 的Menelaus 线. Menelaus -1定理:X,Y,Z 分别是⊿ABC 的三边BC,CA,AB 上或其延长线上的三点,如果1=⋅⋅YACYXC BX ZB AZ ,那么X,Y,Z 三点共线. C15.Desargues 定理:在⊿ABC 和⊿A ’B ’C ’中若AA ’,BB ’,CC ’相交于一点S,则BC 与B ’C ’,CA 与C ’A ’,AB 与A ’B ’的交点D,E,F 三点共线.16.Pascal 定理:设圆内接六边形ABCDEF 的对边的延长线相交于三点X,Y ,Z,则这三点在一条直线上.17.Pappus 定理:有相异两直线l,m,若在l 上依次有A,E,C 三点,在m 上依次有D,B,F 三点,且AB 和DE 的交点为P;BC 和EF 的交点为Q;CD 和FA 的交点为R,则P,Q,R 三点共线.18.Simson 定理:从一点向三角形的各边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上.此直线称为此点关于三角形的.Simson 线.19.清宫定理:设P,Q,为三角形ABC 外接圆上异于A,B,C 的两点,P 点关于三边BC,CA,AB 的对称点分别为U,V ,W,若QU,QV ,QW 和边BC,CA,AB 或其延长线的交点分别为D,E,F,则D,E,F 三点在同一直线上.F20.欧拉Euler 关于垂足三角形的面积公式:P 是⊿ABC 所在平面上任意一点,过P 向⊿ABC 的三边做垂线,垂足分别是A 1,B 1,C 1,若OP=d,则ABC C B A S Rd R S 2221114-=,其中O 是⊿ABC 的外心,R 为其半径.21.Opiel 奥倍儿定理:通过三角形ABC 的顶点A,B,C 引三条互相平行的直线,设他们和三角形ABC 的外接圆的交点分别为A1,B1,C1,在三角形ABC 的外接圆周上取一点P,设PA1,PB1,PC1与三角形的三边BC,CA,AB 或其延长线的交点分别为D,E,F,则D,E,F22.Steiner (斯坦纳)定理:设三角形为P,则P 关于三角形ABC A 1CEP23 Steiner(斯坦纳)定理2:若P为三角形ABC内任意一点,作PD垂直于BC,交BC于D,PE垂直于CA,交CA于E,PF垂直于AB,交AB于F,则AF2+BD2+CE2=AE2+CD2+BF2.24.Weitzenbock外森皮克不等式:⊿ABC的三边分别为a,b,c,面积为S,则22c24.+≥S3a+b25.Finsler-Hadwiger定理:⊿ABC的三边分别为a,b,c,面积为S,则22)22224--a---+≥S3+b-a)()(c(abcbc26.Monge(蒙日)定理:三个圆每两个的根轴或平行或交于一点。
斯坦纳定理推广的猜想证明

斯坦纳定理推广的猜想证明
黄岩
【期刊名称】《安康师专学报》
【年(卷),期】1999(11)1
【总页数】1页(P57-57)
【关键词】Steiner定理;等腰梯形;三角形;中线
【作者】黄岩
【作者单位】陕西绥德四十铺中学
【正文语种】中文
【中图分类】O123.6
【相关文献】
1.斯坦纳定理一个猜想的证明 [J], 马念珠
2.斯坦纳定理推广猜想的证明及再讨论 [J], 洪盈平;崔树峰
3.斯坦纳定理的一个猜想的推广 [J], 周新民
4.关于斯坦纳定理推广的猜想的再研究 [J], 瞿素飞
5.圆中的斯坦纳──莱麦斯定理推广的猜想证明 [J], 魏春强
因版权原因,仅展示原文概要,查看原文内容请购买。
再谈斯坦纳——雷米欧斯定理的纯几何证法

再谈斯坦纳——雷米欧斯定理的纯几何证法作者:令标来源:《中学数学杂志(初中版)》2011年第05期《中学数学杂志》(初中)2011年第8期登载的“对称地处理对称性问题——斯坦纳——雷米欧斯定理的最佳证法”一文(下称文[1]),用间接方法——反证法,并结合两条引理,证明了平面几何中的一个令人痴迷甚久、脍炙人口的著名定理——斯坦纳——雷米欧斯(Steiner—Lehmes)定理.该定理当时甫一面世,便受到了数学爱好者、数学家的青睐,特别是斯坦纳的首证公开之后,在数学界产生了极大的反响,诸多证法纷至沓来,形式各异的推广如雨后春笋.其间出现了一些耐人寻味、发人深省的精妙证法,让人惊叹不已,它确是盛开在平面几何百花园里一朵绚丽多彩的奇葩!文[1]的证明是否“最佳”,笔者不敢妄断,读者定会评判.作为几何问题,探寻其原汁原味的纯几何证法,乃不失其几何神韵(实在难以寻觅,间接方法也是明智的选择),这也正是平面几何的魅力所在.斯坦纳——雷米欧斯定理也不例外,自它问世以来的一百多年里,人们孜孜以求,潜心于新证法的不断探究,尤为引人入胜的是其直接证法——纯几何方法.下面将介绍一个为日本数学家颇感兴趣、高度赞赏的直接证法[2],供读者参考.定理已知△ABC中,BE平分∠ABC,CD平分∠ACB,且BE=CD.求证:AB=AC.证明如图1,作∠BEF=∠BCD,使得EF=BC,点F、C位于BE的两侧,连结BF、CF.由BE=CD,得△FEB≌△BCD.于是∠FBE=∠BDC,BF=BD.又∠ABC=2∠CBE,∠DCE=∠BCD,知∠FBC=∠FBE+∠CBE=∠BDC+∠CBE=(180°-∠ABC-∠BCD)+∠CBE=180°-(∠CBE+∠BCD).①∠CEF=∠CEB+∠BEF=∠CEB+∠BCD=∠CEB+∠DCE=(180°-∠CBE-2∠DCE)+∠DCE=180°-(∠CBE+∠BCD).②由∠ABC+∠ACB<180°,知∠CBE+∠BCD<90°. ③由①、②、③得∠FBC=∠CEF>90°.在钝角△FBC与△CEF中,FC=CF,BC=EF.故△FBC≌△CEF,BF=CE.即BD=CE.因此△BCD≌△CBE,∠ABC=∠ACB.故AB=AC.上述证法仅用有限的直线形知识,浅显简单,通俗易懂,确乎精彩,难怪日本数学家秋山武太郎在他的著作《平面、立体几何学》一书中有“确实是巧妙简洁的证明,今后,能够超过这个证明的,恐怕不会再有了”的较高评价. 斯坦纳——雷米欧斯定理尽管从现行的初中数学课程中已隐退多年,作为数学教师,对它的历史情形的了解和解法的把握是不可或缺的,也能透视教师自身的数学素养.许多经久不衰的历史经典几何名题,仿佛一颗颗闪烁的明珠,璀璨夺目,异彩纷呈,推动着几何学乃至整个数学的发展.伟大的物理学家爱因斯坦曾言:“如果欧几里得未能激起你少年时代的热情,那你就不是一个天才的科学家.”平面几何在数学教育中占有重要的地位,它是培养、训练学生思维能力无可替代的极好素材.愿我们教学一线的数学教师,竭尽所能地介绍一些适合学生知识水平的历史名题(不限于几何方面),拓展学生的知识视野,丰富课堂教学的内容,“激活”学生自主学习的内动力,真正地充实素质教育.参考文献[1]程诗春. 对称地处理对称性问题——斯坦纳——雷米欧斯定理的最佳证法[J].中学数学杂志(初中),2011,(8).[2]郭要红,戴普庆.中学数学研究[M].安徽:安徽大学出版社,1998∶11.。
世界顶级思维之斯坦纳定理

世界顶级思维之斯坦纳定理斯坦纳定理:说的愈少,听到的就愈多提出者:美国心理学家斯坦纳。
内容精解:在哪里说得愈少,在哪里听到的就愈多。
只有很好听取别人的,才能更好说出自己的。
说得过多了,说的就会成为做的障碍。
应用要诀:第一,虚心听取别人的意见是一个人进步必要条件。
第二,自己意见不成熟时不能发表,说得过多了,说的就会成为做的障碍。
第三,多听、多做、少说是一个人成熟的表现。
兼听则明,偏听则暗倾听是获取信息的方法,只有认真倾听,才会获得准确的信息,而许多准确的信息可为准确的决策提供依据。
英国作家拉迪亚德·吉卜林曾经这样描述恰当的提问与回答:“我有6个忠实的仆人,他们可以告诉我所有想知道的事情。
他们的名字是:什么、为什么、何时、何地、怎么样、谁。
”在你倾听别人谈话的时候,如果你确保掌握了吉卜林的6个“忠实仆人”的要素,会对你有很大帮助。
国王收到了三个一模一样的金人,但进贡人要求国王回答问题:三个金人哪个最有价值?无论是称重量还是看做工,都是一模一样。
最后,一位老臣拿着三根稻草,插入第一个金人耳朵里,稻草从另一边耳朵出来。
第二个金人的稻草从嘴巴里掉出来。
第三个金人的稻草掉进肚子里。
老臣说:第三个金人最有价值!答案正确,使者默默无语。
善于倾听,才是最有价值,是成熟的人应具备的基本素质。
英国联合航空公司总裁L·费斯诺归纳类似的现象说,人有两只耳朵却只有一张嘴巴,这意味着人应多听少讲。
这就是“费斯诺定理”。
“金人”故事的实质其实是“善于倾听,才是最有价值;讲一定要讲得精悍。
”这也就给“费斯诺定理”下了个概念:人要善于倾听,获取对方的信息越多,理解对方的意思就越明确,才能给予对方精确的答案。
作为一位领导者,首先要倾听问题,然后再去指导,这是田纳西州BUN公司总裁兼CEO给出的最有价值的建议。
只有很好听取别人的,才能更好说出自己的,虚心听取别人的意见是一个人进步必要条件。
自己意见不成熟时不能发表,说得过多了,说的就会成为做的障碍。
斯坦纳定理

斯坦纳定理
斯坦纳定理:"如果三角形中两内角平分线长度相等,则必为等腰三角形"。
这一命题的逆命题:"等腰三角形两底角的平分线长在相等",早在二千多年前的《几何原本》中就已作为定理,证明是很容易的。
但上述命题在《几何原本》中只字未提,直到1840年,莱默斯
(C.L.Lehmus)在他给斯图姆(C.Sturm)的信中提出请求给出一个纯几
何证明。
斯图姆没有解决,就向许多数学家提出这一问题。
首先给出证明的是瑞士几何学家斯坦纳(J.Steiner,1796~1863),因而这一定
理就称为斯坦纳-莱默斯定理。
扩展资料:
证明:
在△ABC中,BD,CE为其角平分线,且BD=CE
设∠ABD=∠CBD=x,∠ACE=∠BCE=y
根据张角定理,有
2cosx/BD=1/AB+1/BC
2cosy/CE=1/AC+1/BC
则2*AB*BC*cosx/(AB+BC)=BD=CE=2*AC*BC*cosy/(AC+BC)
即(AB*(AC+BC))/(AC*(AB+BC))=cosy/cosx
利用分比定理。
并对cosy-cosx使用和差化积
AB-AC=(-(2*AC*(AB+BC))/(BC*cosx))*sin((y+x)/2)*sin((y-x
)/2)
若AB>AC,则上式左端为正,右端为负若AB<AC,则上式左端为负,右端为正故AB=AC。
斯坦纳(Steiner)比猜想

斯坦纳(Steiner)比猜想
吴振奎
【期刊名称】《中等数学》
【年(卷),期】1997(000)006
【摘要】17世纪初,法国数学家费尔马(Fermat)曾提出一个有趣的几何问题: 求平面上一点至给定三角形三顶点距离和最小。
这个问题后由麦森(Mersenne)带到意大利。
1640年前后,对于已给三角形三内角皆小于120°的情形,被伽利略的高足托里拆利
【总页数】3页(P27-29)
【作者】吴振奎
【作者单位】天津商学院 300122
【正文语种】中文
【中图分类】G634.605
【相关文献】
1.斯坦纳(Steiner)定理及推广 [J], 吴彰烈
2.斯坦纳定理的一个猜想的推广 [J], 周新民
3.关于斯坦纳定理推广的猜想的再研究 [J], 瞿素飞
4.斯坦纳定理推广的猜想证明 [J], 黄岩
5.圆中的斯坦纳──莱麦斯定理推广的猜想证明 [J], 魏春强
因版权原因,仅展示原文概要,查看原文内容请购买。
stein定理

Stein定理是一种用于估计随机变量的均值不等式,由美国数学家Ernst W. Stein在1937年提出。
该定理可以用于估计一些随机变量的均值、方差、协方差等统计量的上界和下界。
Stein定理的一般形式如下:
设X和Y是两个随机变量,Z是一个实数,且X和Y满足一定的条件,那么有:
|E[X|Z] - E[Y|Z]| ≤σ²/σ²(Z)
其中,σ²(Z)是Z的谱均方。
该定理的意义在于,它提供了一种方法来估计随机变量的均值,即使这些随机变量不是独立的。
它也可以用于估计其他统计量的上界和下界,例如方差和协方差等。
Stein定理的应用非常广泛,例如在金融领域中用于估计资产的风险度量、在物理学中用于估计随机波动的能量等。
它也是概率论和统计学中的一个重要工具,对于理解和应用概率论和统计学的基本原理有着重要的作用。
斯坦纳定理(My God)

斯坦纳-雷米欧司定理斯坦纳-雷米欧司定理:两内角的平分线相等的三角形是等腰三角形设在三角形ABC中,有B、C的角平分线CF、BE交于OBE是角平分线推出:BC/CE=AB/AE,同理:BC/BD=AC/AD,因为BD=CE,所以等量代换得出:AB/AE=AC/AD,角A是公共角,所以三角形ACD与ABE相似,所以LACD=LABE,同理LBDC=LBEC,再加上BD=CE,所以三角形BOD全等于三角形OEC,所以OB=OC且LDBE=LECD,OB=OC推出LOBC=LOCB,再等量代换得到LABC=LACB,所以AB=AC注:"L"为角的符号证明一:已知:三角形ABC,角B、角C的平分线是BE、CD作∠BEF=∠BCD;并使EF=BC∵BE=DC∴△BEF≌△DCB,BF=BD,∠BDC=∠EBF设∠ABE=∠EBC=α,∠ACD=∠DCB=β∠FBC=∠BDC+α=180°-2α-β+α=180°-(α+β);∠CEF=∠FEB+∠CEB=β+180-2β-α=180°-(α+β);∴∠FBC=∠CEF∵2α+2β<180°,∴α+β<90°∴∠FBC=∠CEF>90°∴过C点作FB的垂线和过F点作CE的垂线必都在FB和CE的延长线上.设垂足分别为G、H;∠HEF=∠CBG;∵BC=EF,∴Rt△CGB≌Rt△FHE∴CG=FH,BG=HE连接CF∵CF=FC,FH=CG∴Rt△CGF≌△FHC∴FG=CH,∴BF=CE,∴CE=BD∵BD=CE,BC=CB,∴△BDC≌△CEB∴∠ABC=∠ACB∴AB=AC证明二:设二角的一半分别为α、βsin(2α+β)/ sin2α= BC/CE = BC/BD = sin(α+2β)/ sin2β,∴2sinαcosαsin(α+2β) - 2sinβcosβsin(2α+β) =0→sinα[sin2(α+β)+sin 2β]- sinβ[sin2(α+β)+ sin2α]=0 →sin2(α+β)[sinα-sinβ]+2 sinαsinβ[cosβ- cosα]=0→sin [(α-β)/2][sin2(α+β) cos[(α+β)/2] + 2 sinαsinβsin [(α+β)/2]=0,∴sin[(α-β)/2]=0∴α=β,∴AB=AC.证明三:用张角定理:2cosα/BE=1/BC+1/AB2cosβ/CD=1/BC+1/AC若α>β可推出AB>AC矛盾!若α<β可推出AB<AC矛盾!所以AB=AC定理来源:1840年,德国数学家雷米欧斯给当时的大数学家斯图姆的一封信中说到:“几何题在没有证明之前,很难说它是难还是容易。
史坦纳定理

史坦纳定理
史坦纳定理
设△ABC的垂心为H,点D为△ABC外接圆上任意点,则点D关于△ABC的西姆松线通过线段DH的中点.
史坦纳定理的应用定理
△ABC的外接圆上的一点D的关于边BC、CA、AB的对称点和△ABC的垂心H同在一条(与西姆松线平行的)直线上。
这条直线被叫做点D关于△ABC的镜象线.史坦纳定理证明
相比直接证明史坦纳定理,证明史坦纳定理的应用定理更为简便!
如图,设点D关于边BC、CA、AB的对称点分别为P、Q、R,则有:
∠BPC=∠BDC=∠BAC=180°-∠BHC(垂心的性质)
所以H、B、C、P四点共圆,同理有:
所以H、C、A、Q四点共圆.
所以H、A、B、R四点共圆.
证明垂心H在PQ上只要证明∠CHP与∠CHQ互补或相等.
由四点共圆和对称性
∠CHP=∠CBP=∠CBD
∠CHQ=∠CAQ=∠CAD
∠CBD与∠CAD互补
所以有∠CHP与∠CHQ互补,即H在PQ上.
史坦纳定理的应用定理证毕,显然西姆松线是三角形DPQ的中位线,所以DH与西姆松线的交点一定是DH的中点,史坦纳定理得证.。
【管理学定律】之八:斯坦纳定理

【管理学定律】之八:斯坦纳定理斯坦纳定理,指在哪里说得愈少,在哪里听到的就愈多。
只有很好听取别人的,才能更好说出自己的。
说得过多了,说的就会成为做的障碍。
一个人的智慧是有限的,只有不断地从别人的见解中吸取合理、有益的成分,以弥补自己的不足,才能减少失误,取得成绩。
故善于倾听别人的意见是每一个有志者必须具备的品格。
倾听别人的意见,还要防止因人废言的恶习,不要因为别人的地位卑微或文化程度等不如自己便听不进去。
启示:启示1:善于倾听,会受人欢迎;启示2:积极倾听,可以化解矛盾;启示3:不要自以为是、不听劝告。
社会交际中,使用斯坦纳定理可以搞好社会关系:⛳首先,要使自己让人喜爱,并希望成为其他人的好朋友。
1)遇上烦恼时不妨假设正处在快乐逍遥的状态,久而久之,自然可养成乐天的性格;2)尽量利用空闲时间做自己喜爱做的事,参加不同的活动,这样可以扩大交际圈子,增长见识;3)对自己不奢求十全十美,另外还要注意本身的幽默感。
⛳其次,在着手于他人建立友谊前,要想一想自己是否真正对他人感兴趣,能不能令他人感到愉快。
1)要持友善态度;2)接纳他人的性格和观点,不可强求改变他人;3)注重个人风格,不可一味向朋友作出奉献,朋友相交要以互助为原则;4)向朋友叙说你的感觉和想法,但因注意彼此相交的深浅程度,以免出现尴尬局面;5)要明白真正的朋友有这样一些特点:不会贬低你来抬高自己;会保守你的秘密;不会恶言中伤你,不会介意你的衣着如何;不会断然断交。
⛳另外,在社会交际中运用语言交谈的同时,还有一种不可忽视的因素,就是非语言因素。
交谈和交际过程的动作、表情、环境等,这些因素每时每刻都在影响着的交际。
从一道教材习题到斯坦纳—雷米欧斯定理

从一道教材习题到斯坦纳—雷米欧斯定理
刘志凤
【期刊名称】《中国数学教育(初中版)》
【年(卷),期】2016(000)009
【摘要】完成一道教材习题后的反思与探究,追溯到了数学家的发现——著名的斯坦纳—雷米欧斯定理.通过对该定理多种证法的研究及分析,进一步了解了相关数学史知识.作为数学教师应在教学中适时渗透数学史教育,这也是教师必备的专业素养之一.
【总页数】4页(P30-33)
【作者】刘志凤
【作者单位】河南省基础教育教学研究室
【正文语种】中文
【相关文献】
1.关于斯坦纳-雷米欧斯定理的三种证明方法 [J], 肖敏
2.脍炙人口的“斯坦纳—雷米欧司”定理 [J], 李奇特
3.脍炙人口的“斯坦纳—雷米欧司”定理 [J], 李奇特
4.基于初中生的\"斯坦纳-莱默斯定理\"证明 [J], 徐小建
5.斯坦纳—莱默斯定理新证 [J], 宋佳亮
因版权原因,仅展示原文概要,查看原文内容请购买。
数学斯坦纳定理

数学斯坦纳定理
数学斯坦纳定理(MathematicalStark'sTheorem)是一个关于数
论有关的定理,由美国数学家斯坦纳提出。
它证明了一个有趣的结论:任何边缘数量指数(Mersenne)只有在特定的指数值上才能成为完全
数(perfectnumber)。
该定理还指出,完全数的边根素数的形式只有
两种:二进制1(2)后接奇数个0,和二进制1(2)后接偶数个0。
此外,它也可以用来证明其他数学结论,如费马多边形的边数的关系。
斯坦纳定理的证明是以他的研究为基础,其中包括更一般化的概念,例如素数拆分、反义数字(inversenumbers)和模型理论(modulartheory)。
他认为,有效的证明可以通过分析反义数字的几率,也可以通过有关Mersenne指数的模型来实现。
研究发现,能够被
两个整数拆分的值的发生率可以用来证明数学斯坦纳定理。
斯坦纳定理的重要性在于可以用它来预测哪些数字可以被拆分成
完全数。
它有助于人们理解这类值的发生率,以及完全数和Mersenne
指数之间的关系,这种关系在数论领域中是不断发展的。
此外,斯坦
纳定理也有助于科学家和研究者们更好地理解其他有关Mersenne指数的相关定理及其结果,这也为数论研究和实践奠定了基础。
综上所述,斯坦纳定理对数论的研究和实践有莫大的帮助,它对于更好地理解数学知识和发现数学定理都有着重要的意义。
它的重要性正是由于它的证明过程的完整性,并能准确的揭示Mersenne指数和完全数之间的关系。
数学斯坦纳定理无疑是数论领域中一项重要的成就,它对于这一学科的发展有着莫大的贡献。
100个最伟大的定理

100个最伟大的定理这一千年似乎刺激了许多人去编辑许多东西的“最重要的100个”或是“最好的100个”的列表,包括电影(由美国电影学会)和书(由现代图书馆)。
数学家并没有免疫这些影响,在1999年7月的一个数学会议中,Paul 和Jack Abad 提出了他们的“一百个最伟大的定理”名单。
他们给出的排列是基于一下标准;“定理在文献中的地位、证明的质量与结果的意外性”。
这个排列当然同电影还有书排列的一样的武断,但是这里的定理必定都是很有价值的结果。
我希望随着时间的推移能够包含所有证明的链接;现在,你将会满足于这个表格本身与主角们的传记。
1根号2的无理性毕达哥拉斯 和他的学派公元前500年2 代数基本定理卡尔·弗里德里希·高斯(Karl Frederich Gauss ) 1799 3 实数集的不可数 康托(Georg Cantor ) 1867 4勾股定理毕达哥拉斯 和他的学派公元前500 年5 素数定理阿达玛(Jacques Hadamard ) 和普森Charles-Jean de la Vallee Poussin (分别地) 1896 6 哥德尔不完全性定理 哥德尔(Kurt Godel )19317 二次互反律高斯(Karl Frederich Gauss ) 1801 8 三分角 与倍立方体的不可能 旺策尔(P ierre Wantzel ) 1837 9 圆的面积阿基米德(Archimedes )公元前225 10费马小定理的欧拉推广(Fermat’s Little Theorem)欧拉(Leonhard Euler )(费马Pierre de Fermat ) 1760 (1640)11 素数是无穷的 欧几里德(Euclid )公元前30012第五公设的独立性高斯(Karl Frederich Gauss), J,波约(Janos Bolyai ), 尼古拉.罗巴切夫斯基(Nikolai Lobachevsky ), G 离曼(G.F. Bernhard Riemann collectively1870-188013多面体的欧拉公式欧拉(Leonhard Euler)175114欧拉对级数1 + (1/2)^2 + (1/3)^2 + ….的求欧拉(Leonhard Euler)1734和168615微积分基本定理莱布尼兹(Gottfried Wilhelmvon Leibniz)【译注】:此定理由牛顿与莱布尼兹分别得出16一般的高次方程无根式解阿贝尔(Niels Henrik Abel)182417棣莫弗定理棣莫弗(Abraham DeMoivre)173018刘维尔定理和超越数的构造刘维尔(Joseph Liouville)1844177019四平方和定理拉格朗日(Joseph-LouisLagrange)20所有素数都可以写成两个熟的平方和??21格林定理格林(George Green)182822连续统的不可数性康托(Georg Cantor)187423勾股数公式欧几里德(Euclid)公元前300 24连续统假设的不可判定性【译注】:对ZF科恩(Paul Cohen)1963公理系统25施罗德-伯恩斯坦定理??26莱布尼兹的pi的级数莱布尼兹(Gottfried Wilhelm1674von Leibniz)27三角形内角和欧几里德(Euclid)300 B.C. 28帕斯卡六边形定理帕斯卡(Blaise Pascal)1640182229费尔巴哈定理费尔巴哈(Karl WilhelmFeuerbach)30投票问题贝特朗(J.L.F. Bertrand)188731拉姆塞定理拉姆塞(F.P. Ramsey)1930197632四色问题阿佩尔(Kenneth Appel)与哈肯(Wolfgang Haken)33费马大定理怀尔斯(Andrew Wiles)199334调和级数的发散性奥里斯姆(Nicole Oresme)135035泰勒定理泰勒(Brook Taylor)171536Brouwer 不动点定理L.E.J. Brouwer191037三次方程解法希皮奥内·德尔·费罗(ScipioneDel Ferro)150038算术平均值/几何平均值(Proof by Backward Induction)(Polya Proof)柯西(Augustin-Louis Cauchy)波利亚(George Polya)??39佩尔方程的解欧拉(Leonhard Euler)175940闵可夫斯基基本定理闵可夫斯基(HermannMinkowski)189641皮瑟定理皮瑟(Victor Puiseux) (建立在牛顿 1671年的一个发现的基础上)185042三角形数的倒数和莱布尼兹(Gottfried Wilhelmvon Leibniz)167243等周定理斯坦纳(Jacob Steiner)183844二项式定理牛顿(Isaac Newton)166545分解定理欧拉(Leonhard Euler)174046一般四次方程的解费拉里(Lodovico Ferrari)154547中心极限定理??48狄利克雷定理狄利克雷(Peter LejuneDirichlet)183749Cayley-Hamilton 定理Arthur Cayley185850正多面体的数量西厄蒂特斯(Theaetetus)400 B.C. 51Wilson定理拉格朗日(Joseph-LouisLagrange)177352集合的子集数??53Pi是超越数林德曼(FerdinandLindemann)188254哥尼斯堡七桥问题欧拉(Leonhard Euler)173655切割弦定理欧几里德(Euclid)300 B.C. 56埃尔米特-林德曼超越数定理林德曼(FerdinandLindemann)188257海伦公式海伦(Heron of Alexandria)7558 组合数公式 ? ? 59 大数定理 <many><many> 60 裴蜀定理 裴蜀(Etienne Bezout ) ? 61 赛瓦定理 赛瓦(Giovanni Ceva ) 1678 62 公平博弈定理 ?? 63 康托定理 康托(Georg Cantor ) 1891 64 洛必达法则 伯努利(John Bernoulli ) 1696? 65 等腰三角形定理 欧几里德(Euclid ) 公元前300 66几何级数和阿基米德(Archimedes )公元前260 ?67 e 是超越数 厄尔米特(Charles Hermite ) 1873 68等差数列求和巴比伦人公元前170069 辗转相除法 欧几里德(Euclid ) 公元前300 70 完美数定理 欧几里德(Euclid )公元前30071子集的阶拉格朗日(Joseph-Louis Lagrange ) 1802 72 Sylow 定理Ludwig Sylow187073上升或下降序列(Ascending or Descending Sequences ) 厄尔朵思(Paul Erdos ) 和 G . Szekeres 193574 数学归纳法原理 热尔松(Levi ben Gerson ) 1321 75平均值定理柯西(Augustine-Louis Cauchy )1823 76 傅里叶级数 傅里叶(Joseph Fourier )181177 k 次方的和伯努利(Jakob Bernouilli ) 1713 78Cauchy-Schwarz 不等式柯西(Augustine-Louis Cauchy )1814? 79 中值定理柯西(Augustine-Louis Cauchy ) 1821 80 算数基本定理 欧几里德(Euclid ) 300 B.C. 81素数的倒数和是分散的欧拉(Leonhard Euler )1734?82 立方和的分解 (J.E. Littlewood 的优美证明) R .L. Brooks 194083朋友定理厄尔朵思(Paul Erdos ), Alfred Renyi, Vera Sos 1966 84 莫利定理 莫利(Frank Morley ) 1899 85 被三整除性 ??86 Lebesgue 测度与积分 勒贝格(Henri Lebesgue ) 1902 87 笛沙格定理 笛沙格(Gerard Desargues ) 1650 88 错位排列公式 ? ? 89 因数与余数定理 ?? 90 斯特林公式 斯特林(James Stirling ) 1730 91 三角不等式 ? ? 92 皮克定理 George Pick 1899 93 生日问题 ?? 94 余弦定理 韦达(Francois Viete ) 1579 95 托勒密定理 托勒密(Ptolemy ) 120? 96 容斥原理 ??97 克莱姆法则克莱姆(Gabriel Cramer ) 175098Bertrand 假设【译注】对n>3,在n 和2n-2之间必有素数 J.L.F. Bertrand 1860?99 蒲丰投针问题蒲丰(Comte de Buffon )1733100 笛卡尔符号原则【译注】一种确定正根与负根个数的方法笛卡尔(Rene Descartes ) 1637()/2S p a b c d e ==++++。
斯坦纳定理的证明

斯坦纳定理的证明斯坦纳定理:两内角平分线相等的三角形必为等腰三角形。
这一命题的逆命题:“等腰三角形两底角的平分线长在相等”,早在二千多年前的《几何原本》中就已作为定理,证明过程想必大家都会。
但上述命题在《几何原本》中只字未提,直到1840年,雷米欧斯(C.L.Lehmus)在他给斯图姆(C.Sturm)的信中提出请求给出一个纯几何证明。
斯图姆没有解决,就向许多数学家提出这一问题。
据说连欧几里德都不会证!!首先给出证明的是瑞士几何学家斯坦纳(J.Steiner,1796~1863),因而这一定理就称为斯坦纳—雷米欧斯定理。
继斯坦纳之后,这一定理的丰富多彩的证明陆续发表,但大多是间接证法,直接证法难度颇大。
一百多年来,吸引了许多数学家和数学爱好者。
德国数学家海塞(L.O.Hesse,1811~1874)的证法:作∠BDF=∠BCE;并使DF=BC,∵BD=EC,∴△BDF≌△ECB,BF=BE,∠BEC=∠DBF.设∠ABD=∠DBC=α,∠ACE=∠ECB=β,∠FBC=∠BEC+α=180°-2α-β+α=180°-(α+β);∠CDF=∠FDB+∠CDB=β+180-2β-α=180°-(α+β);∴∠FBC=∠CDF,∵2α+2β<180°,∴α+β<90°,∴∠FBC=∠CDF>90°∴过C点作FB的垂线和过F点作CD的垂线必都在FB和CD的延长线上.设垂足分别为G、H;∠HDF=∠CBG;∵BC=DF,∴Rt△CGB≌Rt△FHD,∴CG=FH,BC=HD连接CF,∵CF=FC,FH=CG,∴Rt△CGF≌△FHC(HL),∴FG=CH, 又∵BG=DH,∴BF=CD, 又∵BF=BE,∴CD=BE,∵BE=CD,BC=CB,EC=DB,∴△BEC≌△CDB,∴∠ABC=∠ACB∴AB=AC.。
“斯坦纳-雷米欧斯”定理

设三角形ABC,角B、角C的平分线是BE、CD作∠BEF=∠BCD;并使EF=BC∵BE=DC∴△BEF≌△DCB,BF=BD,∠BDC=∠EBF设∠ABE=∠EBC=α,∠ACD=∠DCB=β∠FBC=∠BDC+α=180°-2α-β+α=180°-(α+β);∠CEF=∠FEB+∠CEB=β+180-2β-α=180°-(α+β);∴∠FBC=∠CEF∵2α+2β<180°,∴α+β<90°∴∠FBC=∠CEF>90°∴过C点作FB的垂线和过F点作CE的垂线必都在FB和CE的延长线上. 设垂足分别为G、H;∠HEF=∠CBG;∵BC=EF,∴Rt△CGB≌Rt△FHE∴CG=FH,BC=HE连接CF∵CF=FC,FH=CG∴Rt△CGF≌△FHC∴FG=CH,∴BF=CE,∴CE=BD∵BD=CE,BC=CB,∴△BDC≌△CEB∴∠ABC=∠ACB∴AB=AC设三角形ABC,角B、角C的平分线是BE、CD作∠BEF=∠BCD;并使EF=BC∵BE=DC∴△BEF≌△DCB,BF=BD,∠BDC=∠EBF设∠ABE=∠EBC=α,∠ACD=∠DCB=β∠FBC=∠BDC+α=180°-2α-β+α=180°-(α+β);∠CEF=∠FEB+∠CEB=β+180-2β-α=180°-(α+β);∴∠FBC=∠CEF∵2α+2β<180°,∴α+β<90°∴∠FBC=∠CEF>90°∴过C点作FB的垂线和过F点作CE的垂线必都在FB和CE的延长线上. 设垂足分别为G、H;∠HEF=∠CBG;∵BC=EF,∴Rt△CGB≌Rt△FHE∴CG=FH,BC=HE连接CF∵CF=FC,FH=CG∴Rt△CGF≌△FHC∴FG=CH,∴BF=CE,∴CE=BD∵BD=CE,BC=CB,∴△BDC≌△CEB∴∠ABC=∠ACB∴AB=AC证明1如图,则在△EBC与△DBC中:sin(2β+γ)/ sin2β= BC/CE = BC/BD = sin(β+2γ)/ sin2γ,∴2sinβcosβsin(β+2γ) - 2sinγcosγsin(2β+γ) =0→sinβ sin2(β+γ)+sin 2γ】- sinγ【 sin2(β+γ)+ sin2β】=0(积化和差)→sin2(β+γ)【sinβ-sinγ】+2 sinβsinγ【cosγ- cosβ】=0(重新分组并提取公因式)→sin [(β-γ)/2]【sin2(β+γ) cos[(β+γ)/2] + 2 sinβsinγsin [(β+γ)/2]=0(和差化积)又显然上式的后一个因式的值大于零,∴sin[(β-γ)/2]=0,∴β=γ,∴AB=A C. 证毕!证明2设三角形ABC,∠B=2a,∠C=2b,角平分线BD=CE分别以BD,CE为底边,以a+b为底角向上做两个等腰三角形BDF,CEG 连接AF,AG则ADBF四点共圆,AGCE四点也共圆因∠1+∠2=∠1+∠3=∠1+b+a=180度所以FAG共线∠4+∠BCG=∠4+(b+b+a)=∠5+(b+b)+a=180度所以BCGF四点共圆因△FBD≌△GEC所以BF=CG,结合共圆条件得FG//BC,等腰梯形,∠FBC=∠GCBb+a+a=b+b+a整理得∠B=∠C证明3如图,将△AEC绕点O(点O为BI和CI的中垂线的交点)逆时针旋转,使CE与BD重合,A的对应点为A'。
四面体斯坦纳定理及其应用

四面体斯坦纳定理及其应用
四面体斯坦纳定理是图论中的一种重要定理,它给出了四面体内部所有边的最小生成树的权值和。
该定理不仅有理论意义,而且在实际应用中也有广泛的应用。
四面体斯坦纳定理的一个重要应用是在计算化学中,用于计算分子的稳定性和化学反应的能量。
此外,它还可以用于计算机图形学中的三维建模和路由算法中的最短路径问题等。
在计算化学中,四面体斯坦纳定理可以用于计算分子中所有原子间的距离。
在分子中,原子可以看作是点,它们之间的化学键可以看作是边。
通过四面体斯坦纳定理可以计算出分子中所有原子之间的最短距离,从而得到分子的稳定性和化学反应的能量。
在计算机图形学中,四面体斯坦纳定理可以用于三维建模。
在三维建模中,需要计算三维空间中各个点之间的距离和最短路径。
通过四面体斯坦纳定理可以快速地计算出最短路径,从而加快了三维建模的速度。
在路由算法中,四面体斯坦纳定理可以用于计算网络中两个节点之间的最短路径。
通过四面体斯坦纳定理可以快速地计算出最短路径,从而提高了网络路由的效率。
综上所述,四面体斯坦纳定理在化学、计算机图形学和路由算法等领域中有着广泛的应用。
- 1 -。
斯太纳定理

斯太纳定理
斯太纳定理,也称为平行轴定理,是刚体动力学中的一个定理,它通过物体的重心和轴线之间的垂直距离在平行轴上的转动惯量,可用于确定给定刚体的质量惯性矩或面积的二次矩。
施泰纳定理指出,如果主体围绕与第一轴平行并且偏离距离的新轴旋转,则惯性矩相对于新轴是与通过下式相关:显然,是轴和之间的垂直距离。
此外,施泰纳定理也适用于平面区域的面积的第二矩(面积惯性矩):其中是相对于平行轴的面积惯性矩,是相对于其质心的面积惯性矩,是平面区域的面积,是距离新的距离轴到平面区域的质心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
斯坦纳-雷米欧司定理
斯坦纳-雷米欧司定理:
两内角的平分线相等的三角形是等腰三角形
设在三角形ABC中,有B、C的角平分线CF、BE交于O
BE是角平分线推出:BC/CE=AB/AE,同理:BC/BD=AC/AD,因为BD=CE,所以等量代换得出:
AB/AE=AC/AD,角A是公共角,所以三角形ACD与ABE相似,所以
LACD=LABE,同理LBDC=LBEC,再加上BD=CE,所以三角形BOD全等于三角形OEC,所以OB=OC且LDBE=LECD,OB=OC推出LOBC=LOCB,再等量代换得到LABC=LACB,所以AB=AC
注:"L"为角的符号
证明一:
已知:三角形ABC,角B、角C的平分线是BE、CD
作∠BEF=∠BCD;并使EF=BC
∵BE=DC
∴△BEF≌△DCB,BF=BD,∠BDC=∠EBF
设∠ABE=∠EBC=α,∠ACD=∠DCB=β
∠FBC=∠BDC+α=180°-2α-β+α=180°-(α+β);
∠CEF=∠FEB+∠CEB=β+180-2β-α=180°-(α+β);
∴∠FBC=∠CEF
∵2α+2β<180°,∴α+β<90°
∴∠FBC=∠CEF>90°
∴过C点作FB的垂线和过F点作CE的垂线必都在FB和CE的延长线上.
设垂足分别为G、H;
∠HEF=∠CBG;
∵BC=EF,
∴Rt△CGB≌Rt△FHE
∴CG=FH,BG=HE
连接CF
∵CF=FC,FH=CG
∴Rt△CGF≌△FHC
∴FG=CH,∴BF=CE,∴CE=BD
∵BD=CE,BC=CB,∴△BDC≌△CEB
∴∠ABC=∠ACB
∴AB=AC
证明二:
设二角的一半分别为α、β
sin(2α+β)/ sin2α= BC/CE = BC/BD = sin(α+2β)/ sin2β,
∴2sinαcosαsin(α+2β) - 2sinβcosβsin(2α+β) =0
→sinα[sin2(α+β)+sin 2β]- sinβ[sin2(α+β)+ sin2α]=0 →sin2(α+β)[sinα-sinβ]+2 sinαsinβ[cosβ- cosα]=0
→sin [(α-β)/2][sin2(α+β) cos[(α+β)/2] + 2 sinαsinβsin [(α+β)/2]=0
,∴sin[(α-β)/2]=0
∴α=β,∴AB=AC.
证明三:
用张角定理:
2cosα/BE=1/BC+1/AB
2cosβ/CD=1/BC+1/AC
若α>β可推出AB>AC矛盾!
若α<β可推出AB<AC矛盾!
所以AB=AC
定理来源:
1840年,德国数学家雷米欧斯给当时的大数学家斯图姆的一封信中说到:“几何题在没有证明之前,很难说它是难还是容易。
等腰三角形的两
底角平分线相等,初中生都会证明。
但反过来,三角形的两内角平分线相等,这个三角形一定是等腰三角形吗?我至今还没想出来。
”此后,斯图
姆又向许多数学家提出了这个问题,请求给出一个纯几何证明。
一年多后,
瑞士达几何学家斯坦纳(1796-1873)首次证明了它,于是,这个问题以“斯坦纳-雷米欧斯”定理而闻名于世。
后世发展:
斯坦纳的证明发表后,引起了数学界极大反响。
论证这个定理的文章发表在1842年到1864年的几乎每一年的各种杂志上。
后来,一家数学刊物公开征解,竟然收集并整理了60多种证法,编成一本书。
直到1980年,美国《数学老师》月刊还登载了这个定理的研究现状,随后又收到了2000多封来信,增补了20多种证法并收到了一个最简单的直接证法。
经过几代人的努力,100多年的研究,“斯坦纳-雷米欧斯”定理已成为数学百花园中最惹人喜爱的瑰丽花朵!
答案(1)
△ABC中,BD CE为角平分线,若BD=CE,求证:AB=AC
证明:(反证法)
设AB<AC,则∠ABC>∠ACB,从而∠ABD>∠ACE.在∠ABD内作∠DBF=∠ACE,则在△FBC中,由∠FBC>∠FCB得FB<FC。
在CF上取CH=BF,过H作HK‖BF交CE于K。
在△BFD和△CHK中,BF=CH,∠BFD=∠CHK,∠FBD=∠HCK,故△BFD≌△CHK
所以BD=CK<CE,与已知BD=CE矛盾。
又若AB>AC,同理可得BD>CE,也与BD=CE矛盾。
所以AB=AC
若用直接证法证明命题“两内角平分线相等的三角形是等腰三角形”,在很多资料上表明问题已被用不同方法得到完全解决,但证题过程较为复杂,寻找简捷的证明方法有待于进一步探索,在间接证法中最多见的是反证法,读者在阅读、理解方面都存在诸多不便,如果选用间接证法中的“同一法”,可使证题过程简化,且便于理解,于是将该证法整理如下,并作一些探讨.定理两内角平分线相等的三角形是等腰三角形.已知:如图1,△ABC中,BD平分∠ABC,CE平分∠ACB,且BD=CE.求证:AB=AC.图1分析结合题目的条件,要证AB=AC,必先证∠ABC=∠ACB,又两角被平分,且平分后的角不易找到直接的相等关系,仔细观察发现∠EBD与∠ECD所对的是同一条边DE,若转化在圆中就是两圆周角所对的公共弦,便可找出互相之间的联系,于是可以考虑B、E、C、D是否在同一个圆上,恰好用“同一法”可以解决这一点,问题就得到简化.证明过点B、D、C作⊙O交CE或其延长线于点H因为BD平分∠ABC,CE平分∠ACB,所以CD=HD,HD=BH,所以CDH=BHD.所以CH=BD.因为BD=CE所以CH=CE,又。
