第18章答案

合集下载

第18章正比例函数和反比例函数 - 答案

课本导学一、略．二、略．三、略．四、略．五、在s ＝60t 中，60是常量，t 是自变量，s 是t 的函数．六、我们把一块橡皮泥（体积V 一定）搓成一个圆柱体．（1）h 是S 的函数．（2）h 是r 的函数．（3）S 是h 的函数．七、m 是n 的函数．在解析式m ＝1＋3n 中，n 是自变量，1和3是常量．八、最高气温是日期的函数．九、成绩随是学号的函数．十、y 是x 的函数，x 是自变量，－2和1是常量．课堂导练十一、解析式是1200n p =，n 是自变量，11200是常量．p 是n 的函数．十二、对于s ＝vt ．（1）①如果速度v 不变，那么s 是t 的函数，t 是自变量，v 是常量．②如果时间t 不变，那么s 是v 的函数，v 是自变量，t 是常量．（2）如果路程s 不变， s v t=，t 是自变量，s 是常量．十三、（1）CD 是变量，AB 是常量．（2）12S ah =，S 是h 的函数，h 是自变量，12a 是常量．课本导学一、略．二、允许取值的范围．（1）全体实数（一切实数，所以实数）；（2）不为0；（3）大于等于0．三、略．四、略．五、周长y ＝10＋x ．课堂导练六、（1）全体实数；（2）x ≠2；（3）x ≥43；（4）x ＞4．七、（1）(2)f -＝12-；（2）1()2f -＝47；（3）(0)f ＝34；（4）f ．八、y ＝180－2x ．定义域是0＜x ＜90．课本导学一、略．二、（1）y＝kx．（2）比例系数．（3）全体实数．（4）解析式．三、f (－5)＝20；f (－2)＝8；f (0)＝0；f (3)＝－12．四、略．课堂导练五、正比例函数有（1）（2）．（5）不是；（6）是．六、y＝6x．七、（1）商一定（不为0），被除数与除数成正比例．（2）除数不变（不为0），被除数与商成正比例．（3）一个因数（不为0）不变，另一个因数与它们的积成正比例．（4）等腰三角形的周长一定，它的腰长与它底边的长不成正比例．（5）一个人的体重与它的年龄不成正比例．课本导学一、结论：正比例函数y＝2x的图像是一条直线．二、结论：正比例函数y＝－2x的图像是一条直线．课堂导练三、四、五、六、七、y＝－10x，直线经过第二、四象限．课本导学一、画图略．（1）二、四；（2）下降；减小；减小．二、画图略．（1）一、三；（2）上升；增大；增大．三、（1）一、三，增大．（2）二、四，减小．四、（1）＞，增大．＜，减小．（2）＞，一、三．＜，二、四．课堂导练五、（1）一、三，增大．（2）一、三，增大．（3）二、四，减小．（4）a＞－1．（5）12a ．（6）一、三．（7）a＜4．（8）a＞3．六、画图略．结论：直线y＝5x和y＝－5x既关于x轴对称，也关于y轴对称．直线y＝x和y＝－x既关于x轴对称，也关于y轴对称；这两条直线与坐标轴的夹角都是45°，这两条直线的位置关系是互相垂直．课本导学一、略．二、（1）kyx =．（2）比例系数．（3）x≠0．（4）解析式．三、略．课堂导练四、反比例函数有（3）（4）．五、15-；反比例函数．六、（1）28yx =；（2）285y=．七、（1）6yx=-；（2）2yx =；（3）－6；（4）52．八、（1）面积S一定时，a与h成反比例；（2）存煤量Q一定时，m与n成反比例；（3）货物的总价A一定时，a与x成反比例；（4）行驶的路程s一定时，d与n成反比例．九、20yx=．定义域是x＞0．课本导学一、画图略．（1）一、三．（2）下降；减小；减小．（3）不会．二、画图略．结论：双曲线，两，二、四．上升；增大；增大．课堂导练三、略．四、五、原题：＜；二、四．改编：（A）（D）．六、（1）(－2, －3)；（2）(4, 2)．课本导学一、一、三，＞．2k＋1．二、略．课堂导练三、增大，＜，2k－1．2k－1＜0，12 <．四、3yx=，32，34y x=．五、（1）x≠0；（2）(1)f-=0，f=．六、略．课本导学一、0＜x＜20．二、（1）甲，甲，甲．（2）乙，甲，甲，甲．甲、乙两人在中点相遇，在各自的中间时刻相遇．（3）甲、乙两人同时出发，同时到达终点，乙的速度快，乙比甲多走了一些路．课堂导练三、（1）0，2；（2）2， 5.5，17.5；（3）5.5，8．四、y＝30x．定义域是0＜x≤40．课本导学一、（1）tx．（2）tx．90x．（3）10；6；6≤x≤10．二、对这个问题的图像是图②．三、略．课堂导练四、（1）y＝2.4x．（2）y＝200x．五、4．六、100，y＝100x．。

《管理学》习题与答案——第18章沟通

第十八章沟通一、教学要点1、解释沟通过程。

2、各种类型沟通的内涵及其优缺点。

3、非正式沟通的特点及其如何管理。

4、有效沟通的障碍因素。

5、如何克服沟通中的障碍？6、冲突产生的原因。

7、冲突处理的方法。

8、谈判及其如何谈判。

9、关键名词：沟通、发送者、接受者、噪音、口头沟通、书面沟通、非言语沟通、电子媒介沟通、正式沟通、非正式沟通、下行沟通、上行沟通、平等沟通、单向沟通、双向沟通、沟通网络、冲突、谈判二、习题(一)填充题1. 沟通是指可理解的_________或__________在两个人或两人以上的人类中传递或交换的过程。

2.按照功能划分，沟通可以分成________和___________。

3.按照方法，沟通可以分为：____________，______________，_____________，_____________，______________。

4.按照组织系统，沟通可分为____________和_______________。

5.沟通过程中存在许多干扰和扭曲信息传递的因素，通常将这些因素称为__________。

6.按照方向，沟通可分为__________，__________，___________-。

7.按照是否进行反馈，沟通可以分为______________和____________。

8.非正式沟通的主要功能是________________，体现的是职工的________和________，与企业正式的要求无关。

9.所谓沟通网络，是指组织中沟通渠道的_______和_________。

10.一种网络不同于另一种网络的基本特征在于：__________，________以及__________。

11. 选择哪一种网络取决于_____________和________________。

12.影响有效沟通的个人因素包括_____________和______________。

第18章法律责任与行政执法

考点1.劳动法律责任形式一、单项选择题1.违反劳动法的民事责任，即劳动关系一方当事人违反了劳动法的规定或劳动合同的约定应承担的民事责任，称为（）。

A.行政责任B.民事责任C.刑事责任D.经济责任正确答案:B解析:民事责任是指违反劳动法的民事责任，即劳动关系一方当事人违反了劳动法的规定或劳动合同的约定而应承担的民事责任，B项符合题意；行政责任是指行为人因违反劳动法律规定、不履行法律规定时，依法应当承担，并由有关行政机关或行为人所在单位以行政制裁方式予以追究的法律责任，A项与题意不符；刑事责任的主要内容是对违法行为人的人身进行制裁，是最严厉的一种法律责任，具有强制性，C项与题意不符；经济责任，是指经济法律关系主体违反经济法义务或经济合同义务依法应承担的法律责任，其形式包括违约金、赔偿金、罚款、没收和某些行政处分，D项与题意不符。

2.行为人因违反劳动法律规定、不履行法律规定时，依法应当承担并由有关行政机关或行为人所在单位以行政制裁方式予以追究的法律责任，称为（）。

A.行政责任B.民事责任C.刑事责任D.经济责任正确答案:A解析:行政责任是指行为人因违反劳动法律规定，不履行法律规定时，依法应当承担，并由有关行政机关或行为人所在单位以行政制裁方式予以追究的法律责任，A项符合题意；民事责任是指违反劳动法的民事责任，即劳动关系一方当事人违反了劳动法的规定或劳动合同的约定而应承担的民事责任，B项与题意不符；刑事责任的主要内容是对违法行为人的人身进行制裁，是最严厉的一种法律责任，具有强制性，C项与题意不符；经经济责任，是指经济法律关系主体违反经济法义务或经济合同义务依法应承担的法律责任，其形式包括违约金、赔偿金、罚款、没收和某些行政处分，D项与题意不符。

3.刑事责任只能由（）追究。

A.国家司法机关B.劳动行政部门C.公安行政部门D.工商行政部门正确答案:A解析:刑事责任是最严厉的一种法律责任，具有强制性；刑事责任只能由国家司法机关追究，任何单位和个人都无权对他人实施，否则也将被追究法律责任。

第18章《项目风险管理》问答习题(含答案)

第18章《项目风险管理》1、风险识别的原则包括哪些？风险识别的原则包括：（1）由粗及细，由细及粗；（2）严格界定风险内涵并考虑风险因素之间的相关性；（3）先怀疑，后排除；（4）排除与确认并重。

对于肯定不能排除又不能肯定予以确认的风险按确认考虑；（5）必要时，可作实验论证。

2、识别风险的工具和技术包括哪些？①文档审查②信息收集技术③核对单分析④假设分析⑤图解技术⑥SWORT分析⑦专家判断3、实施定性风险分析是评估并综合分析风险的概率和影响，对风险进行优先排序，为实施定量风险分析奠定基础。

4、项目模拟旨在使用一个模型，计算项目各细节方面的不确定性对项目目标的潜在影响。

模拟通常釆用蒙特卡洛技术。

5、敏感性分析有助于确定哪些风险对项目具有最大的潜在影响。

典型表现形式是龙卷风图。

6、预期货币价值（EMV）分析是当某些情况在未来可能发生或不发生时，计算平均结果的一种统计方法（不确定性下的分析）。

机会的EMV通常表示为正值，而威胁的EMV则表示为负值。

把每个可能结果的数值与其发生的概率相乘，再把所有乘积相加，就可以计算出项目的EMV。

7、消极风险或威胁的应对策略包括哪些？并简要说明。

①规避：如延长进度、改变策略或缩小范围等。

②转移：可以利用合同或协议把某些具体风险转移给另一方。

成本补偿合同可把成本风险转移给买方，而总价合同可把风险转移给卖方。

③减轻：减轻措施的例子包括采用不太复杂的流程，进行更多的测试，或者选用更可靠的供应商。

例如，在一个系统中加入冗余部件，可以减轻主部件故障所造成的影响。

④接受：风险接受是指项目团队决定接受风险的存在，该策略可以是被动或主动的。

最常见的主动接受策略是建立应急储备8、积极风险或机会的应对策略包括哪些？并简要说明。

①开拓：直接开拓包括把组织中最有能力的资源分配给项目来缩短完成时间，或者采用全新或改进的技术来节约成本，缩短实现项目目标的持续时间。

②提高：本策略旨在提高机会的发生概率和积极影响。

第18章 Logistic回归思考与练习参考答案

第18章 Logistic 回归思考与练习参考答案一、最佳选择题1. Logistic 回归与多重线性回归比较，（ A ）。

A ．logistic 回归的因变量为二分类变量 B ．多重线性回归的因变量为二分类变量C ．logistic 回归和多重线性回归的因变量都可为二分类变量D ．logistic 回归的自变量必须是二分类变量E ．多重线性回归的自变量必须是二分类变量 2. Logistic 回归适用于因变量为（ E ）。

A ．二分类变量B ．多分类有序变量C ．多分类无序变量D ．连续型定量变量E ．A 、B 、C 均可 3. Logistic 回归系数与优势比OR 的关系为（ E ）。

A ．>β0等价于OR ＞1B ．>β0等价于OR ＜1C ．β＝0等价于OR ＝1D ．β＜0等价于OR ＜1E ．A 、C 、D 均正确 4. Logistic 回归可用于（ E ）。

Ａ．影响因素分析 B ．校正混杂因素 C ．预测 D ．仅有A 和C E ．A 、B 、C 均可5. Logistic 回归中自变量如为多分类变量，宜将其按哑变量处理，与其他变量进行变量筛选时可用（ D ）。

A ．软件自动筛选的前进法B ．软件自动筛选的后退法C ．软件自动筛选的逐步法D ．应将几个哑变量作为一个因素，整体进出回归方程E ．A 、B 、C 均可二、思考题1. 为研究低龄青少年吸烟的外在因素，研究者采用整群抽样，在某中心城区和远城区的初中学校，各选择初一年级一个班的全部学生进行调查，并用logistic 回归方程筛选影响因素。

试问上述问题采用logistic 回归是否妥当？答：上述问题采用logistic回归不妥当，因为logistic回归中参数的极大似然估计要求样本结局事件相互独立，而研究的问题中低龄青少年吸烟行为不独立。

2. 分类变量赋值不同对logistic回归有何影响? 分析结果一致吗？答：（1）若因变量交换赋值，两个logistic回归方程的参数估计绝对值相等，符号相反；优势比互为倒数，含义有所区别，实质意义一样；模型拟合检验与回归系数的假设检验结果相同。

【完整版】华师大版八年级下册数学第18章平行四边形含答案

华师大版八年级下册数学第18章平行四边形含答案一、单选题(共15题，共计45分)1、如图，过平行四边形ABCD对角线交点O的线段EF，分别交AD，BC于点E，F，当AE＝ED时，△AOE的面积为4，则四边形EFCD的面积是（）A.8B.12C.16D.322、在平行四边形、矩形、菱形、正方形中，对角线相等的图形有( )A.4个B.3个C.2个D.1个3、平行四边形的周长为50，设它的长为x ，宽为y ，则y与x的函数关系为（）A. y=25- xB. y=25+ xC. y=50- xD. y=50+ x4、如图，▱ABCD中，AE平分∠BAD，交BC于E，DE⊥AE，下列结论：：①DE平分∠ADC；②E是BC的中点；③AD=2CD；④梯形ADCE的面积与△ABE的面积比是3：1，其中正确的结论的个数有（）A.4B.3C.2D.15、如图，点E是▱ABCD的边CD的中点，AD，BE的延长线相交于点F，DF=3，DE=2，则▱ABCD的周长为（）A.5B.7C.10D.146、如图，在Rt△ABC中，∠B＝90°，AB＝6，BC＝8，点D在BC上，以AC为对角线的所有▱ADCE中，DE的最小值是（）A.4B.6C.8D.107、下列判断正确的是（）A.一组对边平行，另一组对边相等的四边形一定是平行四边形B.两条对角线互相平分的四边形一定是平行四边形C.两组邻角分别互补的四边形一定是平行四边形D.两条对角线相等的四边形一定是平行四边形8、▱ABCD中，对角线AC与BD交于点O，∠DAC=42°，∠CBD=23°，则∠COD 是（）A.61°B.63°C.65°D.67°9、如图，在中，如果点是边的中点，且，那么下列结论错误的是（）A. B. C. D.10、下列是假命题的是（）A.平行四边形对边平行B.矩形的对角线相等C.两组对边分别平行的四边形是平行四边形D.对角线相等的四边形是矩形11、如图，在△ABC中，AB=BC=10，AC=12，BO⊥AC，垂足为点O,过点A作射线AE∥BC，点P是边BC上任意一点，连结PO并延长与射线AE相交于点Q，设B，P两点之间的距离为x，过点Q作直线BC的垂线，垂足为R. 下面五个结论，正确的有( )个①△AOB≌△COB；②当0<x<10时，△AOQ≌△COP；③当x =5时，四边形ABPQ是平行四边形；④当x =0或x =10时，都有△PQR∽△CBO；⑤当时，△PQR与△CBO一定相似.A.2B.3C.4D.512、如图，E，F分别是▱ABCD的边AD、BC上的点，EF=6，∠DEF=60°，将四边形EFCD沿EF翻折，得到EFC′D′，ED′交BC于点G，则△GEF的周长为（）A.6B.12C.18D.2413、已知▱ABCD中，AC、BD交于点O．下列结论中，不一定成立的是（）A.▱ABCD关于点O对称B.OA=OCC.AC=BDD.∠B=∠D14、□ABCD中，∠B＝50°，则∠C＝( )A.40°B.50°C.130°D.140°15、四边形中，对角线、相交于点，下列条件不能判定这个四边形是平行四边形的是（）A.AB∥DC，AD∥BCB.AO＝CO，BO＝DOC.AB∥DC，AD＝BC D.AB＝DC，AD＝BC二、填空题(共10题，共计30分)16、如图，在平行四边形ABCD中，AD＝5，AB＝2 ，∠B是锐角，AE⊥BC于点E，F是AB的中点，连接DF，EF，若∠EFD＝90°，则AE的长为________．17、如图，在□ABCD中，对角线AC，BD交于点O，若DO＝1.5 cm，AB＝5 cm，BC＝4 cm，则□ABCD的面积为________cm2.18、如图，在平行四边形ABCD中，AB=8cm，BC=12cm，∠ABC的平分线交AD于点E，∠BCD的平分线交AD于点F。

人教五四学制版七年级下册数学第18章全等三角形含答案

人教五四学制版七年级下册数学第18章全等三角形含答案一、单选题(共15题，共计45分)1、如图，AB=AC，点D，E分别在线段AB，AC上，CD与BE相交于点O，添加以下选项中的一个条件仍不能判定△ABE≌△ACD的是（）A.∠B=∠CB.AD=AEC.BD=CED.BE=CD2、已知：如图，△OAD≌△OBC，且∠O＝70°，∠C＝25°，则∠AEB＝（）A.95°B.120°C.55°D.60°3、下列定理中，逆命题是假命题的是（）A.在一个三角形中，等角对等边B.全等三角形对应角相等C.有一个角是60度的等腰三角形是等边三角形 D.等腰三角形两个底角相等4、如图，△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB，DE⊥AB于点E，连接CE交AD于点H，则图中的等腰三角形有（）A.5个B.4个C.3个D.2个5、如图，AB∥CD，E，F分别为AC，BD的中点，若AB=5，CD=3，则EF的长是（）A.4B.3C.2D.16、如图，在△ABC中，∠C=90 ，BD是∠ABC的平分线，DE⊥AB，垂足为E，CD=5cm，则DE的长是（）A.3cmB.4cmC.5cmD.6cm7、如图，在Rt△ABC中，∠C=90°，∠CAB的平分线AD交BC于点D，DE⊥AB 于点E，若CD=4，则DE的长为（）A.2B.3C.4D.58、如图，在△ABC中，∠C＝90°，BC＝1，AC＝2，BD是∠ABC的平分线，设△ABD，△BCD的面积分别是S1， S2，则S1：S2等于（）A.2：1B. ：1C.3：2D.2：9、如图，两棵大树间相距13m，小华从点B沿BC走向点C，行走一段时间后他到达点E，此时他仰望两棵大树的顶点A和D，两条视线的夹角正好为90°，且EA=ED．已知大树AB的高为5m，小华行走的速度为lm/s，小华走的时间是（）A.13B.8C.6D.510、如图，将正方形OABC放在平面直角坐标系中，O是原点，A的坐标为（1，），则点C的坐标为（）A.（-1，）B.（- ，1）C.（-2，1）D.（-1，2）11、如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（）A.△ABC的三条中线的交点B.△ABC三边的中垂线的交点C.△ABC 三条角平分线的交点D.△ABC三条高所在直线的交点12、如图，△ ≌△ ，∠ ，∠ ，则的度数为（）A.80°B.100°C.50°D.110°13、如图，在△ABC中AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH=EB=3，AE=4，则CH的长是（）A.1B.2C.3D.414、下列可以判定两个直角三角形全等的条件是（）A.斜边相等B.面积相等C.两对锐角对应相等D.两对直角边对应相等15、如图，若△ABC≌△DEF，四个点B、E、C、F在同一直线上，BC＝7，EC＝5，则CF的长是（）A.2B.3C.5D.7二、填空题(共10题，共计30分)16、如图，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D．AD=5cm，DE=3cm，BE的长度是________．17、如图，已知A、B两点的坐标分别为（2，0）、（0，4），P是△AOB外接圆⊙C上的一点，且∠AOP=45°，则点P的坐标为________．18、如图，相等的线段有________，理由是________.19、如图，将标号为A，B，C，D的正方形沿图中的虚线剪开后，得到标号为N，P，Q，M的四个图形，试按照“哪个正方形剪开后与哪个图形”的对应关系填空：A与________对应；B与________对应；C与________对应；D与________对应．20、如图，在平行四边形中，的平分线与的平分线交于点E，若点E恰好在边上，则的值为________．21、如图所示，有一块三角形的镜子，小明不小心弄破裂成1、2两块，现需配成同样大小的一块．为了方便起见，需带上________块，其理由是________．22、如图，已知正方形ABCD的边长为12，BM=CN=5，CM，DN交于点O．则下列结论：①DN⊥MC；②DN垂直平分MC；③sin∠OCD= ；④S△ODC =S四边形BMON中，正确的有________（填写序号）23、如图，在△ABC和△BAD中，BC=AD，请你再补充一个条件，使△ABC≌△BAD．你补充的条件是________（只填一个）．24、下列语句：①有一边对应相等的两个直角三角形全等；②一般三角形具有的性质，直角三角形都具有；③有两边相等的两直角三角形全等；④两直角三角形的斜边为5cm，一条直角边都为3cm，则这两个直角三角形必全等．其中正确的有________个．25、命题“等腰三角形底边上的中点到两腰的距离相等”的逆命题是________,该逆命题是________.(写真命题或假命题）三、解答题(共5题，共计25分)26、如图，∠C=∠D=90°，DA=CB，∠CBA=28°，求∠DAC．27、小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD， BE，当他将一个等腰直角三角板ABC如图垂直放入时，直角顶点C正好在水平线DE上，锐角顶点A和B分别与木墙的顶端重合，求两堵木墙之间的距离。

人教版初中数学《第18章整数几何》竞赛专题复习含答案

第18章整数几何18.1.1★已知ABC △的两条高长分别是5、15，第三条高的长数，求这条高之长的所有可能值．解析由面积知，三条高的倒数可组成三角形三边，这是它们的全部条件．设第三条高为h ，则 111,155111.515h h⎧+>⎪⎪⎨⎪+>⎪⎩ 解得151545h <<，h 可取4、5、6、7这四个值． 18.1.2★已知ABC △的三边长分别为3AB n x =+，2BC n x =+，CA n x =+，且BC 边上的高AD 的长为n ，其中n 为正整数，且01x <≤，问：满足上述条件的三角形有几个？解析注意AB 为ABC △之最长边，故90B ∠<︒，设BD y =，CD z =，则0y >，而z 可正可负．由2y z n x +=+，及()()()22223242y z n x n x n x x -=+-+=+⋅，得4y z x -=，32ny x =+，由勾股定理，知()222332n x n n x ⎛⎫++=+ ⎪⎝⎭，展开得12n x =，由01x <≤及n 为正整数，知1n =，2，…，12，这样的三角形有12个．18.1.3★已知一个直角三角形的三条边均为正整数，其中一条直角边不超过20，其外接圆半径与内切圆半径之比为52∶，求此三角形周长的最大值．解析设该直角三角形直角边长为a 、b ，斜边为c ，则外接圆半径2cR =，内切圆半径2a b cr +-=，不妨设20a ≤．由条件知52c a b c =+-，557a b c +=，平方，得()()222225249a b ab a b ++=+，即()2212250a b ab +-=，()()34430a b a b --=，于是3a k =，4b k =，5c k =，或4a k =，3b k =，5c k =，周长为12k ，k 为正整数．k 的最大值为6，此时各边为18、24、30，周长最大值为72．AB D C18.1.4★ABC △为不等边三角形，60A ∠=︒，7BC =，其他两边长均为整数，求ABC △的面积．解析设AB x =，AC y =，则由余弦定理，有2249x y xy +-=．由条件x y ≠，不妨设x y <，则AB 为ABC △之最小边，x 只能取值1、2、3、4、5、6，分别代入，发现当3x =或5时，8y =，其余情形均无整数解．于是1sin 602ABC S xy =︒=△． 18.1.5★★一点P 与半径为15的圆的圆心距离是9，求经过P 且长为整数的弦的条数．解析如图，O 半径为15，9OP =，过P 的弦ST 长为整数，APB 为直径，6AP =，24PB =，则144SP TP PA PB ⋅=⋅=，因此24ST SP TP =+≥．又30ST AB =≤，故这样的弦共有()302412212-+⨯-=条，其中与AB 垂直的弦及AB 各一条，其余的弦每种长度有两条（关于AB 对称）．18.1.6★★在直角三角形ABC 中，各边长都是整数，90C ∠=︒，CD 为边AB 上的高，D 为垂足，且3BD p =（p 奇素数），求ACAB的值（用p 表示）．解析由2BC BD AB =⋅知2BD BC ，故设2BC p t =（t 为正整数），则2BA pt =，又由勾股定理，知22442AC p t p t =-，故tp AC ．A Bx y60°C设AC kpt =，代入得()()222p t k t k t k =-=+-，易知只能有2t k p +=，1t k -=，解得212p t +=，212p k -=，于是2211AC p AB p -=+． 18.1.7★★设正三角形ABC ，M 、N 分别在AB 、AC 上，MN BC ∥，两端延长MN ，交ABC △外接圆于P 、Q ，若PM 、MN 、AB 长均为正整数，求AB 的最小值．解析如图，易知NQ PM =也是整数．设AM x =，BM y =，PM NQ z ==，则MN x =，于是由相交弦定理，得()xy z x z =+，2z x y z=-．设y ks =，z kt =，(),k y z =，s t >，(),1s t =，则2kt x s t=-，由于()2,1s t t -=，故s t k -，要使2t AB x y k ks s t=+=+-达到最小，k 得取s t -，于是()2AB t s t s =+-．由于s t >，2s ≥，1t ≥，知()223t s t s t s +-+≥≥．当1AM =，2BM =时AB 取到最小值3，此时1PM =．18.1.8★★已知凸四边形ABCD 的四边长是两两不相等的整数，对边乘积之和等于四边形面积的两倍，且22250AD BC +=，求该四边形面积、对角线长度．解析不妨设AB α=，BC b =，CD c =，DA d =，AC 与BD 交于O ，则sin 2ABCD AC BD AOB S ac bd AC BD ⋅⋅∠==+⋅≥，于是由托勒密定理，知A 、B 、C 、D 必共圆，且满足AC BD ⊥．又由已知条件，22250b d +=，22250a c +=．经搜索知250表为平方和只有两组：22515+和22913+．由对称性，不妨设5a =，13b =，15c =，9d =，则19622ABCD ac bdS AC BD +=⋅==．由余弦定理，因cos cos 0BAD BCD ∠+∠=，得222222591315045195BD BD +-+-+=，得BD =AC =18.1.9★★是否存在一个三边长恰是三个连续正整数，且其中一个内角等于另一个内角2倍的ABC △？证明你的结论．解析存在满足条件的三角形．当ABC △的三边长分别为6a =，4b =，5c =时，2A B ∠=∠．如图，当2A B ∠=∠时，延长BA 至点D ，使AD AC b ==．连结CD ，ACD △为等腰三角形．APQM NB C因为BAC ∠为ACD △的一个外角，所以2BAC D ∠=∠．由已知，2BAC B ∠=∠，所以B D ∠=∠．所以CBD △为等腰三角形．又D ∠为ACD △与CBD △的一个公共角，有~ACD CBD △△，于是AD CD CD BD =，即b aa b c=+，所以()2a b b c =+．而()26445=⨯+，所以此三角形满足题设条件，故存在满足条件的三角形．评注满足条件的三角形是唯一的．若2A B ∠=∠，可得()2a b b c =+．有如下三种情形：（ⅰ）当a c b >>时，设1a n =+，c n =，1b n =-（n 为大于1的正整数），代入()2a b bc =+，得()()()21121n n n +=--，解得5n =，有6a =，4b =，5c =；（ⅱ）当c a b >>时，设1c n =+，c n =，1b n =-（n 为大于1的正整数），代入()2a b bc =+，得()212n n n =-⋅．解得2n =，有2a =，1b =，3c =，此时不能构成三角形；（ⅲ）当a b c >>时，设1a n =+，b n =，1c n =-（n 为大于1的正整数），代入()2a b b c =+，得()()2121n n n +=-，即2310n n --=，此方程无整数解．所以，三边长恰为三个连续的正整数，且其中一个内角等于另一个内角的2倍的三角形存在，而且只有三边长分别为4、5、6构成的三角形满足条件．18.1.10★★三边长为连续整数、周长不大于100、且面积是有理数的三角形共有多少个？解析设三角形三边依次为1n -、n 、1n +，则333n ≤≤， ()131122p n n n n =-+++=，S △==于是()234n -是平方数，令()()22343n k -=，得2243n k -=，则32n ≤，CD A224102034033n k -==≤，18k ≤．又k 不可能是奇数，否则()222343n k k =+≡，得2243n k -=，则32n ≤，224102034033n k -==≤，18k ≤．又k 不可能是奇数，否则()22343mod 4n k =+≡，将2k =，4，6，8，10，12，14，16，18代入，发现仅当2k =，8时满足要求．因此这样的三角形共有两个，三边长依次为3、4、5与13、14、15．18.1.11★★某直角三角形边长均为整数，一直角边比斜边小1575，求其周长的最小值．解析设直角三角形直角边长a 、b ，斜边为1575a +，则 ()2221575a b a +=+，()2157521575b a =+．由于221575357=⨯⨯，设105b k =，则2721575k a =+，设7a s =，则22225k s =+，于是k 的最小值为17，此时32s =，224a =，1785b =，1799c =．此时的最小周长为3808． 18.1.12★★已知ABC △，AD 是角平分线，14AB =，24AC =，AD 也是整数，求AD 所有可取的值．解析如图，作DE AB ∥，E 在AC 上，则易知AE ED =．又ED CD AC AB BC AB AC ==+，故 22AB ACAD AE DE ED AB AC⋅<+==+33617.6819==…，故17AD ≤．又当17AD ≤时，不难通过AED △构造出ABC △，故AD 所有可取的值为1，2， (17)18.1.13★面积为c 的正方形DEFG 内接于面积为1的正三角形ABC ，其中a 、b 、c 是整数，且b 不能被任何质娄的平方整除，求a cb-的值． AEB DC解析设正方形DEFG 的边长为x ，正三角形ABC 的边长为m ，则2m =，由ADG ABC △∽△，可得xx m -=．解得()3x m =．于是()222348x m ==．由题意得28a =，3b =，48c =，所以 203a cb -=-． 17.1.14★★如图，AD 是ABC △的高，四边形PQRS 是ABC △的内接正方形，若BC ab =（即两位数），SRc =，ADd =，且a 、b 、c 、d 恰为从小到大的4个连续正整数，求ABC S △的所有可能值．解析易知11SR AR CR SR BC AC AC AD ==-=-，于是有110c c a b d +=+，或11111132a a a +=+++，移项，得()()1111123a a a =+++，或2650a a -+=，解得1a =或5．于是有两解： 12,3,4;BC SR AD =⎧⎪=⎨⎪=⎩56,7,8.BC SR AD =⎧⎪=⎨⎪=⎩易知这两组数据都符合要求，故24ABC S =△或224．ADGB E F CAS RB P D Q18.1.15★★已知ABC △中，B ∠是锐角．从顶点A 向BC 边或其延长线作垂线，垂足为D ；从顶点C 向AB 边或其延长线作垂线，垂足为E ．当2BD BC 和2BEAB均为正整数时，ABC △是什么三角形？并证明你的结论．解析设2BD m BC =，2BEn AB=，m 、n 均为正整数，则 244cos 4BD BE mn B AB BC=⋅⋅=<，所以，1mn =，2，3．（1）当1mn =时，1cos 2B =，60B ∠=︒，此时1m n ==．所以AD 垂直平分BC ，CE 垂直平分AB ，于是ABC △是等边三角形．（2）当2mn =时，cos B =45B ∠=︒，此时1m =，2n =，或2m =1n =，所以点E 与点A 重合，或点D 与点C 重合．故90BAC ∠=︒，或90BCA ∠=︒，于是ABC △是等腰直角三角形．（3）3mn =时，cos B =，30B ∠=︒，此时1m =，3n =，或3m =，1n =．于是AD 垂直平分BC ，或CE 垂直平分AB ．故30ACB ∠=︒，或30BAC ∠=︒，于是ABC △是顶角为120︒的等腰三角形．18.1.6★★某直角三角形两直角边长均为整数，周长是面积的整数倍（就数字上讲），问问这样的直角三角形有多少个？解析设直角边分别为a 、b ，则斜边c =，由条件知它是有理数，故必定是整数．设2ka b ab +=，k 为正整数，于是k =．由于a b +1、2或4，记作k '．由a b k +-'()2220ab k a b k -'++'=，()()22a k b k k -'-'='，1k '=时无解；2k '=时，有()()222a b --=，{a ，b }={3，4}；4k '=时，()()448a b --=，{a ，b }={5，12}或{6，8}，所以这样的直角三角形共有3个．18.1.17★★在等腰ABC △中，已知AB AC kBC ==，这里k 为大于1的自然数，点D 、E 依次在AB 、AC 上，且DB BC CE ==，CD 与BE 相交于O ，求使OCBC为有理数的最小自然数k ．解析如图，连结DE ，则DE BC ∥，11DE AD AB BC BC AB AB k -===-，1k DE BC k-=．由于四边形DBCE 为等腰梯形，则由托勒密定理（或过D 、E 作BC 垂线亦可），2222121k k CD CD BE DE BC DB CE BC BC BC k k--=⋅=⋅+⋅=+=，又21CO BC kCD DE BC k ==+-，于是CO BC =k 与21k -互质，由题设知其必须均为平方数，1k >，25k =适合，这是满足要求的最小自然数．18.1.18★★★对于某些正整数n 来说，只有一组解xyz n =（不计顺序），这里，x 、y 、z 是正整数且可构成三角形的三边长，这样的()100n ≤共有多少个？解析显然，当n p =（素数）时无解；当2n p =或1时只有一组解（1，p ，p ）或（1，1，1）；当n pq =（p 、q 为不同素数）时无解；当4n p =（p 为大于3的素数）时也无解．剩下的数为8，12，16，18，24，27，30，32，36，40，42，45，48，50，54，56，60，63，64，66，70，72，75，78，80，81，84，88，90，96，98，99，100．易验证，无解的n 有：30，42，54，56，63，66，70，78，88，99；唯一解的n 有：8，12，16，18，24，27，32，40，45，48，50，75，80，81，84，90，96，98；不止一组解的n 有：36，60，64，72，100．注意：判定无解的主要依据是，abc n =，c ab >时无解，困为1c ab a b ++≥≥．因此，有解的n 共有23个．18.1.19★★面积为整数的直角三角形周长为正整数k ，求k 的最小值，并求此时这个直角三角形的两条直角边的可取值（如不止一组解，只需举了一组即可）．解析设该直角三角形的直角三角形周长分别为a 、b ，则112ab ≥，a b +≥2，2k a b =+，故5k ≥．下令5k =，2ab =，如有解，则可．()5a b -+，平方得()222225102a b a b a b ab +=-++++．ADEBCO取2ab =，得29,102.a b ab ⎧+=⎪⎨⎪=⎩因此a 、b 为方程21029200x x -+=的根，解得a 、bk 的最小值是5．18.1.20★★若ABC △的三边长a 、b 、c 均为整数，且140abc =，求ABC △内切圆半径．解析不妨设a b c ≤≤，于是7c ≥．又14011c a b ab c<++=+≤，故140c c ≤，得10c ≤．于是c 只可能为7或10．7c =时，20ab =，只可能4a =，5b =，()182p a b c =++=，内切圆半径r ==． 10c =时，14ab =，没有满足要求的解．18.1.21★★证明：若a 、b 、c 是一组勾股数()222a b c +=，则存在正整数k 、u 、v 、u v >，(),1u v =使得()22c k u v =+，而()22a k u v =-，2b kuv =；或2a kuv =，()22b k u v =-．解析222a b c +=，设（a ，b ，c ）k =，则1a ka =，1b kb =，1c kc =，222111a b c +=．易知1a 、1b 、1c 两两互质；1a 与1b 不可能同偶，否则12a ，1b ，1c ；1a 与1b 也不会同奇，否则()212mod 4c =，矛盾．于是1a 与1b 必一奇一偶，不妨设1a 奇而1b 偶，于是1c 为奇数．从而()()211111a c b c b =+-，11c b +与11c b -必互质，否则有一奇素数11|p c b +，11c b -，得|2p c ，12b ，故|p （1c ，1b ），与（1c ，1b ）=1矛盾．于是可设2111c b u +=，2111c b v -=，（1u ，1v ）=1，且1u 、1v 均为奇数，解得221111122u v u v c +-⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，11111222u v u v b +-=⋅⋅，221111122u v u v a +-⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭，令112u v u +=，112u v v -=，即得结论． 18.1.22★★★如图，F 、E 在ABC △的边AB 、AC 上，FE 的延长线与BC 的延长线交于D ，求证：AF 、BF 、CB 、CD 、AE 、EC 、FE 、ED 的长度不可能是1～8的排列．解析如果1EF =，则1AE AF EF -<=，得AE AF =，矛盾，故1EF ≠，同理AF 、AE 、ED 、CD 、EC 都不等于1．因此1只可能等于FB 或BC 之长，不失对称性，设1BF =，则1FD BD BF -<=，FD BD =，作CG AB ∥，G 在ED 上，四边形FBCG 乃一等腰梯形，于是EG FG EF BC EF =-=-为正整数．又1EG EC CG BF -<<=，故EG EC =，但BFD ∠为等腰三角形DFB 的底角，90BFD <︒∠，18090EGC BFD =︒->︒∠∠，为EGC △的最大内角，EC EG >，矛盾，因此结论证毕． 18.1.23★★★已知梯形ABCD 中，AD BC <，E 、F 分别在AB 、CD 上，EF AD BC ∥∥，ED BF ∥，如果AD 、EF 、BC 均为正整数，称该梯形为“整数梯形”．现对于正整数n ，有正整数x x <′<y ′<y ，x y x +=′+y ′=n ，且x 、y 为一“整数梯形”的上、下底， x ′、y ′为另一“整数梯形”的上、下底，求n 的最小值．解析如图，由AED EFD △∽△ DEF FBC △∽△ 得AD AE DF EFEF BE FC BC===，得EF =，于是问题变为求最小的n ，使xy 与x ′y ′均为平方数．xy 、x ′y ′不可能都为4，故至少有一组≥9，显然另一组也不可能为4，于是xy ，x ′y ′≥9．如果xy 或x ′y ′25≥，则10n =≥．若xy 或x ′y ′=9或16，则19n =+或2810+=．于是n 的最小值为10，1x =，x ′=2，y ′=8，y =9．18.1.24★★★求证：存在无穷多个每边及对角线长均为不同整数的、两两不相似的凸四边形．AFE GDCB A DEFB CABDPC解析如图，作圆内接四边形ABCD ，AC 与BD 垂直于P ，设a 为一整数，2a >，4AP a =，24BP a =-，241DP a =-，则24AB a =+，241AD a=+，，由此知()()224414aa CP a--=，而由ABP DCP △∽△，BPC APD △∽△知，()224414a BC a a-=+，()224144a CD a a -=+．同时乘以系数4a ，得()244AB a a =+，()2441AD a a =+，()()22441BC a a =-+，()()22414CD a a =-+，4244AC a a =-+，()2201BD a a =-．易知上述6个多项式无二者恒等，于是任两者相等只能得有限个a ，但正整数有无限个，因此有无限个a ，使6个多项式两两不等，又当a →+∞时，0BDAC→，因此有无限个这样的凸四边形两两不相似． 18.1.25★★★已知PA 、PB 为圆的切线，割线过P ，与圆交于M 、N ，与AB 交于S ，若PA 、PM 、MS 、SN 均为正整数，求PA 的最小值．解析如图，易知有PM PNMS SN=(调和点列)．设PM a =，MS b =，SN c =，则()b a b c ac ++=，()b c b c a b+=-，从而PA === 设a ks =，b kt =，k =（a ，b ），则（s ，t ）=1，s t >，s tc kts t+=-，PA =易见（s t +，s t -）=1，则s 、t 一奇一偶．于是由（()t s t +，s t -）=1，得|s t k -，且由PA 为整数知2s t x +=，2s t y -=，x 、y 为奇数．因为|s t k -，于是k 的最小值为s t -，()c t s t =+，PA sxy =，当s =1，2，3，4时，t 无解(即PA 不是整数)，故5s ≥，又3x ≥，1y ≥，于是PA ≥15，当a =5，b =4，c =36时取到15PA =．若（s t +，s t -）=2，此时s 、t 同奇，k 的最小值为2s t-，此时()2t s t c +=，PA =，22s t x +=，22s t y -=，当1s =，3时，无t 使PA 为整数，于是5s ≥，又x y >，所以1y ≥，2x ≥，5210PA sxy =⨯=≥．当5a =，3b =，12c =时取到PA =10．PMABSN综上，PA 的最小值是10．18.1.26★★★一圆内接四边形的四边长及对角线长都是整数，求这类四边形中周长最小者．解析显然长与宽为4、3的矩形满足要求，其周长=14．若等腰梯形上、下底分别为3、4，腰为2，则由托勒密定理，对角线长为4，满足要求，此时周长为11．故最小周长≤11．显然对圆内接凸四边形ABCD ，无边长为1．否则若设1AB =，—1AD BD AB <=，得AD BD =，同理AC CB =，于是C 、D 均在AB 中垂线上，构不成凸四边形．因此最小周长≥2×4=8．四边均为2，得正方形，对角线为2，另一边为3，得等腰梯形，10．当周长为10时，显然至少有两边为2．若是2、2、2、4能为2、2、3、3故最小周长为11．18.1.27★★★在Rt ABC △中，90BCA =︒∠，CD 是高，已知ABC △的三边长都是整数，且311BD =，求BCD △与ACD △的周长之比．解析设ABC △的三边长分别为a 、b 、c ．由题设知 2BC BD BA =⋅，故2311a c =．于是设211a l =，得211l c =由勾股定理得11b 2211l -是完全平方数，设为()20t t >，则22211l t -=，()()211l t l t -+=．由于0l t l t <-<+，所以21,11.l t l t -=⎧⎨+=⎩解得61,60.l t =⎧⎨=⎩于是21161a =⨯，116160b =⨯⨯．因为BCD CAD △∽△，所以它们的周长比等于它们的相似比，即1160a b =． 18.1.28★★★已知锐角三角形ABC 中，AD 是高，矩形SPQR 的面积是ABC △的1／3，其顶点S 、P 在BC 上，Q 、R 分别在AC 、AB 上，且BC 、AD 及矩形SPQR 的周长均为有理数，求AB ACBC+的最小值．解析如图，设ABC △的三边长依次为a 、b 、c ，AD h =，PQ x =，RS y =，则16xy ah =，及1x y AQ CQ a h AC AC+=+=．由条件，知a 、h 、x y +均为有理数． CB D由16x aa x+=，得x a ，33y h =，)2a h x y a h ++=±-，因此只能有a h =．若过A 作BC 的平行线l ，再作C 关于l 的对称点C '，则AB AC AB AC +=+′≥BC′=，于是AB ACBC+，仅当AB AC =时取到． 18.1.29★★★★整数边三角形ABC 中，90BAC =︒∠，AD 是斜边上的高，BD 也是整数．若对同一个BD 能长度，有两个不全等的直角整数边三角形ABC 满足要求，求BD 的最小值．解析不妨设ABC △的三边长为a 、b 、c ，AD h =，BD d =，首先bch a=为有理数，又222h c d =-为整数，因此h 也是整数．又CD 为整数，故2h d也是整数．又ABD CBA △∽△故h b d c=．因此，只需正整数h 、c 、d 满足222h c d =-及2|d h ，这样的整数边三角形就存在．因为此时hcb d=是有理数，而222b h CD =+为整数，从而b 为整数．易知由2|d h 可得2|d c ．设21d d σ=，σ、1d 为正整数，且σ无平方因子，于是由2|h σ及2c 知|h σ，c ．设1h h σ=，1c c σ=，代入得422111d c h =-，又由2|d h ，2c 得2211|d h σ，21c σ，今对1d 的任一素因子p ，其在1d 的指数()1s d 不会比1h 的指数高，否则()()111s d s h +≥，()()22112s d s h +≥，而()s σ最多为1，于是()()2211s d s h σ>，这是不可能的．于是11|d h ，同理11|d c ．又令112h d h =，112c d c =，代入422111d c h =-得222122d c h =-．于是对1d 有两组不同的2c 、2h 满足222122d c h =-．经计算18d ≥，故64d ≥．当64d =时，确实有满足要求的两组解：80AB =，60AC =，100BC =，和136AB =，255AC =，289BC =．故BD 的最小值是64．AR QB S D P CAB D C18.1.30★★★★试找一不等边三角形ABC ，使BC 及BC 边上的中线、角平分线、高的长度都是整数，BC 可以是多少(此时的中线、角平分线、高的长度分别为多少)?若要求BC 不是整数，但2BC 是整数，则BC 可为多少(此时中线、角平分线、高的长度分别为多少)?解析首先处理BC 为整数的问题，我们选择的是直角三角形ABC ，对应边为a 、b 、c ，中线AM ，角平分线AD ，高AH ，2aAM =，bc AH a =，又ABC ABD ACD S S S =+△△△，得)2bc b c AD =+，故AD b c =+，于是a 为偶数2k，b =，c =，mnAH k =而2mn AD m n =+，2222m n k +=，这个方程有解1m =，7n =，5k =，得75AH =，5AM =，74AD =．乘以一个系数20，即得直角三角形ABC ，它的斜边为200，斜边上的中线为100，角平分线为35，高为28．下面处理BC 为无理数、2BC 为整数的情形，如图，延长AD ，与M P 交于P ，此处MP BC ⊥．易知A 、B 、P 、C 共圆(P 是ABC △外接圆弧BC 之中点)．今从基本勾股数出发构造．取12AH =，13AD =，15AM =，则5DH =，9MH =，4MD =，485MD MP AH HD =⋅=，45255PD AD ==．易知BPD APB △∽△，于是25211760845525BP PD PA =⋅=⨯=，()22222608448302444425255BC BM PB MP ⎛⎫==-=-= ⎪⎝⎭．再乘以系数5，得所求三角形的高60AH =，角平分线65AD =，中线75AM =，边BC =是无理数，但15120BC =．18.1.31★★作圆外切凸五边形ABCDE ，现知该五边形每边长均为整数，1AB =，又圆与BC切于K ，求BK ．解析如图，设CD 、DE 、EA 、AB 分别与圆切于P 、Q 、R 、S ．则RE DP ED +=为整数，于是由题设，AR CP +亦为整数，而AR CP AS KC +=+．于是22BK BS BK BS ==+为整数，由于1BS AB <=，故22BS <，221BK BS ==，12BK =． ABMD HCPAS RB EQ KC P D。

人教五四学制版七年级下册数学第18章全等三角形含答案(满分必刷)

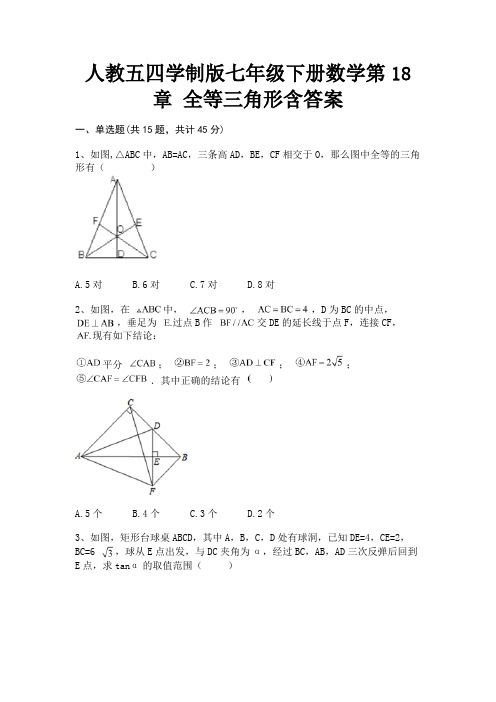
人教五四学制版七年级下册数学第18章全等三角形含答案一、单选题(共15题，共计45分)1、如图,△ABC中，AB=AC，三条高AD，BE，CF相交于O，那么图中全等的三角形有（）A.5对B.6对C.7对D.8对2、如图，在中，，，D为BC的中点，，垂足为过点B作交DE的延长线于点F，连接CF，现有如下结论：平分；；；；．其中正确的结论有A.5个B.4个C.3个D.2个3、如图，矩形台球桌ABCD，其中A，B，C，D处有球洞，已知DE=4，CE=2，BC=6 ，球从E点出发，与DC夹角为α，经过BC，AB，AD三次反弹后回到E点，求tanα的取值范围（）A. ≤tanα＜B. ＜tanα＜C.tanα=D. ＜tanα＜34、如图，AB＝AC，BE⊥AC于点E，CF⊥AB于点F，BE，CF交于点D，则下列结论中不正确的是（）A.△ABE≌△ACFB.点D在∠BAC的平分线上 C.△BDF≌△CDE D.D是BE的中点5、如图，在△ABC中，AB=AC，∠ABC=40°，BD是∠ABC的平分线，延长BD至E，使DE=AD，则∠ECA的度数为（）A.30°B.35°C.40°D.45°6、如图，AB∥CD，AC∥DB，AD 与 BC 交于点 O，AE⊥BC 于点 E，DF⊥BC 于点 F，那么图中全等的三角形有( )对A.5B.6C.7D.87、如图，在菱形ABCD中，∠A＝60°，E、F分别是AB、AD的中点，DE、BF相交于点G，连接BD、CG．给出以下结论：①∠BGD＝120°；②BG+DG＝CG；＝AB2．其中正确的有（）③△BDF≌△CGB；④S△ADEA.1个B.2个C.3个D.4个8、如图，在矩形ABCD中，P是BC上一点，E是AB上一点，PD平分∠APC，PE⊥PD，连接DE交AP于F，在以下判断中，不正确的是（）A.当P为BC中点，△APD是等边三角形B.当△ADE∽△BPE时，P为BC 中点C.当AE=2BE时，AP⊥DED.当△APD是等边三角形时，BE+CD=DE9、如图，在矩形ABCD中，E，F分别是边AB，CD上的点，AE=CF，连接EF，BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC，FC=2，则AB的长为（）A.8B.8C.4D.610、如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD=6，则点P到边OB的距离为（）A.5B.6C.3D.411、若△ABC≌△DEF，且△ABC的周长为20，AB=5，BC=8，则DF长为（）A.5B.8C.7D.5或812、对于△ABC嘉淇用尺规进行了如下操作：如图：⑴分别以点B和点C为圆心，BA，CA为半径作弧，两弧相交于点D；⑵作直线AD交BC边于点E.根据嘉淇的操作方法，可知线段AE是（）A.△ABC的高线B.△ABC的中线C.边BC的垂直平分线 D.△ABC的角平分线13、如图，正方形ABCD中，AB＝6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：＝3．其中正确结论的个数是①△ABG≌△AFG；②BG＝GC；③AG∥CF；④S△FGC( )A.1B.2C.3D.414、正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK 上，正方形BEFG的边长为4，则△DEK的面积为（）A.10B.12C.14D.1615、如图，△ABC≌△DCB，若AC=7，BE=5，则DE的长为（）A.2B.3C.4D.5二、填空题(共10题，共计30分)16、如图，在△ABC中，AC=BC，∠C=90°，BD为∠ABC的平分线，若A点到直线BD的距离为a，则BE的长为________17、如图，在△ABC和△DEF中，已知：AC=DF,，BC=EF，要使△ABC≌△DEF，还需要的条件可以是________ ；(只填写一个条件)18、如图，△ABC≌△DCB，A、B的对应顶点分别为点D、C，如果AB＝6cm，BC ＝12cm，AC＝10cm，DO＝3cm，那么OC的长是________cm．19、如图，有一池塘，要测池塘两端A、B两点的距离，可先在平地上取一个可以直接到达A、B两点的C，连接AC并延长AC到点D，使CD=CA，连结BC并延长BC到点E，使CE=CB，连接DE，那么量出DE的长就等于AB的长. 这是因为可根据________方法判定△ABC≌△DEC；20、如图，A、C、B、D在同一条直线上，MB=ND，MB∥ND，要使△ABM≌△CDN，还需要添加一个条件为________21、如图，∠AOE=∠BOE=15°，EF∥O B，EC⊥OB，若EC=3，则EF的长为________22、如图，在△ABC中，AB＝AC，AD平分∠BAC，则________≌________，理由是________．23、如图，在正方形ABCD中，E为BC上的点，F为CD边上的点，且AE=AF，AB=4，设EC=x，△AEF的面积为y，则y与x之间的函数关系式是________．24、如图，在平面直角坐标系中，直线与轴、轴分别交于A、B两点，以AB为边在第一象限作正方形，点D恰好在双曲线上，则值为________．25、正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB 于F，则EF的长为________．三、解答题(共5题，共计25分)26、如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，AB=6，FC=4，求线段DB的长．27、如图，已知：AB⊥BD，ED⊥BD，AB=CD，BC=DE，那么AC与CE有什么关系？写出你的猜想并说明理由.28、如图，AE=DB，BC=EF，BC∥EF，求证：△ABC≌△DEF．29、如图，CA=CD，∠B=∠E，∠BCE=∠ACD．求证：AB=DE．30、如图，，，．求证：．参考答案一、单选题(共15题，共计45分)1、C2、B3、C4、D5、C6、C7、B8、B9、D10、B11、C12、A13、C14、D15、A二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、30、。

华师大版八年级下册数学第18章平行四边形含答案

华师大版八年级下册数学第18章平行四边形含答案一、单选题(共15题，共计45分)1、平行四边形的对角线一定具有的性质是（）A.相等B.互相平分C.互相垂直D.互相垂直且相等2、如图，平行四边形ABCD中，E是CD的延长线上一点，CD=2DE，BE与AD交于点F，若△DEF的面积为1，则平行四边形ABCD的面积为（）A.8B.10C.12D.143、如图，在▱ABCD中，EF∥AB，点F为BD的中点，EF=4，则CD的长为( )A. B.8 C.10 D.164、如图，已知直线l//AB，l与AB之间的距离为2.C，D是直线l上两个动点（点C在D点的左侧），且AB=CD=5.连接AC，BC，BD，将△ABC沿BC折叠得到△A′BC.下列说法：①四边形ABDC的面积始终为10；②当A′与D重合时，四边形ABDC是菱形；③当A′与D不重合时，连接A′、D，则∠CA′D+∠BCA′=180°；④若以A′，C，B，D为顶点的四边形为矩形，则此矩形相邻两边之和为3 或7.其中正确的是( )A.①②③④B.①③④C.①②④D.①②③5、 ABCD中，A: B: C: D的值可以是（）A.1:2:3:4B.1:2:2:1C.2:2:1:1D.3:2:3:26、如图，已知的四个内角的平分线分别相交于点E、F、G、H，连接，若，则的长是（）A.12B.13C.D.7、下列命题中假命题是（）A.正六边形的外角和等于360°B.位似图形必定相似C.对角线相等的四边形是矩形D.两组对角相等的四边形是平行四边形8、如图，在平行四边形ABCD中，AB=3，AD=2，则CD=（）A.3B.2C.1D.59、如图，在给定的一张平行四边形纸片上作一个菱形．甲、乙两人的作法如下：甲：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形。

乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于E，F，连接EF，则四边形ABEF是菱形。

审计学（第二版）-第18章内部审计习题答案

本章复习思考题1．试述内部审计的定义与特征。

答：一、内部审计的定义中国《审计署关于内部审计工作的规定》对内部审计的定义为：“内部审计是独立监督和评价本单位及所属单位财政收支、财务收支、经济活动的真实、合法和效益的行为，以促进加强经济管理和实现经济目标。

”国际内部审计师协会（IIA）认为，“内部审计是一种独立、客观的确认（Assurance）和咨询（Consulting）活动，旨在增加价值和改善组织运营。

它通过应用系统的、规范的方法，评价并改善风险管理、控制和治理过程的效果，帮助组织实现其目标。

”虽然对内部审计的定义部完全系统，但均包含以下要点：（一）内部审计的独立性要求独立性是审计的本质特征。

内部审计机构在实施审计过程中仍然要保持其独立性，但内部审计的独立性比外部审计要弱。

由于内部审计机构属于本部门、本单位的内部机构，与同属于本部门、本单位的被审计单位有着关联关系，因而只具有相对独立性。

（二）内部审计的职能内部审计只具有经济监督与评价职能，不具有经济鉴证职能。

这是因为内部审计机构与被审计单位同属于一个部门或单位，在外人看来，不具有形式上的独立性，因而其签发的审计报告对外就不具有经济鉴证作用。

在审计职能的侧重点方面，内部审计应当侧重于经济评价职能。

（三）内部审计的范围内部审计的范围只能局限于本部门、本单位及其所属单位内部。

（四）内部审计的对象内部审计的对象是本单位及所属单位内部受托经济责任履行情况，即本单位及所属单位为履行内部受托经济责任而发生的财务收支活动及其相关经济活动的真实性、合法性和效益性以及相关经济资料的合法性、正确性和公允性。

（五）内部审计根本目的内部审计的根本目的是促进本部门、本单位将其经济管理和实现经济目标。

2．内部审计机构应当履行哪些职责？应当赋予内部审计机构哪些职权？答：为充分发挥内部审计的职能，实现内部审计的根本目标，内部审计机构应当在本单位主要负责人或者权力机构的领导下，在本部门、本单位内部履行下列职责：1．开展财政财务审计，即对本单位及所属单位（含占控股地位或者主导地位的单位，下同）的财政收支、财务收支及其有关的经济活动进行审计；2．开展资金管理审计，即对本单位及所属单位预算内、预算外资金的管理和使用情况进行审计；3．开展经济责任审计，即对本单位内设机构及所属单位领导人员的任期经济责任进行审计；4．开展固定资产投资审计，即对本单位及所属单位固定资产投资项目进行审计；5．开展内部控制审计与风险管理审计，即对本单位及所属单位内部控制制度的健全性和有效性以及风险管理进行审计；6．开展管理审计与效益审计，即对本单位及所属单位经济管理和效益情况进行审计；7．开展其他审计，即法律、法规规定和本单位主要负责人或者权力机构要求办理的其他审计事项。

第18章答案

第18章 正比例函数和反比例函数 - 答案

《管理学》习题与答案——第18章 沟通