ABAQUS帮助文档轮胎磨损例子翻译
4abaqus里的单词翻译包括音标方便记忆
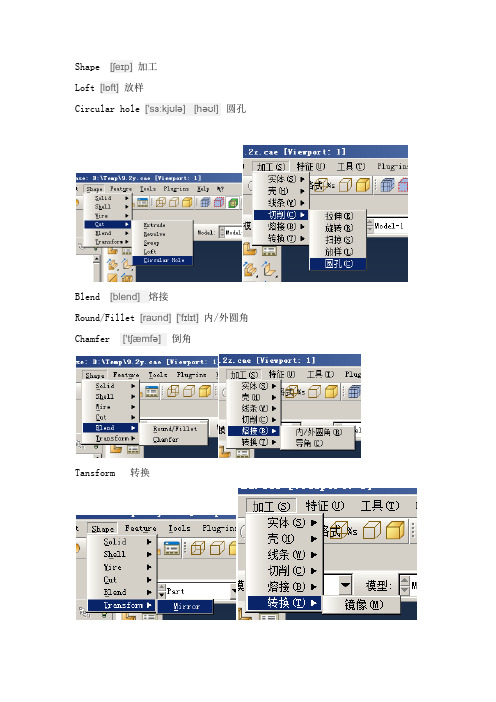
Shape [ʃeɪp]加工Loft [lɒft]放样Circular hole ['sɜːkjʊlə] [həʊl] 圆孔Blend [blend] 熔接Round/Fillet [raʊnd]['fɪlɪt]内/外圆角Chamfer ['tʃæmfə] 倒角Tansform 转换Suppress [sə'pres]禁用Attachment [ə'tætʃm(ə)nt]附加Partition [pɑː'tɪʃ(ə)n]分区CAD Parameters ~ [pə'ræmɪtɚ] CAD参数View Cut 视图切片Points from file/By picking ~ ['pɪkɪŋ]来自文件的或拾取的点Point along direction ~ [ə'lɒŋ] [daɪˈrekʃn]沿某一方向的点Remove attachments ~ [ə'tætʃm(ə)nt]删除附加体Mid surface 中面Assign [ə'saɪn]指定Assign thickness and offset ~['θɪknɪs]~~指定厚度和偏移量On context ~['kɒntekst]上下文帮助On module ~ ['mɒdjuːl]模块帮助Getting started ~ ['stɑːtɪd]入门指南Keyword browser ['braʊzə]关键字浏览器Release notes [rɪ'liːs] [nəʊt]发布记录Invoke context sensitive help [ɪn'vəʊk] ['kɒntekst]['sensɪtɪv]~打开上下文帮助Composite ['kɒmpəzɪt]复合Beam section orientation [biːm]梁截面方向Rebar reference orientation ['riːbɑː]['ref(ə)r(ə)ns] 钢筋参考方向Element normal ['elɪm(ə)nt] ['nɔːm(ə)l]单元法向Element tangent ~[ˈtændʒənt]单元切向Profile ['prəʊfaɪl]剖面Special ['speʃ(ə)l]特殊设置Stringer ['strɪŋə]纵梁Inertia [ɪ'nɜːʃə]惯性Springs/Dashpots [sprɪŋ] ['dæʃpɒt]弹簧/阻尼器Regenerate [rɪ'dʒenəreɪt]重生成Resume [rɪ'zju:m]恢复Evaluate [ɪ'væljʊeɪt]评估Elasticity [elæ'stɪsɪtɪ; iː-; ɪ-]弹性Elastic [ɪ'læstɪk]弹性Hyperelastic ['haɪpə]~超弹性Plasticity [plæ'stɪsɪtɪ]塑性Plastic ['plæstɪk]塑性Isotropic [,aɪsə(ʊ)'trɒpɪk]各向同性Engineering constants ~ ['kɔnstənts]工程常数Lamina ['læmɪnə]单层板Orthotropic [,ɔːθə(ʊ)'trəʊpɪk; -'trɒpɪk]正交Anisotropic [,ænaɪsə(ʊ)'trɒpɪk]各向异性Traction ['trækʃ(ə)n]面作用力Coupled traction ['kʌpld] ['trækʃ(ə)n]耦合表面作用力Shear [ʃɪə]剪力Moduli time scale (for viscoelasticity) ['mɑdʒə,lai] ~ [skeɪl]~ ['viskəu,ilæs'tisiti]模量时间尺度(用于粘弹性)No compression ~ [kəm'preʃ(ə)n]无压缩No tension ~ ['tenʃ(ə)n]无拉伸Modulus ['mɒdjʊləs]模量Ratio ['reɪʃɪəʊ]比Long-term ~ [tɜːm]长期Instantaneous [,ɪnst(ə)n'teɪnɪəs]瞬态Suboptions 子选项Fail stress ~ [stres]破坏应力Fail strain ~ [streɪn]破坏应变Ten stress (fiber dir) ~~ ['faɪbɚ]~拉应力(纤维方向)Com stress (fiber dir) 压应力(纤维方向)Ten stress (transv dir) 拉应力(传递方向)trans英[trɑːnz]美[trænz]•abbr. 翻译(translate)•pref. 表“横穿”;表“进入”•n. 传动装置;变速箱Shear strength [ʃɪə] [streŋθ;streŋkθ]剪切强度Stress limit [stres] ['lɪmɪt]应力限制塑性变形还没写。
轮胎结构设计技术过程讲课文档

第1页,共80页。
目
Ⅰ. PC 结构设计技术 1. PCR Tire 结构 2. Tire 各部位功能及特性
3. 开发FLOW(PCR OE)
1) 新产品开发 PROCEDURE
2) 新产品开发组织图 3) 设计目标设定
4) 开发过程
5) 轮胎实车性能改善
6) 耐久品质验证
7) PCR 结构设计检讨事项
Copyright ⓒ 2002 by Kumho Tire All Rights reserved
第8页,共80页。
Steel Belt 主要Factor 特性
- Wire 材质 - Wire Diameter, 缠结方法 - Wire 密度
- Coating Compound 种 类 - Coating Compound Ga. - Angle & Direction - Width
第17页,共80页。
2) 新产品开发组织图
Copyright ⓒ 2002 by Kumho Tire
All Rights reserved
第18页,共80页。
<参照> OE vs. RE TIRE 比较
OE TIRE
RE TIRE(例示)
Tire
概念
▶ 装配给特定轮胎的专用轮胎
▶ 可装配多种车辆的代替 Tire
3) 带束曾 (Belt) : 位置在胎面和car cass之间,由 Steel Wire构成,缓和外部冲击,当然使Tread接地面维
持在一定宽度,以致运行稳定性良好 。
4) 胎侧(SideWall) : 指的是胎肩下部分到胎圈之间的橡胶,起保护内部car cass的作用。
汽车轮胎稳态滚动中的磨损分析专题资料集锦

轮胎磨损与车轮定位关系研究和探讨.rar 借鉴已有的理论基础和科研成果,主要从摩擦学、宏观动力学的角度来研究轮 胎的磨损及非正常磨损。通过相关理论和方法,进行较为系统和科学的研究, 发现可‘针对不同的悬架形式的定位参数和特点预见和预防车轮的非正常磨 损,也可以通过不同的胎面磨损现象来判断悬架、转向系统的机件故障,为以 减少轮胎非正常磨损为目的的轮胎和悬架的设计和维修保养提供理论分析和 操作指导。
K、开合次数、硬度、材料、Bottom Die移动速度以及温度间的关系,为
建立磨损模型打下了坚实的基础。(3)通过UG建立斜平面导向活络模中套 耐磨板及弓形座的三维造型,将其导入到Deform-3D中并根据真实工况设
置边界条件进行磨损模拟,最终确定磨损系数K的值。(4)根据均匀设计理
论,将修正系数a、b、c设计为十二水平。结合回归分析理论及Deform的 模拟最终确定修正系数的值。
全钢子午线轮胎活络模磨损模型的研究.rar
(1)从斜平面导向活络模的结构、运动、准配准则及试压检测要求等几个 方面论述了活络模的加工要求及使用性能;详细的总结了斜平面导向活络 模在硫化生产中容易出现的问题及相应的解决措施。(2)通过有限元分析 软件Deform-3D的模拟,分析总结了磨损量与修正系数a、b、c、磨损系数
子午线轮胎胎面花纹块滑动磨损有限元分析.pdf
以205/55R16半钢子午线轮胎为参考轮胎,通过建立带纵向和横向简单花纹的 轮胎模型,使用ABAQUS/Standard进行了轮胎自由滚动、制动工况的有限元分 析,分析了与胎面磨损分布相关的粘着滑移区域随滚动角速度变化的分布情况 。结果显示:轮胎在制动状态下,胎面各花纹块沿滑动方向前端出现接触大变 形。但由于整体轮胎模型胎面花纹部分网格较粗糙,计算得到的花纹块变形受 力分布特征不够准确。为此,采用整体到局部的分析方法,建立采用精细网格 的二维平面应变花纹块模型,由整体轮胎模型提供其简化边界条件,使用 ABAQUS/explicit进行了滑动的热力耦合有限元分析。结果显示:采用精细网 格的局部花纹块模型能反映出滑动前端卷曲大变形以及表面卷曲自接触的变 形特征。最后,通过模拟ABS(防抱死制动系统)控制下轮胎胎面花纹块磨损过
ABAQUS帮助文档翻译

节选-ABAQUS帮助文档翻译 reference to: user manual 18.62008-10-10 12:5918.6 理解自适应网格(adaptive meshing)自适应网格可以通过移动独立的材料网格(allowing the mesh to move independently of the material),让你在整个分析过程中即使发生大变形,也能保持高质量的网格。
通常自适应网格只移动节点,网格的拓扑并不改变。
注意:通常自适应网格多用在Dynamic (动态分析),Explicit and Dynamic(显示动态分析), Temp-disp, Explicit 中。
定义模型中某个区域采用自适应网格的设置:other-->Adaptive Mesh Domain 自适应网格的选项控制设置:Other--〉Adaptive Mesh Controls 通常,在每一个step中只能有一个自适应网格区域。
21.2.1 ABAQUS/Standard defines contact between two bodies in terms of two surfaces that may interact; these surfaces are called a “contact pair.”ABAQUS/Standard defines “self-contact,” which is available only in two-dimensional analysis, in terms of a single surface. [if gte vml 1]><![endif][if !vml][endif]Figure 21.2.1–1 Contact and interaction discretization. 从the first surface (the “slave” surface)的节点向the second surface (the “master” surface)做垂线,寻找最近的垂线的垂足,The interaction is then discretized between the point on the master surface and the slave node. Strict master-slave contact 在这种关系下,主面的节点可以穿入从面(副面),但副面不可以穿入主面。
基于Python语言和Abaqus软件的轮胎有限元分析结果自动后处理插件的研发

第 1 期曹金凤等.基于Python语言和Abaqus软件的轮胎有限元分析结果自动后处理插件的研发9基于Python语言和Abaqus软件的轮胎有限元分析结果自动后处理插件的研发曹金凤1,王志文1,高 明2,贾舒安1,孙志伟1,薛茂林1,张泽明1(1.青岛理工大学机械与汽车工程学院,山东青岛266520;2.赛轮集团股份有限公司,山东青岛264200)摘要:基于Abaqus软件的Python语言二次开发功能,采用录制并修改宏文件的方法,开发了一款轮胎有限元仿真分析结果自动后处理插件,用户只需选择要处理的Odb文件,按照需求指定输出数据,单击OK按钮,数据即自动保存到指定的文件夹中。
所开发插件与Abaqus软件无缝连接,用户使用Abaqus软件对轮胎模型仿真分析得到Odb文件后,可直接在Plug-ins菜单下选用插件对数据结果进行整理,实现有限元分析结果的自动后处理,减少了数据提取和整理工作量,缩短了后处理时间,极大地提高了仿真分析效率。
本研究成果可推广应用于其他有限元模型仿真结果的自动后处理。
关键词:轮胎;有限元分析;自动后处理;插件;Python语言;Abaqus软件中图分类号:TQ336.1;O241.82 文章编号:1006-8171(2024)01-0009-06文献标志码:A DOI:10.12135/j.issn.1006-8171.2024.01.0009进入新世纪,国内各大轮胎企业为提高产品质量,降低生产成本,在轮胎设计与研发过程中投入了大量的人力和财力。
随着计算机技术的发展,CAE仿真作为一项成熟的计算机工程辅助技术被越来越多地应用到轮胎设计研发过程中[1]。
轮胎性能的研究也由单纯的试验逐渐转变为试验与仿真技术相结合。
Abaqus软件作为目前国际上最为先进的通用非线性有限元仿真分析软件之一,广泛应用于机械制造、石油化工、航空航天、汽车交通、土木工程以及电子工程等科学研究领域[2-3]。
abaqus 轮胎建模教程

Abaqus 轮胎建模教程简介Abaqus是一种强大的有限元分析软件,常用于模拟复杂的结构力学问题。
在这个教程中,我们将介绍如何使用Abaqus进行轮胎建模和分析。
轮胎是车辆中至关重要的部件之一,建立准确的轮胎模型可以帮助我们更好地理解轮胎的性能和行为。
步骤1:创建轮胎几何模型在Abaqus中,我们可以使用多种方法来创建几何模型。
在这个教程中,我们将使用简单的方法来创建轮胎的二维轮廓。
首先,打开Abaqus软件并创建一个新的模型。
接下来,选择创建几何模型的方法。
我们可以使用Abaqus 提供的绘图工具,也可以导入已经准备好的CAD模型。
在这个教程中,我们将使用绘图工具来创建轮胎几何模型。
创建几何模型的关键是确定轮胎的基本形状,例如总体尺寸、轮胎壁厚、胎纹等。
我们可以根据实际需求和数据来定义这些参数。
在实际应用中,通常需要使用更复杂的方法来获取轮胎几何参数。
完成轮胎几何模型的创建后,我们可以对其进行进一步的编辑和调整,以确保其符合设计要求。
在Abaqus中,我们可以使用各种编辑工具来修改几何模型的各个方面。
步骤2:设置轮胎材料属性完成轮胎几何模型的创建后,我们需要为轮胎指定材料属性。
Abaqus提供了许多预定义的材料模型,我们可以根据实际材料的力学性质来选择合适的材料模型。
在设定材料属性时,我们需要指定材料的弹性模量、泊松比、密度等参数。
这些值通常可以从实验数据或文献中获取。
Abaqus还允许我们定义材料的非线性行为,例如超弹性和塑性行为。
步骤3:创建轮胎网格完成轮胎几何模型和材料属性的设置后,我们需要对轮胎进行网格划分。
网格划分决定了模型在有限元分析中的精度和计算效率。
Abaqus提供了多种网格划分方法,例如等尺度划分和非等尺度划分。
我们可以根据实际需求和计算资源来选择合适的网格划分方法。
在网格划分过程中,我们还可以调整网格的密度和形状,以进一步优化有限元模型的精度和计算效率。
步骤4:定义轮胎加载条件在进行轮胎分析之前,我们需要定义轮胎的加载条件。
ABAQUS帮助文档

初始损伤对应于材料开场退化,当应力或应变满足于定义的初始临界损伤准则,则此时退化开场。
Abaqus 的Damage for traction separation laws 中包括:Quade Damage、Ma*e Damage、Quads Damage、Ma*s Damage、Ma*pe Damage、Ma*ps Damage 六种初始损伤准则,其中前四种用于一般复合材料分层模拟,后两种主要是在扩展有限元法模拟不连续体〔比方crack 问题〕问题时使用。
前四种对应于界面单元的含义如下: Ma*e Damage 最大名义应变准则: Ma*s Damage 最大名义应力准则: Quads Damage 二次名义应变准则: Quade Damage 二次名义应力准则最大主应力和最大主应变没有特定的联系,不同材料适用不同准则就像强度理论有最大应力理论和最大应变理论一样~ABAQUS帮助文档10.7.1 Modeling discontinuities as an enriched feature using the e*tended finite element method 看看里面有没有你想要的Defining damage evolution based on energy dissipated during the damage process根据损伤过程中消耗的能量定义损伤演变You can specify the fracture energy per unit area,, to be dissipated during the damage process directly.您可以指定每单位面积的断裂能量,在损坏过程中直接消散。
Instantaneous failure will occur if is specified as 0.瞬间失效将发生However, this choice is not remended and should be used with care because it causes a sudden drop in the stress at the material point that can lead to dynamic instabilities.但是,不推荐这种选择,应慎重使用,因为它会导致材料点的应力突然下降,从而导致动态不稳定。
ABAQUS在轮胎研发中的应用_2006年会

Vertical Load (N)
静负荷特性曲线
接地面积与负荷关系曲线
佳通轮胎
谢谢!
佳通轮胎
应用实例: 胎肩部应力分布优化
初始设计:
最大应力为 1.4MPa
优化设计:
最大应力为 1.0MPa.
佳通轮胎
应用实例: 轮廓优化
Max.=1.09MPa
Max.=0.78MPa
佳通轮胎
Strain Energy of whole model (J)
佳通轮胎
ห้องสมุดไป่ตู้
有限元模拟的接地压力 分布与实测结果的对比
佳通轮胎
利用轮廓优化来改变接地形状和压力分布特征,以达到不同的设计目 标。例如:
相对优点:舒适 性好,噪音低, 排水性能好 相对缺点:操纵 性欠佳,易磨耗
相对优点:操纵 性好,磨耗性能 好 相对缺点:舒适 性、噪音、排水 性能欠佳
兼备两者优 点,综合性 能最佳
LLM M M M SSLSSSSSSLLLLLSM M M SSSM LLLLM M M M LSLLLSSSSSM SSSSLLLLSSSLM M LM M SSSSLLM M M M M M SSSSSSSLLLLSSSSSSLM M M M M M M LSSLSSSSM LLLSSSSM M M LM M SSM M M M M M M LSSSSM LLLLLM M LSSSSSSM LLLSSSSSSSLLLLLLM SSLSSSSM M M M M M
Experience Design Optimal Design
40 30 20 10 0 0.0
优化轮廓
0.2
0.4
0.6
0.8
Inflated Pressure (MPa)
ABAQUS帮助文档轮胎磨损例子翻译_New

ABAQUS帮助文档轮胎磨损例子翻译_NewABAQUS帮助文档轮胎磨损例子翻译外胎是由胎体、缓冲层(或称带束层)、胎面、胎侧和胎圈组成1、Bead:胎唇部;2、sidewall:胎侧;3、tread:胎面;4belt:缓冲层;5、carcass:胎体帘布层。
3.1.8 Tread wear simulation using adaptive meshing in Abaqus/Standard 3.1.8使用自适应网格在Abaqus/Standard中进行轮胎磨损仿真分析软件:Abaqus/Standard这个例子在Abaqus/Standard中使用自适应网格技术对稳态滚动的轮胎进行建模。
这次分析使用类似“Steady-state rolling analysis of a tire”Section 3.1.2来建立稳态滚动轮胎的接地印迹和状态。
接着,进行稳态传输分析来计算和推测持续分析步,在稳态过程中产生一个近似瞬态磨损解。
问题描述和建模轮胎描述和有限元建模和“Import of asteady-state rolling tire,”Section 3.1.6一样,但是有一些不一样,在这里需要指出。
由于这次分析的中心是轮胎磨损,所以胎面建模需要更加精细。
另外台面使用线性弹性材料模型来避免超弹性材料在网格自适应过程中不收敛。
图1所示的是轴对称175SR14轮胎的一半模型。
橡胶层用CGAX4和 CGAX3单元建模。
加强层使用带有rebar层的SFMGAX1单元模拟。
橡胶层和加强层之间潜入单元约束。
橡胶层的弹性模量为6Mpa,泊松比为0.49。
剩下的轮胎部分用超弹性材料模型模拟。
多应变能使用系数C10=10^6,C01=0和D1=2*10^8。
用来模拟骨架纤维的刚性层和径向成0°,弹性模量为9.87Gpa。
压缩系数设置成受拉系数的百分之一。
名义应力应变数据用马洛超弹性模型定义材料本构关系。
Abaqus教程之cohesive单元损伤模拟可修改文字

位移U2-时间曲线
支反力RF2-时间曲线
分析载荷位移曲线(基于能量准则且施加位移刚好等于cohesive完全损伤时的张开距离)
支反力RF2-位移U2曲线
Stress2-位移U2曲线
从Stress2与位移U2中发现,当达到100MPa时开始损伤,cohesive张开达到1e-5mm时, cohesive单元完全失效,此时的SDEG=1,此时的cohesive不能再承受力将被删除掉, 这个与我们开始的预期是完全一致的。
abaqus中 cohesive模型 的建立及设置
下面我们将给出abaqus不同模块下的实例设置步骤,方便快速理解和学习 Part模块:
Property模块:
Assembly模块:
Step模块:
Load模块:
Mesh模块:
下面结合实例全 面解读cohesive
分析载荷位移曲线(基于能量准则且施加位移刚好等于cohesive完全损伤时的张开距离)
对模型进行网格划分,我们既然是验证,
那么我们就要采用单个cohesive单元进行 分析,因为我们只需要对平板模型进行
切分,然后在中间那层插入cohesive单元 即可,每个边都布置一个种子,这样上下
两层实体单元就分别划分成了一个实体
单元,然后在中间插入一层0厚度的 cohesive单元(采用0厚度cohesive单元 更容易观察cohesive张开位移的变化),
Cohesive element理论
abaqus6.14在线帮助文档 http://ivt-abaqusdoc.ivt.ntnu.no:2080/v6.14/books/usb/default.htm
cohesive element是基于损伤力学理论,自己去帮助文档补充相关基础知识
基于ABAQUS的多工况下轮胎接地特性分析
基于ABAQUS的多工况下轮胎接地特性分析作者:全振强李波王文豪韩霄贝绍轶张兰春顾甜莉茅海剑杭玉迪来源:《江苏理工学院学报》2022年第02期摘要:研究了多工况下轮胎的接地特性。
首先,通过ABAQUS软件搭建了205/55R16子午线轮胎的有限元模型;然后,设计、搭建了有限元轮胎模型验证平台,通过对比二者的径向刚度曲线验证了模型的有效性;最后,通过设置多种仿真工况,研究了不同负载、充气压力、驱动状态以及侧偏角度下轮胎的接地特性。
结果表明:负载越大,轮胎接地面积和接触面应力越大,且应力最大值位于中间纵向沟槽内;胎压越高,轮胎接地面积越小,接触面应力越大,应力最大值逐渐转移至接触中心点;当轮胎由静置转为滚动,接触面积和接触应力均减小,应力最大值位于中间纵向沟槽内,且车速与应力大小无关;加速或制动都会使得接触面应力最大值移至接地印记末端,且应力最大值与角速度呈正相关;接触面应力最大值位置与轮胎侧偏方向相反,与纵向车速方向相同,且接触面应力最大值与侧偏角呈正相关,但接触面横向应力增长会首先趋于饱和。
关键词:子午线轮胎;有限元;多工况;接地特性中图分类号:U463.361文献标识码:A文章编号:2095-7394(2022)02-0063-16轮胎是汽车与地面接触的唯一部件,其性能对汽车行驶安全性、乘坐舒适性和燃油经济性等都有很大的影响[1]。
车轮不仅承载了车身的重量,而且通过轮胎-地面接触面的相互作用,实现了车辆的导向、加速和制动等性能[2];因此,开展轮胎在不同工况下的接地特性研究至关重要。
轮胎的接地特性研究是轮胎领域研究的基石,国内外学者已经就此开展了多项研究。
首先,轮胎接地特性研究可以为轮胎制造提供更好的设计、优化思路。
张伟伟等人[3]通过研究全钢轮胎的接地印痕,认为不同的胎冠弧设计方案对接地印痕的形状影响很大,此结论可以用于轮胎设计初期的结构优化,以提高轮胎的性能。
王琳等人[4]研究了轮胎花纹在不同工况下的接地特性,发现轮胎在侧偏、启动等复杂工况下易发生偏磨,这一结论有助于优化轮胎的花纹结构,以应对复杂工况下轮胎的偏磨现象。
3.1.8在Abaqus-tandard中使用自适应网格的胎面磨损模拟

3.1.8 Tread wear simulation using adaptive meshing in Abaqus/Standard3.1.8在Abaqus / Standard中使用自适应网格的胎面磨损模拟Product: Abaqus/StandardThis example illustrates the use of adaptive meshing in Abaqus/Standard as part of a technique to model treadwear in a steady rolling tire. The analysis follows closely the techniques used in “Steady-state rolling analysis of a tire,” Section 3.1.2, to establish first the footprint and then the state of the steady rolling tire. These steps are then followed by a steady-state transport step in which a wear rate is calculated and extrapolated over the duration ofthe step, providing an approximate consideration of the transient process of wear in this steady-state procedure.本示例说明了在Abaqus / Standard中使用自适应网格划分作为用于对稳定滚动轮胎中的胎面磨损进行建模的技术的一部分。
该分析紧接着使用在“轮胎的稳态滚动分析”第3.1.2节中使用的技术,以首先建立轮胎的足迹,然后建立稳定滚动轮胎的状态。
基于Abaqus的轮-轴强度分析

基于Abaqus的轮-轴强度分析摘要:基于Abaqus软件,在考虑材料非线性和几何非线性的情况下,进行轮-轴强度分析。
对应力集中区域进行加强及结构优化,提高轮-轴强度。
关键词:Abaqus,轮-轴,非线性Abstract: Based on Abaqus,consider nonlinear about material and geometry,analysis strength of wheel-shaft. Strengthen the areas of stress concentration and optimizing structure, improving wheel - shaft strength.Key words: Abaqus,wheel-shaft,nonlinear1引言轮-轴用于支撑整台设备,同时兼为设备提供动力来源,因此对轮-轴的强度有一定要求。
轮-轴的强度分析是模拟设备在静止及运动这2种工况下轮-轴抵抗破坏的能力。
以验证设计的正确性。
2分析对象分析模型为驱动车轮+驱动轴+平键。
整台设备靠4组车轮(驱动车轮,从动车轮各2组)支撑,设备(图1所示)总重160吨,设备重心偏于驱动车轮组侧,承受主要支撑作用,因此,需要对驱动车轮组进行重点分析,确保能够满足支撑设备的要求。
各轮组受力分布(图2所示)。
当设备悬臂处于水平位置取料时,每个驱动车轮组承受400KN最大压力(合40吨)。
由此需运用Abaqus软件模拟这一过程。
3分析方法3.1分析思路运用Abaqus/CAE或者其它CAD软件建立需要作分析的轮-轴三维模型,然后用Abaqus/Standard 和Abaqus/Explicit对需要作分析的2种工况进行分析。
当提交分析时,会发现个人电脑根本无法承受如此巨大规模的计算。
除非用工作图1图2站分析,否则不予考虑此种方案。
这就需要设计人员换一种思路来考虑这个问题。
本次计算采取“各个击破”的方案来分析。
基于Abaqus软件的轮胎有限元模型建立及仿真分析

124
橡 胶 工 业
2019年第66卷
3. 2 胎肩应力分布 从胎肩应力分布云图上可以直观地分析
E-mail:754318973@qq. com
的制高点。国内轮胎企业以及高校和科研院所应 加大相关技术研发力度。
本 工 作 基 于Abaqus软 件 建 立 轮 胎 有 限 元 模 型,对305/75R24. 5全钢载重子午线轮胎的外缘尺 寸、胎 肩 应 力、带 束 层 应 力 分 布、胎 圈 与 轮 辋 接 触 应力分布进行预测分析,以期确保305/75R24. 5全 钢载重子午线轮胎设计的可靠性。
基 金 项 目 :国 家 重 点 研 发 计 划 项 目(2 0 1 6 Y F C 0 3 0 2 2 0 4);国 家 重点研发计划项目(2016YFC0302201);国家自然科学基金资助项 目(41306103)
作者简介:宿晓峰(1989—),男,山东平度人,青岛科技大学硕 士研究生,主要从事机械工程方面的研究。
至 于 模 拟 充 气 过 程 中 气 压 的 加 载,为 了 保 证 计 算 过 程 的 收 敛,本 研 究 设 置 初 始 加 载 气 压 为 0. 01 kPa,求解初始增量步设置为0. 01,然后逐渐 加载至标准充气压力850 kPa,气压方向与轮胎内 壁应始终垂直,Basic选项卡打开nlgeom。由于充 气 过 程 中 轮 胎 要 发 生 较 大 的 变 形,因 此 在 模 拟 过 程中,迭代方法选用Full Newton-Raphason法,分 析选项选用大变形几何非线性。 2. 3 静负荷状态仿真模拟过程
305/75R24. 5载重子午线轮胎的静负荷状态 仿真建模主要是在充气状态仿真模拟的基础上加 入静负荷条件进行的。在完成305/75R24. 5载重 子 午 线 轮 胎 的 充 气 状 态 模 拟 后,将 充 气 状 态 的 仿 真模型通过关键字转换成305/75R24. 5载重子午 线 轮 胎 的 三 维 轴 对 称 模 型,同 时 将 充 气 状 态 的 仿 真 模 拟 结 果 映 射 到 该 三 维 轴 对 称 模 型 中,最 后 引 入 路 面(在 此 可 以 把 路 面 视 为 刚 形 体,不 发 生 形 变)进行静负荷状态的模拟。
基于ABAQUS的子午线轮胎的非线性有限元分析

基于ABAQUS的子午线轮胎的非线性有限元分析一、本文概述随着汽车工业和交通运输业的快速发展,轮胎作为汽车的关键组成部分,其性能与安全性对车辆行驶的稳定性和安全性具有重要影响。
子午线轮胎因其优异的性能,如耐磨、抗爆、抗湿滑等,在现代汽车工业中得到了广泛应用。
然而,子午线轮胎的设计和优化是一个复杂的问题,涉及材料非线性、几何非线性、接触非线性等多种因素。
因此,对子午线轮胎进行精确的非线性有限元分析显得尤为重要。
本文旨在利用ABAQUS这一先进的有限元分析软件,对子午线轮胎进行非线性有限元分析。
我们将介绍ABAQUS软件在轮胎分析中的应用及其优势。
然后,我们将详细阐述轮胎的非线性特性,包括材料非线性、几何非线性和接触非线性等。
接着,我们将介绍如何建立子午线轮胎的有限元模型,包括轮胎的几何建模、材料定义、边界条件设置和接触定义等。
在此基础上,我们将通过具体的案例分析,展示如何利用ABAQUS对子午线轮胎进行非线性有限元分析,并探讨分析结果对轮胎设计和优化的指导意义。
本文的研究不仅有助于深入理解子午线轮胎的非线性特性,为轮胎的设计和优化提供理论支持,同时也为其他类似复杂结构的非线性分析提供了参考和借鉴。
二、ABAQUS软件介绍ABAQUS是一款功能强大的工程模拟软件,广泛应用于各个工程领域的非线性有限元分析。
它以其高效、稳定、精确的特点,成为了工业界和学术界进行复杂结构分析的首选工具。
ABAQUS提供了丰富的材料模型库,支持多种材料类型,包括但不限于金属、塑料、橡胶、复合材料等。
这使得它特别适用于轮胎这种由多种材料组成的复杂结构的分析。
在ABAQUS中,用户可以根据实际需求定义材料属性、设置边界条件、划分网格、选择求解器以及后处理结果等。
特别是在处理轮胎这类橡胶制品的非线性行为时,ABAQUS提供了多种本构模型,如Mooney-Rivlin模型、Yeoh模型等,以准确模拟橡胶材料的应力-应变关系。
ABAQUS还提供了接触算法,用于模拟轮胎与地面之间的摩擦和接触行为。
Abaqus在轮胎中应用的10大算例

第三讲. 模拟接触 .................................................................................................................................13
接触分析中的一般考虑 ....................................................................................................................13 接触面的定义 .................................................................................................................................... 13 有限滑动中面需要考虑的一些问题 ................................................................................................13
abaqus帮助文档_shear damage

Shear damageThe Shear damage initiation criterion is a model for predicting the onset of damage due to shear band localization. The model assumes that the equivalent plastic strain at the onset of damage is a function of the shear stress ratio and strain rate. The shear criterion can be used in conjunction with the Mises, Johnson-Cook, Hill, and Drucker-Prager plasticity models, including equation of state.1. From the menu bar in the Edit Material dialog box, select MechanicalDamage for Ductile Metals Shear Damage.(For information on displaying the Edit Material dialog box,see �Creating or editing a material,�Section 12.7.1.)2. Enter the material parameter, .3. To define material damage data that depend on temperature, toggleon Use temperature-dependent data.A column labeled Temp appears in the Data table.4. To define behavior data that depend on field variables, click the arrowsto the right of the Number of field variables field to increase ordecrease the number of field variables.Field variable columns appear in the Data table.5. Enter damage parameters in the Data table:Fracture StrainEquivalent fracture strain at damage initiation.Shear Stress RatioThe shear stress ratio is defined as , where q is the Mises equivalent stress, p is the pressure stress, and is the maximum shear stress.Strain RateThe equivalent plastic strain rate, .TempTemperature, .Field nPredefined field variables.You may need to expand the dialog box to see all the columns inthe Data table. For detailed information on how to enter data,see �Entering tabular data,�Section 3.2.7.6. Select Suboptions Damage Evolution to define the materialdegradation that takes place once damage begins.For more information, see “Damage evolution.”7. Click OK to exit the material editor.。
基于ABAQUS 的子午线轮胎有限元分析

基于 ABAQUS 的子午线轮胎有限元分析
冯聪利 1 解小松 2 1. 陕西能源职业技术学院 机电与信息工程学院 陕西省咸阳市 712000 2. 西安市城市照明管理处 陕西省西安市 710086
摘 要:轮胎是橡胶工业生产中重要的产品之一,汽车在行驶过程中,与地面接触的唯一的执行部件就是轮胎。轮 胎的各项技术参数对汽车的使用性能有着重要影响与决定作用。随着当代社会车辆对轮胎的安全性能和使 用寿命要求越来越高,因此研究轮胎对汽车燃油的动力性、制动性、操纵的稳定性、经济性等各项指标很 有意义。本文以 ABAQUS 软件为载体,以 12.00R20 18PR 载重子午线轮胎为研究对象,模拟轮胎在静载 状态下的应变量和下沉量,为后续研究轮胎在不同速度、载荷、轮胎气压及地面摩擦系数的工况下应力场 和温度场的变化规律奠定一定理论基础。
关键词:载重子午线轮胎;有限元分析;静载状态
1 引言
轮胎作为汽车的重要支撑部件,影响着 汽车的舒适性和安全性,随着对高速性和越 野性要求的不断增强,对轮胎的要求也更高 [1]。 子午线轮胎的带束层、帘布层是主要受力部 件,承受气压、载荷并且缓冲轮胎受到的外 部冲击 [2]。轮胎在使用过程中力学性能会逐渐 降低,一直以来,国内外科研机构及轮胎生 产制造厂家都把轮胎失效机理的研究与如何 降低成本提高轮胎的使用寿命作为重点问题 进行不断的研究探讨 [3]。文献 [4] 主要是对子 午线轮胎胎面磨损性能进行有限元分析 , 以 及在 ABS 制动状态下对胎面花纹磨损进行研 究。文献 [5] 研究了不同工况参数对轮胎磨损 性能的影响,并对轮胎的帘线参数和胶料性 能进行优化,得出了轮胎在不同工况下的磨 损特征。文献 [6] 考虑轮胎材料、几何及其与 地面接触的非线性 , 借助 ABAQUS 软件建立 了子午线轮胎滚动瞬态碰撞的三维有限元模 型 , 并与轮胎径向刚度试验结果对比验证了 模型的有效性。因此利用有限元分析软件解 决轮胎问题的可靠性和准确性受到人们的广 泛关注,同时也为开发、设计制造出更加安全、 稳定、舒适的轮胎提供了有力的工具和重要 的参数。
abaqus在轮胎中应用的10大算例

abaqus在轮胎中应用的10大算例轮胎是汽车中非常重要的部件之一,它直接影响着车辆的操控性能、舒适性和安全性。
为了更好地研究轮胎的性能和行为,许多工程师和研究人员利用有限元分析软件Abaqus来进行轮胎模拟。
在这篇文章中,我们将介绍10个在轮胎中应用Abaqus的算例,从而深入了解轮胎的性能和行为。
1. 轮胎接地模型在轮胎模拟中,准确地描述轮胎与路面的接触非常重要。
通过Abaqus的接触算法,可以建立轮胎与路面之间的接触模型,研究轮胎在不同路面上的接地性能。
2. 轮胎结构分析轮胎的结构对其性能有着重要影响。
利用Abaqus的弹性力学分析功能,可以对轮胎的内部结构进行分析,了解不同材料和结构参数对轮胎性能的影响。
3. 轮胎热分析在高速行驶或制动时,轮胎会产生大量的热量。
利用Abaqus的热分析功能,可以模拟轮胎在不同工况下的温度分布,从而评估轮胎的热耐久性和性能变化。
4. 轮胎静态载荷分析轮胎在停车和静止状态下也会受到一定载荷的作用。
通过Abaqus的静态分析功能,可以模拟轮胎在不同载荷下的形变和应力分布,为轮胎设计和使用提供参考。
5. 轮胎动态载荷分析在行驶过程中,轮胎会受到复杂的动态载荷作用,如转弯、加速和制动等。
利用Abaqus的动态分析功能,可以模拟轮胎在不同工况下的动态响应和应力变化,为轮胎的操控性能评估提供依据。
6. 轮胎磨耗分析轮胎的磨耗会直接影响其使用寿命和性能。
通过Abaqus的摩擦接触分析功能,可以模拟轮胎与路面之间的摩擦磨耗过程,研究不同工况下轮胎的磨耗规律和寿命预测。
7. 轮胎破坏分析轮胎在使用过程中可能会出现破裂、爆胎等失效情况。
利用Abaqus的破坏力学分析功能,可以模拟轮胎在不同载荷下的破坏行为,评估轮胎的安全性和可靠性。
8. 轮胎振动分析轮胎在行驶过程中会产生振动,影响车辆的舒适性和操控性。
通过Abaqus的动态分析功能,可以模拟轮胎的振动响应,了解不同工况下轮胎的振动特性和减振措施的效果。
ABAQUS帮助文档轮胎磨损例子翻译
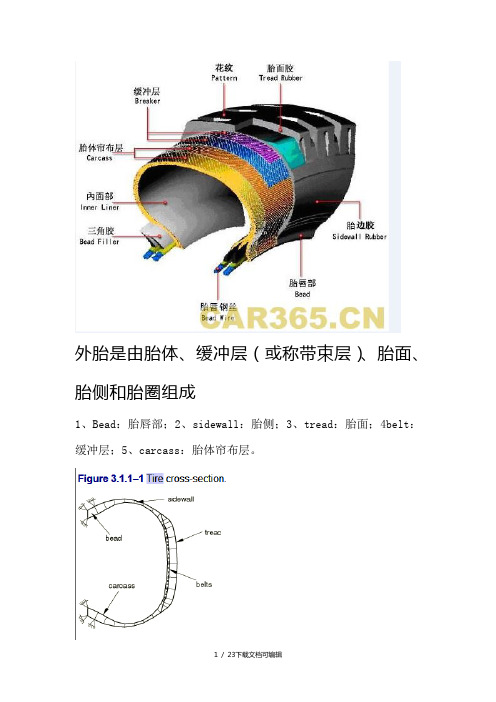
外胎是由胎体、缓冲层(或称带束层)、胎面、胎侧和胎圈组成1、Bead:胎唇部;2、sidewall:胎侧;3、tread:胎面;4belt:缓冲层;5、carcass:胎体帘布层。
3.1.8 Tread wear simulation using adaptive meshing in Abaqus/Standard3.1.8使用自适应网格在Abaqus/Standard中进行轮胎磨损仿真分析软件:Abaqus/Standard这个例子在Abaqus/Standard中使用自适应网格技术对稳态滚动的轮胎进行建模。
这次分析使用类似“Steady-state rolling analysis of a tire”Section 3.1.2来建立稳态滚动轮胎的接地印迹和状态。
接着,进行稳态传输分析来计算和推测持续分析步,在稳态过程中产生一个近似瞬态磨损解。
问题描述和建模轮胎描述和有限元建模和“Import of a steady-state rolling tire,”Section 3.1.6一样,但是有一些不一样,在这里需要指出。
由于这次分析的中心是轮胎磨损,所以胎面建模需要更加精细。
另外台面使用线性弹性材料模型来避免超弹性材料在网格自适应过程中不收敛。
图1所示的是轴对称175SR14轮胎的一半模型。
橡胶层用CGAX4和CGAX3单元建模。
加强层使用带有rebar层的SFMGAX1单元模拟。
橡胶层和加强层之间潜入单元约束。
橡胶层的弹性模量为6Mpa,泊松比为0.49。
剩下的轮胎部分用超弹性材料模型模拟。
多应变能使用系数C10=10^6,C01=0和D1=2*10^8。
用来模拟骨架纤维的刚性层和径向成0°,弹性模量为9.87Gpa。
压缩系数设置成受拉系数的百分之一。
名义应力应变数据用马洛超弹性模型定义材料本构关系。
Belt fibers材料的拉伸弹性模量为172.2Gpa。
压缩系数设置成拉伸系数的的百分之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
外胎是由胎体、缓冲层(或称带束层)、胎面、胎侧和胎圈组成1、Bead:胎唇部;2、sidewall:胎侧;3、tread:胎面;4belt:缓冲层;5、carcass:胎体帘布层。
3.1.8 Tread wear simulation using adaptive meshing in Abaqus/Standard3.1.8使用自适应网格在Abaqus/Standard中进行轮胎磨损仿真分析软件:Abaqus/Standard这个例子在Abaqus/Standard中使用自适应网格技术对稳态滚动的轮胎进行建模。
这次分析使用类似“Steady-state rolling analysis of a tire”Section 3.1.2来建立稳态滚动轮胎的接地印迹和状态。
接着,进行稳态传输分析来计算和推测持续分析步,在稳态过程中产生一个近似瞬态磨损解。
问题描述和建模轮胎描述和有限元建模和“Import of a steady-state rolling tire,”Section 3.1.6一样,但是有一些不一样,在这里需要指出。
由于这次分析的中心是轮胎磨损,所以胎面建模需要更加精细。
另外台面使用线性弹性材料模型来避免超弹性材料在网格自适应过程中不收敛。
图1所示的是轴对称175SR14轮胎的一半模型。
橡胶层用CGAX4和CGAX3单元建模。
加强层使用带有rebar层的SFMGAX1单元模拟。
橡胶层和加强层之间潜入单元约束。
橡胶层的弹性模量为6Mpa,泊松比为0.49。
剩下的轮胎部分用超弹性材料模型模拟。
多应变能使用系数C10=10^6,C01=0和D1=2*10^8。
用来模拟骨架纤维的刚性层和径向成0°,弹性模量为9.87Gpa。
压缩系数设置成受拉系数的百分之一。
名义应力应变数据用马洛超弹性模型定义材料本构关系。
Belt fibers材料的拉伸弹性模量为172.2Gpa。
压缩系数设置成拉伸系数的的百分之一。
Belt的纤维走向在轴向±20°内。
旋转前面的轴对称一半模型可得到局部三位模型,如图2所示。
我们关注轮胎印迹区域的网格。
将局部模型镜像后可得到完整的三维模型。
自适应网格在轮胎磨损计算中的局限性在这个例子中使用自适应网格必须严格遵守以下条件:1、圆柱网格不支持自适应网格并且在本例子也没有使用2、由于梯度状态变量的变形错误严重,自适应网格使用超弹性材料时表现很差。
因此胎面用弹性材料定义3、在自适应网格的范围内不能用包含刚性层的嵌入网格。
4、自适应网格通过网格几何特征来决定自适应网格在自由面光滑的方向,网格几何的特征通常不容易和描述的磨损方向一致。
因此,下面将讨论到,通常你需要做额外的工作来明确地描述磨损的方向。
加载分析分为5个阶段,用轴对称模型开始,以使用symmetric model generation生成的完整三维模型结束。
前4阶段和“Steady-state rolling analysis of a tire,” Section 3.1.2和类似。
1、对称充气:轮胎内部施加200kpa的压力,中间平面使用对称条件。
2、一半三维接地印迹分析:轴对称模型沿着对称轴旋转。
3、完整的三维模型接地印迹分析:一半三维模型镜像生成完整的三维模型4、稳态滚动:在稳定速度32km/h车速进行完整模型分析,这是轮胎的滚动速度为25rad/s。
这些条件符合制动工况,本次分析考虑惯性和迟滞作用。
5、胎面磨损分析:胎面磨损分析在最后一步进行,本次分析轮胎速度保持为一定值,考虑轮胎表面的磨损,使用损耗的摩擦能来计算磨损。
惯性和迟滞同样是本次分析中的考虑因素。
本次分析在车速32km/h的情况下,持续进行3.6*10^6秒,轮胎前进32000公里。
最后的分析为磨损分析,来预测磨损或者面消融,根据稳态侧倾轮胎得到评估。
我们关注由磨损评估结果得到的轮胎外形的改变;因此我们需要介绍在稳态过程中允许瞬态效果的建模假设。
基本的假设是用当前实时持续的滚动角速度来解释稳态前进分析步。
我们认为在任何时候轮胎滚动时轮胎的磨损造成的轮胎外形变化仅仅有很小的效果。
因此在整个分析步的每一步稳态的结果都是合适的。
有了这些假设,我们就能同时考虑两个不同时间范围的效果:短的轮胎转动时间范围和长的轮胎寿命时间范围。
磨损模型为了举例说明磨损的过程,假设磨损率是局部接触压力和滑移率的线性函数,进行一个简单的磨损例子。
尽管我们能计算这些工程量,由于在稳态移动状态下使用欧拉公式,他们必须应用于胎面流线来模拟轮胎周长磨损。
磨损率计算磨损模型如下:q是体积损失量或者磨损量;k是无量纲磨损系数;H是材料硬度;P是接触压力;A是接触面积;Y是接触滑移率。
在这里我们可以认为用PAy描述摩擦耗损率。
对于轮胎橡胶,我们假设磨损系数k=10^-3,材料硬度H=2GPa。
下面开发的目标是材料的磨损表达式能应用于磨损分析的节点上。
首先,考虑用一条带状物围绕着轮胎,带状物的中心用包含胎面花纹的有序节点来定义。
这条中心线是以和每个节点联系的辅助面的任意一边作为边界。
这样的带状物包含轮胎与路面接触的所有面。
我们认为发生在带状物上的磨损是均匀的;因此我们用下式表达整个带状物的磨损率,其中t是时间,x是当前配置位置。
因为我们使用欧拉稳态传输处理,现在表达式可以表示为只依赖于时间的方程,其中S是沿着流线的位置,T(s)是带状物在S位置的宽度。
我们也可以见表达式q写成局部材料衰减率的函数,在整个带状物的离散化方程的处理的结果相等,得到其中h是节点的消融速度,A是节点的接触区域。
这个方程表明沿着带状物h是不均匀的,推导出的结论是带状物进入和离开接地印迹的宽度是不一样的。
然而,因为我们为了维持一个合理的轮胎磨损后的结构,我们假定节点消融的速度是均匀的。
设个假定使得如下表达式成立:再次假定沿着带状物宽度方向的变化可以忽略,既Ti=T,同时认为节点接触区域,则表达式可以简化为没有接地面积的方程:磨损过程实现用曲面消融速度的磨损量方程,现在我们可以在稳态移动分析中应用磨损分析了。
用户子程序UMESHMOTION用来指定轮胎外表面节点的磨损速度向量。
UMESHMOTION用来定义自适应网格约束速度和用来连接自适应网格,每个收敛的增量步之后使用网格光滑技术。
通过子程序指定胎面节点的消融速度,自适应网格技术用来调整橡胶层内部的节点来保持好的网格网格形状。
为了积累沿着每个胎面花纹的磨损量,必须在子程序中记录沿着花纹的节点编号。
使用一个公共模块变量记录,公共模块记录属于集合NADAPT(图4)的节点和那些在整个模型横截面(0°)的参照点。
普通模块变量同时也包括将模型旋转和镜像后节点的编号方式,和参考截面一起,完整地描述了轮胎表面的节点编号。
如下的变量需要在外部公共模块中定义:1、nStreamlines:轮胎磨损分析中整个参考截面的节点数。
2、nGenElem:在模型中沿着带状物体网格划分的数目。
3、nRevOffset:通过*SYMMETRIC MODEL GENERATION, REVOLVE指定节点偏移。
4、nReflOffset:通过*SYMMETRIC MODEL GENERATION, REFLECT指定节点偏移。
(如果模型不用镜像,这个参数设置为0)。
5、jslnodes:在参考截面下所有可能发生磨损的节点的节点信息数组。
这个数组的大小为(2,nStreamlines)。
每个流线的第一个分量是“根节点”的节点编号(节点a在下面讨论),根节点是指在参考截面上细化流线部分的节点。
第二个分量是指提供磨损方向的节点(节点b在下面讨论)。
第二个分量仅仅在胎面的拐角处需要,将他设置成等于在参考截面的节点编号来定义磨损的方向。
对于不在胎面拐角处的节点,第二个分量设置等于0。
那些远离胎面拐角的节点将沿着局部坐标系的3方向进行磨损。
磨损表达式的变量通过函数GETVRN 和 GETVRMAVGATNODE从分析数据库中获得。
P从变量CSTRESS中获得;y从变量CDISP中获得;由带状物的节点坐标决定,从变量COORD中获得。
磨损运动的方向磨损速率h是网格约束矢量变量ULOCAL的分量。
这个变量通过在局部坐标系ALOCAL中定义的默认网格光滑运动传递到用户子程序中,这个局部坐标系测量出当前节点在曲面的法向。
3的方向根据在节点附近网格表面法向的平均值定义为外法向的方向。
在绝大部分情况下,这个法向方向对于描述和这个方向相反的消融和节点衰减的磨损结果是足够的。
然而,在胎面拐角的区域,这个平均的法向方向不能准确的描述磨损的方向。
这种情况下的法向应该像Figure 3.1.8–5所示,它计算如下:假设a是胎面拐角的节点。
就有可能辨认出在胎面边上的节点b。
在这种情况下,磨损的方向就是矢量ab。
因为知道节点a和节点b的坐标,磨损方向就能通过整体坐标系计算得到,也就能转化为局部坐标系(ALOCAL)的方向。
结果和讨论轮胎模型仿真分析持续进行 3.6×106s或者1000小时,等价于在32km/h下行驶32000公里。
下图表示的是轮胎磨损效果的轮廓结果。
下面第二个图片表示的是新轮胎和磨损后轮胎接地印迹分布的情况。
3.1.2 Steady-state rolling analysis of a tire3.1.2 轮胎稳态转动分析产品:Abaqus/Standard本例子在abaqus中使用*STEADY STATE TRANSPORT来建立转动轮胎和刚性平面之间的稳定动态接触模型。
稳态运动分析使用局部参考坐标系,在这个局部参考坐标系中使用欧拉方法来描述刚性体的旋转运动,用拉格朗方法描述变形。
这个运动学描述将稳态的移动接触问题转化为一个纯粹的依赖于空间的仿真。
因此,仅仅需要在接触的区域建立精确的网格——稳态运动通过网格传输材料。
在*STEADY STATE TRANSPORT分析中考虑的因素有:摩擦、惯性和累积效果。
本次分析的目的是获得在地面速度10.0km/h(2.7778m/s)时,相对于平面刚性面不用的侧偏角时轮胎175SR14自由转动的平衡解决方案。
侧偏角是指轮胎前进方向和轮胎中心平面的夹角。
在侧偏角为0°时,轮胎直线行驶。
为了对比测试,我们也进行轮胎在直径在 1.5m 的刚性圆柱上旋转的分析。
圆柱以3.7 rad/s的速度旋转,也就是圆柱表面的瞬时速度为10km/h(2.7778m/s)。
另外一个工况是在轮胎自由转动的情况下检测由轮胎外倾角引起地外倾推力。
本工况允许我们计算外倾推力刚度。
施加到轮胎中心轴的扭矩为0时的平衡状态被称为自由转动状态。
轮胎中心轴的扭矩不为0是的平衡状态被称为驱动或者制动状态。
制动状态:轮胎的角速度足够小以至于轮胎和路面之间的所有或者部分的接触点发生滑动,同时作用在轮胎上的总扭矩与轮胎自由转动的角速度方向相反。
