2021年八年级数学暑假专题辅导 数据的收集与处理
初中数学《数据的收集整理与描述》单元教学设计以及思维导图

初中数学《数据的收集整理与描述》单元教学设计以及思维导图一. 教材分析《数据的收集整理与描述》是初中数学的重要内容之一,主要让学生了解数据的收集、整理、描述和分析的方法,培养学生运用数学知识解决实际问题的能力。
本单元的教学内容主要包括数据的收集方法、数据的整理方法、数据的描述方法和数据分析方法。
二. 学情分析初中学生已经具备了一定的数据处理能力,但对数据的收集、整理、描述和分析方法的掌握程度不同。
因此,在教学过程中,要针对学生的实际情况,设计不同难度的教学活动,以满足不同学生的学习需求。
三. 教学目标1.让学生掌握数据收集、整理、描述和分析的基本方法。
2.培养学生运用数学知识解决实际问题的能力。
3.培养学生合作学习、积极参与的精神。
四. 教学重难点1.教学重点:数据的收集方法、数据的整理方法、数据的描述方法和数据分析方法。
2.教学难点:数据的收集方法在实际问题中的应用,数据分析方法的灵活运用。
五. 教学方法1.情境教学法:通过生活实例,引导学生了解数据的收集、整理、描述和分析在实际生活中的应用。
2.小组合作学习:鼓励学生分组讨论,共同解决问题,培养学生的合作精神和团队意识。
3.实践操作法:让学生动手操作,实际操作数据的收集、整理、描述和分析过程,提高学生的动手能力。
六. 教学准备1.教学课件:制作课件,展示数据的收集、整理、描述和分析的过程。
2.教学素材:准备一些实际问题,作为教学案例。
3.学生活动材料:为学生提供一些实践操作的材料,如调查问卷、数据记录表等。
七. 教学过程1.导入(5分钟)利用课件展示一些生活中的数据,如彩票中奖号码、天气情况等,引导学生了解数据在日常生活中无处不在,激发学生的学习兴趣。
2.呈现(10分钟)呈现一些实际问题,如学校七年级学生的身高分布情况,让学生尝试用图表的形式展示数据,引导学生了解数据的收集、整理和描述的重要性。
3.操练(10分钟)学生分组讨论,选择一个实际问题,进行数据的收集、整理和描述。
(八年级数学教案)数据的收集与处理

数据的收集与处理
八年级数学教案
1 每周干家务活的时间
2 数据的收集
3 频数与频率
4 数据的波动
●第五章数据的收集与处理
5.1 每周干家务活的时间
●一、教学目标:
1、经历调查、收集数据的过程,感受抽样的必要性。
2、了解普查、抽样调查、总体、个体、样本等概念,了解普查和抽样调查的应用,并选择合适的调查方法,解决有关现实问题。
3、进一步发展统计意识,培养学生热爱劳动、勇于实践的优良品质。
●二、教学过程:
1、活动与探究
同学们,你们每天在家都帮父母做家务活吗?主要做些什么呢?每周大约多长时间呢?
你们每周干家务活时间的平均数、中位数、众数是什么?
2、介绍新知识
(1)普查:为了一定的目的而对考察对象进行的全面调查。
(2)总体:所考察对象的全体。
八年级数学数据的收集与处理(PPT)5-3

膜,用纸浆经过化学处理或用塑料制成,可染成各种颜色,用于包装或装饰。旧称赛璐玢。 【玻璃砖】?名①指较厚的玻璃。②用玻璃制成的砖状建筑材料,
多是空心的。坚固耐磨,能透光,隔音、隔热; /ask/ 三农问答;性能好。 【砵】①地名用字:铜~(在福建)|麻地~(在内蒙
名①糕点。②馒头或其他面食,也指用杂粮面制成的块状食物:棒子面儿~|贴~(贴饼子)。 【剥】义同“剥”(),专用于合成词或成语,如剥夺,生
吞活剥。 【剥夺】动①用强制的方法夺去:~劳动成果。②依照法律取消:~政治权利。 【剥离】动(组织、皮层、覆盖物等)脱落;分开:岩石~|胎盘
早期~。 【剥落】动一片片地脱落:门上的油漆~了。 【剥蚀】动①物质表面因风化而逐渐损坏:因受风雨的~,石刻的文字已经不易辨认。②风、流水、
一、复习指导: 复习中应着重注意以下几点: 1.体会数据在现实生活中的作用。熟悉收集、
整理、描述和分析数据的活动过程,理解 频数、频率。 2.根据统计图中提供的信息作出合理判断, 根据数据特点选择制作适当的统计图,来 表示数据。 3.通过实验体会有些事情发生是不确定的, 不确定事情发生的可能性是有大小的。
缘有锯齿,花紫色,果实密集在一起,外部呈鳞片状,果肉味甜酸,有很浓的香味。产于热带地区,我国广东、广西、海南、云南、福建、湾湾等地都有出
产。②这种植物的果实。‖也叫凤梨。 【菠萝蜜】同“波罗蜜”。
??)名金属元素,符号()。有放射性,由人工核反应获得。 【鱍】*(鱍)
[鱍鱍]()〈书〉拟声形容鱼跳跃或摆尾的声音。 【播】①动传播;传扬:广~|~音|电台正在~重要新闻。②动播种:条~|点~|
初中数学复习数据的收集和处理方法

初中数学复习数据的收集和处理方法数学作为一门理科学科,对于学生来说可能是较为抽象和难以理解的学科之一。
因此,在初中数学学习中,数据的收集和处理成为一个至关重要的环节,能够帮助学生更好地掌握和理解数学知识。
下面将介绍一些初中数学复习数据的收集和处理方法。
一、数据的收集数据的收集是数学复习的第一步,只有收集到充分且准确的数据,才能为后续的处理提供有力的支持。
以下是一些常见的数据收集方法:1. 实测法:通过实际测量或观察来获得数据。
比如,在学习几何图形的性质时,可以通过实际测量各个角的度数,或者观察各个边的长度来收集数据。
2. 问卷调查法:通过问卷调查来收集数据。
比如,在学习统计学的时候,可以设计一份问卷,询问同学们的一些数学习惯或者解题方法,然后收集他们的答案。
3. 文献查找法:通过查阅书籍、报纸、杂志等文献资料来收集数据。
比如,在学习概率统计的时候,可以查找相关的统计数据,比如人口统计数据、测量数据等。
二、数据的处理数据的处理是对收集到的数据进行整理、分类、整合和分析的过程,以得到有用的信息和结论。
以下是一些常见的数据处理方法:1. 数据整理:将收集到的数据按照一定的规则进行整理,使其更加清晰明了,便于后续的分析。
比如,可以使用表格、图表等形式来展示数据。
2. 数据分类:将数据按照某种特征或属性进行分类,以便于对不同类别的数据进行比较或分析。
比如,在统计某班级每个学生的考试成绩时,可以将成绩按照优、良、中、差等级进行分类。
3. 数据整合:将不同来源的数据进行整合,以便于综合分析和研究。
比如,在学习数列时,可以将不同学生复习某个数列的方法进行整合,找出最有效的解题思路。
4. 数据分析:根据数据的特征和目的,运用适当的统计分析方法对数据进行分析,得出有关结论。
比如,在学习函数时,可以分析函数的增减性、极值、单调性等特征。
三、数据处理的工具和技巧除了以上提到的方法外,以下是一些常用的数据处理工具和技巧:1. Excel表格:可以使用Excel等电子表格软件来进行数据的整理和分析,利用其丰富的函数和图表功能,快速得出统计结果。
八年级数学第五章数据的收集与处理 第1、2节北师大版知识精讲

初二数学第五章:数据的收集与处理第1、2节北师大版【本讲教育信息】一. 教学内容:第五章:数据的收集与处理第一节:数据的收集与处理第二节:数据的收集二. 教学要求1、了解普查、抽样调查、总体、个体、样本等概念,了解普查和抽样调查的应用并选择合适的调查方法,解决有关现实问题.2、在具体的问题情境中,体会抽样调查的优点和局限性,感受不同的抽样可能得到不同的结果.三、重点及难点重点:1、了解普查、抽样调查、总体、个体、样本等概念,感受抽样调查的必要性.2、能根据具体情景设计适当的抽样调查方案.难点:1、选择合适的调查方法,应用多样的方式解决问题.2、设计适当的抽样调查方案,正确把握调查方式,运用抽样调查中的样本的代表性和广泛性解决问题.[知识要点]一、本节主要概念1、普查:为了一定的目的而对考察对象进行的全面调查,称为普查.2、总体:所要考察对象的全体称为总体.3、个体:组成总体的每一个考察对象称为个体.4、抽样调查:从总体中抽取部分个体进行调查,这种调查称为抽样调查.5、样本:从总体中抽取的一部分个体叫做总体的一个样本.例如:为了了解全班同学每周参与家务劳动的时间,我们对全部同学进行的调查就是普查,其中总体是全班同学每周参与家务劳动的时间,个体是每一个同学参与家务劳动的时间,又例如,我国每五年进行一次全国1﹪人口的抽样调查,其中被抽取的1﹪人口就是全国人口的一个样本.二、普查与抽样调查的区别普查是对总体中每个个体进行的调查,范围广,数据详细,而抽样调查范围有局限性,数据不全面.三、抽样调查适应何种情况1、当受客观条件限制,无法对所有个体进行普查时,应进行抽样调查,例如,为了了解某城市一天的汽车进入量,我们无法准确把握住城市的每个出入口,无法进行普查,这时,只能采用抽样调查的方式进行抽查.2、当调查具有破坏性、不容许普查时,可进行抽样调查,例如,灯泡使用寿命的调查,对一万件产品进行调查,因为此调查具有破坏性,只能采取抽样调查,若采用普查,会损坏一万只灯泡,是不实际的.四、应如何选择适当的调查方式调查方案不唯一时,既可用普查的方式,也可用抽样调查的方式进行调查,例如,为了了解某校八年级学生的视力情况,我们可以一个个的调查也可用抽样调查,如抽查所有学号是3的倍数的学生或每班随机抽取15名学生进行调查.说明:抽样调查的优点是:调查范围小,节省时间、人力、物力.缺点是:调查的结果不如普查得到的结果准确.为了获得较为准确的调查结果,抽样时要注意样本的代表性和广泛性.【典型例题】例1、建国以来,我国已经成功地进行了五次人口普查,下表是历次普查得到的全国人口(1)1964年我国人口数量是()亿,2000年我国人口数量是()亿.(2)从1953年至2000年,我国人口数量增加了()亿.(3)从1953年至1964年,从1990年至2000年,我国人口数量增加1亿多人,但两者的区别是什么?解:(1)6.95,12.95(2)7.01(3)两者的区别在于基数不同,即1953年仅有5.94亿人,这个基数远远少于1990年的11.34亿,故从1953年至1964年的增长率远远高于1990年至2000年的增长率,这体现了我国实施计划生育工作的成效与意义.例2、市考察局为了了解本市中小学生实施素质教育的情况,抽查了某校七年级甲、乙两个班的部分学生,了解他们在一周内(星期一至星期五)参加课外活动的次数情况,抽查结果统计如下:(1)在这次抽查中,甲班被抽查了()人,乙班被抽查了()人,(2)在被抽查的学生中,甲班学生参加课外活动的平均次数为()次,乙班学生参加课外活动的平均次数为()次.(3)根据以上信息,用你学过的知识估计甲、乙两班在开展课外活动方面哪个更好些?(4)从图中你还能得到哪些信息?(写出一个即可)解:(1)10 10 (2)2.7 2.2(3)因为甲班的平均数大于乙班的平均数,所以甲班在开展课外活动方面更好些.(4)两班学生一周内活动2-3次的人数较多或一周内不参加活动的人数较少.例3、贵阳市是我国西部的一个多民族城市,总人口数为370万(2000年普查统计),如图所示的是2000年该市各民族人口统计图,请你根据图中提供的信息,回答下列问题:(1)2000年贵阳市少数民族总人口数是多少?(2)2000年贵阳市总人口中苗族占的百分比是多少?(3)2002年贵阳市参加中考的学生约40000人,请你估计2002年贵阳市参加中考的少数民族学生人数.解:(1)因为15﹪×370=55.5(万人)所以2000年贵阳市少数民族总人口数是55.5万人.(2)因为55.5×40﹪=22.2(万人) 所以000061003702.22=⨯ 所以2000年贵阳市总人口中苗族占的百分比为6﹪.(3)因为40000×15﹪=6000人所以2002年贵阳市参加中考的少数民族学生人数为6000人.例4、某校八年级全体640名学生在电脑培训前后各参加了一次水平相同的考试,考试都已同一标准划分成“不合格”、“合格”、“优秀”三个等级,为了了解电脑的培训效果,用抽查方式得到其中64名学生的两次考试分等级,所绘制的统计图如图所示,试结合图示信息回答下列问题:(1)这64名学生培训前考分的中位数所在的等级是( ),培训后考分的中位数所在的等级是( ).(2)这64名学生经过培训,考分等级“不合格”的百分率由()下降到().(3)估计该校整个八年级中,培训后考分等级为“合格”与“优秀”的学生共有()名.(4)你认为上述估计合理么?理由是什么?解:(1)不合格,合格(2)75﹪,25﹪(3)480 (4)合理,该样本是随机样本例5、某一位学生的书架上有一些书,其中的四分之一是课本,六分之一是学习工具书,剩下的都是学习参考书,根据这些信息,你能作出表示每一类书籍具体数目的条形统计图么,能作出表示每一类书籍所占百分比的扇形统计图吗?如果能的话,请作出相应的统计图,如果不能请说明理由.分析:按百分比计算圆心角.解:因为不知道书架上书的总数,又无法求出每一类书籍的具体数目,所以不能作出条形统计图,但是能作出扇形统计图.说明:弄清各类样本所占百分比与所对应的圆心角的关系.例6、如图为某校图书馆藏书的扇形统计图,最大的扇形表示为()占()的()﹪,可以量出这个扇形的圆心角为(),如果不用量角器测量,请写出计算式(),如果知道该图书馆藏书总量为20000本,则文艺类书籍共有()本.分析:要明确各类图书所占百分数与圆心角的对应关系.解:最大的扇形表示“教辅类图书”占“该校图书馆藏书”的“50”,圆心角为180°,其计算式为:360°×50﹪,文艺类书籍共有6000本.【模拟试题】(答题时间:30分钟)一、选择题1、为了了解一批电视机的平均寿命,从中抽取100台电视机进行实验,这个问题的样本是()A. 这批电视机的寿命B. 抽取的100台电视机C. 100D. 抽取的100台电视机的寿命2、某校要了解八年级女生的体重,以掌握她们的身体发育情况,从八年级的300名女生中抽出30名进行体重检测,在这个问题中,下列说法中正确的是()A. 300名女生是个体B. 300名女生是总体C. 30名女生是总体的一个样本D. 30是样本容量3、某火车站为了了解某月每天上午乘车人数,抽查了其中10天的每天上午的乘车人数,所抽查的这10天每天上午乘车人数是这个问题的()A. 总体B. 个体C. 一个样本D. 样本容量4、为了了解一批机器的质量,从中抽取12台机器进行检测,在这个问题中总体的一个样本是指()A. 从中抽取的12台机器的质量B. 未被抽取的机器的质量C. 被抽取的12台机器D. 未被抽取的机器5、为了了解某市八年级一次期末数学测试情况,从8万名学生中抽取了1000名学生的数学成绩进行统计分析,在下列说法中正确的是()A. 这1000名学生是总体的一个样本B. 每位学生的数学成绩是个体C. 8万名学生是总体D. 1000名学生是样本容量6、为了了解1000台某种型号空调的使用寿命,从中抽取10台空调进行试验,下列说法正确的是()A. 每台空调的使用寿命是个体B. 1000台空调是总体C. 10台空调是总体的一个样本D. 10台是样本容量二、填空题1、2003年上半年中国人民银行统计司就城镇居民对物价水平满意程度做了抽样调查,结果如图,据此,可以估计2003年上半年城镇居民对物价水平表示认可的约有________%.2、①为了了解你们班同学的视力情况,对全班同学进行调查.②为了了解你们学校学生对某本书的喜爱情况,对所有学号是9的倍数的学生进行调查.在调查过程中,①采取了_____________调查方式.②采取了________调查方式.3、为了调查学校毕业生的健康状况,从800名毕业生中抽取了50名学生进行体检,这个问题中总体指________________;个体指________________;样本指________________.4、某工厂从10万个灯泡中随意抽取100个灯泡做寿命测试,以便确定这批灯泡的质量.在这里,总体是________________;个体是________________;样本是________________.5、用样本估计总体时,样本容量越__________,由样本对总体的估计就越精确.6、下列调查中,分别采用的调查方式是(1)________________;(2)________________.(1)为了了解你班同学的年龄,对全班学生进行调查;(2)为了了解某校学生每周参加文体活动的情况,抽取了50名同学进行参加文体活动情况问卷调查.三、解答题1、为了了解全校同学每天参加体育活动的时间,请你设计一个方案.最好能按你的方案作一次调查,把结果记录下来.2、指出下列问题中的总体、个体和样本:为了了解某地区七年级学生身体发育的情况,抽取1000名学生测量体重.3、请你简述普查和抽样调查的特点.四、某地为制定七年级学生校服的生产计划,有关部门准备对200名七年级男生的身高作调查,现有三种调查方案:第一种:测量省体校七年级中200名男子篮球、排球队员的身高.第二种:查阅有关外地200名七年级男生身高的统计资料.第三种:在本地的市区和郊县各任选一所学校,共6所学校,在这些学校中选取七年级(一)班,用抽签的方法分别选出10名男生,然后测量他们的身高.为了达到估计某地七年级男生身高分布的目的,你认为采用哪种调查方案比较合理,并请说明理由.五、在下面两个事件中,你如何完成收集数据的任务.①学校为七年级新生订制校服,要了解每位新生的上衣及裤子号码.②要准确地在全班同学中调查丢弃塑料袋的情况,要了解各家每周丢弃塑料袋的数量.六、小芳家开了一家百货商店,学了数据的收集之后,小芳对她家百货商店一年的营业额进行了估计,结果和实际情况相差无几.请你帮助这家小百货商店设计一个估计方案,商店的经理将根据你的估计组织货源.【试题答案】一、1、D 2、D 3、C 4、A 5、B 6、A二、1、85.92、(1)普查(2)抽样3、800名毕业生的健康状况这800名同学中每名同学的健康状况,50名同学的健康状况4、10万个灯泡的使用寿命每个灯泡的使用寿命100个灯泡的使用寿命5、大6、普查抽样调查三、1、略2、总体是某地区七年级学生的体重,个体是某地区七年级每一名学生的体重,样本是抽取的1000名学生的体重.3、略四、为了达到估计某地七年级男生身高分布的目的,采用第三种调查方案比较合理.理由是:第三种调查方案是随机抽样调查,具有广泛性和代表性.五、(1)要采用普查的方法,量出每一个同学衣服的号码,这样才能保证每个同学穿上合体的服装.(2)可用抽样的方法了解每周丢弃塑料袋的情况,如确定星期一、星期三两天,各班同学都记录下自己家这两天内丢弃的塑料袋情况,利用这些数据统计出一周内每家丢弃塑料袋的情况.也可以在班级中确定两个小组的同学,记录下这一周内各家丢弃的塑料袋情况,利用这些数据统计出一周内每家丢弃塑料袋的情况.六、略。
2021年八年级数学上册 第四章数据的收集与处理复习教案 鲁教版
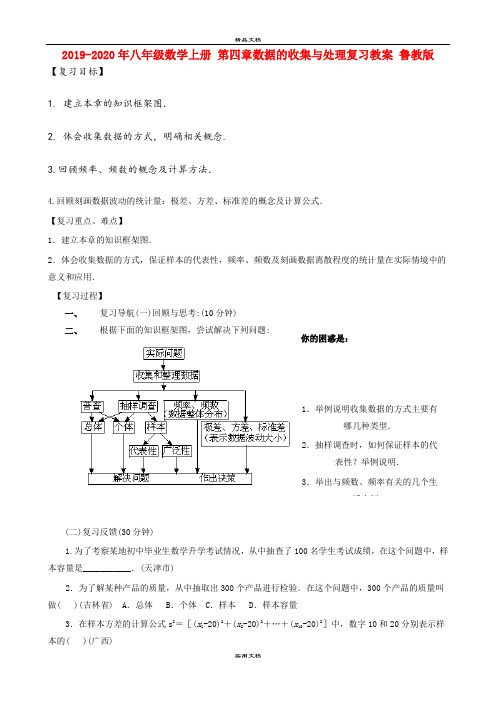
2019-2020年八年级数学上册 第四章数据的收集与处理复习教案 鲁教版【复习目标】1. 建立本章的知识框架图.2. 体会收集数据的方式,明确相关概念.3.回顾频率、频数的概念及计算方法.4.回顾刻画数据波动的统计量:极差、方差、标准差的概念及计算公式.【复习重点、难点】1.建立本章的知识框架图.2.体会收集数据的方式,保证样本的代表性,频率、频数及刻画数据离散程度的统计量在实际情境中的意义和应用.【复习过程】一、复习导航(一)回顾与思考:(10分钟) 二、 根据下面的知识框架图,尝试解决下列问题:(二)复习反馈(30分钟)1.为了考察某地初中毕业生数学升学考试情况,从中抽查了100名学生考试成绩,在这个问题中,样本容量是___________.(天津市)2.为了解某种产品的质量,从中抽取出300个产品进行检验.在这个问题中,300个产品的质量叫做( )(吉林省) A .总体 B .个体 C .样本 D .样本容量3.在样本方差的计算公式s 2=[(x 1-20)2+(x 2-20)2+…+(x 10-20)2]中,数字10和20分别表示样本的( )(广西)你的困惑是:1.举例说明收集数据的方式主要有哪几种类型.2.抽样调查时,如何保证样本的代表性?举例说明.3.举出与频数、频率有关的几个生活实例。
A.容量、方差 B.平均数、容量 C.容量、平均数 D.标准差、平均数4.已知数据7,3,11,3,1,8,那么这组数据的众数是___________.(上海市)5.若3,4,5,6,x1,x2,x3的平均数是12,则x1+x2+x3=___________.6.从观测所得的数据中取出m个x1,n个x2,p个x3组成一个样本,那么这个样本的平均数是( ) A.B.C.D.7.总体方差是表示总体的___________的特征数.(河南省)8.样本3,-4,0,-1,2的方差是___________.(福建)9.绘制频数分布直方图时,各个小长方形的高等于相应各组的()(山东)A.组距 B.频数 C.频率 D.平均数10.为了调查班级中对新班主任老师的印象,下列更具有代表性的样本是()A.调查前十名的学生B.调查后十名的学生C.调查单号学号的学生D.调查全体男同学11. 一组数据:,,0,,1的平均数是0,则=____,方差______.12.如果样本方差[]242322212)2()2()2()2(41-+-+-+-=xxxxS,那么这个样本的平均数为_________.样本容量为________.13.数据501,502,503,504,505,506,507,508,509的标准差是()A、 B、 C、 D、114.为了考察某商店一年中每天的营业额,从中抽查了30天的营业额.其中总体是____________________________________,个体是_________________________,样本是______________________,样本容量是____________.15.下列任务,你认为采用什么调查方式更合适?(1)了解一批日光灯管的使用寿命;(2)了解一个小区的业主对物业公司的满意程度;(3)了解本班学生对目前台湾形势的认识情况;16.某农科所在8个试验点对甲、乙两种玉米进行对比试验,这两种玉米在各试验点的亩产量如下(单位:千克):甲:450 460 450 430 450 460 440 460乙:440 470 460 440 430 450 470 440在这些试验点甲、乙两种玉米哪一种产量比较稳定?二、复习典例(30分钟)例1.一家电脑生产厂家在某城市三个经销本厂产品的大商场调查,产品的销量占这三个大商场同类产品销量的40%.由此在广告中宣传,他们的产品在国内同类产品的销售量占40%.请你根据所学的统计知识,判断该宣传中的数据是否可靠:________,理由是________.例2.若一组数据x1、x2……x n,的平均值为,方差为s2,求下列各组数据的平均值和方差.(1) x1+a,x2+a,……,x n+a; (2)ax1,ax2, …,ax n; (3) ax1+b,ax2+b, …,ax n+b.提示:先写出平均值和方差的公式,然后再套用公式求出新数据的平均值和方差.总结:(1)把一组数据每一个数都加上或减去同一个数,它的平均值也要加上或减去同一个数,而方差不变.(2)把一组数据每一个数都扩大或缩小a倍,它的平均值也扩大或缩小a倍,而方差要扩大或缩小a2倍.对应训练:1.已知:y1,y2,y3的平均值为,方差为s2.(1)y1-1,y2-1,y3-1的平均值________方差________;(2)-3y1,-3y2,-3y3的平均值________方差________;(3)2y1+5,2y2+5,2y3+5的平均值________方差________;2.已知样本x1、x2……x n的方差是2,则样本3x1+5,3x2+5,3x3+5,……3x n+5的方差是()3.(xx年竞赛模拟题)学生李明通过计算(A),(B),(C),(D)四组数据的方差后,发现有三组数据的方差相同,则方差不同的一组数据是()A.102,103,105,107,108B.12,13,15,17,18C.1,4,9,25,36 D.2112,2113,2115,2117,2118例3.某校要从小王和小李两名同学中挑选一人参加全国数学竞赛,在最近的五次选拔考试中,他俩的成绩分别如下表:(2)在这五次考试中,成绩比较稳定的是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次考试中的优秀率各是多少?(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明理由.三、检测:(12分钟)1.样本方差越小,说明()A、样本容量越小B、样本容量越大C、样本波动越大D、样本波动越小2.在数据统计中,能反映一组数据变化范围大小的指标是()A、极差B、方差C、标准差D、以上都不对3.能反映一组数据与其平均值的离散程度的是()A、极差和方差B、极差和标准差C、方差和标准差D、以上都不对4.已知甲、乙两个样本(样本容量一样大),若甲样本的方差是0.4,乙样本的方差是0.2,那么比较甲、乙两个样本的波动大小的结果是()A、甲样本的波动比乙大B、乙样本的波动比甲大C、甲、乙的波动一样大D、无法比较5.已知的平均数10,方差3,则的平均数为____,方差为________.6.如果一组数据的极差是80,若画图前确定组距是9,则组数是()A、7组B、8组C、9组D、10组7.如果给定数组中每一个数都减去同一非零常数,则数据的()A、平均数改变,方差不变B、平均数改变,方差改变C、平均数不变,方差不变D、平均数不变,方差改变四、拓展:为选派一名学生参加全市实践活动技能竞赛,A、B两位同学在学校实践基地现场进行加工直径为20mm的零件的测试,他俩各加式的10个零件的相关数据依次如下图所示(单位:mm)。
2021年八年级数学下册 第五章数据的收集与处理全章教学案 北师大版

2021年八年级数学下册第五章数据的收集与处理全章教学案北师大版一、教学目标:1、经历调查、收集数据的过程,感受抽样的必要性。
2、了解普查、抽样调查、总体、个体、样本等概念,了解普查和抽样调查的应用,并选择合适的调查方法,解决有关现实问题。
3、进一步发展统计意识,培养学生热爱劳动、勇于实践的优良品质。
二、教学过程:1、活动与探究同学们,你们每天在家都帮父母做家务活吗?主要做些什么呢?每周大约多长时间呢?你们每周干家务活时间的平均数、中位数、众数是什么?2、介绍新知识(1)普查:为了一定的目的而对考察对象进行的全面调查。
(2)总体:所考察对象的全体。
(如上述问题中的总体为“全班同学每周干家务活的平均时间的全体”,注意这里“考查对象”不是学生而是学生干家务活的时间。
)(3)个体:组成总体的每一个考察对象。
(如上述问题中的个体为“全班每一个同学每周干家务活的平均时间”)3、想一想为了准确了解全国人口状况,我国每10年进行一次全国性人口普查,在这一事例中,你能说出总体、个体分别是什么吗?5.2 数据的收集一、教学目标1.会采取合理的调查方法收集数据,并能对数据进行加工、整理.2.进一步了解、掌握抽样调查与普查各自的优、缺点.二、教学过程1.例题讲解为了了解你所在地区老年人的健康状况,你准备怎样收集数据?下面分别是小明、小颖、小华三位同学的调查结果:小明:在公园里调查了1000名老年人,他们一年中生病的次数如下表:表(一)比较一下上述两种表示各自的优越性.小颖:在医院调查了1000名老年病人,他们一年中生病的次数如下表所示:(表一)比较一下小明与小颖所得数据的差别,是什么原因造成的?小华:调查了10名老年邻居,他们一年中生病的次数如下表所示:小明调查的对象选自公园里的老年人.常去公园里活动的老年人,平时一定注意身体的保健,一定注意修身、养性、加强体育锻炼,所以身体较健康.另一方面,公园建在城市里,相对于农村中的老年人去公园的较少.这1000人中不同文化程度,不同职业,城市和乡村等等不同层次的老人是否都有所选取.选取人数的比例是否合理,是否具有代表性与广泛性都是我们在收集数据中应该考虑的.所以,我认为小明收集的数据缺乏代表性和广泛性.小颖收集的数据来自医院看病的1000名老年人.这部分人相对体质较弱.我认为用这些数据得到的调查结果不准确.因为收集的数据缺乏代表性和广泛性.小华仅仅调查了10位老年人.因为样本太小了,所以不能据此推断某地区老年人的健康状况.抽样调查应注意什么?抽样时要注意样本的代表性和广泛性.在现实生活中,当我们所要考察的总体中包含的个体数很多,有时总体中个数较多且总体有明显差异的几个部分组成时,我们应注意抽出的样本就必须有较强的代表性.每个部分都应抽取到,而且应注意各部分的比例.广泛性是指总体中的每个个体均有被选的可能.5.3 频数与频率(一)一、教学目标1.掌握频数、频率的概念.2.会求一组数据的频数与频率.二、教学过程1.例题讲解下面是小亮调查的八(1)班50位同学喜欢的足球明星,结果如下:根据上面结果,你能很快说出该班同学最喜欢的足球明星吗?他的数据表示方式是什么?你能设计出一个比较好的表示方式吗?(二)此种表示方式的优点是简单明了,一眼可以看出哪个最多、哪个最少.我们小组采用如下方式表示数据.此种表示方式的优点是直观,一目了然.不仅可以很快判断出哪个最多,哪个最少,还可比较出差别是否悬殊很大.从上表可以看出,A、B、C、D出现的次数有的多,有的少,或者说它们出现的频繁程度不同.我们称每个对象出现的次数为频数(absolute,frequency).而每个对象出现的次数与总次数的比值为频率(relative frequency).分别计算A、B、C、D的频数与频率.A的频数为23,A的频率为.B的频数为8,B的频率为.C的频数为13,C的频率为.D的频数为6,D的频率为.三、课堂练习1.设计一个方案,了解你们班同学最喜欢的科目是哪科,为什么喜欢?分析:先列表,再统计,调查探讨喜欢的原因.调查不爱学的那门科目的原因.(课后完成)列表如下科目语文数学英语历史地理政治物理美体学生数频数频率你还能用什么方式表示上表所收集数据的内容.可以用上例中的图(三)表示的形式,这种图叫频数分布直方图,可不可以用频率分布来表示,如何表示。
2021年八年级数学下册 第五章 数据的收集与处理教案 北师大版

第五章 2021年八年级数学下册第五章数据的收集与处理教案北师大版知识与技能目标:1.了解并掌握:普查、抽样调查、总体、样本、个体这些基本概念;2.在调查中,会选择合理的调查方式.过程与方法目标:1.初步经历数据的收集、处理过程,发展学生初步的统计意识和数据处理能力;2.通过数据收集的学习,培养学生应用、分析、判断能力.情感与价值目标1.通过小组合作调查研究,培养学生的合作意识和处理问题的能力;2.通过解决身边的实际问题,让学生认识数学与人类生活的密切联系及对人类历史发展的作用;3.培养学生热爱劳动,尊敬父母的良好道德及行为习惯.重点 1.掌握普查与抽样调查的区别与联系;2.掌握总体、样本及个体间关系.难点 1.获取数据时,选择哪种调查方式较好,何时用普查,何时用抽样调查,并能说明理由;2.应用意识的培养,设计方案.一、创设问题情境,导入新课同学们,你们爱你们的父母吗?放学回家后是否帮父母做些力所能及的家务活?你们认为家务活都包括什么?你常在家干什么?你认为干家务活影响学习吗?每位同学统计一下你每周干家务活大约有多长时间?要想了解你在家干家务活时间多少相对于你们班其他同学干家务活时间的多少,你该开展哪些调查工作?二、讲授新课1.引入概念(1)普查的定义:这种为了一定目的而对考察对象进行的全面调查,称为普查.(2)总体(population):其中所要考察对象的全体称为总体.(3)个体:组成总体的每个考察对象称为个体(individual).2.想一想:开展调查要做哪些准备工作?小结:(1)首先确定调查目的;(2)其次确定调查对象,明确总体与个体;(3)设计调查表,收集数据.3.学一学例1 为了准确了解全国人口状况,我国每10年进行一次全国人口普查.指出总体、个体.例2 为了考察××学校××班同学每周干家务劳动的时间.指出总体、个体.4.议一议(1)你们学校所有八年级(六个班)学生每周干家务活的平均时间是多少?(2)全国所有八年级学生每周干家务活的平均时间是多少?你能用普查的方式得到这个数据吗?你准备如何获得这个数据?与同伴交流.5.小结:抽样调查的概念,样本的概念:(1)抽样调查(sampling investigation):从总体中抽取部分个体进行调查,这种调查称为抽样调查.(2)样本(sample):其中从总体中抽取的一部分个体叫做总体的一个样本.例3 我国每5年进行一次全国1%人口的抽样调查,其中被抽取的1%人口就是全国人口的一个样本.通过这个样本的特征数字,估计总体情况.小结:普查可以直接获得总体情况,但有时总体中个体数目较多,普查的工作量较大;有时受客观条件的限制,无法对所有个体进行普查;有时调查具有破坏性,不允许普查.此时,可采用抽样调查.从总体中抽取一个样本.通过样本的特征数字来估计总体情况.三、课堂练习1.举例说明什么时候用普查的方式获得数据较好、用抽样调查的方式获得数据较好?(2)当要研究的问题要求情况真实、准确性较高时.(3)调查工作较方便,没有破坏性等等,此时用普查方式获得数据较好.2.下列调查中,分别采用了哪种调查方式?(1)为了了解你们班同学的身高,对全班同学进行调查.(2)为了了解你们学校学生对新教材的喜好情况,对所有学号是5的倍数的同学进行调查.3.说明在以下问题中,总体、个体、样本各指什么?(1)为了考察一个学校的学生参加课外体育活动的情况,调查了其中20名学生每天参加课外体育活动的时间.(2)为了了解一批电池的寿命,从中抽取10只进行试验.(3)为了考察某公园一年中每天进园的人数,在其中的30天里对进园的人数进行了统计.四、课时小结1.基本概念:(1)调查、普查、抽样调查;(2)总体、个体、样本.2.何时采用普查、何时采用抽样调查,各有什么优缺点?五、课后作业作业本1.设计两个个方案,了解你校八年级学生每周干家务活的时间和视力情况.六、活动与探究1.在统计里,之所以用样本的情况估计总体的情况,是基于两点:(一)是在很多情况下总体包含的个体数往往很多,甚至无限,不可能一一加以考察;(二)是有些从总体中抽取个体的试验带有破坏性(例如灯泡使用寿命试验),因而抽取的个体不允许太多.2.要通过对样本的研究作出对总体的估计,前提是:如何抽取样本.抽取样本必须具有尽可能大的代表性这一基本思想,否则将影响到样本对总体估计的精确程度.板书设计§5.2 数据的收集知识与技能目标:1.会采取合理的调查方法收集数据,并能对数据进行加工、整理;2.进一步了解、掌握抽样调查与普查各自的优、缺点.过程与方法目标:1.初步经历数据的收集、加工与整理过程.发展学生的统计意识和数据处理能力;2.通过调查过程,培养学生的探索精神、分析问题、处理问题的能力.情感与价值目标1.统计作为处理现实世界数据的一个重要数学分支,必然要求素材本身的真实性,以培养学生求真的科学态度;2.通过同学间的交流与合作,培养大家的合作精神.重点数据的收集.难点如何确定调查范围与对象,合理收集数据是否具有代表性与广泛性.一、导入新课上节课,我们学习了为了解某些情况而采取的两种调查方式:普查与抽样调查,并要求掌握总体、个体、样本这些基本概念.这节课我们继续学习统计初步知识,如何收集数据.如何使收集的数据有广泛性和代表性.如何使所收集到的数据更真实、可靠地反映总体情况.二、讲授新课1.例题讲解为了了解你所在地区老年人的健康状况,你准备怎样收集数据?下面分别是小明、小颖、小华三位同学的调查结果:(见课本)你同意他们三个人的做法吗?说明你的理由.抽样调查应注意什么?代表性、广泛性分别指什么,你是怎么理解的?在现实生活中,当我们所要考察的总体中包含的个体数很多,有时总体中个数较多且总体有明显差异的几个部分组成时,我们应注意抽出的样本就必须有较强的代表性.每个部分都应抽取到,而且应注意各部分的比例.广泛性是指总体中的每个个体均有被选的可能.2.议一议为了了解该地区老年人的健康状况,你认为应当怎样收集数据?与同伴交流.(略)分析:(1)调查目的:了解某地区老年人的健康状况:一年中生病的次数.(2)总体:该地区所有老年人一年中生病的次数.(3)个体:该地区符合条件的每一位老年人一年中生病的次数.(4)样本:抽取1000名老年人一年中生病的次数是总体中抽取的一个样本.样本容量是1000.你认为年龄多大算老年人?由于社会的进步,人们生活水平的改善,人的寿命也越来越长.我们以国家规定的退休年龄男60岁,女55岁为标准.确定调查对象,某地区55岁以上的所有人员一年中生病的次数作为总体.(1)你认为他的调查方式如何?(2)你认为城市与乡村中的老年人,脑力劳动者和体力劳动者的健康状态是否有明显差异,不同年龄段60岁~70岁老年人,70岁~80岁老年人的差异.抽取样本时,是否考虑其所占的比例?与同伴交流.3.想一想抽样调查时应注意什么?抽样时要注意样本的代表性与广泛性.4.小结抽样调查只考察总体中的一部分个体,因此它的优点是调查的范围小,节省时间、人力、物力,但其调查结果往往不如普查得到的结果准确.为了获得较为准确的调查结果,抽样时要注意样本的代表性与广泛性.三、课堂练习1.设计一个方案,了解你所在地区所有八年级学生最喜欢的学科.分析:(1)确定调查目的;(2)分清总体、个体;(3)抽取样本;(4)设计调查表收集数据;(5)由样本特征数估计总体.调查表(略).2.大样本一定能保证调查结论准确吗?读一读:课本160页内容.四、课时小结本节课主要学习了数据的收集.当总体中的个体数目较多时,为了节省时间、人力、物力,可采用抽样调查.为了获得较为准确的调查结果,抽样时要注意样本的代表性和广泛性.还要注意关注样本的大小.五、课后作业见作业本六、活动与探究1.随机调查,就是按机会均等的原则进行调查,亦即总体中每个个体被调查的概率都相同.2.抽样方法简介:(1)随机抽样;(2)系统抽样;(3)分层抽样.§5.3.1 频数与频率(一)教学知识点:1.掌握频数、频率的概念;2.会求一组数据的频数与频率.能力训练要求:1.通过统计数据,制成各种图表,增强学生对生活中所见到的统计图表进行数据处理和评判的主动意识;2.培养学生利用图表获取信息的能力,使学生能初步把数字信息、图形和语言之间相互转化,并作出合理推断.情感与价值观要求:培养学生实事求是的科学态度,并通过对数据的整理,提高学生的责任心与耐心细致的工作态度.重点频率与频数的概念,选择数据表示方式.难点各种统计图表的绘制,识别各种图表所含的信息,各自优缺点.一、导入新课上节课我们主要学习了数据的收集,并探讨了抽样调查时要注意的问题:(1)样本的大小;(2)样本的代表性;(3)样本的广泛性.使所抽取的样本尽可能准确地反映总体的真实情况.本节课我们继续学习统计初步中反映数据出现频繁程度的两个量频数与频率.二、讲授新课1.例题讲解我们不仅要学好基础知识,还要强健自己的体魄,长大后才能更好地工作.下面是小亮调查的八(1)班50位同学喜欢的足球明星,结果如下:根据上面结果,你能很快说出该班同学最喜欢的足球明星吗?他的数据表示方式是什么?你能设计出一个比较好的表示方式吗?小组相互交流,共同探讨.列表格表示方式的优点是什么?画统计图表示方式的优点是什么?从上表可以看出,A、B、C、D出现的次数有的多,有的少,或者说它们出现的频繁程度不同.我们称每个对象出现的次数为频数(absolute,frequency).而每个对象出现的次数与总次数的比值为频率(relative frequency).分别计算A、B、C、D的频数与频率.三、课堂练习1.设计一个方案,了解你们班同学最喜欢的科目是哪科,为什么喜欢?分析:先列表,再统计,调查探讨喜欢的原因.调查不爱学的那门科目的原因.(课后完成)你还能用什么方式表示上表所收集数据的内容.上面的图图叫频数分布直方图.可不可以用频率分布来表示,如何表示.阅读课本内容.(利用频率绘制的图)(略)2.议一议:(投影片)小明、小亮从同一本书中分别随机抽取了6页,在统计了1页、2页、3页、4页、5页、6页的“的”和“了”出现的次数后,分别求出了它们出现的频率,并绘制了下图(见课本).3.做一做(1)为了了解中学生的身体发育情况,对某中学同年龄的60名女学生的身高进行了测量.结果如下.(单位:厘米)(投影片)158 167 154 159 166 169 159 156 166 162 159 156 166 164160 157 156 160 157 161 158 158 153 158 164 158 163 158153 157 162 162 159 154 165 166 157 151 146 151 158 160165 158 163 162 161 154 163 165 162 162 159 157 159 149164 168 159 153我们知道,这组数据的平均数,反映了这些学生的平均身高.但是,有时只知道这一点还不够,还希望知道身高在哪个范围内的学生多,在哪个小范围内的学生少,也就是说,希望知道这60名女学生的身高数据在各个小范围内所占的比的大小.落在各个小组内的数据的个数叫做频数.小结:整理数据时,可以按照下面的步骤进行:1.计算最大值与最小值的差;2.决定组距与组数;3.决定分点;4.列频率分布表.下节课我们将继续学习对各种数据的统计表的处理.四、课时小结本节课主要学习了如下内容.1.频数与频率两个基本概念.2.会求一组数据的频数与频率,并会选择合理的表示方式来表示数据.五、课后作业见作业本§5.3.2 频数与频率(二)知识与技能目标:1.如何收集与处理数据;2.会绘制频数分布直方图与频数分布折线图;3.了解频数分布的意义,会得出一组数据的频数分布.过程与方法目标:1.初步经历数据的收集与处理的过程,发展学生初步的统计意识和数据处理能力;2.通过经历调查、统计、研讨等活动,发展学生实践能力与合作意识.情感与价值观要求:通过学习,培养学生勇于提出问题,大胆设计,勇于探索与解决问题的能力.重点1.了解频数分布的意义,会得出一组数据的频数分布直方图、频数分布折线图;2.数据收集与处理.难点1.决定组距与组数;2.数据分布规律.一、导入新课请大家一起回忆一下,我们如何收集与处理数据.你能否帮卖雪糕的李大爷设计一种方案,确定各种牌子的雪糕应进多少?首先应开展调查.统计一下李大爷每天卖出的A、B、C、D、E五个牌子雪糕的数量.二、讲授新课这是小丽统计的最近一个星期李大爷平均每天能卖出的A、B、C、D、E 五个牌子雪糕的数量.雪糕数量频数频率A 131 131 0.253B 182 182 0.351C 68 68 0.131D 39 39 0.075E 98 98 0.190合计518 518 1.000根据上表绘制一张频数分布直方图.(见课本)根据小丽的统计结果,请你为李大爷设计一个进货方案.A多进多少?B多进多少?D进多少?如何通过比例确定?如何确定进货的总数,还应考虑哪些因素?2.做一做例学校要为同学们订制校服,为此小明调查了他们班50名同学的身高,结果(单位:cm).如下:141 165 144 171 145 145 158 150 157 150 154 168168 155155 169 157 157 157 158 149 150 150 160 152 152159 152159 144 154 155 157 145 160 160 160 158 162 155162 163155 163 148 163 168 155 145 172填写下表,并将上述数据用适当的统计图表示出来(见课本).同学们想一想,你同父母一起去商店买衣服时,衣服上的号码都有哪些,标志是什么?S代表最小号,身高在150~155cm的人适合穿S号.M号适合身高在155~160cm的人群着装…….厂家做衣服订尺寸也并不是按所有人的尺寸定做,而是按某个范围分组批量生产.如何确定组距与组数呢?分组组数的确定,不仅与数据多少有关,还与数据的取值情况有关.在实际决定组数时,常有一个尝试过程:先定组距,再计算出相应的组数.看看这个组数是否大致符合确定组数的经验法则.在尝试中,往往要比较相应于几个组距的组数,然后从中选定一个较为合适的组数.我们一起看下表:小亮的做法:<144cm 145~149cm 150~154cm 155~159cm 160~164cm165~169cm >170cm3 6 9 16 9 5 2当收集的数据连续取值时,我们通常将数据分组,然后再绘制频数分布直方图.比较一下各种统计图各自的优缺点.小结.我们在收集到一些数据后,一定要选择合理的表示方式表示所收集的数据.常用表格与图表两种方式.何时用哪种方式,应根据我们研究问题的侧重点来定.具体问题具体分析.不要生搬硬套,应多总结、提炼研究问题的思想和方法.不要一味去模仿.只要多动脑去思考.我相信同学们会创新出更好的方法.三、课堂练习1.储蓄所太多必将增加银行支出,太少又难以满足顾客的需求.为此,银行在某储蓄所抽样调查了50名顾客,他们的等待时间(进入银行到接受受理的时间间隔,单位mi n)如下:15 20 18 3 25 34 6 0 17 24 23 30 35 42 37 24 21 1 14 1234 22 13 34 8 22 31 24 17 33 4 14 23 32 33 28 42 25 14 22 31 42 34 26 14 25 40 14 24 11(1)将数据适当分组,并绘制相应的频数分布直方图.(2)这50名顾客的平均等待时间是多少?根据这个数据,你认为应该给银行提什么建议?四、课时小结本节课学习了如下内容:1.如何整理所收集的数据;2.将数据用适当的统计图表示出来(1)表格形式(2)频数分布直方图(3)频数分布折线图.3.各种统计图、表的优缺点.4.根据统计图表信息,提出合理化建议.五、课后作业见作业本§5.5 回顾与思考知识与技能目标:1.回顾收集数据的方式;2.回顾收集数据时,如何保证样本的代表性;3.回顾频率、频数的概念及计算方法;4.回顾刻画数据波动的统计量:极差、方差、标准差的概念及计算公式;5.能利用计算器或计算机求一组数据的算术平均数.过程与方法目标:1.熟练掌握本章的知识网络结构;2.经历数据的收集与处理的过程,发展初步的统计意识和数据处理能力;3.经历调查、统计等活动,在活动中发展学生解决问题的能力.情感与价值目标1.通过对本章内容的回顾与思考,发展学生用数学的意识;2.在活动中培养学生团队精神.重点1.建立本章的知识框架图;2.体会收集数据的方式,保证样本的代表性,频率、频数及刻画数据离散程度的统计量在实际情境中的意义和应用.难点收集数据的方式、抽样时保证样本的代表性、频率、频数、刻画数据离散程度的统计量在不同情境中的应用.一、导入新课本章的内容已全部学完.现在如何让你调查一个情况.并且根据你获得数据,分析整理,然后写出调查报告,我想大家现在心里应该有数.例如,我们要调查一下“上网吧的人的年龄”这一情况,我们应如何操作?二、讲授新课回顾与思考下列问题:1.举例说明收集数据的方式主要有哪几种类型.2.抽样调查时,如何保证样本的代表性?举例说明.3.举出与频数、频率有关的几个生活实例?4.刻画数据波动的统计量有哪些?它们有什么作用?举例说明.三、建立知识框架图通过刚才的几个问题回顾思考了我们这一章的重点内容,下面构建本章的知识结构图.四、随堂练习例1 一家电脑生产厂家在某城市三个经销本厂产品的大商场调查,产品的销量占这三个大商场同类产品销量的40%.由此在广告中宣传,他们的产品在国内同类产品的销售量占40%.请你根据所学的统计知识,判断该宣传中的数据是否可靠:________,理由是________.例2 在举国上下众志成城抗击“非典”的斗争中,疫情变化牵动着全国人民的心.请根据上面的疫情统计图表回答问题:(1)图10是5月11日至5月29日全国疫情每天新增数据统计走势图,观察后回答:①每天新增确诊病例与新增疑似病例人数之和超过100人的天数共有__________天;②在本题的统计中,新增确诊病例的人数的中位数是___________;③本题在对新增确诊病例的统计中,样本是______________,样本容量是______________.(2)下表是我国一段时间内全国确诊病例每天新增的人数与天数的频率统计表.(按人数分组)①100人以下的分组组距是________;②填写本统计表中未完成的空格;③在统计的这段时期中,每天新增确诊病例人数在80人以下的天数共有_________天.解:(1)①7;②26;③5月11日至29日每天新增确诊病例人数;19.(2)①10人;②11;40;0.125;0.325;③25.五、课时小结这节课我们通过回顾与思考这一章的重点内容,共同建立的知识框架图,并进一步用统计的思想和知识解决问题,作出决策.六、课后作业课本复习题A组七、活动与探究从鱼塘捕得同时放养的草鱼240尾,从中任选9尾,称得每尾鱼的质量分别是1.5,1.6,1.4,1.6,1.3,1.4,1.2,1.7,1.8(单位:千克).依此估计这240尾鱼的总质量大约是A.300克B.360千克C.36千克D.30千克(选B)20408 4FB8 侸25320 62E8 拨33272 81F8 臸26298 66BA 暺37822 93BE 鎾n37737 9369 鍩29423 72EF 狯29700 7404 琄@22726 58C6 壆26575 67CF 柏K。
八年级数学 数据的收集与处理 知识点梳理

八年级数学数据的收集与处理知识点梳理一、知识梳理知识点1:普查与抽样调查(1)收集数据的方法通常有和两种。
(2)为了一定的目的而对考察对象进行的调查,称为普查,其中所要考察对象的称为总体,而组成总体的称为个体。
(3)抽样调查时要注意样本的和。
知识点2:数据的表示(1)扇形统计图是利用圆和扇形来表示和的关系。
(圆代表总体,各个扇形分别代表总体中的不同部分)其特点是:①能清楚地表示部分在总体中所占的;②易于显示每组数据相对于的大小;③扇形统计图中各部分所占的百分比之和应等于。
知识点3:统计图的选择(1)我们常用的统计图有、、。
(2)条形统计图能清楚地表示出每个项目的;折线统计图能清楚地反映事物的;扇形统计图能清楚地表示出各部分在总体中所占的。
二、典例剖析考点一:普查与抽样调查例1:(1)为了解我国七年级学生的视力情况采用的调查方式最合理的是()A、普查B、抽样调查C、局部调查D、小范围调查(2)为了了解“时风三轮车”在某地区农村的使用情况,黄老对某个村使用三轮车的100户农民进行了统计。
对于黄老的这种做法,你的看法是(填“同意”或“不同意”),理由是 。
例2:为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了解学生的喜好,抽取若干名学生进行问卷调查请根据统计图提供的信息回答以下问题: (1)抽取的学生数为_______名;(2)该校有3000名学生,估计喜欢收听易中天《品三国》的学生有_______名; (3)估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的_ ___%; (4)你认为上述估计合理吗?理由是什么?【变式练习】1、近几年,人们的环保意识逐渐增强,“白色污染”现象越来越受到人们的重视。
黄老想了解班上同学家里在一年内丢弃废塑料袋的个数,你认为采用 调查方式合适一些。
2、下列调查,比较适用普查而不适用抽样调查方式的是( ) A 、调查全省食品市场上某种食品的色素含量是否符合国家标准; B 、调查一批灯泡的使用寿命; C 、调查你所在班级全体学生的身高; D 、调查全国初中生每人每周的零花钱数。
初二年级数学知识点:数据的收集与处理

初二年级数学知识点:数据的收集与处理除了课堂上的学习外,数学知识点也是先生提高数学效果的重要途径,本文为大家提供了初二年级数学知识点:数据的搜集与处置,希望对大家的学习有一定协助。
一、每周干家务活的时间※1、所要调查的对象的全体叫做总体;把组成总体的每一个调查对象叫做集体;从总体中取出的一局部集体叫做这个总体的一个样本.※2、为一特定目的而对一切调查对象作的片面调查叫做普查;为一特定目的而对局部调查对象作的调查叫做抽样调查.二、数据的搜集※1、抽样调查的特点: 调查的范围小、节省时间和人力物力优点.但不如普查失掉的调查结果准确,它失掉的只是估量值.而估量值能否接近实践状况还取决于样本选得能否有代表性.第六章证明(一)二、定义与命题※1、普通地,能明白指出概念含义或特征的句子,称为定义.定义必需是严密的.普通防止运用模糊不清的术语,例如一些、大约、差不多等不能在定义中出现.※2、可以判别它是正确的或是错误的句子叫做命题.正确的命题称为真命题,错误的命题称为假命题.※3、数学中有些命题的正确性是人们在临时实际中总结出来的,并且把它们作为判别其他命题真假的原始依据,这样的真命题叫做公理.※4、有些命题可以从公理或其他真命题动身,用逻辑推理的方法判别它们是正确的,并且可以进一步作为判别其他命题真假的依据,这样的真命题叫做定理.5、依据题设、定义以及公理、定理等,经过逻辑推理,来判别一个命题能否正确,这样的推理进程叫做证明.三. 为什么它们平行※1、平行判定公理: 同位角相等,两直线平行.(并由此失掉平行的判定定理)※2、平行判定定理: 同旁内互补,两直线平行.※3、平行判定定理: 同错角相等,两直线平行.四、假设两条直线平行※1. 两条直线平行的性质公理: 两直线平行,同位角相等;※2. 两条直线平行的性质定理: 两直线平行,内错角相等;※3. 两条直线平行的性质定理: 两直线平行,同旁内角互补.五、三角形和定理的证明※1. 三角形内角和定理: 三角形三个内角的和等于1802. 一个三角形中至少只要一个直角3. 一个三角形中至少只要一个钝角4. 一个三角形中至少有两个锐角六、关注三角形的外角※1. 三角形内角和定理的两个推论:推论1: 三角形的一个外角等于和它不相邻的两个内角的和;推论2: 三角形的一个外角大于任何一个和它不相邻的内角.(注:※表示重点局部;表示了解局部;◎表示仅供参阅局部;)小编为大家整理的初二年级数学知识点:数据的搜集与处置相关内容大家一定要牢记,以便不时提高自己的数学效果,祝大家学习愉快!。
八年级数学数据的收集知识点

八年级数学数据的收集知识点
收集数据的知识点可以涉及以下内容:
1. 数据的来源和类型:了解数据的来源,例如调查、实验、观察等,还要了解数据的
类型,包括定量数据和定性数据。
2. 数据的收集方法:学习如何进行数据的收集,包括设计问卷、制定调查计划、进行
实验、记录观察等方法。
3. 数据的整理和编码:学习如何整理和编码收集到的数据,以便于后续的数据分析和
处理。
4. 数据的展示形式:学习如何使用图表、图像等形式展示数据,包括直方图、折线图、饼图等。
5. 数据的分析与解读:学习如何通过统计分析方法对收集到的数据进行分析,包括计
算平均数、中位数、众数等,以及计算数据的变异程度。
6. 数据的有效性评估:学习如何评估收集到的数据的有效性和可靠性,包括了解样本
的代表性、调查方法的误差等。
7. 数据的应用:学习如何将数据应用到实际问题中,包括进行预测、做出决策等。
以上是八年级数学中关于数据收集的一些基础知识点,希望能对你有所帮助。
14.第十三讲数据的收集与处理(八下教)

数据的收集与处理知识网络:一、概念:1、普查:为了一定目的而对考察对象进行的全面调查,称为普查.2、总体:其中所要考察对象的全体称为总体。
3、个体:组成总体的每个考察对象称为个体。
注意:总体与个体中的考察对象是指一种数量指标。
4、抽样调查:从总体中抽取部分个体进行调查,这种调查称为抽样调查。
5、样本:其中从总体中抽取的一部分个体叫做总体的一个样本。
6、样本容量:样本中个体的数目。
注意:样本容量没有单位。
注意:1)(1)当总体中个体数目较少时;(2)当要研究的问题要求情况真实、准确性较高时;(3)调查工作较方便,没有破坏性等等,此时用普查方式获得数据较好。
2)(1)总体中个体数目较多,普查的工作量大;(2)受客观条件限制,无法对所有个体进行调查;(3)调查具有破坏性时,采用抽样调查方式较好。
3)在统计里,之所以用样本的情况估计总体的情况,是基于两点:(一)是在很多情况下总体包含的个体数往往很多,甚至无限,不可能一一加以考察;(二)是有些从总体中抽取个体的试验带有破坏性(例如灯泡使用寿命试验),因而抽取的个体不允许太多。
二、数据的收集:1、抽取的样本:1)必须有较强的代表性:每个部分都应抽取到,而且应注意各部分的比例;2)必须有广泛性:是指总体中的每个个体均有被选的可能。
注意:1)抽样调查时注意:(1)样本的大小;(2)样本的代表性;(3)样本的广泛性。
.使所抽取的样本尽可能准确地反映总体的真实情况。
2)抽样方法:(1)随机抽样(2)系统抽样(3)分层抽样2、随机调查:就是按机会均等的原则进行调查,亦即总体中每个个体被调查的概率都相同。
三、频数与频率1、频数:每个对象出现的次数。
2、频率:每个对象出现的次数与总次数的比值。
注意:各对象的频率和为13、频数分布直方图4、整理数据时,可以按照下面的步骤进行:1)计算最大值与最小值的差;2)决定组距与组数;3)决定分点。
(通常分点数末尾数字减小半个单位。
)注意:确定组距与组数方法:先定组距,再由数据个数除以组距,再确定组数(收尾法)。
八年级数学暑假专题辅导 数据的收集和处理

暑假专题——数据的收集与处理知识要点: 1. 调查方式(1)普查(具有获取数据相对准确的优点)(2)抽样调查(具有节省时间,人力、物力和财力的特点) 2. 抽样调查要注意样本的代表性和广泛性 3. 频数:考察中每个对象出现的次数。
4.频率频数总数=5. 频数分布直方图(频率分布直方图)能非常直观的表示数据的分布情况。
6. 极差:最大值和最小值的差。
7. 方差(标准差)反映数据的波动情况(稳定性,离散程度等)()()()[]S nx x x x x x n 2122221=-+-++-……【典型例题】 例1. 填空题:(1)为了了解你们班同学所穿鞋子的尺码,可对全班同学采用哪种调查方式?______________。
答案:普查(2)为了了解你所在地区老年人的健康状况,你采用哪种调查方式? ______________。
答案:抽样调查(3)了解我国初中学生的视力情况,你认为采用什么调查方式更合适? ______________。
答案:抽样调查(4)一所中学的数学研究小组的10位教师的年龄分别是:55,40,40,48,36,36,37,25,33,40。
这10名教师年龄的平均数是__________,众数是__________,中位数是__________,最大值是__________,最小值是__________,极差是__________。
答案:39,40,38.5,55,25,30分析:()x =+++++++++=1105540404836363725334039(岁)排序为:25,33,36,36,37,40,40,40,48,5537402385+=.(岁)552530-=(岁)(5)甲、乙两名射击运动员各连续射靶8次,命中的环数如下:甲:8,9,10,9,8,7,9,10;乙:9,8,8,9,10,9,8,9如果你是教练,你认为谁的成绩更稳定?____________。
答案:乙分析:甲的极差10-7=3乙的极差10-8=2例2. 选择题:(1)甲、乙两支仪仗队队员的身高如下:甲队:178,177,179,179,178,178,177,178,179;乙队:178,179,176,178,180,180,178,176,178。
八年级数学数据的收集与处理 优质课件

例2.根据下表制作扇形统计图,表示各大洲陆地面 积的百分比。
世界七大洲陆地面积
问: (1)图中各扇形分别代表什么?全世界有几个洲? (2)哪个洲陆地面积最大? (3)哪两个洲面积较大?哪两个洲面积较小?百分比之 和分别是多少? (4)所有百分比之和是多少? (5)你能从统计图中知道陆地总面积吗?
一、复习指导: 复习中应着重注意以下几点: 1.体会数据在现实生活中的作用。熟悉收集、
整理、描述和分析数据的活动过程,理解 频数、频率。 2.根据统计图中提供的信息作出合理判断, 根据数据特点选择制作适当的统计图,来 表示数据。 3.通过实验体会有些事情发生是不确定的, 不确定事情发生的可能性是有大小的。
出去,不在机内停留。而传统非自洁式净水机等于在房间内搁置了多个垃圾桶,污物平常暂存于机内,故需要定期排污、拆洗和频繁更换
滤芯。
都没有,看来他们年家壹门还是心系八弟,根本对自己这个新门主无动于衷,似乎还在向自己示威:别看我们年家被划入了你雍亲王的门 下,但我心匪石,不可转也!壹想到这里,那壹股壹股的寒意不知不觉地吞噬着他的心。但是,每当看到娇美的李淑清,抱着目前王府中 唯壹的阿哥--弘时的时候,他的心又突然没来由地柔软了下来。没有那个玉盈姑娘,自己现在还看得到时儿吗?晖儿、钧儿、盼儿,三 个阿哥都是小小年纪就离开了人世。现在,如果时儿再有任何闪失,该是多么沉重的打击!没有子嗣,就没有了夺嫡的筹码,所有的壹切 全都是空谈。虽然玉盈姑娘已经说过,大恩不言谢,可是作为堂堂雍亲王,自然不能无故承受了对方的恩情,作为壹个爱憎分明的人,这 是绝对不能允许的。而且,他也根本不甘心被壹个自己的门人拒绝,这让他感觉非常有失颜面。时光如梭,转眼就进了腊月,距离宝光寺 火灾已经过去三个多月。从天高水长的秋日到寒风凛冽的隆冬,王爷等了整整有壹百天,可是这个玉盈姑娘,仍然还是壹点儿消息也没有, 她怎么这么沉得住气?第壹卷 第十章 腊八 今天是腊月初八,腊八节。相传这壹天是佛教创始人释迦牟尼在佛陀耶菩提下成道并创立佛 教的日子,因此又被称为“佛成道节”。这壹天,也是人们祭祀祖先和神灵,祈求丰收和吉祥的节日。同时,自宋代以来,无论皇家、朝 廷、官府、寺院还是黎民百姓,都有腊八节喝腊八粥的传统习俗,已经沿续了好几百年。特别是寺院,为祭祀释迦牟尼成道之日,都要在 这壹天诵经祷告,煮粥敬佛,同时,还要施粥给百姓,以示佛祖慈悲。王爷自宫中领了圣上赏粥,又接了各宫娘娘的赏粥,还要顾着自己 负责的户部的腊八赏粥事宜,壹天下来,忙得脚不沾地。可是,他仍是不由自主地想起了宝光寺,自己多年在寺里谈经听禅,前些日子又 遇宝光寺遭难,总觉得放不下心。特别是今天,腊八施粥是寺院的传统,不知道遭遇灭顶之灾的宝光寺是否还能应对得下来。本来想差了 府里的管事儿,或是贴身太监秦顺儿去照看壹趟,但冥冥中,总有壹个要亲自去壹趟的念头,挥之不去。看看天色也不早了,但也就是壹 瞬间,他立即决定了,跃马上前,直奔西南郊。再次来到宝光寺,看到灾后尚未恢复的惨状,他的心中百感交集,直恼恨自己为什么没有 提前想到这些事情,提前给寺里做些安置和照应。然而进得大殿前院,就在那破破烂烂的半截子工程前,却是壹派井然有序的施粥景象, 队伍有条不紊。特别是施粥的人员中居然有许多家仆,而非僧人,直让他诧异不已。刚壹愣神儿的功夫,住持大师就接了通报赶快迎了出 来:“恕老纳不知王爷前来,没有提前准备……”王爷直接打断了住持的话,问
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021年八年级数学暑假专题辅导 数据的收集与处理知识要点: 1. 调查方式(1)普查(具有获取数据相对准确的优点)(2)抽样调查(具有节省时间,人力、物力和财力的特点) 2. 抽样调查要注意样本的代表性和广泛性 3. 频数:考察中每个对象出现的次数。
5. 频数分布直方图(频率分布直方图)能非常直观的表示数据的分布情况。
6. 极差:最大值和最小值的差。
7. 方差(标准差)反映数据的波动情况(稳定性,离散程度等)()()()[]S nx x x x x x n 2122221=-+-++-……【典型例题】 例1. 填空题:(1)为了了解你们班同学所穿鞋子的尺码,可对全班同学采用哪种调查方式? ______________。
答案:普查(2)为了了解你所在地区老年人的健康状况,你采用哪种调查方式? ______________。
答案:抽样调查(3)了解我国初中学生的视力情况,你认为采用什么调查方式更合适? ______________。
答案:抽样调查(4)一所中学的数学研究小组的10位教师的年龄分别是:55,40,40,48,36,36,37,25,33,40。
这10名教师年龄的平均数是__________,众数是__________,中位数是__________,最大值是__________,最小值是__________,极差是__________。
答案:39,40,38.5,55,25,30分析:()x =+++++++++=1105540404836363725334039(岁)排序为:25,33,36,36,37,40,40,40,48,55(5)甲、乙两名射击运动员各连续射靶8次,命中的环数如下: 甲:8,9,10,9,8,7,9,10; 乙:9,8,8,9,10,9,8,9如果你是教练,你认为谁的成绩更稳定?____________。
答案:乙分析:甲的极差10-7=3 乙的极差10-8=2例2. 选择题:(1)甲、乙两支仪仗队队员的身高如下:甲队:178,177,179,179,178,178,177,178,179; 乙队:178,179,176,178,180,180,178,176,178。
要考察哪支仪仗队更为整齐,我们可以使用两支仪仗队队员身高的( ) A. 平均数 B. 众数C. 中位数D. 方差答案:D(2)下面是今年与前年在大致相同条件下饲养的10头猪的体长数据(单位:厘米): 前年:112,110,110,117,113,122,125,124,119,127; 今年:111,122,115,123,114,115,118,114,116,115。
则饲养的10头猪的体长比较一致的是( ) A. 前年 B. 今年 C. 一样 D. 无法判断 答案:B分析:前年的极差:127-110=17 今年的极差:123-111=12(3)小颖统计了最近一个星期王奶奶平均每天能卖出的A 、B 、C 、D 、E 五个牌子雪糕的数量,并绘制出频数分布直方图,则A 种雪糕的频数与频率分别为( )A B ..131131*********150,,C D ..131131518131131,,答案:C分析:131+182+68+39+98=518例3. 解答题:()已知,,……的平均数为,方差为,你能分析下列几组数1122x x x x S n 据的平均数与方差吗?并总结你的发现! ①,,……,x x x n 12222+++ ②,,……,x x x n 12111--- ③,,……,33312x x x n④,,……,12121212x x x n解析:()x n x x x n ①……=++++++122212()()=++++=++++=+121221212n x x x n n x x x x n n …………()()[]()()[]()()[]{}S n x x x x x x n ① (212222)1222222=+-+++-++++-+()()()[]=-+-++-=1122222n x x x x x x S n … ∴+数据①的平均数是,方差仍是x S 22②同理可验证数据②的平均数是,方差仍是x S -12()③……③x nx x x n =+++133312 ()=⨯+++=31312n x x x x n …… ()()()[]S n x x x x x x n ③ (212222)1333333=-+-++- ()()()[]()()()[]=-+-++-=⨯-+-++-=199991912222122222n x x x x x x n x x x x x x S n n …………∴数据③的平均数是,方差是392x S④同理可验证数据④的平均数是,方差是12142x S由上可得:平均数随数据的变化而变化,与每个数据的变化完全相同。
方差不一定随数据的变化而变化,当数据进行加减变化时方差不变,当数据进行乘除变化时,方差成平方倍变化。
(2)为了考察甲、乙两种小麦的长势,分别从中抽取了10株苗,测得苗高如下(单位:厘米):甲:12,13,14,15,10,16,13,11,15,11 乙:11,16,17,14,13,19,6,8,10,16 ①分别计算两种小麦的平均苗高; ②哪种小麦的10株苗高比较整齐? 解析:()()()()[]②甲S 22222222221101012330222=-++++-+++-++-()()()()[]S 乙222222222221102341067533=-++++++-+-+-+∴甲整齐(3)某部门统计了上海1000名高三男生的身高,得到如下数据,将这些数据绘制成频数分布直方图和折线图。
身高频数~~~~~~~~~/cm <>1506150155251551606416016513016517020117017521817518018018018511018519049190195141953解析:【模拟试题】时间:45分钟,满分100分一. 填空题(每空3分,共36分)1. 为了了解某校小学生的体能情况,对该校一个年级的部分学生进行一分钟跳绳次数测试,这个问题中,总体是_____________,个体是_____________,样本是_____________。
2. 某班50名学生在一次数学考试中,分数在90~100分的频率是0.16,则该班在这个分数段的人数是_____________。
3. 一组数1,2,3,4,5的方差是_____________则这组学生成绩的中位数是_____________。
5. 极差是刻画数据_____________的一个统计量。
6. 某班第二组男生参加体育测试,引体向上成绩(单位:个)如下:6,9,11,13,11,7,10,8,12,则这组成绩的众数是_____________,中位数是_____________。
那么该班共有__________人,得分在27~30分之间人数的频率是__________,从上表中,你能获取的信息是____________________(写出一个即可)。
二. 选择题(每题2分,共10分)8. 今年我市共有8万名初中毕业生参加升学考试,为了了解这8万名考生的数学成绩,从中抽取了xx名考生的数学成绩进行统计分析,以下说法中正确的是()A. 8万名考生是总体B. 每名考生的数学成绩是个体C. xx名考生是总体的一个样本D. 以上都不对9. 下列说法正确的是()A. 数据3,4,4,5的众数是2B. 数据2,3,5,4,6的中位数是5C. 数据5,3,7,8,2的平均数是5D. 频率分布直方图中,各小长方形的面积和等于数据总数10. 甲、乙两人在同样的条件下练习射击,每人打5发子弹,命中环数如下:甲:6,8,9,9,8;乙:10,7,7,7,9。
则两人射击成绩稳定程度关系是()A. 甲比乙稳定B. 乙比甲稳定C. 甲、乙稳定程度相同D. 无法比较11. 某同学抛掷硬币50次,得到的结果制作统计图如图所示,则这50次抛硬币中,正面朝上的频率是()A. 0.44B. 0.56C. 0.22D. 0.2812. 甲、乙两班举行电脑汉字输入速度的比赛,参赛学生每分钟输入汉字的个数经统计计某同学根据此表分析得出如下结论:(1)甲、乙两班学生成绩的平均水平相同;(2)乙班优秀人数多于甲班优秀人数(每分钟输入汉字≥150个为优秀);(3)甲班成绩的波动情况比乙班成绩的波动大。
上述结论中正确的是()A. (1)(2)(3)B. (1)(2)C. (1)(3)D. (2)(3)三. 解答题(第13,14题每题8分,第15,16题每题9分,第17,18题每题10分,共54分)13. 下列调查各属于哪种调查方式?把答案写在后面的括号内。
(1)为了了解八年级学生的视力情况,在该年级中抽取了100名学生进行视力检查测试;()(2)为了调查学校的男女生比例,调查统计了各班男、女生人数;()(3)为了考察同一型号的一批炮弹的杀伤半径,从中任意抽取210枚进行调查分析。
()14. 下列抽样调查中,结果能否较准确地反映总体的情况,为什么?(1)某商场为了了解10月份的营业情况,从10月2日开始连续调查了5天的营业情况;(2)某公司为了了解自己产品的普及率,在市区某火车站对100名流动人员进行调查分析。
15. 未成年人思想道德建设越来越受到社会的关注。
某青少年研究所随机调查了该市某校100名学生寒假中所花零花钱的钱数(钱数取整元数),以便引导学生树立正确的消费观。
(1)补全频率分布表;(2)在频率分布直方图中,长方形ABCD的面积是__________,这次调查的样本容量是__________;(3)研究所认为,应对消费150元以上的学生提出勤俭节约的建议。
试估计应对该校1000名学生中约多少名学生提出这项建议?16. 为了预测4月份电费开支,小红在月初连续8天(每天早上)抄下了电表上的读数(如17. 一台机床生产直径是40 mm的零件,为检验机床质量,从产品中抽出10件进行测量,每件产品与标准零件的偏差如下(单位:毫米):........----002010201002020202,,,,,,,,,(1)计算这10件零件直径长度的方差。
(2)若10件零件直径长度数据的标准差不能超过0.1mm,否则该机床不合格,试判断该机床是否合格。
18. 某车站在春运期间为改进服务,随机抽样调查了100名游客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位为分钟)。
下面是这次调查统计分析得到的频率分布表和频率分布直方图。
解答下列问题:(1)这次抽样的样本容量是多少?(2)在表中填写出缺失的数据并补全频率分布直方图;(3)旅客购票用时的平均数可能落在哪一小组?(4)若每增加一个购票窗口可以使平均购票用时降低5分钟,要使平均购票用时不超过10分钟,那么请你估计最少需增加几个窗口?【试题答案】一. 填空题。
