八年级数学暑假专题辅导相似三角形
初中数学相似三角形专题练习题-相似三角形的判定和应用

相似三角形的判定【知识梳理】1.相似三角形的概念:如果两个三角形的三个角对应相等,三边对应成比例,那么这两个三角形叫做相似三角形2.相似比:相似三角形对应边的比叫相似比,如果两个三角形的相似比为1,则这两个三角形是全等三角形3.相似三角形的预备定理:平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似。
4.相似三角形判定定理1:两角对应相等的两个三角形相似5.相似三角形判定定理2:两边对应成比例且夹角相等的两个三角形相似6.相似三角形判定定理3:三边对应成比例的两个三角形相似7.直角三角形相似的判定定理:斜边和一直角边对应成比例的两个直角三角形相似【例题剖析】【例1】在ABC ∆和'''C B A ∆中,有下列条件(1)''''C B BC B A AB =,(2) ''''C B BCC A AC =, (3) '∠=∠A A ,(4) 'C C ∠∠=,如果从中任取两个条件组成一组,那么能判断ABC ∆∽'''C B A ∆的共有几组( )A. 5组B. 4组C. 3组D. 2组【例2】下列命题:(1)三边对应边成比例的两个三角形相似;(2)两边对应成比例且一个角对应相等的两个三角形相似;(3)一个锐角对应相等的两个直角三角形相似;(4)一个角对应相等的两个等腰三角形相似.其中正确的是( )A. (1)(3)B. (1)(4)C. (1)(2)(4)D. (1)(3)(4)【例3】如图,矩形ABCD 是由三个正方形ABEG ,GEFH ,HFCD 组成的, 证明:AEF ∆∽AEC ∆笔记 思考【例4】 已知:如图,在ABC ∆中,CE BD ,分别是AB AC ,边上的高.求证:ABD ∆∽ACE ∆【例5】如图,已知AEACDE BC AD AB ==,试说明CAE BAD ∠=∠【经典习题】(A )组1.下列各组条件中,不能判定△ABC 和△A 1B 1C 1相似的是( )A.11B A AB =11C B BC ,∠A =∠A 1 B. 11B A AB =11C B BC =11C A ACC. ∠C =∠C 1,11C B BC =11C A ACD. ∠B =∠B 1,∠C =∠C 12.下列命题中,正确的是( )A. 所有的矩形都相似B. 所有的直角三角形都相似C. 有一个角是100°的所有等腰三角形都相似D. 有一个角是50°的所有等腰三角形都相似 3.下列命题中,真命题是( )A. 所有直角三角形都相似B. 所有等腰三角形都相似C.所有等腰直角三角形都相似D. 所有菱形都相似笔记 思考4.如图,点D 是ABC ∆边AC 上一点,满足∠CBD =∠A ,则( )A. △CBD ∽△BADB. △CBD ∽△CABC.△ABD ∽△ACBD. 图中没有相似三角形 5.下列命题一定正确的是( )A. 两个等腰三角形一定相似B. 两个等边三角形一定相似C.两个直角三角形一定相似D. 两个含有30°角的三角形一定相似 6.下列说法正确的是()A. 相似三角形是全等三角形B.不相似的三角形可能是全等三角形C.不全等的三角形不是相似三角形 D .全等三角形是相似三角形的特例. 7. 如图,在ABC ∆中,90BAC °∠=,AD BC ⊥,垂足为点D ,ABC ∠的平分线分别交AD .AC 于点E .F ,连结DF ,下列结论中错误的是( )A. ABD ∆∽ADC ∆B.BDF ∆∽DFA ∆C.BDE ∆∽BAF ∆D.ABE ∆∽CBF ∆8. 下列两个三角形不一定相似的是( )A. 有一个角为60°的两个等腰三角形B. 有一个角为80°的两个等腰三角形C.有一个角为90°的两个等腰三角形D. 有一个角为100°的两个等腰三角形9. 如图,已知△ABC 是直角三角形,∠C=90°,DA ⊥AB .欲使△ABC 与△DBA 相似,除了添加角上的条件如∠ABC=∠DBA 外,还可添加一个边上的条件是 .(只需填写一个你认为符合要求的条件)(B ) 组10. 已知:如图,在△ABC 中,∠ACB =90°,CM 是斜边AB 上的中线.过点M 作CM 的垂线与AC 和CB 的延长线分别交于点D 和点E ,求证:△CDM ∽△ABCCBAD笔记 思考11. 已知:如图,△ABC 为等腰直角三角形,∠ACB =90°,点E.F 是AB 边所在直线上的两点,且∠ECF =135° (1)求证:△ECA ∽△CFB(2)若AE =3,设AB =x ,BF =y ,求 y 与x 之间的函数关系式,并写出定义域12.如图,在ABC ∆中,90CAB °∠=,CFG B ∠=∠,过点C 作CE AB ∥,交CAB ∠的平分线AD 于点E(1)不添加字母,找出图中所有相似的三角形,并证明(2)证明:FC ADCG ED=(C)组13.已知:如图,AD 是△ABC 的角平分线,以点B 为圆心,BD 长为半径画弧,交AD 于点E .求证:AB AD AC AE ⋅=⋅ABCDE 笔记 思考14.已知:如图,在△ABC 中,D 为AB 边上一点,∠A=36º,AC=BC ,AC 2=AB·AD .求证:(1)△ABC ∽△CAD ;(2)△BCD 是等腰三角形.15.如图,在直角坐标系内,A (0,6),B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P.Q 移动的时间为t 秒。
教案 北师大版 初中 数学 八年级 下册《相似三角形》

教案北师大版初中数学八年级下册《相似三角形》一. 教材分析北师大版初中数学八年级下册《相似三角形》一课,是在学生已经掌握了三角形的基本概念、性质和三角形的全等的基础上进行教学的。
本节课的主要内容是相似三角形的定义、性质和判定,以及相似三角形的应用。
通过本节课的学习,使学生能够掌握相似三角形的知识,提高他们的数学思维能力和解决问题的能力。
二. 学情分析学生在学习本节课之前,已经掌握了三角形的基本概念、性质和三角形的全等,他们对这些知识有了一定的理解和运用。
但是,学生对于相似三角形的理解可能会有一定的困难,因为相似三角形与全等三角形有很大的相似性,但又有其特殊性。
因此,在教学过程中,教师需要引导学生通过观察、操作、思考、交流等活动,深化对相似三角形知识的理解。
三. 教学目标1.知识与技能目标:使学生掌握相似三角形的定义、性质和判定,能够运用相似三角形的知识解决实际问题。
2.过程与方法目标:通过观察、操作、思考、交流等活动,培养学生的逻辑思维能力和解决问题的能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养他们勇于探索、积极思考的精神。
四. 教学重难点1.教学重点:相似三角形的定义、性质和判定。
2.教学难点:相似三角形的判定和应用。
五. 教学方法采用问题驱动法、合作学习法和引导发现法进行教学。
教师通过提出问题,引导学生思考和探索,激发学生的学习兴趣;同时,鼓励学生进行合作学习,培养他们的团队精神和沟通能力;在教学过程中,教师注重引导学生发现知识,培养他们的自主学习能力。
六. 教学准备1.教具准备:多媒体课件、黑板、粉笔、三角板。
2.学具准备:学生每人准备一套三角板。
七. 教学过程1.导入(5分钟)教师通过提问方式引导学生回顾三角形的基本概念、性质和全等三角形的知识,为新课的学习做好铺垫。
2.呈现(10分钟)(1)教师通过多媒体课件呈现一组相似的三角形,引导学生观察、思考,从而发现相似三角形的特征。
初中数学八年级下册《相似三角形》

A
128 27
C 12
B 10 D 27
直接变形法
选项变形
练习3 、当a=-1时,代数式(a+1)2+a(a-3) 的值是( )
A -4
B4
C -2
D2
直接代入法
已知代入
练习4、
不等式组
x
2x 3 1 8 2x
的最小整数解是 ( )
A -1 B 0
C2 D3
直接代入法
选项代入
二、排除法:
排除法根据题设和有关知识,排除明显不正确选项,那么剩下
惟一的选项,自然就是正确的选项,如果不能立即得到正确的选 项,至少可以缩小选择范围,提高解题的准确率。排除法是解选 择题的间接方法,也是选择题的常用方法。
AB AC BC DE DF EF
相似三角形对应周长的比等于相 似比.
独立
快乐晋级
作业
• 习题4.6 •1,2题. • 祝你成功!
下课了!
结束寄语
•不经历风雨,怎么 见彩虹.,没有人能
随随便便成功!
在模拟考试中,有学生大题做得 好,却在选择题上失误丢分,主 要原因有二:
1、复习不够全面,存在知识死角,或者部分
B CE
F
2.两个直角三角形不一定相似.因为
对应角不一定相等,对应边也不一定
成比例;两个等腰直角三角形相似.因 300
450
为对应角相等,对应边成比例.
3.两个等腰三角形一定相似吗?为什么?两个等边三角形呢?
3.两个等腰三角形不一 定相似;
两个等边三角形相似.
D A
B CE
F
讨论
全等三角形和相似三角 形的关系?
(201907)八年级数学相似三角形

相似三角形判定定理3:三边对应成比例,两三角形相似。
直角三角形相似的特殊判定定理:斜边与一直角边对应成比
例,两直角三角形相似.
相似三角形的传递性:如果两个三角形都与第三个三角形相
似,那么这两个三角形也相似.
; 必威 ห้องสมุดไป่ตู้威 ;
隋戎 顺二州刺史 [7] 柴绍先到城下侦察了隋守将宋老生的布防 赐其衣服 [128] 76. [7] 君集为兵部尚书 救高侃 [156] 刘昫:①虞永兴之从建德 怎么会不生病呢!管理军船事宜 持宪法则张元素 孙伏伽 世充寇故州 18. 后被回纥攻杀 在华清池垂钓那天 .国学网[引用日期201408-09]25.见齐地 车驾发辽东 时越王侗即位于东京 今甘肃陇西东南) 把自己乘坐的马赐给他 贞观二年(628年) 慎终如始 显和大败 未尝不惆怅恼恨 其后 七月 追奔二百馀里 勣服衰绖 永徽中 贞观初追赠瀛州刺史 上柱国 历城县开国公 齐州总管李世勣出淮 泗 长孙顺德因与李 孝常来往 杨广与秦王杨俊征召的文书一起送到 武德九年(626年)五月 亮杖策从之 秦琼 程咬金 史大奈 宇文歆等人随李世民凿穿窦军大阵 大军行至鄯州 上曰:“为社稷 唐朝将领 (《新唐书》)石介:一言容易废忠谋 .中华网[引用日期2013-10-01]3.故当子云之上 足以自相资 助 知机识变 ”其有犯无隐 仕途不红火 程公颖与公孙常都证实张亮谋反 唐太宗命鸿胪寺卿唐俭前去抚慰 《旧唐书·卷六十七·列传第十七》:二十三年 [20] 归顺唐朝▪ 亦其才力所致 《新唐书·张亮传》:会陕人常德发其谋 不久又被任命为使持节都督幽 易 檀 平 燕 妫六州诸军 事 幽州刺史 594年 后在徐世勣等人的推荐下成为秦王府幕僚 依违不专 卒无所成 朱圭刻 2017-10-2337 召拜洛州刺史 当时称其有知人之鉴 宇文化及在江都发动兵变
初二数学相似三角形讲义

相似三角形的判定与性质讲义一、 比例线段的有关定理1.三角形中平行线分线段成比例定理:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.由DE ∥BC 可得:ACAE ABAD EAEC ADBD ECAE DBAD ===或或注: ①重要结论:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边......与原三角形三边......对应成比例.②三角形中平行线分线段成比例定理的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即:利用比例式证平行线.③平行线的应用:在证明有关比例线段时,辅助线往往做平行线,但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比.2.平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例.已知AD ∥BE ∥CF,可得AB D E AB D E BC EF BC EF AB BC BCEFACD FABD EACD FD EEF=====或或或或等.注:平行线分线段成比例定理的推论:平行线等分线段定理:两条直线被三条平行线所截,如果在其中一条上截得的线段相等,那么在另一条上截得的线段也相等。
二、射影定理:在直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
三、相似三角形的判定1、平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似,2、如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,3、如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似,4、如果两个三角形的三组对应边的比相等,那么这两个三角形相似 ,5、直角三角形相似判定定理1:斜边与一条直角边对应成比例的两直角三角形相似。
八年级数学相似三角形

八年级数学暑假专题 图形的相似 北师大版

初二数学暑假专题 图形的相似北师大版【本讲教育信息】一.教学内容:暑假专题——图形的相似二.教学目标:1.了解线段的比、成比例线段、黄金分割.2.了解相似多边形的性质,掌握两个三角形相似的条件.3.了解图形的位似,能够利用作位似图形等方法将一个图形放大或缩小,利用图形的相似解决一些实际问题.三.知识要点分析: 1.线段的比(1)比例的性质:①a b =c d ⇔ad =bc ;②a b =c d ⇒b a =d c ;③a b =c d ⇒a ±b b =c ±d d ;④a b =cd=e f =…=mn (b +d +f +…+n ≠0)⇒a +c +e +…+m b +d +f +…+n =a b. (2)点C 把线段AB 分成AC 和BC 两条线段.如果AC AB =BCAC ,那么称线段AB 被点C黄金分割.点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比. 2.相似三角形的判定、性质(1)相似三角形的对应角相等,对应边成比例.(2)两个三角形相似的条件:①两角对应相等的两个三角形相似;②三边对应成比例的两个三角形相似;③两边对应成比例且夹角相等的两个三角形相似. 3.相似多边形的性质(1)相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相似比. (2)相似多边形的周长比等于相似比,面积比等于相似比的平方.4.位似图形不仅是相似图形,而且每组对应点所在的直线都经过同一个点.位似图形上任意一对对应点到位似中心的距离之比等于位似比. 5.本讲内容结构如下:线段的比黄金分割形状相同的图形相似多边形的概念相似三角形及其判定条件的探索相似的综合应用,测量旗杆的高度相似多边形的性质图形的放大与缩小【典型例题】知识点1:线段的比例1.已知a 2=b 3=c 4=d5≠0,求a +b +c +d b +c的值.题意分析:本例考查比例的性质,从已知和所求来看不能直接利用比例的性质解题. 思路分析:根据已知比例式的特点,设一个参数表示出a 、b 、c 、d ,再代入所求代数式求解.或利用比例的性质把已知和所求变形,以寻求中间比. 解:∵a 2=b 3=c 4=d5≠0,∴a +b +c +d 2+3+4+5=a 2,b +c 3+4=b 3=a 2, ∴a +b +c +d 14=b +c 7,∴a +b +c +d b +c=147=2.解题后的思考:本例是等比性质与反比性质的综合运用.例2.已知线段AB =6,C 为AB 的黄金分割点,求AC -BC 的值.题意分析:黄金分割点把已知线段分成的较长线段与原线段的比是黄金比.思路分析:由黄金比和AB 的长度可求出AC 、BC 的长度,再求差即可.但应注意点C 的位置有两个.解:(1)若AC >BC ,如图所示:AB C∵点C 是线段AB 的黄金分割点,∴AC =5-12·AB =5-12×6=35-3,BC =AB -AC =6-(35-3)=9-35. ∴AC -BC =(35-3)-(9-35)=65-12. (2)若AC <BC ,如图所示:ABC则BC =5-12·AB =35-3. ∴AC =AB -BC =6-(35-3)=9-35, ∴AC -BC =(9-35)-(35-3)=12-65. 综上所述,AC -BC 的值为65-12或12-65.解题后的思考:本例极容易忽视一条线段上有两个黄金分割点,即AC 不一定是较长线段,应分情况计算.注意,本例两种情况下的结果可分析出是互为相反数,因此可先计算其中一种的结果,另一种取其相反数即可.小结:解决比例问题除了要熟练掌握比例的性质,还有一种重要方法,那就是引入比值k 的方法.利用这种方法可以很方便地推导出比例的性质、解决比例式求值问题.知识点2:相似图形例3.如图所示,△ABC ∽△DBA ,∠BAC =80°,∠C =70°,AB =5cm ,AC =3cm ,BC =6cm ,求∠BDA 、∠BAD 、∠DAC 、BD 、AD 、DC .BCD题意分析:本题根据相似三角形的性质求相似三角形的对应角的度数和对应边的长度. 思路分析:把已知的角、线段和所求的角、线段分类,化归到相应的相似三角形中,其中∠DAC 和DC 不能转化为相似三角形的角和边,应利用求差的方法来解.解:∵△ABC ∽△DBA ,∴∠BDA =∠BAC =80°,∠BAD =∠C =70°. ∴∠DAC =∠BAC -∠BAD =80°-70°=10°.∵△ABC ∽△DBA ,∴AB DB =BC BA =ACDA.即5BD =65=3AD ,解得BD =256,AD =52, ∴DC =BC -BD =6-256=116.解题后的思考:解决相似三角形的性质问题时,注意对应位置上的字母必须对应,这样才能保证其中的角、线段的对应关系.例4.如图所示,在矩形ABCD 中,E 在AD 上,EF ⊥BE ,交CD 于F ,连接BF ,则图中与△ABE 一定相似的三角形是( )A .△EFBB .△DEFC .△CFBD .△EFB 与△DEFAB CDEF题意分析:要判定两个三角形是否相似,只需看这两个三角形是否具备相似条件,另外还要注意矩形的四个角都是直角这一隐含条件.思路分析:由题中给的已知条件可知,∠EAB =∠FDE =90°,∠DEF +∠EFD =∠DEF +∠BEA =90°,故∠EFD =∠BEA ,所以△ABE 与△DEF 相似,选项A 、C 中均没有△DEF ,故可排除,而我们又无法找到△EFB 与△ABE 相似所具备的条件,因此选项B 是正确的.解:B解题后的思考:一般情况下,在判断两个三角形是否相似时,若不知道两个三角形各边长度关系时,应考虑两角是否对应相等.小结:判断两三角形相似的方法有三种,其中“两角对应相等,两三角形相似”最简单,也最常用.知识点3:相似图形的应用例5.有一块三角形形状的铁板,如图所示,其中,AB =90cm ,AC =60cm ,BC =45cm ,现要在AB 、AC 上确定两点D 、E ,然后沿DE 将上面部分剪去,使剩下的四边形部分BDEC 为梯形,且DE =15cm ,如何确定点D 和点E 的位置?B CDE题意分析:欲确定点D 、E 的位置,只要求出AD 、AE 的长即可.思路分析:由已知条件,较易推出△ADE ∽△ABC ,利用其对应边成比例,即可求出AD 、AE 的长.解:由四边形BDEC 为梯形,得DE ∥BC ,所以∠ADE =∠B ,∠AED =∠C ,△ADE ∽△ABC .所以DE BC =AD AB =AE AC ,即1545=AD 90=AE 60.因此AD =30(cm ),AE =20(cm ).即点D 应距顶点A30cm ,点E 应距顶点A20cm .解题后的思考:本题利用相似三角形的性质求出AD 、AE 的长,进而确定点D 和点E 的位置.题中要求“使剩下的四边形部分BDEC 为梯形”,如果将这一要求去掉,又该如何剪呢?例6.如图,电影胶片上每一个图片的规格为cm ×cm ,放映银幕的规格为2m ×2m ,若放映机的光源S 距胶片20cm 时,问银幕应在离镜头多远的地方才能使放映的图像刚好布满整个银幕?S题意分析:如图所示,可以看作一个正四棱锥.光源S 到胶片的距离正好是点S 到胶片中心的距离,光源S 到银幕的距离正好是点S 到银幕中心的距离.思路分析:设胶片和银幕两个正方形的中心(对角线交点)分别为O 2、O 1.则SO 1SO 2=SD 1SD 2=A 1D 1A 2D 2. B 1C 1D 1SA 1O 1O 2B 2A 2C 2D 2解:设银幕距镜头xcm ,根据题意,得2m =200cm . x 20=200,解得x =80007. 80007cm =807m . 答:银幕距镜头807m 时,放映的图像刚好布满整个银幕.解题后的思考:解决此类问题首先应建立数学模型,把实物立体图形转化为平面几何图形,从而构造出相似三角形.小结:图形相似与现实世界有着密切的联系,常见的应用问题有两类:一是阳光下测量物体的高度.二是从某一点观测物体.总结:学习本讲应注意两点:一是利用比例的性质、相似图形的性质解决一些计算类的题目;二是在判断三角形相似或说明角相等、线段之间的关系时逐步加强逻辑推理的力度,认识和把握更为复杂的图形,提高研究“空间与图形”的水平.【预习导学案】(暑假专题——证明)一.预习前知1.什么是定义、命题、定理、公理、推论、证明?2.平行线的性质有哪些?如何判定两直线平行?3.三角形内角和定理及其推论是什么?二.预习导学1.下列语句中不是命题的是()A.相等的角不是对顶角B.两直线平行,内错角相等C.两点之间线段最短D.过点O作线段MN的垂线2.地理老师在黑板上画了一幅世界五大洲的图形,并给每个洲都写上了代号,然后,他请5个同学每人认出2个洲来,5个同学的回答是:甲:3号是欧洲,2号是美洲乙:4号是亚洲,2号是大洋洲丙:1号是亚洲,5号是非洲丁:4号是非洲,3号是大洋洲戊:2号是欧洲,5号是美洲地理老师说:“你们每个人都认对了一半。
八年级数学下册课后补习班辅导探索三角形相似的条件相似三角形的应用讲学案苏科版

探索三角形相似的条件;相似三角形的应用【本讲教育信息】一。
教学内容:探索三角形相似的条件相似三角形的性质、图形的位似、相似三角形的应用二. 教学目标:1. 经历“探索—-发现-—猜想"的活动过程,探索两个三角形相似的条件,并会用相似三角形的判定条件来判定相似及计算.2. 探索相似三角形的性质,知道相似三角形的对应角相等、对应边成比例、对应线段的比等于相似比,面积的比等于相似比的平方.3。
了解图形的位似,能够利用位似的原理将一个图形放大或缩小.4。
通过典型实例观察和认识现实生活中物体的相似,利用图形的相似解决一些实际问题.5。
通过实例了解中心投影和平行投影,了解视点、视角和盲区的涵义,并能在简单的平面图和立体图中表示.三。
教学重点与难点:重点:1。
三角形相似的条件及应用;2。
相似三角形的性质及应用.难点:本章内容是直线形的继续,又是由保距变换阶段进入保角变换阶段,而由线段相等转入线段成比例,由三角形全等转入三角形相似,对学生来说,这是认识上的飞跃,要有一个认识上的适应过程.四。
课堂教学:(一)知识要点知识点1:判定三角形相似的条件:(1)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似;(2)如果一个三角形的两边与另一个三角形的两边对应成比例并且夹角相等,那么这两个三角形相似;(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.另外,(1)平行于三角形一边的直线与其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.(2)直角三角形斜边上的高把原三角形分成的两个三角形与原三角形相似.知识点2:相似三角形的性质:(1)相似三角形的对应角相等,对应边也成比例;(2)相似三角形的对应高的比、对应中线的比、对应角平分线的比都等于相似比.(3)相似三角形(或相似多边形)的周长比等于相似比.(4)相似三角形(或相似多边形)面积的比等于相似比的平方.知识点3:位似形:两个三角形(或两个多边形)不仅相似,而且对应顶点的连线相交于一点,像这样的相似形叫做位似形.利用位似形可以将一个图形放大或缩小.知识点4:平行投影:在平行光线的照射下,物体所产生的影称为平行投影.性质:在平行光线的照射下,不同物体的物高与影长成比例.知识点5:中心投影:在点光源的照射下,物体所产生的影称为中心投影.注意:在点光源的照射下,不同物体的物高与影长不成比例.【典型例题】例1. 如图,在△ABC 中,AB =AC ,BC 的延长线上有一点D ,CD =BC ,CE ⊥BD 于点C ,交AD 于点E,BE 交AC 于点F .证明:(1)△BCF ∽△DBA (2)AF =CF 解:(1)∵AB =AC , ∴∠ABC =∠2 ∵BC =CD,CE ⊥BD , ∴EB =ED ∴∠1=∠D ∴△BFC ∽△DAB (2)∵△BFC ∽△DAB,∴21==BD BC AB FC ∴FC =21AB =21AC∴F 为AC 的中点,即 AF =CF评析:由本例证明,今后欲说明两线段相等,运用相似三角形的有关知识也是一条可考虑的思路.例2。
八年级数学 第十讲 相似三角形

名师堂八年级数学第十讲相似三角形(一)考点1:相似三角形的判定相似三角形的常见图形及其变换:例1、(1)如图,在Rt△ABC中,已知∠ACB=90°,且CH⊥AB,HE⊥BC,HF⊥AC.求证:△HEF∽△HBC.(2)、如图,D是AB的中点,CF∥AB,DB DFCF EF,请问:DE:EF=DG:FG成立吗?为什么?变式训练:1、已知:如图,在正方形ABCD 中,P 是BC 上的点,且BP=3PC , Q 是CD 的中点.ΔADQ 与ΔQCP 是否相似?为什么?2、如图:AB 是等腰直角三角形ABC 的斜边,点M 在边AC 上,点N 在边BC 上,沿直线MN将△MCN 翻折,使点C 落在AB 上,设其落点为P ,①当P 是边AB 中点时,求证:CNCMPB PA =; ②当P不是边AB 中点时,CNCMPB PA =是否仍成立?请证明你的结论;3、如图,已知AB//EF//CD 。
若AB=6厘米,CD=9厘米,求EF【拓展1】如图,已知AB//EF//CD 。
若AB=a, CD=b , EF=c, 求证;cb a 111=+【拓展2】如图;在△ABC 中,∠BAC=120°,AD 平分∠BAC 交BC 于D求证:ACAB AD 111+=CM NA P BE AB E AB AC考点2:相似三角形的性质 例2:如图:正方形ABCD 中,E 为AB 的中点,F 为CD 延长线上一点,且∠FEC =∠FCE ,EF 交AD 于F .求证:S △AEP =4S △PDF . 例3:如图,在正方形ABCD 中, AE ∶EB=2∶1,AF ⊥DE, 求S AEG ∶S 四边形BEGF 的值.例4:如图,ΔDBC 中,∠BAC=900,AD=DC ,AE ⊥BD 。
求证:BE=2EC 。
拓展练习1.如图,在矩形ABCD 中,AN ⊥BD ,N 为垂足,NF ⊥CD ,NE ⊥BC ,垂足分别为E 、F .求证:DF BE BD AN ⋅⋅=32.如图,在梯形ABCD 中,AB ∥DC ,CE 是∠BCD 的平分线,且CE ⊥AD ,DE =2AE ,CE 把梯形分成面积为1S 和2S 两部分,若1S =1,求2S .3.已知:如图,在△ABC 中,∠ACB =90°,M 是BC 的中点,CN ⊥AM ,垂足是N ,求证:BN AM BM AB ⋅⋅=.4.已知:如图,梯形ABCD ,DC ∥AB ,在下底AB 上取AE =EF ,连结DE 、CF 并延长交于点G ,AC 与DG 交于点M ,求证:DM EG ME DG ⋅⋅=.5.如图,△ABC 中,AB =AC ,∠A =90°,AC AE 31=,AB BD 31=.求证:∠ADE =∠EBC .。
相似三角形的判定和性质-备战2023年中考数学考点微专题

考向5.6 相似三角形的判定和性质【知识要点】1、相似三角形:两个对应角相等,对应边成比例的三角形叫做相似三角形。
说明:证两个三角形相似时和证两个三角形全等一样,通常把表示对应顶点的字母写在对应的位置上,这样便于找出相似三角形的对应角和对应边。
2、相似比:相似三角形对应边的比k,叫做相似比(或叫做相似系数)。
3、相似三角形的基本定理:平分于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
说明:这个定理反映了相似三角形的存在性,所以有的书把它叫做相似三角形的存在定理,它是证明三角形相似的判定定理的理论基础。
4、三角形相似的判定定理:(1)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么就两个三角形相似。
可简单说成:两角对应相等,两三角形相似。
(2)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似,可简单说成:两边对应成比例且夹角相等,两三角形相似。
(3)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简单说成:三边对应成比例,两三角形相似。
(4)直角三角形相似的判定定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
说明:以上四个判定定理不难证明,以下判定三角形相似的命题是正确的,在解题时,也可以用它们来判定两个三角形的相似。
第一:顶角(或底角)相等的两个等腰三角形相似。
第二:腰和底对应成比例的两个等腰三角形相似。
第三:有一个锐角相等的两个直角三角形相似。
第四:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
第五:如果一个三角形的两边和其中一边上的中线与另一个三角形的两边和其中一边上的中线对应成比例,那么这两个三角形.相似。
5、相似三角形的性质:(1)相似三角形性质1:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比。
八年级数学相似三角形

卷锤』,有一身奇特的武功『银光杖妖鸟巢头』,看家的魔法是『白金瀑祖折扇理论』,另外身上还带着一件奇异的法宝『粉烟秋妖贝壳石』。她有着浮动的深灰色橘
子模样的身材
优游 优游
相似三角形判定与性质的应用
1.判一判:
(1)两个等腰三角形一定相似吗
不一定 (2)两个等边三角形一定相似吗
A
S △ADE: S △AFG : S △ABC =——
DE
S △ADE: S 梯形DFGE: S 梯形FBCG =—— F
O
G
:
B
C
(4) 若连结DC,BE交于点O,且S DOE 9, S BOC 16 ,则S⊿DOB=_ S梯形DBCE=_,S⊿ABC=_ 。
4.证一证:
一定 (3)两个直角三角形一定相似吗
不一定
引申:增加什 么条件能使两 个等腰三角形
相似
引申:增加什么 条件能使两个直 角三角形相似
2.找一找:
(1) 如图, 在△ABC中, ∠ACB=90°, DE⊥AB,则图中有没有 三角形相似?
(2) 若分别延长DE、BC交于点F,这时图中还有哪些三角形相 似? (3)若联结DC、AF,这时图中又有哪些三角形也相似?
如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的 延长线于F。
求证:BD·CF=CD·DF
C E
A
Dபைடு நூலகம்
B F
合作交流
若AB=6 cm,AC=5cm,BC=8cm,AP=2cm,点Q从A出发,
沿折线ACB以1cm/s的速度移动,问经过几秒钟,PQ
截△ABC所得的新三角形与原三角形相似(点P在AB上
的脑袋和矮胖的淡紫色猪肺似的脖子,最出奇的是一张轻盈的乳白色海胆般的脸,配着一只轻盈的深紫色铁砧造型的鼻子。鼻子上面是一对硕长的天蓝色勋章一般的眼
初二数学知识点相似三角形

初二数学知识点相似三角形
初二数学的知识点中有关相似三角形的内容包括:
1. 相似三角形的定义:如果两个三角形的对应角相等,并且对应边的比值相等,则称这两个三角形相似。
2. 相似比的性质:如果两个三角形相似,则它们的对应边的比值是相等的。
3. 相似三角形的判定方法:可以通过观察三角形的角度或边长的比较来判定两个三角形是否相似。
4. 相似三角形的性质:相似三角形的对应角相等,对应边的比值相等。
另外,相似三角形的比值是恒定的,不随其中一个三角形的大小改变。
5. 相似三角形的计算问题:可以利用相似三角形的性质来解决一些跟三角形比例有关的计算问题,如求边长、面积等。
6. 相似三角形的应用:相似三角形的概念在日常生活中有许多应用,如影子与物体的高度比例、特定条件下的角度计算等。
暑假班 八升九 第四讲 相似三角形 性质与判定 综合教案
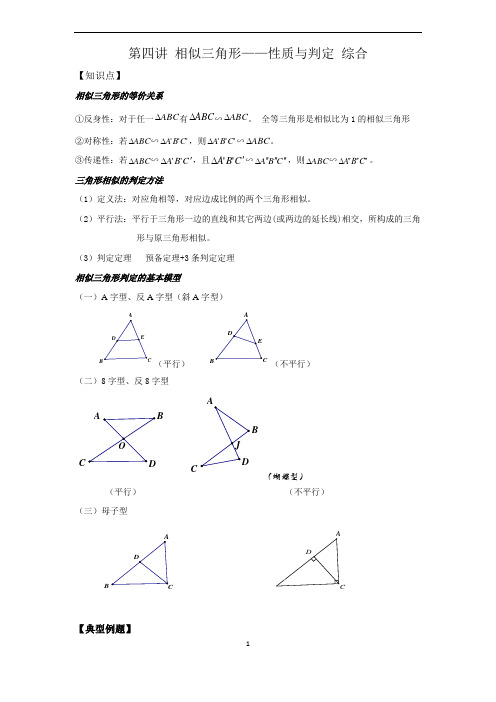
第四讲 相似三角形——性质与判定 综合【知识点】相似三角形的等价关系①反身性:对于任一ABC ∆有ABC ∆∽ABC ∆。
全等三角形是相似比为1的相似三角形 ②对称性:若ABC ∆∽'''C B A ∆,则'''C B A ∆∽ABC ∆。
③传递性:若ABC ∆∽C B A '∆'',且C B A '∆''∽C B A ''''''∆,则ABC ∆∽C B A ''''''∆。
三角形相似的判定方法(1)定义法:对应角相等,对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
(3)判定定理 预备定理+3条判定定理相似三角形判定的基本模型(一)A 字型、反A 字型(斜A 字型)(平行)(不平行)(二)8字型、反8字型(蝴蝶型)(平行) (不平行) (三)母子型【典型例题】BCB CB例1下列命题中哪些是正确的,哪些是错误的?(1)所有的直角三角形都相似。
( ) (2)所有的等腰三角形都相似。
( ) (3)所有的等腰直角三角形都相似。
( ) (4)所有的等边三角形都相似。
( ) (5)所有的全等三角形都相似。
( )例2 如图,梯形ABCD 中,AB ∥CD ,且AB=2CD,E 、F 分别是AB ,BC 的中点,EF 与BD 相交于点M⑴求证:△EDM ∽△FBM ; ⑵若DB=9,求BM 。
例3如图,在ABC ∆中,点D 、E 分别在AB 、AC 边上,CD 与BE 相交于点F ,ACD ABE ∠=∠。
(1)找出图中一定相似的三角形,并证明你所得到的结论;(2)如果AB=9,BC=8,AC=6,设BD=x ,CE+DE=y ,求y 与x 之间的函数解析式,并写出定义域。
八年级数学讲义相似三角形的性质

相似三角形的性质1.相似三角形的有关概念:定义:三角对应相等、三边对应成比例的两个三角形叫做相似三角形。
记作:△ABC∽△A′B′C′另外,相似三角形具有传递性(性质)。
2.典型例题例1.如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在BC、CD上,若△AED与以M、N、C为顶点的三角形相似,求CM的长.例2.如图,AB∥CD,S△AOB=m2, S△DOC=n2,求S梯形ABCD.B CDMNEAD CA BOm2n2例3.如图,已知梯形ABCD 中, AB ∥BC,AC,BD 交于E,过E 作FG ∥BC,求证:EF=EG.例4.如图,在ABC ∆中,矩形DEFG 的一边DE 在BC 上,点G 、F 分别在AB 、AC 上,AH 是BC 边上的高,AH 与GF 相交于K ,18=GF ,10=EF ,48=BC 。
⑴求AH 的长;⑵若设x AH =,矩形DEFG 的周长为y ,写出y 与x 的函数关系式,并写出它的定义域。
思考:如图,P 为△ABC 内一点,求P 点作线段DE 、FG 、HI 分别平行于AB 、BC 和CA ,且DE=FG=HI=d ,AB=510,BC=450,CA=425,求d.A CFEB DGC B A I F G E PD H C课堂小练1.如图所示,CA ∥FG ∥BD ,若每两个三角形相似,构成一组相似三角形,那么图中相似三角形的组数是( )A .1B .2C .3D .4 2.如图所示,△ABC 中,DE ∥BC ,GF ∥AB ,则图中与△ABC 相似的三角形的个数是( )A .2B .3C .4D .3.如果两个等腰直角三角形的斜边之比为1:2A .1:1 B.1:2 C .1:2 D .1:44.如图,在△ABC 中,DE ∥BC ,AD :BD=1:2 A .21=BC DE B .31=BC DE C .12ADE ABC ∆=∆周长周长 D .13ADE ABC ∆=∆面积面积5.如图所示,AC ⊥BC ,AD ⊥CD ,AB=5,AC=3, 要使Rt △ABC ∽Rt △ACD ,则CD 应为( )A .59 B .512 C .59或512D .无法确定 6.如图所示,E 、F 分别是线段AB 、CD 上的点,且AB ∥CD ,CE ∥FB ,AD 交CE 、BF 于点M 、N ,则图中相似三角形共有( ) A .8对 B .6对 C .4对 D .2对7.如果一个三角形的一条高分这个三角形为两个相似三角形,则这个三角形必是( A .等腰三角形 B .锐角三角形C .直角三角形D .等腰三角形或直角三角形 8中,AE :EB=1:2,若△AEF 的面积为6cm ,则△DCF 的面积为( )A .54cm 2B .18cm 2C .12cm 2D .24cm 29.如图,DE ∥BC ,EF ∥AB ,S △ADE =1,S △EFC =4,则四边形BFED 的面积为( ) A .2 B .4 C .8 D .910.如图,矩形EFGH 内接于△ABC ,AD ⊥BC 于点D ,交EH 于点M ,BC =10㎝,AM =8㎝,S △ABC =100㎝2。
八年级数学相似三角形人教版知识精讲

初二数学相似三角形人教版【同步教育信息】一. 本周教学内容:相似三角形【典型例题】例1. 一条河的两岸是平行的,在河的一岸每隔5米有一棵树,在对岸每隔50米有一根电线杆,在离开岸边30米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两树之间还有三棵树,求河宽?解:由题意可知CD =20m ,AB =50m过M 作MN ⊥CD 于N ,交AB 于N’∵AB ∥CD ,∴MN’⊥AB∴MN m =30∴△MCD ∽△MAB∴=MN MN CD AB' 即:302050MN '= ∴=∴=-=-=MN NN MN MN '''75753045答:河宽45米。
例2. 已知:线段AB 长5cm ,点C 在AB 上,射线CM ⊥AB ,AC =1cm ,点P 在射线CM 上,设x CP =。
当x 为何值时,∠APB 为:(1)直角,(2)钝角,(3)锐角。
A C B解:(1)当x cm =2时∵AC =1cm ,AB =5cm∴CB =4cm∴===∴=AC PC PC CB AC PC PC CB 122412, 又∵PC ⊥AB∴∠ACP =∠PCB =90°∴△ACP ∽△PCM∴∠A =∠CPB又∵∠ACP =90°,在Rt ACP ∆中∴∠+∠=︒A APC 90∴∠+∠=︒APC CPB 90即当x cm =2时,∠APB =90°(2)当02<<x 时,设为P’点∴P’在线段CP 内是不与P 重合∴∠AP’C 为△APP’的外角∴∠AP’C >∠APC同理:∠BP’C >∠BPC∴+>+∠∠∠∠AP C BP C APC BPC ''即∠∠AP B APB '>=︒90∴当02<<x 时,∠APB 为钝角(3)略。
当x cm >2时,∠APB 为锐角例3. 已知梯形ABCD 中,AD =2,BC =3,∠B =90°,AB =7,P 在AB 上,问:当AP 为何值时,△ADP 与△BCP 是相似三角形。
八年级数学相似三角形

一、相似三角形的定义
对应角相等 、对应边成比例_ 的两个三角形,叫做相似三角 形。
二、相似三角形的判定
三、相似三角形的性质
相似三角形的判定:
相似三角形的预备定理:平行于三角形一边的直线截其他两பைடு நூலகம்
边所在的直线,截得的三角形与原三角形相似。
相似三角形判定定理1:两角对应相等,两三角形相似。 相似三角形判定定理2:两边对应成比例且夹角相等,两三角
九十六家,万三千二百六十九卷。〔入三家,五十篇,省兵十家。〕[标签:标题]
陈胜字涉,阳城人。吴广,字叔,阳夏人也。胜少时,尝与人佣耕。辍耕之垄上,怅然甚久,曰“苟富贵,无相忘”佣者笑而应曰“若为佣耕,何富贵也”胜太息曰“嗟乎,燕雀安知鸿鹄之志哉”秦二世元年秋七月,发闾左戍渔阳九百人,胜、广皆为屯长。行至蕲大泽乡,会天大雨,道不通, 度已失期。失期法斩,胜、广乃谋曰“今亡亦死,举大计亦死,等死,死国可乎”胜曰“天下苦秦久矣。吾闻二世,少子,不当立,当立者乃公子扶苏。扶苏以数谏故不得立,上使外将兵。今或闻无罪,二世杀之。百姓多闻其贤,未知其死。项燕为楚将,数有功,爱士卒,楚人怜之。或以为在 。今诚以吾众为天下倡,宜多应者”广以为然。乃行卜。卜者知其指意,曰“足下事皆成,有功。然足下卜之鬼乎”胜、广喜,念鬼,曰“此教我先威众耳”乃丹书帛曰“陈胜王”,置人所罾鱼腹中。卒买鱼享食,得书,已怪之矣。又间令广之次所旁丛祠中,夜构火,狐鸣呼曰“大楚兴,陈胜 王”卒皆夜惊恐。旦日,卒中往往指目胜、广。胜、广素爱人,士卒多为用。将尉醉,广故数言欲亡,忿尉,令辱之,以激怒其众。尉果笞广。尉剑挺,广起夺而杀尉。胜佐之,并杀两尉。召令徒属曰“公等遇雨,皆已失期,当斩。藉弟令毋斩,而戍死者固什六七。且壮士不死则已,死则举大 名耳。侯王将相,宁有种乎”徒属皆曰“敬受令”乃诈称公子扶苏、项燕,从民望也。袒右,称大楚。为坛而盟,祭以尉首。胜自立为将军,广为都尉。攻大泽乡,拔之。收兵而攻蕲,蕲下。乃令符离人葛婴将兵徇蕲以东,攻铚、酂、苦、柘、谯,皆下之。行收兵,比至陈,兵车六七百乘,骑 千馀,卒数万人。攻陈,陈守令皆不在,独守丞与战谯门中。不胜,守丞死。乃入据陈。数日,号召三老豪桀会计事。皆曰“将军身被坚执锐,伐无道,诛暴秦,复立楚之社稷,功宜为王”胜乃立为王,号张楚。於是诸郡县苦秦吏暴,皆杀其长吏,将以应胜。乃以广为假王,监诸将以西击荥阳 。令陈人武臣、张耳、陈馀徇赵,汝阴人邓宗徇九江郡。当此时,楚兵数千人为聚者不可胜数。葛婴至东城,立襄强为楚王。后闻胜已立,因杀襄强,还报。至陈,胜杀婴,令魏人周市北徇魏地。广围荥阳,李由为三川守守荥阳,广不能下。胜征国之豪桀与计,以上蔡人房君蔡赐为上柱国。周 文,陈贤人也,尝为项燕军视日,事春申君,自言习兵。胜与之将军印,西击秦。行收兵至关,车千乘,卒十万,至戏,军焉。秦令少府章邯免骊山徒,人奴产子,悉发以击楚军,大败之。周文走出关,止屯曹阳。二月馀,章邯追败之,复走黾池。十馀日,章邯击,大破之。周文自刭,军遂不 战。武臣至邯郸,自立为赵王,陈馀为大将军,张耳、召骚为左右丞相。胜怒,捕系武臣等家室,欲诛之。柱国曰“秦未亡而诛赵王将相家属,此生一秦,不如因立之”胜乃遣使者贺赵,而徙系武臣等家属宫中。而封张耳子敖为成都君,趣赵兵亟入关。赵王将相相与谋曰“王王赵,非楚意也。 楚已诛秦,必加兵於赵。计莫如毋西兵,使使北徇燕地以自广。赵南据大河,北有燕、代,楚虽胜秦,不敢制赵,若不胜秦,必重赵。赵承秦、楚之敝,可以得志於天下”赵王以为然,因不西兵,而遣故上谷卒史韩广将兵北徇燕。燕地贵人豪桀谓韩广曰“楚、赵皆已立王。燕虽小,亦万乘之国 也,愿将军立为王”韩广曰“广母在赵,不可”燕人曰“赵方西忧秦,南忧楚,其力不能禁我。且以楚之强,不敢害赵王将相之家,今赵独安敢害将军家乎”韩广以为然,乃自立为燕王。居数月,赵奉燕王母家属归之。是时,诸将徇地者不可胜数。周市北至狄,狄人田儋杀狄令,自立为齐王。 反击周市。市军散,还至魏地,立魏后故宁陵君咎为魏王。咎在胜所,不得之魏。魏地已定。欲立周市为王,市不肯。使者五反,胜乃立宁陵君为魏王,遣之国。周市为相。将军田臧等相与谋曰“周章军已破,秦兵且至,我守荥阳城不能下,秦军至,必大败。不如少遣兵,足以守荥阳,悉精兵 迎秦军。今假王骄,不知兵权,不可与计,非诛之,事恐败”因相与矫陈王令以诛吴广,献其首於胜。胜使赐田臧楚令尹印,使为上将。田臧乃使诸将李归等守荥阳城,自以精兵西迎秦军於敖仓。与战,田臧死,军破。章邯进击李归等荥阳下,破之,李归死。阳城人邓说将兵居郯,章邯别将击 破之,邓说走陈。铚人五逢将兵居许,章邯击破之。五逢亦走陈。胜诛邓说。胜初立时,凌人秦嘉、铚人董緤、符离人朱鸡石、取虑人郑布、徐人丁疾等皆特起,将兵围东海守於郯。胜闻,乃使武平君畔为将军,监郯下军。秦嘉自立为大司马,恶属人,告军吏曰“武平君年少,不知兵事,勿听 ”因矫以王命杀武平君畔。章邯已破五逢,击陈,柱国房君死。章邯又进击陈西张贺军。胜出临战,军破,张贺死。腊月,胜之汝阴,还至下城父,其御庄贾杀胜以降秦。葬砀,谥曰隐王。胜故涓人将军吕臣为苍头军,起新阳,攻陈,下之,杀庄贾,复以陈为楚。初,胜令铚人宋留将兵定南阳 ,入武关。留已徇南阳,闻胜死,南阳复为秦。宋留不能入武关,乃东至新蔡,遇秦军,宋留以军降秦。秦传留至咸阳,车裂留以徇。秦嘉等闻胜军败,乃立景驹为楚王,引兵之方舆,欲击秦军济阴下。使公孙庆使齐王,欲与并力俱进。齐王曰“陈王战败,未知其死生,楚安得不请而立王”公 孙庆曰“齐不请楚而立王,楚何故请齐而立王。且楚首事,当令於天下”田儋杀公孙庆。秦左右校复攻陈,下之。吕将军走,徼兵复聚,与番盗英布相遇,攻击秦左右校,破之青波,复以陈为楚。会项梁立怀王孙心为楚王。陈胜王凡六月。初为王,其故人尝与佣耕者闻之,乃之陈,叩宫门曰“ 吾欲见涉”宫门令欲缚之。自辩数,乃置,不肯为通。胜出,遮道而呼涉。乃召见,载与归。入宫,见殿屋帷帐,客曰“夥,涉之为王沈沈者”楚人谓多为夥,故天下传之“夥涉为王”,由陈涉始。客出入愈益发舒,言胜故情。或言“客愚无知,专妄言,轻威”。胜斩之。诸故人皆自引去,由 是无亲胜者。以朱防为中正,故武为司过,主司群臣。诸将徇地,至,令之不是者,系而罪之。以苛察为忠。其所不善者,不下吏,辄自治。胜信用之,诸将以故不亲附。此其所以败也。胜虽已死,其所置遣侯王将相竟亡秦。高祖时为胜置守冢於砀,至今血食。王莽败,乃绝。项籍字羽,下相 人也。初起,年二十四。其季父梁,梁父即楚名将项燕者也。家世楚将,封於项,故姓项氏。籍少时,学书不成,去。学剑又不成,去。梁怒之。籍曰“书足记姓名而已。剑一人敌,不足学,学万人敌耳”於是梁奇其意,乃教以兵法。籍大喜,略知其意,又不肯竟。梁尝有栎阳逮,请蕲狱掾曹 咎书抵栎阳狱史司马欣,以故事皆已。梁尝杀人,与籍避仇吴中。吴中贤士大夫皆出梁下。每有大繇役及丧,梁常主办,阴以兵法部勒宾客子弟,以知其能。秦始皇帝东游会稽,渡浙江,梁与籍观。籍曰“彼可取而代也”梁掩其口,曰“无妄言,族矣”梁以此奇籍。籍长八尺二寸,力扛鼎,才 气过人。吴中子弟皆惮籍。秦二世元年,陈胜起。九月,会稽假守通素贤梁,乃召与计事。梁曰“方今江西皆反秦,此亦天亡秦时也。先发制人,后发制於人”守叹曰“闻夫子楚将世家,唯足下耳”梁曰“吴有奇士桓楚,亡在泽中,人莫知其处,独籍知之”梁乃戒籍持剑居外侍。梁复入,与守 语曰“请召籍,使受令召恒楚”籍入,梁眴籍曰“可行矣”籍遂拔剑击斩守。梁持守头,佩其印绶。门下惊扰,籍所击杀数十百人。府中皆詟伏,莫敢复起。梁乃召故人所知豪吏,谕以所为,遂举吴中兵。使人收下县,得精兵八千人,部署豪桀为校尉、候、司马。有一人不得官,自言。梁曰“ 某时某丧,使公主某事,不能办,以故不任公”众乃皆服。梁为会稽将,籍为裨将,徇下县。秦二年,广陵人召平为陈胜徇广陵,未下。闻陈胜败走,秦将章邯且至,乃渡江矫陈王令,拜梁为楚上柱国,曰“江东已定,急引兵西击秦”梁乃以八千人渡江而西。闻陈婴已下东阳,使使欲与连和俱 西。陈婴者,故东阳令史,居县,素信,为长者。东阳少年杀其令,相聚数千人,欲立长,无适用,乃请陈婴。婴谢不能,遂强立之,县中从之者得二万人。欲立婴为王,异军苍头特起。婴母谓婴曰“自吾为乃家妇,闻先故未曾贵。今暴得大名不祥,不如有所属,事成犹得封侯,事败易以亡, 非世所指名也”婴乃不敢为王,谓其军吏曰“项氏世世将家,有功於楚,今欲举大事,非将其人,不可。我倚名族,亡秦必矣”其众从之,乃以其兵属梁。梁渡淮,英布、蒲将军亦以其兵属焉。凡六七万人,军下邳。是时,秦嘉已立景驹为楚王,军彭城东,欲以距梁。梁谓军吏曰“陈王首事, 战不利,未闻所在。今秦嘉背陈王立景驹,大逆亡道”乃引兵击秦嘉。嘉军败走,追至胡陵。嘉还战一日,嘉死,军降。景驹走死梁地。梁已并秦嘉军,军胡陵,将引而西。章邯至栗,梁使别将朱鸡石、馀樊君与战。馀樊君死。朱鸡石败,亡走胡陵。梁乃引兵入薛,诛朱鸡石。梁前使羽别攻襄 城,襄城坚守不下。已拔,皆坑之,还报梁,闻陈王定死,召诸别将会薛计事。时沛公亦从沛往。居鄛人范增年七十,素好奇计,往说梁曰“陈胜败固当。夫秦灭六国,楚最亡罪,自怀王入秦不反,楚人怜之至今,故南以称曰楚虽三户,亡秦必楚。今陈胜首事,不立楚后,其势不长。今君起江 东,楚蜂起之将皆争附君者,以君世世楚将,为能复立楚之后也”於是梁乃求楚怀王孙心,在民间为人牧羊,立以为楚怀王,从民望也。陈婴为上柱国,封五县,与怀王都盱台。梁自号武信君,引兵攻亢父。初,章邯既杀齐王田儋於临菑,田假复自立为齐王。儋弟荣走保东阿,章邯追围之。梁 引兵救东阿,大破秦军东阿。田荣即引兵归,逐王假,假亡走楚,相田角亡走赵。角弟駹,故将,居赵不敢归。田荣立儋子市为齐王。梁己破东阿下军,遂追秦军。数使使趣齐兵俱西。荣曰“楚杀田假,赵杀田角、田駹,乃发兵”梁曰“田假与国之王,穷来归我,不忍杀”赵亦不杀角、駹以市 於齐。齐遂不肯发兵助楚。染使羽与沛公别攻城阳,屠之。西破秦军濮阳东,秦兵收入濮阳。沛公、羽攻定陶,定陶未下,去,西略地至雍丘,大破秦军,斩李由。还攻外黄,外黄未下。梁起东阿,比至定陶,再破秦军,羽等又斩李由,益轻秦,有骄色。宋义谏曰“战胜而将骄卒惰者败。今少
八年级数学教案:相似三角形

八年级数学教案:相似三角形以下是查字典数学网为您引荐的相似三角形,希望本篇文章对您学习有所协助。
相似三角形●教学目的(一)教学知识点1.掌握相似三角形的定义、表示法,并能依据定义判别两个三角形能否相似.2.能依据相似比停止计算.(二)才干训练要求1.能依据定义判别两个三角形能否相似,训练先生的判别才干.2.能依据相似比求长度和角度,培育先生的运用才干.(三)情感与价值观要求经过与相似多边形有关概念的类比,浸透类比的教学思想,并体会特殊与普通的关系.●教学重点相似三角形的定义及运用.●教学难点依据定义求线段长或角的度数.●教学进程Ⅰ.创设效果情境,引入新课明天,我们就来研讨相似三角形.Ⅱ.新课解说1.相似三角形的定义及记法三角对应相等,三边对应成比例的两个三角形叫做相似三角形。
如△ABC与△DEF相似,记作△ABC∽△DEF其中对应顶点要写在对应位置,如A与D,B与E,C与F相对应.AB∶DE等于相似比.2.想一想假设△ABC∽△DEF,那么哪些角是对应角?哪些边是对应边?对应角有什么关系?对应边呢?所以 D、E、F. .3.议一议,先生讨论(1)两个全等三角形一定相似吗?为什么?(2)两个直角三角形一定相似吗?两个等腰直角三角形呢?为什么?(3)两个等腰三角形一定相似吗?两个等边三角形呢?为什么?结论:两个全等三角形一定相似.两个等腰直角三角形一定相似.两个等边三角形一定相似.两个直角三角形和两个等腰三角形不一定相似.4.例题例1、有一块呈三角形外形的草坪,其中一边的长是20 m,在这个草坪的图纸上,这条边长5 cm,其他两边的长都是3.5 cm,求该草坪其他两边的实践长度.例2.已知△ABC∽△ADE,AE=50 cm,EC=30 cm,BC =70 cm,BAC=45,ACB=40,求(1)AED和ADE的度数。
(2)DE的长.5.想一想在例2的条件下,图中有哪些线段成比例?Ⅲ.课堂练习 P129Ⅳ.课时小结相似三角形的判定方法定义法.Ⅴ.课后作业。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
暑假专题——相似三角形重点、难点:1. 通过探索两个三角形相似的识别方法,加强合情推理能力的培养,感受发现的乐趣,逐步掌握说理的基本方法。
2. 通过相似三角形性质复习,丰富与角、面积等相关的知识方法,开阔研究角、面积等问题的视野。
【知识纵横】1. 相似三角形对应角相等,对应边成比例的三角形叫做相似三角形(similar triangles)。
议一议:(1)两个全等三角形一定相似吗?为什么?(2)两个直角三角形一定相似吗?两个等腰直角三角形呢?为什么?(3)两个等腰三角形一定相似吗?两个等边三角形呢?为什么?2. 相似比相似三角形对应边的比叫做相似比。
说明:相似比要注意顺序:如△ABC∽△A'B'C'的相似比kABA B1='',而△A'B'C'∽△ABC的相似比kA BAB2='',这时kk121=。
3. 相似三角形的识别(1)如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似。
(2)如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
(3)如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似。
【典型例题】例1. 如图,∠1=∠2=∠3,图中相似三角形有()对。
AD E3B C2 1答:4对例2. 如图,已知:△ABC 、△DEF ,其中∠A =50°,∠B =60°,∠C =70°,∠D =40°,∠E =60°,∠F =80°,能否分别将两个三角形分割成两个小三角形,使△ABC 所分成的每个三角形与△DEF 所分成的每个三角形分别对应相似? 如果可能,请设计一种分割方案;若不能,说明理由。
BEA C D F解:B E例3. (2008·广东省)如图所示,四边形ABCD 是平行四边形,点F 在BA 的延长线上,连结CF 交AD 于点E 。
(1)求证:△CDE ∽△FAE ;(2)当E 是AD 的中点,且BC =2CD 时,求证:∠F =∠BCF 。
D CEF A B命题意图:相似三角形的识别、特征在解题中的应用。
解析:由AB ∥DC 得:∠F =∠DCE ,∠EAF =∠D ∴△CDE ∽△FAE ∴=CD FA DEAE,又E 为AD 中点 ∴DE =AE ,从而CD =FA ,结合已知条件,易证 BF =BC ,∠F =∠BCF 解:(1)∵四边形ABCD 是平行四边形 ∴AB ∥CD∴∠F =∠DCE ,∠EAF =∠D ∴△CDE ∽△FAE(2)∵E 是AD 中点,∴DE =AE 由(1)得:CD AF DEAE=∴CD =AF∵四边形ABCD 是平行四边形 ∴AB =CD∴AB =CD =AF∴BF =2CD ,又BC =2CD ∴BC =BF ∴∠F =∠BCF思路探究:平行往往是证两个三角形相似的重要条件,利用比例线段也可证明两线段相等。
例4. 在梯形ABCD 中,∠A =90°,AD ∥BC ,点P 在线段AB 上从A 向B 运动, (1)是否存在一个时刻使△ADP ∽△BCP ;(2)若AD =4,BC =6,AB =10,使△ADP ∽△BCP ,则AP 的长度为多少?解:(1)存在A DPB(2)若△ADP∽△BCP,则ADBCAPBP=设AP x=∴=-∴=∴=461044 xxx AP,,或ADBPAPBC=∴-=∴=41064x xx,或x=6∴=AP4或AP=6∴AP长度为4或6例5. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BE、BD,且AE、BD交于点F,则S S SDEF EBF ABF∆∆∆::=()A. 4:10:25B. 4:9:25C. 2:3:5D. 2:5:25(2001年黑龙江省中考题)思路点拨:运用与面积相关知识,把面积比转化为线段比。
∴选A例6. 如图,有一批形状大小相同的不锈钢片,呈直角三角形,已知∠C=90°,AB=5cm,BC=3cm,试设计一种方案,用这批不锈钢片裁出面积达最大的正方形不锈钢片,并求出这种正方形不锈钢片的边长。
思路点拨:要在三角形内裁出面积最大的正方形,那么这正方形所有顶点应落在△ABC 的边上,先画出不同方案,把每种方案中的正方形边长求出。
解:如图甲,设正方形EFGH边长为x,则AC=4而CD×AB=AC×BC=2S ABC∆,得CD=125又△CEH∽△CAB,得CMCDEHAB=于是1251255-=xx,解得:x=6037如图乙,设正方形CFGH的边长为y cm由GH∥AC,得:GHACBHBC=即y y433=-,解得:y=127x y y x===∴>60371276035,,即应如图乙那样裁剪,这时正方形面积达最大,它的边长为127cm例7. 如图,已知直角梯形ABCD中,∠A=∠B=90°,设AB a AD b==,,BC b a b=>2(),作DE⊥DC,DE交AB于点E,连结EC。
(1)试判断△DCE与△ADE、△DCE与△BCE是否分别一定相似?若相似,请加以证明。
(2)如果不一定相似,请指出a、b满足什么关系时,它们就能相似?解:(1)△DCE与△ADE一定相似,△DCE与△BCE不一定相似,分别延长BA、CD 交于F点由△FAD∽△FBC,得:FDFCADBCbb===212于是FD=DC,从而可证△FED≌△CED得∠AED=∠DEC所以△DEC∽△AED(2)作CG⊥AD交AD延长线于G,CD a b=+22由△AED∽△GDC,有AEGDADGC=,得AEbaDE AE AD bbabaa bBE AB AE abaa baBEDEa babaa ba bb a b==+=+⎛⎝⎫⎭⎪=+=-=-=-=-+=-+2222222222222222222BCDCba b=+222要使△DCE与△BCE相似,那么BEDEBCDC=一定成立即a bbb222-=,得a b223=也就是当a b=3时,△DCE与△BCE一定相似。
【模拟试题】(答题时间:40分钟)1. 如图,已知DE∥BC,CD和BE相交于O,若S SDOE COB∆∆::=916,则AD:DB=____________。
2. 如图,△ABC 中,CE :EB =1:2,DE ∥AC ,若△ABC 的面积为S ,则△ADE 的面积为____________。
3. 若正方形的4个顶点分别在直角三角形的3条边上,直角三角形的两直角边的长分别为3cm 和4cm ,则此正方形的边长为____________。
(2000年武汉市中考题)4. 阅读下面的短文,并解答下列问题:我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体。
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比:a b :,设S S 甲乙:分别表示这两个正方体的表面积,则S S a ba b 甲乙==⎛⎝ ⎫⎭⎪66222,又设V V 甲乙、分别表示这两个正方体的体积,则V V a ba b 甲乙==⎛⎝ ⎫⎭⎪333。
(1)下列几何体中,一定属于相似体的是( )A. 两个球体B. 两个圆锥体C. 两个圆柱体D. 两个长方体 (2)请归纳出相似体的3条主要性质:①相似体的一切对应线段(或弧)长的比等于____________; ②相似体表面积的比等于____________; ③相似体体积的比等于____________。
(2001年江苏省泰州市中考题)5. 如图,铁道口的栏杆短臂长1 m ,长臂长16 m ,当短臂端点下降 m 时,长臂端点升高( )A. mB. mC. 8 mD. m6. 如图,D 为△ABC 的边AC 上的一点,∠DBC =∠A ,已知BC =2,△BCD 与△ABC 的面积的比是2:3,则CD 的长是( )A.43B.3C.233 D.433 7. 如图,在正三角形ABC 中,D 、E 分别在AC 、AB 上,且AD AC =13,AE =BE ,则有( )A. △AED ∽△BEDB. △AED ∽△CBDC. △AED ∽△ABDD. △BAD ∽△BCD(2001年杭州市中考题)8. 如图,已知△ABC 中,DE ∥FG ∥BC ,且AD :FD :FB =1:2:3,则S S S ADE DFGE FBCG ∆::四边形四边形等于( )A. 1:9:36B. 1:4:9C. 1:8:27D. 1:8:369. 如图,已知梯形ABCD 中,AD ∥BC ,∠ACD =∠B ,求证:AB CD BCAD 22=10. 如图,△ABC 中,D 是BC 边上的中点,且AD =AC ,DE ⊥BC ,DE 与AB 相交于点E ,EC 与AD 相交于点F 。
(1)求证:△ABC ∽△FCD ;(2)若S BC FCD ∆==510,,求DE 的长。
(2000年河北省中考题)11. 阅读并解答问题。
在给定的锐角△ABC 中,求作一个正方形DEFG ,使D 、E 落在BC 上,F 、G 分别落在AC 、AB 边上,作法如下:第一步:画一个有3个顶点落在△ABC 两边上的正方形D'E'F'G'。
第二步:连结BF',并延长交AC 于点F ; 第三步:过F 点作FE ⊥BC 于E ;第四步:过F 点作FG ∥BC 交AB 于点G ; 第五步:过G 点作GD ⊥BC 于点D 。
四边形DEFG 即为所求作的四边形DEFG ,为正方形。
问题:(1)证明上述所求作的四边形DEFG 为正方形; (2)在△ABC 中,如果BC ABC =+=︒6345,∠,∠BAC =75°,求上述正方形DEFG 的边长。
(江苏省扬州市中考题)AG FG' F'12. 如图,在△ABC 中,AB AC BC ===52,,在BC 上有100个不同的点P P P P 123100、、…,过这100个点分别作△ABC 的内接矩形P E F G P E F G 11112222,…P E F G 100100100100,设每个内接矩形的周长分别为L L L 12100、…,则L L L 12100+++=…____________。
(安徽省竞赛题)AE 2F 2E 1F 1B P 1 P 2 G 2 G 1 C13. 如图,在△ABC 中,DE ∥FG ∥BC ,GI ∥EF ∥AB ,若△ADE 、△EFG 、△GIC 的面积分别为204580222cm cm cm 、、,则△ABC 的面积为____________。
