固体物理老师说以前出但现在基本不出的习题
固体物理习题第二章

U U R N M Q V V ( ) V0 ( ) R0 [ ( m 1) m m 2 ( n 1) n n 2 ] V R V 2 R0 R0 ( 1 N M Q 1 1 2 ) ( m n )( 2 )( )( ) 2 m 1 n 1 3 2 2 3 NAR0 R0 R0 3 NAR0 3 NAR0
2
每个氢分子可以当做球 形来处理.结合能实验值为 0.75KJ / mol, 试与计算值比较 . 解:林纳德- 琼斯势:u (r ) 4 [( )12 ( ) 6 ] r r N N个气体分子间的互作用 能为:U '{4 [( )12 ( ) 6 ]} 2 j rj rj
第二章:固体的结合
2.1证明两种一价离子组成的一维晶格的马德隆常数为:α=2㏑2. 证明:设由两种一价离子组成一无限长的一维晶格,取任一一个 负离子作为参考,用r表示相邻离子间的间距,则有: 1 1 1 1 '
r
j
2 ... aj r 2r 3r
(+、-号分别对应正离子和负离子间的相互作用) 前面有个因子2是因为以负离子作为参考左右两边都存在相互作 用. 1 1 2 1 ... 则: 2 3
j
1 12 6 ' 1 A 则 U ( R ) 2 N [ A ( ) A ( ) ] 12 12 6 6 12 R R aj aj j
U ( R ) 12 6 2 A12 16 在平衡位置处有:( ) 6 A6 7 ) 0 有:R0 ( ) R0 2 N (12 A 12 13 R A6 R0 R0 A6 A6 A6 1 代入U ( R)有:U ( R0 ) 2 N ( ) N 4 A12 2 A12 2 A12 U ( R) bcc A6 A12 12.25 2 12.13 则: 2 ( ) 0.957 U ( R) fcc A12 A6 14.45 9.11
固体物理学基础知识训练题及其参考答案

《固体物理》基础知识训练题与其参考答案说明:本内容是以黄昆原著、韩汝琦改编的《固体物理学》为蓝本,重点训练读者在固体物理方面的基础知识,具体以19次作业的形式展开训练。
第一章作业1:1.固体物理的研究对象有那些?答:(1)固体的结构;(2)组成固体的粒子之间的相互作用与运动规律;(3)固体的性能与用途。
2.晶体与非晶体原子排列各有什么特点?答:晶体中原子排列是周期性的,即晶体中的原子排列具有长程有序性。
非晶体中原子排列没有严格的周期性,即非晶体中的原子排列具有短程有序而长程无序的特性。
3.试说明体心立方晶格,面心立方晶格,六角密排晶格的原子排列各有何特点?试画图说明。
有那些单质晶体分别属于以上三类。
答:体心立方晶格:除了在立方体的每个棱角位置上有1个原子以外,在该立方体的体心位置还有一个原子。
常见的体心立方晶体有:Li,Na,K,Rb,Cs,Fe等。
面心立方晶格:除了在立方体的每个棱角位置上有1个原子以外,在该立方体每个表面的中心还都有1个原子。
常见的面心立方晶体有:Cu, Ag, Au, Al等。
六角密排晶格:以ABAB形式排列,第一层原子单元是在正六边形的每个角上分布1个原子,且在该正六边形的中心还有1个原子;第二层原子单元是由3个原子组成正三边形的角原子,且其中心在第一层原子平面上的投影位置在对应原子集合的最低凹陷处。
常见的六角密排晶体有:Be,Mg,Zn,Cd等。
4.试说明, NaCl,金刚石,CsCl, ZnS晶格的粒子排列规律。
答:NaCl:先将两套相同的面心立方晶格,并让它们重合,然后,将一套晶格沿另一套晶格的棱边滑行1/2个棱长,就组成Nacl晶格;金刚石:先将碳原子组成两套相同的面心立方体,并让它们重合,然后将一套晶格沿另一套晶格的空角对角线滑行1/4个对角线的长度,就组成金刚石晶格;Cscl::先将组成两套相同的简单立方,并让它们重合,然后将一套晶格沿另一套晶格的体对角线滑行1/2个体对角线的长度,就组成Cscl晶格。
固体物理复习题

.简要回答下列问题:1.氯化钠与金刚石是复式格子还是简单格子,各自的基元中包含多少原子?分别是什么原子?复式格子,氯化钠基元包含一个钠原子和一个氯原子;金刚石基元包含2个碳原子。
2.在固体物理中为什么要引入“倒空间”的概念?波的最主要指标是波矢K,波矢K的方向就是波传播方向,波矢的模值与波长成反比,波矢的量纲是m-1。
讨论晶体与波的相互作用是固体物理的基本问题之一。
一般情况下晶体的周期性、对称性等均在正空间描述,及在m的量纲中描述。
为了便于讨论晶体与波的相互作用,必须把二者放到同一空间,同一坐标系下。
我们的选择是把晶体变换到量纲是m-1空间即倒空间来,也就是说在倒空间找到正空间的“映射”。
3.在晶体的物相分析中,为什么使用X光衍射而不使用红外光?52页在晶体衍射中,为什么不能用可见光?解答晶体中原子间距的数量级为10-10米,要使原子晶格成为光波的衍射光栅,光波的波长应小于10米但可见光的波长为米是晶体中原子间距的100倍因此,在晶体衍射中,不能用可见光。
.4.碳化硅是一种常见的半导体材料,当产生晶格振动时,会形成多少支格波,其中声学支和光学支格波各多少支?3声学支 3*8-3=21光学支5.共价键的定义和特点是什么?共价键包括配位键,是化学键的一种,两个或多个原子共同使用它们的外层电子,在理想情况下达到电子饱和的状态,由此组成比较稳定的化学结构叫做共价键。
其本质是原子轨道重叠后,高概率地出现在两个原子核之间的电子与两个原子核之间的电性作用。
再加p169闫饱和性在共价键的形成过程中,因为每个原子所能提供的未成对电子数是一定的,一个原子的一个未成对电子与其他原子的未成对电子配对后,就不能再与其它电子配对,即,每个原子能形成的共价键总数是一定的,这就是共价键的饱和性。
共价键的饱和性决定了各种原子形成分子时相互结合的数量关系是定比定律的内在原因之一。
方向性除s 轨道是球形的以外,其它原子轨道都有其固定的延展方向,所以共价键在形成时,轨道重叠也有固定的方向,共价键也有它的方向性,共价键的方向决定着分子的构形。
固体物理13年复习题考试重点1

固体复习题型:一.简答题(共30分,每小题6分)5道小题二.证明题(共25分)两道小题三.计算题(共45分)分布在第四章2道,第二章、第三章各一道。
一.简答题1简述晶体的定义,说明晶体的5条宏观性质。
晶体:原子按一定的周期排列规则的固体,在微米量级的范围是有序排列的①一定的熔点;②晶体的规则外形;③在不同的带轴方向上,晶体的物理性质不同——晶体的各向异性;④晶面角守恒——同一品种的晶体,两个相应的晶面间夹角恒定不变;⑤晶体的解理性-—晶体常具有沿某些确定方位的晶面劈裂的性质.2列举晶体结合的基本类型.离子性结合、共价结合、金属性结合、范德瓦尔斯结合和氢键结合。
3.说出简立方晶体、面心立方晶体和体心立方晶体的原胞和晶胞中所包含的原子数。
4。
说出氯化钠、氯化铯和金刚石结构晶体它们的原胞的晶格类型,每个原胞中包含的原子数.5.下面几种种典型的晶体由哪种布拉菲格子套构而成?6。
下面几种典型的晶体结构的配位数(最近邻原子数)是多少?体心立方8 金刚石型结构 4简立方 6 立方硫化锌结构 47。
画出体心立方结构的金属在)111(,)(面上原子排列.100(,)110体心立方8画出面心立方晶格结构的金属在)111(,)(面上原子排列.100(,)110面心立方9试述晶态、非晶态、准晶、多晶和单晶的特征性质。
解:晶态固体材料中的原子有规律的周期性排列,或称为长程有序.非晶态固体材料中的原子不是长程有序地排列,但在几个原子的范围内保持着有序性,或称为短程有序。
准晶态是介于晶态和非晶态之间的固体材料,其特点是原子有序排列,但不具有平移周期性.另外,晶体又分为单晶体和多晶体:整块晶体内原子排列的规律完全一致的晶体称为单晶体;而多晶体则是由许多取向不同的单晶体颗粒无规则堆积而成的。
10晶格点阵与实际晶体有何区别和联系?解:晶体点阵是一种数学抽象,其中的格点代表基元中某个原子的位置或基元质心的位置,也可以是基元中任意一个等价的点.当晶格点阵中的格点被具体的基元代替后才形成实际的晶体结构。
(参考资料)固体物理习题带答案

D E ( ) ,其中 , 表示沿 x , y , z 轴的分量,我们选取 x , y , z
沿立方晶体的三个立方轴的方向。
显然,一般地讲,如果把电场 E 和晶体同时转动, D 也将做相同转动,我们将以 D' 表示转
动后的矢量。
设 E 沿 y 轴,这时,上面一般表达式将归结为:Dx xyE, Dy yyE, Dz zy E 。现在
偏转一个角度 tg 。(2)当晶体发生体膨胀时,反射线将偏转角度
tg , 为体胀系数
3
解:(1)、布拉格衍射公式为 2d sin ,既然波长改变,则两边同时求导,有
2d cos ,将两式组合,则可得 tg 。
(2)、当晶体发生膨胀时,则为 d 改变,将布拉格衍射公式 2d sin 左右两边同时对 d
考虑把晶体和电场同时绕 y 轴转动 / 2 ,使 z 轴转到 x 轴, x 轴转到 z 轴, D 将做相同
转动,因此
D'x Dz zy E
D'y Dy yyE
D'z Dx xy E 但是,转动是以 E 方向为轴的,所以,实际上电场并未改变,同时,上述转动时立方晶体
的一个对称操作,所以转动前后晶体应没有任何差别,所以电位移矢量实际上应当不变,即
第一章:晶体结构 1. 证明:立方晶体中,晶向[hkl]垂直于晶面(hkl)。
证 明 : 晶 向 [hkl] 为 h1 k2 l3 , 其 倒 格 子 为
b1
2
a1
a2
a3
(a2 a3 )
b2
2
a1
a3 a1 (a2 a3)
b3
2
a1
a1
a2
(a2 a3)
。可以知道其倒格子矢量
固体物理期末复习题目

固体物理期末复习题目一、名词解释:1、晶体;2、非晶体;3、点阵;4、晶格;5、格点;6、晶体的周期性;7、晶体的对称性8、密勒指数;9、倒格子;10、配位数;11、致密度;12、固体物理学元胞;13、结晶学元胞;14、布拉菲格子;15、复式格子;16、声子;17、布洛赫波;18、布里渊区;19、格波;20、电子的有效质量二、计算证明题1. 晶体点阵中的一个平面hkl ,试证:(1)晶格的两个相邻平行平面(这些平面通过格点)之间的距离为2||hkl d K π=此处123K hb kb lb =++;(2)利用上述关系证明,对于简单立方格子,22d l =+ a 为晶格常数;(3)说明什么样的晶面容易解理,为什么?2、金刚石晶胞的立方边长为m 101056.3-?,求最近邻原子间的距离、平均每立方厘米中的原子数和金刚石的密度。
(碳原子的重量为2310*99.1-g )3. 试证:在晶体中由于受到周期性的限制,只能有1、2、3、4、6重旋转对称轴,5重和大于6重的对称轴不存在。
4、晶体点阵中的一个平面.hkl(a )证明倒易点阵矢量321b l b k b h G ++=垂直于这个平面。
(b )证明正格子原胞体积与倒格子原胞体积互为倒数5. 证明体心立方格子和面心立方格子互为正、倒格子。
6. 在六角空间格子中选取一平行六面体为原胞,试求:(1)基矢321,,a a a的表示式;(2)原胞的体积;(3)倒格子基矢321,,b b b 。
7、氪原子组成惰性晶体为体心立方结构,其总势能可写为()- ??=6612122R A R A N R U σσε,其中N 为氪原子数,R 为最近邻原子间距离,点阵和A 6=12.25,A 12=9.11;设雷纳德—琼斯系数ε=0.014eV ,σ=3.65。
求:(1)平衡时原子间最近距离R 0及点阵常数a ;(2)每个原子的结合能(eV )。
8. 设两原子间的互作用能可表示为()n m r r r u βα+-=式中,第一项为引力能;第二项为排斥能;βα,均为正常数。
固体物理经典复习题及答案

固体物理经典复习题及答案⼀、简答题1.理想晶体答:内在结构完全规则的固体是理想晶体,它是由全同的结构单元在空间⽆限重复排列⽽构成的。
2.晶体的解理性答:晶体常具有沿某些确定⽅位的晶⾯劈裂的性质,这称为晶体的解理性。
3.配位数答: 晶体中和某⼀粒⼦最近邻的原⼦数。
4.致密度答:晶胞内原⼦所占的体积和晶胞体积之⽐。
5.空间点阵(布喇菲点阵)答:空间点阵(布喇菲点阵):晶体的内部结构可以概括为是由⼀些相同的点⼦在空间有规则地做周期性⽆限重复排列,这些点⼦的总体称为空间点阵(布喇菲点阵),即平移⽮量123d 、d 、h h h d 中123,,n n n 取整数时所对应的点的排列。
空间点阵是晶体结构周期性的数学抽象。
6.基元答:组成晶体的最⼩基本单元,它可以由⼏个原⼦(离⼦)组成,整个晶体可以看成是基元的周期性重复排列⽽构成。
7.格点(结点)答: 空间点阵中的点⼦代表着结构中相同的位置,称为结点。
8.固体物理学原胞答:固体物理学原胞是晶格中的最⼩重复单元,它反映了晶格的周期性。
取⼀结点为顶点,由此点向最近邻的三个结点作三个不共⾯的⽮量,以此三个⽮量为边作的平⾏六⾯体即固体物理学原胞。
固体物理学原胞的结点都处在顶⾓位置上,原胞内部及⾯上都没有结点,每个固体物理学原胞平均含有⼀个结点。
9.结晶学原胞答:使三个基⽮的⽅向尽可能的沿空间对称轴的⽅向,以这样三个基⽮为边作的平⾏六⾯体称为结晶学原胞,结晶学原胞反映了晶体的对称性,它的体积是固体物理学原胞体积的整数倍,V=n Ω,其中n 是结晶学原胞所包含的结点数, Ω是固体物理学原胞的体积。
10.布喇菲原胞答:使三个基⽮的⽅向尽可能的沿空间对称轴的⽅向,以这样三个基⽮为边作的平⾏六⾯体称为布喇菲原胞,结晶学原胞反映了晶体的对称性,它的体积是固体物理学原胞体积的整数倍,V=n Ω,其中n 是结晶学原胞所包含的结点数, Ω是固体物理学原胞的体积11.维格纳-赛兹原胞(W-S 原胞)答:以某⼀阵点为原点,原点与其它阵点连线的中垂⾯(或中垂线) 将空间划分成各个区域。
固体物理习题及解答

固体物理习题及解答⼀、填空题1. 晶格常数为a 的⽴⽅晶系 (hkl)晶⾯族的晶⾯间距为a该(hkl)晶⾯族的倒格⼦⽮量hkl G 为 k al j a k i a h πππ222++ 。
2. 晶体结构可看成是将基元按相同的⽅式放置在具有三维平移周期性的晶格的每个格点构成。
3. 晶体结构按晶胞形状对称性可划分为 7 ⼤晶系,考虑平移对称性晶体结构可划分为 14 种布拉维晶格。
4. 体⼼⽴⽅(bcc )晶格的结构因⼦为 []{})(ex p 1l k h i f S hkl ++-+=π,其衍射消光条件是奇数=++l k h 。
5. 与正格⼦晶列[hkl]垂直的倒格⼦晶⾯的晶⾯指数为 (hkl) ,与正格⼦晶⾯(hkl )垂直的倒格⼦晶列的晶列指数为 [hkl] 。
6. 由N 个晶胞常数为a 的晶胞所构成的⼀维晶格,其第⼀布⾥渊区边界宽度为a /2π,电⼦波⽮的允许值为 Na /2π的整数倍。
7. 对于体积为V,并具有N 个电⼦的⾦属, 其波⽮空间中每⼀个波⽮所占的体积为 ()V /23π,费⽶波⽮为 3/123?=V N k F π。
8. 按经典统计理论,N 个⾃由电⼦系统的⽐热应为 B Nk 23,⽽根据量⼦统计得到的⾦属三维电⼦⽓的⽐热为 F B T T Nk /22,⽐经典值⼩了约两个数量级。
9.在晶体的周期性势场中,电⼦能带在布⾥渊区边界将出现带隙,这是因为电⼦⾏波在该处受到布拉格反射变成驻波⽽导致的结果。
10. 对晶格常数为a 的简单⽴⽅晶体,与正格⽮R =a i +2a j +2a k 正交的倒格⼦晶⾯族的⾯指数为 (122) , 其⾯间距为 .11. 铁磁相变属于典型的⼆级相变,在居⾥温度附近,⾃由能连续变化,但其⼀阶导数(⽐热)不连续。
13.等径圆球的最密堆积⽅式有六⽅密堆(hcp )和⾯⼼⽴⽅密堆(fcc )两种⽅式,两者的空间占据率皆为74%。
14. ⾯⼼⽴⽅(fcc )晶格的倒格⼦为体⼼⽴⽅(bcc )晶格;⾯⼼⽴⽅(fcc )晶格的第⼀布⾥渊区为截⾓⼋⾯体。
固体物理习题解答-完整版
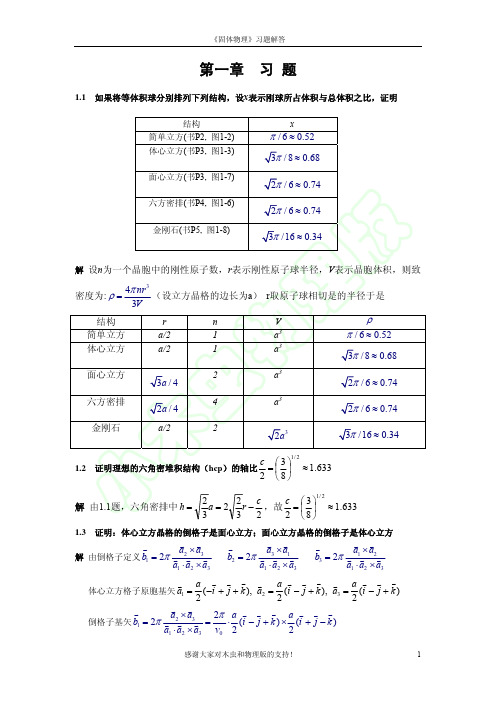
ρ
π / 6 ≈ 0.52
3π / 8 ≈ 0.68 2π / 6 ≈ 0.74 2π / 6 ≈ 0.74 3π /16 ≈ 0.34
1/ 2
3a / 4
2a / 4
a/2
2a 3
c ⎛3⎞ 1.2 证明理想的六角密堆积结构(hcp)的轴比 = ⎜ ⎟ 2 ⎝8⎠
ε A ,对六角晶系,绕 x 轴
(即 a 轴)旋转 180 度和绕 z 轴(即 c 轴)旋转 120 度都是对称操作,坐标变换矩阵分别为
⎛1 0 0⎞ ⎜ ⎟ Ax = ⎜ 0 − 1 0 ⎟ ⎜0 0 1⎟ ⎝ ⎠
⎛ −1/ 2 ⎜ Az = ⎜ − 3 / 2 ⎜ ⎜ 0 ⎝
3 / 2 0⎞ ⎟ −1/ 2 0⎟ ⎟ 0 1⎟ ⎠
6 a
3a / 2
6 a
2a
1.7
画体心立方和面心立方晶格结构的金属在 (100) , (110) , (111) 面上 解:
原子排列.
感谢大家对木虫和物理版的支持!
3
《固体物理》习题解答
体心立方
面心立方
1.9 指出立方晶格(111)面与(100)面,(111)面与(110)面的交线的晶向 解 (111)面与(100)面的交线的 AB-AB 平移, A 与 O 重合。B 点位矢 RB = −aj + ak (111) 与 (100) 面的交线的晶向 AB = − aj + ak —— 晶 向指数 ⎡011⎤
面指数越简单的晶面,其晶面的间距越大 晶面上格点的密度越大,这样的晶面越容易解理 1.7 写出体心立方和面心立方晶格结构中,最近邻和次近邻的原子数,若立方边长为a,写 出最近邻和次近邻原子间距 解 简立方 最近邻数 最近邻间距 次近邻数 次近邻间距 6 a 12 面心立方 12 体心立方 8
固体物理学习题答案朱建国版完整版

固体物理学习题答案朱建国版HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】《固体物理学》习题参考第一章1.1 有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以R f和R b代表面心立方和体心立方结构中最近邻原子间的距离,试问R f/R b等于多少?答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a:对于面心立方,处于面心的原子与顶角原子的距离为:R f=2a 对于体心立方,处于体心的原子与顶角原子的距离为:R b那么,RfRb=31.2 晶面指数为(123)的晶面ABC是离原点O最近的晶面,OA、OB和OC分别与基失a1,a2和a3重合,除O点外,OA,OB和OC上是否有格点若ABC面的指数为(234),情况又如何答:根据题意,由于OA、OB和OC分别与基失a1,a2和a3重合,那么1.3 二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型:正方、矩形、六角、有心矩形和斜方。
分别如图所示:正方a=b 六方a=b矩形带心矩形a=b平行四边1.4 在六方晶系中,晶面常用4个指数(hkil )来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a 1,a 2,a 3上的截距a 1/h ,a 2/k ,a 3/i ,第四个指数表示该晶面的六重轴c 上的截距c/l.证明:i=-(h+k ) 并将下列用(hkl )表示的晶面改用(hkil )表示:(001)(133)(110)(323)(100)(010)(213) 答:证明设晶面族(hkil )的晶面间距为d ,晶面法线方向的单位矢量为n °。
因为晶面族(hkil )中最靠近原点的晶面ABC 在a 1、a 2、a 3轴上的截距分别为a 1/h ,a 2/k ,a 3/i ,因此123o o o a n hda n kd a n id=== ……… (1) 由于a 3=–(a 1+ a 2) 把(1)式的关系代入,即得 根据上面的证明,可以转换晶面族为(001)→(0001),(133)→(1323),(110)→(1100),(323)→(3213),(100)→(1010),(010)→(0110),(213)→(2133)1.5 如将等体积的硬球堆成下列结构,求证球可能占据的最大面积与总体积之比为(1)简立方:6π(2)体心立方:8(3)面心立方:6(4)六方密堆积:6(5)。
固体物理总复习资料及答案

固体物理总复习资料及答案固体物理总复习题⼀、填空题1.原胞是的晶格重复单元。
对于布拉伐格⼦,原胞只包含个原⼦。
2.在三维晶格中,对⼀定的波⽮q ,有⽀声学波,⽀光学波。
3.电⼦在三维周期性晶格中波函数⽅程的解具有形式,式中在晶格平移下保持不变。
4.如果⼀些能量区域中,波动⽅程不存在具有布洛赫函数形式的解,这些能量区域称为 ;能带的表⽰有、、三种图式。
5.按结构划分,晶体可分为⼤晶系,共布喇菲格⼦。
6.由完全相同的⼀种原⼦构成的格⼦,格⼦中只有⼀个原⼦,称为格⼦,由若⼲个布喇菲格⼦相套⽽成的格⼦,叫做格⼦。
其原胞中有以上的原⼦。
7.电⼦占据了⼀个能带中的所有的状态,称该能带为;没有任何电⼦占据的能带,称为;导带以下的第⼀满带,或者最上⾯的⼀个满带称为;最下⾯的⼀个空带称为 ;两个能带之间,不允许存在的能级宽度,称为。
8.基本对称操作包括 , ,三种操作。
9.包含⼀个n重转轴和n 个垂直的⼆重轴的点群叫。
10.在晶体中,各原⼦都围绕其平衡位置做简谐振动,具有相同的位相和频率,是⼀种最简单的振动称为。
11.具有晶格周期性势场中的电⼦,其波动⽅程为。
12.在⾃由电⼦近似的模型中,随位置变化⼩,当作来处理。
13.晶体中的电⼦基本上围绕原⼦核运动,主要受到该原⼦场的作⽤,其他原⼦场的作⽤可当作处理。
这是晶体中描述电⼦状态的模型。
14.固体可分为 , ,。
15.典型的晶格结构具有简⽴⽅结构, , , 四种结构。
16.在⾃由电⼦模型中,由于周期势场的微扰,能量函数将在K= 处断开,能量的突变为。
17.在紧束缚近似中,由于微扰的作⽤,可以⽤原⼦轨道的线性组合来描述电⼦共有化运动的轨道称为,表达式为。
18.爱因斯坦模型建⽴的基础是认为所有的格波都以相同的振动,忽略了频率间的差别,没有考虑的⾊散关系。
19.固体物理学原胞原⼦都在,⽽结晶学原胞原⼦可以在顶点也可以在即存在于。
20.晶体的五种典型的结合形式是、、、、。
固体物理基础参考解答精编版

孙会元主编的《固体物理基础》中的习题参考解答
e CV =(
∂u π2 2 0 k B g (ε F )V = )T = γ T ∂T 3
式中 γ =
π2
3
2 0 kB g (ε F ) ,称 为 电 子 比 热 容 系 数 。由 于 电 子 比 热 容 系 数 与 费 米 面 处 的 能
态密度有关, 所以利用电子比热容系数可以直接提供费米面附近能态密度的信息。 8. 求 一 维 、二 维 和 三 维 情 形 下 ,自 由 电 子 的 能 态 密 度 。分 别 示 意 画 出 一 维 ,二 维 , 三维自由电子气的能态密度曲线,并由此说明对于一维系统是否具有长程序, 为什么? 答:三维下单位体积的能态密度为
0 εF = εF [1 −
π 2 k BT 2 ( 0 ) ] 12 ε F
所以,随着温度的升高,会导致费米能稍稍下降。也就是说,自由电子费米气体 对应的费米球略有变小。 4. 试 说 明 电 子 密 度 在 金 属 自 由 电 子 气 体 模 型 中 的 作 用 ? 答:自由电子气体模型可用价电子密度 n 来描述,而且,n 是仅有的一个独 立参量。对于给定的金属,价电子密度是已知的。由此,我们可以求得具体的费 米波矢、费米能量、费米速度、费米温度等。 5. 如 何 理 解 金 属 自 由 电 子 气 体 的 简 并 性 ? 答 :在 统 计 物 理 中 ,把 体 系 与 经 典 行 为 的 偏 离 ,称 为 简 并 性 (degeneracy) 。在 绝对零度时电子仍有相当大的平均能量,这与经典的结果是截然不同的。按照经 典 的 自 由 电 子 气 体 (Drude) 的 模 型 ,电 子 在 T =0 时 的 平 均 能 量 为 零 。因 此 ,在 T =0K 时,金属自由电子气是完全简并的。系统简并性的判据是:
固体物理复习题(已解答)

1 简述Drude 模型的基本思想把金属中的电子看做气体,金属由可以自由运动的电子和固定不动的离子实两部分组成,这些可以自由运动的电子使金属导电的成分。
将自由电子看做带电的小硬球,它们的运动遵循牛顿第二定律。
应用独立自由电子气假设:在忽略电子-电子和电子-离子间电磁相互作用(内场)的情况下,它们在金属中运动或并发生碰撞。
2 简述Drude 模型的三个基本假设并解释 独立电子近似:电子与电子无相互作用自由电子近似:除碰撞的瞬间外,电子与离子无相互作用弛豫时间近似:一给定的电子在单位时间内受一次碰撞的几率为1/τ 3在Drude 模型下,固体如何建立热平衡 碰撞前后速度无关联 碰撞后获得的速度方向随机 速率与碰撞后的温度相适应4 Drude 模型中对金属导电率的表达式为:mnq τσ2=5 在自由电子气模型中,由能量均分定理知在特定温度T 下电子的动能为: 1.5K B T6 在Drude 模型当中,按照理想气体理论,自由电子气的密度为n ·cm -3,比Cv= 1.5 nK B7 1853年维德曼和弗兰兹在研究金属性质时发现一个定律,即在给定温度下金属的 导热率 和 电导率 的比值为常数。
8 简述Drude 模型的不足之处?电子对比热的贡献与温度无关,被严重高估(210) 对电子速度 2v 低估(210)误认磁化率与温度成反比,而实际无关 什么决定传到电子的数目?价电子? 导体?绝缘体?半导体?他之所以解释 维德曼-弗兰兹 成功,是因为对比热的高估正好抵消对速度的低估 9 对于自由电子气体,系统的化学势随温度的增大而 降低 。
10 请给出Fermi-Dirac 统计分布中,温度T 下电子的能量分布函数,并进一步解释电子能量分布的特点。
11)(/)('+=-TK E E FD B F eE f在温度T 下,能量为E 的状态被占据的几率。
式中EF 是电子的化学势,是温度的函数。
当温度为零时,电子最高占据状态能量,称为费米能级。
固体物理习题及解答

一、填空题1. 晶格常数为a 的立方晶系 (hkl>晶面族的晶面间距为;222/l k h a ++该(hkl>晶面族的倒格子矢量为 。
hkl G k al j a k i a hπππ222++2. 晶体结构可看成是将 基元 按相同的方式放置在具有三维平移周期性的 晶格 的每个格点构成。
3. 晶体结构按晶胞形状对称性可划分为 7 大晶系,考虑平移对称性晶体结构可划分为 14 种布拉维晶格。
4. 体心立方<bcc )晶格的结构因子为,[]{})(exp 1l k h i f S hkl ++-+=π 其衍射消光条件是。
奇数=++l k h 5. 与正格子晶列[hkl]垂直的倒格子晶面的晶面指数为 (hkl> , 与正格子晶面<hkl )垂直的倒格子晶列的晶列指数为 [hkl] 。
6. 由N 个晶胞常数为a 的晶胞所构成的一维晶格,其第一布里渊区边界宽度为,电子波矢的允许值为 的整数倍。
a /2πNa /2π7. 对于体积为V,并具有N 个电子的金属, 其波矢空间中每一个波矢所占的体积为,费M 波矢为()V/23π 。
3/123⎪⎪⎭⎫⎝⎛=V N k F π8. 按经典统计理论,N 个自由电子系统的比热应为,而根据量子统计得到的金属三维电子气的比热为 B Nk 23,比经典值小了约两个数量级。
F B T T Nk /22π9.在晶体的周期性势场中,电子能带在 布里渊区边界 将出现带隙,这是因为电子行波在该处受到 布拉格反射 变成驻波而导致的结果。
10. 对晶格常数为a 的简单立方晶体,与正格矢R =a i +2a j +2a k 正交的倒格子晶面族的面指数为 (122> , 其面间距为.11. 铁磁相变属于典型的 二级 相变,在居里温度附近,自由能连续变化,但其 一阶导数<比热) 不连续。
12. 晶体结构按点对称操作可划分为 32 个点群,结合平移对称操作可进一步划分为 230 个空间群。
固体物理复习题整理

第二章
基本概念:
1、固体的结合可以概括为离子性结合、共价结合、金属性结合和范德瓦尔结合这四种基本形式。
2、离子性结合是指固体中原子与原子之间的结合方式是以离子形式结合的单位。
3、结合能:两粒子结合成稳定结构时所释放出来的能量,或者是破坏稳定结构所需要的最小能量。也就是两粒子处在平衡状态时所具有的势能。
所以,能态密度为
5、例3:求简单立方s态能带的能态密度。
解:简单立方s态能带为
很明显, 。
在长波区域 时, ,此时等能面是一个半径为 的球面,
在 的其他地方,颇为复杂。从其等能面图上可以看到,有些地方, ,也就是 的地方,这些地方,导致能态密度发散,这样的点称为范霍夫奇点,也叫临界点。
6、作业:(1)求二维自由电子的能态密度。
方向性是指原子只在特定的方向上形成共价键。
7、电离度:描述共价结合中离子性的成份。
8、原子的负电性是用来标志原子得失电子能力的物理量,负电性越大越容易得到电子,负电性越小,越容易失去电子。负电性=0.18(电离能+亲和能),(单位:电子伏特)
9、亲和能用来度量原子束缚电子能力的量,即一个中性原子获得一个电子成为负离子时所放出的能量。
4.(作业)一维双原子链中, , ,计算: 1、光学波 和 以及声学波 ;
5.(作业)计算相应的声子能量 ( 声子的能量 )
6.(作业)在T=300K下,三种声子的数目各为多少?(利用 来求声子数)
7.课本p.580.第3.4题:考虑一个全同原子组成的平面方格子,用 记第 行,第m列的原子垂直于格平面的位移,每个原子质量为M,最近邻原子的力常源自为c,解:两格点连线的位矢为
固体物理学习题解答(完整版)

《固体物理学》部分习题参考解答第一章1.1 有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以R f 和R b 代表面心立方和体心立方结构中最近邻原子间的距离,试问R f /R b 等于多少?答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a :对于面心立方,处于面心的原子与顶角原子的距离为:R f=2 a 对于体心立方,处于体心的原子与顶角原子的距离为:R b=2a 那么,Rf Rb31.2 晶面指数为(123)的晶面ABC 是离原点O 最近的晶面,OA 、OB 和OC 分别与基失a 1,a 2和a 3重合,除O 点外,OA ,OB 和OC 上是否有格点?若ABC 面的指数为(234),情况又如何?答:根据题意,由于OA 、OB 和OC 分别与基失a 1,a 2和a 3重合,那么 1.3 二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型:正方、矩形、六角、有心矩形和斜方。
分别如图所示:1.4 在六方晶系中,晶面常用4个指数(hkil )来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a 1,a 2,a 3上的截距a 1/h ,a 2/k ,a 3/i ,第四个指数表示该晶面的六重轴c 上的截距c/l.证明:i=-(h+k ) 并将下列用(hkl )表示的晶面改用(hkil )表示:(001)(133)(110)(323)(100)(010)(213)答:证明设晶面族(hkil )的晶面间距为d ,晶面法线方向的单位矢量为n °。
因为晶面族(hkil )中最靠近原点的晶面ABC 在a 1、a 2、a 3轴上的截距分别为a 1/h ,a 2/k ,a 3/i ,因此123o o o a n hda n kd a n id=== ……… (1) 正方 a=b a ^b=90° 六方 a=b a ^b=120° 矩形 a ≠b a ^b=90° 带心矩形 a=b a ^b=90° 平行四边形 a ≠b a ^b ≠90°由于a 3=–(a 1+ a 2)313()o o a n a a n =-+把(1)式的关系代入,即得()id hd kd =-+ ()i h k =-+根据上面的证明,可以转换晶面族为(001)→(0001),(133)→(1323),(110)→(1100),(323)→(3213),(100)→(1010),(010)→(0110),(213)→(2133)1.5 如将等体积的硬球堆成下列结构,求证球可能占据的最大面积与总体积之比为(1)简立方:6π(2(3)面心立方:6(4)六方密堆积:6(5)金刚石:。
《固体物理学》概念和习题 答案

《固体物理学》概念和习题固体物理基本概念和思考题:1.给出原胞的定义。
答:最小平行单元。
2.给出维格纳-赛茨原胞的定义。
答:以一个格点为原点,作原点与其它格点连接的中垂面(或中垂线),由这些中垂面(或中垂线)所围成的最小体积(或面积)即是维格纳-赛茨原胞。
3.二维布喇菲点阵类型和三维布喇菲点阵类型。
4. 请描述七大晶系的基本对称性。
5. 请给出密勒指数的定义。
6. 典型的晶体结构(简单或复式格子,原胞,基矢,基元坐标)。
7. 给出三维、二维晶格倒易点阵的定义。
8. 请给出晶体衍射的布喇格定律。
9. 给出布里渊区的定义。
10. 晶体的解理面是面指数低的晶面还是指数高的晶面?为什么?11. 写出晶体衍射的结构因子。
12. 请描述离子晶体、共价晶体、金属晶体、分子晶体的结合力形式。
13. 写出分子晶体的雷纳德-琼斯势表达式,并简述各项的来源。
14. 请写出晶格振动的波恩-卡曼边界条件。
15. 请给出晶体弹性波中光学支、声学支的数目与晶体原胞中基元原子数目之间的关系以及光学支、声学支各自的振动特点。
(晶体含N个原胞,每个原胞含p个原子,问该晶体晶格振动谱中有多少个光学支、多少个声学支振动模式?)16. 给出声子的定义。
17. 请描述金属、绝缘体热容随温度的变化特点。
18. 在晶体热容的计算中,爱因斯坦和德拜分别做了哪些基本假设。
19. 简述晶体热膨胀的原因。
20. 请描述晶体中声子碰撞的正规过程和倒逆过程。
21. 分别写出晶体中声子和电子分别服从哪种统计分布(给出具体表达式)?22. 请给出费米面、费米能量、费米波矢、费米温度、费米速度的定义。
23. 写出金属的电导率公式。
24. 给出魏德曼-夫兰兹定律。
25. 简述能隙的起因。
26. 请简述晶体周期势场中描述电子运动的布洛赫定律。
27. 请给出在一级近似下,布里渊区边界能隙的大小与相应周期势场的傅立叶分量之间的关系。
28. 给出空穴概念。
29. 请写出描述晶体中电子和空穴运动的朗之万(Langevin)方程。
固体物理考题汇总(无答案)

固体物理考题汇总(⽆答案)第⼀章晶体结构⼀、填空1、晶⾯有规则,对称配置的固体,具有长程有序特点的固体称为;在凝结过程中不经过结晶(即有序化)的阶段,原⼦的排列为长程⽆序的固体称为。
由晶粒组成的固体,称为。
2、化合物半导体材料GaAs晶体属于闪锌矿类结构,晶格常数为a,其配位数为。
⼀个惯⽤元胞(结晶学元胞)内的原⼦数,其布喇菲格⼦是。
其初基原胞(固体物理学原胞)包含原⼦数,体积为。
初基元胞的基⽮为,,。
3、半导体材料Si具有⾦刚⽯型晶体结构,晶格常数为a,其配位数为。
⼀个惯⽤元胞(结晶学元胞)内的原⼦数。
属于布喇菲格⼦。
写出其初基元胞(固体物理学元胞)的基⽮________,_______,_______。
晶格振动⾊散关系中⽀声学波,⽀光学波,其总的格波数。
4、简⽴⽅结构如果晶格常数为a,其倒格⼦元胞基⽮为是_______,______,_________ 。
在倒格⼦空间中是结构,第⼀布⾥渊区的形状为______,体积为______ 。
5、某元素晶体的结构为体⼼⽴⽅布喇菲格⼦,其格点⾯密度最⼤的晶⾯的密勒指数____ ,并求出该晶⾯系相邻晶⾯的⾯间距________。
(设其晶胞参数为a )。
6、根据三个基⽮的⼤⼩和夹⾓的不同,⼗四种布喇菲格⼦可归属于_____ 晶系,其中当 90,=====γβαc b a 时称为 _____类晶系,该晶系的布喇菲格⼦有 ______ 。
7、NaCl 晶体是由两个 _ 格⼦沿体对⾓线滑移1/4长度套构⽽成;设惯⽤原胞的体积为a 3,⼀个惯⽤元胞内的原⼦数;其配位数为,最近邻距离;初基原胞体积为,第⼀布⾥渊区体积为______;晶体中有⽀声学波,⽀光学波。
8、对晶格常数为a 的SC ,与倒格⽮ 242K i j k a a aπππ=+- 正交的晶⾯族的晶⾯指数为____,其⾯间距为 __ 。
9、半导体材料Si 具有⾦刚⽯型晶体结构,晶格常数为a ,⼀个惯⽤元胞内的原⼦数,⼀个固体物理学原胞内的原⼦数;固体物理学原胞的体积,倒格⼦原胞的体积 __ ,第⼀布⾥渊区的体积为;晶格振动⾊散关系中⽀声学波,______ ⽀光学波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
16 能带计算中的紧束缚法是在晶格点间距 ,电子的运动被看 成绕其原子的运动,而其他原子的作用被看成为微扰。其微扰值 u (r) –v (r- Rn)为 。其中 u (r) 为原子周期场,v (r –Rn)为某一 原子对电子的势。 (P 191) A 较宽,正值 B较窄,正值 C较宽,负值 D较窄,负值 17 电子在周期性势场中运动的波函数是布洛赫函数, 它是 周期函数的乘积。(P154) (A)平面波 (B)球面波 (C)柱面波 (D)其他 和
例2:二维正方格子的布里渊区
(2/a) j
-(2/a) i
(2/a) i
-(2/a) j
杜隆-珀替定律
热容理论
爱恩斯坦的热容公式
假设所有原子都具有同一频率,振动是相互独立的。
根据经典统计理论的能量均分定律,每个简谐振子的 平均能量为kBT,若晶体有N个原子,则共有3N个振动模式, 每个振动模式平均能量为kBT,则晶体的平均动能为 E=3NkBT.
理论反映了在低温时下降的趋势。但在低温范围,爱因斯坦 理论值下降很陡,与实验不符合。
缺陷:
爱因斯坦把固体中各原子的振动看作是相互独立的,即3N个 振动频率是相同的,是一个相对简单的假设。实际固体中原 子相互作用很强。频率不完全相同,有一个分布。
A.晶态 B. 非晶态 C.准晶态 D. 不确定的新形态
*:指数简单的晶面系(如(100),(010)(001)面),其 面间距d就会很大,因此晶体往往在这些面劈裂,形成解理面。 这些面间距比较大的晶体,面密度也就大。x-射线衍射就发生 在这些面上。硅的解理面通常是(111)面
5. 声子是( D ) A.晶体中的原子 B.晶体中的真实粒子 C.光子 D. 描述晶体原子集体运动状态的物理量
CV 3Nk B (
0 2 e0 / k BT ) k BT (e0 / k BT 1) 2
E CV 3Nk B 3R 25.12 J / mol.K T V
是一个与温度及材料的性质无关的常数,在常温和高温下 与晶体的比热实验数值符合比较好,但在低温下不符合, 无法解释Cv随温度变化的实验规律。
18 你认为在T=0 K时,晶体的比热将如何? 固体的内能又如何? A 都将变为零 B 比热将不为零,但内能将为零。 C 比热将变为零,而内能具有零点能。 D 都将不为零。
19 正四面体共有 个对称操作。 A 12 B 24 C 36
D 48
1
2014/6/18
20 晶体的对称性是指晶体经过某种操作以后恢复原状的性质, 其任意操作可以看成以下几个基本操作的组合,在这几个基本操 作的线性变换中,那一种变换不正确:
(A)也是单纯的共价结合 (D) 共价结合中含有金属键成分 (C) 共价结合中含有离子键成分 (B) 变为离子性结合
2. 晶体的完全理解面是( B/C ) A. 晶体的高指数面 B. 晶体的低指数面 C. 晶体中面间距较大的晶面 D. 晶体中的任意一个晶面
4. 某种固体材料的X射线衍射图样显示,其具有n=5的对称性,这 种材料属于 ( ) C
a (其中V为体
D V3 / 2π
A 25 J/mol,CT 3 B 40 J/mol, CT3 C 25 J/mol , CT2 D 40J/mol ,CT
29 晶体的电子是 d ,由自由电子组成的系统,在T = 0 K 时,在K状态空间中形成半径为k f 的费米球,其大小只与 有关 。(P 220) (A) 费米子,系统体积 (B) 玻色子,系统电子密度 (C) 玻色子,系统体积 (D) 费米子,系统电子密度
31 在排斥势不变的情况下,离子电荷增加一倍将使NaCl晶 体的晶格常数变 ,而结合能将变 b 。 (P 579) A 宽 ,小 B 窄 ,大 C 宽 ,大 D 窄 ,小 32 你认为晶体的晶格常数(即原子间的间距)约为多少?用什么 来研究晶体的点陈结构比较好? d 。 A 约10-12米,X射线 B 约10-8米,可见光 C 约10-10米, 电子射线 D 约10-10米,X射线
6 下列可表示一个晶面的是 D A <010> B [101] C {001}
D (110)
10 声子是( B/C ) A 费米子 B 玻色子 C 晶格振动的能量量子 D 是真实的粒子 *:声子是玻色子,因此不受费米系统的泡利规则限制。 遵守Bose统计。 11. 晶体的最大的配位数是:( C ) A 16 B 18 C 12 D8 *:晶格排列最密集的是六角密排和面心立方,它们的配位 数都是12. *:晶体的可能配位数是2,3,4,6,8,12。 *:通常用配位数和致密度来描述晶体中粒子的排列紧密 程度。
倒
以第一布里渊区边界相连就是第二布里渊区,以第二布里 渊区边界相连就是第三布里渊区,由此类推。
3
2014/6/18
例1: 二维长方格子 的布里渊区
2 b2 j b
步骤二: 垂直平分线
最近邻 次近邻 再次近邻
2 b1 i a
步骤一: 长方倒格 子点阵
步骤三: 布里渊区 第一布里渊区 第二布里渊区 第三布里渊区 第四布里渊区 以第一布里渊 区边界相连的 是第二布里渊 区,由此类推
1 0 x1 x 0 cos A.转动: 2 x3 0 sin 0 x1 sin x2 cos x3 1 0 0 x1 x1 x 0 1 0 x B.中心反演: 2 2 x3 0 0 1 x3 1 l1a1 0 0 x1 x1 x 0 .D.平移操作: 1 l 2 a2 0 2 x2 x3 0 x3 0 1 l3a3
25 在晶体的宏观对称性中,由 对称素组成了 对称操作 群。 (P 31) A. 8种,30种 B. 10种,30种 C. 12种,32种 D 10种,32种 26 对于晶体的比热Cv,在常温下,由杜龙—帕绨律,CV = a 。在低温极限(T<3K )下,根据德拜理论,CV 与成正 比。 (P 131)
d2 a2 常数: 例如 已知200C时铁的密度为7860kg/m3,原子 量为55.847,求晶格常数a
如(111)面晶面间距:
d a2 a 12 12 12 3
如(121)面晶面间距:
d a2 a 12 2 2 12 6
布里渊区
认识布里渊区: • 由原点出发的各倒格子矢量的垂直平分面 所围成的区域。
• 各个布里渊区体积相等。等于 格子原胞 的体积 • 包围原点。 • 能带在布里渊区边界处劈裂。(能带理论)
步骤:
布里渊区的几何作图法
1。画倒格子点阵,任取一个倒格点为原点; 2。由近到远作各倒格矢的垂直平分面(线); 3。在原点周围围成一个包含原点在内的最小封闭体积,即 为简约区或第一布里渊区。
2
2014/6/18
36 孤立原子的电子能级在晶体中由于周期微扰的存在变 成了一系列分立的能带。绝缘体和半导体的导带都是a ,其 区别是能隙的大小,而金属导体的导带是 a 。 A 全空,部分空 B 全空,全空 C 部分空,全空 D 部分空,部分空 37 对于一维单原子链,由玻恩- 卡曼条件(Born-von Karman), 波向量k取 。(其中L取整数 ) (p 158) A Lπ/N a B 2 Lπ/N a C Lπ/2N a D N a / Lπ 38 布拉菲格子的单胞按宏观对称性分为 布拉菲格子。 (P 34) A 10 ,14 B 14 ,28 C 7 ,14 种晶系 , D 5 ,14 种
30
半导体发光二极管LED 的发光机理是:在加正向偏压下,N 型导带中的电子向下跃迁与P 型价带中的空穴复合,并以光子 的形式释放能量,发光的颜色只与 d 有关。 A 电子密度 B 材料的体积 C 所加的电压 D 禁带隙的宽度
33 结构是体心立方的倒格子,其结构是 d 。 (P 578) A 体心立方 B 简单立方 C 六角密排 D 面心立方 34 体心立方结构中,一个原子的最临近原子的个数 ( 配位数 ) 是 B 。 (P 578) (A) 6个 (B)8个 (C)12 个 (D)16个 35 在低温下对晶体比热的两种修正中,爱恩斯坦模型把每一个 原子的振动看成是独立的,其具有相同的振动频率,而德拜 模型则认为: a 。 (P 126) A 原子的振动不是独立而是相互影响的,且振动频率有一个分 布。 B 原子的振动是独立的,但有一个频率分布。 C 原子的振动不是独立而相互影响的,但频率却是相同的 D 和爱恩斯坦一样,只是作了一些数学公式上的修改。
39 从 一 个 格 点 沿 晶 向 到 最 近 一 个 格 点 的 平 移 矢 量 为 : l1a1+l2a2+l3a3,则其晶向可表示为: A.(l1,l2,l3) B.[l1,l2,l3] C.{l1,l2,l3} D.<l1,l2,l3>
晶面间距的计算
习题1.6给出了对简单立方晶格各种晶面系晶面间距的计算:
21 对格波的量子——声子的描述正确的为: A.声子不仅是一个能量子,而且还是具有动量 q的真实粒子 B.声子的动量 q是确定的; C.声子是玻色子,在一定温度下声子数目服从玻色——爱因斯坦 统计; D.一种晶格的振动模式可以与多种声子相对应
24 ______是晶体的宏观对称性的微观原因。 A 晶体周期性 B 晶体生长 C 晶体结构 D 晶体基元
2014/6/18
多项或单项选择题
1 对于一维双原子链,在长波极限q →0 下,相邻的A 、B 原子 在声学波及光学波中振动方向分别是 ( C )。 (P96) (A) 相同,相同 (B) 相反,相同 C) 相同,相反 (D) 相反,相反
3 共价结合是一种较强的结合,金钢石就是由碳原子共价结 合成的,而对于由异种原子结合的 III-V 族化合物GaAs , 其结合是 ( C ) 。 (P 62)
